七年级数学下册 8.1 同底数幂的乘法课件2(新版)苏科版
沪科版七年级下册数学精品教学课件 第8章整式乘法与因式分解 第2课时 零次幂、负整数次幂及科学记数法

例2 若 (x - 1)x+1 = 1,求 x 的值. 解:①当 x+1 = 0,即 x = -1 时,(x - 1)x+1 = (-2)0 = 1;
②当 x - 1 = 1,即 x = 2 时,(x - 1)x+1 = 13 = 1; ③当 x - 1 = -1,即 x = 0 时,(x - 1)x+1 = (-1)1 = -1. 故 x 的值为 -1 或 2.
算一算: 10-2 = ____0_._0_1____;
10-4 = ___0_.0_0_0_1____;
10-8 = _0_._0_0_0_0_0_0_0_1_.
议一议:指数与运算结果的 0 的个数有什么关系? 通过上面的探索,你发现了什么?
一般地,10 的 -n 次幂,在 1 前面有__n___个 0.
想一想:10-21 的小数点后的位数是几位? 1 前面有几个零?
知识要点 用科学记数法表示一些绝对值小于 1 的数的方法:
利用 10 的负整数次幂,把一个绝对值小于 1 的数表 示成 a×10-n 的形式,其中 n 是正整数,1≤|a|<10. n 等于原数第一个非零数字前所有零的个数(特别注 意:包括小数点前面那个零).
a0 an a0n 1 an.
即 an 1(a 0,n 是正整数). an
特别地,a1 1 (a 0). a
例4
若
a
=
2 3
-2
,b
=
(-1)-1,c
=
3 2
0
,则
a,b,
c 的大小关系是( B )
A.a>b=c
B.a>c>b
C.c>a>b
D.b>c>a
解 析32:0a==1,故23
a-n=
同底数幂的乘法教学课件

知识要点
同底数幂的乘法的应用
练一练:一个长方体的长为4×103厘米,宽为2×102厘米,高为
2.5×103厘米,则它的体积为( A )
A.2×109 立方厘米
B.20×108立方厘米
C.20×1018立方厘米
D.8.5×108立方厘米
知识要点
CONTENTS
练一练:计算: (1)b5·b;
(2)a2 ·a6 ;
解:(1)b5·b=b6.
(2)a2 ·a6=a8.
(3)y2n·yn+1=y3n+1.
(3)y2n·yn+1.
知识要点
同底数幂的乘法的应用 例2 一颗卫星绕地球运行的速度是7.9×103 m/s,求这颗卫星运行 1h的路程.
解:因为1h=3.6×103s,所以这颗卫星运行1h的路程为 (7.9×103)×(3.6×103) =(7.9×3.6)×(103×103) =28.44×106 =2.844×107(m).
七年级数学下册苏科版
第8章 幂的运算
8.1 同底数幂的乘法
知识要点
1 2
知识要点
CONTENTS
1
知识要点
情境引入
“嫦娥二号”发射升空后,飞行速度: 1.5×103米/秒,预计5日内到达指定轨道, 若到达轨道时飞行了4.32×105秒,那么 “嫦娥二号”共飞行了多少的路程 ?
1.5×103×4.32×105米
知识要点
CONTENTS
4
知识要点
同底数幂 的乘法
同底数幂的 乘法
同底数幂的 乘法的应用
am ·an = am+n (m、n都是正整数). 即同底数幂相乘,底数不变,指数相加.
8.1同底数幂的乘法(课件)七年级数学下册(苏科版)

am·an·ap
=am+n·ap
=am+n+p。
02
知识精讲
【运算性质推广】
am·an·ap=am+n+p(m、n、p是正整数)。
同底数幂的乘法的运算性质
03
知识精讲
典例精析
例1、下列计算正确的是( D )
A.a2+a3=a5
B.a4·a2=a8
C.a6-a4=a2
D.4ab2-5b2a=-ab2
【分析】B、a4·a2=a4+2=a6。
03
知识精讲
典例精析
例2、计算:
(1)x3·(-x)2;(2)(-3)4×243×(-3)6;(3)(a-b)2·(b-a)3+(a-b)4·(b-a)。
【分析】(1)原式=x3·x2=x3+2=x5;
(2)原式=34×35×36=34+5+6=315;
将(b-a)看作整体
文字语言:同底数幂相乘,底数不变,指数相加。
【注意点】
(1)底数不变——幂的底数必须相同,才能进行乘法运算;
(2)指数相加——千万不能把指数相乘;
(3)am·an=am+n中的a可以是一个数,也可以是一个式。
【运算性质的逆用】
am+n=am·an(m、n是正整数);
am+n+p=am·an·ap(m、n、p是正整数)。
= × × ⋯ ×
(+)个
=am+n
02
知识精讲
同底数幂的乘法的运算性质
【运算性质】
符号语言:am·an=am+n(m、n是正整数);
文字语言:同底数幂相乘,底数不变,指数相加。
七级数学下册 8.1 幂的运算《同底数幂的乘法》教案1 (新版)沪科版

《同底数幂的乘法》教学目标:1、经历探索同底数幂乘法运算性质的过程,发展符号感和推理意识.2、能用符号语言和文字语言表述同底数幂乘法的运算性质,会根据性质计算同底数幂的乘法.教学重点:同底数幂的乘法运算法则.教学难点:同底数幂的乘法运算法则的灵活运用.教学过程设计一、复习旧知a n表示的意义是什么?其中a、n、a n分别叫做什么?a n= a× a× a×… a(n个a相乘)25表示什么?10×10×10×10×10可以写成什么形式?10×10×10×10×10 =?式子103×102的意义是什么?这个式子中的两个因式有何特点?二、探究新知1、探究算法103×102=(10×10×10)×(10×10)(乘方意义)=10×10×10×10×10(乘法结合律)=105 (乘方意义)2、寻找规律请同学们先认真计算下面各题,观察下面各题左右两边,底数、指数有什么关系?①103×102= ②23×22= ③a3×a2=归纳规律:底数不变,指数相加.3、定义法则①你能根据规律猜出答案吗?猜想:a m·a n=?(m、n都是正整数)写出计算过程,证明你的猜想是正确的.a m·a n=(aa…a)·(aa…a)(乘方意义)n个a= aa…a(m+n)个a(乘法结合律)=a m+n(乘方意义)即:a m·a n= a m+n(m、n都是正整数)②用自己的语言归纳法则A、a m·a n是什么运算?——乘法运算B、数a m、a n形式上有什么特点?——都是幂的形式C、幂a m、a n有何共同特点?——底数相同D、所以a m·a n叫做同底数幂的乘法.引出课题:这就是这节课要学习的内容《同底数幂的乘法》它的运算法则应该是同底数幂相乘,底数不变,指数相加.幂的底数必须相同,相乘时指数才能相加.例如:43×45=43+5=484、知识应用计算(1)32×35(2)(-5)3×(-5)5练习一例1:计算:(抢答)105×106当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?怎样用公式表示?例2:计算(1)a8·a3·a (2)(a+b)2(a+b)3底数也可以是一个多项式.例3:世界海洋面积约为3.6亿平方千米,约等于多少平方米?练习二下面的计算对不对?如果不对,怎样改正?(1)b5· b5= 2b5()(2)b5+ b5 = b10()(3)x5·x5= x25()(4)y5· y5= 2y10()(5)c· c3= c3()(6)m + m3= m4()。
第八章 幂的运算(小结思考)(课件)七年级数学下册(苏科版)

①③④ (填序号).
11.若a=1.01×10-6,b=1.01×10-5,c=9.99×10-4,则a,b,c按从
解:∵a=1.01×10-6=0.00000101,
a<b<c
小到大的顺序排列为________________.
12.如果等式(2a-1)a+2=1,则a的值为
-2或1或0
____________.
A. x2m
B. x2m+1
C. x2m+2
D. xm+2
3.等式− = (−) ( ≠ )成立的条件是( A )
A. n是奇数 B. n是偶数
C.n是正整数
D. n是整数
课堂检测
4.生物学家发现一种病毒,用1015个这样的病毒首尾连接起来,
可以绕长约为4万km的赤道1周,一个这样的病毒的长度为( B )
加、减法
合并同类项(见七上第三章)
n个 am
乘
法
同底数幂的乘法运算性质:
am·an=am+n (m、n是正整数)
除
法
同底数幂的除法运算性质:
am÷an=am-n (m、n是整数,a≠0)
乘
方
am … am= amn
(am)n = am·
幂的乘方运算性质:
(am)n=amn (m、n是正整数)
积的乘方运算性质:
课堂检测
(2) 1+3+32+33+34+…+3n-1+3n(其中n为正整数).
解:(2) 设S=1+3+32+33+34+…+3n-1+3n①.
将等式两边同时乘3,
得3S=3+32+33+34+35+…+3n+3n+1②.
②-①,得3S-S=3n+1-1.
初中数学七年级下册苏科版8.1同底数幂的乘法教学设计

(3)教师点评:对各小组的讨论成果进行点评,指出优点和不足,引导学生深入思考。
(四)课堂练习
1.教学内容:设计梯度性、层次性的练习题,让学生在练习中巩固同底数幂的乘法知识,形成技能。
2.教学过程:
(1)基础练习:设计一些简单的同底数幂乘法题目,让学生独立完成,巩固基础知识。
初中数学七年级下册苏科版8.1同底数幂的乘法教学设计
一、教学目标
(一)知识与技能
1.理解同底数幂的概念,掌握同底数幂的乘法法则,能够熟练进行同底数幂的乘法运算。
2.能够运用同底数幂的乘法法则解决实际问题,提高运算速度和准确性。
3.能够运用同底数幂的乘法法则推导出相关性质,如幂的乘方、积的乘方等,并应用于解决问题。
2.重点解析:同底数幂的乘法是基础幂运算的重要组成部分,对于后续学习幂的除法、乘方等高级运算具有基石作用。因此,掌握同底数幂的乘法法则是本章节的核心。
难点解析:学生在理解同底数幂乘法法则时,可能会对指数相加的原理感到困惑,需要通过直观的教具或图形辅助,以及实际例子的引导,帮的教具演示、详细的步骤讲解,帮助学生突破难点,掌握同底数幂的乘法法则。
5.练习巩固:设计梯度性、层次性的练习题,让学生在练习中巩固知识,形成技能。
6.课堂小结:引导学生总结同底数幂乘法的学习要点,培养学生的归纳总结能力。
7.课后拓展:布置开放性、挑战性的课后作业,激发学生的学习兴趣,提高学生的自主学习能力。
4.引导学生运用类比、归纳等方法,发现幂的乘方、积的乘方等性质,提高数学思维能力。
(三)情感态度与价值观
1.培养学生对数学学习的兴趣,激发学生的学习积极性,使其主动投入到同底数幂的学习中。
苏科版数学七年级下册同底数幂的乘法课件(共17张)

10
( m n ) 个10
m n
n个10
幂的
意义
乘法结合律
幂的意义
5
探索活动
3.当m,n是正整数时,2 2 等于什么?
m
m
n
n
1 1
呢?
2 2
m
n
1 1 1 1
2 2 2 2
1 1 1
光的速度约为3×105 km/s,太阳系以外距离地球最近的一颗恒星(比邻
7
)
4
.
3×
10
s计算,则这
星 发出的光需要 年的时间才能到达地球 若一年以
颗恒星到地球的距离是_______km.
【详解】
这颗恒星到地球的距离为
4×3×107×3×105,
=(4×3×3)×(107×105),
=3.6×1013km.
8.1 同底数幂的运算
1
复习旧知
n
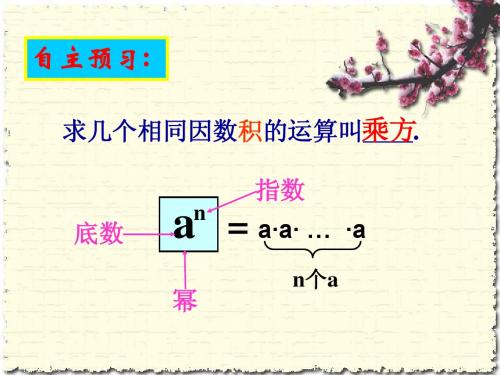
1.a 表示的意义是什么?其中a、n、a 分
别叫做什么?
底数
n
a
n
幂
a
n=
a × a × a ×… a
n个a
指数
注:(1)是幂的
一般情势,读作a
的n次方(幂)
(2)现在我们学
的幂指数n都是正
整数
2
复习旧知
将下列运算结果写成幂的情势
(1)10 10 10 10 10
(2)a a a a a
(3)(5) (5) (5)
3 3 3 3
(4)
5 5 5 5
(5) b b b b
8.1同底数幂的乘法
a · =a a
m
n
m+n
(m,n都是正整数)
同底数幂相乘,底数不变,指数相加.
m· n =a m+n a a
m+n =am· n a a
同底数幂 相乘,底数 不变,指数 相加.
指数为和的 幂等于以和 中每个加数 为指数的同 底数幂的积.
同底数幂的推广
a a a ?(m,n,p是正整数)
p m+n+p
m
n
a · · =a a a 正整数)
m
n
(m,n,p都是
1.下面的计算对不对?如果不对,怎样改正?
(1)x3 · 3= 2x6( × (2)a5 + a5 = a10 (×) x ) x3 · 3=x6 x (3)x4 ·2 = x8 ( ×) x x4 · 2 = x6 x a5 + a5 = 2a5
3 2
2
(3) (-2) ×(-2)2×23 (4) (-x) · ·(-x) x
2 3
(5) (x-y) ·(y-x) ·(y-x)
课堂小结
同底数幂的乘法性质: 同底数幂相乘,底数 不变 ,指数 相加 .
m n m+n
a · =a a
m+n = a
(m,n都是正整数)
a · (m,n都是正整数) a
m n p
可得
a a a a
m n p
m n p
理解、识记这一性质时,应该注意什么? 幂的底数必须相同,相乘时指数才能相加。
刚才提出的问题大家会解决了吗?
310 510 ?
8 2
(3 5) (10 10 ) 8 2 15 (10 10 )
苏科版七年级下册数学《幂的运算》课件

你还记得吗?
4.同底数幂的除法法则
文字叙述: 同底数幂相除,底数不变,指数相减
字母表示: am÷an=am-n (a≠0 m,n是正整数 m>n)
扩大:
am÷an÷ap=am-n-p (a≠0 m,n,p是整数)
考考你
a8 ÷a3 =a8-3=a5
(½)5÷(½)3 =(1/2)5-3=(1/2)2=1/4 (-s)7÷(-s)2 =(-s)7-2=(-s)5=-s5
=4b4
(5) a8÷a4=a2 ×
=a4
(6) (-z)6÷(-z)2=-z4 ×
=z4
幂的运算中的方法与技能
类型一:熟练使用公式,正确进行各种计算
(1)m19÷m14·m3÷m2
=m5·m3÷m2 =m8÷m2
或=m19-14+3-2 =m6
=m6
(2)(x-y)8÷(x-y)4÷(y-x)3
am-n=am÷an amn= (an)m anbn= (ab)n
幂的运算中的方法与技能
类型二:逆用公式进行计算
例1.已知am=4,an=2.
求①am+n的值.②am-n的值.③ a3m+2n的值.④ a2m-n的值=am·an=m÷an=a3m·a2n
=a2m÷an
=4×2 =4÷2
=(am)3·(an)2
=(-x2n-2 ) ·(-x5) ÷x2n+1 =x2n+3÷x2n+1 =x2 (4)4-(-1/2)-2-32÷(-3)0 =4-4-9÷1 =4-4-9 =-9
注意:运算时第一确定
所含运算类型,理清运 算顺序,用准运算法则
幂的运算中的方法与技能
类型二:逆用公式进行计算
七年级数学下册苏科版第8章幂的运算同底数幂的除法

第8章 幂的运算
8.3 同底数幂的除法
第1课时 同底数幂的除法
1
CONTENTS
1
复习引入
回顾所学知识,完成下面内容. 1.同底数幂的乘法法则 :
am·an= am+n ( m,n都是正整数). 2.幂的乘方法则:
(am)n= amn (m,n都是正整数). 3.积的乘方法则:
A.m=4,n=3
B.m=4,n=1பைடு நூலகம்
C.m=1,n=3
D.m=2,n=3
3.计算: (1)x13÷x2÷x7; (3)6x2y3÷(-3xy); (4)(6x3y4z-4x2y3z+2xy3)÷2xy3.
(2)(-x4)3÷(x2)5;
解:(1) x13÷x2÷x7= x13-2-7=x7. (2)(-x4)3÷(x2)5= -x12÷x10=-x2. (3) 6x2y3÷(-3xy)=-2xy2. (4) (6x3y4z-4x2y3z+2xy3)÷2xy3 =6x3y4z÷2xy3-4x2y3z÷2xy3+2xy3÷2xy3 =3x2yz-2xz+1.
CONTENTS
4
课堂小结
同底数幂的除法法则:
am÷an=a( m-n ),其中m、n都是正整数,且m>n.
同底数幂相除,底数不变,指数相减.
同底数幂的除法
练一练:下列计算正确的是( D ) A.(-a)5÷a3= a2 C.(-a5)2÷a3= -a7
B.(-a)5÷(-a)3= -a2 D.(-a)5÷(-a)3=a2
CONTENTS
3
1.计算(a2)3÷a2的结果是( B )
A.a3
B.a4
苏科版数学七年级下册8.1《同底数幂的乘法》说课稿

苏科版数学七年级下册8.1《同底数幂的乘法》说课稿一. 教材分析《同底数幂的乘法》是苏科版数学七年级下册第8.1节的内容。
这一节主要介绍同底数幂的乘法法则,是指数相同且底数相同的幂相乘时,底数不变,指数相加的规律。
这是幂的运算法则的基础,对于学生理解和掌握幂的运算非常重要。
教材通过简单的例子引导学生发现同底数幂的乘法法则,然后通过大量的练习让学生熟练掌握这个法则。
在教材的安排上,既有理论的讲解,也有大量的实践操作,使得学生在学习的过程中能够理论和实践相结合,更好地理解和掌握这个法则。
二. 学情分析学生在学习这一节内容时,已经学习了幂的基本概念,对于幂的运算有一定的了解。
但是,对于同底数幂的乘法法则,他们可能是第一次接触,需要通过实例来理解和掌握。
同时,由于同底数幂的乘法涉及到指数的加法,学生可能对于这个运算规则不是很理解,需要通过具体的例子来解释和说明。
三. 说教学目标1.知识与技能目标:理解同底数幂的乘法法则,能够熟练地进行同底数幂的乘法运算。
2.过程与方法目标:通过观察、分析和归纳,培养学生的抽象思维能力和运算能力。
3.情感态度与价值观目标:激发学生对数学的兴趣,培养他们积极探究、勇于挑战的精神。
四. 说教学重难点1.教学重点:同底数幂的乘法法则的推导和理解。
2.教学难点:同底数幂的乘法运算的熟练掌握,以及对于指数加法的理解。
五. 说教学方法与手段在教学过程中,我将采用讲授法、引导法、实践法等多种教学方法。
通过实例的展示和分析,引导学生观察、思考和归纳同底数幂的乘法法则。
同时,我会利用多媒体教学手段,如PPT等,来展示和解释实例,使得学生能够更直观地理解和掌握这个法则。
六. 说教学过程1.导入:通过简单的例子,引导学生发现同底数幂的乘法法则。
2.新课讲解:讲解同底数幂的乘法法则,并通过大量的实例来解释和说明。
3.练习巩固:让学生进行同底数幂的乘法运算,巩固所学知识。
4.拓展延伸:引导学生思考和探索同底数幂的其他运算规则。
苏科版数学七年级下册第八章《幂的运算》复习 教学课件(共20张PPT)

考考你
a8 ÷a3 (½ )5÷(½ )3 (-s)7÷(-s)2
a3 ÷a8 (a≠0) (-3)2÷(-3)4 (-99)8 ÷(-99)8
换个方式考考你哦!
a8 .a()=a 12
a .an .a()=a n+5
(p-q)5 .(q-p)2
82=2( )=22.2( )
找错误并改正
(1) a3 .a3=2a6 (2) (a3)2=a5 (3) (xy2)3=xy6
考考你
(-0.003)0 (3x)0 (x≠0) 20170
4-2 (-4)-2 (0.1)-3
你还记得吗?
5.同底数幂的除法法则
文字叙述:同底数幂相除,底数不变,指数相减 字母表示:am÷an=am-n (a≠0 m,n是正整数 m>n) 扩展: am÷an=am-n (a≠0 m,n是整数)
(-bm)7 (m是正整数) [(-a)2 ]3 .(a4)2 -[(m-n)3]7
你还记得吗?
3.积的乘方法则
文字叙述:积的乘方,把积的每一个因式分别 乘方,再把所得的幂相乘
字母表示:(ab)n=anbn (n是正整数) 扩展: (abc)n=anbncn (n是正整数)
注意它的逆运算
考考你
(5a)8 (-xy3)3 (-2a3b6c2)3
-b6.b6 (-a)2 .(-a) .(-a)3 (m+n)3.(m+n)7
你还记得吗?
2.幂的乘方法则
文字叙述:幂的乘方,底数不变,指数相乘 字母表示: (an)m=amn (m,n是正整数) 扩展: ((an)m)p=amnp (m,n,p是正整数)
考你
(a5)4 -(a8)2 [(-2)3]10
苏科版七年级数学下册同底数幂的乘法课件

练一练
1.一个长方体的长为4×103厘米,宽为2×102厘米,高为 2.5×103厘米,求它的体积(结果用科学记数法表示).
例题讲授 计算:
(1) (y-x)3·(x-y)5 ;
(2) (x+y)3·(-x-y)2.
解:(1) 原式= - (x-y)3·(x-y)5 = - (x-y)3+5 = - (x-y)8
通过小这节结课的学习你有什么
收获?
谢谢
注意x的指数是1
(4) 原式 = (m+n)3+2 = (m+n)5
练一练 1.计算:
(1) a8·a3 (3) (-2)10×(-2)13
(5) (- a)2·(- a)·(- a)3
(2) x5·x
(4) - b6·b6
6
1
2
1
5
1
3
2 2 2 .
练一练
2.下面的计算是否正确?如有错误,请改正.
8.1 同底数幂的乘法
复习回顾
(1) 3333333
(2)
2 3
2 3
2 3
2 3
(3) a a a a a
指数
an
底数
幂
情景导入
速度×时间=距离
太阳光照射到地球表面所需的时间约是5 ×102 s,光
的速度约是3×108 m/s.地球与太阳之间的距离约是多少?
(3×108)×(5×102) = (3×5)×(108×102)
= 15 × (108×102) =?
情景导入
108 ×102 = ( 10× … ×10 ) × (10×10)
苏科版数学七下同底数幂的乘法课件

7
温故1:
表示的意义是什么?其中 、、 分别叫做什么?
底数
幂
= × × × ⋯×
个
指数
温故2:
25表示什么?
10×10×10×10×10 可以写成什么情势?
25 = 2×2×2×2×2
.
10×10×10×10×10 = 105
.
思考:
103与102 的积
· =( … )·( … ) (乘方的意义)
个
个
= …
(乘法结合律)
( + )个
(乘方的意义)
=+
即
+
· =
(当、都是正整数)
同底数幂的乘法运算性质
a a a
m
n
m n
(m, n都是正整数 ).
同底数幂相乘,底数不变,指数相加.
,(为偶数)
−,(为奇数)
随堂练习
3.计算
(1) 4 ⋅ 6 + 5 ⋅ 5
(2) ⋅ 7 − 4 ⋅ 4
4.填空
7
(1) ⋅
5
(______)
(2) ⋅ ⋅
=12
−1
(
_______)
=2
能力拓展
计算 (1) x 3 x x 2
(2)
( p q) (q p)
5
2
例题讲授
例3
(1)已知 = , = ,求+ 的值.
解:∵+ = · ,
又 = , = ,
∴+ = × = .
(2)已知3+1=81,求.
七年级数学下册 8.1 同底数幂的乘法 怎样理解“同底数幂相乘,底数不变,指数相加”素材 苏科版(

七年级数学下册8.1 同底数幂的乘法怎样理解“同底数幂相乘,底数不变,指数相加”素材(新版)苏科版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(七年级数学下册8.1 同底数幂的乘法怎样理解“同底数幂相乘,底数不变,指数相加”素材(新版)苏科版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为七年级数学下册8.1 同底数幂的乘法怎样理解“同底数幂相乘,底数不变,指数相加”素材(新版)苏科版的全部内容。
怎样理解“同底数幂相乘,底数不变,指数相加”?幂的运算性质的表达式是a m·a n =a m+n(m,n均为正整数)(1)左边两个幂的底数相同,而且是相乘的关系;右边所得到的一个幂,底数仍不变,指数相加.可见,这一性质由乘法运算降为加法运算(指数相加).对于这一性质,不仅要记住结论,更重要的是掌握结论导出过程。
因为这个推导过程体现了“由特殊到一般的数学思想方法"。
掌握这一方法对于学好数学(当然也包括其他学科)是非常重要的.(2)公式中的字母a既可以表示数,也可以表示单项式,还可表示多项式。
(3)当三个或三个以上同底数幂相乘时,法则仍成立,即a m·a n·a p=a m+n+p(m,n,p都是正整数)。
(4)只有“同底数”的幂相乘才能用这个法则。
千万不要出现类似下面的错误: a2·(-a)3=a5。
这里出错的原因是因为这两个底数不同,一个是a,一个是-a,而强用了法则。
(5)注意可逆用公式a m+n=a m·a n(m,n都是正整数)。
七年级数学下册 8.1 同底数幂的乘法 怎样理解“同底数幂相乘,底数不变,指数相加”素材 苏科版(

七年级数学下册8.1同底数幂的乘法怎样理解“同底数幂相乘,底数不变,指数相加”素材(新版)苏科版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(七年级数学下册8.1 同底数幂的乘法怎样理解“同底数幂相乘,底数不变,指数相加”素材(新版)苏科版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为七年级数学下册8.1 同底数幂的乘法怎样理解“同底数幂相乘,底数不变,指数相加”素材(新版)苏科版的全部内容。
怎样理解“同底数幂相乘,底数不变,指数相加”?幂的运算性质的表达式是am·a n =am+n(m,n均为正整数)(1)左边两个幂的底数相同,而且是相乘的关系;右边所得到的一个幂,底数仍不变,指数相加.可见,这一性质由乘法运算降为加法运算(指数相加).对于这一性质,不仅要记住结论,更重要的是掌握结论导出过程。
因为这个推导过程体现了“由特殊到一般的数学思想方法"。
掌握这一方法对于学好数学(当然也包括其他学科)是非常重要的.(2)公式中的字母a既可以表示数,也可以表示单项式,还可表示多项式。
(3)当三个或三个以上同底数幂相乘时,法则仍成立,即a m·a n·a p=am+n+p(m,n,p都是正整数)。
(4)只有“同底数”的幂相乘才能用这个法则。
千万不要出现类似下面的错误: a2·(-a)3=a5。
这里出错的原因是因为这两个底数不同,一个是a,一个是-a,而强用了法则。
(5)注意可逆用公式am+n=a m·a n(m,n都是正整数)。
以上就是本文的全部内容,可以编辑修改。
高尔基说过:“书是人类进步的阶梯。
