复旦附中高二期中(2018.11)
上海复旦大学附属中学2018年高二化学联考试题含解析

上海复旦大学附属中学2018年高二化学联考试题含解析一、单选题(本大题共15个小题,每小题4分。
在每小题给出的四个选项中,只有一项符合题目要求,共60分。
)1. 下列各组混合物中,能用分液漏斗进行分离的是A.酒精和水 B.碘和四氯化碳 C.水和四氯化碳 D.汽油和植物油参考答案:C略2. 已知25℃时,电离常数Ka(HF)=3.6×10-4mol/L,溶度积常数Ksp(CaF2)=1.46×10-10mol3/L3。
现向1L 0.2mol/LHF溶液中加入1L 0.2mol/LCaCl2溶液,则下列说法中,正确的是A.25℃时,0.1 mol/LHF溶液中pH=1B.Ksp(CaF2)随温度和浓度的变化而变化C.该体系中,Ksp(CaF2)=D.该体系中有CaF2沉淀产生参考答案:D3. 著名化学家付鹰说:“化学是实验的科学,只有实验才是最高法庭”。
下列实验装置图操作正确的是参考答案:C4. 下列条件下铁钉最容易生锈的是A.浸泡在植物油中B.浸泡在海水中C.置于干燥的空气中D.浸泡在蒸馏水中参考答案:B5. 在四个相同的容器中,在不同的温度下(其它条件相同)进行合成氨的反应,根据下列在相同时间内测得的结果判断,该反应所处的温度最高的是()A.v(NH3)=0.1mol/(L?min)B.v(H2)=0.6mol/(L?min)C.v(N2)=0.3mol/(L?min)D.v(H2)=0.3mol/(L?min)参考答案:C考点:反应速率的定量表示方法;化学反应速率的影响因素.专题:化学反应速率专题.分析:根据化学反应速率之比等化学计量数之比进行计算,以同一个物质的化学反应速率进行比较;升高温度,加快化学反应速率.解答:解:A.v(NH3)=0.1mol/(L?min);B.v(H2):v(NH3)=3:2,故v(NH3)=v(H2)=×0.6mol/(L?min)=0.4mol/(L?min);C.v(NH3):v(N2)=2:1,故v(NH3)=2v(N2)=2×0.3mol/(L?min)=0.6mol/(L?min);D.v(H2):v(NH3)=3:2,故v(NH3)=v(H2)=×0.3mol/(L?min)=0.2mol/(L?min),故C的反应速率最快,故C反应所处的温度最高,故选C.点评:本题考查化学反应速率的相关计算以及温度对化学反应速率的影响,难度不大.要注意比较化学反应速率快慢要以同一个物质进行比较.6. 下列离子方程式书写正确的是()A.显蓝色的淀粉溶液中通入足量SO2后变成无色溶液:I2 +SO2+2H2O==2I-+SO42-+4H+B.已知电离平衡常数:H2CO3>HClO>HCO3-,向NaClO溶液中通入少量二氧化碳:2ClO-+CO2+ H2O =2HClO+CO32-C.NH4HCO3溶液与过量NaOH溶液反应:+OH-= NH3↑+H2OD.FeI2溶液中通入过量Cl2:2Fe2++2I-+2Cl2=2Fe3++I2+4Cl-参考答案:A略7. 下列有机分子中可形成顺反异构的是()A.CH3—CH2Cl B.CH3CH=CHBr C.CH3C≡CCH3D.CH3CH=C( CH3)2参考答案:B略8. 盛放浓硝酸的试剂瓶里出现黄色是因为硝酸具有()A、酸性B、不稳定性C、强氧化性D、挥发性参考答案:B略9. 下列说法不正确的是()A.苯和甲苯分子中所有原子均在同一平面上B.苯不可以使KMnO4酸性溶液褪色而甲苯可以C.苯和甲苯都能与卤素单质、硝酸等发生取代反应D.苯的同系物的分子通式是C n H2n﹣6(n≥7)参考答案:A【考点】有机物的结构和性质.【分析】A.甲苯含有甲基,具有甲烷的结构特点;B.苯性质稳定,但甲苯可被氧化;C.苯、甲苯在催化条件下可发生取代反应;D.苯的同系物含有一个苯环,且烃基为烷基.【解答】解:A.苯为平面形结构,但甲苯含有甲基,具有甲烷的结构特点,不可能在同一个平面上,故A错误;B.苯性质稳定,但甲苯中苯环对甲基的影响,导致甲苯可被氧化,可使高锰酸钾褪色,故B正确;C.苯、甲苯在催化条件下可发生取代反应,可生成硝基苯、三硝基甲苯等,故C正确;D.苯的同系物含有一个苯环,且烃基为烷基,通式为C n H2n﹣6(n≥7),故D正确.故选A.10. 下列各项比较中,正确的是A.原子核外电子数:H>O>Al B.元素非金属性:F>Cl>Br C.热稳定性:PH3>H2S>HCl D.碱性:LiOH>NaOH>KOH参考答案:B略11. 随着人们生活质量的不断提高,废电器必须进行集中处理的问题被提到议事日程,其首要原因是()A.利用电器中的金属材料B.防止电器造成污染C.废电器经过处理后还可以重新使用 D.回收其中非金属材料参考答案:B12. 下列属于物理变化的是A.石油的分馏 B.苯酚使蛋白质变性C.煤的干馏 D.重油的裂化参考答案:A略13. 下列有关除杂质(括号中为杂质)的操作中,错误的是A.福尔马林(蚁酸):加入足量饱和碳酸钠溶液充分振荡,蒸馏,收集馏出物B.乙醇(水):加入足量生石灰,蒸馏,收集馏出物C.苯(苯酚):加溴水,振荡,过滤除去沉淀D.乙酸乙酯(乙酸):加饱和碳酸钠溶液,充分振荡,分液,弃水层参考答案:C14. 下列基态原子的电子构型中,正确的是A.3d94s2 B.3d44s2 C.3d104s0 D.3d83s2参考答案:A15. 已知Ksp(AgCl) = 1.56×10-10,Ksp(AgBr) = 7.7×10-13,Ksp(Ag2CrO4) = 9.0×10-12。
2018复旦附中2018学年高二第一学期数学期中考试

复旦大学附属中学2018学年第一学期高二年级数学期中考试试卷一. 填空题(本大题共12题,满分54分,第1~6题每题4分,第7~12题每题5分) 1. 直线0132=-+y x 的倾斜角是____________.2. 若矩阵110A ⎛⎫ ⎪=- ⎪ ⎪⎝⎭,()121B =,则AB =__________.3. 行列式43125142k --的元素3-的代数余子式的值为7,则k =________.4. 已知,x m y t =⎧⎨=⎩是增广矩阵为3122012-⎛⎫⎪⎝⎭的二元一次方程组的解,则=+t m ________。
5. 直线143:-=x y l 的一个单位方向向量......是. 6. 已知直线12:(1)30,:(1)(23)20l kx k y l k x k y +--=-++-=,若12l l ⊥,则______k =.7. 已知点P 在直线6014x y -=-上,且点P 到()2,5A 、()4,3B 两点的距离相等,则点P 的坐标是__________.8. 若222lim 11=+--+∞→n n nn n t t ,则实数t 的取值范围是_____________.9. 已知R a ∈,则“61=a ”是“两直线1:210l x ay +-=与2:(31)10l a x ay ---=平行”的___________条件(填“充分非必要”、“必要非充分”、“充要”、“既不充分也不必要”). 10. 过点)2,3(-P 且与直线012=++y x 的夹角为21arctan 的直线的一般式方程.....是____________. 11. 已知实数2211,,,b a b a 满足:1,012211=+-=+-b a b a ,且222221212121)(2b a b a b b a a +⨯+=+,其中21a a >,则以向量),(11b a 为法向量的直线的倾斜角的取值范围是____________.12. 如图,边长为4的正方形ABCD 中,半径为1的动圆Q 的圆心Q 在边CD 和DA 上移动(包含端点D C A ,,),P 是圆Q 上及其内部的动点,设),(R n m BA n BC m BP ∈+=,则n m +的取值范围是_____________.二. 选择题(本大题共4题,每题5分,共20分)13. 函数)(x f y =的图像如图所示,在区间],[b a 上可找到)2(≥n n 个不同的数n x x x ,,,21 ,使得nn x x f x x f x x f )()()(2211=== ,则n 的取值范围为( )(第13题图)A .{3,4}B .{2,3,4}C .{3,4,5}D .{2,3}14. 给出下列命题:①非零向量满足,则的夹角为30°; ②将函数|1|-=x y 的图像按向量)0,1(-=平移,得到函数||x y =的图像; ③在中,若0)(=⋅+BC AC AB ,则为等腰三角形; 其中正确命题的个数是( )A.0B.1C.2D.315. 在平面直角坐标系xOy 中,)0,1(-A ,)0,1(B ,)1,0(C ,经过原点的直线l 将△ABC分成左、右两部分,记左、右两部分的面积分别为1S 、2S ,则22211)1(S S -+取得最小值时,直线l 的斜率( )A .等于1B .等于1-C .等于21D .不存在 16. 如图所示,已知)0,4(),0,0(10A A ,对任何N n ∈,点2+n A 按照如下方式生成:a b、a b a b ==- 与a a b + ABC ∆ABC ∆(第12题图)321π=∠++n n n A A A ,||21||121+++=n n n n A A A A ,且21,,++n n n A A A 按逆时针排列,记点n A 的坐标为()(),n n a b n N ∈,则)lim ,lim (n n n n b a ∞→∞→为( ) A.)734,720(B.)734,3(C.)835,3(D.)835,720((第16题图)三. 解答题(本大题共5题,共76分)17. (本题14分)已知R m ∈,直线1l 的方程为(1)(21)3m x m y m +--=,直线2l 的方程为(31)(41)54m x m y m +--=+.当m 变化时, (1)分别求直线1l 和2l 经过的定点坐标; (2)讨论直线1l 和2l 的位置关系.18. (本题14分)已知直线l 过点(1,3),且与x 轴、y 轴都交于正半轴,当直线l 与坐标轴围成的三角形面积取得最小值时,求: (1)直线l 的方程;(2)直线l 关于直线12:-=x y m 对称的直线方程.19. (本题14分)类似于平面直角坐标系,我们可以定义平面斜坐标系:设数轴,x y 的交点为O ,与,x y 轴正方向同向的单位向量分别是,i j,且与的夹角为θ,其中),2()2,0(πππθ ∈。
上海市复旦大学附属中学2019届高二第二学期期中考试数学试题.docx
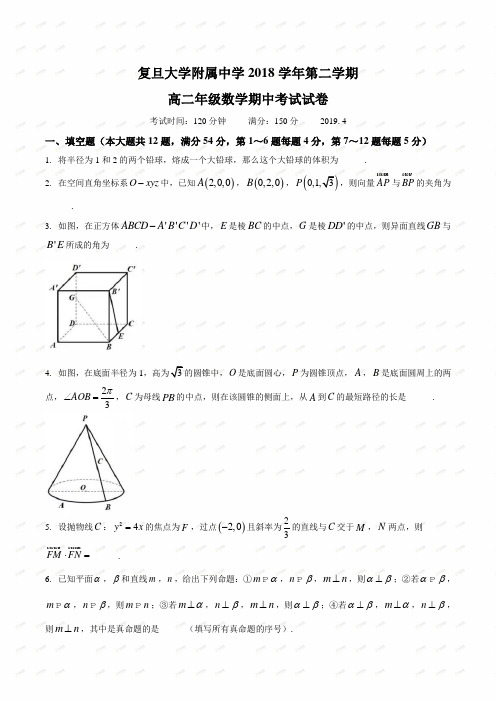
复旦大学附属中学2018学年第二学期高二年级数学期中考试试卷考试时间:120分钟 满分:150分 2019.4一、填空题(本大题共12题,满分54分,第1~6题每题4分,第7~12题每题5分)1. 将半径为1和2的两个铅球,熔成一个大铅球,那么这个大铅球的体积为______.2. 在空间直角坐标系O xyz -中,已知()2,0,0A ,()0,2,0B ,()0,1,3P ,则向量AP uu u r 与BP uu r 的夹角为______.3. 如图,在正方体''''ABCD A B C D -中,E 是棱BC 的中点,G 是棱'DD 的中点,则异面直线GB 与'B E 所成的角为______.4. 如图,在底面半径为1,高为3的圆锥中,O 是底面圆心,P 为圆锥顶点,A ,B 是底面圆周上的两点,23AOB π∠=,C 为母线PB 的中点,则在该圆锥的侧面上,从A 到C 的最短路径的长是______.5. 设抛物线C :24y x =的焦点为F ,过点()2,0-且斜率为23的直线与C 交于M ,N 两点,则FM FN ⋅=uuu r uuu r ______.6. 已知平面α,β和直线m ,n ,给出下列命题:①m αP ,n βP ,m n ⊥,则αβ⊥;②若αβP ,m αP ,n βP ,则m n P ;③若m α⊥,n β⊥,m n ⊥,则αβ⊥;④若αβ⊥,m α⊥,n β⊥,则m n ⊥,其中是真命题的是______(填写所有真命题的序号).7. 如图,在棱长为1的正方体1111ABCD A B C D -中,l 是平面11AB D 与平面ABCD 的交线,则点1D 到l 的距离是______.8. 如图,已知正三棱锥P ABC -的底面边长为2,侧棱长为4,则二面角A PB C --的大小为______.9. 已知球O 的表面上三点A 、B 、C 满足:12AB =,16BC =,20AC =,且球心到该截面的距离为球的半径的一半,则A 、C 两点的球面距离是______.10. 如图是复且附中旦华楼的大致形状,它可看作是一个半球与两个长方体拼接而成,若半球的半径3米,50AB =米,10BC =米,15CD =米,4GF =米,30EF =米,由于年久失修,需要用涂料刷满其外表面(不计地面),则需要______平方米的涂料.11. 已知a ,b ,h 是正常数,由直线0y =、直线y h =、双曲线22221x y a b -=及其一条渐近线围成如图阴影部分所示的图形,该图形绕y 轴旋转一周所得几何体的体积为______.12. 如图,已知直四棱柱1111ABCD A B C D -的所有棱长等于1,60ABC ∠=o ,O 和1O 分别是上下底面对角线的交点,H 在线段1OB 上,13OH HB =,点M 在线段BD 上移动,则三棱锥11M C O H -的体积最小值为______.二、选择题(本大题共4题,每题5分,共20分)13. 已知()1,1,0a =r ,()1,0,2b =-r ,且ka b +r r 与2a b -r r 垂直,则k 的值为( )A . 15 B . 1 C . 35 D . 7514. 过点()0,1P 与圆22230x y x +--=相交的所有直线中,被圆截得的弦最长时的直线方程是( )A . 0x =B . 1y =C . 10x y +-=D . 10x y -+=15. 下列四个结论中正确的是( )①若两个平面有无数多个公共点,则它们重合;②垂直于同一条直线的两条直线平行;③若两平行线中的一条与第三条直线垂直,则另一条也与这条直线垂直;④若a ,b 是异面直线,直线c ,d 与a ,b 都相交,则c ,d 也是异面直线;A . ①②B . ②③C . ③D . ③④16. 如图,在棱长为2的正方体1111ABCD A B C D -中,E ,F ,G 分别是棱AB ,BC ,1CC 的中点,P 是底面ABCD 内一动点,若直线1D P 与平面EFG 平行,则1PBB ∆的面积最小值为( )A . 22B . 1C . 2D . 2三、解答题(本大题共5题,共76分)17. 如图,在四棱锥中P ABCD -中,PA ⊥底面ABCD ,AD DC ⊥,AB DC P ,2AD DC AP ===,1AB =,点E 为棱PC 的中点.(1)证明:BE PD ⊥;(2)若F 为棱PC 上一点,满足BF AC ⊥,求线段PF 的长.18. 已知椭圆C :()222122x y a a +=>过点()2,1T ,左、右顶点分别为A ,B ,点M 是椭圆C 上异于A ,B 的一点,直线AM 与y 轴交于点P .(1)求椭圆C 的方程;(2)设椭圆C 的右焦点为F ,点Q 在y 轴上,且AQ BM P ,求证:PFQ ∠为定值.19. 如图,已知点P 在圆柱1OO 的底面圆O 上,120AOP ∠=o,圆O 的直径4AB =,圆柱的高13OO =.(1)求圆柱的表面积;(2)求点A 到平面1A PO 的距离;(3)求直线1A P 与AB 所成的角.20. 如图,在多面体111ABCA B C 中,1AA 、1BB 、1CC 均垂直于平面ABC ,14AA =,13CC =,12BB AB AC ===,120BAC ∠=o ,D ,E 分别是线段BC 和11B C 上的点.(1)求1AB 与111A B C 所成角的大小;(2)求二面角111A A B C --的大小;(3)求AD DE +的最小值.21. 已知双曲线C :()222210,0x y a b a b -=>>,设P 是双曲线C 上任意一点,O 为坐标原点,F 为双曲线右焦点,1A ,2A 为双曲线的左右顶点.(1)已知:无论点P 在右支的何处,总有PO PF >,求ba 的取值范围;(2)设过右焦点F 的直线l 交双曲线于M ,N 两点,若存在直线l ,使得OMN ∆为等边三角形,求22b a 的值;(3)若2a =,3b =,动点Q 与双曲线的顶点不重合,直线1QA 和直线2QA 与直线l :1x =分别相交于点S 和T ,试问:是否存在定点E ,使得ES ET ⊥恒成立?若存在,请求出定点E 的坐标;若不存在,试说明理由.参考答案一、填空题l . 12π 2. 2arccos 4 3. 90o 4. 3 5. 8 6. ③④ 7. 628. 7arccos 15 9. 4039π 10. 26209π+ 11. 2a h π 12. 348 二、选择题13-16:DCCC三、解答题17.(1)略;(2)3218.(1)22142x y +=;(2)90o19.(1)20π;(2)32;(3)21arccos 720.(1)15arcsin 5;(2)10arccos 5;(3)7391321.(1)()0,3;(2)1136+;(3)1,02⎛⎫- ⎪⎝⎭或5,02⎛⎫⎪⎝⎭。
2017-2018-高二上期中复旦附中

复旦大学附属中学2017学年第一学期期中考试试卷高二数学 满分120分一、填空题(每题4分)1.计算矩阵乘积:则3001a b c d ⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭__________2.若线性方程组的增广矩阵为3110m n -⎛⎫ ⎪-⎝⎭,解为12x y =⎧⎨=⎩,则m n -=__________ 3.平行于直线2350x y -+=,且过点()2,1的直线的点方向式方程为__________4.ABC ∆中,若90C ∠= ,2AC BC ==,则AB BC ⋅=__________5.已知1124(3)211201734n n n n n na n +++---=+-,则lim n n a →∞=__________ 6.已知直角坐标平面内的两个向量()2,1a =- ,()1,3b m m =-+,使得平面内的任意一个c 都可以唯一分解成(,)c a b R λμλμ=+∈,则m 的取值范围是__________ 7.若行列式124cos 50116θ中元素2的代数余子式的值为3,且[]0,2θπ∈,则θ=__________ 8.设0,0a b >>,若关于,x y 的方程组1010ax y x by +-=⎧⎨+-=⎩无解,则a b +的取值范围为__________9. 在ABC ∆中,()()(),1,2,,38,10A a a B a C ---,若ABC ∆的面积不超过2,则a 的取值范围是__________10.平面直角坐标平面系中,已知()()013,1,5,2P P ,且111()2n n n n P P P P n N *+-=-∈,当n →∞时,点n P 无限接近于点M ,则点M 的坐标为__________11.如图,八个边长为1的小正方形拼成一个24⨯的矩形,,,,A B D E 均为小正方形的顶点。
12. 在ABC ∆中,6AC =,7BC =,1cos 5A =,点O 是ABC ∆的内心,若OP xOA yOB =+ ,其中01,01x y ≤≤≤≤,则动点P 的轨迹所覆盖的面积为__________二、选择题(每题4分)13.下列命题正确的的是( )A. 若数列{}n a 、{}n b 的极限都存在,且(0)nn n na cb b =≠,则数列{}n c 的极限存在 B. 若数列{}n a 、{}n b 的极限都不存在,则数列{}n n a b +的极限也不存在 C. 若数列{}n n a b +、{}n n a b -的极限都存在,则数列{}n a 、{}n b 的极限也都存在 D.设12....n n S a a a =+++,若数列{}n a 的极限存在,则数列{}n S 的极限也存在14.设123,,e e e 为单位向量,且3121(0)2e e ke k =+>,若以向量12,e e 为邻边的三角形的面积为12,则k 的值为( )15.已知无穷等比数列{}n a 的公比为q ,前n 项和为n S ,且lim n n S S →∞=,下列条件中使得3()n S S n N *<∈恒成立的是( )A. 10a >,0.80.9q <<B. 10a <,0.90.8q -<<-C. 10a >,0.70.8q <<D. 10a <,0.80.7q -<<-16.设关于123,,x x x 的线性方程组2123123123000x x x x x x x x x λλλλ⎧++=⎪++=⎨⎪++=⎩的系数矩阵记为A ,且该方程组存在非零解。
2018-2019学年复旦附中高二上英语期中

2018-2019学年复旦附中⾼⼆上英语期中复旦⼤学附属中学2018学年第⼀学期⾼⼆年级英语期中考试试卷Ⅱ. Grammar and VocabularyDirections:Beneath each of the following sentences there are four choices marked A, B, C and D. Choose the one answer that best completes the sentence.21. The movie is not quite as good as the play ____ was adapted from.A. thatB. whichC. itD. what22. Never in my wildest dreams ____ lead to a career of writing novels, which has allowed me to share myexperience with people like me.A. I thought the chance wouldB. I thought would the chanceC. did I think the chance wouldD. did I think would the chance23. The charity fund has raised an adequate sum of money, ____ the family of the sick child can buy the kidney,which is urgently needed for the transplant surgery.A. by whichB. with whichC. whichD. for which24. You’d rather I ___ her the news, ____?A. told…wouldn’t youB. told…hadn’t youC. tell…wouldn’t youD. tell…hadn’t you25. –You must have felt dizzy when you stepped on the glass-bottomed bridge, ___?–No, I wasn’t scared of the height since it was foggy on that day.A. mustn’t youB. haven’t youC. weren’t youD. didn’t you26. After I settled in, a man approached me and insisted that I ____ in his seat. I ignored him and told him to goaway.A. wasB. wereC. beD. would be27. Finding that Big Jim was always daydreaming when working, the manager was surprised that theabsent-minded worker _____.A. should have been firedB. should be firedC. should not have been firedD. should not be fired28. If you behave well from now on, you ___ have an Apple Watch for your 18th birthday.A. willB. shallC. canD. must29. Most domestic car rental reservations can be canceled with no penalty ___ you find a better rate even on the day of the trip.A. mayB. shallC. wouldD. should30. She is probably better off fainting. She _____ the pain if she ____ conscious.A. couldn’t stand…wereB. cannot stand…will beC. couldn’t have stood…had beenD. cannot have stood…is31. So many closings, evacuations, shutdowns, ___ emergency response teams, the heroes of 9/11, the country virtually stopped what it was doing and gathered around TV screens.A. except thatB. except forC. besidesD. besides when32. Being a docile son, I didn’t argue with my parents when I was in elementary school and all I had to do was ____ my room _____ every time at their suggestions.A. to keep…being tidyB. to keep…to be tidyC. keep…to be tidyD. kee p…tidy33. His strong sense of humor was _____ make everyone in the room burst ____ laughing.A. so as to…intoB. so as to…outC. such as to…intoD. such as to…out34. The speech on urban pollution is rather a _____ speech, as I can judge from the ___ look of all the listeners.A. disturbing…disturbedB. disturbed…disturbingC. distracting…distractedD. distracted…disturbing35. You can cite examples to ______ the importance of being participants rather than ____ onlookers in life.A. illustrate…vagueB. illustrate…mereC. involve…vagueD. involve…mere36. Looking at images of caloric food can incite a person’s desire to eat. If you’ve fallen victim to this trap, you might consider unsubscribing to accounts that frequently post _____ images.A. indulgentB. radicalC. distractingD. irresistible37. A student activist at the time, toyed with communism, rebelling against Germany’s postwar elites which, as he put it,“still ______ of the Nazis”—only to become par t of the country’s cultural mainstream.A. echoedB. temptedC. assembledD. stank38. Ouyang Xiu repeatedly asked to be _____ his duties, but instead the new emperor sent him to be magistrate successively in Anhui, Shandong and Henan.A. engrossed inB. qualified forC. free fromD. relieved of39. No cash kept on hand is saving a significant amount on security of a large number of banks by removing the_____ for bank robberies.A. inspectionB. investmentC. incentiveD. involvement40. Even ____ of detecting dark matter not in their favor, astrophysicists maintain an unwavering optimism.A. beating the oddsB. against all oddsC. at oddsD. with the oddsSection BDirections:Complete the following passage by using the words in the box. Each word can only be used once. Note that there is one word more than you need.Archaeologists have long thought that stone ships served as graves for one or several individuals, and have even been viewed as death ships ___41___ to take the dead to living eternally. However, a new study conducted by researchers from the University of Gothenburg shows a different picture. It suggests Bronze Age stone monuments in the form of ships were built by sailors as a symbol of their practices at sea.The study indicates that the stone ships and the activities that took place there point to people who were ___42___ focused on practices at sea. Details found within the stone structures show they were built to ___43___ real ships. The stone ships offer up ___44___ about the ship-building techniques of the time and about the ships that sailed on the Baltic Sea during the Bronze Age.“These consist of areas that ___45___ hill forts and are located near easily ___46___ points in the landscape—that is, near well-known waterways leading inland,” Wehlin, head of the team, said. “While these areas have previously been thought to be much younger, recent age ___47___ have dated them to the Bronze Age.”Archaeologists have believed that bronze was ___48___ to Scandinavia from the south, and recent analyses have helped confirm this notion. However, the people who distributed the bronze objects are rarely ___49___ in these thoughts.“One reason why the meeting places of the Bronze Age are not discussed very often is that we haven’t beenable to find them,” Wehlin said. “This is in ___50___ contrast to the trading places of the Viking Age, which have been easy to locate as they left behind such rich archaeological mat erial.”Ⅲ. Reading ComprehensionSection ADirections:For each blank in the following passages there are four words or phrases marked A, B, C, and D. Fill in each blank with the word or phrase that best fits the context.Li-Fi, an alternative to Wi-Fi that transmits data using the spectrum of visible light, has achieved a new breakthrough, with UK scientists reporting transmission speeds of 10Gbit/s—more than 250 times faster than ‘superfast’broadband. The fastestspeed ___51___ reported was 3Gbit/s, achieved earlier this year in Germany. Chinese researchers also claimed this month to have produced a 150Mbp/s connection, but some experts were doubtful without seeing further ___52___.The term Li-Fi was ___53___ by Edinburg University’s Prof Harald Haas thoug ht the technology is also known as visible light communications(VLC). Many experts claim that Li-Fi represents the future of mobile internet ___54___ its reduced costs and greater efficiency compared to traditional Wi-Fi. Both Wi-Fi and Li-Fi transmit data over the electromagnetic spectrum, but ___55___ Wi-Fi utilizes radio waves, Li-Fi uses visible light. This is a ___56___ advantage in that the visible light is far more plentiful than the radio spectrum(10,000 times more in fact)and can achieve far greater data ___57___. Li-Fi signals work by switching bulbs on and off ___58___ quickly---too quickly to be noticed by the human eye. This most recent breakthrough builds upon this by using tiny micro-LED bulbs to ___59___ several lines of data in parallel. The research was carried out by the Ultra Parallel Visible Light Communications project, and funded by the Engineering and Physical Sciences Research Council.Existing LED light bulbs could be ___60___ to transmit Li-Fi signals with a single microchip, and the technology would also be of use in situations where radio frequencies cannot be used for fear of ___61___ with electronic circuit. And although Li-Fi bulbs would have to be kept on to transmit data, the bulbs could be ___62___ to the point that they were not visible to humans and yet still functional. One draw-back is that the data receiver would have to be in sight of the transmitter-bulb as visible light does not ___63___ solid materials.The makers of Li-Fi note that this quality might actually be an advantage in some ___64___, making Li-Fi more ___65___ than Wi-Fi with hackers unable to access unsecured internet connections from out of sight of the transmitter.51. A. subsequently B. presently C. lately D. previously52. A. truth B. proof C. act D. development53. A. produced B. coined C. composed D. designed54. A. thanks to B. in spite of C. but for D. except for55. A. although B. if C. whereas D. because56. A. dubious B. additional C. distinguishable D. distinct57. A. density B. structure C. analysis D. collection58. A. identifiably B. incredibly C. constantly D. frankly59. A. stream B. move C. stir D. float60. A. controlled B. created C. converted D. regulated61. A. combining B. connecting C. competing D. interfering62. A. lowered B. brightened C. sparkled D. dimmed63. A. alter B. reflect C. penetrate D. tough64. A. plots B. scenarios C. places D. settings65. A. secure B. risky C. definite D. dangerousSection BDirections:Read the following passages. Each passage is followed by questions or unfinished statements. For each of them there are four choices marked A, B, C and D. Choose the one that fits best according to the information given in the passage you have just read.AShould parents send their freshmen off to campus armed with a debt or credit card to learn how to handle money? Or is it better to keep firm control through the Bank of Mom and Dad? The "correct" answer will vary by family and personal preference.The Credit Card Act that took effect 2.5 years ago made it much harder for anyone under 21 to get a card. Gone are the days of card issuers collecting plenty of new customers on campus by handing out free T-shirts or rewards points for spring break. Under-21s can still obtain a credit card if they have a qualified co-signer or proof of sufficient income to repay the debt. Andcard issuers still market aggressively to college students, targeting them with pre-screened mail offers. That makes parents, as the likeliest co-signers, more involved in the card-or-no-card decision.Robyn Kahn Federman of Rochester, N.Y., says there’s “no way” she’ll let either of her two daughters have a credit card at such a financially t ender age. Her daughter Sarah, who’s 19 and about to start her second year of college, uses Robyn’s PayPal card instead. That lets her mom fund the balance and see how she spends her money.“I don’t think anything related to debt belongs in the hands of a college kid,” says Federman, communications director of a marketing agency. “The vast majority are not experienced enough with money or aware enough of the risks.”Some students, though, have shown they’re disciplined enough to have their own card on campu s.Scott Gamm, 20, a junior at New York University's Stern School of Business, used his income from freelance work and blogging to obtain a Visa card and then an American Express card. He charges $200 to $300 on them monthly and pays every bill in full.But he has friends who obtained three or four cards within a year and now have big debts.“The more credit you have access to, especially at that young age, the higher the probability you’ll use that card to finance fancy clothes, restaurants and entertainme nt.” says Gamm.66. According to the passage, which of the following statement is true?A. People hold different opinions about their kids using credit cards.B. Credit cards are useful in helping deal with money matters.C. It is better to have Mom and Dad who now run a bank.D. The new Act made it impossible to get a credit card for freshmen.67. To obtain a credit card, an under-21 has to _____.A. own a credit card of his own previouslyB. have someone to repay the possible debtC. turn to their parents to get their permissionD. ask their parents to write the application letter68. We may infer from the case of Sarah that PayPal card ____.A. is a kind of credit cardB. funds the balance automaticallyC. has access to creditD. keeps records of money spent69. What is the passage mainly about?A. The Credit Card ActB. Students and credit cardsC. Card issuers and studentsD. Parents and choice of cardsB70. Which of the following best describes Roth’s feeling in Book 1?A. FrightenedB. CuriousC. PainfulD. Disappointed71. Which of the following is TRUE according to the passage?Twelve-year-old Roth becomes a friend of Dr. Banting and his assistant, Mr. Best, whoare in search of a cure for diabetes for the animals being experimented on and her friendship with Banting and Best. Meet professor who made over 325 products out of peanuts. Through his agricultural research,he States. See also Macleod’s Albert Einstein: A Life of Genius.The Inuit Thought of It: Amazing Arctic Innovationsto intelligent people. Also see other books; The Chinese Thought of It by Tingxing Ye and ANative American Thought of It by Rocky Landon and David MacDonald.Made in Canada: 101 Amazing AchievementsWhat things that were invented in Canada or by a Canadian, including the Blackberry, alkaline(碱性)Ten-year-old disappears on a test run with his two huge friends, King Herbert and Queen Certunde, init! Can he save them before time runs out?A. Book 3 introduced 40 inventive concepts.B. Animals are mentioned in Book 1 and Book 5.C. Alkaline batteries were invented by Dr. Banting.D. George Washington Carver was a black farmer in the US.72. In Book 5, King Herbert and Queen Gertrude are ____.A. Newton’s human friendsB. the names of the time machineC. the inventions of the time machineD. two dinosaurs73. If you are interested in native Americans, you may read the book by ______.A. Elizabeth MacleodB. Eric WaltersC. Rocky Landon & David MacDonaldD. Bev SpencerCGoogle must be the most ambitious company in the world. Its stated goal, "to organize the world’s information and make it universally accessible and useful," deliberately omits the word "web" to indicate that the company is reaching for absolutely all information everywhere and in every form. From books to health records and videos, from your friendships to your click patterns and physical location, Google wants to know. To some people this sounds uplifting, with promises of free access to knowledge and help in managing our daily lives. To others, it is somewhat like another Big Brother, no less frightening than its (极权主义者) ancestors for being in the private information.Randall Stross, a journalist at the New York Times, does a good job of analyzing this unbounded ambition in his book "Planet Google". One chapter is about the huge data centers that Google is building with a view to storing all that information, another about the sets of rules at the heart of its web search and advertising technology, another about its approach to information bound in books, its vision for geographical information and so forth. He is at his best when explaining how Google’s mission casually but fatally smashes into long-existing institutions such as, say, copyright law or privacy norms.And yet, it’s puzzling that he mostly omits the most fascinating component of Google, its people. Google is what it is because of its two founders, Sergey Brin and Larry Page, who see themselves as kindly elites and embody the limitless optimism about science and technology and human nature that is native to Silicon Valley. The world is perfectible, and they are the ones who will do much of the perfecting, provided you let them.Brin and Page set out to create a company and an entire culture in their image. From the start, they claimed that they would innovate as much in managing—rewarding, feeding, motivating, entertaining and even transporting (via Wi-Fi-enabled free shuttle buses) their employees—as they do in internet technology. If Google is in danger of becoming a caricature (讽刺画), this is first apparent here--in the over-engineered day-care centers, the shiatsu massages and kombucha teas (康普茶). In reality Google’s are as prone to power struggl e and office politics as anyone else.None of that makes it into Mr. Stross’ account, which at times reads like a diligent summary of news articles. At those moments, "Planet Google" takes a risk similar to trying to board a speeding train: the Google story changes so fast that no book can stay up to date for long. Even so, a reasonable description of this moment in Google’s quest is welcome. Especially since Google fully expects, as its chief executive, Eric Schmidt, says at the end of the book, to take 300 years completing it.74. By describing Google as a“Big Brother”,people think that Google ______.A. is a pioneer in IT industryB. is an invader of privacyC. breaks its promise of free accessD. overestimates its own influence75. According to Randall Stross, Google’s influence on copyright law or privacy norm is ___.A. inevitableB. undeniableC. long-lastingD. unintentional76. What does the author think of Brin and Larry Page?A. They are the most crucial component of Google.B. They are deliberately omitted in the book“Planet Google”.C. They bring Silicon Valley the most advanced science and technology.D. They are the persons who never stop pursuing a better world.77. What do we know about the Google employees in reality?A. They play tricks on each other in the office.B. They are all hard-working and talented.C. They appreciate the managing techniques.D. They feel encouraged by the company’s benefits.78. What does the author imply by saying“‘Planet Google’takes a risk similar to trying to board a speeding train”?A.“Planet Google”will be in danger if it stays up to date for long.B.“Planet Google”has to take 300 years to catch the speeding train.C. The board of Google welcomes Randall Stross to cover Google story.D. A written book can only cover a little part of the on-going technology.Section CDirections:Read the following passage. Fill in each blank with a proper sentence given in the box. Each sentence can be used only once. Note that there are two more sentences than you need.Most of us are taught to pay attention to what is said—the words. Words do provide us with some information, but meanings are derived from so many other sources that it would hinder our effectiveness as a partner to a relationship to rely too heavily on words alone. Words are used to describe only a small part of the many ideas we associate with any given message. Sometimes we can gain insight into some of those associations if we listen for more than words. ___79___. Sometimes our words don’t mean anything except “ I‘m letting off some steam. I don’t really want you to pay close attention to what I‘m saying. Just pay attention to what I’m feeling.” Mostly we mean several things at once. A person wanting to purchase a house says to the current owner,“This step has to be fixed before I’ll buy.” The owner says,“ It’s been like that for years.” Actually, the step hasn‘t been like that for years,but the unspoken message is: “ I don’t want to fix it. We put up with it. Why can‘t you?” The search for a more expansive view of meaning can be developed of examining a message in terms of who said it, when it occurred,the related conditions or situation, and how it was said.___80___. Let us assume two couples do exactly the same amount of kissing and arguing. But one couple always kisses after an argument and the other couple always argues after a kiss. The ordering of the behaviors may mean a great deal more than the frequency of the behavior. A friend‘s unusually docile behavior may only be understood by noting that it was preceded by situations that required an abnormal amount of assertiveness. ___81___ For example, a person who says “No!”to a serials of charges like “You’re dumb, ” “You‘re lazy, ” and “You’re dishonest, ” may also say “No!” and try to justify his or her response if the next statement is “And you‘re good looking.”___82___ The words, “If sure nice to have you over, ” can be said with emphasis and excitement or ritualistically. The phrase can be said once or repeated several times. And the meanings we associate with the phrase will change accordingly. Sometimes if we say something infrequently it assumes more importance; sometimes the more we say something the less importance it assumes.。
2023-2024学年上海市复旦大学附属中学高二上学期期中考试数学试卷含详解

复旦大学附属中学2023学年第一学期高二年级数学期中考试试卷(A )时间:120分钟满分:150分一、填空题(本大题共有12小题,第1-6题每题4分,第7-12题每题5分,满分54分)1.直线210x y --=的倾斜角是__________.2.抛物线224y x =-的准线方程是__________.3.直线l 过点(1,2)-且与直线2340x y -+=平行,则直线l 的方程是__________.4.椭圆22145x y +=的离心率是__________.5.过点(5,3)作圆22(3)4x y -+=的切线,则切线的方程为__________.6.在ABC 中,(3,0)A -,(3,0)B ,3sin 3sin sin B A C -=,则顶点C 的轨迹方程是__________.7.直线12x t y t =-⎧⎨=+⎩(t 为参数,R t ∈)和曲线:x C y θθ⎧=⎪⎨=⎪⎩,(θ为参数,R θ∈)交于P 、Q 两点,则||PQ =__________.8.已知直线1:2160l x y --=和直线2:10l x +=,则抛物线24y x =上的动点P 到直线1l 和2l 的距离之和的最小值为__________.9.已知双曲线22:41C x y -=,过点(0,0)作直线l 和双曲线C 交于A ,B 两点.点A 在第一象限,过点A 作x 轴的垂线,垂足为H ,则直线BH 倾斜角的取值范围是__________.10.如图,圆柱的底面直径与高均为2,一平面截圆柱,其截面为椭圆,该平面与圆柱的底面所成的二面角为45 ,该椭圆的内接六边形ABCDEF 的最大面积为__________.11.一质点在矩形ABCD 内运动,从AB 的中点O 沿一确定方向发射该质点,依次由线段BC 、CD 、DA 反射.反射点分别为1P 、2P 、3P (入射角等于反射角),最后落在线段OA 上的4P (不包括端点).若()1,0A -、()10B ,、()1,1C 和()11D -,,则1OP 的斜率的取值范围是_______.12.已知椭圆22221(0)x y a b a b +=>>的两个焦点为1F 、2F ,P 为该椭圆上一点,O 为坐标原点且||OP a λ=,满足21212F F PF PF =⋅,则λ的取值范围为__________.二、选择题(本大题共有4小题,第13-14题每题4分,第15-16题每题5分,满分18分)每题有且只有一个正确选项.考生应在答题纸的相应位置,将正确选项用2B 铅笔涂黑.13.关于方程2220x xy y -+=所表示的曲线,下列说法正确的是()A.关于x 轴对称B.关于y 轴对称C.关于y x =轴对称D.关于原点中心对称14.已知直线:0l ax by c ++=,点()11,M x y 、()22,N x y ,设111ax by c λ=++,222ax by c λ=++,以下选项中命题都正确的为()(1)若120λλ+=,则线段MN 的中点在直线l 上(2)若120λλ-=,则直线MN 与直线l 平行(3)若120λλ⋅<,则点M 、 N 分布在直线l 的两侧(4)若121λλ>,则直线l 与线段MN 的延长线相交A .(1)(2)(3) B.(2)(3)(4) C.(1)(3)(4) D.(1)(2)(3)(4)15.12,x x 是关于x 的二次方程22830mx x m -+-=的两个不同实数根,则经过两点()211,A x x ,()222,B x x 的直线与抛物线28y x =公共点的个数是()A.2 B.1 C.0 D.不确定16.足球教练带领运动员对“带球射门”进行专项训练.如图,教练员指导运动员沿着与边路DC 平行的路线带球并起脚射门,教练员强调要在路线上的相应位置P 处起脚射门进球的可能性最佳(即点P 对球门AB 所张的角APB ∠最大),假如每条虚线都表示在规定的区域BCDE 内为运动员预设的带球路线,而每条路线上都有一个最佳起脚射门点P ,为了研究方便,如图建立坐标系,设()1,0A -、()10B ,,请你判断:每条虚线上的最一佳起脚射门点(),P x y 应在怎样的曲线上()A.圆B.椭圆C.双曲线D.抛物线三、解答题(本大题共5题,满分78分)解答下列各题须在答题纸的相应位置写出必要的步骤.17.已知两条直线1:(1)20l t x y t -+-=和2:40l x ty t ++-=.(1)讨论直线1l 与2l 的位置关系;(2)当直线1l 与2l 平行时,求它们之间的距离;当直线1l 与2l 相交时,求它们之间夹角的最大值,并指出相应t 的取值.18.已知拋物线C 的方程为24y x =.(1)求过点(0,2)且与抛物线C 只有一个公共点的直线的方程;(2)已知直线l 过焦点,且与抛物线交于A ,B 两点,点M 为该抛物线准线上一点,求证:0MA MB ⋅≥19.如图,设直线l 为公海与领海的分界线,一巡逻艇在A 处发现了海面B 处有一艘走私船,A 与公海相距20海里.走私船可能向任一方向逃窜,若它进入公海则逃脱成功.假设走私船和巡逻艇都是沿直线航行,巡逻艇的航速是走私船航速的()1λλ>倍.(1)当2λ=,()0,0A ,()6,6B 时,走私船能被截获的点在一个圆上,求这个圆的标准方程;(2)可知非截获区域是一个圆的内部,如果此圆和分界线l 没有公共点,则巡逻艇可以成功截获走私船.已知B 在A 的北偏东45︒,相距102海里处,为了成功截获走私船,求λ的最小整数值.20.已知直线30x y ++=与椭圆222:1x E y a+=有且只有一个公共点.(1)求椭圆E 的方程;(2)是否存在实数λ,使椭圆E 上存在不同两点P 、Q 关于直线20x y λ--=对称?若存在,求λ的取值范围;若不存在,请说明理由;(3)椭圆E 的内接四边形ABCD 的对角线AC 与BD 垂直相交于椭圆的左焦点,S 是四边形ABCD 的面积,求S 的最小值.21.平面上,直线1l 和2l 相交于点O ,它们的夹角为2θ.已知动点P 到直线1l 与2l 的距离之积为定值2(0)m m >,动点P 的轨迹记为曲线E .我们以O 为坐标原点,以直线1l 与2l 夹角的平分线为x 轴,建立直角坐标系,如图.(1)求曲线E 的方程;(2)当1m =,π4θ=时,直线l 与曲线E 顺次交于A 、B 、C 、D 四点,求证:AB CD = ;(3)当125m =,3arctan 4θ=时,是否存在直线l 与曲线E 只有A 、B 、C 三个不同公共点(点B 在线段AC 上),使得OA OC ⊥ ?若存在,求出直线l 的方程;若不存在,请说明理由.复旦大学附属中学2023学年第一学期高二年级数学期中考试试卷(A )一、填空题(本大题共有12小题,第1-6题每题4分,第7-12题每题5分,满分54分)考生应在答题纸的相应位置直接填写结果.1.直线210x y --=的倾斜角是__________.【答案】arctan 2【分析】直接根据斜率可得倾斜角.【详解】210x y --=即21y x =-,设倾斜角为,0παα≤<,则tan 2α=所以arctan 2α=.故答案为:arctan 2.2.抛物线224y x =-的准线方程是__________.【答案】6x =【分析】根据抛物的标准方程,直接求出结果.【详解】因为抛物线的方程为224y x =-,所以准线方程为6x =,故答案为:6x =.3.直线l 过点(1,2)-且与直线2340x y -+=平行,则直线l 的方程是__________.【答案】2380x y -+=【分析】设与直线2340x y -+=平行的直线方程为230x y c -+=,代入已知点计算即可.【详解】设与直线2340x y -+=平行的直线方程为230x y c -+=,带入点(1,2)-得2320c --⨯+=,得8c =,所以直线l 的方程是2380x y -+=.故答案为:2380x y -+=.4.椭圆22145x y +=的离心率是__________.【答案】55【分析】根据条件,求出,a c ,再利用离心率的定义即可求出结果.【详解】由椭圆方程22145x y +=,知a =,1c ==,所以,离心率55c e a ===,5.过点(5,3)作圆22(3)4x y -+=的切线,则切线的方程为__________.【答案】5x =或512110x y -+=【分析】考虑所作切线斜率是否存在,存在时,设出其方程,利用圆心到切线的距离等于半径,列式计算,求得参数,即可求得答案.【详解】由圆22(3)4x y -+=可知圆心为(3,0),半径为2r =,当过点(5,3)的直线斜率不存在时,直线方程为5x =,此时圆心(3,0)到5x =的距离为532-=,此时5x =和圆22(3)4x y -+=相切;当过点(5,3)的直线斜率存在且和圆22(3)4x y -+=相切时,设其方程为3(5)y k x -=-,即530kx y k --+=,2=,解得512k =,即切线方程为525301212x y --+=,即512110x y -+=,故切线的方程为5x =或512110x y -+=,故答案为:5x =或512110x y -+=6.在ABC 中,(3,0)A -,(3,0)B ,3sin 3sin sin B A C -=,则顶点C 的轨迹方程是__________.【答案】2281(0)y x x -=>【分析】由正弦定理化角为边后确定点的轨迹,由双曲线的标准方程求解.【详解】∵(3,0)A -,(3,0)B ,∴6c AB ==,∵3sin 3sin sin B A C -=,∴由正弦定理得33b a c -=,即23c b a -==,2CA CB -=,所以C 点轨迹是以,A B 为焦点的双曲线的右支.该双曲线的半焦距为3,实半轴长为212==,所以轨迹方程为2281(0)y x x -=>.故答案为:2281(0)y x x -=>.7.直线12x t y t =-⎧⎨=+⎩(t 为参数,R t ∈)和曲线:x C y θθ⎧=⎪⎨=⎪⎩,(θ为参数,R θ∈)交于P 、Q 两点,则||PQ =__________.【答案】5【分析】将参数方程化为直角坐标方程,再求出圆心到直线的距离,最后由勾股定理、垂径定理计算可得.【详解】直线12x t y t =-⎧⎨=+⎩(t 为参数,R t ∈),即210x y +-=,曲线:x C y θθ⎧=⎪⎨=⎪⎩,(θ为参数,R θ∈),即222x y +=,表示圆心为坐标原点,半径r =其中坐标原点到直线210x y +-=的距离55d ==,所以5PQ ===.故答案为:6558.已知直线1:2160l x y --=和直线2:10l x +=,则抛物线24y x =上的动点P 到直线1l 和2l 的距离之和的最小值为__________.【答案】【分析】利用抛物线的定义将距离和最小值转化为点到直线的距离求解即可.【详解】直线2:10l x +=为抛物线24y x =的准线,()1,0F 为抛物线24y x =的焦点,过点P 作2PH l ⊥于H ,作1⊥PM l 于M ,过F 作1FN l ⊥于N ,由抛物线的定义可得PF PH =,PH PM PF PM FN ∴+=+≥,当,,F P N '三点共线时等号成立,又FN ==即动点P 到直线1l 和2l 的距离之和的最小值为.故答案为:.9.已知双曲线22:41C x y -=,过点(0,0)作直线l 和双曲线C 交于A ,B 两点.点A 在第一象限,过点A 作x 轴的垂线,垂足为H ,则直线BH 倾斜角的取值范围是__________.【答案】π(0,)4【分析】由题意设l 的方程为,(02)y kx k =<<,设11(,)A x y ,从而表示出BH 的斜率,推得2BH k k =,即可确定其取值范围,从而求得倾斜角的取值范围.【详解】由题意知双曲线22:41C x y -=的渐近线方程为2y x =±,由于直线l 过点(0,0),点A 在第一象限,故设直线l 的方程为,(02)y kx k =<<,设11(,)A x y ,则111(,),(,0)B x y H x --,故1122BH y k k x ==,则(0,1)2BH k k =∈,由于直线倾斜角范围为[0,π),则直线BH 倾斜角的取值范围是π(0,4,故答案为:π(0,410.如图,圆柱的底面直径与高均为2,一平面截圆柱,其截面为椭圆,该平面与圆柱的底面所成的二面角为45 ,该椭圆的内接六边形ABCDEF 的最大面积为__________.【答案】362362【分析】根据题意求出椭圆的长轴长和短轴长,即确定,a b 的值,结合当椭圆的内接六边形ABCDEF 为正六边形时,其面积最大,即可求得答案.【详解】如图,由题意可知截面与圆柱的底面所成的二面角为45 ,即45CAB ∠= ,圆柱的底面直径与高均为2,故2AC =,则椭圆的长轴长222,2a a =∴=而椭圆的短轴长2b 即等于圆柱底面圆的直径,即22,1b b =∴=,当椭圆的内接六边形ABCDEF 为正六边形时,其面积最大,最大值为621π36sin 232⨯=,故答案为:36211.一质点在矩形ABCD 内运动,从AB 的中点O 沿一确定方向发射该质点,依次由线段BC 、CD 、DA 反射.反射点分别为1P 、2P 、3P (入射角等于反射角),最后落在线段OA 上的4P (不包括端点).若()1,0A -、()10B ,、()1,1C 和()11D -,,则1OP 的斜率的取值范围是_______.【答案】12,23⎛⎫ ⎪⎝⎭【分析】根据题意线段123OP P P ,1234PP P P ,分别找出4P 点落在线段OA 上的临界位置,即可求解.【详解】由题意知:123OP P P ,1234PP P P ,设()11,P b ,则线段1OP 的斜率:010b k b -==-,为使4P 点落在线段OA 上(不包括端点),所以得:当4P 落到点O ,点A 时为相应的两种临界位置,当4P 落到点O 时:由题意知:O 点为AB 的中点,且从O 点出发又回到O 点,所以可得:此时1P 位于线段BC 的中点位置,所以得此时1OP 的斜率:112k b ==;当4P 落到点A 时:4P 点与3P 点重合,如下图所示,设1POB θ∠=,可得:1223PP C DP P θ∠=∠=,且tan b θ=,所以得:11CP b =-,2111b CP b b -==-,213DP b =-,所以得:321tan 13DP b DP b θ===-,解之得:23b =,所以此时斜率:223k =,综上所述:可得1OP 的斜率范围为:1223k <<,即12,23⎛⎫ ⎪⎝⎭.故答案为:12,23⎛⎫ ⎪⎝⎭.12.已知椭圆22221(0)x y a b a b+=>>的两个焦点为1F 、2F ,P 为该椭圆上一点,O 为坐标原点且||OP a λ=,满足21212F F PF PF =⋅,则λ的取值范围为__________.【答案】312λ≤≤【分析】设出00(,)P x y ,利用条件21212F F PF PF =⋅和点在椭圆上得到22224c a e x =-,再根据条件||OP a λ=,得到22253b aλ=-,再利用b a λ≤,即可建立不等关系求出结果.【详解】如图,设00(,)P x y ,易知,12(,0),(,0)F c F c -,则1PF =,又2200221x y a b +=,得到222002(1)x y b a-⨯=,代入1PF =10PF ex a =+,同理可得,10PF ex a =-,又0a x a -≤≤,21212F F PF PF =⋅,得到2222222004c e x a a e x =-=-,又||OP a λ=,则222200x y a λ+=,由2222002200221x y a x y ab λ⎧+=⎪⎨+=⎪⎩,消0y 得到,222202e a b x λ=-,又222204c a e x =-,所以2222222453a a b c b a λ=+-=-,得到22253b aλ=-,又由||OP a λ=,易知,b a a λ≤≤,得到baλ≤且01λ<≤,所以22225353b a λλ=-≤-,得到234λ≤,所以312λ≤≤,故答案为:312λ≤≤.二、选择题(本大题共有4小题,第13-14题每题4分,第15-16题每题5分,满分18分)每题有且只有一个正确选项.考生应在答题纸的相应位置,将正确选项用2B 铅笔涂黑.13.关于方程2220x xy y -+=所表示的曲线,下列说法正确的是()A.关于x 轴对称B.关于y 轴对称C.关于y x =轴对称D.关于原点中心对称【答案】D【分析】根据题意,由曲线方程,依次分析选项即可得出答案.【详解】对于A ,将方程中y 换为y -,则有()()2220x x y y --+-=,则2220x xy y ++=,与原方程不同,所以方程2220x xy y -+=不关于x 轴对称;对于B ,将方程中x 换为x -,则有()()2220x x y y ---+=,则2220x xy y ++=,与原方程不同,所以方程2220x xy y -+=不关于y 轴对称;对于C ,将方程中x 换为y ,y 换为x ,则有2220y yx x -+=,与原方程相同,所以方程2220x xy y -+=不关于y x =轴对称;对于D ,将方程中x 换为x -,y 换为y -,则有()()()2220x x y y ----+=,则2220x xy y -+=,与原方程相同,所以方程2220x xy y -+=关于原点中心对称.故选:D .14.已知直线:0l ax by c ++=,点()11,M x y 、()22,N x y ,设111ax by c λ=++,222ax by c λ=++,以下选项中命题都正确的为()(1)若120λλ+=,则线段MN 的中点在直线l 上(2)若120λλ-=,则直线MN 与直线l 平行(3)若120λλ⋅<,则点M 、 N 分布在直线l 的两侧(4)若121λλ>,则直线l 与线段MN 的延长线相交A.(1)(2)(3) B.(2)(3)(4) C.(1)(3)(4) D.(1)(2)(3)(4)【答案】C【分析】根据条件,再合(1)(2)(3)(4)中所给条件,逐一分析判断即可得出结果.【详解】对于(1),因为120λλ+=,所以121211221212()()22[(()]022x x y y ax by c ax by c a x x b y y c a b c +++++++=++++=++=,即1212()()022x x y y a b c ++++=,所以(1)正确;对于(2),当120λλ==时,满足120λλ-=,此时有110ax by c ++=,220ax by c ++=,即()11,M x y 、()22,N x y均在直线l 上,所以(2)错误;对于(3),由120λλ⋅<,得到1122()()0ax by c ax by c ++⋅++<,由直线分平面区域的点满足“同侧同号,异侧异号”,知选项C 正确;对于(4),由121λλ>,得到11221ax by c ax by c ++>++,则有1122()()0ax by c ax by c ++⋅++>,由直线分平面区域的点满足“同侧同号,异侧异号”,知点M 、 N 分布在直线l 的同侧,且由11221ax by cax by c ++>++,得到121222[()()]()0a x x b y y ax by c -+-++>,所以1212()()0a x x b y y -+-≠,从而有1212y y a b x x --≠-,所以(4)正确,故选:C.15.12,x x 是关于x 的二次方程22830mx x m -+-=的两个不同实数根,则经过两点()211,A x x ,()222,B x x 的直线与抛物线28y x =公共点的个数是()A.2B.1C.0D.不确定【答案】A【分析】先利用二次方程根与系数的关系求出1212,,x x x x +,然后代入经过两点()211,A x x ,()222,B x x 的直线方程,整理后可得直线恒过定点,根据定点和抛物线的关系可得直线与抛物线的公共点个数.【详解】12,x x 是关于x 的二次方程22830mx x m -+-=的两个不同实数根,121228383x x m m x x m m ⎧+=⎪⎪∴⎨-⎪==-⎪⎩,又()44830m m ∆=-->,得4133m <或4133m >,且0m ≠,经过两点()211,A x x ,()222,B x x 的直线为()222211121x x y x x x x x --=--,整理得()1212y x x x x x =+-即()282343y x x m m m⎛⎫=--=-+ ⎪⎝⎭该直线恒过点()4,3A ,且斜率不为零,根据图像可得直线与抛物线28y x =公共点的个数是2,故选:A.16.足球教练带领运动员对“带球射门”进行专项训练.如图,教练员指导运动员沿着与边路DC 平行的路线带球并起脚射门,教练员强调要在路线上的相应位置P 处起脚射门进球的可能性最佳(即点P 对球门AB 所张的角APB ∠最大),假如每条虚线都表示在规定的区域BCDE 内为运动员预设的带球路线,而每条路线上都有一个最佳起脚射门点P ,为了研究方便,如图建立坐标系,设()1,0A -、()10B ,,请你判断:每条虚线上的最一佳起脚射门点(),P x y 应在怎样的曲线上()A.圆B.椭圆C.双曲线D.抛物线【答案】B【分析】根据椭圆定义即可判断.【详解】设PA a =,PB b =,在APB 中,()22224424cos 222a b ab a b ab APB ab ab ab+--+--∠==≥,因为cos APB ∠随着APB ∠增大而减小,所以∠APB 最大时,则cos ∠APB 最小,由基本不等式可知,当且仅当a b +为定值时,cos ∠APB 有最小值,即PA PB +为定值且2PA PB +>,所以射门点P 应该在椭圆上.故选:B .三、解答题(本大题共5题,满分78分)解答下列各题须在答题纸的相应位置写出必要的步骤.17.已知两条直线1:(1)20l t x y t -+-=和2:40l x ty t ++-=.(1)讨论直线1l 与2l 的位置关系;(2)当直线1l 与2l 平行时,求它们之间的距离;当直线1l 与2l 相交时,求它们之间夹角的最大值,并指出相应t 的取值.【答案】(1)答案见解析;(2)平行时距离为924,相交时最大夹角为90︒.【分析】(1)由两相交求得t 的范围,再讨论平行与重合的情形即可;(2)由平行线间距离公式求距离,考虑特殊情形即两直线能否垂直,垂直时夹角最大为90︒.【小问1详解】(1)20t t --≠,2t ≠且1t ≠-时,两直线相交,2t =时,两直线方程分别为220x y +-=和220x y +-=,两直线重合,1t =-时,两直线方程分别为2210x y -++=和50x y --=,两直线平行.综上,2t ≠且1t ≠-时,两直线相交,2t =时,两直线重合,1t =-时,两直线平行.【小问2详解】由(1)两直线平行时,两直线方程分别为2210x y -++=和50x y --=即为2210x y --=和22100x y --=,距离为924d ==,两直线相交时,2t ≠且1t ≠-,0t ≠时,1l 的斜率为112t k -=-,2l 的斜率为21k t =-,由11(12t t --⋅-=-得13t =,即13t =时两直线垂直,夹角最大为90︒.18.已知拋物线C 的方程为24y x =.(1)求过点(0,2)且与抛物线C 只有一个公共点的直线的方程;(2)已知直线l 过焦点,且与抛物线交于A ,B 两点,点M 为该抛物线准线上一点,求证:0MA MB ⋅≥【答案】(1)122y x =+,0x =和2y =;(2)证明见解析.【分析】(1)考虑直线斜率不存在和与抛物线对称轴平行的直线,再在斜率存在时,设方程2y kx =+,由它与抛物线相切得结论.(2)直线l 方程为1x my =+,设1122(,),(,)A x y B x y ,设(1,)M t -,直线方程代入抛物线方程应用韦达定理,代入MA MB ⋅计算可得.【小问1详解】显然直线0x =和直线2y =都是与抛物线只有一个公共点,再设直线方程为2y kx =+,代入抛物线方程得224(1)40k x k x +-+=,由2216(1)160k k ∆=--=得12k =,直线方程为122y x =+,它与抛物线相切.只有一个公共点.所以所求直线方程为122y x =+,0x =和2y =;【小问2详解】由已知抛物线焦点为(1,0)F ,设直线l 方程为1x my =+,设1122(,),(,)A x y B x y ,由214x my y x=+⎧⎨=⎩得2440y my --=,124y y m +=,124y y =-,准线方程是=1x -,设(1,)M t -,所以11221212(1,)(1,)(1)(1)()()MA MB x y t x y t x x y t y t ⋅=+-⋅+-=+++--1212(2)(2)()()my my y t y t =++---221212(1)(2)()4m y y m t y y t =++-+++22244(2)0t mt m t m =++=+≥.19.如图,设直线l 为公海与领海的分界线,一巡逻艇在A 处发现了海面B 处有一艘走私船,A 与公海相距20海里.走私船可能向任一方向逃窜,若它进入公海则逃脱成功.假设走私船和巡逻艇都是沿直线航行,巡逻艇的航速是走私船航速的()1λλ>倍.(1)当2λ=,()0,0A ,()6,6B 时,走私船能被截获的点在一个圆上,求这个圆的标准方程;(2)可知非截获区域是一个圆的内部,如果此圆和分界线l 没有公共点,则巡逻艇可以成功截获走私船.已知B 在A 的北偏东45︒,相距海里处,为了成功截获走私船,求λ的最小整数值.【答案】(1)22(8)(8)32x y -+-=;(2)3【分析】(1)设(,)P x y ,用坐标表示出2PA PB =,化简即得;(2)建立如图的直角坐标系,设(,)P x y ,用坐标表示出PA PB λ=,化简即得圆方程,从而求得圆心坐标和半径,该圆外部是截获区域,因此该圆与分界线不能相交,从而可求得λ的范围得出最小整数值.【小问1详解】设(,)P x y 是截获点,则2PA PB =,=22(8)(8)32x y -+-=;【小问2详解】以海岸线为x 轴,A 为坐标原点建立如图所示的平面直角坐标系,则(10,10)B ,设(,)P x y 是截获点,则PA PB λ=,即=,化简得2222222221010200()()11(1)x y λλλλλλ-+-=---,截获点所在圆为以22221010(,)11λλλλ--为圆心,21021λ-为半径的圆,该圆外部为截获区域,要能成功截获走私船,则该圆与分界线不能相交,所以222101022011λλλ+≤--,因为1λ>,故解得21022λ≥+,所以λ的最小整数值为3.20.已知直线0x y ++=与椭圆222:1x E y a+=有且只有一个公共点.(1)求椭圆E 的方程;(2)是否存在实数λ,使椭圆E 上存在不同两点P 、Q 关于直线20x y λ--=对称?若存在,求λ的取值范围;若不存在,请说明理由;(3)椭圆E 的内接四边形ABCD 的对角线AC 与BD 垂直相交于椭圆的左焦点,S 是四边形ABCD 的面积,求S的最小值.【答案】(1)2212x y +=(2)存在,66,33⎛⎫- ⎪ ⎪⎝⎭(3)2【分析】(1)将直线方程和椭圆方程联立,利用Δ0=求解即可;(2)假设存在实数λ,设:20PQ l x y t ++=,通过0∆>求出t 的范围,然后与椭圆联立,求出线段PQ 的中点,代入直线20x y λ--=,求出t 与λ的关系,进而可得λ大范围;(3)先求出对角线AC 与BD 中有一个斜率不存在,另一个斜率为零时的S ,再求对角线AC 与BD 的斜率即存在,又不为零时的S ,对于这种情况,设:1,0AC l x ty t =-≠,与椭圆联立,然后利用弦长公式求出AC ,同理求出BD ,通过12S AC BD =计算求其范围,然后综合可得S 的最小值.【小问1详解】联立22201x y x y a⎧++=⎪⎨+=⎪⎩,消去y 得()2222120a x x a +++=直线0x y ++=与椭圆222:1x E y a+=有且只有一个公共点,∴()()2222810a a ∆=-+=,解得22a =即椭圆E 的方程为2212x y +=;【小问2详解】假设存在实数λ,使椭圆E 上存在不同两点P 、Q 关于直线20x y λ--=对称,设:20PQ l x y t ++=,()()1122,,,P x y Q x y 联立222012x y t x y ++=⎧⎪⎨+=⎪⎩,消去x 得226420y ty t ++-=,则()22162420t t ∆=-->,解得t <<由韦达定理得1223t y y +=-,()12122223t x x y y t ∴+=-+-=-,121222022333x x y y t t tλλλ++∴⨯--=-+-=--=,66,333t λ⎛⎫∴=-∈- ⎪ ⎪⎝⎭,∴存在实数λ,使椭圆E 上存在不同两点P 、Q 关于直线20x y λ--=对称,且λ的取值范围是6633⎛⎫-⎪ ⎪⎝⎭.【小问3详解】椭圆的左焦点为()1,0-,当对角线AC 与BD中有一个斜率不存在,另一个斜率为零时,2112122222b S AC BD a a ==⨯⨯=⨯,当对角线AC 与BD 的斜率即存在,又不为零时,设:1,0AC l x ty t =-≠,()()()()11223344,,,,,,,A x y C x y B x y D x y 则1:1BD l x y t=--,联立22112x ty x y =-⎧⎪⎨+=⎪⎩,消去x 得()222210t y ty +--=,则12122221,22t y y y y t t +==-++,)2212t AC t +∴=+,同理:)22221111212t t BD t t ⎫+⎪+⎝⎭==++,))()()()2222222211411122221221t t t S AC BD t t t t +++∴==⋅⋅=++++令21,1t m m +=>,则()()()()()2222222241422212211221t m m m m m m t t +===++---++,2222121,1,10,0,2211m m m m m >∴>∴->∴>∴+>-- ,综合得2S ≥,即S 的最小值为2.21.平面上,直线1l 和2l 相交于点O ,它们的夹角为2θ.已知动点P 到直线1l 与2l 的距离之积为定值2(0)m m >,动点P 的轨迹记为曲线E .我们以O 为坐标原点,以直线1l 与2l 夹角的平分线为x 轴,建立直角坐标系,如图.(1)求曲线E 的方程;(2)当1m =,π4θ=时,直线l 与曲线E 顺次交于A 、B 、C 、D 四点,求证:AB CD = ;(3)当125m =,3arctan 4θ=时,是否存在直线l 与曲线E 只有A 、B 、C 三个不同公共点(点B 在线段AC 上),使得OA OC ⊥?若存在,求出直线l 的方程;若不存在,请说明理由.【答案】(1)22222sin cos x y m θθ-=(2)证明见解析(3)直线l 不存在,理由见解析【分析】(1)根据题意建立关于,x y 的等式化简即可求得;(2)根据题意求得曲线E 的方程,直线与曲线联立方程组,消掉一个未知数y ,得到关于x 的一元二次方程,利用根与系数的关系表示A D B C x x x x +=+,即可得证;(3)根据题意求得曲线E 的方程,讨论直线斜率与双曲线渐近线方程斜率的关系即可求解.【小问1详解】由题意,直线1l 的方程为tan y x θ=,即tan 0x y θ-=,直线2l 的方程为tan y x θ=-,即tan 0x y θ+=,设动点(,)P x y 是所求轨迹上的任意一点,2m =,整理得22222sin cos x y m θθ-=,即动点P 的轨迹方程为22222sin cos x y m θθ-=.【小问2详解】当π41,m θ==,时,可得曲线E 的方程为222x y -=,即222x y -=或222y x -=,当直线l 的斜率存在时,设直线l 的方程为y kx t =+,联立方程组222y kx t x y =+⎧⎨-=⎩,整理得()2221220k x ktx t ----=,则10∆>,221A D kt x x k +=-,联立方程组222y kx t y x =+⎧⎨-=⎩,整理得()2221220k x ktx t -++-=,则20∆>,221B C kt x x k+=-,可得A D B C x x x x +=+,即AD 与BC 的中点重合,所以AB CD = ;当直线l 不存在时,显然线段AD 与BC 的中点重合,所以AB CD = ,综上可得,当直线l 与曲线E 顺次交于A 、B 、C 、D 四点,则AB CD =成立.【小问3详解】当125m =,3arctan 4θ=时,可得22916sin ,cos 2525θθ==,所以曲线E 的方程为22916144252525x y -=,即221169x y -=,即曲线E 的方程为221:1169x y C -=或222:1916y x C --=,所以双曲线E 的渐近线为:34y x =±,1、当直线l 的斜率34k <时,有题意可知,此时直线l 与2C 相切于点B ,于1C 相交于点A ,C ,设直线l 的方程为y kx m =+,联立方程组221169y kx m x y =+⎧⎪⎨-=⎪⎩,整理得222(916)32161440k x kmx m ----=,设1122(,),(,)A x y C x y ,可得12232916km x x k +=-,212216144916m x x k--=-,因为OA OC ⊥ ,可得1OA OC k k ⋅=-,即12120x x y y +=,可得2212121212()()(1)()0x x kx m kx m k x x km x x m +++=++++=,可得222221614432(1)0916916m km k km m k k --+⨯+⨯+=--,整理可得:22271441440916m k k---=-,即2271441440m k ++=,此时方程无解,2、当直线l 的斜率34k >时,有题意可知,此时直线l 与1C 相切于点B ,于2C 相交于点A ,C ,设直线l 的方程为y kx m =+,联立方程组221169y kx m x y =+⎧⎪⎨-=⎪⎩,整理得222(916)32161440k x kbx m ----=,则222Δ(32)4(916)(16144)0km k m =-⨯---=,整理得221449810k m -++=①联立方程组221916y kx m y x =+⎧⎪⎨-=⎪⎩,整理得222(169)32161440k x kmx m -++-=,设1122(,),(,)A x y C x y ,可得12232169km x x k -+=-,212216144169m x x k -=-,因为OA OC ⊥ ,可得1OA OC k k ⋅=-,即12120x x y y +=,可得2212121212()()(1)()0x x kx m kx m k x x km x x m +++=++++=,可得222221614432(1)0169169m km k km m k k --+⨯+⨯+=--,整理可得:22271441440916m k k--=-,即2271441440m k --=,②由①-②可知222250m +=,此方程无解,3、当34k =时,直线l 与渐近线平行,此时直线l 与曲线E 有且最多只有两个交点,不满足题意,综上所述:直线l 方程不存在.【点睛】关键点点睛:本题第三问解题关键是以渐近线的斜率为标准对直线l 的斜率进行分类讨论,讨论切点与交点的位置情况,考查学生分类讨论的思想以及数学运算能力.。
2018年高二下学期期中考试英语试题(含答题卡及答案)

2018年高二下学期期中考试英语试题(含答题卡及答案)(满分150分,时间120分钟)第一部分阅读理解(共两节,满分60分)第一节(共15小题;每小题3分,满分45分)阅读下列短文,从每题所给的四个选项(A、B、C和D)中,选出最佳选项,并在答题卡上将该项涂黑。
A1. When Array can we visit Music Club?A. 11 :00 am— 7:00 pm every day.B. 8 :00 am一6:00 pm on weekdays.C. 8 :30 am― 9 :30 am every Sunday.D. 8 :00 am― 6:00 pm on weekends.2. You can go to ,if you want to go boating .A. 25 Jiefang Road.B. 95 the Fifth Avenue.C. 120 Xinjin Street.D. Thermopolis Town.3. You are 9 years old . If you and your parents visit Art Museum how much should you pay?A. $ 15.B. $25.5.C. $38.D. $45.BIt was difficult for Dave Cutlip to forget the man who walked into his tattoo (纹身)office in Brooklyn Park. His face had a gang (帮派)tattoo. The man looked for Cutlip‟s help to cover up his past.“I could see the pain in his eyes,” Cutlip said. Cutlip couldn‟t help the man --- the tattoo was too close to the eyes. But it got him thinking. Many young pe ople get tattoos that they come to regret. A few, like the man‟s , may have to stay with them for the rest of their days. Cutlip said,“If I can help, that‟ s my goal.”Cutlip decided he would help by hiding tattoos for free. He wrote on Facebook,” “Sometimes people make bad choices and sometimes people change. We believe there is enough hate in this world, and we want to make a difference.”One man, Casey Schaeffer, showed up with two bad words on his arms. He‟d served a year in prison for fighting and got to know a group there. “Because they took care of me,I thought of it as paying them back,” Casey said. But employers would take one look at the tattoos and turn him down. So he had Cutlip cover up one of the words with a heart and tattoo a horse over the other.Cutlip has done nine such jobs, each of which took several hours. A man let him know that he quickly found a job once his tattoo was hidden. Such victories encouraged Cutlip to found the Acts of Tattoo project with three like-minded tattoo studios from around the country, and now hundreds of people are on the waiting list. He said, “If we can just remove one bad tattoo at a time, then we‟re doing something.”4. What can we learn about the man with a gang tattoo?A. He suffered a lot in society.B. The tattoo made his eyes hurt.C. He had his tattoo hidden at last.D. The tattoo made him jobless.5. Why did Cutlip decide to help people deal with their tattoos?A. To give them a new chance.B. To cover up their characters.C. To spread out his own business.D. To reduce their hate for tattoos.6. What does the underlined word“it” in Paragraph 3 refer to?A. Finding a job.B. Getting the tattoos.C. Fighting for the group.D. Facing his past bravely.7. What is the main idea of the last paragraph?A. Removing a tattoo is difficult.B. Many people with tattoos regret.C. Cutlip has carried out his work well.D. There‟re many people with bad tattoos.CEmojis(表情符号)are worth a thousand words. They are most technology user‟s favorite digital expressions ,after all. There‟s even a scientific reason why we love emojis so much.And we don‟t play favorites, either; we use one of the 1,800 emojis when we‟re sad, happy or angry.(You might want to think twice using an emoji in a work email.)But according to Apple, there is one emoji that rises above the rest. Their list of the most popular emojis was drawn from some data. The most popular emoji among U.S. English speakers is officially called the “face with tears of joy”,though most of us know it as the “laugh/cry” emoji, which many people use to express the fact that they are extremely happy. Coming in second place, the red heart follows well behind the laugh/cry emoji, while the “loudly crying” expression receives the No.3 spot. Smiling face with heart-eyes” is No.4 ,which is used as an expressions of love ,for example: “I love you ”or “I love this”.This isn‟t the first time the laugh/cry emoji has gained its recognition. In 2015,Oxford Dictionaries named the “face with tears of joy” the word of the year. While it was the first time a “pictograph(象形文字)” had been selected as a “word”, they believed this emojis came with an important message.“There were other strong competitors ,but the laugh/cry emoji was chosen as the …word‟ that best showed the mood(心情) of 2015.”t he company wrote. It‟s safe to say that the feeling has continued in 2017, too.8. What does the underlined part “play favorites” in Paragraph 1 mean?A. Find out the difference.B. Know how to choose them.C. Understand their importance.D. Prefer one thing to others.9. According to Apple, what‟s the right order of the most popular emojis?10. What can be learned from Paragraph 3?A. Emojis were meaningless before 2015.B. The laugh/cry emoji has been popular since 2015.C. The laugh/cry emoji was officially accepted in 2015.D. Oxford Dictionaries introduced many new words in 2015.11. Why is the laugh/cry emoji so popular?A. It can show people‟s feeling perfectly.B. It is used to express people‟s happiness.C. It gained its recognition at an early time.D. It was the only one to be chosen as a “word”.DEveryone remembers their first day at a new school , It seems like just yesterday when I was walking up to join Millfield Senior school on a Monday morning. Although the journey took less than five minutes, it seemed like hours.I didn‟t know what if no one liked me or what if I did something wrong . On theway to the Johnson Hall for our first year group gathering ,I became nervous about meeting the rest of my class but I was excited as well .The first day seemed to go in an instant; I made lots of new friends and the activities we did in groups made it easier for us to know each other. The teachers seemed to be friendly and helpful. I hoped tomorrow would be as successful as today. That week I experienced so much: lots of different lessons in small groups, lectures delivered by well-known professors, exciting sport games, etc.In the following weeks, our class had a lot of things going on: we made a beach trip and held a sandcastle-building competition there. The competition was a bit terrible as we forgot to bring buckets and spades (铁锹) to build our sandcastle. We all enjoyed it, though. However, we made a great victory in the singing contest later in that same week.Now I can say that I enjoyed my time so much in Millfield Senior School, It offered so muchacademically as well as in other fields. The timetable was an improvement which allowed me to focus more on my favorite subjects. The extracurricular(课外的)activities were also wonderful. The highlight for me had been making the A team in hockey(曲棍球)。
2017-2018学年上海市复旦大学附属中学高二下学期期中考数学试卷含详解

复旦附中2017学年第二学期高二年级数学期中考试试卷一、填空题(每题4分,满分48分)1.两条异面直线所成角的取值范围是________2.设()()4511i z +=-+,则Im z =________3.若复数z 是纯虚数,且满足226z z -++=,则z =__________4.正方体1111ABCD A B C D -的棱长为1,则点1B 到平面11AA C C 的距离是__________5.如图,三角形ABC 为直角三角形,90C ∠=︒,SA ⊥平面ABC ,则在四面体S ABC -的四个面中,共有______对互相垂直的平面.6.正方体1111ABCD A B C D -中,E 为棱AB 的中点,则异面直线1B E 与1BC 所成角的大小为______(用反余弦函数表示)7.关于x 的实系数方程210x x -+=的一个根为α,则arg α=________8.已知直线a ,如果直线b 同时满足:(1)和a 异面;(2)和a 所成的角是30︒;(3)和a 的距离为2,这样的直线b 有_____条.9.空间四边形ABCD 中,1AB AC AD BC BD CD ======,则二面角B AC D --的大小为_______(用反余弦函数表示)10.若变量x ,y 满足约束条件4y x x y y k ≤⎧⎪+≤⎨⎪≥⎩,且2z x y =+的最小值为6-,则k =_________.11.已知()()111...1n z i n Z +⎛⎛⎛=++++∈ ⎝⎝⎝,则20172018z z -的值是____12.已知11z i =-+,235z i =+,32z i =+,44=-z i ,若在复平面中1z ,2z ,3z ,4z 所对应的点分别为1Z ,2Z ,3Z ,4Z ,过直线12Z Z 作一个与复平面所成的锐角为30︒的平面α,则线段34Z Z 在平面α内的射影长为____________二、选择题(每题4分,满分16分)13.对于以下四个命题:①两条异面直线有无数条公垂线;②直线在平面内的射影是直线;③如果两条直线在同一个平面内的射影平行,那这两条直线平行;④过两条异面直线的一条有且仅有一个平面与已知直线平行;上述命题中为真命题的个数为()个A.1B.2C.3D.414.设(),z a bi a b R =+∈,那么11z z -+为纯虚数的充要条件是()A.1a = B.1a =且0b ≠ C.1z = D.1z =且0b ≠15.对不等式组124x y x y +≥⎧⎨-≤⎩的解集为D ,有下面四个命题:①对于任意(),x y D ∈,都有22x y +≥-;②存在(),x y D ∈,使得22x y +≥;③对于任意(),x y D ∈,都有23x y +≤;④存在(),x y D ∈,使得21x y +≤-,其中的真命题是()A.②③B.①②C.①④D.①③16.给出下列两个命题:(1)设a ,b ,c 都是复数.如果222a b c +>,则2220a b c +->;(2)设a ,b ,c 都是复数,如果2220a b c +->,则222a b c +>.那么,下述说法正确的是A.命题(1)正确,命题(2)也正确B.命题(1)正确,命题(2)错误C.命题(1)错误,命题(2)也错误D.命题(1)错误,命题(2)正确三、解答题(满分56分)17.如图,在长方体1111ABCD A B C D -中,13BB BC ==,4AB =;(1)求证:平面11//AB D 平面1BDC ;(2)求11A B 与平面11AB C D 所成的角.18.复数z 满足224z iz ti -=+,t R ∈,(1)当2t =时,求z ;(2)若复数z 在复平面内所对应的点在第二象限,求实数t 的取值范围.19.在棱长为2的正方体1111ABCD A B C D -中,(如图)E 是棱11C D 的中点,F 是侧面11AA D D 的中心.(1)求三棱锥11A D EF -的体积;(2)求异面直线1A E 与AB 的夹角;(3)求EF 与底面1111D C B A 所成的角的大小.(结果用反三角函数表示)20.若关于x 的二次方程2120x z x z m +++=的两根为α,β,满足7αβ-=.(1)若1z ,2z ,m 均是实数,且212416z z -=,求m 的值;(2)若1z ,2z ,m 均是复数,且21241620z z i -=+,求m 的最大值和最小值.21.已知非零复数(),z x yi x y R =+∈,(),x y i x y R ω''''=+∈,()010z mi m =->;若z ,ω,0z 满足0z z ω=⋅,2z ω=.(1)求m 的值;(2)若z 所对应点(),x y 在圆2240x y x +-=,求ω所对应的点的轨迹;(3)是否存在这样的直线l ,z 对应点在l 上,ω对应点也在直线l 上?若存在,求出所有这些直线;若不存在,若不存在,说明理由.复旦附中2017学年第二学期高二年级数学期中考试试卷一、填空题(每题4分,满分48分)1.两条异面直线所成角的取值范围是________【答案】(0,2π【分析】由异面直线所成角的定义求解.【详解】解:由异面直线所成角的定义可知:过空间一点,分别作相应直线的平行线,两条相交直线所成的直角或锐角为异面直线所成的角,故两条异面直线所成的角的取值范围是0,2π⎛⎤ ⎥⎝⎦故答案为:0,2π⎛⎤ ⎥⎝⎦【点睛】本题主要考查异面直线所成的角,同时还考查了转化思想,属于基础题.2.设()()4511i z +=-+,则Im z =________【答案】16-【分析】先对根据复数的运算法则,得到11616=-z i ,即可得出其虚部.【详解】()()()()42521(2)131616121+=====--+---i i z i因此其虚部为16-.故答案为16-【点睛】本题主要考查复数的运算,以及复数的概念,熟记复数运算法则,以及复数的概念即可,属于基础题型.3.若复数z 是纯虚数,且满足226z z -++=,则z =__________【答案】【分析】先设复数z bi =,其中b ∈R ,且0b ≠,根据题意得到226-+++=bi bi ,根据复数的计算公式,即可求出结果.【详解】设复数z bi =,其中b ∈R ,且0b ≠,由226z z -++=得226-+++=bi bi ,6=,即3=,解得b =.所以=z ;故答案为【点睛】本题主要考查由复数的模求复数,熟记复数模的计算公式即可,属于常考题型.4.正方体1111ABCD A B C D -的棱长为1,则点1B 到平面11AA C C 的距离是__________【答案】2【分析】连结11B D 交11A C 于点O ,根据线面垂直的判定定理,证明11B D ⊥平面11AA C C ;再根据题中数据,即可求出结果.【详解】连结11B D 交11A C 于点O ,所以在正方体1111ABCD A B C D -中,1111B D A C ⊥;又侧棱1AA ⊥底面1111D C B A ,所以111⊥B D AA ;因为1111AA AC A ⋂=,且1AA ⊂平面11AA C C ,11AC ⊂平面11AA C C ,所以11B D ⊥平面11AA C C ;因为正方体的棱长为1,所以11=B D ,因此点1B 到平面11AA C C 的距离是111122==B O B D .故答案为22【点睛】本题主要考查求点到平面距离,熟记线面垂直的判定定理,以及正方体的结构特征即可,属于常考题型.5.如图,三角形ABC 为直角三角形,90C ∠=︒,SA ⊥平面ABC ,则在四面体S ABC -的四个面中,共有______对互相垂直的平面.【答案】3【分析】根据线面垂直,面面垂直的判定定理,直接判断,即可得出结果.【详解】因为SA ⊥平面ABC ,SA ⊂平面SAC ,SA ⊂平面SAB ,所以平面SAC ⊥平面ABC ,平面SAB ⊥平面ABC ;又三角形ABC 为直角三角形,90C ∠=︒,即⊥CB CA ,又SA ⊥平面ABC ,所以⊥SA CB ;因为SA AC A ⋂=,所以CB ⊥平面SAC ;又CB ⊂平面SBC ,所以平面SAC ⊥平面SCB ;综上,共3对互相垂直的平面.故答案为3【点睛】本题主要考查面面垂直的判定,熟记线面垂直,面面垂直的判定定理即可,属于常考题型.6.正方体1111ABCD A B C D -中,E 为棱AB 的中点,则异面直线1B E 与1BC 所成角的大小为______(用反余弦函数表示)【答案】10arccos5【分析】记F 为棱CD 的中点,连结1C F ,EF ,BE ,根据题意得到11//C F B E ,所以1FC B Ð即是异面直线1B E 与1BC 所成角,设正方体棱长为2,结合余弦定理求解,即可得出结果.【详解】记F 为棱CD 的中点,连结1C F ,EF ,BE ,因为正方体1111ABCD A B C D 中,E 为棱AB 的中点,所以EF 与11B C 平行且相等,即四边形11EFB C 为平行四边形,所以11//C F B E ,因此1FC B Ð即是异面直线1B E 与1BC 所成角,设正方体棱长为2,则2211415C F CC CF =+=+=,22114422C B CC CB =+=+=,22415BF CB CF =+=+=,所以158510cos 52522FC B +-Ð==×,所以110arccos5FC B Ð=.即异面直线1B E 与1BC 所成角的大小为10arccos5.故答案为10arccos5【点睛】本题主要考查求异面直线所成的角,在几何体中作出异面直线所成的角,结合余弦定理求解即可,属于常考题型.7.关于x 的实系数方程210x x -+=的一个根为α,则arg α=________【答案】3π±【分析】先设αa bi =+(,a b R ∈)为方程210x x -+=的一个根,根据复数相等的充要条件,得到1322αi =,根据arg α表示复数αa bi =+的辐角,结合辐角的概念,即可求出结果【详解】设αa bi =+(,a b R ∈)为方程210x x -+=的一个根,则()210+--+=a bi a bi ,整理得:()()22120-++--=a b a ab b i ,所以221020a b a ab b ⎧--+=⎨-=⎩,解得122a b ⎧=⎪⎪⎨⎪=⎪⎩或122a b ⎧=⎪⎪⎨⎪=-⎪⎩,即1322αi =因为arg α表示复数αa bi =+的辐角,记为θ,因此tan θ==ba又复数的辐角是复数所对应的向量与x 轴正方向的夹角,因此3πθ=±.故答案为3π±【点睛】本题主要考查求复数的辐角,以及解复数系下的方程,熟记复数相等的充分条件,以及复数辐角的概念即可,属于常考题型.8.已知直线a ,如果直线b 同时满足:(1)和a 异面;(2)和a 所成的角是30︒;(3)和a 的距离为2,这样的直线b 有_____条.【答案】无数【分析】明确异面直线的定义,夹角及距离,即可作图分析出结果.【详解】作出平面α,β,其中//αβ,不妨令a α⊂,b β⊂,且直线a 与直线b 满足题中条件;则平面β内任一条与b 平行的直线,都能满足题意.因此这样的直线b 有无数条.故答案为无数【点睛】本题主要考查异面直线,熟记异面直线的定义即可,属于常考题型.9.空间四边形ABCD 中,1AB AC AD BC BD CD ======,则二面角B AC D --的大小为_______(用反余弦函数表示)【答案】1arccos3【分析】先取AC 中点为O ,连结,OB OD ,根据题意得到OB AC ⊥,OD AC ⊥,推出BOD ∠即是二面角B AC D --的平面角,再由题中数据,结合余弦定理,即可求出结果.【详解】取AC 中点为O ,连结,OB OD ,因为AB BC AD CD ===,所以OB AC ⊥,OD AC ⊥,因此BOD ∠即是二面角B AC D --的平面角,又1AB AC AD BC BD CD ======,所以213122⎛⎫==-= ⎪⎝⎭BO OD ,因此222331144cos 32324--+-∠===⋅⨯OB OD BD BOD OB OD .所以1arccos 3∠=BOD ,即二面角B AC D --的大小为1arccos 3.故答案为1arccos3【点睛】本题主要考查求二面角的大小,根据题意作出二面角的平面角,结合余弦定理即可求解,属于常考题型.10.若变量x ,y 满足约束条件4y x x y y k ≤⎧⎪+≤⎨⎪≥⎩,且2z x y =+的最小值为6-,则k =_________.【答案】2-【详解】试卷分析:画出如图所示的可行域,由可得,由图像可知当直线经过点A时,直线截距最小,即最小,则目标函数为因为解得即,因为点A也在直线上,所以11.已知()()111...123n z i n Z n +⎛⎛⎛=++++∈ ⎝⎝⎝,则20172018z z -的值是____【答案】1【分析】先由题意得到()20172018112017201...11823⎛⎛⎛=++++- ⎪ ⎝⎝-⎝⎝z z i ,根据复数模的计算公式,即可得出结果.【详解】由题意,()2017111...1⎛⎛⎛=++++ ⎝⎝⎝z i ,()2018111...1⎛⎛⎛=++++⎝⎝⎝z i ,所以()20172018111...1⎛⎛⎛=++++- ⎝⎝-⎝⎝z z i ,因此20172018111...1z z i -=+⋅++⋅+-...1==故答案为1【点睛】本题主要考查复数模的计算,熟记公式即可,属于常考题型.12.已知11z i =-+,235z i =+,32z i =+,44=-z i ,若在复平面中1z ,2z ,3z ,4z 所对应的点分别为1Z ,2Z ,3Z ,4Z ,过直线12Z Z 作一个与复平面所成的锐角为30︒的平面α,则线段34Z Z 在平面α内的射影长为____________【答案】【分析】先由题意,得到1(1,1)-Z ,()23,5Z ,()32,1Z ,()44,1-Z ,根据题意,得到直线34Z Z 与平面α所成角为30︒;进而可求出结果.【详解】由题意可得:1(1,1)-Z ,()23,5Z ,()32,1Z ,()44,1-Z ,则121=Z Z k ,121=-Z Z k ,所以1234⊥Z Z Z Z ;又12Z Z ,34Z Z 都在复平面内,过直线12Z Z 所作的平面α与复平面所成的锐角为30︒,所以直线34Z Z 与平面α所成角为30︒;因此线段34Z Z 在平面α内的射影长为343cos302== Z Z .故答案为【点睛】本题主要考查线段在平面内的投影,以及复数的几何意义,熟记复数的几何意义,以及线面角的概念即可,属于常考题型.二、选择题(每题4分,满分16分)13.对于以下四个命题:①两条异面直线有无数条公垂线;②直线在平面内的射影是直线;③如果两条直线在同一个平面内的射影平行,那这两条直线平行;④过两条异面直线的一条有且仅有一个平面与已知直线平行;上述命题中为真命题的个数为()个A.1B.2C.3D.4【答案】A【分析】根据异面直线的概念与性质,以直线与平面位置关系,逐项判断即可得出结果.【详解】①任意两条异面直线的公垂线有且仅有一条;故①错;②当直线与平面垂直时,直线在平面内的射影是点,故②错;③当两条直线在同一个平面内的射影平行,那这两条直线可能平行,或异面;故③错;④过两条异面直线的一条如果有两个平面与已知直线平行,则第一条直线即是这两个平面的交线,且第二条直线与两平面都平行,则第二条直线平行与两平面的交线,即两直线平行,与两直线异面矛盾,所以过两条异面直线的一条有且仅有一个平面与已知直线平行;故④正确;故选A【点睛】本题主要考查直线与直线,以及直线与平面位置关系的判定,熟记直线与直线,以及直线与平面的位置关系即可,属于常考题型.14.设(),z a bi a b R =+∈,那么11z z -+为纯虚数的充要条件是()A.1a =B.1a =且0b ≠ C.1z = D.1z =且0b ≠【答案】D【分析】先由题意,根据复数的运算得到()222211211-+-+=+++z a b bi z a b ,再由11z z -+为纯虚数,得到221020a b b ⎧+-=⎨≠⎩,进而可得出结果.【详解】因为(),z a bia b R =+∈,所以()()()()11111111a bi a bi z a bi z a bi a bi a bi -++---+==++++++-()2222121+-+=++a b bia b,又11z z -+为纯虚数,所以221020a b b ⎧+-=⎨≠⎩,即1z =且0b ≠.故选D【点睛】本题主要考查复数是纯虚数的充要条件,熟记复数的运算法则,以及复数的类型即可,属于常考题型.15.对不等式组124x y x y +≥⎧⎨-≤⎩的解集为D ,有下面四个命题:①对于任意(),x y D ∈,都有22x y +≥-;②存在(),x y D ∈,使得22x y +≥;③对于任意(),x y D ∈,都有23x y +≤;④存在(),x y D ∈,使得21x y +≤-,其中的真命题是()A.②③B.①②C.①④D.①③【答案】B【分析】先作出不等式组124x y x y +≥⎧⎨-≤⎩所表示的平面区域,根据图像,逐项判断,即可得出结果.【详解】作出不等式组124x y x y +≥⎧⎨-≤⎩所表示的平面区域如下:由图知,区域D 为直线1x y +=与24x y -=相交的上部角型区域;显然区域D 所有的部分都在直线22+=-x y 的上方,有一部分在22x y +=的上方;显然①②正确;区域D 有一部分在23x y +=的下方,故③错误;区域D 所有的部分都在直线21x y +=-的上方,所以21+≥-x y ;故④错误;综上①②正确.故选B【点睛】本题主要考查命题的真假判断,以及不等式所表示的平面区域,熟记二元一次不等式所表示的平面区域即可求解,属于常考题型.16.给出下列两个命题:(1)设a ,b ,c 都是复数.如果222a b c +>,则2220a b c +->;(2)设a ,b ,c 都是复数,如果2220a b c +->,则222a b c +>.那么,下述说法正确的是A.命题(1)正确,命题(2)也正确B.命题(1)正确,命题(2)错误C.命题(1)错误,命题(2)也错误D.命题(1)错误,命题(2)正确【答案】B【详解】命题(1)是正确的.222a b c +>表明22a b +与2c 都是实数,因此,根据移项法则有2220a b c +->.命题(2)是错误的.2220a b c +->仅表明222a b c +-是实数,并不能保证22a b +与2c 都是实数,故222a b c +>不一定成立.例如,取2a i =+,b i =,c =,则有()()222341420a b c i i +-=++--=>,但并没有222244a b i i c +=+>=.三、解答题(满分56分)17.如图,在长方体1111ABCD A B C D -中,13BB BC ==,4AB =;(1)求证:平面11//AB D 平面1BDC ;(2)求11A B 与平面11AB C D 所成的角.【答案】(1)证明见详解;(2)3arctan4【分析】(1)根据面面平行的判定定理,直接证明,即可得出结论成立;(2)过点1A 作1A O ⊥1AB 于点O ,证明1A O ⊥平面11AB C D ,得到11∠A B A 为11A B 与平面11AB C D 所成的角,再由题中数据,即可求出结果.【详解】(1)因为在长方体1111ABCD A B C D -中,易知:11//BB DD 且11BB DD =,11//AB C D 且11AB C D =,所以四边形11BB D D 为平行四边形,四边形11ABC D 也是平行四边形;因此11//BD B D ,11//AD BC ;又BD ⊂平面1C BD ,11B D ⊄平面1C BD ;1BC ⊂平面1C BD ,1AD ⊄平面1C BD ;所以11//B D 平面1C BD ;1//AD 平面1C BD ;又11B D ⊂平面11AB D ,1AD ⊂平面11AB D ,1111AD B D D ⋂=,所以平面11//AB D 平面1BDC ;(2)过点1A 作1A O ⊥1AB 于点O ,因为在长方体1111ABCD A B C D -中,易知:AD ⊥平面11B BAA ,所以1⊥AD A O ,又1AB ⊂平面11AB C D ,AD ⊂平面11AB C D ,所以1A O ⊥平面11AB C D ,因此,11∠A B A 为11A B 与平面11AB C D 所成的角;又在长方体1111ABCD A B C D -中,13BB BC ==,4AB =,因此111113tan 4∠==A A A B A A B ,所以113arctan4∠=A B A ;即11A B 与平面11AB C D 所成的角为3arctan4.【点睛】本题主要考查面面垂直的证明,以及求直线与平面所成的角,熟记面面垂直的判定定理,以及直线与平面所成角的几何求法即可,属于常考题型.18.复数z 满足224z iz ti -=+,t R ∈,(1)当2t =时,求z ;(2)若复数z 在复平面内所对应的点在第二象限,求实数t 的取值范围.【答案】(1或;(2)()0,4.【分析】先设z a bi =+,(,a b R ∈),(1)根据题意,得到222()42+-+=+a b i a bi i ,根据复数相等的充要条件,列出方程组222422a b b a ⎧++=⎨-=⎩,求解,即可得出结果;(2)先由题意得到222()4+-+=+a b i a bi ti ,根据复数相等的充要条件,得到22242a b b a t ⎧++=⎨-=⎩,再由复数z 在复平面内所对应的点在第二象限,得到00b a >⎧⎨<⎩,推出2200b b a ⎧+>⎨<⎩,从而可得出结果.【详解】设z a bi =+,(,a b R ∈),(1)当2t =时,224z iz ti -=+可化为:222()42+-+=+a b i a bi i ;整理得:()222242++-=+a b b ai i ,所以222422a b b a ⎧++=⎨-=⎩,解得11a b =-⎧⎨=⎩或13a b =-⎧⎨=-⎩,因此==z;(2)由224z iz ti -=+,可得:222()4+-+=+a b i a bi ti ,整理得:()22224++-=+a b b ai ti ,所以22242a b b a t ⎧++=⎨-=⎩,解得:222442t b b ta ⎧+=-⎪⎪⎨⎪=-⎪⎩,因为复数z 在复平面内所对应的点在第二象限,所以00b a >⎧⎨<⎩,因此2200b b a ⎧+>⎨<⎩,即240402t t ⎧->⎪⎪⎨⎪-<⎪⎩,解得:04t <<;即实数t 的取值范围为()0,4.【点睛】本题主要考查求复数的模,以及已知复数对应点的位置求参数,熟记复数模的计算公式,以及复数的几何意义即可,属于常考题型.19.在棱长为2的正方体1111ABCD A B C D -中,(如图)E 是棱11C D 的中点,F 是侧面11AA D D的中心.(1)求三棱锥11A D EF -的体积;(2)求异面直线1A E 与AB 的夹角;(3)求EF 与底面1111D C B A 所成的角的大小.(结果用反三角函数表示)【答案】(1)13;(2)arccos 5;(3)2.【分析】(1)对三棱锥11A D EF -换底,换成以F 为顶点,11A D E 为底的三棱锥,求出底面11A D E 的面积和对应的高,得到所求的体积.(2)找到异面直线1A E 与AB 所成的角,在11EA B 内由余弦定理求出.(3)取11A D 中点M ,连接MF ,通过证明MF ⊥平面1111D C B A ,找到FEM ∠即为EF 与底面1111D C B A 所成的角,求解即可.【详解】(1)11111113A D EF F A D E A D E V V S h --==⋅⋅=111211323⎛⎫⨯⨯⨯⨯=⎪⎝⎭(2)11A B AB ,11EA B ∴∠或其补角即为异面直线1A E 与AB 所成角,在11EA B,11A E EB ==,112A B =,222111111111cos 25A E AB EB EA B A E A B +-∴∠==⋅,∴异面直线1A E 与AB 所成角为5arccos 5(3)取11A D 中点M ,连接MF ,1MF A A 且1A A ⊥平面1111D C B A ,MF ∴⊥平面1111D C B A ,FEM ∴∠即为EF 与底面1111D C B A 所成的角,1112MF AA ==,ME=tan 2MF FEM ME ∠===,EF ∴与底面1111D C B A所成的角的大小为arctan2.【点睛】本题考查三棱锥等体积转化,求异面直线所成的角,直线与平面所成的角,熟记棱锥的体积公式,异面直线所成的角,以及线面角的求法即可,属于中档题.20.若关于x 的二次方程2120x z x z m +++=的两根为α,β,满足αβ-=.(1)若1z ,2z ,m 均是实数,且212416z z -=,求m 的值;(2)若1z ,2z ,m 均是复数,且21241620z z i -=+,求m 的最大值和最小值.【答案】(1)3m =-;(2)7,最小值为7【分析】(1)先由题意,根据根与系数关系得到1αβz +=-,2αβz m =+,求出12284()2+-=z z m ,再由题意,得出42816+=m ,即可得出结果;(2)先由题意设m a bi =+,(,a b R ∈),得到[]212444(4)(5)--=-+-z z m a b i ,再结合题中条件,得到222(4)(5)7-+-=a b ,将复数模的问题,转化为圆上的点到与定点的距离问题,进而可求出结果.【详解】(1)因为1z ,2z ,m 均是实数,关于x 的二次方程2120x z x z m +++=的两根为α,β,所以1αβz +=-,2αβz m =+,又αβ-=,所以()2428αβαβ=-+,即12284()2+-=z z m ,即1228442=+-z z m ,又212416z z -=,所以42816+=m ,解得:3m =-;(2)因为1z ,2z ,m 均是复数,设m a bi =+,(,a b R ∈),则[]212441620444(4)(5)--=+--=-+-z z m i a bi a b i ,由αβ-=得228αβ-=,即()2428αβαβ+-=,所以1228442-=-z z m ,即(4)(5)7-+-=a b i ,所以222(4)(5)7-+-=a b ,即复数m 对应的点(,)a b 在圆222(4)(5)7-+-=a b 上,该点与原点距离的最大值为77+=+,最小值为:77=因此=m 的最大值为7+,最小值为7【点睛】本题主要考查根与系数关系的应用,以及复数模的计算,熟记复数的运算法则,以及复数的几何意义即可,属于常考题型.21.已知非零复数(),z x yi x y R =+∈,(),x y i x y R ω''''=+∈,()010z mi m =->;若z ,ω,0z 满足0z z ω=⋅,2z ω=.(1)求m 的值;(2)若z 所对应点(),x y 在圆2240x y x +-=,求ω所对应的点的轨迹;(3)是否存在这样的直线l ,z 对应点在l 上,ω对应点也在直线l 上?若存在,求出所有这些直线;若不存在,若不存在,说明理由.【答案】(1(2)ω所对应的点的轨迹是以(为圆心,以4为半径的圆;(3)这样的直线l 存在,且有两条y =或3y x =.【分析】(1)先由题意,得到02==z ,求解,即可得出结果;(2)先由0z z ω=⋅得到()()1''+=+-x y i x yi ,推出3434x x y y ''⎧'=⎪⎪⎨+='-⎪⎪⎩代入2240x y x +-=,得到()(22216''-+-=x y ,进而可得出结果;(3)先设直线l 存在,且为y kx b =+,根据()()1''+=+-x y i x yi得到'=+x x,'=-y y ;再由ω对应点也在直线l 上,y kx b ''=+,推出()-=++y k x b,得到k b ⎧=⎪=⎪⎩,求解,即可得出结果.【详解】(1)因为2z ω=,0z z ω=⋅得002=⋅=z z z z z ,又()010z mi m =->,所以02==z ,所以m =;(2)由(),x y i x y R ω''''=+∈,0z z ω=⋅,得()()1''+=+-x y i x yi ,即44''''''+--==+x y x yi ,所以3434x x y y ''⎧'=⎪⎪⎨+='-⎪⎪⎩,因为2240x y x +-=,所以2233340444⎛⎫⎛⎫⎛⎫''''''+-+++-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭x y x ,即2240''''+--=x y x ,即()(22216''-+-=x y ;所以ω所对应的点的轨迹是以(为圆心,以4为半径的圆;(3)设直线l 存在,且为y kx b =+,由()()1''+=+-x y i x yi得'=+x x,'=-y y ;因为ω对应点也在直线l 上,所以y kx b ''=+,()-=++y k x b,所以=-y因此k b ⎧=⎪=⎪⎩,解得0b k =⎧⎪⎨=⎪⎩或03b k =⎧⎪⎨=⎪⎩,所以这样的直线l存在,且有两条y =或3y x =.【点睛】本题主要考查复数代数形式的混合运算,以及点的轨迹问题,熟记复数的运算法则,复数的几何意义,以及点的轨迹方程的求法等即可,属于常考题型.。
上海市复旦附中高二上学期期中考试数学---精校解析Word版

上海市2018-2019学年复旦附中高二上学期期中考试数学试卷一、填空题(本大题共12题,满分54分,第1~6题每题4分,第7~12题每题5分)1.直线的倾斜角是____________.【答案】【解析】【分析】先求直线2x+3y﹣1=0的斜率,进而转化为倾斜角,【详解】解:直线2x+3y﹣1=0的斜率为k=﹣,倾斜角为α,所以tanα=﹣,则α=π﹣arctan,故答案为:π﹣arctan.【点睛】本题关键是倾斜角以及反三角函数的问题,考查计算能力.2.若矩阵,,则__________.【答案】【解析】【分析】根据矩阵的乘法运算法则,计算积矩阵中的每一项即可.【详解】解:矩阵,B=(1 2 1),则AB=.故答案为:.【点睛】本题考查了矩阵的乘法运算问题,是基础题.3.行列式的元素的代数余子式的值为,则______.【答案】3【解析】【分析】根据余子式的定义可知,M12=﹣ ,求出其表达式列出关于x的方程解之即可.【详解】解:由题意得M12=﹣=﹣(﹣4﹣k)=7,解得:k=3.故答案为:3.【点睛】此题考查学生掌握三阶行列式的余子式的定义,会进行行列式的运算,是一道基础题.4.已知是增广矩阵为的二元一次方程组的解,则________【答案】10【解析】【分析】首先根据二元一次方程组的增广矩阵,写出二元线性方程组的表达式,然后根据方程求解m,t即可;【详解】解:是增广矩阵为的二元一次方程组的解,则 ,解得m=8,t=2,则m+t=10,故答案为:10.【点睛】此题主要考查了二元一次方程组的矩阵形式,计算量小,解答的关键是理解二元线性方程组的增广矩阵的含义,并由此写出二元线性方程组的表达式.5.直线的一个单位方向向量......是________.【答案】【解析】【分析】取直线的方向向量:=±(1,).利用该直线的单位方向向量=即可得出.【详解】解:取直线的方向向量:=±(1,).∴该直线的单位方向向量== ,故答案为:.【点睛】本题考查了直线的方向向量、单位向量,考查了推理能力与计算能力,属于基础题.6.已知直线,若,则.【答案】1或-3【解析】【分析】利用l1⊥l2,得出k•(k﹣1)+(1﹣k)•(2k+3)=0,求出k的值即可.【详解】解:因为l1⊥l2,所以k•(k﹣1)+(1﹣k)•(2k+3)=0,解得k=1或k=﹣3故答案为:1或﹣3【点睛】本题考查直线的垂直条件的应用,考查计算能力.7.已知点在直线上,且点到、两点的距离相等,则点的坐标是__________.【答案】(1,2)【解析】【分析】由二项展开式性质得点P在直线4x+y﹣6=0,设P(a,﹣4a+6),由点P到A(2,5)、B(4,3)两点的距离相等,能求出点P的坐标.【详解】解:∵点P在直线=0上,∴点P在直线4x+y﹣6=0,设P(a,﹣4a+6),∵点P到A(2,5)、B(4,3)两点的距离相等,∴,解得a=1,∴点P的坐标是(1,2).故答案为:(1,2).【点睛】本题考查点的坐标的求法,考查行列式、直线方程、两点间距离公式等基础知识,考查运算求解能力,是基础题.8.若,则实数t的取值范围是_____________.【答案】【解析】【分析】利用数列的极限的运算法则,转化求解即可.【详解】解:当|t|≥2时,,可得,可得t=﹣2.当|t|<2时,可得:,综上可得:实数t的取值范围是:[﹣2,2).故答案为:[﹣2,2).【点睛】本题考查数列的极限的运算法则的应用,考查计算能力.9.已知,则“”是“两直线与平行”的___________条件(填“充分非必要”、“必要非充分”、“充要”、“既不充分也不必要”). 【答案】_充分非必要【解析】【分析】由两直线l1:x+2ay﹣1=0与l2:(3a﹣1)x﹣ay﹣1=0平行列式求得a值,再由充分必要条件的判定得答案.【详解】解:由两直线l1:x+2ay﹣1=0与l2:(3a﹣1)x﹣ay﹣1=0平行,可得,即a=0或a= .∴“a=”是“两直线l1:x+2ay﹣1=0与l2:(3a﹣1)x﹣ay﹣1=0平行”的充分非必要条件.故答案为:充分非必要.【点睛】本题考查充分必要条件的判定,考查两直线平行与系数的关系,是基础题.10.过点且与直线的夹角为的直线的一般式方程.....是____________. 【答案】【解析】【分析】由题意,设夹角为为θ,可得tanθ=,利用夹角公式求解k可得方程;【详解】解:由题意,设夹角为为θ,可得tanθ=当k存在时,设过点P(3,﹣2)直线斜率为k,直线2x+y+1=0的斜率为-由tanθ== ,解得:k=;当k不存在时,x=3.此时两直线夹角tanθ=,∴所求的直线方程为:x﹣3=0或3x+4y﹣1=0;故答案为:x﹣3=0或3x+4y﹣1=0;【点睛】本题主要考查直线方程的求解,结合直线夹角公式利用待定系数法是解决本题的关键11.已知实数满足:,且其中,则以向量为法向量的直线的倾斜角的取值范围是__________.【答案】【解析】【分析】由已知可得,向量=(a1,b1)的终点在直线x﹣y+1=0上,向量=(a2,b2)的终点在直线x﹣y+1=0上,把已知等式变形求得,,的夹角为,再由a1>a2可得A的位置,数形结合可得以向量(a1,b1)为法向量的直线的倾斜角的取值范围.【详解】解:向量=(a1,b1)的终点在直线x﹣y+1=0上,向量=(a2,b2)的终点在直线x﹣y+1=0上,由得 ,即向量与向量的夹角为,又a1>a2,可得点A在曲线x﹣y+1=0(x>﹣1)上,如图,则OA所在直线的斜率为(﹣∞,0)∪(1,+∞),∴以向量(a1,b1)为法向量的直线的斜率为(0,+∞)∪(﹣1,0),倾斜角的范围为(0,)∪(,π),当A为(0,1)时,以向量(a1,b1)为法向量的直线的倾斜角为0.∴以向量(a1,b1)为法向量的直线的倾斜角的范围为[0,)∪(,π),故答案为: [0,)∪(,π).【点睛】本题考查由数量积求向量的夹角,考查数形结合的解题思想方法.12.如图,边长为4的正方形中,半径为1的动圆Q的圆心Q在边CD和DA上移动(包含端点A,C,D),P是圆Q上及其内部的动点,设,则的取值范围是_____________.【答案】【解析】【分析】建立如图所示平面直角坐标系,可得,=( 4,0),.由图可知,当动圆Q的圆心经过点D时,P.此时m+n取得最大值:4m+4n=8+,可得m+n=2+.当动圆Q的圆心为点C或点A时,利用三角函数求m+n的最小值.【详解】解:如图所示,边长为4的长方形ABCD中,动圆Q的半径为1,圆心Q在边CD和DA上移动(包含端点A,C,D),P是圆Q上及内部的动点,向量(m,n为实数),=(0,4),=( 4,0),可得=( 4m,4n).当动圆Q的圆心经过点D时,如图:P.此时m+n取得最大值:4m+4n=8+,可得m+n=2+.当动圆Q的圆心为点C时,BP与⊙C相切且点P在x轴的下方时,=(4+cosθ,sinθ),此时,4m+4n=4﹣ sin(θ+),m+n取得最小值为:1﹣,此时P( 4﹣,﹣).同理可得,当动圆Q的圆心为点A时,BP与⊙A相切且点P在y轴的左方时,m+n取得最小值为:1﹣,此时P(-,4﹣).∴则m+n的取值范围为故答案为:.【点睛】本题考查了向量的坐标运算、点与圆的位置关系,考查了分类讨论思想方法,考查了推理能力与计算能力.二、选择题(本大题共4题,每题5分,共20分)13.函数的图像如图所示,在区间上可找到个不同的数,使得则n的取值范围为( )A. {3,4}B. {2,3,4}C. {3,4,5}D. {2,3}【答案】B【解析】【分析】由表示(x,f(x))点与原点连线的斜率,结合函数y=f(x)的图象,数形结合分析可得答案.【详解】解:令y=f(x),y=kx,作直线y=kx,可以得出2,3,4个交点,故k=(x>0)可分别有2,3,4个解.故n的取值范围为2,3,4.故选:B.【点睛】本题考查的知识点是斜率公式,正确理解表示(x,f(x))点与原点连线的斜率是解答的关键.14.给出下列命题:①非零向量满足,则和的夹角为30°;②将函数的图像按向量平移,得到函数的图像;③在三角形ABC中,若,则三角形ABC为等腰三角形;其中正确命题的个数是()A. 0B. 1C. 2D. 3【答案】D【解析】【分析】①由加法的平行四边形法则可知为菱形,又菱形对角线平分对角可得结论;②根据图象平移的口诀左加右减,得到的是函数y=|x﹣2|的图象;③由加法的平行四边形法则可知为菱形,可得结论.【详解】解:①∵,∴所对应的平行四边形是菱形,∴与+的夹角为30°;②将函数y=|x﹣1|的图象按向量=(1,0)平移,得到函数y=|x﹣2|的图象;③在△ABC中,若,则以AB、AC为邻边所作的平行四边形是菱形,∴△ABC为等腰三角形;故选:C.【点睛】本题以命题的真假判断为载体,考查了向量的基本运算,图象的平移,难度不大,属于基础题.15.在平面直角坐标系中,经过原点的直线l将△ABC分成左、右两部分,记左、右两部分的面积分别为,则取得最小值时,直线l的斜率()A. 等于1B. 等于-1C. 等于D. 不存在【答案】D【解析】【分析】分别计算k=1,k=﹣1,k=,和k不存在时,原式的值,比较大小可知选D.【详解】解:当k=1时,l:y=x,此时S2=S△ABC=,S1=,∴=,当k=﹣1时,l:y=﹣x,此时,S1=,S2=,∴=,当k=时,l:y=x,此时,S2=,S1=,∴=,当k不存在时,l:x=0,此时,S1=S2=,∴=3,比较可知,当k不存在时,原式值最小.故选:D.【点睛】本题考查了正弦定理.属中档题.16.如图所示,已知,对任何,点按照如下方式生成:,且按逆时针排列,记点的坐标为,则为()A. B. C. D.【答案】A【解析】【分析】利用向量的定义,推导知的向量坐标,然后求出a n,b n的表达式,然后进行计算即可.【详解】由题意可知,(k 0)都是在上一个点的基础上横坐标发生变化,纵坐标不变.(k 0)都是在上一个点的基础上横坐标减小,纵坐标增加.(k 0)都是在上一个点的基础上横坐标减小,纵坐标也减小.又,所以=4-===3-=+=所以选A.【点睛】本题是新定义题目,首先读懂新定义的实质,转化成我们已有的知识并解决.本题实质考查向量的坐标运算,几何运算,难度较大.三、解答题(本大题共5题,共76分)17.已知,直线的方程为,直线的方程为.当m变化时,(1)分别求直线和经过的定点坐标;(2)讨论直线和的位置关系.【答案】(1) 直线过定点;同理,直线过定点(3,1);(2)见解析.【解析】【分析】(1)将直线l1的方程改写为m(x﹣2y﹣3)+(x+y)=0,令,求解x,y的值,可得答案;同理,直线l2一样求法;(2)联立方程,得求解交点D,讨论即可;【详解】(1)将直线的方程改写为,令得直线过定点(1,-1);同理,直线过定点(3,1);(2)联立方程,得D=2m(m-2),D x=-2(m-1)(m-2),D y=-2(2m+1)(m-2)当m和2时,D,两直线相交;当m=0时,D=0,,两直线平行;当m=2时,,两直线重合。
2018-2019学年上海市复旦大学附属中学高二下学期期中数学试题(解析版)

2018-2019学年上海市复旦大学附属中学高二下学期期中数学试题一、单选题1.已知向量()()1,1,0,1,0,2,a b ==-且2ka b a b +-与互相垂直,则k =( ) A.75B.1C.35D.15【答案】A 【解析】【详解】因为2ka b a b +-与互相垂直,所以()()71,,23,2,2033240,5k k k k k -⋅-=∴-+-==,选A. 2.过点P (0,1)与圆22230x y x +--=相交的所有直线中,被圆截得的弦最长时的直线方程是( )A .0x = B.1y = C.10x y -+= D .10x y +-= 【答案】D【解析】试题分析:配方得22(1+4x y -=),依题意,被圆截得的弦最长时的直线过圆心1,0(),由因为过点,1P (0),故所求的直线方程为10x y +-=.【考点】1、直线和圆的位置关系;2、直线和圆的方程. 3.下列四个结论中正确的是( )①若两个平面有无数多个公共点,则它们重合; ②垂直于同一条直线的两条直线平行;③若两平行线中的一条与第三条直线垂直,则另一条也与这条直线垂直; ④若a ,b 是异面直线,直线c ,d 与a ,b 都相交,则c ,d 也是异面直线; A.①② B.②③C.③D.③④【答案】C【解析】根据直线和平面的性质对四个结论依次分析即可。
【详解】①当这无数个公共点共线时,两个平面相交,结论错误。
②在正方体ABCD -A 1B 1C 1D 1中,A 1D 1,AB 都与AA 1垂直,但AD 1与AB 不平行,结论错误。
③由异面直线所成角的定义知结论成立 ④反例如图,结论错误故选:C 【点睛】本题考查了直线和平面的位置关系,对于不正确的命题,应该去找出反例。
属于基础题。
4.如图,在棱长为2的正方体1111ABCD A B C D 中,,,E F G 分别是棱1,,AB BC CC 的中点,P 是底面ABCD 内一动点,若直线1D P 与平面EFG 不存在公共点,则三角形1PBB 的面积的最小值为A .2B .1C D .2【答案】C【解析】延展平面EFG ,可得截面EFGHOR ,其中H Q R 、、分别是所在棱的中点,可得1//D P 平面EFGHQR ,再证明平面1//D AC 平面EFGHQR ,可知P 在AC 上时,符合题意,从而得到P 与O 重合时三角形1PBB 的面积最小,进而可得结果. 【详解】延展平面EFG ,可得截面EFGHQR ,其中H Q R 、、分别是所在棱的中点, 直线1D P 与平面EFG 不存在公共点, 所以1//D P 平面EFGHQR , 由中位线定理可得AC//EF ,EF 在平面EFGHQR 内,AC 在平面EFGHQR 外,所以AC //平面EFGHQR ,因为1D P 与AC 在平面1D AC 内相交, 所以平面1//D AC 平面EFGHQR ,所以P 在AC 上时,直线1D P 与平面EFG 不存在公共点, 因为B O 与AC 垂直,所以P 与O 重合时BP 最小, 此时,三角形1PBB 的面积最小,最小值为122⨯= C. 【点睛】本题主要考查线面平行的判定定理、面面平行的判定定理,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面.二、填空题5.将半径为1和2的两个铅球,熔成一个大铅球,那么这个大铅球的体积为______.【答案】12π【解析】由熔前熔后总体积不变,可得新的大铅球体积等于原来两个小铅球的体积之和。
2017-2018学年复旦附中高二上期中等级考物理试卷

复旦大学附属中学第一学期 高二年级 物理期中等级性考试试卷一、单项选择题(第1-8小题,每小题3分,第9-12小题,每小题4分) 1. 下列能源中属于常规能源的是( ) A. 太阳能B. 天然气C. 核能D. 地热能2.如图,在电荷量为Q 的点电荷产生的电场中,电荷量为q的负检验电荷在A 点受到的电场力为F ,方向水平向左。
则A 点的电场强度( ) A. /E F q =,方向水平向左 B. /E F q =,方向水平向右C./E F Q =,方向水平向左D./E F Q =,方向水平向右3. 下列说法正确的是( ) A. 温度低的物体内能少B. 温度低的物体分子运动的平均速率大C. 0℃的铁和0℃的冰的分子平均动能相同D. 做加速运动的物体,由于速度越来越大,因此物体分子的平均动能越来越大4. 三个阻值相同的电阻R ,额定功率均为10W 。
接入如图电路,改变电压U ,使各电阻实际功率均不超过额定功率,则三电阻最大总功率为( )A. 30WB. 20WC. 15WD. 10W5. 清晨,草叶上的露珠是由空气中的水汽凝结成的水珠,这一物理过程中,水分子间引力和斥力变化情况是( )A. 引力减小,斥力增大B. 斥力减小,引力增大C. 引力、斥力都增大D. 引力、斥力都减小6.在某点电荷形成的电场中有一点A ,当一个q -的检验电荷从电场中的A 点被移到电场的无限远处时,电场力做的功为W -,则该检验电荷在A 点的电势能PA E 及电场中A 点的电势A ϕ分别为( )A.,PA A W E W qϕ=-=B.,PA A W E W qϕ==-C.,PA A W E W qϕ==D.,PA A W E W qϕ=-=-7. 如图为a 、b 两个电阻的伏安特性图线,由图可断定( ) A. a 的电阻比b 的电阻小B. 若将a 、b 两电阻串联入电路时,a 电阻功率较大C. 若将a 、b 两电阻并联入电路时,a 电阻功率较大D. a 、b 两电阻分别加上相同电压后,a 电阻产生的焦耳热较多8. 在“用单分子油膜估测分子的大小”实验中,下列不必要的步骤是( ) A. 测出油滴的体积B. 将油滴滴到水面上,使其在水面上散开C. 让油膜形成一个圆,测出圆的直径D. 测出油膜的面积9. 导热性能良好的气缸和活塞,密封一定质量的理想气体,气缸固定不动,保持环境温度不变,现在将活塞向下缓慢移动一段距离,则( )A. 外界对气体做功,内能不变B. 气体放出热量,内能增大C. 气缸内每个气体分子的动能保持不变D. 单位时间内撞击到器壁上单位面积的分子数减小10. 带电粒子仅在电场力作用下,从电场中a 点以初速度0v 进入电场并沿虚线所示的轨迹运动到b 点,如图所示,可以判断( ) A. 粒子的加速度在a 点时较大 B. 粒子的电势能在b 点时较大 C. 粒子带负电,在b 点时速度较大 D. 粒子带正电,动能先变小后变大11. 如图(a )所示,A 、B 为用两个绝缘细线悬挂起来的带电绝缘小球,质量A B m m <。
上海市复旦附中2018-2019学年高二下学期开学考试英语试题(解析版)

fashion and hence in a(n) _____ manner.
A efficient
B. unefficient
C. non-efficient
D. inefficient
【答案】D 【解析】
【详解】考查形容词词义辨析。句意:如果有任何这样的调整,这将意味着投资者对信息的解释是有偏见
4. I suspect_____ Facebook has done to invade our privacy is only the beginning, _____ is why I am considering
cancelling my account.
A. that, which
B. that whatever, which C. that what, that
of the city center — can have the effect of diverting them from already saturated landmarks, or discouraging short
break away in the first place.
A. positive
B. substitute
C. alternative
D. selection
【详解】考查名词词义辨析。句意:地方政府可以通过优先考虑负责任的经营者,甚至是高收入的消费者 来促进这种可持续的活动。A. preference 偏爱,优先权;B. substitute 替代品;C. alternative 二中择一;D. selection 选择。根据“Local governments can foster this sustainable activity”可知,促进这种可持续的活动,政府会优 先考虑负责任的经营者和高收入的消费者,give preference to 表示“优先选择/考虑”,故 A 项正确。
精品解析:【全国百强校】上海市复旦附中2018-2019学年高二上学期期中考试数学试题(解析版)

上海市2018-2019学年复旦附中高二上学期数学期中考试一、填空题(本大题共12题,满分54分,第1~6题每题4分,第7~12题每题5分)1.直线2310x y+-=的倾斜角是____________.【答案】2arctan3 p-【解析】【分析】先求直线2x+3y﹣1=0的斜率,进而转化为倾斜角,【详解】解:直线2x+3y﹣1=0的斜率为k=﹣,倾斜角为α,所以tanα=﹣,则α=π﹣arctan,故答案为:π﹣arctan.【点睛】本题关键是倾斜角以及反三角函数的问题,考查计算能力.2.若矩阵11A骣琪琪=-琪琪桫,()121B=,则AB=__________.【答案】121 121 000骣琪琪---琪琪桫【解析】【分析】根据矩阵的乘法运算法则,计算积矩阵中的每一项即可.【详解】解:矩阵11A骣琪琪=-琪琪桫,B=(1 2 1),则AB=121 121 000骣琪琪---琪琪桫.故答案为:121 121 000骣琪琪---琪琪桫.【点睛】本题考查了矩阵的乘法运算问题,是基础题.3.行列式43125142k--的元素3-的代数余子式的值为7,则k=______.【答案】3 【解析】【分析】根据余子式的定义可知,M12=﹣212k-,求出其表达式列出关于x的方程解之即可.【详解】解:由题意得M12=﹣212k-=﹣(﹣4﹣k)=7,解得:k=3.故答案为:3.【点睛】此题考查学生掌握三阶行列式的余子式的定义,会进行行列式的运算,是一道基础题.4.已知,x my tí=ïì=ïî是增广矩阵为3122012骣-琪琪桫的二元一次方程组的解,则m t+=________【答案】10【解析】【分析】首先根据二元一次方程组的增广矩阵,写出二元线性方程组的表达式,然后根据方程求解m,t 即可;【详解】解:,x my tí=ïì=ïî是增广矩阵为3122012骣-琪琪桫的二元一次方程组的解,则3222m ttí-=ïì=ïî,解得m=8,t=2,则m+t=10,故答案为:10.【点睛】此题主要考查了二元一次方程组的矩阵形式,计算量小,解答的关键是理解二元线性方程组的增广矩阵的含义,并由此写出二元线性方程组的表达式.5.直线3:14l y x =-的一个单位方向向量......是________. 【答案】43,55骣琪±琪桫【解析】 【分析】取直线的方向向量:a =±(1,34).利用该直线的单位方向向量d =aa即可得出. 【详解】解:取直线的方向向量: a=±(1,34). ∴该直线的单位方向向量d =a a =4355骣琪±琪桫, , 故答案为: 4355骣琪±琪桫,. 【点睛】本题考查了直线的方向向量、单位向量,考查了推理能力与计算能力,属于基础题. 6.已知直线12:(1)30,:(1)(23)20l kx k y l k x k y +--=-++-=,若12l l ^,则______k =. 【答案】1或-3 【解析】 【分析】利用l 1⊥l 2,得出k •(k ﹣1)+(1﹣k )•(2k +3)=0,求出k 的值即可.【详解】解:因为l 1⊥l 2,所以k •(k ﹣1)+(1﹣k )•(2k +3)=0,解得 k =1或k =﹣3 故答案为:1或﹣3【点睛】本题考查直线的垂直条件的应用,考查计算能力. 7.已知点P 在直线6014x y -=-上,且点P 到()2,5A 、()4,3B 两点的距离相等,则点P 的坐标是__________.【答案】(1,2) 【解析】 【分析】由二项展开式性质得点P 在直线4x +y ﹣6=0,设P (a ,﹣4a +6),由点P 到A (2,5)、B (4,3)两点的距离相等,能求出点P 的坐标.【详解】解:∵点P 在直线614x y --=0上,∴点P 在直线4x +y ﹣6=0, 设P (a ,﹣4a +6),∵点P 到A (2,5)、B (4,3)两点的距离相等,, 解得a =1,∴点P 的坐标是(1,2). 故答案为:(1,2).【点睛】本题考查点的坐标的求法,考查行列式、直线方程、两点间距离公式等基础知识,考查运算求解能力,是基础题.8.若,则实数的取值范围是_____________.【答案】【解析】 【分析】利用数列的极限的运算法则,转化求解即可.【详解】解:当|t |≥2时,n+1nn n-1n 2-t lim =22+t,可得2n 22()11t lim 2121n t t t ?-==骣琪+琪桫,可得t =﹣2. 当|t |<2时,n+1nn n-1n 2-t lim =22+t 可得: 22()2lim 211?()2n nt t t +=+ , 综上可得:实数t 的取值范围是:[﹣2,2). 故答案为:[﹣2,2).【点睛】本题考查数列的极限的运算法则的应用,考查计算能力.9.已知,则“”是“两直线1:210l x ay +-=与2:(31)10l a x ay ---=平行”的___________条件(填“充分非必要”、“必要非充分”、“充要”、“既不充分也不必要”).【答案】_充分非必要 【解析】 【分析】由两直线l 1:x +2ay ﹣1=0与l 2:(3a ﹣1)x ﹣ay ﹣1=0平行列式求得a 值,再由充分必要条件的判定得答案.【详解】解:由两直线l 1:x +2ay ﹣1=0与l 2:(3a ﹣1)x ﹣ay ﹣1=0平行,可得()23101310a a a a í---=ïì-+-?ïî ,即a =0或a =16 .∴“a =16”是“两直线l 1:x +2ay ﹣1=0与l 2:(3a ﹣1)x ﹣ay ﹣1=0平行”的充分非必要条件.故答案为:充分非必要.【点睛】本题考查充分必要条件的判定,考查两直线平行与系数的关系,是基础题. 10.过点且与直线的夹角为的直线的一般式方程.....是____________. 【答案】【解析】 【分析】由题意,设夹角为为θ,可得tan θ=12,利用夹角公式求解k 可得方程; 【详解】解:由题意,设夹角为为θ,可得tan θ=12当k 存在时,设过点P (3,﹣2)直线斜率为k ,直线2x +y +1=0的斜率为-12由tan θ=12=12112k k +- , 解得:k =34- ;当k 不存在时,x =3.此时两直线夹角tan θ=12,∴所求的直线方程为:x ﹣3=0或3x +4y ﹣1=0; 故答案为:x ﹣3=0或3x +4y ﹣1=0;【点睛】本题主要考查直线方程的求解,结合直线夹角公式利用待定系数法是解决本题的关键11.已知实数满足:,且,其中,则以向量为法向量的直线的倾斜角的取值范围是__________.【答案】【解析】 【分析】由已知可得,向量OA =(a 1,b 1)的终点在直线x ﹣y +1=0上,向量OB=(a 2,b 2)的终点在直线x ﹣y +1=0上,把已知等式变形求得,OA ,OB 的夹角为4p,再由a 1>a 2可得A 的位置,数形结合可得以向量(a 1,b 1)为法向量的直线的倾斜角的取值范围.【详解】解:向量OA =(a 1,b 1)的终点在直线x ﹣y +1=0上,向量OB =(a 2,b 2)的终点在直线x ﹣y +1=0上,1212)a a b b +2=,即向量OA 与向量OB 的夹角为4p,又a 1>a 2,可得点A 在曲线x ﹣y +1=0(x >﹣1)上, 如图,则OA 所在直线的斜率为(﹣∞,0)∪(1,+∞),∴以向量(a 1,b 1)为法向量的直线的斜率为(0,+∞)∪(﹣1,0), 倾斜角的范围为(0,2p )∪(34p ,π), 当A 为(0,1)时,以向量(a 1,b 1)为法向量的直线的倾斜角为0. ∴以向量(a 1,b 1)为法向量的直线的倾斜角的范围为[0,2p )∪(34p,π), 故答案为: [0,2p )∪(34p ,π). 【点睛】本题考查由数量积求向量的夹角,考查数形结合的解题思想方法. 12.如图,边长为4的正方形中,半径为1的动圆的圆心在边和上移动(包含端点),是圆上及其内部的动点,设,则的取值范围是_____________.【答案】【解析】 【分析】建立如图所示平面直角坐标系,可得()0,4BA =,BC =( 4,0),()()()4,00,44,4BP m n m n =+=.由图可知,当动圆Q 的圆心经过点D 时,P (4)22.此时m +n 取得最大值:4m +4n =m +n =2+4.当动圆Q 的圆心为点C 或点A 时,利用三角函数求m +n 的最小值.【详解】解:如图所示,边长为4的长方形ABCD 中,动圆Q 的半径为1,圆心Q 在边CD 和DA 上移动(包含端点A ,C ,D ),P 是圆Q 上及内部的动点,向量BP mBC nBA =+(m ,n 为实数),BA =(0,4),BC =( 4,0),可得BP=( 4m ,4n ). 当动圆Q 的圆心经过点D 时,如图:P (422.此时m +n 取得最大值:4m +4n =8+,可得m +n =.当动圆Q 的圆心为点C 时,BP 与⊙C 相切且点P 在x 轴的下方时,BP=(4+cos θ,sin θ),此时,4m +4n =4sin (θ+4p), m +n 取得最小值为:1P ( 4).同理可得,当动圆Q 的圆心为点A 时,BP 与⊙A 相切且点P 在y 轴的左方时, m +n 取得最小值为:1﹣4,此时P (-2,4﹣2). ∴则m +n的取值范围为12轾犏-犏臌故答案为:1244轾犏-犏臌.【点睛】本题考查了向量的坐标运算、点与圆的位置关系,考查了分类讨论思想方法,考查了推理能力与计算能力.二、选择题(本大题共4题,每题5分,共20分)13.函数的图像如图所示,在区间上可找到个不同的数,使得,则的取值范围为( )A. {3,4}B. {2,3,4}C. {3,4,5}D. {2,3} 【答案】B 【解析】 【分析】由 表示(x ,f (x ))点与原点连线的斜率,结合函数y =f (x )的图象,数形结合分析可得答案. 【详解】解:令y =f (x ),y =kx , 作直线y =kx ,可以得出2,3,4个交点, 故k =()f x x(x >0)可分别有2,3,4个解.故n 的取值范围为2,3,4. 故选:B .【点睛】本题考查的知识点是斜率公式,正确理解 表示(x ,f (x ))点与原点连线的斜率是解答的关键. 14.给出下列命题:①非零向量,a b 满足a b a b ==- ,则a 和a b +的夹角为30°;②将函数的图像按向量平移,得到函数的图像;③在三角形ABC 中,若,则三角形ABC 为等腰三角形;其中正确命题的个数是( )A. 0B. 1C. 2D. 3 【答案】D 【解析】 【分析】①由加法的平行四边形法则可知为菱形,又菱形对角线平分对角可得结论;②根据图象平移的口诀左加右减,得到的是函数y =|x ﹣2|的图象; ③由加法的平行四边形法则可知为菱形,可得结论.【详解】解:①∵a b a b==- ,∴所对应的平行四边形是菱形,∴a 与a +b 的夹角为30°; ②将函数y =|x ﹣1|的图象按向量a =(1,0)平移,得到函数y =|x ﹣2|的图象;③在△ABC 中,若()?0AB AC BC +=,则以AB 、AC 为邻边所作的平行四边形是菱形, ∴△ABC 为等腰三角形; 故选:C .【点睛】本题以命题的真假判断为载体,考查了向量的基本运算,图象的平移,难度不大,属于基础题. 15.在平面直角坐标系中,,,,经过原点的直线将△分成左、右两部分,记左、右两部分的面积分别为、,则取得最小值时,直线的斜率( )A. 等于B. 等于C. 等于D. 不存在【答案】D 【解析】 【分析】分别计算k =1,k =﹣1,k =12,和k 不存在时,原式的值,比较大小可知选D . 【详解】解:当k =1时,l :y =x ,此时S 2=14S △ABC =14,S 1=34,∴()212211s s +-=4915 , 当k =﹣1时,l :y =﹣x ,此时,S 1=14,S 2=34,∴()212211s s +-=257, 当k =12时,l :y =12x ,此时,S 2=16,S 1=56,∴()212211s s +-=12135, 当k 不存在时,l :x =0,此时,S 1=S 2=12,∴()212211s s +-=3, 比较可知,当k 不存在时,原式值最小. 故选:D .【点睛】本题考查了正弦定理.属中档题. 16.如图所示,已知,对任何,点按照如下方式生成:,,且按逆时针排列,记点n A 的坐标为()(),nna b n N Î,则为( )A. B. C. D.【答案】A 【解析】 【分析】利用向量的定义,推导知112231n n n OA OA A A A A A A -=+++的向量坐标,然后求出a n ,b n 的表达式,然后进行计算即可.【详解】解:向量,经过1次变换后得到12222cos ,2sin 33A A p p 骣琪=琪桫=(-,则(2A -,所以221,a b =- 由几何性质可得:332a =-,3b = ,41,a =-4b 则由题意可知112231n n n OA OA A A A A A A -=+++ =()4,0+22(2cos ,2sin )33p p +44cos ,sin 33p p骣琪琪桫+所以选A.【点睛】本题是新定义题目,首先读懂新定义的实质,转化成我们已有的知识并解决.本题实质考查向量的坐标运算,几何运算,难度较大. 三、解答题(本大题共5题,共76分)17.已知,直线的方程为(1)(21)3m x m y m +--=,直线的方程为(31)(41)54m x m y m +--=+.当变化时,(1)分别求直线和经过的定点坐标; (2)讨论直线和的位置关系.【答案】(1) 直线过定点;同理,直线过定点(3,1);(2)见解析.【解析】 【分析】(1)将直线l 1的方程改写为m (x ﹣2y ﹣3)+(x +y )=0,令2300x y x y í--=ïì+=ïî,求解x ,y 的值,可得答案;同理,直线l 2一样求法;(2)联立方程,得()1(21)3(31)(41)54m x m y m m x m y m í+--=ïì+--=+ïî求解交点D ,讨论即可; 【详解】(1)将直线1l 的方程改写为()()230m x y x y --++= ,令2300x y x y í--=ïì+=ïî 得直线1l 过定点(1,-1);同理,直线2l 过定点(3,1); (2)联立方程,得()1(21)3(31)(41)54m x m y m m x m y m í+--=ïì+--=+ïîD=2m(m-2),D x =-2(m-1)(m-2),D y =-2(2m+1)(m-2) 当m 0¹和2时,D 0¹ ,两直线相交;当m=0时,D=0,0x D ¹,两直线平行;当m=2时,0x y D D D === ,两直线重合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复旦附中高二期中数学试卷2018.11一. 填空题1. 直线2310x y +-=的倾斜角是2. 若矩阵110A ⎛⎫ ⎪=- ⎪ ⎪⎝⎭,()121B =,则AB =3. 行列式43125142k --的元素3-的代数余子式的值为7,则k =4. 已知x m y t =⎧⎨=⎩是增广矩阵为3122012-⎛⎫ ⎪⎝⎭的二元一次方程组的解,则m t += 5. 直线3:14l y x =-的一个单位方向向量是 6. 已知直线1:(1)30l kx k y +--=,2:(1)(23)20l k x k y -++-=,若12l l ⊥,则k =7. 已知点P 在直线6014x y -=-上,且点P 到(2,5)A 、(4,3)B 两点的距离相等,则点P 的坐标是 8. 若112lim 22n nn n n t t+-→∞-=+,则实数t 的取值范围是 9. 已知a ∈R ,则“16a =”是“两直线1:210l x ay +-=与2:(31)10l a x ay ---=平行” 的 条件(填“充分非必要”、“必要非充分”、“充要”、“既不充分也不必要”)10. 过点(3,2)P -且与直线210x y ++=的夹角为1arctan 2的直线的一般式方程是 11. 已知实数1a 、1b 、2a 、2b 满足:1110a b -+=,2210a b -+=,且1212)a a b b +=其中12a a >,则以向量11(,)a b 为法向量的直线的倾 斜角的取值范围是12. 如图,边长为4的正方形ABCD 中,半径为1的动圆Q的圆心Q 在边CD 和DA 上移动(包含端点A 、C 、D ),P 是圆Q 上及其内部的动点,(,)BP mBC nBA m n =+∈R u u u r u u u r u u u r,则m n +的取值范围是二. 选择题13. 函数()y f x =的图像如图所示,在区间[,]a b 上可找到n (2n ≥)个不同的数1x , 2x , ⋅⋅⋅ , n x ,使得 1212()()()n n f x fx f x x x x ==⋅⋅⋅=,则n 的范围为( ) A. {3,4} B. {2,3,4}C. {3,4,5}D. {2,3}14. 给出下列命题:① 非零向量a r 、b r 满足||||||a b a b ==-r r r r ,则a r 与a b +r r 的夹角为30°;② 将函数|1|y x =-的图像按向量(1,0)a =-r 平移,得到函数||y x =的图像;③ 在△ABC 中,若()0AB AC BC +⋅=u u u r u u u r u u u r ,则△ABC 为等腰三角形;其中正确命题的个数是( )A. 0B. 1C. 2D. 315. 在平面直角坐标系xOy 中,(1,0)A -,(1,0)B ,(0,1)C ,经过原点的直线l 将△ABC分成左、右两部分,记左、右两部分的面积分别为1S 、2S ,则2122(1)1S S +-取得最小值时,直 线l 的斜率( )A. 等于1B. 等于1-C. 等于12D. 不存在 16. 如图所示,已知0(0,0)A ,1(4,0)A ,对任何n ∈N ,点2n A +按照如下方式生成:123n n n A A A π++∠=,1211||||2n n n n A A A A +++=u u u u u u u u r u u u u u u r ,且n A ,1n A +,2n A +按逆时针排列, 记点n A 的坐标为(,)n n a b (n ∈N ),则(lim ,lim )n n n n a b →∞→∞为( )A. 2043(,)77B. 43(3,)7C. 53(3,) D. 2053(,)7三. 解答题17. 已知m ∈R ,直线1l 的方程为(1)(21)3m x m y m +--=,直线2l 的方程为(31)(41)54m x m y m +--=+,当m 变化时,(1)分别求直线1l 和2l 经过的定点坐标;(2)讨论直线1l 和2l 的位置关系.18. 已知直线l 过点(1,3),且与x 轴、y 轴都交于正半轴,当直线l 与坐标轴围成的三角形面积取得最小值时,求:(1)直线l 的方程;(2)直线l 关于直线:21m y x =-对称的直线方程.19. 类似于平面直角坐标系,我们可以定义平面斜坐标系:设数轴x 、y 的交点为O ,与x 、y 轴正方向同向的单位向量分别是i r 、j r ,且i r 与j r 的夹角为θ,其中(0,)(,)22ππθπ∈U , 由平面向量基本定理,对于平面内的向量OP u u u r ,存在唯一有序实数对(,)x y ,使得OP xi y j =+u u u r r r ,把(,)x y 叫做点P 在斜坐标系xOy 中的坐标,也叫做向量OP u u u r 在斜坐标系xOy 中的坐标,在平面斜坐标系内,直线的方向向量、法向量、点方向式方程、一般式方 程等概念与平面直角坐标系内相应概念以相同方式定义,如45θ=︒时,方程2145x y --=- 表示斜坐标系内一条过点(2,1),且方向向量为(4,5)-的直线. (1)若1arccos()3θ=-,(2,1)a =r ,(,6)b m =r ,a r 与b r 夹角为锐角,求实数m 的取值范围; (2)若60θ=o ,已知点(2,1)A 和直线:320l x y -+=,① 求l 的一个法向量;② 求点A 到直线l 的距离.20. 在平面直角坐标系中,O 为原点,两个点列123,,,A A A L 和123,,,B B B L 满足:①1(5,0)A ,2(4,0)A ,12145n n n n A A A A +++=u u u u u u u u r u u u u u u r (*n ∈N );② 1(1,1)B ,1(1,1)n n B B +=u u u u u u r (*n ∈N ). (1)求点3A 和3B 的坐标;(2)求向量n OA u u u u r ,n OB u u u u r 的坐标;(3)对于正整数k ,用k a 表示无穷数列{||}n OA u u u u r 中从第1k +项开始的各项之和,用k b 表示 无穷数列11n n OB OB +⎧⎫⎪⎪⎨⎬⋅⎪⎪⎩⎭u u u u r u u u u u r 中从第k 项开始的各项之和,即123||||||k k k k a OA OA OA +++=+++u u u u u r u u u u u u r u u u u u u r L ,11223111k k k k k k k b OB OB OB OB OB OB +++++=+++⋅⋅⋅u u u u r u u u u u r u u u u u r u u u u u u r u u u u u u r u u u u u u r L , 若存在正整数k 和p ,使得k k a b p =,求k 、p 的值.21. 已知点P 和非零实数λ,若两条不同的直线1l 、2l 均过点P ,且斜率之积为λ,则称直 线1l 、2l 是一组“P λ共轭线对”,如直线1:2l y x =和21:2l y x =-是一组“1O -共轭线对”, 其中O 是坐标原点.(1)已知1l 、2l 是一组“3O -共轭线对”,求1l 、2l 的夹角的最小值;(2)已知点(0,1)A 、点(1,0)B -和点(1,0)C 分别是三条直线PQ 、QR 、RP 上的点(A 、B 、C 与P 、Q 、R 均不重合),且直线PR 、PQ 是“1P 共轭线对”,直线QP 、QR 是 “4Q 共轭线对”,直线RP 、RQ 是“9R 共轭线对”,求点P 的坐标;(3)已知点(1,Q -,直线1l 、2l 是“2Q -共轭线对”,当1l 的斜率变化时,求原点O 到 直线1l 、2l 的距离之积的取值范围.参考答案一. 填空题 1. 2arctan 3π- 2. 121121000⎛⎫ ⎪--- ⎪ ⎪⎝⎭3. 34. 105. 43(,)55± 6. 1或3- 7. (1,2) 8. [2,2)- 9. 充分非必要 10. 30x -=,3410x y +-= 11. 3[0,)(,)24πππU12. [1+二. 选择题13. B 14. D 15. D 16. A三. 解答题17. (1)将直线1l 的方程改写为0)()32(=++--y x y x m ,令⎩⎨⎧=+=--,0,032y x y x 得直线1l 过定点)1,1(-;同理,直线2l 过定点(3,1); (2)联立方程,得⎩⎨⎧+=--+=--+,45)14()13(,3)12()1(m y m x m m y m x m 2(2)D m m =-,2(1)(2)x D m m =---,2(21)(2)y D m m =-+-当0≠m 和2时,0≠D ,两直线相交;当0=m 时,0,0≠=x D D ,两直线平行;当2=m 时,0===y x D D D ,两直线重合。
18.(1)由已知,直线l 的斜率存在,且小于0,设直线)1(3-=-x k y ,其中0<k与x 轴交于点)0,31(k-,与y 轴交于点)3,0(k -, 故6]9)(6[21)3)(31(21≥-+-+=--=k k k k S ,等号成立的条件是3-=k , 相应地,:360l x y +-=;(2)显然所求直线的斜率存在,设为k ,则k k 2122)3(123+-=⨯-+--,得31=k又由⎩⎨⎧-==-+,12,063x y y x 得l 与m 的交点为)59,57(,该点也在所求直线上, 故所求直线为043=+-y x ;19.(1)由已知,2,6a i j b mi j =+=+r r r r r r ,且526(12)()203a b m m i j m ⋅=+++⋅=+>r r r r , 得56->m ;若a r 和b r 同向,则存在正数t ,使得(2)6t i j mi j +=+r r r r , 由i r 和j r 不平行得,⎩⎨⎧==,6,2t m t 得12=m ,故所求为12,56≠->m m ; (2)① 方程可变形为3210-=-y x ,方向向量为(1,3)d =u r , 设法向量为(,)n a b =r ,由0n d ⋅=r u r ,得02725)3(213=+=+++b a b a b a , 令5,7=-=b a ,(7,5)n =-r ; ② 取直线l 上一点)2,0(B ,则(2,1)BA =-u u u r,所求为||||BA n n ⋅==u u u r r r r r .20.(1)231244(,0)55A A A A ==-u u u u u r u u u u r ,故32416(,0)(,0)55OA OA =+-=u u u u r u u u u r ,即)0,516(3A ; 2312(1,1)B B B B ==u u u u u r u u u u r ,故312(1,1)(3,3)OB OB =+=u u u u r u u u u r ,即)3,3(3B ;(2)由已知,1111244()((),0)55n n n n A A A A --+==-u u u u u u r u u u u r ,故 112231221444(5,0)(1()(),0)5554(5(),0)5n n nn n OA OA A A A A A A ---=++++=-++++=u u u u r u u u r u u u u r u u u u u r u u u u u u r L L 而112231(,)n n n OB OB B B B B B B n n -=++++=u u u u r u u u u r u u u u r u u u u u r u u u u u u r L ;(3)14||5()5n n OA -=u u u u r ,111111()2(1)21n n n n n n OB OB +==-++⋅u u u u r u u u u u r ,故45()4525()4515k k k a ==-, 112k b k =⨯,由已知,kp k 2)54(25=,所以,左边为正整数,故1=k 或2; 当1=k 时,202=p ,得10=p ;当2=k 时,164=p ,得4=p21.(1)设1l 的斜率为k ,则2l 的斜率为k3-,两直线的夹角为α,则 3)||3|(|21|)3(13|tan ≥+=-+--=k k k k α, 等号成立的条件是3±=k ,所以最小值为3π; (2)设直线QR PQ PR ,,的斜率分别为321,,k k k , 则⎪⎩⎪⎨⎧===,9,4,1133221k k k k k k 得6,32,23321===k k k 或6,32,23321-=-=-=k k k . 当6,32,23321===k k k 时,直线PR 的方程为)1(23-=x y , 直线PQ 的方程为132+=x y ,联立得,)3,3(P ; 当6,32,23321-=-=-=k k k 时,,直线PR 的方程为)1(23--=x y ,直线PQ 的方程为 132+-=x y ,联立得,)53,53(P ;故所求为)3,3(P 或)53,53(P ; (3)设)1(22:),1(2:21+-=++=+x ky l x k y l ,其中0≠k ,故 549124591245442)4)(1(|2|241|22|1|2|2224224242222221++-=++-=+++-=++-=+--⨯+-=k k k k k k k k k k k k kk k k d d 由于95422≥++kk (等号成立的条件是22=k ), 故2291[0,1)45k k-∈++,)2,0[21∈d d .。
