5.1.4多跨静定梁内力计算讲解
第二节多跨粱
解:梁AB、CF是基本部分,梁BC、FG是附属部分。梁的支承关系如图所 示,求得附属部分的竖向反力VB、VC、VF后,将其反向作用于基本部分。 作用在铰B上的集中荷载,可认为它略偏左(或右)作用于梁AB(或BC) 上,这样处理对梁的内力图没有影响。
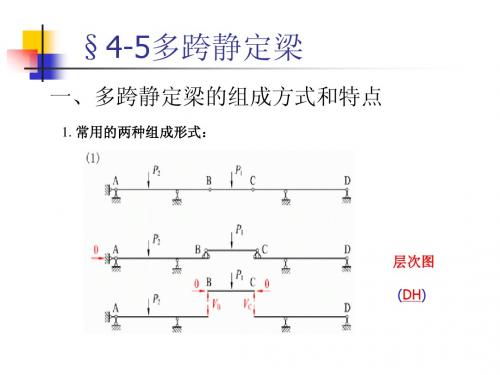
§4-5多跨静定梁
一、多跨静定梁的组成方式和特点
1. 常用的两种组成形式: 常用的两种组成形式:
层次图 (DH)
层次图
2. 组成特点: 组成特点: 从受力分析来看,多跨静定梁可分为基本部分和附序部分。 基本部分:不依靠其它部分的支承而能独立维持平衡。 附属部分:需依靠它部分的支承才能承受荷载。
二、多跨静定梁的内力计算
静定结构的内力计算图文

30 30
4m
4m
4m
4m
12kN
12kN 12kN
M 图(kN·m)
9kN
9kN
2kN/m
7kN
5kN
9kN
4.5kN
7.5kN
39
第40页/共76页
作业
习题3-5、3-6、3-9 习题3-10、3-12
40
第41页/共76页
§3-3 三铰拱
41
第42页/共76页
一、 概述
1、定义:
通常杆轴线为曲线,在竖向荷载作用下,支座产生水平反力的结构。
AC段受力图:
q
MC
t
C
FNC
FQC
n
x
FAY
FAYSinα
(2)求内力方程:
MC = 0 Ft = 0 Fn= 0
M = 1 qlx 1 qx2 (0 x l) 22
FN
=
q(1 l 2
x) sin
(0 x l)
FQ
=
q(1 2
l
x) cos
(0 x l)
FAYcosα
FAY
M中 =162 / 8 6.23/ 2 =1.385kN.m(下拉)
弯矩图见下图。
1kN/m
6.23 D
C 1.385
6.23 E
1.385kN A
4.5kN
M 图(kN.m)
B 1.385kN
1. 5kN
38
第39页/共76页
例:主从刚架弯矩图。
12kN
2kN/m
36 36
6m
12 42 30
F
F
曲梁
拱
f / l : 高跨比(1~1/10)
分析多跨静定梁的步骤(精)

分析多跨静定梁的步骤
计算多跨静定梁的步骤可归纳为以下三步:
(1)先对结构进行几何组成分析,按几何组成分析中刚片的选取次序确定基本部分和附属部分,作出层次图。
(2)根据所作层次图,从上层向下层依次取研究对象,计算各梁的约束力。
(3)按照作单跨梁内力图的方法,分别作出各梁段的内力图,然后再按原顺序连接在一起,即得多跨静定梁的内力图。
例题作如图(a)所示多跨静定梁的剪力图和弯矩图。
解:(1)进行几何组成分析并作层次图。
选地基为刚片Ⅰ,ABE梁为刚片Ⅱ,FCD 梁为刚片Ⅲ。
几何组成分析如下:
作层次图如图(b)所示
(2)计算约束力。
先取EF梁为研究对象,再取FCD梁为研究对象,后取ABE梁为研究对象。
例题图(c)所示为各梁段的受力图。
应用平衡条件依次求出各梁的约束力。
求解过程这里不再详述。
将所求得的各约束反力值标在受力图中。
(3)作内力图。
根据各梁的荷载及约束力情况,分别画出各梁段的剪力图和弯矩图,最后分别把它们按原顺序连在一起。
多跨静定梁的剪力图和弯矩图如图(d)、(e)所示。
例题图。
本章主要介绍了单跨静定梁和多跨静定梁的内力分析计算1

图10
图11
图12
3.3.2
多跨静定梁的内力计算
由层次图可见,作用于基本部分上的荷载,并不 影响附属部分,而作用于附属部分上的荷载,会以支 座反力的形式影响基本部分,因此在多跨静定梁的内 力计算时,应先计算高层次的附属部分,后计算低层 次的附属部分,然后将附属部分的支座反力反向作用 于基本部分,计算其内力,最后将各单跨梁的内力图 联成一体,即为多跨静定梁的内力图。
例6 试作出如图13(a)所示的四跨静定梁的弯矩图和剪 力图。
解:(1) 绘制层次图,如图13(b)所示。
(2) 计算支座反力,先从高层次的附属部分开 始,逐层向下计算:
① EF段:由静力平衡条件得
∑ME=0: ∑Y=0: YF×4-10×2=0 YF=5kN YE=20+10-YF=25kN
解:(1)求支座反力 先假设反力方向如图所示,以 整梁为研究对象: ∑X=0: XA-P=0 XA=P=4kN ∑MB=0: YA*l-q*l*0.5*l=0 YA=0.5ql =0.5×3×4kN=6kN ∑Y=0: YA+YB=ql YB=ql-VA =(3×4-6) kN=6kN
即:
q′l′=ql q=q′l′/l=q′/cosα
下面以承受沿水平向分布的均布荷载的斜梁为例进 行内力分析,如图(b)所示。 根据平衡条件,可以求出支座反力为: XA=0, YA=YB=1/2ql
则距A支座距离为x的截面上的内力可由取隔离体求出。 如图(c)所示,荷载qx、YA,在梁轴方向(t方向)的分 力分别为qxsinα、YAsinα;在梁法线方向(n方向) 的分力分别为:qxcosα、YAcosα。则由平衡条件得: ∑T=0: YAsinα-qxsinα+NX=0 NX=(qx-1/2ql)sinα ∑N=0: YAcosα-qxcosα-QX=0 QX=(1/2ql-qx)cosα ∑MX=0: YAx-qx· x/2-MX=0 MX=1/2qx(1-x)
分析多跨静定梁的步骤

分析多跨静定梁的步骤
计算多跨静定梁的步骤可归纳为以下三步:
(1)先对结构进行几何组成分析,按几何组成分析中刚片的选取次序确定基本部分和附属部分,作出层次图。
(2)根据所作层次图,从上层向下层依次取研究对象,计算各梁的约束力。
(3)按照作单跨梁内力图的方法,分别作出各梁段的内力图,然后再按原顺序连接在一起,即得多跨静定梁的内力图。
例题作如图(a.所示多跨静定梁的剪力图和弯矩图。
解:(1)进行几何组成分析并作层次图。
选地基为刚片Ⅰ,ABE 梁为刚片
Ⅱ,FCD 梁为刚片Ⅲ。
几何组成分析如下:
作层次图如图(b.所示
(2)计算约束力。
先取EF 梁为研究对象,再取FCD 梁为研究对象,后取ABE 梁为研究对象。
例题图(c.所示为各梁段的受力图。
应用平衡条件依次求出各梁的约束力。
求解过程这里不再详述。
将所求得的各约束反力值标在受力图中。
(3)作内力图。
根据各梁的荷载及约束力情况,分别画出各梁段的剪力图和弯矩图,最后分别把它们按原顺序连在一起。
多跨静定梁的剪力图和弯矩图如图(d.、(e.所示。
例题图。
静定结构内力计算全解[详细]
![静定结构内力计算全解[详细]](https://img.taocdn.com/s3/m/290a22ba7cd184254b3535d4.png)
从组成的观点,静定结构的型式: ✓悬臂式、简支式(两刚片法则) ✓三铰式(三刚片法则) ✓组合式(两种方式的结合)
悬臂式 三铰式
简支式 组合式
组合式结构中:
✓基本部分:结构中先组成的部分,能独立承载; ✓附属部分:后组成的以基本部分为支承的部分,不能独立 承载。
三铰拱作业:
y
100kN
1
A O
2m
20kN/m
4m 8m
2
B x
Hale Waihona Puke 2m求图示抛物线拱的1、2截面的内力。
三、三铰拱的合理拱轴线
使拱在给定荷载下只
M M 0 FH y 0 产生轴力的拱轴线,被
y M0
称为与该荷载对应的合 理拱轴
FH
三铰拱的合理拱轴线 的纵坐标与相应简支梁弯 矩图的竖标成正比。
Mik
i
FQik
Mik
i
Fiy
q Mki
k
FQki q
Mki
k
Fky
叠加法作弯矩图: 叠加法作弯矩图:
+
要点:先求出杆两端 截面弯矩值,然后在 两端弯矩纵距连线的 基础上叠加以同跨度、 同荷载简支梁的弯矩 图。
§3 静定多跨梁与静定平面刚架
一、静定多跨梁 多根梁用铰连接组成的静定体系。
AB、CD梁为基本部分 BC梁为附属部分。
2、求支座反力和内部约束力
根据组成和受力情况,取整个结构或部分结构为隔离 体,应用平衡方程求出。
B
B
F
F
FBy
A FC
FAx A FAy
《工程力学》课题十二:静定结构的内力计算

只需求出与杆轴线垂直的反力。
1.悬臂刚架
可以不求反力,由自由端开始直接 求作内力图。
L
q ½qL²↓↓↓↓↓↓↓↓↓
L
qL² qL²
2.简支刚架弯矩图
简支型刚架绘制弯矩图时,往往
只须求出一个与杆件垂直的支座
反力,然后由支座作起。
q
l
D
qa2/2
C
l/2
l/2
q
↓↓↓↓↓↓↓↓↓↓↓↓
ql2/2
qL2/2
(3)绘制内力图(弯矩图 剪力图 轴力图)
由已求得各杆端力,分别按各杆件作内力图。
弯矩图可由已知杆端弯矩,按直杆段的区段叠加法作杆
件的弯矩图。
连接两个杆端的刚结点,若 结点上无外力偶作用,则两 个杆端的弯矩值相等,方向 相反.
M图(KN·m)
拆成单个杆,求出杆两端的所 有内力,按与单跨梁相同的方法 画内力图.
铰拱的合理拱轴线的纵
只限于三铰平拱受 竖向荷载作用
坐标与相应简支梁弯矩 图的竖标成正比。
试求图示对称三铰拱在均布荷载作用下 的合理拱轴线。
MC0=ql2/8 H=ql2/8f M0(x)=qlx/2-qx2 /2 =qx(l-x)/2
y=4fx(l-x)/l2
抛物线
拱的合理拱轴线的形状与相应的简支梁的弯矩 图相似。
三铰拱在竖向集中荷载作用下的的无荷载区段上, 合理拱轴是一条直线,并在集中荷载作用点出现转折; 在均布荷载作用区段上,合理拱轴是一条抛物线。
(2)计算杆端力 取AB杆B截面以下部分, 计算该杆B端杆端力:
MBA = 160kN·m (右侧受拉) 同理:取BD杆B截面以右部 分,计算该杆B端杆端力: MBD = 160kN·m (下侧受拉)
多跨静定梁的内力计算

☆ 多跨梁的内力分析
基本部分
附属部分
基本部分
解题步骤: 1)画组成关系图。(层叠图、层次图) 2)先附属后基本求约束反力。 3)画内力图。
【例 题】 画内力图
58kN
18kN
120kN
画层叠图
求支座反力
FA
FB
FCBiblioteka FDF’C画剪力图
58kN
18kN
120kN
BC
D
A
E
画
弯
矩
图
58kN
A
A
18kN
多跨静定梁的内力计算
多跨静定梁:若干根梁,用中间铰连接在一起, 并以若干支座与地基相连。
1、结构特点
多跨静定梁由两部分组成,即基本部分和附属部分 组成的次序是先固定基本部分,再固定附属部分。
附属部分
基本部分
基本部分
2. 受力特点
附属部分
基本部分
基本部分
多跨静定梁的内力分析顺序:先附属后基本
(1)若荷载作用在基本部分上,则附属部分不受力 (2)若荷载作用在附属部分上,则基本部分同样受力
120kN
BC
D E
B C
DE
总结
•中间铰处弯矩为零
•各中间铰处的约束力属于内力, 不会使剪力图发生突变
利用上述两条,可简化计算工作,即不 用再算铰处的约束力就能迅速地绘制多跨静 定梁的内力图。
多跨静定梁 相互独立的系列简支梁相连
3-1_梁的内力计算与多跨静定梁

2、刚结点上各杆端弯矩及集中力偶应满足结点的力矩平衡。两杆相交刚结 点无 m 作用时,两杆端弯矩等值,同侧受拉。
3、具有定向连结的杆端剪力等于零,如无横向荷载作用,该端弯矩为零。 4.无何载区段 5.均布荷载区段 ↓↓↓↓↓↓
+
-
6.集中力作用处 发生突变
F + -
7.力偶作用处
FQ图
平行轴线
无变化
l-x
B q(l-x)/2 q B C FyC
D
FyD
x 2 6lx l 2 0
对于BD杆:
1 1 2 1 FyD ( ql 0.414215ql 0.17157l q [0.17157l ]2 ) 0.414215ql l 2 2
CD跨最大弯矩为:
M
x 0.17157l , M C M E 0.085787ql 2
20
10 40
M 图(kN· m)
例3-2-3 求 x 的值,使梁正、负弯矩相等。 解:BD跨为基本部分, A E B AB跨为附属部分。
q
C x l D
AB跨跨中弯矩 ME 为: 1 q M E q(l x )2 8 A E BD跨支座C负弯矩 MC 为: 1 1 q(l-x)/2 M C q(l x ) x qx 2 2 2 令 ME = MC 得: 1 1 1 q(l x)2 q(l x) x qx 2 8 2 2
FRA 17kN
17
m=16kNm
F G B
1m 1m FyB 7kN
⑵ 求控制截面的内力值 取AC部分为隔离体,可计算得:
A C FQC
9
+
C D E F G B
MC
单跨静定梁、多跨静定梁受力分析

E 1m B 1m C 20
取AD为隔离体
20kN/m QD
A 1m D 10
MC ND
Σx=0 Σy=0
ND=0
10-20×1-QD=0 QD=-10kN
ΣMD=0
MD=10×1-
20×1×0.5=0kN·m
精选可编辑ppt
12
20kN/m
10kN·m
10kN
A 1m D 1m E 1m B 1m C
剪力方程 弯矩方程
22
20kN/m
A
C
x
1m
20
A
10 2.5
A
QC=20(1-x) B
0≤x≤1
MC=-10(1-x)2
x=0 B Q图(kN) x=1
Q=20 Q=0
B
M图 (kN·m)
精选可编辑ppt
x=0
x=0.5 x=1
M=-10
M=-2.5 M=0
23
20kN/m
A 1m
20
A
10 2.5
19
AC x 1m
20
A
20
A
20kN B
Q=20 M=-20×(1-x)
注意: 弯矩图不标正负, 标在受拉侧
B Q图(kN) Q=20
B
M图 (kN·m)
精选可编辑ppt
x=0 M=-20
x=1 M=0
20
A
1m
20
A
20
A
20kN B
受力特征
仅在杆件端部有集中 荷载,而AB间无荷载
内力图特征
1m
10kN·m BA
1m
10kN·m 2m
A 5
多跨静定连续梁受力分析

多跨铰接连续静定梁内力分析第1跨内力分析:R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i ),i=1 M i =qL i 2*[1-(A i /L i )2]2/8,i=1 第2跨内力分析: P i =R Bi-1,i=2R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i ),i=2M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ],i=2 M A2=-(P i *A i +qA i 2/2),(i=2) 第3跨内力分析:P i =R Bi-1,i=3R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i ),i=3M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ],i=3 M A3=-(P i *A i +qA i 2/2),(i=3) 第4跨内力分析:P i =R Bi-1,i=4R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i ),i=4M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ],i=4 M A4=-(P i *A i +qA i 2/2),(i=4) 第5跨内力分析: P i =R Bi-1,i=5R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i ),i=5M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ],i=5 M A5=-(P i *A i +qA i 2/2),(i=5) 第6跨内力分析: P i =R Bi-1,i=6R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i ),i=6M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ],i=6 M A6=-(P i *A i +qA i 2/2),(i=6) 第7跨内力分析: P i =R Bi-1,i=7R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i ),i=7M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ],i=7 M A7=-(P i *A i +qA i 2/2),(i=7) 第8跨内力分析: P i =R Bi-1,i=8R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i ),i=8M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ],i=8 M A8=-(P i *A i +qA i 2/2),(i=8) 第9跨内力分析: P i =R Bi-1,i=9R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i ),i=9M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ],i=9 M A9=-(P i *A i +qA i 2/2),(i=9)第10跨内力分析: P i =R Bi-1,i=10R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i ),i=10M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ],i=10 M A10=-(P i *A i +qA i 2/2),(i=10)希望以上资料对你有所帮助,附励志名言3条: 1、理想的路总是为有信心的人预备着。
学习任务4 多跨静定梁的内力计算与内力图绘制

5.2 多跨静定梁的内力计算与内力图绘制
• 在任意荷载作用下,用静力学平衡方程可以 求出全部约束力和内力的结构称为静定结构 ;仅用静力学平衡方程不能求出全部约束力 和内力的结构称为超静定结构。
• 从几何组成方面来讲:没有多余联系(约束 )的几何不变体系称为静定结构;具有多余 联系(约束)的几何不变体系称为超静定结 构。
F1 A
F2
B
C
F1 A
F1 A
F1 A
F2 C B
F2
C F2 C
F3 E
D
F3 E D
F4
F F4
F
层 G次
图
G
F3 E
F4 G
F
F3
E
F4
G F
二、多跨静定梁的内力计算
10kN
10kN
A
BC
60° D
2m 4m
F1 A
2m 2m
B C
2m
F2 D
4kN/m
4kN
A
DE
F
4m C 2mBiblioteka 2m 2mq ABA
q
B
C
D
一、 多跨静定梁的组成
(由两段及以上构件组成的梁称为多跨梁)
• 基本部分:直接与地基构成 几何不变体系,能够单独承 担荷载的部分。
• 附属部分:须依靠基本部分 才能成为几何不变的部分
• 层次图:基本部分画在第一 层,附属部分画在第二层
……
F1
F2
A
BC
D
F1 A
F2
C B
D
层次图
作图示多跨梁 的内力图。
大谢家谢辛欣苦赏!了!
Thanks
多跨静定梁的计算顺序

计算多跨静定梁时,可以按照以下步骤进行计算顺序:
1. 确定梁的支座类型和位置:首先确定梁的支座类型,例如固定支座、铰支座或滑动
支座,并确定它们的位置。
2. 划分梁的跨数:根据实际情况,将梁划分为多个跨。
3. 确定每个跨的边界条件:对于每个跨,确定其边界条件,如支座反力、弯矩、剪力等。
4. 单独计算每个跨的内力:对于每个跨,使用适当的方法(如力法、位移法或弯矩法)计算其内力分布。
5. 跨间连续性条件的处理:对于相邻的两个跨,考虑它们之间的连续性条件,例如弯
矩连续性条件。
6. 解算未知反力:根据边界条件和连续性条件,解算出所有跨的未知反力。
7. 检验静定条件:检查所得到的反力是否符合静定条件,即受力平衡和变形平衡。
8. 计算梁的内力分布:根据已知的反力和边界条件,计算梁的内力分布,如弯矩、剪
力和轴力。
9. 校验计算结果:检查计算结果是否满足设计要求,如强度、刚度和稳定性等。
请注意,以上仅为一般情况下多跨静定梁计算的顺序,具体问题具体分析,可能需要
根据实际情况进行调整。
同时,如果你有特定的问题或需要更详细的计算步骤,请提
供更多信息,我将尽力提供帮助。
多跨静定梁的内力分析
-3qa/4
9qa/4
不求反力或少求反力绘制内力图
14
qa2
qa
q
qa2/2
qa
↓↓↓↓↓↓↓↓↓↓↓
qa2
qa2/2
qa2/2
M图(kN.m)
qa
qa 3qa/4
+ qa/4
qa/2
+
qa -
- qa
qa/2 - qa/2
3qa/4
7qa/4
Q图(kN)
15
40k N
80k N·m
20k N/m
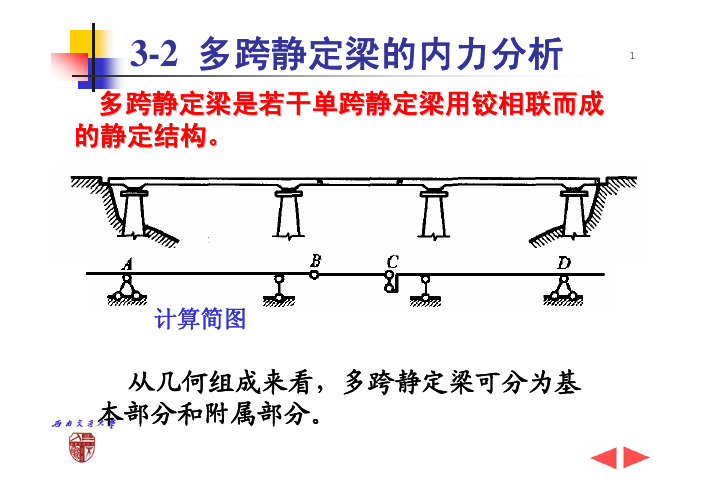
3-2 多跨静定梁的内力分析 1
多跨静定梁是若干单跨静定梁用铰相联而成 的静定结构。
计算简图
从几何组成来看,多跨静定梁可分为基 本部分和附属部分。
多跨静定梁的几何组成
2
基本部分:不依赖结构的其他部分而能独立地维持其 几何不变的结构部分。
附属部分: 必须依赖基本部分的支承才能维持其几何 不变性的结构部分。
地基
机动分析:地基 内力分析:BC梁
ቤተ መጻሕፍቲ ባይዱ
AB梁、CD梁 AB梁、CD梁
BC梁
弯矩图的作法:先作出各个单跨梁的弯矩图;再把 各单跨梁的弯矩图联在一起,就得到多跨静定梁的 弯矩图。
例1 作图示多跨静定梁的内力图 5
10kN
4kN/m
1m 2m
层叠图
BC
D
2m
1m 2m
10kN
4kN/m
附属部分
基本部分
10kN 4 10
8
4kN/m
42
4
M图、Q图
6
4
10
BC
8
4
4
+
+
多跨连续梁板的内力计算方法

多跨连续梁板的内力计算方法1.静力法静力法是根据力的平衡条件进行内力计算的一种方法。
它将整个连续梁板分成多个简支梁,然后根据每个简支梁的自由度和受力情况,利用静力平衡方程来计算内力。
静力法的计算步骤如下:1.1确定荷载情况:根据施工过程中的荷载情况,包括永久荷载、临时荷载、活荷载等,确定在每个简支梁上的作用荷载。
1.2确定支座反力:根据简支梁的支座类型和约束条件,利用静力平衡方程计算得到每个简支梁的支座反力。
1.3确定剪力和弯矩分布:根据简支梁的自由度和受力平衡条件,分别计算每个简支梁的剪力和弯矩分布,并绘制剪力和弯矩图。
1.4超程状态求解:对于超程段,根据断面力和弯矩图的性质,分别计算超程段的剪力和弯矩值。
1.5内力计算:根据每个简支梁上的受力条件和简支梁的自由度,依次计算出每个简支梁的内力值,包括剪力、弯矩和轴力。
1.6跨中内力的计算:将每个简支梁上的内力加权平均,得到整个连续梁板跨中截面所受的内力值。
注意事项:在使用静力法计算连续梁板的内力时,需要注意简支梁之间的相互作用和连梁处的内力传递。
2.变形法变形法是根据结构变形的平衡条件进行内力计算的一种方法。
它将整个连续梁板看作一个整体,利用结构变形平衡方程来计算内力。
变形法的计算步骤如下:2.1建立变形方程:根据连续梁板的几何形状和材料特性,建立连续梁板的位移和变形关系。
2.2确定加载形态:根据施工过程中的荷载情况,确定连续梁板的加载形态,包括简支挠度和弯矩分布。
2.3利用变形方程求解:根据变形方程和加载形态,利用几何和材料力学关系,求解出每个简支梁的弯矩和剪力分布。
2.4变形体内力计算:根据连续梁板的几何和材料力学关系,将每个简支梁上的弯矩和剪力分布转化为变形体上的内力分布。
2.5跨中内力的计算:将变形体上的内力分布加权平均,得到整个连续梁板跨中截面所受的内力值。
注意事项:在使用变形法计算连续梁板的内力时,需要考虑材料的非线性特性和位移场的复杂性,适用于较复杂的结构形式。
工程力学30-多跨静定梁内力计算

(2)求各支反力。先从附属部分GH开始计算,G点反 力求出后,反其指向就是EG梁的荷载。再计算出EG梁 E点的反力后,反其指向就是梁AE的荷载。各支反力的 具体数值如例图中所示。
(3)作各单跨梁的弯矩图和剪力图,并分别连在一起, 即得该多跨静定梁的M和FQ图,如例图所示。
例1计算下图所示多跨静定梁
(3)根据其整体受力图,利用剪力、弯矩和荷载集度之间的微分 关系,再结合区段叠加法,绘制出整个多跨静定梁的内力图。
因此,计算多跨静定梁时应该是先附属后基本,这样可简化计算, 取每一部分计算时与单跨静定梁无异。
多跨静定梁的内力分析及内力图绘制
列题:多跨静定梁的内力图
(1)画出关系图,如例图所示。AE为基本部分,EG 相对于AE来讲为附属部分,而EG相对于GH来讲又是 基本部分,而GH为附属部分。
解:首先分析几何组成:AB、CF为基本部分,BC为附 属部分。画层叠图(b)。
按照先附属后基本部分的原则计算各部分的支座反力, 如图(c)。
然后,逐段作出梁的剪力图和弯矩图。
例2 作此多跨静定梁的内力图。
解:(1)计算支座反力 (2)作弯矩图 (3)在此基础上,剪力图可根据微分关系或平衡条件
求得。 例如:FQC左=2kN,FQB右=7.5kN
多跨静定梁内 力计算
目的及要求
掌握多跨梁层叠图的画法 掌握多跨静定梁的内力计算和内力图的绘制。
重点难点
重点:多跨静定梁的层叠图,内力图 难点:梁受复杂荷载作用下内力图的绘制
多跨静定梁的特点
多跨静定梁是由若干根伸臂梁和简支梁用绞联结而成, 并用来跨越几个相连跨度的静定梁。这种梁常被用于桥 梁和房屋的檩条中,如图
受力分析方面
作用在基本部分上的力不传递给附属部分,而作用在附 属部分上的力传递给基本部分,如图示
结构力学课件-多跨静定梁的内力分析

三、多跨静定梁的计算
ቤተ መጻሕፍቲ ባይዱ
①计算次序与几何构造次序相反
②计算关键:基本部分和附属部分之间相互连接力(作用力和反作用力), 求出这些连接力后,各部分当作单跨静定梁来计算。
q
F1
F2
A①
B C ② D E③F
F2
E ③F
F1
FE
C ②D
q
FC
基本部分不仅承受本身所 受的外荷载,还承受其附 属部分传递来的铰约束力 作用。
M E 6 21 12kN.m(上拉)
M图(kN.m)
10
4kN 10kN AB
H
2m 2m 2m
CD 2m
G 2m
6kN/m
E
F
2m 2m
10kN
B
C
H
FBy 5kN
5kN AB
4kN
9 5
FCy 5kN
5kN
6kN/m
C
DG E
F
FDy 7.5kN
FEy 21.5kN
12
2.5
③ 作 FS 图 : 由 附 属 部 分 到 基本部分依次分析
2、几何构造次序 先固定基本部分,后固定附属部分
①
A
BC
A
①
C B
②
③
DE
F
②E D
③ F
层次图
3、力的传递特点
基本部分上所 受到的荷载对 其附属部分受 力没有影响
F1 ①
A
BC
②
③
DE
F
F1 A
C ①B
E ②
D
③ F
附属部分上 作用的外荷 载必然传递 到其基本部 分
结构力学——静定多跨梁讲解

RAY2
RBY2
由 MB 0 得
1 RAY2 2 ql
由 M A 0
得
1 RBY 2 2 ql
注意:1. 为什么两端支座反力(剪力)计算公式反号?
2. 如果为悬臂梁,须特殊讨论吗?
第三章 静定结构的 受力分析
3-2 静定多跨梁
多跨静定梁
(multi-span statically determinate beam)
FPy
FPz
FPz
k
FP
FPx
FPy
FPz
x
FPxi FPy j FPzk
y
FPx
B
A FPy
力的投影、分解和合成
已知:FP=100 kN,AB的倾角为30o。 试求图示力在坐标轴上的投影。如果 倾角为210o,投影又为多少?
y
BB FPx 100 kN cos 30o
R
力系的平衡条件为
A
如果 MA 0
M
主矢 R 在OA线上
BO 三矩式
如果B不在OA线上
MB 0 则主矢R 0 主矩 M MO 0
平面任意力系对O简化的结果得主矢和主矩
刚体上一个力系的平衡条件
理力、材力相关内容复习
简支梁AB受图示荷载作用,试求A、B
的支座反力。
都是 FP AC
力偶与力偶矩
理力、材力相关内容复习
简支梁AB受图示荷载作用,以AB为隔
离体,求全部外力对A、B的矩。
M
q
A
B
FAx l
FAy
FBy
M A ql 2 / 2 M FByl
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
F1
B F2 B
F2 C
F3
D
E F E F
F4 G F4 G F4
A A
F1 F1CFra bibliotekF3D
F2 C
F3 F3
E
F E
F
层次图
G
A
F1
F2 C
F4
G
二、多跨静定梁的内力计算
10kN A 2m F1 A 4kN/m A B C 4kN D C E F 2m 2m 4m B 2m C 2m
10kN
60° D 2m
作 图 示 多 跨 静 定 梁 的 内 力 图
F2
D
4m
2m
大家辛苦了!
Thanks
q
A
q
A B
B
C
D
(由两段及以上构件组成的梁称为多跨梁)
A F1 B C C F2
一、 多跨静定梁的组成
D F2
D
A
F1
B
层次图
基本部分:直接与地基构成几何不变体系,能够 单独承担荷载的部分。 附属部分:须依靠基本部分才能成为几何不变的 部分 层次图:基本部分画在第一层,附属部分画在第 二层……
工程力学应用
我们加油!
5.2 多跨静定梁的内力计算与内力图绘制 在任意荷载作用下,用静力学平衡方程可以求 出全部约束力和内力的结构称为静定结构;仅 用静力学平衡方程不能求出全部约束力和内力 的结构称为超静定结构。 从几何组成方面来讲:没有多余联系(约束) 的几何不变体系称为静定结构;具有多余联系 (约束)的几何不变体系称为超静定结构。
