中考数学专题训练四边形(含解析)
(易错题精选)初中数学四边形专项训练解析含答案(1)

(易错题精选)初中数学四边形专项训练解析含答案(1)一、选择题1.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )A .7B .7或8C .8或9D .7或8或9【答案】D【解析】试题分析:设内角和为1080°的多边形的边数是n ,则(n ﹣2)•180°=1080°,解得:n=8. 则原多边形的边数为7或8或9.故选D .考点:多边形内角与外角.2.如图,足球图片正中的黑色正五边形的内角和是( ).A .180°B .360°C .540°D .720°【答案】C【解析】【分析】 根据多边形内角和公式2180()n -⨯︒即可求出结果.【详解】解:黑色正五边形的内角和为:5218540(0)-⨯︒=︒,故选:C .【点睛】本题考查了多边形的内角和公式,解题关键是牢记多边形的内角和公式.3.如图,在菱形ABCD 中,60ABC ∠=︒,1AB =,点P 是这个菱形内部或边上的一点,若以点P ,B ,C 为顶点的三角形是等腰三角形,则P ,D (P ,D 两点不重合)两点间的最短距离为( )A .12B .1C 3D 31【答案】D【解析】【分析】分三种情形讨论①若以边BC为底.②若以边PC为底.③若以边PB为底.分别求出PD 的最小值,即可判断.【详解】解:在菱形ABCD中,∵∠ABC=60°,AB=1,∴△ABC,△ACD都是等边三角形,①若以边BC为底,则BC垂直平分线上(在菱形的边及其内部)的点满足题意,此时就转化为了“直线外一点与直线上所有点连线的线段中垂线段最短“,即当点P与点A重合时,PD值最小,最小值为1;②若以边PC为底,∠PBC为顶角时,以点B为圆心,BC长为半径作圆,与BD相交于一点,则弧AC(除点C外)上的所有点都满足△PBC是等腰三角形,当点P在BD上时,PD1③若以边PB为底,∠PCB为顶角,以点C为圆心,BC为半径作圆,则弧BD上的点A与点D均满足△PBC为等腰三角形,当点P与点D重合时,PD最小,显然不满足题意,故此种情况不存在;上所述,PD的最小值为1故选D.【点睛】本题考查菱形的性质、等边三角形的性质、等腰三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.4.在平面直角坐标系中,A,B,C三点坐标分别是(0,0),(4,0),(3,2),以A,B,C三点为顶点画平行四边形,则第四个顶点不可能在().A.第一象限B.第二象限C.第三象限D.第四象限【答案】C【解析】A点在原点上,B点在横轴上,C点在第一象限,根据平行四边形的性质:两组对边分别平行,可知第四个顶点可能在第一、二、四象限,不可能在第三象限,故选C5.一个多边形的每一个外角都是72°,那么这个多边形的内角和为( )A.540°B.720°C.900°D.1080°【答案】A【解析】【详解】解:∵多边形的每一个外角都是72°,∴多边形的边数为:360572=,∴该多边形的内角和为:(5-2)×180°=540°.故选A.【点睛】外角和是360°,除以一个外角度数即为多边形的边数.根据多边形的内角和公式可求得该多边形的内角和.6.如图,正方形ABCD的边长为4,点E、F分别在AB、BC上,且AE=BF=1,CE、DF交于点O,下列结论:①∠DOC=90°,②OC=OE,③CE=DF,④tan∠OCD=43,⑤S△DOC=S四边形EOFB中,正确的有()A.1个B.2个C.3个D.4个【答案】D【解析】分析:由正方形ABCD的边长为4,AE=BF=1,利用SAS易证得△EBC≌△FCD,然后全等三角形的对应角相等,易证得①∠DOC=90°正确,③CE=D F正确;②由线段垂直平分线的性质与正方形的性质,可得②错误;易证得∠OCD=∠DFC,即可求得④正确;由①易证得⑤正确.详解:∵正方形ABCD的边长为4,∴BC=CD=4,∠B=∠DCF=90°.∵AE=BF=1,∴BE=CF=4﹣1=3.在△EBC和△FCD中,BC CDB DCFBE CF=⎧⎪∠=∠⎨⎪=⎩,∴△EBC≌△FCD(SAS),∴∠CFD=∠BEC,CE=DF,故③正确,∴∠BCE+∠BEC=∠BCE+∠CFD=90°,∴∠DOC=90°;故①正确;连接DE,如图所示,若OC=OE.∵DF⊥EC,∴CD=DE.∵CD=AD<DE(矛盾),故②错误;∵∠OCD+∠CDF=90°,∠CDF+∠DFC=90°,∴∠OCD=∠DFC,∴tan∠OCD=tan∠DFC=DCFC=43,故④正确;∵△EBC≌△FCD,∴S△EBC=S△FCD,∴S△EBC﹣S△FOC=S△FCD﹣S△FOC,即S△ODC=S四边形BEOF.故⑤正确;故正确的有:①③④⑤.点睛:本题考查了正方形的性质、全等三角形的判定与性质、直角三角形的性质以及三角函数等知识.此题综合性较强,难度适中,注意掌握数形结合思想与转化思想的应用.7.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为()A.4 B.8 C.6 D.10【答案】B【解析】【分析】【详解】解:设AG与BF交点为O,∵AB=AF,AG平分∠BAD,AO=AO,∴可证△ABO≌△AFO,∴BO=FO=3,∠AOB=∠AOF=90º,AB=5,∴AO=4,∵AF∥BE,∴可证△AOF≌△EOB,AO=EO,∴AE=2AO=8,故选B.【点睛】本题考查角平分线的作图原理和平行四边形的性质.8.下列说法中正确的是()A.有一个角是直角的四边形是矩形B.两条对角线互相垂直的四边形是菱形C.两条对角线互相垂直平分的四边形是正方形D.两条对角线相等的菱形是正方形【答案】D【解析】【分析】本题考查了菱形,矩形,正方形的判定方法,熟练掌握菱形,矩形,正方形的判定方法是解题的关键.A. 有一个角是直角的四边形是矩形,错误;B. 两条对角线互相垂直的四边形是菱形,错误;C. 两条对角线互相垂直平分的四边形是正方形,错误;D. 两条对角线相等的菱形是正方形,正确.故选D.【点睛】本题考查了菱形,矩形,正方形的判定方法,熟练掌握菱形,矩形,正方形的判定方法是解题的关键,考查了学生熟练运用知识解决问题的能力.9.如图,11,,33AB EF ABP ABC EFP EFC ∠=∠∠=∠∥,已知60FCD ∠=︒,则P ∠的度数为( )A .60︒B .80︒C .90︒D .100︒【答案】B【解析】【分析】 延长BC 、EF 交于点G ,根据平行线的性质得180ABG BGE +=︒∠∠,再根据三角形外角的性质和平角的性质得60180120EFC FCD BGE BGE BCF FCD =+=︒+=︒-=︒∠∠∠∠,∠∠,最后根据四边形内角和定理求解即可.【详解】延长BC 、EF 交于点G∵//AB EF∴180ABG BGE +=︒∠∠∵60FCD ∠=︒∴60180120EFC FCD BGE BGE BCF FCD =+=︒+=︒-=︒∠∠∠∠,∠∠ ∵11,33ABP ABC EFP EFC ∠=∠∠=∠ ∴360P PBC BCF PFC =︒---∠∠∠∠2236012033ABG EFC =︒---︒∠∠ ()223606012033ABG BGE =︒--︒+-︒∠∠223604012033ABG BGE =︒--︒--︒∠∠ ()22003ABG BGE =︒-+∠∠ 22001803=︒-⨯︒ 80=︒故答案为:B .【点睛】本题考查了平行线的角度问题,掌握平行线的性质、三角形外角的性质、平角的性质、四边形内角和定理是解题的关键.10.如图,ABCD Y 的对角线AC 与BD 相交于点O ,AD BD ⊥,30ABD ∠=︒,若23AD =.则OC 的长为( )A .3B .3C 21D .6【答案】C【解析】 【分析】 先根据勾股定理解Rt ABD △求得6BD =,再根据平行四边形的性质求得3OD =,然后根据勾股定理解Rt AOD △、平行四边形的性质即可求得21OC OA ==【详解】解:∵AD BD ⊥∴90ADB ∠=︒∵在Rt ABD △中,30ABD ∠=︒,23AD =∴243AB AD ==∴226BD AB AD =-=∵四边形ABCD 是平行四边形∴132OB OD BD ===,12OA OC AC ==∴在Rt AOD △中,AD =3OD =∴OA =∴OC OA ==故选:C【点睛】本题考查了含30°角的直角三角形的性质、勾股定理、平行四边形的性质等知识点,熟练掌握相关知识点是解决问题的关键.11.在四边形ABCD 中,AD ∥BC ,要使四边形ABCD 是平行四边形,可添加的条件不正确的是( )A .AB ∥CDB .∠B =∠DC .AD =BC D .AB =CD【答案】D【解析】【分析】根据平行四边形的判定解答即可.【详解】∵AD ∥BC ,AB ∥CD ,∴四边形ABCD 是平行四边形,故A 正确;∵AD ∥BC ,AD=BC ,∴四边形ABCD 是平行四边形,故C 正确;∵AD ∥BC ,∴∠D+∠C=180°,∵∠B=∠D ,∴∠B+C=180°,∴AB ∥CD ,∴四边形ABCD 是平行四边形,故B 正确;故选:D .【点睛】此题考查平行四边形的判定,解题关键是根据平行四边形的判定解答.12.如图,菱形OBCD 在平面直角坐标系中的位置如图所示,顶点B (0,DOB =60°,点P 是对角线OC 上的一个动点,已知A (﹣1,0),则AP +BP 的最小值为( )A.4 B.5 C.33D.19【答案】D【解析】【分析】点B的对称点是点D,连接AD,则AD即为AP+BP的最小值,求出点D坐标解答即可.【详解】解:连接AD,如图,∵点B的对称点是点D,∴AD即为AP+BP的最小值,∵四边形OBCD是菱形,顶点B(0,23),∠DOB=60°,∴点D的坐标为(3,3),∵点A的坐标为(﹣1,0),∴AD=22+=,(3)419故选:D.【点睛】此题考查菱形的性质,关键是根据两点坐标得出距离.13.如图,四边形ABCD的对角线为AC、BD,且AC=BD,则下列条件能判定四边形ABCD 为矩形的是()A.BA=BCB.AC、BD互相平分C.AC⊥BDD.AB∥CD【答案】B【解析】试题分析:根据矩形的判定方法解答.解:能判定四边形ABCD是矩形的条件为AC、BD互相平分.理由如下:∵AC、BD互相平分,∴四边形ABCD是平行四边形,∵AC=BD,∴▱ABCD是矩形.其它三个条件再加上AC=BD均不能判定四边形ABCD是矩形.故选B.考点:矩形的判定.14.如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则AMMD等于()A.35B.23C.38D.45【答案】A【解析】试题分析:设AB=a,根据题意知AD=2a,由四边形BMDN是菱形知BM=MD,设AM=b,则BM=MD=2a-b.在Rt△ABM中,由勾股定理即可求值.试题解析:∵四边形MBND是菱形,∴MD=MB.∵四边形ABCD是矩形,∴∠A=90°.设AB=a,AM=b,则MB=2a-b,(a、b均为正数).在Rt△ABM中,AB2+AM2=BM2,即a2+b2=(2a-b)2,解得a=4b3,∴MD=MB=2a-b=53 b,∴3553AM bMD b==.故选A.考点:1.矩形的性质;2.勾股定理;3.菱形的性质.15.如图,在菱形ABCD 中,60BCD ∠=︒,BC 的垂直平分线交对角线AC 于点F ,垂足为E ,连接BF 、DF ,则DFC ∠的度数是( )A .130︒B .120︒C .110︒D .100︒【答案】A【解析】【分析】 首先求出∠CFB=130°,再根据对称性可知∠CFD=∠CFB 即可解决问题;【详解】∵四边形ABCD 是菱形,∴∠ACD =∠ACB =12∠BCD=25°, ∵EF 垂直平分线段BC ,∴FB=FC ,∴∠FBC=∠FCB=25°,∴∠CFB=180°-25°-25°=130°,根据对称性可知:∠CFD=∠CFB=130°,故选:A .【点睛】此题考查菱形的性质、线段的垂直平分线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.16.如图,在 ABCD 中,CD=2AD ,BE ⊥AD 于点E ,F 为DC 的中点,连结EF 、BF ,下列结论:①∠ABC=2∠ABF ;②EF=BF ;③S 四边形DEBC =2S △EFB ;④∠CFE=3∠DEF,其中正确结论的个数共有( ).A .1个B .2个C .3个D .4个 【答案】D【解析】分析:如图延长EF 交BC 的延长线于G ,取AB 的中点H 连接FH .证明△DFE ≌△FCG 得EF=FG ,BE ⊥BG ,四边形BCFH 是菱形即可解决问题;详解:如图延长EF 交BC 的延长线于G ,取AB 的中点H 连接FH .∵CD=2AD,DF=FC,∴CF=CB,∴∠CFB=∠CBF,∵CD∥AB,∴∠CFB=∠FBH,∴∠CBF=∠FBH,∴∠ABC=2∠ABF.故①正确,∵DE∥CG,∴∠D=∠FCG,∵DF=FC,∠DFE=∠CFG,∴△DFE≌△FCG,∴FE=FG,∵BE⊥AD,∴∠AEB=90°,∵AD∥BC,∴∠AEB=∠EBG=90°,∴BF=EF=FG,故②正确,∵S△DFE=S△CFG,∴S四边形DEBC=S△EBG=2S△BEF,故③正确,∵AH=HB,DF=CF,AB=CD,∴CF=BH,∵CF∥BH,∴四边形BCFH是平行四边形,∵CF=BC,∴四边形BCFH是菱形,∴∠BFC=∠BFH,∵FE=FB,FH∥AD,BE⊥AD,∴FH⊥BE,∴∠BFH=∠EFH=∠DEF,∴∠EFC=3∠DEF,故④正确,故选D.点睛:本题考查平行四边形的性质和判定、菱形的判定和性质、直角三角形斜边中线的性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考选择题中的压轴题.17.如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为()A.6cm B.4cm C.3cm D.2cm【答案】D【解析】分析:根据翻折的性质可得∠B=∠AB1E=90°,AB=AB1,然后求出四边形ABEB1是正方形,再根据正方形的性质可得BE=AB,然后根据CE=BC-BE,代入数据进行计算即可得解.详解:∵沿AE对折点B落在边AD上的点B1处,∴∠B=∠AB1E=90°,AB=AB1,又∵∠BAD=90°,∴四边形ABEB1是正方形,∴BE=AB=6cm,∴CE=BC-BE=8-6=2cm.故选:D.点睛:本题考查了矩形的性质,正方形的判定与性质,翻折变换的性质,判断出四边形ABEB1是正方形是解题的关键.18.如图a是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是()A.110°B.120°C.140°D.150°【答案】B【解析】【详解】解:∵AD∥BC,∴∠DEF=∠EFB=20°,图b中∠GFC=180°-2∠EFG=140°,在图c中∠CFE=∠GFC-∠EFG=120°,故选B.19.下列说法正确的是()A.对角线相等的四边形一定是矩形B.任意掷一枚质地均匀的硬币10次,一定有5次正面向上C.如果有一组数据为5,3,6,4,2,那么它的中位数是6D.“用长分别为5cm、12cm、6cm的三条线段可以围成三角形”这一事件是不可能事件【答案】D【解析】【分析】根据矩形的判定定理,数据出现的可能性的大小,中位数的计算方法,不可能事件的定义依次判断即可.【详解】A.对角线相等的平行四边形是矩形,故该项错误;B. 任意掷一枚质地均匀的硬币10次,不一定有5次正面向上,故该项错误;C. 一组数据为5,3,6,4,2,它的中位数是4,故该项错误;D. “用长分别为5cm、12cm、6cm的三条线段可以围成三角形” 这一事件是不可能事件,正确,故选:D.【点睛】此题矩形的判定定理,数据出现的可能性的大小,中位数的计算方法,不可能事件的定义,综合掌握各知识点是解题的关键.20.如图,△ABC中,AB=AC=10,BC=12,D是BC的中点,DE⊥AB于点E,则DE的长为()A.65B.85C.125D.245【答案】D【解析】【分析】连接AD,根据已知等腰三角形的性质得出AD⊥BC和BD=6,根据勾股定理求出AD,根据三角形的面积公式求出即可.【详解】解:连接AD∵AB=AC,D为BC的中点,BC=12,∴AD⊥BC,BD=DC=6,在Rt△ADB中,由勾股定理得:22221068AB BD=+=,∵S△ADB=12×AD×BD=12×AB×DE,∴DE=8624105 AD BDAB⨯⨯==,故选D.【点睛】本题考查了等腰三角形的性质(等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合)、勾股定理和三角形的面积,能求出AD的长是解此题的关键.。
2020年九年级数学中考复习:《四边形》压轴专题训练(解析版)

《四边形》压轴专题训练1.已知:在△ABC中,∠C=90°,BC=AC.(1)如图1,若点D、E分别在BC、AC边上,且CD=CE,连接AD、BE,点O、M、N分别是AB、AD、BE的中点.求证:△OMN是等腰直⻆三角形;(2)将图1中△CDE绕着点C顺时针旋转90°如图2,O、M、N分别为AB、AD、BE中点,则(1)中的结论是否成⽴,并说明理由;(3)如图3,将图1中△CDE绕着点C顺时针旋转,记旋转⻆为α(0<α<360°),O、M、N分别为AB、AD、BE中点,当MN=,请求出四边形ABED的⾯积.2.如图,在等边△ABC中,AB=6cm,动点P从点A出发以1cm/s的速度沿AB匀速运动.动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动,当点P到达点B时,点P、Q同时停止运动.设运动时间为t(s).过点P作PE⊥AC于E,连接PQ交AC边于D.以CQ、CE为边作平行四边形CQFE.(1)当t为何值时,△BPQ为直角三角形;(2)是否存在某一时刻t,使点F在∠ABC的平分线上?若存在,求出t的值,若不存在,请说明理由;(3)求DE的长.3.已知,在▱ABCD中,AB⊥BD,AB=BD,E为射线BC上一点,连接AE交BD于点F.(1)如图1,若点E与点C重合,且AF=2,求AD的长;(2)如图2,当点E在BC边上时,过点D作DG⊥AE于G,延长DG交BC于H,连接FH.求证:AF=DH+FH;(3)如图3,当点E在射线BC上运动时,过点D作DG⊥AE于G,M为AG的中点,点N 在BC边上且BN=1,已知AB=4,请直接写出MN的最小值.4.如图,在△ABC中,tan∠ABC=,∠C=45°,点D、E分别是边AB、AC上的点,且DE ∥BC,BD=DE=5,动点P从点B出发,沿B﹣D﹣E﹣C向终点C运动,在BD﹣DE上以每秒5个单位长度的速度运动,在EC上以每秒个单位长度的速度运动,过点P作PQ ⊥BC于点Q,以PQ为边作正方形PQMN,使点B、点N始终在PQ同侧.设点P的运动时间为t(s)(t>0),正方形PQMN与△ABC重叠部分图形的面积为S.(1)当点P在BD﹣DE上运动时,用含t的代数式表示线段DP的长.(2)当点N落在AB边上时,求t的值.(3)当点P在DE上运动时,求S与t之间的函数关系式.(4)当点P出发时,有一点H从点D出发,在线段DE上以每秒5个单位长度的速度沿D ﹣E﹣D连续做往返运动,直至点P停止运动时,点H也停止运动.连结HN,直接写出HN 与DE所夹锐角为45°时t的值.5.如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE.(1)发现:当正方形AEFG绕点A旋转,如图②所示.①线段DG与BE之间的数量关系是;②直线DG与直线BE之间的位置关系是;(2)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE 时,上述结论是否成立,并说明理由.(3)应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果).6.如图将正方形ABCD绕点A顺时针旋转角度α(0°<α<90°)得到正方形AB′C′D′.(1)如图1,B′C′与AC交于点M,C′D′与AD所在直线交于点N,若MN∥B′D′,求α;(2)如图2,C′B′与CD交于点Q,延长C′B′与BC交于点P,当α=30°时.①求∠DAQ的度数;②若AB=6,求PQ的长度.7.在四边形ABCD中,E为BC边中点.(Ⅰ)已知:如图1,若AE平分∠BAD,∠AED=90°,点F为AD上一点,AF=AB.求证:(1)△ABE≌AFE;(2)AD=AB+CD;(Ⅱ)已知:如图2,若AE平分∠BAD,DE平分∠ADC,∠AED=120°,点F,G均为AD 上的点,AF=AB,GD=CD.求证:(1)△GEF为等边三角形;(2)AD=AB+BC+CD.8.如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E,BP=BE.作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.(1)求证:∠BAP=∠BGN;(2)若AB=6,BC=8,求;(3)如图2,在(2)的条件下,连接CF,求tan∠CFM的值.9.矩形ABCD中,AB=2,AD=4,将矩形ABCD绕点C顺时针旋转至矩形EGCF(其中E、G、F分别与A、B、D对应).(1)如图1,当点G落在AD边上时,直接写出AG的长为;(2)如图2,当点G落在线段AE上时,AD与CG交于点H,求GH的长;(3)如图3,记O为矩形ABCD对角线的交点,S为△OGE的面积,求S的取值范围.10.如图,已知在Rt△ABC中,∠C=90°,AC=8,BC=6,点P、Q分别在边AC、射线CB 上,且AP=CQ,过点P作PM⊥AB,垂足为点M,联结PQ,以PM、PQ为邻边作平行四边形PQNM,设AP=x,平行四边形PQNM的面积为y.(1)当平行四边形PQNM为矩形时,求∠PQM的正切值;(2)当点N在△ABC内,求y关于x的函数解析式,并写出它的定义域;(3)当过点P且平行于BC的直线经过平行四边形PQNM一边的中点时,直接写出x的值.11.在正方形ABCD中,AB=6,M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作MN⊥CM,交AB(或AB的延长线)于点N,连接CN.感知:如图①,当M为BD的中点时,易证CM=MN.(不用证明)探究:如图②,点M为对角线BD上任一点(不与B、D重合).请探究MN与CM的数量关系,并证明你的结论.应用:(1)直接写出△MNC的面积S的取值范围;(2)若DM:DB=3:5,则AN与BN的数量关系是.12.已知△ACB和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,以CE、BC为边作平行四边形CEFB,连CD、CF.(1)如图1,当E、D分别在AC和AB上时,求证:CD=CF;(2)如图2,△ADE绕点A旋转一定角度,判断(1)中CD与CF的数量关系是否依然成立,并加以证明;(3)如图3,AE=,AB=,将△ADE绕A点旋转一周,当四边形CEFB为菱形时,直接写出CF的长.13.如图,在菱形ABCD中,对角线AC与BD相交于点M,已知BC=5,点E在射线BC上,tan∠DCE=,点P从点B出发,以每秒2个单位沿BD方向向终点D匀速运动,过点P作PQ⊥BD交射线BC于点O,以BP、BQ为邻边构造▱PBQF,设点P的运动时间为t(t >0).(1)tan∠DBE=;(2)求点F落在CD上时t的值;(3)求▱PBQF与△BCD重叠部分面积S与t之间的函数关系式;(4)连接▱PBQF的对角线BF,设BF与PQ交于点N,连接MN,当MN与△ABC的边平行(不重合)或垂直时,直接写出t的值.14.在△ABC中,AB=AC,点M在BA的延长线上,点N在BC的延长线上,过点C作CD∥AB 交∠CAM的平分线于点D.(1)如图1,求证:四边形ABCD是平行四边形;(2)如图2,当∠ABC=60°时,连接BD,过点D作DE⊥BD,交BN于点E,在不添加任何辅助线的情况下,请直接写出图2中四个三角形(不包含△CDE),使写出的每个三角形的面积与△CDE的面积相等.15.探索发现:如图①,△DEC与△ABC均为等腰直角三角形,∠E=∠ABC=90°,点A在边CD上,B在边EC上,把△DEC绕C点旋转α(0°<α<180°)得到图②,在图②中连接AD、BE交于点P,则图②中:(1)∠APB=;△BCE与△ACD的关系为.(2)连接图②中的AE、BD,如图③所示,若CE=3BC=3,则在旋转的过程中,四边形ABDE的面积是否存在最大值?若存在,请求出最大值并说明理由;若不存在,请说明理由;创新应用:(3)如图④,四边形ABCE中,AB=BC,∠ABC=90°,CE=2,AE=4,连接BE,请求出BE的最大值,并说明理由.(4)如图⑤,BE、AC为四边形ABCE的对角线,CE=2,∠CAE=60°,∠CAB=90°,∠CBA=30°,连接BE,请直接写出BE的最大值.参考答案1.解:(1)∵BC=AC,CD=CE,∴BD=AE,∵O、M、N分别为AB、AD、BE中点,∴OM∥BD且OM=BD,ON∥AE且ON=AE,∴OM=ON,∠AOM=∠ABD=45°,∠BON=∠BAE=45°,∴∠MON=180°﹣(∠AOM+∠BON)=180°﹣(45°+45°)=90°∴△OMN是等腰直角三角形.(2)(1)中的结论成⽴.理由如下:如图2,连接BD,∵△CDE顺时针旋转90°,∴∠ACE=∠ACB=90°,在△BCD和△ACE中,,∴△BCD≌△ACE(SAS),∴BD=AE,∠CBD=∠CAE,∵O、M、N分别为AB、AD、BE中点,∴OM∥BD且OM=BD,ON∥AE且ON=AE,∴OM=ON,∠AOM=∠ABD,∠BON=∠BAE,∴∠MON=180°﹣(∠AOM+∠BON)=180°﹣(∠ABD+∠BAE)=180°﹣(∠ABD+∠CBD+∠BAC)=180°﹣(∠ABC+∠BAC),∵∠ACB=90°,∴∠ABC+∠BAC=180°﹣∠ACB=180°﹣90°=90°,∴∠MON=180°﹣90°=90°,∴△OMN是等腰直角三角形.(3)如图,连接AE、BD,由(2)同理可证△OMN为等腰直角三角形.∴MN=OM.又∵OM=BD,∴MN=BD,BD=MN==2,∵AC=BC,∠BCD=∠ACE,CE=CD,∴△ACE≌△BCD(SAS),∴BD=AE,∠CBD=∠CAE,∵∠BCA=90°,∴∠AHB=90°,∴BD⊥AE,∴四边形ABED的面积为.2.解:(1)∵△ABC是等边三角形,∴∠B=60°,∴当BQ=2BP时,∠BPQ=90°,∴6+t=2(6﹣t),∴t=2,∴t=2时,△BPQ是直角三角形.(2)存在.理由:如图1中,连接BF交AC于M.∵BF平分∠ABC,BA=BC,∴BF⊥AC,AM=CM=3cm,∵EF∥BQ,∴∠EFM=∠FBC=∠ABC=30°,∴EF=2EM,∴t=2•(3﹣t),解得t=3.(3)如图2中,作PK∥BC交AC于K.∵△ABC是等边三角形,∴∠B=∠A=60°,∵PK∥BC,∴∠APK=∠B=60°,∴∠A=∠APK=∠AKP=60°,∴△APK是等边三角形,∴PA=PK,∵PE⊥AK,∴AE=EK,∵AP=CQ=PK,∠PKD=∠DCQ,∠PDK=∠QDC,∴△PKD≌△QCD(AAS),∴DK=DC,∴DE=EK+DK=(AK+CK)=AC=3(cm).3.(1)解:如图1中,∵AB=BD,∠BAD=45°,∴∠BDA=∠BAD=45°,∴∠ABD=90°,∵四边形ABCD是平行四边形,∴E、C重合时BF=BD=AB,在Rt△ABF中,∵AF2=AB2+BF2,∴(2)2=(2BF)2+BF2,∴BF=2,AB=4,在Rt△ABD中,AD==4;(2)证明:如图2中,在AF上截取AK=HD,连接BK,∵∠AFD=∠ABF+∠2=∠FGD+∠3,∠ABF=∠FGD=90°,∴∠2=∠3,在ABK和△DBH中,,∴△ABK≌△DBH,∴BK=BH,∠6=∠1,AK=DH,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠4=∠1=∠6=45°,∴∠5=∠ABD﹣∠6=45°,∴∠5=∠1,在△FBK和△FBH中,,∴△FBK≌△FBH,∴KF=FH,∵AF=AK+KF,∴AF=DH+FH;(3)解:连接AN并延长到Q,使NQ=AN,连接GQ,取AD的中点O,连接OG,∵∠AGD=90°,∴点G的轨迹是以O为圆心,以OG为半径的弧,且OG=4,∴OQ=10,OG=4,∴GQ最小值为6,∵MN是△AGQ的中位线,∴MN的最小值为3.4.解:(1)当0<t≤1时,DP=5﹣5t.当1<t≤2时,DP=5t﹣5.(2)如图1中,在Rt△BDM中,∵∠DMB=90°,tan B==,BD=5,∴DM=4,BM=3,∵DP=DM,∴5t﹣5=4,解得:.(3)①如图2﹣1中,当1≤t≤时,重叠部分是四边形BQPD,S=.②如图2﹣2中,当<t≤时,重叠部分是五边形MQPDK,S=.③如图2﹣3,当<t≤2时,重叠部分是正方形PQMN,S=16.综上所述,S=.(4)如图3﹣1中,作HK⊥NP交NP的延长线于K.由题意∠HNK=45°,∵HK⊥NK,∴△NHK是等腰直角三角形,∴NK=HK,可得4t+3﹣3t+5t=4﹣4t,解得t=0.1.如图3﹣2中,当2<t<3时,满足EH=PN,条件成立.可得:5﹣5(t﹣2)=(4﹣2(t﹣2)),解得.如图3﹣2中,当t>3时,满足EH=PN,条件成立.可得5(t﹣3)=(4﹣2(t﹣2),解得.综上所述,满足条件的t的值为0.1或或.5.解:(1)①如图②中,∵四边形ABCD和四边形AEFG是正方形,∴AE=AG,AB=AD,∠BAD=∠EAG=90°,∴∠BAE=∠DAG,在△ABE和△DAG中,,∴△ABE≌△DAG(SAS),∴BE=DG;②如图2,延长BE交AD于T,交DG于H.由①知,△ABE≌△DAG,∴∠ABE=∠ADG,∵∠ATB+∠ABE=90°,∴∠ATB+∠ADG=90°,∵∠ATB=∠DTH,∴∠DTH+∠ADG=90°,∴∠DHB=90°,∴BE⊥DG,故答案为:BE=DG,BE⊥DG;(2)数量关系不成立,DG=2BE,位置关系成立.如图③中,延长BE交AD于T,交DG于H.∵四边形ABCD与四边形AEFG都为矩形,∴∠BAD=∠EAG,∴∠BAE=∠DAG,∵AD=2AB,AG=2AE,∴==,∴△ABE∽△ADG,∴∠ABE=∠ADG,=,∴DG=2BE,∵∠ATB+∠ABE=90°,∴∠ATB+∠ADG=90°,∵∠ATB=∠DTH,∴∠DTH+∠ADG=90°,∴∠DHB=90°,∴BE⊥DG;(3)如图④中,作ET⊥AD于T,GH⊥BA交BA的延长线于H.设ET=x,AT=y.∵△AHG∽△ATE,∴===2,∴GH=2x,AH=2y,∴4x2+4y2=4,∴x2+y2=1,∴BG2+DE2=(2x)2+(2y+2)2+x2+(4﹣y)2=5x2+5y2+20=25.6.解:(1)如图1中,∵MN∥B′D′,∴∠C′MN=∠C′B′D′=45°,∠C′NM=∠C′D′B′=45°,∴∠C′MN=∠C′NM,∴C′M=C′N,∵C′B′=C′D′,∴MB′=ND′,∵AB′=AD′,∠AB′M=∠AD′N=90°,∴△AB′M≌△AD′N(SAS),∴∠B′AM=∠D′AN,∵∠B′AD′=90°,∠MAN=45°,∴∠B′AM=∠D′AN=22.5°,∵∠BAC=45°,∴∠BAB′=22.5°,∴α=22.5°.(2)①如图2中,∵∠AB′Q=∠ADQ=90°,AQ=AQ,AB′=AD,∴Rt△AQB′≌Rt△AQD(HL),∴∠QAB′=∠QAD,∵∠BAB′=30°,∠BAD=90°,∴∠B′AD=30°,∴∠QAD=∠B′AD=30°.②如图2中,连接AP,在AB上取一点E,使得AE=EP,连接EP.设PB=a.∵∠ABP=∠AB′P=90°,AP=AP,AB=AB′,∴Rt△APB≌Rt△APB′(HL),∴∠BAP=∠PAB′=15°,∵EA=EP,∴∠EAP=∠EPA=15°,∴∠BEP=∠EAP+∠EPA=30°,∴PE=AE=2a,BE=a,∵AB=6,∴2a+a=6,∴a=6(2﹣).∴PB=6(2﹣),∴PC=BC﹣PB=6﹣6(2﹣)=6﹣6,∵∠CPQ+∠BPB′=180°,∠BAB′+∠BPB′=180°,∴∠CPQ=∠BAB′=30°,∴PQ===12﹣4.7.(Ⅰ)证明:(1)如图1中,∵AE平分∠BAD,∴∠BAE=∠FAE,在△ABE和△AFE中,,∴△ABE≌△AFE(SAS),(2)∵△ABE≌△AFE,∴∠AEB=∠AEF,BE=BF,∵AE平分BC,∴BE=CE,∴FE=CE,∵∠AED=∠AEF+∠DEF=90°,∴∠AEB+∠DEC=90°,∴∠DEF=∠DEC,在△DEF和△DEC中,,∴△DEF≌△DEC(SAS),∴DF=DC,∵AD=AF+DF,∴AD=AB+CD;(Ⅱ)证明:(1)如图2中,∵E是BC的中点,∴BE=CE=BC,同(1)得:△ABE≌△AFE(SAS),△DEG≌△DEC(SAS),∴BE=FE,∠AEB=∠AEF,CE=EG,∠CED=∠GED,∵BE=CE,∴EF=EG,∵∠AED=120°,∠AEB+∠CED=180°﹣120°=60°,∴∠AEF+∠GED=60°,∴∠FEG=60°,∴△FEG是等边三角形.(2)由(1)可知FG=GE=EF=BC,∵AD=AG+GH+HD,∴AD=AB+CD+BC.8.(1)证明:如图1中,∵四边形ABCD是矩形,∴∠ABC=90°,∴∠BAP=∠APB=90°∵BP=BE,∴∠APB∠BEP=∠GEF,∵MN垂直平分线段AP,∴∠GFE=90°,∴∠BGN+∠GEF=90°,∴∠BAP=∠BGN.(2)解:∵四边形ABCD是矩形,∴∠BAD=∠ABP=90°,AD∥BC,AD=BC=8,∴BD===10,∵AD∥BC,∴∠DAE=∠APB,∵∠APB=∠BEP=∠DEA,∴∠DAE=∠DEA,∴DA=DE=8,∴BE=BP=BD﹣DE=10﹣8=2,∴PA===2,∵MN垂直平分线段AP,∴AF=PF=,∵PB∥AD,∴===,∴PE=PA=,∴EF=PF﹣PE=﹣=,∴==.(3)解:如图3中,连接AM,MP.设CM=x.∵四边形ABCD是矩形,∴∠ADM=∠MCP=90°,AB=CD=6,AD=BC=8,∵MN垂直平分线段AP,∴MA=MP,∴AD2+DM2=PC2+CM2,∴82+(6﹣x)2=62+x2,∴x=,∵∠PFM=∠PCM=90°,∴P,F,M,C四点共圆,∴∠CFM=∠CPM,∴tan∠CFM=tan∠CPM===.9.解:(1)如图1中,∵四边形ABCD是矩形,∴BC=AD=CG=4,∠B=90°,∵AB=CD=2,∴DG===2,∴AG=AB﹣BG=4﹣2,故答案为4﹣2.(2)如图2中,由四边形CGEF是矩形,得到∠CGE=90°,∵点G在线段AE上,∴∠AGC=90°,∵CA=CA,CB=CG,∴Rt△ACG≌Rt△ACB(HL).∴∠ACB=∠ACG,∵AB∥CD∴∠ACG=∠DAC,∴∠ACH=∠HAC,∴AH=CH,设AH=CH=m,则DH=AD﹣AH=5﹣m,在Rt△DHC中,∵CH2=DC2+DH2,∴m2=22+(4﹣m)2,∴m=,∴AH=,GH===.(3)如图,当点G在对角线AC上时,△OGE的面积最小,最小值=×OG×EG=×2×(4﹣)=4﹣.当点G在AC的延长线上时,△OE′G′的面积最大.最大值=×E′G′×OG′=×2×(4+)=4+综上所述,4﹣≤S≤4+.10.解:(1)在Rt△ACB中,∵∠C=90°,AC=8,BC=6,∴AB===10,当四边形PQMN是矩形时,PQ∥AB.∴tan∠PQM===.(2)如图1中,延长QN交AB于K.由题意BQ=6﹣x,QN=PM=x,AM=x,KQ=BQ=,BK=BQ=,∴MK=AB﹣AM﹣BK=,∵QN<QK,∴x<,∴x<,∴y=PM•MK=(0≤x<).(3)①如图3﹣1中,当平分MN时,D为MN的中点,作NE∥BC交PQ于E,作NH⊥CB 交CB的延长线于H,EG⊥BC于G.∵PD∥BC,EN∥BC,∴PD∥NE,∵PE∥DN,∴四边形PDNE是平行四边形,∴PE=DN,∵DN=DM,PQ=MN,∴PE=EQ,∵EG∥PC,∴CG=GQ,∴EG=PC,∵四边形EGHN是矩形,∴NH=EG=NQ=PM=x,PC=8﹣x,∴x=•(8﹣x),解得x=.②如图3﹣2中,当平分NQ时,D是NQ的中点,作DH⊥CB交CB的延长线于H.∵DH=PC,∴8﹣x=•x,解得x=,综上所述,满足条件x的值为或.11.解:探究:如图①中,过M分别作ME∥AB交BC于E,MF∥BC交AB于F,则四边形BEMF是平行四边形,∵四边形ABCD是正方形,∴∠ABC=90°,∠ABD=∠CBD=∠BME=45°,∴ME=BE,∴平行四边形BEMF是正方形,∴ME=MF,∵CM⊥MN,∴∠CMN=90°,∵∠FME=90°,∴∠CME=∠FMN,∴△MFN≌△MEC(ASA),∴MN=MC;应用:(1)当点M与D重合时,△CNM的面积最大,最大值为18,当DM=BM时,△CNM的面积最小,最小值为9,综上所述,9≤S<18.(2)如图②中,由(1)得FM∥AD,EM∥CD,∴===,∵AN=BC=6,∴AF=3.6,CE=3.6,∵△MFN≌△MEC,∴FN=EC=3.6,∴AN=7.2,BN=7.2﹣6=1.2,∴AN=6BN,故答案为AN=6BN.12.(1)证明:连接FD,∵AD=ED,∠ADE=90°,∴∠DAC=∠AED=45°,∵四边形BCEF是平行四边形,∠BCE=90°,∴四边形BCEF是矩形,∴∠CEF=∠AEF=90°,BC=EF=AC,∴∠DEF=45°,∴∠A=∠DEF,∴△ADC≌△EDF(SAS),∴DC=DF,∠DCA=∠DFE,∴∠FDC=∠FEC=90°,从而△DFC为等腰直角三角形,∴CD=CF.(2)解:成立.理由:连接FD,∵AD⊥DE,EF⊥AC,∴∠DAC=∠DEF,又AD=ED,AC=EF,∴△ADC≌△EDF(SAS),∴DC=DF,∠ADC=∠EDF,即∠ADE+∠EDC=∠FDC+∠EDC,∴∠FDC=∠ADE=90°∴△DFC为等腰直角三角形,∴CD=CF.(3)解:如图3﹣1中,设AE与CD的交点为M,∵CE=CA,DE=DA,∴CD垂直平分AE,∴=,DM=,∴CD=DM+CM=3,∵CF=CD∴CF=6.如图3﹣2中,设AE与CD的交点为M,同法可得CD=CM﹣DM=﹣=2,∴CF=CD=4,综上所述,满足条件的CF的值为6或4.13.解:(1)如图1中,作DH⊥BE于H.在Rt△BCD中,∵∠DHC=90°,CD=5,tan∠DCH=,∴DH=4,CH=3,∴BH=BC+CH=5+3=8,∴tan∠DBE===.故答案为.(2)如图2中,∵四边形ABCD是菱形,∴AC⊥BD,∵BC=5,tan∠CBM==,∴CM=,BM=DM=2,∵PF∥CB,∴=,∴=,解得t=.(3)如图3﹣1中,当0<t ≤时,重叠部分是平行四边形PBQF ,S =PB •PQ =2t •t=10t 2.如图3﹣2中,当<t ≤1时,重叠部分是五边形PBQRT ,S =S平行四边形PBQF ﹣S △TRF =10t 2﹣•[5t ﹣(5﹣t )]•[5t ﹣(5﹣t )]=﹣t 2+30t ﹣10.如图3﹣3中,当1<t ≤2时,重叠部分是四边形PBCT ,S =S △BCD ﹣S △PDT =×5×4﹣•(5﹣t )•(4﹣2t )=﹣t 2+10t .(4)如图4﹣1中,当MN ∥AB 时,设CM 交BF 于T .∵PN∥MT,∴=,∴=,∴MT=,∵MN∥AB,∴===2,∴PB=BM,∴2t=×2,∴t=.如图4﹣2中,当MN⊥BC时,易知点F落在DH时,∵PF∥BH,∴=,∴=,解得t=.如图4﹣3中,当MN⊥AB时,易知∠PNM=∠ABD,可得tan∠PNM==,∴=,解得t=,当点P与点D重合时,MN∥BC,此时t=2,综上所述,满足条件的t的值为或或或2.14.(1)证明:∵AB=AC,∠ABC=∠ACB,∴∠CAM=∠ABC+∠ACB=2∠ABC,∵AD平分∠CAM,∴∠CAM=∠MAD,∴∠ABC=∠MAD,∴AD∥BC,∵CD∥AB,∴四边形ABCD是平行四边形;(2)∵∠ABC=60°,AC=AB,∴△ABC是等边三角形,∴AB=BC,∴四边形ABCD是菱形,∴AC⊥BD,∵DE⊥BD,∴AC∥DE,∵AD∥CE,∴四边形ACED是平行四边形,∴BC=AD=CE,∴图中所有与△CDE面积相等的三角形有△BCD,△ABD,△ACD,△ABC.15.解:(1)如图2中,设EC交AD于O.∵△ABC,△CDE都是等腰直角三角形,∴AC=CB,CD=CE,∠ACB=∠ECD=45°,∴=,∠ACD=∠BCE,∴△ACD∽△BCE,∴∠ODC=∠OEP,∵∠COD=∠EOP,∴∠OPE=∠OCD=45°,故答案为45°,△BCE∽△ACD.(2)如图③中,作EH⊥BA交BA的延长线于H,作BG⊥DE交DE的延长线于G.由题意CE=3BC=3,∴AB=BC=1,EC=DE=3,∵BE ≤BC +EC ,∴BE ≤4,∴当点E 在BC 的延长线上时BE 的值最大,最小值为4,∵S 四边形ABDE =S △ABE +S △BDE =•AB •EH +DE •BG ,又∵EH ≤BE ,BG ≤BE ,∴EH 与BG 的最大值为4,∴四边形ABDE 的面积的最大值=×1×4+×4×3=8.(3)如图④中,以EC 为直角边,向下作等腰直角△CEH (EC =EH ,∠CEH =90°),连接AH .∵△ABC ,△CEH 都是等腰直角三角形,∴∴AC =CB ,CH =CE ,∠ACB =∠ECD =45°, ∴=,∠ACH =∠BCE ,∴△ACH ∽△BCE , ∴==,∴BE =AH ,∵AH ≤EH +AE ,∴AH ≤2+4=6,∴AH 的最大值为6,∴BE 的最大值=6×=3.故答案为3.。
中考数学模拟题汇总《四边形》专项练习(附答案解析)

中考数学模拟题汇总《四边形》专项练习(附答案解析)一、单选题1.如图,四边形ABCD 是正方形,E 是BC 的中点,连接AE 与对角线BD 相交于点G ,连接CG 并延长,交AB 于点F ,连接DE 交CF 于点H .以下结论:①CDE BAE ∠=∠;②CF DE ⊥;③AF BF =;④22CE CH CF =⋅.其中正确结论的个数有( )A .1B .2C .3D .42.如图,正方期ABCD 的边长为4,点E 在对角线BD 上,且22.5,BAE EF AB ︒∠=⊥为F ,则EF 的长为( )A .2BC .D .4-3.如图,已知正方形ABCD 的边长为12,BE =EC ,将正方形边CD 沿DE 折叠到DF ,延长EF 交AB 于G ,连接DG ,现在有如下4个结论:①△ADG ≌△FDG ;②GB =2AG ;③∠GDB =45°;④S △BEF =725.在以上4个结论中,正确的有( )A .1B .2C .3D .44.如图,已知正方形ABCD 的边长为4,P 是对角线BD 上一点,PE //CD 于点E ,PF //BC 于点F ,连接AP ,EF.给出下列结论:①PD =;②四边形PECF 的周长为8;③APD 一定是等腰三角形;④AP EF =;⑤EF 的最小值为其中正确结论的序号为( )A .①②④⑤B .①③④⑤C .②④⑤D .②③⑤5.如图,在正方形ABCD 中,点M 是AB 上一动点,点E 是CM 的中点,AE 绕点E 顺时针旋转90°得到EF ,连接DE ,DF 给出结论:①DE EF =;②45CDF ∠=︒;③75AM DF =;④若正方形的边长为2,则点M 在射线AB 上运动时,CF .其中结论正确的是( )A .①②③B .①②④C .①③④D .②③④6.如图,E 、F 分别是正方形ABCD 的边BC 、CD 的中点,连接AF 、DE 交于点P ,过B 作BG ∥DE 交AD 于G ,BG 与AF 交于点M .对于下列结论:①AF ⊥DE ;②G 是AD 的中点;③∠GBP =∠BPE ;④S △AGM :S △DEC =1:4.正确的个数是( )A .1个B .2个C .3个D .4个7.如图,在正方形ABCD 中,点E 是边BC 上的点,且CE =2BE ,连接AE 、DE ,分别交BD 、AC 于点P 、Q ,过点P 作PF ⊥AE 交CB 的延长线于点F ,下列结论:①∠AED +∠EAC +∠EDB =90°;②AP =FP ;③AE =10AO ;④若四边形OPEQ 的面积为2,则该正方形的面积为36;⑤CE ·EF =EQ ·DE .其中正确的结论有( )A .1个B .2个C .3个D .4个8.如图,四边形ABCD 是边长为2的正方形,点P 为线段AB 上的动点,E 为AD 的中点,射线PE 交CD 的延长线于点Q ,过点E 作PQ 的垂线交CD 于点H 、交BC 的延长线于点F ,则以下结论:①AEP CHF ;②EHQ CHF ;③当点F 与点C 重合时3PA PB ;④当PA PB =时,CF =( )A .①③④B .②③④C .①③D .②④二、填空题9.如图,已知矩形ABCD 中,3AB =,4BC =,点M ,N 分别在边AD ,BC 上,沿着MN 折叠矩形ABCD ,使点A ,B 分别落在E ,F 处,且点F 在线段CD 上(不与两端点重合),过点M 作MH BC ⊥于点H ,连接BF .当四边形CDMH 为正方形时,NC =______;若13DF DC =,则折叠后重叠部分的面积为______.10.如图,将边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AEFC的位置,则图中阴影部分的面积为_______.11.如图,正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠AEB=75°,③EG=FG且∠AGE=90°,④BE=FG⑤S△ABE=1 2S△CEF.其中正确结论是_____(填序号).12.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为_____________________ .13.如图,已知正方形ABCD的边长为2,对角线AC、BD相交于点O,AE平分∠BAC交BD于点E,则BE的长为_________.14.如图,正方形ABCD中,AB=3,点E为对角线AC上一点,EF⊥DE交AB于F,若四边形AFED的面积为4,则四边形AFED的周长为______.15.如图,正方形ABCD的边长为1,AC、BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①四边形AEGF是菱形;②△HED的面积是1﹣;③∠AFG=135°;④BC+FG其中正确的结论是_____.(填2入正确的序号)16.如图,以Rt ABC的斜边AB为一边,在AB的右侧作正方形ABED,正方形对角线交于点O,BC=______.连接CO,如果AC=4,CO=三、解答题17.已知正方形ABCD,点E在AB上,点G在AD,点F在射线BC上,点H在CD上.(1)如图1,DE⊥FG,求证:BF=AE+AG;(2)如图2,DE⊥DF,P为EF中点,求证:BE=2PC;(3)如图3,EH交FG于O,∠GOH=45°,若CD=4,BF=DG=1,则线段EH的长为.18.已知正方形ABCD中AC与BD交于点O,点M在线段BD上,作直线AM交直线DC于点E,过D作DH⊥AE于H,设直线DH交AC于点N.(1)如图1,当M在线段BO上时,求证:OM=ON;(2)如图2,当M在线段OD上,连接NE和MN,当EN//BD时,求证:四边形DENM是菱形;(3)在(2)的条件下,若正方形边长为4,求EC的长.19.如图,在正方形ABCD 中,E 、F 是对角线BD 上两点,且∠EAF =45°,将△ADF 绕点A 顺时针旋转90°后,得到△ABQ ,连接EQ .(1)求证:EA 是∠QED 的平分线; (2)已知BE =1,DF =3,求EF 的长.20.如图1,在正方形ABCD 中,E 为边BC 上一点(不与点B 、C 重合),垂直于AE 的一条直线MN 分别交AB 、AE 、CD 于点M 、P 、N .(1)求证AE =MN ;(2)如图2,若垂足P 恰好为AE 的中点,连接BD ,交MN 于点Q ,连接EQ ,并延长交边AD 于点F .求∠AEF 的度数;(3)如图3,若该正方形ABCD 边长为10,将正方形沿着直线MN 翻折,使得BC 的对应边B ′C ′恰好经过点A ,过点A 作AG ⊥MN ,垂足分别为G ,若AG =6,请直接写出AC ′的长________.21.如图,在平面直角坐标系中,边长为4的正方形OABC 的顶点A 、C 分别在y 轴、x 轴的正半轴上,点O 在原点.现将正方形OABC 绕点O 按顺时针方向旋转,旋转角为θ,当点A 第一次落在直线y x =上时停止旋转,旋转过程中,AB 边交直线y x =于点M ,BC 边交x 轴于点N .θ=︒时,求点A的坐标;(1)若30(2)设MBN△的周长为P,在旋转正方形OABC的过程中,P值是否有变化?请证明你的结论;22.在ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD的右侧作正方形ADEF,连接CF.(1)观察猜想如图1,当点D在线段BC上时,①BC与CF的位置关系为:;②BC,CD,CF之间的数量关系为:.(将结论直接写在横线上)(2)数学思考如图2,当点D在线段CB的延长线上时,结论①②是否仍然成立?若成立,请给予证明:若不成立,请你写出正确结论再给予证明,(3)拓展延伸如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若AB=,CD=1,请求出GE的长.23.如图1,已知正方形ABCD 顶点A ,B 分别在y 轴和x 轴上,边CD 交x 轴的正半轴于点E .(1)若()20,45A a a -+,且2a =,求A 点的坐标.(2)在(1)的条件下,若34AO EO =,D 点的坐标.(3)如图2,连结AC 交x 轴于点F ,点H 是A 点上方轴上一动点,以AF ,AH 为边作平行四边形AFGH ,使G 点恰好落在AD 边上.求证:22224HG DG BF +=.24.已知,四边形ABCD 是正方形,点E 是正方形ABCD 所在平面内一动点(不与点D 重合),AB =AE ,过点B 作DE 的垂线交DE 所在直线于F ,连接CF .提出问题:当点E运动时,线段CF与线段DE之间的数量关系是否发生改变?探究问题:(1)首先考察点E的一个特殊位置:当点E与点B重合(如图①)时,点F与点B也重合.用等式表示线段CF与线段DE之间的数量关系:;(2)然后考察点E的一般位置,分两种情况:情况1:当点E是正方形ABCD内部一点(如图②)时;情况2:当点E是正方形ABCD外部一点(如图③)时.在情况1或情况2下,线段CF与线段DE之间的数量关系与(1)中的结论是否相同?如果都相同,请选择一种情况证明;如果只在一种情况下相同或在两种情况下都不相同,请说明理由;拓展问题:(3)连接AF,用等式表示线段AF、CF、DF三者之间的数量关系:.25.如图1,在正方形ABCD中,E,F分别是AD,CD上两点,BE交AF于点G,且DE=CF.(1)写出BE与AF之间的关系,并证明你的结论;(2)如图2,若AB=2,点E为AD的中点,连接GD,试证明GD是∠EGF的角平分线,并求出GD的长.26.基础探究:如图①,在正方形ABCD中,点E为AD上一点,DF⊥CE交AB于F,垂足为点O.求证:CE=DF.应用拓展:如图②,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为点O.若正方形ABCD的边长为12,DE=5,则四边形EFCG的面积为_______.参考答案与解析一、单选题1.【答案】D【分析】证明△ABE≌△DCE,可得结论①正确;由正方形的性质可得AB=AD=BC=CD,BE=CE,∠DCE=∠ABE=90°,∠ABD=∠CBD=45°,可证△ABE≌△DCE,△ABG≌△CBG,可得∠BCF=∠CDE,由余角的性质可得结论②;证明△DCE≌△CBF可得结论③,证明△CHF∽△CBF即可得结论④正确.【详解】解:∵四边形ABCD是正方形,点E是BC的中点,∴AB=AD=BC=CD,BE=CE,∠DCE=∠ABE=90°,∠ABD=∠CBD=45°,∴△ABE≌△DCE(SAS)∴∠DEC=∠AEB,∠BAE=∠CDE,DE=AE,故①正确,∵AB=BC,∠ABG=∠CBG,BG=BG,∴△ABG≌△CBG(SAS)∴∠BAE=∠BCF,∴∠BCF=∠CDE,且∠CDE+∠CED=90°,∴∠BCF+∠CED=90°,∴∠CHE=90°,∴CF⊥DE,故②正确,∵∠CDE=∠BCF,DC=BC,∠DCE=∠CBF=90°,∴△DCE≌△CBF(ASA),∴CE=BF,∵CE=12BC=12AB,∴BF=12 AB,∴AF=BF,故③正确,∵∠BCF+∠BFC=90°,∠DEC=∠BFC ∴∠BCF+∠DECC=90°,∴∠CHE=90°∴∠CHE=∠FBC又∠DEC=∠BFC∴△CHF∽△CBF∴CH CE BC CF=∵BC=2CE,∴2BC CE CE CE CHCF CF==∴22CE CH CF=⋅故选:D.【点评】本题考查了正方形的性质,全等三角形的判定和性质,相似三角形的判定和性质,直角三角形的性质,勾股定理等知识,熟练运用这些性质进行推理是本题的关键.2.【答案】D【分析】在AF上取FG=EF,连接GE,可得△EFG是等腰直角三角形,根据等腰直角三角形的性质可得,∠EGF=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BAE+∠AEG=∠EGF,然后求出∠BAE=∠AEG=22.5°,根据等角对等边可得AG=EG,再根据正方形的对角线平分一组对角求出∠ABD=45°,然后求出△BEF是等腰直角三角形,根据等腰直角三角形的性质可得BF=EF,设EF=x,最后根据AB=AG+FG+BF列方程求解即可.【详解】解:如图,在AF上取FG=EF,连接GE,∵EF⊥AB,∴△EFG是等腰直角三角形,∴,∠EGF=45°,由三角形的外角性质得,∠BAE+∠AEG=∠EGF,∵∠BAE=22.5°,∠EGF=45°,∴∠BAE=∠AEG=22.5°,∴AG=EG,在正方形ABCD中,∠ABD=45°,∴△BEF是等腰直角三角形,∴BF=EF,设EF=x,∵AB=AG+FG+BF,∴,解得x=4故选:D.【点评】本题考查了正方形的性质,等腰直角三角形的判定与性质,难点在于作辅助线构造出等腰直角三角形并根据正方形的边长AB列出方程.3.【答案】C【解析】试题解析:由折叠可知,DF=DC=DA,∠DFE=∠C=90°,∴∠DFG=∠A=90°,∴△ADG≌△FDG,①正确;∵正方形边长是12,∴BE=EC=EF=6,设AG=FG=x,则EG=x+6,BG=12-x,由勾股定理得:EG2=BE2+BG2,即:(x+6)2=62+(12-x)2,解得:x=4∴AG=GF=4,BG=8,BG=2AG,②正确;BE=EF=6,△BEF是等腰三角形,易知△GED不是等腰三角形,③错误;S△GBE=12×6×8=24,S△BEF=EFEGS△GBE=62410⨯=725,④正确.故选C.考点:正方形综合题.4.【答案】A【分析】①根据正方形的对角线平分对角的性质,得PDF是等腰直角三角形,在Rt DPF中,2222222DP DF PF EC EC EC=+=+=,求得DP=;②根据等腰直角三角形和矩形的性质可得其周长为2BC,则四边形PECF的周长为8;③根据P的任意性可以判断APD△不一定是等腰三角形;④由PECF为矩形,则通过正方形的轴对称性,证明AP EF=;⑤当AP最小时,EF最小,EF的最小值等于【详解】①如图,延长FP交AB与G,连PC,延长AP交EF与H,∵PE ⊥BC ,PF ⊥CD ,∠BCD=90°, ∴四边形PECF 为矩形,∴PF=CE , ∵GF ∥BC ,∴∠DPF=∠DBC ,∵四边形ABCD 是正方形, ∴∠DBC=45°∴∠DPF=∠DBC=45°, ∴∠PDF=∠DPF=45°, ∴PF=EC=DF ,∴在Rt △DPF 中,DP 2=DF 2+PF 2=EC 2+EC 2=2EC 2,∴. 故①正确;②∵四边形PECF 为矩形,∴四边形PECF 的周长=2CE+2PE=2CE+2BE=2BC=8, 故②正确;③∵点P 是正方形ABCD 的对角线BD 上任意一点,∠ADP=45︒, ∴当∠PAD=45︒或67.5︒或90︒时,△APD 是等腰三角形, 除此之外,△APD 不是等腰三角形, 故③错误;④∵四边形PECF 为矩形, ∴PC=EF ,由正方形为轴对称图形, ∴AP=PC , ∴AP=EF , 故④正确;⑤=由EF=PC ,∴当PC 最小时,EF 最小,则当PC ⊥BD 时,即PC=12BD=12⨯=EF 的最小值等于故⑤正确;综上所述,①②④⑤正确,故选:A.【点评】本题考查了正方形的性质,等腰三角形的判定和性质,勾股定理的应用.本题难度较大,综合性较强,在解答时要认真审题.5.【答案】B【分析】①延长AE交DC的延长线于点H,由“AAS”可证△AME≌△HCE,可得AE=EH,由直角三角形的性质可得AE=EF=EH,即可判断;②由四边形内角和定理可求2∠ADE+2∠EDF=270°,可得∠ADF=135°,即可判断;③由连接AC,过点E作EP⊥AD于点P,过点F作FN⊥EP于N,交CD于G,连接CF,由梯形中位线定理可求PE=12(AM+CD),由“AAS”可证△APE≌△ENF,可得AP=NE=12AD,即可求AM=2DG=2,即可判断;④由垂线段最短,可得当CF⊥DF时,CF有最小值,由等腰直角三角形的性质可求CF的最小值,即可判断.【详解】①如图,延长AE交DC的延长线于点H,∵点E是CM的中点,∴ME=EC,∵AB∥CD,∴∠MAE=∠H,∠AME=∠HCE,∴△AME≌△HCE(AAS),∴AE=EH,又∵∠ADH=90°,∴DE=AE=EH,∵AE绕点E顺时针旋转90°得到EF,∴AE=EF,∠AEF=90°,∴AE=DE=EF,故①正确;②∵AE=DE=EF,∴∠DAE=∠ADE,∠EDF=∠EFD,∵∠AEF+∠DAE+∠ADE+∠EDF+∠EFD=360°,∴2∠ADE+2∠EDF=270°,∴∠ADF=135°,∴∠CDF=∠ADF−∠ADC=135°−90°=45°,故②正确;③∵EP⊥AD,AM⊥AD,CD⊥AD,∴AM∥PE∥CD,∴AP ME=PD EC=1,∴AP=PD,∴PE是梯形AMCD的中位线,∴PE=12(AM+CD),∵∠FDC=45°,FN⊥CD,∴∠DFG=∠FDC=45°,∴DG=GF,DF,∵∠AEP+∠FEN=90°,∠AEP+∠EAP=90°,∴∠FEN=∠EAP,又∵AE=EF,∠APE=∠ENF=90°,∴△APE≌△ENF(AAS),∴AP =NE =12AD , ∵PE =12(AM +CD )=NE +NP =12AD +NP , ∴12AM =NP =DG ,∴AM =2DG =2DF ,∴AMDF,故③错误; ④如图,连接AC ,过点E 作EP ⊥AD 于点P ,过点F 作FN ⊥EP 于N ,交CD 于G ,连接CF ,∵EP ⊥AD ,FN ⊥EP ,∠ADC =90°, ∴四边形PDGN 是矩形, ∴PN =DG ,∠DGN =90°, ∵∠CDF =45°, ∴点F 在DF 上运动,∴当CF ⊥DF 时,CF 有最小值, ∵CD =2,∠CDF =45°,∴CF故选:B .【点评】本题考查了正方形的性质,全等三角形的判定和性质,矩形的判定和性质,旋转的性质,平行线分线段成比例,梯形中位线的定理等知识,灵活运用这些性质解决问题是本题的关键. 6.【答案】C【分析】根据正方形性质得出AD BC DC ==;12EC DF BC ==;ADF DCE ∠=∠,证ADF ≌()DCE SAS ,推出AFD DEC ∠=∠,求出90DGF ∠=︒即可判断①;证明四边形GBED 为平行四边形,则可知②正确;由平行线的性质可得③正确;证明AGM ∽AFD ,可得出AGMS:1DECS=:5.则④不正确.【详解】解:∵正方形ABCD ,E ,F 均为中点 ∴AD =BC =DC ,EC =DF =12BC , ∵在△ADF 和△DCE 中,AD DC ADF DCE DF CE =⎧⎪∠=∠⎨⎪=⎩, ∴△ADF ≌△DCE (SAS ), ∴∠AFD =∠DEC , ∵∠DEC +∠CDE =90°, ∴∠AFD +∠CDE =90°=∠DGF , ∴AF ⊥DE ,故①正确, ∵//BG DE ,//GD BE , ∴四边形GBED 为平行四边形, ∴GD =BE , ∵BE =12BC , ∴GD =12AD , 即G 是AD 的中点,故②正确, ∵//BG DE , ∴∠GBP =∠BPE , 故③正确.∵//BG DG ,AF ⊥DE , ∴AF ⊥BG ,∴∠ANG =∠ADF =90°, ∵∠GAM =∠FAD , ∴△AGM ∽△AFD ,设AG =a ,则AD =2a ,AF,∴21()5AGM AFDS AG SAF ==. ∵△ADF ≌△DCE , ∴S △AGM :S △DEC =1:5. 故④错误. 故选:C .【点评】本题主要考查了正方形的性质,全等三角形的性质和判定,相似三角形的性质和判定,平行线的性质,平行四边形的判定与和性质等知识,熟练掌握正方形的性质是解题的关键. 7.【答案】B【分析】①先根据正方形的性质证得∠AOP 是直角,再利用三角形的外角的性质即可判定;②直接利用四点共圆可证∠AFP=∠ABP=45°;③设BE=a 则EC=2a ,然后利用勾股定理得到AE 和OA 的长,即可得出结论;④利用相似得到BP 与DP 的比导出BP 与OP 的比,同理求出OQ 与QC 的比,设△BEP 的面积为S ,再利用同高时面积比即为底的比求出△OPE 和△OQE 的面积,表示出四边形OPEQ 的面积,求出S 的值,再通过正方形面积是24S 即可求出结果;⑤如果当E 是BC 边中点时可得△FPE ∽DCE ,可得结论,因为已知中EC=2BE 时,所以△FPE 与△DCE 不相似,所以错误.【详解】解:如图,连接OE 、 AF , ∵ABCD 是正方形, ∴AC ⊥BD ,∴∠AOP=90°,∵∠AED+∠EDB=∠APO,∴∠AED+∠EAC+∠EDB=∠APO+∠EAC=90°,故①正确;∵PF⊥AE,∴∠APF=∠ABF=90°,即A、P、B、F四点共圆,∴∠AFP=∠ABP=45°,∴∠PAF=∠PFA=45°,∴PA=PF,故②正确;设BE=a,则EC=2a,则a,a,∴3AEAO,∴,故③错误;连接OE,∵CE=2BE,∴BE:EC:BC==1:2:3∵AD//BC∴△BEP∽△DAP,△EQC∽△DQA,∴BP:DP=1:3,CQ:AQ=2:3,∴BP:OP=1:1,OQ:CQ=1:4,∴设S△BEP=S,则S△OPE=S,则S△BEO=2S,S△ECO=4S,∴S△OEQ =45S,S△BCO=2S+4S=6S,∵四边形OPEQ的面积是2,∴S+45S=2,∴S=109,∴正方形ABCD的面积=4S△BCO =24S=803,故④错误;∵BE=2EC∴∠PEB≠∠CED,且PE EC PF CD∴△FPE不一定与△DCE相似,∴EF PEED EC≠,又∵EQ≠PE,∴CE·EF≠EQ·DE,故⑤错误;共有2个正确.故选:B.【点评】本题主要考查正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识,综合性强,难度大,灵活运用所学知识解决问题是解答本题的关键.8.【答案】C【点评】本题考查正方形的性质、全等三角形的判定和性质、相似三角形的性质和判定、勾股定理等知识,解题的关键是学会利用全等三角形解决问题.二、填空题 9.【答案】32 5512【分析】根据正方形的性质证明MHN BCF △△,令HN x =,则3CN x =-,1FN BN x ==+,求得FGN MHN △△,得到2GN =,再证明MEO NCF △△,得到43EO =,即可得到结果;【详解】解:∵四边形CDMH 为正方形, ∴3MH HC ==, ∴1BH =, ∵MHN BCF △△,∴MH BCHN CF=, 令HN x =,则3CN x =-,1FN BN x ==+,∴CF ==∴3x =∴132x =,23x =(不符合题意,舍去), ∴12HN HC =,即N 为HC 的中点, ∴1322NC CH ==,∵13DF DC =,3AB CD ==,∴1DF =,2CF =,∴BF ===∴BG GF == ∵MHN BCF △△,∴MH BCHN CF=, ∴32HN =, ∴FGN MHN △△,∴GN =,∴52FN ===,∴32CN ===, ∴334122BH BC HN NC =--=--=,∵EMO CNF ∠=∠,90MEO NCF ∠=∠=︒, ∴MEO NCF △△, ∴ME NCEO CF=, ∴43EO =, ∴折叠后重叠部分的面积为:()1122MEO MEFN S S ME FN ME EO +=+-⨯△梯形,151455*********⎛⎫=+⨯-⨯⨯= ⎪⎝⎭. 故答案为:32;5512. 【点评】本题主要考查了正方形的性质,相似三角形的判定与性质,准确分析计算是解题的关键.10.【分析】过点M 作MH DE ⊥于点H ,利用正方形的性质和旋转的性质可证得△ADE 为等边三角形,由等腰三角形的判定可得△MDE 为等腰三角形,继而求得12DH EH ==,然后设MH x =,则2DM x =,根据勾股定理列方程求解可得MH =,进而由三角形面积公式即可求解. 【详解】如图,过点M 作MH DE ⊥于点H , ∵四边形ABCD 为正方形,∴1AB AD ==,90B BAD ADC ∠=∠=∠=︒,∵正方形ABCD 绕点A 逆时针旋转30°到正方形AEFG 的位置, ∴1AE AB ==,30BAE ∠=︒,90AEF B ∠=∠=° ∴60DAE ∠=︒∴△ADE 为等边三角形,∴60AED ADE ∠=∠=︒,1DE AD == ∴30MED MDE ∠=∠=︒, ∴△MDE 为等腰三角形, ∴12DH EH ==. 在Rt MDH 中,设MH x =,则2DM x =,∴221(2)4x x =+解得:16x =,26x =-(舍去),∴MH =, ∴1.2MDE S DE MH ∆=⨯⨯1126=⨯⨯12=.故答案为:12【点评】本题考查了旋转的性质,正方形的性质,等边三角形判定与性质,解直角三角形,利用等边三角形和等腰三角形的性质求出12DH EH ==,30MED MDE ∠=∠=︒是解题的关键.11.【答案】①②③⑤.【分析】通过条件可以得出△ABE ≌△ADF ,从而得出∠BAE =∠DAF ,BE =DF ,∠AEB =75°;由正方形的性质就可以得出EC =FC ,得AC 垂直平分EF ,得EG =FG 且∠AGE =90°;设EC =x ,BE =y ,由勾股定理就可以得出x 与y 的关系,表示出BE 与EF ,利用三角形的面积公式分别表示出S △CEF 和2S △ABE ,再通过比较大小就可以得出结论. 【详解】解:∵四边形ABCD 是正方形,∴AB =BC =CD =AD ,∠B =∠BCD =∠D =∠BAD =90°. ∵△AEF 等边三角形, ∴AE =EF =AF ,∠EAF =60°. ∴∠BAE +∠DAF =30°.在Rt △ABE 和Rt △ADF 中,AE AFAB AD =⎧⎨=⎩, ∴Rt △ABE ≌Rt △ADF (HL ), ∴BE =DF , 所以故①正确;∵∠BAE =∠DAF ,∠BAE +∠DAF =30°, ∴∠BAE =∠DAF =15°, ∴∠AEB =75°, 所以②正确; ∵BC =CD ,∴BC ﹣BE =CD ﹣DF ,即CE =CF , ∵AE =AF , ∴AC 垂直平分EF , ∴EG =FG 且∠AGE =90°, 所以③正确;设EC =x ,由勾股定理,得EF ,∴AE =EF ,∴FG =BG =CG =2x , ∵∠EAG =30°,AG ,∴AC =AG +CG +2x ,∴AB=2x ,∴BE =BC ﹣CE ﹣x =, ∴BE ≠FG , 所以④错误; ∵S △CEF =12CE 2=12x 2,S △ABE =12AB •BE =12•2x =14x 2,∴S △ABE =12×12x 2=12S △CEF , 所以⑤正确.综上所述,①②③⑤正确, 故答案为:①②③⑤.【点评】本题考查正方形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,等边三角形的性质的运用,三角形的面积公式的运用,解答本题时运用勾股定理的性质解题时关键.12.【答案】72【分析】由直角三角形的中线,求出DE 的长度,利用三角形中位线定理和勾股定理,求出BE 的长度,即可求出答案.【详解】解:∵四边形ABCD 是正方形, ∴∠DCE=90°,OD=OB , ∵DF=FE , ∴CF=FE=FD ,∵EC+EF+CF=18,EC=5, ∴EF+FC=13, ∴DE=13,∴12=, ∴BC=CD=12, ∴BE=BC-EC=7, ∵OD=OB ,DF=FE ,∴OF=12BE=72;故答案为:72. 【点评】本题考查正方形的性质,三角形的中位线定理,直角三角形斜边中线的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.13.【答案】2【分析】过E 作EM AB ⊥于M ,根据正方形性质得出AO BD ⊥,AO OB OC OD ===,由勾股定理求出AO OB ==Rt BME ∆中,由勾股定理得:222ME BE =,求出即可. 【详解】解:过E 作EM AB ⊥于M ,四边形ABCD 是正方形,AO BD ∴⊥,AO OB OC OD ===,则由勾股定理得:222AO BO AB +=, ∴AO OB ==EM AB ⊥,BO AO ⊥,AE 平分CAB ∠,∴,90OAE MOE AOE AME ∠=∠∠=∠=︒, ∵AE=AE,∴AOE AME ≅△△,EMEO ,AM AO ==四边形ABCD是正方形,∴∠=︒=∠,MBE MEB45∴==,BM ME OE在Rt BME∆中,由勾股定理得:22=,2ME BE即22=,2(2BEBE=,2故答案为:2.【点评】本题考查了角平分线性质和正方形性质,勾股定理的应用,注意:角平分线上的点到线段两个端点的距离相等.14.【答案】【分析】连接BE,DF,过E作EN⊥BF于点N,证明△DCE≌△BCE和△BEF为等腰三角形,设AF=x,用x表示DE与EF,由根据四边形ADEF的面积为4,列出x的方程求得x,进而求得四边形ADEF的周长.【详解】解:如图,连接BE,DF,过E作EN⊥BF于点N,∵四边形ABCD为正方形,∴CB=CD ,∠BCE=∠DCE=45°, 在△BEC 和△DEC 中,DC BC DCE BCE CE CE =⎧⎪∠=∠⎨⎪=⎩, ∴△DCE ≌△BCE (SAS ), ∴DE=BE ,∠CDE=∠CBE , ∴∠ADE=∠ABE ,∵∠DAB=90°,∠DEF=90°, ∴∠ADE+∠AFE=180°, ∵∠AFE+∠EFB=180°, ∴∠ADE=∠EFB , ∴∠ABE=∠EFB , ∴EF=BE , ∴DE=EF ,设AF=x ,则BF=3-x ,∴FN=BN=12BF=32x -,∴AN=AF+FN=32x+, ∵∠BAC=∠DAC=45°,∠ANF=90°,∴EN=AN=32x+,∴=∵四边形AFED 的面积为4, ∴S △ADF +S △DEF =4,∴12×3x+12×24=⎝⎭, 解得,x=-7(舍去),或x=1, ∴AF=1,DE=EF=2= ∴四边形AFED 的周长为:故答案为:4+【点评】本题考查正方形的性质、全等三角形的判定和性质、勾股定理,等腰三角形的性质,解题的关键是由面积列出x 的方程,属于中考选择题中的压轴题. 15.【答案】①②③【分析】依据四边形AEGF 为平行四边形,以及AE GE =,即可得到平行四边形AEGF 是菱形;依据1AE =,即可得到HED 的面积)11111122DH AE =⨯=+=边形AEGF 是菱形,可得267.5135AFG GEA ∠=∠=⨯︒=︒;根据四边形AEGF 是菱形,可得1FG AE ==,进而得到11BC FG +=+=. 【详解】解:正方形ABCD 的边长为1,90BCD BAD ∴∠=∠=︒,45CBD ∠=︒,BD =,1AD CD ==.由旋转的性质可知:90HGD BCD ∠==︒,45H CBD ∠=∠=︒,BD HD =,GD CD =,1HA BG ∴==,45H EBG ∠=∠=︒,90HAE BGE ∠=∠=︒,HAE ∴和BGE 1的等腰直角三角形,AE GE ∴=.在Rt AED 和Rt GED 中, DE DEAD GD =⎧⎨=⎩, Rt AED ∴≌()Rt GED HL ,()118067.52AED GED BEG ∴∠=∠=︒-∠=︒,AE GE =, 1801804567.567.5AFE EAF AEF AEF ∴∠=︒-∠-∠=︒-︒-︒=︒=∠, AE AF ∴=.AE GE =,AF BD ⊥,EG BD ⊥, AF GE ∴=且//AF GE ,∴四边形AEGF 为平行四边形, AE GE =,∴平行四边形AEGF 是菱形,故①正确;21HA =,45H ∠=︒,1AE ∴=,HED ∴的面积)11111122DH AE =⨯=+=②正确; 四边形AEGF 是菱形,267.5135AFG GEA ∴∠=∠=⨯︒=︒,故③正确; 四边形AEGF 是菱形,1FG AE ∴==,11BC FG ∴+==④不正确. 故答案为:①②③.【点评】本题考查旋转的性质,正方形的性质,全等三角形的判定和性质,菱形的判定和性质,等腰直角三角形的性质等知识,解题的关键是掌握旋转的性质:对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等. 16.【答案】8【分析】通过作辅助线使得△CAO ≌△GBO ,证明△COG 为等腰直角三角形,利用勾股定理求出CG 后,即可求出BC 的长.【详解】如图,延长CB 到点G ,使BG=AC . ∵根据题意,四边形ABED 为正方形, ∴∠4=∠5=45°,∠EBA=90°, ∴∠1+∠2=90°又∵三角形BCA 为直角三角形,AB 为斜边, ∴∠2+∠3=90°∴∠1=∠3∴∠1+∠5=∠3+∠4,故∠CAO =∠GBO , 在△CAO 和△GBO 中,CA GB CAO GBO AO BO =⎧⎪∠=∠⎨⎪=⎩故△CAO ≌△GBO , ∴CO =GO=7=∠6, ∵∠7+∠8=90°, ∴∠6+∠8=90°,∴三角形COG 为等腰直角三角形, ∴,∵CG=CB+BG ,∴CB=CG -BG=12-4=8, 故答案为8.【点评】本题主要考查正方形的性质,等腰三角形的判定和性质,勾股定理,全等三角形的判定和性质,根据题意建立正确的辅助线以及掌握正方形的性质,等腰三角形的判定和性质,勾股定理,全等三角形的判定和性质是解答本题的关键. 三、解答题17.【答案】(1)见解析;(2)见解析;(3 【分析】(1)作GM ⊥BC 于M .证△DAE ≌△GMF ,得AE =FM ,AG =BM .所以BF =AE+AG . (2)作EQ ∥CP 交BC 于Q .证EQ =2CP ,EQ可得BE .(3)作BM ∥GF 交AD 于M ,作BN ∥EH 交CD 于N ,得BM =GF ,BF =MG =1,BN =EH ,延长DC 到P ,使CP =AM =2,证△BAM ≌△BCP 得∠ABM =∠CBP ,BM =BP ,再证△MBN ≌△PBN 得MN =PN ,设CN =x ,则MN =PN =CN+PC =x+2,DN =4﹣x ,在Rt △DMN 中,由DM 2+DN 2=MN 2求得x =43,再在△BCN 中利用勾股定理求解可得.【详解】解:(1)如图1,过点G作GM⊥BC于M,则∠GMB=∠GMF=90°,∵四边形ABCD是正方形,∴AD=AB,∠A=∠B=90°,∴四边形ABMG是矩形,∴AG=BM,∵DE⊥GF,∴∠ADE+∠DGF=∠ADE+∠AED=90°,∴∠AED=∠DGF,又∠DGF=∠MFG,∴∠AED=∠MFG,∴△DAE≌△GMF(AAS),∴AE=MF,则BF=BM+MF=AG+AE;(2)如图2,过点E作EQ∥PC,交BC于点Q,∵P是EF的中点,∴PC是△EQF的中位线,则EQ=2PC,QC=CF,∵∠ADC=∠EDF=90°,∴∠ADE=∠CDF,又∵∠A=∠DCF=90°,AD=CD,∴△ADE≌△CDF(ASA),∴AE=CF=QC,∵AB=BC,∴BE=BQ,则∠BEQ=45°,∴EQ,则2PC BE,∴BE;(3)如图3所示,作BM∥GF交AD于M,作BN∥EH交CD于N,则四边形BFGM和四边形BEHN是平行四边形,∴BM=GF,BF=MG=1,BN=EH,∵DG=1,CD=AD=4,∴AM=2,延长DC到P,使CP=AM=2,∵BA=BC,∠A=∠BCP=90°,∴△BAM≌△BCP(SAS),∴∠ABM=∠CBP,BM=BP,∵∠GOH=45°,BN∥EH,BM∥GF,∴∠MBN=45°,∴∠ABM+∠CBN =45°,∴∠CBP+∠CBN =45°,即∠PBN =45°, ∴△MBN ≌△PBN (SAS ), ∴MN =PN ,设CN =x ,则MN =PN =CN+PC =x+2,DN =4﹣x ,在Rt △DMN 中,由DM 2+DN 2=MN 2可得22+(4﹣x )2=(x+2)2,解得x =43,则EH =BN =3,. 【点评】本题考查正方形背景中的线段和差,线段倍分,求线段长问题,掌握垂线的性质,平行线的性质,全等三角形的性质与判定,勾股定理等知识,引垂线构造全等,转化线段的相等关系,利用平行线,构造中位线与等腰直角三角形,确定倍数关系,利用勾股定理解决线段的长度问题.18.【答案】(1)见解析;(2)见解析;(3)8-.【分析】(1)先证明:ODN NAH ∠=∠, 再证明:DON AOM ≌,可得结论;(2)利用正方形的性质证明:AC BD ⊥, 45CDO ∠=︒, 结合:DON AOM ≌,利用全等三角形的性质证明:45NMO ∠=︒, 可得://,ED MN 结合://EN BD , DH AE ⊥, 从而可得结论;(3)利用正方形的性质先求解AC = 再利用菱形的性质可得:AH 是DN 的垂直平分线,证明4AN AD ==,求解4NC =, 再证明:,CN EN = 利用勾股定理可得答案. 【详解】(1)证明:∵DH ⊥AE , ∴∠DHA =90°, ∴∠NAH +∠ANH =90°,∵∠ODN +∠DNO =90°,∠ANH =∠DNO , ∴∠ODN =∠NAH , 在DON △和AOM 中,ODN HAN DON AOM OD OA ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴DON AOM ≌(AAS ), ∴OM =ON ;(2)证明: 正方形ABCD ,AC BD ∴⊥, 45CDO ∠=︒,由(1)可知,DON AOM ≌, ∴OM =ON ,∴∠NMO =45°=∠CDO , ∴ED ∥NM , ∵EN ∥DM ,∴四边形DENM 是平行四边形, ∵DN ⊥AE ,∴平行四边形DENM 是菱形;(3)∵四边形ABCD 为正方形,AD =4, ∴AC= ∵四边形DENM 是菱形,∴AH 是DN 的垂直平分线, ∴AN =AD =4, ∴NC=4, ∵EN ∥DM ,∴∠ENC =∠DOC =90°, ∵∠ECN =45°,∴EC=8==-【点评】本题考查的是三角形全等的判定与性质,垂直平分线的性质,勾股定理的应用,平行四边形的判定,菱形的判定,正方形的性质,掌握以上知识是解题的关键. 19.【答案】(1)见解析;(2【分析】(1)直接利用旋转的性质得出△AQE ≌△AFE (SAS ),进而得出∠AEQ =∠AEF ,即可得出答案;(2)由全等三角形的性质可得QE =EF ,∠ADF =∠ABQ ,再结合勾股定理得出答案. 【详解】证明:(1)∵将△ADF 绕点A 顺时针旋转90°后,得到△ABQ , ∴QB =DF ,AQ =AF ,∠BAQ =∠DAF , ∵∠EAF =45°, ∴∠DAF +∠BAE =45°, ∴∠QAE =45°, ∴∠QAE =∠FAE , 在△AQE 和△AFE 中,AQ AF QAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩, ∴△AQE ≌△AFE (SAS ), ∴∠AEQ =∠AEF , ∴EA 是∠QED 的平分线;(2)由(1)得△AQE≌△AFE,∴QE=EF,∠ADF=∠ABQ,∵四边形ABCD是正方形,∴∠ADB=∠ABD=45°,∴∠ABQ=45°,∴∠QBE=∠ABQ+∠ABD=90°,在Rt△QBE中,QB2+BE2=QE2,又∵QB=DF,∴EF2=BE2+DF2=1+9=10,∴EF.【点评】本题考查了旋转的性质,全等三角形的判定与性质,勾股定理等知识,证明△AQE≌△AFE是解题关键.20.【答案】(1)见解析;(2)∠AEF=45°;(3)10﹣【分析】(1)过点B作BF∥MN交CD于点F,则四边形MBFN为平行四边形,得出MN=BF,BF ⊥AE,由ASA证得△ABE≌△BCF,得出AE=BF,即可得出结论;(2)连接AQ,过点Q作HI∥AB,分别交AD、BC于点H、I,则四边形ABIH为矩形,得出HI ⊥AD,HI⊥BC,HI=AB=AD,证△DHQ是等腰直角三角形,得HD=HQ,AH=QI,由HL证得Rt △AHQ≌Rt△QIE,得∠AQH=∠QEI,证∠AQE=90°,得△AQE是等腰直角三角形,即可得出结果;(3)延长AG交BC于E,则EG=AG=6,得AE=12,由勾股定理得BE=,则CE=BC﹣BE=10﹣,由折叠的性质即可得出结果.【详解】(1)证明:∵四边形ABCD是正方形,∴∠ABE=∠BCD=90°,AB=BC,AB∥CD,过点B作BF∥MN交CD于点F,如图1所示:∴四边形MBFN 为平行四边形, ∴MN =BF ,BF ⊥AE , ∴∠ABF +∠BAE =90°, ∵∠ABF +∠CBF =90°, ∴∠BAE =∠CBF , 在△ABE 和△BCF 中,90BAE CBF AB BC ABE BCF ︒∠=∠⎧⎪=⎨⎪∠=∠=⎩, ∴△ABE ≌△BCF (ASA ), ∴AE =BF , ∴AE =MN ;(2)解:连接AQ ,过点Q 作HI ∥AB ,分别交AD 、BC 于点H 、I ,如图2所示:∵四边形ABCD 是正方形, ∴四边形ABIH 为矩形,∴HI ⊥AD ,HI ⊥BC ,HI =AB =AD ,∵BD 是正方形ABCD 的对角线, ∴∠BDA =45°,∴△DHQ 是等腰直角三角形, ∴HD =HQ ,AH =QI , ∵MN 是AE 的垂直平分线, ∴AQ =QE ,在Rt △AHQ 和Rt △QIE 中,AQ QEAH QI =⎧⎨=⎩, ∴Rt △AHQ ≌Rt △QIE (HL ), ∴∠AQH =∠QEI , ∴∠AQH +∠EQI =90°, ∴∠AQE =90°,∴△AQE 是等腰直角三角形,∴∠EAQ =∠AEQ =45°,即∠AEF =45°; (3)解:延长AG 交BC 于E ,如图3所示:则EG =AG =6, ∴AE =12,在Rt △ABE 中,BE ==∴CE=BC﹣BE=10﹣,由折叠的性质得:AC'=CE=10﹣,故答案为:10﹣.【点评】本题是四边形综合题,主要考查了正方形的性质、平行四边形的判定与性质、矩形的判定与性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、折叠的性质、垂直平分线的性质、勾股定理、平行线的性质等知识;熟练掌握正方形的性质和折叠的性质是解题的关键.21.【答案】(1)(2,);(2)不变【详解】解:(1)如图1,过A作AD⊥y轴,交y轴于点Dθ=︒,正方形OABC的边长是4∵AD⊥y轴,30∴AD=2,∴A的坐标是(2,(2)P值无变化.证明:延长BA交y轴于E点.(如图2)在△OAE 与△OCN 中90?AOE CON OAE OCN OA OC =⎧⎪==⎨⎪=⎩∠∠∠∠∴△OAE ≌△OCN (AAS ) ∴OE=ON ,AE=CN .在△OME 与△OMN 中45?OE ON MOE MON OM OM =⎧⎪∠=∠=⎨⎪=⎩,∴△OME ≌△OMN (SAS ) ∴MN=ME=AM+AE , ∴MN=AM+CN ,∴P=MN+BN+BM=AM+CN+BN+BM=AB+BC=8.∴在旋转正方形OABC 的过程中,P 值无变化.【点评】此题主要考查了一次函数的综合应用、全等三角形的判定与性质等知识,利用图形旋转的变化规律得出对应边之间关系是解题关键.22.【答案】(1)①BC ⊥CF ;②BC =CF+CD ;(2)BC ⊥CF 成立;BC =CD+CF 不成立,CD =CF+BC ,见解析;(3.【分析】(1)①由题意易得∠BAC =∠DAF =90°,则有∠BAD =∠CAF ,进而可证△DAB ≌△FAC ,然后根据三角形全等的性质可求解;②由△DAB ≌△FAC 可得CF =BD ,然后根据线段的数量关系可求解;(2)由题意易证△DAB ≌△FAC ,则可得∠ACB =∠ABC =45°,进而可得BC ⊥CF ,然后根据线段的数量关系可求解;(3)过A 作AH ⊥BC 于H ,过E 作EM ⊥BD 于M ,EN ⊥CF 于N ,则有DH =CH+CD =3,进而可求四边形CMEN 是矩形,然后可得△ADH ≌△DEM ,则可证△BCG 是等腰直角三角形,最后根据勾股定理可求解.【详解】解:(1)①∵正方形ADEF 中,AD =AF ,∠DAF =90°, ∴∠BAC =∠DAF =90°, ∴∠BAD =∠CAF ,在△DAB 与△FAC 中,AD AFBAD CAF AB AC =⎧⎪∠=∠⎨⎪=⎩,∴△DAB ≌△FAC (SAS ),。
中考数学专题测试-四边形的证明与计算(答案解析)

【考点分析】一、证明两线段相等1.两全等三角形中对应边相等。
2.同一三角形中等角对等边。
3.等腰三角形顶角的平分线或底边的高平分底边。
4.平行四边形的对边或对角线被交点分成的两段相等。
5.直角三角形斜边的中点到三顶点距离相等。
6.线段垂直平分线上任意一点到线段两段距离相等。
7.角平分线上任一点到角的两边距离相等。
8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。
9.同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。
10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。
11.两前项(或两后项)相等的比例式中的两后项(或两前项)相等。
12.两圆的内(外)公切线的长相等。
二、证明两角相等1.两全等三角形的对应角相等。
2.同一三角形中等边对等角。
3.等腰三角形中,底边上的中线(或高)平分顶角。
4.两条平行线的同位角、内错角或平行四边形的对角相等。
5.同角(或等角)的余角(或补角)相等。
6.同圆(或圆)中,等弦(或弧)所对的圆心角相等,圆周角相等,弦切角等于它所夹的弧对的圆周角。
7.圆外一点引圆的两条切线,圆心和这一点的连线平分两条切线的夹角。
8.相似三角形的对应角相等。
9.圆的内接四边形的外角等于内对角。
10.等于同一角的两个角相等三、证明两直线平行1.垂直于同一直线的各直线平行。
2.同位角相等,内错角相等或同旁内角互补的两直线平行。
3.平行四边形的对边平行。
4.三角形的中位线平行于第三边。
5.梯形的中位线平行于两底。
6.平行于同一直线的两直线平行。
7.一条直线截三角形的两边(或延长线)所得的线段对应成比例,则这条直线平行于第三边。
四、证明两直线互相垂直1.等腰三角形的顶角平分线或底边的中线垂直于底边。
2.三角形中一边的中线若等于这边一半,则这一边所对的角是直角。
3.在一个三角形中,若有两个角互余,则第三个角是直角。
4.邻补角的平分线互相垂直。
中考数学压轴题专项训练:四边形的综合(含答案)

2020年数学中考压轴题专项训练:四边形的综合1.如图,四边形ABCD是直角梯形,AD∥BC,AB⊥AD,且AB=AD+BC,E是DC的中点,连结BE并延长交AD的延长线于G.(1)求证:DG=BC;(2)F是AB边上的动点,当F点在什么位置时,FD∥BG;说明理由.(3)在(2)的条件下,连结AE交FD于H,FH与HD长度关系如何?说明理由.(1)证明:∵AD∥BC,∴∠DGE=∠CBE,∠GDE=∠BCE,∵E是DC的中点,即DE=CE,∴△DEG≌△CEB(AAS),∴DG=BC.(2)解:当F运动到AF=AD时,FD∥BG.理由:由(1)知DG=BC,∵AB=AD+BC,AF=AD,∴BF=BC=DG,∴AB=AG,∵∠BAG=90°,∴∠AFD=∠ABG=45°,∴FD∥BG.(3)解:结论:FH=HD.理由:由(1)知GE=BG,又由(2)知△ABG为等腰直角三角形,所以AE⊥BG,∵FD∥BG,∴AE⊥FD,∵△AFD为等腰直角三角形,∴FH=HD.2.如图,在矩形ABCD中,过BD的中点O作EF⊥BD,分别与AB、CD交于点E、F.连接DE、BF.(1)求证:四边形BEDF是菱形;(2)若M是AD中点,联结OM与DE交于点N,AD=OM=4,则ON的长是多少?(1)证明:∵四边形ABCD是矩形,∴AB∥CD,∴∠DFO=∠BEO,∵∠DOF=∠EOB,OD=OB,∴△DOF≌△BOE(AAS),∴DF=BE,∴四边形BEDF是平行四边形,∵EF⊥BD,∴四边形BEDF是菱形.(2)解:∵DM=AM,DO=OB,∴OM∥AB,AB=2OM=8,∴DN=EN,ON=BE,设DE=EB=x,在Rt△ADE中,则有x2=42+(8﹣x)2,解得x=5,∴ON=.3.(1)如图1,四边形EFGH中,FE=EH,∠EFG+∠EHG=180°,点A,B分别在边FG,GH 上,且∠AEB=∠FEH,求证:AB=AF+BH.(2)如图2,四边形EFGH中,FE=EH,点M在边EH上,连接FM,EN平分∠FEH交FM 于点N,∠ENM=α,∠FGH=180°﹣2α,连接GN,HN.①找出图中与NH相等的线段,并加以证明;②求∠NGH的度数(用含α的式子表示).(1)证明:如图1中,延长BH到M,使得HM=FA,连接EM.∵∠F+∠EHG=180°,∠EHG+∠EHM=180°,∴∠F=∠EHM,∵AE=HE,FA=HM,∴△EFA≌△EHM(SAS),∴EA=EM,∠FEA=∠HEM,∵∠EAB=∠FEH,∴∠FEA+∠BEH=∠HEM+∠BEH=∠BEM=∠FEH,∴∠AEB=∠BEM,∵BE=BE,EA=EM,∴△AEB≌△MEB(SAS),∴AB=BM,∵BM=BH+HM=BH+AF,∴AB=AF+BH.(2)解:①如图2中,结论:NH=FN.理由:∵NE平分∠FEH,∴∠FEN=∠HEN,∵EF=EH,EN=EN,∴△ENF≌△ENH(SAS),∴NH=FN.②∵△ENF≌△ENH,∴∠ENF=∠ENH,∵∠ENM=α,∴∠ENF=∠ENH=180°﹣α,∴∠MNH=180°﹣α﹣α=180°﹣2α,∵∠FGH=180°﹣2α,∴∠MNH=∠FGH,∵∠MNH+∠FNH=180°,∴∠FGH+∠FNH=180°,∴F,G,H,N四点共圆,∵NH=NF,∴=,∴∠NGH=∠NGF=∠FGH=90°﹣α.4.如图,已知△ABC中,∠ACB=90°,AC=4,BC=3,点M、N分别是边AC、AB上的动点,连接MN,将△AMN沿MN所在直线翻折,翻折后点A的对应点为A′.(1)如图1,若点A′恰好落在边AB上,且AN=AC,求AM的长;(2)如图2,若点A′恰好落在边BC上,且A′N∥AC.①试判断四边形AMA′N的形状并说明理由;②求AM、MN的长;(3)如图3,设线段NM、BC的延长线交于点P,当且时,求CP的长.解:(1)如图1中,在Rt△ABC中,∵∠C=90°,AC=4,BC=3,∴AB===5,∵∠A=∠A,∠ANM=∠C=90°,∴△ANM∽△ACB,∴=,∴=,∴AM=.(2)①如图2中,∵NA′∥AC,∴∠AMN=∠NMA′,由翻折可知:MA=MA′,∠AMN=∠NMA′,∴∠MNA′=∠A′MN,∴A′N=A′M,∴AM=A′N,∵AM∥A′N,∴四边形AMA′N是平行四边形,∵MA=MA′,∴四边形AMA′N是菱形.②连接AA′交MN于O.设AM=MA′=x,∵MA′∥AB,∴=,∴=,解得x=,∴AM=,∴CM=,∴CA′===,∴AA′===,∵四边形AMA′N是菱形,∴AA′⊥MN,OM=ON,OA=OA′=,∴OM===,∴MN=2OM=.(3)如图3中,作NH⊥BC于H.∵NH∥AC,∴==∴==∴NH=,BH=,∴CH=BC﹣BH=3﹣=,∴AM=AC=,∴CM=AC﹣AM=4﹣=,∵CM∥NH,∴=,∴=,∴PC=1.5.如图,四边形ABCD为平行四边形,AD=1,AB=3,∠DAB=60°,点E为边CD上一动点,过点C作AE的垂线交AE的延长线于点F.(1)求∠D的度数;(2)若点E为CD的中点,求EF的值;(3)当点E在线段CD上运动时,是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.解:(1)如图1中,∵四边形ABCD是平行四边形,∴AB∥CB,∠ADC+∠DAB=180°,∵∠DAB=60°,∴∠ADC=120°.(2)如图1中,作AH⊥CD交CD的延长线于H.在Rt△ADH中,∵∠H=90°,∠ADH=60°,AD=2,∴AH=AD•sin60°=,DH=AD•cos60°=,∵DE=EC=,∴EH=DH+DE=2,∴AE===,∵CF⊥AF,∴∠F=∠H=90°,∵∠AEH=∠CEF,∴△AEH∽△CEF,∴=,∴=,∴EF=.(3)如图2中,作△AFC的外接圆⊙O,作AH⊥CD交CD的郯城县于H,作OK⊥CD于K,交⊙O于M,作FP∥CD交AD的延长线于P,作MN∥CD交AD的延长线于M,作NQ⊥CD于Q.∵DE∥PF,∴=,∵AD是定值,∴PA定值最大时,定值最大,观察图象可知,当点F与点M重合时,PA定值最大,最大值=AN的长,由(2)可知,AH=,CH=,∠H=90°,∴AC===,∴OM=AC=,∵OK∥AH,AO=OC,∴KH=KC,∴OK==,∴MK=NQ=﹣,在Rt△NDQ中,DN===﹣,∴AN=AD+DN=+,∴的最大值==+.6.如图,在边长为2的正方形ABCD中,点P是射线BC上一动点(点P不与点B重合),连接AP、DP,点E是线段AP上一点,且∠ADE=∠APD,连接BE.(1)求证:AD2=AE•AP;(2)求证BE⊥AP;(3)直接写出的最小值.(1)证明:∵∠DAE=∠PAD,∠ADE=∠APD,∴△ADE∽△APD,∴=,∴AD2=AE•AP(2)证明:∵四边形ABCD是正方形,∴AD=AB,∠ABC=90°,∴AB2=AE•AP,∴=,∵∠BAE=∠PAB,∴△ABE∽△APB,∴∠AEB=∠ABP=90°,∴BE⊥AP.(3)∵△ADE∽△APD,∴=,∴=,∵AD=2,∴DE最小时,的值最小,如图,作△ABE的外接圆⊙O,连接OD,OE,易知OE=1,OD=,∴DE≥OD﹣OE=﹣1,∴DE的最小值为﹣1,∴的最小值=.7.在正方形ABCD中,点E是BC边上一点,连接AE.(1)如图1,点F为AE的中点,连接CF.已知tan∠FBE=,BF=5,求CF的长;(2)如图2,过点E作AE的垂线交CD于点G,交AB的延长线于点H,点O为对角线AC 的中点,连接GO并延长交AB于点M,求证:AM+BH=BE.解:(1)Rt△ABE中,BF为中线,BF=5,∴AE=10,FE=5,作FP⊥BC于点P,Rt△BFP中,,∴BP=3,FP=4,在等腰三角形△BFE中,BE=2BP=6,由勾股定理求得,∴CP=8﹣3=5,∴;(2)∵∠ACD=∠BAC=45°,AO=CO,∠AOM=∠COG,∴证明△AMO≌△CGO(ASA),∴AM=GC,过G作GP垂直AB于点P,得矩形BCGP,∴CG=PB,∵AB=PG,∠AEB=∠H,∠ABE=∠GPH,∴△ABE≌△GPH(ASA),∴BE=PH=PB+BH=CG+BH=AM+BH.8.阅读理解:如图1,若一个四边形的两条对角线互相垂直,则称这个四边形为垂美四边形.(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;(2)性质探究:如图1,试在垂美四边形ABCD中探究AB2,CD2,AD2,BC2之间的关系,并说明理由;(3)解决问题:如图3,分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE,连结CE、BG、GE、CE交BG于点N,交AB于点M.已知AC=,AB=2,求GE的长.解:(1)如图2,四边形ABCD是垂美四边形;理由如下:连接AC、BD交于点E,∵AB=AD,∴点A在线段BD的垂直平分线上,∵CB=CD,∴点C在线段BD的垂直平分线上,∴直线AC是线段BD的垂直平分线,∴AC⊥BD,即四边形ABCD是垂美四边形;(2)猜想结论:AB2+CD2=AD2+BC2,证明:如图1,在四边形ABCD中,∵AC⊥BD,∴∠AOD=∠AOB=∠BOC=∠COD=90°,由勾股定理得:AB2+CD2=AO2+BO2+OD2+OC2AD2+BC2=AO2+BO2+OD2+OC2∴AB2+CD2=AD2+BC2,(3)如图3,连接CG,BE,∵∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB和△CAE中,FMNG图 3EDCAB∴△GAB≌△CAE(SSS),∴∠ABG=∠AEC,∵∠AEC+∠AME=90°,∴∠ABG+∠BMN=90°,∴∠BNC=90°,即BG⊥CE,∴四边形CGEB是垂美四边形,由(2)得:EG2+BC2=CG2+BE2∵,AB=2,∴BC=1,,,∴EG2=CG2+BE2﹣BC2=6+8﹣2=13,∴.9.已知:如图,长方形ABCD中,∠A=∠B=∠B=∠D=90°,AB=CD=4米,AD=BC=8米,点M是BC边的中点,点P从点A出发,以1米/秒的速度沿AB方向运动再过点B沿BM方向运动,到点M停止运动,点O以同样的速度同时从点D出发沿着DA方向运动,到点A停止运动,设点P运动的时间为x秒.(1)当x=2秒时,线段AQ的长是 6 米;(2)当点P在线段AB上运动时,图中阴影部分的面积发生改变吗?请你作出判断并说明理由.(3)在点P,Q的运动过程中,是否存在某一时刻,使得BP=DQ?若存在,求出点P 的运动时间x的值;若不存在,请说明理由.解:(1)∵四边形ABCD是矩形,∴AD=BC=8,∵DQ=2,∴AQ=AD﹣DQ=8﹣2=6,故答案为6.(2)结论:阴影部分的面积不会发生改变.理由:连结AM,作MH⊥AD于H.则四边形ABMH是矩形,MH=AB=4.∵S阴=S△APM+S△AQM=×x×4+(8﹣x)×4=16,∴阴影面积不变;(3)当点P在线段AB上时,BP=4﹣x,DQ=x.∵BP=DQ,∴4﹣x=x,∴x=3.当点P在线段BM上时,BP=x﹣4,DQ=x.∵BP=DQ,∴x﹣4=x,∴x=6.所以当x=3或6时,BP=DQ.10.A,B,C,D是长方形纸片的四个顶点,点E、F、H分别是边AB、BC、AD上的三点,连结EF、FH.(1)将长方形纸片ABCD按图①所示的方式折叠,FE、FH为折痕,点B、C、D折叠后的对应点分别为B'、C'、D',点B'在FC'上,则∠EFH的度数为90°;(2)将长方形纸片ABCD按图②所示的方式折叠,FE、FH为折痕,点B、C、D折叠后的对应点分别为B'、C'、D',若∠B'FC'=18°,求∠EFH的度数;(3)将长方形纸片ABCD按图③所示的方式折叠,FE、FH为折痕,点B、C、D折叠后的对应点分别为B'、C'、D',若∠EFH=m°,求∠B'FC'的度数为180°﹣2m°.解:(1)∵沿EF,FH折叠,∴∠BFE=∠B'FE,∠CFH=∠C'FH,∵点B′在FC′上,∴∠EFH=(∠BFB'+∠CFC')=×180°=90°,故答案为:90°;(2)∵沿EF,FH折叠,∴可设∠BFE=∠B'FE=x,∠C'FH=∠CFH=y,∵2x+18°+2y=180°,∴x+y=81°,∴∠EFH=x+18°+y=99°;(3)∵沿EF,FH折叠,∴可设∠BFE=∠B'FE=x,∠C'FH=∠CFH=y,∴∠EFH=180°﹣∠BFE﹣∠CFH=180°﹣(x+y),即x+y=180°﹣m°,又∵∠EFH=∠EFB'﹣∠B'FC'+∠C'FH=x﹣∠B'FC'+y,∴∠B'FC'=(x+y)﹣∠EFH=180°﹣m°﹣m°=180°﹣2m°,故答案为:180°﹣2m°.11.勾股定理是数学史上非常重要的一个定理.早在2000多年以前,人们就开始对它进行研究,至今已有几百种证明方法.在欧几里得编的《原本》中证明勾股定理的方法如下,请同学们仔细阅读并解答相关问题:如图,分别以Rt△ABC的三边为边长,向外作正方形ABDE、BCFG、ACHI.(1)连接BI、CE,求证:△ABI≌△AEC;(2)过点B作AC的垂线,交AC于点M,交IH于点N.①试说明四边形AMNI与正方形ABDE的面积相等;②请直接写出图中与正方形BCFG的面积相等的四边形.(3)由第(2)题可得:正方形ABDE的面积+正方形BCFG的面积=正方形ACHI的面积,即在Rt△ABC中,AB2+BC2=AC2.(1)证明:∵四边形ABDE、四边形ACHI是正方形,∴AB=AE,AC=AI,∠BAE=∠CAI=90°,∴∠EAC=∠BAI,在△ABI和△AEC中,,∴△ABI≌△AEC(SAS);(2)①证明:∵BM⊥AC,AI⊥AC,∴BM∥AI,∴四边形AMNI的面积=2△ABI的面积,同理:正方形ABDE的面积=2△AEC的面积,又∵△ABI≌△AEC,∴四边形AMNI与正方形ABDE的面积相等.②解:四边形CMNH与正方形BCFG的面积相等,理由如下:∵Rt△ABC中,AB2+BC2=AC2,∴正方形ABDE的面积+正方形BCFG的面积=正方形ACHI的面积,由①得:四边形AMNI与正方形ABDE的面积相等,∴四边形CMNH与正方形BCFG的面积相等;(3)解:由(2)得:正方形ABDE的面积+正方形BCFG的面积=正方形ACHI的面积;即在Rt△ABC中,AB2+BC2=AC2;故答案为:正方形ACHI,AC2.12.在长方形纸片ABCD中,点E是边CD上的一点,将△AED沿AE所在的直线折叠,使点D 落在点F处.(1)如图1,若点F落在对角线AC上,且∠BAC=54°,则∠DAE的度数为18 °.(2)如图2,若点F落在边BC上,且AB=6,AD=10,求CE的长.(3)如图3,若点E是CD的中点,AF的沿长线交BC于点G,且AB=6,AD=10,求CG 的长.解:(1)∵四边形ABCD是矩形,∴∠BAD=90°,∵∠BAC=54°,∴∠DAC=90°﹣54°=36°,由折叠的性质得:∠DAE=∠FAE,∴∠DAE=∠DAC=18°;故答案为:18;(2)∵四边形ABCD是矩形,∴∠B=∠C=90°,BC=AD=10,CD=AB=6,由折叠的性质得:AF=AD=10,EF=ED,∴BF===8,∴CF=BC﹣BF=10﹣8=2,设CE=x,则EF=ED=6﹣x,在Rt△CEF中,由勾股定理得:22+x2=(6﹣x)2,解得:x=,即CE的长为;(3)连接EG,如图3所示:∵点E是CD的中点,∴DE=CE,由折叠的性质得:AF=AD=10,∠AFE=∠D=90°,FE=DE,∴∠EFG=90°=∠C,在Rt△CEG和△FEG中,,∴Rt△CEG≌△FEG(HL),∴CG=FG,设CG=FG=y,则AG=AF+FG=10+y,BG=BC﹣CG=10﹣y,在Rt△ABG中,由勾股定理得:62+(10﹣y)2=(10+y)2,解得:y=,即CG的长为.13.如图,矩形ABCD中,AB=6cm,AD=8cm,点P从点A出发,以每秒一个单位的速度沿A→B→C的方向运动;同时点Q从点B出发,以每秒2个单位的速度沿B→C→D的方向运动,当其中一点到达终点后两点都停止运动.设两点运动的时间为t秒.(1)当t=7 时,两点停止运动;(2)设△BPQ的面积面积为S(平方单位)①求S与t之间的函数关系式;②求t为何值时,△BPQ面积最大,最大面积是多少?解:(1)∵四边形ABCD是矩形,∴AD=BC=8cm,AB=CD=6cm,∴BC+AD=14cm,∴t=14÷2=7,故答案为7.(2)①当0<t<4时,S=•(6﹣t)×2t=﹣t2+6t.当4≤t<6时,S=•(6﹣t)×8=﹣4t+24.当6<t≤7时,S=(t﹣6)•(2t﹣8)=t2﹣10t+24.②当0<t<4时,S=•(6﹣t)×2t=﹣t2+6t=﹣(t﹣3)2+9,∵﹣1<0,∴t=3时,△PBQ的面积最大,最小值为9.当4≤t<6时,S=•(6﹣t)×8=﹣4t+24,∵﹣4<0,∴t=4时,△PBQ的面积最大,最大值为8,当6<t≤7时,S=(t﹣6)•(2t﹣8)=t2﹣10t+24=(t﹣5)2﹣1,t=7时,△PBQ的面积最大,最大值为3,综上所述,t=3时,△PBQ的面积最大,最大值为9.14.综合实践:问题情境数学活动课上,老师和同学们在正方形中利用旋转变换探究线段之间的关系探究过程如下所示:如图1,在正方形ABCD中,点E为边BC的中点.将△DCE以点D为旋转中心,顺时针方向旋转,当点E的对应点E'落在边AB上时,连接CE'.“兴趣小组”发现的结论是:①AE'=C'E';“卓越小组”发现的结论是:②DE=CE',DE⊥CE'.解决问题(1)请你证明“兴趣小组”和“卓越小组”发现的结论;拓展探究证明完“兴趣小组”和“卓越小组”发现的结论后,“智慧小组”提出如下问题:如图2,连接CC',若正方形ABCD的边长为2,求出CC'的长度.(2)请你帮助智慧小组写出线段CC'的长度.(直接写出结论即可)(1)证明:①∵△DE'C'由△DEC旋转得到,∴DC'=DC,∠C'=∠DCE=90°.又∵四边形ABCD是正方形,∴DA=DC,∠A=90°,∴DA=DC',∵DE'=DE',∴Rt△DAE≌Rt△DC'E′(HL),∴AE'=C'E'.②∵点E为BC中点,C'E'=AE'=CE,∴点E'为AB的中点.∴BE′=CE,又∵DC=BC,∠DCE=∠CBE'=90°,∴△DCE≌△CBE'(SAS),∴DE=CE',∠CDE=∠E'CB,∵∠CDE+∠DEC=90°,∴∠E'CB+∠CED=90°,∴DE⊥CE'.(2)解:如图2中,作C′M⊥CD于M,交AB于N.∵AB∥CD,C′M⊥CD,∴C′M⊥AB,∴∠DMC′=∠C′NE′=∠DC′E′=90°,∴∠MDC′+∠DC′M=90°,∠DC′M+∠E′CN=90°,∴∠MDC′=∠E′C′N,∴△DMC′∽△C′NE′,∴===2,设NE′=x,则AM=AN=1+x,C′M=2x,C′N=(1+x),∵MN=AD=2,∴2x+(1+x)=2,解得x=,∴CM=2﹣(1+)=,MC=,∴CC′===.15.在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,且DM=DN.(1)如图甲,若∠C=90°,∠BAC=60°,AC=9,∠MDN=120°,ND∥AB.①写出∠MDA=90 °,AB的长是18 .②求四边形AMDN的周长.(2)如图乙,过D作DF⊥AC于F,先补全图乙再证明AM+AN=2AF.解:(1)①∵AD平分∠BAC,∴∠BAD=∠CAD=∠BAC=30°,∵ND∥AB,∴∠NDA=∠BAD=30°,∴∠MDA=∠MDN﹣∠NDA=120°﹣30°=90°,∵∠C=90°,∠BAC=60°,∴∠ABC=30°,∴AC=AB,∴AB=2AC=18,故答案为:90,18;②∵∠ABC=30°,ND∥AB,∴∠NDC=30°,又∵∠MDN=120°,∴∠MDB=30°,∴∠MAD=∠NAD=∠ADN=∠MBD=30°,∴BM=MD,DN=AN,∵DM=DN,∴BM=MD=DN=AN,在Rt△ADM中,设MD=x,则AM=2x,BM=MD=DN=AN=x,∵AB=18,∴3x=18,∴x=6,∴AM=12,MD=DN=AN=6,∴四边形AMDN的周长=AM+MD+DN+AN=12+6+6+6=30;(2)补全图如图乙所示:证明:过点D作DE⊥AB于E,如图丙所示:∵DE⊥AB,DF⊥AC,AD平分∠BAC,∴∠DEM=∠DFN=90°,DE=DF,在Rt△DEA和Rt△DFA中,,∴Rt△DEA≌Rt△DFA(HL),∴AE=AF,在Rt△DEM和Rt△DFN中,,∴Rt△DEM≌Rt△DFN(HL),∴EM=FN,∴AM+AN=AE+EM+AF﹣NF=2AF.。
2021届中考数学热点题型专练12 四边形【含答案】
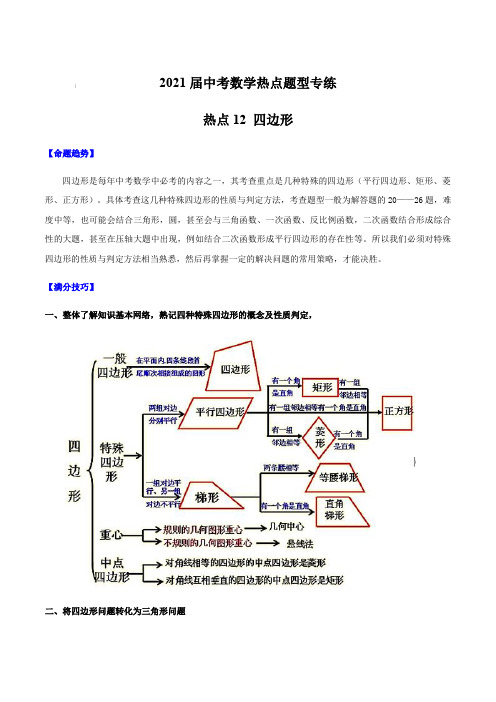
2021届中考数学热点题型专练热点12 四边形【命题趋势】四边形是每年中考数学中必考的内容之一,其考查重点是几种特殊的四边形(平行四边形、矩形、菱形、正方形)。
具体考查这几种特殊四边形的性质与判定方法,考查题型一般为解答题的20——26题,难度中等,也可能会结合三角形,圆,甚至会与三角函数、一次函数、反比例函数,二次函数结合形成综合性的大题,甚至在压轴大题中出现,例如结合二次函数形成平行四边形的存在性等。
所以我们必须对特殊四边形的性质与判定方法相当熟悉,然后再掌握一定的解决问题的常用策略,才能决胜。
【满分技巧】一、整体了解知识基本网络,熟记四种特殊四边形的概念及性质判定,二、将四边形问题转化为三角形问题其实四边形问题的解决最终都会转化到三角形的问题,所以思考问题时一定不能只想着四边形,只要考查四边形的综合题一定会利用到三角形的相关知识,一定要想着将四边形的问题转化成三角形的问题,然后利用三角形的相关知识解决。
三、做一定量的基础练习,培养分析问题和分析图形的能力【限时检测】(建议用时:30分钟)一、选择题1.如图,足球图片正中的黑色正五边形的内角和是()A.180°B.360°C.540°D.720°【答案】C【解析】黑色正五边形的内角和为:(5﹣2)×180°=540°,故选:C2.如图,在ABCD中,全等三角形的对数共有()A.2对B.3对C.4对D.5对【答案】C【解析】四边形ABCD是平行四边形,∴AB=CD,AD=BC,OD=OB,OA=OC∴OD=OB,OA=OC,∴AOD=∴BOC∴∴AOD∴∴COB同理可得∴AOB∴∴COD∴BC=AD,CD=AB,BD=BD∴∴ABD∴∴CDB同理可得∴ACD∴∴CAB因此本题共有4对全等三角形故选:C.3.已知一个多边形的内角和是1080°,则这个多边形是()A.五边形B.六边形C.七边形D.八边形【答案】D【解析】设所求多边形边数为n,则(n﹣2)•180°=1080°,解得n=8.故选:D.4.如图,在正方形ABCD中,点O是对角线AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∴EOF=90°,OC、EF交于点G.给出下列结论:∴∴COE∴∴DOF;∴∴OGE∴∴FGC;∴四边形CEOF的面积为正方形ABCD面积的;∴DF2+BE2=OG•OC.其中正确的是()A .∴∴∴∴B .∴∴∴C .∴∴∴D .∴∴【答案】B【解析】∴∴四边形ABCD 是正方形, ∴OC =OD ,AC ∴BD ,∴ODF =∴OCE =45°, ∴∴MON =90°, ∴∴COM =∴DOF , ∴∴COE ∴∴DOF (ASA ), 故∴正确;∴∴∴EOF =∴ECF =90°, ∴点O 、E 、C 、F 四点共圆, ∴∴EOG =∴CFG ,∴OEG =∴FCG , ∴OGE ∴∴FGC , 故∴正确;∴∴∴COE ∴∴DOF , ∴S ∴COE =S ∴DOF ,∴S 四边形CEOF =S∴OCD=14S 正方形ABCD ,故∴正确;∴)∴∴COE ∴∴DOF , ∴OE =OF ,又∴∴EOF =90°, ∴∴EOF 是等腰直角三角形, ∴∴OEG =∴OCE =45°,∴∴OEG ∴∴OCE , ∴OE :OC =OG :OE , ∴OG •OC =OE 2, ∴OC =12 AC ,OE =EF ,∴OG •AC =EF 2, ∴CE =DF ,BC =CD , ∴BE =CF ,又∴Rt∴CEF 中,CF 2+CE 2=EF 2, ∴BE 2+DF 2=EF 2, ∴OG •AC =BE 2+DF 2, 故∴错误, 故选:B .5.如图,在平行四边形ABCD 中,M 、N 是BD 上两点,BM =DN ,连接AM 、MC 、CN 、NA ,添加一个条件,使四边形AMCN 是矩形,这个条件是( )A .OM =ACB .MB =MOC .BD ∴ACD .∴AMB =∴CND【答案】A【解析】∴四边形ABCD 是平行四边形,∴对角线BD上的两点M、N满足BM=DN,∴OB﹣BM=OD﹣DN,即OM=ON,∴四边形AMCN是平行四边形,∴OM=AC,∴MN=AC,∴四边形AMCN是矩形.故选:A.6.如图,四边形ABCD为菱形,A,B两点的坐标分别是(2,0),(0,1),点C,D在坐标轴上,则菱形ABCD的周长等于()A.B.4C.4D.20【答案】C【解析】∴A,B两点的坐标分别是(2,0),(0,1),∴AB=,∴四边形ABCD是菱形,∴菱形的周长为4,故选:C.7. .一个十二边形的内角和等于()A.2160°B.2080°C.1980°D.1800°【答案】D【解析】十二边形的内角和等于:(12﹣2)•180°=1800°;故选:D.8. .下列命题正确的是()A.有一个角是直角的平行四边形是矩形B.四条边相等的四边形是矩形C.有一组邻边相等的平行四边形是矩形D.对角线相等的四边形是矩形【答案】A【解析】A、有一个角是直角的平行四边形是矩形,是真命题;B、四条边相等的四边形是菱形,是假命题;C、有一组邻边相等的平行四边形是菱形,是假命题;D、对角线相等的平行四边形是矩形,是假命题;故选:A.9. .如图,E是∴ABCD边AD延长线上一点,连接BE,CE,BD,BE交CD于点F.添加以下条件,不能判定四边形BCED为平行四边形的是()A.∴ABD=∴DCE B.DF=CF C.∴AEB=∴BCD D.∴AEC=∴CBD【答案】C【解析】∴四边形ABCD是平行四边形,∴AD∴BC,AB∴CD,∴DE∴BC,∴ABD=∴CDB,∴∴ABD=∴DCE,∴∴DCE=∴CDB,∴BD∴CE,∴BCED为平行四边形,故A正确;∴DE∴BC,∴∴DEF=∴CBF,在∴DEF与∴CBF中,,∴∴DEF∴∴CBF(AAS),∴EF=BF,∴DF=CF,∴四边形BCED为平行四边形,故B正确;∴AE∴BC,∴∴AEB=∴CBF,∴∴AEB=∴BCD,∴∴CBF=∴BCD,∴CF=BF,同理,EF=DF,∴不能判定四边形BCED为平行四边形;故C错误;∴AE∴BC,∴∴DEC+∴BCE=∴EDB+∴DBC=180°,∴∴AEC=∴CBD,∴∴BDE=∴BCE,∴四边形BCED为平行四边形,故D正确,故选:C.10..菱形不具备的性质是()A.是轴对称图形B.是中心对称图形C.对角线互相垂直D.对角线一定相等【答案】D【解析】A、是轴对称图形,故正确;B、是中心对称图形,故正确;C、对角线互相垂直,故正确;D、对角线不一定相等,故不正确;故选:D.11..如图,菱形ABCD周长为20,对角线AC、BD相交于点O,E是CD的中点,则OE的长是()A .2.5B .3C .4D .5【答案】A【解析】∴四边形ABCD 为菱形, ∴CD =BC ==5,且O 为BD 的中点,∴E 为CD 的中点, ∴OE 为∴BCD 的中位线, ∴OE =CB =2.5,故选:A .12. .如图,在正方形ABCD 中,E 是BC 边上的一点,4BE =,8EC =,将正方形边AB 沿AE 折叠到AF ,延长EF 交DC 于G ,连接AC ,现在有如下4个结论: ∴45EAC ∠=︒;∴FG FC =;∴//FC AG ;∴14GFC S ∆=. 其中正确结论的个数是( )A .1B .2C .3D .4【答案】B【解析】如图,连接DF .四边形ABC 都是正方形,AB AD BC CD ∴===,90ABE BAD ADG ECG ∠=∠=∠=∠=︒,由翻折可知:AB AF =,90ABE AFE AFG ∠=∠=∠=︒,2BE EF ==,BAE EAF ∠=∠, 90AFG ADG ∠=∠=︒,AG AG =,AD AF =, Rt AGD Rt ∴∆≅∴()AGF HL ∆,DG FG ∴=,GAF GAD ∠=∠,设GD GF x ==,1()452EAG EAF GAF BAF DAF ∴∠=∠+∠=∠+∠=︒,故∴正确,在Rt ECG ∆中,222EG EC CG =+,222(2)8(12)x x ∴+=+-, 6x ∴=,12CD BC BE EC ==+=, 6DG CG ∴==, FG GC ∴=,易知GFC ∆不是等边三角形,显然FG FC ≠,故∴错误, GF GD GC ==, 90DFC ∴∠=︒, CF DF ∴⊥,AD AF =,GD GF =,AG DF ∴⊥,//CF AG ∴,故∴正确,168242ECG S ∆=⨯⨯=,:6:43:2FG FE ==,:3:5FG EG ∴=,3722455GFC S ∆∴=⨯=,故∴错误,故选:B . 二、填空题13.如图,矩形ABCD 中,AC 、BD 交于点O ,M 、N 分别为BC 、OC 的中点.若4MN =,则AC 的长为 .【答案】16【解析】M 、N 分别为BC 、OC 的中点, 28BO MN ∴==.四边形ABCD 是矩形, 216AC BD BO ∴===.故答案为16.14. .如图,该硬币边缘镌刻的正九边形每个内角的度数是 .【答案】140° 【解析】该正九边形内角和=180°×(9﹣2)=1260°, 则每个内角的度数==140°.故答案为:140°.15.如图,正方形纸片ABCD 的边长为12,E 是边CD 上一点,连接AE 、折叠该纸片,使点A 落在AE 上的G 点,并使折痕经过点B ,得到折痕BF ,点F 在AD 上,若DE =5,则GE 的长为 .【答案】4913【解析】∴四边形ABCD 为正方形, ∴AB =AD =12,∴BAD =∴D =90°,由折叠及轴对称的性质可知,∴ABF ∴∴GBF ,BF 垂直平分AG , ∴BF ∴AE ,AH =GH , ∴∴F AH +∴AFH =90°, 又∴∴F AH +∴BAH =90°, ∴∴AFH =∴BAH ,∴∴ABF∴∴DAE(AAS),∴AF=DE=5,在Rt∴ADF中,BF===13,S∴ABF=AB•AF=BF•AH,∴12×5=13AH,∴AH=,∴AG=2AH=,∴AE=BF=13,∴GE=AE﹣AG=13﹣=,故答案为:.16.在平行四边形ABCD中,∴A=30°,AD=4,BD=4,则平行四边形ABCD的面积等于.【答案】16 3【解析】过D作DE∴AB于E,在Rt∴ADE中,∴∴A=30°,AD=4,∴DE=AD=2,AE=AD=6,在Rt∴BDE中,∴BD=4,∴BE===2,∴AB=8,∴平行四边形ABCD的面积=AB•DE=8×2=16 3 ,故答案为:16 3 .17.三个形状大小相同的菱形按如图所示方式摆放,已知∴AOB=∴AOE=90°,菱形的较短对角线长为2cm.若点C落在AH的延长线上,则∴ABE的周长为cm.【答案】12+8 2【解析】如图所示,连接IC,连接CH交OI于K,则A,H,C在同一直线上,CI=2,∴三个菱形全等,∴CO=HO,∴AOH=∴BOC,又∴∴AOB=∴AOH+∴BOH=90°,∴∴COH=∴BOC+∴BOH=90°,即∴COH是等腰直角三角形,∴∴HCO=∴CHO=45°=∴HOG=∴COK,∴∴CKO=90°,即CK∴IO,设CK=OK=x,则CO=IO=x,IK=x﹣x,∴Rt∴CIK中,(x﹣x)2+x2=22,解得x2=2+,又∴S菱形BCOI=IO×CK=IC×BO,∴x2=×2×BO,∴BO=2+2,∴BE=2BO=4+4,AB=AE=BO=4+2,∴∴ABE的周长=4+4+2(4+2)=12+8,故答案为:12+8.三、解答题18.如图1,在正方形ABCD中,点E是AB边上的一个动点(点E与点A,B不重合),连接CE,过点B 作BF CE⊥于点G,交AD于点F.(1)求证:ABF BCE∆≅∆;(2)如图2,当点E运动到AB中点时,连接DG,求证:DC DG=;(3)如图3,在(2)的条件下,过点C作CM DG⊥于点H,分别交AD,BF于点M,N,求MNNH的值.【解析】(1)证明:BF CE ⊥, 90CGB ∴∠=︒, 90GCB CBG ∴∠+∠=,四边形ABCD 是正方形, 90CBE A ∴∠=︒=∠,BC AB =, 90FBA CBG ∴∠+∠=, GCB FBA ∴∠=∠,()ABF BCE ASA ∴∆≅∆;(2)证明:如图2,过点D 作DH CE ⊥于H , 设2AB CD BC a ===, 点E 是AB 的中点, 12EA EB AB a ∴===, 5CE a ∴,在Rt CEB ∆中,根据面积相等,得BG CE CB EB =,25BG ∴=, 2245CG CB BG ∴=-,90DCE BCE ∠+∠=︒,90CBF BCE ∠+∠=︒, DCE CBF ∴∠=∠,CD BC =,90CQD CGB ∠=∠=︒,()CQD BGC AAS ∴∆≅∆,25CQ BG ∴==, 25GQ CG CQ CQ ∴=-=, DQ DQ =,90CQD GQD ∠=∠=︒, ()DGQ CDQ SAS ∴∆≅∆, CD GD ∴=;(3)解:如图3,过点D 作DH CE ⊥于H , 1122CDG S DQ CH DG ∆==, 85CG DQ CH a DG ∴==, 在Rt CHD ∆中,2CD a =, 2265DH CD CH a ∴=-=,90MDH HDC ∠+∠=︒,90HCD HDC ∠+∠=︒, MDH HCD ∴∠=∠, CHD DHM ∴∆∆∽, ∴34DH DH CH HM ==, 910HM a ∴=,在Rt CHG ∆中,45CG =,85CH a =, 2245GH CG CH a ∴-=,90MGH CGH ∠+∠=︒,90HCG CGH ∠+∠=︒,QGH HCG ∴∠=∠, QGH GCH ∴∆∆∽, ∴HN HGHG CH=, 225HG HN a CG ∴==,12MN HM HN a ∴=-=,∴152245aMN NH a ==19.如图,在四边形ABCD 中,AD ∴BC ,延长BC 到E ,使CE =BC ,连接AE 交CD 于点F ,点F 是CD 的中点.求证:(1)∴ADF∴∴ECF.(2)四边形ABCD是平行四边形.【解析】(1)∴AD∴BC,∴∴DAF=∴E,∴点F是CD的中点,∴DF=CF,在∴ADF与∴ECF中,,∴∴ADF∴∴ECF(AAS);(2)∴∴ADF∴∴ECF,∴AD=EC,∴CE=BC,∴AD=BC,∴AD∴BC,∴四边形ABCD是平行四边形.20.如图,在正方形ABCD中,分别过顶点B,D作//BE DF交对角线AC所在直线于E,F点,并分别延长EB,FD到点H,G,使BH DG,连接EG,FH.(1)求证:四边形EHFG是平行四边形;(2)已知:22AB =4EB =,tan 23GEH ∠=EHFG 的周长.【解析】(1)四边形ABCD 是正方形, AB CD ∴=,//AB CD ,DCA BAC ∴∠=∠, //DF BE ,CFD BEA ∴∠=∠,BAC BEA ABE ∠=∠+∠,DCA CFD CDF ∠=∠+∠, ABE CDF ∴∠=∠,在ABE ∆和CDF ∆中,ABE CDF AEB CFD AB CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ABE CDF AAS ∴∆≅∆,BE DF ∴=,BH DG =,BE BH DF DG ∴+=+,即EH GF =,//EH GF ,∴四边形EHFG 是平行四边形;(2)如图,连接BD ,交EF 于O ,四边形ABCD 是正方形,BD AC ∴⊥,90AOB ∴∠=︒, 22AB =2OA OB ∴==,Rt BOE ∆中,4EB =,30OEB ∴∠=︒,∴EO=2 3 ,OD OB =,EOB DOF ∠=∠, //DF EB ,DFC BEA ∴∠=∠,()DOF BOE AAS ∴∆≅∆,23OF OE ∴==43EF ∴= 23FM ∴=,6EM =,过F 作FM EH ⊥于M ,交EH 的延长线于M , ∴EG//FH ,FHM GEH ∴∠=∠,tan tan 23FM GEH FHM HM∠=∠== ∴2323= ∴HM=1,∴EH=EM -HM=6-1=52222(23)113FH FM HM ++ ∴四边形EHFG 的周长222521310213EH FH =+=⨯+=+。
2021年中考数学压轴题专项训练 四边形(含解析)

2021年中考数学压轴题专项训练《四边形》1.如图①,在矩形ABCD中,已知BC=8cm,点G为BC边上一点,满足BG=AB=6cm,动点E以1cm/s的速度沿线段BG从点B移动到点G,连接AE,作EF⊥AE,交线段CD于点F.设点E移动的时间为t(s),CF的长度为y(cm),y与t的函数关系如图②所示.(1)图①中,CG= 2 cm,图②中,m= 2 ;(2)点F能否为线段CD的中点?若可能,求出此时t的值,若不可能,请说明理由;(3)在图①中,连接AF,AG,设AG与EF交于点H,若AG平分△AEF的面积,求此时t 的值.解:(1)∵BC=8cm,BG=AB=6cm,∴CG=2cm,∵EF⊥AE,∴∠AEB+∠FEC=90°,且∠AEB+∠BAE=90°,∴∠BAE=∠FEC,且∠B=∠C=90°,∴△ABE∽△ECF,∴,∵t=6,∴BE=6cm,CE=2cm,∴∴CF=2cm,∴m=2,故答案为:2,2;(2)若点F是CD中点,∴CF=DF=3cm,∵△ABE∽△ECF,∴,∴∴EC2﹣8EC+18=0∵△=64﹣72=﹣8<0,∴点F不可能是CD中点;(3)如图①,过点H作HM⊥BC于点M,∵∠C=90°,HM⊥BC,∴HM∥CD,∴△EHM∽△EFC,∴∵AG平分△AEF的面积,∴EH=FH,∴EM=MC,∵BE=t,EC=8﹣t,∴EM=CM=4﹣t,∴MG=CM﹣CG=2﹣,∵,∴∴CF=∵EM=MC,EH=FH,∴MH=CF=∵AB=BG=6,∴∠AGB=45°,且HM⊥BC,∴∠HGM=∠GHM=45°,∴HM=GM,∴=2﹣,∴t=2或t=12,且t≤6,∴t=2.2.问题提出:(1)如图1,△ABC的边BC在直线n上,过顶点A作直线m∥n,在直线m上任取一点D,连接BD、CD,则△ABC的面积=△DBC的面积.问题探究:(2)如图2,在菱形ABCD和菱形BGFE中,BG=6,∠A=60°,求△DGE的面积;问题解决:(3)如图3,在矩形ABCD中,AB=12,BC=10,在矩形ABCD内(也可以在边上)存在一点P,使得△ABP的面积等于矩形ABCD的面积的,求△ABP周长的最小值.解:问题提出:(1)∵两条平行线间的距离一定,∴△ABC与△DBC同底等高,即△ABC的面积=△DBC的面积,故答案为:=;问题探究:(2)如图2,连接BD,∵四边形ABCD,四边形BGFE是菱形,∴AD∥BC,BC∥EF,AD=AB,BG=BE,∴∠A=∠CBE=60°,∴△ADB是等边三角形,△BGE是等边三角形,∴∠ABD=∠GBE=60°,∴BD∥GE,∴S△DGE=S△BGE=BG2=9;(3)如图3,过点P作PE∥AB,交AD于点E,∵△ABP的面积等于矩形ABCD的面积的,∴×12×AE=×12×10∴AE=8,作点A关于PE的对称点A',连接A'B交PE于点P,此时△ABP周长最小,∴A'E=AE=8,∴AA'=16,∴A'B===20,∴△ABP周长的最小值=AP+AB+PB=A'P+PB+AB=20+12=32.3.(1)方法感悟:如图①,在正方形ABCD中,点E、F分别为DC、BC边上的点,且满足∠EAF=45°,连接EF.将△ADE绕点A顺时针旋转90°得到△ABG,易证△GAF≌△EAF,从而得到结论:DE+BF=EF.根据这个结论,若CD=6,DE=2,求EF的长.(2)方法迁移:如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=∠BAD,试猜想DE,BF,EF之间有何数量关系,证明你的结论.(3)问题拓展:如图③,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD,试探究线段EF、BE、FD之间的数量关系,请直接写出你的猜想(不必说明理由).解:(1)方法感悟:∵将△ADE绕点A顺时针旋转90°得到△ABG,∴GB=DE=2,∵△GAF≌△EAF∴GF=EF,∵CD=6,DE=2∴CE=4,∵EF2=CF2+CE2,∴EF2=(8﹣EF)2+16,∴EF=5;(2)方法迁移:DE+BF=EF,理由如下:如图②,将△ADE绕点A顺时针旋转90°得到△ABH,由旋转可得,AH=AE,BH=DE,∠1=∠2,∠D=∠ABH,∵∠EAF=∠DAB,∴∠HAF=∠1+∠3=∠2+∠3=∠BAD,∴∠HAF=∠EAF,∵∠ABH+∠ABF=∠D+∠ABF=180°,∴点H、B、F三点共线,在△AEF和△AHF中,∴△AEF≌△AHF(SAS),∴EF=HF,∵HF=BH+BF,∴EF=DE+BF.(3)问题拓展:EF=BF﹣FD,理由如下:在BC上截取BH=DF,∵∠B+∠ADC=180°,∠ADC+∠ADF=180°,∴∠B=∠ADF,且AB=AD,BH=DF,∴△ABH≌△ADF(SAS)∴∠BAH=∠DAF,AH=AD,∵∠EAF=∠BAD,∴∠DAE+∠BAH=∠BAD,∴∠HAE=∠BAD=∠EAF,且AE=AE,AH=AD,∴△HAE≌△FAE(SAS)∴HE=EF,∴EF=HE=BE﹣BH=BE﹣DF.4.如图1,在▱ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当△PNM停止平移时,点Q也停止移动,如图2,设移动时间为t(s)(0<<4),连结PQ,MQ,解答下列问题:(1)当t为何值时,PQ∥MN?(2)当t为何值时,∠CPQ=45°?(3)当t为何值时,PQ⊥MQ?解:(1)∵AB=3cm,BC=5cm,AC⊥AB,∴AC==4cm,∵MN∥AB,PQ∥MN,∴PQ∥AB,∴,∴,∴t=s(2)如图2,过点Q作QE⊥AC,则QE∥AB,∴,∴,∴CE=,QE=t,∵∠CPQ=45°,∴PE=QE=t,∴t+t+t=4,∴t=s(3)如图2,过点P作PF⊥BC于F点,过点M作MH⊥BC,交BC延长线于点H,∴四边形PMHF是矩形,∴PM=FH=5,∵∠A=∠PFC=90°,∠ACB=∠PCF,∴△ABC∽△FPC,∴,∴=∴PF=,CF=,∴QH=5﹣FQ=5﹣(CF﹣CQ)=,∵PQ⊥MQ,∴∠PQF+∠MQH=90°,且∠PQF+∠FPQ=90°,∴∠FPQ=∠MQH,且∠PFQ=∠H=90°,∴△PFQ∽△QHM,∴,∴∴t=s.5.问题背景:如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得四边形EFGH是正方形.类比探究:如图2,在正△ABC的内部,作∠1=∠2=∠3,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合).(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;(2)△DEF是否为正三角形?请说明理由;(3)如图3,进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.(1)△ABD≌△BCE≌△CAF;理由如下:∵△ABC是正三角形,∴∠CAB=∠ABC=∠BCA=60°,AB=BC=AC,又∵∠1=∠2=∠3,∴∠ABD=∠BCE=∠CAF,在△ABD、△BCE和△CAF中,,∴△ABD≌△BCE≌△CAF(ASA);(2)△DEF是正三角形;理由如下:∵△ABD≌△BCE≌△CAF,∴∠ADB=∠BEC=∠CFA,∴∠FDE=∠DEF=∠EFD,∴△DEF是正三角形;(3)c2=a2+ab+b2.作AG⊥BD于G,如图所示:∵△DEF是正三角形,∴∠ADG=60°,在Rt△ADG中,DG=b,AG=b,在Rt△ABG中,c2=(a+b)2+(b)2,∴c2=a2+ab+b2.6.如图,在四边形ABCD中,AC是对角线,∠ABC=∠CDA=90°,BC=CD,延长BC交AD 的延长线于点E.(1)求证:AB=AD;(2)若AE=BE+DE,求∠BAC的值;(3)过点E作ME∥AB,交AC的延长线于点M,过点M作MP⊥DC,交DC的延长线于点P,连接PB.设PB=a,点O是直线AE上的动点,当MO+PO的值最小时,点O与点E是否可能重合?若可能,请说明理由并求此时MO+PO的值(用含a的式子表示);若不可能,请说明理由.(1)证明:∵∠ABC=∠CDA=90°,∵BC=CD,AC=AC,∴Rt△ABC≌Rt△ADC(HL).∴AB=AD.(2)解:∵AE=BE+DE,又∵AE=AD+DE,∴AD=BE.∵AB=AD,∴AB=BE.∴∠BAD=∠BEA.∵∠ABC=90°,∴∠BAD═45°.∵由(1)得△ABC≌△ADC,∴∠BAC=∠DAC.∴∠BAC═22.5°.(3)解:当MO+PO的值最小时,点O与点E可以重合,理由如下:∵ME∥AB,∴∠ABC=∠MEC=90°,∠MAB=∠EMA.∵MP⊥DC,∴∠MPC=90°.∴∠MPC=∠ADC=90°.∴PM∥AD.∴∠EAM=∠PMA.由(1)得,Rt△ABC≌Rt△ADC,∴∠EAC=∠MAB,∴∠EMA=∠AMP.即MC平分∠PME.又∵MP⊥CP,ME⊥CE,∴PC=EC.如图,连接PB,连接PE,延长ME交PD的延长线于点Q.设∠EAM=α,则∠MAP=α.在Rt△ABE中,∠BEA=90°﹣2α.在Rt△CDE中,∠ECD=90°﹣∠BEA=2α.∵PC=EC,∴∠PEB=∠EPC=∠ECD=α.∴∠PED=∠BEA+∠PEB=90°﹣α.∵ME∥AB,∴∠QED=∠BAD=2α.当∠PED=∠QED时,∵∠PDE=∠QDE,DE=DE,∴△PDE≌△QDE(ASA).∴PD=DQ.即点P与点Q关于直线AE成轴对称,也即点M、点E、点P关于直线AE的对称点Q,这三点共线,也即MO+PO的值最小时,点O与点E重合.因为当∠PED=∠QED时,90°﹣α=2α,也即α=30°.所以,当∠ABD=60°时,MO+PO取最小值时的点O与点E重合.此时MO+PO的最小值即为ME+PE.∵PC=EC,∠PCB=∠ECD,CB=CD,∴△PCB≌△ECD(SAS).∴∠CBP=∠CDE=90°.∴∠CBP+∠ABC=180°.∴A,B,P三点共线.当∠ABD=60°时,在△PEA中,∠PAE=∠PEA=60°.∴∠EPA=60°.∴△PEA为等边三角形.∵EB⊥AP,∴AP=2AB=2a.∴EP=AE=2a.∵∠EMA=∠EAM=30°,∴EM=AE=2a.∴MO+PO的最小值为4a.7.已知:如图,在正方形ABCD中,点E在AD边上运动,从点A出发向点D运动,到达D 点停止运动.作射线CE,并将射线CE绕着点C逆时针旋转45°,旋转后的射线与AB边交于点F,连接EF.(1)依题意补全图形;(2)猜想线段DE,EF,BF的数量关系并证明;(3)过点C作CG⊥EF,垂足为点G,若正方形ABCD的边长是4,请直接写出点G运动的路线长.解:(1)补全图形如图1所示:(2)线段DE,EF,BF的数量关系为:EF=DE+BF.理由如下:延长AD到点H,使DH=BF,连接CH,如图2所示:∵四边形ABCD是正方形,∴∠BCD=∠ADC=∠B=90°,BC=DC,∴∠CDH=90°=∠B,在△CDH和△CBF中,,∴△CDH≌△CBF(SAS).∴CH=CF,∠DCH=∠BCF.∵∠ECF=45°,∴∠ECH=∠ECD+∠DCH=∠ECD+∠BCF=45°.∴∠ECH=∠ECF=45°.在△ECH和△ECF中,,∴△EC H≌△ECF(SAS).∴EH=EF.∵EH=DE+DH,∴EF=DE+BF;(3)由(2)得:△ECH≌△ECF(SAS),∴∠CEH=∠CEF,∵CD⊥AD,CG⊥EF,∴CD=CG=4,∴点G的运动轨迹是以C为圆心4为半径的弧DB,∴点G运动的路线长==2π.8.如图,在正方形ABCD中,P是边BC上的一动点(不与点B,C重合),点B关于直线AP的对称点为E,连接AE.连接DE并延长交射线AP于点F,连接BF.(1)若∠BAP=α,直接写出∠ADF的大小(用含α的式子表示);(2)求证:BF⊥DF;(3)连接CF,用等式表示线段AF,BF,CF之间的数量关系,并证明.(1)解:由轴对称的性质得:∠EAP=∠BAP=α,AE=AB,∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∴∠DAE=90°﹣2α,AD=AE,∴∠ADF=∠AED=(180°﹣∠DAE)=(90°+2α)=45°+α;(2)证明:∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∵点E与点B关于直线AP对称,∴∠AEF=∠ABF,AE=AB.∴AE=AD.∴∠ADE=∠AED.∵∠AED+∠AEF=180°,∴在四边形ABFD中,∠ADE+∠ABF=180°,∴∠BFD+∠BAD=180°,∴∠BFD=90°∴BF⊥DF;(3)解:线段AF,BF,CF之间的数量关系为AF=BF+CF,理由如下:过点B作BM⊥BF交AF于点M,如图所示:∵四边形ABCD是正方形,∴AB=CB,∠ABC=90°,∴∠ABM=∠CBF,∵点E与点B关于直线AP对称,∠BFD=90°,∴∠MFB=∠MFE=45°,∴△BMF是等腰直角三角形,∴BM=BF,FM=BF,在△AMB和△CFB中,,∴△AMB≌△CFB(SAS),∴AM=CF,∵AF=FM+AM,∴AF=BF+CF.9.如图1,已知等腰Rt△ABC中,E为边AC上一点,过E点作EF⊥AB于F点,以为边作正方形,且AC=3,EF=.(1)如图1,连接CF,求线段CF的长;(2)将等腰Rt△ABC绕点旋转至如图2的位置,连接BE,M点为BE的中点,连接MC,MF,求MC与MF关系.解:(1)如图1,∵△ABC是等腰直角三角形,AC=3,∴AB=3,过点C作CM⊥AB于M,连接CF,∴CM=AM=AB=,∵四边形AGEF是正方形,∴AF=EF=,∴MF=AM﹣AF=﹣,在Rt△CMF中,CF===;(2)CM=FM,CM⊥FM,理由:如图2,过点B作BH∥EF交FM的延长线于H,连接CF,CH,∴∠BHM=∠EFM,∵四边形AGEF是正方形,∴EF=AF∵点M是BE的中点,∴BM=EM,在△BMH和△EMF中,,∴△BMH≌△EMF(AAS),∴MH=MF,BH=EF=AF∵四边形AGEF是正方形,∴∠FAG=90°,EF∥AG,∵BH∥EF,∴BH∥AG,∴∠BAG+∠ABH=180°,∴∠CBH+∠ABC+∠BAC+∠CAG=180°.∵△ABC是等腰直角三角形,∴BC=AC,∠ABC=∠BAC=45°,∴∠CBH+∠CAG=90°,∵∠CAG+∠CAF=90°,∴∠CBH=∠CAF,在△BCH和△ACF中,,∴△BCH≌△ACF(SAS),∴CH=CF,∠BCH=∠ACF,∴∠HCF=∠BCH+∠BCF=∠ACF+∠BCF=90°,∴△FCH是等腰直角三角形,∵MH=MF,∴CM=FM,CM⊥FM;10.如图将正方形ABCD绕点A顺时针旋转角度α(0°<α<90°)得到正方形AB′C′D′.(1)如图1,B′C′与AC交于点M,C′D′与AD所在直线交于点N,若MN∥B′D′,求α;(2)如图2,C′B′与CD交于点Q,延长C′B′与BC交于点P,当α=30°时.①求∠DAQ的度数;②若AB=6,求PQ的长度.解:(1)如图1中,∵MN∥B′D′,∴∠C′MN=∠C′B′D′=45°,∠C′NM=∠C′D′B′=45°,∴∠C′MN=∠C′NM,∴C′M=C′N,∵C′B′=C′D′,'∴MB′=ND′,∵AB′=AD′,∠AB′M=∠AD′N=90°,∴△AB′M≌△AD′N(SAS),∴∠B′AM=∠D′AN,∵∠B′AD′=90°,∠MAN=45°,∴∠B′AM=∠D′AN=22.5°,∵∠BAC=45°,∴∠BAB′=22.5°,∴α=22.5°.(2)①如图2中,∵∠AB′Q=∠ADQ=90°,AQ=AQ,AB′=AD,∴Rt△AQB′≌Rt△AQD(HL),∴∠QAB′=∠QAD,∵∠BAB′=30°,∠BAD=90°,∴∠B′AD=30°,∴∠QAD=∠B′AD=30°.②如图2中,连接AP,在AB上取一点E,使得AE=EP,连接EP.设PB=a.∵∠ABP=∠AB′P=90°,AP=AP,AB=AB′,∴Rt△APB≌Rt△APB′(HL),∴∠BAP=∠PAB′=15°,∵EA=EP,∴∠EAP=∠EPA=15°,∴∠BEP=∠EAP+∠EPA=30°,∴PE=AE=2a,BE=a,∵AB=6,∴2a+a=6,∴a=6(2﹣).∴PB=6(2﹣),∴PC=BC﹣PB=6﹣6(2﹣)=6﹣6,∵∠CPQ+∠BPB′=180°,∠BAB′+∠BPB′=180°,∴∠CPQ=∠BAB′=30°,∴PQ===12﹣4.11.已知,如图1,在边长为2的正方形ABCD中,E是边AB的中点,点F在边AD上,过点A作AG⊥EF,分别交线段CD、EF于点G、H(点G不与线段CD的端点重合).(1)如图2,当G是边CD中点时,求AF的长;(2)设AF=x,四边形FHGD的面积是y,求y关于x的函数关系式,并写出x的取值范围;(3)联结ED,当∠FED=45°时,求AF的长.解:(1)∵E是AB的中点,AB=2,∴AE=AB=1,同理可得DG=1,∵AG⊥EF,∴∠AHF=∠HAF+∠AFH=90°,∵四边形ABCD是正方形,∴∠ADG=90°=∠DAG+∠AGD,∴∠AFH=∠AGD,∵∠EAF=∠ADG=90°,∴△EAF∽△ADG,∴,即,∴AF=;(2)如图1,由(1)知:△EAF∽△ADG,∴,即,∴DG=2x,∵∠HAF=∠DAG,∠AHF=∠ADG=90°,∴∠AHF∽△ADG,∴=,∴=,∴AH==,FH==,∴y=S△ADG﹣S△AFH,=,=2x﹣,如图2,当G与C重合时,∵EF⊥AG,∴∠AHE=90°,∵∠EAH=45°,∴∠AEH=45°,∴AF=AE=1,∴0<x<1;∴y关于x的函数关系式为:y=2x﹣(0<x<1);(3)如图3,过D作DM⊥AG,交BC于M,连接EM,延长EA至N,使AN=CM,连接DN,设CM=a,则AN=a,∵AD=CD,∠NAD=∠DCM=90°,∴△NAD≌△MCD(SAS),∴∠ADN=∠CDM,DN=DM,∵EF⊥AG,DM⊥AG,∴EF∥DM,∴∠EDM=∠FED=45°,∴∠ADE+∠CDM=∠EDM=45°,∴∠NDA+∠ADE=∠NDE=∠EDM,∵ED=ED,∴△NDE≌△MDE(SAS),∴EN=EM=a+1,∵BM=2﹣a,在Rt△EBM中,由勾股定理得:BE2+BM2=EM2,∴12+(2﹣a)2=(a+1)2,a=,∵∠AEF+∠EAG=∠EAG+∠DAG,∴∠AEF=∠DAG=∠CDM,∴tan∠AEF=tan∠CDM,∴,∴,∴AF=.12.如图1,对角线互相垂直的四边形叫做垂美四边形.(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;(2)性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.试证明:AB2+CD2=AD2+BC2;(3)解决问题:如图3,△ACB中,∠ACB=90°,AC⊥AG且AC=AG,AB⊥AE且AE=AB,连结CE、BG、GE.已知AC=4,AB=5,求GE的长.解:(1)四边形ABCD是垂美四边形,理由如下:连接AC,BD,∵AB=AD,∴点A在线段BD的垂直平分线上,∵CB=CD,∴点C在线段BD的垂直平分线上,∴AC是线段BD的垂直平分线,∴四边形ABCD是垂美四边形;(2)∵AC⊥BD,∴∠AOD=∠AOB=∠BOC=∠COD=90°,由勾股定理得,AD2+BC2=AO2+DO2+BO2+CO2,AB2+CD2=AO2+BO2+CO2+DO2,∴AD2+BC2=AB2+CD2;故答案为:AB2+CD2=AD2+BC2;(3)∵∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB和△CAE中,,∴△GAB≌△CAE(SAS),∴∠ABG=∠AEC,又∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,即CE⊥BG,∴四边形CGEB是垂美四边形,由(2)得,CG2+BE2=CB2+GE2,∵AC=4,AB=5,∴BC=3,CG=4,BE=5,∴GE2=CG2+BE2﹣CB2=73,∴GE=.13.如图1,四边形ACEB,连接BC,∠ACB=∠BEC=90°,D在AB上,连接CD,∠ACD=∠ABC,BE=CD.(1)求证:四边形CDBE为矩形;(2)如图2,连接DE,DE交BC于点O,若tan∠A=2,在不添加任何辅助线和字母的情况下,请直接写出图中所有长度与AD的长度相等的线段.(1)证明:∵∠ACB=90°,∴∠A+∠ABC=90°,∵∠ACD=∠ABC,∴∠A+∠ACD=90°,∴∠ADC=90°,∴∠BDC=180°﹣90°=90°=∠BEC,在Rt△BCD和Rt△CBE中,,∴Rt△BCD≌Rt△CBE(HL),∴BD=CE,∵CD=BE,∴四边形CDBE是平行四边形,又∵∠BEC=90°,∴四边形CDBE为矩形;(2)解:图中所有长度与AD的长度相等的线段为AC=OC=OB=OD=OE=AD.理由如下:由(1)得:四边形CDBE为矩形,∠ADC=90°,∴BC=DE,OD=OE,OB=OC,∴OC=OB=OD=OE=BC,∵∠ADC=∠ACB=90°,∴tan∠A=2==,∴CD=2AD,BC=2AC,∴AC===AD,∴DE=BC=2AC,∴OC=OB=OD=OE=BC=AC=AD,∴AC=OC=OB=OD=OE=AD.14.如图在直角坐标系中,四边形ABCO为正方形,A点的坐标为(a,0),D点的坐标为(0,b),且a,b满足(a﹣3)2+|b﹣|=0.(1)求A点和D点的坐标;(2)若∠DAE=∠OAB,请猜想DE,OD和EB的数量关系,说明理由.(3)若∠OAD=30°,以AD为三角形的一边,坐标轴上是否存在点P,使得△PAD为等腰三角形,若存在,直接写出有多少个点P,并写出P点的坐标,选择一种情况证明.解:(1)∵(a﹣3)2+|b﹣|=0,∴a=3,b=,∴D(0,),A(3,0);(2)DE=OD+EB;理由如下:如图1,在CO的延长线上找一点F,使OF=BE,连接AF,在△AOF和△ABE中,,∴△AOF≌△ABE(SAS),∴AF=AE,∠OAF=∠BAE,又∵∠OAB=90°,∠DAE=,∴∠BAE+∠DAO=45°,∴∠DAF=∠OAF+∠DAO=45°,∴∠DAF=∠EAD,在△AFD和△AED中,,∴△AFD≌△AED(SAS),∴DF=DE=OD+EB;(3)有3种情况共6个点:①当DA=DP时,如图2,Rt△ADO中,OD=,OA=3,∴AD===2,∴P1(﹣3,0),P2(0,3),P3(0,﹣);②当AP4=DP4时,如图3,∴∠ADP4=∠DAP4=30°,∴∠OP4D=60°,Rt△ODP4中,∠ODP4=30°,OD=,∴OP4=1,∴P4(1,0);③当AD=AP时,如图4,∴AD=AP5=AP6=2,∴P5(3+2,0),P6(3﹣2,0),综上,点P的坐标为:∴P(﹣3,0)或(0,3)或(0,﹣)或(1,0)或(3+2,0)或(3﹣2,0).证明:P5(3+2,0),∵∠OAD=30°且△ADO是直角三角形,又∵AO=3,DO=,∴DA=2,而P5A=|3+2﹣3|=2,∴P5A=DA,∴△P5AD是等腰三角形.15.已知,在四边形ABCD中,点M、N、P、Q分别为边AB、AD、CD、BC的中点,连接MN、NP、PQ、MQ.(1)如图1,求证:四边形MNPQ为平行四边形;(2)如图2,连接AC,AC分别交MN、PQ于点E、F,连接BD,BD分别交MQ、NP于点G、H,AC与BD交于点O,且AC⊥BD,若tan∠ADB=,在不添加任何辅助线的情况下,请直接写出图2中所有长度等于OD的线段.(1)证明:如图1,连接BD.∵Q,P分别是BC,CD的中点,所以PQ∥BD,PQ=BD.∵M,N分别是AB,AD的中点.∴MN∥BD,MN=BD.∴PQ∥MN,且PQ=MN.∴四边形MNPQ是平行四边形.(2)解:∵四边形MNPQ是平行四边形,AC⊥BD,∴四边形MNPQ是矩形,∴四边形NHOE和四边形EOGM都是矩形,∴NH=OE=MG=AE=,∵tan∠ADB=,∴,∴NH=OE=MG=AE=.即长度等于OD的线段有NH,OE,MG,AE.。
2020年九年级数学中考三轮冲刺复习:《四边形综合训练》(含解析)

中考三轮冲刺复习:《四边形综合训练》1.如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=32,DC=24,AD=42,动点P 从点D出发,沿射线DA的方向以每秒4个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒2个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).(1)设△BPQ的面积为S,求S与t之间的函数关系式;(2)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?(3)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由.解:(1)如图1,过点P作PM⊥BC,垂足为M,则四边形PDCM为矩形.∴PM=DC=24.∵QB=32﹣t,∴S=×24×(32﹣2t)=384﹣24t(0≤t<16);(2)由图可知:CM=PD=4t,CQ=2t.以B、P、Q三点为顶点的三角形是等腰三角形,可以分三种情况:①若PQ=BQ.在Rt△PMQ中,PQ2=4t2+242,由PQ2=BQ2得4t2+242=(32﹣2t)2,解得t=;②若BP=BQ.在Rt△PMB中,BP2=(32﹣4t)2+242.由BP2=BQ2得:(32﹣4t)2+242=(32﹣2t)2即3t2﹣32t+144=0.由于△=﹣704<0,∴3t2﹣32t+144=0无解,∴PB≠BQ.③若PB=PQ.由PB2=PQ2,得4t2+242=(32﹣4t)2+242整理,得3t2﹣64t+256=0.解得t1=,t2=16(舍去)综合上面的讨论可知:当t=秒或t=秒时,以B、P、Q三点为顶点的三角形是等腰三角形.(3)设存在时刻t,使得PQ⊥BD.如图2,过点Q作QE⊥AD于E,垂足为E.∵AD∥BC∴∠BQF=∠EPQ,又∵在△BFQ和△BCD中∠BFQ=∠C=90°,∴∠BQF=∠BDC,∴∠BDC=∠EPQ,又∵∠C=∠PEQ=90°,∴Rt△BDC∽Rt△QPE,∴=,即=,解得t=9.所以,当t=9秒时,PQ⊥BD.2.综合与实践在Rt△ABC中,∠ACB=90°,点D为斜边AB上的动点(不与点A,B重合).(1)操作发现:如图①,当AC=BC=8时,把线段CD绕点C逆时针旋转90°得到线段CE,连接DE,BE.①∠CBE的度数为45°;②当BE=4时,四边形CDBE为正方形;(2)探究证明:如图②,当BC=2AC时,把线段CD绕点C逆时针旋转90°后并延长为原来的两倍,记为线段CE,连接DE,BE.①在点D的运动过程中,请判断∠CBE与∠A的大小关系,并证明;②当CD⊥AB时,求证:四边形CDBE为矩形.解:(1)①∵∠ACB=90°,AC=BC,∴∠A=∠CBA=45°,∵∠ACB=90°,∠DCE=90°,∴∠ACB=∠DCE,∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,即∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS)∴∠CBE=∠A=45°,故答案为:45°;②∵∠ACB=90°,AC=BC=8,∴AB==8,当四边形CDBE为正方形时,CD⊥AB,BE=BD=AD,∴BE=AB=4,故答案为:4;(2)①∠CBE=∠A.理由如下:∵BC=2AC,CE=2CD,∴==,∵∠ACB=∠DCE=90°,∴∠ACD+∠DCB=∠DCB+∠BCE,∴∠ACD=∠BCE,∴△ACD∽△BCE,∴∠CBE=∠A;②证明:∵∠CBE=∠A,∠DBC+∠A=90°,∴∠DBE=∠DBC+∠CBE=∠DBC+∠A=90°,∵CD⊥AB,∴∠CDB=90°,又∵∠DCE=90°,∴四边形CDBE是矩形.3.如图,边长为5的正方形OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合)EF⊥CE,且与正方形外角平分线AG 交于点P.(1)求证:CE=EP(2)若点E坐标为(3、0)时.①在y轴上是否存在点M使得四边形BMEP是平行四边形?若存在,求出点M的坐标;若不存在,说明理由.②在平面内是否存在点Q,使四边形CEPQ为正方形,若存在,请直接写出Q点坐标,若不存在,说明理由.(1)证明:如图1,在OC上截取OK=OE.连接EK,∵OC=OA,∠COA=∠BA0=90°,∠OEK=∠OKE=45°,∵AP为正方形OCBA的外角平分线,∴∠BAP=45°,∴∠EKC=∠PAE=135°,∴CK=EA,∵EC⊥EP,∴∠CEF=∠COE=90°,∴∠CEO+∠KCE=90°,∠CEO+∠PEA=90°,∴∠KCE=∠CEA,在△CKE和△EAP中,,∴△CKE≌△EAP(ASA),∴EC=EP;(2)①解:y轴上存在点M,使得四边形BMEP是平行四边形.如图2,过点B作BM∥PE交y轴于点M,连接BP,EM,则∠CQB=∠CEP=90°,所以∠OCE=∠CBQ,∵在△BCM和△COE中,∵,∴△BCM≌△COE(ASA),∴BM=CE,∵CE=EP,∴BM=EP.∵BM∥EP,∴四边形BMEP是平行四边形,∵△BCM≌△COE,∴CM=OE=3,∴OM=CO﹣CM=2.故点M的坐标为(0,2).②如图3,存在点Q使四边形CEPQ是正方形,过点Q作QH⊥y轴于点Q,则∠QHC=∠COE=90°,∴∠HQC+∠HCQ=90°,∴∠HCQ+∠ECO=90°,∴∠ECO=∠CHQ,∵四边形CEPQ是正方形,∴CQ=EC,∴△HCQ≌△OEC(AAS),∴HC=OE=2,HQ=OC=5,则HO=7,∴点Q的坐标为(5,7).4.如图,正方形ABCD中,E为BC边上任意点,AF平分∠EAD,交CD于点F.(1)如图1,若点F恰好为CD中点,求证:AE=BE+2CE;(2)在(1)的条件下,求的值;(3)如图2,延长AF交BC的延长线于点G,延长AE交DC的延长线于点H,连接HG,当CG=DF时,求证:HG⊥AG.解:(1)如图1,延长BC交AF的延长线于点G,∵AD∥CG,又∵AF平分∠DAE,∴∠DAF=∠EAF,∴∠G=∠EAF,∴EA=EG,∵点F为CD的中点,∴CF=DF,又∵∠DFA=∠CFG,∠FAD=∠G,∴△ADF≌△GCF(AAS),∴AD=CG,∴CG=BC=BE+CE,∴EG=BE+CE+CE=BE=2CE=AE;(2)设CE=a,BE=b,则AE=2a+b,AB=a+b,在Rt△ABE中,AB2+BE2=AE2,即(a+b)2+b2=(2a+b)2,解得b=3a,b=﹣a(舍),∴==;(3)如图2,连接DG,∵CG=DF,DC=DA,∠ADF=∠DCG,∴△ADF≌△DCG(SAS),∴∠CDG=∠DAF,∴∠HAF=∠FDG,又∵∠AFH=∠DFG,∴△AFH∽△DFG,∴=,又∵∠AFD=∠HFG,∴△ADF∽△HGF,∴∠ADF=∠FGH,∵∠ADF=90°,∴∠FGH=90°,∴AG⊥GH.5.已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=60°,将∠MBN绕点B旋转,它的两边分别交边AD、DC(或它们的延长线)于点E、F.(1)当∠MBN绕点B旋转到AE=CF时(如图1),①求证:△ABE≌△CBF;②求证:AE+CF=EF;(2)当∠MBN绕点B旋转到如图2所示的位置时,AE≠CF,此时,(1)中的两个结论是否还成立?请直接回答.(1)①证明;∵AB⊥AD,BC⊥CD,∴∠A=∠BCF=90°,在△ABE和△CBF中,,∴△ABE≌△CBF(SAS);②证明:∵△ABE≌△CBF,∴BE=BF,∠ABE=∠CBF,∵∠MBN=60°,∴△BEF是等边三角形.∠ABE=∠CBF=(∠ABC﹣∠MBN)=(120°﹣60°)=30°.∴BE=BF=EF,AE=BE,CF=BF,∴AE+CF=BE+BF=EF;(2)解:①△ABE≌△CBF不成立;②AE+CF=EF成立,理由如下:∵AE≠CF,∴△ABE≌△CBF不成立延长DC至点K,使CK=AE,连接BK,如图2所示:在△BAE与△BCK中,,∴△BAE≌△BCK(SAS),∴BE=BK,∠ABE=∠CBK,∵∠FBE=60°,∠ABC=120°,∴∠FBC+∠ABE=60°,∴∠FBC+∠CBK=60°,∴∠KBF=∠FBE=60°,在△KBF与△EBF中,,∴△KBF≌△EBF(SAS),∴KF=EF,∴AE+CF=KC+CF=KF=EF.6.已知:如图①,在矩形ABCD中,AB=3,AD=4,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.(1)求AF和BE的长;(2)若将△ABF沿着射线BD方向平移,设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).当点F分别平移到线段AB、AD上时,直接写出相应的m的值.(3)如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的△ABF 为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AD交于点P,与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.解:(1)∵四边形ABCD是矩形,∴∠BAD=90°,在Rt△ABD中,AB=3,AD=4,由勾股定理得:BD===5,=BD•AE=AB•AD,∵S△ABD∴AE===,∵点F是点E关于AB的对称点,∴AF=AE=,BF=BE,∵AE⊥BD,∴∠AEB=90°,在Rt△ABE中,AB=3,AE=,由勾股定理得:BE===.(2)设平移中的三角形为△A′B′F′,如图①﹣1所示:由对称点性质可知,∠1=∠2.BF=BE=,由平移性质可知,AB∥A′B′,∠4=∠1,BF=B′F′=.①当点F′落在AB上时,∵AB∥A′B′,∴∠3=∠4,∴∠3=∠2,∴BB′=B′F′=,即m=;②当点F′落在AD上时,∵AB∥A′B′,∴∠6=∠2,∵∠1=∠2,∠5=∠1,∴∠5=∠6,又易知A′B′⊥AD,∴△B′F′D为等腰三角形,∴B′D=B′F′=,∴BB′=BD﹣B′D=5﹣=,即m=.(3)存在.理由如下:在旋转过程中,等腰△DPQ依次有以下4种情形:①如图③﹣1所示,点Q落在BD延长线上,且PD=DQ,则∠Q=∠DPQ,∴∠2=∠Q+∠DPQ=2∠Q,∵∠1=∠3+∠Q,∠1=∠2,∴∠3=∠Q,∴A′Q=A′B=3,∴F′Q=F′A′+A′Q=+3=.在Rt△BF′Q中,由勾股定理得:BQ===.∴DQ=BQ﹣BD=﹣5;②如图③﹣2所示,点Q落在BD上,且PQ=DQ,则∠2=∠P,∵∠1=∠2,∴∠1=∠P,∴BA′∥PD,则此时点A′落在BC边上.∵∠3=∠2,∴∠3=∠1,∴BQ=A′Q,∴F′Q=F′A′﹣A′Q=4﹣BQ.在Rt△BQF′中,由勾股定理得:BF′2+F′Q2=BQ2,即:()2+(﹣BQ)2=BQ2,解得:BQ=,∴DQ=BD﹣BQ=5﹣=;③如图③﹣3所示,点Q落在BD上,且PD=DQ,则∠3=∠4.∵∠2+∠3+∠4=180°,∠3=∠4,∴∠4=90°﹣∠2.∵∠1=∠2,∴∠4=90°﹣∠1.∴∠A′QB=∠4=90°﹣∠1,∴∠A′BQ=180°﹣∠A′QB﹣∠1=90°﹣∠1,∴∠A′QB=∠A′BQ,∴A′Q=A′B=3,∴F′Q=A′Q﹣A′F′=3﹣=.在Rt△BF′Q中,由勾股定理得:BQ===,∴DQ=BD﹣BQ=5﹣;④如图④﹣4所示,点Q落在BD上,且PQ=PD,则∠2=∠3.∵∠1=∠2,∠3=∠4,∠2=∠3,∴∠1=∠4,∴BQ=BA′=3,∴DQ=BD﹣BQ=5﹣3=2.综上所述,存在4组符合条件的点P、点Q,使△DPQ为等腰三角形;DQ的长度分别为2或或或.7.如图,在Rt△ABD中,∠BAD=90°,AB=5,过点A作AC⊥BD,垂足为C,且AC=4,E是线段CD上一点,过E作EF⊥AD,垂足为F﹒(1)请直接写出AD的长为;(2)如图1,若点F在∠ABD的角平分线上,求DF的长;(3)如图2,连接CF,点G为点A关于CF的对称点.①连结DG,CG,当四边形CGDF中有两边互相平行时,求CE的长;②连结AG交BD于点H,点H在点E的上方,若∠BAC﹣∠EAH=30°,则=.解:(1)∵AC⊥BD,∴∠ACB=90°,∵AB=5,AC=4,∴BC===3,∵∠ABC=∠ABD,∠ACB=∠BAD=90°,∴△BAC∽△BDA,∴==,∴==,∴BD=,AD=.故答案为.(2)如图1中,作FH⊥BD于H.∵∠FAB=∠FHB=90°,∠FBA=∠FBH,BF=BF,∴△FBA≌△FBH(AAS),∴AF=FH,BA=BH=5,∵BD=,∴DH=﹣5=,设AF=FH=x,则DF=﹣x,在Rt△DFH中,∵DF2=DH2+FH2,∴(﹣x)2=()2+x2,∴x=,∴DF=﹣=.(3)①如图2﹣1中,当DG∥CF时,设CF交AG于P.∵A,G关于CF对称,∴CF垂直平分线段CF,∴AP=PG,∠APF=90°,∵PF∥DG,AP=PG,∴AF=DF,∵EF∥AB,∴DE=BE=,∴EC=BE﹣CB=﹣3=.如图2﹣2中,当DF∥CG时,∵CG∥AD,∴∠AFC=∠FCG,∵∠FCG=∠FCA,∴∠AFC=∠ACF,∴AF=AC=4,∵EF∥AB,∴=,∴=,∴BE=5,∴EC=BE﹣BC=5﹣3=2,综上所述,满足条件的EC的值为2或.②如图3中,设CF交AG于P.∵∠ACH=∠APC=90°,∴∠PCH+∠ACP=90°,∠ACP+∠PAC=90°,∴∠PCH=∠PAC,设∠PAC=∠PCH=α,∵∠AFE=90°,∴∠AFE+∠PCE=180°,∴A,F,E,C四点共圆,∴∠FAE=∠ECF=α,设∠CAB=β,∵∠DAB=90°,∴α﹣∠EAG+α+β=90°,∵β﹣∠EAG=30°,∴2α=60°,∴α=30°,设PC=k,则AP=PG=k,PH=k,∴GH=k﹣k=k,AH=k+k=k,∴==.故答案为.8.问题背景:峰兄在探究几何图形的时候,发现了一组非常神奇的性质:如图1,等边三角形△ABC,△CDE中,连接AD,BE可以得到△ACD≌△BCE,好学的他发问取AD,BE的中点,得到的△CMN是特殊三角形吗?请说明理由;迁移应用:如图2,在正方形ABCD中,点O为CB的中点,构造正方形EHMF绕O点进行旋转,OE=OF,连接AH,BE,DM,求的值;联系拓展:如图3,等腰Rt△ABC,△BDE中,AB=AC,BD=DE,∠BDE=∠BAC=90°,当△BDE绕B点旋转的过程中取AD,CE的中点M,N,连接MN,若AB=BD,且∠ABD=30°,BD=1时,直接写出MN的长度.解:问题背景:如图1中,△CMN是等边三角形.理由如下:∵△ACB,△DCE都是等边三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=60°,∴∠ACD=∠BCE,∴△ACD≌△BCE(SAS),∴AD=BE,∠CAD=∠CBE,∵AM=AD,BN=BE,∴AM=AN,∵AC=CB,∴△ACM≌△BCN(SAS),∴CM=CN,∠ACM=∠BCN,∴∠ACB=∠MCN=60°,∴△MCN是等边三角形.迁移应用:如图2中,连接AO,OH.∵四边形ABCD,四边形EFMH是正方形,∴∠ABO=∠HEO=90°,AB=BC,HE=,∵OB=OC,OE=OF,∴AB=2BO,EH=2OE,OA=OB,OH=OE,∴=,∴=,∴△ABO∽△HEO,∴∠AOB=∠HOE,∴∠BOE=∠AOH,∵==,∴△AOH∽△BOE,∴==.联系拓展:如图3中,连接BM,延长BM到K,使得MK=BM,连接DK,AK,BN,作KJ⊥BD交BD的延长线于J.∵AB=BD,BD=1,∴AB=,∵AM=DM,BM=MK,∴四边形ABDK是平行四边形,∴AB=DK=,AB∥DK,∴∠KDJ=∠ABD=30°,∵KJ⊥BJ,∴∠J=90°,∴KJ=DK=,DJ=KJ=,BJ=BD+DJ=1+=,∴BK===,∴BM=MK=BK=,∵△BDE,△ABC都是等腰直角三角形,∴∠ABC=∠DBE=45°,BC=AB,BE=BD,∴=,∠CBE=∠ABD,∴△ABD∽△CBE,∴∠ADB=∠CEB,=,∵AM=DM,EN=CN,∴=,∵∠BDM=∠BEN,∴△BDM∽△BEN,∴∠MBD=∠EBN,==,∴∠MBN=∠DBE=45°,作NM′⊥BK于M′,在Rt△BNM′中,BM′=BN•cos45°=BN,∵BM=BN,∴BM=BM′,∴M与M′重合,∴△BMN是等腰直角三角形,∴MN=BM=.9.如图,在长方形OABC中,O为平面直角坐标系的原点,点A,点C分别在x轴,y轴上,点B坐标为(4,6),点P从点O出发,以每秒2个单位长度的速度沿O→C→B 方向运动,到点B停止设点P运动的时间为t(秒).(1)点A的坐标为(4,0);(2)当t=1秒时,点P的坐标(0,2);(3)当点P在OC上运动,请直接写出点P的坐标(用含有t的式子表示);(4)在移动过程中,当点P到y轴的距离为1个单位长度时,求t的值.解:(1)∵四边形OABC是矩形,∴∠OAB=90°,∵B(4,6),∴AB=6,OA=4,∴A(4,0),故答案为(4,0).(2)t=1时,OP=2×1=2,∴OP=2,此时点P在线段OC上,∴P(0,2),故答案为(0,2).(3)当点P在OC上运动时,P(0,2t).(4)当点P到y轴的距离为1个单位长度时,可知点P在BC上,∴点P的坐标为(2t﹣6,6),∴2t﹣6=1,解得:t=3.5.答:当点P到y轴的距离为1个单位长度时,t的值为3.5.10.在矩形ABCD中,AB=6,AD=8,点E是对角线BD上一动点.(1)如图1,当CE⊥BD时,求DE的长;(2)如图2,作EM⊥EN分别交边BC于M,交边CD于N,连MN.①若,求tan∠ENM;②若E运动到矩形中心O,连CO.当CO将△OMN分成两部分面积比为1:2时,直接写出CN的长.解:(1)∵矩形ABCD中,AB=6,AD=8∴∠BCD=90°,BC=AD=8,CD=AB=6∴BD==10∵CE⊥BD∴∠CED=∠BCD=90°∵∠CDE=∠BDC∴△CDE∽△BDC∴∴DE=(2)①如图1,过点M作MF⊥BD于点F,过点N作NG⊥BD于点G ∵,BD=10∴BD=BE+DE=3DE+DE=4DE=10∴DE=,BE=设MF=a,NG=b∵∠BFM=∠C=90°,∠FBM=∠CBD∴△FBM∽△CBD∴∴BF==a∴EF=BE﹣BF=a同理可证:△GDN∽△CDB∴∴DG==b∴EG=DE﹣DG=b∵EM⊥EN∴∠MEN=∠MFE=∠NGE=90°∴∠MEF+∠NEG=∠MEF+∠EMF=90°∴∠EMF=∠NEG∴∴EF•EG=NG•MF∴(a)(b)=ba整理得:16a=90﹣27b∴在Rt△MEN中,tan∠ENM==②如图2,过点M作MF⊥BD于点F,MP⊥OC于点P,过点N作NG⊥BD于点G,NQ⊥OC 于点Q,设OC与MN交点为H∵点O为矩形中心,BD=10∴OB=OD=OC=BD=5由①可得,设MF=a,NG=b,则BF==a,DG==b,OF•OG=NG•MF ∴OF=OB﹣BF=5﹣a,OG=OD﹣DG=5﹣b∴(5﹣a)(5﹣b)=ab整理得:16a=60﹣9b∴=设CN=5x∵∠NCQ=∠BDC,∠NQC=∠BCD=90°∴△NCQ∽△BDC∴=∴CQ=CN=3x,NQ=CN=4x∴OQ=OC﹣CQ=5﹣3x∵∠MPO=∠MON=∠OQN=90°∴∠MOP+∠NOQ=∠NOQ+∠ONQ=90°∴∠MOP=∠ONQ∴i )若S △OMH =2S △ONH ,且两三角形都以OH 为底∴MP =2NQ =8x ∴解得:x =∴CN = ii )若2S △OMH =S △ONH ,则MP =NQ =2x ∴解得:x =∴CN =综上所述,CN 的长为或.11.如图,菱形ABCD 中,BE ⊥AD ,且BE =,∠ABE =30°,连接BD 、CE ,作DF ⊥CE ,垂足为F . (1)判断△BCD 的形状(直接写出即可);(2)求DF 的长度.(3)若动点P ,Q 同时从点B 出发,在△ABD 边上运动,P 沿B →A →D 路径匀速运动,Q 沿B →D +A 路径匀速运动,当两点相遇时运动停止,已知点P 的运动速度为2单位/秒,点Q 的运动速度为1单位/秒,设运动时间为x 秒,△PBQ 的面积为y ,求当x 为何值时,y取得最大值?最大值为多少?解:(1)∵BE⊥AD,∴∠BEA=90°,∵∠ABE=30°,∴∠A=60°,∵四边形ABCD是菱形,∴AB=AD=BC=CD,∠BCD=∠A=60°,∴△BCD是等边三角形;(2)在Rt△ABE中,∵BE=,∠A=60°,∴AB===4,∵∠ABE=30°,∴AE=AB=×4=2,∵AB=AD,∠A=60°,∴△ABD是等边三角形,∵BE⊥AD,∴DE=AE=2,∵四边形ABCD是菱形,∴AD∥BC,∴S=DE•BE=×2×2=2,△CED∵AD∥BC,BE⊥AD,∴BC⊥BE,在Rt△BCE中,CE===2,∵DF⊥CE,∴S=DF•EC=DF,△CED∴DF=2,∴DF=;(3)∵AB=AD=4,点P的运动速度为2单位/秒,点Q的运动速度为1单位/秒,∴P到达A点时为2s,到达D得时为4s,则Q在BQ上;P到达D时,Q也到达D;①当0<x≤2时,P在BA上运动,Q在BD上运动,过点Q作QG⊥AB于G,如图1所示:则QG=BQ•sin60°=x,∴y=BP•QG=×2x×x=x2,∴x=2时,y有最大值,最大值为2;②2≤x<4时,P在AD上运动,Q在BD上运动,过点P作PH⊥BD于H,如图2所示:∵DP=8﹣2x,∴PH=DP•sin60°=(8﹣2x)=4﹣x,∴y=PH•BQ=(4﹣x)x=﹣x2+2x=﹣(x2﹣4x)=﹣(x﹣2)2+2,∴当x=2时,y取最大值,最大值为2;综上所述,当x=2时,y有最大值,最大值为2.12.如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交于y轴于点H.(1)连接BM,动点P从点A出发,沿折线ABC方向以1个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);(2)在(1)的情况下,当点P在线段AB上运动时,是否存在以BM为腰的等腰三角形BMP?如存在,求出t的值;如不存在,请说明理由.解:(1)设点M到BC的距离为h,由S△ABC =S△ABM+S△BCM,即×5×4=×5×+×5h,∴h=,①当P在直线AB上运动时△PBM的面积为S与P的运动时间为t秒关系为:S=(5﹣t)×,即S=﹣t+(0≤t<5);②当P运动到直线BC上时△PMB的面积为S与P的运动时间为t秒关系为:S=[5﹣(10﹣t)]×,即S=t﹣(5<t≤10);(2)存在①当MB=MP时,∵点A的坐标为(﹣3,4),AB=5,MB=MP,MH⊥AB,∴PH=BH,即3﹣t=2,∴t=1;②当BM=BP时,即5﹣t=,综上所述,当t=1或时,△PMB为以BM为腰的等腰三角形.13.如图,以矩形OABC的顶点O为坐标原点,OA所在直线为x轴,OC所在直线为y轴建立平面直角坐标系.已知,OA=2,OC=4,点D为x轴上一动点,以BD为一边在BD右侧作正方形BDEF.(1)若点D与点A重合,请直接写出点E的坐标;(2)若点D在OA的延长线上,且EA=EB,求点E的坐标;(3)若OE=2,求点E的坐标.解:(1)当点D与点A重合时,如图1,∴BD=OC=4,∵四边形BDFE是正方形,∴BD=DE=4,∠BDE=90°,∵OA=2,∴OE=OA+AE=2+4=6,∴E(6,0);(2)如图2,过E作EG⊥AB于G,作EH⊥x轴于H,∵EB=EA,∴AG=BG=2,∵∠AGC=∠GAH=∠AHE=90°,∴四边形AGEH是矩形,∴EH=AG=2,∵四边形BDEF是正方形,∴BD=DE,∠BDE=90°,∴∠ADB+∠EDH=∠ADB+∠ABD=90°,∴∠EDH=∠ABD,∵∠BAD=∠DHE=90°,∴△BAD≌△DHE(ASA),∴DH=AB=4,AD=EH=2,∴OH=8,∴E(8,2);(3)分两种情况:①D在点A的右侧时,如图3,过E作EH⊥x轴于H,由(2)知:△BAD≌△DHE,∴DH=AB=4,AD=EH,设AD=x,则EH=x,OH=2+4+x=6+x,在Rt△OEH中,由勾股定理得:OE2=OH2+EH2,∴,解得:x=2或﹣8(舍),∴E(8,2);②D在点A的左侧时,如图4,过E作EH⊥x轴于H,由(2)知:△BAD≌△DHE,∴DH=AB=4,AD=EH,设AD=x,则EH=x,OH=x﹣2﹣4=x﹣6,在Rt△OEH中,由勾股定理得:OE2=OH2+EH2,∴=x2+(x﹣6)2,解得:x=﹣2或8(舍),∴OH=﹣2﹣6=﹣8,∴E(﹣2,﹣8);综上,点E的坐标是(8,2)或(﹣2,﹣8).14.如图,已知点B(a,b),且a,b满足|2a+b﹣13|+=0.过点B分别作BA⊥x 轴、BC⊥y轴,垂足分别是点A、C.(1)求出点B的坐标;(2)点M是边OA上的一个动点(不与点A重合),∠CMA的角平分线交射线CB于点N,在点M运动过程中,的值是否变化?若不变,求出其值;若变化,说明理由;(3)在四边形OABC的边上是否存在点P,使得BP将四边形OABC分成面积比为1:4的两部分?若存在,请直接写出点P的坐标;若不存在,说明理由.解:(1)∵|2a+b﹣13|+=0.∴,∴,∴B(5,3);(2)的值不变,其值为1,理由:∵BC⊥y轴,∴BC∥x轴,∴∠CNM=∠AMN,∵MN是∠CMA的平分线,∴∠CMN=∠AMN,∴∠CNM=∠CMN,∴=1;(3)由(1)知,B(5,3),∵BA⊥x轴、BC⊥y,∴A(5,0),C(0,3),∵BA⊥x轴、BC⊥y,∴∠OCB=∠OAB=90°=∠AOC,∴四边形AOBC是矩形,∴AB=OC=3,BC=OA=5,∴S四边形OABC=OA•OC=15,当点P在OC上时,设P(0,m),∴CP=3﹣m,∴S△BPC=BC•CP=×5(3﹣m)=(3﹣m),∵BP将四边形OABC分成面积比为1:4的两部分,∴S△BPC =S四边形OABC=3,∴(3﹣m)=3,∴m=,∴P(0,)当点P在OA上时,设P(0,n),∴AP=5﹣n,∴S△BPC=AB•AP=×3(5﹣n)=(5﹣n),∵BP将四边形OABC分成面积比为1:4的两部分,∴S△BPA =S四边形OABC=3,∴(5﹣n)=3,∴n=3,∴P(3,0),即:满足条件的点P的坐标为(0,)或(3,0).15.如图1,正方形ABCD中,O是对角线BD的中点,点E在边AB上,点F在边AD上,且OE⊥OF(1)求证:BE=AF;(2)如图2,延长FO交BC于H,连结EH,若BE=12,DF=5,求EH的长;(3)如图3,连结EF,若AB=16,求△AEF的面积的最大值.解:(1)如图1,连接AO,∵四边形ABCD是正方形,且O是BD中点,∴OA=OB,∠OBE=∠OAF=45°,∠AOB=90°,即∠BOE+∠AOE=90°,又∵OE⊥OF,即∠AOF+∠AOE=90°,∴∠BOE=∠AOF,∴△BOE≌△AOF(ASA),∴BE=AF;(2)∵∠OBH=∠ODF=45°,OB=OD,∠BOH=∠DOF,∴△BHO≌△DFO(ASA),∴BH=DF=5,∵BE=12,∠EBH=90°,∴EH=13;(3)如图3,作ON⊥AD于N,则ON=8,∵S △AEF =S 四边形AEOF ﹣S △EOF ,又S 四边形AEOF =S △AOE +S △AOF =S △AOE +S △BOE =S △BOA =64, ∴S △AEF =64﹣OF 2, ∵OF ≥ON ,∴S △AEF ≤64﹣×82=32, ∴△AEF 面积的最大值为32.16.在综合与实践课上,老师组织同学们以“矩形纸片的折叠”为主题开展数学活动. (1)奋进小组用图1中的矩形纸片ABCD ,按照如图2所示的方式,将矩形纸片沿对角线AC 折叠,使点B 落在点B ′处,则△ADC 与△AB ′C 重合部分的三角形的形状是 等腰三角形 .(2)勤学小组将图2中的纸片展平,再次折叠,如图3,使点A 与点C 重合,折痕为EF ,然后展平,则以点A 、F 、C 、E 为顶点的四边形是什么特殊四边形?请说明理由. (3)创新小组用图4中的矩形纸片ABCD 进行操作,其中AD =8cm ,AB =6cm ,先沿对角线BD 对折,点C 落在点C '的位置,BC ′交AD 于点G ,再按照如图5所示的方式折叠一次,使点D 与点A 重合,得折痕EN ,EN 交AD 于点M ,则EM 的长为cm .解:(1)∵四边形ABCD是矩形,∴AB∥CD,∴∠ACD=∠BAC,由折叠知,∠BAC=∠B'AC,∴∠B'AC=∠DAC,∴AM=CM∴△MAC是等腰三角形,故答案为:等腰三角形;(2)菱形,理由:如图3,连接AE,CF,设EF与AC的交点为M,由折叠知,∠AME=∠CME=90°,AM=CM,∴AE=CE,AF=CF,∵四边形ABCD是矩形,∴EC∥AF,∴∠ECM=∠FAM,∠CEM=∠AFM,∴△ECM≌△FAM(AAS),∴EC=FA,∴AE=EC=FC=FA,∴以点A,F,C,E为顶点的四边形是菱形;(3)∵AD=8cm,AB=6cm,∴BD==10cm由(1)可知BG=GD,∵BG2=AB2+AG2,∴BG2=36+(8﹣BG)2,∴BG=cm∴AG=cm由折叠的性质可得AM=MD=4cm,EM⊥AD∵∠BAD=∠BC'D=90°,∠AGB=∠C'GD∴∠ABG=∠C'DG,且∠BAG=∠EMD=90°∴△ABG∽△EMD∴∴∴EM=cm故答案为:17.某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点.(1)该学习小组成员意外的发现图①中(三角板一边与OC重合),BN、CN、CD这三条线段之间存在一定的数量关系:CN2=BN2+CD2,请你对这名成员在图①中发现的结论说明理由;(2)在图③中(三角板一直角边与OD重合),试探究图③中BN、CN、CD这三条线段之间的数量关系,直接写出你的结论.(3)试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由.(1)证明:连结AN,∵矩形ABCD∴AO=CO,∠ABN=90°,AB=CD,∵ON⊥AC,∴NA=NC,∵∠ABN=90°,∴NA2=BN2+AB2,∴CN2=BN2+CD2.(2)如图2,连接DN.∵四边形ABCD是矩形,∴BO=DO,∠DCN=90°,∵ON⊥BD,∴NB=ND,∵∠DCN=90°,∴ND2=NC2+CD2,∴BN2=NC2+CD2.(3)CM2+CN2=DM2+BN2理由如下:延长MO交AB于E,∵矩形ABCD,∴BO=DO,∠ABC=∠DCB=90°,AB∥CD,∴∠ABO=∠CDO,∠BEO=∠DMO,∴△BEO≌△DMO(AAS),∴OE=OM,BE=DM,∵NO⊥EM,∴NE=NM,∵∠ABC=∠DCB=90°,∴NE2=BE2+BN2,NM2=CN2+CM2,∴CN2+CM2=BE2+BN2 ,即CN2+CM2=DM2+BN2 .18.如图,在平面直角坐标系中,边长为3的正方形OABC的边OC落在x轴的正半轴上,边OA落在y轴的正半轴上,点E从点A出发以每秒1个单位长度的速度沿着射线AB 的方向运动,点A关于OE的对称点为点F.运动时间为t秒,连接OF、EF、BF、CF.(1)如图1、当∠AOE=30°时,求∠CFB的度数;(2)如图2,当t=1时,求证:BF⊥CF.(3)如图3,过点F作FG⊥CF,且FG=CF,连接AG.M为AG的中点,连接CM.则当t=(3+3)s时,CM有最小值,CM的最小值为3﹣.解:(1)如图1中,连接AF.由翻折想性质可知:∠AOE=∠EOF=30°,OA=OF,∴∠AOF=60°,∴△AOF是等边三角形,∴AF=FO,∠OAF=60°,∵四边形OABC是正方形,∴AB=OC,∠OAB=∠AOC=∠ABC=∠OCB=90°,∴∠BAF=∠COF=30°,∵AB=AF=OF=OC,∴∠ABF=∠AFB=∠OCF=∠OFC=75°,∴∠FCB=∠FBC=15°,∠CFB=180°﹣15°﹣15°=150°.(2)如图2中,作FM⊥AB于M,交OC于N.设FM=x,EM=y.∵∠OAM=∠AMN=∠AON=90°,∴四边形AMNO是矩形,∴MN=AO=3,AM=ON=1+y,FN=3﹣x,在Rt△EFM和Rt△OFM中,则有,解得,∴BM=CN=3﹣1﹣=,∴BF==,CF==,∴CF2+BF2=+=9=BC2,∴∠CFB=90°,∴CF⊥BF.(3)如图3中,AO的延长线上截取OK=OC,连接KC,KG,OM.∵OC=OF=OK,∠COK=90°,∴∠CFK=135°,∵CF⊥FG,∴∠CFG=90°,∴∠KFG=360°﹣135°﹣90°=135°,∴∠KFC=∠KFG,∵KF=KF,FC=FG,∴△KFC≌△KFG(SAS),∴KC=KG=3,∵OA=OC=OK,AM=MG,∴OM=KG=,∴点M的运动轨迹是以O为圆心,OM长为半径的圆弧,∴当点M落在线段OC上时,CM定值最小,最小值=3﹣,此时易证:∠AOE=∠EOF=67.5°,可得BE=OB=3,∴AE=3+3,∴t=(3+3)s.故答案为:3+3,3﹣.19.如图,在△ABC中,∠ABC=90°,AB=3cm,BC=4cm,点P从点C出发,沿折线CA ﹣AB﹣BC以5cm/s的速度运动,当点P与点B不重合时,连结PB,以线段PB为对角线作正方形PDBE,设点P的运动时间为t(s),正方形PDBE的面积为S(cm2).(1)当正方形PDBE有两边同时落在△ABC的边上时,求t的值;(2)当点P沿折线CA﹣AB运动时,求S与t之间的函数关系式以及自变量t的取值范围;(3)在整个运动过程中,正方形PDBE至少有一个顶点落在∠A的平分线上时,直接写出t的值.解:(1)当正方形PDBE有两边同时落在△ABC的边上时,设正方形的边长为x,如图1所示:∵PE∥AB,∴=,即:=,解得:x=,∴PE=,∴EC=BC﹣BE=4﹣=,∴PC===,∴t==s;(2)①当0≤t≤1时,作PH⊥BC于H,如图2所示:则PH∥AB,∴△CPH∽△CAB,∴==,∵∠ABC=90°,AB=3cm,BC=4cm,∴AC===5(cm),∵CP=5t,∴HC=4t,PH=3t,∴BH=BC﹣HC=4﹣4t,在Rt△PHB中,PB2=PH2+BH2=(3t)2+(4﹣4t)2=25t2﹣32t+16,∴S=PB2=t2﹣16t+8;②当1<t<时,如图3所示:∵PB=8﹣5t,∴S=PB2=(8﹣5t)2=t2﹣40t+32,综上所述,S=;(3)①当D、E在∠BAC的平分线上时,如图4所示:∵AH⊥PB,PH=BH,∴△ABP是等腰三角形,∴AB=AP=3,∴PC=AC﹣AP=5﹣3=2,∴t=s;②当点P运动到点A时,满足条件,此时t=1s;③当点E在∠BAC的平分线上时,作EH⊥BC于H,如图5所示:∵四边形PDBE是正方形,∴∠EBP=45°,∴EB平分∠ABC,∴点E是△ABC的内心,四边形EOBH是正方形,∴OB=EH=EO=BH===1,∴PB=2OB=2,∴AP=1,∴CA+AP=6,∴t=s;④当点P在边BC上,点D在∠BAC的平分线上时,作DN⊥BC于N,作DM⊥AB于M,如图6所示:∵四边形PDBE是正方形,∴∠DBP=45°,∴DB平分∠ABC,∴点D是△ABC的内心,四边形DMBN是正方形,四边形PDBE是正方形,∴DM=BN=PN==1,∴CA+AB+BP=5+3+1+1=10,∴t=2s;⑤当点P在边BC上,且AP是∠BAC的平分线时,作CM∥AP交BA的延长线于M,如图7所示:则∠ACM=∠PAC,∠M=∠BAP,∵AP是∠BAC的平分线,∴∠BAP=∠PAC,∴∠ACM=∠M,∴AM=AC,∵CM∥AP,∴=,∴==,∴BP=BC=,∴CA+AB+BP=5+3+=,∴t=÷5=;综上所述:在整个运动过程中,正方形PDBE至少有一个顶点落在∠A的平分线上时,t 的值为s或1s或s或2s或s.20.如图1,在三角形△ABC中,BA=BC,△ADC和△ABC关于AC对称(1)将图1中的△ACD以A为旋转中心,逆时针方向旋转角α,使α=∠BAC,得到如图2所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是菱形;(2)将图1中的△ACD以A为旋转中心,按逆时针方向旋转角α,使α=2∠BAC,得到如图3所示的△AC′D,连接DB和CC′,得到四边形BCC′D,请判断四边形BCC′D的形状,并说明理由;(3)如图3中,BC=,AC=10,将△AC′D沿着射线DB方向平移a,得到△A′C″D′,進接BD′,CC″,使四边形BCC″D′恰好为正方形,请直接写出a的值.解:(1)∵△△ADC和△△ABC关于AC对称,∴DC=BC,DA=AB,∠BAC=∠DAC,∠BCA=∠DCA,∵BA=BC,∴DC=BC=DA=AB,∠BAC=∠DAC=∠BCA=∠DCA,∵△ACD以A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到△AC′D,∴∠CAC′=∠BAC=∠AC′D=∠BCA,∴AC∥DE,AC′∥BE,∴四边形ACEC′是平行四边形,由旋转可得:AC=AC′,∴四边形ACEC′是菱形,故答案为:菱形;(2)四边形BCC′D是矩形;理由如下:过点A作AE⊥C′C于点E,如图3所示:由旋转的性质,得AC′=AC,∴∠CAE=∠C′AE=α=∠ABC,∠AEC=90°,∵BA=BC,∴∠BCA=∠BAC∴∠CAE=∠BCA,∴AE∥BC.同理,AE∥DC′,∴BC∥DC′,∵BC=DC′,∴四边形BCC′D是平行四边形,∵AE∥BC,∠AEC′=90°,∴∠BCC′=90°,∴四边形BCC′D是矩形;(3)过点B作BF⊥AC于F,∵BA=BC,∴CF=AF=AC=×10=5,在Rt△BCF中,BF=10,∵∠CAE=∠BCF,∠CEA=∠BFC=90°,∴△ACE∽△CBF,∴=,即=,解得:EC=4,∵AC=AC′,AE⊥CC′,∴CC′=2CE=2×4=8,。
【精编版】数学中考专题训练——四边形的综合

中考专题训练——四边形的综合1.四边形ABCD为平行四边形,点P为平面内一点(1)若AP=BC,连AP、DP;①如图1,点P在边BC上,求证:PD平分∠APC;②如图2,过P作PD的垂线交DC的延长线于点F,FP交AB于点E,求证:DF=2AE.(2)如图3,∠ABC=60°,点P在对角线DB上,点M在边AD上,MP=CD且∠AMP =∠ABD,AB=5,BP=3,直接写出平行四边形ABCD的面积.2.在正方形ABCD中,AB=6,E为直线AB上一点,EF⊥AB交对角线AC于F,点G为AF中点,连接CE,点M为CE中点,连接BM并延长交直线AC于点O.(1)如图1,E在边AB上时,=,∠GBM=;(2)将(1)中△AEF绕A逆时针旋转任意一锐角,其他条件不变,如图2,(1)中结论是否仍然成立?请加以证明.(3)若BE=2,则CO长为.3.平面直角坐标系中,菱形ABCD.(1)若点A坐标是(0,2),点B坐标(﹣2,0),求∠ABC及菱形边长:(2)在(1)的条件下,连接OD,过C点向OD作垂线,垂足为E,求CE;(3)如图3所示,∠ABO=60°,在y轴负半轴上取一点P,使得∠BPO=15°,延长BD至Q,使得DQ=CD,连接AQ,若AP=BQ=a,求线段AQ的长(用含a的式子表示).4.矩形ACBD对角线AC、BD相交于点O,点P是对角线BD上的一个动点(不与B,D 重合),∠AOB=α,过P点作PF∥AC,交AB于F,连接AP.将AP绕P点逆时针旋转α得到EP,连接BE.(1)若点P在BD上,∠AOB=50°①求证:AF=BE;②求∠ABE=.(2)若点P在OD上,求∠ABE(用α表示);(3)若BC=8,将A绕点P顺时针方向旋转(180°﹣α)得到EP,连接DE,当DP=3OP时,DE=.5.如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N,连接CN.(1)如图1,求证:E,N、C三点在同一直线上;(2)如图1,若△CMN的面积与△CDN的面积比为3:1,求的值.(3)如图2,已知点P、Q、T分别是CM、CN、MN上的动点,若AN=3,BM=1,试直接写出PT+QT的最小值.6.已知平行四边形ABCD中,N是边BC上一点,延长DN、AB交于点Q,过A作AM⊥DN于点M,连接AN,则AD⊥AN.(1)如图①,若tan∠ADM=,MN=3,求BC的长;(2)如图②,过点B作BH∥DQ交AN于点H,若AM=CN,求证:DM=BH+NH.7.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2.动点P以每秒2个单位长度的速度从点A出发,沿A→C→B的方向向终点B运动(点P不与△ABC的顶点重合).点P 关于点C的对称点为点D,过点P作PQ⊥AB于点Q,以PD、PQ为边作▱PDEQ.设▱PDEQ与△ABC.重叠部分的面积为S,点P的运动时间为t(s)(1)当点P在AC上运动时,用含t的代数式表示PD的长;(2)当点E落在△ABC的直角边上时,求t的值;(3)当▱PDEQ与△ABC重叠部分的图形是四边形时,求S与t之间的函数关系式.8.在菱形ABCD中,∠ABC=60°(1)如图1,P是边BD延长线上一点,以AP为边向右作等边△APE,连接BE、CE.①求证:CE⊥AD;②若AB=,BE=,求AE的长;(2)如图2,P是边CD上一点,点D关于AP的对称点为E,连接BE并延长交AP的延长线于点F,连接DE、DF.若BE=11,DE=5,求△ADF的面积.9.如图,四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=30°,将AC绕着点A顺时针旋转60°得AE,连接BE,CE.(1)求证:△ADC≌△ABE;(2)求证:AC2=DC2+BC2;(3)若AB=2,点Q在四边形ABCD内部运动,且满足AQ2=BQ2+DQ2,求点Q运动路径的长度.10.【阅读】如图1,四边形OABC中,OA=a,OC=8,BC=6,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC 的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].【理解】若点D与点A重合,则这个操作过程为FZ[45°,8];【尝试】(1)若点D与OA的中点重合,则这个操作过程为FZ[,];(2)若点D恰为AB的中点(如图2),求θ的值;【应用】经过FZ[45°,a]操作,点B落在点E处,若点E在四边形OABC的边AB上,直线l 与AB相交于点F,试画出图形并解决下列问题:①求出a的值;②若P为边OA上一动点,连接PE、PF,请直接写出PE+PF的最小值.(备注:等腰直角三角形的三边关系满足1:1:或::2)11.如图,四边形ABCD为正方形,△AEF为等腰直角三角形,∠AEF=90°,连接FC,G为FC的中点,连接GD,ED.(1)如图①,E在AB上,直接写出ED,GD的数量关系.(2)将图①中的△AEF绕点A逆时针旋转,其它条件不变,如图②,(1)中的结论是否成立?说明理由.(3)若AB=5,AE=1,将图①中的△AEF绕点A逆时针旋转一周,当E,F,C三点共线时,直接写出ED的长.12.如图,在平面直角坐标系中,已知A(﹣2,0),B(0,m)两点,且线段AB=2,以AB为边在第二象限内作正方形ABCD.(1)求点B的坐标.(2)在x轴上是否存在点Q,使△QAB是以AB为腰的等腰三角形?若存在,请直接写出点Q的坐标,若不存在,请说明理由;(3)如果在坐标平面内有一点P(a,3),使得△ABP的面积与正方形ABCD的面积相等,求a的值.13.如图,矩形ABCD中,AB=a,AD=b,点P是对角线BD上的一个动点(点P不与B、D重合),连接AP并延长交射线BC于点Q,(1)当AP⊥BD时,求△ABQ的面积(用含a、b的代数式表示);(2)若点M为AD边的中点,连接MP交射线BC于点N,证明:点N也为线段BQ的中点;(3)如图,当为何值时,△ADP与△BPQ的面积之和最小.14.如图1,AC⊥CH于点C,点B是射线CH上一动点,将△ABC绕点A逆时针旋转60°得到△ADE(点D对应点C)(1)延长ED交CH于点F,求证F A平分∠CFE;(2)如图2,当∠CAB>60°时,点M为AB的中点,连接DM,请判断DM与DA、DE的数量关系,并证明;(3)如图3,作▱ABGE,连接DG,点N为DG的中点,连接EN.若AC=EN=3,直接写出四边形ADGE的面积.15.【操作】如图①,在矩形ABCD中,E为对角线AC上一点(不与点A重合).将△ADE 沿射线AB方向平移到△BCF的位置,E的对应点为点F,易知△ADE≌△BCF(不需要证明)【探究】过图①的点E作BG∥BC交FB延长线于点G,连接AG,其它条件不变,如图②.求证:△EGA≌△BCF【拓展】将图②中的△BCF沿BC翻折得到△BCF′,连接GF′,其它条件不变,如图③当GF′最短时,若AB=4,BC=2,直接写出FF′的长和此时四边形BFCF′的周长.16.如1,在矩形ABCD中,AB=6,AD=10,E为AD上一点且AE=6,连接BE.(1)将△ABE绕点B逆时针旋转90°至△ABF(如图2),且A、B、C三点共线,再将△ABF沿射线BC方向平移,平移速度为每秒1个单位长度,平移时间为t(s)(t≥0),当点A与点C重合时运动停止.①在平移过程中,当点F与点E重合时,t=(s).②在平移过程中,△ABF与四边形BCDE重叠部分面积记为S,求s与t的关系式.(2)如图3,点M为直线BE上一点,直线BC上有一个动点P,连接DM、PM、DP,且EM=5,试问:是否存在点P,使得△DMP为等腰三角形?若存在,请直接写出此时线段BP的长;若不存在,请说明理由.17.如图1,△ABC和△CDE均为等边三角形,BC=a,CD=b(a>b).(1)当B、C、D共线时,BA、DE交于点M,①判断四边形ACEM的形状,并说明理由.②a、b为方程x2﹣(m﹣1)x+m2﹣2m﹣8=0的两根,F为AE的中点,求CF的长.(2)将△CDE绕点C旋转(如图3所示),点E在△ABC内部,连接AE,∠BEC=105°,若=n,直接写出n的最小值.18.如图1,四边形ABCD中,对角线AC平分∠DCB,且AD=AB,CD<CB (1)求证:∠B+∠D=180°;(2)如图2,在AC上取一点E,使得BE∥CD,且BE=CE,点F在线段BC上,连接AF,且AB=AF,求证:AE=CF;(3)如图3,在(2)的条件下,若BE与AF交于点G,BF:AB=2:7,求tan∠BGF 的值.19.已知四边形ABCD中,AD∥BC,∠D=90°,AC平分∠BAD,∠ACD=30°(1)如图1,求证:△ABC是等边三角形;(2)如图2,点E在边BA的延长线上,在边BC上取一点F,连接EC、EF且EC=EF,求证:BF=AE;(3)如图3,在(2)的条件下,连接AF,取AF的中点G,连接BG并延长交线段EC 于M,交线段AD于R,过点A作AN∥EC交线段BR于N,若GN=2,EM=5,求CM 的长.20.阅读材料题:浙教版九上作业本①第18页有这样一个题目:已知,如图一,P是正方形ABDC内一点,连接P A、PB、PC,若PC=2,P A=4,∠APC=135°,求PB的长.小明看到题目后,思考了许久,仍没有思路,就去问数学老师,老师给出的提示是:将△P AC绕点A顺时针旋转90°得到△P'AB,再利用勾股定理即可求解本题.请根据数学老师的提示帮小明求出图一中线段PB的长为.【方法迁移】:已知:如图二,△ABC为正三角形,P为△ABC内部一点,若PC=1,P A=2,PB=,求∠APB的大小.【能力拓展】:已知:如图三,等腰三角形ABC中∠ACB=120°,D、E是底边AB上两点且∠DCE=60°,若AD=2,BE=3,求DE的长.21.问题发现:(1)如图①,四边形ABCD中,∠DAB=∠BCD=90°,CB=CD,对角线AC的长为6,则四边形ABCD的面积为.问题探究:(2)如图②,Rt△ABC中,∠CAB=90°,AC=5,AB=12,点D和E都是边BC上的动点,且满足CD=BE,连接AD、AE.求AD+AE的最小值;问题解决:(3)某校准备组织八年级同学开展一次去大明宫遗址公园的考古研学活动.小凯和小鹏在去之前先做了一个模拟“藏宝图”的游戏,为了使宝物隐藏得更神秘,小凯利用学过的数学知识,设计了如下方案,让小鹏破解.如图③,点B在点A的正东方向12m处,点P和Q都为平面内的动点,且满足P A=8m,PB=BQ,∠PBQ=90°,当线段AQ长度最大时,点Q的位置即为藏宝地.请你帮助小鹏破解,藏宝地在点A的什么方向?距离点A多远?22.已知:如图,正方形ABCD,点E是DC边上的一动点,过点C作AE的垂线交AE延长线于点F,过D作DH⊥CF,垂足为H,点O是AC中点,连HO.(1)如图1,当∠CAE=∠DAE时,证明:AE=2CF;(2)如图2,当点E在DC上运动时,线段AF与线段HO之间是否存在确定的数量关系?若存在,证明你发现的结论:若不存在,请说明理由;(3)当E为DC中点时,AC=2,直接写出AF的长.23.如图,在平面直角坐标系中,矩形ABCO的顶点O与坐标原点重合,顶点A、C在坐标轴上,B(18,6),将矩形沿EF折叠,使点A与点C重合.(1)求点E的坐标;(2)点P从O出发,沿折线O﹣A﹣E方向以每秒2个单位的速度匀速运动,到达终点E时停止运动,设P的运动时间为t,△PCE的面积为S,求S与t的关系式,直接写出t的取值范围;(3)在(2)的条件下,当P A=PE时,在平面直角坐标系中是否存在点Q,使得以点P、E、G、Q为顶点的四边形为平行四边形?若不存在,请说明理由;若存在,请求出点Q的坐标.24.在▱ABCD中,∠ADC的平分线交直线BC于点E,交直线AB于点F.(1)如图①,证明:BE=BF.(2)如图②,若∠ADC=90°,O为AC的中点,G为EF的中点,试探究OG与AC的位置关系,并说明理由.(3)如图③,若∠ADC=60°,过点E作DC的平行线,并在其上取一点K(与点F位于直线BC的同侧),使EK=BF,连接CK,H为CK的中点,试探究线段OH与HA 之间的数量关系,并对结论给予证明.参考答案与试题解析1.四边形ABCD为平行四边形,点P为平面内一点(1)若AP=BC,连AP、DP;①如图1,点P在边BC上,求证:PD平分∠APC;②如图2,过P作PD的垂线交DC的延长线于点F,FP交AB于点E,求证:DF=2AE.(2)如图3,∠ABC=60°,点P在对角线DB上,点M在边AD上,MP=CD且∠AMP =∠ABD,AB=5,BP=3,直接写出平行四边形ABCD的面积.【分析】(1)①如图1中,由AP=AD,推出∠ADP=∠APD,再证明∠ADP=∠DPC 即可解决问题.②如图2中,取DF的中点M,连接MA、MP.想办法证明四边形AEFM是平行四边形即可解决问题.(2)在BD上取点K,使AB=AK,作DF⊥BA交BA的延长线于F.证明△ADK≌△PDM (AAS),推出DP=DA,设DP=DA=x,则AF=AD=x.DF=AF=x,在Rt△BDF中,根据BD2=BF2+DF2,构建方程求出x即可解决问题.【解答】解:(1)①如图1中,∵四边形ABCD是平行四边形,∴AD=BC,∵AP=BC,∴AP=AD,∴∠APD=∠ADP∵AD∥BC,∴∠ADP=∠DPC,∴PD平分∠APC.②如图2中,取DF的中点M,连接MA、MP.∵PD⊥PF,∴∠DPF=90°,∴PM=DM=MF,∵AP=AD,∴AM为线段PD的垂直平分线,∴AM∥EF,∵EF⊥PD,∵AE∥FM,∴四边形AEFM为平行四边形,∴AE=MF,∴DF=2AE.(3)在BD上取点K,使AB=AK,作DF⊥BA交BA的延长线于F.∵AB=AK,∵∠AMP=∠ABD,∴∠AMP=∠AKB,∴∠DMP=∠DKA,∵∠ADK=∠PDM,PM=CD=AB=AK,∴△ADK≌△PDM(AAS),∴DP=DA,设DP=DA=x,∵AD∥BC,∴∠F AD=∠ABC=60°,∴AF=AD=x.DF=AF=x,在Rt△BDF中,∵BD2=BF2+DF2,∴(3+x)2=(5+x)2+(x)2,解得x=16,∴S平行四边形ABCD=AB•DF=5××16=.2.在正方形ABCD中,AB=6,E为直线AB上一点,EF⊥AB交对角线AC于F,点G为AF中点,连接CE,点M为CE中点,连接BM并延长交直线AC于点O.(1)如图1,E在边AB上时,=,∠GBM=45°;(2)将(1)中△AEF绕A逆时针旋转任意一锐角,其他条件不变,如图2,(1)中结论是否仍然成立?请加以证明.(3)若BE=2,则CO长为或3.【分析】(1)连接EG、GM.想办法证明△GBM是等腰直角三角形即可解决问题.(2)成立.延长GM到H,使得MH=GM,连接BH,HC,延长HC交AF的延长线于I,设AI交CD于J.利用全等三角形的性质证明△GBM是等腰直角三角形即可解决问题.(3)分两种情形①点E在线段AB上.②点E在AB的延长线上,分别求解即可解决问题.【解答】解:(1)连接EG、GM.∵四边形ABCD是正方形,∴∠ABC=90°,∠CAB=∠ACB=45°,∵EF⊥AB,∴∠AEF=90°,∴∠EAF=∠EF A=45°,∵AG=GF,∴EG⊥AF,∴∠EGC=90°∵EM=MC,∴GM=BM=CE,∴∠MCG=∠MGC,∠MBC=∠MCB,∴∠BMG=∠BME+∠GME=2∠BMC+2∠GCM=2∠ACB=90°.故△GMB为等腰直角三角形.∴=.故答案为,45°.(2)成立.理由:延长GM到H,使得MH=GM,连接BH,HC,延长HC交AF的延长线于I,设AI交CD于J.∵EM=MC,GM=MH,∠EMG=∠HMC,∴△EMG≌△CMH(SAS),∴EG=CH,∠EGM=∠MHC,∴EC∥CH,∴∠AGE=∠AIH=90°,∵AG=EG,∴AG=CH,∵∠D=∠I=90°,∠AJD=∠CJI,∴∠ICD=∠IAD,∵∠BAG+∠IAD=90°,∠BCH+∠ICF=90°∴∠BCH=∠BAG,∵BA=BC∴△BAG≌△BCH(SAS),∴BG=DH,∠ABG=∠CBH,∴∠∠GBH=∠ABC=90°故△GBH是等腰直角三角形,∴=,∠GBM=45°.(3)当E在B上方时,如图3﹣1中,延长BO交CD于T.∴BE∥CT,∴∠MEB=∠MCT,∵∠EMB=∠CMT,EM=CM,∴△EMB≌△CMT(ASA),∴BE=CT=2,∵CT∥AB,∴==,∵AC=6,∴OC=×6∴CO=当E在B下方时同法可得CO=.综上所述,OC的长为或3.故答案为或3.3.平面直角坐标系中,菱形ABCD.(1)若点A坐标是(0,2),点B坐标(﹣2,0),求∠ABC及菱形边长:(2)在(1)的条件下,连接OD,过C点向OD作垂线,垂足为E,求CE;(3)如图3所示,∠ABO=60°,在y轴负半轴上取一点P,使得∠BPO=15°,延长BD至Q,使得DQ=CD,连接AQ,若AP=BQ=a,求线段AQ的长(用含a的式子表示).【分析】(1)在Rt△AOB中,解直角三角形求出AB,∠ABO即可.(2)根据S△ODC=•OD•CE=•OC•OA求解即可.(3)设菱形ABCD的边长为2x,过Q点作QM⊥AD交AD的延长线于M,过DN⊥x轴于N,根据AP=BQ=a,构建方程求解即可.【解答】解:(1)如图1中,∵A(0,2),B(﹣2,0),∴OA=2,OB=2,∴tan∠ABO==,∴∠ABC=60°,∴∠OAB=90°﹣60°=30°,∴AB=2OB=4,∴菱形的边长为4.(2)如图2中,∵四边形ABCD是菱形,AB=AD=CD=BC=4,∴C(2,0),D(4,2),∴OD==2,∵CE⊥OD,∴S△ODC=•OD•CE=•OC•OA,∴EC==.(3)设菱形ABCD的边长为2x,过Q点作QM⊥AD交AD的延长线于M,过DN⊥x 轴于N,在△QDM中,∠QDM=30°,DQ=2x,∴QM=DQ=x,DM=x,AM=2x+x=(2+)x,又QM⊥AM,利用勾股定理可求AQ=(+)x,BD=2x,∵AP=BQ=a,∴2x+2x=a,得x=,继而得AQ=(+)x=a.4.矩形ACBD对角线AC、BD相交于点O,点P是对角线BD上的一个动点(不与B,D 重合),∠AOB=α,过P点作PF∥AC,交AB于F,连接AP.将AP绕P点逆时针旋转α得到EP,连接BE.(1)若点P在BD上,∠AOB=50°①求证:AF=BE;②求∠ABE=50°.(2)若点P在OD上,求∠ABE(用α表示);(3)若BC=8,将A绕点P顺时针方向旋转(180°﹣α)得到EP,连接DE,当DP=3OP时,DE=2或4.【分析】(1)①证明△APF≌△EPB(SAS)可得结论.②利用全等三角形的性质以及三角形内角和定理解决问题即可.(2)如图2中,证明△FP A≌△BPE(SAS),推出∠F AP=∠PEB,由∠F AP+∠P AB=180°,推出∠P AB+∠PEB=180°,推出∠ABE+∠APE=180°可得结论.(3)分两种情形:如图3中,当点P在OD上时,如图3所示,过点P作PF∥OA,交AD于点F,如图4所示,当点P在OB上时,过点P作PF∥OA,交DA的延长线于点F,分别求解即可解决问题.【解答】(1)①证明:∵四边形ABCD是矩形,∴OA=OC=OB=OD,∵PF∥OA,∴=,∠FPB=∠AOB=α,∴PF=PB,∠EPB=∠FPB﹣∠FPE=α﹣∠FPE,∵AP=EP,∠APE=α,∴∠APF=α﹣∠FPE,∴∠APF=∠EPB,∴△APF≌△EPB(SAS),∴AF=BE.②∵△APF≌△EPB,∴∠AFP=∠EBP,∵∠AFP=∠FPB+∠OBA,∠EBP=∠ABE+∠OBA,∴∠ABE=∠FPB,∴∠ABE=α=50°.故答案为50°.(2)如图2中,∵P A=PE,∠APE=α,同法可证PF=PB,∠FPB=α,∴∠FPB=∠APE,∴∠FP A=∠BPE,∴△FP A≌△BPE(SAS),∴∠F AP=∠PEB,∵∠F AP+∠P AB=180°,∴∠P AB+∠PEB=180°,∴∠ABE+∠APE=180°,∴∠ABE=180°﹣α.(3)如图3中,当点P在OD上时,如图3所示,过点P作PF∥OA,交AD于点F,∵DP=3OP,即OD=4OP,∴===,∴AF=AD=BC=2.类比(1)①得:△APF≌△EPD,∴DE=AF=2.如图4所示,当点P在OB上时,过点P作PF∥OA,交DA的延长线于点F,∵DP=3OP,即OD=2OP,∴===,∴AF=AD=BC=4.类比(1)①得:△APF≌△EPD,∴DE=AF=4.综上所述,DE的长为2或4.故答案为2或4.5.如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N,连接CN.(1)如图1,求证:E,N、C三点在同一直线上;(2)如图1,若△CMN的面积与△CDN的面积比为3:1,求的值.(3)如图2,已知点P、Q、T分别是CM、CN、MN上的动点,若AN=3,BM=1,试直接写出PT+QT的最小值2.【分析】(1)证明∠ENM+∠CNM=∠DNM+∠ANM=180°,可得结论.(2)如图1中,首先过点N作NH⊥BC于点H,由△CMN的面积与△CDN的面积比为3:1,易得MC=3ND=3HC,然后设DN=x,由勾股定理,可求得MN的长,继而求得答案,(3)如图2中,由(1)得出△CMN是等腰三角形,而TQ+TA最小就是点T到等腰三角形的两腰的距离之和最小就是等腰三角形腰上的高.【解答】(1)证明:如图1中,由折叠的性质可得:∠ENM=∠DNM,即∠ENM=∠ENA+∠ANM,∠DNM=∠DNC+∠CNM,∵∠ENA=∠DNC,∴∠ANM=∠CNM,∴∠ENM+∠CNM=∠DNM+∠ANM=180°,∴E,N、C三点在同一直线上.(2)解:如图1中,过点N作NH⊥BC于点H,则四边形NHCD是矩形,∴HC=DN,NH=DC,∵△CMN的面积与△CDN的面积比为3:1,∴===3,∴MC=3ND=3HC,∴MH=2HC,设DN=x,则HC=x,MH=2x,∴CM=3x=CN,在Rt△CDN中,DC==2x,∴HN=2x,在Rt△MNH中,MN==2x,∴==2.(3)如图2中,∵CM=CN∴△CMN是等腰三角形,要使PT+QT的最小值,也就是等腰三角形的底边上一点到两腰上距离之和最短,即:TQ⊥CN,TP⊥CM,而等腰三角形的底边上一点到两腰的距离之和等于腰上的高,过点N作NH⊥BC,∴PT+QT的最小值就是NH=AB,由折叠得,AM=CM=AN=3,∴BM=AN=1在Rt△ABM中,根据勾股定理得,AB==2.∴NH=2,即:PT+QT的最小值为2.故答案为2.6.已知平行四边形ABCD中,N是边BC上一点,延长DN、AB交于点Q,过A作AM⊥DN于点M,连接AN,则AD⊥AN.(1)如图①,若tan∠ADM=,MN=3,求BC的长;(2)如图②,过点B作BH∥DQ交AN于点H,若AM=CN,求证:DM=BH+NH.【分析】(1)如图①中,设AM=3k,DM=4k,则AD=5k,由△ADM∽△NDA,可得AD2=DM•AN,由此构建方程即可解决问题.(2)如图②中,连接CH,在DM上取一点K,使得DK=BH.证明△ADK≌△CBH (SAS),推出AK=CH,再证明Rt△AMK≌Rt△CNH(HL),推出MK=HN即可解决问题.【解答】(1)解:如图①中,∵AM⊥DN,∴∠AMD=90°,∵tan∠ADM==,∴可以假设AM=3k,DM=4k,则AD=5k,∵AD⊥AN,∴∠DAN=90°=∠AMD,∵∠ADM=∠ADN,∴△ADM∽△NDA,∴AD2=DM•AN,∴(5k)2=4k(4k+3),解得k=,∴AD=,∵四边形ABCD是平行四边形,∴BC=AD=.(2)证明:如图②中,连接CH,在DM上取一点K,使得DK=BH.∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠ADK=∠BNQ,∵BH∥DQ,∴∠CBH=∠BNQ,∴∠ADK=∠CBH,∵DK=BH,DA=BC,∴△ADK≌△CBH(SAS),∴AK=CH,∵AM⊥DQ,AN⊥AD,AD∥BC,∴AN⊥BC,∴∠AMK=∠CNH=90°,∵AM=CN,∴Rt△AMK≌Rt△CNH(HL),∴MK=NH,∴DM=DK+MK=BH+HN.7.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2.动点P以每秒2个单位长度的速度从点A出发,沿A→C→B的方向向终点B运动(点P不与△ABC的顶点重合).点P 关于点C的对称点为点D,过点P作PQ⊥AB于点Q,以PD、PQ为边作▱PDEQ.设▱PDEQ与△ABC.重叠部分的面积为S,点P的运动时间为t(s)(1)当点P在AC上运动时,用含t的代数式表示PD的长;(2)当点E落在△ABC的直角边上时,求t的值;(3)当▱PDEQ与△ABC重叠部分的图形是四边形时,求S与t之间的函数关系式.【分析】(1)由题意,可先写出AP的长,再写出CP的长,由对称的性质即可写出PD 的长;(2)①如图2﹣1,当点E落在BC边上时,过点Q作QH⊥AD于H,证明CE=HQ=AP=CD,即可列出关于t方程,求出t的值;②如图2﹣2,当点E落在AC边上时,过点Q作QG⊥BC于G,证明CE=GQ=BP=CD,即可列出关于t的方程,求出t的值即可;(3)如图3﹣1,当0<t≤时,求出梯形PQMC的面积即可;如图3﹣2,当≤t≤2时,求出梯形PQCN的面积即可.【解答】解:(1)由题意,得AP=2t,CP=2﹣2t,∴PD=2CP=4﹣4t;(2)①如图2﹣1,当点E落在BC边上时,过点Q作QH⊥AD于H,由题意知,△AQP和△CED为等腰直角三角形,∴CE=HQ=AP,CE=CD,∵HQ=AP=t,CD=PC=2﹣2t,∴t=2﹣2t,∴t=;②如图2﹣2,当点E落在AC边上时,过点Q作QG⊥BC于G,由题意知,△BQP和△CED为等腰直角三角形,∴CE=GQ=BP,CE=CD,∵GQ=BP=(4﹣2t)=2﹣t,CD=PC=2t﹣2,∴2﹣t=2t﹣2,∴t=,综上所述,点E落在△ABC的直角边上时,t的值为或;(3)如图3﹣1,当0<t≤时,S=S梯形PQMC=t(2﹣2t+2﹣t)=﹣t2+2t;如图3﹣2,当≤t≤2时,S=S梯形PQNC=(2﹣t)(2t﹣2+t)=﹣t2+4t﹣2,综上所述,S=.8.在菱形ABCD中,∠ABC=60°(1)如图1,P是边BD延长线上一点,以AP为边向右作等边△APE,连接BE、CE.①求证:CE⊥AD;②若AB=,BE=,求AE的长;(2)如图2,P是边CD上一点,点D关于AP的对称点为E,连接BE并延长交AP的延长线于点F,连接DE、DF.若BE=11,DE=5,求△ADF的面积.【分析】(1)①证△ADC和△ABC是等边三角形,再证△BAP≌△CAE,推出∠ACE=30°,由∠ACE+∠CAD=90°即可证明结论;②如图1,设AC与BD交于点O,证∠BCE=90°,由勾股定理求出CE,BP的长,由锐角三角函数等分别求出OA,OP的长,由勾股定理即可求出AP的长,即AE的长;(2)如图2,连接AE,过点A作AH⊥BF于点H,证∠HAF=∠BAD=60°,再证△DEF为等边三角形,即可求出HF,AH的长,进一步求出△AEF的面积,证△ADF≌△AEF即可.【解答】(1)①证明:在菱形ABCD中,∠ABC=60°,∴∠ADC=60°,且AB=BC=DA=DC,∴△ADC和△ABC是等边三角形,∴AB=AC,∠BAC=∠CAD=60°,又∵△APE是等边三角形,∴AE=AP,∠EAP=60°,∴∠BAC+∠CAP=∠P AE+∠CAP,即∠BAP=∠CAE,∴△BAP≌△CAE(SAS),∴∠ACE=∠ABP=∠ABC=30°,∵∠CAD=60°,∴∠ACE+∠CAD=90°,∴CE⊥AD;②解:如图1,设AC与BD交于点O,由①知,∠ACE=30°,且∠ACB=60°,∴∠ACE+∠ACB=∠BCE=90°,∵在Rt△BCE中,BC=AB=,BE=,∴CE==4,由①知,△BAP≌△CAE,∴BP=CE=4,在Rt△BOC中,∠ACB=60°,∴BO=BC=,CO=AO=BC=,∴OP=BP﹣BO=,∴在Rt△AOP中,AP===,∴AE=AP=;(2)解:如图2,连接AE,过点A作AH⊥BF于点H,∵点D关于AP的对称点为E,∴AP垂直平分DE,∴AD=AE,FD=FE,∴∠EAF=∠DAF=∠EAD,∠DF A=∠EF A=∠DFE,又∵在菱形ABCD中,AB=AD,∴AB=AE,∴AH垂直平分BE,∴EH=BH=BE=,∠BAH=∠EAH=∠BAE,∴∠HAF=∠EAH+∠EAF=∠BAD,∵∠ABC=60°,∴∠BAD=180°﹣∠ABC=120°,∴∠HAF=60°,∴∠AFH=90°﹣∠HAF=30°,∴∠DFE=60°,∴△DEF为等边三角形,∴EF=DE=5,∴HF=HE+EF=+5=,在Rt△AHF中,∠AFH=30°,∴AH=HF=,∴S△AEF=EF•AH=×5×=,∵AD=AE,FD=FE,AF=AF,∴△ADF≌△AEF(SSS),∴△ADF的面积为.9.如图,四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=30°,将AC绕着点A顺时针旋转60°得AE,连接BE,CE.(1)求证:△ADC≌△ABE;(2)求证:AC2=DC2+BC2;(3)若AB=2,点Q在四边形ABCD内部运动,且满足AQ2=BQ2+DQ2,求点Q运动路径的长度.【分析】(1)推出∠DAC=∠BAE,则可直接由SAS证明△ADC≌△ABE;(2)证明△BCE是直角三角形,再证DC=BE,AC=CE即可推出结论;(3)如图2,设Q为满足条件的点,将AQ绕着点A顺时针旋转60度得AF,连接QF,BF,QB,DQ,AF,证△ADQ≌△ABF,由勾股定理的逆定理证∠FBQ=90°,求出∠DQB=150°,确定点Q的路径为过B,D,C三点的圆上,求出的长即可.【解答】(1)证明:∵∠CAE=∠DAB=60°,∴∠CAE﹣∠CAB=∠DAB﹣∠CAB,∴∠DAC=∠BAE,又∵AD=AB,AC=AE,∴△ADC≌△ABE(SAS);(2)证明:在四边形ABCD中,∠ADC+∠ABC=360°﹣∠DAB﹣∠DCB=270°,∵△ADC≌△ABE,∴∠ADC=∠ABE,CD=BE,∴∠ABC+ABE=∠ABC+∠ADC=270°,∴∠CBE=360°﹣(∠ABC+ABE)=90°,∴CE2=BE2+BC2,又∵AC=AE,∠CAE=60°,∴△ACE是等边三角形,∴CE=AC=AE,∴AC2=DC2+BC2;(3)解:如图2,设Q为满足条件的点,将AQ绕着点A顺时针旋转60度得AF,连接QF,BF,QB,DQ,AF,则∠DAQ=∠BAF,AQ=QF,△AQF为等边三角形,又∵AD=AB,∴△ADQ≌△ABF(SAS),∴AQ=FQ,BF=DQ,∵AQ2=BQ2+DQ2,∴FQ2=BQ2+BF2,∴∠FBQ=90°,∴∠AFB+∠AQB=360°﹣(∠QAF+∠FBQ)=210°,∴∠AQD+∠AQB=210°,∴∠DQB=360°﹣(∠AQD+∠AQB)=150°,∴点Q的路径为过B,D,C三点的圆上,如图2,设圆心为O,则∠BOD=2∠DCB=60°,连接DB,则△ODB与△ADB为等边三角形,∴DO=DB=AB=2,∴点Q运动的路径长为:=π.10.【阅读】如图1,四边形OABC中,OA=a,OC=8,BC=6,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC 的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].【理解】若点D与点A重合,则这个操作过程为FZ[45°,8];【尝试】(1)若点D与OA的中点重合,则这个操作过程为FZ[45°,16];(2)若点D恰为AB的中点(如图2),求θ的值;【应用】经过FZ[45°,a]操作,点B落在点E处,若点E在四边形OABC的边AB上,直线l 与AB相交于点F,试画出图形并解决下列问题:①求出a的值;②若P为边OA上一动点,连接PE、PF,请直接写出PE+PF的最小值.(备注:等腰直角三角形的三边关系满足1:1:或::2)【分析】【尝试】(1)如图1所示,若点D恰为AO的中点,证明Rt△OCP≌Rt△ODP,进而得到OD=OC=AD=8,a=16,可得结论;则θ=30°;(2)如图2所示,若点D恰为AB的中点,作辅助线,证明△BDM≌△ADN(ASA),得DM=DN,根据线段垂直平分线的性质可得OM=ON,根据等腰三角形的性质可得∠MOD=∠NOD,所以∠MOD=∠MOC=θ,可得结论;【应用】①如图3,作辅助线,根据点B与点E关于直线l对称,知∠OF A=∠OFB=90°,证明四边形BCOH是平行四边形,得BH=CO=8,OH=CB=6,可得OA的值,即a的值;②作辅助线,如图4,则有∠QAO=∠F AO=45°,QA=F A,从而可得∠QAF=90°.然后根据勾股定理可求出AB、AF、AQ、OF、OB、BF,由折叠可求出EF,从而可求出AE长,在Rt△QAE中,运用勾股定理可求出EQ2长,然后根据两点之间线段最短可得:当点E、P、Q三点共线时,PE+PF=PE+PQ最短,最小值为线段EQ长,问题得以解决.【解答】解:(1)点D与OA的中点重合,如图1,由折叠得:∠COP=∠DOP=45°,∠C=∠ODP=90°,∴CP=PD,∵OP=OP,∴Rt△OCP≌Rt△ODP(HL),∴OC=OD=8,∵D为OA的中点,∴OA=a=16,则这个操作过程为FZ[45°,16];故答案为:45°,16;(2)延长MD、OA,交于点N,如图2.∵∠AOC=∠BCO=90°,∴∠AOC+∠BCO=180°,∴BC∥OA,∴∠B=∠DAN.在△BDM和△ADN中,,∴△BDM≌△ADN(ASA),∴DM=DN.∵∠ODM=∠OCM=90°,∴根据线段垂直平分线的性质可得OM=ON,∴根据等腰三角形的性质可得∠MOD=∠NOD.由折叠可得∠MOD=∠MOC=θ,∴∠COA=3θ=90°,∴θ=30°;【应用】①过点B作BH⊥OA于点H,如图3.∵∠COA=90°,∠COF=45°,∴∠FOA=45°.∵点B与点E关于直线l对称,∴∠OF A=∠OFB=90°,∴∠OAB=45°,∴∠HBA=90°﹣45°=45°=∠HAB,∴BH=AH.∵CO⊥OA,BH⊥OA,∴CO∥BH.∵BC∥OA,∴四边形BCOH是平行四边形,∴BH=CO=8,OH=CB=6,∴OA=OH+AH=OH+BH=6+8=14.∴a的值为14.②过点B作BH⊥OA于点H,过点F作OA的对称点Q,连接AQ、EQ,OB,如图4,则有∠QAO=∠F AO=45°,QA=F A,∴∠QAF=90°.在Rt△BHA中,AB==8.在Rt△OF A中,∠AFO=90°,∠AOF=∠OAF=45°∴AF=OF==7,∴AQ=AF=7.在Rt△OCB中,OB===10.在Rt△OFB中,BF=AB﹣AF=8﹣7=.由折叠可得EF=BF=,∴AE=AF﹣EF=7﹣=6.在Rt△QAE中,EQ2=AE2+AQ2=(6)2+(7)2=170.根据两点之间线段最短可得:当点E、P、Q三点共线时,PE+PF=PE+PQ最短,最小值为线段EQ长.∴PE+PF的最小值的是.11.如图,四边形ABCD为正方形,△AEF为等腰直角三角形,∠AEF=90°,连接FC,G为FC的中点,连接GD,ED.(1)如图①,E在AB上,直接写出ED,GD的数量关系.(2)将图①中的△AEF绕点A逆时针旋转,其它条件不变,如图②,(1)中的结论是否成立?说明理由.(3)若AB=5,AE=1,将图①中的△AEF绕点A逆时针旋转一周,当E,F,C三点共线时,直接写出ED的长.【分析】(1)结论:DE=DG.如图1中,连接EG,延长EG交BC的延长线于M,连接DM.证明△CMG≌△FEG(AAS),推出EF=CM,GM=GE,再证明△DCM≌△DAE(SAS)即可解决问题.(2)如图2中,结论成立.连接EG,延长EG到M,使得GM=GE,连接CM,DM,延长EF交CD于R.证明方法类似.(3)分两种情形:①如图3﹣1中,当E,F,C共线时.②如图3﹣2中,当E,F,C 共线时,分别求解即可.【解答】解:(1)结论:DE=DG.理由:如图1中,连接EG,延长EG交BC的延长线于M,连接DM.∵四边形ABCD是正方形,∴AD=CD,∠B=∠ADC=∠DAE=∠DCB=∠DCM=90°,∵∠AEF=∠B=90°,∴EF∥CM,∴∠CMG=∠FEG,∵∠CGM=∠EGF,GC=GF,∴△CMG≌△FEG(AAS),∴EF=CM,GM=GE,∵AE=EF,∴AE=CM,∴△DCM≌△DAE(SAS),∴DE=DM,∠ADE=∠CDM,∴∠EDM=∠ADC=90°,∴DG⊥EM,DG=GE=GM,∴△EGD是等腰直角三角形,∴DE=DG.(2)如图2中,结论成立.理由:连接EG,延长EG到M,使得GM=GE,连接CM,DM,延长EF交CD于R.∵EG=GM,FG=GC,∠EGF=∠CGM,∴△CGM≌△FGE(SAS),∴CM=EF,∠CMG=∠GEF,∴CM∥ER,∴∠DCM=∠ERC,∵∠AER+∠ADR=180°,∴∠EAD+∠ERD=180°,∵∠ERD+∠ERC=180°,∴∠DCM=∠EAD,∵AE=EF,∴AE=CM,∴△DAE≌△DCM(SAS),∴DE=DM,∠ADE=∠CDM,∴∠EDM=∠ADC=90°,∵EG=GM,∴DG=EG=GM,∴△EDG是等腰直角三角形,∴DE=DG.(3)①如图3﹣1中,当E,F,C共线时,在Rt△ADC中,AC===5,在Rt△AEC中,EC===7,∴CF=CE﹣EF=6,∴CG=CF=3,∵∠DGC=90°,∴DG===4.∴DE=DG=4.②如图3﹣2中,当E,F,C共线时,同法可得DE=3.综上所述,DE的长为4或3.12.如图,在平面直角坐标系中,已知A(﹣2,0),B(0,m)两点,且线段AB=2,以AB为边在第二象限内作正方形ABCD.(1)求点B的坐标.(2)在x轴上是否存在点Q,使△QAB是以AB为腰的等腰三角形?若存在,请直接写出点Q的坐标,若不存在,请说明理由;(3)如果在坐标平面内有一点P(a,3),使得△ABP的面积与正方形ABCD的面积相等,求a的值.【分析】(1)在直角三角形AOB中,由OA与AB的长,利用勾股定理求出OB的长即可;(2)存在,以AB为腰,有两种情况:分别以A、B为顶点作等腰三角形的顶角,根据AB=2,结合图形可得Q的坐标;(3)作辅助线,构建高线PG,分两种情况:P在y轴的左侧和右侧,根据三角函数可得PH的长,从而得a的值.【解答】解:(1)∵A(﹣2,0),∴OA=2,∵AB=2,由勾股定理得:OB==4,∴B(0,4);(2)分两种情况:①以AB为腰,∠BAQ为顶角时,如图1,AB=AQ=2,∴Q1(﹣2﹣2,0),Q2(2﹣2,0),②以AB为腰,∠ABQ为顶角时,如图1,A与Q3关于y轴对称,∴Q3(2,0);综上,点Q的坐标是(﹣2﹣2,0)或(2﹣2,0)或(2,0),(3)分两种情况:①当P在y轴的右边时,如图2,作直线l:y=3,直线l交AB于H,交y轴于E,∵P(a,3),∴点P在直线l上,过P作PG⊥AB于G,∵S△ABP=S正方形ABCD,∴•AB•PG=AB2,PG=2AB=4,∵l∥x轴,∴∠PHG=∠OAB,∴sin∠PHG=sin∠OAB,即,∴,PH=10,∵EH∥OA,∴,即,∴EH=,∴PE=10﹣0.5=9.5,∴P(9.5,3)即a=9.5;②当点P在y轴的左侧时,如图3,同理可得PH=10,∴P(﹣10.5,3),∴a=﹣10.5,综上,a的值是9.5或﹣10.5.13.如图,矩形ABCD中,AB=a,AD=b,点P是对角线BD上的一个动点(点P不与B、D重合),连接AP并延长交射线BC于点Q,(1)当AP⊥BD时,求△ABQ的面积(用含a、b的代数式表示);(2)若点M为AD边的中点,连接MP交射线BC于点N,证明:点N也为线段BQ的中点;(3)如图,当为何值时,△ADP与△BPQ的面积之和最小.【分析】(1)利用相似三角形的性质求出BQ即可解决问题.(2)证明△AMP∽△QNP,△DMP∽△BNP推出,可得,因为点M是AD的中点,所以AM=DM.(3)如图②,过点P作EF⊥AD交AD、BC于E、F.构建一元二次方程,利用根的判别式解决最值问题即可.【解答】(1)解:如图①:。
2023年中考数学专题练——四边形练习(含解析)
2023年浙江省温州市中考数学专题练——四边形一.选择题(共15小题)1.(2022•温州校级模拟)如图,菱形ABCD 中,过点C 作CE ⊥BC 交BD 于点E ,若∠BAD =118°,则∠CEB =( )A .59°B .62°C .69°D .72°2.(2022•乐清市三模)如图,在正方形ABCD 内有一点E ,∠AEB =90°,以CE ,DE 为邻边作▱CEDF ,连结EF ,若A ,E ,F 三点共线,且△ADF 的面积为10,则CF 的长为( )A .2B .5C .22D .103.(2022•鹿城区校级三模)如图,以Rt △ABC 各边为边向外做正方形,把三个正方形如图2叠放,图2中①号L 型和②号L 型面积分别为1和4,则图1中sin ∠ABC 的值为( )A .12B .25C .55D .664.(2022•洞头区模拟)由四个全等的矩形围成了一个大正方形ABCD ,如图所示.连结CH ,延长EF 交CH 于点G ,作PG ⊥CH 交AB 于点P ,若AH =2DH ,则AP BP 的值为( )A .97B .1611C .32D .25.(2022•永嘉县模拟)如图1,矩形方框内是一副现代智力七巧板,它由两个相同的半圆①和⑦、等腰直角三角形②、角不规图形③、直角梯形④、圆不规图形⑤、圆⑥组成,已知AJ =BK .为庆祝北京冬奥会,小明将这个智力七巧板拼成一个滑冰运动员的图案,如图2所示,若AB 平行地面MN ,AJ =2,则该图案的高度是( )A .8B .9―22C .7+2D .10―26.(2022•瑞安市二模)如图,在△ABC 中,∠ACB =90°,分别以AC ,BC 为边向外作正方形ACDE 与正方形BCFG ,H 为EG 的中点,连结DH ,FH .记△FGH 的面积为S ,△CDH 的面积为S ,若S ﹣S =6,则AB 的长为( )A .26B .32C .33D .427.(2022•文成县一模)如图▱ABCD 中,AB =4,BD =6,BD ⊥AB ,则AC 的长为( )A .10B .213C .5D .258.(2022•温州模拟)在数学拓展课上,小华同学将正方形纸片的顶点A ,B ,C ,D 与各边的中点E ,F ,G ,H 分别连结,形成四边形MNST ,直线MS ,TN 与正方形ABCD 各边相交构成一个如图的“风车”图案.若正方形的边长为25,则阴影部分面积之和为( )A .43B .2C .355D .21059.(2022•瑞安市一模)由四个全等的直角三角形和一个小正方形组成的大正方形ABCD 如图所示,延长AH 交CD 于点P ,若AP ⊥HF ,AP =52,则小正方形边长GF 的长是( )A .52B .22C .3D .1010.(2022•龙港市一模)矩形纸片ABCD 按如图1的方式分割成三个直角三角形①,②,③,又把这三个直角三角形按如图2的方式重叠放置在一起,其中直角三角形①的斜边一端点恰好落在直角三角形②的斜边上,若BD =5,则图2中CP 的长为( )A .45B .35C .34D .3211.(2022•瓯海区一模)如图把两张宽度均为3的纸条交错叠在一起,相交成角α,则重叠部分的周长为( )A.12tanαB.12sinαC.12sinαD.12tanα12.(2022•温州模拟)如图,在正方形ABCD中,延长DC至点G,以CG为边向下画正方形CEFG.延长AB交边FG于点H,连结CF,AF分别交AH,CE于点M,N.收录在清朝四库全书的《几何通解》利用此图得:2AB+2BH=AH+MH.若正方形ABCD与CEFG 的面积之和为68,CN=3NE,则AH的长为( )A.42B.8C.82D.16 13.(2022•乐清市一模)如图,在▱ABCD中,AB=BE,∠C=70°,则∠BAE的度数为( )A.35°B.45°C.55°D.65°14.(2022•鹿城区校级一模)如图,在△ABC中以AC,BC为边向外作正方形ACFG与正方形BCDE,连结DF,并过C点作CH⊥AB于H并交FD于M.若∠ACB=120°,AC =3,BC=2,则MD的长为( )A.72B.2C.32D.315.(2021•温州模拟)如图,矩形ABCD 中,AB :AD =2:1,点E 为AB 的中点,点F 为EC 上一个动点,点P 为DF 的中点,连接PB ,当PB 的最小值为32时,则AD 的值为( )A .2B .3C .4D .6二.填空题(共7小题)16.(2022•永嘉县三模)如图,在正方形ABCD 中,BC =6,点P 在正方形内,PF ⊥PC ,交边AD 于点F ,ED ∥PC ,交PF 延长线于点E ,且PC =PE ,连结AP ,AE .若五边形AEDCP 的面积为24,则∠AEP 的度数为 ,PC 的长为 .17.(2022•永嘉县三模)如图,在平行四边形ABCD 中,AB =6,BC =8,∠B =30°,点E 从点D 出发沿DC 方向匀速向终点C 运动,同时点F 从点C 出发沿CB 方向匀速向终点B 运动,它们同时到达终点,记ED =x ,则△CEF 的面积为 (用含x 的代数式表示).18.(2022•鹿城区校级二模)如图,在平面直角坐标系xOy 中,▱ABCD 的边AB 在x 轴上,顶点D 在y 轴的正半轴上,点C 在第一象限,将△AOD 沿y 轴翻折,使点A 落在x 轴上的点E 处,BE =2OB ,DE 与BC 交于点F .若y =k x(k ≠0)图象经过点C ,且S =4,则k 的值为 .19.(2022•龙湾区模拟)如图,点E,F,G,H分别是矩形ABCD各边上的中点,将矩形ABCD 向右平移得矩形A′B′C′D′,点E,F,G,H的对应点分别为点E′,F′,G′,H′.若AD′=7HH′,矩形ABC′D′的面积为84,则图中阴影部分的面积为 .20.(2022•鹿城区二模)如图1是一种彭罗斯地砖图案,它是由形如图2的两种“胖”“瘦”菱形拼接而成(不重叠、无缝隙),则图2中的∠α为 度.21.(2022•永嘉县校级一模)如图,若∠1+∠2+∠3+∠4=278°,则∠5+∠6+∠7+∠8= .22.(2022•温州模拟)如图,菱形ABCD的面积为20,AB=5,AE⊥CD于E,连结BD,交AE于F,连结CF,记△AFD的面积为S,△BFC的面积为S,则S1S2的值为 .三.解答题(共8小题)23.(2022•瑞安市校级三模)如图,在平行四边形ABCD中,以BC为直径的半⊙O经过点A,交AD于点F,过点D作DE⊥AB,交BA的延长线于点E,连接CE.(1)求证:BC=CE;(2)连接EF,CF,若tanB=2,CD=5,求EF的长.24.(2022•鹿城区校级三模)如图,在正方形ABCD中,AB=6,E为AB的中点,连结CE,作CF⊥EC交射线AD于点F,过点F作FG∥CE交射线CD于点G,连结EG交AD 于点H.(1)求证:CE=CF.(2)求HD的长.(3)如图2,连结CH,点P为CE的中点,Q为AF上一动点,连结PQ,当∠QPC与四边形GHCF中的一个内角相等时,求所有满足条件的DQ的长.25.(2022•龙港市模拟)如图,在菱形ABCD中,∠ABC=80°,点E在BA的延长线上,对角线AC与BD交于点M,EM交AD于点F,且∠EFD=105°.(1)求∠E的度数.(2)求证:AM =AE .26.(2022•鹿城区校级二模)如图,在▱ABCD 中,点E 是边AB 的中点,连结DE 并延长,交CB 延长线于点F ,且DE 平分∠ADC .(1)求证:△ADE ≌△BFE .(2)若BF =5,EF =53,求△FCD 的面积.27.(2022•龙湾区模拟)如图,在矩形ABCD 中,AE ⊥BD 于点E ,交BC 边于点F .AG 平分∠DAF 交BD 于点G ,并经过CD 边的中点H .(1)求证:BG =AB .(2)求tan ∠HFC 的值.(3)若CF =255,试在BD 上找一点M (不与B ,D 重合),使直线MC 经过四边形DEFH 一边的中点,求所有满足条件的BM 的值.28.(2022•瓯海区模拟)如图,在Rt △ABC 中,∠BAC =90°,以AB 为一边构造▱ABDE ,DA ∥BC ,连结EC 交DA 的延长线于点F ,DF ⊥EC ,延长EA 交BC 于点G .(1)求证:点A 是EG 的中点.(2)若tan ∠ABC =12,DA =6,求BC 的长.29.(2022•鹿城区二模)如图1,在矩形ABCD中,AB=3,AD=4.P为对角线BD上的点,过点P作PM⊥AD于点M,PN⊥BD交BC于点N,Q是M关于PD的对称点,连结PQ,QN.(1)如图2,当Q落在BC上时,求证:BQ=MD.(2)是否存在△PNQ为等腰三角形的情况?若存在,求MP的长;若不存在,请说明理由.(3)若射线MQ交射线DC于点F,当PQ⊥QN时,求DF:FC的值.30.(2022•鹿城区校级二模)在四边形ABCD中,AD=BC=1,AB=CD=2,BD= 5.点E为线段BD上一动点(不与点B,D重合),连结AE,过E作CE的垂线交边AB 于点F.(1)求证:四边形ABCD是矩形.(2)设DE=x,求△AEF的面积S关于x的函数表达式.(3)在点E运动过程,当△AEF的某一个内角等于∠BDC时,求所有满足条件的AF 的长.2023年浙江省温州市中考数学专题练——7四边形参考答案与试题解析一.选择题(共15小题)1.(2022•温州校级模拟)如图,菱形ABCD 中,过点C 作CE ⊥BC 交BD 于点E ,若∠BAD =118°,则∠CEB =( )A .59°B .62°C .69°D .72°【解答】解:∵四边形ABCD 是菱形,∴AB =AD ,∠ABD =∠CBE ,∴∠ABD =∠ADB ,∵∠BAD =118°,∴∠ABD =180°―118°2=31°,∴∠CBE =31°,∵CE ⊥BC ,∴∠BCE =90°,∴∠CEB =90°﹣31°=59°.故选:A .2.(2022•乐清市三模)如图,在正方形ABCD 内有一点E ,∠AEB =90°,以CE ,DE 为邻边作▱CEDF ,连结EF ,若A ,E ,F 三点共线,且△ADF 的面积为10,则CF 的长为( )A .2B .5C .22D .10【解答】解:设EF 、CD 的交点为G ,过E 作EH ⊥AD 交于H ,∵四边形ECFD 是平行四边形,∴DG =CG =12DG ,设正方形的边长为2x ,则AD =AB =CD =2x ,DG =CG =x ,∵∠AEB=90°,∴∠BAE+∠DAE=90°,∵∠ABE+∠BAE=90°,∴∠BAE=∠DAE,∴△ABE∽△GAD,∴ABAG=AEDG,即2x5x=AEx,∴AE=255x,∴EG=355x,∴EGAG=35,∴S△ADGS△DEG=53,设S=5m,则S=3m,∵G点是CD的中点,∴S=S=3m,∴S=6m,∵S=S=6m,∴S=12m,∴S=6m,∴S=6m+2m=8m,∵S=10,∴8m=10,∴m=5 4,∴S=5m=254=x,∴x=5 2,∴AD=5,EA=5,∵S=12×5×HE=52,∴HE=1,在Rt△AHE中,AH=2,∴HD=3,故选:D .3.(2022•鹿城区校级三模)如图,以Rt △ABC 各边为边向外做正方形,把三个正方形如图2叠放,图2中①号L 型和②号L 型面积分别为1和4,则图1中sin ∠ABC 的值为( )A .12B .25C .55D .66【解答】解:设AB =c ,BC =a ,AC =b ,由题意得,①号L 型面积=c ﹣a =1,②号L 型面积=a ﹣b =4,两式相加得:c ﹣b =5,在Rt △ABC 中,由勾股定理得:c ﹣b =a ,∴a =5,∴b =1,c =6,∴sin ∠ABC =AC AB =b c =16=66.故选:D .4.(2022•洞头区模拟)由四个全等的矩形围成了一个大正方形ABCD ,如图所示.连结CH ,延长EF 交CH 于点G ,作PG ⊥CH 交AB 于点P ,若AH =2DH ,则AP BP 的值为( )A .97B .1611C .32D .2【解答】解:设DH =x ,则AK =FH =x ,AH =BK =FK =2x ,CD =3x ,∵PG ⊥CH ,∴∠FGP+∠HGF =90°,∵∠HGF+∠FHG =90°,∴∠FGP =∠FHG ,由矩形的性质可得CD ∥FH ,∴∠DCH =∠FHG ,∴∠DCH =∠FHG =∠FGP ,∵tan ∠DCH =DH CD =x 3x =13,∴tan ∠FHG =FG FH=FG x =13,解得FG =13x ,∴KG =KF+FG =2x +13x =73x ,∴tan ∠FGP =13=KP KG =KP73x,解得KP =79x ,∴AP =AK+KP =x +79x =169x ,BP =BK ﹣KP =2x ―79x =119x ,∴APBP=169x119x=1611.故选:B.5.(2022•永嘉县模拟)如图1,矩形方框内是一副现代智力七巧板,它由两个相同的半圆①和⑦、等腰直角三角形②、角不规图形③、直角梯形④、圆不规图形⑤、圆⑥组成,已知AJ=BK.为庆祝北京冬奥会,小明将这个智力七巧板拼成一个滑冰运动员的图案,如图2所示,若AB平行地面MN,AJ=2,则该图案的高度是( )A.8B.9―22C.7+2D.10―2【解答】解:如图,作RP⊥AB,OT⊥MN,RQ⊥OT,由已知可得③⑤⑥的高度都为2,MN是半圆⑦的切线,∵∠KBA=45°,∴∠GBC=45°=∠HGB,即直角梯形④的锐角为45°,∴∠PRO=∠ORQ=45°,∵点B到HG 距离为2,∴RP=2,∵半圆⑦的直径为2,∴OR=1,OQ=22OR=22,∴QT=1―2 2,∴高度为6+PR+QT=9―2 2;故选:B.6.(2022•瑞安市二模)如图,在△ABC中,∠ACB=90°,分别以AC,BC为边向外作正方形ACDE与正方形BCFG,H为EG的中点,连结DH,FH.记△FGH的面积为S,△CDH的面积为S,若S﹣S=6,则AB的长为( )A.26B.32C.33D.42【解答】解:过F作FT⊥CG于T,过D作DK⊥EC于K,如图:设BC=a,AC=b,则CG=2a,EC=2b,∴EG=2(a+b),∵H为EG的中点,∴HG=HE=22(a+b),∴CH=HE﹣EC=22(a﹣b),∵FT=12CG=22a,DK=12EC=22b,∴S=12HG•FT=12×22(a+b)×22a=14a+14ab,S=12CH•DK=12×22(a﹣b)×22b=14ab―14b,∵S﹣S=6,∴14a+14ab﹣(14ab―14b)=6,∴14a+14b=6,∴a+b=24,即BC+AC=24,∴AB=24,∴AB=26,故选:A.7.(2022•文成县一模)如图▱ABCD中,AB=4,BD=6,BD⊥AB,则AC的长为( )A.10B.213C.5D.25【解答】解:∵▱ABCD的对角线AC与BD相交于点O,∴BO=DO,AO=CO,∵BD=6,∴BO=3,∵AB⊥BD,AB=4,∴AO=42+32=5,∴AC=2OA=10,故选:A.8.(2022•温州模拟)在数学拓展课上,小华同学将正方形纸片的顶点A,B,C,D与各边的中点E,F,G,H分别连结,形成四边形MNST,直线MS,TN与正方形ABCD各边相交构成一个如图的“风车”图案.若正方形的边长为25,则阴影部分面积之和为( )A.43B.2C.355D.2105【解答】解:如图,∵四边形ABCD是正方形,∴AB=BC=CD=25,AB∥CD,∠ABC=∠BCD=90°,∵E是BC的中点,F是CD的中点,∴BE=CF=12BC=5,由勾股定理得:AE=AB2+BE2=(25)2+(5)2=5,同理得:DH=5,∵AB=BC,∠ABC=∠BCF=90°,BE=CF,∴△ABE≌△BCF(SAS),∴∠BAE=∠CBF,∵∠BAE+∠AEB=90°,∴∠CBF+∠AEB=90°,∴∠BME=90°,同理得∠ATH=90°,tan∠TAH=BEAB=THAT=12,∵AH=5,∴TH=1,AT=2,∴△ATH的面积=12×1×2=1,DT=5﹣1=4,∵CD∥AB,∴DQPH=DTTH=41=4,设PH=x,则FQ=x,DQ=4x,∴DF=AH=3x,∴S△ATHS△PTH=AHPH=3xx=3,∴S=1 3,∴阴影部分面积之和为4S =43.故选:A .9.(2022•瑞安市一模)由四个全等的直角三角形和一个小正方形组成的大正方形ABCD 如图所示,延长AH 交CD 于点P ,若AP ⊥HF ,AP =52,则小正方形边长GF 的长是( )A .52B .22C .3D .10【解答】解:∵△ADE ≌△DCH ≌△CBG ≌△BAF ,∴AE =DH ,DE =CH ,∵四边形GFEH 是正方形,∴EH =EF =HG =GF ,∠HFA =45°=∠EHF ,∵AP ⊥HF ,∴∠FAH =∠AFH =45°=∠AHE ,∴AH =FH ,AE =HE ,∴AF =2AE ,设AE =a ,则AF =DE =2a ,如图过点H 作HM ⊥AD 于M ,∴AD =AE 2+DE 2=5a ,∵∠DMH =∠AED =90°,∠ADE =∠MDH ,∴△AED ∽△HMD ,∴DH AD =MH AE ,∴MH =55a ,DM =255a ,∴AM =AD ﹣DM =355a ,∵AD ⊥CD ,∴MH ∥DP ,∴AH HP =AM DM =32,∵AP =52,∴AH =32,∴EH =3=GF ,故选:C .10.(2022•龙港市一模)矩形纸片ABCD 按如图1的方式分割成三个直角三角形①,②,③,又把这三个直角三角形按如图2的方式重叠放置在一起,其中直角三角形①的斜边一端点恰好落在直角三角形②的斜边上,若BD =5,则图2中CP 的长为( )A .45B .35C .34D .32【解答】解:如图1,设AB =2a ,∵四边形ABCD 是矩形,∴AB =CD =2a ,AD =BC ,∠BAD =90°,AB ∥CD ,∴AD =BD 2―AB 2=25―4a 2,∠ABD =∠BDC ,如图2,HP =AB =2a ,QN =AD =25―4a 2,MN =BD =5,MP =BE ,∴∠MPH =∠NMP ,∠HMP =90°,∴MQ =PQ ,∠H =∠HMQ ,∴HQ =MQ ,∴HQ =HQ =PQ =a ,∴25―4a 2+a =5,∴a =2,a =0(舍去),∴AB =4,AD =3,如图1,∵cos∠ABD=BEAB=ABBD,∴BE4=45,∴BE=165=MP,∴PC=4―165=45,故选:A.11.(2022•瓯海区一模)如图把两张宽度均为3的纸条交错叠在一起,相交成角α,则重叠部分的周长为( )A.12tanαB.12sinαC.12sinαD.12tanα【解答】解:由题意可知:重叠部分是菱形,设菱形ABCD,则∠ABE=α,过A作AE⊥BC于E,则AE=3,∵∠ABE=α,∴AB=AEsinα=3sinα,∴BC=AB=AD=CD=3sinα,∴重叠部分的周长=4×3sinα=12sinα,故选:C.12.(2022•温州模拟)如图,在正方形ABCD中,延长DC至点G,以CG为边向下画正方形CEFG.延长AB交边FG于点H,连结CF,AF分别交AH,CE于点M,N.收录在清朝四库全书的《几何通解》利用此图得:2AB+2BH=AH+MH.若正方形ABCD与CEFG的面积之和为68,CN =3NE ,则AH 的长为( )A .42B .8C .82D .16【解答】解:∵四边形ABCD 和四边形CEFG 是正方形,延长AB 交边FG 于点H ,∴AB ∥EF ,∴△ABN ∽△FEN ,∴AB EF =BN NE ,设AB =a ,CG =b ,∵CN =3NE ,∴NE =14b ,CN =34b ,∴BN =CN ﹣CB =34b ﹣a ,∴a b =34b ―a 14b ,∴b =53a ,∵正方形ABCD 与CEFG 的面积之和为68,∴a+b =68,∴a+(35a )=68,解得a =32,∴b =52,∴a+b =82,则AH 的长为82.故选:C .13.(2022•乐清市一模)如图,在▱ABCD 中,AB =BE ,∠C =70°,则∠BAE 的度数为( )A .35°B .45°C .55°D .65°【解答】解:∵四边形ABCD是平行四边形,∴∠BAD=∠C=70°,AD∥BC,∴∠BEA=∠DAE,∵AB=BE,∴∠BEA=∠BAE,∴∠BAE=∠DAE=12∠BAD=12×70°=35°,故选:A.14.(2022•鹿城区校级一模)如图,在△ABC中以AC,BC为边向外作正方形ACFG与正方形BCDE,连结DF,并过C点作CH⊥AB于H并交FD于M.若∠ACB=120°,AC =3,BC=2,则MD的长为( )A.72B.2C.32D.3【解答】解:如图所示,过D作DN⊥CF于点N,作DP⊥HM于点P,过点F作FQ⊥HM,交HM的延长线于点Q,∵∠ACB=120°,∠ACF=∠BCD=90°,∴∠DCN=60°,∠CDN=30°,又∵BC=DC=2,AC=FC=3,∴CN=12CD=1,FN=CF﹣CN=3﹣1=2,DN=CD2―CN2=3,Rt△DFN中,DF=FN2+DN2=22+(3)2=7.∵四边形BCDE是正方形,∴BC=CD,∠BCD=90°,又∵CH⊥AB,∴∠DCP+∠BCH=∠CBH+∠BCH=90°,∴∠DCP=∠CBH,又∵∠DPC=∠BHC=90°,∴△DCP≌△CBH(AAS),∴DP=CH,同理可得△ACH≌△CFQ,∴FQ=CH,∴FQ=DP,又∵∠Q=∠DPM=90°,∠FMQ=∠DMP,∴△FQM≌△DPM(AAS),∴FM=DM,即M是FD的中点,∴DM=12DF=72.故选:A.15.(2021•温州模拟)如图,矩形ABCD中,AB:AD=2:1,点E为AB的中点,点F 为EC上一个动点,点P为DF的中点,连接PB,当PB的最小值为32时,则AD的值为( )A.2B.3C.4D.6【解答】解:如图,当点F与点C重合时,点P在P处,CP=DP,当点F与点E重合时,点P在P处,EP=DP,∴PP∥CE且PP=12 CE.且当点F在EC上除点C、E的位置处时,有DP=FP.由中位线定理可知:PP∥CE且PP=12 CF,∴点P的运动轨迹是线段PP,.∴当BP⊥PP时,PB取得最小值.∵矩形ABCD中,AB:AD=2:1,设AB=2t,则AD=t,∵E为AB的中点,∴△CBE、△ADE、△BCP为等腰直角三角形,CP=t,∴∠ADE=∠CDE=∠CPB=45°,∠DEC=90°.∴∠DPP=90°.∴∠DPP=45°.∴∠PPB=90°,即BP⊥PP,∴BP的最小值为BP的长.在等腰直角△BCP中,CP=BC=t,∴BP=2t=32,∴t=3.故选:B.二.填空题(共7小题)16.(2022•永嘉县三模)如图,在正方形ABCD中,BC=6,点P在正方形内,PF⊥PC,交边AD于点F,ED∥PC,交PF延长线于点E,且PC=PE,连结AP,AE.若五边形AEDCP的面积为24,则∠AEP的度数为 45° ,PC的长为 26 .【解答】解:过C作CG⊥ED于G,过A作AM⊥DE于M,AN⊥PE于N,连结PB,∵PF⊥PC,ED∥PC,PC=PE,CG⊥ED,∴四边形PCGE是正方形,∴PC=PE=CG=EG,∠PCG=90°,∵正方形ABCD,∴BC=CD=AD=AB,∠BCD=90°,∴∠PCB=∠DCG=90°﹣∠PCD,∴△DCG≌△BCP(SAS),∴∠DGC=∠BPC=90°,∴∠CPE+∠BPC=180°,∴E、F、P、B四点在一条直线上,∴∠PCB=∠DCG=∠ABN=∠ADM,∵AM⊥DE于M,AN⊥PE,∴四边形AMEN是矩形,∴△ABN≌△ADM(AAS),∴AM=AN,∴矩形AMEN是正方形,AE平分∠MEN,∴∠AEP=45°,AM=AN=EM,设AM=AN=EM=x,PC=PE=CG=EG=y,∵∠DCG=∠ADM,∴△DCG≌△ADM(AAS),∴AM=AN=DG=PB=x,∵S五边形AEDCP=S正方形PCGE+S△APE―S△DGC=PC2+12AN⋅PE―12DG⋅CG,∴24=y2+12xy―12xy,∴y=26,即PC=26.17.(2022•永嘉县三模)如图,在平行四边形ABCD中,AB=6,BC=8,∠B=30°,点E从点D出发沿DC方向匀速向终点C运动,同时点F从点C出发沿CB方向匀速向终点B运动,它们同时到达终点,记ED=x,则△CEF的面积为 ―13x2+2x (用含x的代数式表示).【解答】解:∵平行四边形ABCD,AB=6,BC=8,∴CD=AB=6,又∵点E和点F分别同时从点D和点C出发,同时到达终点,∴点E和点F的路程比为6:8=3:4,又∵DE=x,∴CE=6﹣x,CF=43 x,如图,△CEF中,过点E作边CF上的高EH,交CF的反向延长线于点H,∵AB∥CD,∠B=30°,∴∠DCH=∠B=30°,∴在△CHE中,EH=12CE=6―x2,∴S△CEF=12CF⋅EH=12×43x×6―x2=―13x2+2x,故答案为:―13x2+2x.18.(2022•鹿城区校级二模)如图,在平面直角坐标系xOy中,▱ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限,将△AOD沿y轴翻折,使点A落在x轴上的点E处,BE=2OB,DE与BC交于点F.若y=kx(k≠0)图象经过点C,且S=4,则k的值为 12 .【解答】解:如图,连接OC,BD,∵将△AOD沿y轴翻折,使点A落在x轴上的点E处,∴OA=OE,∵BE=2OB,∴OE=3OB,∴OA=3OB,设OB=x,则OA=3x,AB=4x,∵四边形ABCD是平行四边形,∴CD=AB=4x,∵CD∥AB,∴△CDF∽△BEF,∴BECD=2x4x=12=BFCF,∵S=4,∴S=2,∴S=4+2=6,∵CD∥AE,∴S=S=6,即12|k|=6,而k>0,∴k=12.故答案为:12.19.(2022•龙湾区模拟)如图,点E,F,G,H分别是矩形ABCD各边上的中点,将矩形ABCD 向右平移得矩形A′B′C′D′,点E,F,G,H的对应点分别为点E′,F′,G′,H′.若AD′=7HH′,矩形ABC′D′的面积为84,则图中阴影部分的面积为 29 .【解答】解:如图所示,连接EG′,由平移的性质可知:AA′=HH'=DD',AD′∥EG′,∵AD′=7HH′,∴A′D=5HH′,∵H是AD的中点,∴AH=12AD=3HH′,∴A′H=2HH′,∵A′H∥EE′,∴△A′HP∽△E′EP,∴E′PA′P=EE′A′H=12,∴PE′=13A′E′,∴S=16 S,同理可证△HH′Q~ΔGE′Q,设AGEQ边EG上的高为h,HHQ边HH上的高为h,∴hh1=E′GH′H=5,∴h=56 DG,∴S=512S,∵矩形ABC′D′的面积为84,∴矩形AA′B′B的面积为12,矩形A′DCB′的面积为60,∵、E、G、H、F分别是对应边的中点,∴由对称性可知S=4S+2S=4×12×12×16+2×12x60x512=29.故答案为:29.20.(2022•鹿城区二模)如图1是一种彭罗斯地砖图案,它是由形如图2的两种“胖”“瘦”菱形拼接而成(不重叠、无缝隙),则图2中的∠α为 36 度.【解答】解:如图,∵∠DEP=∠DAP=360°5=72°,∠CAB=(10―2)×180°10=144°,∴α=144°―72°2=36°.故答案为:36.21.(2022•永嘉县校级一模)如图,若∠1+∠2+∠3+∠4=278°,则∠5+∠6+∠7+∠8= 442° .【解答】解:如图,∵∠1+∠2+∠3+∠4=278°,∴∠9+∠DCE=180°+180°﹣278°=82°,∴∠CAB+∠ACB=∠9+∠DCE=82°,∴∠NBM=∠ABC=180°﹣82°=98°,∴∠5+∠6+∠7+∠8=(5﹣2)×180°﹣98°=442°,故答案为:442°.22.(2022•温州模拟)如图,菱形ABCD的面积为20,AB=5,AE⊥CD于E,连结BD,交AE于F,连结CF,记△AFD的面积为S,△BFC的面积为S,则S1S2的值为 35 .【解答】解:∵菱形ABCD的面积为20,AB=5,AE⊥CD于E,∴5AE=20,∴AE=4,∴DE=AD2―AE2=52―42=3,∵AB∥CD,∴△ABF∽△EDF,∴AFEF=BFDF=ABED=53,∴S1=58S△ADE=58×12×3×4=154,S2=58S△BCD=58×12×20=254,∴S1S2=154×425=35,故答案为:3 5.三.解答题(共8小题)23.(2022•瑞安市校级三模)如图,在平行四边形ABCD中,以BC为直径的半⊙O经过点A,交AD于点F,过点D作DE⊥AB,交BA的延长线于点E,连接CE.(1)求证:BC=CE;(2)连接EF,CF,若tanB=2,CD=5,求EF的长.【解答】(1)证明:∵BC为直径,∴∠BAC=90°,∴AC⊥AB,∵DE⊥AB,∴AC∥DE,∵四边形ABCD是平行四边形,∴AB∥CD,AD=BC,∴四边形ACDE是矩形,∴CE=AD,∵AD=BC,∴BC=CE;(2)过点C作CG⊥AD于点G,过点F作FH⊥DE于点H,在平行四边形ABCD中,∠B=∠ADC,∵四边形ABCF内接于⊙O,∴∠DFC=∠B,∴∠ADC=∠DFC,∴CF=CD,∵CD=5,tan∠ADC=CGDG=ACCD=tanB=2,∴DG=1,AC=25,∴DF=2DG=2,∵∠FDH+∠ADC=90°,∠ADC+∠DCG=90°,∴∠FDH=∠DCG,又∠FHD=∠DGC=90°,∴△FDH∽△DCG,∴FHDG=DHCG=DFCD,∴FH=255,DH=455,∴EH=65 5,∴EF=EH2+FH2=22.24.(2022•鹿城区校级三模)如图,在正方形ABCD中,AB=6,E为AB的中点,连结CE,作CF⊥EC交射线AD于点F,过点F作FG∥CE交射线CD于点G,连结EG交AD 于点H.(1)求证:CE=CF.(2)求HD的长.(3)如图2,连结CH,点P为CE的中点,Q为AF上一动点,连结PQ,当∠QPC与四边形GHCF中的一个内角相等时,求所有满足条件的DQ的长.【解答】(1)证明:∵四边形ABCD为正方形,∴BC=CD=AB=6,∠ABC=∠BCD=∠ADC=∠CDF=90°.∵CF⊥EC,∴∠ECF=90°,∴∠DCF+∠ECD=90°,∴∠BCE+∠ECD=90°,∴∠BCE=∠DCF,∴△BCE≌△DCF(ASA),∴CE=CF.(2)解:∵E为AB的中点,AE=6,∴AE=BE=3,∴tan∠BCE=BEBC=36=12,∵GF∥EC,CF⊥EC,∴GF⊥CF,∴∠GFC=90°,∵∠GDF=∠ADC=90°,∴∠GFD+∠DGF=∠DCF+∠DGF=90°,∴∠GFD=∠DCF=∠BCE,∴tan∠GFD=tan∠DCF=tan∠ECB=1 2,∵tan∠GFD=DGDF=12,∴DG=12 DF,由(1)可知,△BCE≌△DCF,∴BE=DF=3,∴DG=3 2,∵四边形ABCD是正方形,∴AD=AB=6,AB∥CD,∴△AEH∽△DGH,∴AHDH=AEDG=332=2,∴AH=2HD,∴HD=13AD=2;(3)解:∵HD=2,DF=3,∴FH=5,AH=AD﹣HD=4,∵四边形ABCD是正方形,∴∠A=90°,∴EH=AE2+AH2=32+42=5,∴EH=FH,∵CE=CF,CH=CH,∴△ECH≌△FCH(SSS),∴∠ECH=∠FCH=12×90°=45°,∠HEC=∠HFC.分三种情况:①如图2,∠QPC=∠GFC=90°时,则PQ⊥EC,∵CF⊥EC,∴PQ∥CF,∴∠AQP=∠DFC,∴tan∠AQP=PMQM=tan∠DFC=CDDF=63=2,∴QM=12 PM,过点P作MN⊥AD于点M,则PN∥AB,∵P为CE的中点,∴M为AD的中点,N为BC的中点,∴MD=12AD=3,PN是△BCE的中位线,∴PN=12BE=32,∴PM=6―32=92,∴QM=9 4,∴DQ=MD―QM=3―94=34;②如图3,∠QPC=∠HGF时,∵GF∥EC,∴∠HGF+∠HEC=180°,∵∠QPC+∠QPE=180°.∠QPC=∠HGF,∴∠QPE=∠HEC,由(2)可知,△ECH≌△FCH,∴∠HEC=∠HFC,∴∠QPE=∠HFC=∠BEC,∴PQ∥AB,∵P为CE的中点,∴Q为AD的中点,∴DQ=12AD=3;③如图4,∠QPC=∠GHC时,∵HD=2,DC=6,∠ADC=90°,∴tan∠DHC=CDHD=62=3.由(2)可知,△ECH≌△FCH,∴∠HEC=∠HFC,∠EHC=∠FHC,∵∠QPC=∠GHC,∴∠EHC=∠QPE=∠FHC,∴∠EMP=∠ECH=45°,tan∠QPE=tan∠DHC=3.过点M作MN⊥EP于点N,∵tan∠QPE=MNNP=3,∴MN=2NP,设NP=a,则MN=3a,∵tan∠HEC=MNEN=tan∠HFC=CDDF=2,∴EN=12MN=32a,∵∠ABC=90°,BC=6,BE=3,∴CE=BC2+BE2=62+32=35,∵P为CE的中点,∴EP=12CE=352,∵EN+NP=EP,∴32a+a=352,解得:a=35 5,∴MN=955,EN=9510,∴EM=MN2+EN2=(955)2+(9510)2=92,∴MH=EH﹣EM=5―92=12,在△QMH中,过点Q作QJ⊥MH于点J,则△MQJ是等腰直角三角形,tan∠QHJ=QJJH=AEAH=34,设QJ=3b,∴JH=4b,MJ=QJ=3b,∵MJ+JH=MH,∴3b+4b=1 2,解得:b=1 14,∴QJ=314,JH=414=27,∴QH=QJ2+JH2=(314)2+(27)2=514,∴DQ=HD+QH=2+514=3314;综上所述,DQ的长为34或3或3314.25.(2022•龙港市模拟)如图,在菱形ABCD中,∠ABC=80°,点E在BA的延长线上,对角线AC与BD交于点M,EM交AD于点F,且∠EFD=105°.(1)求∠E的度数.(2)求证:AM=AE.【解答】(1)解:∵四边形ABCD是菱形,∴AD∥BC,∴∠EAD=∠ABC=80°,∴∠E=∠EFD﹣∠EAD=105°﹣80°=25°.(2)证明:∵四边形ABCD是菱形,∴∠DAB=180°﹣∠B=100°,AC平分∠DAB,∴∠BAC=12∠DAB=50°,∴∠AME=∠BAC﹣∠E=50°﹣25°=25°=∠E,∴AM=AE.26.(2022•鹿城区校级二模)如图,在▱ABCD中,点E是边AB的中点,连结DE并延长,交CB延长线于点F,且DE平分∠ADC.(1)求证:△ADE≌△BFE.(2)若BF=5,EF=53,求△FCD的面积.【解答】(1)证明:在▱ABCD中,AD∥BC,∴∠ADF=∠F,∠A=∠ABF,∵点E是边AB的中点,∴AE=BE,在△ADE和△BFE中,∠ADF=∠F∠A=∠ABFAE=BE,∴△ADE≌△BFE(AAS);(2)解:连结CE,如图所示:∵△ADE≌△BFE,∴DE=EF,AD=BF=5,∵四边形ABCD是平行四边形,∴BC=AD=5,∵DE平分∠ADC,∴∠ADF=∠CDF,∵AD∥BC,∴∠ADF=∠F,∴∠CDF=∠F,∴CD=CF=10,∴△DCF是等腰三角形,∵E是DF的中点,∴CE⊥DF,∵DE=EF=53,在Rt△DEC中,根据勾股定理,得CE=5,∵DF=2EF=103,∴S△FCD=DF×CE2=103×52=253,∴△DCF的面积为253.27.(2022•龙湾区模拟)如图,在矩形ABCD中,AE⊥BD于点E,交BC边于点F.AG 平分∠DAF交BD于点G,并经过CD边的中点H.(1)求证:BG=AB.(2)求tan∠HFC的值.(3)若CF=255,试在BD上找一点M(不与B,D重合),使直线MC经过四边形DEFH一边的中点,求所有满足条件的BM的值.【解答】(1)证明:∵AE⊥BD,∴∠AEB=90°,∴∠1+∠2=90°,∵∠BAD=90°,∴∠2+∠5=90°,∴∠1=∠5,∵AG平分∠BAE,∴∠3=∠4,∵∠BAG=∠1+∠3,∠BGA=∠4+∠5,∴∠BAG=∠BGA,∴AB=BG,(2)解:∵H为CD中点,∴设DH=CH=a,CD=AB=2a,由(1)知BG=AB,∴BG=2a,又∵AB∥CD,∴∠BAH=∠DHA,∵∠BGA=∠DGH=∠BAH,∴∠DGH=∠DHA,∴DG=DH=a,∴BD=3a,∴BC=AD=BD2―AB2=5a,又∵S=12AB×AD=12AE×BD,∴AE=AB×ADBD=2a×5a3a=235a,∴BE=AB2―AE2=43 a,DE=BD﹣BE=53 a,∵AD∥BC,∴△AED∽△FEB,∴BFAD=BEDE=45,∴BF=45AD=455a,∴CF=BC﹣BF=55 a,在Rt△HFC中,∠HCF=90°,∴tan∠HFC=HCCF=a55a=5;(3)若CF=255,则55a=255,∴a=2,∴AB=CD=2x2=4,BD=3a=6,BE=83,DE=103,BF=855,CH=DH=2=DG,分三种情况:①当M为DE中点时,即CM平分ED,此时DM=12DE=53,∴BM=6―53=133,②当CM平分EF时,如图所示,设EF中点为O,过F作FN∥BD交CM于N,∴△EOM∽△FON,∴EOOF=MENF=1,∴ME=NF,∵FN∥BM,∴△CNF∽△CMB,∴NFBM=CFBC=25525=15.∴NF=15BM,又EM=MF,EM+BM=BE=83,∴65BM=83,∴BM=20 9,③当CM平分FH时,设FH的中点为I,过M作从MN⊥BC于N,∴∠MNB=∠BCD=90°,∵∠MBN=∠DBC,∴△MBN∽△DBC,∴MN=25 BN,∵I为EH中点,∴CI=IF=IH,∴∠IFC=∠ICF,tan∠MCN=tan∠HFC=5,又在Rt△MNC中,MNCN=tan∠MCN=5,∴MN=5CN,∴25BN=5CN,∴2BN=5CN,又∵BN+CN=BC=25,∴BN=1075,CN=475,∴MN=5a=20 7,∴BM=BN2+MN2=30 7,综上:BM=307,或209,或133.28.(2022•瓯海区模拟)如图,在Rt△ABC中,∠BAC=90°,以AB为一边构造▱ABDE,DA∥BC,连结EC交DA的延长线于点F,DF⊥EC,延长EA交BC于点G.(1)求证:点A是EG的中点.(2)若tan∠ABC=12,DA=6,求BC的长.【解答】(1)证明:∵四边形ABDE是平行四边形,∴BD∥AE,BD=AE,∴BD∥AG,∵DA∥BG,∴四边形ADBG是平行四边形,∴BD=AG,∴AE=AG,∴点A是EG的中点;(2)解:∵四边形ADBG是平行四边形,∴BG=DA=6,∵DA∥BC,DF⊥EC,∴BC⊥EC,∴∠ECG=90°,由(1)可知,点A是EG的中点,∴AC=12EG=AG,∴∠ACG=∠AGC,∵∠BAC=90°,∴∠BAC=∠ECG,∴△BAC∽△ECG,∴ACAB=CGCE,∵tan∠ABC=ACAB=12,∴CGCE=12,设AC=a,则AB=2a,EG=2AC=2a,设CG=b,则CE=2b,∵CE+CG=EG,即(2b)+b=(2a),∴b=255a,∵AB+AC=BC,即(2a)+a=(6+255a),解得:a=25,∴BC=6+255×25=10.29.(2022•鹿城区二模)如图1,在矩形ABCD中,AB=3,AD=4.P为对角线BD上的点,过点P作PM⊥AD于点M,PN⊥BD交BC于点N,Q是M关于PD的对称点,连结PQ,QN.(1)如图2,当Q落在BC上时,求证:BQ=MD.(2)是否存在△PNQ为等腰三角形的情况?若存在,求MP的长;若不存在,请说明理由.(3)若射线MQ交射线DC于点F,当PQ⊥QN时,求DF:FC的值.【解答】(1)证明:如图1,连结DQ.在矩形ABCD中,AD∥BC,∴∠ADB=∠DBC.∵Q是M关于PD的对称点,∴∠ADB=∠BDQ,MD=QD,∴∠DBC=∠BDQ,∴QD=BQ,∴BQ=MD.(2)(I)如图2,当NP=NQ时,设PN=3a,则BP=4a,MP=PQ=245a,∴PD=53MP=8a,∴BD=BP+PD=4a+8a=5,∴a=5 12,∴MP=2;(II)如图3,当PQ=PN时,设PN=3a,则BP=4a,MP=PQ=3a,∴PD=53MP=5a,∴BD=BP+PD=4a+5a=5,∴a=5 9,MP=5 3.(Ⅲ)如图4,当QP=QN时,设PN=3a,则BP=4a,MP=PQ=158a,∴PD=258a,∴BD=BP+PD=4a+258a=5,∴a=40 57,∴MP=25 19.(3)如图5,设PN=3a,则BP=4a,MP=PQ=125a,∴PD=4a,∴BD=BP+PD=8a=5,∴a=5 8,∴MP=3 2,∴MD=43MP=2,∴DF=43MD=83,FC=13,∴DF:FC=8.30.(2022•鹿城区校级二模)在四边形ABCD中,AD=BC=1,AB=CD=2,BD= 5.点E为线段BD上一动点(不与点B,D重合),连结AE,过E作CE的垂线交边AB 于点F.(1)求证:四边形ABCD是矩形.(2)设DE=x,求△AEF的面积S关于x的函数表达式.(3)在点E运动过程,当△AEF的某一个内角等于∠BDC时,求所有满足条件的AF 的长.【解答】(1)证明:∵AD=BC,AB=CD,∴四边形ABCD是平行四边形,∵AD=1,AB=2,BD=5,∴AD+AB=BD,∴∠DAB=90°,∴四边形ABCD是矩形;(2)过点E作EJ⊥AB于点J,交CD于点K.∵四边形ABCD是矩形,∴∠DAJ=∠ADK=∠AJK=90°,∴四边形ADKJ是矩形,∴AJ=DK,AD=JK,AD∥JK∥BC,∴DEDB=EKCB=DKCB,∴x5=EK1=DK2,∴EK=55x,DK=255x,∴EJ=JK=EK=1―55 x,∵EF⊥EC,∴∠EJF=∠FEC=∠EKC=90°,∴∠JEF+∠CEK=90°,∠CEK+∠ECK=90°,∴∠JEF=∠ECK,∴△EJF∽△CKE,∴EJCK=JFEK,∴1―55x2―255x=JF55x,∴JF=510x,∴AF=AJ+JF=255x+510x=52x,∴S=12•AF•EJ=12×52x×(1―55x)=―14x+54x(0<x<5);(3)当∠EAF=∠CDB时,∵AB∥CD,∴∠CDB=∠ABD,∴∠EAB=∠EBA,∴EA=EB,∵∠DAE+∠EAB=90°,∠ADE+∠ABE=90°,∴∠DAE=∠ADE,∴AE=DE,∴DE=EB=5 2,∴x=5 2,∴AF=52×52=54.当∠AEF=∠BDC=∠ABE时,∵∠EAF=∠EAB,∴△EAF∽△BAE,∴AE=AF•AB,∴(1―55x)+(255x)=52x×2,解得x=5±1 2,∴AF=52×5±12=5±54,、当∠AFE=∠BDC时,F与B重合,此时EC与BD垂直,此时AF=AB=2,综上所述,AF的长为34或5±54或2.。
2020年中考数学复习专题练:《四边形综合 》(包含答案)

2020年中考数学复习专题练:《四边形综合 》1.如图①所示,已知正方形ABCD 和正方形AEFG ,连接DG ,BE .(1)发现:当正方形AEFG 绕点A 旋转,如图②所示.①线段DG 与BE 之间的数量关系是 ;②直线DG 与直线BE 之间的位置关系是 ;(2)探究:如图③所示,若四边形ABCD 与四边形AEFG 都为矩形,且AD =2AB ,AG =2AE 时,上述结论是否成立,并说明理由.(3)应用:在(2)的情况下,连接BG 、DE ,若AE =1,AB =2,求BG 2+DE 2的值(直接写出结果).2.如图1,在正方形ABCD 中,点E 是CD 上一点(不与C ,D 两点重合),连接BE ,过点C 作CH ⊥BE 于点F ,交对角线BD 于点G ,交AD 边于点H ,连接GE ,(1)求证:△DHC ≌△CEB ;(2)如图2,若点E 是CD 的中点,当BE =8时,求线段GH 的长;(3)设正方形ABCD 的面积为S 1,四边形DEGH 的面积为S 2,当的值为时,的值为 .3.在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(6,0),点B(0,8).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F,记旋转角为α(0°<α<90°).(I)如图①,当α=30°时,求点D的坐标;(Ⅱ)如图②,当点E落在AC的延长线上时,求点D的坐标;(Ⅲ)当点D落在线段OC上时,求点E的坐标(直接写出结果即可).4.如图,BD是平行四边形ABCD的对角线,DE⊥AB于点E,过点E的直线交BC于点G,且BG=CG.(1)求证:GD=EG.(2)若BD⊥EG垂足为O,BO=2,DO=4,画出图形并求出四边形ABCD的面积.(3)在(2)的条件下,以O为旋转中心顺时针旋转△GDO,得到△G′D'O,点G′落在BC上时,请直接写出G′E的长.5.(1)【探索发现】如图1,在正方形ABCD中,点M,N分别是边BC,CD上的点,∠MAN=45°,若将△DAN 绕点A顺时针旋转90°到△BAG位置,可得△MAN≌△MAG,若△MCN的周长为8,则正方形ABCD的边长为.(2)【类比延伸】如图2,在四边形ABCD中,AB=AD,∠BAD=120°,∠B+∠D=180°,点M,N分别在边BC,CD上的点,∠MAN=60°,请判断线段BM,DN,MN之间的数量关系,并说明理由.(3)【拓展应用】如图3,在四边形ABCD中,AB=AD=2,∠ADC=120°,点M,N分别在边BC,CD上,连接AM,MN,AN,△ABM是等边三角形,AM⊥AD于点A,∠DAN=15°,请直接写出△CMN 的周长.6.(1)如图1,在△ABC中,AB>AC,点D,E分别在边AB,AC上,且DE∥BC,若AD=2,AE=,则的值是;(2)如图2,在(1)的条件下,将△ADE绕点A逆时针方向旋转一定的角度,连接CE 和BD,的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;(3)如图3,在四边形ABCD中,AC⊥BC于点C,∠BAC=∠ADC=θ,且tanθ=,当CD=6,AD=3时,请直接写出线段BD的长度.7.如图1,长方形ABCD中,∠DAB=∠B=∠DCB=∠D=90°,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,把△ADE沿直线AE翻折得△AD′E.(1)当D′点落在AB边上时,∠DAE=°;(2)如图2,当E点与C点重合时,D′C与AB交点F,①求证:AF=FC;②求AF长.(3)连接D′B,当∠AD′B=90°时,求DE的长.8.在平面直角坐标系中,点O是坐标原点,A(0,m),B(n,O),AC∥OB,且AC=OB,连接BC交x轴于点F,其中m、n满足方程+n2+8n+16=0.(1)求A、B两点坐标;(2)过A做AE⊥BC于E,延长AE交x轴于点D,动点P从点B出发以每秒2个单位的速度向x轴正半轴方向运动,设△PFD的面积为S,请用含t的式子表示S,并直接写出t的取值范围;(3)在(2)的条件下,连接PE,将△PED沿PE翻折到△PEG的位置(点D与点G对应),当四边形PDEG为菱形时,求点P和点G的坐标.9.已知四边形ABCD和四边形CEFG都是正方形,且AB>CE.(1)如图1,连接BG、DE.求证:BG=DE;(2)如图2,如果正方形CEFG绕点C旋转到某一位置恰好使得CG∥BD,BG=BD.①求∠BDE的度数;②若正方形ABCD的边长是,请求出△BCG的面积.10.【综合与实践】如图①,在正方形ABCD中,点E、F分别在射线CD、BC上,且BF=CE,将线段FA绕点F顺时针旋转90°得到线段FG,连接EG,试探究线段EG和BF的数量关系和位置关系.【观察与猜想】任务一:“智慧小组”首先考虑点E、F的特殊位置如图②,当点E与点D重合,点F与点C重合时,易知:EG与BF的数量关系是,EG与BF的位置关系是.【探究与证明】任务二:“博学小组”同学认为E、F不一定必须在特殊位置,他们分两种情况,一种是点E、F分别在CD、BC边上任意位置时(如图③);一种是点E、F在CD、BC边的延长线上的任意位置时(如图④),线段EG与BF的数量关系与位置关系仍然成立.请你选择其中一种情况给出证明.【拓展与延伸】“创新小组”同学认为,若将“正方形ABCD”改为“矩形ABCD,且=k(k≠1)”,点E、F分别在射线CD、BC上任意位置时,仍将线段FA绕点F顺时针旋转90°,并适当延长得到线段FG,连接EG(如图⑤),则当线段BF、CE、AF、FG满足一个条件时,线段EG与BF的数量关系与位置关系仍然成立.(请你在横线上直接写出这个条件,无需证明)11.在平面直角坐标系xOy中,四边形OADC为正方形,点D的坐标为(4,4),动点E沿边AO从A向O以每秒1cm的速度运动,同时动点F沿边OC从O向C以同样的速度运动,连接AF、DE交于点G.(1)试探索线段AF、DE的关系,写出你的结论并说明理由;(2)连接EF、DF,分别取AE、EF、FD、DA的中点H、I、J、K,则四边形HIJK是什么特殊平行四边形?请在图①中补全图形,并说明理由.(3)如图②当点E运动到AO中点时,点M是直线EC上任意一点,点N是平面内任意一点,是否存在点N使以O,C、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.12.综合与实践动手操作:第一步:在矩形纸片ABCD的边BC,AD上分别取两点E,F,使CE=AF;第二步:分别以DE,BF为对称轴将△CDE与△ABF翻折得到△C'DE与△A'BF,且边C'E 与A'B交于点G,边A'F与C'D交于一点H.问题解决:(1)求证:△BEG≌△DFH;(2)请判断四边形A'HC'G的形状,并证明你发现的结论;(3)已知tan∠EBG=,A'G=6,C'G=1,求矩形纸片ABCD的面积.13.如图1,矩形ABCD中,∠ACB=30°,将△ACD绕C点顺时针旋转α(0°<α<360°)至△A'CD'位置.(1)如图2,若AB=2,α=30°,求S△BCD′.(2)如图3,取AA′中点O,连OB、OD′、BD′.若△OBD′存在,试判定△OBD′的形状.(3)当α=α1时,OB=OD′,则α1=°;当α=α2时,△OBD′不存在,则α2=°.14.已知矩形ABCD 中,AB =2,BC =m ,点E 是边BC 上一点,BE =1,连接AE .(1)沿AE 翻折△ABE 使点B 落在点F 处,①连接CF ,若CF ∥AE ,求m 的值;②连接DF ,若≤DF ≤,求m 的取值范围.(2)△ABE 绕点A 顺时针旋转得△AB 1E 1,点E 1落在边AD 上时旋转停止.若点B 1落在矩形对角线AC 上,且点B 1到AD 的距离小于时,求m 的取值范围.15.如图1,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,连接BE 、DG .(1)BE 和DG 的数量关系是 ,BE 和DG 的位置关系是 ;(2)把正方形ECGF 绕点C 旋转,如图2,(1)中的结论是否还成立?若成立,写出证明过程,若不成立,请说明理由;(3)设正方形ABCD 的边长为4,正方形ECGF 的边长为3,正方形ECGF 绕点C 旋转过程中,若A 、C 、E 三点共线,直接写出DG 的长.16.如图,正方形ABCD的边长为a,射线AM是∠BAD外角的平分线,点E在边AB上运动(不与点A、B重合),点F在射线AM上,且AF=BE,CF与AD相交于点G,连结EC、EF、EG.(1)求证:CE=EF;(2)求△AEG的周长(用含a的代数式表示);(3)试探索:点E在边AB上运动至什么位置时,△EAF的面积最大.17.问题情境:矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别与边AB、BC所在的直线相交,交点为E、F.探究1:如图1,当PE⊥AB,PF⊥BC时,则=.探究2:如图2,在(1)的基础上,将三角板绕点P逆时针旋转,旋转角为α,(0°<α<60°),试求的值.探究3:在(2)的基础上继续旋转,当60°<α<90°时,将顶点P在AC上移动且使=时,如图3,试求的值.18.在Rt△ABC中,∠B=90°,AB=6,BC=8,点D从点B出发,以每秒3个单位的速度沿B→A→C运动,到点C停止.在点D运动的过程中,过点D作DE⊥BC,垂足为E,以DE为一边在右侧作矩形DEFG,点F在BC边上,且EF:DE=4:3,连结AG,CG,设运动时间为t(秒),矩形DEFG与△ABC重叠部分面积为S.(1)当AG=CG时,求t的值.(2)当点D在边AB上运动时,求S与t的函数关系式.(3)当△ACG的面积为6时,直接写出t的值.19.如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=32,DC=24,AD=42,动点P从点D出发,沿射线DA的方向以每秒4个单位长的速度运动,动点Q从点C出发,在线段CB 上以每秒2个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).(1)设△BPQ的面积为S,求S与t之间的函数关系式;(2)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?(3)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由.20.(1)【发现证明】如图1,在正方形ABCD中,点E,F分别是BC,CD边上的动点,且∠EAF=45°,求证:EF=DF+BE.小明发现,当把△ABE绕点A顺时针旋转90°至△ADG,使AB与AD重合时能够证明,请你给出证明过程.(2)【类比引申】①如图2,在正方形ABCD中,如果点E,F分别是CB,DC延长线上的动点,且∠EAF=45°,则(1)中的结论还成立吗?请写出证明过程.②如图3,如果点E,F分别是BC,CD延长线上的动点,且∠EAF=45°,则EF,BE,DF之间的数量关系是(不要求证明)(3)【联想拓展】如图1,若正方形ABCD的边长为6,AE=3,求AF的长.参考答案1.解:(1)①如图②中,∵四边形ABCD和四边形AEFG是正方形,∴AE=AG,AB=AD,∠BAD=∠EAG=90°,∴∠BAE=∠DAG,在△ABE和△DAG中,,∴△ABE≌△ADG(SAS),∴BE=DG;②如图2,延长BE交AD于T,交DG于H.由①知,△ABE≌△DAG,∴∠ABE=∠ADG,∵∠ATB+∠ABE=90°,∴∠ATB+∠ADG=90°,∵∠ATB=∠DTH,∴∠DTH+∠ADG=90°,∴∠DHB=90°,∴BE⊥DG,故答案为:BE=DG,BE⊥DG;(2)数量关系不成立,DG=2BE,位置关系成立.如图③中,延长BE交AD于T,交DG于H.∵四边形ABCD与四边形AEFG都为矩形,∴∠BAD=∠EAG,∴∠BAE=∠DAG,∵AD=2AB,AG=2AE,∴==,∴△ABE∽△ADG,∴∠ABE=∠ADG,=,∴DG=2BE,∵∠ATB+∠ABE=90°,∴∠ATB+∠ADG=90°,∵∠ATB=∠DTH,∴∠DTH+∠ADG=90°,∴∠DHB=90°,∴BE⊥DG;(3)如图④中,作ET⊥AD于T,GH⊥BA交BA的延长线于H.设ET=x,AT=y.∵△AHG∽△ATE,∴===2,∴GH=2x,AH=2y,∴4x2+4y2=4,∴x2+y2=1,∴BG2+DE2=(2x)2+(2y+2)2+x2+(4﹣y)2=5x2+5y2+20=25.2.证明(1)∵四边形ABCD是正方形,∴CD=BC,∠HDC=∠BCE=90°,∴∠DHC+∠DCH=90°,∵CH⊥BE,∴∠EFC=90°,∴∠ECF+∠BEC=90°,∴∠CHD=∠BEC,∴△DHC≌△CEB(AAS).(2)解:∵△DHC≌△CEB,∴CH=BE,DH=CE,∵CE=DE=CD,CD=CB,∴DH=BC,∵DH∥BC,∴.∴GC=2GH,设GH=x,则,则CG=2x,∴3x=8,∴x=.即GH=.(3)解:∵,∴,∵DH=CE,DC=BC,∴,∵DH∥BC,∴,∴,,设S△DGH =9a,则S△BCG=49a,S△DCG=21a,∴S△BCD=49a+21a=70a,∴S1=2S△BCD=140a,∵S△DEG :S△CEG=4:3,∴S△DEG=12a,∴S2=12a+9a=21a.∴.故答案为:.3.解:(I)过点D作DG⊥x轴于G,如图①所示:∵点A(6,0),点B(0,8).∴OA=6,OB=8,∵以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,∴AD=AO=6,α=∠OAD=30°,DE=OB=8,在Rt△ADG中,DG=AD=3,AG=DG=3,∴OG=OA﹣AG=6﹣3,∴点D的坐标为(6﹣3,3);(Ⅱ)过点D作DG⊥x轴于G,DH⊥AE于H,如图②所示:则GA=DH,HA=DG,∵DE=OB=8,∠ADE=∠AOB=90°,∴AE===10,∵AE×DH=AD×DE,∴DH===,∴OG=OA﹣GA=OA﹣DH=6﹣=,DG===,∴点D的坐标为(,);(Ⅲ)连接AE,作EG⊥x轴于G,如图③所示:由旋转的性质得:∠DAE=∠AOC,AD=AO,∴∠OAC=∠ADO,∴∠DAE=∠ADO,∴AE∥OC,∴∠GAE=∠AOD,∴∠DAE=∠GAE,在△AEG和△AED中,,∴△AEG≌△AED(AAS),∴AG=AD=6,EG=ED=8,∴OG=OA+AG=12,∴点E的坐标为(12,8).4.证明:(1)如图1,延长EG交DC的延长线于点H,∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,AB=CD,AB∥CD,∵AB∥CD,∴∠H=GEB,且BG=CG,∠BGE=∠CGH,∴△CGH≌△BGE(AAS)∴GE=GH,∵DE⊥AB,DC∥AB,∴DC⊥DE,且GE=GH,∴DG=EG=GH;(2)如图1:∵DB⊥EG,∴∠DOE=∠DEB=90°,且∠EDB=∠EDO,∴△DEO∽△DBO,∴∴DE×DE=4×(2+4)=24,∴DE=2,∴EO===2,∵AB∥CD,∴, ∴HO =2EO =4, ∴EH =6,且EG =GH , ∴EG =3,GO =EG ﹣EO =, ∴GB ===,∴BC =2=AD , ∴AD =DE ,∴点E 与点A 重合,如图2:∵S 四边形ABCD =2S △ABD ,∴S 四边形ABCD =2××BD ×AO =6×2=12;(3)如图3,过点O 作OF ⊥BC ,∵旋转△GDO ,得到△G ′D 'O ,∴OG =OG ',且OF ⊥BC ,∴GF =G 'F ,∵OF ∥AB ,∴==,∴GF=BG=,∴GG'=2GF=,∴BG'=BG﹣GG'=,∵AB2=AO2+BO2=12,∵EG'=AG'==,=.5.解:(1)如图1中,∵△MAN≌△MAG,∴MN=GM,∵DN=BG,GM=BG+BM,∴MN=BM+DN,∵△CMN的周长为:MN+CM+CN=8,∴BM+CM+CN+DN=8,∴BC+CD=8,∴BC=CD=4,故答案为4;(2)如图2中,结论:MN=NM+DN.延长CB至E,使BE=DN,连接AE,∵∠ABC+∠D=180°,∠ABC+∠ABE=180°,∴∠D=∠ABE,在△ABE和△ADN中,,∴△ABE≌△ADN(SAS),∴AN=AE,∠DAN=∠BAE,∵∠BAD=2∠MAN,∴∠DAN+∠BAM=∠MAN,∴∠MAN=∠EAM,在△MAN和△MAE中,,∴△MAN≌△MAE(SAS),∴MN=EM=BE+BM=BM+DN,即MN=BM+DN;(3)如图3,延长BA,CD交于G,∵∠BAM=60°,∠MAD=90°,∴∠BAD=150°,∴∠GAD=30°,∵AD=2,∴DG=1,AG=,∵∠DAN=15°,∴∠GAN=45°,∴AG=GN=,∴BG=2+,∴BC=2BG=4+2,CG=BG=2+3,∴CD=CG﹣DG=2+2,由(2)得,MN=BM+DN,∴△CMN的周长=CM+CN+MN=CN+DN+CM+BM=BC+CD=4+2+2+2=6+4.6.解:(1)∵DE∥BC,∴===;故答案为:;(2)的值不变化,值为;理由如下:由(1)得:DE∥B,∴△ADE∽△ABC,∴=,由旋转的性质得:∠BAD=∠CAE,∴△ABD∽△ACE,∴==;(3)在AB上截取AM=AD=3,过M作MN∥BC交AC于N,把△AMN绕A逆时针旋转得△ADE,连接CE,如图所示:则MN⊥AC,DE=MN,∠DAE=∠BAC,∴∠AED=∠ANM=90°,∵AC⊥BC于点C,∠BAC=∠ADC=θ,且tanθ==,∴BC:AC:AB=3:4:5,同(2)得:△ABD∽△ACE,∴==,∵MN∥BC,∴△AMN∽△ABC,∴=,∴MN=×AM=×3=,∵∠BAC=∠ADC=θ,∴∠DAE=∠ADC=θ,∴AE∥CD,∴∠CDE+∠AED=180°,∴∠CDE=90°,∴CE===,∴BD=CE=×=.7.解:(1)由题意知△ADE≌△AD′E,∴∠DAE=∠D′AE,∵D′点落在AB边上时,∠DAE+∠D′AE=90°,∴∠DAE=∠D′AE=45°,故答案为:45;(2)①如图2,由题意知∠ACD=∠ACD′,∵四边形ABCD是矩形,∴AB∥CD,∴∠ACD=∠BAC,∴∠ACD′=∠BAC,∴AF=FC;②设AF=FC=x,则BF=10﹣x,在Rt△BCF中,由BF2+BC2=CF2得(10﹣x)2+62=x2,解得x=6.8,即AF=6.8;(3)如图3,∵△AD′E≌△ADE,∴∠AD′E=∠D=90°,∵∠AD′B=90°,∴B、D′、E三点共线,又∵△ABD′∽△BEC,AD′=BC,∴△ABD′≌△BEC,∴BE=AB=10,∵BD′===8,∴DE=D′E=10﹣8=2;如图4,∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,∴∠CBE=∠BAD″,在△ABD″和△BEC中,∵,∴△ABD″≌△BEC,∴BE=AB=10,∴DE=D″E=8+10=18.综上所知,DE=2或18.8.解:(1)∵,,(n+4)2≥0,∴m﹣4=0,n+4=0,∴m=4,n=﹣4,∴A(0,4),B(﹣4,0);(2)∵AC∥OB,∴∠C=∠CBO,∠CAF=∠BOF,∵AC=OB,∴△ACF≌△OBF(ASA),∴AF=OF=2,∵OA=OB,∠OAD=∠OBF,∠BOF=∠AOD,∴△BOF≌△AOD(ASA),∴OF=OD=2,∴BD=6,①当0≤t<3时,S=PD•OF=(6﹣2t)×2=6﹣2t;②当t>3时,S=PD•OF=(2t﹣6)×2=2t﹣6;(3)①当0≤t<3,如图2,∵AO=4,OD=2,∴AD=,∵BD×OA=AD×BE,∴BE=,∴DE=,∵四边形PDEG为菱形,∴DP=DE=EG=,∵D(2,0),∴P(2﹣,0),作EH⊥BD于H,∵BE×DE=BD×EH,∴EH=,∴HD=,∴OH=,∴E(,),∵EG∥OB,∴G与E的纵坐标相同,∴G(﹣,)②当t>3时,如图3,同理求得P(2+,0),G(+,).9.(1)证明:∵四边形ABCD和四边形CEFG为正方形,∴BC=DC,CG=CE,∠BCD=∠GCE=90°.∴∠BCD+∠DCG=∠GCE+∠DCG,∴∠BCG=∠DCE.在△BCG和△DCE中,,∴△BCG≌△DCE(SAS).∴BG=DE;(2)解:①连接BE,如图2所示:由(1)可知:BG=DE,∵CG∥BD,∴∠DCG=∠BDC=45°,∴∠BCG=∠BCD+∠DCG=90°+45°=135°,∵∠GCE=90°,∴∠BCE=360°﹣∠BCG﹣∠GCE=360°﹣135°﹣90°=135°,∴∠BCG=∠BCE,在△BCG和△BCE中,,∴△BCG≌△BCE(SAS),∴BG=BE,∵BG=BD=DE,∴BD=BE=DE,∴△BDE为等边三角形,∴∠BDE=60°;②延长EC交BD于点H,过点G作GN⊥BC于N,如图3所示:在△BCE和△DCE中,,∴△BCE≌△BCG(SSS),∴∠BEC=∠DEC,∴EH⊥BD,BH=BD,∵BC=CD=,∴BD=BC=2,∴BE=2,BH=1,∴CH=1,在Rt△BHE中,由勾股定理得:EH===,∴CE=﹣1,∵∠BCG=135°,∴∠GCN=45°,∴△GCN是等腰直角三角形,∴GN=CG=(﹣1),=BC•GN=××(﹣1)=.∴S△BCG10.【观察与猜想】解:∵四边形ABCD是正方形,∴∠B=∠BCD=∠ADC=90°,AB=BC=CD=AD,∠ACB=∠ACD=45°,由旋转的性质得:GC=AC,∠ACG=90°,∴∠ACB=∠GCD=45°,在△ABC和△GDC中,,∴△ABC≌△GDC(SAS),∴AB=GD,∠GDC=∠B=90°,∴DG∥BC,△CDG是等腰直角三角形,∴DG=CD=BC,∵点E与点D重合,点F与点C重合,∴EG=BF,EG∥BF;故答案为:EG=BF,EG∥BF;【探究与证明】证明:点E、F分别在CD、BC边上任意位置时,如图③所示:作GM⊥BC,交BC延长线于M,则∠GMF=90°,MG∥DC,∵四边形ABCD是正方形,∴AB=BC,∠BCD=∠B=90°,∴∠BAF+∠BFA=90°,由旋转的性质得:GF=AF,∠AFG=90°,∴∠BFA+∠MFG=90°,∴∠BAF=∠MFG,在△ABF和△FMG中,,∴△ABF≌△FMG(AAS),∴AB=FM,BF=MG,∵AB=BC,∴BF=CM,∵BF=CE,∴MG=CE,∵MG∥CE,∴四边形CEGM是平行四边形,又∵∠GMF=90°,∴四边形CEGM是矩形,∴EG=CM,EG∥CM,∴EG=BF,EG∥BF;点E、F在CD、BC边的延长线上的任意位置时,如图④所示:作GM⊥BC,交BC延长线于M,则∠GMF=90°,MG∥DC,∵四边形ABCD是正方形,∴AB=BC,∠BCD=∠B=90°,∴∠BAF+∠BFA=90°,由旋转的性质得:GF=AF,∠AFG=90°,∴∠BFA+∠MFG=90°,∴∠BAF=∠MFG,在△ABF和△FMG中,,∴△ABF≌△FMG(AAS),∴AB=FM,BF=MG,∵AB=BC,∴BF=CM,∵BF=CE,∴MG=CE,∵MG∥CE,∴四边形CEGM是平行四边形,又∵∠GMF=90°,∴四边形CEGM是矩形,∴EG=CM,EG∥CM,∴EG=BF,EG∥BF;【拓展与延伸】解:==k(k≠1)时,线段EG与BF的数量关系与位置关系仍然成立;理由如下:作GM⊥BC,交BC延长线于M,如图⑤所示:则∠GMF=90°,MG∥DC,∵四边形ABCD是正方形,∴AB=BC,∠BCD=∠B=90°,∴∠BAF+∠BFA=90°,∠B=∠GMF,由旋转的性质得:∠AFG=90°,∴∠BFA+∠MFG=90°,∴∠BAF=∠MFG,∴△ABF∽△FMG,∴==,∵==k,∴==k,==k,∴FM=BC,GM=CE,∴BF=CM,∵MG∥CE,∴四边形CEGM是平行四边形,又∵∠GMF=90°,∴四边形CEGM是矩形,∴EG=CM,EG∥CM,∴EG=BF,EG∥BF;故答案为:==k(k≠1).11.解:(1)AF=DE.理由如下:∵四边形OADC是正方形,∴OA=AD,∠DAE=∠AOF=90°,由题意得:AE=OF,在△AOF和△DAE中,,∴△AOF≌△DAE(SAS),∴AF=DE.(2)四边形HIJK是正方形.理由如下:如图①所示:∵H、I、J、K分别是AE、EF、FD、DA的中点,∴HI=KJ=AF,HK=IJ=ED,HI∥AF,HK∥ED,∵AF=DE,∴HI=KJ=HK=IJ,∴四边形HIJK是菱形,∵△AOF≌△DAE,∴∠ADE=∠OAF,∵∠ADE+∠AED=90°,∴∠OAF+∠AED=90°,∴∠AGE=90°,∴AF⊥ED,∵HI∥AF,HK∥ED,∴HI⊥HK,∴∠KHI=90°,∴四边形HIJK是正方形.(3)存在,理由如下:∵四边形OADC为正方形,点D的坐标为(4,4),∴OA=AD=OC=4,∴C(4,0),∵点E为AO的中点,∴OE=2,E(0,2);分情况讨论:如图②所示,①当OC是以O,C、M、N为顶点的菱形的对角线时,OC与MN互相垂直平分,则M为CE 的中点,∴点M的坐标为(2,1),∵点M和N关于OC对称,∴N(2,﹣1);②当OC是以O,C、M、N为顶点的菱形的边时,若M在y轴的左侧时,∵四边形OCM'N'是菱形,∴OM'=OC=4,M'N'∥OC,∴△M'FE∽△COE,∴==2,设EF=x,则M'F=2x,OF=x+2,在Rt△OM'F中,由勾股定理得:(2x)2+(x+2)2=42,解得:x=,或x=﹣2(舍去),∴M'F=,FN=4﹣M'F=,OF=2+=,∴N'(,);若M在y轴的右侧时,作N''P⊥OC于P,∵ON''∥CM'',∴∠PON''=∠OCE,∴tan∠PON''==tan∠OCE==,设PN''=y,则OP=2y,在Rt△OPN''中,由勾股定理得:y2+(2y)2=42,解得:y=,∴PN''=,OP=,∴N''(,﹣);综上所述,存在点N使以O,C、M、N为顶点的四边形是菱形,点N的坐标为(2,﹣1)或(,)或(,﹣).12.(1)证明:∵四边形ABCD为矩形,∴BC=AD,CD=AB,∠C=∠ABC=∠A=∠ADC=90°,∵CE=AF,∴BC﹣CE=AD﹣AF,即BE=DF,在△DCE和△BAF中,,∴△DCE≌△BAF(SAS),∴∠CDE=∠ABF,∠CED=∠AFB,由折叠的性质得:∠CDE=∠C′DE,∠ABF=∠A′BF,∠CED=∠C′ED,∠AFB=∠A′FB,∵∠CDE+∠C′DE+∠HDF=90°,∠ABF+∠A′BF+∠GBE=90°,∠CED+∠C′ED+∠GEB=180°,∠AFB+∠A′FB+∠HFD=180°,∴∠HDF=∠GBE,∠GEB=∠HFD,在△BEG和△DFH中,,∴△BEG≌△DFH(ASA);(2)解:四边形A'HC'G的形状是矩形;理由如下:由折叠的性质得:∠C=∠DC′E=∠A=∠BA′F=90°,由(1)得:△BEG≌△DFH,∴∠BGE=∠DHF,∵∠BGE=∠A′GC′,∠DHF=∠A′HC′,∴∠A′GC′=∠A′HC′,∵∠DC′E+∠BA′F+∠A′GC′+∠A′HC′=90°+90°+∠A′GC′+∠A′HC′=360°,∴∠A′GC′+∠A′HC′=180°,∴∠A′GC′=∠A′HC′=90°,∴∠DC′E=∠BA′F=∠A′GC′=∠A′HC′=90°,∴四边形A'HC'G是矩形;(3)解:由(2)知:∠BGE=∠A′GC′=90°,∵tan∠EBG=,∴设EG=3x,则BG=4x,BE==5x,由折叠的性质得:CE=C′E=EG+C′G=3x+1,CD=AB=A′B=BG+A′G=4x+6,∴BC=CE+BE=3x+1+5x=8x+1,S矩形ABCD=CD•BC=4×CD•CE+2×EG•BG﹣A'G•C'G,即(4x+6)(8x+1)=4×(3x+1)(4x+6)+2×3x•4x﹣6×1,整理得:x2﹣2x=0,解得:x1=2,x2=0(不合题意舍去),∴CD=4×2+6=14,CB=8×2+1=17,∴S矩形ABCD=CD•BC=14×17=238.13.解:(1)作D'E⊥BC交BC的延长线于E,如图2所示:则∠E=90°,∵四边形ABCD是矩形,∴∠ABC=90°,AB∥CD,AD∥BC,CD=AB=2,∴∠ACD=∠BAC,∠DAC=∠ACB=30°,∵∠ACB=30°,∴BC=AB=2,∠ACD=∠BAC=60°,由旋转的性质得:CD'=CD=2,∠ACA'=30°,∴∠D'CE=180°﹣30°﹣30°﹣60°=60°,∴∠CD'E=30°,∴CE=CD'=1,D'E=CE=,∴S=BC×D'E=×2×=3;△BCD′(2)△OBD′是直角三角形,理由如下:连接OC,如图3所示:由旋转的性质得:CA'=CA,∠AD'C=∠ADC=90°,∠D'A'C=∠DAC=30°,∵O是AA′的中点,∴OC⊥AA',∴∠AOC=∠AOC=90°=∠ABC=∠AD'C,∴∠ABC+∠AOC=180°,∴A、B、C、O四点共圆,∴∠BOC=∠BAC=60°,同理;A、D'、C、O四点共圆,∴∠D'OC=∠D'A'C=30°,∴∠BOD'=90°,∴△BOD'是直角三角形;(3)若B、C、D'三点不共线,如图3所示:由(2)得:∠OBC=∠OAC,∠OD'C=∠OA'C,∠OAC=∠OA'C,∴∠OBC=∠OD'C,∵OB=OD,∴∠OBD'=∠OD'B,∴∠CBD'=∠CD'B,∴CB=CD',∵CD'=CD,∴BC=CD,这与已知相矛盾,∴B、C、D'三点共线;分两种情况:当点D'在BC的延长线上时,如图4所示:=90°;α=α1当点D'在边BC上时,如图5所示:=360°﹣90°=270°;α=α1故答案为:90°或270;时,△OBD′不存在时,分两种情况:当α=α2当O与D'重合时,如图6所示:∵CA'=CA,∠CAD'=∠CA'D'=30°,∴∠ACA'=120°,=360°﹣120°=240°;∴α=α2当O与B重合时,如图7所示:则AA'=2AB=4,∵CA=CA'=2AB=4=AA',∴△ACA'是等边三角形,∴∠A'CA=60°,=360°﹣60°=300°;∴α=α2故答案为:240°或300.14.解:(1)①如图1,∵CF∥AE ∴∠FCE=∠AEB,∠CFE=∠AEF∵△ABE翻折得到△AFE∴EF=BE=1,∠AEF=∠AEB∴∠FCE=∠CFE∴CE=EF=1∴m=BC=BE+CE=2∴m的值是2.②如图2,过点F作GH⊥AD于点G,交BC于点H ∴GH⊥BC∴∠AGF=∠FHE=90°∵四边形ABCD是矩形∴∠BAD=∠B=90°∴四边形ABHG是矩形∴GH=AB=2,AG=BH∵△ABE翻折得到△AFE∴EF=BE=1,AF=AB=2,∠AFE=∠B=90°∴∠AFG+∠EFH=∠AFG+∠FAG=90°∴∠EFH=∠FAG∴△EFH∽△FAG∴设EH=x,则AG=BH=x+1∴FG=2EH=2x∴FH=GH﹣FG=2﹣2x∴解得:x=∴AG=,FG=∵AD=BC=m∴DG=|AD﹣AG|=|m﹣|∴DF 2=DG 2+FG 2=(m ﹣)2+2≥,即可把DF 2看作关于m 的二次函数,抛物线开口向上,最小值为∵∴∵(m ﹣)2+2= 解得:m 1=,m 2=1 ∴根据二次函数图象可知,1≤m(2)如图3,过点B 1作MN ⊥AD 于点M ,交BC 于点N ∴MN ∥AB ,MN =AB =2∵AC = ∴sin ∠ACB =∵AD ∥BC ,点B 1在AC 上∴∠MAB 1=∠ACB∴sin ∠MAB 1= ∴∵点B 1到AD 的距离小于∴MB 1= 解得:∵m>0 ∴m>如图4,当E1落在边AD上,且B1在AC上时,m最大,此时,∠ACB=∠B1AE1=∠BAE∴tan∠ACB=tan∠BAE∴∴m=BC=2AB=4∴m的取值范围是<m≤415.解:(1)BE=DG.BE⊥DG;理由如下:∵四边形ABCD和四边形CEFG为正方形,∴CD=BC,CE=CG,∠BCE=∠DCG=90°,在△BEC和△DGC中,,∴△BEC≌△DGC(SAS),∴BE=DG;如图1,延长GD交BE于点H,∵△BEC≌△DGC,∴∠DGC=∠BEC,∴∠DGC+∠EBC=∠BEC+∠EBC=90°,∴∠BHG=90°,即BE⊥DG;故答案为:BE=DG,BE⊥DG.(2)成立,理由如下:如图2所示:同(1)得:△DCG≌△BCE(SAS),∴BE=DG,∠CDG=∠CBE,∵∠DME=∠BMC,∠CBE+∠BMC=90°,∴∠CDG+∠DME=90°,∴∠DOB=90°,∴BE⊥DG;(3)由(2)得:DG=EB,分两种情况:①如图3所示:∵正方形ABCD的边长为4,正方形ECGF的边长为3,∴AC⊥BD,BD=AC=AB=4,OA=OC=OB=AC=2,CE=3,∴AE=AC﹣CE=,∴OE=OA﹣AE=,在Rt△BOE中,由勾股定理得:DG=BE==;②如图4所示:OE=CE+OC=2+3=5,在Rt△BOE中,由勾股定理得:DG=BE==;综上所述,若A、C、E三点共线,DG的长为或.16.(1)证明:过点F作FH⊥AB于H,如图1所示:则∠AHF=90°,∵AM平分∠DAH,∴∠FAH=45°,∴△AFH是等腰直角三角形,∴FH=AH,AF=AH=FH,∵AF=BE,∴FH=AH=BE,∴AH+AE=BE+AE,∴HE=AB=BC,在△FEH和△ECB中,,∴△FEH≌△ECB(SAS),∴CE=EF;(2)解:∵△FEH≌△ECB,∴∠FEH=∠ECB,∵在Rt△BCE中,∠ECB+∠CEB=90°,∴∠FEH+∠CEB=90°,∴∠CEF=90°,由(1)知,CE=EF,∴△CEF是等腰直角三角形,∠ECF=∠EFC=45°,把Rt△CDG绕点C逆时针旋转90°至Rt△CBN位置,如图2所示:则∠GCN=90°,CG=CN,DG=BN,∴∠NCE=∠GCN﹣∠GCE=45°,∴∠NCE=∠GCE,在△CEG和△CEN中,,∴△CEG≌△CEN(SAS),∴GE=NE=EB+BN=EB+DG,∴△AEG的周长=AE+GE+AG=AE+EB+DG+AG=AB+AD=2a;(3)解:设AE=x,由(1)得:FH=BE=a﹣x,则△EAF的面积=AE×FH=x(a﹣x)=﹣(x﹣)2+,∴当x=,即点E在AB边中点时,△EAF的面积最大,最大值为.17.解:(1)∵矩形ABCD,∴AB⊥BC,PA=PC;∵PE⊥AB,BC⊥AB,∴PE∥BC,∴∠APE=∠PCF;∵PF⊥BC,AB⊥BC,∴PF∥AB,∴∠PAE=∠CPF.∵在△APE与△PCF中,,∴△APE≌△PCF(ASA),∴PE=CF.在Rt△PCF中,=tan30°=,∴=,故答案为:.(2)如答图1,过点P作PM⊥AB于点M,PN⊥BC于点N,则PM⊥PN.0°~30°时∵PM⊥PN,PE⊥PF,∴∠EPM=∠FPN,又∵∠PME=∠PNF=90°,∴△PME∽△PNF,∴=,由(1)知,=,∴=.同理30°~60°时,=;(3)当60°<α<90°时,将顶点P在AC上移动且使=时,如答图2,过点P作PM⊥AB于点M,PN⊥BC于点N,则PM⊥PN,PM∥BC,PN∥AB.∵PM∥BC,PN∥AB,∴∠APM=∠PCN,∠PAM=∠CPN,∴△APM∽△PCN,∴==,得CN=2PM.在Rt△PCN中,==tan30°=,∴=.∵PM⊥PN,PE⊥PF,∴∠EPM=∠FPN,又∵∠PME=∠PNF=90°,∴△PME∽△PNF,∴==.18.解:(1)∵四边形DEFG是矩形,∴DG=BF,GF=BD,∠BDG=∠BFG=90°,∴∠ADG=∠CFG=90°,由题意得:BD=3t,则AD=6﹣3t,DG=4t,CF=8﹣4t,FG=BD=3t,当AG=CG时,由勾股定理得:AG2=AD2+DG2,CG2=FG2+FC2,∴AD2+DG2=FG2+FC2,即(6﹣3t)2+(4t)2=(3t)2+(8﹣4t)2,解得:t=1,即当AG=CG时,t=1秒;(2)分两种情况:①当0<t≤1时,如图1所示:S=矩形DEFG的面积=3t×4t=12t2;即S=12t2(0<t≤1);②当1<t≤2时,如图2所示:∵∠ADH=∠B=90°,∠A=∠A,∴△ADH∽△ABC,∴=,即=,解得:DH=8﹣4t,同理得:FM=6﹣3t,∴S=×6×8﹣×2×(6﹣3t)(8﹣4t)=﹣12t2+48t﹣24;即S=﹣12t2+48t﹣24(1<t≤2);(3)分三种情况:①如图1所示:由题意得:×6×8﹣12t2﹣×4t×(6﹣3t)﹣×3t×(8﹣4t)=6,解得:t=;②如图3所示:由题意得:×4t×(6﹣3t)+×3t×(8﹣4t)+3t×4t﹣×6×8=6,解得:t=;③如图4所示:由勾股定理得:AC===10,∴CD=6+10﹣3t=16﹣3t,同(2)得:△CDE∽△CAB,∴==,即==,解得:DE=(16﹣3t),CE=(16﹣3t),由题意得EF=(16﹣3t),∴C与F重合,∴×8×(16﹣3t)=6,解得:t=;综上所述,当△ACG的面积为6时,t的值为秒或秒或秒.19.解:(1)如图1,过点P作PM⊥BC,垂足为M,则四边形PDCM为矩形.∴PM=DC=24.∵QB=32﹣t,∴S=×24×(32﹣2t)=384﹣24t(0≤t<16);(2)由图可知:CM=PD=4t,CQ=2t.以B、P、Q三点为顶点的三角形是等腰三角形,可以分三种情况:①若PQ=BQ.在Rt△PMQ中,PQ2=4t2+242,由PQ2=BQ2得4t2+242=(32﹣2t)2,解得t=;②若BP=BQ.在Rt△PMB中,BP2=(32﹣4t)2+242.由BP2=BQ2得:(32﹣4t)2+242=(32﹣2t)2即3t2﹣32t+144=0.由于△=﹣704<0,∴3t2﹣32t+144=0无解,∴PB≠BQ.③若PB=PQ.由PB2=PQ2,得4t2+242=(32﹣4t)2+242整理,得3t 2﹣64t +256=0.解得t 1=,t 2=16(舍去)综合上面的讨论可知:当t =秒或t =秒时,以B 、P 、Q 三点为顶点的三角形是等腰三角形.(3)设存在时刻t ,使得PQ ⊥BD .如图2,过点Q 作QE ⊥AD 于E ,垂足为E .∵AD ∥BC∴∠BQF =∠EPQ ,又∵在△BFQ 和△BCD 中∠BFQ =∠C =90°,∴∠BQF =∠BDC ,∴∠BDC =∠EPQ ,又∵∠C =∠PEQ =90°,∴Rt △BDC ∽Rt △QPE , ∴=,即=,解得t =9.所以,当t =9秒时,PQ ⊥BD .20.(1)【发现证明】证明:把△ABE 绕点A 顺时针旋转90°至△ADG ,如图1,∴∠BAE=∠DAG,AE=AG,∵∠EAF=45°,∴∠BAE+∠FAD=45°,∴∠DAG+∠FAD=45°,∴∠EAF=∠FAG,∵AF=AF,∴△EAF≌△GAF(SAS),∴EF=FG=DF+DG,∴EF=DF+BE;(2)【类比引申】①不成立,结论:EF=DF﹣BE;证明:如图2,将△ABE绕点A顺时针旋转90°至△ADM,∴∠EAB=∠MAD,AE=AM,∠EAM=90°,BE=DM,∴∠FAM=45°=∠EAF,∵AF=AF,∴△EAF≌△MAF(SAS),。
初中数学四边形专题训练50题含答案

中考数学四边形专题训练50题含答案(单选、填空、解答题)一、单选题1.平行四边形不一定具有的性质是( )A .对角线互相垂直B .对边平行且相等C .对角线互相平分D .对角相等 2.如图,在MON ∠的两边.上分别截取,OA OB ,使OA OB =;分别以点A ,B 为圆心,OA 长为半径作弧,两弧交于点C ;连接,,,AC BC AB OC .若2AB =,四边形OACB 的面积为4.则OC 的长为( )A .2B .3C .4D .5 3.在ABCD 中,下列结论错误的是( )A .//AB CD B .B D ∠=∠C .AC BD =D .180C D ∠+∠=︒ 4.如图,在平行四边形ABCD 中,E 是AB 延长线上的一点,若∠A=60°,则∠1的度数为( )A .120°B .60°C .45°D .30° 5.若平行四边形中两个内角的度数比为1∠2,则其中较大的内角是( ) A .100° B .60° C .120° D .90° 6.如图,正方形OABC 与正方形ODEF 是位似图形,点O 为位似中心,位似比为2:3,点B 、E 在第一象限.若点A 的坐标为()1,0,则点E 的坐标是( )A .0)B .33,22⎛⎫ ⎪⎝⎭C .D .(2,2) 7.四边形ABCD 中,对角线AC ,BD 交于点O ,AD//BC ,为了判定四边形是平行四边形,还需一个条件,其中错误..的是( ) A .AB//CD B .∠A=∠C C .AB=CD D .AO=CO 8.一个多边形的内角和等于外角和,则这个多边形的边数为( )A .10B .8C .6D .49.顺次连接等腰梯形各边中点所围成的四边形是( )A .平行四边形B .矩形C .菱形D .正方形 10.已知平行四边形ABCD 的周长为32,AB =4,则BC 的长为( )A .4B .12C .24D .48 11.如图,四边形ABCD 是矩形,,把矩形沿直线AC 折叠,点B 落在点E处,连结DE,则的值是( )A .B .C .8D .7:25 12.如图,在平行四边形ABCD 中,AB=4,CE 平分∠BCD 交AD 边于点E ,且AE=3,则BC 的长为( )A .4B .6C .7D .813.如图,在矩形ABCD ,对角线AC 与BD 相交于点O ,EO AC ⊥于点O ,交BC 于点E ,若ABE ∆的周长为8,3AB =,则AD 的长为 ( )A .2B .5.5C .5D .414.如图,矩形ABCD 中,4AB =,2BC =.点E 在边AB 上,点F 在边CD 上,点G 、H 在对角线AC 上.若四边形EGFH 是菱形,则BE 的长是( )A .B C .2.5 D .1.5 15.如图,在平行四边形ABCD 中,过点P 作直线EF 、GH 分别平行于AB 、BC ,那么图中共有( )平行四边形.A .4个B .5个C .8个D .9个 16.如图,已知直线PQ CD ⊥于点P ,B 是CPQ ∠内部一点,过点B 作BA PQ ⊥于点A ,BC CD ⊥于点C ,四边形PABC 是边长为8cm 的正方形,N 是AB 的中点,动点M 从点P 出发,以2cm/s 的速度,沿P A B C →→→方向运动,到达点C 停止运动,设运动时间为()s t ,当CM PN =时,t 等于( )A .2B .4C .2或4D .2或617.如图,在菱形中,,,是的中点.过点作,垂足为.将沿点到点的方向平移,得到.设、分别是、的中点,当点与点重合时,四边形的面积为A .B .C .D . 18.如图,点EF 、分别是菱形ABCD 的边AD 、DC 的中点,如果阴影部分的面积和是10,则菱形对角线AC 与BD 的乘积AC BD ⋅等于( )A .10B .32C .20D .1619.如图,在正方形1ABCB 中,AB =AB 与直线l 所夹锐角为60,延长1CB 交直线l 于点1A ,作正方形1112A B C B ,延长12C B 交直线l 于点2A ,作正方形2223A B C B ,延长23C B 交直线l 于点3A ,作正方形3334A B C B ⋯,依次规律,则线段20212022A A =( )A .20192⨯⎝⎭B .20202⨯⎝⎭C .20212⨯⎝⎭D .20222⨯⎝⎭20.如图,平行四边形ABCD 的对角线AC 与BD 相交于点O ,添加一个条件使平行四边形ABCD 为矩形的是( )A .AD AB = B .AB AD ⊥C .AB AC =D .CA BD ⊥二、填空题21.如图,这个图案是用形状、大小完全相同的等腰梯形密铺而成的,则这个图案中的等腰梯形的底角(指锐角)是_________度.22.如图,点E 在矩形ABCD 的对角线BD 上,EF BC ⊥于点F ,连接AF ,若5BC =,2EF =,则ABF △的面积为_________.23.已知菱形的两条对角线长分别为3和4,则菱形的面积为______.24.有一个边长为50cm 的正方形洞口,要用一个圆盖去盖住这个洞口,那么圆盖的直径至少应为_____.25.如图,Rt ABC 中,90C BC AC ∠=︒>,,以AB BC AC ,,三边为边长的三个正方形面积分别为1S ,2S ,3S .若ABC 的面积为7,140S =,则32S S -的值等于______.26.如图,将长方形ABCD沿AE折叠,已知50∠=︒,则BADCED'∠'的大小是_____27.如图,在菱形ABCD中,AB=1,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为CC',则图中阴影部分的面积为__.28.用直角边分别为3和4的两个直角三角形拼成一个平行四边形(非矩形),所得的平行四边形的周长是______.29.如图,菱形ABCD中,点O为对角线AC的三等分点且AO=2OC,连接OB,OD,OB=OC=OD,已知AC=3,那么菱形的边长为_____.30.如图,将四边形ABCD沿BD、AC剪开,得到四个全等的直角三角形,已知,OA =4,OB=3,AB=5将这四个直角三角形拼为一个没有重叠和缝隙的四边形,则重新拼成的四边形的周长为_____.31.在长方形ABCD中,10AB=,将长方形ABCD折叠,折痕为EF.AD=,8(1)如图1,当A'与B重合时,EF=_______;(2)如图1,当直线EF过点D时,点A的对应点A'落在线段BC上,则线段EF的长为______.32.如图,P 是▱ABCD 内的任意一点,连接P A 、PB 、PC 、PD ,得到△P AB 、△PBC 、△PCD 、△PDA ,设它们的面积分别是S 1、S 2、S 3、S 4,给出如下结论:∠S 1+S 3=S 2+S 4,∠若S 3=2S 1,则S 2=2S 4,∠若S 1+S 3=5,则ABCD 的面积为10;∠S 1+S 2=S 3+S 4.其中正确的结论的序号是____________(把所有正确结论的序号都填在横线上).33.如图, 直线l 是四边形ABCD 的对称轴,若AB CD =,有下面的结论:∠AB BC ⊥;∠AC BD ⊥;∠//AB CD ;∠AO OC =.其中正确的结论有__.34.如图1是三国时期的数学家赵爽创制的一幅“勾股圆方图”.将图2的矩形分割成四个全等三角形和一个正方形,恰好能拼成这样一个“勾股圆方图”,则该矩形与拼成的正方形的周长之比为________.35.如图,平行四边形ABCD 中,45B ∠=︒,7BC =,CD =E ,F 分别是边AB ,BC 的中点,连接CE ,DF ,取CE ,DF 的中点G ,H ,连接GH ,则GH 的长度为__________.36.如图,正方形ABCD的边长为1,AC,BD是对角线,将∠DCB绕着点D顺时针旋转45°得到∠DGH,HG交AB于点E,连接DE交AC于点F,连接FG,则下列结论:∠DE平分∠ADB;∠BE∠四边形AEGF是菱形;∠BC+FG=1.5.其中结论正确的序号是_______.37.如图,点E、F是平行四边形ABCD的边AB、DC上的点,F与DE相交于点P,BF与CE相交于点Q若S△APD=14cm2,S△BCQ=16cm2,四边形PEQF的面积为______.38.如图,在正方形ABCD中,AB=4,G是BC的中点,点E是正方形内一个动点,且EG=2,连接DE,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,则线段CF长的最小值为_____.39.如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为__________.三、解答题40.□ABCD 的对角线AC 的垂直平分线与边AD 、BC 分别交于E 、F ,四边形AFCE 是否是菱形?为什么?41.如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,延长CD 到E ,使DE CD =,连接AE .(1)求证:四边形ABDE 是平行四边形;(2)连接OE ,若60ABC ∠=︒,且8AD DE ==,求OE 的长.42.如图,点E 、F 分别在ABCD 的边AB 、CD 的延长线上,且BE =DF ,连接AC 、EF 、AF 、CE ,AC 与EF 交于点O .(1)求证:AC 、EF 互相平分;(2)若EF 平分∠AEC ,判断四边形AECF 的形状并证明.43.正方形ABCD 的对角线交点为O ,连AE 交BC 于E ,交OB 于F ,2EC FO =,求证:AE 平分BAC ∠.44.如图,在三角形ABC 中,90C ∠=︒,四边形DEFC 是边长为4的正方形,且D 、E 、F 分别在边AC AB BC 、、上.把三角形ADE 绕点E 逆时针旋转一定的角度.(1)当点D 与点F 重合时,点A 的对应点G 落在边BC 上,此时四边形ACGE 的面积为___________;(2)当点D 的对应点1D 落在线段BE 上时,点A 的对应点为点1A ,在旋转过程中点A 经过的路程为1l ,点D 经过的路程为2l ,且12:3:2l l =,求线段1AD 的长. 45.如图所示,已知四边形ABCD 是平行四边形,在AB 的延长线上截取BE=AB ,BF=BD ,连接CE ,DF ,相交于点M .求证:CD=CM .46.如图,在直角梯形ABCD 中,AD ∠BC ,AD ∠CD ,M 为腰AB 上一动点,联结MC 、MD ,AD =10,BC =15,cot B 512=.(1)求线段CD 的长.(2)设线段BM 的长为x ,∠CDM 的面积为y ,求y 关于x 的函数解析式,并写出它的定义域.47.在Rt ABC 与Rt BDE 中,90ABC DBE ∠=∠=︒,AB BC =,BD BE =.(1)如图1,若点D ,B ,C 在同一直线上,连接AD ,CE ,则AD 与CE 的关系为_________;(2)如果将图1中的BDE △绕点B 在平面内顺时针旋转到如图2的位置,那么请你判断AD 与CE 的关系,并说明理由;(3)如图3,若6AB =,2BD =,连接AE ,分别取DE ,AE ,AC 的中点M ,P ,N ,连接MP ,NP ,MN ,将BDE △绕点B 在平面内顺时针旋转一周,请直接写出旋转过程中MPN△面积的最小值和最大值.48.如图,在矩形ABCD中,AD=4,CD=3,点E为AD的中点.连接CE,将∠CDE 沿CE折叠得∠CFE,CE交BD于点G,交BA的延长线于点M,延长CF交AB于点N.(1)求DG的长;(2)求MN的长.49.如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B.(1)求抛物线的解析式.(2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标.(3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E.是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED 的边长;如果不存在,请说明理由.参考答案:1.A【分析】结合平行四边形的性质即可判定.【详解】结合平行四边形的性质可知选项B、C、D均正确,但平行四边形的对角线不垂直,则A不正确.故选A.【点睛】本题考查了平行四边形的性质,熟练掌握平行四边形的性质是正确解题的关键.2.C【分析】根据作法判定出四边形OACB是菱形,再根据菱形的面积等于对角线乘积的一半列式计算即可得解.【详解】解:根据作图,AC=BC=OA,∠OA=OB,∠OA=OB=BC=AC,∠四边形OACB是菱形,∠AB=2,四边形OACB的面积为4,∠12AB•OC=12×2×OC=4,解得OC=4.故选:C.【点睛】本题主要考查菱形的性质与判定,熟练掌握菱形的性质与判定是解题的关键.3.C【分析】根据平行四边形的性质逐项判断即可.【详解】解:A、由平行四边形行两组对边分别平行可得//AB CD,故A正确;B、由平行四边形对角相等可得B D∠=∠,故B正确;C、AC、BD为平行四边形对角线,平行四边形对角线互相平分,但不一定相等,故C错误;D、由平行四边形行两组对边分别平行可得//AD BC,两直线平行同旁内角互补,可得180C D∠+∠=︒,故D正确.故选:C.【点睛】本题主要考查平行四边形的性质及其推论,熟练掌握平行四边形的性质是解题关键.4.B【详解】解:∠四边形ABCD 是平行四边形,∠AD∠BC ,∠∠1=∠A=60°.故选B .5.C【分析】据平行四边形的性质得出AB //CD ,推出∠B +∠C =180°,根据∠B :∠C =1:2,求出∠C 即可.【详解】解:∠四边形ABCD 是平行四边形∠AB //CD ,∠∠B +∠C =180°,∠∠B :∠C =1:2,∠∠C =23×180°=120°,故选:C .【点睛】本题考查了平行线的性质和平行四边形的性质的应用,能熟练地运用性质进行计算是解此题的关键,题目比较典型,难度不大.6.B【分析】由题意可得:2:3OA OD =,又由点A 的坐标为()1,0,即可求得OD 的长,又由正方形的性质,即可求得E 点的坐标.【详解】解:∠正方形OABC 与正方形ODEF 是位似图形,O 为位似中心,相似比为2:3, ∠:2:3OA OD =,∠点A 的坐标为()1,0,即1OA =, ∠32OD =, ∠四边形ODEF 是正方形,∠32 DE OD==.∠E点的坐标为:33,22⎛⎫ ⎪⎝⎭.故选:B.【点睛】此题考查了位似变换的性质与正方形的性质.此题比较简单,注意理解位似变换与相似比的定义是解此题的关键.7.C【分析】根据平行四边形的判定定理逐项判断即可.【详解】解:A.根据两组对边分别平行可判定是平行四边形,不符合题意;B.根据平行线性质可得另一对内角相等,根据两组对角分别相等可判定是平行四边形,不符合题意;C.不能判定是平行四边形,可能是等腰梯形,符合题意;D.可通过全等证对角线互相平分,能判定是平行四边形,不符合题意;故选:C.【点睛】本题考查了平行四边形的判定,解题关键是熟知平行四边形的判定定理,准确进行判断.8.D【分析】设这个多边形的边数为n,根据内角和等于外角和列方程解答即可.【详解】解:设这个多边形的边数为n,则()2180360n-⨯︒=︒,解得4n=,故选:D.【点睛】此题考查了多边形内角和与外角和的计算,熟练掌握多边形内角和公式及外角和是解题的关键.9.C【分析】由E、F、G、H分别为AB、BC、CD、DA的中点,得出EF,HG,FG,EH是中位线,再得出四条边相等,根据“四条边都相等的四边形是菱形”进行证明.【详解】解:如图所示,因为E、F、G、H分别为AB、BC、CD、DA的中点,连接AC、BD,因为E、F分别是AB、BC的中点,所以EF=12AC ,且EF∠AC同理可得HG=12AC ,且HG∠AC , FG=12BD ,且FG∠BD , EH=12BD ,且EH∠BD , ∠EF∠HG ,HE ∠FG ,∠四边形EFGH 是平行四边形,又因为等腰梯形的对角线相等,即AC=BD ,因此有EF=FG=GH=HE ,所以连接等腰梯形各中点所得四边形为菱形.故选:C【点睛】此题考查三角形中位线的性质,解题的关键是掌握三角形的中位线定理及菱形的判定.10.B【详解】由题意得:2()32,4,12AB BC AB BC +===得: .故选B.11.D【详解】试题分析:从D,E 处向AC 作高DF,EH .设AB=4k,AD=3k,则AC=5k .由∠AEC的面积=4k×3k=5k×EH,得EH=95k k;根据勾股定理得CH=,∠四边形ACED是等腰梯形,∠CH=AF=95 k,所以DE=5k﹣95k×2=75k.所以DE:AC=75k:5k=7:25.故选D.考点:翻折变换.12.C【分析】由平行四边形的性质可得AD∠BC,且AD=BC,结合角平分线的性质可求得DE=DC=AB=4,则可求得AD的长,可求得答案.【详解】解:∠四边形ABCD为平行四边形,∠AB=CD=4,AD∠BC,AD=BC,∠∠DEC=∠BCE.∠CE平分∠BCD,∠∠DCE=∠BCE,∠∠DEC=∠DCE,∠DE=DC=4.∠AE=3,∠AD=BC=3+4=7.故选C.【点睛】本题主要考查平行四边形的性质,利用平行线的性质及角平分线的性质求得DE=DC是解题的关键.13.C【分析】由矩形的性质可得AO=CO,由线段垂直平分线的性质可得AE=EC,即可求解.【详解】解:∵四边形ABCD是矩形,∴AO=CO,BC=AD,∵EO⊥AC,∴AE=EC,∵△ABE的周长为8,∴AB+AE+BE=8,∴3+BC=8,∴AD =BC =5,故选:C .【点睛】本题考查了矩形的性质,线段垂直平分线的性质,掌握矩形的性质是本题的关键.14.D【分析】由矩形ABCD 中,四边形EGFH 是菱形,易证得()COF AOE AAS ≌,即可得OA OC =,然后由勾股定理求得AC 的长,继而求得OA 的长,又由AOE ABC ∽△△,利用相似三角形的对应边成比例,即可求得答案.【详解】解:如图,连接EF ,交AC 于O ,∠四边形EHFG 是菱形,EF AC OE OF ∴⊥=,,∠四边形ABCD 是矩形,90B D ∴∠=∠=︒,AB CD ∥,ACD CAB ∴∠=∠,在COF 与AOE △中,FCO OAE FOC AOE OF OE ∠=∠⎧⎪∠=∠⎨⎪=⎩,()COF AOE AAS ∴≌,AO CO ∴=,AC AB ==12AO AC ∴==, 90CAB CAB AOE B ∠=∠∠=∠=︒,,AOE ABC ∴∽,∠AO AE AB AC=,=, 2.5AE ∴=,1.5BE ∴=,故选:D .【点睛】本题考查了菱形的性质、矩形的性质、全等三角形的判定与性质以及相似三角形的判定与性质,准确作出辅助线是解此题的关键.15.D【详解】∠AD∠BC 、AB∠CD ,EF∠AB ,GH∠BC ,∠AB∠EF∠DC ,AD∠GH∠BC ,∠共有9个平行四边形,如平行四边形AGPE ,平行四边形BGPF ,平行四边形PEDH ,平行四边形PFCH ,平行四边形ABFE ,平行四边形EFCD ,平行四边形AGHD ,平行四边形BGHC ,平行四边形ABCD ,故选D.16.D【分析】分点M 是AP 的中点和点M 与点N 重合两种情况讨论,由全等三角形的性质和正方形的性质即可求解.【详解】解:当点M 是AP 的中点时,∵四边形P ABC 是正方形,∴PC =P A =AB ,∠CP A =∠P AN =90°,∵N 是AB 的中点,点M 是AP 的中点,∴PM =AN =4,在△CPM 和△P AN 中,PA CP CPA PAN PM AN =⎧⎪∠=∠⎨⎪=⎩∴△CPM ≌△P AN (SAS ),∴PN =CM ,∴t 42==2, 当点M 与点N 重合时,由正方形的对称性可得PN =CM ,∴t842+==6,故选:D【点睛】本题考查了正方形的性质,全等三角形的性质,利用分类讨论思想解决问题是解题的关键.17.A【详解】试题分析:作在菱形中,,,是的中点是的中点,故答案选A.考点:平行四边形的面积,三角函数.18.B【分析】设EF交BD于G,AC交BD于O,由三角形中位线的性质可得EF=12AC,EF//AC,可得EG为∠AOD的中位线,可得DG=12OD,根据菱形的性质可得BG=34BD,根据菱形的面积公式列方程即可得答案.【详解】设EF交BD于G,AC交BD于O,∠点E F 、分别是菱形ABCD 的边AD 、DC 的中点, ∠EF=12AC ,EF//AC ,∠EG 为∠AOD 的中位线, ∠OG=12OD ,∠四边形ABCD 是菱形, ∠OD=OB=12BD ,BD∠AC , ∠BG=34BD ,BG∠EF , ∠S 菱形ABCD =S 阴影+S △BEF ,阴影部分的面积和是10, ∠12AC·BD=10+12EF·BG=10+12·12AC·34BD , 解得:AC·BD=32.故选:B【点睛】本题考查菱形的性质、三角形中位线的性质及菱形的面积公式,菱形的对角线互相垂直且平分;菱形的面积等于两条对角线乘积的一半;三角形的中位线平行于第三边且等于第三边的一半;熟练掌握相关性质及公式是解题关键.19.C【分析】利用特殊角的三角函数值分别求出11A B 、22A B 、33A B ,以此类推找到规律求出20222022A B ,最后根据202120222022Rt A A B 中20212022202290A B A ∠=︒,20222021202230A A B ∠=︒,即可求解.【详解】解:∠AB 与直线l 所夹锐角为60︒,且1BAB ∠是正方形1ABCB 的一个顶角, ∠11180609030B AA ∠=︒-︒-︒=︒,又∠1190AB A ∠=︒,∠在11Rt AB A △中,11111tan A B AB A AB =⨯∠,∠正方形1ABCB 的边长AB∠11111tan A B AB A AB =⨯∠同理可求得: 222A B =⎝⎭,333A B =⎝⎭,以此类推可知: 20222021202120222022A B ===⎝⎭⎝⎭⎝⎭,∠202120222022Rt A A B 中20212022202290A B A ∠=︒,20222021202230A A B ∠=︒,∠2021202120222022202222A A A B ==⨯⎝⎭,故C 正确.故选:C . 【点睛】本题主要考查了正方形的性质、含特殊角的锐角三角函数等知识,含30°的直角三角形的性质.利用从特殊到一般寻找规律是解题的关键.20.B【分析】根据矩形的判定和平行四边形的性质分别对各个选项进行判断即可.【详解】解: A 、AD AB =时,平行四边形ABCD 是菱形,故选项A 不符合题意; B 、AB AD ⊥时,∠BAD =90°,则平行四边形ABCD 是矩形,故选项B 符合题意; C 、AB AC =时,平行四边形ABCD 不一定是矩形,故选项C 不符合题意;D 、CA BD ⊥时,平行四边形ABCD 是菱形,故选项D 不符合题意;故选:B .【点睛】此题考查的是平行四边形的性质、矩形的判定以及等腰三角形的判定等知识;熟练掌握矩形的判定和平行四边形的性质是解答此题的关键.21.60°【分析】根据图案的特点,可知密铺的一个顶点处的周角,由3个完全相同的等腰梯形的较大内角组成,即可求出等腰梯形的较大内角的度数,进而即可得到答案.【详解】由图案可知:密铺的一个顶点处的周角,由3个完全相同的等腰梯形的较大内角组成,∠等腰梯形的较大内角为360°÷3=120°,∠等腰梯形的两底平行,∠等腰梯形的底角(指锐角)是:180°-120°=60°.故答案是:60°.【点睛】本题主要考查等腰梯形的性质以及平面镶嵌,掌握平面镶嵌的性质是解题的关键.22.5【分析】证明∠BEF∠∠BCD,由相似三角形的性质求得BF•CD,即求得BF•AB,进而由三角形的面积公式求得结果.【详解】解:∠四边形ABCD是矩形,∠AB=CD,∠ABC=∠BCD=90°,∠EF∠BC,∠EF∠CD,∠∠BEF∠∠BDC,∠BF EF BC CD=,∠BC=5,EF=2,∠BF•CD=BC•EF=5×2=10,∠BF•AB=10,∠∠ABF的面积=12BF•AB=5,故答案为:5.【点睛】本题主要考查了矩形的性质,相似三角形的判定与性质,三角形的面积计算,关键是由相似三角形求得BF•AB的值.23.6【分析】根据菱形的面积等于对角线乘积的一半列式进行计算即可得解.【详解】解:∠菱形的两条对角线长分别为3和4,∠菱形的面积为134=6 2⨯⨯故答案为:6【点睛】本题考查了菱形的性质,菱形的面积通常有两种求法,可以用底乘以高,也可以用对角线乘积的一半求解,计算时要根据具体情况灵活运用.24.【分析】根据圆与其内切正方形的关系,易得圆盖的直径至少应为正方形的对角线的长,已知正方形边长为50cm,进而由勾股定理可得答案.【详解】解:根据题意,知圆盖的直径至少应为正方形的对角线的长;再根据勾股定理,50故答案为:.【点睛】题主要考查正多边形和圆的相关知识;注意:熟记等腰直角三角形的斜边是直角边的 倍,可以给解决此题带来方便.25.【分析】结合正方形面积公式,平方差公式,勾股定理,三角形面积公式,可知()()2223S S BC AC BC AC BC AC -=-=+-,2240BC AC +=,14BC AC ⋅=,然后运用完全平方公式()2222a b a b ab ±=+±求解即可.【详解】解:根据题意,2140S AB ==,22S BC =,23S AC = ∠()()2223S S BC AC BC AC BC AC -=-=+-在Rt ABC 中,根据勾股定理,222BC AC AB +=∠2240BC AC +=∠7Rt ABC S = ∠172BC AC ⋅⋅= ∠14BC AC ⋅=∠BC AC +==BC AC -====∠()()BC AC BC AC +-==即23S S -=故答案为:【点睛】本题考查勾股定理与三角形、正方形的面积,完全平方公式与平方差公式的灵活应用,掌握并熟练应用勾股定理和各类公式是解题的关键.26.40【详解】试题分析:先根据折叠的性质求得、的度数,即可求得、的度数,再根据长方形的性质求解即可.∠50CED ∠='︒,AE 为折痕∠∠∠BAD ∠'. 考点:折叠的性质点评:折叠的性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.27.342π+【分析】根据菱形的性质以及旋转角为30°,连接CD ′和BC ',可得A 、D′、C 及A 、B 、C′分别共线,求出扇形的面积,再根据AAS 证得两个小三角形全等,求得面积,最后根据扇形ACC '的面积-两个小的三角形的面积即可.【详解】解:连接CD ′和BC '∠∠DAB =60°∠30DAC CAB ∠=∠=︒∠30C AB ∠''=︒∠A 、D′、C 及A 、B 、C′分别共线∠AC =∠扇形ACC′的面积为:2303604ππ⨯=∠AC =AC ′,AD′=AB在OCD OC B ''和中CD BC ACD AC D COD C OB '='⎧⎪∠=∠''⎨⎪∠'=∠'⎩∠()OCD OC B AAS ''≌∠OB =OD′,CO =C′O又∠60,30CBC BC O ︒∠'∠=='︒∠90BOC ∠'=︒在Rt BOC '中,())22211BO BO +-=解得13,22BO C O ='=∠S △OCB=12BO C O '⨯⨯=,∠322442C B AC OC S S Sππ''=-=-=+阴影扇形 故答案为:342π+ 【点睛】本题考查了旋转的性质,菱形的性质,扇形的面积公式,熟练掌握旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键.28.18或16【分析】首先由直角边分别为3和4,求得其斜边,然后分别从以边长为3,4,5的边为对角线拼成一个平行四边形(非矩形),去分析求解即可求得答案. 【详解】解:直角边分别为3和4,∴5=,若以边长为3的边为对角线,则所得的平行四边形的周长是:2(54)18⨯+=; 若以边长为4的边为对角线,则所得的平行四边形的周长是:2(53)16⨯+=;若以边长为5的边为对角线,则所得的平行四边形的周长是:2(34)14⨯+=(此时是矩形,舍去);综上可得:所得的平行四边形的周长是:16或18.故答案为:16或18.【点睛】此题考查了平行四边形的性质以及勾股定理.注意掌握分类讨论思想的应用是解此题的关键.29【分析】如图,连接BD交AC于E,由四边形ABCD是菱形,推出AC∠BD,AE=EC,在Rt△EOD中,利用勾股定理求出DE,在Rt△ADE中利用勾股定理求出AD即可.【详解】如图,连接BD交AC于E.∠四边形ABCD是菱形,∠AC∠BD,AE=EC,∠OA=2OC,AC=3,∠CO=DO=2EO=1,AE=32,∠EO=12,DE=EB==,∠AD=【点睛】本题考查菱形的性质、勾股定理等知识,解题的关键是灵活应用勾股定理解决问题.30.20,22,26,28【分析】以直角三角形边长相等的边为公共边,拼接四边形,再计算周长;【详解】解:∠如图周长=20;∠如图周长=22;∠如图周长=26;∠如图周长=28;∠如图周长=22;∠四边形的周长为:20,22,26,28;故答案为:20,22,26,28.【点睛】本题考查了图形的拼接,四边形的周长;作出拼接图形是解题关键.31.10【分析】(1)根据题意结合图形直接写出答案即可解决问题;(2)根据勾股定理首先求出A C'的长度;再次利用勾股定理求出AE的长度,即可解决问题.【详解】解:(1)如图1,当A'与B重合时,EF=10;(2)如图2,设AE=x,则BE=8-x;∠四边形ABCD为矩形,∠BC=AD=10,DC=AB=8;∠B=∠C=90°;由题意得:=A D AD '=10;由勾股定理得:222A C A D DC 1006436''=-=-=∠A C 6BA 1064''==-=, ,在Rt∠A BE '中,由勾股定理得:222(8)4x x =-+解得:x=5,由勾股定理得:222EF =10+5=125∠EF =【点睛】该命题主要考查了翻折变换及其应用问题;能根据翻折变换的性质准确找出命题图形中隐含的等量关系是解题的关键.32.∠∠【分析】根据平行四边形的的性质可以得到AB =CD ,AD =BC ,设点P 到AB 、BC 、CD 、DA 的距离分别为h 1、h 2、h 3、h 4,然后利用三角形的面积公式列式整理判断即可得到答案.【详解】解:∠四边形ABCD 是平行四边形,∠AB =CD ,AD =BC ,设点P 到AB 、BC 、CD 、DA 的距离分别为h 1、h 2、h 3、h 4,hAB 、hBC 分别为平行四边形的AB 边和BC 边的高则S 1=12AB •h 1,S 2=12BC •h 2,S 3=12CD •h 3,S 4=12AD •h 4,hAB = h 1+h 3,hBC =h 2+h 4 ∠12AB •h 1+12CD •h 3=12AB •hAB ,12BC •h 2+12AD •h 4=12BC •hBC ,又∠S 平行四边形ABCD =AB •hAB =BC •hBC ,∠S 2+S 4=S 1+S 3,故∠正确;根据S 3=2S 1只能判断h 3=2h 1,不能判断h 2=2h 4,即不能得出S 2=2S 4,故∠错误; 根据S 1+S 3=S 2+S 4,S 1+S 3=5,能得出ABCD 的面积为5×2=10,故∠正确;由题意只能得到S 2+S 4=S 1+S 3无法得到S 1+S 2=S 3+S 4,故∠错误;故答案为:∠∠.【点睛】本题主要考查了平行四边形的性质,三角形的面积,用平行四边形的面积表示出相对的两个三角形的面积是解题的关键.33.∠∠∠【分析】根据轴对称的性质得到直线l 垂直平分BD ,则根据线段垂直平分线的性质得AB AD =,CD CB =,由于AB=CD ,则AB BC CD BC ===,于是可判断四边形ABCD 为菱形,然后根据菱形的性质对4个结论进行判断.【详解】证明:∠直线l 是四边形ABCD 的对称轴,∴直线l 垂直平分BD ,AB AD ∴=,CD CB =,AB CD =,AB BC CD BC ∴===,∴四边形ABCD 为菱形,AC BD ∴⊥,//AB CD ,OA OC =,所以∠∠∠正确 .故答案为∠∠∠.【点睛】本题考查了轴对称的性质:如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.也考查了菱形的判定与性质.34.35)【分析】设图2的矩形分割成四个全等三角形的两直角边为a 、b (a >b ),由图1与图2的两个小正方形相同,得出a 与b 的关系,再求出矩形的边长和大正方形的边长,应用周长公式求得其周长,最后便可求得其比值.【详解】解:设图2的矩形分割成四个全等三角形的两直角边为a 、b (a >b ),小正方形的边长为a-b ,矩形的长为2a+a-b=3a-b ,宽为b ,∠矩形的周长为:2(3a-b+b )=6a ,由图2知,中间小正方形的边长为b ,∠a-b=b ,∠a=2b ,∠大正方形的周长为,==∠该矩形与拼成的正方形的周长之比:=故答案为:3:5).【点睛】本题主要考查了勾股定理,矩形的性质,正方形的性质,关键是根据图形求得全等直角三角形的两直角边与矩形和大正方形的边长的关系.35.134【分析】连接DG 并延长,交于AB 延长线于点M ,过点M 作MN ∠CB ,交于CB 延长线于点N ,首先根据平行四边形的性质证明(),CGD EGM AAS ≅得出,DG GM =即可得出1,2HG FM =再利用勾股定理求出FM ,即可求得答案. 【详解】连接DG 并延长,交于AB 延长线于点M ,过点M 作MN ∠CB ,交于CB 延长线于点N ,如图,∠四边形ABCD 为平行四边形,∠CD ∠AB,AB CD ==∠CDG EMG ∠=∠又∠G 为CE 中点,∠,CG GE =在CGD △和EGM 中∠CDG EMG DGC MGE CG GE ∠=∠⎧⎪∠=∠⎨⎪=⎩∠(),CGD EGM AAS ≅∠,DG GM = ,CD EM = ∠1,2HG FM = AB EM =, ∠,AE BM =∠点E 为AB 的中点,∠1,2AE EB AB ==∠12EB BM AB ===, 又∠45,B ∠=︒∠45,MBN ∠=︒∠,BN MN =设,BN MN x ==在Rt BMN 中,∠222,BN MN BM +=∠222x x +=, 解得,5,2x = 即5,2BN MN == ∠点F 为BC 的中点, ∠17,22BF BC == ∠75622FN BF BN =+=+=, 在Rt MNF △中,∠222,NF MN MF +=∠13,2MF = ∠113,24HG FM == 故填:134. 【点睛】本题考查平行四边形的性质,全等三角形的判定与性质,三角形中位线定理,勾股定理,解题关键是熟练掌握平行四边形的性质和三角形中位线定理.36.∠∠∠【分析】根据旋转的性质可知,∠DGH ∠∠DCB ,进而得知DH =DB ,∠H =∠CBD =45°,∠DGH =∠DCB =90°,DG =DC =AD ,之后可证∠ADF ∠∠GDF ,四边形AEGF 是菱形,再根据勾股定理可知AE 的长度,进而可以一一判断选出答案.【详解】解:根据旋转的性质可知,∠DGH ∠∠DCB ,∠DH =DB ,∠H =∠CBD =45°,∠DGH =∠DCB =90°,DG =DC =AD ,在Rt ∠AED 与Rt ∠GED 中,AD =DG ,ED =ED∠Rt ∠AED ∠Rt ∠GED (HL )∠∠ADE =∠GDE ,即DE 平分∠ADB ,故∠正确;在∠ADF 和∠GDF 中,AD =DG ,∠ADF =∠GDF ,DF =DF ,∠∠ADF ∠∠GDF (SAS )∠AF =GF ,∠DAF =∠DGF =45°又∠∠ABD =45°∠FG ∠AE∠∠DAC =45°,∠∠DAC =∠H ,∠AF ∠EG∠四边形AEGF 是平行四边形,又∠AF =GF∠平行四边形AEGF 是菱形,故∠正确;∠∠H =45°,∠HAE =90°∠AE =AH∠AE =AF =HD -AD =BD -AD∠正方形ABCD 的边长为1,根据勾股定理可知BD ==即HD∠AE 1∠BE =)11=2-∠正确; ∠四边形AEGF 是菱形∠FG =AE 1∠BC +FG =1∠错误;综上答案为:∠∠∠.【点睛】本题考查的是正方形的性质,菱形的判定与性质,勾股定理和直角三角形的性质,是一道综合性较强的题,能够充分调动所学知识是解题的关键.37.30cm 2。
2022年中考数学《四边形》专题训练及答案

2022年中考数学《四边形》专题训练及答案一.选择题(共17小题)1.如图是一个由5张纸片拼成的平行四边形ABCD,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张矩形纸片EFGH的面积为S3,FH与GE 相交于点O.当△AEO,△BFO,△CGO,△DHO的面积相等时,下列结论一定成立的是()A.S1=S2B.S1=S3C.AB=AD D.EH=GH2.数学兴趣小组同学从“中国结”的图案(图1)中发现,用相同的菱形纵向排列放置,可得到更多的菱形.如图2,用2个相同的菱形放置,得到3个菱形.下面说法正确的是()A.用3个相同的菱形放置,最多能得到6个菱形B.用4个相同的菱形放置,最多能得到16个菱形C.用5个相同的菱形放置,最多能得到27个菱形D.用6个相同的菱形放置,最多能得到41个菱形3.如图,菱形ABCD中,∠B=60°,点P从点B出发,沿折线BC﹣CD方向移动,移动到点D停止.在△ABP 形状的变化过程中,依次出现的特殊三角形是()A.直角三角形→等边三角形→等腰三角形→直角三角形B.直角三角形→等腰三角形→直角三角形→等边三角形C.直角三角形→等边三角形→直角三角形→等腰三角形D.等腰三角形→等边三角形→直角三角形→等腰三角形4.如图,在矩形ABCD 中,AB =6,BC =10,E 是BC 边上一动点(不含端点B ,C ),连接EA ,F 是CD 边上一点,设DF =a ,若存在唯一的点E ,使∠FEA =90°,则a 的值是( )A .256B .116C .103D .35.如图,E ,F 是正方形ABCD 的边BC 上两个动点,BE =CF .连接AE ,BD 交于点G ,连接CG ,DF 交于点M .若正方形的边长为1,则线段BM 的最小值是( )A .12B .√3−12C .√2−12D .√5−126.如图,在矩形ABCD 中,以对角线AC 为斜边作Rt △AEC ,过点E 作EF ⊥DC 于点F ,连结AF ,若AD =DF ,S △AEF =3,S △ACF =5,则矩形ABCD 的面积为( )A .18B .19C .20D .217.如图,在▱ABCD 中,BD =6,AC =10,BD ⊥AB ,则AD 的长为( )A .8B .√42C .2√5D .2√138.如图,在Rt △ABC 中(AC >BC ),∠ACB =90°,过C 作CD ⊥AB 于点D ,分别以AD ,AC ,BC 为边向上作正方形ADQP,正方形ACEF,正方形CBGH,其中CE与PQ相交于点O,连接PF,QH,EH.若点F,P,Q,H在同一直线上,且△OCQ的面积为1,则六边形ABGHEF的面积为()A.5+3√5B.15+7√5C.20+10√5D.30+14√59.已知四边形ABCD为平行四边形,要使四边形ABCD为矩形,则可增加条件为()A.AB=BC B.AC=BD C.AC⊥BD D.AC平分∠BAD10.如图,矩形ABCD中,AB:AD=2:1,点E为AB的中点,点F为EC上一个动点,点P为DF的中点,连接PB,当PB的最小值为3√2时,则AD的值为()A.2B.3C.4D.611.如图,在矩形ABCD中,点F为边AD上一点,过F作EF∥AB交边BC于点E,P为边AB上一点,PH⊥DE 交线段DE于H,交线段EF于Q,连接DQ.当AF=AB时,要求阴影部分的面积,只需知道下列某条线段的长,该线段是()A.EF B.DE C.PH D.PE12.如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,里面放置两个大小相同的正方形CDEF与正方形GHIJ,点F在边BC上,点D,H在边AC上,点G在边DE上,点I,J在斜边AB上,则正方形CDEF的边长为()A .3613B .3013C .2413D .181313.已知,矩形ABCD 中,E 为AB 上一定点,F 为BC 上一动点,以EF 为一边作平行四边形EFGH ,点G ,H 分别在CD 和AD 上,若平行四边形EFGH 的面积不会随点F 的位置改变而改变,则应满足( )A .AD =4AEB .AD =2ABC .AB =2AED .AB =3AE14.如图,矩形ABCD 由两直角边之比皆为1:2的三对直角三角形纸片甲、乙、丙拼接而成它们之间互不重叠也无缝隙,则AD AB的值为( )A .23B .34C .45D .2√5515.如图,已知大矩形ABCD 由①②③④四个小矩形组成,其中AE =CG ,则只需要知道其中一个小矩形的面积就可以求出图中阴影部分的面积,这个小矩形是( )A .①B .②C .③D .④16.将一个边长为4的正方形ABCD 分割成如图所示的9部分,其中△ABE ,△BCF ,△CDG ,△DAH 全等,△AEH ,△BEF ,△CFG ,△DGH 也全等,中间小正方形EFGH 的面积与△ABE 面积相等,且△ABE 是以AB 为底的等腰三角形,则△AEH 的面积为( )A .2B .169C .32D .√217.一张矩形纸板和圆形纸板按如图方式分别剪得同样大定理特例图(AC =3,BC =4,AB =5,分别以三边为边长向外作正方形),图1中边HI 、LM 和点K 、J 都恰好在矩形纸板的边上,图2中的圆心O 在AB 中点处,点H 、I 都在圆上,则矩形和圆形纸板的面积比是( )A .400:127πB .484:145πC .440:137πD .88:25π二.填空题(共7小题)18.如图,在矩形ABCD 中,点E 在边AB 上,△BEC 与△FEC 关于直线EC 对称,点B 的对称点F 在边AD 上,G 为CD 中点,连结BG 分别与CE ,CF 交于M ,N 两点.若BM =BE ,MG =1,则BN 的长为 ,sin ∠AFE 的值为 .19.图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图2),则图1中所标注的d 的值为 ;记图1中小正方形的中心为点A ,B ,C ,图2中的对应点为点A ′,B ′,C ′.以大正方形的中心O 为圆心作圆,则当点A ′,B ′,C ′在圆内或圆上时,圆的最小面积为 .20.如图,在▱ABCD中,对角线AC,BD交于点O,AB⊥AC,AH⊥BD于点H,若AB=2,BC=2√3,则AH的长为.21.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=10,BD=24,则OE的长为.22.如图,在▱ABCD中,P为AB上的一点,E、F分别是DP、CP的中点,G、H为CD上的点,连接EG、FH,若▱ABCD的面积为24cm2,GH=12AB,则图中阴影部分的面积为.23.如图1,某学校楼梯墙面上悬挂了四幅全等的正方形画框,画框下边缘与水平地面平行.如图2,画框的左上角顶点B,E,F,G都在直线AB上,且BE=EF=FG,楼梯装饰线条所在直线CD∥AB,延长画框的边BH,MN得到▱ABCD.若直线PQ恰好经过点D,AB=275cm,CH=100cm,∠A=60°,则正方形画框的边长为cm.24.如图,F是矩形ABCD内一点,AF=BF.连接DF并延长交BC于点G,且点C与AB的中点E恰好关于直线DG 对称.若AD =9,则AB 的长为 .三.解答题(共13小题) 25.【推理】如图1,在正方形ABCD 中,点E 是CD 上一动点,将正方形沿着BE 折叠,点C 落在点F 处,连结BE ,CF ,延长CF 交AD 于点G . (1)求证:△BCE ≌△CDG . 【运用】(2)如图2,在【推理】条件下,延长BF 交AD 于点H .若HD HF=45,CE =9,求线段DE 的长.【拓展】(3)将正方形改成矩形,同样沿着BE 折叠,连结CF ,延长CF ,BF 交直线AD 于G ,H 两点,若AB BC=k ,HD HF=45,求DE EC的值(用含k 的代数式表示).26.【证明体验】(1)如图1,AD 为△ABC 的角平分线,∠ADC =60°,点E 在AB 上,AE =AC .求证:DE 平分∠ADB . 【思考探究】(2)如图2,在(1)的条件下,F 为AB 上一点,连结FC 交AD 于点G .若FB =FC ,DG =2,CD =3,求BD 的长. 【拓展延伸】(3)如图3,在四边形ABCD 中,对角线AC 平分∠BAD ,∠BCA =2∠DCA ,点E 在AC 上,∠EDC =∠ABC .若BC =5,CD =2√5,AD =2AE ,求AC 的长.27.小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD.[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.[探究2]如图2,连结AC′,过点D′作D′M∥AC′交BD于点M.线段D′M与DM相等吗?请说明理由.[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P,N(如图3),发现线段DN,MN,PN存在一定的数量关系,请写出这个关系式,并加以证明.28.如图,在菱形ABCD中,∠ABC是锐角,E是BC边上的动点,将射线AE绕点A按逆时针方向旋转,交直线CD于点F.(1)当AE⊥BC,∠EAF=∠ABC时,①求证:AE=AF;②连结BD,EF,若EFBD =25,求S△AEFS菱形ABCD的值;(2)当∠EAF=12∠BAD时,延长BC交射线AF于点M,延长DC交射线AE于点N,连结AC,MN,若AB=4,AC=2,则当CE为何值时,△AMN是等腰三角形.29.如图,在四边形ABCD中,AB∥CD,AD∥BC,过B作BE⊥BD与DA的延长线交于点E.(1)若点A为DE中点,求证:四边形ABCD为菱形.(2)若BA=BE,tan∠EDB=√22,求△ABE与四边形ABCD面积的比值.30.如图,四边形ABCD是菱形,E是AB的中点,AC的垂线EF交AD于点M,交CD的延长线于点F.(1)求证:AM=AE;(2)连接CM,DF=2.①求菱形ABCD的周长;②若∠ADC=2∠MCF,求ME的长.31.如图1,在正方形ABCD中,BD为对角线,点E为边AB上的点,连结DE,过点A作AG⊥DE交BC于点G,交BD于点H,垂足为F,连结EH.(1)AE与BG相等吗,请说明理由;(2)若BE:AE=n,求证:DH:BH=n+1;(3)在(2)的基础上,如图2时,当EH∥AD时,求n的值.32.如图,在矩形ABCD中,点E在射线CB上,连结AE,∠DAE的平分线AG与CD交于点G,与BC的延长线交于F点.设CEEB =λ(λ>0),ABBC=k(k>0且k≠2).(1)若AB=8,λ=1,k=43,求线段CF的长.(2)连结EG,若EG⊥AF,①求证:点G为CD边的中点;②求λ的值(用k表示).33.在正方形ABCD中,点E为边AB上的点,连结DE,过点A作AG⊥DE交BC于G.(1)如图1,AE与BG相等吗?请说明理由;(2)如图2,连接BD,交AG于H,ED于F,连接EH,若BE:AE=n,求DH:BH;(3)在(2)的基础上,如图3,当EH∥AD时,求n的值.34.如图,在△ABC中,AC=BC=2√5,tan∠CAB=12,P为AC上一点,PD⊥AB交AB于点E,AD⊥AC交PD于点D,连结BD,CD,CD交AB于点Q.(1)若CD⊥BC,求证:△AED∽△QCB;(2)若AB平分∠CBD,求BQ的长;(3)连结PQ并延长交BD于点M.①当点P是AC的中点时,求tan∠BQM的值;②当PM平行于四边形ADBC中的某一边时,求BMDM的值.35.在三角形中,一个角两夹边的平方和减去它对边的平方所得的差,叫做这个角的勾股差.(1)概念理解:在直角三角形中,直角的勾股差为 ;在底边长为2的等腰三角形中,底角的勾股差为 ;(2)性质探究:如图1,CD 是△ABC 的中线,AC =b ,BC =a ,AB =2c ,CD =d ,记△ACD 中∠ADC 的勾股差为m ,△BCD 中∠BDC 的勾股差为n ;①求m ,n 的值(用含a ,b ,c ,d 的代数式表示); ②试说明m 与n 互为相反数;(3)性质应用:如图2,在四边形ABCD 中,点E 与F 分别是AB 与BC 的中点,连接BD ,DE ,DF ,若DF AB=34,且CD ⊥BD ,CD =AD ,求DE DF的值.36.【发现问题】小聪发现图1所示矩形甲与图2所示矩形乙的周长与面积满足关系:C 乙C 甲=S 乙S 甲=12.【提出问题】对于任意一个矩形A ,是否一定存在矩形B ,使得C B C A=S B S A=12成立?【解决问题】(1)对于图2所示的矩形乙,是否存在矩形丙(可设两条邻边长分别为x 和7﹣x ),使得C 丙C 乙=S 丙S 乙=12成立.若存在,求出矩形丙的两条邻边长;若不存在,请说明理由; (2)矩形A 两条邻边长分别为m 和1,若一定存在矩形B ,使得C B C A=S B S A=12成立,求m 的取值范围;(3)请你回答小聪提出来的问题.若一定存在,请说明理由;若不一定存在,请直接写出矩形A 两条邻边长a ,b 满足什么条件时一定存在矩形B .37.如图,矩形ABCD 中,AB =7,AD =3,点E 是AD 边上的一点,DE =2AE ,连接EB ,F 是EB 的中点,连接CF ,点M 为DC 边上的一点,当动点P 从点C 匀速运动到点F 时,动点Q 恰好从点M 匀速运动到点C .(1)求tan∠DCF的值;(2)若点P运动到CF的中点时,Q,P,B三点恰好共线,求此时DM的长;(3)连接EM,BM,当∠EMB=90°且DM<CM时,记MQ=x,CP=y.①求y关于x的函数关系式;②当PQ平行于△BEM的某一边时,求所有满足条件的x的值.参考答案与试题解析一.选择题(共17小题)1.【解答】解:如图,连接DG,AH,过点O作OJ⊥DE于J.∵四边形EFGH是矩形,∴OH=OF,EF=GH,∠HEF=90°,∵OJ⊥DE,∴∠OJH=∠HEF=90°,∴OJ∥EF,∵HO=OF,∴HJ=JE,∴EF=GH=2OJ,∵S△DHO=12•DH•OJ,S△DHG=12•DH•GH,∴S△DGH=2S△DHO,同法可证S△AEH=2S△AEO,∵S△DHO=S△AEO,∴S△DGH=S△AEH,∵S△DGC=12•CG•DH,S△ADH=12•DH•AE,CG=AE,∴S△DGC=S△ADH,∴S△DHC=S△ADE,∴S1=S2,故A选项符合题意;S3=HE•EF≠S1,故B选项不符合题意;AB=AD,EH=GH均不成立,故C选项,D选项不符合题意,故选:A.2.【解答】解:如图所示,用2个相同的菱形放置,最多能得到3个菱形;用3个相同的菱形放置,最多能得到8个菱形,用4个相同的菱形放置,最多能得到16个菱形,用5个相同的菱形放置,最多能得到29个菱形,用6个相同的菱形放置,最多能得到47个菱形.故选:B.3.【解答】解:∵∠B=60°,故菱形由两个等边三角形组合而成,当AP⊥BC时,此时△ABP为直角三角形;当点P到达点C处时,此时△ABP为等边三角形;当P为CD中点时,△ABP为直角三角形;当点P 与点D 重合时,此时△ABP 为等腰三角形, 故选:C .4.【解答】解:∵∠FEA =90°, ∴∠AEB +∠FEC =90°, ∵∠B =90°,∴∠AEB +∠EAB =90°, ∴∠EAB =∠FEC , ∵∠B =∠C =90°, ∴△ABE ∽△ECF , ∴AB EC=BE CF,设BE =x ,则EC =BC ﹣BE =10﹣x , ∵DF =a ,∴FC =DC ﹣DF =6﹣a , ∴x (10﹣x )=6(6﹣a ), ∴x 2﹣10x +36﹣6a =0, 由题意判别式b 2﹣4ac =0, ∴24a ﹣44=0, ∴a =116, 故选:B .5.【解答】解:如图,在正方形ABCD 中,AB =AD =CB ,∠EBA =∠FCD ,∠ABG =∠CBG ,在△ABE 和△DCF 中, {AB =CD∠EBA =∠FCD BE =CF, ∴△ABE ≌△DCF (SAS ), ∴∠BAE =∠CDF , 在△ABG 和△CBG 中,{AB =BC∠ABG =∠CBG BG =BG, ∴△ABG ≌△CBG (SAS ), ∴∠BAG =∠BCG , ∴∠CDF =∠BCG ,∵∠DCM +∠BCG =∠FCD =90°, ∴∠CDF +∠DCM =90°, ∴∠DMC =180°﹣90°=90°, 取CD 的中点O ,连接OB 、OF , 则OF =CO =12CD =12,在Rt △BOC 中,OB =√CB 2+OC 2=√12+(12)2=√52,根据三角形的三边关系,OM +BM >OB , ∴当O 、M 、B 三点共线时,BM 的长度最小, ∴BM 的最小值=OB ﹣OF =√52−12=√5−12. 故选:D .6.【解答】解:过点E 作EG 垂直AD 延长线于点G , ∵EF ⊥DC ,∴S △AEF =12EF •DF =3,S △ACF =12CF •AD =5, ∵DF =AD , ∴EF :CF =3:5,设EF =3b ,CF =5b ,AD =DF =a ,∵∠G =90°,∠EFD =90°,∠GDF =90°, ∴四边形EFDG 是矩形, ∴GE =DF =a ,GD =EF =3b , 在Rt △GEA 中,GE 2+AG 2=AE 2, 在Rt △EFC 中,EF 2+FC 2=EC 2, 在Rt △CEA 中,AE 2+CE 2=AC 2,∴AC 2=GE 2+AG 2+EF 2+FC 2=a 2+(a +3b )2+(3b )2+(5b )2=2a 2+43b 2+6ab , 在Rt △DAC 中,AC 2=AD 2+CD 2=a 2+(a +5b )2=2a 2+25b 2+10ab , ∴2a 2+43b 2+6ab =2a 2+25b 2+10ab , ∴18b 2=4ab ,∵b>0,∴a=92b,∴S△AEF=12EF•DF=12×3b×a=12×3b×92b=3,∴b=2 3,∴a=92×23=3,∴S矩形ABCD=AD•CD=a(a+5b)=3×(3+5×23)=19.故选:B.7.【解答】解:AC与BD相交于点O,∵四边形ABCD是平行四边形,∴2AO=AC,2OB=BD,∵BD=6,AC=10,∴OA=5,OB=3,∵DB⊥AB,在Rt△AOB中,由勾股定理得,AB=√OA2−OB2=√52−32=4,在Rt△ADB中,由勾股定理得,AD=√DB2+AB2=√62+42=2√13,故选:D.8.【解答】解:设CQ=x,∵∠CQO=90°,S△OCQ=1,∴12•CQ•OQ=1,∴OQ=2 x,∵∠CDB=∠CQH=∠BCH=90°,∴∠DCB +∠HCQ =90°,∠HCQ +∠CHQ =90°, ∴∠DCB =∠CHQ , 在Rt △CDB 和△HQC 中, {∠CDB =∠HQC∠DCB =∠CHQ CB =HC, ∴△CDB ≌△HQC (AAS ), ∴BD =CQ =x , ∵QO ∥BD , ∴△QCO ∽△DCB , ∴OQ BD=CQCD, ∴CD =x×x2x=12x 3,∵∠CAD +∠ACD =90°,∠DCB +∠ACD =90°, ∴∠CAD =∠DCB , ∵∠ADC =∠CDB =90°, ∴△ACD ∽△CBD , ∴AD CD=CD BD,∴CD 2=AD •DB , ∴(12x 3)2=(x +12x 3)•x ,解得x 2=1+√5或1−√5(舍弃), ∴CD =1+√52x ,AD =√5+32x , ∴AB =AD +BD =5+√52x , ∴AB 2=(5+√52)2×(1+√5)=20+10√5, ∴S 正方形ACEF +S 正方形BCHG =AB 2=20+10√5, ∵S △ACB =12•AB •CD =12×1+√52x ×5+√52x =5+2√5, ∴S 六边形ABGHEF =S 正方形ACEF +S 正方形CBGH +2S △ABC =20+10√5+2(5+2√5)=30+14√5, 故选:D .9.【解答】解:A 、∵四边形ABCD 是平行四边形,AB =BC , ∴四边形ABCD 是菱形,故A 不符合题意; B 、∵四边形ABCD 是平行四边形,AC =BD , ∴四边形ABCD 是矩形,故B 符合题意;C、∵四边形ABCD是平行四边形,AC⊥BD,∴四边形ABCD是菱形,故C不符合题意;D、∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAC=∠ACB,∵AC平分∠BAD,∴∠DAC=∠BAC,∴∠BAC=∠ACB,∴AB=AC,∴四边形ABCD是菱形,故D不符合题意;故选:B.10.【解答】解:如图,当点F与点C重合时,点P在P1处,CP1=DP1,当点F与点E重合时,点P在P2处,EP2=DP2,∴P1P2∥CE且P1P2=12CE..且当点F在EC上除点C、E的位置处时,有DP=FP.由中位线定理可知:P1P∥CE且P1P=12CF,∴点P的运动轨迹是线段P1P2,.∴当BP⊥P1P2时,PB取得最小值.∵矩形ABCD中,AB:AD=2:1,设AB=2t,则AD=t,∵E为AB的中点,∴△CBE、△ADE、△BCP1为等腰直角三角形,CP1=t,∴∠ADE=∠CDE=∠CP1B=45°,∠DEC=90°.∴∠DP2P1=90°.∴∠DP1P2=45°.∴∠P2P1B=90°,即BP1⊥P1P2,∴BP的最小值为BP1的长.在等腰直角△BCP1中,CP1=BC=t,∴BP 1=√2t =3√2, ∴t =3. 故选:B .11.【解答】解:过点P 作PM ⊥EF 于点M ,如图:∵四边形ABCD 为矩形,∴AB ∥DC ,AD ∥BC ,∠C =90°, ∵EF ∥AB , ∴EF ∥DC , ∴∠EDC =∠DEF , ∵PH ⊥DE ,PM ⊥EF , ∴∠PMQ =∠EHQ =90°, 又∵∠PQM =∠EQH , ∴∠QPM =∠DEF =∠EDC , 在△PMQ 和△DCE 中, {∠MPQ =∠EDCPM =CD∠PMQ =∠C,∴△PMQ ≌△DCE (ASA ), ∴PQ =DE ,∴阴影部分的面积=S △PDE ﹣S △QED =12×DE ×PH −12DE ×QH =12DE 2, ∴故选:B .12.【解答】解:在Rt △ABC 中, ∵∠ACB =90°,BC =6,AC =8, ∴AB =√AC 2+BC 2=10.∴sin ∠A =BCAB =35,cos ∠A =ACAB =45. ∵四边形GHIJ 为正方形, ∴GH ∥AB . ∴∠GHD =∠A .∴cos ∠GHD =cos ∠A =45.设正方形CDEF 与正方形GHIJ 的边长为x ,则HI =CD =x .在Rt △AHI 中,∵sin ∠A =HI AH , ∴x AH =35.∴AH =53x .在Rt △GHD 中,∵cos ∠GHD =DH GH , ∴DH x =45. ∴DH =45x .∵AC =CD +DH +AH =8,∴x +45x +53x =8.解得:x =3013. 故选:B .13.【解答】解:设AB =a ,BC =b ,BE =c ,BF =x ,∴S 平行四边形EFGH =S 矩形ABCD ﹣2(S △BEF +S △AEH )=ab ﹣2[12cx +12(a ﹣c )(b ﹣x )] =ab ﹣(cx +ab ﹣ax ﹣bc +cx )=ab ﹣cx ﹣ab +ax +bc ﹣cx=(a ﹣2c )x +bc ,∵F 为BC 上一动点,∴x 是变量,(a ﹣2c )是x 的系数,∵平行四边形EFGH 的面积不会随点F 的位置改变而改变,为固定值,∴x 的系数为0,bc 为固定值,∴a ﹣2c =0,∴a =2c ,∴E 是AB 的中点,∴AB =2AE ,故选:C .14.【解答】解:如图所示设丙的短直角边为x,乙的短直角边为y,则HG=2x,DG=2x+y,CG=12DG=2x+y2,∵BF=DH=y,FG=EH=x,∴CF=2BF=2y,CF=CG+FG=2x+y2+x,∴2y=2x+y2+x,∴x=34y,∵AB=DC=√CG2+DG2=√(2x+y2)2+(2x+y)2=√(54y)2+(52y)2=5√54y,AD=√DH2+AH2=√y2+(2y)2=√5y,∴ADAB=√5y5√54y=45.故选:C.15.【解答】解:如图所示:∵四边形ABCD和四边形③是矩形,∴AB=CD,FP=CG,∵AE=CG,∴BE=DG,∴阴影部分的面积=△BFD的面积﹣△BFP的面积=12BF×CD−12BF×FP=12BF×(CD﹣CG)=12BF×DG=12BF×BE=12矩形②面积,故选:B.16.【解答】解:连接EG,向两端延长分别交AB、CD于点M、N,如图,∵△ABE,△BCF,△CDG,△DAH全等,△ABE是以AB为底的等腰三角形,∴AE=BE=CG=DG,∴EG是AB、CD的垂直平分线,∴MN⊥AB,∴EM=GN(全等三角形的对应高相等),∵四边形ABCD是正方形,∴∠BAD=∠ADC=90°,∴四边形AMND是矩形,∴MN=AD=4,设ME=x,则EG=4﹣2x,∵中间小正方形EFGH的面积与△ABE面积相等,∴12(4−2x)2=12×4x,解得,x=1或x=4(舍),∵△ABE,△BCF,△CDG,△DAH全等,△AEH,△BEF,△CFG,△DGH也全等,∴△AEH的面积=S正方形ABCD−5S△ABE4=42−5×12×4×14=32,故选:C.17.【解答】解:在图1中延长CA与GF交于点N,延长CB与EF交于点P,在图2中,连接OH,过O作OQ⊥AC于点Q,则,在图1中,∵四边形ABJK是正方形,∴AB=BJ,∠ABJ=90°,∴∠ABC +∠PBJ =90°=∠ABC +∠BAC ,∴∠BAC =∠JBP ,∵∠ACB =∠BPJ =90°,∴△ABC ≌△BJK (AAS ),∴AC =BP =3,∵AC =MC =3,BC =4,∴DE =MP =3+4+3=10,同理得,DG =HN =4+3+4=11,∴矩形DEFG 的面积为11×10=110,在图2中,OQ =12CB =2,CQ =12AC =1.5,∴HQ =4+1.5=5.5,∴OH =√22+5.52=√1372,∴⊙O 的面积为:π×(√1372)2=137π4, ∴矩形和圆形纸板的面积比是:110:137π4=440:137π,故选:C .二.填空题(共7小题)18.【解答】解:∵BM =BE ,∴∠BEM =∠BME ,∵AB ∥CD ,∴∠BEM =∠GCM ,又∵∠BME =∠GMC ,∴∠GCM =∠GMC ,∴MG =GC =1,∵G 为CD 中点,∴CD =AB =2.连接BF ,FM ,由翻折可得∠FEM=∠BEM,BE=EF,∴BM=EF,∵∠BEM=∠BME,∴∠FEM=∠BME,∴EF∥BM,∴四边形BEFM为平行四边形,∵BM=BE,∴四边形BEFM为菱形,∵∠EBC=∠EFC=90°,EF∥BG,∴∠BNF=90°,∵BF平分∠ABN,∴F A=FN,∴Rt△ABF≌Rt△NBF(HL),∴BN=AB=2.∵FE=FM,F A=FN,∠A=∠BNF=90°,∴Rt△AEF≌Rt△NMF(HL),∴AE=NM,设AE=NM=x,则BE=FM=2﹣x,NG=MG﹣NM=1﹣x,∵FM∥GC,∴△FMN∽△CGN,∴CGFM=GNNM,即12−x=1−xx,解得x=2+√2(舍)或x=2−√2,∴EF=BE=2﹣x=√2,∴sin∠AFE=AEEF=√2√2=√2−1.故答案为:2;√2−1.19.【解答】解:如图,连接FW,由题意可知点A′,O,C′在线段FW上,连接OB′,B′C′,过点O作OH ⊥B′C′于H.∵大正方形的面积=12,∴FG=GW=2√3,∵EF=WK=2,∴在Rt△EFG中,tan∠EGF=EFFG=2√3=√33,∴∠EGF=30°,∵JK∥FG,∴∠KJG=∠EGF=30°,∴d=JK=√3GK=√3(2√3−2)=6﹣2√3,∵OF=OW=12FW=√6,C′W=√2,∴OC′=√6−√2,∵B′C′∥QW,B′C′=2,∴∠OC′H=∠FWQ=45°,∴OH=HC′=√3−1,∴HB′=2﹣(√3−1)=3−√3,∴OB′2=OH2+B′H2=(√3−1)2+(3−√3)2=16﹣8√3,∵OA′=OC′<OB′,∴当点A′,B′,C′在圆内或圆上时,圆的最小面积为(16﹣8√3)π.故答案为:6﹣2√3,(16﹣8√3)π.20.【解答】解:如图,∵AB⊥AC,AB=2,BC=2√3,∴AC=√(2√3)2−22=2√2,在▱ABCD中,OA=OC,OB=OD,∴OA=OC=√2,在Rt△OAB中,OB=√22+(√2)2=√6,又AH⊥BD,∴12OB •AH =12OA •AB ,即12×√6⋅AH =12×2×√2, 解得AH =2√33. 故答案为:2√33. 21.【解答】解:∵DE ∥AC ,CE ∥BD ,∴四边形OCED 为平行四边形,∵四边形ABCD 是菱形,∴AC ⊥BD ,OA =OC =12AC =5,OB =OD =12BD =12, ∴∠DOC =90°,CD =√OC 2+OD 2=√52+122=13, ∴平行四边形OCED 为矩形,∴OE =CD =13,故答案为:13.22.【解答】解:如图,设EG ,FH 交于点O ,∵四边形ABCD 为平行四边形,且▱ABCD 的面积为24cm 2, ∴S △PCD =12S ▱ABCD =12cm 2,AB =CD ,AB ∥CD , ∵E 、F 分别是DP 、CP 的中点,∴EF 为△PCD 的中位线,∴CD =2EF ,EF ∥CD ∥AB ,∴S △PEF :S △PCD =1:4,∴S △PEF =3,∵GH =12AB ,∴EF =GH ,EF ∥GH ,∴S △OEF =S △OGH =12S △PEF =1.5cm 2,∴S 阴影=3+2×1.5=6cm 2,故答案为6cm 2.23.【解答】解:延长EP ,与CD 交于点K ,如图, ∵AB ∥CD ,BC ∥EK ,∴四边形BCKE 是平行四边形,∴PK=CH=100cm,∵∠A=60°,四边形ABCD是平行四边形,∴∠C=∠A=60°,AB=CD=275cm,∵BC∥EK,∴∠PKD=∠C=60°,∴DK=PKcos60°=200cm,∴BE=CK=CD﹣DK=75cm,∵BE=EF=FG,∴AG=AB﹣3BE=275﹣75×3=50cm,∴GM=AG•sin∠A=50×√32=25√3cm.正方形画框的边长为25√3cm.故答案为:25√3.24.【解答】解:连接EF、EG、EC,如图所示:∵四边形ABCD是矩形,∴BC=AD=9,AD∥BC,∠BAD=∠ABC=90°,∴AB⊥AD,∵AF=BF,点E是AB的中点,∴EF⊥AB,∴EF∥AD∥BC,∴EF是梯形ABGD的中位线,∠EFG=∠CGF,∴EF=12(AD+BG),设BG=x,则CG=9﹣x,EF=12(9+x),∵点C与AB的中点E关于直线DG对称,∴EG=CG,∠CGF=∠EGF,∴EF=CG,∴12(9+x)=9﹣x,解得:x=3,∴BG=3,EG=CG=6,∴BE=√EG2−BG2=√62−32=3√3,∴AB=2BE=6√3;故答案为:6√3.三.解答题(共13小题)25.【解答】(1)证明:如图1中,∵△BFE是由△BCE折叠得到,∴BE⊥CF,∴∠ECF+∠BEC=90°,∵四边形ABCD是正方形,∴∠D=∠BCE=90°,∴∠ECF+∠CGD=90°,∴∠BEC=∠CGD,∵BC=CD,∴△BCE≌△CDG(AAS).(2)如图2中,连接EH.∵△BCE≌△CDG,∴CE=DG=9,由折叠可知BC=BF,CE=FE=9,∴∠BCF=∠BFC,∵四边形ABCD是正方形,∴AD∥BC,∴∠BCG=∠HGF,∵∠BFC=∠HFG,∴∠HFG=∠HGF,∴HF=HG,∵HDHF=45,DG=9,∴HD=4,HF=HG=5,∵∠D=∠HFE=90°,∴HF2+FE2=DH2+DE2,∴52+92=42+DE2,∴DE=3√10或﹣3√10(舍弃),∴DE=3√10.(3)如图3中,连接HE.由题意HD HF =45,可以假设DH =4m ,HG =5m ,设DE EC =x .①当点H 在点D 的左侧时,∵HF =HG ,∴DG =9m ,由折叠可知BE ⊥CF ,∴∠ECF +∠BEC =90°,∵∠D =90°,∴∠ECF +∠CGD =90°,∴∠BEC =∠CGD ,∵∠BCE =∠D =90°,∴△CDG ∽△BCE ,∴DG CE =CD BC , ∵CD BC =AB BC =k , ∴9m CE =k 1,∴CE =9m k=FE , ∴DE =9mx k , ∵∠D =∠HFE =90°∴HF 2+FE 2=DH 2+DE 2,∴(5m )2+(9m k )2=(4m )2+(9mx k )2, ∴x =√k 2+93或−√k 2+93(舍弃), ∴DE EC =√k 2+93.②当点H 在点D 的右侧时,如图4中,同理HG =HF ,△BCE ∽△CDG ,∴DG =m ,CE =m k =FE ,∴DE =mx k, ∵HF 2+FE 2=DH 2+DE 2,∴(5m )2+(m k )2=(4m )2+(mx k )2,∴x =√9k 2+1或−√9k 2+1(舍弃),∴DE EC =√9k 2+1.综上所述,DE EC =√k 2+93或√9k 2+1.26.【解答】(1)证明:如图1,∵AD 平分∠BAC ,∴∠EAD =∠CAD ,∵AE =AC ,AD =AD ,∴△EAD ≌△CAD (SAS ),∴∠ADE =∠ADC =60°,∵∠BDE =180°﹣∠ADE ﹣∠ADC =180°﹣60°﹣60°=60°, ∴∠BDE =∠ADE ,∴DE 平分∠ADB .(2)如图2,∵FB =FC ,∴∠EBD =∠GCD ;∵∠BDE =∠CDG =60°,∴△BDE ∽△CDG ,∴BD CD =DE DG ;∵△EAD ≌△CAD ,∴DE =CD =3,∵DG =2,∴BD =CD 2DG =322=92. (3)如图3,在AB 上取一点F ,使AF =AD ,连结CF . ∵AC 平分∠BAD ,∴∠F AC =∠DAC ,∵AC =AC ,∴△AFC ≌△ADC (SAS ),∴CF =CD ,∠FCA =∠DCA ,∠AFC =∠ADC ,∵∠FCA +∠BCF =∠BCA =2∠DCA ,∴∠DCA=∠BCF,即∠DCE=∠BCF,∵∠EDC=∠ABC,即∠EDC=∠FBC,∴△DCE∽△BCF,∴CDBC=CECF,∠DEC=∠BFC,∵BC=5,CF=CD=2√5,∴CE=CD2BC=(2√5)25=4;∵∠AED+∠DEC=180°,∠AFC+∠BFC=180°,∴∠AED=∠AFC=∠ADC,∵∠EAD=∠DAC(公共角),∴△EAD∽△DAC,∴AEAD=ADAC=12,∴AC=2AD,AD=2AE,∴AC=4AE=43CE=43×4=163.27.【解答】解:[探究1]如图1,设BC=x,∵矩形ABCD绕点A顺时针旋转90°得到矩形AB′C′D′,∴点A,B,D'在一条线上,∴AD'=AD=BC=x,D'C'=AB'=AB=1,∴D'B=AD'﹣AB=x﹣1,∵∠BAD=∠D'=90°,∴D'C'∥DA,又∵点C'在DB的延长线上,∴△D'C'B∽△ADB,∴D′C′AD=D′BAB,∴1x=x−11,解得x1=1+√52,x2=1−√52(不合题意,舍去),∴BC=1+√5 2.[探究2]D'M=DM.证明:如图2,连接DD',∵D'M∥AC',∴∠AD'M=∠D'AC',∵AD'=AD,∠AD'C'=∠DAB=90°,D'C'=AB,∴△AC'D'≌△DBA(SAS),∴∠D'AC'=∠ADB,∴∠ADB=∠AD'M,∵AD'=AD,∴∠ADD'=∠AD'D,∴∠MDD'=∠MD'D,∴D'M=DM;[探究3]关系式为MN2=PN•DN.证明:如图3,连接AM,∵D'M=DM,AD'=AD,AM=AM,∴△AD'M≌△ADM(SSS),∴∠MAD'=∠MAD,∵∠AMN=∠MAD+∠NDA,∠NAM=∠MAD'+∠NAP,∴∠AMN=∠NAM,∴MN=AN,在△NAP和△NDA中,∠ANP=∠DNA,∠NAP=∠NDA,∴△NP A∽△NAD,∴PNAN=ANDN,∴AN2=PN•DN,∴MN2=PN•DN.28.【解答】(1)①证明:∵四边形ABCD是菱形,∴AB=AD,∠ABC=∠ADC,AD∥BC,∵AE⊥BC,∴AE⊥AD,∴∠ABE+∠BAE=∠EAF+∠DAF=90°,∵∠EAF=∠ABC,∴∠BAE=∠DAF,∴△ABE≌△ADF(ASA),∴AE=AF;②解:连接AC,如图1所示:∵四边形ABCD是菱形,∴AB=BC=DC,AC⊥BD,由①知,△ABE≌△ADF,∴BE=DF,∴CE=CF,∵AE=AF,∴AC⊥EF,∴EF∥BD,∴△CEF∽△CBD,∴ECBC=EFBD=25,设EC=2a,则AB=BC=5a,BE=3a,∴AE=√AB2−BE2=√(5a)2−(3a)2=4a,∵AEAB=AFBC,∠EAF=∠ABC,∴△AEF∽△BAC,∴S△AEFS△BAC=(AEAB)2=(4a5a)2=1625,∴S△AEFS菱形ABCD=S△AEF2S△BAC=12×1625=825;(2)解:∵四边形ABCD是菱形,∴∠BAC=12∠BAD,∵∠EAF=12∠BAD,∴∠BAC=∠EAF,∴∠BAE=∠CAM,∵AB∥CD,∴∠BAE=∠ANC,∴∠ANC=∠CAM,同理:∠AMC=∠NAC,∴△MAC∽△ANC,∴ACCN=AMNA,△AMN是等腰三角形有三种情况:①当AM=AN时,如图2所示:∵∠ANC =∠CAM ,AM =AN ,∠AMC =∠NAC , ∴△ANC ≌△MAC (ASA ),∴CN =AC =2,∵AB ∥CN ,∴△CEN ∽△BEA ,∴CE BE =CN AB =24=12, ∵BC =AB =4,∴CE =13BC =43;②当NA =NM 时,如图3所示:则∠NMA =∠NAM ,∵AB =BC ,∴∠BAC =∠BCA ,∵∠BAC =∠EAF ,∴∠NMA =∠NAM =∠BAC =∠BCA ,∴△ANM ∽△ABC ,∴AM AN =AC AB =12, ∴AC CN =AM NA =12, ∴CN =2AC =4=AB ,∴△CEN ≌△BEA (AAS ),∴CE =BE =12BC =2;③当MA =MN 时,如图4所示:则∠MNA =∠MAN =∠BAC =∠BCA ,∴△AMN ∽△ABC ,∴AM AN =AB AC =42=2, ∴CN =12AC =1,∵△CEN ∽△BEA ,∴CE BE =CN AB =14, ∴CE =15BC =45;综上所述,当CE 为43或2或45时,△AMN 是等腰三角形.29.【解答】(1)证明:∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形,∵BE⊥BD,∴∠EBD=90°,∵A为DE的中点,∴AB=AD=12DE,∴四边形ABCD是菱形;(2)解:过B作BF⊥DE于F,tan ∠EDB =√22=BE BD, 设BE =√2x ,BD =2x ,由勾股定理得:DE =√BE 2+BD 2=√(√2x)2+(2x)2=√6x , ∵S △BDE =12×BE ×BD =12×DE ×BF , ∴12×√2x ×2x =12×√6x ×BF , 解得:BF =2√33x , ∴△ABE 与四边形ABCD 面积的比值是(12×√2x ×2x ):(√62x •2√33x )=√2x 2:√2x 2=1:1. 30.【解答】(1)证明:如图,连接BD , ∵四边形ABCD 是菱形,∴AC ⊥DB ,AD =AB ,∵EM ⊥AC ,∴ME ∥BD ,∵点E 是AB 的中点,∴点M 是AD 的中点,AE =12AB ,∴AM =12AD ,∴AM =AE .(2)解:①由(1)得,点M 是AD 的中点, ∴AM =MD ,∵四边形ABCD 是菱形,∴AB ∥CD ,∴∠F =∠AEM ,∠EAM =∠FDM ,∴△MDF ≌△MAE (AAS ),∴AE =DF ,∵AB =2AE ,DF =2,∴AB =4,∴菱形ABCD 的周长为4AB =4×4=16.②如图,连接CM ,记EF 与AC 交点为点G ,∵AM=AE,△MAE≌△MDF,∴DF=DM,MF=ME,∴∠DMF=∠DFM,∴∠ADC=2∠DFM,∵∠ADC=2∠MCD,∴∠MCD=∠DFM,∴MF=MC=ME,∠EMC=2∠FDM=∠MDC,∵ME⊥AC,AM=AE,∴∠MGC=90°,ME=2MG,∴MC=2MG,∴∠GMC=60°,∴∠ADC=60°,∴∠MCD=30°,∴∠DMC=90°,∴△DMC为直角三角形,∵DF=2,∴DM=2,CD=4,∴CM=√DM2+CM2=√22+42=2√3,∴ME=2√3.31.【解答】(1)解:相等,理由如下:∵四边形ABCD是正方形,∴AD=AB,∠DAB=∠ABC=90°,∴∠DAG+∠BAG=90°,∵AG⊥DE,∴∠DAG+∠ADF=90°,∴∠BAG=∠ADF,∵AD=AB,∠DAB=∠ABG,∴△ADE≌△BAG(ASA),∴AE =BG .(2)解:∵△ADE ≌△BAG ,∴BG =AE ,∵四边形ABCD 是正方形,∴AD ∥BC ,∴△ADH ∽△GBH ,∴DH BH =AD BG ,∵BE :AE =n ,BG =AE ,AD =AB ,∴DH BH =AD AG =AB AE =AE+BE AE =AE+nAE AE =n +1.(3)解:设BG =AE =k ,则BE =nk ,∵EH ∥AD ,∴∠BEH =∠BAD =90°,∠EHB =∠ADB =45°,∵∠ABD =45°,∴∠EHB =∠ABD ,∴BE =EH =nk ,∵EH ∥AD ,∴△AEH ∽△ABG ,∴AE AB =EH BG , ∴k k+nk =nk k, ∵n >0,∴n =√5−12.32.【解答】解:(1)∵AB BC =k ,k =43, ∴BC =6,∵CE EB =λ,λ=1,∴CE =EB ,∴点E 为BC 的中点,∵在矩形ABCD 中,AD ∥BC ,∴∠DAG =∠F ,又∵AG 平分∠DAE ,∴∠DAG =∠EAG ,∴∠EAG =∠F ,∴EA =EF ,∵AB =8,∠B =90°,点E 为BC 的中点,∴BE =EC =3,∴AE =√AB 2+BE 2=√73,∴EF =√73,∴CF =EF ﹣EC =√73−3;(2)①证明:∵EA =EF ,EG ⊥AF ,∴AG =FG ,在△ADG 和△FCG 中,{∠D =∠GCF ∠AGD =∠FGC AG =FG,∴△ADG ≌△FCG (AAS ),∴DG =CG ,即点G 为CD 的中点;②设CD =2a ,则CG =a ,∵AB BC =k (k >0且k ≠2).AB =CD ,AD =BC ,∴CF =AD =BC =2a k ,∵EG ⊥AF ,∠GCF =90°,∴∠EGC +∠CGF =90°,∠F +∠CGF =90°,∠ECG =∠GCF =90°,∴∠EGC =∠F ,∴△EGC ∽△GFC ,∴EC GC =GC FC ,∵GC =a ,FC =2a k , ∴GC FC =k 2, ∴EC GC =k 2,∴EC =k 2•a =ka 2,BE =BC ﹣EC =2a k −ka 2=4−k 22k a ,∴λ=CEEB=k24−k2.33.【解答】解:(1)AE=BG,理由如下:∵四边形ABCD是正方形,∴AD=AB,∠DAB=∠ABC=90°,∴∠DAG+∠BAG=90°,∵AG⊥DE,∴∠DAG+∠ADF=90°,∴∠BAG=∠ADF,∵AD=AB,∠DAB=∠ABG,∴△ADE≌△BAG(ASA),∴AE=BG;(2)∵△ADE≌△BAG,∴BG=AE,∵四边形ABCD是正方形∴AD∥BC∴△ADH∽△GBH∴DHBH=ADBG,∵BE:AE=n,BG=AE,AD=AB,∴DHBH=ADAE=ABAE=AE+BEAE,∵BE:AE=n,∴DHBH=AE+nAEAE=n+1;(3)设BG=AE=k,则BE=nk,∵EH∥AD,∴∠BEH=∠BAD=90°,∠EHB=∠ADB=45°,∵∠ABD=45°,∴∠EHB=∠ABD,∴BE=EH=nk,∵EH∥AD,AD∥BC,∴EH∥BC,∴△AEH∽△ABG,∴AEAB=EHBG,∴kk+nk=nkk,∵n>0,∴n=√5−1 2.34.【解答】(1)证明:∵AD⊥AC,CD⊥BC,PD⊥AB,∴∠DAP=∠DEA=∠BCQ=90°,∵∠P AE+∠DAE=90°,∠ADE+∠DAE=90°,∴∠P AE=∠ADE,∵CA=CB,∴∠CAB=∠CBA,∴∠ADE=∠QBC,∴△AED∽△QCB;(2)解:过点C作CH⊥AB于H,∵tan∠CAB=CHAH=12,∴设CH=a,则AH=2a,∴AC=√AH2+CH2=√5a=2√5,∴a=2,∴CH=2,AH=4,∵CA=CB,CH⊥AB,∴AH=BH=4,∠CAB=∠CBA,∴AB=8,∵AB平分∠CBD,∴∠CBA=∠DBA,∴∠CAB=∠DBA,∴AC∥BD,∵AD⊥AC,∴AD⊥BD,∴tan∠ABD=ADBD=tan∠CAB=12,∴AB=√5AD=8,∴AD=8√55,BD=2AD=16√55,∵△AQC∽△BQD,∴AQBQ=ACBD=√516√55=58,∴BQAB=813,∴BQ=813AB=6413;(3)解:①作QG⊥AD于G,∵点P是AC的中点,∴AP=12AC=√5,∵∠CAB=∠CBA=∠ADP,tan∠CAB=1 2,∴AD=2AP=2√5,∴AC=AD,∠ACD=∠ADC=45°,设AG=x,则QG=2x,DG=QG=2x,∴x+2x=2√5,解得:x=2√5 3,∴AQ=√5x=10 3,在Rt△APE中,AP=√5,PE=1,AE=2,∴EQ=AQ﹣AE=103−2=43,∴tan∠BQM=PEEQ=143=34;②作CH⊥AB于H,则CH ∥PD ,∴△CHQ ∽△DEQ ,∴CQ DQ =CH DE =QH EQ ,由(2)知,CH =2,AH =4,若PM ∥BC ,∴BM DM =CQ DQ ,∵CH ∥PD ,∴QH EQ =CH DE =CQ DQ ,∠PQA =∠CBA =∠CAB ,设PE =x ,∵tan ∠CAB =12,∴AE =QE =2x ,DE =4x ,∴QH =4﹣4x ,又∵QH EQ =CH DE , ∴24x =4−4x 2x , ∴x =34,∴BM DM =CQ DQ =CH DE =12x =23; 若PM ∥AD ,如图,∴BMMD=BQAQ,PCAP=CQDQ,∵CH∥PD,∴△CHQ∽△EDQ,∴CHDE=CQDQ=HQEQ,∴PCAP=CHDE,∵∠CAB=∠ADE,∴tan∠CAB=tan∠ADE=1 2,∵CH=2,AH=4,设PE=x,则AE=2x,DE=4x,由勾股定理得:AP=√5x,∴PC=2√5−√5x=√5(2﹣x),∵PCAP=CHDE,∴√5(2−x)√5x=24x,∴x=3 2,∵PM∥AD,AD⊥AC,∴PM⊥AC,∴∠EPQ=∠CAB,∴EQ=12PE=34,∴AQ=AE+EQ=3+34=154,BQ=8−154=174,∴BMMD=BQAQ=1715,综上所述,若PM∥BC,BMDM =23,若PM∥AD,BMDM =17 15.35.【解答】解:(1)∵一个角两夹边的平方和减去它对边的平方所得的差,叫做这个角的勾股差,∴直角的勾股差为两直角边的平方和与斜边的平方的差.∴等腰三角形的底角的勾股差为腰的平方+底边的平方+另一腰的平方.∵等腰三角形的两个腰相等,∴等腰三角形的底角的勾股差为底边的平方=22=4.故答案为:两直角边的平方和与斜边的平方的差;4;(2)①∵CD是△ABC的中线,AB=2c,∴AD=BD=c.依据勾股差的定义可得:m=c2+d2﹣b2,n=c2+d2﹣a2;②过点C作CM⊥AB于点M,如图,在Rt△ACM中,由勾股定理得:b2=CM2+AM2,同理可得:a2=CM2+BM2,CM2=d2﹣MD2.∴a2+b2=2CM2+AM2+BM2.∵AD=BD=c,∴AM=AD﹣MD=c﹣MD,BM=BD+MD=c+MD.∴a2+b2=2(d2﹣MD2)+(c﹣MD)2+(c+MD)2=2d2﹣2MD2+c2﹣2cMD+MD2+c2+2cMD+MD2=2d2+2c2.由(1)知:m=c2+d2﹣b2,n=c2+d2﹣a2,∴m+n=c2+d2﹣b2+c2+d2﹣a2=2c2+2d2﹣(a2+b2)=0.∴m与n互为相反数.(3)∵DF AB =34, ∴设DF =3m ,AB =4m .∵F 是BC 的中点,CD ⊥BD ,∴DF =12BC .∴BC =2DF =6m .∵点E 与F 分别是AB 与BC 的中点,∴CF =DF =BF =3m ,BE =AE =2m .∵点E 与F 分别是AB 与BC 的中点,∴利用(2)中的结论可得:BF 2+DF 2﹣BD 2+CF 2+DF 2﹣CD 2=0,BE 2+DE 2﹣BD 2+AE 2+DE 2﹣AD 2=0.∴4DF 2=BD 2+CD 2,2AE 2+2DE 2=BD 2+AD 2.∵CD =AD ,∴BD 2+CD 2=BD 2+AD 2.∴4DF 2=2AE 2+2DE 2.∴2×(3m )2=(2m )2+DE 2.解得:DE =√14m .∴DE DF =√14m 3m √143. 36.【解答】解:(1)不存在矩形丙,使得C 丙C 乙=S 丙S 乙=12成立.理由: 假定存在矩形丙,∵C 丙C 乙=S 丙S 乙=12, ∴矩形丙的两个邻边之和为7,它的面积为24.设两条邻边长分别为x 和7﹣x ,由题意得:x (7﹣x )=24.∴x 2﹣7x +24=0.∵Δ=(﹣7)2﹣4×1×24=﹣47<0,∴此方程没有实数根,∴不存在矩形丙,使得C 丙C 乙=S 丙S 乙=12成立. (2)∵矩形A 两条邻边长分别为m 和1,∴若存在矩形B ,使得C BC A =S B S A =12成立,则矩形B 的邻边之和为m+12. 设矩形B 的一边为x ,则另一边为m+12−x ,由题意得: x (m+12−x )=m×12. 化简得:2x 2﹣(m +1)x +m =0.由题意方程2x 2﹣(m +1)x +m =0一定有实数根.∴Δ=[﹣(m +1)]2﹣4×2m ≥0.解得:m ≥3+2√2或m ≤3﹣2√2.∵m 为矩形A 的边长,∴m >0.∴m 的取值范围为:0<m ≤3﹣2√2或m ≥3+2√2.(3)由(2)可知:对于任意一个矩形A ,不一定存在矩形B ,使得C BC A =S B S A =12成立. 当矩形A 两条邻边长a ,b 满足0<b a ≤3﹣2√2或b a≥3+2√2时,一定存在矩形B . 37.【解答】解:(1)如图1,∵AD =3,DE =2AE ,∴AE =1,DE =2,取AB 的中点G ,连接GF ,并延长交CD 于H ,∵F 是BE 的中点,∴FG =12AE =12,FG ∥AD ,在矩形ABCD 中,AB ∥CD ,∠A =90°,∴四边形AGHD 是平行四边形,∴▱AGHD 是矩形,。
中考数学二轮专题复习试卷:四边形(含答案)
中考数学二轮专题复习试卷:四边形(时间:120分钟 满分:120分)一、选择题(本大题共15个小题,每小题3分,共45分)1.(山东烟台)一个多边形截去一个角后, 形成另一个多边形的内角和为720°,那么原多边形的边数为( )A.5B.5或6C.5或7D.5或6或7 2.(浙江宁波)如图,梯形ABCD 中,AD ∥BC ,5AB 2=,BC=4,连接BD ,∠BAD 的平分线交BD 于点E ,且AE ∥CD ,则AD 的长为( )435A. B. C. D.23233.(江苏扬州)如图,在菱形ABCD 中, ∠BAD=80°,AB 的垂直平分线交对角线AC 于 点F ,垂足为E ,连接DF ,则∠CDF 等于( )A .50°B .60°C .70°D .80° 4.(福建漳州)用下列一种多边形不能铺满地面的是( ) A.正方形 B .正十边形 C .正六边形 D .等边三角形 5.(云南曲靖)如图,在ABCD 中,对角线AC 与BD 相交于点O ,过点O 作EF ⊥AC 交BC 于点E ,交AD 于点F ,连接AE 、CF .则四边形AECF 是( ) A.梯形 B.矩形 C.菱形 D.正方形 6.菱形OABC 在平面直角坐标系中的位置如图所示, 若OA=2,∠AOC=45°,则B 点的坐标是( )((((A.22,2 B.22,2C.22,2 D.22,2+ --+--7.(湖南邵阳)如图所示,点E 是矩形ABCD 的边AD 延长线上的一点,且AD=DE ,连接BE 交CD 于 点O ,连接AO ,下列结论不正确...的是( ) A.△AOB ≌△BOC B.△BOC ≌△EOD C.△AOD ≌△EOD D.△AOD ≌△BOC8.(重庆)下列图形都是由同样大小的矩形按一定的规律组成,其中第1个图形的面积为2 cm 2,第2个图形的面积为8 cm 2,第3个图形的面积为18 cm 2,…,则第10个图形的面积为( )A.196 cm2B.200 cm2C.216 cm2D.256 cm29.(山东菏泽)如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则S1+S2的值为( )A.16B.17C.18D.1910.(湖南襄阳)如图,平行四边形ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是( )A.18 B.28 C.36 D.4611.(四川雅安)如图,正方形 ABCD中,点E、F 分别在 BC、CD上,△AEF是等边三角形,连接AC 交 EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC 垂直平分EF,④BE+DF=EF,⑤S△C E F=2S△ABE.其中正确结论有( )个A.2B.3C.4D.512.(重庆)如图,矩形纸片ABCD中,AB=6 cm,BC=8 cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )A.6 cmB.4 cmC.2 cm D.1 cm13.(贵州黔南州)如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )A.AB=CDB.AD=BCC.AB=BCD.AC=BD14.(四川巴中)如图,在梯形ABCD中,AD∥BC,点E、F分别是AB、CD的中点,且EF=6,则AD+BC的值是( )A.9B.10.5C.12D.1515.(湖北十堰)如图,梯形ABCD中,AD∥BC,AB=DC=3,AD=5,∠C=60°,则下底BC的长为( )A.8B.9C.10D.11二、填空题(本大题共6个小题,每小题3分,共18分)16.(四川遂宁)若一个多边形内角和等于1 260°,则该多边形边数是.17.(浙江舟山)如图,正方形ABCD的边长为3,点E、F分别在边AB、BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程为.18.(江苏苏州)如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A,C分别在x,y轴的正半轴上.点Q在对角线OB上,且OQ=OC,连接CQ并延长CQ交边AB于点P,则点P的坐标为( , ).19.(江苏苏州)如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部,将AF延长交边BC于点G.若CG1ADGB k AB,则= (用含k的代数式表示).20.(贵州六盘水)如图,梯形ABCD中,AD∥BC,AD=4,AB=5,BC=10,CD的垂直平分线交BC于E,连接DE,则四边形ABED的周长等于.21.(云南曲靖)如图,在直角梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4,则CD= .三、解答题(本大题共5个小题,共57分)22.(本小题满分10分)(广东深圳)如图,在等腰梯形ABCD中,已知AD∥BC,AB=DC,AC与BD交于点O,廷长BC到E,使得CE=AD,连接DE.(1)求证:BD=DE.(2)若AC⊥BD,AD=3,S梯形ABCD=16,求AB的长.23.(本小题满分10分)(重庆)如图,在矩形ABCD中,E、F分别是AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.(1)求证:OE=OF;(2)若BC=23,求AB的长.24.(本小题满分10分)(山东济宁)如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.(1)求证:AF=BE;(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.25.(本小题满分12分)(江苏苏州)如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交边AD于点F,交CD的延长线于点G.(1)求证:△APB≌△APD;(2)已知DF∶FA=1∶2,设线段DP的长为x,线段PF的长为y.①求y与x的函数关系式;②当x=6时,求线段FG的长.26.(本小题满分15分)(江苏苏州)如图,点O为矩形ABCD的对称中心,AB=10 cm,BC=12 cm.点E、F、G分别从A、B、C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为 1 cm/s,点F的运动速度为3 cm/s,点G的运动速度为1.5 cm/s.当点F到达点C(即点F与点C 重合)时,三个点随之停止运动.在运动过程中,△EBF 关于直线EF 的对称图形是△EB ′F ,设点E 、F 、G 运动的时间为t (单位:s ). (1)当t =______s 时,四边形EBFB ′为正方形;(2)若以点E 、B 、F 为顶点的三角形与以点F 、C 、G 为顶点的三角形相似,求t 的值; (3)是否存在实数t ,使得点B ′与点O 重合?若存在,求出t 的值;若不存在,请说明理由.参考答案1.D2.B3.B4.B5.C6.D7.A8.B9.B 10.C 11.C 12.C 13.D 14.C 15.A 16.9 17.65(2422)-,19.k 12+ 20.19 21.3222.(1)证明:∵AD ∥BC ,CE=AD , ∴四边形ACED 是平行四边形, ∴AC=DE ,∵四边形ABCD 是等腰梯形,AD ∥BC ,AB=DC , ∴AC=BD , ∴BD=DE .(2)解:过点D 作DF ⊥BC 于点F ,∵四边形ACED 是平行四边形, ∴CE=AD=3,AC ∥DE , ∵AC ⊥BD , ∴BD ⊥DE , ∵BD=DE ,2BDE ABCD 111S BD DE BD BE DF.22211BC CE DF BC AD DF 22S 16∴====+=+==梯形()(),∴BD= 42, ∴2,221DF BF EF BE 42CF EF CE 1AB CD CF DF 17.∴====∴=-=∴==+=,,23.证明:(1)∵四边形ABCD 是矩形,∴CD ∥AB , ∴∠FCO=∠EAO. 在△FCO 与△EAO 中,FOC EOA FCO EAO CF AE ∠=∠⎧⎪∠=∠⎨⎪=⎩,,, ∴△FCO ≌△EAO(AAS), ∴OF=OE ; (2)解:连接OB , ∵∠BEF=2∠BAC, 又∠BEF=∠BAC+∠AOE , ∴∠BAC=∠AOE , ∴△EAO 为等腰三角形, ∴AE=OE.∵△FCO ≌△EAO(已证), ∴△FCO 为等腰三角形, ∴OF=CF=AE=OE, ∴O 为EF 的中点. ∵BE=BF, ∴BO 垂直平分EF,∴Rt △BCF ≌Rt △BOF ≌Rt △BOE(HL), ∴∠CBF=∠OBF=∠OBE=30°. ∵BC=3,∴CF=AE=2,BF=BE=4,∴AB=AE+BE=2+4=6.24.证明:(1)设AF与BE交于点G,∵四边形ABCD是正方形,∴AB=AD,∠BAD=∠D=90°,∴Rt△ADF中,∠FAD+∠AFD=90°.∵AF⊥BE,∴∠AGE=90°,∴Rt△AGE中,∠EAG+∠AEG=90°,∴∠AFD=∠AEG,∴△DAF≌△ABE,∴AF=BE;(2)解:过点A作AF∥MP交CD于点F,过点B作BE∥NQ交AD于E,得到,∴AF=MP,BE=NQ.由(1)得AF=BE,∴MP=NQ.25.(1)证明:∵四边形ABCD是菱形,∴AB=AD,AC平分∠DAB,∴∠DAP=∠BAP.在△APB和△APD中,AB AD,BAP DAP,AP AP,=⎧⎪∠=∠⎨⎪=⎩∴△APB ≌△APD;(2)解:①∵四边形ABCD 是菱形,∴AD ∥BC ,AD=BC. ∴△AFP ∽△CBP ,AF FP.BC BP∴= ∵DF ∶FA=1∶2,∴AF ∶BC=2∶3,∴FP ∶BP=2∶3. 由(1)知PB=PD=x , 又∵PF=y ,y 22y x x 33∴=∴=,,即y 与x 的函数关系式为2y x 3=; ②当x=6时,2y 643=⨯=,∴FB=FP+PB=10. FG FD 1DG AB DFG AFB FB FA 21FG 10 5.2∴∴==∴=⨯=,∽,,∴线段FG 的长为5.26.解:(1)2.5(2)由题意知AE=t ,BF=3t ,CG=1.5t. ∵AB=10,BC=12,∴BE=10-t ,FC=12-3t.∵点F 在BC 上运动,∴0≤t ≤4. ①当△EBF ∽△FCG 时,得EB BF 10t 3t 14:,t ;FC CG 123t 1.5t 5-==∴=-,即 ②当△EBF ∽△GCF 时,得EB BF 10t 3t,CG FC 1.5t 123t-==-,即: 整理得:t 2+28t-80=0, ∴t 1=-14+269,2t 14269=--.∵0≤t ≤4,(14t s t 1469 s 5∴==-+或符合题意. (3)不存在.理由如下: 连接BD.∵点O 为矩形ABCD 的对称中心, ∴点O 为BD 的中点.假设存在这样的实数t ,使得点B ′与点O 重合,此时EF 是OB 的垂直平分线,垂足为点H.BD 61BD 261BH 42EHB BHF BCD,BE BH BF BH,,DB DC BD BC6161BE BF 1012∴===∴==∴==易知,易证∽∽,,∴AE=10-BE=3.9.∵点F 的运动速度是点E 运动速度的3倍,但BF3,AE≠∴不存在实数t,使得点B′与点O重合.11 / 11。
中考数学四边形专题训练50题(含答案)

中考数学四边形专题训练50题含答案(单选、填空、解答题)一、单选题1.若正多边形的一个外角是24°,则这个正多边形( )A .正十二边形B .正十五边形C .正十八边形D .正二十边形 2.若平行四边形中两个相邻内角的度数比为1:2,则其中较小的内角是( ) A .120︒ B .90︒ C .60︒ D .45︒ 3.如图,四边形ABCD ∽四边形EFGH ,80E ∠=︒,90G ∠=︒,120D ∠=︒,则B ∠等于( )A .50︒B .60︒C .70︒D .80︒ 4.已知三角形的3条中位线分别为3cm 、4cm 、6cm ,则这个三角形的周长是( )A .13cmB .26cmC .24cmD .65cm 5.如图,正方形ABCD 中,E ,F 分别在边AD ,CD 上,AF ,BE 相交于G ,若34AE ED =,DF CF =,则AG GF 的值是( )A .59B .611C .713D .1115 6.在平行四边形ABCD 中,∠B =60°,那么下列各式中,不能成立的是( ) A .∠D =60° B .∠A =120° C .∠C +∠D =180° D .∠C +∠A =180°7.下列说法中,不正确的是()A.对角线互相平分的四边形是平行四边形B.对角线相等的四边形是矩形C.对角线互相垂直的矩形是正方形D.对角线互相垂直的平行四边形是菱形8.对角线互相平分且相等的四边形是()A.菱形B.矩形C.正方形D.等腰梯形9.如图,过O外一点P作O的两条切线PD、PB,切点分别为D、B,作直径∠的度数为()AB,连接AD、BD,若80P∠=︒,则AA.50°B.60°C.70°D.80°10.如图,在∠ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE∠AB于E,PF∠AC于F,M为EF中点,则AM的最小值为()A.1B.1.3C.1.2D.1.5∠=︒,11.如图,将平行四边形ABCD沿对角线AC折叠,使点B落在点B'处,若148∠=︒,则B232∠的度数为().A.124°B.114°C.104°D.56°12.下列说法正确的是()A.矩形的对角线相互垂直B.菱形的对角线相等C.平行四边形是轴对称图形D.等腰梯形的对角线相等13.如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE 对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:∠△EAG=45°:∠CE=3DE;∠AG∠CF;∠S△FGC=725,其中正确结论的个数是()A.1个B.2个C.3个D.4个14.如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,若AB=6,EF=2,则BC的长为()A.8B.10C.12D.1415.如图,在四边形ABCD中,∠A=90°,AB=AD=3,M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),E、F分别为D M,MN的中点,则EF长度的最大值为() .A.4B.3C.D.16.下列说法错误的是()A.菱形的面积等于两条对角线乘积的一半B.矩形的对角线相等C.对角线互相垂直的平行四边形是矩形D.对角线相等的菱形是正方形17.如图所示,将正六边形与正五边形按此方式摆放,正六边形与正五边形的公共顶点为O,且正六边形的边AB与正五边形的边DE共线,则∠COF的度数是()A.86°B.84°C.76°D.74°18.如图,在矩形ABCD中,点E、F分别在边AD、DC上,ABE DEF,AB=,26DF=,则BE的长是()DE=,3D.A.12B.15C.19.如图,在一张矩形纸片ABCD中4BC=,点E,F分别在AD,BC上,AB=,8将纸片ABCD沿直线EF折叠,点C落在AD上的点H处,点D落在点G处,连接CE,CH.有以下四个结论:∠四边形CFHE是菱形;∠CE平分∠DCH;∠线段BF的EF=.以上结论中,其中正确结取值范围为34BF≤≤;∠当点H与点A重合时,5论的个数有()A.1个B.2个C.3个D.4个二、填空题=,连接AE交CD于F,那么20.四边形ABCD是正方形,延长BC至E,使CE AC∠的度数为________.AFC21.M为矩形ABCD中AD的中点,P为BC上一点,PE∠MC,PF∠MB,当AB、BC 满足_________时,四边形PEMF为矩形.22.如图,在矩形ABCD中,E,F分别是边AB,BC上的点.将∠A,∠B,∠C按如图所示的方式向内翻折,EQ ,EF ,DF 为折痕.若A ,B ,C 恰好都落在同一点P 上,AE =1,则ED =___.23.如图,△ABC 内接于∠O ,∠BAC =120°,AB =AC ,BD 为∠O 的直径,CD =8,OA 交 BC 于点 E ,则 AE 的长度是________.24.如图,在正五边形ABCDE 中,AC 为对角线,以点A 为圆心,AE 为半径画圆弧交AC 于点F ,连结EF ,则∠1的度数为__.25.如图,小靓用七巧板拼成一幅装饰图,放入长方形ABCD 内,装饰图中的三角形顶点E ,F 分别在边AB ,BC 上,三角形∠的边GD 在边AD 上,若图1正方形中MN=1,则CD=____.26.如图,在正方形ABCD 中,点E ,F 分别是BC ,CD 上的点,连接AE ,EF ,AF ,若DF BE EF +=,则EAF ∠=______︒.27.如图,已知抛物线24=-+的顶点为D,与y轴交于点C,过点C作x轴的y x x c平行线AC交抛物线于点A,过点A作y轴的平行线AB交射线OD于点B,若OA OB=,则c的值为_____________.28.如图,点E、F、G、H分别是矩形ABCD边AB、BC、CD、DA上的点,且HG 与EF交于点I,连接HE、FG,若AB=7,BC=6,EF//AD,HG//AB,则HE+FG的最小值是______.29.在□ABCD中,∠A:∠B=2:3,则∠B=____,∠C=_____,∠D=____.30.如图,菱形ABCD中,∠BCD=50°,BC的垂直平分线交对角线AC于点F,垂足为E,连接BF、DF,则∠DFC的度数是_____.'沿对角线AC折叠,得到如图所示的图形.若∠BAO=34°,则31.把长方形AB CD∠BAC的大小为_______.32.如图,M 是▭ABCD 的AB 的中点,CM 交BD 于E ,则图中阴影部分的面积与▱ABCD 的面积之比为_____.33.如图,矩形ABCD 中,AD=6,P 为边AD 上一点,且AP=2,在对角线BD 上寻找一点M ,使AM+PM 最小,则AM+PM 的最小值为_____.34.如图,在▱ABCD 中,BE 、CE 分别平分∠ABC 、∠BCD ,E 在AD 上,BE=12cm ,CE=5cm .则▱ABCD 的周长为_____,面积为_____.35.在平面直角坐标系中,对于不在坐标轴上的任意一点(),P x y ,我们把点11,Q y x ⎛⎫ ⎪⎝⎭称为点P 的“逆倒数点”.如图,在矩形OABC 中,点B 的坐标为(48),,反比例函数()0k y x x =>的图象经过矩形对角线交点M .点D 是该反比例函数图象上的点,点E 是对角线上的一点,且点E 是点D 的“逆倒数点”,点E 的坐标为______.36.如图,正方形ABCD 的对角线AC ,BD 交于点O ,M 是边AD 上一点,连接OM ,过点O 作ON ∠OM ,交CD 于点N .若四边形MOND 的面积是1,则AB 的长为 _____.37.如图,点E 为正方形ABCD 外一点,且ED CD =,连接AE ,交BD 于点F .若40CDE ∠=,则∠DCF 的度数为_______.38.如图,在矩形ABCD 中,5,3AB BC ==,将矩形ABCD 绕点B 按顺时针方向旋转得到矩形GBEF ,点A 落在矩形ABCD 的边CD 上,连接CE ,则CE 的长是 _____ .39.如图,点E 、F 分别为正方形ABCD 的边AB 、BC 上的点,满足∠EDF =45°.连接DE 、DF 分别交正方形对角线AC 于点H 、G ,再连接EG ,有如下结论:∠AE CF EF +>;∠ED 始终平分∠AEF ;∠∠AEH ∠∠DGH ;∠DE ;∠14DGH DEF S S =△△.在上述结论中,正确的有______.(请填正确的序号)三、解答题40.如图,方格纸中每个小正方形的边长均为1,ABC 的顶点和线段的端点均在小正方形的顶点上.(利用格点和没有刻度的直尺作图,保留作图痕迹)(1)在方格纸1中画出ADC △,使ADC △与ABC 关于直线AC 对称;(2)在方格纸2中画出以EF 线段为一边的平行四边形(点G ,点H 均在小正方形的顶点上),且平行四边形面积为4;(3)在方格纸3中,连接FM ,在FM 上确定一点P ,使得点P 为FM 中点. 41.如图,在平行四边形ABCD 中,∠BAD 的平分线交CD 于点E ,连接BE 并延长交AD 延长线于点F ,若AB =AF .(1)求证:点D 是AF 的中点;(2)若∠F =60︒,CD =6,求∠ABF 的面积.42.如图1,在等腰ABO 中,AB AO =,分别延长AO 、BO 至点C 、点D ,使得CO AO =、DO BO =,连接AD 、BC .()1如图1,求证:AD BC =;()2如图2,分别取边AD 、CO 、BO 的中点E 、F 、H ,猜想EFH 的形状,并说明理由.43.如图,在矩形ABCD 中,M ,N 分别是AD ,BC 的中点,E ,F 分别是线段BM ,CM 的中点,若AB=8,AD=12,则四边形ENFM 的周长是多少?44.如图∠,在矩形OACB 中,点A 在x 轴正半轴上,点B 在y 轴正半轴上,点C 在第一象限,8OA =,6OB =.(1)直接写出点C 的坐标:________;(2)如图∠,点G 在BC 边上,连接AG ,将ACG 沿AG 折叠,点C 恰好与线段AB 上一点C '重合,求线段CG 的长度;(3)如图∠,P 是直线26y x =-上一点,PD PB ⊥交线段AC 于D .若P 在第一象限,且PB PD =,试求符合条件的所有点P 的坐标.45.直线443y x =-+与x 轴交于点A ,与y 轴交于点B ,菱形ABCD 如图放置在平面直角坐标系中,其中点D 在x 轴负半轴上,直线y =x +m 经过点C ,交x 轴于点E .(1)请直接写出点C ,点D 的坐标,并求出m 的值;(2)点P (0,t )是线段OB 上的一个动点(点P 不与O 、B 重合),经过点P 且平行于x 轴的直线交AB 于M ,交CE 于N .当四边形NEDM 是平行四边形时,求点P 的坐标;(3)点P (0,t )是y 轴正半轴上的一个动点,Q 是平面内任意一点,t 为何值时,以点C 、D 、P 、Q 为顶点的四边形是菱形?46.如图,在Rt ∠ABC 中,∠C =90°,AC =8,BC =6.动点P 从点A 出发,沿AB 以每秒5个单位长度的速度向终点B 运动.当点P 不与点A 重合时,过点P 作PD ∠AC 于点D ,以AP ,AD 为边作▱APED .设点P 的运动时间为t 秒.(1)线段AD的长为(用含t的代数式表示).(2)当点E落在BC边上时,求t的值.(3)连结BE,当tan∠CBE=13时,求t的值.(4)若线段PE的中点为Q,当点Q落在∠ABC一边垂直平分线上时,直接写出t的值.47.如图,BC为∠O的直径,BD平分∠ABC交∠O于点D,DA∠AB于点A.(1)求证:AD是∠O的切线;(2)∠O交AB于点E,若AD=2AE,求sin ABC∠的值.48.如图1,已知在四边形ABCD中,AB//CD,90ABC∠=︒,8BC=,6CD=,1tan2A=.动点P从点D DA方向运动,到A点结束;点Q同时从点A出发,以3个单位的速度沿射线AB运动,点P停止运动后,点Q 也随之停止.以AP,AQ为边作平行四边形AQGP.设运动时间为t.(1)求AB的长;(2)连接GC 、GB ,当CGB △为等腰三角形时,求t 的值;(3)如图2,以PQ 为直径作圆与AD 、PG 分别交于点M 、N ,连接MQ 交PG 于点F ,连接NQ 、DG ,∠当点N 为弧MQ 的中点时,求PMQPNQ S S △△的值;∠当PQM CDG ∠=∠时,求PQ =______(请直接写出答案).49.思维启迪:(1)如图1,A ,B 两点分别位于一个池塘的两端,小亮想用绳子测量A ,B 间的距离,但绳子不够长,聪明的小亮想出一个办法:先在地上取一个可以直接到达B 点的点C ,连接BC ,取BC 的中点P (点P 可以直接到达A 点),利用工具过点C 作CD∠AB 交AP 的延长线于点D ,此时测得CD =100米,那么A ,B 间的距离是_____米.思维探索:(2)在∠ABC 和∠ADE 中,AC =BC ,AE =DE ,且AE <AC ,∠ACB =∠AED =90°,将∠ADE 绕点A 逆时针方向旋转,把点E 在AC 边上时∠ADE 的位置作为起始位置(此时点B 和点D 位于AC 的两侧),设旋转角为α,连接BD ,点M 是线段BD 的中点,连接MC ,ME .∠如图2,当∠ADE 在起始位置时,猜想:MC 与ME 的数量关系和位置关系分别是______;∠如图3,当α=90°时,点D 落在AB 边上,请判断MC 与ME 的数量关系和位置关系,并证明你的结论;参考答案:1.B【详解】分析:利用任意凸多边形的外角和均为360°,正多边形的每个外角相等即可求出答案.详解:∠多边形的每个外角相等,且其和为360°,∠这个正多边形的边形为3602415o o ÷=,∠这个正多边形是正十五边形.故选B.点睛:考查了正多边形外角和的知识,正多边形的每个外角相等,且其和为360°,用360除以一个外角的度数,结果即为正多边形的边形.2.C【分析】根据平行四边形的性质来解答即可.【详解】解:∠平行四边形,∠两个相邻内角互补,又∠两个相邻内角的度数比为1:2,∠两个相邻的内角为60°、120°,∠较小的内角为60°.故选:C .【点睛】本题考查平行四边形的性质,熟练掌握平行四边形的相关性质是解题的关键. 3.C【分析】根据相似多边形的对应角相等以及四边形的内角和为360︒解答即可.【详解】解:∠四边形ABCD ∽四边形EFGH∠120H D ∠=∠=︒∠360()70B F E G H ∠=∠=︒-∠+∠+∠=︒故选:C .【点睛】本题考查了相似多边形的性质、多边形的内角和;理解相似多边形的对应角相等是解题的关键.4.B【分析】根据三角形的中位线平行于第三边并且等于第三边的一半求出三角形的三边,再求解即可.【详解】解:∠三角形的三条中位线分别为3cm、4cm、6cm,∠三角形的三边分别为6cm,8cm,12cm,∠这个三角形的周长=6+8+12=26cm.故选:B.【点睛】本题考查了三角形中位线的性质,解题的关键是熟记三角形中位线的性质定理.5.B【分析】延长AF交BC的延长线于点H,证明∠ADF∠∠HCF,得到CH=AD,设AE=3x,则DE=4x,AD=7x,证得∠AEG∠∠HBG,得到AE AGBH HG==314,即可求出AGGF【详解】解:延长AF交BC的延长线于点H,∠四边形ABCD是正方形,∠∠D=∠DCH=90°,AD∥BC,∠∠DAF=∠H,∠DF CF=,∠∠ADF∠∠HCF(AAS),∠CH=AD,设AE=3x,则DE=4x,AD=7x,∠CH=AD=BC=7x,∠AD∥BC,∠∠AEG∠∠HBG,∠AE AGBH HG==314,∠AGGF =6 11,故选:B.【点睛】此题考查了正方形的性质,相似三角形的性质,全等三角形的判定及性质,熟记各定理是解题的关键.6.D【详解】解:∠四边形ABCD是平行四边形,∠∠D=∠B=60°.故A成立;∠AD△BC,∠∠A+∠B=180°,∠∠A=180°-∠B=120°,故B成立;∠AD△BC,∠∠C+∠D=180°,故C成立;∠四边形ABCD是平行四边形,∠∠C=∠A=120°,故D不成立,故选D.7.B【分析】根据各四边形的性质对各个选项进行分析从而得出最后答案.【详解】解:A、对角线互相平分的四边形是平行四边形,正确;B、错误,对角线相等的四边形不一定是矩形,对角线相等的平行四边形才是矩形;C、对角线互相垂直的矩形是正方形,正确;D、对角线互相垂直的平行四边形是菱形,正确.故选:B.【点睛】本题主要考查了正方形、平行四边形、菱形的判定方法.解决此题的关键是熟练掌握运用这些判定.8.B【分析】根据平行四边形的判定与矩形的判定定理,即可求得答案.【详解】∠对角线互相平分的四边形是平行四边形,对角线相等的平行四边形是矩形,∠对角线相等且互相平分的四边形一定是矩形.故选B.【点睛】此题考查了平行四边形,矩形,菱形以及等腰梯形的判定定理.此题比较简单,解题的关键是熟记定理.9.A【分析】如图,连接OD ,可得90ODP OBP ∠=∠=︒,再利用四边形的内角和定理求解BOD ∠,从而可得答案.【详解】解:如图,连接OD ,∠过O 外一点P 作O 的两条切线PD 、PB ,∠90ODP OBP ∠=∠=︒,∠80P ∠=︒,∠360909080100DOB ∠=︒-︒-︒-︒=︒, ∠1502A DOB ∠=∠=︒, 故选A .【点睛】本题考查的是切线的性质,四边形的内角和定理的应用,圆周角定理的应用,作出过切点的半径是解本题的关键.10.C【分析】首先证明四边形AEPF 为矩形,可得AM =12AP ,最后利用垂线段最短确定AP 的位置,利用面积相等求出AP 的长,即可得AM .【详解】在△ABC 中,因为AB 2+AC 2=BC 2,所以△ABC 为直角三角形,∠A =90°,又因为PE ∠AB ,PF ∠AC ,故四边形AEPF 为矩形,因为M 为 EF 中点,所以M 也是 AP 中点,即AM =12AP ,故当AP ∠BC 时,AP 有最小值,此时AM 最小, 由1122ABC S AB AC BC AP ∆=⨯⨯=⨯⨯,可得AP =125,AM =12AP =6 1.25= 故本题正确答案为C.【点睛】本题考查了矩形的判定和性质,确定出AP ∠BC 时AM 最小是解题关键.11.A【分析】根据折叠、平行四边形的性质,三角形的内角和定理,即可求出答案.【详解】解:由折叠得,45∠=∠,∠四边形ABCD 是平行四边形,∠AB CD ,∠53∠=∠,∠3=4∠∠,又∠13448∠=∠+∠=︒, ∠154348242∠=∠=∠=⨯︒=︒, 在ABC 中,180521802432124B ∠=︒-∠-∠=︒-︒-︒=︒,故选:A .【点睛】本题考查折叠的性质、平行四边形的性质,三角形的内角和定理等知识,由图形直观得出各个角之间的关系是正确解答的关键.12.D【分析】根据矩形、菱形、平行四边形、等腰梯形的性质进行逐一分析解答即可.【详解】A 、错误,矩形的对角线相等;B 、错误,菱形的对角线相互垂直;C 、错误,平行四边形是中心对称图形;D 、正确,等腰梯形的对角线相等.故选D . 【点睛】此题考查命题与定理,解题关键在于掌握正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉其性质定理.13.C【分析】∠由正方形的性质和翻折的性质可证明Rt△ABG∠Rt△AFG(HL),推出∠BAG=∠F AG,根据∠DAE=∠F AE,可得∠EAG=12∠BAD=45°;∠由题意得EF=DE,GB=CG=GF=6,设DE=EF=x,则CE=12-x,在Rt△ECG中,(12-x)2+36=(x+6)2,求出x,则可得到CE=2DE;∠由CG=BG,BG=GF,可得CG=GF,则∠GFC=∠GCF,因为∠AGB+∠AGF=2∠AGB=∠GFC+∠GCF=2∠GCF,可推出∠AGB=∠GCF,则AG∠CF;∠由S△GCE=12×GC×CE,又因为△GFC和△FCE等高,可得S△GFC:S△FEC=3:2,S△GFC=3 5×24=725.【详解】解:∠∠正方形ABCD,∠AB=BC=CD=AD=12,∠B=∠GCE=∠D=90°,由折叠的性质可得,AF=AD,∠AFE=∠D=90°,∠∠AFG=90°=∠B,AB=AF,又∠AG=AG,∠Rt△ABG∠Rt△AFG(HL),∠∠BAG=∠F AG,∠∠DAE=∠F AE,∠∠EAG=12∠BAD=45°,故∠正确;∠由题意得EF=DE,GB=CG=GF=6,设DE=EF=x,则CE=12-x,在Rt∠ECG中,(12-x)2+62=(x+6)2,∠x=4,∠DE=4,CE=8,∠CE=2DE,故∠错误;∠∠CG=BG,BG=GF,∠CG=GF,∠∠GFC=∠GCF,∠Rt∠ABG∠Rt∠AFG,∠∠AGB=∠AGF,∠∠AGB+∠AGF=2∠AGB=∠GFC+∠GCF=2∠GCF,∠∠AGB=∠GCF,∠AG∠CF,故∠正确;∠∠S△GCE=12×GC×CE=12×6×8=24,又∠GF=6,EF=4,∠GFC和∠FCE等高,∠S△GFC:S△FEC=3:2,∠S△GFC=35×24=725,故∠正确;综上,正确的是∠∠∠,共3个.故选:C.【点睛】本题考查翻折变换的性质、正方形的性质,本题综合性很强,熟练掌握全等三角形的判定和性质,勾股定理,三角形面积的计算方法是解题的关键.14.B【详解】试题分析:根据平行四边形的性质可知AB=CD,AD∠BC,AD=BC,然后根据平行线的性质和角平分线的性质可知AB=AF,DE=CD,因此可知AF+DE=AD+EF=2AB=12,解得AD=BC=12-2=10.故选B.点睛:此题主要考查了平行四边形的性质和等腰三角形的性质,解题关键是把所求线段转化为题目中已知的线段,根据等量代换可求解.15.B【分析】根据三角形的中位线定理得出EF=12DN,从而可知DN最大时,EF最大,因为N与B重合时DN最大,此时根据勾股定理求得DN=DB=6,从而求得EF的最大值为3.【详解】解:∠ED=EM,MF=FN,∠EF=12DN,∠DN最大时,EF最大,∠N与B重合时DN最大,此时DN=DB=6,∠EF的最大值为3.故选:B.【点睛】本题考查了三角形中位线定理,勾股定理的应用,熟练掌握定理是解题的关键.16.C【分析】根据有关的定理和定义找到错误的命题即可得到答案;【详解】A、菱形的面积等于对角线乘积的一半,故正确,不符合题意;B、矩形的对角线相等,正确,不符合题意;C、对角线平分且相等的平行四边形是矩形,错误,符合题意;D、对角线相等的菱形是正方形,正确,不符合题意;故选C.【点睛】考查了命题与定理的知识,在判断一个命题正误的时候可以举出反例.17.B【分析】利用正多边形的性质求出∠EOF,∠BOC,∠BOE即可解决问题.【详解】解:由题意:∠EOF=108°,∠BOC=120°,∠OEB=72°,∠OBE=60°,∠∠BOE=180°﹣72°﹣60°=48°,∠∠COF=360°﹣108°﹣48°﹣120°=84°,故选:B.【点睛】本题考查正多边形,三角形内角和定理等知识,解题的关键是熟练掌握基本知识,属于常考题型.18.C【分析】利用相似三角形的性质求出AE的长,再利用勾股定理求解即可.【详解】解:∠ABE DEF,∠AB AE DE DF,∠623AE =,∠9AE=,∠矩形ABCD中,90A∠=︒,∠BE故选:C.【点睛】本题考查了矩形的性质、相似三角形的性质、勾股定理,解题关键是求出AE的长后利用勾股定理求解.19.B【分析】先根据翻折的性质可得CF=FH,∠HFE=∠CFE,可证∠FEH是等腰三角形,可得HE=HF=FC,判断出四边形CFHE是平行四边形,然后根据邻边相等的平行四边形是菱形证明,判断出∠正确;根据菱形的对角线平分一组对角线可得∠BCH=∠ECH,然后求出只有∠DCE=30°时CE平分∠DCH,判断出∠错误;过点F作FM∠AD于M,点H与点A 重合时,设BF=x,表示出AF=FC=8﹣x,利用勾股定理列出方程求解得到BF的最小值,点G与点D重合时,CF=FM=MD=CD,求出BF=4,然后写出BF的取值范围,判断出∠正确;求出ME,再利用勾股定理列式求解得到EF,判断出∠正确.【详解】解:∠将纸片ABCD沿直线EF折叠,∠FC=FH,∠HFE=∠CFE,∠AD△BC,∠∠HEF=∠EFC=∠HFE,HE△FC,∠∠HFE为等腰三角形,∠HE=HF=FC,∠EH与CF都是矩形ABCD的对边AD、BC的一部分,∠EH△CF,且HE=FC,∠四边形CFHE是平行四边形,∠FC=FH,∠四边形CFHE是菱形,故∠正确;∠HC为菱形的对角线,∠∠BCH=∠ECH,∠BCD=90°,∠只有∠DCE=30°时CE平分∠DCH,故∠错误;过点F作FM∠AD于M,点H与点A重合时,BF最小,设BF=x,则AF=FC=8﹣x,在Rt∠ABF中,AB2+BF2=AF2,即42+x2=(8﹣x)2,解得:x=3,点G与点D重合时,点H与点M重合,BF最大,CF=FM=DM=CD=4,∠BF=4,∠线段BF的取值范围为3≤BF≤4,故∠正确;当点H与点A重合时,由∠中BF=3,∠AF=AE=CF=EC=8-3=5,则ME=5﹣3=2,由勾股定理得,EF=∠错误;综上所述,结论正确的有∠∠共2个,故B正确.故选:B.【点睛】本题考查矩形折叠性质,等腰三角形的判定,菱形的判定与性质,勾股定理,掌握矩形折叠性质,菱形的判定与性质,勾股定理是解题关键.20.112.5【分析】根据正方形的性质有∠ACD=∠ACB=45°=∠CAE+∠AEC,根据CE=AC就可以求出∠CAE=22.5°,在△AFC中由三角形的内角和就可以得出∠AFC的度数.【详解】解:∠四边形ABCD是正方形,∠∠ACD=∠ACB=45°.∠∠ACB═∠CAE+∠AEC,∠∠CAE+∠AEC=45°.∠CE=AC,∠∠CAE=∠AEC,∠∠CAE=22.5°.∠∠CAE+∠ACD+∠AFC=180°,∠∠AFC=180°-22.5°-45°=112.5°.故答案为112.5°.【点睛】本题考查了正方形的性质的运用,等腰三角形的性质的运用,三角形的外角与内角的关系的运用及三角形内角和定理的运用.21.12AB BC =##2BC AB =【详解】∠在矩形ABCD 中,M 为AD 边的中点,AB=12BC ,∠AB =DC =AM =MD ,∠A =∠D =90°,∠∠ABM =∠MCD =45°,∠∠BMC =90°,又∠PE ∠MC ,PF ∠MB ,∠∠PFM =△PEM =90°,∠四边形PEMF 是矩形.故答案为:AB =12BC .22.3【分析】连接,EP DP ,根据折叠的性质得出三角形全等,根据三角形全等的性质得出对应边相等,由ED EP PD =+,利用等量代换分别求出,EP PD .【详解】解:连接,EP DP 如下图所示:根据A ,B ,C 恰好都落在同一点P 上及折叠的性质,有,,AQE PQE EBF EPF FPD FCD ≌≌≌,1,1,AE PE EB EP CD PD ∴=====,2AB AE EB =+=,根据正方形的性质得:2AB DC ==,2PD ∴=,ED EP PD =+,123ED ∴=+=,故答案是:3.【点睛】本题考查了翻折的性质,三角形全等的性质,解题的关键是添加辅助线,通过等量代换的思想进行解答.23.4【分析】证明△OAB 是等边三角形,OA ∠BC 即可推出OE =AE ,再利用三角形中位线定理即可解决问题.【详解】解:∠AB =AC ,∠AB AC =,∠OA ∠BC ,BE =EC ,AB =AC∠∠ABC 是等腰三角形∠∠BAE =∠CAE =12∠BAC =60°,∠OA =OB ,∠∠OAB 是等边三角形,∠BE ∠OA ,∠OE =AE ,∠OB =OD ,BE =EC ,∠ OE是△BCD的中位线∠OE=AE=12CD=4.故答案为:4.【点睛】本题考查三角形的外接圆与外心,圆周角定理,垂径定理,三角形的中位线定理,等边三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.24.54°【分析】根据五边形的内角和公式求出∠ABC,根据等腰三角形的性质,三角形内角和的定理计算∠BAC,再求∠EAF,利用圆的性质得AE=AF,最后求出∠1即可.【详解】解:∠五边形ABCDE是正五边形,∠∠EAB=∠ABC=()5-21805⨯︒=108°,∠BA=BC,∠∠BAC=∠BCA=180-1082︒︒=36°,∠∠EAF=108°﹣36°=72°,∠以点A为圆心,AE为半径画圆弧交AC于点F,∠AE=AF,∠∠1=180-722︒︒=54°.故答案为:54°.【点睛】本题考查了正多边形的内角与圆,熟练掌握正多边形的内角的计算公式、和圆的性质,等腰三角形的性质是解题的关键.25122【分析】根据七巧板中图形分别是等腰直角三角形和正方形计算PH的长,即FF'的长,作高线GG',根据直角三角形斜边中线的性质可得GG'的长,即AE的长,可得结论.【详解】解:如图:∠四边形MNQK是正方形,且MN=1,∠∠MNK=45°,在Rt△MNO中,OM=ON∠NL=PL=OL∠PN=12,∠PQ=12,∠∠PQH是等腰直角三角形,∠PH=FF'BE,过G作GG'∠EF',∠GG'=AE=12MN=12,∠CD=AB=AE+BE=12122.故答案为122.【点睛】本题主要考查了正方形的性质、七巧板、等腰直角三角形的性质及勾股定理等知识.熟悉七巧板是由七块板组成的,完整图案为一正方形:五块等腰直角三角形(两块小形三角形、一块中形三角形和两块大形三角形)、一块正方形和一块平行四边.26.45【分析】延长CB到G,使BG=DF,根据正方形的性质得到AD=AB,∠D=∠ABE=90°,求得∠ABG=∠D=90°,根据全等三角形的性质得到AG=AF,∠GAB=∠DAF,求得GE=EF,推出∠AGE∠∠AFE(SSS),根据全等三角形的性质得到∠GAE=∠EAF,根据全等三角形的性质即可得到结论.【详解】解:延长CB到G,使BG=DF,∠四边形ABCD是正方形,∠AD=AB,∠D=∠ABE=90°,∠∠ABG =∠D =90°,在∠ADF 与∠ABG 中,AB AD ABG D BG DF =⎧⎪∠=∠⎨⎪=⎩,∠∠ADF ∠∠ABG (SAS ),∠AG =AF ,∠GAB =∠DAF ,∠DF +BE =EF ,EG =BG +BE =DF +BE ,∠GE =EF ,在∠AGE 与∠AFE 中,AG AF AE AE GE EF =⎧⎪=⎨⎪=⎩,∠∠AGE ∠∠AFE (SSS ),∠∠GAE =∠EAF ,∠∠GAE =∠GAB +∠BAE =∠DAF +∠BAE =∠EAF ,∠∠BAD =90°,∠∠EAF =45°,故答案为:45.【点睛】本题考查了正方形的性质,全等三角形的判定和性质,正确的作出辅助线构造全等三角形是解题的关键.27.83【分析】根据抛物线的解析式求得4DH c =-,BF AF OC c ===,然后根据三角形中位线定理得到142c c -=,解得即可. 【详解】解:作抛物线的对称轴,交OA 于E ,交x 轴于H ,∠224()42y x x c x c =-+=-+-,∠顶点为(2)4c -,,∠4DH c =-,∠AC x ∥轴,∠AF OC c AB x ==⊥,轴,∠OA OB =,∠AF BF c ==,∠OH FH =, ∠12DH BF =, ∠142c c -= ∠83c =, 故答案为:83. 【点睛】本题考查了二次函数与几何的综合运用,熟练掌握三角形的中位线定理是解决本题的关键.28【分析】由EF ∠AD ,HG ∠AB ,结合矩形的性质可得四边形AHIE 和四边形IFCG 为矩形,然后根据矩形的性质可的HE +FG 的长度即为AI +CI 的长度,最后利用两点之间,线段最短,求出AC 的长即可.【详解】解:如图所示,连接AI ,CI ,AC ,在矩形ABCD 中,∠BAD =∠BCD =∠B =90°,AB ∠CD ,AD ∠BC ,又∠EF ∠AD ,HG ∠AB ,∠四边形AHIE和四边形IFCG为矩形,∠HE=AI,FG=CI,∠HE+FG的长度即为AI+CI的长度,又∠AI+CI≥AC,∠当A,I,C三点共线时,AI+CI最小值等于AC的长度,在Rt∠ABC中,AC∠HE+FG【点睛】本题考查矩形的判定和性质以及两点之间,线段最短的运用,正确判定四边形AHIE和四边形IFCG为矩形,运用矩形的对角线相等是解题的关键.29.108º,72º,108º【详解】解:∠平行四边形ABCD中,∠A+∠B=180°,又∠∠A:∠B=2:3,∠∠A=72°,∠B=108°,∠∠D=∠B=108°,∠C=∠A=72°.故答案为108º,72º,108º.30.130°【分析】首先求出∠CFB=130°,再根据对称性可知∠CFD=∠CFB即可解决问题.【详解】∠四边形ABCD是菱形,∠BCD=25°,∠∠ACD=∠ACB=12∠EF垂直平分线段BC,∠FB=FC,∠∠FBC=∠FCB=25°,∠∠CFB=180°﹣25°﹣25°=130°,根据对称性可知:∠CFD=∠CFB=130°,故答案为130°.【点睛】本题考查菱形的性质、线段的垂直平分线的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.31.62°【分析】先利用AAS 证明∠AOB∠∠COD ,得出∠BAO=∠DCO=34°,∠B′CO=68°,结合折叠的性质得出∠B′CA=∠BCA=34°,则∠BAC=∠B′AC=56°.【详解】由题意,得∠B′CA∠∠BCA ,∠AB′=AB ,∠B′CA=∠BCA ,∠B′AC=∠BAC .∠长方形AB′CD 中,AB′=CD ,∠AB=CD .在∠AOB 与∠COD 中,90B D AOB COD AB CD ∠∠︒⎧⎪∠∠⎨⎪⎩==== , ∠∠AOB∠∠COD (AAS ),∠∠BAO=∠DCO=34°,∠∠B′CO=90°-∠DCO=56°,∠∠B′CA=∠BCA=28°,∠∠B′AC=90°-∠B′CA=62°,∠∠BAC=∠B′AC=62°.【点睛】考查了折叠的性质、矩形的性质和全等三角形的判定与性质,解题关键是证明∠AOB∠∠COD ,得出∠BAO=∠DCO=34°是解题的关键.32.1:3【详解】试题解析:设平行四边形的面积为1,∠四边形ABCD 是平行四边形, ∠12DAB ABCD S S =,又∠M 是ABCD 的AB 的中点, 则1124DAM DAB ABCD S S S ==,1,2BE MB DE CD == ∠EMB △上的高线与DAB 上的高线比为1.3BE BD ==∠1113212 EMB DABS S=⨯=,∠143 DEC MEBS S,==S阴影面积1111141233 =---=,则阴影部分的面积与▱ABCD的面积比为13.故填空答案:13.33.【详解】分析:作DH平分∠BDC交BC于H.连接AH交BD于M.首先证明P、H关于BD对称,连接AH交BD于M,则AM+PM的值最小,最小值=AH.详解:作DH平分∠BDC交BC于H.连接AH交BD于M.∠四边形ABCD是矩形,∠∠C=∠BAD=∠ADC=90°,∠tan∠ADB=ABAD∠∠ADB=30°,∠∠BDC=60°,∠∠CDH=30°,∠CD∠CH2,△DH=2CH=4,∠DP=DH,∠∠MDP=∠MDH,∠P、H关于BD对称,连接AH交BD于M,则AM+PM的值最小,最小值=AH=点睛:本题考查了矩形的性质,解直角三角形,勾股定理,含30º角的直角三角形的性质,轴对称的性质,作DH平分∠BDC交BC于H.连接AH交BD于M.说明P和H关于BD成轴对称是解答本题的关键.34.39cm60cm2【分析】根据角平分线的定义和平行线的性质得到等腰三角形ABE和等腰三角形CDE和直角三角形BCE.根据直角三角形的勾股定理得到BC=13cm,根据等腰三角形的性质得到AB=CD=12AD=12CD=6.5cm,从而求得该平行四边形的周长;根据直角三角形的面积可以求得平行四边形BC边上的高.【详解】∠BE、CE分别平分∠ABC、∠BCD,∠∠1=∠3=12∠ABC,∠DCE=∠BCE=12∠BCD,在▱ABCD中,AB=CD,AD=BC,AD∠BC,AB∠CD,∠AD∠BC,AB∠CD,∠∠2=∠3,∠BCE=∠CED,∠ABC+∠BCD=180°,∠∠1=∠2,∠DCE=∠CED,∠3+∠BCE=90°,∠AB=AE,CD=DE,∠BEC=90°,在Rt△BCE中,根据勾股定理得:BC=13cm,∠平行四边形的周长等于:AB+BC+CD+AD=6.5+13+6.5+13=39cm;作EF∠BC于F,根据直角三角形的面积公式得:EF=·6013BE CEBC=cm,∠平行四边形ABCD的面积=BC·EF=601313⨯=60cm2,故答案为39cm,60cm2.【点睛】本题考查了平行四边形的性质、等腰三角形的判定与性质、勾股定理等,在平行四边形中,当出现角平分线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.。
2020年浙江省绍兴市中考数学第22题四边形专题训练含答案

2020年浙江省绍兴市中考数学第22题四边形专题训练1.(1)如图,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,若AB=AC=2,求DE的长;(2)如图,在(1)的条件下,连结AG、AF分别交DE于M、N两点,求MN的长;(3)如图,在△ABC中,AB=AC=BN=2,∠BAC=108°,若AM=AN,请直接写出MN的长.2.如图正方形ABCD的边长为4,E、F分别为DC、BC中点.(1)求证:△ADE≌△ABF.(2)求△AEF的面积.3.小儒在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后做了如下思考:(1)他认为该定理有逆定理,即“如果一个三角形某条边上的中线等于该边长的一半,那么这个三角形是直角三角形”应该成立,你能帮小儒证明一下吗?如图①,在△ABC中,AD是BC边上的中线,若AD=BD=CD,求证:∠BAC=90°.(2)接下来,小儒又遇到一个问题:如图②,已知矩形ABCD,如果在矩形外存在一点E,使得AE⊥CE,求证:BE⊥DE,请你作出证明,可以直接用到第(1)问的结论.(3)在第(2)问的条件下,如果△AED恰好是等边三角形,直接用等式表示出此时矩形的两条邻边AB与BC的数量关系.4.(1)问题发现:如图①,在△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,以点D为顶点作正方形DFGE,使点A、C分别在DE和DF上,连接BE、AF.则线段BE和AF数量关系________.(2)类比探究:如图②,保持△ABC固定不动,将正方形DFGE绕点D旋转α(0°<α≤360°),则(1)中的结论是否成立?如果成立,请证明;如果不成立,请说明理由.(3)解决问题:若BC=DF=2,在(2)的旋转过程中,连接AE,请直接写出AE的最大值.5.操作与证明:如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点c重合,点E,F分别在正方形的边CB,CD上,连接AF.取AF中点M,EF的中点N,连接MD,MN.(1)连接AE,求证:△AEF是等腰三角形;(2)猜想与发现:在(1)的条件下,请判断DM,MN的数量关系和位置关系,得出结论.结论1:DM,MN的数量关系是________;结论2:DM,MN的位置关系是________;(3)拓展与探究:如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,则(2)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.6.如图,在矩形ABCD中,AB=3cm,AD=4cm,EF经过对角线BD的中点O,分别交AD,BC于点E,F.(1)求证:△BOF≌△DOE;(2)当EF⊥BD时,求AE的长.7.定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°.①若AB=CD=1,AB∥CD,则对角线BD的长为________;②若AC⊥BD,求证:AD=CD;________(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形.直接写出AE的长为________.8.如图,在▱ABCD中,BC=2AB,E,F分别是BC,AD的中点,AE,BF交于点O,连接EF,OC.(1)求证:四边形ABEF是菱形;(2)若BC=8,∠ABC=60°,求OC的长.9.如图,矩形纸片ABCD中,AB=4,点E在边CD上移动连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′CE,点B、C的对应点分别为点B′、C′(1)当点E与点C重合时,设B′C′与AD的交点为F,若AD=4DF,则AD=________(2)若AD=6,B′C′的中点记为P,则DP的取值范围是________10.类比等腰三角形的定义,我们定义:有三条边相等的凸四边形叫做“准等边四边形”(1)已知:如图1,在“准等边四边形”ABCD中,BC≠AB,BD⊥CD,AB=3,BD=4,求BC的长;(2)在探究性质时,小明发现一个结论:对角线互相垂直的“准等边四边形”是菱形.请你判断此结论是否正确,若正确,请说明理由;若不正确,请举出反例;(3)如图2,在△ABC中,AB=AC,∠BAC=90°,BC=2.在AB的垂直平分线上是否存在点P使得以A,B,C,P为顶点的四边形为“准等边四边形”?若存在,请求出该“准等边四边形”的面积;若不存在,请说明理由.11.现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,点B落在四边形AECD内,记为点B′,过E作EF垂直B′C,交B′C于F.(1)求AE、EF的位置关系;(2)求线段B′C的长,并求△B′EC的面积.12.(1)【问题探究】如图①,在正方形ABCD中,点E在边AD上,点F在边CD上,且AE=DF.线段BE与AF相交于点G,GH是△BFG的中线.①求证:△ABE≌△DAF.②判断线段BF与GH之间的数量关系,并说明理由.(2)【问题探究】如图②,在矩形ABCD中,AB=4,AD=6.点E在边AD上,点F在边CD上,且AE=2,DF=3,线段BE与AF相交于点G.若GH是△BFG的中线,则线段GH的长为________.13.已知,如图所示,在矩形ABCD中,点E在BC边上,△AEF=90°(1)如图①,已知点F在CD边上,AD=AE=5,AB=4,求DF的长;(2)如图②,已知AE=EF,G为AF的中点,试探究线段AB,BE,BG的数量关系;(3)如图③,点E在矩形ABCD的BC边的延长线上,AE与BG相交于O点,其他条件与(2)保持不变,AD=5,AB=4,CE=1,求△AOG的面积.14.定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,①若AB=CD=1,AB//CD,求对角线BD的长.②若AC⊥BD,求证:AD=CD.(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形.求AE的长.15.如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.(1)求证:四边形BFEP为菱形;(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;①当点Q与点C重合时(如图2),求菱形BFEP的边长;②若限定P、Q分别在边BA、BC上移动,求Rt△CED的内切圆半径的取值范围.16.如图1,在矩形ABCD中,AC为对角线,延长CD至点E使CE=CA,连接AE.F为AB上的一点,且BF=DE,连接FC.(1)若DE=1,CF= 2√2,求CD的长;(2)如图2,点G为线段AE的中点,连接BG交AC于H,若∠BHC+∠ABG=60°,求证:AF+CE= √3 AC.17.如图1,在矩形ABCD中,AC为对角线,延长CD至点E使CE=CA,连接AE.F为AB上的一点,且BF=DE,连接FC.(1)若DE=1,CF= 2√2,求CD的长;(2)如图2,点G为线段AE的中点,连接BG交AC于H,若∠BHC+∠ABG=60°,求证:AF+CE= √3 AC.18.如图,在矩形ABCD中,AB=4,BC=5,E是BC边上的一个动点,DF⊥AE,垂足为点F,连结CF(1)若AE=BC①求证:△ABE≌△DFA;②求四边形CDFE的周长;③求tan∠FCE的值;(2)探究:当BE为何值时,△CDF是等腰三角形.19.如图1,在正方形ABCD中,点E为边AB上的点,BE:AE=n,连结DE、BD,过点A作AG⊥DE,垂足为点F,与BC、BD分别交于点G、H,连结EH.(1)①求证:△ADE≌△BAG;②求证:DH:BH=n+1;(2)如图2,当EH∥AD时,求n的值.20.在Rt△ABC中,∠ACB=90°,AC=12.点D在直线CB上,以CA,CD为边作矩形ACDE,直线AB与直线CE,DE的交点分别为F,G.(1)如图,点D在线段CB上,四边形ACDE是正方形.①若点G为DE的中点,求FG的长.②若DG=GF,求BC的长.(2)已知BC=9,是否存在点D,使得△DFG是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.答案1. (1)解:∵AB =AC =2,∠A =90°,∴∠B =∠C =45°,BC = 2√2 ,∵四边形DEFG 是正方形,∴DE =DG =GF =EF ,∠DGF =∠EFG =90°,∴∠BGD =∠CFE =90°,∴∠B =∠BDG =45°,∠C =∠CEF =45°,∴BG =DG , CF =EF ,∴BG=FG=FC=DE ,∴DE = 13 BC =2√23 .(2)解:∵DE ∥BC ,∴ MN GF =AN AF =AE AC =DE BC , ∴ 2√23=13 ,∴MN =2√29(3)解:∵AB =AC ,∠BAC =108°,∴∠B =∠C =36°,∵BA =NB ,∴∠ANB =∠BAN =72°,∵AM =AN ,∴∠AMN =∠ANM =72°,∴∠B =∠BAM =∠MAN =36°,∴BM =AM =AN ,设MN =x ,则AN =AM =BM =2﹣x.∵△NAM ∽△NBA ,∴AN 2=NM •NB ,∴(2﹣x )2=2x , ∴x =3﹣ √5 或3+ √5 (舍弃) ∴MN =3﹣ √5 .2. (1)证明:∵四边形ABCD 为正方形,∴AB=AD ,∠D=∠B=90°,DC=CB ,∵E 、F 为DC 、BC 中点,∴DE= 12 DC ,BF= 12 BC ,∴DE=BF ,在△ADE和△ABF中,{AD=AB∠B=∠DDE=BF,∴△ADE≌△ABF(SAS)(2)解:由题知△ABF、△ADE、△CEF均为直角三角形,且AB=AD=4,DE=BF= 12×4=2,CE=CF= 12×4=2,∴S△AEF=S正方形ABCD﹣S△ADE﹣S△ABF﹣S△CEF=4×4﹣12×4×2﹣12×4×2﹣12×2×2=63. (1)证明:∵AD=BD,∴∠B=∠BAD,∵AD=CD,∴∠C=∠CAD,在△ABC中,∠B+∠C+∠BAC=180°,∴∠B+∠C+∠BAD+∠CAD=∠B+∠C+∠B+∠C=180°∴∠B+∠C=90°,∴∠BAC=90°(2)解:如图②,连接AC,BD,OE,∵四边形ABCD是矩形,∴OA=OB=OC=OD =12 AC =12BD,∵AE⊥CE,∴∠AEC=90°,∴OE =12AC,∴OE =12BD,∴∠BED=90°,∴BE⊥DE(3)解:如图3,∵四边形ABCD是矩形,∴AD=BC,∠BAD=90°,∵△ADE是等边三角形,∴AE=AD=BC,∠DAE=∠AED=60°,由(2)知,∠BED=90°,∴∠BAE=∠BEA=30°,过点B作BF⊥AE于F,∴AE=2AF,在Rt△ABF中,∠BAE=30°,∴AB=2BF,AF=√3 BF,∴AE=2 √3 BF,∴AE=√3 AB,∴BC=√3 AB.4.(1)BE=AF(2)解:成立;理由如下:当正方形DFGE在BC的上方时,如图②所示,连接AD,∵在Rt△ABC中,AB=AC,D为斜边BC的中点,∴AD=BD,AD⊥BC,∴∠ADE+∠EDB=90°,∵四边形DFGE为正方形,∴DE=DF,且∠EDF=90°,∴∠ADE+∠ADF=90°,∴∠BDE=∠ADF,在△BDE和△ADF中,{BD=AD∠BDE=∠ADFDE=DF,∴△BDE≌△ADF(SAS),∴BE=AF;当正方形DFGE在BC的下方时,连接AD,如图③所示:∵∠BDE=∠BDF+90°,∠ADF=∠BDF+90°,∴∠BDE=∠ADF,在△BDE和△ADF中,{BD=AD∠BDE=∠ADFDE=DF,∴△BDE≌△ADF(SAS),∴BE=AF;综上所述,(1)中的结论BE=AF成立(3)AE的最大值为3.5. (1)证明:四边形ABCD是正方形,AB=AD=BC=CD,∠B=∠ADF=90°,△CEF是等腰直角三角形,∠C=90°,CE=CF。
2020年中考数学复习专题练:《四边形综合 》(含答案)

2020年中考数学复习专题练:《四边形综合 》1.如图①所示,已知正方形ABCD 和正方形AEFG ,连接DG ,BE .(1)发现:当正方形AEFG 绕点A 旋转,如图②所示.①线段DG 与BE 之间的数量关系是 ;②直线DG 与直线BE 之间的位置关系是 ;(2)探究:如图③所示,若四边形ABCD 与四边形AEFG 都为矩形,且AD =2AB ,AG =2AE 时,上述结论是否成立,并说明理由.(3)应用:在(2)的情况下,连接BG 、DE ,若AE =1,AB =2,求BG 2+DE 2的值(直接写出结果).2.如图1,在正方形ABCD 中,点E 是CD 上一点(不与C ,D 两点重合),连接BE ,过点C 作CH ⊥BE 于点F ,交对角线BD 于点G ,交AD 边于点H ,连接GE ,(1)求证:△DHC ≌△CEB ;(2)如图2,若点E 是CD 的中点,当BE =8时,求线段GH 的长;(3)设正方形ABCD 的面积为S 1,四边形DEGH 的面积为S 2,当的值为时,的值为 .3.在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(6,0),点B(0,8).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F,记旋转角为α(0°<α<90°).(I)如图①,当α=30°时,求点D的坐标;(Ⅱ)如图②,当点E落在AC的延长线上时,求点D的坐标;(Ⅲ)当点D落在线段OC上时,求点E的坐标(直接写出结果即可).4.如图,BD是平行四边形ABCD的对角线,DE⊥AB于点E,过点E的直线交BC于点G,且BG=CG.(1)求证:GD=EG.(2)若BD⊥EG垂足为O,BO=2,DO=4,画出图形并求出四边形ABCD的面积.(3)在(2)的条件下,以O为旋转中心顺时针旋转△GDO,得到△G′D'O,点G′落在BC上时,请直接写出G′E的长.5.(1)【探索发现】如图1,在正方形ABCD中,点M,N分别是边BC,CD上的点,∠MAN=45°,若将△DAN 绕点A顺时针旋转90°到△BAG位置,可得△MAN≌△MAG,若△MCN的周长为8,则正方形ABCD的边长为.(2)【类比延伸】如图2,在四边形ABCD中,AB=AD,∠BAD=120°,∠B+∠D=180°,点M,N分别在边BC,CD上的点,∠MAN=60°,请判断线段BM,DN,MN之间的数量关系,并说明理由.(3)【拓展应用】如图3,在四边形ABCD中,AB=AD=2,∠ADC=120°,点M,N分别在边BC,CD上,连接AM,MN,AN,△ABM是等边三角形,AM⊥AD于点A,∠DAN=15°,请直接写出△CMN 的周长.6.(1)如图1,在△ABC中,AB>AC,点D,E分别在边AB,AC上,且DE∥BC,若AD=2,AE=,则的值是;(2)如图2,在(1)的条件下,将△ADE绕点A逆时针方向旋转一定的角度,连接CE 和BD,的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;(3)如图3,在四边形ABCD中,AC⊥BC于点C,∠BAC=∠ADC=θ,且tanθ=,当CD=6,AD=3时,请直接写出线段BD的长度.7.如图1,长方形ABCD中,∠DAB=∠B=∠DCB=∠D=90°,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,把△ADE沿直线AE翻折得△AD′E.(1)当D′点落在AB边上时,∠DAE=°;(2)如图2,当E点与C点重合时,D′C与AB交点F,①求证:AF=FC;②求AF长.(3)连接D′B,当∠AD′B=90°时,求DE的长.8.在平面直角坐标系中,点O是坐标原点,A(0,m),B(n,O),AC∥OB,且AC=OB,连接BC交x轴于点F,其中m、n满足方程+n2+8n+16=0.(1)求A、B两点坐标;(2)过A做AE⊥BC于E,延长AE交x轴于点D,动点P从点B出发以每秒2个单位的速度向x轴正半轴方向运动,设△PFD的面积为S,请用含t的式子表示S,并直接写出t的取值范围;(3)在(2)的条件下,连接PE,将△PED沿PE翻折到△PEG的位置(点D与点G对应),当四边形PDEG为菱形时,求点P和点G的坐标.9.已知四边形ABCD和四边形CEFG都是正方形,且AB>CE.(1)如图1,连接BG、DE.求证:BG=DE;(2)如图2,如果正方形CEFG绕点C旋转到某一位置恰好使得CG∥BD,BG=BD.①求∠BDE的度数;②若正方形ABCD的边长是,请求出△BCG的面积.10.【综合与实践】如图①,在正方形ABCD中,点E、F分别在射线CD、BC上,且BF=CE,将线段FA绕点F顺时针旋转90°得到线段FG,连接EG,试探究线段EG和BF的数量关系和位置关系.【观察与猜想】任务一:“智慧小组”首先考虑点E、F的特殊位置如图②,当点E与点D重合,点F与点C重合时,易知:EG与BF的数量关系是,EG与BF的位置关系是.【探究与证明】任务二:“博学小组”同学认为E、F不一定必须在特殊位置,他们分两种情况,一种是点E、F分别在CD、BC边上任意位置时(如图③);一种是点E、F在CD、BC边的延长线上的任意位置时(如图④),线段EG与BF的数量关系与位置关系仍然成立.请你选择其中一种情况给出证明.【拓展与延伸】“创新小组”同学认为,若将“正方形ABCD”改为“矩形ABCD,且=k(k≠1)”,点E、F分别在射线CD、BC上任意位置时,仍将线段FA绕点F顺时针旋转90°,并适当延长得到线段FG,连接EG(如图⑤),则当线段BF、CE、AF、FG满足一个条件时,线段EG与BF的数量关系与位置关系仍然成立.(请你在横线上直接写出这个条件,无需证明)11.在平面直角坐标系xOy中,四边形OADC为正方形,点D的坐标为(4,4),动点E沿边AO从A向O以每秒1cm的速度运动,同时动点F沿边OC从O向C以同样的速度运动,连接AF、DE交于点G.(1)试探索线段AF、DE的关系,写出你的结论并说明理由;(2)连接EF、DF,分别取AE、EF、FD、DA的中点H、I、J、K,则四边形HIJK是什么特殊平行四边形?请在图①中补全图形,并说明理由.(3)如图②当点E运动到AO中点时,点M是直线EC上任意一点,点N是平面内任意一点,是否存在点N使以O,C、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.12.综合与实践动手操作:第一步:在矩形纸片ABCD的边BC,AD上分别取两点E,F,使CE=AF;第二步:分别以DE,BF为对称轴将△CDE与△ABF翻折得到△C'DE与△A'BF,且边C'E 与A'B交于点G,边A'F与C'D交于一点H.问题解决:(1)求证:△BEG≌△DFH;(2)请判断四边形A'HC'G的形状,并证明你发现的结论;(3)已知tan∠EBG=,A'G=6,C'G=1,求矩形纸片ABCD的面积.13.如图1,矩形ABCD中,∠ACB=30°,将△ACD绕C点顺时针旋转α(0°<α<360°)至△A'CD'位置.(1)如图2,若AB=2,α=30°,求S△BCD′.(2)如图3,取AA′中点O,连OB、OD′、BD′.若△OBD′存在,试判定△OBD′的形状.(3)当α=α1时,OB=OD′,则α1=°;当α=α2时,△OBD′不存在,则α2=°.14.已知矩形ABCD 中,AB =2,BC =m ,点E 是边BC 上一点,BE =1,连接AE .(1)沿AE 翻折△ABE 使点B 落在点F 处,①连接CF ,若CF ∥AE ,求m 的值;②连接DF ,若≤DF ≤,求m 的取值范围.(2)△ABE 绕点A 顺时针旋转得△AB 1E 1,点E 1落在边AD 上时旋转停止.若点B 1落在矩形对角线AC 上,且点B 1到AD 的距离小于时,求m 的取值范围.15.如图1,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,连接BE 、DG .(1)BE 和DG 的数量关系是 ,BE 和DG 的位置关系是 ;(2)把正方形ECGF 绕点C 旋转,如图2,(1)中的结论是否还成立?若成立,写出证明过程,若不成立,请说明理由;(3)设正方形ABCD 的边长为4,正方形ECGF 的边长为3,正方形ECGF 绕点C 旋转过程中,若A 、C 、E 三点共线,直接写出DG 的长.16.如图,正方形ABCD的边长为a,射线AM是∠BAD外角的平分线,点E在边AB上运动(不与点A、B重合),点F在射线AM上,且AF=BE,CF与AD相交于点G,连结EC、EF、EG.(1)求证:CE=EF;(2)求△AEG的周长(用含a的代数式表示);(3)试探索:点E在边AB上运动至什么位置时,△EAF的面积最大.17.问题情境:矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别与边AB、BC所在的直线相交,交点为E、F.探究1:如图1,当PE⊥AB,PF⊥BC时,则=.探究2:如图2,在(1)的基础上,将三角板绕点P逆时针旋转,旋转角为α,(0°<α<60°),试求的值.探究3:在(2)的基础上继续旋转,当60°<α<90°时,将顶点P在AC上移动且使=时,如图3,试求的值.18.在Rt△ABC中,∠B=90°,AB=6,BC=8,点D从点B出发,以每秒3个单位的速度沿B→A→C运动,到点C停止.在点D运动的过程中,过点D作DE⊥BC,垂足为E,以DE为一边在右侧作矩形DEFG,点F在BC边上,且EF:DE=4:3,连结AG,CG,设运动时间为t(秒),矩形DEFG与△ABC重叠部分面积为S.(1)当AG=CG时,求t的值.(2)当点D在边AB上运动时,求S与t的函数关系式.(3)当△ACG的面积为6时,直接写出t的值.19.如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=32,DC=24,AD=42,动点P从点D出发,沿射线DA的方向以每秒4个单位长的速度运动,动点Q从点C出发,在线段CB 上以每秒2个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).(1)设△BPQ的面积为S,求S与t之间的函数关系式;(2)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?(3)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由.20.(1)【发现证明】如图1,在正方形ABCD中,点E,F分别是BC,CD边上的动点,且∠EAF=45°,求证:EF=DF+BE.小明发现,当把△ABE绕点A顺时针旋转90°至△ADG,使AB与AD重合时能够证明,请你给出证明过程.(2)【类比引申】①如图2,在正方形ABCD中,如果点E,F分别是CB,DC延长线上的动点,且∠EAF=45°,则(1)中的结论还成立吗?请写出证明过程.②如图3,如果点E,F分别是BC,CD延长线上的动点,且∠EAF=45°,则EF,BE,DF之间的数量关系是(不要求证明)(3)【联想拓展】如图1,若正方形ABCD的边长为6,AE=3,求AF的长.参考答案1.解:(1)①如图②中,∵四边形ABCD和四边形AEFG是正方形,∴AE=AG,AB=AD,∠BAD=∠EAG=90°,∴∠BAE=∠DAG,在△ABE和△DAG中,,∴△ABE≌△ADG(SAS),∴BE=DG;②如图2,延长BE交AD于T,交DG于H.由①知,△ABE≌△DAG,∴∠ABE=∠ADG,∵∠ATB+∠ABE=90°,∴∠ATB+∠ADG=90°,∵∠ATB=∠DTH,∴∠DTH+∠ADG=90°,∴∠DHB=90°,∴BE⊥DG,故答案为:BE=DG,BE⊥DG;(2)数量关系不成立,DG=2BE,位置关系成立.如图③中,延长BE交AD于T,交DG于H.∵四边形ABCD与四边形AEFG都为矩形,∴∠BAD=∠EAG,∴∠BAE=∠DAG,∵AD=2AB,AG=2AE,∴==,∴△ABE∽△ADG,∴∠ABE=∠ADG,=,∴DG=2BE,∵∠ATB+∠ABE=90°,∴∠ATB+∠ADG=90°,∵∠ATB=∠DTH,∴∠DTH+∠ADG=90°,∴∠DHB=90°,∴BE⊥DG;(3)如图④中,作ET⊥AD于T,GH⊥BA交BA的延长线于H.设ET=x,AT=y.∵△AHG∽△ATE,∴===2,∴GH=2x,AH=2y,∴4x2+4y2=4,∴x2+y2=1,∴BG2+DE2=(2x)2+(2y+2)2+x2+(4﹣y)2=5x2+5y2+20=25.2.证明(1)∵四边形ABCD是正方形,∴CD=BC,∠HDC=∠BCE=90°,∴∠DHC+∠DCH=90°,∵CH⊥BE,∴∠EFC=90°,∴∠ECF+∠BEC=90°,∴∠CHD=∠BEC,∴△DHC≌△CEB(AAS).(2)解:∵△DHC≌△CEB,∴CH=BE,DH=CE,∵CE=DE=CD,CD=CB,∴DH=BC,∵DH∥BC,∴.∴GC=2GH,设GH=x,则,则CG=2x,∴3x=8,∴x=.即GH=.(3)解:∵,∴,∵DH=CE,DC=BC,∴,∵DH∥BC,∴,∴,,设S△DGH =9a,则S△BCG=49a,S△DCG=21a,∴S△BCD=49a+21a=70a,∴S1=2S△BCD=140a,∵S△DEG :S△CEG=4:3,∴S△DEG=12a,∴S2=12a+9a=21a.∴.故答案为:.3.解:(I)过点D作DG⊥x轴于G,如图①所示:∵点A(6,0),点B(0,8).∴OA=6,OB=8,∵以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,∴AD=AO=6,α=∠OAD=30°,DE=OB=8,在Rt△ADG中,DG=AD=3,AG=DG=3,∴OG=OA﹣AG=6﹣3,∴点D的坐标为(6﹣3,3);(Ⅱ)过点D作DG⊥x轴于G,DH⊥AE于H,如图②所示:则GA=DH,HA=DG,∵DE=OB=8,∠ADE=∠AOB=90°,∴AE===10,∵AE×DH=AD×DE,∴DH===,∴OG=OA﹣GA=OA﹣DH=6﹣=,DG===,∴点D的坐标为(,);(Ⅲ)连接AE,作EG⊥x轴于G,如图③所示:由旋转的性质得:∠DAE=∠AOC,AD=AO,∴∠OAC=∠ADO,∴∠DAE=∠ADO,∴AE∥OC,∴∠GAE=∠AOD,∴∠DAE=∠GAE,在△AEG和△AED中,,∴△AEG≌△AED(AAS),∴AG=AD=6,EG=ED=8,∴OG=OA+AG=12,∴点E的坐标为(12,8).4.证明:(1)如图1,延长EG交DC的延长线于点H,∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,AB=CD,AB∥CD,∵AB∥CD,∴∠H=GEB,且BG=CG,∠BGE=∠CGH,∴△CGH≌△BGE(AAS)∴GE=GH,∵DE⊥AB,DC∥AB,∴DC⊥DE,且GE=GH,∴DG=EG=GH;(2)如图1:∵DB⊥EG,∴∠DOE=∠DEB=90°,且∠EDB=∠EDO,∴△DEO∽△DBO,∴∴DE×DE=4×(2+4)=24,∴DE=2,∴EO===2,∵AB∥CD,∴, ∴HO =2EO =4, ∴EH =6,且EG =GH , ∴EG =3,GO =EG ﹣EO =, ∴GB ===,∴BC =2=AD , ∴AD =DE ,∴点E 与点A 重合,如图2:∵S 四边形ABCD =2S △ABD ,∴S 四边形ABCD =2××BD ×AO =6×2=12;(3)如图3,过点O 作OF ⊥BC ,∵旋转△GDO ,得到△G ′D 'O ,∴OG =OG ',且OF ⊥BC ,∴GF =G 'F ,∵OF ∥AB ,∴==,∴GF=BG=,∴GG'=2GF=,∴BG'=BG﹣GG'=,∵AB2=AO2+BO2=12,∵EG'=AG'==,=.5.解:(1)如图1中,∵△MAN≌△MAG,∴MN=GM,∵DN=BG,GM=BG+BM,∴MN=BM+DN,∵△CMN的周长为:MN+CM+CN=8,∴BM+CM+CN+DN=8,∴BC+CD=8,∴BC=CD=4,故答案为4;(2)如图2中,结论:MN=NM+DN.延长CB至E,使BE=DN,连接AE,∵∠ABC+∠D=180°,∠ABC+∠ABE=180°,∴∠D=∠ABE,在△ABE和△ADN中,,∴△ABE≌△ADN(SAS),∴AN=AE,∠DAN=∠BAE,∵∠BAD=2∠MAN,∴∠DAN+∠BAM=∠MAN,∴∠MAN=∠EAM,在△MAN和△MAE中,,∴△MAN≌△MAE(SAS),∴MN=EM=BE+BM=BM+DN,即MN=BM+DN;(3)如图3,延长BA,CD交于G,∵∠BAM=60°,∠MAD=90°,∴∠BAD=150°,∴∠GAD=30°,∵AD=2,∴DG=1,AG=,∵∠DAN=15°,∴∠GAN=45°,∴AG=GN=,∴BG=2+,∴BC=2BG=4+2,CG=BG=2+3,∴CD=CG﹣DG=2+2,由(2)得,MN=BM+DN,∴△CMN的周长=CM+CN+MN=CN+DN+CM+BM=BC+CD=4+2+2+2=6+4.6.解:(1)∵DE∥BC,∴===;故答案为:;(2)的值不变化,值为;理由如下:由(1)得:DE∥B,∴△ADE∽△ABC,∴=,由旋转的性质得:∠BAD=∠CAE,∴△ABD∽△ACE,∴==;(3)在AB上截取AM=AD=3,过M作MN∥BC交AC于N,把△AMN绕A逆时针旋转得△ADE,连接CE,如图所示:则MN⊥AC,DE=MN,∠DAE=∠BAC,∴∠AED=∠ANM=90°,∵AC⊥BC于点C,∠BAC=∠ADC=θ,且tanθ==,∴BC:AC:AB=3:4:5,同(2)得:△ABD∽△ACE,∴==,∵MN∥BC,∴△AMN∽△ABC,∴=,∴MN=×AM=×3=,∵∠BAC=∠ADC=θ,∴∠DAE=∠ADC=θ,∴AE∥CD,∴∠CDE+∠AED=180°,∴∠CDE=90°,∴CE===,∴BD=CE=×=.7.解:(1)由题意知△ADE≌△AD′E,∴∠DAE=∠D′AE,∵D′点落在AB边上时,∠DAE+∠D′AE=90°,∴∠DAE=∠D′AE=45°,故答案为:45;(2)①如图2,由题意知∠ACD=∠ACD′,∵四边形ABCD是矩形,∴AB∥CD,∴∠ACD=∠BAC,∴∠ACD′=∠BAC,∴AF=FC;②设AF=FC=x,则BF=10﹣x,在Rt△BCF中,由BF2+BC2=CF2得(10﹣x)2+62=x2,解得x=6.8,即AF=6.8;(3)如图3,∵△AD′E≌△ADE,∴∠AD′E=∠D=90°,∵∠AD′B=90°,∴B、D′、E三点共线,又∵△ABD′∽△BEC,AD′=BC,∴△ABD′≌△BEC,∴BE=AB=10,∵BD′===8,∴DE=D′E=10﹣8=2;如图4,∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,∴∠CBE=∠BAD″,在△ABD″和△BEC中,∵,∴△ABD″≌△BEC,∴BE=AB=10,∴DE=D″E=8+10=18.综上所知,DE=2或18.8.解:(1)∵,,(n+4)2≥0,∴m﹣4=0,n+4=0,∴m=4,n=﹣4,∴A(0,4),B(﹣4,0);(2)∵AC∥OB,∴∠C=∠CBO,∠CAF=∠BOF,∵AC=OB,∴△ACF≌△OBF(ASA),∴AF=OF=2,∵OA=OB,∠OAD=∠OBF,∠BOF=∠AOD,∴△BOF≌△AOD(ASA),∴OF=OD=2,∴BD=6,①当0≤t<3时,S=PD•OF=(6﹣2t)×2=6﹣2t;②当t>3时,S=PD•OF=(2t﹣6)×2=2t﹣6;(3)①当0≤t<3,如图2,∵AO=4,OD=2,∴AD=,∵BD×OA=AD×BE,∴BE=,∴DE=,∵四边形PDEG为菱形,∴DP=DE=EG=,∵D(2,0),∴P(2﹣,0),作EH⊥BD于H,∵BE×DE=BD×EH,∴EH=,∴HD=,∴OH=,∴E(,),∵EG∥OB,∴G与E的纵坐标相同,∴G(﹣,)②当t>3时,如图3,同理求得P(2+,0),G(+,).9.(1)证明:∵四边形ABCD和四边形CEFG为正方形,∴BC=DC,CG=CE,∠BCD=∠GCE=90°.∴∠BCD+∠DCG=∠GCE+∠DCG,∴∠BCG=∠DCE.在△BCG和△DCE中,,∴△BCG≌△DCE(SAS).∴BG=DE;(2)解:①连接BE,如图2所示:由(1)可知:BG=DE,∵CG∥BD,∴∠DCG=∠BDC=45°,∴∠BCG=∠BCD+∠DCG=90°+45°=135°,∵∠GCE=90°,∴∠BCE=360°﹣∠BCG﹣∠GCE=360°﹣135°﹣90°=135°,∴∠BCG=∠BCE,在△BCG和△BCE中,,∴△BCG≌△BCE(SAS),∴BG=BE,∵BG=BD=DE,∴BD=BE=DE,∴△BDE为等边三角形,∴∠BDE=60°;②延长EC交BD于点H,过点G作GN⊥BC于N,如图3所示:在△BCE和△DCE中,,∴△BCE≌△BCG(SSS),∴∠BEC=∠DEC,∴EH⊥BD,BH=BD,∵BC=CD=,∴BD=BC=2,∴BE=2,BH=1,∴CH=1,在Rt△BHE中,由勾股定理得:EH===,∴CE=﹣1,∵∠BCG=135°,∴∠GCN=45°,∴△GCN是等腰直角三角形,∴GN=CG=(﹣1),=BC•GN=××(﹣1)=.∴S△BCG10.【观察与猜想】解:∵四边形ABCD是正方形,∴∠B=∠BCD=∠ADC=90°,AB=BC=CD=AD,∠ACB=∠ACD=45°,由旋转的性质得:GC=AC,∠ACG=90°,∴∠ACB=∠GCD=45°,在△ABC和△GDC中,,∴△ABC≌△GDC(SAS),∴AB=GD,∠GDC=∠B=90°,∴DG∥BC,△CDG是等腰直角三角形,∴DG=CD=BC,∵点E与点D重合,点F与点C重合,∴EG=BF,EG∥BF;故答案为:EG=BF,EG∥BF;【探究与证明】证明:点E、F分别在CD、BC边上任意位置时,如图③所示:作GM⊥BC,交BC延长线于M,则∠GMF=90°,MG∥DC,∵四边形ABCD是正方形,∴AB=BC,∠BCD=∠B=90°,∴∠BAF+∠BFA=90°,由旋转的性质得:GF=AF,∠AFG=90°,∴∠BFA+∠MFG=90°,∴∠BAF=∠MFG,在△ABF和△FMG中,,∴△ABF≌△FMG(AAS),∴AB=FM,BF=MG,∵AB=BC,∴BF=CM,∵BF=CE,∴MG=CE,∵MG∥CE,∴四边形CEGM是平行四边形,又∵∠GMF=90°,∴四边形CEGM是矩形,∴EG=CM,EG∥CM,∴EG=BF,EG∥BF;点E、F在CD、BC边的延长线上的任意位置时,如图④所示:作GM⊥BC,交BC延长线于M,则∠GMF=90°,MG∥DC,∵四边形ABCD是正方形,∴AB=BC,∠BCD=∠B=90°,∴∠BAF+∠BFA=90°,由旋转的性质得:GF=AF,∠AFG=90°,∴∠BFA+∠MFG=90°,∴∠BAF=∠MFG,在△ABF和△FMG中,,∴△ABF≌△FMG(AAS),∴AB=FM,BF=MG,∵AB=BC,∴BF=CM,∵BF=CE,∴MG=CE,∵MG∥CE,∴四边形CEGM是平行四边形,又∵∠GMF=90°,∴四边形CEGM是矩形,∴EG=CM,EG∥CM,∴EG=BF,EG∥BF;【拓展与延伸】解:==k(k≠1)时,线段EG与BF的数量关系与位置关系仍然成立;理由如下:作GM⊥BC,交BC延长线于M,如图⑤所示:则∠GMF=90°,MG∥DC,∵四边形ABCD是正方形,∴AB=BC,∠BCD=∠B=90°,∴∠BAF+∠BFA=90°,∠B=∠GMF,由旋转的性质得:∠AFG=90°,∴∠BFA+∠MFG=90°,∴∠BAF=∠MFG,∴△ABF∽△FMG,∴==,∵==k,∴==k,==k,∴FM=BC,GM=CE,∴BF=CM,∵MG∥CE,∴四边形CEGM是平行四边形,又∵∠GMF=90°,∴四边形CEGM是矩形,∴EG=CM,EG∥CM,∴EG=BF,EG∥BF;故答案为:==k(k≠1).11.解:(1)AF=DE.理由如下:∵四边形OADC是正方形,∴OA=AD,∠DAE=∠AOF=90°,由题意得:AE=OF,在△AOF和△DAE中,,∴△AOF≌△DAE(SAS),∴AF=DE.(2)四边形HIJK是正方形.理由如下:如图①所示:∵H、I、J、K分别是AE、EF、FD、DA的中点,∴HI=KJ=AF,HK=IJ=ED,HI∥AF,HK∥ED,∵AF=DE,∴HI=KJ=HK=IJ,∴四边形HIJK是菱形,∵△AOF≌△DAE,∴∠ADE=∠OAF,∵∠ADE+∠AED=90°,∴∠OAF+∠AED=90°,∴∠AGE=90°,∴AF⊥ED,∵HI∥AF,HK∥ED,∴HI⊥HK,∴∠KHI=90°,∴四边形HIJK是正方形.(3)存在,理由如下:∵四边形OADC为正方形,点D的坐标为(4,4),∴OA=AD=OC=4,∴C(4,0),∵点E为AO的中点,∴OE=2,E(0,2);分情况讨论:如图②所示,①当OC是以O,C、M、N为顶点的菱形的对角线时,OC与MN互相垂直平分,则M为CE 的中点,∴点M的坐标为(2,1),∵点M和N关于OC对称,∴N(2,﹣1);②当OC是以O,C、M、N为顶点的菱形的边时,若M在y轴的左侧时,∵四边形OCM'N'是菱形,∴OM'=OC=4,M'N'∥OC,∴△M'FE∽△COE,∴==2,设EF=x,则M'F=2x,OF=x+2,在Rt△OM'F中,由勾股定理得:(2x)2+(x+2)2=42,解得:x=,或x=﹣2(舍去),∴M'F=,FN=4﹣M'F=,OF=2+=,∴N'(,);若M在y轴的右侧时,作N''P⊥OC于P,∵ON''∥CM'',∴∠PON''=∠OCE,∴tan∠PON''==tan∠OCE==,设PN''=y,则OP=2y,在Rt△OPN''中,由勾股定理得:y2+(2y)2=42,解得:y=,∴PN''=,OP=,∴N''(,﹣);综上所述,存在点N使以O,C、M、N为顶点的四边形是菱形,点N的坐标为(2,﹣1)或(,)或(,﹣).12.(1)证明:∵四边形ABCD为矩形,∴BC=AD,CD=AB,∠C=∠ABC=∠A=∠ADC=90°,∵CE=AF,∴BC﹣CE=AD﹣AF,即BE=DF,在△DCE和△BAF中,,∴△DCE≌△BAF(SAS),∴∠CDE=∠ABF,∠CED=∠AFB,由折叠的性质得:∠CDE=∠C′DE,∠ABF=∠A′BF,∠CED=∠C′ED,∠AFB=∠A′FB,∵∠CDE+∠C′DE+∠HDF=90°,∠ABF+∠A′BF+∠GBE=90°,∠CED+∠C′ED+∠GEB=180°,∠AFB+∠A′FB+∠HFD=180°,∴∠HDF=∠GBE,∠GEB=∠HFD,在△BEG和△DFH中,,∴△BEG≌△DFH(ASA);(2)解:四边形A'HC'G的形状是矩形;理由如下:由折叠的性质得:∠C=∠DC′E=∠A=∠BA′F=90°,由(1)得:△BEG≌△DFH,∴∠BGE=∠DHF,∵∠BGE=∠A′GC′,∠DHF=∠A′HC′,∴∠A′GC′=∠A′HC′,∵∠DC′E+∠BA′F+∠A′GC′+∠A′HC′=90°+90°+∠A′GC′+∠A′HC′=360°,∴∠A′GC′+∠A′HC′=180°,∴∠A′GC′=∠A′HC′=90°,∴∠DC′E=∠BA′F=∠A′GC′=∠A′HC′=90°,∴四边形A'HC'G是矩形;(3)解:由(2)知:∠BGE=∠A′GC′=90°,∵tan∠EBG=,∴设EG=3x,则BG=4x,BE==5x,由折叠的性质得:CE=C′E=EG+C′G=3x+1,CD=AB=A′B=BG+A′G=4x+6,∴BC=CE+BE=3x+1+5x=8x+1,S矩形ABCD=CD•BC=4×CD•CE+2×EG•BG﹣A'G•C'G,即(4x+6)(8x+1)=4×(3x+1)(4x+6)+2×3x•4x﹣6×1,整理得:x2﹣2x=0,解得:x1=2,x2=0(不合题意舍去),∴CD=4×2+6=14,CB=8×2+1=17,∴S矩形ABCD=CD•BC=14×17=238.13.解:(1)作D'E⊥BC交BC的延长线于E,如图2所示:则∠E=90°,∵四边形ABCD是矩形,∴∠ABC=90°,AB∥CD,AD∥BC,CD=AB=2,∴∠ACD=∠BAC,∠DAC=∠ACB=30°,∵∠ACB=30°,∴BC=AB=2,∠ACD=∠BAC=60°,由旋转的性质得:CD'=CD=2,∠ACA'=30°,∴∠D'CE=180°﹣30°﹣30°﹣60°=60°,∴∠CD'E=30°,∴CE=CD'=1,D'E=CE=,∴S=BC×D'E=×2×=3;△BCD′(2)△OBD′是直角三角形,理由如下:连接OC,如图3所示:由旋转的性质得:CA'=CA,∠AD'C=∠ADC=90°,∠D'A'C=∠DAC=30°,∵O是AA′的中点,∴OC⊥AA',∴∠AOC=∠AOC=90°=∠ABC=∠AD'C,∴∠ABC+∠AOC=180°,∴A、B、C、O四点共圆,∴∠BOC=∠BAC=60°,同理;A、D'、C、O四点共圆,∴∠D'OC=∠D'A'C=30°,∴∠BOD'=90°,∴△BOD'是直角三角形;(3)若B、C、D'三点不共线,如图3所示:由(2)得:∠OBC=∠OAC,∠OD'C=∠OA'C,∠OAC=∠OA'C,∴∠OBC=∠OD'C,∵OB=OD,∴∠OBD'=∠OD'B,∴∠CBD'=∠CD'B,∴CB=CD',∵CD'=CD,∴BC=CD,这与已知相矛盾,∴B、C、D'三点共线;分两种情况:当点D'在BC的延长线上时,如图4所示:=90°;α=α1当点D'在边BC上时,如图5所示:=360°﹣90°=270°;α=α1故答案为:90°或270;时,△OBD′不存在时,分两种情况:当α=α2当O与D'重合时,如图6所示:∵CA'=CA,∠CAD'=∠CA'D'=30°,∴∠ACA'=120°,=360°﹣120°=240°;∴α=α2当O与B重合时,如图7所示:则AA'=2AB=4,∵CA=CA'=2AB=4=AA',∴△ACA'是等边三角形,∴∠A'CA=60°,=360°﹣60°=300°;∴α=α2故答案为:240°或300.14.解:(1)①如图1,∵CF∥AE ∴∠FCE=∠AEB,∠CFE=∠AEF∵△ABE翻折得到△AFE∴EF=BE=1,∠AEF=∠AEB∴∠FCE=∠CFE∴CE=EF=1∴m=BC=BE+CE=2∴m的值是2.②如图2,过点F作GH⊥AD于点G,交BC于点H ∴GH⊥BC∴∠AGF=∠FHE=90°∵四边形ABCD是矩形∴∠BAD=∠B=90°∴四边形ABHG是矩形∴GH=AB=2,AG=BH∵△ABE翻折得到△AFE∴EF=BE=1,AF=AB=2,∠AFE=∠B=90°∴∠AFG+∠EFH=∠AFG+∠FAG=90°∴∠EFH=∠FAG∴△EFH∽△FAG∴设EH=x,则AG=BH=x+1∴FG=2EH=2x∴FH=GH﹣FG=2﹣2x∴解得:x=∴AG=,FG=∵AD=BC=m∴DG=|AD﹣AG|=|m﹣|∴DF 2=DG 2+FG 2=(m ﹣)2+2≥,即可把DF 2看作关于m 的二次函数,抛物线开口向上,最小值为∵∴∵(m ﹣)2+2= 解得:m 1=,m 2=1 ∴根据二次函数图象可知,1≤m(2)如图3,过点B 1作MN ⊥AD 于点M ,交BC 于点N ∴MN ∥AB ,MN =AB =2∵AC = ∴sin ∠ACB =∵AD ∥BC ,点B 1在AC 上∴∠MAB 1=∠ACB∴sin ∠MAB 1= ∴∵点B 1到AD 的距离小于∴MB 1= 解得:∵m>0 ∴m>如图4,当E1落在边AD上,且B1在AC上时,m最大,此时,∠ACB=∠B1AE1=∠BAE∴tan∠ACB=tan∠BAE∴∴m=BC=2AB=4∴m的取值范围是<m≤415.解:(1)BE=DG.BE⊥DG;理由如下:∵四边形ABCD和四边形CEFG为正方形,∴CD=BC,CE=CG,∠BCE=∠DCG=90°,在△BEC和△DGC中,,∴△BEC≌△DGC(SAS),∴BE=DG;如图1,延长GD交BE于点H,∵△BEC≌△DGC,∴∠DGC=∠BEC,∴∠DGC+∠EBC=∠BEC+∠EBC=90°,∴∠BHG=90°,即BE⊥DG;故答案为:BE=DG,BE⊥DG.(2)成立,理由如下:如图2所示:同(1)得:△DCG≌△BCE(SAS),∴BE=DG,∠CDG=∠CBE,∵∠DME=∠BMC,∠CBE+∠BMC=90°,∴∠CDG+∠DME=90°,∴∠DOB=90°,∴BE⊥DG;(3)由(2)得:DG=EB,分两种情况:①如图3所示:∵正方形ABCD的边长为4,正方形ECGF的边长为3,∴AC⊥BD,BD=AC=AB=4,OA=OC=OB=AC=2,CE=3,∴AE=AC﹣CE=,∴OE=OA﹣AE=,在Rt△BOE中,由勾股定理得:DG=BE==;②如图4所示:OE=CE+OC=2+3=5,在Rt△BOE中,由勾股定理得:DG=BE==;综上所述,若A、C、E三点共线,DG的长为或.16.(1)证明:过点F作FH⊥AB于H,如图1所示:则∠AHF=90°,∵AM平分∠DAH,∴∠FAH=45°,∴△AFH是等腰直角三角形,∴FH=AH,AF=AH=FH,∵AF=BE,∴FH=AH=BE,∴AH+AE=BE+AE,∴HE=AB=BC,在△FEH和△ECB中,,∴△FEH≌△ECB(SAS),∴CE=EF;(2)解:∵△FEH≌△ECB,∴∠FEH=∠ECB,∵在Rt△BCE中,∠ECB+∠CEB=90°,∴∠FEH+∠CEB=90°,∴∠CEF=90°,由(1)知,CE=EF,∴△CEF是等腰直角三角形,∠ECF=∠EFC=45°,把Rt△CDG绕点C逆时针旋转90°至Rt△CBN位置,如图2所示:则∠GCN=90°,CG=CN,DG=BN,∴∠NCE=∠GCN﹣∠GCE=45°,∴∠NCE=∠GCE,在△CEG和△CEN中,,∴△CEG≌△CEN(SAS),∴GE=NE=EB+BN=EB+DG,∴△AEG的周长=AE+GE+AG=AE+EB+DG+AG=AB+AD=2a;(3)解:设AE=x,由(1)得:FH=BE=a﹣x,则△EAF的面积=AE×FH=x(a﹣x)=﹣(x﹣)2+,∴当x=,即点E在AB边中点时,△EAF的面积最大,最大值为.17.解:(1)∵矩形ABCD,∴AB⊥BC,PA=PC;∵PE⊥AB,BC⊥AB,∴PE∥BC,∴∠APE=∠PCF;∵PF⊥BC,AB⊥BC,∴PF∥AB,∴∠PAE=∠CPF.∵在△APE与△PCF中,,∴△APE≌△PCF(ASA),∴PE=CF.在Rt△PCF中,=tan30°=,∴=,故答案为:.(2)如答图1,过点P作PM⊥AB于点M,PN⊥BC于点N,则PM⊥PN.0°~30°时∵PM⊥PN,PE⊥PF,∴∠EPM=∠FPN,又∵∠PME=∠PNF=90°,∴△PME∽△PNF,∴=,由(1)知,=,∴=.同理30°~60°时,=;(3)当60°<α<90°时,将顶点P在AC上移动且使=时,如答图2,过点P作PM⊥AB于点M,PN⊥BC于点N,则PM⊥PN,PM∥BC,PN∥AB.∵PM∥BC,PN∥AB,∴∠APM=∠PCN,∠PAM=∠CPN,∴△APM∽△PCN,∴==,得CN=2PM.在Rt△PCN中,==tan30°=,∴=.∵PM⊥PN,PE⊥PF,∴∠EPM=∠FPN,又∵∠PME=∠PNF=90°,∴△PME∽△PNF,∴==.18.解:(1)∵四边形DEFG是矩形,∴DG=BF,GF=BD,∠BDG=∠BFG=90°,∴∠ADG=∠CFG=90°,由题意得:BD=3t,则AD=6﹣3t,DG=4t,CF=8﹣4t,FG=BD=3t,当AG=CG时,由勾股定理得:AG2=AD2+DG2,CG2=FG2+FC2,∴AD2+DG2=FG2+FC2,即(6﹣3t)2+(4t)2=(3t)2+(8﹣4t)2,解得:t=1,即当AG=CG时,t=1秒;(2)分两种情况:①当0<t≤1时,如图1所示:S=矩形DEFG的面积=3t×4t=12t2;即S=12t2(0<t≤1);②当1<t≤2时,如图2所示:∵∠ADH=∠B=90°,∠A=∠A,∴△ADH∽△ABC,∴=,即=,解得:DH=8﹣4t,同理得:FM=6﹣3t,∴S=×6×8﹣×2×(6﹣3t)(8﹣4t)=﹣12t2+48t﹣24;即S=﹣12t2+48t﹣24(1<t≤2);(3)分三种情况:①如图1所示:由题意得:×6×8﹣12t2﹣×4t×(6﹣3t)﹣×3t×(8﹣4t)=6,解得:t=;②如图3所示:由题意得:×4t×(6﹣3t)+×3t×(8﹣4t)+3t×4t﹣×6×8=6,解得:t=;③如图4所示:由勾股定理得:AC===10,∴CD=6+10﹣3t=16﹣3t,同(2)得:△CDE∽△CAB,∴==,即==,解得:DE=(16﹣3t),CE=(16﹣3t),由题意得EF=(16﹣3t),∴C与F重合,∴×8×(16﹣3t)=6,解得:t=;综上所述,当△ACG的面积为6时,t的值为秒或秒或秒.19.解:(1)如图1,过点P作PM⊥BC,垂足为M,则四边形PDCM为矩形.∴PM=DC=24.∵QB=32﹣t,∴S=×24×(32﹣2t)=384﹣24t(0≤t<16);(2)由图可知:CM=PD=4t,CQ=2t.以B、P、Q三点为顶点的三角形是等腰三角形,可以分三种情况:①若PQ=BQ.在Rt△PMQ中,PQ2=4t2+242,由PQ2=BQ2得4t2+242=(32﹣2t)2,解得t=;②若BP=BQ.在Rt△PMB中,BP2=(32﹣4t)2+242.由BP2=BQ2得:(32﹣4t)2+242=(32﹣2t)2即3t2﹣32t+144=0.由于△=﹣704<0,∴3t2﹣32t+144=0无解,∴PB≠BQ.③若PB=PQ.由PB2=PQ2,得4t2+242=(32﹣4t)2+242整理,得3t 2﹣64t +256=0.解得t 1=,t 2=16(舍去)综合上面的讨论可知:当t =秒或t =秒时,以B 、P 、Q 三点为顶点的三角形是等腰三角形.(3)设存在时刻t ,使得PQ ⊥BD .如图2,过点Q 作QE ⊥AD 于E ,垂足为E .∵AD ∥BC∴∠BQF =∠EPQ ,又∵在△BFQ 和△BCD 中∠BFQ =∠C =90°,∴∠BQF =∠BDC ,∴∠BDC =∠EPQ ,又∵∠C =∠PEQ =90°,∴Rt △BDC ∽Rt △QPE , ∴=,即=,解得t =9.所以,当t =9秒时,PQ ⊥BD .20.(1)【发现证明】证明:把△ABE 绕点A 顺时针旋转90°至△ADG ,如图1,∴∠BAE=∠DAG,AE=AG,∵∠EAF=45°,∴∠BAE+∠FAD=45°,∴∠DAG+∠FAD=45°,∴∠EAF=∠FAG,∵AF=AF,∴△EAF≌△GAF(SAS),∴EF=FG=DF+DG,∴EF=DF+BE;(2)【类比引申】①不成立,结论:EF=DF﹣BE;证明:如图2,将△ABE绕点A顺时针旋转90°至△ADM,∴∠EAB=∠MAD,AE=AM,∠EAM=90°,BE=DM,∴∠FAM=45°=∠EAF,∵AF=AF,∴△EAF≌△MAF(SAS),。
中考数学专题训练:特殊平行四边形(附参考答案)

中考数学专题训练:特殊平行四边形(附参考答案)1.如图,在矩形ABCD和△BDE中,点A在BE上.若矩形ABCD的面积为20,△BDE的面积为24,则△ADE的面积为( )A.10 B.12C.14 D.162.如图,矩形ABCD的对角线AC,BD交于点O,AB=3,BC=4,过点O作OM⊥AC,交BC于点M,过点M作MN⊥BD,垂足为点N,则OM+MN的值为( )A.245B.165C.125D.653.如图,在四边形ABCD中,AB∥CD,AB⊥BD,AB=5,BD=4,CD=3,E是AC 的中点,则BE的长为( )A.2 B.52C.√5D.34.关于菱形的性质,以下说法不正确的是( )A.四条边相等B.对角线相等C.对角线互相垂直D.是轴对称图形5.下列选项中能使□ABCD成为菱形的是( )A.AB=CD B.AB=BCC.∠BAD=90°D.AC=BD6.如图,在菱形ABCD中,∠B=60°,点P从点B出发,沿折线BC-CD方向移动,移动到点D停止.在△ABP形状的变化过程中,依次出现的特殊三角形是( )A.直角三角形→等边三角形→等腰三角形→直角三角形B.直角三角形→等腰三角形→直角三角形→等边三角形C.直角三角形→等边三角形→直角三角形→等腰三角形D.等腰三角形→等边三角形→直角三角形→等腰三角形7.如图,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连接OE.若AC=6,BD=8,则OE=( )A.2 B.52C.3 D.48.如图,在菱形ABCD中,E,F分别是边BC,CD的中点,连接AE,AF,EF.若菱形ABCD的面积为8,则△AEF的面积为( )A.2 B.3C.4 D.59.如图,将矩形ABCD对折,使边AB与DC,BC与AD分别重合,展开后得到四边形EFGH.若AB=2,BC=4,则四边形EFGH的面积为( )A.2 B.4C.5 D.610.一个四边形顺次添加下列条件中的三个条件便得到正方形:a.两组对边分别相等;b.一组对边平行且相等;c.一组邻边相等;d.一个角是直角.顺次添加的条件:①a→c→d ②b→d→c ③a→b→c,则正确的是( )A.仅①B.仅③C.①②D.②③11.如图,在正方形ABCD中,点E,F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则CG的长是( )A.2 B.√5C.3√22D.12512.如图,已知F,E分别是正方形ABCD的边AB与BC的中点,AE与DF交于点P,则下列结论成立的是( )A.BE=12AE B.PC=PDC.∠EAF+∠AFD=90°D.PE=EC13.如图,在边长为3的正方形ABCD中,∠CDE=30°,DE⊥CF,则BF的长是( )A.1 B.√2C.√3D.214.如图,O为正方形ABCD对角线AC的中点,△ACE为等边三角形.若AB=2,则OE的长度为( )A.√6B.√62C.2√2D.2√315.如图,在△ABC中,D,E,F分别是边AB,BC和AC的中点,请添加一个条件________________________,使四边形BEFD为矩形.(填一个即可)16.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.若AC=12,BD=16,则OE的长为______.17.如图,在矩形ABCD中,对角线AC,BD相交于点O,E是边AD的中点,点FAC,连接EF.若AC=10,则EF=______.在对角线AC上,且AF=1418.如图,E是矩形ABCD边AD上一点,F,G,H分别是BE,BC,CE的中点,AF=3,则GH的长为_____.19.如图,菱形ABCD的对角线AC,BD相交于点O,OE⊥AD,垂足为点E,AC=8,BD=6,则OE的长为______.20.如图,菱形ABCD的边长为6 cm,∠BAD=60°,将该菱形沿AC方向平移2√3 cm得到四边形A′B′C′D′,A′D′交CD于点E,则点E到AC的距离为_____cm.21.如图,已知菱形ABCD的边长为2,∠DAB=60°,E为AB的中点,F为CE 的中点,AF与DE相交于点G,则GF的长等于______.22.如图,将边长为1的正方形ABCD绕点A顺时针旋转30°得到正方形AB1C1D1,则阴影部分的面积是_________.23.如图,在正方形ABCD中,点E,F分别在BC,CD上,连接AE,AF,EF,∠EAF=45°.若∠BAE=α,则∠FEC一定等于______.24.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是_______.参考答案1.C 2.C 3.C 4.B 5.B 6.C 7.B 8.B 9.B 10.C 11.D 12.C 13.C 14.B15.AB⊥BC(答案不唯一) 16.10 17.52 18.3 19.12520.221.√19422.2-2√3323.2α 24.8√5。
2023年中考数学专题复习——专项训练(五)四边形
2023年中考数学专题复习——专项训练(五)四边形一、选择题(本大题共10小题,每小题3分,共30分)1. 从七边形的一个顶点作对角线,把这个七边形分成三角形的个数是()A. 7B. 6C. 5D. 42. “花影遮墙,峰峦叠窗.”苏州园林空透的窗棂中蕴含着许多的数学元素.图①中的窗棂是冰裂纹窗,图②是这种窗棂中的部分图案.若∠1=∠2=75º,∠3=∠4=65º,则∠5的度数是()A. 80ºB. 75ºC. 65ºD. 60º①②第2题图第3题图第4题图第5题图3. 如图,已知四边形ABCD和四边形AEFG都是矩形.若∠BAG=20°,则∠DGF的度数是()A.70°B.60°C.80°D.45°4. 如图,已知四边形ABCD是平行四边形,下列结论中正确的是()A. 当AB=BC时,四边形ABCD是矩形B. 当AC=BD时,四边形ABCD是菱形C. 当∠ABC=90º时,四边形ABCD是矩形D. 当AC=BD时,四边形ABCD是正方形5. 如图,四边形ABCD为菱形,若CE为边AB的垂直平分线,则∠ADB的度数为()A. 20°B. 25°C. 30°D. 40°6. 用图①所示两种图形可以无缝隙拼接成图②所示的正方形ABCD.已知图①所示图形,∠F=45°,∠H=15°,MN=2,则图②中正方形的对角线AC的长为()A. B. C.1 D.2①②第6题图第8题图第9题图第10题图7. 已知E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,对角线AC,BD相交于点O.根据下列条件,不能证明四边形EFGH是矩形的是()A. AC⊥BDB. AB=BC,OB=ODC. AB=BC,OA=OCD. AB=BC,CD=AD8. 如图,菱形ABCD的边长为2,∠ABC=60º,CE∥BD,则△BDE的面积为()A. 1B. 2C. 3D.9. 如图,在平面直角坐标系中,四边形ABCD是正方形,点A的坐标为(0,2),∠ABO=30º,E为CD的中点,则点E的坐标为()21 B.)2 C. D.2A. )10. 如图,菱形ABCD的边长为12,∠ABC=60°,直线EF⊥AC,垂足为H,分别与AD,AB及CB的延长线交于点E,M,F.若AE∶BF=1∶2,则CH的长为()A. 12B. 10C. 8D. 6二、填空题(本大题共6小题,每小题4分,共24分)11. 六边形的内角和比它的外角和多__________度.12. 如图,在△ABC中,∠ACB=120º,分别以AC,BC为边,向△ABC外作正方形ACDE和正五边形BCFGH,则∠DCF的度数是.第12题图第13题图第14题图13. 如图,矩形OABC的边OA,OC分别在x轴、y轴的正半轴上,点D在OA的延长线上.若A(2,0),D(4,0),以点O为圆心,OD长为半径的弧经过点B,交y轴正半轴于点E,连接DE,BE,则∠BED的度数是.14. 如图,小明同学将边长为6的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移得到△A'B'C'.当两个三角形重叠部分为菱形时,A'D的长为.15. 把一张宽为2 cm的矩形纸片ABCD折叠成如图所示的阴影图案,顶点A,D互相重合,中间空白部分是以E为直角顶点,腰长为4 cm的等腰直角三角形,则纸片的长AD为cm.第15题图第16题图16. 如图13,在□ABCD中,AE⊥BC于点E,N是EC的中点,M是AB的中点.已知S△ABD=6,BC=4,则MN的长为.三、解答题(本大题共4小题,共46分)17. (10分)如图,在□ABCD中,AE⊥BC于点E,延长BC至点F,使CF=BE,连接AF,DE,DF.求证:四边形AEFD是矩形.第17题图第18题图第19题图第20题图18. (10分)如图,在□ABCD中,AB<BC.(1)利用尺规作图,在BC边上确定点E,使点E到边AB,AD的距离相等;(不写作法,保留作图痕迹)(2)若BC=8,CD=5,求CE的长.19. (12分)如图,在四边形ABCD中,AB∥CD,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C 作CE⊥AB,交AB的延长线于点E.(1)求证:四边形ABCD是菱形;(2)若AB=6,BD=8,求CE的长.20.(14分)如图,在正方形ABCD中,E,F分别是边AD,BC的中点,连接DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G.(1)猜想DG与CF的数量关系,并证明你的结论;(2)过点H作MN∥CD,分别交AD,BC于点M,N.若正方形ABCD的边长为10,P是MN上一点,求△PDC周长的最小值.参考答案专项训练(五)答案详解9. A 解析:先分别求出点C,D的坐标,再利用中点坐标求解.10. B 解析:因为四边形ABCD是菱形,所以AD∥BC,AB=BC=12,∠MAH=∠EAH.因为EF⊥AC,所以∠AHM=∠AHE=∠CHE= 90°.因为AH=AH,所以△AHM≌△AHE.所以AM=AE.因为AD∥BC,所以△AME∽△BMF.所以AM AEBM BF==12.所以AM=AE=4,BM=8.所以BF=8.所以CF=20.因为∠ABC=60°,所以△ABC是等边三角形.所以∠ACB=60°.所以CH=CF•cos 60°=10.16.52【解析】连接AC交BD于点O,连接ON,OM,取BE的中点M′,连接MM′,如图所示.易得四边形OMM′N 是矩形,则∠MON=90º.因为S□ABCD=2S△ABD=12,BC=4,所以BC•AE=12.所以AE=3.利用三角形中位线定理,得OM=2,ON=32.由勾股定理,得MN=52.第16题图三、17.证明:因为CF=BE,所以CF+EC=BE+EC,即EF=BC.因为四边形ABCD是平行四边形,所以AD∥BC,AD=BC.所以AD∥EF,AD=EF.所以四边形AEFD是平行四边形. 因为AE⊥BC,所以∠AEF=90°.所以□AEFD是矩形.18. 解:(1)如图所示,点E即为所求.第18题图(2)因为四边形ABCD是平行四边形,所以AB=CD=5,AD∥BC.所以∠DAE=∠BEA.因为AE是∠BAD的平分线,所以∠DAE=∠BAE.所以∠BAE=∠BEA.所以BE=AB=5.所以CE=BC﹣BE=3.19.(1)证明:因为AB∥CD,所以∠OAB=∠DCA.因为AC 平分DAB ∠,所以∠OAB=∠DAC.所以∠DAC=∠DCA.所以CD=AD.因为AB=AD ,所以CD=AB. 因为AB ∥CD ,所以四边形ABCD 是平行四边形.因为AD=AB ,所以□ABCD 是菱形. (2)解:因为四边形ABCD 是菱形,BD=8,所以OA=OC ,BD ⊥AC ,OB=OD=12BD=4.所以∠AOB=90°.所以所以AC=2OA=所以菱形ABCD 的面积为12AC•BD=12×8=.因为CE ⊥AB ,所以菱形ABCD 的面积为AB •CE=,解得. 20. 解:(1)结论:CF=2DG.证明:因为四边形ABCD 是正方形,所以AD=BC=CD=AB ,∠ADC=∠C=90º. 因为E 是AD 的中点,所以DE=AE.所以AD=CD=2DE.因为EG ⊥DF ,所以∠DHG=90º.所以∠CDF+∠DGE=90º,∠DGE+∠DEG=90º. 所以∠CDF=∠DEG.所以△DEG ∽△CDF.所以12DG DE CF CD ==.所以CF=2DG. (2)作点C 关于直线NM 的对称点K ,连接DK 交MN 于点P ,连接PC ,此时△PDC 的周长值最小,最小值为CD+PD+PC=CD+PD+PK=CD+DK.由(1),知CD=AD=10,ED=AE=5,DG=52,所以.因为12DE •DG=12EG •DH ,所以DH=DE DGEG⋅所以EH=2DH=同法可得2DH EHHM DE⋅==,所以DM=CN=NK==1.在Rt △DCK 中,所以△PCD 的周长的最小值为10+第20题图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题训练(四边形)(120分钟120分)一、选择题(本大题共20小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个,均记零分)1.(2019·益阳中考)将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )A.360°B.540°C.720°D.900°【解析】选D.①将矩形沿对角线剪开,得到两个三角形,两个多边形的内角和为:180°+180°=360°;②将矩形从一顶点剪向对边,得到一个三角形和一个四边形,两个多边形的内角和为:180°+360°=540°;③将矩形沿一组对边剪开,得到两个四边形,两个多边形的内角和为:360°+ 360°=720°.2.(2019·眉山中考)如图,EF过▱ABCD对角线的交点O,交AD于点E,交BC于点F,若▱ABCD的周长为18,OE=1.5,则四边形EFCD的周长为( )A.14B.13C.12D.10【解析】选C.因为四边形ABCD是平行四边形,周长为18,所以AB=CD,BC=AD,OA=OC,AD∥BC,所以CD+AD=9,∠OAE=∠OCF,在△AEO和△CFO中,所以△AEO≌△CFO(ASA),所以OE=OF=1.5,AE=CF,则四边形EFCD的周长=ED+CD+CF+EF=(DE+CF)+CD+EF=AD+CD+EF=9+3=12.3.若一个多边形的每一个外角都等于40°,则这个多边形的边数是( )A.7B.8C.9D.10【解析】选C.∵360°÷40°=9,∴这个多边形的边数是9.4.如图,四边形ABCD,AEFG是正方形,点E,G分别在AB,AD上,连接FC,过点E作EH∥FC交BC于点H.若AB=4,AE=1,则BH的长为( )A.1B.2C.3D.3【解析】选C.在正方形ABCD与正方形AEFG中,EF∥AG∥BC,又EH∥FC,∴四边形EFCH是平行四边形,∴HC=EF=1,∴BH=3.5.(2019·菏泽东明模拟)如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( ) A.AB=BE B.BE⊥DCC.∠ADB=90°D.CE⊥DE【解析】选B.因为四边形ABCD为平行四边形,所以AD∥BC,AD=BC,又因为AD=DE,所以DE∥BC,且DE=BC,所以四边形BCED为平行四边形;A.因为AB=BE,DE=AD,所以BD⊥AE,所以▱DBCE为矩形,故本选项不符合题意;B.因为对角线互相垂直的平行四边形为菱形,不一定为矩形,故本选项符合题意;C.因为∠ADB=90°,所以∠EDB=90°,所以▱DBCE为矩形,故本选项不符合题意;D.因为CE⊥DE,所以∠CED=90°,所以▱DBCE为矩形,故本选项不符合题意.6.如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠ACP的度数是A.45°B.22.5°C.67.5°D.75°【解析】选B.∵四边形ABCD是正方形,∴∠DBC=∠BCA=45°,∵BP=BC,∴∠BCP=∠BPC=67.5°,∴∠ACP=∠BCP-∠BCA=67.5°-45°=22.5°.7.如图,四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点.若四边形EFGH 为菱形,则对角线AC,BD应满足的条件是( )A.AC⊥BDB.AC=BDC.AC⊥BD且AC=BDD.不确定【解析】选B.满足的条件应为:AC=BD.理由如下:∵E,F,G,H分别是边AB,BC,CD,DA的中点,∴在△ADC中,HG为△ADC的中位线,所以HG∥AC且HG=AC;同理EF∥AC且EF=AC,同理可得EH=BD,则HG∥EF且HG=EF,∴四边形EFGH为平行四边形,又AC=BD,所以EF=EH,∴四边形EFGH为菱形.8.(2019·胶州市一模)如图,在▱ABCD中,AB=4,BC=5,∠ABC=60°,对角线AC,BD 交于点O,过点O作OE⊥AD交AD于点E,则OE等于( )A. B.2 C.2 D.2.5【解析】选A.作CF⊥AD交AD于点F,如图所示:因为四边形ABCD是平行四边形, 所以∠ADC=∠ABC=60°,CD=AB=4,OA=OC,所以∠DCF=30°,所以DF=CD=2,所以CF=DF=2,因为CF⊥AD,OE⊥AD,所以CF∥OE,因为OA=OC,所以OE是△ACF的中位线,所以OE=CF=.9.(2019·兰州中考)如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2,DE=2,则四边形OCED的面积为( )A.2B.4C.4D.8【解析】选A.∵CE∥BD,DE∥AC,∴四边形OCED为平行四边形,∵ABCD为矩形,∴OC=OD,∴四边形OCED为菱形,∴OD=DE=2,∴BD=2OD=4,∴CD=2,三角形OCD为等边三角形,高为,所以四边形OCED的面积为2.10.(2019·淄博临淄模拟)将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为( )A.1B.2C.2D.4【解析】选C.因为四边形AECF是菱形,AB=3,所以假设BE=x,则AE=3-x,CE=3-x,因为四边形AECF是菱形,所以∠FCO=∠ECO,因为∠ECO=∠ECB,所以∠ECO=∠ECB=∠FCO=30°,2BE=CE,所以CE=2x,所以2x=3-x,解得x=1,所以CE=2,利用勾股定理得出:BC2+BE2=EC2,BC===,又因为AE=AB-BE=3-1=2,则菱形的面积是AE·BC=2.11.如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA等于A.30°B.36°C.45°D.32°【解析】选B.在正五边形ABCDE中,∠C=×(5-2)×180°=108°,∵正五边形ABCDE的边BC=CD,∴∠CBD=∠CDB,∴∠CDB=(180°-108°)=36°,∵AF∥CD,∴∠DFA=∠CDB=36°.12.(2019·岱岳区模拟)如图,将正方形纸片ABCD沿FH折叠,使点D与AB的中点E重合,则△FAE与△EBG的面积之比为( )A.4∶9B.2∶3C.3∶4D.9∶16【解析】选D.因为四边形ABCD是正方形,所以设AB=BC=CD=AD=16,因为AE=EB=8,EF=FD,所以设EF=DF=x.则AF=16-x,在Rt△AEF中,因为AE2+AF2=EF2,所以82+(16-x)2=x2,所以x=10,所以AF=16-10=6,因为将正方形纸片ABCD沿FH折叠,使点D与AB的中点E重合,∠A=∠B=∠D=90°,所以∠FEG=90°,所以∠AEF+∠BEG=∠AEF+∠AFE=90°,所以∠AFE=∠BEG,所以△AFE∽△BEG,所以==.13.如图,D,E,F分别是△ABC的边AB,BC,AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是( )A.AB⊥ACB.AB=ACC.AB=BCD.AC=BC【解析】选B.AB=AC,理由是:∵AB=AC,E为BC的中点,∴AE⊥BC,∵D,F分别为AB和AC的中点,∴DF∥BC,∴AE⊥DF,∵D,E,F分别是△ABC的边AB,BC,AC的中点,∴EF∥AD,DE∥AF,∴四边形ADEF是平行四边形,∵AE⊥DF,∴四边形ADEF是菱形,即只有选项B的条件能推出四边形ADEF是菱形,选项A,C,D的条件都不能推出四边形ADEF是菱形.14.如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )A.10B.12C.18D.24【解析】选B.∵CE∥BD,DE∥AC,∴四边形CODE是平行四边形,∵四边形ABCD是矩形,∴OC=AC,OD=BD,AC=BD=6,∴OC=OD=3,∴四边形CODE是菱形,∴DE=OC=OD=CE=3,∴四边形CODE的周长=4×3=12.15.如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( )A.4B.8C.6D.9【解析】选C.∵AB∥CD,∴∠EAF=∠AED.又AE是∠DAB的平分线,∴∠DAE=∠EAF,∴∠DAE=∠AED,∴AD=ED.∵AB∥CD,EF∥AD∥BC,∴四边形ADEF和四边形BCEF是平行四边形.∴四边形ADEF是菱形.∴AD=AF=9-4=5,AO=AE=4,AE⊥DF.∴DO==3,∴DF=2DO=2×3=6.16.如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD于M,N两点,若AM=2,则正方形的边长为( )A.4B.3C.2+D.+1【解析】选C.过点M作MF⊥AC于点F,如图所示.∵MC平分∠ACB,四边形ABCD为正方形,∴∠CAB=45°,FM=BM.在Rt△AFM中,∠AFM=90°,∠FAM=45°,AM=2,∴FM=AM·sin∠FAM=.∴BM=,∴AB=AM+MB=2+.17.(2019·绍兴模拟)如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )A.1B.2C.3D.4【解析】选C.作F点关于BD的对称点F′,则PF=PF′,连接EF′交BD于点P.由两点之间线段最短可知:当E,P,F′在一条直线上时,EP+FP的值最小,此时EP+FP=EP+F′P=EF′.因为四边形ABCD为菱形,周长为12,所以AB=BC=CD=DA=3,AB ∥CD,因为AF=2,AE=1,所以DF′=DF=AE=1,所以四边形AEF′D是平行四边形,所以EF′=AD=3.所以EP+FP的最小值为3.18.如图,菱形ABCD中,点E,F分别是边AB,AD的中点,连接CE,CF,EF,若四边形ABCD的面积是40cm2,则△CEF的面积为( )A.5 cm2B.10 cm2C.15 cm2D.20 cm2【解析】选C.如图,连接AC,分别交EF,BD于点M,O.∵四边形ABCD为菱形,∴AC⊥BD,AO=CO(设为λ).∵点E,F分别是边AB,AD的中点,∴EF为△ABD的中位线,∴EF∥BD,EF=BD,AO⊥EF.∴△ABD∽△AEF,∴==2,∴OM=OA=0.5λ,CM=1.5λ,∴==,∵S四边形ABCD=40,∴S△EFC=15(cm2).19.如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )A.8B.8C.4D.6【解析】选D.如图,连接OB,由题意易证△OFC≌△OEA,∴OF=OE,OC=OA,∵BE=BF,OE=OF,∴BO⊥EF,∠EBO=∠FBO,∴在Rt△BEO中,∠BEF+∠ABO=90°,由直角三角形斜边上的中线等于斜边的一半可知:OA=OB=OC, ∴∠BAC=∠ABO,又∵∠BEF=2∠BAC,即2∠BAC+∠BAC=90°,解得∠BAC=30°,∴∠EBO=∠FBO=30°,∴∠FBC=30°,∵FC=2,∴BC=2,∴AC=2BC=4,∴AB===6.20.(2019·昆明中考)如图,在正方形ABCD中,AC为对角线,E 为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH,下列结论:①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若=,则3S△EDH=13S△DHC,其中结论正确的有( )A.1个B.2个C.3个D.4个【解析】选D.由题意得HF=HG,∠HFD=∠HGE,DF=AE=EG,∴△DHF≌△EHG,∴EG=DF,∴∠HEG=∠HDF,∴∠HEA+∠ADH=180°,若AE∶AB=2∶3可得④正确;∴正确的结论有4个.二、填空题(本大题共4小题,满分12分,只要求填写最后结果,每小题填对得3分)21.(2019·连云港中考)如图,在平行四边形ABCD中,AE⊥BC于点E,AF⊥CD于点F,若∠EAF=56°,则∠B=________°.【解析】因为AE⊥BC,AF⊥CD,所以∠AEC=∠AFC=90°,在四边形AECF中,∠C=360°-∠EAF-∠AEC-∠AFC=360°-56°-90°-90°= 124°,在▱ABCD中,∠B=180°-∠C=180°-124°=56°.答案:5622.(2019·临沂兰山模拟)如图,▱ABCD的周长为36,对角线AC,BD相交于点O.点E是CD的中点,BD=12,则△DOE的周长为________.【解析】因为▱ABCD的周长为36,所以2(BC+CD)=36,则BC+CD=18.因为四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,所以OD=OB=BD=6.又因为点E是CD的中点,所以OE是△BCD的中位线,DE=CD,所以OE=BC,所以△DOE的周长=OD+OE+DE=BD+(BC+CD)=6+9=15,即△DOE的周长为15.答案:1523.(2019·东平县一模)如图,在菱形ABCD中,点M,N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AN的长度为________.【解题指南】由△MAE∽△NAF,推出=,列方程即可解决问题.【解析】设AN=x,因为四边形ABCD是菱形,所以∠MAE=∠NAF,因为∠AEM=∠AFN=90°,所以△MAE∽△NAF,所以=,所以=,所以x=4,所以AN=4.答案:424.如图,在正方形ABCD中,AB=,点P为边AB上一动点(不与A,B重合),过A,P在正方形内部作正方形APEF,交边AD于F点,连接DE,EC,当△CDE为等腰三角形时,AP=________.【解析】连接AE,∵四边形ABCD,APEF是正方形,∴A,E,C共线,①当CD=CE=时,AE=AC-EC=2-,∴AP=AE=-1;②当ED=EC时,∠DEC=90°,∠EDC=∠ECD=45°,EC=CD=1,∴AE=AC-EC=1,∴AP=AE=;③当DE=DC时,不符合题意,∴当△CDE为等腰三角形时,AP=-1或.答案:-1或三、解答题(本大题共5个小题,满分48分.解答应写出必要的文字说明、证明过程或推演步骤)25.(8分)(2019·陕西中考)如图,在▱ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF = DE,连接AF,CE.求证:AF∥CE.【证明】∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∴∠1=∠2.又∵BF=DE,∴BF+BD=DE+BD.∴DF=BE.∴△ADF≌△CBE.∴∠AFD=∠CEB.∴AF∥CE.26.(8分)(2019·长春中考)如图,在▱ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.(1)求证:BD∥EF.(2)若=,BE=4,求EC的长.【解析】(1)∵四边形ABCD是平行四边形,∴AD∥BC.∵DF=BE,∴四边形BEFD是平行四边形,∴BD∥EF.(2)∵四边形BEFD是平行四边形,∴DF=BE=4,∵DF∥EC,∴△DFG∽△CEG,∴=,∴CE==4×=6.27.(10分)(2019·济南章丘模拟)如图,四边形ABCD为菱形,点E为对角线AC上的一个动点,连接DE并延长交AB所在直线于点F,连接BE.(1)如图①:求证∠AFD=∠EBC.(2)如图②,若DE=EC且BE⊥AF,求∠DAB的度数.(3)若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数.(只写出条件与对应的结果)【解析】(1)因为四边形ABCD为菱形,所以DC=CB,在△DCE和△BCE中,所以△DCE≌△BCE(SAS),所以∠EDC=∠EBC,因为DC∥AB,所以∠EDC=∠AFD,所以∠AFD=∠EBC.(2)因为DE=EC,所以∠EDC=∠ECD,设∠EDC=∠ECD=∠CBE=x°,则∠CBF=2x°,由BE⊥AF得2x+x=90,解得x=30,所以∠DAB=∠CBF=60°.(3)分两种情况:①如图1,当F在AB延长线上时,因为∠EBF为钝角,所以只能是BE=BF,设∠BEF=∠BFE=x°,可通过三角形内角和为180°得90+x+x+x=180,解得x=30,所以∠EFB=30°;②如图2,当F在线段AB上时,因为∠EFB为钝角,所以只能是FE=FB,设∠BEF=∠EBF=x°,则有∠AFD=2x°,可证得∠AFD=∠FDC=∠CBE,得x+2x=90,解得x=30,所以∠EFB=120°,综上∠EFB=30°或120°.28.(10分)(2019·兰州中考)阅读下面材料:在数学课上,老师请同学们思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?小敏在思考问题时,有如下思路:连接AC.结合小敏的思路作答:(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由;参考小敏思考问题的方法,解决问题.(2)如图2,在(1)的条件下,若连接AC,BD.①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.【解析】(1)四边形EFGH还是平行四边形,理由如下:连接AC.∵E,F分别是AB,BC 的中点,∴EF∥AC,EF=AC,∵G,H分别是CD,AD的中点,∴GH∥AC,GH=AC,∴EF∥GH,EF=GH,∴四边形EFGH是平行四边形.(2)①当AC=BD时,四边形EFGH是菱形,理由如下:由(1)可知四边形EFGH是平行四边形,当AC=BD时,FG=BD,EF=AC,∴FG=EF,∴四边形EFGH是菱形.②当AC⊥BD时,四边形EFGH是矩形.29.(12分)如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.①求证:△AGE≌△AFE;②若BE=2,DF=3,求AH的长.(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.【解析】(1)①由旋转的性质可知:AF=AG,∠DAF=∠BAG.∵四边形ABCD为正方形,∴∠BAD=90°.又∵∠EAF=45°,∴∠BAE+∠DAF=45°.∴∠BAG+∠BAE=45°.∴∠GAE=∠FAE.在△GAE和△FAE中,∴△GAE≌△FAE.②∵△GAE≌△FAE,AB⊥GE,AH⊥EF,∴AB=AH,GE=EF=5.设正方形的边长为x,则EC=x-2,FC=x-3.在Rt△EFC中,由勾股定理得:EC2+FC2=EF2,即(x-2)2+(x-3)2=25.解得:x=6.∴AB=6.∴AH=6.(2)MN2=ND2+BM2.理由如下:如图所示:将△ABM逆时针旋转90°得△ADM′,连接NM′.∵四边形ABCD为正方形,∴∠ABD=∠ADB=45°.由旋转的性质可知:∠ABM=∠ADM′=45°,BM=DM′. ∴∠NDM′=90°.∴NM′2=ND2+DM′2.∵∠EAM′=90°,∠EAF=45°,∴∠EAF=∠FAM′=45°.在△AMN和△ANM′中,∴△AMN≌△ANM′.∴MN=NM′.∴MN2=ND2+BM2.。
