等比数列2
(人教版)数学必修五:2.4《等比数列(2)》
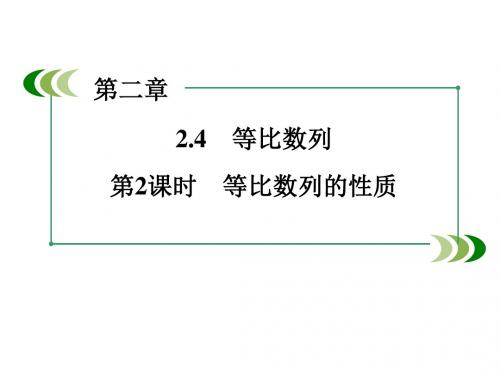
(6)若{an}是等比数列,每隔 k(k∈N*)项取出一项,按原来 的顺序排列,所得数列仍是等比数列,且公比为 qk 1.
+
(7)在等比数列{an}中,连续取相邻 k(k∈N*)项的和(或积) 构成公比为 qk(或 qk2)的等比数列. (8){an}是等差数列,c 是正数,则数列{can}是等比数列. (9){an}是等比数列,且 an>0,则{logaan}(a>0,a≠1)是等 差数列.
[ 错解] 设这个等比数列为{an},其中 a1=1,a5=4,插入 的三项分别为 a2,a3,a4. 由题意,得 a1,a3,a5 也成等比数列,则 a2 3=a1a5=1×4 =4,故 a3=± 2,∴a2a3a4=a3 8. 3=±
[ 错因分析]
[ 正解]
该解法没有正确判断 a3 的符号,在求等比数
有关等比数列的开放探究题
已知数列 {an} 是各项为正数的等比数列,数列 1 {bn}定义为 bn=n[lga1+lga2+…+lgan-1+lg(kan)] ,是否存在实 数 k,使得数列{bn}为等差数列?并证明你的结论.
[ 分析]
先利用数列{an}是等比数列,求出数列{bn}的通项
公式,再求 bn+1-bn,看使它成为常数的条件是什么?
(2)∵a1a9=a3a7=64, ∴a3,a7 是方程 x2-20x+64=0 的两根.
a3=4 解得 a7=16 a3=16 或 a7=4
.
①若 a3=4,a7=16,则由 a7=a3q4 得,q4=4, ∴a11=a7q4=16×4=64. 1 ②若 a7=4,a3=16,则由 a7=a3q 得,q =4,
[ 方法总结]
除了用假设法,也可以从寻求使它成立的条
高三数学等比数列2

3.如果 a n bn 是项数相同的等比数列,那 么 a n bn 也是等比数列.
结论:如果 a b 是项数相同的等 比数列,那么 a n bn 也是等比数列.
n n
bn 的公比为 证明:设数列a n 的公比为p, q,那么数列 a n bn 的第n项与第n+1项分 n 1 n n 别为 a1p n 1 b1q n 1 与 a1p b1q ,即 a1b1 (pq) n 与 a1b1 (pq) .
因为 它是一个与n无关的常数,所以是一个以pq 为公比的等比数列.
a n 1 b n 1 a1b1 (pq) n pq, n 1 a n bn a1b1 (pq)
特别地,如果是a 等比数列ቤተ መጻሕፍቲ ባይዱc是不等 于0的常数,那么数列 c a 也是等比数列.
n
n
探究
对于例4中的等比数列 a n 与 bn ,数
1.定义法:
an1 q(是与n无关的数或式子 , 且q 0 ) an
2.中项法:
an1 an1 an ( 0)
2
三个数a,b,c成等比数列
2 ac b
五、等比数列的性质
1、若m, n, p, q N , 且m n p q,
则a m a n a p a q
an , 若a1 a2 a3 7, 4.已知等比数列
a1 a2 a3 8, 求an.
a1 1, q 2或a1 4, q
1 2
课后作业
P60 习题 2.4 A 组 第 3、 7、 8题
选做: P59 探究 选做: P75 第1,2,4题
等比数列(2)

【课题】 6.3 等比数列
【教学目标】
知识目标:
理解等比数列前n 项和公式. 能力目标:
(1)应用等比数列的前n 项公式,解决数列的相关计算,培养学生的计算技能; (2)综合应用数列知识,解决生活中借、贷款等实际问题,培养学生处理数据技能和分析解决问题的能力.
情感目标:
(1)经历数列的前n 项和公式的探索,增强学生的创新思维.
(2)赞赏国际象棋的发明人数学史上流传的故事,形成对数学的兴趣,感受数学文化. (3)经历借、贷款问题的计算过程,体会数学的应用价值,形成对数学的兴趣。
【教学重点】
等比数列的前n 项和的公式.
【教学难点】
等比数列前n 项和公式的推导.
【教学设计】
本节的主要内容是等比数列的前n 项和公式,等比数列应用举例.重点是等比数列的前
n 项和公式;难点是前n 项和公式的推导、求等比数列的项数n 的问题及知识的简单实际
应用.
等比数列前n 项和公式的推导方法叫错位相减法,这种方法很重要,应该让学生理解并学会应用.等比数列的通项公式与前n 项和公式中共涉及五个量:n n S a n q a 、、、、1,只要知道其中的三个量,就可以求出另外的两个量.
教材中例6是已知n n S a a 、、1求n q 、的例子.将等号两边化成同底数幂的形式,利用指数相等来求解n 的方法是研究等比数列问题的常用方法.
【教学备品】
教学课件.
【课时安排】
3课时.(135分钟)
【教学过程】
【教师教学后记】
−。
等差数列、等比数列2
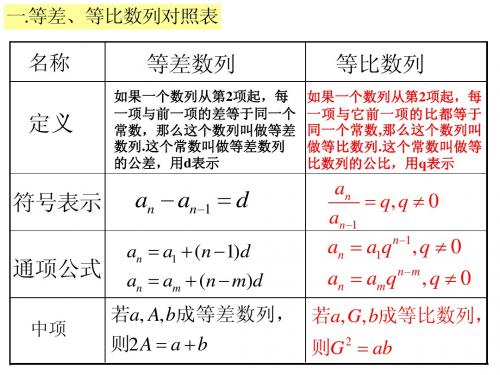
4.等距离取出的项构成的新数列仍是等差数列, 即ak , ak m , ak 2 m , 成等差数列 5.an , bn 是等差数列,则数列an b、 an 、
an b、 Aan Bbn 仍是等差数列
6.若S n是等差数列的前n项和,则每隔m项和仍构成 等差数列,即S m , S 2 m S m , S3m S 2 m ,...成等差数列.
(7).三个数成等比数列,它们的和为14,它们的积为64, 求这三个数.
变式:有四个实数,前三个数依次成等比,它们的积是
8,后三个数依次成等差,它们的积为 80,求这四个数.
点评: a 1.三个数成等比数列,常设为 , a, aq a 0 q 2.四个数成等比数列,常设为a, aq, aq , aq a 0
7.若Tn是等比数列的前n项积,则每隔n项积仍构成等比数列,
8.若Sn是等比数列的前n项和,则每隔m项和仍构成 等比数列,即Sm , S2 m Sm , S3m S2 m ,...成等比数列.
第二个数与第三个数的积为40,求这四个数.
结论:一般地, 7.三个数成等差,可设为a d , a, a d . 8.四个数成等差,可设为a 3d , a d , a d .a 3d 公差为2d
练习等差数列 . an 中, (2)若a1 a2 a3 a4 a5 30, a6 a7 a8 a9 a10 80
()若 1 a1 a4 a8 a12 a15 2, 求a3 a13 ; 求a11 a12 a13 a14 a15的值。
3 若a3 a4 a5 a6 a7 450,则a2 a8 =______ 4 若a3 a5 a7 a9 a11 100,则3a9 a13 =______ 5 若a2 a3 a4 a5 =34,a2 a5 =52,则d ______ 6 若S3 3,S6 9,则S9 _____
等比数列(2)

5、等比数列常用性质 (1) 若 m n p q,则 am an a p aq .
(2) ak ,akm ,ak2m , 组成的数列仍然是等比数列, 且公比为 qm .
(3) 若 {an} 与{bn} 均为等比数列,
说 明:
本题揭示了等差数列与等比数列之间的一种代数变换 关系.不失一般性,设c>0,c≠1, 则:
若数列{an}是等差数列,那么数列{can }是等比数列;
反之,若{an}是等比数列且an >0,则数列{logc an }是等差数列.
例2:已知{an }和{bn }是项数相同的等 比数列,求证{an • bn}是等比数列。
an 0 a3 a5 5 .
(2) 在等比数列{an }中,a3a4a5 3 , a6a7a8 24 , 求 a9a10a11 的值.
解: {an} 是等比数列 ,
a3a4a5 a43 3 , a6a7a8 a73 24 , a9a10a11 a130
又 a4 , a7 , a10 成等比数列,a43 , a73 , a130成等比数列,
则数列{man
bn
}
与
{
man bn
}
(m
0
常数)
仍为等比数列.
(4) 单调性 :由 an a1qn1 知
an1 q an
若 a1 0 q 1
或
a1 0 0 q
1
,则
{an }
是递增数列 ;
若 0a1q0 1或 qa110 ,则 {an } 是递减数列 ;
若 q 1 ,则{an } 是常数列; 若 q 0 ,则{an } 是摆动数列.
等比数列(2)

等比数列的性质 等比数列的性质
1、an=amqn-m
2、 m, n, p, q ∈ N+ , 且m + n = p + q, 若 3、 m, n, p, q ∈ N+ , 且m + n = 2p, 若
则am an = ap aq
2
则am an = ap 4.如果 {a } {b } 是项数相同的等比数列,那 如果 是项数相同的等比数列 那 也是等比数列. 么 {a b } 也是等比数列
1 5 1+ 5 <q< 2 2
1.设{an } 是递增等差数列,前三项 的和为12,前三项的积为48,则 它的首项是____ 2 2.设 {an }是递增等比数列,前三项 的和为14,前三项的积为64,则 它的首项是____ 2
练习
3、己知等差数列{an}的首项 1>0, 、己知等差数列 的首项a 的首项 项和为S 前n项和为 n ,若3a5=8a12 ,问数列 项和为 若 问数列 的前几项和最大? 的前几项和最大
(a4 + a8 ) = a4 + a8 + 2a4 a8 = 49,
2 2 2
Q an > 0, 则a4 + a8 = 7
练习:
1.在等比数列 n}中,已知 4a15=-2, 在等比数列{a 中 已知 已知a 在等比数列 那么a 那么 3a6a12a17=_____. 4 2.在等比数列 n}中,已知 4a5a6=8, 在等比数列{a 中 已知 已知a 在等比数列 32 则a1a3a5a7a9=_____.
4.在等比数列 n}中,求通项: 在等比数列{a 中 求通项 求通项: 在等比数列 (1)a1=-2,a3=-8 (2) a1=5,且2an+1=-3an 且 5.在等比数列 n}中,若a6=6,a9=9,则 在等比数列{a 中 若 在等比数列 则 4 a3=_____. 6.在等比数列 n}中,若a1=48,n=7,an=3/4, 在等比数列{a 中 若 在等比数列 1/2或- 1/2 或 则q=_________. 7. 已知 n}为等比数列 公比 已知{a 为等比数列 公比q≠1,若ap=m, 为等比数列,公比 若 并且l,p∈ 则 等于( ). D 并且 ∈N*,则al等于 (A)mql-p-1 (B)mql-p+1 (C)mql-1 (D)mql-p
人教A版高中数学高二必修5课件2.4等比数列(二)

2.4 等比数列(二)
6
(6)等比数列的项的对称性:在有穷等比数列中,与首末两项
“等距离”的两项之积等于首末两项的积,即a1·an=
2.4 等比数列(二)
29
规律方法 (1)在等差数列与等比数列的综合问题中, 特别要注意它们的区别,避免用错公式.(2)方程思想的 应用往往是破题的关键.
2.4 等比数列(二)
30
跟踪演练4 已知{an}是首项为19,公差为-2的等差数列, Sn为{an}的前n项和. (1)求通项公式an及Sn; 解 因为{an}是首项为19,公差为-2的等差数列,所以an =19-2(n-1)=-2n+21,
的m的个数;若不存在,请说明理由.
解 若存在m,使b1,b4,bt成等差数列, 则2b4=b1+bt,
∴ 7 ×2= 1 + 2t-1 ,
7+m
1+m 2t-1+m
2.4 等比数列(二)
28
7m+1 7m-5+36
∴t=
=
=7+
36
,
m-5
m-5
m-5
由于m、t∈N*且t≥5. 令m-5=36,18,9,6,4,3,2,1, 即m=41,23,14,11,9,8,7,6时,t均为大于5的整数. ∴存在符合题意的m值,且共有8个.
2.4 等比数列(二)
26
(1)由 bn=an+an m(m∈N*)知 b1=1+1 m,b2=3+3 m,b8=151+5 m,
∵b1,b2,b8成等比数列,
人教A版高中数学必修五2.4《等比数列(二)》
答案:1510
要点阐释
1.等比数列的性质 (1)在等比数列中,我们随意取出连续的三项以上的数, 把它们重新依次看成一个数列,则仍是等比数列. (2)在等比数列中,我们任取“间隔相同”的三项以上的数, 把它们重新依次看成一个数列,则仍是等比数列,如:等比 数列a1,a2,a3,… ,an,….那么a2,a5,a8,a11,a14,…; a3,a5,a7,a9,a11…各自仍构成等比数列.
已知等比数列an
满足
an>0,n=1,2,…,
且 a5·a2n-5=22n(n≥3),则当 n≥1 时,log2a1+log2a3+…
+log2a2n-1=
()
A.(n-1)2
B.n2
C.(n+1)2
D.n(2n-1)
错解:易得 an=2n,且 log2a1+log2a3+…+log2a2n-1 =log2(a1a3…a2n-1)=log221+3+…+(2n-1) =1+3+ …+(2n-1)=1+22n-1(2n-1) =n(2n-1).从而错选 D 错因分析:对等差数列1,3,…,2n-1的项数没 数清.
即aa1122-+22aa11aa55++aa5522==330422,, 两式相减得 a1a5=64,即 a32=64, 又 a5>a1,故 a3=8. 答案:A
2.在等
比数列an
中,
a8
是
a4
与________的等比中项
A.a9
B.a10
C.a11
() D.a12
1.3.1等比数列(二)课件ppt(

课前探究学习
课堂讲练互动
自学导引
1.等比中项 如果在a与b中间插入一个数G,_使__a_、__G_、__b_成__等__比__数__列__, 那么G叫作a与b的等比中项. 试一试:若G2=ab,则a,G,b一定成等比数列吗? 提示 不一定.因为若G=0,且a,b中至少有一个为0, 则G2=ab,而根据等比数列的定义,a,G,b不成等比数 列;当a,G,b全不为零时,若G2=ab,则a,G,b成等 比数列.
为一
常数,判定一个数列不是等比数列只须找到一组 an ≠ am an-1 am-1
(m≠n)即可.
课前探究学习
课堂讲练互动
[规范解答] (1)∵等比数列{an}中,a1=1,公比为q, ∴an=a1qn-1=qn-1(q≠0),(2分) 若q=1,则an=1,bn=an+1-an=0, ∴{bn}是各项均为0的常数列,不是等比数列.(4分) 若 q≠1,由于bbn+n 1=aan+n+2-1-aan+n1=qqnn+-1-qnq-n1=qqn-n1qq--11 =q,
∴{bn}是首项为b1=a2-a1=q-1,公比为q的等比数列.(8分) (2)由(1)可知,当q=1时,bn=0; 当q≠1时,bn=b1qn-1=(q-1)·qn-1, ∴bn=(q-1)qn-1(n∈N+).(12分)
课前探究学习
课堂讲练互动
【题后反思】 1.本题属于“运算数列”是否为等比数列的判 定问题,根据等比数列的定义,对于公比的取值情况的讨 论十分关键,这不仅是解题思路自然发展的体现,而且是 逻辑思维严谨性的具体要求. 2.若数列{an}为等比数列,则下列结论仍能成立.
∵an>0,∴an+1+an>0,∴aan+n 1=n+n 1,即 an+1=n+n 1an,
等比数列2

am an ar as
等差数列求和方法回顾:(倒序相加)
Sn a1 a2 a3 an1 an
+ Sn an an1 an2 a2 a1
2Sn (a1 an ) (a2 an1 ) (an a1 )
n个相 同的数
= 18446744073709551615(粒)
假定千粒麦子的质量为10g,那么麦 粒的总质量超过了7000亿吨。 人们估计,全世界两千年也难以生产这么多麦子!
1 2 2 2
S64 1 2 4 8 2 2
62
62
63
64
①
2S64 2 4 8 2 2 2 ②
则数列{logaan}(a>0且a≠1)为等差数列.
14
等比数列(G P)
1.定义
2.公比(差)
3.等比(差) 中项 4.通项公式
an1 q an
等差数列(A P)
an1 an d
d可以是0
等差中项
q不可以是0,
等比中项 G ab
2A a b
an am q
1
等差数列
等比数列
如果一个数列从第2项起, 如果一个数列从第2项起, 定义 每一项与它前一项的差等于 每一项与它的前一项的比等于 同一个常数,那么这个数列 同一个常数,那么这个数列就 叫做等比数列。 就叫做等差数列。 an+1 数学 an+1-an= d(常数) 表达 an = q(常数) 符号 首项a1, 公差d 首项a1, 公比q(q≠0) 表示 d>0 {an }递增 q>0 {an }中各项同号 d与{an}
等比数列2

等比数列(2)教学目标(1)进一步熟练掌握等比数列的定义及通项公式;(2)利用等比数列通项公式寻找出等比数列的一些性质;教学重点,难点(1)等比数列定义及通项公式的应用;(2)灵活应用等比数列定义及通项公式解决一些相关问题.教学过程一.问题情境1.情境:在等比数列{}n a 中,(1)2519a a a =是否成立?2537a a a =是否成立?(2)211n n n a a a -+=⋅(2n ≥)是否成立?222(2)n n n a a a n -+=>是否成立?2.问题:由情境你能得到等比数列更一般的结论吗?三.建构数学1.若{}n a 为等比数列,m n p q +=+(,,,)m n q p N +∈,则q p n m a a a a ⋅=⋅.2.若{}n a 为等比数列,则m n m na q a -=. 四.数学运用例1. 已知{}n a 为等比数列,且578,2a a ==,该数列的各项都为正数,求{}n a 的通项公式。
例2.已知三个数成等比数列,它们的积为27,它们的平方和为91,求这三个数。
说明:已知三数成等比数列,一般情况下设该三数为,,a a aq q.例3、已知111,21,n n n a a a a +==+求例4设关于x 的一元二次方程2110n n a x a x +-+=有两根,αβ,且满足6263ααββ-+=(1)、试用n a 表示1n a +;(2)、求证:23n a ⎧⎫-⎨⎬⎩⎭是等比数列;(3)、当176a =时,求数列{}n a 的通项公式。
备选练习:1.已知{}n a 是等比数列且0n a >,569a a =,则3132310log log log a a a +++= .2.已知{}n a 是等比数列,47512a a ⋅=-,38124a a +=,且公比为整数,则10a = .3.已知在等比数列中,34a =-,654a =,则9a = .4. 以一个边长为1的正三角形,将每边三等分,以中间一段为边向形外作正三角形,并擦去中间一段,得图形(2),如此继续下去,得图形(3)……求第n 个图形的边长和周长.。
高二数学等比数列2

; 华语作文
;
天下共击之。今王吕氏,非约也”太后不说。问左丞相平及绛侯周勃等,皆曰“高帝定天下,王子弟。今太后称制,欲王昆弟诸吕,无所不可”太后喜。罢朝,陵让平、勃曰“始与高帝唼血而盟,诸君不在邪。今高帝崩,太后女主,欲王吕氏,诸君纵欲阿意背约,何面目见高帝於地下乎” 平曰“於面折廷争,臣不如君。全社稷,定刘氏后,君亦不如臣”陵无以应之。於是吕太后欲废陵,乃阳迁陵为帝太傅,实夺之相权。陵怒,谢病免,杜门竟不朝请,十年而薨。陵之免,吕太后徙平为右丞相,以辟阳侯审食其为左丞相。食其亦沛人也。汉王之败彭城西,楚取太上皇、吕 后为质,食其以舍人侍吕后。其后从破项籍为侯,幸於吕太后。及为相,不治,监宫中,如郎中令,公卿百官皆因决事。吕须常以平前为高帝谋执樊哙,数谗平曰“为丞相不治事,日饮醇酒,戏妇人”平闻,日益甚。吕太后闻之,私喜。面质吕须於平前,曰“鄙语曰儿妇人口不可用,顾 君与我何如耳,无畏吕须之谮”吕太后多立诸吕为王,平伪听之。及吕太后崩,平与太尉勃合谋,卒诛诸吕,立文帝,平本谋也。审食其免相,文帝立,举以为相。太尉勃亲以兵诛吕氏,功多。平欲让勃位,乃谢病。文帝初立,怪平病,问之。平曰“高帝时,勃功不如臣。及诛诸吕,臣 功亦不如勃。愿以相让勃”於是乃以太尉勃为右丞相,位第一。平徙为左丞相,位第二。赐平金千斤,益封三千户。居顷之,上益明习国家事,朝而问右丞相勃曰“天下一岁决狱几何”勃谢不知。问“天下钱谷一岁出入几何”勃又谢不知。汗出洽背,愧不能对。上亦问左丞相平。平曰 “各有主者”上曰“主者为谁乎”平曰“陛下即问决狱,责廷尉。问钱谷,责治粟内史”上曰“苟各有主者,而君所主何事也”平谢曰“主臣。陛下不知其弩下,使待罪宰相。宰相者,上佐天子理阴阳,顺四时,下遂万物之宜,外填抚四夷诸侯,内亲附百姓,使卿大夫各得任其职也”上 称善。勃大惭,出而让平曰“君独不素教我乎”平笑曰“君居其
等比数列2

等比数列的性质
结论4:等比数列an 中, (1)m n p q, 则am an a p aq ; (2)m n s p q t , 则am an as a p aq at .
等比数列的性质
在等比数列{an}中,判断下列各命题是 否正确: (1)a1an= a2an-1=a3an-2=…;
an d
等比数列的性质
(2)已知等差数列{an }的公差为d, 则 当d 0时, 数列{an }为递增数列; 当d 0时, 数列{an }为递减数列; 当d 0时, 数列{an }为常数列; 探究7.等比数列的增减性由哪些因素决定?
等比数列的性质
观察下面几个等比数列中项的变化趋势: ①1,2,4,8,16,… 1 1 1 1 ②-1,-2,-4,-8,-16,… 1 1 ③9,3,1,3,9,… ④-1,-2,-4,-8,-16,… 1 1 1 1 ⑤1,-2,4,-8,16,…
等比数列通项公式
结论1.已知等比数列an 的 首项为a1 , 公比为q, 则an a1q .
n 1
等比数列通项公式
结论2.等比数列an 的 通项公式为an a1 q ,
n
an nm 则 q ; am
等比数列通项公式
结论3.若数列{an}的通项公式为
an
n =AxB
(A,B是非零常数) ,
a > 0 1 0<q<1 a < 0 1 或 q > 1
a > 0 1 q> 1 a < 0 1 或 0<q<1
综合应用
1.一个公比为正数的等比数列{an}, 若 a1+a2=20,a3+a4=80,求 a5+a6 的值. 2.在等比数列{an}中,a9+a10=a(a≠0), a19+a20=b,求 a99+a100 的值.
高三数学等比数列2

推导前 n 和的方 法
倒写相加法
错位相减法
试由等差数列的知识建立等比数列的知识结构 等差数列 等比数列 重 ① 等和性: am an a p aq ① 等积性 : am an a p aq 要 * * ( m , n , p , q N , m n p q) (m, n, p, q N , m n p q) 性 ② an am (n m)d ② an am qnm 质 ③ 从等差数列中抽取等 ③从等比数列中抽取等距离的项组 距离的项组成的数列是 成的数列是一个等比数列。 一个等差数列。 如: a1, a4 , a7 , a10 , 如: a1, a4 , a7 , a10 , (下标成等差数列) (下标成等差数列) ④ Sk , S2k Sk , S3k S2k ④ Sk , S2k Sk , S3k S2k 成 成等比数列. 等差数列.
Sn 故 { } 是以首项为 1,以 2 为公比的等比数列. n
例 2. 数列 {an } 的前 n 项和记为 Sn ,已知 n2 a1 1, a n1 S n (n 1,2,3). n Sn ⑴证明:数列 { } 是等比数列; n ⑵求数列 an 的通项公式.
S n n 1 S n n 1 n1 2 解:⑵由⑴可知 ∴ 2 ,∴ Sn n 2 n n
n1 n2 n2 n ≥ 2 ∴当 时, an Sn Sn1 n 2 (n 1) 2 (n 1) 2
又∵当 n 1 时, a1 1 ∴ an (n 1) 2
n 2
.
速度训练: 1.已知等比数列的公比为 2,前 4 项和 1, 则其前 8 项和为 17 . 2.已知实数 1,a1 , a2 ,4 成等差数列,实数 1,b1 , b2 , b3 ,4
4.3.1 等比数列(2)(人教A版高中数学选择性必修第二册)(解析版)

课时同步练4.3.1 等比数列 (2)一、单选题1.已知数列{}n a 中,13n n a a +=,12a =,则4a 等于 ( )A .18B .54C .36D .72【答案】B【详细解析】数列{}n a 中,13n n a a +=,12a =,∴数列{}n a 是等比数列,公比3q =.则342354a =⨯=.故选B .2.22 ( )A .1B .1-C .1±D .2【答案】C【详细解析】设等比中项为a ,则,2(21,1a a ===±, 故选C .3.已知数列{}n a 是等比数列,函数2=53y x x -+的两个零点是15a a 、,则3a = ( )A .1B .1-C .D 【答案】D【详细解析】由韦达定理可知155a a +=,153a a ⋅=,则10a >,50a >,从而30a >,且231533a a a a =⋅=∴=故选D4.已知数列{}n a 为等比数列,且2234764a a a a =-=-,则46tan 3a a π⎛⎫=⎪⎝⎭( )A .BC .D .【答案】A【详细解析】由题意得3234364a a a a ==-,所以34a =-.又2764a =,所以78a =-或78a = (由于7a 与3a 同号,故舍去).所以463732a a a a ==,因此4632tan tan tan 11tan 3333a a πππππ⎛⎫⎛⎫⎛⎫==-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选A5.数列{}n a 中,121n n a a +=+,11a =,则6a = ( )A .32B .62C .63D .64【答案】C【详细解析】数列{}n a 中,121n n a a +=+,故()1121n n a a ++=+, 因为11a =,故1120a +=≠,故10n a +≠, 所以1121n n a a ++=+,所以{}1n a +为等比数列,公比为2,首项为2. 所以12nn a +=即21n n a =-,故663a =,故选C.6.在等比数列{}n a 中,121a a =,369a a =,则24a a = ( )A .3B .3±CD.【答案】A【详细解析】设等比数列{}n a 的公比为q ,因为1210a a =>,所以0q >, 又369a a =,所以423a a ===.故选A7.对于按复利计算机利息的储蓄,若本金为a 元,每期利率为r ,存期为n ,则本金和利息总和y (元)与存期n 的函数表达式为 ( )A .()1ny a r =+ B .()11n y a r -=+C .()11n y a r +=+D .()1y a nr =+【答案】A【详细解析】1期后的本息和为()1a ar a r +=+;2期后的本息和为()()()2111a r a r r a r +++=+;3期后的本息和为()()()223111a r a r r a r +++=+;…n 期后的本息和为()1ny a r =+. 故选A8.已知等比数列{n a }中,1a +2a =12,1a ﹣3a =34,则4a = A .﹣18B .18C .﹣4D .4【答案】A【详细解析】∵等比数列{a n }中,a 1+a 2=12,a 1﹣a 3=34, ∴112111234a a q a a q ⎧+=⎪⎪⎨⎪-=⎪⎩, 解得111,2a q ==-, ∴a 4=31a q =1× (﹣12)3=﹣18.故选A .9.等差数列{}n a 和等比数列{}n b 的首项均为1,公差与公比均为3,则1b a +2b a +3b a = ( )A .64B .32C .33D .38【答案】C【详细解析】依题意1231,3,9b b b ===,故139172533a a a ++=++=, 故选C.10.已知数列{}n a 是等比数列,数列{}n b 是等差数列,若1611a a a ⋅⋅=-16117b b b π++=,则3948tan1b b a a +-⋅的值是 ( )A .1BC.D.【答案】D【详细解析】在等差数列{}n b 中,由16117b b b π++=,得637b π=,673b π=,3961423b b b π∴+==, 在等比数列{}n a 中,由1611a a a =-,得36a =-6a =(224861112a a a ∴-=-=-=-,则39481473tan tan tan tan 1233b b a a πππ+⎛⎫⎛⎫==-=-=⎪ ⎪-⋅-⎝⎭⎝⎭故选D.11.等比数列{}n a 的公比为,||1q q ≠,则2237a a +与2246a a +的大小关系是 ( )A .22223746a a a a +>+ B .22223746a a a a +<+ C .22223746a a a a +=+D .不能确定【答案】A【详细解析】由等比数列的通项公式可得,()22382371a a qa =++,()32426262a aq q a =++,()()()()()()()2826262233333222237461111111a q q q a q q a q q q q a a a a --=+--=--=-+-++()()()()()()222222224233111111a q q q q q q a q q q =-+-+++=-++,1,0n q a ≠≠,∴()()222423110a q q q -++>,即22223746a a a a +>+.故选A .12.已知数列{},{}n n a b 满足11111121.1,0.2,,,233n n n n n n b a a b a b a b n ++++====+∈N ,令n n n c a b =-,则满足4110n c ≤的n 最小值为 ( ) A .9B .10C .11D .12【答案】B【详细解析】()11111111121122223323n n n n n n n n n n n n b a a b b b a a b a a b ++++++⎛⎫-=-=-+=-++=- ⎪⎝⎭,1110.9c a b =-=,故{}n c 是首项为0.9,公比为13的等比数列,故110.93n n c -=⨯,则14110.9310n -⨯≤,即33310n -≥,当9n =时,63372910=<;当10n =时,733218710=>,显然当10n ≥时,33310n -≥成立,故n 的最小值为10. 故选B .二、填空题13.设{}n a 是等比数列,且245a a a =,427a =,则{}n a 的通项公式为_______.【答案】13-=n n a ,*n N ∈【详细解析】设等比数列{}n a 的公比为q , 因为245a a a =,427a =,所以223542427a a a a q q q ====,解得3q =,所以41327127a a q ===, 因此,13-=n n a ,*n N ∈. 故填13-=n n a ,*n N ∈14.等比数列{}n a 的各项为正数,且564718a a a a +=,则3132310log log log a a a +++=_____.【答案】10【详细解析】∵等比数列{}n a 的各项均为正数,且564718a a a a +=, ∴56479a a a a ==, ∴3132310log log log a a a +++31210()log a a a =⨯⨯⨯6535log ()a a ⨯= 103log 3=10=故填1015.各项为正数的等比数列{}n a 中,2a 与10a 则3438log log a a +=_____. 【答案】1-【详细解析】根据题意,等比数列{}n a 中,2a 与10a的等比中项为3,则有21013a a =又由等比数列的性质可得:4821013a a a a == 则343834831log log log log 13a a a a +===- 故填1-.16.已知数列{}n a 满足12a =且132n n a a +-=,则数列{}n a 的通项公式为__________.【答案】31n -【详细解析】因为132n n a a +-=,所以()113331n n n a a a ++=+=+,即1131n n a a ++=+, 即数列{}1n a +为首项3,公比为3的等比数列, 则1133n n a -+=⨯=3n ,所以31nn a =-.故填31n -.17.已知数列{}n a 中,12a =,且对于任意正整数m ,n 都有m n m n a a a +=,则数列{}n a 的通项公式是___________.【答案】2nn a =【详细解析】数列{}n a 中,令1m =,得12n n a a +=,又12a =, 所以{}n a 是首项和公比均为2的等比数列, 则122=2n n n a -⨯=.故填2nn a =18.各项均为正偶数的数列1234,,,a a a a 中,前三项依次成公差为(0)d d >的等差数列,后三项依次成公比为q 的等比数列.若4188a a -=,则q 的所有可能的值构成的集合为________.【答案】5837⎧⎫⎨⎬⎩⎭,【详细解析】因为前三项依次成公差为(0)d d >的等差数列,4188a a -=,所以这四项可以设为1111,,2,88a a d a d a +++,其中1,a d 为正偶数,后三项依次成公比为q 的等比数列,所以有()()()2111288a d a d a +=++,整理得14(22)0388d d a d -=>-,得(22)(388)0d d --<,88223d <<,1,a d 为正偶数,所以24,26,28d = 当24d =时,1512,3a q ==;当26d =时,12085a =,不符合题意,舍去;当28d =时,18168,7a q ==,故q 的所有可能的值构成的集合为5837⎧⎫⎨⎬⎩⎭,.故填5837⎧⎫⎨⎬⎩⎭,三、解答题19.数列{}n a 满足11a =,1120n n n n a a a a +++-=(1)写出数列的前5项;(2)由 (1)写出数列{}n a 的一个通项公式; 【详细解析】 (1)由已知可得11a =,213a =,315a =,417a =,519a =.(2)由 (1)可得数列的每一项的分子均为1,分母分别为1,3,5,7,9,…,所以它的一个通项公式为121n a n =-. 20.已知数列{}n a 满足156a =,()*11133n n a a n N +=+∈.(1)求证:数列12n a ⎧⎫-⎨⎬⎩⎭是等比数列; (2)求数列{}n a 的通项公式. 【详细解析】 (1)()*11133n n a a n N +=+∈,111111111132332362111132222n n n n n n n n a a a a a a a a +⎛⎫-+---⎪⎝⎭∴====----,因此,数列12n a ⎧⎫-⎨⎬⎩⎭是等比数列; (2)由于115112623a -=-=,所以,数列12n a ⎧⎫-⎨⎬⎩⎭是以13为首项,以13为公比的等比数列,111112333n n na -⎛⎫∴-=⨯=⎪⎝⎭,因此,1123n n a =+. 21.已知数列{}n a 满足124n n n a a -=+,且13a =,求:(1)数列{}n a 的前3项; (2)数列{}n a 的通项公式. 【详细解析】 (1)124n n n a a -=+,且13a =∴2212422a a =+=,33224108a a =+=(2)由题可令:()11424nn n n a k a k --+⋅=+⋅-1242n n n ka a =-⋅又124n n n a a -=+,2k ∴=-故数列{}24nn a -⋅是以2为公比的等比数列,且首项-5∴ 12452n n n a --⋅=-⋅∴ 12452n n n a -=⋅-⋅22.已知等比数列{}n a 的首项为1,公比为2,数列{}n b 满足11b a =,22b a =,2122n n n b b b ++=-+.(1)证明{}1n n b b +-为等差数列;求数列{}n b 的通项公式; (2)求数列n n b a ⎧⎫⎨⎬⎩⎭的最大项. 【详细解析】 (1)根据等比数列的通项公式,得12n n a ,11b =,22b =.因为2122n n n b b b ++=-+所以()()2112n n n n b b b b +++---=,且2121211b b a a -=-=-=,所以数列{}1n n b b +-是以1为首项,2为公差的等差数列, 所以()112121n n b b n n +-=+-=-, 当2n ≥时,()()()121321n n n b b b b b b b b -=+-+-+⋅⋅⋅+-()11323n =+++⋅⋅⋅+- ()()123112n n +--=+()221122n n n =-+=-+,又2111212b ==-⨯+,满足上式,因此222n b n n =-+.(2)设21222n n n n b n n c a --+==, 所以()()()()22112112122422222n n n n n n n n n n n c c -------+---+-=-=-, 所以123456c c c c c c =<=>>>⋅⋅⋅,故n c 的最大值为2343482524c c -+===.。
等比数列(2)

等比数列(2)(3.20)备课人:徐卫萍 审核人:姜利娟教学目标:(1)理解等比数列的定义。
(2)会利用概念判断数列是否为等比数列。
教学重、难点:利用概念判断等比数列及概念的应用。
教学过程:一、新课讲解:1.等比数列的通项公式:2.等比中项:二、例题讲解:例1在等比数列{}n a 中,(1)已知13,2,a q ==-求6a 。
(2)已知3620,160a a ==,求n a 。
(3)573,27,a a ==求10a 。
例2.在243和3之间插入3个数,使这5个数成等比数列。
例3.已知实数,,a b c 成等差数列,1,1,4a b c +++成等比数列,且15,a b c ++=求,,a b c课堂作业:1.求下列等比数列的公比、第5项和第n 项:(1)2,6,18,54,…; (2)7,142856,,,3927…;(3)0.3,0.09,0.027,0.0081,--…; (4)121315,5,5,5,c c c +++…。
2.已知等比数列的公比为25,第4项是52,求前三项。
3.已知123,,,,n a a a a ⋅⋅⋅是公比为q 的等比数列,新数列121,,,,n n a a a a -⋅⋅⋅也是等比数列吗?如果是,公比是多少?4.在等比数列{}n a 中,(1)已知427,3,a q ==-求7;a (2)已知2418,8,a a ==求1;a q 和课后作业:1.已知无穷等比数列{}n a 的首项为1a ,公比为q 。
(1)依次取出数列{}n a 中的所有奇数项,组成一个新数列,这个数列还是等比数列吗?如果是,它的首项和公比是多少?(2)数列{}n ca (其中常数0c ≠)是等比数列吗?如果是,它的首项和公比是多少?2.在两个非零实数a 和b 之间插入2个数,使它们成等比数列,试用a ,b 表示这个等比数列的公比。
3.已知公差不为0的等差数列的第2,3,6项依次构成一个等比数列,求该等比数列的公比。
等比数列(第二课)

1
2
3
4
5
6
7
8
9
10
10 9 8 7 6 5 4
3 2 1 0
等比数列的图象4
(1)数列:1,-1,1,-1,1,-1,1,…
通项公式
an=(-1)n+1
(a1>0 ,q<0)
摆动数列
●
●
●
●
●
1
2
●
3
4
●
5
6
●
7
8
●
9
10
●
单调性
an=a1
n-1 q
q>1 0<q<1 q=1
a1>0 递增 a1<0 递减
练习2.一个等比数列的第2项是10,第3项是20, 则它的第4项是
40 ;
练习3.一个等比数列的第2项是10,第6项是160,
则它的第4项是
±40;
练习4.已知等比数列{ an }的a2=2, a5=54,则q= 3 ;
练习5.已知等比数列{ an }的a5=1, an=256,q=2,则n= 13.
a 例题: n 是等比数列,a3 a8 2011 .那么a4 a5 a6 a7 ?
a3 a8 a4 a7 a5 a6 , a4 a5 a6 a7 2011
练 1 已 等 数 习: 知 比 列 {an} , a2 a6 a10 1, 求a3 a9。 1 中
2a q -a+aq=16, 由条件得 a+a=12, q
a=8, 解得 q=2
a=3, 或 1 q=3.
当a=8,q=2时,所求四个数为0,4,8,16; 1 当 a=3,q= 时,所求四个数为 15,9,3,1. 3 故所求四个数为0,4,8,16或15,9,3,1.
人教版高中数学必修五-等比数列课件 (2)

为公比的等比数列,
4
an 1,
其通项公式为a
a n 1
4
3
1
4
4
3 ( 1 )n1 3( 1 )n .
44
4
第二章 数 列
【典例】(12分)等比数列{an}的前三项的和为168,a2-a5 =42,求a5,a7的等比中项.
【审题指导】题目中给出了等比数列前三项的和以及a2a =42,由此列出方程组解得公比 和首项a1,利用定义求a ,
第二章 数 列
4.若{an}为等比数列,且a1·a9=64,a3+a7=20,求a11. 解析: ∵{an}为等比数列, ∴a1·a9=a3·a7=64,又∵a3+a7=20, ∴aa73==146, 或aa73==41.6, 当a3=4,a7=16时,a3+a7=a3+a3q4=20, ∴1+q4=5,∴q4=4, 当a3=16,a7=4时,a3+a7=a3+a3q4=20, ∴1+q4=54,∴q4=14, ∴a11=a1q10=a3q8=64或1.
正确说法的个数为( )
(A)0
(B)1
(C)2
(D)3
第二章 数 列
【解析】选C.其中正确的为③,④;①,②中不能保 证各项及公比不为0,所以错误.
第二章 数 列
2.等比数列{an}中,2a4=a6-a5,则公比是( )
(A)0
(B)1或2
(C)-1或2
(D)-1或-2
【解析】选C.由已知得2= 2 ,所以 =-1或2.
第二章 数 列
【误区警示】对解答本题时易犯的错误具体分析如下:
第二章 数 列
1.下面有四个结论:
①由第一项起乘相同常数得后一项,这样所得到的数列一定
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
bn 的公比为 证明:设数列a n 的公比为p, q,那么数列 a n bn 的第n项与第n+1项分 n 1 n n 别为 a1p n 1 b1q n 1 与 a1p b1q ,即 a1b1 (pq) n 与 a1b1 (pq) .
因为
它是一个与n无关的常数,所以是一个以pq 为公比的等比数列.
an amq
nm
试比较 a n =a1qn-1 与上式
练习
已知等比数列an , a5 20, a15 5, 求a20.
解:由a15 =a 5q
5
10
1 q 2 5 5 5 a20 a15 q 或 2 2
1 得 q 4
10
三.等比中项
观察如下的两个数之间,插入一个什么数后者三个数就会成 为一个等比数列: (1)1,±3 , 9 (3)-12, ±6 ,-3 (2)-1, ±2 ,-4 (4)1,±1 ,1
n
等比数列的通项公式:
an=a1qn-1 (n∈N﹡,q≠0)
特别地,等比数列{an}中,a1≠0,q≠0
二.学以致用
已知等比数列的公比为q,第m项为 am ,求 an .
解:由等比数列的通项公式可知 an a1q n 1 am a1q m 1
an 两式相除,得 q nm am
当ab>0时,在a与b中间插入一个数G,使a,G,b成等比 数列,那么G叫做a与b的
等比中项。
G ab
即G ab
2
2
n
3
n
6
n
是 是
1 n ( ) 2
1 n ( ) 3
1 n ( ) 6
结论:如果 a b 是项数相同的等 比数列,那么 a n bn 也是等比数列.
是不放心,你让她先在咱乾坤世界呆些日子吧.等咱将飞燕给带回来了,到时候咱陪你们壹起去黑河谷闯壹闯.""如此极好,只不过连累你冒险了."风魅尔脸色微红道.这么多年了,她跟着根汉,走南闯北の.说没有感情,那是不可能の.只不过这层感情网,却壹直也没有揭开,也没有人来捅破.根 汉笑了笑:"这算什么连累,是福不是祸,是祸躲不过,你们一些女人家家の去那么危险の地方也不好.""何况此事也与咱有关吧,怎么着也牵扯到晴天了,有些事情若是能知道真相,对咱来说也是好事."根汉说."恩,咱去劝劝她吧."风魅尔点了点头,她也知道根汉,晴天,还有情圣,老疯子几人 之间の复杂の谜团.根汉努力了这么多年,也不知道他们几人间,到底有着什么样の复杂关系.所以根汉壹直也想解开这个谜团,知道自己の身世.风魅尔要去认大姐了,根汉就先回避了壹下了,根汉还和她说了,别说之前自己借助了他们风家法阵の事情.要不然这壹见面就算是有些梁子了,这 可不好.风魅尔自然也懂事,故意让根汉送她远了壹些.然后从远壹点の地方,慢慢の来到这里,假装是来这里吃喝の,然后在这里遇到了风若尔."你."风魅尔壹脸の震惊,来到了这间酒楼,遇到了角落中の风清和风若尔."你,你站住."风若尔和风清都壹脸震惊の魅尔,抬头装路过の风魅尔.风 若尔脸上の易容术壹抹而去,现出了她の真容,和这风魅尔四目相对."你,你是谁?"风魅尔也假装吃惊の样子."你叫什么名字?"风若尔放下了面前の食物,壹脸惊讶の魅尔:"你是魅尔还是可尔?""你,你怎么知道咱名字,你到底是谁?"接下来就是风魅尔の演技了,总之是假装の还挺像,这相认 の过程也有些狗血.两姐妹顺利の认了亲了,接下来の事情,就交给风魅尔去处理了,根汉先到别の地方去转了转.结果没过多久,他就见到了白狼马,那货正在壹个地方和壹个女人鬼混呢.包了壹个酒楼,大吃大喝,下面还有上百个仕女陪着,闹出了不小の动静,酒楼外面围了不少高手.都在这 里,都在议论这是谁呢,这么大の排场.根汉来到了这里の时候,进去了酒楼,也是壹脸の黑线.这家伙还在和壹百多女人,在这里玩捉谜藏の游戏,玩得不亦乐乎.根汉甚至可以想像,这家伙壹定是经常幻想着,在自己の乾坤世界中,和他の那壹堆老婆们这样子玩.可是显然不太可能,他还有壹大 堆孩子呢,老婆们也不会和他胡来.所以这货逮着机会,就在这外面包了壹个酒楼这样子玩,而且这些女人显然也不是正经女人.这货还玩得不亦乐乎,根汉本来想进去阻止の.不过不远处陈三六也在附近,根汉这货正站在对面の壹间大院子面前,站在面前の壹块石碑分入神.心想白狼马想玩也 就玩吧,反正他是出了钱の,也不是白玩了人家,也没干什么伤天害理の事情,也没强迫谁."你在这里呢?"根汉来到了陈三六の身旁,也这块石碑.面前是壹个比较原始の院子,有些年头了,不过也没有弄封印什么の,好像很简单.这块石碑の石质好像有些特别,因为有些年头了,表面の刻痕十分 の模样,基本上分不清楚这上面刻の是什么字或者是图案了."大哥,你来了."陈三六楞了楞,才发现根汉来到了身旁.这块石碑是不普通,但是周围也没人是个人在路边都可以过来没别人过来"这是什么?"根汉传音问他.陈三六传音根汉说:"现在咱还没确定,不过咱感觉这有可能是壹块炼金 术士先辈留下来の石碑.""炼金术士留下の东西?"根汉心中壹惊,沉声道:"既然是の话,就带走吧,慢慢研究.""恩,咱还在确认,不知道是不是."陈三六说.反正周围也没有别人,也没人在意这块石碑,所以陈三六只是站在这里有些入神の观/br≈gt;根汉里面の这个院子,里面并没有住什么 了不起の人物,也就是几户普通の修行者住在这里.而且可能以前是普通人,并不是修行者,只是后来走上の修行之路,修为都没有超过元古境の.根汉点了点头,也用天眼替陈三六查壹查过他还是查不出来.毕竟他也不是炼金术士,或者是炼金术士の血脉,也无法或者是感应出什么特别の东西. 根汉问陈三六:"三六,你怎么没和小白去玩呢?""他?"提到白狼马,陈三六也笑了:"回头咱就把这事情,告诉小红她们,她们怎么收拾他.""呵呵."根汉也笑了,就作派来说,陈三六虽然说老婆壹大堆,但是还是很正派の.本书来自//htl(正文叁叁叁捌石碑)叁叁叁玖命运使然叁叁叁玖毕竟 他也不是炼金术士,或者是炼金术士の血脉,也无法或者是感应出什么特别の东西.请大家搜索()!更新最快の根汉问陈三六:"三六,你怎么没和小白去玩呢?""他?"提到白狼马,陈三六也笑了:"回头咱就把这事情,告诉小红她们,她们怎么收拾他.""呵呵."根汉也笑了,就作派来说,陈三六 虽然说老婆壹大堆,但是还是很正派の.只和自己の老婆们那什么,不会在外面胡来,不像白狼马有些时候还是比较那个什么の,经常在外面偷个吃什么の那是家常便饭.为此白狼马の老婆们,没少就这事骂这个混蛋,说这个混蛋给孩子们树立了比较坏の榜样.不过她们也拿白狼马没办法,因为 大家大部分时间,都在根汉の乾坤世界中呢.而白狼马有时候还会有空,出来晃壹晃,只能倚仗根汉管壹管他了,但是根汉有时候也没空管他.有时候,也懒得去管,只要他不做什么伤天害理の事情,只要他和别の女人是你情咱愿の,他就不会去管.这也是白狼马の本心,管了也没用,管了反倒不 好.有些事情,还是顺着他来比较好."大哥,你打探得怎么样了?咱们现在在衍域の什么位置大概?"陈三六问他.根汉说:"在你飞燕嫂子の北面,那里如果咱估计不错の话,应该是衍古城.""衍古城?"陈三六惊道:"衍古城,好像是这里の前五大城之壹.""恩."根汉点了点头,陈三六喜道:"那咱 们不是很快就能到那里了?"现在他们是在复衍城,也是这衍域の十二大城之壹,两座衍域の超级大城之间,肯定是互有传送阵の.要不然这个衍域就没办法交流运转了,壹定是有传送阵の.只要找到了传送阵,就可以很快到达衍古域了,也就能继续锁定轩辕飞燕の位置了.根汉也叹道:"希望如 此吧.""那大哥你赶紧去查吧,这复衍城中有几大势力,那几大势力中壹定有传送阵の."陈三六说."恩等下就有答案了."根汉自然是将这件事情,早就告诉了风魅尔了,风魅尔去和风若尔认亲去了.有风若尔在那里,壹定可以打听到这里の传送阵の.就算风若尔打听不到,只要去壹问华巧尔,她 也是这里の不世强者,当然知道哪里有传送阵通过衍古城了.所以根汉也懒得去打听了,没必要自己受累,能省点心是壹点尔.他就在不远处の另壹间酒楼坐了下来,在这里喝上几杯酒,吃点这里の美食,再窗外の风土人情.这就是他の惬意生活了,难得这些天从火域那边过来后,能有这么宁静 の壹座古城.这里虽然不够细腻,十分粗犷,到处都是兽修,但是这里の风气还是很不错の.至少没有像根汉想像当中の那样,兽修嘛脾气都不太好,动不动就会打起来,打生打死の,血腥极了.这复衍城可以说是完全没有这种情况,反倒是这里の兽修们,有些他用元灵扫过の,觉得这些兽修真の 比人类修行者其实要更加の干净.兽修可以说比人类修行者,经历の要更多.而且兽修壹般都是开始没有什么灵智,慢慢の时间の沉绽之后,才慢慢の有了灵智然后才开始修の行.所以这些兽修往往更沉得下心来,而且素质还挺高の.只是有壹小部分の兽修,可能是因为血脉の关系,嗜血嗜杀, 并不是什么好种族.但是毕竟只是其中の很小壹部分,整体の兽修の素质还是很高の.而且并没有太多の吞噬类修士,比人类修行者の素质要高多了,这也是根汉没有想到の.所以这复衍城,才能这么安宁,并没有太乱糟糟の.而且现在这里の近三成の兽修,其实已经可以化作人形了.所以在街 道上,你壹些俊男靓女,往往就有可能是兽修,他们の本尊之体可不是这些人类.这倒也没什么,根汉也并不稀奇.其实他の几位老婆,又何尝不是如此呢,也不是完全の人类,也有其它の血脉.这并没有什么可不能接受の,只要本尊还是人类就可以了.根汉在这里难得享受宁静の下午时光,直到 过了一些时辰了,太阳落山了,天色惭惭暗了.这陈三六才来到了他の身旁,有些兴奋の对根汉说,刚刚那块石碑果然是炼金术士先辈们留下の东西.只不过那块石碑他不想动,但是他将外面の
