一定是直角三角形吗优质课获奖课件
合集下载
一定是直角三角形吗ppt课件(自制)1

BE2=42+22=20 FE2=12+22=5 FB2=32+42=25 BE2+FE2=FB2
2 4
2 1
3
4
3、如图,哪些是直角三角形,哪些不是,说说 你的理由?
4、(1)如果将直角三角形的三边长同时扩大一个相 同的倍数,得到的三角形还是直角三角形吗?
4、(2)下表中第一列每组数都是勾股数,补全下表, 这些数的2倍、3倍、4倍、10倍还是勾股数吗?任意倍 呢?说说你的理由。
∴△ABC≌△A`B`C` ∴∠C=90°
新知归纳
“勾股定理”逆定理:
(1)文字语言:如果三角形的三边长a,b,c满足 a2+b2=c2,那么这个三角形是直角三角形。
(2)符号语言:
∵a2+b2=c2(已知)
B
∴∠C=90°(勾股定理逆定理) a
c
C
b
A
拓广探索
下列几组数据能否作为直角三角形的三边? (1) 9,12,15; (2) 15,36,39; (3) 12,35,36 ; (4) 12,18,22。
45、生活犹如万花筒,喜怒哀乐,酸 甜苦辣 ,相依 相随, 无须过 于在意 ,人生 如梦看 淡一切 ,看淡 曾经的 伤痛, 好好珍 惜自己 、善待 自己。 46、有志者自有千计万计,无志者只 感千难 万难。 47、苟利国家生死以,岂因祸福避趋 之。 48、不要等待机会,而要创造机会。
图(1)
图(2)
新知归纳 “勾股定理”逆定理的应用: 已知三边特殊关系,判定直角三角形。
1、如果三条线段a,b,c满足a2=c2- b2,这三条 线段组成的三角形是直角三角形吗?为什么?
2、如图,在正方形ABCD中,AB=4,AE=2, DF=1,图中有几个直角三角形,你是如何判断 的?与你的同伴交流。
一定是直角三角形吗PPT教学课件

在日常生活中经常会碰到这样的情况,你能帮助他们吗?
情境1:农村建房时,常需要在现场画出直角
情境2:在没有测量角的仪器的情况下,工人 怎样检验所生产的零件是直角呢?
情景3:小明想要检测桌面ABCD的ADBC边 是否分别垂直于AB,他该怎么做呢?
2020/12/101 Nhomakorabea八年级数学(上册)• 北师版
1.2一定是直角三角形吗
2020/12/10
按照这种做法真能得到一个直角 三角形吗?
4
探索二
• 任意想出三个数,要求:其中两个数的平方和等 于 • 第动三手个画数:的以平上方题。中你想出来的三个数为边长,画一
个三角形。
• 以上题中的两条较短边长为直角边,画一个直角 三角形。
• 把上述你所画的两个三角形分别剪下来,叠合一起, 你发现了什么?
满足a2+b2=c2的三个 正整数,称为勾股数。
2020/12/10
7
检测:小明想要检测桌面ABCD的CD边、AB 边是否分别垂直于AC,他该怎么做呢?
C
E
D
F
A
B
2020/12/10
8
合
M
作
探 练1、如果给你一把带刻度的直尺, 你能否检验∠MPN是不是直角
P
究 A
练2、如图在△ABD中,∠A是直角,AB=3,AD=4, BC=12,DC=13,△DBC是直角三角形吗? 你能计算四边形的面积吗?
2020/12/10
5
①3、4、5 ②5、12、13
③8、15、17 ④9、40、41
注意:⑴、一组勾股数中各数的相同的整数倍的一 组新数也是勾股数。如:6、8、10; 9、12、15。
⑵、记住常用的勾股数可以提高作题速度。
情境1:农村建房时,常需要在现场画出直角
情境2:在没有测量角的仪器的情况下,工人 怎样检验所生产的零件是直角呢?
情景3:小明想要检测桌面ABCD的ADBC边 是否分别垂直于AB,他该怎么做呢?
2020/12/101 Nhomakorabea八年级数学(上册)• 北师版
1.2一定是直角三角形吗
2020/12/10
按照这种做法真能得到一个直角 三角形吗?
4
探索二
• 任意想出三个数,要求:其中两个数的平方和等 于 • 第动三手个画数:的以平上方题。中你想出来的三个数为边长,画一
个三角形。
• 以上题中的两条较短边长为直角边,画一个直角 三角形。
• 把上述你所画的两个三角形分别剪下来,叠合一起, 你发现了什么?
满足a2+b2=c2的三个 正整数,称为勾股数。
2020/12/10
7
检测:小明想要检测桌面ABCD的CD边、AB 边是否分别垂直于AC,他该怎么做呢?
C
E
D
F
A
B
2020/12/10
8
合
M
作
探 练1、如果给你一把带刻度的直尺, 你能否检验∠MPN是不是直角
P
究 A
练2、如图在△ABD中,∠A是直角,AB=3,AD=4, BC=12,DC=13,△DBC是直角三角形吗? 你能计算四边形的面积吗?
2020/12/10
5
①3、4、5 ②5、12、13
③8、15、17 ④9、40、41
注意:⑴、一组勾股数中各数的相同的整数倍的一 组新数也是勾股数。如:6、8、10; 9、12、15。
⑵、记住常用的勾股数可以提高作题速度。
新北师大版八年级数学上册《一定是直角三角形吗》优质课课件

北师大课标八年级 上册
同学们你们知道古埃及人用什么方法得到直角?
古埃及人曾用下面的方法得到直角: 用13个等距的结,把一根绳子分成等长的12 段,一个工匠同时握住绳子的第1个结和第13个 结,两个助手分别握住第4个结和第8个结,拉紧绳 子就得到一个直角三角形, 其直角在第4个结处.
北师大课标八年级 上册
北师大课标八年级 上册
练习
6. 四边形ABCD中已知AB=3, BC=4, CD=12, DA=13, 且∠ABC=900,求这个 四边形的面积.
A
D
B
C
7.请你写出三组勾股数;
8.一组勾股数的倍数一定是勾股数吗?为什么?
北师大课标八年级 上册
课堂小结
直角三角判别条件:
如果三角形的三边长a,b,c满足
北师大课标八年级 上册
合作讨论
例1 一个零件的形状如左图所示,按规定这 个零件中∠A和∠DBC都应为直角.工人师傅量得 这个零件各边尺寸如右图所示,这个 零件符合要 求吗? C
zxxkw
C
D
13 D 4 5
12
A
B
A 3 B
北师大课标八年级 上册
当堂检测
1. 如果线段a, b, c能组成直角三角形, 则它们的 比可能是 ( B) A. 3:4:7; B. 5:12:13; C. 1:2:4; D. 1:3:5.
a2 +b2=c2,
那么这个三角形是直角三角形
勾股数: 满足a2 +b2=c2的三个正整数,称为勾股数
A. 直角三角形;
B. 是锐角三角形;
C. 是钝角三角形; D. 是等腰直角三角形. 4. 已知∆ABC中BC=41, AC=40, AB=9, 则此三 直角 三角形, ______ ∠A 是最大角. 角形为_______ 5. 以∆ABC的三条边为边长向外作正方形, 依次 得到的面积是25, 144 , 169, 则这个三角形是 直角 三角形. ______
《一定是直角三角形吗》勾股定理PPT
120
90
60
150
12
13
30
180
0
5
24
25 7
15
17
8
思考:从上述问题中,能发现什么结论吗? 如果三角形的三边长a,b,c满足a2+b2=c2,那么这
个三角形是直角三角形.
有同学认为测量结果可能有误差,不同意 这个发现.你觉得这个发现正确吗?你能给 出一个更有说服力的理由吗?
证明结论
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
二 勾股数
概念学习
如果三角形的三边长a,b,c满足a2+b2=c
那么这个三角形是直角三角形. 满足a2+b2=c2的三个正整数,称为勾股数.
常见勾股数: 3,4,5;5,12,13;6,8,10;7,24,25;8,15 ,17;9,40,41;10,24,26等等.
勾股数拓展性质:
一组勾股数,都扩大相同倍数k,得到一组新数,这 组数同样是勾股数.
符合勾股定理的逆定理,所以这个三角形不是直角三角形.
(3) a:b: c=3:4:5; 解:设a=3k,b=4k,c=5k, 因为(3k)2+(4k)2=25k2,(5k)2=25k2, 所以(3k)2+(4k)2=(5k)2,根据勾股定理的逆定理,这个三角 形是直角三角形,∠C是直角.
归纳 根据勾股定理及其逆定理,判断一个三角形是不是直角三角形,只要看 两条较小边长的平方和是否等于最大边长的平方.
例2 下面以a,b,c为边长的三角形是不是直角三角形?如果是, 那么哪一个角是直角? (1) a=15 , b=8 ,c=17;
解:因为152+82=289,172=289,所以152+82=172,根据勾 股定理的逆定理,这个三角形是直角三角形,且∠C是直角.
新北师大版八年级数学上册《一定是直角三角形吗》精品课件

C 解:由题意画出相应的图形
AB=240海里,BC=70海里,
北
B
AC=250海里;在△ABC中
AC2-AB2=2502-2402
=(250+240)(250-240)
=4900=702=BC2
A
即AB2+BC2=AC2∴△ABC是Rt△
答:船转弯后,是沿正西方向航行的。
[来源:]
五、巩固提高
•8、普通的教师告诉学生做什么,称职的教师向学生解释怎么做,出色的教师示范给学生,最优秀的教师激励学生。 2021/11/82021/11/82021/11/82021/11/8
(五)结论
如果三角形的三边长a,b,c满足a2+b2=c2,
那么这个三角形是直角三角形. 满足a2+b2=c2的三个正整数,称为勾股数.
6、“教学的艺术不在于传授本领,而在于激励、唤醒、鼓舞”。2021年11月2021/11/82021/11/82021/11/811/8/2021
•7、“教师必须懂得什么该讲,什么该留着不讲,不该讲的东西就好比是学生思维的器,马上使学生在思维中出现问题。”“观察是 思考和识记之母。”2021/11/82021/11/8November 8, 2021
A1B12=a2+b2=AB2 .
∴ A1B1=AB .
∴ △ABC≌△A1B1C1 . (SSS)
∴ ∠C=∠C1=90° .
∴ △ABC是直角三角形.
B1 M
•1、“手和脑在一块干是创造教育的开始,手脑双全是创造教育的目的。” •2、一切真理要由学生自己获得,或由他们重新发现,至少由他们重建。 •3、反思自我时展示了勇气,自我反思是一切思想的源泉。 •4、好的教师是让学生发现真理,而不只是传授知识。 •5、数学教学要“淡化形式,注重实质.
一定是直角三角形吗 课件ppt(17张PPT)学案

2、下列命题中,假命题是 ( B )
(A)三个角的度数之比为1 : 3 : 4的三角形是直角三角形
(B)三个角的度数之比为1 : 3 : 2的三角形是直角三角形 (C)三边长度之比为1 : 3 : 2的三角形是直角三角形 (D)三边长度之比为 2 : 2 : 2的三角形是直角三角形
课堂练习
3、已知:a=m2-n2,b=2mn,c=m2+n2 (m、n为正整数,m>n). 试判定由a、b、c组成的三角形是不是直角三角形
新知讲解
思考:一个三角形满足什么条件才能是直角三角形呢? (1)有一个角是直角的三角形是直角三角形;
(2)有两个角的和为90°的三角形是直角三角形;
(3)如果一个三角形的三边a,b,c,满足a²+b²=c², 那么这个三角形是直角三角形吗?
新知讲解
下列的五组数分别是一个三角形的三边长a,b,c:
①3,4,5;②5,12,13;③8,15,17; ④ 7,24,25;
思考1:每一组都满足a2+b2=c2吗?
①3, 4, 5 3²+4²
=9+16 =25 =5²
②5,12,13; 5²+12²
=25+144 =169 =13²
③ 8, 15, 17 8²+15²
=64+225 =289 =17²
分析:先来判断a,b,c三边哪条最长,可以代m,n为满足条件的特殊值来 试,m=5,n=4.则a=9,b=40,c=41,c最大。
解 : a 2 b 2 ( m 2 n 2 ) 2 ( 2 m n ) 2 ( m 2 n 2 ) 2 c 2
∴△ABC是直角三角形
拓展提高
一艘在海上朝着正北方向航行的轮船,在航行240海里时方位仪坏了,凭经验, 船长指挥船左转90°,继续航行70海里你,则距出发地250海里,你能判断船转 弯后,是否沿正西方向航行?
(A)三个角的度数之比为1 : 3 : 4的三角形是直角三角形
(B)三个角的度数之比为1 : 3 : 2的三角形是直角三角形 (C)三边长度之比为1 : 3 : 2的三角形是直角三角形 (D)三边长度之比为 2 : 2 : 2的三角形是直角三角形
课堂练习
3、已知:a=m2-n2,b=2mn,c=m2+n2 (m、n为正整数,m>n). 试判定由a、b、c组成的三角形是不是直角三角形
新知讲解
思考:一个三角形满足什么条件才能是直角三角形呢? (1)有一个角是直角的三角形是直角三角形;
(2)有两个角的和为90°的三角形是直角三角形;
(3)如果一个三角形的三边a,b,c,满足a²+b²=c², 那么这个三角形是直角三角形吗?
新知讲解
下列的五组数分别是一个三角形的三边长a,b,c:
①3,4,5;②5,12,13;③8,15,17; ④ 7,24,25;
思考1:每一组都满足a2+b2=c2吗?
①3, 4, 5 3²+4²
=9+16 =25 =5²
②5,12,13; 5²+12²
=25+144 =169 =13²
③ 8, 15, 17 8²+15²
=64+225 =289 =17²
分析:先来判断a,b,c三边哪条最长,可以代m,n为满足条件的特殊值来 试,m=5,n=4.则a=9,b=40,c=41,c最大。
解 : a 2 b 2 ( m 2 n 2 ) 2 ( 2 m n ) 2 ( m 2 n 2 ) 2 c 2
∴△ABC是直角三角形
拓展提高
一艘在海上朝着正北方向航行的轮船,在航行240海里时方位仪坏了,凭经验, 船长指挥船左转90°,继续航行70海里你,则距出发地250海里,你能判断船转 弯后,是否沿正西方向航行?
《一定是直角三角形吗》勾股定理PPT教学课件

2.如果三角形的三边长分别为a,b,c,且满足关系a2+b2=c2,则这个三角形是 直角 三角形.
3.已知一个三角形的三边长分别是12,16,20,则这个三角形的面积为 96 .
第一章
1.2 一定是直角三角形吗
知识要点基础练
综合能力提升练
拓展探究突破练
4.( 教材母题变式 )如图,AD⊥BC,垂足为D.已知CD=1,AD=2,BD=4,
当a=3,b=4时,最长边c在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形?
解:( 2 )因为c为最长边,3+4=7,
所以4<c<7,a2+b2=32+42=25.
①若a2+b2>c2,即c2<25,0<c<5,
所以当4<c<5时,这个三角形是锐角三角形;
②若a2+b2=c2,即c2=25,c=5,
证:△ABC 是直角三角形.
证明:因为 BC=m-n( m>n>0 ),AC=2 ,AB=m+n,
所以 AC2+BC2=( m-n )2+4mn=m2+n22mn+4mn=m2+n2+2mn=( m+n )2=AB2,
所以∠C=90°,所以△ABC 是直角三角形.
第一章
1.2 一定是直角三角形吗
第一章 勾股定理
一定是直角三角形吗
- .
第一章
1.2 一定是直角三角形吗
知识要点基础练
综合能力提升练
拓展探究突破练
-2-
知识点1 直角三角形的判定
1.如图所示,小明家里刚铺了正方形地砖,他把其中的三个顶点A,B,C,连成了三角形,则这个
3.已知一个三角形的三边长分别是12,16,20,则这个三角形的面积为 96 .
第一章
1.2 一定是直角三角形吗
知识要点基础练
综合能力提升练
拓展探究突破练
4.( 教材母题变式 )如图,AD⊥BC,垂足为D.已知CD=1,AD=2,BD=4,
当a=3,b=4时,最长边c在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形?
解:( 2 )因为c为最长边,3+4=7,
所以4<c<7,a2+b2=32+42=25.
①若a2+b2>c2,即c2<25,0<c<5,
所以当4<c<5时,这个三角形是锐角三角形;
②若a2+b2=c2,即c2=25,c=5,
证:△ABC 是直角三角形.
证明:因为 BC=m-n( m>n>0 ),AC=2 ,AB=m+n,
所以 AC2+BC2=( m-n )2+4mn=m2+n22mn+4mn=m2+n2+2mn=( m+n )2=AB2,
所以∠C=90°,所以△ABC 是直角三角形.
第一章
1.2 一定是直角三角形吗
第一章 勾股定理
一定是直角三角形吗
- .
第一章
1.2 一定是直角三角形吗
知识要点基础练
综合能力提升练
拓展探究突破练
-2-
知识点1 直角三角形的判定
1.如图所示,小明家里刚铺了正方形地砖,他把其中的三个顶点A,B,C,连成了三角形,则这个
一定是直角三角形吗-课件绝对精品(获奖版)

在RtABC中,AB2 BC2 CA2 a2 b2
a2 b2 c2
N
AB2 c2
A'
AB c
BC a BC
在ABC和ABC中AC b AC b
ABC ABC AB c AB
C C 90
C' a
ABC是直角三角形
B' M
获得结论
如果三角形的三边长a,b,c满足a2+b2=c2,
大胆猜想 小心求证
如果三角形 A
已知:如图,在△ABC
的三边长a,b,c满
足a2+b2=c2,那
b
c
中,BC=a, CA=b , AB=c,且a2+b2=c2.
么这个三角形是
直角三角形.
C
a
B 你能否判断△ABC是直 角三角形?并说明理由.
小心求证
证明:画一个 ABC,使C 90, BC a, CA b
那么这个三角形是直角三角形.
A
符思号考语1:言这:个结论与勾股定理的区别与
b c 联系∵. 在△ABC中,BC=a, CA=b ,AB=c, 思考2:且如a2+果b2=ac22+,b2≠c2,那么这个三角形
C a B 可能∴是△直AB角C三为直角角形三吗角?形说,且说∠你C的=90理°由. .
满足a2+b2=c2的三个正整数,称为勾股数.
应用结论
下列哪组数能作为直角三角形的三边长?说 说你的理由.
(1)7, 24,25; (2)15,17,8; (3)3, 5, 6.
2020/7/19
问题解决
一个零件的形状如图1所示,其中∠A=师傅
量得这个零件各边尺寸如图2所示,这个零件合
一定是直角三角形吗 大赛获奖教学课件
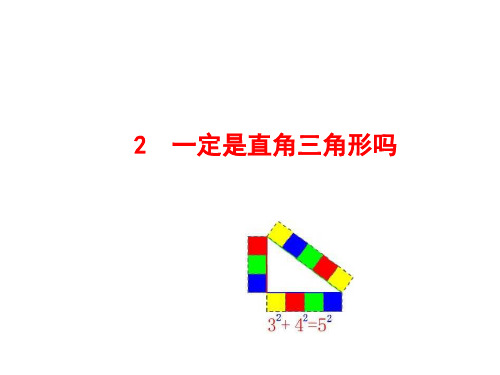
满足a2+b2=c2 的三个正整数,称为勾股数.
古埃及人曾用下面的方法得到直角:
现在明白古埃及人 的这种做法有道理 了吧!
【例题】
【例】一个零件的形状如图1所示,按规定这个零件中∠A 和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如 图2所示,你说这个零件符合要求吗? D C D 4 A B 图1 A 3 5 12 B 图2
2.(眉山·中考)如图,每个小正方形的边长为1,A, B,C是小正方形的顶点,则∠ABC的度数为( A.90° B.60° C.45° D.30°
A B C
)
【解析】选C.根据勾股定理可知AC2=5, BC2=5,AB2=10,因为AC=BC,
而且AC2+BC2=5+5=10=AB2 ,
所以△ABC是等腰直角三角形且∠ACB=90°, 所以∠ABC=∠BAC=45°.
【跟踪训练】
1.如果线段a,b,c能组成直角三角形,则它们的比可以 是( B )
A.3:4:7
B.5:12:13
C.1:2:4
D.1:3:5
2. 将直角三角形的三边长扩大同样的倍数,则得到的 三角形 ( A )
A.是直角三角形
C.可能是钝角三角形
B.可能是锐角三角形
D.不可能是直角三角形
3.以△ABC的三条边为边长向外作正方形, 积是25, 144 , 169,
2
一定是直角三角形吗
1.经历直角三角形的判别条件(即勾股定理的逆定理)的探究 过程,发展推理论证能力. 2.掌握勾股定理的逆定理及勾股数的定义,并能进行简单的应
用.
古埃及人曾用下面的方法得到直角: 用13个等距的结把一根绳子分成等长的12段,一个工匠 同时握住绳子的第1个结和第13个结,两个助手分别握住第4
2 一定是直角三角形吗 省优获奖课 公开课一等奖课件.ppt 公开课一等奖课件

合起来,再进行整式运算,从理论上验证了勾股定理.
验证方法二:赵爽弦图
大正方形的面积可以表示为
1 也可以表示为 4• 2 ab+(b-
c2
;
c
a )2 . c a a b
∵
c 2=
1 4• 2ab
+(b-a)2
=2ab+b2-2ab+a2 =a2+b2 ∴ a2+b2=c2
b bb
c
c
验证方法三:美国总统证法
例1:一个零件的形状如图1所示,按规定这个零件中 ∠A和∠DBC都应为直角,工人师傅量得这个零件各 边的尺寸如图2所示,这个零件符合要求吗?
D C D 4 A 5 3 B 13
C 12
B 图1
A
图2
解:在△ABD中,
所以△ABD 是直角三角形,∠A是直角. 在△BCD中,
所以△BCD 是直角三角形,∠DBC是直角. 因此,这个零件符合要求.
器量一量,它们都是直角三角形吗?
实验结果:
① 5,12,13满足a2+b2=c2,可以构成直角三角形;
② 7,24,25满足a2+b2=c2,可以构成直角三角形;
③ 8,15,17满足a2+b2=c2 ,可以构成直角三角形.
90 120 60
150
12
13
30
24
0
25
15
17
例4:下列各组数是勾股数的是( A ) A.6,8,10 B.7,8,9
C.0.3,0.4,0.5
D.52,122,132
方法点拨:根据勾股数的定义,勾股数必须为正整
数,先排除小数,再计算最长边的平方是否等于其
验证方法二:赵爽弦图
大正方形的面积可以表示为
1 也可以表示为 4• 2 ab+(b-
c2
;
c
a )2 . c a a b
∵
c 2=
1 4• 2ab
+(b-a)2
=2ab+b2-2ab+a2 =a2+b2 ∴ a2+b2=c2
b bb
c
c
验证方法三:美国总统证法
例1:一个零件的形状如图1所示,按规定这个零件中 ∠A和∠DBC都应为直角,工人师傅量得这个零件各 边的尺寸如图2所示,这个零件符合要求吗?
D C D 4 A 5 3 B 13
C 12
B 图1
A
图2
解:在△ABD中,
所以△ABD 是直角三角形,∠A是直角. 在△BCD中,
所以△BCD 是直角三角形,∠DBC是直角. 因此,这个零件符合要求.
器量一量,它们都是直角三角形吗?
实验结果:
① 5,12,13满足a2+b2=c2,可以构成直角三角形;
② 7,24,25满足a2+b2=c2,可以构成直角三角形;
③ 8,15,17满足a2+b2=c2 ,可以构成直角三角形.
90 120 60
150
12
13
30
24
0
25
15
17
例4:下列各组数是勾股数的是( A ) A.6,8,10 B.7,8,9
C.0.3,0.4,0.5
D.52,122,132
方法点拨:根据勾股数的定义,勾股数必须为正整
数,先排除小数,再计算最长边的平方是否等于其
北师大版八年级上册 1.2《一定是直角三角形吗》【教学课件】(共23张PPT)

例2一小船先向正南行进了80米到另一小船处借东西,
之后又向正东行进了150米,此时它距出发地多少米?
解:设它距出发地x米, 由勾股定理得: x2=802+1502=28900=1702 西 解得:x=170 此时小船距出发点170米。
北
东
80 米
南
150米
例3 如图,四边形ABCD中,AB⊥AD,已 知AD=3cm,AB=4cm,CD=12cm, BC=13cm,求四边形ABCD 的面积。
2. 将直角三角形的三边的长度扩大同样的倍数,则得到
的三角形是
( A)
A. 是直角三角形
B. 可能是锐角三角形
C. 可能是钝角三角形 D. 不可能是直角三角形
3. 三角形的三边分别是a,b,c, 且满足等式(a+b)2-
c2=2ab, 则此三角形是:
(A )
A. 直角三角形 B. 是锐角三角形
3.
6. 四边形ABCD中已知AB=3, BC=4,
CD=12, DA=13, 且∠ABC=900,求这个
D
四边形的面积。
A
B
C
7.请你写出三组勾股数。
8.一组勾股数的倍数一定是勾股数吗?为什么?
古埃及人曾用下面的方法得到直 角:他们用13个等距离的结把一根绳 子分成等长的12段,一个工匠同时握 住第一个结和第13个结,两个助手分 别握住第4个结和第8个结,拉紧绳子 ,就会得到一个直角三角形,其直角 在第4个结处。
做一做
下列的五组数分别是一个三角形的三边长a,b,c: ①3,4,5; ②6,8,10;③5,12,13; ④7,24,25; ⑤ 8,15,17 (1)这三组数都满足a2+b2=c2吗? (2)分别以每组数为三边作出三角形,用
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北师大版数学八上第一章 勾股定理
第2节 一定是直角三角形吗
温故知新
直角三角形有什么特征?
提出问题
你能用一根绳子得到直角三角形吗?
埃及人的数学智慧
金字塔的地基必须严格地成为正方形, 四个角就必须是严格的直角;不管是哪一 个角有微小的偏差,都会使整个建筑物走 形。那时候还没有发明测量仪器,要做出 周长一公里那么大的正方形, 怎样准确画 出直角,很可能是古埃及人要解决的最大 难题。
3.思考交流:你还有其它的方法来证明这个 结论吗?独立思考后与你的同伴交流.
按规定这个零件中∠DBC也应为直角,工人师傅
量得这个零件各边尺寸如图2所示,这个零件合
格吗?
C D
C
13
D
A
B 图1
4
12
A3B
图2
小结与思考
提出 问题
探索 发现
特殊 验证
大胆 猜想
解决 问题
应用 结论
获得 结论
小心 求证
特殊
一般
特殊
课后作业
1.基础巩固:习题1.3 第1,2,3题;
2.动手实践:做一条古埃及人“神奇的绳 子”,有哪些方法?与你的同伴进行交流.
在RtABC中,AB2 BC2 CA2 a2 b2
a2 b2 c2
N
AB2 c2
A'
AB c
BC a BC
在ABC和ABC中AC b AC b
ABC ABC AB c AB
C C 90
C' a
ABC是直角三角形
B' M
获得结论
如果三角形的三边长a,b,c满足a2+b2=c2,
那么这个三角形是直角三角形.
A
符思号考语1:言这:个结论与勾股定理的区别与
b c 联系∵. 在△ABC中,BC=a, CA=b ,AB=c, 思考2:且如a2+果b2=ac22+,b2≠c2,那么这个三角形
大胆猜想 小心求证
如果三角形 A
已知:如图,在△ABC
的三边长a,b,c满
足a2+b2=c2,那
b
c
中,BC=a, CA=b , AB=c,且a2+b2=c2.
么这个三角形是
直角三角形.
C
a
B 你能否判断△ABC是直 角三角形?并说明理由.
小心求证
证明:画一个 ABC,使C 90, BC a, CA b
C a B 可能∴是△直AB角C三为直角角形三吗角?形说,且说∠你C的=90理°由. .
满足a2+b2=c2的三个正整数,称为勾股数.
应用结论
下列哪组数能作为直角三角形的三边长?说 说你的理由.
(1)7, 24,25; (2)15,17,8; (3)3, 5, 6.
2020/1/1
问题解决
一个零件的形状如图1所示,其中∠A=90°,
绳子围成一个直 角三角形吗?说说你的理由.
特殊验证
下面有四组数分别是一个三角形的三边长 a,b,c(单位:cm): ①5,12,13 ②1.5,2, 2.5 ③4,7.5,8.5 ④6,8,10,这四组数都 满足a2+b2=c2.
分别以每组数为三边长作出三角形,它 们都是直角三角形吗?你是怎么判断的?
第2节 一定是直角三角形吗
温故知新
直角三角形有什么特征?
提出问题
你能用一根绳子得到直角三角形吗?
埃及人的数学智慧
金字塔的地基必须严格地成为正方形, 四个角就必须是严格的直角;不管是哪一 个角有微小的偏差,都会使整个建筑物走 形。那时候还没有发明测量仪器,要做出 周长一公里那么大的正方形, 怎样准确画 出直角,很可能是古埃及人要解决的最大 难题。
3.思考交流:你还有其它的方法来证明这个 结论吗?独立思考后与你的同伴交流.
按规定这个零件中∠DBC也应为直角,工人师傅
量得这个零件各边尺寸如图2所示,这个零件合
格吗?
C D
C
13
D
A
B 图1
4
12
A3B
图2
小结与思考
提出 问题
探索 发现
特殊 验证
大胆 猜想
解决 问题
应用 结论
获得 结论
小心 求证
特殊
一般
特殊
课后作业
1.基础巩固:习题1.3 第1,2,3题;
2.动手实践:做一条古埃及人“神奇的绳 子”,有哪些方法?与你的同伴进行交流.
在RtABC中,AB2 BC2 CA2 a2 b2
a2 b2 c2
N
AB2 c2
A'
AB c
BC a BC
在ABC和ABC中AC b AC b
ABC ABC AB c AB
C C 90
C' a
ABC是直角三角形
B' M
获得结论
如果三角形的三边长a,b,c满足a2+b2=c2,
那么这个三角形是直角三角形.
A
符思号考语1:言这:个结论与勾股定理的区别与
b c 联系∵. 在△ABC中,BC=a, CA=b ,AB=c, 思考2:且如a2+果b2=ac22+,b2≠c2,那么这个三角形
大胆猜想 小心求证
如果三角形 A
已知:如图,在△ABC
的三边长a,b,c满
足a2+b2=c2,那
b
c
中,BC=a, CA=b , AB=c,且a2+b2=c2.
么这个三角形是
直角三角形.
C
a
B 你能否判断△ABC是直 角三角形?并说明理由.
小心求证
证明:画一个 ABC,使C 90, BC a, CA b
C a B 可能∴是△直AB角C三为直角角形三吗角?形说,且说∠你C的=90理°由. .
满足a2+b2=c2的三个正整数,称为勾股数.
应用结论
下列哪组数能作为直角三角形的三边长?说 说你的理由.
(1)7, 24,25; (2)15,17,8; (3)3, 5, 6.
2020/1/1
问题解决
一个零件的形状如图1所示,其中∠A=90°,
绳子围成一个直 角三角形吗?说说你的理由.
特殊验证
下面有四组数分别是一个三角形的三边长 a,b,c(单位:cm): ①5,12,13 ②1.5,2, 2.5 ③4,7.5,8.5 ④6,8,10,这四组数都 满足a2+b2=c2.
分别以每组数为三边长作出三角形,它 们都是直角三角形吗?你是怎么判断的?
