(全优试卷)湖南省郴州市高三第四次质量检测数学(理)试题 Word版含答案
2024届湖南省郴州市高三上学期第一次质检全真演练物理试题

2024届湖南省郴州市高三上学期第一次质检全真演练物理试题一、单选题:本题共7小题,每小题4分,共28分 (共7题)第(1)题如图所示为一走时准确的时钟,分别是分针和时针的端点,在时钟正常工作时()A.B.C.D.第(2)题北京时间2024年1月9日,我国在西昌卫星发射中心采用长征二号丙运载火箭,成功将“爱因斯坦探针”空间科学卫星发射升空,卫星顺利进入高度为、倾角为的近地轨道,发射任务取得圆满成功。
已知同步卫星距地球表面高度约为。
下列说法正确的是( )A.该卫星的运行速度大于第一宇宙速度B.该卫星的运行周期大于C.该卫星轨道处的重力加速度大于D.该卫星运行的角速度大于同步卫星的角速度第(3)题下列物理量中属于矢量的是()A.速率B.电势C.电流D.位移第(4)题一水平固定的水管,水从管口以不变的速度源源不断地喷出,水管距地面高,水落地的位置到管口的水平距离,不计空气及摩擦阻力,水从管口喷出的初速度大小是( )A.1.2m/s B.2.0m/s C.3.0m/s D.4.9m/s第(5)题光纤通信有传输容量大、传输衰减小、抗干扰性及保密性强等多方面的优点,我国的光纤通信起步较早,现已成为技术先进的几个国家之一,如图甲是光纤的示意图,图乙是光纤简化示意图(内芯简化为长直玻璃丝,外套简化为真空),玻璃丝长为AC=L,折射率为n,AB、CD代表端面,光从AB端面以某一入射角θ进入玻璃丝,在玻璃丝内部恰好发生全反射,知光在真空中传播速度为c,下列选项正确的是( )A.内芯相对于外套是光疏介质B.C.光在玻璃丝中传播的速度为c sinθD.光在玻璃丝中从AB端面传播到CD端面所用的时间为第(6)题如图所示,、间所接电源电压恒定,理想变压器原副线圈匝数比为,电路中两个灯泡完全相同,都标有“,”,电表都是理想电表。
调节滑动变阻器,当触头位于某位置时,两个灯泡都正常发光,下列说法正确的是( )A.此时原副线圈中电流相同B.此时滑动变阻器接入电路的阻值与灯泡的阻值相同C.滑动变阻器的触头向下滑动,电压表、的示数不变D.滑动变阻器的触头向下滑动,电流表示数减小第(7)题总质量为m的返回式人造地球卫星沿半径为R的圆轨道绕地球运动到某点时,向原来运动方向喷出气体以降低卫星的速度,随后卫星转到与地球相切的椭圆轨道,要使卫星相对地面的速度变为原来的k倍(k<1),则卫星在该点将质量为的气体喷出的对地速度大小应为(将连续喷气等效为一次性喷气,地球半径为,地球表面重力加速度为g)A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题2021年10月16日,神舟十三号载人飞船发射取得圆满成功,顺利将翟志刚、王亚平、叶光富三位航天员送入太空。
湖南省湘潭市2024高三冲刺(高考数学)部编版质量检测(拓展卷)完整试卷

湖南省湘潭市2024高三冲刺(高考数学)部编版质量检测(拓展卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题已知,若为奇函数,则实数()A.0B.C.1D.2第(2)题的展开式中的系数为()A.40B.C.80D.第(3)题如图是的大致图象,则的解析式可能为()A.B.C.D.第(4)题若P是一个质数,则像这样的正整数被称为梅森数.从50以内的所有质数中任取两个数,则这两个数都为梅森数的概率为()A.B.C.D.第(5)题已知、、,,,,则()A.B.C.D.第(6)题设集合,,则()A.B.C.D.第(7)题已知函数,点为平面内一点,则下列说法错误的是()A.当,时,过点可作曲线的三条切线B.当,时,过点可作曲线的三条切线C.若过点不能作曲线的切线,则,D.若过点可作曲线的两条切线,则,第(8)题小明同学决定在暑假期间花两个月的时间学习5本书,且每个月最多学习3本,至少学习2本,每次学完1本完整的书籍后,再学习下一本,则小明同学恰好在同一个月学习《三国演义》和《水浒传》的概率为()A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题如图,点是直线上的动点,点在直线外,点在直线上,则()A.有最小值B.有最大值C.D.直线上有且只有一点(不同于点),使得第(2)题已知为虚数单位,下列关于复数的命题正确的有()A.B.复数的虚部为C.若,互为共轭复数,则D.若复数为纯虚数,则第(3)题如图,在方格中,向量的始点和终点均为小正方形的顶点,则()A.B.C.D.三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题已知函数,则曲线在处的切线方程为______________.第(2)题设、、均为正数且,则使得不等式总成立的的取值范围为______.第(3)题已知函数,则函数的最大值为____,若函数在上为增函数,则w的取值范围为______.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题如图所示,为的直径,为的中点,为的中点.(1)求证:;(2)求证:第(2)题如图,在梯形中,,,,四边形为矩形,平面平面,.(1)证明:平面;(2)设点在线段上运动,平面与平面的夹角为,求的取值范围.第(3)题如图(1),在梯形中,,,,为中点,现沿将折起,如图(2),其中分别是的中点.(1)求证:平面;(2)若,求二面角的余弦值.第(4)题猜灯谜,是我国独有的民俗文娱活动,是从古代就开始流传的元宵节特色活动.每逢农历正月十五传统民间都要把谜语写在纸条上并贴在彩灯上供人猜.在一次猜灯谜活动中,若甲、乙两名同学分别独立竞猜,甲同学猜对每个灯谜的概率为,乙同学猜对每个灯谜的概率为.假设甲、乙猜对每个灯谜都是等可能的,试求:(1)甲、乙任选1个独立竞猜,求甲、乙恰有一人猜对的概率;(2)活动规定:若某人任选2个进行有奖竞猜,都猜对则可以在箱中参加抽取新春大礼包的活动,中奖概率是;没有都猜对则在箱中参加抽取新春大礼包的活动,中奖概率是,求甲同学抽中新春大礼包的概率;(3)甲、乙各任选2个独立竞猜,设甲、乙猜对灯谜的个数之和为,求的分布列与数学期望.第(5)题猜灯迷是我国一种民俗娱乐活动,某社区在元宵节当天举行了猜灯谜活动,工作人员给每位答题人提供了5道灯谜题目,答题人从中随机选取2道灯迷题目作答,若2道灯谜题目全答对,答题人便可获得奖品.(1)若甲只能答对工作人员所提供的5道题中的2道,求甲能获得类品的概率;(2)若甲不能获得奖品的概率为,求甲能答对所提供灯谜题目的数量.。
湖南省长沙市四县区2024届高三下学期3月调研考试 数学试卷(含解析)

2024年3月高三调研考试试卷数学(长沙县、望城区、浏阳市、宁乡市联合命制)注意事项:1.本试题卷共5页,共四个大题,19个小题.总分150分,考试时量120分钟.2.接到试卷后,请检查是否有缺页、缺题或字迹不清等问题.如有,清及时报告监考老师.3.答题前,务必将自己的姓名、考号写在答题卡和该试题卷的封面上,并认真核对条形码的姓名、考号和科目.4.作答时,请将答案写在答题卡上.在草稿纸、试题卷上答题无效.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}|12A x x =-≤≤,{}|1B x x =<,则()A B ⋃R ð=()A .{}|1x x >B .{}1|x x ≥-C .{}|12<≤x x D .{}|12x x ≤≤2.已知n S 为等差数列{}n a 的前n 项和,若366,3a a ==,则8S =()A .76B .72C .36D .323.设α,β是两个不同的平面,a ,b 是两条不同的直线,且a α⊥,b β⊂,则“//a b ”是“αβ⊥”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.已知双曲线222:1(0)4x y C b b-=>的一个焦点到一条渐近线的距离为2,则双曲线C 的离心率为()A .2B C D 5.将甲、乙、丙、丁4个人全部分配到,,A B C 三个地区工作,每个地区至少有1人,则不同的分配方案为()A .36种B .24种C .18种D .16种6.过点()00,与圆224240x y x y +--+=相切的两条直线夹角为α,则cos α=()A .35B .45C D 7.钝角ABC 中,sin cos a C c B =,则()cos A B -=()A .1B .12C .2D .08.已知抛物线()2:20C y px p =>的焦点为F ,斜率为k 的直线l 经过点F ,并且与抛物线C 交于A B 、两点,与y 轴交于点M ,与抛物线的准线交于点N ,若2AF MN =,则k =()AB C .D .二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得2分,有选错的得0分.9.设z 为非零复数,则下列命题中正确的是()A .22||z z =B .2||z zz=C .22z z=D .若1z =,则i z +的最大值为210.已知函数()1πcos 223f x x ⎛⎫=- ⎪⎝⎭,把()y f x =的图象向右平移π3个单位长度,得到函数()y g x =的图象,以下说法正确的是()A .π6x =是()y f x =图象的一条对称轴B .()f x 的单调递减区间为()π2ππ,π63k k k ⎡⎤++∈⎢⎥⎣⎦Z C .()y g x =的图象关于原点对称D .()()f x g x +的最大值为1211.已知()f x 是定义在R 上的连续函数,且满足()()()2f x y f x f y xy +=+-,当0x >时,()0f x >,设()()2g x f x x =+()A .若()()113f f ⋅-=-,则()11f =B .()g x 是偶函数C .()g x 在R 上是增函数D .()()10x g x ->的解集是()(),01,-∞⋃+∞三、填空题:本题共3小题,每小题5分,共15分.12.已知一组数据如下:4,4,4,7,7,8,8,9,9,10,则这组数据的第75百分位数是.13.一个正四棱锥底面边长为2,则该四棱锥的内切球表面积为.14.已知对任意()12,0,x x ∈+∞,且当12x x <时,都有:()212112ln ln 11a x x x x x x -<+-,则a 的取值范围是.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.如图,在圆锥SO 中,AB 是圆O 的直径,且SAB △是边长为4的等边三角形,,C D 为圆弧AB 的两个三等分点,E 是SB 的中点.(1)证明:DE //平面SAC ;(2)求平面SAC 与平面SBD 所成锐二面角的余弦值.16.已知函数()()22ln f x x ax x a =+-∈R (1)当0a =时,求函数()f x 的极值;(2)若函数()f x 在区间[]1,2上是减函数,求实数a 的取值范围;17.春节临近,为了吸引顾客,我市某大型商超策划了抽奖活动,计划如下:有A 、B 、C 三个抽奖项目,它们之间相互不影响,每个项目每位顾客至多参加一次,项目A 中奖的概率是14,项目B 和C 中奖的概率都是25.(1)若规定每位参加活动的顾客需要依次参加A 、B 、C 三个项目,如果A 、B 、C 三个项目全部中奖,顾客将获得100元奖券;如果仅有两个项目中奖,他将获得50元奖券;否则就没有奖券.求每位顾客获得奖券金额的期望;(2)若规定每位顾客等可能地参加三个项目中的一个项目.已知某顾客中奖了,求他参加的是A 项目的概率.18.如图,已知,A B 分别是椭圆2222:1x y E a b +=的右顶点和上顶点,椭圆E 的离心率为ABO 的面积为1.若过点(),P a b 的直线与椭圆E 相交于,M N 两点,过点M 作x 轴的平行线分别与直线,AB NB 交于点,C D .(1)求椭圆E 的方程.(2)证明:,,M C D 三点的横坐标成等差数列.19.若存在常数t ,使得数列{}n a 满足1123n n a a a a a t +-⋅⋅⋅=(1n ≥,n ∈N ),则称数列{}n a 为“()H t 数列”.(1)判断数列:1,2,3,8,49是否为“()1H 数列”,并说明理由;(2)若数列{}n a 是首项为2的“()H t 数列”,数列{}n b 是等比数列,且{}n a 与{}n b 满足212321log ni n n i aa a a ab ==+∑ ,求t 的值和数列{}n b 的通项公式;(3)若数列{}n a 是“()H t 数列”,n S 为数列{}n a 的前n 项和,11a >,0t >,试比较ln n a 与1n a -的大小,并证明1e n S n n n t S S -+>--.1.B 【分析】由补集和并集的定义直接求解.【详解】集合{}|12A x x =-≤≤,{}|1B x x =<,则{}1|B x x =≥R ð,(){}1|=A B x x ≥-R ð.故选:B 2.C 【分析】根据题意,结合等差数列的求和公式,即可求解.【详解】在等差数列的求和公式,可得()()1836888S 3622a a a a ++===.故选:C.3.A 【分析】由空间中的线面关系结合充分必要条件的判断得答案【详解】由a α⊥,//a b ,则b α⊥,又b β⊂,所以αβ⊥,故“//a b ”是“αβ⊥”的充分条件.当满足αβ⊥,a α⊥,b β⊂时,直线,a b 可能平行,可能相交,也可能异面.故“//a b ”不是“αβ⊥”的必要条件.故选:A 4.B 【分析】根据题意,利用双曲线的几何性质,求得2b =,结合c e a ==.【详解】由双曲线222:1(0,0)4x y C a b b-=>>,可得其渐近线为2b y x =±,不妨取2by x =,即20bx y -=,且焦点(c,0)F ,因为焦点到一条渐近线的距离为22bcb c===,所以双曲线C的离心率c e a ===故选:B.5.A 【分析】把4个人按2:1:1分成3组,再分配到三个不同地区即可.【详解】依题意,,,A B C 三个地区中必有一个地区有2人,先在甲、乙、丙、丁4个人中选2个人有24C 种组合,将这两个人捆绑在一起看作一个元素,与其他2个人一起分配到,,A B C 三个地区,共有2343C A 36=种.故选:A 6.A 【分析】先求圆心和半径,然后设出切线方程,利用圆心到直线的距离等于半径,求出切线方程,再根据两直线的夹角公式即可求出.【详解】224240x y x y +--+=化为标准方程为22(2)(1)1x y -+-=,圆心为(2,1),半径为1,过点(0,0)与圆224240x y x y +--+=相切的两条直线夹角为α,设切线为y kx =,点线距离为d,则1d =,解得43k =或0k =,故切线为43y x =或0y =,故根据两直线的夹角公式得4043tanα43103-==+⨯,且易知α一定为第一象限角,解得cos α=35.故选:A7.D【分析】根据题意,利用正弦定理化简得到sin sin sin cos A C C B ⋅=⋅,进而得到22cos sin A B =,进而判定得到A 为钝角,得出cos sin A B =-,结合两角差的余弦公式,即可求解.【详解】因为sin cos a C c B ⋅=⋅,由正弦定理得sin sin sin cos A C C B ⋅=⋅,在钝角ABC 中,sin 0C ≠,所以sin cos 0A B =>,即22sin cos A B =且B 为锐角,所以221cos 1sin A B -=-,所以22cos sin A B =,若C 为钝角,则090,09090A B A B <+<<<-< ,可得sin cos A B <,这与sin cos A B =矛盾,所以只可能A 为钝角,所以cos sin A B =-,所以()cos cos cos sin sin 0A B A B A B -=+=.故选:D.8.D【分析】设准线与x 轴的交点为P ,过A 作准线的垂线,垂足为A ',,根据抛物线的定义以及三角形的性质可得2AN AA =',根据含30 角的直角三角形的性质可得答案.【详解】当A 在第一象限时,设准线与x 轴的交点为P ,过A 作准线的垂线,垂足为A ',因为OM PN ∥,且O 为PF 的中点,所以OM 为三角形PFN 的中位线,即FM MN =,所以2N AF MN F ==,又根据抛物线的定义AF AA =',所以22AN AF AA ==',所以在直角三角形AA N '中,60A AN '∠=o ,所以60AFx ∠= ,此时k =根据对称性,当A 在第四象限时,k =故选:D.9.BD 【分析】对于A ,结合题意进行判断,举反例即可,对于B ,设()i ,z a b a b R =+∈,先求出共轭复数和模的平方,求解即可,故B 正确,对于C,举反例证明即可,对于D ,利用1z =画出图形,利用几何意义求解即可.【详解】对于A ,设()i ,z a b a b =+∈R ,当,a b 均不为0时,2222(i)2i z a b a b ab =+=-+为虚数,而||222z a b =+为实数,所以22||z z =不成立,故A 错误;对于B ,则i z a b =-,所以22222,||z a b z a b =+=+,而()()22i i zz a b a b a b =+-=+,所以2||z zz =成立,故B 正确;对于C ,设22i,i 1z z ===,又221z i ==-,所以22z z ≠,故C 错误.对于D ,1z =,则复数z 对应的点P 的轨迹是以()0,0O 为圆心,1为半径的圆,()i i z z +=--的几何意义为复数z 对应的点P 与()0,1Q -两点间的距离PQ ,所以,如图可知,当点P 为()0,1时,PQ 最大,i z +取最大值,则最大值为2,故D 正确.故选:BD.10.ABD【分析】根据题意,求得()1cos22g x x =-的图象,结合三角函数的图象与性质,以及两角差的正弦公式,逐项判定,即可求解.【详解】将函数()1πcos 223f x x ⎛⎫=- ⎪⎝⎭的图象向右平移π3个单位长度,得到函数()()11cos 2πcos222y g x x x ==-=-的图象,对于A 中,令π6x =,求得()12f x =,即为函数()y f x =最大值,所以直线π6x =是函数()f x 图象的一条对称轴,所以A 正确;对于B 中,令π2π22ππ,Z 3k x k k ≤-≤+∈,解得π2πππ,Z 63k x k k +≤≤+∈,可得()f x 的单调减区间为π2ππ,π,Z 63k k k ⎡⎤++∈⎢⎥⎣⎦,所以B 正确.对于C 中,由于()1cos22g x x =-是偶函数,可得函数()g x 的图象关于y 轴对称,所以C 错误.对于D 中,由()()1π1cos 2cos2232f x g x x x ⎛⎫⎛⎫+=-+- ⎪ ⎪⎝⎭⎝⎭111cos2cos2222x x x ⎡⎤=-⎢⎥⎣⎦11π1cos2sin 244262x x x ⎛⎫=-=-≤ ⎪⎝⎭,即()()f x g x +的最大值为12,所以D 正确.故选:ABD.11.ACD 【分析】取0x y ==得到()00f =,取1x =,1y =-计算得到A 正确,确定()()22x f x f x -+=-,计算()()g 0x g x +-=得到B 错误,取12x x <,计算()()21g x g x >得到C 正确,考虑1x >,1x =和1x <三种情况,根据函数单调性解得D 正确,得到答案.【详解】对选项A :取0x y ==得到()()()000f f f =+,即()00f =,取1x =,1y =-得到()()()00211f f f +-=+=,又()()113f f ⋅-=-,()10f >,解得()11f =,正确;对选项B :取y x =-得到()()()202f f x f x x -=++,即()()22x f x f x -+=-,()()()()220g x g x f x x f x x +-=++-+=,函数定义域为R ,函数为奇函数,错误;对选项C :设12x x <,则()()()()22212211g x g x f x x f x x -=+--()()()()222221121121211212f x x x x f x x f x x x x x x x =-++--=---+-()()()22221211221122f x x x x x x f x x x x =--++=-+-,0x >时,()0f x >,故()210f x x ->,()1220x x ->,故()()210g x g x ->,即()()21g x g x >,函数单调递增,正确;对选项D :()()0000g f =+=,()()10x g x ->,当1x >时,()0g x >,则0x >,故1x >;当1x =时,不成立;当1x <时,()0g x <,则0x <,故0x <;综上所述:()(),01,x ∞∞∈-⋃+,正确;故选:ACD.12.9【分析】根据题意,利用百分位数的计算方法,即可求解.【详解】由题意,数据4,4,4,7,7,8,8,9,9,10,可得75%107.5⨯=,故第75百分位数是第8个数,即为9.故答案为:9.13.43π##43π【分析】根据三角形相似求出内切球半径,再利用球的表面积公式求其表面积.【详解】由题意可知该几何体为正四棱锥,如图,O 为内切球的球心,PH 是棱锥的高,,E F 分别是,AB CD 的中点,连接,PF G 是球与侧面PCD 的切点,可知G 在PF 上,OG PF ⊥,设内切球半径为r ,则,1,2OH OG r HF PH PF ====,由△PGO ∽△PHF 可知OG PO HF PF =,即12r r=,解得3r =,所以内切球表面积224π4π4π3S r ==⨯=⎝⎭.故答案为:4π3.14.(],2-∞【分析】依题意可得22112111ln ln a x x a x x x x -+<-+对任意的()12,0,x x ∈+∞当12x x <恒成立,令()()1ln ,0,f x a x x x x∞=-+∈+,即可得到()f x 在()0,∞+上单调递减,求出函数的导函数,即可得到()0f x '≤在()0,∞+上恒成立,参变分离可得1a x x≤+在()0,∞+上恒成立,利用基本不等式求出1x x+的最小值,即可得解.【详解】因为对任意()12,0,x x ∈+∞,且当12x x <时()212112ln ln 11a x x x x x x -<+-恒成立,所以21212112ln ln x x a x a x x x x x --<-+恒成立,所以21211211ln ln a x a x x x x x -<-+-恒成立,所以22112111ln ln a x x a x x x x -+<-+恒成立①,令()()1ln ,0,f x a x x x x∞=-+∈+,由①式可得()()21f x f x <,所以()f x 在()0,∞+上单调递减,所以()2210x ax f x x -+'=-≤在()0,∞+上恒成立,所以210x ax -+≥在()0,∞+上恒成立,所以1a x x ≤+在()0,∞+上恒成立,又12x x +≥=,当且仅当1x x =,即1x =时取等号,2a ∴≤.故答案为:(],2-∞【点睛】关键点点睛:本题关键是将式子变形得到22112111ln ln a x x a x x x x -+<-+对任意的()12,0,x x ∈+∞当12x x <恒成立,从而将问题转化为函数在区间上单调递减求参数问题.15.(1)证明见解析(2)15【分析】(1)证明:取SA 的中点F ,连接,,CF EF CD ,由题意可证得DE //CF ,再由线面平行的判定定理证明即可;(2)以O 为坐标原点,,OB OS的方向分别为,y z 轴的正方向,建立如图所示的空间直角坐标系.求出平面SAC 与平面SBD 的法向量,由二面角的向量公式求解即可.【详解】(1)证明:取SA 的中点F ,连接,,CF EF CD .因为,C D 为圆弧AB 的两个三等分点,所以CD //1,2AB CD AB =.因为,E F 分别为,SB SA 的中点,所以EF //1,2AB EF AB =,则CD //,EF EF CD =,从而四边形CDEF 为平行四边形,故DE //CF .因为DE ⊄平面,SAC CF ⊂平面SAC ,所以DE //平面SAC .(2)解:以O 为坐标原点,,OB OS的方向分别为,y z 轴的正方向,建立如图所示的空间直角坐标系.因为4AB SA ==,所以()())0,2,0,0,2,0,3,1,0A B C --,)(3,1,0,0,0,3DS ,则)()3,1,0,0,2,3,3,1,0,AC AS BD BS ====(0,2,3-.设平面SAC 的法向量为()111,,m x y z =,则111130,230,m AC x y m AS y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩ 令11x =,得()1,3,1m = .设平面SBD 的法向量为()222,,n x y z =,则222230,230,n BD x y n BS y z ⎧⋅=-=⎪⎨⋅=-+=⎪⎩ 令21x =,得()3,1n = .设平面SAC 与平面SBD 所成锐二面角为θ,则||1cos |cos ,|||||5m n m n m n θ⋅=〈〉==.故平面SAC 与平面SBD 所成锐二面角的余弦值为15.16.(1)极小值为1,无极大值(2)3a ≤-【分析】(1)求定义域,求导,根据导函数求出单调区间,从而得到极值情况;(2)由题意得在区间[]1,2上()0f x '≤,参变分离,构造函数()22g x x x=-,求出最小值,得到答案.【详解】(1)0a =时,()22ln f x x x =-,定义域为()0,∞+,()22222x f x x x x-'=-=,令()0f x ¢>,解得1x >,令()0f x '<,解得01x <<,故()f x 在1x =处取得极小值,()11f =,()f x \的极小值为()11f =,无极大值.(2)()f x 在区间[]1,2上为减函数,∴在区间[]1,2上()0f x '≤,()22202f x x a a x x x∴=+-⇒≤-'≤,令()22g x x x =-,只需min ()a g x ≤,显然()22g x x x=-在区间[]1,2上为减函数,()min ()2143g x g ∴==-=-,3a ∴≤-17.(1)16(2)521【分析】(1)根据题意先写出获得奖券金额的可能取值,再根据相互独立事件的概率乘法公式计算得出对应的概率后即可计算数学期望;(2)根据条件概率定义及计算公式计算可得.【详解】(1)设一位顾客获得X 元奖券,则X 的可能取值为100,50,0,()122110045525P X ==⨯=,()21212332650C 4554525P X ⎛⎫==⨯⨯⨯+⨯= ⎪⎝⎭,()161801252525P X ==--=,所以每位顾客获得奖券金额的期望是()16100500162525E X =⨯+⨯+=(元)(2)设“该顾客中奖”为事件M ,参加项目A ,B ,C 分别记为事件1N ,2N ,3N ,则()()()31111212734353520i i i P M P N P M N ===⨯+⨯+⨯=∑,所以()()()()()()11111153472120P N P M N P N M P N M P M P M ⨯====,即已知某顾客中奖了,则他参加的是A 项目的概率是521.18.(1)2214x y +=(2)证明见解析【分析】(1)根据已知条件列出方程组222112,ab c a a b c ⎧=⎪⎪⎪=⎨⎪=+⎪⎪⎩计算即可得出结果;(2)设直线MN 方程与椭圆方程联立,设()()1122,,,M x y N x y ,()()11,,,C D C x y D x y 进而利用韦达定理证明12D C x x x +=即可得出结果.【详解】(1)依据题意,222112,ab c a a b c⎧=⎪⎪⎪=⎨⎪=+⎪⎪⎩解得:21,a b c ⎧=⎪=∴⎨⎪=⎩椭圆E 的方程为2214x y +=.(2)解法1:设直线:,MN x my n =+ 直线过点()2,1,2P m n ∴+=.联立方程组2244x my n x y =+⎧⎨+=⎩可得:()2224240m y mny n +++-=,()()()222222Δ44441640m n m n m n =-+-=-+>设()()1122,,,M x y N x y ,则:212122224,44mn n y y y y m m --+==++,():11220,22,AB l x y C y y +-=∴- ,2211BN y l y x x -=+ :,令1y y =可得:()12211D y x x y -=-,下面证明:12D C x x x +=.即证:()121121441y x x yy -+=--,即证:()()()()()()12121211441my n y y my n y y +-+-+=--整理可得即证:()()()1212244240m y y n m y y n ++--+-+=,即证:()()2224224424044n mnm n m n m m --+⋅+--⋅-+=++,整理可得即证:()2248480m mn n m n ++-+=,即证:()2()20m n m n +-+=,2,m n +=∴ 上式成立,原式得证.解法2:设()()()112212,,,1,1,M x y N x y y y MD ≠≠ x 轴,()()11,,,D C D x y C x y ∴,设直线()11,MN MN l mx n y l +-= :过点()12,1,212P m m ∴=⇒=.由方程组()221044mx n y x y ⎧+-=⎨+=⎩可得:当1y ≠时,2848011x xm n y y ⎛⎫+⋅++= ⎪--⎝⎭,12128411x xm y y ∴+=-=---,又,,B D N 三点共线,22111D x xy y ∴=--,111411D x xy y ∴+=---,即()1141D x x y +=--. 点()1,C C x y 在直线:12xAB y +=上,112C x y ∴-=-,142C D x x x ⎛⎫∴+=-⨯- ⎪⎝⎭,即12.,,D C x x x M C D +=∴三点的横坐标成等差数列.解法3:设直线:,MN x my n =+ 直线过点()2,1,2P m n ∴+=.联立方程组2244x my n x y =+⎧⎨+=⎩可得:()2224240m y mny n +++-=,设()()()112212,,,1,1M x y N x y y y ≠≠,则:212122224,,44mn n y y y y m m --+==++()()()()()1221122121211841111()x y x y m n x xy y y y m n -+--+∴+===-----+,又,,B D N 三点共线,21211112,4211111CD D AB x x x x x y y y y k y ∴=∴-==⋅-----12,,,D C x x x M C D ∴+=∴三点的横坐标成等差数列.【点睛】关键点点睛:本题第二问的关键是采用设线法,联立椭圆方程得到韦达定理式,再计算121211x x y y +--为定值,最后再利用,,B D N 三点共线即可证明.19.(1)不是“()1H ”数列(2)1t =-,12n n b +=(3)ln 1n n a a <-,证明见解析【分析】(1)根据“()H t 数列”的定义进行判断,说明理由;(2)根据{}n a 是首项为2的“()H t 数列”,求出23,a a ,由{}n b 是等比数列,设公比为q ,由212321log nin n i aa a a ab ==+∑ ,可得212321111log n n n i n i a a a a a a b +=++=+∑ ,作差可得()2211132121log log n n n n n a a a a a b b a +++--=+ ,利用{}n b 前三项数列,可以求解t 和q ,进而求解等比数列{}n b 的通项公式;(3)根据题意构造函数()ln 1f x x x =-+,求导并判断()f x 在()1,+∞上单调递增,由{}n a 是“()H t 数列”与11,0a t >>,反复利用1231n n a a a a t a +=+ ,可得对于任意的1,n n ≥∈N ,1n a >,进而得到ln 1n n a a <-,推出()12ln n n a a a S n <- ,再利用ln y x =在()0,x ∈+∞上单调递增,得到12e n S nn a a a -< ,通过已知条件变形推出1e n S n n n t S S -+>--.【详解】(1)根据“()H t 数列”的定义,则1t =,故11231n n a a a a a +-= ,因为211a a -=成立,3211a a a -=成立,432181238621a a a a -=-⨯⨯=-=≠不成立,所以1,2,3,8,49不是“()1H 数列”.(2)由{}n a 是首项为2的“()H t 数列”,则22a t =+,334a t =+,由{}n b 是等比数列,设公比为q ,由212321log ni n n i a a a a a b ==+∑ ,则212321111log n n n i n i a a a a a a b +=++=+∑ ,两式作差可得()2211132121log log n n n n n a a a a a b b a +++--=+ ,即()1123212o 1l g n n n qa a a a a a ++-=+ 由{}n a 是“()H t 数列”,则1231n n a a a a t a +-= ,对于1,n n ≥∈N 恒成立,所以()()121121log n n n a t a q a ++++--=,即()1212log log 1n n n t t b b a ++-=++对于1,n n ≥∈N 恒成立,则()()22321log 1log t a t q t a t q ⎧+-=⎪⎨+-=⎪⎩,即()()()()2212log 134log t t t q t t t q ⎧++-=⎪⎨++-=⎪⎩,解得,1t =-,2q =,又由12a =,21121log a a b =+,则14b =,即12n n b +=故所求的1t =-,数列{}n b 的通项公式12n n b +=(3)设函数()ln 1f x x x =-+,则()11f x x'=-,令()0f x '=,解得1x =,当1x >时,()0f x '<,则()ln 1f x x x =-+在区间()1,+∞单调递减,且()1ln1110f =-+=,又由{}n a 是“()H t 数列”,即1231n n a a a a t a +-= ,对于1,n n ≥∈N 恒成立,因为11,0a t >>,则211a t a =+>,再结合121,0,1a t a >>>,反复利用1231n n a a a a t a +=+ ,可得对于任意的1,n n ≥∈N ,1n a >,则()()10n f a f <=,即ln 10n n a a -+<,则ln 1n n a a <-,即11ln 1a a <-,22ln 1a a <-,L ,ln 1n n a a <-,相加可得1212ln ln ln n n a a a a a a n +++<+++- ,则()12ln n n a a a S n <- ,又因为ln y x =在()0,x ∈+∞上单调递增,所以12e n S nn a a a -< ,又1231n n a a a a t a +-= ,所以1e n S nn a t -+-<,即1e n S nn n S S t -+--<,故1en S nn n t S S -+>--.【点睛】关键点睛:本题主要数列的新定义题型,紧扣题意进行求解,同时构造函数,利用导数判断单调是证明不等式的关键.。
湖南省岳阳市2024高三冲刺(高考数学)人教版质量检测(备考卷)完整试卷

湖南省岳阳市2024高三冲刺(高考数学)人教版质量检测(备考卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题在中,点是边的中点,且,点满足(),则的最小值为()A.B.C.D.第(2)题已知,,,则()A.B.C.D.第(3)题已知,分别为双曲线C:的左右焦点,且到渐近线的距离为1,过的直线与C的左、右两支曲线分别交于两点,且,则下列说法正确的为()A.的面积为2B.双曲线C的离心率为C.D.第(4)题数列中,则数列的极限值( )A.等于B.等于C.等于或D.不存在第(5)题已知二面角的平面角为,AB与平面所成角为.记的面积为,的面积为,则的取值范围为()A.B.C.D.第(6)题设,,,则a,b,c的大小关系正确的是()A.B.C.D.第(7)题已知,且,则的最小值为()A.B.C.D.第(8)题已知m、n是不重合的直线,α、β是不重合的平面,有下列命题:①若mα,n∥α,则m∥n;②若m∥α,m∥β,则α∥β;③若α∩β=n,m∥n,则m∥α且m∥β;④若m⊥α,m⊥β,则α∥β.其中真命题的个数是()A.0B.1C.2D.3二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题已知的展开式中各项系数的和为1,则下列结论正确的有()A.B.展开式中二项式系数之和为256C.展开式中常数项为D.展开式系数的绝对值的和为第(2)题如图,在平面四边形ABCD中,△BCD是等边三角形,AB⊥BD且AB=BD,M是AD的中点.沿BD将△BCD翻折,折成三棱锥C﹣ABD,连接BM,翻折过程中,下列说法正确的是()A.存在某个位置,使得CM与BD所成角为锐角B.棱CD上总恰有一点N,使得MN∥平面ABCC.当三棱锥C﹣ABD的体积最大时,AB⊥BCD.∠CMB一定是二面角C﹣AD﹣B的平面角第(3)题下列命题中正确是()A.线性相关系数越大,两个变量的线性相关性越强B.在经验回归方程中,当解释变量每增加1个单位时,响应变量将平均增加0.5个单位C.若随机变量的期望,则D .若,且,则三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题已知数列的前项和为,且,则____________.第(2)题已知向量,,,则与的夹角为______.第(3)题若“,”为真命题,则实数a的取值范围为___________.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题已知函数.(1)若,求的极小值;(2)若对任意的和,不等式恒成立,求的最大值.第(2)题已知的三个内角、、所对的边分别为、、,且,.(Ⅰ)求的值;(Ⅱ)当时,求函数的最大值.第(3)题已知椭圆C.()与抛物线()共焦点,以椭圆的上下顶点M、N和左右焦点F1、F2所围成的四边形MF1NF2的面积为8,经过F2的直线交抛物线于A、B,交椭圆于C、D,且满足.(1)求出椭圆和抛物线的标准方程;(2)若点D在第三象限,且点A在点B上方,点C在点D上方,当△BF 1D面积取得最大值S时,求的值.第(4)题某地兴建一休闲商业广场,欲在如图所示的一块不规则用地规划建成一个矩形的商业楼区,余下作为休闲区域,已知,且AB=BC=2AO=4km,曲线段OC是以O为顶点且开口向上的抛物线的一段,如果要使矩形的相邻两边分别落在AB、BC上,且一个顶点落在曲线段OC上,应如何规划才能使矩形商业楼区的用地面积最大?第(5)题已知椭圆的方程为,由其个顶点确定的三角形的面积为,点在上,为直线上关于轴对称的两个动点,直线与的另一个交点分别为.(1)求的标准方程;(2)证明:直线经过定点;(3)为坐标原点,求面积的最大值.。
2024届湖南省郴州市高三下学期第二次教学质量监测理综全真演练物理试题

2024届湖南省郴州市高三下学期第二次教学质量监测理综全真演练物理试题一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题如图所示,两个半径不等的均匀带电圆环P、Q带电荷量相等,P环的半径大于Q环的,P带正电,Q带负电。
两圆环圆心均在O点,固定在空间直角坐标系中的yOz平面上。
a、b在x轴上,到O点的距离相等,c在y轴上,到O点的距离小于Q环的半径。
取无限远处电势为零,则( )A.O点场强不为零B.a、b两点场强相同C.电子从c处运动到a处静电力做功与路径无关D.电子沿x轴从a到b,电场力先做正功后做负功第(2)题如图所示,导热性能良好的气缸竖直放置,气缸内用轻质活塞封闭了一定质量的理想气体,活塞可沿气缸无摩擦滑动,现往活塞上缓慢增加砂子,当砂子的质量为时,活塞下降的高度为,此过程中气体向外放出的热量为,继续缓慢添加砂子,当砂子的质量为时,活塞又下降了高度,此过程中气体向外放出的热量为,整个过程中环境的气压和温度均保持不变。
关于上述各量的关系,下列说法正确的是( )A.B.C.D.第(3)题在火星上太阳能电池板发电能力有限,因此科学家用放射性材料PuO 2作为发电能源为火星车供电。
PuO2中的Pu元素是,半衰期是87.7年,有75%的原子核发生衰变需经过( )A.43.85年B.87.7年C.175.4年D.263.1年第(4)题如图甲所示是古代用牛车灌溉时的场景,其简化图如图乙所示,已知A、B、C三个圆的半径分别为,C每转一圈能将8个相同竹筒中的水(质量均为m)灌溉到农田中,已知牛每分钟牵引中柱转动n圈,则一个小时内该牛车对农田灌溉水的质量为( )A.B.C.D.第(5)题自然界中氚()是宇宙射线与上层大气间作用,通过核反应生成的,含量极微,工业上一般用中子轰击获取,核反应为。
氚核()具有放射性,其中衰变产生的He核处于高能级,能量不稳定,总衰变方程为,则下列判断正确的是( )A.核反应为衰变B.氚核衰变中释放的γ光子来自C.X、Y由原子核释放,因此原子核中含有X、Y粒子D.X、Y、γ光子三种粒子在真空中传播速度大小相同第(6)题如图所示,理想变压器原线圈与副线圈的匝数比为,ab端接交流电源,此时电路消耗的总功率为P。
湖南省郴州市2024高三冲刺(高考物理)人教版质量检测(培优卷)完整试卷

湖南省郴州市2024高三冲刺(高考物理)人教版质量检测(培优卷)完整试卷一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题关于平抛运动,下列说法中正确的是( )A.平抛运动是匀速运动B.平抛运动是匀变速曲线运动C.平抛运动不是匀变速运动D.作平抛运动的物体落地时速度方向一定是竖直向下的第(2)题“守株待兔”是众所周知的寓言故事。
假设兔子质量为2kg,以15m/s的速度奔跑,撞树后不反弹,作用时间为0.01s,则兔子受到平均撞击力大小为( )A.3N B.30N C.300N D.3000N第(3)题用光电管探究光电效应规律的实验中,当用不同频率的光照射两种光电管的阴极时,得到的遏止电压与入射光的频率的关系分别为图中a、b图线所示。
由图中数据可知( )A.B.C.普朗克常量D.a图线对应的阴极材料的逸出功为第(4)题细绳拴一个质量为m的小球,小球用固定在墙上的水平弹簧支撑,小球与弹簧不粘连,平衡时细绳与竖直方向的夹角为53°,如图所示。
(已知cos 53°=0.6,sin 53°=0.8)以下说法正确的是( )A.小球静止时弹簧的弹力大小为mgB.小球静止时细绳的拉力大小为mgC.细线烧断瞬间小球的加速度立即为gD.细线烧断瞬间小球的加速度立即为第(5)题如图所示是一玻璃球体,其半径为R,O为球心,AB为水平直径。
M点是玻璃球的最高点,来自B点的光线BD从D点射出,出射光线平行于AB,已知∠ABD=30°,光在真空中的传播速度为c,则玻璃的折射率为( )A.B.2C.1.5D.第(6)题“地震预警”是指在地震发生以后,抢在地震波传播到受灾地区前,向受灾地区提前几秒至数十秒发出警报,通知目标区域从而实现预警。
科研机构对波的特性展开研究,如图甲所示为研究过程中简谐波t=0时刻的波形图,M 是此波上的一个质点,平衡位置处于4m处,图乙为质点M的振动图像,则( )A.该列波的传播方向沿x轴正向传播B.该列波的传播速度为4m /sC.质点M在7s内通过的路程为280cmD.质点M在2s内沿x轴运动了8m第(7)题我国北斗卫星导航系统定位精度可达米级,如图P是纬度为的地球表面上一点,质量相同的北斗导航卫星A、B均绕地心O做匀速圆周运动,卫星B是地球静止轨道卫星(同步地球卫星)。
湖南省郴州市2023-2024学年高二下学期期末教学质量监测数学试题(含答案)

郴州市2023-2024学年高二下学期期末教学质量监测数学(试题卷)注意事项:1.试卷分试题卷和答题卡.试卷共6页,有四大题,19小题,满分150分.考试时间120分钟.2.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上,并将准者证条形码粘贴在答题卡的指定位置,3.考生作答时,选择题和非选择题均须作在答题卡上,在试题卷上作答无效考生在答题卡上按答题卡中注意事项的要求答题.4.考试结束后,将试题卷和答题卡一并交回.一、单项选择题(本大题共8小题,每小题5分,共40分,在所给的四个选项中,只有一个最佳答案,多选或不选得0分)1.设x ∈R ,则“3x >”是“2x >”的( )A.必要而不充分条件B.充分而不必要条件C.充要条件D.既不充分也不必要条件2.已知i 为虚数单位,若复数12,z z 在复平面内对应的点分别为()()2,1,1,2-,则复数12z z ⋅=( )A.5iB.5i -C.45i +D.45i-+1sin170=( )A.-4B.4C.-2D.24.已知P 为椭圆2222:1(0)x y C a b a b+=>>上一动点,12F F 、分别为其左右焦点,直线1PF 与C 的另一交点为2,A APF 的周长为16.若1PF 的最大值为6,则该椭圆的离心率为( )A.14 B.13 C.12 D.235.若n 为一组数8,2,4,9,3,10的第六十百分位数,则二项式1nx ⎫+⎪⎭的展开式的常数项是( )A.28B.56C.36D.406.三位老师和4名同学站一排毕业留影,要求老师们站在一起,则不同的站法有:( )A.360种B.540种C.720种D.900种7.已知函数()2(0,0)f x x bx c b c =-+>>的两个零点分别为12,x x ,若12,,2x x -三个数适当调整顺序后可为等差数列,也可为等比数列,则不等式0x bx c-≤-的解集为( )A.(](),45,∞∞-⋃+B.[]4,5C.()[),45,∞∞-⋃+D.(]4,58.设函数()f x 在R 上存在导数(),f x x '∀∈R ,有()()2f x f x x -+=,在()0,∞+上()f x x '<,若()()932262f m f m m --≥-,则实数m 的取值范围是( )A.1,4∞⎡⎫+⎪⎢⎣⎭B.1,2∞⎡⎫+⎪⎢⎣⎭C.[)1,∞+D.3,4∞⎡⎫+⎪⎢⎣⎭二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)9.如图,正方体1111ABCD A B C D -的边长为2,M 为11A D 的中点,动点P 在正方形ABCD 内(包含边界)运动,且MP =.下列结论正确的是( )A.动点P 的轨迹长度为π;B.异面直线MP 与1BB 所成角的正切值为2;C.MP AB ⋅的最大值为2;D.三棱锥P MAD -的外接球表面积为25π4.10.已知定义域在R 上的函数()f x 满足:()1f x +是奇函数,且()()11f x f x -+=--,当[]()21,1,1x f x x ∈-=-,则下列结论正确的是( )A.()f x 的周期4T =B.5324f ⎛⎫=⎪⎝⎭C.()f x 在[]5,4--上单调递增D.()2f x +是偶函数11.锐角ABC 中,角,,A B C 的对边为,,a b c .且满足4,2a b c ==+.下列结论正确的是()A.点A的轨迹的离心率e =3c <<C.ABC 的外接圆周长()4π,5πl ∈D.ABC 的面积()3,6ABC S ∈ 三、填空题(本题共3小题,每小题5分,共15分.)12.若直线:220l kx y k -+-=与曲线:C y =k 的取值范围是__________.13.已知数列{}n a 满足:()()111,11n n a na n a n n +=-+=+.若()1n nnb n a =+,则数列{}n b 的前n 项和n S =__________.14.暑假将临,大学生小明同学准备利用假期探访名胜古迹.已知某座山高䇯入人云,整体呈圆锥形,其半山腰(母线的中点)有一座古寺,与上山入口在同一条母线上,入口和古寺通过一条盘山步道相连,且当时为了节省资金,该条盘山步道是按“到达古寺的路程最短”修建的.如图,已知该座山的底面半径()2km R =,高)km h =,则盘山步道的长度为__________,其中上山(到山顶的直线距离减小)和下山(到山顶的直线距离增大)路段的长度之比为__________.(第一空2分,第二空3分)四、解答题(本大题共5小题,共77分)15.(本题满分13分)在锐角ABC 中,内角,,A B C 所对的边分别为,a b ,c ,且满足()sin cos sin 1cos c A B b C A =+.(1)证明:2A B =;(2)求ca的取值范围.16.(本题满分15分)如图,在四棱锥P ABCD -中,底面ABCD 为正方形,PA ⊥平面,2,ABCD PA AD E ==为线段PD 的中点,F 为线段PC (不含端点)上的动点.(1)证明:平面AEF ⊥平面PCD ;(2)是否存在点F ,使二面角P AF E --的大小为45 ?若存在,求出PFPC的值,若不存在,请说明理由.17.(本题满分15分)已知函数()2cos e ,xf x ax x a =+-∈R .(1)若()f x 在()0,∞+上单调递减,求实数a 的取值范围;(2)当0a =时,求证()1f x <在ππ,22x ⎛⎫∈- ⎪⎝⎭上恒成立.18.(本题满分17分)已知()2,A a 是抛物线2:2C y px =上一点,F 是抛物线的焦点,已知4AF =,(1)求抛物线的方程及a 的值;(2)当A 在第一象限时,O 为坐标原点,B 是抛物线上一点,且AOB 的面积为1,求点B 的坐标;(3)满足第(2)问的条件下的点中,设平行于OA 的两个点分别记为12,B B ,问抛物线的准线上是否存在一点P 使得,12PB PB ⊥.19.(本题满分17分)材料一:在伯努利试验中,记每次试验中事件A 发生的概率为p ,试验进行到事件A 第一次发生时停止,此时所进行的试验次数为ξ,其分布列为()()1(1)1,2,3,k P k p p k ξ-==-⋅=⋯,我们称ξ服从几何分布,记为()GE p ξ~.材料二:求无穷数列的所有项的和,如求2311111112222k k S ∞-==++++=∑ ,没有办法把所有项真的加完,可以先求数列前n 项和11112122nn k nk S -=⎛⎫==- ⎪⎝⎭∑,再求n ∞→时n S 的极限:1lim lim 2122n nn n S S →∞→∞⎛⎫==-= ⎪⎝⎭根据以上材料,我们重复抛掷一颗均匀的骰子,直到第一次出现“6点”时停止.设停止时抛掷骰子的次数为随机变量X.(1)证明:1()1k P X k∞===∑;(2)求随机变量X的数学期望()E X;(3)求随机变量X的方差()D X.郴州市2023-2024学年高二下学期期末教学质量监测数学参考答案和评分细则一、单项选择题(本大题共8小题,每小题5分,共40分,在所给的四个选项中,只有一个最佳答案,多选或不选得0分)1-5BABCA6-8CDD二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)9.ACD 10.BC11.CD三、填空题(本题共3小题,每小题5分,共15分)12.10,2⎛⎤ ⎥⎝⎦13.1nn +14.5:2四、解答题(本大题共5小题,共77分)15.(本题满分13分)(1)由()sin cos sin 1cos c A B b C A =+,结合正弦定理得()sin sin cos sin sin 1cos ,sin 0C A B C B A C =+≠ 可得sin cos cos sin sin A B A B B -=,所以()sin sin A B B -=,所以A B B -=或()πA B B -+=(舍去),所以2A B=(2)在锐角ABC 中,02022032B A B C B ππππ⎧<<⎪⎪⎪<<<⎨⎪⎪<=-<⎪⎩,即ππ64B <<,cos B <<sin sin3sin2cos cos2sin 12cos sin sin2sin22cos c C B B B B B B a A B B B+====-.令1cos ,2,2B t y t t t ==-∈,因为122y t t =-在上单调递增,所以y y>=<=,所以ca∈.16.(1)证明: 底面ABCD为正方形,CD AD∴⊥.PA⊥平面,ABCD PA CD∴⊥.PA AD A⋂=CD∴⊥平面PAD.又AE⊂平面,PAD CD AE∴⊥.,PA PD E=为PD的中点,AE PD∴⊥.,CD PD D AE⋂=∴⊥平面PCD.AE⊂平面,AEF∴平面AEF⊥平面PCD.(2)以AB AD AP、、分别为x轴、y轴、z轴建立空间直角坐标系,()()0,0,0,2,0,0A B,()()()()2,2,0,0,2,0,0,0,2,0,1,1C D P E设(01)PF PCλλ=<<,()()2,2,22,0,1,1AF AP PF AP PC AEλλλλ=+=+=-=,设平面AEF的法向量()111,,m x y z=,则(),12,,m AEmm AFλλλ⎧⋅=⎪=--⎨⋅=⎪⎩()()2,2,0,0,0,2AC AP==,设平面APF的法向量()222,,n x y z=,则,n ACn AP⎧⋅=⎪⎨⋅=⎪⎩解得()1,1,0n=-由题意得:cos45m nm n⋅===,即13λ-=,解得23λ=.从而23PFPC=.17.(1)解:函数(),2cos e xf x ax x=+-,则()2sin e xf x a x=--',对任意的()()0,,0x f x∞∈+'≤恒成立,所以()2e sinxa x g x≤+=,故()e cos1cos0xg x x x x=+≥++>',所以()min 2()01a g x g ≤==,故实数a 的取值范围为1,2∞⎛⎤- ⎥⎝⎦;(2)证明:由题意知,要证在ππ,22x ⎛⎫∈-⎪⎝⎭,上,cos e 1x x -<,令()cos e xh x x =-,则()sin e xh x x =--',显然在ππ,22x ⎛⎫∈-⎪⎝⎭上()h x '单调减,()π0,002h h ⎛⎫->< ⎪⎝⎭'',所以存在0π,02x ⎛⎫∈-⎪⎝⎭,则()000sin e 0x h x x '=--=,所以当0π,2x x ⎛⎫∈-⎪⎝⎭时,()0h x '>,则()h x 单调递增,当0π,2x x ⎛⎫∈ ⎪⎝⎭时,()0h x '<,则()h x 单调递减,所以()0max 00000π()cos ecos sin 04x h x h x x x x x ⎛⎫==-=+=+< ⎪⎝⎭,故()1f x <在ππ,22x ⎛⎫∈-⎪⎝⎭,上恒成立.18.解:(1)由题意242pAF =+=,解得4p =,因此抛物线的方程为2:8C y x =点()2,A a 在抛物线上可得216a =,故4a =±(2)设点B 的坐标为()11,,x y OA 边上的高为h ,我们知道AOB 的面积是:112S h =⨯=1h h =⇒==直线OA 的方程是2y x =,利用B 到直线OA 的距离公式可得:化简得:1121x y -=由于点B 在抛物线上,代入条件可得:22111121184y y y y ⋅-=⇒-=可以得到211440y y --=或211440y y -+=,解这个方程可以得到12y ===±12y =代入拋物线方程可以得到:1x ==或1x ==112x =综上所述,点B的坐标有三个可能的值:12312,2,,22B B B ⎛⎫+- ⎪⎝⎭(3)不存在,理由如下:由(2)知122,2B B +-则12,B B 的中点3,22M ⎛⎫⎪⎝⎭12B B ===M 到准线2x =-的距离等于37222+=因为73.52=>所以,以M 为圆心122B B 为半径的圆与准线相离,故不存在点P 满足题设条件.19.(1)证明:可知()()1151,1,2,3,666k X GE P X k k -⎛⎫⎛⎫~⋅==⋅=⋯ ⎪ ⎪⎝⎭⎝⎭012515151515115615666666666616nn nn S ⎛⎫- ⎪⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎝⎭=⋅+⋅+⋅+⋯+⋅=⨯=- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭-则15()lim lim 1 1.6n n n n k P X k S ∞→∞→∞=⎛⎫⎛⎫===-= ⎪ ⎪ ⎪⎝⎭⎝⎭∑.(2)设1()nn k T k P X k ==⋅=∑0121152535566666666n n -⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⨯+⋯+⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭12151525155666666666n nn n n T --⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⋯+⨯+⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭两式相减,0121115151515566666666666n nn n T -⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⨯+⋯+⨯-⨯ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭01215555555616666666n n n nn T n n -⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+++⋯+-⨯=--⨯ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭则随机变量X 的数学期望55()lim lim 61666n nn n n E X T n →∞→∞⎛⎫⎛⎫⎛⎫⎛⎫==--⨯= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭;(3)1221151()(6)()lim (6)66k nn k k D X k P X k k -∞→∞==⎛⎫=-⋅==-⋅⋅⎪⎝⎭∑∑()2211111236()()(12)()36()k k k k k k P X k k P X k k P X k P X k ∞∞∞∞=====-+⋅===+-=+⋅=∑∑∑∑2211()12636()36;k k k P X k k P X k ∞∞====-⨯+==-∑∑【也可利用()()()22D XE XE X =-】而012122222151515151()123466666666n k k P X k n -∞=⎛⎫⎛⎫⎛⎫⎛⎫==+++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭∑ 121222215515151()12(1)6666666n k k P X k n -∞=⎛⎫⎛⎫⎛⎫⨯==+++-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑ 两式相减:012121151515151()135(21)666666666n k k P X k n -∞=⎛⎫⎛⎫⎛⎫⎛⎫==++++-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭∑ 112()()2()111k k k P X k P X k E X ∞∞===⋅=-==-=∑∑从而:21()66k kP X k ∞===∑.那么21()()3630k D X k P X k ∞===-=∑.。
湖南省郴州市高考数学一模试卷(理科)含答案

湖南省郴州市高考数学一模试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分.1.已知z是纯虚数,是实数,那么z等于()A.2i B.i C.﹣i D.﹣2i2.已知命题p,q,则“¬p为假命题”是“p∧q是真命题”的()A.充分而不必要条件 B.必要而不充分条件C.充要条件 D.既不充分也不必要条件3.某几何体的三视图如图所示,且该几何体的体积是,则正视图中的x的值是()A.B.C.2 D.34.执行如图所示的程序框图,输出的S的值为30,则输入的n为()A.2 B.3 C.4 D.55.已知函数的图象经过点(0,﹣1),则该函数的一个单调递增区间为()A.[﹣,]B.[,]C.[﹣,]D.[,]]6.一个三位自然数的百位,十位,个位上的数字依次为a,b,c,当且仅当a>b且c>b时称为“凹数”.若a,b,c∈{4,5,6,7,8},且a,b,c互不相同,任取一个三位数,则它为“凹数”的概率是()A.B.C.D.7.要得到函数f (x)=sin2x的导函数f′(x)的图象,只需将f (x)的图象()A.向左平移个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变)B.向左平移个单位,再把各点的纵坐标缩短到原来的倍(横坐标不变)C.向左平移个单位,再把各点的纵坐标伸长到原来的倍(横坐标不变)D.向左平移个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变)8.对一批产品的长度(单位:mm)进行抽样检测,下图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在区间[15,20)和区间[25,30)上的为二等品,在区间[10,15)和[30,35)上的为三等品.用频率估计概率,现从该批产品中随机抽取一件,则其为二等品的概率为()aaA.0.09 B.0.20 C.0.25 D.0.459.若双曲线﹣=1的焦距为10,点P(﹣2,1)在其渐近线上,则双曲线的方程为()A.﹣=1 B.﹣=1C.﹣=1 D.﹣=110.已知e是自然对数的底数,函数f(x)=e x+x﹣2的零点为a,函数g(x)=lnx+x﹣2的零点为b,则下列不等式成立的是()A.f(1)<f(a)<f(b)B.f(a)<f(b)<f(1)C.f(a)<f(1)<f(b)D.f(b)<f(1)<f(a)11.若(1+x)+(1+x)2+…+(1+x)5=a0+a1(1﹣x)+a2•(1﹣x)2+…+a5(1﹣x)5,则a1+a2+a3+a4+a5等于()A.5 B.62 C.﹣57 D.﹣5612.已知定义在R上的偶函数f(x)满足f(x+4)=f(x)+f(2),且当x∈[0,2]时,y=f(x)单调递减,给出以下四个命题:①f(2)=0;②y=f(x)在[8,10]单调递增;③x=4为函数y=f(x)图象的一条对称轴;④若方程f(x)=m在[﹣6,﹣2]上的两根为x1,x2,则x1+x2=﹣8以上命题中不正确命题的序号为()A.①B.②C.③D.④二、填空題:本大题共4小题,每小题5分,共20分.13.设x,y满足约束条件,则z=的最大值为.14.如图,在边长为e(e为自然对数的底数)的正方形中随机撒一粒黄豆,则它落到阴影部分的概率为.15.已知⊙M:x2+y2﹣4x﹣4y﹣1=0及圆外一点P(5,5),过P点作⊙M的切线PA,PB,切点分别为A,B,则弦AB的长为.16.对于两个实数a,b,min{a,b}表示a,b中的较小数.设f (x)=min{x,}(x>0),则不等式f (x)≥log42的解集是.三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤17.在数列{a n}中,前n项和为S n,且.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设,求数列{b n}的前项和T n.18.已知△ABC的内角为A、B、C,其对边分别为a、b、c,已知B为锐角,向量,且∥.(Ⅰ)求角B的大小及当时,△ABC的外接圆半径R的取值范围;(Ⅱ)如果b=2,求S△ABC的最大值.19.若f(x)=cos2ax﹣sinaxcosax(a>0)的图象与直线y=m(m>0)相切,并且切点横坐标依次成公差为π的等差数列.(1)求a和m的值;(2)△ABC中a、b、c分别是∠A、∠B、∠C的对边.若(,)是函数f(x)图象的一个对称中心,且a=4,求△ABC周长的取值范围.20.如图,在△ABC中,记,∠B=,AB=8,点D在BC边上,且CD=2,cos∠ADC=.(Ⅰ)试用表示;(Ⅱ)若以B点为坐标原点,BC所在的直线为x轴(正方向为向右)建立平面直角坐标系,使得点A落在第一象限.点P(x,y)在△ABC三边围成的区域(含边界)上,设,求m﹣n的最大值.21.已知数列{a n}中,a1=1,且当x=时,函数f(x)=a n•x2+(2﹣n﹣a n+1)•x取得极值.(1)若b n=2n﹣1•a n,证明数列{b n}为等差数列;(2)设数列c n=,{c n}的前n项和为S n,若不等式mS n<n+4(﹣1)n对任意的正整数n 恒成立,求m的取值范围.22.已知函数.(Ⅰ)若x=3是函数f(x)的极值点,求曲线y=f(x)在点(1,f(1))处的切线方程;(Ⅱ)若函数f(x)在(0,+∞)上为单调增函数,求a的取值范围;(Ⅲ)设m,n为正实数,且m>n,求证:.湖南省郴州市高考数学一模试卷(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.1.已知z是纯虚数,是实数,那么z等于()A.2i B.i C.﹣i D.﹣2i【考点】复数的基本概念;复数代数形式的乘除运算.【专题】计算题.【分析】设出复数z,代入,它的分子、分母同乘分母的共轭复数,化简为a+bi(a,b∈R)的形式.【解答】解:由题意得z=ai.(a∈R且a≠0).∴==,则a+2=0,∴a=﹣2.有z=﹣2i,故选D【点评】本题考查复数的基本概念,复数代数形式的乘除运算,考查计算能力,是基础题.2.已知命题p,q,则“¬p为假命题”是“p∧q是真命题”的()A.充分而不必要条件 B.必要而不充分条件C.充要条件 D.既不充分也不必要条件【考点】复合命题的真假.【专题】对应思想;综合法;简易逻辑.【分析】根据复合命题之间的关系结合充分条件和必要条件的定义即可得到结论.【解答】解:若p∧q是真命题,则p,q都是真命题,则¬p是假命题,即必要性成立,若¬p是假命题,则p是真命题,此时p∧q是真命题,不一定成立,即充分性不成立,故“¬p为假命题”是“p∧q是真命题”的必要不充分条件,故选:B.【点评】本题主要考查充分条件和必要条件的判断,根据复合命题真假之间的关系是解决本题的关键.3.某几何体的三视图如图所示,且该几何体的体积是,则正视图中的x的值是()A.B.C.2 D.3【考点】由三视图求面积、体积.【专题】计算题;空间位置关系与距离.【分析】三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,该几何体为四棱锥.【解答】解:该几何体为四棱锥,其底面为直角梯形,面积S=×(1+2)×2=3,则该几何体的体积V=•3•x=,故x=.故选A.【点评】三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,本题考查了学生的空间想象力,识图能力及计算能力.4.执行如图所示的程序框图,输出的S的值为30,则输入的n为()A.2 B.3 C.4 D.5【考点】程序框图.【专题】计算题;图表型;试验法;算法和程序框图.【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.【解答】解:模拟执行程序,可得k=1,S=0,满足条件k≤n,S=2,k=2满足条件k≤n,S=6,k=3满足条件k≤n,S=14,k=4满足条件k≤n,S=30,k=5由题意,此时应该不满足条件5≤n,退出循环,输出S的值为30,则输入的n为4.故选:C.【点评】本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.5.已知函数的图象经过点(0,﹣1),则该函数的一个单调递增区间为()A.[﹣,]B.[,]C.[﹣,]D.[,]]【考点】正弦函数的图象.【专题】转化思想;综合法;三角函数的图像与性质.【分析】由条件求得φ的值,可得函数的解析式,再利用正弦函数的单调性求得该函数的单调递增区间.【解答】解:∵函数的图象经过点(0,﹣1),∴2sinφ=﹣1,求得sinφ=﹣,可得φ=﹣,∴f(x)=2sin(2x﹣),令2kπ﹣≤2x﹣≤2kπ+,求得kπ﹣≤x≤kπ+,故函数的增区间为[kπ﹣,kπ+],k∈Z.故选:A.【点评】本题主要考查正弦函数的单调性,属于基础题.6.一个三位自然数的百位,十位,个位上的数字依次为a,b,c,当且仅当a>b且c>b时称为“凹数”.若a,b,c∈{4,5,6,7,8},且a,b,c互不相同,任取一个三位数,则它为“凹数”的概率是()A.B.C.D.【考点】列举法计算基本事件数及事件发生的概率.【专题】计算题;整体思想;定义法;概率与统计.【分析】根据题意,分析“凹数”的定义,根据十位数分类讨论即可求出凹数的个数,再利用古典概型概率计算公式即可得到所求概率.【解答】解:根据题意,当且仅当a>b且c>b时称为“凹数”,在{4,5,6,7,8}的5个整数中任取3个不同的数组成三位数,有A53=60种取法,在{4,5,6,7,8}的5个整数中任取3个不同的数,将4放在十位上,再排2个数排在百、个位上,有A42=12种情况,将5放在十位上,再排2个数排在百、个位上,有A32=6种情况,将6放在十位上,再排2个数排在百、个位上,有A22=2种情况,根据分类计数原理可得12+6+2=20种,故它为“凹数”的概率是=.故选:C.【点评】本题考查组合数公式的运用,关键在于根据题干中所给的“凹数”的定义,再利用古典概型概率计算公式即得答案.7.要得到函数f (x)=sin2x的导函数f′(x)的图象,只需将f (x)的图象()A.向左平移个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变)B.向左平移个单位,再把各点的纵坐标缩短到原来的倍(横坐标不变)C.向左平移个单位,再把各点的纵坐标伸长到原来的倍(横坐标不变)D.向左平移个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变)【考点】函数y=Asin(ωx+φ)的图象变换;导数的运算.【专题】计算题;数形结合;数形结合法;导数的概念及应用;三角函数的图像与性质.【分析】求出导函数的解析式,由条件利用诱导公式,函数y=Asin(ωx+φ)的图象变换规律,可得结论.【解答】解:∵f (x)=sin2x,f′(x)=2cos2x=2sin(2x+)=2sin[2(x+)],∴将f (x)的图象向左平移个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变),即可得到导函数f′(x)的图象.故选:D.【点评】本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.8.对一批产品的长度(单位:mm)进行抽样检测,下图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在区间[15,20)和区间[25,30)上的为二等品,在区间[10,15)和[30,35)上的为三等品.用频率估计概率,现从该批产品中随机抽取一件,则其为二等品的概率为()A.0.09 B.0.20 C.0.25 D.0.45【考点】频率分布直方图.【分析】在频率分布表中,由频率与频数的关系,计算可得各组的频率,根据频率的和等于1可求得二等品的概率.【解答】解:由频率分布直方图知识可知:在区间[15,20)和[25,30)上的概率为0.04×5+[1﹣(0.02+0.04+0.06+0.03)×5]=0.45.故选:D.【点评】本小题主要考查样本的频率分布直方图的知识和分析问题以及解决问题的能力.统计初步在近两年高考中每年都以小题的形式出现,基本上是低起点题.9.若双曲线﹣=1的焦距为10,点P(﹣2,1)在其渐近线上,则双曲线的方程为()A.﹣=1 B.﹣=1C.﹣=1 D.﹣=1【考点】双曲线的简单性质.【专题】计算题;圆锥曲线的定义、性质与方程.【分析】利用双曲线C:﹣=1的焦距为10,点P(﹣2,1)在其渐近线上,建立方程组,求出a,b的值,即可求得双曲线的方程.【解答】解:∵双曲线C:﹣=1的焦距为10,点P(﹣2,1)在其渐近线上,∴a2+b2=25,a=2b,∴b=,a=2∴双曲线的方程为﹣=1.故选:C.【点评】本题考查双曲线的标准方程,考查双曲线的几何性质,考查学生的计算能力,属于基础题.10.已知e是自然对数的底数,函数f(x)=e x+x﹣2的零点为a,函数g(x)=lnx+x﹣2的零点为b,则下列不等式成立的是()A.f(1)<f(a)<f(b)B.f(a)<f(b)<f(1)C.f(a)<f(1)<f(b)D.f(b)<f(1)<f(a)【考点】函数零点的判定定理.【专题】计算题;函数的性质及应用.【分析】首先判断两个函数的单调性,再由定义知f(a)=0,f(1)=e+1﹣2>0,g(b)=0,g(1)=0+1﹣2<0,从而可判断0<a<1<b;从而再利用单调性判断大小关系.【解答】解:易知函数f(x)=e x+x﹣2在R上是增函数,g(x)=lnx+x﹣2在(0,+∞)上也是增函数;又∵f(a)=0,f(1)=e+1﹣2>0,g(b)=0,g(1)=0+1﹣2<0,∴0<a<1<b;故f(a)<f(1)<f(b);故选C.【点评】本题考查了函数的单调性的判断与应用及函数零点的判定定理的应用,属于基础题.11.若(1+x)+(1+x)2+…+(1+x)5=a0+a1(1﹣x)+a2•(1﹣x)2+…+a5(1﹣x)5,则a1+a2+a3+a4+a5等于()A.5 B.62 C.﹣57 D.﹣56【考点】二项式定理的应用.【专题】转化思想;综合法;二项式定理.【分析】在所给的等式中,分别令x=1,可得a0=62;令x=0,可得a0+a1+a2+a3+a4+a5 =5,从而求得a1+a2+a3+a4+a5 的值.【解答】解:∵(1+x)+(1+x)2+…+(1+x)5=a0+a1(1﹣x)+a2•(1﹣x)2+…+a5(1﹣x)5,令x=1,可得a0=2+22+23+24+25=62,再令x=0,可得a0+a1+a2+a3+a4+a5 =5,∴a1+a2+a3+a4+a5 =﹣57,故选:C.【点评】本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式的系数和常用的方法是赋值法,属于基础题.12.已知定义在R上的偶函数f(x)满足f(x+4)=f(x)+f(2),且当x∈[0,2]时,y=f(x)单调递减,给出以下四个命题:①f(2)=0;②y=f(x)在[8,10]单调递增;③x=4为函数y=f(x)图象的一条对称轴;④若方程f(x)=m在[﹣6,﹣2]上的两根为x1,x2,则x1+x2=﹣8以上命题中不正确命题的序号为()A.①B.②C.③D.④【考点】奇偶性与单调性的综合.【专题】函数思想;综合法;函数的性质及应用.【分析】根据条件,令x=﹣2便可得到f(2)=2f(2),从而得出f(2)=0,从而得出f(x)是周期为4的周期函数,而f(x)在[0,2]上单调递减,从而得到f(x)在[8,10]上单调递减.容易得到x=4和x=﹣4为f(x)的对称轴,从而便可以得到,即得到x1+x2=﹣8,这样便可得出不正确命题的序号.【解答】解:f(x)为R上的偶函数,且f(x+4)=f(x)+f(2),令x=﹣2得:f(2)=2f(2);∴f(2)=0,∴①正确;∴f(x+4)=f(x);∴f(x)为周期为4的周期函数;f(x)在[0,2]上单调递减,∴f(x)在[0+4×2,2+4×2]=[8,10]上单调递减,∴②错误;f(x)关于y轴对称,即x=0是f(x)的一条对称轴;∴x=4为函数f(x)图象的一条对称轴,∴③正确;x=﹣4为f(x)的一条对称轴,∴;∴x1+x2=﹣8,∴④正确;∴不正确的命题序号为②.故选B.【点评】考查偶函数的定义,周期函数的定义,周期函数的单调性,本题中f(x)的对称轴为x=4n,n∈Z,以及中点坐标公式.二、填空題:本大题共4小题,每小题5分,共20分.13.设x,y满足约束条件,则z=的最大值为2.【考点】简单线性规划.【专题】计算题;对应思想;数形结合法;不等式.【分析】由约束条件作出可行域,利用z=的几何意义,即可行域内的动点与原点连线的斜率求得答案.【解答】解:由约束条件作出可行域如图,联立,解得A(1,2),,∴z=的最大值为2.故答案为:2.【点评】本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题.14.如图,在边长为e(e为自然对数的底数)的正方形中随机撒一粒黄豆,则它落到阴影部分的概率为.【考点】几何概型.【专题】综合题;概率与统计.【分析】利用定积分计算阴影部分的面积,利用几何概型的概率公式求出概率.【解答】解:由题意,y=lnx与y=e x关于y=x对称,∴阴影部分的面积为2(e﹣e x)dx=2(ex﹣e x)=2,∵边长为e(e为自然对数的底数)的正方形的面积为e2,∴落到阴影部分的概率为.故答案为:.【点评】本题考查几何概型,几何概型的概率的值是通过长度、面积、和体积的比值得到.15.已知⊙M:x2+y2﹣4x﹣4y﹣1=0及圆外一点P(5,5),过P点作⊙M的切线PA,PB,切点分别为A,B,则弦AB的长为3.【考点】直线与圆的位置关系.【专题】数形结合;数形结合法;直线与圆.【分析】根据题意,画出图形,结合图形,利用半径r,圆心M到点P的距离MP以及切线长组成直角三角形,即可求出弦长AB.【解答】解:如图所示,⊙M:x2+y2﹣4x﹣4y﹣1=0可化为(x﹣2)2+(y﹣2)2=9,∴圆心为M(2,2),半径为r=3;则圆心M到点P的距离为d=MP==3,∴切线长PA===3,∴弦AB的长为2×=2×=3.故答案为:3.【点评】本题考查了直线与圆的应用问题,也考查了勾股定理的应用问题,是基础题目.16.对于两个实数a,b,min{a,b}表示a,b中的较小数.设f (x)=min{x,}(x>0),则不等式f (x)≥log42的解集是[,2].【考点】其他不等式的解法.【专题】计算题;数形结合;数形结合法;不等式的解法及应用.【分析】先根据,min{a,b}表示a,b中的较小数求得函数f(x),再按分段函数的图象解得用满足f(x)<时x的集合.【解答】解:根据,min{a,b}表示a,b中的较小数,得到函数f(x)=min{x,}(x>0)的图象,如图所示:当x=或2时,y=,由图象可知,f (x)≥log42的解集是[,2],故答案为:[,2]【点评】本题考查了其他不等式的解法,是一道新定义题,首先要根据新定义求得函数图象,再应用函数图象解决相关问题,这类问题的解决,正确转化是关键.三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤17.在数列{a n}中,前n项和为S n,且.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设,求数列{b n}的前项和T n.【考点】数列的求和;数列递推式.【专题】综合题;方程思想;转化思想;等差数列与等比数列..【分析】(I)由,可得n=1时,a1=S1=1;n≥2时,a n=S n﹣S n﹣1(II)=,利用“错位相减法”与等比数列的前n项和公式即可得出.=﹣【解答】解:(I)∵,∴n=1时,a1=S1=1;n≥2时,a n=S n﹣S n﹣1=n.n=1时也成立.∴a n=n.(II)=,∴数列{b n}的前项和T n=++…+,=+…++,∴=+…+﹣=﹣=,∴T n=2﹣.【点评】本题考查了等比数列的通项公式及其前n项和公式、“错位相减法”、递推关系,考查了推理能力与计算能力,属于中档题.18.已知△ABC的内角为A、B、C,其对边分别为a、b、c,已知B为锐角,向量,且∥.(Ⅰ)求角B的大小及当时,△ABC的外接圆半径R的取值范围;(Ⅱ)如果b=2,求S△ABC的最大值.【考点】余弦定理;平面向量共线(平行)的坐标表示.【专题】计算题;转化思想;解三角形;不等式的解法及应用;平面向量及应用.【分析】(Ⅰ)由平面向量共线(平行)的坐标表示可得2sinB•(2cos2﹣1)+cos2B=0,利用三角函数恒等变换的应用化简可得2sin(2B+)=0,结合B为锐角可求B,由正弦定理即可得解.(Ⅱ)由余弦定理可得ac=a2+c2﹣4,利用基本不等式可得ac≤4,根据三角形面积公式即可求其最大值.【解答】(本题满分为12分)解:(Ⅰ)∵∥,⇒2sinB•(2cos2﹣1)+cos2B=0,…⇒sin2B+cos2B=0⇒2sin(2B+)=0(B为锐角)⇒2B=⇒B=,…∴R=[1,2]…(Ⅱ)由cosB==,可得:ac=a2+c2﹣4,…∵a2+c2≥2ac,∴ac≤4,…∴S△ABC=acsinB≤=,即S△ABC的最大值为.…【点评】本题主要考查了平面向量共线(平行)的坐标表示,三角函数恒等变换的应用,正弦定理,余弦定理,基本不等式,三角形面积公式在解三角形中的应用,考查了转化思想和数形结合思想的应用,属于中档题.19.若f(x)=cos2ax﹣sinaxcosax(a>0)的图象与直线y=m(m>0)相切,并且切点横坐标依次成公差为π的等差数列.(1)求a和m的值;(2)△ABC中a、b、c分别是∠A、∠B、∠C的对边.若(,)是函数f(x)图象的一个对称中心,且a=4,求△ABC周长的取值范围.【考点】正弦定理;两角和与差的正弦函数;二倍角的正弦;y=Asin(ωx+φ)中参数的物理意义.【专题】综合题;解三角形.【分析】(1)由题意,函数f(x)的周期为π,且最大(或最小)值为m,利用三角恒等变换可化简f(x),从而可求结果;(2)由(,)是函数f(x)图象的一个对称中心可求A,利用正弦定理可把周长化为三角函数,进而可求答案;【解答】解:(1)=,由题意,函数f(x)的周期为π,且最大(或最小)值为m,而m>0,,∴a=1,;(2)∵(是函数f(x)图象的一个对称中心,∴,又∵A为△ABC的内角,∴,△ABC中,则由正弦定理得:,∴,∵,∴b+c+a∈(8,12].【点评】该题考查正弦定理、两角和与差的正弦函数、倍角公式等知识,考查学生综合运用知识解决问题的能力.20.如图,在△ABC中,记,∠B=,AB=8,点D在BC边上,且CD=2,cos∠ADC=.(Ⅰ)试用表示;(Ⅱ)若以B点为坐标原点,BC所在的直线为x轴(正方向为向右)建立平面直角坐标系,使得点A落在第一象限.点P(x,y)在△ABC三边围成的区域(含边界)上,设,求m﹣n的最大值.【考点】平面向量数量积的运算.【专题】计算题;数形结合;向量法;平面向量及应用;不等式.【分析】(Ⅰ)可设(0<λ<1),从而,这便可得到,而,根据条件即可得到,从而便可求出,这样便可解出,从而用表示出向量;(Ⅱ)根据题意便可求出点B,A,C三点的坐标,从而求出向量的坐标,这样根据便可求出,从而得到,这样即可求出,从而由线性规划的知识即可求出m﹣n的最大值.【解答】解:(Ⅰ)由题意不妨设,则;∴;;又;∴;∴==,;∴=;解得;∴;(Ⅱ)由题意知;∴;∴=;又P(x,y),∴;∴;∴;∵点P(x,y)在△ABC三边围成的区域(含边界)上,由线性规划知识知,当点P处于点A()位置时m﹣n最大,且最大值为1.【点评】考查向量数乘的几何意义,向量数量积的运算及计算公式,向量长度的求法:,以及向量夹角的余弦公式,完全平方式的运用,能求平面直角坐标系下点的坐标,根据点的坐标可求向量的坐标,向量坐标的加法和数乘运算,以及线性规划的方法求变量的最值.21.已知数列{a n}中,a1=1,且当x=时,函数f(x)=a n•x2+(2﹣n﹣a n+1)•x取得极值.(1)若b n=2n﹣1•a n,证明数列{b n}为等差数列;(2)设数列c n=,{c n}的前n项和为S n,若不等式mS n<n+4(﹣1)n对任意的正整数n 恒成立,求m的取值范围.【考点】数列的求和;等差关系的确定.【专题】等差数列与等比数列.【分析】(1)通过对f(x)=a n•x2+(2﹣n﹣a n+1)•x求导,利用,计算可知b n+1=b n+1,进而可知数列{b n}是首项、公差均为1的等差数列;(2)通过(1)可知b n=n,裂项可知c n=﹣,并项相加得S n=,进而问题转化为求f(n)=的最小值,进而计算可得结论.【解答】(1)证明:∵f(x)=a n•x2+(2﹣n﹣a n+1)•x,∴f′(x)=,∴,即a n+﹣a n+1=0,∴2n a n+1=2n﹣1a n+1,即b n+1=b n+1,又∵=1,∴数列{b n}是首项、公差均为1的等差数列;(2)解:由(1)可知b n=n,∴c n===﹣,∴S n=1﹣+﹣+…+﹣=1﹣=,∵不等式mS n<n+4(﹣1)n对任意的正整数n恒成立,∴m<=1+n+对任意的正整数n恒成立,记f(n)=1+n+,则f(1)=﹣6,f(2)=9,f(3)=﹣,f(4)=10,…,显然当n=1时f(n)取最小值,∴m<f(1)=﹣6,∴m的取值范围是(﹣∞,﹣6).【点评】本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.22.已知函数.(Ⅰ)若x=3是函数f(x)的极值点,求曲线y=f(x)在点(1,f(1))处的切线方程;(Ⅱ)若函数f(x)在(0,+∞)上为单调增函数,求a的取值范围;(Ⅲ)设m,n为正实数,且m>n,求证:.【考点】利用导数研究曲线上某点切线方程;利用导数研究函数的极值.【专题】方程思想;分析法;导数的概念及应用;不等式的解法及应用.【分析】(Ⅰ)求出导数,由题意可得f′(3)=0,代入可得a=,可得切线的斜率和切点,进而得到切线的方程;(Ⅱ)由函数f(x)在(0,+∞)上为单调增函数,可得f′(x)≥0在x>0恒成立,即有x2+(2﹣2a)x+1≥0,当x>0时,2a﹣2≤x+,求得右边函数的最小值,即可得到a的范围;(Ⅲ)运用分析法证明.要证,只需证<,即证ln﹣>0,设h(x)=lnx﹣,求出导数判断单调性,运用单调递增,即可得证.【解答】解:(Ⅰ)f(x)的导数为f′(x)=﹣=,由题意可得f′(3)=0,代入可得a=,检验成立.可得切线的斜率为f′(1)=﹣,切点为(1,0),可得切线的方程为x+3y﹣1=0;(Ⅱ)f′(x)=,由函数f(x)在(0,+∞)上为单调增函数,可得f′(x)≥0在x>0恒成立,即有x2+(2﹣2a)x+1≥0,当x>0时,2a﹣2≤x+,由x+≥2=2,当且仅当x=1时,取得最小值2,即有2a﹣2≤2,可得a≤2,可得a的取值范围是(﹣∞,2];(Ⅲ)证明:要证,只需证<,即证ln>,即证ln﹣>0,设h(x)=lnx﹣,由(Ⅱ)知,h(x)在(1,+∞)递增,又>1,可得h()>h(1)=0,即ln﹣>0,故.【点评】本题考查导数的运用:求切线的斜率和单调区间、极值,考查不等式的证明,注意运用分析法,以及构造函数,判断单调性,考查化简整理的运算能力,属于中档题.。
湖南省郴州市部分学校2024-2025学年高二上学期第一次月考数学试题含答案

高二数学试卷(答案在最后)注意事项:1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.4.本试卷主要考试内容:人教A 版必修第一、二册占60%,选择性必修第一册第一章至第二章第4节占40%.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集{}1,2,3,4,5U =,{}2,4A =,{}1,4,5B =,则()UB A ⋂=ð()A.{}3B.{}4C.{}1,4 D.{}1,5【答案】D 【解析】【分析】利用补集与交集的定义可求解.【详解】因为全集{}1,2,3,4,5U =,{}2,4A =,所以{}U 1,3,5A =ð,又因为{}1,4,5B =,(){}{}{}U 51,3,51,4,51,A B == ð.故选:D.2.已知复数1i z a =+(0a >),且3z =,则a =()A.1B.2C.D.【答案】D 【解析】【分析】利用复数的模的定义即可求解.【详解】因为1i z a =+,3z =3=,解得a =±,因为0a >,所以a =故选:D,3.已知1sin 3α=,π0,2α⎛⎫∈ ⎪⎝⎭,则πcos 22α⎛⎫-= ⎪⎝⎭()A.9B.19-C.79-D.9-【答案】A 【解析】【分析】根据同角三角函数关系得出余弦值,再结合诱导公式化简后应用二倍角正弦公式计算即可.【详解】因为221sin ,sin cos 13ααα=+=,又因为π0,2α⎛⎫∈ ⎪⎝⎭,所以cos 3α===,所以π12242cos 2sin22sin cos 22339αααα⎛⎫-===⨯⨯ ⎪⎝⎭.故选:A.4.已知定义在R 上的函数()f x 满足()()0f x f x -+=,且当0x ≤时,()22x af x =+,则()1f =()A.2B.4C.2- D.4-【答案】A 【解析】【分析】利用题意结合奇函数的定义判断()f x 是奇函数,再利用奇函数的性质求解即可.【详解】因为定义在R 上的函数()f x 满足()()0f x f x -+=,所以()f x 是奇函数,且()00f =,故0202a+=,解得2a =-,故当0x ≤时,()222x f x =-+,由奇函数性质得()()11f f =--,而()121222f --=-+=-,故()()112f f =--=,故A 正确.故选:A5.在正方体1111ABCD A B C D -中,二面角1B AC B --的正切值为()A.2B.3C.3D.【答案】D 【解析】【分析】取AC 的中点M ,连接1,MB MB ,可得1B MB ∠是二面角1B AC B --的平面角,求解即可.【详解】取AC 的中点M ,连接1,MB MB ,由正方体1111ABCD A B C D -,可得11,AB B C AB BC ==,所以1,B M AC BM AC ⊥⊥,所以1B MB ∠是二面角1B AC B --的平面角,设正方体1111ABCD A B C D -的棱长为2,可得AC =,所以BM =在1Rt B B M 中,11tan B B B MB BM =∠==,所以二面角1B AC B --.故答案为:D.6.已知线段AB 的端点B 的坐标是()3,4,端点A 在圆()()22124x y -+-=上运动,则线段AB 的中点P的轨迹方程为()A.()()22232x y -+-= B.()()22231x y -+-=C.()()22341x y -+-= D.()()22552x y -+-=【答案】B 【解析】【分析】设出动点P 和动点A 的坐标,找到动点P 和动点A 坐标的关系,再利用相关点法求解轨迹方程即可.【详解】设(,)P x y ,11(,)A x y ,由中点坐标公式得1134,22x y x y ++==,所以1123,24x x y y =-=-,故(23,2)A x y --4,因为A 在圆()()22124x y -+-=上运动,所以()()222312424x y --+--=,化简得()()22231x y -+-=,故B 正确.故选:B7.我国古代数学名著《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的棱柱称为堑堵.已知在堑堵111ABC A B C -中,π2ABC ∠=,1AB BC AA ==,,,D E F 分别是所在棱的中点,则下列3个直观图中满足BF DE ⊥的有()A.0个B.1个C.2个D.3个【答案】B 【解析】【分析】建立空间直角坐标系,利用空间位置关系的向量证明逐个判断即可.【详解】在从左往右第一个图中,因为π2ABC ∠=,所以AB BC ⊥,因为侧棱垂直于底面,所以1AA ⊥面ABC ,如图,以B 为原点建立空间直角坐标系,设12AB BC AA ===,因为,,D E F 分别是所在棱的中点,所以(0,0,0),(0,1,0),(1,0,2),(1,1,0)B E D F所以(1,1,0)BF = ,(1,1,2)DE =-- ,故110BF DE ⋅=-+=,即BF DE ⊥得证,在从左往右第二个图中,我们建立同样的空间直角坐标系,此时(0,0,0),(1,1,0),(1,0,2),(0,1,1)B E D F ,所以(0,1,1)BF = ,(0,1,2)DE =-,故121BF DE ⋅=-=-,所以,BF DE 不垂直,在从左往右第三个图中,我们建立同样的空间直角坐标系,此时(0,0,0),(1,1,0),(1,0,0),(1,1,2)B E D F ,故(1,1,2)BF = ,(0,1,0)DE = ,即1BF DE ⋅=,所以,BF DE 不垂直,则下列3个直观图中满足BF DE ⊥的有1个,故B 正确.故选:B8.已知过点()1,1P 的直线l 与x 轴正半轴交于点A ,与y 轴正半轴交于点B ,O 为坐标原点,则22OA OB+的最小值为()A.12B.8C.6D.4【答案】B 【解析】【分析】根据题意可知直线l 的斜率存在设为(0)k k <,分别解出,A B 两点的坐标,表示出22OA OB +的表达式由基本不等式即可求得最小值.【详解】由题意知直线l 的斜率存在.设直线的斜率为(0)k k <,直线l 的方程为1(x 1)y k -=-,则1(1,0),(0,1)A B k k--,所以222222121(1)(1)112OA OB k k kk k k+=-+-=-++-+22212(2)28k k k k =+--++≥++=,当且仅当22212,k k k k-=-=,即1k =-时,取等号.所以22OA OB +的最小值为8.故选:B.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得分分,有选错的得0分.9.已知函数()πsin 24f x x ⎛⎫=+ ⎪⎝⎭,则()A.()f x 的最小正周期为πB.()f x 的图象关于直线π85x =对称C.()f x 的图象关于点π,18⎛⎫- ⎪⎝⎭中心对称D.()f x 的值域为[]1,1-【答案】ABD 【解析】【分析】求得最小正周期判断A ;求得对称轴判断B ;求得对称中心判断C ;求得值域判断D.【详解】因为()πsin 24f x x ⎛⎫=+ ⎪⎝⎭,所以的最小正周期为2ππ2T ==,故A 正确;由ππ2π,Z 42x k k +=+∈,可得ππ,Z 28k x k =+∈,所以()f x 图象的对称轴为ππ,Z 28k x k =+∈,当1k =时,图象的关于π85x =对称,故B 正确;由Z 2ππ,4k x k =∈+,可得ππ,Z 28k x k =-∈,所以()f x 图象的对称中心为ππ(,0),Z 28k k -∈,当0k =时,图象的关于点()π8,0-对称,故C 不正确;由()πsin 2[1,1]4f x x ⎛⎫=+∈- ⎪⎝⎭,故()f x 的值域为[]1,1-,故D 正确.故选:ABD.10.若数据1x ,2x ,3x 和数据4x ,5x ,6x 的平均数、方差、极差均相等,则()A.数据1x ,2x ,3x ,4x ,5x ,6x 与数据1x ,2x ,3x 的平均数相等B.数据1x ,2x ,3x ,4x ,5x ,6x 与数据1x ,2x ,3x 的方差相等C.数据1x ,2x ,3x ,4x ,5x ,6x 与数据1x ,2x ,3x 的极差相等D.数据1x ,2x ,3x ,4x ,5x ,6x 与数据1x ,2x ,3x 的中位数相等【答案】ABC 【解析】【分析】运用平均数,方差,极差,中位数的计算方法和公式计算,通过已知两组数据的平均数、方差、极差均相等这个条件,来分析这两组数据组合后的相关统计量与原数据的关系.【详解】设数据123,,x x x 的平均数为x ,数据456,,x x x 的平均数也为x .那么数据123456,,,,,x x x x x x 的平均数为123456()()3366x x x x x x x xx ++++++==,所以数据123456,,,,,x x x x x x 与数据123,,x x x 的平均数相等,A 选项正确.设数据123,,x x x 的方差为2s ,数据456,,x x x 的方差也为2s .对于数据123456,,,,,x x x x x x ,其方差计算为2222221234561[()((()()()]6x x x x x x x x x x x x -+-+-+-+-+-2222221234561[3(()(())3(((())]6x x x x x x x x x x x x =⨯-+-+-+⨯-+-+-2221(33)6s s s =+=,所以数据123456,,,,,x x x x x x 与数据123,,x x x 的方差相等,B 选项正确.设数据123,,x x x 的极差为R ,数据456,,x x x 的极差也为R .对于数据123456,,,,,x x x x x x ,其极差是这六个数中的最大值减去最小值,由于前面两组数据的极差相等,所以组合后数据的极差依然是R ,所以数据123456,,,,,x x x x x x 与数据123,,x x x 的极差相等,C 选项正确.设数据123,,x x x 按从小到大排列为123x x x ≤≤,中位数为2x .设数据456,,x x x 按从小到大排列为456x x x ≤≤,中位数为5x .对于数据123456,,,,,x x x x x x 按从小到大排列后,中位数不一定是2x ,所以数据123456,,,,,x x x x x x 与数据123,,x x x 的中位数不一定相等,D 选项错误.故选:ABC11.已知四棱柱1111ABCD A B C D -的底面是边长为6的菱形,1AA ⊥平面ABCD ,13AA =,π3DAB ∠=,点P 满足1AP AB AD t AA λμ=++,其中λ,μ,[]0,1t ∈,则()A.当P 为底面1111D C B A 的中心时,53t λμ++=B.当1t λμ++=时,AP 长度的最小值为2C.当1t λμ++=时,AP 长度的最大值为6D.当221t λμλμ++==时,1A P为定值【答案】BCD 【解析】【分析】根据题意,利用空间向量进行逐项进行分析求解判断.【详解】对于A ,当P 为底面1111D C B A 的中心时,由1AP AB AD t AA λμ=++ ,则11,,122t λμ===故2t λμ++=,故A 错误;对于B ,当1t λμ++=时,()22222222112·AP AB AD t AA AB AD t AA AB ADλμλμλμ=++=+++()()222223693636936t t λμλμλμλμ=+++=++-22245723636457236362t t t t λμλμ+⎛⎫=-+-≥-+- ⎪⎝⎭223273654273644t t t ⎛⎫=-+=-+⎪⎝⎭当且仅当13,84t λμ===,取最小值为2,故B 正确;对于C ,当1t λμ++=时,1AP AB AD t AA λμ=++,则点P 在1A BD 及内部,而AP是以A 为球心,以AP 为半径的球面被平面1A BD 所截图形在四棱柱1111ABCD A B C D -及内的部分,当=1=0t λμ=,时,=6AP ,当=0=10t λμ=,,时,=6AP ,可得1A P最大值为6,故C 正确;对于D ,221t λμλμ++==,()22223693636945AP t λμλμ=+++=+= ,而11=A P A A AP +,所以()22222111111=+2·=+2A P A A AP A A AP A A AP A A AB AD t AA λμ++⋅++ 22211=29452936A A AP t A A +-=+-⨯= ,则16A P = 为定值,故D 正确.故答案选:BCD.三、填空题:本题共3小题,每小题5分,共15分.12.已知向量()1,2a =- ,(),4b m =-.若()a ab ⊥+ ,则m =__________.【答案】3-【解析】【分析】利用平面向量的坐标运算结合平面向量垂直的性质建立方程,求解参数即可.【详解】因为向量()1,2a =- ,(),4b m =- ,所以()1,2a b m +=--,因为()a ab ⊥+,所以(1)40m ---=,解得3m =-.故答案为:3-13.已知在正四棱台1111ABCD A B C D -中,()0,4,0AB = ,()13,1,1CB =- ,()112,0,0A D =-,则异面直线1DB 与11A D 所成角的余弦值为__________.【答案】19【解析】【分析】利用向量的线性运算求得1DB,根据向量的夹角公式可求异面直线1DB 与11A D 所成角的余弦值.【详解】111(0,4,0)(3,1,1)(3,3,1)DB DC CB AB CB =+=+=+-=,所以111111111·cos ,19·DB A D DB A D DB A D ==-,所以异面直线1DB 与11A D所成角的余弦值为19.故答案为:1914.已知函数()21xg x =-,若函数()()()()()2121f x g x a g x a =+--+⎡⎤⎣⎦有三个零点,则a 的取值范围为__________.【答案】()2,1--【解析】【分析】令()0f x =,可得()2g x =或()1g x a =--,函数有三个零点,则需方程()1g x a =--有两个解,则=与1y a =--的图象有两个交点,数形结合可求解.【详解】令()0f x =,可得()()()()21210g x a g x a ⎡⎤+--+=⎣⎦,所以()()()[2][1]0g x g x a -++=,所以()2g x =或()1g x a =--,由()2g x =,又()21xg x =-,可得212x -=,解得21x =-或23x =,方程21x =-无解,方程23x =有一解,故()2g x =有一解,要使函数()()()()()2121f x g x a g x a ⎡⎤=+--+⎣⎦有三个零点,则()1g x a =--有两解,即=与1y a =--的图象有两个交点,作出函数=的图象的示图如下:由图象可得011a <--<,解得21a -<<-.所以a 的取值范围为(2,1)--.故答案为:(2,1)--.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.在ABC V 中,角A ,B ,C 的对边分别为a ,b ,c ,已知2cos c b a B +=.(1)若π2A =,求B ;(2)若a =1b =,求ABC V 的面积.【答案】(1)π4(2)12【解析】【分析】(1)利用正弦定理化边为角,再结合内角和定理与两角和与差的正弦公式化简等式得sin sin()B A B =-,代入π2A =求解可得;(2)由sin sin()B A B =-根据角的范围得2A B =,由正弦定理结合二倍角公式可得2cos 2B =,从而得π4B =,再利用余弦定理求边c ,由面积公式可求结果.【小问1详解】因为2cos c b a B +=,所以由正弦定理得,sin sin 2sin cos C B A B +=,又sin sin()sin cos cos sin C A B A B A B =+=+代入上式得,所以()sin sin cos cos sin sin =-=-B A B A B A B ,由π2A =,则B 为锐角,且c sin s os n π2i B B B ⎛⎫-= ⎭=⎪⎝,所以π4B =.【小问2详解】由(1)知,()sin sin B A B =-,因为a =1b =,所以A B >,则0πA B <-<,π02B <<,故B A B =-,或πB A B A +-==(舍去).所以2A B =,又a =1b =,由正弦定理得sin sin 22cos sin sin A B aB B B b====,则2cos 2B =,则π4B =,由余弦定理得2222cos b a c ac B =+-,则2122c =+-,化简得2210c c -+=,解得1c =,所以111sin 2222ABC S ac B === .故ABC V 的面积为12.16.甲、乙、丙三人打台球,约定:第一局由甲、乙对打,丙轮空;每局比赛的胜者与轮空者进行下一局对打,负者下一局轮空,如此循环.设甲、乙、丙三人水平相当,每场比赛双方获胜的概率都为12.(1)求甲连续打四局比赛的概率;(2)求在前四局中甲轮空两局的概率;(3)求第四局甲轮空的概率.【答案】(1)18(2)14(3)38【解析】【分析】(1)由题意知甲前三局都要打胜,计算可得甲连续打四局比赛的概率;(2)甲轮空两局的情况为,第一局甲败,第二局轮空,第三局甲败,第四局轮空,计算即可;(3)分析可得甲第四轮空有两种情况:第1种情况,第一局甲败,第二局轮空,第三局甲败,第四局轮空,第2种情况,第一局甲胜,第二局甲胜,第三局甲败,第四局轮空,计算即可.【小问1详解】若甲连续打四局,根据比赛规则可知甲前三局都要打胜,所以甲连续打四局比赛的概率311(28=;【小问2详解】在前四局中甲轮空两局的情况为,第一局甲败,第二局轮空,第三局甲败,第四局轮空,故在前四局中甲轮空两局的概率111(1(1)224-⨯-=;【小问3详解】甲第四轮空有两种情况:第1种情况,第一局甲败,第二局轮空,第三局甲败,第四局轮空,第2种情况,第一局甲胜,第二局甲胜,第三局甲败,第四局轮空,第1种情况的概率111(1)(1224-⨯-=;第2种情况的概率1111(12228⨯⨯-=;由互斥事件的概率加法公式可得第四局甲轮空的概率为113488+=.17.如图,在几何体PABCD 中,PA ⊥平面ABC ,//PA DC ,AB AC ⊥,2PA AC AB DC ===,E ,F 分别为棱PB ,BC 的中点.(1)证明://EF 平面PAC .(2)证明:AB EF ⊥.(3)求直线EF 与平面PBD 所成角的正弦值.【答案】(1)证明见解析(2)证明见解析(3)6【解析】【分析】(1)构造线线平行,证明线面平行.(2)先证AB ⊥平面PACD ,得到AB PC ⊥,结合(1)中的结论,可得AB EF ⊥.(3)问题转化为直线PC 与平面PBD 所成角的正弦值.设1CD =,表示CP 的长,利用体积法求C 到平面PBD 的距离,则问题可解.【小问1详解】如图,连接CP .在BCP 中,E ,F 分别为棱PB ,BC 的中点,所以//EF CP ,,又EF ⊄平面PAC ,CP ⊂平面PAC .所以//EF 平面PAC .【小问2详解】因为PA ⊥平面ABC ,AB ⊂平面ABC ,所以PA AB ⊥,又AB AC ⊥,,PA AC ⊂平面PAC ,且PA AC A = ,所以AB ⊥平面PAC .因为CP ⊂平面PAC ,所以AB CP ⊥.又因为//EF CP ,所以AB EF ⊥.【小问3详解】因为//EF CP ,所以直线EF 与平面PBD 所成角与直线PC 与平面PBD 所成角相等,设为θ.不妨设1CD =,则=PC 设C 到平面PBD 的距离为h .则13C PBD PBD V S h -=⋅ .又11212333C PBDB PCD PCD V V S AB --==⋅=⨯⨯= .在PBD △中,PB =BD PD ==,所以12PBD S =⨯= .所以33C PBD PBD V h S -=== .所以63sin θ6h PC ===.故直线EF 与平面PBD.18.设A 是由若干个正整数组成的集合,且存在3个不同的元素a ,b ,c A Î,使得a b b c -=-,则称A 为“等差集”.(1)若集合{}1,3,5,9A =,B A ⊆,且B 是“等差集”,用列举法表示所有满足条件的B ;(2)若集合{}21,,1A m m =-是“等差集”,求m 的值;(3)已知正整数3n ≥,证明:{}23,,,,nx x x x ⋅⋅⋅不是“等差集”.【答案】(1)答案见解析(2)2m =(3)证明见解析【解析】【分析】(1)根据等差集的定义结合子集的定义求解即可;(2)根据等差集定义应用a b b c -=-,即2a c b +=逐个计算判断即可;(3)应用反证法证明集合不是等差集.【小问1详解】因为集合{}1,3,5,9A =,B A ⊆,存在3个不同的元素a ,b ,c B ∈,使得a b b c -=-,则{}1,3,5,9B =或{}1,3,5B =或{}1,5,9B =.【小问2详解】因为集合{}21,,1A m m =-是“等差集”,所以221m m =+-或2211m m =+-或()2221m m +=-,计算可得12m -±=或0m =或2m =或14m =,又因为m 正整数,所以2m =.【小问3详解】假设{}22,,,,nx x x x⋅⋅⋅是“等差集”,则存在{},,1,2,3,,,m n q n m n q ∈<< ,2n m q x x x =+成立,化简可得2m n q n x x --=+,0m n x ->因为*N ,1x q n ∈-≥,所以21q n x x ->≥≥,所以=1与{}22,,,,nx x x x ⋅⋅⋅集合的互异性矛盾,所以{}22,,,,nx x x x⋅⋅⋅不是“等差集”.【点睛】方法点睛:解题方法是定义的理解,应用反证法设集合是等差集,再化简计算得出矛盾即可证明.19.过点()00,A x y 作斜率分别为1k ,2k 的直线1l ,2l ,若()120k k μμ=≠,则称直线1l ,2l 是()A K μ定积直线或()()00,x y K μ定积直线.(1)已知直线a :()0y kx k =≠,直线b :13y x k=-,试问是否存在点A ,使得直线a ,b 是()A K μ定积直线?请说明理由.(2)在OPM 中,O 为坐标原点,点P 与点M 均在第一象限,且点()00,M x y 在二次函数23y x =-的图象上.若直线OP 与直线OM 是()()0,01K 定积直线,直线OP 与直线PM 是()2P K -定积直线,直线OM 与直线PM 是()00,202x y K x ⎛⎫-⎪⎝⎭定积直线,求点P 的坐标.(3)已知直线m 与n 是()()2,44K --定积直线,设点()0,0O 到直线m ,n 的距离分别为1d ,2d ,求12d d 的取值范围.【答案】(1)存在,理由见解析(2)()1,2(3)[)0,8【解析】【分析】(1)由定积直线的定义运算可求结论;(2)设直线OM 的斜率为()0λλ≠,则直线OP 的斜率为1λ,利用定积直线的定义可得01x λ=或1-,进而2003x x λ-=,计算即可;(3)设直线():42m y t x -=+,直线()4:42n y x t-=-+,其中0t ≠,计算得12d d =,利用基本不等式可求12d d 的取值范围.【小问1详解】存在点()0,0A ,使得a ,b 是()A K μ定积直线,理由如下:由题意可得1133k k ⎛⎫⋅-=- ⎪⎝⎭,由()013y kx k y x k ⎧=≠⎪⎨=-⎪⎩,解得00x y =⎧⎨=⎩,故存在点()0,0A ,使得a ,b 是()A K μ定积直线,且13μ=-.【小问2详解】设直线OM 的斜率为()0λλ≠,则直线OP 的斜率为1λ,直线PM 的斜率为2λ-.依题意得()2022x λλ⋅-=-,得2201x λ=,即01x λ=或1-.直线OM 的方程为y x λ=,因为点()200,3M x x -在直线OM 上,所以2003x x λ-=.因为点M 在第一象限,所以20031x x λ-==,解得02x =或2-(舍去),12λ=,()2,1M ,所以直线OP 的方程为12y x x λ==,直线PM 的方程为()2213y x x λ=--+=-+,由23y x y x =⎧⎨=-+⎩,得12x y =⎧⎨=⎩,即点P 的坐标为()1,2.【小问3详解】设直线():42m y t x -=+,直线()4:42n y xt-=-+,其中0t ≠,则12d d ===2216171725t t ++≥=,当且仅当2216t t =,即24t =时,等号成立,所以08≤<,即1208d d ≤<,故12d d 的取值范围为[)0,8.【点睛】思路点睛:理解新定义题型的含义,利用定积直线的定义进行计算求解,考查了运算求解能力,以及基本不等式的应用.。
湖南2023-2024学年高三上学期月考卷(四)数学试题含答案

湖南2024届高三月考试卷(四)数学(答案在最后)一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数12z i =+,其中i 为虚数单位,则复数2z 在复平面内对应的点的坐标为()A.()4,5- B.()4,3 C.()3,4- D.()5,4【答案】C 【解析】【分析】根据题意得234i z =-+,再分析求解即可.【详解】根据题意得:()22212i 14i 4i 34i z =+=++=-+,所以复数2z 在复平面内对应的点的坐标为:()3,4-.故选:C.2.若随机事件A ,B 满足()13P A =,()12P B =,()34P A B ⋃=,则()P A B =()A.29B.23C.14D.16【答案】D 【解析】【分析】先由题意计算出()P AB ,再根据条件概率求出()P A B 即可.【详解】由题意知:()3()()()4P A B P A P B P AB ==+- ,可得1131()32412P AB =+-=,故()1()1121()62P AB P A B P B ===.故选:D.3.设{}n a 是公比不为1的无穷等比数列,则“{}n a 为递减数列”是“存在正整数0N ,当0n N >时,1n a <”的()A.充分而不必要条件B.必要而不充分条件C .充分必要条件D.既不充分也不必要条件【答案】A【解析】【分析】根据充分条件、必要条件的定义判断即可.【详解】解:因为{}n a 是公比不为1的无穷等比数列,若{}n a 为递减数列,当11a >,则01q <<,所以11n n a a q -=,令111n n a a q -=<,则111n qa -<,所以1111log log qq n a a ->=-,所以11log q n a >-时1n a <,当101a <<,则01q <<,所以111n n a a q -=<恒成立,当11a =,则01q <<,所以11n n a a q -=,当2n ≥时1n a <,当10a <,则1q >,此时110n n a a q -=<恒成立,对任意N*n ∈均有1n a <,故充分性成立;若存在正整数0N ,当0n N >时,1n a <,当10a <且01q <<,则110n n a a q -=<恒成立,所以对任意N*n ∈均有1n a <,但是{}n a 为递增数列,故必要性不成立,故“{}n a 为递减数列”是“存在正整数0N ,当0n N >时,1n a <”的充分不必要条件;故选:A4.设π(0,2α∈,π(0,)2β∈,且1tan tan cos αβα+=,则()A.π22αβ+=B.π22αβ-=C.π22βα-= D.π22βα+=【答案】D 【解析】【分析】根据给定等式,利用同角公式及和角的正弦公式化简变形,再利用正弦函数性质推理即得.【详解】由1tan tan cos αβα+=,得sin sin 1cos cos cos αβαβα+=,于是sin cos cos sin cos αβαββ+=,即πsin()sin()2αββ+=-,由π(0,)2α∈,π(0,2β∈,得20π,0<ππ2αββ<+-<<,则π2αββ+=-或ππ2αββ++-=,即π22βα+=或π2α=(不符合题意,舍去),所以π22βα+=.故选:D5.若52345012345(12)(1)(1)(1)(1)(1)x a a x a x a x a x a x -=+-+-+-+-+-,则下列结论中正确的是()A.01a = B.480a =C.50123453a a a a a a +++++= D.()()10024135134a a a a a a -++++=【答案】C 【解析】【分析】利用二项式定理,求指定项的系数,各项系数和,奇次项系数和与偶数项系数和.【详解】由()52345012345(12)1(1)(1)(1)(1)x a a x a x a x a x a x -=+-+-+-+-+-,对于A 中,令1x =,可得01a =-,所以A 错误;对于B 中,[]55(12)12(1)x x -=---,由二项展开式的通项得44145C (2)(1)80a =⋅-⋅-=-,所以B 错误;对于C 中,012345a a a a a a +++++与5(12(1))x +-的系数之和相等,令11x -=即50123453a a a a a a +++++=,所以C 正确;对于D 中,令2x =,则50123453a a a a a a +++++=-,令0x =,则0123451a a a a a a -+-+-=,解得5024312a a a -+++=,5135312a a a --++=,可得()()10024135314a a a a a a -++++=,所以D 错误.故选:C.6.函数()()12cos 2023π1f x x x ⎡⎤=++⎣⎦-在区间[3,5]-上所有零点的和等于()A.2B.4C.6D.8【答案】D【分析】根据()y f x =在[]3,5-的零点,转化为11y x =-的图象和函数2cosπy x =的图象在[]3,5-交点的横坐标,画出函数图象,可得到两图象关于直线1x =对称,且()y f x =在[]3,5-上有8个交点,即可求出.【详解】因为()()112cos 2023π2cosπ11f x x x x x ⎡⎤=++=-⎣⎦--,令()0f x =,则12cosπ1x x =-,则函数的零点就是函数11y x =-的图象和函数2cosπy x =的图象在[]3,5-交点的横坐标,可得11y x =-和2cosπy x =的函数图象都关于直线1x =对称,则交点也关于直线1x =对称,画出两个函数的图象,如图所示.观察图象可知,函数11y x =-的图象和函数2cosπy x =的图象在[]3,5-上有8个交点,即()f x 有8个零点,且关于直线1x =对称,故所有零点的和为428⨯=.故选:D7.点M 是椭圆()222210x y a b a b+=>>上的点,以M 为圆心的圆与x 轴相切于椭圆的焦点F ,圆M 与y 轴相交于P ,Q ,若PQM 是钝角三角形,则椭圆离心率的取值范围是()A.(0,2B.0,2⎛⎫⎪ ⎪⎝⎭ C.,12⎛⎫⎪ ⎪⎝⎭D.(2-【解析】【分析】依据题目条件可知圆的半径为2b a ,画出图形由PQMc >,即可求得椭圆离心率的取值范围.【详解】依题意,不妨设F 为右焦点,则(),M c y ,由圆M与x 轴相切于焦点F ,M 在椭圆上,易得2b y a =或2b y a =-,则圆的半径为2b a.过M 作MN y ⊥轴垂足为N ,则PN NQ =,MN c =,如下图所示:PM ,MQ 均为半径,则PQM为等腰三角形,∴PN NQ ==∵PMQ ∠为钝角,∴45PMN QMN ∠=∠> ,即PN NQ MN c =>=c >,即4222b c c a ->,得()222222a a c c ->,得22a c ->,故有210e -<,从而解得6202e <<.故选:B8.已知函数22,0,()414,0,x x f x x x ⎧⎪=⎨-++<⎪⎩ 若存在唯一的整数x ,使得()10f x x a -<-成立,则所有满足条件的整数a 的取值集合为()A.{2,1,0,1}--B.{2,1,0}--C.{1,0,1}-D.{2,1}-【答案】A 【解析】【分析】作出()f x 的图象,由不等式的几何意义:曲线上一点与(,1)a 连线的直线斜率小于0,结合图象即可求得a 范围.【详解】作出()f x 的函数图象如图所示:()10f x x a-<-表示点()(),x f x 与点(),1a 所在直线的斜率,可得曲线()f x 上只有一个点()(),x f x (x 为整数)和点(),1a 所在直线的斜率小于0,而点(),1a 在动直线1y =上运动,由()20f -=,()14f -=,()00f =,可得当21a -≤≤-时,只有点()0,0满足()10f x x a -<-;当01a ≤≤时,只有点()1,4-满足()10f x x a-<-.又a 为整数,可得a 的取值集合为{}2,1,0,1--.故选:A.二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分、9.已知双曲线C过点(,且渐近线方程为3y x =±,则下列结论正确的是()A.C 的方程为2213x y -= B.CC.曲线21x y e -=-经过C 的一个焦点D.直线10x --=与C 有两个公共点【答案】AC 【解析】【分析】由双曲线的渐近线为3y x =±,设出双曲线方程,代入已知点的坐标,求出双曲线方程判断A ;再求出双曲线的焦点坐标判断B ,C ;联立方程组判断D .【详解】解:由双曲线的渐近线方程为33y x =±,可设双曲线方程为223x y λ-=,把点代入,得923λ-=,即1λ=.∴双曲线C 的方程为2213x y -=,故A 正确;由23a =,21b =,得2c ==,∴双曲线C3=,故B 错误;取20x -=,得2x =,0y =,曲线21x y e -=-过定点(2,0),故C 正确;联立221013x x y ⎧-=⎪⎨-=⎪⎩,化简得220,0y -+-=∆=,所以直线10x -=与C 只有一个公共点,故D 不正确.故选:AC .10.已知向量a ,b 满足2a b a += ,20a b a ⋅+= 且2= a ,则()A.2b =B.0a b +=C.26a b -= D.4a b ⋅=【答案】ABC 【解析】【分析】由2a b a += ,得20a b b ⋅+= ,又20a b a ⋅+= 且2= a ,得2b = ,4a b ⋅=- ,可得cos ,1a b a b a b⋅==- ,,πa b = ,有0a b += ,26a b -= ,可判断各选项.【详解】因为2a b a += ,所以222a b a += ,即22244a a b b a +⋅+= ,整理可得20a b b ⋅+= ,再由20a b a ⋅+= ,且2= a ,可得224a b == ,所以2b = ,4a b ⋅=- ,A 选项正确,D 选项错误;cos ,1a b a b a b⋅==- ,即向量a ,b 的夹角,πa b = ,故向量a ,b 共线且方向相反,所以0a b += ,B 选项正确;26a b -=,C 选项正确.故选:ABC11.如图,正方体1111ABCD A B C D -的棱长为2,点M 是其侧面11ADD A 上的一个动点(含边界),点P是线段1CC 上的动点,则下列结论正确的是()A.存在点,P M ,使得二面角--M DC P 大小为23πB.存在点,P M ,使得平面11B D M 与平面PBD 平行C.当P 为棱1CC 的中点且PM =时,则点M 的轨迹长度为23πD.当M 为1A D 中点时,四棱锥M ABCD-外接球的体积为3【答案】BC 【解析】【分析】由题意,证得1,CD MD CD DD ⊥⊥,得到二面角--M DC P 的平面角1π0,2MDD ⎡∠∈⎤⎢⎥⎣⎦,可得判定A 错误;利用线面平行的判定定理分别证得11//B D 平面BDP ,1//MB 平面BDP ,结合面面平行的判定定理,证得平面//BDP 平面11MB D ,可判定B 正确;取1DD 中点E ,证得PE ME ⊥,得到2ME ==,得到点M 在侧面11ADD A 内运动轨迹是以E 为圆心、半径为2的劣弧,可判定C 正确;当M 为1AD 中点时,连接AC 与BD 交于点O ,求得OM OA OB OC OD ====,得到四棱锥M ABCD -外接球的球心为O ,进而可判定D 错误.【详解】在正方体1111ABCD A B C D -中,可得CD ⊥平面11ADD A,因为MD ⊂平面11ADD A ,1DD ⊂平面11ADD A ,所以1,CD MD CD DD ⊥⊥,所以二面角--M DC P 的平面角为1∠MDD ,其中1π0,2MDD ⎡∠∈⎤⎢⎥⎣⎦,所以A 错误;如图所示,当M 为1AA 中点,P 为1CC 中点时,在正方体1111ABCD A B C D -中,可得11//B D BD ,因为11B D ⊄平面BDP ,且BD ⊂平面BDP ,所以11//B D 平面BDP ,又因为1//MB DP ,且1MB ⊄平面BDP ,且DP ⊂平面BDP ,所以1//MB 平面BDP ,因为1111B D MB B = ,且111,B D MB ⊂平面11MB D ,所以平面//BDP 平面11MB D ,所以B 正确;如图所示,取1DD 中点E ,连接PE ,ME ,PM ,在正方体1111ABCD A B C D -中,CD ⊥平面11ADD A ,且//CD PE ,所以PE ⊥平面11ADD A ,因为ME ⊂平面11ADD A ,可得PE ME ⊥,则2==ME ,则点M 在侧面11ADD A 内运动轨迹是以E 为圆心、半径为2的劣弧,分别交AD ,11A D 于2M ,1M ,如图所示,则121π3D E D M M E ∠=∠=,则21π3M M E ∠=,劣弧12M M 的长为π3π223⨯=,所以C 正确当M 为1A D 中点时,可得AMD 为等腰直角三角形,且平面ABCD ⊥平面11ADD A ,连接AC 与BD 交于点O ,可得OM OA OB OC OD =====,所以四棱锥M ABCD -外接球的球心即为AC 与BD 的交点O ,所以四棱锥M ABCD -,其外接球的体积为348233π⨯=,所以D 错误.故选:BC.12.若存在实常数k 和b ,使得函数()F x 和()G x 对其公共定义域上的任意实数x 都满足:()F x kx b≥+和()G x kx b ≤+恒成立,则称此直线y kx b =+为()F x 和()G x 的“隔离直线”,已知函数()()2f x x R x =∈,()()10g x x x=<,()2ln h x e x =(e 为自然对数的底数),则()A.()()()m x f x g x =-在x ⎛⎫∈ ⎪⎝⎭内单调递增;B.()f x 和()g x 之间存在“隔离直线”,且b 的最小值为4-;C.()f x 和()g x 之间存在“隔离直线”,且k 的取值范围是[]4,1-;D.()f x 和()h x 之间存在唯一的“隔离直线”y e =-.【答案】ABD 【解析】【分析】令()()()m x f x g x =-,利用导数可确定()m x 单调性,得到A 正确;设()f x ,()g x 的隔离直线为y kx b =+,根据隔离直线定义可得不等式组22010x kx b kx bx ⎧--≥⎨+-≤⎩对任意(),0x ∈-∞恒成立;分别在0k =和0k <两种情况下讨论b 满足的条件,进而求得,k b 的范围,得到B 正确,C 错误;根据隔离直线过()f x 和()h x 的公共点,可假设隔离直线为y kx e =-;分别讨论0k =、0k <和0k >时,是否满足()()e 0f x kx x ≥->恒成立,从而确定k =,再令()()e G x h x =--,利用导数可证得()0G x ≥恒成立,由此可确定隔离直线,则D 正确.【详解】对于A ,()()()21m x f x g x x x=-=-,()212m x x x '∴=+,()3321221m x x x ⎛⎫''=-=- ⎪⎝⎭,当x ⎛⎫∈ ⎪⎝⎭时,()0m x ''>,()m x '∴单调递增,()2233220m x m ⎛'∴>-=--+= ⎝,()m x ∴在x ⎛⎫∈ ⎪⎝⎭内单调递增,A 正确;对于,B C ,设()f x ,()g x 的隔离直线为y kx b =+,则21x kx bkx bx ⎧≥+⎪⎨≤+⎪⎩对任意(),0x ∈-∞恒成立,即22010x kx b kx bx ⎧--≥⎨+-≤⎩对任意(),0x ∈-∞恒成立.由210kx bx +-≤对任意(),0x ∈-∞恒成立得:0k ≤.⑴若0k =,则有0b =符合题意;⑵若0k <则有20x kx b --≥对任意(),0x ∈-∞恒成立,2y x kx b =-- 的对称轴为02kx =<,2140k b ∆+∴=≤,0b ∴≤;又21y kx bx =+-的对称轴为02bx k =-≤,2240b k ∴∆=+≤;即2244k b b k⎧≤-⎨≤-⎩,421664k b k ∴≤≤-,40k ∴-≤<;同理可得:421664b k b ≤≤-,40b ∴-≤<;综上所述:40k -≤≤,40b -≤≤,B 正确,C 错误;对于D , 函数()f x 和()h x 的图象在x =处有公共点,∴若存在()f x 和()h x 的隔离直线,那么该直线过这个公共点.设隔离直线的斜率为k,则隔离直线方程为(y e k x -=,即y kx e =-+,则()()e 0f x kx x ≥->恒成立,若0k =,则()2e 00x x -≥>不恒成立.若0k <,令()()20u x x kx e x =-+>,对称轴为02k x =<()2u x x kx e ∴=-+在(上单调递增,又0ue e =--=,故0k <时,()()e 0f x kx x ≥->不恒成立.若0k >,()u x 对称轴为02kx =>,若()0u x ≥恒成立,则()(22340k e k ∆=-=-≤,解得:k =.此时直线方程为:y e =-,下面证明()h x e ≤-,令()()2ln G x e h x e e x =--=--,则()x G x x-'=,当x =时,()0G x '=;当0x <<()0G x '<;当x >()0G x '>;∴当x =()G x 取到极小值,也是最小值,即()min 0G x G==,()()0G x e h x ∴=--≥,即()h x e ≤-,∴函数()f x 和()h x 存在唯一的隔离直线y e =-,D 正确.故选:ABD .【点睛】本题考查导数中的新定义问题的求解;解题关键是能够充分理解隔离直线的定义,将问题转化为根据不等式恒成立求解参数范围或参数值、或不等式的证明问题;难点在于能够对直线斜率范围进行准确的分类讨论,属于难题.三、填空题:本题共4小题,每小题5分,共20分.13.已知函数()y f x =的图像在点()()11M f ,处的切线方程是122y x =+,则()()11f f '+=______.【答案】3【解析】【分析】根据导数的几何意义,可得'(1)f 的值,根据点M 在切线上,可求得(1)f 的值,即可得答案.【详解】由导数的几何意义可得,'1(1)2k f ==,又()()11M f ,在切线上,所以15(1)1222f =⨯+=,则()()11f f '+=3,故答案为:3【点睛】本题考查导数的几何意义的应用,考查分析理解的能力,属基础题.14.如图,由3个全等的钝角三角形与中间一个小等边三角形DEF 拼成的一个较大的等边三角形ABC ,若3AF =,33sin 14ACF ∠=,则DEF 的面积为________.【解析】【分析】利用正弦定理以及余弦定理求得钝角三角形的三边长,根据等边三角形的性质以及面积公式,可得答案.【详解】因为EFD △为等边三角形,所以60EFD ∠= ,则120EFA ∠= ,在AFC △中,由正弦定理,则sin sin AF ACACF AFC=∠∠,解得sin 7sin 23314AF AC AFC ACF =⋅∠==∠,由余弦定理,则2222cos AC AF FC AF FC AFC =+-⋅⋅∠,整理可得:21499232FC FC ⎛⎫=+-⨯⋅⋅- ⎪⎝⎭,则23400FC FC +-=,解得5FC =或8-(舍去),等边EFD △边长为532-=,其面积为122sin 602⨯⨯⋅=o .15.已知数列{}n a 的首项132a =,且满足1323n n n a a a +=+.若123111181n a a a a +++⋅⋅⋅+<,则n 的最大值为______.【答案】15【解析】【分析】应用等差数列定义得出等差数列,根据差数列通项公式及求和公式求解计算即得.【详解】因为12312133n n n n a a a a ++==+,所以1112,3n n a a +=+,即11123n n a a +-=,且1123a =,所以数列1n a ⎧⎫⎨⎬⎩⎭是首项为23,公差为23的等差数列.可求得()12221333n nn a =+-=,所以()()1232211111212222333n n n n n n a a a a ++⨯+⨯++⨯+++⋅⋅⋅+===,即()()181,12433n n n n +<+<且()*1,N n n n +∈单调递增,1516240,1617272⨯=⨯=.则n 的最大值为15.故答案为:15.16.在棱长为3的正方体1111ABCD A B C D -中,点E 满足112A E EB =,点F 在平面1BC D 内,则|1||A F EF +的最小值为___________.【答案】6【解析】【分析】以点D 为原点,建立空间直角坐标系,由线面垂直的判定定理,证得1A C ⊥平面1BC D ,记1AC 与平面1BC D 交于点H ,连接11A C ,1,C O ,AC ,得到12A H HC =,结合点()13,0,3A 关于平面1BC D 对称的点为()1,4,1G --,进而求得1A F EF +的最小值.【详解】以点D 为原点,1,,DA DC DD所在直线分别为,,x y z 轴,建立空间直角坐标系D xyz -,如图所示,则()13,0,3A ,()3,2,3E ,()0,3,0C,因为BD AC ⊥,1BD A A ⊥,且1AC A A A ⋂=,则BD ⊥平面1A AC ,又因为1AC ⊂平面1A AC ,所以1BD A C ⊥,同理得1BC ⊥平面11A B C ,因为1AC ⊂平面11A B C ,所以11BC A C ^,因为1BD BC B = ,且1,BD BC ⊂平面1BC D ,所以1A C ⊥平面1BC D ,记1AC 与平面1BC D 交于点H ,连接11A C ,1C O ,AC ,且AC BD O = ,则11121A H A C HC OC ==,可得12A H HC =,由得点()13,0,3A 关于平面1BC D 对称的点为()1,4,1G --,所以1A F EF +的最小值为6EG ==.故答案为:6.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.已知函数()23sin 2cos 2xf x x m ωω=++的最小值为2-.(1)求函数()f x 的最大值;(2)把函数()y f x =的图象向右平移6πω个单位,可得函数()y g x =的图象,且函数()y g x =在0,8π⎡⎤⎢⎥⎣⎦上为增函数,求ω的最大值.【答案】(1)2(2)4【解析】【分析】(1)化简函数为()2sin 16f x x m πω⎛⎫=+++ ⎪⎝⎭,再根据函数()f x 的最小值为2-求解;(2)利用平移变换得到()2sin g x x ω=的图象,再由()y g x =在0,8π⎡⎤⎢⎥⎣⎦上为增函数求解.【小问1详解】解:()23sin 2cos 2xf x x m ωω=++,3sin cos 1x x m ωω=+++,2sin 16x m πω⎛⎫=+++ ⎪⎝⎭,函数()f x 的最小值为2-212m ∴-++=-,解得1m =-,则()2sin 6f x x πω⎛⎫=+⎪⎝⎭,∴函数()f x 的最大值为2.【小问2详解】由(1)可知:把函数()2sin 6f x x πω⎛⎫=+ ⎪⎝⎭向右平移6πω个单位,可得函数()2sin y g x x ω==的图象.()y g x = 在0,8π⎡⎤⎢⎥⎣⎦上为增函数,∴函数()g x 的周期22T ππω=4ω∴ ,即ω的最大值为4.18.为了丰富在校学生的课余生活,某校举办了一次趣味运动会活动,学校设置项目A “毛毛虫旱地龙舟”和项目B “袋鼠接力跳”.甲、乙两班每班分成两组,每组参加一个项目,进行班级对抗赛.第一个比赛项目A 采取五局三胜制(即有一方先胜3局即获胜,比赛结束);第二个比赛项目B 采取领先3局者获胜。
湖南省郴州市2025届高三数学下学期3月第三次教学质量监测试题

湖南省郴州市2025届高三数学下学期3月第三次教学质量监测试题(本试卷共4页,22题,全卷满分150分,考试用时120分钟)留意事项:1.答题前,先将自己的姓名、准考证号写在试题卷和答题卡上,并将准考证条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡,上相应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔干脆答在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,将本试题卷和答题卡一并上交。
一、单项选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={x|x2-5x-6<0},B={x|y,则A∩B等于A.(2,3)B.[2,3)C.[2,6)D.(-1,2]2.若复数z满意z(1+i)=1-i,其中i为虚数单位,则复数z的虚部为A.1B.-1C.iD.-i3.设非零向量a,b满意|a|=4|b|,cos<a,b>=14,a·(a-b)=30,则|b|=4.地铁某换乘站设有编号为m1,m2,m3,m4的四个平安出口,若同时开放其中的两个平安出。
口,疏散1000名乘客所需的时间如下:则疏散乘客最快的一个平安出口的编号是A.m1B.m2C.m3D.m45.函数f(x)=2xxe1-的图象大致是6.习近平同志提出:乡村振兴,人才是关键。
要主动培育本土人才,激励外出能人返乡创业。
2024年1月8日,人力资源和社会保障部、财政部、农业农村部印发《关于进一步推动返乡入乡创业工作的看法》。
看法指出,要实行党中心、国务院的决策部署,进一步推动返乡入乡创业,以创新带动创业,以创业带动就业,促进农村一、二、三产业融合发展,实现更充分、更高质量就业。
为激励返乡创业,某镇政府确定投入“创业资金”和开展“创业技术培训”帮扶返乡创业人员。
2024届湖南省郴州市高三上学期第一次教学质量监测全真演练物理试题

2024届湖南省郴州市高三上学期第一次教学质量监测全真演练物理试题一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题用带正电的导体球去接触不带电的验电器,验电器的金属箔片会张开,是因为验电器( )A.失去质子而带负电B.失去电子而带正电C.得到电子而带负电D.得到质子而带正电第(2)题如图所示,金属导轨上的导体棒ab在匀强磁场中沿导轨做下列哪种运动时,线圈c中将有感应电流产生( )A.向右做匀速运动B.向右做加速运动C.静止不动D.向左做匀速运动第(3)题为探讨磁场对脑部神经组织的影响及临床医学应用,某小组查阅资料知:“将金属线圈放置在头部上方几厘米处,给线圈通以上千安培、历时约几毫秒的脉冲电流,电流流经线圈产生瞬间的高强度脉冲磁场,磁场穿过头颅对脑部特定区域产生感应电场及感应电流,而对脑神经产生电刺激作用,其装置如图所示。
”同学们讨论得出的下列结论不正确的是( )A.脉冲电流流经线圈会产生高强度的磁场是电流的磁效应B.脉冲磁场使脑部特定区域产生感应电流是电磁感应现象C.若将脉冲电流改为恒定电流,可持续对脑神经产生电刺激作用D.若脉冲电流最大强度不变,但缩短脉冲电流时间,则在脑部产生的感应电场及感应电流会增强第(4)题如图1所示,先使开关S与1端相连,给电容器充电。
然后把开关S掷向2端,电容器通过电阻R放电,电流传感器将电流信息传入计算机,屏幕上显示出电流随时间变化的I-t图像,如图2所示。
若第5s末时电容器电荷等于零,图2中1s~2s内图线下的面积为S,第1s末和第2s末电压传感器的示数分别为4.5V和3.0V,则1s~5s内图线下的面积为()A.1.5S B.2S C.3S D.4.5S第(5)题两种单色光a和b,a光照射某金属时有光电子逸出,b光照射该金属时没有光电子逸出,则( )A.水对b光的折射率较大B.当光从水中斜射入空气中时,b光比a光更容易发生全反射C.以相同角度斜射到同一玻璃板透过平行表面后,b光侧移量大D.用同样的装置做双缝干涉实验,b光的干涉条纹间距大第(6)题如图所示,t时刻神舟十六号载人飞船从A点开始沿顺时针方向运动,运动半个椭圆到B点变轨,恰好与天和核心舱成功对接,则t时刻,天和核心舱可能在轨道II上的()A.B点B.C点C.D点D.E点第(7)题如图所示,A、B是绕地球做圆周运动的两颗卫星,A、B两卫星与地心的连线在相等时间内扫过的面积之比为,则A、B两卫星的周期的比值为( )A.B.k C.k2D.k3第(8)题一个LC振荡电路中,线圈的自感系数为L,电容器电容为C,一个振荡周期内电容器上电压能达到的最大值为U m,则从电容器上电压达到最大值U m开始计时( )A.至少经过π,磁场能达到最大B .在时间内,电路中的平均电流是C.经过π时间,线圈的自感电动势达到最大D.在时间内,电容器放电电荷量为二、多项选择题(本题包含4小题,每小题4分,共16分。
湖南省多校2024届高三下学期4月大联考数学试题含答案

2024届高三4月大联考数学(答案在最后)(试题卷)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试题卷上无效.3.本试题卷共7页,19小题,满分150分,考试用时120分钟.如缺页,考生须及时报告监考老师,否则后果自负.4.考试结束后,将本试题卷和答题卡一并交回.姓名______.准考证号______.祝你考试顺利!机密★启用前一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.6(2)x -的展开式中,3x 的系数是()A.160B.160- C.220D.220-【答案】B 【解析】【分析】利用二项式定理直接列式求出3x 的系数.【详解】二项式6(2)x -的展开式中,3x 系数为333366C 2(1)C 8160⨯⨯-=-⨯=-.故选:B2.已知集合{}{}27120,14M x x x N x x =-+<=-<,则M N ⋂=()A.(),5-∞ B.[]3,4- C.()6,8 D.()3,4【答案】D 【解析】【分析】解集合中的不等式,得到这两个集合,再由交集的定义求解.【详解】不等式27120x x -+<解得34x <<,不等式14x -<,即414x -<-<,解得35x -<<,可得()()()3,4,3,5,3,4M N M N ==-⋂=.故选:D.3.若复数z 满足i zz=,则z 可以是()A.1i +B.2i+ C.1i- D.12i+【答案】A 【解析】【分析】设i z a b =+,由此写出z ,根据z 与z 的关系得到a 与b 的关系,从而选出正确选项.【详解】设i,,R z a b a b =+∈,则i,i zz a b z=-=,即()i i i ,i i a b a b a b a b +=-+=+,即a b =,故选:A.4.原核生物大肠杆菌存在于人和动物的肠道内,在适宜的环境和温度下会迅速繁殖导致肠道内生态环境失衡从而引发腹泻等症状,已知大肠杆菌是以简单的二分裂法进行无性繁殖,在适宜的条件下分裂一次(1个变为2个)需要约24分钟,那么在适宜条件下1个大肠杆菌增长到1万个大肠杆菌至少需要约()(参考数据:lg20.3≈)A.4小时 B.5小时C.6小时D.7小时【答案】C 【解析】【分析】依据题意列出方程,利用对数的运算性质结合给定的特殊对数值处理即可.【详解】设适宜条件下1个大肠杆菌增长到1万个大肠杆菌大约需要x 分钟,则241210000x⋅=,两边取对数得lg2lg10000424x⋅==,解得42496320lg20.3x ⨯=≈≈,所以大约需要320165.3603=≈小时,故在适宜条件下1个大肠杆菌增长到1万个大肠杆菌至少需要6小时.故选:C.5.已知直线220x y ++=与抛物线2:C y ax =有唯一交点,则C 的准线方程为()A.=1x -B.1x = C.12x =-D.12x =【答案】C 【解析】【分析】直线与抛物线联立方程组消去x ,由Δ0=求出a 的值,由抛物线方程求其准线方程.【详解】依题意,联立2220x y y ax++=⎧⎨=⎩,消去x 得2220y ay a ++=,则2Δ480a a =-=,由0a ≠得2a =,故抛物线C 的方程为22y x =,其准线方程为12x =-.故选:C.6.在不断发展的过程中,我国在兼顾创新创造的同时,也在强调已有资源的重复利用,废弃资源的合理使用,如土地资源的再利用是其中的重要一环.为了积极响应国家号召,某地计划将如图所示的四边形荒地ABCD 改造为绿化公园,并拟计划修建主干路AC 与BD .为更好的规划建设,利用无人机对该地区俯视图进行角度勘探,在勘探简化图中,,,AD AC AB BC AC ⊥⊥平分,BCD BD CD ∠=,则cos ACD ∠=()A.3B.9C.3D.3【答案】A 【解析】【分析】设ACD θ∠=,则2BCD θ∠=,根据余弦定理及二倍角公式求得22cos 3θ=,根据θ的范围即可得解.【详解】设ACD θ∠=,则2BCD θ∠=,设CD BD a ==,则2cos ,cos AC a BC a θθ==.故在BCD △中,由余弦定理可得224222cos 1cos22cos 2a a a a a θθθθ+-==⋅,而2cos22cos 1θθ=-,故2212cos 1cos 2θθ-=,解得221cos ,cos233θθ==,在直角三角形ACD 中,θ为锐角,故cos 0θ>,故cos 3θ=.故选:A.7.将编号为1,2,3,4的4个小球随机放入编号为1,2,3,4的4个凹槽中,每个凹槽放一个小球,则至少有2个凹槽与其放入小球编号相同的概率是()A.14B.724 C.712D.1724【答案】B 【解析】【分析】利用排列组合,先求出将编号为1,2,3,4的4个小球随机放入编号为1,2,3,4的4个凹槽中的放法数,再求出至少有2个凹槽与其放入小球编号相同的放法数,再利用古典概率公式,即可求出结果.【详解】将编号为1,2,3,4的4个小球随机放入编号为1,2,3,4的4个凹槽中,共有44A 24=种放法,恰有2个凹槽与其放入小球编号相同的有24C 6=种放法,4个凹槽与其放入小球编号相同的有1种放法,所以至少有2个凹槽与其放入小球编号相同的概率是2444C 17A 24P +==,故选:B.8.使得不等式()()()()()sin sin2cos sin cos cos sin sin sin cos θθθθθ≤⋅-⋅成立的一个充分不必要条件是()A.π0,4θ⎡⎤∈⎢⎥⎣⎦B.ππ,42θ⎡⎤∈⎢⎣⎦C.3π,π4θ⎡⎤∈⎢⎥⎣⎦D.5ππ,4θ⎡⎤∈⎢⎥⎣⎦【答案】C 【解析】【分析】换元sin cos t θθ=+,利用二倍角公式和两角和的余弦公式的逆用将题干不等式转化为关于t 的不等式,解出t 满足的关系进而排除得到正确选项.【详解】令πsin cos 4t θθθ⎛⎫⎡=+=+∈ ⎪⎣⎝⎭,则()()2222sin 22sin cos sin cos sincos 1t θθθθθθθ==+-+=-,()()()()()cos sin cos cos sin sin sin cos cos sin cos cos tθθθθθθ⋅-⋅=+=所以已知不等式化为()2πsin 1cos sin 2t t t ⎛⎫-≤=+⎪⎝⎭.[]2πππ11,1,222t t ⎡-∈-+∈+⎢⎣,故原不等式的解分两段:①πππ122t -≤+≤-得π12t ⎡⎤∈-⎢⎥⎣⎦,原不等式化为2π12t t -≤+,即2π102t t ---≤.②πππ122t -≤+≤+得π2t ⎡∈-⎢⎣,原不等式化为2π1π2t t ⎛⎫-≤-+ ⎪⎝⎭,即2π102t t +--≤.四个选项对应的t 取值范围分别为[[][,,1,0,1⎡⎤---⎣⎦,当t =时,由②2ππ11022+--=->t t 不符合题意,排除A 、B ;当t =2ππ11022--=+->-t t 不符合题意,排除D ;[]1,0t ∈-时易验证满足①,故选:C.二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对得6分,部分选对得3分,有选错得0分9.已知直线()():2240l m x m y +---=,圆22:4690C x y x y ++-+=,则()A.l 过定点()1,1B.圆C 与y 轴相切C.若l 与圆C 有交点,则m 的最大值为0D.若l 平分圆C ,则25m =-【答案】ABD 【解析】【分析】利用直线方程与m 的取值无关,求解定点判A ,利用直线与圆的位置关系判断B ,C ,先发现直线必过圆心,后将圆心代入直线,求解参数,判断D 即可.【详解】对A ,整理直线l 的方程,得()()240m x y x y -++-=,令0x y -=,解得x y =,当x y =时,直线方程与m 的取值无关,又2x y +=,解得1x y ==,即l 必过定点()1,1,故A 正确;对B ,整理圆C 的方程,得22(2)(3)4x y ++-=,易知圆心到y 轴的距离为2,又2r =,故得圆C 与y 轴相切,故B 正确;对C ,若l 与圆C 有交点,设圆心C 到直线l 的距离为d ,可得2d =,解得142,,17m ⎡⎤∈-⎢⎥⎣⎦故C 错误;对D ,若l 平分圆C ,则l 必过圆心,易知圆心为()2,3-,将()2,3-代入直线l 的方程,得5240m -+-=,解得25m =-,故D 正确.故选:ABD.10.的正方形ABCD 沿对角线AC 折起,当以,,,A B C D 四点为顶点的三棱锥体积最大时()A.AB CD⊥B.直线BD 与平面ABC 所成角的大小为π4C.平面ABD 与平面BCD 夹角的余弦值为13D.四面体ABCD的内切球的半径为2【答案】BCD 【解析】【分析】根据题意画出图形,再由几何法求解异面直线垂直、线面成角、面面成角和内切球半径即可.【详解】如图所示,当平面BAC ⊥平面DAC时,三棱锥体积最大,记E 为AC 中点,此时DE ⊥平面BAC ,因为AB ⊂平面BAC ,所以AB DE ⊥,因为CD DE D = ,所以AB 与CD 不垂直,A 错误.对于B :直线BD 和平面ABC 所成角即为EBD ∠,因为tan 1ED EBD BE ∠==,故π4EBD ∠=,B 正确.对于C :由于BC CD BA AD ===,取BD 中点G ,则有,CG BD AG BD ⊥⊥,故CGA ∠为平面ABD 与平面BCD 所成角的平面角.则2221cos 23AG CG AC CGA AG CG +-∠==⨯,C 正确.对于D :设内切球球心为I ,内切球半径为r ,由等体积法知,13ABCD I ABC I BCD I ACD I ABD ABCD V V V V V rS ----=+++=其中,1133ABCD ACD V BE S =⨯=,1122222ABCD S ⎡⎤⎛⎫⎛=⨯⨯+⨯= ⎪ ⎢⎥⎝⎭⎝⎣⎦,故32ABCD ABCD V r S ===D 正确.故选:BCD.11.已知函数()f x 是定义在()1,+∞上的连续函数,且在定义域上处处可导,()f x '是()f x 的导函数,且()()1f x x f x x'>>>,则()A.()()()42f f f < B.()()422f f >C.()2f < D.()()24e 2>f f 【答案】BC 【解析】【分析】根据()10f x '>>可判断()f x 在()1,∞+单调递增,即可判断A ,构造()()f x g x x=,利用导数求解()g x 在()1,∞+单调递增,即可判断BC,构造()()exf x h x =,求导求解()h x 在()1,∞+单调递减,即可判断D.【详解】由已知得()f x x x>,故()()22,422f f >>,又因为()10f x '>>,所以()f x 在()1,∞+单调递增,所以()()()42,f f f >A 错误;构造函数()()f x g x x=,则()()()10f x g x f x x x ⎛⎫=⋅-> ⎪⎝⎭'',所以()g x 在()1,∞+单调递增,因此()()42g g >,即()()()()42,42242f f f f >>,B 正确;由于()()1,1f x f x x x>>>,故()()()()()()()()()()2,,()f f x f x g f x g x f x xf f x f x x>><,因此()2f <,C 正确;构造函数()()exf x h x =,则()()()exf x f x h x '='-,而()()f x x f x >>',故()()0,h x h x '<在()1,∞+单调递减,因此()()()()()()2424242,4e 2e e f f h h f f <<<,D 错误.故选:BC.【点睛】方法点睛:利用导数比较大小的基本步骤(1)作差或变形;(2)构造新的函数()h x ;(3)利用导数研究()h x 的单调性或最值;(4)根据单调性及最值,得到所证不等式.三、填空题:本题共3小题,每小题5分,共15分.12.已知公比为2的等比数列{}n a 满足2341a a a ++=,则1a =______.【答案】114【解析】【分析】利用等比数列的通项公式可得答案.【详解】由题意可得()2323411141a a a a q q q a++=++==,解得1114a =,故答案为:114.13.函数()cos (0)f x x ωω=>的图象在x ω=与2x ω=处的切线斜率相同,则ω的最小值为______.【答案】【解析】【分析】对()f x 求导,可得()2f f ωω⎛⎫=⎪⎝'⎭',则2sin sin2ω=,即可得出ω的最小值.【详解】因为()cos (0)f x x ωω=>,所以()sin f x x ωω=-',因为函数()cos (0)f x x ωω=>的图象在x ω=与2x ω=处的切线斜率相同,所以()2sin f ωωω'=-,2sin2f ωω⎛⎫=-⎪⎝⎭',故有2sin sin2ωωω-=-,即2sin sin2ω=,则()222πk k ω=+∈Z 或()22π2πk k ω+=+∈Z ,解得)k ω=∈Z 或)k ω=∈Z ,当0k =,<,故ω的最小值为..14.若函数()log (0,0x f x a a x =>>,且1)x ≠的图象与直线2ln x y a +=没有交点,则a 的取值范围是______.【答案】{}e 1⎛⎫⋃ ⎪ ⎪⎝⎭【解析】【分析】由题意可得方程log 2ln x a x a =-+在()()0,11,x ∞∈⋃+无解,即函数()ln 2ln ln ln g x x x a x a =-⋅+在()()0,11,x ∞∈⋃+无零点,当1a =时直接判断,当1a ≠时求出函数的导函数,再分1a >、01a <<两种情况讨论,当1a >时利用导数说明函数的单调性,求出函数的最小值,依题意只需()()0min 0g x g x =>,从而求出0x 的取值范围,再结合()0011ln ln 2x x a +=求出a 的范围.【详解】由题意可得方程log 2ln x a x a =-+在()()0,11,x ∞∈⋃+无解,将方程变形得ln 2ln ln ln 0x x a x a -⋅+=,即函数()ln 2ln ln ln g x x x a x a =-⋅+在()()0,11,x ∞∈⋃+无零点,易得()g x 的定义域为()0,∞+,仅在讨论零点时舍去1x =的情况;若1a =时,则()ln g x x x =,当01x <<时()0g x <,当1x >时()0g x >,故在()()0,11,∞⋃+无零点,因此1a =符合题意;当1a ≠时,则()2ln 1ln a g x x x =+-',设()2ln 1ln a x x x ϕ=+-,则()22ln x ax x ϕ='+,当1a >时()0x ϕ'>,则()x ϕ在()0,∞+单调递增,即()g x '在()0,∞+单调递增,由于0x →时()g x ∞'→-,x →+∞时()g x ∞'→+,由零点存在性定理可知()g x 在()0,∞+必有、且只有一个零点,设为0x ,则当()00,x x ∈时()0g x '<,当()0,x x ∞∈+时()0g x '>,所以()g x 在()00,x 上单调递减,在()0,x ∞+上单调递增,其中()0011ln ln 2x x a +=,故只需令()00g x >,当01x =时()0ln 0g x a =>符合题意,因此()()()000000001ln ln 1ln 1ln 2g x x x x x x x x =-+++()200012ln ln 102x x x ⎡⎤=--->⎣⎦,即()2002ln ln 10x x --<,解得01ln 12x -<<,则0e x <<,设()()11ln2h x x x =+,e x ⎫<<⎪⎭,则()()12ln 02h x x =+>',所以()h x 在⎫⎪⎭上单调递增,又h =,()e e h =,ln ea <<,则ee a <<;当01a <<时,()1ln 0g a =<,02g=>,故()g x 在区间1,2⎛⎫ ⎪ ⎪⎝⎭必有零点,与所求不符.综上,a 的取值范围为{}e 1⎛⎫⋃ ⎪ ⎪⎝⎭.故答案为:{}e 1⎛⎫⋃ ⎪ ⎪⎝⎭【点睛】方法点睛:导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理.四、解答题:本题共5小题,共77分.解答应写出必要的文字说明、证明过程及演算步骤.15.已知函数()213ex x f x --=.(1)求()f x 的单调区间;(2)求()f x 的极值.【答案】(1)单调递减区间为()(),1,3,∞∞--+,单调递增区间为()1,3-(2)极大值为26e,极小值为22e -【解析】【分析】(1)根据函数求出导函数,再由导函数解出原函数的单调区间即可;(2)根据第1问的单调性求出极值即可.【小问1详解】因为()213e x x f x --=,所以()()()2113123e ex x x x x x f x --'--+-+==,令()0f x '=,解得3x =或=1x -,令()0f x '<得3x >或1x <-,令()0f x '>得13x -<<,列表如下:x(),1∞---1()1,3-3()3,∞+()f x '-0+-()f x极小值极大值故()f x 的单调递减区间为()(),1,3,∞∞--+,单调递增区间为()1,3-.【小问2详解】由(1)可得()f x 的极大值为()263ef =,极小值为()212e f -=-.16.多样性指数是生物群落中种类与个体数的比值.在某个物种数目为S 的群落中,辛普森多样性指数211si i n D N =⎛⎫=- ⎪⎝⎭∑,其中i n 为第i 种生物的个体数,N 为总个体数.当D 越大时,表明该群落的多样性越高.已知,A B 两个实验水塘的构成如下:绿藻衣藻水绵蓝藻硅藻A66666B124365(1)若从,A B 中分别抽取一个生物个体,求两个生物个体为同一物种的概率;(2)(i )比较,A B 的多样性大小;(ii )根据(i )的计算结果,分析可能影响群落多样性的因素.【答案】(1)15(2)(i )A 的多样性大于B (ii )答案见解析【解析】【分析】(1)利用古典概型的求法可得答案;(2)根据给出211si i n D N =⎛⎫=- ⎪⎝⎭∑求出,然后比较即可.【小问1详解】记事件C 为“两个生物个体为同一物种”,则C 发生的概率为()11155P C =⨯=.【小问2详解】(i )由表可知30,5,A B A B N N S S ==⎧⎨==⎩所以2214156305A D =-⨯⨯=,()22222216711243653090B D =-⨯++++=;即A BD D >,故A 的多样性大于B ;(ii )在(i )中两群落物种数目相同,各物种数量不同,而A 中各物种数量均相同,即物种均匀度更大,分析可得物种均匀度也会影响群落多样性.17.如图所示,正四棱锥P ABCD -中,,AB PA M N ==分别为,PA PC 的中点,2=PE BE ,平面EMN 与PD 交于G .(1)证明:PD ⊥平面EMGN ;(2)求二面角P ME N --的余弦值.【答案】(1)证明见解析(2)4515【解析】【分析】(1)先通过PHE PGS ∽,证PD GE ⊥,再通过MN ⊥平面PBD ,证MN PD ⊥,最后通过线面垂直判定定理即可证PD⊥平面EMGN ;(2)建立空间直角坐标系,利用空间向量的方法求二面角P ME N --的余弦值即可.【小问1详解】连接,AC BD ,设AC BD O = ,连接PO ,有PO ⊥平面ABCD ,由题意得,ME NE MG NG ==,且6,6BD PO ===,连接MN ,EG ,设EG MN S ⋂=,则MS NS =,故S 在PO 上,过E 作,EH PO H ⊥为垂足,在POB 中,23PE EH PB OB ==,故2EH =,因为MN AC ,所以13,12PS PO SH PH PS ===-=,故1tan tan 2SEH DPO ∠==∠,所以PHE PGS ∽,所以90,PGE PHE PD GE ∠∠==⊥ ,又,,MN OP MN BD ^^OP ⊂平面PBD ,BD ⊂平面PBD ,BD OP O = ,故MN ⊥平面PBD ,因为PD ⊂平面PBD ,故MN PD ⊥.又,MN GE S GE ⋂=⊂平面,EMGN MN ⊂平面EMGN ,故PD ⊥平面EMGN .【小问2详解】以,,OA OB OP 所在的直线分别为,,x y z 轴建立空间直角坐标系可得()()()()3,0,0,0,3,0,0,0,6,0,3,0A B P D -,由(1)得PD ⊥平面EMGN ,故平面EMGN 的一个法向量为()0,3,6DP =其中()()3,0,6,3,3,0AP AB =-=-设平面PAB 的一个法向量为(),,n x y z =,则03603300n AP x z x y n AB ⎧⋅=-+=⎧⎪⇒⎨⎨-+=⋅=⎩⎪⎩,令1z =可得()2,2,1n =设θ为二面角P ME N --的平面角,则cos cos ,15n DP θ==,由图可知所求二面角为锐角,故二面角P ME N --的余弦值为15.18.已知椭圆221:12x C y +=,焦点在x 轴上的双曲线2C,且过点),点()00,P x y 在2C 上,且002x y >>,2C 在点P 处的切线交1C 于,A B 两点.(1)求直线AB 的方程(用含00,x y 的式子表示);(2)若点()0,3Q ,求QAB 面积的最大值.【答案】(1)0002x y x y y =-(22+【解析】【分析】(1)由离心率和所过的点求出双曲线的方程为222:2C x y -=,由点P 在第一象限,将双曲线2C变形为y =,利用导数求切点处的切线方程.(2)直线与双曲线联立方程组,利用弦长公式和点到直线距离表示出QAB 面积,消元后由基本不等式求最大值.【小问1详解】焦点在x 轴上的双曲线2C,则双曲线为等轴双曲线,设双曲线方程为222x y a -=,由双曲线过点),代入方程,解得双曲线222:2C x y -=,点()00,P x y 在2C 上,有22002x y -=,因为点P 在第一象限,所以可以将双曲线2C变形为y =.求导有y '=当0x x =时,000x x x y y =='=,所以AB 的方程为:()0000x y y x x y -=-,化简有0002x y x y y =-.【小问2详解】设()()01122002,,,,,x k m A x y B x y y y ==-,有2222k m -=,联立2212x y y kx m ⎧+=⎪⎨⎪=+⎩,消去y 得()222124220k x kmx m +++-=,有12221224212221km x x k m x x k ⎧+=-⎪⎪+⎨-⎪=⎪+⎩,()22Δ821240k m =+-=>,12AB x =-=222121k k =++,点Q 到直线AB的距离d =,则12QABS AB d == 0002,x k m y y ==-代入,有QAB S =△)200203234y y y ++()()()0002200222411343212216y y y y y ⎡⎤⎫--=+=+⎢⎥⎪⎪+-+-+⎢⎥⎝⎭⎣⎦()0021116232122y y ⎡⎤⎡⎤⎢⎥⎥⎢⎥=+≤+=⎢⎥-++⎢⎢⎥-⎣⎦⎢⎣当且仅当023y =+时取等号,故QAB 面积的2+.【点睛】方法点睛:把两个曲线的方程联立,消去x (或y )建立一元二次方程,然后借助根与系数的关系,并结合题设条件建立有关参变量的等量关系,涉及到直线方程的设法时,务必考虑全面,不要忽略直线斜率为0或不存在等特殊情形,强化有关直线与圆锥曲线联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.19.若数列{}n a 在某项之后的所有项均为一常数,则称{}n a 是“最终常数列”.已知对任意()*,n m m n ≥∈N ,函数()f x 和数列{}n a 满足{}()11min n i i na f a +≤≤=.(1)当()f x x >时,证明:{}n a 是“最终常数列”;(2)设数列{}n b 满足11m b a +=,对任意正整数()1,n n n b f b +=.若方程()0f x x-=无实根,证明:{}n a 不是“最终常数列”的充要条件是:对任意正整数i ,i m i b a +=;(3)若(){}21,,n m f x x a ==不是“最终常数列”,求1a 的取值范围.【答案】(1)证明见解析(2)证明见解析(3)()0,1【解析】【分析】(1)利用“最终常数列”定义即可证明;(2)利用反证法结合“最终常数列”新定义证明必要性,利用“最终常数列”定义证明必要性;(3)利用第二问的证明结论即可求出1a 的取值范围.【小问1详解】因为()f x x >,所以对任意{}(){}111,min min n i i i ni nn m a f a a +≤≤≤≤≥=>,故数列最小值不变.即对于任意{}{}{}(){}()11111,min min ,min min i i n i i i ni mi ni mn m a a a f a f a +≤≤≤≤≤≤≤≤≥===恒成立.故对于任意1n m ≥+,有{}()1min n i i ma f a ≤≤=,故{}n a 是“最终常数列”.【小问2详解】必要性,若{}n a 不为“最终常数列”,假设存在一个n m ≥使得{}11min n i i n a a +≤≤≥,则由(1)同理可知其最小值不变,故{}n a 为“最终常数列”,矛盾.所以对任意{}11,min n i i nn m a a +≤≤≥<.故对任意1n m ≥+,均有{}1min n i i na a ≤≤=成立,故()1n n a f a +=对任意1n m ≥+成立,又由{}nb 定义递推,知对任意正整数,i m i i b a +=.充分性:若任意正整数,i m i i b a +=,则()1n n a f a +=对任意1n m ≥+成立,又由{}n a 定义知任意1n m ≥+,均有{}1min n i i n a a ≤≤=成立.由此知{}{}1111min min n i i n i n i na a a a +≤≤+≤≤=≤=.又由()0f x x -=知1+≠n n a a ,故1n n a a +<,即{}n a 在第1m +项后严格递减,故不是“最终常数列”.综上,原命题得证.【小问3详解】由(2)知:要求(){}12111min i i f a a a a ≤≤=<=,解得()10,1a ∈.下面证明:()11,4a ∈即为所求.由()11,4a ∈时,()()22110,1a f a a ==∈,由递推可知,对任意*n ∈N 均有()0,1n a ∈.进而()1n n a f a +=对任意*n ∈N 均成立,结合(2)结论知{}n a 不是“最终常数列”.故1a 的取值范围是()0,1.【点睛】关键点点睛:本题求解的关键是:一要准确理解给定的新定义;二要利用反证法得出矛盾.。
湖南省郴州市一中2025届高三3月份模拟考试数学试题含解析

湖南省郴州市一中2025届高三3月份模拟考试数学试题注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设01p <<,随机变量ξ的分布列是则当p 在(,)34内增大时,( )A .()E ξ减小,()D ξ减小B .()E ξ减小,()D ξ增大C .()E ξ增大,()D ξ减小D .()E ξ增大,()D ξ增大2.已知函数()2ln 2,03,02x x x x f x x x x ->⎧⎪=⎨+≤⎪⎩的图像上有且仅有四个不同的点关于直线1y =-的对称点在 1y kx =-的图像上,则实数k 的取值范围是( ) A .1,12⎛⎫⎪⎝⎭B .13,24⎛⎫⎪⎝⎭C .1,13⎛⎫ ⎪⎝⎭D .1,22⎛⎫⎪⎝⎭3.已知△ABC 中,22BC BA BC =⋅=-,.点P 为BC边上的动点,则()PC PA PB PC ⋅++的最小值为( ) A .2B .34-C .2-D .2512-4.若复数()()31z i i =-+,则z =( ) A .B .CD .205.设一个正三棱柱ABC DEF -,每条棱长都相等,一只蚂蚁从上底面ABC 的某顶点出发,每次只沿着棱爬行并爬到另一个顶点,算一次爬行,若它选择三个方向爬行的概率相等,若蚂蚁爬行10次,仍然在上底面的概率为10P ,则10P 为( )A .10111432⎛⎫⋅+ ⎪⎝⎭B .111132⎛⎫+ ⎪⎝⎭C .111132⎛⎫- ⎪⎝⎭D .10111232⎛⎫⋅+ ⎪⎝⎭6.若直线240x y m ++=经过抛物线22y x =的焦点,则m =( ) A .12B .12-C .2D .2-7.要得到函数1cos 2y x =的图象,只需将函数1sin 223y x π⎛⎫=+ ⎪⎝⎭的图象上所有点的( )A .横坐标缩短到原来的12(纵坐标不变),再向左平移3π个单位长度B .横坐标缩短到原来的12(纵坐标不变),再向右平移6π个单位长度C .横坐标伸长到原来的2倍(纵坐标不变),再向左平移6π个单位长度 D .横坐标伸长到原来的2倍(纵坐标不变),再向右平移3π个单位长度 8.已知52i 12ia =+-(a ∈R ),i 为虚数单位,则a =( ) A .3 B .3 C .1D .59.若,则( ) A .B .C .D .10.某几何体的三视图如图所示,其中正视图是边长为4的正三角形,俯视图是由边长为4的正三角形和一个半圆构成,则该几何体的体积为( )A .4383π+B .2383π+C .343π+D .8343π+11.过抛物线()220y px p =>的焦点F 作直线与抛物线在第一象限交于点A ,与准线在第三象限交于点B ,过点A 作准线的垂线,垂足为H .若tan 2AFH ∠=,则AF BF=( )A .54B .43C .32D .212.双曲线C :2215x y m-=(0m >),左焦点到渐近线的距离为2,则双曲线C 的渐近线方程为( ) A .250x y ±=B .250x y ±=C .520x y ±=D .50x y ±=二、填空题:本题共4小题,每小题5分,共20分。
湖南省郴州市2024高三冲刺(高考数学)统编版(五四制)真题(综合卷)完整试卷

湖南省郴州市2024高三冲刺(高考数学)统编版(五四制)真题(综合卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题已知函数,且关于的方程有6个不同的实数解,若最小的实数解为-1,则的值为A.-2B.-1C.0D.1第(2)题已知实数,若,且这四个数的中位数是3,则这四个数的平均数是()A.B.3C.D.4第(3)题下列不等式一定成立的是A.B.C.D.第(4)题已知,,则()A.B.C.D.第(5)题下列说法中正确的是()A.一组数据3,4,2,8,1,5,8,6,9,9,的第60百分位数为6B.将一组数据中的每一个数据加上同一个正数后,方差变大C.若甲、乙两组数据的相关系数分别为和,则甲组数据的线性相关程度更强D.在一个列联表中,由计算得的值,则的值越接近1,判断两个变量有关的把握越大第(6)题某三棱锥的三视图如图所示,该三棱锥的表面积是A.B.C.D.第(7)题已知,且,则的最小值为()A.B.C.D.第(8)题已知命题,;命题,,则()A.和都是真命题B.和都是真命题C.和都是真命题D.和都是真命题二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题已知函数,则下列说法正确的是().A.函数的最小正周期为B.点是图像的一个对称中心C .的图像关于直线对称D.在区间单调递减第(2)题已知椭圆上有不同两点,,,则()A.若过原点,则B.,的最小值为C.若,则的最大值为9D.,,异于点,若线段的垂直平分线与轴相交于点,则直线的斜率为第(3)题如图,点是棱长为2的正方体的表面上一个动点,是线段的中点,则()A.当在平面上运动时,三棱锥的体积为定值B.当在线段上运动时,与所成角的取值范围是C.当直线与平面所成的角为时,点的轨迹长度为D.当在底面上运动,且满足平面时,线段长度的取值范围是三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题已知椭圆的左、右焦点分别为,离心率为.若和为椭圆上在轴上方的两点,且,则直线的斜率为______.第(2)题已知,则________.第(3)题在中,,,当取最大值时,的面积为______.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题已知双曲线与直线:()有唯一的公共点,直线与双曲线的两条渐近线分别交于,两点,其中点,在第一象限.(1)探求参数,满足的关系式;(2)若为坐标原点,为双曲线的左焦点,证明:.第(2)题在直角坐标系中,已知曲线(为参数),曲线,以坐标原点为极点,轴的正半轴为极轴建立极坐标系.(1)曲线的极坐标方程及曲线的直角坐标方程;(2)已知是曲线上的两个动点(异于原点),且,若曲线与直线有且仅有一个公共点,求的值.第(3)题已知数列中,,(n).(1)分别比较下列每组中两数的大小:①和;②和;(2)当n≥3时,证明:.第(4)题设数列的前项和,(1)求数列的通项公式;(2)令,记数列前n项和为,求;(3)利用第二问结果,设是整数,问是否存在正整数n,使等式成立?若存在,求出和相应的值;若不存在,说明理由.第(5)题中国探月工程自2004年批准立项以来,聚焦“自主创新、重点跨越、支撑发展、引领未来”的目标,创造了许多项中国首次.2020年12月17日凌晨,嫦娥五号返回器携带“月壤”着陆地球,首次实现了我国地外天体无人采样返回.为了了解某中学高三学生对此新闻事件的关注程度,从该校高三学生中随机抽取了100名学生进行调查,调查样本中有40名女生.如图是根据样本的调查结果绘制的等高条形图(阴影区域表示关注“嫦娥五号”的部分).(1)完成下面的列联表,并判断是否有95%的把握认为对“嫦娥五号”的关注程度与性别有关?关注没关注合计男生女生合计(2)若将频率视为概率,现从该中学高三女生中随机抽取2人.记被抽取的2名女生中对“嫦娥五号”新闻关注的人数为随机变量X,求X的分布列及数学期望.附:,其中.0.1500.1000.0500.0100.0052.072 2.7063.841 6.6357.879。
2024届湖南省郴州市高三上学期第一次质检高效提分物理试题(强化版)
2024届湖南省郴州市高三上学期第一次质检高效提分物理试题(强化版)一、单项选择题(本题包含8小题,每小题4分,共32分。
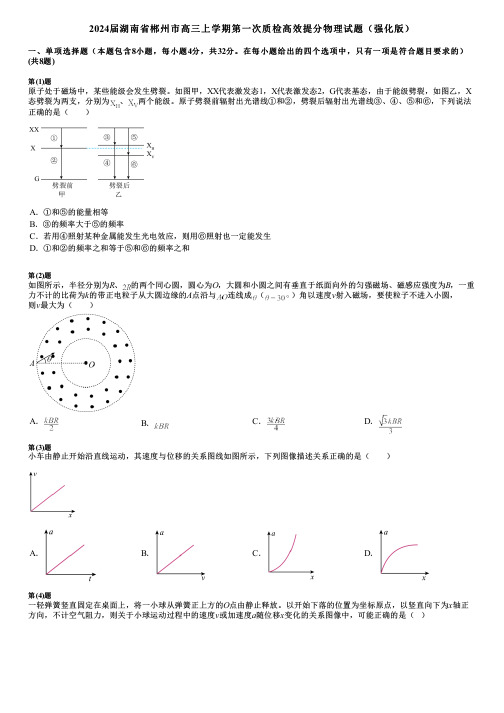
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题原子处于磁场中,某些能级会发生劈裂。
如图甲,XX代表激发态1,X代表激发态2,G代表基态,由于能级劈裂,如图乙,X 态劈裂为两支,分别为、两个能级。
原子劈裂前辐射出光谱线①和②,劈裂后辐射出光谱线③、④、⑤和⑥,下列说法正确的是( )A.①和⑤的能量相等B.③的频率大于⑤的频率C.若用④照射某种金属能发生光电效应,则用⑥照射也一定能发生D.①和②的频率之和等于⑤和⑥的频率之和第(2)题如图所示,半径分别为R、的两个同心圆,圆心为O,大圆和小圆之间有垂直于纸面向外的匀强磁场、磁感应强度为B,一重力不计的比荷为k的带正电粒子从大圆边缘的A点沿与连线成()角以速度v射入磁场,要使粒子不进入小圆,则v最大为( )A.B.C.D.第(3)题小车由静止开始沿直线运动,其速度与位移的关系图线如图所示,下列图像描述关系正确的是( )A.B.C.D.第(4)题一轻弹簧竖直固定在桌面上,将一小球从弹簧正上方的O点由静止释放。
以开始下落的位置为坐标原点,以竖直向下为x轴正方向,不计空气阻力,则关于小球运动过程中的速度v或加速度a随位移x变化的关系图像中,可能正确的是()A.B.C.D.第(5)题一质量为1kg的物体受水平拉力F作用,在粗糙水平面上做加速直线运动时的a-t图像如图所示,t=0时其速度大小为2m/s,滑动摩擦力大小恒为2N,则( )A.t=3s时,水平拉力F的大小为3NB.在0~6 s内,合力对物体做的功为200JC.在0~6 s内,合力对物体的冲量为36N·sD.t=6s时,拉力F的功率为120W第(6)题一质量不计的直角形支架两端分别连接质量为m和2m的小球A和B。
支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示。
2024届湖南省郴州市高三上学期第一次质检物理核心考点试题

2024届湖南省郴州市高三上学期第一次质检物理核心考点试题一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题直流电动机通电后,使线圈发生转动的力是( )A.重力B.电场力C.磁场力D.摩擦力第(2)题原子核俘获一个中子,生成一个核并释放一个质子.由此可知A.A=13 Z=6B.A= 13 Z=7C.A=14 Z=6D.A=14 Z=7第(3)题科学思维在物理问题的研究中十分重要,历史上有一位物理学家受到万有引力定律的启发,运用类比创建了另一个物理定律,该定律是( )A.牛顿第二定律B.库仑定律C.楞次定律D.闭合电路欧姆定律第(4)题广东大亚湾核电站是我国首座利用核裂变发电的大型商用核电站,核裂变反应方程中( )A.为电子,B.为质子,C.为质子,D.为中子,第(5)题用中子轰击静止的锂核,核反应方程为。
已知光子的频率为v,锂核的比结合能为,氦核的比结合能为,X核的比结合能为,普朗克常量为h,真空中光速为c、下列说法中正确的是( )A.X核为核B.光子的动量C.释放的核能D.质量亏损第(6)题如图,玻璃管内开口向下置于水银槽内,管内封闭了一段气体,在槽内缓慢加入水银过程中,管内封闭气体状态变化可能是下图中的( )A.B.C.D.第(7)题如图所示,真空中有一个三棱锥,三棱锥各边长均为,在A、三点分别放置电荷量为的正点电荷,现在要外加一个匀强电场,使点的场强为0,则匀强电场的场强为( )A .B .C .D .第(8)题2022年2月27日,我国长征八号运载火箭一次发射了22颗卫星,假设其中卫星1、卫星2分别沿圆轨道、椭圆轨道绕地球逆时针运动,圆的半径与椭圆的半长轴相等,两轨道面在同一平面内且两轨道相交于A 、B 两点,某时刻两卫星与地球在同一直线上,如图所示。
下列说法正确的是( )A .两卫星在图示位置的速度v 1>v 2B .两卫星在图示位置时,卫星1受到的地球引力较大C .卫星1在A 处的加速度比卫星2在A 处的加速度大D .若不及时调整轨道,两卫星可能发生相撞二、多项选择题(本题包含4小题,每小题4分,共16分。
湖南省长沙市(新版)2024高考数学统编版(五四制)质量检测(自测卷)完整试卷

湖南省长沙市(新版)2024高考数学统编版(五四制)质量检测(自测卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题算盘是我国一类重要的计算工具.下图是一把算盘的初始状态,自右向左前四位分别表示个位、十位、百位、千位,上面一粒珠子(简称上珠)代表5,下面一粒珠子(简称下珠)代表1,即五粒下珠的代表数值等于同组一粒上珠的代表数值,例如,个位拨动一粒上珠至梁上,十位未拨动,百位拨动一粒下珠至梁上,表示数字105.现将算盘的千位拨动一粒珠子至梁上,个位、十位、百位至多拨动一粒珠子至梁上,其它位置珠子不拨动.设事件“表示的四位数为偶数”,事件“表示的四位数大于5050”,则()A.B.C.D.第(2)题如图所示的几何体各自的三视图中,有且仅有两个视图相同的为A.①②B.②④C.①④D.①③第(3)题菱形中,现将菱形沿对角线折起,当时,此时三棱锥的体积为,则三棱锥外接球的表面积为()A.B.C.D.第(4)题已知且,若函数在上单调递减,则实数a的取值范围为()A.B.C.D.第(5)题已知双曲线的中心在原点且一个焦点为,直线与其相交于,两点,若中点的横坐标为,则此双曲线的方程是A.B.C.D.第(6)题油纸伞是中国传统工艺品,至今已有1000多年的历史,为宣传和推广这一传统工艺,北京市文化宫开展油纸伞文化艺术节活动中,某油纸伞撑开后摆放在户外展览场地上,如图所示,该伞伞沿是一个半径为2的圆,圆心到伞柄底端距离为2,当阳光与地面夹角为时,在地面形成了一个椭圆形影子,且伞柄底端正好位于该椭圆的长轴上,若该椭圆的离心率为e,则()A.B.C.D.第(7)题已知双曲线的左、右焦点分别为,,,P为C上一点,的中点为Q,为等边三角形,则双曲线C的方程为().A.B.C.D.第(8)题已知点,在直线和轴上各找一点和,则的周长的最小值为()A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题如图,点是函数的图象与直线相邻的三个交点,且,则()A.B.C.函数在上单调递减D.若将函数的图象沿轴平移个单位,得到一个偶函数的图像,则的最小值为第(2)题已知直线平面,直线平面,则()A.若与不垂直,则与一定不垂直B.若与所成的角为,则与所成的角也为C.是的充分不必要条件D.若与相交,则与一定是异面直线第(3)题现有十个点的坐标为,它们分别与关于点对称已知的平均数为,中位数为,方差为,极差为,则这组数满足()A.平均数为B.中位数为C.方差为D.极差为三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题如图是我国古代测量粮食的容器“升”,其形状是正四棱台,“升”装满后用手指或筷子沿升口刮平,这叫“平升”,若该“升”内粮食的高度为“平升”的一半时,粮食的体积约为“平升”时体积的,则该“升”升口边长与升底边长的比值为______.第(2)题如图,在菱形中,,沿将折起到的位置,得到三棱锥,若三棱锥的体积最大时,则此时三棱锥的外接球的表面积为______.第(3)题记为正项等比数列的前项和,若,,则的值为__________.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题如图,在多面体中,四边形为正方形,平面,,,.(1)求证:;(2)求直线与平面所成角的正弦值;(3)在线段上是否存在点,使得直线与所成角的余弦值为,若存在,求出点到平面的距离,若不存在,请说明理由.第(2)题平面直角坐标系中,曲线的参数方程为(为参数),以坐标原点为极点,以轴正半轴为极轴,建立极坐标系,曲线的极坐标方程为.(1)写出曲线的普通方程和曲线的直角坐标方程;(2)曲线与交于两点,求直线的极坐标方程及三角形面积.第(3)题如图,在三棱柱中,底面是边长为2的正三角形,平面底面,,,E,F分别是,的中点,P是线段上的动点.(1)当P是线段的中点时,求点P到平面的距离;(2)当平面与平面的夹角的余弦值为时,求.第(4)题设函数.(1)证明:当时,有唯一零点;(2)若任意,不等式恒成立,求实数a的取值范围.第(5)题长距离跑简称长跑,英文是.最初项目为英里、英里跑,从世纪中叶开始,逐渐被跑和跑替代.长跑对于培养人们克服困难,磨炼刻苦耐劳的顽强意志具有良好的作用,特别是对那些冬季怕冷爱睡懒觉不想锻炼的人起到促进作用,从而使他们尝到健身长跑锻炼的好处,某校开展阳光体育“冬季长跑活动”,为了解学生对“冬季长跑活动”是否感兴趣与性别是否有关,某调查小组随机抽取该校名高中学生进行问卷调查,所得数据制成下表;感兴趣不感兴趣合计男生女生合计(1)完成上面的列联表,并依据小概率值的独立性检验,能否认为学生对“冬季长跑活动”是否感兴趣与性别有关联?(2)若不感兴趣的男生中恰有名是高三学生,现从不感兴趣的男生中随机选出名进行二次调查,记选出高三学生的人数为,求的分布列与数学期望.参考公式,其中.附:。
郴州市2022-2023学年高三上学期第一次教学质量监测数学试题

郴州市2023届高三第一次教学质量监测试卷数 学一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合{}2560A x x x =+-<,120232023xB x ⎧⎫=>⎨⎬⎩⎭,则A B =( ) A .(3-,1-) B .(2-,1)C .(1-,1)D .(1-,6)2.已知复数z 满足13i1i z+=-(i 为虚数单位),z 是z 的共轮复数,则z z ⋅=( ) A .5 B 5C .10 D .103.△ABC 中,D 为BC 中点,设向量AB a =,AC b =,32AE BC =,则DE =( )A .2a b -+B .2a b -C .2a b -D .2a b -+4.某种疾病的患病率为5%,通过验血诊断该病的误诊率为2%,即非患者中有2%的人诊断为阳性,患者中有2%的人诊断为阴性随机抽取一人进行验血,则其诊断结果为阳性的概率为( ) A .0.46 B .0.046 C .0.68 D .0.068 5.设正项等比数列{}n a 的前n 项和为n S ,若321238S a a =+,8722S S =+,则2a =( ) A .4B .3C .2D .16.设函数()sin 6f x x πω⎛⎫=-⎪⎝⎭(0ω>),已知()f x 在区间[]0,π上有且仅有3个零点,下列结论正确的是( )A .直线76x πω=是函数()f x 的图象的一条对称轴 B .ω的取值范围是1319,66⎡⎫⎪⎢⎣⎭C .()f x 的图象向右平移3πω个单位后所得图象的函数是奇函数 D .()f x 在区间()0,π上有且仅有2个极值点7.F 1、F 2是双曲线C :22221x y a b-=(0a b >>)的左、右焦点,过左焦点F 1的直线l 与双曲线C 的左、右两支分别交于A 、B 两点,若|AB|:|BF 2|:|AF 2|=12:5:13,则双曲线的离心率为( ) A 5B .2 C 6D 10 8.某村计划修建一条横断面为等腰梯形(上底大于下底)的水渠,为了降低建造成本,必须尽量减少水与渠壁的接触面.已知水渠横断面面积设计为6平方米,水渠深2米,水渠壁的倾角为α(02πα<<),则当该水渠的修建成本最低时α的值为( )A .6π B .4π C .3π D .512π二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分) 9.如图1,在四棱锥P −ABCD 中,底面ABCD 是菱形,且∠DAB =60°,侧面PAD 为正三角形,且平面PAD ⊥平面ABCD ,则下列说法正确的是( )A .在棱AD 上存在点M ,使AD ⊥平面PMB B .异面直线PA 与DC 所成的角的余弦值为14C .直线PB 与平面PAD 所成的角为45° D .BD ⊥平面PAC10.已知无穷等差数列{}n a 的首项为1,它的前n 项和为n S ,且89S S <,910S S >,则( )A .数列{}n a 是单调递减数列B .116S S =C .数列{}n a 的公差的取值范围是11,89⎛⎫-- ⎪⎝⎭D .当16n ≤时,0n S >11.已知抛物线24x y =的焦点为F ,M (4,0y )在抛物线上,延长MF 交抛物线于点N ,抛物线准线与y 轴交于点Q ,则下列叙述正确的是( ) A .6MF =B .点N 的坐标为(1-,14) C .94QM QN ⋅=D .在x 轴上存在点R ,使得∠MRF 为钝角 12.已知函数()f x ,()g x 的定义域为R ,()'g x 为()g x 的导函数,且()()'100f x g x +-=,()()'4100f x g x ---=,若()g x 为偶函数,则下列一定成立的有( ) A .()()130f f += B .()40f =C .()()13f f -=-D .()20220f =三、填空题(本题共4小题,每小题5分,共20分)13.若()3sin cos 0θπθ--=,则2sin 2cos θθ-=________.14.已知12nx x ⎫⎪⎭(n *∈N )展开式中第5项和第6项的二项式系数最大,则其展开式中常数项是________. 15.如图2,已知△ABC 的外接圆为圆O ,AB 为直径,PA 垂直圆O 所在的平面,且PA =AB =1,过点A 作平面PB α⊥,分别交PB 、PC 于点M 、N ,则三棱锥P −AMN 的外接球的体积为________.16.已知函数()x f x e =,()1ln33x g x =+,对任意m ∈R ,存在()0,n ∈+∞,使()()f m g n =,则n m -的最小值为________.四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分)已知数列{}n a 中,11a =,其前n 项和为n S ,131n n S S +=+. (1)求数列{}n a 的通项公式; (2)设31log n n b a +=,若数列21n n b b +⎧⎫⎨⎬⎩⎭的前n 项和为n T ,求证:34n T <.18.(本小题满分12分)△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且满足cos cos sin 2sin A C Ba c C+=. (1)求a ;(2)若AD ⊥BC 于D ,且AD 3A 的最大值.19.(本小题满分12分) 在图3(1)五边形ABCDE 中,ED =EA ,AB△CD ,CD =2AB ,∠CDE =150°,将△ADE 沿AD 折起到△SAD 的位置,得到如下图3(2)所示的四棱锥S −ABCD ,F 为线段SC 的中点,且BF ⊥平面SCD .(1)求证:CD ⊥平面SAD ;(2)若CD =2SD ,求直线BF 与平面SBD 所成角的正弦值.20.2022年北京冬季奥运会,是由中国举办的国际性奥林匹克赛事,于2022年2月4日开幕,2月20日闭幕。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
郴州市2017届高三第四次教学质量监测试卷数学理科 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}|(5)4A x x x =->,{}|B x x a =≤,若A B B =,则a 的值可以是( )A .1B .2C .3D .42.已知复数322a i z i+=-在复平面内对应的点在第四象限,则实数a 的取值范围是( )A .(,1)-∞-B .(4,)+∞C .(1,4)-D .(4,1)--3.为考察某种药物对预防禽流感的效果,在四个不同的实验室取相同的个体进行动物试验,根据四个实验室得到的列联表画出如图四个等高条形图,最能体现该药物对预防禽流感有效果的图形是( )4.已知23cos tan 3θθ=+,且k θπ≠(k Z ∈),则[]sin 2()πθ-等于( ) A .13-B .13C .23D .23-5.我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的 1.5S =(单位:升),则输入k 的值为( )A .4.5B .6C .7.5D .96.已知双曲线C :22221x y a b-=(0a >,0b >)过点,过点(0,2)-的直线l 与双曲线C 的一条渐进线平行,且这两条平行线间的距离为23,则双曲线C 的实轴长为( )A .2B .C .4D .7.若()f x 为奇函数,且0x 是()xy f x e =-的一个零点,则下列函数中,0x -一定是其零点的函数是( ) A .()1xy f x e-=-⋅-B .()1xy f x e =⋅+ C .()1x y f x e =⋅-D .()1xy f x e =-⋅+8.某几何体的三视图如图所示,则该几何体的体积为( )A .103B .113C .4D .1439.在ABC ∆中,60BAC ∠=︒,5AB =,4AC =,D 是AB 上一点,且5AB CD ⋅=,则||BD 等于( ) A .6B .4C .2D .110.已知椭圆C :22221(0)x y a b a b+=>>的右焦点为2F ,O 为坐标原点,M 为y 轴上一点,点A 是直线2MF 与椭圆C 的一个交点,且2||||2||OA OF OM ==,则椭圆C 的离心率为( )A .13B .25C D 11.如图,矩形ABCD 中,2AB AD =,E 为边AB 的中点,将ADE ∆沿直线DE 翻转成1A DE ∆(1A ∉平面ABCD ).若M 、O 分别为线段1A C 、DE 的中点,则在ADE ∆翻转过程中,下列说法错误的是( )A .与平面1A DE 垂直的直线必与直线BM 垂直B .异面直线BM 与1A E 所成角是定值C .一定存在某个位置,使DE MO ⊥D .三棱锥1A ADE -外接球半径与棱AD 的长之比为定值 12.若曲线1()ln(1)f x a x =+(211e x e -<<-)和32()g x x x =-+(0x <)上分别存在点A 、B ,使得OAB ∆是以原点O 为直角顶点的直角三角形,且斜边AB 的中点在y 轴上,则实数a 的取值范围是( ) A .2(,)e eB .2(,)2e eC .2(1,)eD .[1,)e第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知实数x ,y 满足条件30,240,3,x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩则22(1)z x y =++的最小值为 .14.把3男2女共5名新生分配给甲、乙两个班,每个班分配的新生不少于2名,且甲班至少分配1名女生,则不同的分配方案种数为 . 15.函数()sin()f x A x ωϕ=+(0ω>,||2πϕ<)的部分图象如图所示,将函数()f x 的图象向右平移724π个单位后得到函数()g x 的图象,若函数()g x 在区间,3πθ⎡⎤-⎢⎥⎣⎦(3πθ>-)上的值域为[]1,2-,则θ= .16.在ABC ∆中,a ,b ,c 分别是角A ,B ,C 的对边,ABC ∆的面积为S ,22()tan 8a b C S +=,且sin cos 2cos sin A B A B =,则cos A = .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.已知等差数列{}n a 的前n (*n N ∈)项和为n S ,33a =,且1n n n S a a λ+=,在等比数列{}n b 中,12b λ=,3151b a =+. (Ⅰ)求数列{}n a 及{}n b 的通项公式;(Ⅱ)设数列{}n c 的前n (*n N ∈)项和为n T ,且()12n n n S c +=,求n T .18.某地区拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从6个招标问题中随机抽取3个问题,已知这6个招标问题中,甲公司可正确回答其中的4道题目,而乙公司能正确回答每道题目的概率均为23,甲、乙两家公司对每题的回答都是相互独立,互不影响的. (Ⅰ)求甲、乙两家公司共答对2道题目的概率;(Ⅱ)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大? 19.如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,底面ABCD 是直角梯形,90ADC ∠=︒,//AD BC ,AB AC ⊥,AB AC ==点E 在AD 上,且2AE ED =.(Ⅰ)已知点F 在BC 上,且2CF FB =,求证:平面PEF ⊥平面PAC ;(Ⅱ)当二面角A PB E --的余弦值为多少时,直线PC 与平面PAB 所成的角为45︒? 20.已知A 是抛物线24y x =上的一点,以点A 和点(2,0)B 为直径的圆C 交直线1x =于M ,N 两点,直线l 与AB 平行,且直线l 交抛物线于P ,Q 两点.(Ⅰ)求线段MN 的长;(Ⅱ)若3OP OQ ⋅=-,且直线PQ 与圆C 相交所得弦长与||MN 相等,求直线l 的方程. 21.设函数2()xf x e =,()1g x kx =+(k R ∈).(Ⅰ)若直线()y g x =和函数()y f x =的图象相切,求k 的值;(Ⅱ)当0k >时,若存在正实数m ,使对任意(0,)x m ∈,都有|()()|2f x g x x ->恒成立,求k 的取值范围.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线C 的参数方程为cos ,2sin x a t y t =⎧⎨=⎩(t 为参数,0a >).以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,已知直线l 的极坐标方程为cos()4πρθ+=-(Ⅰ)设P 是曲线C 上的一个动点,当2a =时,求点P 到直线l 的距离的最小值; (Ⅱ)若曲线C 上的所有点均在直线l 的右下方,求a 的取值范围. 23.选修4-5:不等式选讲已知函数()|1||3|f x x x =++-,()|2|g x a x =--.(Ⅰ)若关于x 的不等式()()f x g x <有解,求实数a 的取值范围; (Ⅱ)若关于x 的不等式()()f x g x <的解集为7(,)2b ,求a b +的值.郴州市2017届高三第四次教学质量监测试卷数学理科答案一、选择题1-5:DCDCB 6-10:ABACD 11、12:CB 二、填空题13.5 14.16 15.4π三、解答题17.解:(Ⅰ)∵1n n n S a a λ+=,33a =,∴112a a a λ=,且12232()3a a a a a λ+==, ∴2a λ=,1233a a a +==,①∵数列{}n a 是等差数列,∴1322a a a +=,即2123a a -=,② 由①②得11a =,22a =,∴n a n =,2λ=,∴14b =,316b =,则12n n b +=.(Ⅱ)∵(1)2n n n S +=,∴2(2)n c n n =+,∴22222132435(1)(1)(2)n T n n n n =+++++⨯⨯⨯-++… 111111111132435112n n n n =-+-+-++-+--++2323232n n n +=-++. 18.解:(Ⅰ)由题意可知,所求概率122111234242333662221()(1)(1)33315C C C C P C C C =⨯-+⨯-=. (Ⅱ)设甲公司正确完成面试的题数为X ,则X 的取值分别为1,2,3.1242361(1)5C C P X C ===,2142363(2)5C C P X C ===,3042361(3)5C C P X C ===. 则X 的分布列为:X 1 2 3P15 35 15∴131()1232555E X =⨯+⨯+⨯=, 2221312()(12)(22)(32)5555D X =-⨯+-⨯+-⨯=.设乙公司正确完成面试的题数为Y ,则Y 取值分别为0,1,2,3.1(0)27P Y ==,123212(1)()339P Y C ==⨯⨯=,223214(2)()339P Y C ==⨯⨯=,328(3)()327P Y ===. 则Y 的分布列为:Y 0 1 2 3P127 29 49 827∴1248()01232279927E Y =⨯+⨯+⨯+⨯=, 222212482()(02)(12)(22)(32)2799273D Y =-⨯+-⨯+-⨯+-⨯=.由()()E X E Y =,()()D X D Y <可得,甲公司竞标成功的可能性更大. 19.(Ⅰ)证明:∵AB AC ⊥,AB AC =,∴45ACB ∠=︒, ∵底面ABCD 是直角梯形,90ADC ∠=︒,//AD BC , ∴45ACD ∠=︒,即AD CD =,∴2BC AD ==,∵2AE ED =,2CF FB =,∴23AE BF AD ==, ∴四边形ABFE 是平行四边形,则//AB EF , ∴AC EF ⊥,∵PA ⊥底面ABCD ,∴PA EF ⊥, ∵PAAC A =,∴EF ⊥平面PAC ,∵EF ⊂平面PEF , ∴平面PEF ⊥平面PAC .(Ⅱ)解:∵PA AC ⊥,AC AB ⊥,∴AC ⊥平面PAB ,则APC ∠为直线PC 与平面PAB 所成的角,若PC 与平面PAB 所成夹角为45︒,则tan 1ACAPC PA∠==,即PA AC == 取BC 的中点为G ,连接AG ,则AG BC ⊥,以A 为坐标原点建立如图所示的空间直角坐标系A xyz -,则(1,1,0)B -,(1,1,0)C ,2(0,,0)3E,P ,∴5(1,,0)3EB =-,2(0,3EP =-,设平面PBE 的法向量(,,)n x y z =,则0,0,n EB n EP ⎧⋅=⎪⎨⋅=⎪⎩即50,320,3x y y ⎧-=⎪⎪⎨⎪-+=⎪⎩令3y =,则5x =,z =,∴(5,3,2)n =,∵(1,1,0)AC =是平面PAB 的一个法向量,∴cos ,3n AC <>==, 即当二面角A PB E --的余弦值为3时,直线PC 与平面PAB 所成的角为45︒. 20.解:(Ⅰ)设200(,)4y A y ,圆C 方程为200(2)()()04y x x y y y --+-=, 令1x =,得2200104y y y y -+-=,∴0M N y y y +=,2014M N y y y =-,||||2M NMN y y=-===.(Ⅱ)设直线l的方程为x my n=+,11(,)P x y,22(,)Q x y,则由2,4,x my ny x=+⎧⎨=⎩消去x,得2440y my n--=,124y y m+=,124y y n=-,∵3OP OQ⋅=-,∴12123x x y y+=-,则21212()316y yy y+=-,∴2430n n-+=,解得1n=或3n=,当1n=或3n=时,当(2,0)B到直线l的距离d=∵圆心C到直线l的距离等于直线1x=的距离,∴28y=,又224ymy-=,消去m得420646416yy+⋅=,求得28y=,此时,2240ymy-==,直线l的方程为3x=,综上,直线l的方程为1x=或3x=.21. 解:(Ⅰ)设切点的坐标为2(,)tt e,由2()xf x e=,得2'()2xf x e=,∴切线方程为222()t ty e e x t-=-,即222(12)t ty e x t e=+-.由已知222(12)t ty e x t e=+-和1y kx=+为同一直线,所以22t e k=,2(12)1tt e-=,令()(1)xh x x e=-,则'()xh x xe=-,当(,0)x∈-∞时,'()0h x>,()h x单调递增,当(0,)x∈+∞时,'()0h x<,()h x单调递减,∴()(0)1h x h≤=,当且仅当0x =时等号成立,∴0t =,2k =.(Ⅱ)①当2k >时,由(Ⅰ)结合函数的图象知:存在00x >,使得对于任意0(0,)x x ∈,都有()()f x g x <,则不等式|()()|2f x g x x ->等价于()()2g x f x x ->,即2(2)10x k x e-+->.设2()(2)1x t x k x e =-+-,2'()22x t x k e =--, 由'()0t x >,得12ln 22k x -<;由'()0t x <,得12ln 22k x ->. 若24k <≤,12ln 022k -≤,∵012(0,)(ln ,)22k x -⊆+∞,∴()t x 在0(0,)x 上单调递减, ∵(0)0t =,∴对任意0(0,)x x ∈,()0t x <,与题设不符.若4k >,12ln 022k ->,1212(0,ln )(,ln )2222k k --⊆-∞,∴()t x 在12(0,ln )22k -上单调递增, ∵(0)0t =,∴对任意12(0,ln )22k x -∈,()0t x >符合题设, 此时取0120min ,ln 22k m x -⎧⎫<≤⎨⎬⎩⎭,可得对任意(0,)x m ∈,都有|()()|2f x g x x ->. ②当02k <≤时,由(Ⅰ)结合函数的图象知2(21)0x e x -+≥(0x >),22()()1(21)(2)x x f x g x e kx e x k x -=--=-++-(2)0k x ≥-≥对任意0x >都成立, ∴|()()|2f x g x x ->等价于2(2)10x ek x -+->. 设2()(2)1x x e k x ϕ=-+-,则2'()2(2)x x e k ϕ=-+w ,由'()0x ϕ>,得12ln 022k x +>>;'()0x ϕ<,得12ln 22k x +<, ∴()x ϕ在12(0,ln )22k +上单调递减,注意到(0)0ϕ=, ∴对任意12(0,ln )22k x +∈,()0x ϕ<,不符合题设. 综上所述,k 的取值范围为(4,)+∞.22.解:(Ⅰ)由cos()4πρθ+=-cos sin )ρθρθ-=-)x y -=-,即直线l 的方程为40x y -+=, 依题意,设(2cos ,2sin )P t t ,则P 到直线l的距离|)4|2cos()4t d t ππ++===+. 当24t k πππ+=+,即324t k ππ=+,k Z ∈时,min 2k =. 故点P 到直线l的距离的最小值为2.(Ⅱ)∵曲线C 上的所有点均在直线l 的右下方,∴t R ∀∈,有cos 2sin 40a t t -+>恒成立,)4t ϕ+>-(其中2tan aϕ=)恒成立,4<,又0a >,解得0a <<故a的取值范围为(0,.23.解:(Ⅰ)当2x =时,()|2|g x a x =--取最大值为a ,∵()|1||3|f x x x =++-4≥,当且仅当13x -≤≤,()f x 取最小值4, ∵关于x 的不等式()()f x g x <有解,∴4a >,即实数a 的取值范围是(4,)+∞. (Ⅱ)当72x =时,()5f x =, 则77()2522g a =-++=,解得132a =, ∴当2x <时,9()2g x x =+, 令9()42g x x =+=,得12x =-(1,3)∈-, ∴12b =-,则6a b +=.。
