高二数学暑假作业7

合集下载

高二数学暑假作业最新的高二数学暑假作业试卷练习题

高二数学暑期作业最新的高二数学暑期作业试卷练习题第Ⅰ卷 (选择题：共60 分 )一、选择题 ( 共 12 小题，每题 5 分，每题四个选项中只有一项切合要求。

)1.的值为A. B. C. D.2.已知会合,则 =A. B. C. D.3.若，此中 a、b∈ R， i 是虚数单位，则A. B. C. D.4.命题 r：假如则且.若命题r的否命题为p，命题 r 的否定为 q，则A.P 真 q 假B. P 假 q 真C. p， q 都真D. p,q 都假5.扔掷一枚均匀硬币和一枚均匀骰子各一次，记“硬币正面向上”为事件 A ，“骰子向上的点数是3”为事件 B，则事件A,B 中起码有一件发生的概率是A. B. C. D.6.设，，， (e 是自然对数的底数)，则A.B.C.D.7.将名学生疏别安排到甲、乙，丙三地参加社会实践活动，每个地方起码安排一名学生参加，则不一样的安排方案共有A.36 种B.24 种C.18 种D.12 种8. 一个袋子里装有大小同样的 3 个红球和 2 个黄球，从中同时拿出 2 个，则此中含红球个数的数学希望是A. B. C. D.9.设函数，曲线在点处的切线方程为，则曲线在点处切线的斜率为A. B. C. D.10.已知样本 9，10，11，x,y 的均匀数是10，标准差是，则的值为A.100B.98C.96D.9411.现有四个函数：① ;② ;③ ;④的图象 (部分 )以下：则依据从左到右图象对应的函数序号安排正确的一组是A. ①④②③B.①④③②C.④①②③D.③④②①12.若函数在R上可导，且知足，则ABCD第 II 卷 (非选择题，共90 分 )二、填空题 (每题 5 分)13.已知偶函数的定义域为R,知足，若时，，则14.设 a= 则二项式的常数项是15.下边给出的命题中：①已知则与的关系是②已知听从正态散布，且，则③将函数的图象向右平移个单位，获得函数的图象。

此中是真命题的有_____________ 。

2017高二数学暑假假期作业1-7套

- 25 -衡水五中2017年高中部高二数学暑假作业第＿1＿套一、选择题1．(2013·四川高考)设集合A ＝{x |x ＋2＝0}，集合B ＝{x |x 2－4＝0}，则A ∩B ＝( ) A ．{－2} B ．{2} C ．{－2,2} D ．∅ 2．下列函数中与函数y ＝x 表示同一函数的是( )A ．y ＝(x )2B ．y ＝x 2C ．y ＝3x 3D ．y ＝x 2x3．已知函数f (x )＝⎩⎪⎨⎪⎧2x ，x ≥0x 2，x ＜0，则f (f (－2))的值是( )A ．4B ．－4C ．8D ．－8 4．下列图形中不是函数的图象的是( )5．已知f (x )的定义域为[－2,2]，则f (x 2－1)的定义域为( ) A ．[－1，3] B ．[0，3] C ．[－3，3] D ．[－4,4] 6．已知函数f (x ＋1)＝3x ＋2，则f (x )的解析式是( ) A ．3x ＋2 B ．3x ＋1 C ．3x －1 D ．3x ＋47．函数f (x )＝|x －1|的图象是( )8．已知f (x )是奇函数，g (x )是偶函数，且f (－1)＋g (1)＝2，f (1)＋g (－1)＝4，则g (1)＝( )A ．4B ．3C ．2D ．19．函数f (x )＝1x －2x 在区间⎣⎢⎡⎦⎥⎤－2，－12上的最小值为( ) A ．1 B ．72 C ．－72 D ．－110．函数f (x )＝1x－x ＋x 3的图象关于( )A ．y 轴对称B ．直线y ＝x 对称C ．坐标原点对称D ．直线y ＝－x 对称11．已知集合M ＝{－1,0,1}，N ＝{x |x ＝ab ，a ，b ∈M ，且a ≠b }，则集合N 的真子集个数为( )A ．8B ．7C ．4D ．312．已知函数f (x )＝－x 5－3x 3－5x ＋3，若f (a ) ＋f (a －2)＞6，则实数a 的取值范围是( ) A ．(－∞，1) B ．(－∞，3) C ．(1，＋∞) D ．(3，＋∞) 二、填空题13．已知集合A ＝{－2,1,2}，B ＝{a ＋1，a }，且B ⊆A ，则实数a 的值是________． 14．已知函数f (x )的图象如图所示，则此函数的定义域是________，值域是________．15．若函数f (x )＝(m －2)x 2＋(m －1)x ＋2是偶函数，则f (x )的单调递增区间是________． 16．对任意的两个实数a ，b ，定义min(a ，b )＝⎩⎪⎨⎪⎧a a ＜b ba ≥b，若f (x )＝4－x 2，g (x )＝3x ，则min(f (x )，g (x ))的最大值为________．三、解答题17．已知全集U＝{x∈Z|－2＜x＜5}，集合A＝{－1,0,1,2}，集合B＝{1,2,3,4}；(1)求A∩B，A∪B；(2)求(∁U A)∩B，A∪(∁U B)．18．已知函数f(x)＝xx－1.(1)求f(1＋x)＋f(1－x)的值；(2)用函数单调性的定义证明函数f(x)在(1，＋∞)上是减函数．19．已知函数f(x)＝|－x2＋3x－2|，试作出函数的图象，并指出它的单调增区间(不需证明)，求出函数在x∈[－1,3]时的最大值．20．已知二次函数f(x)＝－x2＋2ax－a在区间[0,1]上有最大值2，求实数a的值．- 26 -- 27 -衡水五中高中部高二数学暑假作业第＿2＿套一、选择题1．(2013·重庆高考)函数y ＝1log 2x －2的定义域是( )A ．(－∞，2)B ．(2，＋∞)C ．(2,3)∪(3，＋∞) D．(2,4)∪(4，＋∞) 2．下列关于函数f (x )＝x 3的性质表述正确的是( ) A ．奇函数，在(－∞，＋∞)上单调递增 B ．奇函数，在(－∞，＋∞)上单调递减 C ．偶函数，在(－∞，＋∞)上单调递增 D ．偶函数，在(－∞，＋∞)上单调递减3．设集合S ＝{y |y ＝3x，x ∈R }，T ＝{(x ，y )|y ＝x 2－1，x ∈R }，则S ∩T 是( ) A ．(0，＋∞) B ．(－1，＋∞) C ．∅ D ．R 4．已知函数f (x )＝⎩⎪⎨⎪⎧log 3x x ＞0⎝ ⎛⎭⎪⎫12xx ≤0，则f ⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫127＝( )A ．－18B ．18C ．－8D ．85．若P ＝log 23·log 34，Q ＝lg 2＋lg 5，M ＝e 0，N ＝ln 1，则正确的是( ) A ．P ＝Q B ．Q ＝M C ．M ＝N D ．N ＝P6．已知函数f (x )＝⎝ ⎛⎭⎪⎫12x，则函数f (x ＋1)的反函数的图象可能是( )7．设f (x )是定义在R 上的奇函数，当x ≥0时，f (x )＝2x＋2x ＋b (b 为常数)，则f (－1)＝( )A ．1B ．－1C ．3D ．－38．(2013·北京高考)函数f (x )的图象向右平移1个单位长度，所得图象与曲线y ＝e x关于y 轴对称，则f (x )＝( )A ．ex ＋1B ．ex －1C ．e－x ＋1D ．e－x －19．函数f (x )＝log 2(x ＋x 2＋1)(x ∈R )的奇偶性为( ) A ．奇函数而非偶函数 B ．偶函数而非奇函数 C ．非奇非偶函数D ．既是奇函数又是偶函数10．若log (a －1)(2x －1)＞log (a －1)(x －1)，则有( ) A ．a ＞1，x ＞0 B ．a ＞1，x ＞1 C ．a ＞2，x ＞0 D ．a ＞2，x ＞111．关于x 的方程a x＝log 1ax (a ＞0，且a ≠1)( )A ．无解B ．必有唯一解C ．仅当a ＞1时有唯一解D ．仅当0＜a ＜1时有唯一解12．设函数f (x )定义在R 上，f (2－x )＝f (x )，且当x ≥1时，f (x )＝log 2x ，则有( )A ．f (－3)＜f (2)＜f ⎝ ⎛⎭⎪⎫12B ．f ⎝ ⎛⎭⎪⎫12＜f (2)＜f (－3)C ．f ⎝ ⎛⎭⎪⎫12＜f (－3)＜f (2)D ．f (2)＜f ⎝ ⎛⎭⎪⎫12＜f (－3)二、填空题13．若x 12 ＋x －12 ＝3则x ＋x －1＝______. 14．函数y ＝(2)1x 的单调递减区间是______． 15．已知函数f (x )＝a2x －4＋n (a ＞0且a ≠1)的图象恒过定点P (m,2)，则m ＋n ＝______.16．定义在R 上的偶函数f (x )在[0，＋∞)上单调递减，且f ⎝ ⎛⎭⎪⎫12＝0，则满足f (log 14x )＜0的集合为______．- 28 -三、解答题(本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤) 17．计算：(1)2723 －2log 23×log 2 18＋2lg (3＋5＋3－5)；(2)810＋41084＋411.18．设y 1＝log a (3x ＋1)，y 2＝log a (－3x )，其中0＜a ＜1. (1)若y 1＝y 2，求x 的值； (2)若y 1＞y 2，求x 的取值范围．19．已知函数f (x )＝b ·a x(其中a ，b 为常量且a ＞0，a ≠1)的图象经过点A (1,6)，B (3,24)． (1)试确定f (x )；(2)若不等式⎝ ⎛⎭⎪⎫1a x ＋⎝ ⎛⎭⎪⎫1b x－m ≥0，在x ∈(－∞，1]时恒成立，求实数m 的取值范围．20．设函数f (x )＝(log 2x ＋log 24)(log 2x ＋log 22)的定义域为⎣⎢⎡⎦⎥⎤14，4. (1)若t ＝log 2x ，求t 的取值范围；(2)求y ＝f (x )的最大值与最小值，并求出取最值时对应的x 的值．- 29 -衡水五中高中部高二数学暑假作业第＿3＿套一、选择题1．已知全集U ＝{1,2,3,4,5,6,7,8,9}，M ＝{1,3,5,6}，N ＝{1,2,4,7,9}，则M ∪(∁U N )等于( )A ．{3,5,8}B ．{1,3,5,6,8}C ．{1,3,5,8}D ．{1,5,6,8} 2．如图，I 是全集，A ，B ，C 是它的子集，则阴影部分所表示的集合是()A ．(∁I A ∩B )∩C B ．(∁I B ∪A )∩C C ．(A ∩B )∩∁I CD ．(A ∩∁I B )∩C 3．已知函数f (x )＝7＋ax －1的图象恒过点P ，则P 点的坐标是( )A ．(1,8)B ．(1,7)C ．(0,8)D ．(8,0) 4．下列各组函数中，表示同一函数的是( )A ．y ＝x 2和y ＝(x )2B ．y ＝lg(x 2－1)和y ＝lg(x ＋1)＋lg(x －1) C ．y ＝log a x 2和y ＝2log a x D ．y ＝x 和y ＝log a a x5．若x ＝1是函数f (x )＝ax＋b (a ≠0)的一个零点，则函数h (x )＝ax 2＋bx 的零点是( ) A ．0或－1 B ．0或－2 C ．0或1 D ．0或2 6．若lg x －lg y ＝a ，则lg ⎝ ⎛⎭⎪⎫x 23－lg ⎝ ⎛⎭⎪⎫y 23＝( )A ．3aB ．32aC ．aD ．a27．设a ＝22.5，b ＝log 122.5，c ＝⎝ ⎛⎭⎪⎫12 2.5，则a ，b ，c 之间的大小关系是( )A ．c >b >aB ．c >a >bC ．a >c >bD ．b >a >c 8．函数f (x )＝3x21－x＋lg(3x ＋1)的定义域是( ) A.⎝ ⎛⎭⎪⎫－13，＋∞ B ．⎝ ⎛⎭⎪⎫－13，1 C.⎝ ⎛⎭⎪⎫－13，13 D ．⎝⎛⎭⎪⎫－∞，－139．若实数x ，y 满足|x |－ln 1y＝0，则y 关于x 的函数的图象形状大致是( )10．设函数若f (x 0)＞1，则x 0的取值范围是( )A ．(－1,1)B ．(－1，＋∞)C ．(－∞，－2)∪(0，＋∞)D ．(－∞，－1)∪(1，＋∞)11．已知f (x )为奇函数，且当x ＜0时，f (x )＝x 2＋3x ＋2.则当x ∈[1,3]时，f (x )的最小值是( )A ．2B ．14C ．－2D ．－1412．对于定义域为R 的函数f (x )，若存在非零实数x 0，使函数f (x )在(－∞，x 0)和(x 0，＋∞)上与x 轴均有交点，则称x 0为函数f (x )的一个“界点”．则下列四个函数中，不存在“界点”的是( )A ．f (x )＝x 2＋bx －1(b ∈R ) B ．f (x )＝|x 2－1| C ．f (x )＝2－|x －1| D ．f (x )＝x 3＋2x 二、填空题13．已知集合M ＝{(x ，y )|y ＝－x ＋1}，N ＝{(x ，y )|y ＝x －1}，那么M ∩N 为______．14．已知函数f (x )＝⎩⎪⎨⎪⎧1，x ∈Q0，x ∈∁R Q，则f (f (2π))＝____________.15．对于函数f (x )＝ln x 的定义域中任意的x 1，x 2(x 1≠x 2)，有如下结论：- 30 -①f (x 1＋x 2)＝f (x 1)·f (x 2)；②f (x 1·x 2)＝f (x 1)＋f (x 2)；③f x 1－f x 2x 1－x 2>0.上述结论中正确结论的序号是______．16．已知直线y ＝mx 与函数f (x )＝⎩⎪⎨⎪⎧2－⎝ ⎛⎭⎪⎫13x，x ≤012x 2＋1，x >0的图象恰好有3个不同的公共点，则实数m 的取值范围是______．三、解答题17．已知全集U ＝R ，A ＝{x |2x －4>0}，B ＝{x |2≤2x<16}，C ＝{0,1,2}． (1)求∁U (A ∩B )；(2)如果集合M ＝(A ∪B )∩C ，写出M 的所有真子集．18．已知f (x )＝log 2x ＋1x －1； (1)求f (x )的定义域和值域；(2)判断f (x )的奇偶性并证明．19．已知函数f (x )是定义在R 上的奇函数，当x >0时，f (x )＝log 2x . (1)求f (x )的解析式；(2)解关于x 的不等式f (x )≤12.、衡水五中高中部高二数学暑假作业第＿4＿套一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的)1．长方体ABCD－A1B1C1D1中，异面直线AB，A1D1所成的角等于( )A．30° B．45° C．60° D．90°2．已知平面α和直线l，则α内至少有一条直线与l( )A．平行 B．相交 C．垂直 D．异面3．下列命题中，错误的是( )A．一条直线与两个平行平面中的一个平面相交，则必与另一个平面相交B．平行于同一平面的两个不同平面平行C．若直线l不平行于平面α，则在平面α内不存在与l平行的直线D．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β4．已知α、β是两个平面，直线l⊄α，l⊄β，若以①l⊥α；②l∥β；③α⊥β中两个为条件，另一个为结论构成三个命题，则其中正确的命题有( )A．①③⇒②；①②⇒③B．①③⇒②；②③⇒①C．①②⇒③；②③⇒①D．①③⇒②；①②⇒③；②③⇒①5．对于两条不相交的空间直线a与b，必存在平面α，使得( )A．a⊂α，b⊂α B．a⊂α，b∥α C．a⊥α，b⊥α D．a⊂α，b⊥α6．设直线l⊂平面α，过平面α外一点A与l，α都成30°角的直线有( )A．1条 B．2条 C．3条 D．4条7．如图，A是平面BCD外一点，E、F、G分别是BD、DC、CA的中点，设过这三点的平面为α，则在图中的6条直线AB、AC、AD、BC、CD、DB中，与平面α平行的直线有( )A．0条 B．1条 C．2条 D．3条8．已知三棱柱ABC－A1B1C1的侧棱与底面边长都相等，A1在底面ABC内的射影为△ABC的中心O，则AB1与底面ABC所成角的正弦值为( )A．13B．23C．33D．239．等腰Rt△ABC中，AB＝BC＝1，M为AC的中点，沿BM把它折成二面角，折后A与C的距离为1，则二面角C－BM－A的大小为( )A．30° B．60° C．90° D．120°10．如图，α⊥β，α∩β＝l，A∈α，B∈β，A，B到l的距离分别是a和b ，AB与α，β所成的角分别是θ和φ，AB在α，β内的射影长分别是m和n，若a＞b，则( )A．θ＞φ，m＞n B．θ＞φ，m＜n C．θ＜φ，m＜n D．θ＜φ，m＞n11．如图，在三棱柱ABC－A′B′C′中，点E，F，H，K分别为AC′，CB′，A′B，B′C′的中点，G为△ABC的重心，从K，H，G，B′中取一点作为P，使得该三棱柱恰有2条棱与平面PEF平行，则点P为( )A．K B．H C．G D．B′12．如图，四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，将△ABD沿BD 折起，使平面ABD⊥平面BCD，构成四面体ABCD，则在四面体ABCD中，下列结论正确的是( )- 31 -- 32 -A ．平面ABD ⊥平面ABCB ．平面ADC ⊥平面BDC C ．平面ABC ⊥平面BDCD ．平面ADC ⊥平面ABC二、填空题13．直线l 与平面α所成角为30°，l ∩α＝A ，m ⊂α，A ∉m ，则m 与l 所成角取值范围是________.14．如图所示，在正方体ABCD －A 1B 1C 1D 1中，M 、N 分别是棱AA 1和AB 上的点，若∠B 1MN 是直角，则∠C 1MN 等于________.15．如图所示，在四棱锥P －ABCD 中，PA ⊥底面ABCD ，且底面各边都相等，M 是PC 上的一动点，当点M 满足________时，平面MBD ⊥平面PCD (只要填写一个你认为是正确的条件即可)．16．(2013·高考安徽卷)如图正方体ABCD －A 1B 1C 1D 1，棱长为1，P 为BC 中点，Q 为线段CC 1上的动点，过A 、P 、Q 的平面截该正方体所得的截面记为S ，则下列命题正确的是________.(写出所有正确命题的编号)①当0<CQ <12时，S 为四边形②当CQ ＝12时，S 为等腰梯形③当CQ ＝34时，S 与C 1D 1交点R 满足C 1R 1＝13④当34<CQ <1时，S 为六边形⑤当CQ ＝1时，S 的面积为62.三、解答题17．(2014·全国高考江苏卷)如图，在三棱锥P －ABC 中，D 、E 、F 分别为棱PC 、AC 、AB 的中点，已知PA ⊥AC ，PA ＝6，BC ＝8，DF ＝5.求证：(1)直线PA ∥面DEF ； (2)平面BDE ⊥平面ABC ．18．如下图所示，在直三棱柱ABC －A 1B 1C 1中，AC ＝3，BC ＝4，AB ＝5，AA 1＝4，点D 是AB 的中点．(1)求证：AC ⊥BC 1； (2)求证：AC 1∥平面CDB 1；(3)求异面直线AC 1与B 1C 所成角的余弦值．- 33 -衡水五中高中部高二数学暑假作业第＿5＿套一、选择题1．(2015·吉林省高二期末)已知点A (1，3)，B (－1，33)，则直线AB 的倾斜角是( ) A ．60° B ．30° C ．120° D ．150°2．直线l 过点P (－1,2)，倾斜角为45°，则直线l 的方程为( ) A ．x －y ＋1＝0 B ．x －y －1＝0 C ．x －y －3＝0 D ．x －y ＋3＝0 3．如果直线ax ＋2y ＋2＝0与直线3x －y －2＝0平行，则a 的值为( ) A ．－3 B ．－6 C ．32 D ．234．直线x a 2－yb2＝1在y 轴上的截距为( )A ．|b |B ．－b 2C ．b 2D ．±b5．已知点A (3,2)，B (－2，a )，C (8,12)在同一条直线上，则a 的值是( ) A ．0 B ．－4 C ．－8 D ．46．(2015·福州八中高一期末)如果AB <0，BC <0，那么直线Ax ＋By ＋C ＝0不经过( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 7．(2015·江苏淮安高一期末)已知点A (1，－2)，B (m,2)，且线段AB 的垂直平分线的方程是x ＋2y －2＝0，则实数m 的值是( )A ．－2B ．－7C ．3D ．18．(2015·兰州一中高一期末)经过直线l 1：x －3y ＋4＝0和l 2：2x ＋y ＝5＝0的交点，并且经过原点的直线方程是( )A ．19x －9y ＝0B ．9x ＋19y ＝0C ．3x ＋19y ＝0D ．19x －3y ＝09．已知直线(3k －1)x ＋(k ＋2)y －k ＝0，则当k 变化时，所有直线都通过定点( ) A ．(0,0) B ．(17，27) C ．(27，17) D ．(17，114)10．(2015·广东省高一期末)直线x －2y ＋1＝0关于直线x ＝1对称的直线方程是( ) A ．x ＋2y －1＝0 B ．2x ＋y －1＝0 C ．2x ＋y －3＝0 D ．x ＋2y －3＝011．(2015·吉林模拟)已知直线l 的倾斜角为135°，直线l 1经过点A (3,2)，B (a ，－1)，且l 1与l 垂直，直线l 2：2x ＋by ＋1＝0与直线l 1平行，则a ＋b 等于( )A ．－4B ．－2C ．0D ．212．等腰直角三角形ABC 中，∠C ＝90°，若点A ，C 的坐标分别为(0,4)，(3,3)，则点B 的坐标可能是( )A ．(2,0)或(4,6)B ．(2,0)或(6,4)C ．(4,6)D ．(0,2)二、填空题13．直线l 与直线y ＝1，x －y －7＝0分别交于A ，B 两点，线段AB 的中点为M (1，－1)，则直线l 的斜率为_________.14．点A (3，－4)与点B (5,8)关于直线l 对称，则直线l 的方程为_________.15．若动点A ，B 分别在直线l 1：x ＋y －7＝0和l 2：x ＋y －5＝0上移动，则AB 的中点M 到原点的距离的最小值为_________.16．(2009·高考全国卷Ⅰ)若直线m 被两平行线l 1：x －y ＋1＝0与l 2：x －y ＋3＝0所截得的线段的长为22，则m 的倾斜角可以是①15° ②30° ③45° ④60° ⑤75°，其中正确答案的序号是_________.(写出所有正确答案的序号)三、解答题17． (2015·河南省郑州市高一上学期期末试题)已知直线l 经过点P (－2,5)且斜率为－34，(1)求直线l 的方程；(2)若直线m 平行于直线l ，且点P 到直线m 的距离为3，求直线m 的方程．18．求经过两直线3x－2y＋1＝0和x＋3y＋4＝0的交点，且垂直于直线x＋3y＋4＝0的直线方程．19．)已知A(4，－3)，B(2，－1)和直线l：4x＋3y－2＝0，求一点P，使|PA|＝|PB|，且点P到直线l的距离等于2.20．(2015·甘肃兰州一中期末)△ABC中，A(0,1)，AB边上的高CD所在直线的方程为x＋2y－4＝0，AC边上的中线BE所在直线的方程为2x＋y－3＝0.(1)求直线AB的方程；(2)求直线BC的方程；(3)求△BDE的面积．21．直线过点P(43，2)且与x轴、y轴的正半轴分别交于A，B两点，O为坐标原点，是否存在这样的直线同时满足下列条件：(1)△AOB的周长为12；(2)△AOB的面积为6.若存在，求直线的方程；若不存在，请说明理由．- 34 -- 35 -衡水五中高中部高二数学暑假作业第＿6＿套一、选择题1．(2014·全国高考卷Ⅰ)某几何体的三视图，如图所示，则这个几何体是( )A ．三棱锥B ．三棱柱C ．四棱锥D ．四棱柱2．如图，△O ′A ′B ′是水平放置的△OAB 的直观图，则△OAB 的面积为( )A ．6B ．3 2C ．6 2D ．123．已知一个底面是菱形的直棱柱的侧棱长为5，菱形的对角线的长分别是9和15，则这个棱柱的侧面积是( )A ．3034B ．6034C ．3034＋135D ．135 4．半径为R 的半圆卷成一个圆锥，则它的体积为( ) A ．324πR 3 B ．38πR 3 C ．525πR 3 D ．58πR 35．已知圆柱与圆锥的底面积相等，高也相等，它们的体积分别为V 1和V 2，则V 1V 2＝( ) A ．1 3 B ．11 C ．21 D ．316．若一个底面是正三角形的三棱柱的正视图如右图所示，其顶点都在一个球面上，则该球的表面积为( )A ．163πB ．193πC ．1912πD ．43π7．一个正方体的体积是8，则这个正方体的内切球的表面积是( ) A ．8π B ．6π C ．4π D ．π8．如图是一个空间几何体的三视图，如果直角三角形的直角边长均为1，那么这个几何体的体积为( )A ．1B ．12C ．13D ．169．圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小底面的半径为( )A ．7B ．6C ．5D ．310．正三棱柱有一个半径为 3 cm 的内切球，则此棱柱的体积是( ) A ．9 3 cm 3B ．54 cm 3C ．27 cm 3D ．18 3 cm 311．(2014·课标全国Ⅱ)如图，网格纸上正方形小格的边长为1(表示1 cm)，图中粗线画出的是某零件的三视图，该零件由一个底面半径为3 cm ，高为6 cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为( )A ．1727B ．59C ．1027D ．1312．(2013·全国Ⅰ·理科)如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm ，如果不计容器的厚度，则球的体积为( )- 36 -A ．500π3 cm 3B ．866π3 cm 3C ．1372π3 cm 3D ．2048π3cm 3二、填空题13．在几何体①圆锥；②正方体；③圆柱；④球；⑤正四面体中，三视图完全一样的是__________ 14．用斜二测画法画边长为2的正三角形的直观图时，如果在已知图形中取的x 轴和正三角形的一边平行，则这个正三角形的直观图的面积是__________ ________.15．棱锥的高为16，底面积为512，平行于底面的截面面积为50，则截得的棱台的高为__________ 16．如图是一个组合几何体的三视图，则该几何体的体积是__________ ________.三、解答题17．把一个圆锥截成圆台，已知圆台的上、下底面半径的比是14，母线长为10 cm.求圆锥的母线长．18．如图是一个几何体的正视图和俯视图．(1)试判断该几何体是什么几何体？ (2)画出其侧视图，并求该平面图形的面积； (3)求出该几何体的体积．19．如下图，一个圆锥形的空杯子上面放着一个半球形的冰淇淋，如果冰淇淋融化了，会溢出杯子吗？请用你的计算数据说明理由．- 37 -衡水五中高中部高二数学暑假作业第＿7＿套一、选择题1．若角600°的终边上有一点(－4，a )，则a 的值是( ) A ．－4 3 B ．±4 3 C. 3 D ．4 32．已知cos(π2＋φ)＝32，且|φ|<π2，则tan φ＝( )A ．－33 B.33C ．－ 3 D. 3 3．下列函数中，最小正周期为π，且图象关于直线x ＝π3对称的是( )A ．y ＝sin(2x ＋π6)B ．y ＝sin(x 2＋π6)C ．y ＝sin(2x －π6)D ．y ＝sin(2x －π3)4．若2k π＋π<θ<2k π＋5π4(k ∈Z )，则sin θ，cos θ，tan θ的大小关系是( ) A ．sin θ<cos θ<tan θ B ．cos θ<tan θ<sin θ C ．cos θ<sin θ<tan θD ．sin θ<tan θ<cos θ5．已知A 是三角形的内角，且sin A ＋cos A ＝52，则tan A 等于( )A ．4＋15B ．4－15C ．4±15D ．以上均不正确 6．函数y ＝2sin(π6－2x )(x ∈[0，π])的单调递增区间是( )A ．[0，π3]B ．[π12，7π12]C ．[π3，5π6]D ．[5π6，π]7．为得到函数y ＝cos ⎝⎛⎭⎪⎫x ＋π3的图象，只需将函数y ＝sin x 的图象( )A ．向左平移π6个单位长度B ．向右平移π6个单位长度C ．向左平移5π6个单位长度D ．向右平移5π6个单位长度8．已知函数f (x )＝2sin(ωx ＋φ)(ω>0，|φ|<π2)的部分图象如图所示，则函数f (x )的一个单调递增区间是( )A.⎣⎢⎡⎦⎥⎤－7π12，5π12B.⎣⎢⎡⎦⎥⎤－7π12，－π12C.⎣⎢⎡⎦⎥⎤－π4，π6D.⎣⎢⎡⎦⎥⎤11π12，17π129．设a 为常数，且a >1,0≤x ≤2π，则函数f (x )＝cos 2x ＋2a sin x －1的最大值为( ) A ．2a ＋1 B ．2a －1 C ．－2a －1 D ．a 210.函数y ＝cos(ωx ＋φ)(ω>0,0<φ<π)为奇函数，该函数的部分图象如图所示，A ，B 分别为最高点与最低点，并且两点间的距离为22，则该函数图象的一条对称轴方程为( )A ．x ＝2πB ．x ＝π2C ．x ＝1D ．x ＝211．中国最高的摩天轮是“南昌之星”，它的最高点离地面160米，直径为156米，并以每30分钟一周的速度匀速旋转，若从最低点开始计时，则摩天轮进行5分钟后离地面的高度为( )A ．41米B ．43米C ．78米D ．118米12．设ω>0，函数y ＝sin(ωx ＋π3)＋2的图象向右平移4π3个单位后与原图象重合，则ω的最小值是( )- 38 -A.23B.43C.32D ．3 第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题，每小题5分，共20分，把答案填在题中横线上)13．在扇形中，已知半径为8，弧长为12，则圆心角是________弧度，扇形面积是________． 14．方程sin x ＝lg x 的解的个数为________．15．设f (x )＝a sin(πx ＋α)＋b cos(πx ＋β)，其中a ，b ，α，β为非零常数．若f (2 013)＝－1，则f (2 014)＝________.16．关于函数f (x )＝cos ⎝ ⎛⎭⎪⎫2x ＋π3＋1有以下结论：①函数f (x )的值域是[0,2]；②点⎝ ⎛⎭⎪⎫－512π，0是函数f (x )的图象的一个对称中心；③直线x ＝π3是函数f (x )的图象的一条对称轴；④将函数f (x )的图象向右平移π6个单位长度后，与所得图象对应的函数是偶函数．其中，所有正确结论的序号是________．三、解答题(本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤) 17．(10分)已知sin θ＝45，π2<θ<π，(1)求tan θ；(2)求sin 2θ＋2sin θcos θ3sin 2θ＋cos 2θ的值．18．(12分)(1)已知cos(75°＋α)＝13，其中α为第三象限角，求cos(105°－α)＋sin(α－105°)的值；(2)已知π<θ<2π，cos(θ－9π)＝－35，求tan(10π－θ)的值．19．(12分)已知函数f (x )＝2cos(2x －π4)，x ∈R .(1)求函数f (x )的最小正周期和单调递增区间．(2)求函数f (x )在区间[－π8，π2]上的最小值和最大值，并求出取得最值时x 的值．- 39 -。

参考高二数学暑假作业答案

参考高二数学暑假作业答案自己整理的参考高二数学暑假作业答案相关文档，希望能对大家有所帮助，谢谢阅读！[一]1?1变化率和导数1.1.1变化率1 . D2 . D3 . C4-3t-65 .x 26.3？317.(1)0?1(2)0?21(3)2?18.11m/s，10？1m/s 9.25 3t 10.128 a 64 a2 t 11 . f(x)-f(0)x=1x(x0)，-1-x(x0)1?1?2导数的概念1 . D2 . C3 . C4-15 . x0，x；x06.67.a=18.a=2 9.-410.(1)2t-6(2)初速度为v0=-6，初位置为x0=1(3)运动开始3秒，在原点向左变化8m (4)x=1，v=611.水面上升速度为0？16m/min，表明 v= h75 15 h ( h) 23，那么 v t= h t 75 15 h ( h) 23，即limt0vt=limt0ht75 15h(h)23=limt0ht25，那就是v’(t)=25h’(t)，那么h’(t)=1254=0？16(米/分钟)1?1?三阶导数的几何意义(一)1.C2切线的斜率。

B3。

B4。

f (x)在x0，y-f(x0)=f’(x0)(x-x0)5.36.1357.割线的斜率是3？31，正切的斜率为38.k=-1，x y 2=09.2x-y 4=010.k=14，切点坐标为12，1211.有两个交点，交点的坐标是(1，1)，(-2，-8)1?1?3阶导数的几何意义(2)1.C2 a3 . B4 . y=x15。

16.37.y=4x-18.1039.1910.a=3，b=-11，c=9。

提示：首先找出a、b、c之间的关系，即c=3 2a。

B=-3a-2，然后求点(2，-1)处的斜率，得到k=a-2=1，即a=3 11.(1)y=-13x-229(2)125121?导数2的计算1?2?1几种常用函数的导数1.C2。

步步高高二数学暑假作业：【理】作业7 三角恒等变换、解三角形

等于( )
C．
D．
6.
的内角
的对边分别为，，，若
的面积为
，则
A．
B．
C．
D．
7. 已知 A． C．
二、填空题
8. 在
中，
，则
（）
B．
D．
，
，则
________．
9. 在
中，
，
，
，则 ________．
10. 在
中，
，
，，则
__________．
11. 小华同学骑电动自行车以
的速度沿着正北方向的公路行驶，在点处望见电视塔在电动车的北偏东30°方向上，
步步高高二数学暑假作业：【理】作业7 三角恒等变换、解三角形
一、单选题
1. 若
，则
A．
B．
C．
D．
2.
（）
A．1
B．
C．
D．
3. 在
中，
,BC=1,AC=5，则AB=
A．
B．
C．
4. 化简：
（）
A．1
B．
C．
D． D．2
5. 已知 A．-2
,
,则
B．-1
步步高高二数学暑假作业：【理】作业7 三角恒等变换、解三角形
处望见电视塔在电动车的北偏东75°方向上，则电动车在点时与电视塔的距离是___________ ．
后到点
12. 已知
，
，若
步步高高二数学暑假作业：【理】作业7 三角恒等变换、解三角形
，则 ________．
三、解答题
13. 已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边过点P（（Ⅰ）求sin（α+π）的值；（Ⅱ）若角β满足sin（α+β）= ，求cosβ的值．

新教材2021_2022学年高二数学下学期暑假巩固练习7随机变量及其分布二

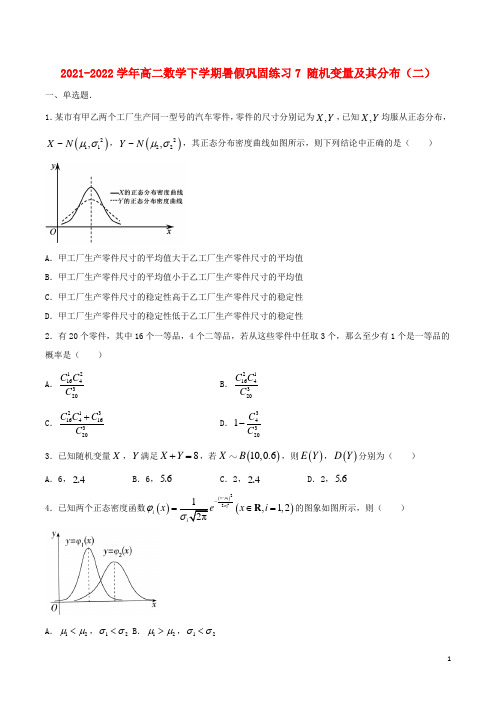
2021-2022学年高二数学下学期暑假巩固练习7 随机变量及其分布（二）一、单选题．1．某市有甲乙两个工厂生产同一型号的汽车零件，零件的尺寸分别记为,X Y ，已知,X Y 均服从正态分布，()211~,X N μσ，()222~,Y N μσ，其正态分布密度曲线如图所示，则下列结论中正确的是（）A ．甲工厂生产零件尺寸的平均值大于乙工厂生产零件尺寸的平均值B ．甲工厂生产零件尺寸的平均值小于乙工厂生产零件尺寸的平均值C ．甲工厂生产零件尺寸的稳定性高于乙工厂生产零件尺寸的稳定性D ．甲工厂生产零件尺寸的稳定性低于乙工厂生产零件尺寸的稳定性2．有20个零件，其中16个一等品，4个二等品，若从这些零件中任取3个，那么至少有1个是一等品的概率是（）A ．12164320C C CB ．21164320C C C C ．21316416320C C C C +D ．343201C C -3．已知随机变量X ，Y 满足8X Y +=，若()10,0.6X B ，则()E Y ，()D Y 分别为（）A ．6，24．B ．6，56．C ．2，24．D ．2，56．4．已知两个正态密度函数()()()222,1,2x i i i x x i μσϕ--=∈=R 的图象如图所示，则（）A ．12μμ<，12σσ<B ．12μμ>，12σσ<C ．12μμ<，12σσ>D ．12μμ>，12σσ>5．在()*n n ∈N 次独立重复试验中，每次试验的结果只有A ，B ，C 三种，且A ，B ，C 三个事件之间两两互斥．已知在每一次试验中，事件A ，B 发生的概率均为25，则事件A ，B ，C 发生次数的方差之比为（） A ．5：5：4B ．4：4：3C ．3：3：2D ．2：2：16．考察下列两个问题：①已知随机变量(),XB n p ，且()4E X =，()2D X =，记()1P X a ==；②甲、乙、丙三人随机到某3个景点去旅游，每人只去一个景点，设A 表示“甲、乙、丙所去的景点互不相同”，B 表示“有一个景点仅甲一人去旅游”，记()|P A B b =，则（）A ．311,22a b ==B ．4211,22a b ==C ．511,22a b ==D ．6211,22a b ==7．有N 件产品，其中有M 件次品，从中不放回地抽n 件产品，抽到的正品数的数学期望值是（） A ．Mn N⋅B ．N MnN- C ．()1M n N-⋅D ．()1N Mn N--⋅8．设随机变量(),1N ξμ，函数()22f x x x ξ=+-没有零点的概率是05．，则()01P ξ<<≈（）附：若()2,N ξμσ，则()0.6827P X μσμσ-<<+≈，()220.9545P X μσμσ-<<+≈．A ．01587．B ．01359．C ．02718．D ．03413．二、多选题．9．下列随机变量中，服从超几何分布的有（） A ．抛掷三枚骰子，向上面的点数是6的骰子的个数XB ．有一批种子的发芽率为70％，任取10颗种子做发芽试验，试验中发芽的种子的个数XC ．盒子中有3个红球、4个黄球、5个蓝球，任取3个球，不是红球的个数XD ．某班级有男生25人，女生20人，选派4名学生参加学校组织的活动，班长必须参加，其中女生的人数X10．一个口袋内有12个大小、形状完全相同的小球，其中有n 个红球，若有放回地从口袋中连续取四次（每次只取一个小球），恰好两次取到红球的概率大于827，则n 的值可能为（） A ．5B ．6C ．7D ．811．一射手对同一目标独立地进行4次射击，已知至少命中1次的概率为8081，则下列结论正确的是（） A ．该射手第一次射击命中的概率为13 B ．该射手第二次射击命中的概率为23C ．该射手4次射击中恰好命中1次的概率为881 D ．该射手4次射击中至多命中1次的概率为1912．设随机变量ξ服从正态分布()0,1N ，则下列结论正确的是（） A ．()()()()0P a P a P a a ξξξ<=<+>-> B ．()()()210P a P a a ξξ<=<-> C ．()()()120P a P a a ξξ<=-<> D ．()()()10P a P a a ξξ<=-≥>三、填空题．13．已知随机变量ξ服从正态分布()2,N μσ，若()()31P P ξξ>=<，则μ=______．14．为了监控某种食品的生产包装过程，检验员每天从生产线上随机抽取()*k k ∈N 包食品，并测量其质量（单位：g ）．根据长期的生产经验，这条生产线正常状态下每包食品质量服从正态分布()2,N μσ．假设生产状态正常，记ξ表示每天抽取的k 包食品中其质量在(3,3)μσμσ-+之外的包数，若ξ的数学期望()0.05E ξ>，则k 的最小值为________．附：若随机变量X 服从正态分布()2,N μσ，则(33)0.9973P X μσμσ-<<+≈．15．投壶是从先秦延续至清末的汉民族传统礼仪和宴饮游戏，在春秋战国时期较为盛行．如图所示的为一幅唐朝的投壶图，假设甲､乙是唐朝的两位投壶游戏参与者，且甲､乙每次投壶投中的概率分别为11,23，每人每次投壶相互独立．若约定甲投壶2次，乙投壶3次，投中次数多者胜，则乙最后获胜的概率为_________．四、解答题．16．网上购物已经成为一种重要的消费方式．某网络公司通过随机问卷调查，得到不同年龄段的网民在网上购物的情况，并从参与的调查者中随机抽取了150人．经统计得到如下表格：若把年龄大于或等于15而小于35岁的视为青少年，把年龄大于或等于35而小于65岁的视为中年人，把年龄大于或等于65岁的视为老年人，将频率视为概率．（1）在青少年、中年人、老年人中，哪个群体网上购物的概率最大？（2）现从某市青少年网民（人数众多）中随机抽取4人，设其中网上购物的人数为X，求X的分布列及期望．17．甲乙两人参加某种选拔测试，在备选的10道题中，甲答对其中每道题的概率都是35，乙能答对其中的8道题，规定每次考试都从备选的10道题中随机抽出4道题进行测试，只有选中的4个题目均答对才能入选．（1）求甲恰有2个题目答对的概率；（2）求乙答对的题目数X 的分布列；（3）试比较甲，乙两人平均答对的题目数的大小，并说明理由．18．口琴是一种大众熟知的方便携带的乐器．独奏口琴有三种，分为半音阶口琴(有按键)、复音口琴、十孔口琴(又名布鲁斯口琴、蓝调口琴)．“口琴者联盟”团队为了解口琴爱好者的练琴情况，提高口琴爱好者的音乐素养，推动口琴发展，在全国范围内进行了广泛调查．“口琴者联盟”团队随机调查了200名口琴爱好者每周的练琴时间x (单位：小时)并绘制如图所示的频率分布直方图．（1）由频率分布直方图可以看出，目前口琴爱好者的练琴时间x 服从正态分布2(,)N μσ，其中μ近似为样本平均数x ，2σ近似为样本方差2s （同一组的数据用该组区间中点值代表），据此，估计1万名口琴爱好者每周练琴时间在160分钟到320分钟的人数；（2）从样本中练琴时间在[0.5,1.5)和[5.5,6.5)内的口琴爱好者中用分层抽样的方法抽取8人，再从这8人中随机抽取4人进行培训，设Y 表示抽取的4人中练琴时间在[5.5,6.5)内的人数，求Y 的分布列和数学期望．参考数据：样本方差21.78s =43≈，()0.6827P X μσμσ-<≤+=，(22)0.9545P X μσμσ-<≤+=，330.997()3P X μσμσ-<≤+=．参考答案一、单选题． 1．【答案】C【解析】由随机变量,X Y 均服从正态分布，()211~,X N μσ，()222~,Y N μσ，结合正态概率密度函数的图象，可得12μμ=，12σσ<，即甲工厂生产零件尺寸的平均值等于乙工厂生产零件尺寸的平均值，甲工厂生产零件尺寸的稳定性高于乙工厂生产零件尺寸的稳定性，故选C ． 2．【答案】D【解析】全部都是二等品的概率为34320C C ，故至少有1个是一等品的概率为343201C C -，故选D ． 3．【答案】C 【解析】∵()10,0.6XB ，∴()100.66E X =⨯=，()100.60.4 2.4D X =⨯⨯=． ∵8X Y +=，∴8Y X =-，∴()()()882E Y E X E X =-=-=，()()()8 2.4D Y D X D X =-==，故选C ． 4．【答案】A【解析】正态曲线关于直线x μ=对称，且在x μ=由题图易得12μμ<，因为()1x ϕ的图象更“瘦高”，()2x ϕ的图象更“矮胖”，则12σσ<，故选A ． 5．【答案】C【解析】根据,,A B C 事件的互斥性可得：每一次试验中，事件C 发生的概率为15，设事件A ，B ，C 发生的次数分别为随机变量,,X Y Z ，则有：2~,5X B n ⎛⎫ ⎪⎝⎭，2~,5Y B n ⎛⎫ ⎪⎝⎭，1~,5Z B n ⎛⎫ ⎪⎝⎭，则事件A ，B ，C 发生次数的方差分别为625n ，625n ，425n ，故事件A ，B ，C 发生次数的方差之比为3:3:2，故选C ． 6．【答案】C 【解析】问题①，由()()()412E X np D X np p ==⎧⎪⎨=-=⎪⎩，解得1,82p n ==，则()171885118112222a P X C ⎛⎫⎛⎫===⋅⋅== ⎪⎪⎝⎭⎝⎭．问题②，根据题意，事件B 的可能情况有()123212n B C =⨯=种，事件AB 发生的可能情况为()33n AB A =种，所以，()()()331231|22n AB A b P A B n B C ====⨯．故选C ． 7．【答案】B【解析】由题意，有N 件产品，其中有M 件次品，从中不放回地抽n 件产品，则抽到正品数X 服从超几何分布，所以抽到的正品数的数学期望值是()N MD X n N-=⋅，故选B ． 8．【答案】B【解析】若函数()22f x x x ξ=+-没有零点，∴二次方程220x x ξ+-=无实根，∴()440∆ξ=-⨯-<，∴1ξ<-．又∵()22f x x x ξ=+-没有零点的概率是05．，∴()10.5P ξ<-=．由正态曲线的对称性知1μ=-， ∴()1,1N ξ-，∴1μ=-，1σ=，∴2μσ-=-，0μσ+=，23μσ-=-，21μσ+=， ∴()200.6827P ξ-<<≈，()310.9545P ξ-<<≈，∴()()()10131202P P P ξξξ<<=-<<--<<⎡⎤⎣⎦()10.95450.68270.13592≈⨯-=，故选B ．二、多选题． 9．【答案】CD【解析】AB 是重复试验问题，服从二项分布，不服从超几何分布，故AB 不符题意；CD 符合超几何分布的特征，样本都分为两类，随机变量X 表示抽取n 件样本中某类样本被抽取的件数，服从超几何分布，故选CD ． 10．【答案】ABC【解析】设每次取到红球的概率为()01p p <<，由题意得()22248C 127p p ->，即()219p p ->，解得1233p <<，因为12np =，所以()124,8n p =∈，所以5n =或6或7，故选ABC ． 11．【答案】BCD【解析】设该射手命中的概率为p ，则至少命中1次的概率为()4801181p --=，解得23p =，则该射手每一次射击命中的概率都为23，故A 错误，B 正确；该射手4次射击中恰好命中1次的概率为3142133C ⎛⎫⨯⨯ ⎪⎝⎭881=，故C 正确；该射手4次射击中至多命中1次的概率为41813819⎛⎫+= ⎪⎝⎭，故D 正确，故选BCD ． 12．【答案】BD【解析】因为()()P a P a a ξξ<=-<<，所以A 不正确；因为()()P a P a a ξξ<=-<<()()()()()()()1P a P a P a P a P a P a ξξξξξξ=<-<-=<->=<--<()21P a ξ=<-，所以B 正确，C 不正确；因为()()1P a P a ξξ<+≥=，所以()()()10P a P a a ξξ<=-≥>，所以D 正确，故选BD ．三、填空题． 13．【答案】2【解析】因为随机变量ξ服从正态分布()2,N μσ，所以正态密度函数图象关于x μ=对称，因为()()31P P ξξ>=<，所以3122μ+==，故答案为2． 14．【答案】19【解析】依题意(33)0.9973P X μσμσ-<<+≈，所以在(3,3)μσμσ-+之外的概率10.99730.0027P =-=，则(),0.0027B k ξ，则()0.0027E k ξ=，因为()0.05E ξ>，所以0.00270.05k >，解得50018.5227k >≈，因为*k ∈N ，所以k 的最小值为19，故答案为19． 15．【答案】1754【解析】若乙只投中1次，则甲投中0次时乙获胜，其概率为12231111(1)(1)3329C ⋅-⋅-=；若乙只投中2次，则甲投中0次或1次时乙获胜，其概率为22213211111()(1)[(1)]33222C C ⋅--+⨯16=；若乙投中3次，则乙必获胜，其概率为311()327=，综上所述：乙最后获胜的概率为1115117962716254++==，故答案为1754．四、解答题．16．【答案】（1）青少年网上购物的概率最大；（2）分布列见解析，期望为3．【解析】（1）由题表中的数据知，青少年网上购物的概率为12334531545604+==+，中年人网上购物的概率为35153534530883=++++，老年人网上购物的概率为27，因为35324837>>，所以青少年网上购物的概率最大．（2）由题意及（1）知，X 可能取值为0，1，2，3，4，34,4X B ⎛⎫~ ⎪⎝⎭，()404110C 4256P X ⎛⎫=== ⎪⎝⎭，()1314311231C 4425664P X ⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭，()22243154272C 44256128P X ⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭，()3134********C 4425664P X ⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭，()4443814C 4256P X ⎛⎫=== ⎪⎝⎭．故X 的分布列为()434E X =⨯=．17．【答案】（1）216625；（2）见解析；（3）甲平均答对的题目数小于乙平均答对的题目数．【解析】（1）∵甲在备选的10道题中，答对其中每道题的概率都是35，∴选中的4个题目甲恰有2个题目答对的概率22243221655625P C ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭．（2）由题意知乙答对的题目数X 的可能取值为2，3，4，()2228410282221015C C P X C ====，()13284101128321015C C P X C ====，()4841070142103C P X C ====，X 的分布列为：（3）∵乙平均答对的题目数8116234151535EX =⨯+⨯+⨯=，甲答对题目34,5Y B ⎛⎫ ⎪⎝⎭，甲平均答对的题目数312455EY =⨯=． EX EY >，∴甲平均答对的题目数小于乙平均答对的题目数．18．【答案】（1）6827人；（2）分布列见解析，3．【解析】（1）这200名口琴爱好者每周的练琴时间的平均时间10.0320.130.240.3550.1960.0970.044x =⨯+⨯+⨯+⨯+⨯+⨯+⨯=，由于样本方差2 1.78s =，所以，结合题意知4μ=，2 1.78σ=，∴~(4,1.78)X N ，43σ=≈， 48433-=小时160=分钟，416433+=小时320=分钟， 44(44)0.682733P X -<≤+=，100000.68276827⨯=，可以估计1万名口琴爱好者每周练琴时间在160分钟到320分钟的人数约为6827人．（2）由频率分布直方图可知，练琴时间在[0.5,1.5)，[5.5,6.5)内的口琴爱好者人数比例为0.03:0.091:3=，用分层抽样的方法抽取8人，则练琴时间在[0.5,1.5)内的有2人，练琴时间在[5.5,6.5)内的有6人． ∴Y 的所有可能取值为2，3，4，则2262483(2)14C C P Y C ===，3162484(3)7C C P Y C ===，()4062483414C C P Y C ===， ∴Y 的分布列为：故()234314714E Y =⨯+⨯+⨯=．。

高二数学暑假作业7附答案

高二数学暑假作业七一、选择题1.如图，点O 为正方体ABCD -A 'B 'C 'D '的中心，点E 为面B 'BCC '的中心，点F 为B 'C '的中点，则空间四边形D 'OEF 在该正方体的面上的正投影不可能是（）A.B.C.D.2.已知球O 与正方体各棱均相切，若正方体棱长为2，则球O 的表面积为（）A.34πB. 2πC. 4πD. 6π 3.如图为某几何体的三视图，则该几何体的表面积为（A ）20+3π （B ）24+3π （C ）20+2π （D ）24+2π4.对于直线,m n 和平面,αβ，下列条件中能得出αβ⊥的是（） A ．,//,//m n m n αβ⊥ B ．,,m n m n αβα⊥⋂=⊂ C ．//,,m n n m βα⊥⊂ D ．//,,m n m n αβ⊥⊥5.若αβ、是两个相交平面，则在下列命题中，真命题的序号为（） ①若直线m α⊥，则在平面β内，一定不存在与直线m 平行的直线． ②若直线m α⊥，则在平面β内，一定存在无数条直线与直线m 垂直． ③若直线m α⊂，则在平面β内，不一定存在与直线m 垂直的直线． ④若直线m α⊂，则在平面β内，一定存在与直线m 垂直的直线． A ．①③ B ．②③ C ．②④ D ．①④6.某几何体的三视图如图所示，则该几何体的体积为（） A ．13π+ B ．23π+ C ．123π+ D ．223π+ 7..已知直线,m l ,平面,αβ,且,m l αβ⊥⊂，给出下列命题： ①若//αβ，则m l ⊥； ②若αβ⊥，则//m l ； ③若m l ⊥，则αβ⊥； ④若//m l ，则αβ⊥. 其中正确的命题是（） A.①④ B.③④ C.①② D.②③ 8.在空间中，下列命题正确的是（）A ．若平面α内有无数条直线与直线l 平行，则//l αB ．若平面α内有无数条直线与平面β平行，则//αβC ．若平面α内有无数条直线与直线l 垂直，则l α⊥D ．若平面α内有无数条直线与平面β垂直，则αβ⊥9.已知正方形ABCD 的边长为2，若将正方形ABCD 沿对角线BD 折叠为三棱锥A -BCD ，则在折叠过程中，不能出现（）A ．AC BD ⊥B ．平面⊥ABD 平面CBD C. 32=-CBD A V D ．CD AB ⊥ 10.如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直线AB 与平面MNQ 不平行的是（）．A ．N QBAB ．MNQBAC ．M NQBAD ．MNQBA11.如图1，四棱柱1111D C B A ABCD -中，E 、F 分别是1AB 、1BC 的中点．下列结论中，正确的是 ( ) A ．1BB EF ⊥ B ．//EF 平面11A ACC C ．BD EF ⊥D ．⊥EF 平面11B BCC12.三条不重合的直线c b a ,,及三个不重合的平面γβα,,，下列命题正确的是（）A ．若n m n ⊥=⋂⊥,,βαβα，则α⊥mB ．若n m n m //,,βα⊂⊂，则βα//C ．若n m n m ⊥,//,//βα，则βα⊥D ．若ββα⊥⊥⊥m n n ,,，则α⊥m 13.设m l ,是两条不同的直线，βα,是两个不同的平面，给出下列条件，其中能够推出m l //的是（）A ．α//l ，β⊥m ，βα⊥B ．α⊥l ，β⊥m ，βα//C ．α//l ，β//m ，βα//D ．α//l ，β//m ，βα⊥14.四面体ABC S -中，三组对棱的长分别相等，依次为5，4，x ，则x 的取值范围是 A ．)41,2( B ．)9,3( C ．)41,3( D ．)9,2( 15.空间两条直线a 、b 与直线l 都成异面直线，则a 、b 的位置关系是（）． A ．平行或相交 B ．异面或平行 C ．异面或相交 D ．平行或异面或相交 16.下列说法正确的是（）（1）任意三点确定一个平面；（2）圆上的三点确定一个平面；（3）任意四点确定一个平面；（4）两条平行线确定一个平面 A ．（1）（2） B ．（2）（3） C ．（2）（4） `D ．（3）（4） 17.列结论正确的是（）．A ．各个面都是三角形的几何体是三棱锥B ．以三角形的一条边所在直线为旋转轴，其余两边旋转形成的曲面所围成的几何体叫圆锥C ．棱柱即是两个底面全等且其余各面都是矩形的多面体D ．任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥18..设,a b 是互不垂直的两条异面直线，则下列命题成立的是（）A ．存在唯一直线l ，使得l a ⊥，且l b ⊥B ．存在唯一直线l ，使得//l a ，且l b ⊥C ．存在唯一平面α，使得a α⊂，且//b αD ．存在唯一平面α，使得a α⊂，且b α⊥ 19.已知,m n 为两条不同的直线，,αβ为两个不同的平面，则下列命题中正确的是（） A.若,m αββ⊥⊥，则//m αB.若平面α内有不共线的三点到平面β的距离相等，则//αβC.若,m m n α⊥⊥，则//n αD.若//,m n n α⊥，则m α⊥20.在梯形ABCD 中，AB CD ∥，AB ⊂平面α，CD ⊄平面α，则直线CD 与平面α内的直线的位置关系只能是（）． A ．平行 B ．平行或异面 C ．平行或相交 D ．异面或相交二、填空题21. 如图，在一个60°的二面角的棱上有两个点A，B，AC，B D分别是在这个二面角的两个半平面内垂直于AB的线段，且AB=4，AC=6，BD=8，则CD的长为_________。

高二数学暑假作业检测试题含解析试题

卜人入州八九几市潮王学校麓山国际实验2021届新高二数学暑假作业检测试题〔含解析〕时量：120分钟总分值是：150分一．选择题〔一共15小题，每一小题4分〕1．设集合A={x||x﹣a|＜1}，B={x|1＜x＜5，x∈R}，A∩B=∅，那么实数a的取值范围是〔〕A．{a|0≤a≤6}B．{a|a≤2或者a≥4}C．{a|a≤0或者a≥6}D．{a|2≤a≤4}2．设x1，x2分别是方程xa x=1和xlog a x=1的根〔其中a＞1〕，那么x1+2x2的取值范围〔〕A．〔2，+∞〕B．[2，+∞〕C．〔3，+∞〕D．[3，+∞〕3．函数〔a＞0，且a≠1〕的值域为R，那么实数a的取值范围是〔〕A．〔0，1〕∪〔1，2] B．〔2，+∞〕C．〔4，+∞〕D．〔0，1〕∪〔1，4]4．在△ABC中，a，b，c分别为内角A，B，C所对的边，S为△ABC的面积．假设向量，满足，那么tan=〔〕A．B．C．2 D．45．A，B，C三点不在同一条直线上，O是平面ABC内一定点，P是△ABC内的一动点，假设，λ∈[0，+∞〕，那么直线AP一定过△ABC的〔〕A．重心B．垂心C．外心D．内心6．三棱柱的侧棱AA1和BB1上各有一动点P，Q满足A1P=BQ，过P、Q、C三点的截面把棱柱分成两局部，那么其体积比为〔〕A．3：1 B．2：1 C．4：1 D．7．完成以下两项调查：①一项对“小彩旗春晚连转四小时〞的调查中有10000人认为这是成为优秀演员的必经之路，有9000人认为太残酷，有1000人认为无所谓．现要从中随机抽取200人做进一步调查．②从某的15名艺术特长生中选出3名调查学习负担情况，宜采用的抽样方法依次是〔〕A．①简单随机抽样，②系统抽样B．①分层抽样，②简单随机抽样C．①系统抽样，②分层抽样D．①②都用分层抽样8．等比数列{a n}的前n项和S n=2n﹣1，那么数列{a n2}的前n项和T n=〔〕A．〔2n﹣1〕2B．4n﹣1 C．D．9．程序框图如图：假设上述程序运行的结果为S=132，那么判断框中应填入〔〕A．k≤10B．k≤9C．k＜10 D．k＜910．假设a＞b＞0，且ab=1，那么以下不等式成立的是〔〕A．a+＜＜log2〔a+b〕〕B．＜log2〔a+b〕＜a+C．a+＜log2〔a+b〕＜D．log2〔a+b〕〕＜a+＜11．设x，y满足约束条件，那么z=x+y的最大值为〔〕A．0 B．1 C．2 D．312．直线l：〔m+2〕x+〔m﹣1〕y+4﹣4m=0上总存在点M，使得过M点作的圆C：x2+y2+2x﹣4y+3=0的两条切线互相垂直，那么实数m的取值范围是〔〕A．m≤1或者m≥2B．2≤m≤8C．﹣2≤m≤10 D．m≤﹣2或者m≥813．假设α，β是两个不同平面，m，n是两条不同直线，那么以下结论错误的选项是〔〕A．假设m∥n，α∥β，那么m与α所成的角和n与β所成的角相等B．假设m⊥n，m⊥α，n∥β，那么α⊥βC．假设α∥β，m⊂α，那么m∥βD．假设m⊥α，n∥α，那么m⊥n14．一个三棱锥的三视图如下列图，其中正视图和侧视图是全等的等腰三角形，那么此三棱锥外接球的外表积为〔〕A．B．9πC．4πD．π15．定义在R上的函数f〔x〕是奇函数且满足f〔﹣x〕=f〔x〕，f〔﹣2〕=﹣3，数列{a n}满足a1=﹣1，且=2×+1，〔其中S n为{a n}的前n项和〕．那么f〔a5〕+f〔a6〕=〔〕A．﹣3 B．﹣2 C．3 D．2二．填空题〔一共5小题，每一小题5分〕16．sinα，cosα是关于x的方程x2﹣ax+a=0的两个根，那么sin3α+cos3α=．17．两点A〔﹣1，0〕，B〔1，3〕，向量=〔2k﹣1，2〕，假设∥，那么实数k的值是．18．如下列图，在棱长为2的正方体ABCD﹣A1B1C1D1中，O是底面ABCD的中心，E、F分别是CC1，AD的中点，那么异面直线OE和FD1所成角的余弦值等于．19．在平面直角坐标系xOy中，假设直线l：x+2y=0与圆C：〔x﹣a〕2+〔y﹣b〕2=5相切，且圆心C在直线l的上方，那么ab最大值为．20．在△ABC中，角A，B，C所对的边分别为a，b，c，假设△ABC为锐角三角形，且满足b2﹣a2=ac，那么﹣的取值范围是．三．解答题〔一共5小题〕〔12+12+13+14+14〕21．函数f〔x〕=log4〔4x+1〕+kx〔k∈R〕是偶函数〔1〕求k的值；〔2〕设g〔x〕=log4〔a•2x﹣a〕，假设函数f〔x〕与g〔x〕的图象有且只有一个公一共点，务实数a的取值范围．22．如图，直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形，E，F分别是BC，CC1的中点，〔Ⅰ〕证明：平面AEF⊥平面B1BCC1；〔Ⅱ〕假设直线A1C与平面A1ABB1所成的角为45°，求三棱锥F﹣AEC的体积．23．{x n}是各项均为正数的等比数列，且x1+x2=3，x3﹣x2=2．〔Ⅰ〕求数列{x n}的通项公式；〔Ⅱ〕如图，在平面直角坐标系xOy中，依次连接点P1〔x1，1〕，P2〔x2，2〕…P n+1〔x n+1，n+1〕得到折线P1P2…P n+1，求由该折线与直线y=0，x=x1，x=x n+1所围成的区域的面积T n．24．直线x﹣y+3=0与圆心为〔3，4〕的圆C相交，截得的弦长为2．〔1〕求圆C的方程；〔2〕设Q点的坐标为〔2，3〕，且动点M到圆q的切线长与|MQ|的比值为常数k〔k＞0〕．假设动点M的轨迹是一条直线，试确定相应的k值，并求出该直线的方程．25．如图是我国2021年至2021年生活垃圾无害化处理量〔单位：亿吨〕的折线图〔Ⅰ〕由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以说明；〔Ⅱ〕建立y关于t的回归方程〔系数准确到0.01〕，预测2021年我国生活垃圾无害化处理量．参考数据：y i=2，t i y i=40.17，=0.55，≈46．参考公式：相关系数r=回归方程=+t中斜率和截距的最小二乘估计公式分别为：=，=﹣．麓山国际实验二零二零—二零二壹新高二暑假作业测试数学试卷参考答案1．解：由|x﹣a|＜1得﹣1＜x﹣a＜1，即a﹣1＜x＜a+1．如图由图可知a+1≤1或者a﹣1≥5，所以a≤0或者a≥6．应选C2．解：由题意可得，x1a x1=1，x2log a x2=1；故a x1=，=x2，又∵y=a x在〔0，+∞〕上单调递增，故=x2，x2＞1；故x1+2x2=+2x2，而y=+2x2在〔1，+∞〕上是增函数，故+2x2＞3；应选C．3．解：函数〔a＞0，且a≠1〕的值域为R⇔y=〔a＞0，且a≠1〕的值域为〔0，+∞〕⇔y=x2﹣4x+a〔a＞0，且a≠1〕的值域为〔0，+∞〕⇔△=〔﹣4〕2﹣4a≥0，a＞0且a ≠1．解得0＜a≤4且a≠1．应选D．4．解：∵向量，，由，得S=〔a+b〕2﹣c2=2ab+a2+b2﹣c2，即，也就是，∴．那么．应选：D．5．解：如图，取BC的中点P并连结AD，那么+=、﹣=，∵，λ∈[0，+∞〕，∴=λ，即A、P、D三点一共线，又∵AD为BC边上的中线，∴直线AP一定过△ABC的重心，应选：A．6．解：设三棱柱ABC﹣A1B1C1的体积为V∵侧棱AA1和BB1上各有一动点P，Q满足A1P=BQ，∴四边形PQBA与四边形PQB1A1的面积相等故四棱椎C﹣PQBA的体积等于三棱锥C﹣ABA1的体积等于V那么四棱椎C﹣PQB1A1的体积等于V故过P、Q、C三点的截面把棱柱分成两局部，那么其体积比为2：1应选B7．解：①一项对“小彩旗春晚连转四小时〞的调查中有10000人认为这是成为优秀演员的必经之路，有9000人认为太残酷，有1000人认为无所谓．现要从中随机抽取200人做进一步调查，此项抽查的总体数目较多，而且差异很大，符合分层抽样的适用范围；②从某的15名艺术特长生中选出3名调查学习负担情况，此项抽查的总体个数不多，而且差异不大，符合简单随机抽样的适用范围．∴宜采用的抽样方法依次是：①分层抽样，②简单随机抽样．应选；B．8．解：等比数列{a n}的前n项和S n=2n﹣1，∴a1=S1=1，a1+a2=22﹣1=3，解得a2=2．∴公比q=2．∴a n=2n﹣1．∴=4n﹣1，那么数列{a n2}为等比数列，首项为1，公比为4．其前n项和T n==．应选：C．9．解：按照程序框图依次执行：k=12，s=1；进入循环，s=1×12=12，k=11；s=12×11=132，k=10，跳出循环，故k=10满足判断框内的条件，而k=11不满足，故判断框内的条件应为k≤10或者k＜11应选A 10．解：∵a＞b＞0，且ab=1，∴可取a=2，b=．那么=4，==，log2〔a+b〕==∈〔1，2〕，∴＜log2〔a+b〕＜a+．应选：B．11．解：x，y满足约束条件的可行域如图：，那么z=x+y经过可行域的A时，目的函数获得最大值，由解得A〔3，0〕，所以z=x+y的最大值为：3．应选：D．12．解：如图，设切点分别为A，B．连接AC，BC，MC，由∠AMB=∠MAC=∠MBC=90°及MA=MB知，四边形MACB为正方形，故，假设直线l上总存在点M使得过点M的两条切线互相垂直，只需圆心〔﹣1，2〕到直线l的间隔，即m2﹣8m﹣20≤0，∴﹣2≤m≤10，应选：C．13．解：A、假设m∥n，α∥β，那么m，n与α所成的角和m，n与β所成的角均相等，故正确；B、假设m⊥n，m⊥α，n∥β，不能得出α⊥β，故错误；C、假设α∥β，m⊂α，那么m与β无公一共点，那么m∥β．故正确；D、假设n∥α，那么存在直线l⊂α，使n∥l，由m⊥α，可得m⊥l，那么m⊥n．故正确，应选B．14．解：由题意，三棱锥的一个侧面垂直于底面，底面是等腰直角三角形，顶点在底面中的射影是底面斜边的中点，设三棱锥外接球的半径为r，那么r2=〔1﹣r〕2+〔〕2，∴r=，∴三棱锥外接球的外表积为4=，应选：A．15．解：∵函数f〔x〕是奇函数∴f〔﹣x〕=﹣f〔x〕∵f〔﹣x〕=f〔x〕，∴f〔﹣x〕=﹣f〔﹣x〕∴f〔3+x〕==﹣f〔〕=﹣f[]=﹣f〔﹣x〕=f〔x〕∴f〔x〕是以3为周期的周期函数．∵数列{a n}满足a1=﹣1，且=2×+1，∴a1=﹣1，且S n=2a n+n，∴a5=﹣31，a6=﹣63∴f〔a5〕+f〔a6〕=f〔﹣31〕+f〔﹣63〕=f〔2〕+f〔0〕=f〔2〕=﹣f〔﹣2〕=3应选C．16．解：由题意利用韦达定理可得sinα+cosα=a，sinα•cosα=a，∴1+2a=a2，解得a=1±．再根据判别式△=a2﹣4a≥0，可得a≤0，或者a≥4，∴a=1﹣．∴sin3α+cos3α=〔sinα+cosα〕〔1﹣sinαcosα〕=a〔1﹣a〕=a﹣a2=〔1﹣〕﹣〔1﹣〕2=﹣2+，故答案为：．17．解：两点A〔﹣1，0〕，B〔1，3〕，向量=〔2k﹣1，2〕，=〔2，3〕，∥，3〔2k﹣1〕=4，解得：k=故答案为：．18．解：取BC的中点G．连接GC1，那么GC1∥FD1，再取GC的中点H，连接HE、OH，那么∵E是CC1的中点，∴GC1∥EH∴∠OEH为异面直线所成的角．在△OEH中，OE=，HE=，OH=．由余弦定理，可得cos∠OEH===．故答案为：19．解：∵直线和圆相切，∴，∵圆心C在直线l的上方，∴a+2b＞0，从而a+2b=5，∴ab，当且仅当a=2b，即a=，b=时取等号，故ab的最大值为，故答案为：20．解：∵b2﹣a2=ac，∴由正弦定理得，sin2B﹣sin2A=sinAsinC，，，由和差化积公式得cos2A﹣cos2B=﹣2sin〔A+B〕sin〔A﹣B〕，代入上式得，﹣sin〔A+B〕sin〔A﹣B〕=sinAsinC，∵sin〔A+B〕=sinC≠0，∴﹣sin〔A﹣B〕=sinA，即sin〔B﹣A〕=sinA，在△ABC中，B﹣A=A，得B=2A，那么C=π﹣3A，∵△ABC为锐角三角形，∴，解得，那么，∴====，由得，sinB∈〔，1〕，那么，∴取值范围是，故答案为：．21．解〔1〕∵函数f〔x〕=log4〔4x+1〕+kx〔k∈R〕〕是偶函数∴f〔﹣x〕=log4〔4﹣x+1〕﹣kx〕=log4〔〕﹣kx=log4〔4x+1〕+kx〔k∈R〕恒成立∴﹣〔k+1〕=k，那么k=．〔5分〕〔2〕g〔x〕=log4〔a•2x﹣a〕，函数f〔x〕与g〔x〕的图象有且只有一个公一共点，即方程f〔x〕=g〔x〕只有一个解由得log4〔4x+1〕x=log4〔a•2x﹣a〕，∴log4〔〕=log4〔a•2x﹣a〕，方程等价于，设2x=t，t＞0，那么〔a﹣1〕t2﹣﹣1=0有一解，假设a﹣1＞0，设h〔t〕=〔a﹣1〕t2﹣﹣1，∵h〔0〕=﹣1＜0，∴恰好有一正解∴a＞1满足题意假设a﹣1=0，即a=1时，h〔t〕=﹣﹣1，由h〔t〕=0，得t=﹣＜0，不满足题意假设a﹣1＜0，即a＜1时，由，得a=﹣3或者a=，当a=﹣3时，t=满足题意当a=时，t=﹣2〔舍去〕综上所述实数a的取值范围是{a|a＞1或者a=﹣3}．〔12分〕〔少些a=-3扣2分〕22．〔Ⅰ〕证明：∵几何体是直棱柱，∴BB1⊥底面ABC，AE⊂底面ABC，∴AE⊥BB1，∵直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形，E分别是BC的中点，∴AE⊥BC，BC∩BB1=B，∴AE⊥平面B1BCC1，∵AE⊂平面AEF，∴平面AEF⊥平面B1BCC1；〔6分〕〔Ⅱ〕解：取AB的中点G，连结A1G，CG，由〔Ⅰ〕可知CG⊥平面A1ABB1，直线A1C与平面A1ABB1所成的角为45°，就是∠CA1G，那么A1G=CG=，∴AA1==，CF=．三棱锥F﹣AEC的体积：×==．〔12分〕23．解：〔I〕设数列{x n}的公比为q，那么q＞0，由题意得，两式相比得：，解得q=2或者q=﹣〔舍〕，∴x1=1，∴x n=2n﹣1．〔6分〕〔II〕过P1，P2，P3，…，P n向x轴作垂线，垂足为Q1，Q2，Q3，…，Q n，记梯形P n P n+1Q n+1Q n的面积为b n，那么b n==〔2n+1〕×2n﹣2，∴T n=3×2﹣1+5×20+7×21+…+〔2n+1〕×2n﹣2，①∴2T n=3×20+5×21+7×22+…+〔2n+1〕×2n﹣1，②①﹣②得：﹣T n=+〔2+22+…+2n﹣1〕﹣〔2n+1〕×2n﹣1=+﹣〔2n+1〕×2n﹣1=﹣+〔1﹣2n〕×2n﹣1．∴T n=．〔13分〕24．解：〔1〕圆心C到直线l的间隔为=，∵截得的弦长为2，∴半径为2，∴圆C：〔x﹣3〕2+〔y﹣4〕2=4；〔6分〕〔2〕设动点M〔x，y〕，那么由题意可得=k，即=k，化简可得〔k2﹣1〕•x2+〔k2﹣1〕•y2+〔6﹣4k2〕x+〔8﹣6k2〕y+13k2﹣21=0，假设动点M的轨迹方程是直线，那么k2﹣1=0，∴k=1，直线的方程为x+y﹣4=0．〔14分〕25．解：〔Ⅰ〕由折线图看出，y与t之间存在较强的正相关关系，∵y i=2，t i y i=40.17，=0.55，∴r≈≈0.993，∵＞0.75，故y与t之间存在较强的正相关关系；〔5分〕〔Ⅱ〕由≈31及〔Ⅰ〕得=≈0.103，×4=0.92．所以，y关于t的回归方程为：+0.10t．〔11分〕将2021年对应的t=10代入回归方程得：+×所以预测2021年我国生活垃圾无害化处理量将约2亿吨．〔14分〕。

高二数学下册暑假作业及答案

高二数学下册暑假作业及答案【导语】着眼于眼前，不要沉迷于玩乐，不要沉迷于学习进步没有别*的痛苦中，进步是一个由量变到质变的过程，只有足够的量变才会有质变，沉迷于痛苦不会改变什么。

无忧考网高二频道为你整理了《高二数学下册暑假作业及答案》，希望对你有所帮助！【一】1.（09年重庆高考）直线与圆的位置关系为（）A．相切B．相交但直线不过圆心C．直线过圆心D．相离2.方程x2+y2+2ax-by+c=0表示圆心为C（2，2），半径为2的圆，则a、b、c的值依次为（）A．2、4、4；B．-2、4、4；C．2、-4、4；D．2、-4、-43（2011年重庆高考）圆心在轴上，半径为1，且过点（1，2）的圆的方程为（）A．B．C．D．4.直线3x-4y-4=0被圆(x-3)2+y2=9截得的弦长为（）A．B．4C．D．25.M（x0，y0）为圆x2+y2=a2（a>0）内异于圆心的一点，则直线x0x+y0y=a2与该圆的位置关系是（）A．相切B．相交C．相离D．相切或相交6、圆关于直线对称的圆的方程是（）.A．B．C．D．7、两圆x2+y2－4x+6y=0和x2+y2－6x=0的连心线方程为（）.A．x+y+3=0B．2x－y－5=0C．3x－y－9=0D．4x－3y+7=08.过点的直线中,被截得最长弦所在的直线方程为（）A.B.C.D.9.（2011年四川高考）圆的圆心坐标是10.圆和的公共弦所在直线方程为____.11.（2011年天津高考）已知圆的圆心是直线与轴的交点，且圆与直线相切，则圆的方程为．12（2010山东高考）已知圆过点，且圆心在轴的正半轴上，直线被该圆所截得的弦长为，则圆的标准方程为____________ 13．求过点P（6，－4）且被圆截得长为的弦所在的直线方程．14、已知圆C的方程为x2＋y2＝4.(1)直线l过点P(1,2)，且与圆C交于A、B两点，若|AB|＝23，求直线l的方程；(2)圆C上一动点M(x0，y0)，ON→＝(0，y0)，若向量OQ→＝OM→＋ON→，求动点Q的轨迹方程"人"的结构就是相互支撑，"众"人的事业需要每个人的参与。

【推荐下载】新课标最新年高二数学暑假作业7(必修5-选修2-3)

[键入文字]
新课标最新年高二数学暑假作业 7（必修 5-选修 2-3）
知识的学习除了理论知识外，还要多练习，准备了 2015 年高二数学暑假作业，希望你喜欢。一选择题(本大题共小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符合题目要求的。1.已知复数满足：(是虚数单位)，则的虚部为( ) A. B. C. D. 2.曲线的参数方程为(t 是参数)，则曲线是( ) A.线段 B.双曲线的一支 3.不等式的解集为( ) A. C. D. 4.如右图，A、B 是⊙O 上的两点，AC 是⊙O 的切线，&ang;B=70°，则 &ang;BAC 等于( ) A. 70° B. 20° C. 35° D. 10°
5
B.1-p C.1-2p
D. -p
B. C. D.
C.472 D.484
B. C. D.或
[键入文字]
A. 8.已知函数上任一点处的切线斜率，则该函数的单调递减区间为( ) A. 10.已知随机变量ξ服从二项分布ξ～B(n，)，且 Eξ=7，Dξ=6，则等于。 11.5 个人排成一排，要求甲、乙两人之间至少有一人，则不同的排法有________种. 12.在平面直角坐标系 xOy 中，点 M 是椭圆上的点，以 M 为圆心的圆与 x 轴相切于椭圆的焦点 F，圆 M 与 y 轴相交于 P，Q 两点.若△PQM 是锐角三角形，则该椭圆离心率的取值范围是 .本大题共小题，每小题分，13.(本小题满分 1 分) 已知复数，当实数为何值时: (1)为实数;(2)为虚数;(3)为纯虚数;(4)复数对应的点在第四象限. 14.(本小题满分 12 分) (1)若的展开式中，的系数是的系数的倍，求; (2)已知的展开式中, 的系数是的系数与的系数的等差中项,求;

高二数学暑假作业

DB1 B上大附中新高三暑假作业1班级________ 姓名_______ 学号________ 成绩________一．填空题（本大题满分48分）1．函数xxylg42-=的定义域为______________2．直线133=-yx的倾斜角等于__________3．各棱长都等于2的正三棱柱的体积为____________4．方程)8ln()3ln(ln+=++xxx的实数解是____________5．抛物线pxy22=过点（3，2），则)(lim32nnpppp++++∞→=_________6．若1lglg=+yx，则yx+2的最小值为_________7．设3sin)(xxfπ=，则)2005()3()2()1(ffff++++ =_________8．下面由火柴杆拼成的一系列图形中，第n个图形由n个正方形组成：n=1 n=2 n=3 n=4通过观察可以发现，第n个图形中，火柴杆共有___________根。

9．函数122-+-=aaxxy在区间[2，3]上单调递增，则实数a的取值范围是_______ 10．从集合},1218|{Zxxxx∈≥--中随机取出两个不同的数，则这两个数互质的概率为___________（结果用分数表示）11．如图，长方体ABCD-A1B1C1D1中，AA1=3，AB=4，AD=5，则长方体被过对角线AC1的平面所截，所得截面四边形的周长的最小值等于___________12．构造一个函数)(xf，同时满足条件：①定义域为R，②值域为[0，1），③不是偶函数，则这样的函数解析式可以为_________________二．单项选择题（本大题满分16分）13．已知点A （-1，0），B （1，0），动点P 满足|PA|2 +|PB|2=2，则点P 的轨迹是（）（A ）一个圆（B ）一个椭圆（C ）一条直线段（D ）一个点14．△ABC 中，若⋅=⋅，则△ABC 为（）（A ）直角三角形（B ）锐角三角形（C ）钝角三角形（D ）等腰三角形15．已知集合}34|{2+-==x x y y A ，}2|{2x x y y B --==，则B A ⋂为（）（A ）}11|{≤≤-x x （B ）R （C ）∅ （D ）以上结论都不对16．F 1、F 2为椭圆)0(12222>>=+b a by a x 的左、右焦点，|F 1F 2|=2c ，P 为椭圆上一点，若有|PF 1|=3|PF 2|，则下面四个命题中，正确的是（）（A ）这样的点P 总共有两点（B ）∠F 1PF 2不可能是钝角（C ）a ，b ，c 可以成等差数列（D ）a c 有最大值21三．解答题（本大题满分86分）本大题共有6题，解答下列各题必须写出必要的步骤。

高中二年级数学暑期作业专题练习

高中二年级数学暑期作业专题练习以下是查字典数学网为大家整理的高中二年级数学暑期作业，希望同窗们多加练习，加油，查字典数学网不时陪伴您。

(一)选择题(每个题5分，共10小题，共50分)1、抛物线上一点的纵坐标为4，那么点与抛物线焦点的距离为 ( )A 2B 3C 4D 52、关于抛物线y2=2x上恣意一点Q, 点P(a, 0)都满足|PQ||a|, 那么a的取值范围是( )A (0, 1)B (0, 1)CD (-, 0)3、抛物线y2=4ax 的焦点坐标是 ( )A (0, a)B (0,-a)C (a,0)D (-a, 0)4、设A(x1,y1),B(x2,y2)是抛物线y2=2px(p0)上的两点,并且满足OAOB. 那么y1y2等于A 4p2B 4p2C 2p2D 2p25、点P在抛物线y2 = 4x上，那么点P到点Q(2，-1)的距离与点P到抛物线焦点距离之和取得最小值时，点P的坐标为( )A. ( ，-1)B. ( ，1)C. (1，2)D. (1，-2)6、抛物线的焦点为，准线与轴的交点为，点在上且，那么的面积为( )(A) (B) (C) (D)7、直线y=x-3与抛物线交于A、B两点，过A、B两点向抛物线的准线作垂线，垂足区分为P、Q ，那么梯形APQB的面积为( )(A)48. (B)56 (C)64 (D)72.8、(2021年高考广东卷文科8)设圆C与圆外切，与直线相切.那么C的圆心轨迹为( )A. 抛物线B. 双曲线C. 椭圆D. 圆9、双曲线：的离心率为2.假定抛物线的焦点到双曲线的渐近线的距离为2，那么抛物线的方程为(A) (B) (C) (D)10、(2021年高考山东卷文科9)设M( ， )为抛物线C：上一点，F为抛物线C的焦点，以F为圆心、为半径的圆和抛物线C的准线相交，那么的取值范围是(A)(0，2) (B)[0，2] (C)(2，+) (D)[2，+)(二)填空题：(每个题5分，共4小题，共20分)11、点P是抛物线y2 = 4x上的动点，那么点P到点A(-1 ,1)的距离与点P到直线x=-1距离之和最小值是。

新高二数学暑假练习题

新高二数学暑假练习题【暑假作业】尊敬的高二同学们：暑假将至，作为新高二学生的你们即将面临数学学科的挑战。

为了帮助大家更好地复习与巩固知识，我们为你们准备了一套新高二数学暑假练习题。

本练习题分为四个部分，分别涵盖代数、几何、概率与统计以及数学推理等内容。

请同学们按照要求完成练习并于暑假结束后提交作业。

【第一部分：代数】1. 解方程：求解以下方程组(a) 2x + 3y = 7x - 2y = 1(b) x^2 - 5x + 6 = 02. 算式转化：将指数函数f(x) = 3^(x+1)写成对数函数的形式。

3. 因式分解：将以下多项式进行因式分解(a) x^2 + 5x + 6(b) 2x^3 - 8x^2 +12x【第二部分：几何】1. 直角三角形：已知直角三角形ABC，角A为直角，BC = 8 cm，AC = 6 cm，求AB的长度。

2. 平面几何证明：已知三角形ABC的三边分别为AB = 5 cm，BC = 6 cm，AC = 7 cm，证明该三角形为等腰三角形。

3. 三视图：根据给定的三视图绘制物体的正视图、侧视图和俯视图，并利用三视图还原物体。

【第三部分：概率与统计】1. 抽样调查：设计一个合理的调查问题，并对你的同学进行抽样调查，根据调查结果绘制统计图表。

2. 概率计算：有一批产品，其中20%存在质量问题。

如果从中随机抽取5个产品，计算至少有1个产品存在质量问题的概率。

3. 随机变量：已知某次抛掷一枚硬币，正面朝上的概率为0.6，反面朝上的概率为0.4。

定义随机变量X为连续抛掷硬币直到出现2次反面朝上的次数。

计算X取值为2的概率。

【第四部分：数学推理】1. 证明题：证明在任意一个三角形中，任意两边之差小于第三边，并推导出三角形的两个内角之和等于第三个角的补角。

2. 数列综合：已知数列an的通项公式为an = 2n^2 - 3n + 1，求前n项的和Sn。

3. 数学归纳法证明：证明对于任意正整数n，2n + 1为奇数。

2021年高考高二数学复习假期作业7

假期作业七出题：第二组审核：王琪 1．如图，棱长为1的正方体1111ABCD A B C D -中，P 为线段1AB 的中点，,M N 分别为线段1AC 和棱 11C D 上任意一点，则2PM MN +的最小值为（） A ．2 B ．2 C ．1 D ．2 2．在四面体ABCD 中，BCD ∆与ACD ∆均是边长为4的等边三角形，二面角A CD B --的大小为60，则四面体ABCD 外接球的表面积为（）
A ．2089π
B ．529π
C ．643π
D ．523
π 3．如图，平面四边形ABCD 中，1AB AD CD ===，2BD =，BD CD ⊥，将其沿对角线BD 折成四面体A BCD '-，使平面A BD '⊥平面BCD ，若四面体A BCD '-的顶点在同一个球面上，则该球的表面积为（）
A ．3π
B ．32
π B ．C ．4π D ．
3π 4．如图，四棱锥S ABCD -中，底面是边长为2的正方形ABCD ，
AC 与BD 的交点为O ，SO ⊥平面ABCD 且2SO =，E 是边BC
的中点，动点P 在四棱锥表面上运动，并且总保持PE AC ⊥，
则动点P 的轨迹的周长为( )
A ．22
B ．23
C ．12+
D ．13+
5．如图，四面体ABCD 中，AB ，BC ，BD 两两垂直，2BC BD == ，
点E 是CD 的中点，若直线AB 与平面ACD 所成角的正切值为24
，。

湖南省长沙市长郡中学2024-2025学年高二上学期入学考试数学试题(含答案)

长郡中学2024年高二暑假作业检测试卷数学得分：________本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共6页。

时量120分钟。

满分150分。

第Ⅰ卷一、选择题（本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．命题“对任意，”的否定为A ．对任意， B ．存在，C ．对任意，D ．存在，2．已知，，则A ． B ．C ．D ．3．已知，则A ．2B ．C ．4D ．★4．已知函数f （x ）是定义在R 上的偶函数，且在（-∞，0]上单调递增，若对任意的，不等式恒成立，则a 的取值范围是A ．B ．C ．（-2，2） D ．（-∞，-2）∪（2，＋∞）5．已知，，则A．B ．C ．D ．★6．若函数有两个零点，则实数m 的取值范围是A ．（-1，2）B ．（-1，1）C ．（0，1）D ．（-1，0）7．如图，圆锥底面半径为3，母线，，一只蚂蚁从A 点出发，沿圆锥侧面绕行一周，到达B 点，最短路线长度为x ∈R 2240x x -+≤x ∈R 2240x x -+≥0x ∈R 200240x x -+>x ∉R 2240x x -+≥0x ∉R 200240x x -+>{}|43A x x =-≤≤(){}|lg 10B x x =->A B = {}|42x x -<≤{}|42x x -≤≤{}|23x x <<{}|23x x <≤3i1iz +=-|1|z +=x ∈R ()()21f ax f x >+11,22⎛⎫-⎪⎝⎭11,,22⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭π1tan 44α⎛⎫-= ⎪⎝⎭()2tan 5αβ+=πtan 4β⎛⎫+=⎪⎝⎭3221318161322()|e 1|xf x m =-+12PA =23AB AP =A ．B ．16C ．D ．128．在△ABC 中，，O 是△ABC 的外心，M 为BC 的中点，，N 是直线OM 上异于M ，O 两点的任意一点，则A ．3B ．6C ．7D ．9二、选择题（本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分）9．已知事件A ，B 发生的概率分别为，，则A ．若，则事件与B 相互独立 B ．若A 与B 相互独立，则C ．若A 与B 互斥，则 D ．若B 发生时A10．，，若在上的投影向量为，则A ． B ． C ． D ．11．已知，，且，则A ． B ．C ．的最大值为2D ．选择题答题卡题号1234567891011得分答案第Ⅱ卷三、填空题（本题共3小题，每小题5分，共15分）12．已知函数则________．AC =8AB AO ⋅=AN BC ⋅=()13P A =()16P B =()19P AB =A ()49P A B = ()49P A B =(),1a λ= ()1,1b =-a b b 3λ=a b P ()a ab ⊥- ||a b -=1x >1y >4xy =45x y +<≤220log log 1x y <⋅≤2log yx21log log 2x x y -+<≤()()3,0,2,0,x x f x f x x ⎧>⎪=⎨+⎪⎩≤31log 16f ⎛⎫= ⎪⎝⎭13．一组数据42，38，45，43，41，47，44，46的第75百分位数是________．★14．直三棱柱的各顶点都在同一球面上，若，，，则此球的表面积等于________．四、解答题（本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤）★15．（13分）记△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，分别以a ，b ，c 为边长的三个正三角形的面积依次为，，，已知，．（1）求△ABC 的面积；（2）若b ．16．（15分）已知函数，．（1）解不等式；（2）若对任意的恒成立，求m 的取值范围．★17．（15分）如图，已知四棱锥P-ABCD 的底面ABCD 是菱形，，，E 为AD 的中点，点F 在PA 上，．（1）证明：；（2）若，且PD 与平面ABCD 所成的角为45°，求平面AEF 与平面BEF 夹角的余弦值．18．（17分）已知函数f （x ）满足：，，且当时，，函数．（1）求实数m 的值；111ABC A B C -1AB =12AC AA ==2π3BAC ∠=1S 2S 3S 123S S S -+=1sin 3B=sin sin A C =()πcos 1224x x f x ⎛⎫=++ ⎪⎝⎭()sin 2g x x =()1f x ≥()()mf x g x ≤π0,4x ⎡⎤∈⎢⎥⎣⎦PBC ABCD ⊥平面平面30ACD ∠=︒3AP AF =PC BEF 平面P PDC PDB ∠=∠x ∀∈R ()()132f x f x +=-[]0,3x ∈()2f x x x m =--+()()21xg x =-（2）若，且，求x 的取值范围；（3）已知，其中，是否存在实数λ，使得恒成立？若存在，求出实数λ的取值范围；若不存在，请说明理由．19．（17分）设整数集合，其中，且对任意i ，j （），若，则．（1）请写出一个满足条件的集合A ；（2）证明：对任意，；（3）若，求满足条件的集合A 的个数．长郡中学2024年高二暑假作业检测试卷数学参考答案一、二、选择题题号1234567891011答案BDBCADCBABADABC8．B 【解析】因为O 是△ABC 的外心，M 为BC 的中点，设AC 的中点为D ，连接OD ，所以，，设，则，又O 是△ABC 的外心，所以，所以．故选B ．(0,3]x ∈()()0g x f x ->()223h x x x λλ=-+-+[]0,1x ∈()()()()g h x f h x >{}12100,,,A a a a = 121001205a a a <<< ≤≤1100i j ≤≤≤i j A +∈i j a a A +∈{}101,102,,200x ∈ x A ∉100205a =OM BC ⊥OD AC ⊥ON OM λ= ()AN BC AO ON BC AO BC OM BCλ⋅=+⋅=⋅+⋅ ()AO BC AO BA AC=⋅=⋅+AO BA AO AC AO AB AO AC =⋅+⋅=-⋅+⋅ ()(2211||||cos ||cos ||||1422AO AC AO AC CAO AO CAO AC AC ⋅=⋅∠=∠⋅==⨯= 8146AN BC AO AB AO AC ⋅=-⋅+⋅=-+=11．ABC 【解析】因为，所以，因为所以，对于A ，，令，，由双勾函数的性质可得函数f （x ）在（1，2）上单调递减，在（2，4）上单调递增，所以，又，，所以，即，故A 正确；对于B ，，由，得，所以，即，故B 正确；对于C ，令，则，即，即，则，由，得，所以当时，lg k 取得最大值lg2，所以k 的最大值为2，即的最大值为2，故C 正确；对于D ，，令，，则，4xy =4y x=1,41,x y x >⎧⎪⎨=>⎪⎩14x <<4x y x x +=+()4f x x x=+14x <<()()min 24f x f ==()15f =()45f =()[4,5)f x ∈45x y +<≤()()222222224log log log log log 2log log 11x y x x x x x⋅=⋅=⋅-=--+14x <<20log 2x <<()220log 111x <--+≤220log log 1x y <⋅≤2log yxk =224log log log x y k x==4lglg lg 2lg k x x =2lg 2lg lg lg 2lg x kx -=()()()22lg 2lg 2lg lg lg 2lg 2lg lg 2lg 2x x x k -+⋅--+==14x <<0lg 2lg 2x <<lg lg 2x =2log yx2224log log log log log 2log 21x xx x y x x x+=+=+-2log t x ∈()0,2t ∈1log 2x t=则，令，，由双勾函数的性质可得函数g （t ）在上单调递减，在上单调递增所以，当x →0时，g （t ）→＋∞，所以，即，故D 错误．故选ABC ．三、填空题12．13．45.5 14．四、解答题15．【解析】（1）由题意得，，，则，即，由余弦定理得，整理得，则，又，所以，即，则．（2）由正弦定理得，则，222log log log 2log 211x xx y x t t+=+-=+-()21g t t t=+-()0,2t ∈()2()min 1g t g==()1,)g t ∈-+∞2log log 1x x y +≥811640π322112S a =⋅=22S =23S =222123S S S a -+=-+=2222a c b +-=222cos 2a c b B ac+-=cos 1ac B =cos 0B >1sin 3B =cos B ==1cos ac B ==1sin 2ABC S ac B ==△sin sin sin b a cB A C==229sin sin sin sin sin 4b a c ac B A C A C =⋅===则，所以．16．【解析】（1）依题意，，由，得则，，解得，，所以不等式的解集为（）．（2）由，得，由，得，令，，原不等式化为，即，显然函数在上单调递增，则当时，，因此，所以m 的取值范围为．17．【解析】（1）设AC ，BE 的交点为O ，连接FO ，易知O 为△ABD 的重心，所以，而，所以在△APC 中，，所以，又，，所以．（2）因为，所以，所以△DCB 为等边三角形，所以，又因为，所以，所以，取BC 的中点为H ，连接PH ，则，3sin 2b B =31sin 22b B ==()212sin cos 12sin 222222x x x x x x f x ⎫=-+=+-⎪⎪⎭πsin cos 4x x x ⎛⎫=+=+ ⎪⎝⎭()1f x ≥πsin 4x ⎛⎫+⎪⎝⎭ππ3π2π2π444k x k +++≤≤k ∈Z π2π2π2k x k +≤≤k ∈Z ()1f x ≥π2π,2π2k k ⎡⎤+⎢⎥⎣⎦k ∈Z ()()mf x g x ≤()sin cos sin 2m x x x +≤π0,4x ⎡⎤∈⎢⎥⎣⎦πππ442x +≤≤πsin 14x ⎛⎫+ ⎪⎝⎭≤πsin cos 4t x x x ⎛⎫=+=+∈ ⎪⎝⎭2sin 22sin cos 1x x x t ==-21mt t -≤211t mt t t t-=-≤1y t t =-1t =min 0y =0m ≤0m ≤12AO OC =12AF FP =12AO AF OC FP ==FO PC P FO BEF ⊂平面PC BEF ⊄平面PCBEF 平面P 30ACD ∠=︒30ACB ∠=︒DC DB =PDC PDB ∠=∠PDB PDC △≌△PB PC =PH BC ⊥因为，，所以，以H 为坐标原点，HD ，HB ，HP 为x ，y ，z 轴，建立如图所示的空间直角坐标系，因为PD 与平面ABCD 所成的角为，所以，设菱形ABCD 的边长为2，则，B （0，1，0），，，，因为，所以，，，，设平面AEF 的法向量为，则令，，，所以，设平面BEF 的法向量为，则令，，所以，则PBC ABCD ⊥平面平面PBC ABCD BC = 平面平面PH ABCD ⊥平面45PDH ∠=︒PH DH =PH DH ==(P )2,0A )D)E3AP AF = 43F 13EF ⎛= ⎝ ()0,1,0AE =-)BE =(),,n x y z =0,0,10,03y n AE x y z n EF -=⎧⎧⋅=⎪⎪⇒⎨⎨++=⋅=⎪⎪⎩⎩ 1x =0y =1z =()1,0,1n =()222,,m x y z =22220,0,100,3m BE m EF x y z =⎧⋅=⎪⇒⎨⎨⋅=+=⎪⎪⎩⎩ 2y =20x =21z =-()1m =-cos ,||||m n m n m n ⋅==所以平面AEF 与平面BEF．18．【解析】（1）由题意得，即，解得．（2）时，，即，令，定义域为，可以看出，又在上单调递增，在上单调递增，所以在上单调递增，故的解集为（2，3]．（3）的定义域为（0，＋∞），要使恒成立，首先满足在上恒成立，由于开口向下，只需解得，此时，故当时，对任意时恒成立，令，则恒成立，即恒成立，由（2）可知，的解集为（2，3]，故只需解得，综上，存在满足条件．19．【解析】（1）答案不唯一．如．()()1302f f =-21332m m --+=-8m =(0,3]x ∈()()0g x f x ->()22180xx x -++->()()2218xu x x x =-+-(0,3]x ∈()234280u =++-=()()21xg x =-(0,3]x ∈22133824y x x x ⎛⎫=+-=+- ⎪⎝⎭(0,3]x ∈()()2218xu x x x =-++-(0,3]x ∈()()0g x f x ->()()21xg x =-()()()()g h x f h x >()0h x >[0,1]x ∈()223h x x x λλ=-+-+()()22030,1130,h h λλλ⎧=-+>⎪⎨=-+-+>⎪⎩1λ-<<()22233333244h x x λλλ⎛⎫=---+-+ ⎪⎝⎭≤≤1λ-<<()03h x <≤[0,1]x ∈()()03s h x s =<≤()()g s f s >()()0g s f s ->()()0g s f s ->()()22032,1132,h h λλλ⎧=-+>⎪⎨=-+-+>⎪⎩01λ<<01λ<<{}1,2,3,,100A =（2）假设存在一个使得，令，其中且，由题意，得，由为正整数，得，这与为集合A 中的最大元素矛盾，所以对任意．（3）设集合中有个元素，，由题意，得，，由（2）知，．假设，则．因为，由题设条件，得，因为，所以由（2）可得，这与为A 中不超过100的最大元素矛盾，所以，又因为，，所以．任给集合{201，202，203，204}的元子集B ，令，以下证明集合符合题意：对于任意i ，j （），则．若，则有，所以，，从而．故集合符合题意，所以满足条件的集合A 的个数与集合{201，202，203，204}的子集个数相同，{}0101,102,,200x ∈ 0x A ∈0100x s =+s ∈N 1100s ≤≤100s a a A +∈s a 100100s a a a +>100a {}101,102,,200x ∈ x A ∉{}201,202,,205A ()15m m ≤≤100m a b -=12100200m a a a -<<< ≤10011002100200m m a a a -+-+<<<< 100100m a b -=≤100b m >-1000b m -+>10010010055100b m m -+-+=<-≤100100m b m a a A --++∈100100100100200m b m a a --+++=≤100100100m b m a a --++≤100m a -100100m a m --≤121001m a a a -<<< ≤i a ∈N ()1100i a i i m =-≤≤1m -{}{}01,2,,100205A m B =- 0A 1100i j ≤≤≤200i j +≤0i j A +∈100i j m +-≤i a i =j a j =0i j a a i j A +=+∈0A故满足条件的集合A 有个．4216。

全新暑假作业：高中高二数学暑假作业答案.doc

全新暑假作业：高中高二数学暑假作业答案为大家整理的2014年全新暑假作业：高中高二数学暑假作业答案文章,供大家学习参考！更多最新信息请点击高二考试网、选择题：(本大题共10小题，每小题4分，共40分)题号1 2 3 4 5 6 7 8 9 10答案B D A A D B D B C D二、填空题(本大题共5小题，每小题4分，共20分，把答案填在相应横线上.)11. 12. 180 13. 14. 为参数) 15. 480三、解答题(本大题共5小题，共44分.解答应写出文字说明、证明过程或演算步骤.)16.(本小题满分6分)解：(Ⅰ)直线的方程可化为，即化为直角坐标方程为，将点代人上式满足，故点在直线上. …………………2分(Ⅱ)直线的参数方程为为参数)，…………………3分曲线的直角坐标方程为，将直线的参数方程代人曲线的方程并整理得，所以…………………………6分17. (本小题满分8分)解：(Ⅰ)当时，当时，可化为，解得;当时，可化为，解得.综上可得，原不等式的解集为…………………………4分(Ⅱ) ………………6分函数有最小值的充要条件为即………………8分18. (本大题满分8分)解：(1)设选手甲答对一个问题的正确率为，则故选手甲回答一个问题的正确率……………2分(2)选手甲答了4道题进入决赛的概率为; ………………3分选手甲答了5道题进入决赛的概率为; ……………5分选手甲答了6道题进入决赛的概率为; …… …7分故选手甲可进入决赛的概率………… …8分19.(本小题满分8分)解(Ⅰ)男生女生合计收看10 6 16不收看6 8 14合计16 14 30由已知数据得:所以,没有充足的理由认为“通过电视收看世界杯”与性别有关. …………4分(Ⅱ) 的可能取值为，……6分所以的分布列为:0 1 2的均值为: …………………………8分20. ,因为.所以切线方程是……………3分(Ⅱ)函数的定义域是当时，令得…………………………5分①当，所以在上的最小值是，满足条件，于是;②当，即时，在上的最小值是，不合题意;③当，即时，在上单调递减，所以在上的最小值是，不合题意.综上所述有，. …………………………………10分。

高二数学暑假作业7试题

新课标2021年高二数学暑假作业7必修5—选修2-3创作人：历恰面日期：2020年1月1日一选择题〔本大题一一共8小题，每一小题5分，在每一小题给出的四个选项里面，只有一项是哪一项符合题目要求的。

〕1.复数满足：〔是虚数单位〕，那么的虚部为〔〕A． B． C． D．2.曲线的参数方程为(t是参数)，那么曲线是〔〕3.不等式的解集为〔〕A． B．C． D．4.如右图，A、B是⊙O上的两点，AC是⊙O的切线，∠B=70°，那么∠BAC等于〔〕A. 70°B. 20°C.35° D. 10°5.从0,1,2,3,4,5,6,7,8,9这10个数字中任取3个不同的数字构成空间直角坐标系中的点的坐标，假设是3的倍数，那么满足条件的点的个数为( )A. 216B. 72C.42 D. 2526.函数的图象如图(其中是函数的导函数),下面四个图象中,的图象可能是BA． B．C． D．7.设(2－x)6＝a0＋a1x＋a2x2＋…＋a6x6，那么|a1|＋|a2|＋…＋|a6|的值是( )A．665 B．729 C．728D．638.设圆(x＋1)2＋y2＝25的圆心为C，A(1，0)是圆内一定点，Q为圆周上任一点，线段AQ的垂直平分线与CQ的连线交于点M，那么M的轨迹方程为( )二．填空题〔本大题一一共4小题，每一小题5分，一共20分。

把答案填在题中横线上〕9.随机变量X服从二项分布X～B(6，)，那么P(X＝2)等于10.为定义在(0，+∞)上的可导函数，且，那么不等式的解集为___________．11.先后掷一枚质地均匀骰子〔骰子的六个面上分别标有、、、、、个点〕两次，落在程度桌面后，记正面朝上的点数分别为,,设事件为“为偶数〞，事件为“,中有偶数且〞，那么概率等于。

12.椭圆E:与双曲线D: (a>0，b>0)，直线：与双曲线D的两条渐近线分别交于点A，B.假设椭圆E的右焦点F在以线段AB为直径的圆内，那么椭圆的离心率的取值范围是________.三．解答题〔本大题一一共4小题，每一小题10分，解容许写出文字说明，证明过程或者演算步骤〕13.〔本小题满分是10分〕椭圆：与抛物线：有一样焦点．〔Ⅰ〕求椭圆的HY方程；〔Ⅱ〕直线过椭圆的另一焦点，且与抛物线相切于第一象限的点，设平行的直线交椭圆于两点，当△面积最大时，求直线的方程．14.〔10分〕为了下一次的航天飞行，现准备从10名预备队员〔其中男6人，女4人〕中选4人参加“神舟十一号〞的航天任务。

山东省高二数学暑假作业(七)理

2013高二数学（理）暑假作业（七）一、选择题1．复数22()i i+= A ．34i -- B ．34i -+ C ．34i - D ．34i +2.设全集U是自然数集N ，集合{}{}1,2,3,1A B x N x ==∈≤，则如图所示的阴影部分的集合为A.{}0,1B.{}1,2C.{}2,3D.{}0,1,23. x 0 1 23 y 1 35 7则y 与x 的线性回归方程+=a x b y 必过点( ) A.(1.5 ,4) B. (2,2) C.(1.5 ,0) D.(1,2)4. 曲线⎪⎩⎪⎨⎧+-=++-=λλλλ11132y x (λ为参数)与y 坐标轴的交点是（） A ．,0( )52 B ．,0( )51 C ．,0( )4- D ．,0( )95 5 .在ABC △中，60,6,10A b c ===o，则ABC △的面积为A. 156B.153C.15D.306. 已知抛物线24y x =的准线与双曲线()2221,0x y a a-=＞交于A,B 两点，点F 为抛物线的焦点，若FAB ∆为直角三角形，则双曲线的离心率是A.3B.6C.2D.37.如图，某几何体的正视图与侧视图都是边长为1的正方形且体积为12，则该几何体的俯视图可以是8. 在各项都为正数的等比数列{}n a 中，首项31=a ，前三项和为321S =，则4a =A ．32 B.24 C.27 D ．549．函数f (x )＝e x－1x的零点所在的区间是( )A.⎝ ⎛⎭⎪⎫0，12B.⎝ ⎛⎭⎪⎫12，1C.⎝ ⎛⎭⎪⎫1，32D.⎝ ⎛⎭⎪⎫32，2 10．如果上述程序运行的结果为S ＝132，那么判断框中应填入（） A. k≤11 B.k≥11 C .k≤10 D .k≥1011.在平面直角坐标系xoy 中，圆C 的方程为228150x y x +-+=，若直线2y kx =+上至少存在一点，使得以该点为圆心，半径为1的圆与圆C 有公共点，则k 的最小值是A.43-B.54-C.35-D.53-12在下列函数中，最小值是22的是 A.12lg (0)lg y x x x =+> B. 2sin sin y x x=+()0,x π∈ C. 223y x =+ D.2xxy e e-=+二、填空题13. 若不等式220ax bx ++>的解集是11(,)23-，则a b +的值为 .14.在复平面内，记复数3i +对应的向量为OZ uuu r ，若向量OZ uuu r绕坐标原点逆时针旋转60o得到向量'OZ u u u u r所对应的复数为___________________．15.已知实数[]0,10x ∈，执行如右图所示的程序框图，则输出的x 不小于47的概率为16.过点A(4,1)的圆C 与直线10x y --=相切于点B(2,1),则圆C 的方程为三、解答题17.已知函数121)(+-=x a x f .（1）证明：不论a 为何实数()f x 总为增函数（2）确定a 的值, 使)(x f 为奇函数；18．(本小题满分12分)如图所示，直角梯形ACDE 与等腰直角ABC ∆所在平面互相垂直，F 为BC 的中点， 90BAC ACD ∠=∠=︒，AE ∥CD ，22DC AC AE ===.（1）求证：平面BCD ⊥平面ABC ; （2）求证：AF ∥平面BDE ；（3）求四面体B CDE -的体积.19．己知等比数列{}n a 所有项均为正数，首11a =，且435,3,a a a 成等差数列．(I)求数列{}n a 的通项公式；(II)数列{}1n n a a λ+-的前n 项和为n S ，若*21()n n S n N =-∈，求实数λ的值．20.已知抛物线24y x =的焦点为F 2，点F 1与F 2关于坐标原点对称，直线m 垂直于x 轴（垂足为T ），与抛物线交于不同的两点P,Q 且125F P F Q ⋅=-u u u r u u u u r.（I ）求点T 的横坐标0x ；（II ）若以F 1,F 2为焦点的椭圆C 过点21,2⎛⎝⎭. ①求椭圆C 的标准方程；②过点F 2作直线l 与椭圆C 交于A,B 两点，设22F A F B λ=u u u u r u u u u r，若[]2,1,TA TBλ∈--+u u r u u r 求的取值范围.2013高二数学（理）暑假作业（七）参考答案一、选择题1-5 ACABB 6-10 BABBD 11-12AD 二、填空题 13.14- 14． 2i 15．1/216.223)2x y -+=（三、解答题17． (1) 依题设)(x f 的定义域为),(+∞-∞原函数即121)(+-=xa x f ，设12x x <, 则121211()()2121x x f x f x a a -=--+++=121222(12)(12)x x x x -++, 12x x <Q , 1212220,(12)(12)0x x x x ∴-<++>,12()()0,f x f x ∴-<即12()()f x f x <,所以不论a 为何实数()f x 总为增函数.(2) ()f x Q 为奇函数, ()()f x f x ∴-=-,即112121x xa a --=-+++ 则11221211211212=+++=+++=-x xx x xa ，∴1.2a = 11().221x f x ∴=-+18．（1）∵面ABC ⊥面ACDE ，面ABC I 面ACDE AC =，CD AC ⊥, ∴DC ⊥面ABC ，又∵DC ⊂面BCD ，∴平面BCD ⊥平面ABC . （2）取BD 的中点P ，连结EP 、FP ，则FP 12DC , 又∵EA12DC ，∴EA FP ， ∴四边形AFPE 是平行四边形，∴AF ∥EP ，又∵EP ⊂面BDE 且AF ⊄面BDE ，∴AF ∥面BDE .（3）∵BA ⊥AC ，面ABC I 面ACDE =AC ， ∴BA ⊥面ACDE . ∴BA 就是四面体B CDE -的高，且BA =2. ∵DC =AC =2AE =2，AE ∥DC ，∴11(12)23,121,22ACE ACDE S S ∆=+⨯==⨯⨯=梯形∴312,CDE S ∆=-= ∴1422.33E CDE V -=⨯⨯=19．（Ⅰ）设数列{}n a 的公比为q ，由条件得423,3,q q q 成等差数列，所以4326q q q +=解得2,3=-=q q 或由数列{}n a 的所有项均为正数,则q =2 数列{}n a 的通项公式为n a =12n -(*)n N ∈（Ⅱ）记n n n a a b λ-=+1,则112)2(22---=⋅-=n n n n b λλ 若0,0,2===n n S b λ不符合条件；若2≠λ，则21=+nn b b ，数列{}n b 为等比数列，首项为λ-2，公比为2,此时)12)(2()21(21)2(--=---=n n n S λλ 又n S ＝21(*)n n N -∈,所以1=λ20．解：（Ⅰ）由题意得)0,1(2F ，)0,1(1-F ，设),(00y x P ，),(00y x Q -，则),1(001y x P F +=，),1(002y x Q F --=. 由521-=⋅Q F P F ，得512020-=--y x 即42020-=-y x ，① 又),(00y x P 在抛物线上，则0204x y =，②联立①、②易得20=x （Ⅱ）（ⅰ）设椭圆的半焦距为c ，由题意得1=c ，设椭圆C 的标准方程为)0(12222>>=+b a by a x ，则121122=+b a ③ 122+=b a ④将④代入③，解得12=b 或212-=b （舍去）所以2122=+=b a故椭圆C 的标准方程为1222=+y x （ⅱ）方法一：容易验证直线l 的斜率不为0，设直线l 的方程为1x ky =+将直线l 的方程代入2212x y +=中得：22(2)210k y ky ++-= 设112212(,),(,),00A x y B x y y y ≠≠且，则由根与系数的关系，可得：12222ky y k +=-+ ⑤12212y y k =-+ ⑥因为F F 22λ=，所以12yy λ=，且0λ<.将⑤式平方除以⑥式，得：221222214142222y y k k y y k k λλ++=-⇒++=-++ 由[]51112,1+22022λλλλλ∈--⇒-≤≤-⇒-≤++≤2214022k k ⇒-≤-≤+所以 7202≤≤k因为1122(2,),(2,)TA x y TB x y =-=-u u r u u r ，所以1212(4,)TA TB x x y y +=+-+u u r u u r，又12222ky y k +=-+，所以2121224(1)4()22k x x k y y k ++-=+-=-+，故2222221212222216(1)4||(4)()(2)(2)k k TA TB x x y y k k ++=+-++=+++u u r u u r 2222222216(2)28(2)828816(2)2(2)k k k k k +-++==-++++，令212t k =+，所以2207k ≤≤ 所以27111622k ≤≤+，即71[,]162t ∈，所以222717||()828168()42TA TB f t t t t +==-+=--u u r u u r .而71[,]162t ∈，所以169()[4,]32f t ∈.所以||[2,8TA TB +∈u u r u u r . 方法二：1）当直线l 的斜率不存在时，即1-=λ时，)22,1(A ，)22,1(-B ，又T )0,2(，所以((1,2TA TB +=-+-=u u r u u r2）当直线l 的斜率存在时，即[)1,2--∈λ时，设直线l 的方程为)1(-=x k y由⎪⎩⎪⎨⎧=+-=1222y x kkx y 得0224)21(2222=-+-+k x k x k设()()1122,,,A x y B x y ，显然120,0y y ≠≠，则由根与系数的关系，可得：2221214k k x x +=+，22212122kk x x +-=⋅ 221212122)(kkk x x k y y +-=-+=+ ⑤ 22212122121)1)((k k x x x x k y y +-=++-=⋅ ⑥因为F F 22λ=，所以12yy λ=，且0λ<.将⑤式平方除以⑥式得：221421k +-=++λλ由[)1,2--∈λ得⎪⎭⎫⎢⎣⎡--∈+2,251λλ即⎪⎭⎫⎢⎣⎡-∈++0,2121λλ 故0214212<+-≤-k ，解得272≥k 因为1122(2,),(2,)TA x y TB x y =-=-u u r u u r，所以1212(4,)TA TB x x y y +=+-+u u r u u r，又222121)1(44k k x x ++-=-+，2222222221221)21(4)21()1(16)()4(k k k k y y x x ++++=++-+=+ 22222222)21(221104)21(2)21(10)21(4k k k k k ++++=+++++= 令2211k t +=，因为272≥k 所以8121102≤+<k ，即⎥⎦⎤ ⎝⎛∈81,0t ，所以22251721042()22TA TB t t t +=++=+-u u r u u r 1694,32⎛⎤∈ ⎥⎝⎦.⎥⎦⎤⎝⎛+8213,2综上所述：||TA TB +∈u u r u u r .。

高二数学暑假作业第7天文-人教版高二全册数学试题

第7天函数与方程课标导航：1.结合二次函数的图象，了解函数零点与方程根的关系；2.了解指数函数、对数函数、幂函数的增长特点，了解函数模型的广泛运用. 一、选择题1. 求函数132)(3+-=x x x f 零点的个数为（） A ．1B ．2C ．3D ．42. 若函数)(x f y =在区间[],a b 上的图象为连续不断的一条曲线，则下列说法正确的是（）A ．若0)()(>b f a f ，不存在实数),(b a c ∈使得0)(=c f ；B ．若0)()(<b f a f ，存在且只存在一个实数),(b a c ∈使得0)(=c f ；C ．若0)()(>b f a f ，有可能存在实数),(b a c ∈使得0)(=c f ；D ．若0)()(<b f a f ，有可能不存在实数),(b a c ∈使得0)(=c f ；3. 函数f(x)=3ax-2a+1在［-1，1］上存在一个零点，则a 的取值范围是（） A.a≥51 B.a≤1 C.-1≤a≤51D. a≥51或a≤-14. 若方程310x x -+=在区间(,)(,,1)a b a b Z b a ∈-=且上有一根，则a b +的值为（）A ．1-B ．2-C ．3-D ．4-5．已知0＜a ＜1，则方程a |x |=|log a x |的实根个数是（）A ．1个B ．2个C ．3个D ．1个或2个或3个 6. 已知函数()22f x x ax a =-+在区间(),1-∞上有最小值，则函数()f x x在区间()1,+∞上（）A ．有两个零点B ．有一个零点C ．无零点D ．无法确定7. 若方程0xa x a --=有两个实数解，则a 的取值范围是（）A ．(1,)+∞B ．(0,1)C ．(0,2)D ．(0,)+∞8. 设()f x 是定义在R 上的偶函数，对任意x R ∈，都有(2)(2),f x f x -=+且当[2,0]x ∈-时，1()()1,(2,6]2x f x =--若在区间内关于x的方程()log (2)0(1)a f x x a -+=>恰有3个不同的实数根，则a 的取值范围是（）A ．（1，2）B ．(2,)+∞C．D．二、填空题9. 关于x 的实系数方程x 2-ax+2b=0的一根在区间［0，1］上，另一根在区间［1，2］上，则2a+3b 的最大值为 10. 已知函数b x a x f x+-=)(的零点))(1,(0Z k k k x ∈+∈，其中常数,a b 满足493,23==b a ，则k = ； 11. 已知函数221,0,()2,x x f x x x x ⎧->⎪=⎨--⎪⎩≤0.若函数()()g x f x m =-有3个零点，则实数m 的取值范围是；12. 设函数22,0,()log ,0x x f x x x ⎧≤=⎨>⎩，若关于x 的方程2()()0f x af x -=恰有三个不同的实数解，则实数a 的取值范围为______ __．三、解答题13. 设二次函数2()f x ax bx c =++在区间[]2,2-上的最大值、最小值分别是M 、m ，集合{}|()A x f x x ==．（1）若{1,2}A =，且(0)2f =，求M 和m 的值；（2）若{1}A =，且1a ≥，记()g a M m =+，求()g a 的最小值．14. 设1x 与2x 分别是实系数方程20ax bx c ++=和20ax bx c -++=的一个根，且1212,0,0x x x x ≠≠≠ ，求证：方程202a x bx c ++=有仅有一根介于1x 和2x 之间．15.已知0a >且1a ≠，求使方程222log ()log ()a a x ak x a -=-有解时的k 的取值范围．16. 设函数()2()4ln 1f x x x =--．（1）求函数)(x f 的单调递增区间；（2）若关于x 的方程()240f x x x a +--=在区间[]1,e 内恰有两个相异的实根，求实数a 的取值范围．【链接高考】函数f(x)=xcos2x 在区间[0,2π]上的零点个数为（）A ．2B ．3C ．4D ．5第7天1~8 CCDC BCAD ; 9. 9; 10. 1; 11. （0，1）; 12. {}01a a <<; 13．（1）1,10m M ==;（2）43114．令2(),2a f x x bx c =++由题意可知2211220,0ax bx c ax bx c ++=-++= 221122,,bx c ax bx c ax +=-+=2222111111(),222a a af x x bx c x ax x =++=-=-22222222223(),222a a a f x x bx c x ax x =++=+=因为120,0,0a x x ≠≠≠∴12()()0f x f x <，即方程202ax bx c ++=有仅有一根介于1x 和2x 之间。

新高二数学暑假作业-7+8

新高二暑假第七次作业一、选择题（单选题）1．cos 4π12 －sin 4π12 等于( ) A ．－12 B ．－32 C ．12 D ．322．已知sin α＝3cos α，那么tan 2α的值为( )A ．2B ．－2C ．34D ．－343．已知函数f (x )＝cos 2⎝ ⎛⎭⎪⎫x －π12 ＋sin 2⎝ ⎛⎭⎪⎫x ＋π12 －1，则f (x )( ) A ．是奇函数 B ．是偶函数C ．既是奇函数又是偶函数D ．既不是奇函数又不是偶函数4．将函数y ＝sin x 的图象向左平移π4 个单位长度，再向上平移2个单位长度，得到的图象的解析式是( )A ．y ＝sin ⎝ ⎛⎭⎪⎫x －π4 ＋2B ．y ＝sin ⎝⎛⎭⎪⎫x ＋π4 －2 C ．y ＝sin ⎝ ⎛⎭⎪⎫x －π4 －2 D ．y ＝sin ⎝⎛⎭⎪⎫x ＋π4 ＋2 5．要得到函数 y ＝3sin 2x 的图象，可将函数 y ＝3cos ⎝⎛⎭⎪⎫2x －π4 的图象( ) A ．沿 x 轴向左平移π8 个单位长度B ．沿 x 轴向右平移π8 个单位长度C ．沿 x 轴向左平移π4 个单位长度D ．沿 x 轴向右平移π4 个单位长度6．已知函数f (x )＝sin ⎝⎛⎭⎪⎫2x ＋π3 ，以下命题中为假命题的是( ) A ．函数f (x )的图象关于直线x ＝π12 对称B ．x ＝－π6 是函数f (x )的一个零点C ．函数f (x )的图象可由g (x )＝sin 2x 的图象向左平移π3 个单位长度得到D ．函数f (x )在⎣⎢⎡⎦⎥⎤0，π12 上是增函数 7．已知点P 是单位圆上的一个质点，它从初始位置P 0⎝ ⎛⎭⎪⎫12，－32 开始，按逆时针方向以角速度1 rad/s 做圆周运动，则点P 的纵坐标y 关于运动时间t (单位：s )的函数关系式为( )A ．y ＝sin ⎝ ⎛⎭⎪⎫t －π3 ，t ≥0B ．y ＝sin ⎝⎛⎭⎪⎫t －π6 ，t ≥0 C ．y ＝－cos ⎝ ⎛⎭⎪⎫t －π3 ，t ≥0 D ．y ＝－cos ⎝⎛⎭⎪⎫t －π6 ，t ≥0 8．已知向量a ∥b ，且|a |＞|b |＞0，则向量a ＋b 的方向( )A ．与向量a 方向相同B ．与向量a 方向相反C ．与向量b 方向相同D ．与向量b 方向相反9．在下列命题中，正确的个数是( )①若|a |＝|b |，则a ＝b ；②若a ＝b ，则a ∥b ；③|AB→ |＝|BA → |；④若a ∥b ，b ∥c ，则a ∥c .A ．1B ．2C ．3D ．4二、解答题 10.已知向量a ⃗ =(cosx +sinx,√3cosx)，b ⃗ =(cosx −sinx,−2sinx)，记函数f(x)=a ⃗ ⋅b ⃗ ． (Ⅰ)求函数f(x)在[0,π2]上的取值范围；(Ⅱ)若g(x)=f(x +t)为偶函数，求|t|的最小值．新高二暑假第八次作业一、选择题（单选题）1．设D ，E ，F 分别为△ABC 的三边BC ，CA ，AB 的中点，则＋＝( )A ．B ．12C ．12D ．2．已知向量a ，b 是两个非零向量，在下列四个条件中，一定能使a ，b 共线的是()①2a－3b＝4e且a＋2b＝－2e；②存在相异实数λ，μ，使λa－μb＝0；③x a＋y b＝0(其中实数x，y满足x＋y＝0)；④已知梯形ABCD，其中＝a，＝b.A．①②B．①③C．②D．③④3．已知向量a，b满足|a|＝2，|b|＝3，a·(b－a)＝－1，则a与b的夹角为()A．π6B．π4C．π3D．π24．若向量a，b的夹角为120°，|a|＝1，|a－2b|＝7，则|b|＝()A．12B．72C．1 D．25．已知菱形ABCD的边长为a，∠ABC＝60°，则·＝()A．－32a2B．－34a2C．34a2D．32a26．在▱ABCD中，E，F分别为边BC，CD的中点，若＝x＋y(x，y∈R)，则x ＋y＝()A．2 B．1 C．32D．237．已知点A(1，－2)，B(－1，3)，若向量－k与a＝(2，3)共线，则实数k的值为()A．79B．－79C．47D．－8118．若向量b与向量a＝(2，－1)是共线向量，且|b|＝35，则b＝() A．(6，－3) B．(－6，3)C．(6，－3)或(－6，3) D．(3，－6)或(－3，6)9．在△ABC中，cos A＝12，a＝43，b＝42，则B等于()A．45°或135°B．135°C．45°D．60°二、解答题10.某海上养殖基地A，接到气象部门预报，位于基地南偏东60°方向相距20(3＋1)n mile的海面上有一台风中心，影响半径为20 n mile，正以102n mile/h的速度沿某一方向匀速直线前进，预计台风中心将从基地东北方向刮过且(3＋1)h后开始影响基地持续2 h．求台风移动的方向．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

新课标2015年高二数学暑假作业7必修5—选修2-3
一选择题（本大题共8小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

）
1.已知复数满足：（是虚数单位），则的虚部为（）
A． B． C． D．
2.曲线的参数方程为(t是参数)，则曲线是（）
A.线段
B.双曲线的一支
C.圆
D.射线
3.不等式的解集为（）
A． B．
C． D．
4.如右图，A、B是⊙O上的两点，AC是⊙O的切线，∠B=70°，则∠BAC等于（）
A. 70°
B. 20°
C.
35° D. 10°
5.从0,1,2,3,4,5,6,7,8,9这10个数字中任取3个不同的数字构成空间直角坐标系中的点的
坐标，若是3的倍数，则满足条件的点的个数为( )
A. 216
B. 72
C.
42 D. 252
6.已知函数的图象如图(其中是函数的导函数),下面四个图象中,的图象可能是B
A． B． C． D．
7.设(2－x)6＝a0＋a1x＋a2x2＋…＋a6x6，则|a1|＋|a2|＋…＋|a6|的值是( )
A．665 B．729 C．728
D．63
8.设圆(x＋1)2＋y2＝25的圆心为C，A(1，0)是圆内一定点，Q为圆周上任一点，线段AQ的垂直平分线与CQ的连线交于点M，则M的轨迹方程为( )
二．填空题（本大题共4小题，每小题5分，共20分。

把答案填在题中横线上）
9.已知随机变量X服从二项分布X～B(6，)，则P(X＝2)等于
10.已知为定义在(0，+∞)上的可导函数，且，则不等式
的解集为___________．
11.先后掷一枚质地均匀骰子（骰子的六个面上分别标有、、、、、个点）两次，落在水平桌面后，记正面朝上的点数分别为,,设事件为“为偶数”，事件为“,中有偶数且”，则概率等于。

12.已知椭圆E:与双曲线D: (a>0，b>0)，直线：
与双曲线D的两条渐近线分别交于点A，B.若椭圆E的右焦点F在以线段AB为直径的
圆内，则椭圆的离心率的取值范围是________.
三．解答题（本大题共4小题，每小题10分，解答应写出文字说明，证明过程或演算步骤）
13.（本小题满分10分）已知椭圆：与抛物线：有相同焦点．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）已知直线过椭圆的另一焦点，且与抛物线相切于第一象限的点，设平行的直线交椭圆于两点，当△面积最大时，求直线的方程．
14.（10分）为了下一次的航天飞行，现准备从10名预备队员（其中男6人，
女4人）中选4人参加“神舟十一号”的航天任务。

（Ⅰ）若男甲和女乙同时被选中，共有多少种选法？
（Ⅱ）若至少两名男航天员参加此次航天任务,问共有几种选法?
（Ⅲ）若选中的四个航天员分配到A、B、C三个实验室去，其中每个实验室至少一个航天员,共有多少种选派法?
15.(本小题满分10分)
设其中a为正实数．
(1)当a＝时，求f(x)的极值点；
(2)若f(x)为R上的单调函数，求a的取值范围．
16.(本题满分10分)
如图，设椭圆 (a＞b＞0)的右焦点为F(1，0)，A为椭圆的上顶点，椭圆上的点到右焦点的最短距离为1．过F作椭圆的弦PQ，直线AP，AQ分别交直线x y2＝0于点M，N．
(Ⅰ) 求椭圆的方程；
(Ⅱ) 求当|MN|最小时直线PQ的方程．
新课标2015年高二数学暑假作业7必修5—选修2-3参考答案
1.D
2.D
3.D
4.B
5.D
6.B
7.A
8.D
9.
10.
11.
12.
13.（Ⅰ）由于抛物线的焦点为，得到，又得到．（Ⅱ）思路一：设，，
直线的方程为即且过点
，
切线方程为
由，设直线的方程为，联立方程组
由，消整理得
设，，应用韦达定理
得，由点到直线的距离为
,应用基本不等式等号成立的条件求得
思路二：，由已知可知直线的斜率必存在，设直线
由消去并化简得
根据直线与抛物线相切于点．得到，．
根据切点在第一象限得；由∥，设直线的方程为
由，消去整理得，思路同上．
试题解析：（Ⅰ）抛物线的焦点为，
，又
椭圆方程为．
（Ⅱ）（法一）设，，
直线的方程为即且过点
，
切线方程为
因为，所以设直线的方程为，
由，消整理得
，解得①
设，，则
∴
直线的方程为，
点到直线的距离为
，
由①，
（当且仅当即时，取等号）最大
所以，所求直线的方程为：．
（法二），由已知可知直线的斜率必存在，
设直线
由消去并化简得
∵直线与抛物线相切于点．
∴，得．
∵切点在第一象限．
∴
∵∥
∴设直线的方程为
由，消去整理得，
，解得．
设，，则
，
．
又直线交轴于
10分
当，即时，．
所以，所求直线的方程为． 12分考点：1．椭圆、抛物线标准方程及几何性质；2．直线与圆锥曲线的位置关系．14.————————3分
——————6分
（3）————————10分
15.对f(x)求导得f′(x)＝
(2)若f(x)为R上的单调函数，则f′(x)在R上不变号，结合①与条件a>0，知1＋ax2－2ax≥0在R上恒成立，即Δ＝4a2－4a＝4a(a－1)≤0，由此并结合a>0，知0<a≤1.
所以a的取值范围为{a|0<a≤1}．
16.(Ⅰ) 由题意知，c＝1，a－c＝－1，所以椭圆方程为＋y2＝1．
(Ⅱ) 设P(x1，y1)，Q(x2，y2)，直线PQ：x－my－1＝0，由
消去x，得(m2＋2)y2＋2my－1＝0，
设点M，N的坐标分别为(x M，y M)，(x N，y N)．
因为直线AP的方程为y－1＝x，由
得x M＝．同理可得x N＝．
所以，|MN|＝＝12．记m－7＝t，则|MN|＝12，
当＝－，即m＝－时，|MN|取最小值．
所以，当|MN|取最小值时PQ的方程为y＝－7x＋7．。