安徽省六安市2016年高二数学文暑假作业第23天Word版含答案
安徽省六安市2016年高二数学文暑假作业第13天Word版含答案

第13天 三角恒等变换课标导航:1.会推导和差公式,二倍角公式; 2.能运用公式进行简单的三角变换. 一、选择题 1. 计算«Skip Record If...»的结果等于( )A.«Skip Record If...»B.«Skip Record If...»C.«SkipRecord If...» D.«Skip Record If...» 2. “1sin 2α=”是“1cos 22α=”的( )A .充分不必要条件.B .必要不充分条件.C .充要条件.D .既不充分也不必要条件3. 在△ABC 中,C =120°,tan A +tan B =233,则tan A ·tan B 的值为( )4. 已知sin cos 2αα-=α∈(0,π),则sin 2α=( )A .-1B .22-C .22D .15. 已知43sin()sin 0,352ππααα++=--<<则2cos()3πα+等于( ) A .45-B .35- C .35 D .456. [2012·重庆卷] sin47°-sin17°cos30°cos17°=( )A .3B .-123 7. 设tan ,tan αβ是方程2320x x -+=的两个根,则tan()αβ+的值为( ) A .3-B .1-C .1D .38.23sin 702cos 10-=-( )A .12B .22C .2D .32二、填空题 9. 函数23cos sin y x x x =-的最大值为 ;10.0003sin 701cos 40+= ;11. 设«Skip Record If...»,利用三角变换,估计«Skip Record If...»在k=l ,2,3时的取值情况,对k ∈N*时猜想«Skip Record If...»的值域为 (结果用k 表示). 12. 已知角αβ、的顶点在坐标原点,始边与x 轴的正半轴重合,(0)αβπ∈、,,角β的终边与单位圆交点的横坐标是13-,角αβ+的终边与单位圆交点的纵坐标是45,则cos α= .三、解答题13. 某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:(1)sin 213°+cos 217°-sin13°cos17°; (2)sin 215°+cos 215°-sin15°cos15°; (3)sin 218°+cos 212°-sin18°cos12°; (4)sin 2(-18°)+cos 248°-sin(-18°)cos48°; (5)sin 2(-25°)+cos 255°-sin(-25°)cos55°.(1)试从上述五个式子中选择一个,求出这个常数;(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.14.已知函数.2sin 2cos 2cos 2sin 2)(22x x x x x f -+⋅= (1)求函数f (x )的最小正周期; (2)若xx ,x f x 4tan 14tan 126)(,160-+=<<求时当π的值.15. 已知在△ABC 中,sin A (sin B +cos B )-sin C =0,sin B +cos2C =0,求角A 、B 、C 的大小.16. 已知(0,)2πα∈,(,)2πβπ∈,7cos 29β=-,7sin()9αβ+=(1) 求cos β的值; (2) 求sin α的值.【链接高考】设α为锐角,若cos 6a π⎛⎫+ ⎪⎝⎭=45,则sin 212a π⎛⎫+ ⎪⎝⎭的值为________.第13天1~8 BABA DCAC ;9.12; 10. 211[,1]2k -; 12. 38215; 13.(2)三角恒等式为sin 2α+cos 2(30°-α)-sin αcos(30°-a )=34.证明如下:sin 2α+cos 2(30°-α)-sin αcos(30°-α)=sin 2α+(cos30°cos α+sin30°sin α)2-sin α(cos30°cos α+sin30°sin α)=sin 2α+34cos 2α3sin αcos α+14sin 2α3sin αcos α-12sin 2α=34sin 2α+34cos 2α=34. «Skip Record If...» 14.(1)2)(π的最小正周期是x f ;(2315. ,4π=A .125,3ππ==C B 16.(1)1cos 3β=-;(2)1sin 3α=;链接高考:172。
安徽省六安市2016年高二数学文暑假作业第25天Word版含答案

第2题第1题主视图俯视图左视图第25天 空间几何体的结构特征、三视图、表面积、体积课标导航:1.认识常见几何体,并能画出直观图、三视图; 2.了解柱、锥、台、球的面积与体积计算公式.一、选择题1. 如下图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为 ( ) A .π3 B .π2 C .π23 D .π42. 如图,在空间四边形ABCD 中,点E 、H 分别是边AB 、AD 的中点,F 、G 分别是边BC 、CD 上的点,且CF CB =CG CD =23,则( )A .EF 与GH 互相平行B .EF 与GH 异面C .EF 与GH 的交点M 可能在直线AC 上,也可能不在直线AC 上D .EF 与GH 的交点M 一定在直线AC 上3. 如下图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为12。
则该几何体的俯视图可以是( )4. 一个圆柱的轴截面为正方形,其体积与一个球的体积比是3:2,则这个圆柱的侧面积与这个球的表面积之比为( )第3题A. 1:1B . 1:2C .2:3 D. 3:25. 某四面体的三视图如图所示,该四面体四个面的面积中最大的是( )A .8B .62C .10D .826. 一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积等于( )A .3B .23C .33D .637. 一个几何体的三视图如图所示,则此几何体的体积是( )A .112 B.80 C.72 D.648. 已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =;则此棱锥的体积为( )A .26B .36C .23 D .22二、填空题9. 一个空间几何体的三视图及部分数据如下图所示,则这个几何体的体积是 ; 第5题第7题10. 某几何体的三视图,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是 ;11. 一个几何体的三视图如图所示,则该几何体的体积(单位:3cm )为 3cm ;12. 一空间几何体的三视图如图所示,则该几何体的体积为 .三、解答题13. 已知四棱锥P ABCD -的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.E 是侧棱PC 上的动点. (1)求证:BD AE ⊥;(2)若五点,,,,A B C D P 在同一球面上,求该球的体积.第11题 ABCD P E第13题14. 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.(1) 求该几何体的体积V ; (2) 求该几何体的侧面积S15. 一个多面体的直观图和三视图如下:(其中N M ,分别是BC AF ,中点)(1) 求证://MN 平面CDEF ; (2) 求多面体CDEF A 的体积. 第14题16. 如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点(1)证明:平面BDC 1⊥平面BDC ;(2)平面BDC 1分此棱柱为两部分,求这两部分体积的比.【链接高考】如图,ABCDEFG 为多面体,平面ABED 与平面AGFD 垂直,点O 在线段AD 上,1,2,OA OD ==OAB ,△OAC ,△ODE ,△ODF 都是正三角形.(1)证明直线BC ∥EF ; (II )求棱锥F-OBED 的体积。
安徽省六安市舒城中学高二数学暑假作业 第二十三天 理

第二十三天 圆锥曲线【课标导航】1:圆锥曲线的定义与标准方程的求法; 2:圆锥曲线的几何性质; 3:圆锥曲线的综合问题。
一、选择题1错误!未指定书签。
.已知 A B 、为平面内两定点,过该平面内动点M 作直线AB 的垂线,垂足为N .若2MN AN NB λ=⋅u u u u r u u u r u u u r,其中λ为常数,则动点M 的轨迹不可能是( )A .圆B .椭圆C .抛物线D .双曲线2. 双曲线2214x y -=的顶点到其渐近线的距离等于( )A .25B .45C .255D .4553.椭圆22:143x y C +=的左、右顶点分别为12,A A ,点P 在C 上且直线2PA 的斜率的取值范围是[]2,1--,那么直线1PA 斜率的取值范围是 ( )A .1324⎡⎤⎢⎥⎣⎦,B .3384⎡⎤⎢⎥⎣⎦,C .112⎡⎤⎢⎥⎣⎦,D .314⎡⎤⎢⎥⎣⎦,4.已知04πθ<<,则双曲线22122:1cos sin x y C θθ-=与222222:1sin sin tan y x C θθθ-=的 ( )A .实轴长相等B .虚轴长相等C .焦距相等D .离心率相等5.抛物线24y x =的焦点到双曲线2213yx -=的渐近线的距离是( )A .12B 3C .1D 36.如图,21,F F 是椭圆14:221=+y x C 与双曲线2C 的公共焦点,B A , 分别是1C ,2C 在第二、四象限的公共点.若四边形21BF AF 为矩形,则2C 的离心率是( )A .26 B .3C .23 D .27.已知抛物线2:8C y x =与点()2,2M -,过C 的焦点且斜率为k 的直线与C 交于,A B 两点,若0MA MB =u u u r u u u rg ,则k =( )A .12B .2 C .2D .28错误!未指定书签。
.设抛物线2:2(0)C y px p =>的焦点为F ,点M 在C 上,5MF =,若以MF 为直径的圆过点)2,0(,则C 的方程为 ( )A .24y x =或28y x =B .22y x =或28y x =C .24y x =或216y x =D .22y x =或216y x =二、填空题9错误!未指定书签。
安徽省六安市2016年高二数学(文)暑假作业 第20天

第20天 数列的求和课标导航:了解常见数列求和方法,掌握和公式的运用 一、选择题1. 已知数列{a n }的前n 项和S n =312n a n +=+,则()A .201B .241C .281D .3212. 已知等差数列}{n a 的前n 项和为n S ,若45818,a a S =-=则( )A .18 B. 36C. 54D. 723. 两等差数列{a n }、{b n }的前n 项和的比'5327n n S n S n +=+,则55a b 的值是( ) A .2817B .4825C .5327D .23154. 已知等差数列{}n a 的前n 项和为n S ,且3711315a a a ++=,则13S =( ) A .104B .78C .52D .395.等差数列{}n a 的通项公式为21n a n =+,其前n 项和为n S ,则数列{}n Sn的前10项和为 ( )A .70B .75C .100D .1206. 满足*12121,log log 1()n n a a a n +==+∈N ,它的前n 项和为n S ,则满足1025n S >的最小n 值是( )A .9B .10C .11D .127. 已知函数()bx x x f 22+=过(1, 2)点,若数列()⎭⎬⎫⎩⎨⎧n f 1的前n 项和为n S ,则2012S 的值为( )A.20112012B.20112010C.20122013D.201320128. 已知数列{a n }满足3a n +1+a n =0,a 2=-43,则{a n }的前10项和等于( ) A .-6(1-3-10) B.19(1-310)C .3(1-3-10) D .3(1+3-10)二、填空题9. 已知等差数列{}n a 的前n 项和为n S ,且13140,0,S S ><若10t t a a +<则t = ; 10. 设等差数列{}n a (*n N ∈)的前n 项和为n S ,该数列是单调递增数列,若4510,15S S ≥≤,则4a 的取值范围是 ;11. 数列,41,41,41,41,31,31,31,21,21,1……,的前100项的和等于 ; 12. 设{a n }是等比数列,公比q =S n 为{a n }的前n 项和。
安徽省六安市2016年高二数学文暑假作业第18天Word版含答案-精品

安徽省六安市2016年高二数学文暑假作业第18天Word 版含答案-精品课标导航:1.了解数列的概念和几种简单的表示法; 2.了解数列是自变量为整数的一类函数. 一、选择题1. 下面是关于公差d>0的等差数列{a n }的四个命题:p 1:数列{a n }是递增数列; p 2:数列{na n }是递增数列;p 3:数列a nn 是递增数列;p 4:数列{a n +3nd}是递增数列,其中的真命题为 ( ) A .p 1,p 2B .p 3,p 4C .p 2,p 3D .p 1,p 42. 已知数列 ,12,,7,5,3,1-n ,则53是它的( )A. 第22项B. 第23项C. 第24项D. 第28项 3. 已知031=--+n n a a ,则数列{}n a 是( )A. 递增数列B. 递减数列C. 常数列D. 摆动数列4. 数列{}n a 的通项公式为n n a n 2832-=,则数列{}n a 各项中最小项是( )A. 第4项B. 第5项 C . 第6项 D. 第7项5. 数列1,0,1,0,1,0,……的一个通项公式是( )A. ()2111+--=n n a B. ()2111+-+=n n a C. ()211--=n na D. ()211nn a ---=6. 已知数列{}n a 满足()nn n n a a a 111-+=--且11=a ,则=35a a( ) A.1516B.34 C. 158 D. 38 7. 已知()*1133,21N n a a a a n n n ∈+==+,则=n a( ) A.52+n B.42+n C. 53+n D. 43+n 8. 数列{a n }的通项a n =)(9998N n n n ∈--,则数列{a n }的前30项中最大项是( ) A .30a B .10a C . 9a D . 1a 二、填空题9. 数列{}n a 满足11=a ,13321++=-+n n a a n n ,根据这个数列的前4项并归纳通项公式得n a = ;10. 设{a n }是首项为1的正项数列,且(n +1)a n +12-na n 2+a n +1a n =0(n ∈N *),则它的通项公式a n =______________;11. 数列{}n a 中,已知()*1221,2,1N n a a a a a n n n ∈-===++,则=2002a ;12. 数列{}n a 满足⎪⎪⎩⎪⎪⎨⎧<≤-<≤=+)121(12)210(21n n n n n a a a a a ,若761=a ,则=8a .三、解答题13.已知数列{}n a 满足q pa a a n n +==+11,1,且15,342==a a ,求q p ,的值.14. 设数列{}n a 的前n 项和为n S ,已知()21nn n ba b S -=-(1)证明:当2b =时,{}12n n a n --⋅是等比数列; (2)求{}n a 的通项公式.15. 已知公差不为0的等差数列{}n a 的前3项和3S =9,且125,,a a a 成等比数列. (1)求数列{}n a 的通项公式和前n 项和n S ; (2)设n T 为数列11{}n n a a +的前n 项和,若1n n T a λ+≤对一切n N *∈恒成立,求实数λ的最小值.16. 设同时满足条件:①122++≥+n n n b b b ;②n b M ≤(N n +∈,M 是与n 无关的常数)的无穷数列{}n b 叫“仁风”数列.已知数列{}n a 的前n 项和n S 满足: (1)1n n aS a a =--(a 为常数,且0a ≠,1a ≠). (1)求{}n a 的通项公式;(2)设21n n n S b a =+,若数列{}n b 为等比数列,求a 的值,并证明此时⎭⎬⎫⎩⎨⎧n b 1为“仁风”数列.【链接高考】[2013·安徽卷] 设数列{a n }满足a 1=2,a 2+a 4=8,且对任意n ∈N *,函数f(x)=(a n -a n+1+a n +2)x +a n +1cos x -a n +2sin x 满足'()2f π=0. (1)求数列{a n }的通项公式; (2)若,求数列{b n }的前n 项和S n .第18天1~8 DBAB BBCB ;9. 3n ; 10.n 1;11. 1-; 12. 75;13.⎩⎨⎧=-=63q p 或⎩⎨⎧==12q p ’14.(1)证明:由题意知12a =,且()21nn n ba b S -=-,()11121n n n ba b S +++-=-两式相减得()()1121nn n n b a a b a ++--=-,即12n n n a ba +=+ ① 当2b =时,由①知122n n n a a +=+,于是()()1122212n n n n n a n a n +-+⋅=+-+⋅()122n n a n -=-⋅又111210n a --⋅=≠,所以{}12n n a n --⋅是首项为1,公比为2的等比数列。
【暑假作业】安徽省六安市2016年高二数学文暑假作业第35天Word版含答案

【关键字】暑假作业第35天综合训练(1)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知复数,则它的共轭复数等于()A.B.C.D.2.最小二乘法的原理是()A.使得yi-(a+bxi)]最小B.使得yi+(a+bxi)2]最小C.使得y-(a+bxi)2]最小D.使得yi-(a+bxi)]2最小3.如果对于任意实数,表示不超过的最大整数,例如,那么“”是“”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4.如图所示的程序框图输出的所有点都在函数()A.y=x+1的图像上B.y=2x的图像上C.y=2x的图像上D.y=2x-1的图像上5.天气预报说,在今后的三天中,每一天下雨的概率均为40%.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683431 257 393 027 556 488 730 113 537 989据此估计,这三天中恰有两天下雨的概率近似为()A.0.35 B..0.20 D.0.156.已知等差数列的前项和为,且,则()A. B. C. D.7.某三棱锥的三视图如图所示,该三棱锥的表面积是()B.C.D.8.定义行列式运算:将函数的图象向左平移个单位,所得图象对应的函数为偶函数,则的最小值()A..B.C.D.9.在中,已知分别为内角, ,所对的边,为的面积.若向量满足,则( ) A .B .C .D .A .0.2B .C .0.6D .0.8 二、填空题:本大题共5小题,每小题5分,共25分。
11.将一张画了直角坐标系(两坐标轴单位长度相同)的纸折叠一次,使点与点重合,则与点重合的点坐标是12. 已知f(x)=log3x+3,x ∈[1,9],则y=[f(x)]2+f(x2)的最大值是_ 13. 在斜三角形中,角所对的边分别为,且.则角 为14. 已知是坐标原点,点,若点为平面区域上的一个动点,则的最小值是 . 15.在棱长为1的正方体ABCD ﹣A1B1D1中,过对角线BD1的一个平面交AA1于E ,交CC1于F ,得四边形BFD1E ,给出下列结论: ①四边形BFD1E 有可能为等腰梯形 ②四边形BFD1E 有可能为菱形③四边形BFD1E 在底面ABCD 内的投影的面积是定值 ④四边形BFD1E 有可能笔直于平面BB1D1D ⑤四边形BFD1E 面积的最小值为其中正确的是 .(请写出所有正确结论的序号)三、解答题:本大题共6个小题,满分75分,解答应写出必要的文字说明、证明过程或演算步骤.16. (本小题满分12分)写出两角差的余弦公式并用向量的数量积证明它。
安徽省六安市2016年高二数学(文)暑假作业 第28天

第28天 椭圆课标导航:1.掌握椭圆定义、标准方程及简单性质; 2.能解决直线与椭圆的位置关系等问题.一、选择题1.若方程1162522=++-my m x 表示焦点在y 轴上的椭圆,则实数m 的取值范围是( ) A .)25,16(-B .)25,29(C .)29,16(-D .),29(+∞2. 设椭圆的两个焦点分别为1F ,2F ,过2F 作椭圆长轴的垂线与椭圆相交,其中的一个交点为P ,若△12F PF 为等腰直角三角形,则椭圆的离心率是( )A 1B .12+ C . D .23. 已知圆(x +2)2+y 2=36的圆心为M ,设A 为圆上任一点,N (2,0),线段AN 的垂直平分线交MA 于点P ,则动点P 的轨迹是 ( ) A .圆 B .椭圆 C .双曲线 D .抛物线4. 椭圆22142x y +=上有一点P ,12,F F 是椭圆的左、右焦点,12F PF ∆为直角三角形,则这样的点P 有( ) A .3个 B .4个C .6个D .8个5. 若点O 和点F 分别为椭圆22143x y +=的中心和左焦点,点P 为椭圆上的任意一点,则OP FP ⋅的最大值为( ) A.2 B.3C.6D.86. 设斜率为1的直线l 与椭圆124:22=+y x C 相交于不同的两点A 、B ,则使||AB 为整数的直线l 共有( ) A .4条 B .5条C .6条D .7条7. 已知椭圆:C 22221x y a b+= (0)a b >>的离心率为2,过右焦点F 且斜率为k (0k >)的直线于C 相交于,A B 两点,若 3AF FB =,则k =( )A .1B CD .28. 已知点P 是椭圆22221(0,0)x y a b xy a b+=>>≠上的动点,1(,0)F c -、2(,0)F c 为椭圆的左、右焦点, O 为坐标原点,若M 是12F PF ∠的角平分线上的一点,且1F M MP ⊥,则||OM 的取值范围是( ) A .(0,)c B .(0,)a C .(,)b a D .(,)c a二、填空题9. 椭圆141622=+y x 上的点到直线022=-+y x 的最大距离是10. 过椭圆22221x y a b+=的左焦点1F 的弦AB 的长为3,42=AF 且02=⋅AF AB ,则该椭圆的离心率为 ;11. 已知P 为椭圆192522=+y x 上的点,且P 点与两焦点的连线互相垂直,则P 点的坐标为 ;12. 在平面直角坐标系中,椭圆x 2a 2+y 2b 2=1(a >b >0)的焦距为2,以O 为圆心,a 为半径的圆,过点2,0a c ⎛⎫⎪⎝⎭作圆的两切线互相垂直,则离心率e =________;三、解答题13. 已知椭圆E 的中心在坐标原点O ,两个焦点分别为)0,1(-A 、)0,1(B ,一个顶点为)0,2(H .(1)求椭圆E 的标准方程;(2)对于x 轴上的点)0,(t P ,椭圆E 上存在点M ,使得MH MP ⊥,求t 的取值范围.14. 已知椭圆22221(0)x y a b a b+=>>的离心率为3,短轴的一个端点到右焦点的距离为直线:l y kx m =+交椭圆于不同的两点A ,B .(1)求椭圆的方程; (2)若坐标原点O 到直线l 的距离为2,求A O B ∆面积的最大值.15. 已知点(4, 0)M ,(1, 0)N ,若动点P 满足6MN MP PN ⋅=. (1)求动点P 的轨迹C 的方程;(2)设过点N 的直线l 交轨迹C 于A ,B 两点,若181275NA NB -≤⋅≤-,求直线l 的斜率的取值范围.16. 在平面直角坐标系xOy 中,经过点(0且斜率为k 的直线l 与椭圆2212x y +=有两个不同的交点P 和Q . (1)求k 的取值范围;(2)设椭圆与x 轴正半轴、y 轴正半轴的交点分别为A B ,,是否存在常数k ,使得向量OP OQ +与AB 共线?如果存在,求k 值;如果不存在,请说明理由.【链接高考】已知椭圆C :2233x y +=,过点()D 1,0且不过点()2,1E 的直线与椭圆C 交于A ,B两点,直线AE 与直线3x =交于点M . (Ⅰ)求椭圆C 的离心率;(Ⅱ)若AB 垂直于x 轴,求直线BM 的斜率;(Ⅲ)试判断直线BM 与直线D E 的位置关系,并说明理由. .第28天1~8 BABC CCBA 9. 10 10.35; 11. (475,49)或(475-,49);13.(1)22143x y +=;(2)12-<<-t . 14.(1)22 1.3x y += ; (2) 2222222212223612(1)(1)()(1)[](31)31k m m AB k x x k k k -=+-=+-++ 242221212123334(0)196123696k k k k k k=+=+≤+=≠++⨯+++ 2219k k =当且仅当,3k =±即. 12222AB AOB S ∴∆=⨯⨯=当最大时的面积取最大值,15.(1)13422=+y x ;(2)设过N 的直线l 的方程为(1)y k x =-,得NA NB ⋅=229(1)34k k -++,故.得213k ≤≤,1k -≤或1k ≤≤16.(1)222⎛⎛⎫--+ ⎪ ⎪⎝⎭⎝⎭,,∞∞; (2)设1122()()P x y Q x y ,,,,则1212(,)OP OQ x x y y +=++, 所以OP OQ +与AB 共线等价于1212)x x y y +=+,解得2k =. 由(1)知2k <-或2k >,故没有符合题意的常数k .2 3;(2) x29+y25=1.链接高考:(1(2)1;(3)直线BM与直线DE平行(1) e=。
安徽省六安市2016年高二数学文暑假作业第24天Word版含答案

第24天 不等式的应用与线性打算课标导航:1.会从实际情境起身,抽象出二元一次不等关系;2.在线性约束条件下求目标函数最值.一、选择题1. 在下列函数中,最小值是2的是 ( )A .y =x 2+2xB .y =21x x ++(x >0) C .y =sin x +cos x ,x ∈(0,π2) D .y =7x +7-x 2. 已知0,0a b >>,则112ab a b ++的最小值是 ( ) A .2 B .22 C .4 D .53. 已知0,0>>b a ,若不等式ba mb a +≥+212恒成立,则m 的最大值等于 ( ) .9 C4. 设双曲线122=-y x 的两条渐近线与直线22=x 围成的三角形区域(包括边界)为D , P (y x ,)为D 内的一个动点,则目标函数y x z 2-=的最小值为( ) A .2- B .22- C .0 D .223 5. 若正数x ,y 知足x+3y=5xy ,则3x+4y 的最小值是( ) A. 245 B . 2856. 若x ,y 知足约束条件1122x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩,目标函数2z ax y =+仅在点(1,0)处取得最小值,则a 的取值范围是( )A .(1-,2 )B . (4-,2 )C .(4,0]-D .(2,4)-7. 若实数x ,y 知足不等式组330,230,10,x y x y x my +-≥⎧⎪--≤⎨⎪-+≥⎩且x y +的最大值为9,则实数m = ( )A .2-B .1-C .1D .28. 点(,)a b 在两直线1-=x y 和3-=x y 之间的带状区域内(含边界),则(,)f a b =22244a ab b a b -++-的最小值为 ( )A .2-B .5C .22D .223 二、填空题9. 若实数对(x ,y )知足约束条件0230x y x x y >⎧⎪≥⎨⎪+-≤⎩,则x y 1+的最小值为 ; 10. 已知变量,x y ,知足240280x y x x y -+≤⎧⎪≥⎨⎪+-≤⎩,则22x y +的取值范围为 ;11. 已知实数,,a b c 知足9a b c ++=,24ab bc ca ++=,则b 的取值范围是 ;12. 曲线1:=+y x C 上的点到原点的距离的最小值为 .三、解答题13. 已知向量(,3),(2,)a x z b y z =+=-,且a b ⊥,若,x y 知足不等式1x y +≤,求实数z 的取值范围.14. 某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,双侧墙砌砖,每米长造价45元,顶部每平方米造价20元,求:(1)仓库面积S 的最大许诺值是多少?(2)为使S 达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?15. 某公司租赁甲、乙两种设备生产A,B 两类产品,甲种设备天天能生产A 类产品5件和B 类产品10件,乙种设备天天能生产A 类产品6件和B 类产品20件.已知设备甲天天的租赁费为200元,设备乙天天的租赁费为300元,现该公司至少要生产A 类产品50件,B 类产品140件,所需租赁费最少为多少元?16. 已知,,0,1a b c a b c >++=≥。
安徽省六安市2016年高二数学(文)暑假作业 第25天 Word版含答案
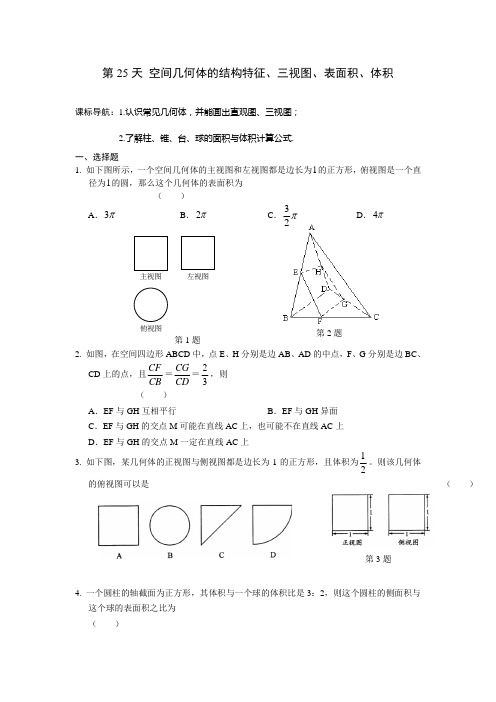
第2题第1题主视图俯视图左视图第25天 空间几何体的结构特征、三视图、表面积、体积课标导航:1.认识常见几何体,并能画出直观图、三视图; 2.了解柱、锥、台、球的面积与体积计算公式.一、选择题1. 如下图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为 ( ) A .π3 B .π2 C .π23D .π42. 如图,在空间四边形ABCD 中,点E 、H 分别是边AB 、AD 的中点,F 、G 分别是边BC 、CD 上的点,且CF CB =CG CD =23,则( )A .EF 与GH 互相平行B .EF 与GH 异面C .EF 与GH 的交点M 可能在直线AC 上,也可能不在直线AC 上D .EF 与GH 的交点M 一定在直线AC 上3. 如下图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为12。
则该几何体的俯视图可以是( )4. 一个圆柱的轴截面为正方形,其体积与一个球的体积比是3:2,则这个圆柱的侧面积与这个球的表面积之比为( )A. 1:1 B .C . D. 3:25. 某四面体的三视图如图所示,该四面体四个面的面积中最大的是( )A .8B .C .10D .826. 一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积等于( )A B . C .D .7. 一个几何体的三视图如图所示,则此几何体的体积是( )A .112 B.80 C.72 D.648. 已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =;则此棱锥的体积为( )A .6B .6C .3 D .2二、填空题9. 一个空间几何体的三视图及部分数据如下图所示,则这个几何体的体积是 ;第7题10. 某几何体的三视图,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是 ;11. 一个几何体的三视图如图所示,则该几何体的体积(单位:3cm )为 3cm ;12. 一空间几何体的三视图如图所示,则该几何体的体积为 .三、解答题13. 已知四棱锥P ABCD -的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.E 是侧棱PC 上的动点. (1)求证:BD AE ⊥;(2)若五点,,,,A B C D P 在同一球面上,求该球的体积.第11题ABCD P E14. 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.(1) 求该几何体的体积V ; (2) 求该几何体的侧面积S15. 一个多面体的直观图和三视图如下:(其中N M ,分别是BC AF ,中点)(1) 求证://MN 平面CDEF ; (2) 求多面体CDEF A 的体积.16. 如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点(1)证明:平面BDC 1⊥平面BDC ;(2)平面BDC 1分此棱柱为两部分,求这两部分体积的比.【链接高考】如图,ABCDEFG 为多面体,平面ABED 与平面AGFD 垂直,点O 在线段AD 上,1,2,OA OD ==OAB V ,△OAC ,△ODE ,△ODF 都是正三角形.(1)证明直线BC ∥EF ; (2)求棱锥F-OBED 的体积。
安徽省六安市2016年高二数学(文)暑假作业 第7天 Word版含答案

第7天 函数与方程课标导航:1.结合二次函数的图象,了解函数零点与方程根的关系;2.了解指数函数、对数函数、幂函数的增长特点,了解函数模型的广泛运用. 一、选择题 1. 求函数132)(3+-=x x x f 零点的个数为( )A .1B .2C .3D .42. 若函数)(x f y =在区间[],a b 上的图象为连续不断的一条曲线,则下列说法正确的是( )A .若0)()(>b f a f ,不存在实数),(b a c ∈使得0)(=c f ;B .若0)()(<b f a f ,存在且只存在一个实数),(b a c ∈使得0)(=c f ;C .若0)()(>b f a f ,有可能存在实数),(b a c ∈使得0)(=c f ;D .若0)()(<b f a f ,有可能不存在实数),(b a c ∈使得0)(=c f ; 3. 函数f(x)=3ax-2a+1在[-1,1]上存在一个零点,则a 的取值范围是 ( )A.a ≥51B.a ≤1C.-1≤a ≤51D. a ≥51或a ≤-14. 若方程310x x -+=在区间(,)(,,1)a b a b Z b a ∈-=且上有一根,则a b +的值为( )A .1-B .2-C .3-D .4- 5.已知0<a <1,则方程a |x |=|log a x |的实根个数是( )A .1个B .2个C .3个D .1个或2个或3个 6. 已知函数()22f x x ax a =-+在区间(),1-∞上有最小值,则函数()f x x在区间()1,+∞上 ( )A .有两个零点B . 有一个零点C .无零点D .无法确定7. 若方程0xa x a --=有两个实数解,则a 的取值范围是( )A .(1,)+∞B .(0,1)C .(0,2)D .(0,)+∞8. 设()f x 是定义在R 上的偶函数,对任意x R ∈,都有(2)(2),f x f x -=+且当[2,0]x ∈-时,1()()1,(2,6]2xf x =--若在区间内关于x 的方程()log (2)0(1)a f x x a -+=>恰有3个不同的实数根,则a 的取值范围是( )A .(1,2)B .(2,)+∞C .D .二、填空题9. 关于x 的实系数方程x 2-ax +2b =0的一根在区间[0,1]上,另一根在区间[1,2]上,则2a +3b的最大值为10. 已知函数b x a x f x +-=)(的零点))(1,(0Z k k k x ∈+∈,其中常数,a b 满足493,23==b a ,则k = ;11. 已知函数221,0,()2,x x f x x x x ⎧->⎪=⎨--⎪⎩≤0.若函数()()g x f x m =-有3个零点,则实数m 的取值范围是 ;12. 设函数22,0,()log ,0x x f x x x ⎧≤=⎨>⎩,若关于x 的方程2()()0f x af x -=恰有三个不同的实数解,则实数a 的取值范围为______ __.三、解答题 13. 设二次函数2()f x ax bx c =++在区间[]2,2-上的最大值、最小值分别是M 、m ,集合{}|()A x f x x ==.(1)若{1,2}A =,且(0)2f =,求M 和m 的值;(2)若{1}A =,且1a ≥,记()g a M m =+,求()g a 的最小值.14. 设1x 与2x 分别是实系数方程20ax bx c ++=和20ax bx c -++=的一个根,且1212,0,0x x x x ≠≠≠ ,求证:方程202a x bx c ++=有仅有一根介于1x 和2x 之间.15.已知0a >且1a ≠,求使方程222log ()log ()a ax ak x a -=-有解时的k 的取值范围.16. 设函数()2()4ln 1f x x x =--.(1)求函数)(x f 的单调递增区间;(2)若关于x 的方程()240f x x x a +--=在区间[]1,e 内恰有两个相异的实根,求实数a 的取值范围.【链接高考】函数f(x)=xcos2x 在区间[0,2π]上的零点个数为 ( ) A .2 B .3C .4D .5第7天1~8 CCDC BCAD ; 9. 9; 10. 1; 11. (0,1); 12. {}01a a <<;13.(1)1,10m M ==;(2)431 14.令2(),2a f x x bx c =++由题意可知2211220,0ax bx c ax bx c ++=-++= 221122,,bx c ax bx c ax +=-+=2222111111(),222a a af x x bx c x ax x =++=-=-22222222223(),222a a a f x x bx c x ax x =++=+=因为120,0,0a x x ≠≠≠∴12()()0f x f x <,即方程202a x bx c ++=有仅有一根介于1x 和2x 之间。
安徽省六安市2016年高二数学(文)暑假作业 第20天 Word版含答案

第20天 数列的求和课标导航:了解常见数列求和方法,掌握和公式的运用 一、选择题1. 已知数列{a n }的前n 项和S n =312n a n +=+,则()A .201B .241C .281D .3212. 已知等差数列}{n a 的前n 项和为n S ,若45818,a a S =-=则( )A .18 B. 36C. 54D. 723. 两等差数列{a n }、{b n }的前n 项和的比'5327n n S n S n +=+,则55a b 的值是( ) A .2817B .4825C .5327D .23154. 已知等差数列{}n a 的前n 项和为n S ,且3711315a a a ++=,则13S =( ) A .104B .78C .52D .395.等差数列{}n a 的通项公式为21n a n =+,其前n 项和为n S ,则数列{}n Sn的前10项和为 ( )A .70B .75C .100D .1206. 满足*12121,log log 1()n n a a a n +==+∈N ,它的前n 项和为n S ,则满足1025n S >的最小n 值是( )A .9B .10C .11D .127. 已知函数()bx x x f 22+=过(1, 2)点,若数列()⎭⎬⎫⎩⎨⎧n f 1的前n 项和为n S ,则2012S 的值为( )A.20112012B.20112010C.20122013D.201320128. 已知数列{a n }满足3a n +1+a n =0,a 2=-43,则{a n }的前10项和等于( ) A .-6(1-3-10) B.19(1-310)C .3(1-3-10) D .3(1+3-10)二、填空题9. 已知等差数列{}n a 的前n 项和为n S ,且13140,0,S S ><若10t t a a +<则t = ; 10. 设等差数列{}n a (*n N ∈)的前n 项和为n S ,该数列是单调递增数列,若4510,15S S ≥≤,则4a 的取值范围是 ;11. 数列,41,41,41,41,31,31,31,21,21,1……,的前100项的和等于 ; 12. 设{a n }是等比数列,公比q =S n 为{a n }的前n 项和。
安徽省六安市2016年高二数学(文)暑假作业 第21天 Word版含答案

第21天 数列的综合应用课标导航:1.会用数列解决一些实际问题; 2.熟悉数列的综合运用 一、选择题1. 数列{a n }中,a 1=1,a n =1a n -1+1,则a 4等于( )A.53B.43 C .1 D.23 2. 已知数列{}n a 满足*111,2()n n n a a a n N +=⋅=∈,则10a =( )A .64B .32C .16D .83. 若数列{}()为常数满足d N n d a a a nn n ,111*+∈=-,则称数列{}n a 为“调和数列”.已知正项数列⎭⎬⎫⎩⎨⎧n b 1为“调和数列”,且90921=+⋅⋅⋅⋅⋅⋅++b b b ,则64b b ⋅的最大值是( ) A.10B.100C.200D.4004. 已知数列{}n a 满足:22111, 0, 1(*)n n n a a a a n +=>-=∈N ,那么使5n a <成立的n 的最大值为( )A .4B .5C .24D .255.已知数列{}n a 满足11a =,且111()(233n n n a a n -=+≥,且)n ∈*N ,则数列{}n a 的通项公式为( )A .n a =32nn +B .n a =23n n +C .n a =2n +D .n a =(2)3nn + 6. 已知数列{}n a 的各项均为正数,其前n 项和为n S ,若2{log }n a 是公差为1-的等差数列,且613,8S a =则等于( ) A .421B .631 C .821 D .12317. 已知等差数列{}n a 的前项和为n S ,若1200OB a OA a OC =+,且,,A B C 三点共线(该直线不过原点O ),则200S =( )A .100 B. 101 C. 200 D. 201 8. 已知数列{}n a 满足1133,2,+-==n na a a n则n a n 的最小值为( )A .10B .10.5C .9D .8二、填空题 9. 函数2(0)y x x =>的图像在点2(,)k k a a 处的切线与x 轴交点的横坐标为1k a +, k 为正整数,116a =,则135a a a ++=___________ ;10. 若数列2(4)()3n n n ⎧⎫+⎨⎬⎩⎭中的最大项是第k 项,则k =__________; 11. 在数列}{n a 中,311=a ,n S 为数列}{n a 的前项和且n n a n n S )12(-=,则n S = ;12. 对于正项数列{}n a ,定义n n na a a a nH +⋯+++=32132为{}n a 的“光阴”值,现知某数列的 “光阴”值为22+=n H n ,则数列{}n a 的通项公式为 .三、解答题13. 已知数列{}n a 中,11a =,前n 项和为*131,()2n n n S S S n N +=+∈且(1)求数列{}n a 的通项公式; (2)设数列1{}n a 的前n 项和为n T ,求满足不等式122n n T S <+的n 值。
安徽省六安市舒城中学2016年高二数学(文)暑假作业 第20天 含答案

第20天 数列的求和课标导航:了解常见数列求和方法,掌握和公式的运用 一、选择题1. 已知数列{a n }的前n 项和S n =312n an +=+,则( )A .201 B .241 C .281 D .321 2。
已知等差数列}{na 的前n 项和为nS ,若45818,a a S =-=则( )A .18B 。
36 C. 54 D. 723. 两等差数列{a n }、{b n }的前n 项和的比'5327n n Sn Sn +=+,则55a b的值是 ( )A .2817B .4825C .5327D .23154。
已知等差数列{}na 的前n 项和为nS ,且3711315aa a ++=,则13S =( )A .104B .78C .52D .395.等差数列{}na 的通项公式为21n a n ,其前n 项和为nS ,则数列{}nS n的前10项和为 ( )A .70B .75C .100D .1206. 满足*12121,log log 1()n na a a n +==+∈N ,它的前n 项和为nS ,则满足1025nS >的最小n 值是 ( )A .9B .10C .11D .127. 已知函数()bx xx f 22+=过(1, 2)点,若数列()⎭⎬⎫⎩⎨⎧n f 1的前n 项和为n S ,则2012S 的值为( )A.20112012 B.20112010 C 。
20122013 D 。
201320128。
已知数列{a n }满足3a n +1+a n =0,a 2=-错误!,则{a n }的前10项和等于 ( ) A .-6(1-3-10) B 。
错误!(1-310) C .3(1-3-10)D .3(1+3-10) 二、填空题9. 已知等差数列{}na 的前n 项和为nS ,且13140,0,S S ><若10t t a a +<则t = ;10。
安徽省六安市2016年高二数学文暑假作业第22天Word版含答案

第22天 不等式的概念与性质课标导航:1.不等式的性质及应用;2.利用不等式的性质证明不等关系;3.了解基本不等式的证明过程,会用基本不等式解决简单的最值问题一、选择题 1. 若0a b >>,则( )A .22()a c b c c R >∈ B .1b a>C .lg()0a b ->D .11()()22ab<2. 若b a c b a >∈,R 、、,则下列不等式成立的是( )A .ba 11< B .22b a >C .1122+>+c bc aD .||||c b c a >3. 已知0<a<b<1,则( )A .3b <3aB .log 3a >log 3bC .(lga)2<(lgb)2D .(1e )a <(1e)b4. 如果01a <<,那么下列不等式中正确的是( )A .1132(1)(1)a a ->-B .(1)log (1)0a a -+>C .32(1)(1)a a ->+D .1(1)1aa +->5 若关于x 的不等式m x x ≥-42对任意]1,0[∈x 恒成立,则实数m 的取值范围是( )A .03≥-≤m m 或B .03≤≤-mC . 3-≥mD .3-≤m 6. 定义在R 上的偶函数)(x f 满足)()2(x f x f =-,且在[-3,-2]上是减函数,βα,是钝角三角形的两个锐角,则下列不等式关系中正确的是 ( )A .(sin )(cos )f f αβ>B .(cos )(cos )f f αβ<C .(cos )(cos )f f αβ>D .(sin )(cos )f f αβ< 7. 已知ln x π=,5log 2y =,12z e -=,则( )A .x y z <<B .z x y <<C .z y x <<D .y z x <<8. 设 a >b >1,0c <,给出下列三个结论: ①c a >cb;② c a <c b ; ③ log ()log ()b a a c b c ->-, 其中所有的正确结论的序号是( ) A .① B.①② C.②③D.①②③二、填空题9. 设10<<a ,函数)22(log )(2--=xx a a a x f ,则使0)(<x f 的x 的取值范围是 ;10. 设关于x 的方程22230kx x k --=的两个实根一个大于1,另一个小于1,则实数k的取值范围是 ;11. 若正数,a b 满足3ab a b =++,则ab 的取值范围是 ;12. 若1x 和2x 是方程220x mx --=的两个实根,不等式21253a a x x --≥- 对任意实数[1,1]m ∈-恒成立,则a 的取值范围是 .三、解答题13. 已知,x y 都是正实数,求证:3322x y x y xy +≥+14. 若二次函数y=f(x)的图象经过原点,且1≤f(-1)≤2,3≤f(1)≤4,求f(-2)的范围.15. ,,a b c 为互不相等的正数,222a c bc +=,判断下列关系中可能成立的有哪几个?①.a b c >>;②.b a c >>;③.a c b >> ; ④.b c a >>16. 已知函数()(1)ln 1f x x x x =+-+.(1)若2'()1xf x x ax ≤++,求a 的取值范围;(2)证明:(1)()0x f x -≥ .【链接高考】已知2log 3log 3a =+2log 9log 3b =-,3log 2c =,则a,b,c 的大小关系是( )(A ) a b c =<(B )a b c => (C )a b c <<(D )a b c >>第22天1~8 DCAA DDDD; 9. 3(,log )a -∞; 10. 04k k ><-或; 11. [9,)+∞; 12.(,1][6,)-∞-⋃+∞13.332222()()()()x y x y xy x x y y y x +-+=-+-222()()()()x y x y x y x y =--=-+,∵,x y R +∈,∴2()0,0x y x y -≥+>,∴2()()0x y x y -+≥,∴3322x y x y xy +≥+14. f(-2)的取值范围是[6,10].15.若a b >,则22222a c b c bc +>+≥,不符合条件,排除①④;又由()222a c c b c -=-,故a c -与b c -同号,排除③;且当b a c >>时,222a c bc +=有可能成立,例如取()(),,3,5,1a b c =,故②可能成立。
【暑假作业】安徽省六安市2016年高二数学文暑假作业第20天Word版含答案

【关键字】暑假作业第20天数列的求和课标导航:了解常见数列求和方法,掌握和公式的运用一、选择题1. 已知数列{an}的前n项和Sn=()A.B.C.D.2. 已知等差数列的前n项和为,若()A.18 B. C. 54 D. 723. 两等差数列{an}、{bn}的前n项和的比,则的值是()A.B.C.D.4. 已知等差数列的前项和为,且,则()A.B.C.D.5.等差数列的通项公式为,其前项和为,则数列的前10项和为()A.70 B.C.100 D.1206. 满足,它的前项和为,则满足的最小值是()A.9 B.C.11 D.127. 已知函数过(1,2)点,若数列的前n项和为,则的值为()A. B. C. D.8. 已知数列{an}满足3an+1+an=0,a2=-,则{an}的前10项和等于( )A.-6(1-3-10) B.(1-310) C.3(1-3-10) D.3(1+3-10)二、填空题9. 已知等差数列的前项和为,且若则;10. 设等差数列()的前n项和为,该数列是单调递加数列,若,则的取值范围是;11. 数列……,的前100项的和等于;12. 设{an}是等比数列,公比,Sn为{an}的前n项和。
记设为数列{}的最大项,则= .三、解答题13.已知数列的前项和是,且.(1)求数列的通项公式;(2)记,求数列的前项和.14. 在等差数列中,(1)求数列的通项公式;(2)设数列的前项和为,求15. 已知数列满足(1)求(2)设求证:;(3)求数列的通项公式.16. 已知各项均不相等的等差数列的前四项和为14,且恰为等比数列的前三项。
(1)分别求数列的前n项和(2)记为数列的前n项和为,设,求证:【链接高考】[2013·江西卷] 正项数列{an}满足:a-(2n-1)an-2n=0.(1)求数列{an}的通项公式an; (2)令bn=,求数列{bn}的前n项和Tn.第20天1~8 ADBD BCDC ;9. 7; 10. ; 11. ; 12. 4;13.(1);(2)由(Ⅰ)知,14.(1)an=n+1;(2)==(-),∴++…+=[(1-)+(-)+…+(-)]=.15.(1),,证明略;(2)由(1):,有;(3)16.(1),(2),链接高考:(1)an=2n. (2)Tn=.此文档是由网络收集并进行重新排版整理.word可编辑版本!。
【暑假作业】安徽省六安市2016年高二数学文暑假作业第36天Word版含答案

【关键字】暑假作业第36天综合训练(2)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知复数满足的复数的对应点的轨迹是()A. 1个圆B.线段C. 2个点D. 2个圆(2)定义若,,则等于()(3)设m、n是两条不同的直线,是两个不同的平面,以下命题正确的是()A.若 B.若C.若D.若(4)已知x,y满足不等式组,则的最大值为()A. B. C. D.(5)设a,b,c∈R+,则“abc=1”是“≤a+b+c”的()A.充分条件但不是必要条件B.必要条件但不是充分条件C.充分必要条件D.既不充分也不必要条件(6)函数的图象大致是()(7)设,若直线与圆相切,则的取值范围是()A. B.C. D.(8)在集合中任取3个不同的数,其中这三个数的和能被3整除的概率为()A. B. C. D.(9)设抛物线的焦点为F,准线为,P为抛物线上一点,,A为垂足,如果直线AF的斜率为,那么= ()A. B. C. D.(10)设△AnBnCn的三边长分别为an,bn,cn,△AnBnCn的面积为Sn,n=1,2,3,…若b1>c1,b1+c1=1,an+1=an,bn+1=,cn+1=,则()A.{Sn}为递减数列B.{Sn}为递加数列C.{S2n-1}为递加数列,{S2n}为递减数列 D.{S2n-1}为递减数列,{S2n}为递加数列第II卷(非选择题,共100分)二、填空题:本大题共5小题,每小题5分,共25分。
(11)如果执行程序框图(右图所示),那么输出的_______(12)定义在R上的函数满足则=_________ .(13)在圆中有结论:如图所示,“AB是圆O的直径,直线AC,BD是圆O过A,B的切线,P是圆O上任意一点,CD是过P的切线,则有PO2=PC·PD”.类比到椭圆:“AB是椭圆的长轴,直线AC,BD是椭圆过A,B的切线,P是椭圆上任意一点,CD是过P的切线,则有________________.”第13题图第14题图(14)如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,的坐标为_____ .(15)已知函数,且是它的最大值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第23天 不等式的解法
课标导航:1.会从实际问题抽象出不等关系;
2.通过函数图象了解不能式及与方程的关系. 一、选择题
1. 不等式0232>-+-x x 的解集是
( ) A .
{}
21x x x <->-或 B .
{}
12x x x <>或 C .
{}12x x <<
D .{
}
21x x -<<-
2. 不等式22
x x x x
-->
的解集是
( )
A. (02),
B. (0)-∞,
C. (2)+∞,
D. (0)∞⋃+∞(-,0),
3. 不等式26
01
x x x --->的解集为
( )
A.{}
2,3x x x -<或> B.{}
213x x x -<,或<< C.{}213x x x -<<,或> D.{}
2113x x x -<<,或<< 4. 2
211x x +≤的解集是
( ) A.{}20|≤≤x x B.
{}
|12x x -≤≤ C.
{}|01x x ≤≤
D.{}
|02x x x ≤≥或
5. 设函数f (x )=()212
log log x x ⎧⎪
⎨-⎪⎩
0,0x x >< 若()()f a f a >-,则实数a 的取值范围是
( )
A.(-1,0)∪(0,1)
B.(-∞,-1)∪(1,+∞)
C.(-1,0)∪(1,+∞)
D.(-∞,-1)∪(0,1)
6. 不等式2()0f x ax x c =-->的解集为{|21}x x -<<,则函数()y f x =-的图象为
( )
7. 设0a >,不等式||ax b c +<的解集是{|21}x x -<<,则::a b c 等于
( ) A.1:2:3
B.2:1:3
C.3:1:2
D.3:2:1
8. 已知函数x x f x
2log 31)(-⎪⎭
⎫
⎝⎛=,正实数,,a b c 是公差为正数的等差数列,且满足
()()()0f a f b f c <.若实数d 是方程()0f x =的一个解,那么下列四个判断:①d a <;
②d b <;③d c <;④d c >中有可能成立的个数为
( ) A.1
B.2
C.3
D.4
二、填空题
9. 不等式组221030x x x ⎧-<⎪⎨-+>⎪⎩的解集是 ;
10. 不等式2
1x x
+≥的解集为 ;
11. 若a+1>0,则不等式2x 2x a
x x 1
--≥-的解集为 ;
12. 已知函数)(x f 是R 上的偶函数,且在(0,+∞)上有()0f x '>,若(1)0f -=,那么关于x 的不等式x f (x )< 0 的解集是____________. 三、解答题
13. 已知函数()|2||5|f x x x =---
(1)证明:-3≤()f x ≤3;(2)求不等式()f x ≥2
815x x -+的解集.
14. 解关于x 的不等式:()09
22
>≤-a a a x x
15. 已知函数2
()(lg 2)lg f x x a x b =+++满足(1)2f -=-且对于任意x R ∈, 恒有
()2f x x ≥成立.
(1) 求实数,a b 的值; (2) 解不等式()5f x x <+.
16. 甲、乙两公司同时开发同一种新产品,经测算,对于函数f (x )和g (x ),当甲公司投入x 万元作宣传时,若乙公司投入的宣传费小于f (x )万元,则乙公司对这一新产品的开发有失败的风险,否则没有失败的风险;当乙公司投入x 万元作宣传时,若甲公司投入的宣传费小于g (x )万元,则甲公司对这一新产品的开发有失败的风险,否则没有失败的风险. (1)试解释f (0)=10,g (0)=20的实际意义;
(2)设f (x )=1
4x +10,g (x )x +20,甲、乙公司为了避免恶性竞争,经过协商,同意在
双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司应投入多少宣传费?
【链接高考】
已知函数2()()f x x ax b a b =++∈R ,的值域为[0)+∞,,若关于x 的不等式()f x c <的
解集为(6)m m +,,则实数c 的值为 .
第23天
1~8 CACA CCBC ; 9. (0,1); 10. [1,)+∞; 11. (,](1,)a -∞-⋃+∞ ;12.
)1,0()1,(⋃--∞
13.(1)略;(2){}
|536x x ≤; 14. 2317(,][]33a
a +-∞⋃ 15. (1)10=
b ,100=a ; (2)}14|{<<-x x .
16. (1)f (0)=10表示当甲公司不投入宣传费时,乙公司要避免新产品的开发有失败风险,至少要投入10万元宣传费;g (0)=20表示当乙公司不投入宣传费时,甲公司要避免新产品的开发有失败的风险,至少要投入20万元宣传费.
(2)设甲公司投入宣传费x 万元,乙公司投入宣传费y 万元,依题意,当且仅当
成立,双方均无失败的风险. 由①②得y ≥1
4y +20)+10⇒4y y -60≥0,∴y -y +15)≥0.
∵y +15>0y ≥4.∴y ≥16.∴x y +20≥4+20=24.∴x min =24,y min =16.
即要使双方均无失败风险,甲公司至少要投入24万元,乙公司至少要投入16万元. 链接高考:9。
