中职数学解析几何部分重要题型练习
中职数学解析几何测试卷

中职数学解析几何测试卷一.选择题1.过点(1,-3)且与直线4x -3y+2=0平行的直线方程为( )A.3x+4y+13=0B.3x-4y+13=0C.4x+3y+13=0D.4x-3y-13=02.下列4条直线中与直线2x+3y-6=0垂直的直线方程( )A.2x-3y-5=0B.3x-2y+1=0C.4x+6y+11=0D.3x+2y-5=03.直线3x-4y-2=0与圆x 2+y 2+2x=0之间的位置关系是( )A.相离B.相切C.相交且直线过圆心D.相交且直线不过圆心4.方程x 2+y 2-x-y+m=0表示一个圆。
则m 的值( )A.m<2B. m ≤-2C. 21<mD.21>m5.求A (3,2) B(5,1)的距离是( ) A.152 B. 5 C. 73 D.7326.椭圆的长轴是短轴的2倍,则椭圆的离心率是( ) A.21B. 31C. 22D.23 7.F 1、F 2是椭圆x 2+4y 2=1的两个焦点。
A 是椭圆上任意一点,AF 1的延长线交椭圆于B 。
则△ABF 2的周长是( )A.4B. 3C. 2D.18.过抛物线y 2=4x 的焦点且倾斜角为300的直线方程是( ) A.)1(33-=x y B. )2(33-=x y C. )1(3-=x y D.)2(3-=x y9.如果方程12322=+++ky k x 表示椭圆。
那么实数k 的取值范围是( ) A.k>-3 B. -3<k<-2 C. k>-2 D.k<-310.抛物线y 2=-12x 上一点P 到焦点的距离是6.则点P 的坐标是( )A. (-3,6)B. (3,6)C. (-3,±6)D.(±3,6)11.F 1、F 2分别是双曲线191622=-y x 的左右焦点。
点P 是双曲线上一点,|PF 1|=10, |PF 2|=( )A.4B. 18C. 2或18D.8或1812.若椭圆的长轴为8.短轴的一个顶点与两个焦点构成等边三角形。
平面解析几何职高专题

选择题在平面直角坐标系中,点P(3, -2)关于x轴对称的点Q的坐标是()。
A. (-3, 2)B. (3, 2)C. (-3, -2)D. (2, -3)直线y = 2x + 3与x轴的交点坐标为()。
A. (-3/2, 0)B. (0, 3)C. (-3, 0)D. (3/2, 0)若直线l的斜率为-1,且过点(1, 2),则直线l的方程是()。
A. y = -x + 3B. y = -x - 1C. y = x + 1D. y = x - 3圆x² + y² = 9与直线y = 2x的交点个数为()。
A. 0B. 1C. 2D. 无法确定两点A(1, 2)和B(4, 5)之间的距离是()。
A. √10B. 3√2C. 5D. √26填空题若点A(-2, y)在直线y = 3x + 1上,则y = _______。
直线y = mx + b与直线y = 2x平行,且过点(1, 3),则m = _______,b = _______。
圆(x - 2)² + (y + 3)² = 4的圆心坐标是_______。
在平面直角坐标系中,点P到x轴的距离为4,到y轴的距离为3,且点P在第三象限,则点P的坐标是_______。
已知两直线l₁: y = 2x + 1 和l₁: y = kx - 3 互相垂直,则k = _______。
简答题求直线y = 2x - 4与坐标轴围成的三角形的面积。
已知两点A(1, 2)和B(3, 4),求线段AB的中点坐标。
已知圆的方程为x² + y² - 6x - 8y + 21 = 0,求该圆的圆心和半径。
证明:两条平行线分别被第三条直线所截,所得的对应线段成比例。
已知直线l过点P(1, 2)且与直线y = -x + 3垂直,求直线l的方程。
职高解析几何测试题

对口班数学检测姓名姓名______________________________________________________成绩成绩成绩_________________ _________________一、选择题一、选择题1.正三棱锥的底面边长为6,高为3,则这个三棱锥的全面积为( ( )A .9 3B .18 3C .9(3+6) D.9 322.下图是某几何体的三视图,则该几何体的体积为.下图是某几何体的三视图,则该几何体的体积为( ( ( )A.92π+12B.92π+18 C .9π+42 D .36π+18 3.圆锥母线长为1,侧面展开图的圆心角为240240°,则圆锥的体积为°,则圆锥的体积为( ( )A.2 2π81B.8π81C.4 5π81D.10π814.在空间中,下列命题正确的是.在空间中,下列命题正确的是( ( ( )A .平行直线的平行投影重合.平行直线的平行投影重合B .平行于同一直线的两个平面平行.平行于同一直线的两个平面平行C .垂直于同一平面的两个平面平行.垂直于同一平面的两个平面平行D .垂直于同一平面的两条直线平行.垂直于同一平面的两条直线平行5.已知m ,n 为异面直线,m ⊂平面α,n ⊂平面β,α∩β=l ,则l ( () A .与m ,n 都相交都相交 B B .与m ,n 中至少一条相交中至少一条相交C .与m ,n 都不相交都不相交D D .至多与m ,n 中的一条相交中的一条相交6.若直线l 不平行于平面α,且l ⊄α,则,则( ( ( )A .α内存在直线与l 异面异面B B .α内存在与l 平行的直线平行的直线C .α内存在唯一的直线与l 平行平行D D .α内的直线与l 都相交都相交7.7.已知已知m ,n 是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是题中正确的是( ( ( )A .若m ∥α,n ∥α,则m ∥nB .若α⊥γ,β⊥γ,则α∥βC .若m ∥α,m ∥β,则α∥βD .若m ⊥α,n ⊥α,则m ∥n9.设直线m 与平面α相交但不垂直,则下列说法中正确的是相交但不垂直,则下列说法中正确的是( ( ( )A .在平面α内有且只有一条直线与直线m 垂直垂直B .过直线m 有且只有一个平面与平面α垂直垂直C .与直线m 垂直的直线不可能与平面α平行平行D .与直线m 平行的平面不可能与平面α垂直垂直1010.在三棱柱.在三棱柱ABC -A 1B 1C 1中,各棱长相等,侧棱垂直于底面,点D是侧面BB 1C 1C 的中心,则AD 与平面BB 1C 1C 所成角的大小是所成角的大小是( ( ( )A .3030°°B .4545°°C .6060°°D .9090°°11.11.下列语句中,表示随机事件的是(下列语句中,表示随机事件的是(下列语句中,表示随机事件的是() A 、掷三颗骰子出现点数之和为19B 、从54张扑克牌中任意抽取5张C 、型号完全相同的红、白球各3个,从中任取一个是红球个,从中任取一个是红球D 、异性电荷互相吸引、异性电荷互相吸引12.12.下列语句中,不表示复合事件的是(下列语句中,不表示复合事件的是(下列语句中,不表示复合事件的是()A 、掷三颗骰子出现点数之和为8B 、掷三颗骰子出现点数之和为奇数、掷三颗骰子出现点数之和为奇数C 、掷三颗骰子出现点数之和为3D 、掷三颗骰子出现点数之和大于1313.13.在掷一颗骰子的试验中,下列在掷一颗骰子的试验中,下列A 和B 是互斥事件的是(是互斥事件的是() A 、A=A={{1,51,5}},B=,B={{3,5,6} B 、A=A={{2,32,3}},B=,B={{1,3,5}C 、A=A={{2,3,4,54,5}},B=,B={{1,2}D 、A=A={{2,4,6},B=,B={{1,3} 14.100张奖券中有2张中奖,从中任抽一张,中奖的概率是( )A 、1100B 、150C 、125D 、1515.15.任选一个两位数,它既是奇数,又是偶数的概率是(任选一个两位数,它既是奇数,又是偶数的概率是(任选一个两位数,它既是奇数,又是偶数的概率是( ) A 、797 B 、2190 C 、5190D 、0 16.16.某中职学校共有某中职学校共有20名男足球运动员,从中选出3人调查学习成绩情况,调查应采用的抽样方法是(情况,调查应采用的抽样方法是() A 、随机抽样法、随机抽样法 B B 、分层抽样法、分层抽样法 C C 、系统抽样法、系统抽样法 D D 、无法确定、无法确定二、解答题二、解答题17.17.请用抽签法从某班请用抽签法从某班40人中抽出8人参加学校的教学质量调查会议,写出抽取的过程。
职业高中数学第九章解析几何测试卷

4. 过点 M(1,2)作圆x 2 + y 2 = 9的弦 AB,则 AB 的最小值为________________ 5. 根据下图所示条件,且椭圆的离心率e = 5,则椭圆的标准方程为_________________ y
4
x
6. 在双曲线中, 若实轴长、 虚轴长、 焦距成等差数列, 那么此双曲线的离心率是___________ 三.解答题(30 分)
1.直线经过点(2,3) ,且倾斜角的余弦值为5 ,求该直线的方程。(7 分)
3
2.过点 P(2,1)作圆x 2 + y 2 — 6x − 2y + 9 = 0的切线,求切线方程。 (7 分)
3.求与双曲线 −
9
x2
y2 16
Hale Waihona Puke = 1有共同的渐近线,且经过点(−3,2 3)的双曲线方程。 (8 分)
第九章解析几何测试卷
学号____________ 姓名________________ 一、选择题(4*10=40 分) 1.直线 x+1=0 的倾斜角为( ) ° ° ° A.0 B.90 C.30 D.不存在 2 若直线过点 A(0,1),B(2,3),则直线方程是( ) A.x − y − 1 = 0 B. x + y − 1 = 0 C. x − y + 1 = 0 3.圆x + y − 6y + m = 0的半径为 2,则 m 等于( A.−5 B. 5 C. −7 D.7 4. (x − 3)2 + (y + 2)2 = 13的周长是( ) )
1 4
)
)
B.−4
C.4
D.
1 4
二、填空题(5*6=30 分) 1.抛物线y 2 =4x上一点 A 到焦点的距离为 3,则点 A 到 x 轴的距离是_______________ 2.已知点 M(−3,1)是等轴双曲线上的一点,则该双曲线的标准方程是______________ 3.倾斜角为 ,且与点(−1, −1)的距离为 2的直线方程是________________
中职数学复习——解析几何

二、填空题
14.(2014年)已知点A(1,3)和点B(3,-1),则线段AB的垂直平分
线的方程是
.
【答案】 x 2 y 0 AB的中点为(2,1),法向量n AB (3, 1) (1,3) (2, 4), 由直线的点法式方程得2(x 2) 4( y 1) 0, 整理得x 2 y 0.
心,且与直线x+y=5相切的圆的标准方程是
.
【答案】 (x 2)2 ( y 1)2 8 AB的中点为O(2, 1),
又 直线x y 5与圆相切, 圆心O(2, 1)到直线的距离等于半径,即r | 2 1 5 | 2 2,
12 12 故圆的标准方程为(x 2)2 ( y 1)2 8.
12.(2016年)抛物线x2=4y的准线方程 ( ) A.y=-1 B.y=1 C.x=-1 D.x=1
【答案】A 抛物线的焦点坐标为(0,1), 准线方程为y 1, 故选A.
13.(2017年)抛物线y2= -8x的焦点坐标是 ( ) A.(-2,0) B.(2,0) C.(0,-2) D.(0,2)
三、解答题
19.(2012年)已知椭圆C的焦点F1(1, 0)和F2 (1, 0), P为椭圆C上的点, 且 | F1F2 | 是 | PF1 | 和 | PF2 |的等差中项. (1)求椭圆C的方程;
(2)若P1为椭圆C在第一象限上一点, F1F2P1
2
3
,求
tan
P1F1F2 .
【解】(1)设所求椭圆C的方程为 x2 y2 1, a2 b2
PF1 2
|)2
25 .
22.(2015年)已知中心在坐标原点,两个焦点F1, F2在x轴上的椭圆E
2020届中职数学单元检测08《解析几何》-对口升学复习题含答案

B、1
1
C、
3
3. 经过点(1,2)且倾斜角为 450 的直线方程为
)
D、0
()
A、 y x 1
B、 y 2x
C、 y x 3
D、 y 2x
4.直线 3x y 1 0 的倾斜角为(
)
A、300
B、 1500
C、 60 0
D、1200
5. 直线4x 5y 10 0的斜率和在y轴上的截距分别为( )
)
) D. m 4
1
A、 3,0
B、 - 3 ,0 2
C、 0, 3 2
D、 0,- 3 2
二.填空题(本大题 8 小题,每小题 4 分,共 32 分)
1.过点 A(1,-1)且与 x 轴平行的直线方程为
2.双曲线 x 2 y 2 1 的离心率是 100 125
3.已知 A(7,4),B(3,2),则线段 AB 的中点坐标是
3
3
第八单元《解析几何》参考答案
一.选择题(本大题 10 小题,每小题 3 分,共 30 分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
A
A
C
C
D
A
C
A
D
二.填空题(本大题共 8 小题,每小题 4 分,共 32 分)
3
1.
y=-1
.2.
2
.3.
(5,3)
-3
.4.
2
.
5.
(1,-2) .6.(x -1)2 y2 3 . 7. x 2 y 2 9 .8.
题号
1
2
中职数学立体几何部分重要题型练习
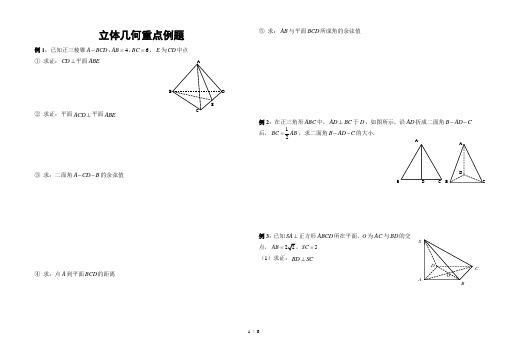
立体几何重点例题例1:已知正三棱锥46A BCD AB BC-==,,,E为CD中点①求证:CD⊥平面ABE②求证:平面ACD⊥平面ABE③求:二面角A CD B--的余弦值④求:点A到平面BCD的距离⑤求:AB与平面BCD所成角的余弦值例2:在正三角形ABC中,AD BC⊥于D,如图所示,沿AD折成二面角B AD C--后,12BC AB=,求二面角B AD C--的大小.例3:已知SA⊥正方形ABCD所在平面,O为AC与BD的交点,5AB SC==(1)求证:BD SC⊥ABCDEABDCDABSO(2)求证:平面SBC⊥平面SAB(3)求:点S到平面ABCD的距离(4)求:点S到直线BC的距离(5)求:直线SC与AB所成角的余弦值(6)求:直线SB与平面ABCD所成角的正切值(7)求:平面SAB与平面SAC所成的二面角的度数例4:已知正方体1111ABCD A B C D-中,E是AB的中点(1)求1BA与1CC夹角的度数;DAB CD1A1B1C1E(2)求1BA 与1CB 夹角的度数;(3)求1A E 与1CB 夹角的余弦例5:已知正方体1111ABCD A B C D -中,O 是底面ABCD 对角线的交点 (1)求证:1//C O 平面11AB D (2)求证:1A C ⊥平面11AB DCDBC 1D 1A 1B 1OA立体几何重点例题 答案例1:已知正三棱锥46ABCD AB BC -==,,,E 为CD 中点 ① 求证:CD ⊥平面ABE .证明:连接BE AE ,,因为E 为CD 中点,在正三棱锥中AC AD BC BD ==,所以AE CD BE CD AE BE E ⊥⊥=I ,且 所以CD ⊥平面ABE .② 求证:平面ACD ⊥平面ABE .证明:由上题可知,CD ⊥平面ABE又CD ⊂平面ACD所以平面ACD ⊥平面ABE .③ 求:二面角A CD B --的余弦值.解:由AE CD BE CD ⊥⊥,所以AEB ∠即二面角A CD B --的平面角 在Rt ACE ∆中,可求得AE ===在BCD ∆中,可求得622BE BC === 所以222cos 27AE BE AB AEB AE BE +-∠===g g 所以所求二面角A CD B --的余弦值为7. ④ 求:点A 到平面BCD 的距离. 解:过点A 作AF BE ⊥于点F由CD ⊥平面ABE ,得CD AF ⊥,又因为BE CD E =I 所以AF ⊥平面BCD所以AF 即所求点A 到平面BCD 的距离由正三棱锥的定义可得,F 是BCD ∆的中心,也是重心可得2233BF BE =⨯=⨯=,2AF == 所以所求点A 到平面BCD 的距离为2. ⑤ 求:AB 与平面BCD 所成角的余弦值. 解:由上题可知,AF ⊥平面BCD故BF 为AB 在平面BCD 内的射影所以ABF ∠即AB 与平面BCD 所成的角在ABF ∆中,24AF AB ==, 所以可知21sin 42ABF ∠== 所以30ABF ∠=︒,cos cos302ABF ∠=︒=. 例2:在正三角形ABC 中,AD BC ⊥于D ,如图所示,沿AD 折成二面角B AD C--后,12BC AB =,求二面角B AD C --的大小.解:由已知可得BD AD CD AD ⊥⊥,所以BDC ∠即二面角B AD C --的平面角由正三角形ABC 可得,12BD DC AB ==,又因为12BC AB = 所以BD DC BC ==,所以BDC ∆为等边三角形 故60BDC ∠=︒所以所求二面角B AD C --为60︒. 所以SA BD ⊥又四边形ABCD 为正方形所以BD AC ⊥,又SA AC A =I所以BD SAC ⊥平面 所以BD SC ⊥(2)求证:平面SBC ⊥平面SAB . 证明:因为SA ⊥正方形ABCD 所在平面ABCDEABCDCDABSO所以SA BC ⊥,又因为BC AB ⊥,AB BC B =I 所以BC SAB ⊥平面又BC SBC ⊂平面,所以平面SBC ⊥平面SAB .(3)求:点S 到平面ABCD 的距离. 解:因为SA ⊥正方形ABCD 所在平面所以SA 即所求点S 到平面ABCD 的距离在Rt SBC ∆中,SB =所以在Rt SAB ∆中,3SA ==因此所求点S 到平面ABCD 的距离为3.(4)求:点S 到直线BC 的距离.解:由前面所证可知BC SAB ⊥平面,所以BC SB ⊥所以SB 即所求点S 到直线BC 的距离 由前可知SB =所以点S 到直线BC .(5)求:直线SC 与AB 所成角的余弦值.解:因为//AB CD所以SCD ∠即SC 与AB 所成的角由前可知SD ==所以222cos 25SC CD SD SCD SC CD +-∠===g g 因此所求直线SC 与AB 所成角的余弦值为5.(6)求:直线SB 与平面ABCD 所成角的正切值. SA ⊥ABCD 所以AB 即为SB 在平面ABCD 内的射影所以SBA ∠即所求的直线SB 与平面ABCD 所成的角 在Rt SAB ∆中,tan 4SA SBA AB ∠===(7)求:平面SAB 与平面SAC 所成的二面角的度数. 解:因为SA ⊥正方形ABCD 所在平面所以SA AC SA AB ⊥⊥,所以CAB ∠即二面角C SA B --的平面角 因为ABCD 为正方形,所以45CAB ∠=︒即所求平面SAB 与平面SAC 所成的二面角的度数为45︒.例4:已知正方体1111ABCD A B C D -中,E 是AB 的中点 (1)求1BA 与1CC 夹角的度数; (2)求1BA 与1CB 夹角的度数; (3)求1A E 与1CB 夹角的余弦.解:(1)因为11//BB CC所以11B BA ∠即所求1BA 与1CC 的夹角 因为四边形11BAA B 为正方形 所以1145B BA ∠=︒即所求1BA 与1CC 夹角的度数为45︒(2)连接111CD B D ,因为1111//A D BC A D BC =且 所以四边形11A D CB 为平行四边形 所以11//BA CD所以11B CD ∠即所求1BA 与1CB 所成的角 易证1111B D CD B C ==所以1160B CD ∠=︒,即所求的1BA 与1CB 所成的角为60︒DA B CD 1A 1B 1C 1E(3)连接1A D ED ,,易证11//A D B C 所以1DA E ∠即所求的1A E 与1CB 所成的角 设正方体的棱长为2则11ED A D A E ======所以22211111cos 2A D A E DE DA E A D A E +-∠===⨯⨯即所求角的余弦为5.例5:已知正方体1111ABCD A B C D -中,O 是底面ABCD 对角线的交点 (1)求证:1//C O 平面11AB D . (2)求证:1A C ⊥平面11AB D .证明:(1)连接11BC DC ,因为1111//DD BB DD BB =且 所以四边形11BB D D 为平行四边形 所以11//D B DB又因为1111//D C AB D C AB =且 所以四边形11AD C B 为平行四边形 所以11//AD BC所以可得平面11//AB D 平面1BDC 所以两平面没有公共点 又因为11OC BDC ⊂平面 所以111OC AB D 与平面没有公共点所以111OC AB D //平面 (2)连接1A D由已知可知正方形11ADD A 中,11AD A D ⊥又因为CD ⊥平面11ADD A ,所以1A D CD ⊥ 所以11AD A DC ⊥平面,所以11AD AC ⊥ 同理,连接11A C可以证得1111111B D AC B D CC ⊥⊥,所以1111B D AC C ⊥平面所以111B D AC ⊥ 所以111AC AB D ⊥平面.CDBC 1D 1A 1B 1OA。
解析几何练习题及答案

解析几何一、选择题1.已知两点A (-3,3),B (3,-1),则直线AB 的斜率是()A.3B.-3C.33D.-33解析:斜率k =-1-33--3=-33,故选D.答案:D2.已知直线l :ax +y -2-a =0在x 轴和y 轴上的截距相等,则a 的值是()A.1B.-1C.-2或-1D.-2或1解析:①当a =0时,y =2不合题意.②a ≠0,x =0时,y =2+a .y =0时,x =a +2a,则a +2a=a +2,得a =1或a =-2.故选D.答案:D3.两直线3x +y -3=0与6x +my +1=0平行,则它们之间的距离为()A.4B.21313C.51326D.71020解析:把3x +y -3=0转化为6x +2y -6=0,由两直线平行知m =2,则d =|1--6|62+22=71020.故选D.4.(2014皖南八校联考)直线2x -y +1=0关于直线x =1对称的直线方程是()A.x +2y -1=0B.2x +y -1=0C.2x +y -5=0D.x +2y -5=0解析:由题意可知,直线2x -y +1=0与直线x =1的交点为(1,3),直线2x -y +1=0的倾斜角与所求直线的倾斜角互补,因此它们的斜率互为相反数,直线2x -y +1=0的斜率为2,故所求直线的斜率为-2,所以所求直线的方程是y -3=-2(x -1),即2x +y -5=0.故选C.答案:C5.若直线l :y =kx -3与直线2x +3y -6=0的交点位于第一象限,则直线l 的倾斜角的取值围是()A.π6,D.π3,π2解析:由题意,可作直线2x +3y -6=0的图象,如图所示,则直线与x 轴、y 轴交点分别为A (3,0),B (0,2),又直线l 过定点(0,-3),由题知直线l 与线段AB 相交(交点不含端点),从图中可以看出,直线l B.答案:B6.(2014一模)过点A (2,3)且垂直于直线2x +y -5=0的直线方程为()A.x -2y +4=0B.2x +y -7=0C.x -2y +3=0D.x -2y +5=0解析:直线2x +y -5=0的斜率为k =-2,∴所求直线的斜率为k ′=12,∴方程为y -3=12(x -2),即x -2y +4=0.答案:A7.过点(2,1)且在x 轴上截距与在y 轴上截距之和为6的直线方程为____________.解析:由题意知截距均不为零.设直线方程为x a +yb =1,b =6,+1b=1,=3=3=4=2.故所求直线方程为x +y -3=0或x +2y -4=0.答案:x +y -3=0或x +2y -4=08.(2014质检)若过点A (-2,m ),B (m,4)的直线与直线2x +y +2=0平行,则m 的值为________.解析:∵过点A ,B 的直线平行于直线2x +y +2=0,∴k AB =4-m m +2=-2,解得m =-8.答案:-89.若过点P (1-a,1+a )与Q (3,2a )的直线的倾斜角为钝角,则实数a 的取值围是________.解析:由直线PQ 的倾斜角为钝角,可知其斜率k <0,即2a -1+a 3-1-a <0,化简得a -1a +2<0,∴-2<a <1.答案:(-2,1)10.已知k ∈R ,则直线kx +(1-k )y +3=0经过的定点坐标是________.解析:令k =0,得y +3=0,令k =1,得x +3=0.+3=0,+3=0,=-3,=-3,所以定点坐标为(-3,-3).答案:(-3,-3)三、解答题11.已知两直线l 1:x +y sin α-1=0和l 2:2x sin α+y +1=0,试求α的值,使(1)l 1∥l 2;(2)l 1⊥l 2.解:(1)法一当sin α=0时,直线l 1的斜率不存在,l 2的斜率为0,显然l 1不平行于l 2.当sin α≠0时,k 1=-1sin α,k 2=-2sin α.要使l 1∥l 2,需-1sin α=-2sin α,即sin α=±22,∴α=k π±π4,k ∈Z .故当α=k π±π4,k ∈Z 时,l 1∥l 2.法二由l 1∥l 22α-1=0,α≠0,∴sin α=±22,∴α=k π±π4,k ∈Z .故当α=k π±π4,k ∈Z 时,l 1∥l 2.(2)∵l 1⊥l 2,∴2sin α+sin α=0,即sin α=0.∴α=k π,k ∈Z .故当α=k π,k ∈Z 时,l 1⊥l 2.12.设直线l 1:y =k 1x +1,l 2:y =k 2x -1,其中实数k 1,k 2满足k 1k 2+2=0.(1)证明l 1与l 2相交;(2)证明l 1与l 2的交点在椭圆2x 2+y 2=1上.证明:(1)假设l 1与l 2不相交,则l 1∥l 2即k 1=k 2,代入k 1k 2+2=0,得k 21+2=0,这与k 1为实数的事实相矛盾,从而k 1≠k 2,即l 1与l 2相交.(2)法一=k 1x +1,=k 2x -1解得交点P而2x 2+y 2=8+k 22+k 21+2k 1k 2k 22+k 21-2k 1k 2=k 21+k 22+4k 21+k 22+4=1.即P (x ,y )在椭圆2x 2+y 2=1上.即l 1与l 2的交点在椭圆2x 2+y 2=1上.法二交点P 的坐标(x ,y-1=k 1x ,+1=k 2x ,故知x ≠0.1=y -1x,2=y +1x.代入k 1k 2+2=0,得y -1x ·y +1x+2=0,整理后,得2x 2+y 2=1.所以交点P 在椭圆2x 2+y 2=1上.第八篇第2节一、选择题1.圆心在y 轴上,半径为1,且过点(1,2)的圆的方程为()A.x 2+(y -2)2=1B.x 2+(y +2)2=1C.(x -1)2+(y -3)2=1D.x 2+(y -3)2=1解析:由题意,设圆心(0,t ),则12+t -22=1,得t =2,所以圆的方程为x 2+(y -2)2=1,故选A.答案:A2.(2014模拟)动点P 到点A (8,0)的距离是到点B (2,0)的距离的2倍,则动点P 的轨迹方程为()A.x 2+y 2=32B.x 2+y 2=16C.(x -1)2+y 2=16D.x 2+(y -1)2=16解析:设P (x ,y ),则由题意可得2x -22+y 2=x -82+y 2,化简整理得x 2+y 2=16,故选B.答案:B3.(2012年高考卷)已知圆C :x 2+y 2-4x =0,l 是过点P (3,0)的直线,则()A.l 与C 相交B.l 与C 相切C.l 与C 相离D.以上三个选项均有可能解析:x 2+y 2-4x =0是以(2,0)为圆心,以2为半径的圆,而点P (3,0)到圆心的距离为d =3-22+0-02=1<2,点P (3,0)恒在圆,过点P (3,0)不管怎么样画直线,都与圆相交.故选A.答案:A4.(2012年高考卷)将圆x 2+y 2-2x -4y +1=0平分的直线是()A.x +y -1=0B.x +y +3=0C.x -y +1=0D.x -y +3=0解析:由题知圆心在直线上,因为圆心是(1,2),所以将圆心坐标代入各选项验证知选项C 符合,故选C.答案:C5.(2013年高考卷)垂直于直线y =x +1且与圆x 2+y 2=1相切于第一象限的直线方程是()A.x +y -2=0B.x +y +1=0C.x +y -1=0D.x +y +2=0解析:与直线y =x +1垂直的直线方程可设为x +y +b =0,由x +y +b =0与圆x 2+y 2=1相切,可得|b |12+12=1,故b =± 2.因为直线与圆相切于第一象限,故结合图形分析知b =-2,则直线方程为x +y -2=0.故选A.答案:A6.(2012年高考卷)直线x +3y -2=0与圆x 2+y 2=4相交于A 、B 两点,则弦AB 的长度等于()A.25B.23C.3D.1解析:因为圆心到直线x +3y -2=0的距离d =|0+3×0-2|12+32=1,半径r =2,所以弦长|AB |=222-12=2 3.故选B.答案:B 二、填空题7.(2013年高考卷)直线y =2x +3被圆x 2+y 2-6x -8y =0所截得的弦长等于________.解析:圆的方程可化为(x -3)2+(y -4)2=25,故圆心为(3,4),半径r =5.又直线方程为2x -y +3=0,∴圆心到直线的距离为d =|2×3-4+3|4+1=5,∴弦长为2×25-5=220=4 5.答案:458.已知直线l :x -y +4=0与圆C :(x -1)2+(y -1)2=2,则圆C 上各点到l 的距离的最小值为________.解析:因为圆C 的圆心(1,1)到直线l 的距离为d =|1-1+4|12+-12=22,又圆半径r = 2.所以圆C 上各点到直线l 的距离的最小值为d -r = 2.答案:29.已知圆C 的圆心在直线3x -y =0上,半径为1且与直线4x -3y =0相切,则圆C 的标准方程是________.解析:∵圆C 的圆心在直线3x -y =0上,∴设圆心C (m,3m ).又圆C 的半径为1,且与4x -3y =0相切,∴|4m -9m |5=1,∴m =±1,∴圆C 的标准方程为(x -1)2+(y -3)2=1或(x +1)2+(y +3)2=1.答案:(x -1)2+(y -3)2=1或(x +1)2+(y +3)2=110.圆(x -2)2+(y -3)2=1关于直线l :x +y -3=0对称的圆的方程为________.解析:已知圆的圆心为(2,3),半径为1.则对称圆的圆心与(2,3)关于直线l 对称,由数形结合得,对称圆的圆心为(0,1),半径为1,故方程为x 2+(y -1)2=1.答案:x 2+(y -1)2=1三、解答题11.已知圆C :x 2+(y -2)2=5,直线l :mx -y +1=0.(1)求证:对m ∈R ,直线l 与圆C 总有两个不同交点;(2)若圆C 与直线相交于点A 和点B ,求弦AB 的中点M 的轨迹方程.(1)证明:法一直线方程与圆的方程联立,消去y 得(m 2+1)x 2-2mx -4=0,∵Δ=4m 2+16(m 2+1)=20m 2+16>0,∴对m ∈R ,直线l 与圆C 总有两个不同交点.法二直线l :mx -y +1恒过定点(0,1),且点(0,1)在圆C :x 2+(y -2)2=5部,∴对m ∈R ,直线l 与圆C 总有两个不同交点.(2)解:设A (x 1,y 1),B (x 2,y 2),M (x ,y ),由方程(m 2+1)x 2-2mx -4=0,得x 1+x 2=2mm 2+1,∴x =mm 2+1.当x =0时m =0,点M (0,1),当x ≠0时,由mx -y +1=0,得m =y -1x,代入x =m m 2+1,得+1=y -1x,化简得x 2=14.经验证(0,1)也符合,∴弦AB 的中点M 的轨迹方程为x 2=14.12.已知圆C :x 2+y 2-8y +12=0,直线l :ax +y +2a =0.(1)当a 为何值时,直线l 与圆C 相切;(2)当直线l 与圆C 相交于A 、B 两点,且|AB |=22时,求直线l 的方程.解:将圆C 的方程x 2+y 2-8y +12=0配方得标准方程为x 2+(y -4)2=4,则此圆的圆心为(0,4),半径为2.(1)若直线l 与圆C 相切,则有|4+2a |a 2+1=2.解得a =-34.(2)过圆心C 作CD ⊥AB ,则根据题意和圆的性质,|=|4+2a |a 2+1,|2+|DA |2=22,|=12|AB |=2,解得a =-7,或a =-1.故所求直线方程为7x -y +14=0或x -y +2=0.第八篇第3节一、选择题1.设P 是椭圆x225+y216=1上的点.若F 1、F 2是椭圆的两个焦点,则|PF 1|+|PF 2|等于()A.4B.5C.8D.10解析:由方程知a =5,根据椭圆定义,|PF 1|+|PF 2|=2a =10.故选D.答案:D2.(2014二模)P 为椭圆x24+y23=1上一点,F 1,F 2为该椭圆的两个焦点,若∠F 1PF 2=60°,则PF 1→·PF 2→等于()A.3B.3C.23D.2解析:由椭圆方程知a =2,b =3,c =1,1|+|PF 2|=4,1|2+|PF 2|2-4=2|PF 1||PF 2|cos 60°∴|PF 1||PF 2|=4.∴PF 1→·PF 2→=|PF 1→||PF 2→|cos 60°=4×12=2.答案:D3.(2012年高考卷)椭圆x 2a 2+y2b 2=1(a >b >0)的左、右顶点分别是A 、B ,左、右焦点分别是F 1,F 2.若|AF 1|,|F 1F 2|,|F 1B |成等比数列,则此椭圆的离心率为()A.14B.55C.12D.5-2解析:本题考查椭圆的性质与等比数列的综合运用.由椭圆的性质可知|AF 1|=a -c ,|F 1F 2|=2c ,|F 1B |=a +c ,又|AF 1|,|F 1F 2|,|F 1B |成等比数列,故(a -c )(a +c )=(2c )2,可得e =c a =55.故应选B.答案:B4.(2013年高考卷)已知椭圆C :x 2a 2+y2b2=1(a >b >0)的左焦点为F ,C 与过原点的直线相交于A ,B 两点,连接AF ,BF .若|AB |=10,|BF |=8,cos∠ABF =45,则C 的离心率为()A.35B.57C.45D.67解析:|AF |2=|AB |2+|BF |2-2|AB ||BF |cos∠ABF =100+64-2×10×8×45=36,则|AF |=6,∠AFB =90°,半焦距c =|FO |=12|AB |=5,设椭圆右焦点F 2,连结AF 2,由对称性知|AF 2|=|FB |=8,2a =|AF 2|+|AF |=6+8=14,即a =7,则e =c a =57.故选B.答案:B5.已知椭圆E :x2m +y24=1,对于任意实数k ,下列直线被椭圆E 截得的弦长与l :y =kx+1被椭圆E 截得的弦长不可能相等的是()A.kx +y +k =0B.kx -y -1=0C.kx +y -k =0D.kx +y -2=0解析:取k =1时,l :y =x +1.选项A 中直线:y =-x -1与l 关于x 轴对称,截得弦长相等.选项B 中直线:y =x -1与l 关于原点对称,所截弦长相等.选项C 中直线:y =-x +1与l 关于y 轴对称,截得弦长相等.排除选项A、B、C,故选D.答案:D6.(2014省实验中学第二次诊断)已知椭圆x 2a 2+y2b 2=1(a >b >0)的左、右焦点分别为F 1(-c,0),F 2(c,0),若椭圆上存在点P ,使asin∠PF 1F 2=csin∠PF 2F 1,则该椭圆的离心率的取值围为()A.(0,2-1)D.(2-1,1)解析:由题意知点P 不在x 轴上,在△PF 1F 2中,由正弦定理得|PF 2|sin∠PF 1F 2=|PF 1|sin∠PF 2F 1,所以由a sin∠PF 1F 2=csin∠PF 2F 1可得a|PF 2|=c |PF 1|,即|PF 1||PF 2|=c a =e ,所以|PF 1|=e |PF 2|.由椭圆定义可知|PF 1|+|PF 2|=2a ,所以e |PF 2|+|PF 2|=2a ,解得|PF 2|=2a e +1.由于a -c <|PF 2|<a +c ,所以有a -c <2ae +1<a +c ,即1-e <2e +1<1+e ,1-e 1+e<2,1+e2,解得2-1<e .又0<e <1,∴2-1<e <1.故选D.答案:D 二、填空题7.设F 1、F 2分别是椭圆x225+y216=1的左、右焦点,P 为椭圆上一点,M 是F 1P 的中点,|OM |=3,则P 点到椭圆左焦点距离为________.解析:∵|OM |=3,∴|PF 2|=6,又|PF 1|+|PF 2|=10,∴|PF 1|=4.答案:48.椭圆x 2a 2+y2b2=1(a >b >0)的左、右焦点分别是F 1、F 2,过F 2作倾斜角为120°的直线与椭圆的一个交点为M ,若MF 1垂直于x 轴,则椭圆的离心率为________.解析:不妨设|F 1F 2|=1,∵直线MF 2的倾斜角为120°,∴∠MF 2F 1=60°.∴|MF 2|=2,|MF 1|=3,2a =|MF 1|+|MF 2|=2+3,2c =|F 1F 2|=1.∴e =ca=2- 3.答案:2-39.(2014模拟)过点(3,-5),且与椭圆y225+x29=1有相同焦点的椭圆的标准方程为________________.解析:由题意可设椭圆方程为y225-m+x29-m=1(m <9),代入点(3,-5),得525-m +39-m=1,解得m =5或m =21(舍去),∴椭圆的标准方程为y220+x24=1.答案:y220+x24=110.已知F 1,F 2是椭圆C :x 2a 2+y 2b2=1(a >b >0)的两个焦点,P 为椭圆C 上的一点,且PF 1→⊥PF 2→.若△PF 1F 2的面积为9,则b =________.解析:1|+|PF 2|=2a ,1|2+|PF 2|2=4c 2,∴(|PF 1|+|PF 2|)2-2|PF 1||PF 2|=4c 2,即4a 2-2|PF 1||PF 2|=4c 2,∴|PF 1||PF 2|=2b 2,∴S △PF 1F 2=12|PF 1||PF 2|=b 2=9,∴b =3.答案:3三、解答题11.(2012年高考卷)在平面直角坐标系xOy 中,已知椭圆C 1:x 2a 2+y2b2=1(a >b >0)的左焦点为F 1(-1,0),且点P (0,1)在C 1上.(1)求椭圆C 1的方程;(2)设直线l 同时与椭圆C 1和抛物线C 2:y 2=4x 相切,求直线l 的方程.解:(1)由椭圆C 1的左焦点为F 1(-1,0),且点P (0,1)在C 12-b 2=1,=1,2=2,2=1.故椭圆C 1的方程为x22+y 2=1.(2)由题意分析,直线l 斜率存在且不为0,设其方程为y =kx +b ,由直线l 与抛物线C 2=kx +b ,2=4x ,消y 得k 2x 2+(2bk -4)x +b 2=0,Δ1=(2bk -4)2-4k 2b 2=0,化简得kb =1.①由直线l 与椭圆C 1kx +b ,y 2=1,消y 得(2k 2+1)x 2+4bkx +2b 2-2=0,Δ2=(4bk )2-4(2k 2+1)(2b 2-2)=0,化简得2k 2=b 2-1.②=1,k 2=b 2-1,解得b 4-b 2-2=0,∴b 2=2或b 2=-1(舍去),∴b =2时,k =22,b =-2时,k =-22.即直线l 的方程为y =22x +2或y =-22x - 2.12.(2014海淀三模)已知椭圆C :x2a 2+y2b 2=1(a >b >0)的四个顶点恰好是一边长为2,一角为60°的菱形的四个顶点.(1)求椭圆C 的方程;(2)若直线y =kx 交椭圆C 于A ,B 两点,在直线l :x +y -3=0上存在点P ,使得△PAB 为等边三角形,求k 的值.解:(1)因为椭圆C :x 2a 2+y2b2=1(a >b >0)的四个顶点恰好是一边长为2,一角为60°的菱形的四个顶点.所以a =3,b =1,椭圆C 的方程为x23+y 2=1.(2)设A (x 1,y 1),则B (-x 1,-y 1),当直线AB 的斜率为0时,AB 的垂直平分线就是y 轴,y 轴与直线l :x +y -3=0的交点为P (0,3),又因为|AB |=23,|PO |=3,所以∠PAO =60°,所以△PAB 是等边三角形,所以直线AB 的方程为y =0,当直线AB 的斜率存在且不为0时,则直线AB 的方程为y =kx ,y 2=1,kx ,化简得(3k 2+1)x 2=3,所以|x 1|=33k 2+1,则|AO |=1+k233k 2+1=3k 2+33k 2+1.设AB 的垂直平分线为y =-1kx ,它与直线l :x +y -3=0的交点记为P (x 0,y 0),=-x +3,=-1k x ,0=3k k -1,0=-3k -1.则|PO |=9k 2+9k -12,因为△PAB 为等边三角形,所以应有|PO |=3|AO |,代入得9k 2+9k -12=33k 2+33k 2+1,解得k =0(舍去),k =-1.综上,k =0或k =-1.第八篇第4节一、选择题1.设P 是双曲线x216-y220=1上一点,F 1,F 2分别是双曲线左右两个焦点,若|PF 1|=9,则|PF 2|等于()A.1B.17C.1或17D.以上答案均不对解析:由双曲线定义||PF 1|-|PF 2||=8,又|PF 1|=9,∴|PF 2|=1或17,但应注意双曲线的右顶点到右焦点距离最小为c -a =6-4=2>1,∴|PF 2|=17.故选B.答案:B2.(2013年高考卷)已知0<θ<π4,则双曲线C 1:x 2sin 2θ-y 2cos 2θ=1与C 2:y 2cos 2θ-x2sin 2θ=1的()A.实轴长相等B.虚轴长相等C.离心率相等D.焦距相等解析:双曲线C 1的半焦距c 1=sin 2θ+cos 2θ=1,双曲线C 2的半焦距c 2=cos 2θ+sin 2θ=1,故选D.答案:D3.(2012年高考卷)已知双曲线C :x 2a 2-y2b2=1的焦距为10,点P (2,1)在C 的渐近线上,则C 的方程为()A.x220-y25=1B.x25-y220=1C.x280-y220=1D.x220-y280=1解析:由焦距为10,知2c =10,c =5.将P (2,1)代入y =bax 得a =2b .a 2+b 2=c 2,5b 2=25,b 2=5,a 2=4b 2=20,所以方程为x220-y25=1.故选A.答案:A4.已知F 1、F 2为双曲线C :x 2-y 2=2的左、右焦点,点P 在C 上,|PF 1|=2|PF 2|,则cos ∠F 1PF 2等于()A.14B.35C.34D.45解析:∵c 2=2+2=4,∴c =2,2c =|F 1F 2|=4,由题可知|PF 1|-|PF 2|=2a =22,|PF 1|=2|PF 2|,∴|PF 2|=22,|PF 1|=42,由余弦定理可知cos∠F 1PF 2=422+222-422×42×22=34.故选C.答案:C5.设椭圆C 1的离心率为513,焦点在x 轴上且长轴长为26,若曲线C 2上的点到椭圆C 1的两个焦点的距离的差的绝对值等于8,则曲线C 2的标准方程为()A.x242-y232=1B.x2132-y252=1C.x232-y242=1D.x2132-y2122=1解析:在椭圆C 1中,因为e =513,2a =26,即a =13,所以椭圆的焦距2c =10,则椭圆两焦点为(-5,0),(5,0),根据题意,可知曲线C 2为双曲线,根据双曲线的定义可知,双曲线C 2中的2a 2=8,焦距与椭圆的焦距相同,即2c 2=10,可知b 2=3,所以双曲线的标准方程为x242-y232=1.故选A.答案:A6.(2014八中模拟)若双曲线x29-y216=1渐近线上的一个动点P 总在平面区域(x -m )2+y 2≥16,则实数m 的取值围是()A.[-3,3]B.(-∞,-3]∪[3,+∞)C.[-5,5]D.(-∞,-5]∪[5,+∞)解析:因为双曲线x 29-y 216=1渐近线4x ±3y =0上的一个动点P 总在平面区域(x -m )2+y 2≥16,即直线与圆相离或相切,所以d =|4m |5≥4,解得m ≥5或m ≤-5,故实数m 的取值围是(-∞,-5]∪[5,+∞).选D.答案:D 二、填空题7.(2013年高考卷)已知F 为双曲线C :x29-y216=1的左焦点,P ,Q 为C 上的点.若PQ的长等于虚轴长的2倍,点A (5,0)在线段PQ 上,则△PQF 的周长为________.解析:由题知,双曲线中a =3,b =4,c =5,则|PQ |=16,又因为|PF |-|PA |=6,|QF |-|QA |=6,所以|PF |+|QF |-|PQ |=12,|PF |+|QF |=28,则△PQF 的周长为44.答案:448.已知双曲线C :x 2a 2-y2b2=1(a >0,b >0)的离心率e =2,且它的一个顶点到较近焦点的距离为1,则双曲线C 的方程为________.解析:双曲线中,顶点与较近焦点距离为c -a =1,又e =ca=2,两式联立得a =1,c =2,∴b 2=c 2-a 2=4-1=3,∴方程为x 2-y23=1.答案:x 2-y23=19.(2014市第三次质检)已知点P 是双曲线x2a 2-y2b2=1(a >0,b >0)和圆x 2+y 2=a 2+b 2的一个交点,F 1,F 2是该双曲线的两个焦点,∠PF 2F 1=2∠PF 1F 2,则该双曲线的离心率为________.解析:依题意得,线段F 1F 2是圆x 2+y 2=a 2+b 2的一条直径,故∠F 1PF 2=90°,∠PF 1F 2=30°,设|PF 2|=m ,则有|F 1F 2|=2m ,|PF 1|=3m ,该双曲线的离心率等于|F 1F 2|||PF 1|-|PF 2||=2m3m -m =3+1.答案:3+110.(2013年高考卷)设F 1,F 2是双曲线C :x2a 2-y2b 2=1(a >0,b >0)的两个焦点.若在C 上存在一点P ,使PF 1⊥PF 2,且∠PF 1F 2=30°,则C 的离心率为________.解析:设点P 在双曲线右支上,由题意,在Rt△F 1PF 2中,|F 1F 2|=2c ,∠PF 1F 2=30°,得|PF 2|=c ,|PF 1|=3c ,根据双曲线的定义:|PF 1|-|PF 2|=2a ,(3-1)c =2a ,e =ca =23-1=3+1.答案:3+1三、解答题11.已知双曲线x 2-y22=1,过点P (1,1)能否作一条直线l ,与双曲线交于A 、B 两点,且点P 是线段AB 的中点?解:法一设点A (x 1,y 1),B (x 2,y 2)在双曲线上,且线段AB 的中点为(x 0,y 0),若直线l 的斜率不存在,显然不符合题意.设经过点P 的直线l 的方程为y -1=k (x -1),即y =kx +1-k .=kx+1-k,2-y22=1,得(2-k2)x2-2k(1-k)x-(1-k)2-2=0(2-k2≠0).①∴x=x1+x22=k1-k2-k2.由题意,得k1-k2-k2=1,解得k=2.当k=2时,方程①成为2x2-4x+3=0.Δ=16-24=-8<0,方程①没有实数解.∴不能作一条直线l与双曲线交于A,B两点,且点P(1,1)是线段AB的中点.法二设A(x1,y1),B(x2,y2),若直线l的斜率不存在,即x1=x2不符合题意,所以由题得x21-y212=1,x22-y222=1,两式相减得(x1+x2)(x1-x2)-y1+y2y1-y22=0,即2-y1-y2x1-x2=0,即直线l斜率k=2,得直线l方程y-1=2(x-1),即y=2x-1,=2x-1,2-y22=1得2x2-4x+3=0,Δ=16-24=-8<0,即直线y=2x-1与双曲线无交点,即所求直线不合题意,所以过点P(1,1)的直线l不存在.12.(2014质检)中心在原点,焦点在x 轴上的一椭圆与一双曲线有共同的焦点F 1,F 2,且|F 1F 2|=213,椭圆的长半轴长与双曲线实半轴长之差为4,离心率之比为3∶7.(1)求这两曲线方程;(2)若P 为这两曲线的一个交点,求cos∠F 1PF 2的值.解:(1)由已知c =13,设椭圆长、短半轴长分别为a 、b ,双曲线实半轴、虚半轴长分别为m 、n ,-m =4,·13a=3·13m,解得a =7,m =3.∴b =6,n =2.∴椭圆方程为x249+y236=1,双曲线方程为x29-y24=1.(2)不妨设F 1、F 2分别为左、右焦点,P 是第一象限的一个交点,则|PF 1|+|PF 2|=14,|PF 1|-|PF 2|=6,∴|PF 1|=10,|PF 2|=4.又|F 1F 2|=213,∴cos∠F 1PF 2=|PF 1|2+|PF 2|2-|F 1F 2|22|PF 1||PF 2|=102+42-21322×10×4=45.第八篇第5节一、选择题1.(2014模拟)抛物线y =2x 2的焦点坐标为()B.(1,0)解析:抛物线y =2x 2,即其标准方程为x 2=12y C.答案:C2.抛物线的焦点为椭圆x24+y29=1的下焦点,顶点在椭圆中心,则抛物线方程为()A.x 2=-45y B.y 2=-45x C.x 2=-413yD.y 2=-413x解析:由椭圆方程知,a 2=9,b 2=4,焦点在y 轴上,下焦点坐标为(0,-c ),其中c =a 2-b 2=5,∴抛物线焦点坐标为(0,-5),∴抛物线方程为x 2=-45y .故选A.答案:A3.已知抛物线y 2=2px ,以过焦点的弦为直径的圆与抛物线准线的位置关系是()A.相离B.相交C.相切D.不确定解析:如图所示,设抛物线焦点弦为AB ,中点为M ,准线为l ,A 1、B 1分别为A 、B 在直线l 上的射影,则|AA 1|=|AF |,|BB 1|=|BF |,于是M 到l 的距离d =12(|AA 1|+|BB 1|)=12(|AF |+|BF |)=12|AB |,故圆与抛物线准线相切.故选C.答案:C4.(2014高三统一考试)已知F 是抛物线y 2=4x 的焦点,过点F 的直线与抛物线交于A ,B 两点,且|AF |=3|BF |,则线段AB 的中点到该抛物线准线的距离为()A.53B.83C.103D.10解析:设点A (x 1,y 1),B (x 2,y 2),其中x 1>0,x 2>0,过A ,B 两点的直线方程为x =my +1,将x =my +1与y 2=4x 联立得y 2-4my -4=0,y 1y 2=-4,1+1=3x 2+1,1x 2=y 214·y 224=y 1y 2216=1,解得x 1=3,x 2=13,故线段AB 的中点到该抛物线的准线x =-1的距离等于x 1+x 22+1=83.故选B.答案:B5.已知F 是抛物线y 2=x 的焦点,A ,B 是该抛物线上的两点,|AF |+|BF |=3,则线段AB 的中点到y 轴的距离为()A.34B.1C.54D.74解析:∵|AF |+|BF |=x A +x B +12=3,∴x A +x B =52.∴线段AB 的中点到y 轴的距离为x A +x B 2=54.故选C.答案:C6.设M (x 0,y 0)为抛物线C :x 2=8y 上一点,F 为抛物线C 的焦点,以F 为圆心、|FM |为半径的圆和抛物线C 的准线相交,则y 0的取值围是()A.(0,2)B.[0,2]C.(2,+∞)D.[2,+∞)解析:∵x 2=8y ,∴焦点F 的坐标为(0,2),准线方程为y =-2.由抛物线的定义知|MF |=y 0+2.以F 为圆心、|FM |为半径的圆的标准方程为x 2+(y -2)2=(y 0+2)2.由于以F 为圆心、|FM |为半径的圆与准线相交,又圆心F 到准线的距离为4,故4<y 0+2,∴y 0>2.故选C.答案:C 二、填空题7.动直线l 的倾斜角为60°,且与抛物线x 2=2py (p >0)交于A ,B 两点,若A ,B 两点的横坐标之和为3,则抛物线的方程为________.解析:设直线l 的方程为y =3x +b ,=3x +b ,2=2py消去y ,得x 2=2p (3x +b ),即x 2-23px -2pb =0,∴x 1+x 2=23p =3,∴p =32,则抛物线的方程为x 2=3y .答案:x 2=3y8.以抛物线x 2=16y 的焦点为圆心,且与抛物线的准线相切的圆的方程为________.解析:抛物线的焦点为F (0,4),准线为y =-4,则圆心为(0,4),半径r =8.所以,圆的方程为x 2+(y -4)2=64.答案:x 2+(y -4)2=649.(2012年高考卷)在直角坐标系xOy 中,直线l 过抛物线y 2=4x 的焦点F ,且与该抛物线相交于A ,B 两点,其中点A 在x 轴上方,若直线l 的倾斜角为60°,则△OAF 的面积为________.解析:∵抛物线y 2=4x ,∴焦点F 的坐标为(1,0).又∵直线l 倾斜角为60°,∴直线斜率为3,∴直线方程为y =3(x -1).联立方程y =3x -1,y 2=4x ,解得x 1=13,y 1=-233,或x 2=3,y 2=23,由已知得A 的坐标为(3,23),∴S △OAF =12|OF |·|y A |=12×1×23= 3.答案:310.已知点P 是抛物线y 2=2x 上的动点,点P 在y 轴上的射影是M ,点A 72,4,则|PA |+|PM |的最小值是________.解析:设点M 在抛物线的准线上的射影为M ′.由已知可得抛物线的准线方程为x =-12,焦点F 坐标为12,0.求|PA |+|PM |的最小值,可先求|PA |+|PM ′|的最小值.由抛物线的定义可知,|PM ′|=|PF |,所以|PA |+|PF |=|PA |+|PM ′|,当点A 、P 、F 在一条直线上时,|PA |+|PF |有最小值|AF |=5,所以|PA |+|PM ′|≥5,又因为|PM ′|=|PM |+12,所以|PA |+|PM |≥5-12=92.答案:92三、解答题11.若抛物线y =2x 2上的两点A (x 1,y 1)、B (x 2,y 2)关于直线l :y =x +m 对称,且x 1x 2=-12,数m 的值.解:法一如图所示,连接AB ,∵A 、B 两点关于直线l 对称,∴AB ⊥l ,且AB 中点M (x 0,y 0)在直线l 上.可设l AB :y =-x +n ,=-x +n ,=2x 2,得2x 2+x -n =0,∴x 1+x 2=-12,x 1x 2=-n2由x 1x 2=-12,得n =1.又x 0=x 1+x 22=-14,y 0=-x 0+n =14+1=54,即点M -14,由点M 在直线l 上,得54=-14+m ,∴m =32.法二∵A 、B 两点在抛物线y =2x 2上.1=2x 21,2=2x 22,∴y 1-y 2=2(x 1+x 2)(x 1-x 2).设AB 中点M (x 0,y 0),则x 1+x 2=2x 0,k AB =y 1-y 2x 1-x 2=4x 0.又AB ⊥l ,∴k AB =-1,从而x 0=-14.又点M 在l 上,∴y 0=x 0+m =m -14,即-14,m∴AB 的方程是y 即y =-x +m -12,代入y =2x 2,得2x 2+x x 1x 2=-m -122=-12,∴m =3212.已知过抛物线y 2=2px (p >0)的焦点,斜率为22的直线交抛物线于A (x 1,y 1),B (x 2,y 2)(x 1<x 2)两点,且|AB |=9.(1)求该抛物线的方程;(2)O 为坐标原点,C 为抛物线上一点,若OC →=OA →+λOB →,求λ的值.解:(1)直线AB 的方程是y y 2=2px 联立,从而有4x 2-5px +p 2=0,所以x 1+x 2=5p4.由抛物线定义得|AB |=x 1+x 2+p =9,所以p =4,从而抛物线方程是y 2=8x .(2)由p =4知4x 2-5px +p 2=0可化为x 2-5x +4=0,从而x 1=1,x 2=4,y 1=-22,y 2=42,从而A (1,-22),B (4,42).设OC →=(x 3,y 3)=(1,-22)+λ(4,42)=(4λ+1,42λ-22),即C (4λ+1,42λ-22),所以[22(2λ-1)]2=8(4λ+1),即(2λ-1)2=4λ+1,解得λ=0或λ=2.。
中职教育数学《平面解析几何-复习课》练习题

第八章 平面解析几何(知识点)1. 直线:(1) 倾斜角α:一条直线l 向上的方向与x 轴的正方向所成的最小正角叫这条直线的倾斜角。
其范围是),0[π(2) 斜率:①倾斜角为090的直线没有斜率;②αtan =k(倾斜角的正切)③经过两点),(),,(222111y x P y x P 的直线的斜率1212x x y y K --= )(21x x ≠(3) 直线的方程①两点式:121121x x x x y y y y --=-- ② 截距式 1=+b y a x③ 斜截式:b kx y += ④点斜式:)(00x x k y y -=- ⑤一般式:0=++C By Ax注:1.若直线l 方程为3x+4y+5=0,则与l 平行的直线可设为3x+4y+C=0;与l 垂直的直线可设为4X-3Y+C=0 2.求直线的方程最后要化成一般式。
(4) 两条直线的位置关系①点),(00y x P 到直线0=++C By Ax 的距离:2200||B A C By Ax d +++=②0:1=++C By Ax l 与0:2=++C By Ax l 平行2221||BA C C d ++=2. 圆的方程(1) 标准方程:222)()(r b y a x =-+-(0>r)其中圆心),(b a ,半径r 。
(2) 一般方程:022=++++F Ey Dx y x (0422>-+F E D )圆心(2,2E D --) 半径:2422F EDr -+=(4)直线和圆的位置关系:主要用几何法,利用圆心到直线的距离d 和半径r 比较。
相交⇔<r d ; 相切⇔=r d ; 相离⇔>r d3. 二次曲线:定义一:平面内到一个定点和一条定直线的距离的比等于定长e 的点的集合,①当0<e<1时,是椭圆.②当e>1时,是双曲线.③当e=1时,是抛物线. 4. 椭圆注:等轴双曲线:(1)b a =(2)离心率2=e (3)渐近线x y ±=6. 抛物线(如右图示) 注:(1)p 的几何意义表示焦点到准线的距离。
中职数学解析几何部分重要题型练习

数学试题解析几何解答题2x 1.已知椭圆4v2r1,过椭圆的左焦点且平行于向量v 1 ,1的直线交椭圆于A ,B两点, 3求弦AB的长.2.设直线y x2x 22与双曲线y21交于A , B两点,求弦AB的长.23.已知抛物线y 2px p 0的焦点为F,过焦点F的弦AB的长为4p,求直线AB的斜率.24.已知抛物线y 2px p 0与直线y x 1相交于A ,B两点,若AB的中点在圆x2 y25上,求抛物线的方程.2uuu uuu 5.已知过抛物线y 2x的焦点且倾斜角为45的直线交抛物线于A ,B两点,求OAgOB .2 27.已知双曲线—工1上一点P到它的一个焦点F i的距离为15,求点P到另16 9圆,求实数k的取值范围.距离.2 26.求椭圆和1上的点到直线l:x y 7 0的最长距离和最短距离.2X若方程一k 91表示双曲线,求实数k的取值范围;若该方程表示焦点在y轴上的椭个焦点F2的59.在抛物线 y 12x 上求一点P ,使该点P 到焦点的距离等于 9.2 2x V10.若点P 是椭圆 1上的一点,F 1和F 2是焦点,且 F 1PF 2 60,求 FfF 2的面25 16积.11.已知双曲线的中心在原点,焦点F,和F 2在坐标轴上,离心率为,2,且双曲线过点2, 2 ,( 1)求双曲线的方程;(2)若点 M 在第一象限而且是渐近线上的点,又MF 1 MF 2,求点M 的坐标;(3)求 MhF 2的面积.2 212.已知双曲线与椭圆—也 9 251有公共焦点F 1和F 2,它们的离心率之和为14上,(1)求双曲线的标准方程;(2)设点P 是椭圆与双曲线的一个交点,求cos F 1PF 2的值.数学试题解析几何解答题(答案) 23.已知抛物线y 2px p 0的焦点为F ,过焦点F的弦AB的长为4 p,求直线AB的斜2x 1.已知椭圆4 2 y3 1,过椭圆的左焦点且平行于向量 1 ,1的直线交椭圆于A ,B两点,率.解:设A, B两点的坐标为x1 , y1, x2, y2因为AB 4p,由抛物线的定义可得,所以x1x23p4,b23,c21,所以c 1由y22px p 0可得,抛物线的焦点F的坐标为所以左焦点坐标为1,01 X1所以直线AB的方程为设A,B两点的坐标为X1,y1由题意列方程组,得3x24y y X 1所以X18X2 7,1gX287 22X1X2X1X24x1x222288 *y2X1X249所以AB讨X1X22y1得,yX2126449因此所求弦22 y2求弦AB的长.2解:由方程—42 y32a0 0,即y设直线AB的斜率为k,则其方程为y2.设直线y,y20,整理得32 2887 492887x2 8x 8 0 由题意列方程组,得所以x-i x2因此所求直线4.已知抛物线242pxpk,整理得kx -2pk2kAB的斜率为1或1.2p223p,整理得k2y 2px p 0与直线yx2 y25上,求抛物线的方程.k2x2pk22p2| 2p k423k,解得k1相交于A , B两点,若AB的中点在圆24AB的长为一.7解:设A, B两点的坐标为x1 , y1, x2, y2则其中点的坐标为x22x 2与双曲线xr y 1交于A,B两点,求弦AB的长.X1 X22由题意,列方程组,解:由题意列方程组, 即x2 8x 10 8x 10X2所以2pX,整理得x 1 x2 2 2p x 1 0所以X1X28, X1gX210X X22X2X24x1x26440 24*y22X12X224所以AB V X12X2y2y2』24 2 朋2 2得x 2y 2 0,整理得x2y x 20,设A,B两点的坐标为x1 , y1,因此所求弦AB的长为4 3 .y1所以X2 2px1 1 x21 x-1y2AB的中点坐标为p 1因为该中点在圆x2解得p 1或p 2x2 2 2p2y 5上,所以 2小p 2pp2 5(不合题意,舍去),所以所求抛物线的方程为y2 2 px2 uuu uuu5.已知过抛物线 y 2x 的焦点且倾斜角为 45的直线交抛物线于 A ,B 两点,求OAgOB . 解:由 y 2x 得 2p 2 , -12 2 1所以抛物线的焦点坐标为 1,02又直线的倾斜角为45,所以斜率为1,因此直线AB1的方程为y x —2设A,B 两点的坐标为x 1,1 - X 2 ,22y 2xA由题意列方程组,得〔,整理得x 2 3x1 0 y x -42所以 x 1 x 2 3, x ,gx 21 41 111 1yey ? x ! - x 22“22 X 1 X 242uur urn所以 OAgOB 为,y g x 2,y 2 NX 2 y 1y 2 3 1 22 26. 求椭圆一1上的点到直线l : x y 7 0的最长距离和最短距离.916解:1作直线l :x y 7 0的平行线并与椭圆相切, 则所作平行线方程可设为 x y D 0由题意列方程组,得16x 2 9y 2 144 0 整理得 25x 2 18Dx 9D 2144 0x y D 0因为所作直线x y D 0与椭圆相切,所以 =324D 24 25 9D 2 144解得D 2 25 ,D527.已知双曲线—-16 < 291上一点P 到它的一个焦点 F 1的距离为15,求点P 到另一个焦点F 2的距离.2 2解:由双曲线方程—y 21,得 a 16 ,a 4,2a816 9根据双曲线的定义可知,PF 1 | PF 2 8所以PF 28PF18 15PF 2 23或 PF 27因此所求点P 到另一个焦点F 2的距离为23或7.2 28.若方程 xy1表示双曲线,求实数k 的取值范围;k 94 k若该方程表示焦点在 y 轴上的椭圆,求实数k 的取值范围.解: (1) 若方程表示双曲线,则须满足条件k-9 4 k解得4 k 9.k 9 0(2) 若方程表示焦点在 y 轴上的椭圆, 则须满足条件4 k 0k 94 kk 9解得k 4,即k 9.k R9.在抛物线 y 12x 上求一点P ,使该点P 到焦点的距离等于 9.解:设点 P 坐标为 x , y ,由 y 2 12x ,得 2 p 12 , p 6,-P 32因为P 到焦点的距离为9,则由抛物线的定义可知 P 到准线的距离也为 9 所以9 — x 3 x, x 6,把x 6代入方程y 12x ,解得y 6、22所以所求点P 的坐标为 6,6'- 2或6 - 2 .所以所作直线方程x y 5 0或x y 5因此所求最长距离为 6 2,最短距离为 2 .72 210.若点P 是椭圆 — — 1上的一点,F i 和F 2是焦点,且F 1PF 2 60,求 FfF 2的面25 16积. 2 2 解:由椭圆方程-y 1 得:a 2 25 ,b 2 16 c 2 25 16 9,2c 625 16 由椭圆的定义可知|PF 1 PF 2 2a 10 JF 1F 2I 2c 6 UU LU MF 1uuuu MF 2,可得MR uuuu2 x , x ,MF 2所以 2 x 2 xF 1F2所以S2c 4UULLT UUJU ULUUrMF 2 即 MF 1gMF 2 0x 2 0,解得x 2 2 ,x 2,所以点M 的坐标为,2,22 F 1F 2 2PF 1 2PF2 PF 1 P 2平2在 PF 1F 2中,由余弦定理,得 2 PF 」]PF 2 cos602 PF 1 | PF 2|PF ^ PF 2MF 1F 2F 1F 2 近2门.12.已知双曲线与椭圆2 2£ y 9251有公共焦点F 1和F 2,它们的离心率之和为 145 (1)求双曲所以 36 100 3PF 1 PF 2,解得 PF j|PF 264 3 线的标准方程;(2)设点P 是椭圆与双曲线的一个交点,求cos F 1PF 2的值.所以S PRF 2 1 P F JI PF 2 sin602 1 64 16、.3 2 3 2 3 11.已知双曲线的中心在原点,焦点 F 1和F 2在坐标轴上,离心率为 、2,且双曲线过点 2, 2 ,(1)求双曲线的方程; (2)若点 M 在第一象限而且是渐近线上的点,又 解:(1)由椭圆方程xy1得,c 225 9 16 ,c 4925由椭圆方程容易求得椭圆的离心率为 4-,所以双 良曲线的离心率为14 上2,5554由此可求得双曲线中2, a22,所以b2 2c a 16 412,焦点为在y 轴,2 2MF 1 MF 2,求点M 的坐标;(3)求 MF^?的面积. 解:(1)由双曲线离心率为 ,2可知所求双曲线为等轴双曲线, 设其方程为x 2 y 2 a 2或y 2 x 2 a 2,因为双曲线经过点 2, 2 , 所以4 2 a 2或2 4 a 2,可得a 2 2或a 2 2 (不合题意舍去) 因此所求双曲线方程为 x 2 y 2 2 . (2)由题意双曲线的渐近线方程为 y x 因为点M 在第一象限而且是渐近线上的点,所以可设其坐标为 x , x x 022所以双曲线的方程为y —1.412(2)设| PF 」|PF 』PF 1 PF 210 根据双曲线和椭圆的定义可得:PF 1 PF 24解得 PF 1 7 , PF 2 3,又 F 1F 2 2c 8所以 cos F 1PF 2PF 『|PF 2『|吋222 2 272 32 82 1 2|PF 1|PF 22 7 37由双曲线方程x 2y 22,得c 22 2 4 ,c 21因此所求值为 一.所以两焦点坐标为2 ,0, 2,07。
解析几何经典练习题(含答案)

解析几何经典练习题(含答案)题目一:已知平面直角坐标系中两点A(-3,4)和B(5,-2),求直线AB的斜率和方程。
解答:直线AB的斜率可以使用斜率公式计算:斜率 = (y2 - y1) / (x2 - x1)其中,A的坐标为(x1, y1) = (-3, 4),B的坐标为(x2, y2) = (5, -2)。
斜率 = (-2 - 4) / (5 - (-3)) = -6 / 8 = -3/4直线AB的方程可以使用点斜式来表示:y - y1 = m(x - x1)其中,m为斜率,(x1, y1)为直线上的任意一点。
将斜率和点A的坐标代入得到方程:y - 4 = (-3/4)(x + 3)化简得到直线AB的方程为:4y - 16 = -3x - 9整理得到标准形式方程:3x + 4y = 7答案:直线AB的斜率为 -3/4,方程为 3x + 4y = 7。
题目二:已知直线L的斜率为2,经过点A(3,-1),求直线L的方程。
解答:直线L的方程可以使用点斜式来表示:y - y1 = m(x - x1)其中,m为斜率,(x1, y1)为直线上的任意一点。
将斜率和点A的坐标代入得到方程:y - (-1) = 2(x - 3)化简得到直线L的方程为:y + 1 = 2x - 6整理得到标准形式方程:2x - y = 7答案:直线L的方程为 2x - y = 7。
题目三:已知直线L的方程为 3x + y = 5,求直线L的斜率和经过点A (2,-1)的方程。
解答:直线L的斜率可以从方程的标准形式中直接读取:3x + y = 5将方程转化成斜截式形式:y = -3x + 5可以看出直线L的斜率为-3。
经过点A(2,-1)的直线方程可以使用点斜式来表示:y - y1 = m(x - x1)其中,m为斜率,(x1, y1)为直线上的任意一点。
将斜率和点A的坐标代入得到方程:y - (-1) = -3(x - 2)化简得到通过点A的直线方程为:y + 1 = -3x + 6整理得到标准形式方程:3x + y = 5答案:直线L的斜率为-3,经过点A(2,-1)的方程为 3x + y = 5。
职高数学平面解析几何练习

职高数学平面解析几何练习
1.判断下列命题的真假:
(1)点A(-8,8)在曲线х²-у²=0上
(2)一动点到两坐标轴的距离相等的点的轨迹方程方程是х=у
(3)已知点A(1,0)B(-5,0),线段AB的垂直平分线的方程是х=-2
(4)直线垂直平分线的方程是у=3х+5与直线у=-х+5的交点不是点(0,5)(5)直线ι在х轴y轴上的截距分别为a,b(a≠b),则ι的斜率是b/a (6)对任意的m值,直线у=6х+m都与直线у=-1/6х垂直
(7)对任一不等于2的实数k,直线2x+3y+k=0与直线2x+3y+2=0平行
(8)通过坐标原点的任一条直线都是椭圆b²х²+a²y²=a²b²的对称轴
2.解答题
(1)过点(3,5)(5,-5)的直线方程是
(2)过点P(1,1)且与直线2х+3y+1=0平行的直线方程是
(3)椭圆11х²+20y²=220的焦距等于
(4)抛物线х²=4y的准线方程是
3.已知ΔABC顶点的坐标A(3,5)B(0,0)C(6,2),BC边的中点为M,求直线AB,AC 和AM的方程
4.已知点A(2,0)与点B(8,0)动点M与点A的距离等于它与点B距离的⅓,求动点M的轨迹方程
5.已知直线x-2y+2=0与椭圆x²+4y²=4相交于A,B两点,求A,B两点的距离12.求到点A(-1,0)和直线x=3距离相等的点的轨迹方程。
中职解析几何真题大题答案

中职解析几何真题大题答案近年来,中职数学考试中的解析几何真题占据了相当大的比重。
解析几何作为数学中的重要分支,对于学生的几何思维能力和问题解决能力有较高的要求。
下面,我们将解析几何真题中几个常见大题的答案进行分析和解释,帮助学生更好地掌握解析几何的考点和解题技巧。
第一题:已知三角形ABC的三个顶点A(1,-2),B(3,4),C(-5,0),求三角形ABC的周长。
解析:由题目可以得知三角形ABC的三个顶点坐标分别为A(1,-2),B(3,4),C(-5,0)。
根据坐标之间的距离公式d=√((x2-x1)^2+(y2-y1)^2),可以求出AB、BC、AC的长度。
AB的长度为√((3-1)^2+(4-(-2))^2)=√((2^2)+(6^2))=√(4+36)=√40=2√10。
BC的长度为√((-5-3)^2+(0-4)^2)=√((-8)^2+(-4)^2)=√(64+16)=√80=4√5。
AC的长度为√((1-(-5))^2+(-2-0)^2)=√((6^2)+(-2)^2)=√(36+4)=√40=2√10。
三角形ABC的周长为AB+BC+AC=2√10+4√5+2√10=4√10+4√5。
第二题:已知抛物线y=ax^2+bx+c的顶点坐标为V(2,-4),并且经过点P(-1,9),求解析方程y=ax^2+bx+c的系数a、b、c。
解析:首先,根据抛物线的性质,抛物线的顶点坐标V(x0,y0)可以求出抛物线的解析式为y=a(x-x0)^2+y0。
所以,我们将已知的顶点坐标代入解析式中。
将V(2,-4)代入解析式,得到y=a(x-2)^2+(-4)。
然后,我们再将已知的点P(-1,9)代入抛物线的解析式中,得到9=a(-1-2)^2+(-4)。
整理得到9=a(-3)^2+(-4),即9=9a-4。
解方程得到a=1。
所以,抛物线的解析式为y=(x-2)^2-4。
进一步展开,得到y=x^2-4x+4-4,即y=x^2-4x。
(word完整版)中职数学解析几何部分重要题型练习

数学试题 解析几何解答题1. 已知椭圆22143x y +=,过椭圆的左焦点且平行于向量()11v =,的直线交椭圆于A B ,两点,求弦AB 的长.2. 设直线2y x =-与双曲线2212x y -=交于A B ,两点,求弦AB 的长.3. 已知抛物线()220y pxp =>的焦点为F ,过焦点F 的弦AB 的长为4p ,求直线AB 的斜率.4. 已知抛物线()220y pxp =>与直线1y x =-相交于A B ,两点,若AB 的中点在圆225x y +=上,求抛物线的方程.5. 已知过抛物线22y x =的焦点且倾斜角为45︒的直线交抛物线于A B ,两点,求OA OB .6. 求椭圆221916x y +=上的点到直线:70l x y +-=的最长距离和最短距离.7. 已知双曲线221169x y -=上一点P 到它的一个焦点1F 的距离为15,求点P 到另一个焦点2F 的距离.8.若方程22194x yk k-=--表示双曲线,求实数k的取值范围;若该方程表示焦点在y轴上的椭圆,求实数k的取值范围.9.在抛物线212y x=上求一点P,使该点P到焦点的距离等于9.10.若点P是椭圆2212516x y+=上的一点,1F和2F是焦点,且1260F PF∠=︒,求12F PF∆的面积.11. 已知双曲线的中心在原点,焦点1F 和2F 在坐标轴上,,且双曲线过点(2,,(1)求双曲线的方程;(2)若点M 在第一象限而且是渐近线上的点,又12MF MF ⊥,求点M 的坐标;(3)求12MF F ∆的面积.12. 已知双曲线与椭圆221925x y +=有公共焦点1F 和2F ,它们的离心率之和为145,(1)求双曲线的标准方程;(2)设点P 是椭圆与双曲线的一个交点,求12cos F PF ∠的值.数学试题 解析几何解答题(答案)1. 已知椭圆22143x y +=,过椭圆的左焦点且平行于向量()11v =,的直线交椭圆于A B ,两点,求弦AB 的长.解:由方程22143x y +=得,222431a b c ===,,,所以1c = 所以左焦点坐标为()10-,所以直线AB 的方程为()()100x y +--=,即1y x =+ 设A B ,两点的坐标为()()1122x y x y ,,,由题意列方程组,得22341201x y y x ⎧+-=⎨=+⎩,整理得27880x x +-=所以12128877x x x x +=-=-,()()221212126432288449749x x x x x x -=+-=+=()()22121228849y y x x -=-=所以AB =247== 因此所求弦AB 的长为247.2. 设直线2y x =-与双曲线2212x y -=交于A B ,两点,求弦AB 的长. 解:由题意列方程组,得222202x y y x ⎧--=⎨=-⎩,整理得28100x x -+-=即28100x x -+=,设A B ,两点的坐标为()()1122x y x y ,,,所以1212810x x x x +==,()()221212124644024x x x x x x -=+-=-=()()22121224y y x x -=-=所以AB ===因此所求弦AB 的长为3. 已知抛物线()220y pxp =>的焦点为F ,过焦点F 的弦AB 的长为4p ,求直线AB 的斜率.解:设A B ,两点的坐标为()()1122x y x y ,,,因为4AB p =,由抛物线的定义可得,124p p x x =++ 所以123x x p += 由()220y pxp =>可得,抛物线的焦点F 的坐标为02p F ⎛⎫⎪⎝⎭, 设直线AB 的斜率为k ,则其方程为2p y k x ⎛⎫=- ⎪⎝⎭由题意列方程组,得222y pxpk y kx ⎧=⎪⎨=-⎪⎩,整理得()22222204p k k x pk p x -++= 所以212223pk px x p k++==,整理得2223k k +=,解得1k =± 因此所求直线AB 的斜率为1或1-.4. 已知抛物线()220y pxp =>与直线1y x =-相交于A B ,两点,若AB 的中点在圆225x y +=上,求抛物线的方程.解:设A B ,两点的坐标为()()1122x y x y ,,,则其中点的坐标为121222x x y y ++⎛⎫⎪⎝⎭,由题意,列方程组,得221y pxy x ⎧=⎨=-⎩,整理得()22210x p x -++=所以1212221x x p x x +=+=,1212121122y y x x x x p +=-+-=+-= 所以AB 的中点坐标为()1p p +,因为该中点在圆225x y +=上,所以22215p p p +++= 解得1p =或2p =-(不合题意,舍去), 所以所求抛物线的方程为22y px =5. 已知过抛物线22y x =的焦点且倾斜角为45︒的直线交抛物线于A B ,两点,求OA OB . 解:由22y x =得22p =,122p = 所以抛物线的焦点坐标为102⎛⎫⎪⎝⎭, 又直线的倾斜角为45︒,所以斜率为1,因此直线AB 的方程为12y x =-设A B ,两点的坐标为()()1122x y x y ,,,由题意列方程组,得2212y xy x ⎧=⎪⎨=-⎪⎩,整理得21304x x -+= 所以1212134x x x x +==,()12121212111112224y y x x x x x x ⎛⎫⎛⎫=--=-++=- ⎪⎪⎝⎭⎝⎭所以()()11221212312OA OB x y x y x x y y ==+=-=,,6. 求椭圆221916x y +=上的点到直线:70l x y +-=的最长距离和最短距离. 解:作直线:70l x y +-=的平行线并与椭圆相切,则所作平行线方程可设为0x y D ++=由题意列方程组,得2216914400x y x y D ⎧+-=⎨++=⎩,整理得22251891440x Dx D ++-=因为所作直线0x y D ++=与椭圆相切,所以()2232442591440D D ∆-⨯⨯-==解得2255DD ==±,所以所作直线方程5050x yx y ++=+-=或由题意可知,所作直线到:70l x y +-=的距离即为所求距离 所以12d d ====因此所求最长距离为.7. 已知双曲线221169x y -=上一点P 到它的一个焦点1F 的距离为15,求点P 到另一个焦点2F 的距离.解:由双曲线方程221169x y -=,得2164,28a a a ===, 根据双曲线的定义可知,128PF PF -=± 所以218815PF PF =±+=±+22237PF PF ==或因此所求点P 到另一个焦点2F 的距离为23或7.8. 若方程22194x y k k-=--表示双曲线,求实数k 的取值范围;若该方程表示焦点在y 轴上的椭圆,求实数k 的取值范围.解:(1)若方程表示双曲线,则须满足条件()()940k ->k-解得49k <<.(2)若方程表示焦点在y 轴上的椭圆,则须满足条件()904094k k k k⎧->⎪-<⎨⎪-<--⎩解得94k k k R >⎧⎪>⎨⎪∈⎩,即9k >.9. 在抛物线212y x =上求一点P ,使该点P 到焦点的距离等于9.解:设点P 坐标为()x y ,,由212y x =,得212632pp p ===,, 因为P 到焦点的距离为9,则由抛物线的定义可知P 到准线的距离也为9所以93,62px x x =+=+=,把6x =代入方程212y x =,解得y =±所以所求点P的坐标为(6或(6-,. 10. 若点P 是椭圆2212516x y +=上的一点,1F 和2F 是焦点,且1260F PF ∠=︒,求12F PF ∆的面积.解:由椭圆方程2212516x y +=得:222251625169,26a b c c ==∴=-==, 由椭圆的定义可知121221026PF PF a F F c +====,在12PF F ∆中,由余弦定理,得2221212122cos60F F PF PF PF PF =+-︒()21212122PF PF PF PF PF PF =+--所以12361003PF PF =-,解得12643PF PF =所以12121164sin 6022323PF F S PF PF ∆=⨯︒=⨯⨯=. 11. 已知双曲线的中心在原点,焦点1F 和2F 在坐标轴上,离心率为,且双曲线过点(2,,(1)求双曲线的方程;(2)若点M 在第一象限而且是渐近线上的点,又12MF MF ⊥,求点M 的坐标;(3)求12MF F ∆的面积. 解:(1)由双曲线离心率为可知所求双曲线为等轴双曲线,设其方程为222222x y a y x a -=-=或,因为双曲线经过点(2,, 所以224224a a -=-=或,可得2222a a ==-或(不合题意舍去) 因此所求双曲线方程为222x y -=. (2)由题意双曲线的渐近线方程为y x =±因为点M 在第一象限而且是渐近线上的点,所以可设其坐标为()()0x x x >,由双曲线方程222x y -=,得22242c c =+==, 所以两焦点坐标为()()2020-,,, 由12MF MF ⊥,可得12120MF MF MF MF ⊥=即()()1222MF x x MF x x =---=--,,,所以()()222202x x x x x ----===,解得,M的坐标为.1224F c ==所以121212MF F S F F ∆=⨯= 12. 已知双曲线与椭圆221925x y +=有公共焦点1F 和2F ,它们的离心率之和为145,(1)求双曲线的标准方程;(2)设点P 是椭圆与双曲线的一个交点,求12cos F PF ∠的值.解:(1)由椭圆方程221925x y +=得,2259164c c =-==, 由椭圆方程容易求得椭圆的离心率为45,所以双曲线的离心率为144255-=, 由此可求得双曲线中42a=,2a =,所以22216412b c a =-=-=,焦点为在y 轴,所以双曲线的方程为221412y x -=. (2)设12PF PF >根据双曲线和椭圆的定义可得:1212104PF PF PF PF ⎧+=⎪⎨-=⎪⎩解得1273PF PF ==,,又1228F F c == 所以222222121212127381cos 22737PF PF F F F PF PF PF +-+-∠===-⨯⨯因此所求值为17-.。
(完整word)20解析几何A(中职数学春季高考练习题)

学校______________班级______________专业______________考试号______________姓名______________数学试题 解析几何A. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分100分,考试时间90分钟,考试结束后,将本试卷和答题卡一并交回.. 本次考试允许使用函数型计算器,凡使用计算器的题目,最后结果精确到0.01.第Ⅰ卷(选择题,共60分)30小题,每小题2分,共60分.在每小题列出的四个选项中,只有一项. 若圆22(2)()5x y b -+-=经过原点且圆心在第四象限,则b 的值为 A .1B .1-C .3D .3-. 若直线20x ay ++=和230x y +=互相平行,则a 等于 A .23B .23-C .32D .32-. 若直线x y m +=与圆22x y m +=相切,则m 的值为A .2BC .1D .12. 直线250y x -+=与圆224220x y x y +-++=的位置关系是 A .相离B .相切C .相交且过圆心D .相交且不过圆心 . 如果方程222x ky +=表示焦点在y 轴上的椭圆,则实数k 的取值范围是 A .0k >B .1k >C .01k <<D .02k <<. 一椭圆的长轴是短轴的2倍,则其离心率是A .34BCD .12. 直线20mx y -+=经过两条直线2x y +=与0x y -=的交点,则m 的值是 A .1B .1-C .3-D .38.过点(的直线l 与圆221x y +=有两个交点则直线l 斜率的取值范围是A .(0,1)B .(1,0)-C .[1,1]-D .(1,1)-9. 若圆的方程22290x y ax +++=的圆心坐标是(5,0),则它的半径是A .3B C .5D .410. “直线1l 与直线2l 互相平行”是“直线1l 的斜率与直线2l 的斜率相等”的A .充分条件B .必要条件C .充要条件D .既不充分也不必要条件11. 如果点(,)P x y 到两坐标轴距离相等,则,x y 所满足的方程是A .y x =B .y x =-C .y x =D .220x y -=12.方程y =A .一条直线B .一个圆C .两条直线D .半个圆13. 若直线0ax by c ++=在第一、二、三象限,则有A .0,0ab bc >>B .0,0ab bc ><C .0,0ab bc <<D .0,0ab bc <>14. 过圆2262150x y x y ++--=是圆心,法向量为(1,1)n =的直线方程是A .20x y --=B .20x y -+=C .20x y ++=D .20x y +-=15. 直线l 过点(2,0)-,当直线l 与圆222x y x +=有两个交点时,其斜率k 的取值范围是A.(-B.(C.44⎛⎫-⎪ ⎪⎝⎭D .11,88⎛⎫- ⎪⎝⎭16. 点()3,9关于直线3100x y +-=对称的点的坐标是A .()1,3--B .()17,9-C .()1,3-D .()17,9-17. 已知两点()15,0F -、()25,0F ,与它们的距离的差的绝对值等于6的点的轨迹方程是学校______________班级______________专业______________考试号______________姓名______________A .221916y x -= B .221169x y -= C .221916x y -= D .221169y x -= . 方程22121x y k k -=++表示焦点在y 轴上的双曲线,则k 的取值范围是 A .1k >B .1k <-C .2k <D .2k <-. 双曲线22169144x y -=的渐近线方程是 A .43y x =±B .34y x =±C .169y x =±D .916y x =±. 若双曲线的渐近线方程为y =±,则它的离心率是 A .1BC D .不存在. 双曲线2213x y m-=的离心率是方程221150x x -+=的根,则实数m 的值是 A .72-B .9-C .4-D .2-. 双曲线221169x y -=与椭圆2212516x y +=的交点个数是 A .1个B .2个C .3个D .4个. 若0mn >,则方程22mx ny mn -=所表示的曲线是A .焦点在x 轴上的双曲线B .焦点在y 轴上的双曲线C .焦点在x 轴上,也可能在y 轴上D .可能不是双曲线. 若抛物线2y px =的焦点与椭圆221259x y +=的右焦点重合,则p 的值是 A .4B .16C .32D .64. 过抛物线()220y px p =>的焦点F ,作垂直于x 轴的垂线,交抛物线A 、B 两点,则AB的长是A .pB .2pC .4pD .不能确定26. 抛物线218y x =-的准线方程是A .132x =B .12x =C .2y =D .4y =27. 已知抛物线的准线方程是1y =-,则抛物线的方程是A .24y x =B .24y x =-C .24x y =D .24x y =-28. 焦点为F 的抛物线24y x =内有一点()2,1A ,p 为抛物线上一点,则PA PF +的最小值为A .1B .2C .3D .429. 抛物线240y x +=上一点到准线的距离为8,则该点的横坐标是A .7B .6C .7-D .6-30. 过点()2,6A -的抛物线方程是A .218y x =-B .216x y =-C .218y x =-或223x y =D .29y x =- 第Ⅱ卷(非选择题,共40分)二、填空题(本大题共4小题,每小题3分,共12分)31. 若22(1)20x y x y λλλ++-++=表示圆,则λ的取值范围是_______________________.32. 椭圆2255x ky -=的一个焦点是(0,2),则k =_______________________.33. 若22tan sin 1x y αα+=表示双曲线,则α所在的象限为_______________________.学校______________班级______________专业______________考试号______________姓名______________. 设A ,B 为抛物线上两点,他们到抛物线焦点的距离分别是2和4,则AB 中点到准线的距离为_______________________.4小题,共28分). 设直线2310x y ++=和圆22230x y x +--=相交于A ,B 两点,求弦AB 的垂直平分线。
解析几何专项训练试题答案

解析几何专项训练试题答案一、选择题1. 若点A(2,3)关于直线x=3的对称点为A',则A'的坐标为:A. (4,3)B. (2,3)C. (1,3)D. (5,3)答案:D解析:点A(2,3)关于直线x=3的对称点A'的横坐标为3-(2-3)=4,纵坐标不变,因此A'的坐标为(4,3)。
2. 已知圆的标准方程为$(x-a)^2+(y-b)^2=r^2$,则其圆心坐标为:A. (a, b)B. (a, r)C. (b, r)D. (r, a)答案:A解析:根据圆的标准方程$(x-a)^2+(y-b)^2=r^2$,可知圆心坐标为(a, b)。
3. 直线2x-3y=6的斜率为:A. 2/3B. -2/3C. 3/2D. -3/2答案:B解析:直线方程2x-3y=6可以转化为y=(2/3)x-2,其斜率为2/3,因此答案为-2/3。
4. 已知三角形ABC的三个顶点分别为A(1,2),B(4,6),C(7,2),求三角形ABC的面积。
A. 4B. 6C. 8D. 10答案:C解析:首先计算线段AB和AC的斜率,分别为1和-1,说明AB和AC 垂直。
然后计算AB的长度为3,由于AC与AB垂直,所以三角形ABC 为直角三角形,其面积为1/2 * AB长度 * BC长度 = 1/2 * 3 * 5 = 7.5。
选项中没有7.5,但最接近的是8,因此选择C。
5. 已知椭圆的标准方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,则其焦点坐标为:A. (a, 0)B. (0, b)C. (a, b)D. (0, 0)答案:D解析:椭圆的标准方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,其焦点位于y轴上,且焦距为2c,因此焦点坐标为(0, c)或(0, -c)。
由于题目未给出具体数值,无法确定c的值,但焦点坐标的形式为(0, c),因此答案为D。
职中数学第八章---平面解析几何

第八章 平面解析几何1.到两坐标轴的距离相等的点的轨迹方程是y=x.( )2、双曲线离心率e<1 ( )5、椭圆上的任一点到它的两焦点的距离的和都等于短轴长。
( )6、方程x 2+y 2+λx=0表示圆,则λ的取值范围是任意实数。
( )8、任意直线都有斜率。
( )9、直线2x —3y+1=0与圆x 2+y 2=1相交。
( )6、已知m ≠0,则过点(1,-1)的直线ax +3my +2a=0的斜率是 ( )A 、3B 、-3C 、31D 、-31 7、直线L 1:ax +2y +6=0与直线L 2:x +(a -1)y +a 2-1=0平行,则a= ( )A 、-1B 、2C 、-1,2D 、0,18、圆x 2-8x +y 2+12=0与直线3x +y=0的位置关系是 ( )A 、相切B 、相离C 、相交D 、无法确定9、如果椭圆的短轴长、焦距、长轴长依次成等差数列,则其离心率e=( ) A 、54 B 、53 C 、43 D 、32 10、抛物线y=4x 2的焦点坐标是 ( )A 、(1,0)B 、(0,1)C 、(0,161)D 、(161,0) 5、直线L 过点A (-2,-3),且在两坐标轴上的截距相等,则L 的方程为______6、若直线L 1与L 2的斜率是方程4x 2-15x -4=0的两根,则L 1与L 2的夹角为_______。
7、过圆x 2+y 2=13上一点(2,-3)的切线方程是_____________。
8、椭圆m x 2+42y =1的焦距为2,则m 的值为___________。
9、双曲线x 2-3y 2=1的两条渐近线的夹角是______________。
10、顶点在原点,且经过点P (-1,2)的抛物线标准方程为_____________。
三、解答题(共70分)1、已知:求(1)的值(2)(10分)2、已知:ABC 的三顶点为A (6,-2),B (-1,5),C (5,5),求ABC 的外接圆方程。
解析几何 专题训练
解析几何专题训练一、选择题(本大题共12小题,每小题5分,共60分).A. B. C. D.2.过点(-1,3)且垂直于直线x-2y=-3 的直线方程为(A.2x+y-1=0B.2x+y-5=0C.x+2y-5=0D.x-2y+7=03.如果直线ax+2y+2=0与直线3x -y-2=0 平行,那么实数a等于( ).A.-6B.-3y巩固知识提升能力针对训练高效复习C.- 32D.234.点(1,2)到直线x+2y=-5的距离为( )A.52B.√5 C.2√5 D.√525.设圆C的方程为(x−3)2+(y−2)2=2,直线L的方程为y= -x+3,点P的坐标为(2,1),那么( ).A点P在直线L上,但不在圆C上B.点P在圆C上,但不在直线L上C.点P既在圆C上,又在直线L上D.点P既不在直线L上,也不在圆C上6.圆C :x2+y2-4x +6y=0的圆心坐标是( ).A.(-2,3)B.(-2,3)C.(-2, -3)D.(2,-3)7.已知椭圆C的中心在(0,0)点,长轴在x轴上,离心率为√32,且椭圆C上一点到其两个焦点的距离之和为12,则椭圆C的方程为( ).A.x236+y29=1 B.x29+y236=1 C.x24+y29=1 D.x29+y24=1巩固知识提升能力针对训练高效复习巩固知识 提升能力 针对训练 高效复习8.已知椭圆x 225+y 2m 2=1 (m 为正实数)的左焦点为F 1(-4,0),则m=( ). A.2 B.3 C.4 D.99.已知M(2,0),N(- 2,0),||PM|-|PN||= 3,则动点P 的轨迹是( ). A.圆 B.椭圆 C.抛物线 D.双曲线10.双曲线x 2- y 23=1的一个焦点与它的渐近线的距离为( )A.1B.√2C.√3D.2 11.过点P(1,-2)的抛物线的标准方程是( ).A.y 2=4x 或x 2=12y B.y 2=4x C.y 2=4x 或x 2=- 12y D. x 2=- 12y 12.抛物线的标准方程是y 2=-12x,则它的焦点坐标是( ). A.(3,0) B.(-3,0) C.(0,3) D.(0,-3)二、填空题(本大题共5小题,每小题4分,共20分).13.直线l:4x- 3y+1=0平行 ,且距离为2的直线方程 14.过点(-3,0)和(2,m)的直线与x-2y- 1 =0互相垂直的条件是 15.椭圆x 225 + y 29=1的长半轴的长是16.与x 29 - y 216=1有相同的渐近线,且过点(0,-8)的双曲线方程为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学校______________班级______________专业______________考试号______________姓名______________数学试题 解析几何解答题. 已知椭圆22143x y +=,过椭圆的左焦点且平行于向量()11v = ,的直线交椭圆于A B ,两点,求弦AB 的长. . 设直线2y x =-与双曲线2212x y -=交于A B ,两点,求弦AB 的长. 3. 已知抛物线()220y px p =>的焦点为F ,过焦点F 的弦AB 的长为4p ,求直线AB 的斜率.4. 已知抛物线()220y pxp =>与直线1y x =-相交于A B ,两点,若AB 的中点在圆225x y +=上,求抛物线的方程.学校______________班级______________专业______________考试号______________姓名______________. 已知过抛物线22y x =的焦点且倾斜角为45︒的直线交抛物线于A B ,两点,求OA OB.. 求椭圆221916x y +=上的点到直线:70l x y +-=的最长距离和最短距离. 7. 已知双曲线221169x y -=上一点P 到它的一个焦点1F 的距离为15,求点P 到另一个焦点2F 的距离.8. 若方程22194x y k k-=--表示双曲线,求实数k 的取值范围;若该方程表示焦点在y 轴上的椭圆,求实数k 的取值范围.学校______________班级______________专业______________考试号______________姓名______________. 在抛物线212y x =上求一点P ,使该点P 到焦点的距离等于9. . 若点P 是椭圆2212516x y +=上的一点,1F 和2F 是焦点,且1260F PF ∠=︒,求12F PF ∆的面积. 11. 已知双曲线的中心在原点,焦点1F 和2F 在坐标轴上,离心率为,且双曲线过点(2-,,(1)求双曲线的方程;(2)若点M 在第一象限而且是渐近线上的点,又12MF MF ⊥,求点M 的坐标;(3)求12MF F ∆的面积.12. 已知双曲线与椭圆221925x y +=有公共焦点1F 和2F ,它们的离心率之和为145,(1)求双曲线的标准方程;(2)设点P 是椭圆与双曲线的一个交点,求12cos F PF ∠的值.学校______________班级______________专业______________考试号______________姓名______________数学试题 解析几何解答题(答案)22143x y +=,过椭圆的左焦点且平行于向量()11v = ,的直线交椭圆于A B ,两点,AB 的长.22143x y +=得,222431a b c ===,,,所以1c = ()10-,AB 的方程为()()100x y +--=,即1y x =+ A B ,两点的坐标为()()1122x y x y ,,,22341201x y y x ⎧+-=⎨=+⎩,整理得27880x x +-=12128877x x x x +=-=- , )()221212126432288449749x x x x x x -=+-=+=)()22121228849y y x x -=-= AB =247==AB 的长为247.2y x =-与双曲线2212x y -=交于A B ,两点,求弦AB 的长. 222202x y y x ⎧--=⎨=-⎩,整理得28100x x -+-=28100x x -+=,设A B ,两点的坐标为()()1122x y x y ,,,1212810x x x x +== ,)()221212124644024x x x x x x -=+-=-=)()22121224y y x x -=-=AB ===AB 的长为3. 已知抛物线()220y px p =>的焦点为F ,过焦点F 的弦AB 的长为4p ,求直线AB 的斜率.解:设A B ,两点的坐标为()()1122x y x y ,,,因为4AB p =,由抛物线的定义可得,124p p x x =++ 所以123x x p += 由()220y pxp =>可得,抛物线的焦点F 的坐标为02p F ⎛⎫⎪⎝⎭, 设直线AB 的斜率为k ,则其方程为2p y k x ⎛⎫=-⎪⎝⎭由题意列方程组,得222y pxpk y kx ⎧=⎪⎨=-⎪⎩,整理得()22222204p k k x pk p x -++= 所以212223pk px x p k++==,整理得2223k k +=,解得1k =± 因此所求直线AB 的斜率为1或1-.4. 已知抛物线()220y pxp =>与直线1y x =-相交于A B ,两点,若AB 的中点在圆225x y +=上,求抛物线的方程.解:设A B ,两点的坐标为()()1122x y x y ,,,则其中点的坐标为121222x x y y ++⎛⎫⎪⎝⎭, 由题意,列方程组,得221y px y x ⎧=⎨=-⎩,整理得()22210x p x -++=所以1212221x x p x x +=+= ,1212121122y y x x x x p +=-+-=+-=所以AB 的中点坐标为()1p p +,因为该中点在圆225x y +=上,所以22215p p p +++= 解得1p =或2p =-(不合题意,舍去), 所以所求抛物线的方程为22y px =学校______________班级______________专业______________考试号______________姓名______________22y x =的焦点且倾斜角为45︒的直线交抛物线于A B ,两点,求OA OB.22y x =得22p =,122p = 102⎛⎫⎪⎝⎭,45︒,所以斜率为1,因此直线AB 的方程为12y x =-A B ,两点的坐标为()()1122x y x y ,,,2212y xy x ⎧=⎪⎨=-⎪⎩,整理得21304x x -+=1212134x x x x +== ,()12121212111112224y x x x x x x⎛⎫⎛⎫=--=-++=- ⎪⎪⎝⎭⎝⎭()()11221212312OA OB x y x y x x y y ==+=-=,,221916x y+=上的点到直线:70l x y +-=的最长距离和最短距离. :70l x y +-=的平行线并与椭圆相切,则所作平行线方程可设为0x y D ++=2216914400x y x y D ⎧+-=⎨++=⎩,整理得22251891440x Dx D ++-=0x y D ++=与椭圆相切,()2232442591440D D ∆-⨯⨯-==2255D D ==±,5050x y x y ++=+-=或:70l x y +-=的距离即为所求距离12d d ==== 7. 已知双曲线221169x y -=上一点P 到它的一个焦点1F 的距离为15,求点P 到另一个焦点2F 的距离.解:由双曲线方程221169x y -=,得2164,28a a a ===,根据双曲线的定义可知,128PF PF -=± 所以218815PF PF =±+=±+22237PF PF ==或因此所求点P 到另一个焦点2F 的距离为23或7.8. 若方程22194x y k k-=--表示双曲线,求实数k 的取值范围;若该方程表示焦点在y 轴上的椭圆,求实数k 的取值范围.解:(1)若方程表示双曲线,则须满足条件()()940k ->k-解得49k <<.(2)若方程表示焦点在y 轴上的椭圆,则须满足条件()904094k k k k⎧->⎪-<⎨⎪-<--⎩解得94k k k R >⎧⎪>⎨⎪∈⎩,即9k >.9. 在抛物线212y x =上求一点P ,使该点P 到焦点的距离等于9.解:设点P 坐标为()x y ,,由212y x =,得212632pp p ===,, 因为P 到焦点的距离为9,则由抛物线的定义可知P 到准线的距离也为9 所以93,62px x x =+=+=,把6x =代入方程212y x =,解得y =±所以所求点P 的坐标为(6或(6-,.学校______________班级______________专业______________考试号______________姓名______________2212516x y +=上的一点,1F 和2F 是焦点,且1260F PF ∠=︒,求12F PF ∆的面2212516x y +=得:222251625169,26a b c c ==∴=-==, 121221026PF PF a F F c +====,中,由余弦定理,得2221212122cos 60F F PF PF PF PF =+-︒()21212122PF PF PF PF PF PF =+--121003PF PF -,解得12643PF PF = 2121164sin 6022323F PF PF =⨯︒=⨯⨯=1F 和2F 在坐标轴上,离心率为,且双曲线过点,(1)求双曲线的方程;(2)若点M 在第一象限而且是渐近线上的点,又2,求点M 的坐标;(3)求12MF F ∆的面积.222222x y a y x a -=-=或,因为双曲线经过点(2,, 2224a a =-=或,可得2222a a ==-或(不合题意舍去) 222x y -=.y x =±在第一象限而且是渐近线上的点,所以可设其坐标为()()0x x x >, 222x y -=,得22242c c =+==, ()()2020-,,,由12MF MF ⊥,可得12120MF MF MF MF ⊥=即()()1222MF x x MF x x =---=-- ,,,所以()()222202x x x x x ----===,解得,M 的坐标为.1224F c == 所以121212MF F S F F ∆=⨯= 12. 已知双曲线与椭圆221925x y +=有公共焦点1F 和2F ,它们的离心率之和为145,(1)求双曲线的标准方程;(2)设点P 是椭圆与双曲线的一个交点,求12cos F PF ∠的值.解:(1)由椭圆方程221925x y +=得,2259164c c =-==, 由椭圆方程容易求得椭圆的离心率为45,所以双曲线的离心率为144255-=, 由此可求得双曲线中42a=,2a =,所以22216412b c a =-=-=,焦点为在y 轴, 所以双曲线的方程为221412y x -=. (2)设12PF PF >根据双曲线和椭圆的定义可得:1212104PF PF PF PF ⎧+=⎪⎨-=⎪⎩解得1273PF PF ==,,又1228F F c == 所以222222121212127381cos 22737PF PF F F F PF PF PF +-+-∠===-⨯⨯因此所求值为17-.。
