表面涂色的正方体 Microsoft Word 文档
表面涂色的正方体

每条棱被平均分成n份
每个面有 (n-2) 2 个 1面涂色的小正方体。
6个面有 1面涂色的小正方体。
(n-2) 2 ×6 个
每条棱被平均分成n份
没有涂色的小正方体有着怎样的规律呢?
13
棱平均分的份数 没有涂色的个数
23
3 4
33
5
131 =1
238 =8
3327 =27
每条棱被平均分成n份 棱平均分的份数 没有涂色的个数
表面涂色的正方体
棱平均分的份数 小正方体的个数
3面涂色的个数 2面涂色的个数 1面涂色的个数
2
8 8 0 0
3面涂色 ?个
2面涂色?个
1面涂色 ?个
活动一:
仔细观察,找一找,3面涂色的小正方体
有多少个?它们在原正方体的什么位置?
3面涂色
顶点
பைடு நூலகம் 活动二:
2面涂色的是多少个?它们在原正方体的 什么位置?
3
4
5
n (n-2)3
13
23
33
棱平均分的份数 小正方体的个数 3面涂色的个数 2面涂色的个数 1面涂色的个数
4
64 8
棱平均分的份数 小正方体的个数 3面涂色的个数
4
64 8
2面涂色的个数 2×12=24 1面涂色的个数
棱平均分的份数 小正方体的个数 3面涂色的个数
4
64 8
2面涂色的个数 2×12=24 1面涂色的个数
4×6=24
每条棱被平均分成n份
棱平均分的份数 小正方体个数 3面涂色的个数 2面涂色的个数
2 8 8
3 27 8
4 64 8
5 125 8
……
表面涂色的正方体课件

4
两面涂色
棱的中间
PPT学习交流
5
一面涂色
面的中间
PPT学习交流
6
如果正方体的棱长是4、5,其中三 面、两面、一面涂色的小正方体各 有多少个?
PPT学习交流
7
棱长为4 三面涂色 8 两面涂色 一面涂色
PPT学习交流
8
棱长为4 三面涂色 8 两面涂色 2×12=24 一面涂色
PPT学习交流
9
21
PPT学习交流
13
仔细观察表格,比一比,从中你发 现了什么?
棱长为3 棱长为4 棱长为5
三面涂色 8
8
8
两面涂色 12 2×12=24 3×12=36
一面涂色 6
4×6=24 9×6=54
PPT学习交流
14
(棱长-2)×12
棱长为3 棱长为4 棱长为5
三面涂色 8
8
8
两面涂色 12 2×12=24 3×12=36
一面涂色 6
4×6=24 9×6=54 (n -2)2×6
PPT学习交流
17
没有 涂色
棱长为3 13
棱长为4 23
棱长为5 棱长为n
33
( n -2)3
PPT学习交流
18
①
②
③
PPT学习交流
19
PPT学习交流
20
此课件下载可自行编辑修改,供参考! 感谢您的支持,我们努力做得更好!
PPT学习交流
一面涂色 6
4×6=24 9×6=54
PPT学习交流
15
(棱长-2)2×6
12
22
32
棱长为3 棱长为4 棱长为5
三面涂色 8
【素材】《表面涂色的正方体》表面涂色的正方体活动单(苏教) (2)

课题:表面涂色的正方体
活动一:初步感知正方体涂色规律
1、把一个表面涂色的大正方体,每条棱平均分成2份。
观察分成的小正方体的个数及每个小正方体表面涂色的情况,把数据填在下面表格中。
2、把一个表面涂色的大正方体,每条棱平均分成3份。
,观察分成的小正方体的个数及每个小正方体表面涂色的情况,把数据填在下面表格中。
3、观察正方体魔方(3×3×3),研究三面涂色、两面涂色和一面涂色的小正方体的位置?在小组内说一说你的发现
活动二:探究正方体涂色规律。
1、把一个表面涂色的大正方体,每条棱平均分成4份。
三面涂色、两面涂色和一面涂色的小正方体各有几个?(先在头脑中想一想,再验证)把验证后得到的数据填在下面表格中。
2、把一个表面涂色的大正方体,每条棱平均分成5份。
三面涂色、两面涂色和一面涂色的小正方体各有几个?(先在头脑中想一想,再结合各组自带的正方体魔方(3×3×3)进行验证)把验证后得到的数据填在下面表格中。
3、观察比较表中已有的数据,交流想法,在小组说一说你的发现。
活动三:揭示正方体涂色规律
1、运用你的发现在小组内说一说如果把一个表面涂色的正方体,每条棱平均分成10份,三面涂色、两面涂色和一面涂色的小正方体各有几个?
2、如果把一个正方体的棱长n等份,三面涂色、两面涂色和一面涂色的小正方体各有几个?
三面涂色:
两面涂色:
一面涂色:
检测反馈:
如果把一个正方体的棱长n等份,没有涂色的小正方体有()个。
正方体表面涂色共27页

▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者,好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
谢谢!
27
•
46、寓形宇内复几时,曷不委心任去 留。
•
47、采菊东篱下,悠然见南山。
•
48、啸傲东轩下,聊复得此生。
•
49、勤学如春起之苗,不见其增,日 有所长 。
•
50、环堵萧然,不蔽风日;短褐穿结26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
06 表面涂色的正方体(原卷版)
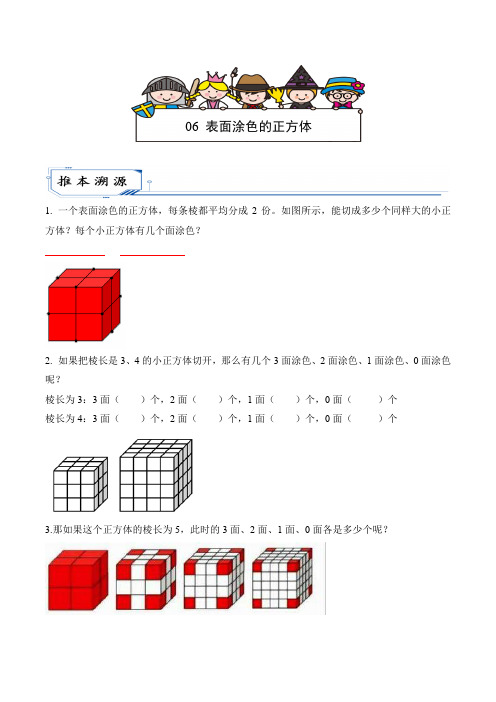
1.一个表面涂色的正方体,每条棱都平均分成2份。
如图所示,能切成多少个同样大的小正方体?每个小正方体有几个面涂色?2.如果把棱长是3、4的小正方体切开,那么有几个3面涂色、2面涂色、1面涂色、0面涂色呢?棱长为3:3面()个,2面()个,1面()个,0面()个棱长为4:3面()个,2面()个,1面()个,0面()个3.那如果这个正方体的棱长为5,此时的3面、2面、1面、0面各是多少个呢?06 表面涂色的正方体【例1】如图,将边长为3和4的两个大正方体的表面刷上红色的漆,再将其分割成边长为1的小正方体,其中三面、两面、一面有红色的小正方体的个数如下表,请尝试找到规律并在【例2】小明将一个表面涂色的正方体木块的棱长平均分成若干份,并锯成同样大的小正方体。
他想要48个两面涂色的小正方体,需要把棱长平均分成多少份?【例3】把一个正方体木块的表面全涂上红色,然后切成27个相同的小正方体(如下图)。
(1)三个面涂红色的有多少个?(2)两个面涂红色的有多少个?(3)一个面涂红色的有多少个?(4)六个面都没有涂色的有多少个?1.(2023秋·六年级课时练习)如图,将一个正方体沿虚线切三刀以后,表面积增加96平方厘米,这个正方体的体积是()立方厘米。
A.32B.64C.128D.2562.(2023秋·六年级课时练习)把一根长1米的长方体木料锯成两段后,表面积增加了200平方厘米,它的体积是()。
A.100立方厘米B.10000立方厘米C.2立方分米3.(2022秋·安徽合肥·六年级统考期末)一个表面涂色的正方体,每条棱都平均分成5份,如果照图的样子把它切开,切成同样大的小正方体。
切成的小正方体中2面涂色的有()个。
A.8B.36C.544.(2022秋·江苏南通·六年级统考期末)小娟用棱长1厘米的小正方体木块拼成一个棱长5厘米的大正方体,并把这个大正方体的表面涂成红色,其中一面涂色的小正方体有()个。
表面涂色的正方体

CONTENTS
• 引言 • 表面涂色正方体的基本概念 • 表面涂色正方体的性质 • 表面涂色正方体的应用 • 表面涂色正方体的制作与展示 • 总结与展望
01
引言
目的和背景
研究正方体表面涂色问题的目的
正方体是一种常见的几何体,研究其表面涂色问题有助于深入理解几何形状和空间结构。此外,该问题在实际应 用中也具有广泛的意义,如建筑设计、艺术创作等领域。
表面涂色的定义
涂色范围
仅限于正方体的外表面,不包括内部。
涂色方式
可以是单一颜色,也可以是多种颜色的组 合或图案。
涂色目的
通常为了美观、标识或特殊功能需求。
正方体的面、棱和顶点
面
正方体有6个面,每个面都 是正方形,且面积相等。
棱
正方体有12条棱,每条棱 连接两个相邻的面。
顶点
正方体有8个顶点,每个顶 点由三条棱交汇而成。
涂色正方体的应用领域
表面涂色的正方体在数学、计算机科学、物理学等多个领域具有广泛的应用,如组合数 学中的计数问题、计算机图形学中的渲染技术、以及物理学中的晶体结构等。
涂色正方体的研究方法
研究表面涂色的正方体主要采用组合数学、图论、群论等方法,通过对涂色模式的分类 和计数,揭示其内在的数学结构和性质。
背景介绍
正方体表面涂色问题是一个经典的数学问题,涉及到组合数学、图论等多个领域。在过去的几十年里,许多数学 家和研究者对此进行了深入的研究,并提出了各种解决方案和算法。随着计算机技术的发展,该问题也得到了更 加广泛和深入的应用。
正方体的定义和性质
• 正方体的定义:正方体是一种特殊的立方体,它的所有棱长都 相等,且每个面都是正方形。在数学上,正方体可以用一个三 维坐标系中的点集来表示,其中每个点的坐标都满足一定的条 件。
2024年公开课《表面涂色的正方体》(带附加条款)

公开课《表面涂色的正方体》(带附加条款)公开课《表面涂色的正方体》一、引言在数学的世界里,几何学是研究空间形式和性质的学科,其中正方体作为一种基本的立体几何图形,具有丰富的性质和广泛的应用。
表面涂色的正方体问题,是几何学中的一个经典问题,涉及数学的多个领域,如组合数学、图论等。
本公开课将围绕表面涂色的正方体问题,探讨其数学原理、解法及其在实际中的应用。
二、正方体的基本性质1.边长:正方体的六个面都是正方形,所以正方体的12条棱的长度相等。
2.面积:正方体的六个面的面积相等,设正方体的边长为a,则每个面的面积为a²。
3.体积:正方体的体积为边长的三次方,即V=a³。
4.对角线:正方体的对角线长度为边长的√3倍,即d=a√3。
5.表面积:正方体的表面积为六个面积之和,即S=6a²。
三、表面涂色的正方体问题表面涂色的正方体问题,即如何用最少的颜色对正方体的表面进行涂色,使得相邻的面颜色不同。
这个问题可以分为两个子问题:1.四色定理:将正方体的表面看作一个平面图,每个面为一个顶点,相邻面之间有一条边相连。
根据四色定理,这个平面图可以用四种颜色进行涂色,使得相邻面的颜色不同。
2.三色定理:当正方体的表面允许有两个对面颜色相同时,可以用三种颜色进行涂色。
具体涂色方法为:选择一个面作为基准面,涂上颜色A,与这个面相对的面涂上颜色B,其余四个面涂上颜色C。
四、表面涂色的正方体问题的应用表面涂色的正方体问题在现实生活中有着广泛的应用,例如:1.地图染色:地图可以看作是一个平面图,每个国家为一个顶点,相邻国家之间有一条边相连。
根据四色定理,地图可以用四种颜色进行染色,使得相邻国家的颜色不同。
2.网络设计:在计算机网络设计中,为了减少数据包的冲突,可以将网络节点看作正方体的顶点,网络链路看作正方体的棱。
根据表面涂色的正方体问题,可以用最少的颜色对网络节点进行标记,使得相邻节点的颜色不同,从而降低数据包的冲突率。
表面涂色的正方体.ppt

谢谢你的观赏
23
(n-2) ×12
(n-2)2 ×6
2020-11-24
谢谢你的观赏
24
回顾探索和发现规律的过程,说说你的体会。
找各种小正方 体时,要注意它 们在大正方体上 的位置。
各种小正方体的 个数与正方体顶点 、面和棱的个(条 )数有关。
要把找、数、算 等方法结合起来, 并根据图形的特征 进行思考。
表面涂色的正方体
2020-11-24
谢谢你的观赏
1
你还记得正方体有 一些基本特征吗?
填空题:
1.正方体有___6___个面. 2.正方体有__1_2___条棱. 3.正方体有___8___个顶点.
2020-11-24
谢谢你的观赏
2
一个表面涂色的正方体,每条棱都平均分成2份。如果 照下图的样子把它切开,能切成多少个同样大的小正方体? 每个小正方体有几个面涂色?
2×12=24
3×12=36
2面涂色的小正方体的个数都是12的倍数。
2020-11-24
谢谢你的观赏
20
12×6=6
22×6=24
32×6=54
1面涂色的小正方体的个数都是6的倍数。
2020-11-24
谢谢你的观赏
21
2020-11-24
8 27 64 125
8 888 0 12 24 36
0 6 24 54
2020-11-24
谢谢你的观赏
16
3×12=36
2面涂色的小正方体有36个。
2020-11-24
谢谢你的观赏
17
32×6=54
3面涂色的小正方体有54个。
2020-11-24
谢谢你的观赏
表面涂色的正方体 文档

《表面涂色的正方体》的教学设计泰州市姜堰区南苑学校小学部曹桂林教学内容:苏教版小学数学六年级上册教科书第26~27页,探索规律《表面涂色的正方体》。
教学目标:1.借助正方体涂色问题,通过实际操作、演示、想象、联想等形式发现小正方体涂色和位置的规律。
2.在探索规律的过程中,经历从特殊到一般的归纳过程,获得一些研究数学问题的方法和经验。
3.在解决问题的过程中,帮助学生感受数学的有趣,培养学生主动探索、勇于实践的精神,培养学生实事求是的科学态度。
教学重点:找出小正方体涂色以及它所在的位置的规律。
教学难点:一面、两面、三面涂色和无色小正方体个数以及它所在位置的规律。
教具准备:配套课件,棱长3厘米、4厘米、5厘米的魔方。
教学过程:一、创设情境,激发兴趣。
1.复习正方体有哪些特征?2.课件演示:一个表面涂色的正方体,将每条棱都平均分成3份,能切成多少个同样大的小正方体?3.引导学生观察,这些小正方体有什么特征?可将它们分为几类?4.提出问题:其中三面、两面、一面涂色的小正方体和没有涂色的小正方体各有多少个?这节课我们就来研究“表面涂色的正方体”。
【设计说明:本节课首先复习正方体的特征,为学生探究发现三面、两面、一面的小正方体所在的位置与大正方体的顶点、棱、面之间的关系,然后通过课件演示将涂色大正方体切开的过程,让学生通过观察,进行分类,初步感知分类的数序思想,为进一步探究活动做好铺垫。
】二、引导探究、感受规律。
1.动手操作,初步感知。
【设计说明:,在学生已经感受涂色的小正方体的个数与大正方体的顶点、棱、面关系,以及没有涂色的小正方体在大正方体的中心的基础之上,这一环节,通过引导学生观察每组算式,自然而然地得出正方体涂色规律,让学生感受新知识的益处,探寻适合自己的学习方法。
】4.完善规律,拓展延伸。
(1).如果用n表示把大正方体的棱平均分的份数,怎样用n来表示3面、2面、1面涂色的小正方体和没有涂色的小正方体各有多少个?小组讨论:3面涂色的小正方体8个;2面涂色的小正方体:(n—2)×12;1面涂色的小正方体:(n—2)²×6;没有涂色的小正方体:(n—2)³(2)一个表面涂色的正方体,将每条棱都平均分成12份,三面、两面、一面涂色的小正方体和没有涂色的小正方体各有多少个?(3)一个表面涂色的正方体,将每条棱都平均分成2份,三面、两面、一面涂色的小正方体和没有涂色的小正方体各有多少个?学生讨论,每条棱都平均分成2份,一共可切成8块小正方体,由于这8块都是3面涂色,所以两面涂色、一面涂色和没有涂色的小正方体就为0个。
六年级上册数学课件-1 表面涂色的正方体(2)

地球无时不刻都在运动,一个人不会永远处在倒霉的位置。 只要你在路上,就不要放弃前进的勇气,走走停停的生活会一直继续。 知道看人背后的是君子;知道背后看人的是小人。 虽然我们不能改变周遭的世界,我们就只好改变自己,用爱心和智慧来面对这一切. 你生命的前半辈子或许属于别人,活在别人的认为里。那把后半辈子还给你自己,去追随你内在的声音。 心如镜,虽外景不断变化,镜面却不会转动,这就是一颗平常心,能景转而心不转。 世上最累人的事,莫过于虚伪的过日子。 沉默是毁谤最好的答复。 每个人身上都有惰性和消极情绪,成功的人都是懂得管理自己的情绪和克服自己的惰性,并像太阳一样照亮身边的人,激励身边的人。 人生如一杯茶,不能苦一辈子,但是总是要苦一阵子。 世界上没有比友谊更美好更令人愉快的东西了;没有友谊,世界仿佛失去了太阳。 征服自己,就能征服一切。 生命力的意义在于拚搏,因为世界本身就是一个竞技场。 这世间最可依赖的不是别人,而是你自己。不要指望他人,一定要坚强自立。
其中三面、两面、一面涂色的 小正方体各有多少个?
8个
三面涂色
12个
两面涂色
6个
一面涂色
三面、两面、一面涂色的小正方体 各在原正方体的什么位置?
三面涂色
顶点
两面涂色
棱的中间
一面涂色
面的中间
如果正方体的每条棱都平均分成4份、 5份,再切成同样大小的小正方体, 结果怎样?
8
8 2×12=24
身体健康,学习进步! 我扑在书上,就像饥饿的人扑在面包上。
书都读得来的人,还怕有什么做不来的。 实现梦想比睡在床上的梦想更灿烂。 生命力的意义在于拚搏,因为世界本身就是一个竞技场。 意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华 成功是一种观念,成功是一种思想,成功是一种习惯,成功是一种心态。
表面涂色的正方体-数学活动共33页文档

6、纪律是自由的第一条件。——黑格 尔 7、纪律是集体的面貌,集体的声音, 集体的 动作, 集体的 表情, 集体的 信念。 ——马 卡连柯
8、我们现在必须完全保持党的纪律, 否则一 切都会 陷入污 泥中。 ——马 克思 9、学校没有纪律便如磨坊没有水。— —夸美 纽斯
10、一个人应该:活泼而守纪律,天 真而不 幼稚, 勇敢而 鲁莽, 倔强而 有原则 ,热情 而不冲 动,乐 观而不 盲目。 ——马 克思
1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确。——培根
表面涂色的正方体

32×6=54
1面涂色的小正方体的个数都是6的倍数。
如果用n表示把大正方体的棱平均分的份数,用a、b分别表示
2面涂色和1面涂色的小正方体的个数,你能用式子分别表示n
和a、b的关系吗?
a=12(n -2) b=6(n -2)2
找各种小正方体时, 各种小正方体的个
要注意它们在大正 数与正方体顶点、
方体上的位置。
谢谢观看
表面涂色的正方体
一个表面涂色的正方体,每条楞都平均分成2 份。如果照下边的样子把它切开,能切成多少个 同样大的小正方体?每个小正方体有几个面涂色?
如果像下图这样把正方体切开,能切成多少个小 正方体?切成的小正方体中,3面涂色、2面涂色、 1面涂色的各有多少个,分别在什么位置?
3面涂色的在每个顶点处,有8个。
3面涂色的小正方体有8个。源自3×12=36(个) 2面涂色的小正方体有36个。
32×6=54(个) 1面涂色的小正方体有54个。
3面涂色的小正方体都在大正方体顶 点的位置,都是8个。
1×12=12
2×12=24
3×12=36
2面涂色的小正方体的个数都是12的倍数。
12×6=6
22×6=24
面和棱的个(条)
数有关。
要把找、数、算等 方法结合起来,并 根据图形的特征进 行思考。
小结: 把棱长为几厘米的小正方体涂色后切成棱长为1厘米的小正 方体,涂色面的规律: (1)3面涂色的小正方体个数=正方体的订点个数=8个; (2)2面涂色的小正方体个数
=正方体棱的条数乘棱长减2的差 =12×(n -2); (3)1面涂色的小正方体个数 =正方体的面数乘棱长将2的差的平方 =6×(n -2)²。
2面涂色的在每条棱的中间位置处,有12个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反思重建
追问:六面都没有涂色的小正方体有多少个?这样的小正方体处在什么位置?它的个数该如何计算?
引导:将大正方体剥去“表皮”,剩下的是什么样子?
指出:六面都没有涂色的小正方体在大正方体的中间。
两种算法:64—8—24—24=8(个),2×2X 2= 8(个)。
学生小组讨论交流
操作教具,验证学生的发现:
(1)将处在顶层的4个顶点上的4个小正方体从教具中取下,让学生见证“三面涂色”。
要求:将正方体的棱长各种正方体的个数及计算方法填在活动记录表。
引导:计算所需的数据与原正方体的棱长有什么关系?
(二)棱长为3的正方体
学生自主完成,将探究结果填在活动记录表。完成后指名汇报交流。
(三)棱长分别为5、6的正方体
学生自主完成,将探究结果填在活动记录表,并在小组内交流。
投影呈现学生的活动记录结果,通过课件呈现实物加以验证。引导学生初步发现正方体表面涂色问题的一般规律。
看来三面涂色、两面涂色、一面涂色的位置是确定的。今天,我们就来一起探究跟表面涂色有关的正方体的计数问题。
板书:分类计数。
课件出示问题:
把一个表面都涂上颜色的正方体木块,切成64块大小相同的小正方体。
(1)三面涂色的小正方体有多少块?
(2)两面涂色的小正方体有多少块?
(3)一面涂色的小正方体有多少块?
课题
表面涂色的正方体
上课时间
一、教学目标
1.通过活动,积累由特殊到一般寻找数学规律的数学经验。
2.进一步培养用分类计数的方法解决问题的能力,发展空间想象力。
二、制定依据(教材、学情分析)
教学重点:找出小正方体涂色以及它所在的位置的规律。
教学难点:一面、两面、三面涂色小正方体个数以及它所在位置的规律。
(四)棱长为a的正方体
提问:如果棱长为n,三面涂色的小正方体有几个?两面涂色、一面涂色和六面都没有涂色的小正方体个数分别怎
(五)延伸思考
课件出示问题:将一个长7厘米、宽5厘米、高4厘米的长方体木块表面涂色后,切成棱长为1厘米的小正方体木块,三面涂色、两面涂色和一面涂色的木块各有几个?
(2)将处在非底层的8条棱上的16个小正方体取下,让学生明确计算方法、见证“两面涂色”。同时追问:还有的两面涂色的小正方体在哪里?
(3)取出其中一面涂色的小正厅体,让学生明确计算方法,见证“一面涂色”。(4)呈现“六面都没有涂色”的小正方体(由8个小正方体组成的棱长为2的正方体)。
(5)将最底层的小正方体按类归位,验证计数的结果及计算方法。
教学过程
教学环节
教师活动
学生活动
设计意图及二次修改
常规积累
开放式导入
核
心
过
程
推
进
一、引入新课
谈话:课前,我们通过魔方认识了三面涂色、两面涂色、一面涂色的相关情况,谁能说说在魔方中三面涂色、两面涂色、一面涂色的部件分别处在魔方的什么位置?能不能通过旋转把魔方中三面涂色的部分移到两面涂色或只有一面涂色的位置?
二、探究正方体中表面涂色的小正方体
(一)棱长为4的正方体
提问:三面涂色的小正方体有多少个?处在什么位置上的小正方体才会是三面涂色的? (课件显示)闭上眼睛想一想三面涂色的小正方体在什么位置。
提问:两面涂色的小正方体有多少个?处在什么位置? (课件显示)
这个数据可以通过怎样的计算获得?
提问:一面涂色的小正方体有多少个?处在什么位置? (课件显示)这个数据该通过怎样的计算获得?
