[计算机]算法分析与设计课程综合实验
实验报告算法分析

实验报告算法分析实验报告:算法分析引言在计算机科学领域中,算法是解决问题的一种方法或步骤的描述。
通过对算法的分析,我们可以评估其效率和性能,从而选择最优的算法来解决特定的问题。
本实验报告旨在介绍算法分析的基本概念和方法,并通过实例来说明其应用。
一、算法分析的背景算法分析是计算机科学中的重要研究领域,它关注如何评估算法的效率和性能。
在实际应用中,我们经常面临着需要在有限的时间内解决大规模问题的挑战。
因此,选择一个高效的算法是至关重要的。
算法分析的目标是通过定量分析算法的时间复杂度和空间复杂度,为选择最佳算法提供依据。
二、算法分析的方法1. 时间复杂度分析时间复杂度是衡量算法执行时间的一种指标。
通常使用大O表示法来表示时间复杂度。
通过计算算法执行所需的基本操作次数,可以得到算法的时间复杂度。
常见的时间复杂度有O(1)、O(log n)、O(n)、O(n log n)和O(n^2)等。
时间复杂度越低,算法执行所需的时间越短。
2. 空间复杂度分析空间复杂度是衡量算法内存使用的一种指标。
通过计算算法执行所需的额外空间大小,可以得到算法的空间复杂度。
常见的空间复杂度有O(1)、O(n)和O(n^2)等。
空间复杂度越低,算法所需的内存空间越小。
三、算法分析的应用算法分析在计算机科学的各个领域都有广泛的应用。
以下是几个常见的应用示例:1. 排序算法排序算法是计算机科学中的经典问题之一。
通过对不同排序算法的时间复杂度进行分析,可以选择最适合特定需求的排序算法。
例如,快速排序算法的平均时间复杂度为O(n log n),在大规模数据排序中表现出色。
2. 图算法图算法是解决图结构相关问题的一种方法。
通过对图算法的时间复杂度和空间复杂度进行分析,可以选择最适合解决特定图问题的算法。
例如,广度优先搜索算法的时间复杂度为O(V+E),其中V和E分别表示图的顶点数和边数。
3. 动态规划算法动态规划算法是解决具有重叠子问题性质的问题的一种方法。
算法设计与分析课程的教学探索与实践

领域的最新进展 , 比如神经网络算法 、 遗传算法等。 本课程 的教学可以尝试从以下四部分展开 , 不同层次的学生可 以 进行相应的调整和取舍 : ( 1 ) 介绍算法的基本概念 、 算法的 数学基础以及算法复杂度分析 ; ( 2 )分别针对排序问题和 组合优化问题 , 讨论各种已有的算法 , 并介绍常用 的算法
况, 我们选择王红梅编写的《 算法设计与分析》 作为教材 , 该教材的特点是不深入讲解高深的理论 , 以易懂的方式阐 述各种经典算法[ 3 1 。建议算法设计与分析课程学时数大约 7 2 学时左右 , 其中课堂教学为4 8 学时 , 实验2 4 学时。 实验学 时要 占到总课时的3 0 %以上, 坚持“ 实践 、 实际 、 实用” 的原 则, 坚持实战教学 , 培养学生的实践能力和创新能力。
文章 编 号 : 1 6 7 4 — 9 3 2 4 ( 2 0 1 3 ) 1 3 - 0 2 1 8 — 0 2
算法设计与分析是计算机专业 的专业基础课 , 是计算
机专业 课 中一 门处 于 核心 地位 的课 程 。 该 课 程 的主要 目的
具有 重要 意 义 。
对于如何解决上述问题以更好地进行教学 , 本文根据 实际的教学经验 , 从教学内容 、 教学方法 、 实践环节和考核 方式等方面来探讨如何对这门课程进行适当的教学改革 。
方 面 的理论 研究 , 如 计算 模 型 、 N P 完 全 问题 和 问题 复 杂 度 等理论 ; ( 3 ) 近年来在并行算法 、 随机算法 、 近似算法 、 加密
算法 、 智能优化算法 、 模式识别算法 、 神经网络算法 、 遗传 算法 以及其他算法领域方面的最新研究成果 。 作为面向计 算机科学与技术专业和软件工程专业的课程 , 算法分析与 设计在 内容组织上应该体现理论与实际应用并重的原则 , 兼顾 串行算法和并行算法两大部分 , 同时介绍一些本学科
算法分析与设计实验报告

算法分析与设计实验报告算法分析与设计实验报告一、引言算法是计算机科学的核心,它们是解决问题的有效工具。
算法分析与设计是计算机科学中的重要课题,通过对算法的分析与设计,我们可以优化计算机程序的效率,提高计算机系统的性能。
本实验报告旨在介绍算法分析与设计的基本概念和方法,并通过实验验证这些方法的有效性。
二、算法分析算法分析是评估算法性能的过程。
在实际应用中,我们常常需要比较不同算法的效率和资源消耗,以选择最适合的算法。
常用的算法分析方法包括时间复杂度和空间复杂度。
1. 时间复杂度时间复杂度衡量了算法执行所需的时间。
通常用大O表示法表示时间复杂度,表示算法的最坏情况下的运行时间。
常见的时间复杂度有O(1)、O(log n)、O(n)、O(n log n)和O(n^2)等。
其中,O(1)表示常数时间复杂度,O(log n)表示对数时间复杂度,O(n)表示线性时间复杂度,O(n log n)表示线性对数时间复杂度,O(n^2)表示平方时间复杂度。
2. 空间复杂度空间复杂度衡量了算法执行所需的存储空间。
通常用大O表示法表示空间复杂度,表示算法所需的额外存储空间。
常见的空间复杂度有O(1)、O(n)和O(n^2)等。
其中,O(1)表示常数空间复杂度,O(n)表示线性空间复杂度,O(n^2)表示平方空间复杂度。
三、算法设计算法设计是构思和实现算法的过程。
好的算法设计能够提高算法的效率和可靠性。
常用的算法设计方法包括贪心算法、动态规划、分治法和回溯法等。
1. 贪心算法贪心算法是一种简单而高效的算法设计方法。
它通过每一步选择局部最优解,最终得到全局最优解。
贪心算法的时间复杂度通常较低,但不能保证得到最优解。
2. 动态规划动态规划是一种将问题分解为子问题并以自底向上的方式求解的算法设计方法。
它通过保存子问题的解,避免重复计算,提高算法的效率。
动态规划适用于具有重叠子问题和最优子结构的问题。
3. 分治法分治法是一种将问题分解为更小规模的子问题并以递归的方式求解的算法设计方法。
算法分析实验指导书(王红梅)

《算法设计与分析》实验指导书计算机科学与技术学院石少俭实验一分治法1、实验目的(1)掌握设计有效算法的分治策略。
(2)通过快速排序学习分治策略设计技巧2、实验要求(1)熟练掌握分治法的基本思想及其应用实现。
(2)理解所给出的算法,并对其加以改进。
3、分治法的介绍任何一个可以用计算机求解的问题所需的计算时间都与其规模有关。
问题的规模越小,越容易直接求解,解题所需的计算时间也越少。
而当n较大时,问题就不那么容易处理了。
要想直接解决一个规模较大的问题,有时是相当困难的。
分治法的设计思想是,将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
如果原问题可分割成k个子问题,1<k≤n ,且这些子问题都可解,并可利用这些子问题的解求出原问题的解,那么这种分治法就是可行的。
由分治法产生的子问题往往是原问题的较小模式,这就为使用递归技术提供了方便。
在这种情况下,反复应用分治手段,可以使子问题与原问题类型一致而其规模却不断缩小,最终使子问题缩小到很容易直接求出其解。
这自然导致递归过程的产生。
分治与递归像一对孪生兄弟,经常同时应用在算法设计之中,并由此产生许多高效算法。
分治法的适用条件(1)该问题的规模缩小到一定的程度就可以容易地解决;(2)该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
(3)利用该问题分解出的子问题的解可以合并为该问题的解;(4)该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
上述的第一条特征是绝大多数问题都可以满足的,因为问题的计算复杂性一般是随着问题规模的增加而增加;第二条特征是应用分治法的前提,它也是大多数问题可以满足的,此特征反映了递归思想的应用;第三条特征是关键,能否利用分治法完全取决于问题是否具有第三条特征,如果具备了第一条和第二条特征,而不具备第三条特征,则可以考虑贪心法或动态规划法。
第四条特征涉及到分治法的效率,如果各子问题是不独立的,则分治法要做许多不必要的工作,重复地解公共的子问题,此时虽然可用分治法,但一般用动态规划法较好。
《计算机算法设计与分析》课程设计

《计算机算法设计与分析》课程设计用分治法解决快速排序问题及用动态规划法解决最优二叉搜索树问题及用回溯法解决图的着色问题一、课程设计目的:《计算机算法设计与分析》这门课程是一门实践性非常强的课程,要求我们能够将所学的算法应用到实际中,灵活解决实际问题。
通过这次课程设计,能够培养我们独立思考、综合分析与动手的能力,并能加深对课堂所学理论和概念的理解,可以训练我们算法设计的思维和培养算法的分析能力。
二、课程设计内容:1、分治法:(2)快速排序;2、动态规划:(4)最优二叉搜索树;3、回溯法:(2)图的着色。
三、概要设计:分治法—快速排序:分治法的基本思想是将一个规模为n的问题分解为k个规模较小的子问题,这些子问题互相独立且与原问题相同。
递归地解这些子问题,然后将各个子问题的解合并得到原问题的解。
分治法的条件:(1) 该问题的规模缩小到一定的程度就可以容易地解决;(2) 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质;(3) 利用该问题分解出的子问题的解可以合并为该问题的解;(4) 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子子问题。
抽象的讲,分治法有两个重要步骤:(1)将问题拆开;(2)将答案合并;动态规划—最优二叉搜索树:动态规划的基本思想是将问题分解为若干个小问题,解子问题,然后从子问题得到原问题的解。
设计动态规划法的步骤:(1)找出最优解的性质,并刻画其结构特征;(2)递归地定义最优值(写出动态规划方程);(3)以自底向上的方式计算出最优值;(4)根据计算最优值时得到的信息,构造一个最优解。
●回溯法—图的着色回溯法的基本思想是确定了解空间的组织结构后,回溯法就是从开始节点(根结点)出发,以深度优先的方式搜索整个解空间。
这个开始节点就成为一个活结点,同时也成为当前的扩展结点。
在当前的扩展结点处,搜索向纵深方向移至一个新结点。
这个新结点就成为一个新的或节点,并成为当前扩展结点。
“算法分析与设计”课程教学改革和实践

通过实践 ,提 高了 学生学习本门课程的学习热情,有利于学生独立分析和解决问题 能力的培 养。 关键词 : 算法分析与设计 ; 启发式 ; 参与式 ;因材施教
随机 化 算 法 、 近 似 算 法 等 。 而在 教 学 计 划 中,课 程 的教 学 课 时 个问题 。同时提 出新 的算法设 计改进问题 ,以便 让学 生进 行思
是有限的,要将这些算法设计的策略全部讲透彻非常困难。
2 课 程 教 学内容难 以跟 上 当 科 技 发 展步伐 . 今
考和研究 。变单向传 输式教学 为双 向互动式教学 ,变 以强调抽 象算法设计为主的理论 讲授为探究解决应用问题为主 的设计引
通过 对计算机算法系统的学 习与研 究,理解和掌握算法设计的
在教学 内容 的选择 上,总的原则是 :内容难度适 中,结合
主要方法 ,培 养对 算法 的计算复杂性 进行正确分析 的能力,为 实际问题和相关课程 的知识讲解 算法设 计技巧及算法分析方法, 独立地设计算法和对给定算法进行复杂性分析奠定 坚实 的理论 使学 生 既能 理 解 ,又 能拓 展 创 新 。
CE E中国 电力教育 P
面
D I O 编码 :1.9 9 j sn 10 — 0 92 1 . .3 03 6 / . s . 7 0 7 .0 01 02 i 0 6
‘ ‘ 算法分析与设计’ ’课程教学改革和实践
李 涵
摘要 : 算法分析与设计”是计算机科 学与技术以及相关专业的重要课 程之・,是理论知 识和能力并重的课程。文中结合算法分析 “
算法设计与分析实验报告

算法设计与分析报告学生姓名学号专业班级指导教师完成时间目录一、课程内容 (3)二、算法分析 (3)1、分治法 (3)(1)分治法核心思想 (3)(2)MaxMin算法分析 (3)2、动态规划 (4)(1)动态规划核心思想 (4)(2)矩阵连乘算法分析 (5)3、贪心法 (5)(1)贪心法核心思想 (5)(2)背包问题算法分析 (6)(3)装载问题算法分析 (7)4、回溯法 (7)(1)回溯法核心思想 (7)(2)N皇后问题非递归算法分析 (7)(3)N皇后问题递归算法分析 (8)三、例子说明 (9)1、MaxMin问题 (9)2、矩阵连乘 (10)3、背包问题 (10)4、最优装载 (10)5、N皇后问题(非递归) (11)6、N皇后问题(递归) (11)四、心得体会 (12)五、算法对应的例子代码 (12)1、求最大值最小值 (12)2、矩阵连乘问题 (13)3、背包问题 (15)4、装载问题 (17)5、N皇后问题(非递归) (19)6、N皇后问题(递归) (20)一、课程内容1、分治法,求最大值最小值,maxmin算法;2、动态规划,矩阵连乘,求最少连乘次数;3、贪心法,1)背包问题,2)装载问题;4、回溯法,N皇后问题的循环结构算法和递归结构算法。
二、算法分析1、分治法(1)分治法核心思想当要求解一个输入规模为n,且n的取值相当大的问题时,直接求解往往是非常困难的。
如果问题可以将n个输入分成k个不同子集合,得到k个不同的可独立求解的子问题,其中1<k≤n, 而且子问题与原问题性质相同,原问题的解可由这些子问题的解合并得出。
那末,这类问题可以用分治法求解。
分治法的核心技术1)子问题的划分技术.2)递归技术。
反复使用分治策略将这些子问题分成更小的同类型子问题,直至产生出不用进一步细分就可求解的子问题。
3)合并技术.(2)MaxMin算法分析问题:在含有n个不同元素的集合中同时找出它的最大和最小元素。
算法分析与设计课程大纲
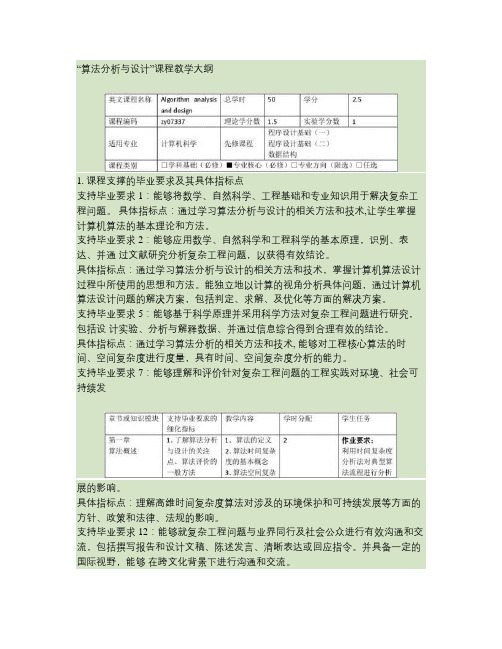
“算法分析与设计”课程教学大纲1. 课程支撑的毕业要求及其具体指标点支持毕业要求1:能够将数学、自然科学、工程基础和专业知识用于解决复杂工程问题。
具体指标点:通过学习算法分析与设计的相关方法和技术,让学生掌握计算机算法的基本理论和方法。
支持毕业要求2:能够应用数学、自然科学和工程科学的基本原理,识别、表达、并通过文献研究分析复杂工程问题,以获得有效结论。
具体指标点:通过学习算法分析与设计的相关方法和技术,掌握计算机算法设计过程中所使用的思想和方法。
能独立地以计算的视角分析具体问题,通过计算机算法设计问题的解决方案,包括判定、求解、及优化等方面的解决方案。
支持毕业要求5:能够基于科学原理并采用科学方法对复杂工程问题进行研究,包括设计实验、分析与解释数据、并通过信息综合得到合理有效的结论。
具体指标点:通过学习算法分析的相关方法和技术, 能够对工程核心算法的时间、空间复杂度进行度量,具有时间、空间复杂度分析的能力。
支持毕业要求7:能够理解和评价针对复杂工程问题的工程实践对环境、社会可持续发展的影响。
具体指标点:理解高维时间复杂度算法对涉及的环境保护和可持续发展等方面的方针、政策和法律、法规的影响。
支持毕业要求12:能够就复杂工程问题与业界同行及社会公众进行有效沟通和交流,包括撰写报告和设计文稿、陈述发言、清晰表达或回应指令。
并具备一定的国际视野,能够在跨文化背景下进行沟通和交流。
具体指标点:让学生在算法设计的时候与同行、领导以及下属等人员沟通,能清晰地表达其想法和思路,并掌握各种国际标准下的算法的撰写方法。
2. 课程教学内容对毕业要求及指标点的支撑3. 考核方式及成绩评定方式该课程的考核采用综合考核方式。
总成绩分为:期末笔试成绩(30%)、过程成绩(30%)、实验成绩(40%)。
过程成绩主要指平时上课出勤及实验态度得分。
本课程设置7 个实验。
前5个实验提前1 周布置给学生,要求学生通过课外进行实验预习,对实验内容进行分析和设计,写出基本程序代码,以保证课堂实验的效果。
数学类专业中《算法分析与设计》课程实验的改革

数学类专业中《算法分析与设计》课程实验的改革摘要:《算法分析与设计》课程是计算机科学和应用数学类专业的核心课程之一,在数学类专业同样起着非常重要的作用。
本文通过对实验课程教学过程中存在的问题进行分析,提出了提高学生上机实现算法的兴趣和能力,改善教学质量的方案,并且通过了课程实践的验证,改革后的措施获得了良好的效果。
关键词:算法分析与设计实验教学改革 python算法1 概述《算法设计与分析》课程是计算机科学和应用数学类专业等的核心课程,其前导课程主要有《面向对象程序设计》、《数据结构》等。
该课程由于涉及大量的抽象数据类型和算法,理论和实践性很强,各种经典算法思想都是从经典问题的解决方案中总结提炼出来的,因此学生学习起来有相当大的难度。
在该课程的教学过程中发现,多数学生对该课程只注重理论学习,忽视了运用实践,没有利用算法思想来思考和解决实际问题,导致实验课的教学效果不理想。
但是,实验课是算法设计与分析课程的一个重要的环节,课堂上所学的内容只有通过实验才能较好的掌握,它是检验教学效果和巩固所学算法的关键。
因此就要求教师思考如何设计与改进实验教学的内容、方法和手段,从而改变算法实验课的现状。
2存在的问题分析当前的算法实验教学效果不理想,学生在实验过程中往往表现为对算法流程无从下手进行实现,并且缺乏信心,主要原因有以下方面:2.1 课程本身内容难度大《算法分析与设计》课程内容丰富,理论性强,学习量大。
课程内容主要是讨论和介绍计算机算法的复杂性理论,结合对一些熟悉的算法进行分析和总结,强化基础理论知识,对一些大型工程软件的分析,会有一定的辅助作用。
它主要介绍计算机科学及应用领域常见的有代表性的非数值算法及算法设计的若干重要方法,同时,介绍算法分析的基本知识。
阐述计算模型和时间复杂性的定义;讨论递归技术和算法分析的基本手段;介绍算法设计的几类方法,如分治法、回溯法、贪心法、动态规划法、分枝限界法等,并结合某些有实用意义的经典算法来加深设计方法的探讨,由浅入深地进行算法效率分析,使学生在掌握各种算法设计方法和分析基本技术的同时,也使逻辑思维得到锻炼。
江西理工大学实验报告(示例)

江西理工大学算法分析与设计课程实验报告实验递归与分治策略专业班级计算机122班实验人xxxx学号XXXXXXXX(8位)实验日期2014年5月12日同组人XXX_____________________________________________________________________________ 一、实验目的1.加深学生对分治法算法设计方法的基本思想、基本步骤、基本方法的理解与掌握;2.提高学生利用课堂所学知识解决实际问题的能力;3.提高学生综合应用所学知识解决实际问题的能力。
二、实验内容设计一个递归和分治算法,找出数组的最大元素,找出x在数组A中出现的次数。
三、实验要求1.用分治法求解问题;2.再选择自己熟悉的其它方法求解本问题;3.上机实现所设计的所有算法。
四、实验过程设计(算法设计过程)1. 设计一个递归算法,找出数组的最大元素。
2. 设计一个分治算法,找出x在数组A中出现的次数。
3. 写一个主函数,调用上述算法。
五、实验结果和分析实验结果:E:\学习\计算机实验\算法\debug\递归.exe数组的最大元素为544输入想要计数的数组元素:77在数组中出现的次数为2次Press any key to continue实验分析(分析时空复杂性,设计测试用例及测试结果):时间复杂性:最好情况下,O(n)最坏情况下:O(nlog(n)空间复杂性分析:O(n)六、实验体会通过写递归与分治策略实验,更加清楚的知道它的运行机理,分治法解题的一般步骤:1.分解,将要解决的问题划分成若干规模较小的同类问题;2.求解,当子问题划分得足够小时,用较简单的方法解决;3.合并,按原问题的要求,将子问题的解逐层合并构成原问题的解。
做实验重在动手动脑,还是要多写写实验,才是硬道理。
七、附录(源代码)#include"stdio.h"#define ElemTypeintintcount(ElemType a[],inti,intj,ElemType x){int k=0,mid; //k用来计数,记录数组中x出现的次数if(i==j){if(a[i]==x) k++;return k;}else{mid=(i+j)/2;k+=count(a,i,mid,x);k+=count(a,mid+1,j,x);}return k;}ElemTypeMaxitem(ElemType a[],int n){ElemType max=a[n-1],j;if(n==1){max=a[n-1];return max;}else{j=Maxitem(a,n-1);if(j>max) max=j;return max;}}void main(void){ElemTypea[]={1,5,2,7,3,7,4,8,9,5,4,544,2,4,123};ElemType b;ElemType x;int n;printf("数组的最大元素为%d\n",b);printf("输入想要计数的数组元素:\n");scanf("%d",&x);n=count(a,0,14,x);printf("%d在数组中出现的次数为%d次\n",x,n); }。
《算法设计与分析》上机实验题目及其解答(可编辑)

《算法设计与分析》上机实验题目及其解答算法设计与分析上机题目解答西安邮电大学计算机学院算法设计与分析上机存在的问题(1 )上机准备工作不足;(2 )程序设计风格不够好;(3 )测试用例设计不够全面;(4 )上机报告撰写不够认真;(5 )上机报告排版不够规范。
西安邮电大学计算机学院算法设计与分析递归与分治策略西安邮电大学计算机学院递归与分治策略基本题 1 : 用分治法查找数组元素的最大值和最小值。
西安邮电大学计算机学院递归与分治策略【问题分析】(1)数组的生成 :许多同学采用固定数组的做法,实际上采用随机数组是一个比较好的做法,一是可以生成随机数字,便于测试代码;二是相对于固定长度数组可以很方便地生成任意长度的数组。
如下:西安邮电大学计算机学院递归与分治策略(2)算法分析 :给同学们的资料上面的算法如下所示:算法中“假定 n 是 2 的指数倍” , 实际算法中可以不局限于此。
许多同学都正确地实现了任意长度数组的最值计算分治算法。
算法的伪代码如下 ( 并非唯一算法 ) :西安邮电大学计算机学院递归与分治策略西安邮电大学计算机学院递归与分治策略(3)小结:大部分同学均能够正确编写程序,但存在一些问题,需要继续努力。
西安邮电大学计算机学院递归与分治策略基本题 2 : 众数问题 ( 课本 P39 算法实现题 2的 2-1 题 ) 。
西安邮电大学计算机学院递归与分治策略西安邮电大学计算机学院递归与分治策略西安邮电大学计算机学院递归与分治策略【问题分析】(1)算法:可以用很直观的思路来求解“众数”问题,即通过扫描输入文件中的各个数据,如果是新数据则建立“记录” ;否则针对老数据累加其出现频度。
最后统计出现频度最高的“数据”即为“众数” ,该频度的值为“重数”。
由于上述算法中涉及到“查找” ,因此一种做法是先将读入的全部数据排序,之后按照上述思路逐个分析、处理。
大部分同学都能正确求解此问题,采用的排序算法有“快速排序”和“合并排序” (均体现了“分治法”思想);数据结构有结构体或者二维数组 ,用来保存出现的数据及其频度。
研究生计算机科学教案:算法分析与设计

研究生计算机科学教案:算法分析与设计1. 导言本教案旨在提供给研究生计算机科学专业的学生一门关于算法分析与设计的课程。
在计算机科学领域中,算法是解决问题的有效方法和步骤。
通过本课程的学习,学生将能够深入了解常见的算法分析技术和设计策略,并掌握如何选择合适的数据结构来实现高效的算法。
此外,本课程还将涵盖一些经典问题和相应的解决方案,以及在实际应用中如何应用这些经典算法。
2. 学习目标•理解基本的算法概念和术语•掌握常见的算法分析技术,如时间复杂度、空间复杂度等•熟练掌握常见的排序和搜索算法•理解动态规划、贪心算法、回溯等设计策略•学会通过递归构建和分析复杂的数据结构和算法•能够应用所学知识解决实际问题3. 教学内容安排第一周:导论及基本概念•算法概述和定义•算法分析的基本概念:时间复杂度和空间复杂度•渐进符号表示法第二周:排序算法•冒泡排序、插入排序、选择排序•快速排序、归并排序、堆排序•排序算法的比较和选择第三周:搜索算法•顺序搜索与二分搜索•深度优先搜索(DFS)和广度优先搜索(BFS)•A*搜索算法第四周:动态规划•基本概念和原理•背包问题和最长公共子序列问题•动态规划解决方案的设计与实现第五周:贪心算法•基本概念和原理•最小生成树问题和背包问题的贪心算法解决方案第六周:回溯算法•基本概念和原理•八皇后问题及其回溯解决方案•迷宫求解问题及其回溯解决方案第七周:递归算法与数据结构•递归思想与应用场景•递归构建和操作链表、二叉树等数据结构•分治策略及其应用第八周:经典算法问题•0/1背包问题•旅行商问题•最短路径问题4. 教学方法与评估方式本课程将采用理论讲授与实践结合的教学方法。
理论讲授部分将以教师演讲、示例分析和交互式讨论等方式进行。
实践部分将通过编程练习、算法案例分析等形式进行,学生需要在课后完成相关的作业和项目,并提交实验报告。
评估方式将包括课堂参与度、作业成绩、项目成果以及期末考试。
5. 参考资料•Cormen, T.H., Leiserson, C.E., Rivest, R.L., and Stein, C. (2009)."Introduction to Algorithms." MIT Press.•Dasgupta, S., Papadimitriou, C.H., and Vazirani, U.V. (2008)."Algorithms." McGraw-Hill Education.以上是本课程《研究生计算机科学教案:算法分析与设计》的大纲内容。
《算法分析与设计》说课

素质 目标
①具备问题抽象和建模的初步能力 ②培养学生逻辑思维能力和想象力 ③培养独立科研的能力和理论联系实践的能力
说课程教学大纲
3、教学总体规划
课内教学总学时:40;课外学习学时:48。 教学内容以算法设计和算法分析作为主线,通过
讲授基本算法技能,总结、归纳算法设计策略, 并系统介绍算法分析技能。 通过学习使学生学会如何评价算法的好坏,帮助 学生完成从“会编程序”到“编好程序”的角色 转变,提高学生实际求解问题的能力。
学生讨论 (8分钟)
教师分析 (7分钟)
说课导航
说课程教学大纲 说教学资源 说教学方法与手段 说学情与学法指导 说教学过程设计
说考核评价
考核评价
总评考核
(100%)
=
平时成绩 (40%)
+
期末考核
(60%)
平时成绩 (100%)
=(考10勤%)
+(作50业%)
43;
学习态度 (10%)
分治策略的应用 分解最优解结构 构造递归关系 判断是否满足贪心性质 回溯法--剪枝函数
解空间树
说课导航
说课程教学大纲 说教学资源 说教学方法与手段 说学情与学法指导 说教学过程设计
说考核评价
说教学资源
1、教材选用原则
国家级规划教材
原则
具有先进性、适用性、时效性
经典教材
说教学资源
王晓东教授编著的 《计算机算法设计与分析》
《算法分析与设计》 课程说课
电子与通信教研室
说课导航
说课程教学大纲 说教学资源 说教学方法与手段 说学情与学法指导 说教学过程设计
说考核评价
说课导航
说课程教学大纲 说教学资源 说教学方法与手段 说学情与学法指导 说教学过程设计
算法设计与分析实验报告

本科实验报告课程名称:算法设计与分析实验项目:递归与分治算法实验地点:计算机系实验楼110专业班级:物联网1601 学号:2016002105 学生姓名:俞梦真指导教师:郝晓丽2018年05月04 日实验一递归与分治算法1.1 实验目的与要求1.进一步熟悉C/C++语言的集成开发环境;2.通过本实验加深对递归与分治策略的理解和运用。
1.2 实验课时2学时1.3 实验原理分治(Divide-and-Conquer)的思想:一个规模为n的复杂问题的求解,可以划分成若干个规模小于n的子问题,再将子问题的解合并成原问题的解。
需要注意的是,分治法使用递归的思想。
划分后的每一个子问题与原问题的性质相同,可用相同的求解方法。
最后,当子问题规模足够小时,可以直接求解,然后逆求原问题的解。
1.4 实验题目1.上机题目:格雷码构造问题Gray码是一个长度为2n的序列。
序列无相同元素,每个元素都是长度为n的串,相邻元素恰好只有一位不同。
试设计一个算法对任意n构造相应的Gray码(分治、减治、变治皆可)。
对于给定的正整数n,格雷码为满足如下条件的一个编码序列。
(1)序列由2n个编码组成,每个编码都是长度为n的二进制位串。
(2)序列中无相同的编码。
(3)序列中位置相邻的两个编码恰有一位不同。
2.设计思想:根据格雷码的性质,找到他的规律,可发现,1位是0 1。
两位是00 01 11 10。
三位是000 001 011010 110 111 101 100。
n位是前n-1位的2倍个。
N-1个位前面加0,N-2为倒转再前面再加1。
3.代码设计:}}}int main(){int n;while(cin>>n){get_grad(n);for(int i=0;i<My_grad.size();i++)cout<<My_grad[i]<<endl;My_grad.clear();}return 0;}运行结果:1.5 思考题(1)递归的关键问题在哪里?答:1.递归式,就是如何将原问题划分成子问题。
《算法设计与分析》实验教学大纲

《算法设计与分析》实验教学大纲
一、实验课的任务、性质与目的:
本课程实验目的是验证、巩固和补充课堂讲授的理论知识。
培养学生初步具备独立设计算法和对给定算法进行复杂性分析的能力,为实际工作打下基础。
实验的安排和要求是:用程序实现经典算法,学习算法设计的主要策略方法、原理并根据实例加以调试,培养动手设计、分析和综合实验结果以及撰写实验报告的能力。
在实验中养成严肃认真的治学态度和踏实细致、实事求是的作风。
二、主要仪器设备及环境:
仪器设备:任何计算机及网络终端。
环境:windows操作系统、任一种编程语言
四、教材、实验教材(指导书):
1. 教材
[1] 郑宗汉等著,算法设计与分析,清华大学出版社,2005年
2. 实验指导书
[1] 王晓东,算法设计与实验题解,电子工业出版社,2006年
[2] 王晓东,计算机算法设计与分析(第三版),电子工业出版社,2007年
五、考核方式与评分办法:
本课程的考核分为平时成绩及期末考试成绩两部分,其中平时成绩包括考勤、实验成绩等,期末考试以闭卷笔试为主。
总成绩按以下公式计算:
总成绩=平时成绩×(30%~40%)+期末成绩×(70%~60%)
六、大纲审核人:
1 / 2。
《算法设计与分析》实验目的

《算法设计与分析》实验指导书曹严元计算机与信息科学学院2007年5月目录实验一递归算法与非递归算法 (2)实验二分治算法 ................................................... 错误!未定义书签。
实验三贪心算法 (3)实验四动态规划 (2)实验五回溯法 (3)实验六分枝—限界算法 (4)实验七课程设计 (4)实验一递归与分治算法实验目的1.了解并掌握递归的概念,掌握递归算法的基本思想;2.掌握分治法的基本思想方法;3.了解适用于用递归与分治求解的问题类型,并能设计相应递归与分治算法;4.掌握递归与分治算法复杂性分析方法,比较同一个问题的递归算法与循环迭代算法的效率。
实验二动态规划实验目的1.掌握动态规划的基本思想方法;2.了解适用于用动态规划方法求解的问题类型,并能设计相应动态规划算法;3.掌握动态规划算法复杂性分析方法。
实验三贪心算法实验目的1.掌握贪心法的基本思想方法;2.了解适用于用贪心法求解的问题类型,并能设计相应贪心法算法;3.掌握贪心算法复杂性分析方法分析问题复杂性。
实验五回溯法实验目的1.掌握回溯法的基本思想方法;2.了解适用于用回溯法求解的问题类型,并能设计相应回溯法算法;3.掌握回溯法算法复杂性分析方法,分析问题复杂性。
实验六 分枝—限界算法实验目的1. 掌握分枝—限界的基本思想方法;2. 了解适用于用分枝—限界方法求解的问题类型,并能设计相应动态规划算法;3. 掌握分枝—限界算法复杂性分析方法,分析问题复杂性。
实验七 课程设计实验目的1. 在已学的算法基本设计方法的基础上,理解算法设计的基本思想方法;2. 掌握对写出的算法的复杂性分析的方法,理解算法效率的重要性;3. 能运用所学的基本算法设计方法对问题设计相应算法,分析其效率,并建立对算法进行改进,提高效率的思想意识。
预习与实验要求1. 预习实验指导书及教材的有关内容,回顾所学过的算法的基本思想;2. 严格按照实验内容进行实验,培养良好的算法设计和编程的习惯;3. 认真听讲,服从安排,独立思考并完成实验。
算法设计与分析实验报告(中南民族大学)

院系:计算机科学学院专业:年级:课程名称:算法设计与分析基础班号:组号:指导教师:年月日实验结果及分析1.求最大数2.递归法与迭代法性能比较递归迭代3.改进算法1.利用公式法对第n项Fibonacci数求解时可能会得出错误结果。
主要原因是由于double类型的精度还不够,所以程序算出来的结果会有误差,要把公式展开计算。
2.由于递归调用栈是一个费时的过程,通过递归法和迭代法的比较表明,虽然递归算法的代码更精简更有可读性,但是执行速度无法满足大数问题的求解。
3.在当前计算机的空间较大的情况下,在一些速度较慢的问题中,空间换时间是一个比较周全的策略。
实验原理(算法基本思想)定义:若A=(a ij), B=(b ij)是n×n的方阵,则对i,j=1,2,…n,定义乘积C=A⋅B 中的元素c ij为:1.分块解法通常的做法是将矩阵进行分块相乘,如下图所示:二.Strassen解法分治法思想将问题实例划分为同一问题的几个较小的实例。
对这些较小实例求解,通常使用递归方法,但在问题规模足够小时,也会使用另一种算法。
如果有必要,合并这些问题的解,以得到原始问题的解。
求解矩阵相乘的DAC算法,使用了strassen算法。
DAC(A[],B[],n){If n=2 使用7次乘法的方法求得解ElseDivide(A)//把A分成4块Divide(B)//把B分成4块调用7次strassen算法求得解的4块合并这4块得到解并返回}伪代码Serial_StrassenMultiply(A, B, C) {T1 = A0 + A3;T2 = B0 + B3;StrassenMultiply(T1, T2, M1);T1 = A2 + A3;StrassenMultiply(T1, B0, M2);T1 = (B1 - B3);StrassenMultiply (A0, T1, M3);T1 = B2 - B0;StrassenMultiply(A3, T1, M4);T1 = A0 + A1;StrassenMultiply(T1, B3, M5);T1 = A2 – A0;T2 = B0 + B1;StrassenMultiply(T1, T2, M6);T1 = A1 – A3;T2 = B2 + B3;StrassenMultiply(T1, T2, M7);C0 = M1 + M4 - M5 + M7C1 = M3 + M5C2 = M2 + M4C3 = M1 - M2 + M3 + M6}实验结果及分析时间复杂度1.分块相乘总共用了8次乘法,因而需要Θ(n log28)即Θ(n3)的时间复杂度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
算法分析与设计课程综合实验Design and Analysis of Algorithms1 Map Routing要求:Mandatory.实验目的:Implement the classic Dijkstra's shortest path algorithm and optimize it for maps. Such algorithms are widely used in geographic information systems (GIS) including MapQuest and GPS-based car navigation systems.实验内容及要求:Maps. For this assignment we will be working with maps, or graphs whose vertices are points in the plane and are connected by edges whose weights are Euclidean distances. Think of the vertices as cities and the edges as roads connected to them. To represent a map in a file, we list the number of vertices and edges, then list the vertices (index followed by its x and y coordinates), then list the edges (pairs of vertices), and finally the source and sink vertices. For example, Input6 represents the map below:Dijkstra's algorithm.Dijkstra's algorithm is a classic solution to the shortest path problem. It is described in section 24.3 in CLRS. The basic idea is not difficult to understand. We maintain, for every vertex in the graph, the length of the shortest known path from the source to that vertex, and we maintain these lengths in a priority queue. Initially, we put all the vertices on the queue with an artificially high priority and then assign priority 0.0 to the source. The algorithm proceeds by taking the lowest-priority vertex off the PQ, then checking all the vertices that can be reached from that vertex by one edge to see whether that edge gives a shorter path to the vertex from the source thanthe shortest previously-known path. If so, it lowers the priority to reflect this new information.Here is a step-by-step description that shows how Dijkstra's algorithm finds the shortest path 0-1-2-5 from 0 to 5 in the example above.process 0 (0.0)lower 3 to 3841.9lower 1 to 1897.4process 1 (1897.4)lower 4 to 3776.2lower 2 to 2537.7process 2 (2537.7)lower 5 to 6274.0process 4 (3776.2)process 3 (3841.9)process 5 (6274.0)This method computes the length of the shortest path. To keep track of the path, we also maintain for each vertex, its predecessor on the shortest path from the source to that vertex. The files EuclideanGraph.java, Point.java, IndexPQ.java, IntIterator.java, and Dijkstra.java provide a bare bones implementation of Dijkstra's algorithm for maps, and you should use this as a starting point. The client program ShortestPath.java solves a single shortest path problem and plots the results using turtle graphics. The client program Paths.java solves many shortest path problems and prints the shortest paths to standard output. The client program Distances.java solves many shortest path problems and prints only the distances to standard output.Your goal.Optimize Dijkstra's algorithm so that it can process thousands of shortest path queries for a given map. Once you read in (and optionally preprocess) the map, your program should solve shortest path problems in sublinear time. One method would be to precompute the shortest path for all pairs of vertices; however you cannot afford the quadratic space required to store all of this information. Your goal is to reduce the amount of work involved per shortest path computation, without using excessive space. We suggest a number of potential ideas below which you may choose to implement. Or you can develop and implement your own ideas.Idea 1.The naive implementation of Dijkstra's algorithm examines all V vertices in the graph. An obvious strategy to reduce the number of vertices examined is to stop the search as soon as you discover the shortest path to the destination. With this approach, you can make the running time per shortest path query proportional to E' log V' where E' and V' are the number of edges and vertices examined by Dijkstra's algorithm. However, this requires some care because just re-initializi ng all of the distances to ∞ would take time proportional to V. Since you are doing repeated queries, you can speed things up dramatically by only re-initializing those values that changed in the previous query.Idea 2.You can cut down on the search time further by exploiting the Euclidean geometry of the problem, as described in section 21.5 in the book of Algorithm in C Part V. For general graphs, Dijkstra's relaxes edge v-w by updating d[w] to the sum of d[v] plus the distance from v to w. For maps, we instead update d[w] to be the sum of d[v] plus the distance from v to w plus the Euclidean distance from w to d minus the Euclidean distance from v to d. This is known as the A* algorithm. This heuristics affects performance, but not correctness.Idea e a faster priority queue. There is some room for optimization in the supplied priority queue. You could also consider using a multiway heap as in Sedgewick Program 20.10.Testing.The file usa.txt contains 87,575 intersections and 121,961 roads in the continental United States. The graph is very sparse - the average degree is 2.8. Your main goal should be to answer shortest path queries quickly for pairs of vertices on this network. Your algorithm will likely perform differently depending on whether the two vertices are nearby or far apart. We provide input files that test both cases. You may assume that all of the x and y coordinates are integers between 0 and 10,000.实验类型:Verification.适用对象:Undergraduate for Computer School2 Document Distance Problem要求:Mandatory.实验目的:Design and implement the document distance problem and optimize it for data.实验内容及要求:Let D be a text document (e.g. the complete works of William Shakespeare).A word is a consecutive sequence of alphanumeric characters, such as "Hamlet" or "2007". We'll treat all upper-case letters as if they are lower-case, so that "Hamlet" and "hamlet" are the same word. Words end at a non-alphanumeric character, so "can't" contains two words: "can" and "t".The word frequency distribution of a document D is a mapping from words w to their frequency count, which we'll denote as D(w).We can view the frequency distribution D as vector, with one component per possible word. Each component will be a non-negative integer (possibly zero).The norm of this vector is defined in the usual way:.The inner-product between two vectors D and D' is defined as usual..Finally, the angle between two vectors D and D' is defined:This angle (in radians) will be a number between 0 and since the vectors are non-negative in each component. Clearly,angle(D,D) = 0.0for all vectors D, andangle(D,D') = π / 2if D and D' have no words in common.Example: The angle between the documents "To be or not to be" and "Doubt truth to be a liar" isWe define the distance between two documents to be the angle between their word frequency vectors.The document distance problem is thus the problem of computing the distance between two given text documents.An instance of the document distance problem is the pair of input text documents.3 Edit Distance要求:Mandatory.实验目的:Many word processors and keyword search engines have a spelling correction feature. If you type in a misspelled word x, the word processor or search engine can suggest a correction y. The correction y should be a word that is close to x. One way to measure the similarity in spelling between two text strings is by “edit distance”. The notion of edit distance is useful in other fields as well. For example, biologists use edit distance to characterize the similarity of DNA or protein sequences.实验内容及要求:The edit distance d(x, y) of two strings of text, x[1..m] and y[1..n], is defined to be the minimum possible cost of a sequence of “transformation operations”(defined below) that transforms string x[1..m] into string y[1..n]. To define the effect of thetransformation operations, we use an auxiliary string z[1..s] that holds the intermediate results. At the beginning of the transformation sequence s = m and z[1..s] = x[1..m] (i.e., we start with string x[1..m]). At the end of the transformation sequence, we should have s = n and z[1..s] = y[1..n](i.e., our goal is to transform into string y[1..n]). Throughout the transformation, we maintain the current length s of string z, as well as a cursor position i, i.e., an index into string z. The invariant 1 ≤i ≤s +1 holds at all times during the transformation. (Notice that the cursor can move one space beyond the end of the string z in order to allow insertion at the end of the string.)Each transformation operation may alter the string z, the size s, and the cursor position i. Each transformation operation also has an associated cost. The cost of a sequence of transformation operations is the sum of the costs of the individual operations on the sequence. The goal of the edit-distance problem is to find a sequence of transformation operation of minimum cost that transforms x[1..m] into y[1..n].There are five transformation operations:Operation Cost Effectleft 0 If i = 1 then do nothing. Otherwise, set i ←i-1right 0 If i = s +1 then do nothing. Otherwise, set i←i-1.replace 4 If i = s +1 then do nothing. Otherwise, replace the character underthe cursor by another character c by setting z[i] ←c, and thenincrementing i.delete 2 If i = s +1 then do nothing. Otherwise, delete the character c underthe cursor by setting z[i..s] ← z[i+1..s+1] and decrementing s. Thecursor position i does not change.insert 3 Insert the character c into string z by incrementing s, setting z[i+1..s] ←z[i..s-1], setting z[i] ←c, and then incrementing index i. As an example, one way to transform the source string algorithm to the target string analysis is to use the sequence of operations shown in Table 1, where the position of the underlined character represents the cursor position i. Many other sequences of transformation operations also transform algorithm to analysis − the solution in Table 1 is not unique − and some other solutions cost more while some others cost less.Operation z Cost Totalinitial string algorithm 0 0right algorithm 0 0right algorithm 0 0replace by y alyorithm 4 4replace by s alysrithm 4 8replace by i alysiithm 4 12replace by s alysisthm 4 16delete alysishm 2 18delete alysism 2 20delete alysis_ 2 22left alysis 0 22left alysis 0 22left alysis 0 22left alysis 0 22left alysis 0 22insert n anlysis 3 25insert a analysis 3 28Table 1: Transforming algorithm into analysis(a)It is possible to transform algorithm to analysis without using the “left” operation.Give a sequence of operations in the style of Table 1 that has the same cost as in Table 1 but does not use the “left” operation.(b)Argue that, for any two strings x and y with edit distance d(x, y), there exists asequence S of transformation operations that transforms x to y with cost d(x, y) where S does not contain any “left” operations.(c)Show that the problem of calculation the edit distance d(x, y) exhibits optimalsubstructure.(Hint: Consider all suffixes of x and y.)(d)Recursively define the value of edit distance d(x, y) in terms of the suffixes of stringsx and y. Indicate how edit distance exhibits overlapping subproblems.(e)Describe a dynamic-programming algorithm that computes the edit distance fromx[1..m] to y[1..n].(Do not use a memoized recursive algorithm. Your algorithm should be a classical, bottom-up, tabular algorithm.) Analyze the running time and space requirements of your algorithm.(f)Implement your algorithm as a computer program in any language you wish. Yourprogram should calculate the edit distance d(x, y) between two strings x and y using dynamic programming and print out the corresponding sequence of transformation operations in the style of Table 1. Run your program on the stringsx= “electrical engineering”,y= “computer science”.Submit the source code of your program electronically on the class website, and hand in a printout of your source code and your results. Sample input and output text is provided on the class website to help you debug your program. These solutions are not necessarily unique: there may be other sequences of transformation operations that achieve the same cost. As usual, you may collaborate to solve this problem, but you must write the program by yourself.(g) Run your program on the three input files provided on the class website. Each inputfile contains the following four lines:1.The number of characters m in the string x.2.The string x.3.The number of characters n in the string y.4.The string y.Compute the edit distance d(x, y) for each input. Do not hand in a printout of the transformation operations for this problem part. (Extra bonus kudos if you can identify the source of all the texts, without searching the web.)(h) If z is implemented using an array, then the “insert” and “delete” operations requiresΘ(n) time. Design a suitable data structure that allow each of the five transformation operations to be implemented in Ο(1) time.实验类型:Synthesis适用对象:Undergraduate for Computer School4 Global Sequence Alignment要求:Optional实验目的:Write a program to compute the optimal sequence alignment of two DNA strings. This program will introduce you to the emerging field of computational biology in which computers are used to do research on biological systems. Further, you will be introduced to a powerful algorithmic design paradigm known as dynamic programming.实验内容及要求:Biology review. A genetic sequence is a string formed from a four-letter alphabet {Adenosine (A), Thymidine (T), Guanosine (G), Cytidine (C)} of biological macromolecules referred to together as the DNA bases. A gene is a genetic sequence that contains the information needed to construct a protein. All of your genes taken together are referred to as the human genome, a blueprint for the parts needed to construct the proteins that form your cells and, by extension, your body. Each new cell produced by your body receives a copy of the genome. This copying process, as well as natural wear and tear, introduces a small number of changes into the sequences of many genes. Among the most common changes are the substitution of one base for another and the deletion of a substring of bases; such changes are generally referred to as point mutations. As a result of these point mutations, the same gene sequenced from closely related organisms will have slight differences.The problem.Through your research you have found the following sequence of a gene in a previously unstudied organism.A A C A G T T A C CWhat is the function of the protein that this gene encodes? You could immediately begin a series of uninformed experiments in the lab to determine what role this gene plays. However, there is a good chance that it is a variant of a known gene in a previously studied organism. Since biologists and computer scientists have laboriously determined (and published) the genetic sequence of many organisms (including humans), you wouldlike to leverage this information to your advantage. We'll compare the above genetic sequence with one which has already been sequenced and whose function is well understood.T A A G G T C AIf the two genetic sequences are similar enough, we might expect them to have similar functions. We would like a way to quantify "similar enough".Edit-distance.We measure the similarity of two genetic sequences by using a very popular method known as the edit distance, a concept which is also widely used in spell checking, speech recognition, plagiarism detection, file revision, and computational linguistics. We align the two sequences, but we are permitted to insert gaps in either sequence (e.g., to make them have the same length). We pay a penalty for each gap that we insert and also for each pair of characters that mismatch in the final alignment. Intuitively, these penalties model the relative likeliness of point mutations arising from deletion/insertion and substitution. We produce a numerical score according to the following simple rule, which is widely used in biological applications:As an example, two possible alignments for the genetic sequences discussed above are:The first alignment has a score of 8, while the second one has a score of 7. The edit-distance is the score of the best possible alignment between the two genetic sequences over all possible alignments. In this example, the second alignment is in fact optimal, so the edit-distance between the two strings is 7. Computing the edit-distance between two strings is a nontrivial computational problem because we must find the best alignment among exponentially many possibilities. For example, if both strings are 100 characters long, then there are more than 10^75 possible alignments.A recursive solution.Your job is to write a program to compute the edit-distance and the optimal alignment of two genetic sequences. We can compute the edit-distancerecursively by breaking up the sequence alignment problem on the two original strings x and y into many alignment problems on the suffixes of the two strings. We use the notation x[i..M] to refer to the suffix of x consisting of the characters x[i], x[i+1], ..., x[M]. Note that x[M] is the string termination character '\0'. For example, consider the two strings x = "AACAGTTACC" and y = "TAAGGTCA" of length M = 10 and N = 8, respectively. Then, x[2..M] is "CAGTTACC" and y[8..N] is the empty string.Now, we return to our recursive solution technique. Consider the zeroth column in an optimal alignment of x[0..M] with y[0..N]. There are three possibilities:1.The optimal alignment matches x[0] = 'A' up with y[0] = 'T'. In this case, we pay apenalty of 1 for a mismatch and still need to align the string x[1..M] with y[1..N].What is the best way to do this? This subproblem is exactly the same as the original sequence alignment problem, except that the two inputs are each suffixes of the original inputs. We can solve this subproblem recursively.2.The optimal alignment matches the x[0] = 'A' up with a gap. In this case, we pay apenalty of 2 for a gap and still need to align the string x[1..M] with y[0..N]. This subproblem is identical to the original sequence alignment problem, except that the first input is a suffix of the original input.3.The optimal alignment matches the y[0] = 'T' up with a gap. In this case, we pay apenalty of 2 for a gap and still need to align the string x[0..M] with y[1..N]. This subproblem is identical to the original sequence alignment problem, except that the second input is a suffix of the original input.All of the resulting subproblems are sequence alignment problem on suffixes of the original inputs. Thus, we need a function, say opt(i, j) that returns the optimum value of aligning the input string x[i..M] with y[j..N]. Using this notation, the optimal value of our original sequence alignment problem is opt(0, 0). In general, to compute opt(i, j), we need to compute the minimum of the following three quantities:opt(i+1, j+1) + 0/1 by aligning x[i] with y[j], add 0 if a match, 1 if a mismatchopt(i+1, j) + 2 by aligning x[i] with a gapopt(i, j+1) + 2 by aligning y[j] with a gapFor our recursive scheme to bottom-out, we need a base case. Aligning an empty string with another string of length j requires inserting j gaps, for a total cost of 2j. Thus, in general we should set opt(M, j) = 2(N-j) and opt(i, N) = 2(M-i). For our example, the final matrix is:6 T 9 87 5 3 3 5 6 87 A 11 9 7 6 4 2 3 4 68 C 13 11 9 7 5 3 1 3 49 C 14 12 10 8 6 4 2 1 210 - 16 14 12 10 8 6 4 2 0The score of the optimal alignment is opt(0, 0) = 7.A dynamic programming approach. A direct implementation of the above recursive scheme will work, but it is spectacularly inefficient. If both input strings have N characters, then the number of recursive calls will exceed 2^N.To overcome this performance bug, we will use dynamic programming. (Read sections 15.1 for an introduction to this technique and 15.4 for the problem.) Dynamic programming is a powerful algorithmic paradigm that forms the core computational engine of many programs, including BLAST(the sequence alignment program almost universally used by molecular biologist in their experimental work). The key idea of dynamic programming is to break a large computational problem up into smaller subproblems, store the answers to those smaller subproblems, and, eventually, using the stored answers to solve the original problem. This avoids recomputing the same quantity over and over again. Specifically, we maintain an array, say c[i][j], that contains a table (or cache) of the solutions to all of the subproblems that the recursive function has already solved. The recursive function computes and fills in the appropriate table entry when it is presented with a new subproblem. However, when the function is presented with a previously solved subproblem, it simply looks up the appropriate value in the table and returns it.Finding the alignment itself.The above procedure above indicates how to compute the value of the optimal alignment. We now describe how to find the optimal alignment itself. In order to reconstruct the optimal alignment, we maintain a character matrix, say bl[i][j], to keep track of where the minimum value for aligning x[i..M] with y[j..N] came from. For example, if the minimum came from aligning x[i] with y[j] (in which case we solved the subproblem c(i+1, j+1), then we can record this fact by drawing an arrow from (i, j) to (i+1, j+1). We can obtain a crude ASCII picture of such an arrow by storing one of the three characters '\', '-', or '|' into b[i][j]. We interpret the three symbols as arrows emanating from (i, j) and terminating at (i+1, j+1), (i+1, j), and (i, j+1), respectively. For the example above, we get the the following solution matrix:5 T \ \ \ \ \ \ \ | |6 T \ \ \ \ \ \ \ | |7 A - \ \ \ \ \ | \ |8 C \ \ \ \ \ \ \ \ |9 C - - - - - - \ \ |10 - - - - - - - - - .Note that all arrows point from top to bottom and left to right. In order to reconstruct the alignment, we follow the arrows from the upper left corner c[0][0] until we arrive at the lower right corner c[M][N]. When we encounter '-', we insert a gap in x; when we encounter '|', we insert a gap in y; and, when we encounter '\', we align the two characters. The optimal alignment is the second candidate alignment in the edit-distance section.Input and output.Read the two input strings from standard input, one per line. Print the edit-distance to standard output. If both strings have length at most 40, also print out a table of optimal values, optimal choices, and an optimal alignment. Test your program using the example provided above, as well as the genomic data sets from GenBank.Analysis.Estimate the running time and memory usage of your program as a function of the lengths of the two input strings M and N.实验类型:Synthesis适用对象:Undergraduate for Computer School。
