数值分析-龙格现象-matlab代码分享
拉格朗日插值龙格现象的matlab实现

拉格朗日插值法在实践中的应 用
在数值分析中的应用
单击此处添加标题
插值法:拉格朗日插值法是数值分析中常用的插值方法之一,具有简单易 行、计算量小等优点。
单击此处添加标题
数据拟合:拉格朗日插值法可以用于数据拟合,通过对已知数据进行插值, 得到未知数据的近似值。
单击此处添加标题
数值微积分:拉格朗日插值法在数值微积分中也有广泛应用,例如在求解 函数的导数、积分等运算时,可以利用拉格朗日插值法进行近似计算。
龙格现象
龙格现象的定义
定义:当插值多项式的阶数过高时, 插值结果可能变得不可预测或出现 剧烈振荡
解决方法:在实际应用中,应避免 使用过高的插值多项式阶数,而应 选择合适的阶数以保证插值结果的 稳定性和准确性
添加标题
添加标题
添加标题
添加标题
原因:由于高阶插值多项式对数据 点的敏感性增强,导致插值结果不 稳定
拉格朗日插值龙格现象的 Matlab实现
汇报人:XX
单击输入目录标题 拉格朗日插值法 龙格现象 拉格朗日插值法在Matlab中的实现 拉格朗日插值法的龙格现象分析 拉格朗日插值法在实践中的应用
添加章节标题
拉格朗日插值法
插值法的定义
插值法是一种数学方法,通过已知的离散数据点,构造一个多项式函数,使得该函数在 数据点处的取值等于已知的数据点值。
算法收敛性:在某些情况下,龙格现象可能导致算法收敛速度减慢,增加计算时间和计算成本。
实际应用限制:由于龙格现象的存在,某些数值方法在实际应用中可能受到限制,无法处理某些 复杂问题。
算法改进需求:为了克服龙格现象的影响,需要研究和发展新的数值方法和算法,提高数值计算 的稳定性和精度。
拉格朗日插值法在Matlab中的 实现
四阶龙格库塔法matlab实现

% hh 是步长
%% ===输入判断===
if (4 == nargin) % == 当没有给步长的时候使用默认步长==
h = 0.1 ;
elseif (5 == nargin)
h = hh ;
end
%% ===参数初始化(可以修改,可从网上找相关参数的值),以下是通用参数===
废话不多说直接复制就可以运行文章底部有参考例子不明白就看看
四阶龙格库塔法matlab实现
% 废话不多说,直接复制就可以运行,文章底部有参考例子,不明白就看看
function [ yy ] = R_K_4( f , y0 , x0 , xn , hh )
% f 是inline function的句柄
% y0 是初始值
end
elseif (1 == nargout)
yy = y ;
else
disp('error : please check your input') ;
return ;
end
end
%% === 例子=======
%
% === input =========
% f = inline('x+y'') ;
% x: 0.800000 y: 2.651042
% x: 1.000000 y: 3.436502
y(k+1) = y(k) + h* ( c(1)*kk(1) + c(2)*kk(2) + c(3)*kk(3) + c(4)*kk(4) ) ;
end
%% ===输出处理===
if (0 == nargout)
MATLAB中龙格库塔(RUNGEKUTTA)方法原理及实现

MATLAB中龙格库塔(RUNGEKUTTA)方法原理及实现函数功能ode是专门用于解微分方程的功能函数,他有ode23,ode45,ode23s等等,采用的是Runge-Kutta算法。
ode45表示采用四阶,五阶runge-kutta单步算法,截断误差为(Δx)3。
解决的是Nonstiff(非刚性)的常微分方程.是解决数值解问题的首选方法,若长时间没结果,应该就是刚性的,换用ode23来解.使用方法[T,Y]=ode45(odefun,tspan,y0)odefun是函数句柄,可以是函数文件名,匿名函数句柄或内联函数名tspan是区间[t0tf]或者一系列散点[t0,t1,...,tf]y0是初始值向量T返回列向量的时间点Y返回对应T的求解列向量[T,Y]=ode45(odefun,tspan,y0,options)options是求解参数设置,可以用odeset在计算前设定误差,输出参数,事件等[T,Y,TE,YE,IE]=ode45(odefun,tspan,y0,options)在设置了事件参数后的对应输出TE事件发生时间YE事件解决时间IE事件消失时间sol=ode45(odefun,[t0tf],y0...)sol结构体输出结果应用举例1求解一阶常微分方程程序:一阶常微分方程odefun=@(t,y)(y+3*t)/t^2;%定义函数tspan=[14];%求解区间y0=-2;%初值[t,y]=ode45(odefun,tspan,y0);plot(t,y)%作图title('t^2y''=y+3t,y(1)=-2,1<t<4')< p="">legend('t^2y''=y+3t')xlabel('t')ylabel('y')%精确解%dsolve('t^2*Dy=y+3*t','y(1)=-2')%ans=一阶求解结果图%(3*Ei(1)-2*exp(1))/exp(1/t)-(3*Ei(1/t))/exp(1/t)2求解高阶常微分方程关键是将高阶转为一阶,odefun的书写.F(y,y',y''...y(n-1),t)=0用变量替换,y1=y,y2=y'...注意odefun方程定义为列向量dxdy=[y(1),y(2)....]程序:function Testode45tspan=[3.94.0];%求解区间y0=[28];%初值[t,x]=ode45(@odefun,tspan,y0);plot(t,x(:,1),'-o',t,x(:,2),'-*')legend('y1','y2')title('y''''=-t*y+e^t*y''+3sin2t')xlabel('t')ylabel('y')function y=odefun(t,x)y=zeros(2,1);%列向量y(1)=x(2);y(2)=-t*x(1)+exp(t)*x(2)+3*sin(2*t);endend高阶求解结果图相关函数ode23,ode45,ode113,ode15s,ode23s,ode23t,ode23tbMatlab中龙格-库塔(Runge-Kutta)方法原理及实现龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法。
matlab-欧拉方法和龙格库塔方法的小实例
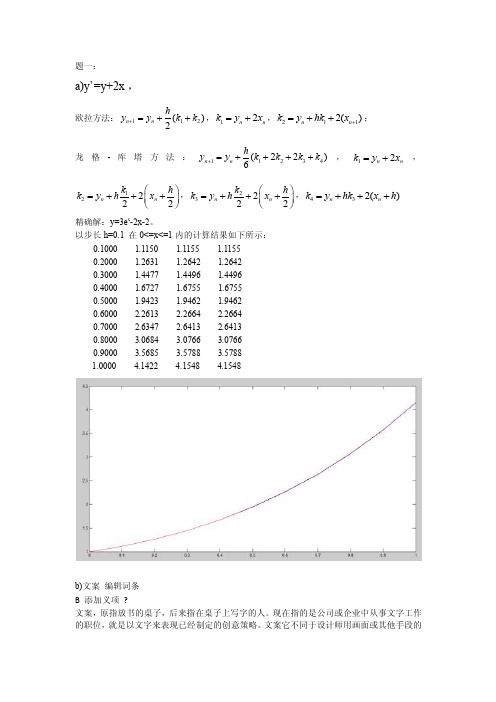
题一:a)y’=y+2x , 欧拉方法:112()2n n h y y k k +=++,12n n k y x =+,2112()n n k y hk x +=++; 龙格-库塔方法:11234(22)6n n h y y k k k k +=++++,12n n k y x =+,12222n n k h k y h x ⎛⎫=+++ ⎪⎝⎭,23222n n k h k y h x ⎛⎫=+++ ⎪⎝⎭,432()n n k y hk x h =+++ 精确解:y=3e x -2x-2。
以步长h=0.1 在0<=x<=1内的计算结果如下所示:0.1000 1.1150 1.1155 1.11550.2000 1.2631 1.2642 1.26420.3000 1.4477 1.4496 1.44960.4000 1.6727 1.6755 1.67550.5000 1.9423 1.9462 1.94620.6000 2.2613 2.2664 2.26640.7000 2.6347 2.6413 2.64130.8000 3.0684 3.0766 3.07660.9000 3.5685 3.5788 3.57881.0000 4.1422 4.1548 4.1548b)文案 编辑词条B 添加义项 ?文案,原指放书的桌子,后来指在桌子上写字的人。
现在指的是公司或企业中从事文字工作的职位,就是以文字来表现已经制定的创意策略。
文案它不同于设计师用画面或其他手段的表现手法,它是一个与广告创意先后相继的表现的过程、发展的过程、深化的过程,多存在于广告公司,企业宣传,新闻策划等。
基本信息中文名称文案外文名称Copy目录1发展历程2主要工作3分类构成4基本要求5工作范围6文案写法7实际应用折叠编辑本段发展历程汉字"文案"(wén àn)是指古代官衙中掌管档案、负责起草文书的幕友,亦指官署中的公文、书信等;在现代,文案的称呼主要用在商业领域,其意义与中国古代所说的文案是有区别的。
微分方程组的龙格库塔公式求解matlab版

微分方程组的龙格-库塔公式求解matlab 版南京大学王寻1.一阶常微分方程组考虑方程组()()()()⎩⎨⎧====0000z x z ,z ,y ,x g 'z y x y ,z ,y ,x f 'y 其经典四阶龙格-库塔格式如下:对于n =0,1,2,...,计算()()⎪⎩⎪⎨⎧++++=++++=++4321143211226226L L L L h z z K K K K h y y n n n n 其中()()()()⎪⎪⎪⎩⎪⎪⎪⎨⎧+++=+++=⎪⎭⎫ ⎝⎛+++=⎪⎭⎫ ⎝⎛+++=⎪⎭⎫ ⎝⎛+++=⎪⎭⎫ ⎝⎛+++===33433422322311211211222222222222hL z ,hK y ,h x g L ,hL z ,hK y ,h x f K hL z ,hK y ,h x g L ,hL z ,hK y ,h x f K hL z ,hK y ,h x g L ,hL z ,hK y ,h x f K z ,y ,x g L ,z ,y ,x f K n n n n n n n n n n n n n n n n n n n n n n n n 下面给出经典四阶龙格-库塔格式解常微分方程组的matlab 通用程序:%marunge4s.m%用途:4阶经典龙格库塔格式解常微分方程组y'=f(x,y),y(x0)=y0%格式:[x,y]=marunge4s(dyfun,xspan,y0,h)%dyfun 为向量函数f(x,y),xspan 为求解区间[x0,xn],%y0为初值向量,h 为步长,x 返回节点,y 返回数值解向量function [x,y]=marunge4s(dyfun,xspan,y0,h)x=xspan(1):h:xspan(2);y=zeros(length(y0),length(x));y(:,1)=y0(:);for n=1:(length(x)-1)k1=feval(dyfun,x(n),y(:,n));k2=feval(dyfun,x(n)+h/2,y(:,n)+h/2*k1);k3=feval(dyfun,x(n)+h/2,y(:,n)+h/2*k2);k4=feval(dyfun,x(n+1),y(:,n)+h*k3);y(:,n+1)=y(:,n)+(h/6).*(k1+2*k2+3*k3+k4);end如下为例题:例1:取h =0.02,利用程序marunge4s.m 求刚性微分方程组()()⎩⎨⎧=-==--=10100209999010z ,z 'z ,y ,z .y .'y 的数值解,其解析解为:xx x .e z ,e e y 100100010---=+=解:首先编写M 函数dyfun.m%dyfun.m function f=dyfun(t,y)f(1)=-0.01*y(1)-99.99*y(2);f(2)=-100*y(2);f=f(:);然后编写一个执行函数:close all ;clear all ;clc;[x,y]=marunge4s(@dyfun,[0500],[21],0.002);plot(x,y);axis([-50500-0.52]);text(120,0.4,'y(x)');text(70,0.1,'z(x)');title('数值解');figure;y1=exp(-0.01*x)+exp(-100*x);%解析解,用来做对比的。
数值分析matlab代码

1、%用牛顿法求f(x)=x-sin x 的零点,e=10^(-6)disp('牛顿法');i=1;n0=180;p0=pi/3;tol=10^(-6);for i=1:n0p=p0-(p0-sin(p0))/(1-cos(p0));if abs(p-p0)<=10^(-6)disp('用牛顿法求得方程的根为')disp(p);disp('迭代次数为:')disp(i)break;endp0=p;endif i==n0&&~(abs(p-p0)<=10^(-6))disp(n0)disp('次牛顿迭代后无法求出方程的解')end2、disp('Steffensen加速');p0=pi/3;for i=1:n0p1=0.5*p0+0.5*cos(p0);p2=0.5*p1+0.5*cos(p1);p=p0-((p1-p0).^2)./(p2-2.*p1+p0);if abs(p-p0)<=10^(-6)disp('用Steffensen加速求得方程的根为')disp(p);disp('迭代次数为:')disp(i)break;endp0=p;endif i==n0&&~(abs(p-p0)<=10^(-6))disp(n0)disp('次Steffensen加速后无法求出方程的解')end1、%使用二分法找到方程 600 x^4 -550 x^3 +200 x^2 -20 x -1 =0 在区间[0.1,1]上的根,%误差限为 e=10^-4disp('二分法')a=0.2;b=0.26;tol=0.0001;n0=10;fa=600*(a.^4)-550*(a.^3)+200*(a.^2)-20*a-1;for i=1:n0p=(a+b)/2;fp=600*(p.^4)-550*(p.^3)+200*(p.^2)-20*p-1;if fp==0||(abs((b-a)/2)<tol)disp('用二分法求得方程的根p=')disp(p)disp('二分迭代次数为:')disp(i)break;endif fa*fp>0a=p;else b=p;endendif i==n0&&~(fp==0||(abs((b-a)/2)<tol))disp(n0)disp('次二分迭代后没有求出方程的根')end2、%使用牛顿法找到方程 600 x^4 -550 x^3 +200 x^2 -20 x -1 =0 在区间[0.1,1]上的根,%误差限为 e=10^-4disp('牛顿法')p0=0.3;for i=1:n0p=p0-(600*(p0.^4)-550*(p0.^3)+200*(p0.^2)-20*p0-1)./(2400*(p0.^3) -1650*p0.^2+400*p0-20);if(abs(p-p0)<tol)disp('用牛顿法求得方程的根p=')disp(p)disp('牛顿迭代次数为:')disp(i)break;endp0=p;endif i==n0&&~(abs(p-p0)<tol)disp(n0)disp('次牛顿迭代后没有求出方程的根')end3、%使用割线法找到方程 600 x^4 -550 x^3 +200 x^2 -20 x -1 =0 在区间[0.1,1]上的根,%误差限为 e=10^-4disp('割线法')p0=0.2;p1=0.25;q0=600*(p0.^4)-550*(p0.^3)+200*(p0.^2)-20*p0-1;q1=600*(p1.^4)-550*(p1.^3)+200*(p1.^2)-20*p1-1;for i=2:n0p=p1-q1*(p1-p0)/(q1-q0);if abs(p-p1)<toldisp('用割线法求得方程的根p=')disp(p)disp('割线法迭代次数为:')disp(i)break;endp0=p1;q0=q1;pp=p1;p1=p;q1=600*(p.^4)-550*(p.^3)+200*(p.^2)-20*p-1;endif i==n0&&~(abs(p-pp)<tol)disp(n0)disp('次割线法迭代后没有求出方程的根')end4、%使用试位法找到方程 600 x^4 -550 x^3 +200 x^2 -20 x -1 =0 在区间[0.1,1]上的根,%误差限为 e=10^-4disp('试位法')p0=0.2;p1=0.25;q0=600*(p0.^4)-550*(p0.^3)+200*(p0.^2)-20*p0-1;q1=600*(p1.^4)-550*(p1.^3)+200*(p1.^2)-20*p1-1;for i=2:n0p=p1-q1*(p1-p0)/(q1-q0);if abs(p-p1)<toldisp('用试位法求得方程的根p=')disp(p)disp('试位法迭代次数为:')disp(i)break;endq=600*(p.^4)-550*(p.^3)+200*(p.^2)-20*p-1;if q*q1<0p0=p1;q0=q1;endpp=p1;p1=p;q1=q;endif i==n0&&~(abs(p-pp)<tol)disp(n0)disp('次试位法迭代后没有求出方程的根')end5、%使用muller方法找到方程 600 x^4 -550 x^3 +200 x^2 -20 x -1 =0 在区间[0.1,1]上的根,%误差限为 e=10^-4disp('muller法')x0=0.1;x1=0.2;x2=0.25;h1=x1-x0;h2=x2-x1;d1=((600*(x1.^4)-550*(x1.^3)+200*(x1.^2)-20*x1-1)-(600*(x0.^4)-55 0*(x0.^3)+200*(x0.^2)-20*x0-1))/h1;d2=((600*(x2.^4)-550*(x2.^3)+200*(x2.^2)-20*x2-1)-(600*(x1.^4)-55 0*(x1.^3)+200*(x1.^2)-20*x1-1))/h2;d=(d2-d1)/(h2+h1);for i=3:n0b=d2+h2*d;D=(b*b-4*(600*(x2.^4)-550*(x2.^3)+200*(x2.^2)-20*x2-1)*d)^0.5;if(abs(d-D)<abs(d+D))E=b+D;else E=b-D;endh=-2*(600*(x2.^4)-550*(x2.^3)+200*(x2.^2)-20*x2-1)/E;p=x2+h;if abs(h)<toldisp('用muller方法求得方程的根p=')disp(p)disp('muller方法迭代次数为:')disp(i)break;endx0=x1;x1=x2;x2=p;h1=x1-x0;h2=x2-x1;d1=((600*(x1.^4)-550*(x1.^3)+200*(x1.^2)-20*x1-1)-(600*(x0.^4)-55 0*(x0.^3)+200*(x0.^2)-20*x0-1))/h1;d2=((600*(x2.^4)-550*(x2.^3)+200*(x2.^2)-20*x2-1)-(600*(x1.^4)-55 0*(x1.^3)+200*(x1.^2)-20*x1-1))/h2;d=(d2-d1)/(h2+h1);endif i==n0%条件有待商榷?!disp(n0)disp('次muller方法迭代后没有求出方程的根')end1、%观察Lagrange插值的Runge现象x=-1:0.05:1;y=1./(1+25.*x.*x);plot(x,y),grid on;n=5;x=-1:2/n:1;y=1./(1+25.*x.*x);for i=1:n+1q(1,i)=y(i);endh=0.05;z=-1:h:1;for k=1:2/h+1for i=2:n+1for j=2:iq(j,i)=((z(k)-x(i-j+1))*q(j-1,i)-(z(k)-x(i))*q(j-1,i-1))/(x(i)-x( i-j+1));endendw(k)=q(n+1,n+1);endhold on, plot(z,w,'r'),grid on;%**** n=10 ****n=10;x=-1:2/n:1;y=1./(1+25.*x.*x);for i=1:n+1q(1,i)=y(i);endh=0.05;z=-1:h:1;for k=1:2/h+1for i=2:n+1for j=2:iq(j,i)=((z(k)-x(i-j+1))*q(j-1,i)-(z(k)-x(i))*q(j-1,i-1))/(x(i)-x( i-j+1));endendw(k)=q(n+1,n+1);endhold on,plot(z,w,'k'),grid on;legend ('原始图','n=5','n=10');2、%固支样条插植%********第一段********x=[1,2,5,6,7,8,10,13,17];a=[3,3.7,3.9,4.2,5.7,6.6,7.1,6.7,4.5];n=numel(a);for i=1:n-1h(i)=x(i+1)-x(i);endA=[2*h(1),h(1),0,0,0,0,0,0,0;h(1),2*(h(1)+h(2)),h(2),0,0,0,0,0,0;0,h(2),2*(h(2)+h(3)),h(3),0,0,0,0,0;0,0,h(3),2*(h(3)+h(4)),h(4),0,0,0,0;0,0,0,h(4),2*(h(4)+h(5)),h(5),0,0,0;0,0,0,0,h(5),2*(h(5)+h(6)),h(6),0,0;0,0,0,0,0,h(6),2*(h(6)+h(7)),h(7),0;0,0,0,0,0,0,h(7),2*(h(7)+h(8)),h(8);0,0,0,0,0,0,0,h(8),2*h(8)];e=[3*(a(2)-a(1))/h(1)-3;3*(a(3)-a(2))/h(2)-3*(a(2)-a(1))/h(1);3*(a(4)-a(3))/h(3)-3*(a(3)-a(2))/h(2);3*(a(5)-a(4))/h(4)-3*(a(4)-a(3))/h(3);3*(a(6)-a(5))/h(5)-3*(a(5)-a(4))/h(4);3*(a(7)-a(6))/h(6)-3*(a(6)-a(5))/h(5);3*(a(8)-a(7))/h(7)-3*(a(7)-a(6))/h(6);3*(a(9)-a(8))/h(8)-3*(a(8)-a(7))/h(7);3*(-0.67)-3*(a(9)-a(8))/h(8)];c=inv(A)*e;for i=1:8b(i)=(a(i+1)-a(i))/h(i)-h(i)*(2*c(i)+c(i+1))/3;d(i)=(c(i+1)-c(i))/(3*h(i));endfor i=1:8z=x(i):0.05:x(i+1);w=a(i)+b(i).*(z-x(i))+c(i).*(z-x(i)).^2+d(i).*(z-x(i)).^3; grid on, plot(z,w),hold on;end%********第二段********x=[17,20,23,24,25,27,27.7];a=[4.5,7,6.1,5.6,5.8,5.2,4.1];for i=1:6h(i)=x(i+1)-x(i);endA=[2*h(1),h(1),0,0,0,0,0;h(1),2*(h(1)+h(2)),h(2),0,0,0,0;0,h(2),2*(h(2)+h(3)),h(3),0,0,0;0,0,h(3),2*(h(3)+h(4)),h(4),0,0;0,0,0,h(4),2*(h(4)+h(5)),h(5),0;0,0,0,0,h(5),2*(h(5)+h(6)),h(6)0,0,0,0,0,h(6),2*h(6)];e=[3*(a(2)-a(1))/h(1)-3*3;3*(a(3)-a(2))/h(2)-3*(a(2)-a(1))/h(1);3*(a(4)-a(3))/h(3)-3*(a(3)-a(2))/h(2);3*(a(5)-a(4))/h(4)-3*(a(4)-a(3))/h(3);3*(a(6)-a(5))/h(5)-3*(a(5)-a(4))/h(4);3*(a(7)-a(6))/h(6)-3*(a(6)-a(5))/h(5);3*(-4)-3*(a(7)-a(6))/h(6)];c=inv(A)*e;for i=1:6b(i)=(a(i+1)-a(i))/h(i)-h(i)*(2*c(i)+c(i+1))/3;d(i)=(c(i+1)-c(i))/(3*h(i));endfor i=1:6z=x(i):0.05:x(i+1);w=a(i)+b(i).*(z-x(i))+c(i).*(z-x(i)).^2+d(i).*(z-x(i)).^3; grid on, plot(z,w),hold on;end%********第三段********x=[27.7,28,29,30];a=[4.1,4.3,4.1,3];for i=1:3h(i)=x(i+1)-x(i);endA=[2*h(1),h(1),0,0;h(1),2*(h(1)+h(2)),h(2),0;0,h(2),2*(h(2)+h(3)),h(3);0,0,h(3),2*h(3)];e=[3*(a(2)-a(1))/h(1)-3*0.33;3*(a(3)-a(2))/h(2)-3*(a(2)-a(1))/h(1);3*(a(4)-a(3))/h(3)-3*(a(3)-a(2))/h(2);3*(-1.5)-3*(a(4)-a(3))/h(3)];c=inv(A)*e;for i=1:3b(i)=(a(i+1)-a(i))/h(i)-h(i)*(2*c(i)+c(i+1))/3;d(i)=(c(i+1)-c(i))/(3*h(i));endfor i=1:3z=x(i):0.05:x(i+1);w=a(i)+b(i).*(z-x(i))+c(i).*(z-x(i)).^2+d(i).*(z-x(i)).^3; grid on, plot(z,w),hold on;endgrid on,title('注:横纵坐标的比例不一样!!!');1、%用不动点迭代法求方程 x-e^x+4=0的正根与负根,误差限是10^-6%disp('不动点迭代法');n0=100;p0=-5;for i=1:n0p=exp(p0)-4;if abs(p-p0)<=10^(-6)if p<0disp('|p-p0|=')disp(abs(p-p0))disp('不动点迭代法求得方程的负根为:')disp(p);break;elsedisp('不动点迭代法无法求出方程的负根.')endelsep0=p;endendif i==n0disp(n0)disp('次不动点迭代后无法求出方程的负根')endp1=1.7;for i=1:n0pp=exp(p1)-4;if abs(pp-p1)<=10^(-6)if pp>0disp('|p-p1|=')disp(abs(pp-p1))disp('用不动点迭代法求得方程的正根为')disp(pp);elsedisp('用不动点迭代法无法求出方程的正根');endbreak;elsep1=pp;endendif i==n0disp(n0)disp('次不动点迭代后无法求出方程的正根')end2、%用牛顿法求方程 x-e^x+4=0的正根与负根,误差限是10^-6 disp('牛顿法')n0=80;p0=1;for i=1:n0p=p0-(p0-exp(p0)+4)/(1-exp(p0));if abs(p-p0)<=10^(-6)disp('|p-p0|=')disp(abs(p-p0))disp('用牛顿法求得方程的正根为')disp(p);break;elsep0=p;endendif i==n0disp(n0)disp('次牛顿迭代后无法求出方程的解')endp1=-3;for i=1:n0p=p1-(p1-exp(p1)+4)/(1-exp(p1));if abs(p-p1)<=10^(-6)disp('|p-p1|=')disp(abs(p-p1))disp('用牛顿法求得方程的负根为')disp(p);break;elsep1=p;endendif i==n0disp(n0)disp('次牛顿迭代后无法求出方程的解')end1、使用欧拉法、改进欧拉法和四阶R-K方法求下列微分方程的解。
一些经典的数值分析(matlab程序)

1、牛顿迭代法此方法一般用来求函数的根,速度比较快,程序比较简单。
文件newton.m 内容如下%n表示迭代次数,ret为返回值function ret=newton(n)format longy=inline('x^3+10*x-20');z=inline('3*x^2+10');x0=1.5;for i=1:na=y(x0);b=z(x0);x1=x0-a/b;x0=x1;endret=x12、复合Simpson求积分很简单的一种求定积分的方法,将求积区间分成很多小的曲边梯形,再累加。
文件mulsimpson.m内容如下%复化simpson求积分%a,b表示区间,n表示区间数function ret=mulsimpson(a,b,n)h=(b-a)/n;detsum=0;for i=1:n-1xk=a+i*h;detsum=detsum+fun(xk);endret=h*(fun(a)+fun(b)+2*detsum)/2;%内建函数function z=fun(x)z=exp(-x*x);3、4阶龙格-库塔法求积分此方法速度较快,编程较方便文件step4Runge.m内容如下%4阶Runge-Kutta 法%a,b为积分区间,N为划分数目,y0为初值,函数由fun定义function ret=step4Runge(a,b,N,y0)format longh=(b-a)/N;n=1;x0=a;for n=1:Nx=x0+h;k1=fun(x0,y0);k2=fun(x0+h/2,y0+h*k1/2);k3=fun(x0+h/2,y0+h*k2/2);k4=fun(x0+h,y0+h*k3);y=y0+h*(k1+2*(k2+k3)+k4)/6;x0=xy0=yend%积分函数定义function z=fun(x,y)z=1+y*y;4、Gauss_Seidel迭代解线性方程相比消元法,编程较为容易文件Gauss_Seidel.m内容如下%此函数演示高斯-赛德尔迭代%a表示系数矩阵,b表示值矩阵,n表示系数矩阵阶数,M表示迭代次数%注意b为列向量function y=Gauss_Seidel(a,b,n,M)format longx0=[0;0;0];for k=1:Mfor i=1:ns=0;t=x0(i);for j=1:nif j~=is=s+a(i,j)*x0(j);endendx0(i)=(b(i)-s)/a(i,i);endendy=x0;5、高斯列主消元法此方法为解线性方程组常用方法,先化简增广矩阵,然后回代求解。
Matlab中龙格-库塔(Runge-Kutta)方法原理及实现

函数功能ode是专门用于解微分方程的功能函数,他有ode23,ode45,ode23s等等,采用的是Runge-Kutta算法。
ode45表示采用四阶,五阶runge-kutta单步算法,截断误差为(Δx)³。
解决的是Nonstiff(非刚性)的常微分方程.是解决数值解问题的首选方法,若长时间没结果,应该就是刚性的,换用ode23来解.使用方法[T,Y] = ode45(odefun,tspan,y0)odefun 是函数句柄,可以是函数文件名,匿名函数句柄或内联函数名tspan 是区间[t0 tf] 或者一系列散点[t0,t1,...,tf]y0 是初始值向量T 返回列向量的时间点Y 返回对应T的求解列向量[T,Y] = ode45(odefun,tspan,y0,options)options 是求解参数设置,可以用odeset在计算前设定误差,输出参数,事件等[T,Y,TE,YE,IE] =ode45(odefun,tspan,y0,options)在设置了事件参数后的对应输出TE 事件发生时间YE 事件解决时间IE 事件消失时间sol =ode45(odefun,[t0 tf],y0...)sol 结构体输出结果应用举例1 求解一阶常微分方程程序:一阶常微分方程odefun=@(t,y) (y+3*t)/t^2; %定义函数tspan=[1 4]; %求解区间y0=-2; %初值[t,y]=ode45(odefun,tspan,y0);plot(t,y) %作图title('t^2y''=y+3t,y(1)=-2,1<t<4')legend('t^2y''=y+3t')xlabel('t')ylabel('y')% 精确解% dsolve('t^2*Dy=y+3*t','y(1)=-2')% ans =一阶求解结果图% (3*Ei(1) - 2*exp(1))/exp(1/t) - (3*Ei(1/t))/exp(1/t)2 求解高阶常微分方程关键是将高阶转为一阶,odefun的书写.F(y,y',y''...y(n-1),t)=0用变量替换,y1=y,y2=y'...注意odefun方程定义为列向量dxdy=[y(1),y(2)....]程序:function Testode45tspan=[3.9 4.0]; %求解区间y0=[2 8]; %初值[t,x]=ode45(@odefun,tspan,y0);plot(t,x(:,1),'-o',t,x(:,2),'-*')legend('y1','y2')title('y'' ''=-t*y + e^t*y'' +3sin2t')xlabel('t')ylabel('y')function y=odefun(t,x)y=zeros(2,1); % 列向量y(1)=x(2);y(2)=-t*x(1)+exp(t)*x(2)+3*sin(2*t);endend高阶求解结果图相关函数ode23, ode45, ode113, ode15s, ode23s, ode23t, ode23tbMatlab中龙格-库塔(Runge-Kutta)方法原理及实现龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法。
matlab龙格库塔法解微分方程组

matlab龙格库塔法解微分方程组
一、引言
龙格库塔法是数值计算中常用的一种求解微分方程的方法,其具有较高的精度和稳定性。
在MATLAB中,可以使用ode45函数来实现龙格库塔法求解微分方程组。
二、龙格库塔法简介
龙格库塔法是一种常用的数值积分方法,也可用于求解微分方程。
该方法将微分方程转化为一个初值问题,并采用逐步逼近的方式计算出数值解。
三、使用ode45函数求解微分方程组
在MATLAB中,可以使用ode45函数来求解微分方程组。
该函数使用了龙格库塔法进行数值计算,并提供了较高的精度和稳定性。
四、MATLAB代码实现
以下是一个使用ode45函数求解微分方程组的示例代码:
function dydt = myfun(t,y)
dydt = zeros(2,1);
dydt(1) = y(2);
dydt(2) = -sin(y(1));
end
[t,y] = ode45(@myfun,[0 10],[0;1]);
plot(t,y(:,1),'-o',t,y(:,2),'-o')
xlabel('Time')
ylabel('Solution')
legend('y_1','y_2')
五、总结
龙格库塔法是一种常用的数值计算方法,可以用于求解微分方程。
在MATLAB中,可以使用ode45函数来实现龙格库塔法求解微分方程组。
通过以上示例代码,我们可以看到MATLAB提供了较为简单的方式来实现龙格库塔法求解微分方程组,并且具有较高的精度和稳定性。
MATLAB龙格库塔法

MATLAB龙格库塔法⾮刚性常微分⽅程的数值解法通常会⽤四阶龙格库塔算法,其matlab函数对应ode45。
对于dy/dx = f(x,y),y(0)=y0。
其四阶龙格库塔公式如下:对于通常计算,四阶已经够⽤,四阶以上函数f(x,y)计算⼯作量⼤⼤增加⽽精度提⾼较慢。
下⾯以龙格库塔法解洛伦兹⽅程为例:matlab代码如下:main.m:1 clear all;2 close all;3 clc;45 %系统龙格库塔法6 [t,h] = ode45(@test_fun,[040],[1240]);7 plot3(h(:,1),h(:,2),h(:,3));8 grid on;910 %⾃定义龙格库塔法11 [t1,h1]=runge_kutta(@test_fun,[1240],0.01,0,40);12 figure;13 plot3(h1(1,:),h1(2,:),h1(3,:),'r')14 grid on;runge_kutta.m(函数参考⽹络):1 %参数表顺序依次是微分⽅程组的函数名称,初始值向量,步长,时间起点,时间终点(参数形式参考了ode45函数)2 function [x,y]=runge_kutta(ufunc,y0,h,a,b)3 n=floor((b-a)/h); %步数4 x(1)=a; %时间起点5 y(:,1)=y0; %赋初值,可以是向量,但是要注意维数6for i=1:n %龙格库塔⽅法进⾏数值求解7 x(i+1)=x(i)+h;8 k1=ufunc(x(i),y(:,i));9 k2=ufunc(x(i)+h/2,y(:,i)+h*k1/2);10 k3=ufunc(x(i)+h/2,y(:,i)+h*k2/2);11 k4=ufunc(x(i)+h,y(:,i)+h*k3);12 y(:,i+1)=y(:,i)+h*(k1+2*k2+2*k3+k4)/6;13 endtest_fun(洛伦兹⽅程):1 %构造微分⽅程2 function dy=test_fun(t,y)3 a = 16;4 b = 4;5 c = 45;67 dy=[a*(y(2)-y(1));8 c*y(1)-y(1)*y(3)-y(2);9 y(1)*y(2)-b*y(3)];得到很经典的洛伦兹吸引⼦,结果如下:。
Matlab版HoG代码

Matlab版HOG代码function F = hogcalculator(img, cellpw, cellph, nblockw, nblockh,...nthet, overlap, isglobalinterpolate, issigned, normmethod)% HOGCALCULATOR calculate R-HOG feature vector of an input image using the % procedure presented in Dalal and Triggs's paper in CVPR 2005.%% Author: timeHandle% Time: March 24, 2010% May 12,2010 update.%% this copy of code is written for my personal interest, which isan% original and inornate realization of [Dalal CVPR2005]'s algorithm% without any optimization. I just want to check whether Iunderstand% the algorithm really or not, and also do some practices for knowing% matlab programming more well because I could be called as'novice'.% OpenCV 2.0 has realized Dalal's HOG algorithm which runs faster% than mine without any doubt, ╮(╯▽╰)╭. Ronan pointed a errorin% the code,thanks for his correction. Note that at the end of this% code, there are some demonstration code,please remove in your work.%% F = hogcalculator(img, cellpw, cellph, nblockw, nblockh,% nthet, overlap, isglobalinterpolate, issigned, normmethod)%% IMG:% IMG is the input image.%% CELLPW, CELLPH:% CELLPW and CELLPH are cell's pixel width and height respectively.%% NBLOCKW, NBLCOKH:% NBLOCKW and NBLCOKH are block size counted by cells number in x and % y directions respectively.%% NTHET, ISSIGNED:% NTHET is the number of the bins of the histogram of oriented% gradient. The histogram of oriented gradient ranges from 0 to pi in% 'unsigned' condition while to 2*pi in 'signed' condition, which can% be specified through setting the value of the variable ISSIGNED by% the string 'unsigned' or 'signed'.%% OVERLAP:% OVERLAP is the overlap proportion of two neighboring block.%% ISGLOBALINTERPOLATE:% ISGLOBALINTERPOLATE specifies whether the trilinear interpolation % is done in a single global 3d histogram of the whole detecting% window by the string 'globalinterpolate' or in each local 3d% histogram corresponding to respective blocks by the string% 'localinterpolate' which is in strict accordance with the procedure% proposed in Dalal's paper. Interpolating in the whole detecting% window requires the block's sliding step to be an integralmultiple% of cell's width and height because the histogram is fixing before% interpolate. In fact here the so called 'global interpolation' is% a notation given by myself. at first the spatial interpolation is% done without any relevant to block's slide position, but when I was% doing calculation while OVERLAP is 0.75, something occurred and% confused me o__O"… . This let me find that the operation Ifirstly% did is different from which mentioned in Dalal's paper. But this% does not mean it is incorrect ^◎^, so I reserve this. As for name,% besides 'global interpolate', any others would be all ok, like 'Lady GaGa'% or what else, :-).%% NORMMETHOD:% NORMMETHOD is the block histogram normalized method which can be % set as one of the following strings:% 'none', which means non-normalization;% 'l1', which means L1-norm normalization;% 'l2', which means L2-norm normalization;% 'l1sqrt', which means L1-sqrt-norm normalization;% 'l2hys', which means L2-hys-norm normalization.% F:% F is a row vector storing the final histogram of all of the blocks% one by one in a top-left to bottom-right image scan manner, the% cells histogram are stored in the same manner in each block's% section of F.%% Note that CELLPW*NBLOCKW and CELLPH*NBLOCKH should be equal to IMG's% width and height respectively.%% Here is a demonstration, which all of parameters are set as the% best value mentioned in Dalal's paper when the window detected is 128*64% size(128 rows, 64 columns):% F = hogcalculator(window, 8, 8, 2, 2, 9, 0.5,% 'localinterpolate', 'unsigned', 'l2hys');% Also the function can be called like:% F = hogcalculator(window);% the other parameters are all set by using the above-mentioned "dalal's% best value" as default.%if nargin < 2% set default parameters value.cellpw = 8;cellph = 8;nblockw = 2;nblockh = 2;nthet = 9;overlap = 0.5;isglobalinterpolate = 'localinterpolate'; issigned = 'unsigned';normmethod = 'l2hys';elseif nargin < 10error('Input parameters are not enough.'); endend% check parameters's validity.[M, N, K] = size(img);if mod(M,cellph*nblockh) ~= 0error('IMG''s height should be an integral multiple ofCELLPH*NBLOCKH.'); endif mod(N,cellpw*nblockw) ~= 0error('IMG''s width should be an integral multiple ofCELLPW*NBLOCKW.'); endif mod((1-overlap)*cellpw*nblockw, cellpw) ~= 0 ||...mod((1-overlap)*cellph*nblockh, cellph) ~= 0str1 = 'Incorrect OVERLAP or ISGLOBALINTERPOLATE parameter';str2 = ', slide step should be an intergral multiple of cell size';error([str1, str2]);end% set the standard deviation of gaussian spatial weight window.delta = cellpw*nblockw * 0.5;% calculate gradient scale matrix.hx = [-1,0,1];hy = -hx';gradscalx = imfilter(double(img),hx);gradscaly = imfilter(double(img),hy);if K > 1gradscalx = max(max(gradscalx(:,:,1),gradscalx(:,:,2)), gradscalx(:,:,3));gradscaly = max(max(gradscaly(:,:,1),gradscaly(:,:,2)), gradscaly(:,:,3)); endgradscal = sqrt(double(gradscalx.*gradscalx + gradscaly.*gradscaly));% calculate gradient orientation matrix.% plus small number for avoiding dividing zero.gradscalxplus = gradscalx+ones(size(gradscalx))*0.0001;gradorient = zeros(M,N);% unsigned situation: orientation region is 0 to pi.if strcmp(issigned, 'unsigned') == 1gradorient =...atan(gradscaly./gradscalxplus) + pi/2;or = 1;else% signed situation: orientation region is 0 to 2*pi.if strcmp(issigned, 'signed') == 1idx = find(gradscalx >= 0 & gradscaly >= 0);gradorient(idx) = atan(gradscaly(idx)./gradscalxplus(idx));idx = find(gradscalx < 0);gradorient(idx) = atan(gradscaly(idx)./gradscalxplus(idx)) + pi; idx = find(gradscalx >= 0 & gradscaly < 0);gradorient(idx) = atan(gradscaly(idx)./gradscalxplus(idx)) + 2*pi; or = 2;elseerror('Incorrect ISSIGNED parameter.');endend% calculate block slide step.xbstride = cellpw*nblockw*(1-overlap);ybstride = cellph*nblockh*(1-overlap);xbstridend = N - cellpw*nblockw + 1;ybstridend = M - cellph*nblockh + 1;% calculate the total blocks number in the window detected, which is% ntotalbh*ntotalbw.ntotalbh = ((M-cellph*nblockh)/ybstride)+1;ntotalbw = ((N-cellpw*nblockw)/xbstride)+1;% generate the matrix hist3dbig for storing the 3-dimensions histogram. the % matrix covers the whole image in the'globalinterpolate' condition or% covers the local block in the 'localinterpolate' condition. The matrix is% bigger than the area where it covers by adding additional elements% (corresponding to the cells) to the surround for calculation convenience. if strcmp(isglobalinterpolate, 'globalinterpolate') == 1ncellx = N / cellpw;ncelly = M / cellph;hist3dbig = zeros(ncelly+2, ncellx+2, nthet+2);F = zeros(1, (M/cellph-1)*(N/cellpw-1)*nblockw*nblockh*nthet);glbalinter = 1;elseif strcmp(isglobalinterpolate, 'localinterpolate') == 1hist3dbig = zeros(nblockh+2, nblockw+2, nthet+2);F = zeros(1, ntotalbh*ntotalbw*nblockw*nblockh*nthet);glbalinter = 0;elseerror('Incorrect ISGLOBALINTERPOLATE parameter.')endend% generate the matrix for storing histogram of one block;sF = zeros(1, nblockw*nblockh*nthet);% generate gaussian spatial weight.[gaussx, gaussy] = meshgrid(0:(cellpw*nblockw-1),0:(cellph*nblockh-1)); weight = exp(-((gaussx-(cellpw*nblockw-1)/2)....*(gaussx-(cellpw*nblockw-1)/2)+(gaussy-(cellph*nblockh-1)/2)....*(gaussy-(cellph*nblockh-1)/2))/(delta*delta));% vote for histogram. there are two situations according to the interpolate % condition('global' interpolate or local interpolate). The hist3d which is % generated from the 'bigger' matrix hist3dbig is the final histogram.if glbalinter == 1xbstep = nblockw*cellpw;ybstep = nblockh*cellph;elsexbstep = xbstride;ybstep = ybstride;end% block slide loopfor btly = 1:ybstep:ybstridendfor btlx = 1:xbstep:xbstridendfor bi = 1:(cellph*nblockh)for bj = 1:(cellpw*nblockw)i = btly + bi - 1;j = btlx + bj - 1;gaussweight = weight(bi,bj);gs = gradscal(i,j);go = gradorient(i,j);if glbalinter == 1jorbj = j;iorbi = i;elsejorbj = bj;iorbi = bi;end% calculate bin index of hist3dbigbinx1 = floor((jorbj-1+cellpw/2)/cellpw) + 1;biny1 = floor((iorbi-1+cellph/2)/cellph) + 1;binz1 = floor((go+(or*pi/nthet)/2)/(or*pi/nthet)) + 1; if gs == 0 continue;endbinx2 = binx1 + 1;biny2 = biny1 + 1;binz2 = binz1 + 1;x1 = (binx1-1.5)*cellpw + 0.5;y1 = (biny1-1.5)*cellph + 0.5;z1 = (binz1-1.5)*(or*pi/nthet);% trilinear interpolation.hist3dbig(biny1,binx1,binz1) =...hist3dbig(biny1,binx1,binz1) + gs*gaussweight... * (1-(jorbj-x1)/cellpw)*(1-(iorbi-y1)/cellph)...*(1-(go-z1)/(or*pi/nthet));hist3dbig(biny1,binx1,binz2) =...hist3dbig(biny1,binx1,binz2) + gs*gaussweight... * (1-(jorbj-x1)/cellpw)*(1-(iorbi-y1)/cellph)...*((go-z1)/(or*pi/nthet));hist3dbig(biny2,binx1,binz1) =...hist3dbig(biny2,binx1,binz1) + gs*gaussweight... * (1-(jorbj-x1)/cellpw)*((iorbi-y1)/cellph)...*(1-(go-z1)/(or*pi/nthet));hist3dbig(biny2,binx1,binz2) =...hist3dbig(biny2,binx1,binz2) + gs*gaussweight... * (1-(jorbj-x1)/cellpw)*((iorbi-y1)/cellph)... *((go-z1)/(or*pi/nthet));hist3dbig(biny1,binx2,binz1) =...hist3dbig(biny1,binx2,binz1) + gs*gaussweight... * ((jorbj-x1)/cellpw)*(1-(iorbi-y1)/cellph)... *(1-(go-z1)/(or*pi/nthet));hist3dbig(biny1,binx2,binz2) =...hist3dbig(biny1,binx2,binz2) + gs*gaussweight... * ((jorbj-x1)/cellpw)*(1-(iorbi-y1)/cellph)... *((go-z1)/(or*pi/nthet));hist3dbig(biny2,binx2,binz1) =...hist3dbig(biny2,binx2,binz1) + gs*gaussweight... * ((jorbj-x1)/cellpw)*((iorbi-y1)/cellph)...*(1-(go-z1)/(or*pi/nthet));hist3dbig(biny2,binx2,binz2) =...hist3dbig(biny2,binx2,binz2) + gs*gaussweight...* ((jorbj-x1)/cellpw)*((iorbi-y1)/cellph)...*((go-z1)/(or*pi/nthet));endend% In the local interpolate condition. F is generated in this block % slide loop. hist3dbig should be cleared in each loop.if glbalinter == 0if or == 2hist3dbig(:,:,2) = hist3dbig(:,:,2)...+ hist3dbig(:,:,nthet+2);hist3dbig(:,:,(nthet+1)) =...hist3dbig(:,:,(nthet+1)) + hist3dbig(:,:,1);endhist3d = hist3dbig(2:(nblockh+1), 2:(nblockw+1), 2:(nthet+1)); for ibin = 1:nblockhfor jbin = 1:nblockwidsF = nthet*((ibin-1)*nblockw+jbin-1)+1;idsF = idsF:(idsF+nthet-1);sF(idsF) = hist3d(ibin,jbin,:);endendiblock = ((btly-1)/ybstride)*ntotalbw +...((btlx-1)/xbstride) + 1;idF = (iblock-1)*nblockw*nblockh*nthet+1;idF = idF:(idF+nblockw*nblockh*nthet-1);F(idF) = sF;hist3dbig(:,:,:) = 0;endendend% In the global interpolate condition. F is generated here outside the% block slide loopif glbalinter == 1ncellx = N / cellpw;ncelly = M / cellph;if or == 2hist3dbig(:,:,2) = hist3dbig(:,:,2) + hist3dbig(:,:,nthet+2);hist3dbig(:,:,(nthet+1)) = hist3dbig(:,:,(nthet+1)) +hist3dbig(:,:,1);endhist3d = hist3dbig(2:(ncelly+1), 2:(ncellx+1), 2:(nthet+1));iblock = 1;for btly = 1:ybstride:ybstridendfor btlx = 1:xbstride:xbstridendbinidx = floor((btlx-1)/cellpw)+1;binidy = floor((btly-1)/cellph)+1;idF = (iblock-1)*nblockw*nblockh*nthet+1;idF = idF:(idF+nblockw*nblockh*nthet-1);for ibin = 1:nblockhfor jbin = 1:nblockwidsF = nthet*((ibin-1)*nblockw+jbin-1)+1;idsF = idsF:(idsF+nthet-1);sF(idsF) = hist3d(binidy+ibin-1, binidx+jbin-1, :);endendF(idF) = sF;iblock = iblock + 1;endendend% adjust the negative value caused by accuracy of floating-point% operations.these value's scale is very small, usually at E-03 magnitude % while others will be E+02 or E+03 before normalization.F(F<0) = 0;% block normalization.e = 0.001;l2hysthreshold = 0.2;fslidestep = nblockw*nblockh*nthet;switch normmethodcase 'none'case 'l1'for fi = 1:fslidestep:size(F,2)div = sum(F(fi:(fi+fslidestep-1)));F(fi:(fi+fslidestep-1)) = F(fi:(fi+fslidestep-1))/(div+e);endcase 'l1sqrt'for fi = 1:fslidestep:size(F,2)div = sum(F(fi:(fi+fslidestep-1)));F(fi:(fi+fslidestep-1)) = sqrt(F(fi:(fi+fslidestep-1))/(div+e)); endcase 'l2'for fi = 1:fslidestep:size(F,2)sF = F(fi:(fi+fslidestep-1)).*F(fi:(fi+fslidestep-1));div = sqrt(sum(sF)+e*e);F(fi:(fi+fslidestep-1)) = F(fi:(fi+fslidestep-1))/div;endcase 'l2hys'for fi = 1:fslidestep:size(F,2)sF = F(fi:(fi+fslidestep-1)).*F(fi:(fi+fslidestep-1));div = sqrt(sum(sF)+e*e);sF = F(fi:(fi+fslidestep-1))/div;sF(sF>l2hysthreshold) = l2hysthreshold;div = sqrt(sum(sF.*sF)+e*e);F(fi:(fi+fslidestep-1)) = sF/div;endotherwiseerror('Incorrect NORMMETHOD parameter.');end% the following code, which can be removed because of having no % contributions to HOG feature calculation, are just for result% demonstration when the trilinear interpolation is 'global' for this % condition is easier to give a simple and intuitive illustration. so in % 'local' condition it will produce error.figure;hold on;axis equal;xlim([0, N]);ylim([0, M]);for u = 1:(M/cellph)for v = 1:(N/cellpw)cx = (v-1)*cellpw + cellpw/2 + 0.5;cy = (u-1)*cellph + cellph/2 + 0.5;hist3d(u,v,:)=0.9*min(cellpw,cellph)*hist3d(u,v,:)/max(hist3d(u,v,: ));for t = 1:nthets = hist3d(u,v,t);thet = (t-1)*pi/nthet + pi*0.5/nthet;x1 = cx - s*0.5*cos(thet);x2 = cx + s*0.5*cos(thet);y1 = cy - s*0.5*sin(thet);y2 = cy + s*0.5*sin(thet);plot([x1,x2],[M-y1+1,M-y2+1]); endendend。
龙格现象matlab算法

实验报告课程名称:___计算方法____________指导老师:___程晓良________成绩:__________________实验名称:___观察龙格现象________________实验类型:________________同组学生姓名:__________一、实验目的和要求(必填) 二、实验内容和原理(必填)三、主要仪器设备(必填) 四、操作方法和实验步骤五、实验数据记录和处理 六、实验结果与分析(必填)七、讨论、心得一、问题描述在计算方法中,有利用多项式对某一函数的近似逼近,这样,利用多项式就可以计算相应的函数值。
例如,在事先不知道某一函数的具体形式的情况下,只能测量得知某一些分散的函数值。
例如我们不知道气温随日期变化的具体函数关系,但是我们可以测量一些孤立的日期的气温值,并假定此气温随日期变化的函数满足某一多项式。
这样,利用已经测的数据,应用待定系数法便可以求得一个多项式函数f (x )。
应用此函数就可以计算或者说预测其他日期的气温值。
一般情况下,多项式的次数越多,需要的数据就越多,而预测也就越准确。
例外发生了:龙格在研究多项式插值的时候,发现有的情况下,并非取节点(日期数)越多多项式就越精确。
著名的例子是f (x )=1/(1+25x^2).它的插值函数在两个端点处发生剧烈的波动,造成较大的误差。
二、相关公式三、MATLAB 程序一、取等距节点,n=5,10,15,20for n = 5:5:20subplot(2,2,n/5)syms x ;专业:___机械工程____姓名:___林炜奕_______学号:_3130102509____ 日期:________________ 地点:_______桌号f = 1/(1+25*x^2);x1=sym(zeros(n+1));W=sym(ones(n+1));L=sym(0);for i=0:nx1(i+1)=-1+2*i/n;endfor i=0:nfor j=0:nif j~=iw=(x-x1(j+1))/(x1(i+1)-x1(j+1));W(i+1)=W(i+1)*w;endendL=L+W(i+1)*(1/(1+25*x1(i+1)^2));endLL(n)=simplify(L);x=-1:0.01:1;y1=subs(f,x);y2=subs(L,x);plot(x,y1,'b');hold on;plot(x,y2,'r');hold off;title(['Ô-º¯Êýf(x)=1/(1+25*x^2)Óë',num2str(n),'´Î²åÖµº¯Êý']); xlabel('x');ylabel('y');legend('Ô-º¯Êý','²åÖµº¯Êý');grid onend二、取节点X j=cosjπ/n,j=0,1,…,n.n分别取5,10,15,20,…,50for n = 5:5:50subplot(2,5,n/5)syms x;f = 1/(1+25*x^2);x1=sym(zeros(n+1));W=sym(ones(n+1));L=sym(0);for i=0:nx1(i+1)=cos(i*pi/n);endfor i=0:nfor j=0:nif j~=iw=(x-x1(j+1))/(x1(i+1)-x1(j+1));W(i+1)=W(i+1)*w;endendL=L+W(i+1)*(1/(1+25*x1(i+1)^2));endLL(n)=simplify(L);x=-1:0.01:1;y1=subs(f,x);y2=subs(L,x);plot(x,y1,'b');hold on;plot(x,y2,'r');hold off;title(['Ô-º¯Êýf(x)=1/(1+25*x^2)Óë',num2str(n),'´Î²åÖµº¯Êý']); xlabel('x');ylabel('y');legend('Ô-º¯Êý','²åÖµº¯Êý');grid onend四、实验分析当采用等距节点时,随着节点数量的增多,插值函数的误差越大。
数值分析Matlab作业龙格库塔欧拉方法解二阶微分方程
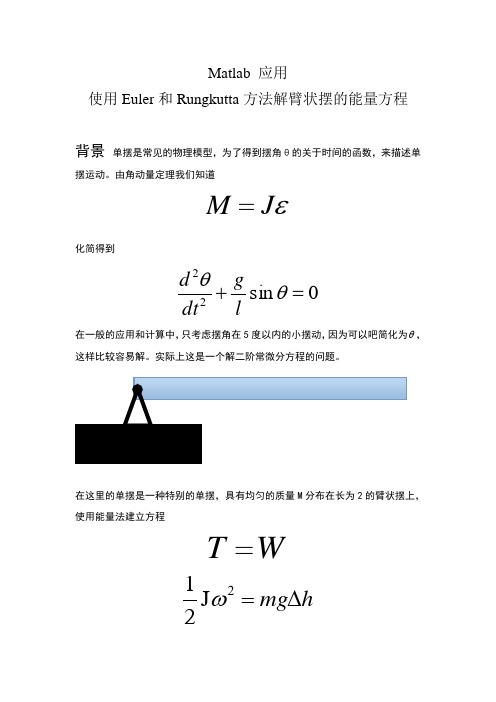
Matlab 应用使用Euler 和Rungkutta 方法解臂状摆的能量方程背景 单摆是常见的物理模型,为了得到摆角θ的关于时间的函数,来描述单摆运动。
由角动量定理我们知道εJ M =化简得到 0sin 22=+θθlg dt d 在一般的应用和计算中,只考虑摆角在5度以内的小摆动,因为可以吧简化为θ,这样比较容易解。
实际上这是一个解二阶常微分方程的问题。
在这里的单摆是一种特别的单摆,具有均匀的质量M 分布在长为2的臂状摆上, 使用能量法建立方程 W T =h mg ∆=2J 21ω化简得到θθcos 35499.722=dtd 重力加速度取1使用欧拉法令dxdy z =,这样降阶就把二阶常微分方程转化为一阶微分方程组,再利用向前Euler 方法数值求解。
y(i+1)=y(i)+h*z(i);z(i+1)=z(i)+h**cos(y(i));y(0)=0z(0)=0精度随着h 的减小而更高,因为向前欧拉方法的整体截断误差与h 同阶,(因为是用了泰勒公式)所以欧拉方法的稳定区域并不大。
2.RK4-四阶龙格库塔方法使用四级四阶经典显式Rungkutta 公式稳定性很好,RK4法是四阶方法,每步的误差是h5阶,而总积累误差为h4阶。
所以比欧拉稳定。
运行第三个程序:在一幅图中显示欧拉法和RK4法,随着截断误差的积累,欧拉法产生了较大的误差h=h=,仍然是开始较为稳定,逐渐误差变大总结:RK4是很好的方法,很稳定,而且四阶是很常用的方法,因为到五阶的时候精度并没有相应提升。
通过这两种方法计算出角度峰值y=,周期是。
三个程序欧拉法clear;clch=;a=0;b=25;x=a:h:b;y(1)=0;z(1)=0;for i=1:length(x)-1 % 欧拉 y(i+1)=y(i)+h*z(i);z(i+1)=z(i)+h**cos(y(i));endplot(x,y,'r*');xlabel('时间');ylabel('角度');A=[x,y];%y(find(y==max(y)))%Num=(find(y==max(y)))[y,T]=max(y);fprintf('角度峰值等于%d',y) %角度的峰值也就是πfprintf('\n')fprintf('周期等于%d',T*h) %周期legend('欧拉');龙格库塔方法先定义函数function w=rightf_sys1(x,y,z)w=*cos(y);clear;clc;%set(0,'RecursionLimit',500)h=;a=0;b=25;x=a:h:b;RK_y(1)=0; %初值RK_z(1)=0; %初值for i=1:length(x)-1K1=RK_z(i);L1=rightf_sys1(x(i),RK_y(i),RK_z(i)); % K1 and L1K2=RK_z(i)+*h*L1; L2=rightf_sys1(x(i)+*h,RK_y(i)+*h*K1,RK_z(i)+*h*L1);K3=RK_z(i)+*h*L2; L3=rightf_sys1(x(i)+*h,RK_y(i)+*h*K2,RK_z(i)+*h*L2);K4=RK_z(i)+h*L3;L4=rightf_sys1(x(i)+h,RK_y(i)+h*K3,RK_z(i)+h*L3); % K4 and L4RK_y(i+1)=RK_y(i)+1/6*h*(K1+2*K2+2*K3+K4);RK_z(i+1)=RK_z(i)+1/6*h*(L1+2*L2+2*L3+L4);endplot(x,RK_y,'b+');xlabel('Variable x');ylabel('Variable y');A=[x,RK_y];[y,T]=max(RK_y);legend('RK4方法');fprintf('角度峰值等于%d',y) %角度的峰值也就是πfprintf('\n')fprintf('周期等于%d',T*h) %周期两个方法在一起对比使用跟上一个相同的函数clear;clc; %清屏h=;a=0;b=25;x=a:h:b;Euler_y(1)=0;Euler_z(1)=0; %欧拉的初值RK_y(1)=0;RK_z(1)=0; %龙格库塔初值for i=1:length(x)-1%先是欧拉法Euler_y(i+1)=Euler_y(i)+h*Euler_z(i);Euler_z(i+1)=Euler_z(i)+h**cos(Euler_y(i));%龙格库塔K1=RK_z(i); L1=rightf_sys1(x(i),RK_y(i),RK_z(i)); % K1 and L1K2=RK_z(i)+*h*L1;L2=rightf_sys1(x(i)+*h,RK_y(i)+*h*K1,RK_z(i)+*h*L1);% K2 and L2K3=RK_z(i)+*h*L2; L3=rightf_sys1(x(i)+*h,RK_y(i)+*h*K2,RK_z(i)+*h*L2); % K3 and L3K4=RK_z(i)+h*L3;L4=rightf_sys1(x(i)+h,RK_y(i)+h*K3,RK_z(i)+h*L3); % K4 and L4 RK_y(i+1)=RK_y(i)+1/6*h*(K1+2*K2+2*K3+K4);RK_z(i+1)=RK_z(i)+1/6*h*(L1+2*L2+2*L3+L4);endplot(x,Euler_y,'r-',x,RK_y,'b-');[y,T]=max(RK_y);fprintf('角度峰值等于%d',y) %角度的峰值也就是πfprintf('\n')fprintf('周期等于%d',T*h) %周期xlabel('时间');ylabel('角度');legend('欧拉','RK4');。
龙格库塔方法及其matlab实现

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载龙格库塔方法及其matlab实现地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容龙格-库塔方法及其matlab实现摘要:本文的目的数值求解微分方程精确解,通过龙格-库塔法,加以利用matlab为工具达到求解目的。
龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法,用于数值求解微分方程。
MatLab软件是由美国Mathworks公司推出的用于数值计算和图形处理的科学计算系统环境。
MatLab 是英文MATrix LABoratory(矩阵实验室)的缩写。
在MratLab环境下,用户可以集成地进行程序设计、数值计算、图形绘制、输入输出、文件管理等各项操作。
关键词:龙格-库塔 matlab 微分方程前言1.1:知识背景龙格-库塔法(Runge-Kutta)是用于非线性常微分方程的解的重要的一类隐式或显式迭代法。
这些技术由数学家卡尔·龙格和马丁·威尔海姆·库塔于1900年左右发明。
通常所说的龙格库塔方法是相对四阶龙格库塔而言的,成为经典四阶龙格库塔法。
该方法具有精度高,收敛,稳定,计算过程中可以改变步长不需要计算高阶导数等优点,但是仍需计算在一些点上的值,比如四阶龙格-库塔法没计算一步需要计算四步,在实际运用中是有一定复杂性的。
Matlab是在20世纪七十年代后期的事:时任美国新墨西哥大学计算机科学系主任的Cleve Moler教授出于减轻学生编程负担的动机,为学生设计了一组调用LINPACK和EISPACK库程序的“通俗易用”的接口,此即用FORTRAN编写的萌芽状态的MATLAB。
经几年的校际流传,在Little的推动下,由Little、Moler、Steve Bangert合作,于1984年成立了MathWorks公司,并把MATLAB正式推向市场。
