11章_化学动力学基础(一3-20150430)
合集下载
11章化学动力学基础一
t0 cA ,0a 0
t t c A a xx
速率方程的微分式为：
rdcA dt
dcP dt
k1cA
或
dx r dt k1(ax)
对微分式进行不定积分
r
dx dt
k1(ax)
dx (a x)
k1dt
dx (ax)
k1dt
ln (a x ) k 1 t 常 数
1950年左右，测时间分辨率小于 1 0 3 s 1970年左右，测时间分辨率到了 1 0 6 s 1980年左右，测时间分辨率到了 1 0 1 2 s 2000年左右，测时间分辨率到了 1 0 1 5 s
•动力学理论尚不够完善，还需继续努力
§11.2 化学反应速率的表示法
速度 velocity 是矢量，有方向性。
r k [ A ] [ B ] 1 /2
1 .5 级 反 应
rk[A ][B ]/(1[B ]1/2) 无 简 单 级 数
反应分子数 在基元反应中，实际参加反应的分子数目称为
反应分子数。反应分子数可区分为单分子反应、双 分子反应和三分子反应，四分子反应目前尚未发现
反应分子数属于微观范畴，通常与反应的级数 一致，但有时单分子反应也可能表现为二级反应
rm1 mFra bibliotekd dt
rV
1 V
d dt
若催化剂用量Q改用表面积表示
rA
1 A
d dt
r A 称为表面反应速率，单位为 molm2s1
绘制动力学曲线
动力学曲线就是反应中各物质浓度随时间的 变化曲线。有了动力学曲线才能在 t 时刻作切线， 求出瞬时速率。测定不同时刻各物质浓度的方法 有： (1) 化学方法
t t c A a xx
速率方程的微分式为：
rdcA dt
dcP dt
k1cA
或
dx r dt k1(ax)
对微分式进行不定积分
r
dx dt
k1(ax)
dx (a x)
k1dt
dx (ax)
k1dt
ln (a x ) k 1 t 常 数
1950年左右，测时间分辨率小于 1 0 3 s 1970年左右，测时间分辨率到了 1 0 6 s 1980年左右，测时间分辨率到了 1 0 1 2 s 2000年左右，测时间分辨率到了 1 0 1 5 s
•动力学理论尚不够完善，还需继续努力
§11.2 化学反应速率的表示法
速度 velocity 是矢量，有方向性。
r k [ A ] [ B ] 1 /2
1 .5 级 反 应
rk[A ][B ]/(1[B ]1/2) 无 简 单 级 数
反应分子数 在基元反应中，实际参加反应的分子数目称为
反应分子数。反应分子数可区分为单分子反应、双 分子反应和三分子反应，四分子反应目前尚未发现
反应分子数属于微观范畴，通常与反应的级数 一致，但有时单分子反应也可能表现为二级反应
rm1 mFra bibliotekd dt
rV
1 V
d dt
若催化剂用量Q改用表面积表示
rA
1 A
d dt
r A 称为表面反应速率，单位为 molm2s1
绘制动力学曲线
动力学曲线就是反应中各物质浓度随时间的 变化曲线。有了动力学曲线才能在 t 时刻作切线， 求出瞬时速率。测定不同时刻各物质浓度的方法 有： (1) 化学方法
物理化学第十一章 化学动力学基础(一)
rA dcA / dt kcAcB
（2）反应级数
rA dcA / dt kcAcB 各浓度的方次、分别为物质A、B
的反应级数。
++ =n，n称为反应的总级数。
➢反应级数的大小表示浓度对反应速率的影 响程度，级数越大，则反应速率受浓度影响 越大。
➢反应级数可为整数、分数、正数、负数或 零。
则：r rA rB rY rZ
A B Y Z
可见：反应速率r与物质B的选择无关，但
反应物的消耗速率或产物的生成速率均随 物质B的选择而不同。
对恒容气相反应，可采用以压力表示的反
应速率：rP=(1/B)(dPB/dt)
A的消耗速率：r’A=-dPA/dt
Z的生成速率：r’Z=dPz/dt
11-2 化学反应速率的表示法
速度 是矢量，有方向性。 速率 是标量，无方向性，总是正值。
对一化学反应
R P
速度 速率
dcR 0 dt
dcP 0 dt
r = dcR dcP 0 dt dt
R P
rR
dcR dt
rp
dc P dt
绘制 ct 关系曲线，在某时刻t 时，作交点处 的切线，就得到 t 时刻的瞬时速率。显然，反应刚
rGm / kJ mol1 16.63 237.12
化学热力学只能判断这两个反应都能发生，但如何 使它发生，热力学无法回答。
11-1 化学动力学的任务和目的
化学动力学是研究化学反应速率和化学反 应机理的学科，主要有四大任务：
1. 研究化学反应进行的速率和外界因素（如 温度、压力、催化剂、溶剂和光照等）对速 率的影响。 2. 揭示化学反应的历程（也叫反应机理）
a
r k cA
（2）反应级数
rA dcA / dt kcAcB 各浓度的方次、分别为物质A、B
的反应级数。
++ =n，n称为反应的总级数。
➢反应级数的大小表示浓度对反应速率的影 响程度，级数越大，则反应速率受浓度影响 越大。
➢反应级数可为整数、分数、正数、负数或 零。
则：r rA rB rY rZ
A B Y Z
可见：反应速率r与物质B的选择无关，但
反应物的消耗速率或产物的生成速率均随 物质B的选择而不同。
对恒容气相反应，可采用以压力表示的反
应速率：rP=(1/B)(dPB/dt)
A的消耗速率：r’A=-dPA/dt
Z的生成速率：r’Z=dPz/dt
11-2 化学反应速率的表示法
速度 是矢量，有方向性。 速率 是标量，无方向性，总是正值。
对一化学反应
R P
速度 速率
dcR 0 dt
dcP 0 dt
r = dcR dcP 0 dt dt
R P
rR
dcR dt
rp
dc P dt
绘制 ct 关系曲线，在某时刻t 时，作交点处 的切线，就得到 t 时刻的瞬时速率。显然，反应刚
rGm / kJ mol1 16.63 237.12
化学热力学只能判断这两个反应都能发生，但如何 使它发生，热力学无法回答。
11-1 化学动力学的任务和目的
化学动力学是研究化学反应速率和化学反 应机理的学科，主要有四大任务：
1. 研究化学反应进行的速率和外界因素（如 温度、压力、催化剂、溶剂和光照等）对速 率的影响。 2. 揭示化学反应的历程（也叫反应机理）
a
r k cA
第11章 化学动力学基础
r def 1 d
Q dt 若催化剂用量Q改用质量表示，则
rm
1 m
d
dt
若催化剂用量
若催化剂用量Q改用表面积表示
rA
1 A
d
dt
rA 称为表面反应速率，单位为 mol m2 s1
化学反应速率与速度
速度 velocity 是矢量，有方向性。
速率 rate 是标量 ，无方向性，都是正值。
§11.1 化学动力学的任务和目的
化学热力学的研究对象和局限性
研究化学变化的方向、能达到的最大限度以及
外界条件对平衡的影响。化学热力学只能预测反应
的可能性，但无法预料反应能否发生？反应的速率
如何？反应的机理如何？例如：
1 2
N2
3 2
H2
NH3 (g)
rGm / kJ mol1 16.63
1 H2 2 O2 H2O(l)
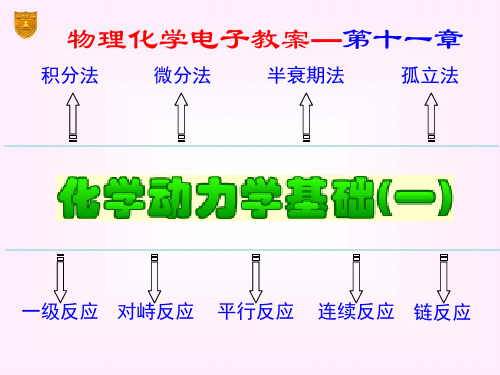
物理化学电子教案—第十一章
积分法
微分法
半衰期法
孤立法
一级反应 对峙反应 平行反应 连续反应 链反应
2020/11/23
第十一章 化学动力学基础(一)
§11.1 化学动力学的任务和目的 §11.2 化学反应速率的表示法 §11.3 化学反应的速率方程 §11.4 具有简单级数的反应 §11.5 几种典型的复杂反应 *§11.6 基元反应的微观可逆性原理 §11.7 温度对反应速率的影响 *§11.8 关于活化能 §11.9 链反应 2020/11*/2§3 11.10 拟定反应历程的一般方法
基元反应和非基元反应 (3) H2 Br2 2HBr 的反应历程为
(10) Br2 M 2Br M (11) Br H2 HBr H (12) H Br2 HBr Br (13) H HBr H2 Br (14) Br Br M Br2 M
物理化学课件-化学动力学基础(一)
基元反應和非基元反應
基元反應簡稱元反應。如果一個化學反應，反 應物分子在碰撞中相互作用，在一次化學行為中就 能轉化為生成物分子，這種反應稱為基元反應。
例如上述反應歷程中，(4)-(14)的反應都是 基元反應。
如果一個化學計量式代表了若干個基元反應 的總結果，那這種反應稱為總包反應或總反應， 是非基元反應。
基元反應和非基元反應
(1) H2 I2 2HI 的反應歷程為
(4) I2 M
2I M
(5) H2 2I 2HI
式中M是指反應器的器壁，或是不參與反應只起 傳遞能量作用的第三物種。
基元反應和非基元反應
(2) H2 Cl2 2HCl 的反應歷程為 (6) Cl2 M 2Cl M (7) Cl H2 HCl H (8) H Cl2 HCl Cl
物理方法有可能做原位反應。
測定反應的初速率，這時干擾少，對研究反 應動力學很有用
對於一些快速反應，要用特殊的測試方法
§11.3 化學反應的速率方程
何謂速率方程？
速率方程又稱動力學方程。它表明了反應速 率與濃度等參數之間的關係或濃度等參數與時間 的關係。速率方程可表示為微分式或積分式。
速率方程必須由實驗來確定
反應機理（reaction mechanism）
反應機理又稱為反應歷程。在總反應中，連續 或同時發生的所有基元反應稱為反應機理，在有些 情況下，反應機理還要給出所經歷的每一步的立體 化學結構圖。
同一反應在不同的條件下，可有不同的反應機 理。瞭解反應機理可以掌握反應的內在規律，從而 更好的駕馭反應。
t1/ 2 ln 2 / k1
3. ln(a x) 與 時間 t 呈線性關係。
引 (1)
伸 的
(2)
11章_化学动力学基础(一2-201504023)
基元反应和非基元反应
不能显示反应历程，只反映了反应的总结果， 此类反应称为非基元反应或总包反应 基元反应简称元反应。如果一个化学反应，反 应物分子在碰撞中相互作用，在一次化学行为中就 能转化为生成物分子，这种反应称为基元反应。
质量作用定律（law of mass action）
由挪威化学家C.M.古德贝格和P.瓦格根据化学反 应的速率与参加反应的活性质量（就是指分压强或浓 度或摩尔分数）成正比的关系于1867年提出。 基元反应的速率与反应物浓度（含有相应的指数） 的乘积成正比。浓度的指数就是基元反应方程中各反 应物的计量系数。这就是质量作用定律，它只适用于 基元反应。 例如： 基元反应 反应速率 r
ln(a x) k1t 常数
t1/ 2
ln2
k1
速率常数 k 的单位为时间的负一次方，时间 t 可以 是秒(s)，分(min)，小时(h)，天(d)和年(a)等。
t1/ 2 : t3/ 4 : t7/8 1: 2 : 3
一级反应应用实例
• • • • 文物鉴定（同位素的衰变） 药物失效问题 放射性元素的安全问题 环境监测
反应级数一致，但有时单分子反应也可能表现为二
级反应。
反应速率常数（重点）
r k[A]
k 称为反应的速率常数，又称为速率系数。
它的物理意义是：当反应物的浓度均为单位浓
度时， 该反应的反应速率。 它的数值与反应物的浓度无关。r = f (T，催化剂， 溶剂种类…) 。在催化剂等其他条件确定时，k 的数值 仅是温度的函数。 k 的单位随着反应级数的不同而不同。 k 的数值直接反映了反应速率的快慢。
r k2[A]
2
(1) A B P t 0 a b 0 t t a- x b- x x
第十一章 化学动力学基础(一)
dx / dt
r k[A]
a ln k1t ax
总包反应：非基元反应, (1) 基元反应: 碰撞中一步转
化为产物。
代表若干基元反应的总结果。
H2 I2 2HI
I2 M 2I M H 2 2I 2HI
此外，反应计量式相似，但反应历程却大不相同。 p160-161
微观可逆性原理：一个基元反应的逆反应， 必然也是一个基元反应，而且正逆反应通过 同样的过渡态。（时间反演对称性）
动力学方程 r kcA cB
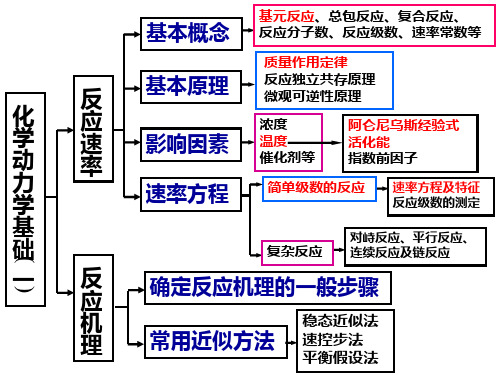
基本概念
基元反应、总包反应、复合反应、 反应分子数、反应级数、速率常数等 质量作用定律 反应独立共存原理 微观可逆性原理 浓度 温度 催化剂等
化 学 动 力 学 基 础 一
反 应 速 率
基本原理 影响因素 速率方程
阿仑尼乌斯经验式 活化能 指数前因子
速率方程及特征 反应级数的测定
简单级数的反应复杂Fra bibliotek应•20世纪前叶，宏观反应动力学向微观反应动力学过 渡阶段。 •20世纪50年代，微观反应动力学阶段。 反应速率的理论探讨、碰撞理论和过渡态理论、势能 面、链反应、基元反应、分子反应动态学。
化学动力学相关成就及诺奖获得者
化学反应机理和链式反应 /
―1956 欣谢尔伍德(UK)、谢苗诺夫(USSR)
对峙反应、平行反应、 连续反应及链反应
( )
反 应 机 理
确定反应机理的一般步骤
常用近似方法
稳态近似法 速控步法 平衡假设法
§11.1 化学动力学的任务和目的
化学热力学的研究对象和局限性
研究对象：化学变化的方向、最大限度及外界条件 对平衡的影响。 局限性：无法预料在给定条件下的反应速率和反应 机理。例如： 1
第十一章-化学动力学一
反应进度为 ξ＝
是任一组分B在反应起始时的物质的量。
是B组分在反应进度为ξ时的物质的量。
是各物质的计量系数，反应物为负值， 生成物为正值。
11
引进反应进度的最大优点:
在反应进行到任意时刻时，可用任一反应物或任意 生成物来表示反应进行的程度，所得的值都相等。
或 当反应按所给反应式的系数比例进行一个单位的化学反应时， 即 ΔnB / mol=ν
r
'
dp N2O5 dt
dp N2O4 dt
2
dpO2 dt
17
Note:
反应速率是描述单位时间内浓度变化的程度； 某时刻的反应速度是C~t关系曲线在该时刻的切线斜率。
C
dc dt
t
18
多相反应
r
r m
1 d Q dt
Q 表示催化剂的量，若用质量 m 表示，则
1 d m dt
rm 为在给定条件下催整数，也可为分数，也为零，也可为负数
如 CO+O2→CO2
对 O2为一级，对CO为负一级
动力学方程为 －d C CO / dt = k C o2 / Cco
只有基元反应的速率与反应物浓度的乘积成正比，其中各浓度的 指数就是反应式中各相应物质的系数－－基元反应的这个规律称为 质量作用定律。
理的有效数据。
8
另一种是分子反应动力学 研究方法。从微观的分子水平来看，一个 化学反应是具有一定量子态的反应物分子间的互相碰撞，进行原子重排， 产生一定量子态的产物分子以至互相分离的单次反应碰撞行为。 用过渡态理论解释，它是在反应体系的超势能面上一个代表体系的 质点越过反应势垒的一次行为。
9
§2 化学反应速率 以前反应速率用单位时间内反应物浓度的减少或生成物浓度的 增加来表示.
物理化学-化学动力学基础
1) 一级反应 2）二级反应 3）零级反应
11.2 具有简单级数的反应
11.2 具有简单级数的反应
对峙反应
11.3 几种典型的复杂反应
平行反应
11.3 几种典型的复杂反应
11.3 几种典型的复杂反应
பைடு நூலகம்连续反应（重要，考题）
11.3 几种典型的复杂反应
11.3 几种典型的复杂反应
真题例题
写出反应AK1B
K2
C的动力学方程式和积分式
K3
KK121
K3
11.4 阿伦尼乌斯公式与活化能
实验活化能（简称活化能）：一个具有平均能量的反应物分子要变成具有平均能量的活化 分子所必须获得的能量。 表观活化能：是组成该总包反应的各基元反应活化能的特定组合，没有确切的意义。
11.2 具有简单级数的反应
11.2 具有简单级数的反应
11.2 具有简单级数的反应
三级反应（P170） 关键就是两步：1.写微分方程 2.做积分（定积分最重要） 积分自己一定要动手积一遍！！！三级反应积分相对复杂一点。
11.2 具有简单级数的反应
11.2 具有简单级数的反应
真题例题 某化合物A在反应容器中反应1小时后，消耗了75%，试问反应2小时后还剩多少？ 假定反应为：
第11章 化学动力学基础
11.1 基础概念 11.2 具有简单级数的反应 11.3 几种典型的复杂反应 11.4 阿伦尼乌斯公式与活化能
11.1 基础概念
11.1 基础概念
11.1 基础概念
一级反应
11.2 具有简单级数的反应
11.2 具有简单级数的反应
二级反应
11.2 具有简单级数的反应
11.2 具有简单级数的反应
11.2 具有简单级数的反应
对峙反应
11.3 几种典型的复杂反应
平行反应
11.3 几种典型的复杂反应
11.3 几种典型的复杂反应
பைடு நூலகம்连续反应（重要，考题）
11.3 几种典型的复杂反应
11.3 几种典型的复杂反应
真题例题
写出反应AK1B
K2
C的动力学方程式和积分式
K3
KK121
K3
11.4 阿伦尼乌斯公式与活化能
实验活化能（简称活化能）：一个具有平均能量的反应物分子要变成具有平均能量的活化 分子所必须获得的能量。 表观活化能：是组成该总包反应的各基元反应活化能的特定组合，没有确切的意义。
11.2 具有简单级数的反应
11.2 具有简单级数的反应
11.2 具有简单级数的反应
三级反应（P170） 关键就是两步：1.写微分方程 2.做积分（定积分最重要） 积分自己一定要动手积一遍！！！三级反应积分相对复杂一点。
11.2 具有简单级数的反应
11.2 具有简单级数的反应
真题例题 某化合物A在反应容器中反应1小时后，消耗了75%，试问反应2小时后还剩多少？ 假定反应为：
第11章 化学动力学基础
11.1 基础概念 11.2 具有简单级数的反应 11.3 几种典型的复杂反应 11.4 阿伦尼乌斯公式与活化能
11.1 基础概念
11.1 基础概念
11.1 基础概念
一级反应
11.2 具有简单级数的反应
11.2 具有简单级数的反应
二级反应
11.2 具有简单级数的反应
化学动力学1
2 r kcA , r kcA cB 3A P , 2A B P , A B C P 3 2 r kcA , r kcA cB , r kcA cB cC
18
基元反应和非基元反应 化学反应的计量式，只反映了参与反应的物质 之间量的关系，如：
(1) H2 I2 2HI
基元反应和非基元反应
(3) H2 Br2 2HBr 的反应历程为
(10) Br2 M 2Br M
(11) Br H2 HBr H
(12) H Br2 HBr Br (13) H HBr H2 Br
(14) Br Br M Br2 M
宏观动力学 —— 从宏观变量出发研究基元反应
和复合反应速率。
10
I. 化学动力学 基本原理
11
§11-2 化学反应速率的表示法
一、表示化学反应速率的要素及其关系
间歇式反应器
连续管式反应器
连续式反应器
时间、空间、物质的量三个要素
12
二、反应速率
dD + eE gG + hH
(-1/d)dnD = (-1/e)dnE = (1/g)dnG = (1/h)dnH
速率方程不同
三、反应级数和反应分子数
dD + eE gG + hH 如果
d[G] r= g dt
1
= k[D][E]
反应级数 n = +
对反应物D来说，级反应
对反应物E来说，级反应 对于基元反应 定义反应分子数，即参加反应的分子数
反应级数 = 反应分子数
§ 11-4
具有简单级数的反应
定义反应进度 d= (1/B)dnB （均相封闭体系） 反应速率 r = 单位时间 浓度变化
化学动力学基础(一)
化学动力学基础（一）教学目的与要求:使学生了解和掌握化学动力学的一些基本概念，测定化学反应速率的一般方法，几种简单级数反应的动力学特征，几种典型的复杂分应的动力学特征，温度对反应速率的影响，有自由基参加的反应的动力学特征，拟定反应动力学方程的一般方法。
重点与难点:化学动力学的一些基本概念：反应的级数与反应的分子数，基元反应与非基元反应以及反应的速率的描述方法等；简单级数反应的动力学特征，几种典型复杂反应的动力学特征，温度对反应速率的影响（反应的活化能的概念），链反应的动力学特征以及动动学方程的推导方法。
§11.1 化学动力学的任务和目的化学反应用于生产实践所遇到的两个方面的问题和热力学的局限性以及化学动力学的必要性，它的实际意义。
化学动力学的基本任务：１．研究化学反应的速率，以及各种因素（浓度，压力，温度，催化剂）对速率的影响。
２．研究反应的机理（历程）。
化学动力学与物质结构的关系：化学动力学和化学热力学的研究方法是不同的。
它要研究反应速率及其影响的因素，必须了解体系的物质结构方面的知识，同时，通过对反应速率以及反应机理的研究，也可以加深人们对物质结构的认识。
化学动力学的发展过程：第一阶段，宏观动力学阶段，主要从宏观上测定化学反应的速率，确定反应的级数，在此阶段，确立了质量作用定律和阿累尼乌斯定律，并提出了活化能的概念。
第二阶段，包括从宏观动力学到微观动力学的过程，以及从微观研究化学反应的速度。
在这一阶段，建立了各种反应的速度理论，如碰撞理论，过渡状态理论，链反应，单分子反应速度等理论，从二十世纪五十年代开始，分子束和激光技术应用于化学动力学的研究，使人们进入到了态--态反应的层次，研究不同量子态的反应物和产物的速率，以及反应的细节。
化学动力学理论还不能象热力学理论那样系统和完善。
§11．2化学反应速率表示法反应系统中反应物的消耗和产物的生成速度随反应的类型的不同而不同，一般情况下，反应系统中反应物和产物的浓度与时间的关系可以用如左图的曲线来表示，化学反应的速度，就是单位时间反应物和产物浓度的改变量，由于反应物产物在反应式中的计量系数不尽一致，所以用不同的物质表示化学反应速率时，其数值也不一致。
11化学动力学基础1
例如上述反应历程中，所有反应历程都是 基元反应。
如果一个化学计量式代表了若干个基元反应 的总结果，那这种反应称为总包反应或总反应， .转化速率和反应速率的定义式
d • 1 dnB
dt
B dt
r 1 d 1 • 1 dcB
V dt V B dt
2.基元反应与非基元反应 基元反应:
(C) - dCNO2/dt = dCNO/dt = dCO2/dt
(D) - dCNO2/2dt = dCNO/2dt = dCO2/dt = 1/V d /dt
§11.3 化学反应的速率方程
何谓速率方程？
速率方程又称动力学方程。它表示反应速率与 浓度等参数之间的关系，或表示浓度等参数与时间 的关系。速率方程可表示为微分式或积分式，其具 体形式随不同反应而异，必须由实验确定。
过渡阶段：宏观向微观过渡阶段（二十世纪前叶） 主要成就：链反应。反应历程中有自由基存在,总包反应由许多基元反 应组成。链反应的发现使动力学的研究从总包反应深入到基元反应，实 现了从宏观向微观的过渡。 第二阶段：微观动力学阶段（二十世纪五十年代后） 主要成就：碰撞理论，过渡态理论
分子束和激光技术的发展和应用，产生分子反应动态学（或分子态反 应动力学）
d.速率系数
它的物理意义是当反应物的浓度均为单位浓度时 k 等
于反应速率，因此它的数值与反应物的浓度无关。在催化
剂等其它条件确定时，k 的数值仅是温度的函数。
注意：k 的单位随着反应级数的不同而不同。
准级数反应（pseudo order reaction）
在速率方程中，若某一物质的浓度远远大于其他反应物的浓度，或 是出现在速率方程中的催化剂浓度项，在反应过程中可以认为没有变 化，可并入速率系数项，这时反应总级数可相应下降，下降后的级数 称为准级数反应。
如果一个化学计量式代表了若干个基元反应 的总结果，那这种反应称为总包反应或总反应， .转化速率和反应速率的定义式
d • 1 dnB
dt
B dt
r 1 d 1 • 1 dcB
V dt V B dt
2.基元反应与非基元反应 基元反应:
(C) - dCNO2/dt = dCNO/dt = dCO2/dt
(D) - dCNO2/2dt = dCNO/2dt = dCO2/dt = 1/V d /dt
§11.3 化学反应的速率方程
何谓速率方程？
速率方程又称动力学方程。它表示反应速率与 浓度等参数之间的关系，或表示浓度等参数与时间 的关系。速率方程可表示为微分式或积分式，其具 体形式随不同反应而异，必须由实验确定。
过渡阶段：宏观向微观过渡阶段（二十世纪前叶） 主要成就：链反应。反应历程中有自由基存在,总包反应由许多基元反 应组成。链反应的发现使动力学的研究从总包反应深入到基元反应，实 现了从宏观向微观的过渡。 第二阶段：微观动力学阶段（二十世纪五十年代后） 主要成就：碰撞理论，过渡态理论
分子束和激光技术的发展和应用，产生分子反应动态学（或分子态反 应动力学）
d.速率系数
它的物理意义是当反应物的浓度均为单位浓度时 k 等
于反应速率，因此它的数值与反应物的浓度无关。在催化
剂等其它条件确定时，k 的数值仅是温度的函数。
注意：k 的单位随着反应级数的不同而不同。
准级数反应（pseudo order reaction）
在速率方程中，若某一物质的浓度远远大于其他反应物的浓度，或 是出现在速率方程中的催化剂浓度项，在反应过程中可以认为没有变 化，可并入速率系数项，这时反应总级数可相应下降，下降后的级数 称为准级数反应。
章化学动力学基础一
r k[A][B]1/2
1.5级反应
r k[A][B]/(1[B]1/2) 无简单级数
第24页/共128页
反应分子数 在基元反应中，实际参加反应的分子数目称为
反应分子数。反应分子数可区分为单分子反应、双 分子反应和三分子反应，四分子反应目前尚未发现
反应分子数属于微观范畴，通常与反应的级数 一致，但有时单分子反应也可能表现为二级反应
第3页/共128页
化学动力学发展简史 •近百年来，由于实验方法和检测手段的日新月异， 如磁共振技术、闪光光解技术等，使化学动力学 发展极快
1950年左右，测时间分辨率小于 103s 1970年左右，测时间分辨率到了 106 s 1980年左右，测时间分辨率到了 1012 s 2000年左右，测时间分辨率到了 1015s
第22页/共128页
k1[Cl2 ][M] k2[Cl][H2 ] k3[H][Cl2 ] k4 [Cl]2 [M]
反应的级数、反应分子数和反应的速率常数
速率方程中，各反应物浓度项上的指数称为该 反应物的级数；
所有浓度项指数的代数和称为该反应的总级数， 通常用n 表示。
n 的大小表明浓度对反应速率影响的大小。
第7页/共128页
反应进度（extent of reaction）
设反应为： R P
t 0 nR (0) nP (0)
t t nR (t) np (t)
nR (t) nR (0) np (t) nP (0)
d dnB B
第8页/共128页
转化速率（rate of conversion）
x
k1t
第15页/共128页
基元反应和非基元反应
化学反应的计量式，只反映了参与反应的物质 之间量的关系，如：
第十一章化学动力学基础一
第十一章化学动力学基础一第十一章化学动力学基础（一）教学目的：1.使学生理解一些动力学基本概念2.掌握简单级数反应以及典型复杂反应的动力学特点。
3.理解并应用阿仑尼乌斯公式。
4.能用稳态近似、平衡假设等处理方法推导一些复杂反应的速率方程基本要求：1.掌握等容反应速率的表示法及基元反应、反应级数等基本概念。
2.对于简单级数反应，要掌握其速率公式的各种特征并能由实验数据确定简单反应的反应级数。
3.对三种典型的复杂反应，要掌握其各自的特点及其中比较简单的反应的速率方程。
4.明确温度、活化能对反应速率的影响，理解阿仑尼乌斯公式中各项的含义。
5.掌握链反应的特点，会用稳态近似、平衡假设等处理方法。
教学重点、难点：简单级数反应以及典型复杂反应的动力计算；反应级数和活化能的测定；从反应机理推导速率方程。
教学内容：§11.1 化学动力学的任务和目的一、化学动力学的任务和目的化学热力学主要研究反应的方向、限度和外界因素对平衡的影响。
解决反应的可能性，即在给定条件下反应能不能发生，及反应进行的程度？而化学动力学主要研究反应的速率及反应机理。
主要解决反应的现实性问题。
化学动力学的基本任务是：了解反应速率；讨论各种因素（浓度、压力、温度、介质、催化剂等）对反应速率的影响；研究反应机理、讨论反应中的决速步等。
二、化学动力学发展概况1850年，人们提出浓度与反应速率的关系；十九世纪末：范特荷夫、阿仑尼乌斯讨论了反应速率与温度的关系；二十世纪化学动力学、催化等有了新的发展，特别是许多新技术如：激光、交叉分子束、计算机等用于动力学的研究，目前动力学的研究已从宏观动力学的研究进入到态-态反应动力学的研究。
§11.2 化学反应速率的表示一、反应速率的表示在等容反应体系中，化学反应速率通常用反应物浓度随时间的变化率来表示，此为瞬时反应速率，但由于反应物浓度随时间的增加而减小，产物浓度随时间的增加而增加，反应速率一般规定为正值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
物理化学电子教案—第十一章
积分法 微分法 半衰期法 孤立法
一级反应 对峙反应
2016/4/15
平行反应
连续反应 链反应
回顾：二级反应（a=b）的特点 k 1 2
1. 速率常数 k 的单位为[浓度] -1 [时间] -1 2. 半衰期与起始物浓度成反比 3.
x t a(a - x)
t1/ 2
1 k2 a
(3)对不同反应，Ea 大，k随T 的变化也大，如 Ea (3) Ea (2)
lnk
20 10
3
2000 1000
2
463 376
1 T /K
1000
1 T /K
2000 100
200，增一倍 10 200，增19倍
ln k2
ln k3
小结
1、对于给定的反应， 低温区反应速率随温度变化更敏感； 2、对于活化能不同的反应，温度增加时， Ea大的反应速率增加的倍数比Ea小的反 应速率增加的倍数大； 3、若几个反应同时进行，升高温度对Ea大的 反应有利。低温有利于活化能较低的反 应。 4、复杂反应，据上述决定适宜的操作温度。
Ea d ln k 2 dT RT
k 值随T 的变化率决定于 Ea 值的大小。
热力学和动力学对 r~T 关系看法
（1）热力学观点 根据van’t Hoff 公式 1. 对于吸热反应 温度升高
d ln K r H m dT RT 2
r H m >0
K 增大
m
k f / kb K 也增大
Tolman 用统计平均的概念对基元反应的活 化能下了一个定义：活化分子的平均能量与反应 物分子平均能量之差值，称为活化能。
Ea E E R
设基元反应为 A P
' 可以用图表示。 正、逆反应的活化能 Ea 和 Ea
*
基元反应的活化能
A*
活化状态
A*
活化状态
Ea
A
Ea '
Ea
A
Ea
Ea '
这两个都是线性方程，从直线斜率可得 E0 Arrhenius公式中，当升高温度，以 lnk 对1/T 作图的直线会发生弯折，这说明活化能还是与温 度有关，所以活化能的定义最好用下式表示：
d ln k Ea RT dT
2
Ea E0 mRT
活化能的估算（了解）
活化能的计算方法有： （1）用实验值作图
（1）如果 Ea,1 Ea,2，升高温度，k1 / k2 也升高，对反应1有利；
（2）如果 Ea,1 Ea,2，升高温度， k1 / k2 下降，对反应2有利。
（3）如果有三个平行反应，主反应的 活化能又处在中间，则不能简单的升高 温度或降低温度，而要寻找合适的反应 温度。
*§11.8
关于活化能
r
r
O
(e)
T
O
(f )
T
（4）速率在随温度升到某一高度时下降，再升 高温度，速率又迅速增加，可能发生了副反应。 （5） 温度升高，速率反而下降。这种类型很少，
如一氧化氮氧化成二氧化氮。
*反应速率与活化能之间的关系(了解)
以 lnk 对 1/T 作图 Ea 直线斜率为 R
lnk/[k]
活化能更高 活化能较低
a t1 2k0 2
零级反应的特点
x
0
dx k0 dt
0
t
x k0 t
1.速率常数 k 的单位为[浓度][时间]-1
2.半衰期与反应物起始浓度成正比：
t1/ 2
3.x 与
a 2k0
t 呈线性关系
4.反应完成所需要的时间 a/k0 零级反应是一个匀速反应。
如何鉴别不同级数的化学反应?(简单级数反应) • • • • 速率公式的定积分形式 浓度与时间的线性关系 半衰期 速率系数k单位
所以
A2 A1 A A1
Ea Ea,2 Ea,1 Ea,1
这就是复杂反应的活化能。
活化能与温度的关系(了解)
Arrhenius在经验式中假定活化能是与温度无 关的常数，这与大部分实验相符。 当升高温度，以 lnk 对1/T 作图的直线会发生 弯折，这说明活化能还是与温度有关。 在速率理论中指出速率常数与温度的关系为
P
作用物
P
Ea 生成物
放热反应
生成物
作用物
吸热反应
复杂反应的活化能
复杂反应的活化能无法用简单的图形表示，它只
是组成复杂反应的各基元反应活化能的特定数学组合。 组合的方式决定于基元反应的速率常数与表观速
率常数之间的关系，这个关系要从反应机理推导而得。
例如：
k (表观） k1k2 / k1
则
E （ Ea,1 Ea,2 Ea,1 a 表观）
有利于正向反应
2. 对于放热反应
温度升高
r H < 0
k f / kb K 也下降
K 下降
不利于正向反应
（2）动力学观点
Ea d ln k 2 dT RT
通常活化能总为正值，所以温度升高，正向
反应速率总是增加。
对于放热反应，实际生产中，为了保证一定 的反应速率，也适当提高温度，略降低一点平衡
如果 Ea 已知，也可以用这公式求另一温度 下的 k 值。
活化能的估算
用键能估算活化能，方法很粗略。
（1） 对于基元反应
A A B B 2(A B)
Ea ( EAA EB B ) 30%
平行反应的特点
4.用合适的催化剂可以改变某一反应的速率， 从而提高主反应产物的产量。 ？？5.用改变温度的办法，可以改变产物的相对含 量。活化能高的反应，速率系数随温度的变
化率也大。
Ea d ln k 2 dT RT
连续反应的c～t关系曲线
因为中间产物既是前一步反应的生成物，又 是后一步反应的反应物，它的浓度有一个先增后 减的过程，中间会出现一个极大值。 这极大值的位置和高度决定于两个速率常数 的相对大小，如下图所示：
E0 k A0T exp RT 式中A0，m 和 E0 都是要由实验测定的参数， 与温度无关。这就称为三参量公式。
m
三参量公式也可表示为
E0 k ln m ln A0 RT T E0 ln k ln A0 m ln T RT
1 与 t 成线性关系。 ax
引伸的特点： 对 a b 的二级反应， t1/ 2
: t3 / 4 : t 7 / 8
=1：3：7
零级反应的微分和积分式
A P t 0 a 0 t =t a - x x
x
0
dx k0dt
0
t
x k0 t
x y a 1 y 2
dx k0 r= dt
（2）对数式：
Ea ln k B RT
描述了速率常数与 1/T 之间的线性关系。可以根据 不同温度下测定的 k 值，以 lnk 对 1/T 作图，从而 求出活化能 Ea 。
阿仑尼乌斯公式
（3）定积分式
k2 Ea 1 1 ln ( ) k1 R T1 T2
设活化能与温度无关，根据两个不同温度 下的 k 值求活化能。 （4）微分式
活化能概念的进一步说明 活化能与温度的关系 活化能的估算
活化能概念的进一步说明
在Arrhenius经验式中，把活化能看作是与温度
无关的常数，这在一定的温度范围内与实验结较复杂的反
应，就不是一条很好的直线，这表明活化能与温度
有关，而且Arrhenius经验式对某些历程复杂的反应 不适用。 对于基元反应，活化能有较明确的物理意义， 而复杂反应的活化能仅是基元反应活化能的特定 组合。
反应级数的确定方法（实验确定）
积分法确定反应级数
微分法确定反应级数
半衰期法确定反应级数
改变反应物数量比例的方法
§11.5 几种典型的复杂反应
对峙反应 对峙反应的净速率等于正向
速率减去逆向速率，当达到
平衡时，净速率为零。
平行反应
总的反应速率等于所有平
行反应速率之和。
连续反应
对峙反应的特点
1.净速率等于正、逆反应速率之差值 2.达到平衡时，反应净速率等于零 3.正、逆速率系数之比等于平衡常数 K= kf/kb 4.在c～t 图上，达到平衡后，反应物和产物的 浓度不再随时间而改变
B 和 A C • 6．已知平行反应 A ，且 Ea,1 Ea,2 ，为提高B的产量，应采取 什么措施？
k1 , Ea,1
k2 , Ea,2
例如：平行反应反应中的温度选择原理
B
A
C
反应1，Ea,1 , k1 反应2， Ea,2 , k2
d ln(k1 / k2 ) dT Ea,1 Ea,2 2 RT
1
活化能较高
从图上可看出
1)直线越陡，活化能越大
Ea (3) Ea (2) Ea (1)
3
1 T /K
2
(2)对同一反应，k 随T 的变化在低温区较敏感。例 如 2。
1 T /K
376 463
活化能更高
ln k
10 20
增加
1倍 1倍
200
活化能较低
100
1
活化能较高
1000-2000 100-200
k
已知碘与氢的反应是复杂反应
H2 I2 2HI d[H 2 ] 总速率表示式为 r k[H 2 ] [I 2 ] dt
已知反应的历程为
垐 1垎 (1) I2 +M 噲 2Ig+M k垐
-1
积分法 微分法 半衰期法 孤立法
一级反应 对峙反应
2016/4/15
平行反应
连续反应 链反应
回顾：二级反应（a=b）的特点 k 1 2
1. 速率常数 k 的单位为[浓度] -1 [时间] -1 2. 半衰期与起始物浓度成反比 3.
x t a(a - x)
t1/ 2
1 k2 a
(3)对不同反应，Ea 大，k随T 的变化也大，如 Ea (3) Ea (2)
lnk
20 10
3
2000 1000
2
463 376
1 T /K
1000
1 T /K
2000 100
200，增一倍 10 200，增19倍
ln k2
ln k3
小结
1、对于给定的反应， 低温区反应速率随温度变化更敏感； 2、对于活化能不同的反应，温度增加时， Ea大的反应速率增加的倍数比Ea小的反 应速率增加的倍数大； 3、若几个反应同时进行，升高温度对Ea大的 反应有利。低温有利于活化能较低的反 应。 4、复杂反应，据上述决定适宜的操作温度。
Ea d ln k 2 dT RT
k 值随T 的变化率决定于 Ea 值的大小。
热力学和动力学对 r~T 关系看法
（1）热力学观点 根据van’t Hoff 公式 1. 对于吸热反应 温度升高
d ln K r H m dT RT 2
r H m >0
K 增大
m
k f / kb K 也增大
Tolman 用统计平均的概念对基元反应的活 化能下了一个定义：活化分子的平均能量与反应 物分子平均能量之差值，称为活化能。
Ea E E R
设基元反应为 A P
' 可以用图表示。 正、逆反应的活化能 Ea 和 Ea
*
基元反应的活化能
A*
活化状态
A*
活化状态
Ea
A
Ea '
Ea
A
Ea
Ea '
这两个都是线性方程，从直线斜率可得 E0 Arrhenius公式中，当升高温度，以 lnk 对1/T 作图的直线会发生弯折，这说明活化能还是与温 度有关，所以活化能的定义最好用下式表示：
d ln k Ea RT dT
2
Ea E0 mRT
活化能的估算（了解）
活化能的计算方法有： （1）用实验值作图
（1）如果 Ea,1 Ea,2，升高温度，k1 / k2 也升高，对反应1有利；
（2）如果 Ea,1 Ea,2，升高温度， k1 / k2 下降，对反应2有利。
（3）如果有三个平行反应，主反应的 活化能又处在中间，则不能简单的升高 温度或降低温度，而要寻找合适的反应 温度。
*§11.8
关于活化能
r
r
O
(e)
T
O
(f )
T
（4）速率在随温度升到某一高度时下降，再升 高温度，速率又迅速增加，可能发生了副反应。 （5） 温度升高，速率反而下降。这种类型很少，
如一氧化氮氧化成二氧化氮。
*反应速率与活化能之间的关系(了解)
以 lnk 对 1/T 作图 Ea 直线斜率为 R
lnk/[k]
活化能更高 活化能较低
a t1 2k0 2
零级反应的特点
x
0
dx k0 dt
0
t
x k0 t
1.速率常数 k 的单位为[浓度][时间]-1
2.半衰期与反应物起始浓度成正比：
t1/ 2
3.x 与
a 2k0
t 呈线性关系
4.反应完成所需要的时间 a/k0 零级反应是一个匀速反应。
如何鉴别不同级数的化学反应?(简单级数反应) • • • • 速率公式的定积分形式 浓度与时间的线性关系 半衰期 速率系数k单位
所以
A2 A1 A A1
Ea Ea,2 Ea,1 Ea,1
这就是复杂反应的活化能。
活化能与温度的关系(了解)
Arrhenius在经验式中假定活化能是与温度无 关的常数，这与大部分实验相符。 当升高温度，以 lnk 对1/T 作图的直线会发生 弯折，这说明活化能还是与温度有关。 在速率理论中指出速率常数与温度的关系为
P
作用物
P
Ea 生成物
放热反应
生成物
作用物
吸热反应
复杂反应的活化能
复杂反应的活化能无法用简单的图形表示，它只
是组成复杂反应的各基元反应活化能的特定数学组合。 组合的方式决定于基元反应的速率常数与表观速
率常数之间的关系，这个关系要从反应机理推导而得。
例如：
k (表观） k1k2 / k1
则
E （ Ea,1 Ea,2 Ea,1 a 表观）
有利于正向反应
2. 对于放热反应
温度升高
r H < 0
k f / kb K 也下降
K 下降
不利于正向反应
（2）动力学观点
Ea d ln k 2 dT RT
通常活化能总为正值，所以温度升高，正向
反应速率总是增加。
对于放热反应，实际生产中，为了保证一定 的反应速率，也适当提高温度，略降低一点平衡
如果 Ea 已知，也可以用这公式求另一温度 下的 k 值。
活化能的估算
用键能估算活化能，方法很粗略。
（1） 对于基元反应
A A B B 2(A B)
Ea ( EAA EB B ) 30%
平行反应的特点
4.用合适的催化剂可以改变某一反应的速率， 从而提高主反应产物的产量。 ？？5.用改变温度的办法，可以改变产物的相对含 量。活化能高的反应，速率系数随温度的变
化率也大。
Ea d ln k 2 dT RT
连续反应的c～t关系曲线
因为中间产物既是前一步反应的生成物，又 是后一步反应的反应物，它的浓度有一个先增后 减的过程，中间会出现一个极大值。 这极大值的位置和高度决定于两个速率常数 的相对大小，如下图所示：
E0 k A0T exp RT 式中A0，m 和 E0 都是要由实验测定的参数， 与温度无关。这就称为三参量公式。
m
三参量公式也可表示为
E0 k ln m ln A0 RT T E0 ln k ln A0 m ln T RT
1 与 t 成线性关系。 ax
引伸的特点： 对 a b 的二级反应， t1/ 2
: t3 / 4 : t 7 / 8
=1：3：7
零级反应的微分和积分式
A P t 0 a 0 t =t a - x x
x
0
dx k0dt
0
t
x k0 t
x y a 1 y 2
dx k0 r= dt
（2）对数式：
Ea ln k B RT
描述了速率常数与 1/T 之间的线性关系。可以根据 不同温度下测定的 k 值，以 lnk 对 1/T 作图，从而 求出活化能 Ea 。
阿仑尼乌斯公式
（3）定积分式
k2 Ea 1 1 ln ( ) k1 R T1 T2
设活化能与温度无关，根据两个不同温度 下的 k 值求活化能。 （4）微分式
活化能概念的进一步说明 活化能与温度的关系 活化能的估算
活化能概念的进一步说明
在Arrhenius经验式中，把活化能看作是与温度
无关的常数，这在一定的温度范围内与实验结较复杂的反
应，就不是一条很好的直线，这表明活化能与温度
有关，而且Arrhenius经验式对某些历程复杂的反应 不适用。 对于基元反应，活化能有较明确的物理意义， 而复杂反应的活化能仅是基元反应活化能的特定 组合。
反应级数的确定方法（实验确定）
积分法确定反应级数
微分法确定反应级数
半衰期法确定反应级数
改变反应物数量比例的方法
§11.5 几种典型的复杂反应
对峙反应 对峙反应的净速率等于正向
速率减去逆向速率，当达到
平衡时，净速率为零。
平行反应
总的反应速率等于所有平
行反应速率之和。
连续反应
对峙反应的特点
1.净速率等于正、逆反应速率之差值 2.达到平衡时，反应净速率等于零 3.正、逆速率系数之比等于平衡常数 K= kf/kb 4.在c～t 图上，达到平衡后，反应物和产物的 浓度不再随时间而改变
B 和 A C • 6．已知平行反应 A ，且 Ea,1 Ea,2 ，为提高B的产量，应采取 什么措施？
k1 , Ea,1
k2 , Ea,2
例如：平行反应反应中的温度选择原理
B
A
C
反应1，Ea,1 , k1 反应2， Ea,2 , k2
d ln(k1 / k2 ) dT Ea,1 Ea,2 2 RT
1
活化能较高
从图上可看出
1)直线越陡，活化能越大
Ea (3) Ea (2) Ea (1)
3
1 T /K
2
(2)对同一反应，k 随T 的变化在低温区较敏感。例 如 2。
1 T /K
376 463
活化能更高
ln k
10 20
增加
1倍 1倍
200
活化能较低
100
1
活化能较高
1000-2000 100-200
k
已知碘与氢的反应是复杂反应
H2 I2 2HI d[H 2 ] 总速率表示式为 r k[H 2 ] [I 2 ] dt
已知反应的历程为
垐 1垎 (1) I2 +M 噲 2Ig+M k垐
-1