山东省2013年高二暑假作业(四)数学(文)
山东省2013年高二暑假作业(二)理科数学

2013高二理科数学暑假作业(二)一、选择题 1.复数11ii+-(i 是虚数单位)的共轭复数的虚部为 A.1-B.0C.1D.22.已知不同的直线m ,n ,l ,不重合的平面,αβ,则下列命题正确的是 A .m//α,n∥α,则m∥nB .m//α,m//β,则α//βC .m⊥l ,n⊥l ,则m∥nD .m⊥α,m⊥β,则α// 3. 曲线33y x x =-和y x =围成的面积为( ).4A .8B .10C .9D4.已知0)](log [log log 237=x ,那么21-x 等于( )A.31B.63C.33D.425.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,根据收集到的数据(如下表),由最小二乘法求得回归直线方程0.6854.6y x =+表中有一个数据模糊不清,请你推断出该数据的值为A .68B . 68.2C .69D .756.函数)1(1)(xx n x f -=的图象是7.如果n a a )13(32-的展开式中各项系数之和为128,则展开式中2a 的系数是 ( )A .-2835 B.2835 C.21 D.-21 8.下列四个判断: ①2,10x R x x ∃∈-+≤;②已知随机变量X 服从正态分布N (3,2σ),P (X ≤6)=0.72,则P (X ≤0)=0.28; ③已知21()nx x+的展开式的各项系数和为32,则展开式中x 项的系数为20;④11e dx x>⎰⎰其中正确的个数有:A .1个B .2个C .3个D .4个9.已知ABC ∆中,三个内角A ,B ,C 的对边分别为a,b,c ,若ABC ∆的面积为S ,且()222,tan S a b c C =+-则等于A.34B.43C.43-D.34-10 . 把正整数按一定的规则排成了如图所示的三角形数表.设*(,)ij a i j N ∈ 是位于这个三角形数表中从上往下数第i 行,从左 往右数第j 个数,若2013ij a =, 则i 与j 的和为( )A .105B .103C .82D .81 11.要得到函数()sin(2)3f x x π=+的导函数'()f x 的图象,只需将()f x 的图象( )A .向左平移2π个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) B .向左平移2π个单位,再把各点的纵坐标缩短到原来的12倍(横坐标不变)C .向左平移4π个单位,再把各点的纵坐标伸长到原来的12倍(横坐标不变)D .向左平移4π个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变)12.等差数列{}n a 前n 项和为n S ,已知310061006(1)2013(1)1,a a -+-=124753121086911131517141618202224310081008(1)2013(1)1,a a -+-=-则A.2013100810062013,S a a => B .2013100810062013,S a a =< C.2013100810062013,S a a =-> D .2013100810062013,S a a =-< 二、填空题 13.若x,y 满足⎩⎨⎧≥+-≤+-,22,0y x y x 则的最大值y x C )(log 21+=为 .14.以椭圆192522=+y x 的焦点为焦点,离心率为2的双曲线方程为15.已知函数()f x 在实数集R 上具有下列性质:①直线1x =是函数()f x 的一条对称轴;②()()2f x f x +=-;③当1213x x ≤<≤时,()()()21f x f x -⋅()210,x x -<则()2012f 、()2013f 从大到小的顺序为_______.16. 已知2()(0)f x ax bx c a =++≠,且方程()f x x =无实数根,下列命题: ①方程[()]f f x x =也一定没有实数根;②若0a >,则不等式[()]f f x x >对一切实数x 都成立; ③若0a <,则必存在实数0x ,使00[()]f f x x >④若0a b c ++=,则不等式[()]f f x x <对一切实数x 都成立. 其中正确命题的序号是 . 三、解答题17. 已知向量2(3sin,1),(cos ,cos ).444x x xm n ==记()f x m n =⋅. (Ⅰ)若3()2f α=,求2cos()3πα-的值; (Ⅱ)在△ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,且满足(2)cos cos a c B b C -=,若13()f A +=,试判断△ABC 的形状. 18.已知函数)0()221(1)(2>-+=a ax x ax n x f .(Ⅰ)若的一个极)(是函数21x f x =值点,求a 的值; (Ⅱ)求证:当0<a ≤2时,f(x)在⎪⎭⎫⎢⎣⎡∞+,21上是增函数;(Ⅲ)若对任意的)2,1(∈a ,总存在]2,1[0∈x ,使不等式)1()(20a m x f ->成立,求实数m的取值范围.19.由世界自然基金会发起的“地球1小时”活动,已发展成为最有影响力的环保活动之一,今年的参与人数再创新高.然而也有部分公众对该活动的实际效果与负面影响提出了疑问.对此,某新闻媒体进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:(1)在所有参与调查的人中,用分层抽样的方法抽取个人,已知从“支持”态度的人中抽取了45人,求n 的值;(2)在持“不支持”态度的人中,用分层抽样的方法抽取5人看成一个总体,从这5人中任意选取2人,求至少有1人20岁以下的概率;20.(本小题满分13分)如图,椭圆22122:1(0)x y C a b a b +=>>的离心率为2,x 轴被曲线22:C y x b =-截得的线段长等于1C 的短轴长。
山东省2013年高二暑假作业(二)理科数学.pdf

2013高二理科数学暑假作业(二) 一、选择题 1.复数(i是虚数单位)的共轭复数的虚部为 A.B.0C.1D.2 2.已知不同的直线m,n,l,不重合的平面,则下列命题正确的是 A.m//,n∥,则m∥n B.m//,m//,则// C.m⊥,n⊥,则m∥n D.m⊥,m⊥,则//和围成的面积为( ) 4.已知,那么等于( ) A. B. C. D. 5.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,根据收集到的数据(如下表),由最小二乘法求得回归直线方程 表中有一个数据模糊不清,请你推断出该数据的值为 A.68 B. 68.2 C.69 D.75 的图象是 7.如果的展开式中各项系数之和为128,则展开式中的系数是 ( ) A.-2835 B.2835 C.21 D.-21 8.; ②已知随机变量X服从正态分布N(3,),P(X≤6)=0.72,则P(X≤0)=0.28; ③已知的展开式的各项系数和为32,则展开式中x项的系数为20; ④ 其中正确的个数有: A.1个 B.2个 C.3个 D.4个 9.已知中,三个内角A,B,C的对边分别为a,b,c,若的面积为S,且等于 A.B.C.D. 10 . 把正整数按一定的规则 排成了如图所示的三角形数表.设是位于这个三角形数表中从上下数第行从左往右数第个数若,则与的和( )A. B.10C. D.的导函数的图象,只需将的图象( ) A.向左平移个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) B.向左平移个单位,再把各点的纵坐标缩短到原来的倍(横坐标不变) C.向左平移个单位,再把各点的纵坐标伸长到原来的倍(横坐标不变) D.向左平移个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) 12.等差数列前项和为,已知 则 A. B. C. D. 二、填空题 13.若x,y满足则为 . 14.以椭圆的焦点为焦点,离心率为2的双曲线方程为 15.已知函数在实数集R上具有下列性质:①直线是函数的一条对称轴;②;③当时, 、从大到小的顺序为_______. 16. 已知,且方程无实数根,下列命题: ①方程也一定没有实数根; ②若,则不等式对一切实数都成立; ③若,则必存在实数,使 ④若,则不等式对一切实数都成立. 其中正确命题的序号是 . 三、解答题 17. 已知向量记. (Ⅰ)若,求的值; (Ⅱ)在△ABC中,角A、B、C的对边分别是、、,且满足,若,试判断△ABC的形状. 18.已知函数. (Ⅰ)若值点,求a的值; (Ⅱ)求证:当0。
山东省2013年高二暑假作业(一)语文

2013高二语文暑假作业(一)一、选择题1.下列词语中加点的字,读音全都正确的一组是:()A. 悚.然(sǒng)庇.护( bì)引吭.高歌(kàng)大腹便.便(pián)B.请帖.(tiě)人寰(huán)刚愎.自用( bì)自怨自艾(ài )C.匮.乏(kuì) 羸.弱(léi)喟.然长叹(kuì)处.心积虑(chŭ)D.鞭挞.(dá)哺.育(bŭ)一蹴.而就(cù)乳臭(xiù)未干2.下列各组词语中没有错别字的一项是()A.延荡恣肆修茸卷帙浩繁B.勋绶情愫馥郁神采熠熠C.忧悒拾掇拖拽纡尊降贵D.砭骨欠收缅怀乌烟瘴气3. 依次填入下面一段文字横线处的语句,衔接最恰当...的一组是()批评文章通常是即兴的随笔,与写意画相通。
,。
;。
在怀有一流技术的画家看来,批评界人士都是眼高手低。
①批评家的文章却不能有败笔②如果形而上地议论,画家又指责批评家不会细微地体味作品③批评家如果引经据典,会被讥之为卖弄④写意画家的作品,不经意的败笔很常见⑤颜真卿打叉画圈的行书或黄宾虹的乱笔,感觉无所谓A.④⑤①③②B.④①②③⑤C.③②①④⑤D.③②④⑤①4.下列各句中,没有语病的一句是()A.近来,“高校母语教育”重新受到重视,许多大学都在开设或准备开设大学语文课程,力图通过该课程帮助学生继续提高母语修养和对母语文化的热爱。
B.这些敢于将自己的遗体捐献出去的人,多是以医护人员、教师、工程师等知识分子为主,他们在日常生活中,也以乐于助人的精神唱响感动人心的奉献之歌。
C.不仅本届运动会以出色的运动成绩、顺畅的组织运作、热情的志愿服务而令人难忘,而且在增强各单位的联系和职工之间的友谊方面也发挥了重要作用。
D.网络安全问题日益为人们所关注,加强网络监管的呼声也日益高涨,而网络监管技术水平则是能否顺利推进网络监管工作的重要因素。
山东省2013年高二暑假作业(五)文科数学

2013高二数学暑假作业(五)一、选择题1.“a=2”是“直线2x +ay -1=0与直线ax +2y -2=0平行”的( )A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件2.直线l 经过点A (2,1)、B (1,2m ) (m )R ∈两点,那么直线l 的倾斜角的范围是( )A . [)π,0B . []()πππ,,024C . []4,0πD .[]4,0π[)ππ,23.若双曲线x 2a 2-y 2b 2=1的焦点到其渐近线的距离等于实轴长,则该双曲线的离心率为( ) A. 5 B .5 C. 2 D .24.已知圆的方程为x 2+y 2-2x +6y +8=0,那么下列直线中经过圆心的直线方程为( )A .2x -y +1=0B .2x +y +1=0C .2x -y -1=0D .2x +y -1=05、直线l 过抛物线y 2=2px(p>0)的焦点F ,且与抛物线交于A 、B 两点,若线段AB 的长是8,AB 的中点到y 轴的距离是2,则此抛物线方程是( )A .y 2=12xB .y 2=8xC .y 2=6xD .y 2=4x6.定义:平面内横坐标为整数的点称为“左整点”.过函数y =9-x 2图象上任意两个“左整点”作直线,则倾斜角大于45°的直线条数为( )A .10B .11C .12D .137.设双曲线y 2m -x 22=1的一个焦点为(0,-2),则双曲线的离心率为( ) A. 2 B .2 C. 6 D .2 28.椭圆x 24+y 2=1的焦点为F 1,F 2,点M 在椭圆上,MF 1→·MF 2→=0,则M 到y 轴的距离为( ) A.233 B.263 C.33 D. 39.已知双曲线的两个焦点为F 1(-10,0),F 2(10,0),M 是此双曲线上的一点,且MF 1→·MF 2→=0,|MF 1→|·|MF 2→|=2,则该双曲线的方程是( )A.x 29-y 2=1 B .x 2-y 29=1 C.x 23-y 27=1 D.x 27-y 23=1 10.设圆C 的圆心在双曲线x 2a 2-y 22=1(a>0)的右焦点上,且与此双曲线的渐近线相切,若圆C 被直线l :x -3y =0截得的弦长等于2,则a =( )A.14B. 6C. 2 D .211.直线y =kx +3与圆(x -3)2+(y -2)2=4相交于M ,N 两点,若|MN|≥23,则k 的取值范围是( )A.⎣⎢⎡⎦⎥⎤-34,0B.⎝⎛⎦⎥⎤-∞,-34∪[0,+∞)C.⎣⎢⎡⎦⎥⎤-33,33 D.⎣⎢⎡⎦⎥⎤-23,0 12.已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的两条渐近线均和圆C :x 2+y 2-6x +5=0相切,且双曲线的右焦点为圆C 的圆心,则该双曲线的方程为( ).A.x 25-y 24=1B.x 24-y 25=1 C.x 23-y 26=1 D.x 26-y 23=1 13.已知曲线C :y =2x 2,点A(0,-2)及点B(3,a),从点A 观察点B ,要使视线不被曲线C 挡住,则实数a 的取值范围是( )A .(4,+∞)B .(-∞,4]C .(10,+∞)D .(-∞,10]二、填空题 14.两圆C1:0101022=--+y x y x 与C 2:0402622=-+++y x y x 的公共弦所在直线方程是______________,公共弦的长等于 .15.到直线49=x 的距离与到定点)0,4(F 的距离之比为43的点的轨迹方程是 .16.已知两点)5,3(-M 、)5,7(-N ,则线段MN 的垂直平分线的方程为______________.17.已知点(x 0,y 0)在直线ax +by =0(a ,b 为常数)上,则(x 0-a)2+(y 0-b)2的最小值为________.三、解答题18.已知:圆C :x 2+y 2-8y +12=0,直线l :ax +y +2a =0.(1)当a 为何值时,直线l 与圆C 相切; (2)当直线l 与圆C 相交于A 、B 两点,且AB =22时,求直线l 的方程.19.如图,直线l :y =x +b 与抛物线C :x 2=4y 相切于点A.(1)求实数b 的值;(2)求以点A 为圆心,且与抛物线C 的准线相切的圆的方程.20.设椭圆C :x 2a 2+y 2b 2=1(a>b>0)的离心率为22,过原点O 斜率为1的直线与椭圆C 相交于M ,N 两点,椭圆右焦点F 到直线l 的距离为 2.(1)求椭圆C 的方程;(2)设P 是椭圆上异于M ,N 外的一点,当直线PM ,PN 的斜率存在且不为零时,记直线PM 的斜率为k 1,直线PN 的斜率为k 2,试探究k 1·k 2是否为定值?若是,求出定值;若不是,说明理由.2013高二数学暑假作业(五)参考答案一、选择题1.B2.B3.A4.B5.B6.B7.A8.B9.A 10.C 11.A 12.A 13.D二、填空题14. 01034=-+y x ;10 15. 17922=-y x16. 02=+-y x 17. a 2+b 2三、解答题 18.解:将圆C 的方程x 2+y 2-8y +12=0配方得标准方程为x 2+(y -4)2=4,则此圆的圆心为(0,4),半径为2.(1)若直线l 与圆C 相切,则有|4+2a|a 2+1=2. 解得a =-34. (2)过圆心C 作CD⊥AB,则根据题意和圆的性质, 得⎩⎪⎨⎪⎧CD =|4+2a|a 2+1,CD 2+DA 2=AC 2=22,DA =12AB = 2. 解得a =-7,或a =-1. 故所求直线方程为7x -y +14=0或x -y +2=0. 19.解:(1)由⎩⎪⎨⎪⎧ y =x +b ,x 2=4y ,得x 2-4x -4b =0,(*)因为直线l 与抛物线C 相切,所以Δ=(-4)2-4×(-4b)=0,解得b =-1.(2)由(1)可知b =-1,故方程(*)为x 2-4x +4=0.解得x =2,代入x 2=4y ,得y =1,故点A(2,1).因为圆A 与抛物线C 的准线相切,所以圆A 的半径r 就等于圆心A 到抛物线的准线y =-1的距离,即r =|1-(-1)|=2,所以圆A 的方程为(x -2)2+(y -1)2=4.20.解:(1)设椭圆的焦距为2c(c>0),焦点F(c,0),直线l :x -y =0,F 到l 的距离为|c|2=2,解得c =2, 又∵e=c a =22,∴a=22,∴b=2. ∴椭圆C 的方程为x 28+y 24=1. (2)由⎩⎪⎨⎪⎧ x 28+y 24=1,y =x ,解得x =y =263,或x =y =-263, 不妨设M ⎝ ⎛⎭⎪⎫263,263,N ⎝ ⎛⎭⎪⎫-263,-263,P(x ,y), ∴k PM ·k PN =y -263x -263·y +263x +263=y 2-83x 2-83, 由x 28+y 24=1,即x 2=8-2y 2,代入化简得k 1·k 2=k PM ·k PN =-12为定值.。
2013高二数学暑假作业答案

2013年高二数学暑假作业答案【快乐暑假】2013年高二数学暑假作业答案一.填空题1.A.2.3.3.(1)(4)..5.212cm4.(1)(2)..6.(2)(4).7.300..8.90°.9.①与③.10.④.11.30.12.2:1.13.3.14.若②③④则①.二.解答题15.S=60+42;V=52-38=314816.证明:作PO,,PEABPFAC,垂足分别为,,OEF,连结,,OEOFOA,∵,PEABPFACPAEPAFRtPAERtPAFAEAFPAPA,POABPOAB,又∵ABPE,∴AB平面PEO,∴ABOE.同理ACOF.在RtAOE和RtAOF,,AEAFOAOA,∴RtAOE RtAOF,∴EAOFAO,即点P在平面上的射影在BAC的平分线上.17.证明:(1)因为E,F分别是11AB,AC的中点,所以EF//BC,又EF面ABC,BC面ABC,所以EF∥ABC平面;(2)因为直三棱柱111ABCABC,所以1111BBABC面,11BBAD,又11ADBC,所以111ADBCC面B,又11ADAFD面,所以111AFDBBCC平面平面.18.证明:(1)连结11AC,设11111ACBDO连结1AO,1111ABCDABCD是正方体11AACC是平行四边形11ACAC且11ACAC,又1,OO分别是11,ACAC的中点,11OCAO且11OCAO11AOCO是平行四边形.111,COAOAO面11ABD,1CO面11ABD1CO面11ABD.(2)证明:////''''''ABDCDCABCDABDCDC是平行四边形'//'''''''BCADBCABDADABD平面平面'//'''//'''''BCABDCDABDBCCDC平面同理,平面平面'//CDB平面''ABD.19.(本小题满分14分)(1)证明: E.P分别为AC.A′C的中点,EP∥A′A,又A′A平面AA′B,EP平面AA′B∴即EP∥平面A′FB(2)证明:∵BC⊥AC,EF⊥A′E,EF∥BC∴BC⊥A′E,∴BC⊥平面A′ECBC平面A′BC∴平面A′BC⊥平面A′EC(3)证明:在△A′EC中,P为A′C的中点,∴EP⊥A′C,在△A′AC中,EP∥A′A,∴A′A⊥A′C由(2)知:BC⊥平面A′EC又A′A平面A′EC∴BC⊥AA′∴A′A⊥平面A′BC20.解:(1)证明:在DD1上取一点N使得DN=1,连接CN,EN,显然四边形CFD1N是平行四边形,所以D1F//CN,同理四边形DNEA是平行四边形,所以EN//AD,且EN=AD,又BC//AD,且AD=BC,所以EN//BC,EN=BC,所以四边形CNEB是平行四边形,所以CN//BE,所以D1F//BE,所以1,,,EBFD四点共面.(2)因为GMBF所以BCF∽MBG,所以MBBGBCCF,即2332MB,所以MB=1,因为AE=1,所以四边形ABME是矩形,所以EM⊥BB1又平面ABB1A1⊥平面BCC1B1,且EM在平面ABB1A1内,所以EM面11BCCB.精心整理,仅供学习参考。
山东2013高二暑假作业试题(四)-数学(理).

2013高二数学(理)暑假作业(四)一、选择题1.设R b a ∈、,是虚数单位,则“0=ab ”是“复数bi a +为纯虚数的”( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件2.已知niim-=+11,其中m,n 是实数,i 是虚数单位,则m+ni=(A)1-2i (B)1+2i (C)2-i (D)2+i3.在6的二项展开式中,x 2的系数为A .427- B .227- C .227 D .4274. 有一段 “三段论”推理是这样的:对于可导函数()f x ,若0()0f x '=,则0x x =是函数()f x 的极值点.因为3()f x x =在0x =处的导数值(0)0f '=,所以0x =是3()f x x =的极值点.以上推理中 ( ) A .大前提错误 B .小前提错误 C .推理形式错误 D .结论正确 5.已知3cos(),sin 245x xπ-=则=( ) A .1825 B .725C .725- D .1625-的y 值.若要使输入的x 值与输出的y 值相等,则这样的x 值有A .1个B .2个C .3个D .4个 8.市内某公共汽车站6个候车位(成一排),现有3名乘客随便坐在某个座位上候车,则恰好有2个连续空座位的候车方式的种数是A.48B.54C.72D.849. 等比数列}{n a 的前n 项和n S ,若36,963==S S ,则=++987a a aA. 72B. 81C. 90D. 99 10::4:3:2a b c =,那么cos C 的值为 A.14B.14- C.78 D.111611. 设12F F 是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点,P 为直线32a x =上一点, ∆21F PF 是底角为30的等腰三角形,则E 的离心率为( )A.12B. 23C.34D.4512.已知函数,)0(1)1()0(12)(⎩⎨⎧〉+-≤-=x x f x x x f ),0(≤x 把函数1)()(+-=x x f x g 的零点从小到大的顺序排列成一个数列,记该数列的前n 项的和为=10,则S S n(A)45 (B)55 (C)129- (D)1210- 二、填空题 13 .若双曲线()222210x y a b a b -=>>的左、右焦点分别为F 1,F 2,线段F 1F 2被抛物线22y bx =的焦点分成5:3两段,则此双曲线的离心率为______.14.由曲线f=x 2-1和直线y=0所围成的封闭图形的面积为 。
【推荐下载】最新年山东省高二暑假作业:文科数学(含答案)

[键入文字]
17.若函数当时,函数极值 (1)求函数的解析式; (2)若函数有 3 个解,求实数的取值范围. 18.(本小题满分 12 分) (1)求证:平面平面; (2)求证:∥平面; (3)求四面体的体积. 19、己知等比数列所有项均为正数,首,且成等差数列. (I)求数列的通项公式; (II)数列的前 n 项和为,若,求实数的值. 20.(本小题满分 12 分) 已知函数.
2
)
B.
C.2
D.3
B.
C.
D.
B.
D.
)
[键入文字]
k≤11?
B.k≥11?
C.k≤10?
D.k≥10?
11.已知动点在椭圆上,若点坐标为,,且,则的最小值是 A. C. 12.已知函数满足:当 A. 二、填空题 13.已知某几何体的三视图如图所示,若该几何体的体积为 24, 则正(主)视图中的值为 . B. C. D. D.
6
∴面.
[键入文字]
∴ ∴ 19.(Ⅰ)设数列的公比为,由条件得成等差数列,所以 解得 由数列的所有项均为正数,则=2 数列的通项公式为= (Ⅱ)记,则 若不符合条件; 若, 则,数列为等比数列,首项为,公比为 2, 此时 又=,所以 20.解:. (1),解得.
8
[键入文字]
由已知, ,由(Ⅱ)可知, ①当时,在上单调递增, 故, 所以, ,解得,故. ②当时,在上单调递增,在上单调递减, 故. 由可知, , , 所以, , , 综上所述,. 这篇山东省高二暑假作业就为大家分享到这里了。希望对大家有所帮助!
2013高二数学暑假作业答案

2013年高二年数学暑假作业答案一、填空题:本大题共14小题。
每小题5分。
共计70分.请把答案填写在答题纸相应位置上1.命题“R,≥”的否定是.2.直线的倾斜角为.3.抛物线的焦点坐标是.4.双曲线的渐近线方程是.5.已知球的半径为3,则球的表面积为.6.若一个正三棱锥的高为5,底面边长为6,则这个正三棱锥的体积为.7.函数在点(1,)处的切线方程为.8.若直线与直线平行,则实数的值等于.9.已知圆与圆相内切,则实数的值为.10.已知直线和圆相交于,两点,则线段的垂直平分线的方程是。
11.已知两条直线和都过点(2,3),则过两点,的直线的方程为.12.已知是椭圆的左焦点,是椭圆上的动点,是一定点,则的最大值为.13.如图,已知(常数),以为直径的圆有一内接梯形,且,若椭圆以,为焦点,且过,两点,则当梯形的周长最大时,椭圆的离心率为.14.设函数,,若的图象与的图象有且仅有两个不同的公共点,则当时,实数的取值范围为.二、解答题:本大题共6小题,共计90分.请在答题纸制定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分14分)如图,在正方体中,,分别为棱,的中点.(1)求证:∥平面;(2)求证:平面⊥平面.16.(本小题满分l4分)已知圆经过三点,,.(1)求圆的方程;(2)求过点且被圆截得弦长为4的直线的方程.17.(本小题满分14分)已知,命题≤,命题≤≤.(1)若是的必要条件,求实数的取值范围;(2)若,“或”为真命题,“且”为假命题,求实数的取值范围.18.(本小题满分l6分)现有一张长80厘米、宽60厘米的长方形铁皮,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为l00%,不考虑焊接处损失.方案一:如图(1),从右侧两个角上剪下两个小正方形,焊接到左侧中闻,沿虚线折起,求此时铁皮盒的体积;方案二:如图(2),若从长方形的一个角上剪下一块正方形铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,求该铁皮盒体积的最大值,并说明如何剪拼?。
山东省高二暑假作业:文科数学(含答案)

山东省高二暑假作业:文科数学(含答案)解答题17.若函数当时,函数极值(1)求函数的解析式;(2)若函数有3个解,求实数的取值范围.18.(本小题满分12分) 与等腰直角所在平面互相垂直,为的中点,,∥,.(1)求证:平面平面;(2)求证:∥平面;(3)求四面体的体积.19、己知等比数列所有项均为正数,首,且成等差数列.(I)求数列的通项公式;(II)数列的前n项和为,若,求实数的值.20.(本小题满分12分)已知函数.(1)若曲线在和处的切线互相平行,求的值;(2)求的单调区间;(3)设,若对任意,均存在,使得,求的取值范围.2019高二文科数学暑假作业(一)答案1-5 ACABC 6-10 BADBD 11-12BB13. 614. 2i15.1/216.17. (1)所以,.即,由此可解得,(2)所以在处取得极大值,在处取得极小值所以18.(1)∵面面,面面,,面,又∵面,平面平面.(2)取的中点,连结、,则 ,又∵,,四边形是平行四边形,∥,又∵面且面,∥面.(3)∵,面面=,面.就是四面体的高,且=2.∵==2=2,∥,19.(Ⅰ)设数列的公比为,由条件得成等差数列,所以解得由数列的所有项均为正数,则=2数列的通项公式为=(Ⅱ)记,则若不符合条件;若,则,数列为等比数列,首项为,公比为2, 此时又=,所以20.解:.(1),解得.(3).①当时,,,在区间上,;在区间上,故的单调递增区间是,单调递减区间是.②当时,,在区间和上,;在区间上,故的单调递增区间是和,单调递减区间是.③当时,,故的单调递增区间是.④当时,,在区间和上,;在区间上,故的单调递增区间是和,单调递减区间是. (Ⅲ)由已知,在上有.由已知,,由(Ⅱ)可知,①当时,在上单调递增,故,所以,,解得,故.②当时,在上单调递增,在上单调递减,故.由可知,,,所以,,,综上所述,.这篇山东省高二暑假作业就为大家分享到这里了。
希望对大家有所帮助!。
山东省2013年高二暑假作业(三)理科数学
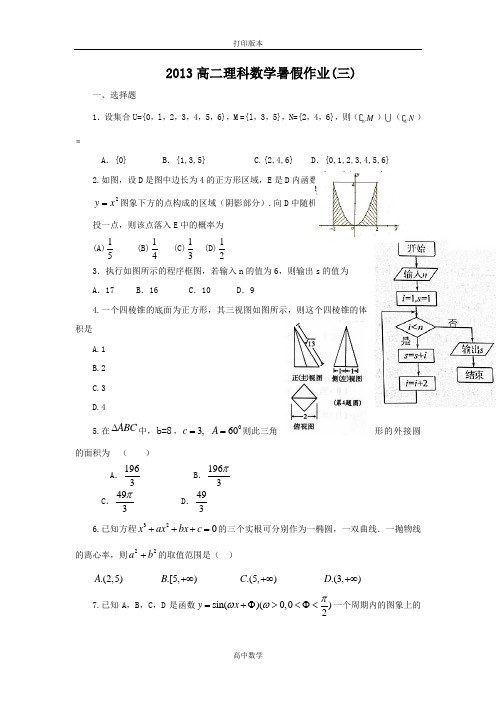
2013高二理科数学暑假作业(三)一、选择题1.设集合U={0,l ,2,3,4,5,6},M ={l ,3,5},N={2,4,6},则(U M )(U N )﹦A .{0}B .{1,3,5}C.{2,4,6} D .{0,1,2,3,4,5,6}2.如图,设D 是图中边长为4的正方形区域,E 是D 内函数2x y =图象下方的点构成的区域(阴影部分).向D 中随机投一点,则该点落入E 中的概率为 (A)51 (B)41 (C)31 (D)213.执行如图所示的程序框图,若输入n 的值为6,则输出s 的值为 A .17 B .16 C .10 D .94.一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是A.1B.2C.3D.45.在ABC ∆中,b=8,3,c = 060A =则此三角形的外接圆的面积为 ( )A .1963 B .1963πC .493πD .4936.已知方程320x ax bx c +++=的三个实根可分别作为一椭圆,一双曲线.一抛物线的离心率,则22a b +的取值范围是( ).(2,5)A .[5,)B +∞ .(5,)C +∞ .(3,)D +∞7.已知A ,B ,C ,D 是函数sin()(0,0)2y x πωω=+Φ><Φ<一个周期内的图象上的四个点,如图所示,(,0),6A π-B 为y 轴上的点,C 为图像上的最低点,E 为该函数图像的一个对称中心,B 与D 关于点E 对称,CD 在x 轴上的投影为12π,则,ωΦ的值为 A.2,3πω=Φ= B . 2,6πω=Φ= C. 1,23πω=Φ= D .1,26πω=Φ=8.各项为正的等比数列{}n a 中,4a 与14a 的等比中项为22,则7112a a +的最小值为( )A .16B .8C .22D .49.已知x,y 满足条件020x y x x y k ≥⎧⎪≤⎨⎪++≤⎩(k 为常数),若目标函数3z x y =+的最大值为8,则k=A.16-B.6-C.83-D.610.已知抛物线的顶点在原点,焦点在x 轴的正半轴上,若抛物线的准线与双曲线5x 2-y 2= 20的两条渐近线围成的三角形的面积等于54,则抛物线的方程为A .y 2=4xB .y 2=8xC .x 2=4yD .x 2=8y11设正实数x,y,z x 2-3xy+4y 2-z=0.则当xyz取得最大值时,212x y z +-为A )0 (B )1 (C ) 94(D )312.若函数()y f x =的导函数...在区间[,]a b 上是增函数,则函数()y f x =在区间[,]a b 上的图象可能是( )二、填空题13.已知0,0x y >>且满足281x y+=,则x y +的最小值为14.某校高三年级的学生共1000人,一次测验成绩的分布直方图如右图所示,现要按右图所示的4个分数段进行分层抽样,抽取50人了解情况,则在80~90分数段应抽取人数为 。
山东省2013年高二暑假作业(三)文科数学.pdf

2013高二数学暑假作业(三) 一、选择题 1.(2011·新课标全国)已知集合M={0,1,2,3,4},N={1,3,5},P=M∩N,则P的子集 共有( ). A.2个 B.4个 C.6个 D.8个 2(2011·陕西)设a,b是向量,命题“若a=-b,则|a|=|b|”的逆命题是( ). A.若a≠-b,则|a|≠|b| B.若a=-b,则|a|≠|b| C.若|a|≠|b|,则a≠-b D.若|a|=|b|,则a=-b 3(山东文)设集合,,则( ) A. B. C. D. 4定义.若,则( ).A.{4,8}B.{1,2,6,10}C.{1}D. {2,6,10}5.设集合,定义,则中元素的个数是( ). A.3 B.7 C.10 D.12 6(2012·湛江模拟)设a,b∈R,则“a>2,且b>1”是“a+b>3,且ab>2”的( ). A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 7给出命题:若函数y=f(x)是幂函数,则函数y=f(x)的图象不过第四象限.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( ). A.3 B.2 C.1 D.0 8命题“?x>0,x2+x>0”的否定是( ). A.?x0>0,x+x0>0 B.?x0>0,x+x0≤0 C.?x>0,x2+x≤0 D.?x≤0,x2+x>0 9“三角函数是周期函数,y=tan x,x∈是三角函数,所以y=tan x, x∈是周期函数.”在以上演绎推理中,下列说法正确的是( ). A.推理完全正确 B.大前提不正确 C.小前提不正确 D.推理形式不正确 10观察下图: 1 2 3 4 3 4 5 6 7 4 5 6 7 8 9 10 …… 则第________行的各数之和等于2 0112( ). A.2 010 B.2 009 C.1 006 D.1 005 11.命题“若函数f(x)=logax(a>0,a≠1)在其定义域内是减函数,则loga2<0”的逆否命题是( ). A.若loga2<0,则函数f(x)=logax(a>0,a≠1)在其定义域内不是减函数 B.若loga2≥0,则函数f(x)=logax(a>0,a≠1)在其定义域内不是减函数 C.若loga2<0,则函数f(x)=logax(a>0,a≠1)在其定义域内是减函数 D.若loga2≥0,则函数f(x)=logax(a>0,a≠1)在其定义域内是减函数 12设a、b、c均为正实数,则三个数a+、b+、c+( ). A.都大于2 B.都小于2 C.至少有一个不大于2 D.至少有一个不小于2 13.已知集合P={(x,y)|y=m},Q={(x,y)|y=,a>0,a≠1},如果P Q有且只有一个元素,那么实数m的取值范围是_________. 14“ω=2”是“函数y=sin (ωx+φ)的最小正周期为π”的________条件(填“充分非必要”、“必要非充分”、“充要”). 15已知:; 通过观察上述两等式的规律,请你写出一般性的命题: ___________________________________________________________ 16已知以下四个命题: ①如果x1,x2是一元二次方程a x+bx+c=0的两个实根,且x<x,那么不等式ax+bx+c<0的解集为{x| x<x2,则x-2x+m>0的解集是实数集R; ④若函数y=x-ax+b在[2,+∞)上是增函数,则a≤4. 其中为真命题的是______.(填上你认为正确的命题序号) 17.已知p:|x-3|≤2,q:(x-m+1)·(x-m-1)≤0,若p是q的充分而不必要条件,求实数m的取值范围. 18设集合A={x|x2+4x=0,x∈R},B={x|x2+2(a+1)x+a2-1=0,a∈R,x∈R},若BA,求实数a的取值范围. 19已知c>0,且c≠1,设p:函数y=cx在R上单调递减;q:函数f(x)=x2-2cx+1在上为增函数,若“p∧q”为假,“p∨q”为真,求实数c的取值范围. 20.若a、b、c是不全相等的正数,求证: lg+lg+lg>lg a+lg b+lg c.1.B2.D3.A4.D5.D6.A7.C8.B9.C 10.C 11.B 12.D 二、填空题 13. (1, +) 14.充分非必要 15. (答案不唯一)一般形式: 16. ③④ 17.解 由题意p:-2≤x-3≤2,∴1≤x≤5.∴p:x<1或x>5. q:m-1≤x≤m+1,∴q:x<m-1或x>m+1. 又∵p是q的充分而不必要条件, ∴∴2≤m≤4,即实数m的取值范围是[2,4]. 18.解 ∵A={0,-4},∴BA分以下三种情况: (1)当B=A时,B={0,-4},由此知0和-4是方程x2+2(a+1)x+a2-1=0的两个根,由根与系数之间的关系,得解得a=1. (2)当BA时,B={0}或B={-4},并且Δ=4(a+1)2-4(a2-1)=0,解得a=-1,此时B={0}满足题意. (3)当B=时,Δ=4(a+1)2-4(a2-1)<0,解得a<-1. 综上所述,所求实数a的取值范围是(-∞,-1]∪{1}. 19.解:∵函数y=cx在R上单调递减,∴0<c<1. 即p:0<c<1.∵c>0且c≠1,∴p:c>1. 又∵f(x)=x2-2cx+1在上为增函数, ∴c≤.即q:0<c≤.∵c>0且c≠1,∴q:c>且c≠1. 又∵“p∨q”为真,“p∧q”为假,∴p真q假或p假q真. ①当p真,q假时,{c|0<c<1}∩=; ②当p假,q真时,{c|c>1}∩=, 综上所述,实数c的取值范围是. 20.证明 ∵a,b,c∈(0,+∞), ∴≥>0,≥>0,≥>0. 又上述三个不等式中等号不能同时成立. ∴··>abc成立.上式两边同时取常用对数,得 lg>lg abc, ∴lg+lg+lg>lg a+lg b+lg c.。
山东省2013年高二暑假作业(四)语文 Word版含答案

2013高二语文暑假作业(四) 一、基础检测 1.给加点的字注音 迷惘( ) 晨曦( ) 沉湎( ) 炫( )耀 眷( )恋 挚( )友 譬( )如 怪癖( ) 摭( )拾 诧( )异 琐( )碎 遨( )游 翱( )翔 磕绊( ) 焦灼( ) 入不敷( )出 枝桠( ) 妥帖( ) 自艾自怜( ) 刻薄( ) 称职( ) 纤巧( ) 碑帖( ) 期期艾艾( ) 薄饼( ) 称赞( ) 纤夫( ) 摭拾( ) 吭声( ) 横幅( ) 衡量( ) 干瘪( ) 拾级而上( ) 引吭高歌( ) 蛮横( ) 量体裁衣( ) 瘪三( ) 2.根据读音写出汉字 晨xī( ) jué( )择 沉miǎn( ) nì( )爱 急zào( )枝yā( ) 痴心wàn( )想 冰báo( ) zhēn( )别 入不fū( )出 完美无xiá( ) 其乐rón rón( ) 3.依次填入下列各句横线上的词语,正确的一项是( ) ①孩子, 地说,我无法抑制对你的期望,我虽不致横蛮专制到干涉你对“志愿”的选择,但也实在希望你能考进大学。
②东东,人到了中年便时有闲愁,怪不得词人会 年华一瞬,容销金镜,壮志消残,我也不免有些 。
③只要我认真地活过,无愧地付出过,人们将无权 我是入不敷出的傻瓜,也不必用他的尺度来衡量我值得或是不值得。
A.坦率 感叹/感触 耻笑B.轻率 感叹/感触 讥笑C.坦率 感触/感叹 讥笑D.轻率 感触/感叹 耻笑 4.下列各句中标点符号使用正确的一项是( ) A.诗人说:“在东方似是晨曦初露,乍回身,已是大地明亮”。
这正可引来描述我突然想起你已是十八岁的心情。
B.美国作家劳伦斯著有一本叫做《我的父亲》的书(你可以在我的书架上找到),在他的描写里,他父亲一样犯有许多惹儿女烦厌的“严父”怪癖。
C.我已经爱过、恨过、哭泣过、体味过、彻悟过……细细想来,便知晴日多于阴雨,收获多于劳作。
山东省2013年高二暑假作业(五)理科数学

2013高二数学(理)暑假作业(五)一、选择题1.已知全集}{1,2,3,4U =,集合{}{}1,2,2,4A B ==,则()UB B =(A ){}1,2 (B ){}2,3,4 (C){}3,4(D){}1,2,3,42. 设全集R U =,集合{}2|lg(1)M x y x==-,{}|02N x x =<<,则()U NM =A .{}|21x x -≤<B .{}|01x x <≤C .{}|11x x -≤≤D .{}|1x x <3.已知3cos ,05ααπ=<<,则tan 4πα⎛⎫+= ⎪⎝⎭A.15B 。
17C 。
1-D 。
7-4.由直线12x =,x=2,曲线1y x =及x 轴所围图形的面积为 A .154 B .174 C .1ln 22D .2ln 2 5。
设,,(,0),a b c ∈-∞则111,,a b c b c a+++( )A.都不大于2- B 。
都不小于2-C 。
至少有一个不大于2- D.至少有一个不小于2-6。
(2013山东卷)给定两个命题p 、q ,若﹁p 是q 的必要而不充分条件,则p 是﹁q 的(A )充分而不必条件 (B )必要而不充分条件(C )充要条件 (D )既不充分也不必要条件 7。
若二项式(x x-θsin )6展开式的常数项为20,则θ的值为(A))(22Z k k ∈+ππ (B))(22Z k k ∈-ππ(C )2π- (D)2π8.若直线x -y =2被圆(x -a)2+y 2=4所截得的弦长为2错误!,则实数a 的值为A.-1或 3 B .1或3 C.-2或6 D .0或49.已知{}na 为等差数列,若34899,aa a S ++==则(A )24 (B )27 (C )15 (D )54 10。
有四个关于三角函数的命题:1p :∃x ∈R , 2sin 2x +2cos2x =122p : ∃x 、y ∈R, sin (x —y)=sinx-siny 3p : ∀x ∈[]0,π,1cos 22x-=sinx4p : sinx=cosy ⇒x+y=2π 11。
山东省高二数学暑假作业(4)

2014高二暑假作业数学四一、填空题1. 已知抛物线24y x =的准线与双曲线()2221,0x y a a-=>交于A,B 两点,点F 为抛物线的焦点,若FAB ∆为直角三角形,则双曲线的离心率是 A.3B.6C.2D.32. 已知动点(,)P x y 在椭圆2212516x y +=上,若A 点坐标为(3,0),||1AM =u u u u r ,且0PM AM ⋅=u u u u r u u u u r ,则||PM u u u u r的最小值是( )A.2B.3C.2D.3 3. 已知0)](log [log log 237=x ,那么21-x 等于( )A.31 B.63 C.33D.424. 要得到函数()sin(2)3f x x π=+的导函数'()f x 的图象,只需将()f x 的图象( )A .向左平移2π个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) B .向左平移2π个单位,再把各点的纵坐标缩短到原来的12倍(横坐标不变)C .向左平移4π个单位,再把各点的纵坐标伸长到原来的12倍(横坐标不变)D .向左平移4π个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变)5. 已知x,y 满足条件020x y x x y k ≥⎧⎪≤⎨⎪++≤⎩(k 为常数),若目标函数3z x y =+的最大值为8,则k= A.16-B.6-C.83-D.66. 如图,设D 是图中边长为4的正方形区域,E 是D 内函数2x y =图象下方的点构成的区域(阴影部分).向D 中随机投一点,则该点落入E 中的概率为 A.51 B. 41 C.31 D.21 7. 已知函数y =f(x)的周期为2,当x∈[-1,1]时f(x)=x 2,那么函数y =f(x)的图象与函数y =|lg x|的图象的交点共有( ) A .10个 B .9个 C .8个 D .1个8. 已知函数1)(23--+-=x ax x x f 在),(+∞-∞上是单调函数,则实数的取值范围是( )A.),3[]3,(+∞--∞YB. ]3,3[-C. ),3()3,(+∞--∞YD. )3,3(-9. 已知全集}{1,2,3,4U =,集合{}{}1,2,2,4A B ==,则()U B B =U ð(A ){}1,2 (B ){}2,3,4(C ){}3,4 (D ){}1,2,3,410. 给定两个命题p 、q ,若﹁p 是q 的必要而不充分条件,则p 是﹁q 的A.充分而不必条件C.充要条件D.既不充分也不必要条件 二、填空题11. 二维空间中圆的一维测度(周长)2l r π=,二维测度(面积)2S r π=,观察发现S l '=;三维空间中球的二维测度(表面积)24S r π=,三维测度(体积)343V r π=,观察发现V S '=.已知四维空间中“超球”的三维测度38V r π=,猜想其四维测度W =________.12.已知0,0x y >>且满足281x y+=,则x y +的最小值为13.i 对应的向量为OZ uuu r ,若向量OZ uuu r绕坐标原点逆时针旋转60o得到向量'OZ u u u u r 所对应的复数为___________________.14.过点A(4,1)的圆C 与直线10x y --=相切于点B(2,1),则圆C 的方程为三、解答题15. 已知函数21()ln 12a f x a x x +=++. (Ⅰ)当21-=a 时,求)(x f 在区间],1[e e 上的最值;(Ⅱ)讨论函数)(x f 的单调性.16. 春节期间,某商场决定从3种服装、2种家电、3种日用品中,选出3种商品进行促销活动。
山东省高二数学暑假作业(四)文

2013高二数学(文)暑假作业(四)一、选择题1.曲线y =-x 3+3x 2在点()1,2处的切线方程为( )A .y =3x -1B .y =-3x +5C .y =3x +5D .y =2x2.(2011·山东)对于函数y =f(x),x∈R,“y=|f(x)|的图象关于y 轴对称”是 “y=f(x)是奇函数”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件3.函数f(x)=11-x+lg(1+x)的定义域是( ) A .(-∞,-1) B .(1,+∞) C .(-1,1)∪(1,+∞) D.(-∞,+∞)4.(2011·江西)若f(x)=x 2-2x -4ln x ,则f′(x)>0的解集为 ( ) A .(0,+∞) B .(-1,0)∪(2,+∞) C .(2,+∞)D .(-1,0)5.(2011·湖北)已知定义在R 上的奇函数f(x)和偶函数g(x)满足f(x)+g(x) =a x-a -x+2(a>0,且a≠1). 若g(2)=a ,则f(2)等于 ( ) A .2B.154C.174D .a 26.(2011·课标全国)在下列区间中,函数f(x)=e x+4x -3的零点所在的区间( ) A .(-14,0)B .(0,14)C .(14,12)D .(12,34)7.已知函数y =f(x)的周期为2,当x∈[-1,1]时f(x)=x 2,那么函数y =f(x)的图象与函数y =|lg x|的图象的交点共有( ) A .10个 B .9个 C .8个D .1个8.设a =log 3π,b =log 23,c =log 32,则 ( ) A .a>b>c B .a>c>b C .b>a>cD .b>c>a 9.若a>0,b>0,且函数f(x)=4x 3-ax 2-2bx +2在x =1处有极值,则ab 的最大值等于( )A .2B .3C .6D .910.已知函数1)(23--+-=x ax x x f 在),(+∞-∞上是单调函数,则实数的取值范围是( )A.),3[]3,(+∞--∞YB. ]3,3[-C. ),3()3,(+∞--∞YD. )3,3(- 11.函数y =2x-x 2的图象大致是( ).12.设函数g(x)=x 2-2(x∈R),f(x)=⎩⎪⎨⎪⎧g(x)+x +4,x<g(x),g(x)-x ,x≥g (x),则f(x)的值域是 ( )A .[-94,0]∪(1,+∞) B.[0,+∞)C .[-94,+∞) D.[-94,0]∪(2,+∞)二、填空题13.如果幂函数y =(m 2-3m +3)x12--m m 的图象不过原点,则m 的取值是________.14.若函数f(x)=a x-x -a(a >0,且a≠1)有两个零点,则实数a 的取值范围是________.15.已知二次函数y =f(x)的顶点坐标为⎝ ⎛⎭⎪⎫-32,49,且方程f(x)=0的两个实根之差的绝对值等于7,则此二次函数的解析式是________.16.奇函数f(x)在定义域(-1,1)上是减函数,且f(1+a)+f(1-a 2)<0,则实数a 的取值范围是____________ 三、解答题17.已知定义在实数集上的函数f(x)满足xf(x)为偶函数,f(x+2)=-f(x), ()x R ∈ 且当13x ≤≤时,3()(2)f x x =-.(1)求10x -≤≤时,函数f(x)的解析式;(2)求f(2008)、f (2008.5)的值。
山东省高二数学暑假作业(五)文

2013高二数学暑假作业(五)一、选择题1.“a=2”是“直线2x +ay -1=0与直线ax +2y -2=0平行”的( )A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件2.直线l 经过点A (2,1)、B (1,2m ) (m )R ∈两点,那么直线l 的倾斜角的范围是( )A . [)π,0B . []()πππ,,0 C . []4,0π D .[]4,0π[)ππ,2 3.若双曲线x 2a 2-y 2b 2=1的焦点到其渐近线的距离等于实轴长,则该双曲线的离心率为( ) A. 5 B .5 C. 2 D .24.已知圆的方程为x 2+y 2-2x +6y +8=0,那么下列直线中经过圆心的直线方程为( )A .2x -y +1=0B .2x +y +1=0C .2x -y -1=0D .2x +y -1=05、直线l 过抛物线y 2=2px(p>0)的焦点F ,且与抛物线交于A 、B 两点,若线段AB 的长是8,AB 的中点到y 轴的距离是2,则此抛物线方程是( )A .y 2=12xB .y 2=8xC .y 2=6xD .y 2=4x6.定义:平面内横坐标为整数的点称为“左整点”.过函数y =9-x 2图象上任意两个“左整点”作直线,则倾斜角大于45°的直线条数为( )A .10B .11C .12D .137.设双曲线y 2m -x 22=1的一个焦点为(0,-2),则双曲线的离心率为( ) A. 2 B .2 C. 6 D .2 28.椭圆x 24+y 2=1的焦点为F 1,F 2,点M 在椭圆上,MF 1→·MF 2→=0,则M 到y 轴的距离为( ) A.233 B.263 C.33 D. 39.已知双曲线的两个焦点为F 1(-10,0),F 2(10,0),M 是此双曲线上的一点,且MF 1→·MF 2→=0,|MF 1→|·|MF 2→|=2,则该双曲线的方程是( )A.x 29-y 2=1 B .x 2-y 29=1 C.x 23-y 27=1 D.x 27-y 23=1 10.设圆C 的圆心在双曲线x 2a 2-y 22=1(a>0)的右焦点上,且与此双曲线的渐近线相切,若圆C 被直线l :x -3y =0截得的弦长等于2,则a =( )A.14B. 6C. 2 D .211.直线y =kx +3与圆(x -3)2+(y -2)2=4相交于M ,N 两点,若|MN|≥23,则k 的取值范围是( )A.⎣⎢⎡⎦⎥⎤-34,0B.⎝⎛⎦⎥⎤-∞,-34∪[0,+∞)C.⎣⎢⎡⎦⎥⎤-33,33 D.⎣⎢⎡⎦⎥⎤-23,0 12.已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的两条渐近线均和圆C :x 2+y 2-6x +5=0相切,且双曲线的右焦点为圆C 的圆心,则该双曲线的方程为( ).A.x 25-y 24=1B.x 24-y 25=1 C.x 23-y 26=1 D.x 26-y 23=1 13.已知曲线C :y =2x 2,点A(0,-2)及点B(3,a),从点A 观察点B ,要使视线不被曲线C 挡住,则实数a 的取值范围是( )A .(4,+∞)B .(-∞,4]C .(10,+∞)D .(-∞,10]二、填空题 14.两圆C1:0101022=--+y x y x 与C 2:0402622=-+++y x y x 的公共弦所在直线方程是______________,公共弦的长等于 .15.到直线49=x 的距离与到定点)0,4(F 的距离之比为43的点的轨迹方程是 .16.已知两点)5,3(-M 、)5,7(-N ,则线段MN 的垂直平分线的方程为______________.17.已知点(x 0,y 0)在直线ax +by =0(a ,b 为常数)上,则(x 0-a)2+(y 0-b)2的最小值为________.三、解答题18.已知:圆C :x 2+y 2-8y +12=0,直线l :ax +y +2a =0.(1)当a 为何值时,直线l 与圆C 相切; (2)当直线l 与圆C 相交于A 、B 两点,且AB =22时,求直线l 的方程.19.如图,直线l :y =x +b 与抛物线C :x 2=4y 相切于点A.(1)求实数b 的值;(2)求以点A 为圆心,且与抛物线C 的准线相切的圆的方程.20.设椭圆C :x 2a 2+y 2b 2=1(a>b>0)的离心率为22,过原点O 斜率为1的直线与椭圆C 相交于M ,N 两点,椭圆右焦点F 到直线l 的距离为 2.(1)求椭圆C 的方程;(2)设P 是椭圆上异于M ,N 外的一点,当直线PM ,PN 的斜率存在且不为零时,记直线PM 的斜率为k 1,直线PN 的斜率为k 2,试探究k 1·k 2是否为定值?若是,求出定值;若不是,说明理由.2013高二数学暑假作业(五)参考答案一、选择题1.B2.B3.A4.B5.B6.B7.A8.B9.A 10.C 11.A 12.A 13.D二、填空题14. 01034=-+y x ;10 15. 17922=-y x16. 02=+-y x 17. a 2+b 2三、解答题 18.解:将圆C 的方程x 2+y 2-8y +12=0配方得标准方程为x 2+(y -4)2=4,则此圆的圆心为(0,4),半径为2.(1)若直线l 与圆C 相切,则有|4+2a|a 2+1=2. 解得a =-34. (2)过圆心C 作CD⊥AB,则根据题意和圆的性质, 得⎩⎪⎨⎪⎧CD =|4+2a|a 2+1,CD 2+DA 2=AC 2=22,DA =12AB = 2. 解得a =-7,或a =-1. 故所求直线方程为7x -y +14=0或x -y +2=0. 19.解:(1)由⎩⎪⎨⎪⎧ y =x +b ,x 2=4y ,得x 2-4x -4b =0,(*)因为直线l 与抛物线C 相切,所以Δ=(-4)2-4×(-4b)=0,解得b =-1.(2)由(1)可知b =-1,故方程(*)为x 2-4x +4=0.解得x =2,代入x 2=4y ,得y =1,故点A(2,1).因为圆A 与抛物线C 的准线相切,所以圆A 的半径r 就等于圆心A 到抛物线的准线y =-1的距离,即r =|1-(-1)|=2,所以圆A 的方程为(x -2)2+(y -1)2=4.20.解:(1)设椭圆的焦距为2c(c>0),焦点F(c,0),直线l :x -y =0,F 到l 的距离为|c|2=2,解得c =2,又∵e=ca =22,∴a=22,∴b=2.∴椭圆C 的方程为x 28+y24=1.(2)由⎩⎪⎨⎪⎧ x 28+y24=1,y =x ,解得x =y =263,或x =y =-263, 不妨设M ⎝ ⎛⎭⎪⎫263,263,N ⎝ ⎛⎭⎪⎫-263,-263,P(x ,y),∴k PM ·k PN =y -263x -263·y +263x +263=y 2-83x 2-83,由x28+y24=1,即x 2=8-2y 2,代入化简得k 1·k 2=k PM ·k PN =-12为定值.。
数学-高二山东省2013年高二暑假作业(一)理科数学

2013高二理科数学暑假作业(一)一.选择题1.复数z 满足(z-3)(2-i)=5(i 为虚数单位),则z 的共轭复数为( D ) A. 2+i B.2-i C. 5+i D.5-i2. 函数xxx f +=1cos )(在)1,0(处的切线方程是( ) A .01=-+y x B .012=-+y x C .012=+-y x D .01=+-y x 3.“x x 22-<0”是“22<-x ”的(A)充分条件 (B)充分而不必要条件 (C)必要而不充分条件 (D)既不充分也不必要条件4.如图,在棱长为1的正方体ABCD -A 1B 1C 1D 1中,M 、N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN 所成的角的余弦值为( )A.32B.1010C.35 D.255.用数学归纳法证明不等式()1111n 1>2322n n N *-++++∈,第二步由k 到k+1时不等式左边需增加( )A.12k B.111212k k -++ C.1111121222k k k --++++ D.1111121222k k k--+++++ 6.利用如图所示程序框图在直角坐标平面上打印一系列点,则打印的点落在坐标轴上的个数是( )A.0B.1C.2D.37.若x x f x f x f ln 4)1(')2(2)(-+-=,则)1(f 等于( )A.2-B.4-C.2D. 08.己知等差数列{a n }的首项为a 1,公差为d ,其前n 项和为S n ,若直线y = a 1x 与圆(x -2)2+ y 2=1的两个交点关于直线x+y+d=0对称,则S n =A . n 2B .-n 2C .2n -n 2D .n 2-2n9.点P 到图形C 上每一个点的距离的最小值称为点P 到图形C 的距离,那么平面内到定圆C 的距离与到定点A 的距离相等的点的轨迹不可能...是( ) A .圆 B .椭圆 C .双曲线的一支 D .直线 10.已知f (x )=41x 2+sin ⎪⎭⎫⎝⎛+x 2π,f '(x )为f (x )的导函数,则f '(x )的图像是11.下列几个命题:①方程0)3(2=+-+a x a x 有一个正实根,一个负实根,则a<0; ②函数2211x x y -+-=是偶函数,但不是奇函数;③函数)(x f 的定义域是[-2,2],则函数)1(+x f 的定义域为[-1,3];④一条曲线23x y -=和直线y=a(a R ∈)的公共点个数是m ,则m 的值不可能是1.其中真命题的个数是(A)1 (B)2 (C)3 (D)412.设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π,且()()f x f x -=,则( )A.()f x 在0,2π⎛⎫ ⎪⎝⎭单调递减 B.()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减 C.()f x 在0,2π⎛⎫⎪⎝⎭单调递增D.()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增二.填空题 13.若423401234(23)x a a x a x a x a x =++++,则2202413()()a a a a a ++-+______=14.已知向量AB 与AC 的夹角为120,且||3,||2,AB AC ==若,AP AB AC λ=+且AP BC ⊥,则实数λ的值为15.如图所示,一个三棱锥的三视图是三个直角三角形,则该三棱锥的外接球的表面积为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013高二数学(文)暑假作业(四) 一、选择题
1.曲线y =-x 3
+3x 2
在点()1,2处的切线方程为( )
A .y =3x -1
B .y =-3x +5
C .y =3x +5
D .y =2x
2.(2011·山东)对于函数y =f(x),x∈R,“y=|f(x)|的图象关于y 轴对称”是 “y=f(x)是奇函数”的( )
A .充分而不必要条件
B .必要而不充分条件
C .充要条件
D .既不充分也不必要条件
3.函数f(x)=
1
1-x
+lg(1+x)的定义域是( ) A .(-∞,-1) B .(1,+∞) C .(-1,1)∪(1,+∞) D.(-∞,+∞)
4.(2011·江西)若f(x)=x 2
-2x -4ln x ,则f′(x)>0的解集为 ( ) A .(0,+∞) B .(-1,0)∪(2,+∞) C .(2,+∞)
D .(-1,0)
5.(2011·湖北)已知定义在R 上的奇函数f(x)和偶函数g(x)满足f(x)+g(x) =a x
-a -x
+2(a>0,且a≠1). 若g(2)=a ,则f(2)等于 ( ) A .2
B.154
C.174
D .a 2
6.(2011·课标全国)在下列区间中,函数f(x)=e x
+4x -3的零点所在的区间( ) A .(-1
4
,0)
B .(0,14)
C .(14,1
2
)
D .(12,3
4
)
7.已知函数y =f(x)的周期为2,当x∈[-1,1]时f(x)=x 2
,那么函数y =f(x)的图象与函数y =|lg x|的图象的交点共有( ) A .10个 B .9个 C .8个
D .1个
8.设a =log 3π,b =log 23,c =log 32,则 ( ) A .a>b>c B .a>c>b C .b>a>c
D .b>c>a 9.若a>0,b>0,且函数f(x)=4x 3
-ax 2
-2bx +2在x =1处有极值,则ab 的最大值等于( )
A .2
B .3
C .6
D .9
10.已知函数1)(23--+-=x ax x x f 在),(+∞-∞上是单调函数,则实数的取值范围是( )
A.),3[]3,(+∞--∞
B. ]3,3[-
C. ),3()3,(+∞--∞
D. )3,3(- 11.函数y =2x
-x 2
的图象大致是( ).
12.设函数g(x)=x 2
-2(x∈R),f(x)=⎩
⎪⎨
⎪⎧
g(x)+x +4,x<g(x),
g(x)-x ,x≥g (x),则f(x)的值
域是 ( )
A .[-9
4,0]∪(1,+∞) B.[0,+∞)
C .[-94,+∞)
D .[-9
4,0]∪(2,+∞)
二、填空题
13.如果幂函数y =(m 2
-3m +3)x
1
2--m m 的图象不过原点,则m 的取值是________.
14.若函数f(x)=a x
-x -a(a >0,且a≠1)有两个零点,则实数a 的取值范围是________.
15.已知二次函数y =f(x)的顶点坐标为⎝ ⎛⎭
⎪⎫-32,49,且方程f(x)=0的两个实根之差的绝
对值等于7,则此二次函数的解析式是________.
16.奇函数f(x)在定义域(-1,1)上是减函数,且f(1+a)+f(1-a 2
)<0,则实数a 的取值范围是____________ 三、解答题
17.已知定义在实数集上的函数f(x)满足xf(x)为偶函数,f(x+2)=-f(x), ()x R ∈ 且当
13x ≤≤时,3
()(2)f x x =-.
(1)求10x -≤≤时,函数f(x)的解析式;
(2)求f(2008)、f (2008.5)的值。
18.已知函数f(x)=x 2
+4ax +2a +6.
(1)若函数f(x)的值域为[0,+∞),求a 的值;
(2)若函数f(x)的函数值均为非负数,求g(a)=2-a|a +3|的值域. 19.(2012年沈阳模拟)已知函数f(x)=ax 2
-|x|+2a -1(a 为实数) (1)若a =1,作出函数f(x)的图象;
(2)设f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式.
20.(1)m 为何值时,f(x)=x 2
+2mx +3m +4,①有且仅有一个零点;②有两个零点且均比-1大;
(2)若函数f(x)=|4x -x 2
|+a 有4个零点,求实数a 的取值范围.
2013高二数学暑假作业(四)
一、选择题
1.A
2.B
3.C
4.C
5.B
6.C
7.A
8.A
9.D 10. B 11. A 12.D 二、填空题
13. 1 14. a>1 15. f (x )=-4x 2
-12x +40. 16. (-1,0) 三、解答题
17.解:(1)由xf(x)为偶函数可知:f(x)是奇函数。
设10,22x x -≤≤≤+≤则1
又f(x+2)=-f(x)可得:3
()f x x =
(2)(2)()()(2)f x f x f x f x +=-⇒=-- 得:f(x+2)=f(x-2)知T=4
得:f(2008)=f(0)=0,f(2008.5)=f(0.5)= -f(-0.5)=1
8
18.解:(1)∵函数的值域为[0,+∞), ∴Δ=16a 2
-4(2a +6)=0 ⇒2a 2
-a -3=0⇒a =-1或a =32.
(2)∵对一切x ∈R 函数值均为非负, ∴Δ=8(2a 2
-a -3)≤0⇒-1≤a ≤32
∴a +3>0,
∴g (a )=2-a |a +3|=-a 2
-3a +2 =-(a +32)2+174(a ∈[-1,3
2]).
∵二次函数g (a )在[-1,3
2]上单调递减,
∴g (32)≤g (a )≤g (-1),即-19
4≤g (a )≤4,
∴g (a )的值域为[-19
4
,4].
19.解:(1)当a =1时,f (x )=x 2
-|x |+1
=⎩
⎪⎨⎪⎧
x 2
+x +1,x <0 x 2
-x +1,x ≥0,作图如右:
(2)当x ∈[1,2]时,f (x )=ax 2
-x +2a -1,
若a =0,则f (x )=-x -1在区间[1,2]上是减函数,
g (a )=f (2)=-3.
若a ≠0,则f (x )=a (x -12a )2+2a -1
4a
-1,f (x )的图象的对称轴是直线
x =1
2a
.
当a <0时,f (x )在区间[1,2]上是减函数,g (a )=f (2)=6a -3. 当0<12a <1,即a >1
2
时,f (x )在区间[1,2]上是增函数,
g (a )=f (1)=3a -2.
当1≤12a ≤2,即14≤a ≤1
2
时,
g (a )=f (12a )=2a -1
4a
-1. 当2<12a ,即0<a <1
4
时,f (x )在区间[1,2]上是减函数,
g (a )=f (2)=6a -3.
∴g (a )=⎩⎪⎨⎪⎧
6a -3,a <1
4
,
2a -1
4a -1, 14≤a ≤1
2
,
3a -2, a >12
.
20.解:(1)①f (x )=x 2
+2mx +3m +4有且仅有一个零点Û方程f (x )=0有两个相等实根ÛΔ=0,即4m 2
-4(3m +4)=0,即m 2
-3m -4=0,∴m =4或m =-1.
②由题意,知⎩⎪⎨⎪
⎧
Δ>0, -m >-1,
f -1>0,
即⎩⎪⎨⎪
⎧
m 2
-3m -4>0, m <1, 1-2m +3m +4>0.
∴-5<m <-1.
∴m 的取值范围为(-5,-1). (2)令f (x )=0,得|4x -x 2
|+a =0, 即|4x -x 2
|=-a .
令g (x )=|4x -x 2
|,h (x )=-a . 作出g (x )、h (x )的图象. 由图象可知,当0<-a <4,
即-4<a <0时,g (x )与h (x )的图象有4个交点,即f (x )有4个零点.故a 的取值范围为(-4,0).。
