【全国校级联考】百校联盟2017届高三4月教学质量检测乙卷理数(原卷版)

合集下载

百校联盟2017届高三4月教学质量检测乙卷理科数学试题含答案

2016—2017学年普通高中高三教学质量监测理科数学第Ⅰ卷（共60分）一、选择题:本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1。

已知集合{}03722<+-=x xx A ,{}1lg <∈=x Z x B ，则阴影部分所表示的集合的元素个数为( ）A ．1B ．2C ．3D ．4 2.已知复数z 的共轭复数为z ，若i i z z 25)221)(223(-=-+（i 为虚数单位),则在复平面内，复数z 所对应的点位于（ )A ．第一象限B ．第二象限C ．第三象限D ．第四象限3。

已知命题x x x p 816),,1(3>++∞∈∀：，则命题p 的否定为（）A ．x x x p 816),,1(3≤++∞∈∀⌝：B ．x x x p 816),,1(3<++∞∈∀⌝：C ．0300816),,1(x x xp ≤++∞∈∃⌝：D ．0300816),,1(x x x p <++∞∈∃⌝：4.62)12)23(---x x x （的展开式中，含3x 项的系数为（）A ．600B ．360 C.600- D ．360-5。

已知双曲线)0,0(1:2222>>=-b a by a x C 的左焦点为F，第二象限的点M 在双曲线C 的渐近线上，且a OM =,若直线 MF 的斜率为ab，则双曲线C 的渐近线方程为（ )A ．x y ±=B ．x y 2±= C.x y 3±= D ．x y 4±= 6。

已知边长为2的菱形ABCD 中,120=∠BAD ，若)10(<<=λλAC AP ，则PDBP ⋅的取值范围为（）A ．]3,0[B ．]3,2[ C.]3,0( D ．]3,2(7.已知2211=+ϕϕos c sin ，若)2,0(πϕ∈，则=-⎰ϕtan 12)2(-dx x x ( ）A ．31 B ．31- C 。

河南省百校联盟2017届高三4月教学质量监测数学(文)试题(附答案)

2016——2017学年普通高中高三教学质量监测文科数学第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，有且只有一项符合题目要求.1.已知集合{}{}2|2730,|lg 1A x x x B x Z x =-+<=∈<，则阴影部分所表示的集合的元素个数为A. 1B. 2C. 3D. 42.已知复数z 的共轭复数为z ，若()31522zz ⎛⎫+-= ⎪⎝⎭（i 为虚数单位），则在复平面内，复数z 所对应的点位于A. 第一象限B. 第二象限C. 第三象限D.第四象限 3.已知命题()2:1,,168p x x x ∀∈+∞+>，则命题p 的否定为A. ()2:1,,168p x x x ⌝∀∈+∞+≤ B. ()2:1,,168p x x x ⌝∀∈+∞+<C. ()2000:1,,168p x x x ⌝∃∈+∞+≤ D.()2000:1,,168p x x x ⌝∃∈+∞+<4.已知等比数列{}n a 满足23210log log 1a a +=，且568916a a a a =，则数列{}n a 的公比为 A. 2 B. 4 C. 2± D.4±5.已知向量()()1,2,1,m n λ=-=，若m n ⊥，则2m n +与m 的夹角为 A.23π B. 34π C. 3π D.4π 6. 已知双曲线()2222:10,0x y C a b a b-=>>的左焦点为F,第二象限的点M 在双曲线C 的渐近线上，且OM a =，若直线MF 的斜率为ba，则双曲线C 的渐近线方程为 A. y x =± B. 2y x =± C.3y x =± D.4y x =±7. 已知23cos 34πα⎛⎫-= ⎪⎝⎭，则sin cos 263ππαα⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭A.332 B. 332- C. 316 D.316- 8. 如图，小正方形的边长为1，粗线画出的是某空间几何体的三视图，则该几何体的体积为 A. 328π+ B. 8323π+C.8163π+ D.168π+ 9. 《九章算术》是我国古代的数学名著，体现了古代劳动人民的数学智慧，其中第六章“均输”中，有一竹节容量问题，谋教师根据这一问题的思想设计了如图所示的程序框图，若输出的m 的值为35，则输入的a 的值为 A. 4 B. 5 C. 7 D. 1110. 某颜料公司生产A,B 两种产品，其中生产每吨A 产品，需要甲染料1吨，乙染料4吨，丙染料2吨，生产每吨B 产品，需要甲染料1吨，乙染料0吨，丙染料5吨，且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨、160吨和200吨，如果A 产品的利润为300元/吨，B 产品的利润为200元/吨，则该颜料公司一天之内可获得的最大利润为 A. 14000元 B. 16000元 C. 16000元 D. 20000元11.已知函数()2x x e af x e=-，若对任意的[]12,1,2x x ∈，且12x x ≠时，()()()12120f x f x x x ⎡⎤-->⎣⎦则实数a 的取值范围是A.22,44e e ⎡⎤-⎢⎥⎣⎦ B.22,22e e ⎡⎤-⎢⎥⎣⎦ C. 22,33e e ⎡⎤-⎢⎥⎣⎦D.22,e e ⎡⎤-⎣⎦12.已知正项数列{}n a 的前n 项和为n S ，且111,61n n n n a S n a m S S +++==-+，现有下列说法： ①25a =；②当n 为奇数时，33n a n m =+-；③224232n a a a n n +++=+.则上述说法正确的个数为A. 0B. 1C. 2D. 3第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题5分，共20分.13.已知函数()()sin 0,0,2f x M x M πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示，其中()2,3A （点A 为图象的一个最高点）5,02B ⎛⎫- ⎪⎝⎭，则函数()f x = . 14.折纸已经成为开发少年儿童智力的一种重要工具和手段，已知在折叠“爱心”活动中，会产生如图所示的几何图形，其中四边形ABCD 为正方形，G 为线段BC 的中点，四边形AEFG 与四边形DGHI 也是正方形，连接EB,CI,则向多边形AEFGHID 中投掷一点，则该点落在阴影部分的概率为 .15.若圆C 过点()()0,1,0,5-，且圆心到直线20x y --=的距离为C 的标准方程为 .16.已知关于x 的方程()221ln 2x x x k k +=++在1,2x ⎡⎫∈+∞⎪⎢⎣⎭上有两个不相等的实数根，则实数k 的取值范围为 .三、解答题：本大题共6小题，共70分.解答应写出必要的文字说明或推理、验算过程. 17.（本题满分12分）在ABC ∆中，()01,3,.3BD mBC m AC AD C π=<<===（1）求ABC ∆的面积；（2）若cos B =，求AB 的长度以及BAC ∠的正弦值.18.（本题满分12分）如图（1）所示，已知四边形SBCD 是由直角SAB ∆和直角梯形ABCD 拼接而成的，其中90SAB SDC ∠=∠=,且点A 为线段SD 的中点，21,AD DC AB SD ===现将SAB ∆沿AB 进行翻折，使得二面角S AB C --的大小为90，得到的图形如图（2）所示，连接SC,点E,F 分别在线段SB,SC 上.（1）证明：BD AF ⊥；（2）若三棱锥B-AEC 的体积为四棱锥S-ABCD 体积的25，求点E 到平面ABCD 的距离.19.（本题满分12分）国内某知名连锁店分店开张营业期间，在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动，随着抽奖活动的有效展开，参与抽奖活动的人数越来越多，该分店经理对开业前7天参加抽奖活动的人数进行统计，y 表示开业第x 天参加抽奖活动的人数，得到统计表格如下：经过进一步的统计分析，发现Y 与X 具有线性相关关系.（1）若从这7天中随机抽取两天，求至少有1天参加抽奖人数超过10天的概率；（2）根据上表给出的数据，用最小二乘法，求出y 与x 的线性回归方程ˆˆˆybx a =+，并估计若该活动持续10天，共有多少名顾客参加抽奖.20.（本题满分12分）已知椭圆()2222:10x y C a b a b +=>>的左、右焦点分别为12,F F，点1,⎛ ⎝是椭圆C 上的点，离心率为e =（1）求椭圆C 的方程；（2）点()()000,0A x y y ≠在椭圆上C 上，若点N 与点A 关于原点对称，连接2AF ,并延长与椭圆C 的另一个交点为M,连接MN,求AMN ∆面积的最大值.21.（本题满分12分）已知函数()ln 1.xf x x x e =-+（1）求函数()f x 在点()()1,1f 处的切线方程；（2）证明：()sin f x x <在()0,+∞上恒成立.请考生在第22、23两题中任选一题作答，如果两题都做，则按照所做的第一题给分；作答时，请用2B 铅笔将答题卡上相应的题号涂黑。

重庆市2017届高三4月调研测试(二诊)数学理试题答案

1 2017一、选择题1～6 DCCCCD 7～12 DABCAD第（11）题解析：xxxf-=')(1()()(xf∴在,(-∞又当-∞→x时故)(xf令txf=)(当e21-=t时恰有32e6-=t，此时1)(txf=有1个根，2)(txf=有2个根；当e21-<t时必有32e60-<<t，此时1)(txf=无根，2)(txf=有3个根；当0e21<<-t时必有32e6->t，此时1)(txf=有2个根，2)(txf=有1个根；综上，对任意Rm∈，方程均有3个根.第（12）题解析：由题知，只需考虑圆柱的底面与正方体的表面相切的情况，由图形的对称性可知，圆柱的上底面必与过A点的三个面相切，且切点分别在线段11,,ADACAB上，设线段1AB上的切点为E，1AC面21OBDA=，圆柱上底面的圆心为1O，半径即为EO1记为r，则2262331312=⨯⨯==DFFO，13112==ACAO，由FOEO21//知EOAOAOEO11112122=⇒=，则圆柱的高为rAO223231-=-，242(3)()()428r rS r r rπ+-=-=-⋅==侧≤.二、填空题（13）2（14）53（15）]1,8[--（16）1306第（15）题解析：函数)(xf当]1,8[--∈m时，,1[)(-∈xf第（16）题解析：1122+=++naann，则2999832+=++++ aaaa2625502550100=+=-=aaa三、解答题（17）（本小题满分12分）解：（Ⅰ）sin1)2cos(1)sin(-=--=-CCBAπ21cossin=∴BA；……6分xyz（Ⅱ）332sin sin ==b a B A ，由（Ⅰ）知212sin 33cos sin 332cos sin ===B B B B A ，232sin =∴B ， 32π=∴B 或32π，6π=∴B 或3π. ……12分（18）（本小题满分12分）解：（Ⅰ）由题知，在矩形ABCD 中，︒=∠=∠45BMC AMD ，︒=∠∴90AMB ，又BM A D ⊥'，⊥∴BM 面AM D '，∴面⊥ABCM 面AM D '； ……6分（Ⅱ）由（Ⅰ）知，在平面AM D '内过M 作直线MA NM ⊥，则⊥NM 平面ABCM ，故以M 为原点，MN MB MA ,,分别为z y x ,,轴的正方向建立空间直角坐标系，则)0,0,0(M ，)0,0,2(A ，)0,2,0(B ，)1,0,1(D '，于是)21,1,21(E ，)0,0,2(=，)21,1,21(=，设平面EAM 的法向量为),,(z y x =，则⎪⎩⎪⎨⎧=++=0212102z y x x 令1=y ，得平面EAM 的一个法向量)2,1,0(-=，显然平面AM D '的一个法向量为)0,1,0(=n ，故51,cos >=<，即二面角D AM E '--的余弦值为55. ……12分（19）（本小题满分12分）解：（Ⅰ）841.3114018222020)861214(4022<=⨯⨯⨯⨯-⨯⨯=K ，故没有95%以上的把握认为二者有关；……6分（Ⅱ）由题知，小王的微信好友中任选一人，其每日走路步数不超过5000步的概率为81，超过10000步的概率为41，且当0==Y X 或1==Y X 时，0=ξ，12551129888464P C =⨯+⋅=；当0,1==Y X 或1,0==Y X 时，1=ξ，6430854185811212=⋅+⋅=C C P ；当0,2==Y X 或2,0==Y X 时，2=ξ， 645)81()41(22=+=P ，即ξ的分布列为：85=ξE . ……12分（20）（本小题满分12分）解：（Ⅰ）设),(00y x P ，则21242220202020000021-=-=-=-⋅+=y y x y x y x y k k ；……4分（Ⅱ）由题知，直线x k y OM 1:=，直线x k y ON 2:=，设),(),,(2211y x N y x M ，则|)(|21||21||2121211122211221x x k k x k x x k x y x y x S -=⋅-⋅=-=，由212112221442k x xk y y x +=⇒⎩⎨⎧==+，同理可得2222214k x +=，故有1)(24)2(16214214)(42221222121222122212212+++-+=+⋅+⋅-=k k k k k k k k k k k k S ，又2121-=k k ，故8)(22)1(164222122212=++++=k k k k S ，2=∴S . ……12分（21）（本小题满分12分）解：（Ⅰ）22ln (2)ln ()x a xf x x -+-'=，由题22122(e)3e e a f a -+-'==-⇒=；……5分（Ⅱ）2ln 3ln 3()x x f x x++=，2ln (ln 1)()x x f x x -+'=，1()01e f x x '>⇒<<，故()f x 在1(0,)e 和(1,)+∞上递减，在1(,1)e上递增， ①当(0,1)x ∈时，1()()e e ≥f x f =，而33(1)()e e x x x x -'=，故3e xx 在(0,1)上递增， 33e e e x x ∴<<，3()e x x f x ∴>即()3ex f x x >； ②当[1,)x ∈+∞时，2ln 3ln 30033≥x x ++++=，令23()ex x g x =，则23(2)()e xx x g x -'=故()g x 在[1,2)上递增，(2,)+∞上递减，212()(2)3e ≤g x g ∴=<，223ln 3ln 3ex x x x ∴++>即()3e x f x x >；综上，对任意0x >，均有()3ex f x x >.……12分（22）（本小题满分10分）解：（Ⅰ）14444cos sin 422222222=+⇒=+⇒=+y x x y θρθρ；……5分（Ⅱ）因为点P 在椭圆C 的内部，故l 与C 恒有两个交点，即R ∈α，将直线l 的参数方程与椭圆C 的直角坐标方程联立，得4)sin 21(4)cos 1(22=+++-ααt t ，整理得02)cos 2sin 4()sin 31(22=--++t t ααα，则]2,21[sin 312||||2∈+=⋅αPB PA . ……10分（23）（本小题满分10分）解：（Ⅰ）|||3||()(3)||2|x a x a x a x a a -+----=≥，当且仅当x 取介于a 和a 3之间的数时，等号成立，故)(x f 的最小值为||2a ，1±=∴a ；……5分（Ⅱ）由（Ⅰ）知)(x f 的最小值为||2a ，故]1,1[-∈∃a ，使||2||2a m m <-成立，即 2||2<-m m ，0)2|)(|1|(|<-+∴m m ，22<<-∴m . ……10分。

山东2017届高三4月月考模拟数学试题(理)(word版含答案)

山东省2017届高三4月月考（模拟）数学试卷（理科）第Ⅰ卷一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若集合}8,6,4,2{=A ，}0189|{2≤+-=x x x B ，则=B A （） A ．}4,2{ B ．}6,4{ C ．}8,6{ D ．}8,2{2.若复数iia 21++（R a ∈）为纯虚数，其中i 为虚数单位，则=a （） A ．2 B ．3 C ．2- D ．3-3.袋中装有大小相同的四个球，四个球上分别标有数字“2”，“3”，“4”，“6”.现从中随机选取三个球，则所选的三个球上的数字能构成等差数列的概率是（）A ．41 B ．21 C ．31 D ．324.等比数列}{n a 的前n 项和为b a S n n +⋅=-13，则=ba（）A ．3-B ．1- C. 1 D ．35.直线l ：)(04R k y kx ∈=++是圆C ：064422=+-++y x y x 的一条对称轴，过点),0(k A 作斜率为1的直线m ，则直线m 被圆C 所截得的弦长为（）A ．22B ．2 C. 6 D ．62 6.祖冲之之子祖恒是我国南北朝时代伟大的科学家，他在实践的基础上提出了体积计算的原理：“幂势既同，则积不容异”.意思是，如果两个等高的几何体在同高处截得面积恒等，那么这两个几何体的体积相等.此即祖恒原理.利用这个原理求球的体积时，需要构造一个满足条件的几何体，已知该几何体三视图如图所示，用一个该几何体的下底面平行相距为h （20<<h ）的平面截几何体，则截面面积为（）A ．π4B ．2h π C. 2)2(h -π D ．2)4(h -π7.函数x x f xx cos 1212)(⋅-+=的图象大致是（）8.已知0>>b a ，0<c ，下列不等关系正确的是（）A ．bc ac >B ．cc b a > C. )(log )(log c b c a b a ->-D ．cb bc a a ->- 9.执行如图所示的程序框图，若输入2017=p ，则输出i 的值为（）A ．335B ．336 C. 337 D ．33810.已知F 是双曲线E ：12222=-by a x (0,0>>b a )的右焦点，过点F 作E 的一条渐近线的垂线，垂足为P ，垂线PF 与E 相交于点Q ，记点Q 到E 的两条渐近线的距离之积为2d ，若d FP 2||=，则该双曲线的离心率（） A ．2 B ．2 C. 3 D ．4第Ⅱ卷二、填空题（每题5分，满分20分，将答案填在答题纸上）11.已知向量)2,1(=p ，)3,(x q =，若q p ⊥，则=+||q p ．12.5)1(xx -的二项展开式中，含x 的一次项的系数为．（用数字作答）13.若实数y x ,满足不等式组⎪⎩⎪⎨⎧≥≤--≤-+1083204x y x y x ，目标函数y kx z -=的最大值为12，最小值为0，则实数=k ．14.已知数列}{n a 满足)2()2(22n n a n na n n +=+-+λ，其中2,121==a a ，若1+<n n a a 对*∈∀N n 恒成立，则实数λ的取值范围为．15.设函数2)2()(x x g x f +=，曲线)(x g y =在点))1(,1(g 处的切线方程为019=-+y x ，则曲线)(x f y =在点))2(,2(f 处的切线方程为．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）16.已知函数)2||,0,0)(sin()(πϕωϕω<>>+=A x A x f 满足下列条件：①周期π=T ；②图象向左平移6π个单位长度后关于y 轴对称；③1)0(=f . （1）求函数)(x f 的解析式；（2）设)4,0(,πβα∈，1310)3(-=-παf ，56)6(=+πβf ，求)22cos(βα-的值. 17. ABC ∆的内角C B A ,,的对边分别为c b a ,,，已知C a A c a cos sin 32-=. （1）求C ；（2）若3=c ，求ABC ∆的面积的最大值.18.如图，四边形ABCD 为菱形，四边形ACEF 为平行四边形，设BD 与AC 相交于点G ，2==BD AB ，3=AE ，EAB EAD ∠=∠.（1）证明：平面⊥ACEF 平面ABCD ；（2）若AE 与平面ABCD 所成角为60，求二面角D EF B --的余弦值.19.某市为了鼓励市民节约用电，实行“阶梯式”电价，将该市每户居民的月用电量划分为三档，月用电量不超过200度的部分按0.5元/度收费，超过200度但不超过400度的部分按0.8元/度收费，超过400度的部分按1.0元/度收费.（1）求某户居民的用电费用y （单位：元）关于月用电量x （单位：度）的函数解析式；（2）为了了解居民的用电情况，通过抽样，获得了今年1月份100户居民每户的用电量，统计分析后得到如图所示的频率分布直方图，若这100户居民中，今年1月份用电量不超过260元的占80%，求b a ,的值；（3）在满足（2）的条件下，若以这100户居民用电量的频率代替该月全市居民用户用电量的概率，且同组中的数据用该组区间的中点值代替，记Y 为该居民用户1月份是用电费用，求Y 的分布列和数学期望.20.已知椭圆C ：)0(12222>>=+b a by a x 的左右顶点21,A A ，上下顶点分别为21,B B ，左右焦点分别为21,F F ，其中长轴长为4，且圆O ：71222=+y x 为菱形2211B A B A 的内切圆. （1）求椭圆C 的方程；（2）点)0,(n N 为x 轴正半轴上一点，过点N 作椭圆C 的切线l ，记右焦点2F 在l 上的射影为H ，若HN F 1∆的面积不小于2163n ，求n 的取值范围. 21.已知函数x x x f ln )(=，e 为自然对数的底数. （1）求曲线)(x f y =在2-=e x 处的切线方程；（2）关于x 的不等式)1()(-≥x x f λ在),0(+∞上恒成立，求实数λ的值；（3）关于x 的方程a x f =)(有两个实根21,x x ，求证：22112||-++<-e a x x .试卷答案一、选择题1-5: BCBAC 6-10: DCDCB二、填空题11.25 12. 5- 13. 3 14. ),0[+∞ 15.062=++y x三、解答题16.解：（1）∵)(x f 的周期为πωπ==2T ，∴2=ω，又函数)(x f 的图象向左平移6π个单位长度，变为])6(2sin[)(ϕπ++=x A x g ，由题意，)(x g 的图象关于y 轴对称，∴ππϕπk +=+⨯262，Z k ∈，又2||πϕ<，∴6πϕ=，∴函数)62sin()(π+=x A x f ，又1)0(=f ，∴16sin=πA ，解得2=A ，∴函数)62sin(2)(π+=x x f .（2）由1310)3(-=-παf ，56)6(=+πβf ，得1310)6322sin(2-=+-ππα，56)632sin(2=++ππβ，∴532cos ,1352cos ==βα，又)2,0(,πβα∈，∴13122sin =α，542sin =β，∴6563541312531352sin 2sin 22cos )22cos(=⨯+⨯=+=-βαβαβαos . 17.解：（1）由已知及正弦定理可得C a A C A cos sin sin 3sin 2-=，在ABC∆中，0sin >A ，∴C C cos sin 32-=，∴1cos 21sin 23=-C C ，从而1)6sin(=-πC ，∵π<<C 0，∴6566πππ<-<-C ，∴26ππ=-C ，∴32π=C . （2）解法1：由（1）知32π=C ，∴23sin =C ，∵C ab S sin 21=，∴ab S 43=，∵abc b a C 2cos 222-+=，∴ab b a -=+322，∵ab b a 222≥+，∴1≤ab （当且仅当1==b a时等号成立），∴4343≤=ab S ；解法2：由正弦定理可知2sin sin sin ===C c B b A a ，∵C ab S sin 21=，∴B A S sin sin 3=， ∴)3sin(sin 3A A S -=π，∴43)62sin(23-+=πA S ，∵30π<<A ，∴65626πππ<+<A ，当262ππ=+A ，即6π=A 时，S 取最大值43.18.解：（1）证明：连接EG ，∵四边形ABCD 为菱形，AB AD =，AC BD ⊥，GB DG =，在EAD ∆和EAB ∆中，AB AD =，AE AE =，EAB EAD ∠=∠，∴EAD ∆EAB ∆≅，∴EB ED =，∴EG BD ⊥，∵G EG AC = ，∴⊥BD 平面ACFE ，∵⊂BD 平面ABCD ，∴平面⊥ACFE 平面ABCD .（2）解法1：过G 作EF 垂线，垂足为M ，连接MB ，MG ，MD ，易得EAC ∠为AE 与面ABCD 所成的角，∴ 60=∠EAC ，∵GM EF ⊥，BD EF ⊥，∴⊥EF 平面BDM ，∴DMB ∠为二面角D EF B --的平面角，可求得23=MG ，213==BM DM ，在DMB ∆中余弦定理可得135cos =∠BMD ，∴二面角D EF B --的余弦值为135.解法2：如图，在平面ABCD 内，过G 作AC 的垂线，交EF 于点M ，由（1）可知，平面⊥ACFE 平面ABCD ，∴⊥MG 平面ABCD ，∴直线GB GA GM ,,两两垂直，分别以GM GB GA ,,为z y x ,,轴建立空间直角坐标系xyz G -，易得EAC ∠为AE 与平面ABCD 所成的角，∴ 60=∠EAC ，则)0,1,0(-D ，)0,1,0(B ，)23,0,23(E ，)23,0,233(-F ，)0,0,32(=FE ，)23,1,23(-=BE ，)23,1,23(=DE ，设平面BEF 的一个法向量为),,(z y x n =，则0=⋅且0=⋅，∴0=x ，且02323=+-z y x ，取2=z ，可得平面BEF 的一个法向量为)2,3,0(=n ，同理可求得平面DEF 的一个法向量为)2,3,0(-=，∴135,>=<m n cis ， ∴二面角D EF B --的余弦值为135. 19.解：（1）当2000≤≤x 时，x y 5.0=；当当400200≤<x 时，608.0)200(8.02005.0-=-⨯+⨯=x x y ；当当400>x 时，140)400(0.12008.02005.0-=-⨯+⨯+⨯=x x y ，所以y 与x 之间的函数解析式为⎪⎩⎪⎨⎧>-≤<-≤≤=140,140400200,608.02000,5.0x x x x x x y .（2）由（1）可知，当260=y 时，400=x ，则80.0)400(=≤x P ，结合频率分布直方图可知⎩⎨⎧=+=+⨯+2.005.01008.03.010021.0a b ，∴0015.0=a ，0020.0=b （3）由题意可知X 可取50，150，250，350，450，550，当50=x 时，25505.0=⨯=y ，∴1.0)25(==y P ，当150=x 时，751505.0=⨯=y ，∴2.0)75(==y P ，当250=x 时，140508.02005.0=⨯+⨯=y ，∴3.0)140(==y P ，当350=x 时，2201508.02005.0=⨯+⨯=y ，∴2.0)220(==y P ，当450=x 时，310500.12008.02005.0=⨯+⨯+⨯=y ，∴15.0)310(==y P ，当550=x 时，4101500.12008.02005.0=⨯+⨯+⨯=y ，∴05.0)410(==y P ，故Y 的概率分布列为所以随机变量X 的数学期望5.17005.041015.03102.02203.01402.0751.025=⨯+⨯+⨯+⨯+⨯+⨯=EY20.解：（1）由题意知42=a ，所以2=a ，所以)0,2(1-A ,)0,2(2A ，),0(1b B -，),0(2b B ，则直线22B A 的方程为12=+b yx ，即022=-+b y bx ，所以7124|2|2=+-b b ，解得32=b ，故椭圆C 的方程为13422=+y x . （2）由题意，可设直线l 的方程为0,≠+=m n my x ，联立⎩⎨⎧=++=124322y x n my x 消去x 得0)4(36)43(222=-+++n mny y m （*），由直线l 与椭圆C 相切，得0)4)(43(34)6(222=-+⨯-=∆n m mn ，化简得04322=+-n m ，设点),(t n mt H +，由（1）知)0,1(),0,1(21F F -，则111)(0-=⋅-+-mn mt t ，解得21)1(m n m t +--=，所以HN F 1∆的面积2221|)1(|21|1)1(|)1(211m n m mn m n S HNF +-=+--+=∆，代入04322=+-n m 消去n 化简得||231m S HN F =∆，所以)43(163163||2322+=≥m n m ，解得2||32≤≤m ，即4942≤≤m ，从而434942≤-≤n ，又0>n ，所以4334≤≤n ，故n 的取值范围为]4,334[.21.解：（1）对函数)(x f 求导得1ln 1ln )('+=⋅+=x xx x x f ，∴11ln )('22-=+=--e e f ，又22222ln )(-----==e e e e f ，∴曲线)(x f y =在2-=e x 处的切线方程为)()2(22----=--e x e y ，即2---=e x y .（2）记)1(ln )1()()(--=--=x x x x x f x g λλ，其中0>x ，由题意知0)(≥x g 在),0(+∞上恒成立，下求函数)(x g 的最小值，对)(x g 求导得λ-+=1ln )('x x g ，令0)('=x g ，得1-=λe x ，当x 变化时，)('x g ，)(x g 变化情况列表如下：∴1111min )1()1()()()(-----=---===λλλλλλλe e e e g x g x g 极小，∴01≥--λλe，记1)(--=λλλe G ，则11)('--=λλe G ，令0)('=λG ，得1=λ. 当λ变化时，)('λG ，)(λG 变化情况列表如下：∴0)1()()(max ===g G G 极大λλ 故01≤--λλe当且仅当1=λ时取等号，又01≥--λλe ，从而得到1=λ；（3）先证2)(---≥e x x f ，记22ln )()()(--++=---=e x x x e x x f x h ，则2ln )('+=x x h ，令0)('=x h ，当x 变化时，)('x h ，)(x h 变化情况列表如下：∴0ln )()()(22222min =++===-----e e e e e h x h x h 极小，0)(≥x h 恒成立，即2)(---≥e x x f ，记直线2---=e x y ，1-=x y 分别与a y =交于),'(),,'(21a x a x ，不妨设21x x <，则21121)('----≥=--=e x x f e x a ，从而11'x x ≤，当且仅当22--=e a 时取等号，由（2）知，1)(-≥x x f ，则1)(1'222-≥=-=x x f x a ，从而22'x x ≤，当且仅当0=a 时取等号，故2212122112)()1(''||--++=---+=-≤-=-e a e a a x x x x x x ，因等号成立的条件不能同时满足，故22112||-++<-e a x x .。

2017届河南省百校联盟高三4月教学质量检测英语试卷(含答案)

英语试题第一部分听力（共两节，满分30分）第一节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. What does the woman ask the man to do?A. Go to a film with her.B. Go to a company.C. Buy a map.2. Where does the conversation most probably take place?A. In a shop.B. In an office.C. In a flat.3. What does the woman want to buy?A. A car.B. Some equipment.C. A bar.4. What will the woman most probably write with?A. A pencil.B. A ball-pen.C. A pen.5. What do you know about the reporter?A. He is old.B. He is generous.C. He is successful.第二节（共15小题；每小题1.5分，满分22.5分）听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第6段材料，回答第6、7题。

6. How does Martin feel?A. Tired.B. Excited.C. Happy.7. Why is Martin so busy?A. Because his boss doesn’t help him.B. Because he has to do everything by himself.C. Because he likes to run an office.听第7段材料，回答第8、9题。

江西省2017届高三4月新课程教学质量监测数学(理)试题含答案

江西省2017年高中毕业班新课程教学质量监测卷理科数学第Ⅰ卷（选择题共60分）一、选择题：本大题共12个小题,每小题5分，共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。

1.已知221iz i +=-+（i 是虚数单位），则复数z 的实部是( )A ．0B ．—1C ．1D ．2 2.已知集合13{|log(4)1}A x x =->-，1{|48}x B x -=>，若全集为实数集R ,则()R A C B =（）A ．5(,]2-∞ B ．(2,4) C ．5(,4)2D ．5(2,]23。

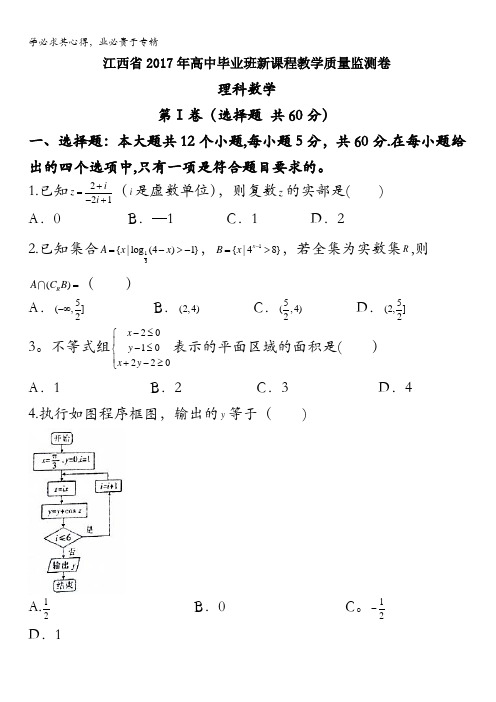
不等式组2010220x y x y -≤⎧⎪-≤⎨⎪+-≥⎩表示的平面区域的面积是(）A ．1B ．2C ．3D ．4 4.执行如图程序框图，输出的y 等于（ )A.12B ．0C 。

12-D ．15。

在公差不为零的等差数列{}na 中，2311722aa a +=，数列{}nb 是各项为正的等比数列，且77ba =则68b b =的最小值为( ）A ．2B ．1C 。

4D ．8 6.在矩形ABCD 中，2AB =，3AD =，点F 为CD 的中点，点E 在BC 边上，若4AF DE ⋅=-，则AE BF ⋅的值为（)A.0 B ．1 C.2 D ．37。

已知点(,)P a b 及圆O ：222xy r +=，则“点P 在圆O 内”是“直线l ：2ax by r +=与圆O 相离"的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 8。

已知函数2()tan 1xx a f x b x x a =+++(0,1)a a >≠，若(1)3f =,则(1)f -等于（）A ．—3B ．—1C 。

0D ．39。

一个三棱锥的三视图如图（图中小正方形的边长为1)，若这个三角棱锥的顶点都在同一个球的球面上，则这个球的表面积是（）A ．16πB ．32πC 。

河南省2017届普通高中高三4月教学质量监测理科数学试卷(含答案)

河南省2017届普通高中高三4月教学质量监测理科（数学）试卷第Ⅰ卷（共60分）一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合2{|2730}A x x x =-+＜，{|lg 1}B x x =∈Z ＜，则阴影部分所表示的集合的元素个数为（） A ．1B ．2C ．3D ．42．已知复z 的共轭复数为z ，若3()(122z z+-（i 为虚数单位），则在复平面内，复数z 所对应的点位于（） A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．已知命题:(1,)p x ∀∈+∞，2168x x +＞则命题p 的否定为（） A ．:(1,)p x ⌝∀∈+∞，2168x x +≤ B ．:(1,)p x ⌝∀∈+∞，2168x x +＜ C ．0(1,):p x ⌝∃∈+∞，200168x x +≤D ．0(1,):p x ⌝∃∈+∞，200168x x +＜4．26(32)(21)x x x ---的展开式中，含3x 项的系数为（） A ．600B ．360C ．600-D ．360-5．已知双曲线2222:1(0,0)x y C a b a b-=＞＞的左焦点为F ，第二象限的点M 在双曲线C 的渐近线上，且||OM a =，若直线MF 的斜率为ba，则双曲线C 的近线方程为（）A ．y x =±B ．2y x =±C ．3y x =±D ．4y x =±6．已知边长为2的菱形ABCD 中，120BAD ∠=︒，若(01)A P A C =λλ＜＜，则BP P D 的取值范围是（）A ．[0,3]B ．[2,3]C ．(0,3]D ．(2,3]7．已知11sin cos +=ϕϕ，若π(0,)2ϕ∈，则2tan (2)1x x dx ϕ--⎰=（） A ．13B ．13-C ．23D ．23-8．《九章算术》是我国古代的数学名著，体现了古代劳动人民的数学智慧，其中第六章“均输”中，有一竹节容量问题，某教师根据这一问题的思想设计了如图所示的程序框图，若输出m 的值为35，则输入a 的值为（）A ．4B ．5C ．7D ．119．某颜料公司生产A ，B 两种产品，其中生产每吨A 产品，需要甲染料1吨，乙染料4吨，丙染料2吨，生产每吨B 产品，需要甲染料1吨，乙染料0吨，丙染料5吨，且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨、160吨和200吨，如果A 产品的利润为300元/吨，B 产品的利润为200元/吨，则该颜料公司一天之内可获得的最大利润为（） A ．14 000元B ．16 000元C ．16 000元D ．20 000元10．已知函数22,20()(1),02x x x f x f x x ⎧+-=⎨-⎩≤≤＜≤，则方程5[()]1x f x -=在[2,2]-上的根的个数为（）A ．3B ．4C ．5D ．611．如图，小正方形的边长为1，粗线画出的是某空间几何体的三视图，则该几何体的体积为（）A ．B ．16C ．D ．3212．已知ABC △的外接圆的半径为R ，角A ，B ，C 的对边分别是a ，b ，c ，若32sin cos sin 2a B C c C R+=，则ABC △面积的最大值为（）A ．25B ．45C D ．125第Ⅱ卷（共90分）二、填空题：本大题共4小题，每小题5分，满分20分．13．已知函数()sin()f x M x =ω+ϕ（0M ＞，0ω＞，π||2ϕ＜）的部分图像如图所示，其中(2,3)A （点A 为图像的一个最高点）5(,0)2B -，则函数()f x =__________．14．折纸已经成为开发少年儿童智力的一种重要工具和手段，已知在折叠“爱心”活动中，会产生如图所示的几何图形，其中四边形ABCD 为正方形，G 为线段BC 的中点，四边形AEFG 与四边形DGHI 也是正方形，连接EB ，CI ，则向多边形AEFGHID 中投掷一点，则该点落在阴影部分的概率为__________．15．已知抛物线2:8C y x =的焦点为F ，准线l 与x 轴交于点M ，过点M 的直线l 与抛物线C 的交点为P ，Q 延长PF 交抛物线C 于点A ，延长QF 交抛物线C 于点B ，若||||22||||PF QF AF BF +=，则直线l 的方程为__________．16．若[1,)x ∈+∞时，关于x 的不等式ln (1)1x xx x λ-+≤恒成立，则实数λ的取值范围是__________．三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．） 17．已知数列{}n a 的前n 项和为n S ，且28a =，112n n a S n -=--．（1）求数列{}n a 的通项公式；（2）求数列123{}nn n a a +⨯的前n 项和n T ． 18．国内某知名连锁店分店开张营业期间，在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动，随着抽奖活动的有效展开，参与抽奖活动的人数越来越多，该分店经理对开业前7天参加抽奖活动的人数进行统计，y 表示开业第x 天参加抽奖活动的人数，得到统计表格如下：经过进一步的统计分析，发现Y 与X 具有线性相关关系．（1）根据上表给出的数据，用最小二乘法，求出y 与x 的线性回归方程ˆˆˆybx a =+；（2）若该分店此次抽奖活动自开业始，持续10天，参加抽奖的每位顾客抽到一等奖（价值200元奖品）的概率为17，抽到二等奖（价值100元奖品）的概率为27，抽到三等奖（价值10元奖品）的概率为47，试估计该分店在此次抽奖活动结束时送出多少元奖品？参考公式：1221ˆni ii nii x ynx y bxnx---=-∑∑，ˆˆay bx =- 19．如图所示的空间几何体中，底面四边形ABCD 为正方形，AF AB ⊥，AF BE ∥，平面ABEF ⊥平面ABCD，DF =CE =，2BC =．（1）求二面角F DE C --的大小；（2）若在平面DEF 上存在点P ，使得BP ⊥平面DEF ，试通过计算说明点P 的位置．20．已知椭圆2222:1(0)x y C a b a b +=＞＞的左、右焦点分别为1F ，2F，点(1,是椭圆C 上的点，离心率为e 2=．（1）求椭圆C 的方程；（2）点000(,)(0)A x y y ≠在椭圆上C 上，若点N 与点A 关于原点对称，连接2AF ，并延长与椭圆C 的另一个交点为M ，连接MN ，求AMN △面积的最大值． 21．已知函数()F x 与()ln f x x =的图象关于直线y x =对称．（1）不等式()1xf x ax -≥对任意(0,)x ∈+∞恒成立，求实数a 的最大值；（2）设()()1f x F x =在(1,)+∞内的实根为0x ，00(),1(),()xf x x x m x x x x F x ⎧⎪=⎨⎪⎩＜≤＞，若在区间(1,)+∞上存在1212()()()m x m x x x =＜，证明：1202x x x +＞．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分；作答时，请用2B 铅笔将答题卡上相应的题号涂黑．22．选修4-4：参数方程与极坐标系已知直线l的参数方程为12t x y +⎧⎪=⎨=⎪⎩（t 为参数），以原点为极点，X轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程是2sin 3cos 0p θ-θ=．（1）求曲线C 的直角坐标方程及直线l 的极坐标方程；（2）求直线l 与曲线C 交点的极坐标（0p ≥，02πθ≤＜）． 23．选修4-5：不等式选讲已知函数()|3||1|f x x x =++-的最小值为m ，且()f a m =．（1）求m 的值以及实数a 的取值集合；（2）若实数p ，q ，r 满足2222p q r m ++=，证明()2q p r +≤．河南省2017届普通高中高三4月教学质量监测理科数学试卷答案一、选择题1~5．BACCA 6~10．DDAAD 11~12．BC 二、填空题13．ππ3sin()36x -14．1315．2)y x =+ 16．1[,]2+∞三、解答题 17．（1）因为112n n a S n +=--，故当1n =时，211122aa =--=；当2n ≥时，1222n n S a n +=--，122(1)2n n S a n -=---两式对减可得132n n a a +=+；经检验，当1n =时也满足132n n a a +=+；故1(1)3(1)n n a a ++=+，故数列{1}n a +是以3为首项，3为公比的等比数列，故13n n a +=，即31n n a =-．（2）由（Ⅰ）可知，111232311(31)(31)3131n n n n n n n n a a +++⨯⨯==-----，故12231111111111313131313131231n n n n T ++=-+-+⋅⋅⋅+-=--------．18．（1）依题意：1(1234567)47x =++++++=，1(58810141517)117y =++++++=，721140i i x ==∑，71364i i i x y ==∑，71722173647411ˆ21407167i ii ii x yx y bxx==--⨯⨯===-⨯-∑∑，ˆˆ11243a y bx=-=-⨯= 则y 关于x 的线性回归方程为ˆ23yx =+．（2）参加抽奖的每位顾客获得奖品金额为X ，X 的分布列为124440200100107777EX =⨯+⨯+⨯=（元）．由y 关于x 的回归直线方程ˆ23yx =+，预测8x =时，ˆ19y =，9x =时，ˆ21y =，10x =时，ˆ23y =，则此次活动参加抽奖的人数约为58810141517192123140+++++++++=人．44014088007⨯=（元）所以估计该分店为此次抽奖活动应准备8 800元奖品．19．（1）因为AF AB ⊥，平面ABCD ⊥平面ABEF ，所以AF ⊥平面ABCD ，所以AF AD ⊥．因为四边形ABCD 为正方形，所以AB AD ⊥，所以AD 、AB 、AF 两两垂直，以A 为原点，AD 、AB 、AF 分别为x 、y 、z 轴建立空间直角坐标系（如图）．由勾股定理可知1AF =，2BE =，所以(0,0,0)A ，(0,2,0)B ，(2,2,0)C ，(2,0,0)D ，(0,2,2)E ，(0,0,1)F ，所以(2,2,0)AC =，(0,2,0)CD =-，(2,0,2)CE =-．设平面CDE 的一个法向量为(,,)m x y z =，由0,0,n CD n CE ⎧=⎪⎨=⎪⎩，得20,220,y x z -=⎧⎨-+=⎩，即0,0,y x z =⎧⎨-=⎩取1x =，得(1,0,1)n =；同理可得平面DEF 的一个法向量(1,1,2)m =-，故3cos ,||||2m n m n m n <>==，因为二面角F DE C --为钝角，故二面角F DE C --的大小为56x ．（2）设DP DE DF λμ=+，因为(2,2,2)DE =-，(2,0,1)DF =-，又(2,2,0)BD =-，(2,2,2)(2,0,)(22,2,2)DP DE DFλμλλλμμλμλλμ=+=-+-=--+，所以(222,22,2)BP BD DP λμλλμ=+=---+，0,0,BP DF BP DE ⎧=⎪⎨=⎪⎩2(222)20,2(222)2(22)2(2)0,λμλμλμλλμ---++=⎧∴⎨---+-++=⎩解得0,2,3μλ=⎧⎪⎨=⎪⎩即23DP DE =．所以P 是线段DE 上靠近E 的三等分点． 20．（1）依题意，221112a b+=，ca =，222abc =+，解得a =，1b c ==，故椭圆C 的方程为2212x y +=，（2）①当直线AM的斜率不存在时，不妨取A，(1,M，(1,N -，故122AMN S =⨯△②当直线AM 的斜率存在时，设直线AM 的方程为()1y kx =-，0k ≠，联立方程22(1)12y k x x y =-⎧⎪⎨+=⎪⎩化简得2222(21)4220k x k x k +-+-=，设11(,)A x y ，22(,)M x y ，则2122421k x x k +=+，21222221k x x k -=+，2222222422||(1)[()4]2221212k k k AM k k k k -==+-=++，点O 到直线AM 的距离d ==，因为O 是线段AN 的中点，所以点N 到直线AM 的距离为2d =222111||2(22)22211AMNk S AM d k k +∴===++△，综上，AMN △面积的最大值为．21．（1）由()1xf x ax -≥，所以1ln a x x+≤，设1()ln g x x x=+，22111()x g x x x x -'∴=-=．由()0g x '＞，1x ∴＞，()g x 在(1,)+∞上单调递增；()0g x '＜，01x ∴＜＜，()g x 在(0,1)上单调递减，所以min ()(1)1g x g ==，则1a ≤，所以实数a 的最大值为1．（2）设(,y)x 为函数()F x 图像上任意一点，则点(,)y x 为函数()f x 图像上的点，所以()e x F x =，所以001ln e x x =，当01x x ＜＜时，()ln m x x x =，()1ln 0m x x '=+＞，因而()m x 在0(1,)x 上单调递增；当0x x ＞时，()e x x m x =，1()0e x xm x -'=＜，因而()m x 在0(,)x +∞上单调递减；又12()()m x m x =，12x x ＜，则10(1,)x x ∈，20(,)x x ∈+∞，显然当2x →+∞时，1202x x x +＞．要证：1202x x x +＞，即证20102x x x x -＞＞，而()m x 在0(,)x +∞上单调递减，故可证201()(2)m x m x x -＜，又由12()()m x m x =，即证101()(2)m x m x x -＜，即01011122ln e x x x x x x --＜，记0022()ln ex x x xh x x x --=-，01x x ＜＜，其中0()0h x =．000002221221()1ln 1ln e e e x x x x x xx x x x h x x x ---+--'=++=++-．记()et tt ϕ=，1()e t t t ϕ-'=，当(0,1)t ∈时，()0t ϕ'＞；(1,)t ∈+∞时，()0t ϕ'＜，故max 1()t eϕ=，而()0t ϕ＞，故10()e t ϕ＜≤，而020x x -＞，从而002210e e x x x x ----≤＜，因此当0000022212211()1ln 1ln 10e e e ex x x x x xx x x x h x x x ---+--'=++=++--＞＞，即()h x 单调递增．从而当01x x ＜＜时，0()()0h x h x =＜即0101122ln e x x x x x x --＜，故1202x x x +＞得证． 22．（1）依题意，22sin 3cos p p θθ=，故23y x =；因为12x t y =+⎧⎪⎨=⎪⎩20y --=，cos 2sin 0p θθ--=．（2）联立2sin 3cos 0cos 2sin 0p p θθθθ⎧-=⎪--=，化简得：2cos cos 3()3()30sin sin θθθθ--=，则cos sin θθcos sin θθ=，即tan θ=tan θ=，又因为0p ≥，02πθ≤＜则π6θ=或5π3θ=，则直线l 与曲线C 的交点的极坐标为π)6和5(2,π)3．23．（1）依题意，()|3||1||31|4f x x x x x =++-+-+=≥，故m 的值为4；当且仅当(3)(1)0x x +-≤，即31x -≤≤时等号成立，则a 的取值集合为[3,1]-．（2）因为2222p q r m ++=，故2222()()4p q q r +++=；因为222p q pq +≥，当且仅当p q =时等号成立；因为222q r qr +≥，当且仅当q r =时等号成立；故2222()()422p q q r pq qr +++=+≥，故()2q p r +≤（当且仅当p q r ==时等号成立）．河南省2017届普通高中高三4月教学质量监测理科数学试卷解析一、选择题1．【解析】依题意，21{|2730}{|(21)(3)0}{|3}2A x x x x x x x x =-+=--=＜＜＜＜，{|lg 1}{|010}{1,2,3,4,5,6,7,8,9}B x x x x =∈=∈=Z Z ＜＜＜，阴影部分表示集合A B ，故{1,2}A B =．2．【解析】依题意，设i (,)z a b a b =+∈R ，则32i 22z z a b +=+，故2i 1a b +==，故12a =，b =则在复平面内，复数z所对应的点为1(2，位于第一象限．3．【解析】全命题的否定为特称命题，故其否定为0:(1,)p x ⌝∃∈+∞，30168x x +≤． 4．【解析】依题意，由排列组合知识可知，展开式中3x 项的系数为3332246632(1)22(1)600C C ⨯--⨯-=-． 5．【解析】设(,0)F c -，依题意，联立,,a b y x a =-⎪⎩解得2(,)a ab M c c -，故20ab b c a a c c-=-+，解得a b =，故所求渐近线方程为y x =±．6．【解析】如图所示，建立平面直角坐标系，故(B，D ，(0,)(11)P m m -＜＜，故(3,m )BP =，(3,m)PD =-，故23BP PD m =-，故(2,3]BP PD ∈．7．【解析】依题意，11πsin cos cos )2sin cos 4ϕϕϕϕϕϕϕϕ+=+=+，因为π(0,)2ϕ∈，所以π4ϕ=，故322211tan 12(2)(2)()|1133x x x dx x x dx x ϕ--=-=-=--⎰⎰． 8．【解析】起始阶段有23m a =-，i 1=，第一次循环后，2(23)349m a a =--=-，i 2=；第二次循环后，2(49)3821m a a =--=-，i 3=；第三次循环后，2(821)31645m a a =--=-，i 4=；接着计算2(1645)33293m a a =--=-，跳出循环，输出3293m a =-．令329335a -=，得4a =．9．【解析】依题意，将题中数据统计如下表所示：设该公司一天内安排生产A 产品x 吨、B 产品吨，所获利润为z 元，依据题意得目标函数为300200z x y =+，约束条件为50,4160,25200,0,0,x y x x y x y +⎧⎪⎪⎨+⎪⎪⎩≤≤≤≥≥欲求目标函数300200100(32)z x y x y =+=+的最大值，先画出约束条件表示的可行域，如图中阴影部分所示，则点(40,0)A ，(40,10)B ，50100(,)33C ，(0,40)D ，作直线320x y +=，当移动该直线过点(40,10)B 时，32x y +取得最大值，则300200z x y =+也取得最大值（也可通过代入凸多边形端点进行计算，比较大小求得）．故max 300402001014000z =⨯+⨯=．所以工厂每天生产A 产品40吨，B 产品10吨时，才可获得最大利润，为14 000元．10．【解析】因为5[()]1x f x -=，故1()5f x x =-；在同一直角坐标系中分别作出函数()y f x =，15y x =-，的图像如图所示，观察可知，两个函数的图像在[2,2]-上有6个交点，故方程5[()]1x f x -=在[2,2]-上有6个根．11．【解析】由三视图可知，该几何体所表示的几何图形为三棱锥A BCD-，作出该几何体的直观图如图所示，取AC的中点E ，连接BE ；可以证明BE ⊥平面A C D ，故三棱锥A B CD-的体积2111633ACD V BE S ==⨯=△．12．【解析】依题意，32sin cos sin 2a B C c C R +=，故23cos 42ab C c +=，故22223422a b c ab c ab +-+=，整理得22228a b c ++=，结合余弦定理可知2832cos c ab C -=①；记ABC △的面积为S ，则42s i n S a b C =②，将①②平方相加可得2222222222(83)164()(82)c S a b a b c ++=+=-≤，故22226416(165)5S c c -≤≤，即245S ≤，S ，当且仅当285c =时等号成立．二、填空题13．【解析】依题意，3M =，3592422T =+=，故6T =，故2ππ3T ω==，将点(2,3)A 代入可得ππ22π()32k k ϕ⨯+=+∈Z ，故π2π()6k k ϕ=-+∈Z ，故ππ()3sin()36f x x =-．14．【解析】设2AB =，则1BG =，AG =故多边形AEFGHID 的面积1222122S =+⨯⨯=；阴影部分为两个对称的三角形，其中90EAB GAB ∠=-∠，故阴影部分的面积12sin 2S AE AB EAB =⨯∠112cos 2422AE AB GAB =⨯∠=⨯=，故所求概率13P =． 15．【解析】设直线:2l x my '=-，联立28,2,y x x my ⎧=⎨=-⎩故28160y my -+=，264640m ∆=-＞，21m ＞，设11(,)P x y ，22(,)Q x y ，则128y y m +=，1216y y =，由抛物线的对称性可知，21221||||4222||||y y PF QF m AF BF y y +=+=-=，解得26m =，故m =，故直线l '的方程为2)y x =+． 16．【解析】2ln (1)ln (1)01x x x x x x x λλ-⇒--+≤≤；设函数2()ln (1)H x x x x λ=--，从而对任意[1,)x ∈+∞，不等式()0(1)H x H =≤恒成立，又()ln 12H x x x λ'=+-，①当()ln 120H x x x λ'=+-≤，即ln 2x x x λ≤恒成立时，函数()H x 单调递减，设ln 1()x r x x+=，则2ln ()0x r x x -'=≤，所以m a x ()(1)1r x r ==，即1122λλ⇒≤≥，符合题意；②当0λ≤时，()ln 120H x x x λ'=+-≥恒成立，此时函数()H x 单调递增．于是，不等式()(1)0H x H =≥对任意[1,)x ∈+∞恒成立，不符合题意；③当102λ＜＜时，设()()ln 12q x H x x x λ'==+-，则11()2012q x x x λλ'=-=⇒=＞，当1(1,)2x λ∈时，1()20q x x λ'=-＞，此时()()ln 12q x H x x x λ'==+-单调递增，所以()ln 12(1)120H x x x H λλ''=+->=-＞，故当1(1,)2x λ∈时，函数()H x 单调递增．于是当1(1,)2x λ∈时，()0H x ＞成立，不符合题意；综上所述，实数λ的取值范围为1[,)2+∞．三、解答题17．【解析】略．18．【解析】略．19．【解析】略．20．【解析】略．21．【解析】略．22．【解析】略．23．【解析】略．。

河南省普通高中2017届高三4月教学质量监测理数试题含答案

河南省2017届普通高中高三4月教学质量监测理科数学试题第Ⅰ卷(共60分）一、选择题：本大题共12个小题,每小题5分，共60分。

在每小题给出的四个选项中,只有一项是符合题目要求的. 1。

已知集合{}2|2730A x xx =-+<,{}|lg 1B x Z x =∈<，则阴影部分所表示的集合的元素个数为（）A ．1B ．2C ．3D ．42.已知复z 的共轭复数为z ，若()312222z z i ⎛⎫+- ⎪⎝⎭（i 为虚数单位),则在复平面内,复数z 所对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3.已知命题():1,p x ∀∈+∞，2168x x+>则命题p 的否定为（）A ．():1,p x ⌝∀∈+∞，2168x x+≤ B ．():1,p x ⌝∀∈+∞，2168xx+<C ．()0:1,p x ⌝∃∈+∞,20168xx +≤ D ．()0:1,p x ⌝∃∈+∞,2168xx +<4. ()()623221x x x ---的展开式中，含3x 项的系数为( ）A ．600B ．360C 。

600- D ．360-5.已知双曲线()2222:10,0x y C a b a b-=>>的左焦点为F ，第二象限的点M 在双曲线C 的渐近线上，且OM a=，若直线MF 的斜率为b a,则双曲线C 的近线方程为（）A ．y x =±B ．2y x =± C. 3y x=± D ．4y x =±6.已知边长为2的菱形ABCD 中，120BAD ∠=，若()01AP AC λλ=<<，则BP PD ⋅的取值范围是( )A ．[]0,3B ．[]2,3 C.(]0,3 D ．(]2,37。

已知1122sin cos ϕϕ+=，若0,2πϕ⎛⎫∈ ⎪⎝⎭，则()2tan 21xx dxϕ--⎰=（）A ．13B ．13-C 。

2017届高三四校联考理科综合四月模拟试题(配答案)

2017年高考模拟试题四校联考2017.04理科综合本试卷分第Ⅰ卷和第Ⅱ卷两部分，共15页。

满分300分。

考试时间150分钟。

答题前，考生务必用0.5毫米黑色签字将自己的姓名、座号、考生号、县区和科类填写在试卷和答题卡规定的位置。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷（必做，共126分）注意事项：1．第Ⅰ卷共21小题，共126分。

2．每小题选出答案后，用2B铅笔把答题纸上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

不涂在答题卡上，只答在试卷上无效。

相对原子质量：Fe 56 Cu 64 S32一、选择题（共13小题，每小题6分，共78分。

每小题只有一个选项符合题意。

）1．下列有关组成生物体的化合物的相关叙述，正确的是A．纤维素和淀粉都是生物体的能源物质B．大肠杆菌细胞质中的遗传物质是DNAC．核糖体的主要组成成分是脱氧核糖核酸和蛋白质D．蛋白质和RNA可以自由通过核膜上的核孔2．如图表示某生态系统一年中CO2的释放和消耗状况，其中①是生产者呼吸释放量，②是分解者呼吸释放量，③是消费者呼吸释放量，④是生产者光合作用消耗量。

有关叙述正确的是A．流经该生态系统的总能量可用①+②+③表示B．②的量越小，说明该生态系统施用的有机肥料越多C．该生态系统中消费者同化量的多少可用③表示D．该生态系统一年中CO2的释放量与消耗量相等，说明该生态系统处于稳定期3．下列关于生物变异的叙述，不正确的是A．基因突变和染色体结构变异都可导致DNA碱基序列的改变B．无子西瓜及无子番茄的培育过程中都有生长素参与C．某DNA分子中丢失一个基因，该变异属于染色体变异D．基因型Aa的个体自交，因基因重组而导致子代性状分离4．下图为基因的作用与性状的表现流程示意图。

请据图分析，正确的选项是A．①过程是转录，它以DNA的一条链为模板、四种脱氧核苷酸为原料合成mRNA B．②过程中共有64种密码子对应着20种氨基酸C．某段DNA上发生了基因突变，则该基因形成的mRNA一定会改变D．白化病是基因对性状的直接控制，使得蛋白质结构发生变化所致5．某兴趣小组为了研究环境因素对绿色植物光合作用的影响，将其置于一密闭玻璃容器内，其他条件适宜时从黑暗到光照条件下容器内氧气含量的变化如下图所示。

【全国省级联考word】河南省2017届普通高中高三4月教学质量监测理科数学试题

绝密★启用前【全国省级联考word 】河南省2017届普通高中高三4月教学质量监测理科数学试题试卷副标题考试范围：xxx ；考试时间：69分钟；命题人：xxx学校:___________姓名：___________班级：___________考号：___________注意事项．1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、选择题（题型注释）1、已知的外接圆的半径为，角的对边分别是，若，则面积的最大值为（）A ．B ．C ．D ．2、如图，小正方形的边长为1，粗线画出的是某空间几何体的三视图，则该几何体的体积为（）A ．B ．C ．D ．323、已知函数，则方程在上的根的个数为（） A ．B ．C ．D ．4、某颜料公司生产两种产品，其中生产每吨产品，需要甲染料1吨，乙染料4吨，丙染料2吨，生产每吨产品，需要甲染料1吨，乙染料0吨，丙染料5吨，且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨、160吨和200吨，如果产品的利润为300元/吨，产品的利润为200元/吨，则该颜料公司一天之内可获得的最大利润为（） A ．14000元B ．16000元C ．16000元D ．20000元5、《九章算术》是我国古代的数学名著，体现了古代劳动人民的数学智慧，其中第六章“均输”中，有一竹节容量问题，某教师根据这一问题的思想设计了如图所示的程序框图，若输出的值为35，则输入的值为（）A ．B ．C ．D ．6、已知，若，则=（）A ．B ．C ．D ．7、已知边长为的菱形中，，若，则的取值范围是（）A ．B ．C ．D ．8、已知双曲线的左焦点为，第二象限的点在双曲线的渐近线上，且，若直线的斜率为，则双曲线的近线方程为（） A ．B ．C ．D ．9、的展开式中，含项的系数为（）A ．B ．C ．D ．10、已知命题，则命题的否定为（）A ．，B ．，C ．，D ．，11、已知复的共轭复数为，若（为虚数单位），则在复平面内，复数所对应的点位于（） A ．第一象限B ．第二象限C ．第三象限D ．第四象限12、已知集合，，则阴影部分所表示的集合的元素个数为（）A ．B ．C ．D ．第II卷（非选择题）二、填空题（题型注释）13、若时，关于的不等式恒成立，则实数的取值范围是__________．14、已知抛物线的焦点为，准线与轴交于点，过点的直线与抛物线的交点为延长交抛物线于点，延长交抛物线于点，若，则直线的方程为__________．15、折纸已经成为开发少年儿童智力的一种重要工具和手段，已知在折叠“爱心”活动中，会产生如图所示的几何图形，其中四边形为正方形，为线段的中点，四边形与四边形也是正方形，连接，则向多边形中投掷一点，则该点落在阴影部分的概率为__________．16、已知函数的部分图像如图所示，其中（点为图像的一个最高点），则函数=__________．三、解答题（题型注释）17、选修4-5：不等式选讲已知函数的最小值为，且.（1）求的值以及实数的取值集合；（2）若实数满足，证明.18、选修4-4：参数方程与极坐标系已知直线的参数方程为（为参数），以原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程是.（1）求曲线的直角坐标方程及直线的极坐标方程；（2）求直线与曲线交点的极坐标.19、已知函数与的图象关于直线对称.（1）不等式对任意恒成立，求实数的最大值；（2）设在内的实根为，，若在区间上存在，证明：.20、已知椭圆的左、右焦点分别为，点是椭圆上的点，离心率为.（1）求椭圆的方程；（2）点在椭圆上上，若点与点关于原点对称，连接，并延长与椭圆的另一个交点为，连接，求△面积的最大值.21、如图所示的空间几何体中，底面四边形为正方形，，，平面平面，，，.（1）求二面角的大小；（2）若在平面上存在点，使得平面，试通过计算说明点的位置.22、国内某知名连锁店分店开张营业期间，在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动，随着抽奖活动的有效展开，参与抽奖活动的人数越来越多，该分店经理对开业前7天参加抽奖活动的人数进行统计，表示开业第天参加抽奖活动的人数，得到统计表格如下：经过进一步的统计分析，发现与具有线性相关关系.（1）根据上表给出的数据，用最小二乘法，求出与的线性回归方程；（2）若该分店此次抽奖活动自开业始，持续10天，参加抽奖的每位顾客抽到一等奖（价值200元奖品）的概率为，抽到二等奖（价值100元奖品）的概率为，抽到三等奖（价值10元奖品）的概率为，试估计该分店在此次抽奖活动结束时送出多少元奖品？参考公式：，23、已知数列的前项和为，且，.（1）求数列的通项公式；（2）求数列的前项和.参考答案1、C2、B3、D4、A5、A6、D7、D8、A9、C10、C11、A12、B13、14、15、16、17、（1）（2）见解析18、（1）（2）和.19、（1）1（2）见解析20、（1）（2）21、（1）（2）是线段上靠近的三等分点.22、（1）（2）8800元23、（1）（2）【解析】1、依题意，，故，故，整理得，结合余弦定理可知①；记△的面积为，则②，将①②平方相加可得，故，即，，当且仅当时等号成立.选C.点睛：三角形中最值问题，一般转化为条件最值问题:先根据正、余弦定理及三角形面积公式结合已知条件灵活转化边和角之间的关系，利用基本不等式或函数方法求最值. 在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用，否则会出现错误.2、由三视图可知，该几何体所表示的几何图形为三棱锥，作出该几何体的直观图如图所示，取的中点，连接；可以证明平面，故三棱锥的体积.选B.点睛:空间几何体体积问题的常见类型及解题策略(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体，则可直接利用公式进行求解．(2)若所给定的几何体的体积不能直接利用公式得出，则常用转换法、分割法、补形法等方法进行求解．(3)若以三视图的形式给出几何体，则应先根据三视图得到几何体的直观图，然后根据条件求解．3、因为，故；在同一直角坐标系中分别作出函数，，的图象如图所示，观察可知，两个函数的图象在上有6个交点，故方程在上有6个根.选D.点睛：涉及函数的零点问题、方程解的个数问题、函数图像交点个数问题，一般先通过研究函数的单调性、最大值、最小值、变化趋势等，再借助函数的大致图象判断零点、方程根、交点的情况，归根到底还是研究函数的性质，如单调性、极值，然后通过数形结合的思想找到解题的思路.4、依题意，将题中数据统计如下表所示：设该公司一天内安排生产产品吨、产品吨，所获利润为元，依据题意得目标函数为，约束条件为欲求目标函数的最大值，先画出约束条件表示的可行域，如图中阴影部分所示，则点，，，，作直线，当移动该直线过点时，取得最大值，则也取得最大值（也可通过代入凸多边形端点进行计算，比较大小求得）.故.所以工厂每天生产产品40吨，产品10吨时，才可获得最大利润，为14000元.选A.点睛：线性规划的实质是把代数问题几何化，即数形结合的思想.需要注意的是：一，准确无误地作出可行域；二，画目标函数所对应的直线时，要注意与约束条件中的直线的斜率进行比较，避免出错；三，一般情况下，目标函数的最大或最小值会在可行域的端点或边界上取得.5、起始阶段有，，第一次循环后，，；第二次循环后，，；第三次循环后，，；接着计算，跳出循环，输出.令，得.选A.6、依题意，，因为，所以，故.选D.7、如图所示，建立平面直角坐标系，故，，，故，，故，故.选D.8、设，依题意，联立解得，故，解得，故所求渐近线方程为.选A.9、依题意，由排列组合知识可知，展开式中项的系数为.选C.10、全命题的否定为特称命题，故其否定为，.选C.11、依题意，设，则，故，故，则在复平面内，复数所对应的点为，位于第一象限.选A.12、依题意，，，阴影部分表示集合，故.选B.13、；设函数，从而对任意，不等式恒成立，又，①当，即恒成立时，函数单调递减，设，则，所以，即，符合题意；②当时，恒成立，此时函数单调递增.于是，不等式对任意恒成立，不符合题意；③当时，设，则，当时，，此时单调递增，所以，故当时，函数单调递增.于是当时，成立，不符合题意；综上所述，实数的取值范围为.点睛：对于求不等式成立时的参数范围问题，在可能的情况下把参数分离出来，使不等式一端是含有参数的不等式，另一端是一个区间上具体的函数，这样就把问题转化为一端是函数，另一端是参数的不等式，便于问题的解决.但要注意分离参数法不是万能的，如果分离参数后，得出的函数解析式较为复杂，性质很难研究，就不要使用分离参数法.14、设直线，联立故，，，设，，则，，由抛物线的对称性可知，，解得，故，故直线的方程为.15、设，则，，故多边形的面积；阴影部分为两个对称的三角形，其中，故阴影部分的面积，故所求概率.16、依题意，，，故，故，将点代入可得，故，故.点睛：已知函数的图象求解析式(1).(2)由函数的周期求(3)利用“五点法”中相对应的特殊点求.17、试题分析：（1）根据绝对值三角不等式可得函数最小值，再根据不等式等于号取法确定实数的取值集合，（2）利用基本不等式可得，，相加即得结论.试题解析：（Ⅰ）依题意，，故的值为；当且仅当，即时等号成立，则的取值集合为. （Ⅱ）因为，故；因为，当且仅当时等号成立；因为，当且仅当时等号成立；故，故（当且仅当时等号成立）.18、试题分析：（1）根据加减消元法将直线的参数方程化为普通方程，根据将曲线的极坐标方程化为直角坐标方程，（2）根据直线的普通方程与曲线的直角坐标方程。

2017届河南省百校联盟高三4月教学质量检测：英语试卷(含答案)

英语试题第一部分听力（共两节，满分30分）第一节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第6段材料，回答第6、7题。

【全国市级联考】浙江省台州市2017届高三4月调研(一模)数学(解析版)

选择题部分（共40分）一、选择题：本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 若集合错误！未找到引用源。

，则错误！未找到引用源。

（）A. 错误！未找到引用源。

B. 错误！未找到引用源。

C. 错误！未找到引用源。

D. 错误！未找到引用源。

【答案】C2. 已知双曲线错误！未找到引用源。

的一条渐近线方程是错误！未找到引用源。

，则双曲线的离心率为（）A. 错误！未找到引用源。

B. 错误！未找到引用源。

C. 错误！未找到引用源。

D. 错误！未找到引用源。

【答案】D【解析】双曲线的渐近线方程是错误！未找到引用源。

，所以错误！未找到引用源。

，即错误！未找到引用源。

，错误！未找到引用源。

，即错误！未找到引用源。

，错误！未找到引用源。

，故选D.3. 若函数错误！未找到引用源。

是定义在错误！未找到引用源。

上的周期为2的奇函数，则错误！未找到引用源。

（）A. -2017B. 0C. 1D. 2017【答案】B【解析】因为周期为2，所以错误！未找到引用源。

，所以错误！未找到引用源。

，而错误！未找到引用源。

，故选B.4. 某空间几何体的三视图如图所示，其中俯视图是半径为1的圆，则该几何体的体积是（）A. 错误！未找到引用源。

B. 错误！未找到引用源。

C. 错误！未找到引用源。

D. 错误！未找引用源。

【答案】A5. 若错误！未找到引用源。

，则“错误！未找到引用源。

”是“错误！未找到引用源。

”的（）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】C【解析】当错误！未找到引用源。

，而错误！未找到引用源。

，反过来也成立，所以是充要条件，故选C. @￥6. 在错误！未找到引用源。

中，内角错误！未找到引用源。

的对边分别为错误！未找到引用源。

，已知错误！未找到引用源。

，错误！未找到引用源。

，则错误！未找到引用源。

的面积为（）A. 错误！未找到引用源。

【河南省】2017届百校联盟4月高考模拟数学(理科)试卷-答案

0＜（t）
1 e
，而
2x0﹣x＞0
，从而

1 e

2x0 x e2 x0 x
＜0
，
因此，当
h（ x）
1

lnx

1
x2 e2x0 x
x0
1 lnx
1 e2x0 x

2x0 x e2x0 x
＞1﹣1 e
＞0
，即
（h x）单调递增．
从而，当1＜x＜x0 时，（ h x）＜（ h x0） 0 ，即
f (a) m ，则实数 a 的取值集合为{a | 3≤a≤1} ；
（Ⅱ）证明： p2 2q2 r2 4≥2 pq 2qr ，
∴ pq qr≤2 ，即 q( p r)≤2 ，当且仅当 p q r 时取等号．
- 4 - / 13
河南省百校联盟 2017 年 4 月高考模拟数学（理科）试卷
- 1 - / 13
∵ DF 5,CE 2 2, BC 2 ， ∴ D(2,0,0), E(0,2,2), F(0,0,1)C(2,2,0) ， DE (2,2,2), DF (2,0,1), DC (0,2,0) ，
设平面 DEF 的法向量 n (x, y, z) ，
BP
DP DE

0 0
，∴
2(2 2(2

2) 2 0 2 2) 2(2 2)

2(2

)

0
，
0
解得

2 3
，即
DP

2 3
DE
．
∴ P 是线段 DE 上靠近 E 的三等分点．

河南省普通高中高三4月教学质量监测理数试题 Word版含答案

河南省2017届普通高中高三4月教学质量监测理科数学试题第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}2|2730A x x x =-+<，{}|lg 1B x Z x =∈<，则阴影部分所表示的集合的元素个数为（）A ．1B ．2C ．3D ．42.已知复z 的共轭复数为z ，若()3122z z ⎛⎫+- ⎪⎝⎭（i 为虚数单位），则在复平面内，复数z所对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 3.已知命题():1,p x ∀∈+∞，2168x x +>则命题p 的否定为（）A ．():1,p x ⌝∀∈+∞，2168x x +≤B ．():1,p x ⌝∀∈+∞，2168x x +<C ．()0:1,p x ⌝∃∈+∞，200168x x +≤D ．()0:1,p x ⌝∃∈+∞，200168x x +< 4. ()()623221x x x ---的展开式中，含3x 项的系数为（） A ．600 B ．360 C. 600- D ．360-5.已知双曲线()2222:10,0x y C a b a b-=>>的左焦点为F ，第二象限的点M 在双曲线C 的渐近线上，且OM a =，若直线MF 的斜率为ba，则双曲线C 的近线方程为（）A ．y x =±B ．2y x =± C. 3y x =± D ．4y x =±6.已知边长为2的菱形ABCD 中，120BAD ∠=，若()01AP AC λλ=<<，则BP PD ⋅的取值范围是（）A ．[]0,3B ．[]2,3 C. (]0,3 D ．(]2,37.已知11sin cos ϕϕ+=0,2πϕ⎛⎫∈ ⎪⎝⎭，则()2tan 21x x dx ϕ--⎰=（） A ．13 B ．13- C. 23 D ．23-8.《九章算术》是我国古代的数学名著，体现了古代劳动人民的数学智慧，其中第六章“均输”中，有一竹节容量问题，某教师根据这一问题的思想设计了如图所示的程序框图，若输出m 的值为35，则输入a 的值为（）A ．4B ．5 C.7 D ．119.某颜料公司生产,A B 两种产品，其中生产每吨A 产品，需要甲染料1吨，乙染料4吨，丙染料2吨，生产每吨B 产品，需要甲染料1吨，乙染料0吨，丙染料5吨，且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨、160吨和200吨，如果A 产品的利润为300元/吨，B 产品的利润为200元/吨，则该颜料公司一天之内可获得的最大利润为（） A ．14000元 B ．16000元 C.16000元 D.20000元10.已知函数()()22,201,02x x x f x f x x ⎧+-≤≤⎪=⎨-<≤⎪⎩，则方程()51x f x -=⎡⎤⎣⎦在[]2,2-上的根的个数为（）A ．3B ．4 C. 5 D ．611.如图，小正方形的边长为1，粗线画出的是某空间几何体的三视图，则该几何体的体积为（）A ．．16 C. ．3212.已知ABC ∆的外接圆的半径为R ，角,,A B C 的对边分别是,,a b c ，若32sin cos sin 2a B C c C R+=，则ABC ∆面积的最大值为（）A ．25 B ．45 C. D ．125第Ⅱ卷（共90分）二、填空题：本大题共4小题，每小题5分，满分20分.13.已知函数()()sin 0,0,||2f x M x M πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图像如图所示，其中()2,3A （点A 为图像的一个最高点）5,02B ⎛⎫- ⎪⎝⎭，则函数()f x = ．14折纸已经成为开发少年儿童智力的一种重要工具和手段，已知在折叠“爱心”活动中，会产生如图所示的几何图形，其中四边形ABCD 为正方形，G 为线段BC 的中点，四边形AEFG 与四边形DGHI 也是正方形，连接,EB CI ，则向多边形AEFGHID 中投掷一点，则该点落在阴影部分的概率为．15.已知抛物线2:8C y x =的焦点为F ，准线l 与x 轴交于点M ，过点M 的直线l 与抛物线C的交点为,P Q 延长PF 交抛物线C 于点A ，延长QF 交抛物线C 于点B ，若22PF QF AFBF+=，则直线l 的方程为． 16.若[)1,x ∈+∞时，关于x 的不等式()ln 11x xx x λ≤-+恒成立，则实数λ的取值范围是．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.已知数列{}n a 的前n 项和为n S ，且28a =，112n n a S n -=--. （1）求数列{}n a 的通项公式；（2）求数列123n n n a a +⎧⎫⨯⎨⎬⎩⎭的前n 项和n T .18. 国内某知名连锁店分店开张营业期间，在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动，随着抽奖活动的有效展开，参与抽奖活动的人数越来越多，该分店经理对开业前7天参加抽奖活动的人数进行统计，y 表示开业第x 天参加抽奖活动的人数，得到统计表格如下：经过进一步的统计分析，发现Y 与X 具有线性相关关系.（1）根据上表给出的数据，用最小二乘法，求出y 与x 的线性回归方程ˆˆˆybx a =+；（2）若该分店此次抽奖活动自开业始，持续10天，参加抽奖的每位顾客抽到一等奖（价值200元奖品）的概率为17，抽到二等奖（价值100元奖品）的概率为27，抽到三等奖（价值10元奖品）的概率为47，试估计该分店在此次抽奖活动结束时送出多少元奖品？参考公式：1221ˆni ii n i i x ynx ybx nx---=-∑∑，ˆˆay bx =- 19. 如图所示的空间几何体中，底面四边形ABCD 为正方形，AF AB ⊥，//AF BE ，平面ABEF ⊥平面ABCD，DF =CE =，2BC =.（1）求二面角F DE C --的大小；（2）若在平面DEF 上存在点P ，使得BP ⊥平面DEF ，试通过计算说明点P 的位置. 20.已知椭圆()2222:10x y C a b a b +=>>的左、右焦点分别为12,F F，点1,⎛ ⎝⎭是椭圆C 上的点，离心率为e . （1）求椭圆C 的方程；（2）点()()000,0A x y y ≠在椭圆上C 上，若点N 与点A 关于原点对称，连接2AF ，并延长与椭圆C 的另一个交点为M ，连接MN ，求△AMN 面积的最大值. 21. 已知函数()F x 与()ln f x x =的图象关于直线y x =对称.（1）不等式()1xf x ax ≥-对任意()0,x ∈+∞恒成立，求实数a 的最大值；（2）设()()1f x F x =在()1,+∞内的实根为0x ，()()()00,1,xf x x x m x xx x F x ⎧<≤⎪=⎨>⎪⎩，若在区间()1,+∞上存在()()()1212m x m x x x =<，证明：1202x x x +>. 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分；作答时，请用2B 铅笔将答题卡上相应的题号涂黑.22.选修4-4：参数方程与极坐标系已知直线l的参数方程为12tx y +⎧⎪=⎨=⎪⎩（t 为参数），以原点为极点，X 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程是2sin 3cos 0p θθ-=. （1）求曲线C 的直角坐标方程及直线l 的极坐标方程；（2）求直线l 与曲线C 交点的极坐标()0,02p θπ≥≤<. 23.选修4-5：不等式选讲已知函数()31f x x x =++-的最小值为m ，且()f a m =. （1）求m 的值以及实数a 的取值集合；（2）若实数,,p q r 满足2222p q r m ++=，证明()2q p r +≤.试卷答案一、选择题1.B 【解析】依题意，{}()(){}21|2730|2130|32A x x x x x x x x ⎧⎫=-+<=--<=<<⎨⎬⎩⎭，{}|lg 1B x Z x =∈<{}{}|0101,2,3,4,5,6,7,8,9x Z x =∈<<=，阴影部分表示集合A B ，故{}1,2AB =.2.A 【解析】依题意，设(),z a bi a b R =+∈，则3222z z a bi +=+，故21a bi +==+，故12a =，b =则在复平面内，复数z所对应的点为12⎛ ⎝，位于第一象限.3.C 【解析】全命题的否定为特称命题，故其否定为()0:1,p x ⌝∃∈+∞，30168x x +≤. 4.C 【解析】依题意，由排列组合知识可知，展开式中3x 项的系数为()()34332266321221600C C ⨯--⨯-=-.5.A 【解析】设(),0F c -，依题意，联立,,a b y x a ==-⎪⎩解得2,a ab M c c ⎛⎫- ⎪⎝⎭，故20ab b c a a c c-=-+，解得a b =，故所求渐近线方程为y x =±.6.D 【解析】如图所示，建立平面直角坐标系，故()B，)D ，()()0,11P m m -<<，故()3,m BP =，()3,m PD =-，故23BP PD m ∙=-，故(]2,3BP PD ∙∈.7.D【解析】依题意，11sin cos cos 2sin cos 4πϕϕϕϕϕϕϕϕ⎛⎫+=⇒+=⇒+= ⎪⎝⎭，因为0,2πϕ⎛⎫∈ ⎪⎝⎭，所以4πϕ=，故()()322211tan 12221133x x x dx x x dx x ϕ-⎛⎫-=-=-=⎪--⎝⎭⎰⎰. 8.A 【解析】起始阶段有23m a =-，1i =，第一次循环后，()223349m a a =--=-，2i =；第二次循环后，()2493821m a a =--=-，3i =；第三次循环后，()282131645m a a =--=-，4i =；接着计算()2164533293m a a =--=-，跳出循环，输出3293m a =-.令329335a -=，得4a =.9.A 【解析】依题意，将题中数据统计如下表所示：设该公司一天内安排生产A 产品x 吨、B 产品y 吨，所获利润为z 元，依据题意得目标函数为300200z x y =+，约束条件为50,4160,25200,0,0,x y x x y x y +≤⎧⎪≤⎪⎨+≤⎪⎪≥≥⎩欲求目标函数()30020010032z x y x y =+=+的最大值，先画出约束条件表示的可行域，如图中阴影部分所示，则点()40,0A ，()40,10B ，50100,33C ⎛⎫⎪⎝⎭，()0,40D ，作直线320x y +=，当移动该直线过点()40,10B 时，32x y +取得最大值，则300200z x y =+也取得最大值（也可通过代入凸多边形端点进行计算，比较大小求得）.故max 300402001014000z =⨯+⨯=.所以工厂每天生产A 产品40吨，B 产品10吨时，才可获得最大利润，为14000元.10.D 【解析】因为()51x f x -=⎡⎤⎣⎦，故()15f x x =-；在同一直角坐标系中分别作出函数()y f x =，15y x =-，的图象如图所示，观察可知，两个函数的图象在[]2,2-上有6个交点，故方程()51x f x -=⎡⎤⎣⎦在[]2,2-上有6个根.11.B 【解析】由三视图可知，该几何体所表示的几何图形为三棱锥A BCD -，作出该几何体的直观图如图所示，取AC 的中点E ，连接BE ；可以证明BE ⊥平面ACD ，故三棱锥A BCD -的体积(2111633ACDV BE S=∙∙=⨯=.12.C 【解析】依题意，32sin cos sin 2a B C c C R +=，故23cos 42ab C c +=，故22223422a b c ab c ab +-∙+=，整理得22228a b c ++=，结合余弦定理可知2832cos c ab C-=①；记△ABC 的面积为S ，则42sin S ab C =②，将①②平方相加可得()()()22222222228316482c S a b a b c ++=≤+=-，故()222264161655S c c ≤-≤，即245S ≤，S 285c =时等号成立. 二、填空题13. 3sin 36x ππ⎛⎫- ⎪⎝⎭【解析】依题意，3M =，3592422T =+=，故6T =，故23T ππω==，将点()2,3A 代入可得()2232k k Z ππϕπ⨯+=+∈，故()26k k Z πϕπ=-+∈，故()3sin 36f x x ππ⎛⎫=- ⎪⎝⎭.14.13【解析】设2AB =，则1BG =，AG =AEFGHID 的面积1222122S +⨯⨯=；阴影部分为两个对称的三角形，其中90EAB GAB ∠=-∠，故阴影部分的面积12sin 2S AE AB EAB =⨯∙∙∠112cos 2422AE AB GAB =⨯∙∙∠=⨯=，故所求概率13P =.15. )2y x =+【解析】设直线:2l x my '=-，联立28,2,y x x my ⎧=⎨=-⎩故28160y my -+=，26464m ∆=-0>，21m >，设()11,P x y ，()22,Q x y ，则128y y m +=，1216y y =，由抛物线的对称性可知，PF QF AFBF+212214222y y m y y =+=-=，解得26m =，故m =l '的方程为)2y x =+. 16. 1,2⎡⎤+∞⎢⎥⎣⎦【解析】()()2ln 1ln 101x x x x x x x λλ≤-⇒--≤+；设函数()()2ln 1H x x x x λ=--，从而对任意[)1,x ∈+∞，不等式()()01H x H ≤=恒成立，又()ln 12H x x x λ'=+-，①当()ln 120H x x x λ'=+-≤，即ln 2x x x λ≤恒成立时，函数()H x 单调递减，设()ln 1x r x x+=，则()2ln 0x r x x -'=≤，所以()()max11r x r ==，即1122λλ≤⇒≥，符合题意；②当0λ≤时，()ln 120H x x x λ'=+-≥恒成立，此时函数()H x 单调递增.于是，不等式()()10H x H ≥=对任意[)1,x ∈+∞恒成立，不符合题意；③当102λ<<时，设()()q x H x '== ln 12x x λ+-，则()112012q x x x λλ'=-=⇒=>，当11,2x λ⎛⎫∈ ⎪⎝⎭时，()120q x x λ'=->，此时()()q x H x '==ln 12x x λ+-单调递增，所以()()ln 121120H x x x H λλ''=+->=->，故当11,2x λ⎛⎫∈ ⎪⎝⎭时，函数()H x 单调递增.于是当11,2x λ⎛⎫∈ ⎪⎝⎭时，()0H x >成立，不符合题意；综上所述，实数λ的取值范围为1,2⎡⎫+∞⎪⎢⎣⎭.三、解答题17.【解析】（Ⅰ）因为112n n a S n +=--，故当1n =时，211122aa =--=；当2n ≥时，1222n n S a n +=--，()12212n n S a n -=---两式对减可得132n n a a +=+；经检验，当1n =时也满足132n n a a +=+；故()()1131n n a a ++=+，故数列{}1n a +是以3为首项，3为公比的等比数列，故13n n a +=，即31n n a =- .（Ⅱ）由（Ⅰ）可知，()()11123231131313131n n n n n n n n a a +++⨯⨯==-----，故12231111111111313131313131231n n n n T ++=-+-+⋅⋅⋅+-=--------. 18.【解析】（Ⅰ）依题意：()1123456747x =++++++=， ()158810141517117y =++++++=，721140i i x ==∑，71364i i i x y ==∑，71722173647411ˆ21407167i ii i i x yx ybx x==--⨯⨯===-⨯-∑∑，ˆˆ11243a y bx =-=-⨯= 则y 关于x 的线性回归方程为ˆ23yx =+. （Ⅱ）参加抽奖的每位顾客获得奖品金额为X ，X 的分布列为124440200100107777EX =⨯+⨯+⨯=（元）. 由y 关于x 的回归直线方程ˆ23yx =+，预测8x =时，ˆ19y =，9x =时，ˆ21y =，10x =时，ˆ23y =，则此次活动参加抽奖的人数约为58810141517192123140+++++++++=人. 44014088007⨯=（元）所以估计该分店为此次抽奖活动应准备8800元奖品.19.【解析】（Ⅰ）因为AF AB ⊥,平面ABCD ⊥平面ABEF ，所以AF ⊥平面ABCD ，所以AF AD ⊥.因为四边形ABCD 为正方形，所以AB AD ⊥，所以AD 、AB 、AF 两两垂直，以A 为原点，AD 、AB 、AF 分别为x 、y 、z 轴建立空间直角坐标系（如图）.由勾股定理可知1AF =，2BE =，所以()0,0,0A ，()0,2,0B ，()2,2,0C ，()2,0,0D ，()0,2,2E ，()0,0,1F ，所以()2,2,0AC =，()0,2,0CD =-，()2,0,2CE =-.设平面CDE 的一个法向量为(),,m x y z =，由0,0,n CD n CE ⎧∙=⎪⎨∙=⎪⎩，得20,220,y x z -=⎧⎨-+=⎩，即0,0,y x z =⎧⎨-=⎩取1x =，得()1,0,1n =；同理可得平面DEF 的一个法向量()1,1,2m =-，故cos ,m n m n m n ∙==，因为二面角F DE C --为钝角，故二面角F DE C --的大小为56x .（Ⅱ）设DP DE DF λμ=+，因为()2,2,2DE =-，()2,0,1DF =-，又()2,2,0,BD =-，()()()2,2,22,0,22,2,2DP DE DF λμλλλμμλμλλμ=+=-+-=--+，所以()222,22,2BP BD DP λμλλμ=+=---+，∵0,0,BP DF BP DE ⎧∙=⎪⎨∙=⎪⎩∴()()()()222220,2222222220,λμλμλμλλμ⎧---++=⎪⎨---+-++=⎪⎩解得0,2,3μλ=⎧⎪⎨=⎪⎩即23DP DE =.所以P 是线段DE 上靠近E 的三等分点. 20.【解析】（Ⅰ）依题意，221112a b+=，c a =222a b c =+，解得a 1b c ==，故椭圆C 的方程为2212x y +=，（Ⅱ）①当直线AM的斜率不存在时，不妨取A ⎛ ⎝⎭，1,M ⎛ ⎝⎭，1,N ⎛- ⎝⎭，故122AMNS=⨯= ②当直线AM 的斜率存在时，设直线AM 的方程为()1y k x =-，0k ≠，联立方程()22112y k x x y =-⎧⎪⎨+=⎪⎩化简得()2222214220k x k x k +-+-=，设()11,A x y ，()22,M x y ,则2122421k x x k +=+，21222221k x x k -∙=+，AM =，点O 到直线AM的距离d ==因为O 是线段AN 的中点，所以点N 到直线AM 的距离为2d =2211122221AMNk SAM d k ⎛⎫+∴=∙=∙= ⎪+⎝⎭，综上，AMN ∆21.【解析】（Ⅰ）由()1xf x ax ≥-，所以1ln a x x≤+，设()1ln g x x x =+，∴()22111x g x x x x-'=-=. 由()0g x '>，∴1x >，()g x 在()1,+∞上单调递增；()0g x '<，∴01x <<，()g x 在()0,1上单调递减，所以()()min 11g x g ==，则1a ≤，所以实数a 的最大值为1.（Ⅱ）设(),y x 为函数()F x 图象上任意一点，则点(),y x 为函数()f x 图象上的点，所以()x F x e =，所以001ln x x e =，当01x x <<时，()ln m x x x =，()1ln 0m x x '=+>，因而()m x 在()01,x 上单调递增；当0x x >时，()x x m x e =，()10xxm x e-'=<，因而()m x 在()0,x +∞上单调递减；又()()12m x m x =，12x x <，则()101,x x ∈，()20,x x ∈+∞，显然当2x →+∞时，1202x x x +>. 要证：1202x x x +>，即证20102x x x x >->，而()m x 在()0,x +∞上单调递减，故可证()()2012m x m x x <-，又由()()12m x m x =，即证()()1012m x m x x <-，即01011122ln x x x x x x e --<，记()0022ln x xx xh x x x e --=-，01x x <<，其中()00h x =. ()0000022212211ln 1ln x x x x x xx x x x h x x x e e e---+--'=++=++-. 记()tt t e ϕ=，()1t t t e ϕ-'=，当()0,1t ∈时，()0t ϕ'>；()1,t ∈+∞时，()0t ϕ'<，故()max 1t eϕ=，而()0t ϕ>，故()10t e ϕ<≤，而020x x ->，从而002210x x x x e e ---≤-<，因此当()00000222122111ln 1ln 10x x x x x xx x x x h x x x e e e e ---+--'=++=++->->，即()h x 单调递增.从而当01x x <<时，()()00h x h x <=即0101122ln x x x x x x e --<，故1202x x x +>得证.22.【解析】（Ⅰ）依题意，22sin 3cos p p θθ=，故23y x =；因为12x ty =+⎧⎪⎨=⎪⎩20y --，cos 2sin 0p θθ--=.（Ⅱ）联立2sin 3cos 0cos 2sin 0p p θθθθ⎧-=⎪--=，化简得：2cos cos330sin sin θθθθ⎛⎫⎫--= ⎪⎪⎝⎭⎭，则c o s s i n θθ或cos sin θθ=，即ta n θ=或tan θ=，又因为0p ≥，02θπ≤<则6πθ=或53θπ=，则直线l 与曲线C 的交点的极坐标为6π⎛⎫ ⎪⎝⎭和52,3π⎛⎫ ⎪⎝⎭.23.【解析】（Ⅰ）依题意，()31314f x x x x x =++-≥+-+=，故m 的值为4；当且仅当()()310x x +-≤，即31x -≤≤时等号成立，则a 的取值集合为[]3,1-. （Ⅱ）因为2222p q r m ++=，故()()22224p q q r +++=；因为222p q pq +≥，当且仅当p q =时等号成立；因为222q r qr +≥，当且仅当q r =时等号成立；故()()2222422p q q r pq qr +++=≥+，故()2q p r +≤（当且仅当p q r ==时等号成立）.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

百校联盟2017届高三4月教学质量检测乙卷
理数试题
第Ⅰ卷（共60分）
一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1.已知集合{}
03722<+-=x x x A ，{}
1lg <∈=x Z x B ，则阴影部分所表示的集合的元素个数为（）
A ．1
B ．2
C ．3
D ．4 2.已知复数z 的共轭复数为z ，若i i z
z 25)221)(2
23(-=-+（i 为虚数单位）
，则在复平面内，复数z 所对应的点位于（）
A ．第一象限
B ．第二象限
C ．第三象限
D ．第四象限 3.已知命题x x x p 816),,1(3
>++∞∈∀：，则命题p 的否定为（）
A ．x x x p 816),,1(3
≤++∞∈∀⌝： B ．x x x p 816),,1(3
<++∞∈∀⌝： C ．0300816),,1(x x x p ≤++∞∈∃⌝： D ． 03
00816),,1(x x x p <++∞∈∃⌝： 4.62
)12)23(---x x x （的展开式中，含3x 项的系数为（） A ．600 B ．360 C.600- D ．360-
5.已知双曲线)0,0(1:22
22>>=-b a b
y a x C 的左焦点为F ，第二象限的点M 在双曲线C 的渐近线上，且
a OM =，若直线 MF 的斜率为a
b
，则双曲线C 的渐近线方程为（）
A ．x y ±=
B ．x y 2±= C.x y 3±= D ．x y 4±=
6.已知边长为2的菱形ABCD 中， 120=∠BAD ，若)10(<<=λλ，则⋅的取值范围为（） A ．]3,0[ B ．]3,2[ C.]3,0( D ．]3,2(
7.已知
2211=+ϕ
ϕos c sin ，若)2,0(π
ϕ∈，则=-⎰ϕtan 12)2(-dx x x ( )
A ．
31 B ．31- C.32 D ．3
2- 8.《九章算术》是中国古代数学名著，体现了古代劳动人民数学的智慧，其中第六章“均输”中，有一竹节容量问题，某教师根据这一问题的思想设计了如图所示的程序框图，若输出的m 的值为35，则输入的a 的值为（）
A ．4
B ．5 C.7 D ．11
9.某颜料公司生产A 、B 两种产品，其中生产每吨A 产品，需要甲染料1吨，乙染料4吨，丙染料2吨，生产每吨B 产品，需要甲染料1吨，乙染料0吨，丙染料5吨，且该公司一天之内甲、乙、丙三种染料的用量分别不超过50吨、160吨、200吨，如果A 产品的利润为300元/吨，B 产品的利润为200元/吨，则该颜料公司一天内可获得的最大利润为（）
A ．14000元
B ．16000元 C. 18000元 D ．20000元
10.已知函数⎩⎨⎧≤<+-≤≤-+=2
0,1)1(,02,2)(2x x f x x x x f 则方程1)]([5=-x f x 在]2,2[-上的根的个数为（）
A ．3
B ．4 C. 5 D ．6
11.如图，小正方形的边长为1，粗线画出的是某空间几何体的三视图，则该几何体的体积为（）
A ．38
B ．16 C. 316 D ．32
12.已知ABC ∆的外接圆半径为R ，角C B A ,,所对的边分别为c b a ,,，若R
C c C B a 2sin 23cos sin =+，则ABC ∆面积的最大值为（） A ．
52 B ．54 C.552 D ．5
12
第Ⅱ卷（共90分）
二、填空题（每题5分，满分20分，将答案填在答题纸上）
13.已知函数)2
,0,0)(sin()(π
ϕωϕω<>>+=M x M x f 的部分图象如图所示，
其中)3,2(A （点A 为图象的一个最高点），)0,2
5
(-
B ，则函数=)(x f ．
14.折纸已经成为开发少年儿童智力的一大重要工具和手段.已知在折叠“爱心”的过程中会产生如图所示的几何图形，其中四边形ABCD 为正方形，G 为线段BC 的中点，四边形AEFG 与四边形DGHI 也为正方形，连接CI EB ,，则向多边形AEFGHID 中投掷一点，该点落在阴影部分内的概率为．
15.已知抛物线x y C 8:2
=的焦点为F ，准线l 与x 轴的交点为M ，过点M 的直线l '与抛物线C 的交点为
Q P ,，延长PF 交抛物线C 于点A ，延长QF 交抛物线C 于点B ，若
22=+
BF
QF AF
PF ，则直线l '的方程
为．
16.若),1[+∞∈x 时，关于x 的不等式
)1(1
ln -≤+x x x
x λ恒成立，则实数λ的取值范围为．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）
17. 已知数列{}n a 的前n 项和为n S ，且82=a ，12
1
--=+n a S n n . （1）求数列{}n a 的通项公式；
（2）求数列⎭
⎬⎫
⎩⎨⎧⨯+132n n n a a 的前n 项和为n T .
18. 国内某知名连锁店分店开张营业期间，在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动，随着抽奖活动的有效开展，参与抽奖活动的人数越来越多，该分店经理对开业前7天参加抽奖活动的人数进行统计，y 表示开业第x 天参加抽奖活动的人数，得到统计表格如下：
经过进一步统计分析，发现y 与x 具有线性相关关系.
（1）根据上表提供的数据，用最小二乘法求出y 关于x 的线性回归方程∧
∧
∧
+=a x b y ；
（2）若该分店此次抽奖活动自开业始，持续10天，参加抽奖的每位顾客抽到一等奖（价值
200元奖品）的概率为
71，抽到二等奖（价值100元奖品）的概率为72，抽到三等奖（价值10元奖品）的概率为7
4. 试估计该分店在此次抽奖活动结束时送出多少元奖品？
参考公式：∑∑==∧
--=
n
i i
n
i i
i x
n x
y x n y
x b 1
2
2
1
，x b y a ∧
∧-=.
19. 如图所示的空间几何体中，底面四边形ABCD 为正方形，AB AF ⊥，BE AF ∥，平面⊥ABEF 平面ABCD ，5=DF ，22=CE ，2=BC .
（1）求二面角C DE F --的大小；
（2）若在平面DEF 上存在点P ，使得⊥BP 平面DEF ，试通过计算说明点P 的位置.
20. 已知椭圆)0(1:2222>>=+b a b y a x C 的左、右焦点分别为21F F 、，点)2
2
,1(-是椭圆C 上的点，离心
率2
2=
e . （1）求椭圆C 的方程；
（2）点)0)(,(000≠y y x A 在椭圆C 上，若点N 与点A 关于原点对称，连接2AF 并延长与椭圆C 的另一个交点为M ，连接MN ，求AMN ∆面积的最大值.
21. 已知函数)(x F 与x x f ln )(=的图象关于直线x y =对称.
（1）不等式1)(-≥ax x xf 对任意),0(+∞∈x 恒成立，求实数a 的最大值；
（2）设1)()(=x F x f 在),1(+∞内的实根为0x ，⎪⎩⎪⎨⎧>≤<=0
0,)
(1),()(x x x f x
x x x xf x m ，若在区间),1(+∞上存在
))(()(2121x x x m x m <=，证明：
02
12
x x x >+.
请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.
22.选修4-4：坐标系与参数方程已知直线l 的参数方程为⎩⎨
⎧
+-=+=t y t
x 3321（t 为参数），以原点为极点，x 轴的正半轴为极轴建立极坐标系.
曲线C 的坐标方程是0cos 3sin 2
=-θθρ.
（1）求曲线C 的直角坐标方程以及直线l 的极坐标方程；（2）求直线l 与曲线C 交点的极坐标（πθρ20,0<≤≥）. 23.选修4-5：不等式选讲
已知函数13)(-++=x x x f 的最小值为m ，且m a f =)(. （1）求m 的值以及实数a 的取值集合；
（2）若实数r q p ,,，满足m r q p =++2
2
2
2，证明：2)(≤+r p q .。