人教版七年级上册2.2《整式的加减》第一课时导学案
2019-2020学年七年级数学上册 2.2《整式的加减》(第1课时)导学案(新版)新人教版.doc

4.合并同类项的法则:______________________________________
我的收获: 我的困惑:
【达标测评】(约8分)1.课本p65练习,可酌情处理.
2.如果5x2y与 xmyn是同类项,那么m= ____,n=______
3.认真阅读课本p65例3,根据思路导航完成此题.
思路导航:例3中(1)水位上升量与水位下降量是具有相反意义的两个量,我们可以把下降的水位量记为负,上升的水位量记为正,那么第一天水位的变化量为________cm,第二天水位的变化量为__________cm,两天水位的总变化量为________ =________________.
(3)3ab2-4ab2=( )ab2
2.观察上述的三个多项式,他们都可以合并为一个单项式,那么具备什么特点的多项式可以合并呢?可结对子交流 .
3.像这样,所含字母相同,并且相同字母的指数也相同的项叫做________,几个常数项也是________.
三、合作交流(约5分)
1.对上述问题中的困惑地方小组交流解决,必要时教师指导.
2019-2020学年七年级数学上册2.2《整式的加减》(第1课时)导学案(新版)新人教版
【学习目标】
1.了解同类项,合并同类项的概念,掌握合并同类项法则,能正确合并同类项.
2.能先合并同类项化简后求 值.
3.培养观察,探究,分类,归纳等能力,养成良好的学习习惯.
【学习重点,难点】
重点:掌握合并同类项法则,熟练地合并同类项.
(2)把进货的数量记为正,售出的数量记为负.故进货后这个商店共有大米________________=___________
整式的加减导学案1

17.当多项式x²+3kxy-2y²+6xy-1中不含xy项时,求k的值。
18.一根铁丝长acm,第一次用去它的一半少2cm,第二次用去剩下的 还多1cm。 (1)用式子表示这根铁丝还剩多少米?
(2)当a=600时,这根铁丝还剩多少米?
(5)3m²n-mn²-mn+n²m-0.8mn-3n²m (6) (7) -5a-2a-(-8a)-(-6a)-a (8) 3(x-y)²-9(y-x)³-8(x-y)² +6(x-y)³
10. 先合并同类项,再求值 (1) 3a²-5a+2-6a²+6a-3, 其中a=-1 (2) , 其中x=-2,y=-
与 是同类项,合并的结果为 8. 合并同类项: 。
3a²+6a²= -2x²y+3x²y-8 x²y= a²-2a²= -2x²y+3xy-8x²y= 9.将下列各式合并同类项。 (1)-x-x-x (2) 2x²y-3x²y+5x²y (3) 2a²-3ab+4b²-5ab (4) -ab³+2a³b+3ab³-4a³b
学习重点、难点:
根据学生的认知水平、认知能力以及教材的特点,确定以下重、难点: 重点:同类项的概念、合并同类项的法则及应用。 难点:正确判断同类项;准确合并同类项。
学习过程:
一、引入: 1、 运用有理数的运算律计算: 100×2+252×2=_ 100×(-2)+252×(-2)= _ 2、根据(1)中的方法完成下面的运算,并说明其中的道理: 100t+252t = _ 3、下列三个多项式由哪些单项式组成?.每个多项式中的单项式有什 么共同特点? (1)3x+2x (2)3ab-4ab (3)100t-252t 二、讲授新课: 1.同类项的定义:所含字母相同,并且相同字母的指数也相同的 项叫做同类项。 特别指出:几个常数项也是同类项。 2.例题:例1:判断下列说法是否正确,正确地在括号内打“√”, 错误的打“×”。
七年级数学上册 第二章 整式的加减 2.2 整式的加减(第1课时)教案 (新版)新人教版

(2)5×66+7×66-66×2
2、将(1)题中3.14用字母a替换,(2)中66用b替换,得到两个多项式,能像刚才那样计算吗?
通过运用乘法分配律简化运算为本节课的新知探究做铺垫,同时利用用字母表示数问题的引入起质疑,激发学习欲望的作用。
教
学
过
程
发现规律,总结规 律,知道什么是同类项
通过观察、思考等活动,总结归纳合并同类项法则
从运用类比方法探究,符合学生的认知规律。发展观察能力,顾纳总结能力。
经历观察,思考,交流,等探究合并同类项的过程,体会数式通性,领悟由特殊到一般及类比思想,发展观察能力,归纳总结能力。
教
学
过
程
结合具体的例子,进一步体会什么是同类项
尝试运用法则解决问题
练习:
1、下列各组是同类项的是()
A 2x3与3x2B 12ax与8bx
(2)4a2+3b2+1-2ab-4a2-4b2-5
4、合并同类项。
(1) 12x-20x
(2) -6ab+ba+8ab
(3) -mn+2mn-3mn2+4mn2
(4) X3 +3X2-1-5X2+2
通过练习,学生能正确识别同类 项,进一步明晰同类项概念。达到本节课的第一个学习目标。
通过不同形式,不同梯次的合并同类项的训练检验是否能正确的合并同类项,突出本节的重点,达到第二个学习目标。
人教版-数学-七年级上册--2.2整式的加减导学案

2.2整式的加减学习目标、重点、难点【学习目标】1.理解同类项的概念,会合并同类项.2.掌握去括号的法则,会去括号.3.会用整式的加减运算法则,能熟练进行整式的加减运算、求值.【重点难点】1.同类项的概念,合并同类项.2.用整式的加减运算法则,能熟练进行整式的加减运算、求值.知识概览图新课导引前面我们学习了单项式、多项式和整式的概念,也学会了用字母表示实际生活中的一些数量关系,那么我们如何解决图中小明提出的问题呢?就让我们一起来学习整式的加减这一节吧!相信你通过这一节的学习,一定会帮助小明找到答案的.教材精华知识点1同类项(重点)★所含字母相同,并且相同字母的指数也相同的项叫做同类项.另外,所有的常数项都是同类项.★同类项要满足两个“同”,第一个“同”是所含字母相同,第二个“同”是相同字母的指数相同.注意:是不是同类项只与所含字母和字母的指数有关,而与该项系数无关(在系数不为零的前提下).如:-m2n与3m2n是同类项,x2y3与2y3x2是同类项.知识点2合并同类项(难点)★把多项式中的同类项合并成一项,叫做合并同类项.合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母部分不变.为了更好地掌握合并同类项的法则,可记住以下口诀:合并同类项,法则不能忘,只求系数和,字母指数不变样.知识点3去括号(难点)★去括号的法则:如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.★在去括号时需要注意:(1)去括号时,要将括号连同它前面的符号一起去掉;(2)在去括号时,首先要明确括号前是“+”还是“-”;(3)该变号时,各项都变号;不该变号时,各项都不变号.知识点4整式的加减(重点)★整式的加减的运算法则:一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.★应用整式的加减的运算法则进行化简求值时,一般先去括号、合并同类项,再代人字母的值进行计算,简记为“一化、二代、三计算”.课堂检测基本概念题1、若-5a 3b m +1与13b 2 a n +1是同类项,求(m -n )100的值.2、求下列代数式的值.(1)3(x 2-2x -1)-4(3x -2)+2(x -1),其中x =-3;(2)2x -y +(2y 2-x 2)-(x 2+2y 2),其中x =l ,y =-2.基础知识应用题3、化简:(32)[5(2)3]x y z x x y z x --+---+-.综合应用题4、一列火车上原有乘客(6a -2b )人,中途有一半乘客下车,又有若干乘客上车,此时车上共有乘客(10a -6b )人,则中途上车的乘客有多少人?当a =200,b =100时,中途上车的乘客有多少人?探索创新题5、规定两种新运算:a *b =a +b ,a #b =a -b ,其中a ,b 为有理数.化简(a 2b )*(3ab )+(5a 2b )#(4ab ),并求出当a =5,b =3时的值是多少?体验中考1、当a =1,b =2时,代数式a 2-ab 的值是 .2、把3+化简得 .学后反思附: 课堂检测及体验中考答案课堂检测1、分析:解:因为-5a 3b m +1与13 b 2 a n +1是同类项,所以12,1 3.m n +=⎧⎨+=⎩ 解得1001001,()(12) 1.2.m m n n =⎧-=-=⎨=⎩则2、分析:此题属于化简求值题,应先去括号,再合并同类项,最后代入求值.解:(1)3(x 2-2x -1)-4(3x -2)+2(x -1)=3x 2-6x -3-12x +8+2x -2=3x 2-16x +3.当x =-3时,原式=3×(-3)2-16×(-3)+3=27+48+3=78.(2)2x -y +(2y 2-x 2)-(x 2+2y 2)=2x -y +2y 2-x 2-x 2 -2y 2=-2x 2+2x -y .当x =1,y =-2时,原式=-2×12+2×1-(-2)=-2+2+2=2.3、 分析:去括号时,可以由里向外去,也可以由外向里去.解:(32)[5(2)3]x y z x x y z x --+---+-32(523)32(2)3224.x y z x x y z x x y z x y z x y z x y z x =-+---+--=-+--+-=-+---+=- 规律对这类题目而言,化简就是先去括号,然后合并同类项.去括号时,一方面注意括号前是“-”时,去掉括号,括号里各项都要改变符号;另一方面是括号前的系数要与括号里的每一项相乘,防止漏乘.4、解:由题意可知,中途上车的乘客人数为(10a -6b )-12(6a -2b )=10a -6b -3a +b =7a -5b . 当a =200,b =100时,中途上车的乘客有7× 200-5×100=900(人);答:中途上车的乘客有(7a -5b )人.当a =200,b =100时,中途上车的乘客有900人.点拨 此题要分清以下几个数量关系:(1)车上原有乘客人数;(2)中途下车的人数;(3)中途上车后车上现有人数;(4)中途上车的人数等于车上现有人数减去中途下车后车上剩余的人数.明确这几个数量关系是解决本题的关键.5、解:(a 2b )*(3ab )+(5a 2b )#(4ab )=a 2b +3ab +5a 2b -4ab =6a 2b -ab .当a =5,b =3时,原式=6×25×3-5×3=450-15=435.说明 读懂规则是解答此题的关键,根据不同的规则,正确列出常规算式.体验中考1、-1 解析:当a =1,b =2时,a 2-ab =12-1×2=-1.2、a +5 解析:3+=3+(3a -2a +2)=3+3a -2a +2=a +5.。
2.2整式的加减(1)-人教版七年级数学上册导学案

2.2整式的加减(1)备课时间: 授课时间: 授课班级: 学习目标:1、知识与技能:理解并掌握同类项的概念;掌握合并同类项的方法,能将简单的式子合并同类项.2过程与方法:经历探索合并同类项法则的过程,体会转化的思想方法.3、情感态度与价值观:培养探究精神,体会探究乐趣.学习重点:掌握合并同类项的方法.学习难点:理解合并同类项法则.学习方法:自主、合作、探究、展示.一、自主学习:自学教材63--65页:1、探究:(1)运用有理数的运算律:=⨯+⨯22522100 ,=−⨯+−⨯)2(252)2(100_________________.(2)根据(1)中的方法完成下面的运算,并说说其中的道理。
=−t t 252100( )t ,=+2223x x ( )2x ,=−2243ab ab ( )2ab观察上面(2)中的多项式的项100t 和-252t ,它们含有相同的字母t ,并且t 的指数都是1,23x 和22x 它们含有相同的字母x ,并且x 的指数都是2;23ab 和24ab −它们都含有字母b a ,,并且a 都是一次,b 都是二次,像这些所含的______ _______________项叫做同类项。
2、(1)说出下列各题的两项是不是同类项,为什么?y x 23与y x 24− ,abc 4与ab 4;y x 22.0与23.0xy ;mn 3−与nm 6;-125与13.(2)用画线的方法标出下列各多项式中的同类项:26358422−+−+−x x x x ; 222234234b a ab b a −−++(3)运用运算律把上面两个多项式中的同类项进行合并。
3、把多项式中的同类项合并成一项叫做 ;合并同类项后,所得 的系数是合并前各同类项的系数的 ,且 部分不变。
二、合作探究、交流展示:1、合并下列各式的同类项:(1)2251xy xy − (2)222234234b a ab b a −−++ 2、下列各组数中,是同类项的是( )xyz A −.与xyz1 B.yz x 22−与y x 23 t s C 24.与23ts − 32.y x D 与32x y 3、计算223a a +的结果是( )23.a A B.24a C.43a D.44a4、下列计算正确的是( )A.x x x x −=+−694B.02121=−a a C.x x x =−23 D.xy xy xy 32=− 5、已知y x 23和n m y x 是同类项,则=m ,=n三、拓展延伸:1、合并同类项:(1)a b ab 2251− (2)222532xy xy y x −+− (3)2237427a ab a ab −++−−2、若M =4x 2-2009x +10,N =3x 2-2009x +9,则M________N(填“>”、“<”、“=”).四、达标检测:1、计算=+−a a 23 ;=−22137xy xy _______________.2、已知n xy 2−与y x m 121+的和是一个单项式,则=m ,=n _________. 3、多项式863322−+−−xy y kxy x 不含xy 项,则=k ____________.4、求下列多项式的值:72322−+ab b a 22224232b a ab b a ++−,其中41,2==b a .五、教(学)后反思:答案一、自主学习:1、探究:(1)704,-704(2)252100−,23+,43− 道理:是逆用分配律 所含字母并且所含字母的指数2、(1)y x 23与y x 24− ,是同类项,因为它们所含字母并且所含字母的指数相同; abc 4与ab 4,不是同类项,因为所含字母不同; y x 22.0与23.0xy ,不是同类项,因为所含字母的指数不同; mn 3−与nm 6,是同类项,因为它们所含字母并且所含字母的指数相同; -125与13,是同类项,因为都是数字,是0次单项式。
人教版七年级上册数学:2.2《整式的加减》第一课时表格式教学设计

2.2《整式的加减》第一课时教学设计
一、教学内容分析:
本节课选自新人教版数学七年级上册§2.2节,是学生进入初中阶段后,在学习了用字母表示数,单项式、多项式以及有理数运算的基础上,对同类项进行合并、探索、研究的一个课题。
合并同类项是本章的一个重点,其法则的应用是整式加减的基础,也是以后学习解方程、解不等式的基础。
另一方面,这节课与前面所学的知识有千丝万缕的联系:合并同类项的法则是建立在数的运算的基础之上;在合并同类项过程中,要不断运用数的运算。
可以说合并同类项是有理数加减运算的延伸与拓广。
因此,这节课是一节承上启下的课。
二、学生情况分析:
本节课的教学内容是《整式的加减》(第1课时),是学生在学习了整式的有关概念之后的一节课。
在七年级上册的学习中,学生已经学了数的运算、字母表示数等内容,具备了学习本节所必须的基本运算技能。
在相关知识学习的过程中,学生已经经历了一些通过代数式的运算来解决问题、进行推理的活动,解决了一些简单的现实问题,获得了一定的运算能力;同时最亲爱以前的数学学习中,经历了很多合作学习的过程,具有了一定的合作学习的经验,具备了一定的合作和交流的能力。
三、教学过程
教学任务分析
教学流程安排。
人教版七年级数学上册2.2 整式的加减(1)导学案

2
与 3 ab 是
2 2 2
2
2
7. 在代数式 4x 4xy 8 y 3x 1 5x 6 7 x 中, 4 x 的同类项 是
2
,6 的同类项是
2
。
8.在 a (2k 6)ab b 9 中,不含 ab 项,则 k= 四、拓展延伸 1.若 2 x y 2.
k k 2
复习回顾
一、 自主学习 1、问题;每本练习本 x 元,小明买 5 本,小红买 3 本,两人一共花 了多少钱?小明比小红多花多少钱? 用代数式表示以上问题; (用两种表示方法) 2、运用有理数的运算定律填空: 100×2+252×2=( ) 100×(-2)+252×(-2)=( ) 100t+252t=( ) 你发现什么规侓了吗?与同伴交流一下。
与 3x y 的和为 5 x y ,则 k=
2
n
2
n
,n=
若-3x y 与
m-1 4
1 2 n2 x y 是同类项,求 m,n. 3
k 2
3.k 取何值时,3x y 与-x y 是同类项? 小结 4.若把(s+t)、(s-t)分别看作一个整体,指出下面式子中的同类项。 (1) (s+t)- (s-t)- (s+t)+ (s-t); (2)2(s-t)+3(s-t) -5(s-t)-8(s-t) +s-t。 五、课堂小结 谈谈学习本节课你有什么收获?。
2 2 2
1 3
2
) ) )
2 2
(2)3x y-2xy + xy - yx 。
1 3
2
3 2
2
三、跟踪训练 1. 1 、与 ( A.
1 2 x y 不仅所含字母相同,而且相同字母的指数也相同的是 2
七年级(人教版)数学上册导学案:2.2整式的加减(1)

⎩⎨⎧_______________:2_______________:1一、前置性小研究有理数可以进行加减计算,那么整式能否可以加减运算呢?怎样化简呢? 我们来看下面的问题:在西宁到拉萨路段,如果列车通过冻土地段的时间是t 小时, 速度是100千米/小时。
它通过非冻土地段所需的时间就是2.1t 小时,速度是120千米/小时。
则这段铁路的全长是100t+120×2.1t,即100t+252t 1.类比数的运算,我们应如何化简式子100t+252t 呢? (1)运用有理数的运算律计算:100×2+252×2= ;100×(-2)+252×(-2)= .(2)根据(1)中的方法完成下面的运算,并说明其中的道理.100t+252t= .2、 仿照上面的计算方法,你能做下面三个题吗?100t -252t = ;10x - 4x = ; 5ab 2-2ab 2= 。
3、 想一想:3x+ 2y 能仿照(2)题的方法计算吗?为什么? 二、合作探究1.观察以上2题每个多项式的项有什么特征?_________________________________________________________ 同类项: 特别提示:同类项应满足的两个条件有:说明:几个常数项也是同类项。
举几个同类项的例子: 归纳:合并同类项法则: 三、展示交流1、下面各组的两项是同类项的是( ) A. -xy 和xyz B. a 3b 和0.2a 3b C. 8x 2y 3和-8x 3y 2 D. x 3和y 32、 下列各组中,不是同类项的是( )。
A. -7x 2y 和21yx 2 B. 100和0.2 C. 0.4ab 和0.2ab 2 D. -3m 和 m3、若5xy m与2x n y 3是同类项,则m= ,n= .4、合并下列同类项:(1)12x x 20- (2) x+7x-5x (3)10y 2-0.5 y 2科目 数学班级:学生姓名 课题 2.2整式的加减(1) 课 型新授课时一课时 主备教师备课组长签字学习目标: 1.了解同类项、合并同类项的概念,掌握合并同类项法则。
七年级数学上册2.2整式的加减导学案1(新版)新人教版

多项式中只有_______才能合并,不是_______不能合并。
4、下列各题合并同类项的结果对不对?若不对,请改正。
(1)2x2+3x2=5x4;(2)3x+2y=5xy;(3)7x2-3x2=4;(4)9a2b-9ba2=0。
【随堂检测】
1、下列各组式子中,是同类项的是()
A、 与 B 、 与 C、 与 D、 与
2、在下列各组式子中,不是同类项的一组是()
A、2,-5 B、-0.5xy2,3x2y
C、-3t,200πt D、ab 2,-b2a
3、写出一个与-3x2y是同类项的式子____________.
4、已知xmy2与-5ynx3是同类项,则m=,n=.
5.判断下列说法是否正确,正确地在括号内打“√”,错误的打“×”。
(1)3x与3mx是同类项。( ) (2)2ab与-5ab是同类项。( ) (3)3x2y与- yx2是同类项。( ) (4)5ab2与-2 ab2c是同类项。( )
(5)23与32是同类项。( ) (6)15abc与 是同类项()
知识点二合并同类项
(1)100×2+252×2=_________ _,
(2)100×(-2)+252×(-2)=__________,
(3)100t+252t=__________,
思路点拨:根据逆用乘法的分配律可得。
2.请根据上面得到结论的方法探究下面各式的结果:
(1)100t-252t=()t
(2)3x2+2x2= ( )x2
5、指出下列多项式中的同类项:
(1)3x-2y+1+3y-2x-5;(2)3x2y-2xy2+ xy2- yx2;
人教版七年级数学上正式的加减教案2.2 整式的加减(1)导学案含配套课时作业

七年级数学教学案 (课时3) 班级_________姓名 _____________ 设计人:黄本华 第二章 《整式的加减》52.2 整式的加减(1)【教学目标】1.理解同类项的概念;2.掌握合并同类项的法则,能熟练进行同类项的合并.3.在经历了从具体问题抽象出同类项、合并同类项法则的过程中,发展抽象概括能力. 探究一:同类项所含 ,并且 也相同的项叫做同类项. 几个常数项也是 . 注意1.字母要完全相同;2.相同字母的指数也必须相同. 探究二:合并同类项把多项式中的同类项合并成一项,即 作为新的系数,而 不变,叫做 合并同类项.注意 1.字母和字母的指数不变;2.系数相加作为新的系数;3.合并同类项的依据是分配律.【典型例题】例1判断下列各组中的两项是不是同类项,并说明为什么?(1)220.20.2x y xy 与;(2) 44abc ac 与;(3)mn 与-nm ;(4)12512-与;(5)221145s t ts 与.练习:1.下面各题中的两项是不是同类项?若不是,请说明理由.(1) 233212a b b a -与; (2)2323a a 与 ; (3)3333a b ab 与; (4)3a 与35; (5)32-与23.2.填空:(1)如果22mx y -与23y x 是同类项,那么m = .(2)如果25mn x y -与213n y x +-是同类项,那么m = ,n = . 例2 先找出下列多项式中的同类项,然后合并同类项:(1)22485362x x x x -+-+-; (2)222243243a b ab a b ++--.练习:1.(口答)合并下列各式的同类项: (1)54x x += ;(2)76ab ba -+= ; (3)57x x --= ;(4)mn mn += . 2.下列各题合并的结果对不对,指出错在哪里?(1)325a b ab +=; (2)22532y y -=; (3)22245x y y x x y -=-; (4)2a a a +=; (5)770ab ab -=; (6)225325x x x +=. 3.合并下列各式的同类项(1)22610125x x x x -+-; (2)222232x y xy yx y x -+-.例3把()()a b x y +-与各当作一个因式,合并各式中的同类项:(1)7a b -+()7()6()a b a b -+++; (2)223()()()6()x y x y x y x y ---+-+-.练习:(1)2224()2()7()a b a b a b +++-+; (2)76n nx x -+(n 是正整数);(3)113786n n n n x x x x ++--++(n 是正整数).例4先合并再求值:22113333a abc c a c +--+,其中16a =-,2b =,3c =-.【巩固练习】1.若3mnx y 与312xy -是同类项,则m = ,n = . 2.合并22381073x x x x ---++中的同类项得 .3.若23322353x y ay x x y +=,则a = .4.若43x y 与232m nx y -可以合并,则mn = . 5.合并下列各式的同类项:(1)433352a a a -+; (2)323322322x x x x x -+-+-;6.求下列各式的值:(1)2225435256x x x x x +----+,其中3x =-.(2)22347321x x x x -+-++,其中2x =.(3)222243322xy x xy y x xy y x --++--+其中13115x =,1y =-.。
人教版七年级数学上册整式的加减(第1课时)教案

(2)各项的系数是多少?
(3)那些项可以合并成一项?为什么?
【设计意图:通过视察、讨论、类比得出合并同类项的方法,并且进行适当的巩固.体会合并同类项的过程就是化简多项式的过程,让学生进一步了解化简过程的根据.】
师生活动:由一学生板演,其他同学独立完成.师生共同订正板演过程,教师详细讲授,并板书示范过程.教师引导学生类比有理数的运算,共同探究归纳合并同类项的法则.教师强调:一般情况,先将多项式按照某个字母进行降幂或升幂排列.
师生活动:学生独立思考,逐一完成各个问题.教师巡回指点,待学生完成后,抽学生口答,其他学生判断评价.
教师强调:
(1)几个单项式是不是同类项与字母和字母的指数有关,与单项式的系数无关.
(2)几个单项式是不是同类项与字母的顺序无关.
想一想:你能写出几个单项式是同类项的例子吗?
【设计意图:这类开放性问题的答案不唯一,但是答案有共性,可拓展学生的思维,帮助每个学生以自己所学的知识为基础,进一步巩固同类项的定义,建构自己的理解,培养学生应用知识的能力.】
(根据实际情况,如果学生已经掌握很好,可以不用这一环节.)
师生活动:学生自己动手独立完成后,小组内交流,视察写出的结果是否符合要求,注意思考答案的共性,教师参与指点.
三、释疑解难、பைடு நூலகம்讲点拨
试着把多项式4x2+2x+7+3x-8x2-2合并同类项:
如果学生对于合并同类项已经掌握很好,教师可以直接让学生处理即可;如果学生感到有些难度,师生共同分析,教师尝试以下问题的引导.
师板书法则,并强调:
(1) 合并的前提是同类项.
(2) 合并指的是系数相加,字母和字母的指数保持不变.
人教版七年级数学上册2.2《整式的加减》教案

-难点二:多项式的简化
-学生可能在合并多项式骤进行,先找出同类项,再进行合并。
-难点三:整式的加减法法则的应用
-学生可能在运用法则时出现混淆,如误用结合律。
-教学策略:通过对比练习,让学生在具体运算中体会法则的应用。
3.重点难点解析:在讲授过程中,我会特别强调同类项的识别和合并,以及多项式简化的方法。对于难点部分,我会通过具体例题和步骤分解来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与整式加减相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的计算活动。这个活动将演示如何将实际问题转化为整式的加减运算。
-难点四:实际问题中的应用
-学生可能不知道如何将实际问题转化为整式的加减问题。
-教学策略:提供实际情境,引导学生学会从问题中抽象出数学模型。
四、教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《整式的加减》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过需要计算两个或多个物品总量的问题?”(例如:购物时计算多件商品的总价)这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索整式的加减的奥秘。
此外,我在课堂上设计了一些开放性问题,旨在启发学生的思维,引导他们主动探索。从学生的回答来看,他们对于整式的加减在实际生活中的应用有了更深的理解。然而,我也发现,部分学生在面对这类问题时,思路不够开阔,可能是因为他们还没有完全将理论知识与实际情境结合起来。因此,我打算在接下来的教学中,多举一些生活中的实例,帮助学生更好地理解和运用整式加减。
人教版七年级数学上册《2.2整式的加减第1课时》教 案

第二章整式的加减2.2 整式的加减第1课时一、教学目标1.理解同类项的概念.2.掌握合并同类项的方法,能通过合并同类项进行多项式的化简.二、教学重点及难点重点:同类项的概念及合并同类项的法则,感受“数式通性”和类比的思想.难点:正确判断同类项,准确合并同类项.三、教学用具相关资源电脑、多媒体、课件四、相关资源微课、知识卡片五、教学过程(一)创设情境问题:青藏铁路西宁到拉萨路段,列车在冻土上的行驶速度是100km/h,在非冻土地段的行驶速度是120km/h,列车通过非冻土地段所需时间是通过冻土地段所需时间的2.1倍,如果通过冻土地段需要t h,你能用含t的式子表示这段铁路的全长吗?师生活动:学生尝试解答.如果学生得到100t+120×2.1t=100t+252t,教师可以追问:这个式子的结果是多少?你是怎样得到的?说明其中的道理.如果学生直接得到352t,教师可以追问:这个结果是怎样得到的?说明其中的道理.此环节教师应关注:(1)学生能否正确列式;(2)学生能否依据分配律化简100t+252t,并说明其中的道理;(3)学生能否体会在实际生活中,经常遇到含有字母的式子的运算问题.教师归纳:在实际生活中,经常遇到含有字母的式子的运算问题,学习含有字母的式子的运算是实际需要,整式的运算是建立在数的运算基础之上的.设计意图:引入实际问题,使学生感受到含有字母的式子的运算是实际需要.理解化简100t+252t的方法是运用有理数的运算律“分配律”,初步体会“数式通性”,促使学生的学习形成正迁移.(二)合作探究1.整式的运算是建立在数的运算基础之上的,对于有理数的运算是怎样做的呢?整式的运算与有理数的运算有什么联系?(1)运用运算律计算:100×2+252×2=,100×(-2)+252×(-2)=;师生活动:学生尝试回答,根据分配律可得:100×2+252×2=(100+252)×2=352×2=704,100×(-2)+252×(-2)=(100+252)×(-2)=-352×2=-704.教师追问:式子100t+252t与问题中的两个算式有什么联系?你是如何理解化简式子100t +252t的方法的?学生尝试解释,教师根据学生回答情况进行引导.教师引导学生归纳:(1)算式100×2+252×2和100×(-2)+252×(-2),式子100t+252t具有相同的结构,由于字母t代表的是一个因(乘)数,因此根据分配律应有100t+252t =(100+252)t=352t;(2)由于整式中的字母表示数,因此可以类比数的运算,运用数的运算法则和运算定律进行整式的运算.设计意图:通过用分配律进行有理数的运算,帮助学生理解用分配律化简式子100t+252t 的方法,为进一步类比学习整式的运算提供方法上的借鉴.通过引导学生观察比较,发现三个算式的联系,理解由于式子100t+252t中的字母表示数,因此可以依据分配律对式子进行化简,理解整式的运算与有理数的运算具有一致性,为更一般的同类项的合并提供方法上的指导.体会由“数”到“式”是由特殊到一般的思想方法,初步感受“数式通性”和类比的数学思想.(2)类比式子100t+252t的运算,化简下列式子:①100t-252t;②3x2+2x2;③3ab2-4ab2.师生活动:学生尝试独立解答,然后学生代表发言.此环节教师应关注:(1)学生在计算100t-252t时,是否能注意分配律的使用,正确区分运算符号和性质符号;(2)学生是否能正确运用分配律化简式子时“系数相加,字母连同它的指数不变”的道理.设计意图:进一步引导学生类比前面关于式子100t+252t的化简,讨论更一般的同类项(多项式中的项的次数高于1,字母不止一个等)的合并,进一步理解分配律的运用,体会“数式通性”和类比的数学思想.通过几组不同形式的同类项,感受不同类型式子的组成,突出同类项的特点,为归纳同类项的概念和合并同类项法则做好铺垫.2.观察多项式100t+252t,100t-252t,3x2+2x2,3ab2-4ab2.(1)上述各多项式的项有什么共同特点?(2)化简上述多项式,你能从中得出什么规律?师生活动:学生先独立思考,然后小组合作讨论,小组代表发言.教师巡视,指导学生归纳和表达.在讨论交流的基础上,教师引导学生归纳同类项的定义、合并同类项的定义和法则.此环节教师应关注:(1)学生能否理解和判断同类项的两条标准:①含有相同的字母;②相同字母的指数也相同;(2)学生能否理解合并同类项的要点,一是“字母连同它的指数不变”,既包括字母不变,也包含字母的指数不变,二是“系数相加”.设计意图:在观察、比较中,发现各多项式的项的共同特征,分析运算特点,归纳出同类项、合并同类项的定义及合并同类项的法则.3.你能举出同类项的例子吗?师生活动:学生代表举出同类项的例子,由其他学生合并所给出的同类项.教师在评价学生举例后,追问合并同类项的结果.设计意图:通过举例,加深对同类项概念和合并同类项法则的理解.4.化简多项式的一般步骤是什么?通过如下问题进行说明:找出多项式中的同类项,并进行合并.师生活动:学生尝试口述解题,教师示范解答过程.解:4x2+2x+7+3x-8x2-2=4x2-8x2+2x+3x+7-2 (交换律)=(4x2-8x2)+(2x+3x)+(7-2)(结合律)=(4-8)x2+(2+3)x+(7-2)(分配律)=-4x2+5x+5.教师引导学生归纳化简多项式的一般步骤:(1)找出同类项并做标记;(2)运用交换律、结合律将多项式的同类项结合;(3)合并同类项;(4)按同一个字母的降幂(或升幂)排列.此环节教师应强调:(1)运用交换律、结合律将多项式变形时,不要丢掉各项系数的符号;(2)不要漏项;(3)运算结果通常按一个字母的指数由大到小(降幂)或者由小到大(升幂)的顺序排列.设计意图:归纳化简多项式的一般步骤.(三)例题分析例1 合并下列各式的同类项:(1)2215xy xy -; (2)22323232x y x y xy xy -++-;(3)222243244a b ab a b ++--.师生活动:学生先独立完成,然后互相纠错、评价,学生代表板演,教师巡视指导. 解:(1)原式=2214155xy xy ⎛⎫-= ⎪⎝⎭; (2)原式=()()22223232x y xy x y xy -++-=-+;(3)原式=()()222443422a b ab b ab -+-+=-+. 例2 (1)求多项式22225432x x x x x ++---的值,其中1;2x =; (2)求多项式22113333a abc c a c ++--的值,其中1236a b c =-==-,,.师生活动:学生独立完成,教师巡视指导.可以引导学生对以下两种方法进行比较:直接代入求值,先化简再求值,看哪种方法更简单.解:(1)原式=()()2213452=2x x x ++-----. 当12x =时,原式=15222--=-. (2)原式=()2113333a abc c abc ⎛⎫+++= ⎪⎝⎭--. 当16a =-,2b =,3c =-时,原式=()12316⎛⎫-⨯⨯-= ⎪⎝⎭. 例3 (1)水库中水位第一天连续下降了a 小时,每小时平均下降2 cm ;第二天连续上升了a 小时,每小时平均上升0.5 cm ,这两天水位总的变化情况如何?(2)某商店原有5袋大米,每袋大米为x 千克.上午卖出3袋,下午又购进同样包装的大米4袋.进货后这个商店有大米多少千克?师生活动:教师引导学生回忆第一章用正负数代表具有相反意义的量,然后由学生独立完成.解:(1)-2a +0.5a =(-2+0.5)a =-1.5a (cm ).答:这两天水位总的变化情况为下降了1.5a cm .(2)把进货的数量记为正,售出的数量记为负.进货后这个商店共有大米5x -3x +4x =(5-3+4)x =6x (千克).设计意图:加深对同类项的概念和合并同类项法则的理解和运用,提高运算能力.(四)练习巩固练习1 判断下列说法是否正确,正确的在括号内打“√”,错误的打 “×”.(1)3x 与3mx 是同类项;( )(2)2ab 与-5ab 是同类项;( )(3)3xy 2与212y x -是同类项;( ) (4)5a 2b 与-2a 2bc 是同类项;( )(5)23与32是同类项.( )答案:(1)×;(2)√;(3)√;(4)×;(5)√.设计意图:进一步巩固同类项的概念练习2 填空:(1)若单项式2x m y 3与单项式-3x 2y n 是同类项,则m =________,n =________.(2)单项式-6ab 2c 3的同类项可以是________(写出一个即可).(3)下列运算中,正确的是________(填序号).2222222223553232651a a a a b ab ab x x x m m +=-= -=-=①;②;③;④.(4)多项式2222223684925ab a b ab a b ab ab --+-+-,其中与2ab 是同类项的是________;与22a b 是同类项的是________;将多项式中的同类项合并后,结果是________.答案:(1)2;3. (2)ab 2c 3;(3)③;(4)2282ab ab -,;222264a b a b -,; 2222665a b ab ab ----.设计意图:进一步巩固同类项的概念和合并同类项法则.五、课堂小结教师与学生一起回顾本节课主要内容,并请学生回答一下问题:(1)本节课学了哪些主要内容?(2)你能举例说明同类项的概念吗?(3)举例说明合并同类项的方法.(4)本节课主要运用了什么思想方法研究问题?设计意图:通过小结,使学生梳理本节课所学内容,掌握本节课的核心——同类项的概念、合并同类项的概念好法则,感受“数式通性”和类比的数学思想.六、板书设计2.2 整式的加减(1)同类项1.同类项的定义:一个多项式中,所含字母相同,并且相同字母的指数也都相同的项叫做同类项.2.合并同类项法则:合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变.。
数学:2.2《整式的加减》 精品导学案(人教版七年级上)

数学:2.2《整式的加减》学案(人教版七年级上)【学习目标】:让学生从实际背景中去体会进行整式的加减的必要性,并能灵活运用整式的加减的步骤进行运算。
【学习重点】:正确进行整式的加减。
【学习难点】:总结出整式的加减的一般步骤。
【导学指导】一、知识链接1.多项式中具有什么特点的项可以合并,怎样合并?2.如何去括号,它的依据是什么?去括号、合并同类项是进行整式加减的基础.二、自主学习例6.计算:(1)(2x-3y)+(5x+4y)(2)(8a-7b)-(4a-5b).(解答由学生自己完成,教师巡视,关注学习有困难的学生)。
.例7.一种笔记本的单价是x(元),圆珠笔的单价是y(元),小红买这种笔记本3本,买圆珠笔2枝;小明买这种笔记本4个,买圆珠笔3枝,买这些笔记本和圆珠笔,小红和小明共花费多少钱?米).(1)做这两个纸盒共用料多少平方厘米?(2)做大纸盒比小纸盒多用料多少平方厘米?(学生小组学习,讨论解题方法.)(思路点拨:让学生自己归纳整式加减运算法则,发展归纳、表达能力.一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.)例9.求12x-2(x-13y2)+(-32x+13y2)的值,其中x=-2,y=23.(思路点拨:先去括号,合并同类项化简后,再代入数值进行计算比较简便,去括号时,特别注意符号问题。
)【课堂练习】1.课本P70页练习1、2、3题。
【要点归纳】:1.整式的加减实际上就是去括号、合并同类项这两个知识的综合。
2.整式的加减的一般步骤:①如果有括号,那么先算括号。
②如果有同类项,则合并同类项。
3.求多项式的值,一般先将多项式化简再代入求值,这样使计算简便。
【拓展训练】:1.如果a-b=12,那么-3(b-a)的值是().A.-35B.23C.32D.162.一个多项式与x2-2x+1的和是3x-2,则这个多项式为().A.x2-5x+3 B.-x2+x-1 C.-x2+5x-3 D.x2-5x-13 3.先化简再求值:4x2y-+1,其中x=2,y=-12;【总结反思】:教学反思在新课改的形式下,如何激发教师的教研热情,提升教师的教研能力和学校整体的教研实效,是摆在每一个学校面前的一项重要的“校本工程”。
人教版七年级数学上册导学案:2.2整式的加减(一)

课型:新课学时:1学时主备人:周朝兰学习目标:1.理解同类项的概念,在具体情景中,认识同类项。
2.初步体会数学与人类生活的密切联系。
3.会合并同类项学习重点:同类项的概念学习难点:同类项合并的方法.一.自主学习1.运用有理数的运算律计算:(1)100×2+252×2=__________,(2)100×(-2)+252×(-2)=__________,(3)100t+252t=__________,思路点拨:根据逆用乘法对加法的分配律可得。
2.请根据上面得到结论的方法探究下面各式的结果:(1)100t—252t=()t(2)3x2+ 2 x2 = ( ) x2(3)3ab2- 4 ab2 = ( ) ab2上述运算有什么共同特点,你能从中得出什么规律?二.合作探究活动1:同类项的定义:1. 观察:3x 2 和 2 x 2 ; 3ab 2 与 -4 ab 2 在结构上有哪些相同点和不同点?注:代数式-4a 2b 与32ab 都含字母,并且都是一次,都是二次,因此-4a 2b 与32ab 是 .若两个单项式为同类项,必须满足几点?2.归纳:_______________________________________________叫做同类项____________________也是同类项。
如3和-5是同类项活动2:1、判断下列说法是否正确,正确地在括号内打“√”,错误的打“×”。
(1)3x 与3mx 是同类项。
( ) (2)2a b 与-5a b 是同类项。
( )(3)3x 2y 与-31yx 2是同类项。
( ) (4)5a b 2与-2a b 2c 是同类项。
( )(5)23与32是同类项。
( )2、下列各组式子中,是同类项的是( )A 、y x 23与23xy -B 、xy 3与yx 2-C 、x 2与22xD 、xy 5与yz 53、在下列各组式子中,不是同类项的一组是()A 、 2 ,-5B 、-0.5xy 2, 3x 2yC 、-3t ,200πtD 、ab 2,-b 2a4、已知x m y 2与-5y n x 3是同类项,则m=,n=。
人教版数学七年级上册2.2 《整式的加减》导学案(无答案)
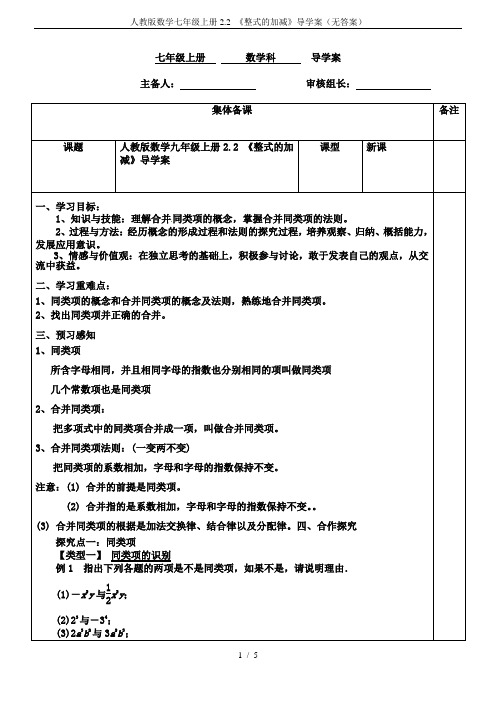
探究点四:合并同类项的应用
例5有一批货物,甲可以3天运完,乙可以6天运完,若共有x吨货物,甲乙合作运输一天后还有________吨没有运完.
解析:甲每天运货物的 ,乙每天运货物的 ,则两个人合作运输一天后剩余的货物为x- x- x= x吨,故填 x.
例2若-5x2ym与xny是同类项,则m+n的值为()
A.1B.2C.3D.4
解析:∵-5x2ym和xny是同类项,
∴n=2,m=1,m+n=1+2=3,
故选C.
方法总结:注意掌握同类项定义中的两个“相同”:(1)所含字母相同;(2)相同字母的指数相同,解题时易混淆,因此成了中考的常考点.
探究点二:合并同类项
探究点三:化简求值
例4化简求值:2a2b-2ab+3-3a2b+4ab,其中a=-2,b= .
解析:原式合并同类项得到最简结果,把a与b的值代入计算即可求出值.
解:2a2b-2ab+3-3a2b+4ab=(2-3)a2b+(-2+4)ab+3=-a2b+2ab+3.将a=-2,b= 代入得原式=-(-2)2× +2×(-2)× +3=-1.
方法总结:体现了数学在生活中的运用.解决问题的关键是读懂题意,找到所求的量之间的关系.
五、检查反馈:
1.化简﹣2a+3a的结果是( )
A.﹣aB.aC.5aD.﹣5a
2.化简:a+a=( )
A.2B.a2C.2a2D.2a
3.如果单项式﹣xa+1y3与 是同类项,那么a、b的值分别为( )
A.a=2,b=3B.a=1,b=2C.a=1,b=3D.a=2,b=2
人教版七年级数学上册2.2.1《整式的加减(1)》教案

人教版七年级数学上册2.2.1《整式的加减(1)》教案一. 教材分析《整式的加减(1)》是人教版七年级数学上册第二章的内容,主要讲述了整式的加减运算。
本节课的内容是学生学习更高级数学知识的基础,对于培养学生的逻辑思维和运算能力具有重要意义。
二. 学情分析七年级的学生已经掌握了整数和分数的加减法运算,具备一定的数学基础。
但他们在处理整式加减法时,可能会遇到符号混乱和运算顺序出错等问题。
因此,在教学中需要注重引导学生理清运算思路,培养他们的运算习惯。
三. 教学目标1.让学生掌握整式的加减法运算规则。
2.培养学生正确、迅速的整式加减运算能力。
3.培养学生的逻辑思维和运算能力。
四. 教学重难点1.重点:整式的加减法运算规则。
2.难点:整式加减法在实际应用中的运算顺序和思路。
五. 教学方法采用“问题驱动”的教学方法,通过引导学生发现问题、分析问题、解决问题,从而培养学生独立思考和合作交流的能力。
同时,运用“案例教学”方法,以具体案例为载体,让学生在实际操作中掌握整式加减法运算。
六. 教学准备1.准备相关案例和练习题。
2.制作PPT,展示整式加减法的运算过程。
七. 教学过程1.导入(5分钟)通过一个实际案例,引导学生思考如何计算整式的加减法。
例如,计算以下表达式的值:(2x + 3) + (x - 1)2.呈现(10分钟)呈现整式加减法的运算规则,引导学生总结出:–同类项的加减法:系数相加(减),字母及指数不变。
–不同类项的加减法:先将它们化为同类项,再进行加减。
3.操练(10分钟)让学生分组讨论,找出以下表达式的运算顺序和步骤:(2x + 3) - (x - 1)每组给出答案后,教师进行点评和讲解。
4.巩固(10分钟)让学生独立完成以下练习题:1.计算以下表达式的值:(3x - 2) + (x + 4)2.计算以下表达式的值:(4y - 5) - (2y + 1)教师巡回指导,解答学生遇到的问题。
5.拓展(10分钟)引导学生思考:在实际应用中,如何运用整式加减法解决问题?举例说明。
人教版七年级上册数学:2.2《整式的加减》导学案(两套)

整式的加减一、学习目标1、了解并掌握合并同类项的概念、去括号法则;2、利用整式的加减法则对整式进行加减运算.二、问题与例题问题(一)填空,并解释等式成立的依据.(1)x +2x +4x -3x =______;___________ (2)3x 2+2x 2=________; ________(3)3ab 2-4ab 2 =_______;___________问题(二): 观察下列式子的变形,你能发现什么?(1)+120(t -0.5)=+120t -60(2)-120(t -0.5)=-120t +60例1:1.化简下列各式:(1)8a +2b +(5a -b ); (2)(5a -3b )-3(a 2-2b ).例2:计算(1)(-x 2+3xy -21y 2)-(-21x 2+4xy -23y 2);(2)(5y +3x -15z 2)-(12y -7x +z 2).三、目标检测1、下列算式正确的是 ( )A 、224=-a aB 、2222a a a -=--C 、 3243a a a =+D 、a a a =-222.下列说法中正确的是( )(A )x 的系数是0 (B )22与42不是同类项(C )-3的次数是0 (D )25x yz 是三次单项式3.下列判断中正确的是( )(A )3a 2bc 与bca 2不是同类项 (B )52n m 不是整式 (C )单项式-x 3y 2的系数是-1 (D )3x 2-y +5xy 2是二次三项式4.下列说法中正确的是( )(A )x 的系数是0 (B )22与42不是同类项(C )y 的次数是0 (D )25x yz 是三次单项式5.a 3b 2c 的系数是 ,次数是 ;6.一个多项式加上-2+x -x 2得到x 2-1,则这个多项式是 。
7.-2x 2y m 与x n y 3是同类项,则 m = ,n = ;四、配餐作业A 组基础巩固1.3ab -5a 2b 2+4a 3-4按a 降幂排列是 ;2.(-a -b +c)(a -b +c)=-[a +( )][a -( )]。
人教版七年级数学上册导学案2.2整式的加减

新人教版七年级数学上册导学案2.2整式的加减学习目的和要求:1.理解合并同类项的概念,掌握合并同类项的法则。
2.经历概念的形成过程和法则的探究过程,培养观察、归纳、概括能力,发展应用意识。
3.渗透分类和类比的思想方法。
4.在独立思考的基础上,积极参与讨论,敢于发表自己的观点,从交流中获益。
学习重点和难点:重点:正确合并同类项。
难点:找出同类项并正确的合并。
一、自主学习1、问题:为了搞好班会活动,李明和张强去购买一些水笔和软面抄作为奖品。
他们首先购买了15本软面抄和20支水笔,经过预算,发现这么多奖品不够用,然后他们又去购买了6本软面抄和5支水笔。
问:①他们两次共买了多少本软面抄和多少支水笔?②若设软面抄的单价为每本x元,水笔的单价为每支y元,则这次活动他们支出的总金额是多少元?2.合并同类项的定义:【提示】(讨论问题2)可根据购买的时间次序列出代数式,也可根据购买物品的种类列出代数式,再运用加法的交换律与结合律将同类项结合在一起,将它们合并起来,化简整个多项式,所得结果都为(21x+25y)元。
由此可得:把多项式中的同类项合并成一项,叫做合并同类项。
二、合作探究1、找出多项式3x2y-4xy2-3+5x2y+2xy2+5种的同类项,并用交换律、结合律、分配律合并同类项。
根据以上合并同类项的实例,讨论归纳,得出合并同类项的法则:把同类项的系数相加,所得的结果作为系数,字母和字母指数保持不变。
2、下列各题合并同类项的结果对不对?若不对,请改正。
(1)2x2+3x2=5x4;(2)3x+2y=5xy;(3)7x2-3x2=4;(4)9a2b-9b a2=0。
3、合并下列多项式中的同类项:①2a2b-3a2b+0.5a2b;②a3-a2b+a b2+a2b-a b2+b3;③5(x+y)3-2(x-y)4-2(x+y)3+(y-x)4。
【提示】(用不同的记号如横线、双横线、波浪线等标出各同类项,会减少运算错误,当然熟练后可以不再标出。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.2 整式的加减
第1课时
1.知道同类项的定义、合并同类项的法则,能运用合并同类项的法则进行有关运算.
2.认识升(降)幂排列,会将一个多项式进行升(降)幂排列.
3.经历探究合并同类项法则的过程,体会类比的数学思想.
4.重点:同类项的概念、合并同类项的法则,以及运用法则进行相关计算.
【旧知回顾】用字母表示乘法分配律:a(b+c)=ab+ac.
【问题探究】阅读教材P62~65“例3”,回答下列问题.
(方法指导:类比数的运算学习式的运算,学习合并同类项的法则.)
探究一:逆用乘法分配律计算:
(1)100×2+252×2=(100+252)×2=704;
(2)100×(-2)+252×(-2)=(100+252)×(-2)=-704;
(3)100t+252t=(100+252)t=352t;
(4)100t-252t=(100-252)t=-152t;
(5)3x2+2x2=(3+2)x2=5x2;
(6)3ab2-4ab2=(3-4)ab2=-ab2.
【归纳】在逆用乘法分配律计算时,共有的因数可以是数,也可以是字母.
【预习自测】计算2a+5a,结果正确的是(B) A.10a B.7a C.10a2 D.7a2
梳理:所含字母相同,并且相同字母的指数也相同的项叫作同类项.
【讨论】4ab2和ba2是同类项吗?为什么?
不是,对应a和b的指数不一样.
【预习自测】判断下列说法是否正确,正确的在括号内打“√”,错误的打“×”.
(1)3x与3mx是同类项.(×)(2)2ab与-5ab是同类项.(√)
(3)x3与53是同类项.(×)(4)23与32是同类项.(√)
探究二:
1.运用交换律、结合律和分配律将下面多项式中的同类项进行合并.
5x-x2-7+3x+2x2+2
=5x+3x-x2+2x2-7+2
=(5x+3x)+(-x2+2x2)+(-7+2)
=(5+3)x+(-1+2)x2+(-7+2)
=8x+x2-5.
2.将多项式8x+x2-5按x的指数从大到小的顺序排列.
x2+8x-5.
【归纳】1.(1)把多项式中的同类项合并成一项,叫作合并同类项;
(2)合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母部分不变.
2.(1)把一个多项式的各项按照字母x的指数从大到小的顺序排列,叫作按字母x 的降幂排列;
(2)把一个多项式的各项按照字母x的指数从小到大的顺序排列,叫作按字母x 的升幂排列.
【预习自测】1.合并同类项:3a2-2a+4a2-7a=7a2-9a;
2.把多项式3x2-x3-5+x按x的降幂排列为-x3+3x2+x-5.
探究三:当a=时,求多项式5a2-5a+4-3a2+6a-5的值.
用两种方法计算,思考哪种比较简便.(1)将a的值直接代入多项式中计算;(2)先化简多项式,然后将a的值代入计算.
两种方法的结果都等于0.第(2)种.
【归纳】求多项式的值时,一般先合并同类项,再代入求值,这样做比较简便.
互动探究1:下列各组式子中的两个单项式,属于同类项的是(D)
A.6xy和6xyz
B.x3与y3
C.2a2b与-ab2
D.-0.85xy4与y4x
[变式训练1]如果2a x b3与-3a4b y是同类项,那么x=4,y=3.
[变式训练2]如果4x m y3与-x2y n-1的和是单项式,那么m=2,n=4.
互动探究2:合并下列多项式中的同类项:(1)2a2b-a2b;(2)2a2-3ab+4b2+5ab-6b2.
解:(1)原式=a2b;(2)原式=2a2+2ab-2b2.
[变式训练]若关于x的多项式5x3-2mx2-2x2+3合并同类项后是三次二项式,则m满足的条件是m=-1.
【方法归纳交流】如果两个同类项的系数互为相反数,那么它们合并后的结果等于0. 互动探究3:将多项式-3ab+a2-4b2按a的升幂排列为-4b2-3ab+a2.
【方法归纳交流】按a的升幂(降幂)排列时,字母b看作常数.
互动探究4:求多项式3x2+4x-2x2+x+x2-3x-1的值,其中x=-2.
解:原式=2x2+2x-1.当x=-2时,原式=2×(-2)2+2×(-2)-1=3.
互动探究5:学校餐厅有10a桶花生油,周一用去1.5a桶,周二用去3.5a桶,周三运进7a桶,现在还有12a桶花生油.
见《导学测评》P27。
