2015年广州市高二数学竟赛试题及答案
广东省广州市2015-2016学年高二学业水平测试数学试题 含解析

2015-2016学年度广州市高中二年级学生学业水平测试2015年12月24日一、选择题:本大题共10小题,每小题5分.1。
已知集合M =-1,0,1{},{}xxx N ==2|,则M ÇN =()A.1{} B 。
0,1{} C 。
-1,0{} D 。
-1,0,1{}2.已知等比数列a n{}的公比为2,则a 4a 2值为()A. 14B 。
12C 。
2 D.43。
直线l 过点1,-2(),且与直线2x +3y -1=0垂直,则l 的方程是()A.2x +3y +4=0B.2x +3y -8=0 C 。
3x -2y -7=0 D.3x -2y -1=04.函数f x ()=12æèçöø÷x-x +2的零点所在的一个区间是()A.-1,0() B 。
0,1() C.1,2() D 。
2,3()5.已知非零向量与的方向相同,下列等式成立的是()BD6.要完成下列两项调查:(1)某社区有100户高收入家庭,210户中等收入家庭,90户低收入家庭,从中抽取100户调查消费购买力的某项指标;(2)从某中学高二年级的10名体育特长生中抽取3人调查学习负担情况,应采取的抽样方法是()A 。
(1)用系统抽样法,(2)用简单随机抽样法C 。
(1)用分层抽样法,(2)用简单随机抽样法 D.(1)(2)都用分层抽样法7.设x ,y 满足约束条件⎪⎩⎪⎨⎧≤-+≥-≥+,03,02,01y x x y x ,则z =x -y 的最大值为()A. 3 B 。
1 C 。
1- D 。
5- 8。
某几何体的三视图及其尺寸图,则该几何体的体积为()A. 6 B 。
9 C 。
12 D. 18 9。
函数f x ()=12-cos2p 4-x æèçöø÷的单调增区间是() A 。
2k p -p 2,2k p +p 2éëêùûú,k ÎZ B. 2k p +p 2,2k p +3p 2éëêùûú,k ÎZC.k p +p 4,k p +3p 4éëêùûú,k ÎZ D.k p -p 4,k p +p 4éëêùûú,k ÎZ 10.设a >1,b >2且ab =2a +b 则a +b 的最小值为()A 。
2015全国高中数学联赛广东初赛试题及答案

y − y1 =
y2 − y1 ( x − x1 ). 当 y = 0 时, x2 − x1
2 x2 − x1 y2 − y12 y2 yy y1 + 1 = − 1 2 , y1 + x1 = − y2 − y1 2 p ( y2 − y1 ) 2p 2p yy ………. 5 分 所以 | OC |= − 1 2 . 2p 另一方面,抛物线在 A、B 两点的切线方程分别为: yy1 = p ( x + x1 ), yy2 = p ( x + x2 ), yy ………. 10 分 求得其交点的横坐标为 x3 = 1 2 . 于是 | OC | + x3 = 0 . 2p
2 2
最小值, 当且仅当 ∆ = a − 4 < 0 . 所以 1 < a < 2 .
2
4. 已 知 数 列 {an } 满 足 a1 = 0, an +1 = an + 1 + 2 an + 2 , 则 该 数 列 的 通 项 公 式
an = ______________.
【答案】 an = n + 2 − 1 − 2 . 【 解 析 】 因 为 an +1 + 2 = an + 2 + 2 an + 2 + 1 =
,有概率 在 0 ≤ x1 , x2 ≤ 1 上考虑满足上述条件的 (x1 , x2)
P=∫
1
0
6 3 α −β 7. 已知 sin α + sin β = , 则 cos , cos α + cos β = = ______________. 2 3 3
【答案】1/4. 【解析】平方求和, 再用倍角公式即得.
广二模理数答案
A
M
第 5 页 共 15 页
ed u. c
B
n/
ì ï-3 y + 3 z = 0, ï î3 3 x - 2 y = 0.
在△ ABA1 中, AM = AN = 1 , AB = AA1 = 3 , 所以
AM AN = , AB AA1
所以 MN P BA1 .…………………………………………………………………………………………4分 所以 MN P DE1 . 所以 M , N , E1 , D 四点共面.………………………………………………………………………6分
取 y = 3 3 ,则 x = 2 , z = 3 3 . 所以 n = 2,3 3,3 3 是平面 MNE1 D 的一个法向量.………………………………………………12分 设直线 BC 与平面 MNE1 D 所成的角为 q ,
(
)
=
2
æ 3 3ö 3 2´ç ÷+ 3 3´ +3 3´0 2 è 2 ø
F
(
)
ed u. c
B D1 C1 B1 D C
ht t
r uuu r æ 3 3 3 ö uuuu 则 BC = ç , DE1 = ( 0, -3,3) , , , 0 ÷ B ç 2 2 ÷ A M è ø x uuuu r DM = 3 3, -2, 0 .……………………………………………………………………………………10分
教
第(1) (2)问均用向量法:
州
(1)证明:以点 E 为坐标原点, EA , ED , EE1 所在的直线 分别为 x 轴, y 轴, z 轴,建立如图的空间直角坐标系,
gu
an gz
F1 A1
2015-2016学年广东实验中学等高二(下)期末考试数学(理)试题(解析版)

2015-2016学年广东实验中学等高二(下)期末考试数学(理)试题一、选择题1.设集合{|06}A x x =≤≤,集合2{|3280}B x x x =+-≤,则A B = ( ) A .4[0,]3 B .4[2,]3- C .[0,6] D .[2,6]- 【答案】D【解析】试题分析:由于42,3B ⎡⎤=-⎢⎥⎣⎦,故[]2,6A B ⋃=-.【考点】1.集合交集、并集和补集;2.一元二次不等式.【易错点晴】确定性、互异性和无序性.研究一个集合,我们首先要看清楚它的研究对象,是实数还是点的坐标还是其它的一些元素,这是很关键的一步.第二步常常是解一元二次不等式,我们首先用十字相乘法分解因式,求得不等式的解集.在解分式不等式的过程中,要注意分母不能为零.元素与集合之间是属于和不属于的关系,集合与集合间有包含关系. 2.若12z i =+,则41izz =-( ) A .1 B .i C .-1 D .-i 【答案】B【解析】试题分析:22125z z ⋅=+=,故451ii =-. 【考点】复数运算.3.设随机变量~(2,9)N ζ,若()(2)P c P c ξξ>=<-,则c 的值是( ) A .1 B .2 C .3 D .4 【答案】C【解析】试题分析:依题意正态分布均值2μ=,故24,3c c c +-==. 【考点】正态分布.4.已知实数,x y 满足1x ya a <<(01a <<),则下列关系式恒成立的是( )A .221111x y >++B .22ln(1)ln(1)x y +>+ C .sin sin x y > D .22x y > 【答案】A【解析】试题分析:由于1x y a a <<且01a <<,所以222222110,,11,11x y x y x y x y >><+<+>++. 【考点】不等式.5.将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张.如果分给同一人的2张参观券连号,那么不同的分法种数是( )A .24B .96C .144D .210 【答案】B【解析】试题分析:如果1,2连,方法数有4424A =中,同理其它连的方法也有24种,故中的方法数有24496⋅=种. 【考点】排列组合.6.已知等比数列{}n a 中,各项都是正数,且1321,,22a a a 成等差数列,则91078a a a a +=+( ) A.3-.3+【答案】C【解析】试题分析:因为1321,,22a a a 成等差数列,所以3122a a a =+,即21112a q a a q=+,2210q q --=,1q =,故()278291078783a a qa a q a a a a ++===+++【考点】等差、等比数列的基本概念.7.执行如图所示的程序框图,则输出的结果是( )A .16B .17C .18D .19【答案】A【解析】试题分析:根据程序框图分析可知,程序框图的作用是计算()333332log 2log 2log log 22n n --+=<+,即21,1428n n <>+,即15n =.由于程序运行时先1n n =+再进行循环的判断,故取16n =. 【考点】算法与程序框图.8.已知函数()sin()f x x ϕ=-且2πϕ<,又230()0,f x d x π=⎰则函数()f x 的图象的一条对称轴是( ) A .56x π= B .712x π= C .3x π= D .6x π=【答案】A【解析】试题分析:由于()2300f x dx π=⎰,即()f x 图象关于,03π⎛⎫⎪⎝⎭对称,所以()sin 0,33f x ππϕϕ⎛⎫=-== ⎪⎝⎭,()sin()3f x x π=-,代入选项验证可知A 正确.【考点】1.定积分;2.三角函数图象与性质.9.已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示(单位: m ),则该四棱锥的体积为( )m 3A .4B .73C .3D .2 【答案】D【解析】试题分析:底面积为212⋅=,高为3,故体积为12323⋅⋅=. 【考点】三视图.10.设F 1,F 2分别为双曲线)0,0(12222>>=-b a b y a x 的左、右焦点,双曲线上存在一点P 使得b PF PF 321=+,ab PF PF 4921=⋅,则该双曲线的离心率为( ) A .43 B .3 C .94 D .53【答案】D【解析】试题分析:设12,PF m PF n ==,依题意有2m n a -=,3m n b +=,94m n ab ⋅=,前两项平方相减得224949mn b a ab =-=,两边除以2a 得249940,3b b b a a a ⎛⎫-⋅-== ⎪⎝⎭,故53e ==.【考点】双曲线离心率.【思路点晴】求解圆锥曲线的离心率问题,主要考虑方程的思想、圆锥曲线的定义,如椭圆的定义是点到两个定点的距离之和等于常数,并且常数大于两个定点的距离.双曲线是点到两个定点的距离之差的绝对值为常数.本题依题意 有2m n a -=,3m n b +=,94m n ab ⋅=,由此解方程组求得43b a =,进而求出离心率.有的题目还需要结合222a bc =+,或者222c a b =+来求解.11.如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t 时刻五角星露出水面部分的图形面积为()S t ,且((0)0)S =,则导函数'()y S t =的图像大致为( )【答案】A【解析】试题分析:五角星向上升起的时候,首先面积缓慢提升,然后突然变大,但是面积提升的速度变换,然后稍微面积提升速度又变快一点,最后面积提升速度变慢.有以上分析过程可知,A 选项正确. 【考点】函数图象与性质.12.设直线l 1,l 2分别是函数f(x)= ln ,01,ln ,1,x x x x -<<⎧⎨>⎩图象上点P 1,P 2处的切线,l 1与l 2垂直相交于点P ,且l 1,l 2分别与y 轴相交于点A ,B ,则△PAB 的面积的取值范围是( )A .)1,0(B .)2,0(C .),0(+∞D .),1(+∞ 【答案】A【解析】试题分析:设()()111222,ln ,,ln P x x P x x -(不妨设121,01x x ><<),则由导数的几何意义易得切线12,l l 的斜率分别为121211,.k k x x ==-由已知得12122111,1,.k k x x x x =-∴=∴=∴切线1l 的方程为()1111ln y x x x x -=-,切线2l 的方程为()2221ln y x x x x +=--,即1111ln y x x x x ⎛⎫-=-- ⎪⎝⎭.分别令0x =得()()110,1ln ,0,1ln .A x B x -++又1l 与2l 的交点为2111221121,ln .11x x P x x x ⎛⎫-+ ⎪++⎝⎭11x >,【考点】1.分段函数;2.函数导数与不等式.【思路点晴】本题首先考查导数的几何意义,其次考查最值问题,解题时可设出切点坐标,利用切线垂直求出这两点横坐标的关系,同时得出切线方程,从而得点,A B 的坐标,由两直线相交得出P 点坐标,从而求得面积,把面积用1x 表示后,可得面积的取值范围.本题的求解是根据题意按部就班一步一步解得结论,这也是我们解决问题的一种基本方法,朴实而基础,简单而实用.二、填空题13.已知向量,a b 夹角为45︒,且1,2a a b =-= ;则_____b = .【答案】【解析】试题分析:2222244410a b a a b b b -=-⋅+=-+= ,解得b =【考点】向量运算.14.72)()(y x y x +-的展开式中63y x 的系数为 (用数字作答). 【答案】0【解析】试题分析:系数为061524272727742350C C C C C C -⋅+⋅=-+=.【考点】二项式定理.15.记不等式组⎪⎩⎪⎨⎧≤+≥+≥43430y x y x x 所表示的平面区域为D ,若直线y =a(x +1)与D 有公共点,则a 的取值范围是________. 【答案】1,42⎡⎤⎢⎥⎣⎦【解析】试题分析:画出可行域和直线图象如下图所示,注意到直线过定点()1,0-.由图象可知,斜率的取值范围在,AB AC k k 之间,1,42AB AC k k ==,所以取值范围是1,42⎡⎤⎢⎥⎣⎦.【考点】线性规划.【思路点晴】对于线性目标函数,必须明确线性目标函数的最值一般在可行域的顶点或边界取得,运用数形结合的思想方法求解.同时注意边界直线斜率与目标函数斜率的关系;对于非线性目标函数,应考虑其具有的几何意义,依平面几何知识解答;对于交汇问题应转化为目标函数最值问题处理.线性规划也是求值的一种,是求在某种限制范围之下的最大值或最小值的问题,其关键是列出所有的限制条件,不能有遗漏的部分,如有时变量要求为正实数或自然数,其次是准确找到目标函数,如果数量关系多而杂,可以用列表等方法把关系理清.16.在平面内,定点A 、B 、C 、D 满足:==,2-=⋅=⋅=⋅,动点P 、M 满足:AP =1,PM =MC ,则BM的最大值是 . 【答案】72【解析】试题分析:依题意可知,,,A B C 三个点在以D 为圆心,半径为R 的圆上,且AOB AOC BOC ∠=∠=∠ 23π=,故222cos 2,4,23R R R π=-==.由题意可知,P 点在以A 为圆心,半径为1的圆上,M 为PC 的中点.以D 为坐标原点,DA 为x 轴建立平面直角坐标系,各点的坐标分别为()2,0A,(1,B -,(C -,依题意P 在圆()2221x y -+=上,设其坐标为()2cos ,sin P θθ+,故1c 3s i n()2M θ+,3cos sin ,22BM θθ⎛⎫+= ⎪ ⎪⎝⎭ ,2223cos sin 22BM θθ⎛⎫+⎛⎫=+ ⎪ ⎪ ⎪⎝⎭⎝⎭3712sin 49644πθ⎛⎫++ ⎪⎝⎭==≤,BM 最大值为72.【考点】向量运算.【思路点晴】本题美妙的考查了向量的几何意义、向量的数量积,数形结合的思想、圆的参数方程,中点坐标公式,两点间的距离公式,三角函数求最值.题目的突破口在于三个向量模相等,并且两两的数量积相等,由此可知,,A B C 三个点在以D 为圆心,半径为R 的圆上,由此计算出圆的半径.根据1PA =,实际上P 点在以A 为圆心,半径为1的圆上,M 为PC 的中点.先设出P 点的参数方程,然后一步一步求出BM的表达式最终求得其最大值.三、解答题17.在ABC ∆中,角A ,B ,C 所对的边分别为c b a ,,,已知c o s (c 3s i n )c o sC A A B +=. (1)求角B 的大小; (2)若1b c ==,求ABC ∆的面积.【答案】(1)3B π=;(2【解析】试题分析:(1)利用sin sin()C A B =+,化简题目给定的已知条件,得到tan B =3B π=;(2)用余弦定理求出2a =,再利用三角形面积公式求得面积. 试题解析:(1)由已知得cos()cos cos cos 0A B A B A B -++=即sin sin cos 0A B A B -=因为sin 0A ≠,所以sin 0tan B B B =⇒=因为0B π<< 所以3B π=(2)因为2222cos b a c ac B =+-⋅所以231a a =+-,即220a a --=⇒2a =所以11sin 212222ABC S ac B ∆==⋅⋅⋅=【考点】解三角形.18.正项数列{}n a 的前项和n S 满足:222(1)()0n n S n n S n n -+--+=.(1)求数列{}n a 的通项公式n a ; (2)令221(2)n nn b n a +=+,数列{}n b 的前n 项和为n T .证明:对于任意的*n N ∈,都有564n T <. 【答案】(1)2n a n =;(2)证明见解析.【解析】试题分析:(1)对222(1)()0n n S n n S n n -+--+=因式分解得2()(1)0n n S n n S ⎡⎤-++=⎣⎦,20,n n S S n n >=+,再根据公式11,1,1n nn S n a S S n -=⎧=⎨->⎩求得2n a n =;(2)将2n a n =代入得222211114(2)16(2)n n b n n n n ⎡⎤+==-⎢⎥++⎣⎦,利用裂项求和法求得()()221111511646412n T n n ⎡⎤=+--<⎢⎥++⎢⎥⎣⎦. 试题解析:(1)由222(1)()0n n S n n S n n -+--+=,得2()(1)0n n S n n S ⎡⎤-++=⎣⎦.由于{}n a 是正项数列,所以20,n n S S n n >=+. 当1n =时,112a S ==当2n ≥221(1)(1)2n n n a S S n n n n n -=-=+----=. 综上可知,数列{}n a 的通项公式2n a n =. (2)证明:由于2212,(2)n n nn a n b n a +==+. 所以222211114(2)16(2)n n b n n n n ⎡⎤+==-⎢⎥++⎣⎦. 222222222111111111111632435(1)(1)(2)n T n n n n ⎡⎤=-+-+-++-+-⎢⎥-++⎣⎦ (2222)11111151(1)162(1)(2)16264n n ⎡⎤=+--<+=⎢⎥++⎣⎦. 【考点】1.数列求通项;2.裂项求和法.19.为了增强环保意识,省实社团从男生中随机抽取了60人,从女生中随机抽取了50(1)试判断是否有99%的把握认为环保知识是否优秀与性别有关;(2)为参加广州市举办的环保知识竞赛,学校举办预选赛,已知在环保测试中优秀的同学通过预选赛的概率为32,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量X 表示这3人中通过预选赛的人数,求X 的分布列与数学期望.附:2K =2()n ad bc - 【答案】(1)有99%的把握认为环保知识是否优秀与性别有关;(2)分布列见解析,2.【解析】试题分析:(1)利用公式计算得22110(40302020)7.8260506050K ⨯-⨯=≈⨯⨯⨯,故有99%把握;(2)X 的可能取值为0,1,2,3,且X 满足二项分布2~(3,)3X B ,由此求得分布列和期望. 试题解析:(1)22110(40302020)7.8260506050K ⨯-⨯=≈⨯⨯⨯因为27.822 6.635K ≈> 2( 6.635)0.01P K >= 所以有99%的把握认为环保知识是否优秀与性别有关. (2)X 的可能取值为0,1,2,3 271)31()0(3===X P ,92)31)(32()1(213===C X P94)32)(31()2(223===C X P278)32()3(3===X P所以的分布列为:因为2~(3,)3X B , 所以2()323E X np ==⨯= 【考点】1.独立性检验;2.二项分布.20.已知梯形BDEF 所在平面垂直于平面ABCD 于BD ,EF ∥BD ,12EF DE BD ==,2BD BC CD =====,DE BC ⊥.A BCDEF(1)求证:DE ABCD ⊥平面;(2)求平面AEF 与平面CEF 所成的锐二面角的余弦值. 【答案】(1)证明见解析;(2 【解析】试题分析:(1)第一问利用面面垂直的性质定理来证明,连接AC 交BD 于O ,BD BC CD == 且,AB AD = AC BD ∴⊥,因为平面BDEF ⊥平面ABCD ,交线为BD ,且AC ⊂平面ABCD AC ∴⊥平面BD EF ,DE ⊂ 平面BDEF ,DE AC ∴⊥,又D E B C ∴⊥且AC BC C = ,DE ∴⊥平面A B C D ;(2)以,,OA OB OF 为x 轴,y 轴,z 轴建立空间直角坐标系,利用平面AEF 与平面CEF 的法向量来求二面角的余弦值. 试题解析:(1)连接AC 交BD 于O ,BD BC CD == 且,AB AD =AC BD ∴⊥因为平面BDEF ⊥平面ABCD ,交线为BD ,且AC ⊂平面ABCD AC ∴⊥平面BDEFDE ⊂ 平面BDEF ,DE AC ∴⊥又DE BC ∴⊥且AC BC C = ,DE ∴⊥平面ABCD (2)1//,,2EF BD EF BD =且O 是BD 中点,ODEF ∴是平行四边形 //,OF DE OF ∴∴⊥平面ABCD分别以,,OA OB OF 为x 轴,y 轴,z 轴建立空间直角坐标系(1,0,0),C(1,1),F(0,0,1)A - 设平面AEF 的法向量(,,)m x y z =,由00m AF m EF ⎧⋅=⎪⎨⋅=⎪⎩ 得(1,0,1)m = 设平面CEF 的法向量(,,)n x y z =, 由00n CF n EF ⎧⋅=⎪⎨⋅=⎪⎩得(1,0,n =所以cos ,m n m n m n⋅<>==即平面AEF 与平面CEF【考点】空间向量法求面面角的余弦值.21.已知椭圆C 的中心在坐标原点,离心率e =且其中一个焦点与抛物线214y x=的焦点重合.(1)求椭圆C 的方程;(2)过点1,03S ⎛⎫- ⎪⎝⎭的动直线l 交椭圆C 于,A B 两点,试问:在坐标平面上是否存在一个定点T ,使得无论l 如何转动,以AB 为直径的圆恒过点T ?若存在,求出点T 的坐标;若不存在,请说明理由.【答案】(1)2212y x +=;(2)存在一个定点()1,0T 满足条件. 【解析】试题分析:(1)注意到焦点在y 轴上,故设椭圆的方程为()222210x y a b b a +=>>,依题意2c a =,焦点为()0,1,求得椭圆方程为2212y x +=;(2)若直线l 与x 轴重合则以AB 为直径的圆是221x y +=,若直线l 垂直于x 轴,则以AB 为直径的圆是2211639x y ⎛⎫++= ⎪⎝⎭,这两个圆都过()1,0T .当直线l 不垂直于x轴时,可设直线1:3l y k x ⎛⎫=+ ⎪⎝⎭,联立直线的方程和椭圆的方程,计算得0TA TB ⋅= ,故在坐标平面上存在一个定点()1,0T 满足条件.试题解析:(1)设椭圆的方程为()222210x y a b b a +=>>,离心率2c e a ==,又抛物线214y x =的焦点为()0,1,所以1,1c a b ===, ∴椭圆C 的方程是2212y x +=. (2)若直线l 与x 轴重合,则以AB 为直径的圆是221x y +=,若直线l 垂直于x 轴,则以AB 为直径的圆是2211639x y ⎛⎫++= ⎪⎝⎭.由22221,116,39x y x y ⎧+=⎪⎨⎛⎫++=⎪ ⎪⎝⎭⎩解得1,0.x y =⎧⎨=⎩即两圆相切于点()1,0. 因此所求的点T 如果存在,只能是()1,0.当直线l 不垂直于x 轴时,可设直线1:3l y k x ⎛⎫=+ ⎪⎝⎭.由221,31,2y k x y x ⎧⎛⎫=+ ⎪⎪⎪⎝⎭⎨⎪+=⎪⎩消去y 得()22222122039k x k x k +++-=.设()()1122,,,A x y B x y ,则2122212223,2129.2k x x k k x x k ⎧-⎪+=⎪⎪+⎨⎪-⎪=⎪+⎩又因为()()11221,,1,TA x y TB x y =-=-,()()121211TA TB x x y y ∴⋅=--+()()()22212122222222111113912211931112329k x x k x x k k kk k k k k ⎛⎫=++-+++ ⎪⎝⎭--⎛⎫=+⋅+-⋅++ ⎪++⎝⎭ 0,=TA TB ∴⊥,即以AB 为直径的圆恒过点()1,0T .故在坐标平面上存在一个定点()1,0T 满足条件. 【考点】直线与圆锥曲线的位置关系.【方法点晴】第一问中,题目给了两个条件,一个是离心率为2c e a ==,另一个条件是过抛物线的焦点.通过分析可以知道,抛物线的焦点在y 轴的正半轴上,所以椭圆的交点也在在y 轴的正半轴上,故设椭圆的方程为()222210x y a b b a+=>>.在求圆锥曲线方程的时候,要特别注意题目中隐藏的焦点所在位置的条件. 22.已知函数)(,ln )(2R a x x a x f ∈-=. (1)求函数)(x f 的单调区间;(2)若1>x 时,0)(≤x f 恒成立,求实数a 的取值范围;(3)设0>a ,若),(11y x A ,),(22y x B 为曲线)(x f y =上的两个不同点,满足210x x <<,且),(213x x x ∈∃,使得曲线)(x f y =在3x x =处的切线与直线AB 平行,求证:2213x x x +<. 【答案】(1)当0≤a 时,)(x f 的减区间是),0(+∞,当0>a 时,)(x f 的减区间是)22(∞+,a ,增区间是)22,0(a;(2)e a 2≤;(3)证明见解析. 【解析】试题分析:(1)先求得定义域0x >,然后求导xa x x x a x f +-=-=2'22)(,对a 分成两类来讨论()f x 的单调区间;(2)当1x >时,2()ln 0f x a x x =-≤等价于2ln x a x ≤,令()2ln x h x x=,利用到处求得()2h x e ≥,故2a e ≤;(3)先求得直线AB的斜率332AB ak x x =-,∵x x a x f 2)('-=在),0(+∞上是减函数, ∴要证:2213x x x +<,即证:)2()(21'3'x x f x f +>,即证2ln 11121212>-+x x x x x x ,令112>=x x t ,即证:)1(2ln )1(->+t t t 在()+∞∈,1t 恒成立,最后通过构造函数)1(2ln )1()(--+=t t t t F 来证明.试题解析:(1)∵函数R a x x x a x f ∈>-=,0,ln )(2∴xax x x a x f +-=-=2'22)(;当0≤a 时,0)('<x f 恒成立,∴)(x f 在定义域上是减函数;当0>a 时,⇒>0)('x f 220a x <<,∴)(x f 在)22,0(a 上是增函数; ⇒<0)('x f 22a x >,∴)(x f 在)22(∞+,a上是减函数; 综上所得, 0≤a 时,)(x f 的减区间是),0(+∞;②0>a 时,)(x f 的减区间是)22(∞+,a ,增区间是)22,0(a ; (2)∵01)1(<=-f ,由(1)可知,0≤a 时,)(x f 的减区间是),0(+∞, ∴0)1()(<<f x f 恒成立,则0≤a 满足题意;当0>a 时,)(x f 的减区间是)22(∞+,a ,增区间是)22,0(a; ①若122≤a,即20≤<a 时)(x f 在),1(+∞上是减函数,∴20≤<a 满足题意; ②当122>a ,即2>a 时,)22()(a f x f ≤,令0)22(≤a f , 即0)22(22ln2≤-⋅a a a ,解得e a 2≤,即e a 22≤<满足题意; 综上所得,a 的取值范围是e a 2≤;(3)∵12121212122112221212))((ln)ln ()ln (x x x x x x x x a x x x x a x x a x x y y k AB-+--=----=--==)(ln 121212x x x xx x a +--;又∵333'2)(x x a x f -=,∴331212122)(ln x x a x x x x x x a -=+-- ∵x xax f 2)('-=在),0(+∞上是减函数, ∴要证:2213x x x +<,即证:)2()(21'3'x x f x f +>, 即证:)(2)(ln 2121121212x x x x a x x x x x x a +-+>+--,即证:2ln 121221>-+x x x x x x ⇔2ln 11121212>-+x x x x x x 令112>=x x t ,即证:)1(2ln )1(->+t t t 在()+∞∈,1t 恒成立 令)1(2ln )1()(--+=t t t t F ,0111)(,11ln )(22'''>-=-=-+=tt t t t F tt t F∴)('t F 在()+∞∈,1t 上单调递增,0)1()(''=>F t F∴函数)(t F 在()+∞∈,1t 上单调递增,0)1()(=>F t F 恒成立, 即)1(2ln )1(->+t t t 成立,故2213x x x +<得证. 【考点】1.函数导数与单调区间;2.函数导数与不等式.【方法点晴】本题第一问考查分类讨论函数的单调性,导数为xax x x a x f +-=-=2'22)(,我们观察它的分子,分子是一个二次函数,且开口向下,那么单调区间只要分成两类就可以解决.分类讨论的问题,关键在于如何得到完整的分类标准.二次函数的分类标准主要在于二次项系数、对称轴、两个根的大小关系.制定分类标准要做到不重不漏.。
广东高二高中数学竞赛测试带答案解析

广东高二高中数学竞赛测试班级:___________ 姓名:___________ 分数:___________一、选择题1.A.B.C.D.2.若A.1B.1或C.D.1或3.在等差数列中,若,则A.14B.15C.16D.174.已知椭圆,若成等差数列,则椭圆的离心率为( )A.B.C.D.5.如图,三棱柱的所有棱长均为2,且点在面上的射影为BC中点O,则异面直线AB与CC所成角的余弦值为( )1A.B.C.D.6.已知函数,则要得到其导函数的图象,只需将函数的图象( )A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位7.已知定义域为的函数,满足;当时,单调递增.如果,对于的值,下列判断正确的是( )A.恒小于0B.恒大于0C.可能为0D.可正可负二、其他如图:向量,点为圆心的圆弧上运动,设,则的最大值为( )A.1B.C.2D.三、填空题1.已知 ;2.不等式的解集为3.把4名大学毕业生分配到A、B、C三个单位实习,每个单位至少一人,已知学生甲只去A 单位,则不同的分配方案有种(用数字作答)4.已知点为抛物线上的一个动点,为圆上的动点,设点到抛物线的准线距离为,则的最小值为5.已知数列,利用如右图所示的程序框图计算的值,则判断框中应填6.下列命题中:①在频率分布直方图中估计平均数,可以用每个小矩形的高乘以底边中点的横坐标之和;②线性相关系数r的的绝对值越接近1,表示两变量的相关性越强③回归直线一定过样本中心;④已知随机变量,则其中正确命题的序号是四、解答题1.、(本小题满分12分)已知函数为偶函数,且其图象两相邻对称轴间的距离为(1)求的解析式;(2)若把图象按向量平移,得到函数的图象,求的单调增区间.2.(本小题满分12分)高二级某次数学测试中,随机从该年级所有学生中抽取了100名同学的数学成绩(满分150分),经统计成绩在的有6人,在的有4人.在,各区间分布情况如右图所示的频率分布直方图,若直方图中,和对应小矩形高度相等,且对应小矩形高度又恰为对应小矩形高度的一半.(1)确定图中的值;(2)设得分在110分以上(含110分)为优秀,则这次测试的优秀率是多少?(3)某班共有学生50人,若以该次统计结果为依据,现随机从该班学生中抽出3人, 则至少抽到一名数学成绩优秀学生的概率是多少?3.(1)、据此说明四棱锥P-ABCD具有的特征及已知条件;(2)、由你给出的特征及条件证明:面PAD⊥面PCD(3)、若PC中点为E,求直线AE与面PCD所成角的余弦值.4.(本小题满分14分)已知为坐标原点,点F、T、M、P分别满足.(1) 当t变化时,求点P的轨迹方程;(2) 若的顶点在点P的轨迹上,且点A的纵坐标,的重心恰好为点F,求直线BC的方程.5.(本小题满分14分)已知函数()(1) 判断函数的单调性;(2) 是否存在实数使得函数在区间上有最小值恰为? 若存在,求出的值;若不存在,请说明理由.6.(本小题满分14分)下表给出的是由n×n(n≥3,n∈N*)个正数排成的n行n列数表,表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为,若已知(1)求的值;(2)求用表示的代数式;=+++……+求使不等式(3)设表中对角线上的数,,,……,组成一列数列,设Tn成立的最小正整数n.广东高二高中数学竞赛测试答案及解析一、选择题1.A.B.C.D.【答案】 D【解析】略2.若A.1B.1或C.D.1或【答案】B【解析】略3.在等差数列中,若,则A.14B.15C.16D.17【答案】C【解析】略4.已知椭圆,若成等差数列,则椭圆的离心率为( )A.B.C.D.【答案】B【解析】略5.如图,三棱柱的所有棱长均为2,且点在面上的射影为BC中点O,则异面直线AB与CC所成角的余弦值为( )1A.B.C.D.【答案】 D【解析】略6.已知函数,则要得到其导函数的图象,只需将函数的图象( )A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位【答案】 C【解析】略7.已知定义域为的函数,满足;当时,单调递增.如果,对于的值,下列判断正确的是( )A.恒小于0B.恒大于0C.可能为0D.可正可负【答案】A【解析】略二、其他如图:向量,点为圆心的圆弧上运动,设,则的最大值为( )A.1B.C.2D.【答案】C【解析】略三、填空题1.已知 ;【答案】【解析】略2.不等式的解集为【答案】(0,2)【解析】略3.把4名大学毕业生分配到A、B、C三个单位实习,每个单位至少一人,已知学生甲只去A 单位,则不同的分配方案有种(用数字作答)【答案】12【解析】略4.已知点为抛物线上的一个动点,为圆上的动点,设点到抛物线的准线距离为,则的最小值为【答案】【解析】略5.已知数列,利用如右图所示的程序框图计算的值,则判断框中应填【答案】【解析】略6.下列命题中:①在频率分布直方图中估计平均数,可以用每个小矩形的高乘以底边中点的横坐标之和;②线性相关系数r的的绝对值越接近1,表示两变量的相关性越强③回归直线一定过样本中心;④已知随机变量,则其中正确命题的序号是【答案】②③④【解析】略四、解答题1.、(本小题满分12分)已知函数为偶函数,且其图象两相邻对称轴间的距离为(1)求的解析式;(2)若把图象按向量平移,得到函数的图象,求的单调增区间.【答案】 y=2cos2x,的单调递增区间为【解析】∴又…………………………………………………7分(或由恒成立) ∴…………………………………………8分(2)由(1)得…………………………………10分令得的单调递增区间为…………………………………12分2.(本小题满分12分)高二级某次数学测试中,随机从该年级所有学生中抽取了100名同学的数学成绩(满分150分),经统计成绩在的有6人,在的有4人.在,各区间分布情况如右图所示的频率分布直方图,若直方图中,和对应小矩形高度相等,且对应小矩形高度又恰为对应小矩形高度的一半.(1)确定图中的值;(2)设得分在110分以上(含110分)为优秀,则这次测试的优秀率是多少?(3)某班共有学生50人,若以该次统计结果为依据,现随机从该班学生中抽出3人, 则至少抽到一名数学成绩优秀学生的概率是多少?【答案】0.024,,0.4,【解析】(1)由题意知,成绩分布在间的频率为0.9,3.(1)、据此说明四棱锥P-ABCD具有的特征及已知条件;(2)、由你给出的特征及条件证明:面PAD⊥面PCD(3)、若PC中点为E,求直线AE与面PCD所成角的余弦值.【答案】①ABCD为直角梯形,其中AB∥CD,AD⊥AB,(AB⊥CD)②PA⊥面ABCD,③PA="AD=CD=2, " AB="1 "【解析】(1)由图可知四棱锥P-ABCD中有①ABCD为直角梯形,其中AB∥CD,AD⊥AB,(AB⊥CD)②PA⊥面ABCD,③PA="AD=CD=2, " AB="1 " ………………………5分⑵由(1)知PA⊥面ABCD ∴PA⊥CD又在直角梯形ABCD中,AD⊥CD而PA,AD面PAD中, ∴CD⊥面PADCD面PCD∴面PAD⊥面PCD ……………………9分⑶取PD中点F,连结EF;则EF在,PA=AD,PA AD∴AF⊥PD且又由(2)知面PAD⊥面PCD∴AF⊥面PCD∴∠AEF为AE与面PCD所成的角…………………………………12分在△AEF中, ∠AFE=900,,EF=1∴即AE与面PCD所成角的余弦值为…………………………………14分(3)由E为PC中点∴E由(2)知面PCD的一个法向量为设AE与面PCD所成角为即AE与面PCD所成角的余弦值为4.(本小题满分14分)已知为坐标原点,点F、T、M、P分别满足.(1) 当t变化时,求点P的轨迹方程;(2) 若的顶点在点P的轨迹上,且点A的纵坐标,的重心恰好为点F, 求直线BC的方程.【答案】,2x+2y+5=0【解析】18、解:(1)设又由…………………………2分由①②消去t得点P的轨迹方程为:……………………………7分5.(本小题满分14分)已知函数()(1) 判断函数的单调性;(2) 是否存在实数使得函数在区间上有最小值恰为? 若存在,求出的值;若不存在,请说明理由.【答案】见详解答案【解析】当,在上为增函数,此时, …………9分当,在上为减函数,在上为增函数;此时, …………11分当,在上为减函数,此时, ……13分综上,存在满足题意. …………………14分6.(本小题满分14分)下表给出的是由n×n(n≥3,n∈N*)个正数排成的n行n列数表,表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为,若已知(1)求的值;(2)求用表示的代数式;=+++……+求使不等式(3)设表中对角线上的数,,,……,组成一列数列,设Tn成立的最小正整数n.【答案】,,4【解析】20、解:⑴由题意有:又由…………………………………4分⑶由(2)知故使原不等式成立的最小正整数为4. …………………………………14分。
2016年广州市高二数学竞赛试卷(附答案)

2016年广州市高二数学竞赛试题考生注意:⒈ 用钢笔、签字笔或圆珠笔作答,答案写在答卷上; ⒉ 不准使用计算器;⒊ 考试用时120分钟,全卷满分150分.一、选择题:本大题共4小题,每小题6分,满分24分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 若sin 2cos 0θθ-=, 则22sin 2cos θθ-的值是A.103 B. 53 C. 54- D. 2- 2. 用min{}a,b 表示a,b 两数中的最小值.若函数()f x =min {}x ,x t -的图象关于直线12x =-对称,则t 的值为 A.2- B. 2 C. 1- D. 13. 设,x y 满足约束条件220,840,0,0.x y x y x y -+≥⎧⎪--≤⎨⎪≥≥⎩ 若目标函数()0,0z abx y a b =+>>的最大值为8, 则41a b+的最小值为 A.1B. C. 2D. 4. 已知动点P(),x y 满足3455x y +-=, 则点P 的轨迹是A. 直线B. 圆C. 抛物线D. 椭圆 二、填空题:本大题共6小题,每小题6分,满分36分.5. 已知复数z=()21i的共轭复数为z , 则z z ⋅= .6. 某战争的模拟训练, 我军两支部队从不同驻地到某攻击点会师, 实行合围, 其到达攻击点 的时刻均在5时与6时之间, 敌军一旦发现情况后只需20分钟集结就会遁逸, 则全歼敌军 胜算的概率是 .7. 在△ABC 中, 角A ,B ,C 的对边分别为a,b ,c ,c =60C ︒=, 则a b -的取值范围是 . 8. 考查集合{}1,2,3,4,5,6,7,8,9的所有非空子集, 若一个非空子集中的偶数的个数不少于YXNMC 1B 1A 1CBA奇数的个数, 称这个子集是“好子集”, 则“好子集”的个数为 . 9.如图,一个箱子的每个面都是矩形且边长都是整数,若它的 主对角线9XY =,则这个箱子的体积的最大值可以是 .10.设函数()f x 是定义在R 上的函数, 若()02016f =, 且对任意x ∈R ,满足()()283x f x f x +-≥⋅, ()()4803x f x f x +-≤⋅, 则()2016f = .三、解答题:本大题共5小题,满分90分.解答须写出文字说明、证明过程和演算步骤. 11.(本小题满分15分)我们规定:对于A ∀∈R , 若存在数列{}n a 和实数()0x x >,使得21123n n A a a x a x a x -=++++ , 则称数A 可以表示成x 进制形式,简记为:()()()()123n A x a a a a = .(1) 已知()()21213(m x x =+-其中0)x >,试将m 表示成x 进制的简记形式;(2) 记()()()()()12312nn n b a a a a a -= (n ∈N *), 若数列{}n a 是等差数列,且满足123a a +=, 347a a +=. 当9217n b =时, 求n 的值.12.(本小题满分15分)如图, 在直三棱柱111ABC A B C -中, 90BAC ︒∠=, ,M N 分别为1A B 和11B C 的中点.(1) 证明:MN ∥平面11A ACC ;(2)若AB AC ==且二面角1A MN C --为直二面角,求三棱锥1A CMN -的体积.13.(本小题满分20分)设椭圆22:11x C y m +=+的两个焦点为()1,0F c -,()2,0F c ()0c >.(1) 设E 是直线2y x =+与椭圆C 的一个公共点, 求使得12EF EF +取最小值时椭圆C 的方程;(2) 已知()0,1N-, 设斜率为()0k k ≠的直线l 与条件(1)下的椭圆C 交于不同的两点,A B , 点Q 满足AQ QB = , 且0NQ AB ⋅=, 求直线l 在y 轴上截距的取值范围.14.(本小题满分20分)设函数()()2ln f x x a x =++.(1) 若曲线()f x 在点()()0,0f 处的切线方程为y x b =+, 求实数a ,b 的值;(2) 若()f x 存在极值, 求实数a 的取值范围, 并证明所有极值之和大于eln2.15.(本小题满分20分)设函数()11(xf x n n ⎛⎫=+∈ ⎪⎝⎭N *, 且1n >, x ∈R ).(1) 设()f x '是函数()f x 的导数, 证明:()()()222f x f f x '+>;(2) 是否存在a ∈N*, 使得()1111knk an a n k =⎛⎫<+<+ ⎪⎝⎭∑恒成立? 若存在, 求a 的值;若不存在, 说明理由.2016年广州市高二数学竞赛试题参考答案与评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:每小题6分,满分24分.1.A 2.C 3.C 4.A 二、填空题:每小题6分,满分36分.5.146.597.( 8.255 9.112 10.201632015+三、解答题:满分90分. 11.(本小题满分15分) (1) 解:()()22312131236m x x x x x =+-=+--()()()()1236x =-- .(2 )解: 设数列{}n a 的公差为d ,由12343,7,a a a a +=⎧⎨+=⎩ 得1123,257,a d a d +=⎧⎨+=⎩解得11a =, 1d =.所以21122322n nb n -=+⨯+⨯++⨯ , ① 于是232222322n nb n =+⨯+⨯++⨯ , ②①-②得2112222n n nb n --=++++-⨯12212nn n -=-⨯- ()112n n =-+-⨯.所以()121n n b n =-⨯+. 因为9217nb =, 所以10n =. 12.(本小题满分15分) (1) 证明: 连接1AB ,1AC ,∵三棱柱111ABC A B C -为直三棱柱, M为1A B 的中点,∴M 为1AB 的中点.∵N 为11B C 的中点,∴MN ∥1AC .∵1AC ⊂平面11A ACC , MN ⊄平面11A ACC ,∴MN ∥平面11A ACC .(2)解: 以AB 所在直线为x 轴, AC 所在直线为y 轴, 1AA 所在直线为z 轴, 建立空间直角坐标系A xyz -.设1AA a =,由于AB AC ==, 则()10,0,A a,()C,2a M ⎫⎪⎪⎝⎭,22N a ⎛⎫⎪ ⎪⎝⎭.∴1,022A N ⎛⎫= ⎪ ⎪⎝⎭, 122a A M ⎛⎫=- ⎪ ⎪⎝⎭,22CN a ⎛⎫=- ⎪ ⎪⎝⎭, 22a CM ⎛⎫= ⎪ ⎪⎝⎭. 设平面1A MN 的法向量为1=n ()111,,x y z ,由1A N ⋅ 10=n , 1AM ⋅ 10=n ,得11110,0.22x y ax z =⎪-=⎪⎩令11x =,则11y =-, 1z =.∴1=n 1,1,a ⎛- ⎝⎭. 设平面CMN 的法向量为2=n ()222,,x y z ,由CN ⋅ 20=n , CM ⋅20=n ,得2222220,0.22x y az ax z +=⎪+=⎪⎩令21y =,则2z =23x =.∴2=n 3,1,⎛ ⎝⎭. ∵二面角1A MN C --为直二面角,∴1⋅n 20=n .∴13110⨯-⨯=. ∴1a =.∴点C 到平面1A MN 的距离d =11⋅CN nn ==∵112MN AC ==, 1112A M A B ==, 111112A N B C ==,∴1112A MNS A N ∆=⨯= ∴三棱锥1A CMN -的体积为13V d =⋅⋅111346A MN S ∆==. 13.(本小题满分20分)(1) 解:由题意, 知11m +>,即0m >.由222,1,1y x x y m =+⎧⎪⎨+=⎪+⎩ 得()()()2241310m x m x m +++++=,由()()()216112210m m m ∆=+-++≥,解得2m ≥或1m ≤-(舍去)所以2m ≥. 此时12EF EF+=≥当且仅当2m =时,12EF EF +取得最小值此时椭圆C 的方程为2213x y +=.(2) 设直线l 的方程为y kx b =+,由22,1,3y kx b x y =+⎧⎪⎨+=⎪⎩ 得()222136330k x kbx b +++-=,因为直线l 与椭圆C 交于不同的两点,A B ,所以()()()2226413330kb k b ∆=-+->, 即2213b k <+. ①设()()1122,,,Ax y B x y , 则122613kbx x k +=-+.由AQ QB = , 得点Q 为线段AB 的中点, 则1223213Q x x kbx k +==-+,213Q Q by kx b k =+=+.因为0NQ AB ⋅=,所以1AB NQ k k ⋅=-.即221131313bk k kb k ++⨯=--+, 化简得2132k b +=,代入①得22b b <,解得02b <<.又23210kb =->,得12b >所以直线l 在y 轴上截距的取值范围为1,22⎛⎫⎪⎝⎭.14.(本小题满分20分) (1)解:由()()2ln f x x a x =++, 得()12f x x x a'=++, 依题意,得()101f a'==, 所以,1a =.所以,()()2ln 1f x x x =++。
广东高二高中数学竞赛测试带答案解析

广东高二高中数学竞赛测试班级:___________ 姓名:___________ 分数:___________一、选择题1.已知集合,则()A.B.C.D.2.已知=b-i, (a,b∈R),其中i为虚数单位,则a+b=()A.-1 B.1 C.2 D.33.已知a、b是实数,则“a>1,b>2”是“a+b>3且ab>2”的A.充分而不必要条件B.必要而不充分条件C.充分且必要条件D.既不充分也不必要条4.函数是()A.周期为的奇函数B.周期为的奇函数C.周期为的偶函数D.非奇非偶函数5.已知平面向量, , 且, 则m=( )A. 4B.-1C. 2D. -46.某几何体的三视图及尺寸如图示,则该几何体的表面积为A. B. C. D.7.已知向量,且,若变量x,y满足约束条,则z的最大值为A.1B.2C.3D.48.等差数列中,,且成等比数列,则A.B.C.D.9.以轴为对称轴,以坐标原点为顶点,准线的抛物线的方程是A.B.C.D.10.起点到终点的最短距离为A.16B.17C.18D.19二、填空题1.的定义域--__________2.校高中部有三个年级,其中高三有学生人,现采用分层抽样法抽取一个容量为的样本,已知在高一年级抽取了人,高二年级抽取了人,则高中部共有学生__ _人.3.在中,,且,则的面积是_____4.(几何证明选讲选做题)如图,已知的两条直角边,的长分别为,,以为直径的圆与交于点,则=.5.(坐标系与参数方程选做题)直线截曲线(为参数)的弦长为_ _三、解答题1.(本小题共12分)已知函数(1)求的最小正周期;(2)若,, 求的值2.(本题满分14分)有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.已知在全部105人中抽到随机抽取1人为优秀的概率为(1)请完成上面的列联表;(2)根据列联表的数据,若按的可靠性要求,能否认为“成绩与班级有关系” .(3)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到6或10号的概率.3.(本题12分)如图所示,在直四棱柱中, ,点是棱上一点.(1)求证:面;(2)求证:;4.(本题满分14分)为赢得2010年广州亚运会的商机,某商家最近进行了新科技产品的市场分析,调查显示,新产品每件成本9万元,售价为30万元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值(单位:万元,)的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.(1)将一个星期的商品销售利润表示成的函数;(2)如何定价才能使一个星期的商品销售利润最大?5.(本小题满分14分)已知椭圆的左焦点为F,左右顶点分别为A,C上顶点为B,过F,B,C三点作,其中圆心P的坐标为.(1) 若FC是的直径,求椭圆的离心率;(2)若的圆心在直线上,求椭圆的方程.6.(本小题满分14分)设不等式组所表示的平面区域为,记内的格点(格点即横坐标和纵坐标均为整数的点)个数为(1)求的值及的表达式;(2)记,试比较的大小;若对于一切的正整数,总有成立,求实数的取值范围;(3)设为数列的前项的和,其中,问是否存在正整数,使成立?若存在,求出正整数;若不存在,说明理由.广东高二高中数学竞赛测试答案及解析一、选择题1.已知集合,则()A.B.C.D.【答案】B【解析】.2.已知=b-i, (a,b∈R),其中i为虚数单位,则a+b=()A.-1 B.1 C.2 D.3【答案】D【解析】,所以b=2,a=1,a+b=3.3.已知a、b是实数,则“a>1,b>2”是“a+b>3且ab>2”的A.充分而不必要条件B.必要而不充分条件C.充分且必要条件D.既不充分也不必要条【答案】A【解析】若a>1,b>2,则a+b>3且ab>2.反之不成立.所以“a>1,b>2”是“a+b>3且ab>2”的充分而不必要条件.4.函数是()A.周期为的奇函数B.周期为的奇函数C.周期为的偶函数D.非奇非偶函数【答案】C【解析】,所以f(x)是周期为的偶函数.5.已知平面向量, , 且, 则m=( )A. 4B.-1C. 2D. -4【答案】D【解析】因为,所以.6.某几何体的三视图及尺寸如图示,则该几何体的表面积为A. B. C. D.【答案】B【解析】.7.已知向量,且,若变量x,y满足约束条,则z的最大值为A.1B.2C.3D.4【答案】C【解析】因为,所以,当直线经过直线和直线的交点A(1,1)时,z取得最大值,最大值为3.8.等差数列中,,且成等比数列,则A.B.C.D.【答案】B【解析】因为成等比数列,所以.9.以轴为对称轴,以坐标原点为顶点,准线的抛物线的方程是A.B.C.D.【答案】A【解析】由题意可知抛物线的开口方向向左,并且p=2,所以应选A.10.起点到终点的最短距离为A.16B.17C.18D.19【答案】B【解析】最短距离应为,长度为4+2+4+7=17.二、填空题1.的定义域--__________【答案】【解析】由,所以定义域为.2.校高中部有三个年级,其中高三有学生人,现采用分层抽样法抽取一个容量为的样本,已知在高一年级抽取了人,高二年级抽取了人,则高中部共有学生__ _人.【答案】3700【解析】由题意知高三抽取了185-75-60=50.所以高中部共有学生.3.在中,,且,则的面积是_____【答案】6【解析】因为,所以,又因为,所以.4.(几何证明选讲选做题)如图,已知的两条直角边,的长分别为,,以为直径的圆与交于点,则=.【答案】【解析】因为AC=3,BC=4,所以AB=5,设BD=x,因为BC为圆O的切线,根据切割线定理可知.5.(坐标系与参数方程选做题)直线截曲线(为参数)的弦长为_ _【答案】【解析】曲线消参后得到普通方程为,由圆心(0,1)到直线3x+4y-7=0的距离,所以弦长.三、解答题1.(本小题共12分)已知函数(1)求的最小正周期;(2)若,, 求的值【答案】(Ⅰ)函数的最小正周期为. (Ⅱ)。
广东省广州市高二数学学业水平测试试卷(含解析)

2015-2016学年度广州市高中二年级学生学业水平测试2015年12月24日一、 选择题:本大题共10小题,每小题5分.1.已知集合M =-1,0,1{},{}x x x N ==2|,则M ÇN =()A.1{}B.0,1{}C.-1,0{}D.-1,0,1{}2.已知等比数列a n {}的公比为2,则a 4a 2值为() A.14 B.12C. 2D.4 3.直线l 过点1,-2(),且与直线2x +3y -1=0垂直,则l 的方程是()A. 2x +3y +4=0B.2x +3y -8=0C.3x -2y -7=0D.3x -2y -1=04.函数f x ()=12æèçöø÷x-x +2的零点所在的一个区间是() A.-1,0() B.0,1() C.1,2() D.2,3()5.已知非零向量与的方向相同,下列等式成立的是()6.要完成下列两项调查:(1)某社区有100户高收入家庭,210户中等收入家庭,90户低收入家庭,从中抽取100户调查消费购买力的某项指标;(2)从某中学高二年级的10名体育特长生中抽取3人调查学习负担情况,应采取的抽样方法是()A.(1)用系统抽样法,(2)用简单随机抽样法B.(1)用分层抽样法,(2)用系统抽样法C.(1)用分层抽样法,(2)用简单随机抽样法D.(1)(2)都用分层抽样法7.设x ,y 满足约束条件⎪⎩⎪⎨⎧≤-+≥-≥+,03,02,01y x x y x ,则z =x -y 的最大值为()A. 3B.1C.1-D.5-8.某几何体的三视图及其尺寸图,则该几何体的体积为()A. 6B. 9C. 12D. 189.函数f x ()=12-cos 2p 4-x æèçöø÷的单调增区间是() A. 2k p -p 2,2k p +p 2éëêùûú,k ÎZ B. 2k p +p 2,2k p +3p 2éëêùûú,k ÎZ C. k p +p 4,k p +3p 4éëêùûú,k ÎZ D. k p -p 4,k p +p 4éëêùûú,k ÎZ 10.设a >1,b >2且ab =2a +b 则a +b 的最小值为()A.22B.22+1C.22+2D.22+3二、填空题:本大题共4小题,每小题5分,满分20分。
2015年全国高中数学联赛试题及答案详解(B卷)

的个数。
2015 年全国高中数学联合竞赛一试(B 卷) 参考答案及评分标准
说明:
1. 评阅试卷时,请依据本评分标准. 填空题只设 8 分和 0 分两档;其他各题的 评阅,请严格按照本评分标准的评分档次给分,不要增加其他中间档次. 2. 如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可 参考本评分标准适当划分档次评分,解答题中第 9 小题 4 分为一个档次,第 10、 11 小题 5 分为一个档次,不要增加其他中间档次.
则 OAi + OAj ≥ 1的概率为
二、解答题
9:(本题满分 16 分)数列 {an}满足 a1 = 3, 对任意正整数 m, n ,均有 am+n = am + an + 2mn (1)求 {an}的通项公式;
∑k
(2)如果存在实数 c 使得
1 < c 对所有正整数 k 都成立,求 c 的取值范围
k 1 k 3
的半径 2 ,故
2.
k2 1
结合图像,应取较小根 k 2 3 .
M(1,1) Γ
O
x
7. 在平面直角坐标系 xOy 中, P 是椭圆 y2 x2 1 上的一个动点,点 A, B 的坐标分 43
别为 (1, 1), (0, 1) ,则 PA PB 最大值为
1)
100
.
a1
a1
16
解得 kmin 34 .
6. 设 k 为实数,在平面直角坐标系 xOy 中有两个点集 A (x, y) | x2 y2 2(x y) 和
广东省广州市2014-2015学年高二下学期期末五校联考理数试题Word版含解析

广东省广州市2014-2015学年高二下学学期期末五校联考数学(理科)试题第Ⅰ卷(共40分)一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}0,2,A a =,{}21,B a =,若{}0,1,2,4,16AB =,则a 的值为( )A.0B.1C.4D.22.复数1z i =+(i 为虚数单位),z 为z 的共轭复数,则下列结论正确的是 A. z 的实部为1- B. z 的虚部为1 C.2z z ⋅= D.zi z=3.已知等差数列}{n a 中,79416,1a a a +==,则12a 的值是( )A . 15B . 30 C. 31 D. 64 【答案】A 【解析】试题分析:根据等差数列的性质,可知79412a a a a +=+,所以有1216115a =-=,故选A. 考点:等差数列的性质.4.如图所示,正四棱锥 (底面是正方形,顶点在底面的射影是底面的中心) P ABCD -的底面边长为6cm ,侧棱长为5cm ,则它的正视图的面积等于A.5.在△ABC 中,4cos 5A =,8AB AC ⋅=,则△ABC 的面积为( ). A.65 B.3 C.125D.66.下列命题中正确的是( )A .若p q ∨为真命题,则p q ∧为真命题B .“0a >,0b >”是“2b aa b+≥”的充分必要条件 C .命题“若2320x x -+=,则1x =或2x =”的逆否命题为“若1x ≠或2x ≠,则2320x x -+≠”D .命题:p R x ∃∈,使得210x x +-<,则:p ⌝R x ∀∈,使得210x x +-≥ 【答案】D 【解析】试题分析:根据p q ∨为真命题,可知,p q 有一个真即可,而p q ∧为真命题,要求,p q 两者都真,故A 不正确,因为2b a a b +≥要求b a 0>,即,a b 同号,所以“0a >,0b >”是“2b aa b+≥”的充分不必要条件,故B 不正确,命题“若2320x x -+=,则1x =或2x =”的逆否命题为“若1x ≠且2x ≠,则2320x x -+≠”,故C 不正确,根据特称命题的否定形式,可知D 是正确的,故选D.考点:复合命题的真值表,充要条件,逆否命题,特称命题的否定.7.将编号为1、2、3、4的四个小球任意地放入A 、B 、C 、D 四个小盒中,每个盒中放球的个数不受限制,恰好有一个盒子是空的概率为( )()169A()41B()43C()167D8.在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数()f x 的图象恰好通过()n n N +∈个整点,则称函数()f x 为n 阶整点函数.有下列函数:①()sin 2f x x =; ②3()g x x = ③1()();3xh x = ④()ln x x φ=,其中是一阶整点函数有( ) 个 A.1 B.2 C.3 D.4第Ⅱ卷(共110分)二、填空题(本题共7小题,考生作答6小题,每小题5分,共30分) (一)必做题(9~13题)9.函数21)(--=x x x f 的定义域为___________.10.关于x 的二项式41(2)x x-展开式中的常数项是11.如右图,是一程序框图,则输出结果为 【答案】511【解析】试题分析:根据题意,可知执行的结果为1111113355779911S =++++=⨯⨯⨯⨯⨯1111115(1)233591111-+-++-=. 考点:程序框图,裂项相消法求和.12.如果关于x 的不等式a x x ≥-+-32的解集为R, 则a 的取值范围是 .13.设平面区域D 是由双曲线1422=-x y 的两条渐近线和抛物线28y x =-的准线所围成的三角形(含边界与内部).若点D y x ∈),(,则目标函数y x z +=的最大值为 .(二)选做题(14、15题,考生只能从中选做一题,两题全答的,只计前一题的得分) 14.(坐标系与参数方程选做题)极坐标系下,直线2)4cos(=-πθρ 与圆2=ρ的公共点个数是________; 【答案】1 【解析】试题分析:直线2)4cos(=-πθρ平面直角坐标方程为20x y +-=,圆2=ρ的平面直角坐标方程为222x y +=,此时圆心(0,0)到直线2x y +=的距离d ==,等于圆的半径,所以直线与圆的公共点的个数为1个.考点:曲线的极坐标方程与平面直角坐标方程的转换,圆与直角的位置关系.15.15(几何证明选讲选做题)如图,AB 是圆O 的直径,DE AD =,6,8==BD AB ,则三、解答题 (本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.) 16.(本题满分12分)已知函数x x a x f cos sin )(+=的图象经过点)1,2(-π.(1)求函数()x f 的最小正周期与单调递增区间. (2)若0,2πθ⎛⎫∈ ⎪⎝⎭,且()12f θ=,求sin 2θ的值.……1分17.(本题满分12分) 数列{}n b ()*∈Nn 是递增的等比数列,且4,53131==+b b b b.(Ⅰ)若3log 2+=n n b a ,求证:数列{}n a 是等差数列; (Ⅱ)若+++3221a a a ……46a a m ≤+,求m 的最大值. 【答案】(Ⅰ)证明略; (Ⅱ) 7【解析】试题分析:第一问根据题意可知13,b b 是方程0452=+-x x 的两根,结合题的条件递增数列,从而确定出1 8.(本题满分14分)某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示.(1)请根据图中所给数据,求出a的值;(2)为了了解学生本次考试的失分情况,从成绩在[50,70)内的学生中随机选取3人的成绩进行分析,用X表示所选学生成绩在[60,70)内的人数,求X的分布列和数学期望.【答案】(1)0.03a=(2)EX=27 11所以X的分布列为第19题图312355555511EX =⨯+⨯+⨯=. …………………14分 考点:频率分布直方图,离散型随机变量的分布列及期望.19.(本题满分14分)如图,已知E ,F 分别是正方形ABCD 边BC 、CD 的中点,EF 与AC 交于点O ,PA 、NC 都垂直于平面ABCD ,且4P A A B ==,2NC =,M 是线段PA上一动点.(Ⅰ)求证:平面PAC ⊥平面NEF ;(Ⅱ)若//PC 平面MEF ,试求:PM MA 的值;(Ⅲ)当M 是PA 中点时,求二面角M EF N --的余弦值.【答案】(Ⅰ)证明略; (Ⅱ)1:3 (Ⅲ)∵//PC 平面MEF ,平面PAC 平面MEF OM ,(Ⅲ)(4,4,2)N ,则(0,2,2)EN =,设平面NEF 的法向量为(,,)m x y z =,则00m EN m EF ⎧⋅=⎪⎨⋅=⎪⎩,即220220y z x y +=⎧⎨-+=⎩,令1x =,则1y =,1z =-,即(1,1,1)m =-,当M 是PA 中点时,2m =,则(1,1,3)n =,∴cos ,m n <>==, ∴二面角M EF N --的余弦值为分 考点:面面垂直的判定,线面平行的性质,二面角的余弦值.20.(本题满分14分)已知椭圆C :)0(12222>>=+b a by a x ,左、右两个焦点分别为1F 、2F,上顶点),0(b A ,21F AF ∆为正三角形且周长为6.(1)求椭圆C 的标准方程及离心率;(2)O 为坐标原点,P 是直线A F 1上的一个动点,求||||2PO PF +的最小值,并求出此时点P 的坐标.||||2PO PF +的最小值为7)023()123(||222=-+--=MF …………… 11分 直线2MF 的方程为)1(123023----=x y 即)1(53--=x y …………… 12分 由⎪⎪⎩⎪⎪⎨⎧=-=⇒⎪⎩⎪⎨⎧+=--=3332)1(3)1(53y x x y x y ,所以此时点P 的坐标为 )33,32(-…… 14分 考点:椭圆的方程,椭圆的性质,点关于直线的对称点问题,距离和的最值.21.(本题满分14分)已知函数32()()f x ax bx b a x =++-(a ,b 是不同时为零的常数),其导函数为()f x '.(1)当13a =时,若不等式1()3f x '>-对任意x R ∈恒成立,求b 的取值范围; (2)若函数()f x 为奇函数,且在1x =处的切线垂直于直线230x y +-=,关于x 的方程1()4f x t =-在[1,](1)t t ->-上有且只有一个实数根,求实数t 的取值范围. 【答案】(1)(0,1)(2)是0t ≤<或0t <<t =【解析】 试题分析:第一问将13a =代入函数解析式,求出函数的导数,将不等式化简为220x bxb ++>,从而根据判别式大于零得出b 所满足条件,从而求得其范围是(0,1),第二问根据函数为奇函数,得出0b =,根据在1x =处的切线垂直于直线230x y +-=,可以得出'(1)2f =-,从而求得a 的值,从而确定出函数的解析式,确定出函数的单调区间,注意对t 的取值进行讨论.试题解析:(1)当13a =时,21()23f x x bx b '=++-,………1分 依题意 21()23f x x bx b '=++-13>- 即220x bx b ++>恒成立 2440b b ∴∆=-<,解得 01b <<所以b 的取值范围是(0,1)………3分。
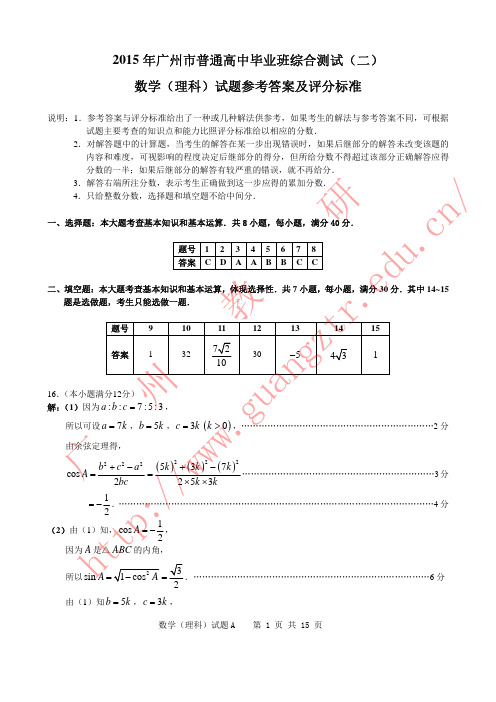
[精品]广东省广州市2015高中毕业班综合测试(二)高中数学理科试题和答案
![[精品]广东省广州市2015高中毕业班综合测试(二)高中数学理科试题和答案](https://img.taocdn.com/s3/m/018a862cbb68a98271fefa98.png)
试卷类型:A2015年广州市普通高中毕业班综合测试(二)数学(理科)2015.4本试卷共4页,21小题, 满分150分.考试用时120分钟 注意事项:1.答卷前,考生务必用2B 铅笔在“考生号”处填涂考生号.用黑色字迹的钢笔或签字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上. 2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上. 3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题题号对应的信息点,再作答.漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回. 参考公式:球的表面积公式24S R =π,其中R 是球的半径.一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.命题“若2x =,则2320x x -+=”的逆否命题是A .若2x ≠,则2320x x -+≠B .若2320x x -+=,则2x =C .若2320x x -+≠,则2x ≠D .若2x ≠,则2320x x -+= 2.已知0a b >>,则下列不等关系式中正确的是A .sin sin a b >B .22log log a b <C .1122a b <D .1133a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭3.已知函数()40,1,0,x f x x x x ⎧≥⎪=⎨⎛⎫-<⎪ ⎪⎝⎭⎩则()2f f =⎡⎤⎣⎦A .14B .12C .2D .44.函数()sin y A x ωϕ=+()0,0,0A ωϕ>><<π的图象的一部分如图1则此函数的解析式为A .3sin y x ππ⎛⎫=+ ⎪44⎝⎭ B .3sin y x π3π⎛⎫=+ ⎪44⎝⎭C .3sin y x ππ⎛⎫=+ ⎪24⎝⎭D .3sin y x π3π⎛⎫=+ ⎪24⎝⎭5.已知函数()223f x x x =-++,若在区间[]4,4-上任取一个实数0x ,则使()00f x ≥成立的概率为 A .425B .12C .23 D .16.如图2,圆锥的底面直径2AB =,母线长3VA =,点C 在母线VB 上,且1VC =, 有一只蚂蚁沿圆锥的侧面从点A 到达点C ,则这只蚂蚁爬行的最短距离是A C .3 D .27.已知两定点()1,0A -,()1,0B ,若直线l 上存在点M ,使得3MA MB +=, 则称直线l 为“M 型直线”.给出下列直线:①2x =;②3y x =+; ③21y x =--;④1y =;⑤23y x =+.其中是“M 型直线”的条数为 A .1 B .2 C .3 D .48.设(),P x y 是函数()y f x =的图象上一点,向量()()51,2x =-a ,()1,2y x =-b ,且//a b .数列{}n a是公差不为0的等差数列,且()()()12936f a f a f a ++⋅⋅⋅+=,则129a a a ++⋅⋅⋅+=图1AV CB图2A.0B.9C.18D.36 二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题) 9.已知i 为虚数单位,复数1i1iz -=+,则z = . 10.执行如图3所示的程序框图,则输出的z 的值是 .11.已知()sin 6f x x π⎛⎫=+ ⎪⎝⎭,若3cos 5α=02απ⎛⎫<< ⎪⎝⎭,则12f απ⎛⎫+= ⎪⎝⎭.12.5名志愿者中安排4人在周六、周日两天参加社区公益活动.若每天安排2人,则不同的安排方案共有_________种(用数字作答).13.在边长为1的正方形ABCD 中,以A 为起点,其余顶点为终点的向量分别为1a ,2a ,3a ;以C()()ijst +∙+a a cc 的最小值,其中{}{},1,2,3i j ⊆,{}{},1,2,3s t ⊆(二)选做题(14~15题,考生只能从中选做一题) 14.(几何证明选讲选做题)如图4,在平行四边形ABCD 中,4AB =,点E 为边DC 的中点,AE 与BC 的延长线交于点F,且AE 平分BAD ∠,作DG AE ⊥,垂足为G ,若1DG =,则AF 的长为 . 15.(坐标系与参数方程选做题)图4在平面直角坐标系中,已知曲线1C 和2C 的方程分别为32,12x t y t =-⎧⎨=-⎩(t 为参数)和24,2x t y t =⎧⎨=⎩(t 为参数),则曲线1C 和2C 的交点有 个. 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)已知△ABC 的三边a ,b ,c 所对的角分别为A ,B ,C ,且::7:5:3a b c =. (1)求cos A 的值;(2)若△ABC的面积为,求△ABC 外接圆半径的大小.17.(本小题满分12分)答一份).现从回收的年龄在20~60份,统计结果如下面的图表所示.(a b c n (2)从第3,4组答对全卷的人中用分层抽样的方法抽取6人,在所抽取的6人中随机抽取2人授予“环保之星”,记X 为第3组被授予“环保之星”的人数,求X 的分布列与数学期望.18.(本小题满分14分)如图5,已知六棱柱111111ABCDEF A BC D E F -的侧棱 垂直于底面,侧棱长与底面边长都为3,M ,N 分别 是棱AB ,1AA 上的点,且1AM AN ==. (1)证明:M ,N ,1E ,D 四点共面;(2)求直线BC 与平面1MNE D 所成角的正弦值.19.(本小题满分14分)已知点(),n n n P a b ()n ∈*N 在直线l :31y x =+上,1P 是直线l 与y 轴的交点,数列{}n a 是公差为1的等差数列.(1)求数列{}n a ,{}n b 的通项公式; (2)求证:22212131111116n PP PP PP ++++<.C 1ABA 1B 1D 1CDMNE FE 1F 1 图520.(本小题满分14分)已知圆心在x 轴上的圆C 过点()0,0和()1,1-,圆D 的方程为()2244x y -+=.(1)求圆C 的方程;(2)由圆D 上的动点P 向圆C 作两条切线分别交y 轴于A ,B 两点,求AB 的取值范围.21.(本小题满分14分)已知函数()ln f x a x =-11x x -+,()e xg x =(其中e 为自然对数的底数). (1)若函数()f x 在区间()0,1内是增函数,求实数a 的取值范围;(2)当0b >时,函数()g x 的图象C 上有两点(),e b P b ,(),e b Q b --,过点P ,Q 作图象C 的切线分别记为1l ,2l ,设1l 与2l 的交点为()00,M x y ,证明00x >.2015年广州市普通高中毕业班综合测试(二)数学(理科)试题参考答案及评分标准说明:1.参考答案与评分标准给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题考查基本知识和基本运算.共8小题,每小题,满分40分.二、填空题:本大题考查基本知识和基本运算,体现选择性.共7小题,每小题,满分30分.其中14~15题是选做题,考生只能选做一题.16.解:(1)因为::7:5:3a b c=,所以可设7b k=,=,5a kk>,…………………………………………………………2分=()0c k3由余弦定理得,222cos 2b c a A bc +-=()()()222537253k k k k k+-=⨯⨯…………………………………………………………3分12=-.………………………………………………………………………………………………4分(2)由(1)知,1cos 2A =-,因为A 是△ABC 的内角, 所以s i A=………6分由(1)知5b k =,3c k =, 因为△ABC的面积为,所以1sin 2bc A =8分即15322k k ⨯⨯⨯= 解得k =…………10分由正弦定理2sina R A =,即71432s n2kR A==,…………………………………………………11分解得14R =. 所以△ABC外接圆半径的大小为14.…………………………………………………………………12分17.(本小题满分12分)解:(1)根据频率直方分布图,得()0.0100.0250.035101c +++⨯=, 解得0.03c =.……………………………………………………………………………………………1分 第3组人数为105.05=÷,所以1001.010=÷=n .…………………………………………………2分第1组人数为1000.3535⨯=,所以28350.8b =÷=.……………………………………………3分第4组人数为2525.0100=⨯,所以250.410a =⨯=.……………………………………………4分(2)因为第3,4组答对全卷的人的比为5:101:2=, 所以第3,4组应依次抽取2人,4人.…………………………………………………………………5分 依题意X的取值为0,1,2.……………………………………………………………………………6分()022426C C 20C 5P X ===,…………………………………………………………………………………7分()112426C C 81C 15P X ===,………………………………………………………………………………8分()202426C C 12C 15P X ===,………………………………………………………………………………9分所以X 的分布列为:………………………………………10分所以280151EX =⨯+⨯+⨯=. ………………………………………………………………12分18.(本小题满分14分)第(1)问用几何法,第(2)问用向量法: (1)证明:连接1A B ,11B D ,BD ,11A E ,在四边形1111A B D E 中,1111A E B D 且1111=A E B D ,在四边形11BB D D 中,11BD B D 且11=BD B D , 所以11A E BD 且11=A E BD ,所以四边形11A BDE 是平行四边形.所以11A B E D .………………………………2分 在△1ABA 中,1AM AN ==,13AB AA ==, 所以1AM ANAB AA =, 所以1MN.…………………………………………………………………………………………4分所以1MN DE .所以M,N,1E ,D四点共面.………………………………………………………………………6分 (2)解:以点E 为坐标原点,EA ,ED ,1EE 所在的直线分别为x 轴,y 轴,z 轴,建立如图的空间直角坐标系, 则()B ,9,02C ⎫⎪⎪⎝⎭,()0,3,0D , ()10,0,3E ,()M 1C 1A BA 1B 1D 1CDMN E FE 1F 1则3,02BC ⎛⎫= ⎪ ⎪⎝⎭,()10,3,3DE =-,()2,0DM =-.……………………………………10分设(),,x y z =n 是平面1MNE D 的法向量,则10,0.DE DM ⎧⋅=⎪⎨⋅=⎪⎩n n即330,20.y z y -+=⎧⎪⎨-=⎪⎩取y =2x =,z = 所以(23,33=n 是平面1MNE D的一个法向量.………………………………………………12分设直线BC 与平面1MNE D 所成的角为θ,则sin BC BCθ⋅=⋅n n116==. 故直线BC与平面1M NE D 所成角的正弦值为116. (14)第(1)(2)问均用向量法:(1)证明:以点E 为坐标原点,EA ,ED ,1EE 分别为x 轴,y 轴,z 则()B ,9,02C ⎫⎪⎪⎝⎭,()0,3,0D ,()10,0,3E ,()M ,()N ,……………2分所以()10,3,3DE =-,()0,1,1MN =-. ………………3分 因为13DE MN =,且MN 与1DE 不重合,所以1DE MN .…………………………………………5分 所以M,N,1E ,D四点共面.………………………………………………………………………6分 (2)解:由(1)知,02BC ⎛⎫= ⎪ ⎪⎝⎭,()10,3,3DE =-,()2,0DM =-.………………10分(特别说明:由于给分板(1)6分(2)8分,相当于把(1)中建系与写点坐标只给2分在此加2分)设(),,x y z =n 是平面1MNE D 的法向量,则10,0.DE DM ⎧⋅=⎪⎨⋅=⎪⎩n n即330,20.y z y -+=⎧⎪⎨-=⎪⎩取y =2x =,z = 所以(23,33=n 是平面1MNE D的一个法向量.………………………………………………12分设直线1BC 与平面1MNE D 所成的角为θ,则sin BC BCθ⋅=⋅n n==. 故直线BC与平面1MN E D 所成角的正弦值为.………………………………………………14分 第(1)(2)问均用几何法:(1)证明:连接1A B ,11B D ,BD ,11A E ,在四边形1111A B D E 中,1111A E B D 且1111=A E B D , 在四边形11BB D D 中,11BD B D 且11=BD B D , 所以11A E BD 且11=A E BD ,C 1BA 1B 1D 1CDNEFE 1F 1所以四边形11A BDE 是平行四边形.所以11A B E D .………………………………2分 在△1ABA 中,1AM AN ==,13AB AA ==, 所以1AM ANAB AA =, 所以1MN.…………………………………………………………………………………………4分所以1MN DE .所以M,N,1E ,D四点共面.………………………………………………………………………6分 (2)连接AD ,因为BCAD ,所以直线AD 与平面1MNE D 所成的角即为直线BC 与平面1MNE D 所成的角.…………………7分连接DN ,设点A 到平面DMN 的距离为h ,直线AD 与平面1MNE D 所成的角为θ,则sin hADθ=.……………………………………………………………………………………………8分因为A V V--=,即1133DMN AMN S h S DB ∆∆⨯⨯=⨯⨯.…………………………………………9分 在边长为3的正六边形ABCDEF中,DB =6DA =, 在△ADM 中,6DA =,1AM =,60DAM ∠=,由余弦定理可得,DM =在Rt △DAN 中,6DA =,1AN =,所以DN 在Rt △AMN 中,1AM =,1AN =,所以MN =在△DMN中,DM =DN =MN =由余弦定理可得,cos DMN ∠=,所以sin DMN ∠=. 所以1s 22DMN S MN DM DMN ∆=⨯⨯⨯∠=.…………………………………………………11分又12AMN S ∆=,……………………………………………………………………………………………12分所以AMN DMN S DB h S ∆∆⨯==.…………………………………………………………………………13分所以sin h AD θ==故直线BC与平面1MN E D 所成角的正弦值为116.………………………………………………14分 19.(本小题满分14分)(1)解:因为()111,P a b 是直线l :31y x =+与y 轴的交点()0,1, 所以10a =,11b =.……………………………………………………………………………………2分因为数列{}n a 是公差为1的等差数列, 所以1n a n =-.……………………………………………………………………………………………4分因为点(),n n n P a b 在直线l :31y x =+上, 所以31n n b a =+32n =-.所以数列{}n a ,{}n b 的通项公式分别为1n a n =-,32n b n =-()*n ∈N .………………………6分(2)证明:因为()10,1P ,()1,32n P n n --,所以()1,31n P n n ++.所以()222211310n PP n n n +=+=.………………………………………………………………………7分所以221211n P P +++211n ⎛⎫=+++⎪⎝⎭.……………………………………8分因为()()2221144112141212121214n n n n n n n ⎛⎫<===- ⎪--+-+⎝⎭-,……………………………10分所以,当2n ≥时,222121311111n PP PP PP ++++111111210352121n n ⎡⎤⎛⎫<+-++- ⎪⎢⎥-+⎝⎭⎣⎦……………………………………………………………11分15110321n ⎛⎫=- ⎪+⎝⎭………………………………………………………………………………………12分16<. 又当1n =时,212111106PP =<.………………………………………………………………………13分所以2212116nP P ++.……………………………………………………………14分20.(本小题满分14分) 解:(1)方法一:设圆C的方程为:()222x a y r -+=()0r >,………………………………………1分因为圆C 过点()0,0和()1,1-, 所以()22222,11.a r a r ⎧=⎪⎨--+=⎪⎩………………………………………………………………………………3分解得1a =-,1r =. 所以圆C的方程为()2211x y ++=.…………………………………………………………………4分方法二:设()0,0O ,()1,1A -,依题意得,圆C 的圆心为线段OA 的垂直平分线l 与x 轴的交点C .………………………………1分因为直线l的方程为1122y x -=+,即1y x =+,……………………………………………………2分所以圆心C的坐标为()1,0-.…………………………………………………………………………3分 所以圆C的方程为()2211x y ++=.…………………………………………………………………4分(2)方法一:设圆D 上的动点P 的坐标为()00,x y ,则()220044x y -+=, 即()2200440y x =--≥,解得026x ≤≤.…………………………………………………………………………………………5分由圆C 与圆D 的方程可知,过点P 向圆C 所作两条切线的斜率必存在, 设PA 的方程为:()010y y k x x -=-, 则点A 的坐标为()0100,y k x -, 同理可得点B 的坐标为()0200,y k x -, 所以120AB k k x =-,因为PA ,PB 是圆C 的切线,所以1k ,2k1=,即1k ,2k 是方程()()2220000022110xx k y x k y +-++-=的两根,………………………………7分即()0012200201220021,21.2y x k k x x y k k x x ⎧++=⎪+⎪⎨-⎪=⎪+⎩所以12A B =-x =9分因为()220044y x =--, 所以AB =………10分设()()0020562x f x x -=+,则()()00305222x f x x -+'=+.………………………………………………………………………………11分由026x ≤≤,可知()0f x 在222,5⎡⎫⎪⎢⎣⎭上是增函数,在22,65⎛⎤⎥⎝⎦上是减函数,……………………12分所以()0max2225564f x f ⎛⎫==⎡⎤ ⎪⎣⎦⎝⎭, ()()(){}min0131min 2,6min ,484f x f f ⎧⎫===⎡⎤⎨⎬⎣⎦⎩⎭, 所以AB的取值范围为4⎦.…………………………………………………………………14分 方法二:设圆D 上的动点P 的坐标为()00,x y ,则()220044x y -+=,即()2200440y x =--≥, 解得026x ≤≤.…………………………………………………………………………………………5分设点()0,A a ,()0,B b , 则直线PA :00y ay a x x --=,即()0000y a x x y ax --+=,因为直线PA 与圆C1=,化简得()2000220x a y a x +--=. ① 同理得()2000220x b y b x +--=, ② 由①②知a,b为方程()2000220x x y x x +--=的两根,…………………………………………7分即00002,2.2y a b x x ab x ⎧+=⎪+⎪⎨-⎪=⎪+⎩所以AB a b =-===…9分因为()220044y x =--, 所以AB =………10分=.………………………………………………………………11分令012t x =+,因为026x ≤≤,所以1184t ≤≤.所以AB ==,………………………………………12分 当532t =时,max AB =, 当14t =时,min AB =所以AB 的取值范围为4⎦.…………………………………………………………………14分 21.(本小题满分14分)(1)解法一:因为函数()ln f x a x =-11x x -+在区间()0,1内是增函数, 所以()()2201a f x x x '=-≥+()01x <<.……………………………………………………………1分即()2120a x x +-≥()01x <<,即()221x a x ≥+……………………………………………………………………………………………2分212x x=++()01x <<, 因为21122x x<++在()0,1x ∈内恒成立, 所以12a ≥.故实数a 的取值范围为1,2⎡⎫+∞⎪⎢⎣⎭.……………………………………………………………………4分 解法二:因为函数()ln f x a x =-11x x -+在区间()0,1内是增函数, 所以()()2201a f x x x '-+≥=()01x <<.……………………………………………………………1分即()2120a x x +-≥()01x <<,即()2210ax a x a +-+≥()01x <<,…………………………………………………………………2分设()()221g x ax a x a =+-+,当0a =时,得20x -≥,此时不合题意.当0a <时,需满足()()00,10,g g ≥⎧⎪⎨≥⎪⎩即()0,210,a a a a ≥⎧⎪⎨+-+≥⎪⎩解得12a ≥,此时不合题意. 当0a >时,需满足()222140a a --≤⎡⎤⎣⎦或()()00,10,10,g g a a ⎧⎪≥⎪≥⎨⎪-⎪-<⎩或()()00,10,11,g g a a⎧⎪≥⎪≥⎨⎪-⎪->⎩ 解得12a ≥或1a >, 所以12a ≥.综上所述,实数a 的取值范围为1,2⎡⎫+∞⎪⎢⎣⎭.……………………………………………………………4分 (2)证明:因为函数()e x g x =,所以()e xg x '=. 过点(),e b P b ,(),e b Q b --作曲线C 的切线方程为:1l :()e e b b y x b =-+,2l :()e e b b y x b --=++,因为1l 与2l 的交点为()00,M x y ,由()()e e ,e e ,b b b b y x b y x b --⎧=-+⎪⎨=++⎪⎩ ………………………………………………………………………………6分消去y ,解得()()()0e +e e e e e b b b b b b b x -----=-. ①…………………………………………7分下面给出判定00x >的两种方法:方法一:设e b t =,………………………………………………………………………………………8分因为0b >,所以1t >,且ln b t =.所以()()2202+1ln 11t t t x t --=-.…………………………………………………………………………9分设()()()22+1ln 1h t t t t =--()1t >,则()12ln h t t t t t'=-+()1t >.………………………………………………………………………10分令()12ln u t t t t t =-+()1t >,则()212ln 1u t t t '=+-. 当1t >时,l n t >,2110t ->,所以()212ln 10u t t t '=+->,………………………………11分 所以函数()u t 在()1,+∞上是增函数,所以()()10u t u >=,即()0h t '>,…………………………………………………………………12分所以函数()h t 在()1,+∞上是增函数,所以()()10h t h >=.…………………………………………………………………………………13分因为当1t >时,210t ->,所以()()2202+1ln 101t t t x t --=>-.…………………………………………………………………14分方法二:由①得0x ()221+e 11e b b b --=--. 设2e b t -=,…………………………………………………………………………………………………8分因为0b >,所以01t <<,且ln 2t b =-.于是21ln b t-=,……………………………………………………………………………………………9分所以()01+221ln 1ln 1b t b t x b t t t t +⎛⎫=+=+ ⎪--⎝⎭.…………………………………………………………10分由(1)知当12a =时,()1ln 2f x x =-11x x -+在区间()0,1上是增函数,…………………………11分所以()ln 2t f t =-()1101t f t -<=+, 即ln 2t <11t t -+. …………………………………………………………………………………………12分 即210ln 1t t t++>-,………………………………………………………………………………………13分已知0b >,所以0210ln 1t x b t t +⎛⎫=+> ⎪-⎝⎭.…………………………………………………………………………14分。
广东省广州市五校2015-2016学年高二数学上学期期末联考试题 理

2015—2016学年度第一学期期末模块考试 五校联考高二年级数学(理科)试题试题说明:本试卷分选择题和非选择题两部分,满分为150分。
考试时间为120分钟。
注意事项:1、 选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
2、 非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内。
第一部分 选择题(共60分)一、选择题:(本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,有且只有一项是符合题目要求的。
) 1.设全集{}1,2,3,4,5,6,7,8U =,集合{1,2,3,5}A =,{2,4,6}B =,则图中的阴影部分表示的集合为 ( ) A .{}2 B .{}4,6C .{}1,3,5D .{}4,6,7,82.函数()lg(31)f x x =+的定义域是( ) 第1题图 A .1(,)3-+∞ B .1(,1)3- C .1(,1]3- D .1(,1)33.已知向量(1,2),(1,0),(3,4)===a b c .若λ为实数,()λ+⊥b a c ,则λ= ( )A .311-B .113- C .12 D .354.下列有关命题的说法正确的是( )A .命题“若21x =,则1=x ”的否命题为:“若21x =,则1x ≠”.B .线性回归直线方程y bx a =+恒过样本中心(,)x y ,且至少经过一个样本点.C .命题“x R ∃∈,使得210x x ++<”的否定是:“x R ∀∈, 均有210x x ++<”.D .命题“若x y =,则sin sin x y =”的逆否命题为真命题.5.已知:p 直线1:10l x y --=与直线2:20l x ay +-=平行,:1q a =-,则p 是q 的( ) A.充要条件 B.充分不必要条件 C. 必要不充分条件 D. 既非充分又非必要条件 6.等差数列}{n a 的前n 项和为n S ,若301272=++a a a ,则13S 的值是( ) A .65B .70C .130D .1407.函数y =sin (2x +π4)的图像可由函数y =sin 2x 的图像( ) A .向左平移π8个单位长度而得到 B .向右平移π8个单位长度而得到C .向左平移π4个单位长度而得到 D .向右平移π4个单位长度而得到 8.设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是( ) A .若αβ⊥,m α⊂,n β⊂,则m n ⊥ B .若//αβ,m α⊂,n β⊂,则//m n C .若m n ⊥,m α⊂,n β⊂,则αβ⊥ D .若m α⊥,//m n ,//n β,则αβ⊥ 9.如图,若程序框图输出的S 是126,则判断框①中应为( ) A .5?n ≤ B .6?n ≤ C .7?n ≤ D .8?n ≤ 10.已知{}n a 为等比数列,n S 是它的前n 项和.若2312a a a ⋅=,且4a 与72a 的等差中项为54,则5S 等于( ) A.314B. 8C. 31D. 32 11.过抛物线24y x =的焦点F 的直线交抛物线于A B 、两点,点O 是坐标原点,若||5AF =,则△AOB 的面积为( )A.5B.52 C.32 D.178第9题图 12.若函数()M f x 的定义域为实数集R,满足()1,0,M x Mf x x M ∈⎧=⎨∉⎩(M 是R 的非空真子集),在R 上有两个非空真子集,A B ,且A B =∅ ,则()()()()11A B A B f x F x f x f x +=++ 的值域为( )A . 20,3⎛⎤ ⎥⎝⎦ B. {}1 C. 12,,123⎧⎫⎨⎬⎩⎭D. 1,13⎡⎤⎢⎥⎣⎦第二部分 非选择题(共90分)二、填空题(本题共4小题,每小题5分,共20分)13.如右图,一个棱长为2的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为__________.14.设,x y 满足约束条件0201x x y x y ≥⎧⎪-≥⎨⎪-≤⎩,则2z x y =-的最大值是________.15.已知椭圆22221(0)x y a b a b+=>>的左焦点为F ,右顶点为A ,点B 在椭圆上,且BF x ⊥轴,直线AB 交y 轴于点P .若2AP PB =,则椭圆的离心率是_________.16.设二次函数2()4()f x ax x c x =-+∈R 的值域为(,0]-∞,则19c a+的最大值为_________. 三、解答题:本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤. 17.(本小题满分10分)A 、B 、C 为△ABC 的三个内角,且其对边分别为a 、b 、c ,若m u r =⎝⎛⎭⎪⎫-cos A 2,sin A 2,n r =⎝⎛⎭⎪⎫cos A 2,sin A 2,且∙m n u r r =12.(Ⅰ)求角A 的大小;(Ⅱ)若a =23且4b c +=,求此三角形的面积.18.(本小题满分12分)某校学生利用元旦节进行社会实践,在[25,55]岁的人群随机抽取n 人,进行了一次“是否已养成垃圾分类习惯”的调查,得到如下统计表和各年龄段人数频率分布直方图:(Ⅰ)补全频率分布直方图并求n 、a 、p 的值;(Ⅱ)从[40,50)岁年龄段的“已养成垃圾分类习惯的人”中采用分层抽样法抽取6人参加垃圾分类宣讲活动,其中选取2人作为领队,求选取的2名领队年龄都在[40,45)岁的概率.19.(本小题满分12分)已知二次函数2()f x x =,数列}{n a 的前n 项和为n S ,点(,)n n S 均在函数()y f x =上的图像上。
2015年全国高中数学联赛广东赛区拟参赛名单

曹鸿艺
广东实验中学
黄凯旋
广东实验中学
朱若珺
广东实验中学
陈悦
广东实验中学
廖铮发
广东实验中学
郑世豪
广东实验中学
杜浩民
广东实验中学
黄家和
广东实验中学
郑言
广东实验中学
李祉涵
广东实验中学
林罗萱
广东实验中学
黄文皓
广东实验中学
邵小姍
广东实验中学
陈鸿峥
省直 广东实验中学 省直 广东实验中学 省直 广东实验中学 省直 广东实验中学 省直 广东实验中学 省直 广东实验中学 省直 广东实验中学 广州市 广州大学附属中学 广州市 广东广雅中学 广州市 广州市执信中学 广州市 广州大学附属中学 广州市 广州大学附属中学 广州市 广州市执信中学 广州市 广州市执信中学 广州市 广州市执信中学 广州市 广州大学附属中学 广州市 广州大学附属中学 广州市 广州市执信中学 广州市 广州市执信中学 广州市 广州大学附属中学 广州市 广东广雅中学 广州市 广东广雅中学 广州市 广东广雅中学 广州市 广州大学附属中学 广州市 广州大学附属中学
华南师范大学附属中学梁逸爽 省直 华南师范大学附属中学 陈俊宏 省直 华南师范大学附属中学 李易安
华南师范大学附属中学戎明远 省直 华南师范大学附属中学 柳纬洋 省直 华南师范大学附属中学 曹以宁
华南师范大学附属中学 洪博
省直 华南师范大学附属中学 邱磊鑫 省直 华南师范大学附属中学 金璋
华南师范大学附属中学胡壮飞 省直 华南师范大学附属中学 许啸天 省直 华南师范大学附属中学 郭欣玮
省直 省直 省直 省直 省直 省直 省直 省直 省直 省直 省直 省直 省直 省直 省直 省直 省直 省直 省直 省直 省直 省直 省直 省直 省直
2014-2015学年广东省广州市高二下学期期末五校联考数学(理)试卷(带解析)

,左、右两个焦点分别为 、 ,上顶点
,
的最小值,并求出此时点 的坐标.
为正三角形且
难度:0.85 组卷:679 题型:解答题 更新:2015/10/8
相似题 纠错 收藏 详情
21 . (本题满分14分)已知函数
(1)当
时,若不等式
(2)若函数
为奇函数,且在
实数根,求实数t的取值范围.
C.12
D.24
难度:0.65 组卷:731 题型:单选题 更新:2011/9/6
相似题 纠错 收藏 详情
5 . 在△ABC中, A.
,
,则△ABC的面积为( ).
B.3
C.
【知识点】平面向量的数量积
D.6
难度:0.64 组卷:615 题型:单选题 更新:2015/10/8
相似题 纠错 收藏 详情
(a,b是不同时为零的常数),其导函数为
.
对任意
恒成立,求b的取值范围;
处的切线垂直于直线
,关于x的方程
在
【知识点】导数在函数中的其他应用
上有且只有一个
难度:0.64 组卷:300 题型:解答题 更新:2015/10/8
相似题 纠错 收藏 详情
设
京ICP备12013499号-24
2014-2015学年广东省广州市高二下学期期末五校联考数学(理)试卷(带解析)
适用年级:高二 试卷类型:期末 试题总数:21 浏览次数:450 上传日期:2017/7/20
1 . 集合
,
,若
,则 的值为( ).
A.
B.
C.
D.
【知识点】根据并集结果求集合或参数 解读
难度:0.85 组卷:379 题型:单选题 更新:2017/12/31
广东省广州市执信中学2015-2016学年高二下学期期末考试理数试题Word版含解析

一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合2{20}A x x x =+-<,{0}B x x =>,则集合A B 等于( )A .{2}x x >-B .{21}x x -<<C .{1}x x <D .{01}x x <<【答案】D【解析】 试题分析:由2{20}A x x x =+-<,得{}12<<-x x ,故{}10<<=⋂x x B A ,故选D. 考点:集合的运算.2.已知复数(1)23i z i +=-(i 为虚数单位),则z 在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】C【解析】考点:复数的性质.3.等差数列{}n a 中,79416,1a a a +==,则16a 的值是( )A .22B .16C .15D .18【答案】A【解析】试题分析:由1697=+a a ,得88=a ,所以7448=-=a a d ,则2212416=+=d a a ,故选A.考点:等差数列的性质.4.已知角θ的顶点与原点重合,始边与x 轴的非负半轴重合,终边在直线2y x =上,则22cos sin θθ-等于( )A .45-B .35-C .35D .45【答案】B【解析】考点:(1)任意角的三角函数;(2)二倍角的余弦.5.如下图所示,1OA =,在以O 为圆心,以OA 为半径的半圆弧上随机取一点B ,则AOB∆的面积小于14的概率为( ) A .13 B .14 C .12 D .16【答案】A【解析】试题分析:∵1=OA ,AOB ∆的面积小于41,∴41s i n 1121<∠⨯⨯⨯A O B ,∴21s i n <∠A O B ,∴60π<∠<AOB 或ππ<∠<AOB 65,∴∆AOB 的面积小于41的概率为31,故选项为A. 考点:几何概型.6.某几何体的三视图如下图所示,则此几何体的体积是( )A .203πB .6πC .103πD .163π【答案】C【解析】考点:由三视图求面积、体积.【思路点晴】本题考查几何体与三视图的对应关系,几何体体积的求法,考查空间想象能力与计算能力.利用三视图判断几何体的形状:由正视图和侧视图易知该图分为上下两部分,一部分的三视图为两个三角形和半个圆,另一部分的三视图为两个矩形和半个圆,故可得上面为圆锥下面为圆柱且被轴截面分割出的一半的组合体,然后通过三视图的数据求解几何体的体积.7.函数22x y x =-的图象大致是( )【答案】A【解析】试题分析:当+∞→x 时,+∞→-=22x y x ,故排除C ;当-∞→x 时,-∞→-=22x y x故排除D ;当3=x 时,01<-=y ,故排除B ,故选A.考点:函数的图象.8.执行下面的程序框图,如果输入的10N =,那么输出的S =( )A .109 B .169 C .95D .2011【答案】C【解析】考点:程序框图.9.设01,1b a c <<<>,则( )A .2ab b bc <<B .log log b a a c b c <C .c cab ba >D .log log a b c c <【答案】D【解析】试题分析:∵0>>b a ,∴2b ab >,故选项A 错误;∵b a lg lg 0>>,∴b a lg 1lg 1<,ac b c lg lg lg lg >,即log log a b c c <,故选项D 正确. 考点:(1)不等式的性质;(2)函数值大小比较.10.直三棱柱111ABC A B C -中,090BCA ∠=,,M N 分别是1111,A B AC 的中点,1BC CA CC ==,则BM 与AN 所成的角的余弦值为( )A .110B .25C .D 【答案】C【解析】考点:异面直线及其所成的角.11.过抛物线22(0)y px p =>的焦点F 的直线l 依次交抛物线及其准线于点,,A B C ,若 2BC BF =,且3AF =,则抛物线的方程为( )A .2y x =B .22y x =C .23y x =D .24y x =【答案】C【解析】试题分析:分别过点A ,B 作准线的垂线,分别交准线于点E ,D ,设a BF =,则由已知得:a BC 2=,由定义得:a BD =,故30=∠BCD ,在直角三角形ACE 中,∵3=AF ,a AC 33+=,∴AC AE =2,∴633=+a ,从而得1=a ,∵FG BD //,∴321=p ,求得23=p ,因此抛物线方程为x y 32=.故选C. 考点:抛物线的标准方程.【思路点晴】本题主要考查了抛物线的标准方程.考查了学生对抛物线的定义和基本知识的综合把握.分别过点A ,B 作准线的垂线,分别交准线于点E ,D ,设a BF =,根据抛物线定义可知a BD =,进而推断出BCD ∠的值,在直角三角形中求得a ,进而根据FG BD //,利用比例线段的性质可求得P ,则抛物线方程可得.12.我们把形如(0,0)b y a b x a =>>-的函数称为“莫言函数”,其图象与y 轴的交点关于原点的对称点称为“莫言点”,以“莫言点”为圆心且与“莫言函数”的图象有公共点的圆称为“莫言圆”,当1a b ==时,“莫言圆”的面积的最小值是( )A .2πB .52π C .e πD .3π【答案】D【解析】考点:(1)圆的标准方程;(2)两点间距离公式的应用.【方法点晴】本题给出“莫言函数”、“莫言点”、“莫言圆”的定义,求圆的最小面积.着重考查了函数的图象、圆的方程、两点的距离公式与圆面积求法等知识,属于中档题.根据已知中关于“莫言函数”,“莫言点”,“莫言圆”的定义,利用1=a ,1=b ,我们易求出“莫言点”坐标,并设出“莫言圆”的方程,根据两点的距离公式求出圆心到“莫言函数”图象上点的最小距离,即可得到结论.第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每题5分,满分20分.)13.设向量(,1),(1,3)a m b ==,且()0a a b ∙-=,则m =___________.【答案】2或1-【解析】试题分析:由(,1),(1,3a m b ==,得()2,1--=-m ,又因为()0a a b ∙-=,得()021=--m m ,解得2=m 或1-.考点:向量垂直的坐标表示.14.已知ABC ∆的面积为2,2AC =,3BAC π∠=,则ACB ∠=___________. 【答案】6π 【解析】考点:正弦定理的应用.15.已知54(12)(1)x ax -+的展开式中2x 的系数为26-,则实数a 的值为___________.【答案】3或311 【解析】试题分析:∵()()()()443322524546413240101121x a x a x a ax x x x ax x ++++⋅+++-=+- 的展开式中2x 的系数为26-,∴264040640410622-=+-=+⋅-a a a a ,即 0382032=--a a ,求得实数3=a 或311=a ,故答案为:3或311. 考点:二项式定理的应用.16.已知实数,x y 满足不等式组2040250x y x y x y -+≥⎧⎪+-≥⎨⎪--≤⎩,则2()x y xy -的取值范围是___________. 【答案】⎥⎦⎤⎢⎣⎡34,0 【解析】考点:线性规划.【方法点晴】平面区域的最值问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案.本题考查的知识点是线性规划,处理的思路为:根据已知的约束条件 ,画出满足约束条件的可行域,将式子2()x y xy-进行变形,再分析x y z =表示的几何意义,结合图象即可给出xy 的取值范围,最后再结合对勾函数的性质,求出式子的取值范围. 三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分12分)设数列{}n a 的前n 项和为n S ,已知213n n S a +=,*n N ∈. (1)求通项公式n a 及n S ;(2)设10n n b a =-,求数列{}n b 的前n 项和n T .【答案】(1)13-=n n a ,213-=n n S ;(2)()()⎪⎪⎩⎪⎪⎨⎧≥+-≤+-=4267203321320n n n n T n n n. 【解析】(2)由 103101n -=--n a ,则()()⎪⎩⎪⎨⎧≥-≤=-=--410333-10101n 1n n n a b n n 讨论:3≤n 时,21310313-11n 10n --=--=n n n T )( 4≥n 时,2672033010227317)3n (10313-133-n 33+-=+--+=---+=n n T T n n n )( 综上则()()⎪⎪⎩⎪⎪⎨⎧≥+-≤+-=42672033n 213n 20n n T n n n 考点:(1)数列通项公式的求法;(2)数列求和.18.(本小题满分12分)在如图所示的几何体中,四边形ABCD 为平行四边形,090ABD ∠=,EB ⊥面ABCD ,//EF AB ,2AB =,EB =1,EF BC =M 是BD 的中点.(1)求证: //EM 平面ADF ; (2)求二面角D AF B --的大小.【答案】(1)证明见解析;(2)60. 【解析】试题解析:因为EB ⊥平面ABD ,AB BD ⊥,故以B 为原点,建立如图所示的空间直角坐标系B xyz -,由已知可得(0,0,0),(0,2,0),(3,0,0)B A D,3(3,2,0),(,0,0)2C E F M - (1)3(,0,3),(3,2,0),(0,2EM AD AF =-=-=-, 设平面ADF 的一个法向量是(,,)n x y z =,由00n AD n AF⎧∙=⎪⎨∙=⎪⎩,得3200x y y -=⎧⎪⎨-+=⎪⎩,令3y =,则n =.又因为3(,0,30302EM n ∙=∙=+-= 所以EM n ⊥,又EM ⊄平面ADF ,所以//EM 平面ADF .考点:(1)直线与平面平行判定;(2)利用空间向量求二面角. 【一题多解】(1)取AD 的中点N ,连接,MN NF ,在DAB ∆中,M 是BD 的中点,N 是AD 的中点,所以1//,2MN AB MN AB =, 又因为1//,2EF AB EF AB =,所以//MN EF 且MN EF =. 所以四边形MNFE 为平行四边形,所以//EM FN .又因为FN ⊂平面ADF ,EM ⊄平面ADF ,故//EM 平面ADF . 19.(本小题满分12分)为及时了解适龄公务员对开放生育二胎政策的态度,某部门随机调查了90位30岁到40岁的公务员,得 到情况如下表:(1)完成表格,并判断是否有99%以上的把握认为“生二胎意愿与性别有关”,并说明理由; (2)现把以上频率当作概率,若从社会上随机独立抽取三位30岁到40岁的男公力员访问,求这三人中至少有一人有意愿生二胎的概率.(3)已知15位有意愿生二胎的女性公务员中有两位来自省妇联,该部门打算从这15位有意愿生二胎的女性公务员中随机邀请两位来参加座谈,设邀请的2人中来自省女联的人数为X ,求X 的公布列及数学 期望()E X .男性公务员女性公务员总计 有意愿生二胎 30 15 无意愿生二胎20 25 总计附:22()()()()()n ad bc k a b c d a c b d -=++++【答案】(1)没有99%以上的把握认为“生二胎意愿与性别有关;(2)125117;(3)分布列见解析,415. 【解析】试题解析:(1)男性公务员女性公务员总计 有意愿生二胎 30 15 45 无意愿生二胎20 25 45 总计504090由于2k =故没有99%以上的把握认为“生二胎意愿与性别有关”.20()P k k ≥0.050 0.010 0.001 0k3.8416.63510.828(2)由题意可得,一名男公务员要生二胎意愿的概率为53203030=+,无意愿的概率为52203030=+,记事件A :这三人中至少有一人要生二胎,且各人意愿相互独立则 ()()12511752525211=⋅⋅-=-=A P A P答:这三人中至少有一人有意愿生二胎的概率为125117.(3) X 可能的取值为2,1,01051)2(;10526)1(;352610578)0(2152221511312215213==========C C X P C C C X P C C X P154105281051210526135260)(==⨯+⨯+⨯=X E 考点:(1)独立性检验;(2)相互独立事件;(3)对立事件;(4)离散型随机变量及其分布列.20.(本小题满分12分)设椭圆2222:1(x y C a a b +=>的右焦点为F ,右顶点为M ,且113eO F O MF M+=,(其中O 为原点,e 为椭圆的离心率.(1)求椭圆C 方程;(2)若过点F 的直线l 与C 相交于,A B 两点,在x 轴上是否存在点N ,使得NA NB ∙为定值?如果有,求出点N 的坐标及相应定值;如果没有,请说明理由.【答案】(1)13422=+y x ;(2)存在,⎪⎭⎫ ⎝⎛0,811N . 【解析】 试题分析:(1)由113e OF OM FM+=得()c a a c a c -=+311,即224c a =,结合222c b a +=及3=b ,可求出c b a ,,的值;(2)设()()1122,,,A x y B x y ,(),0N m .设直线l 的方程为:()1y k x =-(k 存在)联立()⎩⎨⎧=++=1243122y x x k y ,得:()01248342222=-+++k kx x k ,由此利用根的判别式、韦达定理、向量的数量积结合已知条件推导出存在11,08N ⎛⎫⎪⎝⎭,使得13564NA NB =-. 试题解析:(1)由题意:则有()c a a cc a e a c -==+3-311 化简后得224c a =,又3222==-b c a故2221,4,3c a b ===. 所以椭圆方程为13422=+y x .如果要上式为定值,则必须有2248541131238m m m m --=⇒=-验证当直线l 斜率不存在时,也符合. 故存在点11,08N ⎛⎫⎪⎝⎭满足13564NA NB =-. 考点:(1)椭圆的方程;(2)直线与圆锥曲线的综合问题.【方法点晴】本题考查椭圆方程的求法,考查满足条件的点的判断与求法,解题时要认真审题,注意向量的数量积的合理运用.第一问中通过把已知条件中的等式转化为c b a ,,之间的关系,联立出方程组可得解;第二问属于开放性问题,主要考查直线与圆锥曲线的综合问题,首先考虑斜率存在时,设出点斜式,联立方程组,运用韦达定理以及向量数量积的概念,运用整体代换的思想得到在一般情况下的存在性,最后验证在一般情况下,当斜率不存在时也成立.21.(本小题满分12分)已知函数()()xf x e kx k k R =-+∈. (1)试讨论函数()y f x =的单调性;(2)若该函数有两个不同的零点12,x x ,试求: (i )实数k 的取值范围; (ii )证明:124x x +>.【答案】(1)当0≤k 时, )(x f y =的单调递增区间为),(+∞-∞,无单调递减区间,当0>k 时, )(x f y =的单调递增区间为),(ln +∞k ,单调递减区间为)ln ,(k -∞;(2)(i )()+∞,2e ;(ii )证明见解析. 【解析】试题解析:由)()(R k k kx e x f x∈+-=,则k e x f x -=')(,讨论:若0≤k ,则0)(>'x f ,故)(x f y =在定义域上单调递增; 若0>k ,令0)(>'x f ,解得k x ln >;令0)(<'x f ,解得k x ln <,综上:当0≤k 时, )(x f y =的单调递增区间为),(+∞-∞,无单调递减区间; 当0>k 时, )(x f y =的单调递增区间为),(ln +∞k ,单调递减区间为)ln ,(k -∞. (2) (i)由题意:由(1)可知, 当0≤k 时,函数至多只有一个零点,不符合题意,舍去;0>k 时,令0ln )(ln ln <+-=k k k e k f k ,解得2e k >,此时0)1(>=e f ;+∞→x 时, 0)(>+∞→x f ,因此会有两个零点,符合题意.综上:实数k 的取值范围是),(2+∞e由()()01)1(1)1(2)1(21)(222>+-=+--+-='t t t t t t t t h ,)(t h y =单调递增,则0)1()(=>h t h ,故不等式成立,综上 即原不等式成立.考点:(1)利用导数判断函数的单调性;(2)函数零点个数的判断;(3)函数性质的综合应用.【一题多解】本题主要考查利用导数判断函数的单调性,以及函数的图象判断函数零点的个数及函数性质的应用等,综合性较强,难度较大,前面两个问题属于常规题,最后一小问还可采用由1,0)(-=∴=+-=x e k k kx e x f xx,构造函数1)(-=x e x g x ,由()21)2()(--='x x e x g x ,令2,0)(>∴>'x x g ;令2,0)(<∴<'x x g 且1≠x ,2)2(e g =,则函数)(x g y =在)1,(-∞和)2,1(单调递减,在),2(+∞递增,若与直线k y =有两个交点21,x x ,则必有),2(),2,1(21+∞∈∈x x ,要证421>+x x ,即证: 124x x ->,因为函数)(x g y =在),2(+∞递增,只需证)()()4(121x g x g x g =<-即可,即证)2,1(,13111411∈-<--x x e x e x x ,通分后只需证()0)3(111141<----x xe x e x ,构造函数())2,1(,)3(1)(4∈---=-x e x ex x h x x由0))(2()2()2()(44>--=---='--x x x x e e x x e x e x h ,故)(x h y =在)2,1(上单调递增,故0)2()(=<h x h ,故不等式成立,综上则原命题成立.请考生在第22、23二题中任选一题作答,如果多做,则按所做的第一题记分.解答时请写清题号.22.(本小题满分10分)选修4-4:坐标系与参数方程曲线C 的极坐标方程是4sin()6πρθ=-,直线l 的参数方程是32545x t y t ⎧=-+⎪⎪⎨⎪=⎪⎩(t 为参数).(1)将曲线C 的极坐标方程转化为直角坐标方程;(2)设直线l 与x 轴的交点是,M N 为曲线C 上一动点,求MN 的取值范围. 【答案】(1)()()43122=-++y x ;(2)[]232,232+-.【解析】试题解析:(1ρx y y x 23222-=+,化简得:()()43122=-++y x曲线C 的极坐标方程转化为直角坐标方程为:()()43122=-++y x(2)消去参数t ,直线l 的参数方程化为直角坐标方程得:4(2)3y x =-- 令0y =得2x =,即(2,0)M ,又曲线C 为圆,圆C半径2=r ,则则[]232,232+-∈MN . 考点:简单曲线的极坐标方程.23.(本小题满分10分)选修4-5:不等式选讲已知函数()3f x m x =--,不等式()1f x >的解集为(1,5). (1)求实数m 的值;(2)若关于x 的不等式()x a f x -≥恒成立,求实数a 的取值范围. 【答案】(1)3=m ;(2)(][)+∞⋃∞-,60,. 【解析】(2)关于x 的不等式()x a f x -≥恒成立⇔关于x 的不等式33x a x -≥--恒成立33x a x ⇔-+-≥恒成立33a ⇔-≥恒成立,由33a -≥或33a -≤-,解得:6a ≥或0a ≤.即),6[]0,(+∞-∞∈ a . 考点:(1)绝对值不等式的解法;(2)分段函数的应用.。
2015年全国高中数学联合竞赛试题与解答(B卷)

2015年全国高中数学联赛(B 卷)(一试)一、填空题(每个小题8分,满分64分 1:已知函数⎩⎨⎧+∞∈∈-=),3(log ]3,0[)(2x a x xa x f x,其中a 为常数,如果)4()2(f f <,则a 的取值围是2:已知3)(x x f y +=为偶函数,且15)10(=f ,则)10(-f 的值为 3:某房间的室温T (单位:摄氏度)与时间t (单位:小时)的函数关系为:),0(,cos sin +∞∈+=t t b t a T ,其中b a ,为正实数,如果该房间的最大温差为10摄氏度,则b a +的最大值是4:设正四棱柱1111D C B A ABCD -的底面ABCD 是单位正方形,如果二面角11C BD A --的大小为3π,则=1AA 5:已知数列{}n a 为等差数列,首项与公差均为正数,且952,,a a a 依次成等比数列,则使得121100a a a a k >+⋅⋅⋅++的最小正整数k 的值是6:设k 为实数,在平面直角坐标系中有两个点集{})(2),(22y x y x y x A +=+=和{}03),(≥++-=k y kx y x B ,若B A 是单元集,则k 的值为7:设P 为椭圆13422=+x y 上的动点,点)1,0(),1,1(-B A ,则PB PA +的最大值为 8:正2015边形201521A A A ⋅⋅⋅接于单位圆O ,任取它的两个不同顶点j i A A ,,1≥+的概率为 二、解答题9:(本题满分16分)数列{}n a 满足,31=a 对任意正整数n m ,,均有mn a a a n m n m 2++=+ (1)求{}n a 的通项公式; (2)如果存在实数c 使得c a ki i<∑=11对所有正整数k 都成立,求c 的取值围10:(本题满分20分)设4321,,,a a a a 为四个有理数,使得:{}⎭⎬⎫⎩⎨⎧----=≤<≤3,1,81,23,2,2441j i aa ji,求4321a a a a +++的值11:(本题满分20分)已知椭圆)0(12222>>=+b a by a x 的右焦点为)0,(c F ,存在经过点F的一条直线l 交椭圆于B A ,两点,使得OB OA ⊥,求该椭圆的离心率的取值围(加试)1:(本题满分40分)证明:对任意三个不全相等的非负实数c b a ,,都有:21)()()()()()(222222≥-+-+--+-+-a c c b b a ab c ac b bc a ,并确定等号成立的充要条件 2:(本题满分40分)如图,在等腰ABC ∆中,AC AB =,设I 为其心,设D 为ABC ∆的一个点,满足D C B I ,,,四点共圆,过点C 作BD 的平行线,与AD 的延长线交于E 求证:CE BD CD ⋅=23:(本题满分50分)证明:存在无穷多个正整数组)2015,,)(,,(>c b a c b a 满足:1,1,1++-ab c ac b bc a4:(本题满分50分)给定正整数)2(,n m n m ≤≤,设m a a a ,,,21⋅⋅⋅是n ,,2,1⋅⋅⋅中任取m 个互不相同的数构成的一个排列,如果存在{}m k ,,2,1⋅⋅⋅∈使得k a k +为奇数,或者存在整数 )1(,m l k l k ≤<≤,使得l k a a >,则称m a a a ,,,21⋅⋅⋅是一个“好排列”,试确定所有好排列的个数。
2015-2016学年广东省广州二中高二(下)期末数学试卷(理科)(解析版)

2015-2016学年广东省广州二中高二(下)期末数学试卷(理科)一、选择题(本题共12小题,每小题5分,满分60分)1.(5分)若A n3=6∁n4,则n的值为()A.6B.7C.8D.92.(5分)“|x﹣1|<2成立”是“x(x﹣3)<0成立”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件3.(5分)函数y=ax2+1的图象与直线y=x相切,则a=()A.B.C.D.14.(5分)设复数=a+bi(a,b∈R)则a+b=()A.1B.2C.﹣1D.﹣25.(5分)已知随机变量ξ~B(n,p),且Eξ=12,Dξ=2.4,则n与p的值分别是()A.15与0.8B.16与0.8C.20与0.4D.12与0.66.(5分)下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产品x(吨)与相应的生产能耗y(吨)的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程为y=0.7x+0.35,那么表中t的值为()A.4.5B.3.5C.3.15D.37.(5分)已知S1=xdx,S2=e x dx,S3=x2dx,则S1,S2,S3的大小关系为()A.S1<S2<S3B.S1<S3<S2C.S3<S2<S1D.S2<S3<S1 8.(5分)与曲线共焦点,而与双曲线共渐近线的双曲线方程为()A.B.C.D.9.(5分)若(x+)n展开式的二项式系数之和为64,则展开式的常数项为()A.10B.20C.30D.12010.(5分)下列四个命题中真命题的个数是()①若a,b∈[0,1],则不等式a2+b2<4成立的概率是;②命题“∃x∈R,x2﹣x>0”的否定是“∀x∈R,x2﹣x≤0”;③“若am2<bm2,则a<b”的逆命题为真④命题p:∀x∈[0,1],e x≥1,命题q:∃x∈R,x2+x+1<0,则p∨q为真.A.0B.1C.2D.311.(5分)在一条南北方向的步行街同侧有8块广告牌,牌的底色可选用红、蓝两种颜色的一种,若只要求相邻两块牌的底色不都为红色,则不同的配色方案共有()A.55B.54C.46D.4512.(5分)AB是椭圆(a>b>0)的任意一条与x轴不垂直的弦,O是椭圆的中心,e为椭圆的离心率,M为AB的中点,则K AB•K OM的值为()A.e﹣1B.1﹣e C.e2﹣1D.1﹣e2二、填空题(本题共4小题,每小题5分,满分20分)13.(5分)已知随机变量ξ服从正态分布N(2,σ2),P(ξ≤4)=0.84,则P(ξ≤0)=.14.(5分)设(2x+1)4=a0+a1x+a2x2+a3x3+a4x4,则a0﹣a1+a2﹣a3+a4=.15.(5分)椭圆+=1上的点到直线x﹣2y﹣12=0的距离的最小值为.16.(5分)不等式(x+1)(x2﹣4x+3)>0有多种解法,其中有一种方法如下,在同一直角坐标系中作出y1=x+1和y2=x2﹣4x+3的图象然后进行求解,请类比求解以下问题:设a,b∈Z,若对任意x≤0,都有(ax+2)(x2+2b)≤0,则a+b=.三、解答题(本题共6小题,满分70分)17.(12分)袋子里装有6个球,其中红球1个,黄球2个,白球3个,规定每次摸球只能摸出一个球,且摸到红球得4分,摸到黄球得2分,摸到白球不得分.(1)在每次摸出球,记下结果后就放回的情况下,求某人摸3次得分为4分的概率;(2)在每次摸出球,记下结果后就不再放回的情况下,求某人摸3次得分的分布列和数学期望.18.(12分)2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如图频率分布直方图(如图):(Ⅰ)小明向班级同学发出倡议,为该小区居民捐款.现从损失超过6000元的居民中随机抽出2户进行捐款援助,求这两户在同一分组的概率;(Ⅱ)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如表,在表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?附:临界值表参考公式:K2=,n=a+b+c+d.19.(12分)如图,在底面是菱形的四棱锥P﹣ABCD中,∠ABC=60°,P A=AC=a,PB =PD=a,点E在PD上,且PE:ED=2:1.(Ⅰ)求二面角E﹣AC﹣D的大小:(Ⅱ)在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.20.(12分)已知椭圆Γ的中心在坐标原点,且经过点,它的一个焦点与抛物线E:y2=4x的焦点重合.(1)求椭圆Γ的方程;(2)斜率为k的直线l过点F(1,0),且与抛物线E交于A、B两点,设点P(﹣1,k),△P AB的面积为,求k的值;(3)若直线l过点M(0,m)(m≠0),且与椭圆Γ交于C、D两点,点C关于y轴的对称点为Q,直线QD的纵截距为n,证明:mn为定值.21.(12分)已知函数f(x)=xe﹣x(x∈R)(Ⅰ)求函数f(x)的单调区间和极值;(Ⅱ)已知函数y=g(x)的图象与函数y=f(x)的图象关于直线x=1对称,证明:当x>1时,f(x)>g(x);(Ⅲ)如果x1≠x2,且f(x1)=f(x2),证明x1+x2>2.22.(10分)在平面直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,已知圆C的圆心为极坐标:C(,),半径r=.(1)求圆C的极坐标方程;(2)若过点P(0,1)且倾斜角α=的直线l交圆C于A,B两点,求|P A|2+|PB|2的值.2015-2016学年广东省广州二中高二(下)期末数学试卷(理科)参考答案与试题解析一、选择题(本题共12小题,每小题5分,满分60分)1.【解答】解:∵A n3=6∁n4,∴n(n﹣1)(n﹣2)=6×,整理,得n﹣3=4,∴n=7.故选:B.2.【解答】解:由|x﹣1|<2解得:﹣2+1<x<2+1,即﹣1<x<3.由x(x﹣3)<0,解得0<x<3.“|x﹣1|<2成立”是“x(x﹣3)<0成立”必要不充分条件.故选:B.3.【解答】解:把两个解析式联立得方程ax2﹣x+1=0,当a≠0时,由△=0即得a=故选:B.4.【解答】解:,∴,∴a+b=1,故选:A.5.【解答】解:∵随机变量ξ~B(n,p),且Eξ=12,Dξ=2.4,∴np=12,且np(1﹣p)=2.4,解得n=15,p=0.8.故选:A.6.【解答】解:由已知中的数据可得:=(3+4+5+6)÷4=4.5,=(2.5+t+4+4.5)÷4=,∵数据中心点(,)一定在回归直线上∴=0.7×4.5+0.35解得t=3故选:D.7.【解答】解:S1=xdx=x2=(4﹣1)=,S2=e x dx=e x=e2﹣e=e(e﹣1),S3=x2dx==(8﹣1)=,∵<<e(e﹣1),∴S1<S3<S2故选:B.8.【解答】解:由题意知椭圆焦点在y轴上,且c==5,双曲线的渐近线方程为y=±x,设欲求双曲线方程为,则,解得a=4,b=3,所以欲求双曲线方程为.故选:D.9.【解答】解:∵∁n°+∁n1+…+∁n n=2n=64,∴n=6.T r+1=C6r x6﹣r x﹣r=C6r x6﹣2r,令6﹣2r=0,∴r=3,常数项:T4=C63=20,故选:B.10.【解答】解:因为a,b∈[0,1],则a2≤1,b2≤1,所以a2+b2≤2<4,所以事件为必然事件,所以满足不等式a2+b2<4成立的概率为1,故命题①不正确.“∃x∈R,x2﹣x>0”的否定是“∀x∈R,x2﹣x≤0”,所以命题②为真命题.“若am2<bm2,则a<b”的逆命题为:“若a<b,则am2<bm2”,而当m2=0时,由a<b,得am2=bm2,所以“am2<bm2,则a<b”的逆命题为假,故命题③不正确.命题p:∀x∈[0,1],e x≥1,为真命题,命题q:∃x∈R,x2+x+1<0,为假命题,则p∨q 为真,故命题④为真命题.故选:C.11.【解答】解:根据题意,分5种情况讨论:不选用一个红色广告牌,即全部用蓝色广告牌,有1种情况,当广告牌有一个红色的,则有七个蓝色广告牌,不会出现红色相邻的情况,易得有8种配色方案,当广告牌有两个红色的,则有六个蓝色广告牌,只需先排好六个蓝色广告牌,再其形成的7个空位中选2个插入红色广告牌即可,有C72=21种配色方案,当广告牌有三个红色的,则有五个蓝色广告牌,同理可得有C63=20种配色方案,当广告牌有四个红色的,则有四个蓝色广告牌,同理可得有C54=5种配色方案,则共有1+8+21+20+5=55种配色方案;故选:A.12.【解答】解:设直线为:y=kx+c联立椭圆和直线消去y得b2x2+a2(kx+c)2﹣a2b2=0,即(b2+k2a2)x2+2a2kcx+a2(c2﹣b2)=0所以:x1+x2=﹣所以,M点的横坐标为:M x=(x1+x2)=﹣又:y1=kx1+cy2=kx2+c所以y1+y2=k(x1+x2)+2c=所以,点M的纵坐标M y=(y1+y2)=所以:Kom===﹣所以:k AB•k OM=k×(﹣)=﹣=e2﹣1故选:C.二、填空题(本题共4小题,每小题5分,满分20分)13.【解答】解:∵随机变量X服从正态分布N(2,σ2),∴μ=2,∵P(ξ≤4)=0.84,∴P(ξ≥4)=1﹣0.84=0.16,∴P(ξ≤0)=P(ξ≥4)=1﹣P(ξ≤4)=0.16,故答案为:0.16.14.【解答】解:∵(2x+1)4=a0+a1x+a2x2+a3x3+a4x4,令x=﹣1,则(﹣1)4=a0﹣a1+a2﹣a3+a4=1故答案为:1.15.【解答】解:设椭圆的参数方程为,则d==|2cos(θ+)﹣3|,当cos(θ+)=1时,d min=,故答案为:16.【解答】解:类比图象法解不等式的方法,在同一坐标系中,画出y1=ax+2和y2=x2+2b 的图象,若对任意x≤0,都有(ax+2)(x2+2b)≤0,则两个函数图象应如下图所示:则,由a,b∈Z得:,∴a+b=﹣1,故答案为:﹣1三、解答题(本题共6小题,满分70分)17.【解答】解:(1)由题意得某人摸3次得分为4分的情况为:摸到两个黄球一个白球或摸到两个白球一个红球,∴某人摸3次得分为4分的概率:P=+=+=.(2)由题意得某人摸3次得分X的可能取值为0,2,4,6,8,P(X=0)=×=,P(X=2)==,P(X=4)=+=,P(X=6)==,P(X=8)==,∴某人摸3次得分X的分布列为:∴数学期望EX=+8×=4.18.【解答】解:(Ⅰ)由频率分布直方图可得,损失不少于6000元的居民共有(0.00003+0.00003)×2000×50=6户,损失为6000~8000元的居民共有0.00003×2000×50=3户,损失不少于8000元的居民共有0.00003×2000×50=3户,…3分因此,这两户在同一分组的概率为P ==,两户在同一分组的概率;…6分(Ⅱ)如表:…7分K2==≈4.046>3.841,…8分所以有95%以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否项500元有关…12分19.【解答】解:(Ⅰ)由ABCD是菱形,且∠ABC=60°得AB=BC=CD=AD=AC=P A=a由PB=PD=a得PB2=P A2+AB2,PD2=P A2+AD2∴P A⊥AB,P A⊥AD∴P A⊥平面ABCD建立坐标系,则A(0,0,0),B(a,﹣a,0),C(a,a,0),P(0,0,a),D(0,a,0),E(0,a,a),∴=(a,a,0),=(0,a,a),设平面ACE的一个法向量为=(x,y,z),则,可取=(a,﹣a,2a),同理平面ACP的一个法向量为=(a,﹣a,0),∴cos<,>=,∴二面角P﹣AC﹣E的大小为60°;(Ⅱ)设F为PC中点,取PE中点G,连接FG、BG设AC、BD交于O,连接OE由PG=GE,PF=FC得GF∥EC由DO=OB,DE=EG得OE∥BG∴平面BGF∥平面AEC∴BF∥平面AEC∴F是PC中点时,BF∥平面AEC20.【解答】解:(1)设椭圆的方程为,由题设得,∴,∴椭圆Γ的方程是.(2)设直线l:y=k(x﹣1),由,得k2x2﹣2(k2+2)x+k2=0,l与抛物线E有两个交点,k≠0,△=16(k2+1)>0,则,P(﹣1,k)到l的距离,又,∴,∴4k2=3k2+3,故.(3)∵C(x1,y1),D(x2,y2),点C关于y轴的对称点为Q(﹣x1,y1),则直线,设x=0得直线,设x=0得,∴,又,,∴,,∴.21.【解答】解:(Ⅰ)解:f′(x)=(1﹣x)e﹣x令f′(x)=0,解得x=1当x变化时,f′(x),f(x)的变化情况如下表所以f(x)在(﹣∞,1)内是增函数,在(1,+∞)内是减函数.函数f(x)在x=1处取得极大值f(1)且f(1)=.(Ⅱ)证明:由题意可知g(x)=f(2﹣x),得g(x)=(2﹣x)e x﹣2令F(x)=f(x)﹣g(x),即F(x)=xe﹣x+(x﹣2)e x﹣2于是F'(x)=(x﹣1)(e2x﹣2﹣1)e﹣x当x>1时,2x﹣2>0,从而e2x﹣2﹣1>0,又e﹣x>0,所以F′(x)>0,从而函数F(x)在[1,+∞)是增函数.又F(1)=e﹣1﹣e﹣1=0,所以x>1时,有F(x)>F(1)=0,即f(x)>g(x).(Ⅲ)证明:(1)若(x1﹣1)(x2﹣1)=0,由(I)及f(x1)=f(x2),则x1=x2=1.与x1≠x2矛盾.(2)若(x1﹣1)(x2﹣1)>0,由(I)及f(x1)=f(x2),得x1=x2.与x1≠x2矛盾.根据(1)(2)得(x1﹣1)(x2﹣1)<0,不妨设x1<1,x2>1.由(Ⅱ)可知,f(x2)>g(x2),则g(x2)=f(2﹣x2),所以f(x2)>f(2﹣x2),从而f(x1)>f(2﹣x2).因为x2>1,所以2﹣x2<1,又由(Ⅰ)可知函数f(x)在区间(﹣∞,1)内是增函数,所以x1>2﹣x2,即x1+x2>2.22.【解答】解:(1)∵圆C的圆心为极坐标:C(,),∴=1,y==1,∴点C直角坐标C(1,1),∵半径r=,∴圆C的直角坐标方程为(x﹣1)2+(y﹣1)2=3,…(2分)由,得圆C的极坐标方程为ρ2﹣2ρcosθ﹣2ρsinθ﹣1=0.…(5分)(2)∵过点P(0,1)且倾斜角α=的直线l交圆C于A,B两点,∴直线l的参数方程为,…(7分)把直线l的参数方程代入圆C:(x﹣1)2+(y﹣1)2=3,得()2+()2=3,整理,得=0,,t1t2=﹣2,∴|P A|2+|PB|2=+|t2|2=(t1+t2)2﹣2t1•t2=7.…(10分)。
2015B二试

2015年全国高中数学联合竞赛加试(B 卷)参考答案及评分标准说明:1. 评阅试卷时,请严格按照本评分标准的评分档次给分.2. 如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可参考本评分标准适当划分档次评分, 10分为一个档次,不要增加其他中间档次.一、(本题满分40分)证明:对任意三个不全相等的非负实数,,a b c ,有222222()()()1()()()2a bcb cac ab a b b c c a −+−+−≥−+−+−,并确定等号成立的充分必要条件.解:当,,a b c 不全相等时,原不等式等价于2222222()2()2()()()()a bc b ca c ab a b b c c a −+−+−≥−+−+−.上式可化简为22222222212222a b b c c a abc ab bc ca ++−≥−−−,即2222226a b b c c a ab bc ca abc +++++≥.①考虑到222222,,,,,0a b b c c a ab bc ca ≥,故由平均不等式得,2222226a b b c c a ab bc ca abc +++++≥=,②因此原不等式成立. …………………20分下面考虑等号成立的充分必要条件.注意到②中等号成立的充分必要条件是222222a b b c c a ab bc ca =====.若0abc ≠,则abbc ca ==,显然a b c ==,与条件矛盾! 若0abc =,则0abbc ca ===,但,,a b c 不全为0,不妨设0a ≠,则0b c ==.类似可得其余两种情况,即,,a b c 中恰有一个非零.这时原不等式中等式确实成立.因此,原不等式等号成立当且仅当,,a b c 中有两个是0,另一个为正数. …………………40分二、(本题满分40分)如图,在等腰ABC 中,AB AC =,I 为其内心,D 为ABC 内一点,使得,,,I B C D 四点共圆.过点C 作BD 的平行线,与AD 的延长线交于点E .求证:2CD BD CE =⋅.证明:连接,BI CI .设,,,I B C D 四点在圆O 上,延长DE 交圆O 于F ,连接,FB FC .因为BD CE ∥,所以180DCE BDC BFC ∠=°−∠=∠.又由于CDE CDF CBF ∠=∠=∠,所以BFC ∽DCE ,从而DC BFCE FC=. ①…………………10分再证明,AB AC 与圆O 相切.事实上,因为1122ABI ABC ACB ICB ∠=∠=∠=∠,所以AB 与圆O 相切.同理AC 与圆O 相切.…………………20分 因此有ABD ∽AFB ,ACD ∽AFC ,故BD AB AC DCBF AF AF CF===,即 BF BDFC DC=. ② …………………30分结合①、②,得DCBD CE DC=,即2CD BD CE =⋅. (40)分三、(本题满分50分)证明:存在无穷多个正整数组(,,)(,,2015)a b c a b c >,使得|1,|1,|1a bc b ac c ab −++.证明:考虑1c ab =+的特殊情况,此时|1c ab + 成立. ……………10分 由|1a bc −知,|(1)1a b ab +−,故|1a b −.① 由|1b ac +知,|(1)1b a ab ++,故|1b a +.②为满足①、②,取*,1()a k b k k N ==+∈,此时211c ab k k =+=++.…………………40分当正整数2015k >时,2(,,)(,1,1)a b c k k k k =+++均符合条件,因此满足条件的正整数组(,,)a b c 有无穷多个. …………………50分四、(本题满分50分)给定正整数,(2)m n m n .设12,,,m a a a 是1,2,,n中任取m 个互不相同的数构成的一个排列.如果存在{1,2,,}k m 使得k a k 为奇数,或者存在整数,(1)k l k l m ,使得k l a a ,则称12,,,m a a a 是一个“好排列”.试确定所有好排列的个数.解:首先注意,“存在{1,2,,}k m 使得k a k 为奇数”是指存在一个数与它所在的位置序号的奇偶性不同;“存在整数,(1)k l k l m ,使得k l a a ”意味着排列中存在逆序,换言之,此排列不具有单调递增性.将不是好排列的排列称为“坏排列”,下面先求坏排列的个数,再用所有排列数减去坏排列数.注意坏排列同时满足:(1)奇数位必填奇数,偶数位必填偶数;(2)单调递增. ………………10分下面来求坏排列的个数.设P 是坏排列全体,Q 是在1,2,,2n m中任取m 项组成的单调递增数列的全体.对于P 中的任意一个排列12,,,m a a a ,定义121212(,,,),,,222m m a m a a f a a a. 因为,k a n k m ≤≤,故由条件(1)可知,所有的2k a k+均属于集合1,2,,2n m +.再由条件(2)可知,(1,2,,)2k a k k m += 单调递增.故如上定义的f 给出了P Q →的一个映射.显然f 是一个单射. ……………30分下面证明f 是一个满射.事实上,对于Q 中任一个数列12,,,m b b b ,令2(1,2,,)k k a b k k m =−= .因为整数1k k b b +>,故11k k b b +≥+,从而112()11(11)k k k k a a b b k m ++−=−−≥≤≤−,故12,,,m a a a 单调递增.又11a ≥,而22m n m a m n +≤−≤,及2k k a k b +=为偶数,故12,,,m a a a 为P 中的一个排列.显然 1212(,,,),,,m m f a a a b b b ,故f 是一个满射.综上可见,f 是P Q →的一个一一映射,故P Q =. …………40分又Q 中的所有数列与集合1,2,,2n m的所有m 元子集一一对应,故2C n m m Q,从而2C n m mP. 最后,我们用总的排列数!P ()!m n n n m扣除坏排列的数目,得所有的排列的个数为2!C ()!n m m n n m. …………………50分。
2014年广州市高二数学竞赛试卷(含答案)

2014年广州市高二数学竞赛试题2014. 5. 10考生注意:⒈用钢笔、签字笔或圆珠笔作答,答案写在答卷上;⒉不准使用计算器;⒊考试用时120分钟,全卷满分150分.一、选择题:本大题共4小题,每小题6分,满分24分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数,是的共轭复数,则的值是A .B .C .D .2.已知向量与向量的夹角为钝角,则实数的取值范围是A .B .C .D .3. 已知函数,则下列不等式中恒成立的是A .B .C .D .4. 若实数满足,则的取值范围是A .B .C .D .二、填空题:本大题共6小题,每小题6分,满分36分.5. 已知N ,,则数列的前项和 .6.投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件,“骰子向上的点数是”为事件,则事件、中至多有一件发生的概率是 .7. 函数的最大值是 .DC 1B 1A 1CBA 8. 设不等式组所表示的平面区域为,平面区域与关于直线对称,对于中的任意一点与中的任意一点,的最小值等于 . 9. 已知是表面积为的球面上三点,,为球心,则直线与平面所成角的余弦值是 .10.若将函数表示为其中为实数,则的值为 .三、解答题:本大题共5小题,满分90分.解答须写出文字说明、证明过程和演算步骤. 11.(本小题满分15分) 已知函数R ,为常数,且是函数的零点.(1)求的值; (2)若,求的最大值和最小值.12.(本小题满分15分) 已知直三棱柱的底面是正三角形,是的中点.(1)证明:∥平面; (2)若,,求三棱锥的体积.13. (本小题满分20分)已知椭圆的左、右焦点分别为、,点、是直线上的两个动点,且.(1)设圆是以线段为直径的圆,试判断原点与圆的位置关系;(2)若椭圆的离心率为,的最小值为,求椭圆的方程.14. (本小题满分20分)设轴、轴正方向上的单位向量分别为、,为坐标原点. 坐标平面上点、N分别满足下列两个条件:①,且;②,且.(1)求向量及的坐标;(2)若四边形的面积是,求的表达式;(3)对于(2)中的,是否存在最小的自然数,对一切N,都有成立?若存在,求的值;若不存在,说明理由.15.(本小题满分20分)已知函数,为自然对数的底数. (1)证明:;(2)若N,且,证明:.2014年广州市高二数学竞赛试题参考答案与评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:每小题6分,满分24分.1.A 2.C 3.A 4.B二、填空题:每小题6分,满分36分.5. 6. 7. 8. 9. 10.三、解答题:满分90分.11.(本小题满分15分)(1)解:∵是函数的零点,∴. …………2分解得. …………4分(2)解:由(1)得…………6分…………8分. …………10分∵,∴. …………11分OGFDC 1B 1A 1CBA ∴当,即时,取得最大值,其值为; …………13分当,即时,取得最小值,其值为.……15分12.(本小题满分15分) (1)证明:连接,与相交于点,连接,∵四边形是矩形, ∴点是的中点.∵是的中点, ∴∥. …………2分∵平面,平面,∴∥平面. …………4分 (2)解:取的中点,连接,∵△是正三角形,∴.∵平面平面,且平面平面,∴平面. …………6分∵平面,∴. ∵,,平面,平面,∴平面. …………8分 ∵平面, ∴.∵,∴.∵, ∴△~△. …………10分 ∴. ∴.∴. …………12分 取的中点,连接,则∥,且,由于平面,则平面.∴三棱锥的体积为.…15分 13. (本小题满分20分) 解:(1)设,则.∵,∴.∴,即. …………4分∵,∴为锐角.∴原点在圆外. …………8分(2)∵椭圆的离心率为,∴. …………9分∴,且. …………10分,当且仅当或时取等号.…………14分∴的最小值为. …………16分依题意得,,解得,从而. …………19分∴椭圆的方程为. …………20分14.(本小题满分20分)(1)解:,…………4分. …………8分(2)解:由(1)知,直线交轴于点,. …………12分(3)解:. …………14分当时,;当时,;当时,.故等等.即在数列中,是数列的最大项,…………18分所以存在最小的自然数,对一切N,都有成立. …………20分15.(本小题满分20分)(1)证明:要证,只要证明,由于,等价于证明,设,则,等价于证明. …………3分令,则.当时,,故函数在上单调递减.∴当时,.∴当,成立.故成立.…………8分(2)证明:∵,…………14分∴…………16分…………18分. …………20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年广州市高二数学竞赛试题2015.5.16考生注意: 1.用钢笔、签字笔或回珠笔作答,答案写在答卷上;2.不准使用计算器;3.考试用时120分钟,全卷满分150分.一、选择题。
本大题共4小题,每小题5分,满分24分.在每小理给出的四个选项中,只有一项是符合题目要求的. 1.(2013年重庆卷)以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x ,y 的值分别为( ).A .2,5B .5,5C .5,8D .8,8 2.“22x x >”是“2log 1x >”的( )A. 充分而不必要条件B. 必要而不充分条件C.充分且必要条件D. 既不充分也不必要条件3.设集合{(|(1)()0},{|1}A x x x a B x x a =--≥=≥-,且A B R = ,则实数a 的取值范围是( )A. (,2)-∞B. [2,)+∞C. (,2]-∞D. (2,)+∞4.若直线l 过定点P(1,4),且在x 轴正半轴上的截距之和最小,则直线的方程是( )A. 50x y +-=B. 260x y +-=C. 290x y +-=D. 220x y -+= 二、填空题:本大题共6小题,每小题6分,满分36分.5.已知为i 虚数单位,复数z 满足()(2)3z i i --=,则|z | = .6.若函数2()(1)x f x x ax e =++有两个不同的零点,则实数a 的取值范围是 . 7.(2013-2014学年广东省肇庆市高二(上)期末数学试卷(理科))已知水平放置的棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积的取值范围是 .8.设e 1、e 2为单位向量,非零向量b =x e 1+y e 2(,x y R ∈),若e 1、e 2的夹角为4π,则||||b y 的最小值等于 . 9.已知()f x =,若(1)(1)()()(),()[()]()n nfx f x f x f fx n N +==∈,则(48)()f x = .10.(2014年湖北卷理第7题)由不等式⎪⎩⎪⎨⎧≤--≥≤0200x y y x 确定的平面区域记为1Ω,不等式⎩⎨⎧-≥+≤+21y x y x ,确定的平面区域记为2Ω,在1Ω中随机取一点,则该点恰好在2Ω内的概率为 .三、解答题:本大题共 5 小题,满分 90 分.11.(本小题满分15分)在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c,且a=5,b=8,设CA与CB的夹角为θ.(1)当3πθ=时,求c ;(2)当02πθ<≤时,求函数2()122cos ()4f πθθθ=-+的最大值与最小值,并分别求出()f θ取得最大值与最小值时θ的值.12. (本小题满分 15 分)已知数列{n a }的前n 项和为n S ,24n S n n =-. (1)求数列{n a }的通项公式;(2)设3nn n a b =,求数列{n b }的前n 项和为n T .13. (本小题满分 20 分)(2012年山东日照市高考数学二模试卷(文科)A 卷) 如图,已知直四棱柱1111D C B A ABCD -的底面是直角梯形,CD AB BC AB //,⊥,F E ,分别是棱BC ,11C B 上的动点,且3,2,1,//11====BC AB DD CD CC EF .(Ⅰ)证明:无论点E 怎样运动,四边形D EFD 1都为矩形; (Ⅱ)当1=EC 时,求几何体D EFD A 1-的体积.14. (本小题满分20分)(2005年重庆卷文第21题)已知中心在原点的双曲线C 的右焦点为(2,0),右顶点为)0,3(. (1)求双曲线C 的方程;(2)若直线:l y kx =C 恒有两个不同的交点A 和B ,且2O AO B ⋅>(其中O 为原点). 求k 的取值范围.15.(本小题满分20分)已知函数()tan (0)2f x x x x π=-<<.(1)试判断函数()f x 的单调性,并说明理由; (2)若数列{n a }满足*110,(),4n n a a f a n N π+<<=∈,证明:104n n a a π+<<<.2015年广州市高二数学竞赛试题参考答案与评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分. 一、选择题:每小题6分,满分24分。
1.C 2.B 3.C 4.B1.解:由甲组数据中位数为15,可得x =5;而乙组数据的平均数91510182416.85y ++(+)++=,可解得y =8.故选C .4.解:设直线l 的方程为:y-4=k (x-1),其中k <0,令y=0,得41x k=-;令x=0,得y=4-k ,则|OA|+|OB|=(41x k =-)+(4-k )=5+[(k -)+(4k -)]≥5+,当且仅当4k k-=-,即k=-2时,|OA|+|OB|取最小值,此时直线l 的方程为260x y +-=.二、填空题:每小题6分,满分36分。
5.2 6.(,2)(2,)-∞-+∞ 7. 8 9.19 10.787.水平放置的正方体,当正视图为正方形时,其面积最小为1;向左旋转,主视图由正方形变成长方形,因此满足棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积的范围为[1.三、解答题:11.解:(1)由由余弦定理知,222222cos 58258cos493c a b ab C π=+-=+-⨯⨯=,所以c =7.(2)因为2()122cos ()4f πθθθ=+-+2cos 2()4πθθ=-+2cos(2)2πθθ=-+sin 2θθ=12(sin 22)22θθ=+2sin(2)3πθ=+. 因为02πθ<≤,所以42333πππθ<+≤.所以sin(2)123πθ-≤+≤,即()2f θ≤≤.故当2πθ=时,min ()f θ=12πθ=时,max ()2f θ=.12.解:(1)因为24n S n n =-,当1n =时,113a S ==-.当2n ≥时,22(4)[(1)4(1)]25n n n a S S n n n n n =-=-----=-. 当1n =时,12153a =⨯-=-,也适合上式. 所以25n a n =-.(2)因为25n a n =-,所以2533n n n n a n b -==. 1231311272533333n n n n n T -----=+++++L . ①234113112725333333n n n n n T +----=+++++L .② 由①-②得23121112512()33333n n n n T +-=-++++-L 111251333n n n +-=-+--122233n n +-=--. 所以113n n n T -=--.13.解:(Ⅰ)在直四棱柱1111ABCD A B C D -中, 11DD //CC ,∵11EF //CC ,EF //DD ,∴又 ∵ 平面ABCD //平面1111A B C D , 平面ABCD ⋂平面1EFD D ED = 平面1111A B C D ⋂平面11EFD D FD =, ∴1ED //FD ,……………5分∴四边形1EFD D 为平行四边形.……………6分 ∵ 侧棱1DD ⊥底面ABCD , DE ⊂平面A BCD 内,∴ 1DD DE ⊥, ∴四边形1EFD D 为矩形. …………8分 (Ⅱ)证明:连结AE ,∵四棱柱1111ABCE A B C D -为直四棱柱, ∴侧棱1DD ⊥底面ABCD.又AE ⊂平面ABCD 内,∴1DD AE ⊥. ………………………………………10分在Rt A BE ∆中,AB=2,BE=2,则AE =在Rt CDE ∆中,EC=1,CD=1,则……………………12分在直角梯形中ABCD ,∴222AE DE AD AE ED +=∴⊥. ………………………14分 又1ED DD D ⋂=,∴AE ⊥平1EFD D . ………………………………………16分由(Ⅰ)可知,四边形1EFD D 为矩形,且1DE 1==,∴矩形1EFD D 的面积1EFD D 1S DE DD =⋅=…………18分∴几何体1A EFD D -的体积为11A EFD D EFD D 114V S AE 333-=⋅=.…20分14. 解:(Ⅰ)设双曲线方程为22221x y a b-= ).0,0(>>b a由已知得.1,2,2,32222==+==b b a c a 得再由故双曲线C 的方程为.1322=-y x (Ⅱ)将得代入13222=-+=y x kx y .0926)31(22=---kx x k 由直线l与双曲线交于不同的两点得2222130,)36(13)36(1)0.k k k ⎧-≠⎪⎨∆=+-=->⎪⎩即.13122<≠k k 且 ① 设),(),,(B B A A y x B y x A ,则229,,22,1313A B A B A B A B x x x x OA OB x x y y k k -+==⋅>+>-- 由得而2((1)()2A B A B A B A B A B A B x x y y x x kx kx k x x x x +=+=+++2222937(1)2.1331k k k k -+=+++=--于是222237392,0,3131k k k k +-+>>--即解此不等式得.3312<<k ② 由①、②得 .1312<<k故k的取值范围为(1,-⋃15.解: (1)因为''2sin cos cos sin (sin )()()11cos cos x x x x x f x x x--=-=- 222221cos sin tan cos cos x x x x x-===. 所以,当(0,)2x π∈时, '()0f x >.故()f x 在(0,)2π内单调递增.(2)先证04n a π<<(*n N ∈).(用数学归纳法) .①当1=n 时,由已知条件,结论成立.②假设当n k =时结论成立,即04k a π<<.由(1)可知,()f x 在(0,)2π内单调递增,且(0)0f =.因为04k a π<<,所以(0)()()tan 144444k f f a f πππππ<<=-=-<,即104k a π+<<.故当1n k =+时,结论成立.由①、②可知,04n a π<<对一切*n N ∈都成立.再证1n n a a +<(*n N ∈).设()tan 2(0)4g x x x x π=-<<,则'''2()(tan )tan 1g x x x x x =--=-.因为04x π<<,所以20tan 1x <<.所以当04x π<<时,'()0g x <,即()g x 在(0,)4π内单调递减.又(0)0g =,所以当04x π<<时,()tan 20g x x x =-<, 所以()tan 20n n n g a a a =-<,即1n n a a +<. 综上可知,104n n a a π+<<<对*n N ∈都成立.。
