北京市朝阳区2011届高三模拟数学(文)试卷及答案
2011朝阳高三三模数学理

朝阳区2010~2011学年度第二学期高三年级保温测试数 学 试 卷(理工类)(考试时间120分钟,满分150分) 2011.5一、选择题(本大题共8小题,每小题5分,共40分)1.若集合{}A=|1x x x R ≤∈,,{}2B=|y y x x R =∈,,则A B I = ( )A .{}|11x x -≤≤B .{}|0x x ≥C .{}|01x x ≤≤D . ∅2.设l ,m 是两条不同的直线,α是一个平面,则下列命题正确的是 ( ) A .若l m ⊥,m α⊂,则l α⊥ B .若l α⊥,l m //,则m α⊥ C .若l α//,m α⊂,则l m //D .若l α//,m α//,则l m//3.已知ξ~N (0, s 2),若P (ξ >2) = 0.023,则P (-2≤ξ≤2) = ( )A .0.477B .0.628C .0.954D .0.9774.6的展开式中常数项是( )A .-160B .-20C .20D .1605.一空间几何体的三视图如图所示,则该几何体的体积为( ) A .13B .23C .53D .436.a ,b 为非零向量,“函数2()()f x x =+a b 为偶函数”是“⊥a b ”的 ( )A .充分但不必要条件B .必要但不充分条件C .充要条件D .非充非要条件7.设等差数列{}n a 的前n 项和为n S ,若111a =-,466a a +=-,则当n S 取最小值时,n 等于( ) A .6B .7C .8D .98.已知平面上不重合的四点P ,A ,B ,C 满足0PA PB PC ++= ,且AB AC mAP +=,那么实数m 的值为 ( ) A .5 B .4 C .3 D .2二、填空题(本大题共6小题,每小题5分,共30分)9.由直线x y =与曲线2x y =所围图形的面积=S ________.10.样本中共有五个个体,其值分别为a ,0,1,2,3.若该样本的平均值为1,则样本方差为________. 11.已知某程序框图如图所示,则执行该程序后输出的结果是________.12.如图,已知⊙O 的直径5A B =,C 为圆周上一点,4=BC ,过点C 作⊙O 的切线l ,过点A 作l 的垂线AD ,垂足为D ,则C D =________.正视图侧视图俯视图13.若直线l 的参数方程为31,545x t y t ⎧=-⎪⎪⎨⎪=⎪⎩(t 为参数),则直线l 的斜率为________;在极坐标系中,直线m 的方程为sin()42πρθ+=,则点7(2,)4A π到直线m 的距离为________.14.已知点(4, 1)A 和坐标原点O ,若点(,)B x y 满足1133x y x y x y -≥-⎧⎪+≥⎨⎪-≤⎩,则OA OB ⋅ 的最大值是________. 三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤) 15.(13分)设函数()cos(2)6f x x π=+sin 2x +.(Ⅰ)求函数()f x 的单调递增区间;(Ⅱ)设A ,B ,C 为∆ABC 的三个内角,若AB=1,sinB=31,()22C f =,求AC 的长.16.(13分)某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为23.现有10件产品,其中6件是一等品,4件是二等品.(Ⅰ)随机选取1件产品,求能够通过检测的概率;(Ⅱ)随机选取3件产品,其中一等品的件数记为X ,求X 的分布列; (Ⅲ)随机选取3件产品,求这三件产品都不能通过检测的概率.开始a =2,i =1 i ≥2010i =i +1结束输出a是否lOADCB17.(13分)如图,在四棱锥P-ABCD 中,底面ABCD 为直角梯形,AD//BC ,∠ADC=90°,平面PAD ⊥底面ABCD ,Q 为AD 的中点,M 是棱PC 上的点,PA=PD=2,BC=12AD=1,(Ⅰ)若点M 是棱PC 的中点,求证:PA//平面BMQ ; (Ⅱ)求证:平面PQB ⊥平面PAD ;(Ⅲ)若二面角M-BQ-C 为30°,设PM = tMC ,试确定t 的值.18.(13分)已知数列}{n a ,其前n 项和为237()22n S n n n N *=+∈.(Ⅰ)求数列}{n a 的通项公式,并证明数列}{n a 是等差数列;(Ⅱ)如果数列}{n b 满足n n b a 2log =,请证明数列}{n b 是等比数列,并求其前n 项和.19.(14分)已知函数()ln a xf x x x-=+,其中a 为大于零的常数.(Ⅰ)若曲线()y f x =在点(1,(1)f )处的切线与直线12y x =-平行,求a 的值;(Ⅱ)求函数()f x 在区间[1,2]上的最小值.20.(14分)已知椭圆C:22221(0)x y a b ab+=>>的长轴长为,离心率22=e .(Ⅰ)求椭圆C 的标准方程;(Ⅱ)若过点B (2,0)的直线l (斜率不等于零)与椭圆C 交于不同的两点E ,F (E 在B ,F 之间),且∆OBE 与∆OBF 的面积之比为12,求直线l 的方程.PABCD QM高三数学练习题参考答案 (理科)一、选择题:(本大题共8小题,每小题5分,共40分)(1)C (2)B (3)C (4)A (5)D (6)C (7)A (8)C 二、填空题:(本大题共6小题,每小题5分,共30分)(9)61(10) 2 (11)-1 (12)125(13)43-;2(14)11三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15(本小题共13分) 解:()cos(2)6f x x π=+sin 2x +=1cos 2cossin 2sinsin 22sin 2sin(2)66223x x x x x x πππ-+=+=+......3分(I )令222,232k x k k Z πππππ-≤+≤+∈,则5,1212k x k k Z ππππ-≤≤+∈所以函数f(x)的单调递增区间为5[,]().1212k k k Z ππππ-+∈ .............6分(II)由已知()sin()3C f C π+==22, ……………………………………………….8分因为40,333C C ππππ<<∴<+<所以233C ππ+=,3C π=,所以2. ……10分在∆ABC 中,由正弦定理,sin sin AC AB BC=,得1sin sin 92AB B AC C ⋅===. …..13分 16(本小题共13分)解:(Ⅰ)设随机选取一件产品,能够通过检测的事件为A . …………………………1分事件A 等于事件 “选取一等品都通过检测或者是选取二等品通过检测” ……………2分151332104106)(=⨯+=A p …………………………4分(Ⅱ) 由题可知X 可能取值为0,1,2,3.3463101(0)30C C P X C ===,21463103(1)10C C P X C ===,12463101(2)2C C P X C ===,03463101(3)6C C P X C ===. ………………8分……………9分C(Ⅲ)设随机选取3件产品都不能通过检测的事件为B , ……………10分 事件B 等于事件“随机选取3件产品都是二等品且都不能通过检测” 所以,3111()()303810P B =⋅=. ………………………………………………………13分 17(本小题共13分)证明:(Ⅰ)连接AC ,交BQ 于N ,连接MN . ………………………………………1分∵BC ∥AD 且BC=12AD ,即BC //AQ ,∴四边形BCQA 为平行四边形,且N 为AC 中点,又∵点M 在是棱PC 的中点,∴ MN // PA. ……………………………………………………………………2分 ∵ MN ⊂平面MQB ,PA ⊄平面MQB , …………………………………3分 ∴ PA // 平面MBQ . …………………………………………………………………4分 (Ⅱ)∵AD // BC ,BC=12AD ,Q 为AD 的中点,∴四边形BCDQ 为平行四边形,∴CD // BQ .……………………………………6分 ∵∠ADC=90° ∴∠AQB =90° 即QB⊥AD. 又∵平面PAD ⊥平面ABCD且平面PAD ∩平面ABCD=AD , ………………………………………………7分 ∴BQ ⊥平面PAD . …………………………………………………………8分 ∵BQ ⊂平面PQB ,∴平面PQB ⊥平面PAD . …………………………………………………………9分 另证:AD // BC ,BC=12AD ,Q 为AD 的中点∴ BC // DQ 且BC= DQ ,∴ 四边形BCDQ 为平行四边形,∴CD // BQ .∵ ∠ADC=90° ∴∠AQB =90° 即QB⊥AD. …………………………………6分 ∵ PA=PD , ∴PQ ⊥AD . …………………………………………………7分 ∵ PQ ∩BQ=Q ,∴AD ⊥平面PBQ . ………………………………………………8分 ∵ AD ⊂平面PAD ,∴平面PQB ⊥平面PAD . ……………………………………………………9分 (Ⅲ)∵PA=PD ,Q 为AD 的中点, ∴PQ ⊥AD.∵平面PAD ⊥平面ABCD ,且平面PAD ∩平面ABCD=AD , ∴PQ⊥平面ABCD .…10分(不证明PQ⊥平面ABCD 直接建系扣1分) 如图,以Q 为原点建立空间直角坐标系.则平面BQC 的法向量为(0,0,1)n = ;(0,0,0)Q ,(0,0,P ,0)B,(0)C -.………设(,,)M x y z ,则(,,PM x y z =-,(1,)M C x y z=---,∵PM t M C = ,∴(1))(x tx y t yz t z =--⎧⎪=⎨⎪-=-⎩), ∴ 111t x tyt z t ⎧=-⎪+⎪⎪=⎨+⎪⎪=⎪+⎩……12分在平面MBQ 中,0)Q B = ,(,111t Q M t t t=-+++ ,∴ 平面MBQ法向量为0,)m t =.∵二面角M-BQ-C 为30°,cos 302n m t n m ︒⋅===3t =.…………13分 18(本小题共13分)解:(Ⅰ)当1n =时,115a S ==, ……………………………………………………1分当2n ≥时,22137[(1)][(1)]22n n n a S S n n n n -=-=--+--37(21)3222n n =-+=+. ……………………………3分又15a =满足32n a n =+, ……………………………………………………5分 32()n a n n N *∴=+∈. ………………………………………………………6分∵132[3(1)2]3n n a a n n --=+--+= (2,)n n N *≥∈,∴数列{}n a 是以5为首项,3为公差的等差数列. ……………………………7分(Ⅱ)由已知得2na nb = ()n N *∈, …………………………………………8分∵+1+13+12==2=2=82n n nna a -a n a nb b ()n N *∈, ……………………10分又11232a b ==, ∴数列}{n b 是以32为首项,8为公比的等比数列. …………12分∴数列}{n b 前n 项和为32(18)32(81)187nn-=--. …………………………13分19(本小题共14分) 解:2221()1'()x a x ax af x x x x x x----=+=-=(0x >) ………………………………..4分 (I )因为曲线()y f x =在点(1,(1)f )处的切线与直线1-2y x =平行,所以'(1)-2f =,即12, 3.a a -=-=解得 ……………………………………6分(II)当01a <≤时,'()0f x >在(1,2)上恒成立,这时()f x 在[1,2]上为增函数 min ()(1)1f x f a ∴==-. ………………………………………………….8分当12a <<时,由'()0f x =得,(1,2)x a =∈对于(1,)x a ∈有'()0,f x <()f x 在[1,a]上为减函数, 对于(,2)x a ∈有'()0,f x >()f x 在[a ,2]上为增函数,min ()()ln f x f a a ∴==. …………………………………………………..11分当2a ≥时,'()0f x <在(1,2)上恒成立, 这时()f x 在[1,2]上为减函数,m in ()(2)ln 212af x f ∴==+-.综上,()f x 在[1,2]上的最小值为①当01a <≤时,m in ()1f x a =-,②当12a <<时,min ()ln f x a =,③当2a ≥时,m in ()ln 212a f x =+-.…………….14分20(本小题共14分).解:(I )椭圆C 的方程为)0(12222>>=+b a bya x,由已知得22222c e a a a b c ⎧==⎪⎪⎪=⎨⎪=+⎪⎪⎩……..3分解得 1,1a b c ===∴所求椭圆的方程为1222=+yx. ………………………………………………… 5分(II)由题意知l 的斜率存在且不为零,设l 方程为2(0)x my m =+≠ ①,将①代入1222=+yx,整理得22(2)420m y m y +++=,由0>∆得2 2.m > ………….……………….……….7分设),(11y x E ,),(22y x F ,则1221224222m y y m y y m -⎧+=⎪⎪+⎨⎪=⎪+⎩②. …………………………8分由已知,12OBEOBF S S ∆∆=, 则||1||2BE BF =由此可知,2BF BE =,即212y y =. …………………………………………….10分 代入②得,12212432222m y m y m -⎧=⎪⎪+⎨⎪=⎪+⎩,消去1y 得222221629(2)2m m m ⋅=++ 解得,2187m =,满足22.m >即7m =±. ………………………………………………………….13分所以,所求直线l的方程为71407140x x --=+-=或. …….14分。
北京市西城区2011届高三模拟数学(文)试题及答案

北京市西城区2011 年高三一模试卷数学(文科)2011.4第Ⅰ卷(选择题共40分)一、选择题:本大题共 8 小题,每题 5 分,共 40 分 .在每题列出的四个选项中,选出切合题目要求的一项 .1. 已知全集U{1,2,3,4,5} ,会合 A{2,5} , B{4,5} ,则e U( A B) 等于( A){1,2,3,4}( B){1,3}( C){2,4,5}( D){5}2. 函数y2x lg x 的定义域是( A)0,2( B)(0, 2)( C)0,2( D)1,2 3. 为了获得函数y sin x cos x 的图像,只要把y sin x cos x 的图象上全部的点( A)向左平移个单位长度( B)向右平移个单位长度44( C)向左平移个单位长度( D)向右平移个单位长度2124. 设a log2 3, b log 4 3 ,c,则2( A)a c b( C)b ca[ 来( D)c b a ( B)c a b源: 学&科&网]5.一个棱锥的三视图如下图,则这个棱锥的体积是(A)6(B)12(C)24(D)363343正 (主 )视图侧(左)视图34俯视图6.关于平面和异面直线 m,n ,以下命题中真命题是( A)存在平面,使 m, n( B)存在平面,使 m, n( C)存在平面,知足 m, n //( D)存在平面,知足 m //, n //7. 右边茎叶图表示的是甲、乙两人在5 次综合测评中的甲成绩,此中一个数字被污损. 则甲的均匀成绩超出乙9 8 8 3 3 7乙的均匀成绩的概率为2 1 099(A )2(B )7(C )4(D )95105108.某次测试成绩满分为150 分,设 n 名学生的得分分别为 a 1 ,a 2 , , a n ( a i N ,1 i n ),b k ( 1 k150 )为 n 名学生中得分起码为 k 分的人数 . 记 M 为 n 名学生的均匀成绩 . 则 b 1 b 2 b 150 b 1 b 2 b 150(A ) Mn(B ) M 150b 1 b 2b150b 1 b 2b150 (C ) Mn(D ) M150第Ⅱ卷(非选择题共 110 分)二、填空题:本大题共 6 小题,每题 5 分,共 30 分.9. 若复数 (1 i)(1 ai) 是纯虚数,则实数 a 等于 ______.10. 设向量 a(1,sin) , b (1,cos ) ,若 a b3 ______.,则 sin 2511. 双曲线 C :x 2y21的离心率为 ______;若椭圆x 2y 2 1(a 0) 与双曲线 C 有同样2a 2的 焦点,则 a ______.12. 设不等式组2 x 2,2y 表示的地区为 W ,2圆 C : ( x2)2 y 24 及其内部地区记为D .若向地区 W 内投入一点,则该点落在地区 D内的概率为 _____.13. 阅读右边程序框 图,则输出的数据 S 为 _____.14. 已知数列 { a n } 的各项均为正整数, S n 为其前 n 项和,关于 n 1,2,3,,有3a n 5, a n为奇数,an 1a n,,2k a n 为偶数 . 此中 k 为使 a n 1为奇数的正整数当 a 3 5时, a 1 的最小值为 ______;当 a1 1 时, S1S2S20______.三、解答题:本大题共6小题,共 80 分。
朝阳区高考二模数学文试题目及答案

(II)由题意可设直线l方程为y=k(x-3),
由 得(1+2k2)x2-12k2x+18k2-6=0.……………………………7分
因为直线l与椭圆C交于不同的两点M,N,
所以△=144k4-4(1+2k2)(18k2-6)=24(1-k2)>0.解得-1<k<1.………8分
则g(x)在x=1处取得最小值,g(1)=e.则a≤e.
综上所述,x∈[0,+∞)时,f(x)≥0成立的a的范围是(-∞,e].……………13分
(19)(本小题满分14分)
解:(I)由题意得 ………………………………………………………2分
解得a= ,b= .……………………………………………………………4分
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,不能答在试题卷上。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项。
(1)已知全集U=R,集合A={x︱2x>1},B={x︱ >0},则A∩(CUB)=
因为C1D 平面A1C1B1,所以BB1⊥C1D.……………………………………………………6分
又A1C1=C1B1,且D是A1B1的中点,所以C1D⊥A1B1.………………………………………7分
因为A1B1∩BB1=B1,所以C1D⊥平面AA1B1B.………………………………………………8分
由(I)知EF∥C1D.
综上所述,当a≤0时,f(x)的单调增区间为(-∞,+∞);当a>0时,f(x)的单调减区间是(-∞,㏑a),f(x)的单调增区间是(㏑a,+∞).……………………………6分
2011北京市朝阳区高三二模word含答案.

北京市朝阳区高三年级第二次综合练习语文试题2011.5(考试时长150分钟满分150分)本试卷共6页。
考生务必将答案答在机读卡和答题纸上,在试卷上作答无效。
考试结束后,只收回机读卡和答题纸。
第一部分(27分)一、本大题共5小题,每小题3分,共15分。
1.下列词语中,字形和加点的字的读音全都正确的一项是A.顶粱柱身体力行蹚浑.(hún)水模棱.(línɡ)两可B.田径赛寥若辰星一刹.(chà)那令人咋.(zhà)舌C.四和院烟消云散抹.(mǒ)桌子面如冠.(ɡuān)玉D.倒栽葱寒冬腊月女主角.(jué)锲.(qiè)而不舍2.下列句子中,加点的成语和熟语使用不.恰当..的一项是A.阿Q、祥林嫂、孔乙己、闰土这些栩栩如生的人物形象都出自人们耳熟能详....的经典作品。
B.大厅里摆放着一块天然形成的奇石,形状酷似一只憨态可掬的大熊猫,真是巧夺天工....。
C.为应对金融危机,美国政府只好拆东墙补西墙......,挪用巨额资金向濒临破产的银行注资。
D.上大学不是为得到一纸文凭,把它当作求职的敲门砖...,而是为了学习知识、提高素养。
3.下列句子中,没有语病的一句是A.4月1日开始,北京大幅提高重点区域停车费,这是继车辆限行、摇号限购政策之后,北京实施的又一“治堵新政”。
B.随着信息技术的不断发展和进步,使我们可以通过社交服务网站与朋友保持更加直接和方便的联系,扩大交际范围。
C.在连续遭遇本赛季的五连败后,湖人队的处境令人堪忧,如果后两场比赛再失利,湖人队将跌落至西部赛区第四名。
D.房龙善于用轻松俏皮的文字撰写通俗地理著作,所以他的《房龙地理》能够从历史的角度阐释人与地理环境的关系。
4.下列有关文学常识的表述,有错误的一项是A.诸子散文指的是春秋战国时期各学派的代表著作,其中包括儒家的《论语》、道家的《庄子》、法家的《韩非子》和墨家的《墨子》等。
北京市朝阳区2011-2012学年度高三年级第一学期期末统一考试(数学文)

北京市朝阳区2011-2012学年度高三年级第一学期期末统一考试数学试卷(文史类) 2012.1第一部分(选择题 共40分)注意事项:考生务必将答案答在答题卡上,在试卷上答无效。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.已知集合2{|3},{|log 1}M x x N x x =<=>,则M N 等于( )A .φB .}321|{<<x x C .}30|{<<x xD .{|23}x x <<2.已知平面向量(3,1)=a ,(,3)x =b ,且a ⊥b ,则实数x 的值为( )A .9-B .1-C .1D .93. 函数⎪⎩⎪⎨⎧≥-<=)0(12)0(2x x x y x 的图象大致是 ( )4. 设数列{}n a 是公差不为0的等差数列,11a =且136,,a a a 成等比数列,则{}n a 的前n 项和n S 等于 ( )A . 2788n n +B .2744n n + C .2324n n+D .2n n +5.执行如图所示的程序框图,输出的S 值为( )A .1B .1-C . 2-D .06. 函数2()2xf x a x=--的一个零点在区间(1,2)内,则实数a 的取值范围是( ) A .(1,3) B .(1,2) C .(0,3) D . (0,2)7.已知函数()sin f x x x =,设()7a f π=,()6b f π=,()3c f π=,则,,a b c 的大小关系是 ( ) A. a b c << B.c a b << C.b a c << D.b c a << 8. 已知集合{(,)|,,}A x y x n y na b n ===+∈Z ,{(,)|,B x y x m ==2312,y m =+m ∈Z }.若存在实数,a b 使得AB ≠∅成立,称点(,)a b 为“£”点,则“£”点在平面区域22{(,)|108}C x y x y =+≤内的个数是 ( ) A. 0 B. 1 C. 2 D. 无数个第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.9. 若变量x ,y 满足约束条件1,,236,x y x x y ≥⎧⎪≥⎨⎪+≤⎩则2z x y =+的最大值为 .10. 已知有若干辆汽车通过某一段公路,从中抽取200辆汽车进行测速分析,其时速的频率分布直方图如图所示,则时速在区间[60,70)上的汽车大约有 辆.11. 某几何体的三视图如图所示,则这个几何体的体积是 .时速(km/h )01002 003 00440 50 60 70 8012. 设直线10x my --=与圆22(1)(2)4x y -+-=相交于A ,B 两点,且弦AB的长为m 的值是 .13. 某公司购买一批机器投入生产,据市场分析每台机器生产的产品可获得的总利润y (万元)与机器运转时间x (年数,x *∈N )的关系为21825y x x =-+-.则当每台机器运转 年时,年平均利润最大,最大值是 万元.14. 已知两个正数,a b ,可按规则c ab a b =++扩充为一个新数c ,在,,a b c 三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.(1)若1,3a b ==,按上述规则操作三次,扩充所得的数是__________;(2)若0p q >>,经过6次操作后扩充所得的数为(1)(1)1m n q p ++-(,m n 为正整数),则,m n 的值分别为______________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15. (本题满分13分)在锐角三角形ABC 中,a ,b ,c 分别为内角A ,B ,C所对的边,且满足2sin 0b A -=.(Ⅰ)求角B 的大小;(Ⅱ)若b =2c =,求AB AC 的值.16. (本题满分14分)如图,在四棱锥S ABCD -中,平面SAD ⊥平面ABCD .四边形ABCD 为正方形,且P 为AD 的中点,Q 为SB 的中点. (Ⅰ)求证:CD ⊥平面SAD ; (Ⅱ)求证://PQ 平面SCD ;(Ⅲ)若SA SD =,M 为BC 中点,在棱SC 上是否存在点N,使得平面DMN ⊥平面ABCD ,并证明你的结论.17. (本题满分13分) 如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转MSD BCP Q·转盘,转盘停止转动时,箭头A 所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A 指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后各转动一次游戏转盘,得分记为(,)a b (假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动). (Ⅰ)请列出一个家庭得分(,)a b 的所有情况;(Ⅱ)若游戏规定:一个家庭的总得分为参与游戏的两人所得分数之和,且总得分为偶数的家庭可以获得一份奖品.请问一个家庭获奖的概率为多少?18. (本题满分13分)设函数2()ln 2,R 2ax f x a x x a =+-∈. (Ⅰ)当1a =时,试求函数()f x 在区间[1,e]上的最大值; (Ⅱ)当0a ≥时,试求函数()f x 的单调区间. 19. (本题满分13分)已知椭圆2222:1(0)x y C a b a b +=>>的离心率为12,且过点3(1,)2P ,F 为其右焦点.(Ⅰ)求椭圆C 的方程;(Ⅱ)设过点(4,0)A 的直线l 与椭圆相交于M 、N 两点(点M 在,A N 两点之间),若AMF △与MFN △的面积相等,试求直线l 的方程.20. (本题满分14分) 数列{}n a ,{}n b (1,2,3,n =)由下列条件确定:①110,0a b <>;②当2k ≥时,k a 与k b 满足:当011≥+--k k b a 时,1-=k k a a ,211--+=k k k b a b ;当011<+--k k b a 时,211--+=k k k b a a ,1-=k k b b . (Ⅰ)若11a =-,11b =,求2a ,3a ,4a ,并猜想数列}{n a 的通项公式(不需要证明); (Ⅱ)在数列}{n b 中,若s b b b >>> 21(3s ≥,且*s ∈N ),试用11,b a 表示k b ,},,2,1{s k ∈;(Ⅲ)在(Ⅰ)的条件下,设数列}{n c (*)n ∈N 满足211=c ,0n c ≠,2212m n n n mc c c ma -+=-+(其中m 为给定的不小于2的整数),求证:当m n ≤时,恒有1<n c .北京市朝阳区2011-2012学年度高三年级第一学期期末统一考试数学试卷(文史类)答案 2012.1二、填空题:注:若有两空,则第一个空第二个空三、解答题:(15)(本小题满分13分)解:2sin 0b A -=,根据正弦定理得:2sin sin 0A B A -=.………………………………………………………3分因为sin 0A ≠,所以23sin =B . ………………………………………………5分 又B 为锐角, 则3B π=. …………………………………………………6分(Ⅱ)由(Ⅰ)可知,3B π=.因为b =2c =,根据余弦定理,得 2744cos3a a π=+-, ……………………………………8分整理,得2230a a --=.由于0a >,得3a =. ……………………………10分于是222cos214b c a A bc +-===, ………………………………11分所以 cos cos 21AB AC AB AC A cb A ====. ……………13分(16)(本小题满分14分)证明:(Ⅰ)因为四边形ABCD 为正方形,则CD AD ⊥. …………………1分 又平面SAD ⊥平面ABCD , 且面SAD 面ABCD AD =,所以CD ⊥平面SAD . ………………………………………………………3分(Ⅱ)取SC 的中点R ,连QR, DR .由题意知:PD ∥BC 且PD =12BC .…………………4分在SBC ∆中,Q 为SB 的中点,R 为SC 的中点, 所以QR ∥BC 且QR =12BC .所以QR ∥PD 且QR=PD ,则四边形PDRQ 为平行四边形. …………………………………………………7分 所以PQ ∥DR .又PQ ⊄平面SCD ,DR ⊂平面SCD ,所以PQ ∥平面SCD . ……………………………………………………………10分 (Ⅲ)存在点N 为SC 中点,使得平面DMN ⊥平面ABCD . ………………11分连接PC DM 、交于点O ,连接PM 、SP , 因为//PD CM ,并且PD CM =,所以四边形PMCD 为平行四边形,所以PO CO =. 又因为N 为SC 中点,所以//NO SP .………………………………………………………………………12分 因为平面SAD ⊥平面ABCD ,平面SAD 平面ABCD =AD ,并且SP AD ⊥, 所以SP ⊥平面ABCD ,所以NO ⊥平面ABCD , ……………………………………………………13分 又因为NO ⊂平面DMN ,所以平面DMN ⊥平面ABCD .……………………………………………………14分 (17)(本小题满分13分) 解:(Ⅰ)由题意可知,一个家庭的得分情况共有9种,分别为(2,2),(2,3),(2,5),(3,2),(3,3),(3,5),(5,3),(5,2),(5,5). …………………………………………………………7分(Ⅱ)记事件A :一个家庭在游戏中获奖,则符合获奖条件的得分情况包括(2,2),(3,3),(3,5),(5,3),(5,5)共5种, ……………………………………………11分 所以5()9P A =. 所以一个家庭获奖的概率为59. …………………………………………………13分(18)(本小题满分13分)解: (Ⅰ)函数()f x 的定义域为(0,)+∞. ………………………………………………1分当1a =时,2()ln 22x f x x x =+-,因为21(1)()20x f x x x x -'=+-=≥, …3分 M SDBCAPQ·R (N ) O所以函数()f x 在区间[1,e]上单调递增,则当=e x 时,函数()f x 取得最大值2e (e )12e 2f =+-. …………………………………………………………………5分(Ⅱ)22()ax x af x x-+'=. ………………………………………………………6分当0a =时,因为()20f x '=-<,所以函数()f x 在区间(0,)+∞上单调递减;…7分 当0a >时,⑴当2440a ∆=-≤时,即1a ≥时,()0f x '≥,所以函数()f x 在区间(0,)+∞ 上单调递增; …………………………………………………………9分⑵当2440a ∆=->时,即01a <<时,由()0f x '>解得,0x <<,或x >. …………………………………………10分由()0f x '<x <<; ………………………………11分所以当01a <<时,函数()f x 在区间上单调递增;在11(a a +上单调递减,1()a+∞单调递增. ………13分(19)(本小题满分13分)解:(Ⅰ)因为12c a =,所以2a c =,b =. …………………………………1分 设椭圆方程为2222143x y c c+=,又点3(1,)2P 在椭圆上,所以2213144c c +=,解得21c =, …………………………………………………………………………3分所以椭圆方程为22143x y +=. …………………………………………………………4分 (Ⅱ)易知直线l 的斜率存在,设l 的方程为(4)y k x =-, ……………………………………………………………5分由22(4),1,43y k x x y =-⎧⎪⎨+=⎪⎩消去y 整理,得 2222(34)3264120k x k x k +-+-=, ………………………………………………6分由题意知2222(32)4(34)(6412)0k k k ∆=-+->, 解得1122k -<<. ……………………………………………………………………7分 设11(,)M x y ,22(,)N x y ,则21223234k x x k+=+,⋅⋅⋅⋅⋅⋅ ①, 2122641234k x x k -=+.… ②. 因为AMF △与MFN △的面积相等,所以AM MN =,所以1224x x =+.⋅⋅⋅⋅⋅⋅ ③ ……………………………………10分由①③消去2x 得21241634k x k +=+.⋅⋅⋅⋅⋅⋅ ④将2124x x =-代入②得21126412(24)34k x x k --=+.⋅⋅⋅⋅⋅⋅ ⑤ 将④代入⑤2222224164166412(24)343434k k k k k k ++-⨯-=+++,整理化简得2365k =,解得6k =±,经检验成立. …………………………12分 所以直线l的方程为4)y x =-. …………………………………………13分 (20)(本小题满分14分)(Ⅰ)解:因为011=+b a ,所以112-==a a ,02112=+=b a b . ……1分 因为0122<-=+b a ,则212223-=+=b a a ,320b b ==. ………………2分 333421222a b a a +===-. ……………………………………………………3分 猜想当2n ≥时,22221111222n n n n a a ---⎛⎫⎛⎫=⨯=-⋅=-⎪⎪⎝⎭⎝⎭.则21,1,1, 2.2n n n a n -⎧-=⎪=⎨-≥⎪⎩ …………………………………………………………4分(Ⅱ)解:当s k ≤≤2时,假设110k k a b --+<,根据已知条件则有1-=k k b b ,与s b b b >>> 21矛盾,因此110k k a b --+<不成立, ……………………5分所以有110k k a b --+≥,从而有1k k a a -=,所以1a a k =. ……………………6分当011≥+--k k b a 时,1-=k k a a ,211--+=k k k b a b , 所以111111()22k k k k k k k a b b a a b a -----+-=-=-; …………………………8分当s k ≤≤2时,总有111()2k k k k b a b a ---=-成立. 又110b a -≠,所以}{k k a b -(s k ,,2,1 =)是首项为11b a -,公比为12的等比数列, ……9分 11121)(-⎪⎭⎫⎝⎛-=-k k k a b a b ,1,2,,k s =,又因为1a a k =,所以111121)(a a b b k k +⎪⎭⎫⎝⎛-=-. …………………………10分(Ⅲ)证明:由题意得2212m n n n mc c c ma -+=-+n n c c m+=21. 因为211n n n c c c m +=+,所以2110n n n c c c m+-=>.所以数列{}n c 是单调递增数列. ………………………………………………11分 因此要证)(1m n c n ≤<,只须证1<m c . 由2≥m ,则n n n c c m c +=+211<n n n c c c m ++11,即1111n n c c m+->-. …12分因此1122111)11()11()11(1c c c c c c c c m m m m m +-++-+-=--- m m m m 121+=+-->. 所以11m mc m <<+. 故当m n ≤,恒有1<n c . ………………………………………………………14分。
北京市西城区2011届高三第一学期期末考试(数学文)

北京市西城区2010 — 2011学年度第一学期期末试卷高三数学(文科) 2011.1第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分. 在每小题列出的四个选项中,选出符合题目要求的一项. 1. 已知集合{1}A x x =≥-,{3}B x x =<,那么集合A B = [来源:学#科#网Z#X#X#K] (A ){13}x x -≤< (B ){13}x x -<< (C ){1}x x <-(D ){3}x x >2. 下列函数中,图象关于坐标原点对称的是 (A )lg y x =(B )cos y x =(C )||y x =(D )sin y x =3. 若a b >,则下列不等式正确的是 (A )11a b< (B )33a b >(C )22a b >(D )a b >4. 命题“若a b >,则1a b +>”的逆否命题是 (A )若1a b +≤,则a b > (B )若1a b +<,则a b > (C )若1a b +≤,则a b ≤(D )若1a b +<,则a b <5. 设{}n a 是等差数列,若24a =,57a =,则数列{}n a 的前10项和为 (A )12(B )60(C )75(D )1206. 阅读右面程序框图,如果输出的函数值在区间11[,]42内,那么输入实数x 的取值范围是 (A )(,2]-∞- (B )[2,1]-- (C )[1,2]- (D )[2,)+∞7. 如图,四边形ABCD 中,1AB AD CD ===,2BD =BD CD ⊥,将四边形ABCD沿对角线BD 折成四面体A BCD '-,使平 面A BD '⊥平面BCD ,则下列结论正确的是 (A )A C BD '⊥ (B )90BA C'∠=(C )A DC '∆是正三角形(D )四面体A BCD '-的体积为138. 设函数121()log ()2xf x x =-,2121()log ()2xf x x =-的零点分别为12,x x ,则(A )1201x x << (B )121x x = (C )1212x x << (D )122x x ≥第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9. i 为虚数单位,则22(1i)=+______. 10. 已知1==a b ,12⋅=a b ,则平面向量a 与b 夹角的大小为______. 11.若实数,x y 满足条件10,2,1,x y x y x -+≥⎧⎪+≥⎨⎪≤⎩则2x y +的最大值为______.12.在ABC ∆中,若3,3a b =,3B 2π∠=,则c =____. 13. 已知双曲线22221x y a b-=的离心率为2,它的一个焦点与抛物线28y x =的焦点相同,那么双曲线的焦点坐标为______;渐近线方程为_______.14.在平面直角坐标系中,定义1212(,)d P Q x x y y =-+-为两点11(,)P x y ,22(,)Q x y 之间的“折线距离”.在这个定义下,给出下列命题:①到原点的“折线距离”等于1的点的集合是一个正方形; ②到原点的“折线距离”等于1的点的集合是一个圆;③到(1,0),(1,0)M N -两点的“折线距离”之和为4的点的集合是面积为6的六边形; ④到(1,0),(1,0)M N -两点的“折线距离”差的绝对值为1的点的集合是两条平行线. 其中正确的命题是____________.(写出所有正确命题的序号)三、解答题:本大题共6小题,共80分. 解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数2()3sin 22sin f x x x -. (Ⅰ)求()6f π的值;(Ⅱ)若[,]63x ππ∈-,求()f x 的最大值和最小值.16.(本小题满分13分)如图,在三棱柱111ABC A B C -中,侧面11ABB A ,11ACC A均为正方形,90BAC ∠=,D 为BC 中点.(Ⅰ)求证:1//A B 平面1ADC ; (Ⅱ)求证:11C A B C ⊥.[来源:学科网ZXXK] [来源:学|科|网]17.(本小题满分13分)对某校高三年级学生参加社区服务次数进行统计,随机抽取M 名学生作为样本,得到这M 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下: [来源:Z&xx&](Ⅰ)求出表中,M p 及图中a 的值;(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数;(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[25,30)内的概率. [来源:学科网]18.(本小题满分13分)分组[来频数 频率 [10,15) 10 0.25[15,20)24n[20,25)mp[25,30)20.05 合计M1ABCDC 1 A 1B 1已知椭圆2222:1x y C a b+= (0>>b a )的一个焦点坐标为(1,0),且长轴长是短轴长的2.(Ⅰ)求椭圆C 的方程;(Ⅱ)设O 为坐标原点,椭圆C 与直线1y kx =+相交于两个不同的点,A B ,线段AB 的中点为P ,若直线OP 的斜率为1-,求△OAB 的面积.19.(本小题满分14分)已知函数()ln f x ax x =+()a ∈R .(Ⅰ)若2a =,求曲线()y f x =在1x =处切线的斜率; (Ⅱ)求()f x 的单调区间;(Ⅲ)设2()22g x x x =-+,若对任意1(0,)x ∈+∞,均存在[]20,1x ∈,使得12()()f x g x <,求a 的取值范围.[来源:学.科.网Z.X.X.K]20.(本小题满分14分)[来源:Z,xx,]已知数列}{n a 的首项为1,对任意的n ∈*N ,定义n n n a a b -=+1. (Ⅰ) 若1n b n =+,求4a ;(Ⅱ) 若11(2)n n n b b b n +-=≥,且12,(0)b a b b ab ==≠.[来源:学&科&网] (ⅰ)当1,2a b ==时,求数列{}n b 的前3n 项和;(ⅱ)当1a =时,求证:数列}{n a 中任意一项的值均不会在该数列中出现无数次.北京市西城区2010 — 2011学年度第一学期期末高三数学参考答案及评分标准(文科) 2011.1一、选择题:本大题共8小题,每小题5分,共40分.2[来二、填空题:本大题共6小题,每小题5分,共30分.9.i - 10. 6011. 412.3 13. (2,0)±30x y ±= 14. ①③④[来源:] 注:13题第一问2分,第二问3分;14题①③④选对其中两个命题得2分,选出错误的命题即得0分.三、解答题:本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分.15.(本小题满分13分) 解:(Ⅰ)()6f π232sin 36ππ- ………………2分 321241=-⨯=. ………………4分 (Ⅱ)()f x 3sin2cos21x x =+- ………………6分2sin(2)16x π=+-. ………………8分[来源:]因为[,]62x ππ∈-,所以65626πππ≤+≤-x , ………………10分 所以 1sin(2)126x π-≤+≤, ………………11分 所以()f x 的最大值为1 ,最小值为2-. ………………13分16.(本小题满分13分)解:(Ⅰ)连结1AC ,设1AC 交1AC 于点O ,连结OD . ………………2分 因为11ACC A 为正方形,所以O 为1AC 中点,又D 为BC 中点,所以OD 为1A BC ∆的中位线,[来源:学科网]所以1//A B OD . ………………4分 因为OD ⊂平面1ADC ,1A B ⊄平面1ADC , 所以1//A B 平面1ADC . ………………6分 (Ⅱ)由(Ⅰ)可知,11C A CA ⊥ ………………7分因为侧面11ABB A 是正方形,1AB AA ⊥, 且90BAC ∠=, 所以AB ⊥平面11ACC A . 又11//AB A B ,所以11A B ⊥平面11ACC A . ………………9分 又因为1C A ⊂平面11ACC A ,所以111A B C A ⊥. ………………10分 所以111C A A B C ⊥平面. ………………12分 又1B C ⊂平面11A B C ,所以11C A B C ⊥. ………………13分 17.(本小题满分13分)解:(Ⅰ)由分组[10,15)内的频数是10,频率是0.25知,100.25M=, 所以40M =. ………………2分 因为频数之和为40,所以1024240m +++=,4m =. ………………3分40.1040m p M ===. ………………4分 因为a 是对应分组[15,20)的频率与组距的商,所以240.12405a ==⨯.……………6分 (Ⅱ)因为该校高三学生有240人,分组[10,15)内的频率是0.25,所以估计该校高三学生参加社区服务的次数在此区间内的人数为60人. ………8分 (Ⅲ)这个样本参加社区服务的次数不少于20次的学生共有26m +=人,设在区间[20,25)内的人为{}1234,,,a a a a ,在区间[25,30)内的人为{}12,b b . 则任选2人共有1213141112232421(,),(,),(,),(,),(,),(,),(,),(,),a a a a a a a b a b a a a a a b2234(,),(,)a b a a ,3132414212(,),(,),(,),(,),(,)a b a b a b a b b b 15种情况, ………………10分AB CDC 1A 1B 1O而两人都在[25,30)内只能是()12,b b 一种, ………………12分 所以所求概率为11411515P =-=.(约为0.93) ………………13分18.(本小题满分13分)解:(Ⅰ)由题意得1,2c a b ==, ………………2分又221a b -=,所以21b =,22a =. ………………3分所以椭圆的方程为2212x y +=. ………………4分 (Ⅱ)设(0,1)A ,11(,)B x y ,00(,)P x y ,联立2222,1x y y kx ⎧+=⎨=+⎩ 消去y 得22(12)40k x kx ++=……(*), ………………6分解得0x =或2412k x k =-+,所以12412kx k=-+, 所以222412(,)1212k k B k k--++,2221(,)1212k P k k -++, ………………8分 因为直线OP 的斜率为1-,所以112k-=-,[来源:学科网ZXXK] 解得12k =(满足(*)式判别式大于零). ………………10分 O 到直线1:12l y x =+5………………11分 2211(1)AB x y =+-=253………………12分 所以△OAB 的面积为12252335=. ………………13分19.(本小题满分14分)解:(Ⅰ)由已知1()2(0)f x x x'=+>, ………………2分(1)213f '=+=.故曲线()y f x =在1x =处切线的斜率为3. ………………4分[来源:学§科§网](Ⅱ)11'()(0)ax f x a x x x+=+=>. ………………5分 ①当0a ≥时,由于0x >,故10ax +>,'()0f x >所以,()f x 的单调递增区间为(0,)+∞. ………………6分②当0a <时,由'()0f x =,得1x a=-.在区间1(0,)a -上,()0f x '>,在区间1(,)a -+∞上()0f x '<,所以,函数()f x 的单调递增区间为1(0,)a -,单调递减区间为1(,)a-+∞.………………8分(Ⅲ)由已知,转化为max max ()()f x g x <. ………………9分max ()2g x = ………………10分由(Ⅱ)知,当0a ≥时,()f x 在(0,)+∞上单调递增,值域为R ,故不符合题意. (或者举出反例:存在33(e )e 32f a =+>,故不符合题意.) ………………11分当0a <时,()f x 在1(0,)a -上单调递增,在1(,)a -+∞上单调递减,故()f x 的极大值即为最大值,11()1ln()1ln()f a a a-=-+=----, ………13分 所以21ln()a >---, 解得31ea <-. ………………14分 [来源:学科网ZXXK]20.(本小题满分14分)(Ⅰ) 解:11a =,211123a a b =+=+=,322336a a b =+=+=4336410a a b =+=+=. ………………3分(Ⅱ)(ⅰ)解:因为11n n n b b b +-=(2n ≥),所以,对任意的n ∈*N 有5164321n n n n n n n b b b b b b b ++++++====, 即数列{}n b 各项的值重复出现,周期为6. ………………5分又数列}{n b 的前6项分别为21,21,1,2,2,1,且这六个数的和为7.设数列{}n b 的前n 项和为n S ,则,当2()n k k =∈*N 时,36123456()7n k S S k b b b b b b k ==+++++=,当21()n k k =+∈*N 时,363123456616263()n k k k k S S k b b b b b b b b b ++++==++++++++ 123775k b b b k =+++=+ , ………………7分 所以,当n 为偶数时,372n S n =;当n 为奇数时,3732n n S +=. ………………8分(ⅱ)证明:由(ⅰ)知:对任意的n ∈*N 有6n n b b +=,又数列}{n b 的前6项分别为111,,,1,,b b b b,且这六个数的和为222b b ++.设)0(6≥=+n a c i n n ,(其中i 为常数且}6,5,4,3,2,1{∈i ),所以1n n c c +-=66666162636465n i n i n i n i n i n i n i n i a a b b b b b b ++++++++++++++-=+++++222b b=++. 所以,数列}{6i n a +均为以222b b++为公差的等差数列. ………………10分 因为0b >时,2220b b ++>,0b <时,22220b b++≤-<, ………………12分所以{6n i a +}为公差不为零的等差数列,其中任何一项的值最多在该数列中出现一次.所以数列}{n a 中任意一项的值最多在此数列中出现6次,即任意一项的值不会在此数列中重复出现无数次. ………………14分。
北京市朝阳区高三二模数学文科含答案
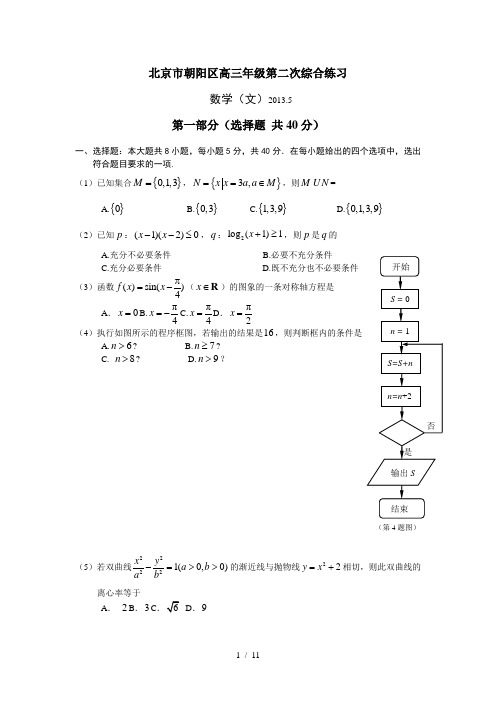
北京市朝阳区高三年级第二次综合练习数学(文)2013.5第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. (1)已知集合{}0,1,3M =,{}3,N x x a a M ==∈,则MN =A.{}0B.{}0,3C.{}1,3,9D.{}0,1,3,9 (2)已知p :(1)(2)0x x --≤,q :2log (1)1x +≥,则p 是q 的 A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件 (3)函数()sin()4f x x π=-(x ∈R )的图象的一条对称轴方程是A .0x = B.π4x =- C.π4x =D .π2x =(4)执行如图所示的程序框图,若输出的结果是16,则判断框内的条件是A.6n >?B.7n ≥?C. 8n >?D.9n >?(第4题图)(5)若双曲线22221(0,0)x y a b a b-=>>的渐近线与抛物线22y x =+相切,则此双曲线的离心率等于A . 2B .3CD .9(6)将一个质点随机投放在关于,x y 的不等式组3419,1,1x y x y +≤⎧⎪≥⎨⎪≥⎩所构成的三角形区域内,则该质点到此三角形的三个顶点的距离均不小于1的概率是 A .12πB .6πC .112π-D .16π- (7)某三棱锥的三视图如图所示,则该三棱锥的体积为A .16B .13 C .12D .1(第7题图)(8)已知函数()21(0)xf x a a =⋅+≠,定义函数(),0,()(),0.f x x F x f x x >⎧=⎨-<⎩给出下列命题:①()()F x f x =;②函数()F x 是奇函数;③当0a <时,若0mn <,0m n +>,总有()()0F m F n +<成立,其中所有正确命题的序号是 A .②B .①③C .②③D .①②正视图侧视图俯视图第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上. (9)i 为虚数单位,计算3i1i+=+. (10)已知向量(2,1),(3,)x ==a b ,若(2)-⊥a b b ,则x 的值为.(11)已知等差数列{}n a 的公差为2-,3a 是1a 与4a 的等比中项,则首项=1a _,前n 项和=n S __.(12)若直线l 与圆22(1)4x y ++=相交于A ,B 两点,且线段AB 的中点坐标是(1,2)-,则直线l 的方程为.(13)某公司一年购买某种货物600吨,每次都购买x 吨(x 为600的约数),运费为3万元/次,一年的总存储费用为2x 万元.若要使一年的总运费与总存储费用之和最小,则每次需购买吨. (14)数列{21}n-的前n 项1,3,7,,21n -组成集合{1,3,7,,21}()n n A n *=-∈N ,从集合n A 中任取k (1,2,3,,)k n =个数,其所有可能的k 个数的乘积的和为k T (若只取一个数,规定乘积为此数本身),记12n n S T T T =+++.例如当1n =时,1{1}A =,11T =,11S =;当2n =时,2{1,3}A =,113T =+,213T =⨯,213137S =++⨯=.则当3n =时,3S =;试写出n S =.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. (15)(本小题满分13分) 在ABC∆中,角,,A B C所对的边分别为,,a b c,且()f A =2cossin()22A A π-22sin cos 22A A+-. (Ⅰ)求函数()f A 的最大值;(Ⅱ)若()0,,12f A C a 5π===b 的值.(16)(本小题满分13分)为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的工程测试.成绩低于6M 为不合格,成绩在6至8M (含6M 不含8M )的为及格,成绩在8M 至12M (含8M 和12M ,假定该市初二学生掷实心球均不超过12M )为优秀.把获得的所有数据,分成[2,4),[4,6),[6,8),[8,10),[10,12]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10M 到12M 之间.(Ⅰ)求实数a 的值及参加“掷实心球”工程测试的人数; (Ⅱ)根据此次测试成绩的结果,试估计从该市初二年级男生中任意选取一人,“掷实心球”成绩为优秀的概率;(Ⅲ)若从此次测试成绩不合格的男生中随机抽取2名学生再进行其它工程的测试,求所抽 取的2名学生来自不同组的概率.(17)(本小题满分14分)如图,已知四边形ABCD 是正方形,EA ⊥平面A B C D ,PD EA ,22AD PD EA ===,F ,G ,H 分别为BP ,BE ,PC 的中点.(Ⅰ)求证:FG平面PDE ;(Ⅱ)求证:平面FGH ⊥平面AEB ;(Ⅲ)在线段PC 上是否存在一点M ,使PB ⊥平面EFM ?若存在,求出线段PM 的长;若不存在,请说明理由.BD CFGHEP频率分布直方图(18) (本小题满分13分)已知函数()axf x a x =++21,()ln g x a x x =-(0a ≠). (Ⅰ)求函数()f x 的单调区间;(Ⅱ)求证:当0a >时,对于任意(]12,0,e x x ∈,总有12()()g x f x <成立.(19) (本小题满分14分)已知椭圆2222:1x y C a b +=()0a b >>的右焦点F (1,0),长轴的左、右端点分别为12,A A ,且121FA FA ⋅=-.(Ⅰ)求椭圆C 的方程;(Ⅱ)过焦点F 斜率为k (0)k ≠的直线l 交椭圆C 于,A B 两点,弦AB 的垂直平分线与x轴相交于点D .试问椭圆C 上是否存在点E 使得四边形ADBE 为菱形?若存在,试求点E 到y 轴的距离;若不存在,请说明理由.(20)(本小题满分13分)已知实数12,,,n x x x (n *∈N 且2n ≥)满足||1i x ≤()1,2,,i n =⋅⋅⋅,记121(,,,)n i j i j nS x x x x x ≤<≤=∑.(Ⅰ)求2(1,1,)3S --及(1,1,1,1)S --的值; (Ⅱ)当3n =时,求123(,,)S x x x 的最小值; (Ⅲ)当n 为奇数时,求12(,,,)n S x x x 的最小值.注:1i j i j nx x ≤<≤∑表示12,,,n x x x 中任意两个数i x ,j x (1i j n ≤<≤)的乘积之和.北京市朝阳区高三年级第一次综合练习数学学科测试答案(文史类)2013.5二、填空题:(注:两空的填空,第一空3分,第二空2分) 三、解答题:(15)(本小题满分13分)(Ⅰ)22()2cos sin sin cos 2222A A A A f A =+-sin cos )4A A A π=-=-. 因为0A <<π,所以444A ππ3π-<-<.则所以当42A ππ-=,即34A π=时,()f A .……7分(Ⅱ)由题意知())04f A A π=-=,所以sin()04A π-=.又知444A ππ3π-<-<,所以04A π-=,则4A π=.因为12C 5π=,所以712A B π+=,则3B π=.由sin sin a b A B =得,sinsin 33sin sin 4a Bb A π===π.……………………13分 (16)(本小题满分13分)解:(Ⅰ)由题意可知(0.20.150.0750.025)21a ++++⨯=,解得0.05a =. (Ⅱ)由图可知,参加此次“掷实心球”的工程测试的初二男生,成绩优秀的频率为(0.150.05)20.4+⨯=,则估计从该市初二年级男生中任意选取一人,“掷实心球”成绩为优秀的概率为0.4.……………………7分(Ⅲ)设事件A :从此次测试成绩不合格的男生中随机抽取2名学生来自不同组. 由已知,测试成绩在[)2,4有2人,记为,a b ;在[)4,6有6人,记为,,,,,A B C D E F . 从这8人中随机抽取2人有,,,,,,,,,,,,ab aA aB aC aD aE aF bA bB bC bD bE bF ,,,,,,,,,,,,,,,AB AC AD AE AF BC BD BE BF CD CE CF DE DF EF 共28种情况.事件A 包括,,,,,,,,,,,aA aB aC aD aE aF bA bB bC bD bE bF 共12种情况.所以123()287P A ==. 答:随机抽取的2名学生来自不同组的概率为37.……………………………13分 (17)(本小题满分14分)(Ⅰ)证明:因为F ,G 分别为PB ,BE 的中点, 所以FGPE .又因为FG ⊄平面PED ,PE ⊂平面PED , 所以FG平面PED . ……………4分(Ⅱ)因为EA ⊥平面ABCD ,所以EA CB ⊥.又因为CB AB ⊥,AB AE A =,所以CB ⊥平面ABE .由已知F ,H 分别为线段PB ,PC 的中点, 所以FH BC .则FH ⊥平面ABE . 而FH⊂平面FGH ,所以平面FGH ⊥平面ABE . …………………………………………………9分 (Ⅲ)在线段PC 上存在一点M ,使PB ⊥平面EFM .证明如下: 在直角三角形AEB 中,因为1AE =,2AB =,所以BE =在直角梯形EADP 中,因为1AE =,2AD PD ==,所以PE =所以PE BE =.又因为F 为PB 的中点,所以EF PB ⊥. 要使PB ⊥平面EFM ,只需使PB FM ⊥.因为PD ⊥平面ABCD ,所以PD CB ⊥,又因为CB CD ⊥,PD CD D =,所以CB ⊥平面PCD ,而PC ⊂平面PCD ,所以CB PC ⊥. 若PB FM ⊥,则PFM ∆∽PCB ∆,可得PM PFPB PC=.由已知可求得PB =,PF =PC =2PM =.……14分 (18)(本小题满分13分)解:(Ⅰ)函数()f x 的定义域为R ,AEBD CPFGHM()()()()()()a x a x x f x x x --+'==++2222211111.当a >0时,当x 变化时,()f x ',()f x 的变化情况如下表:当a <0时,当x 变化时,()f x ',()f x 的变化情况如下表:综上所述,当a >0时,()f x 的单调递增区间为(,)-11,单调递减区间为(,)-∞-1,(,)+∞1; 当a <0时,()f x 的单调递增区间为(,)-∞-1,(,)+∞1,单调递减区间为(,)-11. ……………………………………5分 (Ⅱ)由(Ⅰ)可知,当0a >时,()f x 在(,)01上单调递增,()(0)f x f >;()f x 在(,e]1上单调递减,且2e(e )e 1a f a a =+>+. 所以(0,e]x ∈时,()f x >a . 因为()ln g x a x x =-,所以()1ag x x'=-, 令()0g x '=,得x a =.①当0e a <<时,由()0g x >',得0x a <<;由()0g x <',得x a >, 所以函数()g x 在(0,)a 上单调递增,在(,e]a 上单调递减.所以max ()()ln g x g a a a a ==-.因为(ln )(2ln )(2ln e)0a a a a a a a a --=->-=>, 所以对于任意(]12,0,e x x ∈,总有12()()g x f x <. ②当e a ≥时,()0g x '≥在(0,e]上恒成立,所以函数()g x 在(0,e]上单调递增,max ()(e)e <g x g a a ==-. 所以对于任意(]12,0,e x x ∈,仍有12()()g x f x <.综上所述,对于任意(]12,0,e x x ∈,总有12()()g x f x <.…………………13分 (19)(本小题满分14分)解:(Ⅰ)依题设1(,0)A a -,2(,0)A a ,则1(1,0)FA a =--,2(1,0)FA a =-. 由121FA FA ⋅=-,解得22a =,所以21b =.所以椭圆C 的方程为2212x y +=.…………………………………………4分 (Ⅱ)依题直线l 的方程为(1)y k x =-.由22(1),22y k x x y =-⎧⎨+=⎩得()2222214220k x k x k +-+-=. 设11(,)A x y ,22(,)B x y ,弦AB 的中点为00(,)M x y ,则2122421k x x k +=+,21222(1)21k x x k -=+,202221k x k =+,0221ky k -=+, 所以2222(,)2121k kM k k -++. 直线MD 的方程为22212()2121kk y x k k k +=--++, 令0y =,得2221D k x k =+,则22(,0)21k D k +. 若四边形ADBE 为菱形,则02E D x x x +=,02E D y y y +=.所以22232(,)2121k kE k k -++. 若点E 在椭圆C 上,则2222232()2()22121k kk k -+=++.整理得42k =,解得2k =所以椭圆C 上存在点E 使得四边形ADBE 为菱形.此时点E 到y ………………………………………………14分(20)(本小题满分13分)解:(Ⅰ)由已知得222(1,1,)11333S --=-+-=-. (1,1,1,1)1111112S --=----+=-. ………………………3分(Ⅱ)3n =时,12312132313(,,)i j i j S S x x x x x x x x x x x ≤<≤===++∑.固定23,x x ,仅让1x 变动,那么S 是1x 的一次函数或常函数, 因此2323min{(1,,),(1,,)}S S x x S x x ≥-. 同理2333(1,,)min{(1,1,),(1,1,)}S x x S x S x ≥-.2333(1,,)min{(1,1,),(1,1,)}S x x S x S x -≥---.以此类推,我们可以看出,S 的最小值必定可以被某一组取值1±的123,,x x x 所达到,于是12311,2,3min{(,,)}k x k S S x x x =±=≥.当1k x =±(1,2,3k =)时,22221231231[()()]2S x x x x x x =++-++212313()22x x x =++-. 因为123||1x x x ++≥, 所以13122S ≥-=-,且当121x x ==,31x =-,时1S =-, 因此min 1S =-. ……………………………………………7分11 / 11 (Ⅲ)121(,,,)n i j i j n S S x x x x x ≤<≤==∑121312321n n n n x x x x x x x x x x x x -=++++++++. 固定23,,,n x x x ,仅让1x 变动,那么S 是1x 的一次函数或常函数,因此2323min{(1,,,,),(1,,,,)}n n S S x x x S x x x ≥-.同理2333(1,,,,)min{(1,1,,,),(1,1,,,)}n n n S x x x S x x S x x ≥-.2333(1,,,,)min{(1,1,,,),(1,1,,,)}n n n S x x x S x x S x x -≥---.以此类推,我们可以看出,S 的最小值必定可以被某一组取值1±的12,,,n x x x 所达到,于是1211,2,,min {(,,,)}k n x k n S S x x x =±=≥.当1k x =±(1,2,,k n =)时,222212121[()()]2n n S x x x x x x =+++-+++ 2121()22n n x x x =+++-. 当n 为奇数时,因为12||1n x x x +++≥, 所以1(1)2S n ≥--,另一方面,若取12121n x x x -====,1112221n n n x x x --++====-,那么1(1)2S n =--,因此min 1(1)2S n =--. …………………………………………………………13分。
2011年高考北京市数学试卷-文科(含详细答案)

2011年普通高等学校招生全国统一考试数学(文)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出四个选项中,选出符合题目要求的一项。
(1) 已知全集U=R ,集合{}21P x x =½£,那么U P =ð(A)(,1-¥-) (B)(1,+¥) (C)(-1,1) (D)()()11-¥,-,+¥【解析】:2111x x £Þ-££,U P =ð()()11-¥,-,+¥ ,故选D (2)复数212ii-=+(A)i (B )i - (C)4355i -- (D)4355i -+ 【解析】:22i 2(i 2)(12i)2242(1)2412i (12i)(12i)1414(1)i i i i i i i ---------+====++----,选A 。
(3)如果1122log log 0x y <<,那么,那么(A )1y x << (B)1x y << (C)1x y << (D)1y x << 【解析】:1122log log x y x y <Þ>,12log 01y y <Þ>,即1y x <<故选D(4)若p 是真命题,q 是假命题,则是假命题,则(A )p q Ù是真命题是真命题 (B)p q Ú是假命题是假命题 (C)p Ø是真命题是真命题 (D)q Ø是真命题是真命题 【解析】:或(Ú)一真必真,且(Ù)一假必假,非(Ø)真假相反,故选D(5)某四棱锥的三视图如图所示,该四棱锥的表面积是(A)32 (B)16+162 (C)48 (D)16322+【解析】:由三视图可知几何体为底面边长为4,高为2的正四棱锥,则四棱锥的斜高为22,表面积2142244161622´´´+=+故选B 。
2011朝阳区一模试卷(文)及答案

北京市朝阳区高三年级第一次综合练习数学测试题(文史类) 2011.4 第一部分(选择题 共40分) 注意事项:1.答第一部分前,考生务必将自己的姓名、考试科目涂写在答题卡上。
考试结束时,将试题卷和答题卡一并交回。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,不能答在试题卷上。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. 1.若集合{}20Mx x =->,{}(3)(1)0N x x x =--<,则M N =(A){}23x x << (B ){}1x x < (C ){}3x x > (D ){}12x x <<2. 某校高三一班有学生54人,二班有学生42人,现在要用分层抽样的方法从这两个班随机选出16人参加军训表演,则一班和二班分别选出的人数是(A )8人,8人 (B )15人,1人(C )9人,7人 (D )12人,4人 3.函数2cos 1y x =+在下列哪个区间上为增函数(A )π[0,]2 (B )π[, π]2(C )[]0, π (D )[]π, 2π 4. 已知{}n a 是由正数组成的等比数列,n S 表示{}n a 的前n 项的和,若13a =,24144a a =,则5S 的值是(A )692(B ) 69 (C )93 (D )1895.已知a ,b 是两条不重合的直线,α,β是两个不重合的平面,下列命题中正确的是(A ) //a b ,//b α,则//a α(B ) a ,b α⊂,//a β,//b β,则//αβ(C ) aα⊥,//b α,则a b ⊥(D ) 当a α⊂,且b α⊄时,若b ∥α,则a ∥b6. 已知三棱锥的三视图如图所示,其中侧视图为直角三角形, 俯视图为等腰直角三角形,则此三棱锥的体积等于(A )23(B )33(C )223(D )2337.已知函数()y f x =是奇函数, 当0x >时,()f x =lg x ,则1(())100f f 的值等于(A )1lg 2(B )1lg 2-(C )lg 2 (D )lg 2-8.已知x ∈R ,用[]x 表示不超过x 的最大整数,记{}[]x x x =-,若(0, 1)a ∈,则{}a 与1{}2a +的大小关系是(A )不确定(与a 的值有关) (B ){}a <1{}2a +(C ){}a =1{}2a + (D ){}a >1{}2a +第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上. 9.已知i 为虚数单位,则3i1i+-= . 正视图俯视图侧视图1310.过原点且倾斜角为60︒的直线被圆2240x y x +-= 所截得的弦长为 .11. 已知两点(3, 2)A --,(3,6)B ,点C 满足AC CB = ,则点C 的坐标是 ,AB AC ⋅= .12.抛物线24y x =上一点M与该抛物线的焦点F 的距离||4MF =,则点M 的横坐标x = .13.执行右图所示的程序框图,若输入 5.2x =,则输出y 的值为 .14.对于各数互不相等的整数数组),,,,(321n i i i i (n 是不小于2的正整数),对于任意,{1,2,3,,}p q n ∈ ,当q p <时有q p i i >,则称p i ,q i 是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为该数组的“逆序数”,则数组(2,4,3,1)中的逆序数等于 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.否开始输入x是 1?y ≤输出y结束x y =|2|y x =-15.(本小题满分13分) 在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c .已知2c a =,4C π=. (Ⅰ)求sin A 的值;(Ⅱ)求cos(2)3A π-的值.16.(本小题满分13分) 已知集合A ={-2,0,2},B ={-1,1}.(Ⅰ)若M ={(,)x y |x ∈A ,y ∈B },用列举法表示集合M;(Ⅱ)在(Ⅰ)中的集合M 内,随机取出一个元素(,)x y ,求以(,)x y 为坐标的点位于区域D :20,20,1x y x y y -+⎧⎪+-⎨⎪-⎩≥≤≥内的概率.17.(本小题满分13分) 如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,且//AD BC ,90ABC ∠=︒,侧面PAD ⊥底面ABCD ,90PAD ∠=︒. 若12AB BC AD ==.(Ⅰ)求证:CD ⊥平面PAC ;(Ⅱ)设侧棱PA 的中点是E ,求证:BE 平面PCD .AB PCDE18.(本小题满分13分) 已知函数2()ln f x a x x=+,a ∈R . (Ⅰ)若曲线()y f x =在点(1,(1))P f 处的切线垂直于直线2y x =+,求a 的值;(Ⅱ)求函数()f x 在区间(0, e]上的最小值.19.(本小题满分14分) 已知(2, 0)A -,(2, 0)B 为椭圆C 的左右顶点,(1, 0)F 为其右焦点.(Ⅰ)求椭圆C 的标准方程及离心率;(Ⅱ)过点A 的直线l 与椭圆C 的另一个交点为P (不同于A ,B ),与椭圆在点B 处的切线交于点D .当直线l 绕点A 转动时,试判断以BD 为直径的圆与直线PF 的位置关系,并加以证明.20.(本小题满分14分) 有n (3, )n n *∈N ≥个首项为1,项数为n 的等差数列,设其第m (, )m n m *∈N ≤个等差数列的第k 项为mk a (1,2,3,,)k n = ,且公差为m d . 若11d =,23d =, 123,,,,n n n nn a a a a 也成等差数列.(Ⅰ)求m d (3m n ≤≤)关于m 的表达式;(Ⅱ)将数列{}m d 分组如下:1()d ,234(,,)d d d ,5(d ,6d ,7d ,8d ,9d )…,(每组数的个数组成等差数列),设前m 组中所有数之和为4()(0)m m c c >,求数列{2}m c m d 的前n 项和n S ;(Ⅲ)设N 是不超过20的正整数,当nN>时,对于(Ⅱ)中的n S ,求使得不等式1(6)50n n S d ->成立的所有N 的值.北京市朝阳区高三年级第一次综合练习 数学测试题答案(文史类) 2011.4 一、选择题 题号 (1) (2) (3) (4) (5) (6) (7) (8) 答案 ACBCCBDA二、填空题 题号 (9)(10) (11)(12)(13) (14) 答案 12i +2(0, 2)5030.84三、解答题(共80分) 15.(满分13分) 解:(Ⅰ)因为2ca =,4C π=, 由正弦定理sin sin a c A C =得:2sin 4A =. (5)分(Ⅱ)因为2sin 4A =,2c a =可知a c <,4A π<.则214cos1sin 4A A =-=. 7sin 22sin cos 4A A A ==,23cos 22cos 14A A =-=.则cos(2)3A π-=ππcos 2cos sin 2sin 33A A +=3218+.………………13分 16. (满分13分)解:(Ⅰ)M ={(-2, -1),(-2, 1),(0, -1),(0, 1),(2, -1),(2, 1)}. ……………6分(Ⅱ)记“以(x ,y )为坐标的点位于区域D 内”为事件A .E FA BP CD集合M 中共有6个元素,即基本事件总数为6,区域D 含有集合M 中的元素4个, 所以42()63P A ==. 故以(x ,y )为坐标的点位于区域D 内的概率为23. ……………………………13分17. (满分13分) 解:(Ⅰ)因为 90PAD ∠=︒,所以PAAD ⊥.又因为侧面PAD⊥底面ABCD ,且侧面PAD 底面ABCD AD =,所以PA ⊥底面ABCD .而CD⊂底面ABCD , 所以PA ⊥CD .在底面ABCD 中,因为90ABC BAD ∠=∠=︒,12AB BC AD ==, 所以22AC CD AD ==, 所以AC ⊥CD . 又因为PA AC A = , 所以CD ⊥平面PAC . ……………………………6分(Ⅱ)设侧棱PD 的中点为F , 连结BE ,EF ,FC ,则EFAD ,且12EF AD =. 由已知90ABC BAD ∠=∠=︒,所以BC AD . 又12BC AD =, 所以BC EF . 且BC EF=.所以四边形BEFC 为平行四边形,所以BE CF .因为BE ⊄平面PCD ,CF ⊂平面PCD ,所以BE 平面PCD . ………………………………………………………13分ABP CDE18. (满分13分) 解: (Ⅰ)直线2y x =+的斜率为1.函数()y f x =的导数为22()a f x x x'=-+,则22(1)111af '=-+=-,所以1a =. ………………………………5分(Ⅱ)22()ax f x x-'=,x ∈(0,)+∞.①当0a =时,在区间(0, e]上22()0f x x'=-<,此时()f x 在区间(0, e]上单调递减,则()f x 在区间(0, e]上的最小值为2(e)ef =. ②当20a<,即0a <时,在区间(0, e]上()0f x '<,此时()f x 在区间(0, e]上单调递减,则()f x 在区间(0, e]上的最小值为2(e)ef a =+. ③当20e a<<,即2e a >时,在区间2(0,)a 上()0f x '<,此时()f x 在区间2(0,)a 上单调递减;在区间2(,e]a 上()0f x '>,此时()f x 在区间2(,e]a 上单调递增;则()f x 在区间(0, e]上的最小值为22()ln f a a a a =+.④ 当2e a ≥,即20ea <≤时,在区间(0, e]上()0f x ′≤,此时()f x 在区间(0, e]上为单调递减,则()f x 在区间(0, e]上的最小值为2(e)ef a =+. 综上所述,当2ea ≤时,()f x 在区间(0, e]上的最小值为2e a +;当2e a >时,()f x 在区间(0, e]上的最小值为2ln a a a +. …………………………………………13分19. (满分14分)解:(Ⅰ)由题意可设椭圆C 的方程为22221(0)x y a b a b +=>>,半焦距为c ,因为(2, 0)A -、(2, 0)B 为椭圆C 的左、右顶点,(1, 0)F 为其右焦点, 所以2a=, 1c =.又因为222ab c =+,所以223b a c =-=.故椭圆C 的方程为22143x y +=,离心率为12.……5分(Ⅱ)以BD 为直径的圆与直线PF 相切. 证明如下: 由题意可设直线l 的方程为(2)y k x =+(0)k ≠,则点D 坐标为(2, 4)k ,BD 中点E 的坐标为(2, 2)k .由22(2),1,43y k x x y =+⎧⎪⎨+=⎪⎩得2222(34)1616120k x k x k +++-=. 设点P 的坐标为00(,)x y ,则2021612234k x k --=+.所以2026834k x k -=+,00212(2)34k y k x k =+=+.因为点F 坐标为(1, 0),当12k =±时,点P 的坐标为3(1, )2±,点D 的坐标为(2, 2)±, 直线PFx ⊥轴,此时以BD 为直径的圆22(2)(1)1x y -+= 与直线PF相切.当12k≠±时,则直线PF 的斜率0204114PFy kk x k ==--.所以直线PF 的方程为24(1)14ky x k=--. 点E 到直线PF的距离OF EPD BAy x222228421414161(14)k kk k k d k k ----=+-322228142||14|14|k k k k k k +-==+-.又因为||4||BD k = 所以1||2d BD =. 故以BD 为直径的圆与直线PF 相切. 综上得,当直线l 绕点A 转动时,以BD 为直径的圆与直线PF相切. (14)分20. (满分14分) 解(Ⅰ)由题意知,1(1)mnm a n d =+-.212121[1(1)][1(1)](1)()n n a a n d n d n d d -=+--+-=--,同理,3232(1)()n n a a n d d -=--,4343(1)()n n a a n d d -=--,…,(1)1(1)()nn n n n n a a n d d ---=--. 123,,,,n n n nn a a a a 成等差数列,所以2132(1)n n n n nn n n a a a a a a --=-==- , 故21321n n d d d d d d --=-==- .即{}n d 是公差是21312d d -=-=的等差数列.所以,21md m =-(3m n ≤≤,*,m n ∈N ). ………………………5分 (Ⅱ)由(Ⅰ)知*2 1 ()m d m m =-∈N .数列{}m d 分组如下:(1),(3,5,7),(9,11,13,15,17),…. 按分组规律,第m 组中有21m -个奇数,所以第1组到第m 组共有2135(21)m m ++++-= 个奇数.注意到前k 个奇数的和为2135(21)k k ++++-= ,所以前2m 个奇数的和为224()mm =,即前m 组中所有数之和为4m ,所以44()m c m =.因为0m c >,所以m c m =,从而*2(21)2()m c m m d m m =-⋅∈N .所以234112325272(23)2(21)2n n n S n n -=⋅+⋅+⋅+⋅++-⋅+-⋅ .23412123252(23)2(21)2n n n S n n +=⋅+⋅+⋅++-⋅+-⋅ ,故2341222222222(21)2n n n S n +-=+⋅+⋅+⋅++⋅--⋅ 2312(2222)2(21)2n n n +=++++---⋅12(21)22(21)221n n n +-=⨯---⋅-1(32)26n n +=--, 所以1(23)26n n S n +=-+. ……………………………………10分(Ⅲ)由(Ⅱ)得*2 1 ()n d n n =-∈N ,1(23)26n n S n +=-+* ()n ∈N . 故不等式1(6)50n n S d -> 就是1(23)250(21)n n n +->-. 考虑函数1()(23)250(21)n f n n n +=---1(23)(250)100n n +=---.当1,2,3,4,5n =时,都有()0f n <,即1(23)250(21)n n n +-<-.而(6)9(12850)1006020f =--=>,注意到当6n ≥时,()f n 单调递增,故有()0f n >. 因此当6n ≥时,1(23)250(21)n n n +->-成立,即1(6)50n n S d ->成立. 所以满足条件的所有正整数5,6,7,,20N = .…………………………………14分。
北京市东城2011届高三年级第二学期第一次模拟数学文科试卷

北京市东城区2010-2011学年度综合练习(一)高三数学 (文科)2011.4一、本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知复数z 满足(1i)2z -=,则z 等于(A )1i + (B )1i - (C )1i -+ (D )1i -- (2)命题“0x ∃∈R ,20log 0x ≤”的否定为(A )0x ∃∈R ,20log 0x > (B )0x ∃∈R ,20log 0x ≥ (C )x ∀∈R ,2log 0x ≥ (D )x ∀∈R ,2log 0x >(3)已知函数()f x 是定义在R 上的偶函数,且当0x >时,()ln(1)f x x =+,则函数()f x 的大致图像为(A )(B ) (C )(4)给定下列四个命题:①若一个平面内的两条直线与另一个平面都平行,则这两个平面平行; ②若两个平面都垂直于同一条直线,则这两个平面平行;③若两个平面互相垂直,则在其中一个平面内的直线垂直另外一个平面;其中为真命题的是(A )①和② (B )②和③ (C )③和④ (D )②和④ (5)已知函数()sin y x =ω+ϕ(0,02πω><ϕ≤的部分图象如图所示,则点P (),ωϕ的坐标为 (A )(2,3π(B )(2,6π(C )1(,23π (D )1(,26π(6)若右边的程序框图输出的S 是126,则条件①可为(A )5n ≤ (B )6n ≤(C )7n ≤ (D )8n ≤(7)已知函数131()()2xf x x =-,那么在下列区间中含有函数()f x 零点的为(A )1(0,)3(B )11(,)32(C )1(,1)2(D )(1,2)(8)空间点到平面的距离如下定义:过空间一点作平面的垂线,该点和垂足之间的距离即为该点到平面的距离.平面α,β,γ两两互相垂直,点A ∈α,点A 到β,γ的距离都是3,点P 是α上的动点,满足P 到β的距离是到P 到点A 距离的2倍,则点P 的轨迹上的点到γ的距离的最小值为 (A )3(B )3+(C )6 (D )33-二、填空题:本大题共6小题,每小题5分,共30分。
北京市朝阳区2011年第二学期高三综合练习(一)

北京市朝阳区2011年第二学期高三综合练习(一)数学(理科)(朝阳一模)(时间:120分钟总分: 150分)第1卷(选择题共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小 题列出的四个选项中,选出符合题目要求的一项.1.若集合},,2{{},,|{2R x x y y N R x x y y M ∈+==∈==则=N M ( )),0.[+∞A ),.(∝+-∞B ∅.C )1,1()4,2.(- D2.某校高三一班有学生54人,二班有学生42人,现在要用分层抽样的方法从这两个班抽出16人参加军训表演,则一班和二班分别被抽取的人数是 ( )8,8.A 6,10.B 7,9.C 4,12.D3.极坐标方程θρcos 4=化为直角坐标方程是 ( )4)2.(22=+-y x A 4.22=+y x B 4)2(.22=-+y x C 4)1()1.(22=-+-y x D4.已知}{n a 是由正数组成的等比数列,n s 表示 }{n a 的前n 项和.若,144,3421==a a a 则10s 的值是( )511.A 1023.B 1533.C 3069.D5.函数)2(cos 2π+=x y 的单调递增区间是 ( )Z k k k A ∈+),2,.(πππ z k k k B ∈++),,2.(ππππZ k k k C ∈+),2,2.(πππ z k k k D ∈++),22,2.(ππππ6.已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形,则此三棱锥的体积等于 ( )126.A 33.B 46.C 332.D7.如图,双曲线的中心在坐标原点0,A ,C 分别是双曲线虚轴的上、下顶点,B 是双曲线的左顶点,F 为双曲线的左焦点,直线AB 与FC 相交于点D.若双曲线的离心率为2,则∠BDF 的余弦值是 ( )77.A 775.B 147.C 1475.D 8.定义区间(a ,b ),k ,b ),(a ,b],k ,b]的长度均为,a b d -=多个区间并集的长度为各区间长度之和.例如, )2,1()5,3[的长度.3)35()12(=-+-=d 用][x 表示不超过x 的最大整数,记 ],[||x x x -=其中.R x ∈设=)(x f ,1)(|,|][-=⋅x x g x x 若321,,d d d 分别表示不等式),()(x g x f > 方程),()(x g x f =不等式)()(x g x f <解集区间的长度,则当20110≤≤x 时,有 ( )2008,2,1.321===d d d A 2009,1,1.321===d d d B2003,5,3.321===d d d C 2006,3,2.321===d d d D第Ⅱ卷(非选择题共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.9.复数,1,321i z i z -=+=则21z z等于 10.在二项式6)2(+x 的展开式中,第四项的系数是11.如下图,在三角形ABC 中,D ,E 分别为BC ,AC 的中点,F 为AB 上的点,且.4=若 ,AE y AF x AD +=则实数=x =y ,12.执行下图所示的程序框图,若输入,2.5-=x 则输出y 的值为13.如下图,在圆内接四边形ABCD 中,对角线AC ,BD 相交于点 E.已知=∠===D B C EC AE CD BC ,2,32=∠C A B 则,30 ,AC 的长是14.对于各数互不相等的整数数组n i i i i n (),,,,(321 ⋅是不小于3的正整数),对于任意},,,3,2,1{,n q P ∈ 当P q <时,有,q P i i >则称q P i i ,是该数组的一个“逆序”,一个数据中所有“逆序”的个数称为该数组的“逆序数”,则数组(2,4,3,1)中的逆序数等于____;若数组,,(21i i ),,3n i i 中的逆序数为n ,则数组),,,(11i i i n n -中的逆序数为三、解答题:本大题共6小题,共80分,解答应写在文字说明,演算步骤或证明过程:15.(本小题共13分)在锐角△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知⋅-=432cos C (I)求sinC ;(Ⅱ)当C=2a ,且73=b 时,求a .16.(本小题共13分)如图,在四棱雉P- ABCD 中,底面ABCD 为直角梯形,且=∠=∠PAD ABC BC AD ,// ,90 侧面PAD ⊥底面ABCD.若BC AB PA ==.21AD = (I)求证:CD ⊥平面PAC .(Ⅱ)侧棱PA ⊥是否存在点E ,使得BE∥平面PCD? 若存在,指出点E 的位置并证明;若不存在,请说明理由.(Ⅲ)求二面角A-PD-C 的余弦值.17.(本小题共13分)在某校教师趣味投篮比赛中,比赛规则是:每场投6个球,至少投进 4个球且最后.2个球都投 进者获奖,否则不获奖,已知教师甲投进每个球的概率都是⋅32 (I)记教师甲在每场的6次投球中投进球的个数为X , 求X 的分布列及数学期望;(Ⅱ)求教师甲在一场比赛中获奖的概率;(Ⅲ)已知教师乙在某场比赛中,6个球中恰好投进了4个球,求教师乙在这场比赛中获奖的概率;教师乙 在这场比赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗?18.(本小题共13分)已知函数>-+=a x a xZ x f (2ln )().0 (I)若曲线)(x f y =在点))1(,1(f P 处的切线与直线2+=x y 垂直,求函数)(x f y =的单调区间; (Ⅱ)若对于),0(+∞∈∀x 都有)1(2)(->a x f 成立,试求a 的取值范围;(Ⅲ)记).()()(R b b x x f x g ∈-+=当1=a 时,函数)(x g 在区间].,[1e e -上有两个零点,求实数b的取值范围.19.(本小题共14分)已知A (-2,0),B(2,O)为椭圆C 的左、右顶点,F 为其右焦点,P 是椭圆C 上异于A ,B 的动点,且△APB 面积的最大值为.32(I )求椭圆C 的方程及离心率;(Ⅱ)直线AP 与椭圆在点B 处的切线交于点D ,当直线AP 绕点A 转动时,试判断以BD 为直径的圆与直 线PF 的位置关系,并加以证明.20.(本小题共14分)有n 个首项都是1的等差数列,设第m 个数列的第k 项为),3,,,3,2,1,(≥=n n k m a nk 公差为,m d 并且*,,,,32ln r n n a a a a 成等差数列.(I)证明212211,,3(1P P n m d p d p d m ≤≤+==是m 的多项式),并求21P P +的值; (Ⅱ)当3,121==d d 时,将数列}{m d 分组如下:),(1d ),,,,,(),,,(98765432d d d d d d d d …(每组数的个数构成等差数列),设前m 组中所有数之和为m m c c ()(4),0>求数列}*2{m c d 的前挖项和n s . (Ⅲ)设N 是不超过20的正整数,当N n >时,对于(Ⅱ)中的,n s 求使得不等式n n d S >-)6(501成立的所有N 的值.。
北京市东城区2011高三一模文科数学试题及答案
北京市东城区2011高三一模文科数学试题及答案一、选择题(共1小题;共5分)1. 若下面的程序框图输出的是,则条件①可为______A. B. C. D.二、填空题(共1小题;共5分)2. 抛物线的焦点坐标为______.三、解答题(共2小题;共26分)3. 已知四棱锥的底面是菱形.,为的中点.(1)求证: 平面;(2)求证:平面平面.4. 对于,定义一个如下数阵:其中对任意的,,当能整除时,;当不能整除时,.(1)当时,试写出数阵;(2)设.若表示不超过的最大整数,求证:.四、选择题(共7小题;共35分)5. 已知复数满足,则等于______A. B. C. D.6. 命题" , "的否定为______A. ,B. ,C. ,D. ,7. 已知函数是定义在上的偶函数,且当时,,则函数的大致图像为______A. B.C. D.8. 给定下列四个命题:①若一个平面内的两条直线与另一个平面都平行,则这两个平面平行;②若两个平面都垂直于同一条直线,则这两个平面平行;③若两个平面互相垂直,则在其中一个平面内的直线垂直另外一个平面;④若两个平面互相平行,则在其中一个平面内的直线平行另外一个平面.其中为真命题的是______A. ①和②B. ②和③C. ③和④D. ②和④9. 已知函数(,)的部分图象如图所示,则点的坐标为A. B. C. D.10. 已知函数,那么在下列区间中含有函数零点的为______A. B. C. D.11. 空间点到平面的距离定义如下:过空间一点作平面的垂线,该点和垂足之间的距离即为该点到平面的距离.平面,,两两互相垂直,点,点到,的距离都是,点是上的动点,满足到的距离是点到点距离的倍,则点的轨迹上的点到的距离的最小值为______A. B. C. D.五、填空题(共4小题;共20分)12. 在等差数列中,若,,则 ______.13. 已知,,则 ______.14. 设且,则 ______; ______.15. 设不等式组在直角坐标系中所表示的区域的面积为,则当时,的最小值为______.六、解答题(共4小题;共52分)16. 在中,角,,的对边分别为、、.若,.(1)求证:;(2)若的面积,求的值.17. 某高校在年的自主招生考试成绩中随机抽取名学生的笔试成绩,按成绩分组:第组,第组,第组,第组,第组.得到的频率分布直方图如图所示.(1)分别求第,,组的频率;(2)若该校决定在笔试成绩高的第,,组中用分层抽样抽取名学生进入第二轮面试,求在第,,组中各抽取多少名学生进入第二轮面试?(3)在(2)的前提下,学校决定在这名学生中随机抽取名学生接受甲考官的面试,求第组至少有一名学生被甲考官面试的概率.18. 已知函数,且.(1)求的值;(2)求函数的单调区间;(3)设函数,若函数在上单调递增,求实数的取值范围.19. 已知椭圆的中心在坐标原点,焦点在轴上,离心率为,椭圆上的点到焦点距离的最大值为.(1)求椭圆的标准方程;(2)若过点的直线与椭圆交于不同的两点、,且,求实数的取值范围.答案第一部分1. B第二部分2.第三部分3. (1)因为,分别为,的中点,所以.因为平面,平面,所以 平面.(2).因为,所以.在菱形中,,因为,所以平面.因为平面,所以平面平面.4. (1)依题意可得,(2)由题意可知,是数阵的第列的和,因此是数阵所有数的和.而数阵所有数的和也可以考虑按行相加.对任意的,不超过的倍数有,,…,.因此数阵的第行中有个1,其余是,即第行的和为.所以.第四部分5. A6. D7. D8. D9. A 10. B11. D第五部分12.13.14. ;15.第六部分16. (1)由已知及正弦定理,得由,得将代入上式整理,得由,,得所以即.(2)由(1),得由,得由,得解得由余弦定理,得即得.17. (1)由题设可知,第组的频率为;第组的频率为;第组的频率为.(2)第组的人数为;第组的人数为;第组的人数为.由此,第,,组共有名学生.利用分层抽样在名学生中抽取名学生,其中第组抽取人;第组抽取人;第组抽取人.所以第,,组分别抽取人、人、人.(3)设第组的位同学为、、,第组的位同学为、,第组的位同学为.从六位同学中抽取两位同学的方法有共种可能.其中第组的位同学,至少有一位同学入选的有共种可能.所以第组至少有一名学生被甲考官面试的概率为.18. (1)由已知,得.由,得解得.(2)由(1),得,则列表如下:由此,的增区间是和;极大值极小值减区间是.(3)由已知,得从而函数在上单调递增,等价于在上恒成立.根据二次函数图象的特征,只要即可,解得.因此,的取值范围是.19. (1)设椭圆的方程为.由题意,得解得因此,椭圆的方程为.(2)①若过点的直线的斜率不存在,则.②若过点的直线的斜率为,即时,设直线的方程为.由消去,得因为和椭圆交于不同两点,所以化简,得设,,则由,得从而将代入,消去,得解得,代入式,得解得,即或.综上,实数的取值范围为.。
2011年北京市高考数学试卷(文科)答案与解析

2011年北京市高考数学试卷(文科)参考答案与试题解析一、选择题(共8小题,每小题5分,满分40分)1.(5分)(2011•北京)已知全集U=R,集合P={x|x2≤1},那么∁U P=()A.(﹣∞,﹣1]B.[1,+∞)C.[﹣1,1]D.(﹣∞,﹣1)∪(1,+∞)【考点】补集及其运算.【专题】集合.【分析】先求出集合P中的不等式的解集,然后由全集U=R,根据补集的定义可知,在全集R 中不属于集合P的元素构成的集合为集合A的补集,求出集合P的补集即可.【解答】解:由集合P中的不等式x2≤1,解得﹣1≤x≤1,所以集合P=[﹣1,1],由全集U=R,得到C U P=(﹣∞,1)∪(1,+∞).故选D【点评】此题属于以不等式的解集为平台,考查了补集的运算,是一道基础题.2.(5分)(2011•北京)复数=()A.i B.﹣i C.D.【考点】复数代数形式的混合运算.【专题】数系的扩充和复数.【分析】将分子、分母同乘以1﹣2i,再按多项式的乘法法则展开,将i2用﹣1代替即可.【解答】解:==i故选A【点评】本题考查复数的除法运算法则:分子、分母同乘以分母的共轭复数;再按多项式的乘法法则展开即可.3.(5分)(2011•北京)如果那么()A.y<x<1 B.x<y<1 C.1<x<y D.1<y<x【考点】对数函数的单调性与特殊点.【专题】函数的性质及应用.【分析】本题所给的不等式是一个对数不等式,我们要先将不等式的三项均化为同底根据对数函数的单调性,即可得到答案.【解答】解:不等式可化为:又∵函数的底数0<<1故函数为减函数∴x>y>1故选D【点评】本题考查的知识点是对数函数的单调性与特殊点,其中根据对数函数的性质将对数不等式转化为一个整式不等式是解答本题的关键.4.(5分)(2011•北京)若p是真命题,q是假命题,则()A.p∧q是真命题B.p∨q是假命题C.﹁p是真命题D.﹁q是真命题【考点】复合命题的真假.【专题】简易逻辑.【分析】根据题意,由复合命题真假表,依次分析选项即可作出判断.【解答】解:∵p是真命题,q是假命题,∴p∧q是假命题,选项A错误;p∨q是真命题,选项B错误;¬p是假命题,选项C错误;¬q是真命题,选项D正确.故选D.【点评】本题考查复合命题的真假情况.5.(5分)(2011•北京)某四棱锥的三视图如图所示,该四棱锥的表面积是()A.32 B.16+16 C.48 D.16+32【考点】由三视图求面积、体积.【专题】立体几何.【分析】根据所给的三视图得到四棱锥的高和底面的长和宽,首先根据高做出斜高,做出对应的侧面的面积,再加上底面的面积,得到四棱锥的表面积.【解答】解:由题意知本题是一个高为2,底面是一个长度为4的正方形的四棱锥,过顶点向底面做垂线,垂线段长是2,过底面的中心向长度是4的边做垂线,连接垂足与顶点,得到直角三角形,得到斜高是2,∴四个侧面积是,底面面积是4×4=16,∴四棱锥的表面积是16+16,故选:B.【点评】本题考查有三视图求表面积和体积,考查由三视图得到几何图形,考查简单几何体的体积和表面积的做法,本题是一个基础题.6.(5分)(2011•北京)执行如图所示的程序框图,若输入A的值为2,则输入的P值为()A.2 B.3 C.4 D.5【考点】循环结构.【专题】算法和程序框图.【分析】根据输入A的值,然后根据S进行判定是否满足条件S≤2,若满足条件执行循环体,依此类推,一旦不满足条件S≤2,退出循环体,求出此时的P值即可.【解答】解:S=1,满足条件S≤2,则P=2,S=1+=满足条件S≤2,则P=3,S=1++=满足条件S≤2,则P=4,S=1+++=不满足条件S≤2,退出循环体,此时P=4故选:C【点评】本题主要考查了当型循环结构,循环结构有两种形式:当型循环结构和直到型循环结构,当型循环是先判断后循环,直到型循环是先循环后判断.7.(5分)(2011•北京)某车间分批生产某种产品,每批的生产准备费用为800元.若每批生产x件,则平均仓储时间为天,且每件产品每天的仓储费用为1元.为使平均每件产品的生产准备费用与仓储费用之和最小,每批应生产产品()A.60件B.80件C.100件D.120件【考点】函数模型的选择与应用.【专题】函数的性质及应用.【分析】若每批生产x件,则平均仓储时间为天,可得仓储总费用为,再加上生产准备费用为800元,可得生产x件产品的生产准备费用与仓储费用之和是=元,由此求出平均每件的生产准备费用与仓储费用之和,再用基本不等式求出最小值对应的x值【解答】解:根据题意,该生产x件产品的生产准备费用与仓储费用之和是=这样平均每件的生产准备费用与仓储费用之和为(x为正整数)由基本不等式,得当且仅当时,f(x)取得最小值、可得x=80时,每件产品的生产准备费用与仓储费用之和最小故答案为B【点评】本题结合了函数与基本不等式两个知识点,属于中档题,运用基本不等式时应该注意取等号的条件,才能准确给出答案.8.(5分)(2011•北京)已知点A(0,2),B(2,0).若点C在函数y=x2的图象上,则使得△ABC的面积为2的点C的个数为()A.4 B.3 C.2 D.1【考点】抛物线的应用.【专题】函数的性质及应用.【分析】本题可以设出点C的坐标(a,a2),求出C到直线AB的距离,得出三角形面积表达式,进而得到关于参数a的方程,转化为求解方程根的个数(不必解出这个跟),从而得到点C的个数.【解答】解:设C(a,a2),由已知得直线AB的方程为,即:x+y﹣2=0点C到直线AB的距离为:d=,有三角形ABC的面积为2可得:=|a+a2﹣2|=2得:a2+a=0或a2+a﹣4=0,显然方程共有四个根,可知函数y=x2的图象上存在四个点(如上面图中四个点C1,C2,C3,C4)使得△ABC的面积为2(即图中的三角形△ABC1,△ABC2,△ABC3,△ABC4).故应选:A【点评】本题考查了截距式直线方程,点到直线的距离公式,三角形的面积的求法,就参数的值或范围,考查了数形结合的思想二、填空题(共6小题,每小题5分,满分30分)9.(5分)(2011•北京)在△ABC中.若b=5,,sinA=,则a=.【考点】正弦定理.【专题】解三角形.【分析】直接利用正弦定理,求出a 的值即可.【解答】解:在△ABC中.若b=5,,sinA=,所以,a===.故答案为:.【点评】本题是基础题,考查正弦定理解三角形,考查计算能力,常考题型.10.(5分)(2011•北京)已知双曲线(b>0)的一条渐近线的方程为y=2x,则b=2.【考点】双曲线的简单性质.【专题】圆锥曲线的定义、性质与方程.【分析】利用双曲线的标准方程写出其渐近线方程是解决本题的关键,根据已知给出的一条渐近线方程对比求出b的值.【解答】解:该双曲线的渐近线方程为,即y=±bx,由题意该双曲线的一条渐近线的方程为y=2x,又b>0,可以得出b=2.故答案为:2.【点评】本题考查根据双曲线方程求解其渐近线方程的方法,考查学生对双曲线标准方程和渐近线方程的认识和互相转化,考查学生的比较思想,属于基本题型.11.(5分)(2011•北京)已知向量=(,1),=(0,﹣1),=(k,).若与共线,则k=1.【考点】平面向量共线(平行)的坐标表示.【专题】平面向量及应用.【分析】利用向量的坐标运算求出的坐标;利用向量共线的坐标形式的充要条件列出方程,求出k的值.【解答】解:∵与共线,∴解得k=1.故答案为1.【点评】本题考查向量的坐标运算、考查向量共线的坐标形式的充要条件:坐标交叉相乘相等.12.(5分)(2011•北京)在等比数列{a n}中,a1=,a4=﹣4,则公比q=﹣2;a1+a2+…+a n=.【考点】等比数列的性质;等比数列.【专题】等差数列与等比数列.【分析】根据等比数列的性质可知,第4项比第1项得到公比q的立方等于﹣8,开立方即可得到q的值,然后根据首项和公比,根据等比数列的前n项和的公式写出此等比数列的前n 项和S n的通项公式,化简后即可得到a1+a2+…+a n的值.【解答】解:q3==﹣8∴q=﹣2;由a1=,q=﹣2,得到:等比数列的前n项和S n=a1+a2+…+a n==.故答案为:﹣2;【点评】此题考查学生掌握等比数列的性质,灵活运用等比数列的前n项和公式化简求值,是一道基础题.13.(5分)(2011•北京)已知函数若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是(0,1).【考点】根的存在性及根的个数判断.【专题】函数的性质及应用.【分析】要求程f(x)=k有两个不同的实根是数k的取值范围,根据方程的根与对应函数零点的关系,我们可以转化为求函数y=f(x)与函数y=k交点的个数,我们画出函数的图象,数形结合即可求出答案.【解答】解:函数的图象如下图所示:由函数图象可得当k∈(0,1)时方程f(x)=k有两个不同的实根,故答案为:(0,1)【点评】本题考查的知识点是根的存在性及根的个数判断,其中根据方程的根与对应函数零点的关系,将方程问题转化为函数问题是解答的关键.14.(5分)(2011•北京)设A(0,0),B(4,0),C(t+4,3),D(t,3)(t∈R).记N(t)为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则N(0)=6,N(t)的所有可能取值为6、7、8.【考点】二元一次不等式(组)与平面区域.【专题】不等式的解法及应用.【分析】作出平行四边形,结合图象得到平行四边形中的整数点的个数.【解答】解:当t=0时,平行四边形ABCD内部的整点有(1,1);(1,2);(2,1);(2,2);(3,1);(3,2)共6个点,所以N(0)=6作出平行四边形ABCD将边OD,BC变动起来,结合图象得到N(t)的所有可能取值为6,7,8故答案为:6;6,7,8【点评】本题考查画可行域、考查数形结合的数学思想方法.三、解答题(共6小题,满分80分)15.(13分)(2011•北京)已知函数.(Ⅰ)求f(x)的最小正周期:(Ⅱ)求f(x)在区间上的最大值和最小值.【考点】三角函数的周期性及其求法;两角和与差的余弦函数;三角函数的最值.【专题】三角函数的图像与性质.【分析】(Ⅰ)利用两角和公式和二倍角公式对函数的解析式进行化简整理后,利用正弦函数的性质求得函数的最小正周期.(Ⅱ)利用x的范围确定2x+的范围,进而利用正弦函数的单调性求得函数的最大和最小值.【解答】解:(Ⅰ)∵,=4cosx()﹣1=sin2x+2cos2x﹣1=sin2x+cos2x=2sin(2x+),所以函数的最小正周期为π;(Ⅱ)∵﹣≤x≤,∴﹣≤2x+≤,∴当2x+=,即x=时,f(x)取最大值2,当2x+=﹣时,即x=﹣时,f(x)取得最小值﹣1.【点评】本题主要考查了三角函数的周期性及其求法,三角函数的最值.解题的关键是对函数解析式的化简整理.16.(13分)(2011•北京)以下茎叶图记录了甲、乙两组各四名同学的植树棵树.乙组记录中有一个数据模糊,无法确认,在图中以X表示.(1)如果X=8,求乙组同学植树棵树的平均数和方差;(注:方差,其中的平均数)(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.【考点】茎叶图;众数、中位数、平均数;极差、方差与标准差.【专题】概率与统计.【分析】(1)根据所给的这组数据,利用求平均数的公式,把所有的数据都相加,再除以4,得到平均数,代入求方差的公式,做出方差.(2)本题是一个等可能事件的概率.分别从甲、乙两组中随机选取一名同学,共有16种结果,满足条件的事件是这两名同学的植树总棵数为19,可以列举出共有4种结果,根据等可能事件的概率公式得到结果.【解答】解:(1)当X=8时,由茎叶图可知乙组同学的植树棵树是8,8,9,10,∴平均数是,方差是+=.(2)由题意知本题是一个等可能事件的概率.若X=9,分别从甲、乙两组中随机选取一名同学,共有16种结果,满足条件的事件是这两名同学的植树总棵数为19,包括:(9,10),(11,8),(11,8),(9,10)共有4种结果,∴根据等可能事件的概率公式得到P=.【点评】本题考查一组数据的平均数和方差,考查等可能事件的概率,考查利用列举法来列举出符合条件的事件数和满足条件的事件数,本题是一个文科的考试题目.17.(14分)(2011•北京)如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.(Ⅰ)求证:DE∥平面BCP;(Ⅱ)求证:四边形DEFG为矩形;(Ⅲ)是否存在点Q,到四面体PABC六条棱的中点的距离相等?说明理由.【考点】直线与平面平行的判定;空间中直线与直线之间的位置关系.【专题】空间位置关系与距离;立体几何.【分析】(Ⅰ)根据两个点是两条边的中点,得到这条线是两条边的中位线,得到这条线平行于PC,根据线面平行的判定定理,得到线面平行.(Ⅱ)根据四个点是四条边的中点,得到中位线,根据中位线定理得到四边形是一个平行四边形,根据两条对角线垂直,得到平行四边形是一个矩形.(Ⅲ)做出辅助线,证明存在点Q到四面体PABC六条棱的中点的距离相等,根据第二问证出的四边形是矩形,根据矩形的两条对角线互相平分,又可以证出另一个矩形,得到结论.【解答】证明:(Ⅰ)∵D,E分别为AP,AC的中点,∴DE∥PC,∵DE⊄平面BCP,∴DE∥平面BCP.(Ⅱ)∵D,E,F,G分别为AP,AC,BC,PB的中点,∴DE∥PC∥FG,DG∥AB∥EF∴四边形DEFG为平行四边形,∵PC⊥AB,∴DE⊥DG,∴四边形DEFG为矩形.(Ⅲ)存在点Q满足条件,理由如下:连接DF,EG,设Q为EG的中点,由(Ⅱ)知DF∩EG=Q,且QD=QE=QF=QG=EG,分别取PC,AB的中点M,N,连接ME,EN,NG,MG,MN,与(Ⅱ)同理,可证四边形MENG为矩形,其对角线交点为EG的中点Q,且QM=QN=EG,∴Q为满足条件的点.【点评】本题考查直线与平面平行的判定,考查三角形中位线定理,考查平行四边形和矩形的判定及性质,本题是一个基础题.18.(13分)(2011•北京)已知函数f(x)=(x﹣k)e x.(Ⅰ)求f(x)的单调区间;(Ⅱ)求f(x)在区间[0,1]上的最小值.【考点】利用导数研究函数的单调性;利用导数求闭区间上函数的最值.【专题】导数的综合应用.【分析】(I)求导,令导数等于零,解方程,跟据f′(x)f(x)随x的变化情况即可求出函数的单调区间;(Ⅱ)根据(I),对k﹣1是否在区间[0,1]内进行讨论,从而求得f(x)在区间[0,1]上的最小值.【解答】解:(Ⅰ)f′(x)=(x﹣k+1)e x,令f′(x)=0,得x=k﹣1,f′(x)f(x)随x的变化情况如下:x (﹣∞,k﹣1)k﹣1 (k﹣1,+∞)f′(x)﹣0 +f(x)↓﹣e k﹣1↑∴f(x)的单调递减区间是(﹣∞,k﹣1),f(x)的单调递增区间(k﹣1,+∞);(Ⅱ)当k﹣1≤0,即k≤1时,函数f(x)在区间[0,1]上单调递增,∴f(x)在区间[0,1]上的最小值为f(0)=﹣k;当0<k﹣1<1,即1<k<2时,由(I)知,f(x)在区间[0,k﹣1]上单调递减,f(x)在区间(k﹣1,1]上单调递增,∴f(x)在区间[0,1]上的最小值为f(k﹣1)=﹣e k﹣1;当k﹣1≥1,即k≥2时,函数f(x)在区间[0,1]上单调递减,∴f(x)在区间[0,1]上的最小值为f(1)=(1﹣k)e;综上所述f(x)min=.【点评】此题是个中档题.考查利用导数研究函数的单调性和在闭区间上的最值问题,对方程f’(x)=0根是否在区间[0,1]内进行讨论,体现了分类讨论的思想方法,增加了题目的难度.19.(14分)(2011•北京)已知椭圆G:=1(a>b>0)的离心率为,右焦点为(2,0),斜率为1的直线l与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(﹣3,2).(Ⅰ)求椭圆G的方程;(Ⅱ)求△PAB的面积.【考点】直线与圆锥曲线的综合问题;椭圆的标准方程.【专题】圆锥曲线的定义、性质与方程.【分析】(Ⅰ)根据椭圆离心率为,右焦点为(,0),可知c=,可求出a的值,再根据b2=a2﹣c2求出b的值,即可求出椭圆G的方程;(Ⅱ)设出直线l的方程和点A,B的坐标,联立方程,消去y,根据等腰△PAB,求出直线l方程和点A,B的坐标,从而求出|AB|和点到直线的距离,求出三角形的高,进一步可求出△PAB的面积.【解答】解:(Ⅰ)由已知得,c=,,解得a=,又b2=a2﹣c2=4,所以椭圆G的方程为.(Ⅱ)设直线l的方程为y=x+m,由得4x2+6mx+3m2﹣12=0.①设A,B的坐标分别为(x1,y1),(x2,y2)(x1<x2),AB的中点为E(x0,y0),则x0==﹣,y0=x0+m=,因为AB是等腰△PAB的底边,所以PE⊥AB,所以PE的斜率k=,解得m=2.此时方程①为4x2+12x=0.解得x1=﹣3,x2=0,所以y1=﹣1,y2=2,所以|AB|=3,此时,点P(﹣3,2).到直线AB:y=x+2距离d=,所以△PAB的面积s=|AB|d=.【点评】此题是个中档题.考查待定系数法求椭圆的方程和椭圆简单的几何性质,以及直线与椭圆的位置关系,同时也考查了学生观察、推理以及创造性地分析问题、解决问题的能力.20.(13分)(2011•北京)若数列A n:a1,a2,…,a n(n≥2)满足|a k+1﹣a k|=1(k=1,2,…,n﹣1),则称A n为E数列,记S(A n)=a1+a2+…+a n.(Ⅰ)写出一个E数列A5满足a1=a3=0;(Ⅱ)若a1=12,n=2000,证明:E数列A n是递增数列的充要条件是a n=2011;(Ⅲ)在a1=4的E数列A n中,求使得S(A n)=0成立得n的最小值.【考点】数列的应用.【专题】点列、递归数列与数学归纳法.【分析】(Ⅰ)根据题意,a2=±1,a4=±1,再根据|a k+1﹣a k|=1给出a5的值,可以得出符合题的E数列A5;(Ⅱ)从必要性入手,由单调性可以去掉绝对值符号,可得是A n公差为1的等差数列,再证充分性,由递增数列的性质得出不等式,再利用同向不等式的累加,可得a k+1﹣a k=1>0,A n是递增数列;(Ⅲ)由|a k+1﹣a k|=1,可得a k+1≥a k﹣1,再结合已知条件a1=4,可得n的最小值.【解答】解:(Ⅰ)0,1,0,1,0是一个满足条件的E数列A5(答案不唯一,0,﹣1,0,﹣1,0或0,±1,0,1,2或0,±1,0,﹣1,﹣2或0,±1,0,﹣1,0都满足条件的E数列A5)(Ⅱ)必要性:因为E数列A n是递增数列所以a k+1﹣a k=1(k=1,2, (1999)所以A n是首项为12,公差为1的等差数列.所以a2000=12+(2000﹣1)×1=2011充分性:由于a2000﹣a1999≤1a1999﹣a1998≤1…a2﹣a1≤1,所以a2000﹣a1≤1999,即a2000≤a1+1999又因为a1=12,a2000=2011所以a2000≤a1+1999故a k+1﹣a k=1>0(k=1,2,…,1999),即A n是递增数列.综上所述,结论成立.(Ⅲ)对首项为4的E数列A n,由于a2≥a1﹣1=3a3≥a2﹣1≥2…a8≥a7﹣1≥﹣3…所以a1+a2+…+a k>0(k=2,3,…,8),所以对任意的首项为4的E数列A n,若S(A n)=0,则必有n≥9,又a1=4的E数列A9:4,3,2,1,0,﹣1,﹣2,﹣3,﹣4满足S(A9)=0,所以n的最小值是9.【点评】本题以数列为载体,考查了不等式的运用技巧,属于难题,将题中含有绝对值的等式转化为不等式是解决此题的关键.。
北京市朝阳区2011-2012学年度高三年级第一学期期末统一考试(数学理)

北京市朝阳区2011-2012学年度高三年级第一学期期末统一考试数学试卷(理工类) 2012.1(考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题 共40分)注意事项:考生务必将答案答在答题卡上,在试卷上答无效。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. 1.已知平面向量(3,1)=a ,(,3)x =b ,且a ⊥b ,则实数x 的值为 ( ) A .9 B .1 C .1- D . 9-2.设集合{}U =1,2,3,4,{}25M =x U x x+p =0∈-,若{}2,3U C M =,则实数p 的值 为 ( ) A .4- B . 4 C .6- D .63. 设数列{}n a 是公差不为0的等差数列,11a =且136,,a a a 成等比数列,则{}n a 的前n 项和n S 等于 ( )A . 2788n n +B .2744n n + C .2324n n+D .2n n +4.执行如图所示的程序框图,输出的S 值为( ) A .1 B .1- C . 2- D .05.已知函数()sin f x x x =,设()7a f π=,()6b f π=,()3c f π=,则,,a b c 的大小关系是( )A. a b c <<B.c a b <<C.b a c <<D.b c a << 6.函数2()2xf x a x=--的一个零点在区间(1,2)内,则实数a 的取值范围是( ) A .(1,3) B .(1,2) C .(0,3) D . (0,2)7. 已知正方形ABCD的边长为ABC ∆沿对角线AC 折起,使平面ABC ⊥平面ACD ,得到如图所示的三棱锥B ACD -.若O 为AC 边的中点,M ,N 分别为线段DC ,BO 上的动点(不包括端点),且BN CM =.设BN x =,则三棱锥N AMC-ADBNMOC的体积()y f x =的函数图象大致是( )A .B .C .D .8.已知集合{(,)|,,}A x y x n y na b n ===+∈Z ,{(,)|,B x y x m ==2312,y m =+ m ∈Z }.若存在实数,a b 使得A B ≠∅ 成立,称点(,)a b 为“£”点,则“£”点在平面区域22{(,)|108}C x y x y =+≤内的个数是( )A. 0B. 1C. 2D. 无数个第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在答题卡上. 9.已知有若干辆汽车通过某一段公路,从中抽取200辆汽车进行测速分析, 其时速的频率分布直方图如图所示,则时速在区间[60,70)上的汽车大约 有 辆.10.某几何体的三视图如图所示,则这个几何体的体积是 .11. 在平面直角坐标系中,不等式组0,40,x y x y x a +≥⎧⎪-+≥⎨⎪≤⎩所表示的平面区域的面积是9,则实数a 的值为 .12. 设直线10x my --=与圆22(1)(2)4x y -+-=相交于A ,B 两点,且弦AB的长为m 的值是 .13. 某公司购买一批机器投入生产,据市场分析每台机器生产的产品可获得的总利润y (万元)与机器运转时间x (年数,x *∈N )的关系为21825y x x =-+-.则当每台机器运转 年时,年平均利润最大,最大值是 万元.14. 已知两个正数,a b ,可按规则c ab a b =++扩充为一个新数c ,在,,a b c 三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作. (1)若1,3a b ==,按上述规则操作三次,扩充所得的数是__________;时速(km/h )01002 003 004 40 50 60 70 80(2)若0p q >>,经过6次操作后扩充所得的数为(1)(1)1m n q p ++-(,m n 为正整数),则,m n 的值分别为______________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15. (本题满分13分)在锐角ABC ∆中,a ,b ,c 分别为内角A ,B ,C2sin 0b A -=. (Ⅰ)求角B 的大小;(Ⅱ)若5a c +=,且a c >,b =AB AC的值.16. (本题满分13分)如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A 所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A 指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(,)a b (假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).(Ⅰ)求某个家庭得分为(5,3)的概率?(Ⅱ)若游戏规定:一个家庭的得分为参与游戏的两人得分之和,且得分大于等于8的家庭可以获得一份奖品.请问某个家庭获奖的概率为多少?(Ⅲ)若共有5个家庭参加家庭抽奖活动.在(Ⅱ)的条件下,记获奖的家庭数为X ,求X 的分布列及数学期望.17. (本题满分13分) 如图,在四棱锥S ABCD -中,平面SAD ⊥平面ABCD .底面ABCD 为矩形,,AD AB =,SA SD a ==. (Ⅰ)求证:CD SA ⊥;(Ⅱ)求二面角C SA D --的大小.18. (本题满分13分)已知函数1()ln(1)1xf x ax x-=+++(0x ≥,a 为正实数). (Ⅰ)若1a =,求曲线()y f x =在点(1,(1))f 处的切线方程; (Ⅱ)求函数()f x 的单调区间;(Ⅲ)若函数()f x 的最小值为1,求a 的取值范围.19. (本题满分14分)已知椭圆2222:1(0)x y C a b a b +=>>的离心率为12,直线l 过点(4,0)A ,(0,2)B ,且与椭圆C 相切于点P .(Ⅰ)求椭圆C 的方程;(Ⅱ)是否存在过点(4,0)A 的直线m 与椭圆C 相交于不同的两点M 、N ,使得23635AP AM AN =⋅?若存在,试求出直线m 的方程;若不存在,请说明理由.20. (本题满分14分)数列{}n a ,{}n b (1,2,3,n = )由下列条件确定:①110,0a b <>;②当2k ≥时,k a 与k b 满足:当011≥+--k k b a 时,1-=k k a a ,211--+=k k k b a b ;当011<+--k k b a 时,211--+=k k k b a a ,1-=k k b b . (Ⅰ)若11a =-,11b =,写出234,,a a a ,并求数列}{n a 的通项公式;(Ⅱ)在数列}{n b 中,若s b b b >>> 21(3s ≥,且*s ∈N ),试用11,b a 表示k b },,2,1{s k ∈; (Ⅲ)在(Ⅰ)的条件下,设数列}{n c (*)n ∈N 满足211=c ,0n c ≠, 2212m n n n mc c c ma -+=-+(其中m 为给定的不小于2的整数),求证:当m n ≤时,恒有1<n c .北京市朝阳区2011-2012学年度高三年级第一学期期末统一考试数学试卷答案(理工类) 2012.1一、选择题:二、填空题:三、解答题:(15)(本小题满分13分)解:2sin 0b A -=,2sin sin 0A B A -=, ……………………………………………… 2分因为sin 0A ≠,所以23sin =B . …………………………………………………3分 又B 为锐角, 则3B π=. …………………………………………… 5分(Ⅱ)由(Ⅰ)可知,3B π=.因为b =根据余弦定理,得 2272cos3a c ac π=+-,………………………………………7分整理,得2()37a c ac +-=.由已知 5a c +=,则6ac =.又a c >,可得 3a =,2c =. ……………………………………… 9分于是222cos2b c a A bc +-===, ………………………… 11分所以cos cos 21AB AC AB AC A cb A ==== . …………… 13分 (16)(本小题满分13分)解:(Ⅰ)记事件A :某个家庭得分情况为(5,3).111()339P A =⨯=.所以某个家庭得分情况为(5,3)的概率为19.……………………………… 4分(Ⅱ)记事件B :某个家庭在游戏中获奖,则符合获奖条件的得分包括(5,3),(5,5),(3,5) 共3类情况. 所以1111111()3333333P B =⨯+⨯+⨯=.所以某个家庭获奖的概率为13. ………………………………………… 8分(Ⅲ)由(Ⅱ)可知,每个家庭获奖的概率都是13,所以1~(5,)3X B .00551232(0)()()33243P X C ==⋅=,11451280(1)()()33243P X C ==⋅=,22351280(2)()()33243P X C ==⋅=,33251240(3)()()33243P X C ==⋅=,44151210(4)()()33243P X C ==⋅=,5505121(5)()()33243P X C ==⋅=. ………………………………… 11分 所以X所以533EX np ==⨯=. 所以X 的数学期望为53. ……………………………………………… 13分(17)(本小题满分13分) 证明:(Ⅰ)因为平面SAD ⊥平面ABCD , CD AD ⊥,且面SAD 面ABCD AD =, 所以CD ⊥平面SAD . 又因为SA ⊂平面SAD所以CD SA ⊥. …………………………………………… 6分 (Ⅱ)由(Ⅰ)可知,CD SA ⊥.在SAD ∆中,SA SD a ==,AD =,所以SA SD ⊥,所以SA ⊥平面SDC . 即SA SD ⊥,SA SC ⊥,所以CSD ∠为二面角C SA D --的平面角.在Rt CDS ∆中,tan CDCSD SD ∠===所以二面角C SA D --的大小3π. …………………………………… 13分 法二:取BC 的中点E , AD 的中点P .在SAD ∆中,SA SD a ==,P 为AD 的中点,所以,SP AD ⊥. 又因为平面SAD ⊥平面ABCD ,且平面SAD 平面ABCD AD =所以,SP ⊥平面ABCD .显然,有PE AD ⊥. ……………………………… 1分 如图,以P 为坐标原点,P A 为x 轴,PE 为y 轴,PS为z 轴建立空间直角坐标系,则)S,,0,0)A ,,0)B,(,0)C ,(,0,0)D . ………………………………………………………………3分(Ⅰ)易知(0,,0),,0,)CD SA ==因为0CD SA ⋅=,所以CD SA ⊥. …………………………………………………………… 6分(Ⅱ)设(,,)x y z =n 为平面CSA 的一个法向量,则有0SA CA ⎧⋅=⎪⎨⋅=⎪⎩n n ,即00=⎪-=⎩,所以=n . ……………………………… 7分显然,EP ⊥平面SAD ,所以PE为平面SAD 的一个法向量,所以(0,1,0)=m 为平面SAD 的一个法向量.……………………………………… 9分 所以1cos ,2<>==n m , 所以二面角C SA D --的大小为3π. ………………………………………… 13分 (18)(本小题满分13分)解:(Ⅰ)当1a =时,1()ln(1)1xf x x x-=+++, 则212()1(1)f x x x -'=+++. ………………………………………………… 2分 所以(1)0f '=.又(1)ln 2f =,因此所求的切线方程为ln 2y =. ………… 4分(Ⅱ)22222()1(1)(1)(1)a ax a f x ax x ax x -+-'=+=++++. ………………………… 5分 (1)当20a -≥,即2a ≥时,因为0x ≥,所以()0f x '>,所以函数()f x 在[)0,+∞上单调递增.…… 6分(2)当20a -<,即02a <<时,令()0f x '=,则220ax a +-=(0x ≥),所以x =.因此,当x ∈时,()0f x '<,当)x ∈+∞时,()0f x '>. 所以函数()f x的单调递增区间为)+∞,函数()f x的单调递减区间为. …… 10分 (Ⅲ)当2a ≥时,函数()f x 在[)0,+∞上单调递增,则()f x 的最小值为(0)1f =,满足题意.……… 11分当02a <<时,由(Ⅱ)知函数()f x的单调递增区间为)+∞,函数()f x的单调递减区间为,则()f x的最小值为f ,而(0)1f =,不合题意. 所以a 的取值范围是[)2,+∞. ………………………………………………… 13分(19)(本小题满分14分)解: (Ⅰ)由题得过两点(4,0)A ,(0,2)B 直线l 的方程为240x y +-=.………… 1分 因为12c a =,所以2a c =,b =. 设椭圆方程为2222143x y c c+=,由2222240,1,43x y x y c c+-=⎧⎪⎨+=⎪⎩消去x 得,224121230y y c -+-=. 又因为直线l 与椭圆C 相切,所以221244(123)0c ∆=-⨯-=,解得21c =.所以椭圆方程为22143x y +=. ……………………………………………… 5分 (Ⅱ)易知直线m 的斜率存在,设直线m 的方程为(4)y k x =-,…………………… 6分由22(4),1,43y k x x y =-⎧⎪⎨+=⎪⎩消去y ,整理得2222(34)3264120k x k x k +-+-=. ………… 7分由题意知2222(32)4(34)(6412)0k k k ∆=-+->,解得1122k -<<. ……………………………………………………………… 8分 设11(,)M x y ,22(,)N x y ,则21223234k x x k +=+,2122641234k x x k -=+. …… 9分又直线:240l x y +-=与椭圆22:143x y C +=相切,由22240,1,43x y x y +-=⎧⎪⎨+=⎪⎩解得31,2x y ==,所以3(1,)2P . ……………………………10分则2454AP =. 所以3645813547AM AN ⋅=⨯=.又AM AN ⋅==212(1)(4)(4)k x x =+--21212(1)(4()16)k x x x x =+-++22222641232(1)(416)3434k k k k k -=+-⨯+++2236(1).34k k =++ 所以223681(1)347k k +=+,解得4k =±.经检验成立. …………………… 13分 所以直线m的方程为(4)4y x =±-. …………………………………… 14分 (20)(本小题满分14分)(Ⅰ)解:因为011=+b a ,所以112-==a a ,02112=+=b a b . 因为0122<-=+b a ,所以212223-=+=b a a ,023==b b . 因为33102a b +=-<,所以334124a b a +==-,430b b ==.所以1234111,1,,24a a a a =-=-=-=-. …………………………………… 2分由此猜想,当2≥k 时,011<+--k k b a ,则22111---=+=k k k k a b a a ,10k k b b -==.… 3分 下面用数学归纳法证明:①当2k =时,已证成立.②假设当k l =(l *∈N ,且2l ≥)猜想成立,即110l l a b --+<,10l l b b -==,102l l a a -=<. 当1k l =+时,由102l l a a -=<, 10l l b b -==得0l l a b +<,则10l l b b +==,1022l l ll a b a a ++==<.综上所述,猜想成立.所以22221111(2)222n n n n a a n ---⎛⎫⎛⎫=⨯=-⋅=-≥ ⎪⎪⎝⎭⎝⎭.故211,12.2n n n a n --=⎧⎪=⎨-≥⎪⎩. ……………………………………………… 6分(Ⅱ)解:当s k ≤≤2时,假设110k k a b --+<,根据已知条件则有1-=k k b b ,与s b b b >>> 21矛盾,因此110k k a b --+<不成立, …………… 7分 所以有110k k a b --+≥,从而有1k k a a -=,所以1a a k =. 当011≥+--k k b a 时,1-=k k a a ,211--+=k k k b a b , 所以111111()22k k k k k k k a b b a a b a -----+-=-=-; …………………… 8分 当s k ≤≤2时,总有111()2k k k k b a b a ---=-成立.又110b a -≠,所以数列}{k k a b -(s k ,,2,1 =)是首项为11b a -,公比为12的等比数列, 11121)(-⎪⎭⎫⎝⎛-=-k k k a b a b ,1,2,,k s = ,又因为1a a k =,所以111121)(a a b b k k +⎪⎭⎫⎝⎛-=-. …………………………… 10分(Ⅲ)证明:由题意得2212m n n n mc c c ma -+=-+n n c c m +=21.因为211n n n c c c m +=+,所以2110n n n c c c m+-=>. 所以数列{}n c 是单调递增数列. …………………………………… 11分 因此要证)(1m n c n ≤<,只须证1<m c . 由2≥m ,则n n n c c m c +=+211<n n n c c c m ++11,即1111n n c c m+->-.…… 12分 因此1122111)11()11()11(1c c c c c c c c m m m m m +-++-+-=--- m m m m 121+=+-->.所以11m mc m <<+. 故当m n ≤,恒有1<n c . …………………………………………………14分。
北京市海淀区2011届高三模拟数学(文)试题及答案
海淀区高三年级第二学期期中练习数学 (文科)2011.4选择题 (共 40 分)一、选择题:本大题共8 小题 ,每题 5 分 ,共 40 分.在每题列出的四个选项中 ,选出切合题目要求的一项 .1、已知会合 Ax R 0 x 3 , B xR x 2 4 ,则 A BA. x x2 或 2 x 3B.x 2 x 3C. x 2 x 32. 设 a 30.5, blog 3 2, ccos2,则3A. c b aB. c a bC. a b cD. bx 13.函数 f ( x) 图象的对称中心为xA . (0,0)B.(0,1)C. (1,0)D.(1,1)4. 履行以下图的程序框图,若输入x 的值为 2,则输出的 x 值为A. 25B . 24 C. 23 D . 225.从会合 A { 1,1,2}中随机选用一个数记为k ,从会合 B { 2,1,2} 中随机选用一个数记为b ,则直线 ykx b 不经过第三象限的概率为2 1 C.4 5A .B.9D.9396. 在 同 一 个 坐 标 系 中 画 出 函 数 y a x, y sin ax 的 部 分 图 象 , 其 中a 0且a 1 ,则以下所给图象中可能正确的选项是yy11O12xO 1D. Rc a开始 输入 xn 1n ≤3否 输出 x 结束2n n 1x 2x 1是xAByy11O12xO12xC D7. 已知函数f ( x)x2ax1,x1,则“ 2 a 0 ”是“ f (x)在 R 上单一递加”的ax2x1,x1,A.充足而不用要条件B.必需而不充足条件C.充足必需条件D.既不充足也不用要条件8.若直线 l 被圆 C : x2y2 2 所截的弦长不小于2,则 l 与以下曲线必定有公共点的是A2y 21B..x 2y21 C. y x2D.x2y21. ( x 1)2非选择题(共 110 分)二、填空题 :本大题共 6 小题 ,每题 5 分,共 30 分 .把答案填在题中横线上.29. 计算__________________.1i10.为认识本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每个月平时花费额”的检查.他们将检查所获得的数据分别绘制成频次分布直方图(以下图),记甲、乙、丙所检查数据的标准差分别为s1, s2,s3, 则它们的大小关系为. (用“”连结)频次频次频次组距组距组距0.00080.00080.00080.00060.00060.00060.00040.00040.00040.00020.00020.0002O1000 1500 2000 2500 3000 3500 元O1000 1500 2000 2500 3000 3500 元O10001500 2000 2500 3000 3500 元甲乙丙11.如图,在正方体ABCD A1B1C1D1中,点P是上底面A1B1C1 D1内一动点,则三棱锥P ABC 的主视图与左视图的面积的比值为_________.D1C1A1PB1[根源 :]DC左视A B主视12. 已知函数f ( x) xe x ,则 f ' (x) =________;函数 f ( x) 图象在点 (0, f (0)) 处的切线方程为_______13. 已知向量 a ( x,2), b (1,y) ,此中 x, y 0 .若 agb 4 ,则 y x 的取值范围为.14.如图, 线段 AB =8,点 C 在线段 AB 上,且 AC =2, P 为线段 CB 上一动点, 点 A 绕点 C 旋转后与点B 绕点 P 旋转后重合于点 D .设 CP = x , △ CPD 的面积为 f (x) .则 f (x) 的定义域为 ________; f ( x) 的最大值为________.D ACP B三、解答题 : 本大题共 6 小题 ,共 80 分 .解答应写出文字说明 , 演算步骤或证明过程 .15. (本小题共 13 分)在 ABC 中,内角 A 、B 、 C 所对的边分别为1 , tan C1a 、b 、c ,已知 tan B, 且23c 1 .[ 根源 :Z#xx #](Ⅰ ) 求 tan(B C ) ;(Ⅱ) 求 a 的值 .16. (本小题共 13 分)数列 { a n } 的前 n 项和为 S n ,若 a 12 且 S n S n 1 2n ( n 2 , n N * ) . [根源 :]( I )求 S n ;( II ) 能否存在等比数列{ b n } 知足 b 1 a 1, b 2a 3,b 3 a 9 ?若存在, 则求出数列 { b n } 的通项公式;若不存在,则说明原因.17. (本小题共 13 分)如图:梯形 ABCD 和正△PAB 所在平面相互垂直,此中 AB//DC,ADCD1AB ,且 O 为 AB 中点.P2( I ) 求证: BC // 平面 POD ;OAB(II) 求证:AC PD .18. (本小题共14 分)已知函数 f (x)1a ln x ( a 0, a R) x(Ⅰ)若 a 1,求函数 f ( x) 的极值和单一区间;(II) 若在区间[1,e] 上起码存在一点 x0,使得 f ( x0 )0 建立,务实数 a 的取值范围.19.(本小题共 14 分)已知椭圆 C :x2y2b 0) 经过点 M (1,3), 其离心率为1 . a2b2 1 ( a22(Ⅰ)求椭圆C的方程;( Ⅱ) 设直线l与椭圆C订交于 A、B 两点,以线段OA, OB为邻边作平行四边形OAPB,其中极点 P 在椭圆C上,O为坐标原点 . 求O到直线距离的l 最小值.20.(本小题共 13 分)已知每项均是正整数的数列a1, a2 ,a3 ,L ,a100,此中等于i 的项有k i个(i1,2,3L ) ,设 b j k1 k 2k j( j1,2,3L ) ,g(m) b1b2L b m 100m ( m1,2,3L ).(Ⅰ)设数列 k140, k230, k3 20,k4 10, k5...k1000 ,求 g(1), g(2), g(3), g(4) ;(II)若 a1 ,a2 , a3 ,L , a100中最大的项为50,比较 g(m), g(m1) 的大小;(Ⅲ)若 a1 a2La100200 ,求函数 g( m) 的最小值.[根源:][根源 : ][根源 : ]海淀区高三年级第二学期期中练习数学(文)答案及评分参照2011. 4(共 40 分) [ 根源 :]一、 (本大 共8 小 , 每小 5 分 , 共 40 分) [ 根源 :Z § xx § ]号 12 3 45 6 7 8答案CABC ADBB非(共 110 分)二、填空 (本大 共 6小 , 每小 5分 . 共 30分 . 有两空的 目,第一空3 分,第二空 2分)9.1 i10. s 1 > s 2 > s 3 11. 1 12.xy x13. [ 4,2]14.(1 x e ,,2 2)(2, 4) 三、解答 ( 本大 共 6 小 , 共 80 分)15. (共 13 分)解:( I )因 tan B1 , tanC 1 , tan(B C ) tan B tan C⋯⋯⋯⋯⋯⋯⋯3分231 tan B tan C1 1代入获得, tan(B C) 2 3 1 .⋯⋯⋯⋯⋯⋯⋯6分1 1 12 3( II )因 A180o B C⋯⋯⋯⋯⋯⋯⋯7分因此 tan A tan[180 o(B C )]tan( B C )1⋯⋯⋯⋯⋯⋯⋯9分 又 0oA180o ,因此 A 135o .⋯⋯⋯⋯⋯⋯⋯10分因 tan C1 ,且 0oC180o,因此 sin C10⋯⋯⋯⋯⋯⋯⋯11分0 ,310ac 5 . ⋯⋯⋯⋯⋯⋯⋯13分 [来由,得 asin Asin C源 :学§科§网 ]16. (共 13 分)解:( I )因 S n Sn 12n ,因此有S n S n 1 2n n 2 , nN *建立 ⋯⋯⋯2 分即 a n 2n n 2建立,又 a 1 S 12 1 , 因此 a n2n nN *建立⋯⋯⋯⋯⋯⋯⋯3分 因此 a n 1 a n 2 n N * 建立 ,因此 { a n } 是等差数列,⋯⋯⋯⋯⋯⋯⋯4分 因此有 S na 1annn 2 n , nN *⋯⋯⋯⋯⋯⋯⋯6分2( II )存在 .⋯⋯⋯⋯⋯⋯⋯7分[ 来源 :Z|xx|]由( I ), a n 2n , n N * 建立因此有 a 36, a 9 18 ,又 a 12 ,⋯⋯⋯⋯⋯⋯9分因此由b 1 a 1, b 2 a 3, b 3 a 9 b 2b 3 3⋯⋯⋯⋯⋯⋯⋯11分,b 1b 2因此存在以 b 1 2 首 ,公比 3 的等比数列 {b n } ,其通 公式 b n23n 1.⋯⋯⋯⋯⋯⋯13 分P17. (共 13 分)明 : (I) 因 O AB 中点,因此 BO1AB,⋯⋯⋯⋯⋯⋯⋯1分21又 AB / /CD, CDAB ,AO2B因此有 CD BO,CD / /BO,⋯⋯⋯⋯⋯⋯⋯2分D C因此 ODCB 平行四 形 ,因此 BC / /OD ,⋯⋯⋯⋯⋯⋯⋯3分又 DO 平面 POD, BC 平面 POD,因此 BC//平面 POD . ⋯⋯⋯⋯⋯⋯⋯5分(II) 接 OC .P因 CD BO AO, CD / / AO, 因此 ADCO平行四 形,⋯⋯⋯⋯⋯⋯⋯6分又 ADCD ,因此 ADCO 菱形,OABDC因此AC DO ,⋯⋯⋯⋯⋯⋯⋯7分因正三角形PAB , O AB 中点,因此 PO AB ,⋯⋯⋯⋯⋯⋯⋯8分又因平面 ABCD平面 PAB ,平面 ABCD I 平面 PAB AB ,因此 PO平面 ABCD ,⋯⋯⋯⋯⋯⋯⋯10分而 AC平面 ABCD ,因此 PO AC ,[根源:]又POI DO O ,因此 AC平面 POD .⋯⋯⋯⋯⋯⋯⋯12分又 PD平面 POD ,因此 AC PD .⋯⋯⋯⋯⋯⋯⋯13分 [来源 : ]18. (共 14 分)解:( I)因 f '( x)1a ax 1,⋯⋯⋯⋯⋯⋯⋯2分x2x x2当 a 1 , f '( x)x1,x2令 f'( x)0 ,得x 1 ,⋯⋯⋯⋯⋯⋯⋯3分又 f( x) 的定域(0,) ,f( x) , f (x) 随x的化状况以下表:x(0,1)1(1,)f '( x)0f ( x)]极小Z所以 x 1 , f ( x)的极小 1 .⋯⋯⋯⋯⋯⋯⋯5分f ( x) 的增区(1,) ,减区(0,1) ;⋯⋯⋯⋯⋯⋯⋯6分( II)解法一:因 f '( x)1a ax10 ,x2x x2,且 a令 f '( x)0 ,获得 x 1,a若在区 (0, e] 上存在一点 x0,使得 f ( x0 )0 建立,其充要条件是 f (x) 在区 (0, e] 上的最小小于0 即可 .⋯⋯⋯⋯⋯⋯⋯7分( 1)当 x10 , f '( x)0 x(0,) 建立,0 ,即 aa因此, f ( x) 在区 (0, e] 上 减,故 f ( x) 在区 (0, e] 上的最小 f (e)1 a ln e 1 a ,e由111) e a 0,得 a,即 a (, ⋯⋯⋯⋯⋯⋯⋯9分e1e e( 2)当 x 0 ,即 a0 ,a① 若 e1, f '( x)0 x(0, e] 建立,因此f ( x) 在区 (0, e] 上 减,a11因此, f ( x) 在区 (0, e] 上的最小 f ( e)a ln ea 0 ,e e然, f ( x) 在区 (0, e] 上的最小 小于0 不建立⋯⋯⋯⋯⋯⋯⋯11分② 若 0 1 e ,即 a1, 有aex(0,11( 1)a, e)a af '( x)f ( x)]极小Z因此 f ( x) 在区 (0, e] 上的最小f ( 1) aa ln 1,aa由 f ( 1)a a ln1a(1 ln a) 0 ,aa得 1ln a,解得ae,即 a(e,) .13⋯⋯⋯⋯⋯⋯⋯分上,由 (1)( 2)可知: a(, 1) U (e, ) 切合 意 .⋯⋯⋯⋯⋯⋯⋯14分e(0, e] 上存在一点 x 0 ,使得 f ( x 0 )0 1 a ln x 0 0 ,解法二:若在区建立,即x 0因 x 00 , 因此,只需 1 ax 0 ln x 0 0⋯⋯⋯⋯⋯⋯⋯7分令 g ( x) 1ax ln x ,只需 g(x) 1 ax ln x 在区 (0, e] 上的最小 小于0 即可因 g '(x)a ln x aa(ln x 1) ,令 g '( x)a(ln x1) 0,得 x 1⋯⋯⋯⋯⋯⋯9 分e( 1)当 a 0 :x1 1 (1, e] [ 来(0, )eee源 :]g '( x) [ 来源:学+科+ 网 ]g(x)Z极大][来源 :Z*xx*]因 x(0, 1) , g( x)1 ax ln x 0 ,而 g(e) 1 ae ln e 1 ae ,e11只需 1 ae 0 ,得 a(⋯⋯⋯⋯⋯⋯⋯11分,即 a, )(2 )当 aee:1x [:(0, ) [根源 :11e根源 学,e]#科#网]学+科+网e(eZ+X+X+K]g '( x)g(x)]极小Z因此,当x (0, e] , g( x) 极小 即最小g( 1 ) 1 a 1 ln 11a ,e e ee由1a 0 , 得ae ,即 a(e,).⋯⋯⋯⋯⋯⋯⋯分e131上,由 (1)( 2)可知,有 a( ,) .⋯⋯⋯⋯⋯⋯⋯14 分 [根源 : 学*) U (e,e科 * 网 Z*X*X*K]19. (共 14 分)解:(Ⅰ)由已知, e 2a 2b 2 1 ,因此 3a 2 4b 2,①⋯⋯⋯⋯⋯⋯⋯1分a 2431 9 1 ,⋯⋯⋯⋯⋯⋯⋯2分又点 M (1, ) 在 C 上,因此a 24b 2②2由①②解之,得 a 24, b 23 .故 C 的方程x 2y 2 1 .⋯⋯⋯⋯⋯⋯⋯5分43( Ⅱ ) 当直 l 有斜率 ,y kx m ,y kxm,由y 2x 2 1.43消 去 y 得 , (34k 2 ) x 2 8kmx 4m 2 12 0 ,⋯⋯⋯⋯⋯⋯⋯6分 [ 来源 :]64k 2m 24(3 4k 2 )(4m 2 12) 48(3 4k 2m 2 ) 0 ,③ ⋯⋯⋯⋯7分A 、B 、 P 点的坐 分 (x 1, y 1 )、(x 2 , y 2 )、( x 0 , y 0 ) , :x 0 x 1x 28km 2 , yy 1 y 2k( x 1x 2 ) 2m6m 2 ⋯⋯⋯⋯8分3 4k3 4k ,因为点 P 在 C 上,因此x 02y 02 1 .⋯⋯⋯9 分43进而16k 2m 212m 21 ,化 得 4m 234k 2 , 足③式 .(3 4k 2 )2(3 4k 2 )2⋯⋯⋯10 分又点 O 到直 l 的距离 :| m | 3 k 21 1 34d1 k 212 )121 k 24(1 k 4[根源 :学| 科 | 网]⋯⋯⋯11分当且 当 k 0 等号建立⋯⋯⋯⋯12 分当直 l无斜率 ,由 称性知,点P 必定在 x 上,进而 P 点 (2,0),(2,0) ,直 l x1 ,因此点 O 到直 l 的距离1 ⋯⋯13 分因此点 O 到直 l 的距离最小3 ⋯⋯14 分220. (共 13 分)解:(I)因 数列 k 140, k 2 30, k 3 20, k 4 10 ,因此 b 1 40, b 2 70,b 3 90, b 4 100 ,因此 g (1)60, g(2)90, g(3)100, g(4)100 .⋯⋯⋯⋯⋯⋯⋯3分(II)一方面, g(m 1) g( m) b m 1 100 ,北京市海淀区2011届高三模拟数学(文)试题及答案依据 b j的含知 b m 1100,故 g(m1)g( m) 0 ,即g( m)g (m1) ,①⋯⋯⋯⋯⋯⋯⋯5分当且当 b m 1100 取等号.因 a1, a2 ,a3,L, a100中最大的50,因此当m50必有b m100 ,因此 g (1) g(2)L g(49)g(50)g(51)L L即当 1m49 ,有g( m) g( m1) ;当 m49 ,有g (m)g(m1) .⋯⋯⋯⋯⋯⋯⋯7分( III)Ma1 , a2 ,L ,a100中的最大 .由( II )能够知道,g( m) 的最小 g (M ) .下边算 g (M ) 的.g(M )b1 b2b3L b M100M( b1100)(b2 100) (b3100)L(b M 1 100)( k2k3 L k M ) ( k3k4 L k M ) ( k4 k5L k M ) L( k M )[ k22k3L( M 1)k M ]( k12k23k3 L Mk M ) ( k1k2L k M )( a1a2a3L a100)b M(a1a2a3L a100)100 ,∵ a1a2a3L a100200,∴ g (M )100 ,∴ g (m)最小100.⋯⋯⋯⋯⋯⋯⋯13分明:其余正确解法按相步分.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市朝阳区高三年级第一次综合练习数学测试题(文史类) 2011.4(考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题 共40分)注意事项:1.答第一部分前,考生务必将自己的姓名、考试科目涂写在答题卡上。
考试结束时,将试题卷和答题卡一并交回。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,不能答在试题卷上。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.[来源:] 1.若集合{}20M x x =->,{}(3)(1)0N x x x =--<,则MN =(A) {}23x x << (B ){}1x x < (C ){}3x x > (D ){}12x x <<2. 某校高三一班有学生54人,二班有学生42人,现在要用分层抽样的方法从这两个班随 机选出16人参加军训表演,则一班和二班分别选出的人数是 (A )8人,8人 (B )15人,1人(C )9人,7人 (D )12人,4人 3.函数2cos 1y x =+在下列哪个区间上为增函数 (A )π[0,]2 (B )π[, π]2(C )[]0, π (D )[]π, 2π 4. 已知{}n a 是由正数组成的等比数列,n S 表示{}n a 的前n 项的和,若13a =,24144a a =,则5S 的值是(A )692(B ) 69 (C )93 (D )1895.已知a ,b 是两条不重合的直线,α,β是两个不重合的平面,下列命题中正确的是 (A ) //a b ,//b α,则//a α(B ) a ,b α⊂,//a β,//b β,则//αβ[来源:学科网] (C ) a α⊥,//b α,则a b ⊥[来源:学。
科。
网Z 。
X 。
X 。
K](D ) 当a α⊂,且b α⊄时,若b ∥α,则a ∥b6.已知三棱锥的三视图如图所示,其中侧视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于(A )3(B )3(C )3(D7.已知函数()y f x =是奇函数, 当0x >时,()f x =lg x ,则1(())100f f 的值等于(A )1lg 2(B )1lg 2-(C )lg 2 (D )lg 2-8.已知x ∈R ,用[]x 表示不超过x 的最大整数,记{}[]x x x =-,若(0, 1)a ∈,则{}a 与1{}2a +的大小关系是(A )不确定(与a 的值有关) (B ){}a <1{}2a + (C ){}a =1{}2a + (D ){}a >1{}2a +正视图俯视图第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上. 9.已知i 为虚数单位,则3i1i+-= . 10.过原点且倾斜角为60︒的直线被圆2240x y x +-=所截得的弦长为 .11. 已知两点(3, 2)A --,(3,6)B ,点C 满足AC CB =,则点C 的坐标是 ,[来源:学_科_网Z_X_X_K]AB AC ⋅= .12.抛物线24y x =上一点M 与该抛物线的焦点F 的距离||4MF =,则点M 的横坐标x = .13.执行右图所示的程序框图,若输入 5.2x =,则输出y 的值为 .14.对于各数互不相等的整数数组),,,,(321n i i i i (n 是不小于2的正整数),对于任意,{1,2,3,,}p q n ∈,当q p <时有q p i i >,则称p i ,q i 是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为该数组的“逆序数”,则数组(2,4,3,1)中的逆序数等于 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题满分13分)在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c .已知2c a =,4C π=. (Ⅰ)求sin A 的值; (Ⅱ)求cos(2)3A π-的值.16.(本小题满分13分)已知集合A ={-2,0,2},B ={-1,1}.(Ⅰ)若M ={(,)x y |x ∈A ,y ∈B },用列举法表示集合M ;(Ⅱ)在(Ⅰ)中的集合M 内,随机取出一个元素(,)x y ,求以(,)x y 为坐标的点位于区域D :20,20,1x y x y y -+⎧⎪+-⎨⎪-⎩≥≤≥内的概率. 17.(本小题满分13分)如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,且//AD BC ,90ABC ∠=︒,侧面PAD ⊥底面ABCD ,90PAD ∠=︒. 若12AB BC AD ==. (Ⅰ)求证:CD ⊥平面PAC ; (Ⅱ)设侧棱PA 的中点是E ,求证:BE 平面PCD .[来源:][来源:学科网ZXXK] 18.(本小题满分13分)已知函数2()ln f x a x x=+,a ∈R . (Ⅰ)若曲线()y f x =在点(1,(1))P f 处的切线垂直于直线2y x =+,求a 的值; (Ⅱ)求函数()f x 在区间(0, e]上的最小值. 19.(本小题满分14分)已知(2, 0)A -,(2, 0)B 为椭圆C 的左右顶点,(1, 0)F 为其右焦点.(Ⅰ)求椭圆C 的标准方程及离心率;(Ⅱ)过点A 的直线l 与椭圆C 的另一个交点为P (不同于A ,B ),与椭圆在点B 处的切线交于点D .当直线l 绕点A 转动时,试判断以BD 为直径的圆与直线PF 的位置关系,并加以证明. 20.(本小题满分14分)有n (3, )n n *∈N ≥个首项为1,项数为n 的等差数列,设其第m (, )m n m *∈N ≤个等差数列的第k 项为mk a (1,2,3,,)k n =,且公差为m d . 若11d =,23d =,123,,,,n n n nn a a a a 也成等差数列.(Ⅰ)求m d (3m n ≤≤)关于m 的表达式;(Ⅱ)将数列{}m d 分组如下:1()d ,234(,,)d d d ,5(d ,6d ,7d ,8d ,9d )…,[来源:学科网](每组数的个数组成等差数列),设前m 组中所有数之和为4()(0)m m c c >,求数列{2}m cm d 的前n 项和n S ;[来源:学#科#网](Ⅲ)设N 是不超过20的正整数,当n N >时,对于(Ⅱ)中的n S ,求使得不等式1(6)50n n S d ->成立的所有N 的值.北京市朝阳区高三年级第一次综合练习数学测试题答案(文史类)[来源:Z|xx|]2011.4二、填空题来源Z.X.X.K] 三、解答题(共80分)15.(满分13分)[来源:] 解:(Ⅰ)因为2c a =,4C π=, 由正弦定理sin sin a c A C =得:sin A =. ………………………5分 (Ⅱ)因为sin A =2c a =可知a c <,4A π<.[来源:]则cos 4A ==. sin 22sin cos A A A ==,23cos 22cos 14A A =-=.则cos(2)3A π-=ππcos 2cossin 2sin 33A A +=38. ………………13分 16. (满分13分)[来源:Z+xx+]解:(Ⅰ)M ={(-2, -1),(-2, 1),(0, -1),(0, 1),(2, -1),(2, 1)}. ……………6分 (Ⅱ)记“以(x ,y )为坐标的点位于区域D 内”为事件A .集合M 中共有6个元素,即基本事件总数为6,区域D 含有集合M 中的元素4个, 所以42()63P A ==. 故以(x ,y )为坐标的点位于区域D 内的概率为23. ……………………………13分17. (满分13分)解:(Ⅰ)因为 90PAD ∠=︒, 所以PA AD ⊥.又因为侧面PAD ⊥底面ABCD , 且侧面PAD底面ABCD AD =,所以PA ⊥底面ABCD . 而CD ⊂底面ABCD , 所以PA ⊥CD . 在底面ABCD 中,因为90ABCBAD ∠=∠=︒,12AB BC AD ==, 所以 2AC CD AD ==, 所以AC ⊥CD . 又因为PA AC A =, 所以CD ⊥平面PAC . ……………………………6分(Ⅱ)设侧棱PD 的中点为F ,连结BE ,EF ,FC ,则EFAD ,且12EF AD =. 由已知90ABC BAD ∠=∠=︒,所以BC AD . 又12BC AD =,所以BC EF . 且BC EF =.所以四边形BEFC 为平行四边形,所以BE CF .因为BE ⊄平面PCD ,CF ⊂平面PCD , 所以BE平面PCD . ………………………………………………………13分18. (满分13分)解: (Ⅰ)直线2y x =+的斜率为1.函数()y f x =的导数为22()a f x x x'=-+, 则22(1)111af '=-+=-,所以1a =. ………………………………5分 (Ⅱ)22()ax f x x-'=,x ∈(0,)+∞. ①当0a =时,在区间(0, e]上22()0f x x '=-<,此时()f x 在区间(0, e]上单调递减,则()f x 在区间(0, e]上的最小值为2(e)ef =.②当20a<,即0a <时,在区间(0, e]上()0f x '<,此时()f x 在区间(0, e]上单调递减,则()f x 在区间(0, e]上的最小值为2(e)ef a =+.③当20e a <<,即2e a >时,在区间2(0,)a 上()0f x '<,此时()f x 在区间2(0,)a上单调递减;在区间2(,e]a 上()0f x '>,此时()f x 在区间2(,e]a上单调递增;则()f x 在区间(0, e]上的最小值为22()ln f a a a a=+.④ 当2e a ≥,即20ea <≤时,在区间(0, e]上()0f x ′≤,此时()f x 在区间(0, e]上为单调递减,则()f x 在区间(0, e]上的最小值为2(e)ef a =+.[来源:]综上所述,当2e a ≤时,()f x 在区间(0, e]上的最小值为2e a +;当2ea >时,()f x 在区间(0, e]上的最小值为2ln a a a+. …………………………………………13分19. (满分14分)解:(Ⅰ)由题意可设椭圆C 的方程为22221(0)x y a b a b+=>>,半焦距为c ,因为(2, 0)A -、(2, 0)B 为椭圆C 的左、右顶点,(1, 0)F 为其右焦点,所以2a =, 1c =.又因为222a b c =+,所以b ==故椭圆C 的方程为22143x y +=,离心率为12.……5分 (Ⅱ)以BD 为直径的圆与直线PF 相切. 证明如下:由题意可设直线l 的方程为(2)y k x =+(0)k ≠, 则点D 坐标为(2, 4)k ,BD 中点E 的坐标为(2, 2)k .由22(2),1,43y k x x y =+⎧⎪⎨+=⎪⎩得2222(34)1616120k x k x k +++-=.设点P 的坐标为00(,)x y ,则2021612234k x k --=+.所以2026834k x k-=+,00212(2)34k y k x k =+=+. 因为点F 坐标为(1, 0), 当12k =±时,点P 的坐标为3(1, )2±,点D 的坐标为(2, 2)±, 直线PF x ⊥轴,此时以BD 为直径的圆22(2)(1)1x y -+=与直线PF 相切.当12k ≠±时,则直线PF 的斜率0204114PF y k k x k ==--. 所以直线PF 的方程为24(1)14ky x k=--. 点E 到直线PF的距离d =322228142||14|14|k k k k k k +-==+-. 又因为||4||BD k = 所以1||2d BD =. 故以BD 为直径的圆与直线PF 相切.综上得,当直线l 绕点A 转动时,以BD 为直径的圆与直线PF 相切.………14分20. (满分14分)解(Ⅰ)由题意知,1(1)mn m a n d =+-.212121[1(1)][1(1)](1)()n n a a n d n d n d d -=+--+-=--,同理, 3232(1)()n n a a n d d -=--,4343(1)()n n a a n d d -=--,…,(1)1(1)()nn n n n n a a n d d ---=--. 123,,,,n n n nn a a a a 成等差数列,所以2132(1)n n n n nn n n a a a a a a --=-==-,故21321n n d d d d d d --=-==-.即{}n d 是公差是21312d d -=-=的等差数列.所以,21m d m =-(3m n ≤≤,*,m n ∈N ). ………………………5分 (Ⅱ)由(Ⅰ)知*2 1 ()m d m m =-∈N .[来源:Z&xx&]数列{}m d 分组如下:(1),(3,5,7),(9,11,13,15,17),…. 按分组规律,第m 组中有21m -个奇数, 所以第1组到第m 组共有2135(21)m m ++++-=个奇数. 注意到前k 个奇数的和为2135(21)k k ++++-=,所以前2m 个奇数的和为224()m m =,即前m 组中所有数之和为4m ,所以44()m c m =. 因为0m c >,所以m c m =,从而 *2(21)2()m cm m d m m =-⋅∈N .所以 234112325272(23)2(21)2n n n S n n -=⋅+⋅+⋅+⋅++-⋅+-⋅.[来源:]23412123252(23)2(21)2n n n S n n +=⋅+⋅+⋅++-⋅+-⋅,故2341222222222(21)2n n n S n +-=+⋅+⋅+⋅++⋅--⋅2312(2222)2(21)2n n n +=++++---⋅12(21)22(21)221n n n +-=⨯---⋅-1(32)26n n +=--,[来源:学科网ZXXK]所以 1(23)26n n S n +=-+. ……………………………………10分(Ⅲ)由(Ⅱ)得*2 1 ()n d n n =-∈N ,1(23)26n n S n +=-+* ()n ∈N .故不等式1(6)50n n S d -> 就是1(23)250(21)n n n +->-. 考虑函数1()(23)250(21)n f n n n +=---1(23)(250)100n n +=---. 当1,2,3,4,5n =时,都有()0f n <,即1(23)250(21)n n n +-<-. 而(6)9(12850)1006020f =--=>,注意到当6n ≥时,()f n 单调递增,故有()0f n >.因此当6n ≥时,1(23)250(21)n n n +->-成立,即1(6)50n n S d ->成立. 所以满足条件的所有正整数5,6,7,,20N =.…………………………………14分。
