初中几何经典例题及解题技巧精编版
源于经典而高于经典的初二几何难题解答概要
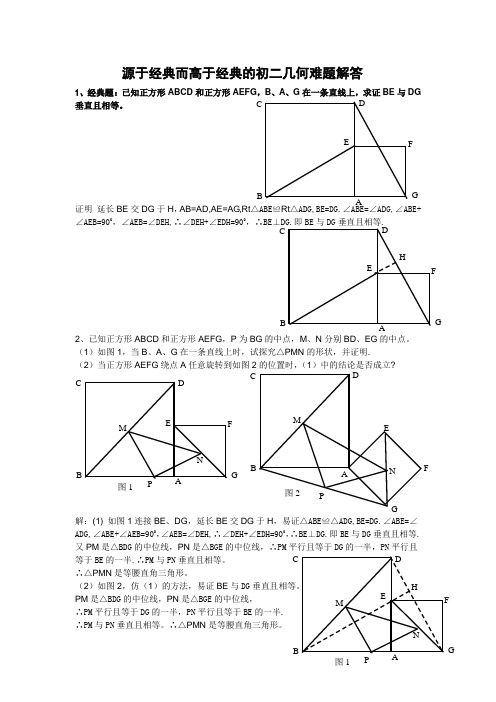
源于经典而高于经典的初二几何难题解答1、经典题:已知正方形ABCD 和正方形AEFG ,B 、A 、G 在一条直线上,求证BE 与DG垂直且相等。
证明 延长BE 交DG 于H ,AB=AD,AE=AG,Rt △ABE ≌Rt △ADG,BE=DG.∠ABE=∠ADG,∠ABE+∠AEB=900,∠AEB=∠DEH,∴∠DEH+∠EDH=900,∴BE ⊥DG.即BE 与DG 垂直且相等.2、已知正方形ABCD 和正方形AEFG ,P 为BG 的中点,M 、N 分别BD 、EG 的中点。
(1)如图1,当B 、A 、G 在一条直线上时,试探究△PMN 的形状,并证明. (2)当正方形AEFG 绕点A 任意旋转到如图2的位置时,(1)中的结论是否成立?解:(1) 如图1连接BE 、DG ,延长BE 交DG 于H ,易证△ABE ≌△ADG,BE=DG.∠ABE=∠ADG,∠ABE+∠AEB=900,∠AEB=∠DEH,∴∠DEH+∠EDH=900,∴BE ⊥DG.即BE 与DG 垂直且相等. 又PM 是△BDG 的中位线,PN 是△BGE 的中位线,∴PM 平行且等于DG 的一半,PN 平行且等于BE 的一半.∴PM 与PN 垂直且相等。
∴△PMN 是等腰直角三角形。
(2)如图2,仿(1)的方法,易证BE 与DG 垂直且相等。
PM 是△BDG 的中位线,PN 是△BGE 的中位线,∴PM 平行且等于DG 的一半,PN 平行且等于BE 的一半. ∴PM 与PN 垂直且相等。
∴△PMN 是等腰直角三角形。
N图1 D M E CPBA F G P 图2 A D M E N CB F G图1HD MEC PBAFGND E C B AF G H D E C B AF G说明:本题的第(2)小题也可看成以△ABG 边AB 、AG 向外作正方形ABCD 和 正方形AEFG 。
可得以上结论。
3、分别以任意四边形ABCD 的各边向外作正方形ABEF 、AGHD 、DIJC 、CKLB 。
初中数学必会的12个几何模型精解精编(222页Word)

中考数学几何模型1:截长补短模型有一类几何题其命题主要是证明三条线段长度的“和”或"差”及其比例关系. 这一类题目一般可以采取“截长”或“补短”的方法来进行求解. 所谓“截长”,就是将三者中最长的那条线段一分为二,使其中的一条线段与已知线段相等,然后证明其中的另一段与已知的另一段的大小关系. 所谓“补短”,就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等. 然后求出延长后的线段与最长的已知线段的关系. 有的是采取截长补短后,使之构成某种特定的三角形进行求解.例题1如图,AB∥CD,BE平分∠ABC,CE平分∠BCD,若E在AD上.求证:(1)BE⊥CE;(2)BC=AB+CD.【解析】证明:如图所示:(1)∵BE、CE分别是∠ABC和∠BCD的平分线,∴∠1=∠2,∠3=∠4,又∵AB∥CD,∴∠1+∠2+∠3+∠4=180°,∴∠2+∠3=90°,∴∠BEC=90°,∴BE⊥CE.(2)在BC上取点F,使BF=BA,连接EF.在△ABE和△FBE中,,∴△ABE≌△FBE(SAS),∴∠A=∠5.∵AB∥CD,∴∠A+∠D=180°,∴∠5+∠D=180,∵∠5+∠6=180°,∴∠6=∠D,在△CDE和△CFE中,,∴△CDE≌△CFE(AAS),∴CF=CD.∵BC=BF+CF,∴BC=AB+CD,变式1已知△ABC的内角平分线AD交BC于D,∠B=2∠C. 求证:AB+BD=AC.答案:略例题2已知△ABC中,∠A=60°,BD,CE分别平分∠ABC和∠ACB,BD、CE交于点O,试判断BE,CD,BC的数量关系,并说明理由.【解析】在BC上取点G使得CG=CD,∵∠BOC=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣60°)=120°,∴∠BOE=∠COD=60°,∵在△COD和△COG中,,∴△COD≌△COG(SAS),∴∠COG=∠COD=60°,∴∠BOG=120°﹣60°=60°=∠BOE,在△BOE和△BOG中,,∴△BOE≌△BOG(ASA),∴BE=BG,∴BE+CD=BG+CG=BC.变式2已知:△ABC中,AB=AC,D为△ABC外一点,且∠ABD=60°,∠ADB=90°﹣∠BDC.试判断线段CD、BD与AB之间有怎样的数量关系?并证明你的结论.【解析】AB=BD+CD,理由是:延长CD到E,使DE=BD,连接AE,∵∠ADB=90°﹣∠BDC,∴∠ADE=180°﹣(90°﹣)﹣∠BDC=90°﹣,∴∠ADB=∠ADE,在△ABD和△AED中,∴△ABD≌△AED(SAS),∴∠E=∠ABD=60°,AB=AE,∵AB=AC,∴AE=AC,∴△ACE是等边三角形,∴AB=CE=CD+DE=BD+CD.例题3如图,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:DA平分∠CDE【解析】连接AC,延长DE到F,使EF=BC,连接AF,∵BC+DE=CD,EF+DE=DF,∴CD=FD,∵∠ABC+∠AED=180°,∠AEF+∠AED=180°,∴∠ABC=∠AEF,在△ABC和△AEF中,,∴△ABC≌△AEF(SAS),∴AC=AF,在△ACD和△AFD中,,∴△ACD≌△AFD(SSS)∴∠ADC=∠ADF,即AD平分∠CDE变式3如图,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,M是AB延长线上一点,N是CA延长线上一点,且∠MDN=60°.试探究BM、MN、CN之间的数量关系,并给出证明.【解析】CN=MN+BM(微信公众号:数学三剑客)证明:在CN上截取点E,使CE=BM,连接DE,∵△ABC为等边三角形,∴∠ACB=∠ABC=60°,又△BDC为等腰三角形,且∠BDC=120°,∴BD=DC,∠DBC=∠BCD=30°,∴∠ABD=∠ABC+∠DBC=∠ACB+∠BCD=∠ECD=90°,在△MBD和△ECD中,,∴△MBD≌△ECD(SAS),∴MD=DE,∠MDB=∠EDC,又∵∠MDN=60°,∠BDC=120°,∴∠EDN=∠BDC﹣(∠BDN+∠EDC)=∠BDC﹣(∠BDN+∠MDB)=∠BDC﹣∠MDN=120°﹣60°=60°,∴∠MDN=∠EDN,在△MND与△END中,,∴△MND≌△END(SAS),∴MN=NE,∴CN=NE+CE=MN+BM例题4在四边形ABDE中,C是BD边的中点.(1)如图(1),若AC平分∠BAE,∠ACE=90°,则线段AE、AB、DE的长度满足的数量关系为AE=AB+DE;(直接写出答案)(2)如图(2),AC平分∠BAE,EC平分∠AED,若∠ACE=120°,则线段AB、BD、DE、AE的长度满足怎样的数量关系?写出结论并证明;(3)如图(3),BD=8,AB=2,DE=8,若ACE=135°,则线段AE长度的最大值是10+4.(直接写出答案).【解析】(1)AE=AB+DE;(2)猜想:AE=AB+DE+BD.证明:在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG.∵C是BD边的中点,∴CB=CD=BD.∵AC平分∠BAE,∴∠BAC=∠F AC.在△ACB和△ACF中,,∴△ACB≌△ACF(SAS),∴CF=CB,∴∠BCA=∠FCA.同理可证:CD=CG,∴∠DCE=∠GCE.∵CB=CD,∴CG=CF∵∠ACE=120°,∴∠BCA+∠DCE=180°﹣120°=60°.∴∠FCA+∠GCE=60°.∴∠FCG=60°.∴△FGC是等边三角形.∴FG=FC=BD.∵AE=AF+EG+FG.∴AE=AB+DE+BD.(3)作B关于AC的对称点F,D关于EC的对称点G,连接AF,FC,CG,EG,FG.∵C是BD边的中点,∴CB=CD=BD.∵△ACB≌△ACF(SAS),∴CF=CB,∴∠BCA=∠FCA.同理可证:CD=CG,∴∠DCE=∠GCE∵CB=CD,∴CG=CF∵∠ACE=135°,∴∠BCA+∠DCE=180°﹣135°=45°.∴∠FCA+∠GCE=45°.∴∠FCG=90°.∴△FGC是等腰直角三角形.∴FC=BD.∵BD=8,∴FC=4,∴FG=4.∵AE=AB+4+DE.∵AB=2,DE=8,∴AE≤AF+FG+EG=10+4.∴当A、F、G、E共线时AE的值最大2,最大值为10+4.故答案为:10+4.例题5在△ABC中,∠BAC=90°.(1)如图1,直线l是BC的垂直平分线,请在图1中画出点A关于直线l的对称点A′,连接A′C,A′B,A′C与AB交于点E;(2)将图1中的直线A′B沿着EC方向平移,与直线EC交于点D,与直线BC交于点F,过点F作直线AB的垂线,垂足为点H.①如图2,若点D在线段EC上,请猜想线段FH,DF,AC之间的数量关系,并证明;②若点D在线段EC的延长线上,直接写出线段FH,DF,AC之间的数量关系.【解析】(1)如图1(2)①DF+FH=CA,证明:如图2,过点F作FG⊥CA于点G,∵FH⊥BA于H,∠A=90°,FG⊥CA,∴∠A=∠FGA=∠FHA=90°,∴四边形HFGA为矩形.∴FH=AG,FG∥AB,∴∠GFC=∠EBC,∵直线l是BC的垂直平分线,∴BE=EC,∴∠EBC=∠ECB,由(1)和平移可知,∠ECB=∠EBC=∠GFC,∠FDC=∠A=90°,∴∠FDC=∠FGC=90°.∵在△FGC和△CDF中∴△FGC≌△CDF,∴CG=FD,∴DF+FH=GC+AG,即DF+FH=AC;②解:FH﹣DF=AC,理由是:过F作FH⊥BA于H,过点C作CG⊥FH于G,∵FH⊥BA于H,∠BAC=90°,CG⊥FH,∴∠CAH=∠CGH=∠FHA=90°,∴四边形ACGH为矩形.∴AC=GH,CG∥AB,∴∠GCF=∠EBC,∵直线l是BC的垂直平分线,∴BE=EC,∴∠EBC=∠ECB=∠FCD,∴∠GCF=∠FCD,由(1)和平移可知,∠FDC=∠A=90°,∴∠FDC=∠FGC=90°.∵在△FGC和△CDF中∴△FGC≌△CDF,∴FG=FD,∵FH﹣FG=GH,∴FH﹣DF=AC.例题6如图1,在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于点D,点H为AO上一动点,过点H作直线l⊥AO于H,分别交直线AB、AC、BC、于点N、E、M.(1)当直线l经过点C时(如图2),求证:BN=CD;(2)当M是BC中点时,写出CE和CD之间的等量关系,并加以证明;(3)请直接写出BN、CE、CD之间的等量关系.【解析】(1)证明:连接ND,如图2所示:∵AO平分∠BAC,∴∠BAD=∠CAD,∵直线l⊥AO于H,∴∠AHN=∠AHE=90°,∴∠ANH=∠AEH,∴AN=AC,∴NH=CH,∴AH是线段NC的中垂线,∴DN=DC,∴∠DNH=∠DCH,∴∠AND=∠ACB,∵∠AND=∠B+∠BDN,∠ACB=2∠B,∴∠B=∠BDN,∴BN=DN,∴BN=DC;(2)解:当M是BC中点时,CE和CD之间的等量关系为CD=2CE,理由如下:过点C作CN'⊥AO交AB于N',过点C作CG∥AB交直线l于点G,如图3所示:由(1)得:BN'=CD,AN'=AC,AN=AE,∴∠ANE=∠AEN,NN'=CE,∴∠ANE=∠CGE,∠B=∠BCG,∴∠CGE=∠AEN,∴CG=CE,∵M是BC中点,∴BM=CM,在△BNM和△CGM中,,∴△BNM≌△CGM(ASA),∴BN=CG,∴BN=CE,∴CD=BN'=NN'+BN=2CE;(3)解:BN、CE、CD之间的等量关系:当点M在线段BC上时,CD=BN+CE;理由如下:过点C作CN'⊥AO交AB于N',如图3所示:由(2)得:NN'=CE,CD=BN'=BN+CE;当点M在BC的延长线上时,CD=BN﹣CE;理由如下:过点C作CN'⊥AO交AB于N',如图4所示:同(2)得:NN'=CE,CD=BN'=BN﹣CE;当点M在CB的延长线上时,CD=CE﹣BN;理由如下:过点C作CN'⊥AO交AB于N',如图5所示:同(2)得:NN'=CE,CD=BN'=CE﹣BN.【练习1】如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,且AC=AB+BD,求∠ABC的度数.【解析】如图,在AC上截取AE=AB,∵AD平分∠BAC,∴∠BAD=∠CAD,在△ABD和△AED中,,∴△ABD≌△AED(SAS),∴BD=DE,∠B=∠AED,∵AC=AE+CE,AC=AB+BD,∴CE=BD,∴CE=DE,∴∠C=∠CDE,即∠B=2∠C,在△ABC中,∠BAC+∠B+∠C=180°,∴60°+2∠C+∠C=180°,解得∠C=40°,∴∠ABC=2×40°=80°.【练习2】如图,在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F,试探究线段AB与AF,CF之间的数量关系,并证明你的结论.【练习3】如图,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角∠NDM,角的两边分别交AB、AC边于M、N两点,连接MN.试探究BM、MN、CN之间的数量关系,并加以证明.【解析】探究结论:BM+CN=NM.证明:延长AC至E,使CE=BM,连接DE,∵△BDC是顶角∠BDC=120°的等腰三角形,△ABC是等边三角形,∴∠BCD=30°,∴∠ABD=∠ACD=90°,即∠ABD=∠DCE=90°,∴在△DCE和△DBM中,∴R t△DCE≌R t△DBM(SAS),∴∠BDM=∠CDE,又∵∠BDC=120°,∠MDN=60°,∴∠BDM+∠NDC=∠BDC﹣∠MDN=60°,∴∠CDE+∠NDC=60°,即∠NDE=60°,∴∠MDN=∠NDE=60°∴DM=DE(上面已经全等)在△DMN和△DEN中,∴△DMN≌△DEN(S A S),∴BM+CN=NM.【练习4】如图,▱ABCD中,E是BC边的中点,连接AE,F为CD边上一点,且满足∠DF A=2∠BAE.(1)若∠D=105°,∠DAF=35°.求∠F AE的度数;(2)求证:AF=CD+CF.【解析】(1)解:∵∠D=105°,∠DAF=35°,∴∠DF A=180°﹣∠D﹣∠DAF=40°(三角形内角和定理).∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD(平行四边形对边平行且相等).∴∠DF A=∠F AB=40°(两直线平行,内错角相等);∵∠DF A=2∠BAE(已知),∴∠F AB=2∠BAE(等量代换).即∠F AE+∠BAE=2∠BAE.∴∠F AE=∠BAE;∴2∠F AE=40°,∴∠F AE=20°;(2)证明:在AF上截取AG=AB,连接EG,CG.∵∠F AE=∠BAE,AE=AE,∴△AEG≌△AEB.∴EG=BE,∠B=∠AGE;又∵E为BC中点,∴CE=BE.∴EG=EC,∴∠EGC=∠ECG;∵AB∥CD,∴∠B+∠BCD=180°.又∵∠AGE+∠EGF=180°,∠AGE=∠B,∴∠BCF=∠EGF;又∵∠EGC=∠ECG,∴∠FGC=∠FCG,∴FG=FC;又∵AG=AB,AB=CD,∴AF=AG+GF=AB+FC=CD+FC.【练习5】如图所示,在正方形ABCD的边CB的延长线上取点F,连结AF,在AF上取点G,使得AG=AD,连结DG,过点A作AE⊥AF,交DG于点E.(1)若正方形ABCD的边长为4,且AB=2FB,求FG的长;(2)求证:AE+BF=AF.【解析】(1)∵四边形ABCD是正方形,且边长为4,∴∠ABF=90°,AB=AD=4,∵在R t△ABF中,AB=2FB,∴FB=×4=2,∴AF==2,∵AG=AD=4,∴FG=AF﹣AG=2﹣4;(2)证明:在BC上截取BM=AE,连接AM,∵AG=AD,AB=AD,∴AG=AB,∵AE⊥AF,∴∠EAG=∠ABM=90°,在△AGE和△BAM中,,∴△AGE≌△BAM(SAS),∴∠AMB=∠AEG,∠BAM=∠AGD,∵AG=AD,∴∠AGD=∠ADG,∴∠BAM=∠ADG,∵∠BAD=90°,∴∠F AB+∠BAE=∠BAE+∠EAD=90°,∴∠F AB=∠EAD,∴∠AEG=∠EAD+∠ADG=∠F AB+∠BAM=∠F AM,∴∠F AM=∠AMB,∴AF=FM=BF+BM=BF+AE.【练习6】如图,在四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°,连接AC,BD交于点E.(1)若BC=CD=2,M为线段AC上一点,且AM:CM=1:2,连接BM,求点C到BM的距离.(2)证明:BC+CD=AC.【解析】(1)∵AB=AD,∠BAD=60°,∴△ABD是等边三角形,∴∠ABD=∠ADB=60°.∵BC=CD,∴△ABC≌△ADC,∴∠BAC=∠DAC=30°,∠ACB=∠ACD=60°.∴∠AEB=∠BEC=90°,∠ABC=90°,∴CE=BC=1,BE=,AC=2BC=4.∵AM:CM=1:2,∴AM=,CM=,∴EM=,在R t△BEM中由勾股定理得BM==.过点C作CF⊥BM于点F.∴.∴,∴CF=.即点C到BM的距离.(2)证明:延长BC到点F,使CF=CB,连接DF,∵AB=AD,∠ABD=60°,∴△ABD是等边三角形,∴∠ADB=60°,AD=BD,∴BC=CD,∴CF=CD.∵∠BCD=120°,∴∠DCF=180°﹣∠BCD=60°,∴△DCF是等边三角形,∴∠CDF=∠ADB=60°,DC=DF,∴∠ADC=∠BDF,又∵AD=BD,∴△ACD≌△BDF,∴AC=BF=BC+CF,即AC=BC+CD.【练习7】如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP交DP的延长线于点E,连接AE,过点A作AF⊥AE交DP于点F,连接BF.(1)若AE=2,求EF的长;(2)求证:PF=EP+EB.【解析】(1)∵四边形ABCD是正方形,且BE⊥DP,AF⊥AE,∴AB=AD,∠BAD=∠EAF=∠BEF=90°,∴∠1+∠F AB=∠2+∠F AB=90°,∴∠1=∠2.∵∠3+∠5=∠4+∠6,且∠5=∠6,∴∠3=∠4.在△AEB和△AFD中,∵,∴△AEB≌△AFD,∴AE=AF=2,在R t△EAF中,由勾股定理,得EF==2.(2)过点A作AM⊥EF于M,且∠EAF=90°,AE=AF,∴△EAF为等腰直角三角形.∴AM=MF=EM.∠AME=∠BEF=90°.∵点P是AB的中点,∴AP=BP.在△AMP和△BEP中,∵,∴△AMP≌△BEP,∴BE=AM,EP=MP,∴MF=BE,∴PF=PM+FM=EP+BE.中考数学几何模型2:共顶点模型共顶点模型,亦称“手拉手模型”,是指两个顶角相等的等腰或者等边三角形的顶点重合,两个三角形的两条腰分别构成的两个三角形全等或者相似。
初中几何题解题技巧(带例题)

初中几何题解题技巧(带例题)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN初中几何题解题技巧在小学阶段,我们学过许多关于几何图形面积计算的知识。
在计算几何图形面积时,除了能正确运用面积计算公式外,还需要掌握一定的解题技巧。
一、割补法割补法是指将一些不规则的、分散的几何图形经过分割、移补,拼成一个规则的几何图形,从而求出面积的方法。
例1如图1,已知正方形的边长是6厘米,求阴影部分的面积。
分析与解:如图2所示,连接正方形的对角线,可以将阴影I分割成I1和I2两部分,然后将阴影I1移至空白I1′处,将阴影I2移至空白I2′处,这样阴影部分就拼成了一个等腰直角三角形。
要求阴影部分的面积,只要求出这个等腰直角三角形的面积即可,列式为:6×6÷2=18(平方厘米)。
练一练1:如图3,已知AB=BC=4厘米,求阴影部分的面积。
二、平移法平移法是指把一些不规则的几何图形沿水平或垂直方向移动,拼成一个规则的几何图形,从而求出面积的方法。
例2如图4,已知长方形的长是12厘米,宽是6厘米,求阴影部分的面积。
分析与解:如图5所示,连结长方形两条长的中点,把阴影部分分成左右两部分,然后把左边的阴影部分向右平移至空白处,这样阴影部分就转化成了一个边长为6厘米的正方形。
要求阴影部分的面积,只要求出这个正方形的面积,列式为:6×6=36(平方厘米)。
练一练2:如图6,求阴影部分的面积(单位:分米)。
三、旋转法旋转法是指把一些几何图形绕某一点沿顺时针(或逆时针)方向转动一定的角度,使分散的、不规则的几何图形合并成一个规则的几何图形,从而求出面积的方法。
例3如图7,已知ABC是等腰直角三角形,斜边AB=20厘米,D是AB的中点,扇形DAE和DBF都是圆的,求阴影部分的面积。
分析与解:如图8所示,把扇形DBF绕D点沿顺时针方向旋转180°后,扇形DBF与扇形DAE就合并成了一个半径为10厘米的半圆,两个空白三角形也合并成了一个直角边为10厘米的等腰直角三角形,要求阴影部分的面积,只要用半圆的面积减去空白部分的面积即可,列式为:3.14×(20÷2)2÷2-(20÷2)2÷2=107(平方厘米)。
七年级数学第四章几何图形初步典型例题及答题技巧

七年级数学第四章几何图形初步典型例题及答题技巧单选题1、一个几何体由大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置小立方块的个数,则从正面看该几何体的形状图为()A.B.C.D.答案:A解析:由已知条件可知,从正面看有3列,每列小正方形数目分别为4,2,3,据此可得出图形.解:根据所给出的图形和数字可得:从正面看有3列,每列小正方形数目分别为4,3,2,则符合题意的是:故选:A.小提示:本题考查了从不同方向看几何体等知识,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平2、下列各角中,是钝角的是( ).A .14周角B .23平角C .平角D .14平角答案:B解析:直接利用角的定义逐项分析即可得出答案.解:A. 14周角= 14×360°=90°,不是钝角,不合题意; B. 23平角=23×180°=120°,是钝角,符合题意;C. 平角=180°,不是钝角,不合题意;D. 14平角=14×180°=45°,不是钝角,不合题意. 故选:B小提示:此题主要考查了角的概念,正确掌握平角、周角、钝角的概念是解题关键.3、已知∠AOB =30°,如果用10倍的放大镜看,这个角的度数将( )A .缩小10倍B .不变C .扩大10倍D .扩大100倍答案:B解析:根据角是从同一点引出的两条射线组成的图形.它的大小与图形的大小无关,只与两条射线形成的夹角有关系,直接判断即可.解:角的大小只与角的两边张开的大小有关,放大镜没有改变顶点的位置和两条射线的方向,所以用10倍放大镜观察这个角还是30度.小提示:本题考查了角的概念.解题关键是掌握角的概念:从同一点引出的两条射线组成的图形叫做角,明确角的大小只与角的两边张开的大小有关.4、如图所示,∠COD的顶点O在直线AB上,OE平分∠COD,OF平分∠AOD,已知∠COD=90°,∠BOC=α,则∠EOF的度数为()A.90°+αB.90°+α2C.45°+αD.90°﹣α2答案:B解析:先利用∠COD=90°,∠BOC=α,求出∠BOD的度数,再求出∠AOD的度数,利用角平分线,分别求出∠FOD和∠EOD的度数,相加即可.解:∵∠COD=90°,∠BOC=α,∴∠BOD=90°-∠BOC=90°-α,∴∠AOD=180°-∠BOD=90°+α,∵OF平分∠AOD,∴∠DOF=12∠AOD=45°+12α,∵OE平分∠COD,∴∠DOE=12∠COD=45°,∴∠EOF=∠FOD+∠DOE=90°+α;2故选:B.小提示:本题考查了角平分线的计算,解题关键是准确识图,弄清角之间的和差关系.5、观察下列图形,其中不是正方体的表面展开图的是()A.B.C.D.答案:B解析:利用正方体及其表面展开图的特点解题.解:A、C、D均是正方体表面展开图;B、是凹字格,故不是正方体表面展开图.故选:B.小提示:本题考查了正方体的展开图,熟记展开图的11种形式是解题的关键,利用不是正方体展开图的“一线不过四、田凹应弃之”(即不能出现同一行有多于4个正方形的情况,不能出现田字形、凹字形的情况)判断也可.6、下列事实可以用“经过两点有且只有一条直线”来说明的是()A.从王庄到李庄走直线最近B.在正常情况下,射击时要保证瞄准的一只眼睛在准星和缺口确定的直线上,才能射中目标C.向远方延伸的铁路给我们一条直线的印象D.数轴是一条特殊的直线答案:B解析:根据两点确定一条直线进而得出答案.在正常情况下,射击时要保证瞄准的一只眼在准星和缺口确定的直线上,才能射中目标,这说明了两点确定一条直线的道理.故选B.小提示:此题主要考查了直线的性质,利用实际问题与数学知识联系得出是解题关键.7、如图是一个正方体的平面展开图,把展开图折叠成正方体后,“红”字的面的对面上的字是()A.传B.国C.承D.基答案:D解析:正方体的平面展开图中,相对面的特点是必须相隔一个正方形,据此作答.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,则:“传”与“因”是相对面,“承”与“色”是相对面,“红”与“基”是相对面.故选:D.小提示:本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.8、如图,是一个几何体的表面展开图,则该几何体中写“英”的面相对面上的字是( )A.战B.疫C.情D.颂答案:B解析:正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“战”与“情”是相对面,“疫”与“英”是相对面,“颂”与“雄”是相对面.故选:B.小提示:本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手分析是解题的关键.填空题9、下列语句表示的图形是(只填序号)①过点O的三条直线与另条一直线分别相交于点B、C、D三点:_____.②以直线AB上一点O为顶点,在直线AB的同侧画∠AOC和∠BOD:_______.③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点:_________.答案:(3)(2)(1)解析:解:观察图形,根据所给的信息可得:①过点O的三条直线与另一条直线分别相交于点B、C、D三点的图形为(3);②以直线AB上一点O为顶点,在直线AB的同侧画∠AOC和∠BOD的图形为(2);③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点的图形为(1).所以答案是:(3);(2);(1).小提示:本题考查了直线、射线与线段的知识,注意掌握三者的特点,给出图形应该能判断出是哪一个.10、一个直角三角形的两条直角边的长分别为3厘米和4厘米,绕它的直角边所在的直线旋转所形成几何体的体积是_____立方厘米.(结果保留π)答案:12π或16π解析:根据题意可得绕它的直角边所在的直线旋转所形成几何体是圆锥,再利用圆锥的体积公式进行计算即可.解:绕它的直角边所在的直线旋转所形成几何体是圆锥,π×32×4=12π,①当绕它的直角边为3cm所在的直线旋转所形成几何体的的体积是:13π×42×3=16π,②当绕它的直角边为4cm所在的直线旋转所形成几何体的的体积是:13所以答案是:12π或16π.小提示:此题主要考查了点、线、面、体,关键是掌握圆锥的体积公式,注意分类讨论.11、如图,将甲、乙、丙、丁四个小正方形中的一个剪掉,使余下的部分不能围成一个正方体,则剪掉的这个小正方形是________答案:丁解析:能围成正方体的“一四一”,“二三一”,“三三”,“二二二”的基本形态要记牢.解题时,据此即可判断答案.解:将如图所示的图形剪去一个小正方形,使余下的部分不能围成一个正方体,编号为甲乙丙丁的小正方形中剪去的是丁,所以答案是:丁.小提示:本题考查了展开图折叠成正方体的知识,解题关键是根据正方体的特征,或者熟记正方体的11种展开图,只要有“田”,“凹”字格的展开图都不是正方体的表面展开图.12、如图,∠AOC=∠BOD=90°,∠AOB=70°,在∠AOB内画一条射线OP得到的图中有m对互余的角,其中∠AOP=x°,且满足0<x<50,则m=_______.答案:3或4或6解析:分三种情况下:①∠AOP=35°,②∠AOP=20°,③0<x<50中的其余角,根据互余的定义找出图中互余的角即可求解.∠AOB =35°时,∠BOP=35°①∠AOP=12∴互余的角有∠AOP与∠COP,∠BOP与∠COP,∠AOB与∠COB,∠COD与∠COB,一共4对;②∠AOP=90°-∠AOB =20°时,∴互余的角有∠AOP与∠COP,∠AOP与∠AOB,∠AOP与∠COD,∠COD与∠COB,∠AOB与∠COB,∠COP与∠COB,一共6对;③0<x<50中35°与20°的其余角,互余的角有∠AOP与∠COP,∠AOB与∠COB,∠COD与∠COB,一共3对.则m=3或4或6.所以答案是:3或4或6.小提示:本题考查了余角和补角:如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角.13、已知∠A=20°18',则∠A的余角等于__.答案:69°42′解析:根据互为余角的两个角之和为90°解答即可.解:∵∠A=20°18',∴∠A的余角为90°﹣20°18′=69°42′.所以答案是:69°42′.小提示:本题考查余角定义,熟知互为余角的两个角之和为90°是解答的关键.解答题14、如图,线段AB=8cm,C是线段AB上一点,M是AB的中点,N是AC的中点.(1)AC=3cm,求线段CM、NM的长;(2)若线段AC=m,线段BC=n,求MN的长度(m<n用含m,n的代数式表示).答案:(1)CM=1cm,NM=2.5cm;(2)12n解析:(1)求出AM长,代入CM=AM-AC求出即可;分别求出AN、AM长,代入MN=AM-AN求出即可;(2)分别求出AM和AN,利用AM-AN可得MN.解:(1)∵AB=8cm,M是AB的中点,∴AM=12AB=4cm,∵AC=3cm,∴CM=AM−AC=4−3=1cm;∵AB=8cm,AC=3cm,M是AB的中点,N是AC的中点,∴AM=12AB=4cm,AN=12AC=1.5cm,∴MN=AM−AN=4−1.5=2.5cm;(2)∵AC=m,BC=n,∴AB=AC+BC=m+n,∵M是AB的中点,N是AC的中点,∴AM =12AB =12(m +n),AN =12AC =12m ,∴MN =AM −AN =12(m +n)−12m =12n . 小提示:本题考查了两点之间的距离,线段中点的定义的应用,解此题的关键是求出AM 、AN 的长.15、已知:如图,点C 在线段AB 上,点M 、N 分别是AC 、BC 的中点.(1)若线段AC =6,BC =4,求线段MN 的长度;(2)若AB =a ,求线段MN 的长度;(3)若将(1)小题中“点C 在线段AB 上”改为“点C 在直线AB 上”,(1)小题的结果会有变化吗?求出MN 的长度. 答案:(1)5cm ;(2)12a ;(3)1或5. 解析:(1)由点M 、N 分别是AC 、BC 的中点.可知MC =3,CN =2,从而可求得MN 的长度.(2)由点M 、N 分别是AC 、BC 的中点,MN =MC +CN =12(AC +BC )=12AB .(3)由于点C 在直线AB 上,所以要分两种情况进行讨论计算MN 的长度.解:(1)∵ AC =6,BC =4,∴ AB =6+4=10,又∵ 点M 是AC 的中点,点N 是BC 的中点,∴ MC =AM =12AC ,CN =BN =12BC ,∴ MN =MC +CN =12AC +12BC =12(AC +BC )=12AB =5(cm ).(2)由(1)中已知AB =10cm 求出MN =5cm ,分析(1)的推算过程可知MN =12AB ,故当AB=a时,MN=12a,从而得到规律:线段上任一点把线段分成的两部分的中点间的距离等于原线段长度的一半.(3)分类讨论:当点C在点B的右侧时,如图可得:MN=MC−NC=12AC−12BC=12(AC−BC)=12×(6−4)=1;当点C在线段AB上时,如(1);当点C在点A的左侧时,不满足题意.综上可得:点C在直线AB上时,MN的长为1或5.小提示:本题考查线段计算问题,涉及线段中点的性质,分类讨论的思想,属于基础题型.。
初中几何经典例题及解题技巧

初中几何证明技巧及经典试题证明两线段相等1. 两全等三角形中对应边相等。
2.同一三角形中等角对等边。
3.等腰三角形顶角的平分线或底边的高平分底边。
4.平行四边形的对边或对角线被交点分成的两段相等。
5.直角三角形斜边的中点到三顶点距离相等。
6.线段垂直平分线上任意一点到线段两段距离相等。
7.角平分线上任一点到角的两边距离相等。
8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。
*9.同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。
*10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。
11.两前项(或两后项)相等的比例式中的两后项(或两前项)相等。
*12.两圆的内(外)公切线的长相等。
13.等于同一线段的两条线段相等。
证明两个角相等1.两全等三角形的对应角相等。
2.同一三角形中等边对等角。
3.等腰三角形中,底边上的中线(或高)平分顶角。
4.两条平行线的同位角、内错角或平行四边形的对角相等。
5.同角(或等角)的余角(或补角)相等。
*6.同圆(或圆)中,等弦(或弧)所对的圆心角相等,圆周角相等,弦切角等于它所夹的弧对的圆周角。
*7.圆外一点引圆的两条切线,圆心和这一点的连线平分两条切线的夹角。
8.相似三角形的对应角相等。
*9.圆的内接四边形的外角等于内对角。
10.等于同一角的两个角相等。
证明两条直线互相垂直1.等腰三角形的顶角平分线或底边的中线垂直于底边。
2.三角形中一边的中线若等于这边一半,则这一边所对的角是直角。
3.在一个三角形中,若有两个角互余,则第三个角是直角。
4.邻补角的平分线互相垂直。
5.一条直线垂直于平行线中的一条,则必垂直于另一条。
6.两条直线相交成直角则两直线垂直。
7.利用到一线段两端的距离相等的点在线段的垂直平分线上。
8.利用勾股定理的逆定理。
9.利用菱形的对角线互相垂直。
*10.在圆中平分弦(或弧)的直径垂直于弦。
初中几何题解题技巧带例题

初中几何题解题技巧带例题Newly compiled on November 23, 2020初中几何题解题技巧在小学阶段,我们学过许多关于几何图形面积计算的知识。
在计算几何图形面积时,除了能正确运用面积计算公式外,还需要掌握一定的解题技巧。
一、割补法割补法是指将一些不规则的、分散的几何图形经过分割、移补,拼成一个规则的几何图形,从而求出面积的方法。
例1如图1,已知正方形的边长是6厘米,求阴影部分的面积。
分析与解:如图2所示,连接正方形的对角线,可以将阴影I分割成I1和I2两部分,然后将阴影I1移至空白I1′处,将阴影I2移至空白I2′处,这样阴影部分就拼成了一个等腰直角三角形。
要求阴影部分的面积,只要求出这个等腰直角三角形的面积即可,列式为:6×6÷2=18(平方厘米)。
练一练1:如图3,已知AB=BC=4厘米,求阴影部分的面积。
二、平移法平移法是指把一些不规则的几何图形沿水平或垂直方向移动,拼成一个规则的几何图形,从而求出面积的方法。
例2如图4,已知长方形的长是12厘米,宽是6厘米,求阴影部分的面积。
分析与解:如图5所示,连结长方形两条长的中点,把阴影部分分成左右两部分,然后把左边的阴影部分向右平移至空白处,这样阴影部分就转化成了一个边长为6厘米的正方形。
要求阴影部分的面积,只要求出这个正方形的面积,列式为:6×6=36(平方厘米)。
练一练2:如图6,求阴影部分的面积(单位:分米)。
三、旋转法旋转法是指把一些几何图形绕某一点沿顺时针(或逆时针)方向转动一定的角度,使分散的、不规则的几何图形合并成一个规则的几何图形,从而求出面积的方法。
例3如图7,已知ABC是等腰直角三角形,斜边AB=20厘米,D是AB的中点,扇形DAE和DBF都是圆的,求阴影部分的面积。
分析与解:如图8所示,把扇形DBF绕D点沿顺时针方向旋转180°后,扇形DBF与扇形DAE就合并成了一个半径为10厘米的半圆,两个空白三角形也合并成了一个直角边为10厘米的等腰直角三角形,要求阴影部分的面积,只要用半圆的面积减去空白部分的面积即可,列式为:×(20÷2)2÷2-(20÷2)2÷2=107(平方厘米)。
初中几何题解题技巧(带例题)

练一练 7: 如图 19 所示,已知平行四边形 EFGH 的底是 8 厘米,高是 6 厘 米,阴影部分的面积是 16 平方厘米,求四边形 ABCD 的面积。
八、两次求差法 两次求差法是指根据图形之间相容相斥的原理,通过两次求差求出面积的方 法。 例 8 如图 20,长方形 ABCD 的长是 6 厘米,宽是 4 厘米,求阴影部分的面积。
分析与解:通过作辅助线,可以将三角形 ABC 平均分成 16 个完全一样的小 三角形(如图 11 所示),阴影部分为其中 3 个小三角形,即阴影部分的面积占 三角形 ABC 的面积的。阴影部分的面积为:48×=9(平方分米)。
练一练 4: 如图 12 所示,长方形 ABCD 的长是 10 厘米,宽是 6 厘米,E、F 分别是 AB 和 AD 的中点,求阴影部分的面积。
七、等量代换法 等量代换法是指根据题目中图形之间面积相等的关系,以此代彼,相互替换, 从而求出面积的方法。 例 7 如图 18,长方形 ABCD 的面积为 1500 平方厘米,阴影部分的面积为 880 平方厘米,求四边形 EFGO 的面积。
分析与解:在长方形 ABCD 中,△ABF 与△DBF 同底(即 BF 的长)、等高(即 长方形的宽),所以 S△ABF= S△DBF 。若从这两个三角形中同时减去△BEF, 则剩下的图形面积相等,即:S△ABE=S△DEF 。这样 S 阴影=S 四边形 EFGO+
分析与解:通过仔细观察图形,我们可以发现:在大圆中,与阴影Ⅰ、阴影 Ⅱ、阴影Ⅲ面积相等的图形均有 4 个,其中阴影 1 个,空白 3 个。要求阴影部分 的面积,就相当于把大圆的面积平均分成 4 份,求其中一份的面积,列式为: 3.ቤተ መጻሕፍቲ ባይዱ4×(20÷2)2÷4=78.5(平方厘米)。
初中经典几何证明练习题(含问题详解)

初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQOP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形 ∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
初中的数学经典几何的题目及问题详解

4e d c 经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F GC EBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 N FE CDPCG FB QA DE 经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)· A D HE M C B O · GAO D B EC Q P NM · O Q PB DE C N M · A AFD E2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)D E DA CB F F EP C B A O D BFAECP AP CBP A D CB DA4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二) 经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA=200,求∠BED 的度数.FP DE CBAAPCBACBPDEDCB A A CBPD经典难题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何题解题技巧

初中数学几何题解题技巧一.添辅助线有二种情况1按定义添辅助线:如证明二直线垂直可延长使它们,相交后证交角为90°;证线段倍半关系可倍线段取中点或半线段加倍;证角的倍半关系也可类似添辅助线。
2按基本图形添辅助线:每个几何定理都有与它相对应的几何图形,我们把它叫做基本图形,添辅助线往往是具有基本图形的性质而基本图形不完整时补完整基本图形,因此“添线”应该叫做“补图”!这样可防止乱添线,添辅助线也有规律可循。
举例如下:(1)平行线是个基本图形:当几何中出现平行线时添辅助线的关键是添与二条平行线都相交的等第三条直线(2)等腰三角形是个简单的基本图形:当几何问题中出现一点发出的二条相等线段时往往要补完整等腰三角形。
出现角平分线与平行线组合时可延长平行线与角的二边相交得等腰三角形。
(3)等腰三角形中的重要线段是个重要的基本图形:出现等腰三角形底边上的中点添底边上的中线;出现角平分线与垂线组合时可延长垂线与角的二边相交得等腰三角形中的重要线段的基本图形。
(4)直角三角形斜边上中线基本图形出现直角三角形斜边上的中点往往添斜边上的中线。
出现线段倍半关系且倍线段是直角三角形的斜边则要添直角三角形斜边上的中线得直角三角形斜边上中线基本图形。
(5)三角形中位线基本图形几何问题中出现多个中点时往往添加三角形中位线基本图形进行证明当有中点没有中位线时则添中位线,当有中位线三角形不完整时则需补完整三角形;当出现线段倍半关系且与倍线段有公共端点的线段带一个中点则可过这中点添倍线段的平行线得三角形中位线基本图形;当出现线段倍半关系且与半线段的端点是某线段的中点,则可过带中点线段的端点添半线段的平行线得三角形中位线基本图形。
(6)全等三角形:全等三角形有轴对称形,中心对称形,旋转形与平移形等;如果出现两条相等线段或两个档相等角关于某一直线成轴对称就可以添加轴对称形全等三角形:或添对称轴,或将三角形沿对称轴翻转。
当几何问题中出现一组或两组相等线段位于一组对顶角两边且成一直线时可添加中心对称形全等三角形加以证明,添加方法是将四个端点两两连结或过二端点添平行线(7)相似三角形:相似三角形有平行线型(带平行线的相似三角形),相交线型,旋转型;当出现相比线段重叠在一直线上时(中点可看成比为1)可添加平行线得平行线型相似三角形。
初中数学全部几何模型汇总+附例题精编

专题一 平行线的五大类拐点模型模型一 铅笔头模型1例题1 (1)如图,若CD AB //,此时,E D B ∠∠∠,,之间有什么关系?请证明【解析】如图,过点E 作AB l //得证360=∠+∠+∠E D B(2)反之,如图,若360=∠+∠+∠E D B ,直线AB 与CD 有什么位置关系?请证明【解析】如图,过点E 作AB l //得证CD l //则CD AB // 【总结】①辅助线:过拐点作平行线②若CD AB //,则360=∠+∠+∠E D B ③若360=∠+∠+∠E D B ,则CD AB //例题2 如图,两直线CD AB ,平行,则=∠+∠+∠+∠+∠+∠654321【解析】如图,过F 作AB l //1,过G 作12//l l ,过H 作23//l l ,过I 作34//l l 得证900654321=∠+∠+∠+∠+∠+∠【总结】①辅助线:过拐点作平行线,且有多少个拐点就作多少条平行线 ②)1(180121-=∠+∠+⋅⋅⋅+∠+∠-n A A A A n n【2-n 个拐点】例题3 (1)如图,若CD AB //,则E D B ∠=∠+∠,你能说明为什么吗?【解析】如图,过点E 作AB l //得证E D B ∠=∠+∠(2)在图中,CD AB //,G E ∠+∠与D F B ∠+∠+∠又有何关系?【解析】如图,过点E 作AB l //1,过点F 作AB l //2,过点G 作AB l //3得证G E ∠+∠=D F B ∠+∠+∠(3)在图中,若CD AB //,又得到什么结论?【解析】同理可得n n E E E D F F F B ∠++∠+∠=∠+∠++∠+∠+∠- 21121 【总结】①辅助线:过拐点作平行线,且有多少个拐点就作多少条平行线 ②所有朝左的角之和等于所有朝右的角之和例题4 如图所示,已知CD AB //,BE 平分ABC ∠,DE 平分ADC ∠,求证:)(21C A E ∠+∠=∠【解析】①方法一:锯齿模型【锯齿ABEDC 】如图,过点E 作AB EF //+转化思想得证 ②方法二:8字模型(详解见第2讲) 【总结】①辅助线:过拐点作平行线,且有多少个拐点就作多少条平行线 ②所有朝左的角之和等于所有朝右的角之和 ③转化思想例题5 如图,已知CD AB //,EAB EAF ∠=∠41,ECD ECF ∠=∠41,求证: AEC AFC ∠=∠43【解析】锯齿BAECD +锯齿BA F CD ;过点E 作AB GE //,过点F 作CD HF //+方程思想【βα,表示角度】得证 【总结】①辅助线:过拐点作平行线,且有多少个拐点就作多少条平行线 ②所有朝左的角之和等于所有朝右的角之和 ③方程思想例题6 如图,CD AB //,61=∠BED ,ABE ∠的平分线与CDE ∠的平分线交于点F ,则=∠DFB ( )A.149 B .5.149 C .150 D .5.150【解析】锯齿CD F BA +铅笔头CDEBA ;得证B 【总结】①辅助线:过拐点作平行线,且有多少个拐点就作多少条平行线 ②铅笔头模型:角之和=180×(拐点个数+1)微信公众号:数学三剑客 ③锯齿模型:所有朝左的角之和等于所有朝右的角之和例题7 如图,已知点P 是矩形ABCD 内一点(不含边界),设21,θθ=∠=∠PBA PAD ,43,θθ=∠=∠PDC PCB ,若 50,80=∠=∠CPD APB ,则( )A .30)()(3241=+-+θθθθB .40)()(3142=+-+θθθθ C .70)()(4321=+-+θθθθD .180)()(4321=+++θθθθ【解析】锯齿ADPCB +锯齿DAPBC ;得证A 【总结】①辅助线:过拐点作平行线,且有多少个拐点就作多少条平行线 ②所有朝左的角之和等于所有朝右的角之和例题8 如图,若CD AB //,E D B ∠∠∠,,之间有什么关系?请证明【解析】如图,过点E 作AB l //得证B E D ∠=∠+∠ 臭脚模型基础(汇总)【总结】①辅助线:过拐点作平行线,且有多少个拐点就作多少平行线例题9 如图,直线CD AB //,50,30,90,30=∠=∠=∠=∠CNP HMN FGH EFA ,则GHM ∠的大小是【解析】①方法一:如图,过点H 作AB QH //则有铅笔头A F GH Q+臭脚Q HMNC 得证40=∠GHM ②方法二:锯齿B F GHMND 得证40=∠GHM 【总结】①辅助线:过拐点作平行线,且有多少个拐点就作多少平行线模型七 蛇型基础例题10 如图,若D C B CD AB ∠∠∠,,,//之间有什么关系?请证明【解析】过点C 作AB l //得证180=∠-∠+∠D C B 【总结】①辅助线:过拐点作平行线,且有多少个拐点就作多少平行线模型八 蜗牛模型基础例题11 如图,若D C B DE AB ∠∠∠,,,//之间有什么关系?请证明【解析】过点C 作AB l //得证180=∠+∠+∠D C B【总结】辅助线:过拐点作平行线,且有多少个拐点就作多少平行线专题二 飞镖模型和8字模型模型一 角的飞镖模型1结论:C B A BDC ∠+∠+∠=∠【解析】①方法一:延长BD 交AC 于点E 得证 ②方法二:延长CD 交AB 于点F 得证③方法三:延长AD 到在其延长方向上任取一点为点G 得证 【总结】利用三角形外角的性质证明模型二 角的8字模型1结论:D C B A ∠+∠=∠+∠【解析】①方法一:三角形内角和得证②方法二:三角形外角【BOD ∠】的性质得证 【总结】①利用三角形内角和等于180 ②利用三角形外角的性质证明模型三 角的飞镖模型和8字模型2例题1 如图,则=∠+∠+∠+∠+∠E D C B A【解析】①方法一:飞镖ACD 得证180=∠+∠+∠+∠+∠E D C B A ②方法二:8字BECD 得证 180=∠+∠+∠+∠+∠E D C B A例题2 如图,则=∠+∠+∠+∠+∠+∠F E D C B A【解析】飞镖AB F+飞镖DEC 得证210=∠+∠+∠+∠+∠+∠F E D C B A例题3 如图,求=∠+∠+∠+∠+∠+∠F E D C B A【解析】8字模型得证360=∠+∠+∠+∠+∠+∠F E D C B A例题4 如图,求=∠+∠+∠+∠D C B A【解析】连接BD 得飞镖BAD +飞镖DBC 得证 220=∠+∠+∠+∠D C B A例题5 如图,求=∠+∠+∠+∠+∠+∠+∠+∠H G F E D C B A【解析】飞镖EHB +飞镖F AC 得证360=∠+∠+∠+∠+∠+∠+∠+∠H G F E D C B A模型四 边的飞镖模型1结论:CD BD AC AB +>+【解析】延长BD 交AC 于点E +三角形三边关系+同号不等式【大的放左边,小的放在右边】模型五 边的8字模型1结论:BC AD CD AB +<+【解析】三角形三边关系+同号不等式【大的放在右边,小的放在左边】 【总结】①三角形两边之和大于第三边模型六 边的飞镖模型和8字模型2例题6 如图,点P 为ABC ∆内一点,试说明AB PC PB PA AC BC AB <++<++)(21AC BC ++【解析】三角形三边关系+边的飞镖模型可证例题7 如图,BD AC ,是四边形ABCD 的对角线,且BD AC ,相交于点O ,求证:AD CD BC AB BD AC AD CD BC AB +++<+<+++)(21【解析】边的8字模型+三角形三边关系可证专题三 三垂直全等模型模型一 K 型三垂直1例题1 如图,DE AE DE AE BC CD BC AB =⊥⊥⊥,,,,求证:BC CD AB =+【解析】易证模型二 K 型三垂直2例题2 如图,等腰90,=∠∆AOB OAB Rt ,斜边AB 交y 轴正半轴于点C ,若)1,3(A ,则点C 的坐标为【解析】K 型三垂直模型+一次函数可得点C 坐标为)25,0(例题3 如图,在EF B ABC Rt ,90,=∠∆是AC 的垂直平分线,且CE EF =,D 是AB 的中点,21tan =A ,若15+=+DE EF ,求DEF ∆的面积【解析】21例题4 如图,在矩形ABCD 中,E AD AB ,12,6==为边AB 上一点,Q P AE ,,2=分别为边BC AD ,上的两点,且45=∠PEQ ,若EPQ ∆为等腰三角形,则AP 的长为【解析】10(该图为PQ EQ =)或6(PQ PE =图略)或224+(EQ EP =)模型三 L 型三垂直1例题5 如图,CE BE CE AD BC AC ACB ⊥⊥==∠,,,90,垂足分别是点1,3,,==BE AD E D ,则DE 的长是( )A .23B .2C .22D .10【解析】B模型四 L 型三垂直2例题6 如图,直线l 过正方形ABCD 的顶点D ,过C A ,分别作直线l 的垂线,垂足分别为F E ,,若a CF a AE ==,4,则正方形ABCD 的面积为【解析】217a例题7 如图,以ABC Rt ∆的斜边AC 为边,在ABC ∆同侧作正方形AEDC ,O 为对角线交点,连接BO ,若22,4==BO AB ,则正方形的面积是【解析】80例题8 如图,在ABC ∆中,BD CD BD CD AB BC AC ACB 3,,52,,90=⊥===∠,则ABD ∆的面积是【解析】①方法一:L 型三垂直+整体减空白 ②方法二:L 型三垂直+面积公式③方法三:铅垂高求面积法【½×(水平高×铅锤高)】 ④方法四:和角模型模型五 十字型三垂直1【解析】垂直⇔相等模型六 十字型三垂直2例题9 如图,已知正方形ABCD 的边长为4,点F E ,分别在边BC AB ,上,且1==BF AE ,则=OC【解析】512例题10 如图,在等腰ABC Rt ∆中,90=∠ACB ,点D 为BC 边上的中点,AD CE ⊥,分别交AD AB ,于点F E ,,连接DE ,求证:BDE ADC ∠=∠【解析】易证专题四 角平分线四大模型角平分线的定义:从一个角的顶点引出的一条射线,把这个叫分成两个相等的角,这条射线叫做这个角的平分线角平分线的性质定理:角平分线上的点到角两边距离相等角平分线的判定定理:角的内部,到角两边距离相等的点,在这个角的平分线上模型一 双垂直模型1角的平分线上的点到这个角的两边的距离相等例题1 已知:43,21∠=∠∠=∠,求证:AP 平分BAC ∠【解析】易证例题2 已知:如图,在四边形中,CD AD AB BC =>,,BD 平分ABC ∠,求证:BAD ∠180=∠+C【解析】①方法一:双垂模型 ②方法二:双等模型例题3 如图,正方形ABCD 的边长为4,DAC ∠的平分线交DC 于点E ,若点Q P ,分别是AD 和AE 上的动点,则PQ DQ +的最小值是【解析】①方法一:双垂模型②方法二:双等模型【将军饮马+垂线段最短】 答案:22有垂直于角平分线的线,果断延长,就会得到一个等腰三角形例题4 如图,在ABC ∆中,BE 是角平分线,BE AD ⊥,垂足为D ,求证:C ∠+∠=∠12【解析】易证例题5 如图,在ABC ∆中,AC AB BAC ==∠,90,BE 平分ABC ∠,BE CE ⊥,求证:BD CE 21=【解析】易证例题6 如图,AD CD AC AB CAD BAD ⊥>∠=∠,,于点D ,H 是BC 的中点,求证:)(21AC AB DH -=【解析】易证例题7 如图所示,OP 平分MON ∠,A 为OM 上一点,C 为OP 上一点,连接AC ,在射线ON 上截取OA OB =,连接BC ,易证:BOC AOC ∆≅∆例题8 如图所示,在ABC ∆中,AB AC >,AD 是内角平分线,P 是AD 上异于点A 的任意一点,求证:AB AC PB PC -<-【解析】易证例题9 在ABC ∆中,108,=∠=A AC AB ,BD 平分ABC ∠,求证:=BC CD AB +【解析】①方法一:双等模型 ②方法二:截长补短例题10 如图,梯形ABCD 中,BC AD //,点E 在CD 上,且AE 平分BAD ∠,BE 平分ABC ∠,求证:BC AB AD -=【解析】①方法一:双等模型+截长 ②方法二:双平模型+补短角平分线、平行线、等腰三角形,三个条件,知二推一例题11 如图,在ABC ∆中,ABC ∠与ACB ∠的角平分线相交于点F ,过F 作BC DE //,交AB 于点D ,交AC 于点E ,若9=+CE BD ,则线段DE 之长为【解析】9例题12 如图,在ABC ∆中,CD BD ,分别平分ABC ∠和ACB ∠,AC FD AB ED //,//,如果cm BC 6=,则DEF ∆的周长【解析】cm 6例题13 如图,在ABC ∆中,AD 平分BAC ∠,点F E ,分别在AD BD ,上,AB EF //,且CD DE =,求证:AC EF =【解析】双平模型+类倍长中线法(延长FD 于点G 使得DG FD =,连接CG ;延长AD 于点G 使得DG AD =,连接EG )∠的平分线交BC于点E,交DC的延长线于点F,例题14 如图,在矩形ABCD中,BAD∠的度数点G是EF的中点,求BDG【解析】①方法一:双平模型+手拉手模型【G点+反推法】②方法二:双平模型+隐形圆模型【共斜边】专题五 截长补短模型截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略。
八年级上 数学几何典型例题 及 解题思路

数学几何是初中数学的一个重要部分,也是学生们比较容易感到困惑的一个知识点。
通过典型例题的学习,可以帮助学生掌握数学几何的解题方法,提高他们的解题能力。
下面就一些典型的数学几何例题进行详细讲解,希望能够对广大学生有所帮助。
【例题一】已知直角三角形ABC中,∠B=90°,AB=5cm,BC=12cm,求AC的长度。
解题思路:1. 根据勾股定理,直角三角形的斜边长度可以通过其两条直角边的长度求得。
2. AC的长度即为三角形ABC的斜边长度,可以使用勾股定理求解。
具体步骤:1. 根据勾股定理,AC的长度可以通过AB和BC的长度求得,即AC²=AB²+BC²。
2. 代入数据,得到AC²=5²+12²=25+144=169。
3. 开平方,得到AC=√169=13cm。
AC的长度为13cm。
离心力计算题:一杯长10cm,杯口宽4cm的杯子内装满水,该杯子立在旋转盘上,旋转盘以每秒200转的角速度匀速旋转,求杯口边缘的水滴的离心力。
解题思路:1. 离心力是一个物体在旋转运动时产生的一种惯性力,可以通过公式计算得出。
2. 对于杯口边缘的水滴,可以看作是在旋转盘上做匀速圆周运动,因此可以利用离心力的公式进行计算。
具体步骤:1. 离心力的公式为F=mω²r,其中m为物体的质量,ω为角速度,r 为旋转半径。
2. 首先计算出水滴的质量,然后根据旋转盘的角速度和杯子的半径计算出离心力的大小。
这里就不再罗列具体计算步骤,具体计算过程略。
最后得出水滴的离心力为XXX。
【例题三】已知矩形ABCD中,AB=8cm,BC=6cm,P是AB的中点,E是BC 上一点,使得PE⊥AB,求PE的长度。
解题思路:1. 首先利用矩形的性质和垂直平分线的性质进行分析。
2. 利用相似三角形的性质,通过比较辅助线的长度来求解PE的长度。
具体步骤:1. 由矩形的性质可知,AD=BC=6cm,同时由垂直平分线的性质可知,PE=EC,且PE⊥AB。
初中数学几何拔高题精编版

专题:角平分线、线段的垂直平分线一、角平分线1定义:2性质:3判定:二、线段的垂直平分线1、定义:2、性质:3、判定:典型例题讲解:1、如图,在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB、BC延长线于F、E求证:(1)∠EAD=∠EDA ;(2)DF∥AC(3)∠EAC=∠B2.如图,在△ABC 中,AB =AC ,∠A =120°,AB 的垂直平分线MN 分别交BC 、AB 于点M 、N .求证:CM =2BM .3、如图,PA=PB ,∠1+∠2=180 。
求证:OP 平分∠AOB 。
21)OPBA4、如图13,△ABC 中,P 、Q 分别是BC 、AC 上的点,PR ⊥AB 于R ,PS ⊥AC 于S ,若AQ=PQ ,RP=PS 。
则PQ 与AB 是否平行?S QRPCB A能力提升:、1.如图,A、B两村在一条小河的的同一侧,要在河边建一水厂向两村供水.(1)若要使自来水厂到两村的距离相等,厂址应选在哪个位置?(2)若要使自来水厂到两村的输水管用料最省,厂址应选在哪个位置?请将上述两种情况下的自来水厂厂址标出,并保留作图痕迹..BA .2.已知∠MON内有一定点P,在角的两边OM、ON上能否分别找到两点A、B,使△APB的周长最短?3.3.如图所示,在△ABC中,CD是AB上的中线,且DA=DB=DC.(1)已知∠A=︒30,求∠ACB的度数;(2)已知∠A=︒40,求∠ACB的度数;(3)已知∠A=︒x,求∠ACB的度数;(4)请你根据解题结果归纳出一个结论.CB4.如图所示,在等边三角形ABC 中,∠B 、∠C 的平分线交于点O ,OB 和OC 的垂直平分线交BC 于E 、F ,试用你所学的知识说明BE =EF =FC 的道理.5.如图,△ABC 中,AB=AC ,∠BAC=120°,AD ⊥AC 交BC•于点D ,•求证:•BC=3AD.DCABABOEFC6.如图,已知点B 、C 、D 在同一条直线上,△ABC 和△CDE•都是等边三角形.BE 交AC 于F ,AD 交CE 于H ,①求证:△BCE ≌△ACD ;②求证:CF=CH ;③判断△CFH•的形状并说明理由.EDCABH F7.如图,已知△ABC 中,AH⊥BC 于H ,∠C=35°,且AB+BH=HC ,求∠B 度数.CABH8.如图,点E 是等边△ABC 内一点,且EA=EB ,△ABC 外一点D 满足BD=AC ,且BE 平分∠DBC ,求∠BDE 的度数.EDCAB9.如图1,△ABC 中,∠ABC 和∠ACB 的平分线交于点D ,过D 作EF//BC, 交AB 于E, 交AC 于F, 易证: EF=BE+CF.当D 为∠ABC 的平分线和∠ACB 的外角平分线的交点(如图2)时,或当D 为∠ABC 的外角平分线和∠ACB 的外角平分线的交点(如图3)时,其它条件都不变,EF 、BE 、CF 的关系又如何?请对图2进行证明.ABC DE FH A BCDEFGABCDEFG。
初中数学经典几何题及答案-附知识点及结论总结
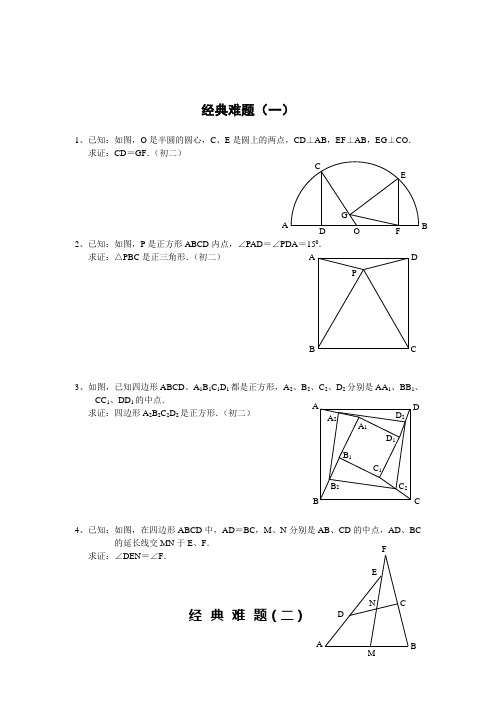
经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难 1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典难1、已知:△ABC 是正三角形,P求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二) 经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC0,∠EBA =200,求∠BED 的度数.经典难题(一)1.如下图做GH ⊥AB,连接EO 。
八年级几何解题技巧

八年级几何解题技巧一、三角形相关(1 - 10题)题1:在△ABC中,∠A = 50°,∠B = 60°,求∠C的度数。
解析:根据三角形内角和为180°,所以∠C=180° - ∠A - ∠B = 180°-50° - 60°= 70°。
题2:已知等腰三角形的一个底角为40°,求这个等腰三角形的顶角的度数。
解析:等腰三角形两底角相等,三角形内角和为180°。
所以顶角的度数为180° - 2×40°=180° - 80° = 100°。
题3:在△ABC中,AB = AC,AD是底边BC上的高,若∠BAC = 100°,求∠BAD的度数。
解析:因为AB = AC,所以△ABC是等腰三角形,AD是底边BC上的高,AD也是∠BAC的角平分线。
所以∠BAD=(1)/(2)∠BAC=(1)/(2)×100° = 50°。
题4:三角形三边分别为3,4,x,求x的取值范围。
解析:根据三角形三边关系,两边之和大于第三边,两边之差小于第三边。
所以4 -3<x<4 + 3,即1<x<7。
题5:如图,在△ABC中,∠ACB = 90°,CD⊥AB于D,若∠A = 30°,BC = 2,求BD 的长。
解析:在Rt△ABC中,∠A = 30°,BC = 2,根据30°所对直角边是斜边的一半,所以AB = 2BC=4。
又因为在Rt△BCD中,∠BCD=∠A = 30°,BC = 2,所以BD=(1)/(2)BC = 1。
题6:证明:三角形的一个外角等于与它不相邻的两个内角之和。
解析:已知△ABC,∠ACD是∠ACB的外角。
延长BC到D,因为∠ACD+∠ACB = 180°(平角定义),∠A+∠B + ∠ACB=180°(三角形内角和定理)。
初中几何经典例题、“解题技巧”大分享!

初中几何经典例题、“解题技巧”大分享!
许许多多的孩子在小学阶段的学习成绩还算不错,但是步入初中之后就开始落后。
特别是数学这门学科,是孩子们成绩下降最严重的科目。
初中数学在小学的基础上难度加深了,学的知识点对孩子的逻辑思维能力的要求也更强了。
特别是函数和几何,是初中孩子最犯难的两个类型。
初中几何是比较抽象的知识点,很多孩子在刚接触的时候会出现跟不上老师节奏的可能。
为了让孩子更好的学习几何知识,掌握其中的重点难点,我将平时课上讲解的10大几何方面的经典例题,与大家分享,希望能够帮到有需要的家长和孩子,培养好孩子学习几何的思
维。
当然,家长如果有关于孩子学习方面的问题,或者需要其他的学习方法和学习资料,都可以添加我的微信号:jiyifa119,直接与我在微信上与我沟通。
我将免费为您解答。
一、分割法
二、添加辅助线法
三、倍比法
四、割补平移法
五、等量代换法
六、等腰直角三角形法
七、扩倍、缩倍法
八、代数法
九、外高法
十、概念法
一个真正好的老师,不是教孩子多少知识点,而是传授好的学习方法。
一个好的学习方法将决定你的学习生涯!
我专注于记忆力提升、中小学学习方法的研究,帮助孩子找到适合的学习方法,有什么问题随时在微信上向我咨询,我都将免费为您解答。
欢迎添加我的微信:jiyifa119 教孩子不一样的学习法,快速提高成绩。
初中几何典型题精编

初中几何典型题精编1. “哎呀,这道几何题可真难啊!”就像我那次找玩具,明明记得放在那里,却怎么也找不到,急得我呀!比如这道题:已知一个三角形,它的两条边分别是 5 厘米和 7 厘米,那第三条边最长能是多少呢?2. “哇塞,这个几何图形好有意思呀!”就像我看到了一个超级酷炫的机器人,充满了新奇。
比如:有一个正方形的花园,边长是 8 米,在里面围一个最大的圆形花坛,这个圆形花坛的面积是多少呢?3. “嘿,这道几何题我一定要把它拿下!”就像我和小伙伴比赛跑步,我非要争第一一样。
比如:一个长方形的长是 12 分米,宽是 8 分米,把它分成两个一样的梯形,每个梯形的面积是多少?4. “天哪,这几何题也太绕了吧!”就好像我在一堆乱七八糟的线团里找线头,好晕啊!比如:有一个圆柱,底面直径是 6 厘米,高是 10 厘米,把它削成一个最大的圆锥,圆锥的体积是多少?5. “哈哈,这道几何题我懂啦!”就如同我终于解开了一个很难的拼图,开心极了。
比如:一个直角三角形的两条直角边分别是 3 厘米和 4 厘米,斜边是 5 厘米,求它的面积。
6. “哎呀呀,这几何题可真让人头疼!”就像我面对一堆作业不知道从哪里开始一样。
比如:一个圆锥的底面半径是 3 厘米,高是 5 厘米,求它的体积。
7. “哇哦,这道几何题感觉好有趣呀!”好像我发现了一个新的游戏,充满了好奇。
比如:有一个圆,它的直径是 10 厘米,在圆里画一个最大的正方形,正方形的面积是多少?8. “哼,我就不信我做不出来这道几何题!”就像我努力去够高处的一个东西,不拿到不罢休。
比如:一个等腰梯形的上底是 5 厘米,下底是 9 厘米,腰是 6 厘米,求它的周长。
9. “哎呀,这初中几何题也太有挑战性了吧!”这不就像我爬山的时候,那陡峭的山坡让我又兴奋又紧张嘛!比如:有一个球体,半径是 4 厘米,求它的表面积。
10. “哈哈,我找到解决这道几何题的方法啦!”就如同我找到了丢失好久的宝贝一样惊喜!比如:一个菱形的两条对角线分别是 6 厘米和 8 厘米,求这个菱形的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中几何证明技巧及经典试题证明两线段相等1.两全等三角形中对应边相等。
2.同一三角形中等角对等边。
3.等腰三角形顶角的平分线或底边的高平分底边。
4.平行四边形的对边或对角线被交点分成的两段相等。
5.直角三角形斜边的中点到三顶点距离相等。
6.线段垂直平分线上任意一点到线段两段距离相等。
7.角平分线上任一点到角的两边距离相等。
8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。
*9.同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。
*10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。
11.两前项(或两后项)相等的比例式中的两后项(或两前项)相等。
*12.两圆的内(外)公切线的长相等。
13.等于同一线段的两条线段相等。
证明两个角相等1.两全等三角形的对应角相等。
2.同一三角形中等边对等角。
3.等腰三角形中,底边上的中线(或高)平分顶角。
4.两条平行线的同位角、内错角或平行四边形的对角相等。
5.同角(或等角)的余角(或补角)相等。
*6.同圆(或圆)中,等弦(或弧)所对的圆心角相等,圆周角相等,弦切角等于它所夹的弧对的圆周角。
*7.圆外一点引圆的两条切线,圆心和这一点的连线平分两条切线的夹角。
8.相似三角形的对应角相等。
*9.圆的内接四边形的外角等于内对角。
10.等于同一角的两个角相等。
证明两条直线互相垂直1.等腰三角形的顶角平分线或底边的中线垂直于底边。
2.三角形中一边的中线若等于这边一半,则这一边所对的角是直角。
3.在一个三角形中,若有两个角互余,则第三个角是直角。
4.邻补角的平分线互相垂直。
5.一条直线垂直于平行线中的一条,则必垂直于另一条。
6.两条直线相交成直角则两直线垂直。
7.利用到一线段两端的距离相等的点在线段的垂直平分线上。
8.利用勾股定理的逆定理。
9.利用菱形的对角线互相垂直。
*10.在圆中平分弦(或弧)的直径垂直于弦。
*11.利用半圆上的圆周角是直角。
证明两直线平行1.垂直于同一直线的各直线平行。
2.同位角相等,内错角相等或同旁内角互补的两直线平行。
3.平行四边形的对边平行。
4.三角形的中位线平行于第三边。
5.梯形的中位线平行于两底。
6.平行于同一直线的两直线平行。
7.一条直线截三角形的两边(或延长线)所得的线段对应成比例,则这条直线平行于第三边。
证明线段的和差倍分1.作两条线段的和,证明与第三条线段相等。
2.在第三条线段上截取一段等于第一条线段,证明余下部分等于第二条线段。
3.延长短线段为其二倍,再证明它与较长的线段相等。
4.取长线段的中点,再证其一半等于短线段。
5.利用一些定理(三角形的中位线、含30度的直角三角形、直角三角形斜边上的中线、三角形的重心、相似三角形的性质等)。
证明角的和差倍分1.与证明线段的和、差、倍、分思路相同。
2.利用角平分线的定义。
3.三角形的一个外角等于和它不相邻的两个内角的和。
证明线段不等1.同一三角形中,大角对大边。
2.垂线段最短。
3.三角形两边之和大于第三边,两边之差小于第三边。
4.在两个三角形中有两边分别相等而夹角不等,则夹角大的第三边大。
*5.同圆或等圆中,弧大弦大,弦心距小。
6.全量大于它的任何一部分。
证明两角的不等1.同一三角形中,大边对大角。
2.三角形的外角大于和它不相邻的任一内角。
3.在两个三角形中有两边分别相等,第三边不等,第三边大的,两边的夹角也大。
*4.同圆或等圆中,弧大则圆周角、圆心角大。
5.全量大于它的任何一部分。
证明比例式或等积式1.利用相似三角形对应线段成比例。
2.利用内外角平分线定理。
3.平行线截线段成比例。
4.直角三角形中的比例中项定理即射影定理。
*5.与圆有关的比例定理---相交弦定理、切割线定理及其推论。
6.利用比利式或等积式化得。
证明四点共圆*1.对角互补的四边形的顶点共圆。
*2.外角等于内对角的四边形内接于圆。
*3.同底边等顶角的三角形的顶点共圆(顶角在底边的同侧)。
*4.同斜边的直角三角形的顶点共圆。
*5.到顶点距离相等的各点共圆知识归纳:1. 几何证明是平面几何中的一个重要问题,它对培养学生逻辑思维能力有着很大作用。
几何证明有两种基本类型:一是平面图形的数量关系;二是有关平面图形的位置关系。
这两类问题常常可以相互转化,如证明平行关系可转化为证明角等或角互补的问题。
2. 掌握分析、证明几何问题的常用方法:(1)综合法(由因导果),从已知条件出发,通过有关定义、定理、公理的应用,逐步向前推进,直到问题的解决;(2)分析法(执果索因)从命题的结论考虑,推敲使其成立需要具备的条件,然后再把所需的条件看成要证的结论继续推敲,如此逐步往上逆求,直到已知事实为止;(3)两头凑法:将分析与综合法合并使用,比较起来,分析法利于思考,综合法易于表达,因此,在实际思考问题时,可合并使用,灵活处理,以利于缩短题设与结论的距离,最后达到证明目的。
3. 掌握构造基本图形的方法:复杂的图形都是由基本图形组成的,因此要善于将复杂图形分解成基本图形。
在更多时候需要构造基本图形,在构造基本图形时往往需要添加辅助线,以达到集中条件、转化问题的目的。
一. 证明线段相等或角相等两条线段或两个角相等是平面几何证明中最基本也是最重要的一种相等关系。
很多其它问题最后都可化归为此类问题来证。
证明两条线段或两角相等最常用的方法是利用全等三角形的性质,其它如线段中垂线的性质、角平分线的性质、等腰三角形的判定与性质等也经常用到。
例1. 已知:如图1所示,∆ABC 中,∠=︒===C AC BC AD DB AE CF 90,,,。
求证:DE =DF分析:由∆ABC ∠=︒DCF 45。
从而不难发现∆ 证明:连结CDAC BC A BACB AD DBCD BD AD DCB B A AE CF A DCB AD CD =∴∠=∠∠=︒=∴==∠=∠=∠=∠=∠=90,,,,∴≅∴=∆∆ADE CDF DE DF说明:在直角三角形中,作斜边上的中线是常用的辅助线;在等腰三角形中,作顶角的平分线或底边上的中线ABC CDA SSS B D AB CD AE CFBE DF∴≅∴∠=∠==∴=,∆∆() 在∆BCE 和∆DAF 中,BE DF B D BC DA BCE DAF SAS E F=∠=∠=⎧⎨⎪⎩⎪∴≅∴∠=∠∆∆()说明:利用三角形全等证明线段求角相等。
常须添辅助线,制造全等三角形,这时应注意:(1)制造的全等三角形应分别包括求证中一量;(2)添辅助线能够直接得到的两个全等三角形。
二. 证明直线平行或垂直在两条直线的位置关系中,平行与垂直是两种特殊的位置。
证两直线平行,可用同位角、内错角或同旁内角的90°,或KH ∥BC。
同理,延长AK交又BH⊥AH ∴==︒∠∠AHB NHB90BH=BH∴≅∴==∆∆ABH NBH ASABA BN AH HN(),同理,CA=CM,AK=KM ∴KH是∆AMN的中位线∴KH MN//即KH//BC例4. 已知:如图4所示,AB求证:FD⊥ED证明一:连结ADAB AC BD DCDAEBAC BD DCBD ADB DAB DAE==∴+=︒=︒=∴=∴==,∠∠,∠∠,∠∠∠129090在∆ADE和∆BDF中,AE BF B DAE AD BD ADE BDF FD ED===∴≅∴∠=∠∴∠+∠=︒∴⊥,∠∠,∆∆313290证明二:如图5所示,延长 BD DCBDM CDE DM BDM CDE CE BM C CBM BM ACA ABM AAB AC BF AE AF CE BM =∠=∠∴≅∴=∠=∠∴∠=︒∴∠=︒=∠==∴==,,,∆∆//9090∴≅∴==∴⊥∆∆AEF BFMFE FM DM DE FD ED说明:证明两直线垂直的方法如下:(1)首先分析条件,观察能否用提供垂直的定理得到,包括添常用辅助线,见本题证二。
(2)找到待证三直线所组成的三角形,证明其中两个锐角互余。
(3)证明二直线的夹角等于90°。
三. 证明一线段和的问题(一)在较长线段上截取一线段等一较短线段,证明其余部分等于另一较短线段。
(截长法)例5. 已知:如图6所示在∆ABC 中,∠=︒B 60,∠BAC 、∠BCA 的角平分线AD 、CE 相交于O 。
求证:AC =AE +CD∠=︒B 60,知,得: ()∴≅∴∠=∠AEO AFO SAS ∆∆42又∠=︒B 60∴∠+∠=︒∴∠=︒∴∠+∠=︒∴∠=∠=∠=∠=︒∴≅∴=566016023120123460∆∆FOC DOC AAS FC DC()即AC AE CD =+(二)延长一较短线段,使延长部分等于另一较短线段,则两较短线段成为一条线段,证明该线段等于较长线段。
(补短法)例6. 已知:如图7求证:EF =BE +DF分析:此题若仿照例1 证明:延长CB 至G ,使BG = 在正方形ABCD 中,∠=ABG∴≅∴=∠=∠∆∆ABG ADF SAS AG AF (),13又∠=︒EAF 45∴∠+∠=︒∴∠+∠=︒23452145即∠GAE =∠FAE∴=∴=+GE EF EF BE DF中考题:,连结CE 、DE 。
∴==BA AF EF即EF =ACAC FDEAC EFD EAC DFE SAS EC ED//()∴∠=∠∴≅∴=∆∆题型展示:DCE B DCE EDE DC BD DC∠>∠∴∠>∠∴>∴>, 证明二:如图10所示,在AB 上截取AF =AC ,连结DFM 为BC 的中点。
4.1. 证明:取CD AC ADAF CDAFC CDE =∴⊥∴∠=∠= 又∠+∠=︒∠14901, ∴∠=∠=∴≅∴=∴=431AC CEACF CED ASA CF EDDE CD∆∆()CD CD CBD CEDB EBAC BBAC E=⎩⎪∴≅∴∠=∠∠=∠∴∠=∠∆∆22又∠=∠+∠BAC ADE E∴∠=∠∴=∴==+=+ADE E AD AE BC CE AC AE AC AD,3. 证明:延长PM 交CQ 于R11 CQ AP BP APBP CQ PBM RCM⊥⊥∴∴∠=∠,//又BM CM BMP =∠=∠, ∴≅∆∆BPM CRM()AD AB AC BC AD AB AC BC ∴<++∴<++414。
