五年级__多边形的面积(知识点整理+典型例题_推荐!!!)

合集下载

苏州苏教版五年级数学上册第二单元《多边形的面积》知识点梳理+典型例题及答案

1☆ 平行四边形的面积＝底×高 ☆ 平行四边形拉伸和平移问题：①把一个长方形框拉成平行四边形，周长不变，高变小，面积也变小；同理，把平行四边形框拉成长方形，周长不变，高变大，面积也变大.②把一个平行四边形剪拼成长方形，面积不变，宽变小，周长也变小. ☆ 两个平行四边形之间的关系：等底等高的两个平行四边形面积必相等；面积相等的两个平行四边形形状不一定相同.1. 填一填. (1) 一张平行四边形的底是30厘米，高是4厘米，那么它的面积为（）平方厘米；(2) 已知一个平行四边形的面积为180平方米，高为15米，那么它的底为（）米； (3) 已知一个平行四边形的底为22厘米，高是底的一半，那么这个平行四边形的面积为（）平方厘米.2. 选一选. (1) 用木条做成一个长方形框，把它拉成一个平行四边形后，它的面积（）A. 比原来小B. 和原来相等C. 比原来大D. 无法确定 (2) 把一个平行四边形的底扩大至4倍，高缩小至一半，那么它的面积（）A. 扩大至3倍B. 不变C. 扩大至2倍D. 缩小至一半3. 计算下列各平行四边形的面积.（单位：厘米）302555323522第二单元多边形的面积知识点一平行四边形的面积【典型例题】2☆ 三角形的面积＝底×高÷2 ☆ 两个三角形的关系：等底等高的两个三角形面积一定相等；面积相等的两个三角形形状不一定相同.☆ 三角形与平行四边形之间的关系：①一个平行四边形能分割成两个完全相同的三角形，两个完全相同的三角形能拼成一个平行四边形；②与平行四边形等底等高的三角形，面积是平行四边形的一半；③等面积且等底（或等高）的三角形和平行四边形，三角形的高（或底）是平行四边形的两倍.1. 判断. (1) 面积相等的两个三角形可以拼成一个平行四边形. （） (2) 两个底和高相等的三角形，面积也相等，两个面积相等的三角形，底和高也分别相等. （） (3) 直角三角形一条直角边上的高，就是这个三角形的另一条直角边. （）2. 计算下列图形的面积.3. 一块三角形玻璃的底为6米，高为4米，每平方米的玻璃售价98元，那么买这块玻璃需要多少元？14171015知识点二三角形的面积【典型例题】3☆ 梯形的面积＝（上底＋下底）×高÷2 ☆ 梯形与平行四边形的面积关系：①两个完全相同的梯形可以拼成一个平行四边形；②要从梯形中剪去一个最大的平行四边形，那么应把梯形的上底作为平行四边形的底，这样去剪才能最大.1. 填一填. (1) 把两个完全一样的梯形拼成一个平行四边形，这个平行四边形的底是16厘米，高是5厘米，每个梯形的面积是（）平方厘米.(2) 一个梯形的上底与下底的和是10厘米，高是4厘米，那么它的面积是（）平方厘米.(3) 一个梯形的上底和下底的平均长度是20厘米，高是17厘米，那么它的面积是（）平方厘米.2. 一个梯形的面积是42平方厘米，高是4厘米，下底是上底的3倍，那么它的上底长多少厘米？正确的算式为（）A. 42÷4÷(3＋1)B. 42×2÷4÷(3＋1)C. 42÷4÷3D. 42×2÷4÷33. 计算下列图形的面积.221113163014121510知识点三梯形的面积【典型例题】知识点四公顷、平方千米的认识☆公顷：1公顷就是边长100米的正方形的面积；1公顷＝10000平方米；一个社区、校园等的面积通常用“公顷”做单位.☆平方千米：1平方千米就是边长1000米的正方形的面积；1平方千米＝100公顷；表示一个国家、省市、地区、湖泊等的面积通常用“平方千米”做单位.【典型例题】1.在下面括号中填上合适的数.5平方千米＝（）公顷9000公顷＝（）平方千米2500平方千米＝（）平方米70000平方米＝（）公顷2.在括号里填上合适的单位.(1) 一间办公室的面积大约是56（）(2) 某大学校园的面积大约是2（）(3) 天安门广场的面积大约是45（）3.在○里面填上“＞”“＜”或“＝”.2公顷○1900平方米300公顷○3平方千米4平方千米○404公顷8000平方米○8公顷0.5公顷○510平方米7.1平方千米○710公顷1平方千米○900000平方米0.68平方米○680平方分米4.判断.(1) 1公顷土地的形状就是边长100米的正方形.（）(2) 测量和计算一个城市的土地面积，一般用平方千米做单位.（）45☆ 求组合图形面积的常见方法： ①分割法：将组合图形分割成几个规则图形，然后分别计算求和； ②添补法：将组合图形补成一个大的规则图形，将其看成是一个大的规则图形减去几个小的规则图形，然后分别计算求差.1. 先说说下面图形是由哪些简单图形拼成的，再计算它们的面积.（单位：厘米）2. 计算下图的面积.3. 计算下图的面积.11112515881610101033561012881640知识点五组合图形的面积【典型例题】参考答案及解析知识点一：平行四边形的面积1.(1) 120；(2) 12；(3) 2422.(1) A；(2) C解析：平行四边形的底扩大至4倍，面积也扩大至4倍；高缩小至一半，面积也缩小至一半，所以相比原来扩大至2倍.3.770；1760解析：平行四边形的面积等于底乘上底对应的高.☆建议：这部分出错，需加强面积公式的练习以及计算，注重面积公式中底和对应高的区分.知识点二：三角形的面积1.(1) ×；(2) ×；(3) √解析：两个完全一样的三角形可以拼成一个平行四边形；两个面积相等的三角形，底和高不一定相等.2.75；119；1923.1176解析：三角形玻璃的面积：6×4÷2＝12平方米；价格：98×12＝1176元.☆建议：第一题出错，需加强对三角形与三角形、平行四边形之间的关系；后两题出错，需加强对三角形面积公式的练习，区分面积公式中底和对应高的区分.知识点三：梯形的面积1.(1) 40；(2) 20；(3) 340解析：上底和下底的平均长度是20厘米，上底和下底的和是20×2＝40厘米；所以面积为40×17÷2＝340平方厘米.2.B解析：梯形上、下底和＝梯形面积×2÷高；梯形上底＝梯形上、下底和÷(3＋1).3.150；352☆建议：这部分出错需加强对梯形面积公式的练习，以及面积公式的正用和反用.67知识点四：公顷、平方千米的认识1. 500；90；2500000000；72. 平方米；平方千米；公顷3. ＞；＝；＜；＜；＞；＝；＞；＜4. (1) ×；(2) √ ☆建议：第一、三两题出错，需加强单位换算之间的练习；第二、四两题出错，需加强对面积单位的感知，因为长度单位易感知，所以可采用将面积转化为长度的方式，如教室面积56＝7×8，应该7米乘8米，所以56后面应该填平方米.知识点五：组合图形的面积1. 正方形和三角形，150；平行四边形和三角形，192；梯形和长方形，385 解析：10×10＋10×10÷2＝150；16×8＋16×8÷2＝192；(15＋25)×11÷2＋15×11＝385 2. 43 解析：3×10＋(6＋7)×2÷2＝433. 576 解析：(16＋8＋40)×(8＋12)÷2－8×8＝576☆建议：这部分出错，需加强对三角形、平行四边形、梯形等图形的认识，能将组合图形分解成学过的图形并计算，多练习分割和添补的方法去解决问题.723336108812881640。

(人教版)五年级数学重难点：多边形的面积(知识点+试题解析)

多边形的面积001多边形的面积1.平行四边形的底和高从平行四边形一条边上的任意一点向它的对边画一条垂直线段，这条垂直线段就是平行四边形的高，这条对边就是这条高所对应的底，如下图所示．注意：平行四边形有无数条高．2.平行四边形的面积计算公式(1)平行四边形的面积=底×高(2)如果用S表示平行四边形的面积，用a表示底，用ℎ表示高，那么平行四边形的面积公式可表示为S=aℎ．(3)注意：面积公式中的底和高必须是相对应的．3.已知面积，反求底或高(1)已知平行四边形的面积和高，求底，可以根据a=S÷ℎ计算．(2)已知平行四边形的面积和底，求高，可以根据ℎ=S÷a计算．0025年级重难点汇编1.在方格纸上数一数，比较平行四边形和长方形的面积大小有什么关系．平行四边形的和长方形的长相等，平行四边形的和长方形的宽相等，所以这两个图形的面积．（填“相等”或“不相等”）2.平行四边形的面积是（）．A.24×20B.15×24C.15×203.已知平行四边形ABCD的面积是72平方厘米，AE=6厘米，AF=8厘米，求平行四边形ABCD的周长．多边形的面积0031.平行四边形的等积变形底和高都相等的平行四边形，就算形状不同，面积也相等．如图所示的3个平行四边形的面积相等．2.平行四边形的压缩变形当一个平行四边形压缩变形时，周长不变，面积改变．4.如图，正方形的周长是28厘米，平行四边形的面积是平方厘米．5.如图，a和b是两条互相平行的直线，已知平行四边形ABCD的底是12厘米，高是8厘米，那么平行四边形CDEF的面积是多少平方厘米？0045年级重难点汇编6.如下图，把一个长7cm，宽5cm的长方形拉成一个平行四边形，图中画出的这个平行四边形的高可能是（）cm．A.4B.5C.6D.77.把一个平行四边形活动框架拉成一个长方形，那么原来平行四边形与现在长方形相比（）A.周长不变，面积不变B.周长变了，面积不变C.周长不变，面积变了1.三角形面积公式的推导（1）角形的面积是等底等高的平行四边形面积的一半，即三角形面积＝底×高÷2．所以三角形的面积＝底×高÷2．（2）如果用字母S表示三角形的面积，用a和ℎ分别表示三角形的底和高，那么三角形的面积计算公式可以写成：S＝aℎ÷2．多边形的面积0052.三角形面积公式的逆应用（1）已知三角形的面积S，高ℎ，求对应的底a：a＝2S÷ℎ．（2）已知三角形的面积S，底a，求对应的高ℎ：ℎ＝2S÷a．8.用两个完全相同的三角形拼成一个平行四边形；平行四边形与三角形的相等，相等，平行四边形的面积=×，所以其中一个三角形的面积=×÷．9.看图回答问题．（1）求下图三角形的面积．（单位：cm）（2）求下图直角三角形的面积和斜边上的高ℎ．10.如图所示，在三角形ABC中，已知AD=12厘米，BE=15厘米，BC=20厘米，则AC的长度为厘米．0065年级重难点汇编如图，三角形ACD和三角形BCD夹在一组平行线之间，由于两个三角形底相等（均为CD），高也相等（平行线间的距离处处相等），所以它们的面积也相等，即S△ACD ＝S△BCD．11.已知两条平行线间的距离是13，求三个阴影三角形的面积之和是（）A.195B.97.5C.195.5D.20012.如图，比较梯形中甲、乙两个阴影部分三角形的面积，甲的面积（）乙的面积．A.大于B.等于C.小于多边形的面积007（1）等底等高时，三角形面积是平行四边形面积的一半；等面积等底时，三角形的高是平行四边形的高的2倍；等面积等高时，三角形的底是平行四边形的底的2倍．（2）三角形与长方形或正方形的面积关系同三角形和平行四边形的面积关系相同．（3）在计算三角形与其他四边形面积关系时，主要底和高的数量关系，然后利用图形的面积公式或面积倍数关系计算．13.一个三角形和一个平行四边形的底和高分别相等．如果平行四边形的面积是200平方厘米，那么三角形的面积是（　）平方厘米．A.50B.100C.40014.一个三角形与一个平行四边形等高，平行四边形的底是三角形的底的3倍，则平行四边形的面积是三角形面积的（）A.1.5倍B.6倍C.3倍1.梯形面积公式如果用字母S表示梯形的面积，用a、b和ℎ分别表示梯形的上底、下底和高，那么梯形的面积计算公式可以写成：S＝（a＋b）×ℎ÷2．0085年级重难点汇编2.梯形面积公式的逆应用（1）已知梯形的面积S，高ℎ，上底a，求下底b：b＝2S÷ℎ－a．（2）已知梯形的面积S，高ℎ，下底b，求上底a：a＝2S÷ℎ－b．（3）已知梯形的面积S，上底a，下底b，求高ℎ：ℎ＝2S÷（a＋b）．15.如下图所示，在探究梯形面积计算公式时，可以将梯形沿两腰中点的连线剪开，将上面部分旋转后与下面部分拼成一个平行四边形，平行四边形的底和梯形的相等，平行四边形的高和梯形的相等，从而根据平行四边形的面积计算公式推导出梯形的面积计算公式．16.将两个完全相同的梯形拼在一起，你能得到什么图形？这个图形和梯形有什么关系？发现：（1）两个完全相同的梯形可以拼成一个平行四边形，拼成的平行四边形的底等于梯形的上底与下底的，平行四边形的高等于梯形的．（2）拼成的平行四边形的面积等于两个梯形的面积．多边形的面积009 17.求下列梯形中的未知量．篱笆围墙的梯形问题，通常能根据已知能得出梯形上、下底之和、然后再根据高的条件，可以直接用上、下底之和×高÷2来计算，而不需要知道上、下底分别具体是多少．18.用40米长的篱笆，在靠墙的地方围一块直角梯形菜地（如图），这块菜地的面积是多少平方米？19.孙大伯家用70米长的竹篱笆在一块靠墙的空地上围了一个花圃（如图）．（1）这个花圃的面积是多少平方米？（2）如果每平方米种菊花9棵，这个花圃一共可以种菊花多少棵？0105年级重难点汇编梯形堆木料问题除了一层一层数出数量，数字求和之外，还可以利用类似梯形面积公式求解：（顶层根数+底层根数）×层数÷220.建筑工地上有一大堆水管（如图），你能算出一共有多少根水管吗？21.自来水公司新购进一批水管，堆成如图的形状．最上层9根，最下层18根，每相邻的两层相差1根，堆了若干层．自来水公司一共购进多少根水管？多边形的面积011求不规则图形的面积，可以用数方格法进行估计．估计时，先数整格的，再数不满整格的，不满整格的按半格计算．22.考考你的估算能力（每一个小方格表示1平方厘米）．（1）下图面积约为cm2．（2）下图面积约为cm2．0125年级重难点汇编4个知识点1.分割法通过分割把不规则图形转化成几个规则图形，再把各规则图形的面积相加．例如：2.添补法把原图形添补成一个规则图形，先算出规则图形和添补图形的面积，然后从规则图形的面积中减去添补图形的面积．例如：3.整体减部分阴影部分的面积＝整个图形的面积－空白部分的面积．例如：4.平移法将两个或多个图形，通过左右平移或上下平移，使它们组合成规则图形．例如：多边形的面积01323.计算阴影部分的面积．（1）整体-部分（2）平移法24.小明将一张长方形纸的一角作如图折叠，你能帮小明求出阴影部分的面积吗？（单位：分米）0145年级重难点汇编答案解析一、平行四边形的面积（一）面积公式1.底；高；相等B2.3.42厘米（二）变形问题4.495.96平方厘米7.A6.C二、三角形面积（一）面积公式8.底高底高底高29.（1）9×6÷2=54÷2=27cm2（2）30×40÷2=1200÷2=600cm2;60×2÷50=1200÷5=24cm10.16答案解析015（二）等积变形12.11.BB（三）与四边形的关系14.B13.B三、梯形面积（一）面积公式15.上底+下底的和高的一半16.（1）和高（2）和17.S=180cm2h=6dm（二）梯形篱笆问题18.128m219.（1）这个花圃的面积是600平方米．（2）这个花圃一共可以种菊花5400棵．（三）堆木料问题20.124根21.自来水公司一共购进135根水管．四、数方格估算面积22.（1）20（2）20五、组合图形的面积23.（1）14dm2（2）120平方米24.18平方分米。

五年级奥数讲义-多边形面积计算二(附答案)

五年级奥数-多边形的面积计算二学员编号：年级：小五课时数：学员姓名：辅导科目：奥数学科教师：课程主题：多边形的面积计算二授课时间：学习目标教学内容知识点一（多边形的面积）【知识梳理】【典型例题】例题精讲例1. 如图△ABC 中，D 是BC 的中点，AC=3EC 。

已知三角形CDE 的面积是6平方厘米，那么三角形ABC 的面积是多少？答案： 362cm例2. 如下图所示，两个完全相同的直角三角形部分重叠，已知AB=10厘米，BD=4cm ，EF=3cm ，求阴影部分的面积。

G 答案：连接AF, =ACGFAEFS SS阴影即可求出，得34A FB D C③ ① EBDCE A知识精讲例3. 直角梯形ABCD 的上底AB=10，高DA=8.，下底上的线段ED=6。

求阴影部分面积。

（单位：厘米）答案：ADFS=6*8/2=24=BCFS例4. 把例3 的问题改为：梯形ABCD 的面积是多少平方厘米？答案：ADFS=24，ABFS=8*10/2-24=16, BCFS=24AF:FC=16:24=2:3ADFS:DCFS=2:3, DCFS=36S=24+24+16+36=100平方厘米【同步练习】1、在平行四边形ABCD 的一角有一个△AEF 。

已知AB=4AF,AD=3AE,△AEF 的面积是5平方厘米，求平行四边形ABCD 的面积。

答案：连接BE,BD,AB=4AF, AEBS=4 AEFS=20,AD=3AE, ADBS=3AEBS=60, S=2ADBS =1202、已知△ABC 的面积是1平方厘米，把AB ，BC ，CA 分别延长2倍到D 、E 、F ，求△DEF 的面积。

答案：连BF,DC,AE,CE=BD=BF=2, S=198A C10 6 BD EF3、下图由两个相同的直角梯形重叠在一起，求图中阴影部分的面积。

（单位：厘米）答案：45厘米4、在下图中，正方形ABCD 的边长为5厘米，又△CEF 的面积比△ADF 的面积大5平方厘米。

南京某校苏教版五年级数学上册第二单元《多边形的面积》练习及解析

第二单元多边形的面积（一）知识点整理1、公式：平行四边形的面积=底×高字母公式： S=ah三角形的面积=底×高÷2 字母公式：S=ah÷2梯形的面积=（上底+下底）×高÷2 字母公式： S=（a+b）h÷22、单位换算的方法：大化小，乘进率；小化大，除以进率。

3、常用的单位间的进率长度单位：1 千米=1000 米 1 米=10 分米 1 分米=10 厘米面积单位：1 平方千米=100 公顷 1 公顷=10000 平方米1 平方米=100 平方分米 1 平方分米=100 平方厘米4、图形之间的关系：一个平行四边形能分割成两个完全相同的三角形；两个完全相同的三角形能拼成一个平行四边形。

一个平行四边形能分割成两个完全相同的梯形；两个完全相同的梯形可能拼成一个平行四边形。

等底等高的三角形的面积相等；一个三角形的面积是与它等底等高的平行四边形面积的一半。

5、求组合图形面积的方法：割补法（二）练习一、填空题。

1.一张平行四边形纸片的底是 20 厘米,高是 15 厘米,它的面积是()平方厘米。

如果将这张纸片剪成两个大小相等的三角形,每个三角形的面积是()平方厘米。

2.一个三角形和一个平行四边形等底等高,如果这个三角形的面积是 48 平方分米,那么这个平行四边形的面积是()平方分米。

3.一个梯形的上底是 5 厘米，下底是 10 厘米,高是 4 厘米,它的面积是()平方厘米。

4.把两个完全一样的梯形拼成一个平行四边形,这个平行四边形的底是 32 厘米, 高是 6 厘米,每个梯形的面积是()平方厘米。

5.一个近似于平行四边形的菜地,面积是 270 平方米,底是 30 米,高是() 米。

二、选择题。

1.用木条做成一个长方形框,把它拉成一个平行四边形后,它的面积()。

A.比原来小 B.和原来相等C.比原来大D.无法确定2.一个三角形和一个平行四边形的面积相等,底也相等,如果平行四边形的高是22 厘米,那么三角形的高是()厘米。

小学五年级多边形的面积知识点总结和精选练习

多边形的面积知识点总结和精选练习【知识梳理】1.长方形公式：周长=(长+宽)×2 用字母表示： C=(a+b)×2 变形式：【长=周长÷2-宽宽=周长÷2-长】面积=长×宽用字母表示：S=ab 变形式：【长=面积÷宽宽=面积÷长】2.正方形公式：周长=边长×4 用字母表示：C=4a 变形式：【边长=周长÷4】面积=边长×边长用字母表示：S=a23.平行四边形的面积平行四边形的面积=底×高用字母表示：s=ah 变形式：【平行四边形的底=面积÷高（a=s÷h)】【平行四边形的高=面积÷底（h=s÷a)】（要点提示：求平行四边形的面积时，底和高要对应。

）4.三角形的面积三角形的面积=底×高÷2 用字母表示：s=ah÷2 变形式：【三角形的底=面积×2÷高（a=2s÷h)】（要点提示：）【三角形的高=面积×2÷底（h=2s÷a)】（任何三角形都有三条高，被高垂直的一边就是相应的底边。

在计算时一定是这条边的高乘以这条边。

）5.梯形的面积梯形的面积=（上底+下底）×高÷2 用字母表示：s=（a+b）h÷2变形式：【梯形的高=面积×2÷（上底+下底) 字母表示为：h=2s÷(a+b) 】【梯形的上底=面积×2÷高-下底字母表示为：a=2s÷h-b 】【梯形的下底=面积×2÷高-上底字母表示为：b=2s÷h-a 】（要点提示：已知梯形的面积，求梯形的高或其中一个底，也可以用方程法解决。

）6.组合图形的面积把求组合图形的面积转化成求几个简单图形的面积的和或差。

数学五年级多边形的面积问题整理单

五年级学生在学习数学课程中，常常遇到多边形的面积问题。

多边形的面积是一个基础而重要的数学概念，能帮助学生加深对几何图形的认识，提高他们的逻辑思维能力。

然而，在教学过程中，我们发现学生对多边形的面积计算存在一定困惑，因此有必要对多边形的面积问题进行整理和总结，以便帮助学生更好地理解和掌握这一知识点。

二、正文1. 多边形的定义多边形是指由三条或者三条以上的线段构成的平面图形，其中相邻的两条线段之间有一个共同端点并且不在同一直线上。

常见的多边形包括三角形、四边形、五边形等。

2. 多边形的面积计算公式(1) 三角形的面积计算公式三角形的面积计算公式为：S = 1/2 * 底 * 高，其中S表示三角形的面积，底表示三角形的底边长度，高表示三角形的高度。

(2) 四边形的面积计算公式① 矩形的面积计算公式为：S = 长 * 宽，其中S表示矩形的面积，长表示矩形的长度，宽表示矩形的宽度。

② 平行四边形的面积计算公式为：S = 底 * 高，其中S表示平行四边形的面积，底表示平行四边形的底边长度，高表示平行四边形的③ 梯形的面积计算公式为：S = (上底 + 下底) * 高 / 2，其中S表示梯形的面积，上底表示梯形的上底长度，下底表示梯形的下底长度，高表示梯形的高度。

(3) 正多边形的面积计算公式对于正多边形而言，我们可以通过以下公式来计算其面积：S = (正多边形的边长)^2 * n / (4 * tan(π/n))，其中S表示正多边形的面积，边长表示正多边形的边长，n表示正多边形的边数。

3. 多边形的面积计算方法(1) 利用公式计算对于简单的多边形来说，我们可以直接利用上述的面积计算公式来进行计算，较为简单直观。

(2) 分割计算法对于复杂的多边形或者特殊形状的多边形，我们可以通过将其分割成多个简单的几何图形，然后分别计算这些几何图形的面积，最后加总得到多边形的总面积。

(3) 应用实例通过实际的示例和练习来帮助学生理解和掌握多边形的面积计算方法，例如通过建模、绘图或者实际测量的方法来求解多边形的面积。

新北师大版五年级上册数学第四单元《多边形的面积》知识点总结(全)

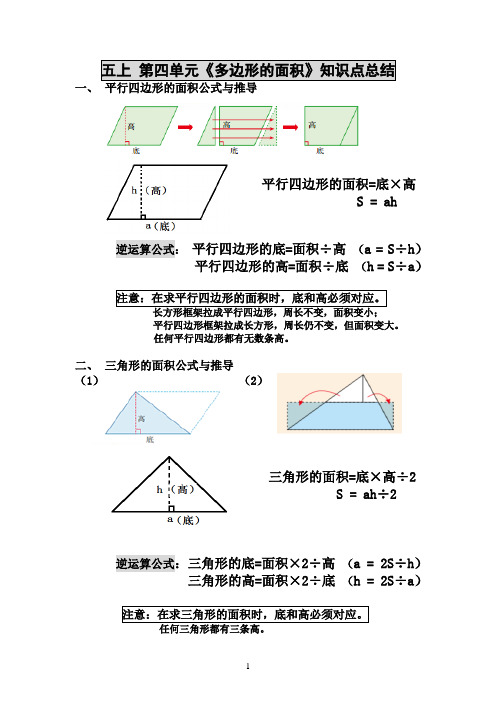
五上第四单元《多边形的面积》知识点总结一、平行四边形的面积=底×高S = ah 逆运算公式：平行四边形的底=面积÷高（a = S÷h）平行四边形的高=面积÷底（h = S÷a）注意：在求平行四边形的面积时，底和高必须对应。

平行四边形框架拉成长方形，周长仍不变，但面积变大。

任何平行四边形都有无数条高。

二、三角形的面积公式与推导（1）（2）三角形的面积=底×高÷2S = ah÷2 逆运算公式：三角形的底=面积×2÷高（a = 2S÷h）三角形的高=面积×2÷底（h = 2S÷a）注意：在求三角形的面积时，底和高必须对应。

三、等底等高的平行四边形与三角形Ⅰ.等底等高的平行四边形的面积相等。

Ⅱ.等底等高的三角形的面积相等。

Ⅲ.等底等高的三角形的面积是平行四边形的面积的一半。

Ⅰ.S 1 = S 2 Ⅱ. S △1 = S △2 Ⅲ. S 1÷2 = S △2四、梯形的面积公式与推导（1）梯形的面积=（上底＋下底）×高÷2S =（a ＋b ）×h ÷2逆运算公式：梯形的上底＋下底的和=面积×2÷高梯形的上底=面积×2÷高－下底（a = 2S ÷h-b ）梯形的下底=面积×2÷高－上底（b = 2S ÷h-a ）梯形的高=面积×2÷（上底＋下底） h = 2S ÷（a ＋b ）注意：任何梯形都有无数条高。

即时练习11.计算下面各图形的面积。

2.填表平行四边形三角形梯形底高面积底高面积上底下底高面积12m 5m 24m 8m 5m 4m 12m3dm 27dm29dm 81dm29dm 4dm48dm27cm 98cm214cm 98cm28cm 10cm 63cm2即时练习2填空：1.下图中，甲、乙两个三角形的面积比较，S甲（）S乙（填＞、＜或者=）。

五年级上册数学《多边形的面积》知识点归纳

五年级上册数学《多边形的面积》知识点归纳五年级上册数学《多边形的面积》知识点1、公式长方形：周长=(长+宽)×2;字母公式：C=(a+b)×2面积=长×宽;字母公式：S=ab正方形：周长=边长×4;字母公式：C=4a面积=边长×边长;字母公式：S=a平行四边形：面积=底×高;字母公式：S=ah三角形：面积=底×高÷2;字母公式：S=ah÷2底=面积×2÷高;高=面积×2÷底梯形：面积=(上底+下底)×高÷2;字母公式：S=(a+b)h÷2上底=面积×2÷高-下底;下底=面积×2÷高-上底;高=面积×2÷(上底+下底)2、单位换算的方法大化小，乘进率;小化大，除以进率。

3、常用单位间的进率1千米=1000米1米=10分米1分米=10厘米1厘米=10毫米1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米4、图形之间的关系(1)、平行四边形可以转化成一个长方形;两个完全相同的三角形可以拼成一个平行四边形。

两个完全相同的梯形可以拼成一个平行四边形。

(2)、等底等高的平行四边形面积相等;等底等高的三角形面积相等。

(3)、等底等高的平行四边形面积是三角形面积的2倍。

如果一个三角形和一个平行四边形等面积，等底，则三角形的高是平行四边形的2倍。

如果一个三角形和一个平行四边形等面积，等高，则三角形的底是平行四边形的2倍。

(4)、把长方形框架拉成平行四边形，周长不变，面积变小了。

5、求组合图形面积的方法(1)仔细观察，确定组合图形可以分割或添补成哪些可以计算面积的基本图形。

(2)找到计算这些基本图形的面积所需要的数据。

(3)分别计算这些基本图形的面积，然后再相加或相减。

人教版五年级数学上册第六单元《多边形的面积》重点难点易错题集锦归类总复习(含答案)

人教版五年级数学上册第六单元多边形的面积重点难点易错题集锦（有答案）一、《平行四边形的面积》专项复习一、单选题（共6题；共12分）1.一个平行四边形，底扩大6倍，高缩小2倍，这个平行四边形的面积（）。

A. 扩大6倍B. 缩小2倍C. 面积不变 D. 扩大3倍2.如图平行线间的三个图形，它们的面积相比（）。

A. 平行四边形的面积大B. 三角形的面积大C. 梯形的面积大 D. 面积都相等3.一个长方形框架拉成一个平行四边形后，面积（）.A. 与原来相等B. 比原来小C. 比原来大4.把一个木条钉成的长方形捏住对角，拉成一个平行四边形，它的面积比原来的面积（）。

A. 大B. 小C. 相等 D. 无法确定5.一个平行四边形与一个长8cm，宽3cm的长方形面积相等．平行四边形的底为6cm，则高为（）cm．A. 5B. 4C. 246.一个平行四边形的底缩小到原来的1，高扩大到原来的2倍，则它的面积2（）。

A. 扩大到原来的2倍B. 扩大到原来的4倍C. 不变二、填空题（共4题；共7分）7.一个三角形和一个平行四边形的面积相等，底也相等。

如果三角形的高是10厘米，那么平行四边形的高是________厘米；如果平行四边形的高是8厘米，那么三角形的高是________厘米。

8.一个三角形的底是10分米，高是8分米，面积是________平方分米；与它等底等高的平行四边形的面积是________平方分米。

9.（如图）一个长方形活动木框变形后成为一个平行四边形。

原来长方形的面积是________ cm2，现在平行四边形的面积是________ cm2。

10.一个三角形和一个平行四边形的高相等，面积也相等，如果三角形的底是6厘米，那么平行四边形的底是________分米．三、计算题（共2题；共20分）11.计算下面图形的面积12.计算下面图形的面积。

（1）（2）（3）四、解答题（共6题；共40分）13.在一块底边长8m、高6.5 m的平行四边形菜地里种萝卜，如果每平方米收萝卜7. 5 kg，这块菜地可收萝卜多少千克？14.一块平行四边形钢板，底是1.8m，高是1.5m，它的面积是多少？15.计算下面各图形的面积。

五年级数学上册《多边形的面积》整理与复习

《多边形的面积》整理与复习一、学习目标：1、会推导平行四边形、三角形、梯形的面积计算公式。

2、掌握平行四边形、三角形、梯形的面积计算公式，会利用公式计算它们的面积。

3、会计算组合图形的面积。

二、重点、难点：重点：掌握平行四边形、三角形、梯形的面积计算公式，会利用公式计算它们的面积。

难点：会推导平行四边形、三角形、梯形的面积计算公式并能灵活应用。

三、考点分析：1、本讲内容涉及的知识点在考试大纲或考试说明中对应的考点及知识细目；本讲所涉及的考点是“空间与图形”，这部分内容需要我们了解、掌握，在考试中会以填空题、选择题、操作题、解决问题等形式出现。

2、每个考点具体到考核目标与要求（了解、理解、掌握、综合运用）；（1）通过观察、操作，认识平行四边形、三角形、梯形。

（2）利用方格纸或割补等方法，探索并掌握平行四边形、三角形、梯形的面积计算公式。

3、每个考点常出现（体现）的题型和大体分值。

平行四边形、三角形、梯形面积公式的推导：填空、选择、操作题（约2—4分）平行四边形、三角形、梯形与组合图形面积的计算：填空、选择题及解决问题（约4—6分）知识梳理长方形面积＝长×宽平行四边形面积＝底×高三角形面积＝底×高÷2梯形面积＝（上底＋下底）×高÷2典型例题方法应用题：例1：思路分析：1）题意分析：求平行四边形的一条高。

2）解题思路：DF为平行四边形的一条高，所以要先求出平行四边形的面积，再除以DF这条高所对应的底边AB的长，就可以求出DF的长度。

解答过程：平行四边形的面积：1.2×2＝2.4（平方厘米）DF的长：2.4÷1.5＝1.6（厘米）解题后的思考：平行四边形的两组底和高的乘积相等。

例2：思路分析：1）题意分析：求平行四边形的周长。

2）解题思路：求铁丝的长也就是求这个平行四边形的周长。

先根据一组对应的底和高求出平行四边形的面积，再除以另一条高就可以求出另一条边的长。

五年级上册数学《多边形的面积》典型例题

《多边形的面积》典型例题1、淘气家在装修客厅，需要一块底是1.3米，高0.8米的平行四边形木板，木板每平方米的售价是120元，淘气家买这块木板需要多少元？平行四边形的面积＝底×高1.3×0.8×120＝124.8（元）答：淘气家买这块木板需要124.8元。

2、一块三角形稻田，底90米，高60米，如果每平方米施肥0.2千克，这块稻田约需施肥多少千克？根据三角形面积公式：面积＝底×高÷290×60÷2×0.2＝540（千克）答：这块稻田约需施肥540千克。

3、乐乐家在一块空地上种满了鲜花（如下图）。

如果每平方米土地的鲜花卖200元，一共可以卖多少元？根据直角三角形面积公式：S＝ab÷2（a、b为两条直角边）3.5×4÷2×200＝1400（元）答：一共可以卖1400元。

《多边形的面积》典型例题4、在城固县南沙湖风景区入口处有一个上底为24m、下底为37m、高为16m的梯形宣传栏。

宣传栏中间留出一个宽为1m，长为16m 的长方形刷黄色油漆，其余的刷白色油漆。

刷白色油漆的面积是多少m2？梯形的面积公式：S＝（a＋b）h÷2，长方形的面积公式：S＝ab （24＋37）×16÷2－16×1＝472（m2）答：刷白色油漆的面积是472m2。

5、一块梯形土地（如图），村里准备在这块地里种蔬菜。

（1）如果在蔬菜地中间铺一条长9m、宽1m的小路，求种蔬菜的面积。

（12.8＋20）×9÷2－9×1＝138.6（平方米）答：种蔬菜的面积是138.6平方米。

（2）如果铺小路改为划出一块最大的三角形地来种生菜求种生菜的面积。

20×9÷2＝90（平方米）答：种植生菜的面积是90平方米。

新北师大版五年级上册数学第四单元《多边形的面积》知识点总结(全)

新北师大版五年级上册数学第四单元《多边形的面积》知识点总结(全)
本文总结了五年级上册第四单元《多边形的面积》的知识点。

其中包括平行四边形、三角形、等底等高的平行四边形和三角形以及梯形的面积公式与推导。

首先介绍了平行四边形的面积公式为底乘高，同时提供了逆运算公式：底等于面积除以高，高等于面积除以底。

需要注意的是，在求平行四边形的面积时，底和高必须对应。

此外，平行四边形框架可以拉成长方形或者拉成面积更小的平行四边形，但周长不变。

接下来是三角形的面积公式，即底乘高除以二。

同样提供了逆运算公式：底等于面积乘以二除以高，高等于面积乘以二除以底。

需要注意的是，在求三角形的面积时，底和高必须对应。

任何三角形都有三条高。

然后介绍了等底等高的平行四边形和三角形。

对于等底等高的平行四边形，它们的面积相等；对于等底等高的三角形，它们的面积也相等，并且是平行四边形面积的一半。

最后介绍了梯形的面积公式为上底加下底乘以高除以二。

同时提供了逆运算公式：上底加下底等于面积乘以二除以高，上底等于面积乘以二除以高减去下底，下底等于面积乘以二除以高减去上底，高等于面积乘以二除以上底加下底。

五年级数学多边形的面积计算公式汇总+练习题(附答案)

五年级数学多边形的面积计算公式汇总+练习题（附答案）面积计算公式1、长方形的面积=长×宽字母表示：S=ab长方形的长=面积÷宽 a=S÷b长方形的宽=面积÷长b=S÷a2、正方形的面积=边长×边长字母表示: S= a²3、平行四边形的面积=底×高字母表示：S=ah平行四边形的高=面积÷底 h=S÷a平行四边形的底=面积÷高 a=S÷h4、三角形的面积=底×高÷2字母表示：S=ah÷2三角形的高= 2×面积÷底h=2S÷a三角形的底= 2×面积÷高a=2S÷h5、梯形的面积=（上底+下底）×高÷2字母表示：S=(a+b)·h ÷2梯形的高=2×面积÷（上底+下底）h=2S÷(a+b)梯形的上底=2×面积÷高—下底a=2S÷h-b梯形的下底=2×面积÷高—上底b=2S÷h-a1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方米=10000平方厘米1米=10分米=100厘米多边形面积同步试题一、填空1．完成下表。

考查目的：平行四边形、三角形和梯形的面积计算及变式练习。

答案：解析：直接利用公式计算这三种图形的面积，对于学生来说完成的难度不大。

对于已知平行四边形的面积和高求底、已知三角形的面积和底求高这两个变式练习，可引导学生进行比较，理解并强化三角形和梯形的类似计算中需要先将“面积×2”这一知识点。

2．下图是一个平行四边形，它包含了三个三角形，其中两个空白三角形的面积分别是15 平方厘米和25 平方厘米。

中间涂色三角形的面积是（）。

考查目的：等底等高的三角形和平行四边形的面积之间的关系。

第14讲多边形的面积计算 (讲义)-2023-2024学年五年级数学人教版

第14讲多边形的面积计算专题概述在掌握三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等基本图形的面积计算公式的基础上，进行多边形的面积计算。

本讲常见的解题方法有：(1)对于多种基本图形的组合，利用已给的线段间的比例关系，求出多边形的面积；(2)把图形进行切分、平移、翻转、补充、变形转化为基本图形，继而求出多边形的面积。

典型例题11. 已知三角形 ABC 的面积为1,BE=2AB,BC=CD,求三角形 BDE 的面积。

分析利用已给的线段间的比例关系、三角形的面积以及三角形的面积公式，设法把三角形BDE 划分成一些与三角形ABC 的面积成相应比例的三角形。

这样，三角形BDE 的面积就能求得了。

解见右图，连接CE。

对于三角形ABC与三角形BEC，分别把AB 和BE 看成底，那么它们的高相等。

此外，BE=2AB。

根据三角形面积公式S=1aℎ可知，,S△BEC=2S△ABC=2。

显然，三角形BEC和三角形CED 是两个等底(BC=CD)、等高2的三角形，因此S△CED=S△BEC=2。

这样,S△BDE=S△BEC+S△CED=4。

思维训练11. 正方形ABCD 的边长是18厘米,已知DE 是EC 长度的2倍,求三角形DEF 的面积。

2.如图所示, DC=2BD,AO=OD,，三角形AOG 的面积与三角形DOC 面积的和是16 平方厘米。

三角形ABC 的面积是多少?典型例题2求图中阴影部分的面积。

(大圆直径为2，单位：厘米，圆周率π取近似值3.14)分析如图所示，解题时可以先将图形下半部分翻转拼接，然后将图中的小圆移至中心。

从图中不难看出，求原图中阴影部分的面积就是求一个圆环的面积。

解大圆半径：2÷2=1(厘米),小圆半径：1÷2=0.5(厘米),阴影面积：3.14×(1²−0.5²)=2.355(平方厘米)。

答：阴影部分的面积是2.355 平方厘米。

五年级__多边形的面积(知识点整理+典型例题_推荐!!!)

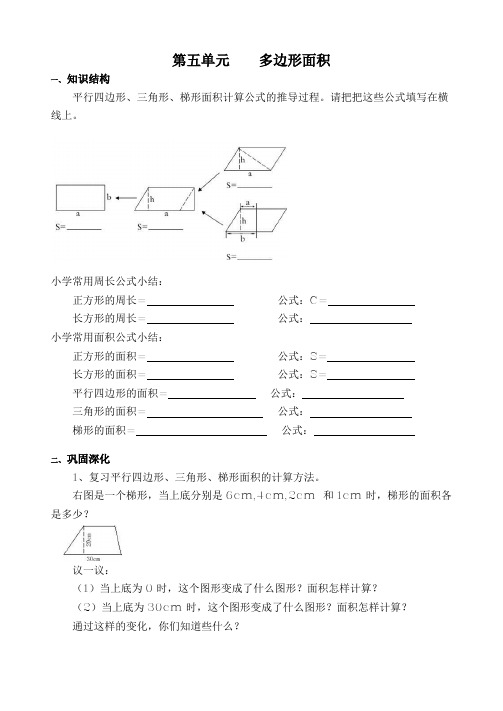
第五单元多边形面积一、知识结构平行四边形、三角形、梯形面积计算公式的推导过程。

请把把这些公式填写在横线上。

小学常用周长公式小结：正方形的周长= 公式：C=长方形的周长= 公式：小学常用面积公式小结：正方形的面积= 公式：S=长方形的面积= 公式：S=平行四边形的面积= 公式：三角形的面积= 公式：梯形的面积= 公式：二、巩固深化1、复习平行四边形、三角形、梯形面积的计算方法。

右图是一个梯形，当上底分别是6cm,4cm,2cm 和1cm时，梯形的面积各是多少？议一议：（1）当上底为0时，这个图形变成了什么图形？面积怎样计算？（2）当上底为30cm时，这个图形变成了什么图形？面积怎样计算？通过这样的变化，你们知道些什么？通过这样的变化，说明了图形之间是相互联系的，在特定的情况下是可以互相转化。

2、复习组合图形的计算方法。

计算下面图形的面积，你能想出几种方法？三、拓展应用理解分割、移补法推导三角形面积计算公式的过程。

你能用类似的方法推导梯形的面积公式吗？具体方法可参考如下：推导过程：从梯形的两腰中点的连线将梯形剪开，拼成一个平行四边形。

平行四边形的底等于（梯形的上底＋梯形的下底）平行四边形的高等于梯形的高÷2梯形的面积等于拼成的平行四边形的面积所以，梯形的面积＝（上底＋下底）×高÷2四、课堂练习1、计算下面每个图形的面积。

2、计算下面组合图形的面积。

小学常用周长公式小结：正方形的周长=边长×4 公式：C=4a长方形的周长=（长+宽）×2 公式：C=（a+b）×2小学常用面积公式小结：正方形的面积=边长×边长公式：S=a×a长方形的面积=长×宽公式：S=a×b平行四边形的面积=底×高公式：S= a×h三角形的面积=底×高÷2。

公式：S= a×h÷2梯形的面积=（上底+下底）×高÷2 公式：S=（a+b）h÷2第五单元多边形面积——课后作业一、填一填1、一个直角三角形的两条直角边分别是6cm和8cm，斜边长10cm，这个直角三角形的面积是（）cm2。

五上多边形面积知识点归纳总结及习题

五年级数学上册第五单元多边形面积知识点归纳总结一、基本图形（一）长方形1、长方形面积=长×宽字母公式：s=ab长方形周长=(长＋宽)×2字母公式：c=(a＋b)×2（长=周长÷2-宽；宽=周长÷2-长）2、★长方形中面积、周长与长和宽之间的变化关系：（1）长方形的长加宽等于长方形周长的一半。

即 a + b = c ÷ 2（2）当长方形的周长不变时，长与宽的差越大，这个长方形的面积就越小；反之，长与宽的差越小，这个长方形的面积就越大。

（3）当长方形的面积不变时，长与宽的差越大，这个长方形的周长就越长；长与宽的差越小，这个长方形的周长就越短。

（4）长方形框架拉成平行四边形，周长不变，面积变小。

（二）正方形1、正方形面积=边长×边长字母公式：s= a²或者s=a×a2、正方形周长=边长×4字母公式：c=4a 或者c= a×4（三）平行四边形1、平行四边形面积=底×高字母公式：s=ah2、★平行四边形面积公式的推导过程：剪拼、平移沿着平行四边形的任意一条高剪开，将其一部分平移与另一部分正好拼成一个长方形，这个长方形的长就是平行四边形的底，这个长方形的宽就是平行四边形的高。

因为长方形的面积=长×宽，所以平行四边形的面积=底×高，用字母表示S=a×h。

3、★等底等高的平行四边形面积相等。

（四）三角形1、三角形面积=底× 高÷2字母公式：s=ah÷2（底=面积×2÷高；高=面积×2÷底）2、★三角形面积公式的推导过程：旋转、平移将两个完全一样的三角形拼成一个平行四边形，拼成的平行四边形的底就是三角形的底，拼成的平行四边形的高就是三角形的高，拼成的平行四边形的面积是三角形面积的2倍。

一个三角形的面积是这个平行四边形的面积一半。

五年级__多边形的面积(知识点整理+典型例题_推荐!!!)

苏州苏教版五年级数学上册第二单元《多边形的面积》知识点梳理+典型例题及答案

(人教版)五年级数学重难点：多边形的面积(知识点+试题解析)

五年级奥数讲义-多边形面积计算二(附答案)

南京某校苏教版五年级数学上册第二单元《多边形的面积》练习及解析

小学五年级多边形的面积知识点总结和精选练习

数学五年级多边形的面积问题整理单

新北师大版五年级上册数学第四单元《多边形的面积》知识点总结(全)

五年级上册数学《多边形的面积》知识点归纳

人教版五年级数学上册第六单元《多边形的面积》重点难点易错题集锦归类总复习(含答案)

五年级数学上册《多边形的面积》整理与复习

五年级上册数学 《多边形的面积》典型例题

新北师大版五年级上册数学第四单元《多边形的面积》知识点总结(全)

五年级数学多边形的面积计算公式汇总+练习题(附答案)

第14讲多边形的面积计算 (讲义)-2023-2024学年五年级数学人教版

五年级__多边形的面积(知识点整理+典型例题_推荐!!!)

五上多边形面积知识点归纳总结及习题

五年级上册数学《多边形的面积》典型例题