8.截面图形性质
常见几何体的截面

常见几何体的截面
常见几何体的截面通常指的是用一个平面截取几何体后与几何体相交得到的平面图形。
在立体几何中,截面问题是一个常见的题型,它要求我们理解和想象三维几何体被切割后的样子。
以下是一些常见几何体及其可能的截面形状:
1. 圆柱体:当用一个平面去截一个圆柱体时,如果截面平行于底面,那么截面形状是一个圆形;如果截面垂直于底面,那么截面形状是一个矩形。
2. 圆锥体:圆锥体的截面可能是圆形、椭圆形或者是抛物线形,这取决于截面的角度和位置。
如果截面平行于圆锥的底面,那么截面是一个小圆形;如果截面是斜截圆锥,那么截面可能是椭圆形或者抛物线形。
3. 球体:球体的截面总是圆形,不论截面的角度和位置如何,因为球体在任何方向上都是对称的。
4. 立方体:立方体的截面可能是正方形或长方形,这取决于截面的方向。
如果截面平行于立方体的一个面,那么截面是一个正方形;如果截面与立方体的一个面成一定角度,那么截面是一个长方形。
总的来说,了解这些常见几何体的截面形状对于解决立体几何问题非常有帮助,尤其是在处理高考或数学竞赛中的综合题目时。
16秋北交《工程力学》(本)在线作业一

B. 3次
C. 4次
D. 12次
正确答案:
4. 构件在拉伸或压缩时的变形特点( )。
A. 仅有轴向变形
B. 仅有横向变形
C. 轴向变形和横向变形
D. 轴向变形和截面转动
正确答案:
5. 弯曲梁上的最大正应力发生在危险截面( )各点处。
A. 中性轴上
B. 离中性轴最远
A. 错误
B. 正确
正确答案:
2. 压杆丧失其直线的平衡形式而过度到曲线的平衡形式,称为失稳,也称屈曲。
A. 错误
B. 正确
正确答案:
3. 挠度和转角的正负号规定为:挠度向下为正,转角逆时针为正。
A. 错误
B. 正确
正确答案:
4. 对于土木工程中的许多梁,除了要满足强度条件意外,还需要满足刚度条件。
正确答案:
3. 下列用到自锁现象的是( )
A. 带式输送机
B. 螺纹
C. 千斤顶
D. 陀螺
正确答案:
4. 下列关于平面汇交力系的说法哪些是正确的( )
A. 所有力的作用线在同一平面内
B. 所有力的作用线平行
C. 所有力的作用线汇交于一点
D. 作用在物体上的平面汇交力系,如果合力为零,则物体处于平衡状态
北交《工程力学》(本)在线作业一
一、单选题(共 10 道试题,共 30 分。)
1. 提高梁的强度和刚度的措施有()。
A. 变分布载荷为集中载荷
B. 将载荷远离支座
C. 将梁端支座向内侧移动
D. 撤除中间支座
正确答案:
2. 平面汇交力系平衡的必要与充分条件是力系的合力( )
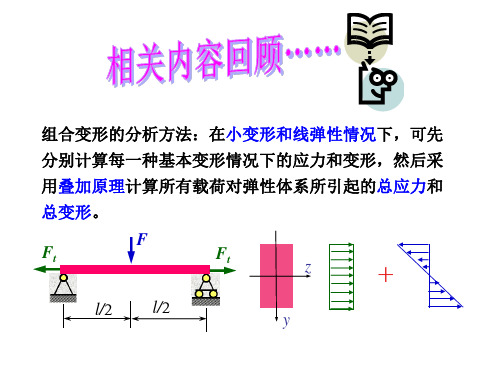
材料力学_第八章截面核心汇总.
a
z
z (4a a)(2a 2a) (2a 4a)(a)
(4a a) (2a 4a)
4a 6a
* C
z
2a
4a
y1
(b)
a
2. 确定形心主惯性轴,并求形心主惯性矩 z
4a 6a
由于z轴为对称轴,且y、z轴的交 点过形心,故图c中y轴和z轴的为形 心主惯性轴。
A Iz
Iy
中性轴方程 az
ay 中性轴 z
F A
FyF y0 Aiz2
FzF z0
Ai
2 y
F (1 A
yF y0 iz2
z
F z0
i
2 y
)
0
y
F(zF , yF )
1
yF y0 izy
0
中性轴在形心主惯性轴y、z上的截距
ay
iz2 yF
az
i
2 y
zF
* C
y
形心主惯性矩Iy为
4a
Iy
a(4a)3 [
12
(a
4a) (2a)2]
4a(2a)3 [
12
(4a
(c)
2a) a2 ]
32a4
Iz
4a(a)3 12
2a(4a)3 12
11a4
3. 计算横截面上的内力
将F力向形心C简化,可得杆的内力分别为 FN=F,My=F·2a, Mz=F·2a
,
az
i
立体几何中的截面(解析版)

立体几何中的截面(解析版)在立体几何中,截面是指用一个平面去截一个几何体(包括圆柱、圆锥、球、棱柱、棱锥、长方体、正方体等),得到的平面图形。
总共有三种截面方式,分别为横截、竖截、斜截。
我们需要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。
正六面体的基本斜截面不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形。
圆柱体的基本截面也有其特殊性质。
我们可以运用线、面平行的判定定理与性质求截面问题,或者结合线、面垂直的判定定理与性质定理求正方体中截面问题。
此外,我们还可以灵活运用一些特殊图形与几何体的特征,“动中找静”,如正三角形、正六边形、正三棱锥等。
建立函数模型也是求最值问题的一种方法。
在一个透明的塑料制成的长方体内灌进一些水,固定底面一边于地面上,再将倾斜,有四个命题。
其中,水的部分始终呈棱柱状,棱AD始终与水面平行,当倾斜到如图5(2)时,BE·BF是定值。
水面的面积在转动过程中会改变,而BC//FG//A1D1,所以A1D1//面EFGH。
因此,正确的命题序号为①③④。
一个容积为1立方单位的正方体,在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G。
若此可以任意放置,则该可装水的最大容积是多少?分析本题,不能用一个平面去截一个正方体,使得截面为五边形。
进一步地,截面也不能为正五边形。
这是因为正方体的每个面都是正方形,而五边形无法与正方形相切。
因此,无论如何调整平面的位置,都不能得到五边形的截面。
而且OE=OC是抛物线的直线准线,所以焦点F在OC上,且OF=OC=1.故选:D二、完形填空在数学课上,老师讲到一个有趣的问题:如何用一个平面去截一个正方体所得截面不能是一个正五边形。
这个问题引起了我的思考,我开始想象一个平面在正方体中穿过的情景。
我发现,如果截面是一个正五边形,那么这个五边形的五条边必须分属于正方体的五个不同的面。
但是,正方体的每两个相对的面是平行的,所以这五条边中必有两条边是平行的。
材料力学 截面的几何性质

1、矩形截面 h
Iz
y2dA
A
2 h
y 2bdy
h
2
dy y
b y 3 2 1 bh3 3 h 12
2
同理
Iy
z2dA 1
A
12
hb3
b h z
y
26
2、实心圆截面
y
已知
IP
A2dA
D 4 32
D
z
则 I P A2 d A A y 2 d A A z 2 d I A z I y
A
Iz Iy
此式说明了极惯性矩与轴惯性矩之间的关系。
z
y
o
A dA
z
y
惯性积
定义
Iyz
yzdA
A
z y
A dA
为图形对y、z轴的惯性积 。
z
o
y
惯性积的数值可正,可负,也可为零。惯性积的量纲是[长 度]4 ,常用单位为m4和mm4。
定理:若有一个轴是图形的对称轴,则图形对这对轴 的惯性积必然为零。
4.3 形心主惯性轴和形心主惯性矩
若主惯性轴通过形心,则该轴称为形心主惯性轴(principal centroidal axis)。
图形对形心主惯性轴的惯性矩称为形心主惯性矩。 由于图形对于对称轴的惯性积等于零,而对称轴又过形心,所以,图形 的对称轴就是形心主惯性轴。
形心主惯性轴的特点可归纳为以下几点: ⑴形心主惯性轴是通过形心,由角定向的一对互 相垂直的坐标轴。
32
32
圆环形对y(或z)轴的惯性矩为
IyIz1 2Ip6 D4414
由于y轴为对称轴,故
Iyz 0
z
y
d D
材料力学填空与判断题解

实用文档第1 章 绪论一、是非判断题1-1 材料力学是研究构件承载能力的一门学科。
( √ ) 1-2 材料力学的任务是尽可能使构件安全地工作。
( × ) 1-3 材料力学主要研究弹性范围内的小变形情况。
( √ )1-4 因为构件是变形固体,在研究构件的平衡时,应按变形后的尺寸进行计算。
(×) 1-5 外力就是构件所承受的载荷。
( × )1-6 材料力学研究的内力是构件各部分间的相互作用力。
( × )1-7 用截面法求内力时,可以保留截开后构件的任一部分进行平衡计算。
( √ ) 1-8 压强是构件表面的正应力。
( × ) 1-9 应力是横截面上的平均内力。
( × )1-10 材料力学只研究因构件变形引起的位移。
( √ ) 1-11 线应变是构件中单位长度的变形量。
( × ) 1-12 构件内一点处各方向线应变均相等。
( × )1-13 切应变是变形后构件中任意两根微线段夹角的变化量。
( × ) 1-14 材料力学只限于研究等截面直杆。
( × )1-15 杆件的基本变形只是拉(压)、剪、扭和弯四种。
如果还有另一种变形,必定是这四种变形的某种组合。
( √ )第 2 章 轴向拉伸与压缩 一、是非判断题2-1 使杆件产生轴向拉压变形的外力必须是一对沿杆轴线的集中力。
(×) 2-2 拉杆伸长后,横向会缩短,这是因为杆有横向应力存在。
(×) 2-3 虎克定律适用于弹性变形范围内。
(×) 2-4 材料的延伸率与试件尺寸有关。
(√)2-5 只有超静定结构才可能有装配应力和温度应力。
(√) 二、填空题2-6 承受轴向拉压的杆件,只有在(加力端一定距离外)长度范围内变形才是均匀的。
2-7 根据强度条件][σσ≤可以进行(强度校核、设计截面、确定许可载荷)三方面的强度计算。
2-8 低碳钢材料由于冷作硬化,会使(比例极限)提高,而使(塑性)降低。
截一个几何体与三视图(4种题型)(解析版)(北师大版)

截一个几何体与三视图(4种题型)【知识梳理】一.截一个几何体(1)截面:用一个平面去截一个几何体,截出的面叫做截面.(2)截面的形状随截法的不同而改变,一般为多边形或圆,也可能是不规则图形,一般的截面与几何体的几个面相交就得到几条交线,截面就是几边形,因此,若一个几何体有几个面,则截面最多为几边形.二.简单几何体的三视图(1)画物体的主视图的口诀为:主、俯:长对正;主、左:高平齐;俯、左:宽相等.(2)常见的几何体的三视图:圆柱的三视图:三.简单组合体的三视图(1)画简单组合体的三视图要循序渐进,通过仔细观察和想象,再画它的三视图.(2)视图中每一个闭合的线框都表示物体上的一个平面,而相连的两个闭合线框常不在一个平面上.(3)画物体的三视图的口诀为:主、俯:长对正;主、左:高平齐;俯、左:宽相等.四.由三视图判断几何体(1)由三视图想象几何体的形状,首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.(2)由物体的三视图想象几何体的形状是有一定难度的,可以从以下途径进行分析:①根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,以及几何体的长、宽、高;②从实线和虚线想象几何体看得见部分和看不见部分的轮廓线;③熟记一些简单的几何体的三视图对复杂几何体的想象会有帮助;④利用由三视图画几何体与有几何体画三视图的互逆过程,反复练习,不断总结方法.【考点剖析】一.截一个几何体(共8小题)1.(2022秋•高新区期末)用一个平面去截一个三棱柱,截面的形状不可能是()A.B.C.D.【分析】根据三棱柱的特点,考虑截面从不同角度和方向截取的情况.【解答】解:A、当截面与底面平行时,得到的截面的形状可能是该图形,故不符合题意;B、当截面与侧面平行时,截面就是长方形,故不符合题意;C、无论如何去截截面,截面的形状不可能是圆形.故符合题意;D、当截面与轴截面斜交时,得到的截面的形状可能是梯形,故不符合题意.故选:C.【点评】本题考查了截一个几何体的应用,主要考查学生的观察图形的能力、空间想象能力和动手操作能力.2.(2022秋•玄武区校级期末)用一个平面去截一个几何体,若截面(截出的面)的形状是四边形,则这个几何体可以是:①三棱柱;②三棱锥;③长方体;④圆柱,其中所有正确结论的序号是.【分析】根据三棱柱,三棱锥,长方体,圆柱的特征,分别分析出用一个平面去截该几何体时,可能得到的截面的形状是四边形.【解答】解:①用一个平面去截一个三棱柱,得到的图形可能是四边形;②用一个平面去截一个三棱锥,得到的图形可能是四边形;③用一个平面去截一个长方体,得到的图形可能是四边形;④用一个平面去截一个圆柱,得到的图形可能是四边形.故答案为:①②③④.【点评】本题考查了截一个几何体,截面的形状随截法的不同而改变,一般为多边形或圆,也可能是不规则图形,一般的截面与几何体的几个面相交就得到几条交线,截面就是几边形,因此,若一个几何体有几个面,则截面最多为几边形.3.(2022秋•礼泉县期末)用一个平面分别去截长方体,圆锥,三棱柱,圆柱,能得到截面是三角形的几何体有个.【分析】当截面的角度和方向不同时,圆柱体的截面无论什么方向截取圆柱都不会截得三角形.【解答】解:长方体沿体面对角线截几何体可以截出三角形;圆锥能截出三角形;三棱柱能截出三角形;圆柱不能截出三角形;所以截面可能是三角形的有3故答案为:3.【点评】本题考查了几何体的截面,掌握常见几何体的截面是解题的关键.4.(2022秋•吉州区期末)如图所示,用经过A、B、C三点的平面截去正方体的一角,变成一个新的多面体,若这个多面体的面数为m,棱数为n,则m+n=.【分析】截去正方体一角变成一个多面体,这个多面体多了一个面,棱数不变,少了一个顶点.【解答】解:由图可得,多面体的面数是7;正方体有12条棱,被截去了3条棱,截面为三角形,增加了3条棱,故棱数不变.所以m+n=7+12=19.故答案为:19.【点评】本题考查了正方体的截面.明确正方体的面数,顶点数,棱的条数,形数结合,求出截去一个角后得到的几何体的面数,顶点数,棱的条数是解题的关键.5.(2022秋•茂南区期末)截一个几何体,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.如图,下列几何体的截面是.【分析】根据圆柱和四棱柱的形状特点解答即可.【解答】解:用一个平面去截圆柱,截面形状是圆;用一个平面去截四棱柱,截面形状是长方形.故答案为:圆,长方形.【点评】此题考查了截一个几何体,截面的形状既与被截的几何体有关,还与截面的角度和方向有关,要熟练掌握各种几何图形.6.(2022秋•柳江区月考)如图,左面立体图形中四边形APQC表示平面截正方体的截面,请在右面展开图中画出四边形APQC的四条边.【分析】根据正方体的特征解答即可.【解答】解:截面的线在展开图中如右图的A﹣C﹣Q﹣P﹣A.【点评】此题考查正方体的展开图,解决此题的关键是抓住四边形APQC四个顶点所在的位置,再进一步确定四边形的四条边所在的平面就可容易地画出.7.(2022秋•金凤区校级月考)如图是一个长为4cm,宽为3cm的长方形纸片,将该长方形纸片绕一条边所在的直线旋转一周,然后用平面沿与AB平行的方向去截所得的几何体,求截面的最大面积(结果保留π).【分析】长方形纸片绕一条边所在的直线旋转一周得到一个圆柱体,沿线段AB的方向截所得的几何体,计算截面比较即可得到最大面积.【解答】解:由题意可得,把长方形ABCD绕AB边所在的直线旋转一周,得到的几何体为圆柱,圆柱的底面半径为4cm,高为3cm,用平面沿与AB平行的方向去截所得的几何体,截面是长方形,所以截面的最大面积为4×2×3=24(cm2);由题可得,把长方形ABCD绕AD边所在的直线旋转一周,得到的几何体为圆柱,圆柱的底面半径为3cm,高为4cm,用平面沿与AB所以截面的最大面积为32×π=9π(cm2);因为9π>24,所以截面的最大面积为9πcm2.【点评】本题主要考查的是截一个几何体,点、线、面、体,能够正确得到截面的图形是解题的关键.8.(2022秋•通川区期末)如图,用一个平面去截一个三棱柱,截面的形状可能是.①三角形②四边形③五边形④六边形【分析】根据三棱柱的截面形状判断即可.【解答】解:矩形:从三棱柱的顶面垂直截下去,就会出现一个矩形截面;三角形:从三菱柱的侧面平移截过去,就可以得到一个三角形的截面;梯形:从三棱柱的顶面斜着截取下去,就可以得到一个梯形截面;五边形:从三角形的顶面往下斜着截,但是必须经过5条线,就可以得到一个五边形截面.用一个平面去截一个三棱柱,截面的形状可能是:三角形,四边形,五边形,不可能是六边形,故答案为:①②③.【点评】本题考查了截一个几何体,熟练掌握三棱柱的截面形状是解题的关键.二.简单几何体的三视图(共8小题)9.(2022秋•大东区期末)下列几何体中,从下面观察看到的形状为三角形的是()A.B.C.D.【分析】根据俯视图的定义判断即可.【解答】解:A.该圆柱的俯视图是圆,故本选项不合题意;B.该圆锥的俯视图是圆(带圆心),故本选项不合题意;C.该三棱柱的俯视图是三角形,故本选项符合题意;D.该正方体的俯视图是正方形,故本选项不合题意;故选:C.【点评】此题主要考查了简单几何体的三视图,正确把握观察角度得出正确视图是解题关键.10.(2022秋•丰润区期末)如图几何体中,从正面看(主视图)是长方形的是()A.B.C.D.【分析】主视图是分别从物体正面看,所得到的图形.【解答】解:A图的主视图是等腰三角形,B图的主视图是长方形,C图的主视图是梯形,D图的主视图是圆形,故选:B.【点评】本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.11.(2022秋•南平期末)如图,从上面看这个圆柱,看到的平面图形是.【分析】根据从上边看得到的图形是俯视图,可得答案.【解答】解:该几何体,从上面看到的平面图形是一个圆.故答案为:圆.【点评】本题考查了几何体的三视图,从上边看得到的图形是俯视图.12.(2022秋•禅城区期末)下列几何体中,①圆柱;②球;③棱锥;④圆锥;⑤长方体.从正面看图形是长方形的是.(填序号)【分析】从正面看图形得到是几何体的主视图,逐一分析解答即可.【解答】解:①圆柱的主视图是长方形,符合题意;②球的主视图是圆,不符合题意;③棱锥的主视图是三角形,不符合题意;④圆锥的主视图是三角形,不符合题意;⑤长方体的主视图是长方形,符合题意.故从正面看图形是长方形的是①⑤.故答案为:①⑤.【点评】本题考查了简单几何体的三视图,解题的关键是掌握常见几何体的三视图.13.(2022秋•丹徒区月考)如图所示,水平放置的长方体的底面是长为4cm、宽为2cm的长方形,它的主视图的面积为12cm2,则长方体的体积等于cm3.【分析】由主视图的面积=长×高,长方体的体积=主视图的面积×宽,得出结论.【解答】解:依题意,得长方体的体积=12×2=24(cm3).故答案为:24.【点评】本题考查了简单几何体的三视图.关键是明确主视图是由长和高组成的.14.(2022秋•密云区期末)分别从正面、上面、左面观察下列物体,得到的平面图形完全相同的是(填写序号).【分析】图①、图②、图③、图④分别是长方体,圆锥,正方体、圆柱,根据它们三视图的形状进行判断即可.【解答】解:图①、图②、图③、图④分别是长方体,圆锥,正方体、圆柱,长方体的三视图虽然都是长方形的,但它们的大小不相同,圆锥体的主视图、左视图是三角形的,而俯视图是圆形的,正方体的三视图都是正方形的,圆柱的主视图、主视图是长方形的,但俯视图是圆形的,因此从正面、上面、左面看所得到的平面图形完全相同的是正方体,故答案为:③.【点评】本题考查简单组合体的三视图,掌握简单组合体的三视图的形状是正确判断的前提.15.(2022秋•清河区校级期末)如图是由棱长都为1cm的6块小正方体组成的简单几何体.(1)请在方格中画出该几何体的三个视图.(2)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,最多可以再添加块小正方体,【分析】(1)根据简单组合体三视图的画法画出相应的图形即可;(2)在俯视图上相应位置备注出相应摆放的数目即可.【解答】解:(1)该几何体的主视图、左视图和俯视图如下:(2所以最多可以添加2个,故答案为:2.【点评】本题考查简单组合体的三视图,理解视图的意义是正确解答的前提.16.(2022秋•历下区期中)如图,若干个大小相同的小立方块搭成的几何体.(1)这个几何体由个小立方块搭成;(2)从正面、左面、上面观察该几何体,分别画出你所看到的几何体的形状图.【分析】(1)根据搭建组合体的形状,或根据“从上面看”所得到的图形相应位置上所摆放的小正方体的个数得出答案;(2)根据简单组合体三视图的画法画出相应的图形即可.【解答】解:由该组合体的“俯视图”相应位置上所摆放的小正方体的个数可得,1+3+1+1+2=8(个),故答案为:8;(2)这个组合体的三视图如下:键.三.简单组合体的三视图(共8小题)17.(2022秋•公安县期末)如图是一个由5个相同的正方体组成的立体图形,从其左面看,得到的平面图形是()A.B.C.D.【分析】找到从左面看的图形即可得出结果.【解答】解:从其左面看,得到的平面图形是:故选:C.【点评】本题考查三视图.熟练掌握从不同的方向观察几何体,确定三视图,是解题的关键.18.(2022秋•秀英区校级期末)如图所示的几何体的左视图是()A.B.C.D.【解答】解:从左边看,是三个长方形组成的图形.故选:B.【点评】本题考查简单几何体的三视图,注意掌握从左边看得到的图形是左视图.19.(2022秋•高邮市期末)用三个大小不等的正方体拼成了一个如图所示的几何体,若该几何体的主视图、左视图和俯视图的面积分别表示为S1、S2、S3,则S1、S2、S3的大小关系是(用“<”从小到大连接).【分析】根据从正面看得到的图形是主视图,从上面看得到的图形是俯视图,从左面看得到的图形是左视图,根据边角面积的大小,可得答案.【解答】解:主视图的面积是三个正方形的面积,左视图是两个正方形的面积,俯视图是一个正方形的面积,故S3<S2<S1,故答案为:S3<S2<S1.【点评】本题考查了简单组合体的三视图,分别得出三视图是解题关键.20.(2022秋•汝州市期末)如图是用7块相同的小长方体搭成的几何体.若拿走一块长方体后,该几何体的主视图和左视图都没改变,则这块长方体的序号是.【分析】根据几何体的主视图和左视图的定义解答即可.【解答】解:若拿走一块长方体后,该几何体的主视图和左视图都没改变,则这块长方体的序号是⑤.故答案为:⑤.【点评】本题考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“主视图疯狂盖,左视图拆违章”就更容易得到答案.21.(2022的小立方体摆成如图所示的几何体,从上面看这个几何体得到的平面图形的面积是.【分析】根据从上边看得到的图形是俯视图,可得答案.【解答】解:从上面看的平面图形是:有3列,从左到右正方形的个数分别为:1、2、1,所以从上面看这个几何体得到的平面图形的面积是4.故答案为:4.【点评】本题考查了简单组合体的三视图,从上边看得到的图形是俯视图.22.(2022秋•市中区期末)如图,请分别画出从正面、左面和上面观察该几何体看到的形状图.【分析】根据三视图的定义结合图形可得.【解答】解:如图所示:【点评】本题考查作图﹣三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.本题画几何体的三视图时应注意小正方形的数目及位置.23.(2022秋•东平县校级期末)如图,在平整的地面上,用多个棱长都为2cm的小正方体堆成一个几何体.(1)共有个小正方体;(2)求这个几何体的表面积;(3)如果现在你还有一些棱长都为2cm的小正方体,要求保持俯视图和左视图都不变,最多可以再添加个小正方体.【分析】(1)根据拼图可直接得出答案;(2)求出主视图、主视图、俯视图的面积,再根据表面积的意义进行计算即可;(3)结合三视图,在俯视图上的相应位置添加相应数量的正方体,直至最多.【解答】解:(1)根据拼图可知,堆成如图所示的几何体需要10个小正方体,故答案为:10;(2)这个组合体的三视图如图所示:因此主视图的面积为2×2×7=28(cm2),左视图为2×2×5=20(cm2),俯视图的面积为2×2×7=28(cm2),∴该组合体的表面积为(28+20+28)×2+2×2×4=168(cm2),(3)在俯视图的相应位置摆放相应数量的小正方体,使其俯视图和左视图都不变,如图所示,所以最多可以添加5个,故答案为:5.【点评】本题考查简单组合体的三视图,理解视图的意义,掌握简单三视图的画法是正确解答的关键.24.(2022秋•吉州区期末)一个几何体由一些大小相同的小正方块儿搭建,如图是从上面看到的这个几何体的形状如图,小正方形的数字表示在该位置的小正方块儿的个数,请在网格中画出从正面和左面看到的几何体的形状图.【分析】根据主视图,左视图的定义画出图形即可.【解答】解:主视图,左视图如图所示:【点评】本题考查简单组合体的三视图,解题的关键是理解三视图的定义,属于中考常考题型.四.由三视图判断几何体(共5小题)25.(2022秋•鄄城县期末)如图①所示的组合几何体,它的下面是一个长方体,上面是一个圆柱.“左”或“俯”);(1)图②和图③是它的两个视图,在横线上分别填写两种视图的名称(填“主”、(2)根据两个视图中的尺寸,计算这个组合几何体的表面积和体积.(结果保留π)【分析】(1)找到从正面和上面看所得到的图形即可,注意所有的看到的棱都应表现在视图中.(2)根据图形中的数据可知,长方体的长为8,宽为5,高为2,圆柱的底面直径为2,高为6,根据体积和表面积表示方法进行计算即可.【解答】解:(1)如图,故答案为:左,俯.(2)表面积为:(8×5+8×2+5×2)×2+2π×6=132+12π,体积为:2×5×8+π×(2÷2)2×6=80+π×1×6=80+6π.答:这个组合几何体的表面积为132+12π,体积是80+6π.【点评】本题考查简单组合体的三视图,根据三视图得出相关数据,依据相关计算方法进行计算是得出正确答案的前提.26.(2023•东城区校级模拟)用3个同样的小正方体摆出的几何体,从三个方向看到的图形分别如图:这个几何体是()A.B.C.D.【分析】根据三视图的得出小正方体摆出的几何体即可.【解答】解:由俯视图可知,小正方体摆出的几何体为:,故选:B.【点评】本题考查实物体的三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.27.一个几何体由若干个大小相同的小立方块搭成,从左边和上边看到的平面图形如图所示,则搭成这个几何体的小立方块的个数为.【分析】根据左面看与上面看的图形,得到俯视图解答即可.【解答】解:根据左视图和俯视图,这个几何体的底层有3个小正方体,第二层有1个小正方体,所以有3+1=4个小正方体,故答案为:4.【点评】本题考查了由三视图判断几何体,也考查了对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就容易得到答案.28.(2022秋•驿城区校级期末)用若干大小相同的小正方体搭一个几何体,使得从正面和从上面看到的这个几何体的形状如图所示完成下列问题:(1)搭成满足如图所示的几何体最多需要个小正方体,最少需要个小正方体;(2)请在网格中画出用最多小正方体搭成的几何体的左视图.【分析】(1)在俯视图中,写出最多时,写出最少时,小正方体的个数,可得结论;(2)利用俯视图,结合主视图的特征,解决问题即可.【解答】解:(1)搭成满足如图所示主视图和俯视图的几何体最多需要:2+2+2+2+2=10(个),最少需要1+2+1+1+2=7(个)小正方体故答案为:10,7;(2)左视图如图所示.【点评】本题考查由三视图判断几何体,解题的关键是理解三视图的定义,属于中考常考题型.29.(2022秋•大竹县期末)如图是分别从正面、左面、上面观察一个几何体得到的图形,请解答以下问题:(1)这个几何体的名称为;(2)若从正面看到的是长方形,其长为10cm;从上面看到的是等边三角形,其边长为4cm,求这个几何体的侧面积.【分析】(1)根据三视图的知识,主视图以及左视图都是长方形,俯视图为三角形,故可判断出该几何体是三棱柱;(2)侧面积为3个长方形,它的长和宽分别为10cm,4cm,计算出一个长方形的面积,乘3即可.【解答】解:(1)这个几何体是三棱柱.故答案为:三棱柱;(2)三棱柱的侧面展开图形是长方形,长方形的长是等边三角形的周长,宽是三棱柱的高,所以三棱柱侧面展开图形的面积为:S=3×4×10=120(cm2).答:这个几何体的侧面积为120cm2.【点评】本题主要考查由三视图确定几何体和求几何体的面积等相关知识,考查学生的空间想象能力.注意:棱柱的侧面都是长方形,上下底面是几边形就是几棱柱.【过关检测】一.选择题(共6小题)1.(2021秋•连州市期末)下列说法正确的是()A.长方体的截面形状一定是长方形B.棱柱侧面的形状可能是一个三角形C.“天空划过一道流星”能说明“点动成线”D.圆柱的截面一定是长方形【分析】分别判断每个选项的对错即可.【解答】解:∵长方体的截面形状可能是长方形也可能是正方形,故A选项不符合题意,∵棱柱侧面的形状是长方形或正方形,故B选项不符合题意,∵“天空划过一道流星”能说明“点动成线”,说法正确,故C选项符合题意,∵圆柱的截面还可以是圆形,故D选项不符合题意,故选:C.【点评】本题主要考查点、线、面、体的知识,熟练利用几何直观得出正确结论是解题的关键.2.(2022•安阳一模)下列几何体的三视图不含矩形的是()A.长方体B.圆柱C.圆锥D.三棱柱【分析】分别找出四个立体图形的三视图即可解答.【解答】解:A.长方体的三视图都是矩形,故不符合题意;B.正立的圆柱的主视图和左视图都是矩形,故不符合题意;C.正立的圆锥的俯视图是圆,主视图和左视图都是等腰三角形,故符合答题;D.正立的三棱柱的主视图和左视图都是矩形,故不符合题意,故选:C.【点评】本题考查了简单几何体的三视图,注意主视图、左视图、俯视图是分别从物体正面、左面、上面看,所得到的图形.3.(2022•五华区二模)由8化前后的两个几何体的左视图和俯视图都不改变,而主视图可能改变,则取走小正方体的方法共有()A.4种B.5种C.6种D.7种【分析】根据主视图是从物体的正面看得到的视图,俯视图是从上面看得到的图形,左视图是左边看得到的图形,可得答案.【解答】解:如图,单独取走1或2或3或同时取走1和2或1和3或2和3,变化前后的两个几何体的左视图和俯视图都不改变,所以取走小正方体的方法共有6种,故选:C.【点评】本题考查了简单组合体的三视图,利用三视图的意义是解题关键.4.(2022•天府新区模拟)下列几何体中,截面形状不可能是圆的是()A.B.C.D.【分析】根据每一个几何体的截面形状,即可判断.【解答】解:因为圆锥、圆柱、球的截面都可能是圆,三棱柱的截面只可能是多边形,不可能是圆,故选:D.【点评】本题考查了截一个几何体,熟练掌握每一个几何体的截面形状是解题的关键.5.(2021秋•井研县期末)如图,四个几何体分别为球体、三棱柱、圆柱体和长方体,这四个几何体中截面不可能是长方形的几何体是()A.球体B.三棱柱C.圆柱体D.长方体【分析】根据球体、三棱柱、圆柱体和长方体的截面形状,即可判断.【解答】解:三棱柱、圆柱体和长方体的截面都有可能是长方形,球体的截面不可能是长方形,故选:A.【点评】本题考查了截一个几何体,熟练掌握球体、三棱柱、圆柱体和长方体的截面形状是解题的关键.6.(2021秋•碑林区校级期末)用一个平面去截下面几个几何体,截面不可能有圆的是()A.圆锥B.圆柱C.棱柱D.球【分析】根据每一个几何体的截面形状判断即可.【解答】解:用一个平面去截几何体,圆锥,圆柱,球的截面都可能是圆,棱柱的截面只可能是多边形,不。
材料力学填空与判断题解

第一章 绪论第1 章 绪论一、是非判断题1-1 材料力学是研究构件承载能力的一门学科。
( √ ) 1-2 材料力学的任务是尽可能使构件安全地工作。
( × ) 1-3 材料力学主要研究弹性范围内的小变形情况。
( √ )1-4 因为构件是变形固体,在研究构件的平衡时,应按变形后的尺寸进行计算。
(×) 1-5 外力就是构件所承受的载荷。
( × )1-6 材料力学研究的内力是构件各部分间的相互作用力。
( × )1-7 用截面法求内力时,可以保留截开后构件的任一部分进行平衡计算。
( √ ) 1-8 压强是构件表面的正应力。
( × ) 1-9 应力是横截面上的平均内力。
( × )1-10 材料力学只研究因构件变形引起的位移。
( √ ) 1-11 线应变是构件中单位长度的变形量。
( × ) 1-12 构件内一点处各方向线应变均相等。
( × )1-13 切应变是变形后构件中任意两根微线段夹角的变化量。
( × ) 1-14 材料力学只限于研究等截面直杆。
( × )1-15 杆件的基本变形只是拉(压)、剪、扭和弯四种。
如果还有另一种变形,必定是这四种变形的某种组合。
( √ )第 2 章 轴向拉伸与压缩 一、是非判断题2-1 使杆件产生轴向拉压变形的外力必须是一对沿杆轴线的集中力。
(×) 2-2 拉杆伸长后,横向会缩短,这是因为杆有横向应力存在。
(×) 2-3 虎克定律适用于弹性变形范围内。
(×) 2-4 材料的延伸率与试件尺寸有关。
(√)2-5 只有超静定结构才可能有装配应力和温度应力。
(√) 二、填空题2-6 承受轴向拉压的杆件,只有在(加力端一定距离外)长度范围内变形才是均匀的。
2-7 根据强度条件][σσ≤可以进行(强度校核、设计截面、确定许可载荷)三方面的强度计算。
2-8 低碳钢材料由于冷作硬化,会使(比例极限)提高,而使(塑性)降低。
材料力学 附录 截面的几何性质

(Properties of Plane Areas) 三、组合截面的静矩和形心 (The first moments ¢roid of a composite area)
由几个简单图形组成的截面称为组合截面.
截面各组成部分对于某一轴的静矩之代数和,等于该截 面对于同一轴的静矩.
(Properties of Plane Areas)
§1-1 截面的静矩和形心 (The first moment of the area & centroid of
an area)
一、静矩(The first moment of the area )
截面对 y , z 轴的静矩为
z
S y
zdA
A
Sz
ydA
A
dA z
静矩可正,可负,也可能等于零.
1
矩形 2
A2 10 80 800mm2
y2
10
80 2
50mm
z2 5mm
所以 y A1 y1 A2 y2 23mm A1 A2
z A1z1 A2z2 38mm A1 A2
y1
z1
2 z2
10
O y2
y
90
(Properties of Plane Areas)
方法2 用负面积法求解,图形分割及坐标如图(b)
yC , zC ̄ 过截面的形心 C 且与 y, z轴平行
的坐标轴(形心轴)
z
Iy , Iz , Iyz — 截面对 y, z 轴的惯性矩和惯性积.
zC
IyC , IzC , IyCzC ̄ 截面对形心轴 yC , zC的惯性矩
n
Ai zi
z
工程力学习题解答(详解版)
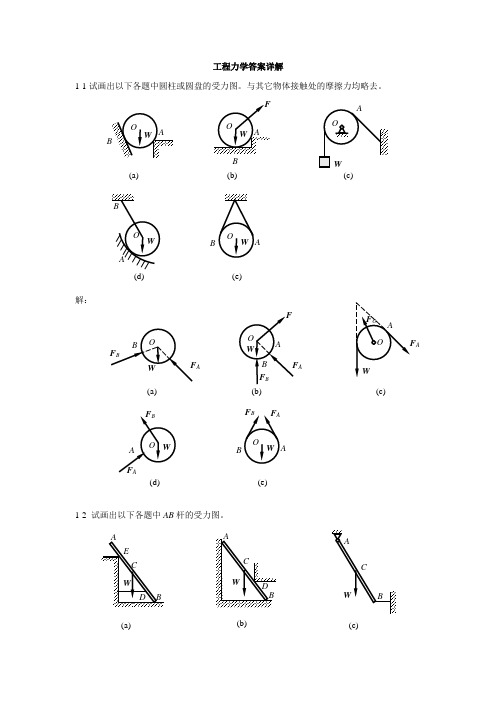
工程力学答案详解1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解:1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(c)(a)(b)解:1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解:1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
解:(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BF D1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ,结点B ;(b) 圆柱A 和B 及整体;(c) 半拱AB ,半拱BC 及整体;(d) 杠杆AB ,切刀CEF 及整体;(e) 秤杆AB ,秤盘架BCD 及整体。
解:(a)(d) FC(e)WB (f)F FBC(c)(d)AT F BAF (b)(e)(b)(c)(d)(e)CAA C’CDDB2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点,如图所示。
如不计刚架重量,试求支座A 和D 处的约束力。
解:(1) 取整体ABCD 为研究对象,受力分析如图,画封闭的力三角形:(2)F 1F FDF F AF D211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ,力的大小等于20KN ,如图所示。
材料力学复习选择题

1、构件的强度、刚度、稳定性 C 。
A:只与材料的力学性质有关B:只与构件的形状尺寸有关C:与二者都有关D:与二者无关2、均匀性假设认为,材料内部各点的 D 是相同的。
A:应力B:应变C:位移D:力学性质3、各向同性认为,材料沿各个方向具有相同的 A 。
A:力学性质B:外力C:变形D:位移4、在下列四种材料中, C 不可以应用各向同性假设。
A:铸钢B:玻璃C:松木D:铸铁5、根据小变形条件,可以认为: DA:构件不变形B:构件不破坏C:构件仅发生弹性变形D:构件的变形远小于原始尺寸6、外力包括: DA:集中力和均布力B:静载荷和动载荷C:所有作用在物体外部的力D:载荷与支反力7、在下列说法中,正确的是 A .A:内力随外力的增大而增大;B:内力与外力无关;C:内力的单位是N或KN;D:内力沿杆轴是不变的;8、静定杆件的内力与其所在的截面的 D 有关.A:形状;B:大小; C:材料; D:位置9、在任意截面的任意点处,正应力σ与剪应力τ的夹角α= A 。
A:α=90O;B:α=45O;C:α=0O; D:α为任意角。
10、图示中的杆件在力偶M的作用下,BC段上 B .A:有变形、无位移; B:有位移、无变形;C:既有位移、又有变形;D:既无变形、也无位移;11、等直杆在力P作用下: DA:Na大B:Nb大C:Nc大D:一样大12、用截面法求内力时,是对 C 建立平衡方程而求解的。
A:截面左段B:截面右段C:左段或右段D:整个杆件13、构件的强度是指 C ,刚度是指 A ,稳定性是指 B 。
A:在外力作用下抵抗变形的能力;B:在外力作用下保持其原有平衡态的能力;C:在外力的作用下构件抵抗破坏的能力;14、计算M-M面上的轴力 D 。
A:-5P B:-2P C:-7P D:-P15、图示结构中,AB为钢材,BC为铝材,在P力作用下 C 。
A:AB段轴力大 B:BC段轴力大 C:轴力一样大16、关于轴向拉压杆件轴力的说法中,错误的是: C 。
第8章 截面的几何性质

b C1 C C2 O a
z y
1 2 1 h bh h ah 2 3 2 3
h
h a 2b 6
2
形心位置
zC 0
辽宁铁道职业技术学院
S z h a 2b yC A 3 ab
工程力学
[练习]求图示阴影部分的面积对y轴的静矩。
其中:A为截面面积,x、 y轴为形心轴, x1、 y1为 分别与x、y轴平行的轴, a、b分别为相应平行轴之 间的距离。
O a
z
O1 b
辽宁铁道职业技术学院
工程力学
证明: 即推导Iy、Iz、Iyz与 Iy1、Iz1、Iy1z1的关系,x、y 轴为形心轴。 根据惯性矩和惯性积的定义显然有
I y 1 z 1 dA
第 8章
截面的几何性质
单元学习目标
静矩、形心及其相互关系 惯性矩的概念及计算方法 惯性矩的平行移轴公式 组合截面惯性矩计算
水利土木工程学院工程力学课程组
工程力学
静矩、形心及其相互关系 惯性矩的概念及计算方法
惯性矩的平行移轴公式 组合截面惯性矩计算
辽宁铁道职业技术学院
建立坐标系如图所示。
zC zA
i i
10
y
A
z1 A1 z 2 A2 A1 A2
120
35 10 110 20.3mm 10 110 80 10
C2
C1(0,0) C2(-35,60)
形心C坐标为(-20.3,34.7)。
80
辽宁铁道职业技术学院
25
18 106 mm4
辽宁铁道职业技术学院
截面的几何性质

S xC AyC 0
I xC 2bSxC b 2 A
I x I xC b 2 A
I y I yC a 2 A
注意: C点必须为形心
I xy I xCyC abA
I r I rC (ab) 2 A
1 面积矩与形心位置 一、面积(对轴)矩:(与力矩类似)
是面积与它到轴的距离之积。 y
dS x dAy
x y x dA
dS y dAx
S x dS x ydA
A A
S y dS y xdA
A A
2 惯性矩、惯性积、极惯性矩 一、惯性矩:(与转动惯量类似) 是面积与它到轴的距离的平方之积。
一、平行移轴定理:(与转动惯量的平行移轴定理类似) 以形心为原点,建立与原坐标轴平行 y
yC x
dA C b xC y x
的坐标轴如图
xa xC yb yC
I x y 2 dA
A
a
r
( yC b) 2 dA
A A 2 ( yC 2byC b 2 )dA
I x I xC b A
Hale Waihona Puke I x y dA2 A
y x
I y x 2 dA
二、极惯性矩:
A
dA y
x
是面积对极点的二次矩。
r
I r r 2dAI x I y
A
三、惯性积:面积与其到两轴距离之积。
I xy xydA
A
y 如果 x 或 y 是对称轴,则Ixy =0 x
dA y
x
r
3 惯性矩和惯性积的平行移轴定理
常用截面几何性质计算公式JX

常用截面几何性质计算公式JX1.矩形截面:矩形截面是一种常见的结构截面形式。
假设矩形截面宽度为b,高度为h,则其面积可以通过以下公式计算:A=b*h质心位置可以通过以下公式计算:x=b/2y=h/2惯性矩可以通过以下公式计算:Ix=(b*h^3)/12Iy=(h*b^3)/12截面模数可以通过以下公式计算:Wx=(b*h^2)/6Wy=(h*b^2)/62.圆形截面:圆形截面是另一种常见的结构截面形式。
假设圆形截面的半径为r,则其面积可以通过以下公式计算:A=π*r^2质心位置在圆心上,即x=0,y=0。
惯性矩可以通过以下公式计算:Ix=(π*r^4)/4Iy=(π*r^4)/4截面模数可以通过以下公式计算:Wx=(π*r^3)/4Wy=(π*r^3)/43.等边三角形截面:等边三角形截面是一个等边三角形形状的结构截面。
假设等边三角形截面的边长为a,则其面积可以通过以下公式计算:A = (sqrt(3) * a^2) / 4质心位置可以通过以下公式计算:x=a/2y = (sqrt(3) * a) / 6惯性矩可以通过以下公式计算:Ix = (a^4 * sqrt(3)) / 48Iy=(a^4)/48截面模数可以通过以下公式计算:Wx = (a^3 * sqrt(3)) / 12Wy=(a^3)/12以上是常见的几种截面几何性质的计算公式,通过这些公式可以方便地计算结构截面的重要性质,为结构设计和分析提供参考。
在实际应用中,还需要根据具体的截面形状和尺寸选择相应的公式进行计算。
切圆柱的12种截面

切圆柱的12种截面1. 圆截面圆截面是指垂直于圆柱轴线的平面与圆柱相交所得截面。
圆截面具有完全对称的形状,其边界是一个圆形。
2. 椭圆截面椭圆截面是指垂直于圆柱轴线的平面与圆柱相交所得截面。
椭圆截面的边界是一个椭圆,具有两个不同的半径。
3. 长方形截面长方形截面是指垂直于圆柱轴线的平面与圆柱相交所得截面。
长方形截面的边界是一个矩形,具有两对相等的边。
4. 正方形截面正方形截面是指垂直于圆柱轴线的平面与圆柱相交所得截面。
正方形截面的边界是一个正方形,具有四条相等的边。
5. 梯形截面梯形截面是指垂直于圆柱轴线的平面与圆柱相交所得截面。
梯形截面的边界是一个梯形,具有两对平行边。
6. 直角三角形截面直角三角形截面是指垂直于圆柱轴线的平面与圆柱相交所得截面。
直角三角形截面的边界是一个直角三角形,其中至少有一个角为90度。
7. 等腰三角形截面等腰三角形截面是指垂直于圆柱轴线的平面与圆柱相交所得截面。
等腰三角形截面的边界是一个等腰三角形,其中至少有两条边相等。
8. 正五边形截面正五边形截面是指垂直于圆柱轴线的平面与圆柱相交所得截面。
正五边形截面的边界是一个正五边形,具有五条相等的边。
9. 正六边形截面正六边形截面是指垂直于圆柱轴线的平面与圆柱相交所得截面。
正六边形截面的边界是一个正六边形,具有六条相等的边。
10. 正多边形截面正多边形截面是指垂直于圆柱轴线的平面与圆柱相交所得截面。
正多边形截面的边界是一个正多边形,具有多条相等的边。
11. 摆线截面摆线截面是指垂直于圆柱轴线的平面与圆柱相交所得截面。
摆线截面的边界呈现出摆线的形状,具有特殊的曲线。
12. 指数曲线截面指数曲线截面是指垂直于圆柱轴线的平面与圆柱相交所得截面。
指数曲线截面的边界呈现出指数曲线的形状,具有特殊的曲线。
以上是切圆柱的12种截面的简要介绍。
这些截面形状各不相同,具有不同的几何特征和应用领域。
熟悉这些截面形状对于工程设计和几何学的学习都有一定的帮助。
材料力学填空与判断题解

第一章 绪论第1 章 绪论一、是非判断题1-1 材料力学是研究构件承载能力的一门学科。
( √ ) 1-2 材料力学的任务是尽可能使构件安全地工作。
( × ) 1-3 材料力学主要研究弹性范围内的小变形情况。
( √ )1-4 因为构件是变形固体,在研究构件的平衡时,应按变形后的尺寸进行计算。
(×) 1-5 外力就是构件所承受的载荷。
( × )1-6 材料力学研究的内力是构件各部分间的相互作用力。
( × )1-7 用截面法求内力时,可以保留截开后构件的任一部分进行平衡计算。
( √ ) 1-8 压强是构件表面的正应力。
( × ) 1-9 应力是横截面上的平均内力。
( × )1-10 材料力学只研究因构件变形引起的位移。
( √ ) 1-11 线应变是构件中单位长度的变形量。
( × ) 1-12 构件内一点处各方向线应变均相等。
( × )1-13 切应变是变形后构件中任意两根微线段夹角的变化量。
( × ) 1-14 材料力学只限于研究等截面直杆。
( × )1-15 杆件的基本变形只是拉(压)、剪、扭和弯四种。
如果还有另一种变形,必定是这四种变形的某种组合。
( √ )第 2 章 轴向拉伸与压缩 一、是非判断题2-1 使杆件产生轴向拉压变形的外力必须是一对沿杆轴线的集中力。
(×) 2-2 拉杆伸长后,横向会缩短,这是因为杆有横向应力存在。
(×) 2-3 虎克定律适用于弹性变形范围内。
(×) 2-4 材料的延伸率与试件尺寸有关。
(√)2-5 只有超静定结构才可能有装配应力和温度应力。
(√) 二、填空题2-6 承受轴向拉压的杆件,只有在(加力端一定距离外)长度范围内变形才是均匀的。
2-7 根据强度条件][σσ≤可以进行(强度校核、设计截面、确定许可载荷)三方面的强度计算。
2-8 低碳钢材料由于冷作硬化,会使(比例极限)提高,而使(塑性)降低。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
I z0 y0 0
§3.5 平行移轴公式和转轴公式
tg 2 0 2I zy Iz I y
可求得 0 和 0 90两个角度,从而确定两根轴y0,,z0。
截面对于惯性矩为极值的一对坐标轴的惯性积必为零
I z0 y0 0
由 tg 2 0
2I zy Iz I y
I z1 y d A
A 2 1
I z1 cos2 y 2 d A sin 2 z 2 d A
A A
2 sin cos zy d A
A
I z cos2 I y sin 2 2 I zy sin cos
利用二倍角函数公式
cos 2 1 1 cos 2 2 1 2 sin 1 cos 2 2 2 sin cos sin 2
i ci
Az
80
z yc
Ay
i
A1 yc1 A2 yc 2 A A1 A2 5 700 60 1200 39.7(mm ) 700 1200
ci
§3.4 静矩、惯性矩、惯性积及其性质
解法二:1)、分割图形及建立坐标系,如图所示
A1 800mm2 , zc1 0, yc1 0.
z
yc
Ay A
A1 yc1 A2 yc 2 A1 A2
60 1100 34.7( mm ) 1100 800
§3.4 静矩、惯性矩、惯性积及其性质
yБайду номын сангаас
10 10
解法三:负面积法
A1 9600 mm2 , zc1 40mm, yc1 60mm A2 70110mm2 , zc 2 45mm, yc 2 65mm
y
y
I z1 y1
2 Iz Iy
A dA C D
2 将前两式相加得
sin 2 I zy cos 2
E O
z
B
z
I z1I y1I z I y
上式表明,截面对于通过同一点的任意一对相互垂直 的坐标轴的惯性矩之和为一常数,并等于截面对该坐标原 点的极惯性矩
§3.5 平行移轴公式和转轴公式
y
求:Iz1、Iy1、Iz1y1。
dA 在坐标系 ozy 和坐标系oz1y1 的 坐标分别为(z,y )和(z1 , y1 )
A dA
y1 y cos z sin
C
y
z1 z cos y sin
代入惯性矩的定义式:
D
E
O
z
B
z
I z1 y d A
A 2 1
§3.5 平行移轴公式和转轴公式
6、惯性矩与极惯性矩的关系:
y
I p 2 dA ( y 2 z 2 )dA
A A
z
dA
y z
y 2 dA z 2 dA I z I y o
A A
图形对任一对相互垂直的坐标系的惯性矩之和恒 等于此图形对该两轴交点的极惯性矩。
§3.4 静矩、惯性矩、惯性积及其性质
A
I y z 2 dA ( zc b)2 dA zc2 dA b 2dA 2b zc dA I yc b2 A
A A A A A
I zy yzdA ( yc a)( zc b)dA
A A
yc zc dA abdA a zc dA b yc dA I zcyc abA
截面几何 材料
载荷
内力
应力
应变
§3.4 静矩、惯性矩、惯性积及其性质
§3.4.1
一、静矩(面积矩)
1、定义:
y
静矩和形心
dSz ydA
dA对z轴的微静矩: dA对y轴的微静矩:
dSy zdA
z
dA
y
Sz
z
Sy
yd A zd A
A A
o
2、量纲:[长度]3;单位:m3、cm3、mm3。
I z1 I y1 Iz Iy 2 Iz Iy Iz Iy 2 Iz Iy 2 cos 2 I zy sin 2 cos 2 I zy sin 2
I z 1 y1
2 Iz Iy 2
sin 2 I zy cos 2
3.5.3 主惯性轴、主惯性矩、形心主惯性矩
求出 sin 2 0 , cos2 0 代入转轴公式可得:
I max I z 0
min y0
Iz I y 2
(
Iz Iy 2
) 2 I zy
2
§3.5 平行移轴公式和转轴公式
I z1
Iz I y 2
Iz I y 2
cos 2 I zy sin 2
Iz I y 2 Iz I y 2
y
A dA y C
E O
z
B
D
z
I z1
cos 2 I zy sin 2
§3.5 平行移轴公式和转轴公式
I z1 I y1 Iz Iy 2 Iz Iy Iz Iy 2 Iz Iy 2 cos 2 I zy sin 2 cos 2 I zy sin 2
求形心: Ai z ci A1 z c1 A2 z c 2 zc A A1 A2 z
80
y
40 9600 45 ( 7700 ) 19.7( mm ) 9600 7700
C0
C2 C1
yc
Ay
i
ci
A
A1 yc1 A2 yc 2 A1 A2
A
z
dA y z
I z y 2 dA,
o
图形对y轴的惯性矩:
2、量纲:m4、mm4。
I y z dA
2 A
2 z2 y2
3、惯性矩是对轴而言(轴惯性矩)。 4、惯性矩的取值恒为正值。 5、极惯性矩:(对o点而言) I p
A
2 dA
§3.4 静矩、惯性矩、惯性积及其性质
z
60 9600 65 ( 7700 ) 39.7( mm ) 9600 7700
§3.4 静矩、惯性矩、惯性积及其性质
§3.4.2
1、惯性矩的定义: dA对z轴的惯性矩:
惯性矩和惯性积
y
dA对y轴的惯性矩:
图形对z轴的惯性矩:
dIz y 2dA dIy z 2dA
3、静矩的值可以是正值、负值、或零。
§3.4 静矩、惯性矩、惯性积及其性质
y
4、静矩和形心的关系
z
dA
y
由平面图形的形心公式
o
z
yC
y dA A , zC
A
z dA A
A
Sz
可知
Sy
A
ydA AyC
静矩和形心的关系
A
zdA Az C
结论: 图形对过形心的轴的静矩为零。
2、形心确定的规律:
(1)图形有对称轴时,形心必在此对称轴上。 (2)图形有两个对称轴时,形心必在这两对称轴的交点处。
§3.4 静矩、惯性矩、惯性积及其性质
三、组合图形(由若干个基本图形组合而成的图形)的静矩:
基本图形----指面积、形心位置已知的图形
Szz Szizi A yci S S A ci iiy
哈尔滨工业大学本科生课
截面图形的几何性质
§3.4.1 静矩和形心 §3.4.2 惯性矩和惯性积 §3.5.1 平移轴公式
§3.5.2 转轴公式
§3.5.3 主惯性轴、主惯性矩、形心主惯性矩
哈尔滨工业大学本科生课
静矩,惯性矩,惯性积 特性:
(1) 纯几何量,与材料的力学性质无关
(2) 从不同角度反映了截面的几何特征——称为截面的几何性质
根据惯性矩和惯性积的定义易得组合截面对于某轴的惯性矩 (或惯性积)等于其各组成部分对于同一轴的惯性矩(或惯性积) 之和:
I z I zi ,I y I yi ,I zy I ziyi
§3.5 平行移轴公式和转轴公式 3.5.2 惯性矩和惯性积的转轴公式
已知:A、Iz、Iy、Izy、。
S y S yi Ai zci
四、组合图形的形心:
yc
S zi A
i
zc
S A
yi i
A Az
A
Ai yci
i ci
利用基本图形 的结果, 可使组合图形 的形心计算简单
§3.4 静矩、惯性矩、惯性积及其性质
例 试确定下图的形心。 解法1:1)、建立坐标如图示,分割图形 y
7、简单图形惯性矩的计算 ⑴ 圆形截面:
1 4 实心(直径D)—— I z I y D 64
yc c zc
1 空心(外径D,内径d)——I z I y ( D 4 d 4 ) 64 ⑵ 矩形截面: h h 1 2 2 1 bh3 2 2 2 3 2 3 2 I y dA y bdy Izz A y dA h y bdy bh h A 12 2 12 yc 2
10
A1 700mm2 , zc1 45mm, yc1 5mm A2 1200 mm2 , zc 2 5mm, yc 2 60mm
2)、求形心
120
C2
c(19.7;39.7)
C1
A1 z c1 A2 z c 2 zc A A1 A2 45 700 5 1200 19.7(mm) 700 1200
