23-26 统计方法建模
统计师如何进行统计建模

统计师如何进行统计建模统计建模是统计学中一项重要的技术,它用于分析数据和推断未知的关系。
统计建模可以帮助统计师分析数据、发现模式,并根据这些模式做出预测和决策。
在本文中,将介绍统计师如何进行统计建模的步骤和方法。
一、问题定义在进行统计建模之前,统计师首先需要明确问题的定义。
问题定义可以包括以下几个方面:数据的背景和来源、需要解决的具体问题、所用的数据类型以及预期的建模结果。
明确问题的定义有助于统计师更好地理解问题,并有针对性地选择适当的建模方法。
二、数据采集与处理数据是统计建模的基础,统计师需要采集与问题相关的数据。
采集数据可以通过实地调查、问卷调查、实验设计等方式进行。
数据采集完成后,统计师还需要对数据进行处理,包括数据清洗、数据变换、数据归一化等操作,以保证数据的质量和准确性。
三、特征选择与变量筛选在进行统计建模之前,统计师需要选择合适的特征和变量。
特征选择是指从大量的特征中选择出对问题具有重要影响的特征,而变量筛选是指选择与建模目标相关的变量。
特征选择和变量筛选可以通过统计方法、机器学习算法等进行,如相关性分析、主成分分析、逻辑回归等。
四、模型选择与建立根据问题的性质和特征选择的结果,统计师需要选择合适的模型进行建立。
常见的统计建模方法包括线性回归、逻辑回归、决策树、支持向量机等。
在选择模型时,需要考虑模型的适用性、复杂度、稳定性以及解释性等因素。
模型建立完成后,统计师需要对模型进行参数估计和显著性检验,以确定模型的准确性和可靠性。
五、模型评估与优化建模完成后,统计师需要对模型进行评估和优化。
模型评估可以通过交叉验证、拟合优度检验、AIC、BIC等指标进行,以评估模型的拟合程度和预测准确性。
如果模型评估结果不理想,统计师需要对模型进行优化,如调整模型参数、改进特征工程等。
六、模型应用与预测优化后的模型可以用于实际应用和预测。
统计师可以利用已建立好的模型对新数据进行预测和推断,以解决实际问题。
数学建模 最短路程

交巡警服务平台的设置与调度摘要本论文主要是关于图论中的“最短路径问题”和“最优搜索问题”。
问题所述的模型已经很自然地用图表示出来,所以我们运用图的性质和算法来求解问题。
图论中求最短路径通常采用dijkstra 算法,但本题涉及的交巡警平台数量较多,即求多个源点到其它所有顶点的距离,所以采用floyd 算法求解比较简单,其基本思想是通过程序得到每个节点到其他节点的最优距离。
针对问题一,用floyd 算法算出每个交巡警平台3分钟内所能到达的全部节点,这些节点就是平台的管辖范围,但仍有3分钟内不能到达的节点,这些节点处就应该增设交巡警服务平台。
在快速封锁13条交通要道时,要遵循封锁时间最短、每个平台的警力最多封锁一个路口的原则,运用LINGO 程序解答。
最后分析得到出警时间至少大于3分钟的节点,及工作量最大的平台,在这些节点处需要增加3个服务平台。
针对问题二,需要对发案率进行降序排列,筛选出发案率较高,但是未设置交巡警服务平台的节点。
根据六个城区的基本数据,得到每个平台管辖的面积和人口,比较各平台的工作量,从而找出不合理的理由。
在搜捕犯罪嫌疑人时要遵循两个原则:搜捕时间最短和围堵区域最小。
根据逃犯的位置和逃跑的可能路径建立关于时间T 的目标函数和初始概率密度函数,001()0p X vt v ⎧∈⎪=⎨⎪∉⎩其中 t (0,6)其中s (0,6)对交巡警的搜捕区域建立探测函数,32(,,)j kz b x t z r ≈模型应该满足以下约束条件:22211223()()j i j i j Z X Z X r Z h -+-≡=最后运用拉格朗日乘数法求得围堵嫌疑人的最佳围堵方案。
模型的建立提高了交巡警服务平台的工作效率,同时这个模型也可以运用于最优选址、搜索正在执行任务的敌方潜艇等问题,并可将该模型的算法扩展到其他领域。
关键字:交巡警 最短路径 最优搜索 动态规划 floyd 算法1、问题重述交巡警为了更有效地贯彻落实四大职能,需要在市区的交通要道和重要部位设置交巡警服务平台。
统计方法建模

第八章 统计方法建模数理统计研究的对象是受随机因素影响的数据,以下数理统计就简称统计,统计是以概率论为基础的一门应用学科。
数据样本少则几个,多则成千上万,人们希望能用少数几个包含其最多相关信息的数值来体现数据样本总体的规律。
描述性统计就是搜集、整理、加工和分析统计数据,使之系统化、条理化,以显示出数据资料的趋势、特征和数量关系。
它是统计推断的基础,实用性较强,在统计工作中经常使用。
面对一批数据如何进行描述与分析,需要掌握参数估计和假设检验这两个数理统计的最基本方法。
我们将用Matlab 的统计工具箱(Statistics Toolbox)来实现数据的统计描述和分析。
§1 统计的基本概念1.1 总体和样本总体是人们研究对象的全体,又称母体,如工厂一天生产的全部产品(按合格品及废品分类),学校全体学生的身高。
总体中的每一个基本单位称为个体,个体的特征用一个变量(如x )来表示,如一件产品是合格品记0=x ,是废品记1=x ;一个身高170(cm )的学生记170=x 。
从总体中随机产生的若干个个体的集合称为样本,或子样,如n 件产品,100名学生的身高,或者一根轴直径的10次测量。
实际上这就是从总体中随机取得的一批数据,不妨记作n x x x 21,,n 称为样本容量。
简单地说,统计的任务是由样本推断总体。
1.2 频数表和直方图一组数据(样本)往往是杂乱无章的,作出它的频数表和直方图,可以看作是对这组数据的一个初步整理和直观描述。
将数据的取值范围划分为若干个区间,然后统计这组数据在每个区间中出现的次数,称为频数,由此得到一个频数表。
以数据的取值为横坐标,频数为纵坐标,画出一个阶梯形的图,称为直方图,或频数分布图。
若样本容量不大,能够手工作出频数表和直方图,当样本容量较大时则可以借助Matlab 这样的软件了。
让我们以下面的例子为例,介绍频数表和直方图的作法。
例1 学生的身高和体重(i) 数据输入数据输入通常有两种方法,一种是在交互环境中直接输入,如果在统计中数据量比较大,这样作不太方便;另一种办法是先把数据写入一个纯文本数据文件data.txt中,格式如例1的表格,有20行、10列,数据列之间用空格键或Tab键分割,该数据文件data.txt存放在matlab\work子目录下,在Matlab中用load命令读入数据,具体作法是:load data.txt20×个数据的矩阵。
Leslie模型

Leslie 人口模型现在我们来建立一个简单的离散的人口增长模型,借用差分方程模型,仅考虑女性人口的发展变化。
如果仅把所有的女性分成为未成年的和成年的两组,则人口的年龄结构无法刻划,因此必须建立一个更精确的模型。
20世纪40年代提出的Leslie 人口模型,就是一个预测人口按年龄组变化的离散模型。
模型假设(1) 将时间离散化,假设男女人口的性别比为1:1,因此本模型仅考虑女性人口的发展变 化。
假设女性最大年龄为S 岁,将其等间隔划分成m 个年龄段,不妨假设S 为m 的整数倍,每隔m S /年观察一次,不考虑同一时间间隔内人口数量的变化;(2) 记)(t n i 为第i 个年龄组t 次观察的女性总人数,记)](,),(),([)(21t n t n t n t n m =第i 年龄组女性生育率为i b (注:所谓女性生育率指生女率),女性死亡率为i d ,记1,i i s d =-假设,i i b d 不随时间变化;(3) 不考虑生存空间等自然资源的制约,不考虑意外灾难等因素对人口变化的影响;(4) 生育率仅与年龄段有关,存活率也仅与年龄段有关。
建立模型与求解根据以上假设,可得到方程 )1(+t n =∑=mi ii t n b 1)( )()1(1t n s t n i i i =++ 1=i ,2.…,m -1 写成矩阵形式为)()1(t Ln t n =+其中,L =⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--000000000121121m m m s s s b b b b (1) 记)]0(,),0(),0([)0(21m n n n n = (2)假设n (0)和矩阵L 已经由统计资料给出,则()(0),0,1,2,t n t Ln t ==t1+t为了讨论女性人口年龄结构的长远变化趋势,我们先给出如下两个条件:(i) s i > 0,i =1,2,…,m -1;(ii) b i 0≥,i =1,2,…,m ,且b i 不全为零。
数学建模中的统计方法介绍

维度归约
• 维度归约使用数据编码或变换,以便得到 原数据的归约或“压缩”表示。分为无损 和有损两种。
• 主要方法:
– 串压缩:无损,但只允许有限的数据操作。 – 小波变换(DWT):有损,适合高维数据。 – 主成分分析(PCA):有损,能更好地处理稀
* Smoothing by bin boundaries: - Bin 1: 4, 4, 4, 15 - Bin 2: 21, 21, 25, 25 - Bin 3: 26, 26, 26, 34
同济大学 数学系
• 回归:用一个函数(回归函数)拟合数据来光滑 数据。 –线性回归 –多元线性回归
• 聚类:将类似的值聚集为簇。检测离群点
–反映了每个数与均值相比平均相差的数值
同济大学 数学系
18
度量数据的离散程度…
• 盒图boxplot,也称箱线图 • 从下到上五条线分别表示最小值、下四分
位数Q1 、中位数、上四分位数Q3和最大值 • 盒的长度等于IRQ • 中位数用盒内的横线表示 • 盒外的两条线(胡须) 分别延伸到最小和
最大观测值。
同济大学 数学系
局部回归(Loess)曲线 • 添加一条光滑曲线到散布图
同济大学 数学系
数据清理
•现实世界的数据一般是不完整的、有噪 声的和不一致的。 •数据清理的任务:
填充缺失的值,光滑噪声并识别离群 点,纠正数据中的不一致。
同济大学 数学系
缺失值
• 忽略元组 • 人工填写空缺值 • 使用一个全局常量填充空缺值 • 使用属性的平均值填充空缺值 • 使用与给定元组属同一类的所有样本的平均
• 含噪声的
– 包含错误或存在偏离期望的离群值。
• 不一致的
数学建模的相关问题求解方法

数学建模的相关问题求解方法:1.量纲分析法是在物理领域建立数学模型的一种方法,主要是依据物理定律的量纲齐次原则来确定个物理量之间的关系,量纲齐次原则是指一个有意义的物理方程的量纲必须一致的,也就是说方程的两边必须具有相同的量纲,即: dim左=dim右并且,方程中每一边的每一项都必须有相同的量纲。
例子见书《数学建模方法与实践》P17—P232.线性规划法线性规划法是运筹学的一个重要分支应用领域广泛。
从解决各种技术领域中的优化问题,到工农业生产、商业经济、交通运输、军事等的计划和管理及决策分析。
线性规划所解决的问题具有以下共同的特征:(1)每一个问题都有一组未知数(x1,x2,……,xn)表示某一方案;这些未知数的一组定值就代表一个具体方案。
由于实际问题的要求,通常这些未知数取值都是非负的。
(2)存在一定的限制条件(即约束条件),这些条件是关于未知数的一组线性等式或线性不等式来表示。
(3)有一个目标要求,称为目标函数。
目标函数可表示为一组未知数的线性函数。
根据问题的需要,要求目标函数实现最大化或最小化。
例子见书《数学建模方法与实践》P26—P303.0—1规划法用于解决指派问题,是线性规划的特殊情况。
例子见书《数学建模方法与实践》P314.图解法用于求解二维线性规划的一种几何方法,其方法步骤见书《数学建模方法与实践》P345.单纯形法也是一种求解线性规划的常用方法,其基本原理和方法见书《数学建模方法与实践》P37——P39,计算步骤P40。
6.非线性规划法在目标函数和(或)约束条件很难用线性函数表示时,如果目标函数或约束条件中,有一个或多个是变量的非线性函数,则称这种规划问题为非线规划问题。
例子见书《数学建模方法与实践》P44——P457.最短路及狄克斯特拉算法狄克斯特拉算法是图论中用于计算最短路的一种方法,详见书《数学建模方法与实践》P588.克罗斯克尔算法克罗斯克尔算法是用来求解一个连通的赋权图的最小生成树的方法,详见书《数学建模方法与实践》P599.普莱姆算法同上10.欧拉回路及弗洛来算法欧拉回路是指若存在一条回路。
【国家自然科学基金】_轨道分布_基金支持热词逐年推荐_【万方软件创新助手】_20140803

科研热词 有限元 铁道工程 轨道交通 模拟 密度泛函 高斯曲率 重试轨道 辙叉 轮轨接触 轨道 稳态分布 环境振动 机器人 旋风分离器 密度泛函理论 吸收光谱 可修 参数二次规划法 ybco块材 高速铁路 高能质子 高能电子 马氏链 颗粒随机轨道模型 颗粒间相互交换耦合 颗粒浓度分布 颗粒浓度 频域 预测方法 预案评估 非解离电荷转移过程 非线性光学 随机加权法 阻尼 长寿命产品 镍连二硫烯 锌配位聚合物 铁路轨道 铁电性 钢轨 钟漂 金属碳化物 量子化学计算 速度误差 近月点高度 运筹学 过渡区噪声 载波相位观测误差 软着陆 轮对 转向架 轨道随机不平顺
107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
数学建模-多元统计模型专题(最新版)

河南科技大学数学与统计学院 (2010-07-23) 武新乾
一、前言
24 年前(1986 年) ,美国出现了大学生数学建模竞赛。随着改革开放的进程,数模竞赛 逐渐传入我国。1992 年,开始国内第一届大学生数学建模比赛。数模竞赛一经传入,便受 到了全国高校的普遍关注,引起了大学生的广泛兴趣。特别是近年来,虽然试题难度不断增 大,但是,参赛的学生规模空前膨胀,获奖的组队也日益增加,论文质量不断提高。 综观 18 年的竞赛试题,问题广泛,解决方案多种多样,其中基于统计分析的问题屡见 不鲜。比如:1992 年 A 题(简单记为 1992A,下同) “施肥方案对作物、蔬菜的影响” ,采 用多元二次回归、全回归、逐步回归和二次响应面回归;1993A“非线性交调的频率设计” , 采用最小二乘方法(简单记为 LS) ;1998A“资产投资收益与风险模型”和 2000A“DNA 序 列的分类” ,都采用多元分析方法;2001A“血管管道的三维重建”和“血管切片的三维重 建” ,分别采用 LS 方法和非线性拟合;2001B“公交车调度的规划数学模型” ,采用聚类分 析、 平滑方法和随机过程的有关知识; 2003A “SARS 传播的数学原理及预测与控制” 和 “SARS 传播的研究” ,均考虑了时间序列的应用;2003A“SARS 传播预测的数学模型” ,采用非线 性拟合,建立了指数模型;2004A“ MS 网点的合理布局”采用了聚类分析, “基于利润最大 化的实运商业网点分布微观经济模型”采用多元统计分析方法,另外, “临时超市网点的规 划模型研究”考虑了经验分布的应用;2004B“电力市场的输电阻塞优化管理(指导教师: 肖华勇) ”和“电力市场输电阻塞管理模型” ,均使用了多元线性回归;2005A“长江水质的 评价和预测” 、 “长江水质的评价预测模型” (二元线性回归预测) 、 “基于回归分析的长江水 质预测与控制” ,均考虑了回归分析,此外, “长江水质评价和预测的研究” 、 “水质的评价和 预测模型” ,均考虑了时间序列分析方法和多元线性回归模型;2005B“DVD 在线租赁系统 的优化设计”应用了抽样统计和随机服务模型, “DVD 在线租赁问题”和“DVD 租赁优化 方案(指导教师:孙浩) ”考虑了二项分布和随机模拟;2005B“DVD 在线租赁问题研究” 和 2005C“雨量预报方法的评价模型”考虑了均值的应用;2006B“艾滋病疗法评价及疗效 预测模型”使用了二次曲线和多元方差分析, “艾滋病疗法评价及疗效的预测模型”使用了 逐步回归方法, “艾滋病疗法的评价及疗效的预测模型”应用了假设检验和方差分析, “艾滋 病疗法的评价及疗效的预测”使用了线性拟合、二次和三次曲线拟合与非线性回归, “基于 数据统计分析的艾滋病疗效评价方法”采用了 F-检验和二次多项式回归;2007A“中国人口 区域结构向量模型”采用了倒数曲线模型拟合, “基于 Les lie 模型的中国人口预测及蒙特卡 罗仿真(指导教师:梅长林) ”应用了概率方法;2008A“数码相机定位”应用了多元线性 回归分析;2008B“高等教育学费标准探讨(华南农业大学,编号 1910) ”应用了因子分析、 主成分分析和聚类分析, “高等教育学费标准的探讨(华南农业大学,编号 1920) ”采用了 多元回归分析、数据挖掘和模拟退火算法, “关于高等教育学费标准的评价及建议(编号 cumcm0849) ”和“高校学费合理性研究(编号 cumcm0860) ”分别考虑了回归分析和曲线 拟合。 由是可知, 多元统计分析是常见的解决数模竞赛的主要工具之一, 务必给以充分的重视 和加强训练指导。
高教社杯全国大学生数学建模竞赛D题获奖论文之欧阳文创编

2014高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):D我们的报名参赛队号为(8位数字组成的编号):所属学校(请填写完整的全名):参赛队员 (打印并签名) :1.(隐去论文作者相关信息等)2.3.指导教师或指导教师组负责人 (打印并签名):(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。
以上内容请仔细核对,提交后将不再允许做任何修改。
如填写错误,论文可能被取消评奖资格。
)日期:2014年月日赛区评阅编号(由赛区组委会评阅前进行编号):2014高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国评阅编号(由全国组委会评阅前进行编号):储药柜的设计摘要面向消费者的药品零售药房,日常运行中需要执行大量的药品存储和分拣工作,目前自动化药房的研发及逐渐应用提高了药品存储和分拣效率,为医疗工作提供了极大地便利。
储药通道即为自动化药房的重要部分,合理的储药槽设计可以减少储药槽的设计成本、合理的利用储存处空间、提高药品的存储率和分拣效率。
(附专家点评)2009年全国大学生统计建模大赛获奖名单
马天然、刘静、张田 王焕英、王尚坤、王灿 叶少峰、何沛钊、王希哲 王文静、张明喆、侍湾湾 惠昌强、唐海峰、王诗庆 潘振宇、陈忆文、陈丹丹 闫凤梅、孙小冬、杨志华 王军伟、马歆玮、谢欣燕 贾旭东、王海燕、武宏伟 张吉良、于雪、马远超 王晓沛、马晓燕、李凯丽 魏文灵、陈银平、刘艳艳 徐雨茜、徐瑞文、林天逸 陈思易、奚潭、王亚民 汪维维、任萍、温婷婷
黄成、张磊、刘文林 杨少娜、孙鹏、袁妍 田昊枢、牛启昆、彭沁 王维玲、蔡金鑫、周晓婷 邬琼、刘寅、张静宇 柴亮、李壮壮、党建令 吴文娟、李宏生、张美丽 陈飞、柴家友、陈婷 袁蒂、蒋莉莉、牛胜男 葛盛荣、寸晓洁、李丽丽 朱璐璐、卢苏娟、薛亚楠 乔宁宁、韩雨珊、任严岩 李予娇、张丽、李玉玉
南京人口管理干部学院 浙江工商大学 北京大学 浙江财经学院 北京工商大学 河北经贸大学 广东外语外贸大学 厦门大学 华北电力大学 云南财经大学 中南财经政法大学 山西财经大学 山东工商学院
基于变参数模型的山东省消费需求与经济增长关系的实证研究 >>点 评 工业“三废”排放量与经济增长的关系 >>点评 广东省科技贡献力与经济增长关系的实证研究 >>点评 亚运会对广州旅游业前景趋势预测研究 >>点评 基于 AIC 准则的合理的汽油价格的制定使得社会与环境协调发展 >> 点评 基于 GARCH 模型的中国股市收益实证研究 >>点评 金融危机对中国出口的影响 >>点评
二等奖
序号 1 2 3 4 5 6 7 8 9 10 11 论文题目 中国地区经济增长收敛性分位数回归分析 >>点评 大学生休闲态度、休闲参与和休闲阻碍调查研究 >>点评 用天气发生器对我国主要城市天气指标的模拟和预测(附件) >>点 评 中国环保投资废气治理效率差异及其影响因素研究 >>点评 流动性信息与资产收益:基于非参数模型的分析 >>点评 2009 年上半年货币过多投放是否将导致未来通货膨胀? >>点评 外部经济变量对我国货币需求模型影响程度的实证分析 >>点评 紧凑型城市:中国城市经济可持续发展的新视角 >>点评 研究生教育收费改革实证研究 >>点评 我国各地区教育支出与经济增长的空间计量分析 >>点评 中国内陆甲型 H1N1 流感的预测和控制模型 >>点评 参赛队员 黄蓓、范悍彪、宋峰 张凤、肖粤志、许长淑 吴蔚、王磊、李树良 吴淑丽、昌先宇、谭竿荣 李攀登、刘海燕、高赟玥 柳玲娣、胡月、赵颖 李玮、郁婷婷、李双双 夏青、陈佳、游碧芙 高勇标、林亮、黄宝辉 宛立杰、胡洪胜、陶淘 刘玉方、律清萍、高培安 参赛学校 安徽财经大学 山东工商学院 华东师范大学 中南财经政法大学 浙江工商大学 安徽大学 中南财经政法大学 浙江工商大学 西南财经大学 中央民族大学 鲁东大学
数学建模题

自习教室开放的优化管理西安科技大学卢凯鹏吴修振翟文豪摘要近年来,大学用电浪费比较严重,集中体现在学生上晚自习上,一种情况是去某个教室上自习的人比较少,但是教室内的灯却全部打开,第二种情况是晚上上自习的总人数比较少,但是开放的教室比较多。
这样的话,就产生了一个问题,怎么样才能让教室开放的程度和学生上自习的情况合理的匹配,做到不“浪费”教室,不浪费电?对于问题1,从表格分析,得到了对每一个教室是否开放的重要重要指标:座位数和用电功率(教室用电功率 = 灯管数 * 每只灯管的功率)。
依据这两个指标,再结合上自习的学生人数以及教室的有效座位数,利用0-1整数规划,在满足节约用电的目的,我们建立了相应的线性目标函数及相应的约束条件。
用lingo求解,得到的最后结果是,需要关闭的教室是:1,2,15,16,20,22,31,44,45对于问题 2,如果将学生对自习室满意程度加入考虑范畴,那么一间教室是否开放就有了三个指标:座位数,用电总功率和学生满意度。
在建立模型时尽量使开放的教室在同一区,那么可以理解为某区是没有开放的。
此观点可以将模型大幅简化。
然后引用1题中的数学思想,以lingo求解,即可得到最后结果,需要关闭的教室是1,15,31,41,42,43,44,45。
针对问题3,由于考试的原因,上自习的学生人数增加,我们首先计算出要搭建教室的座位数至少为241个,结合问题2的结论,再进行数学建模,主要考虑学校成本花费的问题和座位是否能够满足学生需求的问题,次要考虑学生满意度的问题,最后得出结论:只要搭建2间教室,即在自习区B5搭建和教室24一样的教室和在自习区B4搭建和教室19一样的教室。
最后我们对建立的模型优缺点进行了分析,并说明了该模型在实际生活中的广泛应用,对决策者具有一定的指导意义。
关键字0-1整数规划一、问题重述近年来,大学用电浪费比较严重,集中体现在学生上晚自习上,一种情况是去某个教室上自习的人比较少,但是教室内的灯却全部打开,第二种情况是晚上上自习的总人数比较少,但是开放的教室比较多,这要求我们提供一种最节约、最合理的管理方法。
第三讲 DPS应用(3、多元统计分析)

多元统计分析是运用数理统计方法来研究解决多指标问题 的理论和方法。在采用多元统计分析进行数据处理、建立 宏观或微观系统模型时,主要研究以下几个方面的问题:
简化系统结构,探讨系统内核。可采用主成分分析、因子分析、 对应分析等方法,在众多因素中找出各个变量最佳的子集合,从 子集合所包含的信息描述多变量的系统结果及各个因子对系统的 影响。 构造预测模型,进行预报控制。探索多变量系统运动的客观规律 及其与外部环境的关系,进行预测预报,以实现对系统的最优控 制,是应用多元统计分析技术的主要目的。在多元分析中,用于 预报控制的模型有两大类。一类是预测预报模型,通常采用多元 线性回归或逐步回归分析、判别分析、双重筛选逐步回归分析等 建模技术。另一类是描述性模型,通常采用聚类分析的建模技术。 进行数值分类,构造分类模式。在多变量系统的分析中,往往需 要将系统性质相似的事物或现象归为一类,以便找出它们之间的 联系和内在规律性。过去许多研究多是按单因素进行定性处理, 以致处理结果反映不出系统的总的特征。进行数值分类,构造分 类模式一般采用聚类分析和判别分析技术。
(二)逐步回归分析
数据的输入格式是一行为一个样本,一列为一个变量,因变量放在 最右边,输完一个样本后再输下一个样本。将输入待分析的所有数 据定义成数据矩阵块。
在逐步回归分析时,系统首先在 0.1 的置信水平下挑选自变量, 并自动调整F值以保证选入一个 自变量因子,在当前所取的Fx 值 下,进行逐步回归(引入或剔除变 量)。在当前F值分析结束时,系 统会出现如图界面,并询问用户 是继续引入变量、剔除变量还是 结束变量的引入、剔除工作。
如何选择适当的方法来解决实际问题?需要对问题进行综合考 虑。对一个问题可以综合运用多种统计方法进行分析。 例如一个预报模型的建立,可先根据有关生物学、生态学原理, 确定理论模型和试验设计;根据试验结果,收集试验资料;对 资料进行初步提炼;然后应用统计分析方法(如相关分析、逐步 回归分析、偏最小二乘回归分析、主成分分析等)研究各个变量 之间的相关性,选择最佳的变量子集合;在此基础上构造预报 模型,最后对模型进行诊断和优化处理,并应用于生产实际。
第一章 统计建模

聚类分析
聚类分析是一种数值分类方法。所研究的样 本或者变量之间存在程度不同的相似性,要 求设法找出一些能够度量它们之间相似程度 的统计量作为分类的依据,将相似程度大的 样本聚合为一类,把另外一些彼此之间相似 程度大的样本聚合为另外一类⋯⋯关系密切 的聚合到一个小的分类单位,关系疏远的聚 合到一个大的分类单位,直到把所有样品都 聚合完毕,把不同的类型一个个划分出来, 形成一个由小到大的分类系统。
判别分析
判别分析是在已知研究对象分成若干类型(或 组别)并已取得各种类型的一批已知样品的观 测数据,在此基础上根据某些准则建立判别式, 然后对未知类型的样品进行判别分类。对于聚 类分析来说,一批给定样品要划分的类型事先 并不知道,正需要通过聚类分析来给以确定类 型的。正因为如此,判别分析和聚类分析往往 联合起来使用,例如判别分析是要求先知道各 类总体情况才能判断新样品的归类,当总体分 类不清楚时,可先用聚类分析对原来的一批样 品进行分类,然后再用判别分析建立判别式以 对新样品进行判别。
第三部分
往年试题分析
历年来的CUMCM题
1992年A题:施肥效果分析 B题:实验数据分解 1993年A题:非线性交调的频率设计 B题:足球队排名次 1994年A题:逢山开路 B题:锁具装箱 1995年A题:一个飞行管理问题 B题:天车与冶炼炉的作业调度
第二部分
统计学基础知识简介
统计学基础知识简介
统计是“认识社会的最有力的武器之 一”——列宁 什么是统计学?
一封统计学博士的情书
亲爱的莲: 我们的感情,在组织的亲切关怀下、 在领导的亲自过问下,一年来正沿着健康 的道路蓬勃发展。这主要表现在: (一)我们共通信121封,平均3.01天一 封。其中你给我的信51封,占42.1%; 我给你的信70封,占57.9%。每封信平 均1502字,最长的达5215字,最短的也 有624字。
中级经济师—经济基础 第二十三章 统计与数据科学-课件新

① 结构化数据是指存储在数据库里,可以用二维表结构实现 表达的数据;
35
四、统计调查
(二)统计调查的方式 ★ ★ ★
4.重点调查 (1)重点调查是一种非全面调查,它是在所要调查的总体中
选择一部分重点单位进行的调查。所选择的重点单位虽然只是全 部单位中的一部分,但就调查的标志值来说在总体中占绝大比重, 调查这一部分单位的情况,能够大致反映被调查对象的基本情况。
(2)重点调查能以较少的投入、较快的速度取得某些现象主 要标志的基本情况或变动趋势。
统计学
第二十 三章 统 计与数 据科学
变量和数据 数据的来源
统计调查 数据科学与大数据
描述统计与推断统计 定性、定量变量 数据 概念、分类、方式
6
一、统计学
7
一、统计学
(一)统计学 ★
1.定义 统计学是关于收集、 整理、分析数据和从数据中得出结论的
科学。
统计有两个分支: 描述统计和推断统计。
8
一、统计学
数据
信息
知识
47
五、数据科学与大数据
(二)大数据 ★
1.大数据 大数据(big data )指无法在一定时间范围内用常规软件工
具进行捕捉、管理和处理的数据集合,是需要新处理模式才能具 有更强的决策力、洞察发现力和流程优化能力的海量、高增长率 和多样化的信息资产。
48
五、数据科学与大数据
(二)大数据 ★
一方面研究数据本身的特性和变化规律,另一方面通过对数 据的研究为自然科学和社会科学提供一种新的方法,从而揭示自 然界和人类行为的现象和规律。数据科学的研究对象是数据,研 究目标是获得洞察力和理解力,通过对数据的分析,来解释、预 测、洞见和决策,为现实世界服务。
统计学课件 第三章 统计整理

2013-7-26
人数(人) 男 1 4 9 7 2 23 女 1 6 9 5 1 22 合计 2 10 18 12 3 45
9
(四)编表(或绘图)
编表是把汇总的资料按一定的规则在表格 上表现出来。
成绩 50~60 60~70 70~80 80~90 90以上 合计 人数 (人) 2 7 11 8 2 30
(一)数据的预处理
包括数据的审核 、筛选、 排序等. 数据的审核:
1. 数据的审核
检查数据中的错误
2. 数据的筛选
找出符合条件的数据
3. 数据排序
升序和降序 寻找数据的基本特征
2013-7-26 7
(二)统计分组
• 分组是根据研究任务的要 求,对调查所得的原始资 料,确定要进行哪些分组 或分类。 • 如右表是对统计学考试成 绩进行分组。
2013-7-26 4
二、统计整理的意义
统计工作
统计调查
统计整理
统计分析
作用:是统计调查的继续,是统计分 析的前提和基础,在整个统计工作中 发挥着承上启下的作用。
2013-7-26 5
三、统计整理的步骤
1.数据的预处理
2.统计分组
3.编制分配数列
4.汇总统计资料
5.制作统计表或统计图
2013-7-26 6
组别
2013-7-26
øÔýËý ½¶ÊÈÊ 30 10 40
次数
È × (%) ±Ö 75 25 100
频率
28
变量数列
±3-6 Ä ³ Ú ¶ » ¶ ¸ Ë Æ ½ È ² Á í ³ §µ þ ½ È ¤È ¼ ù Õ ú ¾ ¤È ¼ ù Õ ú Á þ ¸ Ë Æ ½ È ² ¾ (» ) ¸ Ë Ê ¤È ý ø Ô ý ½ ¶ Ê È × ±Ö (%) 2 10 8.7 3 15 13.0 4 30 26.1 5 40 34.8 6 20 17.4 Ï Æ ¹ » 115 100.0
统计师如何进行统计模型选择

统计师如何进行统计模型选择统计模型选择是统计学中的重要环节,它对于数据分析和预测模型的构建具有重要意义。
统计师在进行统计模型选择时需要考虑多个因素,包括数据的特征、研究目的、可用的统计方法等。
本文将探讨统计师在进行统计模型选择时的一些常见策略和方法。
一、了解数据的特征在进行统计模型选择时,统计师首先需要全面了解所处理的数据的特征。
这包括数据的类型(是连续型数据还是离散型数据)、数据的分布形态、数据的缺失情况等。
统计师可以借助统计图表和描述性统计量来获得对数据的初步认识,从而更好地选择适用的统计模型。
二、明确研究目的统计模型选择的一个关键因素是研究目的。
不同的研究目的需要使用不同类型的统计模型。
例如,如果研究目的是预测某个变量的值,可以选择回归模型;如果研究目的是比较两组数据的差异,可以选择方差分析模型。
明确研究目的有助于统计师更准确地选择适用的统计模型。
三、考虑统计方法的可用性在选择统计模型时,统计师还需要考虑可用的统计方法。
有些统计模型对于特定的数据类型或特定的数据分布形态更为适用。
例如,对于正态分布型的连续型数据,可以选择使用线性回归模型;对于二分类变量的数据,可以选择使用逻辑回归模型。
统计师需要根据实际情况,选择适用的统计方法进行模型选择。
四、尝试不同的模型在进行统计模型选择时,统计师可以尝试多个不同的模型,并进行比较。
这有助于找到最佳的模型,提高模型的准确度和预测能力。
常见的模型比较方法包括交叉验证、残差分析等。
通过比较不同模型的表现,可以选择出最适合的统计模型。
五、评估模型的拟合度在进行统计模型选择时,统计师还需要评估模型的拟合度。
拟合度是衡量统计模型对数据拟合程度的指标,常见的拟合度指标包括均方根误差(RMSE)、决定系数(R-squared)等。
评估模型的拟合度有助于判断模型的优劣,进而选择最佳的统计模型。
总结:统计模型选择在统计学中具有重要作用。
统计师在进行模型选择时,需要了解数据的特征、明确研究目的、考虑统计方法的可用性,尝试不同的模型,并评估模型的拟合度。
数学建模之需求预测

A
23
A
24
二重指数平滑法
适用范围:市场需求具有一定的线性趋势时, 可以考虑采用
基本原理:每期结束时先预测基数和斜率,基 于所得的基数和斜率计算下一期的需求预测值
A
25
第t期结束时,按下列一重指数平滑法的原理 分别计算基数和斜率
st dt (1)(st1 gt1) gt (st st1) (1)gt1 , 为平滑系数
适合较长期的预测,如对新产品的未来需求进行预测
4 销售人员意见法
作为基层工作人员直接面对市场和顾客
适用于公司短期预测
注意主观因素影响,可能出于对自己完成指标有利考虑,将上报的需 求预测结果偏离真实的需求结果,对公司长期运营造成损失
A
15
定量预测方法:
时间序列分析:
以时间为独立变量,把过去需求和时间的关 系作为需求模式来估计未来需求。
A
26
基于上述基数和斜率值,预测第t+1期的需 求 Ft1 st gt
若在第t期结束预测第t+2期的需求 Ft2 st 2gt
在第t期结束预测第t+n期的需求
Ftn st ngt
A
27
例2-4 某产品的销售量呈现一定的线性增长趋 势,假设
试取 进行预测
d02 7 ,s 12 3 ,g 14
包括方法: 移动平均法 指数平滑法 周期性波动预测方法
A
16
2.3 移动平均法:
最适合的预测期:短期。
对过去的实际需求数据进行适当的加权处理来推测未 来的需求,即取最近的N期实际需求进行平均作为 下一期的需求预测值。
数学表达式:
Ft1N 1nttN1dn
(2.6)
A
数学建模——投篮命中率的数学模型

投篮命中率的数学模型摘要随着篮球运动的普及,篮球比赛中紧张、激烈的气氛和更加具有攻击性的防守等因素导致投篮命中率大大降低。
根据研究显示,影响投篮命中率有两个关键因素:出手角度和出手速度。
本文主要运用运动力学的知识,建立有效的篮球投射模型, 从篮球投射时球的出手角度、出手速度、出手高度和篮球球心与篮框中心的水平距离、篮球入射角之间的关系入手,分析各种因素对投篮命中率的影响,并作适当的假设,在合理估计出手点与篮框中心距离并保持出手速度稳定的情况下, 确定投篮的最佳出手角度和最佳出手速度,得出一个既能使投篮时不过多耗费体力又能提高投篮命中率的结论。
首先,本文将三角函数、导数、微分等数学知识及运动学、力学等物理知识相互结合,在罚球投篮这一具体问题的相应具体情境下对此进行了深入分析。
其次,本文建立了与之相关的数学模型,通过不同投篮情况的图表分析归纳出对应的公式,在多重公式的累加条件下最后整理得到满足要求的最终条件范围,得出模型的结果。
在求解过程中,本文使用了MathType数学软件对所用的数学符号作了系统的整理,借此列出了各组公式,同时给出了详细的计算及分析过程,并得出最终结果。
本文在第一问中所设定的不考虑球出手后自身的旋转及球碰篮板或篮框的情况,即在只针对空心球的情况下又限制变量,分别讨论篮框大小、篮球大小、空气阻力及出手角度和速度的最大偏差这四个不同变量下命中率受到的的影响,给出公式,计算出结果。
最终,本文探讨出提高罚球命中率的方法是控制投篮时的出手角度和出手速度,使之分别限制在一定的范围内。
出手角度和速度的过高或过低都会使罚球命中率不能保持在较高水平。
在第二问中本文针对篮球擦板后进篮的情况,假定篮球在碰撞过程中没有能量损耗的理想情况,讨论出了分别在限制区边线距篮框中心30度、45度、90度(罚球线)位置上这三种不同情境下出手角度、出手速度与投篮的命中率之间的关系。
当运动员所站的位置改变时,即投篮出手点到篮框的距离改变时,出手角度和出手速度的增加或减少都影响了投篮的命中率。
数学建模_电梯调度问题2

数学建模参选题目:A题:电梯的运载效率的分析与建模参赛队员:熊程燃丁建佳聂红松信电10-5班电梯调度问题摘要:本文提出了一个如何合理调配现有电梯,使电梯运送效率更高的方案。
运用运筹学的基本知识,我们建立了非线性整数规划模型,并运用概率统计法计算出了模型的解,最后运用综合评价的方法从时间评价指标和能耗评价指标进行评价和优化。
针对问题(1),通过分析电梯运行的整个过程,我们可以得到评价电梯服务效率的评价指标有:时间评价指标、能耗评价指标、乘客状态评价指标和乘客容忍度评价指标。
上下班高峰期,衡量系统优劣的主要指标有时间评价指标和能耗评价指标。
我们运用目标规划的基本知识对系统建立综合评价模型。
针对本案例中出现的问题是工作日里每天早晚高峰时期均是非常拥挤,而且等待电梯的时间明显增加;由文献可知,电梯的主要能量消耗发生在启停阶段,因此通过减少启停次数可以较少能耗。
综上所述,本文以电梯运行的平均时间和总的启停次数作为主要评价指标,对模型进行分析评价。
针对问题(2),在合理假设的前提下,运用非线性整数规划的基础知识,建立了非线性整数规划模型(2)。
为了简化模型,我们将电梯往返平均时间作为时间评价指标的主要依据,以电梯往返运行总时间作为目标函数,建立数学模型。
再对模型进行合理的简化处理后,在matlab中运用模拟退火算法进行求解得到每个电梯运行的平均时间为5489秒,启停的平均总次数为924次,六部电梯分配方案如下:电梯编号允许停靠楼层1 2、3、17、18 282 19、20、21、22 263 5、6、7、9 254 8、12、14 235 10、11、16 246 4、13、15 27由排队论的知识可知,原模型是一个多对多服务,运用概率统计的知识,可以求解出没有优化前的状态,每个电梯运行的平均时间是10811秒,启停总次数为3939次。
针对上述两个指标,我们通过综合评价的方法,对改进后和改进前的状态做出了评价,得分分别是7407.3,3228.可知优化后的方案很好的解决了实际的拥堵和能源损耗过多的问题针对问题(3),我们进一步联系实际,考虑到电梯能够运行到地下1层,地下2层。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
u( X ) aT ( X ) (X的线性函数)
称为线性判别函数. a称为判别系数.
注
在判别分析中,实质是利用线性判别函数把 样本空间划分成两个部分:
D1 X | u( X ) 0,D2 X | u( X ) 0
当样本 X落入D1时,则判断 X G1 ; 当样本X落入D2时,则判断 X G2 。
Department of Mathematics
HUST
Mathematical Modeling
Release 1.0
例题 判别分析问题
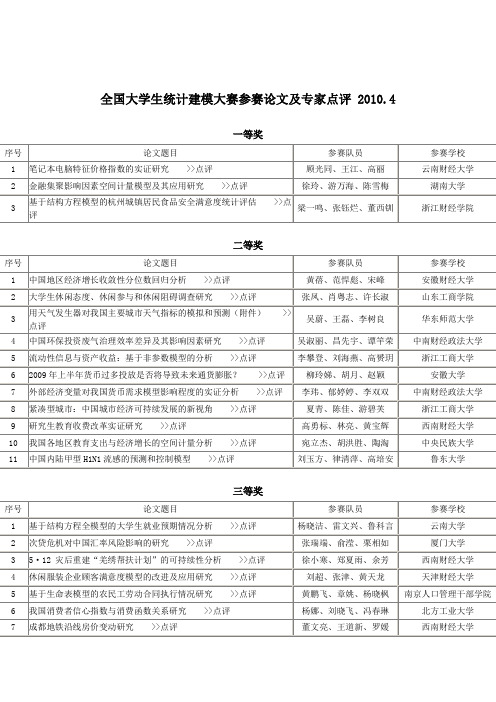
1981年生物学家格若根(W.Grogan)和维什(W.Wirth)发现 了两类蚊子.他们测量了这两类蚊子每个个体的翼长和触角 长,把翼长作纵坐标,触角长作横坐标,每个蚊子的翼长和触 角决定了坐标平面的一个点. 共测量了15个蚊子的数据,其 中6个蚊子属于Apf类,用黑点“.”表示;9个蚊子属Af类,用 小圆圈“。”表示,得到的结果见图6.5.
判别分析问题
af apf
有k个总体 G1 , , Gk , 分布函数分别
F1 ( x ), , Fk ( x )
这里 x Î R p表示p维指标 对给定的一个新样本 判断它来自哪个总体?
图6.5 蚊子的触角长和翼长图
Department of Mathematics HUST
Mathematical Modeling
x1
1 2 3 4 5 6 7 8 9 10 -1.9 -6.9 5.2 5.0 7.3 6.8 0.9 -12.5 1.5 3.8 9.2
2 i
X ( 1) x2
3.2 10.4 2.0 2.5 0.0 12.7 -15.4 -2.5 1.3 6.8 21 581.28
x1 x2
-6.08 -71.76 10.4 12.5 0 86.36 -13.86 31.25 1.95 25.84 76.60 0.2 -0.1 0.4 2.7 2.1 -4.6 -1.7 -2.6 2.6 -2.8 -3.8
Department of Mathematics HUST
Mathematical Modeling
Release 1.0
减小误差概率以改变判断准则
如果 x c ,判断 X G2 如果x d , 判断X G1
如果 c x d , 则有待进一步判定。 判别准则只能减少误差发生的概率而不能杜绝错判 因为事实上如果X来自G1,而 因为事实上如果X来自G2,而
9.2.1 9.2.2
距离判别法 费歇判别法
9.2.3
蚊子的费歇判别法
Department of Mathematics
HUST
Mathematical Modeling
Release 1.0
9.2 统计识别方法
常见的识别(或判别) 问题
(1)诊断疾病
(2)天气预报
(3)在考古方面的应用 (4)昆虫分类
问题现在变为: 今有一个样本 X Rp
问X属于G1总体还是属于G2总体?
Department of Mathematics HUST
Mathematical Modeling
Release 1.0
距离判别的根据与原则 距离判别法是根据X与G1和G2的距离决定X的归属 距离判别法原则: 若X与G1 距离小,则X属于G1 ; 若X与G2 距离小,则X属于G2 ;
Release 1.0
例9.6 对于下雨天和非雨天两类天气情况收集如下数据
雨 x 1 湿度差
-1.9 -6.9 5.2 7.3 6.8 0.9 -12.5 1.5 3.8
Department of Mathematics
天 x2 温度
3.2 10.4 2.0 0.0 12.7 -15.4 -2.5 1.3 6.8
Department of Mathematics HUST
Mathematical Modeling
Release 1.0
例如
距离判别法
T
设X x1 , x2 , u( X ) 规定了Rn 的一个分划如图6.6
x2
D1
u(X
)=0
x1
O
D2
图9.6
Department of Mathematics
(1) ( 2 ) T 1 (1) 2( X ) S ( ( 2) ) 2
2( X ) S (
T 1 (1)
)
( 2)
(1) ( 2 ) ( 令 ) 2
Department of Mathematics
HUST
Mathematical Modeling
( x )( (1) ( 2) )
2
Department of Mathematics
HUST
Mathematical Modeling
Release 1.0
判别误差
误差产生的原因
G1的分布密度 G2的分布密度
μ
(1)
c dμ
(2)
x
μ
(1)
μ
μ
(2)
x
可见 判别规则符合直观判断的合理性; 判别方法会发生误判的情况. 该错误的情况发生在X当来自G1而落入阴影部分 (如图6.8所示的情形) 而根据判别法则判为 X G2
如果u( X ) 0, 有X G1
如果u( X ) 0, 有X G2
Department of Mathematics HUST
Mathematical Modeling
Release 1.0
距离判别的根据与原则
若 (1) , ( 2) 和S已知, 令
a S 1 ( (1) ( 2) )
u ( X )规定的分划
HUST
Mathematical Modeling
Release 1.0
判别误差 误差产生的原因 考察当p=1时的情形
G1 , G2 : G1 N ( (1) , 2 ), G2 N ( ( 2 ) , 2 )
其线性判别函数为 u( x ) 不妨假设 (1) ( 2 ) ,则 判断 X G1 当 x 0 即x , 判断 X G2 当 x 0 即x ,
若抓到三只新的蚊子,它们的触角长和翼 长分别为 (1.24,1.80), (1.28,1.84),(1.40,2.04) . 问它们应分别属于哪一个种类?
Department of Mathematics HUST
Mathematical Modeling
Release 1.0
2.1 2.0 1.9 1.8 1.7 1.1 1.2 1.3 1.4 1.5 1.6
则判别函数:
X (1) X (2) T ˆ 1 (1) ˆ (2) u( X ) ( X ) S (X X ) 2
当 u( X ) 0时,判断 X G1
Department of Mathematics HUST
当 u( X ) 0时, 判断 X G2
Mathematical Modeling
这里采用马氏距离 d ( X , Gi )
d 2 ( X , Gi )( X ( i ) )T S 1( X ( i ) ), i 1, 2
Department of Mathematics
HUST
Mathematical Modeling
Release 1.0
距离判别的根据与原则 计算X与G1和X与G2的距离平方之差
d 2 ( X , G1 ) d 2 ( X , G2 ) ( X (1) )T S 1 ( X (1) ) ( X ( 2 ) )T S 1 ( X ( 2 ) ) X T S 1 X 2 X T 1 (1) (1)T S 1 (1) ( X T S 1 X 2 X T S 1 ( 2 ) ( 2 )T S 1 ( 2 ) 2 X T S 1 ( ( 2 ) (1) ) (1)T S 1 (1) ( 2 )T S 1 ( 2 ) 2 X T S 1 ( ( 2 ) (1) ) ( (1) ( 2 ) )T S 1 ( (1) ( 2 ) )
x1
X ( 2) x2
6.2 7.5 14.6 8.3 0.8 4.3 10.9 13.1 12.8 10.0 88.5 950.13
x1 x2
1.24 -0.75 5.84 22.41 1.68 -19.78 -18.53 -34.06 33.28 -28 -36.67
x
376.54
57.32
Release 1.0
距离判别的根据与原则
d 2 ( X , G1 ) d 2 ( X , G2 ) 2( X )T S 1( (1) ( 2) )
定义一个函数 u( X ) ( X )T S 1 ( (1) ( 2 ) ) 距离判别准则 如果 d ( X , G1 ) d ( X , G2 ) 则判断 X G1 如果 d ( X , G2 ) d ( X , G1 ) 则判断 X G2 由 ( X ) 确定判别准则为
Release 1.0
9.2.1 距离判别法
距离判别法中的数学模型
G1 , G2 表示两个总体 , 是取值于 Rp中的随机变量
它们的数学期望和方差分别为
EG1 (1) , EG2 ( 2 ) VarG1 S (1) ,VarG2 S ( 2 )
(1) ( 2) S S S 假设
Department of Mathematics
HUST
Mathematical Modeling
