四年级奥数+长方形与正方形

合集下载

四年级奥数教材第4讲____长方形和正方形(二)

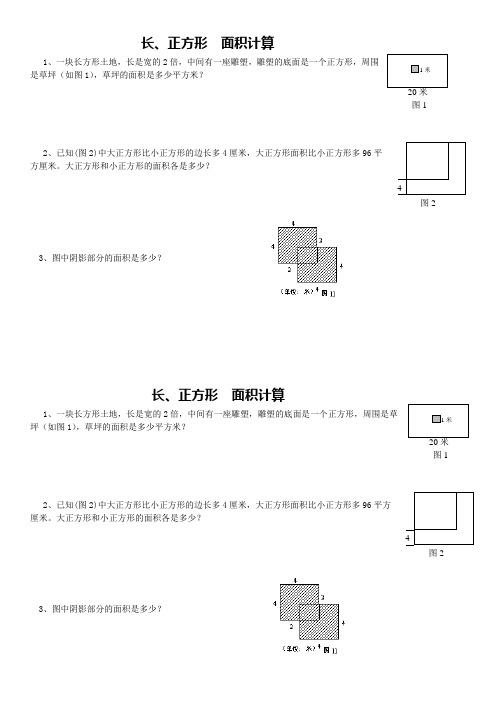
长、正方形面积计算1、一块长方形土地，长是宽的2倍，中间有一座雕塑，雕塑的底面是一个正方形，周围是草坪（如图1），草坪的面积是多少平方米？2、已知(图2)中大正方形比小正方形的边长多4厘米，大正方形面积比小正方形多96平方厘米。

大正方形和小正方形的面积各是多少？3、图中阴影部分的面积是多少？长、正方形面积计算1、一块长方形土地，长是宽的2倍，中间有一座雕塑，雕塑的底面是一个正方形，周围是草坪（如图1），草坪的面积是多少平方米？2、已知(图2)中大正方形比小正方形的边长多4厘米，大正方形面积比小正方形多96平方厘米。

大正方形和小正方形的面积各是多少？3、图中阴影部分的面积是多少？图1图24图1图244、如图8，已知大正方形的面积比小正方形多52平方分米，大正方形比小正方形的边长多2分米。

小正方形的面积是多少？大正方形的面积是多少？5.图9是由9个小长方形组成的，按图中编号，第1，2，3，4，5号的面积分别是1平方米，2平方米，3平方米，4平方米，5平方米，那么，第6号长方形和面积是多少呢？6、如图，正方形中套着一个长方形，正方形的边长是15厘米，长方形的四个角的顶点，恰好分别把正方形四条边都分成两段，其中长的一段是短的2倍。

这个长方形的面积是多少？4、如图，已知大正方形的面积比小正方形多52平方分米，大正方形比小正方形的边长多2分米。

这个长方形的面积是多少？。

四年级奥数巧数长正方形的个数

第 4 讲巧数长（正）方形的个数数图形时要有次序、有条理，才能不遗漏、不重复，一般步骤应是：仔细观察，发现规律，应用规律。

长方形是用“点”或者“线”来数的，而正方形是用“块”来数的。

数长方形的公式：长边上的线段和×宽边上的线段和数正方形的公式：1、一个被划分成m×n 的小正方形的长方形中共可以数出的正方形的个数是：m×n＋（m-1）×（n-1）＋（m-2）×（n-2 ）＋⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯＋1×【n-（m-1）】（其中m<n）2 、当m=n时，即一个划分成n×n=n2个小正方形的正方形中，共可以数出正方形的个数是：n2＋（n-1）2＋⋯⋯⋯⋯⋯⋯⋯⋯＋22＋12典型例题：1、长方形的构成必须有长和宽，下图中有许多长方形，你能数出它们有多少个？分析与解答:因为长方形的构成与长的线段数有关，也与宽的线段数有关，所以数长方形的个数必须要看长与宽两个因素上图上长有6 条线段，即3＋2＋1=6（个）宽边上有3 条线段，即2＋1=3（个）因此，根据数长方形公式：6×3=18（个）答：上图中共有18 个长方形。

2、下图中共有多少个长方形？分析与解答：这道题比例1 横竖都多了一条线，那么长方形的个数明显增多了，利用公式仍然要数出长边上的线段数和宽边上的线段数即长边上的线段和：4＋3＋2＋1＝10 个宽边上的线段和：3+2+1=6个因此根据数长方形公式：10×6=60 个答：上图中共有60 个长方形。

3、下图中共有多少个正方形？分析与解答：我们先来数一数：只含一个正方形的有9个（即3×3=9）；含有4个正方形的有4个（即2×2=4）；含有9 个正方形的有1个通过刚才的数，我们发现图中正方形的个数为1× 1+2× 2+3×3=1+4+9=14 个，以后我们碰到类似的题目可以用这种方法数出正方形的个数。

1小学奥数暑假提高衔接(长方形和正方形周长与面积)

1小学奥数暑假提高衔接（长方形和正方形周长与面积）小学奥数暑假提高衔接姓名：第一部分四年级下册课本知识复习与提高第1讲长方形和正方形的周长与面积重点点拨我们已经学会了长方形和正方形的周长与面积计算，掌握了“长方形周长=(长宽)×2”，“正方形周长=边长×4”“长方形面积=长×宽”，“正方形面积=边长×边长”。

在运用这些基本知识解决相关问题时，一定要仔细观察，认真思考，找出条件和问题之同有什么联系，应先求什么，再什么，最后灵活运用公式进行计算。

【例1】把两个边长是6厘米的正方形拼成一个长方形，这个长方形的周长是多少厘米? 分析在解决这类关于图形剪拼问题时，可以借助画示意图的方法帮助理解题意，找到问题解决的方法。

如题目中两个边长是6米的正方形拼成一个长方形，可以这样拼，要求这个长方形的周长可以先求出这个长方形的长和宽，然后再用长方形周长公式进行计算，这是方法一;也可以把这个长方形的周长看成由6个6厘米长的线段围成的，这样也可以求出这个长方形的周长。

解答 (1)6×2=12(厘米) (2)6X6=36(厘米) (12+6)×2 =18X2=36(厘米）答:这个长方形的周长是36厘米。

【例2】一根铁丝正好可以围成一个边长是18厘米的正方形，如果用它重新围一个长是24厘米的长方形、这个长方形的宽是多少厘米? 分析用一根铁丝正好国成一个正方形，那么这个正方形的周长就是这根铁丝的长度，又用这根铁丝国成一个长方形，那么这根铁丝的长度就是围成的这个长方形的周长，然后根据长方形周长公式，求出长方形的宽。

解答 18X4=72(厘米) 72÷2－24=12(厘米) 答：这个长方形的宽12厘米。

【例3】把一个边长是16分米的正方形纸裁成4个完全一样的小正方形，这4个小正方形的周长和比原来的大正方形周长增加了多少? 分析将边长是16分米的正方形沿水平方向裁一刀，周长和比原来大正方形周长增加2个边长；再沿竖直方向裁一刀，又增加2个边长，一共增加了4个边长。

小学奥数系列：第2讲长方形、正方形、三角形、角

数学书的面、课桌的面、黑板的面都是长方形。

形状如下图。

长方形是由四条线段连接起来的。

这四条线段就是长方形的四条边。

用折纸的办法就会发现，长方形相对的边一样长。

长方形长边的长度叫做长方形的“长”，短边的长度叫做长方形的“宽”。

长方形有四个角，用三角板的直角去量，就会知道，长方形的四个角都是直角。

长方形有四条边，对边相等；长方形有四个角，都是直角。

四条边都相等的长方形叫做正方形。

正方形的四条边都相等，四个角都是直角。

动一动手，用折纸的办法，把长方形剪成正方形。

三角板的面是三角形。

如下图。

三角形是由三条线段连接成的，这三条线段就是三角形的三条边。

在一个三角形中，若有两条边相等，这个三角形就叫做等腰三角形。

上面图中图(2)就是等腰三角形。

三角形有三个角。

在一个三角形中，若有一个角是直角，这个三角形就叫做直角三角形。

图中两个三角形都是直角三角形。

上面图中图(2)不但是等腰三角形，而且是直角三角形，因此这个三角形就叫做等腰直角三角形。

看一看，下面实物中圆的图形。

请你把硬币放在纸上，用左手按住不动，右手拿笔，沿硬币的边画一周，就画出一个圆。

你还可以用圆糖盒等有圆图形的物体，照样描画出圆。

画圆有专门的工具——圆规。

图中，点O叫做圆心，线段OA的长叫做半径。

圆心O不动，半径越长画出的圆就越大。

图中(2)画出以O为圆心的三个同心圆。

【例1】说出下图中每个图的名称。

解：在图中，(1)、(2)是长方形；(3)、(6)是正方形；(4)、(8)是直角三角形；(5)、(10)是折线；(7)、(8)是等腰三角形；(8)还是等腰直角三角形；(9)是圆；(11)是三角形；(12)是线段。

【例2】数一数，下图中图(1)有几个正方形?图(2)有几个长方形?。

小学四年级奥数讲义专题一正方形

小学四年级奥数讲义专题一正方形小学四年级奥数讲义专题一: 正方形
简介
正方形是一种特殊的四边形，它具有四条边相等且四个角均为90度的特点。

在数学奥林匹克竞赛中，正方形常常是一个重要的考察对象。

本讲义将重点介绍关于正方形的性质、运算和问题解决方法。

正方形的性质
1. 边长：正方形的四条边长度相等，可以用一个变量a表示。

2. 内角：正方形的四个内角都是直角（90度），记为
∠A=∠B=∠C=∠D=90度。

3. 对角线：正方形的对角线相等且垂直平分，记为BD=AC且BD⊥AC。

正方形的运算
1. 周长：正方形的周长等于4倍的边长，即周长=4a。

2. 面积：正方形的面积等于边长的平方，即面积=a²。

正方形的问题解决方法
1. 求边长：当已知正方形的周长时，可以通过周长除以4得到
边长。

2. 求面积：当已知正方形的边长时，可以将边长平方得到面积。

练题
1. 若一个正方形的边长为5cm，求其周长和面积。

2. 若正方形的周长为24cm，求其边长和面积。

答案
1. 边长为5cm的正方形，其周长为20cm，面积为25cm²。

2. 周长为24cm的正方形，其边长为6cm，面积为36cm²。

希望本讲义能够帮助同学们更好地理解正方形的性质和运算，
并在日常学习和解决问题中灵活运用。

下一讲义将继续介绍正方形
的相关知识，请大家继续关注。

奥数四年级—长方形和正方形面积市公开课一等奖省赛课获奖PPT课件

长方形和正方形（面积）
上节我们学了长方形、正方形周长计算，本
节我们学习，怎样将复杂图形变成我们熟悉长
方形和正方形, 计算面积。
长方形面积=长×宽正方形面积=边长×边长
方法有：减法、拆分、分块、分段、等技巧，使大家在解题中能顺利地找到突破口，化难为易，化繁为简。
第1页
减法
例1、有一块长方形土地，长是宽2倍，中间有一座雕塑，雕塑底面是一个正方形，周围是草坪，草坪面积是多少平方米？(单位：米)
第9页
画图
例5、一张边长7厘米正方形纸片，最多能裁出多少张长4厘米，宽1厘米纸条？并画图说明。
最多能裁出12张长4宽1厘米纸条
第10页
练 1.用48厘米长一根铁丝围成一个正方形，它习面积是多少？用这根铁丝围成一个长15厘米
长方形，它面积是多少？
48÷4=12 12×12=144
15×2=30
点恰好把正方形四条边都分成两段，其中长一段是短4倍。阴影部分面积是多少？
20×20=400
20÷5=4 4×4=16 4×4÷2×2=16 16×16÷2×2 =256 16＋256=272
第17页
练 6、如图，一个正方形中套着一个长方形，已知正方形边长是20分习米，长方形四个角顶点恰好把正方形四条边都分成两段，其中长一
求长方形面积，必须知道长和宽，这题长和宽，都极难求解。
换个角度：正方形-4个三角形。
第7页
分段
例4、如图，正方形中套一长方形，正方形边长是15，
长方形四个顶点恰好分别把正方形四条边都分成两段，
其中长一段都是短2倍。这个长方形面积是多少？
(单位:厘米)
15÷3=5 5×2=10。

四年级数学奥赛起跑线第4讲长方形与正方形(二)

四年级数学奥赛起跑线
第4讲长方形与正方形（二）
1、用48厘米长的一根铁丝围成一个正方形，它的面积是多少？如果用这根铁丝围成一个长15
厘米的长方形，它的面积是多少？
2、有一个长方形的市民广场，长100米，宽80米。

广场中间留了宽4米的人行道，把广场平均分成四块（如下图），每一块的面积是多少？
3、如下图，是由12个相同的等腰直角三角形拼成的，这个图形的面积是多少（单位：厘米）？
4、如下图，已知大正方形的面积比小正方形的面积多52平方分米，大正方形的边长比小正方形
多2分米。

小正方形和大正方形的面积各是多少？
5、下图是由9个小长方形组成的，按图中编号，第1、2、3、4、5号的面积分别是1平方米，2平方米、3平方米、4平方米、5平方米。

那么，第6号长方形的面积是多少呢？
6、如下图，一个正方形中套着一个长方形，已知正方形的边长是20分米，长方形的四个顶点恰
好把正方形四条边都分成两段，其中长的一段都是短的4倍。

阴影部分的面积是多少？
7、求下图中阴影部分的面积（单位：米）
8、把一块长6分米，宽5分米的长方形钢板，截成长3分米，宽2分米的小长方形钢板，最多能截成几块？请画图说明。

四年级奥数第10次课长方形和正方形面积

第11次课长方形和正方形的面积知识点简析：利用“割补”、“平移”、“旋转”等方法，使复杂的问题简单化。

切实掌握有关概念，利用“割补”、“平移”、“旋转”等方法，使复杂的问题转化为普通的求长方形、正方形面积的问题，从而正确解答。

例1 已知大正方形比小正方形边长多2厘米，大正方形比小正方形的面积大40平方厘米。

求大、小正方形的面积各是多少平方厘米？例2 一个大长方形被两条平行于它的两条边的线段分成四个较小的长方形，其中三个长方形的面积如下图所求，求第四个长方形的面积。

例3 把20分米长的线段分成两段，并且在每一段上作一正方形，已知两个正方形的面积相差40平方分米，大正方形的面积是多少平方分米？例4 有一个正方形ABCD如下图，请把这个正方形的面积扩大1倍，并画出来。

例5 有一个周长是72厘米的长方形，它是由三个大小相等的正方形拼成的。

一个正方形的面积是多少平方厘米？A. 基础题自测1.有一块长方形草地，长20米，宽15米。

在它的四周向外筑一条宽2米的小路，求小路的面积。

2.下图一个长方形被分成四个小长方形，其中三个长方形的面积分别是24平方厘米、30平方厘米和32平方厘米，求阴影部分的面积。

3.一块正方形，一边划出1.5米，另一边划出10米搞绿化，剩下的面积比原来减少了1350平方米。

这块地原来的面积是多少平方米？4.四个完全一样的长方形和一个小正方形组成了一个大正方形，如果大、小正方形的面积分别是49平方米和4平方米，求其中一个长方形的宽。

5.五个同样大小的正方形拼成一个长方形，这个长方形的周长是36厘米，求每个正方形的面积是多少平方厘米？B.中档题演1.正方形的一组对边增加30厘米，另一组对边减少18厘米，结果得到一个与原正方形面积相等的长方形。

原正方形的面积是多少平方厘米？2.下面一个长方形被分成六个小长方形，其中四个长方形的面积如图所示（单位：平方厘米），求A 和B 的面积。

B1224A 45153.一个正方形，如果它的边长增加5厘米，那么，面积就比原来增加95平方厘米。

四年级奥数专题第13讲长方形与正方形的面积(二)

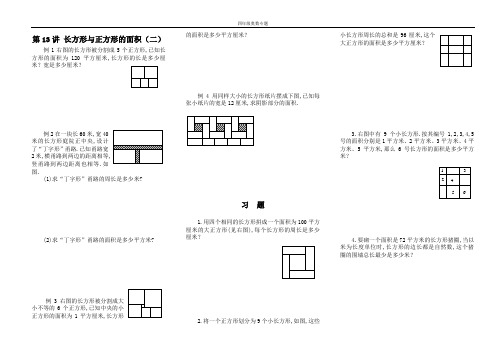
第13讲长方形与正方形的面积（二）例1右图的长方形被分割成5个正方形,已知长方形的面积为120平方厘米,长方形的长是多少厘米？宽是多少厘米？例2在一块长60米,宽40米的长方形庭院正中央,设计了“丁字形”甬路.已知甬路宽2米,横甬路到两边的距离相等,竖甬路到两边距离也相等.如图.(1)求“丁字形”甬路的周长是多少米?(2)求“丁字形”甬路的面积是多少平方米?例3右图的长方形被分割成大小不等的6个正方形,已知中央的小正方形的面积为1平方厘米,长方形的面积是多少平方厘米？例4用同样大小的长方形纸片摆成下图,已知每张小纸片的宽是12厘米,求阴影部分的面积.习题1.用四个相同的长方形拼成一个面积为100平方厘米的大正方形(见右图),每个长方形的周长是多少厘米？2.将一个正方形划分为9个小长方形,如图,这些小长方形周长的总和是96厘米,这个大正方形的面积是多少平方厘米？3.右图中有9个小长方形.按其编号1,2,3,4,5号的面积分别是1平方米、2平方米、3平方米、4平方米、5平方米,那么6号长方形的面积是多少平方米？4.要砌一个面积是72平方米的长方形猪圈,当以米为长度单位时,长方形的边长都是自然数,这个猪圈的围墙总长最少是多少米？5.右图中5个阴影所示的图形都是正方形,所标的数字是邻近线段的长度.那么阴影所示的5个正方形面积之和是多少？6.下图大正方形的面积是128平方厘米,阴影部分的总面积是多少平方厘米？7.四个一样的长方形和一个小正方形拼成一个大正方形,大小正方形的面积分别为64平方厘米和9平方厘米.长方形的面积是多少平方厘米？8.一个长方形,如果宽不变,长增加8米,面积增加72平方米,如长不变,宽减少4米,面积减少48平方米.原长方形面积是多少？9.有两个完全相同的长方形,如果把它们的长连在一起拼成一个新长方形,周长比原一个长方形增加10厘米;如果宽连一起拼成一个新长方形,周长比原一个长方形增加16厘米.求原每个长方形的面积.10.某工厂的一座新厂房建筑在一块边长是25米的正方形场地上,厂房的横竖都宽5米,如图.(1)求工字形新厂房的周长是多少米?(用最简单的方法解答)(2)工字形新厂房的面积是多少平方米?8 cm米。

四年级奥数巧求长方形和正方形周长KK

7．如图，长方形的长为
120厘米，截去一个正方形后，剩下一个长方形，即阴影部分，求剩下的长方形的周长。

8、.右图是某小学教学楼的平面示意图，设计者在图上只标明了三条线段的长度(单位：米)。

请你算出它的周长。

9、.如右图所示，一个正方形被分成了三个相同的长方形。

如果其中一个长方形的周长是16米，那么这个正方形的周长是多少米？
10
、(2007年“希望杯”第一试）右图中的阴影部分BCGF 是正方形，线段FH 长18
厘米，线段AC 长24厘米，则长方形ADHE 的周长是多少厘米？
A C
B。

高斯小学奥数四年级上册含答案第03讲_基本直线形面积公式

第三讲基本直线形面积公式在几何中，所谓直线形就是指由线段构成的图形．在日常生活中，我们最常见的直线形有以下几种：正方形、长方形、平行四边形、三角形、梯形．在有关直线形的计算中，计算周长和计算面积是最常见的两类．我们已经学过了如何计算直线形的周长，接下来我们将学习如何计算直线形的面积．№1. 正方形和长方形的面积正方形的面积和长方形的面积公式是我们所熟悉的，如下图：例题1如下图，有一块长方形田地被分成了五小块，分别栽种了茄子、黄瓜、豆角、莴笋和苦瓜．其中栽种茄子的面积是16平方米，栽种黄瓜的面积是28平方米，栽种豆角的面积是32平方米，栽种莴笋的面积是72平方米，而且左上角栽种茄子的田地恰好是一个正方形．请问：剩下的栽种苦瓜的田地面积是多少？「分析」左上角是面积为16的正方形，那么它的边长是多少？你还能求出哪些线段的长度呢？练习1如图，有一块长方形田地被分成了四小块，分别栽种了冬瓜、西瓜、南瓜、黄瓜，其中冬瓜地的面积是24平方米，西瓜地的面积是36平方米，南瓜地的面积是18平方米，而且左下角西瓜地恰好是一个正方形．请问：剩下的黄瓜地的宽面积是多少？№2. 平行四边形的面积如下图，平行四边形的两组对边平行且相等，我们把两组对边用不同颜色标出来．为了计算平行四边形的面积，我们可以把平行四边形切成两块，然后拼成一个长方形，如下图．这个平行四边形的面积和拼成的长方形的面积相同，都等于长方形的长乘以宽．长方形的长和宽在平行四边形中都可以找到对应线段．在平行四边形中，这两条线段分别叫做底和高．于是我们有：如图所示，同学们可以画出这条底对应的若干条高，并且这些高是相等的，都等于上下两条平行线间的距离．36 1824底当然我们可以用另一种方式把上面的平行四边形剪拼成一个长方形，如下面左图所示．同样得到相对于这条底的若干条高，如下面右图所示，这些高也是相等的，都等于左右两条平行线间的距离．要计算平行四边形的面积，需要知道一条底，以及它所对应的高．大家看看下面的几个图形，试着画出与底边相对应的高．例题2下图是由两个边长分别为4和7的正方形拼成的，请求出阴影平行四边形的面积．「分析」阴影部分是平行四边形，应该选哪条边作为底呢？相应的高是多少呢？练习2如图，大正方形里有一个小正方形还有一个阴影平行四边形．如果大正方形的边长是20厘米，小正方形的边长是8厘米．那么阴影平行四边形的面积是多少？BCF底高高高№3. 三角形的面积三角形中也有相对应的底和高．过三角形的一个顶点向所对的边做一条垂线，所得的垂线段叫做三角形的高，所对的边叫做三角形的底．每个三角形有三组对应的底和高．要计算三角形的面积，同样要利用底和高的长度．观察下图，我们把一个三角形倒过来和原图形拼在一起，可以得到一个平行四边形．平行四边形的底与三角形的底相等，高也与三角形的高相等．而平行四边形的面积等于“⨯底高”，正好是三角形面积的2倍，所以我们有三角形面积公式：从形状上讲，三角形有三类：锐角三角形、直角三角形、钝角三角形．由于三角形的形状多变，在初学阶段要找准三角形相对应的底和高很不容易．因此要想算出三角形的面积，最关键的还在于准确地找到底与相应的高．．．．．．．．．．．．下面是一个简单的作图练习，大家不妨画一画．例题3如下图所示，两个正方形并排放在一起，大正方形的边长是8厘米，小正方形的边长是6厘米．请问：阴影三角形的面积是多少？「分析」阴影部分是三角形，应该选哪条边作为底呢？相应的高是多少呢？练习3右图是由两个边长分别为4和6的正方形拼成的，请求出阴影三角形的面积．№4. 梯形的面积三角形和平行四边形都有“底”和“高”的概念，梯形中也有．在梯形中，平行的一组对边分别叫做上底和下底，不平行的一组对边叫做腰，上底和下底之间的距离叫做梯形的高．如下图所示，把两个相同的梯形拼在一起，可以得到一个平行四边形．从图中可以看出，这个平行四边形的面积是梯形面积的2倍．同时平行四边形的底由梯形的上底和下底拼接而成，高与梯形的高相等．所以：86下底例题4一个正方形和一个长方形按下图的方式排放，已知正方形的面积是49平方厘米，长方形的长为11厘米，宽为8厘米，那么阴影部分的面积是多少？「分析」阴影部分是梯形，要求面积，关键是找清楚它的上底、下底、高分别是多少．练习4如下图，大正方形的边长是8厘米，小正方形的边长是6厘米．请问：图中的阴影图形的面积是多少平方厘米？例题5如下图所示，两个边长10厘米的正方形相互错开3厘米，那么图中阴影平行四边形的面积是多少？「分析」阴影部分是平行四边形，应该选哪条边作为底呢？相应的高是多少呢？例题6如图，把两个正方形拼在一起，小正方形的边长是5厘米，大正方形的边长是7厘米．请问：阴影部分的面积是多少？「分析」阴影部分由两个三角形组成，你能分别求出这两个三角形的面积吗？以哪条边作为底最容易计算呢？11课堂内外小欧拉与大羊圈欧拉是著名的数学家，他在数论、几何学、天文数学、微积分等好几个数学的分支领域中都取得了出色的成就．不过，这个大数学家在孩提时代却一点也不讨老师的喜欢，他是一个被学校除了名的小学生．小欧拉因为问老师天上星星有多少颗，老师也答不上来，只知道天上的星星是上帝镶上去的．小欧拉感觉上帝真是太粗心了，竟然忘记了星星的数目！在欧拉的年代，对上帝是绝对不能怀疑的，人们只能做思想的奴隶，绝对不允许自由思考．小欧拉没有与上帝“保持一致”，老师就让他离开学校回家．回家后无事，他就帮助爸爸放羊，成了一个牧童．他一面放羊，一面读书．他读的书中，有不少数学书．爸爸的羊渐渐增多了，达到了100只．原来的羊圈有点小了，爸爸决定建造一个新的羊圈．他用尺量出了一块长方形的土地，长40米，宽15米，他一算，面积正好是600平方米，平均每一头羊占地6平方米．正打算动工的时候，他发现他的材料只够围100米的篱笆，不够用．若要围成长40米，宽15米的羊圈，其周长将是110米．父亲感到很为难，若要按原计划建造，就要再添10米长的材料；要是缩小面积，每头羊的面积就会小于6平方米．小欧拉却向父亲说，不用缩小羊圈，也不用担心每头羊的领地会小于原来的计划．他有办法．父亲不相信小欧拉会有办法，听了没有理他．小欧拉急了，大声说，只要稍稍移动一下羊圈的桩子就行了．父亲听了直摇头，心想：“世界上哪有这样简单的事情？”但是，小欧拉却坚持说，他一定能两全齐美．父亲终于同意让儿子试试看．小欧拉见父亲同意了，站起身来，跑到准备动工的羊圈旁．他以一个木桩为中心，将原来的40米边长截短，缩短到25米．父亲着急了，说：“那怎么成呢？那怎么成呢？这个羊圈太小了，太小了．”小欧拉也不回答，跑到另一条边上，将原来15米的边长延长，又增加了10米，变成了25米．经这样一改，原来计划中的羊圈变成了一个25米边长的正方形．然后，小欧拉很自信地对爸爸说：“现在，篱笆也够了，面积也够了．”父亲照着小欧拉设计的羊圈扎上了篱笆，100米长的篱笆真的够了，不多不少，全部用光．面积也足够了，而且还稍稍大了一些．父亲心里感到非常高兴．孩子比自己聪明，真会动脑筋，将来一定大有出息．父亲感到让这么聪明的孩子放羊实在是太可惜了．后来，他想办法让小欧拉认识了一个大数学家伯努利．通过这位数学家的推荐，1720年，小欧拉成了巴塞尔大学的大学生．这一年，小欧拉13岁，是这所大学最年轻的大学生．作业1. 在下面的每个平行四边形与三角形中，作出以AB 为底的高．2. 如图，大正方形被分成三块区域．左上角的正方形面积为4，右上角的长方形面积为6，请问：大正方形的面积是多少？3.下图中，大正方形的面积是64，小正方形的面积是36．求平行四边形的面积．4. 下面两幅图都是边长为8和6的两个正方形拼成的，根据图中所示的线段长度，求两个阴影三角形的面积．5. 如图，两个正方形并排放在一起，小正方形的边长是9厘米，大正方形的边长是13厘米．请问阴影梯形的面积是多少平方厘米？66 846BD C第三讲基本直线形面积公式1.例题1答案：8平方米详解：方法一：正方形的面积是16平方米，所以正方形的边长是4米，黄瓜的面积是28平方米，黄瓜的宽是4米，长就是2847÷=米．豆角的面积是32平方米，豆角的宽是4米，所以长是3248÷=米．所以苦瓜的宽是÷=米，莴笋的宽是8米，面积是72平方米，所以长是7289⨯=平方米；方法二：豆角是茄子面积的2倍，972-=米，长是4米，所以苦瓜的面积是248所以莴笋是黄瓜和苦瓜面积和的2倍，黄瓜和苦瓜的面积是72236÷=平方米，所以苦瓜的面积是36288-=平方米．2.例题2答案：28详解：阴影平行四边形的底BC是4，高FG是7，所以平行四边形的面积是4728⨯=．3.例题3答案：42平方厘米详解：阴影三角形的底是6厘米，高是6814+=厘米，所以阴影三角形的面积是614242⨯÷=平方厘米．4.例题4答案：30平方厘米详解：阴影部分是一个梯形，这个梯形的上底是正方形上面的边，正方形的面积是49平方厘米，所以正方形的边长是7厘米，梯形的下底是长方形的宽即8厘米，梯形的高即长方形长与正方形边长之差，为1174-=厘米，所以梯形的面积是()+⨯÷=平方厘米．7842305.例题5答案：91平方厘米详解：由于两个大小一样的正方形错开了3厘米，可以知道图中两个小的直角三角形的直角边都是3厘米，所以阴影平行四边形的底就是1037+=厘米，所以其面积-=厘米，高就是10313是71391⨯=平方厘米．6.例题6答案：12平方厘米详解：小正方形的边长是5厘米，大正方形的边长是7厘米．阴影部分是由两个三角形组成的，这两个三角形的底都是752-=厘米，左面三角形的高是5厘米，右面三角形的高是7厘米，所以面积分别是2525⨯÷=平方厘米，2727+=平⨯÷=平方厘米，所以阴影部分的面积是5712方厘米．7.练习1答案：12平方米详解：西瓜地是正方形，面积为36平方米，所以边长为6米；冬瓜地面积为24平方米，长为6米，所以宽为2464÷=米；南瓜地面积为18平方米，长为6米，所以宽为1863÷=米；黄瓜地长为4米，宽为3米，所以面积为4312⨯=平方米．8. 练习2答案：96平方厘米详解：阴影平行四边形的底是小正方形边长即8厘米，高是两正方形边长之差，即20812-=厘米，所以平行四边形的面积是81296⨯=平方厘米．9. 练习3答案：30简答：阴影三角形的底是6，高是6410+=，所以阴影三角形的面积是610230⨯÷=．10. 练习4答案：14平方厘米简答：阴影部分是一个梯形，这个梯形的上底是小正方形的边长，即6厘米；梯形的下底是大正方形的边长即8厘米，梯形的高即两正方形边长之差，为862-=厘米，所以梯形的面积是()682214+⨯÷=平方厘米．11. 作业1答案：如图所示简答：12. 作业2答案：25简答：小正方形的边长为2，小长方形的长为3，那么大正方形的边长为5，面积为5525⨯=．13. 作业3答案：48简答：小正方形的边长为6，大正方形的边长为8，平行四边形的面积是6848⨯=．14. 作业4答案：24；18简答：左图阴影三角形的底选为6，高为8，面积是68224⨯÷=．右图阴影三角形的底选为6，高为6，面积是66218⨯÷=．15.作业5答案：242平方厘米简答：梯形的上底为小正方形的边长，即9厘米．梯形的下底为大正方形的边长，即13厘米．梯形的高为大、小正方形边长和为22厘米．梯形的面积为(913)222242+⨯÷=平方厘米．6.。

小学奥数奥林匹克起跑线（四年级）共34讲

第3讲长方形和正方形（一）例题例1 用一块长8分米，宽4分米的长方形纸板与两块边长4分米的正方形纸板拼成一个正方形。

拼成的正方形的周长是多少分米？例 2 两个大小相同的正方形拼成一个长方形后，周长比原来的两个正方形周长的和减少了6厘米。

原来一个正方形的周长是多少厘米？例3 求图3和图4的周长。

图3 图4例4图7是一座厂房的平面图，求这座厂房平面图的周长。

例5 图9是个多边形，图中每个角都是直角，它的周长是多少？图9 例6 一个正方形被分成3个大小，形状完全一样的长方形(如图10)，每个小长方形的周长都是24厘米，求这个正方形的周长。

图10例7 图11是由四个一样大的长方形和一个周长是4分米的小正方形拼成的一个边长是11分米的大正方形。

每个长方形的长和宽各是多少？周长是多少？(图11单位:分米) 例8 一根铁丝长12厘米，能围几种长和宽都是整厘米数和长方形，每种长方形的长和宽各是几厘米？围成的正方形的边长是几厘米？练习1、把一个长10厘米，宽5厘米的长方形，分成两个大小一样的正方形，每个正方形的周长是多少？2、用一个长8厘米，宽4厘米的长方形与7个边长4厘米的正方形，拼成一个大正方形。

3、求图12、图13（单位：厘米）图12 图134、图14是一座楼房的平面图，这座楼房平面图的周长是多少米？5、把一个正方形分成甲、乙两个部分（如图15），比较甲、乙两个部分周长的长短，并求出乙的周长。

（单位：米）（单位：分米）图14 图156、有两个相同的长方形，长7厘米，宽3厘米，把它们按图16的样子重叠在一起，这个图形的周长是多少厘米？7、一个正方形被分成6个大小、形状完全一样的长方形（如图17），每个长方形的周长都是14厘米。

原来正方形的周长是多少厘米？（单位：分米）图17 图188、一块长方形布，周长是18米，长比宽多1米，这块布的长是几米？宽是几米？9、用4个一样大的长方形和一个小正方形，拼成一个边长是16分米的大正方形（如图18），每个长方形的周长是多少？第4讲长方形和正方形(二)例题例1 有一块长方形土地，长是宽的2倍，中间有一座雕塑的底面是一个正方形，周围是草坪(如图1)，草坪的面积是多少平方米？例2 图2是由6个相等于的三角形拼成的图形，求这个图形的面积。

奥数教程(第八版)四年级第21讲长方形、正方形的周长(二)

例6 如图所示是一个“工”字形大楼的平面图，请你求出它的周长。(单位：米)
谢谢!
例2 沿直线边剪三刀，将长为60厘米、宽为30厘米的长方形剪成若干个小长方形，这些小长方形的周长之和最小是多少厘米？解：根据题意，长方形沿直线边剪三刀的情况如图所示：
第21讲长方形，正方形的周长（二）
例3 一张长方形纸长20厘米，宽12厘米，现在沿着对角线对折(如图)，阴影部分图形的周长是多少？
第21讲长方形，正方形的周长（二）
例4 有一块长方形的牧场，它的周长为700米。将它分隔为六块完全相同的小长方形的牧场，如图所示。求每一块小长方形牧场的周长。解：设小长方形的长为a，宽为b，
第21讲长方形，正方形的周长（二）
例5 如图是一座楼房的平面图，求这座楼房平面图的周长。
第21讲 ቤተ መጻሕፍቲ ባይዱ方形，正方形的周长（二）
小学（第八版）
经典例题精讲四年级
第21讲长方形，正方形的周长（二）
主讲老师： Mathematical Olympiad Tutorial
第21讲长方形，正方形的周长（二）
例1 如图所示，4个一样的宽为2厘米的小长方形拼成一个大长方形。那么这个大长方形的周长是多少厘米？
第21讲长方形，正方形的周长（二）

四年级数学奥赛训练题第3讲长方形和正方形(一)

四年级数学奥赛训练题第3讲长方形和正方形(一)A卷1. 求右面这块水稻田的周长(单位: 米) 。

50502. 右图是一座楼房的平面图, 这座楼房平面图的周长是多少米?5080 3. 把一个长24厘米、宽12厘米的长方形, 分成两个大小一样的正方形, 每个正方形的周长是多少?4. 如右图, 用一块长16分米、宽8分米的长方形纸板与两块边长8分米的正方形纸板拼成一一个正方形。

拼成的正方形周长是多少?5. －个正方形被分成6个大小、形状完全一样的长方形(如右图) , 每个长方形的周长都是14厘米。

原来正方形的周长是多少厘米?B卷1. 将一个边长为5分米的正方形分成甲、乙两个部分(如右图) , 比较甲、乙两个部分周长的长短, 并求出乙的周长(单位: 分米) 。

2. 两个相同的长方形, 长7厘米, 宽3厘米, 把它们按右图的样子重叠在一起, 这个图形的周长是多少厘米?3. 一块长方形布, 周长是28米, 长比宽多2米, 这块布的长是几米?宽是几米?4. 用4个一样大的长方形, 拼成一个边长是32分米的大正方形(如右图) , 每个长方形的周长是多少?5. 一根铁丝长16厘米, 能團成几种长和宽都是整厘米数的长方形, 每种长方形的长和宽各是几厘米?围成的正方形的边长是几厘米?第3讲长方形和正方形(一)A卷1. 200米2. 320米3. 48厘米4. 64分米5. 24厘米B卷1. 乙的周长大于甲；乙的周长是20分米2. 28厘米3. 长是6米；宽是8米4. 64分米5. 能围成3种长方形：(1) 长7厘米，宽1厘米；(2) 长6厘米，宽2厘米；(3) 长5厘米，宽3厘米。

围成的正方形的边长是4厘米。

四年级奥数第11次课长方形和正方形周长

第10次课长方形和正方形的周长知识点简析：通过分解、平移、合并等技巧，将一些较复杂图形的周长问题转化为简单的长方形、正方形周长问题求解。

重点：如何应用所学知识巧求表面上看起来不是长方形或正方形的图形的周长，难点：灵活应用已学知识，掌握转化的思考方法，把复杂的问题转化为标准的图形，以便计算它们的周长。

1. 长方形、正方形周长的基本公式为：长方形周长=（长+宽）×2正方形周长=边长×42.解题思想：要求出长方形或正方形周长，一般都要先求出图形的边长。

周长问题中，常常通过面积或线段之间的倍数关系先求图形的边长，再求周长。

例题讲解例1 有5张同样大小的纸如下图（a）重叠着，每张纸都是边长6厘米的正方形，重叠的部分为边长的一半，求重叠后图形的周长。

例2 一块长方形木板，沿着它的长度不同的两条边各截去4厘米，截掉的面积为192平方厘米。

现在这块木板的周长是多少厘米？例3 已知下图中，甲是正方形，乙是长方形，整个图形的周长是多少？例4 下图是边长为4厘米的正方形，求正方形中阴影部分的周长。

例5 如下图，阴影部分是正方形，DF=6厘米，AB=9厘米，求最大的长方形的周长。

A.基础题自测1.下图由8个边长都是2厘米的正方形组成，求这个图形的周长。

2.下图中的每一小段的长度都是相等，求图形的周长。

3.求下面图形的周长（单位：厘米）。

5cm8cm4.有一块长方形广场，沿着它不同的两条边各划出2米做绿化带，剩下的部分仍是长方形，且周长为280米。

求划去的绿化带的面积是多少平方米？5.在（）里填上“＞”、“＜”或“=”。

甲的周长（）乙的周长B.中档题演练1.下图由1个正方形和2个长方形组成，求这个图形的周长。

2.有一个长方形，如果长减少4米，宽减少2米，面积就比原来减少44 平方米，且剩下部分正好是一个正方形。

求这个正方形的周长。

3.有两个相同的长方形，长是8厘米，宽是3厘米，如果按下图叠放在一起，这个图形的周长是多少？50cm4.下面是一个零件的平面图，图中每条短线段都是5厘米，零件长35厘米，高30厘米。

(完整)四年级奥数+长方形与正方形

长方形与正方形长方形和正方形（一）：周长计算长方形、正方形的周长与面积的计算，利用公式很容易算出它们的面积与周长。

但在遇到一些较复杂的有关长方形和正方形的周长和面积计算时需要灵活应用平移、转化、分解、合并等技巧。

【例1】有一块长8分米，宽4分米的长方形纸板与两块边长 4分米的正方形拼也一个正方形。

拼成的正方形的周长是多少分米？【例2】两个大小数点相同的正方形拼成一个长方形后，周长比原来的两个正方形周长的和减少米。

原来一个正方形的周长是多少厘米？【例3】求图1和图2的周长。

（单位：米）【例4】右图是一座厂房的平面图，求这座厂房平面图的周长。

【例5】下图是个多边形，图中每个角都是直角，它的周长是多少?【例6】一个正方形被分成3个大小、形状完全不一样的长方形（如下图），每个小长方形的周长都是24厘米，求这个正方形的周长。

10图1【例7】下图是由四个一样大的长方形和一个周长是4分米的小正方形拼成的一个边长是 11分米的大正方形。

每个长方形的长和宽各是多少？周长是多少？【例8】一根铁丝长12厘米，能围成几种长和宽都是整厘米数的长方形，每种长方形的长和宽各是几厘米？围成的正方形的边长是几厘米？练习与思考：1、把一个长10厘米，宽5厘米的长方形，分成两个大小一样的正方形，每个正方形的周长是多少?2、用一个长8厘米，宽4厘米的长方形与7个边长4厘米的正方形，拼成一个大正方形。

拼成的大正方形的周长是多少？4、图14是一座楼房的平面图，这座楼房平面图的周长是多少米?15），比较甲、乙两个部分周长的长短，并求出乙的周1米长方形和正方形（二）：面积计算3、5、把一个正方形分成甲、乙两个部分（如图长。

求图12、图13的周长。

【例1】一块长方形土地，长是宽的2倍，中间有一座雕塑，雕塑的底面是一个正方形，周围是草坪（如图1），草坪的面积是多项式少平方米？20米图1【例2】图2是由6个相等的三角形拼成的图形，求这个图形的面积【例5】如图5,已知正方形ABCD 勺边长为6分米，长方形BCEF 和长方形AGH 啲面积分别为24平方分米和20平方分米，求阴影部分和面积。