4.1.1圆的标准方程
中职数学 圆的标准方程
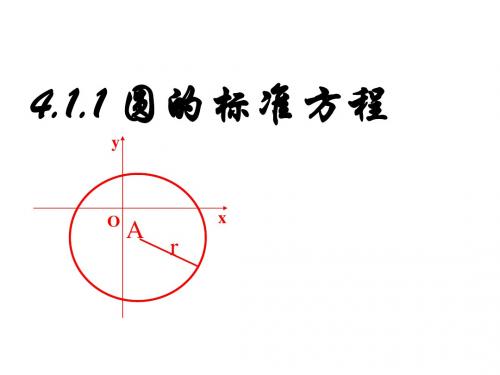
程,并判断点 M1(5,7) , M 2 ( 5,1)是否在这个圆上。
解:圆心是 A(2,3) ,半径长等于5的圆的标准方程 是:
(x 2)2 ( y 3)2 25
把M1(5,7) 的坐标代入方程(x 2)2 (y 3)2 25 左右两边相等,点M 1 的坐标适合圆的方程,所以点
M 1 在这个圆上;
把点M 2 ( 5,1) 的坐标代入此方程,左右两边 不相等,M点2 的坐标不适合圆的方程,所以点M 2 不 在这个圆上.
点与圆的位置关系
怎样判断点 M0 (x0, y0 ) 在圆 (x a)2 ( y b)2 r2
内呢?圆上?还是在圆外呢? M0
M0 O
O M0
O
点在圆内
点在圆上
点在圆外
| OM 0 | <r
| OM 0 | =r
(x0-a)2+(y0-b)2<r2; (x0-a)2+(y0-b)2=r2
| OM 0 | >r
(x0-a)2+(y0-b)2>r2
点与圆的位置关系
练习3.请判断点A(m, 4)与圆x2 + y2 =16的位置关 系是( D )
A、圆内
B、圆上
C、圆外
D、圆上或圆外
待定系数法
y P(3,4)
x O
小结
1.圆的标准方程
(x a)2 (y b)2 r2 (圆心C(a,b),半径r)
2.点与圆的位置关系
3.求圆的标准方程的方法:
4.1.1 圆的标准何定义圆的?
平面内到定点距离等于定长的点的轨迹是圆.
4.1.1 圆的标准方程

5.如图,已知隧道的截面是半径为4米的半圆,车 辆只能在道路中心线一侧行驶,一辆宽为2.7米, 高为3米的货车能不能驶入这个隧道?
解:以某一截面半圆的圆心为 坐标原点,半圆的直径AB所在 的直线为x轴,建立直角坐标系
y
(如右图).
2 2
A
0
2.7
B
x
那么半圆的方程为 x y 16( y 0), 将x=2.7代入,得 y 16 2.7 8.71 <3.
【解】设圆M的方程为(x-a)2+(y-b)2=r2(r>0),
1- a 2 + -1- b 2 = r2 , 2 2 2 -1a + 1b = r , a + b - 2 = 0,
根据题意得
解得a=b=1,r=2, 故所求圆M的方程为(x-1)2+(y-1)2=4.
第四章 圆与方程
4.1 圆的方程
4.1.1 圆的标准方程
生活掠影
一石激起千层浪
乐在其中
生活掠影
奥运五环
福建土楼
生活中,我们经常接触一些圆形,下面我们就 一起来认识一下圆吧!
1.掌握圆的标准方程.(重点)
2.会由圆的标准方程写出圆的半径和圆心坐标,
能根据条件写出圆的标准方程.
3.会用待定系数法求圆的标准方程.(难点)
2
即在离中心线2.7米处,隧道的高度低于货车的
高度.因此,货车不能驶入这个隧道.
圆 的
推导步骤 特点
求法
建系设点→写条件→列方程→化简→说明
标
准 方 程
圆心(a,b)、半径r 待定系数法和直接法
不想当元帅的士兵不是好士兵。
A.(x-1)2+(y-1)2=1
§4.1.1 圆的标准方程

作业: P124习题4.1 A组 2、3、4、5
2 2
两边平方得: (x-a)2+(y-b)2=r2
圆的标准方程:
(x-a)2+(y-b)2=r2
若点 M ( x, y) 在圆上,由上述讨论可知, 点M的坐标适合方程;反之,若点 M ( x, y) 的 坐标适合方程,这就说明点M与圆心A的距离 为r,即点M在圆心为A的圆上。
圆心是A(a,b), 半径是r
解:设所求圆的方程是(x-a)2+(y-b)2=r2 根据题意,可得 △ ABC 外接圆 (5 a ) 2 (1 b) 2 r 2 的圆心是三边 2 2 2 垂直平分线的 (7 a ) (3 b) r (2 a ) 2 (8 b) 2 r 2 交点
(2) (x+3)2+(y-4)2=5
8
练习
3.已知圆经过P(5,1),圆心在C(8,3),求圆方程. y
C(8,3)
P(5,1)5) (3 1) 13
2 2 (x-8) +(y-3) =13
例2.△ABC的三个顶点的坐标分别是A(5,1), B(7,-3),C(2,-8),求它的外接圆的方程.
§4.1.1 圆的标准方程
课件制作 广安二中
何 琥
我们知道,在平面直角坐标系中,两 点确定一条直线,一点和倾斜角也能确定 一条直线。 思考 在平面直角坐标系中,如何确定一个 圆呢? 问题1:你知道圆的定义吗? 平面内与定点距离等于定长的点的集合 (轨迹)是圆. 定点就是圆心, 定长就是半径。 显然,当圆心位置与半径大小确定后, 圆就唯一确定了。
解此方程组,得 a=2 , b=-3 , r2=25 所以, △ABC的外接圆的方程是 (x-2)2+(y+3)2=25
圆的标准方程

圆
与 方程
圆的方程 圆的标准方程
问题1--什么是圆? 圆的定义:平面内与定点距离等于定 长的点的集合(轨迹)是圆。定点就 是圆心,定长就是半径 问题2-- 确定圆需要 哪几个要素? 圆心--确定圆的位置 半径--确定圆的大小
圆 的 标 准 方 程
y
r
O
C(a,b)
x
探索:圆心是C(a,b),半径是r的圆上的动点满足怎 样的关系式?圆的方程是什么? 解:
特点: (确定圆的方程必须具备二个独立条
件,即圆心和半径 .) 2、是关于x、y的二元二次方程。 3.若圆心在坐标原点,则圆方程为 x2 + y 2 = r2
二:数学运用--确定圆的标准方程
练习1:试写出下列圆 (x-1)2+(y-3)2=9 的圆心及半径
解:圆心为点(1,3)半径为r=3
变式1:判断下列方程是否为圆的方程如果 是,写出下列各圆的圆心坐标和半径 (1) (x-1)2+y2=6 (2) (x+1)2-(y-2)2=9
解:因为圆C经过坐标原点,所以圆C 的半径是 r=2 (3)2 Nhomakorabea2
=
方程为: (x-2) 2 + (y+3) 2 = 13
13
变式1: 求圆心在(-2,3)又过点(1,7)的圆的 方程 解:圆的半径r= (1+2) 2 + (7-3) 2 =5
圆的方程为: (x+2) 2 + (y-3) 2 = 25
圆心:两条弦的中垂线的交点
半径:圆心到圆上一点
例3:己知圆心为C的圆经过点A(1,1)和B(2,2),且圆心在直线l:x-y+1=0 上 , 求圆心为 C 的圆 y 的标准方程. A(1,1)
高中数学4.1.1圆的标准方程优秀课件

b
3
(2 a)2 (8 b)2 r2
待r 定 5系数
所求圆的方程为
法
(x2)2(y3)225
几何方法
y
O E
A(5,1)
x
B(7,-3)
C(2,-8)
圆心:两条弦的中垂线的交点
半径:圆心到圆上一点
练习:△AOB的三个顶点的坐标 分别是A(4, 0),B(0, 3),O(0, 0), 求它的外接圆的方程.
A.是圆心
B.在圆上
C.在圆内
D.在圆外
3、点P(1,-1)在圆(x+2) 2+y 2 =m的外部,那
么实数m的取值范围是m10 .
4、圆C:(x-5) +(y+21) =3,那2 么圆C的周长等
于 2 3 .
:
一、圆的标准方
程
(x
a)2
(
y
b)2
r2
y
M
C
O
x
圆心C(a,b),半径r
特别的假设圆心为O(0,0),那么圆的标准x方2 y2 r 2
(3 2
,
1 ), 2
直线AB的斜率:
kAB22113
因此线段AB的垂直平分线 l ' 的方程是
y11(x3) 23 2
即x3y30
x x
3y 30
y 10
x y
3 2
C(3,2)
r |A| C(13 )2(12 )25
所以,圆心为C的圆的标准方程是
(x3 )2(y2)225
练习: 求经过A(6,5),B(0,1)两点,并且圆心在
程二为 、:点与圆的位置关 系:
(1)点M在圆上 x0a2y0b2r2 (2)点M在圆内 x0a2y0b2r2
必修二4.1.1圆的标准方程

复习与作业: 复习与作业:
1.复习初中有关点与圆的位置关系 直线与圆的位置 复习初中有关点与圆的位置关系,直线与圆的位置 复习初中有关点与圆的位置关系 关系,圆与圆的位置关系有关内容 圆与圆的位置关系有关内容. 关系 圆与圆的位置关系有关内容 2.课本习题 课本习题4.1 A组第 、3题. 组第2、 题 课本习题 组第
得: 整理得: 整理得:
( x − 0) + ( y − 0) = r
2 2
2
x +y =r
2 2
2
典型例题
半径长等于5的圆的 例1 写出圆心为 A(2,−3) ,半径长等于 的圆的 方程, 方程,并判断点 M 1 (5,−7) , M 2 ( − 5 ,−1) 是否在这 个圆上. 个圆上. 解:圆心是 A(2,−3) ,半径长等于5的圆的标准 半径长等于 的圆的标准 方程是: 方程是: 2 2
特殊位置的圆方程
圆心在坐标原点,半径长为 的圆的方程是什么? 圆心在坐标原点,半径长为r 的圆的方程是什么? 因为圆心是原点O(0, 0),将x=0,y=0和半径 r 因为圆心是原点 , = , = 和半径 带入圆的标准方程: 带入圆的标准方程:
( x − a ) 2 + ( y − b) 2 = r 2
圆的方程
圆上任意点M(x, y)与圆心 (a,b)之间的距离能 与圆心A 圆上任意点 与圆心 之间的距离能 用什么公式表示? 用什么公式表示? 根据两点间距离公式: 根据两点间距离公式: 则点M、 间的距离为 MA = 间的距离为: 则点 、A间的距离为: 即:
(x − a )2 + ( y − b )2 .
p ={M | M |= r} A
( x − a ) + ( y − b) = r
4.1.1 圆的标准方程

目标导航
知识梳理
重难聚焦
典例透析
题型一 题型二 题型三
(2)(方法一)由题意,得线段 AB 的垂直平分线的方程为
3x+2y-15=0.
由
3������ + 2������-15 = 0, 解得 3������ + 10������ + 9 = 0,
������ = 7, ������ = -3.
所以圆心 C 的坐标为(7,-3).
求圆的标准方程时,一般先从确定圆的两个要素入手,即先求出圆 心的坐标和半径,再写出圆的标准方程.
②确定圆心和半径时,常用到中点坐标公式、两点间的距离公式,
有时还用到平面几何知识,如“弦的中垂线必过圆心”“两条弦的中 垂线的交点为圆心”等.
(2)待定系数法,步骤是:
①设圆的标准方程为(x-a)2+(y-b)2=r2(r>0); ②由条件列方程(组)解得a,b,r的值; ③写出圆的标准方程.
������
������
<
-
5 2
.
-12-
4.1.1 圆的标准方程
目标导航
知识梳理
重难聚焦
典例透析
题型一 题型二 题型三
题型二 求圆的标准方程
【例2】 求下列圆的标准方程: (1)圆心是(4,-1),且过点(5,2); (2)经过A(6,5),B(0,1)两点,并且圆心C在直线l:3x+10y+9=0上. 解:(1)(方法一)由题意知圆的
-11-
4.1.1 圆的标准方程
题型一 题型二 题型三
目标导航
知识梳理
重难聚焦
典例透析
【变式训练1】 已知点A(1,2)在圆C:(x-a)2+(y+a)2=2a2的内部,求
4.1.1圆的标准方程

思 考:
通过圆的方程形式我们能得到什么信息? 当圆心在原点时,圆的方程是什么?
例1.写出下列各圆的方程: (1) 圆心在原点,半径是3; (2) 经过点P(5, 1),圆心在点C(8, -3).
课堂小结
1. 圆的方程的推导步骤: 建系设点→写条件→列方程→化简→说明
4.1.1 圆的 标准方程
情景引入
1.在直角坐标系中,确定一条直线的基本要素 是什么? 2.在平面直角坐标系中,那么圆是否也可用一 个方程来表示呢?
讲授新课 讨 论:
具有什么性质的点的轨迹称为圆?
到定点的距离等于定长的点的集合
思 考:
在平面直角坐标系中,如何确定 一个圆呢?
思 考:
已知圆心为A(a,b),半径为r,设圆上任一 点M坐标为(x,y),如何求该圆的方程?
2. 圆的方程的特点:点(a, b)、r分别表示 圆心坐标和圆的半径;
课后作业
1. 阅读教材P.118到P.120; 2. 《习案》二十五.
y rM
A
O
x
思 考:
已知圆心为A(a,b),半径为r,设圆上任一 点M坐标为(x,y),如何求该圆的方程?
求方程的一般步骤:
建系设点
y rM
列方程
A
化简方程
O
x
圆的标准方程: (x-a)2+(y-b)2=r2.
圆的标准方程的两个基本要素: 圆心坐标和半径.
圆的标准方程:
(x-a)2+(y-b)2=r2.
4.1.1圆的标准方程

(1) x2+y2=9
(2) (x+3)2+(y-4)2=5
理论迁移
例1 写出圆心为 A(2, 3),半径长等于5的圆的方程, 并判断点 M1 (5, 7) ,M2 ( 5, 1)是否在这个圆上.
解:圆心是 A(2, 3) ,半径长等于5的圆的标准 2 2 方程是:( x 2) ( y 3) 25
知识探究
例1 写出圆心为 A(2, 3) ,半径长等于5的圆的 方程,并判断点 M1 (5, 7) ,M2 ( 5, 1) 是否在这 个圆上. 解:圆心是 A(2, 3) ,半径长等于5的圆的标准 2 2 ( x 2) ( y 3) 25 方程是:
y
M2
o
A M1
x
知识探究
把这个方程称为圆心为A(a, b),半径长为r 的圆 的方程,把它叫做圆的标准方程.
知识探究
圆心在坐标原点,半径长为r 的圆的方程是什么?
因为圆心是原点O(0, 0),将a=0,b=0和半径 r 代入圆的标准方程:
( x a )2 ( y b)2 r 2
得: 整理得:
( x 0) ( y 0) r
例2 ABC 的三个顶点的坐标分 别A(5,1), B(7,-3),C(2, -8),求 它的外接圆的方程.
分析:不在同一条直线上的三个点可 以确定一个圆,三角形有唯一的外接圆.
理论迁移
解:设所求圆的方程是 ( x a )2 ( y b)2 r 2 (1)
因为A(5,1), B(7,-3),C(2, -8) 都在圆上,所以它们的坐 标都满足方程(1).于是
即: p M / | MA | r
( x a)2 ( y b)2 r
4.1.1 圆的标准方程2

方法二:待定系数法 设圆的方程为:(x-a)2+(y-b)2=r2.
1 a 2 2 b 2 r 2 , a 3, 2 2 2 则 ⇒ b 2, 1 a 4 b r , r 2 20. 2a b 4 0.
【规律总结】利用数形结合巧解最值问题
(1)形如u=
yb 型的,可转化为直线的斜率的最值问题求解. xa
(2)形如t=ax+by型的,可转化为动直线截距的最值问题求解.
(3)形如m=(x-a)2+(y-b)2型的,可转化为两点间的距离的平方
求解.
提醒:若A(x0,y0)是圆C外一定点,则该点与圆上的点的最大距 离dmax=|AC|+r,最小距离dmin=|AC|-r.
【解题指南】1.考虑利用两点间的距离公式的几何意义探求 (x-5)2+(y+4)2的最大值. 2.方程x2+(y-1)2=1表示的曲线是以(0,1)为圆心,以1为半径的 圆.(1) y 1 的几何意义是圆上一点P(x,y)与点(2,1)连线的斜
x2
率.(2)x2+y2的几何意义是圆上一点到原点距离的平方.
【解析】1.选D.(x-5)2+(y+4)2的几何意义是点P(x,y)到点 Q(5,-4)的距离的平方,由于点P在圆(x-2)2+y2=1上,C(2,0),所 以这个最大值是(|QC|+1)2=36.
2.(1)设 y 1 =k,则k表示点P(x,y)与点(2,1)连线的斜率.
x2
当直线y-1=k(x-2)与圆相切时,k取得最大值与最小值.如图 所示,
【探究总结】对圆的标准方程的两点说明 (1)圆的标准方程是由两点间的距离公式推导出来的,它是圆的 定义的直观反映,是代数与几何结合的完美体现. (2)由圆的标准方程可直接写出圆的圆心和半径,反之,已知圆 的圆心和半径可以写出圆的标准方程,这一点体现了圆的标准 方程的优越性.
最新人教版高中数学必修二第四章圆与方程第一节第1课时圆的标准方程

第四章 圆 与 方 程 4.1 圆 的 方 程 4.1.1 圆的标准方程圆的标准方程圆心为C(x 0,y 0),半径为r 的圆的标准方程为(x -x 0)2+(y -y 0)2=r 2,特别地,圆心在原点时,圆的标准方程为x 2+y 2=r 2.(1)如果圆的标准方程为(x +x 0)2+(y +y 0)2=a 2(a ≠0),那么圆的圆心、半径分别是什么? 提示:圆心为(-x 0,-y 0),半径为|a|.(2)如果点P(x 0,y 0)在圆x 2+y 2=r 2上,那么x 20 +y 20 =r 2,若点P 在圆内呢?圆外呢?提示:若点P 在圆内,则x 20 +y 20 <r 2;若点P 在圆外,则x 20 +y 20 >r 2.1.辨析记忆(对的打“√”,错的打“×”) (1)圆的标准方程由圆心、半径确定.( √ ) (2)方程(x -a)2+(y -b)2=m 2一定表示圆.( × )(3)原点在圆(x -x 0)2+(y -y 0)2=r 2上,则x 20 +y 20 =r 2.( √ ) 提示:(1)如果圆的圆心位置、半径确定,圆的标准方程是确定的. (2)当m =0时,表示点(a ,b).(3)原点在圆上,则(0-x 0)2+(0-y 0)2=r 2,即x 20 +y 20 =r 2. 2.圆(x -1)2+y 2=3的圆心坐标和半径分别是( ) A .(-1,0),3B .(1,0),3C .()-1,0, 3D .()1,0 , 3【解析】选D.根据圆的标准方程可得,(x -1)2+y 2=3的圆心坐标为(1,0),半径为 3 . 3.到原点的距离等于 3 的点的坐标所满足的方程是________.【解析】设点的坐标为(x ,y),根据到原点的距离等于 3 以及两点间的距离公式,得(x -0)2+(y -0)2= 3 ,两边平方得x 2+y 2=3,是半径为 3 的圆. 答案:x 2+y 2=3类型一 圆的标准方程的定义及求法(数学抽象、数学运算)1.以点(2,-1)为圆心,以 2 为半径的圆的标准方程是( ) A .(x +2)2+(y -1)2= 2 B .(x +2)2+(y -1)2=2 C .(x -2)2+(y +1)2=2D .(x -2)2+(y +1)2= 2【解析】选C.由题意,圆的标准方程是(x -2)2+(y +1)2=2. 2.圆心在y 轴上,半径为1,且过点(1,3)的圆的方程是( ) A .x 2+(y -2)2=1 B .x 2+(y +2)2=1 C .x 2+(y -3)2=1D .x 2+(y +3)2=1【解析】选C.由题意,设圆的标准方程为x 2+(y -b)2=1,由于圆过点(1,3),可得1+(3-b)2=1,解得b =3,所以所求圆的方程为x 2+(y -3)2=1.3.已知圆C :(x -6)2+(y -8)2=4,O 为坐标原点,则以OC 为直径的圆的方程为( ) A .(x -3)2+(y +4)2=100 B .(x +3)2+(y -4)2=100 C .(x -3)2+(y -4)2=25D .(x +3)2+(y -4)2=25【解析】选C.圆C 的圆心坐标C(6,8),则OC 的中点坐标为E(3,4),半径|OE|=32+42=5,则以OC 为直径的圆的方程为(x -3)2+(y -4)2=25.4.圆心在直线x -2y -3=0上,且过点A(2,-3),B(-2,-5)的圆的标准方程为________. 【解析】方法一(几何性质法):设点C 为圆心,因为点C 在直线x -2y -3=0上,所以可设点C 的坐标为(2a +3,a). 因为该圆经过A ,B 两点,所以|CA|=|CB|,所以(2a +3-2)2+(a +3)2 =(2a +3+2)2+(a +5)2 , 解得a =-2,所以圆心为C(-1,-2),半径长r =10 . 故所求圆的标准方程为(x +1)2+(y +2)2=10.方法二(待定系数法):设所求圆的标准方程为(x -a)2+(y -b)2=r 2,由题设条件知,⎩⎨⎧a -2b -3=0,(2-a )2+(-3-b )2=r 2,(-2-a )2+(-5-b )2=r 2,解得a =-1,b =-2,r =10 (负值舍去), 故所求圆的标准方程为(x +1)2+(y +2)2=10.方法三(几何性质法):线段AB 的中点的坐标为(0,-4), 直线AB 的斜率k AB =-3+52+2 =12, 所以弦AB 的垂直平分线的斜率为k =-2,所以弦AB 的垂直平分线的方程为y +4=-2x ,即2x +y +4=0. 又圆心是直线2x +y +4=0与直线x -2y -3=0的交点, 所以圆心坐标为(-1,-2),所以圆的半径长r =(2+1)2+(-3+2)2 =10 , 故所求圆的标准方程为(x +1)2+(y +2)2=10. 答案:(x +1)2+(y +2)2=101.直接法求圆的方程圆的方程由圆心、半径决定,因此求出圆心和半径即可写出圆的标准方程. 2.待定系数法求圆的方程(圆心(a ,b)、半径为r)特殊位置 标准方程 圆心在x 轴上 (x -a)2+y 2=r 2 圆心在y 轴上 x 2+(y -b)2=r 2 与x 轴相切 (x -a)2+(y -b)2=b 2 与y 轴相切(x -a)2+(y -b)2=a 23.利用圆的性质求方程求圆的方程时,可以利用圆的性质求圆心、半径,如弦的垂直平分线过圆心,过切点垂直于切线的直线过圆心等.类型二点与圆的位置关系的判断(数学抽象、数学运算)1.点P(m,5)与圆x2+y2=24的位置关系是( )A.在圆外 B.在圆内C.在圆上 D.不确定【解析】选A.把P(m,5)代入x2+y2=24,得m2+25>24,所以点P在圆外.2.已知圆的方程是(x-2)2+(y-3)2=4,则点P(3,2)满足( )A.是圆心B.在圆上C.在圆内D.在圆外【解析】选C.因为(3-2)2+(2-3)2=2<4,所以点P(3,2)在圆内.3.点(1,1)在圆(x+2)2+y2=m上,则圆的方程是________.【解析】因为点(1,1)在圆(x+2)2+y2=m上,故(1+2)2+12=m,所以m=10.则圆的方程为(x+2)2+y2=10.答案:(x+2)2+y2=10.4.已知点A(1,2)不在圆C:(x-a)2+(y+a)2=2a2的内部,求实数a的取值范围.【解析】由题意知,点A在圆C上或圆C的外部,所以(1-a)2+(2+a)2≥2a2,所以2a+5≥0,所以a≥-52.因为a≠0,所以a的取值范围为⎣⎢⎡⎭⎪⎫-52,0∪(0,+∞).【思路导引】1.将点P的坐标代入圆的方程,看方程的等于号变成了什么符号,然后进行判断.2.验证点P与圆心的距离与半径之间的关系.3.将点的坐标代入圆的方程,解方程即可得出m的值,进而得方程.4.不在圆的内部,即在圆上或圆外.点与圆位置关系的判断与应用(1)位置关系的判断:①几何法:判断点到圆心的距离与半径的大小;②代数法:将点的坐标代入圆的方程左边,判断与r 2的大小. (2)位置关系的应用:代入点的坐标,利用不等式求参数的范围.【补偿训练】1.若点(3,a)在圆x 2+y 2=16的内部,则a 2的取值范围是( ) A .[0,7) B .(-∞,7) C .{7}D .(7,+∞)【解析】选A.由点在圆的内部,得9+a 2<16得a 2<7,又a 2≥0,所以0≤a 2<7. 2.若点(2a ,a -1)在圆x 2+(y -1)2=5的内部,则a 的取值范围是( ) A .(-1,1) B .(0,1) C .⎝ ⎛⎭⎪⎫-1,15 D .⎝ ⎛⎭⎪⎫-15,1【解析】选D.因为点(2a ,a -1)在圆的内部,所以d =(2a )2+(a -2)2 =4a 2+a 2-4a +4 =5a 2-4a +4 < 5 , 解得-15 <a <1,所以a 的取值范围是⎝ ⎛⎭⎪⎫-15,1 .3.若点A(a +1,3)在圆C :(x -a)2+(y -1)2=m 外,则实数m 的取值范围是( ) A .(0,+∞) B .(-∞,5) C .(0,5)D .[0,5]【解析】选C.由题意,得(a +1-a)2+(3-1)2>m ,即m<5, 又由圆的方程知m>0,所以0<m<5.类型三 与圆有关的最值问题(数学抽象、数学运算)角度1 与几何意义有关的最值问题【典例】已知x 和y 满足(x +1)2+y 2=14,试求x 2+y 2的最值.【思路导引】首先由条件观察x 、y 满足的条件,然后分析x 2+y 2的几何意义,求出其最值. 【解析】由题意知,x 2+y 2表示圆上的点到坐标原点距离的平方,显然当圆上的点与坐标原点的距离取得最大值和最小值时,其平方也相应取得最大值和最小值.原点O(0,0)到圆心C(-1,0)的距离d =1,故圆上的点到坐标原点的最大距离为1+12 =32 ,最小距离为1-12 =12.因此x2+y2的最大值和最小值分别为94,14.1.本例条件不变,试求yx的取值范围.【解析】设k=yx,变形为k=y-0x-0,此式表示圆上一点(x, y)与点(0, 0)连线的斜率,由k=yx,可得y=kx,此直线与圆有公共点,圆心到直线的距离d≤r,即|-k|k2+1≤12,解得-33≤k≤33.即yx的取值范围是⎣⎢⎡⎦⎥⎤-33,33.2.本例条件不变,试求x+y的最值.【解析】令y+x=b并将其变形为y=-x+b,问题转化为斜率为-1的直线在经过圆上的点时在y轴上的截距的最值.当直线和圆相切时,在y轴上的截距取得最大值和最小值,此时有|-1-b|2=12,解得b=±22-1,即最大值为22-1,最小值为-22-1.角度2 距离的最值问题【典例】1.设P是圆(x-3)2+(y+1)2=4上的动点,Q是直线x=-3上的动点,则|PQ|的最小值为( )A.6 B.4 C.3 D.2【解析】选B.|PQ|的最小值为圆心到直线的距离减去半径长.因为圆的圆心为(3,-1),半径长为2,所以|PQ|的最小值为3-(-3)-2=4.2.已知圆O的方程为(x-3)2+(y-4)2=25,则点M(2,3)到圆上的点的距离的最大值为________.【解析】由题意知,点M在圆O内,O为圆心,MO的延长线与圆O的交点到点M(2,3)的距离最大,最大距离为(2-3)2+(3-4)2+5=5+ 2 .答案:5+ 2【思路导引】1.转化为圆心到直线x=-3的距离减去半径;2.转化为M到圆心的距离加半径.1.与圆有关的最值问题的常见类型及解法(1)形如u=y-bx-a形式的最值问题,可转化为过点(x, y)和(a, b)的动直线斜率的最值问题.(2)形如l=ax+by形式的最值问题,可转化为动直线y=-abx+lb在y轴上的截距的最值问题.(3)形如(x-a)2+(y-b)2形式的最值问题,可转化为动点(x, y)到定点(a, b)的距离的平方的最值问题.2.求圆外一点到圆的最大距离和最小距离的方法采用几何法,先求出该点到圆心的距离,再加上或减去圆的半径,即可得距离的最大值或最小值.1.圆(x-1)2+(y-1)2=1上的点到直线x-y=2的距离的最大值是( )A.2 B.1+ 2 C.2+22D.1+2【解析】选B.圆(x-1)2+(y-1)2=1的圆心为(1,1),圆心到直线x-y=2的距离为 2 ,圆心到直线的距离加上半径就是圆上的点到直线的最大距离,即最大距离为1+ 2 .2.若实数x,y满足(x+5)2+(y-12)2=142,则x2+y2的最小值为( )A.2 B.1 C.0 D.-1【解析】选B.x2+y2表示圆上的点(x,y)与(0,0)间距离的平方,由几何意义可知最小值为(14-13)2=1.3.如果实数x,y满足(x-2)2+y2=3,求yx的最大值和最小值.【解析】方法一:如图,当过原点的直线l与圆(x-2)2+y2=3相切于上方时yx最大,过圆心A(2,0)作切线l的垂线交于B,在Rt△ABO中,OA=2,AB= 3 .所以切线l的倾斜角为60°,所以yx的最大值为 3 .同理可得yx的最小值为- 3 .方法二:令yx=n,则y=nx与(x-2)2+y2=3联立,消去y得(1+n2)x2-4x+1=0,Δ=(-4)2-4(1+n2)≥0,即n2≤3,所以- 3 ≤n≤ 3 ,即yx的最大值和最小值分别为 3 ,- 3 .【补偿训练】1.已知圆C的圆心为C(x0,x),且过定点P(4,2).(1)求圆C的标准方程.(2)当x为何值时,圆C的面积最小?求出此时圆C的标准方程.【解析】(1)设圆C的标准方程为(x-x0)2+(y-x)2=r2(r≠0).因为圆C过定点P(4,2),所以(4-x0)2+(2-x)2=r2(r≠0).所以r2=2x2-12x+20.所以圆C的标准方程为(x-x0)2+(y-x)2=2x2-12x+20.(2)因为(x-x0)2+(y-x)2=2x2-12x+20=2(x-3)2+2,所以当x=3时圆C的半径最小,则圆C的面积最小.此时圆C的标准方程为(x-3)2+(y-3)2=2.2.已知实数x,y满足方程x2+(y-1)2=14,求(x-2)2+(y-3)2的取值范围.【解析】(x-2)2+(y-3)2可以看成圆上的点P(x,y)到A(2,3)的距离.圆心C(0,1)到A(2,3)的距离为d=(0-2)2+(1-3)2=2 2 ,由图可知,圆上的点P(x ,y)到A(2,3)的距离的范围是⎣⎢⎡⎦⎥⎤22-12,22+12 .即(x -2)2+(y -3)2 的取值范围是⎣⎢⎡⎦⎥⎤22-12,22+12 .。
第4章 4.1 4.1.1 圆的标准方程

4.1.1圆的标准方程1.圆的标准方程(1)圆的定义:平面内到定点的距离等于定长的点的集合叫做圆,定点称为圆心,定长称为圆的半径.(2)确定圆的基本要素是圆心和半径,如图所示.(3)圆的标准方程:圆心为A(a,b),半径长为r的圆的标准方程是(x-a)2+(y-b)2=r2.当a=b=0时,方程为x2+y2=r2,表示以圆点O为圆心、半径为r的圆.思考:平面内确定圆的要素是什么?2. 点与圆的位置关系圆的标准方程为(x-a)2+(y-b)2=r2,圆心A(a,b),半径为r.设所给点为M(x0,y0),则位置关系判断方法几何法代数法点在圆上│MA│=r⇔点M在圆A上点M(x0,y0)在圆上⇔(x0-a)2+(y0-b)2=r2点在圆内│MA│<r⇔点M在圆A内点M(x0,y0)在圆内⇔(x0-a)2+(y0-b)2<r2点在圆外│MA│>r⇔点M在圆A外点M(x0,y0)在圆外⇔(x0-a)2+(y0-b)2>r21.圆(x-2)2+(y+3)2=2的圆心和半径分别是()A.(-2,3),1 B.(2,-3),3 C.(-2,3), 2 D.(2,-3), 22.以原点为圆心,2为半径的圆的标准方程是()A.x2+y2=2 B.x2+y2=4 C.(x-2)2+(y-2)2=8 D.x2+y2= 23.点P(m,5)与圆x2+y2=24的位置关系是()A.在圆外B.在圆内C.在圆上D.不确定4.点(1,1)在圆(x+2)2+y2=m上,则圆的方程是________.求圆的标准方程【例1】求过点A(1,-1),B(-1,1)且圆心在直线x+y-2=0上的圆的方程.确定圆的方程的方法:确定圆的标准方程就是设法确定圆心C(a,b)及半径r,其求解的方法:一是待定系数法,如法一,建立关于a,b,r的方程组,进而求得圆的方程;二是借助圆的几何性质直接求得圆心坐标和半径,如法二、法三.一般地,在解决有关圆的问题时,有时利用圆的几何性质作转化较为简捷.1.求下列圆的标准方程:(1)圆心是(4,0),且过点(2,2);(2)圆心在y 轴上,半径为5,且过点(3,-4);(3)过点P (2,-1)和直线x -y =1相切,并且圆心在直线y =-2x 上.命题角度1 直接法求圆的标准方程例1 (1)已知圆C 的圆心在x 轴的正半轴上,点M (0,5)在圆C 上,且圆心到直线2x -y =0的距离为455,则圆C 的方程为________.(2)与y 轴相切,且圆心坐标为(-5,-3)的圆的标准方程为________.反思与感悟 (1)确定圆的标准方程只需确定圆心坐标和半径,因此用直接法求圆的标准方程时,要首先求出圆心坐标和半径,然后直接写出圆的标准方程.(2)确定圆心和半径时,常用到中点坐标公式、两点间距离公式,有时还用到平面几何知识,如“弦的中垂线必过圆心”“两条弦的中垂线的交点必为圆心”等.跟踪训练1 以两点A (-3,-1)和B (5,5)为直径端点的圆的方程是( )A .(x +1)2+(y +2)2=10B .(x -1)2+(y -2)2=100C .(x +1)2+(y +2)2=25D .(x -1)2+(y -2)2=25命题角度2 待定系数法求圆的标准方程例2 求经过点P (1,1)和坐标原点,并且圆心在直线2x +3y +1=0上的圆的方程.反思与感悟 待定系数法求圆的标准方程的一般步骤跟踪训练2 已知△ABC 的三个顶点坐标分别为A (0,5),B (1,-2),C (-3,-4),求该三角形的外接圆的方程.点与圆的位置关系【例2】 已知圆心为点C (-3,-4),且经过原点,求该圆的标准方程,并判断点P 1(-1,0),P 2(1,-1),P 3(3,-4)和圆的位置关系.例3 (1)点P (m 2,5)与圆x 2+y 2=24的位置关系是( )A .点P 在圆内B .点P 在圆外C .点P 在圆上D .不确定(2)已知点M (5a +1,a )在圆(x -1)2+y 2=26的内部,则a 的取值范围是_________.1.判断点与圆的位置关系的方法(1)只需计算该点与圆的圆心距离,与半径作比较即可;(2)把点的坐标代入圆的标准方程,判断式子两边的符号,并作出判断.2.灵活运用若已知点与圆的位置关系,也可利用以上两种方法列出不等式或方程,求解参数范围.2.已知点A (1,2)不在圆C :(x -a )2+(y +a )2=2a 2的内部,求实数a 的取值范围.跟踪训练3 已知点(1,1)在圆(x -a )2+(y +a )2=4的外部,则a 的取值范围是________.与圆有关的最值问题[探究问题]1.怎样求圆外一点到圆的最大距离和最小距离?2.若点P (x , y )是圆C :(x -2)2+(y +2)2=1上的任一点,如何求点P 到直线x -y =0的距离的最大值和最小值?【例3】 已知x 和y 满足(x +1)2+y 2=14,试求x 2+y 2的最值.1.本例条件不变,试求y x的取值范围.2.本例条件不变,试求x +y 的最值.与圆有关的最值问题的常见类型及解法: (1)形如u =y -b x -a形式的最值问题,可转化为过点(x , y )和(a , b )的动直线斜率的最值问题. (2)形如l =ax +by 形式的最值问题,可转化为动直线y =-a b x +l b截距的最值问题. (3)形如(x -a )2+(y -b )2形式的最值问题,可转化为动点(x , y )到定点(a , b )的距离的平方的最值问题.例4 已知实数x ,y 满足方程(x -2)2+y 2=3,求y x的最大值和最小值.引申探究1.若本例条件不变,求y -x 的最大值和最小值.2.若本例条件不变,求x 2+y 2的最大值和最小值.反思与感悟 与圆有关的最值问题,常见的有以下几种类型(1)形如u =y -b x -a形式的最值问题,可转化为过点(x ,y )和(a ,b )的动直线斜率的最值问题. (2)形如l =ax +by 形式的最值问题,可转化为动直线y =-a b x +l b截距的最值问题. (3)形如(x -a )2+(y -b )2形式的最值问题,可转化为动点(x ,y )到定点(a ,b )的距离的平方的最值问题.跟踪训练4 已知x 和y 满足(x +1)2+y 2=14,试求: (1)x 2+y 2的最值;(2)x +y 的最值.1.判断点与圆位置关系的两种方法(1)几何法:主要利用点到圆心的距离与半径比较大小.(2)代数法:主要是把点的坐标代入圆的标准方程来判断:点P (x 0,y 0)在圆C 上⇔(x 0-a )2+(y 0-b )2=r 2;点P (x 0,y 0)在圆C 内⇔(x 0-a )2+(y 0-b )2<r 2;点P (x 0,y 0)在圆C 外⇔(x 0-a )2+(y 0-b )2>r 2.2.求圆的标准方程时常用的几何性质求圆的标准方程,关键是确定圆心坐标和半径,为此常用到圆的以下几何性质:(1)弦的垂直平分线必过圆心.(2)圆内的任意两条弦的垂直平分线的交点一定是圆心.(3)圆心与切点的连线长是半径长.(4)圆心与切点的连线必与切线垂直.3.求圆的标准方程常用方法(1)待定系数法.(2)直接法.一、选择题1.圆(x +1)2+(y -2)2=4的圆心与半径分别为( )A .(-1,2),2B .(1,-2),2C .(-1,2),4D .(1,-2),42.已知一圆的圆心为点A (2,-3),一条直径的端点分别在x 轴和y 轴上,则圆的标准方程为( )A .(x +2)2+(y -3)2=13B .(x -2)2+(y +3)2=13C .(x -2)2+(y +3)2=52D .(x +2)2+(y -3)2=523.过点A (1,-1),B (-1,1),且圆心在直线x +y -2=0上的圆的标准方程是( )A .(x -3)2+(y +1)2=4B .(x +3)2+(y -1)2=4C .(x -1)2+(y -1)2=4D .(x +1)2+(y +1)2=44.点(5a +1,12a )在圆(x -1)2+y 2=1的内部,则实数a 的取值范围是( )A .|a |<1B .a <13C .|a |<15D .|a |<1135.若圆心在x 轴上,半径为5的圆C 位于y 轴左侧,且与直线x +2y =0相切,则圆C 的标准方程为( )A .(x -5)2+y 2=5B .(x +5)2+y 2=5C .(x -5)2+y 2=5D .(x +5)2+y 2=56.若直线y =ax +b 通过第一、二、四象限,则圆(x +a )2+(y +b )2=1的圆心位于( )A .第一象限B .第二象限C .第三象限D .第四象限7.已知圆C 与圆(x -1)2+y 2=1关于直线y =-x 对称,则圆C 的标准方程为( )A .(x +1)2+y 2=1B .x 2+y 2=1C .x 2+(y +1)2=1D .x 2+(y -1)2=18.设P 是圆(x -3)2+(y +1)2=4上的动点,Q 是直线x =-3上的动点,则|PQ |的最小值为( )A .6B .4C .3D .2二、填空题9.若圆C 与圆M :(x +2)2+(y -1)2=1关于原点对称,则圆C 的标准方程为________.10.圆O 的方程为(x -3)2+(y -4)2=25,则点(2,3)到圆上的最大距离为________.11.若圆C 的半径为1,圆心在第一象限,且与直线4x -3y =0和x 轴都相切,则该圆的标准方程是________________________.12.若实数x ,y 满足x 2+y 2=1,则y -2x -1的最小值是______. 三、解答题13.求过点A (1,2)和B (1,10)且与直线x -2y -1=0相切的圆的标准方程.四、探究与拓展14.设P(x,y)是圆C:(x-2)2+y2=1上任意一点,则(x-5)2+(y+4)2的最大值为() A.6 B.25 C.26 D.3615.已知x,y满足x2+(y+4)2=4,求(x+1)2+(y+1)2的最大值与最小值.。
4.1.1圆的标准方程

2 2 2
( x a) ( y b) m
2 2
2.下列方程表示的曲线分别是什么? 2 2 y 4 ( x 1)
y 4 ( x 1)
2
21
方程 ( x a)2 ( y b)2 r 2 , 叫做以点 (a , b) 为圆心, r为半径 的圆的标准方程。 作用:
O
y
A
r
x M
需要几个量?
a,b,r.需三个条件
(1)已知圆心坐标和半径可写出圆的方程; (2)可由标准方程直接看出圆心和半径。
6
知识应用
(1) ( x 2) ( y 1) 2,
10
探究新知
对于点 M(x0 , y0) 和圆A: ( x a)2 ( y b)2 r 2 , (1)点在圆上 ( x 0 a ) 2 ( y 0 b ) 2 r 2 ; (2)点在圆内 ( x 0 a ) 2 ( y 0 b ) 2 r 2 ; 2 2 2 (3)点在圆外 ( x 0 a ) ( y 0 b ) r ;
8
知识应用
( x a) ( y b) r
2 2
2
练习3:写出满足下列条件的圆的标准方程. (1)圆心为(2 , -3),半径是 5的圆 ; (2)圆心为(-1 , 2),且过原点的圆 ; (3)以(0 , 0), (6 , -8)为直径端点的圆 ; (4)圆心为原点,且与直线x=1相切的圆. 解:(1) ( x 2) ( y r
2 2
2
练习1:说出下列方程表示的圆的圆心和半径. (2) x ( y 2) ( 2) ,
课件9:4.1.1 圆的标准方程

解此方程组,得b=1 . r2=4
故所求圆的标准方程为(x-1)2+(y-1)2=4. 解法二:设点C为圆心, ∵点C在直线x+y-2=0上, ∴可设点C的坐标为(a,2-a).
又∵该圆经过 A、B 两点, ∴|CA|=|CB|. ∴ (a-1)2+(2-a+1)2= (a+1)2+(2-a-1)2, 解得 a=1. ∴圆心坐标为 C(1,1),半径长 r=|CA|=2. 故所求圆的标准方程为(x-1)2+(y-1)2=4.
例 4 已知 x,y 满足(x-1)2+(y-2)2=16,则 x2+y2 的 取值范围是___[_2_1_-__8__5_,__2_1_+__8__5_]_____. 【解析】 x2+y2 表示圆 C:(x-1)2+(y-2)2=16 的动点 P(x,y)与原点 O(0,0)连线段长度 d 的平方, 由于 r-|OC|≤d≤r+|OC|, ∴4- 5≤d≤4+ 5,∴21-8 5≤d2≤21+8 5. ∴21-8 5≤x2+y2≤21+8 5.
解法三:由已知可得线段 AB 的中点坐标为(0,0), kAB=1--1(--11)=-1, ∴弦 AB 的垂直平分线的斜率为 k=1, ∴AB 的垂直平分线的方程为 y-0=1·(x-0), 即 y=x,则圆心是直线 y=x 与 x+y-2=0 的交点,
由yx= +xy-2=0 ,得xy= =11 .即圆心为(1,1), 圆的半径为 (1-1)2+[1-(-1)]2=2, 故所求圆的标准方程为(x-1)2+(y-1)2=4.
命题方向3 ⇨圆的标准方程的综合应用
例3 求过点A(1,-1)、B(-1,1),且圆心在直线x+y-2 =0上的圆的标准方程. 解:解法一:设所求圆的标准方程为(x-a)2+(y-b)2=r2,
圆的标准方程

3.解:∵圆心在y轴上, 3.解:∵圆心在y轴上, 圆心在 可设圆心坐标为(0,b),则圆的方程为: (0,b),则圆的方程为 ∴可设圆心坐标为(0,b),则圆的方程为: +(yx2+(y-b)2=r2. 圆经过A 两点, ∵圆经过A、B两点,
∴圆的方程是x2+(y-1)2=10. 圆的方程是x +(y-
所以,所求圆的方程为
练习: 、写出下列各圆的方程: 练习:1、写出下列各圆的方程:
( x − 3) 2 + ( y − 4) 2 = 16 (1)圆心在点 圆心在点C(3, 4 ),半径是 圆心在点 ,半径是4
(2) 经过点 经过点P(5,1),圆心在点 圆心在点C(8,-3) 圆心在点
( x − 8) + ( y + 3) = 25
再( x − 2) + ( y + 3) = 25
2 2
左右两边不等,则M2 不在圆上
思考:M2 的位 置在哪里?
探究 点与圆的位置关系
点 M ( x0 , y0 ) 在圆 ( x − a ) + ( y − b) = r 内的条件是什么?圆外呢?
2 2 2
结论: 结论 若 ( x0 − a ) + ( y0 − b) < r ,则M在圆内 则 在圆内 在圆内.
2
x
两边同时平方, 两边同时平方,得
(x-a)2+(y-b)2=r2 - -
( x − a ) + ( y − b) = r
2 2
2
(1)
在圆上, 若M(x,y)在圆上,由以上讨论 点M的坐标满 在圆上 由以上讨论,点 的坐标满 );反之 的坐标满( ), ),即 足(1);反之,若M(x,y)的坐标满(1),即 );反之, 的坐标满 M到A点的距离为 M点在圆上。 点的距离为r, 点在圆上 点在圆上。 到 点的距离为 我们把( )称为以 为圆心, 我们把(1)称为以A(a,b)为圆心,r为半 , 为圆心 为半 径的圆的标准方程 特别地, 表示以原点为圆心, 为 特别地,x2+y2=r2 表示以原点为圆心,r为 半径的圆. 半径的圆
圆的方程中的典型问题与方法:圆的方程中的典型问题与方法——4.1.1圆的标准方程

2 2 2
则圆的标准方程为(x-4)2+(y+1)2=10. (2)由已知可设圆的标准方程为 x2+(y-b)2=25,则 32+(-4-b)2=25, 解得 b=0 或 b=-8, 则圆的标准方程为 x2+y2=25 或 x2+(y+8)2=25. (3)由已知设所求圆的标准方程为(x-a)2+y2=r2,
)Байду номын сангаас
故圆的标准方程为(x-2)2+(y+3)2=13. 3.点 P(m2,5)与圆 x2+y2=24 的位置关系是( ) A.在圆内 B.在圆外 C.在圆上 D.不确定 4 2 2 2 解析:选 B.由 m +25>24 可知,点 P(m ,5)在圆 x +y =24 的外部. 4.(2014· 滨州调研)已知圆 C 经过 A(5,2),B(-1,4)两点,圆心在 x 轴上,则圆 C 的标准方程是( A.(x-2)2+y2=13 B.(x+2)2+y2=17 C.(x+1)2+y2=40 D.(x-1)2+y2=20 解析:选 D.∵圆心在 x 轴上,∴设圆心坐标为 C(a,0). 又∵圆 C 经过 A(5,2),B(-1,4)两点, ∴半径 r=|AC|=|BC|,可得 (a-5)2+(-2)2= (a+1)2+(-4)2, 解之得 a=1,可得半径 r= (a-5)2+(-2)2= 20, ∴圆 C 的标准方程是(x-1)2+y2=20. 5.圆(x-1)2+y2=1 的圆心到直线 y= 1 A. 2 B. 3 2 C.1 3 x 的距离为( 3 D. 3 ) )
2.用待定系数法求圆的标准方程 例 2 △ABC 的三个顶点的坐标分别是 A(5,1),B(7,-3),C(2,-8),求它的外接圆的标准方程. (链接教材 P119 例 2) [解析] 设所求圆的标准方程是(x-a)2+(y-b)2=r2,① 因为 A(5,1),B(7,-3),C(2,-8)都在圆上, 所以它们的坐标都满足方程①, (5-a) +(1-b) =r a=2 2 2 2 于是(7-a) +(-3-b) =r ,解此方程组,得b=-3, (2-a)2+(-8-b)2=r2 r2=25 所以△ABC 的外接圆的标准方程是:(x-2)2+(y+3)2=25. 【方法归纳】待定系数法求圆的标准方程的一般步骤: (1)设:设所求圆的标准方程为(x-a)2+(y-b)2=r2; (2)列:由已知条件,建立关于 a,b,r 的方程组; (3)解:解方程组,求出 a,b,r; (4)代:将 a,b,r 代入所设方程,得所求圆的标准方程. 【跟踪练习】 2.求下列圆的标准方程: (1)圆心是(4,-1),且过点(5,2); (2)圆心在 y 轴上,半径长为 5,且过点(3,-4); (3)求过两点 C(-1,1)和 D(1,3),圆心在 x 轴上的圆的标准方程. 解:(1)设圆的标准方程为(x-a)2+(y-b)2=r2,
第四章 4.1.1圆的标准方程

问题 4 如果把圆看成是点的集合, M(x, y)为这个圆上任意一点,
用坐标表示点 M 适合的条件并化简将得到什么等式?
|MA|=r,由两点间的距离公式,得 x-a2+y-b2 =r,
答
Байду номын сангаас
化简可得:(x-a)2+(y-b)2=r2.
问题 6
如何说明(x-a)2+(y-b)2=r2 就是圆心坐标为 A(a, b),
设圆的圆心坐标为 A(a,b),半径为 r(其中 a、b、r 都
是常数,r>0).设 M(x,y)为这个圆上任意一点,那么点 M 满足的条件是什么? 答 |MA|=r.
研一研·问题探究、课堂更高效
那么圆心为 A 的圆如何表示? 答 P={M||MA|=r}.
问题 5
本 课 时 栏 目 开 关
4.1.1
练一练·当堂检测、目标达成落实处
4.1.1
2.已知以点 A(2,-3)为圆心,半径长等于 5 的圆 O,则点 M(5,-7)与圆 O 的位置关系是
本 课 时 栏 目 开 关
( B )
A.点在圆内 C.点在圆外
B.点在圆上 D.无法判断
解析 点 M(5,-7)到圆心 A(2,-3)的距离为 5,恰好等 于半径长,故点在圆上.
写出圆心为 A(2,-3),半径长等于 5 的圆的方程,并
判断点 M1(5,-7),M2(- 5,-1)是否在这个圆上. 解 圆心是 A(2,-3),半径长等于 5 的圆的标准方程是(x-
2)2+(y+3)2=25.把点 M1(5,-7)的坐标代入方程(x-2)2+(y
本 课 时 栏 目 开 关
+3)2=25,左右两边相等,点 M1 的坐标适合圆的方程,所以 点 M1 在这个圆上;把点 M2(- 5,-1)的坐标代入方程(x- 2)2+(y+3)2=25,左右两边不相等,点 M2 的坐标不适合圆的 方程,所以点 M2 不在这个圆上. 小结 判断点与圆的位置关系,通常用两种方法,一种是利 用点与圆心的距离 d 与半径 r 的大小关系来判定, d>r 时, 当 点在圆外;当 d=r 时,点在圆上;当 d<r 时,点在圆内.另 一种方法是把点 P(x0,y0)代入圆的方程.若(x-x0)2+(y-y0)2 >r2,则点 P 在圆外;若(x-x0)2+(y-y0)2=r2,则点 P 在圆 上;若(x-x0)2+(y-y0)2<r2,则点 P 在圆内,这种方法实质 上就是第一种方法的另外一种表达形式.
高考数学第四章圆与方程4.1.1圆的标准方程课件新人教A版必修2ppt版本

解析答案
谢谢
2019/11/13
答案
(2)代数法:可利用圆C的标准方程(x-a)2+(y-b)2=r2来确定: 点M(m,n)在 圆C上 ⇔(m-a)2+(n-b)2=r2; 点M(m,n)在 圆C外 ⇔(m-a)2+(n-b)2>r2; 点M(m,n)在 圆C内 ⇔(m-a)2+(n-b)2<r2. 思考 确定点与圆的位置关系的关键是什么?
自主学习
(x-a)2+(y-b)2=r2 x2+y2=r2
答案
思考 方程(x-a)2+(y-b)2=m2一定表示圆吗? 答 不一定.当m=0时表示点(a,b),当m≠0时,表示圆.
答案
知识点二 点与圆的位置关系 点与圆有三种位置关系,即点在圆外、点在圆上、点在圆内,判断点与 圆的位置关系有两种方法: (1)几何法:将所给的点M与圆心C的距离跟半径r比较: 若|CM|=r,则点M在 圆上; 若|CM|>r,则点M在 圆外; 若|CM|<r,则点M在 圆内.
反思与感悟
解析答案
跟踪训练2 若点(1,1)在圆(x-a)2+(y+a)2=4的内部,则a的取值范围 是( A ) A.-1<a<1 B.0<a<1 C.a<-1或a>1 D.-1<a<0 解析 直接利用点与圆的位置关系来判断. ∵点(1,1)在圆的内部, ∴(1-a)2+(1+a)2<4. 解得-1<a<1.
解析答案
题型二 点与圆的位置关系的判断 例2 已知点A(1,2)不在圆C:(x-a)2+(y+a)2=2a2的内部,求实数a的 取值范围. 解 由题意,得点A在圆C上或圆C的外部, ∴(1-a)2+(2+a)2≥2a2, ∴2a+5≥0, ∴a 的取值范围是-52,0∪(0,+∞). 解 由已知,得 C(3,0),r=|A2B|=2,
4.1.1圆的标准方程

1.圆的标准方程: 设圆心坐标为A(a,b),圆上任 意一点M(x,y),则|MA|=r,即: y r A o x M
√(x-a)2+(y-b)2=r
பைடு நூலகம்
(x-a)2+(y-b)2=r2
特别地,当圆心为坐标原点时, 圆的方程为:
x2+y2=r2
2.点与圆的位置关系:
设平面内任意一点坐标为A(x0,y0),则圆C的圆心 坐标为O(a,b),圆半径为r,则: A
4.1.1 圆的标准方程
(1)在平面直角坐标系中,两点确定 一条直线,一点和倾斜角也确定一条 直线,那么在什么条件下可以确定一 个圆呢? 圆心和半径
(2)直线可以用一个方程表示,圆也可以用一个方程来 表示,怎样建立圆的方程呢? 建立平面直角坐标系 (3)若圆心坐标用A(a,b)表示,圆上有任意一点M(x,y),圆 的半径为r,如何列出等式? |MA|=r
A O |OA|<r
(x0-a)2+(y0-b)2<r2
点M在圆C内
A
O |OA|=r
(x0-a)2+(y0-b)2=r2
点M在圆C上
O |OA|>r
(x0-a)2+(y0-b)2>r2
点M在圆C外
例1 写出圆心为A(2,-3),半径长等于5的圆的方 程,并判断点M(5, -7),N( 5 ,-1)是否在这 个圆上? 例2 △ABC的三个顶点的坐标分别是 A(5,1),B (7,-3),C(2,-8),求它的外接圆的方程. 三角形的外心是三边中垂线的交点 例3 已知圆心为C的圆经过点A(1,1)和B(2,-2), 且圆心C在直线l :x-y+1=0上,求圆C的标准方程.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学必修2 4.1.1圆的标准方程【学习目标】1、能根据圆心、半径写出圆的标准方程;由标准方程求圆心和半径;会用待定系数法求圆的标准方程.2、进一步培养学生能用解析法研究几何问题的能力,渗透数形结合思想.3、通过运用圆的知识解决实际问题的学习,从而激发学生学习数学的热情和兴趣.【学习重点】圆的标准方程;【学习难点】会根据不同的已知条件,利用待定系数法求圆的标准方程. 【课前预习】 1、圆的定义2、两点间距离公式3、尝试推导圆的标准方程圆心A(a,b),半径为r ,点M(x,y)为圆上任意一点,则点M 满足的集合为 ,由两点间距离公式可得点M 满足的方程为 ,化简得 。
4、圆心为原点,半径为r 的圆的标准方程 。
5、(1)写出圆心在原点,半径是3的圆的标准方程 ; (2)写出(x-3)2+(y-2)2=5的圆心坐标 和半径 。
【尝试解答】一、点到圆心的距离探究一:点00(,)M x y 与圆222()()x a y b r -+-=的关系的判断方法: (1)点在圆外 (2)点在圆上 (3)点在圆内总结:从圆的标准方程222()()x a y b r -+-= 可知,要确定圆的标准方程,可用待定系数法确定a b r 、、三个参数。
探究二: (1)确定一个圆只需确定圆心为C 的圆经过点(1,1)A 和(2,2)B -,由于圆心C 与A,B 两点的距离相等,所以圆心C 在线段AB 的垂直平分线m 上,又圆心C 在直线l 上,因此圆心C 是直线l 与直线m 的交点,半径长等于CA 或CB 。
(2)总结归纳:ABC 外接圆的标准方程的两种求法:①根据题设条件,列出关于a b r 、、的方程组,解方程组得到a b r 、、得值,写出圆的标准方程.②根据确定圆的要素,以及题设条件,分别求出圆心坐标和半径大小,然后再写出圆的标准方程.例 1 写出圆心为(2,3)A -半径长等于5的圆的方程,并判断点12(5,7),(1)M M --是否在这个圆上.例2△ABC 的三个顶点的坐标是(5,1),(7,3),(2,8),A B C --求它的外接圆的方程.例3已知圆心为C 的圆:10l x y -+=经过点(1,1)A 和(2,2)B -,且圆心在:10l x y -+=上,求圆心为C 的圆的标准方程.【达标检测】1、已知两点)9,4(1P ,)3,6(2P ,求以线段21P P 为直径的圆的方程,并判断点M(6,9),N(3,3),Q(5,3)在圆上、在圆内、还是在圆外?2、已知AOB ∆的顶点坐标分别为A(4,0),B(0,3),O(0,0),求A O B ∆外接圆的方程.3、已知圆C 的圆心在直线012:=--y x l 上,并且经过原点和 A(2,1),求圆C 的标准方程.【课堂作业】课本P124 A 组2、4【拓展延伸】1、求下列圆的标准方程(1)圆心为点C(8,-3),且过点A(5,1) (2)过A(-1,5),B(5,5),C(6,-2)三点2、圆心在x 轴,并且过点A(-1,1),B(1,3),求此圆的方程.*3、平面直角坐标系中有A(0,1),B(2,1),C(3,4),D(-1,2)四点,这四点是否在同一圆上?为什么?*4、等腰三角形的顶点A的坐标为(4,2),底边一个端点B的坐标为(3,5),求另一个端点C的轨迹方程,并说明是什么图像。
数学必修24.1.2圆的一般方程【学习目标】1、掌握圆的一般方程的特征,由圆的一般方程确定圆的圆心半径。
2、掌握二元二次方程与圆的一般方程的关系及根据不同的已知条件,利用待定系数法求圆的一般方程。
3、进一步培养学生能用解析法研究几何问题的能力,渗透数形结合思想。
【重点难点】重点:掌握圆的一般方程,用待定系数法求圆的一般方程;难点:二元二次方程与圆的一般方程的关系及根据不同的已知条件,利用待定系数法求圆的一般方程。
【课前预习】C a b,半径为r ,则圆的标准方程为,若圆心1.已知圆的圆心为(,)在坐标原点上,则圆的方程就是.A B C的圆的方程.2.求过三点(0,0),(1,1),(4,2)问题1.方程222410x y x y+-++=表示+-++=表示什么图形?方程222460x y x y什么图形?问题2.方程220++++=在什么条件下表示圆?x y Dx Ey F方程220x y Dx Ey F ++++= 表示的轨迹:(1)当_____________ 时,方程表示以(,)22D E --的圆(2)当_____________ 时,方程只有实数解,22D Ex y =-=-,即只表示一个点(,)22D E-- (3) 当_____________时,方程没有实数解,因而它不表示任何图形 【尝试解答】 1、圆222420x y x y ++-+=的圆心坐标和半径分别为 ( )()A (1,2),3- ()B (1,2),3- ()C (1,3- ()D (1,3-2、圆心为(1,2),半径为2的圆的标准方程是_______________________.3、如果圆220x y Dx Ey F ++++=圆心在直线2y x =上,则( )()A 2D E = ()B 2E D = ()C 20E D += ()D D E =4、若方程x 2+y 2+ax+2ay+2a 2+a-1=0表示圆,则a 的取值范围是( )A.a <-2或a >32B.-32<a <0C.-2<a <0D.-2<a <325. 判断下列二元二次方程是否表示圆的方程?如果是,求出圆的圆心及半径.(1)4x 2+4y 2-4x+12y+9=0; (2)4x 2+4y 2-4x+12y+11=0.【达标检测】1.配方法求下列方程表示圆的圆心坐标和半径:(1)22250x y x +--= (2)222440x y x y ++--=(3)2240x y x ++= (4)22510x y y +-+=2、已知∆ABC 的顶点坐标分别是A(1,1)、B(3,1)、C(3,3),求∆ABC 外接圆的方程。
3、求点(4,2)P -与圆224x y +=上任一点Q 连线所成线段的中点M 的轨迹方程。
【课堂作业】P123 1. 2.【拓展延伸】1、将圆222410x y x y +--+=平分的直线是( )A.10x y +-=B. 30x y ++=C. 10x y -+=D. 30x y -+= 2.若直线30x y a ++=过圆22240x y x y ++-=的圆心,则a 的值为( )A.-1B.1C.3D.-33.经过圆2220x x y ++=的圆心C ,且与直线0x y +=垂直的直线方程是( )A.10x y ++=B. 10x y +-=C. 10x y -+=D. 10x y --= 4.求与两定点A(-1,2),B(3,2)P 的轨迹方程5.求经过三点A (1,-1)、B (1,4)、C (4,-2)的圆的方程。
6、已知线段AB 的端点B 的坐标是(4,3),端点A 在圆上()2214x y ++=运动,求线段AB 的中点M 的轨迹方程。
数学必修24.2.1直线与圆的位置关系(1)【学习目标】1、理解直线与圆的位置关系;会利用点到直线的距离公式求圆心到直线的距离2、会判断直线和圆的位置关系3、通过例题的分析讨论,提高学生的综合运用知识的能力【重点难点】重点:根据给定直线和园的方程,判断直线与圆的位置关系难点:判断方法的选择【课前预习】阅读课本教材,完成下面填空:1、 直线方程的一般式为:__ _________________2、 圆的标准方程为:______ ________圆心为:___ ____半径为:__ _____3、 圆的一般方程为:_____ _________圆心为:_____ ___半径为:_________4、 点),(y x P 到直线0=++C By Ax 的距离为:_______ _________例1 已知直线l :3x+y-6=0和圆心为C 的圆x 2+y 2-2y-4=0,判断直线l 与圆的位置关系.如果相交,求出它们的交点坐标.变式:()()()224:,3C :x y l y x b l +==+已知圆和直线 ,b 为何值时,直线与圆C 1相交,2相切相离.222(3,3)4210.M l x y y l --++-=例已知过点的直线被圆所截得的弦长为求直线的方程变式:求与x 轴相切,圆心在直线3x-y=0上,且被直线x-y=0所截弦长为2的圆的方程.【达标检测】1.直线3x +4y +12=0与圆(x +1)2+(y +1)2=9的位置关系是( )A .过圆心B .相切C .相离D .相交2.直线l 将圆x 2+y 2-2x -4y =0平分,且与直线x +2y =0垂直,则直线l 的方程为( )A .y =2xB .y =2x -2C .y =12x +32D .y =12x -323.若圆C 半径为1,圆心在第一象限,且与直线4x -3y =0和x 轴都相切,则该圆的标准方程是( )A .(x -2)2+(y -1)2=1B .(x -2)2+(y +1)2=1C .(x +2)2+(y -1)2=1D .(x -3)2+(y -1)2=14.若直线ax +by =1与圆x 2+y 2=1相交,则点P (a ,b )的位置是( )A .在圆上B .在圆外C .在圆内D .都有可能5.过原点O 作圆x 2+y 2-6x -8y +20=0的两条切线,设切点分别为P 、Q ,则线段PQ 的长为________.6.已知圆C 过点(1,0),且圆心在x 轴的正半轴上,直线l :y =x -1被该圆所截得的弦长为22,则圆C 的标准方程为____________.【课堂作业】 课本P132 5 6【拓展延伸】1.圆x 2+y 2+2x +4y -3=0上到直线l :x +y +1=0的距离为2的点有( )A .1个B .2个C .3个D .4个2.已知直线l :y=x+b 与曲线C :y=21x 有两个不同的公共点,求实数b 的取值范围;3.已知,圆C :x 2+y 2﹣8y+12=0,直线l :ax+y+2a=0. (1)当a 为何值时,直线l 与圆C 相切;(2)当直线l 与圆C 相交于A 、B 两点,且AB=2时,求直线l 的方程.数学必修24.2.1直线与圆的位置关系(2)【学习目标】1、能根据给定直线、圆的方程判断直线与园的位置关系2、能用直线和圆的方程解决一些简单的问题3、体会数形结合思想,初步形成代数方法处理几何问题能力。
【重点难点】重点:根据给定直线和园的方程,判断直线与圆的位置关系难点:用直线和圆的方程解决一些简单的问题【课前预习】完成下面填空: 与圆有关的最值问题(1)若00P x y (,)是圆222x +y =r 上的一点,则00x y ,的范围是0x Î( ),0y Î( )(2)若P 是半径为r 的圆C 外一点,则圆上的点到P 点距离的最小值为 ,最大值为(3)若P 是圆C 内一点,则过点P 的弦中,最长值为 ,最短值为 (4)若直线l 与半径为r 的圆相离,且圆心到直线的距离为d ,则圆上的点到直线的距离的最大值为 ,最小值为【尝试解答】例1. 求经过点A(-2,-4),且与直线l:x+3y-26=0相切于点B(8,6)的圆的方程.例2.自点A(-3,3)发出的光线l射到x轴上,被x轴反射,其反射光线所在直线与圆22x+y-4x-4y+7=0相切,求光线l所在直线的方程.例3.设点P(,x y)在圆22x+(y-1)=1上.(1)求.(2)求21yx++的最小值.变式:设点P(x,y)是圆x2+(y+4)2=4上任意一点,则的最大值为( )【达标检测】1.求圆心在直线23x y -=上,且与两坐标轴相切的圆的方程 . 2.已知圆C 的半径为2,圆心在x 轴的正半轴上,直线0443=++y x 与圆C 相切,则圆C 的方程为( )A 22230x y x +--=B 2240x y x ++=C 22230x y x ++-=D .2240x y x +-= 3.点P (x,y )在圆x 2+y 2=4 上,则44y x --的最大值是 4.已知x 2+y 2+4x -2y-4=0,则x 2+y 2的最大值为____________5.一束光线从点A (-1,1)发出,经x 轴反射到圆C :22x 2(3)1y -+-=()上,其最短路程是( )A .4 B.5 C. 1 D. 6.在平面直角坐标系中,A ,B 分别是x 轴和y 轴上的动点,若以AB 为直径的圆C 与直线课本P132 7 8 【拓展延伸】1.直线x-2y-3=0与圆22x-2+(y+3)=9()交于E 、F 两点,则EOF D (O 是原点)的面积为( ) A.32 B.34 C. D.5224.已知直线l :(2m+1)x+(m+1)y=7m+4,圆C : 22x 1(2)25y -+-=().证明:当m RÎ时,l 与圆必相交,并求相交弦最短时对应的m 值.数学必修22.3.4圆与圆的位置关系【学习目标】1.了解圆与圆的位置关系及其判定方法2.掌握判定圆与圆的位置关系的代数与几何判别方法3.利用圆与圆、直线与圆的位置关系解决一些简单的相关问题【重点难点】圆与圆的位置关系的判断 【课前预习】1.知识链接:1.圆和圆的位置关系有2.圆与圆的位置关系,设两圆的半径分别为)(,2121r r r r ,圆心距为d2.教材导读:阅读教材第129-130面。
