柯桥区鲁迅中学城南校区 高三(理)数学学科期中质量检测卷
鲁迅中学城南校区高三专题练(非金属)

绍兴县鲁迅中学城南校区高三化学学科结营考检测卷命题人:×××复核人×××考生须知:1、本卷共××大题,××小题,满分100分,时间90分钟,1.下列说法正确的是() A.光缆在信息产业中有广泛应用,制造光缆的主要材料是二氧化硅B.金刚石是自然界中硬度最大的物质,不可能与氧气发生反应C.浓H2SO4具有强氧化性,常温下就能与金属Cu发生剧烈反应D.将SO2通入品红溶液,溶液褪色后加热恢复原色;将SO2通入溴水,溴水褪色后加热也能恢复原色2.勤洗手和经常对环境进行消毒是预防传染病的有效途径。
2009年4月,猪流感疫情爆发,可以用某种消毒液进行消毒,预防传染。
已知该消毒液为无色液体,用红色石蕊试纸检验,发现试纸先变蓝后褪色,则该消毒液的主要成分可能是() A.KMnO4B.H2O2C.NaClO D.NH3·H2O3. 化学无处不在,下列与化学有关的说法不正确的是A.侯氏制碱法的工艺过程中应用了物质溶解度的差异B.可用蘸浓盐酸的棉棒检验输送氨气的管道是否漏气C.碘是人体必需微量元素,所以要多吃富含高碘酸的食物D.黑火药由硫黄、硝石、木炭三种物质按一定比例混合制成4.化学与生产、生活、社会密切相关,下列叙述错误的是() A.食品保鲜膜、一次性食品袋的主要成分是聚氯乙烯B.在家用燃煤中加入适量的生石灰能有效减少二氧化硫的排放量C.若使用氯气处理水,能达到消毒杀菌的目的D.我国“神舟九号”宇航员所穿航天服的主要成分是碳化硅、陶瓷和碳纤维,它们都属于新型无机非金属材料5.下列说法不正确的是() A.在食品袋中放入盛有硅胶和铁粉的透气小袋,可防止食物受潮、氧化变质B.海水中提取镁、溴、精制食盐等过程中包含化学变化C.低碳经济就是以低能耗、低污染、低排放为基础的经济发展模式D.大量排放SO2或CO2都会导致温室效应、形成酸雨等6.目前,人类已经发现的非金属元素除稀有气体元素外共有16种,下列对这16种非金属元素的判断不正确的是()①都是主族元素,原子的最外层电子数都大于3②单质在反应中都只能作氧化剂③最高价氧化物对应的含氧酸都是强酸④氢化物常温下都是气态,所以又叫气态氢化物⑤气态氧化物与水反应都不会再生成气体 A .全部B .①②C .①②③④D .①②④⑤7.如图把气体缓慢通过盛有足量试剂的试剂瓶M ,在试管N 中可以观察到明显现象的是8.研究发现,空气中少量的NO 2能参与硫酸型酸雨的形成,反应过程如下:①SO 2+NO 2―→SO 3+NO ②SO 3+H 2O ―→H 2SO 4③2NO +O 2―→2NO 2NO 2在上述过程中的作用,与H 2SO 4在下列变化中的作用相似的是( )A .加入少量H 2SO 4使淀粉水解B .碳酸钠与硫酸反应C .向铜和双氧水的混合物中加入硫酸D .潮湿的氯气通过盛有浓H 2SO 4的洗气瓶 9.下列说法不正确的是( ) A .在稀硫酸中加入铜粉,铜粉不溶解,再加入Cu(NO 3)2固体,铜粉仍不溶解 B .某气体能使湿润的红色石蕊试纸变蓝,该气体的水溶液一定显碱性C .铜与稀硝酸反应的离子方程式为3Cu +8H ++2NO -3===3Cu 2++2NO ↑+4H 2O D .HNO 3―→NO ―→NO 2,以上各步变化均能通过一步实现10. X 、Y 、Z 是三种常见的单质,甲、乙是两种常见的化合物。
浙江省绍兴鲁迅中学2025届高三第二次调研数学试卷含解析

浙江省绍兴鲁迅中学2025届高三第二次调研数学试卷注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.复数5i12i+的虚部是 ( ) A .iB .i -C .1D .1-2.历史上有不少数学家都对圆周率作过研究,第一个用科学方法寻求圆周率数值的人是阿基米德,他用圆内接和外切正多边形的周长确定圆周长的上下界,开创了圆周率计算的几何方法,而中国数学家刘徽只用圆内接正多边形就求得π的近似值,他的方法被后人称为割圆术.近代无穷乘积式、无穷连分数、无穷级数等各种π值的表达式纷纷出现,使得π值的计算精度也迅速增加.华理斯在1655年求出一个公式:π2244662133557⨯⨯⨯⨯⨯⨯=⨯⨯⨯⨯⨯⨯,根据该公式绘制出了估计圆周率π的近似值的程序框图,如下图所示,执行该程序框图,已知输出的 2.8T >,若判断框内填入的条件为?k m ≥,则正整数m 的最小值是A .2B .3C .4D .53.函数()y f x =在区间,22ππ⎛⎫- ⎪⎝⎭上的大致图象如图所示,则()f x 可能是( )A .()ln sin f x x =B .()()ln cos f x x =C .()sin tan f x x =-D .()tan cos f x x =-4.二项式52x⎫⎪⎭的展开式中,常数项为( )A .80-B .80C .160-D .1605.已知向量(3sin ,2)a x =-,(1,cos )b x =,当a b ⊥时,cos 22x π⎛⎫+= ⎪⎝⎭( ) A .1213-B .1213C .613-D .6136.大衍数列,米源于我国古代文献《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释我国传统文化中的太极衍生原理,数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和.已知该数列前10项是0,2,4,8,12,18,24,32,40,50,…,则大衍数列中奇数项的通项公式为( )A .22n n -B .212n -C .212n (-)D .22n7.M 、N 是曲线y=πsinx 与曲线y=πcosx 的两个不同的交点,则|MN|的最小值为( )A .πB πC πD .2π8.已知函数31()sin ln 1x f x x x x +⎛⎫=++⎪-⎝⎭,若(21)(0)f a f ->,则a 的取值范围为( ) A .1,2⎛⎫+∞ ⎪⎝⎭B .()0,1C .1,12⎛⎫⎪⎝⎭D .10,2⎛⎫⎪⎝⎭9.已知复数11iz i+=-,则z 的虚部是( ) A .iB .i -C .1-D .110.已知[]2240a b a b +=⋅∈-,,,则a 的取值范围是( ) A .[0,1]B .112⎡⎤⎢⎥⎣⎦,C .[1,2]D .[0,2]11.已知数列{}n a 是公差为()d d ≠0的等差数列,且136,,a a a 成等比数列,则1a d=( ) A .4B .3C .2D .112.如图是国家统计局于2020年1月9日发布的2018年12月到2019年12月全国居民消费价格的涨跌幅情况折线图.(注:同比是指本期与同期作对比;环比是指本期与上期作对比.如:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比)根据该折线图,下列结论错误的是( )A .2019年12月份,全国居民消费价格环比持平B .2018年12月至2019年12月全国居民消费价格环比均上涨C .2018年12月至2019年12月全国居民消费价格同比均上涨D .2018年11月的全国居民消费价格高于2017年12月的全国居民消费价格 二、填空题:本题共4小题,每小题5分,共20分。
浙江省绍兴市绍兴县鲁迅中学城南校区高三数学上学期期中试卷理(含解析)

2014-2015学年浙江省绍兴市绍兴县鲁迅中学城南校区高三(上)期中数学试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)(2014•诸暨市模拟)已知集合A={x|y=+},B={y|y=log 2x,x∈A},则(∁R A)∩B等于()A.(0,1) B. [0,1) C.(0,1] D. [0,1]考点:交、并、补集的混合运算.专题:集合.分析:求函数的定义域得到A,根据补集的定义求得∁R A,求函数的值域得到B,从而求得可得(∁R A)∩B.解答:解:∵集合A={x|y=+}={x|}={x|1≤x≤2},∴∁R A={x|x<1,或x>2},又 B={y|y=log2x,x∈A}={y|0≤y≤1},∴(∁R A)∩B=[0,1),故选:B.点评:本题主要考查求函数的定义域、求函数的值域,求集合的补集,两个集合的交集的定义和求法,属于基础题.2.(5分)(2014秋•绍兴县校级期中)设等差数列{a n}的前n和为S n,若已知a3+3a5﹣a6的值,则下列可求的是()A. S5 B. S6 C. S7 D. S8考点:等差数列的前n项和.专题:等差数列与等比数列.分析:已知式子化简可得a4为定值,由求和公式和性质可得S7=7a4,可得答案.解答:解:设等差数列{a n}的公差为d,则a3+3a5﹣a6=a3+3(a3+2d)﹣(a3+3d)=3(a3+d)=3a4,∴S7===7a4,故选:C点评:本题考查等差数列的性质和求和公式,属基础题.3.(5分)(2014•浙江模拟)已知a∈R,则“a>2”是“a2>2a”的() A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件考点:不等关系与不等式.专题:常规题型.分析:我们分别判断“a>2”⇒“a2>2a”与“a2>2a”⇒“a>2”的真假,然后根据充要条件的定义,即可得到答案.解答:解:∵当“a>2”成立时,a2﹣2a=a(a﹣2)>0∴“a2>2a”成立即“a>2”⇒“a2>2a”为真命题;而当“a2>2a”成立时,a2﹣2a=a(a﹣2)>0即a>2或a<0∴a>2不一定成立即“a2>2a”⇒“a>2”为假命题;故“a>2”是“a2>2a”的充分非必要条件故选A点评:本题考查的知识点是必要条件、充分条件与充要条件的判断,即若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件.4.(5分)(2014秋•绍兴县校级期中)将函数y=sin2x的图象向左平移个单位,再将图象上各点的横坐标伸长到原来的2倍,纵坐标不变,则所得图象对应的函数解析式是() A. y=cos4x B. y=cosx C. y=sin(x+) D. y=sinx考点:函数y=Asin(ωx+φ)的图象变换.专题:计算题.分析:函数y=sin2x的图象向左平移个单位,推出y=cos2x,横坐标伸长到原来的2倍,纵坐标不变,得到y=cosx的图象即可.解答:解:将函数y=sin2x的图象向左平移个单位,得到函数y=sin2(x+)=cos2x的图象,再将其周期扩大为原来的2倍,得到函数y=cosx的图象,故选B.点评:本题考查函数y=Asin(ωx+φ)的图象变换,基础题.5.(5分)(2014秋•绍兴县校级期中)设为向量,若+与的夹角为60°,与的夹角为45°,则=()A. B. C. D.考点:平面向量数量积的运算.专题:平面向量及应用.分析:作,,以OA,OB为邻边作平行四边形OACB,可得=.利用已知及其正弦定理可得:=.解答:解:作,,以OA,OB为邻边作平行四边形OACB,则=.∵+与的夹角为60°,与的夹角为45°,由正弦定理可得:==.故选:B.点评:本题考查了向量的平行四边形法则、正弦定理,考查了推理能力与计算能力,属于中档题.6.(5分)已知定义域为R的函数f(x)在(8,+∞)上为减函数,且函数y=f(x+8)函数为偶函数,则()A. f(6)>f(7) B. f(6)>f(9) C. f(7)>f(9) D. f(7)>f(10)考点:函数奇偶性的性质;函数单调性的性质.专题:压轴题.分析:根据y=f(x+8)为偶函数,则f(x+8)=f(﹣x+8),即y=f(x)关于直线x=8对称.又f(x)在(8,+∞)上为减函数,故在(﹣∞,8)上为增函数,故可得答案.解答:解:∵y=f(x+8)为偶函数,∴f(x+8)=f(﹣x+8),即y=f(x)关于直线x=8对称.又∵f(x)在(8,+∞)上为减函数,∴f(x)在(﹣∞,8)上为增函数.由f(8+2)=f(8﹣2),即f(10)=f(6),又由6<7<8,则有f(6)<f(7),即f(7)>f(10).故选D.点评:本题主要考查偶函数的性质.对偶函数要知道f(﹣x)=f(x).7.(5分)已知,则f[f(x)]≥1的解集是()A. B. C.D.考点:其他不等式的解法.专题:计算题.分析:先对x分段讨论,求出f[f(x)]的表达式,然后代入不等式f[f(x)]≥1求出x的范围,写出集合形式即为解集.解答:解:当x≥0时,有f[f(x)]=∴f[f(x)]≥1即解得x≥4当x<0时,有f[f(x)]=∴f[f(x)]≥1即解得∴不等式的解集为故选D点评:解决分段函数的有关问题,应该分段来解决,然后将各段的结果并起来即为函数的对应结果.8.(5分)(2014•杭州一模)若α∈(,π),且3cos2α=sin(﹣α),则sin2α的值为()A. B. C. D.考点:二倍角的余弦;二倍角的正弦.专题:三角函数的求值.分析:由条件可得3(cos2α﹣sin2α)=cosα﹣sinα,化简求得cosα+sinα=,再平方即可求得sin2α的值.解答:解:∵α∈(,π),3cos2α=sin(﹣α),∴3(cos2α﹣sin2α)=cosα﹣sinα,即3(cosα+sinα)•(cosα﹣sinα)=(cosα﹣sinα),∴cosα+sinα=,或cosα﹣sinα=0(不合题意,舍去),∴1+s in2α=,∴sin2α=﹣,故选:D.点评:本题主要考查两角和差的正弦公式、二倍角公式的应用,属于中档题.9.(5分)(2014秋•绍兴县校级期中)在△ABC中,角A,B,C所对的边分别为a,b,c,若△ABC的三边a,b,c成等比数列,则cos2B+cosB+cos(A﹣C)的值为() A. 0 B. 1 C. 2 D.不能确定考点:两角和与差的余弦函数.专题:计算题;等差数列与等比数列;三角函数的求值;解三角形.分析:运用等比数列的性质和正弦定理可得,sin2B=sinAsinC,利用三角形的内角和,两角和与差的三角函数化简cos(A﹣C)+cosB+cos2B,然后利用二倍角公式化简即可.解答:解:∵在△ABC中,若a,b,c成等比数列,∴b2=ac,利用正弦定理可得sin2B=sinAsinC.∴cos(A﹣C)+cosB+cos2B=cos(A﹣C)﹣cos(A+C)+cos2B=2sinAsinC+cos2B=2sin2B+(1﹣2sin2B)=1.故选B.点评:本题考查三角函数和正弦定理及等比数列的知识,解题时要注意公式的合理选用,考查计算能力,属于中档题.10.(5分)(2014秋•绍兴县校级期中)已知向量均为单位向量,它们的夹角为600,实数x,y满足|x+y|=,那么x+2y的最大值为()A. 3 B. C. D.考点:平面向量数量积的运算.专题:等差数列与等比数列.分析:向量均为单位向量,它们的夹角为600,可得=1,=1×1×cos60°=.由|x+y|=,可得x2+y2+xy=3,设x+2y=t,则x=t﹣2y,可得3y2﹣3ty+t2﹣3=0,利用△≥0,解出即可.解答:解:∵向量均为单位向量,它们的夹角为600,∴=1,=1×1×cos60°=.∵|x+y|=,∴=,化为x2+y2+xy=3,设x+2y=t,则x=t﹣2y,∴(t﹣2y)2+y2+(t﹣2y)y=3,化为3y2﹣3ty+t2﹣3=0,∵y∈R,∴△=9t2﹣12(t2﹣3)≥0,解得,∴t即x+2y的最大值为2.故选:C.点评:本题考查了向量的数量积定义及其运算性质、一元二次方程有实数根与判别式的关系,考查了推理能力与计算能力,属于中档题.二、填空题:本大题共7小题,每小题4分,共28分11.(4分)(2012•江苏模拟)已知,向量与垂直,则实数λ= .考点:数量积判断两个平面向量的垂直关系.专题:计算题.分析:首先由向量坐标运算表示出λ与的坐标,再由它们垂直列方程解之即可.解答:解:由题意知λ=λ(﹣3,2)+(﹣1,0)=(﹣3λ﹣1,2λ),=(﹣3,2)﹣2(﹣1,0)=(﹣1,2),又因为两向量垂直,所以(﹣3λ﹣1,2λ)(﹣1,2)=0,即3λ+1+4λ=0,解得λ=.故答案为解得.点评:本题考查向量坐标运算及两向量垂直的条件,是一道基础题.12.(4分)(2014秋•绍兴县校级期中)在各项均为正数的等比数列{a n}中,若公比为,且满足a3•a11=16,则log2a16= 5 .考点:等比数列的通项公式.专题:计算题.分析:设出等比数列的首项,由a3•a11=16,得到首项与公比的关系,把首项用公比表示,然后代入要求的式子化简即可.解答:解:设等比数列的首项为a1,由公比为,且满足a3•a11=16,得:,即,所以,所以==5.故答案为5.点评:本题考查了等比数列的通项公式,考查了等比数列的概念,考查了学生的运算能力,此题是基础题.13.(4分)(2014秋•绍兴县校级期中)已知lga=lg(2a+b)﹣lgb,则ab的最小值为8 .考点:基本不等式在最值问题中的应用;基本不等式.专题:函数的性质及应用.分析:先由对数的和等于乘积的对数化积,去掉对数符号后解得a与b的关系,然后求解log2a ﹣log2b的值.解答:解:由lga=lg(2a+b)﹣lgb,可得lga+lgb=lg(2a+b),得ab=2a+b,解得:ab≥8,当且仅当2a=b时取等号.则ab的最小值为:8.故答案为:8.点评:本题考查了对数式的运算性质,考查了对数方程的解法,是基础的计算题.14.(4分)(2014秋•绍兴县校级期中)若不等式≤k的解集是空集,则正整数k 的取值集合为{1} .考点:其他不等式的解法.专题:不等式的解法及应用.分析:根据不等式的解集是空集,转化为一元二次不等式,进行求解即可.解答:解:不等式≤k的解集是空集,等价为3x2+2x+2≤k(x2+x+1),即(3﹣k)x2+(2﹣k)x+2﹣k≤0的解集是空集,若k=3,不等式等价为x≥1,此时不满足条件.若3﹣k<0,即k>3,不等式(3﹣k)x2+(2﹣k)x+2﹣k≤0的解集不是空集,不满足条件,若3﹣k>0,即k<3,若(3﹣k)x2+(2﹣k)x+2﹣k≤0的解集是空集,则等价为判别式△=(2﹣k)2﹣4(3﹣k)(2﹣k)=(2﹣k)(3k﹣10)<0,解得k>或k<2,∵k<3,∴k<2,∵k是正整数,∴k=1,故答案为:{1}点评:本题主要考查不等式的求解,根据不等式的解集,转化为不等式恒成立是解决本题的关键.15.(4分)(2014秋•绍兴县校级期中)若实数x,y满足,则z=|x|﹣2y的最大值为.考点:简单线性规划.专题:不等式的解法及应用.分析:作出不等式组对应的平面区域,利用z的几何意义,利用数形结合即可得到结论.解答:解:作出不等式组对应的平面区域如图:由z=|x|﹣2y,得y=|x|,作出直线y=|x|,平移直线y=|x|,由图象可知当直线y=|x|经过点C时,直线y=|x|的截距最小,此时z最大,由,解得,即C(,),此时z max=||﹣2×==,故答案为:点评:本题主要考查线性规划的应用,作出平面区域,利用数形结合是解决本题的关键.16.(4分)(2014•浙江二模)等差数列{a n}中,a1=1,公差为d,a3>0,当且仅当n=3时,|a n|取到最小值,则d的取值范围是.考点:等差数列的性质.专题:等差数列与等比数列.分析:根据已知条件:a3>0,当且仅当n=3时,|a n|取到最小值,利用等差数列的通项公式列出不等式组,求出d的范围.解答:解:∵a3>0,当且仅当n=3时,|a n|取到最小值,∴a4<0,且a4+a3>0,∴解得,故答案为:.点评:本题考查等差数列的性质及通项公式,解本题的关键是据已知条件,|a n|取到最小值得到a4<0,且a4+a3>0,属于中档题.17.(4分)(2014秋•绍兴县校级期中)在△ABC中,已知•=9,sinB=cosA•sinC,S△ABC=6,P为线段AB上的点,且=x•+y•,则+的最小值为 3 .考点:利用导数求闭区间上函数的最值;平面向量的基本定理及其意义;平面向量数量积的运算.专题:导数的综合应用;解三角形;平面向量及应用.分析:由•=9,可得bccosA=9.又6=S△ABC=sinA,可得tanA=,bc=15.由sinB=cosA•sinC,利用正弦定理可得b=c,联立解得b,c.利用余弦定理可得a.由于=x•+y•,可得=+,利用向量共线定理可得x+y=1.可得+===f(x),利用导数研究函数的单调性即可得出.解答:解:∵•=9,∴bccosA=9,∵6=S△ABC=sinA,∴t anA=,∴sinA=,cosA=.∴bc=15.∵sinB=cosA•sinC,∴b=c,,解得.∴a2=b2+c2﹣2bccosA=32+52﹣18=16.∴a=4.∵=x•+y•,∴=+,∴x+y=1.∴3y=12﹣4x>0.解得0<x<3.则+===f(x),f′(x)=﹣+=,当时,f′(x)>0,函数f(x)单调递增;当时,f′(x)<0,函数f (x)单调递减.∴当x=时,f(x)取得最小值,=3.故答案为:3.点评:本题考查了向量数量积运算性质、正弦定理、余弦定理、向量共线定理、利用导数研究函数的单调性,考查了推理能力与计算能力,属于难题.三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或运算步骤.18.(14分)(2014秋•绍兴县校级期中)已知集合A={x|<1},B={x|log6(x+a)<1}.(1)若A∪B=R,求实数a的取值范围;(2)若x∈A是x∈B的必要不充分的条件,求实数a的取值范围.考点:集合的包含关系判断及应用;必要条件、充分条件与充要条件的判断.专题:函数的性质及应用;集合.分析:(1)先求出集合A={x|x<﹣2,或x>3},B={x|﹣a<x<6﹣a},若A∪B=R,则有,解不等式组即可;(2)根据条件便知B⊊A,所以便有6﹣a≤﹣2,或﹣a≥3,所以解不等式即可得到a的取值范围.解答:解:(1)A={x|x2﹣x﹣6>0}={x|x<﹣2,或x>3};B={x|0<x+a<6}={x|﹣a<x<6﹣a};若A∪B=R,则:;解得2<a<3;∴a的取值范围为(2,3);(2)x∈A是x∈B的必要不充分条件;∴x∈B能得到x∈A,而x∈A得不到x∈B;∴B⊊A;∴6﹣a≤﹣2,或﹣a≥3;∴a≥8,或a≤﹣3;∴实数a的取值范围为(﹣∞,﹣3]∪[8,+∞).点评:考查指数函数的单调性,对数函数的定义域及单调性,以及并集、子集的概念.19.(14分)(2014秋•绍兴县校级期中)已知函数f(x)=2sin2(x+)﹣cos2x﹣1,x∈[,].(1)求f(x)的单调递增区间;(2)若存在x∈[,],使得f(x)<m成立,求实数m的取值范围.考点:三角函数中的恒等变换应用;正弦定理.专题:三角函数的求值;三角函数的图像与性质.分析:(1)首先对三角函数的关系式进行恒等变换,把函数关系式变形成正弦型函数,进一步利用正弦型函数的整体思想求出函数的单调区间.(2)首先根据函数的定义域求出函数的值域,进一步利用函数的恒成立问题求出参数的取值范围.解答:解:(1)(x)=2sin2(x+)﹣cos2x﹣1=2(sin2x﹣cos2x)=所以:由x∈[,].所以:,得,故递增区间为;(2)∵,∴,使得f(x)<m成立,只需满足m>f(x)min即可,进一步求出f(x)的最小值为,∴m>1点评:本题考查的知识要点:三角函数的恒等变换,利用函数的整体思想求出函数的单调区间,恒成立问题的应用,属于基础题型.20.(14分)(2014秋•绍兴县校级期中)在△ABC中,角A,B,C所对的边分别为a,b,c,已知角A,B,C成等差数列.(1)若b=,求a+c的取值范围;(2)若,,也成等差数列,求证:a=c.考点:等差数列的性质;正弦定理.专题:综合题;等差数列与等比数列;解三角形.分析:(1)由已知得B=60°,由正弦定理得,利用A的范围,即可求a+c的取值范围;(2)若,,成等差数列,,得,结合b2=a2+c2﹣2accos60°=a2+c2﹣ac,化简可得a=c.解答:(1)解:由已知得B=60°.由正弦定理,得,∵A∈(0°,120°),∴60°﹣A∈(﹣60°,60°),则,因此.(2)证明:由已知,得.又b2=a2+c2﹣2accos60°=a2+c2﹣ac,将代入此式得,化简此式得(a2+c2)2+ac(a2+c2)﹣6a2c2=0,即(a2+c2+3ac)(a2+c2﹣2ac)=0.∵a2+c2+3ac>0,∴a2+c2﹣2ac=0,得a=c.点评:本题考查正弦定理、余弦定理,考查等差数列的性质,考查学生分析解决问题的能力,属于中档题.21.(15分)(2013•宁波模拟)数列{a n}中,a3=1,a1+a2+…+a n=a n+1(n=1,2,3…).(1)求a1,a2的值;(2)求数列{a n}的前n项和S n及数列{a n}的通项公式;(3)设b n=log2S n,存在数列{c n}使得c n•b n+3•b n+4=1+n(n+1)(n+2)S n,试求数列{c n}的前n项和T n.考点:等差数列与等比数列的综合.专题:计算题;等差数列与等比数列.分析:(1)由a1+a2+…+a n=a n+1,a3=1,分别令n=1可求a1,a2(2)由已知可得,s n=a n+1=s n+1﹣s n,结合等比数列的通项公式可求s n,进而可求a n(3)由(2)可求b n=log2S n=n﹣2,代入已知可求c n,然后利用分组求和及裂项求和、错位相减即可求解数列的和解答:解:(1)∵a1+a2+…+a n=a n+1,a3=1令n=1可得,a1=a2令n=2可得,a1+a2=a3=1∴;….(2分)(2)∵a1+a2+…+a n=a n+1,即s n=a n+1=s n+1﹣s n∴s n+1=2s n∵a1=s1=∴{s n}是以为首项,以2为公比的等比数列∴即;….(3分)∴a n+1=s n=2n﹣2∴…(3分)(3)∵b n=log2S n=n﹣2又∵c n•b n+3•b n+4=1+n(n+1)(n+2)S n,∴∴…(3分)∵==设A=1•2﹣1+2•20+…+n•2n﹣2∴2A=1•20+2•2+…+(n﹣1)•2n﹣2+n•2n﹣1两式相减可得,﹣A=2﹣1+20+…+2n﹣2﹣n•2n﹣1=×2=×2=∴A=(n﹣1)•2n﹣1∴c1+c2+…+c n=+1•2﹣1+2•20+…+n•2n﹣2==∴….(3分)点评:本题主要考查了利用数列的递推公式求解数列的通项、等比数列的通项公式的应用及数列的分组求和、裂项求和、错位相减求和方法的应用.22.(15分)(2014秋•绍兴县校级期中)已知函数f(x)=|x2﹣1|+x2+kx.(1)若函数f(x)在(﹣∞.﹣1]单调递减,求实数k的取值范围;(2)若关于x的方程f(x)=0在(0,2)上有两个不同的解x1,x2,求k的取值范围,并证明+<4.考点:绝对值不等式的解法.专题:计算题;函数的性质及应用;不等式的解法及应用.分析:(1)运用绝对值的含义,化f(x)为分段函数,再由二次函数的单调性,解不等式即可得到k的范围;(2)运用参数分离,讨论0<x<1,1≤x<2时,函数的单调性及值域,并求出相应方程的根,即可得到k的范围,以及两根的倒数之和小于4.解答:解:(1),当x≥1或x≤﹣1时,f(x)=2(x+)2﹣1﹣,由函数f(x)在(﹣∞.﹣1]单调递减,则,可得k≤4.(2)方程f(x)=0,即为.∵x∈(0,1)时,单调递增,且;x∈[1,2)时,单调递减,且.∴要使方程f(x)=0在(0,2)上有两个不同的解x1,x2,必须且只须.此时,.则.因为=在上单调递减,所以.即有+<4.点评:本题考查绝对值函数的单调性,考查函数与方程的转化思想的运用,考查一次函数和二次函数的单调性的运用,考查运算能力,属于中档题和易错题.四、B卷23.(2014秋•绍兴县校级期中)某人制定了一项旅游计划,从7个旅游城市中选择5个进行游览.如果A,B为必选城市,并且在游览过程中必须先A后B的次序经过A,B两城市(A,B两城市可以不相邻),则有不同的游览路线600 种.考点:计数原理的应用.专题:应用题;排列组合.分析:首先确定5个入选的城市,需要再从剩下的5个城市中抽取3个,有C53=10种不同情况,再对5个入选的城市全排列,又由A、B顺序一定,要使用倍分法,结合根据分步计数原理,计算可得答案.解答:解:已知AB必选,则从剩下的5个城市中,再抽取3个,有C53=10种不同情况,此时5个城市已确定,将其全排列,可得共A55=120种情况,又由A、B顺序一定,则根据分步计数原理,可得不同的游览线路有=600种.故答案为:600.点评:本题考查排列、组合的综合运用,注意要根据题意,选用特殊的方法,如插空法、捆绑法、倍分法.24.若二项式的展开式中各项系数的和是512,则展开式中的常数项为() A.﹣27C93 B. 27C93 C.﹣9C94 D. 9C94考点:二项式系数的性质.专题:计算题.分析:在中,令x=1可得,其展开式各项系数的和,又由题意,可得2n=512,解可得n=9,进而可得其展开式的通项,在其中令x的指数为0,可得r的值为6,即可得其展开式中的常数项,即可得答案.解答:解:在中,令x=1可得,其展开式各项系数的和是2n,又由题意,可得2n=512,解可得n=9,则二项式的展开式的通项为T r+1=C9r(3x2)9﹣r(﹣)r=(﹣1)r•C9r•39﹣r x18﹣3r,令18﹣3r=0可得,r=6,则其展开式中的常数项为第7项,即T7=(﹣1)6•C96•33=27C93,故选B.点评:本题考查二项式定理的应用,解题时需要区分展开式中各项系数的和与各二项式系数和.25.(2014秋•绍兴县校级期中)将五名插班生安排到A,B,C三个班级,要求每个班级至少安排一人.(1)求A班恰好安排三人的概率;(2)求甲、乙不安排在同一个班级的概率.)P=;=。
2020-2021学年浙江省绍兴市鲁迅中学高三(上)期中数学试卷

2020-2021学年浙江省绍兴市鲁迅中学高三(上)期中数学试卷一、1.若集合A={x|1<x<2},集合B={x|2≤2x<4},则A∪B=()A.(1,2)B.[1,2)C.[0,2)D.(0,2)2.已知复数(i为虚数单位),则复数z的模|z|=()A.1B.C.2D.43.已知双曲线C:=1(a>0,b>0)的离心率为22(2,0),则双曲线C的方程为()A.B.C.D.4.已知实数x,y满足,则z=x+y的最大值为()A.4B.3C.D.25.设x,y∈R,则“0<xy<1”是“|x|<()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件6.函数的图象可能是()A.B.C.D.7.已知直线x+y﹣k=0(k>0)与圆x2+y2=4交于不同的两点A、B,O是坐标原点,且有()A.B.C.D.8.甲箱子里装有3个白球和2个红球,乙箱子里装有2个白球和2个红球.从这两个箱子里分别摸出一个球,设摸出的白球的个数为X,则()A.P(X=1),且E(X)>E(Y)B.P(X=1),且E(X)<E(Y)C.P(X=1)=,且E(X)>E(Y)D.P(X=1)=,且E(X)<E(Y)9.在△ABC中,∠ACB=90°,BC=2,点D在斜边AB上,以CD为棱把它折成直二面角A﹣CD﹣B()A.B.C.2D.310.已知点P是曲线y=sin x+lnx上任意一点,记直线OP(O为坐标系原点)的斜率为k,则()A.至少存在两个点P使得k=﹣1B.对于任意点P都有k<0C.对于任意点P都有k<1D.存在点P使得k≥1二、填空题11.计算:log2=,2=.12.已知多项式(x+b)5=(x﹣1)5+a1(x﹣1)4+a2(x﹣1)3+a3(x﹣1)2+a4(x﹣1)﹣32,则b=,a2=.13.一个几何体的三视图如图所示,则该几何体的体积为,表面积为.14.已知抛物线y=x2上两点A,B(A在第二象限),O为原点,且OA⊥AB,△OAB的面积为.15.平面向量,,满足||=|,|﹣|=|﹣|=|﹣||的最大值为.16.在△ABC中,AB=2,AC=3,AC的中点分别为F,E,则的取值范围是.17.设S n为数列{a n}的前n项和,S n=(﹣1)n a n﹣,n∈N*,则:(1)a3=;(2)S1+S2+…+S100=.三、解答题(共5小题,满分0分)18.A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与x轴正半轴的交点,△AOB为正三角形.记∠AOC=α.(Ⅰ)若A点的坐标为.求的值;(Ⅱ)求|BC|2的取值范围.19.如图,四棱锥P﹣ABCD中,CD∥AB,,P A=PB=10,,,点E为PD中点.(1)求证:PD⊥CD;(2)求直线BE与平面PCD所成角的正弦值.20.设各项均为正数的数列{a n}的前n项和为S n,已知数列是首项为1,公差为1的等差数列.(Ⅰ) 求数列{a n}的通项公式;(Ⅱ)令b n=,若不等式b1+b2+b3+…+b n≥对任意n∈N*都成立,求实数m的取值范围.21.如图,F1,F2是椭圆C:+y2=1的左、右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线l:x=﹣(1)若B的坐标为(0,1),求点M的坐标;(2)求•的取值范围.22.已知f(x)=e x﹣ax﹣1,x∈(0,2).(1)若f(x)无零点,求a的取值范围;(2)当a=1时,证明:﹣<f(x)2<1.(参考数据:7<e2<8)2020-2021学年浙江省绍兴市鲁迅中学高三(上)期中数学试卷参考答案与试题解析一、1.若集合A={x|1<x<2},集合B={x|2≤2x<4},则A∪B=()A.(1,2)B.[1,2)C.[0,2)D.(0,2)【分析】先求出集合A,B,由此能求出A∪B.【解答】解:∵集合A={x|1<x<2},集合B={x|6≤2x<4}={x|7≤x<2},∴A∪B={x|1≤x<5}=[1,2).故选:B.【点评】本题考查并集的求法,考查并集定义等基础知识,考查运算求解能力,是基础题.2.已知复数(i为虚数单位),则复数z的模|z|=()A.1B.C.2D.4【分析】直接利用商的模等于模的商求解.【解答】解:∵,∴|z|=||=.故选:C.【点评】本题考查复数模的求法,考查数学转化思想方法,是基础题.3.已知双曲线C:=1(a>0,b>0)的离心率为22(2,0),则双曲线C的方程为()A.B.C.D.【分析】通过双曲线的离心率以及焦点坐标,求出c,a,然后求解b,即可得到双曲线方程.【解答】解:双曲线C:=1(a>2,且其右焦点为F2(2,0),可得c=2,a=,所以双曲线方程为:.故选:A.【点评】本题考查双曲线的简单性质的应用,双曲线方程的求法,考查计算能力,是基础题.4.已知实数x,y满足,则z=x+y的最大值为()A.4B.3C.D.2【分析】作出不等式组对应的平面区域,利用z的几何意义,利用数形结合即可得到结论.【解答】解:作出不等式组对应的平面区域如图:设z=x+y得y=﹣x+z,平移直线y=﹣x+z,由图象可知当直线y=﹣x+z经过点B(4,直线y=﹣x+z的截距最大,此时z最大,此时z=3,故选:B.【点评】本题主要考查线性规划的应用,利用z的几何意义,通过数形结合是解决本题的关键5.设x,y∈R,则“0<xy<1”是“|x|<()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【分析】“0<xy<1”⇒0<|xy|<1⇒“|x|<”.反之不成立.【解答】解:“0<xy<1”⇒4<|xy|<1⇒“|x|<”.,反之不成立,例如﹣8<xy<0,∴“0<xy<7”是“|x|<”的充分不必要条件,故选:A.【点评】本题考查了不等式的基本性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.6.函数的图象可能是()A.B.C.D.【分析】由f(﹣3)=0直接可以得出答案.【解答】解:函数的定义域为{x|x≠±1},令f(x)=0,符合要求的只有选项B.故选:B.【点评】本题考查由函数解析式确定函数图象,属于基础题.7.已知直线x+y﹣k=0(k>0)与圆x2+y2=4交于不同的两点A、B,O是坐标原点,且有()A.B.C.D.【分析】利用平行四边形法则,借助于直线与圆的位置关系,利用直角三角形,即可求得结论.【解答】解:设AB中点为D,则OD⊥AB∵,∴∴∵∴∵直线x+y﹣k=2(k>0)与圆x2+y3=4交于不同的两点A、B,∴∴4>∴4>∵k>0,∴故选:C.【点评】本题考查向量知识的运用,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.8.甲箱子里装有3个白球和2个红球,乙箱子里装有2个白球和2个红球.从这两个箱子里分别摸出一个球,设摸出的白球的个数为X,则()A.P(X=1),且E(X)>E(Y)B.P(X=1),且E(X)<E(Y)C.P(X=1)=,且E(X)>E(Y)D.P(X=1)=,且E(X)<E(Y)【分析】由题意计算P(X=1)和X、Y的数学期望E(X)、E(Y)即可.【解答】解:由题意知,P(X=1)=+=+=;又P(X=0)==,P(X=4)==,∴X的数学期望为E(X)=0×+1×=;P(Y=0)==,P(Y=4)=+=+=,P(Y=2)==,∴Y的数学期望为E(Y)=0×+1×=;∴E(X)>E(Y).故选:C.【点评】本题考查了离散型随机变量的概率分布与数学期望的计算问题,是基础题.9.在△ABC中,∠ACB=90°,BC=2,点D在斜边AB上,以CD为棱把它折成直二面角A﹣CD﹣B()A.B.C.2D.3【分析】设∠ACD=θ,则∠BCD=90°﹣θ,作AM⊥CD于M,BN⊥CD于N,于是AM =3sinθ,CN=2sinθ,MN=|2sinθ﹣3cosθ|,由此能求出当θ=45°,AB有最小值,最小值是.【解答】解:设∠ACD=θ,则∠BCD=90°﹣θ,作AM⊥CD于M,BN⊥CD于N,于是AM=3sinθ,CN=2sinθ,∴MN=|5sinθ﹣3cosθ|,∵A﹣CD﹣B是直二面角,AM⊥CD,∴AM与BN成90°角,∴AB==≥.∴当θ=45°,即CD是∠ACB的平分线时,AB有最小值,最小值是.故选:B.【点评】本题考查线段长最小值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.10.已知点P是曲线y=sin x+lnx上任意一点,记直线OP(O为坐标系原点)的斜率为k,则()A.至少存在两个点P使得k=﹣1B.对于任意点P都有k<0C.对于任意点P都有k<1D.存在点P使得k≥1【分析】结合正弦函数的值域和对数函数y=lnx和直线y=x﹣1的关系,即可判断D;当≤x<π时,y=sin x+lnx>0,即可判断B;=﹣1,即sin x+lnx+x=0至少存在两解,运用导数判断单调性,即可判断A,由排除法思想即可得到结论.【解答】解:任意取x为一正实数,一方面y=sin x+lnx≤lnx+1,另一方面由y=lnx和直线y=x﹣1的图象容易证lnx+7≤x成立,所以y=sin x+lnx≤x,因为y=sin x+lnx≤lnx+1与lnx+1≤x中两个等号成立条件不一样,所以y=sin x+lnx<x恒成立,所以k<6;当≤x<π时,所以k>0;对于A选项,至少存在两个点P使得k=﹣3=﹣1至少存在两解,即sin x+lnx+x=0至少存在两解,(sin x+lnx+x)′=cos x+,所以sin x+lnx+x=0至多存在一解,故排除A,故选:C.【点评】本题考查直线的斜率的范围,考查分类讨论思想方法,以及正弦函数的性质、函数的导数与单调性的运用,考查分析问题和判断能力、推理能力,属于中档题.二、填空题11.计算:log2=,2=.【分析】进行对数的运算即可.【解答】解:,=.故答案为:.【点评】本题考查了对数的运算性质,对数的换底公式,考查了计算能力,属于基础题.12.已知多项式(x+b)5=(x﹣1)5+a1(x﹣1)4+a2(x﹣1)3+a3(x﹣1)2+a4(x﹣1)﹣32,则b=﹣3,a2=40.【分析】根据(x+b)5=[(x﹣1)+b+1]5,利用二项展开式的通项公式,求得b和a2的值.【解答】解:∵(x+b)5=[(x﹣1)+b+5]5=(x﹣1)8+a1(x﹣1)2+a2(x﹣1)6+a3(x ﹣1)8+a4(x﹣1)﹣32,∴•(b+1)8=﹣32,∴b=﹣3.∴a2=•(b+1)6=40,故答案为:﹣3;40.【点评】本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于中档题.13.一个几何体的三视图如图所示,则该几何体的体积为,表面积为.【分析】几何体是四棱锥,几何直观图判断四棱锥的底面四边形的形状及相关几何量的数据;再由侧视图判断几何体的高,把数据代入棱锥的体积公式计算.【解答】解:由三视图知:几何体是四棱锥,如图:四棱锥的底面四边形为直角梯形,直角梯形的底边长分别为2、1;四棱锥的高为:,AB=2,BC=1,P A=PB=4,DC=,CP=,∴几何体的体积V=×=.表面积为:×++++=.故答案为:;.【点评】本题考查了由三视图求几何体的体积,根据三视图判断几何体的形状及数据所对应的几何量是解题的关键.14.已知抛物线y=x2上两点A,B(A在第二象限),O为原点,且OA⊥AB,△OAB的面积为3.【分析】设出点A的坐标,即可直线OA的斜率以及直线AB的斜率,所以求出直线AB 的方程,代入抛物线方程求出x的最小值,此时点距离y轴的距离最近,距离为2,进而求出点A,B的坐标,从而可以求解.【解答】解:由题意设点A(﹣m,m2),(m>0),所以k,则直线AB的方程为:y﹣m2=,即y=,代入抛物线方程可得:mx7﹣x﹣m(m2+1)=8,即(x+m)(mx﹣m2﹣1)=2=0,解得x=m+,此时点距离y轴的距离最近,距离为2,此时x A=﹣m=﹣1,y,x,即A(﹣1,1),2),所以|OA|=,|AB|=,所以三角形AOB的面积为S=,故答案为:3.【点评】本题考查了直线与抛物线的位置关系的应用,涉及到利用基本不等式求解最值的问题,考查了学生的运算能力,属于中档题.15.平面向量,,满足||=|,|﹣|=|﹣|=|﹣||的最大值为2.【分析】由题意||=||=1,设,,,利用向量的夹角运算,OA=OB,AC=CB=AB,可得△CAO≌△CBO,从而OC垂直平分AB,结合三角函数化简,即可求解||的最大值.【解答】解:由题意,设,,,向量与,根据||=|,|﹣|=|﹣﹣|,如图:OA=OB,AC=CB=AB,可得△CAO≌CBO,即OC垂直平分AB,设AB=t,那么t=2sin,等边三角形ABC的高CH为,那么==2sin(),当=时,||的最大值为2.故答案为:2.【点评】本题考查了向量夹角和数量积的关系、向量的坐标运算,属于基础题.16.在△ABC中,AB=2,AC=3,AC的中点分别为F,E,则的取值范围是(,).【分析】在△ABE和在△ACF中,利用余弦定理分别求出BE2,CF2,再做除法,利用三角形角A的范围,得出cos A∈(﹣1,1),进行合理变形可求解.【解答】解:∵F,E分别为AB,∴AE=,在△ABE中,BE5=AB2+AE2﹣5AB•AE•cos A=4+﹣2×2×﹣8cos A,在△ACF中,CF2=AC2+AF8﹣2AC•AF•cos A=9+5﹣2×3×2×cos A=10﹣6cos A,∴===1﹣×,∵A∈(0,π),7),16),∴,),∴∈(,),∴,).故答案为:(,).【点评】本题考查知道两边和夹角利用余弦定理求出第三边,要进行合理变形,准确确定比值的范围,是中档题.17.设S n为数列{a n}的前n项和,S n=(﹣1)n a n﹣,n∈N*,则:(1)a3=﹣;(2)S1+S2+…+S100=.【分析】(1)把给出的数列递推式先分n=1和n≥2讨论,由此求出首项和n≥2时的关系式.对此关系式再分n为偶数和奇数分别得到当n为偶数和奇数时的通项公式,则a3可求;(2)把(1)中求出的数列的通项公式代入,n∈N*,则利用数列的分组求和和等比数列的前n项和公式可求得结果.【解答】解:由,n∈N*,当n=1时,有,得.当n≥2时,.即.若n为偶数,则.所以(n为正奇数);若n为奇数,则=.所以(n为正偶数).所以(1).故答案为﹣;(2)因为(n为正奇数),又(n为正偶数).则.,.则.….所以,S1+S2+S6+S4+…+S99+S100====.故答案为.【点评】本题考查了数列的求和,考查了数列的函数特性,解答此题的关键在于当n为偶数时能求出奇数项的通项,当n为奇数时求出偶数项的通项,此题为中高档题.三、解答题(共5小题,满分0分)18.A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与x轴正半轴的交点,△AOB为正三角形.记∠AOC=α.(Ⅰ)若A点的坐标为.求的值;(Ⅱ)求|BC|2的取值范围.【分析】(Ⅰ)利用任意角的三角函数的定义,三角恒等变换,求得所给式子的值.(Ⅱ)由题意可得∠AOB=,α∈(,),由余弦定理以及余弦函数的定义域和值域,求得|BC|2的取值范围.【解答】解:(Ⅰ)若A点的坐标为,则cosα=,∴===20.(Ⅱ)由题意可得∠AOB=,∴由余弦定理可得|BC|2=OB2+OC3﹣2OB•OC•cos(+α)=4+1﹣2cos(,∵∠AOC=α∈(,),∴+α∈(,)+α)∈(﹣,∴﹣2cos(+α)∈(3,)+α)∈(4).【点评】本题主要考查任意角的三角函数的定义,三角恒等变换,余弦定理,余弦函数的值域,属于中档题.19.如图,四棱锥P﹣ABCD中,CD∥AB,,P A=PB=10,,,点E为PD中点.(1)求证:PD⊥CD;(2)求直线BE与平面PCD所成角的正弦值.【分析】(1)取AB中点F,连接PF、FD,证明AB⊥PF,AB⊥FD,推出AB⊥平面PFD,说明AB⊥PD,然后证明PD⊥CD.(2)过P做PO⊥FD于O,过O做OG∥AB交BC于G,则PO、OF、OG两两垂直,以OF、OG、OP分别为x、y、z轴建立如图所示空间直角坐标系o﹣xyz,求出,平面PCD的法向量,然后利用空间向量的数量积求解直线BE与平面PCD所成角的正弦值即可.【解答】(1)证明:取AB中点F,连接PF,∵P A=PB=10,,∴AB⊥PF,AB⊥FD,∵PF∩FD=F,∴AB⊥平面PFD,PD⊂平面PFD,∴AB⊥PD,又∵CD∥AB,∴PD⊥CD.(2)解:过P做PO⊥FD于O,∵AB⊥平面PFD,PO⊂平面PFD,∴AB⊥PO,∵AB∩FD=F.过O做OG∥AB交BC于G,则PO、OG两两垂直,以OF、OG、y、z轴建立如图所示空间直角坐标系o﹣xyz,∵AB=16,P A=PB=10,,,∴PF=6,FD=12,∴PF6+PD2=FD2,∴PF⊥PD,∴,OF=3.∵CD∥AB,,∴CD∥OG∥FB,CD=FB,∴四边形FBCD是矩形,CD=OG=FB=8,∴,D(﹣9,0,B(2,8,C(﹣9,3,∵E为PD中点,∴,∴,,.设平面PCD的法向量,由,得,令x2=1,得,则,则与所成角设为α,设为β,∴直线BE与平面PCD所成角的正弦值为.【点评】本题考查直线与平面所成角的求法,直线与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.20.设各项均为正数的数列{a n}的前n项和为S n,已知数列是首项为1,公差为1的等差数列.(Ⅰ) 求数列{a n}的通项公式;(Ⅱ)令b n=,若不等式b1+b2+b3+…+b n≥对任意n∈N*都成立,求实数m的取值范围.【分析】(Ⅰ)利用等差数列通项公式,推出前n项和,然后求解数列的通项公式.(Ⅱ)化简b n=,求出数列的和,然后求出m的不等式,推出结果即可.【解答】解:(Ⅰ)∵数列是首项为1,∴.∴.当n=1时,a2=S1=1; 当n≥4时,a n=S n﹣S n﹣1=n2﹣(n﹣6)2=2n﹣3.又a1=1适合上式.∴a n=5n﹣1.…(4分)(Ⅱ)==,∴b1+b7+…+b n===.∴对任意n∈N*都成立,得对任意n∈N*都成立.令,则.∴c n+1>c n.∴.∴.∴实数m的取值范围为.…(10分)【点评】本题考查数列的应用,数列求和以及数列与不等式相结合,考查计算能力.21.如图,F1,F2是椭圆C:+y2=1的左、右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线l:x=﹣(1)若B的坐标为(0,1),求点M的坐标;(2)求•的取值范围.【分析】(1)先求得A点的横坐标为﹣1,代入椭圆方程+y2=1,解得y的值,可得A的纵坐标,再根据中点公式求得M的坐标.(2)当AB垂直于x轴时,易得•的值.当AB不垂直于x轴时,设AB的斜率为k,M(﹣,m),由可得k=,可得AB的方程为y=x+①.把①代入椭圆方程化简利用韦达定理,由判别式大于零,求得m2的范围,化简•为.令t=1+8m2,则1<t<8,再根据函数的单调性求得•=[3t+]的范围.【解答】解:(1)∵B的坐标为(0,1)上,∴A点的横坐标为﹣1,代入椭圆方程+y2=5,解得y=±,)或点A(﹣1,﹣).∴线段AB的中点M(﹣,+)或(﹣,﹣).(2)由于F1(﹣6,0),F2(5,0),AB的方程为x=﹣,﹣)、B(﹣,),求得•=.当AB不垂直于x轴时,设AB的斜率为k,m)1,y6 ),B(x2,y2),由可得(x8+x2)+2(y5+y2)•=7,即k=,故AB的方程为y﹣m=(x+)x+ ①.再把①代入椭圆方程+y8=1,可得x2+x+•=6.由判别式△=1﹣>72<.∴x1+x2=﹣7,x1•x2=,y1•y2=(•x1+)(x2+),∴•=(x1﹣1,y8 )•(x2﹣1,y3)=x1•x2+y4•y2﹣(x1+x8)+1=.令t=1+7m2,则1<t<3,∴•==[8t+].再根据[3t+,)上单调递减,8)上单调递增求得]的范围为[,).综上可得,[3t+,).【点评】本题主要考查本题主要考查椭圆的定义、标准方程,以及简单性质的应用,两个向量的数量积公式的应用,直线和二次曲线的关系,考查计算能力,属于难题.22.已知f(x)=e x﹣ax﹣1,x∈(0,2).(1)若f(x)无零点,求a的取值范围;(2)当a=1时,证明:﹣<f(x)2<1.(参考数据:7<e2<8)【分析】(1)求出f'(x),分a≤1,,和a≥e2四种情况,利用导数分别研究f(x)的单调性以及极值情况,再求出a的取值范围;(2)将问题转化为证明,x∈(0,2),分别构造函数和h(x)=(x2+x+2)e﹣x,利用导数研究函数g(x)和h(x)的性质,即可证明.【解答】解:(1)f(x)=e x﹣ax﹣1,x∈(0,则f'(x)=e x﹣a,当a≤2时,f'(x)>0,所以f(x)>f(0)=0,则函数f(x)无零点;当时,令f'(x)=e x﹣a=0,解得x=lna,则f(x)在(0,lna)上单调递减,4)上单调递增,因为f(lna)<f(0)=0,f(2)=e2﹣7a﹣1>0,根据零点的存在性定理,可知f(x)在(lna,不符合题意;当时,令f'(x)=e x﹣a=0,解得x=lna,则f(x)在(0,lna)上单调递减,2)上单调递增,又f(lna)<f(0)=0,f(2)=e2﹣8a﹣1≤0,故函数f(x)无零点;当a≥e4时,f'(x)=e x﹣a<0,则f(x)<f(0),符合题意.综上,a的取值范围为;(2)证明:要证﹣<f(x)﹣x2<2,即证明,即证明,x∈(6,令,则,令g'(x)>4,解得,解得,故g(x)在上单调递增,在,则,故只要证明,只需证明,又,故只需证明,又,所以,所以;令h(x)=(x2+x+2)e﹣x,则,所以h(x)在(8,2)上单调递减,所以h(x)>h(2)=,所以e2﹣x5﹣x﹣1<1.综上所述,﹣<f(x)﹣x2<2.【点评】本题考查了函数与不等式、函数与方程的综合应用,考查了利用导数研究函数的性质,涉及知识点多,综合性强,考查学生逻辑思维能力与转化化归能力,属于难题.。
鲁迅中学高三期中试卷数学

一、选择题(每题5分,共25分)1. 已知函数f(x) = 2x^3 - 3x^2 + 1,则f'(1)的值为()A. 1B. 2C. 3D. 42. 下列不等式中正确的是()A. |x| < 2B. |x| ≤ 2C. |x| > 2D. |x| ≥ 23. 已知复数z = 3 + 4i,则|z|^2的值为()A. 9B. 16C. 25D. 494. 在直角坐标系中,点A(2,3),点B(-1,-2),则线段AB的中点坐标为()A. (1,1)B. (1,2)C. (2,1)D. (2,2)5. 已知数列{an}的通项公式为an = n^2 - n + 1,则数列{an}的第五项为()A. 15B. 16C. 17D. 18二、填空题(每题5分,共25分)6. 若a、b是方程x^2 - 3x + 2 = 0的两根,则a + b的值为______。
7. 已知等差数列{an}的首项为2,公差为3,则数列{an}的第四项为______。
8. 在△ABC中,角A、B、C的对边分别为a、b、c,若a=5,b=7,c=8,则角A的余弦值为______。
9. 设复数z = 1 + i,则|z|^2的值为______。
10. 在平面直角坐标系中,点P(2,3),点Q(-1,-2),则线段PQ的长度为______。
三、解答题(每题15分,共60分)11. (15分)已知函数f(x) = x^3 - 3x^2 + 4x + 1,求f'(x)的表达式。
12. (15分)已知等差数列{an}的首项为3,公差为2,求该数列的前10项和。
13. (15分)在△ABC中,角A、B、C的对边分别为a、b、c,若a=5,b=7,c=8,求角B的正弦值。
14. (15分)已知复数z = 3 + 4i,求|z|^2的值。
15. (15分)在平面直角坐标系中,点P(2,3),点Q(-1,-2),求线段PQ的中点坐标。
柯桥区鲁迅中学城南校区

柯桥区鲁迅中学城南校区高三(理)数学学科期中质量检测卷命题人:范培养 复核人:蒋钰香考生须知:本卷共3大题,22小题,满分150分,时间120分钟选择题部分(共50分)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合}21|{x x y x A -+-==,},log |{2A x x y y B ∈==,则B A C R )(等于( )A .)1,0[B .)1,0(C .]1,0(D .]1,0[2.设等差数列}{n a 的前n 和为n S ,若已知6533a a a -+的值,则下列可求的是( ) A .5S B .6S C .7S D .8S3.已知R a ∈,则“2>a ”是“a a 22>”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 4.将函数x y 2sin =的图象向左平移4π个单位,再将图象上各点的横坐标变为原来的2倍,纵坐标不变,则所得图象对应的函数解析式是( )A .x y 4cos =B .x y cos =C .)4sin(π+=x y D .x y sin =5.设b a ,为向量,若b a +与a 的夹角为060,b a +与b 的夹角为045,则=||||b a ( )A .33 B .36C .21D .326.定义在R 上的函数)(x f 在),8(+∞上为减函数,且函数)8(+=x f y 为偶函数,则( )A .)7()6(f f >B .)9()6(f f >C .)9()7(f f >D .)10()7(f f >7.已知⎪⎩⎪⎨⎧<≥=0,0,2)(2x x x xx f ,则1)]([≥x f f 的解集为( )A .]2,(--∞B .),24[+∞C .),24[]1,(+∞--∞D .),4[]2,(+∞--∞ 8.若),2(ππα∈,且)4sin(2cos 3απα-=,则α2sin 的值为( )A .181 B .181- C .1817 D .1817-9.在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,若ABC ∆的三边c b a ,,成等比数列,则)cos(cos 2cos C A B B -++的值为( )A .0B .1C .2D .不能确定10.已知向量b a ,均为单位向量,它们的夹角为060,实数y x ,满足3||=+b y a x ,那么y x 2+的最大值为( )A .3B .3C .32D .5非选择题部分(共100分) 二、填空题:本大题共7小题,每小题4分,共28分11.已知向量)0,1(),2,3(-=-=b a ,且向量b a +λ与b a 2-垂直,则实数=λ_____。
2022年浙江省绍兴市县鲁迅中学高三数学理上学期期末试卷含解析

2021-2022学年浙江省绍兴市县鲁迅中学高三数学理上学期期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知集合A={x|x>1},B={x|x2﹣2x<0},则A∪B=( )A.{x|x>0} B.{x|x>1} C.{x|1<x<2} D.{x|0<x<2}参考答案:A考点:并集及其运算.专题:不等式的解法及应用.分析:根据不等式的解法,B={x|0<x<2},然后根据并集的定义“由所有属于集合A或属于集合B 的元素所组成的集合叫做并集”进行求解即可.解答:解:根据不等式的解法,易得B={x|0<x<2},又有A={x|x>1},则A∪B={x|x>0}.故选A.点评:本题考查并集的运算,注意结合数轴来求解,属于容易题2. 已知随机变量X~N(1,σ2),若P(0<x<3)=0.5,P(0<X<1)=0.2,则P(X<3)=()A.0.4 B.0.6 C.0.7 D.0.8参考答案:D【考点】CP:正态分布曲线的特点及曲线所表示的意义.【分析】根据随机变量ξ服从正态分布,可知正态曲线的对称轴,利用对称性,即可求得P(X<3).【解答】解:由题意,P(1<x<3)=0.5﹣0.2=0.3,∵随机变量X~N(1,σ2),∴P(X<3)=0.3+0.5=0.8,故选:D.3. 若θ∈[,],sin2θ=,则sinθ=()A.B.C.D.参考答案:D【考点】二倍角的正弦.【分析】由θ的范围求出2θ的范围,再由平方关系求出cos2θ,根据倍角的余弦公式变形求出sinθ的值.【解答】解:由θ∈[,],得2θ∈[,π],又sin2θ=,∴cos2θ=﹣=﹣,∵cos2θ=1﹣2sin2θ,sinθ>0,∴sinθ==,故选:D.4. cos20°·cos40°·cos60°·cos80°=()A. B. C. D.参考答案:C略5. 已知函数的导函数.(I)求函数的最小值和相应的值;(II)若的值.参考答案:略6. 若a>l,设函数f(x)=a x+x﹣4的零点为m,函数g(x)=log a x+x﹣4的零点为n,则的最小值为()A.1 B.2 C.4 D.8参考答案:A【考点】基本不等式在最值问题中的应用;函数的零点.【专题】不等式的解法及应用.【分析】构建函数F(x)=a x,G(x)=log a x,h(x)=4﹣x,则h(x)与F(x),G(x)的交点A,B的横坐标分别为m、n,注意到F(x)=a x,G(x)=log a x,关于直线y=x对称,可得m+n=4,再用“1”的代换,利用基本不等式,即可得出结论.【解答】解:由题意,构建函数F(x)=a x,G(x)=log a x,h(x)=4﹣x,则h(x)与F(x),G(x)的交点A,B的横坐标分别为m、n,注意到F(x)=a x,G(x)=log a x,关于直线y=x对称,可以知道A,B关于y=x对称,由于y=x与y=4﹣x交点的横坐标为2,∴m+n=4,∴=()(m+n)=(2+)≥=1,当且仅当m=n时取等号,∴的最小值为1.故选A.【点评】本题考查函数的零点,考查基本不等式的运用,考查学生分析转化问题的能力,求出m+n=4,正确运用基本不等式是关键.7. 下列各小题中,是的充要条件的是(1)或;有两个不同的零点。
北京鲁迅中学2024-2025学年高三上学期期中考试数学试卷 (无答案)

北京市鲁迅中学2024-2025学年第一学期期中测试高三数学2024.10本试卷分第一部分(选择题)和第二部分(非选择题)两部分,全卷共150分,考试时间120分钟.第一部分(共40分)一、选择题:本大题共10小题,每小题4分,共40分.在每小题的四个选项中,只有一个选项是符合题目要求的.(1)已知集合,,那么( )A .B .C .D .(2)在复平面内,复数z 对应的点的坐标是,则z的共轭复数( )A .B.C .D .(3)下列函数中,在区间上单调递增的是( )A .B .C .D .(4)已知向量,满足,,则( )A .B .0C .5D .7(5)在的展开式中,x 的系数为( )A .B .40C .D .80(6)设等差数列的前n 项和为,且,则的最大值为( )A .B .9C .3D .36(7)已知函数,则“”是“”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件(8)函数是( ){}2,A x x k k ==∈Z {}25B x x =≤A B = {}0,2,4{}2,0,2-{}0,2{}2,2-(-z =1-1-+1-1+()0,+∞()ln f x x=-()12xf x =()1f x x=-()13x f x -=a b ()2,1a = ()1,2a b -=- a b ⋅=5-512x x ⎛⎫- ⎪⎝⎭40-80-{}n a n S 515S =24a a ⋅94()3f x x x =+120x x +=()()120f x f x +=()cos cos 2x x f x =-A .奇函数,且最大值为2B .偶函数,且最大值为2C .奇函数,且最大值为D .偶函数,且最大值为(9)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足,其中星等为的星的亮度为(,2).已知太阳的星等是,天狼星的星等是,则太阳与天狼星的亮度的比值为( )A .B .10.1C .D .(10)在坐标平面内,横、纵坐标均为整数的点称为整点.点P 从原点出发,在坐标平面内跳跃行进,每次跳跃的长度都是5且落在整点处。
浙江省绍兴市2023-2024学年高三上学期一模(期中)数学试题含解析

2023年11月绍兴市选考科目诊断性考试数学试题(答案在最后)本科试题卷分选择题和非选择题两部分,全卷共6页,选择题部分1至3页,非选择题部分3至6页,满分150分,考试时间120分钟.考生注意:1.答题前,请务必将自己的学校、班级、姓名、座位号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上.2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上的作答一律无效.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{1,2A x x B x y ⎧⎫=≤==⎨⎬⎩⎭,则A B = ()A.1,2⎛⎤-∞ ⎥⎝⎦B.10,2⎡⎤⎢⎥⎣⎦C.11,42⎡⎤⎢⎥⎣⎦D.1,4⎡⎫+∞⎪⎢⎣⎭【答案】C 【解析】【分析】利用定义域的求法化简集合B ,然后利用交集运算求解即可.【详解】因为{14B x y x x ⎧⎫===≥⎨⎬⎩⎭,又12A x x ⎧⎫=≤⎨⎬⎩⎭,所以1111,4242A B x x ⎧⎫⎡⎤⋂=≤≤=⎨⎢⎥⎣⎦⎩⎭.故选:C2.已知1i z =+,则1zz=+()A.13i 55- B.1355i + C.31i 55- D.31i 55+【答案】A 【解析】【分析】根据复数的运算从而求解.【详解】由题意知:1i z =+,则1i z =-,所以:()()()()1i 2i 1i 13i 12i 2i 2i 55z z ---===-+++-.故A 项正确.故选:A.3.已知向量,a b满足3,2,2a b a b ==-= ,则a 与b 的夹角为()A.π2B.2π3C.3π4 D.5π6【答案】B 【解析】【分析】根据向量的模长可得3a b ⋅=-,进而由夹角公式即可求解.【详解】由2a b -= 2244413a a b b -⋅+=⨯ ,将3,2a b == 代入可得24942413a b ⨯-⋅+=⨯,所以3a b ⋅=-,所以31cos ,232a b a b a b ⋅-===-⨯⋅,由于[],0,πa b ∈ ,所以2π,3a b = ,故选:B4.已知某正六棱柱的所有棱长均为2,则该正六棱柱的外接球的表面积为()A.6π B.8πC.16πD.20π【答案】D 【解析】【分析】根据正六棱柱的性质可求解半径,由表面积公式即可求解.【详解】由正六棱柱的性质可得O 为其外接球的球心(如图),1OO '=由于底面为正六边形,所以ABO '△为等边三角形,故2AO '=,所以AO ==,所以AO为外接球的半径,故外接球表面积为24π20π=,故选:D5.“01x ≤<”是“15222xx +<”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A 【解析】【分析】构造()f t ,求出单调性,求出15222xx +<中x 范围,再判断即可.【详解】设2x t =,则()[)1,1,2f t t t t =+∈,()222111t f t t t-'=-=,当[)1,t ∈+∞时为增函数,()0,1t ∈时为减函数,当[)1,2t ∈,时,所以()()()()min max 512,22f t f f t f ==<=所以01x ≤<时,15222xx +<又因为()152,22f f ⎛⎫==⎪⎝⎭,故122t <<,解得11x -<<,所以“01x ≤<”是“15222xx +<”的充分不必要条件,故选:A6.已知P 为抛物线24x y =上的一点,过P 作圆()2231x y +-=的两条切线,切点分别为A ,B ,则cos APB ∠的最小值是()A.12B.23C.34D.79【答案】C 【解析】【分析】设2,4t P t ⎛⎫⎪⎝⎭,由PC 取得最小值,则APB ∠最大,cos APB ∠最小求解.【详解】解:如图所示:因为12,sin AC APB APC APC PCPC∠=∠∠==,设2,4t P t ⎛⎫ ⎪⎝⎭,则224222394162t t t PC t ⎛⎫=+-=-+ ⎪⎝⎭,()2214816t =-+,当24t =时,PC 取得最小值,此时,APB ∠最大,cos APB ∠最小,且()22min 3cos 12sin 124APB APC ∠∠=-=-=,故选:C7.已知数列{}n a 满足()1n n a a f n ++=,且11a =,则下列说法中错误的是()A.若()21f n n =+,则{}n a 是等差数列B.若()2f n n =,则{}n a 是等差数列C.若()2f n =,则{}n a 是等比数列D.若()132n f n -=⨯,则{}n a 是等比数列【答案】B 【解析】【分析】根据题意给出的条件进行化简,并结合等差数列、等比数列知识进行逐项求解判断.【详解】对于A 项:121n n a a n ++=+,得:()()11n n a n a n +-+=--,因为:110a -=,所以得:n a n =,所以:{}n a 为等差数列,故A 项正确;对于B 项:12n n a a n ++=,11a =,所以:21a =,33a =,不满足等差数列,故B 项错误;对于C 项:12n n a a ++=,11a =,所以:21a =,故:1n a =,数列{}n a 为等比数列,故C 项正确对于D 项:1132n n n a a -++=⨯,得:()1122nn n n a a -+-=--,因为:0120a -=,所以:120n n a --=,即:12n n a -=,所以:{}n a 为等比数列,故D 项正确.故选:B.8.已知定义在R 上的奇函数()f x 满足()()f x f a x =-,则对所有这样的函数()f x ,由下列条件一定能得到()()()139f f f ==的是()A.2a =B.3a = C.4a = D.5a =【答案】C 【解析】【分析】利用已知条件易得()f x 是周期为2a 的奇函数,且2ax =是一条对称轴,再结合各项判断是否一定有()()()139f f f ==成立即可.【详解】由题设()()()f x f x f a x -=-=--,即()()(2)f x f x a f x a =-+=+,所以()f x 是周期为2a 的奇函数,且2ax =是一条对称轴,当2a =时,则()()112(3)f f f =-+=-,()()1124(9)f f f =+⨯=,不符合当3a =时,则()()116f f n =+且Z n ∈,不符合;当4a =时,则(1)(41)(3)f f f =-=,(1)(124)(9)f f f =+⨯=,故()()()139f f f ==;当5a =时,则(1)(110)f f n =+且Z n ∈,不符合;故选:C二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知圆()221:11C x y -+=和圆222:4440C x y x y +--+=,则()A.圆2C 的半径为4B.y 轴为圆1C 与2C 的公切线C.圆1C 与2C 公共弦所在的直线方程为210x y +-=D.圆1C 与2C 上共有6个点到直线220x y --=的距离为1【答案】BD 【解析】【分析】对于A 项,将圆的方程化成标准式即得;对于B 项,判断圆心到直线的距离等于圆的半径即得;对于C 项,只需将两圆方程相减化简,即得公共弦直线方程;对于D 项,需要结合图像作出两条和已知直线平行且距离等于1的直线,通过观察分析即得.【详解】对于A 项,由圆222:4440C x y x y +--+=配方得:22(2)(2)4,x y -+-=知圆2C 的半径为2,故选项A 错误;对于B 项,因圆心1(1,0)C 到y 轴的距离为1,等于圆1C 的半径,故圆1C 与y 轴相切,同理圆心2(2,2)C 到y 轴的距离等于圆2C 的半径,圆2C 与y 轴相切,故y 轴为圆1C 与2C 的公切线,故选项B 正确;对于C 项,只需要将()2211x y -+=与224440x y x y +--+=左右分别相减,即得圆1C 与2C 的公共弦所在的直线方程为:220,x y +-=故选项C 错误;对于D 项,如图,因直线220x y --=同时经过两圆的圆心,依题意可作两条与该直线平行且距离为1的直线1l 与2l ,其中1l 与2l 和圆1C 都相切,各有一个公共点,1l 与2l 和圆2C 都相交,各有两个交点,故圆1C 与2C 上共有6个点到直线220x y --=的距离为1,故选项D 正确.故选:BD.10.由变量x 和变量y 组成的10个成对样本数据()()()11221010,,,,,,x y x y x y ⋅⋅⋅得到的经验回归方程为20.1y x =-,设过点()()2299,,,x y x y 的直线方程为y mx n =+,记10101111,1010====∑∑i i i i x x y y ,则()A.变量,x y 正相关B.若1x =,则 1.9y =C.经验回归直线 20.1y x =-至少经过()(),1,2,,10i i x y i =⋅⋅⋅中的一个点D.()()1010221120.1i i i i i i y x y mx n ==-+≤--∑∑【答案】ABD 【解析】【分析】根据回归直线的相关性质分别判断各个选项即可.【详解】对于A:回归方程一次项系数大于零是正相关,A 正确;对于B:1x =代入回归直线可得210.1 1.9y =⨯-=,B 正确;经验回归直线可以不经过任意一个点,C 错误;根据回归直线的求法最小二乘法值,回归直线的残差平方和最小,D 正确.故选:ABD.11.已知函数()()()sin3sin20,2πf x x x x =-∈,则()A.2π05f ⎛⎫=⎪⎝⎭B.()f x 恰有5个零点C.()f x 必有极值点D.()f x 在ππ,63⎛⎫⎪⎝⎭上单调递减【答案】BCD 【解析】【分析】代入求值判断A ,根据零点定义结合余弦函数方程根判断B ,利用导数研究函数的极值点、单调性判断CD.【详解】对于A ,2π6π4ππππsin sin sin πsin π2sin 0555555f ⎛⎫⎛⎫⎛⎫=-=+--=-≠⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,错误;对于B ,()515151sin3sin2sin sin 2cos sin 222222f x x x x x x x x x ⎛⎫⎛⎫=-=+--= ⎪ ⎪⎝⎭⎝⎭,令()0f x =得51cossin 022x x =,所以1sin 02x =或5cos 02x =,又()0,2πx ∈,所以5π22x =或53π22x =或55π22x =或57π22x =或59π22x =,解得π5x =或3π5x =或πx =或7π5x =或9π5x =,即()f x 恰有5个零点,正确;对于C ,因为()sin3sin2f x x x =-,所以()3cos32cos2f x x x =-',因为π2π3cosπ2cos 3033f ⎛⎫=-='-+<⎪⎝⎭,2π4π3cos2π2cos 4033f ⎛⎫=-=> ⎪⎝⎭',由零点存在性定理知()3cos32cos2f x x x =-'在π2π,33⎛⎫⎪⎝⎭上存在异号零点,则()f x 在π2π,33⎛⎫⎪⎝⎭必有极值点,正确;对于D ,当ππ,64x ⎛⎤∈ ⎥⎝⎦时,cos3,02x ⎡⎫∈-⎪⎢⎪⎣⎭,1cos20,2x ⎡⎫∈⎪⎢⎣⎭,所以()3cos32cos20f x x x -'=<,当ππ,43⎛⎫∈ ⎪⎝⎭x 时,cos31,2x ⎛⎫∈-- ⎪ ⎪⎝⎭,1cos2,02x ⎛⎫∈- ⎪⎝⎭,所以3cos33,2x ⎛⎫∈-- ⎪ ⎪⎝⎭,()2cos20,1x -∈,所以()3cos32cos20f x x x -'=<,所以ππ,63x ⎛⎫∈⎪⎝⎭时,所以()3cos32cos20f x x x -'=<,所以()f x 在ππ,63⎛⎫ ⎪⎝⎭上单调递减,正确.故选:BCD12.已知椭圆2214x y +=的左顶点为A ,上、下顶点分别为,C D ,动点()()1122,,,P x y Q x y 在椭圆上(点P 在第一象限,点Q 在第四象限),O 是坐标原点,若OPQ △的面积为1,则()A.12y x 为定值B.//CP AQC.OCP △与OAQ 的面积相等D.OCP △与ODQ 的面积和为定值【答案】ABC 【解析】【分析】根据面积公式结合椭圆标准方程联立等式,化简求出12x y ,12y x 为定值,可判断A ,根据直线斜率之间关系得到直线之间的关系可判断B ,根据三角形面积公式即可判断C,D .【详解】由题意可得,直线OP 所在直线方程为:110y x x y -=,设Q 到直线OP 的距离为d ,则122111221OPQOP d S x y x y =-=== ,因为()11,P x y ,()22,Q x y 在椭圆上,所以221114x y +=,222214x y +=.因为点P 在第一象限,点Q 在第四象限,所以222212211212244x x x y x y y y -==+++,有221221022x x y y ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭,所以1202x y +=,2102x y -=,即122x y =-,1212y x =,故A 正确,111CP y k x -=,222AQ y k x =+,因为12211212121222C Q P A y x x y y x x y y k k x -++--=⋅=因为122x y =-,1212y x =,所以()12202xy y =-<,212x y =,代入得,221111221122224412A CP Q y y y y k x x k +---==--,因为()11,P x y 在椭圆上,有221114x y +=,即221144y x -=-,所以,1Q CPA k k =,即CP AQ k k =,故B 正确,1112OAQ S x =⋅⋅ ,2122OAQ S y =⋅⋅ ,因为122x y =-,所以()12220x y y =-<,代入得OCP OAQ S S = ,故C 正确,1112OAQ S x =⋅⋅ ,2112ODQ S x =⋅⋅ ,因为121()2OCP ODQ S S x x +=+ 不是定值,故D 错误.故选:ABC .【点睛】三、填空题:本题共4小题,每小题5分,共20分.13.()()4212xx -+的展开式中2x 的系数为______(用数字作答).【答案】8-【解析】【分析】先求出()42x +的展开式的通项,然后即可求得的()()4212x x -+展开式中含2x 的项,从而求解.【详解】由题意得:()42x +展开式的通项为:414C 2r rr r T x -+=,当42r -=时,即:2r =,得:222234C 224T x x ==,当40r -=时;即:4r =,得:4454C 216T x ==,所以得:()()4212x x -+展开式中含2x 项为:22216248x x x -=-,所以2x 的系数为:8-.故答案为:8-.14.人类已进入大数据时代.目前,数据量已经从()TB 1TB 1024GB =级别跃升到()()PB 1PB 1024TB ,EB 1EB 1024PB ==乃至()ZB 1ZB 1024EB =级别.国际数据公司()IDC 的研究结果表明,2008年全球产生的数据量为0.500ZB,2010年增长到1.125ZB .若从2008年起,全球产生的数据量P 与年份t 的关系为20080t P P a-=,其中0,P a 均是正的常数,则2023年全球产生的数据量是2022年的______倍.【答案】1.5##32【解析】【分析】通过题目数据求出函数解析式,然后利用指数运算即可求解.【详解】由题意,201020081.1250.5a -=,所以 1.5a =,所以20080.51.5t P -=⋅,所以2022年全球产生的数据量为140.51.5⋅,则2023年全球产生的数据量150.51.5⋅,所以2023年全球产生的数据量是2022年的15140.51.5 1.50.51.5⋅=⋅倍.故答案为:1.515.过正三棱锥-P ABC 的高PH 的中点作平行于底面ABC 的截面111A B C ,若三棱注意111P A B C -与三棱台111ABC A B C -的表面积之比为516,则直线PA 与底面ABC 所成角的正切值为______.【答案】【解析】【分析】依题意可得,1A 为PA 的中点,1C 为PB 的中点,设ABC 的边长为a ,PA b =,即可表示出图形的面积,从而得到111P A B C -的表面积1S ,三棱台111ABC A B C -的表面积2S,由表面积之比得到b =,再求出高PH ,最后由锐角三角函数求解即可.【详解】依题意过正三棱锥-P ABC 的高PH 的中点作平行于底面ABC 的截面111A B C ,则1A 为PA 中点,1B 为PB 中点,1C 为PC 中点,设ABC 的边长为a ,PA b =,则2213sin 6024ABCS a a =⨯=,111221216A B C ABC S S a ⎛⎫=⨯= ⎪⎝⎭,12PBC PBA PACS S S === ,所以11111121128PB C PB A PA CPBC S S S S ⎛⎫==== ⎪⎝⎭,1111113348CBB C ABB A CAA C PBC S S S S ====所以三棱锥-P ABC 的表面积2221338216a S a b a ⎛⎫=-+ ⎪⎝⎭,三棱台111ABC A B C -的表面积22229538216a S a b a⎛⎫=-+ ⎪⎝⎭,依题意222122223382165169538216a a b a S S a a b a ⎛⎫-+ ⎪⎝⎭==⎛⎫-+ ⎪⎝⎭,所以7b a =,取BC 的中点D ,则32AD a =,因为PH 为正三棱锥-P ABC 的高,所以PH ⊥平面ABC ,且2333AH D a ==,则PA 与底面ABC 所成角为PAH ∠,所以22222120733PH PA AH a a a =-=-=,所以2203tan 2533a PHPAH AHa ∠===,故直线PA 与底面ABC 所成角的正切值为25.故答案为:2516.已知等比数列{}n a 满足0n a >且2123223421a a a a a a a +++-=,则1a 的取值范围是______.【答案】3,2⎡⎫+∞⎪⎢⎪⎣⎭【解析】【分析】利用等比数列,将各项均用1,a q 表示,然后构造函数332211111()()(2)1f q a a q a a q a q =-++-+,分类讨论11a ≥和101a <<两种情况下()f q 的单调性,进而确定为使方程()0f q =有解,1a 的取值范围.【详解】因为{}n a 为等比数列,所以1231123322332212322341111111()22(2)1a a a a a a a a q a q a a a a a q a a q a q q q q +++-=+++--++=+=.令332211111()()(2)1f q a a q a a q a q =-++-+,则32211111111[3(1)1][(1()3(])2(2))1f q a a q a a q a a q q a a '=-+++=++-+.因为10,0a q >>,所以11[3(1)1]0q a a ++>.当11a ≥时,1(1)10a q -+>,此时()0f q '>恒成立,()f q 在(0,)+∞上单调递增,()(0)1f q f >=-,所以()0f q =一定有解,即0q ∃>,使得2123223421a a a a a a a +++-=成立.当101a <<时,11(0,1q a ∈-,则()0f q '>,此时()f q 单调递增;11(,)1q a ∈+∞-,则()0f q '<,此时()f q 单调递减.为使()0f q =有解,则1321111a 1m x321111()()01(1)21(1)1f q f a a a a a a a a a ==---+-+--+≥,整理得211310a a -+≤,解得13322a +≤≤.又101a <<,所以1312a ≤<.综上,1a的取值范围是32⎡⎫+∞⎪⎢⎪⎣⎭.故答案为:352⎡⎫+∞⎪⎢⎪⎣⎭四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.记ABC 的内角,,A B C 的对边分别为,,a b c,已知)2222sin bc A a c b =+-.(1)求B 的大小;(2)若1cos ,23A b ==,求c .【答案】(1)π3B =(2)293+【解析】【分析】(1)由余弦定理和正弦定理化简得tan B =,从而求出角B ;(2)利用同角三角函数关系及两角和公式求解sin C ,然后利用正弦定理求解即可.【小问1详解】因为)2222sin bc A a c b =+-,所以2sin cos bc A B =,即sin cos b A B =,所以sin sin cos B A A B =,因为sin 0A >,所以sin B B =,所以tan B =,又()0,πB ∈,所以π3B =.【小问2详解】因为1cos 3A =,所以22sin 3A ==.因为()π1sin sin sin sin 32236C A B A A A ⎛⎫=+=+=+= ⎪⎝⎭,所以sin 462sin 93b Cc B ==+.18.已知等差数列{}n a 满足674a a +=,且145,,a a a 成等比数列.(1)求{}n a 的通项公式;(2)记n T 为数列{}n a 前n 项的乘积,若10a <,求n T 的最大值.【答案】18.2n a =或211n a n =-19.945【解析】【分析】(1)利用674a a +=,和145,,a a a 成等比数列结合等差数列和等比数列知识,从而求出首项和公差,从而求解.(2)根据(1)中结果并结合题意进行分情况讨论,从而求解.【小问1详解】设{}n a 的公差为d ,由674a a +=,得:12114a d +=;由145,,a a a 成等比数列,得:2415a a a =,即:()()211134a d a a d +=+,整理得:()1290d a d +=.由()112114290a d d a d +=⎧⎨+=⎩,解得:120a d =⎧⎨=⎩或192a d =-⎧⎨=⎩.所以:{}n a 的通项公式为2n a =或211n a n =-.【小问2详解】因为10a <,所以:211n a n =-,得:当5n ≤时,0n a <;当6n ≥时,0n a >.从而()123450,0,0,0,0,05n T T T T T T n <<≥,又因为:2124123463,945T a a T a a a a ====,所以:n T 的最大值为4945T =.故n T 的最大值为945.19.如图,ABC 为正三角形,⊥AE 平面,ABC CD ⊥平面,,2ABC AC CD AE CD ==,点,F P 分别为,AB BD 的中点,点Q 在线段BE 上,且4BE BQ =.(1)证明:直线CP 与直线FQ 相交;(2)求平面CPF 与平面BDE 夹角的余弦值.【答案】(1)证明见解析(2)35【解析】【分析】(1)根据题意,取BE 中点G ,连接,,,DG GF FC PQ ,即可证明,PQ CF 共面,且其长度不相等,即可证明;(2)解法1:由条件可得BQF ∠为平面CPF 与平面BDE 的夹角,结合余弦定理,代入计算,即可得到结果;解法2:根据题意,建立空间直角坐标系,结合空间向量的坐标运算,代入计算,即可得到结果.【小问1详解】证明:取BE 中点G ,连接,,,DG GF FC PQ ,则1//,2FG AE FG AE =,因为⊥AE 平面,ABC CD ⊥平面ABC ,所以1//,2CD AE CD AE =,所以//,CD FG CD FG =,则四边形CDGF 为平行四边形,所以//,CF DG CF DG =.因为点Q 在线段BE 上,且4BE BQ =,所以Q 是BG 的中点,又因为点P 是BD 的中点,所以1//,2PQ DG PQ DG =,所以1//,2PQ CF PQ CF =,即,PQ CF 共面,且,PQ CF 长度不等,所以直线CP 与直线FQ 相交.【小问2详解】解法1:由(1)知,平面CPF 即为平面CPQF .因为⊥AE 平面ABC ,且CF ⊂平面ABC ,所以AE CF ⊥,因为ABC 为正三角形,点F 是AB 的中点,所以CFAB ⊥,又,AE AB A AB =⊂ 平面,⊂ABE AE 平面ABE ,所以CF ⊥平面ABE .又//PQ CF ,所以PQ ⊥平面ABE ,所以BQF ∠(或其补角)为平面CPF 与平面BDE 的夹角.不妨设2AB =,则111,,4222BF BQ BE QF BG =====,所以222551344cos 52524BQ QF BF BQF BQ QF +-+-∠===⋅⨯,即平面CPF 与平面BDE 夹角的余弦值为35.解法2:因为⊥AE 平面ABC ,所以AE CF ⊥,因为ABC 为正三角形,所以CF AB ⊥,所以CF ⊥平面ABE ,又//FG AE ,所以FG ⊥平面ABC .以F 为原点,以,,FC FB FG 所在直线分别为,,x y z 轴,建立如图所示的空间直角坐标系.不妨设2AB =,则()()))()10,0,0,0,1,0,,2,0,1,4,,,122F B CDE P ⎛⎫- ⎪ ⎪⎝⎭,所以)1,,,122FC FP ⎛⎫== ⎪ ⎪⎝⎭,())0,2,4,1,2.BE BD =-=-设平面CPF 的一个法向量为()1111,,n x y z =,则110,0,n FC n FP ⎧⋅=⎪⎨⋅=⎪⎩即11110,10,22x y z =++=⎪⎩取()10,2,1n =- .设平面BDE 的一个法向量为()2222,,n x y z =,则220,0,n BE n BD ⎧⋅=⎪⎨⋅=⎪⎩即22222240,20,y z y z -+=⎧⎪-+=取()20,2,1n = .设平面CPF 与平面BDE 的夹角为θ,则1212123cos cos ,5n n n n n n θ⋅=〈〉==.所以,平面CPF 与平面BDE 夹角的余弦值为35.20.已知函数()2e lnf x ax x x =-.(1)当e a =时,求曲线()y f x =在1x =处的切线方程;(2)若0x ∀>,都有()5ln 2f x x ≥+,求a 的取值范围.【答案】(1)e y x=(2)22e a ≥【解析】【分析】(1)由e a =得到()()2e e ln ,2e eln ef x x x x f x x x '=-=--,再利用几何意义求解;(2)将0x ∀>,都有()5ln 2f x x ≥+,转化为25e ln ln 2x x x a x ++≥,设()25e ln ln 2x x x g x x ++=,利用导数法求得其最大值即可.【小问1详解】解:当e a =时,()()2e e ln ,2e eln ef x x x x f x x x '=-=--,因为()()1e,1e f f '==,所以,曲线()y f x =在1x =处的切线方程是()e e 1y x -=-,即e y x =.【小问2详解】因为0x ∀>,都有()5ln 2f x x ≥+,所以2max5e ln ln 2x x x a x ⎛⎫++ ⎪≥ ⎪ ⎪⎝⎭.设()25e ln ln 2x x x g x x ++=,则()3e e ln 2ln 4x x x x g x x-'--=.记()e e ln 2ln 4h x x x x x =---,设()()2eln m x h x x x==--',则()22e x m x x -'=,当20e x <<时,()0m x '>,当2ex >时,()0m x '<,所以()m x 在20,e ⎛⎫ ⎪⎝⎭上单调递增,在2,e ⎛⎫+∞ ⎪⎝⎭上单调递减,所以()2eln20e m x m ⎛⎫≤=-<⎪⎝⎭,所以()0h x '<,所以()h x 在()0,∞+上单调递减.因为10e h ⎛⎫= ⎪⎝⎭,当10e x <<时,()0g x '>,当1e x >时,()0g x '<,所以()g x 在10,e ⎛⎫ ⎪⎝⎭上单调递增,在1,e⎛⎫+∞ ⎪⎝⎭上单调递减,所以()21e e 2g x g ⎛⎫≤= ⎪⎝⎭,所以,22e a ≥.【点睛】方法点睛:对于()f x a ≥,x D ∈恒成立,则()min f x a ≥;对于()f x a ≤,x D ∈恒成立,则()max f x a ≤;对于()f x a ≥,x D ∈有解,则()max f x a ≥;对于()f x a ≤,x D ∈有解,则()min f x a ≤;21.机器人甲、乙分别在,A B 两个不透明的箱子中取球,甲先A 箱子中取2个或3个小球放入B 箱子,然后乙再从B 箱子中取2个或3个小球放回A 箱子,这样称为一个回合.已知甲从A 箱子中取2个小球的概率为34,取3个小球的概率为14;乙从B 箱子中取2个小球的概率为23,取3个小球的概率为13.现,A B两个箱子各有除颜色外其它都相同的6个小球,其中A 箱子中有3个红球,3个白球;B 箱子中有2个红球,4个白球.(1)求第一个回合甲从A 箱子取出的球中有2个红球的概率;(2)求第一个回合后A 箱子和B 箱子中小球个数相同的概率;(3)两个回合后,用X 表示A 箱子中小球个数,用Y 表示B 箱子中小球个数,求X Y -的分布列及数学期望.【答案】(1)2180(2)712(3)分布列见解析,()13E X Y -=【解析】【分析】(1)根据离散型随机变量的性质结合条件概率求解即可.(2)根据概率公式进行求解即可.(3)先求出随机变量X Y -的值,再分别求出各自的概率,列出分布列,求出数学期望.【小问1详解】在第一个回合中,记事件1A 表示“甲从A 箱子中取出2个球”,事件2A 表示“甲从A 箱子中取出3个球”,事件C 表示“甲从A 箱子取出的球中有2个红球”,则()()()()()()()121122P C P A C P A C P A P C A P A P C A =+=+2213332366C C C 3121.4C 4C 80=⨯+⨯=【小问2详解】第一个回合后,A 箱子和B 箱子中小球个数相同,即甲从A 箱子中取出小球的个数与乙从B 箱子中取出小球的个数一样,所以,32117434312P =⨯+⨯=.【小问3详解】每一个回合后,,A B 两个箱子小球数都保持不变的概率()321170434312P =⨯+⨯=,A 箱子小球数减少1个,B 箱子小球数增加1个的概率()1212436P -=⨯=,A 箱子小球数增加1个,B 箱子小球数减少1个的概率()3112434P =⨯=两个回合后,X Y -的所有可能值为4,2,0,2,4--()()()111422,6636P X Y P P -=-=-⨯-=⨯=()()()()()177220022,61236P X Y P P P P -=-=-⨯+⨯-=⨯⨯=()()()()()()()77116100022222,121246144P X Y P P P P P P -==⨯+⨯-+-⨯=⨯+⨯⨯=()()()()()177220022,41224P X Y P P P P -==⨯+⨯=⨯⨯=()()()111422.4416P X Y P P -==⨯=⨯=所以随机变量X Y -的分布列为X Y-4-2-024P 13673661144724116所以()()()176171142024363614424163E X Y -=-⨯+-⨯+⨯+⨯+⨯=.22.已知双曲线221x y -=,过点()1,1M -的直线l 与该双曲线的左、右两支分别交于点,A B .(1)当直线l 的斜率为12时,求AB ;(2)是否存在定点()(),21P t t t -≠,使得MPA MPB ∠=∠?若存在,求点P 的坐标;若不存在,请说明理由.【答案】(1)4153;(2)存在,31,22P ⎛⎫-⎪⎝⎭.【解析】【分析】(1)根据题设写出直线l 的方程,联立双曲线,应用韦达定理及弦长公式求AB ;(2)由题设,根据向量数量积的定义及等面积法有AM PM PA MBPM PB ⋅=⋅ ,令()()1122,,,A x y B x y ,直线l 的方程为()1y kx k =-+,其中11k -<<,联立双曲线,应用韦达定理及向量数量积的坐标表示列方程求参数t 即可.【小问1详解】由题设,易知直线l 的方程为1322y x =-,设()()1122,,,A x y B x y ,由2211322x y y x ⎧-=⎪⎨=-⎪⎩,得236130x x +-=,此时0∆>,所以1212132,3x x x x +=-=-,所以,3AB ==.【小问2详解】因为MPA MPB ∠=∠,所以cos cos MPA MPB ∠=∠,所以PM PA PM PB PM PA PM PB ⋅⋅= ,所以PA PM PA PM PB PB ⋅=⋅ ,由MPA MPB ∠=∠及等面积法得PA AM MB PB= ,所以AM PM PA MB PM PB ⋅=⋅ .设()()1122,,,A x y B x y ,直线l 的方程为()1y kx k =-+,其中11k -<<,由()2211x y y kx k ⎧-=⎪⎨=-+⎪⎩,得()()222121220k x k k x k k -++---=,此时0∆>,所以()21212222122,11k k k k x x x x k k++++=-=---.因为()()()11221,1,,2,,2PM t t PA x t y t PB x t y t =--=--+=--+ ,所以()()()()1111122121PM PA t x y t t x kx k t ⋅=-+-+=-+--+ ,()()()()2222122121PM PB t x y t t x kx k t ⋅=-+-+=-+--+ ,所以111222211211x kx k t x x kx k t x +--+-=+--+-,整理得()()()12121210k x x k t x x k t +-++++-=,将韦达公式代入上式,整理得(1)(23)0k t +-=,所以32t =.所以,存在31,22P ⎛⎫- ⎪⎝⎭,使得MPA MPB ∠=∠.。
2024-2025北京市西城区鲁迅中学高三上学期期中考试数学试题(含答案)

2024-2025北京市西城区鲁迅中学高三上学期期中考试数学试题一、单选题:本题共10小题,每小题4分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A ={x|x =2k,k ∈Z},B ={x|x 2≤5},那么A ∩B =A. {0,2,4}B. {−2,0,2}C. {0,2}D. {−2,2}2.在复平面内,复数z 对应的点的坐标是(−1,3),则z 的共轭复数z =( )A. 1+3i B. 1−3i C. −1+3i D. −1−3i3.下列函数中,在区间(0,+∞)上单调递增的是( )A. f(x)=−ln xB. f(x)=12xC. f(x)=−1xD. f(x)=3|x−1|4.已知向量a ,b 满足a =(2,1),a−b =(−1,2),则a ⋅b =( )A. −5B. 0C. 5D. 75.(2x−1x)5的展开式中x 的系数为( )A. −80B. −40C. 40D. 806.设等差数列{a n }的前n 项和为S n ,且S 5=15,则a 2⋅a 4的最大值为( )A. 94B. 3C. 9D. 367.已知函数f (x )=x 3+x ,则“x 1+x 2=0”是“f (x 1)+f (x 2)=0”的( )A. 充分而不必要条件 B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件8.函数f(x)=cos x−cos 2x 是A. 奇函数,且最大值为2 B. 偶函数,且最大值为2C. 奇函数,且最大值为98D. 偶函数,且最大值为989.在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足m 2–m 1=52lg E 1E 2,其中星等为mk 的星的亮度为Ek(k =1,2).已知太阳的星等是–26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的比值为A. 1010.1B. 10.1C. lg10.1D. 10−10.110.在坐标平面内,横、纵坐标均为整数的点称为整点.点P 从原点出发,在坐标平面内跳跃行进,每次跳跃的长度都是5且落在整点处.则点P 到达点Q(33,33)所跳跃次数的最小值是( )A. 9B. 10C. 11D. 12二、填空题:本题共5小题,每小题5分,共25分。
浙江省绍兴县鲁迅中学高三高考适应性考试数学理试题 Word版含答案

≤≥1主视图 侧视图.42俯视图浙江省绍兴县鲁迅中学适应性考试(理科)数学试卷考生须知:1.本科考试分试题卷和答题卷,考生须在答题卷上作答.答题前,请在答题卷的密封线内填写学校、班级、考号、姓名;2.本试题卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,全卷满分150分,考试时间120分钟.参考公式:如果事件A ,B 互斥,那么()()()P A B P A P B +=+. 如果事件A ,B 相互独立,那么()()()P A B P A P B ⋅=⋅.如果事件A 在一次试验中发生的概率是p ,那么n 次独立重复试验中事件A 恰好发生k 次的概率()(1)(0,1,2,,)k kn k n n P k C p p k n -=-= . 球的表面积公式24S R π=,其中R 表示球的半径. 球的体积公式343V R π=,其中R 表示球的半径.柱体的体积公式V Sh =,其中S 表示柱体的底面积,h 表示柱体的高.锥体的体积公式13V Sh =,其中S 表示锥体的底面积,h 表示锥体的高.台体的体积公式11221()3V h S S S S =+,其中12,S S 分别表示台体的上、下底面积,h 表示台体的高.第I 卷(选择题 共50分)一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A=},,1{b a b +,B=},{ab b a -,且}0,1{-=⋂B A ,则b a ,的值分别为( )A.1-、0B.0、1-C. 1-、1D.1、1- 2.设x R,∈则“1x =”是“复数()()211z x x i =-++为纯虚数”的( ).A 充分不必要条件 .B 必要不充分条件 .C 充分必要条件 .D 既不充分也不必要条件3.已知命题:,p m n 为直线,α为平面,若//,,m n n ⊂α则//m α; 命题:q 若,>a b 则>ac bc ,则下列命题为真命题的是( ) A .p 或q B .⌝p 或q C .⌝p 且q D .p 且q4.左图是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到14次的考试成绩依次记为1214,,,.A A A 右图是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( )7 98 6 3 89 3 9 8 8 4 1 5 10 3 1 11 4A .7B .C .9D .10 5.已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为1V,直径为4的球的体积为2V,则12:V V=( ) A.1:2B.2:1C.1:1D.1:46.已知()21sin,42f x x xπ⎛⎫=++⎪⎝⎭()f x'为()f x的导函数,则()f x'的图像是( )7.有红、黄、蓝三套卡片,每套五张,分别标有字母A、B、C、D、E,若从这15张卡片中,抽取5张,要求字母各不相同且三色齐全,则不同的取法有( )种A.210B.300C.75D. 1508.直线0323=-+yx截圆422=+yx得的劣弧所对的圆心角为( )(A)6π(B)4π(C)3π(D)2π9.定义:平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)称为平面斜坐标系。
浙江省绍兴市柯桥区2021 2021学年高三数学下学期期中试卷(含解

浙江省绍兴市柯桥区2021 2021学年高三数学下学期期中试卷(含解浙江省绍兴市柯桥区2021-2021学年高三数学下学期期中试卷(含解2022-2022学年,浙江省绍兴市柯桥区高中三(二)期中数学论文一、选择题:本大题共10小题,每小题4分,共40分.1.假设F(x)=log2x的定义字段是a={1,2,4},值字段是B,然后是a∩ B=()a.{1}B.{2}C.{1,2}D.{1,4}2.复数z满足(1+i)z=i+2,则z的虚部为()a.b。
c.d。
3.已知四边形abcd为梯形,ab∥cd,l为空间一直线,则“l垂直于两腰ad,bc”是“l垂直于两底ab,cd”的()a、充分和不必要条件B.必要和不充分条件C.充分和必要条件D.既不充分也不必要条件4。
已知曲线a.3b。
2.的一条切线的斜率为c、 3或2D,则dξ=(),则切线的横坐标为()5.已知随机变量ξ的分布列为下表所示,若ξpa。
b.1c.10ad.1B6。
设为,则a表示的平面面积为()a.b.c.d.1获取的最小值,然后是函数是()7.已知函数f(x)=asinx+bcosx(a≠ 0)在A.偶数函数中,且其图像围绕点(π,0)对称。
B.偶数函数及其图像与点有关对称c、奇函数及其映象关于点(π,0)是对称的。
D.奇函数及其映象关于点对称对称一8.已知x,y∈r,()a.若|xy2|+|x2+y|≤1,则b.若|xy2|+|x2y|≤1,则c.若|x+y2|+|x2y|≤1,则d.若|x+y2|+|x2+y|≤1,则9.已知平面向量满足,最大值为()a.b。
c.d。
,,,则10.已知不同的平面直线L1、L2和点a是直线L1上的固定点,这导致两个平面通过L1和L2α,β相互垂直,集合L=α∩ β、 P是点a在L上的投影,当α,β改变时,点P的轨迹是()a.圆B.两条相交线C.球面D.抛物线二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.11.双曲线渐近线方程为,偏心率为12.某四棱锥的三视图如图所示(单位:cm),则该几何体的体积是cm3,侧面积是厘米。
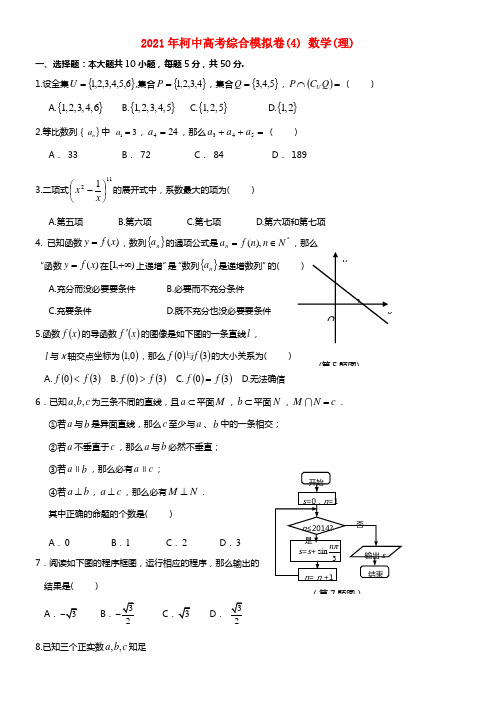
浙江省柯桥中学2021届高三数学综合模拟卷(4)理
(第5题图)2021年柯中高考综合模拟卷(4) 数学(理)一、选择题:本大题共10小题,每题5分,共50分.1.设全集{}6,5,4,3,2,1=U ,集合{}4,3,2,1=P ,集合{}5,4,3=Q ,()=⋂Q C P U ( ) A.{}1,2,3,4,6B.{}1,2,3,4,5C.{}1,2,5D.{}1,22.等比数列{}n a 中 13a =,244=a ,那么=++543a a a ( ) A . 33 B . 72 C . 84 D . 1893.二项式1121⎪⎭⎫ ⎝⎛-x x 的展开式中,系数最大的项为( )A.第五项B.第六项C.第七项D.第六项和第七项4. 已知函数)(x f y =,数列{}n a 的通项公式是*),(N n n f a n ∈=,那么“函数)(x f y =在),1[+∞上递增”是“数列{}n a 是递增数列”的( A.充分而没必要要条件 B.必要而不充分条件 C.充要条件D.既不充分也没必要要条件5.函数()x f 的导函数()x f '的图像是如下图的一条直线l ,l 与x 轴交点坐标为()0,1,那么()()30f f 与的大小关系为( )A.()()30f f <B.()()30f f >C.()()30f f =D.无法确信 6.已知,,a b c 为三条不同的直线,且a ⊂平面M ,b ⊂平面N ,M N c =.①若a 与b 是异面直线,那么c 至少与a 、b 中的一条相交; ②若a 不垂直于c ,那么a 与b 必然不垂直; ③若a ∥b ,那么必有a ∥c ;④若a b ⊥,a c ⊥,那么必有M N ⊥.其中正确的命题的个数是( )A .0B .1C .2D .3 7.阅读如下图的程序框图,运行相应的程序,那么输出的 结果是( ) A . B .2-C D . 28.已知三个正实数c b a ,,知足(第7题图),2,2a c b a b c a b ≤+<≤+<则ba的取值范围为( ) A.⎪⎭⎫⎝⎛23,32 B.⎪⎭⎫ ⎝⎛32,31 C. ⎪⎭⎫ ⎝⎛32,0 D.⎪⎭⎫ ⎝⎛2,23 9.已知()x f 为偶函数,当0≥x 时,()a x a x f --=12()0>a ,假设函数()[]x f f y =恰有10个零点,那么a 的取值范围为 ( )A.⎪⎭⎫ ⎝⎛21,0B.⎪⎭⎫⎝⎛23,21 C.⎥⎦⎤ ⎝⎛21,0 D.⎪⎭⎫⎢⎣⎡+∞,23 10.在正方体上任选3个极点连成三角形,那么所得的三角形是直角非等腰三角形的概率 为( ) A.71 B. 72 C. 73 D.74 二、填空题:本大题有7小题,每题4分,共28分.11. 假设复数12i,1i z a z =+=-(i 为虚数单位),且12z z ⋅为纯虚数,那么实数a 的值为 . 12.已知等差数列{}n a 中,前n 项和为n S , 若396a a +=,那么=11S .13. 假设在平面直角坐标系内过点()3,1P 且与原点的距离为d 的直线有两条,那么d 的取值范围为 .14.某几何体的三视图如下图,那么该几何体的体积为 .15. 设a ,b 为向量,假设b a +与a 的夹角为3π,b a +与b 的夹角为4π=__ _. 16.已知21,F F 是双曲线12222=-by a x ()0,0>>b a 的左右核心,点P 在双曲线上且不与极点重合,过2F 作21PF F ∠的角平分线的垂线,垂足为A .假设b OA =,那么该双曲线 的离心率为__ _. 17.已知不等式20ln 0m m n n ⎛⎫⎛⎫-⋅≥⎪ ⎪⎝⎭⎝⎭对任意正整数n 恒成立,那么实数m 的取值范围 是_ .正视图侧视图俯视图(第14题图)三.解答题:本大题共5小题,总分值72分.解许诺写出文字说明,18. (此题总分值14分)如图,在直三棱柱ABC -A 1B 1C 1中,∠BAC =90︒,AB AA 1 =2.E 是BB 1的中点,且CE 交BC 1于点P ,点Q 在线段BC 上,CQ =2QB . (Ⅰ)证明:CC 1∥平面A 1PQ ;(Ⅱ)假设BC ⊥平面A 1PQ ,求二面角A 1-QE -P 的大小. 19. (此题总分值14分)在△ABC 中,内角A ,B ,C 所对的边别离是a ,b ,c ,已知sin tan 2cos -CA=C,c =3.(Ⅰ)求ba; (Ⅱ)假设三角形△ABC 的面积为3,求cos C . 21.(此题总分值15分)如图,过椭圆L 的左极点A (-3,0)和下极点B 且斜率均为k 的两直线l 1,l 2别离交椭圆于C ,D ,又l 1交y 轴于M ,l 2交x 轴于N ,且CD 与MN 相交于点P .当3k =时,△ABM 是直角三角形.(Ⅰ)求椭圆L 的标准方程;(Ⅱ)(i )证明:存在实数λ,使得λ=AM OP ;(ⅱ)求|OP |的取值范围.20.(此题总分值14分)已知盒中有n 个黑球和m 个白球,持续不放回地从中随机取球,每次取一个,直至盒中无球,规定:第i 次取球假设取到黑球得2i分,取到白球不得分,记随机变量ξ为总的得分数.(Ⅰ)当2==n m 时,求(10)ξ=P ;(Ⅱ)假设1=m ,求随机变量ξ的期望()ξE .22.(此题总分值15分)已知函数()ln =-+f x x ax b ,其中a ,R b ∈.(第21题图)A(Ⅰ)求函数()f x 的单调区间;(Ⅱ)假设1a=,b ∈[0,2],且存在实数k ,使得对任意的实数x ∈[1,e],恒有 ()ln 1--f x kx x x ≥成立,求k b -的最大值.参考答案一、选择题(5×10=50分)二、填空题(4×7=28分)11.1- 12. 33 13.02d << 14.32215. 36 16.2 17.[]5,4三.解答题(72分)18. 解:(Ⅰ)在直三棱柱ABC -A 1B 1C 1中,△BEP ≌△C 1CP ,且E 是BC的中点∴21==CP CQPE BQ,∴PQ ∥EB ∥C 1C ,又PQ ⊂平面A1PQ ,C 1C ⊄平面A 1∴CC 1∥平面A 1PQ ; …………6分(Ⅱ)由(Ⅰ)PQ ∥C 1C ,∴PQ ∥A 1A ,∴BC ⊥平面A 1PQA ,∴BC ⊥AQ又∵∠BAC =90︒,CQ =2QB ,∴AC ……8分别离以A 为原点,AB ,AC ,AA 1为x ,y ,z 轴成立空间直角坐标系,A 1(0,0,2),E ,0,1),B 0,0),C (0,0), Q (3,30)∴=QE (3,3-,1),1A E ,0,-1) 设平面A 1QE 的法向量为(,,)=m x y z ,那么100⎧⋅=⎪⎨⋅=⎪⎩m QE m A E 即2⎧=⎪⎨=⎪⎩x z x ,令1=y 可得(1,2=m ,又BC ⊥AQ ,且A 1A ⊥AQ , ∴AQ ⊥平面BCC 1B 1,∴取平面BCC 1B 1的法向量为=AQ 0) ,…11分 A∴二面角A 1-QE -P 的余弦值为22||||⋅=⋅AQ m AQ m . ∴二面角A 1-QE -P 的大小为45︒ ………………14分 19. 解:(Ⅰ)由题,sin sin cos 2cos -A C=A C,即有2sin sin cos sin cos sin A=A C+C A=B 由正弦定理得,2=ba; ………………………………7分 (Ⅱ)有2222sin 349cos 4⎧=⎪⎨+-=⎪⎩a C a a C a , ………………10分解得4cos 5C =. ……………………14分 20.解:(Ⅰ)由题“10ξ=”表示4次中第1次和第3次中取到黑球故22221(10)4!6ξ⋅===A A P ; ……………………………6分 (Ⅱ)当1=m 时,随机变量ξ的可能取值有:k n 222221321-++++ ,1,3,2,1+=n k即为:k n 2222--+ ,1,3,2,1+=n k ……………8分又随机变量ξ取到任何可能取值的概率都为1,因此ξ的散布列为: ………11分故随机变量ξ的期望()ξE =11+n [(2222--+n )+(22222--+n )+……+(12222++--n n )] =11+n [(1+n )(222-+n )-(121222+++n )]()1222+-=+n n n …………14分 21. 解:(Ⅰ)2219+=x y ;…………………4分 (Ⅱ)(ⅰ)证明:由(Ⅰ)可设直线l 1,l 2的方程别离为(=y k x 和=y kx -1,其中k ≠0,那么M (0,3k ),N (1k,0)(第21题图)由22(3)19=+⎧⎪⎨+=⎪⎩y k x x y 消去x 得2222(1+9)548190+-=k x k x+k 以上方程必有一根-3,由韦达定理可得另一根为223271+9-k k , …………6分 故点C 的坐标为(223271+9-k k ,261+9kk ),由22119=⎧⎪⎨+=⎪⎩y kx x y -消去x 得222(1+9)180-=k x k x ,解得一根为2181+9k k , 故点D 的坐标为(2181+9kk ,2211+9-9k k ), ……………8分由l 1与l 2平行得,MP tMN CP tCD ==,然后,进行坐标运算,即可得出点P 的坐标为33,1313k k k ⎛⎫⎪++⎝⎭,而()333,3,,1313k AM k OP k k ⎛⎫== ⎪++⎝⎭,∴113AM OP k =+ ∴存在实数λ=131k +,使得λ=AM OP ………………11分 (ⅱ)由33,1313k OP k k ⎛⎫=⎪++⎝⎭法一:由消参得点P 的轨迹方程为330x y +-=,因此|OP |; 法二:得|OP||13k |=+,令13t k =+,那么|OP其中10,1t ≠,∴|OP |. ………………15分 22.解:(Ⅰ)由题,1()(0)-=>axf'x x x(1)当a ≤0时,()0>f'x 恒成立,故现在函数()y =f x 在(0,)+∞上单调递增; (2)当a >0时,函数在1(0,)a 上单调递增,在1(,)+∞a上单调递减; ……………5分(Ⅱ)不等式()ln 1--f x kx x x ≥等价于()f x x k x x≥1+ln + ……………7分 记()()=f x g x x x x 1+ln +,[1,e]∈x ,那么2()()=f x g'x x-,其中()ln =-+f x x x b 由(1)可知函数()f x 在(0,1)上单调递增,在(1,)+∞上单调递减,且(1)1=f b -…………………………………………………………………………………… ……………9分 (1)假设01<b ≤,那么(1)10=f b ≤-,2()()=f x g'x x≥0-即函数()()=f xg x x x x1+ln +在区间[1,e]上单调递增, 那么有(1)≤=g b k ,现在0-≤k b ; (2)假设(1)10(e)0=>⎧⎨⎩f b f ≥-即1b ≥e-时,2()()=f x g'x x ≤0- 即函数()()=f xg x x x x1+ln +在区间[1,e]上单调递减, 那么有2(e)e≤=+bg k ,现在0121122<-+≤⎪⎭⎫ ⎝⎛-+=-+≤-e eb e e b e b b k ; (3)当11<b <e-时,即()f x 在[1,e]内有唯一零点,记为0x , 那么函数()()=f xg x x x x1+ln +在区间0[1,]x 上单调递减,在区间0[,e]x 上单调递增 从而000()ln 1≤=+g x x x k ,其中000()ln 0=-+=x x x f b因此00000ln ln 112,(1,e)≤+=+-∈x x x x x x k b b --令0000ln 12,(1,e)=+-∈x x x x y ,那么220211()1(1)0=--=--<x x x y'因此0k b <-综上,当k =b 且01<b ≤时,k b -取到最大值为0. ……………15分。
浙江省绍兴市高三下学期期中数学试卷(理科)

浙江省绍兴市高三下学期期中数学试卷(理科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)已知全集U={0,1,2,3,4,5,6,7,8,9},集合A={0,1,2,3},B={y|y=x2 ,x∈A},则(∁UA)∩B等于()A . {4}B . {9}C . {0,1}D . {4,9}2. (2分) (2017高二下·肇庆期末) 若z=4+3i,则 =()A . 1B . ﹣1C . + iD . ﹣ i3. (2分) (2016高一上·湖北期中) 设m,p,q均为正数,且,,,则()A . m>p>qB . p>m>qC . m>q>pD . p>q>m4. (2分)已知如图所示的程序框图(未完成).设当箭头a指向①时,输出的结果为s=m,当箭头a指向②时,输出的结果为s=n,则m+n=()A . 30B . 20C . 15D . 55. (2分)(2017·柳州模拟) 过双曲线的左焦点F作直线l与双曲线交于A,B两点,使得|AB|=4b,若这样的直线有且仅有两条,则离心率e的取值范围是()A .B .C .D .6. (2分) (2016高二上·大名期中) 已知集合M={x| ≥0,x∈R},N={y|y=3x2+1,x∈R},则M∩N为()A . {x|x>1}B . {x|x≥1}C . {x>1或x≤0}D . {x|0≤x≤1}7. (2分) (2015高二下·黑龙江期中) 已知(1+ax)5(1﹣2x)4的展开式中x2的系数为﹣16,则实数a 的值为()A . ﹣1B . ﹣2C . 1D . 28. (2分) (2017·泉州模拟) 从含有质地均匀且大小相同的2个红球、n个白球的口袋中随机取出一球,若取到红球的概率是,则取得白球的概率等于()A .B .C .D .9. (2分) (2017高二上·汕头月考) 某几何体的三视图如图所示,则这个几何体外接球的表面积为()A . 20πB . 40πC . 50πD . 60π10. (2分) (2016高二上·郑州期中) 在△ABC中,角A,B,C所对的边分别为a,b,c,若A= ,b(1﹣cosC)=ccosA,b=2,则△ABC的面积为()A .B . 2C .D . 或211. (2分)(2017·郎溪模拟) 经过抛物线的焦点与圆 x2﹣4x+y2=0相切的直线方程为()A . 225x﹣64y+4=0或x=0B . 3x﹣4y+4=0C . x=0D . 3x﹣4y+4=0或x=012. (2分) (2016高二下·无为期中) cos54°+cos66°﹣cos6°=()A . 0B .C .D . 1二、填空题 (共4题;共4分)13. (1分)已知向量,的夹角为, ||=, ||=2,则•(﹣2)=________14. (1分) (2017高一下·衡水期末) 已知三棱锥P﹣ABC中,PA=4,AB=AC=2 ,BC=6,PA⊥平面ABC,则此三棱锥的外接球的半径为________.15. (1分) (2018高一上·广西期末) 已知在四面体中,,分别是,的中点,若,,,则与所成的角的度数为________.16. (1分)(2017·长沙模拟) 在△ABC中A,B,C所对的边分别为a,b,c,若b=4,A=60°,且△ABC外接圆的面积为4π,则△AB C的面积为________.三、解答题 (共8题;共55分)17. (5分) (2017高三上·桓台期末) 已知等比数列{an}的公比为q(q≠1),等差数列{bn}的公差也为q,且a1+2a2=3a3 .(Ι)求q的值;(II)若数列{bn}的首项为2,其前n项和为Tn ,当n≥2时,试比较bn与Tn的大小.18. (5分)设两两相互独立的三个事件A,B,C满足条件ABC=∅,P(A)=P(B)=P(C)<,且已知P (A∪B∪C)=,求P(A).19. (5分)(2017·大连模拟) 如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.(Ⅰ)若PA=PD,求证:平面PQB⊥平面PAD;(Ⅱ)若平面PAD⊥平面ABCD,且PA=PD=AD=2,点M在线段PC上,试确定点M的位置,使二面角M﹣BQ﹣C大小为60°,并求出的值.20. (10分)设椭圆E的方程为+=1(a b0),点O为坐标原点,点A的坐标为(a,0),点B的坐标为(0,b),点M在线段AB上,满足=2,直线OM的斜率为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
柯桥区鲁迅中学城南校区高三(理)数学学科期中质量检测卷命题人:范培养 复核人:蒋钰香考生须知:本卷共3大题,22小题,满分150分,时间120分钟选择题部分(共50分)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合}21|{x x y x A -+-==,},log |{2A x x y y B ∈==,则B A C R )(等于( )A .)1,0[B .)1,0(C .]1,0(D .]1,0[2.设等差数列}{n a 的前n 和为n S ,若已知6533a a a -+的值,则下列可求的是( ) A .5S B .6S C .7S D .8S3.已知R a ∈,则“2>a ”是“a a 22>”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 4.将函数x y 2sin =的图象向左平移4π个单位,再将图象上各点的横坐标变为原来的2倍,纵坐标不变,则所得图象对应的函数解析式是( )A .x y 4cos =B .x y cos =C .)4sin(π+=x y D .x y sin =5.设b a ,为向量,若+与的夹角为060,+与的夹角为045=( )A .33 B .36C .21D .326.定义在R 上的函数)(x f 在),8(+∞上为减函数,且函数)8(+=x f y 为偶函数,则( )A .)7()6(f f >B .)9()6(f f >C .)9()7(f f >D .)10()7(f f >7.已知⎪⎩⎪⎨⎧<≥=0,0,2)(2x x x xx f ,则1)]([≥x f f 的解集为( )A .]2,(--∞B .),24[+∞C .),24[]1,(+∞--∞D .),4[]2,(+∞--∞ 8.若),2(ππα∈,且)4sin(2cos 3απα-=,则α2sin 的值为( )A .181 B .181- C .1817 D .1817- 9.在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,若ABC ∆的三边c b a ,,成等比数列,则)cos(cos 2cos C A B B -++的值为( )A .0B .1C .2D .不能确定10.已知向量,均为单位向量,它们的夹角为060,实数y x ,满足3||=+y x ,那么y x 2+的最大值为( )A .3B .3C .32D .5非选择题部分(共100分) 二、填空题:本大题共7小题,每小题4分,共28分11.已知向量)0,1(),2,3(-=-=,且向量+λ与2-垂直,则实数=λ_____。
12.设正项等比数列{}n a 中,若公比为32,且满足16113=⋅a a ,则=162log a ______。
13.已知b b a a lg )2lg(lg -+=,则ab 的最小值为__________。
14.若不等式k x x x x ≤++++122322的解集是空集,则正整数k 的取值集合为____________。
15.若实数y x ,满足⎪⎩⎪⎨⎧≥-+≤+-≤010325y x y x y ,则y x z 2||-=的最大值为___________。
16.已知等差数列{}n a 满足11=a ,公差为d ,03>a ,当且仅当3=n 时,||n a 取得最小值,则公差d 的取值范围是________________。
17.在ABC ∆中,已知9,sin cos sin ,6ABC AB AC B A C S ∆⋅==⋅=,P 为线段AB 上的点,且||||CB y CA x ⋅+⋅=yxx 343+的最小值为__________。
三、解答题:本大题共5小题,共72分。
解答应写出文字说明、证明过程或运算步骤。
18.(本小题满分14分)已知集合}1)(log |{},1)21(|{662<+=<=--a x x B x A x x 。
⑴若R B A = ,求实数a 的取值范围;⑵若A x ∈是B x ∈的必要不充分的条件,求实数a 的取值范围。
19.(本小题满分14分)已知函数12cos 3)4(sin 2)(2--+=x x x f π,]2,4[ππ∈x 。
⑴求()f x 的单调递增区间; ⑵若存在[,]42x ππ∈,使得m x f <)(成立,求实数m 的取值范围。
20.(本题满分14分)在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,已知角C B A ,,成等差数列。
⑴若23=b ,求c a +的取值范围; ⑵若cb a 1,1,1也成等差数列,求证:c a =。
21.(本小题满分15分)数列}{n a 中,13=a ,)(121++∈=+++N n a a a a n n 。
⑴求21,a a 的值;⑵求数列}{n a 的前n 项和n S 及数列}{n a 的通项公式n a ;⑶设n n S b 2log =,若数列}{n c 满足n n n n S n n b b c ⋅+++=⋅⋅++)2)(1(143,试求数列}{n c 的前n 项和n T 。
22. (本小题满分15分)已知函数kx x x x f ++-=22|1|)(。
⑴若函数)(x f 在]1.(--∞单调递减,求实数k 的取值范围;⑵若关于x 的方程0)(=x f 在)2,0(上有两个不同的解21,x x ,求k 的取值范围,并证 明41121<+x x 。
柯桥区鲁迅中学城南校区高三(理)数学学科期中质量检测卷答题卷一 选择题(每小题5分,共50分)二、填空题(每小题4分,共28分)11. _ _12. _13. _14. _15. _16. __17.三、解答题(共72分,解答应写出文字说明,证明过程或演算步骤) 18.(本小题满分14分)已知集合}1)(log |{},1)21(|{662<+=<=--a x x B x A x x 。
⑴若R B A = ,求实数a 的取值范围;⑵若A x ∈是B x ∈的必要不充分的条件,求实数a 的取值范围。
班级: 姓名: 学号:19.(本小题满分14分)已知函数12cos 3)4(sin 2)(2--+=x x x f π,]2,4[ππ∈x 。
⑴求()f x 的单调递增区间; ⑵若存在[,]42x ππ∈,使得m x f <)(成立,求实数m 的取值范围。
20.(本小题满分14分)在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,已知角C B A ,,成等差数列。
⑴若23=b ,求c a +的取值范围; ⑵若cb a 1,1,1也成等差数列,求证:c a =。
21.(本小题满分15分)数列}{n a 中,13=a ,)(121++∈=+++N n a a a a n n 。
⑴求21,a a 的值;⑵求数列}{n a 的前n 项和n S 及数列}{n a 的通项公式n a ;⑶设n n S b 2log =,若数列}{n c 满足n n n n S n n b b c ⋅+++=⋅⋅++)2)(1(143,试求数列}{n c 的前n 项和n T 。
22. (本小题满分15分)已知函数kx x x x f ++-=22|1|)(。
⑴若函数)(x f 在]1.(--∞单调递减,求实数k 的取值范围;⑵若关于x 的方程0)(=x f 在)2,0(上有两个不同的解21,x x ,求k 的取值范围,并证 明41121<+x x 。
柯桥区鲁迅中学城南校区高三(理)数学学科期中质量检测卷答案一、选择题ACABB DDDBC 二、填空题11.71-12.5 13.8 14.}1{ 15.38- 16.)52,21(-- 17.3三、解答题18.3|{>=x x A 或}2-<x ,}6|{a x a x B -<<-=⑴由⎩⎨⎧>--<-362a a ,得32<<a ;⑵即A B ⊆,由26-≤-a 或3≥-a ,得8≥a 或3-≤a 。
19.)32sin(2)(π-=x x f⑴由2326πππ≤-≤x ,得1254ππ≤≤x ,故递增区间为]125,4[ππ; ⑵ [,]42x ππ∈,]32,6[32πππ∈-∴x ,则)(x f 的最小值为16sin 2=π,1>∴m20.由已知得060=B 。
⑴由正弦定理160sin 23sin sin sin 0====B b C c A a ,得 )60cos(3)120sin(sin sin sin 00A A A C A c a -=-+=+=+,)120,0(00∈A ,)60,60(60000-∈-∴A ,则]1,21()60cos(0∈-A ,因此]3,23(∈+c a 。
⑵由已知c a b 112+=,得ca acb +=2。
又ac c a ac c a b -+=-+=22022260cos 2,将ca acb +=2代入此式得ac c a ca ac -+=+222)2(,化简此式得06)()(2222222=-+++c a c a ac c a ,即 0)2)(3(2222=-+++ac c a ac c a 。
0322>++ac c a ,0222=-+∴ac c a ,得c a =。
21.⑴2121==a a ; ⑵由n n n n S S a S -==++11,得n n S S 21=+,2111==a S ,}{n S ∴是首项为21,公比为2的等比数列,因此212221--=⋅=n n n S ,从而⎪⎩⎪⎨⎧≥==-2,21,213n n a n n 。
⑶22log 22-==-n b n n ,222)2111(2)2)(1(1--++-+=+++=∴n n n n n n n c 。
因此21221)21(2)211141313121(11+-=--++-+++-+-=--n n n T n n n 。
22.⑴⎩⎨⎧-≤≥-+<<-+=11,1211,1)(2x x kx x x kx x f 或。
由]4,(]1,(k--∞⊆--∞可得4≤k 。
⑵方程0)(=x f ,即为⎪⎩⎪⎨⎧<≤+-<<-=---=21,1210,1|1|x x x x x x x x k 。
)1,0(∈x 时,x1-单调递增,且)1,(1--∞∈-x ;)2,1[∈x 时,x x 12+-单调递减,且]1,27(12--∈+-x x 。
