江苏省淮安市淮阴中学2021届高三数学期中数学模拟测试

2021届江苏省淮安市淮阴中学高三上学期8月测试数学试题(解析版)

2021届江苏省淮安市淮阴中学高三上学期8月测试数学试题一、单选题1．设集合={1,2,3}A ，B={45}，，={x|x=a+b,a A,b B}M ∈∈，则M 中元素的个数为（） A ．3 B ．4 C ．5 D ．6【答案】B 【解析】【详解】由题意知x a b =+，,a A b B ∈∈，则x 的可能取值为5,6,7,8.因此集合M 共有4个元素，故选B. 【考点定位】集合的概念2．以下四个命题既是特称命题又是真命题的是 A ．锐角三角形的内角是锐角或钝角 B ．至少有一个实数x ，使20x ≤ C ．两个无理数的和必是无理数 D ．存在一个负数x ，使12x> 【答案】B【解析】先确定命题中是否含有特称量词，然后利用判断特称命题的真假．【详解】对于A ，锐角三角形中的内角都是锐角，所以A 为假命题；对于B ，为特称命题，当0x =时，20x =成立，所以B 正确；对于C ，(0=，所以C 为假命题；对于D ，对于任何一个负数x ，都有10x<，所以D 错误．故选B ．【点睛】本题以命题的真假判断与应用为载体，考查了全称命题和特称命题的定义，难度不大，属于基础题．3．汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程s 看作时间t 的函数，其图象可能是( )A ．B ．C ．D ．【答案】A【解析】试题分析：汽车启动加速过程，随时间增加路程增加的越来越快，汉使图像是凹形，然后匀速运动，路程是均匀增加即函数图像是直线，最后减速并停止，其路程仍在增加，只是增加的越来越慢即函数图像是凸形．故选A ．【考点】函数图像的特征．4．对任意R x ∈，函数()327f x ax ax x =++不存在极值点的充要条件是（）A ．021a ≤≤B ． 021a <<C ． 0a ≤或21a ≥D ．0a <或21a > 【答案】A【解析】求出导函数()'f x ，由方程()0f x '=没有变号的实数解即可得．【详解】由题意()2327f x ax ax '=++，()f x 不存在极值点，0a =时，()70f x '=>，()f x 单调递增，无极值点；0a ≠时，则24840a a ∆=-≤，解得021a <≤，综上021a ≤≤．故选：A ．【点睛】本题考查用导数与函数的极值的关系，对于可导函数，如果导函数存在变号的零点，则原函数有极值．如果没有变号的零点，则原函数无极值．5．将甲桶中的a 升水缓慢注入空桶乙中，t 分钟后甲桶中剩余的水符合指数衰减曲线y＝a e nt .假设过5分钟后甲桶和乙桶的水量相等，若再过m 分钟甲桶中的水只有8a，则m 的值为( ) A ．7 B ．8C ．9D ．10【答案】D【解析】由题意，函数y=f （t ）=ae nt ,满足f （5）=2a ，f （m+5）=8a , 可解出m 的值. 【详解】根据题意得2a＝a e 5n ，令8a ＝a e nt ，即18＝e nt ，因为12 ＝e 5n ，故18＝e 15n ，故t ＝15，m ＝15－5＝10. 故选D 【点睛】对实际情景，根据已知或建立的相应函数模型，将实际问题转换为函数的求解.，最后解决实际问题.6．函数()()log 6a f x ax =-（0a >且1a ≠）在[]0,2上为减函数，则实数a 的取值范围是（） A ．()1,3 B ．()0,1C ．(] 1,3D ．[)3+∞，【答案】A【解析】根据对数函数性质与复合函数的单调性求解．【详解】首先6t ax =-是减函数，∴log a y t =应是增函数，()f x 才可能是减函数， ∴1a >，函数()f x 在[0,2]上减函数，由对数函数性质知620a ->，3a <，综上13a <<．故选：A ．【点睛】本题考查复合函数的单调性，掌握对数函数性质是解题关键．7．如果已知0<a <1，则方程a |x |＝|log a x |的实根个数为( ) A ．2 B ．3C ．4D ．与a 的值有关【答案】A【解析】设,0(),()log ,0x xa xa x f x a g x x a x -⎧≥===⎨≤⎩分别作出它们的图象如图所示：由图可知有两个交点，故选A.8．已知函数()()2ln15f x x x x =++-[]()2020,2020x ∈-的最大值为M ，最小值为m ，则M m +=（） A ．5- B ．10-C ．5D ．10【答案】B【解析】构造新函数()()5g x f x =+，证明它是奇函数，然后利用奇函数的性质求值．【详解】设2()()5ln(1)g x f x x x x =+=++，则2222()()ln(1)ln(1)ln (1)(1)0g x g x x x x x x x x x x x ⎡⎤+-=++-++=++=⎣⎦，∴()()g x g x -=，()g x 是奇函数，又min min ()()55g x f x m =+=+，max max ()()55g x f x M =+=+， ∴min max ()()550g x g x M m +=+++=，10M m +=-．故选：B ．【点睛】本题考查函数的奇偶性，解题关键是构造新函数是奇函数，然后利用奇函数的性质求得结论．二、多选题9．下列说法中，正确的命题是（）． A ．已知随机变量X 服从正态分布()22,N σ，()40.8P X <=，则()240.2P X <<= B ．线性相关系数r 越大，两个变量的线性相关性越强；反之，线性相关性越弱 C ．已知两个变量具有线性相关关系，其回归直线方程为y a bx =+，若2b =，1x =，3y =，则1a =D ．若样本数据121x +，221x +，…，1621x +的方差为8，则数据1x ，2x ，…，16x 的方差为2 【答案】CD【解析】利用正态分布的对称型可以求得()24P X <<的值，进而判定A 错误;根据相关系数的意义可以判定B 错误；利用回归直线方程过样本中心点，可以求得回归常数的估计值，从而判定C 正确；利用线性相关的数据组的方差之间的关系可以求得数据1x ，2x ，…，16x 的方差，进而判定D 正确.【详解】A. 已知随机变量X 服从正态分布()22,N σ，()40.8P X <=，则()410.80.2P X ≥=-=，所以()00.2P X ≤=，所以()04120.20.6P X <<=-⨯=, ∴()0.6240.32P X <<==，故A 错误； B. 线性相关系数r 的范围在1-到1之间，有正有负，相关有正相关和负相关，相关系数的绝对值的大小越接近于1，两个变量的线性相关性越强；反之，线性相关性越弱，故B 错误；C. 已知两个变量具有线性相关关系，其回归直线方程为y a bx =+，若2b =，1x =，3y =，则y 1a bx =-=，故C 正确；D. 设数据1x ，2x ，…，16x 的方差为2S ,样本数据121x +，221x +，…，1621x +的方差为222S =8，则22S =，即数据1x ，2x ，…，16x 的方差为2，故D 正确. 故选:CD. 【点睛】本题考查正态分布的概率计算问题，相关系数问题，回归直线方程问题，数据的方差关系问题，属小综合题，难度一般. 10．下列不等式，其中正确的是（） A ．2 32x x +>（R x ∈） B ．3322 a b a b ab +≥+（a ，R b ∈）C ．22 2a b +≥（1a b --）D ．()22211f x x x =+≥- 【答案】AC【解析】,,A B C 三个选项用作差法比较，D 选项通过举例判断．【详解】2232(1)20x x x +-=-+>，所以232x x +>，A 正确；332222222()()()()()()a b a b ab a a b b a b a b a b a b a b +--=---=--=-+，当0a b +<时，33220a b a b ab +--≤，B 错误；22222(1)(1)(1)0a b a b a b +-+-=-+-≥，即222(1)a b a b +≥+-，C 正确；222()1f x x x =+-中(0)21f =-<+，D 错误．故选：AC ．【点睛】本题考查不等式的性质，考查两实数比较大小，作差法是解题的基本方法． 11．若()f x 满足对任意的实数a ，b 都有()()()f a b f a f b +=且()12f =，则下列判断正确的有（） A ．()f x 是奇函数B ．()f x 在定义域上单调递增C ．当()0,x ∈+∞时，函数()1f x >D ．()()()()()()()()()()()()2462016201820202020135201520172019f f f f f f f f f f f f +++⋅⋅⋅++= 【答案】BCD【解析】利用新定义结合函数的性质进行判断．计算出(1)f 判断A ；先利用(1)21f =>证明所有有理数p ，有()1f p >，然后用任意无理数q 都可以看作是一个有理数列的极限，由极限的性质得()1f q >，这样可判断C ，由此再根据单调性定义判断B ，根据定义计算(2)(21)f n f n -（n N ∈），然后求得D 中的和，从而判断D ．【详解】令0,1a b ==，则(1)(10)(1)(0)f f f f =+=，即22(0)f =，∴(0)1f =，()f x 不可能是奇函数，A 错；对于任意x ∈R ，()0f x ≠，若存在0x R ∈，使得0()0f x =，则0000(0)(())()()0f f x x f x f x =+-=-=，与(0)1f =矛盾，故对于任意x ∈R ，()0f x ≠，∴对于任意x ∈R ，2()022222x x x x x f x f f f f ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+==> ⎪ ⎪⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦， ∵(1)21f =>，∴对任意正整数n ，11111111121nn n f n n f f f f f n n n n n n n ⎛⎫ ⎪⎝⎭⎛⎫ ⎪⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫ ⎪+++===> ⎪ ⎪ ⎪ ⎪⎢⎥ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎪ ⎪⎝⎭个个，∴11f n ⎛⎫> ⎪⎝⎭，同理()(111)(1)(1)(1)21n f n f f f f =+++==>，对任意正有理数p ，显然有m p n=（,m n 是互质的正整数），则1()1mm f p f fn n ⎡⎤⎛⎫⎛⎫==> ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，对任意正无理数q ，可得看作是某个有理数列123,,,p p p 的极限，而()1i f p >，i N ∈，∴()f q 与()i f p 的极限，∴()1f q >，综上对所有正实数x ，有()1f x >，C 正确，设12x x <，则210x x ->，∴21()1f x x ->，则21211211()(())()()()f x f x x x f x f x x f x =+-=⋅->，∴()f x 是增函数，B 正确；由已知(2)(211)(21)(1)2(21)f n f n f n f f n =-+=-=-，∴(2)2(21)f n f n =-，∴()()()()()()()()()()()()10102246201620182020222210102020135201520172019f f f f f f f f f f f f +++⋅⋅⋅++=+++=⨯=个，D 正确．故选：BCD ．【点睛】本题考查新定义函数，考查学生分析问题，解决问题的能力，逻辑思维能力，运算求解能力，对学生要求较高，本题属于难题． 12．已知定义在0,2π⎛⎫⎪⎝⎭上的函数()f x ，()'f x 是()f x 的导函数，且恒有cos ()sin ()0xf x xf x '+<成立，则( )A．64f ππ⎛⎫⎛⎫>⎪ ⎪⎝⎭⎝⎭B63f ππ⎛⎫⎛⎫>⎪ ⎪⎝⎭⎝⎭C．63f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭D64ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭【答案】CD【解析】根据题意，令()()cos f x g x x =，0,2x π⎛⎫∈ ⎪⎝⎭，对其求导分析可得()0g x '<，即函数()g x 为减函数，结合选项分析可得答案．【详解】解：根据题意，令()()cos f x g x x =，0,2x π⎛⎫∈ ⎪⎝⎭，则其导数2()cos sin ()()f x x x f x g x cos x '+'=，又由(0,)2x π∈，且恒有cos ()sin ()0x f x x f x '+<，则有()0g x '<，即函数()g x 为减函数，又由63ππ<，则有()()63g g ππ>，即()()63cos cos 63f f ππππ>，分析可得()()63f ππ>；又由64ππ<，则有()()64g g ππ>，即()()64cos cos 64f f ππππ>()()64ππ>．故选：CD ．【点睛】本题考查函数的单调性与函数导数的关系，注意构造函数()()cos f x g x x=，并借助导数分析其单调性，属于中档题．三、填空题13．若1<a<3，－4<b<2，那么a －|b|的取值范围是_______ 【答案】(－3,3)【解析】先算出|b |的范围，再算出a +（﹣|b |）的范围．【详解】由﹣4＜b ＜2⇒0≤|b |＜4，﹣4＜﹣|b |≤0，又1＜a ＜3． ∴﹣3＜a ﹣|b |＜3．所求范围为（﹣3，3）. 故答案为（﹣3，3）. 【点睛】本题考查了不等式性质的应用，注意同向不等式只能相加，不能相减的特点． 14．已知0a >，0b >，若不等式3103m a b a b--≤+恒成立，则m 的最大值为______ 【答案】16【解析】不等式变形后用基本不等式求最小值后可得结论．【详解】∵0a >，0b >，3103m a b a b--≤+恒成立， ∴3133(3)()10a b m a b a b b a≤++=++， ∵0,0a b >>，33101016b a a b ++≥+=，当且仅当33b aa b=，即a b =时，等号成立， ∴16m ≤，即m 的最大值为16．故答案为：16 【点睛】本题考查不等式恒成立，考查用基本不等式求最小值．解题方法是分离参数法．15．定义运算“⊗”22x y x y xy-⊗=，（,R x y ∈，0xy ≠）.当0x >，0y >时，()2x y y x ⊗+⊗的最小值为______【解析】根据新定义，把()2x y y x ⊗+⊗用通常的运算表示，然后用基本不等式求得最小值．【详解】由题意()222222422222x y y x x y x y x y y x xy xy xy y x --+⊗+⊗=+==+≥=当且仅当2x yy x=，即x =时等号成立．．．【点睛】本题考查新定义运算，求新定义运算下的最值，解题方法是利用新定义把新定义表达式转化为通常的运算，然后由基本不等式求得最小值．四、双空题16．设1,3a ⎛⎤∈-∞ ⎥⎝⎦，R b ∈，()3g x ax x =-，[]1,1x ∈-，则()g x 的值域是______，函数()()f x g x b =-在[]1,1-的最大值是23，则22a b +的值是______ 【答案】[1,1]a a --19【解析】求出导数()'g x ，由已知条件得()0g x '≤，从而确定()g x 的单调性，得函数()g x 值域，由最大值得2()3f x ≤恒成立，从而2(1)32(1)3f f ⎧-≤⎪⎪⎨⎪≤⎪⎩，由此化简变形后求得,a b ，得22a b +，【详解】由题意2()31g x ax '=-，∵13a ≤，[1,1]x ∈-，∴2()310g x ax '=-≤，()g x 在[1,1]-上单调递减，max ()(1)1g x g a =-=-，min ()(1)1g x g a ==-，∴()g x 值域为[1,1]a a --；函数()()f x g x b =-在[]1,1-的最大值是23，即2()3f x ≤在[1,1]-上恒成立， ∴()()21132113f a b f a b ⎧-=-+-≤⎪⎪⎨⎪=--≤⎪⎩，两式相加得4113a b a b -+-++-≤，又1122a b a b a -+-++-≥-，∴4223a -≤，解得1533a ≤≤，又∵13a ≤，∴13a =，可得1213312133b b ⎧-+-≤⎪⎪⎨⎪--≤⎪⎩，即22332233b b ⎧-≤⎪⎪⎨⎪--≤⎪⎩，解得403403b b ⎧≤≤⎪⎪⎨⎪-≤≤⎪⎩，∴0b =，∴2219a b +=．故答案为：[1,1]a a --；19．【点睛】本题考查用导数研究函数的单调性与最值，研究函数恒成立问题，着重考查了逻辑推理能力，运算求解能力，难度中等．五、解答题17．已知函数y =R ．()1求a 的取值范围；()2解关于x 的不等式220x x a a --+<．【答案】()[]1?0,1；(2)见解析.【解析】()1由函数的定义域是R ，得出2210ax ax ++≥恒成立，求出a 的取值范围；()2分类讨论，即可求出不等式的解集．【详解】()1函数y =R ，2210ax ax ∴++≥恒成立．①当0a =时，10≥，不等式恒成立；②当0a ≠时，则02440a a a >⎧=-≤⎨⎩解得01a <≤．综上可知，a 的取值范围是[]0,1．()2由220x x a a --+<，得()()10x a x a ⎡⎤---<⎣⎦．01a ≤≤，∴①当1a a ->，即102a ≤<时，1a x a <<-； ②当1a a -=，即12a =时，)21(02x -<，不等式无解；③当1a a -<，即112a <≤时，1a x a -<<．综上，当102a ≤<时，原不等式的解集为(),1a a -；当12a =时，原不等式的解集为；当112a <≤时，原不等式的解集为()1,a a - 【点睛】本题考查了函数的性质与应用以及不等式的解法与应用问题，解题时应根据题意，适当地转化条件，从而获得解答问题的途径，是综合性题目．解含参数的一元二次不等式，要把握好分类讨论的层次，一般按下面次序进行讨论：首先根据二次项系数的符号进行分类，其次根据不等式的判别式的符号进行分类，最后在根存在的条件下，再根据根的大小进行分类．18．（1）已知不等式1x m -<成立的充分不必要条件是1132x <<，求实数m 的取值范围.（2）已知()2log f t t =，t ∈⎤⎦，对于()f t 值域内的所有实数m ，不等式2424x mx m x ++>+恒成立，求x 的取值范围.【答案】（1）1423m -≤<；（2）()(),12,-∞-+∞.【解析】（1）先求得不等式1x m -<解集，结合题意，列出不等式组，即可求解；（2）根据题意，求得()1,32f t ⎡⎤∈⎢⎥⎣⎦，得到1,32m ⎡⎤∈⎢⎥⎣⎦，转化为()()2220x m x -+->对任任意的1,32m ⎡⎤∈⎢⎥⎣⎦恒成立，令()()()222g x m m x =-+-，结合一次函数的性质，即可求解. 【详解】（1）由题意，不等式1x m -<，解得11m x m -<<+，因为1x m -<成立的充分不必要条件是1132x <<，所以113112m m ⎧-≤⎪⎪⎨⎪+>⎪⎩①，或113112m m ⎧-<⎪⎪⎨⎪+≥⎪⎩②，由①得：1423m -<≤；由②得：1423m -≤<，综合①②得：1423m -≤<.（2）因为()2log f t t =，t ∈⎤⎦，所以()1,32f t ⎡⎤∈⎢⎥⎣⎦，即1,32m ⎡⎤∈⎢⎥⎣⎦，因为2424x mx m x ++>+对任意的1,32m ⎡⎤∈⎢⎥⎣⎦恒成立，所以()()2220x m x -+->对任意的1,32m ⎡⎤∈⎢⎥⎣⎦恒成立，令()()()222g x m m x =-+-，因为()()2220x m x -+->对任意的1,32m ⎡⎤∈⎢⎥⎣⎦恒成立，可得()()()()()()()22112202233220g x x g x x ⎧⎛⎫=-+->---* ⎪⎪⎝⎭⎨⎪=-+->---**⎩，由()* 可得：()()2230x x -->，则2x >或23x <；由()**可得：()()120x x +->，则2x >或1x <-，综上所述：x 的范围()(),12,-∞-+∞.【点睛】本题主要考查了绝对值不等式的求解，二次函数的图象与性质，以及不等式的恒成立问题，其中解答中熟记绝对值不等式的解法，以及二次函数的图象与性质是解答的关键，着重考查推理与运算能力.19．美国2018年3月挑起“中美贸易争端”，剑指“中国制造2025”，中国有“缺芯”之痛.今有三个研究机构A ，B ，C 对某“AI 芯片”做技术攻关，A 能攻克的概率34为，B 能攻克的概率为23，C 能攻克的概率为12，（1）求这一技术难题被攻克的概率；（2）先假设一年后该技术难题已被攻克，上级会奖励m 万元.奖励规则如下：若只有1个机构攻克，则此机构获得全部奖金m 万元；若只有两个机构攻克，则奖金奖给此两个机构，每个机构各得2m万元；若三个机构均攻克，则奖金奖给三个机构，每个机构各得3m万元.设A ，B 得到的奖金数为X ，求X 的分布列和数学期望. 【答案】（1）2324；（2）分布列见解析，()3548E X m =. 【解析】（1）对立事件是这一技术难题没有被攻克即每个队都没有攻克技术难题，由对立事件的概率公式求解；（2）根据规则X 的可能取值为：0，2m ，23m，m ，X 0=表示,A B 均未攻克技术难题，C 可能攻克也可以未攻克，2mX =表示A 未攻克，,B C 同时攻克或B 未攻克，,A C 同时攻克，23mX =表示,,A B C 同时攻克，X m =表示C 未攻克，,A B 中至少1个机构攻克这个技术难题，由此可计算出概率，得分布列，从而可计算出期望．【详解】（1）记这一技术难题被攻克的事件为A ；()111123114322424P A =-⨯⨯=-=.（2）X 的可能取值为：0，2m ，23m ，m 2321134324m P X ⎛⎫==⨯⨯= ⎪⎝⎭；3111215243243224m P X ⎛⎫==⨯⨯+⨯⨯=⎪⎝⎭； ()3111213211143243243224P X m ==⨯⨯+⨯⨯+⨯⨯=；()1111111043243212P X ==⨯⨯+⨯⨯=X 的分布列：()15211135012224342448m m E X m m =⨯+⨯+⨯+⨯=. 【点睛】本题考查相互独立事件同时发生的概率公式和对立事件的概率公式，考查随机变量的概率分布列和数学期望，解题关键是确定变量X 的可能取值．20．设二次函数()2f x ax bx c =++，函数()()F x f x x =-的两个零点为m ，n（m n <）.（1）若1m =-，2n =，求不等式()0F x >的解集. （2）若0a >，且10x m n a<<<<，比较()f x 与m 的大小. 【答案】（1）答案见解析；（2）()f x m <.【解析】（1）由二次方程的根与一元二次不等式的解之间的关系直接得出结论；（2）设()()()F x a x m x n =--，得()()()f x a x m x n x =--+，作差()f x m -可得它与0的大小，从而得出()f x 与m 的大小．【详解】（1）()0F x =的两个根分别为1-和2 当0a >时，()0F x >的解集为()(),12,-∞-+∞；当0a <时，()0F x >的解集为()1,2-；（2）()()()F x a x m x n =--，()()()f x a x m x n x =--+()()()()()1f x m a x m x n x m x m ax an -=--+-=--+∵10x m n a<<<<，∴0x m -<，10an -+>，0ax > ∴10ax an -+>，()0f x m -< ∴()f x m <. 【点睛】本题考查二次方程的根与一元二次不等式的解之间的关系，考查二次函数的解析式，掌握三个二次的关系是解题关键． 21．已知函数()1ln x f x x a-=-（1）当1a =时，求()f x 的最大值；（2）若()f x 在区间()2,e 上存在零点，求实数a 的取值范围.【答案】（1）0；（2）1,1ln 2e ⎛⎫-⎪⎝⎭. 【解析】（1）先求导数，再求导函数零点，根据导函数符号变化规律确定函数单调性，最后根据单调性求最大值；（2）先变量分离转化求对应函数()1ln x g x x-=值域，利用导数求其单调性，再根据单调性求其值域，即得结果. 【详解】（1）()()ln 1f x x x =--，()111x f x x x-=-='，令0fx，得1x =所以()f x 在0,1上单调递增，1,上单调递减∴()()max 10f x f ==.（2）()f x 在区间()2,e 上存在零点，∴1ln 0x x a--=在()2,e 上有解，1ln x a x -=令()1ln x g x x-=（()2x e ∈,），()()21ln 1ln ,x x x x g +='-设2211111ln 1,(2,)0ln 2102x y x x e y y x x x x -'=-+∈∴=-=>∴>-+=> 因此0g x,∴()g x 在()2,e 上单调递增，即()()12ln 2g x g >=，()()1g x g e e <=- ∴1,1ln 2a e ⎛⎫∈-⎪⎝⎭. 【点睛】本题考查利用导数求函数单调性、利用导数研究函数零点，考查综合分析求解能力，属中档题.22．设函数()32f x x ax bx =++（a ，R b ∈）的导函数为()f x .已知1x ，2x 是()f x 的两个不同的零点. （1）证明：23a b >；（2）当0b =时，若对任意0x >，不等式()ln f x x x >恒成立，求a 的取值范围；（3）求关于x 的方程()()()1211()2x f x f x f x x x '=-++的实根的个数. 【答案】（1）证明见解析；（2）1a ≥-；（3）1.【解析】（1）先求导数，再根据导函数必有两个不同零点列不等式，解得结果；（2）先分离变量，转化为求对应函数()2ln x x F x x-=最值，利用导数确定其单调性，根据单调性确定最值，即得结果；（3）先求122x x f +⎛⎫' ⎪⎝⎭，再构造差函数()()321211()2x x G x x ax bx f x x f x +⎛⎫'=++--- ⎪⎝⎭，再利用导数确定其单调性，最后根据单调性以及()10G x =确定零点个数，即得结果. 【详解】（1）证明：()232f x x ax b '=++，令()2320f x x ax b '=++=∵0f x有两个不等的实根，∴2241203a b a b ∆=->⇒>.（2）0b =时，()32f x x ax =+，由()ln f x x x ≥得32ln x ax x x +≥∴22ln ln x x x ax x x a x-+≥⇒≥令()2ln x x F x x-=，()222212ln 1ln x x x x x x x F x x x ⎛⎫--+ ⎪--⎝⎭'== 令()21ln g x x x =--，()120g x x x'=--< ∴()g x 在0,上单调递减，注意到10g∴当01x <<时，()0gx >，()0F x '>，()F x '单调递增；当1x >时，()0g x <，()0F x '<，()F x 单调递减： ∴()()max 11F x F ==-，∴1a ≥-. （3）()()3212112x x x ax bx f x x f x +⎛⎫'++=-+⎪⎝⎭()()32121102x x x ax bx f x x f x +⎛⎫'⇒++---= ⎪⎝⎭212233x x a a f f b +⎛⎫⎛⎫''=-=- ⎪ ⎪⎝⎭⎝⎭令()()321211()2x x G x x ax bx f x x f x +⎛⎫'=++---⎪⎝⎭()()2222221211323296(3)02333x x a G x x ax b f x ax b b x ax a x a +⎛⎫''=++-=++-+=++=+≥ ⎪⎝⎭∴()G x 在R 上单调递增，故()G x 在R 上至多只有一个零点，注意到()10G x = ∴()G x 在R 上只有1个零点，即()()1211()2x x f x f x x f x '+⎛⎫=-+⎪⎝⎭的实根个数为1. 【点睛】本题考查利用导数研究不等式恒成立、利用导数研究函数零点、利用导数证明不等式，考查综合分析求解能力，属中档题.。

江苏省淮安市淮阴中学2021届高三数学期中测试数学试题及答案

淮阴中学2020/2021学年度高三第一学期期中考试数学一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的。

１.已知集合M ={x||2x +1|>3},N ={x|x 2+x −6≤0}，则M ∩N 等于（） A ．(−3,−2]∪[1,2]B ．(−3,−2)∪(1,+∞)C ．[−3,−2)∪(1,2]D ．(−∞,−3)∪(1,2]2．已知向量a →=(1,2),a →⋅b →=5,|a →−b →|=2√5，则|b →|等于（） A ．√5 B ．2√5C ．25D ．5３．长方体AC 1的长、宽、高分别为3、2、1，则从A 到C 1沿长方体的表面的最短距离为（）A ．1+√3B ．2+√10C ．3√2D ．2√3４.已知函数f(x)={x 2+2x −1,x ≥0x 2−2x −1,x <0，则对任意x 1,x 2∈R ，若0<|x 1|<|x 2|，下列不等式成立的是（）A. f(x 1)+f(x 2)<0B. f(x 1)+f(x 2)>0C. f(x 1)−f(x 2)>0D. f(x 1)−f(x 2)<0５．三个共面向量a 、b 、c 两两所成的角相等，且|a |=1，|b |=2，|c |=3，则|a +b +c | 等于（）A ．√3B ．6C ．√3或6D ．3或6６．正方形ABCD 的边长为2，点E 、F 分别在边AB 、BC 上，且AE =1，BF =12，将此正方形沿DE 、DF 折起，使点A 、C 重合于点P ，则三棱锥P −DEF 的体积是A ．13 B ．√56C ．2√39D ．√23 ７.函数−2+i 的零点所在的区间为 ( )A ．2+iB ．(1+2iC ．1−2iD ．(12,34)８.设点P 是椭圆x 29+y 25=1上的一点，点M 、N 分别是两圆：(x +2)2+y 2=1和(x −2)2+y 2=1上的点，则的最小值、最大值分别为 ( )A. 4，8B.2，6 C) 6，8 D.8，12二、多项选择题：本题共４小题，每小题５分，共２０分，在每小题给出的选项中，有多项符合要求，全部选对的得５分，部分选对的得３分，有选错的得０分）９.若函数f(x)具有性质:,则称f(x)是满足“倒负”变换的函数.下列四个函数: 其中,满足“倒负”变换的所有函数的选项是 ( )A.(a>0且a ≠1); B.(a>0且a ≠1);C.;D..10.定义在R 上的偶函数在[—1，0]上是增函数，给出下列关于的判断: 其中正确的选项是 ( )A ．关于直线对称； B ．是[0，1]上是增函数；Ｃ．在[1，2]上是减函数；Ｄ．．11．设、是不同的直线，、、是不同的平面，有以下四个命题：A ．B ．C ．D ．，其中正确的选项是 ( )（A ）（1）（2）（B ）（1）（3）（C ）（2）（3）（D ）（2）（4）12.如图所示，在长方体ABCD −A 1B 1C 1D 1，若AB =BC ，E ，F 分别是AB 1，1BC 的中点，则下列结论中不成立的是（）A. EF 与1BB 垂直B. EF ⊥平面BDD 1B 1C. EF 与C 1D 所成的角为45°D. EF//平面A 1B 1C 1D 1三、填空题：本大题共４小题，每小题5分，共２0分，请将答案填在题中横线上1３．已知{x ≥1x −y +1≤02x −y −2≤0则x 2+y 2的最小值是______．14．已知F 是双曲线的左焦点，是双曲线右支上的动点，则的最小值为 .15．用0，1，2，3，4这五个数字组成无重复数字的五位数，其中恰有一个偶数夹在两个奇数之间的五位数共有16．圆柱形容器的内壁底半径是10cm ，有一个实心铁球浸没于容器的水中，若取出这个铁球，测得容器的水面下降了53cm ，则这个铁球的表面积为 cm 2.四、解答题：本大题共６个小题共70分17．设条件：实数满x 2—4ax+3a 2<0(a>0)条件：实数满足;已知q 是p 的必要不充分条件，求实数的取值范围。

江苏省淮阴中学2021届高三第一学期数学测试卷

淮阴中学2021届高三数学测试卷2020年8月29日一、选择题:本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.设集合4={1，2，3}，B={4，5}，M={x|x=a+b，a∈，b∈B}，则M中元素的个数为( )A. 3B. 4C.5D.62.以下四个命题既是存在性命题又是真命题的是( )A.锐角三角形的内角是锐角或钝角B.至少有一个实数x0，使x02≤0>2C.两个无理数的和必是无理数D.存在一个负数x0，使1x03.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这-过程中汽车的行驶路程s看作时间t的函数，其图象可能是( )4.对任意x∈R，函数f(x)=ax3+ax2+7x不存在极值点的充要条件是( )A.0≤a≤21B. 0<a<21C. a≤0或a≥21D. a<0或a> 215.将甲桶中的a升水缓慢注入空桶乙中，t 分钟后甲桶中剩余的水符合指数衰减曲线升，则y=ae m，假设过5分钟后甲桶和乙桶的水量相等，若再过m分钟甲桶中的水只有a8m的值为( )A.7B. 8C.9D.10(6-ax)(a>0且a≠1)在[0，2] 上为减函数，则实数a的取值范围是6.函数f(x)=loga( )A. (1,3)B. (0,1)C. (1，3]D. [3，+∞)7. 如果已知0<a<1,则方程a|x|=|logx|的实根个数为( )aA.2B.3C.4D.与a的值有关8.已知函数f(x)=x+ln(√x2+1-x)-5(x∈[-2020，2020]) 的最大值为M ,最小值为m,则M+m=( )A.-5B.-10C.5D.10二、选择题:本题共4小题，每小题5分，共20分。

在每小题给出的选项中,有多项符合题目要求。

全部选对的得5分，有选错的得0分，部分选对的得3分。

9.下列说法中，正确的命题是( )A.已知随机变量X服从正态分布N(2,σ2)，P(X<4)=0.8，则P(2<X<4)=0.2B.线性相关系数r越大，两个变量的线性相关性越强;反之，线性相关性越弱C.已知两个变量具有线性相关关系，其回归直线方程为y=â+ b̂x，若b̂=2x⃗, x⃗=1，y⃗=3，则a=1D.若样本数据2x 1+1，2x 2+1， ... 2x 16+1的方差为8，则数据x 1,x 2，.，. x 16 的方差为210.下列不等式，其中正确的是( )A. x 2+3>2x(x∈R)B. a 3 +b 3≥a 2b + ab 2 (a,b∈R)C. a 2 +b 2≥2(a -b-1)D.f(x)=x 2+2x 2−1≥2√2+111.若f(x)满足对任意的实数a ，b 都有f(a+b)= f(a)*f(b)且f(1)=2，则下列判断正确的有( )A. f(x)是奇函数B. f(x) 在定义域上单调递增C.当x∈(0,+∞)时，函数f(x)>1D.f(2)f(1)+f(4)f(3)+f(6)f(5)+…f(2016)f(2015)+f(2018)f(2017)+f(2020)f(2019)=2020 12.定义在(0,π2)上的函数f(x)，f , " (x) 是它的导函数，且恒有cosx.f"(x)+ sinx*f(x)<0成立，则有( )A.f(π6)> √2f(π4)B. √3f(π6)> f(π4)C. f(π6)> √3f(π3)D. √2f(π6)> √3f(π4) 三、填空题:本题共4小题，每小题5分，共20分。

江苏省淮安市淮阴中学高三(上)期中数学试卷含答案

∴ 푥|푥−2| ≤ 1，
{ { ∴
푥2−2푥 푥 ≥2
≤ 1或
2푥−푥2 푥 <2
≤
1，解得푥
≤
2 +1，
∴ 푓(2푥) ≤ 푓(2)的解集为{푥|푥 ≤ 2 +1}．
故答案为：{푥|푥 ≤ 2 +1}
{ { 可由푓(2푥)
． ≤ 푓(2)得出푥|푥−2|
≤
1，从而得到
푥2−2푥 푥 ≥2
≤ 1或
21. 已知矩阵퐴 = [0 13]，퐵 = [2 08]，求퐴−1퐵
2
1
22. 已知矩阵퐴 = [ 1
−1
24]，向量푎 = [53]，计算퐴5푎．
23. 已知四棱锥푃−퐴퐵퐶퐷的底面为直角梯形，퐴퐵//퐷퐶，∠퐷퐴퐵 = 90°，푃퐴 ⊥ 底面
ABCD，且푃퐴 = 퐴퐷 = 퐷퐶 = 1，퐴퐵 = 2，M 是 PB 的中点． (Ⅰ)求 AC 与 PB 所成角的余弦值； (Ⅱ)求面 AMC 与面 BMC 所成二面角的余弦值的大小．
第 3 页，共 21 页
19. 已知函数푓(푥) = 푥3 +3|푥−푎|，푎 ∈ 푅
(1)当푎 = 1时，求曲线푦 = 푓(푥)在푥 = 2处的切线方程；
(2)当푥 ∈ [−1,1]时，求函数푓(푥)的最小值； (3)已知푎 > 0，且任意푥 ≥ 1有푓(푥 + 푎)−푓(1 + 푎) ≥ 15푎2푙푛푥，求实数 a 的取值范
3.【答案】(−1,2)
{푥 + 1 > 0
【解析】解：依题意，
2−푥 2−푥
≠0 ≥0
，解得−1 < 푥
< 2，
所以푦 = ln(푥 + 1) + 22−푥的定义域为(−1,2)，

江苏省淮安市楚中、新马、清浦、洪泽高中四校2021届高三数学上学期期中联考试题文(含解析).doc

江苏省淮安市楚中、新马、清浦、洪泽高中四校2021届高三数学上学期期中联考试题文（含解析）一、填空题（本大题共14小题）1.已知R为实数集，集合A={-1，0，1}，集合B={x|x≤0}，则A∩∁R B=______．2.“∀x∈R，x2+2x+1＞0”的否定是______．3.已知向量，若，则=______．4.已知函数，则函数的最小正周期为______．5.已知函数，则f（f（0）-3）=______．6.设△ABC的内角A，B，C的对边分别为a，b，c，且a=2，cos C=-，3sin A=2sin B，则c=______．7.已知，，则tanα=______．8.将函数f（x）=cos（x+φ）（|φ|＜）的图象上各点的横坐标缩短到原来的倍（纵坐标不变），再把得到的图象向左平移个单位长度，所得函数图象关于原点对称，则φ=______．9.若等比数列{a n}的前n项和S n=2n+1+c，则c=______．10.《算法统宗》中有如下问题：“哑子来买肉，难言钱数目，一斤少三十，八两多十八，试问能算者，合与多少肉”，意思是一个哑子来买肉，说不出钱的数目，买一斤（两）还差文钱，买八两多十八文钱，求肉数和肉价，则该问题中，肉价是每两__________文．11.在△ABC中，M是BC的中点，AM=3，BC=10，则•=______．12.已知函数f（x）=x lnx-x2-x+a（a∈R）在其定义域内有两个不同的极值点，则实数a的取值范围是______．13.已知a，b为正实数，直线y=x-a与曲线y=ln（x+b）相切，则+的最小值为______．14.已知关于x的不等式（x-3）ln x≤2λ有解，则整数λ的最小值为______．二、解答题（本大题共6小题）15.已知sin（α+）=，α∈（，π）．求：（1）cosα的值；（2）sin（2α-）的值．16.在△ABC中，记角A，B，C的对边为a，b，c，角A为锐角，设向量=（cos A，sin A），=（cos A，-sin A），且•=（I）求角A的大小及向量与的夹角；（II）若a=，求△ABC面积的最大值．17.请你设计一个包装盒，如图所示，ABCD是边长为60cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A，B，C，D四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E、F在AB上，是被切去的等腰直角三角形斜边的两个端点，设AE=FB=x（cm）．（1）若广告商要求包装盒侧面积S（cm2）最大，试问x应取何值？（2）若广告商要求包装盒容积V（cm3）最大，试问x应取何值？并求出此时包装盒的高与底面边长的比值．18.函数f（x）=log a（2-ax）（a＞0，a≠1）．（1）当a=3时，求函数f（x）的定义域；（2）若g（x）=f（x）-log a（2+ax），判断g（x）的奇偶性；（3）是否存在实数a，使函数f（x）在[2，3]递增，并且最大值为1，若存在，求出a的值；若不存在，说明理由．19.已知数列{a n}和{b n}满足a1a2a3…a n=（n∈N*）．若{a n}为等比数列，且a1=2，b3=6+b2．（Ⅰ）求a n和b n；（Ⅱ）设c n=（n∈N*）．记数列{c n}的前n项和为S n．（i）求S n；（ii）求正整数k，使得对任意n∈N*均有S k≥S n．20.已知函数f（x）=x2+ax+1，g（x）=e x（其中e为自然对数的底数）．（Ⅰ）若a=1，求函数y=f（x）•g（x）在区间[-2，0]上的最大值；（Ⅱ）若a=-1，关于x的方程f（x）=k•g（x）有且仅有一个根，求实数k的取值范围；（Ⅲ）若对任意的x1，x2∈[0，2]，x1≠x2，不等式|f（x1）-f（x2）|＜|g（x1）-g （x2）|均成立，求实数a的取值范围．答案和解析1.【答案】{1}【解析】解：∵A={-1，0，1}，B={x|x≤0}，∴∁R B={x|x＞0}，A∩∁R B={1}．故答案为：{1}．进行补集、交集的运算即可．考查列举法、描述法的定义，以及交集、补集的运算．2.【答案】∃x0∈R，x02+2x0+1≤0【解析】解：命题为全称命题，则“∀x∈R，x2+2x+1＞0”的否定是：∃x0∈R，x02+2x0+1≤0，故答案为：∃x0∈R，x02+2x0+1≤0．根据含有量词的命题的否定即可得到结论．本题主要考查含有量词的命题的否定，比较基础．3.【答案】【解析】解：向量，若，∴，∴x=4，==．故答案为：．利用斜率的垂直求出x，得到向量，然后求模即可．本题考查斜率的数量积的应用，向量的模的求法，考查计算能力．4.【答案】π【解析】解：函数的最小正周期为：=π．故答案为：π．直接利用三角函数的周期公式求解即可．本题考查三角函数的周期公式的应用，是基础题．5.【答案】-1【解析】解：∵函数，∴f（0）=e0=1，f（0）-3=1-3=-2＜0，∴f（-2）=-2+1=-1，所以f（f（0）-3）=f（-2）=-1，故答案为-1；已知f（x）是分段函数，代入分段函数求出f（0），再把f（0）-3看为一个整体，再进行代入进行求解；此题主要考查分段函数的性质，注意分段函数的定义域，此题是一道基础题；6.【答案】4【解析】解：∵3sin A=2sin B，∴由正弦定理可得：3a=2b，∵a=2，∴可解得b=3，又∵cos C=-，∴由余弦定理可得：c2=a2+b2-2ab cos C=4+9-2×=16，∴解得：c=4．故答案为：4．由3sin A=2sin B即正弦定理可得3a=2b，由a=2，即可求得b，利用余弦定理结合已知即可得解．本题主要考查了正弦定理，余弦定理在解三角形中的应用，属于基础题．7.【答案】【解析】解：∵，∴∈（，），又，∴sin（）==．∴sinα=sin[（）-]=sin（）cos-cos（）sin==，则cosα=，∴tan．故答案为：．由已知求得sin（），再由sinα=sin[（）-]，运用两角差的正弦展开求得sinα，然后利用同角三角函数基本关系式求解．本题考查三角函数的化简求值，考查同角三角函数基本关系式与两角差的三角函数，是基础题．8.【答案】【解析】解：将函数f（x）=cos（x+φ）（|φ|＜）的图象上各点的横坐标缩短到原来的倍（纵坐标不变），得到y=cos（2x+φ），再把得到的图象向左平移个单位长度，得到y=cos[2（x+）+φ]=cos（2x++φ），∵所得函数图象关于原点对称，∴+φ=+kπ，k∈Z，即φ=+kπ，k∈Z，∵|φ|＜，∴当k=0时，φ=，故答案为：．根据函数平移变换关系求出函数解析式，结合函数奇偶性的性质进行求解即可．本题主要考查三角函数的图象和性质，结合三角函数的图象变换求出函数的解析式，以及利用函数对称性的性质是解决本题的关键．9.【答案】-2【解析】【解答】解：依题意，该等比数列的公比不为1，所以S n==-·q n=c+2×2n，所以q=2，=-2，∴c==-2，故填：-2．【分析】显然该等比数列的公比不为1，所以S n==-·q n=c+2×2n，所以q=2，=-2，c=-2，本题考查了等比数列的前n项和，主要考查公式的运用和处理能力，属于基础题．10.【答案】6【解析】【分析】本题考查中国古代著作中的数学问题，属数学文化，正确地理解题意是解题关键．设肉价是每两x文，根据题意列出方程可解得答案【解答】解：设肉价是每两x文，由题意得16x-30=8x+18，解得x=6，即肉价是每两6文．故答案为：6．11.【答案】-16【解析】解：设∠AMB=θ，则∠AMC=π-θ．又=-，=-，∴=（-）•（-）=•-•-•+，=-25-5×3cosθ-3×5cos（π-θ）+9=-16，故答案为-16．设∠AMB=θ，则∠AMC=π-θ，再由=（-）•（-）以及两个向量的数量积的定义求出结果．本题主要考查两个向量的数量积的定义，属于基础题．12.【答案】（0，）【解析】解：由题意知，函数f（x）的定义域为（0，+∞），方程f′（x）=0在（0，+∞）有两个不同根；即方程ln x-ax=0在（0，+∞）有两个不同根；转化为函数y=ln x与函数y=ax的图象在（0，+∞）上有两个不同交点，如右图．可见，若令过原点且切于函数y=ln x图象的直线斜率为k，只须0＜a＜k．令切点A（x0，ln x0），故k=y′=，又k=，故=，解得，x0=e，故k=，故0＜a＜．故答案为：（0，）．由导数与极值的关系知可转化为方程f′（x）=ln x-ax=0在（0，+∞）有两个不同根；再转化为函数y=ln x与函数y=ax的图象在（0，+∞）上有两个不同交点，通过函数的导数利用曲线的斜率，从而求解a的范围；本题考查了导数的综合应用，转化思想，数形结合的思想方法的应用，属于中档题．13.【答案】5+2【解析】解：y=ln（x+b）的导数为y′=，由切线的方程y=x-a可得切线的斜率为1，可得切点的横坐标为1-b，切点为（1-b，0），代入y=x-a，得a+b=1，∵a、b为正实数，则+=（a+b）（+）=2+3++≥5+2=5+2．当且仅当a=b，即a=，b=3-时，取得最小值5+2．故答案为：5+2．求函数的导数，由已知切线的方程，可得切线的斜率，求得切线的坐标，可得a+b=1，再由乘1法和基本不等式，即可得到所求最小值．本题主要考查导数的应用，利用导数的几何意义以及基本不等式是解决本题的关键，属于中档题．14.【答案】0【解析】h（x）=（x-3）ln x，h′（x）=ln x-+1，h″（x）=+＞0恒成立，∴h′（x）在（0，+∞）上单调递增，∴存在x0，h′（x0）=0，即ln x0=-1，h（x）在（0，x0）上单调递减，（x0，+∞）上单调递增，∴h（x）min=h（x0）=-（x0+）+6，∵h′（）＜0，h′（2）＞0，∴x0∈（，2），∴h（x0）∈（-，-），∴存在λ的最小值0，使得关于x的不等式2λ≥h（x）有解；故答案为：0令函数h（x）=（x-3）ln x，求出h（x）的最小值，根据函数的单调性判断即可；本题考查导数知识的综合运用，考查函数的单调性与最值，考查分类讨论的数学思想，属于中档题．15.【答案】解：（1）sin（α+）=，即sinαcos+cosαsin=，化简：sinα+cosα=…①sin2α+cos2α=1…②．由①②解得cosα=-或cosα=∵α∈（，π）．∴cosα=-（2）∵α∈（，π）．cosα=-∴sinα=，那么：cos2α=1-2sin2α=，sin2α=2sinαcosα=∴sin（2α-）=sin2αcos-cos2αsin=．【解析】（1）利用两角和差公式打开，根据同角三角函数关系式可求cosα的值；（2）根据二倍角公式求出cos2α，sin2α，利用两角和差公式打开，可得sin（2α-）的值．本题主要考查了两角和差公式，同角三角函数关系式以及二倍角公式的运用和计算能力．16.【答案】解：（I）在△ABC中，由•=求得cos2A=，可得．再根据=cos＜，＞，求得cos＜，＞=，可得向量与的夹角＜，＞=．（II）∵a=，A=，由余弦定理可得a2=5=b2+c2-2bc•cos A≥2bc-bc，求得bc≤10+5，当且仅当b=c时取等号，故△ABC面积bc•sin A=的最大值为．【解析】本题主要考查两个向量的数量积的定义，余弦定理以及基本不等式的应用，属于中档题．（I）在△ABC中，由•=求得cos2A=，可得A的值．再根据两个向量的数量积的定义求得向量与的夹角．（II）由条件利用余弦定理以及基本不等式求得bc的最大值，可得△ABC面积bc•sin A 的最大值.17.【答案】解：设包装盒的高为h（cm），底面边长为a（cm），则a=x，h=（30-x），0＜x＜30．（1）S=4ah=8x（30-x）=-8（x-15）2+1800，答：当x=15时，S取最大值．（2）V=a2h=2（-x3+30x2），V′=6x（20-x），由V′=0得x=20，当x∈（0，20）时，V′＞0；当x∈（20，30）时，V′＜0；答：当x=20时，包装盒容积V（cm3）最大，此时，．即此时包装盒的高与底面边长的比值是．【解析】（1）可设包装盒的高为h（cm），底面边长为a（cm），写出a，h与x的关系式，并注明x的取值范围．再利用侧面积公式表示出包装盒侧面积S关于x的函数解析式，最后求出何时它取得最大值即可；（2）利用体积公式表示出包装盒容积V关于x的函数解析式，最后利用导数知识求出何时它取得的最大值即可．考查函数模型的选择与应用，考查函数、导数等基础知识，考查运算求解能力、空间想象能力、数学建模能力．属于基础题．18.【答案】解：（1）由题意得：f（x）=log3（2-3x），∴2-3x＞0，即x＜，所以函数f（x）的定义域为（-∞，）；（2）易知g（x）=log a（2-ax）-log a（2+ax），∵2-ax＞0且2+ax＞0，∴关于原点对称，又∵，∴，∴g（x）为奇函数．（3）令μ=2-ax，∵a＞0，a≠1，∴μ=2-ax在[2，3]上单调递减，又∵函数f（x）在[2，3]递增，∴0＜a＜1，又∵函数f（x）在[2，3]的最大值为1，∴f（3）=1，即f（3）=log a（2-3a）=1，∴，∵0＜a＜1，∴符合题意．即存在实数，使函数f（x）在[2，3]递增，并且最大值为1．【解析】本题考查了对数函数的性质，考查复合函数的单调性、最值问题，是一道中档题．（1）根据对数函数的性质求出函数的定义域即可；（2）根据函数奇偶性的定义判断即可；（3）令μ=2-ax，根据复合函数的单调性求出函数的最大值，从而求出对应的a的值即可．19.【答案】解：（Ⅰ）∵a1a2a3…a n=（n∈N*）①，当n≥2，n∈N*时，②，由①②知：，令n=3，则有．∵b3=6+b2，∴a3=8．∵{a n}为等比数列，且a1=2，∴{a n}的公比为q，则=4，由题意知a n＞0，∴q＞0，∴q=2．∴（n∈N*）．又由a1a2a3…a n=（n∈N*）得：，，∴b n=n（n+1）（n∈N*）．（Ⅱ）（i）∵c n===．∴S n=c1+c2+c3+…+c n====；（ii）因为c1=0，c2＞0，c3＞0，c4＞0；当n≥5时，，而=＞0，得，所以，当n≥5时，c n＜0，综上，对任意n∈N*恒有S4≥S n，故k=4．【解析】本题考查了等比数列通项公式、求和公式，还考查了分组求和法、裂项求和法和猜想证明的思想，证明可以用二项式定理，还可以用数学归纳法．本题计算量较大，思维层次高，要求学生有较高的分析问题解决问题的能力．本题属于难题．（Ⅰ）先利用前n项积与前（n-1）项积的关系，得到等比数列{a n}的第三项的值，结合首项的值，求出通项a n，然后现利用条件求出通项b n；（Ⅱ）（i）利用数列特征进行分组求和，一组用等比数列求和公式，另一组用裂项法求和，得出本小题结论；（ii）本小题可以采用猜想的方法，得到结论，再加以证明．20.【答案】解：（Ⅰ）a=1时，y=（x2+x+1）e x，y′=（x+1）（x+2）e x，令y′＞0，解得：x＞-1或x＜-2，令y′＜0，解得：-2＜x＜-1，∴函数y=f（x）•g（x）在[-2，-1]递减，在[-1，0]递增，而x=-2时，y=，x=0时，y=1，故函数在[-2，0]上的最大值是1；（Ⅱ）由题意得：k==有且只有一个根，令h（x）=，则h′（x）=，故h（x）在（-∞，1）上单调递减，（1，2）上单调递增，（2，+∞）上单调递减，所以h（x）极大=h（2）=，h（x）极小=h（1）=，因为h（x）在（2，+∞）单调递减，且函数值恒为正，又当x→-∞时，h（x）→+∞，所以当k＞或0＜k＜时，k=h（x）有且只有一个根．（Ⅲ）设x1＜x2，因为g（x）=e x在[0，2]单调递增，故原不等式等价于|f（x1）-f（x2）|＜g（x2）-g（x1）在x1、x2∈[0，2]，且x1＜x2恒成立，所以g（x1）-g（x2）＜f（x1）-f（x2）＜g（x2）-g（x1）在x1、x2∈[0，2]，且x1＜x2恒成立，即，在x1、x2∈[0，2]，且x1＜x2恒成立，则函数F（x）=g（x）-f（x）和G（x）=f（x）+g（x）都在[0，2]单调递增，则有，在[0，2]恒成立，当a≥-（e x+2x）恒成立时，因为-（e x+2x）在[0，2]单调递减，所以-（e x+2x）的最大值为-1，所以a≥-1；当a≤e x-2x恒成立时，因为e x-2x在[0，ln2]单调递减，在[ln2，2]单调递增，所以e x-2x的最小值为2-2ln2，所以a≤2-2ln2，综上：-1≤a≤2-2ln2．【解析】（Ⅰ）求出函数的导数，得到函数的单调区间，从而求出函数的最大值即可；（Ⅱ）若a=-1，关于x的方程f（x）=k•g（x）有且仅有一个根，即k==，有且只有一个根，令h（x）=，可得h（x）极大=h（2）=，h（x）极小=h（1）=，进而可得当k＞或0＜k＜时，k=h（x）有且只有一个根；（Ⅲ）设x1＜x2，因为g（x）=e x在[0，2]单调递增，故原不等式等价于|f（x1）-f（x2）|＜g（x2）-g（x1）在x1、x2∈[0，2]，且x1＜x2恒成立，当a≥-（e x+2x）恒成立时，a≥-1；当a≤e x-2x恒成立时，a≤2-2ln2，综合讨论结果，可得实数a的取值范围．本题考查的知识点是导数在最大值和最小值中的应用，利用导数分析函数的单调性，利用导数分析函数的极值，运算量大，综合性强，转化困难，属于难题．。

江苏省淮安市楚中、新马、清浦、洪泽高中四校联考2021届高三数学上学期期中试题(含解析)

江苏省淮安市楚中、新马、清浦、洪泽高中四校联考2021届高三数学上学期期中试题（含解析）一、填空题（本大题共14小题）1.已知R 为实数集，集合{}1,0,1A =-，集合{}0B x x =≤，则RA B =______．【答案】{}1 【解析】【分析】利用补集的定义求出集合B R，然后利用交集的定义求出集合RAB .【详解】{}0B x x =≤，{}0R B x x ∴=>，因此，{}1RAB =.故答案为{}1.【点睛】本题考查列举法、描述法的定义，以及交集、补集的运算，考查计算能力，属于基础题.2.“R x ∀∈，2210x x ++>”的否定是____________．【答案】0R x ∃∈，使得200210x x ++≤【解析】【分析】直接利用全称命题的否定得解.【详解】“R x ∀∈，2210x x ++>”的否定是：“0R x ∃∈，使得200210x x ++≤”【点睛】本题主要考查了全称命题的否定，属于基础题． 3.已知向量(1,2),(,2)a b x =-=，若a b ⊥，则b ＝________．【答案】25 【解析】试题分析：因为a b ⊥，所以，所以解得，b ＝考点：向量模的运算． 4.函数()sin(2)6f x x π=+最小正周期为___________ .【答案】π 【解析】函数()sin 26f x x π⎛⎫=+ ⎪⎝⎭的最小正周期为2π2π=，故答案为π.5.已知函数10(){0xx x f x e x +<=≥，则((0)3)f f -= ；【答案】.【解析】试题分析：由0(0)1f e ==得(0)3132f -=-=-，进而求出((0)3)(2)211f f f -=-=-+=-.考点：分段函数的求值.6.设ABC ∆的内角,,A B C 的对边分别为,,a b c ，且12,cos ,3sin 2sin 4a C A B ==-=，则c =________．【答案】4 【解析】试题分析：由3sin 2sin A B =及正弦定理，得32a b =．又因为2a =，所以3b =．由余弦定理得：22212cos 49223()164c a b ab C =+-=+-⨯⨯⨯-=，所以4c =．考点：正余弦定理．7.已知5cos 4πα⎛⎫+= ⎪⎝⎭，0,2πα⎛⎫∈ ⎪⎝⎭，则tan α=______. 【答案】13【解析】【分析】本题首先可根据5cos 45πα⎛⎫+= ⎪⎝⎭计算出sin 4πα⎛⎫+ ⎪⎝⎭的值，然后通过cos 4πα⎛⎫+ ⎪⎝⎭以及sin 4πα⎛⎫+ ⎪⎝⎭计算出tan 4πα⎛⎫+ ⎪⎝⎭的值，最后通过两角差的正切公式即可得出结果．【详解】因为cos 45πα⎛⎫+= ⎪⎝⎭，0,2πα⎛⎫∈ ⎪⎝⎭，所以sin 45πα⎛⎫+== ⎪⎝⎭，()()44sin tan 24cos ππαπαα+⎛⎫+== ⎪+⎝⎭，所以()()4444tan tan 1tan tan 441tan tan 3ππππαππααα+-⎛⎫=+-== ⎪++⎝⎭．【点睛】本题考查三角恒等变换，主要考查同角三角函数关系以及两角差的正切公式，考查的公式有22sin cos 1αα+=、sin tan cos ααα=以及()tan tan tan 1tan tan αβαβαβ--=+，考查计算能力，是中档题．8.将函数()()cos 2f x x πϕϕ⎛⎫=+< ⎪⎝⎭的图象上各点的横坐标缩短到原来的12倍（纵坐标不变），再把得到的图象向左平移6π个单位长度，所得函数图象关于原点对称，则ϕ=___．【答案】6π 【解析】【分析】根据函数平移变换关系求出函数解析式，然后将原点坐标代入解析式得出关于ϕ的表达式，结合条件2πϕ<可得出ϕ的值.【详解】将函数()()cos 2f x x πϕϕ⎛⎫=+< ⎪⎝⎭的图象上各点的横坐标缩短到原来的12倍（纵坐标不变），得到()cos 2y x ϕ=+，再把得到的图象向左平移6π个单位长度，得到cos 2cos 263y x x ππϕϕ⎡⎤⎛⎫⎛⎫=++=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，所得函数图象关于原点对称，()32k k Z ππϕπ∴+=+∈，则()6k k Z πϕπ=+∈，2πϕ<，∴当0k =时，6π=ϕ.故答案为6π．【点睛】本题主要考查三角函数的图象和性质，结合三角函数的图象变换求出函数的解析式，以及利用函数对称性的性质是解决本题的关键，考查分析问题和解决问题的能力，属于中等题.9.若等比数列{}n a 的前n 项和12n n S c +=+，则c =______．【答案】2- 【解析】【分析】先求出1a 的值，然后由1n n n a S S -=-得出n a 在2n ≥时的表达式，然后由1a 满足()2n a n ≥，可求出c 的值. 【详解】等比数列{}n a 的前n 项和12n n S c +=+，则114a S c ==+.当2n ≥且n *∈N ，()()11122222n n n n n n n n a S S c c ++-=-=+-+=-=.14a c =+适合2n n a =，则42c +=，解得2c =-.故答案2-.【点睛】本题考查了利用等比数列的前n 项和表达式求参数，主要考查公式的运用和处理能力，考查计算能力，属于中等题．10.《算法统宗》中有如下问题：“哑子来买肉，难言钱数目，一斤少三十，八两多十八，试问能算者，合与多少肉”，意思是一个哑子来买肉，说不出钱的数目，买一斤（两）还差30文钱，买八两多十八文钱，求肉数和肉价，则该问题中，肉价是每两__________文．【答案】6 【解析】【分析】设肉价是每两x 文，根据题意列出方程可解得答案.【详解】设肉价是每两x 文，由题意得1630818x x -=+，解得6x =，即肉价是每两6文. 【点睛】本题考查中国古代著作中的数学问题，属数学文化，正确地理解题意是解题关键. 11.在∆ABC 中，M 是BC 的中点，AM ＝3，BC ＝10，则AB AC ⋅＝______________．【答案】16-【解析】此题最适合的方法是特例法．假设∆ABC 是以AB ＝AC 的等腰三角形，如图，AM ＝3，BC ＝10，AB ＝AC 34cos∠BAC＝3434100823417+-=-⨯．AB AC ⋅＝cos 16AB AC BAC ⋅∠=-12.已知函数()()2ln 2a f x x x x x a a R =--+∈在其定义域内有两个不同的极值点，则实数a 的取值范围是______．【答案】10,e ⎛⎫ ⎪⎝⎭【解析】【分析】求出函数()y f x =的定义域和导数()ln f x x ax '=-，令()0f x '=，得出ln xa x=，将问题转化为直线y a =与函数()ln xg x x=在()0,∞+上有两个交点，然后利用导数分析函数()ln xg x x=的单调性和极值，作出图象，利用数形结合思想可得出实数a 的取值范围. 【详解】由题意可知，函数()y f x =的定义域为()0,∞+，且()ln f x x ax '=-，令()0f x '=，得ln ax x =，即ln xa x =，构造函数()ln x g x x=，则直线y a =与函数()ln xg x x=在()0,∞+上有两个交点. ()21ln xg x x-'=，令()0g x '=，得x e =，列表如下： x()0,ee(),e +∞()g x ' +-()g x极大值1e所以，函数()ln xg x x=的单调递增区间为()0,e ，单调递减区间为(),e +∞，极大值为()1g e e=，如下图所示：当10a e <<时，直线y a =与函数()ln x g x x=在()0,∞+上有两个交点，因此，实数a 的取值范围是10,e ⎛⎫ ⎪⎝⎭. 故答案为10,e ⎛⎫ ⎪⎝⎭. 【点睛】本题考查了利用导数研究函数的极值点，可将极值点问题转化为导数的零点问题，并借助参变量分离法与数形结合思想求解，属于中等题.13.已知,a b 为正实数，直线y x a =-与曲线ln()y x b =+相切，则23a b+的最小值为__________. 【答案】526+【解析】【分析】设切点的坐标为00(,)x y ，利用导数的几何意义，求得1a b +=，再利用基本不等式，即可求解23a b+的最小值，得到答案. 【详解】由题意，设切点的坐标为00(,)x y ，又由函数ln()y x b =+，则1y x b'=+，又由切线的方程y x a =-可得切线的斜率为1，则011x b=+，解得01x b =-，即切点的横坐标为1b -，所以切点为(1,0)b -，代入直线方程y x a =-，得1a b +=，又因为a 、b 为正实数，则232323()2355b a a b a b a b a b ⎛⎫+=++=+++≥++ ⎪⎝⎭当且仅当a =，即2,3a b ==-5+故答案为5+【点睛】本题主要考查了导数的几何意义的应用，以及利用基本不等式求最值的应用，其中解答中利用导数的几何意义，求得1a b +=，再利用基本不等式求解是解答的关键，着重考查了推理与运算能力，属于中档试题.14.已知关于x 的不等式()3ln 2x x λ-≤有解，则整数λ的最小值为______．【答案】0 【解析】【分析】令函数()()3ln f x x x =-，利用导数求出函数()y f x =的最小值，即可得出整数λ的最小值.【详解】构造函数()()3ln f x x x =-，则()33ln ln 1x f x x x x x-'=+=-+， ()2130f x x x ''=+>对任意的0x >恒成立，所以，函数()y f x '=在()0,∞+上单调递增. 33ln 1022f ⎛⎫'=-< ⎪⎝⎭，()12ln 202f '=->.由零点存在定理知，存在3,22t ⎛⎫∈⎪⎝⎭，使得()3ln 10f t t t '=-+=.当0x t <<时，()0f x '<；当x t >时，()0f x '>. 所以，函数()y f x =在x t =处取得最小值，即()()()()()2min3393ln 316t f x f t t t t t t t t -⎛⎫⎛⎫==-=--=-=-+ ⎪ ⎪⎝⎭⎝⎭，由双勾函数的单调性可知，函数96y t t ⎛⎫=-+⎪⎝⎭在区间3,22⎛⎫ ⎪⎝⎭上单调递增，所以，当322t <<时，391622t t ⎛⎫-<-+<- ⎪⎝⎭，0x ∃>，使得()3ln 2x x λ-≤，926t tλ⎛⎫∴≥-+ ⎪⎝⎭，因此，整数λ的最小值为0. 故答案为0.【点睛】本题考查导数知识的综合运用，考查函数的单调性与最值，解题的关键就是利用极值点所满足的等式来进行代换计算，考查分类讨论的数学思想，属于中档题．二、解答题（本大题共6小题）15.已知sin()410απ+=(,)2παπ∈. （Ⅰ）求cos α的值；（Ⅱ）求sin(2)4πα-的值.【答案】(Ⅰ)35；(Ⅱ). 【解析】试题分析：（1）根据同角满足的不同命的三角公式列出方程组，求解即可．（2）根据两角和差公式得到πππsin 2sin2cos cos2sin 444ααα⎛⎫-=- ⎪⎝⎭，再由二倍角公式得到sin2α，cos2α，代入公式即可．解析：（Ⅰ）由π2sin 410α⎛⎫+= ⎪⎝⎭得，12，即1sin cos 5αα+=. ①22sin cos 1αα+= ② 由①②解得3cos 5α=-或cos α= 45. 因为ππ2α⎛⎫∈ ⎪⎝⎭，，所以3cos 5α=-. （Ⅱ）因为ππ2α⎛⎫∈ ⎪⎝⎭，3cos 5α=-,2234sin 1cos 155αα⎛⎫=-=--= ⎪⎝⎭4324sin22sin cos 25525ααα⎛⎫==⨯⨯-=- ⎪⎝⎭ 2237cos22cos 12525αα⎛⎫=-=⨯-=- ⎪⎝⎭. πππsin 2sin2cos cos2sin 444ααα⎛⎫-=- ⎪⎝⎭ 24272252252⎛⎫⎛⎫=-⨯--⨯ ⎪ ⎪⎝⎭⎝⎭ 17250=-. 点睛：本题主要考查同角三角函数的基本关系、两角和差的三角公式、二倍角的正弦公式的应用，属于基础题．一般sin cos sin cos αααα+-，，sin *cos αα，这三者我们成为三姐妹，结合22sin cos 1αα+=，可以知一求三．16.在∆ABC 中，记角A ，B ，C 的对边为a ，b ，c ，角A 为锐角，设向量(cos ,sin )m A A =，(cos ,sin )n A A =-，且12m n ⋅=．（1）求角A 的大小及向量m 与n 的夹角；（2）若5a =，求∆ABC 面积的最大值．【答案】（1）6A π=，,3m n π=；（2）5(23)4+ 【解析】分析】（1）由数量积的坐标表示得221cos sin cos 22m n A A A ⋅=-==，根据02A π<<，求；（2）三角形ABC 中，知道一边5a =和对角6A π=，利用余弦定理得关于,b c 的等式，利用基本不等式和三角形面积公式1sin 2S bc A =得ABC ∆面积的最大值．【详解】（1）221cos sin cos 22m n A A A ⋅=-==因为角为锐角，所以23A π=，6A π=根据1||cos ,2m n m n m n ⋅=⋅⋅<>=，,3m n π=（2）因为5a =，6A π=22252cos6b c bc π=+-得：5(23)bc ≤+15(23)sin 24S bc A +=≤即ABC ∆面积的最大值为5(23)4+ 17.请你设计一个包装盒，如图所示，ABCD 是边长为60cm 的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得四个点重合于图中的点P ，正好形成一个正四棱柱形状的包装盒，E 、F 在AB 上是被切去的等腰直角三角形斜边的两个端点，设AE=FB=xcm 2（1）若广告商要求包装盒侧面积S （cm ）最大，试问x 应取何值？（2）若广告商要求包装盒容积V （cm ）最大，试问x 应取何值？并求出此时包装盒的高与底面边长的比值．【答案】（1）x=15cm （2）12【解析】【详解】试题分析：（1）先设包装盒的高为，底面边长为，写出a ，h 与x 的关系式，并注明x 的取值范围，再利用侧面积公式表示出包装盒侧面积S 关于x 的函数解析式，最后求出何时它取得最大值即可；（2）利用体积公式表示出包装盒容积V 关于x 的函数解析式，利用导数知识求出何时它取得的最大值即可．设包装盒的高为，底面边长为由已知得6022,2(30),0302xa x h x x -===-<< （1）∵∴当15x =时，S 取得最大值（2）根据题意有222(2)(602)22(30)(030)V x x x x x =-=-<< ∴()6220V x x '=-．由得，(舍)或．∴当()0,?20x ∈时；当()20,?30x ∈时∴当20x时取得极大值，也是最大值，此时包装盒的高与底面边长的比值为26021222x h a x==（－）即包装盒的高与底面边长的比值为12．考点：1．函数的应用问题；2．函数的最值与导数；3．二次函数的图像与性质．18.函数()log (2)a f x ax =-.（1）当3a =时，求函数()f x 的定义域；（2）若()()log (2)a g x f x ax =-+判断()g x 的奇偶性；（3）是否存在实数a 使函数()f x 在[2,3]递增，并且最大值为1，若存在，求出a 值；若不存在，说明理由.【答案】（1）23-∞（，）（2）奇函数(3)12【解析】试题分析：（1）当3a =时，根据230x ->解得32x <；（2）化简()()log (2)log 2a a g x ax ax =--+，先判断定义域关于原点对称，然后利用奇偶性的定义，判断()()g x g x -=-，故函数为奇函数；（3）利用复合函数的单调性可知01a <<，由()31f =解得12a =，经验证符合题意. 试题解析：（1）由题意：()()log 23a f x x =-，∴230x ->，即32x <，所以函数()f x 的定义域为2,3⎛⎫-∞- ⎪⎝⎭.（2）易知()()()log 2log 2a a g x ax ax =--+，∵20ax ->且20ax +>，∴22x a a-<<关于原点对称，又∵()()()2log 2log 2log 2a a a axg x ax ax ax-=--+=+， ∴()()22log log 22aa ax axg x g x ax ax+--==-=--+，∴()g x 奇函数.（3）令2ax μ=-，∵0,1a a >≠，，∴2ax μ=-在[]2,3上单调递减，又∵函数()f x 在[]2,3递增，∴01a <<，又∵函数()f x 在[]2,3的最大值为1，∴()31f =，即()()3log 231a f a =-=，∴12a =，∵01a <<，∴12a =符合题意.即存在实数12a =，使函数()f x 在[]2,3递增，并且最大值为1 .点睛：本题主要考查函数的基本性质，考查奇偶性的判断，考查复合函数的单调性等知识.第一问考查函数的定义域，需要对数的真数大于零.第二问考查函数的奇偶性，判断的时候先判断函数的定义域是否关于原点对称，然后再判断()g x -和()g x 的关系，由此判断()g x 的单调性.复合函数单调性判断主要是根据同增异减. 19.已知数列n a 和n b 满足123(2)().n b n a a a a n N +⋅⋅=∈若n a 为等比数列，且1322,6a b b ==+（1）求n a 和n b ；（2）设11n n nc a b =-，记数列n c 的前n 项和为n S ①求n S ；②求正整数 k ，使得对任意n N +∈均有k n S S ≥.【答案】（1）a n ＝2n(n ∈N *)．b n ＝n (n ＋1)(n ∈N *)．（2）(i) S n ＝1112n n -+ (n ∈N *)．(ii)k ＝4. 【解析】【详解】解：(1)由题意123(2)().n b n a a a a n N +⋅⋅=∈，b 3－b 2＝6，知a 3＝(32(2)b b -)8.设数列{an}的公比为q,又由12a =，得231a q 4a == ，q ＝2(q ＝－2舍去)，所以数列{}n a 的通项为a n ＝2n (n ∈N *)．所以，(1)(1)2123(2)2.n n n n n a a aa ++⋅⋅==故数列{}n b 的通项为b n ＝n (n ＋1)(n ∈N *)． (2)(i)由(1)知11n n n c a b =-n 1112n n 1⎛⎫=-- ⎪+⎝⎭(n∈N*)．所以Sn ＝n 11n 12-+ (n∈N*)． (ii)因为c 1＝0，c 2>0，c 3>0，c 4>0，当n≥5时，cn ＝()()nn n 111n n 12⎡⎤+-⎢⎥+⎣⎦而()()()()()nn 1n 1n n 1n 2n 1n 2n 10222+++++-+-=>得()n5n n 156122+⨯≤<所以，当n≥5时，c n <0.综上，若对任意n∈N*恒有S k ≥S n ，则k ＝4.20.已知函数()()21,xf x x axg x e =++=（其中e 为自然对数的底数）.（1）若1a =,求函数()()·y f x g x =在区间[]2,0-上的最大值；（2）若1a =-,关于x 的方程()()·f x kg x =有且仅有一个根, 求实数k 的取值范围；（3）若对任意[]1212,0,2,x x x x ∈≠,不等式()()()()1212f x f x g x g x -<-均成立, 求实数a 的取值范围.【答案】（1）；（2）2130,,e e ⎛⎫⎛⎫⋃+∞ ⎪ ⎪⎝⎭⎝⎭；（3）[]1,22ln 2a ∈--. 【解析】【详解】试题分析：（1）求出函数的导数，得到函数的单调区间，从而求出函数的最大值即可；（2）若a=-1，关于x 的方程f （x ）=k•g （x ）有且仅有一个根，即()()21xf x x x kg x e -+==，有且只有一个根，令()21xx x h x e-+=，可得h （x ）极大=h （2）=23e ，h （x ）极小=h （1）=1e ，进而可得当k ＞23e或0＜k ＜1e 时，k=h （x ）有且只有一个根；（3）设12x x <，因为()xg x e =在[0，2]单调递增，故原不等式等价于|f （x 1）-f （x 2）|＜g （x 2）-g （x 1）在x 1、x 2∈[0，2]，且x 1＜x 2恒成立，当a≥-（e x+2x ）恒成立时，a≥-1；当a≤e x-2x 恒成立时，a≤2-2ln2，综合讨论结果，可得实数a 的取值范围试题解析：（1）当1a =时,()()()()221,'3221xxxy x x e y x x e x x e =++=++=++, 故()()·y f x g x =在[]2,1--上单调递减,[]1,0-上单调递增, 当2x =-时,23y e=, 当0x =时,1y =, 故在区间[]2,0-上max 1y =．（2）当1a =-时, 关于x 的方程为21xx x ke -+=有且仅有一个实根, 则21xx x k e-+=有且仅有一个实根, 设()21xx x h x e-+=,则()()()()()()2222111232'x xx xxx e x x e x x x x h x e e e ---+---+-===-,因此()h x 在(],1-∞和[)2,+∞上单调递减, 在[]1,2上单调递增,()()2131,2h h e e==, 如图所示, 实数k 的取值范围是2130,,e e ⎛⎫⎛⎫⋃+∞ ⎪⎪⎝⎭⎝⎭．（3）不妨设12x x <,则()()122112xx x x f x f x e ee e -<-=-恒成立．因此()()122112xxxxe ef x f x e e -<-<-恒成立, 即()()1212xxe f x e f x -<-恒成立,且()()1212x x e f x e f x +<+恒成立, 因此()xe f x -和()xe f x +均在[]0,2上单调递增,设()()()()221,1xxxxu x e f x e x ax v x e f x e x ax =+=+++=-=---,则()'20x u x e x a =++≥在上[]0,2上恒成立, 因此2x a e x ≥--在[]0,2上恒成立因此()max2x a e x≥--,而2x e x --在[]0,2上单调递减, 因此0x =时,()max21,1xe xa --=-∴≥-．由()'20x v x e x a =--≥在[]0,2上恒成立, 因此2x a e x ≤-在[]0,2上恒成立, 因此()min2xa e x≤-,设()()202xx e x x ϕ=-≤≤,则'2x e ϕ=-．当()'0x ϕ=时,ln 2x =, 因此()x ϕ在()0,ln 2内单调递减, 在()ln 2,2内单调递增,因此()()min ln 222ln 2,22ln 2x a ϕϕ==-∴≤-．综上述,[]1,22ln 2a ∈--．考点：利用导数求闭区间上函数的最值；根的存在性及根的个数判断；利用导数研究函数的单调性。

2021-2022学年江苏省淮阴中学、海门中学、姜堰中学高三(上)期中数学试卷(学生版+解析版)

2021-2022学年江苏省淮阴中学、海门中学、姜堰中学高三（上）期中数学试卷一、单项选择题：（每题5分，共40分）1．（5分）已知集合A ＝{1，2}，B ＝{a ，1}，若A ∪B ＝{1，2，3}，则实数a 的值为（） A ．1B ．2C ．3D ．42．（5分）若复数z 的满足z （1+2i ）＝﹣3+4i （i 是虚数单位），则复数z 的实部是（） A ．1B ．2C ．iD ．﹣2i3．（5分）在△ABC 中，角A ，B ，C 所对应的边分别为a ，b ，c ，若A ＝60°，B ＝75°，a ＝2，则边长c 的值为（） A ．2√33B ．2√63C ．3√22D ．2√234．（5分）已知非零向量a →，b →满足a →⊥（a →−2b →），且|a →|＝|b →|，则向量a →，b →的夹角为（） A ．π6B ．π4C ．π3D ．2π35．（5分）已知函数f （x ）＝e x ﹣e ﹣x ﹣2sin x ，则关于x 的不等式f （x 2﹣3）+f （2x ）＜0的解集为（） A ．（﹣3，1）B ．（﹣1，3）C ．（﹣∞，﹣3）∪（1，+∞）D ．[﹣1，3]6．（5分）2sin80°−sin20°cos20°的值为（）A ．1B ．√2C ．√3D ．27．（5分）函数f （x ）={log 2x −2x ，x ＞0sin(ωx +π3)，−π≤x ≤0有且仅有2个零点，则正数ω的取值范围是（） A ．(43，73]B ．[43，73)C ．(43，73)D ．[43，73]8．（5分）已知实数a =35，b ＝cos1，c =1−(log 52)21+(log 52)2，则a ，b ，c 的大小关系为（）A ．a ＞b ＞cB ．c ＞a ＞bC ．b ＞a ＞cD ．b ＞c ＞a二、多选题：（选错不得分，漏选得2分，每题5分，共20分） 9．（5分）已知a ＞b ，则下列结论正确的是（）A ．a +b ＞2bB ．1a＜1bC ．ac ＞bcD ．e a ﹣c +a ＞e b ﹣c +b10．（5分）如图，在平行四边形ABCD 中，已知F ，E 分别是靠近C ，D 的四等分点，则下列结论正确的是（）A ．EF →=12AB →B ．AF →=−34AB →+AD →C ．BE →=−34AB →+AD →D ．BE →•AF →=（AD →）2−910（AB →）211．（5分）关于函数f （x ）＝tan （|x |+π4），则下列判断正确的有（） A ．f （x ）的图像关于y 轴对称B ．f （x ）的最小正周期为πC ．f （x ）在区间（0，π4）上单调递增D ．f （x ）的图像关于点（3π4，0）对称12．（5分）红星照耀中国，五角星有着丰富的数学内涵与文化．如图所示，正五边形ABCDE 的边长a 1，正五边形A 1B 1C 1D 1E 1边长为a 2，正五边形A 2B 2C 2D 2E 2边长为a 3，……，依次下去，正五边形A n ﹣1B n ﹣1C n ﹣1D n ﹣1E n ﹣1边长为a n ，记∠ACE ＝α，则下列结论中正确的是（）A ．{a n }是公长对3−√52的等比数列B ．{a n }是公比为√5−12的等比数列C ．cos α=√5+14D ．对任意θ∈R ，cos θ+cos （θ+2α）+cos （θ+4α）+cos （θ+6α）+cos （θ+8α）＝0 三、填空题：（每题5分，共20分）13．（5分）定义R 上的函数f （x ）的周期为4，且x ∈[﹣2，2）时，f （x ）={−tan πx4，0＜x ＜2|x +12|，−2≤x ≤0，则f （f （2021））＝．14．（5分）函数f （x ）＝x ﹣alnx （a ≠0）与直线y ＝2x 相切，则实数a 的值为． 15．（5分）已知a x ＝b 2y ＝2，ab ＝4，a ＞1，b ＞1，则x +y 的最小值为． 16．（5分）已知函数f （x ）=1x−1+1x−2+1x−3，g （x ）＝x ﹣2，则关于x 的方程f （x ）＝g （x ）的实数根之和为；定义区间（a ，b ），[a ，b ），（a ，b ]，[a ，b ]的长度均为b ﹣a ，则f （x ）=1x−1+1x−2+1x−3≥1的解集全部区间长度之和为．四、解答题：本大题共6小题，解答时应写出文字说明、证明过程或演算步骤．17．（10分）在公差不为0的等差数列{a n }中，前n 项和为S n ，S 4＝2（a 4+1），a 22+a 62＝a 42+a 52．（1）求数列{a n }的通项公式；（2）若b n =1a n ⋅a n+1，求数列{b n }的前n 项和为T n ．18．（12分）已知函数f （x ）＝A sin （ωx +φ）（A ＞0，ω＞0，−π2＜φ＜π2)的部分图象如图所示．（1）求函数f （x ）的解析式；（2）若f （θ）=513，求sin2θ的值．19．（12分）如图，在△ABC 中，AE →=12AB →，点D 是AC 上一点，BD 与CE 交于点P ，且AP →=25AB →+15AC →．（1）若AC →=λAD →，求实数λ的值；（2）若AP →•BC →=0，求证：tan B ＝2tan C ．20．（12分）已知函数f （x ）＝lnx ﹣ax 2+x ．（1）若对任意实数x ∈（0，+∞），都有f （x ）＜0恒成立，求实数a 的取值范围；（2）当a =12时，若f （x 1）+f （x 2）＝1，求x 1+x 2的最小值．21．（12分）深圳别称“鹏城”，是中国的窗口，“深圳之光”摩天轮是中国之眼，如图Ⅰ，代表着开拓创新、包容开放的精神，向世界展示着中国自信，摩天轮的半径为6（单位：10m ），圆心O 在水平地面上的射影点为A ，摩天轮上任意一点P 在水平地面上的射影点都在直线l 上，水平地面上有三个观景点B 、C 、D ，如图Ⅱ所示，其中在三角形ABC 中，AB ＝AC ，BD ＝8DC ，∠BAD ＝90°，BC ∥l ，∠OBA ＝45°，记OA ＝a （单位：10m ）．（1）求cos ∠ABC 的值；（2）因安全因素考虑，观景点B 与摩天轮上任意一点P 的之间距离不超过√239（单位：10m ），求实数a 的取值范围．22．（12分）已知函数f （x ）＝（2﹣x ）e x +（1﹣2a ）x ，g （x ）＝ax 2﹣lnx ．（1）讨论函数g （x ）＝ax 2﹣lnx 的单调性；（2）函数h （x ）＝|f （x ）|+g （x ）在x ＝1处取得极小值，求实数a 的取值范围．2021-2022学年江苏省淮阴中学、海门中学、姜堰中学高三（上）期中数学试卷参考答案与试题解析一、单项选择题：（每题5分，共40分）1．（5分）已知集合A ＝{1，2}，B ＝{a ，1}，若A ∪B ＝{1，2，3}，则实数a 的值为（） A ．1B ．2C ．3D ．4【解答】解：∵集合A ＝{1，2}，B ＝{a ，1}，A ∪B ＝{1，2，3}，∴实数a ＝3．故选：C ．2．（5分）若复数z 的满足z （1+2i ）＝﹣3+4i （i 是虚数单位），则复数z 的实部是（） A ．1B ．2C ．iD ．﹣2i【解答】解：∵z （1+2i ）＝﹣3+4i ， ∴z =−3+4i 1+2i =(−3+4i)(1−2i)(1+2i)(1−2i)=1+2i ， ∴复数z 的实部为1．故选：A ．3．（5分）在△ABC 中，角A ，B ，C 所对应的边分别为a ，b ，c ，若A ＝60°，B ＝75°，a ＝2，则边长c 的值为（） A ．2√33B ．2√63C ．3√22D ．2√23【解答】解：由题可得C ＝45°，再由正弦定理asinA =csinC可得c =asinC sinA =2×√2232=2√63，故选：B ．4．（5分）已知非零向量a →，b →满足a →⊥（a →−2b →），且|a →|＝|b →|，则向量a →，b →的夹角为（） A ．π6B ．π4C ．π3D ．2π3【解答】解：根据题意，设向量a →，b →的夹角为θ，若a →⊥（a →−2b →），则有a →•（a →−2b →）=a →2﹣2a →•b →=0，又由|a →|＝|b →|，则cos θ=12，又由0≤θ≤π，则θ=π3，故选：C ．5．（5分）已知函数f （x ）＝e x ﹣e ﹣x ﹣2sin x ，则关于x 的不等式f （x 2﹣3）+f （2x ）＜0的解集为（） A ．（﹣3，1）B ．（﹣1，3）C ．（﹣∞，﹣3）∪（1，+∞）D ．[﹣1，3]【解答】解：∵f （x ）＝e x ﹣e ﹣x ﹣2sin x ，f （﹣x ）＝e ﹣x ﹣e x +2sin x ， ∴f （x ）＝﹣f （﹣x ），故函数f （x ）为奇函数． f ′（x ）＝e x +e ﹣x ﹣2cos x ≥2﹣2cos x ≥0，则f （x ）在R 上为增函数．则f （x 2﹣3）+f （2x ）＜0，化简得f （x 2﹣3）＜﹣f （2x ），即f （x 2﹣3）＜f （﹣2x ），又∵f （x ）为增函数， ∴x 2﹣3＜﹣2x ，解得﹣3＜x ＜1．故选：A ． 6．（5分）2sin80°−sin20°cos20°的值为（）A ．1B ．√2C ．√3D ．2【解答】解：原式=2sin(60°+20°)−sin20°cos20°=√3cos20°+sin20°−sin20°cos20°=√3．故选：C ．7．（5分）函数f （x ）={log 2x −2x ，x ＞0sin(ωx +π3)，−π≤x ≤0有且仅有2个零点，则正数ω的取值范围是（） A ．(43，73]B ．[43，73)C ．(43，73)D ．[43，73]【解答】解：x ＞0时，f （x ）＝log 2x ﹣2x ，∴f '（x ）=1xln2−2=1−xln4xln2，令f '（x ）＝0，x =1ln4， ∴f '（x ）在（0，1ln4）递增，在（1ln4，+∞）递减．∵1ln4∈（0，1），而x ∈（0，1）时，f （x ）＜0，∴f （x ）的最大值为f （1ln4）＜0，∴x ＞0时，f （x ）无零点．∴x ≤0，f （x ）有两个零点，﹣2π＜﹣ωπ+π3≤−π，43≤ω＜73．故选：B ．8．（5分）已知实数a =35，b ＝cos1，c =1−(log 52)21+(log 52)2，则a ，b ，c 的大小关系为（）A ．a ＞b ＞cB ．c ＞a ＞bC ．b ＞a ＞cD ．b ＞c ＞a【解答】解：∵cos x 在（0，π2）上单调递减，∴cos1≈cos57°＜cos53°＝0.6，∴cos1＜35，即b ＜a ； c =1−(log 52)21+(log 52)2=−1+21+(log 52)2；∵0＜log 52＜log 5√5=12，∴35＜−1+21+(log 52)2＜1，∴b ＜a ＜c ．故选：B ．二、多选题：（选错不得分，漏选得2分，每题5分，共20分） 9．（5分）已知a ＞b ，则下列结论正确的是（） A ．a +b ＞2b B ．1a＜1bC ．ac ＞bcD ．e a ﹣c +a ＞e b ﹣c +b【解答】解：对于A ，∵a ＞b ，b ＝b ， ∴a +b ＞b +b ＝2b ，故A 正确，对于B ，令a ＝1，b ＝﹣1，满足a ＞b ，1a＞1b，故B 错误，对于C ，当c ＝0时，ac ＝bc ，故C 错误，对于D ，∵a ﹣c ＞b ﹣c ， ∴e a ﹣c ＞e b ﹣c ，又∵a ＞b ，∴由不等式的可加性可得，e a ﹣c +a ＞e b ﹣c +b ，故D 正确．故选：AD ．10．（5分）如图，在平行四边形ABCD 中，已知F ，E 分别是靠近C ，D 的四等分点，则下列结论正确的是（）A ．EF →=12AB →B ．AF →=−34AB →+AD →C ．BE →=−34AB →+AD →D ．BE →•AF →=（AD →）2−910（AB →）2【解答】解：A ：∵F ，E 分别是靠近C ，D 的四等分点，∴EF →=12AB →，∴A 正确，B ：∵F 是靠近C 的四等分点，∴AF →=AD →+DF →=AD →+34DC →=34AB →+AD →，∴B 错误，C ：∵E 是靠近D 的四等分点，∴BE →=BC →+CE →=AD →+34CD →=−34AB →+AD →，∴C 正确，D ：∵BE →•AF →=（−34AB →+AD →）•（34AB →+AD →）=AD →2−916AB →2，∴D 错误，故选：AC ．11．（5分）关于函数f （x ）＝tan （|x |+π4），则下列判断正确的有（） A ．f （x ）的图像关于y 轴对称B ．f （x ）的最小正周期为πC ．f （x ）在区间（0，π4）上单调递增D ．f （x ）的图像关于点（3π4，0）对称【解答】解：显然f （﹣x ）=tan(|−x|+π4)=tan(|x|+π4)=f （x ），故f （x ）是偶函数，故A 正确；因为f(−π4)=tan π2不存在，而f(−π4+π)=f(3π4)=tan π＝0，显然f （−π4）≠f(3π4)，故B 错误；x ∈(0，π4)时，f(x)=tan(x +π4)满足π4＜x +π4＜π2，因为y ＝tan x 在（π4，π2）上单调递增，故原函数f （x ）在区间（0，π4）上单调递增，故C 正确；因为f （−π3）=√3+11−3=−2−√3，f （3π2+π3）=tan π12，结合tan π6=2tan π121−tan 2(π12)=√33解得tanπ12=2−√3，因为f(−π3)+f(3π2+π3)≠0，故f （x ）的图像不关于点（3π4，0）对称，故D 错误．故选：AC ．12．（5分）红星照耀中国，五角星有着丰富的数学内涵与文化．如图所示，正五边形ABCDE 的边长a 1，正五边形A 1B 1C 1D 1E 1边长为a 2，正五边形A 2B 2C 2D 2E 2边长为a 3，……，依次下去，正五边形A n ﹣1B n ﹣1C n ﹣1D n ﹣1E n ﹣1边长为a n ，记∠ACE ＝α，则下列结论中正确的是（）A ．{a n }是公长对3−√52的等比数列 B ．{a n }是公比为√5−12的等比数列C ．cos α=√5+14D ．对任意θ∈R ，cos θ+cos （θ+2α）+cos （θ+4α）+cos （θ+6α）+cos （θ+8α）＝0 【解答】解：由正五边形的性质得∠ACE =α=π5，所以∠D 1AC 1＝α，作∠AD 1C 1＝α的角平分线D 1M ，取D 1C 1中点N ，连接AN ，则AN ⊥D 1C 1，所以∠AD 1M ＝∠C 1D 1M ＝α，所以MD 1＝MA ＝D 1C 1．令MD 1＝MA ＝D 1C 1＝1，MC 1＝x ，则C 1M C 1D 1=C 1D 1AC 1，所以1＝x （x +1），解得x =√5−12，所以cosC 1=cos2α=C 1N C 1A =√5−14，所以cos 2α=12(1+cos2α)=12⋅√5+34=√5+38=2√5+616=(√5+14)2，所以cosα=√5+14，故C 选项正确；因为a 2＝1，△ABE △C 1AE ，所以AB BE=AC 1AE，即12⋅√5+12+a 2=√5+12a 1，所以a 12=(√5+2)(√5+1)2=7+3√52，所以(a2a 1)2=27+3√5=2(7−3√5)4=(3−√52)2，即q =3−√52，故A 选项正确，B 选项错误；由于5α＝π，则10α＝2π，所以cos θ+cos （θ+2α）+cos （θ+4α）+cos （θ+6α）+cos （θ+8α）＝cos θ+cos （θ+2α）+cos （θ+4α）+cos[（θ﹣4α）+10α]+cos[（θ﹣2α）+10α] ＝cos θ+cos （θ+2α）+cos （θ+4α）+cos （θ﹣4α）+cos （θ﹣2α）＝cos θ+2cos θcos4α+2cos θcos2α＝cos θ（1+2cos4α+2cos2α）＝cos θ[1+2⋅（2cos 22α﹣1）+2cos2α]＝cos θ（4cos 22α+2cos2α﹣1） =cosθ[4×(√5−14)2+√5−12−1]=0，故D 选项正确．故选：ACD ．三、填空题：（每题5分，共20分）13．（5分）定义R 上的函数f （x ）的周期为4，且x ∈[﹣2，2）时，f （x ）={−tan πx4，0＜x ＜2|x +12|，−2≤x ≤0，则f （f （2021））＝12．【解答】解：定义R 上的函数f （x ）的周期为4，且x ∈[﹣2，2）时，f （x ）={−tan πx4，0＜x ＜2|x +12|，−2≤x ≤0，则f （f （2021））＝f （f （505×4+1））＝f （f （1））＝f （﹣tan π4）＝f （﹣1）＝|﹣1+12|=12，故答案为：12．14．（5分）函数f （x ）＝x ﹣alnx （a ≠0）与直线y ＝2x 相切，则实数a 的值为 ﹣e ．【解答】解：设切点为（m ，n ），由f （x ）＝x ﹣alnx ，得f ′（x ）＝1−ax ，则{1−am=22m =m −alnm，解得：m ＝e ，a ＝﹣e ．故答案为：﹣e ．15．（5分）已知a x ＝b 2y ＝2，ab ＝4，a ＞1，b ＞1，则x +y 的最小值为 34+√22．【解答】解：∵a x＝2，b 2y＝2，∴a =21x （a ＞1，x ＞0），b =212y （b ＞1，y ＞0）；∵ab ＝4，∴21x×212y =4，1x+12y=2，∴x +y =12×（1x +12y ）（x +y ）=12×（32+y x +x 2y）， ∵x ＞0，y ＞0，∴y x＞0，x 2y＞0，∴yx +x2y ≥2√yx ×x2y =√2，x +y ≥12×（32+√2）=34+√22，当且仅当y x =x 2y ，1x +12y=2时取等号，∴x +y 的最小值为34+√22．故答案为：34+√22． 16．（5分）已知函数f （x ）=1x−1+1x−2+1x−3，g （x ）＝x ﹣2，则关于x 的方程f （x ）＝g （x ）的实数根之和为 8 ；定义区间（a ，b ），[a ，b ），（a ，b ]，[a ，b ]的长度均为b ﹣a ，则f （x ）=1x−1+1x−2+1x−3≥1的解集全部区间长度之和为 3 ．【解答】解：f （4﹣x ）=13−x +12−x +11−x =−f （x ），f （x ）关于（2，0）对称， f '（x ）=−1(x−1)2−1(x−2)2−1(x−3)2＜0，∴f （x ）在（﹣∞，1），（1，2），（2，3），（3，+∞）递减， x →1+时，x →+∞，x →2﹣时，x →﹣∞，x →2+时，x →+∞，x →3﹣时，x →﹣∞，x →3+时，x →+∞，作出f （x ）图像，作出g （x ）图像，则f （x ）与g （x ）有四个交点，四个实根设为t 1，t 2，t 3，t 4，则t 1+t 2+t 3+t 4＝4+4＝8，令f （x ）＝1，则x 3﹣9x 2+23x ﹣17＝0，由韦达定理可知x 1+x 2+x 3＝9， ∴x 1﹣1+x 2﹣2+x 3﹣3＝9﹣6＝3．故答案为：8；3．四、解答题：本大题共6小题，解答时应写出文字说明、证明过程或演算步骤．17．（10分）在公差不为0的等差数列{a n }中，前n 项和为S n ，S 4＝2（a 4+1），a 22+a 62＝a 42+a 52．（1）求数列{a n }的通项公式；（2）若b n =1a n ⋅a n+1，求数列{b n }的前n 项和为T n ．【解答】解：（1）设公差d 不为0的等差数列{a n }中，首项为a 1，满足S 4＝2（a 4+1），a 22+a 62＝a 42+a 52，所以{4a 1+4×32d =2×(a 1+3d)+2(a 1+d)2+(a 1+5d)2=(a 1+3d)2+(a 1+4d)2，解得{a 1=1d =2；故a n ＝2n ﹣1；（2）由（1）得：b n =1a n ⋅a n+1=1(2n−1)(2n+1)=12(12n−1−12n+1)；所以T n =12(1−13+13−15+...+12n−1−12n+1)=12(1−12n+1)=n2n+1．18．（12分）已知函数f （x ）＝A sin （ωx +φ）（A ＞0，ω＞0，−π2＜φ＜π2)的部分图象如图所示．（1）求函数f （x ）的解析式；（2）若f （θ）=513，求sin2θ的值．【解答】解：（1）根据函数f （x ）＝A sin （ωx +φ）（A ＞0，ω＞0，−π2＜φ＜π2)的部分图象，可得A ＝1，可得：f （0）＝sin φ=√22，可得：φ=π4，可得f （x ）＝sin （ωx +π4），又f （−π4）＝sin （−π4ω+π4）＝0，可得：−π4ω+π4=k π，k ∈Z ，解得ω＝1﹣4k ，k ∈Z ，当k ＝0时，可得ω＝1，可得函数f （x ）的解析式为f （x ）＝sin （x +π4）．（2）因为f （θ）＝sin （θ+π4）=√22×（sin θ+cos θ）=513，所以sin θ+cos θ=5√213，两边平方，可得1+sin2θ=50169，可得sin2θ=−119169．19．（12分）如图，在△ABC 中，AE →=12AB →，点D 是AC 上一点，BD 与CE 交于点P ，且AP →=25AB →+15AC →．（1）若AC →=λAD →，求实数λ的值；（2）若AP →•BC →=0，求证：tan B ＝2tan C ．【解答】解：（1）∵AC →=λAD →，∴AP →=25AB →+15AC →=25AB →+15λAD →， ∵B ，D ，P 三点共线， ∴25+15λ＝1，∴λ＝3．（2）证明：∵AP →=25AB →+15AC →，∴AP →•BC →=（25AB →+15AC →）•（AC →−AB →）=15AC →2−25AB →2+15AB →⋅AC →=0，即b 2﹣2c 2+ab cos A ＝0，∴b 2﹣2c 2+ab ×b 2+c 2−a 22bc=0，∴a 2﹣3b 2+3c 2＝0，即2（a 2+c 2﹣b 2）＝a 2+b 2﹣c 2，∴2c cos B ＝b cos C ，由正弦定理得2sin C cos B ＝sin B cos C ，∴tan B ＝2tan C ． 20．（12分）已知函数f （x ）＝lnx ﹣ax 2+x ．（1）若对任意实数x ∈（0，+∞），都有f （x ）＜0恒成立，求实数a 的取值范围；（2）当a =12时，若f （x 1）+f （x 2）＝1，求x 1+x 2的最小值．【解答】解：（1）函数f （x ）＝lnx ﹣ax 2+x ，对任意实数x ∈（0，+∞），都有lnx ﹣ax 2+x ＜0恒成立，当a ≤0时，则f （1）＝1﹣a ＞0，这与f （x ）＜0在x ∈（0，+∞）上恒成立矛盾，故舍去；当a ＞0时，f '（x ）=1x−2ax +1，因为f '（x ）在（0，+∞）上单调递减，又f ′(12a )=2a ＞0，f′(1+1a )=a a+1−2a −1＜0，故存在唯一的x 0∈(12a ，1+1a )，使得f '（x 0）＝0，即1x 0−2ax 0+1=0，且当x ∈（0，x 0）时，f '（x ）＞0，则f （x ）单调递增，当x ∈（x 0，+∞）时，f '（x ）＜0，则f （x ）单调递减，故当x ＝x 0时，f （x ）取得最大值f （x 0）=lnx 0−ax 02+x 0=lnx 0−x 0+12+x 0=lnx 0+x 02−12＜0，解得0＜x 0＜1，故a =12(1x 0+1x 02)＞1，所以实数a 的取值范围为（1，+∞）；（2）当a =12时，f(x)=lnx −12x 2+x ，若f （x 1）+f （x 2）＝1，则lnx 1−12x 12+x 1+lnx 2−12x 22+x 2=1，故ln(x 1x 2)−12(x 1+x 2)2+x 1x 2+x 1+x 2=1，所以12(x 1+x 2)2−(x 1+x 2)+1=ln （x 1x 2）+x 1x 2≤ln(x 1+x 22)2+(x 1+x 22)2，令t =x 1+x 22，则2t 2﹣2t +1≤lnt 2+t 2，即t 2﹣2t +1﹣2lnt ≤0，令h （t ）＝t 2﹣2t +1﹣2lnt ，则h '（t ）=2t −2−2t =2(t 2−t−1)t，令h '（t ）＝0，解得t =1+√52，所以当0＜t ＜1+√52时，h '（t ）＜0，则h （t ）单调递减，当t ＞1+√52时，h '（t ）＞0，则h （t ）单调递增，又h （1）＝0，h （3）＝4﹣2ln 3＞0，故h （t ）在(1+√52，3)上有唯一的零点t 0，又当1≤t ≤t 0时，h （t ）≤0，故2≤x 1+x 2≤2x 0，所以x 1+x 2的最小值为2，当且仅当x 1＝x 2＝1取等号．21．（12分）深圳别称“鹏城”，是中国的窗口，“深圳之光”摩天轮是中国之眼，如图Ⅰ，代表着开拓创新、包容开放的精神，向世界展示着中国自信，摩天轮的半径为6（单位：10m ），圆心O 在水平地面上的射影点为A ，摩天轮上任意一点P 在水平地面上的射影点都在直线l 上，水平地面上有三个观景点B 、C 、D ，如图Ⅱ所示，其中在三角形ABC 中，AB ＝AC ，BD ＝8DC ，∠BAD ＝90°，BC ∥l ，∠OBA ＝45°，记OA ＝a （单位：10m ）．（1）求cos ∠ABC 的值；（2）因安全因素考虑，观景点B 与摩天轮上任意一点P 的之间距离不超过√239（单位：10m ），求实数a 的取值范围．【解答】解：（1）设DC ＝m ，则BD ＝8m ，所以在△ABD 和△ABC 中，分别利用余弦定理得：cos ∠ABC =a 8m =a 2+8lm 2−a 22⋅9m⋅a =9m 2a，所以a 2＝36m 2⇒a ＝6m ，所以cos ∠ABC =34，（2）根据题意，观景点B 与与摩天轮上任意一点P 之间距离不超过√239，即(PB)max ≤√239，过点P 作PQ ⊥l 于Q ，连接BQ ，PB ，要使PB 尽可能的大，则点P 摩天轮同一竖直线上，且在直线m 的上方部分，且Q 在点A 的右侧，如图，设PQ ＝h ，AQ ＝x ，a ≤h ≤a +6，则（h −a ）2+x 2＝36⇒h 2+a 2+x 2−2ah ＝36，所以PB =√BQ 2+PQ 2=√AB 2+AQ 2−2AB ⋅AQ(−34)+PQ 2=√a 2+x 2+32ax +ℎ2=√36+2a ℎ+32ax =√36+a(2ℎ+32x)，令{ℎ=a +6cosθx =6sinθ，则2ℎ+32x =2a +12cosθ+9sinθ=2a +15sin(θ+φ)≤2a +15，（其中tanφ=34)，所以(PB)max =√36+2a 2+15a ≤√239， 2a 2+15a −203≤0，解得a ≤7，所以实数a的取值范围是（6，7]．22．（12分）已知函数f（x）＝（2﹣x）e x+（1﹣2a）x，g（x）＝ax2﹣lnx．（1）讨论函数g（x）＝ax2﹣lnx的单调性；（2）函数h（x）＝|f（x）|+g（x）在x＝1处取得极小值，求实数a的取值范围．【解答】解：（1）函数g（x）＝ax2﹣lnx的定义域为（0，+∞），则g'（x）=2ax−1x=2ax2−1x，所以当a≤0时，g'（x）＜0，函数g（x）在（0，+∞）上单调递减，当a＞0时，令g'（x）＝0，解得x=√12a，当x∈（0，√12a）时，g'（x）＜0，则g（x）单调递减，当x∈（√12a，+∞）时，g'（x）＞0，则g（x）单调递增，所以f（x）在（0，√12a）上单调递减，在（√12a，+∞）上单调递增．综上所述，当a≤0时，函数g（x）在（0，+∞）上单调递减；当a＞0时，f（x）在（0，√12a）上单调递减，在（√12a，+∞）上单调递增．（2）因为f（1）＝e+1﹣2a，①当f（1）＝e+1﹣2a＜0，即a＞e+12时，存在x∈（1﹣σ，1+σ）（σ为足够小的正数），使得f（x）＜0，此时h（x）＝（x﹣2）e x﹣（1﹣2a）x+ax2﹣lnx，则h'（x）＝（x﹣4）e x﹣（1﹣2a）+2ax−1 x，故h'（1）＝4a﹣2＞0，这与x＝1处取得极小值矛盾；②当f（1）＝e+1﹣2a＞0，即a＜e+12时，存在x∈（1﹣σ，1+σ）（σ为足够小的正数），使得f（x）＞0，此时h（x）＝（2﹣x）e x+（1﹣2a）x+ax2﹣lnx，则h'（x）＝（1﹣x）e x+（1﹣2a）+2ax−1 x，故h'（1）＝0，又h''（x）＝﹣xe x+2a+12，所以h'''（x）＝﹣（x+1）e x−2x3＜0恒成立，则h''（x）在（0，+∞）上单调递减，（i）若h''（x）≤0，即﹣e+2a+1≤0，a≤e−12时，此时当x＞1时，h''（x）＜0，则h'（x）单调递减，则h'（x）＜h'（1）＝0，所以h（x）在（1，+∞）上单调递减，h（x）不可能在x＝1处取得极小值，故舍去；（ii）若h''（x）＞0，即﹣e+2a+1＞0，a＞e−12时，h''（2a）=−2ae2a+2a+14a2＜14a2−4a2＜0，所以存在唯一的x0∈（1，2a），使得h''（x0）＝0，且当0＜x＜x0时，h''（x）＞0，则h'（x）单调递增，注意到h'（1）＝0，则当1﹣σ0＜x＜1时，h'（x）＜0，则h（x）单调递减，当1＜x＜min{x0，1+σ0}时，h'（x）＞0，则h（x）单调递增，所以此时满足函数h（x）在x＝1处取得极小值，故实数a的取值范围为(e−12，e+12)；③当f（1）＝e+1﹣2a＝0，即a=e+12时，存在x∈（1﹣σ1，1+σ1）（σ1为足够小的正数），使得f（x）≥0，此时h（x）＝（2﹣x）e x﹣ex+e+12x2﹣lnx，则h'（x）＝（1﹣x）e x﹣e+（e+1）x−1 x，又h'（1）＝0，则h''（x）＝﹣xe x﹣e+1+1x2，h'''（x）＝﹣（x+1）e x−2x3＜0恒成立，故h''（x）在（0，+∞）上单调递减，由于h''（1）＝2＞0，h''（2）=−2e2+e+1+14＜0所以存在唯一的x1∈（1，2），使得h''（x1）＝0，则当0＜x＜x1时，h''（x）＞0，则h'（x）单调递增，注意到h'（1）＝0，故当0＜x＜1时，h'（x）＜0，则h（x）单调递减，当1＜x＜min{x1，1+σ1}时，h'（x）＞0，则h（x）单调递增，此时满足h（x）在x＝1处取得极小值．综上所述，实数a的取值范围为(e−12，e+12]．。

2021届江苏省淮安市高三高考数学模拟试卷(202105)解析

2021年江苏省淮安市高考数学模拟试卷（5月份）一、选择题（共8小题，每小题5分，共40分）.1．已知M，N均为R的子集，且（∁R N）∩M＝∅，则M∪N＝（）A．N B．M C．∅D．R2．现有甲、乙、丙、丁、戊5种在线教学软件，若某学校要从中随机选取3种作为教师“停课不停学”的教学工具，则其中甲、乙、丙至多有2种被选取的概率为（）A．B．C．D．3．已知a为实数，复数z＝（a﹣2）+ai（ i为虚数单位），复数z的共轭复数为，若z2＜0，则1﹣＝（）A．1﹣2i B．1+2i C．2+i D．2﹣i4．设a＝sin246°，b＝cos235°﹣sin235°，，则a，b，c的大小关系为（）A．b＜c＜a B．c＜a＜b C．a＜b＜c D．b＜a＜c5．比莎斜塔是意大利的著名景点，因斜而不倒的奇特景象而世界闻名，把地球看作一个球（球心记为O），地球上的一点A的纬度是指OA与地球赤道所在平面所成角，OA的方向即为A点处的竖直方向．已知斜塔处于北纬44°，经过测量，比莎斜塔朝正南方向倾斜，且其中轴线与竖直方向的夹角为4°，则中轴线与赤道所在平面所成的角为（）A．50°B．48°C．42°D．40°6．函数f（x）＝e sinx（﹣π≤x≤π）的大致图象为（）A．B．C．D．7．某保鲜封闭装置由储物区与充氮区（内层是储物区用来放置新鲜易变质物品，充氮区是储物区外的全部空间，用来向储物区输送氮气从而实现保鲜功能）．如图所示，该装置外层上部分是半径为2半球，下面大圆刚好与高度为3的圆锥的底面圆重合，内层是一个高度为4的倒置小圆锥，小圆锥底面平行于外层圆锥的底面，且小圆锥顶点与外层圆锥顶点重合，为了保存更多物品，充氮区空间最小可以为（）A．4πB．C．D．8．已知a＞0，b＞0，且，则a，b的值不可能是（）A．B．C．D．二、选择题：本大题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，有选错的得0分，部分选对的得2分．9．若随机变量ξ～N（0，1），则下列结论正确的是（）A．该正态曲线关于直线x＝1对称B．若P（ξ≤1.52）＝0.9357，则P（ξ＞1.52）＝0.0643C．若P（ξ≤1.49）＝0.9319，则P（ξ≤﹣1.49）＝0.9319D．当x＞0时，若P（ξ≥x）＝φ（x），则P（|ξ|≥x）＝2φ（x）10．已知曲线，则下列结论正确的有（）A．曲线C关于原点对称B．曲线C是封闭图形，且封闭图形的面积大于2πC．曲线C不是封闭图形，且图形以x轴和y轴为渐近线D．曲线C与圆x2+y2＝4有4个公共点11．在三维空间中，定义向量的外积：×叫做向量与的外积，它是一个向量，满足下列两个条件：①⊥（×），⊥（×），且，和×构成右手系（即三个向量的方向依次与右手的拇指、食指、中指的指向一致，如图所示）；②×的模|×|＝||||sin＜，＞（＜，＞表示向量，的夹角）．在正方体ABCD﹣A1B1C1D1中，有以下四个结论，正确的有（）A．B．C．与方向相同D．与正方体表面积的数值相等12．甲、乙两人进行围棋比赛，共比赛2n（n∈N*）局，且每局甲获胜的概率和乙获胜的概率均为．如果某人获胜的局数多于另一人，则此人赢得比赛．记甲赢得比赛的概率为P（n），则（）A．B．C．D．P（n）的最大值为三、填空题：本大题共4小题，每小题5分，共20分．13．已知f（x）是定义在R上的周期为3的奇函数，且f（﹣1）＝2f（10）+3，则f（2021）＝．14．已知△ABC内角A，B，C的对边分别为a，b，c，那么当a＝时，满足条件“b＝2，A＝30°”的△ABC有两个．（仅写出一个a的具体数值即可）15．在的二项展开式中，常数项为．16．已知平行四边形ABCD中，AB＝3，AD＝4，∠BAD＝，平面内有动点E，满足|ED|＝2|EC|，则•的取值范围为．四、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．在△ABC中，角A，B，C所对的边分别是a，b，c，已知（a+c）（a﹣c）＝b（b+c）．（1）求角A的大小；（2）在下列三个条件中任选一个，补充在下面问题中的横线上，并解答．若b＝3，c＝4，点D是BC边上的一点，且______．求线段AD的长．①AD是△ABC的高；②AD是△ABC的中线；③AD是△ABC的角平分线．18．已知数列{a n}满足a1＝1，a2＝3，且a n+2﹣2a n+1+a n＝4，n∈N*．（1）求数列{a n}的通项公式；（2）设，n∈N*，求{b n}的最小值．19．机动车行经人行横道时，应当减速慢行；遇行人正在通过人行横道，应当停车让行，俗称“礼让行人”．下表是某市一主干道路口监控设备所抓拍的5个月内驾驶员不“礼让行人”行为统计数据：月份 1 2 3 4 5违章驾驶人次125 105 100 90 80（1）由表中看出，可用线性回归模型拟合违章人次y与月份x之间的关系，求y关于x的回归方程，并预测该路口月份不“礼让行人”违规驾驶人次；（2）交警从这5个月内通过该路口的驾驶员中随机抽查90人，调查驾驶员“礼让行人”行为与驾龄的关系，得到下表：不礼让行人礼让行人驾龄不超过2年24 16驾龄2年以上26 24能否据此判断有90%的把握认为“礼让行人行为与驾龄有关？并用一句话谈谈你对结论判断的体会．附：＝＝＝﹣．，其中n＝a+b+c+d．P（K2≥k0）0.15 0.10 0.05 0.025 0.010k0 2.072 2.706 3.841 5.024 6.63520．已知四棱锥P﹣ABCD的底面为直角梯形，AB∥CD，AD⊥CD，AB＝AD＝1，CD＝2，PD⊥平面ABCD，且PD ＝2，平面PAB与平面PCD的交线为l．（1）求证：l∥AB；（2）试建立适当的空间直角坐标系，并求点A在平面PBC上的射影A'的坐标．21．已知双曲线的离心率为2，F为双曲线C的右焦点，M为双曲线C上的任一点，且点M到双曲线C的两条渐近线距离的乘积为．（1）求双曲线C的方程；（2）设过点F且与坐标轴不垂直的直线l与双曲线C相交于点P，Q，线段PQ的垂直平分线与x轴交于点B，求的值．22．已知函数f（x）＝lnx﹣x+1，g（x）＝e x﹣1．（1）求f（x）的最大值；（2）当x∈[2，+∞）时，证明：g（x）＞2x（x﹣1）；（3）证明：．（参考数据：自然对数的底数e≈2.71828）参考答案一、选择题（共8小题，每小题5分，共40分）.1．已知M，N均为R的子集，且（∁R N）∩M＝∅，则M∪N＝（）A．N B．M C．∅D．R解：结合韦恩图可知，当M⊆N时，（∁R N）∩M＝∅，故M∪N＝N．故选：A．2．现有甲、乙、丙、丁、戊5种在线教学软件，若某学校要从中随机选取3种作为教师“停课不停学”的教学工具，则其中甲、乙、丙至多有2种被选取的概率为（）A．B．C．D．解：甲、乙、丙、丁、戊5种在线教学软件，某学校要从中随机选取3种作为教师“停课不停学”的教学工具，基本事件总数n＝＝10，甲、乙、丙至多有2种被选取包含的基本事件个数m＝＝9，则其中甲、乙、丙至多有2种被选取的概率p＝．故选：D．3．已知a为实数，复数z＝（a﹣2）+ai（ i为虚数单位），复数z的共轭复数为，若z2＜0，则1﹣＝（）A．1﹣2i B．1+2i C．2+i D．2﹣i解：z2＜0，则（a﹣2）2﹣a2+2a（a﹣2）i＜0，即4﹣4a+2a（a﹣2）i＜0，∴4﹣4a＜0，2a（a﹣2）＝0，解得a＝2．∴z＝2i，则1﹣＝1﹣（﹣2i）＝1+2i，故选：B．4．设a＝sin246°，b＝cos235°﹣sin235°，，则a，b，c的大小关系为（）A．b＜c＜a B．c＜a＜b C．a＜b＜c D．b＜a＜c解：因为sin45°＜sin46°＜sin60°，所以＜sin46°＜，所以sin246°＜，可得；因为b＝cos235°﹣sin235°＝1﹣2sin235°，又sin30°＜sin35°＜sin45°，所以＜sin235°＜，所以﹣1＜﹣2sin235°＜﹣，所以1﹣2sin235°∈（0，），即0，所以a＞b，又＝•＝tan64°，因为tan64°＞tan60°，可得tan64°，可得c＝tan64°＞＞，所以c＞a，综上，可得c＞a＞b．故选：D．5．比莎斜塔是意大利的著名景点，因斜而不倒的奇特景象而世界闻名，把地球看作一个球（球心记为O），地球上的一点A的纬度是指OA与地球赤道所在平面所成角，OA的方向即为A点处的竖直方向．已知斜塔处于北纬44°，经过测量，比莎斜塔朝正南方向倾斜，且其中轴线与竖直方向的夹角为4°，则中轴线与赤道所在平面所成的角为（）A．50°B．48°C．42°D．40°解：如图所示，AP为比莎斜塔的中轴线，∠AOD＝44°，∠BAP＝4°，则∠PAC＝40°，即中轴线与赤道所在平面所成的角为40°．故选：D．6．函数f（x）＝e sinx（﹣π≤x≤π）的大致图象为（）A．B．C．D．解：由函数f（x）＝e sinx（﹣π≤x≤π），可知y＝e t是单调递增的函数，而函数y＝sinx在[）和单调递减；在（）单调递增，由此可得原函数函数f（x）＝e sinx在[）和单调递减；在（）单调递增，所以符合的只有B选项，故选：B．7．某保鲜封闭装置由储物区与充氮区（内层是储物区用来放置新鲜易变质物品，充氮区是储物区外的全部空间，用来向储物区输送氮气从而实现保鲜功能）．如图所示，该装置外层上部分是半径为2半球，下面大圆刚好与高度为3的圆锥的底面圆重合，内层是一个高度为4的倒置小圆锥，小圆锥底面平行于外层圆锥的底面，且小圆锥顶点与外层圆锥顶点重合，为了保存更多物品，充氮区空间最小可以为（）A．4πB．C．D．解：设半球的半径为R，则R＝2，小圆锥的高为4，大圆锥的高为3，整个保鲜封闭装置的体积为＝，小圆锥的半径为r，则r2＝R2﹣（4﹣3）2＝22﹣1＝3，所以，故小圆锥的体积为，所以充氮区空间最小可以为．故选：B．8．已知a＞0，b＞0，且，则a，b的值不可能是（）A．B．C．D．解：∵，a＞0，b＞0，∴，y（a）＝在a∈（0，+∞）上为增函数，在b∈（0，+∞）上为减函数，当a＝2时，y（2）＝，∵b＝sin31°＞，y（b）＜＝，即左边大于右边，故选项A错误，＞2，则，，则，即左边大于右边，故选项B错误，当a＝1时，，b＝2＞1，，则左边小于右边，故选项D错误．故选：C．二、选择题：本大题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，有选错的得0分，部分选对的得2分．9．若随机变量ξ～N（0，1），则下列结论正确的是（）A．该正态曲线关于直线x＝1对称B．若P（ξ≤1.52）＝0.9357，则P（ξ＞1.52）＝0.0643C．若P（ξ≤1.49）＝0.9319，则P（ξ≤﹣1.49）＝0.9319D．当x＞0时，若P（ξ≥x）＝φ（x），则P（|ξ|≥x）＝2φ（x）解：由已知得，该分布为标准正态分布曲线，且μ＝0，σ＝1．对称轴为x＝0，故A错；因为P（ξ≤1.52+P（ξ＞1.52）＝1，故B正确；因为对称轴为x＝0，故P（ξ≤1.49）＝0.9319＝P（ξ≥﹣1.49）＝0.9319，故C错误；由对称轴为x＝0可知，当x＞0时，若P（ξ≥x）＝φ（x），则P（ξ≤﹣x）＝P（ξ≥x）＝φ（x），故P（|ξ|≥x）＝2φ（x），D正确．故选：BD．10．已知曲线，则下列结论正确的有（）A．曲线C关于原点对称B．曲线C是封闭图形，且封闭图形的面积大于2πC．曲线C不是封闭图形，且图形以x轴和y轴为渐近线D．曲线C与圆x2+y2＝4有4个公共点解：由于（x，y）与（﹣x，﹣y）都满足方程，故曲线C关于原点对称，A正确；当x→+∞时，|y|→1，∴曲线C不是封闭曲线，且x轴不是图形的渐近线，故BC错误；联立，解得或或或．∴曲线C与圆x2+y2＝4有4个公共点，故D正确．故选：AD．11．在三维空间中，定义向量的外积：×叫做向量与的外积，它是一个向量，满足下列两个条件：①⊥（×），⊥（×），且，和×构成右手系（即三个向量的方向依次与右手的拇指、食指、中指的指向一致，如图所示）；②×的模|×|＝||||sin＜，＞（＜，＞表示向量，的夹角）．在正方体ABCD﹣A1B1C1D1中，有以下四个结论，正确的有（）A．B．C．与方向相同D．与正方体表面积的数值相等解：对于A，由×模的定义知，|×|＝||||sin＜，＞＝||||sin＜，＞＝|×|，所以A对；对于B，由，和×构成右手系知，×与×方向相反，再由A知，×＝﹣×，所以B错；对于C，A1C1⊥B1D1，A1C1⊥BB1⇒A1C1⊥平面BB1D1D，BD1⊂平面BB1D1D⇒BD1⊥A1C1，BD1⊥A1D，再由右手系知，与同向，所以C对；对于D，正方体棱长为a，＝＝6a•a•＝6a2，正方体表面积为6a2，所以D对．故选：ACD．12．甲、乙两人进行围棋比赛，共比赛2n（n∈N*）局，且每局甲获胜的概率和乙获胜的概率均为．如果某人获胜的局数多于另一人，则此人赢得比赛．记甲赢得比赛的概率为P（n），则（）A．B．C．D．P（n）的最大值为解：若甲、乙比赛4局甲获胜，则甲在4局比赛中至少胜3局，∴P（2）＝＝，故A错误；若甲、乙比赛6局甲获胜，则甲在6局比赛中至少胜4局，∴P（3）＝＝，故B错误；在2n局比赛中甲获胜，则甲胜的局数至少为n+1局，∴P（n）＝+•••+＝（）•（）2n＝＝，故C正确；∵P（n）＝，∴当n＝1时，P（n）取最大值，故D正确．故选：CD．三、填空题：本大题共4小题，每小题5分，共20分．13．已知f（x）是定义在R上的周期为3的奇函数，且f（﹣1）＝2f（10）+3，则f（2021）＝ 1 ．解：∵f（x）是定义在R上的周期为3的奇函数，∴f（10）＝f（1）＝﹣f（﹣1），∵f（﹣1）＝2f（10）+3，∴f（﹣1）＝﹣2f（﹣1）+3，∴f（﹣1）＝1，∴f（2021）＝f（﹣1）＝1，故答案为：1．14．已知△ABC内角A，B，C的对边分别为a，b，c，那么当a＝ 1.5 时，满足条件“b＝2，A＝30°”的△ABC有两个．（仅写出一个a的具体数值即可）解：由正弦定理得，所以sinB＝，由△ABC有两个得B有两个，可能为锐角，也可能为钝角，所以B＞A，sinB＜1所以b＞a，＜1，即1＜a＜2，故答案为：1.5．（答案不唯一）．15．在的二项展开式中，常数项为10 ．解：的通项公式为T k+1＝x5﹣k＝（﹣1）k x5﹣2k，∴常数项为x•（﹣1）3x﹣1+••（﹣1）2•x＝2﹣＝10．故答案为：10．16．已知平行四边形ABCD中，AB＝3，AD＝4，∠BAD＝，平面内有动点E，满足|ED|＝2|EC|，则•的取值范围为[12，24] ．解：因为平行四边形ABCD中，AB＝3，AD＝4，∠BAD＝，建立如图所示坐标系，则A（0，0），B（3，0），C（5，2），D（2，2），设E（x，y），∵平面内有动点E，满足|ED|＝2|EC|，∴（x﹣2）2+（y﹣2）2＝4[（x﹣5）2+（y﹣2）2]，即：（x﹣6）2+（y﹣2）2＝4，故（x﹣6）2≤4⇒4≤x≤8，∵•＝＝（3，0）•（x，y）＝3x∈[12，24]．故答案为：[12，24]．四、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．在△ABC中，角A，B，C所对的边分别是a，b，c，已知（a+c）（a﹣c）＝b（b+c）．（1）求角A的大小；（2）在下列三个条件中任选一个，补充在下面问题中的横线上，并解答．若b＝3，c＝4，点D是BC边上的一点，且______．求线段AD的长．①AD是△ABC的高；②AD是△ABC的中线；③AD是△ABC的角平分线．解：（1）在△ABC中，a，b，c分别为A，B，C所对的边，且（a+c）（a﹣c）＝b（b+c），可得a2﹣c2＝b2+bc，由余弦定理可得cosA＝＝﹣．∵0＜A＜π，∴．（2）选②AD是△ABC的中线，∵AD是△ABC的中线，∴，∴，∵b＝3，c＝4，，∴＝，∴＝．18．已知数列{a n}满足a1＝1，a2＝3，且a n+2﹣2a n+1+a n＝4，n∈N*．（1）求数列{a n}的通项公式；（2）设，n∈N*，求{b n}的最小值．解：（1）∵a n+2﹣2a n+1+a n＝4，n∈N*，∴a n+2﹣a n+1﹣（a n+1﹣a n）＝4，n∈N*．∴数列{a n+1﹣a n}为等差数列，首项为a2﹣a1＝3﹣1＝2，公差为4，∴a n+1﹣a n＝2+4（n﹣1）＝4n﹣2，∴a n＝（a n﹣a n﹣1）+（a n﹣1﹣a n﹣2）+……+（a2﹣a1）+a1＝4（n﹣1）﹣2+4（n﹣2）﹣2+……+4×1﹣2+1＝+1＝2（n﹣1）2+1．∴a n＝2（n﹣1）2+1．（2）＝+1＝2n+﹣3≥2×﹣3＝1，当且仅当n＝1时取等号，∴{b n}的最小值为1．19．机动车行经人行横道时，应当减速慢行；遇行人正在通过人行横道，应当停车让行，俗称“礼让行人”．下表是某市一主干道路口监控设备所抓拍的5个月内驾驶员不“礼让行人”行为统计数据：月份 1 2 3 4 5违章驾驶人次125 105 100 90 80（1）由表中看出，可用线性回归模型拟合违章人次y与月份x之间的关系，求y关于x的回归方程，并预测该路口月份不“礼让行人”违规驾驶人次；（2）交警从这5个月内通过该路口的驾驶员中随机抽查90人，调查驾驶员“礼让行人”行为与驾龄的关系，得到下表：不礼让行人礼让行人驾龄不超过2年24 16驾龄2年以上26 24能否据此判断有90%的把握认为“礼让行人行为与驾龄有关？并用一句话谈谈你对结论判断的体会．附：＝＝＝﹣．，其中n＝a+b+c+d．P（K2≥k0）0.15 0.10 0.05 0.025 0.010k0 2.072 2.706 3.841 5.024 6.635解：（1）由已知得：，．，，所以＝，．故．所以x＝9时，，即可预测该路口9月份不“礼让行人”的违章驾驶人次约为46．（2）由题意，得2×2列联表为：不礼让行人礼让行人合计驾龄不超过1年24 16 40驾龄1年以上16 14 30合计40 30 70≈0.311＜2.706．所以没有90%的把握认为礼让行人的行为与驾龄有关．文明驾驶、安全驾驶是行车驾车的基本要求．20．已知四棱锥P﹣ABCD的底面为直角梯形，AB∥CD，AD⊥CD，AB＝AD＝1，CD＝2，PD⊥平面ABCD，且PD ＝2，平面PAB与平面PCD的交线为l．（1）求证：l∥AB；（2）试建立适当的空间直角坐标系，并求点A在平面PBC上的射影A'的坐标．解：（1）证明：因为AB∥CD，AB⊂平面PAB，AB⊄平面PCD，CD⊂平面PCD，所以AB∥平面PCD，因为平面PAB∩平面PCD＝l，所以AB∥l．（2）以D为原点，以DA，DC，DP为坐标轴建立空间直角坐标系，可得A（1，0，0），B（1，1，0），C（0，2，0），P（0，0，2），＝（1，1，﹣2），＝（0，2，﹣2），可得设平面PBC的法向量为＝（x，y，z），所以，即，令y＝1，则x＝1，z＝1，所以（1，1，1），设A′的坐标为（x0，y0，z0），AA′＝（x0﹣1，y0，z0），由AA′∥，可得＝＝，所以x0﹣1＝y0＝z0，可得＝（1﹣x0，1﹣y0，﹣z0），因为⊥，所以1﹣x0+1﹣y0﹣z0＝0，所以2＝x0+y0+z0，所以2＝x0+x0﹣1+x0﹣1，解得x0＝，y0＝，z0＝，所以点A在平面PBC的射影A′的坐标为（，，）．21．已知双曲线的离心率为2，F为双曲线C的右焦点，M为双曲线C上的任一点，且点M到双曲线C的两条渐近线距离的乘积为．（1）求双曲线C的方程；（2）设过点F且与坐标轴不垂直的直线l与双曲线C相交于点P，Q，线段PQ的垂直平分线与x轴交于点B，求的值．解：（1）由题意可得，渐近线的方程为bx±ay＝0，设M（x，y），则•＝＝，又＝2，即c2＝4a2，所以b2＝3a2，所以a2＝1，b2＝3，所以双曲线的方程为x2﹣＝1．（2）由（1）知，F（2，0），设直线l的方程为y＝k（x﹣2），联立x2﹣＝1，得（3﹣k2）x2+4k2x﹣4k2﹣3＝0，所以△＝16k4+4（4k2+3）（3﹣k2）＝36（k2+1）＞0，若P（x1，y1），Q（x2，y2），则x1+x2＝，x1x2＝，所以|PQ|＝|x1﹣x2|＝•＝||，所以y1+y2＝k（x1+x2﹣4）＝，所以PQ的中点坐标为（，），所以线段PQ的垂直平分线的方程为y＝﹣（x﹣）+，整理得y＝﹣x+，所以B（，0），则|BF|＝|﹣2|＝||，所以＝1．22．已知函数f（x）＝lnx﹣x+1，g（x）＝e x﹣1．（1）求f（x）的最大值；（2）当x∈[2，+∞）时，证明：g（x）＞2x（x﹣1）；（3）证明：．（参考数据：自然对数的底数e≈2.71828）（1）解：∵f（x）＝lnx﹣x+1 （x＞0）∴f′（x）＝﹣1＝，∴当0＜x＜1时，f′（x）＞0，x＞1时，f′（x）＜0，∴f（x）≤f（1）＝0，∴f（x）的最大值为0；（2）证明：设h（x）＝e x﹣1﹣2x（x﹣1）＝e x﹣2x2+2x﹣1，故h′（x）＝e x﹣4x+2，h″（x）＝e x﹣4，x∈[2，+∞）时，h″（x）＞0，故h′（x）在[2，+∞）递增，故h′（x）≥h′（2）＝e2﹣6＞0，h（x）在[2，+∞）递增，故h（x）≥h（2）＝e2﹣5＞0恒成立，故当x∈[2，+∞）时：g（x）＞2x（x﹣1）；（3）证明：要证：．即证：ln（1+）+ln（1+）+…+ln（1+）＜ln，由（1）可知：x＞0，lnx≤x﹣1，故ln（1+x）＜x对于x∈（0，+∞）恒成立，∵∀n∈N*，n≥2，0＜＜1，∴ln（1+）＜，而依据第（2）问当x∈[2，+∞）时，e x﹣1＞2x（x﹣1），故n≥2时，＜＝（﹣），故ln（1+）+ln（1+）+…+ln（1+）＜++…+＜（1﹣+﹣+…+﹣）＝﹣＜，又∵e＜＝，∴＜，即＜ln，故ln（1+）+ln（1+）+…+ln（1+）＜ln，∴．。

2021届江苏省淮阴区高三上学期期中调研测试文科数学试卷

2021年江苏省淮阴区高三上学期期中调研测试文科数学试卷学校:___________姓名：___________班级：___________考号：___________一、填空题1．设集合}|{},1|{a x x B x x A <=>=，若R B A =⋃，则实数a 的取值范围为2．复数i i z +-=2)21(的实部为3．某大学为了解在校本科生对参加某项社会实践活动的意向，拟采用分层抽样的方法，从该校四个年级的本科生中抽取一个容量为300的样本进行调查．已知该校一年级、二年级、三年级、四年级的本科生人数之比为4∶5∶5∶6，则应从一年级本科生中抽取________名学生．4．从1、2、3、4这4个数中一次性随机地取两个数，则所取两个数的和为5的概率为5．函数)62sin(2π-=x y 的图像中，离坐标原点最近的一条对称轴的方程为6．阅读如图所示的程序框图，运行相应的程序，则程序运行后输出的结果为7．等比数列}{n a 的公比大于1，6,152415=-=-a a a a ，则=3a8．一个圆柱和一个圆锥同底等高，若圆锥的侧面积是其底面积的2倍，则圆柱的侧面积是其底面积的_________倍.9．在平面直角坐标系中，直线0323=+-y x 被圆422=+y x 截得的弦长为10．设函数1sin )1()(22+++=x x x x x f 的最大值为M ，最小值为m ，则=+m M 11．已知点),1(m P 是函数x ax y 2+=图像上的点，直线b y x =+是该函数图像在P 点处的切线，则=-+m b a12．设P 为ABC ∆中线AD 的中点，D 为边BC 中点，且2=AD ，若3PB PC ⋅=-，则AB AC ⋅=13．若存在正数x 使1)(<-a x e x 成立，则a 的取值范围是14．已知0,0,1≠>=+x y y x ，则1||||21++y x x 的最小值为二、解答题15．（本题满分14分）已知2tan ),,2(-=∈αππα（1）求)4sin(απ+的值；（2）求)232cos(απ-的值 16．（本题满分14分）如图，四边形ABCD 为正方形，PD ⊥平面ABCD ，AD PD =，AF ⊥PC 于点F ，FE ∥CD 交PD 于点E. （1）证明：CF ⊥平面ADF ；（2）若O BD AC =⋂，证明//FO 平面AED17．（本题满分15分）设椭圆)0(12222>>=+b a by a x 的左焦点为F ，短轴上端点为B ，连接BF 并延长交椭圆于点A ，连接AO 并延长交椭圆于点D ，过O F 、、B 三点的圆的圆心为C（1）若C 的坐标为）（1,1-，求椭圆方程和圆C 的方程；（2）若AD 为圆C 的切线，求椭圆的离心率18．为迎接省运会在我市召开，美化城市，在某主干道上布置系列大型花盆，该圆形花盆直径2米，内部划分为不同区域种植不同花草如图所示，在蝶形区域内种植百日红，该蝶形区域由四个对称的全等三角形组成，其中一个三角形OAB 的顶点O 为圆心，A在圆周上，B 在半径OQ 上，设计要求 120=∠ABO（1）请设置一个变量x ，写出该蝶形区域的面积S 关于x 的函数表达式；（2）x 为多少时，该蝶形区域面积S 最大？ P O B QA19．（本题满分16分）设数列}{n a 的前n 项和为n S（1）若数列}{n a 是首项为1，公比为2的等比数列，求常数t m ,的值，使t ma S n n +=对一切大于零的自然数n 都成立（2）若数列}{n a 是首项为1a ，公差0≠d 的等差数列，证明：存在常数b t m ,,使得b ta ma S n n n ++=2对一切大于零的自然数n 都成立，且21=t （3）若数列}{n a 满足b ta ma S n n n ++=2，+∈N n ，b t m 、、（0≠m ）为常数，且0≠n S ，证明：当21=t 时，数列}{n a 为等差数列 20．（本题满分16分）已知函数x e e x f x x 2)(--=-，R x ∈（1）证明)(x f 为奇函数，并在R 上为增函数；（2）若关于x 的不等式322)(-+-≤m x mex f x 在),0(+∞上恒成立，求实数m 的取值范围（3）设)(4)2()(x bf x f x g -=，当0>x 时，0)(>x g ，求b 的最大值参考答案1．1>a【解析】试题分析：当1a ≤时，{|1}AB x x x a R =><≠或，当1a >时，A B R =考点：集合运算2．3-【解析】试题分析：2(12)14433z i i i i i =-+=--+=--，所以实部为3- 考点：复数运算3．60【解析】试题分析：应从一年级本科生中抽取4300604556⨯=+++名学生．考点：分层抽样 4．31【解析】试题分析：从1、2、3、4这4个数中一次性随机地取两个数，共有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)，6种取法，其中所取两个数的和为5的有(1,4),(2,3),2种取法，所以概率为21=63 考点：古典概型概率5．6x π=-【解析】试题分析：由2=+()62x k k Z πππ-∈得对称轴的方程为=+()32k x k Z ππ∈，其中离坐标原点最近的为6x π=-考点：三角函数对称轴6．9【解析】试题分析：第一次循环：1lg ,33S i ==；第二次循环：131lg +lg lg ,5355S i ===；第三次循环：151lg +lg lg ,7577S i ===；第四次循环：171lg +lg lg ,9799S i ===；第二次循环：191lg +lg lg 1,91111S ==<-输出9i =.考点：循环结构流程图7．4【解析】试题分析：由题意得：42511334215151512()146222a a q q q q a a a a q q q --+=⇒=⇒=⇒==⇒=⇒=--或舍考点：等比数列8．【解析】试题分析：因为一个圆柱和一个圆锥同底等高，所以设底面半径为r ，高为h ，因为圆锥的侧面积是其底面面积的2倍，所以22,2rl r l r ππ==，h =，所以圆柱的侧面积22S rl r π==，其底面积为2r π，所以圆柱的侧面积是底面积的.考点：旋转体的侧面积与表面积.【方法点晴】本题主要考查了旋转体的侧面积与表面积的计算，其中解答中涉及到圆柱侧面积、圆锥的侧面积与表面积的计算，圆锥与圆柱的性质等知识点的综合考查，着重考查了学生分析问题和解答问题的能力，以及学生的空间想象能力，解答中利用圆柱和圆锥的侧面积公式，准确计算是解答的关键，试题比较基础，属于基础题.9．2【解析】试题分析：圆心到直线距离为d ==2.= 考点：直线与圆位置关系10．2【解析】试题分析：22sin ()11x x x f x x +=++，所以22sin ()()11x x x g x f x x +=-=+为奇函数，其取值范围为[1,1]m M --，因此(1)12m M M m --=-⇒+=考点：奇函数性质11．2【解析】试题分析：因为22y a x '=-，所以21,1a a -=-=，从而23,14m a b m =+==+=，2.a b m +-= 考点：导数几何意义12．0【解析】试题分析：因为+2,,PB PC PD PB PC CB =-=所以2244,PB PC PD CB ⋅=-同理2244,AB AC AD CB ⋅=-从而222244443410.AB AC PB PC AD PD AB AC PB PC AD PD ⋅-⋅=-⇒⋅=⋅+-=-+-=考点：向量数量积13．1->a【解析】试题分析：由题意得：min (),(0)x a x e x ->->，由于函数x y x e -=-单调递增，所以011x x e -->-=-，因此1a >-考点：不等式恒成立14．43【解析】试题分析：1||||2||1312||12||24||24||444x x y x x y x x x x y x y x x y x x x +++=+=++≥=-=+++-，当且仅当0,22,1x x y x x y <+=-+=即2,3x y =-=时取等号考点：基本不等式求最值15．（12）【解析】试题分析：（1）给值求值问题，首先要分析角之间关系，本题可化为同角，即απαπαπsin 4cos cos 4sin )4sin(+=+，因此只需由2tan ),,2(-=∈αππα根据同角三角函数关系求出：552sin =α，55cos -=α，代入即得)4sin(απ+10101=（2）本题为二倍角关系，可利用二倍角的正余弦公式进行求解：==αααcos sin 22sin 54-，53sin cos 2cos 22-=-=ααα 103432sin 32sin 2cos 32cos )232cos(-=+=-απαπαπ试题解析：解：（1）由2tan ),,2(-=∈αππα 得552sin =α，55cos -=α 4分，每个数据2分 απαπαπsin 4cos cos 4sin )4sin(+=+ 公式2分 10101= 结论2分（2）==αααcos sin 22sin 54- 2分，公式和结论各1分 53sin cos 2cos 22-=-=ααα 2分，也可以用平方关系方法得到103432sin 32sin 2cos 32cos )232cos(-=+=-απαπαπ考点：给值求值16．（1）详见解析，（2）详见解析【解析】试题分析：（1）证明线面垂直，一般利用其判定定理，即证线线垂直：由PD ⊥平面ABCD ，得AD PD ⊥由,,AD PD AD DC PD DC C ⊥⊥=,PD DC PDC ⊂面⊥⇒AD 平面PDC ，CF PDC ⊂面CF AD ⊥⇒由C CF AF CF AF CF AD =⊥⊥ ,,,AF CF ADF ⊂面⊥⇒CF 平面ADF （2）证明线面平行一般利用其判定定理，即证线线平行：因为AD=PD ，由（1）知，F 为PC 中点，从而//AP FO ,因此由,AP ADE ⊂面FO ADE ⊄面得//FO 平面AED试题解析：（1）由PD ⊥平面ABCD ，得AD PD ⊥（1分）由C DC AD DC AD PD AD =⊥⊥ ,,⊥⇒AD 平面PDC（3分，少一个条件扣一分）CF AD ⊥⇒（1分）由C CF AF CF AF CF AD =⊥⊥ ,,⊥⇒CF 平面ADF （2分）（2）因为AD=PD ，由（1）知，F 为PC 中点从而//AP FO ,因此由,AP ADE ⊂面FO ADE ⊄面得//FO 平面AED ，本小题方法较多，关键采分点是证明线面平行的相关要素考点：线面垂直判定定理，线面平行判定定理17．（1）椭圆方程为14822=+y x ，圆方程为2)1()1(22=-++y x（2）【解析】试题分析：（1）求椭圆方程及圆方程，一般利用待定系数法求解：因为三角形BFO 为直角三角形，所以其外接圆圆心为斜边BF 中点C ，由C 点坐标为)1,1(-得，2,2==c b ，所以222c b a +=8=，圆半径2==CO r ，所以椭圆方程为14822=+y x ，圆方程为2)1()1(22=-++y x（2）圆的切线问题一般转化为圆心到切线距离等于半径，本题由于切点为O ，所以转化为AO CO ⊥，先由直线BF 方程与椭圆方程求出A 点坐标),)(2(2232222c a b c a c c a A +-+-，再代入AO CO ⊥得：2242c a b =22221b a c e e ⇒=⇒-=⇒-=⇒=试题解析：（1）因为三角形BFO 为直角三角形，所以其外接圆圆心为斜边BF 中点C ，由C 点坐标为)1,1(-得，2,2==c b ，所以222c b a +=8=，圆半径2==CO r ，所以椭圆方程为14822=+y x ，圆方程为2)1()1(22=-++y x （4分，每个方程2分）（2）由AD 与圆C 相切，得 CO AD ⊥BF 方程为b x c b y +=由⎪⎪⎩⎪⎪⎨⎧=++=12222b y a x b x c b y 得),)(2(2232222c a b c a c c a A +-+- （6分，每个坐标3分）0OA OC ⋅=得2242c a b =，222222)(c a c a =- 044224=+-c c a a，e = （5分）考点：椭圆方程，圆方程，椭圆离心率18．（1）)sin S x x=-（2） 30=x【解析】试题分析：（1）由于蝶形区域由四个对称的全等三角形组成，所以其面积为一个三角形AOB 面积的四倍，表示三角形AOB 面积应设角为自变量，即设x AOB =∠，在三角形AOB 中，由正弦定理得231120sin )60sin(sin ==-= AO x OB x AB ，xx x OB OA S S AOB sin )60sin(34sin 24-=•==∆ ，其定义域为(0,)3x π∈（2）求三角函数最值，先将其化为基本三角函数,这要利用两角差的正弦公式，二倍角公式及配角公式：211cos 211)sin cos sin )2)(sin(2))24264x S x x x x x x x π-=-=-=-=+-，从而30=x 时，蝶形区域面积最大试题解析：（1）设x AOB =∠，在三角形AOB 中，由正弦定理得231120sin )60sin(sin ==-= AO x OB x AB42sin )sinAOB S S OA OB x x x ∆==⋅=-（7分）（2）211cos 211)sin cos sin )2)(sin(2))24264x S x x x x x x x π-=-=-=-=+-整理得+)6S x π（整理过程和结论共6分，过程4分，结论2分）所以30=x 时，蝶形区域面积最大（2分）注：本题也可以用余弦定理和基本不等式解答，参照得分考点：函数解析式，正弦定理，三角函数最值 19．（1）1,2-==t m （2）详见解析（3）详见解析【解析】试题分析：（1）恒等式问题，可列方程组求解，也可用对应项系数相等求解：由等比数列和项公式12212111-=--=--=n nn n a a q qa a S 所以 1,2-==t m （2）同上，利用列方程组求解，也可用对应项系数相等求解：在等差数列}{n a 中，d n a a n )1(1-+=，所以11+-=d a a n n1111111(1)(1)(1)()22n n n n a a a a a a S na n n d a d d d d ---=+-=+++2211112222n n a a a a d d =++- 所以存在d m 21=，21=d ，d a a b 22211-=使得命题成立（3）先由和项与通项关系求数列递推关系，进而利用定义证明数列为等差数列：由题知)2()(21)(1212≥=-+-=----n a a a a a m S S n n n n n i n n0)(21)(1212=+----n n n n a a a a m ，0]21)()[(11=--+--n n n n a a m a a若,01=+-n n a a 则02=S ，与题设矛盾，所以21)(1=--n n a a m ，0≠m ，得m a a n n 211=--所以数列}{n a 为等差数列试题解析：（1）12212111-=--=--=n nn n a a q qa a S所以 1,2-==t m （4分）（2）在等差数列}{n a 中，d n a a n )1(1-+=，所以11+-=d a a n nd a a a a dd da a d a a a d a a d n n na S n n n n n n 222121))(1(21)1()1(21211211111-++=-+-++-=-+=所以存在d m 21=，21=d ，d a a b 22211-=使得命题成立（6分）（3）由题知 )2()(21)(1212≥=-+-=----n a a a a a m S S n n n n n i n n 0)(21)(1212=+----n n n n a a a a m]21)()[(11=--+--n n n n a a m a a若,01=+-n n a a 则02=S ，与题设矛盾所以21)(1=--n n a a m ，0≠m ，得m a a n n 211=--所以数列}{n a 为等差数列（6分）考点：恒等式问题，等差数列定义20．（1）详见解析（2）43211++≥m （3）2【解析】试题分析：（1）根据奇函数定义：定义域关于原点对称，且()()f x f x -=-进行证明：R x ∈，()2()x x f x e e x f x --=-+=-，所以)(x f 为奇函数，利用导数证明其单调性：因为/1()20x x f x e e =+-≥在R 上恒成立，所以)(x f 在R 上为增函数（2）解决不等式恒成立问题，先化简不等式：由322)(-+-≤m x me x f x变形得x xx e e e m 2112+-+≥，再求对应函数最值：2112xxx e y e e -=++，令10xt e =-> 得21113434t y t t t t =+=+++++1≤当且仅当t =43211++≥m （3）本题若用变量分离，则研究的函数较复杂，不易求出其最值，因此从原函数出发为宜：g （x ）＝f （2x ）－4bf （x ）＝e 2x－e－2x－4b （e x －e －x ）＋（8b －4）x ，g ′（x ）＝2[e 2x ＋e－2x－2b （e x ＋e －x）＋（4b －2）]＝2（e x＋e －x－2）（e x＋e －x－2b ＋2）．当b≤2时，g′（x ）≥0，g （x ）在（－∞，＋∞）上单调递增．而g （0）＝0，所以对任意x>0，g （x ）>0. 当b>2时，存在函数值小于g （0）＝0，不满足，所以b 的最大值为2.试题解析：（1）R x ∈，()2()x xf x e e x f x --=-+=-，所以)(x f 为奇函数（2分）不写定义域扣1分 /1()20x x f x e e =+-≥在R 上恒成立，所以)(x f 在R 上增（2分）（2）由322)(-+-≤m x me x f x 变形得x xx e e e m 2112+-+≥令1-=xe t 得43113412+++=+++≥t t t t tm得43211++≥m （本小题共6分）（3）g （x ）＝f （2x ）－4bf （x ）＝e 2x－e －2x－4b （e x －e －x）＋（8b －4）x ，g ′（x ）＝2[e 2x＋e－2x－2b （e x＋e －x）＋（4b －2）]＝2（e x＋e －x－2）（e x＋e －x－2b ＋2）．（i ）当b≤2时，g′（x ）≥0，等号仅当x ＝0时成立，所以g （x ）在（－∞，＋∞）上单调递增．而g （0）＝0，所以对任意x>0，g （x ）>0.（ii ）当b>2时，若x 满足2<e x＋e －x<2b －2，即0<x<ln （b －1）时，g′（x ）<0.而g （0）＝0，因此当0<x<ln （b －1）时，g （x ）<0. 综上，b 的最大值为2.考点：函数奇偶性，利用导数求函数单调性，利用导数求函数最值。

2021届江苏省淮安市淮阴中学高三上学期8月测试数学试题(解析版)

2021届江苏省淮安市淮阴中学高三上学期8月测试数学试题一、单选题1．设集合={1,2,3}A ，B={45}，，={x|x=a+b,a A,b B}M ∈∈，则M 中元素的个数为（） A ．3 B ．4 C ．5 D ．6【答案】B 【解析】【详解】由题意知x a b =+，,a A b B ∈∈，则x 的可能取值为5,6,7,8.因此集合M 共有4个元素，故选B. 【考点定位】集合的概念2．以下四个命题既是特称命题又是真命题的是 A ．锐角三角形的内角是锐角或钝角 B ．至少有一个实数x ，使20x ≤ C ．两个无理数的和必是无理数 D ．存在一个负数x ，使12x> 【答案】B【解析】先确定命题中是否含有特称量词，然后利用判断特称命题的真假．【详解】对于A ，锐角三角形中的内角都是锐角，所以A 为假命题；对于B ，为特称命题，当0x =时，20x =成立，所以B 正确；对于C ，(0=，所以C 为假命题；对于D ，对于任何一个负数x ，都有10x<，所以D 错误．故选B ．【点睛】本题以命题的真假判断与应用为载体，考查了全称命题和特称命题的定义，难度不大，属于基础题．3．汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程s 看作时间t 的函数，其图象可能是( )A ．B ．C ．D ．【答案】A【解析】试题分析：汽车启动加速过程，随时间增加路程增加的越来越快，汉使图像是凹形，然后匀速运动，路程是均匀增加即函数图像是直线，最后减速并停止，其路程仍在增加，只是增加的越来越慢即函数图像是凸形．故选A ．【考点】函数图像的特征．4．对任意R x ∈，函数()327f x ax ax x =++不存在极值点的充要条件是（）A ．021a ≤≤B ． 021a <<C ． 0a ≤或21a ≥D ．0a <或21a > 【答案】A【解析】求出导函数()'f x ，由方程()0f x '=没有变号的实数解即可得．【详解】由题意()2327f x ax ax '=++，()f x 不存在极值点，0a =时，()70f x '=>，()f x 单调递增，无极值点；0a ≠时，则24840a a ∆=-≤，解得021a <≤，综上021a ≤≤．故选：A ．【点睛】本题考查用导数与函数的极值的关系，对于可导函数，如果导函数存在变号的零点，则原函数有极值．如果没有变号的零点，则原函数无极值．5．将甲桶中的a 升水缓慢注入空桶乙中，t 分钟后甲桶中剩余的水符合指数衰减曲线y＝a e nt .假设过5分钟后甲桶和乙桶的水量相等，若再过m 分钟甲桶中的水只有8a，则m 的值为( ) A ．7 B ．8C ．9D ．10【答案】D【解析】由题意，函数y=f （t ）=ae nt ,满足f （5）=2a ，f （m+5）=8a , 可解出m 的值. 【详解】根据题意得2a＝a e 5n ，令8a ＝a e nt ，即18＝e nt ，因为12 ＝e 5n ，故18＝e 15n ，故t ＝15，m ＝15－5＝10. 故选D 【点睛】对实际情景，根据已知或建立的相应函数模型，将实际问题转换为函数的求解.，最后解决实际问题.6．函数()()log 6a f x ax =-（0a >且1a ≠）在[]0,2上为减函数，则实数a 的取值范围是（） A ．()1,3 B ．()0,1C ．(] 1,3D ．[)3+∞，【答案】A【解析】根据对数函数性质与复合函数的单调性求解．【详解】首先6t ax =-是减函数，∴log a y t =应是增函数，()f x 才可能是减函数， ∴1a >，函数()f x 在[0,2]上减函数，由对数函数性质知620a ->，3a <，综上13a <<．故选：A ．【点睛】本题考查复合函数的单调性，掌握对数函数性质是解题关键．7．如果已知0<a <1，则方程a |x |＝|log a x |的实根个数为( ) A ．2 B ．3C ．4D ．与a 的值有关【答案】A【解析】设,0(),()log ,0x xa xa x f x a g x x a x -⎧≥===⎨≤⎩分别作出它们的图象如图所示：由图可知有两个交点，故选A.8．已知函数()()2ln15f x x x x =++-[]()2020,2020x ∈-的最大值为M ，最小值为m ，则M m +=（） A ．5- B ．10-C ．5D ．10【答案】B【解析】构造新函数()()5g x f x =+，证明它是奇函数，然后利用奇函数的性质求值．【详解】设2()()5ln(1)g x f x x x x =+=++，则2222()()ln(1)ln(1)ln (1)(1)0g x g x x x x x x x x x x x ⎡⎤+-=++-++=++=⎣⎦，∴()()g x g x -=，()g x 是奇函数，又min min ()()55g x f x m =+=+，max max ()()55g x f x M =+=+， ∴min max ()()550g x g x M m +=+++=，10M m +=-．故选：B ．【点睛】本题考查函数的奇偶性，解题关键是构造新函数是奇函数，然后利用奇函数的性质求得结论．二、多选题9．下列说法中，正确的命题是（）． A ．已知随机变量X 服从正态分布()22,N σ，()40.8P X <=，则()240.2P X <<= B ．线性相关系数r 越大，两个变量的线性相关性越强；反之，线性相关性越弱 C ．已知两个变量具有线性相关关系，其回归直线方程为y a bx =+，若2b =，1x =，3y =，则1a =D ．若样本数据121x +，221x +，…，1621x +的方差为8，则数据1x ，2x ，…，16x 的方差为2 【答案】CD【解析】利用正态分布的对称型可以求得()24P X <<的值，进而判定A 错误;根据相关系数的意义可以判定B 错误；利用回归直线方程过样本中心点，可以求得回归常数的估计值，从而判定C 正确；利用线性相关的数据组的方差之间的关系可以求得数据1x ，2x ，…，16x 的方差，进而判定D 正确.【详解】A. 已知随机变量X 服从正态分布()22,N σ，()40.8P X <=，则()410.80.2P X ≥=-=，所以()00.2P X ≤=，所以()04120.20.6P X <<=-⨯=, ∴()0.6240.32P X <<==，故A 错误； B. 线性相关系数r 的范围在1-到1之间，有正有负，相关有正相关和负相关，相关系数的绝对值的大小越接近于1，两个变量的线性相关性越强；反之，线性相关性越弱，故B 错误；C. 已知两个变量具有线性相关关系，其回归直线方程为y a bx =+，若2b =，1x =，3y =，则y 1a bx =-=，故C 正确；D. 设数据1x ，2x ，…，16x 的方差为2S ,样本数据121x +，221x +，…，1621x +的方差为222S =8，则22S =，即数据1x ，2x ，…，16x 的方差为2，故D 正确. 故选:CD. 【点睛】本题考查正态分布的概率计算问题，相关系数问题，回归直线方程问题，数据的方差关系问题，属小综合题，难度一般. 10．下列不等式，其中正确的是（） A ．2 32x x +>（R x ∈） B ．3322 a b a b ab +≥+（a ，R b ∈）C ．22 2a b +≥（1a b --）D ．()22211f x x x =+≥- 【答案】AC【解析】,,A B C 三个选项用作差法比较，D 选项通过举例判断．【详解】2232(1)20x x x +-=-+>，所以232x x +>，A 正确；332222222()()()()()()a b a b ab a a b b a b a b a b a b a b +--=---=--=-+，当0a b +<时，33220a b a b ab +--≤，B 错误；22222(1)(1)(1)0a b a b a b +-+-=-+-≥，即222(1)a b a b +≥+-，C 正确；222()1f x x x =+-中(0)21f =-<+，D 错误．故选：AC ．【点睛】本题考查不等式的性质，考查两实数比较大小，作差法是解题的基本方法． 11．若()f x 满足对任意的实数a ，b 都有()()()f a b f a f b +=且()12f =，则下列判断正确的有（） A ．()f x 是奇函数B ．()f x 在定义域上单调递增C ．当()0,x ∈+∞时，函数()1f x >D ．()()()()()()()()()()()()2462016201820202020135201520172019f f f f f f f f f f f f +++⋅⋅⋅++= 【答案】BCD【解析】利用新定义结合函数的性质进行判断．计算出(1)f 判断A ；先利用(1)21f =>证明所有有理数p ，有()1f p >，然后用任意无理数q 都可以看作是一个有理数列的极限，由极限的性质得()1f q >，这样可判断C ，由此再根据单调性定义判断B ，根据定义计算(2)(21)f n f n -（n N ∈），然后求得D 中的和，从而判断D ．【详解】令0,1a b ==，则(1)(10)(1)(0)f f f f =+=，即22(0)f =，∴(0)1f =，()f x 不可能是奇函数，A 错；对于任意x ∈R ，()0f x ≠，若存在0x R ∈，使得0()0f x =，则0000(0)(())()()0f f x x f x f x =+-=-=，与(0)1f =矛盾，故对于任意x ∈R ，()0f x ≠，∴对于任意x ∈R ，2()022222x x x x x f x f f f f ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+==> ⎪ ⎪⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦， ∵(1)21f =>，∴对任意正整数n ，11111111121nn n f n n f f f f f n n n n n n n ⎛⎫ ⎪⎝⎭⎛⎫ ⎪⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫ ⎪+++===> ⎪ ⎪ ⎪ ⎪⎢⎥ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎪ ⎪⎝⎭个个，∴11f n ⎛⎫> ⎪⎝⎭，同理()(111)(1)(1)(1)21n f n f f f f =+++==>，对任意正有理数p ，显然有m p n=（,m n 是互质的正整数），则1()1mm f p f fn n ⎡⎤⎛⎫⎛⎫==> ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，对任意正无理数q ，可得看作是某个有理数列123,,,p p p 的极限，而()1i f p >，i N ∈，∴()f q 与()i f p 的极限，∴()1f q >，综上对所有正实数x ，有()1f x >，C 正确，设12x x <，则210x x ->，∴21()1f x x ->，则21211211()(())()()()f x f x x x f x f x x f x =+-=⋅->，∴()f x 是增函数，B 正确；由已知(2)(211)(21)(1)2(21)f n f n f n f f n =-+=-=-，∴(2)2(21)f n f n =-，∴()()()()()()()()()()()()10102246201620182020222210102020135201520172019f f f f f f f f f f f f +++⋅⋅⋅++=+++=⨯=个，D 正确．故选：BCD ．【点睛】本题考查新定义函数，考查学生分析问题，解决问题的能力，逻辑思维能力，运算求解能力，对学生要求较高，本题属于难题． 12．已知定义在0,2π⎛⎫⎪⎝⎭上的函数()f x ，()'f x 是()f x 的导函数，且恒有cos ()sin ()0xf x xf x '+<成立，则( )A．64f ππ⎛⎫⎛⎫>⎪ ⎪⎝⎭⎝⎭B63f ππ⎛⎫⎛⎫>⎪ ⎪⎝⎭⎝⎭C．63f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭D64ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭【答案】CD【解析】根据题意，令()()cos f x g x x =，0,2x π⎛⎫∈ ⎪⎝⎭，对其求导分析可得()0g x '<，即函数()g x 为减函数，结合选项分析可得答案．【详解】解：根据题意，令()()cos f x g x x =，0,2x π⎛⎫∈ ⎪⎝⎭，则其导数2()cos sin ()()f x x x f x g x cos x '+'=，又由(0,)2x π∈，且恒有cos ()sin ()0x f x x f x '+<，则有()0g x '<，即函数()g x 为减函数，又由63ππ<，则有()()63g g ππ>，即()()63cos cos 63f f ππππ>，分析可得()()63f ππ>；又由64ππ<，则有()()64g g ππ>，即()()64cos cos 64f f ππππ>()()64ππ>．故选：CD ．【点睛】本题考查函数的单调性与函数导数的关系，注意构造函数()()cos f x g x x=，并借助导数分析其单调性，属于中档题．三、填空题13．若1<a<3，－4<b<2，那么a －|b|的取值范围是_______ 【答案】(－3,3)【解析】先算出|b |的范围，再算出a +（﹣|b |）的范围．【详解】由﹣4＜b ＜2⇒0≤|b |＜4，﹣4＜﹣|b |≤0，又1＜a ＜3． ∴﹣3＜a ﹣|b |＜3．所求范围为（﹣3，3）. 故答案为（﹣3，3）. 【点睛】本题考查了不等式性质的应用，注意同向不等式只能相加，不能相减的特点． 14．已知0a >，0b >，若不等式3103m a b a b--≤+恒成立，则m 的最大值为______ 【答案】16【解析】不等式变形后用基本不等式求最小值后可得结论．【详解】∵0a >，0b >，3103m a b a b--≤+恒成立， ∴3133(3)()10a b m a b a b b a≤++=++， ∵0,0a b >>，33101016b a a b ++≥+=，当且仅当33b aa b=，即a b =时，等号成立， ∴16m ≤，即m 的最大值为16．故答案为：16 【点睛】本题考查不等式恒成立，考查用基本不等式求最小值．解题方法是分离参数法．15．定义运算“⊗”22x y x y xy-⊗=，（,R x y ∈，0xy ≠）.当0x >，0y >时，()2x y y x ⊗+⊗的最小值为______【解析】根据新定义，把()2x y y x ⊗+⊗用通常的运算表示，然后用基本不等式求得最小值．【详解】由题意()222222422222x y y x x y x y x y y x xy xy xy y x --+⊗+⊗=+==+≥=当且仅当2x yy x=，即x =时等号成立．．．【点睛】本题考查新定义运算，求新定义运算下的最值，解题方法是利用新定义把新定义表达式转化为通常的运算，然后由基本不等式求得最小值．四、双空题16．设1,3a ⎛⎤∈-∞ ⎥⎝⎦，R b ∈，()3g x ax x =-，[]1,1x ∈-，则()g x 的值域是______，函数()()f x g x b =-在[]1,1-的最大值是23，则22a b +的值是______ 【答案】[1,1]a a --19【解析】求出导数()'g x ，由已知条件得()0g x '≤，从而确定()g x 的单调性，得函数()g x 值域，由最大值得2()3f x ≤恒成立，从而2(1)32(1)3f f ⎧-≤⎪⎪⎨⎪≤⎪⎩，由此化简变形后求得,a b ，得22a b +，【详解】由题意2()31g x ax '=-，∵13a ≤，[1,1]x ∈-，∴2()310g x ax '=-≤，()g x 在[1,1]-上单调递减，max ()(1)1g x g a =-=-，min ()(1)1g x g a ==-，∴()g x 值域为[1,1]a a --；函数()()f x g x b =-在[]1,1-的最大值是23，即2()3f x ≤在[1,1]-上恒成立， ∴()()21132113f a b f a b ⎧-=-+-≤⎪⎪⎨⎪=--≤⎪⎩，两式相加得4113a b a b -+-++-≤，又1122a b a b a -+-++-≥-，∴4223a -≤，解得1533a ≤≤，又∵13a ≤，∴13a =，可得1213312133b b ⎧-+-≤⎪⎪⎨⎪--≤⎪⎩，即22332233b b ⎧-≤⎪⎪⎨⎪--≤⎪⎩，解得403403b b ⎧≤≤⎪⎪⎨⎪-≤≤⎪⎩，∴0b =，∴2219a b +=．故答案为：[1,1]a a --；19．【点睛】本题考查用导数研究函数的单调性与最值，研究函数恒成立问题，着重考查了逻辑推理能力，运算求解能力，难度中等．五、解答题17．已知函数y =R ．()1求a 的取值范围；()2解关于x 的不等式220x x a a --+<．【答案】()[]1?0,1；(2)见解析.【解析】()1由函数的定义域是R ，得出2210ax ax ++≥恒成立，求出a 的取值范围；()2分类讨论，即可求出不等式的解集．【详解】()1函数y =R ，2210ax ax ∴++≥恒成立．①当0a =时，10≥，不等式恒成立；②当0a ≠时，则02440a a a >⎧=-≤⎨⎩解得01a <≤．综上可知，a 的取值范围是[]0,1．()2由220x x a a --+<，得()()10x a x a ⎡⎤---<⎣⎦．01a ≤≤，∴①当1a a ->，即102a ≤<时，1a x a <<-； ②当1a a -=，即12a =时，)21(02x -<，不等式无解；③当1a a -<，即112a <≤时，1a x a -<<．综上，当102a ≤<时，原不等式的解集为(),1a a -；当12a =时，原不等式的解集为；当112a <≤时，原不等式的解集为()1,a a - 【点睛】本题考查了函数的性质与应用以及不等式的解法与应用问题，解题时应根据题意，适当地转化条件，从而获得解答问题的途径，是综合性题目．解含参数的一元二次不等式，要把握好分类讨论的层次，一般按下面次序进行讨论：首先根据二次项系数的符号进行分类，其次根据不等式的判别式的符号进行分类，最后在根存在的条件下，再根据根的大小进行分类．18．（1）已知不等式1x m -<成立的充分不必要条件是1132x <<，求实数m 的取值范围.（2）已知()2log f t t =，t ∈⎤⎦，对于()f t 值域内的所有实数m ，不等式2424x mx m x ++>+恒成立，求x 的取值范围.【答案】（1）1423m -≤<；（2）()(),12,-∞-+∞.【解析】（1）先求得不等式1x m -<解集，结合题意，列出不等式组，即可求解；（2）根据题意，求得()1,32f t ⎡⎤∈⎢⎥⎣⎦，得到1,32m ⎡⎤∈⎢⎥⎣⎦，转化为()()2220x m x -+->对任任意的1,32m ⎡⎤∈⎢⎥⎣⎦恒成立，令()()()222g x m m x =-+-，结合一次函数的性质，即可求解. 【详解】（1）由题意，不等式1x m -<，解得11m x m -<<+，因为1x m -<成立的充分不必要条件是1132x <<，所以113112m m ⎧-≤⎪⎪⎨⎪+>⎪⎩①，或113112m m ⎧-<⎪⎪⎨⎪+≥⎪⎩②，由①得：1423m -<≤；由②得：1423m -≤<，综合①②得：1423m -≤<.（2）因为()2log f t t =，t ∈⎤⎦，所以()1,32f t ⎡⎤∈⎢⎥⎣⎦，即1,32m ⎡⎤∈⎢⎥⎣⎦，因为2424x mx m x ++>+对任意的1,32m ⎡⎤∈⎢⎥⎣⎦恒成立，所以()()2220x m x -+->对任意的1,32m ⎡⎤∈⎢⎥⎣⎦恒成立，令()()()222g x m m x =-+-，因为()()2220x m x -+->对任意的1,32m ⎡⎤∈⎢⎥⎣⎦恒成立，可得()()()()()()()22112202233220g x x g x x ⎧⎛⎫=-+->---* ⎪⎪⎝⎭⎨⎪=-+->---**⎩，由()* 可得：()()2230x x -->，则2x >或23x <；由()**可得：()()120x x +->，则2x >或1x <-，综上所述：x 的范围()(),12,-∞-+∞.【点睛】本题主要考查了绝对值不等式的求解，二次函数的图象与性质，以及不等式的恒成立问题，其中解答中熟记绝对值不等式的解法，以及二次函数的图象与性质是解答的关键，着重考查推理与运算能力.19．美国2018年3月挑起“中美贸易争端”，剑指“中国制造2025”，中国有“缺芯”之痛.今有三个研究机构A ，B ，C 对某“AI 芯片”做技术攻关，A 能攻克的概率34为，B 能攻克的概率为23，C 能攻克的概率为12，（1）求这一技术难题被攻克的概率；（2）先假设一年后该技术难题已被攻克，上级会奖励m 万元.奖励规则如下：若只有1个机构攻克，则此机构获得全部奖金m 万元；若只有两个机构攻克，则奖金奖给此两个机构，每个机构各得2m万元；若三个机构均攻克，则奖金奖给三个机构，每个机构各得3m万元.设A ，B 得到的奖金数为X ，求X 的分布列和数学期望. 【答案】（1）2324；（2）分布列见解析，()3548E X m =. 【解析】（1）对立事件是这一技术难题没有被攻克即每个队都没有攻克技术难题，由对立事件的概率公式求解；（2）根据规则X 的可能取值为：0，2m ，23m，m ，X 0=表示,A B 均未攻克技术难题，C 可能攻克也可以未攻克，2mX =表示A 未攻克，,B C 同时攻克或B 未攻克，,A C 同时攻克，23mX =表示,,A B C 同时攻克，X m =表示C 未攻克，,A B 中至少1个机构攻克这个技术难题，由此可计算出概率，得分布列，从而可计算出期望．【详解】（1）记这一技术难题被攻克的事件为A ；()111123114322424P A =-⨯⨯=-=.（2）X 的可能取值为：0，2m ，23m ，m 2321134324m P X ⎛⎫==⨯⨯= ⎪⎝⎭；3111215243243224m P X ⎛⎫==⨯⨯+⨯⨯=⎪⎝⎭； ()3111213211143243243224P X m ==⨯⨯+⨯⨯+⨯⨯=；()1111111043243212P X ==⨯⨯+⨯⨯=X 的分布列：()15211135012224342448m m E X m m =⨯+⨯+⨯+⨯=. 【点睛】本题考查相互独立事件同时发生的概率公式和对立事件的概率公式，考查随机变量的概率分布列和数学期望，解题关键是确定变量X 的可能取值．20．设二次函数()2f x ax bx c =++，函数()()F x f x x =-的两个零点为m ，n（m n <）.（1）若1m =-，2n =，求不等式()0F x >的解集. （2）若0a >，且10x m n a<<<<，比较()f x 与m 的大小. 【答案】（1）答案见解析；（2）()f x m <.【解析】（1）由二次方程的根与一元二次不等式的解之间的关系直接得出结论；（2）设()()()F x a x m x n =--，得()()()f x a x m x n x =--+，作差()f x m -可得它与0的大小，从而得出()f x 与m 的大小．【详解】（1）()0F x =的两个根分别为1-和2 当0a >时，()0F x >的解集为()(),12,-∞-+∞；当0a <时，()0F x >的解集为()1,2-；（2）()()()F x a x m x n =--，()()()f x a x m x n x =--+()()()()()1f x m a x m x n x m x m ax an -=--+-=--+∵10x m n a<<<<，∴0x m -<，10an -+>，0ax > ∴10ax an -+>，()0f x m -< ∴()f x m <. 【点睛】本题考查二次方程的根与一元二次不等式的解之间的关系，考查二次函数的解析式，掌握三个二次的关系是解题关键． 21．已知函数()1ln x f x x a-=-（1）当1a =时，求()f x 的最大值；（2）若()f x 在区间()2,e 上存在零点，求实数a 的取值范围.【答案】（1）0；（2）1,1ln 2e ⎛⎫-⎪⎝⎭. 【解析】（1）先求导数，再求导函数零点，根据导函数符号变化规律确定函数单调性，最后根据单调性求最大值；（2）先变量分离转化求对应函数()1ln x g x x-=值域，利用导数求其单调性，再根据单调性求其值域，即得结果. 【详解】（1）()()ln 1f x x x =--，()111x f x x x-=-='，令0fx，得1x =所以()f x 在0,1上单调递增，1,上单调递减∴()()max 10f x f ==.（2）()f x 在区间()2,e 上存在零点，∴1ln 0x x a--=在()2,e 上有解，1ln x a x -=令()1ln x g x x-=（()2x e ∈,），()()21ln 1ln ,x x x x g +='-设2211111ln 1,(2,)0ln 2102x y x x e y y x x x x -'=-+∈∴=-=>∴>-+=> 因此0g x,∴()g x 在()2,e 上单调递增，即()()12ln 2g x g >=，()()1g x g e e <=- ∴1,1ln 2a e ⎛⎫∈-⎪⎝⎭. 【点睛】本题考查利用导数求函数单调性、利用导数研究函数零点，考查综合分析求解能力，属中档题.22．设函数()32f x x ax bx =++（a ，R b ∈）的导函数为()f x .已知1x ，2x 是()f x 的两个不同的零点. （1）证明：23a b >；（2）当0b =时，若对任意0x >，不等式()ln f x x x >恒成立，求a 的取值范围；（3）求关于x 的方程()()()1211()2x f x f x f x x x '=-++的实根的个数. 【答案】（1）证明见解析；（2）1a ≥-；（3）1.【解析】（1）先求导数，再根据导函数必有两个不同零点列不等式，解得结果；（2）先分离变量，转化为求对应函数()2ln x x F x x-=最值，利用导数确定其单调性，根据单调性确定最值，即得结果；（3）先求122x x f +⎛⎫' ⎪⎝⎭，再构造差函数()()321211()2x x G x x ax bx f x x f x +⎛⎫'=++--- ⎪⎝⎭，再利用导数确定其单调性，最后根据单调性以及()10G x =确定零点个数，即得结果. 【详解】（1）证明：()232f x x ax b '=++，令()2320f x x ax b '=++=∵0f x有两个不等的实根，∴2241203a b a b ∆=->⇒>.（2）0b =时，()32f x x ax =+，由()ln f x x x ≥得32ln x ax x x +≥∴22ln ln x x x ax x x a x-+≥⇒≥令()2ln x x F x x-=，()222212ln 1ln x x x x x x x F x x x ⎛⎫--+ ⎪--⎝⎭'== 令()21ln g x x x =--，()120g x x x'=--< ∴()g x 在0,上单调递减，注意到10g∴当01x <<时，()0gx >，()0F x '>，()F x '单调递增；当1x >时，()0g x <，()0F x '<，()F x 单调递减： ∴()()max 11F x F ==-，∴1a ≥-. （3）()()3212112x x x ax bx f x x f x +⎛⎫'++=-+⎪⎝⎭()()32121102x x x ax bx f x x f x +⎛⎫'⇒++---= ⎪⎝⎭212233x x a a f f b +⎛⎫⎛⎫''=-=- ⎪ ⎪⎝⎭⎝⎭令()()321211()2x x G x x ax bx f x x f x +⎛⎫'=++---⎪⎝⎭()()2222221211323296(3)02333x x a G x x ax b f x ax b b x ax a x a +⎛⎫''=++-=++-+=++=+≥ ⎪⎝⎭∴()G x 在R 上单调递增，故()G x 在R 上至多只有一个零点，注意到()10G x = ∴()G x 在R 上只有1个零点，即()()1211()2x x f x f x x f x '+⎛⎫=-+⎪⎝⎭的实根个数为1. 【点睛】本题考查利用导数研究不等式恒成立、利用导数研究函数零点、利用导数证明不等式，考查综合分析求解能力，属中档题.。

2020-2021学年江苏淮安高三上数学期中试卷

为提高月总利润，厂家决定下月进行营销策略改革，计划每只售价元，并投入万元作为营销策略改革费用.据市场调查，每只售价每提高元，月销售量将相应减少万只.则当每只售价为多少时，下月的月总利润最大？并求出下月最大总利润.
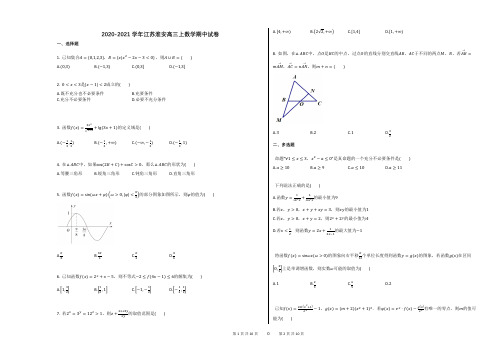
已知函数， .
求函数的值域；
设，，，求函数的最小值；
对中的，若不等式对于任意的时恒成立，求实数的取值范围．
若点的横坐标为，点的纵坐标为，求的值；
若，求的取值范围．
因疫情影响，引起口罩热销．某品牌口罩原来每只成本为元．售价为元，月销售万只．
据市场调查，若售价每提高元，月销售量将相应减少万只，要使月总利润不低于原来的月总利润（月总利润月销售总收入月总成本），该口罩每只售价最多为多少元？
5.函数的部分图象如图所示，则的值为( )
A. B. C. D.
6.已知函数，则不等式的解集为( )
A. B. C. D.
7.若，则的取值范围是( )
A. B. C. D.
8.如图，在中，点是的中点，过点的直线分别交直线，于不同的两点，，若，，则
A. B. C. D.
向明的月响分其几何意义
【解析】
此题暂无解析
【解答】
此题暂无解答
二、多选题
【答案】
此题暂无答案
【考点】
复合命题常育真假判断
必要条水表综分条近与充要条件的判断
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
命题的真三判断州应用
基来雨等式
基本常等式簧最母问赤中的应用
【解析】
此题暂无解析

江苏省淮安市淮阴中学2021届高三数学期中数学模拟测试

2021届江苏省淮安市淮阴中学高三上学期8月测试数学试题(解析版)

江苏省淮安市淮阴中学2021届高三数学期中测试数学试题及答案

江苏省淮阴中学2021届高三第一学期数学测试卷

江苏省淮安市淮阴中学高三(上)期中数学试卷含答案

江苏省淮安市楚中、新马、清浦、洪泽高中四校2021届高三数学上学期期中联考试题 文(含解析).doc

江苏省淮安市楚中、新马、清浦、洪泽高中四校联考2021届高三数学上学期期中试题(含解析)

2021-2022学年江苏省淮阴中学、海门中学、姜堰中学高三(上)期中数学试卷(学生版+解析版)

2021届江苏省淮安市高三高考数学模拟试卷(202105)解析

2021届江苏省淮阴区高三上学期期中调研测试文科数学试卷

2021届江苏省淮安市淮阴中学高三上学期8月测试数学试题(解析版)

2020-2021学年江苏淮安高三上数学期中试卷

江苏省淮安市楚中、新马、清浦、洪泽高中四校2021届高三数学上学期期中联考试题文(含解析).doc