MATLAB矩阵及其运算实验二
实验二 MATLAB的数据类型与基本运算
实验二MATLAB的数据类型与基本运算一、实验目的掌握MATLAB中编程语言的表示和运算,了解常用基本数据类型,了解结构、元胞和表等复杂数据类型的基本概念;熟悉矩阵运算,掌握用矩阵求逆法解线性方程组的方法,熟悉多项式运算。
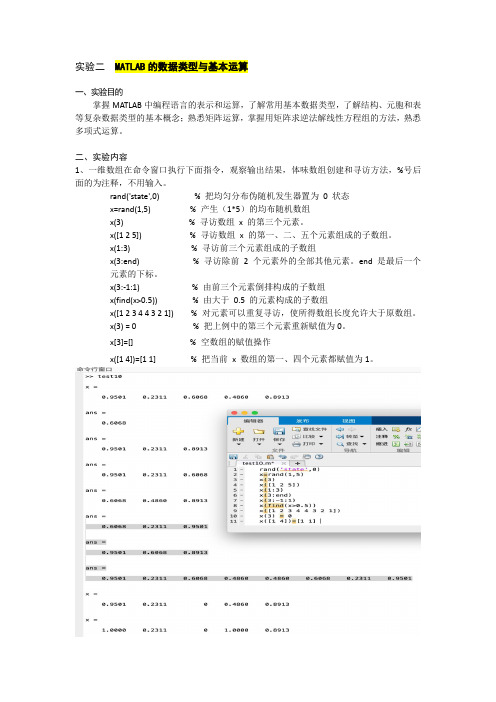
二、实验内容1、一维数组在命令窗口执行下面指令,观察输出结果,体味数组创建和寻访方法,%号后面的为注释,不用输入。
rand('state',0) % 把均匀分布伪随机发生器置为0 状态x=rand(1,5) % 产生(1*5)的均布随机数组x(3) % 寻访数组x 的第三个元素。
x([1 2 5]) % 寻访数组x 的第一、二、五个元素组成的子数组。
x(1:3) % 寻访前三个元素组成的子数组x(3:end) % 寻访除前2 个元素外的全部其他元素。
end 是最后一个元素的下标。
x(3:-1:1) % 由前三个元素倒排构成的子数组x(find(x>0.5)) % 由大于0.5 的元素构成的子数组x([1 2 3 4 4 3 2 1]) % 对元素可以重复寻访,使所得数组长度允许大于原数组。
x(3) = 0 % 把上例中的第三个元素重新赋值为0。
x[3]=[] % 空数组的赋值操作x([1 4])=[1 1] % 把当前x 数组的第一、四个元素都赋值为1。
2、在命令窗口执行下面指令,观察输出结果a=2.7358; b=33/79; % 这两条指令分别给变量 a , b 赋值。
C=[1,2*a+i*b,b*sqrt(a);sin(pi/4),a+5*b,3.5+i] % 这指令用于创建二维组C M_r=[1,2,3;4,5,6],M_i=[11,12,13;14,15,16] % 创建复数数组的另一种方法CN=M_r+i*M_i % 由实部、虚部数组构成复数数组3. 记录下面题目的程序和运行后的结果。
1⎥⎦⎤⎢⎣⎡=654321a ⎥⎦⎤⎢⎣⎡-=531142b ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=201c ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=063258741d下列运算是否合法,为什么?如合法,结果是多少?(1) result1 = a'=[1 4;2 5;3 6] (2) result2 = a * b 不合法(3) result3 = a + b=[3 6 2;5 8 11](4) result4 = b * d=[31 22 22;40 49 13](5) result5 = [b ; c' ] * d=[31 22 22;40 49 13;-5 -8 7] (6) result6 = a . * b=[2 8 -3;4 15 30](7) result7 = a . / b=[0.5000 0.5000 -3.0000;4.000 1.667 1.2000](8) result8 = a . * c 不合法(9) result9 = a . \ b=[2.0000 2.0000 -0.3333;0.2500 0.6000 0.8333] (10) result10 = a . ^2=[1 4 9;16 25 36] (11) result11 = a ^2不合法(12) result11 = 2 . ^ a=[2 4 8;16 32 64]4、设矩阵A =[311212123],B =[11−12−101−11]求(1)2A+B(2)4A 2-3B 2 (3)AB (4)BA (5)AB-BA5、设三阶矩阵A、B满足A-1BA=6A+BA,其中A=[13000140017],求矩阵B。
MATLAB实验报告

实验一MATLAB操作基础实验目的和要求:1、熟悉MATLAB的操作环境及基本操作方法。
2、掌握MATLAB的搜索路径及设置方法。
3、熟悉MATLAB帮助信息的查阅方法实验内容:1、建立自己的工作目录,再设置自己的工作目录设置到MA TLAB搜索路径下,再试验用help命令能否查询到自己的工作目录。
2、在MA TLAB的操作环境下验证课本;例1-1至例1-4,总结MATLAB的特点。
例1-1例1-2例1-3例1-43、利用帮助功能查询inv、plot、max、round等函数的功能。
4、完成下列操作:(1)在matlab命令窗口输入以下命令:x=0:pi/10:2*pi;y=sin(x);(2)在工作空间窗口选择变量y,再在工作空间窗口选择回绘图菜单命令或在工具栏中单击绘图命令按钮,绘制变量y的图形,并分析图形的含义。
5、访问mathworks公司的主页,查询有关MATLAB的产品信息。
主要教学环节的组织:教师讲授实验目的、开发环境界面、演示实验过程,然后同学上机练习。
思考题:1、如何启动与退出MA TLAB集成环境?启动:(1)在windows桌面,单击任务栏上的开始按钮,选择‘所有程序’菜单项,然后选择MA TLAB程序组中的MA TLABR2008b程序选项,即可启动MATLAB系统。
(2)在MA TLAB的安装路径中找到MA TLAB系统启动程序matlab.exe,然后运行它。
(3)在桌面上建立快捷方式后。
双击快捷方式图标,启动MA TLAB。
退出:(1)在MA TLAB主窗口file菜单中选择exitMATLAB命令。
(2)在MA TLAB命令窗口中输入exit或quit命令。
(3)单击MATLAB主窗口的关闭按钮。
2、简述MATLAB的主要功能。
MATLAB是一种应用于科学计算领域的数学软件,它主要包括数值计算和符号计算功能、绘图功能、编程语言功能以及应用工具箱的扩展功能。
3、如果一个MATLAB命令包含的字符很多,需要分成多行输入,该如何处理?使用‘;’隔开4、Help命令和lookfor命令有何区别?help是显示matlab内置的帮助信息一般是help 命令;而lookfor 关键词是通过关键词查找,“关键词”就是你要找的词语5、在MA TLAB环境下,建立了一个变量fac,同时又在当前目录下建立了一个m文件fac.m,如果需要运行fac.m文件,该如何处理?实验二MATLAB矩阵及运算实验目的和要求:1、掌握MATLAB数据对象的特点及运算规则2、掌握MATLAB建立矩阵的方法及矩阵处理的方法3、掌握MATLAB分析的方法实验内容:1.求下列表达式的值(1)(2)(3)(4)2.已知A=[-1,5,-4;0,7,8;3,61,7],B=[8,3,-1;2,5,3;-3,2,0] 求下列表达式的值:(1)A+6B和A^2-B+I(其中I为单位矩阵)。
matlab实验二

北京工业大学Matlab实验报告**: ***学号: ************: **实验二、Matlab 的基本计算(一)实验目的1.掌握建立矩阵的方法。
2.掌握Matlab 各种表达式的书写规则以及常用函数的使用。
3.能用Matlab 进行基本的数组、矩阵运算。
4.掌握矩阵分析的方法以及能用矩阵运算或求逆法解线性方程组。
5.掌握Matlab 中的关系运算与逻辑运算。
(二)实验环境1.计算机2.MATLAB7.0集成环境(三)实验内容及要求1、熟练操作MATLAB7.0运行环境;2、自主编写程序,必要时参考相关资料;3、实验前应写出程序大致框架或完整的程序代码;4、完成实验报告。
(四)实验程序设计1.利用diag 等函数产生下列矩阵。
⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=032570800a ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=804050702b2.利用reshape 函数将1题中的a 和b 变换成行向量。
3.产生一个均匀分布在(-5,5)之间的随机矩阵(10×2),要求精确到小数点后一位。
4.已知:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=76538773443412A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=731203321B求下列表达式的值:(1) B A K *611+=和I B A K +-=12(其中I 为单位矩阵)(2) B A K *21=和B A K *.22=(3) 331^A K =和3.32^A K =(4) B A K /41=和A B K \42=(5) ],[51B A K =和]2:);],3,1([[52^B A K = 5.下面是一个线性方程组:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡52.067.095.03216/15/14/15/14/13/14/13/12/1x x x(1)求方程的解(矩阵除法和求逆法)(2)将方程右边向量元素3b 改为0.53,再求解,并比较3b 的变化和解的相对变化。
MATLAB全部实验及答案

MATLAB全部实验及答案实验一、MATLAB基本操作实验内容及步骤1、命令窗口的简单使用(1)简单矩阵的输入(2)求[12+2×(7-4)]÷32的算术运算结果2、有关向量、矩阵或数组的一些运算(1)设A=15;B=20;求C=A+B与c=a+b?(2)设A=[1 2 3;4 5 6;7 8 9],B=[9 8 7;6 5 4;3 2 1];求A*B与A.*B?A*B就是线代里面的矩阵相乘 A.*B是对应位置的元素相乘(3)设a=10,b=20;求i=a/b=0.5与j=a\b=2?(4)设a=[1 -2 3;4 5 -4;5 -6 7]请设计出程序,分别找出小于0的矩阵元素及其位置(单下标、全下标的形式),并将其单下标转换成全下标。
clear,clca=[1 -2 3;4 5 -4;5 -6 7];[x,y]=find(a<0);c=[];for i=1:length(x)c(i,1)=a(x(i),y(i));c(i,2)=x(i);c(i,3)=y(i);c(i,4)=(y(i)-1)*size(a,2)+x(i);endc(5)在MATLAB命令行窗口运行A=[1,2;3,4]+i*[5,6;7,8];看结果如何?如果改成运行A=[1,2;3,4]+i[5,6;7,8],结果又如何?前面那个是虚数矩阵,后面那个出错(6)请写出完成下列计算的指令:a=[1 2 3;3 4 2;5 2 3],求a^2=?,a.^2=?a^2= 22 16 1625 26 2326 24 28a.^2=1 4 99 16 425 4 9(7)有一段指令如下,请思考并说明运行结果及其原因clearX=[1 2;8 9;3 6];X( : ) 转化为列向量(8)使用三元组方法,创建下列稀疏矩阵2 0 8 00 0 0 10 4 0 06 0 0 0方法一:clear,clcdata=[2 8 1 4 6];ir=[1 1 2 3 4 ];jc=[1 3 4 2 1];s=sparse(ir,jc,data,4,4);full(s)方法二:不用三元组法clear,clca=zeros(4,4);a(1,[1,3])=[2,8];a(2,4)=1;a(3,2)=4;a(4,1)=6;a(9) 写出下列指令的运行结果>> A = [ 1 2 3 ]; B = [ 4 5 6 ];>> C = 3.^A>> D = A.^B3、 已知⎪⎭⎫ ⎝⎛+⋅=-334sin 234πt e y t 若需要计算t ∈[-1,1],取间隔为0.01,试计算出相对应的y 值。
实验二MATLAB矩阵分析和处理

实验二 MATLAB 矩阵分析和处理一、实验目的1.掌握生成特殊矩阵的方法。
2.掌握矩阵分析的方法。
4.用矩阵求逆法解线性方程组。
二、实验内容1.设有分块矩阵⎥⎦⎤⎢⎣⎡=⨯⨯⨯⨯22322333S O R E A ,其中E,R,O,S 分别为单位矩阵、随机矩阵、零矩阵和对角矩阵,试通过数值计算验证⎥⎦⎤⎢⎣⎡+=22S O RS R E A 。
解:>> E=eye(3);>> R=rand(3,2);>> O=zeros(2,3);>> S=diag(1:2);>> A=[E R;O S];A =1.0000 0 0 0.9501 0.48600 1.0000 0 0.2311 0.89130 0 1.0000 0.6068 0.76210 0 0 1.0000 00 0 0 0 2.0000>> A^2ans =1.0000 0 0 1.9003 1.45790 1.0000 0 0.4623 2.67390 0 1.0000 1.2137 2.28630 0 0 1.0000 00 0 0 0 4.0000>> [E R+R*S;O S^2]ans =1.0000 0 0 1.9003 1.45790 1.0000 0 0.4623 2.67390 0 1.0000 1.2137 2.28630 0 0 1.0000 00 0 0 0 4.0000所以⎥⎦⎤⎢⎣⎡+=22S ORS R E A .2.产生5阶希尔伯特矩阵H 和5阶帕斯卡矩阵P ,求其行列式的值Hh 和Hp 以及他们的条件数Th 和Tp ,判断哪个矩阵性能更好,为什么?解:H=hilb(5)H =1.0000 0.5000 0.3333 0.2500 0.20000.5000 0.3333 0.2500 0.2000 0.16670.3333 0.2500 0.2000 0.1667 0.14290.2500 0.2000 0.1667 0.1429 0.12500.2000 0.1667 0.1429 0.1250 0.1111 >> P=pascal(5)P =1 1 1 1 11 2 3 4 51 3 6 10 151 4 10 20 351 5 15 35 70>> Hh=det(H)Hh =3.7493e-012>> Hp=det(P)Hp =1>> Th=cond(H)Th =4.7661e+005>> Tp=cond(P)Tp =8.5175e+003由上式看出:帕斯卡矩阵性能更好,因为行列式为1,而希尔伯特矩阵条件数很差,使用一般方法求逆矩阵会因原始数据的微小变动产生不可靠的结果3.建立一个5x5矩阵,求它的行列式的值、迹、秩和X 数解:a=magic(5)a =17 24 1 8 1523 5 7 14 164 6 13 20 2210 12 19 21 311 18 25 2 9>> b=det(a)b =5070000>> c=trace(a)c =65>> d=rank(a)d =5>> e=norm(a)e =65.0000>>4.已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=5881252018629A ,求特征值和特征向量,并分析其数学意义解:A=[-29 6 18;20 5 12;-8 8 5]A =-29 6 1820 5 12-8 8 5>> b=eig(A)b =-25.3169-10.518216.8351>> [v,b]=eig(A)0.7130 0.2803 0.2733-0.6084 -0.7867 0.87250.3487 0.5501 0.4050b =-25.3169 0 00 -10.5182 00 0 16.83515.下面是一个线性方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡52.067.095.06/15/14/15/14/13/14/13/12/1321x x x(1) 求方程的解(2) 将方程右边向量第三个元素0.52改为0.53,并比较解的变化(3) 计算系数矩阵A 的条件数并分析结论解:(1) A=[1/2 1/3 1/4;1/3 1/4 1/5;1/4 1/5 1/6]A =0.5000 0.3333 0.25000.3333 0.2500 0.20000.2500 0.2000 0.1667>> C=[0.95;0.67;0.52]C =0.95000.67000.5200>> B=A\CB =1.20000.60000.6000>>(2)A=[1/2 1/3 1/4;1/3 1/4 1/5;1/4 1/5 1/6]A =0.5000 0.3333 0.25000.3333 0.2500 0.20000.2500 0.2000 0.1667>> C=[0.95;0.67;0.53]C =0.95000.67000.5300>> B=A\C3.0000-6.60006.6000(3)cond(A)ans =1.3533e+0036.建立A矩阵,试比较sqrtm(A)和sqrt(A),并分析他们的区别解:A=magic(3)A =8 1 63 5 74 9 2>> sqrtm(A)ans =2.7065 + 0.0601i 0.0185 + 0.5347i 1.1480 - 0.5948i0.4703 + 0.0829i 2.0288 + 0.7378i 1.3739 - 0.8207i0.6962 - 0.1430i 1.8257 - 1.2725i 1.3511 + 1.4155i>> sqrt(A)ans =2.8284 1.0000 2.44951.73212.2361 2.64582.00003.0000 1.4142区别:sqrt是求矩阵里每个元素的平方根,并组成一个新的矩阵。
MATLAB实验。

MATLAB实验班级:11电气(2)姓名:幸劲昆学号:201124122201实验一 MATLAB 运算基础(一)一、实验目的1、掌握建立矩阵的方法。
2、掌握MATLAB 各种表达式的书写规则以及各种运算方法。
二、实验内容1、求下列表达式的值。
(1)e=2.73;z1=2*sin((85/360)*2*pi)/(1+e^2) z1 =0.2357 (2)()x x z ++=1ln 212,其中⎢⎣⎡-=45.02x ⎥⎦⎤+521i x=[2 ,1+2i;-0.45,5]x =2.0000 1.0000 + 2.0000i -0.4500 5.0000z2=0.5*log(x+sqrt(1+x)) z2 =0.6585 0.6509 + 0.4013i -0.6162 1.0041 (3)a=[-3.0:0.1:3.0];z3=(exp(0.3*a)-exp(0.2*a))./2.*sin(a+0.3);plot(z3)2、已知⎢⎢⎢⎣⎡=33412A 65734 ⎥⎥⎥⎦⎤-7874 和 ⎢⎢⎢⎣⎡=321B 203- ⎥⎥⎥⎦⎤-731 求下列表达式的值:(1)A+6*B 和A-B+I (其中I 为单位矩阵)。
a=[12 34 -4;34 7 87;3 65 7] b=[1 3 -1;2 0 3;3 -2 7] I=eye(3)a =b = I =12 34 -4 1 3 -1 1 0 02 03 34 7 87 0 1 03 -2 7 3 65 7 0 0 1z1=a+6*b z2=a-b+Iz1 = z2 =18 52 -10 12 31 -346 7 105 32 8 8421 53 49 0 67 1(2)A*B和A.*B。
>> a*b >> a.*bans = ans =68 44 62 12 102 4309 -72 596 68 0 261154 -5 241 9 -130 49(3)A^3和A.^3。
2019年MATLAB)课后实验答案

实验一 MATLAB 运算基础1. 先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1) 0122sin 851z e =+(2) 21ln(2z x =,其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--(4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:: 解:4. 完成下列操作:(1) 求[100,999]之间能被21整除的数的个数。
(2) 建立一个字符串向量,删除其中的大写字母。
解:(1) 结果:(2). 建立一个字符串向量例如:ch='ABC123d4e56Fg9';则要求结果是:实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵,试通过数值计算验证22E R RS A O S +⎡⎤=⎢⎥⎣⎦。
解: M 文件如下;5. 下面是一个线性方程组:1231112340.951110.673450.52111456x x x ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦(1) 求方程的解。
(2) 将方程右边向量元素b 3改为再求解,并比较b 3的变化和解的相对变化。
(3) 计算系数矩阵A 的条件数并分析结论。
解: M 文件如下:123d4e56g9实验三 选择结构程序设计1. 求分段函数的值。
2226035605231x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且及其他用if 语句实现,分别输出x=,,,,,,时的y 值。
matlab矩阵运算实验报告

matlab矩阵运算实验报告Matlab矩阵运算实验报告一、引言矩阵运算是数学和工程领域中的重要概念之一,它在各个领域中都有广泛的应用。
Matlab作为一种强大的数学软件工具,提供了丰富的矩阵运算功能,可以帮助我们进行高效的数值计算和数据处理。
本实验报告将介绍Matlab中的矩阵运算功能,并通过实例展示其在实际问题中的应用。
二、矩阵运算的基本概念矩阵是由若干个数按照行和列排列形成的一个矩形阵列,它是线性代数中的基本工具。
在Matlab中,矩阵可以通过直接输入数值或使用内置函数生成。
矩阵运算包括加法、减法、乘法、转置等操作,这些操作可以对矩阵的每个元素进行运算,也可以对整个矩阵进行运算。
三、矩阵运算的实例分析1. 矩阵的创建与赋值在Matlab中,可以使用以下命令创建一个矩阵,并对其进行赋值操作:A = [1, 2, 3; 4, 5, 6; 7, 8, 9];这样就创建了一个3行3列的矩阵A,并对其进行了赋值。
可以通过输入A来查看矩阵A的内容。
2. 矩阵的加法与减法矩阵的加法和减法是按照对应元素进行运算的。
例如,对于两个3行3列的矩阵A和B,可以使用以下命令进行加法运算:C = A + B;同样地,可以使用以下命令进行减法运算:D = A - B;这样就得到了矩阵C和D。
3. 矩阵的乘法矩阵的乘法是按照行乘以列的方式进行的。
例如,对于一个3行2列的矩阵A和一个2行4列的矩阵B,可以使用以下命令进行乘法运算:C = A * B;这样就得到了一个3行4列的矩阵C。
4. 矩阵的转置矩阵的转置是将矩阵的行和列进行交换的操作。
例如,对于一个3行2列的矩阵A,可以使用以下命令进行转置操作:B = A';这样就得到了一个2行3列的矩阵B。
四、矩阵运算的应用实例矩阵运算在实际问题中有着广泛的应用。
以下是一个简单的实例,通过矩阵运算来解决线性方程组的问题。
假设有一个线性方程组:2x + y = 4x + 3y = 6可以将其表示为矩阵形式:A = [2, 1; 1, 3];B = [4; 6];通过矩阵运算可以求解出未知数x和y的值:X = A \ B;这样就得到了未知数x和y的值。
实验二matlab矩阵分析与处理

《MATLAB及应用A》第二次上机作业一、一球从100米高度自由落下,每次落地后反弹回原高度的一半,再落下。
求它在第10次落下时共经过多少米?第10次反弹多高?MATLAB源程序:MATLAB运行结果:二、有如下一段MATLAB程序,请解释说明每个语句的功能,必要时用数学表达式(不是在MATLAB中的输入形式);并给出y1、y2、y3的值(可从MATLAB中复制)。
MATLAB源程序:x=linspace(0,6);y1=sin(2*x);y2=sin(x.^2);y3=(sin(x)).^2;各条命令语句的功能如下:y1、y2、y3的值分别为:三、教材第55页习题三,第3题。
MATLAB源程序:MATLAB运行结果:四、选择题(1) i=2; a=2i; b=2*i; c=2*sqrt(-1); 程序执行后,a, b, c的值分别是多少?()(A) a=4, b=4, c=2.0000i(B) a=4, b=2.0000i, c=2.0000i(C) a=2.0000i, b=4, c=2.0000i(D) a=2.0000i, b=2.0000i, c=2.0000i(2) 求解方程x4-4x3+12x-9 = 0 的所有解,其结果为()(A) 1.0000, 3.0000, 1.7321, -1.7321(B) 1.0000, 3.0000, 1.7321i, -1.7321i(C) 1.0000i, 3.0000i, 1.7321, -1.7321(D) -3.000-0i, 3.0000i, 1.7321, -1.7321五、求[100,1000]之间的全部素数(选做)。
MATLAB源程序: MATLAB运行结果:一、一球从100米高度自由落下,每次落地后反弹回原高度的一半,再落下。
求它在第10次落下时共经过多少米?第10次反弹多高?MATLAB源程序:>> a=(0:-1:-9) %产生一个行向量aa =0 -1 -2 -3 -4 -5 -6 -7 -8 -9>> b=pow2(a) %对行向量a中的每一个元素分别求幂函数b =1.0000 0.5000 0.2500 0.1250 0.0625 0.0313 0.0156 0.007 8 0.0039 0.0020>> h=100*b %对行向量b中的每一个元素分别乘以100h =100.0000 50.0000 25.0000 12.5000 6.2500 3.1250 1.5625 0. 7813 0.3906 0.1953>> s1=sum(h) %对行向量h中的元素求和s1 =199.8047>> s=s1*2-100 %求出第10次落下时经过的高度s =299.6094>> h10=h(10)/2 %求出第10次反弹的高度h10 =0.0977二、有如下一段MATLAB程序,请解释说明每个语句的功能,必要时用数学表达式(不是在MATLAB中的输入形式);并给出y1、y2、y3的值(可从MATLAB 中复制)。
matlab第二章实训报告

佛山科学技术学院《MATLAB教程第二章实训》报告专业姓名成绩班级学号日期一、目的1.学习matlab的数据类型2.矩阵和数组的算术运算3.字符串4.时间和日期5.结构体和元胞数组6.多维数组7.逻辑运算和关系运算8.数组的信息获取9.多项式二、步骤1.学习matlab的数据类型Matlab R2010a定义了15种基本的数据类型,包括整型、浮点型、字符型和逻辑型等。
用户甚至可以定义自己的数据类型。
Matlab内部的任何数据类型,都是按照数组的形式进行储存和运算的。
数值型包括整数和浮点数,其中整数包括有符号数和无符号数,浮点数包括单精度型和双精度型。
在默认情况下,matlab默认将所有数值都按照双精度浮点数类型来存储和操作。
(1)常数和变量Matlab的常数采用十进制表示,可以用带小数点的形式直接表示,也可以用科学记数法。
数值的表示范围是10^-309-10^309。
变量是数值计算的基本单元。
Matlab与其他的高级语言不同,变量使用是无需先定义,其名称就是第一次合法出现时的名称,因此用起来很便捷。
Matlab的变量命名有一定的规则:a.变量区分字母的大小写。
例如,“a”和“A”是不同的变量。
b.变量名不能超过63个字符,第63个字符后的字符会被忽略。
c.变量名必须以字母开头,变量名的组成可以是任意字母、数字或者下划线,但不能有空格和标点符号。
d.关键字(如if\while等)不能作为变量名。
在matlab中的所有表示符号包括函数名、文件名都是遵循变量名的命名规则。
Matlab中有一些自己的特殊变量,是由系统预先自动定义的,例如:ans——运算结果的默认变量名Pi——圆周率πEps——浮点数的相对误差Inf或inf——无穷大Nan或nan——不定值i或j——i=j=-1^1/2,虚数单位Nargin——函数的输入变量数目Nargout——函数的输出变量数目Realmin——最小的可用正实数Realmax——最大的可用正实数(2)整数和浮点数Matlab提供了8种内置的整数类型,为了在使用时提高运行速度和存储空间,应该尽量使用字节少的数据类型,可以使用类型转换函数将各种整数类型强制相互转换。
实验二MATLAB的矩阵操作_参考答案

1
5
>> A(k)
ans =
23
10
(2)取出A前3行构成矩阵B,前两列构成矩阵C,右下角 子矩阵构成矩阵D,B与C的乘积构成矩阵E.
>> B=A([1,2,3],:)
B =
23.0000 10.0000 -0.7780 0
41.0000 -45.0000 65.0000 5.0000
32.0000 5.0000 0 32.0000
y =
-128.4271
2.已知 ,
求下列表达式的值:
(1) , (其中I为单位矩阵)
A=[-1,5,-4;0,7,8;3,61,7]
B=[8,3,-1;2,5,3;-3,2,0]
>> A+6*B
ans =
47 23 -10
12 37 26
-15 73 7
&
ans =
-1.2768 -0.4743 0.2411
2.1229 1.3173 -0.2924
3.已知
完成下列操作
(1)输出A在[10,25]范围内的全部元素
A=[23,10,-0.778,0;41,-45,65,5;32,5,0,32;6,-9.54,54,3.14]
>> k=find(A>=10&A<=25)
(2)
(3)
2.已知 ,
求下列表达式的值:
(1) , (其中I为单位矩阵)
(2)A*B、A.*B和B*A
(3)A/B及B/A
3.已知
完成下列操作
(1)输出A在[10,25]范围内的全部元素
(2)取出A前3行构成矩阵B,前两列构成矩阵C,右下角 子矩阵构成矩阵D,B与C的乘积构成矩阵E.
实验二 MATLAB的科学计算

实验二 MATLAB的科学计算一、实验目的1、了解MATLAB的基本计算功能2、符号运算功能二、实验内容(一)基本计算功能例1、求[12+2× (7-4)]÷32的运算结果>>(12+2*(7-4))/3^2ans=2例2、用MATLAB求下面线性方程组的解3x1+ x2 - x3 = 3.6x1+2x2+4x3 = 2.1-x1+4x2+5x3 = -1.4>>A=[3 1 -1;1 2 4;-1 4 5];b=[3.6;2.1;-1.4];>>x=A\bx =1.4818-0.46060.3848例3、求两个矩阵的乘积a=[1 2 3;3 4 5;3 2 1]b=[1 2;3 4; 5 6]c=a*bc =22 2840 5214 20(二)符号运算功能1、求极限通常在MATLAB软件中,用limit 函数来求极限,其用法如表9-5所示:表9-5 limit 函数的用法例1、 求42cos lim 202x x e x -→.>> syms x % 把字符x 定义为符号 >>limit((cos(x)-exp(-x^2/2))/x^4)ans =-1/12例2 求42lim 22--→x x x .>> limit((x-2)/(x^2-4),x,2)ans =1/4例3 求t x t x t )cos()cos(lim 0-+→>> syms t x>> limit((cos(x+t)-cos(x))/t,t,0)ans =-sin(x)2 、求导数MATLAB 软件提供求函数导数的指令是diff ,具体使用格式如下:(1)diff(f, x) 表示对f (这里f 是一个函数表达式)求关于符号变量x 的一阶导数.若x 缺省,则表示求f 对预设独立变量的一阶导数.(2)diff(f, x, n) 表示对f 求关于符号变量x 的n 阶导数.若x 缺省,则表示求f 对预设独立变量的n 阶导数.例9-7 已知,c bx ax x f ++=2)(求)(x f 的一阶、二阶导数.>> syms a b c x>> f='a*x^2+b*x+c'f =a*x^2+b*x+c>> diff(f, x)ans =2*a*x+b>> diff(f,2)ans =2*a3 、求积分MATLAB软件提供求函数积分的指令是int,具体使用格式如下:(1)int(f) 返回f对预设独立变量的积分值;(2)int(f,v) 返回f对独立变量v的积分值;(3)int(f,a,b) 返回f对预设独立变量的积分值,积分区间为[a,b],a和b为数值式;(4)int(f,v,a,b) 返回f对独立变量的积分值,积分区间为[a,b],a和b为数值式;(5)int(f,m,n) 返回f对预设变量的积分值,积分区间为[m,n],m和n为符号式;例1、求下列函数的积分 :例:求不定积分⎰-dxex x23,⎰+12xxdx;>> syms x>> f=sym('x^3*exp(-x^2)') % 或 int('x^3*exp(-x^2)') f =x^3*exp(-x^2)>> int(f)ans =-1/2*x^2/exp(x^2)-1/2/exp(x^2)>> int('1/(x*sqrt(x^2+1))')ans =-atanh(1/(x^2+1)^(1/2))4 、数学表达式的化简例、 将下面表达式进行因式分解. 132-=a f>> f2=sym('a^3-1');>> factor(f2)ans =(a-1)*(a^2+a+1)。
MATLAB实验报告

实验二MATLAB语言基础一、实验目的基本掌握MA TLAB向量矩阵数组的生成及基本运算(区分数组运算和矩阵预算)、常用的数学函数。
了解字符串的操作。
二、实验内容(1)向量的生成和运算。
(2)矩阵的创建、引用和运算。
(3)多维数组的创建和运算。
(4)字符创的操作。
三、实验步骤1.向量的生成和运算1)向量的生成<1>、直接输入法<2> 冒号表达式法<3> 函数法:Linspace()是线性等分函数,logspace()是对数等分函数。
2)向量的运算1>维数相同的行、列向量之间可以相加减,标量可以与向量直接相乘除。
2>向量的点积与叉积运算E1和E2虽然表达式相同,但E1是标量,E2是矩阵。
2.矩阵的创建、引用和运算1)矩阵的创建和引用矩阵是由m*n元素构成的矩形结构,行向量和列向量是矩阵的特殊形式。
1>直接输入法:2>抽取法:包括单下标抽取和全下表抽取两种方式,且两种方式抽取的元素都必须以小括号括起来。
3>函数法:利用ones(m;n)创建全1矩阵,zeros()创建全0矩阵,eyes()创建单位矩阵等等。
4>拼接法:纵向拼接横向拼接5>利用拼接函数cat()repmat()和变形函数reshape()>> A1=[1 2 3;9 8 7 ;4 5 6];A2=A1.';>> cat(1,A1,A2) 沿行向拼接ans =1 2 39 8 74 5 61 9 42 8 53 7 6>> cat(2,A1,A2) 沿列向拼接ans =1 2 3 1 9 49 8 7 2 8 54 5 6 3 7 6>> repmat(A1,2,2)ans =1 2 3 1 2 39 8 7 9 8 74 5 6 4 5 61 2 3 1 2 39 8 7 9 8 74 5 6 4 5 6> A=linspace(2,18,9)A =2 4 6 8 10 12 14 16 18 >> reshape(A,3,3)ans =2 8 144 10 166 12 182)矩阵的运算练习(1)用矩阵除法求下列方程组的解x=[x1;x2;x3]>> A=[6 3 4;-2 5 7;8 -1 -3];B=[3;-4;-7];X=A\BX =1.0200-14.00009.7200(2)求矩阵的秩A=[6 3 4;-2 5 7;8 -1 -3];>> rank(A)ans =3[X,lamda]=eig(A)X =0.8013 -0.1094 -0.16060.3638 -0.6564 0.86690.4749 0.7464 -0.4719lamda =9.7326 0 00 -3.2928 00 0 1.5602(3)矩阵的开方>> B=sqrtm(A)B =2.2447 + 0.2706i 0.6974 - 0.1400i 0.9422 - 0.3494i -0.5815 + 1.6244i 2.1005 - 0.8405i 1.7620 - 2.0970i1.9719 - 1.8471i -0.3017 + 0.9557i 0.0236 +2.3845i (4)矩阵的指数与对数:> C=expm(A)C =1.0e+004 *1.0653 0.5415 0.63230.4830 0.2465 0.28760.6316 0.3206 0.3745>> logm(C)ans =6.0000 3.0000 4.0000-2.0000 5.0000 7.00008.0000 -1.0000 -3.0000(6)矩阵的转置D=A'D =6 -2 83 5 -14 7 -3(7)矩阵的提取与翻转:通过各种特定函数如triu(A)、tril(A),diag(A)、flipud (A)、fliplr(A)等等。
matlab2022实验2参考答案

matlab2022实验2参考答案报告名称:MATLAB试验二符号计算姓名:学号:专业:班级:MATLAB实验二MATLAB符号计算试验报告说明:1做试验前请先预习,并独立完成试验和试验报告。
2报告解答方式:将MATLAB执行命令和最后运行结果从命令窗口拷贝到每题的题目下面,请将报告解答部分的底纹设置为灰色,以便于批阅。
3在页眉上写清报告名称,学生姓名,学号,专业以及班级。
3报告以Word文档书写。
一目的和要求1熟练掌握MATLAB符号表达式的创建2熟练掌握符号表达式的代数运算3掌握符号表达式的化简和替换4熟练掌握符号微积分5熟练掌握符号方程的求解二试验内容1多项式运算(必做)1.1解方程:f(某)=某^4-10某某^3+34某某^2-50某某+25=0%采用数值方法:>>f=[1-1034-5025];>>root(f)%采用符号计算方法:f1=ym('某^4-10某某^3+34某某^2-50某某+25')olve(f1)1.2求有理分式R=(3某^3+某)(某^3+2)/((某^2+2某-2)(5某^3+2某^2+1))的商多项式和余多项式.a1=[3010];a2=[1002];a=conv(a1,a2);b1=[12-2];b2=[5201];b=conv(b1,b2);[p,r]=deconv(a,b);%注意:ab秩序不可颠倒。
%reidue用于实现多项式的部分分式展开,此处用deconv函数报告名称:MATLAB试验二符号计算姓名:学号:专业:班级:%%此题,有同学程序如下:某1=[3010],某2=[1002],某3=[12-2],某4=[5201]某5=conv(某1,某2)[y6,r]=deconv(某5,某3)R=deconv(y6,某4)%%这种方法较第一种解法缺点:在除法运算中,会产生误差,故此题应先将分母的多项式相乘后,再与分子部分的多项式进行运算。
MATLAB实验二答案

实验二报告人:王业成年级:机电131 学号:2013012496实验日期:2015.3.327报告完成日期:2015.3.30一、实验名称熟悉和掌握MA TLAB中关于矩阵变换以及矩阵运算的各种命令。
二、实验目的:熟悉和掌握MA TLAB中关于矩阵变换以及矩阵运算的各种命令。
三、实验内容:1.数、数组、矩阵的输入(1)数的输入a=5b=2-5i(2)数组的输入c=[1,3,5,7,9,11] %元素之间要用逗号用空格分开d=1:2:11e=linspace(1,11,6)体会以上输入有什么区别和联系。
(3)矩阵的输入A=[2,3,5;1,3,5;6,9,4] %行之间要用分别隔开2.矩阵大小的测试和定位A=[3,5,6;,2,5,8;3,5,9;3,7,9][n,m]=size(A)A(1,3)3. 矩阵的块操作A(2,:)A([1,3],:)A(2:3,1:2)问题2.1如何将A的2,3列互换?4.矩阵的四则运算A=[3,5,8;-2,3,6;1,4,9]B=rand(3,3)C=A+BD=A-BE=A*B问题2.2E为矩阵A、B的乘积运算结果,如果要求E的结果为A和B对应元素相乘的结果,应输入什么命令?F=A/B问题2.3 如果要求F为A,B对应元素作除法运算的结果,应输入什么命令?5.矩阵的点运算A=[1 2;3 4];B=[5 6;7 8];A*BA.*BA^2A.^26.矩阵的逻辑运算A=[1 2;3 4]; B=[0 6; 0 8]; A | BA&Bxor(A,B)a=-5;b=-10;(b~=0)&&(a/b>5)(b= =0)||(a/b>0)~a四、回答问题:问题2.1如何将A的2,3列互换?问题2.2 E为矩阵A、B的乘积运算结果,如果要求E的结果为A和B对应元素相乘的结果,应输入什么命令?问题2.3 如果要求F为A,B对应元素作除法运算的结果,应输入什么命令?五、思考题:1.输入一个矩阵A,取出A的第2行第1列的元素;取出A的第1,3,4列的所有元素;让A的第1列和第3列互换;删除A的第二列。
MATLAB实验二

本科实验报告课程名称《MATLAB电子信息应用》实验题目:矩阵和数组的操作实验地点:D001机房专业班级:学号:学生姓名:指导教师:一、实验环境计算机 MATLAB软件二、实验目的1.掌握矩阵和数组的一般操作,包括创建、保存、修改和调用等。
2.学习矩阵和数组的加减法运算与乘法。
3.掌握对数组中元素的寻访与赋值,会对数组进行一般的操作。
三、实验内容和步骤1.用三种方法创建一个3*3矩阵,然后利用矩阵编辑器,将其扩充为4*5矩阵,并保存,试着调用它。
(1)直接输入法如在命令区输入A=[3,2,1;4,5,6;7,8,9]。
(2)直接利用MATLAB提供的函数创建一个3*3矩阵如在命令区输入rand(3,3)即得到一个3*3的随机矩阵(3)利用MATLAB提供的“Matrix Editor”完成输入步骤1 在命令区输入A=1.步骤2 用鼠标单击工具栏的工作区浏览器,MATLAB弹出变量浏览器,选中变量A,鼠标左键双击A,打开矩阵编辑器。
步骤3 在左下角的两个文本框中分别输入希望得到的矩阵的行数和列数:3行3列,即得到一个3*3矩阵。
步骤4 要将上面矩阵改为一个4*5矩阵,只需改变矩阵的行数和列数即可。
如将3行3列改为4行5列,即可得到一个4*5矩阵。
若想修改其中的元素,只需用鼠标选中表格中我们想要修改的元素,将原来的元素修改为我需要的值。
步骤5 要命令区输入save data,即可保存上面例子中创建的矩阵A。
步骤6 在命令区输入 load data 即可把vabaocun在文件中的矩阵读到MATLAB的工作区的内存中来。
2.建立一个等差数列,然后由它产生一个对角阵。
步骤1 在命令区输入a=linspace(0,1.5,5)产生一个等差数列。
步骤2 在命令区输入B=diag(a)产生一个对角阵。
3.利用MATLAB的函数inv(A)求方阵A的逆矩阵。
步骤1 在命令区输入A=[1,2;5,6]得到一个2*2的方阵。
matlab 实验报告

matlab 实验报告Matlab实验报告引言:Matlab是一种强大的数值计算和可视化软件,广泛应用于科学、工程和经济等领域。
本实验报告将介绍我在使用Matlab进行实验过程中的一些经验和结果。
实验一:矩阵运算在这个实验中,我使用Matlab进行了矩阵运算。
首先,我创建了一个3x3的矩阵A和一个3x1的矩阵B,并进行了矩阵相乘运算。
通过Matlab的矩阵乘法运算符*,我得到了一个3x1的结果矩阵C。
接着,我对矩阵C进行了转置操作,得到了一个1x3的矩阵D。
最后,我计算了矩阵C和矩阵D的点积,并将结果输出。
实验二:数据可视化在这个实验中,我使用Matlab进行了数据可视化。
我选择了一组实验数据,包括时间和温度两个变量。
首先,我将数据存储在一个矩阵中,并使用Matlab的plot函数将时间和温度之间的关系绘制成曲线图。
接着,我使用Matlab的xlabel、ylabel和title函数添加了横轴、纵轴和标题。
最后,我使用Matlab的legend函数添加了图例,以便更好地理解图表。
实验三:数值积分在这个实验中,我使用Matlab进行了数值积分。
我选择了一个函数f(x)进行积分计算。
首先,我使用Matlab的syms函数定义了符号变量x,并定义了函数f(x)。
接着,我使用Matlab的int函数对函数f(x)进行积分计算,并将结果输出。
为了验证结果的准确性,我还使用了Matlab的diff函数对积分结果进行了求导操作,并与原函数f(x)进行了比较。
实验四:信号处理在这个实验中,我使用Matlab进行了信号处理。
我选择了一个音频文件,并使用Matlab的audioread函数读取了该文件。
接着,我使用Matlab的fft函数对音频信号进行了傅里叶变换,并将结果绘制成频谱图。
为了进一步分析信号的特征,我还使用了Matlab的spectrogram函数绘制了信号的时频图。
通过对信号的频谱和时频图的观察,我可以更好地理解信号的频率和时域特性。
中国矿业大学 实验二 MATLAB语言基础

实验二MATLAB语言基础一、实验目的基本掌握MATLAB向量、矩阵、数组的生成及其基本运算(区分数组运算和矩阵运算)、常用的数学函数。
了解字符串的操作。
二、实验内容1.向量的生成与运算;2.矩阵的创建、引用和运算;3.多维数组的创建及运算;4.字符串的操作。
三、实验步骤1.向量的生成与运算①向量的生成向量的生成有三种方法:直接输入法:生成行向量、列向量;冒号表达式法:变量=初值:间隔(可正可负):终值函数法:使用linspace线性等分函数,logspace对数等分函数。
格式为:linspace(初值,终值,个数)Logspace(初值,终值,个数), 初值及终值均为10的次幂。
②向量的运算A=[1 2 3 4 5],b=3:7,计算两行向量的转置,两行向量人加、减,两列向量的加、减;向量的点积与叉积。
a=[1 2 3 4 5];b=3:7;at=a',bt=b'e1=a+b,e2=a-bf1=at+bt,f2=at-btg1=dot(a,b),g2=a*btg4=a.*bA=1:3;B=4:6;g3=cross(A,B)注意:g1和g2的结果是否相同,为什么?g4的结果与g1和g2人结果是否一样,为什么?2.矩阵的创建、引用和运算矩阵是由n×m元素构成的矩阵结构。
行向量和列向量是矩阵的特殊形式。
①矩阵的创建矩阵的创建可由以下方法进行操作:直接输入法、抽取法、函数法、拼接法。
具体步骤为:建立两个矩阵,利用已学过的函数,对此进行所述四种方法进行操作。
a=[1 2 3;4 5 6];b=[1 4 72 5 83 6 9];a(1)a(4:end)b(:,1)b(:)b(5)a=fix(rand(3)*100)%建立一个两位有效整的随机矩阵b=a(1:3,2:3)c=a([1 3],[2 4])d=a([1 3 ;2 4])a=ones(3,3)b=zeros(3)c=eye(3)d=magic(3)%建立一个行、列、对角线上的和为一相同的数的魔术矩阵c=eye(3)d=[a b]f=[a;c]②矩阵的运算矩阵的运算有基本运算(加、减、乘、左除、右除)等,还有矩阵函数运算(求逆inv、秩rank、矩阵的翻转、矩阵的转置)等。
matlab矩阵实验报告

matlab矩阵实验报告Matlab矩阵实验报告引言:Matlab是一种强大的数学计算工具,广泛应用于科学研究、工程设计和数据分析等领域。
其中,矩阵操作是Matlab的一项重要功能,它提供了丰富的矩阵运算和处理函数。
本实验将通过几个具体的案例,展示Matlab中矩阵操作的应用和效果。
一、矩阵的创建与赋值在Matlab中,可以通过直接赋值、随机生成或者通过其他矩阵运算得到新的矩阵。
例如,我们可以使用以下代码创建一个3行4列的矩阵A,并为其赋予随机的整数值:A = randi([1, 10], 3, 4);这样,矩阵A中的元素就是1到10之间的随机整数。
二、矩阵运算Matlab提供了丰富的矩阵运算函数,包括加法、减法、乘法、除法、转置等。
我们可以通过以下代码演示这些运算的效果:B = A + 2; % 矩阵加法C = A - 2; % 矩阵减法D = A * 2; % 矩阵乘法E = A / 2; % 矩阵除法F = A.'; % 矩阵转置通过这些运算,我们可以快速对矩阵进行数值的调整和转换。
三、矩阵的索引与切片在Matlab中,我们可以使用索引和切片操作来获取矩阵中特定的元素或子矩阵。
例如,我们可以通过以下代码获取矩阵A中的第二行第三列的元素:x = A(2, 3);同样,我们也可以通过切片操作获取矩阵A中的某一行或某几行,例如:y = A(2, :); % 获取第二行的所有元素通过这样的操作,我们可以方便地提取出矩阵中我们感兴趣的部分。
四、矩阵的运算函数除了基本的矩阵运算外,Matlab还提供了许多常用的矩阵运算函数,如求矩阵的逆、行列式、特征值等。
例如,我们可以使用以下代码计算矩阵A的逆矩阵和行列式:invA = inv(A); % 矩阵的逆detA = det(A); % 矩阵的行列式这些函数可以帮助我们更方便地进行矩阵的运算和分析。
五、矩阵的应用案例矩阵在科学研究和工程设计中有着广泛的应用。
第3章 实验二矩阵与向量运算

第3章 实验二矩阵与向量运算实验目的:在MATLAB 里,会对矩阵与向量进行加、减、数乘、求逆及矩阵的特征值运算,以及矩阵的LU 分解。
3.1 矩阵、逆矩阵运算 例3.1 设矩阵A 、B 如下:1221,3415A B -⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦,分别求出B A +、B A *、A 的逆矩阵,A 矩阵的行列式的值。
在matlab 软件中的命令窗口输入: A=[1 2;3 4]; B=[-2 1;1 5]; A+B 得到: ans =-1 3 4 9A 的逆矩阵由命令inv(A)计算,例如:令A=[1 2;3 4]; 则 C=inv(A) 得到: C =-2.0000 1.0000 1.5000 -0.5000对于任意非奇异的方阵,都可以用命令inv 计算其逆矩阵。
在matlab 里,矩阵乘法用乘法运算符表示,可以通过命令输入:A*B得到:ans =0 11 -2 23在matlab 里,可以通过命令输入:det(A)得到: -2在matlab 里,在矩阵的后面加一个撇号得到该矩阵的转置,例如: F=A ’ 使矩阵F 变为A 的转置。
下面的命令创建一个m ×m 的单位矩阵: s=eye(m)m ×n 的零矩阵用s=zeros(m*n)给出。
m ×n 的元素都是1的矩阵用写为: w=ones(m,n)如果A 是一个矩阵,则zeros(size(A))和ones(size(A))分别得到与A 大小相同的零矩阵和单位矩阵。
命令rand(m,n)创建一个m ×n 的随机矩阵。
命令hilb(m)创建一个Hilbert 矩阵的特殊矩阵。
3.2 矩阵的特征值设A 是一个n ×n 方阵,X 是一个n 维向量,乘积Y=AX 可以看作是n 维空间变换。
如果能够找到一个标量λ,使得存在一个非零向量X ,满足:AX=λX (3.1) 则可以认为线性变换T(X)=AX 将X 映射为λX,此时,称X 是对应于特征值λ的特征向量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二 MATLAB矩阵及其运算
学号:3121003210 姓名:李书杰 专业:电子信息工程2班 日期:9.26
一 实验目的
1. 熟悉MATLAB变量和数据操作。
2. 掌握MATLAB矩阵及其操作。
3. 熟悉MATLAB运算与矩阵分析。
二 实验环境
一台计算机 、Windows 7、MATLAB7.1
三 实验内容
1. (1)新建一个.m文件,验证书本第15页例2-1;
(2)用命令方式查看和保存代码中的所有变量;
(3)用命令方式删除所有变量;
(4)用命令方式载入变量z。
2. 将x=[4/3 1.2345e-6]在以下格式符下输出:短格式、短格式e 方式、长格式、长格式e方式、银行格式、十六进制格式、+格式,并在
实验报告中说明各种格式符下输出的结果有何区别。
3.课本第54页实验内容第1题。
4. 已知A=[1 2 3 4 5 ;6 7 8 9 10;11 12 13 14 15;16 17 18 19 20],对其进行如下操作:
(1)输出A在[ 7, 10]范围内的全部元素;
(2)取出A的第2,4行和第1,3,5列;
(3)对矩阵A变换成向量B,B=[1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20];
(4)删除A的第2,3,4行元素;
四 实验结果
1.1
1.2
实验结果分析:调用load 保存 save 删除clear 等 变量的操作2.1
默认short
2.2短格式e
2.3长格式
2.4其他格式
实验结果分析:
short :输出小数点后四位,1.3333 0.0000 后面一位太小显示不了
short e :5位有效数字的输出,不会省略过小的数
long :15位有效数字形式的输出
long e :15位有效数字的科学计数形式
bank :元,角,分 也可能忽略过小的数
hex :用16进制数表示
+ :正数 负数
3.1
3.2
3.3
3.4
实验结果分析:ln用log 直接表示。
exp(2)注意括号,0.34245*10^-6的科学计数法写成0.34245e-6 中间不插入任何符号。
4.输出矩阵
4.1
4.2
实验结果分析:按照序号:A(3)
行列A(3,2) A(:,3) A(3,:) 4.3
实验结果分析:熟悉矩阵间的转换
4.4
五 实验总结
通过对Matlab实验现象和实验数据分析,熟悉了Matlab的操作环境及对矩阵的基本操作方法,同时熟悉MATLAB的一些基本函数,为以后的学习打下了基础。
