18.2 勾股定理的逆定理
《18.2勾股定理的逆定理》作业设计方案-初中数学沪科版12八年级下册

《勾股定理的逆定理》作业设计方案(第一课时)一、作业目标1. 掌握勾股定理的逆定理的基本内容。
2. 理解勾股定理的逆定理在几何图形中的应用。
3. 培养学生的逻辑推理能力和空间想象能力。
二、作业内容1. 知识点复习:回顾勾股定理的基本内容,明确直角三角形三边关系。
2. 预习新知:学习勾股定理的逆定理,即若三角形三边满足一定关系,则该三角形为直角三角形。
重点掌握“两短边的平方和等于最长边的平方”这一条件。
3. 练习题:- 完成课本上的相关练习题,包括判断题、选择题和证明题。
- 结合生活中的实例,如建筑物的斜边与两直角边关系等,进行讨论与解析。
- 完成一份简单的逆定理应用报告,以小组为单位,收集至少三个生活中运用勾股定理逆定理的实例,并分析其应用过程。
三、作业要求1. 认真复习和预习,做好笔记,标记疑难问题。
2. 练习题要求独立完成,不能抄袭他人答案。
如有不懂的问题,可以请教同学或家长。
3. 应用报告需小组合作完成,每个学生至少要负责一个实例的收集与分析。
报告中要注明每个实例的具体情况、如何运用逆定理以及应用的意义。
4. 作业需按时提交,不迟到、不早退。
四、作业评价1. 练习题完成情况:评价学生是否正确理解和掌握了勾股定理的逆定理,以及其应用方法。
2. 应用报告评价:评价学生小组合作的情况、实例收集的多样性和分析的深度。
3. 课堂表现评价:评价学生在课堂上的参与度、发言情况和思维活跃度。
4. 综合评价:综合以上各项评价,给出学生本次作业的总体评价。
五、作业反馈1. 针对学生在练习题和报告中的错误和不足,进行及时的讲解和指导,帮助学生改正错误,提高其解题能力和应用能力。
2. 对于表现优秀的学生和小组,给予表扬和鼓励,激发学生的学习积极性和团队合作精神。
3. 针对学生在课堂上的表现和作业完成情况,及时与家长进行沟通,共同关注学生的学习进步,为下一步的教学工作做好准备。
以上是“初中数学课程《勾股定理的逆定理》作业设计方案(第一课时)”的部分内容。
精品 八年级数学下册 勾股定理逆定理
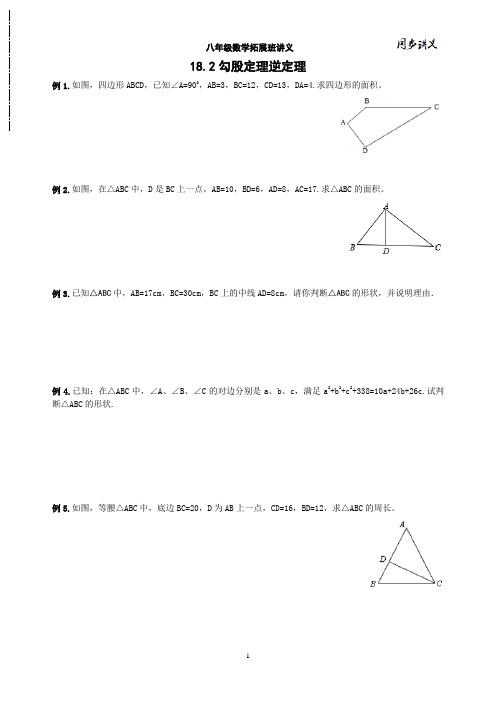
18.2勾股定理逆定理例1.如图,四边形ABCD,已知∠A=900,AB=3,BC=12,CD=13,DA=4.求四边形的面积。
例2.如图,在△ABC中,D是BC上一点,AB=10,BD=6,AD=8,AC=17.求△ABC的面积。
例3.已知△ABC中,AB=17cm,BC=30cm,BC上的中线AD=8cm,请你判断△ABC的形状,并说明理由.例4.已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,满足a2+b2+c2+338=10a+24b+26c.试判断△ABC的形状.例5.如图,等腰△ABC中,底边BC=20,D为AB上一点,CD=16,BD=12,求△ABC的周长。
例6.在正方形ABCD 中, E 为AB 的中点, F 为AD 上一点, 且AF=AD 41, 求证: ∠FEC=90︒例7.有一只喜鹊正在一棵高3 m 的小树的树梢上觅食,它的巢筑在距离该树24 m 且高为14 m 的一棵大树上,巢距离大树顶部1m ,这时,它听到巢中幼鸟求助的叫声,便立即赶过去.如果它飞行的速度为5m/s ,那么它至少需要几秒才能赶回巢中?课堂练习:1.下列三角形中,是直角三角形的是( )A.三角形的三边满足关系a+b=cB.三角形的三边长分别为32,42,52C.三角形的一边等于另一边的一半D.三角形的三边长为7,24,25 2.三角形的三边长为a 、b 、c ,且满足等式(a+b)2-c 2=2ab ,则此三角形是( )A.锐角三角形B.直角三角形C.钝角三角形D.等边三角形 3.满足下列条件的三角形中,不是直角三角形的是( )A.三内角之比为1∶2∶3B.三边长的平方之比为1∶2∶3C.三边长之比为3∶4∶5D.三内角之比为3∶4∶5 4.三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( )A.等边三角形B.钝角三角形C.直角三角形D.锐角三角形.5.适合下列条件的△ABC 中,直角三角形的个数为( ) (1)31=a ,41=b ,51=c (2)b a =,︒=∠45A (3)︒=∠︒=∠58,32B A (4)7=a ,24=b ,25=c (5)25=a ,2=b ,3=c A.2个 B.3个 C.4个 D.5个 6.如图,正方形网格中的△ABC ,若小方格边长为1,则△ABC 是( )A.直角三角形B.锐角三角形C.钝角三角形D.以上答案都不对7.如图,△ABC 中,CD ⊥AB 于D ,若AD=2BD ,AC=6,BC=3,则BD 的长为( )A .3B .12C .1D .48.如图,一电线杆AB 高为10米,当太阳光线与地面夹角为600时,其影长AC 约为(3≈1.732,保留三个有效数字)( ) A .5.00米 B .8.66米 C .17.3米 D .5.77米 9.三角形的三边长分别是15,36,39,这个三角形是 三角形。
18.2 勾股定理的逆定理(二)

八数教学案一、课时学习目标1.灵活应用勾股定理及逆定理解决实际问题。
2.进一步加深性质定理与判定定理之间关系的认识。
重点、难点1.重点:灵活应用勾股定理及逆定理解决实际问题。
2.难点:灵活应用勾股定理及逆定理解决实际问题。
二、课前预习导学1.填空题。
⑴任何一个命题都有 ,但任何一个定理未必都有 。
⑵“两直线平行,内错角相等。
”的逆定理是 。
⑶在△ABC 中,若a 2=b 2-c 2,则△ABC 是 三角形, 是直角; 若a 2<b 2-c 2,则∠B 是 。
⑷若在△ABC 中,a=m 2-n 2,b=2mn ,c= m 2+n 2,则△ABC 是 三角形。
2.下列四条线段不能组成直角三角形的是( )A .a=8,b=15,c=17B .a=9,b=12,c=15C .a=5,b=3,c=2D .a :b :c=2:3:43.已知:在△ABC 中,∠A 、∠B 、∠C 的对边分别是a 、b 、c ,分别为下列长度,判断该三角形是否是直角三角形?并指出那一个角是直角?⑴a=3,b=22,c=5; ⑵a=5,b=7,c=9;⑶a=2,b=3,c=7; ⑷a=5,b=62,c=1。
4.若三角形的三边是 ⑴1、3、2; ⑵51,41,31; ⑶32,42,52⑷9,40,41; ⑸(m +n )2-1,2(m +n ),(m +n )2+1;则构成的是直角三角形的有( ) A .2个 B .3个 C.4个 D.5个 5.叙述下列命题的逆命题,并判断逆命题是否正确。
⑴如果a 3>0,那么a 2>0;⑵如果三角形有一个角小于90°,那么这个三角形是锐角三角形; ⑶如果两个三角形全等,那么它们的对应角相等; ⑷关于某条直线对称的两条线段一定相等。
三、课堂学习研讨例1(P75例2)在军事和航海上经常要确定方向和位置, 从而使用一些数学知识和数学方法。
分析:⑴了解方位角,及方位名词;⑵依题意画出图形;⑶依题意可得PR= ,PQ= ,QR= ;小结:让学生养成“已知三边求角,利用勾股定理的逆定理”的意识。
18.2勾股定理的逆定理3

C
1,一个零件的形状如图,工人师 傅量得一个零件的尺寸如下: AB=3 ,AD=4,BC=13,CD=12 且 ∠DAB=90°,你能求这个零件 的面积吗?
12
D
13
4
5
A 3 B
2.有一块菜地,形状如下,试求它的面积. B 12
C
3
D
13
4 A
3、如图,在正方形ABDC中,E是CD的中点, F为BD上一点,且BF=3FD,求证:∠AEF=90º.
3.三角形ABC中,∠A.∠B.∠C.的对边分别是a.b.c, 且 c+a=2b, c – a= ( )
──
1 b,则三角形ABC的形状是 2
A
A 直角三角形 C 等腰三角形
B 等边三角形 D 等腰直角三角形
已知a.b.c为△ABC的三边,且满足 a2c2 – b2c2=a4 – b4, 试判断△ABC的形状. 解 ∵ ∴ a2c2- b2c2 = a4 – b4 c2(a2 – b2) = (a2+ b2) (a2- b2) (1) (2)
N 海天 R P Q 远航 E
6.如图,点A是一个半径为 400 m的圆形森林公园 的中心,在森林公园附近有 B .C 两个村庄,现要在 B.C 两村庄之间修一条长为 1000 m 的笔直公路 将两村连通,经测得 ∠B=60°,∠C=30°,问此公 路是否会穿过该森林公园?请通过计算说明.
400
A
勾股定理:
直角三角形的两直角边为a ,b , 斜边为 c ,则有
a2+ b2=c2
逆定理:
三角形的三边a,b,c满足a2+b2=c2,则这个三角形 是直角三角形; 较大边c 所对的角是直角.
勾股定理的逆定理

; 乐动体育 LD乐动 ;
大旱。关东民传行西王母筹,经历郡国,西入关至京师。民又会聚祠西王母,或夜持火上屋,击鼓号呼相惊恐。二月,封帝太太后从弟侍中傅商为汝昌侯,太后同母弟子侍中郑业为阳信侯。三月,侍中驸马都尉董贤、光禄大夫息夫躬、南阳太守孙宠皆以告东平王封列侯。语在《贤传》。 夏五月,赐中二千石至六百石及天下男子爵。六月,尊帝太太后为皇太太后。秋八月,恭皇园北门灾。冬,诏将军、中二千石举明兵法有大虑者。元寿元年春正月辛丑朔,日有蚀之。诏曰“朕获保宗庙,不明不敏,宿夜忧劳,未皇宁息。惟阴阳不调,元元不赡,未赌厥咎。娄敕公卿,庶 几有望。至今有司执法,未得其中,或上暴虐,假势获名,温良宽柔,陷於亡灭。是故残贼弥长,和睦日衰,百姓愁怨,靡所错躬。乃正月朔,日有蚀之,厥咎不远,在余一人。公卿大夫其各悉心勉帅百寮,敦任仁人,黜远残贼,期於安民。陈朕之过失,无有所讳。其与将军、列侯、中 二千石举贤良方正能直言者各一人。大赦天下”丁巳,皇太太后傅氏崩。三月,丞相嘉有罪,下狱死。秋九月,大司马票骑将军丁明免。孝元庙殿门铜龟蛇铺首鸣。二年春正月,匈奴单于、乌孙大昆弥来朝。二月,归国,单于不说。语在《匈奴传》。夏四月壬辰晦,日有蚀之。五月,正 三公官公职。大司马卫将军董贤为大司马,丞相孔光为大司徒,御史大夫彭宣为大司空,封长平侯。正司直、司隶,造司寇职,事未定。六月戊午,帝崩於未央宫。秋九月壬寅,葬义陵。赞曰:孝哀自为藩王及充太子之宫,文辞博敏,幼有令闻。赌孝成世禄去王室,权柄外移,是故临朝 娄诛大臣,欲强主威,以则武、宣。雅性不好声色,时览卞射武戏。即位痿痹,末年浸剧,飨国不永,哀哉。[标签:标题] 孝平皇帝,元帝庶孙,中山孝王子也。母曰卫姬。年三岁嗣立为王。元寿二年六月,哀帝崩,太皇太后诏曰“大司马贤年少,不合众心。其上印、绶,罢”贤即日自杀。新都侯王葬为大司马,领尚书事。秋七月,遣车骑将军王舜、大鸿胪左咸使持节迎中山王。辛卯,贬皇太后赵氏为孝成 皇后,退居北宫,哀帝皇后傅氏退居桂宫。孔乡侯傅晏、少府董恭等皆免官爵,徙合浦。九月辛酉,中山王即皇帝位,谒高庙,大赦天下。帝年九岁,太皇太后临朝,大司马莽秉政,百官总己以听於莽。诏曰“夫赦令者,将与天下更始,诚欲令百姓改行洁己,全其性命也。往者有司多举 奏赦前事,累增罪过,诛陷亡辜,殆非重信慎刑,洒心自新之意也。及选举者,其历职更事有名之士,则以为难保,废而弗举,甚谬於赦小过举贤材之义。诸有臧及内恶未发而荐举者,皆勿案验。令士厉精乡进,不以小疵妨大材。自今以来,有司无得陈赦前事置奏上。有不如诏书为亏恩, 以不道论。定著令,布告天下,使明知之”元始元年春正月,越裳氏重译献白雉一,黑雉二,诏使三公以荐宗庙。群臣奏言大司马莽功德比周公,赐号安汉公,及太师孔光等皆益封。语在《莽传》。赐天下民爵一级,吏在位二百石以上,一切满秩如真。立故东平王云太子开明为王,故桃 乡顷侯子成都为中山王。封宣帝耳孙信等三十六人皆为列侯。太仆王恽等二十五人前议定陶傅太后尊号,守经法,不阿指从邪。右将军孙建爪牙大臣,大鸿胪咸前正议不阿,后奉节使迎中山王。及宗正刘不恶、执金吾任岑、中郎将孔永、尚书令姚恂、沛郡太守石诩,皆以前与建策,东迎 即位,奉事周密勤劳,赐爵关内侯,食邑各有差。赐帝征即位所过县邑吏二千石以下至佐史爵,各有差。又令诸侯王、公、列侯、关内侯亡子而有孙若子同产子者,皆得以为嗣。公、列侯嗣子有罪,耐以上先请。宗室属未尽而以罪绝者,复其属。其为吏举廉佐史,补四百石。天下吏比二 千石以上年老致仕者,参分故禄,以一与之,终其身。遣谏大夫行三辅,举籍吏民,以元寿二年仓卒时横赋敛者,偿其直。义陵民冢不妨殿中者勿发。天下吏民亡得置什器储偫。二月,置羲和官,秩二千石。外史、闾师,秩六百石。班教化,禁淫祀,放郑声。乙未,义陵寝神衣在柙中, 丙申旦,衣在外床上,寝令以急变闻。用太牢祠。夏五月丁巳朔,日有蚀之。大赦天下。公卿、将军、中二千石举敦厚能直言者各一人。六月,使少府左将军丰赐帝母中山孝王姬玺书,拜为中山孝王后。赐帝舅卫宝、宝弟玄爵关内侯。赐帝女弟四人号皆曰君,食邑各二千户。封周公后公 孙相如为褒鲁侯,孔子后孔均为褒成侯,奉其祀。追谥孔子曰褒成宣尼公。罢明光宫及三辅驰道。天下女徒已论,归家,顾山钱月三百。复贞妇,乡一人。置少府海丞、果丞各一人。大司农部丞十三人,人部一州,劝农桑。太皇太后省所食汤沐邑十县,属大司农,常别计其租入,以赡贫 民。秋九月,赦天下徒。以中山苦陉县为中山孝王后汤沐邑。二年春,黄支国献犀牛。诏曰“皇帝二名,通於器物,今更名,合於古制。使太师光奉太牢告祠高庙”夏四月,立代孝王玄孙之子如意为广宗王,江都易王孙盱台侯宫为广川王,广川惠王曾孙伦为广德王。封故大司马博陆侯霍 光从父昆弟曾孙阳、宣平侯张敖玄孙庆忌、绛侯周勃玄孙共、舞阳侯樊哙玄孙之子章皆为列侯,复爵。赐故曲周侯郦商等后玄孙郦明友等百一十三人爵关内侯,食邑各有差。郡国大旱,蝗,青州尤甚,民流亡。安汉公、四辅、三公、卿大夫、吏民为百姓困乏献其田宅者二百三十人,以口 赋贫民。遣使者捕蝗,民捕蝗诣吏,以石、斗受钱。天下民赀不满二万及被灾之郡不满十万,勿租税。民疾疫者,舍空邸第,为置医药。赐死者一家六尸以上葬钱五千,四尸以上三千,二尸以上二千。罢安定呼池苑,以为安民县,起官寺市里,募徙贫民,县次给食。至徙所,赐田宅什器, 假与犁、牛、种、食。又起五里於长安城中,宅二百区,以居贫民。秋,举勇武有节明兵法,郡一人,诣公车。九月戊申晦,日有蚀之。赦天下徒。使谒者大司马掾四十四人持节行边兵。遣执金吾侯陈茂假以钲鼓,募汝南、南阳勇敢吏士三百人,谕说江湖贼成重等二百馀人皆自出,送家 在所收事。重徙云阳,赐公田宅。冬,中二千石举治狱平,岁一人。三年春,诏有司为皇帝纳采安汉公莽女。语在《莽传》。又诏光禄大夫刘歆等杂定婚礼。四辅、公卿、大夫、博士、郎、吏家属皆以礼娶,亲迎立轺并马。夏,安汉公奏车服制度,吏民养生、送终、嫁娶、奴婢、田宅、 器械之品。立官稷及学官:郡国曰学,县、道、邑、侯国曰校,校、学置经师一人。乡曰庠,聚曰序,序、庠置《孝经》师一人。阳陵任横等自称将军,盗库兵,攻官寺,出囚徒。大司徒掾督逐,皆伏辜。安汉公世子宇与帝外家卫氏有谋。宇下狱死,诛卫氏。四年春正月,郊祀高祖以配 天,宗祀孝文以配上帝。改殷绍嘉公曰宋公,周承休公曰郑公。诏曰“盖夫妇正则父子亲,人伦定矣。前诏有司复贞妇,归女徒,诚欲以防邪辟,全贞信。及眊掉之人刑罚所不加,圣王之所以制也。惟苛暴吏多拘系犯法者亲属,妇女老弱,构怨伤化,百姓苦之。其明敕百僚,妇女非身犯 法,及男子年八十以上七岁以下,家非坐不道,诏所名捕,它皆无得系。其当验者,即验问。定著令”二月丁未,立皇后王氏,大赦天下。遣太仆王恽等八人置副,假节,分行天下,览观风俗。赐九卿已下至六百石、宗室有属籍者爵,自五大夫以上各有差。赐天下民爵一级,鳏、寡、孤、 独、高年帛。夏,皇后见於高庙。加安汉公号曰“宰衡”。赐公太夫人号曰功显君。封公子安、临皆为列侯。安汉公奏立明堂、辟廱。尊孝宣庙为中宗,孝元庙为高宗,天子世世献祭。置西海郡,徙天下犯禁者处之。梁王立有罪,自杀。分京师置前辉光、后丞烈二郡。更公卿、大夫、八 十一元士官名、位次及十二州名。分界郡国所属,罢、置、改易,天下多事,吏不能纪。冬,大风吹长安城东门屋瓦且尽。五年春正月,祫祭明堂。诸侯王二十八人、列侯百二十人、宗室子九百馀人征助祭。礼毕,皆益户,赐爵及金、帛,增秩、补吏,各有差。诏曰“盖闻帝王以德抚民, 其次亲亲以相及也。昔尧睦九族,舜惇叙之。朕以皇帝幼年,且统国政,惟宗室子皆太祖高皇帝子孙及兄弟吴顷、楚元之后,汉元至今,十有馀万人,虽有王侯之属,莫能相纠,或陷入刑罪,教训不至之咎也。传不云乎。君子笃於亲,则民兴於仁。其为宗室,自太上皇以来族亲,各以世 氏,郡国置宗师以纠之,致教训焉。二千石选有德义者以为宗师。考察不从教令有冤失职者,宗师得因邮亭书言宗信,请以闻。常以岁正月赐宗师帛各十匹”羲和刘歆等四人使治明堂、辟雍,令汉与文王灵台、周公作洛同符。太仆王恽等八人使行风俗,宣明德化,万国齐同。皆封为列侯。 征天下通知逸经、古记、天文、历算、钟律、小学、《史篇》、方术、《本草》及以《五经》、《论语》、《孝经》、《尔雅》教授者,在所为驾一封轺传,遣诣京师。至者数千人。闰月,立梁孝王玄孙之耳孙音为王。冬十二月丙午,帝崩於未央宫。大赦天下。有司议曰“礼,臣不殇君。 皇帝年十有四岁,宜以礼敛,加元服”奏可。葬康陵。诏曰“皇帝仁惠,无不顾哀,每疾一发,气辄上逆,害於言语,故不及有遗诏。其出媵妾,皆归家得嫁,如孝文明故事”赞曰:孝平之世,政自莽出,褒善显功,以自尊盛。观其文辞,方外百蛮,亡思不服。休征嘉应,颂声并作。至 乎变异见於上,民怨於下,莽亦不能文也。[标签:标题] 昔《诗》、《书》述虞、夏之际,舜、禹受禅,积德累功,治於百姓,摄位行政,孝之於天,经数十年,然后在位。殷、周之王,乃繇卨、稷,修仁行义,历十馀世,至於汤、武,然后放杀。秦起襄公,章文、缪、献、孝、昭、严,稍蚕食六国,百有馀载,至始皇,乃并天下。以德若彼, 用力如此其艰难也。秦既称帝,患周之败,以为起於处士横议,诸侯力争,四夷交侵,以弱见夺。於是削去五等,堕城销刃,箝语烧书,内锄雄俊,外攘胡、粤,有一威权,为万世安。然十馀年间,猛敌横发乎不虞,適戍强於五伯,闾阎逼於戎狄,响应於谤议,奋臂威於甲兵,乡秦之禁, 适所以资豪杰而速自毙也。是以汉亡尺土之阶,繇一剑之任,五载而成帝业。书传所记,未尝有焉。何则。古世相革,皆承圣王之烈,今汉独收孤秦之弊。镌金石者难为功,摧枯朽者易为力,其势然也。故据汉受命,谱十八王,月而列之,天下一统,乃以年数。讫於孝文,异姓尽矣。 〔表略〕[标签:标题] 昔周监於二代,三圣制法,立爵五等,封国八百,同姓五十有馀。周公、康叔建於鲁、卫,各数百里。太公於齐,亦五侯九伯之地。《诗》载其制曰“介入惟藩,大师惟垣。大邦惟屏,大宗惟翰。怀德惟宁,宗子惟城。毋俾城坏,毋独斯畏”所以亲亲贤贤,褒表功德,关诸盛衰,深根固
勾股定理的逆定理

我们把这样的两个命题叫做互逆
命另命满题一题足如个.如2:叫”果同做把如位它a其果角2的中相三逆一等b角命个2,形两题叫直的.c做线2三原平边命行长题”,a那与,b么,”c
两那直么线这平个行,三同角位角形相是等直”角是三互角逆形命.题.
一起探究
系:
.
2.52 62 6.52
那么画出的三角形是直角三角形吗? 换成三边分别是4cm,7.5cm,8.5cm 呢?
由以上例子,我们猜想:
命题2 如果三角形的三边长a,b,c
满足 a2 b2 c2
那么这个三角形是直角三角形.
观察思考
(什1命)直么命题?角题它1边1和们长命如有分题什果别2么直的为关角题a系、设三?、b角,斜结形边论的分长两别为是 c,那么
命题1经证明是正确的,你能证 明命题2的正确性吗?练习本上试 一试,与同学交流你的想法.
一般地,如果一个定理的逆命题经 过证明是正确的,它也是一个定理,称 这两个定理互为逆定理.
命题2经证明是正确的,所以我 们把它叫做勾股定理的逆定理.
一个命题一定有逆命题,但逆命 题不一定正确.所以一个定理不一定 有逆定理.
练习
1.如果三条线段a,b,c满足 a2 c2 b2 , 这三条线段组成的三角形是不是 直角三角形?为什么?
练习
2.说出下列命题的逆命题.这些命题的逆命题 成立吗?
(1)两条直线平行,内错角相等; (2)如果两个实数相等,那么它们的绝对值相
等; (3)全等三角形的对应角相等; (4)到角的两边距离相等的点在角的平分线上.
我国古代大禹治水测量工程时,也用 类似方法确定直角.你知道这是为什么 吗?其中蕴涵什么道理?
第18章 勾股定理的逆定理及全章复习

18.2 勾股定理的逆定理(一)教学目标1.体会勾股定理的逆定理得出过程,掌握勾股定理的逆定理。
2.探究勾股定理的逆定理的证明方法。
3.理解原命题、逆命题、逆定理的概念及关系。
重点:掌握勾股定理的逆定理及简单应用。
难点:勾股定理的逆定理的证明。
教学过程:一.预习新知(阅读教材P73 — 75 , 完成课前预习)1.三边长度分别为3 cm 、4 cm 、5 cm 的三角形与以3 cm 、4 cm 为直角边的直角三角形之间有什么关系?你是怎样得到的?2.你能证明以6cm 、8cm 、10cm 为三边长的三角形是直角三角形吗?3.如图18.2-2,若△ABC 的三边长a 、b 、c 满足222c b a =+,试证明△ABC 是直角三角形,请简要地写出证明过程.4.此定理与勾股定理之间有怎样的关系? (1)什么叫互为逆命题(2)什么叫互为逆定理(3)任何一个命题都有 _____,但任何一个定理未必都有 __ 5.说出下列命题的逆命题。
这些命题的逆命题成立吗? (1) 两直线平行,内错角相等;(2) 如果两个实数相等,那么它们的绝对值相等; (3) 全等三角形的对应角相等;(4) 角的内部到角的两边距离相等的点在角的平分线上。
二.课堂展示例1:判断由线段a 、b 、c 组成的三角形是不是直角三角形: (1)17,8,15===c b a ; (2)15,14,13===c b a . (3)25,24,7===c b a ; (4)5.2,2,5.1===c b a ;三.随堂练习1.完成书上P75练习1、2图18.2-22.如果三条线段长a,b,c 满足222b c a -=,这三条线段组成的三角形是不是直角三角形?为什么?3.A,B,C 三地的两两距离如图所示,A 地在B 地的正东方向,C 地在B 地的什么方向?4.思考:我们知道3、4、5是一组勾股数,那么3k 、4k 、5k (k 是正整数)也是一组勾股数吗?一般地,如果a 、b 、c 是一组勾股数,那么ak 、bk 、ck (k 是正整数)也是一组勾股数吗?四.课堂检测1.若△ABC 的三边a ,b ,c 满足条件a 2+b 2+c 2+338=10a+24b+26c ,试判定△ABC 的形状.2.一根24米绳子,折成三边为三个连续偶数的三角形,则三边长分别为多少米?此三角形的形状为?3.已知:如图,在△ABC 中,CD 是AB 边上的高,且CD 2=AD ·BD 。
18.2勾股定理逆定理
教学设计
题目
18.2勾股定理的逆定理
课时
2
学校
星火一中
教者
杨玉杰
年级
八年
学科
数学
设计来源
自我设计及网络
教学时间
2012-4-26
教
材
分
析
本节内容是著名的勾股定理,它是建立在三角形、全等三角形、等腰三角形等有关三角形知识的基础上的,揭示的时直角三角形中三边的数量关系,它是直角三角形的一条非常重要的性质,也是几何中重要定理之一。它把代数和几何很好的结合起来,应用非常广泛。
学生观看
动手画图,体验发现,得到猜想
△再现古人做法
△采用实验、观察、比较的数学手法,突破难点.
总体要求:1.“统一”设计“分段”教学;2.围绕“三维”落实“三问”;3.充实“心案”活化“形案”。
教学流程
分课时
环节
与时间
教师活动
学生活动
△设计意图
◇资源准备
□评价○反思
课堂演练】(投影显示)
1.以下各组数为边长,能组成直角三角形的是(C).
A.12.5 B.12 C. D.9
学生回答
小组合作
△
以例为理解勾股逆定理的应用,再补充“问题探究2”来拓展勾股定理逆定理的应用范围.
勾股定理的逆定理

18.2 勾股定理的逆定理知识点1 互逆命题在两个命题中,如果一个命题的题设和结论分别是另一个命题的结论和题设,那么这两个命题称为互逆命题,如果把其中一个叫做原命题,那么另一个叫做它的逆命题.每个命题都有逆命题,但原命题是真命题,它的逆命题不一定是真命题.原命题和逆命题的真假性一般有四种情况:真、假;真、真;假、假;假、真.知识点2 互逆定理如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理称为互逆定理,其中一个定理称为另一个定理的逆定理.每个命题都有逆命题,但不是所有的定理都有逆定理.知识点3 勾股定理的逆定理——直角三角形的判别条件定理:如果三角形的边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形.解读:(1)作用:可用边的关系来判断一个三角形是否是直角三角形.(2)用较短两边的平方和与最大边的平方进行比较.(3)条件中没有涉及直角三角形,结论是直角三角形.(4)勾股定理与勾股定理的逆定理的联系与区别:联系:①两者都与三角形的三边关系a2+b2=c2有关;②两者都与直角三角形有关.区别:①勾股定理是以“一个三角形是直角三角形”为条件,进而得到这个直角三角形的三边的数量关系,即a2+b2=c2.②勾股定理的逆定理是以“一个三角形的三边满足a2+b2=c2”为条件,进而得到这个三角形是直角三角形,是判断一个三角形是否是直角三角形的一个有效的方法.(5)应用:①现实生活中,在没有测量角的仪器的情况下,常利用勾股定理的逆定理来确定直角(或垂线).②勾股定理与勾股定理的逆定理的综合运用.知识点4 勾股数概念:满足a2+b2=c2的三个正整数,称为勾股数.解读:(1)勾股数满足两个条件:①正整数;②满足a2+b2=c2.(2)常见的勾股数:3,4,5;6,8,10;5,12,13;8,15,17;9,40,41;…(3)小窍门:记住常见的勾股数可以提高做题速度.(4)一组勾股数中各数扩大相同的整数倍能得到一组新的勾股数,如当k=1,2,3,…,n时,下列各组数还是勾股数,{3k,4k,5k},{l5k,l2k,l3k},…延伸:(1)几个求勾股数的常见公式:①n2-1,2n,n2+1(n≥2,n.为正整数);②2n+1,2n2+2n,2n2+2n+1(n是正整数);③m2-n2,2mn,m2+n2(m>n,m、n都是正整数).(2)小窍门:①有最小的勾股数(3,4,5),没有最大的勾股数.②勾股数不能全是奇数,但可以全是偶数.③勾股数中不可能只有两个偶数.一、选择题1.以下面各组数为边长的三角形,能组成直角三角形的个数是( )①6,7,8;②8,15,17;③7,24,25;④12,35,37.A.1B.2C.3D.42.在△ABC 中,a 、b 、c 分别是∠A 、∠B 、∠C 的对边,在满足下列条件下,不是直角三角形的是( )A.a :b :c =3:4:5B.a :b :c =9:12:15C.∠A :∠B :∠C =3:4:5D.∠A :∠B :∠C =1:2:33.在△ABC 中,∠A :∠B :∠C =2:1:3, a 、b 、c 分别为∠A 、∠B 、∠C 的对边,则有( )A.b 2+a 2=c 2B.c 2=3b 2C.3a 2=2c 2D.c 2=2b 24.等腰三角形底边上的高为1cm,周长为4cm,则三角形的面积是( )A.14cm 2B.10cm 2C.1cm 2D.23cm 45.如图所示,已知AB ⊥CD , △ABD 、△BCE 都为等腰三角形,如果CD =7,BE =3,那么AC 的长为( )A.8B.5C.3D.46.下列说法中,正确的是( )A.三角形两条边的平方和等于第三条边的平方B.如果一个三角形两条边的平方差等于第三条边的平方,那么这个三角形是直角三角形C.在△ABC 中,∠A 、∠B 、∠C 的对边分别是a 、b 、c , 若a 2+b 2=c 2,则∠A =90°D.在△ABC 中,∠A 、∠B 、∠C 的对边分别是a 、b 、c ,若c 2-a 2=b 2,则∠B=90°7.把直角三角形的三边都扩大n 倍( n >0),得到的三角形是( )A.等腰三角形B.锐角三角形C.直角三角形D.不能确定8.小丽和小芳二人同时从公园去图书馆,都是每分钟走50米,小丽走直线用了10分钟,小芳先回家拿了钱去图书馆,小芳到家用了6分钟,从家到图书馆用了8分钟.小芳从公园到图书馆拐的角是( )A.锐角B.直角C.钝角D.不能确定9.如图所示,我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如果大正方形的面积是13, 小正方形的面积是1,直角三角形较短的直角边为a ,较长的直角边为b ,那么(a +b )2的值为( )A.13B.19C.25D.16910.长度分别为9cm、12cm、15cm、36cm、39cm的五根木棍,选出三根首尾连接,最多可搭成的直角三角形的个数为( )A.1B.2C.3D.411.在下列长度的各组线段中,能组成直角三角形的是( )A.12,15,27B.32,42,52C.5a, l2a, l3a(a>0)D.1,2,312.满足下列条件的△ABC,不是直角三角形的是( )A.∠A=∠B-∠CB.∠A:∠B:∠C=1:1:2C.a:b:c=1:1:2D.b2=a2-c213.已知在△ABC中,AB=8,BC=15,AC=17,则下列结论无法判断的是( )A.△ABC是直角三角形,且AC为斜边B.△ABC是直角三角形,且∠ABC=90°C.△ABC的面积为60D.△ABC是直角三角形,且∠A=60°14.在△ABC中,∠A:∠B:∠C=1:1:2,则下列说法错误的是( )A.∠C=90°B.a2=b2-c2C.c2=2a2D.a=b15.若△ABC的三边分别为m2-1,2m,m2+1(m>1),则下列结论正确的是( )A.△ABC是直角三角形,且斜边的长为m2+ 1B.△ABC是直角三角形,且斜边的长为2mC.△ABC是直角三角形,但斜边的长需由m的大小确定D.△ABC无法判定是否是直角三角形二、填空题1.若△ABC三边长为a、b、c,且满足(a-b)(a2+b2-c2)=0,则△ABC的形状为_______三角形.2.若三角形三边之比为3:4:5,则该三角形为________三角形;若三角形三角之比为1:2:3,则该三角形为__________三角形.3.三角形三边分别为6、8、10,则最长边上的高为__________.4.三边长为a=m2-n2,b=2mn,c=m2+n2(其中m>n>0)的三角形为_______三角形.5.请任意写出三组勾股数_______,________,_________.6.一直角三角形的两直角边分别为9、12,该三角形的周长为_________.7.在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,则斜边上的高是__________cm.8.如图所示,在△ABC中,AB=AC,D是BC上一点,AD⊥AB,AD=9cm,BD=15cm,则AC=-_________cm.9.一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是_________.10.传说,古埃及人曾用“拉绳”的方法画直角,现有一根长24厘米的绳子,请你利用它拉出一个周长为24厘米的直角三角形,那么你拉出的直角三角形三边的长度分别是______厘米,_________厘米,_________厘米,其中的道理是________.11.一条对角线长39cm,一条边长是36cm的矩形的周长为________cm.12.三角形三边长为a+1,a+2,a+3,当a=_________时,此三角形为直角三角形.13.在△ABC中,三边为a、b、c,且满足a2+b2+c2=ab+ac+bc,则△ABC的形状为________.14.在△ABC中,AB=13cm,BC=10cm,BC边上的中线AD=l2cm,则△ABC的面积为_______.15.如图所示,在Rt△ABC中,∠C=90°,∠1=∠2, CD=1.5,BD=2.5,则AC等于___________.16.将一根长24cm的筷子,置于直径为5cm、高为12cm的圆柱形水杯中(如图所示).设筷子露在杯子外面的长为h cm,则h的取值范围是__________.17.直角三角形的三边长分别是a-b,a,a+b,其周长为24cm,则面积为________cm2.三、解答题1.试判断三边长分别为2n2+2n,2n+1,2n2+2n+1(n>0)的三角形是否是直角三角形.2.已知△ABC的三边的长分别为a、b、c,且满足关系式a2+b2+c2+50=6a+8b+10c,试判断△ABC的形状.3.在△ABC中,∠BAC=90°,AB=AC,P为BC上一点,求证:PB2+PC2=2P A2.4.如图所示,CD是△ABC的边AB上的高,且CD2=AD·DB.求证:∠ACB=90°.5.求证a=m2-n2, b=m2+n2,c=2mn(m>n>0)是一个直角三角形的三边.6.如图所示,如果只给你一把带刻度的直尺,你是否能检验∠MPN是不是直角,简述你的作法.7.如图所示,在四边形ABCD中,AB⊥BC,且AB=9,BC=12,CD=17,AD=8,求四边形ABCD的面积.8.如图所示,学校B前面有一条笔直的公路,学生放学后走AB、BC两条路可到达公路,经测量BC=6km,BA=8km,AC=10km.现需修建一条公路使学校B到公路的距离最短,请你帮助学校B设计一种方案,并求出公路的长.9.如图所示,一个池塘呈三角形形状,三角形的边长分别为6m、8m、10m,距池塘边缘5m 内的土地上栽着树,问池塘连同树木共占土地多少m2?(结果精确到1m2,π=3.14)10.如图所示,在正方形ABCD中,F为DC的中点,E为BC上一点,且1,4EC BC试判断AF与EF的位置关系,并说明理由.11.3,4 ,5 32+42=525, 12 , 13 52+122=327,24 ,25 72+242=2529,40 ,41 92+402=412……21, b ,c212+b2=c2(1)试找出它们的共同点,并说明你的结论;(2)当a=21时,求b、c的值.a b c第一组3=2×1+1 4=2×l×(1+1) 5=2×1×(1+1)+1第二组 5=2×2+1 12=2×2×(2+1) 13=2×2×(2+1)+1 第三组7=2×3+1 24=2×3×(3+1) 25=2×3×(3+1)+1 第四组9=2×4+1 40=2×4×(4+1) 41=2×4×(4+1)+1 … … … …根据以上勾股数组的组成傅点,你能求,出第七组勾股数的a 、b 、c 各是多少吗?第n 组呢?13.如图是一个零件的形状,校规这个零件中必须有AC ⊥BC ,工人师傅量得B 、C 两点距离为36,AD =12,CD =9,AB =39,∠ADC =90°.问:这个零件符合要求吗?并说明理由.14.如图所示,E 、F 分别是正方形ABCD 中BC 和CD 边上的点,并且AB =4,1,4CE BC =F 为CD 的中点,连接AF 、AE 、EF ,△AEF 是什么三角形?请说明理由.15.甲、乙两船从港口A 同时出发,甲船以16海里/时的速度向北偏东35°航行,乙船沿南偏东一角度航行,船速为12海里/时,2小时后,甲、乙两船相距40海里,问乙船的航行方向.16.如图所示,在△ABC 中,AB =40,BC =100,且BC 边上的中线长AD =30.(1)试说明2;ABC ABD S S ∆∆=(2)求△ADC 的面积.17.同学们在数学老师的带领下来到平坦的草原上游玩,他们发现前面有两棵大树,当地的牧'民告诉他们,这是两棵古老而特别的树,两楝树之间的距离为750 m,一部分同学以45 m/min 的速度向一棵大树走去,伺时,剩下的一部分同学以60m/min 的速度向另一棵大树走去,10min 后,两组同学同时到达目的地.问:(1)两组同学行走的方向是否成直角?(2)如果他们仍以原速度行走,至少还需要几分钟才能相遇?18.Tom 和Jerry 去野外宿营,在某地要确定两条互相垂直的路,而身边又没带直角尺,可利用的只有背包带,你能帮他们想一个简单可行的办法吗?19.已知某开发区有一块四边形的空地ABCD ,如图所示,现计划在该空地上种上草皮,经测量,∠A =90°,AB =3m,BC =12m,CD =13m,DA =4m.若每平方米草皮需要200元,问需要投人多少元.20.阅读下列解题过程:已知a 、b 、c 为△ABC 的三边,且满足a 2c 2-b 2c 2=a 4-b 4,试判断△ABC 的形状.解:∵222244a c b c a b -=-① ∴2222222()()()c a b a b a b -=+- ②∴222c a b =+③ ∴△ABC 是直角三角形.问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号:________;(2)错误的原因为___________;(3)本题正确的结论是_____________;21.观察下列两组勾股数:(1)3,4,5;5,12,13;7,24,25;…(2)6,8,10;10,24,26;14,48,50;…你发现上述两组勾股数各有什么特征?请用含有字母m 、n 的式子表示出来,你还能发现勾股数有什么特征?与同学交流.22.已知,如图△ABC 的周长是24,M 是AB 的中点,MC =MA =5,求△ABC 的面积.。
18.2勾股定理的逆定理(1)

具体训练步骤
1、情景引入2、典型例题3、针对性练习4、小结
训练内容实例
一、情景引入一起看书第73页上的故事引出命题2
命题2如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形
思考:这个命题与命题1“如果直角三角形两直角边是a、b,斜边是c,那么a2+b2=c2”
(2)勾股定理的逆定理是:如果两条直角边的平方和等于斜边的平方,那么这个三角形是直角三角形。
(3)△ABC的三边之比是1:1: ,则△ABC是直角三角形。
2.△ABC中∠A、∠B、∠C的对边分别是a、b、c,下列命题中的假命题是()
A.如果∠C-∠B=∠A,则△ABC是直角三角形。
B.如果c2= b2—a2,则△ABC是直角三角形,且∠C=90°。
⑴a= ,b= ,c= ;⑵a=5,b=7,c=9;
⑶a=2,b= ,c= ;⑷a=5,b= ,c=1。
5.若三角形的三边是⑴1、 、2;⑵ ;⑶32,42,52⑷9,40,41;
⑸(m+n)2-1,2(m+n),(m+n)2+1;则构成的是直角三角形的有()
A.2个B.3个 C.4个 D.5个
三、本课知识能力提升训练
四、课堂梳理小结作业说明
小结具体内容
1、命题与逆命题2、勾股定理的逆定理3、直角三角形的判断
详细分层作业
布置要求说明
必做:书76页习题18.2 1、2导航33页18.2随堂练习
选作:书76页习题18.2 4、6
提升能力点
灵活运用“勾股定理的逆定理”解决问题
学生层面
综合运用因式分解等相关知识解决勾股定理的问题
提升内容
1、已知a , b , c是△ABC的三边长,且满足 ,
勾股定理的逆定理

解:∵ 2+122=132,∴ 2+BC2=AC2. 5 AB ∴ △ABC 是直角三角形. ∴ BD·CA=BC·BA. ∴ BD=
������������·������������ 60 = (km). ������������ 13 60 13
∴ 修这条公路的最低造价为 ×26000=120000(元).
返回目录 按Esc键退出
7.如图,四边形 ABCD 中,∠ ADC=90° ,AD=4cm,CD=3cm,AB=13cm,BC=12cm,求这个四边形的面积.
解:连接 AC,如图.
因为∠ADC=90° , 所以△ACD 是直角三角形.
返回目录
按Esc键退出
所以 AC= ������������2 + C������ 2 = 42 + 32 =5(cm). 又因为 AC2+BC2=52+122=132=AB2, 所以 AC2+BC2=AB2. 所以△ACB 是直角三角形. 所以四边形 ABCD 的面积为: S 四边形=S △ACB-S △ADC = AC·BC- AD·CD
返回目录
按Esc键退出
2.勾股定理的逆定理的实际应用 【例 2】 如图,南北向 MN 以西为我国领海,以东为公海.上午 9 时 50 分, 我国反走私艇 A 发现正东方向有一走私艇 C 以 13 海里/时的速度偷偷向我 国领海开来,便立即通知正在 MN 线上巡逻的我国反走私艇 B.已知 A,C 两 艇的距离是 13 海里,A,B 两艇的距离是 5 海里;反走私艇 B 测得离艇 C 的距 离是 12 海里.若走私艇 C 的速度不变,最早会在什么时间进入我国领海?
5.下列真命题中,其逆命题也是真命题的是( A.直角都相等 B.等边三角形是锐角三角形 C.若 a<b<0,则|a|>|b| D.如果 a=b 或 a=-b,那么 a 2=b 2 答案:D
18.2勾股定理的逆定理

(4)全等三角形的对应角相等.
逆命题:对应角相等的两个三角形是全等三角形. 不成立
感悟: 一个命题是真命题,它逆命题却不一定是真命题. 原命题成立时, 逆命题有时成立, 有时不成立
例题解析
例1 判断由a、b、c组成的三角形是不是直角三角形:
2 2 2 2 2 2 2 2 2
2
∴△ABC是直角三角形
想一想:
互逆命题与互逆定理有何关系?
试一试
说出下列命题的逆命题.这些命题的逆命题成立吗? (1)两条直线平行,内错角相等.
逆命题: 内错角相等,两条直线平行. 成立
(2)如果两个实数相等,那么它们的平方相等.
逆命题:如果两个实数的平方相等,那么这两个实数相等.不成立
(3)如果两个实数相等,那么它们的绝对值相等.
例2 一个零件的形状如左图所示,按规定这个零件中 ∠A和∠DBC都应为直角。工人师傅量得这个零件各边 尺寸如图右所示,这个 零件符合要求吗?
C D A B 13 D 4 5 A 3 B 12
C
练一练
1.三角形三边长a、b、c满足条件( a + b )2-c2=2ab,则 此三角形是( B )
A.锐角三角形 C.钝角三角形
如果三角形的三边长a、b、c满足
a2 + b2 = c2
那么这个三角形是直角三角形。且边c所 对的角为直角。
勾股定理
互逆命题 定理
如果直角三角形两直角边分别为a,b, 斜边为c,那么 a2 + b2 = c2
定理与逆定理
如果一个定理的逆命题经过证明是真命题,那么它 是一个定理,这两个定理称为互逆定理,其中一个 定理称另一个定理的逆定理. 我们已经学习了一些互逆的定理,如: 勾股定理及其逆定理, 两直线平行,内错角相等;内错角相等,两直线平行.
勾股定理的逆定理10分钟教案

18.2勾股定理的逆定理一、教学目标知识目标:1、体会勾股定理的逆定理得出过程,掌握勾股定理的逆定理。
2、探究勾股定理的逆定理的证明方法。
3、理解原命题、逆命题、逆定理的概念。
能力目标:(1)通过对勾股定理的逆定理的探索,经历知识的发生、发展和形成的过程;(2)通过用三角形的三边的数量关系来判断三角形的形状,体验数形结合方法的应用。
二、教学重点难点重点:证明勾股定理的逆定理;用勾股定理的逆定理解决具体的问题。
难点:理解勾股定理的逆定理的推导。
三、教学准备一根打了13个等距离结的细绳子四、教学过程(1)复习旧课1、勾股定理:如果直角三角形两直角边分别为a ,b ,斜边为c ,那么222c b a =+(2)情境导入1、在古代,没有直尺、圆规等作图工具,人们是怎样画直角三角形的呢?【实验观察】用一根打了13个等距离结的细绳子,在小黑板上,用钉子钉在第一个结上,再钉在第4个结上,再钉在第8个结上,最后将第十三个结与第一个结钉在一起.然后用三角板量出最大角的度数.可以发现这个三角形是直角三角形。
(这是古埃及人画直角的方法)学生猜想:如果一个三角形的三边长c b a ,,满足下面的关系222c b a =+,那么这个三角形是直角三角形。
2、指出这个命题的题设和结论,对比勾股定理,理解互逆命题。
(3)证明新知在下图中,△ABC 的三边长a ,b ,c 满足222c b a =+。
如果△ABC 是直角三角形,它应该与直角边是a ,b 的直角三角形全等。
实际情况是这样吗?用三角形全等的方法证明这个命题。
(由于难度较大,由教师示范证明过程)已知:在△ABC 中,AB=c ,BC=a ,AC=b ,并且222c b a =+,如上图(1)。
求证:∠C=90°。
证明 : 作△A ’B ’C ’,使∠C ’=90°,A ’C ’=b , B ’C ’=a ,如上图(2),那么A ’B ’2 =22b a +(勾股定理)又∵222c b a =+(已知)∴A ’B ’2=2c ,A ’B ’=c (A ’B ’>0) 在△ABC 和△A ’B ’C ’中,BC=a =B ’C ’CA=b =C ’A ’AB=c =A ’B ’∴△ABC ≌△A ’B ’C ’(SSS)∴∠C=∠C ’=90°,∴△ABC 是直角三角形【强调说明】(1)勾股定理的逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
18.2勾股定理逆定理教案、说课稿、反思--唐艳文

18.2勾股定理的逆定理(1)教案主备人:唐艳文审核人:授课时间:教学内容:18.2勾股定理的逆定理(1)教学时数:第1课时教学目标:1.知识与技能:(1)、体会勾股定理的逆定理得出过程,掌握勾股定理的逆定理。
(2)、探究勾股定理的逆定理的证明方法。
(3)、理解原命题、逆命题、逆定理的概念及关系。
2、过程与方法:经直角三角形判别条件的探究过程体会命题、定理的胡逆性,渗透合情推理得数学意识。
教学重点:掌握勾股定理的逆定理及简单应用。
教学难点:勾股定理的逆定理的证明。
教学课型与教学方法:新授课。
方法:先学后教、适当点拨教学资源的利用及教学准备:多媒体课件、优秀教案、检测题教学过程:一、情境引入:勾股定理的内容是_____________________________________。
古埃及人曾用下面的方法得到直角:用13个等距的结,把一根绳子分成等长的12段,然后以3个结,4个结,5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。
按照这种做法真能得到一个直角三角形吗?二、先学后教出示学习目标:1.理解并掌握勾股定理的逆定理;2.利用勾股定理的逆定理判定一个三角形是否直角三角形.3. 知道什么叫做原命题、逆命题、互逆命题、互逆定理。
自学指导:请同学们看课本73至74页内容及例1思考以下问题:(时间5分钟)1、如何借助尺规画出以已知的三条线段为边的三角形。
2、写出命题2的已知、求证。
3、(1)如何构造△A ′B ′C ′(2)如何证明:△ABC ≌△A ′B ′C ′(3)如何证明 ∠C=9004、什么叫做原命题、逆命题、互逆命题、互逆定理。
5、自学检测:画一画下面的三组数分别是一个三角形的三边长a ,b ,c :5cm ,12cm ,13cm ;(男同学) 6cm ,8cm ,10cm (女同学)。
思考:(1)画出图形,它们都是直角三角吗?(2)这三组数都满足a 2 + b 2 = c 2吗?你猜想到了什么?命题2:勾股定理的逆命题:如果三角形的三边长a 、b 、c 满足a 2 + b 2 = c 2那么这个三角形是直角三角形。
18.2勾股定理的逆定理(1)[精选文档]
![18.2勾股定理的逆定理(1)[精选文档]](https://img.taocdn.com/s3/m/d95b845d4b7302768e9951e79b89680203d86bad.png)
(1)a=6,b=8,c=10; (2)a=5,b=12,c=13;
(3)a=5,b=7,c=9; (4)a=8,b=15,c=17;
尝试应用
4.说出下列命题的逆命题.这些命题的逆命题成立吗? (1)两条直线平行,内错角相等. (2)如果两个实数相等,那么它们的平方相等. (3)如果两个实数相等,那么它们的绝对值相等. (4)全等三角形的对应角相等. 5.如图所示△ABC三边a,b,c为边向外作正方形, 若S1+S2=S3成立,则△ABC是什么三角形?为什么?
情境引入
用一根钉上13个等距离结的细绳子,让同学操作, 用钉子钉在第一个结上,再钉在第4个结上,再钉在第8个结 上,最后将第十三个结与第一个结钉在一起.然后用角尺量 出最大角的度数.可以发现这个三角形是直角三角形.
课中探究
探究一:动手实践.
(一)、画一画.画出边长分别是下列各组数的三角形(单位:厘米).
作用:根据边的 数量关系判定是 否是直角三角形.
尝试应用
1.“如果同旁内角互补,那么两条直线平行”的题设是
_____, 结论是 ,逆命题是_______.
2.“对顶角相等”的的题设是 结论是
,逆命题
是_______.
3. 已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、
c,分别为下列长度,判断该三角形是否是直角三角形?
(1):3、4、5 ;(2):3、6、8;(3):6、8、10
(二)、量一量.用你的量角器分别测量一下小组内同学画出的三个三角形的
最大角的度数,并判断上述你们所画的三角形的形状:(按角分类)
(三)、算一算.请比较上述每个三角形的两条较短边的平方和与最长边的
平方之间的大小关系. 你能发现什么规律?
勾股定理逆定理 (2)

18.2 勾股定理的逆定理(一)教学目标知识与技能:1.体会勾股定理的逆定理得出过程,掌握勾股定理的逆定理。
2.了解勾股定理的逆定理的证明方法和证明过程。
过程与方法通过三角形三边的数量关系来判断三角形的形状,体验数形结合法的应用。
情感态度与价值观1、通过三角形三边的数量关系来判断三角形的形状,体验数与形的内在联系,感受定理与逆定理之间的关系。
2、通过“创设情景—建立模型—实验探究—理论释意—拓展应用”的勾股定理的逆定理的探索过程,经历知识的发生、发展、形成和应用的过程;重点掌握勾股定理的逆定理及证明。
难点勾股定理的逆定理的证明。
教学过程教学设计第一步:复习巩固:创设情境:⑴怎样判定一个三角形是等腰三角形?⑵怎样判定一个三角形是直角三角形?和等腰三角形的判定进行对比,从勾股定理的逆命题进行猜想。
第二步:应用提高:例1(补充)说出下列命题的逆命题,这些命题的逆命题成立吗?⑴同旁内角互补,两条直线平行。
⑵如果两个实数的平方相等,那么两个实数平方相等。
⑶线段垂直平分线上的点到线段两端点的距离相等。
⑷直角三角形中30°角所对的直角边等于斜边的一半。
分析:⑴每个命题都有逆命题,说逆命题时注意将题设和结论调换即可,但要分清题设和结论,并注意语言的运用。
⑵理顺他们之间的关系,原命题有真有假,逆命题也有真有假,可能都真,也可能一真一假,还可能都假。
解略。
例2(P82探究)证明:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。
分析:⑴注意命题证明的格式,首先要根据题意画出图形,然后写已知求证。
⑵如何判断一个三角形是直角三角形,现在只知道若有一个角是直角的三角形是直角三角形,从而将问题转化为如何判断一个角是直角。
⑶利用已知条件作一个直角三角形,再证明和原三角形全等,使问题得以解决。
⑷先做直角,再截取两直角边相等,利用勾股定理计算斜边A1B1=c,则通过三边对应相等的两个三角形全等可证。
勾股定理的逆定理说课稿

18.2勾股定理的逆定理说课稿一、教材分析 :(一)、本节课在教材中的地位作用“勾股定理的逆定理”一节,是在上节“勾股定理”之后,继续学习的一个直角三角形的判断定理,它是前面知识的继续和深化,勾股定理的逆定理是初中几何学习中的重要内容之一,是今后判断某三角形是直角三角形的重要方法之一,在以后的解题中,将有十分广泛的应用,同时在应用中渗透了利用代数计算渗透与他人交流、合作的意识和探究精神(三)、学情分析:尽管已到初二下学期学生知识增多,能力增强,但思维的局限性还很大,能力也有差距,而勾股定理的逆定理的证明方法学生第一次见到,它要求根据已知条件构造一个直角三角形,根据学生的智能状况,学生不容易想到,因此勾股定理的逆定理的证明又是本节的难点,这样如何添辅助线就是解决它的关键,这样就确定了本节课的重点、难点和关键。
重点:勾股定理逆定理的应用难点:勾股定理逆定理的证明关键:辅助线的添法探索二、教学过程:本节课的设计原则是:使学生在动手操作的基础上和合作交流的良好氛围中,通过巧妙而自然地在学生的认识结构与几何知识结构之间筑了一个信息流通渠道,进而达到完善学生的数学认识结构的目的。
(一)、复习回顾: 复习回顾与勾股定理有关的内容,建立新旧知识之间的联系。
直角三角形,通过操作验证两三角形全等,从而不仅显示了符合条件的三角形是直角三角形,还孕育了辅助线的添法,为后面进行逻辑推理论证提供了直观的数学模型。
接下来就是利用这个数学模型,从理论上证明这个定理。
从动手操作到证明,学生自然地联想到了全等三角形的性质,证明它与一个直角三角形全等,顺利作出了辅助直角三角形,整个证明过程自然、无神秘感,实现了从生动直观向抽象思维的转化,同时学生亲身体会了动手操作——观察——猜测——探索——论证的全过程,这样学生不是被动接受勾股定理的逆定理,因而使学生感到自然、亲切,学生的学习兴趣和学习积极性有所提高。
使学生确实在学习过程中享受到自我创造的快乐。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:18.2 勾股定理的逆定理(学案)
一、课前热身【课前复习,回顾旧知】
1、勾股定理:____________________________________________________________.
2、命题: 一件事情的语句,叫做命题。
组成:每个命题都是由 和 两部分组成。
形式:任何一个命题都可以写成“ …… ……”的形式。
种类: 和 ;正确的命题称为 ,错误的命题称为 。
二、学习目标【为了目标,全力以赴】
1. 了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2. 培养在实际生活中发现问题总结规律的意识和能力。
三、学法指导【合作交流,感悟新知】
自学内容:P 73-P 75
知识点1:勾股定理的逆定理
如果三角形的三边长a ,b ,c 满足 ,那么这个三角形是直角三角形。
注意:此定理是直角三角形的判定定理,必须已知三角形的三边,且满足两短边的平方和等于最长边的平方,才可判断这个三角形是直角三角形,且最长边所对的角是直角。
针对性练习:判断由线段a ,b ,c 组成的三角形是不是直角三角形:
⑴a=15,b=8,c=17; ⑵a=25,b=24,c=7;
⑶a=13,b=14,c=15; ⑷a=
43, b=1, c=45.
知识点2:互逆命题 如果两个命题的题设和结论正好相反,那么这样的两个命题叫做互逆命题。
如果把其中一个叫做原命题,那么另一个叫做它的 。
注意:任何一个命题都有逆命题,但是,原命题的真假与逆命题的真假没有必然联系。
针对性练习:写出下列命题的逆命题,并判断这些命题的逆命题是否成立。
⑴两条直线平行,同位角相等;
⑵全等三角形的对应角相等。
知识点3:互逆定理
如果一个定理的逆命题经过证明是正确的,那么这个逆命题也是一个定理,这两个定理叫做互逆定理,把其中一个定理称为另一个定理的逆定理。
注意:⑴逆定理是原定理的逆命题,并且是真命题。
⑵判断一个定理的逆命题与原定理是否为互逆定理,关键是确定它的逆命题的真假。
针对性练习:下列说法正确的是( )
A.任何命题都有逆命题
B.任何定理都有逆定理
C.真命题的逆命题一定是真命题
D.定理的逆命题一定是真命题
四、基础训练【摩拳擦掌,初试牛刀】(必做题)
1、已知△ABC 中,AB=8cm ,AC=6cm ,BC=10cm .则最长边上的高是( )
A 、48cm
B 、4.8cm
C 、0.48cm
D 、5cm
2、满足下列条件的△ABC ,不能构成直角三角形的是( )
A 、b 2=c 2-a 2
B 、a :b :c=3:4:5
C 、∠C=∠A-∠B
D 、∠A :∠B :∠C=12:13:15
3、在下列长度的各组线段中,能组成直角三角形的是( )
A .5,6,7
B .1,4,9
C .5,12,13
D .5,11,12
4、一个直角三角形的三边长的平方分别为:32,42,x 2,则x 2
的值是( )
A .42
B .52
C .7
D .52或7
5、若△ABC 的三边a 、b 、c ,满足(a -b )(a 2+b 2-c 2)=0,则△ABC 是( )
A .等腰三角形
B .直角三角形
C .等腰三角形或直角三角形
D .等腰直角三角形
6、三角形的两边长为3和5,要使这个三角形为直角三角形,则第三边长是 .
7、一根24米绳子,折成三边为三个连续偶数的三角形,则三边长分别为 ,此三角形的形状 .
8、如果△ABC 的三边a,b,c 满足关系式602-+b a +(b-18)2+30-c =0,则△ABC 是 。
9、命题“对顶角相等”.
(1)它的逆命题是: .
(2)这个逆命题正确吗?为什么?
10、如图,在四边形ABCD 中,∠C=90°,AB=13,BC=4,CD=3,AD=12,求证:AD ⊥BD .
五、能力提升【八仙过海,各显神通】(选做题)
11、若△ABC 的三边a ,b ,c 满足条件a 2+b 2+c 2+338=10a+24b+26c ,试判定△ABC 的形状.。
