假期奥数练习六
小学数学六年级简单奥数练习题

小学数学六年级简单奥数练习题以下是一份关于小学数学六年级简单奥数练习题:题一:计算下列各题1. $20 \times 5 =$2. $76 \div 4 =$3. $15 - 8 =$4. $3^2 \times 4 =$5. $30 \div (5-2) =$6. $72 \div 8 \times 2 =$7. $(6 + 2) \times 5 =$8. $(10 - 4) \times 3 =$题二:填空题1. $5 \times \_\_\_ = 30$2. $\_\_\_ + 12 = 25$3. $\_\_\_ \div 4 = 7$4. $9 - \_\_\_ = 3$5. $\_\_\_ \times 6 = 42$6. $\_\_\_ + 16 = 30$7. $45 \div \_\_\_ = 5$8. $80 - \_\_\_ = 56$题三:选择题1. 在下列数中,哪个数是偶数?a) 27b) 46c) 332. 一个正方形的边长是8米,它的面积是多少?a) 32平方米b) 64平方米c) 48平方米3. 小明剪掉一根长为2厘米的线段和一根长为3厘米的线段,他剪下来的线段总长是多少?a) 2厘米b) 3厘米c) 5厘米4. 如果$12 + 3x = 21$,那么x的值为多少?a) 3b) 4c) 5题四:解答题1. 一支蜡烛共燃烧了15小时。
小明先在晚上7点燃了这支蜡烛,然后在次日凌晨熄灭了它。
那么小明熄灭蜡烛的时间是几点?答:凌晨7点2. 有一本书的页码是从1开始连续编号的。
如果总共有120页,那么最后一页的页码是多少?答:120页3. 如果本周的星期六是18号,那么下个星期六是几号?答:25号以上是一份关于小学数学六年级简单奥数练习题,希望能对学生们的数学能力提升有所帮助。
小学四年级奥数练习题(六篇)

小学四年级奥数练习题(六篇)1、30名学生报名参加美术小组或者书法小组。
其中有26人参加了美术组,17人参加了书法组。
问两个组都参加的有多少人?2、用6根短绳连成一条长绳,一共要打()个结。
3、篮子里有10个红萝卜,小灰兔吃了其中的一半,小白兔吃了2个,还剩下()个。
4、围绕桌子一周放了一些苹果和梨,已知每2个苹果之间放有2个梨,一共有5个苹果,梨有多少个。
5、用1、2、3三个数字能够组成()个不同的三位数。
6、有两个数,它们的和是9,差是1,这两个数是()和()7、3个小朋友下棋,每人都要与其他两人各下一盘,他们共要下()盘。
8、把4、6、7、8、9、10填下入面的空格里(三行三列的格子),使横行、竖行、斜行上三个数的和都是18。
9、15个小朋友排成一排报数,报双数的小朋友去打乒乓,队伍里留下()人。
10、一只梅花鹿从起点向前跳5米,再向后跳4米,又朝前跳7米,朝后跳10米;然后停下休息,你知道梅花鹿停在起点前还是起点后?与起点相距几米?小学四年级奥数练习题篇二1、修花坛要用94块砖,第一次搬来36块,第二次搬来38,还要搬多少块?(用两种方法计算)2、王老师买来一条绳子,长20米剪下5米修理球网,剩下多少米?3、食堂买来60棵大白菜,吃了56棵,又买来30棵,现在还有多少棵大白菜?4、小红有41元钱,在文具店买了3支钢笔,每支6元钱,还剩多少元?5、二(1)班从书店买来了89本书,第一组同学借了25本,第二组同学借了38本,还剩多少本?6、果园里有桃树126颗,是梨树棵数的3倍,果园里桃树和梨树一共多少棵?7、1+2+3+4+5+6+7+8+9+10=()8、11+12+13+14+15+16+17+18+19=()9、按规律填数。
(1)1,3,5,7,9,()(2)1,2,3,5,8,13()(3)1,4,9,16,(),36(4)10,1,8,2,6,4,4,7,2,()10、在下面算式适当的位置添上适当的运算符号,使等式成立。
奥数题练习题六年级

奥数题练习题六年级一、填空题1. 小明有12本漫画书,他借给了好友小红3本,还剩下___本漫画书。
2. 爸爸从9点钟开始修理自行车,用了3小时,修理完成的时间是___点钟。
3. 小明有28颗糖果,他平均发给他的4个朋友,每人分到___颗糖果。
4. 小明抄写了45页书籍,他每天抄写5页,一共花了___天。
5. 有一个三角形,第一条边长是6cm,第二条边长比第一条边长长2cm,第三条边长是第一条边长减2cm,这个三角形的周长是___cm。
二、选择题1. 下面哪个数是3的倍数?A. 15B. 18C. 21D. 242. 小明去超市买了一盒牛奶,里面有6瓶牛奶,每瓶牛奶容量是250ml,一共有___ml的牛奶。
A. 1000B. 1250C. 1500D. 17503. 小红每天步行上学,一次步行1.5km,一周上学一共走了___km。
A. 7.5B. 10.5C. 11.5D. 124. 下面哪个数是4的因数?A. 12B. 15C. 18D. 215. 小明家早上6点出发去旅行,一共旅行12小时。
旅行结束的时间是___点。
A. 12B. 14C. 16D. 18三、解答题1. 一个正方形的边长是8cm,求其面积和周长。
2. 计算:8 × 6 - 12 ÷ 43. 小明在超市买了一盒饼干,里面有15块饼干,小明一共吃了3块,还剩下多少块饼干?4. 在一条直角坐标系中,A点坐标是(3, 4),B点坐标是(7, 2),求AB线段的长度。
5. 一辆巴士上载了40名乘客,下车了1/4乘客,又上来了12名乘客,车上还剩下多少名乘客?以上就是奥数题的练习题,希望能够对你的数学能力提升有所帮助。
暑假数学作业【奥数篇】

每日一题奥数1.一个五位数的各位上的数字各不相同,将这个数字乘以4,所得的新五位数刚好是原数的反序数,(如ABCDE 的反序数是EDCBA )。
求原来的五位数?21978*4=879122.在前1000个自然数中,该数各位上的数字和等于15的有多少个?523.某大学有外语教师120名,其中英语教师50名,日语教师45名,法语教师40名,15名教师既教英语又教日语,10名教师既教英语又教法语,8名教师既教日语又教法语,有4名教师这三门外语都会教。
不教这三门外语的教师有多少名? 50+45+40-15-10-8+4+X=120 X=144.一次校友聚会有50人参加,在参加聚会的同学中,每个女生认识男生人数各不相同,而且恰好构成一串连续自然数,最多的全认识,最少的也认识15人,这次聚会中有多少个女生? 50-x-15+1=x x=185.赵强每天上学步行10分钟以后,跑步2分钟,恰好准时到校,有一天,他步行6分钟后开始跑步,结果早到了2分24秒,则他跑步的速度是步行的速度的多少倍?那天跑步时间为10+2-(2+24/60)=9.6分钟 10A+2B=6A+9.6B A=1.9B6.如图,一个长方形将一个正方形的每条边都分成了3厘米和6厘米,求长方形的面积?√3²+3²=3√2 √6²+6²=6√2 3√2×6√2=36 或﹙3+6﹚²=81 81-3×3÷2×2-6×6÷2×2=367.小光和小红同时从相距5千米的甲、乙两地相对而行,小光到达乙地后立刻返回,小红到达后休息了2分钟再返回,已知小光每分钟跑320米,小红每分钟跑305米,从开始跑到两人第二次相遇需多少分钟?8.右图是由8个长2厘米、宽1厘米的长方形拼成的正方形,从A 点出发沿格线到B 点,不能走重复路线,最多走多少厘米?1+1+1+2+1+1+1+2+1+2+2+2+1+2+2=229.3+33+333+3333+…+33……33,和的末三位数是多少? 1995个31995*3+1994*30+1993*300 (个位有1995个3,十位有1994个3,百位有1993个3) =3*(1995+19940+199300)=3*221235=663705所以末三位数字是70510.李小宁参加六次测试,第3、4次的平均分比前两次的平均分多2分,比后两次的平均分少2分,如果后三次跟前这些前三次平均分多3分。
人教版六年级奥数习题

人教版六年级奥数习题人教版六年级奥数习题11、(鸡兔同笼问题)小丽买回0.8元一本和0.4元一本的练习本共50本,付出人民币32元。
0.8元一本的练习本有多少本?2、(年龄问题)5年前父亲的年龄是儿子的7倍。
15年后父亲的年龄是儿子的二倍,父亲和儿子今年各是多少岁?3、(盈亏问题)王老师发笔记本给学生们,每人6本则剩下41本,每人8本则差29本。
求有多少个学生?有多少个笔记本?4、(还原问题)便民水果店卖芒果,第一次卖掉总数的一半多2个,第二次卖掉剩下的一半多1个,第三次卖掉第二次卖后剩下的一半少1个,这时只剩下11个芒果。
求水果店里原来一共有多少个芒果?5、(置换问题)学校买回6张桌子和6把椅子共用去192元。
已知3张桌子的价钱和5把椅子的价钱相等,每张桌子和每把椅子各是多少元?6、(安排)烤面包的架子上一次最多只能烤两个面包,烤一个面包每面需要2分钟,那么烤三个面包最少需要多少分钟?7、(油和桶问题)一桶油连桶共重18千克,用去油的一半后,连桶还重9.75千克,原有油多少千克?桶重多少千克?8、(和倍)青青农场一共养鸡、鸭、鹅共12100只,鸭的只数是鸡的2倍,鹅的只数是鸭的4倍,问鸡、鸭、鹅各有多少只?9、(鸡兔同笼)实验小学举行数学竞赛,每做对一题得9分,做错一题倒扣3分,共有12道题,小旺得了84分,小旺做错了几道题?10、(相遇问题)甲、乙两人同时从相距2000米的两地相向而行,甲每分钟行55米,乙每分钟行45米,如果一只狗与甲同时同向而行,每分钟行120米,遇到乙后,立即回头向甲跑去,遇到甲再向乙跑去。
这样不断来回,直到甲和乙相遇为止,狗共行了多少米?人教版六年级奥数习题21、甲、乙、丙三人在A、B两块地植树,A地要植900棵,B地要植1250棵。
已知甲、乙、丙每天分别能植树24,30,32棵,甲在A地植树,丙在B地植树,乙先在A地植树,然后转到B地植树。
两块地同时开始同时结束,乙应在开始后第几天从A地转到B地?2、有三块草地,面积分别是5,15,24亩。
四年级奥数周末练习六

四年级奥数周末练习六 11、 在一道减法算式中,被减数比减数多1998,差比减数小56,被减数是( )。
2、 被减数、减数、差之和为80,减数与差相等,减数是( )。
3、 在一道减法算式里,被减数、减数与差的和等于120,而差是减数的3倍,那么减数是( )。
4、 一个数除以4,李林在计算时把除号看成了减号,得到的结果是28。
正确的商是( )。
5、 一个数加14,小红在计算时把加号当成了乘号,得到的结果是266,正确的结果是( )。
6、 一个数乘以6再除以5,亮亮在计算时错误地看成除以6再乘以5,结果得数是75,正确的结果应是( )。
7、 两数相乘,若乘数增加14,乘数不变,积增加168,若乘数增加14,被乘数不变,积增加420.那么原来的积是( )。
8、 一个学生做两位数乘两位数乘法时,把一个因数的个位数5误写成3,得到的乘积是516,正确的乘积是540,这两个乘数是( )。
9、 两个数相乘,如果被乘数增加2,乘数不变,积就增加36,如果乘数减少5,被乘数不变,积就减少120,原来的积是( )。
10、乘数是6,被乘数比乘积小140,这个乘法算式是( )。
11、乘数是9,积比被乘数多720,被乘数是( )。
12、一道乘法算式中,乘数是9,把乘数、被乘数和乘得的积相加得319,被乘数是( )。
13、 张妮在计算有余数的除法时,把被除数115当成151,结果商比正确得数大了3,但余数恰好相同,这道除法算式是( )。
14、 刘英在计算有余数的除法时,把被除数113错写成131,结果商比原来多3,但余数恰巧相同,那么该题的余数是( )。
15、 欢欢和莉莉计算从不出差错。
有一天两人同时用同一个数做被除数,欢欢的除数是12,莉莉的除数是15;结果欢欢除得的商是32还余6,莉莉的计算结果是( )。
16、计算下面图形中角的度数。
1、已知∠1=75°,∠2=∠3=∠4=2、∠1= ∠2= ∠3= 35° 2 30° 3 1。
六年级奥数方程练习题

六年级奥数方程练习题在奥数学习过程中,方程是一个重要的概念和技巧。
通过解方程,我们可以找到未知数的值,从而解决各种实际问题。
下面是一些六年级奥数方程练习题,希望能帮助同学们更好地理解和掌握方程的基本知识和解题方法。
1. 请解方程:2x + 3 = 92. 请解方程:5x - 4 = 113. 请解方程:3(x + 1) = 184. 请解方程:2(3x - 7) = 205. 请解方程:4(2x + 5) = 72通过将这些方程转化为适当的等式,我们可以应用一些基本的代数运算得到方程的解。
下面是逐个解答每一个方程的步骤和答案:1. 解方程:2x + 3 = 9首先,我们将方程两边减去3,得到2x = 6然后,我们再把方程两边除以2,得到x = 3因此,方程的解为x = 32. 解方程:5x - 4 = 11首先,我们将方程两边加上4,得到5x = 15然后,我们再把方程两边除以5,得到x = 3因此,方程的解为x = 33. 解方程:3(x + 1) = 18首先,我们将方程两边除以3,得到x + 1 = 6然后,我们再把方程两边减去1,得到x = 5因此,方程的解为x = 54. 解方程:2(3x - 7) = 20首先,我们将括号里的表达式进行运算,得到6x - 14 = 20然后,我们将方程两边加上14,得到6x = 34最后,我们再把方程两边除以6,得到x = 5.67因此,方程的解为x = 5.675. 解方程:4(2x + 5) = 72首先,我们将括号里的表达式进行运算,得到8x + 20 = 72然后,我们将方程两边减去20,得到8x = 52最后,我们再把方程两边除以8,得到x = 6.5因此,方程的解为x = 6.5通过以上的练习题,我们可以看到方程的解题方法其实并不难。
只要运用一些基本的代数运算,就可以得到方程的解。
同学们在学习奥数方程时,可以多进行类似的练习,提高自己的解题能力和逻辑思维能力。
六年级奥数精讲精练典型题训练

六年级奥数精讲精练典型题训练
例1、某裁缝做一件童装、一条裤子、一件上衣,所用时间之比为1:2:3,他一天共能做2件童装、3条裤子、4件上衣,他做2件上衣、10条裤子、14件童装,需要几天时间?
解以做一件童装的时间为1个时间单位。
裁缝一天干1×2+2×3+3×4=20(时间单位)。
做2件上衣、10条裤子、14个童装需3×2+2×10+1×14=40(时间单位)。
所以需40÷20=2(天)。
答:需要2天时间。
练习
1.有三个梯形甲、乙、丙,它们的高之比依次是1:2:3,上底之比依次是6:9:4,下底之比依次是12:15:10。
梯形甲的面积是30平方厘米,乙、丙两个梯形面积之和是多少平方厘米?
2.三批货物共值2250元。
按重量,第一批和第二批的比是1:2,第二批和第三批的比是1:2.5;按单价,第一批和第二批的比是3:1,第二批和第三批的比是7:3。
三批货物的总价分别为多少元?
3.有大、小两筐苹果,大苹果与小苹果的单价比是5:4,质量比是2:3,把两筐苹果混在一起成为100千克的混合苹果。
每千克苹果
4.4元,大、小两筐苹果原来的单价分别是多少元?
4.车过河交渡费3元,马过河交渡费2元,人过河交渡费1元。
某天过河的车和马数目之比为2:9,马和人数目之比为3:7,如果渡口共收渡费315元,这天过河的车、马和人的数量分别是多少?。
奥数题六年级练习题

奥数题六年级练习题第一题:某数加上8等于17,这个数是多少?解析:设这个数为x,根据题意可以得到方程x + 8 = 17。
解这个方程可得x = 17 - 8 = 9。
所以答案是9。
第二题:某书架上有5本数学书,比物理书多3本,比化学书少2本,总共有几本书?解析:假设物理书的本数为x,则数学书的本数为x + 3,化学书的本数为x - 2。
根据题意,数学书、物理书和化学书的总本数为5 + (x + 3) + (x - 2) = 2x + 6。
所以总共有2x + 6本书。
第三题:一个三位数,个位数字为3,十位和百位数字之和为13,这个数是多少?解析:设这个三位数为abc,根据题意可以列出方程系统:a = 3(个位数字为3)b +c = 13(十位和百位数字之和为13)根据第一个方程可以得到a = 3。
将a = 3代入第二个方程,得到b + c = 13。
由于a、b、c分别代表数字,所以b和c的取值范围为0到9之间。
根据题目条件可以得到b和c两个数的组合只有两种可能:4和9、5和8。
即b = 4,c = 9或者b = 5,c = 8。
所以这个三位数可以是349或者358。
第四题:甲数是乙数的2倍,乙数是丙数的3倍,甲数加丙数等于19,求甲、乙、丙三个数。
解析:设甲数为a,乙数为b,丙数为c,根据题意可以列出方程系统:a = 2b(甲数是乙数的2倍)b = 3c(乙数是丙数的3倍)a + c = 19(甲数加丙数等于19)根据第一个方程可以得到b = a/2。
将b = a/2代入第二个方程可以得到a/2 = 3c,化简得到a = 6c。
将a = 6c代入第三个方程可以得到6c + c = 19,化简得到7c = 19,解方程可得到c = 19/7。
由于甲、乙、丙三个数都是整数,所以c只能等于2。
将c = 2代入a = 6c和b = a/2可以得到a = 12和b = 6。
所以甲、乙、丙三个数分别为12、6和2。
小学数学五年级升六年级暑期衔接《奥数题》练习(附名师详解)

五年级升六年级数学奥数题练习班级考号姓名总分1.一本书的页码需要1995个数字,问这本书一共有多少页?2.某礼堂有20 排座位,其中第一排有10 个座位,后面每一排都比它前面的一排多一个座位。
如果允许参加考试的学生坐在任意一行,但是在同一行中不能与其他同学挨着,那么在考试时,这个礼堂最多能安排多少名学生就试?3.一半真一半假A、B、C、D 四人赛跑,三名观众对赛跑成绩做如下估计:王晨说:“B 得第二名,C 得第一名。
”张旭说:“C 得第二名,D 得第三名。
”李光说:“A 得第二名,D 得第四名。
”实际上,每人都说对了一半。
同学们,你能说出A、B、C、D 各是第几名吗?4.下面这串数是按一定规律排列的:6、3、2、4、7、8、……那么这串数的前1995 个数的和是多少?第1995 个数除以5 余几?5.在一道减法算式中,被减数加减数再加差的和是6 74,又知减数比差的3倍多17,求减数。
6.少年宫游乐厅内悬挂着200 个彩色灯泡,这些灯或亮或暗,变幻无穷。
200 个灯泡按1~200 编号。
灯泡的亮暗规则是:第1 秒,全部灯泡变亮;第2 秒,凡编号为2 的倍数的灯泡由亮变暗;第3 秒,凡编号为3 的倍数的灯泡改变原来的亮暗状态(即亮的变暗,暗的变亮);第4 秒,凡编号为4 的倍数的灯泡改变原来亮暗状态。
这样继续下去,……200 秒为一周期。
当第200 秒时,哪些灯是亮着的?7.新年快到了,五年级三个班决定互相赠送一些图书,三个班原有的图书数量各不相同。
如果五(1)班把本班的一部分图书赠给五(2)班和五(3)班,那么这两个班的图书数量各增加一倍;然后五(2)班也把本班的一部分图书赠给五(1)班和五(3)班,这两个班的图书数量也各增加一倍;接着五(3)班又把本班的图书一部分赠给五(1)班和五(2)班,这两个班的图书又各增加一倍。
这时,三个班的图书数量都是72 本,问原来各班各有图书有多少本?8.和平里小学五(1)班有学生40 名,他们在一起做纸花,每人手中的纸从7 张到46 张不等,没有二人拿相同的张数。
5年级升六年年级暑期奥数学习资料及练习

第一讲找规律①1、4、7、10、13、16、()②56、55、53、50、46、41、()③1、1、2、2、3、4、4、7、()、()④2、6、18、54、162、()⑤2、5、11、23、47、()⑥1、1、2、6、24、120、()⑦1、3、4、7、11、18、()⑧3、4、5、7、9、12、16、()⑨0、3、8、15、24、35、()○102、9、28、65、126、()第二讲植树问题①一条直圆柱形的铁条,如果锯成5段需要1.2小时,今天把同样的铁条锯成若干等长的小段,共用去90分钟,这样共锯了几段?②一个老人在公路上散步,从第一根电线杆走到第十二根电线杆共用22分钟,这个老人走了40分钟,他到了第几根电线杆?③某人到高层建筑的10层去,他从1层到5层共用了100秒,如果用同样的速度走到10层,则还需要多少秒?④一个半径是125米的圆形花园周围,以等距离种白杨树157棵,求相邻两树间的距离是多少?第三讲等差数列①3+7+11+15+19+23+27+31+35+39②3+7+11+15+…(共有34项)③78+75+72+69+…(共有20项)⑤54枚硬币,10个盒子,要使每个盒子里边的硬币数目都不相同,应该怎么办?⑥小明在计算从1开始的等差数列时,不小心漏掉了一个数字,所得结果为210.漏掉的数字是?⑦在19和91之间插入5个数字,使这7个数构成一个等差数列。
写出插入的5个数。
第四讲平均数问题①abc三个数的平均数是81,d、e的平均数是96,求5个数的平均数是多少?②前三场游戏中小明得分分别为130分、143分、144分,为了使四场游戏平均分为145分,第四场应得多少分?③一班男生24人,平均分为85分,女生平均分为88分,全班平均分为86分。
那么一班女生有多少人?④五五班30人参加考试,全班平均分为75分,男生平均72分,女生平均81分,那么男女生分别有多少人?⑤五个好朋友A身高174厘米,B身高177厘米,C身高173厘米,D比五人平均身高少6厘米,E比五人平均身高多1厘米。
六年级上册奥数练习题

六年级上册奥数练习题奥数(Olympiad mathematics)是指数学奥林匹克竞赛,是一项面向中小学生的数学竞赛活动。
通过参与奥数练习题,学生可以锻炼自己的数学思维能力,培养逻辑思维和解决问题的能力。
在六年级上册,奥数练习题更加注重灵活运用各种数学知识,培养学生的数学思维。
一、整数运算1. 计算:1234 - 567 + 890 - 345解答:首先计算减法:1234 - 567 = 667,然后进行加法运算:667 + 890 = 1557,最后再减去345得到最终结果:1557 - 345 = 1212。
2. 计算:(-45) + 23 - (-78) + 90解答:首先计算括号内的减法:- (-78) = 78,然后进行加法运算:(-45) + 23 = -22,再加上78得到:-22 + 78 = 56,最后再加上90得到最终结果:56 + 90 = 146。
二、倍数和因数1. 求200的倍数有多少个?解答:200的倍数可以通过乘以任意正整数来得到,所以200的倍数有无限多个。
2. 36的因数有哪些?解答:36的因数为1、2、3、4、6、9、12、18和36。
三、几何图形1. 如图所示,矩形ABCDE中,线段DC的长度为3cm,线段DE的长度为6cm,请问矩形的面积是多少?解答:根据矩形的性质,矩形的面积可以通过长度和宽度相乘来计算。
线段DC和线段DE分别为矩形的宽和高,所以矩形的面积为3cm × 6cm = 18cm²。
2. 如图所示,正方形ABCD的边长为5cm,求正方形的周长和面积。
解答:正方形的周长可以通过边长乘以4来计算,所以正方形的周长为5cm × 4 = 20cm。
正方形的面积可以通过边长的平方来计算,所以正方形的面积为5cm × 5cm = 25cm²。
四、逻辑推理1. 请问36 + 18 = 54是否成立?解答:36 + 18的结果为54,所以36 + 18 = 54是成立的。
三年奥数综合练习六

三年奥数综合练习六1、有两层书架,总共有415本书,其中第二层的书是第一层的4倍,那么两层书架各有多少本?2、某校共有学生560人,其中男生人数是女生的3倍少40人,则该校有男生多少人,女生多少人?3、甲乙丙三数之和是183,乙比丙的2倍少4,甲比丙的3倍多7,求甲乙丙三数各是多少?4、甲乙两个仓库各存粮食若干吨,已知甲库比乙库多496吨,又知甲库存粮是乙库的3倍,问甲乙两个仓库各存粮食多少吨?5、甲筐有苹果400个,乙筐有苹果240个。
现从两筐取出数目相等的苹果,则剩下苹果的数量甲筐是乙筐的5倍。
那么甲筐和乙筐所剩的苹果各是多少个?6、甲校人数比乙校人数的3倍多16人,甲校比乙校多234人,甲校和乙校各有多少人?7、有一条公路长1250米,在公路的一侧从头到尾每隔25米栽一棵槐树。
问:可栽槐树多少棵?8、两座楼房之间相距40米,每隔4米栽一棵雪松,一侧能栽多少棵树?9、一条公路长3600米,在公路两旁每隔9米栽一棵梧桐树,两端都栽,共可栽梧桐树多少棵?10、一条公路的一旁连两端在内共有树91棵,每两棵中间的距离是5米,这条公路长多少米?11、甲乙两船共有1520人,甲船的人数比乙船多200人,甲乙两船各有多少人?12、甲乙两筐共装苹果75千克,从甲筐取出5千克放入乙筐,甲筐苹果还比乙筐多7千克。
两筐原来各有苹果多少千克?13、鸡兔共有100个头,320只脚,鸡兔各有多少只?14、有20道数学题,做对一题得5分,做错一题倒扣2分,小明得了79分,那么他做对了几道题?15、小朋友们分苹果,如果每人分3个就多了11个;如果每人分5个还缺5个,有几个小朋友,多少个苹果?16、小强问老师今年多少岁,老师说:“当我像你这么大的时候,你刚3岁;当你像我这么大的时候,我已经39岁了。
”那么,老师今年多少岁?17、甲乙两列火车同时由相距792千米的两地相向而行,9小时后相遇,甲车每小时行45千米,乙车每小时行多少千米?18、小明用棋子摆空心方阵,最外一层每边摆了20个,共摆了4层,需要多少个棋子?19、同学们组成一个中空方阵,最内层要28人,最外层要56人,这个方阵有多少人?20、弟弟早晨以每分钟50米的速度向学校走去,经过10分钟后。
三年级暑假奥数作业练习题

三年级数学暑假作业(一)姓名: 2014年月日一、计算①竖式计算54×63=25×38=370÷5= 774÷8=23×34=②脱式计算81×7×5 81×7÷9 576÷3÷4 576÷(3×4)③列式计算1、3691加上234与3的商是多少?2、9个31是3的多少倍?三、解决问题1、有1吨水果,一辆微型车一次最多运235千克、4辆这样的微型车一次能运走吗?如果不能,还剩多少千克?2、水果店运来水果380千克,其中苹果比梨的3倍还少40千克,水果店运来苹果和梨各多少千克?3、三年级的学生去茶园里劳动。
女生有56人,男生有64人。
4名学生分成一组,一共可以分成多少组?四、奥数训练甲乙两班共有学生95人,从甲班调8人到乙班,再从乙班掉35人到丙班,这时甲班的人数是乙班的2倍。
原来甲乙两班各有多少人?三年级数学暑假作业(二)姓名: 2014年月日一、计算①竖式计算770÷5=696÷2=882÷4=32×68=56×79=②脱式计算85÷5+33 45×90÷2 65÷(130÷2)112×(15×5)③列式计算1、98与13的积,与46的和是多少?2、999减去999与3的商是多少?三、解决问题1、养一张蚕需要桑叶约600千克,可产茧约50千克,我家养了4张蚕。
可产茧多少千克?需要桑叶多少千克?张村共养40张蚕,可产茧多少千克?2、有一块菜地,长12米,宽8米。
如果每平方米收菜45千克,这块地可以收菜多少千克?若给这块菜地围上篱笆,需要篱笆几米?3、一场排球赛,从19时30分开始,进行了155分钟。
比赛什么时候结束?四、奥数训练两个数的和是91,小玲在抄题时,将其中一个加数个位上的“0”丢掉了,结果算出的和是37,这两个数分别是()和()。
小学奥数6-1-16 盈亏问题(二).专项练习及答案解析

1. 熟练掌握盈亏问题的本质.2. 运用盈亏问题的解题方法解决一些生活实际问题.盈亏问题的特点是问题中每一同类量都要出现两种不同的情况.分配不足时,称之为“亏”,分配有余称之为“盈”;还有些实际问题,是把一定数量的物品平均分给一定数量的人时,如果每人少分,则物品就有余(也就是盈),如果每人多分,则物品就不足(也就是亏),凡研究这一类算法的应用题叫做“盈亏问题”.可以得出盈亏问题的基本关系式:(盈+亏)÷两次分得之差=人数或单位数(盈-盈)÷两次分得之差=人数或单位数(亏-亏)÷两次分得之差=人数或单位数物品数可由其中一种分法和人数求出.也有的问题两次都有余或两次都不足,不管哪种情况,都是属于按两个数的差求未知数的“盈亏问题”.注意:1.条件转换; 2.关系互换.利用条件关系转换解盈亏问题——转化分配单位数(接受分配的人数)【例 1】 小鸣用48元钱按零售价买了若干练习本。
如果按批发价购买,每本便宜2元,恰好多买4本。
问:零售价每本多少元?【考点】盈亏问题 【难度】3星 【题型】解答【关键词】华杯赛,初赛,第9题【解析】 见下图,以横线表示本数,纵线表示单价,因为黄色部分面积与绿色部分面积相等,所以黄色的宽是绿色高的2倍,设批发价为x 元(图中绿色长方形的高),知识精讲教学目标6-1-7.盈亏问题(二)则有:x×(2x+4)=48,即x×(x+2)=24=4×6=4×(4+2),所以,x=4(元),零售价为x+2=6(元)【答案】6元【例2】春节前夕,一富翁想丐帮帮众施舍一笔钱财,一开始他准备给每人100元,结果剩下350元,他决定每人多给20元。
这时从其它地方又闻讯赶来了5个乞丐,如果他们每个人拿到的钱和其它乞丐一样多,富翁还需要再增加550元。
原有()名乞丐。
【考点】盈亏问题【难度】3星【题型】填空【关键词】走美杯,3年级,初赛【解析】如果不来这五个乞丐,富翁能剩下120555050⨯-=元。
二年级奥数练习(六)
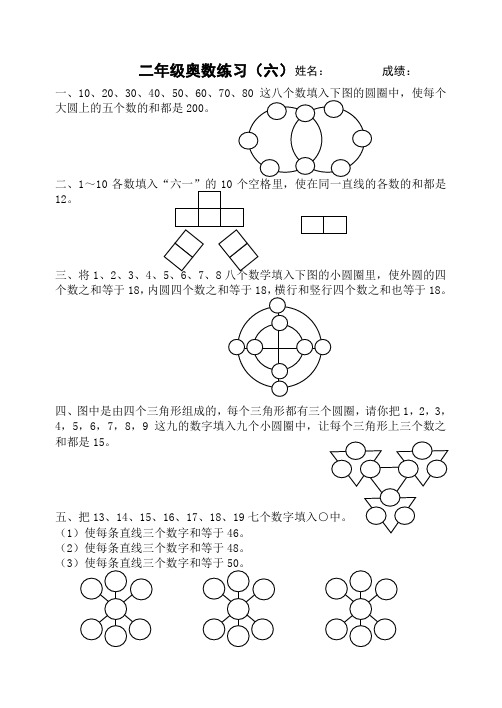
五、把13、14、15、16、17、18、19七个数字填入○中。
(1)使每条直线三个数字和等于46。
(2)使每条直线三个数字和等于48。
(3)使每条直线三个数字和等于50。
二年级奥数练习(六)姓名:成绩:
一、10、20、30、40、50、60、70、80这八个数填入下图的圆圈中,使每个大圆上的五个数的和都是200。
二、1~10各数填入“六一”的10个空格里,使在同一直线的各数的和都是12。
三、将1、2、3、4数之和等于18,内圆四个数之和等于18,横行和竖行四个数之和也等于18。
小学数学下册奥数练习题

小学数学下册奥数练习题奥数练习题一:1. 一辆汽车在1小时内以80公里的速度行驶。
问这辆汽车在10分钟内能行驶多少公里?解法:首先将1小时转换成分钟,即1小时=60分钟。
然后将10分钟除以60分钟,得到0.167小时。
最后将0.167小时乘以80公里/小时,即可得到答案。
计算过程如下:10分钟 ÷ 60分钟/小时 = 0.167小时0.167小时 × 80公里/小时 = 13.36公里答:这辆汽车在10分钟内能行驶约13.36公里。
奥数练习题二:2. 小明喜欢阅读图书,他每天坚持阅读30页。
他计划阅读一本共240页的书,问他需要多少天才能读完?解法:首先将总页数除以每天阅读的页数,即240页 ÷ 30页/天 = 8天。
所以,小明需要8天才能读完这本书。
答:小明需要8天才能读完这本共240页的书。
奥数练习题三:3. 一桶装满汽油的容量为50升。
小明用这桶汽油给自己的摩托车加油,摩托车每升油可以行驶25公里。
问小明用这桶汽油最多可以行驶多少公里?解法:将容量为50升的汽油乘以每升油可以行驶的公里数,即50升 × 25公里/升 = 1250公里。
答:小明可以用这桶汽油最多行驶1250公里。
奥数练习题四:4. 教室里有35个学生,他们需要坐在7排椅子上。
每排椅子上的学生数要尽可能相等且不能有多余的座位。
问每排应该坐几个学生?解法:将学生总数除以排数,即35个学生 ÷ 7排 = 5个学生/排。
所以,每排应该坐5个学生。
答:每排应该坐5个学生。
奥数练习题五:5. 一箱鸡蛋里有168个鸡蛋,小明想把它们平均分给4个朋友。
问每个朋友能分到多少个鸡蛋?解法:将鸡蛋总数除以朋友数,即168个鸡蛋 ÷ 4个朋友 = 42个鸡蛋/朋友。
所以,每个朋友能分到42个鸡蛋。
答:每个朋友能分到42个鸡蛋。
奥数练习题六:6. 小明有40元钱,他买了一本书花了15元,接着又买了一支笔花了6元。
流水行船题练习及答案(六年级奥数)

流水行船题练习及答案(六年级奥数)work Information Technology Company.2020YEAR流水行船题练习及答案1、水流速度是每小时4千米。
现在有一艘船逆水在60千米长的河中航行需5小时,顺水航行需几小时?解:60÷5+4=16(千米/小时)60÷(16+4)=3(小时)答:顺水航行需要3小时。
2、某船在静水中的速度是每小时15千米,它从上游甲地开往下游乙地共花去了8小时,水速每小时3千米,问从乙地返回甲地需要多少时间?解:15+3=18(千米/小时),18×8=144(千米),15—3=12(千米/小时),144÷12=12(小时)。
答:从乙地返回甲地需要12小时。
3、有一艘船行驶于100千米的长河中,逆行需要10小时,顺行需要5小时,求船速和水速。
解:100÷10=10(千米/小时)10÷5=20(千米/小时)(10+20)÷2=15(千米/小时)(20-10)÷2=5(千米/小时)答:船速是每小时15千米,水速是每小时5千米4、甲、乙两港间的水路长208千米,一只船从甲港开往乙港,顺水8小时到达,从乙港返回甲港,逆水13小时到达,求船在静水中的速度和水流速度。
解:顺水速度:208÷8=26(千米/小时)逆水速度:208÷13=16(千米/小时)船速:(26+16)÷2=21(千米/小时)水速:(26—16)÷2=5(千米/小时)答:船在静水中的速度为每小时21千米,水流速度每小时5千米。
5、一艘轮船每小时行21千米,在长120千米的河中逆流航行要10小时到达,返回需要几小时?解:21-120÷10+21=30(千米/小时)120÷30=4(小时)答:返回需要4小时。
6、两个码头相距352千米,一船顺流而下,行完全程需要11小时.逆流而上,行完全程需要16小时,求这条河水流速度。
二年级奥数练习六

二年级练习六
1、填空
2、如图,根据规律填图形和数字
3、找规律填数字
(1)6,0,12,1,18,(),()
(2)1,2,3,5,(),13,()
4、如下图,根据规律接着画
5、观察下面图形中的数的规律,按照此规律,“?”处是()
6、找规律填数,“?”处是()
7、按规律在下划线处画出合适的图形
8、二年级(1)班有学生34人,女生比男生少8人。
问:男、女生各有几人?
9、第一个筐中有15个球,第二个筐中有11个球,从第一个筐中拿出几个球放到第二个筐中,两个筐中的球才能一样多?
10、小丁丁到超市买饮料,每瓶4元,买二送一,他一共买了24瓶,要付多少元钱?
11、新年贺卡每张2元,买4张送1张,学校需要20张,最少需付多少钱?
12、超市搞活动“买五送一”,规定每买5包薯条送1包,小胖买了10包薯条,最多可以得到几包薯条?
13、食品商店搞促销,规定每3个空可乐瓶可以换1瓶可乐,丽丽买了9瓶可乐就,一共可以喝到几瓶可乐?
14、一家冷饮店规定,喝完汽水后,用4个空瓶可以换1瓶汽水。
一天,16名工人叔叔进店买了12瓶汽水,那么,每个工人叔叔能喝到1瓶汽水吗?
15、把27米长的一根绳子分成3段,使后一段都比前一段多3米。
那么,这三段绳子分别长几米?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
奥数练习六
周期问题
在
日常生活中,有一些按照一定的规律不断重复的现象,如:人的十二生肖,一年有春夏秋冬四个季节,一个星期七天等等。
像这样日常生活中常碰到的有一定周期的问题,我们称为简单周期问题。
这类问题一般要利用余数的知识来解答。
在研究这些简单周期问题时,我们首先要仔细审题,判断其不断重复出现的规律,也就是找出循环的固定数,然后利用除法算式求出余数,最后根据余数得出正确的结果。
【例1】:小丁把同样大小的红、白、黑珠子按先2个红的、后1个白的、再3个黑的的规律排列(如下图),请你算一算,第32个珠子是什么颜色?
【思路导航】从上图可以看出,珠子是按“两红一白三黑”的规律重复排列,即6个珠子为一个周期。
32÷6=5(组)……2(个),32个珠子中含有5个周期多2个,所以第32个珠子就是重复5个周期后的第2个珠子,应为( )色。
【课堂随练】如图,算出第20个图形是什么?
○△△□□□○△△□□□○△△……
【例2】:2001年10月1日是星期一,问:10月25日是星期几?
【思路导航】我们知道,每星期有7天,也就是说以7天为一个周期不断地重复。
从10月1日到10月25日经过25-1=24天,24÷7=3(星期)……3(天),说明24天中包括3个星期还多3天。
所以从10月1日开始过3个星期,最后一天还是星期一,从这最后一天起再过3天就应是星期四。
【课堂随练】2017年5月3日是星期三,5月20日是星期几?
【例3】:100个3相乘,积的个位数字是几?
【思路导航】这道题我们只考虑积的个位数字的排列规律。
1个3.积的个位是3;2个3相乘积的个位数字是9;3个3相乘积的个位数字是7;4个3相乘积的个位数字是1;5个3相乘积的个位数字是3……可以发现,积的个位数字分别以3、9、7、1不断重复
出现,即每4个3积的个位数字为一周期。
100÷4=25(个),因此100个3相乘积的个位数字是第25个周期中的最后一个,即是1。
【课堂随练】23个3相乘,积的个位数字是几?
【例4】:有一列数按“432791864327918643279186……”排列,那么前54个数字之和是多少?
【思路导航】上面一列数中,从第1个数字开始重复出现的部分是“43279186”,周期数是8。
要求出这列数字的和,就要先求出这列数里共有多少组“43279186”。
54÷8=6(组)……6(个)
因此,前6组数字和是(4+3+2+7+9+1+8+6)×6=240,余下6个数字之和是
4+3+2+7+9+1=26。
所以,这列数中前54个数字之和是240+26=266。
【课堂随练】一列数按“294736294736294……”排列,那么前40个数字之和是多少?
1、“数学趣味题数学趣味题……”依次重复排列,第
201个字是什么?
2、把38面小三角旗按下图排列,其中有多少面白旗?
3、2017年8月1日是星期二,8月28日是星期几?
4、2017年6月1日是星期四,9月1日是星期几?
5、100个2相乘,积的个位数字是几?
6、50个7相乘,积的个位数字是几?
6、有一列数按“9453672945367294……”排列,那么前50个数字之和是多少?
7、有一列数“7231652316523165……”,请问从左起第2个数字到第25个数字之间(含第2个与第25个数字)所有数字的和是多少?。
