聚类分析(数学建模)讲解
聚类分析简介
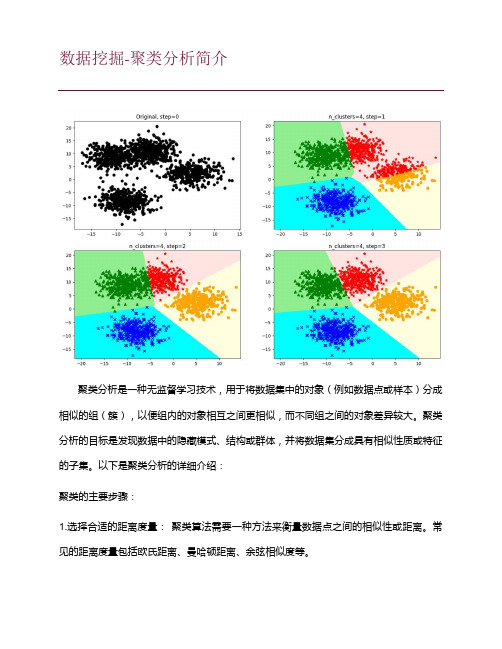
数据挖掘-聚类分析简介聚类分析是一种无监督学习技术,用于将数据集中的对象(例如数据点或样本)分成相似的组(簇),以便组内的对象相互之间更相似,而不同组之间的对象差异较大。
聚类分析的目标是发现数据中的隐藏模式、结构或群体,并将数据集分成具有相似性质或特征的子集。
以下是聚类分析的详细介绍:聚类的主要步骤:1.选择合适的距离度量:聚类算法需要一种方法来衡量数据点之间的相似性或距离。
常见的距离度量包括欧氏距离、曼哈顿距离、余弦相似度等。
2.选择聚类算法:选择适合数据和问题的聚类算法。
常见的聚类算法包括K均值聚类、层次聚类、DBSCAN(基于密度的聚类)、高斯混合模型等。
3.初始化:对于迭代型聚类算法(例如K均值),需要初始化聚类中心或其他参数。
初始值的选择可以影响聚类结果。
4.分配数据点到簇:根据数据点之间的相似性,将每个数据点分配到一个簇中。
不同的算法使用不同的分配策略。
5.更新簇的代表:对于迭代聚类算法,计算每个簇的新代表,通常是簇内所有数据点的平均值。
6.重复迭代:重复步骤4和步骤5,直到满足停止条件,例如簇中心不再改变或达到最大迭代次数。
7.评估聚类结果:使用合适的评估指标来评估聚类的质量。
常用的指标包括轮廓系数、Davies-Bouldin指数、互信息等。
常见的聚类算法:1.K均值聚类(K-Means Clustering):K均值是一种迭代型聚类算法,通过指定簇的数量K来将数据分成K个簇。
它以簇的中心点(均值)作为代表。
2.层次聚类(Hierarchical Clustering):层次聚类是一种层次化的聚类方法,可以创建层次化的聚类结构。
它可以是自底向上的凝聚聚类或自顶向下的分裂聚类。
3.DBSCAN(Density-Based Spatial Clustering of Applications with Noise): DBSCAN 是一种基于密度的聚类算法,能够识别不规则形状的簇,并能处理噪声数据。
数学建模聚类分析

层次聚类
要点一
总结词
一种基于距离的聚类算法,通过构建层次结构来对数据进 行聚类。
要点二
详细描述
层次聚类算法的基本思想是,通过不断将相近的数据点合 并成新的集群,或者将现有的集群分裂成更小的集群,来 构建一个层次结构。算法首先将每个数据点视为一个独立 的集群,然后按照距离的远近逐步合并或分裂集群,直到 达到预设的停止条件。层次聚类算法有多种,其中最常用 的是凝聚层次聚类和分裂层次聚类。
密度峰值聚类
总结词
一种基于密度的聚类算法,通过识别密度峰值点来对 数据进行聚类。
详细描述
密度峰值聚类算法的基本思想是,通过识别数据集中的 密度峰值点来对数据进行聚类。算法首先计算每个数据 点在其邻域内的密度,并将密度最大的点视为密度峰值 点。然后,算法将每个密度峰值点作为中心点,将与其 相近的数据点归入同一个集群。通过这种方式,密度峰 值聚类算法能够识别出任意形状的集群,并处理异常值 和噪声点。与DBSCAN算法相比,密度峰值聚类算法 的计算复杂度较低,因此在处理大规模数据集时具有更 好的性能。
DBSCAN聚类
总结词
一种基于密度的聚类算法,通过识别高密度区域和低 密度区域来对数据进行聚类。
详细描述
DBSCAN聚类算法的基本思想是,通过识别高密度区 域和低密度区域来对数据进行聚类。算法首先从任意一 个未被访问过的数据点开始,搜索其邻域内的所有点, 如果邻域内的点数超过预设的阈值,则将该点标记为核 心点,并将其所在区域视为一个集群。然后,算法继续 搜索核心点的邻域内的点,并将这些点标记为边界点和 噪声点。通过这种方式,DBSCAN算法能够识别出任 意形状的集群,并处理异常值和噪声点。
通过分析不同群体的用户特征和行为模式,电商企业可以 制定更加精准的营销策略和个性化推荐方案,提高用户满 意度和忠诚度。
聚类分析在数学建模中的应用

聚类分析在数学建模中的应用聚类分析是一种无监督学习方法,主要用于发现数据中的潜在分组或模式。
它在数学建模中起着重要的作用,能够帮助研究人员在未知的数据集中发现隐藏的结构和关联。
本文将介绍聚类分析在数学建模中的应用,并详细讨论其几个典型的应用场景。
1.生物医学研究中的应用:聚类分析在生物医学研究中被广泛应用于基因表达数据、蛋白质相互作用网络、疾病分类等方面。
例如,基因表达数据通常具有高维度和复杂性,聚类分析可以将不同的基因分组,找到相关基因集合,从而帮助研究人员发现与特定疾病相关的生物过程和信号通路。
在药物研发过程中,聚类分析还可以帮助研究人员识别潜在药物靶点和候选靶向药物。
2.社交网络分析中的应用:聚类分析在社交网络分析中发挥着重要作用。
通过对社交网络数据进行聚类分析,可以将社交网络中的用户划分为不同的群体或社区,并发现隐藏的社交群体结构。
这可以帮助研究人员了解社交网络用户的行为、兴趣和关系,并为灵活的社交网络设计和推荐系统提供支持。
3.图像分析中的应用:聚类分析在图像分析中也有广泛的应用。
通过对图像数据进行聚类分析,可以将图像分组为具有相似特征的集合,从而实现图像分类、图像和图像压缩等任务。
例如,对于大规模的图像库,聚类分析可以帮助研究人员将图像分组为具有相似主题或特征的集合,从而提高图像的效率和精度。
4.金融风险管理中的应用:聚类分析在金融风险管理中也有着重要的应用。
通过对风险因素进行聚类分析,可以帮助金融机构识别风险因素的潜在结构和关联,并评估不同风险因素之间的相互作用。
这对于制定有效的风险管理策略和规避潜在风险非常重要。
例如,聚类分析可以帮助银行发现具有相似信用风险的客户群体,并采取相应的措施来降低风险。
5.消费者行为分析中的应用:聚类分析在消费者行为分析中也有重要的应用。
通过对消费者数据进行聚类分析,可以将消费者划分为不同的行为类型或偏好群体,并发现不同群体之间的行为模式和趋势。
这可以帮助企业了解消费者的需求和喜好,并制定相应的市场营销策略。
第五讲聚类分析

第五讲聚类分析聚类分析是一种无监督学习方法,旨在将样本数据划分为具有相似特征的若干个簇。
它通过测量样本之间的相似性和距离来确定簇的划分,并试图让同一簇内的样本点相似度较高,而不同簇之间的样本点相似度较低。
聚类分析在数据挖掘、模式识别、生物信息学等领域有着广泛的应用,它可以帮助我们发现隐藏在数据中的模式和规律。
在实际应用中,聚类分析主要包含以下几个步骤:1.选择合适的距离度量方法:距离度量方法是聚类分析的关键,它决定了如何计算样本之间的相似性或距离。
常用的距离度量方法包括欧氏距离、曼哈顿距离、切比雪夫距离等。
2.选择合适的聚类算法:聚类算法的选择要根据具体的问题和数据特点来确定。
常见的聚类算法有K-means算法、层次聚类算法、DBSCAN算法等。
3.初始化聚类中心:对于K-means算法等需要指定聚类中心的方法,需要初始化聚类中心。
初始化可以随机选择样本作为聚类中心,也可以根据领域知识或算法特点选择合适的样本。
4.计算样本之间的相似度或距离:根据选择的距离度量方法,计算样本之间的相似度或距离。
相似度越高或距离越小的样本越有可能属于同一个簇。
5.按照相似度或距离将样本划分为不同的簇:根据计算得到的相似度或距离,将样本划分为不同的簇。
常用的划分方法有硬聚类和软聚类两种。
硬聚类将样本严格地分到不同的簇中,而软聚类允许样本同时属于不同的簇,并给出属于每个簇的概率。
6.更新聚类中心:在K-means等迭代聚类算法中,需要不断迭代更新聚类中心,以找到最优划分。
更新聚类中心的方法有多种,常用的方法是将每个簇内的样本的均值作为新的聚类中心。
7.评估聚类结果:通过评估聚类结果的好坏,可以判断聚类算法的性能。
常用的评估指标有轮廓系数、Dunn指数、DB指数等。
聚类分析的目标是让同一簇内的样本点尽量相似,而不同簇之间的样本点尽量不相似。
因此,聚类分析常常可以帮助我们发现数据中的分组结构,挖掘出数据的内在规律。
聚类分析在市场细分、社交网络分析、基因表达数据分析等领域都有广泛的应用。
数学建模-主成分分析聚类分析

随机抽取管理学院10名学生,对其4门课程的考试成绩进行统计,如下表所示,这4门课程分别为多元统计分析1X ,运筹学2X ,经济学3X ,管理学4X . 使用主成分分析方法对学生成绩进行分析.>> x1=[77 63 75 55 31 67 70 66 70 57]; >> x2=[82 78 73 72 55 81 81 81 68 73]; >> x3=[67 80 71 63 60 82 78 73 72 55]; >> x4=[81 81 81 68 73 67 80 71 63 60];>> data=[x1;x2;x3;x4]'; %输入观测值数据矩阵 >> [n,m]=size(data);>> for i=1:m %将数据矩阵中心标准化sddata(:,i)=(data(:,i)-mean(data(:,i)))./std(data(:,i),1); end>> [P,score,egenvalue,t2]=princomp(sddata) %做主成分分析 P =-0.5511 0.3268 -0.3624 0.6769 -0.5588 0.3358 -0.2089 -0.7289 -0.5110 -0.1193 0.8460 0.0944 -0.3505 -0.8753 -0.3307 -0.0398score =-1.3489 -0.2567 -1.2840 -0.0315 -1.2458 -0.9740 0.5341 -0.2698 -0.8704 -0.7467 -0.5863 0.7336 1.1642 0.3096 -0.2225 -0.2707 3.3634 -1.5690 0.3950 -0.0572 -1.1054 0.8480 1.1534 -0.2345 -1.5954 -0.5212 0.0958 -0.1867 -0.6992 0.4872 0.1005 -0.4105 0.4738 0.9799 0.5768 1.03061.8637 1.4430 -0.7628 -0.3031egenvalue = 2.7502 0.9334 0.5275 0.2334 t2 =3.8620 2.4333 3.8297 1.0034 7.0609 3.9724 1.3834 1.1732 6.29124.9906>> for k=1:mgxl(k)=sum(egenvalue(1:k))/sum(egenvalue); end>> gxl %输出累计贡献率 gxl =0.6188 0.8288 0.9475 1.0000>> plot(score(:,1),score(:,2),'r+') %画出第一第二主成分的散点图 >> gname第一主成分43211X X X X Y 0.3505-0.5110-0.5588--0.5511=,所有科目考试成绩的系数均为负,且差异不大,故1Y 可解释为学生的综合学习成绩,该主成分得分越小(散点图中的位置越靠左),综合成绩越好.第二主成分43212X X X X Y 0.8753-0.1193-0.33580.3268+=,数学科目考试成绩的系数均为正,专业科目考试成绩的系数均为负,故2Y 可解释为学生的数学科目与专业科目学习成绩的差异,该主成分得分绝对值越大则差异越大,由散点图可以看出,10号学生的数学科目明显优于其专业科目成绩,而5号学生的数学科目明显差于其专业科目成绩.>> Y1=score(:,1);ZF=(sum(data'))'; %提取第一主成分得分,求每个学生的总分 >>for k=1:norder(k,1)=find(Y1==min(Y1));Y1(order(k,1))=inf; %按第一主成分得分由高到低排序order(k,2)=find(ZF==max(ZF));ZF(order(k,2))=-inf; %按总分由高到低排序 end >> orderorder =7 7 1 1 2 2 6 3 3 6 8 8 9 9 4 4 10 10 5 5两种排序方式下3号学生和6号学生的排序结果相反,原因在于43211X X X X Y 0.3505-0.5110-0.5588--0.5511可见,这四个科目成绩的重要性是依次递减的,3号学生的总分虽略高于6号学生,但他的最高分出现在重要性最低的第4科.>> R=sddata'*sddata./n %求标准化数据的样本相关矩阵R =1.0000 0.7867 0.5322 0.28900.7867 1.0000 0.5749 0.27680.5322 0.5749 1.0000 0.39750.2890 0.2768 0.3975 1.0000建模2011A主成分分析-聚类分析:data1=[7.84 153.80 44.31 20.56 266.00 18.20 35.38 72.35 5.93 146.20 45.05 22.51 86.00 17.20 36.18 94.594.90 439.20 29.07 64.56 109.00 10.60 74.32 218.376.56 223.90 40.08 25.17 950.00 15.40 32.28 117.356.35 525.20 59.35 117.53 800.00 20.20 169.96 726.02 14.08 1092.90 67.96 308.61 1040.00 28.20 434.80 966.738.94 269.80 95.83 44.81 121.00 17.80 62.91 166.739.62 1066.20 285.58 2528.48 13500.00 41.70 381.64 1417.867.41 1123.90 88.17 151.64 16000.00 25.80 172.36 926.848.72 267.10 65.56 29.65 63.00 21.70 36.94 100.415.93 201.40 45.19 24.90 259.00 14.60 35.88 102.659.17 287.00 43.94 45.77 168.00 19.70 62.74 223.165.72 193.70 80.35 26.57 111.00 19.80 57.64 89.084.49 359.50 258.15 123.27 77.00 12.90 106.47 853.985.51 516.40 91.97 89.04 189.00 19.80 121.72 494.80 11.45 1044.50 94.78 136.97 202.00 22.30 472.48 602.046.14 445.40 82.69 167.39 144.00 18.40 111.24 389.807.84 347.90 57.65 97.14 213.00 19.60 70.82 307.247.41 345.70 159.45 71.03 85.00 18.10 89.34 380.928.50 614.00 744.46 130.55 156.00 32.80 228.64 1013.475.51 257.20 54.64 29.01 104.00 13.20 87.68 223.279.84 1213.50 920.84 1364.85 115.00 142.50 181.48 1818.479.39 325.80 172.29 104.89 82.00 31.50 90.90 429.293.30 212.10 50.13 38.62 139.00 10.60 66.98 186.224.09 90.50 35.02 11.82 16.00 10.40 29.09 46.846.14 583.40 95.25 233.70 155.00 21.10 97.47 311.025.31 366.40 42.34 64.65 188.00 17.40 67.11 182.653.69 323.90 35.14 34.66 50.00 13.90 65.48 253.16 21.87 424.50 73.40 59.72 1520.00 27.80 83.70 175.71 18.38 630.00 96.68 114.81 645.00 34.80 130.36 1626.02 10.53 635.30 64.03 101.35 190.00 28.30 162.64 615.103.50 463.40 112.19 72.93 118.00 14.10 60.60 193.376.35 532.00 57.51 83.76 191.00 19.50 73.46 297.14 5.51 778.70 74.66 92.48 330.00 19.70 110.20 351.63 4.49 754.80 99.88 97.92 243.00 24.90 100.79 323.37 3.50 396.30 138.37 58.97 170.00 24.20 91.76 2893.47 5.51 687.80 85.52 72.85 201.00 19.00 103.20 403.27 4.29 526.00 55.31 81.43 93.00 19.90 100.65 369.80 4.29 449.10 67.22 51.64 315.00 15.70 106.97 294.69 6.56 852.70 72.59 158.67 311.00 21.20 124.24 377.14 16.58 459.00 94.79 47.17 1900.00 19.90 71.32 215.10 7.41 337.30 77.27 248.85 90.00 20.10 99.58 210.00 5.93 568.10 75.14 118.16 135.00 23.80 111.54 572.96 4.69 599.00 69.05 122.18 121.00 19.80 102.72 427.044.90 635.50 68.42 227.76 176.00 19.50 96.33 538.985.31 600.70 44.65 45.10 51.00 15.50 65.87 186.334.29 567.60 60.25 48.67 46.00 16.10 63.74 208.065.51 228.50 49.27 30.85 62.00 22.90 45.93 102.04 4.69 568.60 306.02 70.41 900.00 16.80 79.67 196.737.20 214.70 50.33 40.16 156.00 20.80 47.76 403.98 5.31 151.90 47.24 24.44 140.00 17.30 37.49 92.55 4.90 343.30 42.01 58.81 80.00 13.80 79.07 275.82 4.90 293.90 60.29 51.03 53.00 12.60 75.93 278.37 3.89 312.90 33.79 277.82 55.00 14.00 68.24 295.61 3.69 315.90 45.43 34.05 55.00 12.60 62.84 196.33 3.11 416.30 57.88 47.64 167.00 11.90 116.19 242.04 3.89 374.00 45.17 50.19 35.00 15.00 58.11 157.35 3.89 344.30 35.29 47.87 100.00 15.10 133.72 141.022.91 252.90 45.98 71.54 32.14 14.40 42.99 146.223.30 503.40 38.74 30.46 36.43 7.20 53.73 102.864.90 303.80 56.02 65.86 63.21 40.05 90.69 3760.82 4.09 127.00 27.58 23.99 30.00 11.93 57.47 85.61 2.91 265.00 35.66 29.39 24.64 9.23 60.54 122.962.72 278.90 43.43 32.61 64.29 9.90 53.40 135.713.11 751.20 53.11 53.80 27.86 10.46 60.27 155.00 3.30 361.30 47.54 52.28 25.71 9.11 113.46 218.27 3.30 488.00 51.18 34.55 37.50 10.80 54.62 125.926.14 227.00 42.15 67.04 49.29 16.31 34.28 82.963.69 347.40 37.76 19.97 26.79 10.01 54.41 221.224.49 136.00 36.56 23.07 21.43 14.96 34.19 78.98 3.11 327.10 25.98 23.73 25.71 9.79 63.81 138.06 8.06 113.10 52.40 20.81 65.36 19.69 29.56 62.24 3.69 270.50 33.12 57.85 25.71 13.50 62.04 118.16 3.69 160.30 38.29 26.08 25.71 14.29 40.13 82.86 3.50 305.50 39.50 30.86 31.07 14.74 61.89 148.88 2.72 70.90 19.45 9.12 15.007.09 22.73 32.861.77 119.80 15.32 13.34 8.57 6.19 26.31 47.762.53 468.80 37.04 32.03 45.00 12.15 65.25 178.983.69 150.70 59.61 19.00 34.29 24.98 38.47 89.08 6.14 100.30 37.49 20.23 34.29 14.85 29.29 61.94 10.99 109.80 56.07 69.06 58.93 20.70 38.87 63.27 6.35 91.80 36.12 16.91 36.43 12.49 27.01 47.76 30.13 743.90 49.03 26.18 27.86 17.66 72.76 182.04 3.89 416.80 37.04 23.78 22.50 11.48 54.45 105.00 2.91 369.80 36.34 52.48 22.507.99 42.02 84.08 1.96 194.00 18.08 16.17 26.79 6.98 40.27 94.69 6.98 50.10 41.02 14.25 17.14 13.39 26.57 40.92 2.91 198.80 28.21 19.24 13.93 9.56 47.81 94.80 5.93 886.60 42.69 28.12 43.93 21.15 94.64 163.27 5.93 128.90 47.52 16.31 12.86 17.66 33.51 91.73 7.41 114.30 48.34 21.45 35.36 16.54 35.83 63.88 4.29 232.90 29.17 40.02 1714.29 9.79 38.65 95.414.69 132.80 36.11 17.28 20.36 15.53 37.03 82.765.72 1619.80 43.48 15.50 20.36 15.41 30.99 57.556.77 282.50 41.97 52.80 27.86 18.34 49.10 104.90 4.49 180.60 37.23 18.70 27.86 11.93 36.45 63.98 3.11 386.60 35.93 26.38 24.64 12.26 60.00 157.24 2.91 345.00 40.46 152.21 23.57 15.53 58.05 170.71 4.29 95.60 22.49 17.15 85.71 10.13 27.97 67.24 7.63 87.10 45.83 14.83 30.00 14.63 29.25 48.78 5.93 203.00 35.97 16.88 15.00 14.51 45.83 89.49 2.34 353.00 24.53 12.70 11.79 9.00 58.80 89.08 2.91 233.20 24.92 21.62 85.71 8.33 45.20 100.10 5.72 174.30 33.83 29.45 20.36 13.05 42.10 71.43 2.34 87.60 18.46 9.73 13.93 8.89 24.43 43.37 6.56 245.60 36.73 61.30 55.71 14.18 47.24 114.29 4.69 167.90 33.15 18.96 60.00 15.98 33.46 55.71 6.35 111.40 28.82 59.17 206.79 11.70 28.02 61.53 5.10 94.60 77.92 20.34 23.57 28.69 25.92 58.47 4.69 111.60 24.57 12.09 31.07 8.55 27.12 43.883.50 85.50 26.33 24.88 36.43 11.36 26.77 64.084.69 169.50 39.11 22.51 25.71 15.98 39.53 82.96 4.49 138.00 34.52 35.54 50.36 12.60 25.45 52.45 3.30 131.40 35.97 11.29 43.93 11.03 30.06 61.94 2.91 41.00 41.77 12.50 17.14 17.10 19.68 78.374.09 129.70 26.83 10.12 40.71 7.76 28.84 68.165.72 148.00 36.73 14.21 52.50 12.60 27.15 57.86 4.90 108.10 22.729.40 35.36 8.89 32.39 69.39 4.90 132.50 79.52 18.67 42.86 27.68 28.30 92.245.93 88.80 52.41 15.30 10.71 19.91 28.62 63.88 2.91 206.70 17.46 12.02 31.07 5.51 53.79 79.18 2.72 121.80 19.98 7.71 24.648.10 27.30 57.96 2.34 231.10 36.48 12.80 37.50 17.66 29.02 96.532.53 128.60 21.75 9.10 30.00 9.56 22.77 58.063.89 126.80 50.01 12.74 53.57 18.68 29.40 69.90 2.34 79.70 74.36 27.49 9.64 45.45 21.22 87.65 2.34 294.10 42.68 12.27 79.29 15.53 83.44 99.491.96 238.30 19.71 25.22 19.29 6.64 66.24 142.862.72 109.30 18.52 12.55 19.29 9.79 26.06 61.433.11 69.40 22.93 7.56 26.79 7.65 22.09 53.06 3.50 155.70 33.30 12.08 42.86 11.36 28.05 51.53 2.72 109.30 19.83 14.54 19.29 9.45 34.56 47.55 1.77 205.50 173.34 27.81 41.79 74.03 55.71 229.80 3.50 53.20 35.15 7.91 20.36 11.14 24.90 34.39 2.53 40.00 19.08 2.29 15.00 7.88 24.15 54.29 9.17 82.80 63.88 24.85 11.79 31.50 21.68 76.537.41 222.40 31.10 38.50 142.50 8.66 128.60 133.98 5.72 164.80 49.44 27.98 126.43 13.61 37.64 76.12 8.06 194.00 41.79 31.43 213.21 13.61 45.52 127.35 5.72 310.10 56.40 37.11 138.21 16.43 59.63 154.49 8.72 1024.90 77.61 71.24 128.57 19.35 227.40 1389.39 6.77 492.80 37.86 35.61 142.50 13.39 114.13 118.98 6.56 202.30 33.28 37.67 1339.29 11.36 140.62 110.92 6.77 97.20 38.67 18.12 24.64 14.74 28.77 49.90 6.98 208.60 41.00 28.55 67.50 15.19 93.83 84.59 6.14 143.40 41.67 22.57 88.93 12.49 38.14 65.61 6.69 158.10 36.61 16.22 36.00 12.91 31.67 63.57 8.00 332.60 77.06 46.01 240.00 24.47 68.10 259.29 6.69 401.80 84.94 60.11 138.00 19.16 96.76 227.558.23 756.40 42.73 87.52 63.00 19.26 88.74 184.699.35 407.50 55.54 61.83 112.00 24.05 66.82 208.27 8.90 307.30 54.39 57.21 326.00 25.72 131.93 256.94 3.77 242.10 30.93 32.13 28.00 11.56 50.60 144.69 5.41 178.90 29.54 23.73 52.00 9.89 49.84 118.88 7.78 315.50 49.76 28.03 550.00 18.95 45.73 109.29 5.62 134.60 25.33 19.10 45.00 11.66 40.50 87.14 5.41 235.60 36.88 48.80 43.00 14.06 53.61 213.47 4.58 203.80 39.03 24.18 87.00 16.66 53.09 138.88 6.91 568.50 54.59 113.46 264.00 23.22 82.40 399.90 5.00 506.50 59.45 70.71 202.00 26.13 78.01 334.395.62 880.00 78.29 121.12 293.00 25.61 171.14 540.006.91 250.30 39.09 50.46 81.00 20.41 59.17 172.656.26 249.40 54.70 81.74 75.00 25.51 57.92 171.127.56 248.20 42.23 69.39 57.00 16.56 44.54 165.104.79 156.30 41.16 32.40 83.00 14.58 35.50 103.882.77 120.30 49.85 18.38 43.00 25.51 37.93 115.416.26 429.20 54.47 56.60 45.00 19.78 87.50 230.417.34 205.10 43.63 23.51 47.00 19.78 41.33 104.294.17 113.80 37.27 17.06 34.00 14.47 26.74 64.495.00 221.30 30.75 70.32 47.00 16.14 47.20 185.417.56 580.10 39.78 85.46 270.00 17.49 66.69 315.925.62 171.00 31.23 25.73 292.00 15.72 31.09 110.616.05 365.00 35.92 30.91 110.00 17.91 44.75 147.354.79 289.70 42.12 41.10 57.00 17.49 76.80 237.45 23.72 452.10 37.22 43.61 160.00 16.35 73.27 1635.926.47 847.60 53.17 59.00 96.00 19.05 68.82 186.534.17 310.70 40.70 42.64 58.00 14.99 115.59 177.765.00 317.50 42.46 30.96 162.00 17.81 59.94 221.944.17 357.50 38.78 43.89 14901.00 17.70 98.22 349.80 6.26 387.20 38.03 30.06 85.00 21.97 54.98 142.555.00 196.50 50.03 18.56 29.00 25.82 33.90 84.801.61 295.80 15.40 18.35 19.00 4.27 40.42 106.534.58 129.00 31.09 18.93 38.00 15.10 29.76 69.805.41 204.90 40.16 25.86 41.00 16.24 33.28 80.003.57 174.80 31.13 26.21 26.00 11.14 31.77 94.082.00 197.00 78.36 22.98 19.00 24.05 43.73 104.183.37 106.70 16.31 9.04 17.00 7.60 26.89 37.146.47 738.00 47.35 24.07 135.00 19.58 34.09 101.733.37 788.70 28.90 17.62 34.00 15.51 26.04 91.026.91 133.10 40.58 32.64 27.00 22.39 33.97 115.202.38 149.50 27.18 11.19 54.00 14.47 38.35 59.497.56 206.60 55.79 24.44 22.00 28.63 29.73 81.738.67 78.90 58.87 21.65 26.00 23.43 26.52 70.514.79 178.60 32.31 29.01 45.00 14.26 47.98 104.905.41 250.10 34.32 16.25 15.00 18.53 41.29 90.205.83 89.20 54.90 23.28 19.00 21.76 24.95 53.575.62 453.50 37.22 21.92 40.00 16.56 41.51 87.354.38 92.40 38.70 15.03 21.00 13.85 24.22 47.242.77 198.70 18.11 15.33 19.00 9.68 34.15 95.925.41 260.10 43.81 26.46 33.00 13.22 39.49 87.045.62 101.10 49.01 19.96 23.00 20.82 26.00 71.536.69 146.50 43.39 19.89 36.00 17.49 33.24 60.007.56 66.50 49.24 14.67 19.00 17.08 25.48 41.122.77 119.00 27.49 10.62 44.00 10.52 31.94 53.271.61 434.80 21.29 12.84 18.00 8.85 56.14 106.432.97 77.50 16.91 9.95 34.00 7.50 28.15 41.634.58 130.80 35.61 19.59 23.00 16.14 29.87 61.125.20 134.50 29.37 16.33 32.00 13.54 29.83 59.90 3.17 101.80 32.23 10.68 12.00 12.81 33.20 51.12 5.00 232.00 32.43 24.23 37.00 15.10 36.08 101.84 7.56 121.10 62.91 31.03 44.00 27.28 28.36 88.165.20 238.70 47.18 59.66 24.00 19.68 62.57 108.476.05 151.20 92.76 31.43 79.00 32.07 31.57 130.61 2.77 202.60 56.54 18.09 49.00 28.11 26.14 82.14 2.38 351.60 64.86 28.97 65.00 17.28 112.62 105.31 5.20 173.80 58.28 19.99 51.00 22.49 31.61 69.80 8.67 423.30 61.41 117.83 216.00 30.30 178.88 293.16 5.41 645.30 50.27 80.60 113.00 23.32 99.42 358.27 7.12 967.70 36.41 70.71 66.00 16.87 119.35 457.96 4.58 445.70 28.32 132.05 139.00 12.91 87.44 303.06 8.23 420.60 35.81 73.86 561.00 22.49 60.91 241.63 4.58 257.40 42.25 44.84 260.00 19.58 46.90 192.65 6.05 248.70 44.36 42.79 150.00 19.89 72.20 170.10 8.23 350.30 59.07 36.58 177.00 24.57 52.56 170.00 4.17 109.90 29.09 13.71 31.00 11.35 25.08 51.63 3.97 306.20 38.30 36.22 115.00 13.54 60.63 145.51 10.74 306.50 53.98 97.05 255.00 27.91 69.40 177.86 3.77 515.60 28.74 77.47 1801.00 15.10 70.18 178.57 10.27 175.90 57.88 37.50 65.00 26.97 45.34 100.415.20 417.80 35.71 47.58 801.00 16.03 94.93 204.086.47 368.20 44.22 65.70 91.00 18.33 76.88 247.04 6.47 393.00 35.82 70.17 135.00 18.53 72.96 254.80 8.90 117.50 32.54 20.51 41.00 14.47 41.45 56.33 3.37 379.10 32.13 37.81 49.00 13.74 70.37 208.37 6.69 320.30 87.90 66.99 78.00 21.90 123.60 230.11 4.17 613.40 50.34 149.26 133.00 16.60 110.20 447.83 8.23 220.50 61.48 41.96 84.00 22.40 58.37 153.274.38 229.30 32.69 60.40 64.00 13.70 62.62 204.815.20 334.30 47.05 40.37 76.00 18.40 61.03 211.47 5.20 284.30 40.47 44.73 349.00 16.00 119.46 184.61 5.41 230.10 41.65 35.71 57.00 16.90 43.91 118.70 5.00 551.10 71.75 71.23 74.00 22.30 111.62 209.50 9.58 201.00 39.11 25.26 125.00 10.70 99.35 90.07 3.17 203.80 26.57 24.29 23.00 11.90 41.69 94.34 3.77 355.20 26.25 32.87 14.00 9.60 59.22 117.87 9.13 133.70 52.99 22.10 26.00 24.80 37.73 95.48 7.34 95.60 47.85 19.51 14.00 20.80 28.52 57.68 5.62 352.60 44.57 58.98 51.00 13.30 69.95 531.454.79 556.20 50.87 143.31 92.00 19.10 180.05 388.695.20 113.70 41.85 20.73 12.00 19.00 31.87 57.273.37 240.50 28.04 22.63 261.00 11.70 35.74 92.467.34 120.30 54.19 21.90 27.00 23.00 29.63 81.013.57 514.10 42.34 47.67 13800.00 17.30 69.96 269.894.38 246.30 29.90 21.84 84.00 14.10 59.00 95.175.41 158.00 46.86 24.02 31.00 19.30 36.27 79.244.38 211.30 27.79 19.01 34.00 12.00 38.38 81.425.62 236.50 35.95 66.52 199.00 13.90 40.98 193.676.05 193.00 40.60 24.88 27.00 14.40 33.53 84.866.26 169.70 44.26 88.12 46.00 17.20 42.71 97.675.20 320.10 35.92 36.86 68.00 16.50 58.46 162.856.91 180.20 54.08 27.01 37.00 18.40 44.13 118.914.58 351.80 55.39 78.07 87.00 16.90 69.55 188.888.67 245.70 47.79 27.55 35.00 18.40 53.42 98.816.47 86.80 41.12 15.46 23.00 15.90 37.53 70.187.12 367.80 92.02 49.80 97.00 16.30 41.26 321.123.77 467.10 49.03 34.44 45.00 15.40 60.83 132.865.41 364.70 40.34 40.93 79.00 18.70 83.32 175.34 10.97 248.50 40.61 61.52 81.00 17.20 76.19 168.059.81 171.80 75.38 163.20 30.00 26.30 45.27 125.168.23 409.90 44.67 66.92 80.00 36.00 96.85 197.635.41 302.50 34.22 27.60 408.00 14.80 68.70 218.242.77 236.20 42.67 16.35 62.00 9.40 41.88 149.527.78 114.50 56.38 26.96 36.00 22.40 31.24 75.916.47 165.20 73.40 42.73 40.00 19.70 84.13 95.695.62 380.40 46.63 28.31 48.00 14.60 83.82 155.983.77 398.40 29.57 18.64 60.00 10.50 113.84 172.533.57 268.60 28.11 23.20 64.00 12.20 54.52 101.004.38 126.50 28.57 20.57 19.00 12.10 25.17 53.106.91 290.30 47.87 28.90 34.00 14.80 44.26 94.967.12 228.40 40.29 25.15 37.00 15.30 40.10 83.194.38 305.50 52.44 22.92 13.00 19.10 45.21 109.333.97 407.60 35.65 22.33 11.00 18.60 60.36 121.628.00 96.60 19.42 11.26 12.00 7.50 27.54 47.383.57 185.50 23.15 13.42 34.00 9.50 29.49 92.363.37 288.70 26.12 15.10 18.00 10.30 30.14 63.833.17 90.40 16.20 8.30 32.00 7.00 44.31 44.672.97 285.40 26.86 15.00 65.00 13.30 38.63 68.207.12 100.00 46.15 19.43 14.00 23.00 22.01 65.705.62 306.90 42.02 25.21 40.00 19.20 36.99 141.505.83 319.50 43.32 25.89 54.00 15.80 40.98 83.403.97 100.10 21.69 11.96 40.00 7.90 42.79 69.243.17 218.60 39.51 15.26 34.00 10.50 50.98 84.242.77 239.80 26.06 15.82 35.00 10.20 41.43 80.903.17 156.80 19.73 8.34 42.00 7.60 39.21 71.012.97 281.10 28.56 11.42 48.00 12.60 37.95 81.013.17 142.50 36.75 9.93 43.00 13.30 32.61 61.641.80 195.50 28.53 7.32 36.00 9.70 37.41 50.923.17 153.90 20.90 8.21 37.00 7.60 31.37 38.213.77 104.20 30.34 12.34 24.00 11.80 39.31 57.164.79 72.10 65.54 11.55 35.00 19.80 26.04 47.583.57 190.80 31.33 10.67 65.00 15.70 51.56 94.026.47 282.90 52.68 20.34 25.00 22.90 32.53 103.507.34 149.00 44.22 20.14 33.00 16.00 35.43 147.758.23 121.30 43.29 31.63 86.00 11.40 33.21 46.8610.74 479.20 96.28 29.23 98.00 25.30 80.36 112.3511.68 870.50 70.84 35.17 302.00 29.10 78.15 435.447.34 279.00 51.25 27.95 44.00 22.50 51.20 117.666.05 162.00 36.22 17.91 35.00 14.20 36.41 61.025.41 907.00 43.08 36.48 10.00 14.50 41.02 121.206.26 132.90 42.59 16.58 27.00 16.20 35.52 63.316.47 197.00 38.18 21.09 64.00 18.60 40.18 168.056.47 100.70 36.19 13.31 42.00 11.50 34.34 56.234.79 119.10 35.76 19.71 44.00 9.90 39.66 67.067.56 63.50 33.65 21.90 60.00 12.50 41.29 60.509.35 156.00 57.36 31.06 59.00 25.80 51.03 95.90]; %8种重金属元素的浓度原始数据>> bjz=[3.61303113.23512.33169]'; %8种重金属元素的背景值的均值>>[n,m]=size(data1);>> for i=1:m %求污染程度数据矩阵data2(:,i)=data1(:,i)./bjz(:,i);end>>data3=zscore(data2); %将污染程度数据矩阵中心化标准化>> R3=data3'*data3./n %求污染程度矩阵的相关系数矩阵R3 =0.9969 0.2539 0.1884 0.1592 0.0642 0.3156 0.2890 0.24610.2539 0.9969 0.3513 0.3955 0.2639 0.3283 0.6583 0.42980.1884 0.3513 0.9969 0.5299 0.1029 0.7135 0.3816 0.42300.1592 0.3955 0.5299 0.9969 0.4154 0.4930 0.5184 0.38610.0642 0.2639 0.1029 0.4154 0.9969 0.1026 0.2972 0.19520.3156 0.3283 0.7135 0.4930 0.1026 0.9969 0.3058 0.43500.2890 0.6583 0.3816 0.5184 0.2972 0.3058 0.9969 0.49210.2461 0.4298 0.4230 0.3861 0.1952 0.4350 0.4921 0.9969 >> [P,score,egenvalue,t2]=princomp(data3) %对标准化污染程度数据做主成分分析P =-0.2256 0.1861 -0.6932 0.6286 -0.0346 0.0990 -0.0130 0.1659 -0.3767 -0.2624 -0.2875 -0.3676 -0.3346 -0.4944 0.4024 0.2305 -0.3895 0.4140 0.3089 -0.0527 -0.1442 -0.1494 -0.5203 0.5146 -0.4009 -0.1162 0.3718 0.1569 -0.2034 0.6210 0.4560 0.1674 -0.2165 -0.6279 0.3028 0.5121 0.2027 -0.3585 -0.1862 -0.0236 -0.3831 0.4798 0.1932 0.1561 -0.0183 -0.3038 0.2180 -0.6490 -0.4049 -0.2930 -0.2415 -0.2828 -0.2074 0.3297 -0.5166 -0.4396 -0.3704 0.0349 -0.1254 -0.2750 0.8604 0.0909 0.1005 0.1079score =0.5456 0.4760 -0.2385 0.9238 0.0347 0.0562 -0.0448 -0.00680.7236 0.3890 0.1517 0.4457 0.0965 0.0977 -0.0533 -0.04400.1029 -0.6786 -0.3148 -0.6068 -0.1762 0.0955 0.2073 0.26030.5289 -0.0888 0.0282 0.7029 0.1653 -0.1864 0.0361 0.1829-2.2377 -0.8590 -0.8366 -1.0018 0.5103 0.4119 -0.4269 -0.6101 -7.0283 -2.3626 -4.0263 -1.6355 -1.1503 1.6389 -1.4879 -2.1198 -0.3681 0.5809 -0.5586 0.6635 -0.1787 0.0705 -0.4055 0.3925 -15.5620 -6.6945 5.7248 3.5181 -1.3891 6.1650 2.6337 1.0367 -6.0371 -6.9258 1.2082 2.9402 1.8860 -4.2464 -1.0592 -0.2348 -0.0015 0.7581 -0.4581 0.8739 -0.1659 -0.2192 0.1137 0.09280.6954 0.1341 0.0674 0.3664 0.0591 0.0268 -0.0202 0.1885-0.2674 0.3478 -0.8345 0.7230 0.0449 0.1003 0.0674 -0.06300.1822 0.5162 0.2579 0.2336 -0.1541 -0.0185 -0.3874 -0.1035-2.1906 0.7026 0.6746 -1.3487 0.8725 0.3109 -1.5612 1.6705 -1.5324 -0.2124 -0.3571 -0.9523 0.0396 -0.0076 -0.2709 -0.0697 -6.0460 -2.4069 -3.9522 -2.5619 -2.0637 1.4629 -2.7735 -2.3424 -1.3424 -0.2013 -0.2190 -0.5147 -0.1666 0.4430 -0.0608 0.0551 -0.6321 0.1785 -0.4933 0.2850 0.0627 0.1584 0.1581 0.0416 -1.2540 0.6515 -0.1718 -0.1308 -0.0092 0.0480 -0.8613 0.6978 -7.5796 3.7551 1.3460 -1.7726 -0.6913 -0.9056 -5.5039 3.41100.0944 -0.2025 -0.2070 -0.2764 0.0309 0.3363 -0.4892 -0.0266 -17.4212 8.9703 5.9221 -0.0944 -1.4722 -1.2894 0.8421 0.1725 -2.1046 1.4921 -0.2319 0.4977 0.0202 -0.1274 -0.6136 0.04220.6397 -0.3411 0.4288 -0.5322 0.1214 0.3348 -0.3583 0.12191.4171 0.0243 0.4828 0.1015 0.1464 0.3042 -0.1825 0.2053 -1.7146 -0.1366 -0.0385 -0.4983 -0.6268 0.1689 0.4550 0.2763 -0.0550 -0.1538 -0.0622 -0.2113 -0.1635 -0.0413 0.1809 -0.0872 0.3403 -0.3241 0.1514 -0.6483 0.1454 0.0456 0.0582 -0.0361 -2.2528 0.8758 -3.4344 3.6015 -0.4367 -0.2157 -0.1284 0.2580 -4.7160 1.0707 -3.4565 0.9714 2.5440 0.0534 0.4370 0.1119 -2.7709 -0.0334 -1.8314 -0.2652 -0.0324 0.0437 -0.0380 -0.7412 -0.3140 -0.0641 0.5062 -0.8364 -0.3898 -0.3550 -0.1278 0.7118 -0.7990 -0.1320 -0.4332 -0.3535 -0.2162 -0.3231 0.4275 0.1141 -1.6491 -0.6296 -0.6280 -1.1407 -0.6168 -0.6762 0.3947 0.1354 -1.7686 -0.1825 -0.0992 -1.1970 -0.6814 -0.8994 0.3968 -0.0186 -3.9091 0.7415 -0.2673 -2.9500 6.3803 0.2921 0.2126 0.7461 -1.4647 -0.3831 -0.5316 -1.0731 -0.3343 -0.5569 0.1834 0.2274 -0.9190 -0.3578 -0.1369 -1.0095 -0.1176 -0.1736 0.1963 -0.2639 -0.6199 -0.5094 -0.0971 -0.8925 -0.1719 -0.0425 -0.3181 -0.0942 -2.1994 -0.7106 -0.8728 -1.0604 -0.8158 -0.4901 0.6209 0.1088 -1.6930 0.1943 -2.2379 2.4508 -0.2430 -0.4713 -0.3154 0.7789 -1.1941 0.0654 -0.0643 0.2298 -0.5284 0.8791 0.1192 -0.0071 -1.7783 -0.0857 -0.4393 -0.8688 0.1825 -0.1170 0.2485 -0.2336 -1.3269 -0.3879 -0.1961 -1.0676 -0.1696 -0.1690 0.3273 -0.0182 -1.7262 -0.4834 -0.0588 -1.0235 -0.0390 0.1464 0.7781 0.2450 -0.3146 -0.4307 -0.4538 -0.6836 -0.4914 -0.5546 0.5160 0.2878 -0.3077 -0.3195 -0.0877 -0.8476 -0.4049 -0.5604 0.3973 0.3028 0.2697 0.5142 0.2370 0.2496 -0.0752 -0.1768 0.1170 -0.3981 -2.0172 0.7524 1.0532 -0.7316 -0.9341 -1.0987 -1.6186 1.9530 -0.1381 0.5167 -0.2506 0.3730 0.6859 0.0785 0.1171 -0.0865 0.7240 0.3319 0.3071 0.3205 0.0841 0.0607 -0.0694 -0.0735 -0.0150 -0.3424 -0.1356 -0.4977 0.0635 0.2120 -0.0350 0.0194 0.0576 -0.2000 -0.0237 -0.4499 0.1273 0.2745 -0.2710 0.2023 -0.3202 -0.4893 0.6425 -0.4004 -0.0446 1.0314 0.7140 0.1861 0.4307 -0.3085 0.2150 -0.6014 0.0067 0.0449 -0.0530 0.1206 -0.2662 -0.7819 0.0386 -1.1966 -0.2686 0.1909 -0.4906 -0.1128 0.2713 -0.2298 0.2108 -0.5493 -0.1878 -0.1247 0.1894 0.0785 -0.2246 -0.7164 -0.1448 -0.8876 -0.4672 0.4291 -0.5872 -0.7035 0.6481 -0.0998 0.7073 -0.4511 0.0103 0.1054 0.1706 0.0970 0.5783 -0.7979 -0.0027 -0.9507 -0.4412 -0.2953 0.2737 0.6414 -4.9523 1.3451 -0.8451 -2.9211 8.8247 0.5078 1.3004 -0.6180 1.0347 -0.1646 0.3122 -0.1042 0.0719 0.4338 -0.2773 -0.1365 0.8726 -0.4966 0.3722 -0.6675 -0.0569 0.2092 -0.1495 0.1663 0.8251 -0.4207 0.4898 -0.6795 -0.0298 0.0953 -0.0850 0.2530-0.1942 -0.9026 -0.1482 -1.4141 -0.7682 -0.8284 0.6967 0.7609 0.0322 -0.8372 -0.0282 -1.1085 -0.2348 0.4498 -0.5239 -0.0294 0.3535 -0.5388 0.1385 -0.8978 -0.4007 -0.3706 0.2416 0.4858 0.5465 0.2398 0.0786 0.3970 -0.1003 0.1225 0.2374 0.14640.5999 -0.4428 0.0847 -0.6828 0.0925 -0.0251 0.0617 0.33341.0220 0.1884 0.4185 0.1384 0.1096 0.1586 -0.0265 -0.0356 0.7568 -0.6009 0.1811 -0.7472 -0.1007 0.0866 -0.0003 0.1035 0.5791 0.7669 -0.1772 1.0316 0.0466 0.0941 -0.0653 -0.0231 0.5777 -0.2940 0.3178 -0.4222 -0.1304 0.2144 0.0321 -0.0681 0.9969 0.0506 0.5431 -0.1119 0.0623 0.1465 -0.0594 -0.04600.4834 -0.2277 0.2977 -0.5526 -0.0828 -0.0171 0.0098 -0.09351.8398 -0.2509 0.7183 -0.1471 0.2235 0.3812 -0.1144 0.26030.2548 0.4254 -0.5970 0.7625 -0.1701 -0.0364 0.0853 0.10581.8317 -0.4542 0.8235 -0.4658 0.1887 0.3240 -0.0319 0.2644 0.3311 -0.6401 0.2281 -1.0978 -0.2421 -0.2917 0.2434 0.15270.5054 0.7159 0.8483 0.0558 0.0455 -0.2427 -0.0024 -0.58781.0213 0.3558 0.1137 0.5801 0.1244 0.2419 -0.0707 0.06690.1123 0.9352 -0.7452 1.6501 -0.0884 0.4054 -0.0489 0.06351.1602 0.2701 0.0336 0.6235 0.1197 0.3106 -0.1185 0.2258 -2.5152 1.0417 -6.3439 4.2111 -1.0196 -0.1554 0.5575 1.6064 0.5339 -0.4580 0.0262 -0.6347 -0.3144 -0.2299 0.1989 0.28090.8768 -0.5859 0.3732 -0.7010 -0.2629 -0.0286 0.2501 0.53371.4739 -0.5605 0.6379 -0.6457 0.1290 0.2485 -0.0275 0.2146 1.1412 0.4411 -0.0234 0.8324 0.1481 0.3742 -0.2152 0.1941 1.1723 -0.3646 0.4770 -0.4669 0.0490 0.2327 -0.1095 0.1148 -1.2112 -0.6208 -1.0304 -1.0941 -1.0874 -1.2110 0.8126 -0.0459 0.7708 0.4939 0.1799 0.4678 0.1187 0.0905 -0.0748 -0.0563 0.7194 0.5240 -0.1438 0.8025 0.0400 0.2259 -0.1583 0.0648 0.7944 -0.9189 0.5332 0.3728 0.2052 -0.1612 -0.0980 0.2948 0.9803 0.2176 0.3573 0.1695 0.1169 0.1536 -0.0615 -0.0981 -1.5418 -1.3814 -1.7142 -2.0008 -2.1581 -3.1459 2.5861 1.58680.2234 0.2447 -0.2142 0.3473 -0.1840 0.0135 0.1959 -0.03351.0684 -0.0200 0.2915 0.0147 0.0063 0.1445 -0.0589 0.1836 0.5102 -0.4695 0.2141 -0.8049 -0.1532 -0.1505 0.1388 0.11860.1351 -0.3252 0.6881 -0.6096 -0.2194 0.2954 0.4798 0.03551.4382 -0.0785 0.3928 0.1568 0.2213 0.3376 -0.0624 0.1678 0.9228 0.5060 -0.1865 0.9060 0.0832 0.2852 -0.1856 0.2015 0.7335 0.1135 -0.0839 0.2394 -0.0191 0.1308 -0.0519 0.03200.9324 -0.6877 0.3173 -0.9078 -0.2174 -0.0534 0.0507 0.14601.1803 -0.4970 0.4240 -0.5047 0.0370 0.1793 -0.0235 0.23220.8836 0.0599 0.0175 0.2708 -0.0123 0.2535 -0.0508 0.11051.7497 -0.2216 0.8038 -0.2423 0.2205 0.2957 -0.0487 0.1209 0.4705 0.0381 -0.1928 0.3225 -0.0839 0.2425 0.1211 0.1778 0.9697 0.1825 0.3466 0.1776 0.0190 0.0359 0.0621 -0.08941.0486 0.0656 0.0792 0.6619 0.1062 0.4412 0.0459 0.28020.3823 1.2290 0.8225 0.5786 0.0397 -0.3092 -0.0381 -0.57351.4829 -0.1092 0.2502 0.1891 0.1353 0.3403 -0.0917 0.3202 1.4459 -0.0130 0.6431 0.0268 0.2163 0.3198 -0.0399 0.08020.8508 0.1939 0.3332 0.1067 0.0396 0.0881 -0.0200 -0.08441.1861 0.0885 0.4469 0.1916 0.0722 0.2072 0.0544 0.1862 1.3512 -0.0505 0.6217 -0.1298 0.1299 0.1695 -0.1094 0.1650 1.3321 0.4301 1.0120 0.0658 0.3255 0.1041 -0.0609 -0.2046 1.4784 -0.2019 0.3393 -0.0076 0.1701 0.3084 -0.1081 0.3645 1.0978 0.1706 0.1035 0.3954 0.0722 0.1516 -0.0253 0.2451 1.4059 -0.1147 0.1648 0.1935 0.1880 0.3788 -0.1325 0.25140.3092 1.1165 0.7832 0.4217 0.0644 -0.3575 -0.0249 -0.48011.1689 0.0514 0.4286 0.0063 0.1077 0.0795 0.0210 0.11380.7967 0.7055 0.3276 0.6135 0.1147 0.0563 -0.0939 -0.17531.3591 -0.6709 0.3044 -0.5580 0.0136 0.3660 -0.1928 0.2431 1.6505 -0.2852 0.6425 -0.2593 0.1926 0.2667 -0.0500 0.21670.9654 0.1082 0.8399 -0.4113 0.0687 -0.2751 0.2406 -0.19281.6196 -0.2004 0.7395 -0.2598 0.1962 0.1714 0.0319 0.1721 0.9338 0.4434 0.7083 0.1116 0.1093 -0.0636 -0.0446 -0.1938 -0.0224 1.8951 1.8098 0.3005 0.1527 -0.8642 0.4199 -1.80240.4598 -0.3654 0.4884 -0.8496 -0.2460 -0.0137 -0.3065 -0.42171.1199 -0.7696 0.4580 -0.9040 0.0627 0.3781 -0.1954 0.0908 1.6095 -0.1915 0.6996 -0.2041 0.2183 0.2580 0.0036 0.0999 1.7576 -0.1751 0.6513 -0.0680 0.2704 0.3653 -0.1255 0.2795 1.3236 -0.0558 0.5546 -0.1005 0.0772 0.1055 -0.0197 0.1749 1.5568 -0.2528 0.6675 -0.2453 0.1433 0.3254 -0.0999 0.0547 -2.28193.4783 2.5596 0.0509 -0.0632 -1.9845 0.2218 -3.1007 1.5508 0.0924 0.6973 0.0827 0.1982 0.2972 -0.2033 0.1161 1.8592 -0.1918 0.7847 -0.1554 0.3280 0.4086 -0.1762 0.1513 0.0733 1.5738 -0.0808 1.5086 0.0907 -0.2093 0.1524 -0.6012 0.0548 -0.6737 -0.9257 -0.0157 -0.2853 0.9373 -0.9108 -0.2132 0.8116 0.1771 0.1455 0.3367 0.0141 0.1669 -0.1403 0.2165 0.4910 0.1651 -0.4949 0.7257 0.0634 0.2553 -0.1077 0.2680 0.1334 0.0532 -0.0667 -0.0370 -0.1238 -0.0554 -0.0499 0.0735 -4.3058 -1.2052 -2.7072 -2.4707 1.1227 -0.0943 -0.1468 -0.1098 -0.4295 -0.6749 -0.9341 -0.4303 -0.6773 0.0528 -0.2342 -0.1111-0.1933 -1.0926 -0.4721 0.2073 -0.2135 0.6730 -1.1701 -0.5717 1.0010 0.4069 -0.0233 0.7211 0.0926 0.2576 -0.0931 0.1129 0.1729 -0.0758 -0.4896 0.2159 -0.2704 0.4691 -0.5391 -0.3240 0.9282 0.1422 0.0027 0.4359 0.0325 0.2666 -0.1663 0.2209 0.9517 0.2118 -0.1487 0.5521 0.0370 0.1945 -0.0411 0.2519 -0.7175 0.5932 -0.4110 0.4186 -0.0085 -0.2246 -0.0397 -0.1848 -0.7932 0.0804 -0.3808 -0.2108 -0.3324 -0.0177 -0.3394 -0.0270 -1.2166 -0.4314 -1.2681 -0.3538 -0.9096 -0.6028 0.7595 0.1899。
数学建模里的聚类分析

聚类分析聚类,或称分集,即所谓“物以类聚”,它是按某种相似规则对给定样本集、指标簇进行某种性质的划分,使之成为不同的类.将数据抽象化为样本矩阵()ij n m X X ⨯=,ij X 表示第i 个样本的第j 个变量的值.聚类目的,就是从数据出发,将样本或变量分成类.其方法大致有如下几个.(1) 聚类法.即谱系聚类法.将n 个样本看成n 类,将性质最接近的两类并为一新类,得1-n 类;再从1-n 类中找出最接近的两类加以合并,得2-n 类;继之,最后所有样本都成一类,得一聚类谱系,从谱系中可确定划分多少类,每类含有哪些样本.(2) 分解法.它是系统聚类的逆过程,将所有样本视为一类,按某种最优准则将它分成两类,继之,每一类都分到只含一个样本为止.(3) 动态聚类.即快速聚类法.将n 个样本粗糙地分成若干类,然后用某种最优准则进行调整,直至不能调整为止.(4) 有序样本聚类.按时间顺序,聚在一类的样本必须是次序相邻的样本.(5) 模糊聚类.它是将模糊数学用于样本聚类.(6) 运筹学聚类.它是将聚类问题化为线性规划、动态规划、整数规划模型的聚类.(7) 神经网络聚类.它是将样本按自组织特征映射的方法进行,也是我们要加以叙述的一个重点.(8) 预测中聚类.它是聚类在预测中的应用,以弥补非稳定信号回归的预测与分析.这里主要介绍谱系聚类法和快速聚类法. 一、距离定义样本矩阵()ij n m X x ⨯=,是m 维空间中n 个点,以距离度量样本之间的贴近度,就是距离聚类方法.最常用的第i 个与第j个样本的Minkowski 距离为p mk p jk ik ijx x d /11)||(∑=-=式中p 为一正整数.当2=p , ij d 就是欧几里德距离;当1=p ,ij d 就是绝对距离,或称“布洛克(cityblock )”距离.而切比雪夫距离为||max 1jk ik mk ij x x d -=≤≤设m m C ⨯是变量的协方差矩阵,i x ,j x 为第i 行与第j 行m 个变量构成的向量,则马哈兰罗比斯距离定义为1()()T ij i j i j d x x C x x -=-- 根据距离的定义,就获得距离矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn n n n n d d d d d d d d d d 212222111211 由距离性质可知,d 为实对称矩阵,ij d 越小,两样本就越相似,其中01211====nn d d d ,根据)(j i d ij ≠的n 个点分类,依聚类准则分为不同的类.对d 常用的系统聚类准则有: 1、类间距离定义(1) 最短距离;,min p qpq ij i Gj GD d ∈∈= (2) 最长距离;,maxpqpq ij i G j GD d ∈∈=(3) 质心距离;(,)pq p q D d x x = (4) 平均距离;1p qpq iji G j G p qD d n n ∈∈=∑∑(5) 平方距离:2()()p q T pqp q p q p qn n D x x x x n n =--+2.类间距离的递推公式(1)最短距离:min{,}rk pk qk D D D = (2)最长距离:max{,}rk pk qk D D D = (3)类平均距离:p q rk pk qk rrn n D D D n n =+(4)重心距离:2222pqp q rkpkqkpq r r r rn n n n D D D D n n n n =+-⋅(5)离差平方和距离:2222p k q k krkpk qk pq r kr kr kn n n n n D D D D n n n n n n ++=+-+++二、谱系聚类法例: 假如抽取5个样本,每个样本只测一个指标,即数据为x =[1,0;2,0;4.5,0;6,0;8,0] 试以最短距离准则进行距离聚类说明.解 这时,样本间的绝对距离、欧几里德距离或切比雪夫距离均一致,见表3.1.以最短距离准则聚类.根据定义,当令p Ω与q Ω中分别有pn 与q n 个样本,则最短距离为:},|min{),(q p ij nearj i d q p Ω∈Ω∈=δ于是,对于某步,假定具有样本为p n 的第p 集合与样本为q n 的第q 集合,聚成为具有样本为q p s n n n +=的第s 集合,则第k 集合与第s 集合的最短距离,可写为)},(),,(min{),(q k p k s k near near nearδδδ=(1)表1 绝对距离数据表中数据1、2、4.5、6、8视为二叉树叶子,编号为1、2、3、4、5.当每一个样本看成一类时,则式子(1)变为ij neard j i =),(δ,最小距离为1,即1与2合聚于6号,得表2.表中5.2)5.2,5.3min()}2,3(),1,3(min{)6,3(===δδδnear near near表2 一次合聚表2中最小距离为1.5,即4.5与6合聚于7,得表3.表中(6,7)min{(6,4.5),(6,6)}min(2.5,4) 2.5near nearnearδδδ===.表3 二次合聚表3中最小距离为2,即{4.5,6}元素(为7号)与8(为5号)合聚于8号,得表4.表中5.2)6,4,5.2min()}8,6(),6,6(),5.4,6(min{)8,6(===δδδδnear near near near表4 三次合聚最后集合{1,2}与{4.5,6,8}聚成一集丛.此例的Matlab 程序如下:x =[1,0;2,0;4.5,0;6,0;8,0])();'sin ',();'',(z dendrogram gle y linkage z CityBlock x pdist y ==绘得最短距离聚类谱系如图1所示,由图看出分两类比较合适.1号、2号数据合聚于6号,最小聚距为1;3号、4号数据合聚于7号,最小聚距为1.5;7号于5号数据合聚于8号,最小聚距为2;最后6号和8号合聚,最小聚距为2.5。
数学建模-聚类分析

满足输出;不满足循环;
(7)重复;
初始聚类中心的选择
初始聚类中心的选取决定着计算的迭代 次数,甚至决定着最终的解是否为全局最优, 所以选择一个好的初始聚类中心是很有必要 的。
(1)方法一:选取前k个样品作为初始凝聚点。
(2)方法二: 选择第一个样本点作为第一个聚类 中心。然后选取距离第一个点最远的点作为第二个 聚 类中心。……
数据变换:进行[0,1]规格化得到
初始类个数的选择; 初始类中心的选择;
设k=3,即将这15支球队分成三个集团。现抽取日 本、巴林和泰国的值作为三个类的种子,即初始化三 个类的中心为 A:{0.3, 0, 0.19}; B:{0.7, 0.76, 0.5}; C:{1, 1, 0.5};
样品到类中心的距离; 归类;
计算所有球队分别对三个中心点的欧氏 距离。下面是用程序求取的结果:
第一次聚类结果: A:日本,韩国,伊朗,沙特; B:乌兹别克斯坦,巴林,朝鲜; C:中国,伊拉克,卡塔尔,阿联酋,泰 国,越南,阿曼,印尼。
重新计算类中心;
下面根据第一次聚类结果,采用k-均值法调整各个类的 中心点。
A类的新中心点为:{(0.3+0+0.24+0.3)/4=0.21,
数据变换
(5)极差正规化变换:
x*ij
=
xij
min 1t n
xij
Rj
i 1,,2,...,,n; j 1,..., m
(6)对数变换x*:ij = log xij
i 1,,2,...,,n; j 1,..., m
k
样品间的距离
(1)绝对值距离:
m
dij
xit x jt
t 1
数学建模聚类分析
用的类与类之间距离的定义。
1 、最短距离(Nearest Neighbor)
x11• x12•
x21• x22•
Dpq D(Gp ,Gq ) min dij i Gp , j Gq
即定义 G p 与 Gq 之间的距离为 G p 与 Gq 中最近的两个样品的距
x1, y1
x2, y2
•
•
设聚类到某一步,类p与 q分别有样品 n p 、nq 个,
将p和q合并为k,则k类的样品个数为 nk n p nq
它的重心是
1
xk nk np xp nq xq
某一类 r 的重心是 xr ,它与新类k的距离是
min D(G p , Gk ), D(Gq , Gk )
最短距离法进行聚类分析的步骤如下:
开始各样本自成一类
1、根据样品的特征,规定样品之间的距离 ,共 有 个。将所有列表,记为D(0)表,该表是一张 对称表。所有的样本点各自为一类。
2、选择D(0)表中最小的非零数,不妨假设 ,
于是将 和 合并为一类,记为
nine
ni
ten
ti
ni
negen neun
neuf nueve
nove dziewiec kilenc yhdeksan
ni
tien zehn
dix
diez dieci dziesiec tiz kymmenen
选择适用的距离
在聚类分析中通常要结合实际问题来选择适用的 距离, 有时应根据实际问题定义新的距离,
的距离来衡量各样品点之间的接近程度。
样品 xi 和 x j之间的距离 d (xi , x j ), 一般应满足如下条件:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
聚类分析的基本思想是认为我们所研究的样本或指标(变 量)之间存在着程度不同的相似性(亲疏关系)。于是根据 一批样本的多个观测指标,具体找出一些彼此之间相似程度 较大的样本(或指标)聚合为一类,把另外一些彼此之间相 似程度较大的样本(或指标)又聚合为另一类,关系密切的 聚合到一个小的分类单位,关系疏远的聚合到一个大的分类 单位,直到把所有样本(或指标)都聚合完毕,把不同的类 型一一划分出来,形成一个由小到大的分类系统。最后把整 个分类系统画成一张谱系图,用它把所有样本(或指标)间 的亲疏关系表示出来。这种方法是最常用的、最基本的一种, 称为系统聚类分析。
三维或者更高维的情况也是类似;只不过三维以 上的图形无法直观地画出来而已。在饮料数据中, 每种饮料都有四个变量值。这就是四维空间点的 问题了。
两个距离概念
按照远近程度来聚类需要明确两个概念:一个是点和点之间的距 离,一个是类和类之间的距离。
点间距离有很多定义方式。最简单的是歐氏距离,还有其他的距 离。
x1 x2 x3 x4 x5 x6 x7
二、距离
每个样本有p个指标,因此每个样本可以看成 p维空间中的一个点,n个样本就组成p维空间 中的n个点,这时很自然想到用距离来度量n 个样本间的接近程度。
用 dij 表示第i个样本与第j个样本之间的距 离。一切距离应满足以下条件:
dij 0, 对于一切i, j dij 0,等价于样本i与样本j的指标相同 dij=d ji,对于一切i, j dij dik dkj, 对于一切i, j, k
D
3. 构造个类,每类只含有一个样本;
d ij
4. 合并符合类间距离定义要求的两类为一个新类;
5. 计算新类与当前各类的距离。若类的个数为1,则转 到步骤6,否则回到步骤4;
6.画出聚类图;
7.决定类的个数和类。
系统聚类分析的方法
系统聚类法的聚类原则决定于样品间的距离 以及类间距离的定义,类间距离的不同定义 就产生了不同的系统聚类分析方法。
⒉相似系数 夹角余弦 相关系数
① 夹角余弦
两变量的夹角余弦定义为:
② 相关系数
两变量的相关系数定义为:
系统聚类方法
1 、最短距离(Nearest Neighbor)
x11• x12•
d13
x21•
x22•
16
三、系统聚类法基本步骤
1. 选择样本间距离的定义及类间距离的定义;
2. 计算n个样本两两之间的距离,得到距离矩阵
t 1
chebychev distance 切比雪夫距离
d Max xit xjt t
明氏距离在实际中应用的很多, 但也存在一些缺点:
1、量纲的问题; 处理办法:标准化
2、指标间的相关问题;
改进的办法,采用马氏距离
Mahalanobis 马氏距离
dij (M) (Xi X j )S1(Xi X j )
饮料数据(drink.sav )
16种饮料的热量、咖啡因、钠及价格四种变量
如何度量远近?
如果想要对100个学生进行分类,如果仅仅知道 他们的数学成绩,则只好按照数学成绩来分类; 这些成绩在直线上形成100个点。这样就可以把 接近的点放到一类。
如果还知道他们的物理成绩,这样数学和物理成 绩就形成二维平面上的100个点,也可以按照距 离远近来分类。
聚类分析
对于一个数据,人们既可以对变量(指标)进行 分类(相当于对数据中的列分类),也可以对观测值 (事件,样品)来分类(相当于对数据中的行分 类)。
比如学生成绩数据就可以对学生按照理科或文科 成绩(或者综合考虑各科成绩)分类,
当然,并不一定事先假定有多少类,完全可以按 照数据本身的规律来分类。
聚类分析
分类
俗语说,物以类聚、人以群分。 但什么是分类的根据呢? 比如,要想把中国的县分成若干类,就有很多
种分类法; 可以按照自然条件来分, 比如考虑降水、土地、日照、湿度等各方面; 也可以考虑收入、教育水准、医疗条件、基础
设施等指标; 既可以用某一项来分类,也可以同时考虑多项
指标来分类。
常见的距离有:
minkowski distance (明氏距离):
1
d
tp1xit x jt
q
q
d x x 当 q=1 block distance 绝对值距离:
p
t 1
it
jt
当 q=2 squared euclidean distance 平方欧式距离
当q=
p
x x d
2
it
jt
当然还有一些和距离相反但起同样作用的概念,比如相似性等, 两点越相似度越大,就相当于距离越短。
由一个点组成的类是最基本的类;如果每一类都由一个点组成, 那么点间的距离就是类间距离。但是如果某一类包含不止一个点, 那么就要确定类间距离,
类间距离是基于点间距离定义的:比如两类之间最近点之间的距 离可以作为这两类之间的距离,也可以用两类中最远点之间的距 离作为这两类之间的距离;当然也可以用各类的中心之间的距离 来作为类间距离。在计算时,各种点间距离和类间距离的选择是 通过统计软件的选项实现的。不同的选择的结果会不同,但一般 不会差太多。
一、聚类分析的基本概念
研究对样品或指标进行分类的一种多元统 计方法,是依据研究对象的个体的特征进行 分类的方法。
聚类分析把分类对象按一定规则分成若干 类,这些类非事先给定的,而是根据数据 特征确定的。在同一类中这些对象在某种 意义上趋向于彼此相似,而在不同类中趋 向于不相似。
职能是建立一种能按照样品或变量的相似 程度进行分类的方法。
以下用dij表示样品X(i)和X(j)之间的距离,当样
品间的亲疏关系采用相似系数Cij时,
令 di2j 1 Ci2j
;
以下用D(p,q)表示类Gp和Gq之间的距离。
3.重心法(CENtroid method)
4.类平均法(AVErage method)
例
为了研究辽宁等5省1991年城镇居民生活消费情况 的分布规律,根据调查资料做类型分类,用最短 距离做类间分类。数据如下:
