2020届河北省衡水中学2017级高三下学期九调考试数学(理)试卷参考答案
河北衡水中学2020年第二学期高三年级第九次调研考试理科综合卷参考答案

高三下学期第九次调研考试理科综合生物部分1—6BDCABC29(9分)(1)S M CDK2(2)G0物质和能量的浪费(3)G23(4)71430.(11分)(1)①高脂肪低糖类(KD)②IAV感染3天后,实验组的生存率显著高于对照组(2分)③无明显变化显著增加(2)①a:A基因敲除小鼠b:KD饮食c:KD饮食d:小鼠生存率②1组小鼠的生存率显著低于2组(2分)31.(9分)(1)能量在流动过程中逐级递减,经过五个营养级后剩余的能最不足以维持一个种群的生长发育和繁殖。
(2分)(2)错误(1分);食物链是从生产者开始的(2分)。
(3)直接(1分)(4)不合理(1分):大量捕杀蝙蝠会破坏生态系统原有的营养结构和生物多样性,导致生态系统稳定性降低,不利于生态系统的稳定(2分)。
(答案合理即可)31.(10分)(1)B1对B2、B3为显性,B2对B3为显性Z B2W和Z B3W多节数:中节数:少节数=8:5:3(2)设计方案:F1中多只多节数雄性家蚕蛾分别与中节数雌性家蚕蛾挑选方案:中节数雌性家蚕蛾(或不出现少节数家蚕蛾)37.(15分)(1)乳酸(1分);(2)提供无氧环境(2分);防止杂菌污染(2分);(3)D(2分);(4)玫瑰红(2分);标准显色液(2分);标准显色液设计浓度范围太窄,使待测浓度不在区间内;(2分)增大标准显色液的浓度范围进一步实验(2分)(或者:标准显色液浓度梯度过大,使待测浓度难以找到相近的;缩小浓度梯度至,进一步实验)38、(除标注外,每空2分,共15分)(1)自然界物质循环的规律少消耗、多效益、可持续(2)物质循环再生物种多样性人类的干扰(3)浮床生态工艺法垃圾分类处理掩埋(1分)化学部分7.C8.A9.A10.D11.C12.B13.D26.(14分)(1)CO(NH2)2+H2O2=CO(NH2)2·H2O2(2分)(2)b(1分)温度过高会导致过氧化氢、尿素分解(2分)(3)聚四氟乙烯化学性质稳定,铁质材料易被氧化(1分)(4)4H2O2+Cr2O72-+2H+=2CrO5+5H2O(2分)4CrO5+12H+=4Cr3++6H2O+O2↑(2分)(5)滴入最后一滴KMnO4标准溶液时,溶液变为浅粉色,且半分钟内不褪色(2分)(6)16%(2分)27.(14分)(1)+6(1分)重结晶(1分)(2)MoO3、SO2(2分)(3)MoO3+CO32-=MoO42-+CO2↑(2分)将焙烧产品粉碎、搅拌、适当升高温度或适当提高Na2CO3溶液的浓度等(答出合理的两点即可)(2分)(4)98.5(2分)(5)①Cl-促进碳钢的腐蚀,SO42-抑制碳钢的腐蚀;硫酸浓度增大,会使碳钢钝化(2分)②替代空气中氧气起氧化剂作用(2分)28.(15分)I.(1)-90.77kJ·mol-1(2分)(2)较低温度(1分)(3)①200(L/mol)2(2分)②C(2分)II.(1)<(2分)(2)>(2分)(3)①CH3OCH3-12e-+3H2O=2CO2+12H+(2分)②(2分)35.(15分)[化学——选修3:物质结构与性质](1);17;sp2、sp3;sp2、sp3(每空1分)(2)①羟氯喹仅比氯喹多一个羟基,可以与水形成更多的氢键,故水溶性更好。
2020届河北省衡水中学2017级高三下学期九调考试数学(理)试卷参考答案
5. 某几何体的三视图如图,该几何体表面上的点 P 与点 Q 在正视图与侧视图上 的对应点分别为 A,B,则在该几何体表面上,从点 P 到点 Q 的路径中,最短路 径的长度为( )
A.
B.
C.
D.
解:根据几何体的三视图知,该几何体是长方体,如图所示;
其展开图中,有三种情况,
从点 P(A)到 Q(B)的最短距离为 故选:C.
,
,即 M 为 PA 的中点.
第 11 页 2020届河北省衡水中学2017级高三下学期九调考试数学(理)试卷
19. 某快餐连锁店招聘外卖骑手,该快餐连锁店提供了两种日工资方案:方案① 规定每日底薪 50 元,快递业务每完成一单提成 3 元;方案②规定每日底薪 100 元,快递业务的前 44 单没有提成,从第 45 单开始,每完成一单提成 5 元,该快 餐连锁店记录了每天骑手的人均业务量,现随机抽取 100 天的数据,将样本数据 分为[25,35),[35,45),[45,55),[55,65),[65,75),[75,85),[85,95] 七组,整理得到如图所示的频率分布直方图.
即 sinC(1+3cosA)=0,
因为 sinC≠0,
,且 D.
所以 cosA=﹣ ,
由余弦定理可得 a2﹣b2﹣c2=﹣2bccosA= bc=2,
所以 bc=3,
河北省衡水中学2017届高三下学期期中考试数学(理)试题 Word版含答案

2016—2017学年度高三下学期数学期中考试(理科)第Ⅰ卷一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、设集合{|2,},{|(1)(1)0}xA y y x RB x x x ==∈=-+<,则A B 等于A .(1,1)-B .(0,1)C .(1,)-+∞D .(0,)+∞ 2、若复数z 满足112i z i-=+,则2z 等于 A .25B .35C .105D .153、椅子双曲线2222:1(0)x y C a b a b+=>>的一条渐近线过点(1,2)-,则C 的离心率为A .22B .2C .52D .5 4、已知向量(,)(,),(1,2)a x y x y R b =∈=,若221x y +=,则a b -的最小值为 A .3 B .51- C .31+ D .52+5、某几何体的三视图如图是,其中俯视图为扇形,则该几何体的体积为A .163π B .83π C .89π D .169π6、已知等比数列{}n a 中,12,n a S =是数列{}n a 前n 项的和,若9S 是3S 和6S 的等差中项, 则10a 的值是 A .12 B .12- C .14 D .14- 7、《孙子算经》是中国公元四世纪的数学著作,其中接受了求解依次同余式的方法,他是数论中一个重要的定理,又称《中国剩余定理》,如图所示的程序框图的算法就是源于《中国剩余定理》,执行该程序框图,若正整数N 除以正整数m 后的余数为n ,则记为(mod )N n m ≡,例如113(mod 4)≡,则输出的等于A .8B .16C .32D .648、有5人随机排在一起照相,其中男医生、女以上各1名,男教师、 女教师各1名,男运动员1名,则同职业的人互不相邻,且女的相邻 的概率为 A .215 B .15 C .815 D .7309、已知函数()sin()f x A wx ϕ=+(其中0,2A πϕ><)的部分图象如图所示,将函数的图象向左平移6π个单位长度得到函数()g x 的图象,则函数()g x 的解析式为 A .()2sin(2)3g x x π=- B .()2sin(2)6g x x π=-+C .()2sin(2)3g x x π=--D .()2sin(2)6g x x π=-+10、已知抛物线2:4C y x =的焦点为F ,点在C 的准线l 上,且线段EF 的垂直平分线与抛物线C 及直线l 分别交于P 、Q 两点,若点Q 的纵坐标为3,2O 为原点,则以OP 为直径的圆的方程为 A .22(1)(2)8x y -+-= B .22(2)(1)8x y -+-=C .22(4)(22)96x y -+-=D .22(2)(2)8x y -+-=11、已知三棱锥S-ABC 的所有顶点都在球O 的球面上,底面ABC ∆是边长为1的正三角形,棱SC 是球O 的直径且2SC =,则异面直线SA 与BC 所成角的余弦值为 A .34 B .33 C .36 D .1212、若关于x 的不等式1()x x a m a R -<+∈在(0,1]上恒成立,则实数m 的取值范围为 A .(222,222)-+ B .(1,)-+∞ C .(222,)-+∞ D .(1,222)-+第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上..13、已知2sin()3sin 4παα+=,则2sin 1cos 2αα+= 14、如图,在平面直角坐标系xOy 中,将直线2y x =与直线2x =及x 轴所围成的图形绕x 轴旋转一周得到一个圆锥,圆锥的体积223200432(2)|33V x dx x πππ===⎰, 据此类比:将曲线2(0)y x x =≥与直线1y =及y 轴围成的图形绕 轴旋转一周得到一个旋转体,该旋转体的体积V 等于15、直线20x y a -+=与330x y +-=交于第一象限,当点(,)P x y 在不等式组20330x y a x y -+≥⎧⎨+-≤⎩表示的区域上运动时,43m x y =+的最大值为8,此时3yn x =+的最大值是 16、已知数列{}n a 与{}n b 满足112()n n n n a b b a n N ++++=+∈,若19,3()n n a b n N +==∈且3nn a λ+36(3)3n λ+-+对一切n N +∈恒成立,则实数λ的取值范围是三、解答题:本大题共6小题,满分70分,解答应写出文字说明、证明过程或演算步骤 17、(本小题满分12分).已知,,a b c 是ABC ∆的三个内角,,A B C 的对边,22224sin 3a bc Abc +=+. (1)求角A ;(2)若13,a ABC =∆的面积是33,求ABC ∆的最大角的余弦值.18、(本小题满分12分)500名学生的语文成绩服从正态分布2(100,17.5)N ,数学成绩的频率分布直方图如下: (1)如果成绩大于135的为特别优秀,这500名学生中本次 考试语文、数学特别优秀的大约各多少人?(假设数学成绩在频 率分布直方图中各段是均匀分布的)(2)如果语文和数学两科都特别优秀的共有6人,从(1)中的这些同学中随机抽取3人,设三人中两科都特别优秀的有X 人,求X 的分布列和数学期望.(附参考公式:若2(,)X N μσ,则()0.68P X μσμσ-<≤+=,(22)0.96P X μσμσ-<≤+=)19、(本小题满分12分)如图所示,正方形11AA D D 与矩形ABCD 所在的平面互相垂直,22AB AD ==. (1)若点E ,H 分布为AB ,CD 的中点,求证:平面1//BD H 平面1A DE ; (2)在线段AB 上是否存在点G ,使二面角1D GC D --的大小为3π? 若存在,求出AC 的长;若不存在,请说明理由.20、(本小题满分12分)已知椭圆2222:1(0)x y C a b a b+=>>的离心率为32,椭圆的中心点O 到直线0x y b +-=的距离为522. (1)求椭圆C 的方程;(2)设过椭圆C 的右焦点F ,且倾斜角为045的直线l 和椭圆交于,A B 两点,对于椭圆C 上任一点,若OM OA OB λμ=+,求λμ的最大值.21、(本小题满分12分) 已知函数()21(1)ln ()2f x ax a x x a R =-++-∈. (1)当0a >时,求函数()f x 的单调递减区间;(2)当0a =时,设函数()()g x xf x =,若存在区间1[,][,)2m n ⊆+∞,使得函数()g x 在[,]m n 的值域为[(2),(2])2k m k n ++-,求实数k 的取值范围.请考生在第(22)、(23)题中任选一题作答,如果多做,则按所做的第一题记分,作答时用2B 铅笔在答题卡上把所选题目的题号涂黑,把答案填在答题卡上.22、(本小题满分10分) 选修4-4 坐标系与参数方程在直角坐标系xOy 中,以O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为sin()1)4m πρθ=+=+,而曲线C的参数方程为x y ϕϕ⎧=⎪⎨=⎪⎩(其中ϕ为参数). (1)若直线l 与曲线C 恰好有一个公共点,求实数的值; (2)当34m =-时,求直线l 被曲线C 截得的弦长.23、(本小题满分10分))选修4-5 不等式选讲 设函数()2f x x a x =-+-. (1)若1a =,解不等式()2f x ≤;(2)若存在x R ∈,使得不等式()24t f x t+≤对任意0t >恒成立,求实数a 的取值范围.。
河北衡水中学2020届高三下期第九次调研考试理科综合卷(参考答案)

高三下学期第九次调研考试物理部分二、选择题:本题共8小题,每小题6分。
在每小题给出的四个选项中,第14~18题只有一项符合题目要求,第19~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
14.D [金属的逸出功是由金属自身决定的,与入射光频率无关,A 项错误;光电子的最大初动能E km 与入射光的强度无关,B 项错误;根据爱因斯坦光电效应方程E km =hν-W 0,可知最大初动能E km 随入射光频率增大而增大,但不成正比,C 项错误;E km -ν图线的斜率与普朗克常量有关,D 项正确。
]15.C [由v t 图线可求得两图线交点的横坐标为t =2 s 。
有a 甲=0-105 m/s 2=-2 m/s 2,a乙=6-02-1 m/s 2=6 m/s 2,所以|a 甲|∶a 乙=1∶3,故D 错;由图象可求得甲的位移x 甲=12×10×5 m =25 m ,乙的位移x 乙=12×6×1 m +6×3 m =21 m 。
t =5 s 时两物体位于同一位置,所以t =0时甲物体在乙物体后4 m ,故C 正确;运动过程中,t =2 s 前甲的速度大于乙的速度,t =2 s 后乙的速度大于甲的速度,所以前面甲追乙,后面乙追甲,故A 错;2 s ~5 s 时间内,甲物体位移x 1=12×6×3 m =9 m ,乙物体位移x 2=6×3 m =18 m ,t =5 s 时两物体位于同一位置,所以t =2 s 甲物体在前,乙物体在后,故B 错。
]16.B [粒子运动周期T =2πmqB ,可知速度变化前后,粒子的两次运动周期不变,设以速率v射入磁场时运动轨迹的半径为R 1,画出粒子运动过程图如图甲所示,根据几何关系可知,粒子在磁场中运动所转过的圆心角θ1=90°,半径R 1=r 。
河北省衡水中学2020届高三数学下学期第九次调研试题文(含解析)

【详解】 BC AC AB (1, a 2) ,
由| BC | 1,可得 (1)2 (a 2)2 1 ,解得 a 2 ,
则 AB AC 2 1 2 2 6 ,
故选:C.
【点睛】本题考查了向量的坐标运算,难度不大.
5.已知 a log5 2 , b log0.5 0.2 , c 0.50.2 ,则 a, b, c 的大小关系为( )
c2 2
b2
2
,若
a2
sin
C
5 sin
A
,
(a
c)2
16
b2
,则用“三斜
求积”公式求得 ABC 的面积为( )
3
1
A. 2
B. 3
C. 2
பைடு நூலகம்
D. 2
【答案】D
【解析】
【分析】
由已知利用正弦定理可求得 ac ,进而可求得 a2 c2 b2 6 代入“三斜求积”公式即可求得结
果.
【详解】 a2 sin C 5sin A , a2c 5a , ac 5 ,因为 (a c)2 16 b2 ,
设
2
a
,则 f x的极大值恒小于 0 等价于 g x恒小于 0.
gx a x
∵
x
a x2 x
0
在
0,
a
上在恒成立
∴ g x在 0,
a
上单调递增
g x g a a ln a 3 a 0 ln a 3
∴
2
,即
2.
∴ a e3 .
故选:D.
【点睛】本题主要考查函数极值的应用,求函数的导数,利用函数极值和导数之间的关系转
sin
由 f (x) 在 4 内有且只有两个极值点可得 6 10 ,再由
【河北省衡水中学】2017届高三下学期三调数学(理科)试卷(附答案与解析)

(2)对任意实数 ,都有 成立,求实数 的最大值.
河北省衡水中学2017届度高三下学期三调数学(理科)考试
答案
一、选择题
1~5.CDCAB6~10.BDAAB11~12.DA
二、填空题
13.
14.
15.
16.
三、解答题
17.解:(1)令 ,得 .(1分)
∵ ,∴ ,当 时, .(2分)
由 ,得 ,取 得 的一个法向量 .
假设线段 上存在一点 ,使得直线 与 所成角的正弦值等于 .
所以
.
所以 ,解得 .
因此,线段 上存在一点 ,当点 与点 重合时,直线 与 所成角的余弦值等于 .(12分)
20.解:(1)因为 ,所以 ,所以椭圆的方程为 .
(4分)
(2)将直线 代入椭圆 ,得 .
设 ,则 .
当 时, , 为减函数;
当 时, , 为增函数.
所以 .(10分)
所以 ,与 矛盾.(11分)
综上,得 的最小值为 .(12分)
22.解:(1)由 得 ,
所以曲线 的直角坐标系方程为 .
所以直线 过定点 且斜率为 ,
所以直线 的参数方程为 .(5分)
(2)将直线 的参数方程代入 中,得到 ,
设 对应的参数分别为 ,则 .
(1)求数列 的通项公式;
(2)设 ,当n为何值时,数列 的前 项和最大.
18.(本小题满分12分)
某同学在研究性学习中,收集到某制药厂今年前5个月甲胶囊生产产量(单位:万盒)的数据如下表所示:
x(月份)
1
2
3
4
5
y(万盒)
4
4
5
6
6
【全国百强校】河北省衡水中学2017届高三9月摸底联考(全国卷)理数(解析版)

一、选择题(本大题共8个小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.若集合{}0≥=x x B ,且A B A = ,则集合A 可能是( ) A.{}2,1 B.{}1≤x x C.{}1,0,1- D.R 【答案】A. 【解析】试题分析:∵A B A = ,∴A B ⊆,故只有A 符合题意,故选A. 考点:集合的关系及其运算. 2.复数iiz +=1的共轭复数在复平面上对应的点在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 【答案】D.考点:复数的概念及其运算.3.已知平面向量a ,b 满足()5a a b ⋅+= ,且||2a = ,||1b =,则向量a 与b 夹角的余弦值为( )A.23 B.23- C.21 D.21-【答案】C. 【解析】试题分析:由题意得,215421cos ,5cos ,2a ab a b a b +⋅=⇒+⋅⋅<>=⇒<>= ,故选C.考点:平面向量数量积.4.执行如图所示的程序框图,如输入的a 值为1,则输出的k 的值为( ) A.1 B.2 C.3 D.4【答案】B.考点:程序框图.5.已知数列{}n a 中,11=a ,121()n n a a n N *+=+∈,n S 为其前n 项和,则5S 的值为( ) A.57 B.61 C.62 D.63 【答案】A. 【解析】试题分析:∵112112(1)n n n n a a a a ++=+⇒+=+,∴{1}n a +是首项为2,公比为2的等比数列,∴1221nnn n a a +=⇒=-,∴12(21)2221n n n S n n +-=-=---,∴652757S =-=,故选A.考点:数列的通项公式.6.某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为( ) A.32π B.3π C.92π D.916π【答案】D. 【解析】试题分析:由题意得,该几何体为底面是一扇形的锥体,∴211216243239V ππ=⋅⋅⋅⋅=,故选D. 考点:1.三视图;2.空间几何体的体积. 7.为了得到x y 2cos =,只需要将)32sin(π+=x y 作如下变换( )A.向右平移3π个单位 B.向右平移6π个单位C.向左平移12π个单位D.向右平移12π个单位【答案】C. 【解析】考点:1.诱导公式;2.三角函数的图象变换8.若A 为不等式组⎪⎩⎪⎨⎧≤-≥≤200x y y x 表示的平面区域,则当a 从-2连续变化到1时,动直线a y x =+扫过A 中的那部分区域的面积为( )A.1B.1.5C.0.75D.1.75 【答案】D. 【解析】试题分析:如下图所示,作出不等式组所表示的区域,从而可知,扫过的面积为11722224S =⋅⋅-=,故选D.考点:线性规划.9.焦点在x 轴上的椭圆方程为22221(0)x y a b a b+=>>,短轴的一个端点和两个焦点相连构成一个三角形,该三角形内切圆的半径为3b,则椭圆的离心率为( ) A.41 B.31 C.21 D.32【答案】C. 【解析】考点:1.诱导公式;2.三角函数的图象变换10.在四面体S ABC -中,AB BC ⊥,AB BC ==,2SA SC ==,二面角S AC B --的余弦值是33-,则该四面体外接球的表面积是( ) A.π68 B.π6 C.π24 D.π6 【答案】B. 【解析】考点:1.二面角;2.空间几何体的外接球.【方法点睛】立体几何的外接球中处理时常用如下方法:1.结合条件与图形恰当分析取得球心位置;2.直接建系后,表示出球心坐标,转化为代数;3.化立体为平面,利用平面几何知识求解. 11.已知函数()52log 1,(1)()(2)2,(1)x x f x x x ⎧-⎪=⎨--+≥⎪⎩<,则关于x 的方程()(),f x a a R =∈实根个数不可能为( )A.2B.3C.4D.5 【答案】D.【解析】考点:1.函数与方程;2.分类讨论的数学思想.【方法点睛】运用函数图象结合数形结合思想求解问题的类型:1.对一些可通过平移、对称变换作出其图像的对数型函数,在求解其单调性(单调区间)、值域(最值)、零点时,常利用数形结合思想;2.一些函数型方程、不等式问题常转化为相应的函数图像问题,利用数形结合法求解. 12.函数()sin(2)(,0)2f x A x A πϕϕ=+≤>的部分图象如图所示,且0)()(==b f a f ,对不同的1x ,[]2,x a b ∈,若)()(21x f x f =,有3)(21=+x x f ,则( )A.)(x f 在)12,125(ππ-上是减函数B.)(x f 在)12,125(ππ-上是增函数C.)(x f 在)65,3(ππ上是减函数D.)(x f 在)65,3(ππ上是增函数【答案】B. 【解析】考点:三角函数的图象和性质.【名师点睛】根据sin()y A x ωϕ=+,x R ∈的图象求解析式的步骤:1.首先确定振幅和周期,从而得到A 与ω;2.求ϕ的值时最好选用最值点求:峰点:22x k πωϕπ+=+,谷点:22x k πωϕπ+=-+,也可用零点求,但要区分该零点是升零点,还是降零点,升零点(图象上升时与x 轴的交点):2x k ωϕπ+=;降零点(图象下降时与x 轴的交点):2x k ωϕππ+=+(以上k Z ∈).二、填空题(本大题共4小题,每小题5分,共20分.)13.41(1)(1)x x-+的展开式中2x 项的系数为_______. 【答案】2. 【解析】试题分析:由二项式定理可知4(1)x +中,14r r r T C x +=,令2r =,可知2x 的系数为246C =,令3r =,可知3x 的系数为344C =,故41(1)(1)x x-+的展开式中2x 的系数为642-=,故填:2.考点:二项式定理.14.已知抛物线22(0)y px p =>上一点),1(m M 到其焦点的距离为5,双曲线122=-ay x 的左顶点为A ,若双曲线一条渐近线与直线AM 垂直,则实数a =_______. 【答案】14. 【解析】试题分析:由题意得,2284152m pp p m ⎧==⎧⎪⇒⎨⎨=±+=⎩⎪⎩,又∵(1,0)A -,∴22AMm K ==±,渐近线方程为y =1124a =⇒=,故填:14. 考点:二项式定理.15.如图,为测量出山高MN ,选择A 和另一座山的山顶C 为测量观测点,从A 点测得M 点的仰角60MAN ∠= ,C 点的仰角45CAB ∠= 以及75MAC ∠= ,C 点测得60MCA ∠= ,已知山高100BC =m ,则山高MN =_______m.【答案】150.考点:正余弦定理解三角形.【名师点睛】①这是一道有关解三角形的实际应用题,解题的关键是把实际问题抽象成纯数学问题,根据题目提供的信息,找出三角形中的数量关系,然后利用正、余弦定理求解.②解三角形的方法在实际问题中,有广泛的应用.在物理学中,有关向量的计算也要用到解三角形的方法.近年的高考中我们发现以解三角形为背景的应用题开始成为热点问题之一.③不管是什么类型的三角应用问题,解决的关键都是充分理解题意,将问题中的语言叙述弄明白,画出帮助分析问题的草图,再将其归结为属于哪类可解的三角形.16.设函数x x x f 1)(2+=,x e x x g =)(,对任意1x ,2(0,)x ∈+∞,不等式1)()(21+≤k x f k x g 恒成立,则正数k 的取值范围是________.【答案】1[,)21e +∞-. 【解析】考点:1.导数的运用;2.转化的数学思想.【名师点睛】高考中一些不等式的证明或求解需要通过构造函数,转化为利用导数研究函数的单调性或求最值,从而证得不等式,而如何根据不等式的结构特征构造一个可导函数是用导数证明不等式的关键.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分12分)中国人口已经出现老龄化与少子化并存的结构特征,测算显示中国是世界上人口老龄化速度最快的国家之一,再不实施“放开二胎”新政策,整个社会将会出现一系列的问题.若某地区2015年人口总数为45万,实施“放开二胎”新政策后专家估计人口总数将发生如下变化:从2016年开始到2025年每年人口比上年增加0.5万人,从20216年开始到2035年每年人口为上一年的99%.(1)求实施新政策后第n 年的人口总数n a 的表达式(注:2016年为第一年);(2)若新政策实施后的2016年到2035年人口平均值超过49万,则需调整政策,否则继续实施.问到2035年后是否需要调整政策?(说明:0.9910=(1-0.01)10≈0.9)【答案】(1)10450.5,110500.99,1120n n n n a n -+≤≤⎧=⎨⨯≤≤⎩;(2)详见解析. 【解析】试题分析:(1)分析题意将问题转化为等差数列等比数列的通项公式即可求解;(2)根据题意求得20S 的值,即可得出结论.试题解析:(1)当10n ≤时,数列{}n a 是首项为45.5,公差为0.5的等差数列,∴新政策实施到2035年年人口均值为2048.6320S ≈万,由204920S<,故到2035年不需要调整政策. 考点:等差数列与等比数列的通项公式及其前n 项和. 18.(本小题满分12分)如图,已知矩形ABCD 所在平面垂直于直角梯形ABPE 所在平面于直线AB ,平面ABCD 平面ABPE AB =,且2AB BP ==,1AD AE ==,AE AB ⊥,且//AE BP .(1)设点M 为棱PD 中点,在面ABCD 内是否存在点N ,使得MN ⊥平面ABCD ?若存在, 请证明;若不存在,请说明理由; (2)求二面角D PE A --的余弦值.【答案】(1)详见解析;(2)23. 【解析】试题分析:(1)连接AC ,BD 交于点N ,连接MN ,证明MN ⊥平面ABCD ,从而MN 即为所求;(2)建立空间直角坐标系,求得两个平面的法向量后即可求解.试题解析:(1)连接AC ,BD 交于点N ,连接MN ,则MN ⊥平面ABCD , ∵M 为PD 中点,N 为BD 中点,∴MN 为PDB ∆的中位线,∴//MN PB ,又∵平面ABCD ⊥平面ABPE ,平面ABCD 平面ABPE AB =,BC ⊂平面ABCD ,BC AB ⊥,考点:1.线面垂直的判定与性质;2.面面垂直的性质;3.二面角的求解. 19.(本小题满分12分)某产品按行业生产标准分成8个等级,等级系数X 依次为1,2,…,8,其中5X ≥为标准A ,3X ≥为标准B ,已知甲厂执行标准A 生产该产品,产品的零售价为6元/件;乙厂执行标准B 生产该产品,产品的零售价为4元/件,假定甲、乙两厂的产品都符合相应的执行标准 (1)已知甲厂产品的等级系数1X 的概率分布列如下所示:且1X 的数字期望16EX =,求a ,b 的值;(2)为分析乙厂产品的等级系数2X ,从该厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如下:3 5 3 3 8 5 5 6 34 6 3 4 75 3 4 8 5 3 8 3 4 3 4 4 7 56 7用这个样本的频率分布估计总体分布,将频率视为概率,求等级系数2X 的数学期望.(3)在(1)、(2)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由. 注:①产品的“性价比”=产品的等级系数的数学期望/产品的零售价;②“性价比”大的产品更具可购买性. 【答案】(1)0.30.2a b =⎧⎨=⎩;(2)4.8;(3)详见解析.【解析】(2)由已知得,样本的频率分布表如下:用这个样本的频率分布估计总体分布,将频率视为概率,可得等级系数2X 的概率分布列如下:∴230.340.250.260.170.180.1 4.8EX =⨯+⨯+⨯+⨯+⨯+⨯=,即乙厂产品的等级系数的数学期望等于4.8;(3)乙厂的产品更具可购买性,理由如下:∵甲厂产品的等级系数的数学期望等于6,价格为6元/件,∴其性价比为616=,∵乙厂产品的等级系数的期望等于4.8,价格为4元/件,∴其性价比为4.81.24=,据此,乙厂的产品更具可购买性.考点:离散型随机变量的概率分布及其期望.20.(本小题满分12分)已知椭圆C :22221(0)x y a b a b+=>>短轴的两个顶点与右焦点的连线构成等边三角形,直线0643=++y x 与圆222)(a b y x =-+相切. (1)求椭圆C 的方程;(2)已知过椭圆C 的左顶点A 的两条直线1l ,2l 分别交椭圆C 于M ,N 两点,且12l l ⊥,求证:直线MN 过定点,并求出定点坐标;(3)在(2)的条件下求AMN ∆面积的最大值.【答案】(1)2214x y +=;(2)详见解析;(3)1625. 【解析】试题分析:(1)根据题意列出a ,b 满足的方程组,从而求解;(2)设出直线方程,将直线方程与椭圆方程同理∴222284(,)4141m mN m m --++, i) 1m ≠±时,254(1)MN m k m =-, 256:()4(1)5MNm l y x m =+-过定点6(,0)5-, ii) 1m =±时6:5MN l x =-,过点6(,0)5-, 综上所述,∴MN l 过定点6(,0)5-;(3)由(2)知32242244854414174AMNm m m m S m m m m ∆+=+=++++ 21881194()941m mm m mmm m+==+++++,令121t m m m=+≥=±且时取等号, ∴1625S ∆≤时,当1m =±取等号,即max 1625S ∆=.考点:1.椭圆的标准方程及其性质;2.直线与椭圆的位置关系;3.椭圆的最值问题.【方法点睛】求解范围问题的常见求法(1)利用判别式来构造不等关系,从而确定参数的取值范围;(2)利用已知参数的范围,求新参数的范围,解这类问题的核心是在两个参数之间建立等量关系;(3)利用隐含或已知的不等关系建立不等式,从而求出参数的取值范围;(4)利用基本不等式求出参数的取值范围;(5)利用函数的值域的求法,确定参数的取值范围.21.(本小题满分12分)已知函数))(1()(a e x a x f x --=(常数R a ∈且0≠a ). (1)证明:当0a >时,函数)(x f 有且只有一个极值点; (2)若函数)(x f 存在两个极值点1x ,2x ,证明:1240()f x e <<且2240()f x e <<. 【答案】(1)详见解析;(2)详见解析. 【解析】(,0)-∞不存在极值点;②当0x ≥时,由'()(1)0x h x a x e =+>,故()h x 在[0,)+∞上单调递增,∵2(0)0h a =-<,2()()(1)0aah a a a e a a e =⋅-=->,∴()'()h x f x =在[0,)+∞有且只有一个零点, 又∵'()f x 的零点左侧,'()0f x <,在'()f x 的零点右侧,'()0f x >,∴函数()f x 在[0,)+∞有且只有一个极值点,综上所述,当0a >时,函数()f x 在(,)-∞+∞内有且只有一个极值点;(2)∵为函数()f x 存在两个极值点1x ,2x (不妨设12x x <), ∴1x ,2x 是()'()h x f x =的两个零点,且由(1)知,必有0a <, 令'()(1)0xh x a x e =+=得1x =-;令'()(1)0xh x a x e =+>得1x <-;令'()(1)0x h x a x e =+<得1x >-,∴()'()h x f x =在(,1]-∞-单调递增,在[1,)-+∞单调递减,又∵2(0)'(0)0h f a ==-<,∴必有1210x x <-<<,令'()()0tf t a te a =-=,解得t a te =,又∵122111()(1)0x f x e x x =-->,∴1240()f x e <<, 当10t -<<时,∵210t -<,210t -<,20t e >,∴'()0g t <,则()g t 在(1,0)-(1,0)-单调递减,∵210x -<<,∴22240(0)()()(1)g g x f x g e =<=<-=, 综上可知,1240()f x e <<且2240()f x e <<. 考点:1.导数的综合运用;2.分类讨论的数学思想.【思路点睛】1.证明不等式问题可通过作差或作商构造函数,然后用导数证明;2.求参数范围问题的常用方法:(1)分离变量;(2)运用最值;3.方程根的问题:可化为研究相应函数的图象,而图象又归结为极值点和单调区间的讨论.请考生在第22、23、24题中任意选一题作答。
2020届河北省衡水中学高三下学期第九次调研数学(理科)试题及其详细解析

(3)当 a 0 时, 1
a x2
0
,∴
f
(x) 在 (, 0) 上单调递减,
令1
a x2
0得x
a ,
∴当 x
a
时,1 Biblioteka a x20,当0 x
a
时,1
a x2
0,
第 3 页 共 25 页
∴ f (x) 在 (0, a ) 上单调递减,在 ( a , ) 上单调递增,图象为 B;
故选:C. 【点睛】本题考查了分段函数的图像的识别,考查了分类讨论思想,考查了利用导数研 究函数的单调性,属于中档题.
2020 届河北省衡水中学高三下学期第九次调研 数学(理)试题
一、单选题
1.已知集合 A {x | 0 x 2} , B x | log1 x 2 ,则 AUB ( )
2
A. R
B. x | 0 x 2 C.x | x 0
D.
x
|
1 4
x
2
【答案】C
【解析】先化简集合 A,B,再求 A U B .
【详解】
D. 5 i 26
i 5 i
z
1
5
i ,所以 z
i
的虚部为 5 .
26 26 26
5i
26
故选: A
【点睛】本题考查了复数虚部的计算,属于简单题.
3.某运动制衣品牌为了成衣尺寸更精准,现选择 15 名志愿者,对其身高和臂展进行测 第 1 页 共 25 页
量(单位:厘米),左图为选取的 15 名志愿者身高与臂展的折线图,右图为身高与臂展
Q 1 n3 1 1 1 m1 n 2 m1 n 2
m n3 1
5
1
【4月衡水九调理数】衡水中学2020届高三下学期第九次调研考试理科数学试卷及答案解析

A. 5 26
B. 5 i 26
C. 5 26
D. 5 i 26
3. 某运动制衣品牌为了成衣尺寸更精准,现选择 15 名志愿者,对其身高和臂展进
行测量(单位:厘米),左图为选取的 15 名志愿者身高与臂展的折线图,右图为身
高与臂展所对应的散点图,并求得其回归方程为 1.16x﹣30.75,以下结论中不正 确的为( )
(2)若 A0,1 ,直线 l 与曲线 C 相交于不同的两点 M ,N ,求 1 1 的值.
AM AN
23. 选修 4-5:不等式选讲
已知函数
0,
2
C.
0,
3 4
D.
0,
3 2
第2页
12. 已知函数
﹣
,若方程
有 3 个不同的实根 x1,x2,x3(x1
<x2<x3),则
x2
a
2
的取值范围是(
)
A.
1 e
,
0
B.
e
2
2
,
0
C.
e
2
2
,
2e
2
二、 填空题(本大题共 4 小题,每题 5 分,共 20 分.)
D. 0, 2e 2
17. 设
.
(1)求 的单调区间;
(2)在锐角 中,角 , , 的对边分别为 , , . 若
,,
求 面积的最大值.
18. 如图,在三棱锥
中,已知
,
,顶点 在平面 上的射影为
的外接圆圆心.
(1)证明:平面 ⊥平面 ;
(2)若点 M 在棱 PA 上,
,且二面角
的
余弦值为 ,试求 的值.
19. 某快餐连锁店招聘外卖骑手,该快餐连锁店提供了两种日工资方案:方案①规 定每日底薪 50 元,快递业务每完成一单提成 3 元;方案②规定每日底薪 100 元, 快递业务的前 44 单没有提成,从第 45 单开始,每完成一单提成 5 元,该快餐连锁 店记录了每天骑手的人均业务量,现随机抽取 100 天的数据,将样本数据分为[25, 35),[35,45),[45,55),[55,65),[65,75),[75,85),[85,95]七组,整理 得到如图所示的频率分布直方图.
2019-2020学年河北省衡水中学高三(下)第九次调研数学试卷(理科)(有答案解析)

2019-2020学年河北省衡水中学高三(下)第九次调研数学试卷(理科)一、选择题(本大题共12小题,共60.0分)1.已知集合,,则A. RB.C. D.2.复数上的虚部为A. B. C. D.3.某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量单位:厘米,左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为,以下结论中不正确的为A. 15名志愿者身高的极差小于臂展的极差B. 15名志愿者身高和臂展成正相关关系C. 可估计身高为190厘米的人臂展大约为厘米D. 身高相差10厘米的两人臂展都相差厘米4.函数的图象不可能是A. B.C. D.5.某几何体的三视图如图,该几何体表面上的点P与点Q在正视图与侧视图上的对应点分别为A,B,则在该几何体表面上,从点P到点Q的路径中,最短路径的长度为A.B.C.D.6.设m,n为正数,且,则的最小值为A. B. C. D.7.我国古代数学家秦九韶在数书九章中记述了“三斜求积术”,用现代式子表示即为:在中,角A,B,C所对的边分别为a,b,c,则的面积根据此公式,若,且,则的面积为A. B. C. D.8.执行如图所示的程序框图,则输出的a值为A.B.C.D. 29.若,,,,则x,y,z大小关系正确的是A. B. C. D.10.已知双曲线C:,点是直线上任意一点,若圆与双曲线C的右支没有公共点,则双曲线的离心率取值范围是A. B. C. D.11.直线与函数的图象的相邻两个交点的距离为,若在上是增函数,则m的取值范围是A. B. C. D.12.已知函数,若方程有3个不同的实根,,,则的取值范围是A. B. C. D.二、填空题(本大题共4小题,共20.0分)13.的展开式的第2项为______.14.已知中,,,,若点D满足,则______15.记等差数列的前n项和为,若,,则的前n项和______.16.已知三棱锥的所有顶点都在球O的表面上,平面ABC,,,,,则球O的表面积为______.三、解答题(本大题共7小题,共82.0分)17.设.求函数的单调区间;在锐角中,角A,B,C的对边分别为a,b,c,若,,求面积的最大值.18.如图,在三棱锥中,已知,顶点P在平面ABC上的射影为的外接圆圆心.证明:平面平面ABC;若点M在棱PA上,,且二面角的余弦值为,试求的值.19.某快餐连锁店招聘外卖骑手,该快餐连锁店提供了两种日工资方案:方案规定每日底薪50元,快递业务每完成一单提成3元;方案规定每日底薪100元,快递业务的前44单没有提成,从第45单开始,每完成一单提成5元,该快餐连锁店记录了每天骑手的人均业务量,现随机抽取100天的数据,将样本数据分为,,,,,,七组,整理得到如图所示的频率分布直方图.Ⅱ随机选取一天,估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率;Ⅱ从以往统计数据看,新聘骑手选择日工资方案的概率为,选择方案的概率为若甲、乙、丙三名骑手分别到该快餐连锁店应聘,三人选择日工资方案相互独立,求至少有两名骑手选择方案的概率;Ⅲ若仅从人均日收入的角度考虑,请你利用所学的统计学知识为新聘骑手做出日工资方案的选择,并说明理由.同组中的每个数据用该组区间的中点值代替20.如图,椭圆:的左右焦点分别为的、,离心率为;过抛物线:焦点F的直线交抛物线于M、N两点,当时,M点在x轴上的射影为连结NO,MO并延长分别交于A、B两点,连接AB;与的面积分别记为,,设.Ⅰ求椭圆和抛物线的方程;Ⅱ求的取值范围.21.已知函数.若有两个不同的极值点,,求实数a的取值范围;在的条件下,求证:.22.在平面直角坐标系中,曲线C的参数方程为为参数,直线l的参数方程为为参数,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系.Ⅰ求曲线C以及直线l的极坐标方程;Ⅱ若,直线l与曲线C相交于不同的两点M,N,求的值.23.已知函数.Ⅰ解不等式;Ⅱ已知,,且,求证.-------- 答案与解析 --------1.答案:C解析:【分析】本题考查描述法的定义,对数函数的单调性,以及并集的运算.可以求出集合B,然后进行并集的运算即可.【解答】解:,.故选:C.2.答案:A解析:解:,复数上的虚部为.故选:A.直接利用复数代数形式的乘除运算化简得答案.本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.3.答案:D解析:解:对于A,身高极差大约是25,臂展极差大于等于30,故A正确;对于B,很明显根据散点图以及回归方程得到,身高矮展臂就会短一些,身高高一些,展臂就会长一些,故B正确;对于C,身高为190厘米,代入回归方程可得展臂等于厘米,但不是准确值,故C正确;对于D,身高相差10厘米的两人展臂的估计值相差厘米,但不是准确值,回归方程上的点并不都是准确的样本点,故D错误;故选:D.就会图形对各个选项分别判断即可.本题考查了回归方程问题,考查对应思想,是一道常规题.4.答案:C解析:【分析】本题考查了导数与函数单调性的关系,分类讨论思想,属于中档题.讨论a的范围,利用导数判断的单调性得出答案.【解答】解:,.当时,,图象为A;当时,,在上单调递增,令得,当时,,当时,,在上单调递减,在上单调递增,图象为D;当时,,在上单调递减,令得,当时,,当时,,在上单调递减,在上单调递增,图象为B;故选:C.5.答案:C解析:解:根据几何体的三视图知,该几何体是长方体,如图所示;其展开图中,有三种情况,从点到的最短距离为.故选:C.根据三视图知该几何体是长方体,结合题意画出图形,结合图形求出点P到Q的最短距离.本题考查了三视图和几何体之间的转换问题,也考查了运算与求解能力,是基础题.6.答案:D解析:解:当时,,因为,当且仅当,即时取等号,则,即最小值为.故选:D.由,结合已知可考虑利用基本不等式求解.本题主要考查了利用基本不等式求解最值问题,属于基础试题.7.答案:A解析:【分析】由正弦定理,两角和的正弦函数公式化简已知等式,结合,可得,由余弦定理可得bc的值,根据公式即可求解的面积公式.本题主要考查了正弦定理,两角和的正弦函数公式,余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于中档题.【解答】解:由,可得,即,即,因为,所以,由余弦定理可得,所以,由的面积公式可得.故选:A.8.答案:D解析:解:当时,不满足退出循环的条件,执行循环体后,,;当时,不满足退出循环的条件,执行循环体后,,;当时,不满足退出循环的条件,执行循环体后,,;当时,不满足退出循环的条件,执行循环体后,,;当时,不满足退出循环的条件,执行循环体后,,;a的值是以4为周期的循环,由,故当时,满足退出循环的条件,故输出的a值为2,故选:D.由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量a的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答,本题属于基础题.9.答案:A解析:解:;,;.故选:A.根据即可得出,,从而得出x,y,z的大小关系.考查指数函数、幂函数和对数函数的单调性,增函数和减函数的定义.10.答案:D解析:解:双曲线C:的一条渐近线方程为,即,是直线上任意一点,则直线与直线的距离,圆与双曲线C的右支没有公共点,,,即,故e的取值范围为,故选:D.先求出双曲线的渐近线方程,可得则直线与直线的距离d,根据圆与双曲线C的右支没有公共点,可得,解得即可.本题考查了直线和双曲线的位置关系,以及两平行线间的距离公式,属于中档题.11.答案:B解析:解:直线与函数图象的相邻两个交点的距离为一个周期,则,所以,所以,由,解得,;所以函数在上是单调增函数;又在上是单调增函数,即,解得;所以m的取值范围是故选:B.根据直线与函数图象的相邻两个交点距离为一个周期,求出的值,写出的解析式,求出它的单调增区间,再求m的取值范围.本题考查了正切函数的图象与性质的应用问题,是基础题.12.答案:A解析:解:由,,令,解得,当或,,函数单调递增,当,,函数单调递减,由图象可得,又,设,,,在上是减函数,在上是增函数,由,,,可得的取值范围为,故选:A.先求导,判断函数的单调性,可得的范围,再构造函数,根据导数和函数单调性以及最值的关系即可求出a的范围.本题主要考查方程根的个数的应用,根据方程和函数之间的关系,利用导数和函数的思想,本题难度较大,综合性较强.13.答案:解析:解:的展开式的第2项为,故答案为:.利用二项展开式的通项公式,求得的展开式的第2项.本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.14.答案:解析:【分析】本题考查向量的数量积的应用,向量的加减法的运算,是基本知识的考查.通过余弦定理和向量的数量积转化求解即可.【解答】解:,,,可得,所以.故答案为:.15.答案:解析:解:因为是等数差数列,,而,所以,解得,,则,;数列构成首项为9,公差为9的等差数列;若n为偶数,则,若n为奇数,则,故;故答案为:.根据题意,求出数列的通项公式,进而可得数列构成首项为9,公差为9的等差数列,据此分n为奇数、偶数两种情况讨论,求出的前n项和,综合即可得答案.本题考查等差数列的前n项的计算,涉及数列的求和,属于基础题.16.答案:解析:解:如图:由,可得,则.在中,,,,.则为等腰三角形,设的外心为G,连接BG交AC于E,由正弦定理求得,求解三角形可得,则.取CD中点F,则F为三角形ACD的外心,过F作平面ACD的垂线,过G作平面ABC的垂线,两垂线相交于O,则O为三棱锥的外接球的球心,其半径.球O的表面积为.故答案为:.由题意画出图形,分别设出三角形ABC与ADC的外接圆的圆心,作垂线找到三棱锥外接球的球心,求解三角形得到三棱锥外接球的半径,代入球的表面积公式得答案.本题考查多面体外接球的表面积,关键是找出球心,是中档题.17.答案:解:由题意可知,,由,,得,,由,,得,,所以的单调递增区间是,单调递减区间是;由,可得,由题意知A为锐角,所以,由余弦定理,可得,即,当且仅当时等号成立.因此,所以面积的最大值为.解析:本题主要考查了正弦函数的图象和性质、余弦定理、基本不等式的应用,三角形的面积公式,属于中档题,由三角函数恒等变换化简解析式可得,由,可解得的单调递增区间,由,可解得单调递减区间;由,可得sin A,cos A,由余弦定理并结合基本不等式可得,当时等号成立,从而可求,从而得解,18.答案:解:证明:如图,设AC的中点为O,连接PO,由题意,得,则为直角三角形,点O为的外接圆圆心.又点P在平面ABC上的射影为的外接圆圆心,所以平面ABC,又平面PAC,所以平面平面ABC.解:由可知平面ABC,所以,,,以OC,OB,OP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,则0,,0,,1,,0,,0,,设,,0,,0,,,0,,0,,设平面MBC的法向量为y,,则,令,得1,,设平面PBC的法向量为y,,由,令,得1,,二面角的余弦值为,,解得,即M为PA的中点.解析:设AC的中点为O,连接PO,推导出为直角三角形,点O为的外接圆圆心.平面ABC,由此能证明平面平面ABC.以OC,OB,OP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,利用向量法能求出结果.本题考查面面垂直的证明,考查满足二面角的点是否存在的判断与求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.19.答案:共13分解:Ⅰ设事件A为“随机选取一天,这一天该连锁店的骑手的人均日快递业务量不少于65单”依题意,连锁店的人均日快递业务量不少于65单的频率分别为:,,因为所以估计为.Ⅱ设事件B为“甲、乙、丙三名骑手中至少有两名骑手选择方案”设事件为“甲乙丙三名骑手中恰有1,2,人选择方案”,则所以三名骑手中至少有两名骑手选择方案的概率为Ⅲ方法1:设骑手每日完成快递业务量为X件方案的日工资,方案的日工资所以随机变量的分布列为140170200230260290320P所以100130180230280330P因为,所以建议骑手应选择方案方法2:快餐店人均日快递量的期望是:因此,方案日工资约为方案2日工资约为故骑手应选择方案.解析:Ⅰ设事件A为“随机选取一天,这一天该连锁店的骑手的人均日快递业务量不少于65单”,连锁店的人均日快递业务量不少于65单的频率分别为:,,,由此能估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率.Ⅱ设事件B为“甲、乙、丙三名骑手中至少有两名骑手选择方案”设事件为“甲乙丙三名骑手中恰有1,2,人选择方案”,则,由此能求出三名骑手中至少有两名骑手选择方案的概率.Ⅲ方法1:设骑手每日完成快递业务量为X件,方案的日工资,方案的日工资求出随机变量的分布列、和随机变量的分布列、,由,建议骑手应选择方案.方法2:求出快餐店人均日快递量的期望是62,方案日工资约为,方案2日工资约为,由此得到骑手应选择方案.本题考查概率的求法,考查离散型随机变量的分布列、数学期望、频率分布直方图的性质等基础知识,考查运算求解能力,考查数形结合思想,是中档题.20.答案:解:Ⅰ由抛物线定义可得,代入有,即又得到代入,解得,所以的方程为,的方程为;Ⅱ设直线MN的方程为,,由,得到,则,设,,则,所以,设直线ON的方程为,由,解得,所以,由可知,用代替m,可得,由,可得,所以,用代替m,可得,所以,,,时等号成立所以的取值范围为.解析:Ⅰ根据抛物线的定义,以及双曲线的离心率公式可求出答案,Ⅱ设直线MN的方程为,,,根据韦达定理和弦长公式求出,,的长,再根据三角形的面积公式和基本不等式即可求出的取值范围本题考查了双曲线和抛物线的定义和简单性质,以及直线和抛物线的位置关系,弦长公式和基本不等式,属于难题21.答案:解:由得,因为有两个不同的极值点,,则有两个不同的零点,即方程有两个不同的实根,即直线与的图象有两个不同的交点,设,则,当时,,单调递增,且的取值范围是;当时,,单调递减,且的取值范围是,所以当时,直线与的图象有两个不同的交点,有两个不同的极值点,,故实数a的取值范围是;由知,设,则,由得,即,所以要证,只需证,即证,即证,设,即证,即证,设,则,所以在是增函数,,所以,从而有.解析:本题考查了利用导数研究函数的单调性、极值,考查导数中的不等式证明,属于难题.对函数求导,根据题意可得,方程有两个不同的实根,设,对求导,根据函数单调性可得的取值范围,即可得实数a的取值范围;设,则,结合可得,要证,即证,设,即证,构造函数,根据函数的单调性可得,即可得证.22.答案:解:Ⅰ依题意,曲线C:,故,即,即;直线l:,即,即,故;Ⅱ将直线l的参数方程为参数代入中,化简可得,设M,N所对应的参数分别为,,则,,故.解析:Ⅰ直接利用转换关系的应用,把参数方程极坐标方程和直角坐标方程之间进行转换.Ⅱ利用一元二次方程根和系数关系式的应用求出结果.本题考查的知识要点:参数方程极坐标方程和直角坐标方程之间的转换,一元二次方程根和系数关系式的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.23.答案:解:Ⅰ由,可得,则或或,解得或或,故不等式的解集为,证明Ⅱ,,当且仅当时,即,时取等号,,.解析:Ⅰ利用绝对值的意义,分类讨论解不等式;Ⅱ对于任意,先根据绝对值不等式,再根据基本不等式,即可证明.本题考查绝对值不等式的解法,考查不等式的证明,考查数形结合的数学思想,属于中档题.。
2020届河北省衡水中学2017级高三下学期十调考试数学(理)试卷参考答案

故 E, F, P,Q 四点共面
又 EF // PQ,EF 平面BPQ, PQ 平面BPQ ,
3
2020届河北省衡水中学2017级高关三下注学公期众十调号考《试数春学蕾(盛理)开试》卷 获取更多优质免费资料
0
A
,
cos
A
2 3
,得
sin
A
5 ,…………………………1 分 3
所以 sin B sin 2 A 2 sin A cos A 2 5 2 4 5 ,…………………………3 分 33 9
由正弦定理 a b ,可得 a b sin A 6 .…………………………6 分
sin A sin B
②当k 1时,f (x)在(- ,1)上递减 当x 1时,f (x)有最小值,即f (1) 0 1 0显然成立,此时k 1
(2)当 x 1时, f ( x) ( x k 1)ex e3 f ' ( x) ( x k )ex
①当k 1时,f (x)在(1, )上递增 f ( x) f (1) ke e3 0k e2 此时k 1
关注公众号《春蕾盛开》 获取更多优质免费资料
高三年级第十次调研考试
数学(理科)参考答案
一.选择题: DDCBC DCACA BD
1.【解析】 B x 0 x 4 A x Z x 1 A B 1,2,3故选 D.
2.【解析】 z2 1 b2 2bi 3 4i,b 2, z 1 2i, z 1 2i .故选 D.
DA ) ,化简可以得 DB 4
3
,
3
DAB 90 ,易得 SABD SACD ,故V1 V2 ,由于 ADB ACD 60 ,所以
ABD与ACD 的外接圆相同(四点共圆),所以三棱锥 P ABD ,三棱锥 P ACD 的外
【河北省衡水中学】2017届高三下学期三调数学(理科)试卷-答案

(2)()312545339910540100,1,2,3,0,(1)48428421C C C X P X P X C C =========. ()()2134543399305412,384148421C C C P X P X C C ========. 其分布列为X 0123P542 1021 514 121∴510514()0123422114213E X =⨯+⨯+⨯+⨯=. (12分) 19.(1)因为,,DA AE DA AB AB AE A ⊥⊥=I ,故DA ABFE ⊥平面.故CB ABFE ⊥平面,以B 为原点,BABF BC ,,分别为x 轴,y 轴,z 轴正方向. 建立如图所示的空间直角坐标系,则0,2,0F (),2,0,1D (),11,12G (,),2,1,0E (),0,0,1C() 所以1=1,0,2EG ⎛⎫- ⎪⎝⎭,易知ABCD 平面的一个法向量()0,1,0n =r . 所以()11,0,0,1,002EG n ⎛⎫=-= ⎪⎝⎭u u u r r g g .所以EG n ⊥u u u r r . 又EG ABCD ⊄平面,所以EG ABCD P 平面. (6分) (2)当点N 与点D 重合时,直线BN 与FCD 平面所成角的余弦值等于215.理由如下:直线BN 与FCD 平面所成角的余弦值等于215,即直线BN 与FCD 平面所成角的正弦值等于25,因为()()2,2,1,2,0,0FD CD =-=u u u r .设FCD 平面的法向量为()1=0,1,2n r.由110n FD n CD ⎧=⎪⎨=⎪⎩u u r u u u r g u u r g ,得111122020x y z x -+=⎧⎨=⎩,取11y =得FCD 平面的一个法向量()10,1,2n =u u r .假设线段FD 上存在一点N ,使得直线BN 与FCD 平面所成角的正弦值等于25. 所以sin cos ,BN n α=u u u r r()()()122221222559845222BN n BN n λλλλλ====-+⋅+-+u u u r u u r g u u u r u u r g .所以29810λλ--=,解得11=9λλ=-或(舍去).因此,线段DF 上存在一点N ,当点N 与点D 重合时,直线BN 与FCD 平面所成角的余弦值等于。
河北省衡水中学2020届高三数学下学期第九次调研试题理(含解析)

河北省衡水中学2020届高三数学下学期第九次调研试题 理(含解析)一、选择题(本大题包括12小题,每小题5分,共60分.) 1.已知集合{|0A x x =<<,12|log 2B x x ⎧⎫=<⎨⎬⎩⎭,则A B =( )A. RB. {|0x x <<C. {}|0x x >D.1|4x x ⎧<<⎨⎩ 【答案】C 【解析】 【分析】先化简集合A ,B ,再求AB .【详解】因为{|0A x x =<<,121|log 2|4B x x x x ⎧⎫⎧⎫=<=>⎨⎬⎨⎬⎩⎭⎩⎭,所以{}|0A B x x ⋃=>. 故选:C【点睛】本题主要考查集合的基本运算,属于基础题. 2.复数5iz i=+上的虚部为( ) A.526B. 526i C. 526-D. 526i -【答案】A 【解析】 【分析】 化简得到152626z i =+计算虚部得到答案. 【详解】()515262626i i z i-==+,所以5i z i =+的虚部为526. 故选:A【点睛】本题考查了复数虚部的计算,属于简单题.3.某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为 1.160.5ˆ37yx =-,以下结论中不正确的为( )A. 15名志愿者身高的极差小于臂展的极差B. 15名志愿者身高和臂展成正相关关系,C. 可估计身高为190厘米的人臂展大约为189.65厘米D. 身高相差10厘米的两人臂展都相差11.6厘米, 【答案】D 【解析】 【分析】根据散点图和回归方程的表达式,得到两个变量的关系,A 根据散点图可求得两个量的极差,进而得到结果;B ,根据回归方程可判断正相关;C 将190代入回归方程可得到的是估计值,不是准确值,故不正确;D ,根据回归方程x 的系数可得到增量为11.6厘米,但是回归方程上的点并不都是准确的样本点,故不正确.【详解】A ,身高极差大约为25,臂展极差大于等于30,故正确;B ,很明显根据散点图像以及回归直线得到,身高矮臂展就会短一些,身高高一些,臂展就长一些,故正确;C ,身高为190厘米,代入回归方程可得到臂展估计值等于189.65厘米,但是不是准确值,故正确;D ,身高相差10厘米的两人臂展的估计值相差11.6厘米,但并不是准确值,回归方程上的点并不都是准确的样本点,故说法不正确. 故答案为D.【点睛】本题考查回归分析,考查线性回归直线过样本中心点,在一组具有相关关系的变量的数据间,这样的直线可以画出许多条,而其中的一条能最好地反映x 与Y 之间的关系,这条直线过样本中心点.线性回归方程适用于具有相关关系的两个变量,对于具有确定关系的两个变量是不适用的, 线性回归方程得到的预测值是预测变量的估计值,不是准确值. 4.函数()||()af x x a R x=-∈的图象不可能是( ) A. B.C. D.【答案】C 【解析】 【分析】变成分段函数后分段求导,通过对a 分类讨论,得到函数的单调性,根据单调性结合四个选项可得答案.【详解】,0(),0a x x xf x a x x x ⎧->⎪⎪=⎨⎪--<⎪⎩,∴221,0()1,0a x x f x a x x ⎧+>⎪⎪=⎨⎪-+<⎩'⎪.(1)当0a =时,,0(),0x x f x x x >⎧=⎨-<⎩,图象为A; (2)当0a >时,210ax+>,∴()f x 在(0,)+∞上单调递增, 令210ax -+=得x a =∴当x a <,210ax -+<,当0a x <<时,210ax-+>,∴()f x 在(,)a -∞-上单调递减,在(,0)a -上单调递增,图象为D; (3)当0a <时,210ax-+<,∴()f x 在(,0)-∞上单调递减,令210ax +=得x a =-, ∴当x a >-时,210ax +>,当0x a <<-时,210ax+<,∴()f x 在(0,)a -上单调递减,在(,)a -+∞上单调递增,图象为B; 故选:C.【点睛】本题考查了分段函数的图像的识别,考查了分类讨论思想,考查了利用导数研究函数的单调性,属于中档题.5.某几何体的三视图如图所示,该几何体表面上的点P 与点Q 在正视图与侧视图上的对应点分别为A ,B ,则在该几何体表面上,从点P 到点Q 的路径中,最短路径的长度为( )A. 5B. 6C. 22D. 10【答案】C 【解析】 【分析】画出几何体的图形,然后PQ 的路径有正面和右面以及正面和上面两种路径,分别计算出结果,得出答案.【详解】由题,几何体如图所示(1)前面和右面组成一面此时PQ=222222+=(2)前面和上面再一个平面此时223110+=2210<故选C【点睛】本题考查了几何体的三视图以及相关的计算,解题的关键是PQ 的路径有两种情况,属于较易题.6.设m ,n 为正数,且2m n +=,则1312n m n ++++的最小值为( ) A.32B.53C. 74D.95【答案】D 【解析】 【分析】根据2m n +=,化简135112(1)(2)n m n m n ++=++++⋅+,根据均值不等式,即可求得答案; 【详解】当2m n +=时,131111212n m n m n ++=++++++3511(1)(2)(1)(2)m n m n m n ++=+=++⋅++⋅+21225(1)(2)24m n m n +++⎛⎫+⋅+≤=⎪⎝⎭, 当且仅当12m n +=+时,即3122m n ==,取等号, ∴139125n m n ++≥++. 故选:D【点睛】本题主要考查了根据均值不等式求最值,解题关键是灵活使用均值不等式,注意要验证等号的是否成立,考查了分析能力和计算能力,属于中档题.7.我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,用现代式子表示即为:在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,则ABC ∆的面积S =.根据此公式,若()cos 3cos 0a B b c A ++=,且2222a b c --=,则ABC ∆的面积为( )B.D. 【答案】A 【解析】 【分析】 根据()cos 3cos 0a B b c A ++=,利用正弦定理边化为角得sin cos cos sin 3sin cos 0A B A B C A ++=,整理为()sin 13cos 0C A +=,根据sin 0C ≠,得1cos 3A =-,再由余弦定理得3bc =,又2222a b c --=,代入公式=S . 【详解】由()cos 3cos 0a B b c A ++=得sin cos cos sin 3sin cos 0A B A B C A ++=, 即()sin 3sin cos 0A B C A ++=,即()sin 13cos 0C A +=,因为sin 0C ≠,所以1cos 3A =-, 由余弦定理22222cos 23a b c bc A bc --=-==,所以3bc =, 由ABC ∆的面积公式得()222222211()312424c b a S bc ⎡⎤⎛⎫+-⎢⎥=-=-= ⎪⎢⎥⎝⎭⎣⎦故选:A【点睛】本题主要考查正弦定理和余弦定理以及类比推理,还考查了运算求解的能力,属于中档题.8.执行如图所示的程序框图,则输出的a 值为( )A. 3-B.13C. 12-D. 2【答案】D 【解析】 【分析】由题知,该程序是利用循环结构计算,输出变量a 的值,可发现周期为4,即可得到2020i =,2a =,2021i =,此时输出2a =.【详解】1i =,3a =-.2i =,12a =-.3i =,13a =. 4i =,2a =.5i =,3a =-.可发现周期4,2020i =,2a =,2021i =. 此时输出2a =.故选:D【点睛】本题主要考查程序框图中的循环结构和条件结构,周期是4是解决本题的关键,属于简单题.9.设01a b <<<,b x a =,a y b =,log b z a =,则( ) A. x y z << B. y x z <<C. z x y <<D. z y x <<【答案】A 【解析】 【分析】根据条件01a b <<<,令11,32a b ==,代入,x y 中并取相同的正指数,可得,x y 的范围并可比较,x y 的大小;由对数函数的图像与性质可判断z 的范围,进而比较,,x y z 的大小.【详解】因为01a b <<< 令11,32a b == 则1213b x a ⎛⎫= ⎪⎝⎭=1312a y b ⎛⎫= ⎪⎝⎭=12log log 13b a z == 将式子变形可得61321113327⎡⎤⎛⎫⎛⎫⎢⎥== ⎪ ⎪⎢⎥⎝⎭⎝⎭⎢⎥⎣⎦,6123111224⎡⎤⎛⎫⎛⎫⎢⎥== ⎪ ⎪⎢⎥⎝⎭⎝⎭⎢⎥⎣⎦因为111274<< 所以x y <由对数函数的图像与性质可知112211log log 132>= 综上可得x y z << 故选:A.【点睛】本题考查了指数式与对数式大小比较,指数幂的运算性质应用,对数函数图像与性质应用,属于基础题.10.已知双曲线2222:1(0,0)x y C a b a b-=>>,点()00,P x y 是直线40bx ay a -+=上任意一点,若圆()()22001x x y y -+-=与双曲线C 的右支没有公共点,则双曲线的离心率取值范围是( ). A. (]1,2 B. (]1,4 C. [)2,+∞ D. [)4,+∞ 【答案】B 【解析】 【分析】先求出双曲线的渐近线方程,可得则直线bx ay 2a 0-+=与直线bx ay 0-=的距离d ,根据圆()()2200x x y y 1-+-=与双曲线C 的右支没有公共点,可得d 1≥,解得即可.【详解】由题意,双曲线2222x y C :1(a 0,b 0)a b-=>>的一条渐近线方程为b y x a =,即bx ay 0-=,∵()00P x ,y 是直线bx ay 4a 0-+=上任意一点, 则直线bx ay 4a 0-+=与直线bx ay 0-=的距离4ad c==, ∵圆()()2200x x y y 1-+-=与双曲线C 的右支没有公共点,则d 1≥, ∴41a c ≥,即4ce a=≤,又1e > 故e 的取值范围为(]1,4, 故选:B .【点睛】本题主要考查了直线和双曲线的位置关系,以及两平行线间的距离公式,其中解答中根据圆与双曲线C 的右支没有公共点得出d 1≥是解答的关键,着重考查了推理与运算能力,属于基础题.11.直线y a =与函数()tan (0)4f x x πωω⎛⎫=+> ⎪⎝⎭的图象的相邻两个交点的距离为2π,若()f x 在()(),0m m m ->上是增函数,则m 的取值范围是( )A. (0,]4π B. (0,]2πC. 3(0,]4π D. 3(0,]2π 【答案】B 【解析】 【分析】根据直线y a =与函数()f x 的图象的相邻两个交点的距离为一个周期,得到12ω=,则()1tan 24f x x π⎛⎫=+ ⎪⎝⎭,然后求得其单调增区间,再根据()f x 在()(),0m m m ->上是增函数,由(,)m m -是增区间的子集求解.【详解】因为直线y a =与函数()f x 的图象的相邻两个交点的距离为一个周期, 所以12ω=,()1tan 24f x x π⎛⎫=+ ⎪⎝⎭,由12242k x k πππππ-<+<+,得322()22k x k k ππππ-<<+∈Z , 所以()f x 在3,22ππ⎛⎫-⎪⎝⎭上是增函数, 由3(,),22m m ππ⎛⎫-⊆- ⎪⎝⎭, 解得02m π<≤.故选:B【点睛】本题主要考查正切函数的图象和性质,还考查了运算求解的能力,属于中档题 12.已知函数()()22xf x x x e =-,若方程()f x a =有3个不同的实根()123123,,x x x x x x <<,则22ax -的取值范围是( )A. 1[,0)e-B. ⎛⎫ ⎪ ⎪⎝⎭C. ⎛⎫ ⎪ ⎪⎝⎭D.(【答案】A【解析】 【分析】利用导数法,明确()f x 在(),2-∞-,()2,+∞上是增函数,在()2,2-上是减函数,结合()f x 的图象,得220x -<<,构造函数()()2222222===--x f x a g x x e x x ,再利用导数法求其取值范围.【详解】由()()22xf x x x e =-得()()22xf x x e '=-,所以()f x 在(),2-∞-,()2,+∞上是增函数,在()2,2-上是减函数,结合()f x 的图象可得220x -<<,又()2222222x f x a x e x x ==--, 设()(20)x g x xe x =<<,则()()1xg x x e '=+, 所以()g x 在()2,1--上是减函数,在()1,0-上是增函数, 由()11g e-=-,(222g e --=-,()00g =, 可得22a x -的取值范围是 1[,0)e-故选:A【点睛】本题主要考查导数在函数中的综合应用,还考查了转化化归的思想和运算求解问题的能力,属于难题.二、填空题(本大题共4小题,每题5分,共20分.)13.717x x ⎛⎫- ⎪⎝⎭的展开式的第2项为_______. 【答案】5x - 【解析】 【分析】由二项式定理的通项公式求解即可【详解】由题展开式的第2项为116571C x x 7x ⎛⎫-=- ⎪⎝⎭故答案为5x -【点睛】本题考查二项式定理,熟记公式,准确计算是关键,是基础题. 14.已知ABC ∆中,3AB =,5AC =,7BC =,若点D 满足1132AD AB AC =+,则DB DC ⋅=__________.【答案】12- 【解析】 【分析】 根据1132AD AB AC =+,以,AB AC 为一组基底,由2222()2BC AC AB AC AB AB AC=-=+-⋅,得到152AB AC ⋅=-,再由2111()()3223⎛⎫⎛⎫⋅=-⋅-=-⋅- ⎪ ⎪⎝⎭⎝⎭DB DC AB AD AC AD AB AC AC AB 求解.【详解】因为2222()2BC AC AB AC AB AB AC =-=+-⋅ 又因为3AB =,5AC =,7BC = 所以152AB AC ⋅=-, 所以2111()()3223DB DC AB AD AC AD AB AC AC AB ⎛⎫⎛⎫⋅=-⋅-=-⋅-=⎪ ⎪⎝⎭⎝⎭22211251521294244AB AC AB AC --+⋅=---=-. 故答案为:-12【点睛】本题主要考查平面向量基本定理和向量的线性运算,还考查了运算求解的能力,属于中档题.15.记等差数列{}n a 的前n 项和为n S ,若2418a a +=,17459S =,则(){}31nn a -的前n 项和n T =______.【答案】()()9,229(1),212n nn k k Z T n n k k Z ⎧=∈⎪⎪=⎨+⎪-=+∈⎪⎩【解析】 【分析】由等差数列的通项公式以及前n 项和公式代入可求得n a ,再由分组求和即可求解.【详解】因为{}n a 是等数差数列,17994591745927S a a =⇒=⇒=,而2418a a +=,所以1918272418a d a d +=⎧⎨+=⎩,解得3d =,13a =,则3(1)33n a n n +-⨯==,n *∈N ; 数列{}3n a 构成首项为9,公差为9的等差数列; 若n 为偶数,则991827369(1)92n n T n n =-+-++--+=, 若n 为奇数,则T 91827369(2)9(1)9n n n n =-+-++--+--9(1)9(1)922n n n -+=-=- 故()()9,229(1),212n nn k k Z T n n k k Z ⎧=∈⎪⎪=⎨+⎪-=+∈⎪⎩.故答案为:()()9,229(1),212n nn k k Z T n n k k Z ⎧=∈⎪⎪=⎨+⎪-=+∈⎪⎩【点睛】本题主要考查等差数列的通项公式以及分组求和,需熟记公式,属于基础题. 16.已知三棱锥D ABC -的所有顶点都在球O 的表面上,AD ⊥平面ABC,AC =1BC =,cos ACB ACB ∠=∠,2AD =,则球O 的表面积为__________.【答案】8π 【解析】分析:根据三棱锥的结构特征,求得三棱锥外接球半径,由球表面积公式即可求得表面积.详解:由cos ACB ACB ∠=∠,根据同角三角函数关系式得22sin cos 1ACB ACB ∠+∠= ,解得1sin 2ACB ∠=所以6C π=,因为AC =1BC =,由余弦定理2222cos AB AC BC AC BC C =+-⋅代入得 3121AB =+-=所以△ABC 为等腰三角形,且120B = ,由正弦定理得△ABC 外接圆半径R 2sin120R = ,解得1R =设△ABC 外心为'O ,'OO h = ,过'O 作'O M AD ⊥ 则在'O OA ∆ 中2221h R += 在'O MD ∆中()22221h R -+=解得R =所以外接球面积为22448S R πππ===点睛:本题综合考查了空间几何体外接球半径的求法,通过建立空间模型,利用勾股定理求得半径;结合球的表面积求值,对空间想象能力要求高,综合性强,属于难题. 三、解答题(本大题共6小题,共70分,解答应写出文字说明或演算步骤.)17.设()2sin cos cos 4f x x x x π⎛⎫=-+ ⎪⎝⎭.(Ⅰ)求()f x 的单调区间;(Ⅱ)在锐角ABC ∆中,角,,A B C 的对边分别为,,a b c ,若0,12A f a ⎛⎫== ⎪⎝⎭,求ABC ∆面积的最大值.【答案】(Ⅰ)单调递增区间是(),44k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦;单调递减区间是()3,44k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦(Ⅱ)ABC ∆面积的最大值为24+ 【解析】试题分析:(Ⅰ)首先利用二倍角公式化简函数()f x 的解析式,再利用正弦函数的单调性求其单调区间;(Ⅱ)首先由02A f ⎛⎫= ⎪⎝⎭结合(Ⅰ)的结果,确定角A 的值,然后结合余弦定理求出三角形ABC ∆面积的最大值.试题解析:解:(Ⅰ)由题意知()1cos 2sin 2222x x f x π⎛⎫++ ⎪⎝⎭=-sin 21sin 21sin 2222x x x -=-=- 由222,22k x k k Z ππππ-+≤≤+∈可得,44k x k k Z ππππ-+≤≤+∈由3222,22k x k k Z ππππ+≤≤+∈可得3,44k x k k Z ππππ+≤≤+∈ 所以函数()f x 的单调递增区间是(),44k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦;单调递减区间是()3,44k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦(Ⅱ)由1sin 0,22A f A ⎛⎫=-=⎪⎝⎭得1sin 2A = 由题意知A为锐角,所以cos A =由余弦定理:2222cos a b c bc A =+-可得:22132bc b c bc +=+≥即:23,bc ≤+当且仅当b c =时等号成立.因此123sin 2bc A +≤所以ABC ∆面积的最大值为23+ 考点:1、诱导公式;2、三角函数的二倍角公式;3、余弦定理;4、基本不等式.18.如图,在三棱锥P -ABC 中,已知22====,AC AB BC PA ,顶点P 在平面ABC 上的射影为ABC 的外接圆圆心.(1)证明:平面PAC ⊥平面ABC ; (2)若点M 在棱PA 上,||||=λAM AP ,且二面角P -BC -M 的余弦值为53333,试求λ的值. 【答案】(1)证明见解析 (2)12λ= 【解析】 【分析】(1)设AC 的中点为O ,连接PO ,易知点O 为ABC 的外接圆圆心,从而PO ⊥平面ABC ,即可证明平面PAC ⊥平面ABC ;(2)以OC ,OB ,OP 所在直线分别为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系, 求出平面MBC 与平面PBC 的法向量,代入公式即可建立λ的方程,解之即可. 【详解】(1)证明:如图,设AC 的中点为O ,连接PO ,由题意,得222BC AB AC +=,则ABC 为直角三角形, 点O 为ABC 的外接圆圆心.又点P 在平面ABC 上的射影为ABC 的外接圆圆心, 所以PO ⊥平面ABC ,又PO ⊂平面PAC ,所以平面PAC ⊥平面ABC . (2)解:由(1)可知PO ⊥平面ABC , 所以PO OB ⊥,PO OC ⊥,OB AC ⊥,于是以OC ,OB ,OP 所在直线分别为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系,则(000)O ,,,(100)C ,,,(010)B ,,,(100)A -,,,(001)P ,,, 设[01](101)(10)AM AP AP M λλλλ=∈=-,,,,,,,,,(110)BC =-,,,(101)PC =-,,,(20).MC λλ=--,,设平面MBC 的法向量为111()m x y z =,,, 则·0·0m BC m MC ⎧=⎨=⎩,,得11110(2)0x y x z λλ-=⎧⎨--=⎩,,令11x =,得11y =,12z λλ-=,即211m λλ-⎛⎫= ⎪⎝⎭,,. 设平面PBC 的法向量为222()n x y z =,,,由·0·0n BC n PC ⎧=⎨=⎩,,得222200x y x z -=⎧⎨-=⎩,,令1x =,得1y =,1z =,即(111)n =,,,2222·533cos ||?||(2)3?2n mn m n m λλλλ-+〈〉===-+,, 解得1110222⎛⎫=- ⎪⎝⎭,,,,λM 即M 为PA 的中点. 【点睛】本题考查平面与平面垂直的判定,二面角的平面角的求法,考查空间想象能力以及计算能力.19.某快餐连锁店招聘外卖骑手,该快餐连锁店提供了两种日工资方案:方案(a)规定每日底薪50元,快递业务每完成一单提成3元;方案(b)规定每日底薪100元,快递业务的前44单没有提成,从第45单开始,每完成一单提成5元,该快餐连锁店记录了每天骑手的人均业务量,现随机抽取100天的数据,将样本数据分为[ 25,35),[35,45),[45,55),[55,65),[65,75),[75,85),[85,95]七组,整理得到如图所示的频率分布直方图.(1)随机选取一天,估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率; (2)从以往统计数据看,新聘骑手选择日工资方案(a )的概率为13,选择方案(b )的概率为23.若甲、乙、丙三名骑手分别到该快餐连锁店应聘,三人选择日工资方案相互独立,求至少有两名骑手选择方案(a)的概率;(3)若仅从人均日收入的角度考虑,请你利用所学的统计学知识为新聘骑手做出日工资方案的选择,并说明理由.(同组中的每个数据用该组区间的中点值代替) 【答案】(Ⅰ) 0.4 (Ⅱ) 727(Ⅲ)见解析 【解析】 分析】(Ⅰ)先设事件A 为“随机选取一天,这一天该连锁店的骑手的人均日快递业务量不少于65单”,由频率分布直方图,即可求出结果;(Ⅱ)先设事件B 为“甲、乙、丙三名骑手中至少有两名骑手选择方案(1)”,设事件i C 为“甲乙丙三名骑手中恰有()0,1,2,3i i =人选择方案(1)”,根据题意可得()()()23P B P C P C =+,进而可求出结果;(Ⅲ)先设骑手每日完成快递业务量为X 件,得到方案(1)的日工资()*1503Y X X N=+∈,方案(2)的日工资()*2*100,44,100544,44,X X N Y X X X N ⎧≤∈⎪=⎨+->∈⎪⎩,再由题中条件分别得到1Y 与2Y 的期望,比较大小即可得出结果.【详解】(Ⅰ)设事件A 为“随机选取一天,这一天该连锁店的骑手的人均日快递业务量不少于65单”依题意,连锁店的人均日快递业务量不少于65单的频率分别为:0.20.150.05,, 因为0.20.150.050.4++= 所以()P A 估计为0.4.(Ⅱ) 设事件B 为“甲、乙、丙三名骑手中至少有两名骑手选择方案(1)” 设事件i C 为“甲乙丙三名骑手中恰有()0,1,2,3i i =人选择方案(1)”,则()()()213232333121617333272727P B P C P C C C ⎛⎫⎛⎫⎛⎫=+=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 所以三名骑手中至少有两名骑手选择方案(1)的概率为727(Ⅲ)设骑手每日完成快递业务量为X 件 方案(1)的日工资()*1503Y X X N=+∈,方案(2)的日工资()*2*100,44,100544,44,X X N Y X X X N ⎧≤∈⎪=⎨+->∈⎪⎩所以随机变量1Y 的分布列为11400.051700.052000.22300.32600.22900.153200.05EY =⨯+⨯+⨯+⨯+⨯+⨯+⨯236=;同理随机变量2Y 的分布列为1Y100130 180 230 280 330 P0.10.20.30.20.150.0521000.11300.21800.32300.22800.153300.05EY =⨯+⨯+⨯+⨯+⨯+⨯ 194.5=因为12EY EY >,所以建议骑手应选择方案(1)【点睛】本题主要考查频率分布直方图、离散型随机变量的分布列与期望等,熟记概念,会分析频率分布直方图即可,属于常考题型.20.如图,椭圆1C :22221(0)x y a b a b +=>>的左右焦点分别为12,F F ,离心率为3,过抛物线2C :24x by =焦点F 的直线交抛物线于,M N 两点,当7||4MF =时,M 点在x 轴上的射影为1F ,连接,)NO MO 并延长分别交1C 于,A B 两点,连接AB ,OMN ∆与OAB ∆的面积分别记为OMN S ∆,OAB S ∆,设λ=OMNOABS S ∆∆.(1)求椭圆1C 和抛物线2C 的方程; (2)求λ的取值范围.【答案】(I ) 2214x y +=,24x y =;(II ) [)2,+∞. 【解析】试题分析:(Ⅰ )由题意得得7,4M c b ⎛⎫-- ⎪⎝⎭,根据点M 在抛物线上得2744c b b ⎛⎫=- ⎪⎝⎭,又由2c a =,得 223c b =,可得277b b =,解得1b =,从而得2c a ==,可得曲线方程.(Ⅱ )设ON k m =,'OM k m =,分析可得1'4m m=-,先设出直线ON 的方程为y mx = (0)m >,由24y mxx y=⎧⎨=⎩,解得4N x m =,从而可求得4ON =,同理可得,,OM OA OB ,故可将=OMN OAB ON OMS S OA OBλ∆∆⋅=⋅化为m 的代数式,用基本不等式求解可得结果. 试题解析:(Ⅰ)由抛物线定义可得7,4M c b ⎛⎫--⎪⎝⎭, ∵点M 在抛物线24x by =上, ∴2744c b b ⎛⎫=-⎪⎝⎭,即2274c b b =- ①又由2c a =,得 223c b = 将上式代入①,得277b b = 解得1,b =∴c =2a ∴=,所以曲线1C 方程为2214x y +=,曲线2C 的方程为24x y =.(Ⅱ)设直线MN 的方程为1y kx =+,由214y kx x y=+⎧⎨=⎩消去y 整理得2440x kx --=, 设11,)Mx y (,()2,2N x y . 则124x x =-,设ON k m =,'OM k m =, 则21122111'164y y mm x x x x =⋅==-, 所以1'4m m=-, ② 设直线ON 的方程为y mx = (0)m >,由24y mxx y=⎧⎨=⎩,解得4N x m =,所以4N ON ==, 由②可知,用14m-代替m ,可得M OM == 由2214y mxx y =⎧⎪⎨+=⎪⎩,解得A x =,所以A OA ==用14m-代替m,可得B OB ==所以=OMN OABON OM S S OA OB λ∆∆⋅==⋅==1222m m=+≥,当且仅当1m =时等号成立. 所以λ的取值范围为[)2,+∞.点睛:解决圆锥曲线的最值与范围问题时,若题目的条件和结论能体现一种明确的函数关系,则可首先建立目标函数,再求这个函数的最值.常从以下几个方面考虑: ①利用判别式来构造不等关系,从而确定参数的取值范围;②利用隐含或已知的不等关系建立不等式,从而求出参数的取值范围; ③利用基本不等式求出参数的取值范围; ④利用函数的值域的求法,确定参数的取值范围. 21.已知函数()21xf x x ae =--.(1)若()f x 有两个不同的极值点1x ,2x ,求实数a 的取值范围; (2)在(1)的条件下,求证:124xx e ea+>. 【答案】(1)20,e ⎛⎫⎪⎝⎭;(2)详见解析. 【解析】 【分析】(1)由()21xf x x ae =--得()2xf x x ae '=-,根据()f x 有两个不同的极值点1x ,2x ,则()f x '有两个不同的零点,即方程2x x a e =有两个不同的实根,转化为直线y a =与2xx y e =的图象有两个不同的交点求解.(2)由(1)知20a e <<,设12x x <,则1201x x <<<,由121222x x x ae x ae⎧=⎨=⎩得()()12122x x x x a e e -=-,()12122x x x x a e e -=-,要证124xx e ea +>,将()12122x x x x a e e -=- 代入整理为()()121212121x x x x x x e e ---+>-,再令12(0)x xt t -=<,转化为()2101t t e t e --<+,再构造函数()21()(0)1t t e g t t t e -=-<+,研究其最大值即可.【详解】(1)由()21x f x x ae =--得()2x f x x ae '=-,()f x 有两个不同的极值点1x ,2x ,则()f x '有两个不同的零点,即方程2x xa e=有两个不同的实根, 即直线y a =与2xxy e =的图象有两个不同的交点, 设()2x xg x e =,则()()21xx g x e-'=, (),1x ∈-∞时()0g x '>,()g x 单调递增,且()g x 的取值范围是2,e ⎛⎫-∞ ⎪⎝⎭; ()1,x ∈+∞时()0g x '<,()g x 单调递减,且()g x 的取值范围是20,e ⎛⎫⎪⎝⎭,所以当20a e <<时,直线y a =与2x x y e=的图象有两个不同的交点, ()f x 有两个不同的极值点1x ,2x ,故实数a 的取值范围是20,e ⎛⎫ ⎪⎝⎭. (2)由(1)知20a e<<,设12x x <,则1201x x <<<, 由121222x x x ae x ae ⎧=⎨=⎩得()()12122x x x x a e e -=-,()12122x x x x a e e -=- 所以要证124xx e ea+>,只需证()124x xa e e +>, 即证()()1212122x x x x x x e e e e -+>-,即证()()121212121x x x x x x e e ---+>-,设12(0)x x t t -=<,即证()121t t t e e +>-,即证()2101tt e t e --<+,设()21()(0)1t te g t t t e -=-<+,则21()01t t e g t e '⎛⎫-=> ⎪+⎝⎭, 所以()g t 在(),0-∞是增函数,()()00g t g <=,所以()2101t t e t e --<+,从而有124x x ee a+>. 【点睛】本题主要考查导数与函数的极值,导数法证明不等式,还考查了转化化归的思想和运算求解的能力,属于难题.选考题:共10分.请考生在第22、23两题中任选一题作答.如果多做,则按所做的第一题计分.选修4-4:坐标系与参数方程22.在平面直角坐标系中,曲线C 的参数方程为22cos 2sin x y θθ=+⎧⎨=⎩(θ为参数),直线l 的参数方程为212x y ⎧=-⎪⎪⎨⎪=+⎪⎩t 为参数),以坐标原点为极点,x 轴的非负半轴为极轴建立极坐标系.(Ⅰ)求曲线C 以及直线l 的极坐标方程;(Ⅱ)若()0,1A ,直线l 与曲线C 相交于不同的两点M ,N ,求11+AM AN的值. 【答案】(Ⅰ)4cos ρθ=sin 14πθ⎛⎫+= ⎪⎝⎭;(Ⅱ)【解析】 【分析】(1)消去参数t 可得l 的普通方程,利用平方关系消去参数θ可得曲线C 的直角坐标方程,把ρ2=x 2+y 2,y =ρsin θ代入,可得曲线C 以及直线l 的极坐标方程..(II )把直线l 的参数方程代入曲线C 的直角坐标方程,利用直线参数的几何意义求得结果. 【详解】(Ⅰ)依题意,曲线C :()2224x y -+=,故2240x y x +-=,即24cos 0ρρθ-=,即4cos ρθ=;直线l :1y x =-,即10x y +-=,即cos sin 10ρθρθ+-=,sin 14πθ⎛⎫+= ⎪⎝⎭; (Ⅱ)将直线l的参数方程212x t y ⎧=-⎪⎪⎨⎪=+⎪⎩代入2240x y x +-=中,化简可得210t ++=,设M ,N 所对应的参数分别为1t ,2t ,则12t t +=-121t t =,故11AM AN AM AN AM AN++==【点睛】本题考查了极坐标方程、参数方程与普通方程的互化,考查了直线参数的意义,考查了计算能力,属于中档题. 选修4-5:不等式选讲 23.选修4-5:不等式选讲 已知函数() 1.f x x =+(Ⅰ)解不等式()32f x x >-+; (Ⅱ)已知0,0a b >>,且2a b +=()f x x -≤【答案】(Ⅰ)()(),30,-∞-⋃+∞; (Ⅱ)见解析. 【解析】 【分析】(Ⅰ)整理()32f x x >-+得:123x x +++>,由绝对值的几何意义即可解不等式. (Ⅱ)将问题转化成()max f x x -≤⎡⎤⎣⎦()max 1f x x -=⎡⎤⎣⎦,转化成证明1≤利用基本不等式即可证明结论,问题得解.【详解】(Ⅰ)()32f x x >-+,即123x x +++>, 由绝对值的几何意义得:(,3)(0,)x ∈-∞-⋃+∞; (Ⅱ)()[]11,1f x x x x -=+-∈-,要证()f x x -≤1≤22a b a b +==+≥1,4ab ≤1.==【点睛】本题主要考查了绝对值的几何意义,还考查了转化思想及基本不等式的应用,考查计算能力,属于中档题.。
河北省衡水中学2020届高三下学期第九次调研考试数学(理)试题 含答案
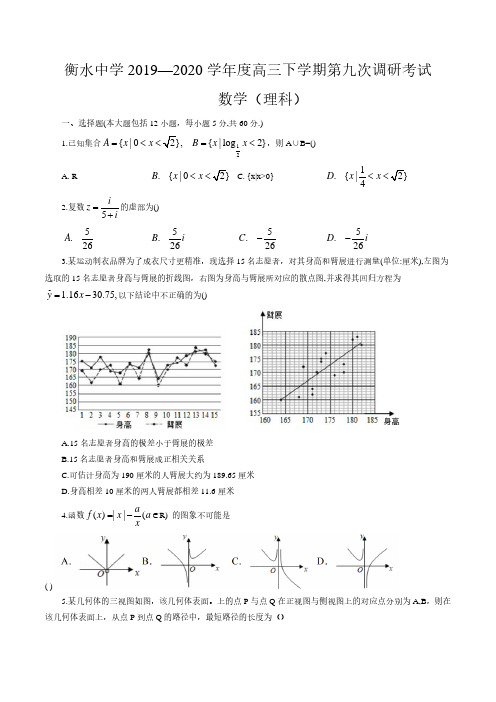
(1)随机选取一天,估计这一天该连锁店的骑手的人均日快递业务量不少于 65 单的概率;
(2)从以往统计数据看,新聘骑手选择日工资方案①的概率为 1 , 选择方案②的概率为 2 . 若甲、乙、丙三名骑
3
3
手分别到该快餐连锁店应聘,三人选择日工资方案相互独立,求至少有两名骑手选择方案①的概率;
(3)若仅从人均日收入的角度考虑,请你利用所学的统计学知识为新聘骑手做出日工资方案的选择,并说明理
5. 某几何体的三视图如图,该几何体表面上的点 P 与点 Q 在正视图与侧视图上 的对应点分别为 A,B,则在该几何体表面上,从点 P 到点 Q 的路径中,最短路 径的长度为( )
A.
B.
C.
D.
解:根据几何体的三视图知,该几何体是长方体,如图所示;
其展开图中,有三种情况,
从点 P(A)到 Q(B)的最短距离为 故选:C.
为身高与臂展所对应的散点图,并求得其回归方程为 中不正确的为( )
1.16x﹣30.75,以下结论
A.15 名志愿者身高的极差小于臂展的极差
第1页
B.15 名志愿者身高和臂展成正相关关系
C.可估计身高为 190 厘米的人臂展大约为 189.65 厘米
D.身高相差 10 厘米的两人臂展都相差 11.6 厘米
A. (1, 2]
B. (1, 4]
C.[2,+∞)
D.[4,+∞)
11.直线 y= a 与函数 f (x) = tan(ω x + π )(ω > 0 )的图象的相邻两个交点的距离为 2π,若 f(x)在(-m,m) (m> 0) 4
上是增函数,则 m 的取值范围是( )
A. (0, π ] 4
河北衡水中学2020年第九次调研考试理数试题含答案

高三下学期九调理科数学一、选择题(本大期包括12小题,每小聊5分,关60分.)A. 15名志愿有身高的极差小丁臂展的极差B. 15名志愿者身高和臂展成正相关关系C. 可估计身高为190闸米的人皆展人约为189.65座米D. 身高相差10厘米的两人臂展都相塑11.6厘米 I .已知集合4 = {寺<.》<回,8 = jx 卜 x<2、则 AU8=(A. RB.河0v*v>/5jC. {A |.V >0|2.筋数二一二的虚部为(>5+/ A. —R. —/C ・-—2626263某运动制衣品牌为了成衣尺寸更粘部.现选择1S 名志电者.对其身高引臀展进行测虽(单位:厘米).左图为选取的15名志愿者身高与肾展的折线图.右国为身 高与宵展所'付应的故点图,并求得其回门方程为;=1.161- 30.75,以卜.结论中不正 确的为(〉4. 6»/(X ) = |A |-- (aeR)的图象不可能是•)5粟几何体的三视图如图.该JL 何体表面上的点P 与点Q 在正视图与侧视图上的 对应点分别为4・R,则在该几何体表而匕从点P 到点Q 的珞容中.最短路径的 长度为( )第I7.我国古代玫学家公九韶在《数书九中记述J'“三斜求积术”.用现代式了及示 I 酎为8在KABC 中,ff]A, B,。
所对的边分别为加b. c.则AZ8C 的而积$ =. HJ 据此公式.77ncos/? + (/)+3c)cos/l = 0. ILa 2 -b 2 -c 2 = 2» 则hlBC 的面枳为()A. y/2 B ・ C. \/b 8执行如图所示的程序框图.则输出的a 值为(A. x/任 R.C.6 .设皿〃为正数,且"5 = 2,则 —+•— 的最小仙为(〃il n + 2A. -B. -C.-2 34D.面D.D. 2V3D. 2=h a . 7. = log 6 a.则x 9 y. r 大小关系正确的是A. x < y < zB. y <x < 2C. z <x < yD. 2 < y < x 10.己知攻曲线C : £一%=1(Q>0・ bX)・点P (Ao- Vo)是直线质-qi 十和二0 上任意一点,若圆<X -AO )2+ <y-y 0) 2 = 1与双的线C 的右支没有公共点.则双 曲线的离心率取值范围是( )A ・(1, 2] B. (1, 4] C. [2・ «) D. [4, +—) 与函牧/lx) = tan(3 + 9(3>0>的图象的相知两个交点的距离为2m 若/(x)在(一仇m)(m>0)上是哗函数. Ug 的取值范国是()C. 11.直技y = aD.。
河北省衡水中学2020届高三下学期第九次调研试题理(数学解析)

一、选择题(本大题包括12小题,每小题5分,共60分.)1.已知集合{|0A x x =<<,12|log 2B x x ⎧⎫=<⎨⎬⎩⎭,则A B =( )A. RB. {|0x x <<C. {}|0x x >D. 1|4x x ⎧<<⎨⎩答案:C 【分析】先化简集合A ,B ,再求A B .解:因为{|0A x x =<<,121|log 2|4B x x x x ⎧⎫⎧⎫=<=>⎨⎬⎨⎬⎩⎭⎩⎭,所以{}|0A B x x ⋃=>. 故选:C点评:本题主要考查集合的基本运算,属于基础题. 2.复数5iz i=+上的虚部为( ) A.526B. 526i C. 526-D. 526i -答案:A 【分析】 化简得到152626z i =+计算虚部得到答案. 解:()515262626i i z i -==+,所以5i z i =+的虚部为526. 故选:A点评:本题考查了复数虚部的计算,属于简单题.3.某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为 1.160.5ˆ37yx =-,以下结论中不正确的为( )A. 15名志愿者身高的极差小于臂展的极差B. 15名志愿者身高和臂展成正相关关系,C. 可估计身高为190厘米的人臂展大约为189.65厘米D. 身高相差10厘米的两人臂展都相差11.6厘米, 答案:D 【分析】根据散点图和回归方程的表达式,得到两个变量的关系,A 根据散点图可求得两个量的极差,进而得到结果;B ,根据回归方程可判断正相关;C 将190代入回归方程可得到的是估计值,不是准确值,故不正确;D ,根据回归方程x 的系数可得到增量为11.6厘米,但是回归方程上的点并不都是准确的样本点,故不正确.解:A ,身高极差大约为25,臂展极差大于等于30,故正确;B ,很明显根据散点图像以及回归直线得到,身高矮臂展就会短一些,身高高一些,臂展就长一些,故正确;C ,身高为190厘米,代入回归方程可得到臂展估计值等于189.65厘米,但是不是准确值,故正确;D ,身高相差10厘米的两人臂展的估计值相差11.6厘米,但并不是准确值,回归方程上的点并不都是准确的样本点,故说法不正确. 故答案为D.点评:本题考查回归分析,考查线性回归直线过样本中心点,在一组具有相关关系的变量的数据间,这样的直线可以画出许多条,而其中的一条能最好地反映x 与Y 之间的关系,这条直线过样本中心点.线性回归方程适用于具有相关关系的两个变量,对于具有确定关系的两个变量是不适用的, 线性回归方程得到的预测值是预测变量的估计值,不是准确值. 4.函数()||()af x x a R x=-∈的图象不可能是( )A. B.C. D.答案:C 【分析】变成分段函数后分段求导,通过对a 分类讨论,得到函数的单调性,根据单调性结合四个选项可得答案.解:,0(),0a x x x f x a x x x ⎧->⎪⎪=⎨⎪--<⎪⎩,∴221,0()1,0a x xf x a x x ⎧+>⎪⎪=⎨⎪-+<⎩'⎪.(1)当0a =时,,0(),0x x f x x x >⎧=⎨-<⎩,图象为A;(2)当0a >时,210ax+>,∴()f x 在(0,)+∞上单调递增, 令210ax-+=得x a =∴当x a <,210ax -+<,当0a x <<时,210ax-+>,∴()f x 在(,a -∞上单调递减,在(,0)a 上单调递增,图象为D; (3)当0a <时,210ax-+<,∴()f x 在(,0)-∞上单调递减, 令210ax +=得x a =-∴当x a >-,210ax +>,当0x a <<-,210ax+<,∴()f x 在)a -上单调递减,在,)a -+∞上单调递增,图象为B;故选:C.点评:本题考查了分段函数的图像的识别,考查了分类讨论思想,考查了利用导数研究函数的单调性,属于中档题.5.某几何体的三视图如图所示,该几何体表面上的点P与点Q在正视图与侧视图上的对应点分别为A,B,则在该几何体表面上,从点P到点Q的路径中,最短路径的长度为()A. 5B. 6C. 22D. 10答案:C【分析】画出几何体的图形,然后PQ的路径有正面和右面以及正面和上面两种路径,分别计算出结果,得出答案. 解:由题,几何体如图所示(1)前面和右面组成一面此时22+=222(2)前面和上面再一个平面此时223110+=2210<故选C点评:本题考查了几何体的三视图以及相关的计算,解题的关键是PQ 的路径有两种情况,属于较易题. 6.设m ,n 为正数,且2m n +=,则1312n m n ++++的最小值为( ) A.32B.53C. 74D.95答案:D 【分析】根据2m n +=,化简135112(1)(2)n m n m n ++=++++⋅+,根据均值不等式,即可求得答案; 解:当2m n +=时,131111212n m n m n ++=++++++ 3511(1)(2)(1)(2)m n m n m n ++=+=++⋅++⋅+21225(1)(2)24m n m n +++⎛⎫+⋅+≤=⎪⎝⎭, 当且仅当12m n +=+时,即3122m n ==,取等号, ∴139125n m n ++≥++. 故选:D点评:本题主要考查了根据均值不等式求最值,解题关键是灵活使用均值不等式,注意要验证等号的是否成立,考查了分析能力和计算能力,属于中档题.7.我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,用现代式子表示即为:在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,则ABC ∆的面积S =.根据此公式,若()cos 3cos 0a B b c A ++=,且2222a b c --=,则ABC ∆的面积为( )B.D. 答案:A 【分析】根据()cos 3cos 0a B b c A ++=,利用正弦定理边化为角得sin cos cos sin 3sin cos 0A B A B C A ++=,整理为()sin 13cos 0C A +=,根据sin 0C ≠,得1cos 3A =-,再由余弦定理得3bc =,又2222a b c --=,代入公式=S . 解:由()cos 3cos 0a B b c A ++=得sin cos cos sin 3sin cos 0A B A B C A ++=, 即()sin 3sin cos 0A B C A ++=,即()sin 13cos 0C A +=, 因为sin 0C ≠,所以1cos 3A =-, 由余弦定理22222cos 23a b c bc A bc --=-==,所以3bc =, 由ABC ∆的面积公式得S ===故选:A点评:本题主要考查正弦定理和余弦定理以及类比推理,还考查了运算求解的能力,属于中档题. 8.执行如图所示的程序框图,则输出的a 值为( )A. 3-B.13C. 12-D. 2答案:D 【分析】由题知,该程序是利用循环结构计算,输出变量a 的值,可发现周期为4,即可得到2020i =,2a =,2021i =,此时输出2a =.解:1i =,3a =-.2i =,12a =-.3i =,13a =.4i =,2a =.5i =,3a =-.可发现周期4,2020i =,2a =,2021i =. 此时输出2a =. 故选:D点评:本题主要考查程序框图中的循环结构和条件结构,周期是4是解决本题的关键,属于简单题. 9.设01a b <<<,b x a =,a y b =,log b z a =,则( ) A. x y z << B. y x z <<C. z x y <<D. z y x <<答案:A 【分析】根据条件01a b <<<,令11,32a b ==,代入,x y 中并取相同的正指数,可得,x y 的范围并可比较,x y 的大小;由对数函数的图像与性质可判断z 的范围,进而比较,,x y z 的大小.解:因为01a b <<< 令11,32a b == 则1213b x a ⎛⎫= ⎪⎝⎭=1312a y b ⎛⎫= ⎪⎝⎭=12log log 13b a z == 将式子变形可得61321113327⎡⎤⎛⎫⎛⎫⎢⎥== ⎪ ⎪⎢⎥⎝⎭⎝⎭⎢⎥⎣⎦,6123111224⎡⎤⎛⎫⎛⎫⎢⎥== ⎪ ⎪⎢⎥⎝⎭⎝⎭⎢⎥⎣⎦因为111274<< 所以x y <由对数函数的图像与性质可知112211log log 132>= 综上可得x y z << 故选:A.点评:本题考查了指数式与对数式大小比较,指数幂的运算性质应用,对数函数图像与性质应用,属于基础题.10.已知双曲线2222:1(0,0)x y C a b a b-=>>,点()00,P x y 是直线40bx ay a -+=上任意一点,若圆()()22001x x y y -+-=与双曲线C 的右支没有公共点,则双曲线的离心率取值范围是( ). A. (]1,2 B. (]1,4C. [)2,+∞D. [)4,+∞ 答案:B 【分析】先求出双曲线的渐近线方程,可得则直线bx ay 2a 0-+=与直线bx ay 0-=的距离d ,根据圆()()2200x x y y 1-+-=与双曲线C 的右支没有公共点,可得d 1≥,解得即可.解:由题意,双曲线2222x y C :1(a 0,b 0)a b-=>>的一条渐近线方程为b y x a =,即bx ay 0-=,∵()00P x ,y 是直线bx ay 4a 0-+=上任意一点, 则直线bx ay 4a 0-+=与直线bx ay 0-=的距离4a d c==, ∵圆()()2200x x y y 1-+-=与双曲线C 的右支没有公共点,则d 1≥, ∴41a c ≥,即4ce a=≤,又1e > 故e 的取值范围为(]1,4, 故选:B .点评:本题主要考查了直线和双曲线的位置关系,以及两平行线间的距离公式,其中解答中根据圆与双曲线C 的右支没有公共点得出d 1≥是解答的关键,着重考查了推理与运算能力,属于基础题. 11.直线y a =与函数()tan (0)4f x x πωω⎛⎫=+> ⎪⎝⎭的图象的相邻两个交点的距离为2π,若()f x 在()(),0m m m ->上是增函数,则m 的取值范围是( )A. (0,]4πB. (0,]2πC. 3(0,]4π D. 3(0,]2π 答案:B 【分析】根据直线y a =与函数()f x 的图象的相邻两个交点的距离为一个周期,得到12ω=,则()1tan 24f x x π⎛⎫=+ ⎪⎝⎭,然后求得其单调增区间,再根据()f x 在()(),0m m m ->上是增函数,由(,)m m -是增区间的子集求解.解:因为直线y a =与函数()f x 的图象的相邻两个交点的距离为一个周期, 所以12ω=,()1tan 24f x x π⎛⎫=+ ⎪⎝⎭,由12242k x k πππππ-<+<+,得322()22k x k k ππππ-<<+∈Z ,所以()f x 在3,22ππ⎛⎫-⎪⎝⎭上是增函数, 由3(,),22m m ππ⎛⎫-⊆- ⎪⎝⎭, 解得02m π<≤.故选:B点评:本题主要考查正切函数的图象和性质,还考查了运算求解的能力,属于中档题12.已知函数()()22xf x x x e =-,若方程()f x a =有3个不同的实根()123123,,x x x x x x <<,则22ax -的取值范围是( )A. 1[,0)e-B. 22,0e ⎛⎫- ⎪ ⎪⎝⎭C. 222,2e e ⎛⎫- ⎪ ⎪⎝⎭D. ()20,2e答案:A 【分析】利用导数法,明确()f x 在(),2-∞-,()2,+∞上是增函数,在()2,2-上是减函数,结合()f x 的图象,得220x -<<,构造函数()()2222222===--x f x a g x x e x x ,再利用导数法求其取值范围. 解:由()()22xf x x x e =-得()()22xf x x e '=-,所以()f x 在(),2-∞-,()2,+∞上是增函数,在()2,2-上是减函数,结合()f x 的图象可得220x -<<,又()2222222x f x a x e x x ==--,设()(0)x g x xe x =<<,则()()1xg x x e '=+,所以()g x 在()1-上是减函数,在()1,0-上是增函数,由()11g e-=-,(g =()00g =, 可得22a x -的取值范围是 1[,0)e- 故选:A点评:本题主要考查导数在函数中的综合应用,还考查了转化化归的思想和运算求解问题的能力,属于难题.二、填空题(本大题共4小题,每题5分,共20分.)13.717x x ⎛⎫- ⎪⎝⎭的展开式的第2项为_______.答案:5x - 【分析】由二项式定理的通项公式求解即可解:由题展开式的第2项为116571C x x 7x ⎛⎫-=- ⎪⎝⎭故答案为5x -点评:本题考查二项式定理,熟记公式,准确计算是关键,是基础题. 14.已知ABC ∆中,3AB =,5AC =,7BC =,若点D 满足1132AD AB AC =+,则DB DC ⋅=__________.答案:12- 【分析】 根据1132AD AB AC =+,以,AB AC 为一组基底,由2222()2BC AC AB AC AB AB AC =-=+-⋅,得到152AB AC ⋅=-,再由2111()()3223⎛⎫⎛⎫⋅=-⋅-=-⋅- ⎪ ⎪⎝⎭⎝⎭DB DC AB AD AC AD AB AC AC AB 求解.解:因为2222()2BC AC AB AC AB AB AC =-=+-⋅又因为3AB =,5AC =,7BC = 所以152AB AC ⋅=-, 所以2111()()3223DB DC AB AD AC AD AB AC AC AB ⎛⎫⎛⎫⋅=-⋅-=-⋅-=⎪ ⎪⎝⎭⎝⎭22211251521294244AB AC AB AC --+⋅=---=-. 故答案为:-12点评:本题主要考查平面向量基本定理和向量的线性运算,还考查了运算求解的能力,属于中档题.15.记等差数列{}n a 的前n 项和为n S ,若2418a a +=,17459S =,则(){}31nna -的前n 项和nT=______.答案:()()9,229(1),212n nn k k Z T n n k k Z ⎧=∈⎪⎪=⎨+⎪-=+∈⎪⎩【分析】由等差数列的通项公式以及前n 项和公式代入可求得n a ,再由分组求和即可求解. 解:因为{}n a 是等数差数列,17994591745927S a a =⇒=⇒=,而2418a a +=,所以1918272418a d a d +=⎧⎨+=⎩,解得3d =,13a =,则3(1)33n a n n +-⨯==,n *∈N ; 数列{}3n a 构成首项为9,公差为9的等差数列; 若n 为偶数,则991827369(1)92n n T n n =-+-++--+=, 若n 为奇数,则T 91827369(2)9(1)9n n n n =-+-++--+--9(1)9(1)922n n n -+=-=- 故()()9,229(1),212n nn k k Z T n n k k Z ⎧=∈⎪⎪=⎨+⎪-=+∈⎪⎩.故答案为:()()9,229(1),212n nn k k Z T n n k k Z ⎧=∈⎪⎪=⎨+⎪-=+∈⎪⎩点评:本题主要考查等差数列的通项公式以及分组求和,需熟记公式,属于基础题.16.已知三棱锥D ABC -的所有顶点都在球O 的表面上,AD ⊥平面ABC,AC =1BC =,cos ACB ACB ∠=∠,2AD =,则球O 的表面积为__________.答案:8π分析:根据三棱锥的结构特征,求得三棱锥外接球半径,由球表面积公式即可求得表面积.详解:由cos ACB ACB ∠=∠,根据同角三角函数关系式得22sin cos 1ACB ACB ∠+∠= ,解得1sin 2ACB ∠=所以6C π=,因为AC =1BC =,由余弦定理2222cos AB AC BC AC BC C =+-⋅ 代入得3121AB =+-= 所以△ABC 为等腰三角形,且120B = ,由正弦定理得△ABC 外接圆半径R2sin120R = ,解得1R = 设△ABC 外心为'O ,'OO h = ,过'O 作'O M AD ⊥ 则在'O OA ∆ 中2221h R += 在'O MD ∆中()22221h R -+=解得R =所以外接球面积为22448S R πππ===点睛:本题综合考查了空间几何体外接球半径的求法,通过建立空间模型,利用勾股定理求得半径;结合球的表面积求值,对空间想象能力要求高,综合性强,属于难题.三、解答题(本大题共6小题,共70分,解答应写出文字说明或演算步骤.) 17.设()2sin cos cos 4f x x x x π⎛⎫=-+⎪⎝⎭. (Ⅰ)求()f x 的单调区间;(Ⅱ)在锐角ABC ∆中,角,,A B C 的对边分别为,,a b c ,若0,12A f a ⎛⎫==⎪⎝⎭,求ABC ∆面积的最大值. 答案:(Ⅰ)单调递增区间是(),44k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦;单调递减区间是()3,44k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦(Ⅱ)ABC ∆试题分析:(Ⅰ)首先利用二倍角公式化简函数()f x 的解析式,再利用正弦函数的单调性求其单调区间; (Ⅱ)首先由02A f ⎛⎫= ⎪⎝⎭结合(Ⅰ)的结果,确定角A 的值,然后结合余弦定理求出三角形ABC ∆面积的最大值. 试题解析:解:(Ⅰ)由题意知()1cos 2sin 2222x x f x π⎛⎫++ ⎪⎝⎭=-sin 21sin 21sin 2222x x x -=-=- 由222,22k x k k Z ππππ-+≤≤+∈可得,44k x k k Z ππππ-+≤≤+∈由3222,22k x k k Z ππππ+≤≤+∈可得3,44k x k k Z ππππ+≤≤+∈ 所以函数()f x 的单调递增区间是(),44k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦; 单调递减区间是()3,44k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦(Ⅱ)由1sin 0,22A f A ⎛⎫=-=⎪⎝⎭得1sin 2A =由题意知A为锐角,所以cos A =由余弦定理:2222cos a b c bc A =+-可得:22132bc b c bc +=+≥即:23,bc ≤+当且仅当b c =时等号成立.因此123sin 2bc A +≤所以ABC ∆面积的最大值为234+ 考点:1、诱导公式;2、三角函数的二倍角公式;3、余弦定理;4、基本不等式.18.如图,在三棱锥P -ABC 中,已知22====,AC AB BC PA ,顶点P 在平面ABC 上的射影为ABC 的外接圆圆心.(1)证明:平面PAC ⊥平面ABC ;(2)若点M 在棱PA 上,||||=λAM AP ,且二面角P -BC -M 533,试求λ的值. 答案:(1)证明见解析 (2)12λ= 【分析】(1)设AC 的中点为O ,连接PO ,易知点O 为ABC 的外接圆圆心,从而PO ⊥平面ABC ,即可证明平面PAC ⊥平面ABC ;(2)以OC ,OB ,OP 所在直线分别为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系, 求出平面MBC 与平面PBC 的法向量,代入公式即可建立λ的方程,解之即可. 解:(1)证明:如图,设AC 的中点为O ,连接PO ,由题意,得222BC AB AC +=,则ABC 为直角三角形, 点O 为ABC 的外接圆圆心.又点P 在平面ABC 上的射影为ABC 的外接圆圆心, 所以PO ⊥平面ABC ,又PO ⊂平面PAC ,所以平面PAC ⊥平面ABC . (2)解:由(1)可知PO ⊥平面ABC , 所以PO OB ⊥,PO OC ⊥,OB AC ⊥,于是以OC ,OB ,OP 所在直线分别为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系,则(000)O ,,,(100)C ,,,(010)B ,,,(100)A -,,,(001)P ,,, 设[01](101)(10)AM AP AP M λλλλ=∈=-,,,,,,,,,(110)BC =-,,,(101)PC =-,,,(20).MC λλ=--,,设平面MBC 的法向量为111()m x y z =,,,则·0·0m BC m MC ⎧=⎨=⎩,,得11110(2)0x y x z λλ-=⎧⎨--=⎩,,令11x =,得11y =,12z λλ-=,即211m λλ-⎛⎫= ⎪⎝⎭,,. 设平面PBC 的法向量为222()n x y z =,,,由·0·0n BC n PC ⎧=⎨=⎩,,得222200x y x z -=⎧⎨-=⎩,,令1x =,得1y =,1z =,即(111)n =,,,2222·533cos ||?||(2)3?2n mn m n m λλλλ-+〈〉===-+,, 解得1110222⎛⎫=- ⎪⎝⎭,,,,λM 即M 为PA 的中点. 点评:本题考查平面与平面垂直的判定,二面角的平面角的求法,考查空间想象能力以及计算能力. 19.某快餐连锁店招聘外卖骑手,该快餐连锁店提供了两种日工资方案:方案(a)规定每日底薪50元,快递业务每完成一单提成3元;方案(b)规定每日底薪100元,快递业务的前44单没有提成,从第45单开始,每完成一单提成5元,该快餐连锁店记录了每天骑手的人均业务量,现随机抽取100天的数据,将样本数据分为[ 25,35),[35,45),[45,55),[55,65),[65,75),[75,85),[85,95]七组,整理得到如图所示的频率分布直方图.(1)随机选取一天,估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率; (2)从以往统计数据看,新聘骑手选择日工资方案(a )的概率为13,选择方案(b )的概率为23.若甲、乙、丙三名骑手分别到该快餐连锁店应聘,三人选择日工资方案相互独立,求至少有两名骑手选择方案(a)的概率;(3)若仅从人均日收入的角度考虑,请你利用所学的统计学知识为新聘骑手做出日工资方案的选择,并说明理由.(同组中的每个数据用该组区间的中点值代替) 答案:(Ⅰ) 0.4 (Ⅱ) 727(Ⅲ)见解析 分析】(Ⅰ)先设事件A 为“随机选取一天,这一天该连锁店的骑手的人均日快递业务量不少于65单”,由频率分布直方图,即可求出结果;(Ⅱ)先设事件B 为“甲、乙、丙三名骑手中至少有两名骑手选择方案(1)”,设事件i C 为“甲乙丙三名骑手中恰有()0,1,2,3i i =人选择方案(1)”,根据题意可得()()()23P B P C P C =+,进而可求出结果; (Ⅲ)先设骑手每日完成快递业务量为X 件,得到方案(1)的日工资()*1503Y X X N=+∈,方案(2)的日工资()*2*100,44,100544,44,X X N Y X X X N⎧≤∈⎪=⎨+->∈⎪⎩ ,再由题中条件分别得到1Y 与2Y 的期望,比较大小即可得出结果.解:(Ⅰ)设事件A 为“随机选取一天,这一天该连锁店的骑手的人均日快递业务量不少于65单”依题意,连锁店的人均日快递业务量不少于65单的频率分别为:0.20.150.05,, 因为0.20.150.050.4++= 所以()P A 估计为0.4.(Ⅱ) 设事件B 为“甲、乙、丙三名骑手中至少有两名骑手选择方案(1)” 设事件i C 为“甲乙丙三名骑手中恰有()0,1,2,3i i =人选择方案(1)”,则()()()213232333121617333272727P B P C P C C C ⎛⎫⎛⎫⎛⎫=+=+=+= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭, 所以三名骑手中至少有两名骑手选择方案(1)的概率为727(Ⅲ)设骑手每日完成快递业务量为X 件 方案(1)的日工资()*1503Y X X N=+∈,方案(2)的日工资()*2*100,44,100544,44,X X N Y X X X N ⎧≤∈⎪=⎨+->∈⎪⎩所以随机变量1Y 的分布列为11400.051700.052000.22300.32600.22900.153200.05EY =⨯+⨯+⨯+⨯+⨯+⨯+⨯ 236=;同理随机变量2Y 的分布列为P0.1 0.20.3 0.2 0.15 0.0521000.11300.21800.32300.22800.153300.05EY =⨯+⨯+⨯+⨯+⨯+⨯ 194.5=因为12EY EY >,所以建议骑手应选择方案(1)点评:本题主要考查频率分布直方图、离散型随机变量的分布列与期望等,熟记概念,会分析频率分布直方图即可,属于常考题型.20.如图,椭圆1C :22221(0)x y a b a b +=>>的左右焦点分别为12,F F ,离心率为3,过抛物线2C :24x by =焦点F 的直线交抛物线于,M N 两点,当7||4MF =时,M 点在x 轴上的射影为1F ,连接,)NO MO 并延长分别交1C 于,A B 两点,连接AB ,OMN ∆与OAB ∆的面积分别记为OMN S ∆,OAB S ∆,设λ=OMNOABS S ∆∆.(1)求椭圆1C 和抛物线2C 的方程; (2)求λ的取值范围.答案:(I ) 2214x y +=,24x y =;(II ) [)2,+∞.试题分析:(Ⅰ )由题意得得7,4M c b ⎛⎫-- ⎪⎝⎭,根据点M 在抛物线上得2744c b b ⎛⎫=- ⎪⎝⎭,又由3c a =得 223c b =,可得277b b =,解得1b =,从而得32c a ==,,可得曲线方程.(Ⅱ )设ON k m =,'OM k m =,分析可得1'4m m =-,先设出直线ON 的方程为y mx = (0)m >,由24y mx x y=⎧⎨=⎩,解得4N x m =,从而可求得4ON =同理可得,,OM OA OB ,故可将=OMN OAB ON OMS S OA OBλ∆∆⋅=⋅化为m 的代数式,用基本不等式求解可得结果. 试题解析:(Ⅰ)由抛物线定义可得7,4M c b ⎛⎫-- ⎪⎝⎭, ∵点M 在抛物线24x by =上,∴2744c b b ⎛⎫=- ⎪⎝⎭,即2274c b b =- ①又由c a =,得 223c b = 将上式代入①,得277b b = 解得1,b =∴c =2a ∴=,所以曲线1C 的方程为2214x y +=,曲线2C 的方程为24x y =.(Ⅱ)设直线MN 的方程为1y kx =+,由214y kx x y=+⎧⎨=⎩消去y 整理得2440x kx --=, 设11,)Mx y (,()2,2N x y . 则124x x =-,设ON k m =,'OM k m =, 则21122111'164y y mm x x x x =⋅==-, 所以1'4m m=-, ② 设直线ON 的方程为y mx = (0)m >,由24y mxx y=⎧⎨=⎩,解得4N x m =,所以4N ON ==, 由②可知,用14m-代替m ,可得M OM == 由2214y mxx y =⎧⎪⎨+=⎪⎩,解得A x =,所以A OA ==用14m-代替m,可得B OB ==所以=OMN OABON OM S S OA OB λ∆∆⋅==⋅==1222m m=+≥,当且仅当1m =时等号成立. 所以λ的取值范围为[)2,+∞.点睛:解决圆锥曲线的最值与范围问题时,若题目的条件和结论能体现一种明确的函数关系,则可首先建立目标函数,再求这个函数的最值.常从以下几个方面考虑: ①利用判别式来构造不等关系,从而确定参数的取值范围;②利用隐含或已知的不等关系建立不等式,从而求出参数的取值范围; ③利用基本不等式求出参数的取值范围; ④利用函数的值域的求法,确定参数的取值范围.21.已知函数()21xf x x ae =--.(1)若()f x 有两个不同的极值点1x ,2x ,求实数a 的取值范围; (2)在(1)的条件下,求证:124xx e ea+>. 答案:(1)20,e ⎛⎫⎪⎝⎭;(2)详见解析. 【分析】(1)由()21xf x x ae =--得()2xf x x ae '=-,根据()f x 有两个不同的极值点1x ,2x ,则()f x '有两个不同的零点,即方程2x x a e =有两个不同的实根,转化为直线y a =与2xx y e=的图象有两个不同的交点求解.(2)由(1)知20a e <<,设12x x <,则1201x x <<<,由121222x x x ae x ae⎧=⎨=⎩得()()12122x x x x a e e -=-,()12122x x x x a e e -=-,要证124x x e e a +>,将()12122x x x x a e e -=- 代入整理为()()121212121x x x x x x e e ---+>-,再令12(0)x x t t -=<,转化为()2101t t e t e --<+,再构造函数()21()(0)1tt e g t t t e -=-<+,研究其最大值即可.解:(1)由()21xf x x ae =--得()2xf x x ae '=-,()f x 有两个不同的极值点1x ,2x ,则()f x '有两个不同的零点,即方程2x xa e=有两个不同的实根, 即直线y a =与2x xy e=的图象有两个不同的交点,设()2x xg x e =,则()()21xx g x e -'=, (),1x ∈-∞时()0g x '>,()g x 单调递增,且()g x 的取值范围是2,e ⎛⎫-∞ ⎪⎝⎭; ()1,x ∈+∞时()0g x '<,()g x 单调递减,且()g x 的取值范围是20,e ⎛⎫⎪⎝⎭,所以当20a e <<时,直线y a =与2x x y e=的图象有两个不同的交点, ()f x 有两个不同的极值点1x ,2x ,故实数a 的取值范围是20,e ⎛⎫ ⎪⎝⎭. (2)由(1)知20a e<<,设12x x <,则1201x x <<<, 由121222x x x ae x ae ⎧=⎨=⎩得()()12122x x x x a e e -=-,()12122x x x x a e e -=- 所以要证124xx e ea+>,只需证()124x xa e e +>, 即证()()1212122x x x x x x e e e e -+>-,即证()()121212121x x x x x x e e ---+>-,设12(0)x x t t -=<,即证()121t t t e e +>-,即证()2101tt e t e --<+,设()21()(0)1t te g t t t e -=-<+,则21()01t t e g t e '⎛⎫-=> ⎪+⎝⎭, 所以()g t 在(),0-∞是增函数,()()00g t g <=,所以()2101t t e t e --<+,从而有124x x ee a+>. 点评:本题主要考查导数与函数极值,导数法证明不等式,还考查了转化化归的思想和运算求解的能力,属于难题.选考题:共10分.请考生在第22、23两题中任选一题作答.如果多做,则按所做的第一题计分. 选修4-4:坐标系与参数方程22.在平面直角坐标系中,曲线C 的参数方程为22cos 2sin x y θθ=+⎧⎨=⎩(θ为参数),直线l的参数方程为212x y ⎧=-⎪⎪⎨⎪=+⎪⎩t 为参数),以坐标原点为极点,x 轴的非负半轴为极轴建立极坐标系. (Ⅰ)求曲线C 以及直线l 的极坐标方程;(Ⅱ)若()0,1A ,直线l 与曲线C 相交于不同的两点M ,N ,求11+AM AN的值. 答案:(Ⅰ)4cos ρθ=sin 14πθ⎛⎫+= ⎪⎝⎭;(Ⅱ) 【分析】(1)消去参数t 可得l 的普通方程,利用平方关系消去参数θ可得曲线C 的直角坐标方程,把ρ2=x 2+y 2,y =ρsin θ代入,可得曲线C 以及直线l 的极坐标方程..(II )把直线l 的参数方程代入曲线C 的直角坐标方程,利用直线参数的几何意义求得结果. 解:(Ⅰ)依题意,曲线C :()2224x y -+=,故2240x y x +-=,即24cos 0ρρθ-=,即4cos ρθ=;直线l :1y x =-,即10x y +-=,即cos sin 10ρθρθ+-=,sin 14πθ⎛⎫+= ⎪⎝⎭; (Ⅱ)将直线l的参数方程212x y ⎧=-⎪⎪⎨⎪=+⎪⎩代入2240x y x +-=中,化简可得210t ++=,设M ,N 所对应的参数分别为1t ,2t ,则12t t +=-,121t t =,故11AM AN AM AN AM AN++==点评:本题考查了极坐标方程、参数方程与普通方程的互化,考查了直线参数的意义,考查了计算能力,属于中档题. 选修4-5:不等式选讲 23.选修4-5:不等式选讲 已知函数() 1.f x x =+(Ⅰ)解不等式()32f x x >-+;(Ⅱ)已知0,0a b >>,且2a b +=()f x x -≤答案:(Ⅰ)()(),30,-∞-⋃+∞; (Ⅱ)见解析. 【分析】(Ⅰ)整理()32f x x >-+得:123x x +++>,由绝对值的几何意义即可解不等式.(Ⅱ)将问题转化成()max f x x -≤⎡⎤⎣⎦求得()max 1f x x -=⎡⎤⎣⎦,转化成证明1≤利用基本不等式即可证明结论,问题得解.解:(Ⅰ)()32f x x >-+,即123x x +++>, 由绝对值的几何意义得:(,3)(0,)x ∈-∞-⋃+∞; (Ⅱ)()[]11,1f x x x x -=+-∈-,要证()f x x -≤1≤22a b a b +==+≥1,4ab ≤1.==≥点评:本题主要考查了绝对值的几何意义,还考查了转化思想及基本不等式的应用,考查计算能力,属于中档题.。
2020届河北省衡水中学2017级高三下学期二调考试数学(理)试卷及解析

2020届河北省衡水中学2017级高三下学期二调考试数学(理)试卷★祝考试顺利★(解析版)一、选择题1.已知集合{1,3,4,5}A =,集合2{}450|B x Z x x =∈--<,则A B 的子集个数为( )A. 2B. 4C. 8D. 16【答案】C试题分析:由2450x x --<,解得15x -<<,所以{}0,1,2,3,4B =,所以{}1,3,4A B ⋂=,所以A B ⋂的子集个数为328=,故选C . 2.如图,复平面上的点1234,,,Z Z Z Z 到原点的距离都相等,若复数z 所对应的点为1Z ,则复数•z i (i 是虚数单位)的共轭复数所对应的点为( )A. 1ZB. 2ZC. 3ZD. 4Z【答案】B 试题分析:z i ⋅为将复数z 所对应的点逆时针旋转90得2Z ,选B.【名师点睛】本题重点考查复数的基本运算和复数的概念,属于基本题.首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如()()()(),(,,.)a bi c di ac bd ad bc i a b c d R ++=-++∈. 其次要熟悉复数相关基本概念,如复数(,)a bi a b R +∈的实部为a 、虚部为b 22a b +、共轭为.a bi -3.下列四个函数,在0x =处取得极值的函数是( )①3y x = ②21y x +=③y x =④2x y =A. ① ②B. ② ③C. ③ ④D. ① ③【答案】B【详解】试题分析:能不能取得极值要看函数在这个导函数的零点处的两边是否异性单调.通过检验②③这两个函数在处的左右两边情况是:左边是减函数,右边是增函数,因此是极值点.而①④两个函数都是单增的,所以应选B.4.已知变量,x y满足:20{230x yx yx-≤-+≥≥,则2(2)xyz+=的最大值为()A. 2B. 22C. 2D. 4【答案】D试题分析:作出满足不等式组的平面区域,如图所示,由图知目标函数12z x y=+经过点(1,2)A时取得最大值,所以212max(2)4z⨯+==,故选D.5.执行如图所示的程序框图,输出的结果是()A. 5B. 6C. 7D. 8。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点 O 为△ABC 的外接圆圆心. 又点 P 在平面 ABC 上的射影为△ABC 的外接圆圆心, 所以 PO⊥平面 ABC, 又 PO⊂平面 PAC,所以平面 PAC⊥平面 ABC. (2)解:由(1)可知 PO⊥平面 ABC, 所以 PO⊥OB,PO⊥OC,OB⊥AC, 以 OC,OB,OP 所在直线分别为 x 轴,y 轴,z 轴建立如图所示的空间直角坐 标系, 则 O(0,0,0),C(1,0,0),B(0,1,0),A(﹣1,0,0),P(0,0, 1), 设 = ,λ∈[0,1], =(1,0,1),M(λ﹣1,0,λ),
.
所以△ABC 面积的最大值为
.
18. 如图,在三棱锥 面 上的射影为
(1)证明:平面
中,已知
,
的外接圆圆心.
⊥平面 ;
(2)若点 M 在棱 PA 上,
,且二面角
求 的值.
,顶点 在平 的余弦值为 ,试
解:(1)证明:如图,设 AC 的中点为 O,连接 PO, 由题意,得 BC2+AB2=AC2,则△ABC 为直角三角形,
第3页
2020届河北省衡水中学2017级高三下学期九调考试数学(理)试卷
=2 .
6. 设 m,n 为正数,且 m+n=2,则 1 n 3 的最小值为( ) m1 n 2
A.
B.
C.
D.
解:当 m+n=2 时,
,
因为
,
当且仅当 m+1=n+2,即
, 时取等号,则
,即最小
值为 .
故选:D.
7. 我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,用现代式子表
=(1,﹣1,0), =(1,0,﹣1), =(2﹣λ,0,﹣λ), 设平面 MBC 的法向量为 =(x,y,z),
则
,令 x=1,得 =(1,1, ),
设平面 PBC 的法向量为 =(x,y,z),
由
,令 x=1,得 =(1,1,1),
∵二面角 P﹣BC﹣M 的余弦值为
,
∴cos< >= 解得
=
=
2. 复数 z i 的虚部为( ) 5i
A. 5 26
B. 5 i 26
解:∵
=
C. 5 26
,
D. 5 i 26
∴复数
上的虚部为 .
故选:A. 3. 某运动制衣品牌为了成衣尺寸更精准,现选择 15 名志愿者,对其身高和臂展 进行测量(单位:厘米),左图为选取的 15 名志愿者身高与臂展的折线图,右图
可得 的取值范围为[﹣ ,0),
故选:A.
第7页 2020届河北省衡水中学2017级高三下学期九调考试数学(理)试卷
二、 填空题(本大题共 4 小题,每题 5 分,共 20 分.)
13.
x
1 7x
7
的展开式的第
2
项为
.
解:(x﹣ )7 的展开式的第 2 项为 T2= •
•x5=﹣x5,
故答案为:﹣x5.
1(a>0,b>0),点 P(x0,y0)是直线 bx﹣ay+4a
=0 上任意一点,若圆(x﹣x0)2+(y﹣y0)2=1 与双曲线 C 的右支没有公共点, 则双曲线的离心率取值范围是( )
A.(1,2]
B.(1,4]
C.[2,+∞) D.[4,+∞)
第5页
2020届河北省衡水中学2017级高三下学期九调考试数学(理)试卷
为身高与臂展所对应的散点图,并求得其回归方程为 中不正确的为( )
1.16x﹣30.75,以下结论
A.15 名志愿者身高的极差小于臂展的极差
第1页
B.15 名志愿者身高和臂展成正相关关系
C.可估计身高为 190 厘米的人臂展大约为 189.65 厘米
D.身高相差 10 厘米的两人臂展都相差 11.6 厘米
14. 已知 中,
,
,
,若点 满足
________.
解: =
,所以:
,
Hale Waihona Puke ,则以及 AB=3,AC=5,BC=7,cos∠BAC=
=﹣
可得 所以 =
= =(
=, )•( ﹣ )
=
=﹣12.
故答案为:﹣12.
15. 记 等 差 数 列 的 前 项 和 为 , 若
1n a3n 的前 项和
.
,
,则数列
解:因为{an}是等数差数列,S17=459⇒17a9=459⇒a9=27,而 a2+a4=18,
即 sinC(1+3cosA)=0,
因为 sinC≠0,
,且 D.
所以 cosA=﹣ ,
由余弦定理可得 a2﹣b2﹣c2=﹣2bccosA= bc=2,
所以 bc=3,
由△ABC 的面积公式可得 S=
=
=
. 故选:A.
第4页
8. 执行如图所示的程序框图,则输出的 a 值为( )
A.
B.
C.
D.2
解:当 i=1 时,不满足退出循环的条件,执行循环体后,a=﹣3,i=2;
当﹣ <x< ,f′(x)<0,函数 f(x)单调递减,
由图象可得﹣ <x2<0,
D. 0, 2e 2
又=
=x2 ,
设 g(x)=xex,(﹣ <x<0), ∴g′(x)=(x+1)ex,
∴g′(x)在(﹣ ,﹣1)上是减函数,在(﹣1,0)上是增函数,
由 g(﹣1)=﹣ ,g(﹣ )=﹣
,g(0)=0,
所以
,解得 d=3,a1=3,
则 an=3+(n﹣1)×3=3n,n∈N*; 数列{a3n}构成首项为 9,公差为 9 的等差数列;
若 n 为偶数,则
,
若 n 为奇数,
则 Tn=﹣9+18﹣27+36+…﹣9(n﹣2)+9(n﹣1)﹣9n=﹣
,
第8页
故 Tn=
;
故答案为:
16. 已知三棱锥 ,
解:如图:
﹣1+ >0,
∴f(x)在(﹣∞,﹣ )上单调递减,在(﹣ ,0)上单调递增,图象为 D;
第2页
(3)当 a<0 时,﹣1+ <0,∴f(x)在(﹣∞,0)上单调递减,
令 1+ =0 得 x= ,∴当 x> 时,1+ >0,当 0<x< 时,1+
<0, ∴f(x)在(0, )上单调递减,在( ,+∞)上单调递增,图象为 B; 故选:C.
即 e 4,
故 e 的取值范围为 , 故选:B.
11. 直线 与函数
(
)的图象的相邻两个交点的距
离为 ,若 在
(
)上是增函数,则 的取值范围是( )
A.
0,
4
B.
0,
2
C.
0,
3 4
D.
0,
3 2
解:直线 y=a 与函数 f(x)=tan(
)图象的相邻两个交点的距离为
一个周期,则 T=2π, 所以 ω= = ,
解:对于 A,身高极差大约是 25,臂展极差大于等于 30,故 A 正确;
对于 B,很明显根据散点图以及回归方程得到,身高矮展臂就会短一些,
身高高一些,
展臂就会长一些,故 B 正确;
对于 C,身高为 190 厘米,代入回归方程可得展臂等于 189.65 厘米,但不
是准确值,故 C 正确;
对于 D,身高相差 10 厘米的两人展臂的估计值相差 11.6 厘米,但不是准
所以 f(x)=tan( x+ ),
由 kπ﹣ < x+ <kπ+ ,
解得 2kπ﹣ <x<2kπ+ ,(k∈Z);
所以函数 f(x)在(﹣ , )上是单调增函数; 又 f(x)在(﹣m,m)上是单调增函数, 即(﹣m,m)⊆(﹣ , ),
解得 0<m≤ ;
所以 m 的取值范围是(0, ].
第6页
故选:B.
【解答】解:双曲线 C:
1(a>0,b>0)的一条渐近线方程为 y x,
即 bx﹣ay=0,
∵P(x0,y0)是直线 bx﹣ay+4a=0 上任意一点,
则直线 bx﹣ay+4a=0 与直线 bx﹣ay=0 的距离 d
,
∵圆(x﹣x0)2+(y﹣y0)2=1 与双曲线 C 的右支没有公共点, ∴,
∴ 1,
三、 解答题(本大题共 6 小题,共 70 分,解答应写出文字说明或演算步骤.)
17. 设
.
(1)求 的单调区间;
(2)在锐角 中,角 , , 的对边分别为 , , . 若
, ,求
面积的最大值.
解:(1)由题意知 f(x)=
-
=
-
=sin2x- .
由- +2kπ≤2x≤ +2kπ,k∈Z,可得- +kπ≤x≤ +kπ,k∈Z; 由 +2kπ≤2x≤ +2kπ,k∈Z,可得 +kπ≤x≤ +kπ,k∈Z.
由 2020÷4=505,
故当 i=2021 时,满足退出循环的条件,故输出的 a 值为 2,
故选:D.
9. 若
,
,
,
,则 x,y,z 大小关系正确的
是( )
A.
B.
C.
D.
解:∵0<a<b<1;
∴ab<aa<ba<b0=1,logba>logbb=1; ∴x<y<z.
故选:A.
10. 已知双曲线 C:
5. 某几何体的三视图如图,该几何体表面上的点 P 与点 Q 在正视图与侧视图上 的对应点分别为 A,B,则在该几何体表面上,从点 P 到点 Q 的路径中,最短路 径的长度为( )
