重庆市2018年中考数学试题b卷(word版无答案)

合集下载

重庆2018中考数学试题B卷含答案解析

重庆市2018年初中学业水平暨高中招生考试数学试题( B 卷)(全卷共五个大题，满分150分。

考试时间120分钟)注意事项:1.试题的答案书写在答题卡上，不得在试卷上直接作答；2.作答前认真阅读答题卡上的注意事项；3.作图(包括作辅助线)请一律用黑色签字笔完成；4.考试结束，由监考人员将试题和答题卡一并收回。

参考公式：抛物线2(0)y ax bx c a =++≠的顶点坐标为24,24b ac b a a ⎛⎫- ⎪⎝⎭,对称轴为2b x a=。

一、选择题：(本大题12 个小题，每小题4分 ,共48分)在每个小题的下面，都给出了代号为A 、B 、C 、D 的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑。

1.下列四个数中，是正整数的是( )A.-1B.0C.21 D.1 2下列图形中，是轴对称图形的是( )3.下列图形都是由同样大小的黑色正方形纸片组成,其中第①个图中有3张黑色正方形纸片，第②个图中有5张黑色正方形纸片,第③个图中有7张黑色正方形纸片,..，按此规律排列下去,第⑥个图中黑色正方形纸片的张数为( )A.11B.13C.15D.174.下列调查中，最适合采用全面调查(普查)的是( )A.对我市中学生每周课外阅读时间情况的调查B.对我市市民知晓“礼让行人”交通新规情况的调查C.对我市中学生观看电影(厉害了，我的国》情况的调查D.对我国首艘国产航母002型各零部件质量情况的调查5.制作一块m m 23⨯长方形广告牌的成本是120元,在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，那么扩大后长方形广告牌的成本是( )A.360元B.720元C.1080元D.2160元6.下列命题是真命题的是( )A.如果一个数的相反数等于这个数本身，那么这个数一定是0 。

B.如果一个数的倒数等于这个数本身，那么这个数一定是1 。

C.如果一个数的平方等于这个数本身，那么这个数定是0 。

2018年重庆市中考数学试卷(B)

2018年重庆市初中学业水平暨高中招生考试数学试题( B 卷)(全卷共五个大题，满分150分。

参考公式：抛物线2(0)y ax bx c a =++≠的顶点坐标为24,24b ac b a a ⎛⎫- ⎪⎝⎭,对称轴为2b x a =。

1.下列四个数中，是正整数的是( ) A.-1 B.0 C.21 D.1 2下列图形中，是轴对称图形的是( )3.下列图形都是由同样大小的黑色正方形纸片组成,其中第①个图中有3张黑色正方形纸片，第②个图中有5张黑色正方形纸片,第③个图中有7张黑色正方形纸片,..，按此规律排列下去,第⑥个图中黑色正方形纸片的张数为( )A.11B.13C.15D.174.下列调查中，最适合采用全面调查(普查)的是( )A.对我市中学生每周课外阅读时间情况的调查B.对我市市民知晓“礼让行人”交通新规情况的调查C.对我市中学生观看电影(厉害了，我的国》情况的调查D.对我国首艘国产航母002型各零部件质量情况的调查5.制作一块m m 23⨯长方形广告牌的成本是120元,在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，那么扩大后长方形广告牌的成本是( )A.360元B.720元C.1080元D.2160元6.下列命题是真命题的是( )A.如果一个数的相反数等于这个数本身，那么这个数一定是0 。

B.如果一个数的倒数等于这个数本身，那么这个数一定是1 。

C.如果一个数的平方等于这个数本身，那么这个数定是0 。

2018年重庆市中考数学试卷(b卷)(解析版)

2018年重庆市中考数学试卷（B卷）一、选择题：（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A，B，C，D的四个答案，其中只有一个是正确的1．（4分）下列四个数中，是正整数的是（）A．﹣1B．0C．D．12．（4分）下列图形中，是轴对称图形的是（）A．B．C．D．3．（4分）下列图形都是由同样大小的黑色正方形纸片组成，其中第①个图中有3张黑色正方形纸片，第②个图中有5张黑色正方形纸片，第③个图中有7张黑色正方形纸片，…，按此规律排列下去第⑥个图中黑色正方形纸片的张数为（）A．11B．13C．15D．174．（4分）下列调查中，最适合采用全面调查（普查）的是（）A．对我市中学生每周课外阅读时间情况的调查B．对我市市民知晓“礼让行人”交通新规情况的调查C．对我市中学生观看电影《厉害了，我的国》情况的调查D．对我国首艘国产航母002型各零部件质量情况的调查5．（4分）制作一块3m×2m长方形广告牌的成本是120元，在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，那么扩大后长方形广告牌的成本是（）A．360元B．720元C．1080元D．2160元6．（4分）下列命题是真命题的是（）A．如果一个数的相反数等于这个数本身，那么这个数一定是0B．如果一个数的倒数等于这个数本身，那么这个数一定是1C．如果一个数的平方等于这个数本身，那么这个数一定是0D．如果一个数的算术平方根等于这个数本身，那么这个数一定是07．（4分）估计5﹣的值应在（）A．5和6之间B．6和7之间C．7和8之间D．8和9之间8．（4分）根据如图所示的程序计算函数y的值，若输入的x值是4或7时，输出的y值相等，则b等于（）A．9B．7C．﹣9D．﹣79．（4分）如图，AB是一垂直于水平面的建筑物，某同学从建筑物底端B出发，先沿水平方向向右行走20米到达点C，再经过一段坡度（或坡比）为i＝1：0.75、坡长为10米的斜坡CD到达点D，然后再沿水平方向向右行走40米到达点E（A，B，C，D，E均在同一平面内）．在E处测得建筑物顶端A的仰角为24°，则建筑物AB的高度约为（参考数据：sin24°≈0.41，cos24°≈0.91，tan24°＝0.45）（）A．21.7米B．22.4米C．27.4米D．28.8米10．（4分）如图，△ABC中，∠A＝30°，点O是边AB上一点，以点O为圆心，以OB 为半径作圆，⊙O恰好与AC相切于点D，连接BD．若BD平分∠ABC，AD＝2，则线段CD的长是（）A．2B．C．D．11．（4分）如图，菱形ABCD的边AD⊥y轴，垂足为点E，顶点A在第二象限，顶点B在y轴的正半轴上，反比例函数y＝（k≠0，x＞0）的图象同时经过顶点C，D．若点C 的横坐标为5，BE＝3DE，则k的值为（）A．B．3C．D．512．（4分）若数a使关于x的不等式组，有且仅有三个整数解，且使关于y的分式方程+＝1有整数解，则满足条件的所有a的值之和是（）A．﹣10B．﹣12C．﹣16D．﹣18二、填空题：（本大题6个小题，每小题4分，共24分）请将每小题的答案直接填在答题卡中对应的横线上13．（4分）计算：|﹣1|+20＝．14．（4分）如图，在边长为4的正方形ABCD中，以点B为圆心，以AB为半径画弧，交对角线BD于点E，则图中阴影部分的面积是（结果保留π）．15．（4分）某企业对一工人在五个工作日里生产零件的数量进行调查，并绘制了如图所示的折线统计图，则在这五天里该工人每天生产零件的平均数是个．16．（4分）如图，在Rt△ABC中，∠ACB＝90°，BC＝6，CD是斜边AB上的中线，将△BCD沿直线CD翻折至△ECD的位置，连接AE．若DE∥AC，计算AE的长度等于．17．（4分）一天早晨，小玲从家出发匀速步行到学校，小玲出发一段时间后，她的妈妈发现小玲忘带了一件必需的学习用品，于是立即下楼骑自行车，沿小玲行进的路线，匀速去追小玲，妈妈追上小玲将学习用品交给小玲后，立即沿原路线匀速返回家里，但由于路上行人渐多，妈妈返回时骑车的速度只是原来速度的一半，小玲继续以原速度步行前往学校，妈妈与小玲之间的距离y（米）与小玲从家出发后步行的时间x（分）之间的关系如图所示（小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计）．当妈妈刚回到家时，小玲离学校的距离为米．18．（4分）为实现营养套餐的合理搭配，某电商推出两款适合不同人群的甲、乙两种袋装的混合粗粮．甲种袋装粗粮每袋含有3千克A粗粮，1千克B粗粮，1千克C粗粮；乙种袋装粗粮每袋含有1千克A粗粮，2千克B粗粮，2千克C粗粮．甲、乙两种袋装粗粮每袋成本分别等于袋中的A、B、C三种粗粮成本之和．已知每袋甲种粗粮的成本是每千克A种粗粮成本的7.5倍，每袋乙种粗粮售价比每袋甲种粗粮售价高20%，乙种袋装粗粮的销售利润率是20%．当销售这两款袋装粗粮的销售利润率为24%时，该电商销售甲、乙两种袋装粗粮的袋数之比是（商品的销售利润率＝×100%）三、解答题：（本大题2个小题，每小题8分，共16分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上19．（8分）如图，AB∥CD，△EFG的顶点F，G分别落在直线AB，CD上，GE交AB于点H，GE平分∠FGD．若∠EFG＝90°，∠E＝35°，求∠EFB的度数．20．（8分）某学校开展以素质提升为主题的研学活动，推出了以下四个项目供学生选择：A．模拟驾驶；B．军事竞技；C．家乡导游；D．植物识别．学校规定：每个学生都必须报名且只能选择其中一个项目．八年级（3）班班主任刘老师对全班学生选择的项目情况进行了统计，并绘制了如下两幅不完整的统计图．请结合统计图中的信息，解决下列问题：（1）八年级（3）班学生总人数是，并将条形统计图补充完整；（2）刘老师发现报名参加“植物识别”的学生中恰好有两名男生，现准备从这些学生中任意挑选两名担任活动记录员，请用列表或画树状图的方法，求恰好选中1名男生和1名女生担任活动记录员的概率．四、解答题：（本大题5个小题，每小题10分，共50分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上21．（10分）计算：（1）（x+2y）2﹣（x+y）（x﹣y）；（2）（a﹣1﹣）÷22．（10分）如图，在平面直角坐标系中，直线l1：y＝x与直线l2交点A的横坐标为2，将直线l1沿y轴向下平移4个单位长度，得到直线l3，直线l3与y轴交于点B，与直线l2交于点C，点C的纵坐标为﹣2．直线l2与y轴交于点D．（1）求直线l2的解析式；（2）求△BDC的面积．23．（10分）在美丽乡村建设中，某县政府投入专项资金，用于乡村沼气池和垃圾集中处理点建设．该县政府计划：2018年前5个月，新建沼气池和垃圾集中处理点共计50个，且沼气池的个数不低于垃圾集中处理点个数的4倍．（1）按计划，2018年前5个月至少要修建多少个沼气池？（2）到2018年5月底，该县按原计划刚好完成了任务，共花费资金78万元，且修建的沼气池个数恰好是原计划的最小值．据核算，前5个月，修建每个沼气池与垃圾集中处理点的平均费用之比为1：2．为加大美丽乡村建设的力度，政府计划加大投入，今年后7个月，在前5个月花费资金的基础上增加投入10a%，全部用于沼气池和垃圾集中处理点建设．经测算：从今年6月起，修建每个沼气池与垃圾集中处理点的平均费用在2018年前5个月的基础上分别增加a%，5a%，新建沼气池与垃圾集中处理点的个数将会在2018年前5个月的基础上分别增加5a%，8a%，求a的值．24．（10分）如图，在▱ABCD中，∠ACB＝45°，点E在对角线AC上，BE＝BA，BF⊥AC 于点F，BF的延长线交AD于点G．点H在BC的延长线上，且CH＝AG，连接EH．（1）若BC＝12，AB＝13，求AF的长；（2）求证：EB＝EH．25．（10分）对任意一个四位数n，如果千位与十位上的数字之和为9，百位与个位上的数字之和也为9，则称n为“极数”．（1）请任意写出三个“极数”；并猜想任意一个“极数”是否是99的倍数，请说明理由；（2）如果一个正整数a是另一个正整数b的平方，则称正整数a是完全平方数．若四位数m为“极数”，记D（m）＝，求满足D（m）是完全平方数的所有m．五、解答题：（本大题1个小题，共12分）解答时每小题必须给出必要的演算过程或推理步骤，请将解答书写在答题卡中对应的位置上26．（12分）抛物线y＝﹣x2﹣x+与x轴交于点A，B（点A在点B的左边），与y轴交于点C，点D是该抛物线的顶点．（1）如图1，连接CD，求线段CD的长；（2）如图2，点P是直线AC上方抛物线上一点，PF⊥x轴于点F，PF与线段AC交于点E；将线段OB沿x轴左右平移，线段OB的对应线段是O1B1，当PE+EC的值最大时，求四边形PO1B1C周长的最小值，并求出对应的点O1的坐标；（3）如图3，点H是线段AB的中点，连接CH，将△OBC沿直线CH翻折至△O2B2C 的位置，再将△O2B2C绕点B2旋转一周，在旋转过程中，点O2，C的对应点分别是点O3，C1，直线O3C1分别与直线AC，x轴交于点M，N．那么，在△O2B2C的整个旋转过程中，是否存在恰当的位置，使△AMN是以MN为腰的等腰三角形？若存在，请直接写出所有符合条件的线段O2M的长；若不存在，请说明理由．2018年重庆市中考数学试卷（B卷）参考答案与试题解析一、选择题：（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A，B，C，D的四个答案，其中只有一个是正确的1．【解答】解：A、﹣1是负整数，故选项错误；B、0是非正整数，故选项错误；C、是分数，不是整数，错误；D、1是正整数，故选项正确．故选：D．2．【解答】解：A、不是轴对称图形，故本选项错误；B、不是轴对称图形，故本选项错误；C、不是轴对称图形，故本选项错误；D、是轴对称图形，故本选项正确．故选：D．3．【解答】解：观察图形知：第一个图形有3个正方形，第二个有5＝3+2×1个，第三个图形有7＝3+2×2个，…故第⑥个图形有3+2×5＝13（个），故选：B．4．【解答】解：A、对我市中学生每周课外阅读时间情况的调查，人数众多，意义不大，应采用抽样调查，故此选项错误；B、对我市市民知晓“礼让行人”交通新规情况的调查，人数众多，意义不大，应采用抽样调查，故此选项错误；C、对我市中学生观看电影《厉害了，我的国》情况的调查，人数众多，意义不大，应采用抽样调查，故此选项错误；D、对我国首艘国产航母002型各零部件质量情况的调查，意义重大，应采用普查，故此选项正确；5．【解答】解：3m×2m＝6m2，∴长方形广告牌的成本是120÷6＝20元/m2，将此广告牌的四边都扩大为原来的3倍，则面积扩大为原来的9倍，∴扩大后长方形广告牌的面积＝9×6＝54m2，∴扩大后长方形广告牌的成本是54×20＝1080m2，故选：C．6．【解答】解：A、如果一个数的相反数等于这个数本身，那么这个数一定是0，是真命题；B、如果一个数的倒数等于这个数本身，那么这个数一定是1，是假命题；C、如果一个数的平方等于这个数本身，那么这个数一定是0，是假命题；D、如果一个数的算术平方根等于这个数本身，那么这个数一定是0，是假命题；故选：A．7．【解答】解：，∵7＜＜8，∴5﹣的值应在7和8之间，故选：C．8．【解答】解：∵当x＝7时，y＝6﹣7＝﹣1，∴当x＝4时，y＝2×4+b＝﹣1，解得：b＝﹣9，故选：C．9．【解答】解：作BM⊥ED交ED的延长线于M，CN⊥DM于N．在Rt△CDN中，∵＝＝，设CN＝4k，DN＝3k，∴CD＝10，∴（3k）2+（4k）2＝100，∴CN＝8，DN＝6，∵四边形BMNC是矩形，∴BM＝CN＝8，BC＝MN＝20，EM＝MN+DN+DE＝66，在Rt△AEM中，tan24°＝，∴0.45＝，∴AB＝21.7（米），故选：A．10．【解答】解：连接OD∵OD是⊙O的半径，AC是⊙O的切线，点D是切点，∴OD⊥AC在Rt△AOD中，∵∠A＝30°，AD＝2，∴OD＝OB＝2，AO＝4，∴∠ODB＝∠OBD，又∵BD平分∠ABC，∴∠OBD＝∠CBD∴∠ODB＝∠CBD∴OD∥CB，∴即∴CD＝．故选：B．11．【解答】解：过点D做DF⊥BC于F由已知，BC＝5∵四边形ABCD是菱形∴DC＝5∵BE＝3DE∴设DE＝x，则BE＝3x∴DF＝3x，BF＝x，FC＝5﹣x在Rt△DFC中，DF2+FC2＝DC2∴（3x）2+（5﹣x）2＝52∴解得x＝1∴DE＝1，FD＝3设OB＝a则点D坐标为（1，a+3），点C坐标为（5，a）∵点D、C在双曲线上∴1×（a+3）＝5a∴a＝∴点C坐标为（5，）∴k＝故选：C．12．【解答】解：，解①得x≥﹣3，解②得x≤，不等式组的解集是﹣3≤x≤．∵仅有三个整数解，∴﹣1≤＜0∴﹣8≤a＜﹣3，+＝13y﹣a﹣12＝y﹣2．∴y＝∵y≠2，∴a≠﹣6，又y＝有整数解，∴a＝﹣8或﹣4，所有满足条件的整数a的值之和是（﹣8）+（﹣4）＝﹣12，故选：B．二、填空题：（本大题6个小题，每小题4分，共24分）请将每小题的答案直接填在答题卡中对应的横线上13．【解答】解：|﹣1|+20＝1+1＝2．故答案为：2．14．【解答】解：S阴＝S△ABD﹣S扇形BAE＝×4×4﹣＝8﹣2π，故答案为8﹣2π．15．【解答】解：，故答案为：3416．【解答】解：由题意可得，DE＝DB＝CD＝AB，∴∠DEC＝∠DCE＝∠DCB，∵DE∥AC，∠DCE＝∠DCB，∠ACB＝90°，∴∠DEC＝∠ACE，∴∠DCE＝∠ACE＝∠DCB＝30°，∴∠ACD＝60°，∠CAD＝60°，∴△ACD是等边三角形，∴AC＝CD，∴AC＝DE，∵AC∥DE，AC＝CD，∴四边形ACDE是菱形，∵在Rt△ABC中，∠ACB＝90°，BC＝6，∠B＝30°，∴AC＝，∴AE＝．17．【解答】解：由图象得：小玲步行速度：1200÷30＝40（米/分），由函数图象得出，妈妈在小玲10分后出发，15分时追上小玲，设妈妈去时的速度为v米/分，（15﹣10）v＝15×40，v＝120，则妈妈回家的时间：＝10，（30﹣15﹣10）×40＝200．故答案为：200．18．【解答】解：设A的单价为x元，B的单价为y元，C的单价为z元，当销售这两款袋装粗粮的销售利润率为24%时，该电商销售甲的销售量为a袋，乙的销售量为b袋，由题意，得A一袋的成本是7.5x＝3x+y+z，化简，得y+z＝4.5x；乙一袋的成本是x+2y+2z＝x+2（y+z）＝x+9x＝10x，乙一袋的售价为10x（1+20%）＝12x，甲一袋的售价为10x．根据甲乙的利润，得（10x﹣7.5x）a+20%×10xb＝（7.5xa+10xb）×24%化简，得2.5a+2b＝1.8a+2.4b0.7a＝0.4b＝，故答案为：．三、解答题：（本大题2个小题，每小题8分，共16分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上19．【解答】解：∵∠EFG＝90°，∠E＝35°，∴∠FGH＝55°，∵GE平分∠FGD，AB∥CD，∴∠FHG＝∠HGD＝∠FGH＝55°，∵∠FHG是△EFH的外角，∴∠EFB＝55°﹣35°＝20°．20．【解答】解：（1）调查的总人数为12÷30%＝40（人），所以C项目的人数为40﹣12﹣14﹣4＝10（人）条形统计图补充为：故答案为40人；（2）画树状图为：共有12种等可能的结果数，其中恰好选中1名男生和1名女生担任活动记录员的结果数为8，所以恰好选中1名男生和1名女生担任活动记录员的概率＝＝．四、解答题：（本大题5个小题，每小题10分，共50分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上21．【解答】解：（1）原式＝x2+4xy+4y2﹣x2+y2＝4xy+5y2；（2）原式＝•＝•＝．22．【解答】解：（1）把x＝2代入y＝x，得y＝1，∴A的坐标为（2，1）．∵将直线l1沿y轴向下平移4个单位长度，得到直线l3，∴直线l3的解析式为y＝x﹣4，∴x＝0时，y＝﹣4，∴B（0，﹣4）．将y＝﹣2代入y＝x﹣4，得x＝4，∴点C的坐标为（4，﹣2）．设直线l2的解析式为y＝kx+b，∵直线l2过A（2，1）、C（4，﹣2），∴，解得，∴直线l2的解析式为y＝﹣x+4；（2）∵y＝﹣x+4，∴x＝0时，y＝4，∴D（0，4）．∵B（0，﹣4），∴BD＝8，∴△BDC的面积＝×8×4＝16．23．【解答】解：（1）设2018年前5个月要修建x个沼气池，则2018年前5个月要修建（50﹣x）个垃圾集中处理点，根据题意得：x≥4（50﹣x），解得：x≥40．答：按计划，2018年前5个月至少要修建40个沼气池．（2）修建每个沼气池的平均费用为78÷[40+（50﹣40）×2]＝1.3（万元），修建每个垃圾处理点的平均费用为1.3×2＝2.6（万元）．根据题意得：1.3×（1+a%）×40×（1+5a%）+2.6×（1+5a%）×10×（1+8a%）＝78×（1+10a%），设y＝a%，整理得：50y2﹣5y＝0，解得：y1＝0（不合题意，舍去），y2＝0.1，∴a的值为10．24．【解答】解：（1）如图，∵BF⊥AC，∠ACB＝45°，BC＝12，∴等腰Rt△BCF中，BF＝sin45°×BC＝12，又∵AB＝13，∴Rt△ABF中，AF＝＝5；（2）如图，连接GE，过A作AP⊥AG，交BG于P，连接PE，∵BE＝BA，BF⊥AC，∴AF＝FE，∴BG是AE的垂直平分线，∴AG＝EG，AP＝EP，∵∠GAE＝∠ACB＝45°，∴△AGE是等腰直角三角形，即∠AGE＝90°，△APE是等腰直角三角形，即∠APE＝90°，∴∠APE＝∠P AG＝∠AGE＝90°，又∵AG＝EG，∴四边形APEG是正方形，∴PF＝EF，AP＝AG＝CH，又∵BF＝CF，∴BP＝CE，∵∠APG＝45°＝∠BCF，∴∠APB＝∠HCE＝135°，∴△APB≌△HCE（SAS），∴AB＝EH，又∵AB＝BE，∴BE＝EH．25．【解答】解：（1）根据“极数”的意义得，1287，2376，8712，任意一个“极数”都是99的倍数，理由：设对于任意一个四位数且是“极数”n的个位数字为x，十位数字为y，（x是0到9的整数，y是0到8的整数）∴百位数字为（9﹣x），千位数字为（9﹣y），∴四位数n为：1000（9﹣y）+100（9﹣x）+10y+x＝9900﹣990y﹣99x＝99（100﹣10y﹣x），∵x是0到9的整数，y是0到8的整数，∴100﹣10y﹣x是整数，∴99（100﹣10y﹣x）是99的倍数，即：任意一个“极数”都是99的倍数；（2）设四位数m为“极数”的个位数字为x，十位数字为y，（x是0到9的整数，y是0到8的整数）∴m＝99（100﹣10y﹣x），∵m是四位数，∴m＝99（100﹣10y﹣x）是四位数，即1000≤99（100﹣10y﹣x）＜10000，∵D（m）＝＝3（100﹣10y﹣x），∴30≤3（100﹣10y﹣x）≤303∵D（m）完全平方数，∴3（100﹣10y﹣x）既是3的倍数也是完全平方数，∴3（100﹣10y﹣x）只有36，81，144，225这四种可能，∴D（m）是完全平方数的所有m值为1188或2673或4752或7425．五、解答题：（本大题1个小题，共12分）解答时每小题必须给出必要的演算过程或推理步骤，请将解答书写在答题卡中对应的位置上26．【解答】解：（1）如图1，过点D作DK⊥y轴于K，当x＝0时，y＝，∴C（0，），y＝﹣x2﹣x+＝﹣（x+）2+，∴D（﹣，），∴DK＝，CK＝﹣＝，∴CD＝＝＝；（4分）（2）在y＝﹣x2﹣x+中，令y＝0，则﹣x2﹣x+＝0，解得：x1＝﹣3，x2＝，∴A（﹣3，0），B（，0），∵C（0，），易得直线AC的解析式为：y＝，设E（x，），P（x，﹣x2﹣x+），∴PF＝﹣x2﹣x+，EF＝，Rt△ACO中，AO＝3，OC＝，∴AC＝2，∴∠CAO＝30°，∴AE＝2EF＝，∴PE+EC＝（﹣x2﹣x+）﹣（x+）+（AC﹣AE），＝﹣﹣x+[2﹣（）]，＝﹣﹣x﹣x，＝﹣（x+2）2+，（5分）∴当PE+EC的值最大时，x＝﹣2，此时P（﹣2，），（6分）∴PC＝2，∵O1B1＝OB＝，∴要使四边形PO1B1C周长的最小，即PO1+B1C的值最小，如图2，将点P向右平移个单位长度得点P1（﹣，），连接P1B1，则PO1＝P1B1，再作点P1关于x轴的对称点P2（﹣，﹣），则P1B1＝P2B1，∴PO1+B1C＝P2B1+B1C，∴连接P2C与x轴的交点即为使PO1+B1C的值最小时的点B1，∴B1（﹣，0），将B1向左平移个单位长度即得点O1，此时PO1+B1C＝P2C＝＝，对应的点O1的坐标为（﹣，0），（7分）∴四边形PO1B1C周长的最小值为+3；（8分）（3）O2M的长度为或或2+或2．（12分）理由是：如图3，∵H是AB的中点，∴OH＝，∵OC＝，∴CH＝BC＝2，∴∠HCO＝∠BCO＝30°，∵∠ACO＝60°，∴将CO沿CH对折后落在直线AC上，即O2在AC上，∴∠B2CA＝∠CAB＝30°，∴B2C∥AB，∴B2（﹣2，），①如图4，AN＝MN，∴∠MAN＝∠AMN＝30°＝∠O2B2O3，由旋转得：∠CB2C1＝∠O2B2O3＝30°，B2C＝B2C1，∴∠B2CC1＝∠B2C1C＝75°，过C1作C1E⊥B2C于E，∵B2C＝B2C1＝2，∴＝B 2O2，B2E＝，∵∠O2MB2＝∠B2MO3＝75°＝∠B2CC1，∠B2O2M＝∠C1EC＝90°，∴△C1EC≌△B2O2M，∴O2M＝CE＝B2C﹣B2E＝2﹣；②如图5，AM＝MN，此时M与C重合，O2M＝O2C＝，③如图6，AM＝MN，∵B2C＝B2C1＝2＝B2H，即N和H、C1重合，∴∠CAO＝∠AHM＝∠MHO2＝30°，∴O2M＝AO2＝；④如图7，AN＝MN，过C1作C1E⊥AC于E，∴∠NMA＝∠NAM＝30°，∵∠O3C1B2＝30°＝∠O3MA，∴C1B2∥AC，∴∠C1B2O2＝∠AO2B2＝90°，∵∠C1EC＝90°，∴四边形C1EO2B2是矩形，∴EO 2＝C1B2＝2，，∴EM＝，∴O2M＝EO2+EM＝2+，综上所述，O2M的长是或或2+或2．。

2018年重庆市中考数学试卷(B)

2018年重庆市初中学业水平暨高中招生考试数学试题( B 卷)(全卷共五个大题，满分150分。

参考公式：抛物线2(0)y ax bx c a =++≠的顶点坐标为24,24b ac b a a ⎛⎫- ⎪⎝⎭,对称轴为2b x a =。

1.下列四个数中，是正整数的是( ) A.-1 B.0 C.21 D.1 2下列图形中，是轴对称图形的是( )3.下列图形都是由同样大小的黑色正方形纸片组成,其中第①个图中有3张黑色正方形纸片，第②个图中有5张黑色正方形纸片,第③个图中有7张黑色正方形纸片,..，按此规律排列下去,第⑥个图中黑色正方形纸片的张数为( )A.11B.13C.15D.174.下列调查中，最适合采用全面调查(普查)的是( )A.对我市中学生每周课外阅读时间情况的调查B.对我市市民知晓“礼让行人”交通新规情况的调查C.对我市中学生观看电影(厉害了，我的国》情况的调查D.对我国首艘国产航母002型各零部件质量情况的调查5.制作一块m m 23⨯长方形广告牌的成本是120元,在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，那么扩大后长方形广告牌的成本是( )A.360元B.720元C.1080元D.2160元6.下列命题是真命题的是( )A.如果一个数的相反数等于这个数本身，那么这个数一定是0 。

B.如果一个数的倒数等于这个数本身，那么这个数一定是1 。

C.如果一个数的平方等于这个数本身，那么这个数定是0 。

2018重庆中考数学试题b卷及答案

2018重庆中考数学试题b卷及答案第一节选择题1. 化简下列代数式：(3x - 2y)² - (x - 3y)²解析：展开后进行简化得：5x² - 8xy + 5y²2. 已知函数 y=f(x) 的图象关于 x 轴对称，且当 x=1 时，y=f(1)=-4，若点 (1,5) 在图象 y=f(2x^2-3) 上，则 y=f(x) 的图象关于 y 轴对称。

3. 一根梯子的上端顶在墙上的高度是1.5m，且距墙底4.6m。

一只猫顺梯子爬上去，当爬到梯子的上端时，发现梯子下端离墙的距离比顶端离墙的距离多0.9m。

求梯子的长。

第二节解答题1. 已知一棵花的种子经过 20 天开花，经过 40 天就会开枯。

已知这样一棵树从 8 月 1 日开始种植，开花之后 20 天会结出 300 个果实，每天结的果实数是上一天结的果实数的 2 倍。

问：9 月 1 日这一天有多少果实？解析：逆推法，从 8 月 25 日（40 天前）开始往回计算每一天的果实数，因此可得 8 月 6 日的果实数为 300 / 2^3 = 37.5（取整为 37），所以 9 月 1 日的果实数是 37 * 2^6 = 2368 个。

2. 一个底面是菱形的金字塔，底面边长为 6，塔尖到底面中心的垂线长为 5，求这个金字塔的体积。

解析：根据勾股定理可得，金字塔的高度是√(5²-3²)=√16=4。

再根据体积计算公式：V = (1/3) * 底面面积 * 高度 = (1/3) * (6²) * 4 = 48。

3. 有一架飞机从 A 地到 B 地，全程 7 千米。

飞机是沿直线航线飞行的，中间途经 C、D 两地。

飞机自起飞后，先行驶 2.5 千米达 C 地，再转向飞行，与水平线呈 30°的上升角继续飞行至 D 地，最后再转向飞行。

已知 AB 的距离等于 BC 的距离，求 CD 的长度。

2018年重庆市中考数学试卷(B)

2018年重庆市初中学业水平暨高中招生考试数学试题( B 卷)(全卷共五个大题，满分150分。

参考公式：抛物线2(0)y ax bx c a =++≠的顶点坐标为24,24b ac b a a ⎛⎫- ⎪⎝⎭,对称轴为2bx a =。

1.下列四个数中，是正整数的是( ) A.-1 B.0 C.21D.1 2下列图形中，是轴对称图形的是( )3.下列图形都是由同样大小的黑色正方形纸片组成,其中第①个图中有3张黑色正方形纸片，第②个图中有5张黑色正方形纸片,第③个图中有7张黑色正方形纸片,..，按此规律排列下去,第⑥个图中黑色正方形纸片的张数为( )A.11B.13C.15D.17 4.下列调查中，最适合采用全面调查(普查)的是( ) A.对我市中学生每周课外阅读时间情况的调查B.对我市市民知晓“礼让行人”交通新规情况的调查C.对我市中学生观看电影(厉害了，我的国》情况的调查D.对我国首艘国产航母002型各零部件质量情况的调查5.制作一块m m 23⨯长方形广告牌的成本是120元,在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，那么扩大后长方形广告牌的成本是( ) A.360元 B.720元 C.1080元 D.2160元6.下列命题是真命题的是( )A.如果一个数的相反数等于这个数本身，那么这个数一定是0 。

B.如果一个数的倒数等于这个数本身，那么这个数一定是1 。

C.如果一个数的平方等于这个数本身，那么这个数定是0 。

2018年重庆中考数学试卷(B卷)(含解析)

重庆市2018年初中学业水平暨高中招生考试数学试题（B卷）（全卷共五个大题，满分150分，考试时间120分钟）注意事项1．试题的答案书写在答题卡上，不得在试卷上直接作答；2．作答前认真阅读答题卡上的注意事项；3．作图（包括作辅助线）请一律用黑色签字笔完成；4．考试结束，由监考人员将试题和答题卡一并收回．参考公式：抛物线y＝ax2＋bx＋c（a≠0）的顶点坐标为（－2ba，244ac ba），对称轴为x＝－2ba．一、选择题（本大题12个小题，每小题4分，共48分．在每小题所给的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置．．．．．．．上）1．（2018·重庆B卷，1，4）下列四个数中，是正整数的是（）A．－1 B．0 C．12D．1【答案】D．【解析】易知－1是负整数，12是分数，1是正整数，而整数包括正整数、0和负整数，故选D．【知识点】实数的概念整数正整数．2．（2018·重庆B卷，2，4）下列图形中，是轴对称图形的是（）【答案】D．【解析】根据轴对称图形的定义，沿某条直线将图形折叠，直线两旁的部分能够完全重合的图形才是轴对称图形，故只有选项D满足要求，因此选D．【知识点】图形的变换轴对称图形．3．（2018·重庆B卷，3，4）下列图形都是由同样大小的黑色正方形纸片组成，其中第①个图形中有3张黑色正方形纸片，第②个图形中有5张黑色正方形纸片，第③个图形中有7张黑色正方形纸片，…，按此规律排列下去，第⑥个图形中黑色正方形纸片的张数为（）③②①A．B．C．D．A．11 B．13 C．15 D．17【答案】B．【解析】根据第1个图形中小正方形的个数为2×1＋1，第1个图形中小正方形的个数为2×1＋1，第2个图形中小正方形的个数为2×2＋1；第3个图形中小正方形的个数为2×3＋1，……，第n个图形中小正方形的个数为2n＋1，故第6个图形中小正方形的个数为2×6＋1＝13，故选B．【知识点】规律探究题代数式代数式的值．4．（2018·重庆B卷，4，4）下列调查中，最适合采用全面调查（普查）的是（）A．对我市中学生每周课外阅读时间情况的调查B．对我市市民知晓“礼让行人”交通新规情况的调查C．对我市中学生观看电影《厉害了，我的国》情况的调查D．对我国首艘国产航母002型各零部件质量情况的调查【答案】D．【解析】选项A、B、C中，调查的对象的数量多，分布广，不适合普查；选项D中，由于对我国首艘国产航母002型各零部件质量情况的调查，每一个零部件都不能有任何的疏忽懈怠，必须一个一个检查，要采用普查方式，故选择D．【知识点】普查与抽样调查5．（2018·重庆B卷，5，4）制作一块3m×2m长方形广告牌的成本是120元，在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大到原来的3倍，那么扩大后长方形广告牌的成本是（）A．360元B．720元C．1080元D．2160元【答案】C．【解析】∵将此广告牌的四边都扩大到原来的3倍后面积为原长方形面积的9倍，而120×9＝1080（元），∴扩大后长方形广告牌的成本是1080元．故选C．【知识点】有理数的应用6．（2018·重庆B卷，6，4）下列命题是真命题的是（）A．如果一个数的相反数等于这个数的本身，那么这个数一定是0B．如果一个数的倒数等于这个数本身，那么这个数一定是1C．如果一个数的平方等于这个数的本身，那么这个数一定是0D．如果一个数的算术平方根等于这个数的本身，那么这个数一定是0【答案】A．【解析】易知A选项正确，因为倒数等于其本身的数是±1，平方数等于其本身的数有0和1，算术平方根等于其本身的数有0和1，故选A．【知识点】有理数的概念相反数倒数平方数算术平方根7．（2018·重庆B卷，7，4）估计的值应在（）A．5和6之间B．6和7之间C．7和8之间D．8和9之间【答案】C．【解析】∵－＝7＝8，∴7和8之间，故选C．【知识点】二次根式的计算估算8．（2018·重庆B卷，8，4）根据如图所示的程序计算函数y的值，若输入的x的值是4或7时，输出的y的值相等，则b 等于（）A ．9B ． 7C ．－9D ．－7【答案】C ．【解析】由题意得2×4＋b ＝6－7，解得b ＝－9，故选C ．【知识点】代数式求代数式的值程序求值题函数值分段函数9．（2018·重庆B 卷，9，4）如图，AB 是一垂直于水平面的建筑物．某同学从建筑物底端B 出发，先沿水平方向向右行走20米到达点C ，再经过一段坡度（或坡比）为i ＝1﹕0.75、坡长为10米的斜坡CD 到达点D ，然后再沿水平方向向右行走40米到达点E （A ，B ，C ，D ，E 均在同一平面内）．在E 处测得建筑物顶端A 的仰角为24°，则建筑物AB 的高度约为（参考数据：sin24°≈0.41，cos24°≈0.91，tan24°≈0.45）（）A ．21.7米B ．22.4米C ．27.4米D ．28.8米【答案】A ．【解析】过点C 作CN ⊥DE 于点N ，延长AB 交ED 的延长线于点M ，则BM ⊥DE 于点M ，则MN ＝BC ＝20米．∵斜坡CD 的坡比i ＝1﹕0.75，∴令CN ＝x ，则DN ＝0.75x ．在Rt △CDN 中，由勾股定理，得x 2＋(0.75x )2＝102，解得x ＝8，从而CN ＝8米，DN ＝6米．∵DE ＝40米，∴ME ＝MN ＋ND ＋DE ＝66米，AM ＝(AB ＋8)米．在Rt △AME 中，tan E ＝AMEM，即8tan 2466AB +=︒，从而0.45＝866AB +，解得AB ＝21.7，故选A ．【知识点】解直角三角形坡度9题图8题图10．（2018·重庆B 卷，10，4）如图，△ABC 中，∠A ＝30°，点O 是边AB 上一点，以点O 为圆心，以OB为半径作圆，⊙O 恰好与AC 相切于点D ，连接BD ．若BD 平分∠ABC ，AD ＝，则线段CD 的长是（）A ．2 BC ．32 D【答案】B ．【解析】如下图，连接OD ，则由AD 切⊙O 于点D ，得OD ⊥AC ．∵在Rt △AOD 中，∠A ＝30°，AD ＝，tan A ＝ODAD， ∴OD ＝AD •，tanA ＝tan30°＝3＝2． ∴AO ＝2OD ＝4，AB ＝OA ＋OB ＝6． ∵∠AOD ＝90°－∠A ＝60°， ∴∠ABD ＝12∠AOD ＝30°． ∵BD 平分∠ABC ，∴∠ABC ＝2∠ABD ＝60°． ∴∠C ＝90°＝∠ADO ． ∴OD ∥BC ． ∴AD AODC OB=42=． ∴DC【知识点】圆圆的切线相似三角形11．（2018·重庆B 卷，11，4）如图，菱形ABCD 的边AD ⊥y 轴，垂足为点E ，顶点A 在第二象限，顶点B10题图在y 轴的正半轴上，反比例函数y ＝kx（k ≠0，x ＞0）的图象同时经过顶点C ，D ．若点C 的横坐标为5，BE ＝3DE ，则k 的值为（） A ．52 B ．3 C ．154D ．5【答案】C ．【解析】．∵菱形ABCD 的边AD ⊥y 轴，点C 的横坐标为5， ∴BC ＝5，DE ＝1． ∵BE ＝3DE ， ∴BE ＝3．令OB ＝m ，则OE ＝m ＋3，C (5，m )，D (1，m ＋3)，由C 、D 两点均在双曲线y ＝kx上，得5m ＝m ＋3，解得m ＝34，从而k ＝5m ＝154，故选C ．【知识点】反比例函数菱形反比例函数的图像与性质12．（2018·重庆B 卷，12，4）若数a 使关于x 的不等式组111(1)3223(1)x x x a x ⎧-≤-⎪⎨⎪-≤-⎩有且仅有三个整数解，且使关于y的分式方程312122y a y y++=--有整数解，则满足条件的所有a 的值之和是（）A ．－10B ．－12C ．－16D ．－18 【答案】B ．【解析】解不等式组，得－3≤x ≤35a +，由该不等式组有且仅有三个整数解，得－1≤35a +＜0，从而－8≤a ＜－3．解方程312122y a y y ++=--，得y ＝2a＋5．又∵y ≠2，即2a＋5≠2， ∴a ≠－6．又∵y 为整数，∴满足条件的整数a 为－8和－4，其和为－12．故选B ．【知识点】一元一次不等式组的解法分式方程的解法11题图二、填空题（本大题6个小题，每小题4分，共24分）请将每小题的答案直接填在答题卡中对应的横线上）．13．（2018·重庆B卷，13，4）计算：1-＋20＝．【答案】2．【解析】∵原式＝1＋1＝2，∴答案为2．【知识点】实数的运算绝对值零指数14．（2018·重庆B卷，14，4）如图，在边长为4的正方形ABCD中，以点B为圆心，以AB为半径画弧，交对角线BD于点E，则图中阴影部分的面积是（结果保留π）．【答案】8－2π．【解析】∵正方形ABCD的边长为4，∴∠BAD＝90°，∠ABD＝45°，AB＝AD＝4．∴S阴影＝S Rt△ABD－S扇形BAE＝12×4×4－2454360π⋅＝8－2π．【知识点】圆的有关计算扇形面积正方形15．（2018·重庆B卷，15，4）某企业对一工人在五个工作日里生产零件的数量进行调查，并绘制了如图所示的折线统计图，则在这五天里该工人每天生产零件的平均数年是个．【答案】34．【解析】由图可知这组数据是36，34，31，34，35，故x＝15(36＋34＋31＋34＋35)＝15×170＝34，因此答案为34．14题图15题图期五期四期三期二期一【知识点】．统计平均数折线统计图16．（2018·重庆B 卷，16，4）如图，在Rt △ABC 中，∠ACB ＝90°，BC ＝6，CD 是斜边AB 上的中线，将△BCD 沿直线CD 翻折至△ECD 的位置，连接AE ．若DE ∥AC ，计算AE 的长度等于．【答案】．【解析】∵在Rt △ABC 中，∠ACB ＝90°，BC ＝6，CD 是斜边AB 上的中线， ∴CD ＝12AB ＝DA ＝DB ．令∠B ＝x °，则∠DCB ＝∠B ＝x °，由翻折知，DE ＝DB ，∠ECD ＝∠DCB ＝x °＝∠CED ． ∵DE ∥AC ，∴∠ACE ＝∠CED ＝x °．∴由∠ACB ＝90°，得3x ＝90，x ＝30，从而∠B ＝30°，于是AC ＝12AB ．在Rt △ABC 中，tan B ＝ACBC，得AC ＝BC tan B ＝6tan30°＝∴AC ∥DE ，AC ＝DE ，从而四边形ACDE 是平行四边形．又∵CD ＝DE ，∴四边形ACDE 是菱形． ∴AE ＝AC ＝OEDC BA【知识点】翻折直角三角形菱形三角函数17．（2018·重庆B 卷，17，4）一天早晨，小玲从家出发匀速步行到学校．小玲出发一段时间后，她的妈妈发现小玲忘带了一件必需的学习用品，于是立即下楼骑自行车，沿小玲行进的路线，匀速去追小玲．妈妈追上小玲将学习用品交给小玲后，立即沿原路线匀速返回家里，但由于路上行人渐多，妈妈返回时骑车的速度只是原来的一半．小玲继续以原速度步行前往学校．妈妈与小玲之间的距离y （米）与小玲从家出发后步行的时间x （分）之间的函数关系如图所示（小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计）．当妈妈刚回到家时，小玲离学校的距离为米．16题图EDCBA【答案】200．【解析】由图可知：玲玲用30分钟从家里步行到距家1200米的学校，因此玲玲的速度为40米/分；妈妈在玲玲步行10分钟后从家时出发，用5分钟追上玲玲，因此妈妈的速度为40×15÷5＝120米/分，返回家的速度为120÷2＝60米/分．设妈妈用x 分钟返回到家里，则60x ＝40×15，解得x ＝10，此时玲玲已行走了25分钟，共步行25×40＝1000米，还离学校1200－1000＝200（米），故答案为200．【知识点】一次函数的实际应用18．（2018·重庆B 卷，18，4）为实现营养套餐的合理搭配，某电商推出两款适合不同人群的甲、乙两种袋装的混合粗粮．甲种袋装粗粮每袋含有3千克A 粗粮，1千克B 粗粮，1千克C 粗粮；乙种袋装粗粮每袋含有1千克A 粗粮，2千克B 粗粮，2千克C 粗粮．甲、乙两种袋装粗粮每袋成本分别等于袋中的A 、B 、C 三种粗粮的成本之和．已知每袋甲粗粮的成本是每千克A 种粗粮成本的7.5倍，每袋乙种粗粮售价比每袋甲种粗粮的售价高20%，乙种袋装粗粮的销售利润率是20%．当销售这两款袋装粗粮的销售利润率为24%时，该电商销售甲、乙两种袋装粗粮的袋数之比是．（商品的销售利润率＝100%-⨯商品的售价商品的成本价商品的成本价）【答案】4﹕7．【解析】设1千克A 粗粮的成本为m 元，则甲袋成本为7.5m 元，且B 、C 两种粗粮各1千克的成本之和为7.5m －3m ＝4.5m 元，从而乙袋粗粮的成本为m ＋2×4.5m ＝10m 元，由乙种袋装粗粮的销售利润率是20%，得乙种袋装粗粮的销售利润为10m ×20%＝2m 元；而由每袋乙种粗粮售价比每袋甲种粗粮的售价高20%，知甲种袋装粗粮的售价为12m ÷(1＋20%)＝10m 元，其利润为2.5m 元，现将以上信息列表如下：2m2.5m10m 12m 10m 7.5m221113CBA每袋粗粮组成成分（千克）每袋售价（元）每袋成本（元）每袋利润（元）乙袋甲袋设甲袋装粗粮销售x 袋，乙袋装粗粮销售y 袋时，销售这两款袋装粗粮的销售利润率为24%，根据题意，得2.5224%7.510m x m ym x m y⋅+⋅=⋅+⋅，整理，得7x ＝4y ，从而x ﹕y ＝4﹕7，故答案为4﹕7．【知识点】方程组的应用销售问题三、解答题（本大题2个小题，每小题8分，共16分）解答时每小题必须给出必要的演算过程或推理步骤，画17题图分出必要的图形，请将解答过程书写在答题卡中对应的位置上．19．（2018·重庆B 卷，19，8）如图，AB ∥CD ，△EFG 的顶点F ，G 分别落在直线AB ，CD 上，GE 交AB 于点H ，GE 平分∠FGD ．若∠EFG ＝90°，∠E ＝35°，求∠EFB 的度数．【思路分析】本题解答分四步走：一是由三角形内角和定理，求出∠EGF ＝55°；二是由角平分线定义，得∠EGD ＝55°；三是由平行线性质，得∠EHB ＝55°；四是由三角形外角性质，求得∠EFB ＝∠EGB －∠E ＝55°－35°＝20°．【解题过程】19．解：∵在△EFG 中，∠EFG ＝90°，∠E ＝35°，∴∠EGF ＝90°－∠E ＝55°． ∵GE 平分∠FGD ，∴∠EGF ＝∠EGD ＝55°． ∵AB ∥CD ，∴∠EHB ＝∠EGD ＝55°．又∵∠EHB ＝∠EFB ＋∠E ，∴∠EFB ＝∠EGB －∠E ＝55°－35°＝20°．【知识点】平行线三角形内角和角平分线20．（2018·重庆B 卷，20，8）某学校开展以素质提升为主题的研学活动，推出了以下四个项目供学生选择：A ．模拟驾驶；B ．军事竞技；C ．家乡导游；D ．植物识别．学校规定：每个学生都必须报名且只能选择其中一个项目．八年级（3）班班主任刘老师对全班学生选择的项目情况进行了统计，并绘制了如下两幅不完整的统计图．请结合统计图中的信息，解决下列问题：（1）八年级（3）班学生总人数是___________，并将条形统计图补充完整；（2）刘老师发现报名参加“植物识别”的学生中恰有两名男生，现准备从这些学生中任意挑选两名担任活动记录员，请用列表或画树状图的方法，求恰好选中1名男生和1名女生担任活动记录员的概率．【思路分析】数．（1）由条形图可知，A 选项有12人；由扇形图可知，A 选项占全班人数的30%，两者相除即可得到全班总人数为40；再用全班人数分别减去A 、B 、D 三个选项的人数可知C 选项的人数为10人，在条形图中补图即可；（2）由条形图知D 选项有4人，且男生有2人，用列表法或画树状图法，可求得恰好选中1名H GFEDCBA19题图20题图DCBA 30%八年级（3）班研学项目选择情况的扇形统计图八年级（3）班研学项目选择情况的条形统计图男生和1名女生担任活动记录员的概率为23．【解题过程】 20．解：（1）∵12÷30%＝40（人），40－12－14－4＝10（人），∴八年级（3）班学生总人数是40，补图如下：八年级（3）班研学项目选择情况的条形统计图（2）由题意可知从4名学生（其中男、女生各2人）任选2人，记男生为a 1，a 2，女生为b 1，b 2，现列表和画树状图分别如下：(b 2,b 1)(b 2,a 2)(b 2,a 1)(b 1,b 2)(b 1,a 1)(a 2,b 2)(a 2,b 1)(a 1,b 2)(b 1,a 2)(a 2,a 1)(a 1,b 1)(a 1,a 2)b 1b 2a 1a 2b 2b 1a 2a 1(b 2,b 1)(b 2,a 2)(b 2,a 1)(b 1,b 2)(b 1,a 2)(b 1,a 1)(a 2,b 2)(a 2,b 1)(a 2,a 1)(a 1,b 2)(a 1,b 1)(a 1,a 2)结果：第2人：第1人：开始b 2a 1a 21a 1a 2b 1b 21a 2b 2a 1a 2b 1b 1b 2由上面表格或树状图可知，共有12种等可能结果，其中“恰好选中1名男生和1名女生担任活动记录员”的共有8种，故P (恰好选中1名男生和1名女生担任活动记录员)＝812＝23．【知识点】统计概率条形统计图扇形统计图列表法或画树状图求概率四、解答题（本大题5个小题，每小题10分，共50分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上．21．（2018·重庆B 卷，21，10）计算：（1）(x ＋2y )2－(x ＋y )(x －y )；（2）(a －1－411a a -+)÷28161a a a -++．【思路分析】（1）利用乘法公式将式子展开，然后合并同类项即可得到结果；（2）按分式的运算法则和运算顺序进行计算即可，注意结果的化简．【解题过程】 21．解：（1）原式＝x 2＋4xy ＋4y 2－(x 2－y 2)＝x 2＋4xy ＋4y 2－x 2＋y 2＝4xy ＋5y 2．（2）原式＝2(1)(1)(41)11(4)a a a a a a -+--+⋅+- ＝2(4)11(4)a a a a a -+⋅+- ＝4a a -．【知识点】整式的乘法乘法公式分式的运算22．（2018·重庆B 卷，22，10）如图，在平面直角坐标系中，直线l 1：y ＝12x 与直线l 2交点A 的横坐标为2，将直线l 1沿y 轴向下平移4个单位长度，得到直线l 3，直线l 3与y 轴交于点B ，与直线l 2交于点C ，点C 的纵坐标为－2，直线l 2与y 轴交于点D ．（1）求直线l 2的解析式；（2）求△BDC 的面积．【思路分析】（1）先求出点A 的坐标，再由平移求出直线l 3的为y ＝12x －4，进而求出点C 的坐标；直线l 2的解析式为y ＝kx ＋b ，将A 、C 两点坐标代入得方程组解答即可锁定直线l 2的解析式；（2）先求出B 、D 两点坐标，进而得到线段BD 的长，C 点的横坐标的绝对值即为△BDC 的边BD 上的高，由三角形的面积公式计算即可．【解题过程】 22．解：（1）在y ＝12x 中，当x ＝2时，y ＝1；易知直线l 3的解析式为y ＝12x －4，当y ＝－2时，x ＝4，故A (2，1)，C (4，－2)．设直线l 2的解析式为y ＝kx ＋b ，则2142k b k b +=⎧⎨+=-⎩，解得324k b ⎧=-⎪⎨⎪=⎩，故直线l 2的解析式为y＝－32x ＋4．（2）易知D (0，4)，B (0，－4)，从而DB ＝8．由C (4，－2)，知C 点到y 轴的距离为4，故S △BDC ＝12BD •C x ＝12×8×4＝16．【知识点】一次函数的应用平移一次函数解析式的求法23．（2018·重庆B 卷，23，10）在美丽乡村建设中，某县政府投入专项资金，用于乡村沼气池和垃圾集中处理点建设．该县政府计划：2018年前5个月，新建沼气池和垃圾集中处理点共计50个，且沼气池的个数不低于垃圾集中处理点个数的4倍．（1）按计划，2018年前5个月至少要修建多少个沼气池？（2）到2018年5月底前，该县按原计划刚好完成了任务，共花费资金78万元，且修建的沼气池个数恰好是原计划的最小值．据核算，前5个月，修建每个沼气池与垃圾集中处理点的平均费用之比为1﹕2．为加大美丽乡村建设的力度，政府计划加大投入，今年后7个月，在前5个月花费资金的基础上增加投入10a %，全部用于沼气池和垃圾集中处理点建设．经测算：从今年6月起，修建每个沼气池与垃圾集中处理点的平均费用在2018年前5个月的基础上分别增加a %，5a %，新建沼气池与垃圾集中处理点的个数将会在2018年前5个月的基础上分别增加5a %，8a %．求a 的值．【思路分析】（1）根据“沼气池的个数不低于垃圾集中处理点个数的4倍”列不等式，并求不等式的最小整数解即可；（2）先求出到2018年5月底前，该县修建的沼气池40个，修建垃圾集中处理点10个；再求出前5个月修建每个沼气池与垃圾集中处理点的平均费用；最后根据题意，列出关于a 的一元二次方程，解方程即可求出a 的值．【解题过程】 23．解：（1）设2018年前5个月要修建x 个沼气池，则修建垃圾集中处理点(50－x )个，根据题意，得x ≥4(50－x )，解得x ≥40．答：按计划，2018年前5个月至少要修建40个沼气池．（2）由题意可知，到2018年5月底前，该县修建的沼气池40个，修建垃圾集中处理点10个，若令修建的沼气池每个y 元，则修建的垃圾集中处理点的每个2y 元，从而由题意得40y ＋10×2y ＝78，解得y ＝1.3，即到2018年5月底前，修建的每个沼气池与垃圾集中处理点的费用分别为1.3万元和2.6万元．根据题意，得40•(1＋5a %)•1.3(1＋a %)＋10•(1＋8a %)•2.6(1＋5a %)＝78•(1＋10a %)．令a %＝t ，则52(1＋5t )(1＋t )＋26(1＋8t )(1＋5t )＝78(1＋10t )，整理，得 10t 2－t ＝0，解得t 1＝0.1，t 2＝0（不合题意，舍去），从而a %＝0.1，a ＝10．答：a 的值为10．【知识点】一元一次不等式的应用一元二次方程的应用24．（2018·重庆B 卷，24，10）如图，在□ABCD 中，∠ACB ＝45°，点E 在对角线AC 上，BE ＝BA ，BF ⊥AC 于点F ，BF 的延长线交AD 于点G ．点H 在BC 的延长线上，且CH ＝AG ，连接EH ．（1）若BC ＝，AB ＝13，求AF 的长；（2）求证：EB ＝EH ．【思路分析】（1）在Rt △FBC 中，由sin ∠FCB ＝BFBC，求出BF ＝×sin45°＝×2＝12；在Rt△ABF 中，由勾股定理，得AF5．（2）本题有两种证法，一是在BF 上取点M ，使AM ＝AG ，连接ME 、GE ．通过证明四边形AMEG 是正方形，进而得到∠AMB ＝∠HCE ＝45°，BM ＝CE ，AM ＝CH ，于是△AMB ≌△CHE ，从而EH ＝AB ，进而EB ＝EH ．第二种方法是连接EG ，GH ．通过证明△GBE ≌△GHE （SAS ）锁定答案．24题图HG FEDC BA【解题过程】 24．解：（1）∵BF ⊥AC ，∴∠BFC ＝∠AFB ＝90°．在Rt △FBC 中，sin ∠FCB ＝BFBC，而∠ACB ＝45°，BC ＝， ∴sin45． ∴BF ＝sin45°＝×2＝12．在Rt △ABF 中，由勾股定理，得AF=5．（2）方法一：如下图，在BF 上取点M ，使AM ＝AG ，连接ME 、GE ．MABC DEF G H∵∠BFC ＝90°，∠ACB ＝45°，∴△FBC 是等腰直角三角形． ∴FB ＝FC ．∵在□ABCD 中，AD ∥BC ， ∴∠GAC ＝∠ACB ＝45°． ∴∠AGB ＝45°．∵AM ＝AG ，AF ⊥MG ，∴∠AMG ＝∠AGM ＝45°，MF ＝GF ． ∴∠AMB ＝∠ECG ＝135°． ∵BA ＝BE ，BF ⊥AE ， ∴AF ＝EF ．∴四边形AMEG 是正方形． ∴FM ＝FE ． ∴BM ＝CE ．又∵CH ＝AG ， ∴CH ＝AM ．∴△AMB ≌△CHE ． ∴EH ＝AB ． ∴EH ＝EB ．方法二：如下图，连接EG ，GH ．A BC DEFG H∵BF ⊥AC 于点F ，BA ＝BE ， ∴∠ABF ＝∠EBF ． ∵GB ＝GB ，∴△GBA ≌△GBE （SAS ）． ∴∠AGB ＝∠EGB ．在△FBC 中，∵∠BFC ＝90°，∠ACB ＝45°， ∴∠FBC ＝45°．∵在□ABCD 中，AD ∥BC ，∴∠GAC ＝∠ACB ＝45°，∠AGB ＝∠FBC ＝45°． ∴∠EGB ＝45°． ∵CH ＝AG ，∴四边形AGHC 是平行四边形． ∴∠BHG ＝∠GAC ＝45°． ∴∠BHG ＝∠GBH ＝45°． ∴GB ＝GH ，∠BGH ＝90°． ∴∠HGE ＝∠BGE ＝45°． ∵GE ＝GE ，∴△GBE ≌△GHE （SAS ）． ∴EH ＝EB ．【知识点】勾股定理等腰三角形的性质全等三角形平行四边形 25．（2018·重庆B 卷，25，10）对任意一个四位数n ，如果千位与十位上的数字之和为9，百位与个位上的数字之和也为9，则称n 为“极数”．（1）请任意写出三个“极数”；并猜想任意一个“极数”是否是99的倍数，请说明理由；（2）如果一个正整数a 是另一个正整数b 的平方，则称正整数a 是完全平方数．若四位数m 为“极数”，记D (m )＝33m，求满足D (m )是完全平方数的所有m ．【思路分析】（1）先根据“极数”的定义，较易写出千位与十位上的数字之和为9且百位与个位上的数字之和为9的四位数三个，答案不唯一；再设n 的千位数字为s ，百位数字为t （1≤s ≤9，0≤t ≤9且s 、t 均为整数），用代数式表示出n ，化简后因式分解，即可证明n 是99的倍数；（2）先求出D (m )＝33m，其中m ＝1000s ＋100t ＋10(9－s )＋9－t ，化简后得D (m )＝33m＝3(10s ＋t ＋1)；再根据D (m )是完全平方数，且10s ＋t ＋1是一个两位数，从而10s ＋t ＋1＝3×22、3×32、3×42、3×52，即10s ＋t ＋1＝12或27或48或75，于是得到方程组112s t =⎧⎨+=⎩或217s t =⎧⎨+=⎩或418s t =⎧⎨+=⎩或715s t =⎧⎨+=⎩，解方程组即可锁定符合条件的所有m ．【解题过程】25．解：（1）答案不唯一，如5346，1782，9405，等．任意一个“极数”都是99的倍数，理由如下：设n 的千位数字为s ，百位数字为t （1≤s ≤9，0≤t ≤9且s 、t 均为整数），则n ＝1000s ＋100t ＋10(9－s )＋9－t ＝990s ＋99t ＋99＝99(10s ＋t ＋1)，而10s ＋t ＋1是整数，故n 是99的倍数．（2）易由（1）设m ＝1000s ＋100t ＋10(9－s )＋9－t ＝990s ＋99t ＋99＝99(10s ＋t ＋1)，其中1≤s ≤9，0≤t ≤9且s 、t 均为整数，从而D (m )＝33m＝3(10s ＋t ＋1)，而D (m )是完全平方数，故3(10s ＋t ＋1)是完全平方数． ∵10＜10s ＋t ＋1＜100， ∴30＜3(10s ＋t ＋1)＜300．∴10s ＋t ＋1＝3×22、3×32、3×42、3×52． ∴(s ，t )＝(1，1)，(2，6)，(4，7)，(7，4)． ∴m ＝1188，2673，4752，7425．【知识点】整式的运算完全平方数不等式的解法新定义运算题二元一次方程的特殊解五、解答题（本大题1个小题，共12分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上． 26．（2018·重庆B 卷，26，12）抛物线y2x与x 轴交于点A ，B （点A 在点B 的左边），与y 轴交于点C ，点D 是该抛物线的顶点．（1）如图1，连接CD ，求线段CD 的长；（2）如图2，点P 是直线AC 上方抛物线上一点，PF ⊥x 轴于点F ，PF 与线段AC 交于点E ；将线段OB 沿x 轴左右平移，线段OB 的对应线段是O 1B 1．当PE ＋12EC 的值最大时，求四边形P O 1B 1C 周长的最小值，并求出对应的点O 1的坐标；（3）如图3，点H 是线段AB 的中点，连接CH ，将△OBC 沿直线CH 翻折至△O 2B 2C 的位置，再将△O 2B 2C 绕点B 2旋转一周，在旋转过程中，点O 2，C 的对应点分别是O 3，C 1，直线O 3C 1分别与直线AC ，x 轴交于点M ，N ．那么，在△O 2B 2C 的整个旋转过程中，是否存在恰当的位置，使△OMN 是以MN 为腰的等腰三角形？若存在，请直接写出所有符合条件的线段O 2M 的长；若不存在，请说明理由．【思路分析】（1）过点D 作DE ⊥y 轴于点E ，由题意易知点C (0)，再根据抛物线的顶点公式求出D 点坐标，最后在Rt △CDE 中，由勾股定理，易求出CD 的长度；（2）①在y2x中，令y ＝0，得到关于x 的一元二次方程，求解得A 、B 两点的坐标；②再设直线AC 的解析式为y ＝kx，将A 点坐标代入即可得到kP (t2t)， E (t)，从而PE2t ，并根据两点间的距离公式求出EC 的长；④计算出PE ＋12EC ＝－6(t ＋22)2＋46，由二次函数的性质易知当t ＝－22时，PE ＋12EC 取最大值463，此时P (－22，6)，且PC ∥x 轴，易知PC ＝22，O 1B 1＝OB ＝2，要使四边形PO 1B 1C 周长的值最小，就是要求PO 1＋B 1C 的值最小，此时利用平移、轴对称知识，先将点P 向右平移2个单位长度，得点P 1（－2，6)，则PO 1＝P 1B 1．再作P 1关于x 轴的对称点P 2（－2，－6)，则P 1B 1＝P 2B 1．连接P 2C 与x 轴的交点即为使PO 1＋B 1C 的值最小的点B 1．⑤在Rt △P 1P 2C 中，由勾股定理，得PO 1＋B 1C ＝P 2C ＝22(26)(2)+＝26，从而四边形P O 1B 1C 周长的最小值为32＋26，所求的点O 1的坐标为(－322，0)．（3）分类讨论如下：如答图3，通过计算可得O 2M ＝226-时，NA ＝NM ；如答图4，若点C 与M 点重合时，MA ＝MN ，此时，O 2M ＝O 2C ＝12AC ＝6；如答图5，通过计算可得O 2M ＝226+时，NA ＝NM ；如答图6，通过计算可得O 2M ＝63时，MA ＝MN ，此时C 1，H ，N 重合．综上，符合条件的O 2M 的长为63或6或22＋6或22－6．【解题过程】26．解：（1）如下图，过点D 作DE ⊥y 轴于点E ，由题意易知点C (0，6)．第26题答图3 第26题答图4第26题答图5 第26题答图6∵2ba-==224((443ac ba⨯-==，∴D()，从而CEDE．∴在Rt△CDE中，由勾股定理，得CD23=．（2）在y2x中，令y＝02x＝0，解得x1＝－，x2，从而A(－，0)，B，0)．令直线AC的解析式为y＝kx，则－k＝0，解得k．∴直线AC的解析式为y．令P(t2t)，E(tt)，从而PE2t，EC3=-．∴PE＋12EC＝－6t2t－3t2－tt＋)2．∴当t＝－时，PE＋12EC，此时P(－)．∴PC＝，O1B1＝OB．要使四边形PO1B1C周长的值最小，就是要求PO1＋B1C的值最小，将点P个单位长度，得点P1)，则PO1＝P1B1．再作P1关于x轴的对称点P2)，则P1B1＝P2B1．连接P2C与x轴的交点即为使PO1＋B1C的值最小的点B1．∴B1（－2，0)，将B1个单位长度即得点O1．此时，PO1＋B1C＝P2CP O1B1C周长的最小值为，所求的点O1的坐标为(－2，0)．2（3）O2M或或．【知识点】二次函数；一元二次方程的解法；勾股定理；平移；旋转；轴对称；最值问题；等腰三角形；分类思想；数形结合思想；探究性问题；压轴题；。

2018年重庆市中考数学试卷(b卷)(答案+解析)

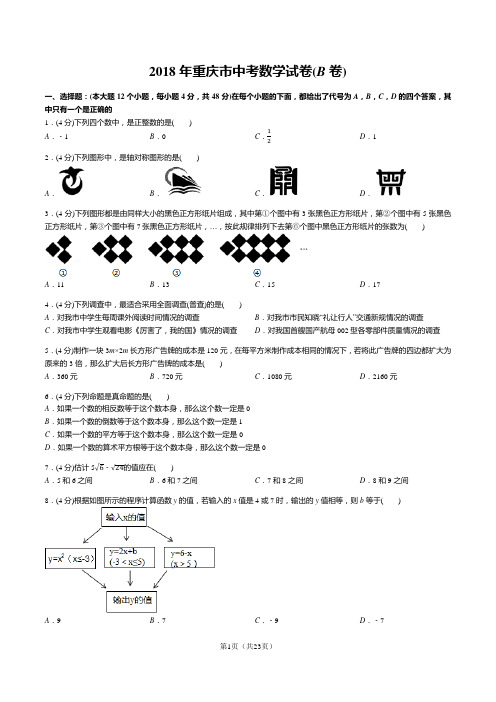
2018年重庆市中考数学试卷(B卷)一、选择题：(本大题12个小题，每小题4分，共48分)在每个小题的下面，都给出了代号为A，B，C，D的四个答案，其中只有一个是正确的1．(4分)下列四个数中，是正整数的是()A．﹣1 B．0 C．D．12．(4分)下列图形中，是轴对称图形的是()A．B．C．D．3．(4分)下列图形都是由同样大小的黑色正方形纸片组成，其中第①个图中有3张黑色正方形纸片，第②个图中有5张黑色正方形纸片，第③个图中有7张黑色正方形纸片，…，按此规律排列下去第⑥个图中黑色正方形纸片的张数为()A．11 B．13 C．15 D．174．(4分)下列调查中，最适合采用全面调查(普查)的是()A．对我市中学生每周课外阅读时间情况的调查B．对我市市民知晓“礼让行人”交通新规情况的调查C．对我市中学生观看电影《厉害了，我的国》情况的调查D．对我国首艘国产航母002型各零部件质量情况的调查5．(4分)制作一块3m×2m长方形广告牌的成本是120元，在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，那么扩大后长方形广告牌的成本是()A．360元B．720元C．1080元D．2160元6．(4分)下列命题是真命题的是()A．如果一个数的相反数等于这个数本身，那么这个数一定是0B．如果一个数的倒数等于这个数本身，那么这个数一定是1C．如果一个数的平方等于这个数本身，那么这个数一定是0D．如果一个数的算术平方根等于这个数本身，那么这个数一定是07．(4分)估计5﹣的值应在()A．5和6之间B．6和7之间C．7和8之间D．8和9之间8．(4分)根据如图所示的程序计算函数y的值，若输入的x值是4或7时，输出的y值相等，则b等于()A．9 B．7 C．﹣9 D．﹣79．(4分)如图，AB是一垂直于水平面的建筑物，某同学从建筑物底端B出发，先沿水平方向向右行走20米到达点C，再经过一段坡度(或坡比)为i=1：0.75、坡长为10米的斜坡CD到达点D，然后再沿水平方向向右行走40米到达点E(A，B，C，D，E均在同一平面内)．在E处测得建筑物顶端A的仰角为24°，则建筑物AB的高度约为(参考数据：sin24°≈0.41，cos24°≈0.91，tan24°=0.45)()A．21.7米B．22.4米C．27.4米D．28.8米10．(4分)如图，△ABC中，∠A=30°，点O是边AB上一点，以点O为圆心，以OB为半径作圆，⊙O恰好与AC相切于点D，连接BD．若BD平分∠ABC，AD=2，则线段CD的长是()A．2 B．C．D．11．(4分)如图，菱形ABCD的边AD⊥y轴，垂足为点E，顶点A在第二象限，顶点B在y轴的正半轴上，反比例函数y=(k≠0，x＞0)的图象同时经过顶点C，D．若点C的横坐标为5，BE=3DE，则k的值为()A．B．3 C．D．512．(4分)若数a使关于x的不等式组，有且仅有三个整数解，且使关于y的分式方程+=1有整数解，则满足条件的所有a的值之和是()A．﹣10 B．﹣12 C．﹣16 D．﹣18二、填空题：(本大题6个小题，每小题4分，共24分)请将每小题的答案直接填在答题卡中对应的横线上13．(4分)计算：|﹣1|+20=．14．(4分)如图，在边长为4的正方形ABCD中，以点B为圆心，以AB为半径画弧，交对角线BD于点E，则图中阴影部分的面积是(结果保留π)．15．(4分)某企业对一工人在五个工作日里生产零件的数量进行调查，并绘制了如图所示的折线统计图，则在这五天里该工人每天生产零件的平均数是个．16．(4分)如图，在Rt △ABC 中，∠ACB =90°，BC =6，CD 是斜边AB 上的中线，将△BCD 沿直线CD 翻折至△ECD 的位置，连接AE ．若DE ∥AC ，计算AE 的长度等于．17．(4分)一天早晨，小玲从家出发匀速步行到学校，小玲出发一段时间后，她的妈妈发现小玲忘带了一件必需的学习用品，于是立即下楼骑自行车，沿小玲行进的路线，匀速去追小玲，妈妈追上小玲将学习用品交给小玲后，立即沿原路线匀速返回家里，但由于路上行人渐多，妈妈返回时骑车的速度只是原来速度的一半，小玲继续以原速度步行前往学校，妈妈与小玲之间的距离y (米)与小玲从家出发后步行的时间x (分)之间的关系如图所示(小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计)．当妈妈刚回到家时，小玲离学校的距离为米．18．(4分)为实现营养套餐的合理搭配，某电商推出两款适合不同人群的甲、乙两种袋装的混合粗粮．甲种袋装粗粮每袋含有3千克A 粗粮，1千克B 粗粮，1千克C 粗粮；乙种袋装粗粮每袋含有1千克A 粗粮，2千克B 粗粮，2千克C 粗粮．甲、乙两种袋装粗粮每袋成本分别等于袋中的A 、B 、C 三种粗粮成本之和．已知每袋甲种粗粮的成本是每千克A 种粗粮成本的7.5倍，每袋乙种粗粮售价比每袋甲种粗粮售价高20%，乙种袋装粗粮的销售利润率是20%．当销售这两款袋装粗粮的销售利润率为24%时，该电商销售甲、乙两种袋装粗粮的袋数之比是 (商品的销售利润率=商品的售价商品的成本价商品的成本价×100%)三、解答题：(本大题2个小题，每小题8分，共16分)解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上19．(8分)如图，AB∥CD，△EFG的顶点F，G分别落在直线AB，CD上，GE交AB于点H，GE平分∠FGD．若∠EFG=90°，∠E=35°，求∠EFB的度数．20．(8分)某学校开展以素质提升为主题的研学活动，推出了以下四个项目供学生选择：A．模拟驾驶；B．军事竞技；C．家乡导游；D．植物识别．学校规定：每个学生都必须报名且只能选择其中一个项目．八年级(3)班班主任刘老师对全班学生选择的项目情况进行了统计，并绘制了如下两幅不完整的统计图．请结合统计图中的信息，解决下列问题：(1)八年级(3)班学生总人数是，并将条形统计图补充完整；(2)刘老师发现报名参加“植物识别”的学生中恰好有两名男生，现准备从这些学生中任意挑选两名担任活动记录员，请用列表或画树状图的方法，求恰好选中1名男生和1名女生担任活动记录员的概率．四、解答题：(本大题5个小题，每小题10分，共50分)解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上21．(10分)计算：(1)(x+2y)2﹣(x+y)(x﹣y)；(2)(a﹣1﹣)÷22．(10分)如图，在平面直角坐标系中，直线l1：y=x与直线l2交点A的横坐标为2，将直线l1沿y轴向下平移4个单位长度，得到直线l3，直线l3与y轴交于点B，与直线l2交于点C，点C的纵坐标为﹣2．直线l2与y轴交于点D．(1)求直线l2的解析式；(2)求△BDC的面积．23．(10分)在美丽乡村建设中，某县政府投入专项资金，用于乡村沼气池和垃圾集中处理点建设．该县政府计划：2018年前5个月，新建沼气池和垃圾集中处理点共计50个，且沼气池的个数不低于垃圾集中处理点个数的4倍．(1)按计划，2018年前5个月至少要修建多少个沼气池？(2)到2018年5月底，该县按原计划刚好完成了任务，共花费资金78万元，且修建的沼气池个数恰好是原计划的最小值．据核算，前5个月，修建每个沼气池与垃圾集中处理点的平均费用之比为1：2．为加大美丽乡村建设的力度，政府计划加大投入，今年后7个月，在前5个月花费资金的基础上增加投入10a%，全部用于沼气池和垃圾集中处理点建设．经测算：从今年6月起，修建每个沼气池与垃圾集中处理点的平均费用在2018年前5个月的基础上分别增加a%，5a%，新建沼气池与垃圾集中处理点的个数将会在2018年前5个月的基础上分别增加5a%，8a%，求a的值．24．(10分)如图，在▱ABCD中，∠ACB=45°，点E在对角线AC上，BE=BA，BF⊥AC于点F，BF的延长线交AD于点G．点H在BC的延长线上，且CH=AG，连接EH．(1)若BC=12，AB=13，求AF的长；(2)求证：EB=EH．25．(10分)对任意一个四位数n，如果千位与十位上的数字之和为9，百位与个位上的数字之和也为9，则称n为“极数”．(1)请任意写出三个“极数”；并猜想任意一个“极数”是否是99的倍数，请说明理由；(2)如果一个正整数a是另一个正整数b的平方，则称正整数a是完全平方数．若四位数m为“极数”，记D(m)=，求满足D(m)是完全平方数的所有m．五、解答题：(本大题1个小题，共12分)解答时每小题必须给出必要的演算过程或推理步骤，请将解答书写在答题卡中对应的位置上26．(12分)抛物线y=﹣x2﹣x+与x轴交于点A，B(点A在点B的左边)，与y轴交于点C，点D是该抛物线的顶点．(1)如图1，连接CD，求线段CD的长；(2)如图2，点P是直线AC上方抛物线上一点，PF⊥x轴于点F，PF与线段AC交于点E；将线段OB沿x轴左右平移，线段OB的对应线段是O1B1，当PE+EC的值最大时，求四边形PO1B1C周长的最小值，并求出对应的点O1的坐标；(3)如图3，点H是线段AB的中点，连接CH，将△OBC沿直线CH翻折至△O2B2C的位置，再将△O2B2C绕点B2旋转一周，在旋转过程中，点O2，C的对应点分别是点O3，C1，直线O3C1分别与直线AC，x轴交于点M，N．那么，在△O2B2C的整个旋转过程中，是否存在恰当的位置，使△AMN是以MN为腰的等腰三角形？若存在，请直接写出所有符合条件的线段O2M的长；若不存在，请说明理由．2018年重庆市中考数学试卷(B卷)参考答案与试题解析一、选择题：(本大题12个小题，每小题4分，共48分)在每个小题的下面，都给出了代号为A，B，C，D的四个答案，其中只有一个是正确的1．(4分)下列四个数中，是正整数的是()A．﹣1 B．0 C．D．1【分析】正整数是指既是正数还是整数，由此即可判定求解．【解答】解：A、﹣1是负整数，故选项错误；B、0是非正整数，故选项错误；C、是分数，不是整数，错误；D、1是正整数，故选项正确．故选：D．2．(4分)下列图形中，是轴对称图形的是()A．B．C．D．【分析】根据轴对称图形的概念对各选项分析判断即可得解．【解答】解：A、不是轴对称图形，故本选项错误；B、不是轴对称图形，故本选项错误；C、不是轴对称图形，故本选项错误；D、是轴对称图形，故本选项正确．故选：D．3．(4分)下列图形都是由同样大小的黑色正方形纸片组成，其中第①个图中有3张黑色正方形纸片，第②个图中有5张黑色正方形纸片，第③个图中有7张黑色正方形纸片，…，按此规律排列下去第⑥个图中黑色正方形纸片的张数为()A．11 B．13 C．15 D．17【分析】仔细观察图形知道第一个图形有3个正方形，第二个有5=3+2×1个，第三个图形有7=3+2×2个，由此得到规律求得第⑥个图形中正方形的个数即可．【解答】解：观察图形知：第一个图形有3个正方形，第二个有5=3+2×1个，第三个图形有7=3+2×2个，…故第⑥个图形有3+2×5=13(个)，故选：B．4．(4分)下列调查中，最适合采用全面调查(普查)的是()A．对我市中学生每周课外阅读时间情况的调查B．对我市市民知晓“礼让行人”交通新规情况的调查C．对我市中学生观看电影《厉害了，我的国》情况的调查D．对我国首艘国产航母002型各零部件质量情况的调查【分析】由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．【解答】解：A、对我市中学生每周课外阅读时间情况的调查，人数众多，意义不大，应采用抽样调查，故此选项错误；B、对我市市民知晓“礼让行人”交通新规情况的调查，人数众多，意义不大，应采用抽样调查，故此选项错误；C、对我市中学生观看电影《厉害了，我的国》情况的调查，人数众多，意义不大，应采用抽样调查，故此选项错误；D、对我国首艘国产航母002型各零部件质量情况的调查，意义重大，应采用普查，故此选项正确；故选：D．5．(4分)制作一块3m×2m长方形广告牌的成本是120元，在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，那么扩大后长方形广告牌的成本是()A．360元B．720元C．1080元D．2160元【分析】根据题意求出长方形广告牌每平方米的成本，根据相似多边形的性质求出扩大后长方形广告牌的面积，计算即可．【解答】解：3m×2m=6m2，∴长方形广告牌的成本是120÷6=20元/m2，将此广告牌的四边都扩大为原来的3倍，则面积扩大为原来的9倍，∴扩大后长方形广告牌的面积=9×6=54m2，∴扩大后长方形广告牌的成本是54×20=1080m2，故选：C．6．(4分)下列命题是真命题的是()A．如果一个数的相反数等于这个数本身，那么这个数一定是0B．如果一个数的倒数等于这个数本身，那么这个数一定是1C．如果一个数的平方等于这个数本身，那么这个数一定是0D．如果一个数的算术平方根等于这个数本身，那么这个数一定是0【分析】根据相反数是它本身的数为0；倒数等于这个数本身是±1；平方等于它本身的数为1和0；算术平方根等于本身的数为1和0进行分析即可．【解答】解：A、如果一个数的相反数等于这个数本身，那么这个数一定是0，是真命题；B、如果一个数的倒数等于这个数本身，那么这个数一定是1，是假命题；C、如果一个数的平方等于这个数本身，那么这个数一定是0，是假命题；D、如果一个数的算术平方根等于这个数本身，那么这个数一定是0，是假命题；故选：A．7．(4分)估计5﹣的值应在()A．5和6之间B．6和7之间C．7和8之间D．8和9之间【分析】先合并后，再根据无理数的估计解答即可．【解答】解：，∵7＜＜8，∴5﹣的值应在7和8之间，故选：C．8．(4分)根据如图所示的程序计算函数y的值，若输入的x值是4或7时，输出的y值相等，则b等于()A．9 B．7 C．﹣9 D．﹣7【分析】先求出x=7时y的值，再将x=4、y=﹣1代入y=2x+b可得答案．【解答】解：∵当x=7时，y=6﹣7=﹣1，∴当x=4时，y=2×4+b=﹣1，解得：b=﹣9，故选：C．9．(4分)如图，AB是一垂直于水平面的建筑物，某同学从建筑物底端B出发，先沿水平方向向右行走20米到达点C，再经过一段坡度(或坡比)为i=1：0.75、坡长为10米的斜坡CD到达点D，然后再沿水平方向向右行走40米到达点E(A，B，C，D，E均在同一平面内)．在E处测得建筑物顶端A的仰角为24°，则建筑物AB的高度约为(参考数据：sin24°≈0.41，cos24°≈0.91，tan24°=0.45)()A．21.7米B．22.4米C．27.4米D．28.8米【分析】作BM⊥ED交ED的延长线于M，CN⊥DM于N．首先解直角三角形Rt△CDN，求出CN，DN，再根据tan24°=，构建方程即可解决问题；【解答】解：作BM⊥ED交ED的延长线于M，CN⊥DM于N．在Rt△CDN中，∵==，设CN=4k，DN=3k，∴CD=10，∴(3k)2+(4k)2=100，∴k=2，∴CN=8，DN=6，∵四边形BMNC是矩形，∴BM=CN=8，BC=MN=20，EM=MN+DN+DE=66，在Rt△AEM中，tan24°=，∴0.45=，∴AB=21.7(米)，故选：A．10．(4分)如图，△ABC中，∠A=30°，点O是边AB上一点，以点O为圆心，以OB为半径作圆，⊙O恰好与AC相切于点D，连接BD．若BD平分∠ABC，AD=2，则线段CD的长是()A．2 B．C．D．【分析】连接OD，得Rt△OAD，由∠A=30°，AD=2，可求出OD、AO的长；由BD平分∠ABC，OB=OD可得OD与BC间的位置关系，根据平行线分线段成比例定理，得结论．【解答】解：连接OD∵OD是⊙O的半径，AC是⊙O的切线，点D是切点，∴OD⊥AC在Rt△AOD中，∵∠A=30°，AD=2，∴OD=OB=2，AO=4，∴∠ODB=∠OBD，又∵BD平分∠ABC，∴∠OBD=∠CBD∴∠ODB=∠CBD∴OD∥CB，∴即∴CD=．故选：B．11．(4分)如图，菱形ABCD的边AD⊥y轴，垂足为点E，顶点A在第二象限，顶点B在y轴的正半轴上，反比例函数y=(k≠0，x＞0)的图象同时经过顶点C，D．若点C的横坐标为5，BE=3DE，则k的值为()A．B．3 C．D．5【分析】由已知，可得菱形边长为5，设出点D坐标，即可用勾股定理构造方程，进而求出k值．【解答】解：过点D做DF⊥BC于F由已知，BC=5∵四边形ABCD是菱形∴DC=5∵BE=3DE∴设DE=x，则BE=3x∴DF=3x，BF=x，FC=5﹣x在Rt△DFC中，DF2+FC2=DC2∴(3x)2+(5﹣x)2=52∴解得x=1∴DE=1，FD=3设OB=a则点D坐标为(1，a+3)，点C坐标为(5，a)∵点D、C在双曲线上∴1×(a+3)=5a∴a=∴点C坐标为(5，)∴k=故选：C．12．(4分)若数a使关于x的不等式组，有且仅有三个整数解，且使关于y的分式方程+=1有整数解，则满足条件的所有a的值之和是()A．﹣10 B．﹣12 C．﹣16 D．﹣18【分析】根据不等式的解集，可得a的范围，根据方程的解，可得a的值，根据有理数的加法，可得答案．【解答】解：，解①得x≥﹣3，解②得x≤，不等式组的解集是﹣3≤x≤．∵仅有三个整数解，∴﹣1≤＜0∴﹣8≤a＜﹣3，+=13y﹣a﹣12=y﹣2．∴y=∵y≠2，∴a≠﹣6，又y=有整数解，∴a=﹣8或﹣4，所有满足条件的整数a的值之和是(﹣8)+(﹣4)=﹣12，故选：B．二、填空题：(本大题6个小题，每小题4分，共24分)请将每小题的答案直接填在答题卡中对应的横线上13．(4分)计算：|﹣1|+20= 2 ．【分析】本题涉及零指数幂、绝对值2个考点．在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．【解答】解：|﹣1|+20=1+1=2．故答案为：2．14．(4分)如图，在边长为4的正方形ABCD 中，以点B 为圆心，以AB 为半径画弧，交对角线BD 于点E ，则图中阴影部分的面积是 8﹣2π (结果保留π)．【分析】根据S 阴=S △ABD ﹣S 扇形BAE 计算即可；【解答】解：S 阴=S △ABD ﹣S 扇形BAE = ×4×4﹣ =8﹣2π，故答案为8﹣2π．15．(4分)某企业对一工人在五个工作日里生产零件的数量进行调查，并绘制了如图所示的折线统计图，则在这五天里该工人每天生产零件的平均数是 34 个．【分析】根据平均数的计算解答即可．【解答】解：，故答案为：3416．(4分)如图，在Rt △ABC 中，∠ACB =90°，BC =6，CD 是斜边AB 上的中线，将△BCD 沿直线CD 翻折至△ECD 的位置，连接AE ．若DE ∥AC ，计算AE 的长度等于．【分析】根据题意、解直角三角形、菱形的性质、翻折变化可以求得AE 的长．【解答】解：由题意可得，DE =DB =CD = AB ，∴∠DEC =∠DCE =∠DCB ，∵DE ∥AC ，∠DCE =∠DCB ，∠ACB =90°，∴∠DEC =∠ACE ，∴∠DCE =∠ACE =∠DCB =30°，∴∠ACD =60°，∠CAD =60°，∴△ACD 是等边三角形，∴AC =CD ，∴AC =DE ，∵AC ∥DE ，AC =CD ，∴四边形ACDE 是菱形，∵在Rt △ABC 中，∠ACB =90°，BC =6，∠B =30°，∴AC = ，∴AE = ．17．(4分)一天早晨，小玲从家出发匀速步行到学校，小玲出发一段时间后，她的妈妈发现小玲忘带了一件必需的学习用品，于是立即下楼骑自行车，沿小玲行进的路线，匀速去追小玲，妈妈追上小玲将学习用品交给小玲后，立即沿原路线匀速返回家里，但由于路上行人渐多，妈妈返回时骑车的速度只是原来速度的一半，小玲继续以原速度步行前往学校，妈妈与小玲之间的距离y (米)与小玲从家出发后步行的时间x (分)之间的关系如图所示(小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计)．当妈妈刚回到家时，小玲离学校的距离为 200 米．【分析】由图象可知：家到学校总路程为1200米，分别求小玲和妈妈的速度，妈妈返回时，根据“妈妈返回时骑车的速度只是原来速度的一半”，得速度为60米/分，可得返回时又用了10分钟，此时小玲已经走了25分，还剩5分钟的总程．【解答】解：由图象得：小玲步行速度：1200÷30=40(米/分)，由函数图象得出，妈妈在小玲10分后出发，15分时追上小玲，设妈妈去时的速度为v 米/分，(15﹣10)v =15×40，v =120，则妈妈回家的时间： =10，(30﹣15﹣10)×40=200．故答案为：200．18．(4分)为实现营养套餐的合理搭配，某电商推出两款适合不同人群的甲、乙两种袋装的混合粗粮．甲种袋装粗粮每袋含有3千克A 粗粮，1千克B 粗粮，1千克C 粗粮；乙种袋装粗粮每袋含有1千克A 粗粮，2千克B 粗粮，2千克C 粗粮．甲、乙两种袋装粗粮每袋成本分别等于袋中的A 、B 、C 三种粗粮成本之和．已知每袋甲种粗粮的成本是每千克A 种粗粮成本的7.5倍，每袋乙种粗粮售价比每袋甲种粗粮售价高20%，乙种袋装粗粮的销售利润率是20%．当销售这两款袋装粗粮的销售利润率为24%时，该电商销售甲、乙两种袋装粗粮的袋数之比是 (商品的销售利润率=商品的售价商品的成本价商品的成本价×100%)【分析】根据每袋甲种粗粮的成本是每千克A 种粗粮成本的7.5倍，可得甲的成本，乙的成本；根据乙种袋装粗粮的销售利润率是20%，可得乙的售价，根据每袋乙种粗粮售价比每袋甲种粗粮售价高20%，可得甲的售价，根据甲的利润+乙的利润=(甲的成本+乙的成本)×24%，根据等式的性质，可得答案．【解答】解：设A的单价为x元，B的单价为y元，C的单价为z元，当销售这两款袋装粗粮的销售利润率为24%时，该电商销售甲的销售量为a袋，乙的销售量为b袋，由题意，得A一袋的成本是7.5x=3x+y+z，化简，得y+z=4.5x；乙一袋的成本是x+2y+2z=x+2(y+z)=x+9x=10x，乙一袋的售价为10x(1+20%)=12x，甲一袋的售价为10x．根据甲乙的利润，得(10x﹣7.5x)a+20%×10xb=(7.5xa+10xb)×24%化简，得2.5a+2b=1.8a+2.4b0.7a=0.4b=，故答案为：．三、解答题：(本大题2个小题，每小题8分，共16分)解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上19．(8分)如图，AB∥CD，△EFG的顶点F，G分别落在直线AB，CD上，GE交AB于点H，GE平分∠FGD．若∠EFG=90°，∠E=35°，求∠EFB的度数．【分析】依据三角形内角和定理可得∠FGH=55°，再根据GE平分∠FGD，AB∥CD，即可得到∠FHG=∠HGD=∠FGH=55°，再根据∠FHG是△EFH的外角，即可得出∠EFB=55°﹣35°=20°．【解答】解：∵∠EFG=90°，∠E=35°，∴∠FGH=55°，∵GE平分∠FGD，AB∥CD，∴∠FHG=∠HGD=∠FGH=55°，∵∠FHG是△EFH的外角，∴∠EFB=55°﹣35°=20°．20．(8分)某学校开展以素质提升为主题的研学活动，推出了以下四个项目供学生选择：A．模拟驾驶；B．军事竞技；C．家乡导游；D．植物识别．学校规定：每个学生都必须报名且只能选择其中一个项目．八年级(3)班班主任刘老师对全班学生选择的项目情况进行了统计，并绘制了如下两幅不完整的统计图．请结合统计图中的信息，解决下列问题：(1)八年级(3)班学生总人数是40人，并将条形统计图补充完整；(2)刘老师发现报名参加“植物识别”的学生中恰好有两名男生，现准备从这些学生中任意挑选两名担任活动记录员，请用列表或画树状图的方法，求恰好选中1名男生和1名女生担任活动记录员的概率．【分析】(1)利用A项目的频数除以它所占的百分比得到调查的总人数，然后计算出C项目的人数后补全条形统计图；(2)画树状图展示所有12种等可能的结果数，再找出恰好选中1名男生和1名女生担任活动记录员的结果数，然后利用概率公式求解．【解答】解：(1)调查的总人数为12÷30%=40(人)，所以C项目的人数为40﹣12﹣14﹣4=10(人)条形统计图补充为：故答案为40人；(2)画树状图为：共有12种等可能的结果数，其中恰好选中1名男生和1名女生担任活动记录员的结果数为8，所以恰好选中1名男生和1名女生担任活动记录员的概率==．四、解答题：(本大题5个小题，每小题10分，共50分)解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上21．(10分)计算：(1)(x+2y)2﹣(x+y)(x﹣y)；(2)(a﹣1﹣)÷【分析】(1)原式利用完全平方公式，平方差公式化简，去括号合并即可得到结果；(2)原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分即可得到结果．【解答】解：(1)原式=x2+4xy+4y2﹣x2+y2=4xy+5y2；(2)原式=•=•=．22．(10分)如图，在平面直角坐标系中，直线l1：y=x与直线l2交点A的横坐标为2，将直线l1沿y轴向下平移4个单位长度，得到直线l3，直线l3与y轴交于点B，与直线l2交于点C，点C的纵坐标为﹣2．直线l2与y轴交于点D．(1)求直线l2的解析式；(2)求△BDC的面积．【分析】(1)把x=2代入y=x，得y=1，求出A(2，1)．根据平移规律得出直线l3的解析式为y=x﹣4，求出B(0，﹣4)、C(4，﹣2)．设直线l2的解析式为y=kx+b，将A、C两点的坐标代入，利用待定系数法即可求出直线l2的解析式；(2)根据直线l2的解析式求出D(0，4)，得出BD=8，再利用三角形的面积公式即可求出△BDC的面积．【解答】解：(1)把x=2代入y=x，得y=1，∴A的坐标为(2，1)．∵将直线l1沿y轴向下平移4个单位长度，得到直线l3，∴直线l3的解析式为y=x﹣4，∴x=0时，y=﹣4，∴B(0，﹣4)．将y=﹣2代入y=x﹣4，得x=4，∴点C的坐标为(4，﹣2)．设直线l2的解析式为y=kx+b，∵直线l2过A(2，1)、C(4，﹣2)，∴，解得，∴直线l2的解析式为y=﹣x+4；(2)∵y=﹣x+4，∴x=0时，y=4，∴D(0，4)．∵B(0，﹣4)，∴BD=8，∴△BDC的面积=×8×4=16．23．(10分)在美丽乡村建设中，某县政府投入专项资金，用于乡村沼气池和垃圾集中处理点建设．该县政府计划：2018年前5个月，新建沼气池和垃圾集中处理点共计50个，且沼气池的个数不低于垃圾集中处理点个数的4倍．(1)按计划，2018年前5个月至少要修建多少个沼气池？(2)到2018年5月底，该县按原计划刚好完成了任务，共花费资金78万元，且修建的沼气池个数恰好是原计划的最小值．据核算，前5个月，修建每个沼气池与垃圾集中处理点的平均费用之比为1：2．为加大美丽乡村建设的力度，政府计划加大投入，今年后7个月，在前5个月花费资金的基础上增加投入10a%，全部用于沼气池和垃圾集中处理点建设．经测算：从今年6月起，修建每个沼气池与垃圾集中处理点的平均费用在2018年前5个月的基础上分别增加a%，5a%，新建沼气池与垃圾集中处理点的个数将会在2018年前5个月的基础上分别增加5a%，8a%，求a的值．【分析】(1)设2018年前5个月要修建x个沼气池，则2018年前5个月要修建(50﹣x)个垃圾集中处理点，根据沼气池的个数不低于垃圾集中处理点个数的4倍，即可得出关于x的一元一次不等式，解之取其最小值即可得出结论；(2)根据单价=总价÷数量可求出修建每个沼气池的平均费用，进而可求出修建每个垃圾集中点的平均费用，设y=a%结合总价=单价×数量即可得出关于y的一元二次方程，解之即可得出y值，进而可得出a的值．【解答】解：(1)设2018年前5个月要修建x个沼气池，则2018年前5个月要修建(50﹣x)个垃圾集中处理点，。

2018年重庆市中考数学试卷(B)含评分标准

2018年重庆市初中学业水平暨高中招生考试数学试题( B 卷)(全卷共五个大题，满分150分。

参考公式：抛物线2(0)y ax bx c a =++≠的顶点坐标为24,24b ac b a a ⎛⎫- ⎪⎝⎭,对称轴为2b x a =。

1.下列四个数中，是正整数的是( ) A.-1 B.0 C.21 D.1 2下列图形中，是轴对称图形的是( )3.下列图形都是由同样大小的黑色正方形纸片组成,其中第①个图中有3张黑色正方形纸片，第②个图中有5张黑色正方形纸片,第③个图中有7张黑色正方形纸片,..，按此规律排列下去,第⑥个图中黑色正方形纸片的张数为( )A.11B.13C.15D.174.下列调查中，最适合采用全面调查(普查)的是( )A.对我市中学生每周课外阅读时间情况的调查B.对我市市民知晓“礼让行人”交通新规情况的调查C.对我市中学生观看电影(厉害了，我的国》情况的调查D.对我国首艘国产航母002型各零部件质量情况的调查5.制作一块m m 23⨯长方形广告牌的成本是120元,在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，那么扩大后长方形广告牌的成本是( )A.360元B.720元C.1080元D.2160元6.下列命题是真命题的是( )A.如果一个数的相反数等于这个数本身，那么这个数一定是0 。

B.如果一个数的倒数等于这个数本身，那么这个数一定是1 。

C.如果一个数的平方等于这个数本身，那么这个数定是0 。

重庆市2018年中考数学试题B卷含答案

重庆市 2018 年初中学业水平暨高中招生考试数学试题(B卷)( 全卷共五个大题，满分150 分。

考试时间120 分钟 )注意事项 :1.试题的答案书写在答题卡上，不得在试卷上直接作答；2.作答前仔细阅读答题卡上的注意事项；3.作图 ( 包含作协助线 ) 请一律用黑色署名笔达成；4.考试结束，由监考人员将试题和答题卡一并回收。

参照公式：抛物线 y ax 2 bx c(ab 4ac b2b 0) 的极点坐标为, ,对称轴为x 。

2a 4a 2a一、选择题： (本大题 12 个小题，每题 4 分 ,共 48 分 )在每个小题的下边，都给出了代号为 A、B、C、 D 的四个答案，此中只有一个是正确的，请将答题卡上题号右边正确答案所对应的方框涂黑。

1. 以下四个数中，是正整数的是()A.-1B.0C. 1D.1 22 以下图形中，是轴对称图形的是( )3. 以下图形都是由相同大小的黑色正方形纸片构成, 此中第①个图中有 3 张黑色正方形纸片，第②个图中有 5 张黑色正方形纸片, 第③个图中有7 张黑色正方形纸片,..，按此规律排列下去 , 第⑥个图中黑色正方形纸片的张数为( )A.11B.13C.15D.174.以下检查中，最合适采纳全面检查( 普查 ) 的是 ( )A.对我市中学生每周课外阅读时间状况的检查B.对我市市民了解“礼让行人”交通新规状况的检查C.对我市中学生观看电影 ( 厉害了，我的国》状况的检查D.对我国首艘国产航母 002 型各零零件质量状况的检查5.制作一块 3m 2m 长方形广告牌的成本是120元,在每平方米制作成真相同的状况下，若将此广告牌的四边都扩大为本来的 3 倍，那么扩大后长方形广告牌的成本是( )A.360 元B.720元C.1080元D.2160元6.以下命题是真命题的是 ( )A. 假如一个数的相反数等于这个数自己，那么这个数必定是0 。

B. 假如一个数的倒数等于这个数自己，那么这个数必定是 1 。

重庆市2018年中考数学试题B卷(无答案)

重庆市2018年初中学业水平暨高中招生考试数学试题( B 卷)(全卷共五个大题，满分150分。

参考公式：抛物线2(0)y ax bx c a =++≠的顶点坐标为24,24b ac b a a ⎛⎫- ⎪⎝⎭,对称轴为2b x a =。

1.下列四个数中，是正整数的是( )A.-1B.0C.21 D.1 2下列图形中，是轴对称图形的是( )3.下列图形都是由同样大小的黑色正方形纸片组成,其中第①个图中有3张黑色正方形纸片，第②个图中有5张黑色正方形纸片,第③个图中有7张黑色正方形纸片,..，按此规律排列下去,第⑥个图中黑色正方形纸片的张数为( )A.11B.13C.15D.174.下列调查中，最适合采用全面调查(普查)的是( )A.对我市中学生每周课外阅读时间情况的调查B.对我市市民知晓“礼让行人”交通新规情况的调查C.对我市中学生观看电影(厉害了，我的国》情况的调查D.对我国首艘国产航母002型各零部件质量情况的调查5.制作一块m m 23 长方形广告牌的成本是120元,在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，那么扩大后长方形广告牌的成本是( )A.360元B.720元C.1080元D.2160元6.下列命题是真命题的是( )A.如果一个数的相反数等于这个数本身，那么这个数一定是0 。

B.如果一个数的倒数等于这个数本身，那么这个数一定是1 。

C.如果一个数的平方等于这个数本身，那么这个数定是0 。

【2018中考真题数学卷】2018年重庆市中考数学试题(B)含答案(word版)

重庆市2018年初中学业水平暨高中招生考试数学试题( B 卷)(全卷共五个大题，满分150分。

参考公式：抛物线2(0)y ax bx c a =++≠的顶点坐标为24,24b ac b a a ⎛⎫- ⎪⎝⎭,对称轴为2b x a =。

B.如果一个数的倒数等于这个数本身，那么这个数一定是1 。

C.如果一个数的平方等于这个数本身，那么这个数定是0 。

2018年重庆市中考数学试题(B卷)及解析

2018年重庆市中考数学试卷（B卷）一.选择题（本大题共12个小题，每小题4分，共48分，每小题的四个选项中只有一个是正确的）1．（4分）（2018•常州）﹣3的绝对值是（）A．3B．﹣3C．D．2．（4分）（2018•重庆）下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（）A．B．C．D．3．（4分）（2018•重庆）下列调查中，最适宜采用全面调查方式（普查）的是（）A．对重庆市中学生每天学习所用时间的调查B．对全国中学生心理健康现状的调查C．对某班学生进行6月5日是“世界环境日”知晓情况的调查D．对重庆市初中学生课外阅读量的调查4．（4分）（2018•重庆）在平面直角坐标系中，若点P的坐标为（﹣3，2），则点P所在的象限是（）A．第一象限B．第二象限C．第三象限D．第四象限5．（4分）（2018•重庆）计算3﹣的值是（）A．2B．3C．D．26．（4分）（2018•重庆）某校为纪念世界反法西斯战争70周年，举行了主题为“让历史照亮未来”的演讲比赛，其中九年级的5位参赛选手的比赛成绩（单位：分）分别为：8.6，9.5，9.7，8.8，9，则这5个数据的中位数是（）A．9.7B．9.5C．9D．8.87．（4分）（2018•重庆）已知一个多边形的内角和是900°，则这个多边形是（）A．五边形B．六边形C．七边形D．八边形8．（4分）（2018•重庆）已知一元二次方程2x2﹣5x+3=0，则该方程根的情况是（）A．有两个不相等的实数根B．有两个相等的实数根C．两个根都是自然数D．无实数根9．（4分）（2018•重庆）如图，AC是⊙O的切线，切点为C，BC是⊙O的直径，AB交⊙O于点D，连接OD．若∠BAC=55°，则∠COD的大小为（）A．70°B．60°C．55°D．35°10．（4分）（2018•重庆）下列图形都是由几个黑色和白色的正方形按一定规律组成，图①中有2个黑色正方形，图②中有5个黑色正方形，图③中有8个黑色正方形，图④中有11个黑色正方形，…，依次规律，图⑩中黑色正方形的个数是（）A．32B．29C．28D．2611．（4分）（2018•重庆）某星期下午，小强和同学小明相约在某公共汽车站一起乘车回学校，小强从家出发先步行到车站，等小明到了后两人一起乘公共汽车回到学校．图中折线表示小强离开家的路程y（公里）和所用的时间x（分）之间的函数关系．下列说法错误的是（）A．小强从家到公共汽车在步行了2公里B．小强在公共汽车站等小明用了10分钟C．公共汽车的平均速度是30公里/小时D．小强乘公共汽车用了20分钟12．（4分）（2018•重庆）如图，在平面直角坐标系中，菱形ABOC的顶点O在坐标原点，边BO在x轴的负半轴上，∠BOC=60°，顶点C的坐标为（m，3），反比例函数y=的图象与菱形对角线AO交D点，连接BD，当DB⊥x轴时，k的值是（）A．6B．﹣6C．12D．﹣12二.填空题（本大题6个小题，每小题4分，共24分）13．（4分）（2018•重庆）据不完全统计，我国常年参加志愿者服务活动的志愿者超过65000000人，把65000000用科学记数法表示为．。