浙江省杭州市2010年第二次高考科目教学质量检测_数学理
杭州市高考科目第二次教学质量检测--数学试卷分析

3
0.76
4
0.73
5
0.91
定量指标:
6
0.84
7
0.86
8
0.80
文科抽样:120人
9
0.52
10
0.70
11
0.37
12
0.71
13
0.46
14
0.22
15
0.88
16
0.69
17
0.88
18
0.40
19
0.79
20
0.25
二、检测情况
题号
难度
1
0.99
2
0.93
3
0.95
4
0.93
5
0.90
20
难度 0.99 0.95 0.93 0.93 0.92 0.91 0.90 0.86 0.74 0.72 0.71 0.63 0.63 0.59 0.55 0.53 0.46 0.46 0.31
0.23
定量指标:理科三类题比例
分值
分类
分值
5
5
5
5
14
容
4
易
70分
5
题
4
14
5
4
5
14
14
中
5
等
61分
二、检测情况
定性分析:(两极差增大) 1) 概念的准确把握. 2)审题理解题意,探索联想方法. 3) 计算能力. 4)考试心理状态. 5)分数定位与解题选择.
二、检测情况
定性分析: 1) 能暴露教学中存在的问题;
实力、策略. 2)能为教学正确定位提供依据.
立足、着力.
三、教学建议
2010年杭州市高二年级教学质量检测

2010年杭州市高二年级教学质量检测化学试题卷(理科)考生须知:1.本试卷分试题卷和答题卷,满分100分,考试时间90分钟。
2.答题前,在答题卷密封区内填写学校、班级和姓名。
3.所有答案必须写在答题卷上,写在试卷上无效。
4.考试结束,只需上交答题卷。
可能用到的相对原子质量:S-32 O-16 C- 12 H- 1 Ca-40 Mg-24 Fe-56 Ba-137一、选择题(每小题只有一个选项符合题意,每小题2分,共40分)1.近年来,我国接连发生多起煤矿矿难,造成重大人员伤亡和财产损失。
其中煤矿发生爆炸事故的元凶是煤矿坑道气中含有的甲烷。
下列关于甲烷的叙述中错误的...是A.甲烷是人类第一个合成的有机物B.甲烷是相对分子质量最小的有机物C.甲烷是重要的化工原料,其分解产物可用于合成氨和橡胶工业D.“抽”出坑道中的甲烷,既可用作清洁燃料,又可防止坑道内爆炸2.有些化学反应反应速率很慢且副反应较多,测定这些反应的焓变可运用A.阿佛加德罗定律 B.勒沙特列原理 C .盖斯定律 D.质量守恒定律3.科学家常用下列哪种方法来研究有机化学反应历程A.质谱法 B.同位素示踪法 C.核磁共振法 D.红外光谱法4.要得到较大颗粒的明矾晶体,在结晶时可如下操作A.进行快速蒸发明矾饱和溶液至有大量晶体析出B.在沸水中配制明矾饱和溶液,然后急速冷却结晶C.室温下,在明矾饱和溶液中浸入悬挂的明矾小晶核,静置过夜D.配制比室温高10~20℃的明矾饱和溶液然后浸入悬挂的明矾小晶核, 静置过夜5. 把①蔗糖②淀粉③纤维素④蛋白质在稀硫酸存在下分别进行水解,最终产物只有1种的是A.①和②B.只有③C.只有④D.②和③6.化学反应可视为旧键断裂和新键形成的过程。
化学键的键能是形成(或拆开)1mol 化学键时释放(或吸收)出的能量。
已知白磷(P4)和P O的分子结构如图所示,已知:4246A.-1638 kJ·mol-1B.+1638 kJ·mol-1C.-126 kJ·mol-1D.+126 kJ·mol-17.最近《美国科学院院刊》发表了关于人体体香的研究文章,文章称人的体味中存在两种名为“AND”和“EST”的荷尔蒙。
2010年杭州市第二次高考科目教学质量检测文综试题

2010年杭州市第二次高考科目教学质量检测文综试题第I卷(选择题,共140分)本卷共35小题。
在每小题给出的四个选项中,只有一项是符合题目要求的。
青藏高原是一种特殊的高原气候,但利用大棚技术使得拉萨的瓜果蔬菜供应充足。
根据材料和图,完成1~2小题。
1.拉萨利用大棚技术种植瓜果蔬菜,主要是改善了当地的A.光照条件B.热量条件C.水分条件D.土壤条件2.拉萨原来不产西瓜,引种后发现:直接“铺”在地上生长的西瓜长不好,只有将西瓜藤蔓架空,西瓜“挂”着才能结果(如图所示)。
西瓜“挂”着的原因是A.可以减少叶子对西瓜的遮掩,增强光照,促进光合作用B.可以充分利用立体空间,节省土地、节省大棚面积,减少农业投入C.土壤的湿度不够、干燥,直接“搁”在地上,容易使西瓜的水分蒸发D.大棚内的地面温度比空气温度低,不有利于西瓜的发育成熟图中大圆为晨昏线,M点维度为70°N,且在东西半球分界线上;P点的线速度不存在;图中阴影与非阴影部分日期不同。
完成3~4题。
3.若图中日期为8日和9日,则北京时间是A.8日2时40分B.9日21时20分C.9日2时40分D.8日21时20分4.有一飞机准备从M点起飞,沿图中虚线所示路线飞行,12小时后在Q点降落A.飞机飞行方向保持不变B.飞机将飞越印度洋上空C.飞行员看到的白天时数比夜短D.图示区域的各地为昼短夜长秦驰道是与长城、兵马俑相媲美的世界奇迹,它始建于公元前212年,是我国历史上最早的一条‚高速公珞‛,读图回答5~6题。
5.秦驰道修建的目的,最有可能是A.加强政治中心与边疆的联系B.促进沿途经济的发展C.加强民族团结D.开发北方地区的矿产资源6.从咸阳到九原郡沿途的景观可能是A.地表形态从多沟壑一平坦B.地表形态从平坦一多沟壑—平坦C.沟谷附近多分布着平顶房的小村落D.降水稀少,荒漠连片,风沙肆虐右图表示我国某水库年内逐月入库水量(a)、月均水位(b)。
读图,完咸7~8题。
浙江省杭州市高三第二次教学质量检测数学(理)试题 Wor

2015学年杭州市第二次高考科目教学质量检测高三数学检测试卷(理科)选择题部分(共40分)一、选择题:本大题共8个小题,每小题5分,共40分.1.设集合{}{}2220,2,A x x x B y y x x x A =-≤==-∈,则A B =( )A .[]1,2-B .[]0,2C .(,2]-∞D .[0,)+∞2.设等比数列{}n a 的前n 项和为n S ,则“20a >且10a >”是“数列{}n S 单调递增”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .即不充分也不必要条件4.设(0,)x π∈,若11sin cos x x +=,则sin(2)3x π+=( )A .12 B .2 C .12- D .2-5.在梯形ABCD 中,//AB DC ,AB AD ⊥,1AD DC ==,2AB =,若1566AP AD AB =+,则()BC tPB t R +∈的取值范围是( )A .)+∞B .)+∞C .D .[1,)+∞ 6.设双曲线2222:1(0,0)x y C a b a b-=>>的顶点为12,A A ,P 为双曲线上一点,直线1PA 交双曲线C 的一条渐近线于M 点,直线2A M 和2A P 的斜率分别为12,k k ,若21A M PA ⊥且1240k k +=,则双曲线C 离心率为( )A .2BCD .47.设函数()f x 与()g x 的定义域为R ,且()f x 单调递增,()()()F x f x g x =+,()()()G x f x g x =-,若对任意12,x x R ∈12()x x ≠,不等式221212[()()][()()]f x f x g x g x ->-恒成立,则( )A .(),()F x G x 都是增函数B .(),()F x G x 都是减函数C .()F x 是增函数,()G x 是减函数D .()F x 是减函数,()G x 是增函数8.在四棱锥P ABCD -中,底面ABCD 是直角梯形,//AD BC ,AB BC ⊥,侧面PAB ⊥底面ABCD ,若PA AD AB kBC ===(01)k <<,则( ) A .当12k =时,平面BPC ⊥平面PCD B .当12k =时,平面APD ⊥平面PCD C .当(0,1)k ∀∈,直线PA 与底面ABCD 都不垂直 D .(0,1)k ∃∈,使直线PD 与直线AC垂直非选择题部分(共110分)二、填空题:本大题共7小题,多空题分题6分,单空题每题4分,满分36分.9.设函数()2sin()6f x x πω=+(0,)x R ω>∈,最小正周期T π=,则实数ω=__________,函数()f x 的图象的对称中心为__________,单调递增区间是__________.10.已知某几何体的三视图如图所示,则这个几何体的体积为__________,表面积为__________.11. 设直线212:260,(1)10l ax y l x a y a ++==+-+-=,若12l l ⊥,则a =__________.12.若实数,x y 满足0120x y x x y +≥⎧⎪≤⎨⎪-≥⎩,则x y +的取值范围是__________.13.设抛物线22(0)y px p =>的焦点为F ,点,A B 在抛物线上,且0120AFB ∠=,弦AB中点M 在准线l 上的射影为1M ,则1MM AB的最大值为__________.14.定义{},(),,()x x y M x y y x y ≥⎧=⎨<⎩,设22,42a x xy x b y xy y =++=++(,)x y R ∈,则{},M a b 的最小值为__________,当M 取到最小值是,x =__________,y =__________.15.在边长为1的正方体,''''ABCD A B C D -中,,,E F G 分别在',,BB BC BA 上,并且满足'34BE BB =,12BF BC =,12BG BA =,若平面'AB F ,平面ACE ,平面'B CG 交于一点O ,BO xBG yBF zBE =++,则x y z ++=__________,OD =__________.三、解答题 :本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.16.(本题满分14分)在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,若sin sin sin m A B C =+ ()m R ∈(1)当3m =时,求cos A 的最小值; (2)当3A π=时,求m 的取值范围.17. (本题满分15分)在底面为正三角形的三棱柱111ABC A B C -,2AB =,1AA ⊥平面ABC ,,,E F G 分别为1,,BB AB AC 的中点.(1)求证://BG 平面1A EC ;(2)若1AA -,求二面角1A EC F --的大小.18.(本题满分15分)设数列{}n a 满足11a =,11n n na a a +=+*()n N ∈. (1)求证:22123n n a a +≤-≤;(2)求证:13123221n n a n nn a n +-≤≤--.19.(本题满分15分)设直线l 与抛物线22x y =交于,A B 两点,与椭圆22143x y +=交于C ,D 两点,直线,,,OA OB OC OD (O 为坐标原点)的斜率分别为1234,,,k k k k ,若OA OB ⊥. (1)是否存在实数t ,满足1234()k k t k k +=+,并说明理由; (2)求OCD ∆面积的最大值.20.(本题满分15分)设函数1()(1,)f x x c b c R x b=++<-∈-,函数()()g x f x =在区间[]1,1-上的最大值为M . (1)若2b =-,求M 的值;(2)若M k ≥对任意的,b c 恒成立,求k 的最大值.2015学年杭州市第二次高考科目教学质量检测理科数学试题参考答案一、选择题:本大题共8个小题,每小题5分,共40分.1.A2.C3. C4.A5.A6.B7.A8.A二、填空题:本大题共7小题,多空题分题6分,单空题每题4分,满分36分.9. 2 ,0212k ππ⎛⎫-⎪⎝⎭ ,,,36k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭ 10. 83 63+11.23 12. [0,2] 13. 14. 16-,13-,16- 15. 43三、解答题 :本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.16.(本题满分14分)所以cos A 的最小值为79,当且仅当b c =时等号成立.(2)当3A π=时,sin sin )26m B C B π=+=+, 所以2sin()6m B π=+.又因为2(0,)3B π∈,所以5(,)666B πππ+∈, 所以1sin (,1]62B π⎛⎫+∈ ⎪⎝⎭, 所以(1,2]m ∈. 17.(本题满分15分)解:(1)取1A C 中点H ,连接,HG EH , 所以1//HG A A ,112HG A A =, 又E 为1BB 的中点, 所以//,BE HG BE HG =, 所以四边形EHGB 为平行四边形, 故//BG EH ,又EH ⊂平面1A EC ,BG ⊄平面1A EC , 所以//BG 平面1A EC .(2)以F 为坐标原点建立空间直角坐标系,设1AA a =,则1(0,0,0),(1,0,),(1,0,),2a F A a E C -,所以11(1,0,),(0,3,0),(2,0,),(1,3,)22a a FE FC A E AC a ===-=-, 设平面ECF 法向量为(,,)m m x y z ==,则由0FE m ∙=及0FC m ∙=,得020a x z ⎧+=⎪=, 不妨取(,0,2)m a =-;类似的,可取平面1A EC 法向量为(,4)n a =, 设二面角1AEC F --的平面角为θ, 则2cos cos,m n θ==当a =cos 0θ=,即090θ=.18.(本题满分15分)解:(1)因为11a =及11(1)n n na a n a +=+≥, 所以1n a ≥,所以2101na <≤. 因为2221211()2n n n n na a a a a +=+=++, 所以221212(2,3]n n na a a +-=+∈,即22123n n a a +≤-≤. (2)由(1)得221123n n a a n +<-≤ 所以212131n n a n ++<≤+,即22132(2)n n a n n -<≤-≥,当1n =时,也满足, 所以22132n n a n -<≤-.所以1213121[,]3221n n n a n na a n n ++=+∈-- 19.(本题满分14分)解:设直线l 方程为y kx b =+,11(,)A x y ,22(,)B x y ,33(,)C x y ,44(,)D x y . 联立y kx b =+和22x y =, 得2220x kx b --=,则122x x k +=,122x x b =,2480k b ∆=+>.由OA OB ⊥,所以12120x x y y +=,得2b =. 联立2y kx =+和223412x y +=,得22(34)1640k x kx +++=,所以3421634k x x k +=-+,342434x x k=-+. 由22192480k ∆=->,得214k >.(1)因为121212y y k k k x x +=+=,3434346y yk k k x x +=+=-所以123416k k k k +=-+.(2)根据弦长公式34CD x =-,得:CD =,根据点O 到直线CD的距离公式,得d =所以12OCDS CD d ∆=∙=,0t =>,则24OCD S t ∆=≤+ 所以当2t =,即k =OCD S ∆. 20.(本题满分15分)解:(1)当2b =-时,1()2f x x c x =+++在区间[]1,1-上是增函数, 所以4(1),(1)3g c g c =+-=, 所以{}2,()3max (1),(1)42,()33c c M g g c c ⎧≤-⎪⎪=-=⎨⎪+≥-⎪⎩.(2)①当2b ≤-时,因为1(1)11M g c b ≥=+++,1(1)11M g c b≥-=+--, 所以112(1)(1)1111M g g c c b b≥+-=+-++++- 21124221113b b b ≥++=+≥+--,所以23M ≥.②当2b -<≤(1)(1)(1)f b f f +<-<,则1max{(1),(1)}max{1,2}1M g g b c b c b=+=++++- 12(1)(1)121M g b g c b c b≥++=+++++-, 1121b b≥++≥-,所以1M ≥.③当1b <≤-时,有(1)(1)(1)f b f f +<<-, 则1max{(1),(1)}max{1,2}1M g g b c b c b=-+=-++++--, 所以12(1)(1)121M g b g c b c b≥++-=-+++++-- 1321b b ≥++≥+,所以1M ≥.综上可知,对任意的,b c 都有1M ≥.。
2010年浙江高考真题(含答案)数学理

绝密★考试结束前2010年普通高等学校招生全国统一考试数 学(理科)本试题卷分选择题和非选择题两部分。
全卷共5页,选择题部分1至2页,非选择题部分3至5页。
满分150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分(共50分)注意事项:1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。
2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用像皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
参考公式:如果事件A 、B 互斥,那么 柱体的体积公式 P (A +B )=P (A )+P (B ) Sh V =如果事件A 、B 相互独立,那么 其中S 表示柱体的底面积,h 表示柱体的高P (A ·B )=P (A )·P (B ) 锥体的体积公式如果事件A 在一次试验中发生的概率是P ,那么n Sh V 31=次独立重复试验中恰好发生k 次的概率 其中S 表示锥体的底面积,h 表示锥体的高kn kkn n P P C k P )1()(=),,2,1,0(n k = 球的表面积公式台体的体积公式 .ξE )(312211S S S S h V ++=球的体积公式其中S 1,S 2分别表示台体的上、下底面积 3π34R V =h 表示台体的高 其中R 表示球的半径一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设}4|{},4|{2<=<=x x Q x x P(A )Q P ⊆(B )P Q ⊆(C )Q C P R ⊆(D )P C Q R ⊆(2)某程序框图如图所示,若输出的S=57,则判断框内为 (A )?4>k (B )?5>k (C )?6>k (D )?7>k (3)设n S 为等比数列}{n a 的前n 项和,0852=+a a ,则=25S S(A )11 (B )5 (C )-8(D )-11(4)设2π0<<x ,则“1sin2<x x ”是“1sin <x x ”的(A )充分而不必不必要条件 (B )必要而不充分条件 (C )充分必要条件(D )既不充分也不必要条件(5)对任意复数i R y x yi x z ),∈,(+=为虚数单位,则下列结论正确的是(A )y z z2||= (B )222y x z += (C )x z z2≥|| (D )||||≤||y x z + (6)设m l ,是两条不同的直线,α是一个平面,则下列命题正确的是 (A )若α⊥,α⊂,⊥l m m l 则 (B )若α⊥,//,α⊥m m l l 则(C )若m l m l //,α⊂,α//则(D )若m l m l //,α//,α//则(7)若实数y x ,满足不等式组++,0≥1,0≤32,0≥33my xyxyx 且y x +的最大值为9,则实数=m(A )-2 (B )-1(C )1(D )2(8)设F 1,F 2分别为双曲线)0,0(12222>>=b a by ax 的左、右焦点。
浙江省杭州市高考数学二模试卷解析版
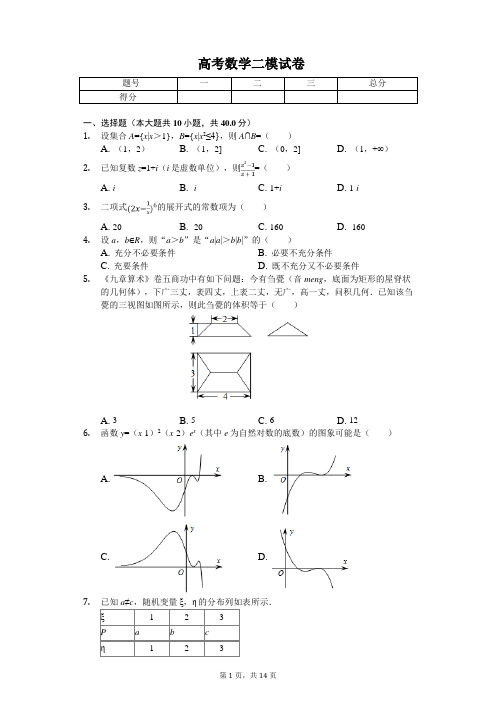
高考数学二模试卷题号一二三总分得分一、选择题(本大题共10小题,共40.0分)1.设集合A={x|x>1},B={x|x2≤4},则A∩B=()A. (1,2)B. (1,2]C. (0,2]D. (1,+∞)2.已知复数z=1+i(i是虚数单位),则=()A. iB. -iC. 1+iD. 1-i3.二项式的展开式的常数项为()A. 20B. -20C. 160D. -1604.设a,b∈R,则“a>b”是“a|a|>b|b|”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件5.《九章算术》卷五商功中有如下问题:今有刍甍(音meng,底面为矩形的屋脊状的几何体),下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何.已知该刍甍的三视图如图所示,则此刍甍的体积等于()A. 3B. 5C. 6D. 126.函数y=(x-1)2(x-2)e x(其中e为自然对数的底数)的图象可能是()A. B.C. D.7.已知a≠c,随机变量ξ,η的分布列如表所示.ξ123P a b cη123P c b a命题p:Eξ=Eη,命题q:Dξ=Dη,则()A. p真q真B. p真q假C. p假q真D. p假q假8.设函数,则函数y=f(f(x))()A. 是偶函数也是周期函数B. 是偶函数但不是周期函数C. 不是偶函数是周期函数D. 既不是偶函数也不是周期函数9.已知数列{a n}满足2a n≤a n-1+a n+1(n∈N*,n≥2),则()A. a5≤4a2-3a1B. a2+a7≤a3+a6C. 3(a7-a6)≥a6-a3D. a2+a3≥a6+a710.已知椭圆,直线x+y=1与椭圆Γ交于M,N两点,以线段MN为直径的圆经过原点,若椭圆Γ的离心率不大于,则a的取值范围为()A. B. C. D.二、填空题(本大题共7小题,共36.0分)11.双曲线的焦距为______;渐近线方程为______.12.设函数,若,则实数a=______,f(f(2))=______.13.在△ABC中,角A,B,C所对的边分别为a,b,c,已知,则sin C=______;当a=2,2sin A=sin C时,则b=______.14.设实数x,y满足不等式组则x+2y的最小值是______;设d=x2+y2,则d的最小值等于______.15.已知集合A={1,3,5},B={0,2,4},分别从A,B中各取2个不同的数,能组成不同的能被3整除的四位偶数的个数是______(用数字作答).16.已知向量,平面向量满足,则的最小值等于______.17.如图,已知矩形ABCD,,AD=1,AF⊥平面ABC,且AF=3.E为线段DC上一点,沿直线AE将△DAE翻折成△D'AE,M为BD'的中点,则三棱锥M-BCF体积的最小值是______.三、解答题(本大题共5小题,共74.0分)18.已知函数.(1)求函数f(x)的单调递增区间;(2)当时,求函数f(x)的值域.19.如图,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=1,点P在线段DF上.(1)证明:AF⊥平面ABCD.(2)若二面角DF-AP-C的余弦值为,求PF的长度.20.设等差数列{a n}前n项和为A n,等比数列{b n}前n项和为B n.若B n+3=8B n+7,a1=b2,a4=b4.(1)求b n和A n;(2)求数列{b n-A n}的最小项.21.如图,已知P(1,1)为抛物线y=x2上一点,斜率分别为k,-k(k>2)的直线PA,PB分别交抛物线于点A,B(不与点P重合).(1)证明:直线AB的斜率为定值;(2)若△ABP的内切圆半径为,(i)求△ABP的周长(用k表示);(ii)求直线AB的方程.22.已知函数f(x)=(x-1)e x.(1)求函数f(x)的单调递增区间;(2)若方程f(x)=ax+b(a,b∈R)有非负实数解,求a2+4b的最小值.答案和解析1.【答案】B【解析】解:B={x|-2≤x≤2};∴A∩B=(1,2].故选:B.可求出集合B,然后进行交集的运算即可.考查描述法、区间的定义,以及交集的运算.2.【答案】A【解析】解:∵z=1+i,∴===i.故选:A.把z=1+i代入,再由复数代数形式的乘除运算化简得答案.本题考查复数代数形式的乘除运算,是基础题.3.【答案】D【解析】解:二项式(2x-)6的展开式的通项公式为T r+1=•(-1)r•26-r•x6-2r,令6-2r=0,求得r=3,可得展开式中的常数项是-8•=-160,故选:D.先求出二项式展开式的通项公式,再令x的幂指数等于0,求得r的值,即可求得展开式中的常数项的值.本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.4.【答案】C【解析】【分析】本题主要考查充分条件和必要条件的判断,利用不等式的性质结合分类讨论是解决本题的关键.根据不等式的性质,结合充分条件和必要条件的定义进行判断即可得到结论.【解答】解:若a>b,①a>b≥0,不等式a|a|>b|b|等价为a•a>b•b,此时成立;②0>a>b,不等式a|a|>b|b|等价为-a•a>-b•b,即a2<b2,此时成立;③a≥0>b,不等式a|a|>b|b|等价为a•a>-b•b,即a2>-b2,此时成立,即充分性成立;若a|a|>b|b|,①当a>0,b>0时,a|a|>b|b|去掉绝对值得,(a-b)(a+b)>0,因为a+b>0,所以a-b>0,即a>b;②当a>0,b<0时,a>b;③当a<0,b<0时,a|a|>b|b|去掉绝对值得,(a-b)(a+b)<0,因为a+b<0,所以a-b>0,即a>b,即必要性成立.综上“a>b”是“a|a|>b|b|”的充要条件,故选C.5.【答案】B【解析】【分析】本题考查由三视图求面积、体积,关键是由三视图还原原几何体,是中档题.由已知中的三视图,可知该几何体是组合体,由一个三棱柱和两个相同的四棱锥构成,分别求出体积累加得答案.【解答】解:由三视图还原原几何体如图:沿上棱两端向底面作垂面,且使垂面与上棱垂直,则将几何体分成两个四棱锥和1个直三棱柱,则三棱柱的体积V1=×3×1×2=3,四棱锥的体积V2=×1×3×1=1,由三视图可知两个四棱锥大小相等,∴此刍甍的体积V=V1+2V2=5(立方丈),故选B.6.【答案】A【解析】【分析】本题主要考查函数图象的识别和判断,结合特殊值的符号的对应性是解决本题的关键.利用特殊值以及函数零点,函数值的符号的对应性进行判断即可.【解答】解:由y=0得x=2或x=1,当x=3时,y=4e3>0,排除C,D,且当1<x<2时,y<0,排除B,故选A.7.【答案】C【解析】【分析】本题考查了离散型随机变量的分布列,期望与方差,抓住a+b+c=1,是解决问题的关键,属于难题.根据题意分别计算出ξ,η的期望与方差,比较即可得到结果.【解答】解:依题意Eξ=a+2b+3c,Eη=c+2b+3a,Eξ-Eη=2c-2a,a≠c,故Eξ-Eη≠0,即p为假命题.E(ξ2)=a+4b+9c,所以D(ξ)=E(ξ2)-E2(ξ)=a+4b+9c-(a+2b+3c)2.同理:D(η)=c+4b+9a-(c+2b+3a)2,∴D(ξ)-D(η)=8(c-a)+(2a-2c)(4a+4b+4c)因为a+b+c=1,所以D(ξ)-D(η)=8(c-a)-8(c-a)=0,即D(ξ)=D(η),故q真.综上p假q真,故选C.8.【答案】A【解析】解:根据题意,f(x)==,则有f(-x)=f(x),即函数f(x)为偶函数,则f(f(-x))=f(f(x)),即函数y=f (f(x))为偶函数;又由f(x)==,当x<-1时,f(x)=2-2x+1,有-<f(x)<,当-1≤x≤1时,f(x)=-,当x>1时,f(x)=2-()x-1,有-<f(x)<,综合可得:-<f(x)<,则f(f(x))=-,其函数值为常数,y=f(f(x))为周期函数;故y=f(f(x))为偶函数且是周期函数;故选:A.根据题意,将f(x)的解析式写成分段函数的形式,分析可得f(x)为偶函数,进而分析f(x)的值域,由此可得f(f(x))=-,其函数值为常数,即可得y=f(f(x))为周期函数;综合即可得答案.本题考查分段函数的应用,涉及函数奇偶性与单调性的综合应用,属于综合题.9.【答案】C【解析】解:∵2a n≤a n-1+a n+1(n∈N*,n≥2),∴a n-a n-1≤a n+1-a n,∴a4-a3≤a5-a4≤a6-a5≤a7-a6,∴a6-a3=a6-a5+a5-a4+a4-a3≤3(a7-a6),即3(a7-a6)≥a6-a3,故选:C.由已知可得a4-a3≤a5-a4≤a6-a5≤a7-a6,则a6-a3=a6-a5+a5-a4+a4-a3≤3(a7-a6),答案可求.本题考查数列递推式,考查不等式的性质,是中档题.10.【答案】D【解析】【分析】本题考查椭圆的方程和性质,主要是离心率的运用,考查直线方程和椭圆方程联立,运用韦达定理,考查化简运算能力,属于中档题.由题意可得a>1,联立直线方程和椭圆方程,运用韦达定理,直径所对的圆周角为直角,化为x1x2+y1y2=0,化简整理,结合离心率公式和不等式的解法,可得a的范围.【解答】解:椭圆,直线x+y=1与椭圆Γ交于M,N两点,可得a>1,由x+y=1联立椭圆方程可得(a2+b2)x2-2a2x+a2-a2b2=0,设M(x1,y1),N(x2,y2),可得x1+x2=,x1x2=,线段MN为直径的圆经过原点,可得OM⊥ON,即有x1x2+y1y2=0,可得x1x2+(1-x1)(1-x2)=0,化为2x1x2+1-(x1+x2)=0,则2•+1-=0,化为a2+b2=2a2b2,由e≤,可得1-≤,即b2≥a2,可得≥a2,即有2a2-1≤4,解得a≤,可得1<a≤,故选:D.11.【答案】;y=【解析】【分析】本题考查双曲线的标准方程,考查双曲线的简单性质,是基础题.由双曲线方程求得a,b,c的值,则其焦距与渐近线方程可求.【解答】解:由题知,a2=4,b2=1,故c2=a2+b2=5,∴双曲线的焦距为:,渐近线方程为:.故答案为;.12.【答案】;【解析】解:函数,若,可得,解得a=;f(2)==-.f(f(2))=f(-)===.故答案为:;.利用分段函数的解析式通过,求解a的值,利用分段函数逐步求解f(f(2))即可.本题考查分段函数的应用,函数值的求法函数解析式的求法,考查计算能力.13.【答案】或2【解析】解:因为cos2C=1-2sin2C=-,及0<C<π,所以解得:sin C=.当a=2,2sin A=sin C时,由正弦定理,解得:c==4.由cos2C=2cos2C-1=-,及0<C<π得cos C=±.由余弦定理c2=a2+b2-2ab cos C,得b2±b-12=0,解得b=,或b=2.故答案为:,或2.根据角C的范围,利用二倍角公式求得sin C的值;利用正弦定理先求出边长c,由二倍角公式求cos C,用余弦定理解方程求边长b.本题主要考查三角变换、正弦定理、余弦定理等基础知识,同时考查运算求解能力,属于基础题.14.【答案】5 10【解析】解:依题意作出实数x,y满足不等式组可行性区域如图,目标函数z=x+2y在点(3,1)处取到最小值:5.d=x2+y2,由图形可知,A到原点的距离最小,则d的最小值等于:10故答案为:5;10.先画出实数x,y满足不等式组的平面区域,然后分析平面区域里各个整点,然后将其代入x+2y中,求出x+2y的最小值.判断最优解A然后求解d=x2+y2,则d的最小值.在解决线性规划的小题时,常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解.15.【答案】32【解析】【分析】本题主要考查排列组合的应用,结合能被3整除的四位偶数的数字规律进行讨论是解决本题的关键.根据能被3整除的四位数相加是3的倍数,结合偶数进行讨论求解即可.【解答】解:若A选1,3,则B中只能选0,2,若个位是0,则有A=6;若个位是2,则有C A=4种,此时有6+4=10种;若A选1,5,则B中只能选4,2,此时偶数有C A=12种;若A选3,5,则B中只能选0,4,若个位是0,则有A=6;若个位是4,则有C A=4种,此时有6+4=10种,综上共有10+12+10=32种,故答案为32.16.【答案】20【解析】【分析】本题考查向量的数量积的性质,考查二次函数的最值求法,属于基础题.由向量的数量积的性质,可得•=||-10,再由二次函数的最值求法,可得最小值.【解答】解:向量,平面向量满足,可得22+•=10+•=||,可得•=||-10,则=2-4•=||2-4||+40=(||-2)2+20,当||=2,可得的最小值为20.故答案为20.17.【答案】【解析】解:选固定点E,可知D′在圆上运动,现E在线段DC上运动,且AD′=1,∴D′的运动轨迹为以A为球心,半径为AD′=1的球面的一部分,∵S△BCF===,∴求三棱锥M-BCF体积的最小值只需求M到面BCF的距离d1的最小值,即求D′到面BCF的距离d的最小值,过A作BF的垂线,垂足为H,当D′为AH与球面的交点G时,D′到面BCF的距离最小,此时点E在DC上,d=AF-1=,d1==,∴三棱锥M-BCF体积的最小值为:V min=S△BCF×d1=.故答案为:.选固定点E,可知D′在圆上运动,现E在线段DC上运动,且AD′=1,从而D′的运动轨迹为以A为球心,半径为AD′=1的球面的一部分,求出S△BCF==,从而求三棱锥M-BCF体积的最小值只需求M到面BCF的距离d1的最小值,即求D′到面BCF的距离d的最小值,过A作BF的垂线,垂足为H,当D′为AH与球面的交点G时,D′到面BCF的距离最小,由此能求出三棱锥M-BCF体积的最小值.本题考查三棱锥的体积的最小值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.18.【答案】(本题满分为14分)解:(1)∵=2sin(2x-)+1,…5分∴2kπ-≤2x-≤2kπ+,k∈Z,解得:kπ-≤x≤kπ+,k∈Z,∴函数f(x)的单调递增区间为:[kπ-,kπ+],k∈Z,…9分(2)因为,∴2x-∈[-,],∴sin(2x-)∈[-1,],∴函数f(x)的值域为:[-1,2].…14分【解析】(1)利用两角差的正弦函数公式化简函数解析式可得f(x)=2sin(2x-)+1,利用正弦函数的单调性即可得解.(2)由,可求2x-∈[-,],利用正弦函数的图象和性质可求函数f(x)的值域.本题主要考查了两角差的正弦函数公式,正弦函数的图象和性质,考查了转化思想和数形结合思想的应用,属于基础题.19.【答案】(I)证明:∵∠BAF=90°,∴AB⊥AF.又平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB,AF⊂平面ABEF,∴AF⊥平面ABCD.(II)解:以A为原点,以AB,AD,AF为坐标轴建立空间坐标系,如图所示,则B(1,0,0),C(1,2,0),D(0,2,0),∵AB⊥平面ADF,∴=(1,0,0)为平面ADF的一个法向量,设=λ,则P(0,2λ,1-λ),∴=(0,2λ,1-λ),=(1,2,0).设平面APC的法向量为=(x,y,z),则,∴,令y=1可得=(-2,1,),∴|cos<>|=||=||=,解得λ=,∴PF=.【解析】(I)根据面面垂直的性质即可得出AF⊥平面ABCD;(II)建立空间坐标系,设=λ,求出平面PAD和平面APC的法向量,令法向量的夹角的余弦值的绝对值等于求出λ.本题考查了面面垂直的性质,空间向量与二面角的计算,属于中档题.20.【答案】解:(1)等差数列{a n}的公差设为d,等比数列的公比设为q,B n+3=8B n+7,可得b1+b2+b3+(b4+…+b n+3)=b1+b2+b3+q3B n=8B n+7,则q3=8,b1+b2+b3=7,解得q=2,b1=1,则b n=2n-1;a1=b2=2,a4=b4=8,可得d==2,A n=2n+•2•n(n-1)=n2+n;(2)设c n=b n-A n=2n-1-n2-n,c n+1-c n=2n-(n+1)2-n-1-(2n-1-n2-n)=2n-1-2(n+1),当n≤4时,c n+1<c n;当n≥5时,c n+1>c n,可得数列{b n-A n}的最小项为c5=-14.【解析】(1)等差数列{a n}的公差设为d,等比数列的公比设为q,运用等比数列的通项公式和求和公式,解方程可得首项和公比,可得所求;由等差数列的通项公式和求和公式,可得所求;(2)设c n=b n-A n=2n-1-n2-n,判断单调性,可得最小值为c5.本题考查等差数列和等比数列的通项公式和求和公式的运用,考查数列的单调性的判断和运用,以及方程思想和运算能力,属于中档题.21.【答案】证明:(1)设直线PA的方程为y=k(x-1)+1,与抛物线联立可得x2-kx+k-1=0,易知A(k-1,(k-1)2),B(-k-1,(k+1)2),∴直线AB的斜率k AB==-2为定值.(2)由(1)可得直线AB的方程为y=-2(x-k+1)+(k-1)2,∴点P到直线AB的距离d=,|AP|=•(k-2),|BP|=(k+2),|AB|=2k,(i)△ABP的周长l=2k+2k,(ii)设△ABP的内切圆半径为r,则r=-,即r===-,即-=-,解得k=5,∴直线AB的方程为y=-2x+24.【解析】(1)设直线PA的方程为y=k(x-1)+1,求出点A,B的坐标,即可证明,(2)(i)由(1)可得直线AB的方程为y=-2(x-k+1)+(k-1)2,根据点到直线的距离,弦长公式,即可求出三角形的周长,(ii)设△ABP的内切圆半径为r,可得-=-,解得即可.本题考查了直线和抛物线的位置关系,考查了运算能力和转化能力,属于中档题.22.【答案】解:(1)由f(x)=(x-1)e x,的f′(x)=xe x,由f′(x)=xe x>0,得x>0,∴函数f(x)的单调递增区间为(0,+∞);(2)设g(x)=(x-1)e x-ax-b,则g′(x)=xe x-a.当a≤0时,g′(x)≥0在[0,+∞)上恒成立,可得g(x)在[0,+∞)上单调递增,∴g(0)=-1-b≤0,得b≥-1,故a2+4b≥-4;当a>0时,存在x0>0,使g′(x0)=0,即,且g(x)在[0,x0]上单调递减,在[x0,+∞)上单调递增.∴≤0,解得.因此,.设h(x)=x2e2x-4(x2-x+1)e x,则h′(x)=2(x2+x)e x(e x-2).∴h(x)在[0,ln2]上单调递减,在[ln2,+∞)上单调递增.∴h(ln2)<h(0)=-4,h(x)≥h(ln2)=-4ln22+8ln2-8.∴当a=2ln2,b=-2ln22+2ln2-2时,a2+4b取到最小值-4(ln2-1)2,此时方程f(x)=ax+b有非负实数解ln2.综上所述,a2+4b的最小值为-4.【解析】(1)求出原函数的导函数,由导函数大于0可得原函数的单调增区间;(2)设g(x)=(x-1)e x-ax-b,则g′(x)=xe x-a.当a≤0时,由导数得到g(x)在[0,+∞)上单调递增,结合g(0)=-1-b≤0,得b≥-1,故a2+4b≥-4;当a>0时,存在x0>0,使g′(x0)=0,即,且g(x)在[0,x0]上单调递减,在[x0,+∞)上单调递增.由g(x0)≤0得到,可得.设h(x)=x2e2x-4(x2-x+1)e x,利用导数求其最小值得答案.本题考查利用导数研究函数的单调性,考查函数最值的求法,考查逻辑思维能力与推理论证能力,属难题.。
年杭州市第二次高考科目教学质量检测数学试题卷(理科)

年杭州市第二次高考科目教学质量检测数学试题卷(理科)考生须知:1. 本卷满分150分, 考试时间120分钟.2. 答题前, 在答题卷密封区内填写学校、班级和姓名.3. 所有答案必须写在答题卷上, 写在试题卷上无效.4. 考试结束, 只需上交答题卷.第I 卷(选择题,共60分)参考公式如果事件B A ,互斥,那么球的表面积公式)()()(B P A P B A P +=+; 24R S π=,如果事件B A ,相互,那么其中R 表示球的半径. )()()(B P A P B A P ⋅=⋅;球的体积公式如果事件A 在一次试验中发生的概率是P , 334R V π=,那么n 次重复试验中恰好发生k 次的概率其中R 表示球的半径.k n k kn n P P C k P --=)1()(.一. 选择题 : 本大题共12小题, 每小题5分, 共60分. 在每小题给出的四个选项中,有且只有一项是符合题目要求的 . 1. 设z 1 = 1 – 2i , z 2 = 1+ i , 则复数z =221z z 在复平面内对应点位于 ( )(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限 2. “| 2x – 1 | < 3”是“)2x ()3x )(1x (-++< 0”的 ( )(A) 必要不充分条件 (B) 充分不必要条件 (C) 充要条件 (D) 既不充分也不必要条件3. 有一条信息, 若1人得知后用1小时将其传给2人, 这2人又用1小时分别传给未知此信息的另外2人, 如此继续下去, 要传遍100万人口的城市, 所需的时间大约是 ( )(A) 10天 (B) 2天 (C) 1天 (D) 半天4. }),3,2()2,1(|{},),2,1(11|{R n n Q R m m P ∈+-==∈+-==ββαα),(是两个向量集合, 则=Q P ( )(A) {(1,-2)} (B) {(-13,-23)} (C) ((1,-2)) (D) {(-23,-13)}5.设a ,b 是两条不同的直线,α,β是两个不同的平面,则下面四个命题: ① 若a ⊥b, a ⊥α, b ⊄ α, 则b ∥α ; ② 若a ∥α, α⊥ β, 则a ⊥β ;③ 若a ⊥β, α⊥β, 则a ∥α或a ⊂ α ; ④ 若a ⊥b, a ⊥α, b ⊥ β, 则α⊥β ; 其中正确的命题是( )(A)仅① (B)仅② (C)①②③ (D) ①③④ 6. 若(x x –x 1)6的展开式中的第五项是215, 设S n = x –1 + x –2 + … + x – n , 则∞→n lim S n 等于( )(A)1 (B)21 (C) 41(D)617. 在△ABC 中,acos 22C+ ccos 22A =23b, 则 ( )(A)a, b , c 依次成等差数列 (B)b , a , c 依次成等差数列(C)a, c , b 依次成等差数列 (D)a , b , c 既成等差数列,也成等比数列8. 将写有1,2,3,4,5的5张卡片分别放入标有1,2,3,4,5的5个盒子内, 每个盒子里放且只放1张卡片. 那么2号卡片不在2号盒内且4号卡片不在4号盒内的放法数等于 ( ) (A) 42 (B) 72 (C)78 (D) 1209. 函数f ( x ) = ax 3 + ( a – 1 )x 2 + 48( b – 3 )x + b 的图象关于原点中心对称,则f ( x) ( ) (A)在[–43,43]上为增函数 (B) 在[–43,43]上非单调 (C) 在[43,+∞)上为增函数, 在 (– ∞, –43]为减函数 (D) 在 (– ∞, –43]为增函数,在[43,+∞)上也为增函数,10. 如图所求,椭圆中心在坐标原点,离心率为21,F 为椭圆左焦点,直线AB 与FC 交于D 点,则∠BDC 的正切值是 ( )(A) –33. (B) 3 –3. (C) 33. (D) 3 +3 11. 甲、乙两人地对同一目标各射击一次,其命中率分别为0.6, 0.5, 现已知目标被击中, 则它是甲射中的概率是 ( ) (A) 0.45 (B) 0.6 (C)0.65 (D)0.75 .12. 把311表示成k 项连续正整数的和,则项数k 的最大值为 ( ) (A) 595 (B) 486 (C) 374 (D) 243第Ⅱ卷(非选择题,共90分)二.填空题: 本大题有4小题, 每小题4分, 共16分. 请将答案填写在答题卷中的横线上. 13. 在直角坐标系xOy 中,设a = ( x , y ) , b = ( cos θ, sin θ ) (θ∈R ) , 则原点O 到直线a · b = p 的距离等于 .14.已知n m n m +,,成等差数列, mn n m ,,成等比数列, 则椭圆122=+ny mx 的准线方程为 _______ _ .15. 已知f ( x )是定义在实数集上的函数,且f ( x + 2) =)x (f 1)x (f 1-+, 若f ( 1 ) = 2 + 3,则f ( ) = . 16. 在下面4个平面图形中, 哪些是右面正四面体的展开图,其序号是 __ ____ . (把你认为正确的序号都填上)三. 解答题: 本大题有6小题, 共74分. 解答应写出文字说明, 证明过程或演算步骤.17. (本小题满分12分)(第10题)第16题① ② ③ ④已知12π< x < 3π, cos ( 2x +3π) = – 135, 求sin2x 的值.18. (本小题满分12分)如图,三棱锥P – ABC 中,PB ⊥底面ABC 于B ,∠BCA = 90︒,PB = BC = CA = 42,点E ,点F 分别是PC ,AP 的中点.(1) 求证:侧面PAC ⊥侧面PBC (2) 求异面直线AE 与BF 所成的角 (3) 求二面角A – BE – F 的平面角.19.(本小题满分12分)△A 1OB 1 , △A 2B 1B 2 , △A 3B 2B 3 , … , △A n B n – 1B n 均为等腰直角三角形, 已知它们的直角顶点A 1,A 2,A 3,…,A n 在曲线xy = 1 ( x > 0 )上,B 1,B 2,B 3,…, B n 在x 轴上(如图).(1) 分别求斜边OB 1,B 1B 2,B 2B 3的长;(2) 求数列OB 1,B 1B 2,B 2B 3,…,B n– 1B n 的通项公式.20 . (本小题满分12分)右表是某班英语及数学成绩的分布表,已知该班有50名学生,成绩分1 至5五个档次. 如:表中所示英语成绩为4分,数学成绩为2分的学生有5人. 现设该班任意一位学生的英语成绩为m ,数学成绩为n.(1) 求m = 4, n = 3的概率; (2) 求在m ≥ 3的条件下,n = 3的概率; (3) 求a + b 的值,并求m 的数学期望;(4) 若m= 2与n = 4是相互的,求a, b 的值. 21. (本小题满分14分)第18题第19题nm 数 学 5 4 3 21 英 语 5 1 3 10 1 4 1 0 7 5 1 3 2 1 09 3 2 1 b 6 0 a 1 0 0 1 1 3设双曲线2222by a x -=1( a > 0, b > 0 )的右顶点为A ,P 是双曲线上异于顶点的一个动点,从A引双曲线的两条渐近线的平行线与直线OP 分别交于Q 和R 两点.(1) 证明:无论P 点在什么位置,总有|→--OP |2 = |→-OQ ·→--OR | ( O 为坐标原点);(2) 若以OP 为边长的正方形面积等于双曲线实、虚轴围成的矩形面积,求双曲线离心率的取值范围;22. (本小题满分12分)已知常数a > 0, n 为正整数,f n ( x ) = x n – ( x + a)n ( x > 0 )是关于x 的函数. (1) 判定函数f n ( x )的单调性,并证明你的结论. (2) 对任意n ≥ a , 证明f `n + 1 ( n + 1 ) < ( n + 1 )f n `(n)第21题年高考科目教学质量第二次检测理科数学参考答案及评分标准一. 选择题 : 本大题共12小题. 每小题5分, 共60分.题 号 1 2 3 4 5 6 7 8 9 10 11 12 答 案CBCBDAACDCDB二. 填空题 : 本大题共4小题. 每小题4分, 共16分.13. |p| 14. 22±=y 15. 3 – 2 16. ① ② 三. 解答题: 本大题共6小题, 共74分. 17. (本小题满分12分)解:∵12π< x < 3π, ∴ 2π< 2x +3π < π , 2分∴sin(2x +3π) = 1312, 3分∴sin2x = sin[(2x +3π) –3π] 3分= sin(2x+3π)cos 3π – cos(2x +3π)sin 3π2分= 1312·21 – (–135)23= 263512+. 2分18. (本小题满分12分)解.(1) ∵PB ⊥平面ABC ,∴平面PBC ⊥平面ABC ,又∵AC ⊥BC , ∴AC ⊥平面PBC∴侧面PAC ⊥侧面PBC. 4分(2)以BP 所在直角为z 轴,CB 所在直线y 轴,建立空间直角坐标系,由条件可设 P ( 0, 0 , 42), B ( 0 , 0 , 0 ), C (0 ,– 42,0),A (42,– 42,0). 则E (0,–22,22),F (22,–22,22)→--AE = (– 42, 22,22),→--BF =(22,–22,22),∴→--AE ·→--BF = – 16, |→--AE |·|→--BF | = 242, ∴ cos<→--AE ,→--BF > = –32, ∴AE 与BF 所成的角是arccos32. 4分 (3) 平面EFB 的法向量为a = (0,1,1) 平面ABE 的法向量为b = (1, 1, 1 ) cos<a , b > =36, ∴二面角A – BE – F 的平面角为arccos 36. 4分 (2)或(3)题,若用几何方法求解,第小题定位正确2分,定量正确2分.19.(本小题满分12分)解1: (1) OB 1 = 2, B 1B 2 = 2(2– 1 ), B 2B 3 = 2(3–2). 4分(2) 设B n – 1B n = a n ,猜想出a n =B n – 1B n = 2 (n –1n -) 当n =1时,由上已证猜想成立.假设n = k 时,猜想成立,即有a k = 2 (k –1k -), 2分 设S k 是{a n }的前k 项和,则有(S k +2a 1k +)·2a1k += 1. ∴(S k – 1 +2a k )·2ak = 1.两式相减,得2a 1k ++2a k =1k a 2+–ka 2, 3分 即4k a k + 1 – 4 = 0,解得a k + 1 = 2 (1k + –k ) , 即n = k + 1时,猜想也成立, 2分综合上述,所求的通项公式a n =B n – 1B n = 2 (n –1n -). 1分 解2 : 设OB 1 = a 1, B 1B 2 = a 2, … , B n – 1B n = a n , {a n }的前n 项和为S n .则B n ( S n , 0 ), ∴A n+1(S n +21a n+1, 21a n+1 ) , 3分 代入曲线方程得:(S n +21a n+1)(21a n+1 ) = 1 , 且 (21a 1)2 = 1, 2分∴2S n a n+1 + (a n+ 1)2 = 4, a 1 = 2,2S n (S n+1 – S n ) +(S n+1 – S n )2 = 4, S 1 = 2.化简得 (S n+1)2 – (S n )2 = 4, 3分∴(S n )2 = (S 1)2 + 4( n – 1 ) = 4n, ∴S n = 2n 2分 ∴a n = 2 (n –1n -) ( n = 1仍适合). 2分20 . (本小题满分14分)解(1) 由表知:英语4分,数学3分是学生有7人,总学生数是50人 ∴所求概率为5073分 (2) m ≥3的条件下,即英语成绩在3分及3分以上的学生为总体, 总体数35人, 又n = 3的学生数为1 + 7 = 8,∴所求概率358. 3分(3) 总学生数是50,表中标出学生总数是47人, ∴a + b = 50 – 47 = 3.Em = 5⨯5010131+++++ 4⨯5015701+++++ 3⨯5039012+++++2⨯50a 06b 1+++++1⨯5031100++++ = 2578 4分(4)∵m= 2与n = 4相互,∴P ( m = 2)·P ( n = 4 ) = P(m = 2, n = 4) 即50a 6b 1+++·50b 13++=50b ,得b = 1, a = 2. 4分21. (本小题满分12分)解:(1) 设OP :y = k x, 又条件可设AR: y =ab(x – a ), 解得:→--OR = (b ak ab --,b ak kab --), 同理可得→-OQ = (b ak ab +,bak kab+),∴|→-OQ ·→--OR | =|b ak ab --b ak ab ++b ak kab --b ak kab+| =|b k a |)k 1(b a 222222-+. 4分设→--OP = ( m, n ) , 则由双曲线方程与OP 方程联立解得:m 2 =22222k a b b a -, n 2= 222222ka b b a k -, ∴ |→--OP|2 = :m 2 + n 2 =22222k a b b a -+ 222222k a b b a k -=222222k a b )k 1(b a -+ ,∵点P 在双曲线上,∴b 2 – a 2k 2 > 0 . ∴无论P 点在什么位置,总有|→--OP|2 = |→-OQ ·→--OR | . 4分(2)由条件得:222222ka b )k 1(b a -+= 4ab, 2分 即k 2 =22a 4ab ab b 4+-> 0 , ∴ 4b > a, 得e > 4172分22. (本小题满分12分)解: (1) f n `( x ) = nx n – 1 – n ( x + a)n – 1 = n [x n – 1 – ( x + a)n – 1 ] ,∵a > 0 , x > 0, ∴ f n `( x ) < 0 , ∴ f n ( x )在(0,+∞)单调递减. 4分 (2)由上知:当x > a>0时, f n ( x ) = x n – ( x + a)n 是关于x 的减函数, ∴ 当n ≥ a 时, 有:(n + 1 )n – ( n + 1 + a)n ≤ n n – ( n + a)n . 2分又 ∴f `n + 1 (x ) = ( n + 1 ) [x n –( x+ a )n ] ,∴f `n + 1 ( n + 1 ) = ( n + 1 ) [(n + 1 )n –( n + 1 + a )n ] < ( n + 1 )[ n n – ( n + a)n ] = ( n + 1 )[ n n – ( n + a )( n + a)n – 1 ] 2分( n + 1 )f n `(n) = ( n + 1 )n[n n – 1 – ( n + a)n – 1 ] = ( n + 1 )[n n – n( n + a)n – 1 ], 2分 ∵( n + a ) > n ,∴f `n + 1 ( n + 1 ) < ( n + 1 )f n `(n) . 2分。
浙江省杭州市高三数学第二次教学质量检测 理 新人教A版

杭 州 市2011届高考科目教学质量检测(二)数学(理)试题考生须知:1. 本卷满分150分, 考试时间120分钟.2. 答题前, 在答题卷密封区内填写学校、班级和姓名.3. 所有答案必须写在答题卷上, 写在试题卷上无效.4. 考试结束, 只需上交答题卷.参考公式:如果事件A , B 互斥, 那么 棱柱的体积公式 P (A +B )=P (A )+P (B )V =Sh如果事件A , B 相互独立, 那么 其中S 表示棱柱的底面积, h 表示棱柱的高 P (A ·B )=P (A )·P (B )棱锥的体积公式如果事件A 在一次试验中发生的概率是p , 那么n V =31Sh次独立重复试验中事件A 恰好发生k 次的概率 其中S 表示棱锥的底面积, h 表示棱锥的高 P n (k )=C kn p k(1-p )n -k(k = 0,1,2,…, n )球的表面积公式棱台的体积公式S = 4πR 2)2211(31S S S S h V ++=球的体积公式其中S 1, S 2分别表示棱台的上、下底面积, V =34πR 3h 表示棱台的高 其中R 表示球的半径选择题部分一、选择题: 本大题共10小题, 每小题5分,共50分.在每小题给出的四个选项中, 只有一项是符合题目要求的. 1.设函数,0,(),0,x f x x ≥=< 若()(1)2f a f +-=,则a =( )A .– 3B .±3C .– 1D .±12.设,,a b c 是三条不同的直线,,αβ是两个不同的平面,则a b ⊥的一个充分条件为( ) A .,a c b c ⊥⊥ B .,,a b αβαβ⊥⊂⊂C .,//a b αα⊥D .,a b αα⊥⊥3. 6名同学安排到3个社区A ,B ,C 参加志愿者服务,每个社区安排两名同学,其中甲同学必须到A 社区,乙和丙同学均不能到C 社区,则不同的安排方法种数为( )A .12B .9C .6D .5 4.已知非零向量a ,b 满足|a + b | =|a –ba |,则a +b 与a –b 的夹角为( ) A .30︒ B .60︒ C .120︒ D .150︒ 5.若正实数,a b 满足1a b +=,则( )A .11a b +有最大值4 B .ab 有最小值14CD .22a b +6.已知1tan()42πα+=,且02πα-<<,则22sin sin 2cos()4ααπα+=-( )A.B.C.D.7.执行如图所示的程序框图,若输出的结果是8,则判断框内m 的取值范围是( )A .(30,42]B .(42,56]C .(56,72]D .(30,72)8.体育课的排球发球项目考试的规则是: 每位学生最多可发球3次,一旦发球成功,则停止发球,否则一直发到3次为止. 设学生一次发球成功的概率为p (p ≠ 0),发球次数为X ,若X 的数学期望EX >1.75,则p 的取值范围是 ( ) A. (0,712) B. (712,1) C. (0,12) D. (12,1) 9.已知双曲线2222:1(,0)x y C a b a b-=>的左、右焦点分别为1F ,2F ,过2F 作双曲线C 的一条渐近线的垂线,垂足为H ,若2F H 的中点M 在双曲线C 上,则双曲线C 的离心率为( ) AB .C .2D .310.已知函数3()31,,f x x x x R =-+∈{|1},{||()|1},A x t x t B x f x =≤≤+=≥集合A B⋂开始 k=1 S=0只含有一个元素,则实数t 的取值范围是( ) A.1} B.1]C.1] D.1)非选择题部分二、填空题:本大题共7小题,每小题4分,共28分. 11.已知i是虚数单位,z =则||z = .12.如图是某赛季甲乙两名篮球运动员每场比赛得分的茎叶图,则甲乙两人比赛得分的中位数之和是 .13.设542345012345(21)(2),x x a a x a x a x a x a x -++=+++++ 则024||||||a a a ++=___________.14.如果以抛物线24y x =过焦点的弦为直径的圆截y 轴所得的弦长为4, 那么该圆的方程是 .15.一个棱锥的三视图如图,则该棱锥的外接球的表面积为 .16.设实数,x y 满足不等式组210,460,220.x y x y x y k --≥⎧⎪--≤⎨⎪+--≥⎩且224x y +的最小值为m ,当925m ≤≤时,实数k 的取值范围是___________.17.由数字1,2,3,4,5,6,7组成一个无重复数字的七位正整数,从中任取一个,所取的数满足首位为1且任意相邻两位的数字之差的绝对值不大于2的概率等于 .三、解答题: 本大题共5小题, 共72分.解答应写出文字说明, 证明过程或演算步骤.18.(本题满分14分)已知函数22()cos sin sin (0,)f x x x x x x R ωωωωω=+->∈图象的两相邻对称轴间的距离为2π. (Ⅰ)求ω的值;(Ⅱ)在ABC ∆中,,,a b c 分别是角,,A B C的对边,若a =()1,f A =求b c +的最大值.(第12题)(第15题)19.(本题满分14分)已知正项数列{},{}n n a b 满足:对任意正整数n ,都有1,,n n n a b a +成等差数列,11,,n n n b a b ++成等比数列,且1210,15.a a ==(Ⅰ)求证:数列}是等差数列; (Ⅱ)求数列{},{}n n a b 的通项公式; (Ⅲ) 设12111,n n S a a a =+++如果对任意正整数n ,不等式22n n nb aS a <-恒成立,求实数a 的取值范围.20.(本题满分14分)如图1,在平面内,ABCD 是60,BAD AB a ∠=︒=且的菱形,ADD ``A 1和CD D `C 1都是正方形.将两个正方形分别沿AD ,CD 折起,使D ``与D `重合于点D 1 .设直线l 过点B 且垂直于菱形ABCD 所在的平面,点E 是直线l 上的一个动点,且与点D 1位于平面ABCD 同侧(图2).(Ⅰ) 设二面角E – AC – D 1的大小为θ,若4π≤ θ ≤ 3π,求线段BE 长的取值范围; (Ⅱ)在线段1D E 上存在点P ,使平面11//PAC 平面EAC ,求1D PPE与BE 之间满足的关系式,并证明:当0 < BE < a 时,恒有1D PPE< 1.(第20题–1)(第20题–2)21.(本题满分14分)已知直线(13)(32)(13)0m x m y m +---+=()m R ∈所经过的定点F 恰好是椭圆C 的一个焦点,且椭圆C 上的点到点F 的最大距离为3.(Ⅰ) 求椭圆C 的标准方程; (Ⅱ) 设过点F 的直线l 交椭圆于A 、B 两点,若1218||||57FA FB ≤⋅≤,求直线l 的斜率的取值范围.22.(本题满分16分) 已知函数21()(3)ln .2f x x a x x =+-+ (Ⅰ)若函数()f x 是定义域上的单调函数,求实数a 的最小值;(Ⅱ)在函数()f x 的图象上是否存在不同两点1122(,),(,)A x y B x y ,线段AB 的中点的横坐标为0x ,直线AB 的斜率为k ,有/0()k f x =成立?若存在,请求出0x 的值;若不存在,请说明理由.参考答案一、选择题 (每小题5分,共50分)二、填空题 (每小题4分,共28分)11.1 12.64 13.110 14.(x – 32)2 + (y ±1)2 = 25415.2894π 16.2,5] 17.1360三、解答题(共72分)18.(本题满分14分)(Ⅰ)()cos 222sin(2).6f x x x x πωωω==+ 4分∵()f x 图象的两条相邻对称轴间的距离为2π,∴()f x 的最小正周期.T π=2.2ππω∴=∴ 1.ω= 7分 (Ⅱ)由()2sin(2)1,6f A A π=+= 得1sin(2).62A π+=∵0<A<π,132.666A πππ∴<+<52..663A A πππ∴+=∴= 11分由余弦定理,得2222cos ,a b c bc A =+- 因此,222222313()3()()().44b c bc b c bc b c b c b c =+-=+-≥+-+=+2()12.b c ∴+≤于是,当b c =即ABC ∆为正三角形时,b c +的最大值为 14分 19.(本题满分14分)(1)由已知,得12n n n b a a +=+ ①,211n n n a b b ++=⋅ ② . 由②得1n a += ③.将③代入①得,对任意*2,n n N ≥∈,有2n b =即=∴是等差数列. 4分(Ⅱ)设数列的公差为d , 由1210,15.a a ==经计算,得1225,18.2b b ==2d ===(1)4).22n n =-⋅=+ 2(4),2n n b +∴=(3)(4).2n n n a ++=9分 (Ⅲ)由(1)得12112().(3)(4)34n a n n n n ==-++++ 111111112[()()()]2().45563444n S n n n ∴=-+-++-=-+++ 不等式22nn nb aS a <-化为1144()2.443n a n n +-<-++ 即2(1)(36)80.a n a n -+--<设()f n =2(1)(36)8a n a n -+--,则()0f n <对任意正整数n 恒成立.当10a ->,即1a >时,不满足条件; 当10a -=,即1a =时,满足条件;当10a -<,即1a <时,()f n 的对称轴为3(2)02(1)a x a -=-<-,()f n 关于n 递减,因此,只需(1)4150.f a =-< 解得15, 1.4a a <∴< 综上, 1.a ≤ 14分 20.(本题满分14分)(方法1)设菱形ABCD 的中心为O ,以O 为原点,对角线AC ,BD 所在直线分别为x,y 轴,建立空间直角坐标系如图1.设BE = t (t > 0) .(Ⅰ)1,0,0),(,0,0),(0,,),(0,,).22a a A C D a E t - 13(,,),(3,0,0),22aAD a a AC a =--=-设平面1D AC 的法向量为111(,,1)n x y =,则111111110,0,0,2 2.0.0.a n AD x y a y n AC ⎧⎧⋅==-+=⎧⎪⎪⇒⇒⎨⎨⎨=⋅=⎩⎪⎪⎩=⎩ 1(0,2,1).n ∴= 3分 (,,),2aAE t =-设平面EAC 的法向量为222(,,1)n x y =-, 则22222220,0,0,22.0.0.a x n AE y t t y n AC a ⎧=⎧⎧⋅=+-=⎪⎪⎪⇒⇒⎨⎨⎨=⋅=⎪⎪⎪⎩=⎩⎩22(0,,1).t n a ∴=- 4分设二面角1E AC D --的大小为θ,则1212cos ||||20n n n n θ⋅==, 6分 ∵cos θ∈1[,22,∴12≤||2≤ ,解得≤ t ≤ 32a . 所以BE 的取值范围是 ,32a ]. 8分(Ⅱ) 设1D P PE λ=,则1(0,,).211a t aP λλλλ-+⋅++1131(,0,),(,,).22211a t a A a a A P λλλλλ--∴=-⋅++ 由平面11//PAC 平面EAC ,得1//A P 平面EAC ,120.A P n ∴⋅=1011t a t λλλλλ--∴⋅-=++,化简得:t a λ=(t ≠ a ),即所求关系式:1D P PEBE a =(BE ≠ a ). ∴当0< t < a 时,1D P PE < 1. 即:当0 < BE < a 时,恒有1D PPE< 1. 14分 (方法2)(Ⅰ)如图2,连接D 1A ,D 1C ,EA ,EC ,D 1O ,EO ,(第20题 – 1 )∵ D 1A= D 1C ,所以,D 1O ⊥AC ,同理,EO ⊥AC ,∴1DOE ∠是二面角1E AC D --的平面角.设其为θ. 3分 连接D 1E ,在△OD 1E 中,设BE = t (t > 0)则有:OD 1= ,OE = D 1E =∴cos θ=. 6分∵cos θ∈1[2, ∴12≤||≤ , 解得≤ t ≤ 32a . 所以BE 的取值范围是,32a ].≤ BE ≤ 32a . 8分(Ⅱ)当点E 在平面A 1D 1C 1上方时,连接A 1C 1,则A 1C 1∥AC ,连接EA 1,EC 1,设A 1C 1的中点为O 1,则O 1在平面BDD 1内,过O 1作O 1P ∥OE 交D 1E 于点P ,则平面11//PAC 平面EAC .作平面BDD 1如图3.过D 1作D 1B 1∥BD 交于l 点B 1,设EO 交D 1B 1于点Q . 因为O 1P ∥OE ,所以1D P PE =111D O O Q =122a aQB -, 由Rt △EB 1Q ∽RtEBO ,得12QB t a a t -=,解得QB 1 = 222a a t -,得1D P PE =t a , 12分 当点E 在平面A 1D 1C 1下方时,同理可得,上述结果仍然成立. 13分 ∴有1D P PE =BE a (BE ≠a ),∴当0 < t < a 时,1D PPE< 1. 14分21.(本题满分14分)(Ⅰ)由(13)(32)(13)0m x m y m +---+=得(31)(323)0x y m x y --++-=,由3103230x y x y --=⎧⎨+-=⎩,解得(1,0)F . 2分设椭圆C 的标准方程为22221(0)x y a b a b +=>>,则22213c a c a b c⎧=⎪+=⎨⎪=+⎩解得2,1a b c ==,(第20题 – 2)(第20题 – 3)从而椭圆C 的标准方程为22143x y +=. 6分 (Ⅱ) 过F 的直线l 的方程为(1)y k x =-,11(,)A x y ,22(,)B x y ,由22(1)143y k x x y =-⎧⎪⎨+=⎪⎩,得2222(34)84120k x k x k +-+-=,因点F 在椭圆内部必有0∆>,有2122212283441234k x x k k x x k ⎧+=⎪⎪+⎨-⎪=⎪+⎩, 8分所以|FA|·|FB| =(1 + k 2)|(x 1 – 1)(x 2 – 1 )|2(1)k =+1212|()1|x x x x -++229(1)34k k +=+11分由22129(1)185347k k +≤≤+, 得213k ≤≤,解得1k ≤-或1k ≤ 所以直线l的斜率的取值范围为11,3⎡⎤⎡⎤-⎣⎦⎣⎦. 14分22.(本题满分16分) (Ⅰ)/1()3(0).f x x a x x=+-+> 2分 若函数()f x 在(0,)+∞上递增,则/()0f x ≥对0x >恒成立,即1()3a x x≥-++对0x >恒成立,而当0x >时,1()323 1.x x-++≤-+= 1.a ∴≥若函数()f x 在(0,)+∞上递减,则/()0f x ≤对0x >恒成立,即1()3a x x≤-++对0x >恒成立,这是不可能的.综上, 1.a ≥ a 的最小值为1. 6分 (Ⅱ)假设存在,不妨设120.x x <<2211122212121211(3)ln (3)ln ()()22x a x x x a x x f x f x k x x x x +-+-----==--12012ln(3).x x x a x x =+-+- 9分/0001()(3).f x x a x =+-+若/0(),k f x =则12120ln1x x x x x =-,即121212ln 2x x x x x x =-+,即11212222ln 1x x x x x x -=+. (*) 12分 令12x t x =,22()ln 1t u t t t -=-+(01t <<), 则22(1)()(1)t u t t t -'=+>0.∴()u t 在01t <<上增函数, ∴()(1)0u t u <=, ∴(*)式不成立,与假设矛盾.∴/0().k f x ≠ 因此,满足条件的0x 不存在. 16分。
2010届浙江杭州高中高三年级第二次月考理

2010届浙江杭州高中高三年级第二次月考数学试卷(理)注意事项:1.本卷答题时间120分钟,满分150分。
2 .本卷不得使用计算器,答案一律做在答卷页上。
、选择题(本大题共 10小题,每小题5分,满分50分•在每小题给出的四个选项中,只有一项是符合题目要求的)2 21 11 .已知命题p :若x y 0,则x 、y 全为0 ;命题q :若a b ,贝U.给出下列a b4.二次函数f (x )的二次项系数为正数,且对任意项 x R 都有f (x ) f (4 x )成立,若f(12x 2)f(1 2x x 2), 则x 的取值范围是()A . x 2B .x 2或0 x2C .2 xD .x2或x 0UJU r umr AC ruuu uurUU LT5.在△ ABC 中, AB c , b .若点 D 满足 BD 2DC , 则AD()2 r 1 r5 r 2 ,r2 r 1 r 1 ,r 2 r A .- b cB . c 一 bC . b cD . - b — c3 33 33 33 36.已知0loga 2logb 2, 则a 、b 的关系:H.A是()A . 0a b 1 B . 0 b a 1C .b a 1D . ab 117 .在△ ABC 中,tanA 是以 4为第3项,4为第7项的等差数列的公差;tanB 是以—为第3项,93为第6项的等比数列的公比,则该三角形为 ()A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形A . 1B . 2C . 3D . 42 .设集合A{x|x2a 1,aN},B {y|yb 2 4b 5,b N},则下列关系中正确的是( )A . AB B . B AC .A BD . A B四个复合命题:①p 且q ,②p 或q ,③ p ④ q ,其中真命题的个数为 ()3.已知等差数列a n 的公差为2,若a-], a 3, a 4成等比数列,则a 2等于 ( )A . 4B . 6C . 8D .10(3), (5, 7), (9, 11, 13), (15, 17, 19, 21), (23), (25, 27), (29, 31, 33), (35, 37, 39 , 41), (43) (45, 47)…则第104个括号内各数之和为()A . 2036B . 2048C . 2060D . 2072二、填空题(本大题共 7小题,每题4分,共28分)1 2111.已知 f(x ) x _____________________ 2,则函数 f(3) .xx212. 在函数f (x) ax bx c 中,若a, b, c 成等比数列且f(0)4,则f (x)有最—值(填“大”或“小”),且该值为 _________________ .■—*■13. 已知复数z a bi,z a bi ( a 、b R ),若z i 在映射f 下的象是z i ,则 2 i在映射f 下的原象是 _______ .14. _____________________________________________________________________ 已知向量a (1,sin ) , b (1,J 3cos ),则a b 的最大值为 ___________________________________ .4; 2715. 计算:Iog3^— lg 25 2lg 2 e ln2 __________________ .1 x16. 函数y a (a 0, a 1)图象恒过定点 A ,若点A 在直线mx ny 8 0(mn 0)1 1上,则 的最小值为__________________ .m n17. 把实数a,b,c,d 排成形如a b的形式,称之为二行二列矩阵, 定义矩阵的一种运算c d&已知 sin x sin y2 ,cosx cosy3且x,y 为锐角,则tan(xy)= 2#14 B .52 14 55. 14 289.已知定义在R 上的函数f ( x )的图象关于点(一 4,0)对称,且满足f (x )=-f (x +3),f (- 1)= 1 , f ( 0 )=- 2,则 f (1)+ f (2)+ •••+ f (2009)的值为10 .把数列{ 2n 1} ( n N )依次按第一个括号一个数,第二个括号两个数,第三个括号三个数,第四个括号四个数, 第五个括号一个数,第六个括号两个数,…循环分别为ax by,该运算的几何意义为平面上的点cx dy x, y在矩阵a b的c d作用下变换成点 ax by,cx dy ,则若曲线x y 1在矩阵1 a的作用下变换 b 1成曲线2x y 1,则a b 的值为三、解答题(本大题共 5题,满分72分,解答应写出文字说明、证明过程或演算步骤) 18. (本题满分14分)2 __设A {x||x| w 1} , B {x|x 4x 3 0},求集合C ,使C 同时满足下列三个条件:(1) C (AU B) I Z ; (2) C 有两个元素;(3) CI B 19. (本题满分14分)2112cos (x 3) 2>g(x) sin (2x y)(1)要得到y f (x)的图像,只需把 y g(x)的图像经过怎样的变换?(2)设h(x) f (x) g(x),求①函数h(x)的最大值及对应的 x 的值;②函数h(x)的单调递增区间。
浙江省杭州市第二次高考科目教学质量检测 数学(理)

杭州市第二次高考科目教学质量检测数学(理)试题考生须知:1.本卷满分150分,考试时间120分钟2.答题前,在答题卷密封区内填写学校、班级和姓名 3.所有答案必须写在答题卷上,写在试题上无效 4.考试结束,只需上交答题卷 参考公式:如果事件A 、B 互斥,那么 棱柱的体积公式 P (A +B )=P (A )+P (B ) V=Sh如果事件A 、B 相互独立,那么 其中S 表示棱柱的底面积,h 表示棱柱的高 P (A - B )=P (A )·P (B ) 棱锥的体积公式 如果事件A 在一次试验中发生的概车是p ,那么 13V Sh = n 次独立重复试验中事件A 恰好发生k 次概率 ()(1)(0,1,2,,)k kn k n n P k C p p k n -=-= 其中S 表示棱锥的底面积,h 表示棱锥的高棱台的体积公式 球的表面公式121()3V h S S =+ 24S R p =其中S 1,S 2分别表示棱台的上、下底面积,h 球的体积公式 表示棱台的高化 343V R p =其中R 表示球的半径一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知i 是虚数单位,则11i ii i++=+( )A .1322i -+ B .1322i - C .3122i + D .3122i - 2.已知集合{|sin()sin ,(0,)},{|cos()cos ,2A k Z k Bk Z k pp q q q pq q q =?=??=?(0,)},()2z A B p =则ðA .{|2,}k k n n Z =?B .{|21,}k k n n Z =-?C .{|4,}k k n n Z =?D .{|41,}k k n n Z =-?3.设P 为函数()sin()f x x p =的图象上的一个最高点,Q 为函数()cos()g x x p =的图象上的一个最低点,则|PQ|最小值是( )AB .2 C.2D .4.设直线::(0)l y kx m m =+?,双曲线2222:1(0,0)x y C a b a b +=>>,则“bk a=-”是“直线l与双曲线C 恰有一个公共点“的( )A .充分不必要条件B .必要不充分条件C .充分条件D .既不充分也不必要条件5.若存在实数x ,y 使不等式组0320,60x y x y x y ì-?ïïï-+?íïï+-?ïïî与不等式20x y m -+?都成立,则实数m 的取值范围是( )A .m≥0B . m≤3C .m≥lD .m≥36.设数列{a n }是首项为l 的等比数列,若11{}2n n a a ++是等差数列,则12231111()()22a a a a +++2012201311()2a a +++的值等于( ) A . 2012B . 2013C . 3018D . 30197.已知双曲线2222:1(0,0)y x C a b a b+=>>,A ,B 是双曲线的两个顶点.P 是双曲线上的一点,且与点B 在双曲线的同一支上.P 关于y 轴的对称点是Q 若直线AP ,BQ 的斜率分别是k 1,k 2, 且k 1·k 2=45-,则双曲线的离心率是() A .5 B .94C .32D .958.若函数()(1).xf x x e =+,则下列命题正确的是( )A .对任意21m e<-,都存在x R Î,使得()f x m < B .对任意21m e >-,都存在x R Î,使得()f x m < C .对任意21m e<-,方程()f x m =只有一个实根 D .对任意21m e >-,方程()f x m =总有两个实根 9.在直角坐标中,A (3,1),B (-3,-3),C (l .4).P 是AB 和AC 夹角平分线上的一点,且AP =2,则AP 的坐标是A .(,1313-B .(-C .(55- D (-10.如图,平面a 与平面b 交于直线l ,A ,C 是平面a 内 不同的两点,B ,D 是平面b 内不同的两点,且A ,B . C .D 不在直线l 上,M ,N 分别是线段AB ,CD 的中点,下列判断正确的是( )A .若AB 与CD 相交,且直线AC 平行于l 时,则直线BD与l 可能平行也有可能相交B .若AB ,CD 是异面直线时,则直线MN 可能与l 平行C .若存在异于AB ,CD 的直线同时与直线AC ,MN ,BD都相交,则AB ,CD 不可能是异面直线D .M ,N 两点可能重合,但此时直线AC 与l 不可能相交 二、填空题(本大题共7小题,每小题4分,共28分) 11.已知2cos ()3x x R =?,则cos()3x p-= 。
2010高考浙江理数(含解析)

2010年普通高等学校招生全国统一考试(浙江卷)数学理解析一. 选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四项中,只有一项是符合题目要求的。
(1)设P={x ︱x <4},Q={x ︱2x <4},则 (A )p Q ⊆ (B )Q P ⊆ (C )Rp Q C⊆(D )RQ P C⊆解析:{}22<<x x Q -=,可知B 正确,本题主要考察了集合的基 本运算,属容易题(2)某程序框图如图所示,若输出的S=57,则判断框内位 (A ) k >4? (B )k >5? (C ) k >6? (D )k >7?解析:选A ,本题主要考察了程序框图的结构,以及与数列有关的简 单运算,属容易题(3)设n S 为等比数列{}n a 的前n 项和,2580a a +=,则52S S =(A )11 (B )5 (C )8- (D )11-解析:解析:通过2580a a +=,设公比为q ,将该式转化为08322=+q a a ,解得q =-2,带入所求式可知答案选D ,本题主要考察了本题主要考察了等比数列的通项公式与前n 项和公式,属中档题(4)设02x π<<,则“2sin 1x x <”是“sin 1x x <”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件 解析:因为0<x <2π,所以sinx <1,故x sin 2x <x sinx ,结合x sin 2x 与x sinx 的取值范围相同,可知答案选B ,本题主要考察了必要条件、充分条件与充要条件的意义,以及转化思想和处理不等关系的能力,属中档题(5)对任意复数()i ,R z x y x y =+∈,i 为虚数单位,则下列结论正确的是(A )2z z y -= (B )222z x y =+ (C )2z z x -≥ (D )z x y ≤+解析:可对选项逐个检查,A 项,y z z 2≥-,故A 错,B 项,xyi y x z 2222+-=,故B 错,C 项,y z z 2≥-,故C 错,D 项正确。
2010年高考理综(浙江卷)(含答案)

(浙江卷)2010年高考理综化学试题1、下列说法中正确的是A. 光导纤维、棉花、油脂、ABS树脂都是由高分子化合物组成的物质B. 开发核能、太阳能等新能源,推广基础甲醇汽油,使用无磷洗涤剂都可直接降低碳排放C. 红外光谱仪、核磁共振仪、质谱仪都可用于有机化合物结构的分析D. 阴极射线、 -粒子散射现象及布朗运动的发现都对原子结构模型的建立作出了贡献2、有X、Y、Z、W、M五种短周期元素,其中X、Y、Z、W同周期,Z、M同主族;X+与M2-具有相同的电子层结构;离子半径:Z2->W-;Y的单质晶体熔点高、硬度大,是一种重要的半导体材料。
下列说法中,正确的是A. X、M两种元素只能形成X2M型化合物B. 由于W、Z、M元素的氢气化物相对分子质量依次减小,所以其沸点依次降低C. 元素Y、Z、W的单质晶体属于同种类型的晶体D. 元素W和M的某些单质可作为水处理中的消毒剂3、Li-Al/FeS电池是一种正在开发的车载电池,该电池中正极的电极反应式为:2Li+FeS+2e-=Li2S+Fe有关该电池的下列中,正确的是A. Li-Al在电池中作为负极材料,该材料中Li的化合价为+1价B. 该电池的电池反应式为:2Li+FeS=Li2S+FeC. 负极的电极反应式为Al-3 e-=Al3+D. 充电时,阴极发生的电极反应式为:Li2S+Fe-2e-=2Li++FeS4、核黄素又称为维生素B2,可促进发育和细胞再生,有利于增进视力,减轻眼睛疲劳。
核黄素分子的结构为:已知:+H2O+有关核黄素的下列说法中,不正确的是:A.该化合物的分子式为C17H22N4O6B.酸性条件下加热水解,有CO2生成C.酸性条件下加热水解,所得溶液加碱后有NH3生成D.能发生酯化反应5、下列关于实验原理或操作的叙述中,不正确的是:A、从碘水中提取单质碘时,不能用无水乙醇代替CCl4B、可用新制的Cu(OH)2悬浊液检验牙膏中存在的甘油C、纸层析实验中,须将滤纸上的试样点浸入展开剂中D、实验室中提纯混有少量乙酸的乙醇,可采用先加生石灰,过滤后再蒸馏的方法6、下列热化学方程式或离子方程式中,正确的是:A、甲烷的标准燃烧热为-890.3kJ·mol-1,则甲烷燃烧的热化学方程式可表示为:CH4(g)+2O2(g)=CO2(g)+2H2O(g) △H=-890.3kJ·mol-1B.500℃、30MPa下,将0.5molN2和1.5mol H2置于密闭容器中充分反应生成NH3(g),放热19.3kJ,其热化学方程式为:N2(g)+3H2(g) 2NH3(g) △H=-38.6kJ·mol-1C.氯化镁溶液与氨水反应:Mg2++2OH-=Mg(OH)2↓D.氧化铝溶于NaOH溶液:Al2O3+2OH-+3H2O=2Al(OH)4-7、某钠盐溶液中可能含有NO2-、SO42-、SO32-、CO32-、Cl-、I-等阴离子。
2010杭州市高三年级二模

浙江省杭州市2010年第二次高考科目教学质量检测理科综合能力试题考生须知:1.本试卷分试题卷和答题卷,满分150分,考试时间150分钟。
2.答题前,在答题卷密封区内填写学校、班级和姓名。
3.所有答案必须写在答题卷上,写在试题卷上无效。
第Ⅰ卷(选择题共120分)相对原子质量:C 12 H l O 16 Na 23一、选择题(本题包括17小题,每小题只有一个选项符合题意,每小题6分)1.已知洋葱根尖细胞有丝分裂一个细胞周期大约需要12h,某学生研究该细胞周期,获得以下4组数据:①分裂期最多的一个视野中,共有30个细胞,其中分裂前期5个,中期2个,后期2个,末期1个,其余为问期;②分裂期最少的一个视野中,共有35个细胞,其中分裂中期1个,其余为间期;③全部共观察了10个视野,平均每个视野有32个细胞;④统计这些视野观察到的结果:分裂前期细胞15个,中期12个,后期10个,末期8个。
对这4组数据的分析,正确的是()A.用第①组数据直接计算分裂期各期持续时间是最准确的B.用第②组数据直接计算分裂间期持续时间产生的误差最大C.①、②组数据没有意义,不能用于细胞周期各期所需时间分析D.③、④组数据分析间期持续时间大约是l0.3h2.图甲是一个发酵装置,甲瓶中装有酵母菌发酵液。
发酵初期不通气,溶液中有气泡产生;中期可以闻到酒香;后期接种醋酸菌,适当升高温度并通气,酒香逐渐变成醋香。
图乙中能正确表示整个发酵过程培养液pH变化的曲线是()A.①B.②C.③D.④3.下图表示免疫反应的某些过程,下列对a、b、c、d四种细胞的分析判断,正确的是()A .a 细胞具有特异性识别能力B .b 细胞可特异性地攻击自身体内某些细胞或者组织C .HIV 病毒主要侵入并破坏c 细胞,最终导致免疫系统崩溃D .d 细胞受攻击后会导致死亡,这种死亡属于伤害死亡4.2008年,澳大利亚墨尔本大学的安德鲁·帕斯克教授领导的科研小组成功地提取了已经于20年前正式宣布灭绝的塔斯马尼亚虎的DNA 片段,将它注入到老鼠的胚胎中,并在这个胚胎形成软骨和其它骨骼的过程中发挥了重要作用。
2010年浙江省高考数学卷试卷(含答案)

2010年浙江省高考数学卷试卷(含答案)参考公式:如果事件A、B互斥,那么柱体的体积公式如果事件A、B相互独立,那么其中S表示柱体的底面积,h 表示柱体的高椎体的体积公式如果事件A在一次实验中发生的概率是p,那么n次独立重复试验中事件A恰好发生k次的概率其中S表示椎体的底面积,h表示台体的体积公式椎体的高球的表面积公式其中分别表示台体的上、下底面积,球的体积公式H表示台体的高其中R表示球的半径一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)设P={x |x<4},Q={x |x2<4},则(A)(B)(C) (D)(2)某程序框图如图所示,若输出的S=57,则判断框内为(A)k>4? (B)k>5?(C) k>6? (D) k>7?(3)设S n 为等比数列{a n}的前n项和,8a2+ a5=0, 则S5/S2=(A)11 (B)5 (C)-8 (D)-11(4)(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件(5)对任意复数z=x+yi (x,y ∈R ),i 为虚数单位,则下列结论正确的是(6)设m,l 是两条不同的直线,α是一个平面,则下列命题正确的是(7)若实数y x ,满足不等式组,且y x +的最大值为9,则实数m 、n(A)-2 (B ) -1 (C)1 (D)2(8)设1F ,2F 分别为双曲线)0,0(12222>>=-b a by a x 的左,右焦点。
若在双曲线右支上存在点P ,满足2PF =21F F ,且2F 到直线1PF 的距离等于双曲线的实轴长,则该双曲线的渐近方程为(A)043=±y x (B ) 053=±y x (C)034=±y x (D) 045=±y x (9)设函数,)12sin(4)(x x x f -+=则)(x f 不存在零点的是(A)][2,4-- (B ) ][0,2-(C) ][2,0 (D) ][4,2(10)设函数的集合{},1,0,1;1,21,0,21)log()(-=-=++==b a b a x x f P 平面上点的集合{},1,0,1;1,21,0,21),(-=-==y x y x Q 则在同一直角坐标系中,P 中函数)(x f 的图像恰好经过Q 中两个点的函数的个数是(A)4 (B ) 6 (C)8 (D)10二、填空题:本大题共7小题,每小题5分,共28分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
≠浙江省杭州市2010年第二次高考科目教学质量检测数学试题(理科)考生须知: 1.本卷满分150分,考试时间120分钟。
2.答题前,在答题卷密封区内填写学校、班级和姓名。
3.所有答案必须写在答题卷上,写在试题卷上无效。
4.考试结束,只需上交答题卷。
参考公式:如果事件A 、B 互斥,那么 球的体积公式24R S π=P(A+B)=P(A)+P(B) V S h =如果事件A 、B 相互独立,那么 其中S 表示棱柱的底面积,h 表示棱柱的高P(A·B)=P(A)·P(B) 棱锥的体积公式如果事件A 在一次试验中发生的概率是 13V Sh =P ,那么n 次独立重复试验中恰好发生k 其中S 表示棱锥的底面积,h 表示棱锥的高 次的概率 棱台的体积公式k n kk n n P P C k P --=)1()(121()3V h S S =+球的表面积公式 其中S 1、S 2分别表示棱台的上、下底面积, 24R S π= h 表示棱台的高 球的体积公式334R V π=球其中R 表示球的半径一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设1(2i ω=-+是虚数单位),设集合{1,0,1}M =-,则下列结论中正确的是( )A .3(1)M ω+∈ B .3M ω⊆C .1M ω⊂ D .2M ωω+∉2.如图,是一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的侧面积为( ) A .6 B.C .24D .33.使“lg 1m <”成立的一个充分不必要条件是 ( )A .(0,)m ∈+∞B .{1,2}m ∈C .010m <<D .m <14.在阳光体育活动中,全校学生积极参加室外跑步,高三(1)班每个学生上个月跑步的路程从大到小排列依次是12350,,,,a a a a (任意11,2,,49,i i i a a +=>),如图是计算该班上个 月跑步路程前10名学生的平均路程的程序框图,则图中判断框①和处理框②内应分别填写( ) A .10,9s i a <=B .11,11si a <=C .11,10si a <=D .10,10si a <=5.在二项式25(1)(1)x x x ++-的展开式中,含4x 项的系数是 ( )A .-25B .-5C .5D .256.平面上A ,B ,C 三点满足():():()1:2:3BA CA CA AB AB BC ⋅⋅⋅=,则这三点( ) A .组成锐角三角形 B .组成直角三角形C .组成钝角三角形D .在同一条直线上7.设函数()ln(1)(2)f x x x =--的定义域是A ,函数()1)g x =的定义域是B ,若A B ≤,则正数a 的取值范围是( )A .3a >B .3a ≥C .a >D .a ≥8.过双曲线22221(0,0)x y a b a b-=>>的一个焦点F 引它的渐近线的垂线,垂足为M ,延长FM 交y 轴于E ,若FM=2ME ,则该双曲线的 离心主经为 ( )A .3B .2C D 9.设一个小物体在一个大空间中可以到达的部分空间与整个空间的体积的比值为可达率,现用半径为1的小球扫描检测棱长为10的正方体内部,则可达率落在的区间是( )A .(0.96,0.97)B .(0.97,0.98)C .(0.98,0.99)D .(0.99,1)10.如图,阴影是集合22{(,)|(cos )(sin )4,0}P x y x y θθθπ=-+-=≤≤在平面直角坐标系上表示的点集,则阴影中间形如“水滴”部分的面积等于( ) A.π+B.73π-C.116π-D .2π+二、填空题:本大题共7小题,每小题4分,共28分。
11.函数0sin(10)cos(40),()y x x x R =+++∈的最大值是 。
12.依次写出数列*1231,,,,()n a a a a n N =∈的法则如下:如果2n a -为自然数且未写过,则写12n n a a +=-,否则就写13n n a a +=+,则6a = 。
(注意:0是自然数) 13.已知A 、B 是圆22:16O x y +=上的两点,且|AB=6,若以AB 为直径的圆M 恰好经过点C (1,-1),则圆心M 的轨迹方程是 。
14.观察下列等式: 20(1)1;x x ++= 212(1)1;x x x x ++=++22432(1)2321;x x x x x x ++=++++2365432(1)367631;x x x x x x x x ++=++++++……;可能以推测,25(1)x x ++展开式中,第五、六、七项的系数和是 。
15.将3个不同的小球放入编号分别为1,2,3,4,5,6的盒子内,6号盒中至少有一个球的方法种数是16.如果实数,x y 满足条件101010x y y x y -+≥⎧⎪+≥⎨⎪++≤⎩,则3251x y x +--的取值范围是17.已知函数()||||||||f x x a x a x b x b c =-+++-++-,若存在正常数m ,使()0f m =,则不等式()()f x f m <的解集是 。
三、解答题:本大题共5小题,共72分,解答应写出文字说明,证明过程或演算步骤。
18.(本题满分14分)口袋中有1个红球、2个黄球、3个白球、3个黑球共9个球,从中任取3个球。
(1)求取出的球的颜色不全相同的概率;(2)记ξ为取出的球的颜色的种数,求随机变量ξ的分布列及其数学期望E ξ。
19.(本题满分14分)在ABC ∆中,角A 、B 、C 的对边分别为,,a b c ,且满足).c BA BC cCB CA -⋅=⋅(1)求角B 的大小; (2)若||6BA BC -=ABC ∆面积的最大值。
20.(本题满分14分)已知如图四棱锥P —ABCD 中,底面ABCD 是平行四边形,PG ⊥平面ABC ,垂足G 在AD 上,且1,.2,43AG GD GB GC GB GC PG =⊥===,E 是BC 的中点。
(1)求证:PC ⊥BG ;(2)求异面直线GE 与PC 所成角的余弦值; (3)若F 是PC 上一点,且,CFDF GC CP⊥求的值。
21.(本小题满分15分)已知椭圆的中心在原点,焦点在x 轴上,长轴长是短轴长的2倍且经过点M (2,1),平行于OM 的直线l 交椭圆于A 、B 两点。
(1)求椭圆的方程; (2)已知(,0),()||||MA MBe t p MA MB λ==+,是否对任意的正实数,t λ,都有0e p ⋅=成立?请证明你的结论。
22.(本题满分15分)设32121()()3(,,0)32x a b f x x x x x a b R a λλ-=+++⋅∈> (1)当121,0λλ==时,设12,x x 是()f x 的两个极值点, ①如果1212x x <<<,求证:(1)3f '->;②如果21122,2(,)a x x x x x ≥-=∈且且时,函数2()()2()g x f x x x '=+-的最小值为()h a ,求()h a 的最大值。
(2)当120,1λλ==时,①求函数()3(ln31)y f x x =-+的最小值。
②对于任意的实数,,a b c ,当3a b c ++=时,求证3339.a b ca b c ++≥参考答案一、选择题: 本题考查基本知识和基本运算.每小题5分, 满分50分. 1—5ACBCB 6—10ABCBC二、填空题: 本题考查基本知识和基本运算.每小题4分, 满分28分. 11.1 12.613. 9)1()1(22=++-y x14.141 15.91 16.[4,7] 17.(– m ,m )三、解答题: 本大题共5小题, 满分72分.18.解(Ⅰ)P=1 – 1/42 =41/42 5分 (Ⅱ)842)1(==ξP , 8443)2(==ξP , 8439)3(==ξP 5分8420538439284431842=⨯+⨯+⨯=ξE 4分19.解:(I )条件可化为 (2)c o s c o sa c Bb C -=根据正弦定理有 s i n s i n )c o s s i n c o s A C B B C-= 3分∴s i n c o s s i n (A B C B=+cos sin A B A =因为 s i n 0A >,所以 c o s2B = 4B π=. 3分 (II )因为 ||6B A BC -= 所以 ||6CA =,即 26b =, 2分根据余弦定理 2222c o s b a c a c B =+-,可得 226a c =+ 2分有基本不等式可知 2262(2a c ac ac =+≥=即 3(2)ac ≤,故△ABC 的面积1sin 2S ac B ==≤ 即当a =c=236+时,△ABC 的面积的最大值为2)12(3+. 4分 20.解:(Ⅰ)因为PG ⊥底面ABCD, 所以 PG ⊥ BG, 又BG ⊥CG , 所以BG ⊥面PGC,所以PC ⊥BG . 4分(Ⅱ)建立如图空间直角坐标系,各点坐标如图所示,)4,2,0(),0,1,1(-==→--→--PC GE∴ 1010|||||||,cos |=⋅=><→--→--→--→--→--→--PC GE PC GE PC GE 。
. 4分 (Ⅲ)设CF = λCP , 则点 )4220(λλ,,-F ,又D (–23,23,0 ), ∴),4,221,23(λλ-=→--DF 3234(,,)2121DF λλλ∴=-++,GC =(0,2,0), 由GC DF ⊥得0=⋅→--→--GC DF ,∴0)221(2=-λ。
得41=λ,所以 CP CF = 41 6分21解:(1)设椭圆方程为)0(12222>>=+b a b y a x则⎪⎩⎪⎨⎧==⎪⎩⎪⎨⎧=+=2811422222b a b a b a 解得 ,∴椭圆方程12822=+y x . 5分(2)若0=⋅p e 成立,则向量||||(MB MA +=λ与x 轴垂直,由菱形的几何性质知,AMB ∠的平分线应与x 轴垂直.为此只需考察直线MA,MB 的倾斜角是否互补即可.由已知,设直线l 的方程为:m x y +=212分由0422128212222=-++∴⎪⎪⎩⎪⎪⎨⎧=++=m m x x y x m x y 3分设直线MA 、MB 的斜率分别为k 1,k 2, 只需证明k 1+k 2=0即可,设21,21),,(),,(2221112211--=--=x y k x y k y x B y x A 则 042222=-++m mx x 由可得,42,222121-=-=+m x x m x x ,而0)2)(2(4442422122=--+-+--=x x m m m m , 3分∴k 1+k 2=0,直线MA,MB 的倾斜角互补.故对任意的正实数λ,t ,都有0=⋅成立. 2分22.解: 解 (Ⅰ)①证明:当11λ=,20λ=时,2()(1)1f x ax b x '=+-+,x 1,x 2是方程()0f x '=的两个根,由1212x x <<<且0a >得(1)0(2)0f f '<⎧⎨'>⎩,即04210a b a b +<⎧⎨+->⎩.所以f `( – 1)= a – b + 2 = – 3(a+b ) + (4a +2b – 1) + 3 > 3 . 3分②设12()()()f x a x x x x '=--,所以212122()()()()()g x a x x x x a x x x x a a=--+=---+,易知20x x ->,120x x a-+>,所以2212()()1()(2)2x x x x a g x a a a ⎛⎫-+-+ ⎪≥-⋅=-++ ⎪ ⎪⎝⎭当且仅当112x x x x a-=-+时, 即1211112x x x x a a+=-=+-时取等号所以1()(2)h a a a=-++(2a ≥).易知当2a =时,()h a 有最大值,即max 9()(2)2h a h ==-. 5分(Ⅱ)①当10λ=,21λ=时,()3x f x x =, 所以33(ln31)x y x x =-+.3(ln3)33(ln31)x x y x '=⋅+-+,容易知道y '是单调增函数,且1x =是它的一个零点,即也是唯一的零点. 当1x >时,0y '>;当1x <时,0y '<,故当1x =时,函数()3(ln31)y f x x =-+有最小值为3ln 3-. 4分 ②由①知 33(l n 31)3l x x x ≥+-,当x 分别取a 、b 、c 时有:33(ln31)3ln3a a a ≥+-;33(ln31)3ln3b b b ≥+-; 33(ln31)3ln3c c c ≥+-三式相加即得. 3分。
