热学第三章麦克斯维速率分布定律及分子热运动规律
合集下载
热学-第三章气体分子热运动速率和能量分布
3 2 2 mv 2 kT 2
得：dN m 4 e 得
N
kT 2
v dv
记忆这个公式分三部分： 第一部分，4v2dv是“球壳”的体积，而“球壳”全方位的高 度对称性正是分子热运动想各个方向几率均等的生动表现；
第二部分 ,
e
mv2 / 2kT
正是分子热运动速率取值不等几率的表现，值得注意，这个 指数衰减律的结果没有单位，mv2/2是分子热运动的动能，kT 既有能量的量纲，所以指数衰减的指数部分是热运动的动能 与体系能量状态特征量之比，对于大的速率，指数衰减的速 度比v2增加的速度快得多，二者共同影响的结果，分布函数 值必然较小。
vf v dv
Nvfvdv
（B）
v2
v1 v2 v1
vf v dv f v dv
（C）
v2
v1
（D）
v2 v1
vf v dv N
（B）
2.麦克斯韦速度分布律
在平衡态下，当气体分子间的相互作用可以 d v的分子 忽略时，分布在速度区间 v ~ v 数占总分子数的比率为
dω＝ 4πv2dv
麦克斯韦速率分布律
将dω＝dvxdvydvz代入
dN m e N 2 kT
x y
3 2 2 2 m ( v v v 2 x y z) 2 2 kT
v dv dv dv x y z
麦克斯韦 速率分布 分布律
2 2 2 2 且： v v v v z
小球在伽 尔顿板中的分 布规律 .
统计规律 当小球数 N 足够大时小球的分布具有 统计规律. . . . . . . . . . 设 N i 为第 i格中的粒子数 .
得：dN m 4 e 得
N
kT 2
v dv
记忆这个公式分三部分： 第一部分，4v2dv是“球壳”的体积，而“球壳”全方位的高 度对称性正是分子热运动想各个方向几率均等的生动表现；
第二部分 ,
e
mv2 / 2kT
正是分子热运动速率取值不等几率的表现，值得注意，这个 指数衰减律的结果没有单位，mv2/2是分子热运动的动能，kT 既有能量的量纲，所以指数衰减的指数部分是热运动的动能 与体系能量状态特征量之比，对于大的速率，指数衰减的速 度比v2增加的速度快得多，二者共同影响的结果，分布函数 值必然较小。
vf v dv
Nvfvdv
（B）
v2
v1 v2 v1
vf v dv f v dv
（C）
v2
v1
（D）
v2 v1
vf v dv N
（B）
2.麦克斯韦速度分布律
在平衡态下，当气体分子间的相互作用可以 d v的分子 忽略时，分布在速度区间 v ~ v 数占总分子数的比率为
dω＝ 4πv2dv
麦克斯韦速率分布律
将dω＝dvxdvydvz代入
dN m e N 2 kT
x y
3 2 2 2 m ( v v v 2 x y z) 2 2 kT
v dv dv dv x y z
麦克斯韦 速率分布 分布律
2 2 2 2 且： v v v v z
小球在伽 尔顿板中的分 布规律 .
统计规律 当小球数 N 足够大时小球的分布具有 统计规律. . . . . . . . . . 设 N i 为第 i格中的粒子数 .
热学--麦克斯韦速率分布
应用：
o
v
计算分子平均自由程、气体分子碰壁数、碰撞频率时经常用到。
3）均方根速率
v
0
2
v
2
N
0
v dN N
2
v 2 Nf ( v)dv N
f ( v)
3kT v m
2
应用：
o
v
计算分子平均自由程、气体分子碰壁数、碰撞频率时经常用到。
速率比较：
3kT 3RT 3RT vrms v 1.73 m Mm Mm
概率定义
基本性质
平均值与涨落
F(x) 分布曲线
§2.3 麦克斯韦速率分布
处于平衡态的气体，虽然每个分子在某一瞬时的 速度大小、方向都在随机地变化着，但是大多数分
子之间存在一种统计相关性，这种统计相关性表现
为平均说来气体分子的速率（指速度的大小）介于v
到v+dv的概率（即速率分布函数）是不会改变的。
v
o
vp 0 vpH
v
N2 分子在不同 温度下的速率分布
同一温度下不同气 体的速率分布
例2.1：设图中的两条曲线分别为氢气（H2）和氧气 （O2）在相同温度下的麦克斯韦气体分子速率分布曲 线。 (1)指出图中哪条曲线是代表氢气的，哪条曲线是 代表氧气的? (2)在同一温度下，氢分子的最概然速率等于氧分 子最概然速率的多少倍？ 问题一:
比较两种不同温度和质量的气体的分布曲线时经常用到。
2）平均速率
(离散型) (连续型)
v
v1dN1 v2dN 2 vi dN i vn dN n v N
v
N
0
vdN N
o
v
计算分子平均自由程、气体分子碰壁数、碰撞频率时经常用到。
3）均方根速率
v
0
2
v
2
N
0
v dN N
2
v 2 Nf ( v)dv N
f ( v)
3kT v m
2
应用：
o
v
计算分子平均自由程、气体分子碰壁数、碰撞频率时经常用到。
速率比较：
3kT 3RT 3RT vrms v 1.73 m Mm Mm
概率定义
基本性质
平均值与涨落
F(x) 分布曲线
§2.3 麦克斯韦速率分布
处于平衡态的气体，虽然每个分子在某一瞬时的 速度大小、方向都在随机地变化着，但是大多数分
子之间存在一种统计相关性，这种统计相关性表现
为平均说来气体分子的速率（指速度的大小）介于v
到v+dv的概率（即速率分布函数）是不会改变的。
v
o
vp 0 vpH
v
N2 分子在不同 温度下的速率分布
同一温度下不同气 体的速率分布
例2.1：设图中的两条曲线分别为氢气（H2）和氧气 （O2）在相同温度下的麦克斯韦气体分子速率分布曲 线。 (1)指出图中哪条曲线是代表氢气的，哪条曲线是 代表氧气的? (2)在同一温度下，氢分子的最概然速率等于氧分 子最概然速率的多少倍？ 问题一:
比较两种不同温度和质量的气体的分布曲线时经常用到。
2）平均速率
(离散型) (连续型)
v
v1dN1 v2dN 2 vi dN i vn dN n v N
v
N
0
vdN N
热学-统计物理3 第3章 气体分子热运动速率和能量的统计分布律
f v
v v pv v 2
讨论
麦克斯韦速率分布中最概然速率 vp 的概念
下面哪种表述正确？
（A） vp 是气体分子中大部分分子所具有的速率. （B） vp 是速率最大的速度值. （C） vp 是麦克斯韦速率分布函数的最大值.
（D） 速率大小与最概然速率相近的气体分子的比 率最大.
例1 计算在 27 C 时，氢气和氧气分子的方均
M
3.方均根速率 v2
v2
N
0
v2dN N
0
v2Nf N
(v)dv
o
v
v2 v2 f (v)dv 4 ( m )3 2 e mv2 2kT v4dv
0
2 kT
0
v4ev2 dv 3
0
8 5
v2 3kT m
v2 3kT 3RT
2kT
v
麦克斯韦速率分布函数的物理意义： f (v) dNv
Nd v
既反映理想气体在热动平衡条件下，分布在速率 v 附近单
位速率区间内的分子数占总分子数的百分比，又表示任意
一分子的速率出现在 v附近单位速率区间内的概率。
如果以速率为横坐标轴，速率分布函数为纵坐标轴，画 出的一条表示f(v) —v之间关系的曲线，称为气体分子的麦 克斯韦速率分布曲线。 ，它形象地描绘出气体分子按速率 分布的情况。
大量分子的速率的算术平均值叫做分子的平均速率.
v
vNf (v)dv
0
vf (v)dv
v 4 (
m
)3 e2 mv2 2kT v2dv
N
0
0
v v pv v 2
讨论
麦克斯韦速率分布中最概然速率 vp 的概念
下面哪种表述正确？
（A） vp 是气体分子中大部分分子所具有的速率. （B） vp 是速率最大的速度值. （C） vp 是麦克斯韦速率分布函数的最大值.
（D） 速率大小与最概然速率相近的气体分子的比 率最大.
例1 计算在 27 C 时，氢气和氧气分子的方均
M
3.方均根速率 v2
v2
N
0
v2dN N
0
v2Nf N
(v)dv
o
v
v2 v2 f (v)dv 4 ( m )3 2 e mv2 2kT v4dv
0
2 kT
0
v4ev2 dv 3
0
8 5
v2 3kT m
v2 3kT 3RT
2kT
v
麦克斯韦速率分布函数的物理意义： f (v) dNv
Nd v
既反映理想气体在热动平衡条件下，分布在速率 v 附近单
位速率区间内的分子数占总分子数的百分比，又表示任意
一分子的速率出现在 v附近单位速率区间内的概率。
如果以速率为横坐标轴，速率分布函数为纵坐标轴，画 出的一条表示f(v) —v之间关系的曲线，称为气体分子的麦 克斯韦速率分布曲线。 ，它形象地描绘出气体分子按速率 分布的情况。
大量分子的速率的算术平均值叫做分子的平均速率.
v
vNf (v)dv
0
vf (v)dv
v 4 (
m
)3 e2 mv2 2kT v2dv
N
0
0
大学物理麦克斯韦分子速率分布定律资料
（D） 速率大小与最概然速率相近的气体分子的比 率最大.
11
例: 设有N个气体分子，其速率分布函数为
f
(
)
A
(0 0
)
0 0 0
求: (1)常数A；(2)最概然速率，平均速率和方均根；
(3)速率介于0~0/3之间的分子数；(4)速率介于0~ 0/3
之间的气体分子的平均速率。
f()
解： (1)气体分子的分布曲线如图
2 1300
N
dN
0
3 Nf ( )d
0
0 3
0
N
6
3 0
(0
)d
7N 27
13
(4)速率介于0~0/3之间的气体分子平均速率为
0~0 3
0
3 dN
0 0
0 3
0
N
6 v03
2
(
0
)d
30
7N 27
14
3 dN 0
注意：速率介于 1~ 2之间的气体分子的平均速率
的计算是
2f ( )d
1~2
1
2 f ( )d
1
而非
1 ~2
2f ( )d
1
14
作业题
设. 有N个粒子，其速率分布函数 f v 为
f
v
Av 30 v
0
v 30 v 30
求: （1）归一化常数A的值；（2）最概然速率
（3）N个粒子的平均速率 v
15
§3.4 麦克斯韦分子速率分布定律
任何一个分子，速度大小和方向都是偶然的， 不可预知。但在平衡态下,大量气体分子的速度分布 将具有稳定的规律 — 麦克斯韦速度分布律。
只考虑速度大小的分布—麦克斯韦速率分布律。
11
例: 设有N个气体分子，其速率分布函数为
f
(
)
A
(0 0
)
0 0 0
求: (1)常数A；(2)最概然速率，平均速率和方均根；
(3)速率介于0~0/3之间的分子数；(4)速率介于0~ 0/3
之间的气体分子的平均速率。
f()
解： (1)气体分子的分布曲线如图
2 1300
N
dN
0
3 Nf ( )d
0
0 3
0
N
6
3 0
(0
)d
7N 27
13
(4)速率介于0~0/3之间的气体分子平均速率为
0~0 3
0
3 dN
0 0
0 3
0
N
6 v03
2
(
0
)d
30
7N 27
14
3 dN 0
注意：速率介于 1~ 2之间的气体分子的平均速率
的计算是
2f ( )d
1~2
1
2 f ( )d
1
而非
1 ~2
2f ( )d
1
14
作业题
设. 有N个粒子，其速率分布函数 f v 为
f
v
Av 30 v
0
v 30 v 30
求: （1）归一化常数A的值；（2）最概然速率
（3）N个粒子的平均速率 v
15
§3.4 麦克斯韦分子速率分布定律
任何一个分子，速度大小和方向都是偶然的， 不可预知。但在平衡态下,大量气体分子的速度分布 将具有稳定的规律 — 麦克斯韦速度分布律。
只考虑速度大小的分布—麦克斯韦速率分布律。
热学-第三章气体分子热运动速率和能量分布
等概率性
在平衡态下，系统从任意一个微观状态转移到另一个 微观状态的概率相等。
宏观态与微观态等概率性的意义
平衡态是系统内部最混乱的状态，即系统内部各个分 子运动状态的分布最均匀，没有明显的有序性。
热力学概率与宏观态的等概率性
热力学概率
宏观态等概率性与热力学概 率的关系
在平衡态下，系统处于各个宏观态的概率相等，即 热力学概率相等。
了解气体分子的能量分布和速度分布有助于深入理解热力学的基本原理，如温度 、内能、熵等概念。
03 气体分子的碰撞和动量传 递
气体分子间的碰撞频率
总结词
气体分子间的碰撞频率与气体分子的速度分布和分子间的距离有关，是气体分子热运动的重要参数。
详细描述
气体分子间的碰撞频率是指在单位时间内，两个分子相互碰撞的次数。由于气体分子的速度分布和分 子间的距离不同，碰撞频率也会有所差异。在理想气体中，碰撞频率可以用公式计算，它与气体分子 的平均自由程和分子速度有关。
定义
气体分子在热运动中具有的 平均能量是指所有气体分子 的总能量除以分子总数。
计算公式
平均能量 = (总能量) / (分子 总数)
影响因素
温度和物质的种类会影响气 体分子的平均能量。
气体分子的最可几能量
01
定义
气体分子在热运动中具有的最可 几能量是指一定温度下，占据一 定数量的分子的主要能量的值。
熵与自然过程的不可逆性
熵与自然过程的不可逆性密切相关，因为高熵状态对应于无序程度较高的状态，低熵状态对应于有序 程度较高的状态。
在自然过程中，由于熵增加原理的作用，系统总是向着高熵状态发展，即从有序向无序发展。因此，许 多自然过程都是不可逆的。
例如，物体受热会膨胀，但自发地收缩；化学反应会进行到底，但自发地逆向反应很困难；生物体衰老 和死亡后不能自发地恢复青春等。这些都是由于系统内部熵增加导致的不可逆过程。
分子热运动的速度和速率统计分布规律
C 1 vo
vvf(v)dvvoC vdvCvo 2
0
0
2
1
v
2 o
vo
vo 2 2
v20 v2f(v)dv0 voC v2dv1 3vo 2
v2
3 3 vo
9.4.2 分子的速度分布函数：
速度空间（如图） 速度空间的体积元 dVxdVydVz 代表如下速度范围
Vz dVxdVy dVz
-
p
a
A
π
a
-
3 2
v
2 x
v
2 x
e
-
a
v
2 x
d
v
x
-
e
-
a
v
2 x
d
v
x
kT m
-
a m 2kT
F (V x,V y,V z)(2π m kT)3 2e-2m kT(V x2+ V y2+ V z2)
麦克斯韦速度分布函数
2. 麦克斯韦速率分布律
处于平衡态的理想气体系统，速率满足下列分布规律
处于平衡态的理想气体系统利用系统的各向同性性三个速度分量的相互独立性dvdvdvdvdvdvdvdvdvaevvvktfvvvkt麦克斯韦速度分布函数处于平衡态的理想气体系统速率满足下列分布规律麦克斯韦速率分布律分子速率处于vdv间的几率是分子速度矢量端点落在和vdv为内外半径球壳内的几率
9.4.1 分子的速率分布函数
2RT M
1.41 kT m
V 0 Vf (V)dV
V 8kT 8RT 1 .6 0 k T
πm πM
m
V2 V2f(V)dV 0
or 1mV2 3kT
第3章 气体分子热运动速率和能量的统计分布
每个分子的速度可用一个以坐标原点为起点的矢量表示
v vxi vy j vzk
速度空间体积元
速率分布是速度矢量大小被限制在一定区间
满足此条件的速度矢量其端点位于半径为 v，厚度为dv的球壳内
球壳体积为
17
用球壳体积
代替
并注意 v2 vx2 v2y vz2 得麦克斯韦速率分布
dN 4π(
n n 1 n
•分子数∆n 越大，涨落的百分数就越小，涨落现象越不显著。
• 麦克斯韦速率分布律只对大量分子组成的体系才成立。 9
三、用麦克斯韦速率分布函数求平均值
平均速率（算术平均值）
离散型
v v1N1 v2N2 viNi vnNn i viNi
N
N
连续型
N
v 0 vdN 0 vNf (v)dv
•当R 以一定的角速度转动，铋分子由S3到达G需用一段时间。 • 这段时间内R己转过一角度，铋分子不再沉积在板上P处。 • 不同速率的分子将沉积在不同的地方．速率大的分子由S3到G所需
的时间短，沉积在距P较近的地方，速率小的分子沉积在距P较远 的地方。
34
•设速率为 v的分子沉积在P’处以s 表示弧PP’的长度。 表示R的
N1, N2,…, Ni, …
小球在槽内的分配情况，称为一种分布。
总数足够大，槽内的小球的数目与小球总数之比
..........
.. . .
.......
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. .
. . .
.
. . .
.
. . .
v vxi vy j vzk
速度空间体积元
速率分布是速度矢量大小被限制在一定区间
满足此条件的速度矢量其端点位于半径为 v，厚度为dv的球壳内
球壳体积为
17
用球壳体积
代替
并注意 v2 vx2 v2y vz2 得麦克斯韦速率分布
dN 4π(
n n 1 n
•分子数∆n 越大，涨落的百分数就越小，涨落现象越不显著。
• 麦克斯韦速率分布律只对大量分子组成的体系才成立。 9
三、用麦克斯韦速率分布函数求平均值
平均速率（算术平均值）
离散型
v v1N1 v2N2 viNi vnNn i viNi
N
N
连续型
N
v 0 vdN 0 vNf (v)dv
•当R 以一定的角速度转动，铋分子由S3到达G需用一段时间。 • 这段时间内R己转过一角度，铋分子不再沉积在板上P处。 • 不同速率的分子将沉积在不同的地方．速率大的分子由S3到G所需
的时间短，沉积在距P较近的地方，速率小的分子沉积在距P较远 的地方。
34
•设速率为 v的分子沉积在P’处以s 表示弧PP’的长度。 表示R的
N1, N2,…, Ni, …
小球在槽内的分配情况，称为一种分布。
总数足够大，槽内的小球的数目与小球总数之比
..........
.. . .
.......
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. .
. . .
.
. . .
.
. . .
麦克斯韦速率分布
一般气体、液体、固体及在恒定外场中的经典系统，
只要系统的能量可写成：
分子的动量分量
E
3N
i 1
Pi2 2m
U
(q1 , q2 ,
qi
,
)
广义坐标
分子间相互作用的能量及在外场中的势能之和
气体分子按速率分布的统计规律最早是由麦克斯韦于1859年 在概率论的基础上导出的，1877年玻耳兹曼由经典统计力学中导 出，1920年斯特恩从实验中证实了麦克斯韦速率分布律。
但由前面 u2 u2 知，vrms v 总成立
例1．速率分布函数 f 的v物理意义为：
（Ａ）具有速率v 的分子占总分子数的百分比． （Ｂ）速率分布在v 附近的单位速率间隔中的
分子数占总分子数的百分比．
（Ｃ）具有速率v 的分子数． （Ｄ）速率分布在 v 附近的单位速率间隔中
的分子数．
3
)2
exp(
m1v12 2kT
)
v12dv1
注意
dN 2 N2
f (v2 )dv2
4
(
m2
2 kT
3
)2
exp(
m2v22 2kT
)
v22dv2
混合气中各组分的麦氏分布率不一样，但有一点一定相同：
混合气达到平衡后，各组分的温度T必然相同。
7. 统计物理证明，麦氏分布率不仅适用于理气，也适用于
速率分布函数为：
麦克斯韦速率分布概率密度
f (v) 4 (
m
)
3 2
exp(
mv
2
)
v
2
2 kT
2kT
ቤተ መጻሕፍቲ ባይዱ
热学第三章
3/ 2
1
1
1
1/ 2
1
1/ 2
1
1 y m −2v2 / kT f (vy ) = e 2πkT 1 m −2vz2 / kT f (vz ) = e 2πkT 1/ 2
1/ 2
f (v) = f (vx ) f (vy ) f (vz )
积分公式：
translation rotation
2
如果某种气体的分子有t个平动自由度，r个转 动由度，s个振动自由度，则分子的平均平动 s t kT ， kT 能，平均转动能和平均振动能就分别为 2 2 r 1 kT 和 2 ，而分子的平均总动能即为 (t + r + s)kT
2
注意：能量均分定理是一种统计规律。对于个别分子，在任一瞬时 它的各种形式动能不具有上述关系。大量粒子通过碰撞，使各种形 式的动能发生传递和转换，从而实现能量均分的统计结果。
e
v dv
m = 4π 2πkT 3RT = M v =
__ 2
3/ 2
∫
1 ∞ − mv2 / kT 4 2 0
e
v dv
3RT M
积分公式：
∫
∞
0
e
−λv2 3
1 v dv = 2 2λ
,
∫
∞
0
e
−λv2 4
v dv =
3 π 8 λ5
比较：
vp =
2RT M
, v=
8RT πM
§2 用分子射线实验验证麦克斯韦速度分布律（1）
一、分子射线
S 金属蒸气
S1
S2
准直器
§2 用分子射线实验验证麦克斯韦速度分布律（2）
气体分子运动论和热力学基础之麦克斯韦速率分布律
极大值在376.6m/s~378.1m/s速率区间，极大值为0.0022044。
速率间 隔不断 减小， 直方条 越来越 窄。
当速率间隔很小时， 直方条很窄，直线 都连成一片，顶部 的阶梯几乎消失。
当速率间隔趋于零时， 顶部将趋于光滑的曲 线，极大值范围趋于 一点，极大值越精确。
速率在0~100m/s之内的分子数 占总分子数比例约为1.35%。
麦克斯韦速率分布的函数曲线 分子的质量是参数，函数曲
会随参数不同而有所改变；
线会随参数而有所改变。
氧气分子在300K时 的最概然速率约为 395m/s，在600K时 的最概然速率约为 558m/s。 对于分子质量一定的气
体，温度升高则峰值降 低，说明：在相同的速 率间隔内，向着各个方 向运动的速率小的分子 数量减少了，速率大的 分子数量增加了，分子 运动得更剧烈了。
{范例8.4} 麦克斯韦速率分布律
[解析](1)在三维速度空间中，在速度间隔vx~vx + dvx、 vy~vy + dvy、vz~vz + dvz内，分子数占总分子数的比例为
dN N0
(m 2πkT
F
)3/
(vx )F (vy )F (vz )dvxdvydvz
2
exp[
m(vx2
v
2 y
2kT
{范例8.4} 麦克斯韦速率分布律
[解析](2)当v = 0时，f(v) = 0；当v→∞时，f(v)→0。
由于f(v)不小于零，因此f(v)必有极大值。 令df(v)/dt = 0，即
df (v) 4π( m )3/2 (2v v2 m2v ) exp( mv2 ) 0
dv
2πkT
2kT
麦克斯韦速度分布定律
麦克斯韦速度分布定律麦克斯韦速度分布定律是描述气体分子速度分布的统计规律之一，由19世纪末的苏格兰物理学家詹姆斯·麦克斯韦提出。
该定律在热力学和统计物理学中有着广泛的应用，能够揭示气体分子运动特征，对于理解气体动力学和热传导等现象具有重要意义。
根据麦克斯韦速度分布定律，理想气体分子的速度服从麦克斯韦-玻尔兹曼速度分布。
其概率密度函数为：f(v) = (m / (2πkT))^(3/2) * 4πv^2 * e^(-mv^2 / (2kT))其中，f(v)表示速度为v的分子的概率密度，m为分子质量，k为玻尔兹曼常数，T为气体温度。
该概率密度函数描述了气体分子速度的分布情况。
根据这一函数，可以得到气体分子不同速度下的概率密度，以及平均速度、平均速度的平方等相关参数。
麦克斯韦速度分布定律具体刻画了速度分布的趋势，从而为研究气体热力学性质提供了重要依据。
根据麦克斯韦速度分布定律可以得到以下几个重要结论：1. 峰值速度：麦克斯韦速度分布定律的概率密度函数在具体速度处取得最大值，即存在一个峰值速度。
这个峰值速度与气体的温度和质量有关，温度越高或质量越小，峰值速度越大。
2. 平均速度：根据麦克斯韦速度分布定律，可以计算出气体分子的平均速度。
平均速度与系统的温度有关，随着温度的升高，平均速度也增加。
3. 速度分散度：麦克斯韦速度分布定律还可以用来计算气体分子速度的分散度。
速度分散度可以通过计算速率最大值附近的速度范围来确定。
由于速度分散度对于描述气体的输运性质至关重要，因此，该定律在研究气体动力学和热学性质时经常被应用。
麦克斯韦速度分布定律是热力学和统计物理学中的重要模型，它将分子速度的概率分布与系统的热力学性质联系在一起。
通过该定律，我们可以更好地理解气体分子的运动规律，研究气体的输运性质和热传导现象。
同时，在工程和科学领域的应用中，麦克斯韦速度分布定律也为材料设计、能源开发和天文物理学等提供了重要指导。
第三章气体分子热运动速率和能量的统计分布律
麦克斯韦严谨的科学态度和科学研究方法是人类极其宝贵的精 神财富。
热学
14
讨论
麦克斯韦速率分布中最概然速率 vp 的概念
下面哪种表述正确？
（A） vp 是气体分子中大部分分子所具有的速率. （B） vp 是速率最大的速度值. （C） vp 是麦克斯韦速率分布函数的最大值.
（D） 速率大小与最概然速率相近的气体分子的比 率最大.
N
N
v
v f (v)dv
8kT
0
πm
v 1.60 kT 1.60 RT
f (v)
m
M
3）方均根速率 v2
o
v
v2
N
0
v2dN N
0
v2
Nf
N
(v)dv
v2 3kT m
热学
8
vp v v2
vrms
v2
3kT m
3RT M
v 1.60 kT 1.60 RT
m
M
vp
2kT m
为清楚起见 , 从正面来
观察。
铁钉
隔板
热学
28
统计规律和方法
伽尔顿板 再投入小球： 经一定段时间后 , 大量小
球落入狭槽。
分布情况：中间多，两边少。
重复几次 ，结果相似。
单个小球运动是随机的 , 大量小球运动分布是确定的。
大量偶然事件整体所遵 循的规律 —— 统计规律。
热学
小球数按空间 位置 分布曲线
v2
dN 4π(
m
)3
2
e
mv2 2 kT
v2
dv
N
2πkT
热学
5
反映理想气体在热动 平衡条件下，各速率区间 分子数占总分子数的百分
热学
14
讨论
麦克斯韦速率分布中最概然速率 vp 的概念
下面哪种表述正确？
（A） vp 是气体分子中大部分分子所具有的速率. （B） vp 是速率最大的速度值. （C） vp 是麦克斯韦速率分布函数的最大值.
（D） 速率大小与最概然速率相近的气体分子的比 率最大.
N
N
v
v f (v)dv
8kT
0
πm
v 1.60 kT 1.60 RT
f (v)
m
M
3）方均根速率 v2
o
v
v2
N
0
v2dN N
0
v2
Nf
N
(v)dv
v2 3kT m
热学
8
vp v v2
vrms
v2
3kT m
3RT M
v 1.60 kT 1.60 RT
m
M
vp
2kT m
为清楚起见 , 从正面来
观察。
铁钉
隔板
热学
28
统计规律和方法
伽尔顿板 再投入小球： 经一定段时间后 , 大量小
球落入狭槽。
分布情况：中间多，两边少。
重复几次 ，结果相似。
单个小球运动是随机的 , 大量小球运动分布是确定的。
大量偶然事件整体所遵 循的规律 —— 统计规律。
热学
小球数按空间 位置 分布曲线
v2
dN 4π(
m
)3
2
e
mv2 2 kT
v2
dv
N
2πkT
热学
5
反映理想气体在热动 平衡条件下，各速率区间 分子数占总分子数的百分
第三章 气体分子热运动速率和能量的统计分布规律
m
v2
v2dNv
4
1
v4ev2 / 2 dv 3 2
N
0
3 3
2
所以： a2 2kT m
所以：速度分布率： F(v)
dNv
( m ) e 3/ 2 mv2 / 2kT
Ndvxdvydvz 2kT
速率分布律：
f (v) dNv 4 ( m ) v e 3/ 2 2 mv2 / 2kT
2.统计规律的数学描述
(1).概率：大量偶然事件中，出现某一结果的可能性
PA
lim
N
NA N
所有结果的概率和等于1，即称概率满足归一化条件。
Pi 1 i
0 Pi 1
(2).物理量的统计平均值
W
lim W1N1 W2 N2 Wn Nn
N
N
W1P1 W2 P2 Wn Pn
一般说来，某次测量值与统计平均值之间存在的偏离， 这种偏离就是涨落。
n
•
F (vx2
v
2 y
vz2 )dxdydz
• vzdAdt
n为分子数密度，F为麦克斯韦速度分布 除以dtdA，积分可得单位时间内碰撞到单位器壁面积上的分子数为：
n • (
m
3
)2
Байду номын сангаас
2kT
0 dvz
dv dv • v e x y
m
(
vx2
v
2 y
vz2
)
/
2
kT
z
n( m )1/2 kT 1 n 8kT 1 nv
N
C3
e dv vx2 / 2 x
e dv vy2 / 2 y
麦克斯韦速率分布定律
1859年, 麦克斯韦用概率论导出了气体分子速率分布 定律，后由玻尔兹曼使用经典统计力学理论导出.
1920年史特恩用分子束实验, 获得分子有着确定的速 度分布的信息, 但未能给出定量的结果. 1934年我国留学 生葛正权在伯克利首次获得此定律的精确实验验证. 此 成功经报界报道, 当时闻名欧美, 在很大程度上改变了外 国人眼中“中国留学生只会读书不能动手, 我们不欢迎” 的形象, 对当时欧美中国留学生有极大的影响和鼓舞.
氧气分子在 0ºC 时的分子速率分布
(m / s)
100以下
N / N (%)
1.4
100－200
8.1
200－300
16.5
300－400
21.4
400－500
20.6
500－600
15.1
600－700
9.2
700－800
4.8
800－900
2.0
二．气体分子速率分布 N /(Nv)
p (O2 ) 500 m/s
例4. 设某气体的速率分布函数为
f (v )
av 2，(0 v v0 )
0 ， (v v 0 )
f (v )
求：（1）常量 a 和υ0 的关系 0 v0
v
（2）平均速率 v
（3）速率在 0 v 0 之间分子的平均速率v
2
解：（1）由归一化条件
N
0 / 4 0
f ()d
5N 32
（3）最可几速率
df () d p
0p
0
2
（4）
f
( )d
0
0
2
rms
2
[
1920年史特恩用分子束实验, 获得分子有着确定的速 度分布的信息, 但未能给出定量的结果. 1934年我国留学 生葛正权在伯克利首次获得此定律的精确实验验证. 此 成功经报界报道, 当时闻名欧美, 在很大程度上改变了外 国人眼中“中国留学生只会读书不能动手, 我们不欢迎” 的形象, 对当时欧美中国留学生有极大的影响和鼓舞.
氧气分子在 0ºC 时的分子速率分布
(m / s)
100以下
N / N (%)
1.4
100－200
8.1
200－300
16.5
300－400
21.4
400－500
20.6
500－600
15.1
600－700
9.2
700－800
4.8
800－900
2.0
二．气体分子速率分布 N /(Nv)
p (O2 ) 500 m/s
例4. 设某气体的速率分布函数为
f (v )
av 2，(0 v v0 )
0 ， (v v 0 )
f (v )
求：（1）常量 a 和υ0 的关系 0 v0
v
（2）平均速率 v
（3）速率在 0 v 0 之间分子的平均速率v
2
解：（1）由归一化条件
N
0 / 4 0
f ()d
5N 32
（3）最可几速率
df () d p
0p
0
2
（4）
f
( )d
0
0
2
rms
2
[
麦克斯韦速率分布
m f (v ) 4 Ndv 2kT dN
3/ 2 mv
2
e
2 kT
v , ( , n均匀）
2
2、分子在势场中，n不均匀，考虑空间分布：
dN ndV n0 e
p
kT
dxdydz
——在x，y，z处得体元dV中的分子数
在势场中，分子总是优先占据势能较低的状态。
N / N 0
0
100－200 200－300 300－400 400－500 500－600 600－700 700－800 800－900
1.4 8.1
16.5 21.4 20.6 15.1 9.2 4.8 2.0
N
Nv
ΔN－在v－v＋Δv区间内 的分子数 N－总分子数 Δv －速率区间
分布
2、公式推导：——流体静力学 h+dh h 今取一垂直于地面的气体圆 P+dP＝P’ 柱体。设地面处分子数密度 为 n 高度为h处的分子数密 0 为度 n P
dP gdh
nm
dP nmgdh —（1）
平衡时， P nkT
h+dh h
P+dP＝P’ P
T处处相等，
dP kT dn —（2）
0
m 4 2kT
3/ 2
mv
2
e
2 kT
v dv
3
__
v 4 2kT
3/ 2
mv
2
e
2 kT
k3dv R / N 0 v
mN0
8kT
m
8 RT 1.60 RT
3/ 2 mv
2
e
2 kT
v , ( , n均匀）
2
2、分子在势场中，n不均匀，考虑空间分布：
dN ndV n0 e
p
kT
dxdydz
——在x，y，z处得体元dV中的分子数
在势场中，分子总是优先占据势能较低的状态。
N / N 0
0
100－200 200－300 300－400 400－500 500－600 600－700 700－800 800－900
1.4 8.1
16.5 21.4 20.6 15.1 9.2 4.8 2.0
N
Nv
ΔN－在v－v＋Δv区间内 的分子数 N－总分子数 Δv －速率区间
分布
2、公式推导：——流体静力学 h+dh h 今取一垂直于地面的气体圆 P+dP＝P’ 柱体。设地面处分子数密度 为 n 高度为h处的分子数密 0 为度 n P
dP gdh
nm
dP nmgdh —（1）
平衡时， P nkT
h+dh h
P+dP＝P’ P
T处处相等，
dP kT dn —（2）
0
m 4 2kT
3/ 2
mv
2
e
2 kT
v dv
3
__
v 4 2kT
3/ 2
mv
2
e
2 kT
k3dv R / N 0 v
mN0
8kT
m
8 RT 1.60 RT
热学 (3 第三章 气体分子热运动速率和能量的统计分布率)
或概率密度。
f ()d dN
N
dN
2
＝
f
( )d
N 1
表示速率分布在→+d内的
分子数占总分子数的概率
表示速率分布在1→2内的分
子数占总分子数的概率
N
0
dN N
0
f
d
1
归一化条件
应注意的问题:
分布函数是一个统计结果，以上各种讨论都是建立在众多分子微 观运动基础上的，分子的数目越大，结论越正确。所以：
1、作速率分布曲线。 2、由N和vo求常数C。 3、求粒子的平均速率。 4、求粒子的方均根速率。
f (v)
C ( vo> v > 0) 0 ( v > vo )
f (v)
解：
f (v)dv
0
vo 0
Cdv
Cvo
1
C
C 1 vo
o
vo v
o f ()d o Cd C o2
3. 方均根速率
2
2
f
d
0
3
2
4
m
2 kT
2
e
m 2 2kT
4
d
3kT
3RT
0
mM
2 3kT 3RT
m
M
4. 三种速率的比较
最概然速率
p
2kT m
2RT M
平均速率
8kT 8RT m M
方均根速率
一、速率分布函数
气体分子处于无规则的热运动之中，由于碰撞，每个分子的速度都
f ()d dN
N
dN
2
＝
f
( )d
N 1
表示速率分布在→+d内的
分子数占总分子数的概率
表示速率分布在1→2内的分
子数占总分子数的概率
N
0
dN N
0
f
d
1
归一化条件
应注意的问题:
分布函数是一个统计结果，以上各种讨论都是建立在众多分子微 观运动基础上的，分子的数目越大，结论越正确。所以：
1、作速率分布曲线。 2、由N和vo求常数C。 3、求粒子的平均速率。 4、求粒子的方均根速率。
f (v)
C ( vo> v > 0) 0 ( v > vo )
f (v)
解：
f (v)dv
0
vo 0
Cdv
Cvo
1
C
C 1 vo
o
vo v
o f ()d o Cd C o2
3. 方均根速率
2
2
f
d
0
3
2
4
m
2 kT
2
e
m 2 2kT
4
d
3kT
3RT
0
mM
2 3kT 3RT
m
M
4. 三种速率的比较
最概然速率
p
2kT m
2RT M
平均速率
8kT 8RT m M
方均根速率
一、速率分布函数
气体分子处于无规则的热运动之中，由于碰撞，每个分子的速度都
第三章 气体分子热运动速率和能量的统计分布
第三章
气体分子热运动速率 和能量的统计分布
1
第三章 气体分子热运动速率和能量的 统计分布
§1 气体分子的速率分布律 §2 用分子射线实验验证麦克斯韦速度分布律 §3 玻尔兹曼分布律 重力场中微粒按高度的分布 §4 能量按自由度均分定理
2
§1 气体分子的速率分布律
一、速率分布函数
设总分子数N，速率区间v ~ v+dv内分子数 dN占总 分子数的比率为： dN f (v)dv ，其中：
1mol理想气体内能为：
Um
1 2
(r
t
2s)RT
，因此：
CV ,m
1 2
(r
t
2s)R
只与自由度有关
单原子分子气体：
CV ,m
3 2
R
双原子分子气体：
7 CV ,m 2 R
35
五、经典理论的缺陷
CV ,m
根据经典理论：
7R 2
一切双原子分子CV,m相同
5R 2
CV,m与温度无关
3R 2
T/K
理论与实验的不符，根本在于它是建立在经典概念，即能量 连续分布的基础上的。只有用量子理论才能进行较完满的解释。
单位时间内碰到单位面积器壁上速度在vx~vx+dv之间的分子数为：
nvx
f
(vx )dvx
nvx
m
2kT
1/ 2
e dv mvx2 / 2kT x
单位时间内碰到单位面积器壁的总分子数为：
0 nvx f (vx )dvx
n
m
1/ 2
2kT
e v dv mvx2 / 2kT
0
xx
n
kT
气体分子在空间位 置不再呈均匀分布
气体分子热运动速率 和能量的统计分布
1
第三章 气体分子热运动速率和能量的 统计分布
§1 气体分子的速率分布律 §2 用分子射线实验验证麦克斯韦速度分布律 §3 玻尔兹曼分布律 重力场中微粒按高度的分布 §4 能量按自由度均分定理
2
§1 气体分子的速率分布律
一、速率分布函数
设总分子数N，速率区间v ~ v+dv内分子数 dN占总 分子数的比率为： dN f (v)dv ，其中：
1mol理想气体内能为：
Um
1 2
(r
t
2s)RT
，因此：
CV ,m
1 2
(r
t
2s)R
只与自由度有关
单原子分子气体：
CV ,m
3 2
R
双原子分子气体：
7 CV ,m 2 R
35
五、经典理论的缺陷
CV ,m
根据经典理论：
7R 2
一切双原子分子CV,m相同
5R 2
CV,m与温度无关
3R 2
T/K
理论与实验的不符，根本在于它是建立在经典概念，即能量 连续分布的基础上的。只有用量子理论才能进行较完满的解释。
单位时间内碰到单位面积器壁上速度在vx~vx+dv之间的分子数为：
nvx
f
(vx )dvx
nvx
m
2kT
1/ 2
e dv mvx2 / 2kT x
单位时间内碰到单位面积器壁的总分子数为：
0 nvx f (vx )dvx
n
m
1/ 2
2kT
e v dv mvx2 / 2kT
0
xx
n
kT
气体分子在空间位 置不再呈均匀分布
03 热学讲义 第三章 气体分子热运动速率和能量的统计分布律
v vf v dv
0
1 即 v N
0
vNf v dv
当分子速率满足麦氏分布时
v
0
m v 4π 2 π kT
32
ve
mv 2 2 2 kT
dv 8kT
m
8RT M mol
3、方均根速率
v v 2 f v dv
N
0
dN f v dv 1 0 N
归一化条件
应注意的问题: 分布函数是一个统计结果，以上各种讨论都是建立在众多分子 微观运动基础上的，分子的数目越大，结论越正确。所以： 1）少数分子谈不上概率分布 偶然事件少了，或分子数少了，就不能表现出稳定的统计特性。 2）统计规律表现出涨落 3）“具有某一速率的分子有多少”是不恰当的说法 f (v)是针对v附近单位速率间隔的，离开速率间隔来谈分子数 有多少就没有意义了。 4 ）气体由非平衡到平衡的过程是通过分子间的碰撞来实现的。 因此，分子间的碰撞是使分子热运动达到并保持确定分布的决 定因素。
f (v)dv
(v)dv
速率在v-v+dv内的分子数占总分子数的百分比 速率在v-v+dv内的分子数
(2) Nf
v2
(3)
v1
v1
f (v)dv 速率在v1→v2内的分子数占总分子数的百分比
速率在v1→v2内的分子数
v2
(4)
Nf (v)dv
练习 在平衡状态下，已知理想气体分子的麦克斯韦速率分 布函数为 f (v ) 、分子质量为 m 、最可几速率为v P ，试说 明下列各式的物理意义： （１）
2
v p 1.41 v 1.60
物理分子热运动
物理分子热运动
物理分子热运动是指物质中微小粒子（分子或原子）的随机运动。
这种运动受到热能的驱动，它使得分子不断碰撞、加速和变换方向。
物质中的分子热运动是在宏观上观察不到的，因为它们是微观尺度的。
然而，这种运动对于物理和化学性质的理解至关重要。
分子热运动具有三个主要特征：随机性、速度多样性和碰撞。
分子根据布朗运动的原理进行无规则的移动，没有固定的轨道。
其速度多样性表现为分子具有各种速度，速度的分布符合麦克斯韦速率分布定律。
碰撞是分子热运动的结果，分子之间的碰撞会改变它们的速度和方向。
分子热运动对于物质的热传导、扩散和扰动等过程起着重要作用。
由于分子随机运动的性质，能量会从热源传递到周围环境，实现热平衡。
在气体状态下，分子的热运动产生气体的压力。
此外，分子热运动还解释了液体和固体的性质，例如液体的黏性和固体的弹性。
总的来说，物理分子热运动是物质微观层面的运动现象，它在许多物理和化学过程中起着重要的作用。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
直线型分子
s 3n 5
例如CO2 s 3 3 5 4
O=C=O
对称伸缩
O=C=O
反对称伸缩
O=C=O
面内变形 分子的平均能量：
O=C=O
面外变形
t r 2 s kT 3 2 2 4 kT 13 kT 2 2 2
二 、能量均分定理
在温度 T 的平衡态下，物质（气体、液体
1 eV 热能相当温度～ 104 K
( kT ~ 1.6 1019 J , k 1.38 1023 J/K)
常温（T~300K，能量~10 －2eV）：振动 能级难跃迁，对能量变化不起作用。 “冻结” 振动自由度，分子可视为刚性。
刚性分子：常温，不计振动自由度
3 2 kT 5 t r kT kT 2 2 3kT 5 2 kT （单 原 子） （双 原 子） （非 直 线 型 多 原 子 ） （直 线 型 多 原 子 ）
平均速率 v
2
0
vf (v )dv
2
v0 6 2 v (v0 v )dv 3 2 v0
v0 0
方均速率 v 方均根速率为
0
v f (v )dv
3 v v0 10
2
6 3 3 2 v (v0 v )dv v0 3 10 v0
(3)速率介于0~v0/3之间的分子数
v1
v2
正确结果为：
W v1 ~ v 2 W (v ) f (v )dv
v1 v2 v2
f (v )dv
0
v1
W 0 ~ W (v ) f (v )dv
0
f (v )dv W (v ) f (v )dv
0
分子速率的三个统计值 1、最概然速率
vp
y
x
1I 2
r 3 , ( , , )
直线型分子（如CO2）转动自由度为2 （3）振动自由度
非直线型分子（如H2O）
由n（>2）个原子组成的分子，一般最多有 3n个自由度，其中3个平动，3个转动，其余为 振动自由度 s 3n 6，例如n=3
s 3 3 6 3 t r 2 s kT 2 3 3 2 3 kT 6kT 28 2
f (v )
0
f (v )dv 1
v0
0
6 A 3 v0
A 3 Av(v0 v )dv v0 1 6
o
v
v0
df (v ) 0 决定，即 (2)最可几速率由 dv v p
df (v ) A(v 0 2v ) v 0 p dv v p
v0 vp 2
v0 0
一、重力场中分子数按高度的（等温）分布
hn p
n0e p / kT , p mgh n
恒温气压公式（高度计原理）：
T
0 n0 p0
p p0e
mgh / kT
,
p0 n0 kT
证明： 平衡态 不同高度处温度相同
p+ dp
S
T
p
mg
dpS nmgdhS 0 dp nmg dh h+dh p nkT dn 1 dp nmg h n dh kT dh kT dn mg 0 n0 dh n kT
m 32 f ( v ) 4 ( ) e 2kT
mv 2 2 kT
v
2
一个分子处于v~v+dv区间的概率为：
dN m 32 f ( v )dv 4 ( ) e N 2kT
mv 2 2 kT
v dv
2
三 计算物理量 W（v）在速率区间v1v2内按 速率的平均值。
解： v1 ~ v 2 W (v ) f (v )dv 对吗？ W
N 1
i
N
----归一化条件
0 Wi 1
2、气体分子的速率分布
研究气体分子的速率分布
•把速率分成若干相等区间
分布函数
•求气体在平衡态下分布在各区间内的分子数
•各区间的分子数占气体分子总数的百分比
（1）分子速率分布的测定—斯特恩实验
j
v
金属 蒸汽 方向选择
ω
t 2 =ω
L
ω
屏
L t1=v ,
与分布函数f(v)的极大值相对应的速率
df (v ) 0 极值条件 dv v v p
vp 2kT m 2 RT RT 1.41 M mol M mol
2、平均速率
v
大量分子速率的统计平均值
v N v
i
i
N
对于连续分布
vdN v
N
dN v N 0 vf (v )dv
v
8kT m
8 RT RT 1.60 M mol M mol
3、方均根速率
v
2
大量分子速率的平方平均值的平方根
v
2
0
v 2 dN N
v f (v )dv
2 0
3kT v m
2
3kT 3 RT RT v 1.73 m M mol M mol
2
f(v) T
和固体）分子的每一个自由度的平均动能都 1 kT。 相等，而且都等于 2 分子运动总平均能量：
i kT , i t r 2s 2
物理解释： 分子频繁碰撞，统计地看，能量 在各个自由度上均分。 转动，振动 。
平动能量连续
转动能级间隔小
振动能级间隔大
10 ~ 10 eV
2
4
100 ~ 102 eV
晶格点阵上的离子：只有振动自由度
2 s kT 2 3 kT 3kT 2 2
I 0
y
m2
C
x
1 I 2
自由度 对能量无贡献 转动 r 2 , ( , )
25
本体坐标系
振动自由度为1
m1
微振动～简谐振动
1 v2 动能 2
1 2 势能 2
？
m2
2个平方项 。
振动自由度 s 1 ，但 s 2 s kT kT 2 双原子分子的平均能量
m f ( v ) 4 2 kT
3/ 2
v e
2
m v 2 / 2 kT
0
v
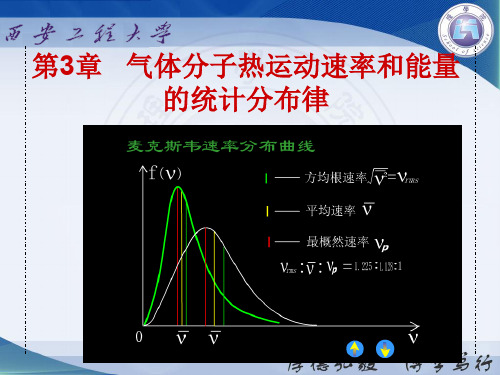
vp v
v2
v p : v : v 2 1.41 : 1.60 : 1.73
四、麦克斯维分布曲线的性质
1、温度与分子速率 f(v) f(vp1) T1 T2 温度越高，分布曲线中的最概然 速率vp增大，但归一化条件要求 曲线下总面积不变，因此分布曲 线宽度增大，高度降低。
Mmol1
T相同
O
vp
v
例设想有N个气体分子，其速率分布函数为
试求: (1)常数A；(2)最可几速率，平均速率和方均根； (3)速率介于0~v0/3之间的分子数；(4)速率介于 0~v0/3之间的气体分子的平均速率。
解： (1)气体分子的分布曲线如图 由归一化条件
Av(v 0 v ) 0 v v 0 f (v ) 0 v v0
分子能量表达式中平方项的数目与自由度有关。
2、双原子分子（如 O2 ，H2 ，CO ）
平动 + 转动 + 振动
刚性分子：平动 + 转动 平动自由度为3
m1
平动 t 3 , ( x, y, z )
m2
C ( x, y, z ) 质心
转动自由度为2
1I 2
对称轴
m1
z
f(vp2) f(vp3)
T3
T1 T2 T3
m 相同
O
vp
v
2、质量与分子速率 f(v) f(vp1) Mmol3 分子质量越大，分布曲线中的最 概然速率vp越小，但归一化条件 要求曲线下总面积不变，因此分 布曲线宽度减小，高度升高。
f(vp2) f(vp3)
Mmol2
M mol 1 M mol 2 M mol 3
两边积分，得
n n0e
mg/ kT
一、气体分子的自由度（degree of freedom） 力学对自由度的定义：确定物体空间位置的 独立坐标的数目。
这里，只考虑那些对能量有贡献的自由度。 1、单原子分子（如 He，Ne） 质点，只有平动自由度 t 3 , ( x, y, z )
能量表达式中包括 3 个平方项。 分子平均能量： t t kT 3 kT 2 2
j
速率选择器
令 t 1 =t 2
v j 得： = L ω
只有满足此条件的分子才能同时通过两缝。 通过改变ω 可获得不同速率区间的分子。
1920年斯特 恩从实验上证 实了速率分布 定律。
分 子 速 率 分 布 的
速率区间 百分数 (m/s) 1.4 % ＜100 100~200 8.1 % 200~300 16.5 % 实 300~400 21.4 % 验 数 400~500 20.6 % 据 500~600 15.1 % 600~700 9.2 % 700~800 4.8 % 800~900 2.0 % 0.9 % ＞ 900
N dN Nf (v )dv
v0 3 0
v0 3 0
6 7N N 3 v (v0 v )dv 27 v0
(4)速率介于0~v0/3之间的气体分子平均速率为