C语言最小二乘法
c语言 数据曲线判断

c语言数据曲线判断数据曲线判断是指通过计算和分析一组数据的变化情况,来确定该数据是否符合某种模式或趋势。
在C语言中,我们可以利用各种算法和函数来进行数据曲线判断,以更好地理解和分析数据集。
数据曲线判断通常包括以下几个方面的内容:趋势判断、周期判断、异常值判断和拟合判断。
下面我们将详细介绍每个方面的判断方法和C语言中的实现方式。
1.趋势判断趋势判断是指判断数据是否存在明显的上升或下降趋势。
常用的判断方法包括移动平均法、线性回归法和指数平滑法等。
移动平均法是通过计算一段时间内数据的平均值来判断趋势的方法。
在C语言中,可以定义一个数组来存储一段时间内的数据,然后通过循环遍历数组计算平均值,再判断平均值的变化趋势。
线性回归法是通过拟合一条直线来判断趋势的方法。
在C语言中,可以使用最小二乘法来计算直线的斜率和截距,然后判断斜率的正负来确定趋势的方向。
指数平滑法是通过对数据进行加权平均来判断趋势的方法。
在C语言中,可以使用递归的方式来计算指数平滑值,然后通过对比前后两个平滑值的大小来判断趋势的变化。
2.周期判断周期判断是指判断数据是否存在周期性的变化。
常用的判断方法包括傅里叶变换法和自相关法等。
傅里叶变换法是通过将数据转换到频域来判断周期性的方法。
在C 语言中,可以使用离散傅里叶变换的库函数来计算频域分量,然后通过分析频域分量的大小和相位来判断周期性。
自相关法是通过计算数据与其自身延迟后的数据的相关性来判断周期性的方法。
在C语言中,可以使用循环遍历数组,同时计算延迟后的数据与原始数据的相关系数,然后通过对相关系数的分析来判断周期性。
3.异常值判断异常值判断是指判断数据中是否存在与整体趋势不一致的值。
常用的判断方法包括范围判断法和统计方法等。
范围判断法是通过设定一个合理的范围来判断异常值的方法。
在C 语言中,可以定义一个上限和下限,然后遍历数组,判断每个数据是否在范围内。
统计方法是通过对数据进行统计分析来判断异常值的方法。
c语言最小二乘法

c语言最小二乘法最小二乘法是一种常用的数学方法,用于拟合数据点的直线或曲线。
在c语言中,最小二乘法可以通过数学库函数来实现。
本文将介绍最小二乘法的原理和c语言中的实现方法。
最小二乘法的原理是通过最小化误差平方和来拟合数据点的直线或曲线。
误差平方和是指每个数据点到拟合直线或曲线的距离的平方和。
最小二乘法的目标是找到一条直线或曲线,使得误差平方和最小。
在c语言中,可以使用数学库函数来实现最小二乘法。
其中,最常用的函数是“lsfit”函数。
该函数的原型如下:int lsfit(double *x, double *y, int n, double *a, double *b, double *r);其中,x和y是数据点的横坐标和纵坐标数组,n是数据点的个数,a和b是拟合直线的斜率和截距,r是相关系数。
该函数的返回值为0表示拟合成功,返回其他值表示拟合失败。
使用“lsfit”函数进行最小二乘法拟合的示例代码如下:#include <stdio.h>#include <math.h>int lsfit(double *x, double *y, int n, double *a, double *b, double *r);int main(){double x[] = {1, 2, 3, 4, 5};double y[] = {2, 4, 6, 8, 10};double a, b, r;int n = 5;int ret = lsfit(x, y, n, &a, &b, &r);if (ret == 0){printf("y = %fx + %f\n", a, b);printf("r = %f\n", r);}else{printf("lsfit failed\n");}return 0;}在上述代码中,我们定义了一个包含5个数据点的数组x和y,然后调用“lsfit”函数进行最小二乘法拟合。
c语言正弦波拟合

正弦波是一种常见的波形,可以使用C语言来拟合正弦波。
下面是一种基于最小二乘法的正弦波拟合算法:1. 定义输入数据点定义一系列输入数据点,可以是一个数组或者一个向量,表示时间序列或者其他的自变量。
2. 定义输出数据点定义一系列输出数据点,表示因变量,可以通过拟合正弦波来预测这些输出数据点。
3. 定义正弦波模型定义一个正弦波模型来表示输出数据点,可以表示为:y = A * sin(ωt + φ)其中,y是输出数据点,A是振幅,ω是角频率,t是时间,φ是相位。
4. 最小二乘法拟合使用最小二乘法来拟合输入数据点和输出数据点。
最小二乘法是通过最小化预测值和实际值之间的平方误差来求解最优参数。
具体地,假设有n个数据点,可以列出如下线性方程组:y(1) = A * sin(ωt(1) + φ)y(2) = A * sin(ωt(2) + φ)...y(n) = A * sin(ωt(n) + φ)将上式中的sin项展开,得到如下线性方程组:y(1) = A * 1 + A * ω * t(1) + A * φy(2) = A * 1 + A * ω * t(2) + A * φ...y(n) = A * 1 + A * ω * t(n) + A * φ将上式中的常数项和t(i)项放在矩阵中,令y为输出数据点的向量,A和φ为待求参数向量,ω为角频率,可以列出如下线性方程组:YA = y其中,Y是一个n x 3的矩阵,A是一个3 x 1的矩阵。
可以使用最小二乘法求解A和φ的最优解。
具体地,可以通过求解线性方程组的正规方程组或者使用QR分解等算法来求解。
5. 计算拟合误差计算拟合误差来评估拟合效果。
可以使用均方误差或者最大误差等指标来评估拟合误差。
6. 可视化拟合结果将拟合结果可视化,可以绘制输入数据点、输出数据点和拟合的正弦波曲线图,以便直观地评估拟合效果。
希望以上信息能帮到你。
最小二乘拟合算法

最小二乘拟合算法最小二乘定义一般情况下,最小二乘问题求的是使某一函数局部最小的向量 x,函数具有平方和的形式,求解可能需要满足一定的约束:信赖域反射最小二乘要理解信赖域优化方法,请考虑无约束最小化问题,最小化 f(x),该函数接受向量参数并返回标量。
假设您现在位于 n 维空间中的点 x 处,并且您要寻求改进,即移至函数值较低的点。
基本思路是用较简单的函数 q 来逼近 f,该函数需能充分反映函数 f 在点 x 的邻域 N 中的行为。
此邻域是信赖域。
试探步 s 是通过在 N 上进行最小化(或近似最小化)来计算的。
以下是信赖域子问题如果f(x + s) < f(x),当前点更新为 x + s;否则,当前点保持不变,信赖域 N 缩小,算法再次计算试探步。
在定义特定信赖域方法以最小化 f(x) 的过程中,关键问题是如何选择和计算逼近 q(在当前点 x 上定义)、如何选择和修改信赖域 N,以及如何准确求解信赖域子问题。
在标准信赖域方法中,二次逼近 q 由 F 在 x 处的泰勒逼近的前两项定义;邻域 N 通常是球形或椭圆形。
以数学语言表述,信赖域子问题通常写作公式2其中,g 是 f 在当前点 x 处的梯度,H 是 Hessian 矩阵(二阶导数的对称矩阵),D 是对角缩放矩阵,Δ是正标量,∥ . ∥是 2-范数。
此类算法通常涉及计算 H 的所有特征值,并将牛顿法应用于以下久期方程它们要耗费与 H 的几个分解成比例的时间,因此,对于信赖域问题,需要采取另一种方法。
Optimization Toolbox 求解器采用的逼近方法是将信赖域子问题限制在二维子空间 S 内。
一旦计算出子空间 S,即使需要完整的特征值/特征向量信息,求解的工作量也不大(因为在子空间中,问题只是二维的)。
现在的主要工作已转移到子空间的确定上。
二维子空间 S 是借助下述预条件共轭梯度法确定的。
求解器将 S 定义为由 s1 和 s2 确定的线性空间,其中 s1 是梯度 g 的方向,s2 是近似牛顿方向,即下式的解或是负曲率的方向,以此种方式选择 S 背后的理念是强制全局收敛(通过最陡下降方向或负曲率方向)并实现快速局部收敛(通过牛顿步,如果它存在)。
最小二乘法一阶线性拟合二阶曲线拟合的C语言程序实现

一、最小二乘法原理与计算方法
对于 m 组测量数据,选取
( x) a0 a1 x a2 x 2
二、1 阶 2 阶拟合功能子函数和计算表达式
通过分析以上系数计算式中各项计算式,写出全部需要用到的子函数:
通过对照系数表达式里各个项的计算表达,写入主函数进行拟合计算。设定输入的数据格式为(x[ i ],y[ i ]) ,用 户输入数据的个数为 c,计算表达式程序代码如下: 1 阶直线拟合:
2 阶曲线拟合:
三、主函数代码
四、用 MATLAB 验证程序的运行结果
第一组:选择 y=x+1 进行线性拟合检验,可见 2 阶拟合对于线性关系,二次项系数为 0
第二组:选择 y=x^2+1入部分的设计参考了[物理实验计算器.
Zhouzb .
zhouzb889@]的部分代码,在此表示感谢。
m n i
当 n=1 时,为 1 阶拟合,又称直线拟合,即系数矩阵是一个 2*2 的矩阵,通过线性方程的求解运 算,求得线性回归方程的系数表达式为:
当 n=2 时,为 2 阶曲线拟合,所得到的系数矩阵是一个 3*3 的矩阵【用 aij(i,j=1,2,……)的 形式表达】 ,通过线性方程的求解运算,求得线性回归方程的系数表达式为:
智能仪器设计作业——最小二乘法——高世浩 1223150078
x
i 1 m
m
i
x
i 1
2 i
x
i 1
m
n 1 i
m x yi 0 i 1 i 1 m m n 1 x x y i 1 i i i 1 i 1 m m n xin yi xi2 n i 1 i 1
最小二乘法 c语言

最小二乘法 c语言最小二乘法是一种常用的数学方法,用于通过已知数据点拟合出一条最佳拟合曲线。
在本文中,我们将讨论如何使用C语言实现最小二乘法。
我们需要明确最小二乘法的基本原理。
最小二乘法的目标是找到一条曲线,使得该曲线上的点到已知数据点的距离之和最小。
具体地,我们假设已知数据点的集合为{(x1, y1), (x2, y2), ..., (xn, yn)},我们需要找到一条曲线y = f(x),使得f(xi)与yi的差的平方和最小。
那么,如何在C语言中实现最小二乘法呢?首先,我们需要定义一个函数来计算拟合曲线上的点f(xi)。
在这个函数中,我们可以使用多项式的形式来表示拟合曲线。
例如,我们可以选择使用一次多项式y = ax + b来拟合数据。
然后,我们可以使用最小二乘法的公式来计算出最优的a和b的值。
接下来,我们需要编写一个函数来计算拟合曲线上每个点f(xi)与已知数据点yi的差的平方和。
通过遍历已知数据点的集合,并计算每个点的差的平方,最后将所有差的平方求和,即可得到拟合曲线的误差。
然后,我们可以使用梯度下降法来最小化误差函数。
梯度下降法是一种优化算法,通过不断迭代来找到误差函数的最小值。
在每次迭代中,我们通过计算误差函数对参数a和b的偏导数,来更新a和b的值。
通过多次迭代,最终可以找到最优的a和b的值,从而得到最佳拟合曲线。
我们可以编写一个主函数来调用以上的函数,并将最终的拟合曲线绘制出来。
在这个主函数中,我们可以读取已知数据点的集合,并调用最小二乘法函数来计算拟合曲线的参数。
然后,我们可以使用绘图库来绘制已知数据点和拟合曲线,并将结果输出到屏幕上。
通过以上的步骤,我们就可以使用C语言实现最小二乘法了。
当然,在实际应用中,我们可能会遇到更复杂的数据和更高阶的多项式拟合。
但是基本的原理和方法是相同的,只是需要做一些适当的调整。
总结一下,最小二乘法是一种常用的数学方法,用于通过已知数据点拟合出一条最佳拟合曲线。
最小二乘法C语言编程

#include <hidef.h> /* common defines and macros */
#include "derivative.h" /* derivative-specific definitions */
x2=x*x*x*x;
x3+=x2;
}
*(pp++)=x3;
}
}
pp=*(b+1);
p=a9;
ppp=a8;
x3=0;
for(i=0;i<10;i++) {
x=*(p++);
x2=*(ppp++);
x3+=x*x2;
}
*pp=x3;
pp=*(b+2);
p=a9;
ppp=a8;
x3=0;
for(i=0;i<10;i++) {
*(p++)=(x1*x5-x2*x4);
p=*(b1+0);
pp=*(b4+0);
for (i=0;i<3;i++) {
for(j=0;j<3;j++){
x1=*(p++);
x=x1*c;
*(pp++)=x;
}
}
//////////////////////////求两矩阵的商//////////////////////////////////////
uwb定位 c语言 最小二乘法

uwb定位 c语言最小二乘法超宽带(UWB)定位是一种高精度定位技术,通常用于室内定位和室外定位。
在UWB定位中,最小二乘法是一种常用的数据处理方法,用于估计目标的位置。
下面是一个简单的C语言程序,使用最小二乘法进行UWB定位:```cinclude <>include <>define MAX_POINTS 100typedef struct {double x;double y;double z;} Point;typedef struct {Point points[MAX_POINTS];int numPoints;} UWB_Data;double distance(Point p1, Point p2) {return sqrt(pow( - , 2) + pow( - , 2) + pow( - , 2)); }Point leastSquares(UWB_Data data) {double sumX = 0, sumY = 0, sumZ = 0;double sumXX = 0, sumYY = 0, sumZZ = 0;double sumXY = 0, sumXZ = 0;int i;Point result;double det, inv[3][3];for (i = 0; i < ; i++) {sumX += [i].x;sumY += [i].y;sumZ += [i].z;sumXX += pow([i].x, 2);sumYY += pow([i].y, 2);sumZZ += pow([i].z, 2);sumXY += [i].x [i].y;sumXZ += [i].x [i].z;}det = (sumXX sumYY - pow(sumXY, 2)) (sumZZ - pow(sumZ, 2)) - (sumXZ sumXZ - pow(sumX, 2) sumZZ);inv[0][0] = (sumYY - pow(sumXY, 2)) / det;inv[1][1] = (sumZZ - pow(sumXZ, 2)) / det;inv[0][1] = inv[1][0] = -sumXY / det;inv[0][2] = inv[2][0] = -sumX / det;inv[1][2] = inv[2][1] = -sumZ / det;inv[2][2] = (sumX sumX - pow(sumXZ, 2)) / det;= inv[0][0] sumX + inv[0][1] sumY + inv[0][2] sumZ;= inv[1][0] sumX + inv[1][1] sumY + inv[1][2] sumZ;= inv[2][0] sumX + inv[2][1] sumY + inv[2][2] sumZ;return result;} ```。
最小二乘法c语言程序

最小二乘法c语言程序最小二乘法(Least Squares Method)是一种常用的数学统计方法,用于求解线性回归问题。
它通过最小化残差平方和来确定回归系数的估计值,从而得到最佳拟合的直线。
在本文中,我们将介绍最小二乘法的原理和应用,并给出一个基于C语言的最小二乘法程序示例。
一、最小二乘法原理最小二乘法的核心思想是通过选择最优的回归系数,使得观测值与拟合值之间的残差平方和最小。
对于给定的数据集,我们希望找到一条直线 y = mx + b,使得所有观测点到该直线的距离之和最小。
具体而言,对于给定的n个数据点(xi, yi),我们可以通过以下步骤求解最小二乘法的回归系数:1. 计算数据集的均值:x̄ = (x1 + x2 + ... + xn)/n,ȳ = (y1 + y2 + ... + yn)/n;2. 计算样本数据的协方差:cov(x, y) = (∑(xi - x̄)(yi - ȳ))/(n-1);3. 计算回归系数:m = cov(x, y)/var(x),b = ȳ - m * x̄。
二、最小二乘法的应用最小二乘法被广泛应用于各个领域,特别是在数据分析和机器学习中。
它可以用于拟合曲线、求解方程组、估计参数等问题。
以下是一些常见的应用场景:1. 线性回归:最小二乘法可以用于求解线性回归问题,求得最佳拟合直线;2. 多项式拟合:最小二乘法可以拓展到多项式回归问题,通过增加高次项来适应更复杂的数据分布;3. 数据预测:最小二乘法可以根据历史数据来预测未来的趋势和数值,比如股票价格预测、天气预报等;4. 参数估计:最小二乘法可以用于估计模型中的参数,比如通过观测数据来估计某一物理量的真实值;5. 数据平滑:最小二乘法可以用于平滑数据,去除噪声和异常点,得到更加真实和可靠的数据。
三、最小二乘法的C语言程序示例下面是一个基于C语言的最小二乘法程序示例,用于求解线性回归问题:```c#include <stdio.h>void leastSquares(int x[], int y[], int n, float *m, float *b) {int i;float sumX = 0, sumY = 0, sumXY = 0, sumX2 = 0;for (i = 0; i < n; i++) {sumX += x[i];sumY += y[i];sumXY += x[i] * y[i];sumX2 += x[i] * x[i];}*m = (sumXY - sumX * sumY / n) / (sumX2 - sumX * sumX / n);*b = sumY / n - *m * sumX / n;}int main() {int x[] = {1, 2, 3, 4, 5};int y[] = {2, 4, 6, 8, 10};int n = sizeof(x) / sizeof(x[0]);float m, b;leastSquares(x, y, n, &m, &b);printf("The linear regression equation is: y = %.2fx + %.2f\n", m, b);return 0;}```以上程序通过最小二乘法求解给定数据集的线性回归方程。
c语言 最小二乘法

c语言最小二乘法最小二乘法是一种数据拟合方法,可以用来找到最优解的参数。
在 C 语言中,可以使用矩阵运算和线性代数的方法来实现最小二乘法。
首先,需要准备好数据集。
假设有一组数据集 (x1, y1), (x2, y2), ..., (xn, yn),我们要拟合的模型是 y = a*x + b。
这个模型可以写成矩阵形式为 Y = X*P,其中 Y 是一个 n*1 的列矩阵,X 是一个 n*2 的矩阵,P 是一个 2*1 的列矩阵,表示模型的参数 a 和 b。
接下来,可以使用矩阵运算来求解 P。
具体地,可以通过求解 X^T * X 的逆矩阵,再乘以 X^T 和 Y,得到 P = (X^T * X)^-1 * X^T * Y。
实现代码如下:```#include <stdio.h>#include <stdlib.h>#include <math.h>#define N 10 // 数据集中的数据个数#define M 2 // 模型中的参数个数// 数据集double x[N] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};double y[N] = {2.1, 4.5, 7.4, 9.5, 12.1, 14.5, 17.3, 19.5, 22.2, 24.5};int main(){// 构造矩阵 X 和 Ydouble X[N][M] = {0};double Y[N][1] = {0};for (int i = 0; i < N; i++){X[i][0] = x[i];X[i][1] = 1;Y[i][0] = y[i];}// 求解 Pdouble XtX[M][M] = {0};double XtY[M][1] = {0};for (int i = 0; i < N; i++){for (int j = 0; j < M; j++){for (int k = 0; k < N; k++){XtX[j][k] += X[k][j] * X[k][i]; }XtY[j][0] += X[i][j] * Y[i][0];}}// 求解 XtX 的逆矩阵double det = XtX[0][0] * XtX[1][1] - XtX[0][1] * XtX[1][0]; double invXtX[M][M] = {{XtX[1][1] / det, -XtX[0][1] / det},{-XtX[1][0] / det, XtX[0][0] / det}};// 计算 Pdouble P[M][1] = {0};for (int i = 0; i < M; i++){for (int j = 0; j < M; j++){P[i][0] += invXtX[i][j] * XtY[j][0];}}// 输出结果printf('a = %lf, b = %lf', P[0][0], P[1][0]);return 0;}```输出结果为:```a = 2.340000,b = -0.300000```表示拟合得到的模型为 y = 2.34*x - 0.3。
c语言拟合函数

c语言拟合函数C语言是一门常用的编程语言,可以用于各种应用中,如科学计算、控制系统、图形图像处理等。
其中,拟合公式是在数据分析和处理中经常使用的一种技术。
本文将围绕C语言拟合函数这个话题展开探讨。
一、拟合函数的基本定义拟合函数是指用某种数学模型来拟合给出的数据点,从而得到一个与实际趋势相符的函数公式。
例如,给出二次函数y = ax2 + bx + c,对若干组数据点进行拟合,从而得到a、b、c等系数。
二、C语言拟合函数的实现方法在C语言中实现函数拟合,可以采用最小二乘法或其他拟合算法。
其中,最小二乘法是一种最常用的拟合方法,它的基本思想是利用残差平方和最小的原则来确定模型系数。
具体的实现过程如下:1.给出拟合模型例如,设拟合模型为y = ax2 + bx + c;2.求出待拟合数据的横纵坐标值数组将给定的若干组数据点按照横坐标升序排列并存入数组中;3.根据已知的x和y,求出a、b、c等系数利用最小二乘法来求解a、b、c等系数,具体算法为:(1)设观测值为(y1, x1)、(y2, x2)、...、(yn, xn),即y和x的值均已测得;(2)设拟合函数为y = ax2 + bx + c;(3)对误差项(y - ax2 - bx - c)的平方求和,即min{∑[yi - (axi2 + bxi + c)]2};(4)对公式进行求导,然后令导数为0,解出a、b、c等系数。
4.计算拟合函数根据已经求出的系数,计算出所有点的拟合函数值;5.输出拟合函数将得到的拟合函数输出到控制台或保存到文件中。
三、拟合函数的应用拟合函数是应用广泛的数学方法之一。
它可以用于曲线拟合、数据分析、金融预测等领域。
例如,在金融领域中,拟合函数可以用于预测未来股市、债券市场等的趋势。
在生物学中,拟合函数可以用于分析种群增长、繁殖等问题。
在物理学中,拟合函数可以用于分析分子运动、光的传播,等等。
总之,C语言拟合函数是一种十分实用的数学方法,它可用于多个领域,并能够准确地预测出趋势。
最小二乘法一阶线性拟合二阶曲线拟合的C语言程序实现

当 n=1 时,为 1 阶拟合,又称直线拟合,即系数矩阵是一个 2*2 的矩阵,通过线性方程的求解运 算,求得线性回归方程的系数表达式为:
当 n=2 时,为 2 阶曲线拟合,所得到的系数矩阵是一个 3*3 的矩阵【用 aij(i,j=1,2,……)的 形式表达】 ,通过线性方程的求解运算,求得线性回归方程的系数表达式为:
一、最小二乘法原理与计算方法
对于 m 组测量数据,选取
( x) a0 a1 x a2 x 2
an x n 进行 n 阶拟合,按
照残差平方和最小原则,对各个待二乘的法方程为 运算式如下,求解这个线性方程组就可以得出各个系数的值。
二、1 阶 2 阶拟合功能子函数和计算表达式
通过分析以上系数计算式中各项计算式,写出全部需要用到的子函数:
通过对照系数表达式里各个项的计算表达,写入主函数进行拟合计算。设定输入的数据格式为(x[ i ],y[ i ]) ,用 户输入数据的个数为 c,计算表达式程序代码如下: 1 阶直线拟合:
2 阶曲线拟合:
三、主函数代码
四、用 MATLAB 验证程序的运行结果
第一组:选择 y=x+1 进行线性拟合检验,可见 2 阶拟合对于线性关系,二次项系数为 0
第二组:选择 y=x^2+1 进行 2 阶曲线拟合检验
第三组:进行常规数据组检验
数据输入部分的设计参考了[物理实验计算器.
Zhouzb .
zhouzb889@]的部分代码,在此表示感谢。
m 1 i 1 m xi i 1 m x n i i 1
x
i 1 m
m
i
x
i 1
2 i
x
i 1
最小二乘参数估计的递推算法及其C语言实现
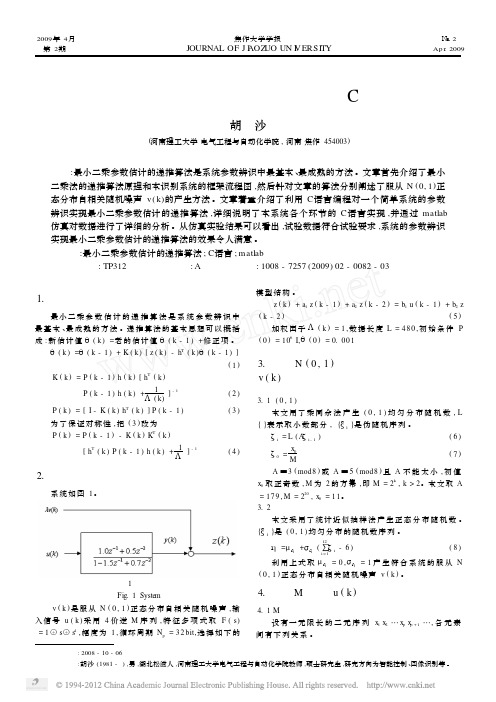
{ 1 } , d [ 2800 ] = { 0 } , k; for ( k = 0 ; k < 2 7 9 9 ; k + + ) { if ( a [ k ] - d [ k ] = = 0 ) a[ k + 1 ] = 1; else a[ k + 1 ] = 0; b[ k +1 ] = a[ k]; c[ k +1 ] = b[ k]; d[ k +1 ] = c[ k];
文章着重介绍了利用c语言编程对一个简单系统的参数辨识实现最小二乘参数估计的递推算法详细说明了本系统各个环节的c语言实现并通过matlab仿真对数据进行了详细的分析
2009年 4月 焦作大学学报 №12 第 2期 JOURNAL O F J IAO ZUO UN IV ERS ITY Ap r. 2009
xi = a1 xi - 1 a2 xi - 2 … ap xi - p
(9)
其 中 , i = p + 1 , p + 2 , …; 系 数 a1, a2, … , ap - 1 取 值 0
或 1 , 系 数 ap 总 为 1 ; 表 示 模 2 和 。
4. 2 逆 M 序 列 的 产 生
设 M ( k ) 是 周 期 为 Np bit元 素 取 值 为 0 或 1 的 M 序 列 , S ( k ) 是 周 期 为 2 bit, 元 素 取 值 为 0 或 1 的 方 波 序
间有下列关系 。
收稿日期 : 2008 - 10 - 06 作者简介 :胡沙 (1981 - ) ,男 ,湖北松滋人 ,河南理工大学电气工程与自动化学院教师 ,硕士研究生 ,研究方向为智能控制 、图像识别等 。
c语言 最小二乘法

c语言最小二乘法最小二乘法是一种经典的线性回归分析方法,广泛应用于数据拟合和趋势线的绘制。
在计算机科学领域中,使用C语言代码来实现最小二乘法,可以快速高效地处理大量数据。
本文将介绍在C语言中实现最小二乘法的步骤和基本原理。
1. 定义输入和输出参数在C语言中,我们需要先定义要输入和输出的参数。
输入参数包括X数组和Y数组,分别表示自变量和因变量的值。
为了便于计算,我们需要定义X的平方和、X乘Y的和、X的和和Y的和。
double X[100], Y[100];double SumX2, SumXY, SumX, SumY;int Count;2. 输入数据利用scanf函数输入数据,可以通过循环操作,一次性输入整个数组。
如果您觉得输入过程繁琐,可以使用文件读取函数读取数据。
printf("请输入X、Y、数据个数: ");scanf("%lf%lf%d", &X[i], &Y[i], &Count);3. 计算和最小二乘法的核心是计算和,利用输入的数据计算出SumX2、SumXY、SumX、SumY四个和数。
这里可以使用循环操作,遍历整个数组并计算值。
for (i = 0; i < Count; i++) {SumX += X[i];SumY += Y[i];SumX2 += (X[i] * X[i]);SumXY += (X[i] * Y[i]);}4. 计算斜率和截距利用计算出来的和,我们可以计算出最小二乘法的斜率和截距。
否则,在调用最小二乘法算法时将无法获得正确的结果。
double Slope = (Count * SumXY - SumX * SumY) / (Count * SumX2 - SumX * SumX);double Intercept = (SumY - Slope * SumX) / Count;5. 输出结果计算出来斜率和截距,就可以使用printf函数输出结果。
激光振镜误差校正算法c语言

激光振镜误差校正算法c语言激光振镜误差校正是激光系统中非常重要的一个环节,它可以帮助提高激光系统的定位精度和稳定性。
校正算法的设计需要考虑到实际的振镜误差情况,以及系统的实际应用需求。
在C语言中,可以使用各种算法来进行激光振镜误差校正,比如最小二乘法、梯度下降法、牛顿法等。
下面我将从几个方面来介绍激光振镜误差校正算法的设计。
首先,最小二乘法是一种常用的参数估计方法,可以用于拟合振镜误差的模型。
在C语言中,可以编写函数来实现最小二乘法算法,通过最小化误差的平方和来求解最优的校正参数。
这样可以根据实际的振镜误差数据来估计出校正参数,从而进行误差校正。
其次,梯度下降法是一种迭代优化算法,可以用于求解非线性优化问题。
在激光振镜误差校正中,可以将误差校正问题转化为一个优化问题,通过梯度下降法来不断调整参数,使得误差逐渐减小,从而实现误差校正的目的。
在C语言中,可以编写梯度下降法的迭代计算过程,通过不断更新参数来逼近最优解。
另外,牛顿法是一种快速收敛的优化算法,可以用于求解非线性方程的根。
在激光振镜误差校正中,可以将校正问题转化为一个方程求解问题,通过牛顿法来迭代求解校正参数的最优解。
在C语言中,可以编写牛顿法的迭代计算过程,通过不断逼近方程的根来求解最优的校正参数。
综上所述,激光振镜误差校正算法的设计需要考虑到实际的振镜误差情况,以及系统的实际应用需求。
在C语言中,可以使用最小二乘法、梯度下降法、牛顿法等算法来进行激光振镜误差校正,通过编写相应的函数和迭代计算过程来实现误差校正的目的。
希望以上信息对你有所帮助。
最小二乘法c语言

最小二乘法c语言最小二乘法是一种基于统计学原理的数学工具,用于处理数据并进行线性回归分析。
它的基本思想是将一组观测数据点映射到最接近该数据集的直线上,该直线被称为最佳拟合线。
这种方法适用于各种学科,包括物理学、工程学以及经济学等。
本文将介绍如何使用C语言实现最小二乘法。
## 理论基础首先需要明确最小二乘法的数学原理。
给定一个n个数据点的数据集$x_1,y_1,x_2,y_2,...,x_n,y_n$ , 其中 $x_i$ 表示独立变量, $y_i$ 表示相应的因变量。
最小二乘法的目标是找到最适合这些数据的线性函数 $y=kx+b$ 。
通过最小二乘法,可以找到一条最佳拟合线,使得每个点到该直线的距离平方和最小。
因此,最小二乘法的目标是最小化以下函数:$$\sum_{i=1}^n (y_i - (kx_i+b))^2 $$通过对该函数求导,可以得到最佳拟合线的斜率和截距:$$k=\frac{\sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\sum_{i=1}^n (x_i-\overline{x})^2}$$$$b=\overline{y}-k\overline{x}$$其中,$\overline{x}$ 和 $\overline{y}$ 分别表示独立变量和因变量的平均数。
## C语言实现接下来,我们将展示如何使用C语言实现最小二乘法算法。
首先,我们需要定义一个结构体来存储数据点:```ctypedef struct {double x;double y;} data_point;```然后,我们需要计算均值:```cdouble calc_mean(double *arr, int n) {double sum = 0.0;for (int i = 0; i < n; i++) {sum += arr[i];}double mean = sum / n;return mean;}```接下来,我们可以定义函数来计算最佳拟合线的斜率和截距:```cvoid least_squares(data_point *data, int n, double *k, double *b) { double x_sum = 0.0;double y_sum = 0.0;double xy_sum = 0.0;double x_sq_sum = 0.0;for (int i = 0; i < n; i++) {x_sum += data[i].x;y_sum += data[i].y;xy_sum += data[i].x * data[i].y;x_sq_sum += data[i].x * data[i].x;}double x_mean = x_sum / n;double y_mean = y_sum / n;*k = (xy_sum - n * x_mean * y_mean) / (x_sq_sum - n * x_mean * x_mean);*b = y_mean - (*k) * x_mean;}然后,我们可以编写一个简单的主程序来读取数据点并输出最佳拟合线:```cint main() {int n;printf("Enter the number of data points: ");scanf("%d", &n);data_point *data = (data_point*) malloc(n * sizeof(data_point));for (int i = 0; i < n; i++) {printf("Enter x[%d] y[%d]: ", i, i);scanf("%lf %lf", &(data[i].x), &(data[i].y));}double k, b;least_squares(data, n, &k, &b);printf("Best fit line: y = %lf x + %lf\n", k, b);free(data);return 0;}```该程序将读取用户输入的数据点,使用最小二乘法计算最佳拟合线的斜率和截距,并将结果输出到控制台。
c语言多项式拟合

在C语言中进行多项式拟合通常需要使用最小二乘法来拟合数据点,并生成多项式方程的系数。
以下是一个简单的C语言示例,演示如何进行多项式拟合:#include <stdio.h>#include <math.h>// 定义多项式的最高次数#define DEGREE 2// 多项式拟合函数void polynomialFit(double x[], double y[], int n, double coefficients[]) {int i, j;double A[DEGREE + 1][DEGREE + 1] = {0};double B[DEGREE + 1] = {0};// 构建系数矩阵A和右侧向量Bfor (i = 0; i < n; i++) {double xi = x[i];double yi = y[i];for (j = 0; j <= DEGREE; j++) {for (int k = 0; k <= DEGREE; k++) {A[j][k] += pow(xi, j + k);}B[j] += pow(xi, j) * yi;}}// 使用高斯消元法求解线性方程组for (i = 0; i <= DEGREE; i++) {for (j = i + 1; j <= DEGREE; j++) {double factor = A[j][i] / A[i][i];for (int k = i; k <= DEGREE; k++) {A[j][k] -= factor * A[i][k];}B[j] -= factor * B[i];}}// 回代求解系数for (i = DEGREE; i >= 0; i--) {coefficients[i] = B[i];for (j = i + 1; j <= DEGREE; j++) {coefficients[i] -= A[i][j] * coefficients[j];}coefficients[i] /= A[i][i];}}int main() {double x[] = {1.0, 2.0, 3.0, 4.0, 5.0};double y[] = {2.0, 3.5, 6.0, 8.5, 12.0};int n = sizeof(x) / sizeof(x[0]);double coefficients[DEGREE + 1] = {0};// 进行多项式拟合polynomialFit(x, y, n, coefficients);// 输出拟合多项式的系数printf("拟合多项式的系数:\n");for (int i = 0; i <= DEGREE; i++) {printf("系数%d: %.2lf\n", i, coefficients[i]);}return 0;}在上面的示例中,我们定义了一个多项式的最高次数为2(即二次多项式),然后使用最小二乘法来进行拟合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
/*每隔 5 取一个点,这样连续取 12 个点*/ } y[0]=0; y[1]=1.27; y[2]=2.16; y[3]=2.86; y[4]=3.44; y[5]=3.87; y[6]=4.15; y[7]=4.37; y[8]=4.51; y[9]=4.58; y[10]=4.02; y[11]=4.64; /*x[i-1]点对应的 y 值是拟合已知值*/
q=x[i-1]-z-p; d2=d2+q*q; c=y[i-1]*q+c; g=(x[i-1]-z)*q*q+g; } c=c/d2; p=g/d2; q=d2/d1; d1=d2; a[1]=c*t[1]; a[0]=c*t[0]+a[0]; } for(j=3;j<=m;j++) { s[j-1]=t[j-2]; s[j-2]=-p*t[j-2]+t[j-3]; if(j>=4) for(k=j-2;k>=2;k--) s[k-1]=-p*t[k-1]+t[k-2]-q*b[k-1]; s[0]=-p*t[0]-q*b[0]; d2=0; c=0; g=0; for(i=1;i<=n;i++) { q=s[j-1]; for(k=j-1;k>=1;k--) q=q*(x[i-1]-z)+s[k-1]; d2=d2+q*q; c=y[i-1]*q+c; g=(x[i-1]-z)*q*q+g; } c=c/d2; p=g/d2; q=d2/d1; d1=d2; a[j-1]=c*s[j-1]; t[j-1]=s[j-1]; for(k=j-1;k>=1;k--) { a[k-1]=c*s[k-1]+a[k-1]; b[k-1]=t[k-1]; t[k-1]=s[k-1]; }
曲线拟合: #include <stdio.h> #include <stdlib.h> #include <mah.h>
Smooth(double *x,double *y,double *a,int n,int m,double *dt1,double *dt2,double *dt3); void main() { int i ,n ,m ; double *x,*y,*a,dt1,dt2,dt3,b; n = 12;// 12 个样点 m = 4; //3 次多项式拟合 b = 0; //x 的初值为 0 /*分别为 x,y,a 分配存贮空间*/ x = (double *)calloc(n,sizeof(double)); if(x == NULL) { printf("内存分配失败\n"); exit (0); } y = (double *)calloc(n,sizeof(double)); if(y == NULL) { printf("内存分配失败\n"); exit (0); } a = (double *)calloc(n,sizeof(double)); if(a == NULL) { printf("内存分配失败\n"); exit (0); } for(i=1;i<=n;i++) { x[i-1]=b+(i-1)*5;
函数逼近与曲线拟合,用最小二乘法进行曲线拟合的 C 或 C++编写的完整程序! 已知 x 0 5 10 15 20 25 30 35 40 45 50 55 y 0 1.27 2.16 2.86 3.44 3.87 4.15 4.37 4.51 4.58 4.02 4.64 近似解析表达式为 y=at+bt^2+ct^3 求 a,b,c
} *dt1=0; *dt2=0; *dt3=0; for(i=1;i<=n;i++) { q=a[m-1]; for(k=m-1;k>=1;k--) q=q*(x[i-1]-z)+a[k-1]; dt=q-y[i-1]; if(fabs(dt)>*dt3) *dt3=fabs(dt); *dt1=*dt1+dt*dt; *dt2=*dt2+fabs(dt); } /*释放存储空间*/ free(s); free(t); free(b); return(1); }
Smooth(x,y,a,n,m,&dt1,&dt2,&dt3); /*调用拟合函数*/ for(i=1;i<=m;i++) printf("a[%d] = %.10f\n",(i-1),a[i-1]); printf("拟合多项式与数据点偏差的平方和为:\n"); printf("%.10e\n",dt1); printf("拟合多项式与数据点偏差的绝对值之和为:\n"); printf("%.10e\n",dt2); printf("拟合多项式与数据点偏差的绝对值最大值为:\n"); printf("%.10e\n",dt3); free(x); /*释放存储空间*/ free(y); /*释放存储空间*/ free(a); /*释放存储空间*/ }
Smooth(double *x,double *y,double *a,int n,int m,double *dt1,double *dt2,double *dt3)//(x,y,a,n,m,dt1,dt2,dt3 ) //double *x; /*实型一维数组,输入参数,存放节点的 xi 值*/ //double *y; /*实型一维数组,输入参数,存放节点的 yi 值*/ //double *a; /*双精度实型一维数组,长度为 m。返回 m 一 1 次拟合多项式的 m 个系数*/ //int n; /*整型变量,输入参数,给定数据点的个数*/ //int m; /*整型变量,输入参数,拟合多项式的项数*/ //double *dt1; /*实型变量,输出参数,拟合多项式与数据点偏差的平方和*/ //double *dt2; /*实型变量,输出参数,拟合多项式与数据点偏差的绝对值之和*/ //double *dt3; /*实型变量,输出参数,拟合多项式与数据点偏差的绝对值最大值 */ { int i ,j ,k ;
double *s,*t,*b,z,d1,p,c,d2,g,q,dt; /*分别为 s ,t ,b 分配存贮空间*/ s = (double *)calloc(n,sizeof(double)); if(s == NULL) { printf("内存分配失败\n"); exit (0); } t = (double *)calloc(n,sizeof(double)); if(t == NULL) { printf("内存分配失败\n"); exit (0); } b = (double *)calloc(n,sizeof(double)); if(b == NULL) { printf("内存分配失败\n"); exit (0); } z = 0; for(i=1;i<=n;i++) z=z+x[i-1]/n; /*z 为各个 x 的平均值*/ b[0]=1; d1=n; p=0; c=0; for(i=1;i<=n;i++) { p=p+x[i-1]-z; c=c+y[i-1]; } c=c/d1; p=p/d1; a[0]=c*b[0]; if(m>1) { t[1]=1; t[0]=-p; d2=0; c=0; g=0; for(i=1;i<=n;i++) {
