高等代数 线性方程组习题课(精选)
线性代数课程习题

《高等代数》课程习题第1章行列式习 题 1.11. 计算下列二阶行列式: (1)2345 (2)2163- (3)xxx x cos sin sin cos - (4)11123++-x x x x(5)2232ab b a a (6)ββααcos sin cos sin (7)3log log 1a b b a2. 计算下列三阶行列式:(1)341123312-- (2)00000d c b a (3)d c e ba 0000 (4)zy y x x 00002121(5)369528741 (6)01110111-- 3. 用定义计算行列式:(1)4106705330200100 (2)1014300211321221---(3)5000000004000300020001000 (4)dcb a 100110011001---.4.用方程组求解公式解下列方程组:(1) ⎪⎩⎪⎨⎧=-+=--=--0520322321321321x x x x x x x x x (2)⎪⎩⎪⎨⎧=+-=-+=++232120321321321x x x x x x x x x习 题 1.21. 计算下列行列式:(1)123112101 (2)15810644372---- (3)3610285140 (4)6555655562.计算行列式(1)2341341241231234(2)12114351212734201----- (3)524222425-----a a a(4)322131399298203123- (5)0532004140013202527102135---- 3.用行列式的性质证明:(1)322)(11122b a b b a ab aba -=+(2)3332221113333332222221111112c b a c b a c b a a c c b b a a c c b b a a c c b b a =+++++++++ 4.试求下列方程的根:(1)022223356=-+--λλλ(2)0913251323221321122=--x x5.计算下列行列式(1)8364213131524273------ (2)efcfbfde cd bdae ac ab---(3)2123548677595133634424355---------- (4)111110000000002211n n a a a a a a ---(5)xaaa x a a a x(6)abb a b a b a 000000000000习 题 1.31. 解下列方程组(1)⎪⎩⎪⎨⎧-=++=+--=++1024305222325321321321x x x x x x x x x (2)⎪⎪⎩⎪⎪⎨⎧=+++-=----=+-+=+++01123253224254321432143214321x x x x x x x x x x x x x x x x2. k 取何值时,下列齐次线性方程组可能有非零:(1) ⎪⎩⎪⎨⎧=+-=++-=++0200321321321x x x x kx x kx x x (2)⎪⎩⎪⎨⎧=+-=++=++0300321321321x x x x kx x x x kx 习 题 五1.41.计算下列行列式(1)3010002113005004, (2)113352063410201-- (3)222111c b a c b a(4)335111243152113------, (5)nn n n n b a a a a a b a a a a D ++=+212112111112.用克莱姆法则解线性方程(1)⎪⎩⎪⎨⎧=+-=-+=--114231124342321321321x x x x x x x x x (2)⎪⎪⎩⎪⎪⎨⎧=++=+-+=+-+=++3322212543143214321321x x x x x x x x x x x x x x3.当λ为何值时,方程组⎪⎩⎪⎨⎧=+-=+-=++0020321321321x x x x x x x x x λλ可能存在非零解?4.证明下列各等式(1) 222)(11122b a b b a a b ab a -=+(2) ))()((4)2()1()2()1()2()1(222222222c b a c a b c c c b b ba a a ---=++++++ (3) ))()()()()()((111144442222d c b a d c d b c b d a c a b a d c b a d c b a d c b a+++------=5.试求一个2次多项式)(x f ,满足1)2(,1)1(,0)1(-==-=f f f .第2章矩阵 习 题 2.21.设 ⎥⎦⎤⎢⎣⎡=530142A , ⎥⎦⎤⎢⎣⎡-=502131B , ⎥⎦⎤⎢⎣⎡--=313210C , 求3A -2B +C 。
高等代数Ⅰ第二章 线性方程组测试题

η1,η2 ,",ηn−1 线性无关。(10 分)
八、已知α1
=
(0,1,0),α 2
=
⎧
(−
3,2,2)
是方程组
⎪ ⎨
x1 − x2 + 2x3 = −1 3x1 + x2 + 4x3 = 1
的两个解,求此方程的
⎪⎩ax1 + bx2 + cx3 = d
一般解。(10 分)
九、设α1,α2 ,",αt 是齐次方程组②的基础解系, β1 = α2 + α3 + "+ αt , β2 = α1 + α3 +
β4
= α4
− α1 ,那么,
β
1
,
β
2
,
β
3
,
β
必线相关
4
。
⒉等价的向量组有相同的极大关组。
() ()
⒊设 A是n级方阵, 那么A的行向量线性无关当且仅当 A 的列向量线性无关。( )
⒋如果非齐次线性方程组①的系数矩阵的秩小于 n ,那么①的基础解系一定存在,但未
必是唯一的。
()
⒌非齐次线性方程组的任意两个解向量的和仍是它的解。
⒊设齐次线性方程组
⎪⎪⎨a21x1 ⎪
+
a22 x2 + "+ a2n xn """"
=
0
②
⎪⎩a s1 x1 + as2 x2 + "+ asn xn = 0
只有零解, A 表示其系数矩阵,那么( )
(A) A 的列向量线性相关;
(B) A 的列向量性无关;
第三章习题与复习题(线性方程组)---高等代数
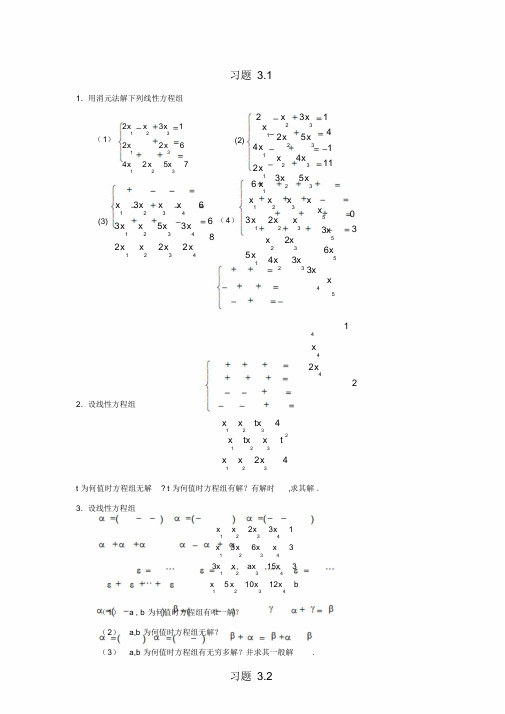
x2x2x0
123
2xxx0
123
3xxx0
123
的解,求的值.
5.已知线性方程组
x2xx2x0
1234
xcxcx
234
0
xcxx
124
0
的基础解系由两个解向量构成,求c的值与该方程组的通解.
6.设
123
A
132
21t
211
B是3阶非零矩阵,且AB=O,求t的值.
(D)若n维向量组1,2,⋯,m(m≥2)线性无关,则对于任意不全为零的数k1,k2,⋯,km
一定有
k11k22
k
m
m
7.已知向量组1,2,3线性无关,向量可由1,2,3线性表示,向量不能由1,2,3
线性表示,则对任意常数k,必有().
(A)1,2,3,k线性无关
(B)1,2,3,k线性相关
(C)1,2,3,k线性无关
(B),,,
12233441
(C),,,
12233441
(D),,,
12233441
5.对任意实数a,b,c下列向量组线性无关的是().
(A) (a,1, 2),(2,b,3),(0, 0, 0)
(B) (b,1, 1),(1,a,3),(2, 3,c),(a,0,c)
(C) (1,a,1, 1),(1,b,1, 0),(1,c,0, 0)
当满足时,
1,2,3线性无关.
8.已知向量组
1111
0112
,,
,
1234
23t24
351t9
线性相关,则t满足.
3.设向量组1,2,3线性无关,则当参数l, m满足时,l21,m32,13也线性无关.
(完整版)高等代数习题集

《高等代数》试题库一、 选择题1.在[]F x 里能整除任意多项式的多项式是( )。
A .零多项式B .零次多项式C .本原多项式D .不可约多项式2.设()1g x x =+是6242()44f x x k x kx x =-++-的一个因式,则=k ( )。
A .1 B .2 C .3 D .43.以下命题不正确的是 ( )。
A . 若()|(),()|()f x g x f x g x 则;B .集合{|,}F a bi a b Q =+∈是数域;C .若((),'())1,()f x f x f x =则没有重因式;D .设()'()1p x f x k -是的重因式,则()()p x f x k 是的重因式4.整系数多项式()f x 在Z 不可约是()f x 在Q 上不可约的( ) 条件。
A . 充分B . 充分必要C .必要D .既不充分也不必要5.下列对于多项式的结论不正确的是( )。
A .如果)()(,)()(x f x g x g x f ,那么)()(x g x f =B .如果)()(,)()(x h x f x g x f ,那么))()(()(x h x g x f ±C .如果)()(x g x f ,那么][)(x F x h ∈∀,有)()()(x h x g x fD .如果)()(,)()(x h x g x g x f ,那么)()(x h x f6. 对于“命题甲:将(1)n >级行列式D 的主对角线上元素反号, 则行列式变为D -;命题乙:对换行列式中两行的位置, 则行列式反号”有( ) 。
A .甲成立, 乙不成立;B . 甲不成立, 乙成立;C .甲, 乙均成立;D .甲, 乙均不成立7.下面论述中, 错误的是( ) 。
A . 奇数次实系数多项式必有实根;B . 代数基本定理适用于复数域;C .任一数域包含Q ;D . 在[]P x 中, ()()()()()()f x g x f x h x g x h x =⇒=8.设ij D a =,ij A 为ij a 的代数余子式, 则112111222212.....................n n n n nn A A A A A A A A A =( ) 。
高等代数学习题集

高等代数学习题集一、线性方程组1. 解下列线性方程组:(1)$3x+2y=7$$2x-3y=4$(2)$2x-y+z=4$$x+3y-2z=5$$2x-y+z=1$(3)$3x+y=5$$4x-y=8$2. 通过矩阵表示以下线性方程组,并求出其解:(1)$4x+2y=6$$-2x+y=3$(2)$x-2y+3z=1$$2x+y+3z=9$$3x+2y+4z=12$(3)$x+y+z=0$$x+2y+3z=1$$x-3y+2z=2$二、矩阵运算与性质1. 计算以下矩阵的乘积:$\begin{bmatrix} 2 & 3 \\ 1 & -1 \end{bmatrix}$$\begin{bmatrix} 4 & 2 \\ -1 & 3 \end{bmatrix}$2. 求下列矩阵的逆矩阵:(1)$\begin{bmatrix} 4 & 2 \\ 1 & 3 \end{bmatrix}$(2)$\begin{bmatrix} 1 & 0 & 2 \\ 0 & 1 & -1 \\ -1 & 0 & 3 \end{bmatrix}$3. 判断下列矩阵是否可逆,并求其逆矩阵:(1)$\begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix}$(2)$\begin{bmatrix} 3 & -2 & 1 \\ 1 & -3 & 2 \\ 2 & -4 & 3 \end{bmatrix}$4. 求矩阵的转置:(1)$\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}$(2)$\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix}$三、特征值与特征向量1. 求矩阵的特征值与特征向量:$\begin{bmatrix} 3 & 1 \\ 2 & 2 \end{bmatrix}$2. 计算以下矩阵的迹:(1)$\begin{bmatrix} 2 & 5 \\ -1 & 3 \end{bmatrix}$(2)$\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{bmatrix}$四、向量空间1. 判断向量组是否线性相关:(1)$\begin{bmatrix} 1 \\ 2 \end{bmatrix}$, $\begin{bmatrix} 2 \\ 4 \end{bmatrix}$(2)$\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}$, $\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}$, $\begin{bmatrix} 2 \\ 3 \\ 4 \end{bmatrix}$2. 求以下向量组的一个极大线性无关组:(1)$\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}$, $\begin{bmatrix} 3 \\ 1 \\ 2 \end{bmatrix}$, $\begin{bmatrix} 2 \\ 3 \\ 1 \end{bmatrix}$(2)$\begin{bmatrix} 1 \\ 1 \\ 0 \\ 1 \end{bmatrix}$, $\begin{bmatrix} 1 \\ 0 \\ 1 \\ 0 \end{bmatrix}$, $\begin{bmatrix} 0 \\ 1 \\ 0 \\ 1\end{bmatrix}$, $\begin{bmatrix} 1 \\ 0 \\ 1 \\ 0 \end{bmatrix}$五、线性变换1. 判断以下线性变换是否为一一映射:(1)$T\left(\begin{bmatrix} x \\ y\end{bmatrix}\right)=\begin{bmatrix} 2x+y \\ 3y \end{bmatrix}$(2)$T\left(\begin{bmatrix} x \\ y \\ z\end{bmatrix}\right)=\begin{bmatrix} x+y \\ y+z \\ x+z \end{bmatrix}$2. 求下列线性变换的矩阵表示:(1)$T\left(\begin{bmatrix} x \\ y\end{bmatrix}\right)=\begin{bmatrix} 2x-y \\ 3x+2y \end{bmatrix}$(2)$T\left(\begin{bmatrix} x \\ y \\ z\end{bmatrix}\right)=\begin{bmatrix} x+y+z \\ 2x+3y-z \\ 3x-2y+2z\end{bmatrix}$六、二次型1. 对以下二次型进行分类:(1)$f(x,y)=2x^2+3y^2-4xy$(2)$f(x,y,z)=x^2+y^2+z^2-2xy+4xz$2. 将以下二次型化为标准形:(1)$f(x,y,z)=3x^2+4y^2+2z^2+4xy+4xz-8yz$(2)$f(x,y,z)=x^2+2y^2+3z^2-2xy+6xz$以上为《高等代数学习题集》的内容,希望对你的学习有所帮助。
高等代数第三章线性方程组知识点复习与相关练习

第三章线性方程组3.1主要方法3.1.1线性相关性的判别线性关系:α1,α2,···,αs线性无关⇐⇒α1,α2,···,αs不线性相关⇐⇒不存在不全为零的数k1,k2,···,k s使成立k1α1+k2α2+···+k sαs=0⇐⇒若k1,k2,···,k s不全为零,则k1α1+k2α2+···+k sαs=0⇐⇒若k1α1+k2α2+···+k sαs=0,则k1=k2=···=k s=0.因此,判断向量组α1,α2,···,αs是否线性相关的方法:令k1α1+k2α2+···+k sαs=0,若k1,k2,···,k s有非零解,则α1,α2,···,αs线性相关;若k1,k2,···,k s只有零解,则α1,α2,···,αs无关。
3.1.2求矩阵与向量组的秩的方法求矩阵秩的方法:A初等行变换−−−−−−→B(阶梯形矩阵)则r(A)=r(B)=B的非零行的行数.求向量组的秩的方法:以α1,α2,···,αs为列做成矩阵A,A=(αT1,αT2,···,αTs)初等行变换−−−−−−→B(阶梯形矩阵)则•r(α1,α2,···,αs)=r(A)=r(B)=B的非零行的行数.•若B的非零行的第一个非零元分别位于i1,i2,···,i r,则αi1,αi2,···,αir就是α1,α2,···,αs的一个极大线性无关组。
高等代数_李海龙_习题第4章线性方程组

第四章 线性方程组4.1 消元法1. 解以下线性方程组:(ⅰ)123412341234212125x x x x x x x x x x x x -++=⎧⎪-+-=-⎨⎪-++=⎩(ⅱ)123123123123233350433136x x x x x x x x x x xx -+=⎧⎪+-=⎪⎨-+=⎪⎪+-=-⎩解:(ⅰ)利用消元法,线性方程组增广矩阵121111211112111000221211500004A --⎛⎫⎛⎫⎪ ⎪=---→-- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭=B由矩阵B 可看出,相当于矩阵B 的线性方程组中有一个方程是: 05.=所以原方程无解.(ⅱ)利用消元法,将线性方程组增广矩阵化为阶梯矩阵.方程组的解为:1231,2,1,x x x === 2. 证明,对矩阵施行第一种行初等变换相当于对它连续施行几次第二种和第三种行初等变换.证明:设交换矩阵的第i 行与第j 行,方法如下: (1) 将第i 行与第j 行分别乘以1加到第1行上 (2) 将第1行乘以-1加到第i 行与第j 行上 (3) 对第1行、第i 行与第j 行分别乘以-1 (4) 将第i 行与第j 行分别乘以-1加到第1行上3.设n 阶行列式1112121222120.n n n n nna a a a a a D a a a =≠证明,用行初等变换能把n 行n 列矩阵111212122212n n n n nna a a a a a aa a ⎛⎫⎪ ⎪ ⎪ ⎪ ⎪⎝⎭化为n 行n 列矩阵100010001⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭证明:因为0,D ≠若111110,a a ≠用乘第一行,若110,a =将第i 行的1111i a a -(设10i a ≠)倍加到第一行,原矩阵变为,''''121121''212222''1221100n n nn nn n n nnn nna a a a a a a a a aa a a a ⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪→⎪⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭则 '''222'''20.nn nna a D a a =≠ 同样的方法,原矩阵变为''''12131'''''232''''333''''311*10111000100n n n n nn a a a a a a a D a a ⎛⎫ ⎪⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪ ⎪ ⎪→→⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭ ⎪⎝⎭4.证明,在前一题的假设下,可以通过若干次第三种初等变换把n 行n 列矩阵111212122212n n n n nna a a a a a aa a ⎛⎫⎪ ⎪ ⎪ ⎪ ⎪⎝⎭ 化为100001000010000D ⎛⎫⎪⎪ ⎪⎪ ⎪ ⎪⎝⎭证明:矩阵可经第三种行初等变换变为:1*10D ⎛⎫⎪ ⎪ ⎪⎪⎝⎭ 又因为0,D ≠,再作第三种列初等变换变为:1010D ⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭ 4.2 矩阵的秩 线性方程组可解的判别法1.对第一和第二种行初等变换证明定理4.2.1证:设矩阵A 经过第一种行的初等变换,交换第i 行和第j 行,得到矩阵B ,矩阵A 经过第二种行的初等变换,用0a ≠乘第i 行得到矩阵C ,并设秩A=r .在B 中任取一个1r +阶子式,从而0D =;若D 包含A 的第i 行或第j 行的元素,那么在A 中有一个与D 的元素相同的1r +阶子式,只是行的顺序不同,它与D 的绝对值相等,所以0D =,若D 包含A 的第i 行和第j 行,则在A 中有一个与D 相差一个符号的1r +阶子式,所以0D =.综上所述,B 的任一1r +阶子式一定为零.所以 秩B ≤秩A=r .因为A 可由B 交换第i 行和第j 行得到,所以 秩A ≤秩B .从而 秩A=秩B ,故第一种初等变换不改变矩阵的秩.在C 中任取一个1r +阶子式D ‘,若D ‘不包含A 的第i 行,它就是A 的一个1r +阶子式,D ‘=0. 若D ‘包含A 的第i 行,则D ‘是A 的相应子式的a 倍,仍是D ‘=0.因而秩C ≤秩A ,又A 可由C 用1a 乘第i 行得到,因而秩A ≤秩C ,所以秩A=秩C ,故第二种初等变换不改变矩阵的秩.2.用初等变换求下列矩阵的秩(ⅰ)2111210411145652156⎛⎫ ⎪- ⎪ ⎪⎪--⎝⎭(ⅱ)112571237101349131451116⎛⎫ ⎪⎪⎪⎪⎝⎭解:(ⅰ) 2;(ⅱ) 2;3.证明:一个线性方程组的增广矩阵的秩比系数矩阵的秩最多大1. 证明:设线性方程组的增广矩阵和系数矩阵分别为1111n n nna a A aa ⎛⎫⎪= ⎪ ⎪⎝⎭11111n n nn na ab A a a b ⎛⎫⎪= ⎪ ⎪⎝⎭且秩A r =,所以A 的所有r +1阶子式全为零.对于A 的r +2阶子式K ,若K 不包含A 中的最后一列元素,则K 是A 的r +2阶子式,K=0.若K 包含A 中的最后一列元素,,将K 按这一列展开,其中都是r +1阶子式A 的r +1阶子式,所以K=0.故秩A ≤r +1.显然r =秩A ≤秩A ≤r +1,故结论成立.4.证明:含有n 个未知量n+1个方程的线性方程组11111111,111,11n n n nn n nn n n n n a x a x b a x a x b a x a x b ++++++=++=++=有解的必要条件是行列式111111,11,1n n nn n n n nn a a b a a b a a b +++=这个条件不是充分的,试举一反倒.证明:反证法.若01,,D A n A n ≠=+≤,则秩秩从而A A ≠秩秩,此与方程组有解矛盾,所以 D=0.例如:线性方程组1212121221331x x x x x x +=⎧⎪+=⎨⎪+=⎩,我们有1112210331=但显然此方程组无解.5.λ取怎样的数值时,线性方程组1234212343123423232121x x x x x x x x x x x x λλλ++-=⎧⎪-++=-⎨⎪-+-=-⎩有解.解:101,2A Aλλλ===-≠当,,时,秩秩方程组无解;1013,2A A λλλ≠≠≠-==当且且时,秩秩方程组有解,且有无穷多解6.λ取何值时,线性方程组 12312321231,,x x x x x x x x x λλλλλ⎧++=⎪++=⎨⎪++=⎩唯一解,没有解,有无穷解?解:当1λ≠且2λ≠-时,方程组有唯一解; 当1λ=时,方程组有无穷多解; 当2λ=-时,方程组无解4.3 线性方程组的公式解1.考虑线性方程组:121342131242x x a x x a x x b x x b +=⎧⎪+=⎪⎨+=⎪⎪+=⎩这里1212.a a b b +=+证明,这个方程组有解,并且它的系数矩阵的秩是3.解:通过计算可知:秩A =秩A =3,所以方程组有解.2.用公式解法解线性方程组:1234123412342121255x x x x x x x x x x x x -++=⎧⎪-+-=-⎨⎪-++=⎩解:1234232,1,,x x x x x x =-=为自由未知量.3.设线性方程组11112211211222221122,,n n n n m m m n n m a x a x a x b a x a x a x b a x a x a x b++=⎧⎪++=⎪⎨⎪⎪++=⎩有解,并且添加一个方程:1122n n a x a xa xb +++= 后所得的方程组与原方程组同解.证明,添加的方程是原方程组中m 个方程的结果.证明:设原方程组为(1);添加一个方程后所得方程组为(2),(1)的系数矩阵 和增广矩阵为,A A ;(2)的系数矩阵 和增广矩阵为,.B B 并设秩A r =.因为(1)有解,设秩A=秩A =r 0≠,则(1)中可选出r 个方程,其余m r -个方程都是这r 个方程的结果.记这r 个方程所组成的方程组为(3),则(1)与(3)同解.因而(2)与(1)同解,所以(2)与(3) 同解,从而(2)中其余m r -+1个方程都是这r 个方程的结果,因而(2)中最后一个方程即添加的方程是前m 个方程的结果.假若设秩A=秩A =r =0,则A =0,由(1)与(2)同解,所以添加方程的各系数和常数项只能全为零,所以添加的方程是(1)中m 个方程的结果.4.设齐次线性方程组1111221211222211220,0,0.n n n n n n nn n a x a x a x a x a x a x a x a x a x +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩ .的系数行列式D=0,而D 中某一元素ija 的代数余子式ij A ≠,证明,这个方程组的解都可以写成12,,,i i in kA kA kA 的形式,此处k是任意数.设12,,,n x x x 是原方程组的一个解,那么它也是以下方程组的解:111111111111,111,111,111,1,1,111,111,111,1,11j j j j n n j j i i j j i j j i n n i j j i i j j i j j i n n i j j n a x a x a x a x a x ax a x a x a x a x a x a x a x a x a x a x --++-----++--++--++++++++++=-+++++=-+++++=-+ ,11,11.n j j n j j nn n nj j a x a x a x a x --++⎧⎪⎪⎪⎪⎨⎪⎪⎪++++=-⎪⎩ 因为0,ij A ≠所以其系数行列式不等到于零.由克莱姆规得 1212,,,.i i in j j n j ijijijA A A x x x x x x A A A === jx 为自由未知量,令j ijx kA =(k 是任意数). 则1122,,,.i i n in x kA x kA x kA === 于是原方程组的任一解都可以写成12,,,i i in kA kA kA 的形式,此处k 是任意数.5.设行列式 111212122212n n n n nna a a a a a a a a =. 令ijA 是元素ija 的代数余子式.证明,矩阵112111222212n n nnnn A A A A A A A A A ⎛⎫⎪ ⎪ ⎪⎝⎭的秩 1.≤解:考虑齐次线性方程组111122111220n n n n nn n a x a x a x a x a x a x +++=⎧⎪⎨⎪+++=⎩因为它的系数行列式D=0,显然,12,,,(1,2,,)i i in A A A i n = 都是方程组的解.若所有0(,1,2,),ij A i j n == 则题中矩阵的秩为0;若有一个0.ij B ≠由上题,方程组的解都有可以写成12,,,i i in kA kA kA .题中所给矩阵各列都与第i 列成正比例,所它的秩为1.4.4 结式和判别式1.设12(),(),()[].f x g x g x C x ∈证明,1212(,)(,)(,).R f g g R f g R f g = 证明:提示:设012()()()(),n f x a x a x a x a =--- 12g g m k +为次多项式,则12012121(,)()()(,)(,).nm k i i i R f g g aga g a R f g R f g +===∏2.问λ取怎样的数值时,多项式32()2,()2f x x x g x x x λλ=-+=++有公根?解:1λ=-或 3.λ=3.求101()n n n f x a x a x a -=+++ 与12011 ()n n n g x a x a x a ---=+++ 结式.解:行列式得结式为10(,).n n n R f g a a -=(解法参见例10)4.解下列方程组:(ⅰ)2222306711120.x y x y x xy y x y ⎧+--=⎪⎨+---+=⎪⎩(ⅱ)2222423041090x y x y x xy y y ⎧++-+=⎪⎨+-+-=⎪⎩(ⅲ)222256516020x xy y x xy y x y ⎧-+-=⎪⎨-+--=⎪⎩解: (ⅰ)312412342302,,,.0112x x x x y y y y ====⎧⎧⎧⎧⎨⎨⎨⎨===-=⎩⎩⎩⎩(ⅱ)1112x y =-⎧⎨=⎩2230x y =-⎧⎨=⎩3355x y ⎧=⎪⎪⎨⎪=⎪⎩4455x y ⎧=⎪⎪⎨⎪=⎪⎩(ⅲ)3122123411121,1,1, 2.x x x x y y y y ==-=-=⎧⎧⎧⎧⎨⎨⎨⎨===-=⎩⎩⎩⎩5.求多项式nx a +的判别式.解:1().n f x nx -'=()f x '的根只有0. 而(0),f a =11(,)(0).nn n n R f f n fn a--'==(1)1(,)(1)(,).n n n n R f fR f fn a --''=-= (1)(1)122()(1)(,)(1).n n n n n n D f R f f n a---'=-=-6.求多项式3x px q ++的判别式.解: 2()3.f x x p '=+ 设()f x 的根为123,,,ααα由韦达定理得:1231223230,p ααααααααα++=++=123,q ααα=- 2221232,p ααα++=-2222222122313,p αααααα++=123222123(,)()()()(3)(3)(3)R f f f f f p p p αααααα''''==+++2333322769427.qppppq =+-+=+32()(,)427.D f R f f p q '=-=--7.证明,多项式1011()n n n nf x a x a xa x a --=++++ 与10()nn g x a x a x a =+++ 0(0,0)n a a ≠≠有相同的判别式.证明:设()f x 在复数域C 上的根为12,,.n ααα 则()g x 在C 上的根为12111,,.nααα(),()f x g x 的判别式分别为12,.D D 22210(),n ij i jD a aa ->=-∏222222222()11()j i n n nni ji jiji jD aaαααααα-->>-=-=∏∏22222121()()n n j i n i jn a ααααα-->=⋅-∏222220[(1)]()n nn ni j i jna a a αα-->=-⋅-∏2221().n ij i ja D αα->=-=∏8.令D 是()f x 的判别式,1D 是()()x a f x -判别式,证明21()D f a D =证:设12()()()(),n n f x a x x x ααα=--- 则222211()()()nn ij n i jD a a a αααα>=---∏2222221[()]()()n nij n n a a a a αααα-=-⋅--∏ 2().D f a =⋅9.令D 是实数域上三次多项式()f x 的判别式.证明: 当D=0时,()f x 有重根;当D>0时,()f x 有三个互不相同的实根; 当D<0时,()f x 有一个实根,两个非实的复根. 证:设12()()()(),f x a xx x ααα=---且0,a a ≠为实数,则4222213132()()().D a αααααα=---当D=0时,因为40,a >所以至少有一个0,i j αα-=从而()f x 有重根;当D>0时,因为40,a >所以 222213132()()()0αααααα--->,从而213132()()()αααααα---为非零实数.因为123,,ααα中至少有一个是实数,不妨设为1,α若23,αα不是实数,则23,αα=那么,2131,αααα-=-32αα-是纯虚数,与它们的积为实数矛盾,所以123,,ααα是三个不同的实数.当D<0时,因为40,a >所以 222213132()()()0.αααααα---< 若123,,ααα都是实数,则()ij i jαα>-∏为实数,矛盾.又因为复根成对出现,故()f x 有一个实根,两个非实的复根.。
《工程高等代数》5第五章线性方程组习题解答

习 题 五A 组1.填空题(1)当方程的个数等于未知数的个数时,=Ax b 有惟一解的充分必要条件是 . 解 因为()()R R n ==A A b 是=Ax b 有惟一解的充要条件.故由()R n =A 可得||0≠A . (2)线性方程组121232343414,,,x x a x x a x x a x x a +=⎧⎪+=⎪⎨+=⎪⎪+=⎩ 有解的充分必要条件是 .解 对方程组的增广矩阵施行初等行变换()12341100011000111001a a a a ⎛⎫⎪⎪== ⎪⎪⎪⎝⎭B A b12341231100011000110000a a a a a a a ⎛⎫⎪⎪→ ⎪ ⎪⎪-+-⎝⎭. 所以方程组有解的充要条件是()()R R =A B ,即43210a a a a -+-=.(3)设n 阶方阵A 的各行元素之和均为零,且()1R n =-A ,则线性方程组=Ax 0的通解为 . 解 令111⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭x显然x 满足方程组,又因为()1R n =-A ,所以()1n R -=A ,即方程组的基础解系中有一个向量,通解为T 11(1,1,,1)1k k ⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪⎝⎭x ,k 为任意常数.(4)设A 为n 阶方阵,||0=A ,且kj a 的代数余子式0kj A ≠(其中,1k n ≤≤;1,2,,j n =),则=Ax 0的通解 .解 因为0=A ,又0kj A ≠,所以()1R n =-A ,并且有11220, ;||0, i k i k in kn i k a A a A a A i k ≠⎧+++=⎨==⎩.A 所以()T12,,,k k kn A A A 是方程组的解,又因为()1R n =-A ,可知方程组的通解为()T12,,,k k kn c A A A =x ,其中c 为任意常数.(5)设11222221231111211111,,11n n n n n n n x a a a x a a a x a a a x ---⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭A x b , 其中,(;,1,2,,)i j a a i j i j n ≠≠=,则非齐次线性方程组T =A x b 的解是=x .解 T (1,0,0,,0)=x .(6)设方程123111111112a x a x a x ⎛⎫⎛⎫⎛⎫⎪⎪ ⎪= ⎪⎪ ⎪ ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭有无穷多个解,则a = .解 2a =-.2.单项选择题(1)齐次线性方程组355⨯⨯1=A x 0解的情况是 .(A) 无解; (B) 仅有零解;(C) 必有非零解; (D) 可能有非零解,也可能没有非零解. 答 (C ).(2) 设n 元齐次线性方程组的系数矩阵的秩()3R n =-A ,且123,,ξξξ为此方程组的三个线性无关的解,则此方程组的基础解系是 .(A) 12312,2,32+- -ξξξξξ; (B) 122331,,+-+ ξξξξξξ;(C)122132-2,-2,32+-+ ξξξξξξ; (D) 12231324,2+,++ - ξξξξξξ.答(A ).(3)要使T 1(1,0,2)=ξ,T 2(0,1,1)=-ξ都是线性方程组=Ax 0的解,只要A 为 . (A) (211)-; (B) 201011⎛⎫⎪⎝⎭;(C) 102011-⎛⎫⎪-⎝⎭; (D)011422011-⎛⎫ ⎪-- ⎪ ⎪⎝⎭. 答(A ).(4)已知12,ββ是=Ax b 的两个不同的解,12,αα是相应的齐次方程组=Ax 0的基础解系,12,k k 为任意常数,则=Ax b 的通解是 .(A) 12()k k 12112-+++2ββααα; (B) 12()k k 12112++-+2ββααα;(C) 12()k k 12112-+-+2ββαββ; (D) 12()k k 12112++-+2ββαββ.答(B ).(5)设n 阶矩阵A 的伴随矩阵*≠A 0 若1234,,,ξξξξ是非齐次线性方程组Ax =b 的互不相等的解,则对应的齐次线性方程组Ax =0的基础解系是 .(A) 不存在; (B) 仅含一个非零解向量;(C) 含有两个线性无关的解向量; (D) 含有三个线性无关的解向量. 答(B ).(6)设有齐次线性方程组Ax =0和Bx =0,其中A ,B 均为m n ⨯矩阵,现有4个命题: ① 若Ax =0的解均是Bx =0的解,则()()R R ≥A B ;② 若()()R R ≥A B ,则Ax =0的解均是Bx =0的解; ③ 若Ax =0与Bx =0同解,则()()R R =A B ;④ 若()()R R =A B ,则Ax =0与Bx =0同解. 以上命题正确的是 .(A ) ①,②; (B )①,③; (C )②,④; (D )③,④. 答(B ).(7)设A 是m n ⨯矩阵,B 是n m ⨯矩阵,则线性方程组()=AB x 0 . (A )当n m >时仅有零解; (B )当n m >时必有非零解; (C )当m n >时仅有零解; (D )当m n >时必有非零解. 答(D ). (8)设A 是n 阶矩阵,α是n 维列向量. 若秩T0⎛⎫=⎪⎝⎭αAα秩()A ,则线性方程组 . (A )=αAx 必有无穷多解; (B )=αAx 必有惟一解;(C )T 0y ⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭αA αx 0仅有零解; (D )T 0y ⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭αA αx 0必有非零解.答(D ).3.求下列齐次线性方程组的一个基础解系(1) 12341234123420,20,2220;x x x x x x x x x x x x ++-=⎧⎪++-=⎨⎪+++=⎩解 对系数矩阵施行初等行变换,有41001121321110103221240013⎛⎫-⎪-⎛⎫⎪ ⎪=-→ ⎪ ⎪ ⎪ ⎪⎝⎭- ⎪⎝⎭A .与原方程组同解的方程组为14243440,330,40,3x x x x x x ⎧-=⎪⎪+=⎨⎪⎪-=⎩或写为1241344343944331x x x k x x ⎛⎫ ⎪ ⎪⎛⎫⎛⎫ ⎪- ⎪ ⎪ ⎪- ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎪ ⎪⎝⎭x ,其中143k =为任意常数.所以,基础解系为 14943⎛⎫ ⎪- ⎪= ⎪ ⎪⎝⎭ξ.(2) 12341234123420,3630,51050;x x x x x x x x x x x x ++-=⎧⎪+--=⎨⎪++-=⎩解1211120136130010510150000--⎛⎫⎛⎫⎪ ⎪=--→ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭A ,与原方程组同解的方程组为12432 0,0,x x x x +-=⎧⎨=⎩或写为124223442,,0,x x x x x x x x =-+⎧⎪=⎪⎨=⎪⎪=⎩, 其中,24,x x 可取任意常数12,k k ,故12123421100001x x k k x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪==+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭x . 所以,基础解系为122110,0001-⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ξξ.(3) 12341234123412342350,3270,4360,2470;x x x x x x x x x x x x x x x x +-+=⎧⎪++-=⎪⎨+-+=⎪⎪-+-=⎩解231512473127012126413600151247000327--⎛⎫⎛⎫ ⎪ ⎪-- ⎪ ⎪=→ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭A , ()4R n ==A ,方程组组只有零解.(4) 123412341234123434570,23320,41113160,7230x x x x x x x x x x x x x x x x +-+=⎧⎪-+-=⎪⎨+-+=⎪⎪-++=⎩.解3131017173457192001233217174111316000072130000⎛⎫-⎪⎪-⎛⎫⎪-⎪⎪--⎪=→ ⎪ ⎪- ⎪⎪ ⎪⎪-⎝⎭ ⎪ ⎪ ⎪⎝⎭A , 与原方程组同解的方程组为134234313 017171920 01717x x x x x x ⎧-+=⎪⎪⎨⎪-+=⎪⎩,. 或写为1342343344313171719201717x x x x x x x x x x ⎧=-⎪⎪⎪=-⎨⎪=⎪⎪=⎩,,,. 故1212343131920170017x x k k x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪==+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭x . 所以基础解系为123131920,170017-⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ξξ. 4.求解下列非齐次线性方程组.(1) 123123124+2232101138x x x x x x x x -=⎧⎪-+=⎨⎪+=⎩,,;解 对增广矩阵施行初等行变换42121338312100101134113080006---⎛⎫⎛⎫ ⎪ ⎪=-→- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭B ,所以()2,()3R R ==A B .无解.(2) 23424538213496x y z x y z x y z x y z ++=⎧⎪-+=-⎪⎨+-=⎪⎪-+=-⎩,,,;解231410211245011238213000041960000-⎛⎫⎛⎫⎪ ⎪---⎪ ⎪=→ ⎪ ⎪- ⎪ ⎪⎪ ⎪--⎝⎭⎝⎭B()()2R R ==A B ,所以原方程组有解.与原方程组同解的方程组为21,2,x z y z z z =--⎧⎪=+⎨⎪=⎩. 故211210x y k z --⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. (3) 21,4222,21x y z w x y z w x y z w +-+=⎧⎪+-+=⎨⎪+--=⎩;解111102222111142212000102111100000⎛⎫- ⎪-⎛⎫ ⎪⎪⎪=-→ ⎪ ⎪⎪-- ⎪⎝⎭⎪ ⎪⎝⎭B ,()()2R R ==A B ,原方程组有解.与原方程组同解的方程组为111222,,0x y z y y z z w ⎧=-++⎪⎪⎪=⎨⎪=⎪=⎪⎩,.所以原方程组的通解为111222100010000x y y z z w ⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭121211020020000k k ⎛⎫ ⎪ ⎪-⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪ ⎪ ⎪=++ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪ ⎪⎝⎭. (4) 21,3234,4352x y z w x y z w x y z w +-+=⎧⎪-+-=⎨⎪+-+=-⎩.解116107772111159532134017771435200000⎛⎫-- ⎪-⎛⎫ ⎪⎪⎪=--→-- ⎪ ⎪ ⎪-- ⎪⎝⎭ ⎪ ⎪⎝⎭B ,()()2R R ==A B ,原方程组有解.与原方程组同解的方程组为116777595777x z w y z w z z w w ⎧=++⎪⎪⎪=--⎨⎪=⎪⎪=⎩,,,. 故通解为1267115597700070x y k k z w ⎛⎫⎪ ⎪⎛⎫⎛⎫⎛⎫ ⎪- ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪=++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎪ ⎪ ⎪⎝⎭. 5.问λ取何值时,非齐次线性方程组12312321231x x x x x x x x x ⎧λ++=⎪+λ+=λ⎨⎪++λ=λ⎩,,(1)有惟一解;(2)无解;(3)有无穷个解?解 系数行列式21111(1)(2)11D λλλλλ==-+.当1≠λ且2-≠λ时0≠D ,方程组有惟一解. 当1=λ时,对增广矩阵施行初等行变换111111111111000011110000⎛⎫⎛⎫ ⎪ ⎪=→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭B ,则()()13R R ==<A B ,故原方程组有解且有无穷多解.当2-=λ时,对增广矩阵施行初等行变换211111241212121211242111--⎛⎫⎛⎫ ⎪ ⎪=--→-- ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭B112411240336033603390003--⎛⎫⎛⎫ ⎪ ⎪→--→-- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭, ()2,()3R R ==A B .所以方程组无解.6.非齐次线性方程组1231231232x x x x x x x x x 2⎧-2++=-⎪-2+=λ⎨⎪+-2=λ⎩,,当λ取何值时有解?并求出它的全部解.解 对增广矩阵施行初等行变换,得222112112121033(1)112000(1)(2)λλλλλλλ⎛⎫---⎛⎫⎪ ⎪=-→-- ⎪ ⎪ ⎪ ⎪--+⎝⎭⎝⎭B ,当1λ≠且2λ≠-时,()2,()3R R ==A B 方程组无解. 当1λ=时,有101101100000-⎛⎫⎪→- ⎪ ⎪⎝⎭B()()2R R ==A B ,方程组有解,且与原方程组同解的方程组为13233310x x x x x x =+⎧⎪=+⎨⎪=⎩,,.故原方程组的解为1213111010x x k x ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪==+ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭x .当2λ=-时,有101201120000-⎛⎫ ⎪→- ⎪ ⎪⎝⎭B与原方程组同解的方程组为13233322x x x x x x =+⎧⎪=+⎨⎪=⎩,,.故方程组的解为123121210x x k x ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪==+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭x .7.设12312312322124224x x x x x x x x x (2-λ)+-=⎧⎪+(5-λ)-=⎨⎪--+(5-λ)=-λ-1⎩,,,问λ为何值时,此方程组有惟一解、无解或有无穷多解?并在有无穷多解时求出其通解. 解 系数行列式2222254(1)(10)245D λλλλλ--=--=------. 当1λ≠且10λ≠时,方程组有惟一解. 当1λ=时,有122112212442000024420000--⎛⎫⎛⎫ ⎪ ⎪=-→ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭B()()1R R ==A B ,方程组有无穷多解,此时123221x x x +-=通解为12123221100010x x k k x -⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪==++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭x .当10=λ时,有8221254225420111245110003----⎛⎫⎛⎫ ⎪ ⎪=--→ ⎪ ⎪ ⎪ ⎪-----⎝⎭⎝⎭B ,()2,()3R R ==A B ,故方程组无解.8.问,a b 为何值时,非齐次线性方程组123423423412340,221,(3)2,321x x x x x x x x a x x b x x x ax +++=⎧⎪++=⎪⎨-+--=⎪⎪+++=-⎩ (1) 有惟一解,求出惟一解;(2) 无解;(3) 有无穷多解,并写出通解.解 方程组的增广矩阵11110111100122101221.013200101321100010a b a b a a ⎛⎫⎛⎫⎪ ⎪⎪ ⎪=→ ⎪ ⎪----+ ⎪ ⎪⎪ ⎪--⎝⎭⎝⎭B当1≠a 时,()()4R R ==A B ,方程组有惟一解.此时2100012301001.10010100010a b a a b a b a -++⎛⎫ ⎪- ⎪-- ⎪ ⎪-→⎪+ ⎪ ⎪- ⎪ ⎪ ⎪⎝⎭B所以,12342231,,,0111a b a b b x x x x a a a -+--++====---.当1=a 时,有11110012210000100000b ⎛⎫⎪⎪→ ⎪+ ⎪⎪⎝⎭B ,所以,当1=a 且1-≠b 时,()2R =A ,()3R =B ,方程组无解.而当1=a 且1b =-时,有10111012210000000000---⎛⎫⎪⎪→ ⎪⎪⎪⎝⎭B ,()()2R R ==A B ,方程组有解,且与原方程组同解的方程组为1342341,221,x x x x x x --=-⎧⎨++=⎩ 或写为13423433441,221,,.x x x x x x x x x x =+-⎧⎪=--+⎪⎨=⎪⎪=⎩ 故原方程组的通解为121234111221100010x x k k x x -⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪==++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭x , 其中12,k k 为任意实数.9.设四元非齐次线性方程组的系数矩阵的秩为3,已知123,,ηηη是它的三个解向量,且1232132,4354⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪=+= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ηηη, 求该方程组的通解.解 4,()3n r R ===A ,所以1n r -=,令11124136242()8351046⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎪ ⎪ ⎪=-+=-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ξηηη,则1ξ为基础解系,故方程组的通解为1132435465k k ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪=+=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭x ξη, 其中k 可取任意常数.10. 设,A B 都是n 阶方阵,且=AB 0.证明()()R R n +≤A B .证明 设12(,,,)n =B b b b ,则有(1,2,,)j j n ==Ab 0.可见每个j b 都是=Ax 0的解向量.因()R r =A ,可知=Ax 0的解空间的维数是n r -,所以向量组12,,,n b b b 的秩小于等于r n -,从而()R n r ≤-B ,于是()()()R R r n r n +≤+-=A B .11.已知非齐次线性方程组1234123412341435131x x x x x x x x ax x x bx +++=-⎧⎪++-=-⎨⎪+++=⎩ 有3个线性无关的解.(1)证明方程组的系数矩阵A 的秩()2R =A ; (2)求,a b 的值及方程组的通解.解 (1) 设123,,ααα是方程组=βAx 的3个线性无关的解,其中111114351,1131a b -⎛⎫⎛⎫ ⎪ ⎪=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭A β.则有1213(),()-=-=ααααA 0A 0,即1213,--αααα是对应齐次线性方程组=Ax 0的解,且线性无关.(否则,易推出123,,ααα线性相关,矛盾).所以()2n R -≥A ,即4()2()2R R -≥⇒≤A A .又矩阵A 中有一个2阶子式111043=-≠,所以()2R ≥A .因此()2R =A .(2) 因为11111111111143510115011513013004245a b a a b a a b a ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-→--→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪----+-⎝⎭⎝⎭⎝⎭A又()2R =A ,则420,2,,450 3.a ab a b -==⎧⎧⇒⎨⎨+-==-⎩⎩ 对原方程组的增广矩阵施行初等行变换,111111024243511011532133100000--⎛⎫⎛⎫ ⎪ ⎪=--→-- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭B ,故原方程组与下面的方程组同解13423424253x x x x x x =-++⎧⎨=--⎩. 选34,x x 为自由变量,则134234334424253x x x x x x x x x x =-++⎧⎪=--⎪⎨=⎪⎪=⎩. 故所求通解为12242153100010k k -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪=++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭x ,12,k k 为任意常数.12.已知三阶矩阵A 的第一行是()a b c ,,,a b c 不全为零,矩阵12324636k ⎛⎫ ⎪⎪ ⎪⎝⎭B =(k 为常数),且AB =0,求线性方程组Ax =0的通解.解 由于AB =0,故()()3R R +≤A B ,又由,,a b c 不全为零,可知()1R ≥A . 当9k ≠时,()2R =B ,于是()1R =A ;当9k =时,()1R =B ,于是()1R =A 或()2R =A . ① 对于9k ≠,由AB =0可得123⎛⎫ ⎪⎪ ⎪⎝⎭A =0和36k ⎛⎫⎪ ⎪ ⎪⎝⎭A =0.由于()()TT121,2,3,3,6,k ==ηη线性无关,故12,ηη为Ax =0的一个基础解系,于是Ax =0的通解为1122c c =+x ηη,其中12,c c 为任意常数.② 对于9k =,分别就()2R =A 和()1R =A 进行讨论.如果()2R =A ,则Ax =0的基础解系由一个向量构成. 又因为123⎛⎫⎪⎪ ⎪⎝⎭A =0,所以Ax =0的通解为()T11,2,3c =x ,其中1c 为任意常数.如果()1R =A ,则Ax =0的基础解系由两个向量构成. 又因为A 的第1行是(),,a b c ,且,,a b c 不全为零,所以Ax =0等价于1230ax bx cx ++=. 不妨设0a ≠,()()TT12,,0,,0,b a c a =-=-ηη是Ax =0的两个线性无关的解,故Ax =0的通解为 1122c c =+x ηη,其中12,c c 为任意常数.13.确定常数a ,使向量组T1(1,1,),a =αT 2(1,,1),a =αT 3(,1,1)a =α可由向量组T 1(1,1,)a =β,T 2(2,,4)a =-β,T 3(2,,)a a =-β线性表示,但向量组123,,βββ不能由向量组123,,ααα线性表示.解 对矩阵123123(,,,,)=B βββααα作初等行变换,有123123(,,,,)=B βββααα=12211111411a aa a a a a --⎛⎫⎪⎪ ⎪⎝⎭ →1221102201000403(1)1a a a a a a a --⎛⎫⎪++- ⎪ ⎪---⎝⎭, 当2a =-时,→B 122112000030006033---⎛⎫⎪- ⎪ ⎪-⎝⎭,显然2α不能由123,,βββ线性表示,因此2-≠a ;当4a =时,→B 122114066030000093--⎛⎫ ⎪⎪ ⎪--⎝⎭, 显然23,αα均不能由123,,βββ线性表示,因此4≠a .而当2-≠a 且4≠a 时,秩123(,,)3R =βββ,此时向量组123,,ααα可由向量组123,,βββ线性表示.又12312311122(,,,,)111114a a a a a a a --⎛⎫⎪== ⎪ ⎪⎝⎭C αααβββ 2111220110220110423a a a a a a a a a --⎛⎫ ⎪→--++ ⎪ ⎪--+⎝⎭21112201102200206342aa a a a a a a a --⎛⎫⎪→--++ ⎪ ⎪--++⎝⎭, 由题设向量组123,,βββ不能由向量组123,,ααα线性表示,必有01=-a 或022=--a a ,即1a =或2-=a .综上所述,满足题设条件的只能是1a =.14.已知齐次线性方程组(Ⅰ)⎪⎩⎪⎨⎧=++=++=++,0,0532,032321321321ax x x x x x x x x (Ⅱ)⎩⎨⎧=+++=++,0)1(2,03221321x c x b x cx bx x 同解,求,,a b c 的值.解 方程组(Ⅱ)的未知量个数大于方程个数,故方程组(Ⅱ)有无穷多解.因为方程组(Ⅰ)与(Ⅱ)同解,所以方程组(Ⅰ)的系数矩阵的秩小于3.对方程组(Ⅰ)的系数矩阵施以初等行变换12310123501111002a a ⎛⎫⎛⎫ ⎪ ⎪→ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭, 从而2a =.此时,方程组(Ⅰ)的系数矩阵可化为123101235011112000⎛⎫⎛⎫ ⎪ ⎪→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 故T (1,1,1)--是方程组(Ⅰ)的一个基础解系.将1,1,1321=-=-=x x x 代入方程组(Ⅱ)可得2,1==c b 或 .1,0==c b当2,1==c b 时,对方程组(Ⅱ)的系数矩阵施以初等行变换,有112101213011⎛⎫⎛⎫→ ⎪ ⎪⎝⎭⎝⎭, 显然此时方程组(Ⅰ)与(Ⅱ)同解.当1,0==c b 时,对方程组(Ⅱ)的系数矩阵施以初等行变换,有101101202000⎛⎫⎛⎫→ ⎪ ⎪⎝⎭⎝⎭, 显然此时方程组(Ⅰ)与(Ⅱ)的解不相同.综上所述,当2,1,2a b c ===时,方程组(Ⅰ)与(Ⅱ)同解. 15.设有齐次线性方程组)2(,0)(,02)2(2,0)1(212121≥⎪⎪⎩⎪⎪⎨⎧=++++=++++=++++n x a n nx nx x x a x x x x a n n n试问a 取何值时,该方程组有非零解,并求出其通解.解 对方程组的系数矩阵A 作初等行变换,有111111112222200.00aa a a a n n n n a na a ++⎛⎫⎛⎫ ⎪ ⎪+- ⎪ ⎪=→= ⎪ ⎪ ⎪ ⎪+-⎝⎭⎝⎭A B 当0a =时,()1R n =<A ,故方程组有非零解,其同解方程组为,021=+++n x x x由此得基础解系为T 1(1,1,0,,0),=-η T 2(1,0,1,,0),=-ηT 1,(1,0,0,,1),n -=-η于是方程组的通解为1111,n n x k k --=++ηη其中11,,-n k k 为任意常数.当0≠a 时,对矩阵B 作初等行变换,有(1)1111000221002100.0101n n a a n n +⎛⎫++⎛⎫ ⎪ ⎪⎪-⎪-→→⎪ ⎪ ⎪ ⎪ ⎪ ⎪- ⎪⎝⎭-⎝⎭B 可知2)1(+-=n n a 时,()1R n n =-<A ,故方程组也有非零解,其同解方程组为⎪⎪⎩⎪⎪⎨⎧=+-=+-=+-,0,03,0213121n x nx x x x x 由此得基础解系为T (1,2,,)n =η,于是方程组的通解为k =x η,其中k 为任意常数.16.设T 1(1,2,0)=α,T 2(1,2,3)a a =+-α, T 3(1,2,2)b a b =---+α, T (1,3,3)=-β, 试讨论当b a ,为何值时,(1) β不能由123,,ααα线性表示;(2) β可由123,,ααα惟一地线性表示, 并求出表示式;(3) β可由123,,ααα线性表示, 但表示式不惟一, 并求出表示式. 解 设有数,,,321k k k 使得112233k k k ++=αααβ.记123(,,)=A ααα.对矩阵(,)A β施以初等行变换, 有1111(,)22230323a b a a b -⎛⎫ ⎪=+-- ⎪ ⎪-+-⎝⎭A β111101000a b a b -⎛⎫ ⎪→- ⎪ ⎪-⎝⎭.(1) 当0=a 时, 有1111(,)0010001b -⎛⎫⎪→- ⎪ ⎪-⎝⎭A β.可知()(,)R R ≠A A β. 故方程组无解, β不能由123,,ααα线性表示.(2) 当0≠a , 且b a ≠时, 有1111(,)01000a b a b -⎛⎫ ⎪→- ⎪ ⎪-⎝⎭A β1100110100010a a ⎛⎫- ⎪ ⎪⎪→ ⎪ ⎪ ⎪ ⎪⎝⎭()(,)3R R ==A A β, 方程组有惟一解:a k 111-=, ak 12=, 03=k .此时β可由123,,ααα惟一地线性表示, 其表示式为1211(1)a a=-+βαα.(3) 当0a b =≠时, 对矩阵(),A β施以初等行变换, 有1111(,)01000a b a b -⎛⎫ ⎪→- ⎪ ⎪-⎝⎭A β1100110110000a a ⎛⎫- ⎪ ⎪⎪→- ⎪ ⎪ ⎪ ⎪⎝⎭, ()(,)2R R ==A A β,方程组有无穷多解,其全部解为a k 111-=, c ak +=12, c k =3, 其中c 为任意常数.β可由123,,ααα线性表示, 但表示式不惟一,其表示式为12311(1)()c c a a=-+++βααα.17.设线性方程组⎪⎩⎪⎨⎧=+++++=+++=+++,14)4()2(3,022,0432143214321x x μx λx x x x x x x μx λx 已知T (1,1,1,1)--是该方程组的一个解,试求(1) 方程组的全部解,并用对应的齐次线性方程组的基础解系表示全部解; (2) 该方程组满足32x x =的全部解.解 将T (1,1,1,1)--代入方程组,得μλ=.对方程组的增广矩阵B 施以初等行变换, 得1101021211200131132441002(21)2121λλλλλλλλλλ---⎛⎫⎛⎫⎪ ⎪=→ ⎪ ⎪ ⎪ ⎪++---⎝⎭⎝⎭B ,(1) 当21≠λ时,有1001011010*********⎛⎫⎪ ⎪⎪→-- ⎪ ⎪ ⎪⎝⎭B ,()()34R R ==<A B ,故方程组有无穷多解,且T 011(0,,,0)22=-ξ为其一个特解,对应的齐次线性方程组的基础解系为 T(2,1,1,2)=--η,故方程组的全部解为T T 011(0,,,0)(2,1,1,2)22k k =+=-+--ξξη (k 为任意常数).当12λ=时,有11101220131100000⎛⎫-- ⎪ ⎪→ ⎪ ⎪ ⎪⎝⎭B ,()()24R R ==<A B ,故方程组有无穷多解,且T 01(,1,0,0)2=-ξ为其一个特解,对应的齐次线性方程组的基础解系为 T 1(1,3,1,0)=-η,T 2(1,2,0,2)=--η,故方程组的全部解为T T T 01122121(,1,0,0)(1,3,1,0)(1,2,0,2)2k k k k =++=-+-+--ξξηη(21,k k 为任意常数).(2) 当21≠λ时,由于32x x =,即k k -=+-2121, 解得21=k ,故方程组的解为T T T 111(1,,,0)(2,1,1,2)(1,0,0,1)222=-+--=-ξ .当21=λ时,由于32x x =,即121231k k k =--,解得212141k k -=,故方程组的全部解为T T T 22111(,1,0,0)()(1,3,1,0)(1,2,0,2)242k k =-+--+--ξT T 2111311(,,,0)(,,,2)444222k =-+---其中2k 为任意常数.18.已知平面上三条不同直线的方程分别为123:230,:230,:230.l ax by c l bx cy a l cx ay b ++=⎧⎪++=⎨⎪++=⎩ 试证这三条直线交于一点的充分必要条件为0a b c ++=.解 必要性.设三条直线321,,l l l 交于一点,则线性方程组23,23,23ax by c bx cy a cx ay b +=-⎧⎪+=-⎨⎪+=-⎩有惟一解,故系数矩阵222a b b c c a ⎛⎫ ⎪= ⎪ ⎪⎝⎭A 与增广矩阵232323a b c b c a c a b -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭B 的秩均为2,于是0=B .由于22223236()[]23a b cb c a a b c a b c ab ac bc c a b-=-=++++----B=])()())[((3222a c cb b ac b a -+-+-++, 但根据题设0)()()(222≠-+-+-a c c b b a ,故.0=++c b a充分性.由0=++c b a ,则从必要性的证明可知,0=B ,故秩()3<B .由于])([2)(22222b b a a b ac cb b a ++-=-==0]43)21[(222≠++-b b a ,故秩()2=B .于是,秩()=A 秩()B 2=.因此方程组有惟一解,即三直线321,,l l l 交于一点.*19.求方程组12311231231,0,1,242,x x x x x x x x x x -+=⎧⎪=⎪⎨++=-⎪⎪++=⎩ 的最小二乘解.解 方程组的系数矩阵和常数项矩阵为111100111124-⎛⎫⎪ ⎪=⎪ ⎪ ⎪⎝⎭A ,1012⎛⎫ ⎪ ⎪= ⎪- ⎪ ⎪⎝⎭b ,记123x x x ⎛⎫ ⎪= ⎪ ⎪⎝⎭x ,则方程组的正规方程TT=A Ax A b 为1234262268268188x x x ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭, 解之得1233/54/51x x x -⎛⎫⎛⎫⎪ ⎪=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 因此,方程组的最小二乘解为12334,, 1.55x x x =-=-=*20.当外加电压E (单位:V )分别为5,8,10,12时,测得电源中对应的电流I (单位:A )分别为4,6,8,9,试根据公式00E E R I =+确定电源内阻0R 与电源的端电势0E .解 根据公式00E E R I =+,把测得的数据代入方程,得0000000045,68,810,912.E R E R E R E R +=⎧⎪+=⎪⎨+=⎪⎪+=⎩ 该方程组的系数矩阵和常数项矩阵为14161819⎛⎫ ⎪ ⎪= ⎪⎪ ⎪⎝⎭A ,581012⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭b ,记00E R ⎛⎫= ⎪⎝⎭x ,则方程组的正规方程TT=A Ax A b 为004273527197256E R ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 解之得0017/5979/59E R -⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭, 即000.288(), 1.339()E V R ≈-≈Ω。
习题与复习题详解线性空间高等代数

习题5. 11.判断全体n 阶实对称矩阵按矩阵的加法与数乘是否构成实数域上的线性空间.答 是.因为是通常意义的矩阵加法与数乘; 所以只需检验集合对加法与数乘运算的封闭性.由n 阶实对称矩阵的性质知;n 阶实对称矩阵加n 阶实对称矩阵仍然是n 阶实对称矩阵;数乘n 阶实对称矩阵仍然是n 阶实对称矩阵; 所以集合对矩阵加法与数乘运算封闭; 构成实数域上的线性空间. 2.全体正实数R +; 其加法与数乘定义为,,k a b ab k a a a b R k R+⊕==∈∈其中判断R +按上面定义的加法与数乘是否构成实数域上的线性空间. 答 是. 设,R λμ∈.因为,a b R a b ab R ++∀∈⇒⊕=∈;,R a R a a R λλλ++∀∈∈⇒=∈;所以R +对定义的加法与数乘运算封闭.下面一一验证八条线性运算规律1 a b ab ba b a ⊕===⊕;2()()()()()a b c ab c ab c abc a bc a b c ⊕⊕=⊕====⊕⊕;3 R +中存在零元素1; ∀a R +∈; 有11a a a ⊕=⋅=;4 对R +中任一元素a ;存在负元素1n a R -∈; 使111a a aa --⊕==;511a a a ==; 6()()a a a a a λμμλμλμλλμ⎛⎫==== ⎪⎝⎭;7 ()a a a a a a a a λμμμλλλμλμ++===⊕=⊕;所以R +对定义的加法与数乘构成实数域上的线性空间. 3. 全体实n 阶矩阵;其加法定义为按上述加法与通常矩阵的数乘是否构成实数域上的线性空间. 答 否.A B B A ∴⊕⊕与不一定相等.故定义的加法不满足加法的交换律即运算规则1; 全体实n 阶矩阵按定义的加法与数乘不构成实数域上的线性空间. 4.在22P ⨯中;{}2222/0,,W A A A P W P ⨯⨯==∈判断是否是的子空间.答 否.121123123345⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭例如和的行列式都为零,但的行列式不为零; 也就是说集合对加法不封闭.习题1.讨论22P ⨯中 的线性相关性.解 设11223344x A x A x A x A O +++=;即123412341234123400ax x x x x ax x x x x ax x x x x ax +++=⎧⎪+++=⎪⎨+++=⎪⎪+++=⎩ . 由系数行列式3111111(3)(1)111111a a a a a a=+- 知; 3 1 , , a a ≠-≠且时方程组只有零解这组向量线性无关; 2.在4R 中;求向量1234ααααα在基,,,下的坐标.其中 解 设11223344x x x x ααααα=+++由()1234100110010111ααααα⎛⎫ ⎪⎪= ⎪- ⎪-⎝⎭2111301010001010000010100010⎛⎫ ⎪ ⎪−−−−→⎪- ⎪⎝⎭初等行变换 得13ααα=-. 故向量1234ααααα在基,,,下的坐标为 1; 0 ; - 1 ; 0 . 解 设11223344x x x x ααααα=+++则有123412341234123402030040007x x x x x x x x x x x x x x x x +++=⎧⎪--+=⎪⎨+++=⎪⎪+++=-⎩. 由101121000711103010011110040010211007000130-⎛⎫⎛⎫⎪ ⎪--⎪ ⎪−−−−→⎪⎪-⎪ ⎪-⎝⎭⎝⎭初等行变换 得12347112130ααααα=-+-+.故向量1234ααααα在基,,,下的坐标为-7;11;-21;30. 4.已知3R 的两组基Ⅰ: 123111ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭11=,=0,=0-11Ⅱ:123121βββ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭23=,=3,=443 (1) 求由基Ⅰ到基Ⅱ的过渡矩阵;(2) 已知向量123123,,,,,αααααβββ⎛⎫⎪⎪ ⎪⎝⎭1在基下的坐标为0求在基下的坐标-1;(3) 已知向量123123,,,,,βββββααα⎛⎫⎪ ⎪ ⎪⎝⎭1在基下的坐标为-1求在基下的坐标2; (4) 求在两组基下坐标互为相反数的向量γ.解1设C 是由基Ⅰ到基Ⅱ的过渡矩阵; 由 ()()321321,,,,αααβββ= C即123111234100143111C ⎛⎫⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭; 知基Ⅰ到基Ⅱ的过渡矩阵为1111123234100234010111143101C -⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪==- ⎪ ⎪ ⎪⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭. 2首先计算得11322201013122C -⎛⎫-- ⎪⎪=- ⎪ ⎪ ⎪-⎝⎭; 于是α 在基321,,βββ 下的坐标为131200112C -⎛⎫ ⎪⎛⎫⎪ ⎪=⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪-⎝⎭. 3β 在基321,,ααα 下的坐标为171123C ⎛⎫⎛⎫⎪ ⎪-= ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭. 4 设γ在基321,,βββ 下的坐标为123y y y ⎛⎫ ⎪ ⎪ ⎪⎝⎭; 据题意有234010101⎛⎫⎪- ⎪⎪--⎝⎭123y y y ⎛⎫ ⎪ ⎪ ⎪⎝⎭123y y y -⎛⎫⎪=- ⎪ ⎪-⎝⎭; 解此方程组可得123y y y ⎛⎫ ⎪ ⎪ ⎪⎝⎭=043k k ⎛⎫⎪ ⎪ ⎪-⎝⎭,为任意常数.231430,7k k k k γββ-⎛⎫⎪∴=-= ⎪ ⎪⎝⎭为任意常数. 5.已知Px 4的两组基Ⅰ:2321234()1()()1()1f x x x x f x x x f x x f x =+++=-+=-=,,,Ⅱ:2323321234()()1()1()1g x x x x x x x x x x x x x =++=++=++=++,g ,g ,g(1) 求由基Ⅰ到基Ⅱ的过渡矩阵;(2) 求在两组基下有相同坐标的多项式fx .解 1 设C 是由基Ⅰ到基Ⅱ的过渡矩阵; 由 ()()12341234,,,,,,g g g g f f f f =C有23230111101110111110(1,,,)(1,,)1101110011101000x x x x x x C ⎛⎫⎛⎫⎪ ⎪-- ⎪ ⎪= ⎪⎪ ⎪ ⎪⎝⎭⎝⎭,. 1110001101121113C ⎛⎫ ⎪-⎪∴= ⎪- ⎪---⎝⎭. 2设多项式fx 在基Ⅰ下的坐标为1234(,,,)T x x x x .据题意有111222333444 ()x x x x x x C C E x x x x x x ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎪ ⎪ ⎪=⇒-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭0 因为01101101100111111001101021021021112C E ---==--==------所以方程组只有零解;则fx 在基Ⅰ下的坐标为(0,0,0,0)T ;所以fx = 0习题证明线性方程组的解空间与实系数多项式空间3[]R x 同构.证明 设线性方程组为AX = 0; 对系数矩阵施以初等行变换.()2()3R A R A =∴=线性方程组的解空间的维数是5-.实系数多项式空间3[]R x 的维数也是3; 所以此线性方程组的解空间与实系数多项式空间3[]R x 同构.习题1.求向量()1,1,2,3α=- 的长度.解α.2.求向量()()1,1,0,12,0,1,3αβ=-=与向量之间的距离.解(,)d αβ=αβ-. 3.求下列向量之间的夹角 1 ()()10431211αβ==--,,,,,,,2 ()()12233151αβ==,,,,,,,3()()1,1,1,2311,0αβ==-,,,解1(),1(1)02413(1)0,,2a παββ=⨯-+⨯+⨯+⨯-=∴=.2(),1321253118αβ=⨯+⨯+⨯+⨯=;,4παβ∴==.3(),13111(1)203αβ=⨯+⨯+⨯-+⨯=;α==β==,αβ∴=3.设αβγ,,为n 维欧氏空间中的向量;证明: (,)(,)(,)d d d αβαγγβ≤+.证明 因为22(,)αβαγγβαγγβαγγβ-=-+-=-+--+- 所以22()αβαγγβ-≤-+-; 从而(,)(,)(,)d d d αβαγγβ≤+.习题1.在4R 中;求一个单位向量使它与向量组()()()1,1,1,11,1,1,11,1,1,1321--=--=--=ααα,, 正交.解 设向量1234123(,,,)x x x x αααα=与向量,,正交;则有 112342123431234(0(,0(,)0x x x x x x x x x x x x αααααα=+--=⎧⎧⎪⎪=--+=⎨⎨⎪⎪=-+-=⎩⎩,)0)0即 . 齐次线性方程组的一个解为 12341x x x x ====.取*1111(1,1,1,1), ,,,2222ααα=将向量单位化所得向量=()即为所求.2.将3R 的一组基1231101,2,1111ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪===- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭化为标准正交基.解 1 正交化; 取11111βα⎛⎫ ⎪== ⎪ ⎪⎝⎭ ; 12221111311(,)111211221(,)11111131113βαβαβββ⎛⎫- ⎪⎛⎫⎛⎫ ⎪⨯+⨯+⨯ ⎪ ⎪ ⎪=-=-= ⎪ ⎪ ⎪⨯+⨯+⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎪- ⎪⎝⎭2 将123,,βββ单位化则*1β;*2β;*3β为R 3的一组基标准正交基. 3.求齐次线性方程组 的解空间的一组标准正交基.分析 因齐次线性方程组的一个基础解系就是其解空间的一组基;所以只需求出一个基础解系再将其标准正交化即可.解 对齐次线性方程组的系数矩阵施行初等行变换化为行最简阶梯形矩阵 可得齐次线性方程组的一个基础解系123111100,,010004001ηηη--⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.由施密特正交化方法; 取11221331211/21/311/21/3111,,011/3223004001βηβηββηββ--⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪===+==-+= ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;将123,,βββ单位化得单位正交向量组因为齐次线性方程组的解向量的线性组合仍然是齐次线性方程组的解;所以*1β;*2β;*3β是解空间的一组标准正交基.3. 设1α;2α ;… ;n α 是n 维实列向量空间n R 中的一组标准正交基; A 是n 阶正交矩阵;证明: 1αA ;2αA ;… ;n A α 也是n R 中的一组标准正交基.证明 因为n ααα,,,21 是n 维实列向量空间n R 中的一组标准正交基; 所以⎩⎨⎧=≠==j i j i j T i j i 10),(αααα (,1,2,,)i j n =. 又因为A 是n 阶正交矩阵; 所以T A A E =. 则故n A A A ααα,,,21 也是n R 中的一组标准正交基.5.设123,,ααα是3维欧氏空间V 的一组标准正交基; 证明 也是V 的一组标准正交基. 证明 由题知123,,βββ所以是单位正交向量组; 构成V 的一组标准正交基.习题五 A一、填空题1.当k 满足 时;()()()31211,2,1,2,3,,3,,3k k R ααα===为的一组基. 解 三个三维向量为3R 的一组基的充要条件是123,,0ααα≠; 即26k k ≠≠且. 2.由向量()1,2,3α=所生成的子空间的维数为 .解 向量()1,2,3α=所生成的子空间的维数为向量组α的秩; 故答案为1. 3.()()()()3123,,1,3,5,6,3,2,3,1,0R αααα====中的向量371在基下的坐标为 . 解 根据定义; 求解方程组就可得答案.设所求坐标为123(,,)x x x ; 据题意有112233x x x αααα=++. 为了便于计算; 取下列增广矩阵进行运算()3213613100154,,133701082025100133αααα⎛⎫⎛⎫⎪ ⎪=−−−−→- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭初等行变换; 所以123(,,)x x x = 33;-82;154.4. ()()()3123123,,2,1,3,1,0,1,2,5,1R εεεααα=-=-=---中的基到基的过渡矩阵为 .解 因为123123212(,,)(,,)105311αααεεε---⎛⎫ ⎪=- ⎪ ⎪-⎝⎭; 所以过渡矩阵为212105311---⎛⎫⎪- ⎪ ⎪-⎝⎭. 5. 正交矩阵A 的行列式为 . 解 21T A A E A =⇒=⇒A =1±.6.已知5元线性方程组AX = 0的系数矩阵的秩为3; 则该方程组的解空间的维数为 .解 5元线性方程组AX = 0的解集合的极大无关组基础解系含5 – 3 =2 个向量; 故解空间的维数为2.()()()()412342,1,1,1,2,1,,,3,2,1,,4,3,2,11,a a a R a αααα====≠7.已知不是的基且a 则满足 .解 四个四维向量不是4R 的一组基的充要条件是1234,,,0αααα=; 则12a =或1.故答案为12a =.二、单项选择题1.下列向量集合按向量的加法与数乘不构成实数域上的线性空间的是 . A (){}R x x x x V n n ∈=,,0,,0,111B (){}R x x x x x x x V i n n ∈=+++=,0,,,21212C (){}R x x x x x x x V i n n ∈=+++=,1,,,21213D (){}411,0,,0,0V x x R =∈解 C 选项的集合对向量的加法不封闭; 故选C.2.331,23P A ⨯⎛⎫⎪= ⎪ ⎪⎝⎭在中由生成的子空间的维数为 .A 1B 2C 3D 4解 向量组A =123⎛⎫⎪ ⎪ ⎪⎝⎭生成的子空间的维数是向量组A 的秩; 故选A.解 因 B 选项1223311231012,23,3=(,,) 220033ααααααααα⎛⎫⎪+++ ⎪ ⎪⎝⎭中(); 又因123101,,220033ααα⎛⎫⎪⎪ ⎪⎝⎭线性无关且可逆, 所以1223312,23,3αααααα+++线性无关. 故选B.解 因122313 ()()()0αααααα-+---=; 所以 C 选项中向量组线性相关; 故选C. 5.n 元齐次线性方程组AX = 0的系数矩阵的秩为r ; 该方程组的解空间的维数为s; 则 .A s=rB s=n-rC s>rD s<r 选B6. 已知A; B 为同阶正交矩阵; 则下列 是正交矩阵. A A+B B A-B C AB D kA k 为数 解 A; B 为同阶正交矩阵()T T T T AB AB ABB A AA E ⇒=== 故选C.7. 线性空间中;两组基之间的过渡矩阵 .A 一定不可逆B 一定可逆C 不一定可逆D 是正交矩阵 选BB1.已知4R 的两组基 Ⅰ: 1234, αααα,,Ⅱ:11234223433444,βααααβαααβααβα=+++=++=+=,, 1 求由基Ⅱ到Ⅰ的过渡矩阵;2 求在两组基下有相同坐标的向量. 解 1设C 是由基Ⅰ到基Ⅱ的过渡矩阵; 已知1234123410001100(,,,)(,,,)11101111ββββαααα⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭; 所以由基Ⅱ到基Ⅰ的过渡矩阵为11000110001100011C -⎛⎫⎪-⎪= ⎪-⎪-⎝⎭. 2设在两组基下有相同坐标的向量为α; 又设α在基Ⅰ和基Ⅱ下的坐标均为),,,(4321x x x x ; 由坐标变换公式可得11223344x x x x C x x x x ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ ; 即 1234()x x E C x x ⎛⎫ ⎪ ⎪-= ⎪ ⎪ ⎪⎝⎭0 齐次线性方程的一个基础解系为(0,0,0,1)η=; 通解为(0,0,0,) ()X k k R *=∈. 故在基Ⅰ和基Ⅱ下有相同坐标的全体向量为12344000 ()k k k R αααααα=+++=∈.解 1 由题有因0011001112220≠;所以123,, βββ线性无关. 故123,,βββ是3个线性无关向量;构成3 R 的基. 2 因为所以从123123,,,,βββααα基到基的过渡矩阵为010-1-12100⎛⎫⎪⎪ ⎪⎝⎭3 123123123101012,,2,,-1-12211001αααααααβββ⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪=+-== ⎪ ⎪⎪ ⎪ ⎪⎪--⎝⎭⎝⎭⎝⎭()()1232,,-51βββ⎛⎫⎪= ⎪ ⎪⎝⎭()所以1232,,5.1αβββ⎛⎫⎪- ⎪ ⎪⎝⎭向量在基下的坐标为 解 1 因为12341234,,,,ααααββββ由基,到基,的过渡矩阵为C = 2100110000350012⎛⎫ ⎪⎪⎪ ⎪⎝⎭; 所以112341234(,,,)(,,,)12001-10013002100-120010000012002-5000100210-13037C ααααββββ-=-⎛⎫⎛⎫⎛⎫⎪⎪ ⎪ ⎪⎪ ⎪==⎪⎪ ⎪⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭所以123413001000,,,00010037αααα-⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭.2112341234123411112(,,,)(,,,)1122C αααααααααββββ-⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪=++-== ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭123401(,,,)127ββββ⎛⎫⎪ ⎪= ⎪ ⎪-⎝⎭;12341234012,,,12-7αααααββββ⎛⎫ ⎪ ⎪∴=++- ⎪ ⎪⎝⎭向量在基下的坐标为.证明 设112233()()()0t f x t f x t f x ++=;则有222123(1)(12)(123)0t x x t x x t x x ++++++++=即123123123011120*11210230123t t t t t t t t t ++=⎧⎪++==-≠⎨⎪++=⎩()因为系数行列式所以方程组只有零解. 故123(),(),()f x f x f x 线性无关; 构成3[]P x 线性空间的一组基.设112233()()()()f x y f x y f x y f x =++则有1231123212336129223143y y y y y y y y y y y y ++=⎧⎛⎫⎛⎫⎪ ⎪ ⎪++=⇒=⎨ ⎪ ⎪⎪ ⎪⎪++=⎝⎭⎩⎝⎭所以()f x 123(),(),()f x f x f x 在基下的坐标为1; 2; 3.5.当a 、b 、c 为何值时;矩阵A= 00010a bc ⎫⎪⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭是正交阵.解 要使矩阵A 为正交阵;应有 T AA E =⇒2221120 1a ac b c ⎧+=⎪⎪=⇒⎪+=⎪⎩①a b c ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩;②a b c ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩;③a b c ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩;④a b c ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩.6.设 是n 维非零列向量; E 为n 阶单位阵; 证明:T T E A αααα)(/2-=为正交矩阵. 证明 因为是n 维非零列向量; T αα所以是非零实数.又22TTT TT T TA E E A αααααααα⎛⎫=-=-= ⎪⎝⎭; 所以22T T T TTA A AA E E αααααααα⎛⎫⎛⎫==--⎪⎪⎝⎭⎝⎭故A 为正交矩阵.7.设T E A αα2-=; 其中12,,,Tn a a a α=(); 若 ααT = 1. 证明A 为正交阵.证明 因为A E E E A T T T T T T T =-=-=-=αααααα2)(2)2(;所以A 为对称阵.又(2)(2)T T T A A E E αααα=--244()T T T E E αααααα=-+=;所以A 为正交阵.证明 因为, ,A B n 均为阶正交矩阵 所以0T A A =≠且。
第三章习题与复习题(线性方程组)---高等代数

习题3.11.用消元法解下列线性方程组(1)123131232312 264257x x x x x x x x -+=⎧⎪+=⎨⎪++=⎩ (2)⎪⎪⎩⎪⎪⎨⎧=+--=+-=+-=+-115361424524132321321321321x x x x x x x x x x x x(3)⎪⎩⎪⎨⎧=-++=-+-=--+8222635363432143214321x x x x x x x x x x x x (4) ⎪⎪⎩⎪⎪⎨⎧=-+++=+++=-+++=++++233453622032315432154325432154321x x x x x x x x x x x x x x x x x x x 2.设线性方程组1232123123424x x tx x tx x t x x x ++=⎧⎪-++=⎨⎪-+=-⎩ t 为何值时方程组无解? t 为何值时方程组有解?有解时,求其解. 3.设线性方程组1234123412341234231363315351012x x x x x x x x x x ax x x x x x b+++=⎧⎪+++=⎪⎨--+=⎪⎪--+=⎩ (1) a , b 为何值时方程组有唯一解? (2) a, b 为何值时方程组无解?(3) a , b 为何值时方程组有无穷多解?并求其一般解.习题3.21.设()()()1231,1,1,22,1,0,11,2,0,2ααα=--=-=--,, ,求 (1) 321ααα++ (2) 321532ααα+- 1211222. (1,0,,0) (0,1,,0)(0,0,,1),.n n n n a a a εεεεεε===+++设 维向量 , ,, 求()()3. 2 02,1 3 1,124αβγαγβ=-=-+=设2,,,4,2, ,,,求向量 ,使.4.设()()122,0,13,1,1αα==-, 满足 12234βαβα+=+ ,求 β .5.342112231231,.αβαβαβ+=+=-设(,,,), (,,,),求习题3.31. 判断向量 β 能否由向量1α,2α,3α,4α 线性表示,若可以,求出表达式. ()()()()()1234(1) 1,1,1,1 ,1,1,1,11,1,1,11,1,1,11,1,3,1βαααα=--==--=--=-,,, ()()()()()1,1,1,11,1,1,11,1,1,11,1,1,1,1,1,2,1 )2(4321--=--=--===ααααβ,,, ()()()()()3,0,1,37,1,1,40,1,0,17,3,1,23,1,3,4 )3(4321---==-==--=ααααβ,,, 1231231232. 120347110,,,011234(1) , , ,,;(2) , , ,,,;(3) , b a a b a b a b αααββαααβααα⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭设取何值时不能由线性表示取何值时能由唯一线性表示写出该表达式取何值123, ,,,βααα时能由线性表示且表达式不唯一写出全体表达式.3.判断下列向量组的线性相关性.⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=70241202152101014 )1(4321αααα,,,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=2131012021013312 )2(4321αααα,,,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=652111113211 )3(321ααα,,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=14044121302101130112 )4(4321αααα,,,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=7932 ,4354327697656324 )5(54321ααααα,,,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=7023120233631121 )6(4321αααα,,,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=431003801053001 )7(321ααα,,12344. 12341234 12341234a a a a αααα+⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪+ ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪+ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭设向量组,,, 12341234(1) , ,,,;2 , ,,,.a a αααααααα为何值时线性相关()为何值时线性无关5.讨论向量组12310112,,21425111a b ααα⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭的线性相关性. 6.已知向量组1,,,,i n ααα线性无关,证明1,,,,(0)i n k k ααα≠线性无关.7.已知向量组12,,,n ααα线性无关, 1121212,,,,n n βαβααβααα==+=+++证明: 12,,,n βββ线性无关.8.设12,,,n ααα线性无关,nnn n n n nn n n a a a a a a a a a αααβαααβαααβ+++=+++=+++=22112222121212121111证明:n βββ,,,21 线性无关的充要条件是行列式D = n n n n nna a a a a a a a a 111212122212≠ 09.已知向量组m ααα,,,21 线性无关,设111322211,,,,ααβααβααβααβ+=+=+=+=--m m m m m证明:(1) 当m 为偶数时, m βββ,,,21 线性相关;(2)当m 为奇数时, m βββ,,,21 线性无关.习题3.41.求下列向量组的秩与一个极大线性无关组.(1)12344212 312101308αααα-⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪==-== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,,, (2)1234511005 2112, 153223ααααα⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪===== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,,,(3)123450********* , 0111111011ααααα-⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪ ⎪===== ⎪ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,,, 2.求下列向量组的秩与一个极大无关组并将其余向量用求出的极大无关组线性表示.(1)12342104113410100124αααα⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,,,(2)123452313712024 , 3283023743ααααα--⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪ ⎪===== ⎪ ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,,, (3)123452183723075, 3258010320ααααα⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪ ⎪===== ⎪ ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,,,3.求向量组123411312000121135a b αααα⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭⎝⎭,,,的秩和一个极大无关组.4.设A 、B 均为m × n 阶矩阵,证明:R (A + B )≤ R (A )+ R (B ) 5.设向量组m ααα,,,21 ( m > 1 )的秩为r ,m m m m βαααβαααβααα-=+++=+++=+++,,,123213121证明:向量组m βββ,,,21 的秩为r .6.设A 为n × m 阶矩阵,B 为m × n 阶矩阵,且n > m ,证明 AB = 0 .习题3.51.求下列齐次线性方程组的一个基础解系并用它表出通解. (1) 123413412313424303 07 730x x x x x x x x x x x x x -+-=⎧⎪+-=⎪⎨++=⎪⎪+-=⎩ (2) 12345123451234512345202 +230322025220x x x x x x x x x x x x x x x x x x x x -+-+=⎧⎪-+-=⎪⎨--+-=⎪⎪-+-+=⎩2.设线性方程组123123123232082021430x x x x x x x x x λλλ---=⎧⎪-+--=⎨⎪+++=⎩()()()问λ为何值时, 该方程组有非零解?并求出它的全部解.3.设n 阶方阵A 的每行元素之和都为零,且R (A )= n -1 ,求方程组A X = 0的通解. 4.已知3阶非零矩阵B 的每个列向量都是线性方程组1231231232202030x x x x x x x x x λ+-=⎧⎪-+=⎨⎪+-=⎩ 的解, 求λ的值. 5.已知线性方程组12342341242200 0x x x x x cx cx x cx x +++=⎧⎪++=⎨⎪++=⎩ 的基础解系由两个解向量构成,求c 的值与该方程组的通解. 6.设12313221211A t ⎛⎫⎪-⎪= ⎪⎪--⎝⎭B 是3阶非零矩阵,且AB=O , 求t 的值.习题3.61.解下列线性方程组(在有无穷多解时求出其结构式通解). (1)12312312312323424538213496x x x x x x x x x x x x ++=⎧⎪-+=-⎪⎨+-=⎪⎪-+=-⎩(2)1234124123401 222461x x x x x x x x x x x --+=⎧⎪⎪--=⎨⎪--+=-⎪⎩2.已知线性方程组1231231232123(2)320x x x x x a x x ax x ++=⎧⎪+++=⎨⎪+-=⎩ 无解,求a 的值.3.参数λμ,取何值时,线性方程组123412341234230327162x x x x x x x x x x x x λμ+-+=⎧⎪+++=⎨⎪---=⎩ 有解、无解?4. 参数a , b 为何值时,线性方程组12345123452345123451323 22635433x x x x x x x x x x a x x x x x x x x x b ++++=⎧⎪+++-=⎪⎨+++=⎪⎪+++-=⎩有解、无解?在有解时,求其解.5. 参数a , b 为何值时,线性方程组1231231234324ax x x x bx x x bx x ++=⎧⎪++=⎨⎪++=⎩ 无解、有唯一解、有无穷多解?在有解时,求其解.6.向量123,,γγγ是四元非齐次线性方程组AX β=的解向量,()2R A =且 121321γγ⎛⎫ ⎪ ⎪+= ⎪ ⎪⎝⎭ ,231102γγ⎛⎫ ⎪ ⎪+= ⎪ ⎪-⎝⎭,132110γγ⎛⎫⎪ ⎪+= ⎪ ⎪⎝⎭求线性方程组AX β=的通解. 7.设线性方程组23112131231222322313233323142434x a x a x a x a x a x a x a x a x a x a x a x a ⎧++=⎪++=⎪⎨++=⎪⎪++=⎩ (1)若1234,,,a a a a 互不相同,证明方程组无解;(2)若1324,(0)a a k a a k k ====-≠,证明方程组有解,并求其通解.8.证明线性方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=-=-=-=-515454343232121a x x ax x a x x a x x a x x 有解的充分必要条件是∑=51i i a = 0 ,并在有解时求其通解.9.设非齐次线性方程组A X = β 的解向量12,,,s γγγ,证明(1) 线性组合1122s s k k k γγγ+++是A X = β 的解的充分必要条件是k 1 + k 2 + … + k s = 1;(2)线性组合1122s s k k k γγγ+++是A X = 0 的解的充分必要条件是k 1 + k 2 + … + k s = 0.习题三 (A)一、填空题1.设123111111λααλαλ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,,当λ满足 时, 123ααα,,线性相关; 当λ满足 时, 123ααα,,线性无关. 2.已知向量组123411110112,23243519t t αααα⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪+ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭,, 线性相关, 则t 满足 .3.设向量组123ααα,,线性无关,则当参数l, m 满足 时,213213l m αααααα---,,也线性无关.4. 已知123ααα,,线性无关,若12123123242m m αααααααα+-++-,,也线性无关, 则m .5.设向量组123(, 0, )(, ,0)(0, , )a c b c a b ααα===,,线性无关, 则a , b , c 满足 . 6. 设向量组1234(2,1,1,1)(2,1,,)(3,2,1,),(4,3,2,1)a a a αααα====,,线性相关,且1a ≠, 则 a = .7. 当k = 时, 向量 ()Tk k 2,,0=β 可由向量组()T k 1,1,11+=α ,()()T T k k +=+=1,1,11,1,132αα, 线性表示且表示方法不唯一.()()()1231,2,1,1,2,0,,0,0,4,5,22, t t ααα=-==--=8.已知的秩为 则 .9. 设A = ⎪⎪⎪⎭⎫ ⎝⎛--11334221t , B 为3阶非零矩阵, 且A B = O , 则t = .10. 设B 为3阶非零矩阵,且B 的每个列向量都是方程组 ⎪⎩⎪⎨⎧=-+=+-=++030202321321321x x x x x x kx x x 的解,则k= ,B = .11. 设123,,ααα是齐次线性方程组AX = 0 的一个基础解系, 则当参数a 满足 时,122331a αααααα+++,,也是该方程组的基础解系.12. 已知向量组1234,,,αααα的秩为3, 且1234,,,αααα可由向量组123,,βββ线性表示, 则向量组123,,βββ必线性 .二、单项选择题1. 已知1143α⎛⎫ ⎪= ⎪ ⎪⎝⎭,221t α⎛⎫ ⎪= ⎪ ⎪-⎝⎭,3231α-⎛⎫⎪= ⎪ ⎪⎝⎭线性相关, 则t =( ) .(A ) 2 (B) -2 (C ) 3 (D ) –3 2.已知向量组1234αααα,,,线性无关, 则向量组( )线性无关.12233441122334411223344112233441A αααααααααααααααααααααααααααααααα+++++++-----++--() ,,,(B ) ,,,(C ) ,,,(D ) ,,,3. 对任意实数a , b , c 下列向量组线性无关的是( ).(A) (a , 1, 2), (2, b , 3), (0, 0, 0)(B) (b , 1, 1), (1, a , 3), (2, 3, c ), (a , 0, c ) (C) (1, a , 1, 1), (1, b , 1, 0), (1, c , 0, 0) (D) (1, 1, 1, a ), (2, 2, 2, b ), (0, 0, 0, c )4.若向量组 α , β , γ 线性无关, α , β , δ 线性相关, 则( ).(A ) α 必可由 β , γ , δ 线性表示 (B ) β 必不可由 α , γ , δ 线性表示 (C ) δ 必可由 α , β , γ 线性表示 (D ) δ 必不可由 α , β , γ 线性表示 5. 设同维向量组12121::,rr r mA B αααααααα+,,,,,,,,则下列说法正确的是( ). (A) A 组与B 组的线性相关性相同 (B) 当A 组线性无关时, B 组也线性无关 (C) 当B 组线性相关时, A 组也线性相关 (D) 当A 组线性相关时, B 组也线性相关 6. 下列说法正确的是( ). (A) 若1α,2α线性相关,1β ,2β线性相关, 则11βα+,22βα+一定线性相关(B) 若1α,2α 线性无关, β为任一向量, 则βα+1,βα+2一定线性无关(C) 若1α,2α ,…,m α( m ≥ 2 )线性相关, 则其中任何一个向量都可由其余向量线性表示 (D) 若n 维向量组1α,2α,… ,m α( m ≥ 2 )线性无关,则对于任意不全为零的数k 1, k 2 ,… , k m 一定有 θααα≠+++m m k k k 22117.已知向量组123ααα,,线性无关, 向量β可由123ααα,,线性表示, 向量γ不能由123ααα,,线性表示, 则对任意常数k , 必有( ).(A) 123,,, k αααβγ+线性无关 (B) 123,,, k αααβγ+线性相关 (C) 123,,, k αααβγ+线性无关 (D) 123,,, k αααβγ+线性相关8. 一个向量组的极大线性无关组( ). (A ) 个数唯一 (B) 个数不唯一(C ) 所含向量个数唯一 (D ) 所含向量个数不唯一9.已知任一n 维向量均可由n ααα,,,21 线性表示, 则n ααα,,,21 ( ).(A) 线性相关 (B) 秩等于n(C) 秩小于n (D) 秩不能确定10. 已知21346639A t ⎛⎫ ⎪= ⎪ ⎪⎝⎭, B 为三阶非零矩阵且AB =O ,则( ).(A)当t = 2时,B 的秩必为1 (B)当t = 2时,B 的秩必为2 (C)当t ≠2时,B 的秩必为1 (D)当t ≠ 2时,B 的秩必为211.设非齐次线性方程组A X = B 中未知量个数为n , 方程个数为m , 系数矩阵A 的秩为r ,则 ( ) .(A ) r = m 时,方程组A X = B 有解 (B) r = n 时,方程组A X = B 有唯一解 (C ) m = n 时,方程组A X = B 有唯一解 (D ) r < n 时,方程组A X = B 有无穷多解12.n 元线性方程组AX=B 有唯一解的充分必要条件是( ).(A ) 导出组AX=0仅有零解 (B ) A 为方阵,且∣A ∣≠0(C ) R(A) = n(D ) 系数矩阵A 的列向量组线性无关,且常数项向量B 可由A 的列向量组线性表示13.设A 是n 阶矩阵, α 是n 维列向量,若R ⎪⎪⎭⎫⎝⎛0TAαα = R (A ) ,则线性方程组 ( ).(A ) A X = α 必有无穷多解(B ) A X = α 必有唯一解 (C ) ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛y X A T0αα = 0仅有零解 (D ) ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛y X A T0αα = 0必有非零解 14.将齐次线性方程组⎪⎩⎪⎨⎧=++=++=++0003213213221x x x x x x x x x λλλλ的系数矩阵记为A , 若存在3阶矩阵B ≠ O使得AB =O , 则 ( ) .(A ) λ = -2且 B = 0 (B ) λ = -2且 B ≠ 0 (C ) λ = 1且 B = 0 (D ) λ = 1且 B ≠ 0 15. 已知123,,ααα是非齐次线性方程组AX=b 的3个解, 则下列( )不是导出组 AX = 0的解.(A) 1232ααα+- (B) 121()3αα- (C) 132αα- (D)311()2αα- 16. 已知123,,ααα是非齐次线性方程组AX=b 的3个解,则下列( )是AX = b 的解. (A) 1232ααα+- (B) 123ααα+- (C) 132αα- (D)311()2αα- 17. 已知123ααα,,是4元非齐次线性方程组AX=b 的3个不同的解且R (A ) =3,则下列( )是导出组AX = 0的基础解系.(A) 12312,ααααα+-- (B) 12αα- (C) 13αα+ (D) 3121,αααα--(B)1.设12312300111a b αααβββ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭1011=,=,010012011=,=,1221求a , b 的值,使向量组123ααα,,与向量组123βββ,,等价.122.,,,.r t t t r n ≤设是互不相同的数,21(1,,,,) (1,2,,)n i i i i t t t i r α-==证明:线性无关.3. ,, , 0. , , , a b c a b c abc αβγαβγθαβαγβγ++=≠设向量,,及数满足且证明和均与等价.4.设向量组123411321326,1511031p p αααα--⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,,(1)p 为何值时,1234,αααα,,线性无关, 并在此时将向量()4,1,6,10Tβ=用该向量组线性表示;(2)p 为何值时,1234,αααα,,线性相关,并在此时求出该向量组的秩和一个极大无关组. 5.求向量组1231111121111k k ααα⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,,的秩和一个极大无关组.6.,,A m n B n m m n AB E B ⨯⨯<=设为矩阵,为矩阵,且若证明的列向量组线性无关. 7.已知向量组123967ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭13=2,=0,-31与1232110a b βββ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭0=1,=,-1具有相同的秩且3β可由123ααα,,线性表示,求a , b 的值. 8.已知3阶矩阵B O ≠且B 的列向量都是线性方程组12312312320200x x x x x x ax x x +-=⎧⎪-+=⎨⎪+-=⎩ 的解.(1) 求a 的值; (2) 证明0B =. 9. 已知线性方程组⎪⎩⎪⎨⎧=++=++=++000322212321321x c x b x a cx bx ax x x x ,(1) 当a , b , c 满足何种关系时,方程组仅有零解?(2)当a , b , c 满足何种关系时,方程组有无穷多组解?求出其通解. 10. 两个齐次线性方程组⎪⎪⎩⎪⎪⎨⎧=++=++=++⎪⎪⎩⎪⎪⎨⎧=++=++=++00000011212111111121211111n tn t n n n n n mn m n n n n x b x b x b x b x b x b x a x a x a x a x a x a 与 的系数矩阵A 与B 的秩都小于n /2. 证明:这两个方程组必有相同的非零解. 11. 设12s ααα,,,为某齐次线性方程组的一个基础解系, 11122,t t βαα=+21223,t t βαα=+ 12112,,,s s t t t t βαα=+其中为任意常数. 问当12,t t 满足什么条件时, 12s βββ,,,也为该方程组的一个基础解系.12.设四元齐次线性方程组(Ⅰ)为 ⎩⎨⎧=-++=-+020324321321x x x x x x x , 且已知另一四元齐次线性方程组(Ⅱ)的一个基础解系为 T T a a )(,)(8,4,2,11,2,1,221+-=+-=αα(1) 求方程组(Ⅰ)的一个基础解系; (2) a 为何值时,(Ⅰ)与(Ⅱ)有非零公共解?在有非零公共解时, 求出全部非零公共解.13.设 r n -γγγγ,,,,210 为非齐次线性方程组A X = β 的n - r +1个线性无关的解向量,其中r = R (A ).证明:00201,,,γγγγγγ----r n 是其导出组AX = 0的一个基础解系. 14.若线性方程组n n n n n nn n n a x a x b a x a x b a x a x b ++=⎧⎪++=⎪⎨⎪⎪++=⎩111112112211 的系数矩阵的秩等于矩阵B =1111110n n nnn na ab a a b b b ⎛⎫⎪⎪ ⎪ ⎪ ⎪⎝⎭的秩. 证明此方程组有解.12312315. 4, ()3, ,,,2200,20028.AX B R A αααααα==⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭设元非齐次线性方程组已知为方程组的解其中求该方程组的通解16. 设线性方程组Ⅰ: 123123212302040x x x x x ax x x a x ++=⎧⎪++=⎨⎪++=⎩Ⅱ: 123 21x x x a ++=-有公共解, 求a 的值及所有公共解.。
高等代数课件(北大版)第三章 线性方程组§3-3

8)向量组线性相关的基本性质定理 定理2 设 1 , 2 ,, r 与 1 , 2 ,, s 为两个 向量组,若 i) 向量组 1 , 2 ,, r 可经 1 , 2 ,, s 线性表出; ii) r s. 则向量组 1 , 2 ,, r必线性相关.
相关,则向量组 1 , 2 , , s 也线性相关. 注:向量组 1 , 2 ,, s 常称为向量组 1 , 2 , , s 的延伸组; 而 1 , 2 , , s 称为 1 , 2 ,, s
的缩短组.
§3.3 线性相关性
2013-8-8 数学与计算科学学院
§3.3 线性相关性
2013-8-8 数学与计算科学学院
(1)
对方程组(1)的增广矩阵作初等行变换化阶梯阵
1 2 A 3 1
5 5 12 11
1 3 6 3
1 2 1 0 0 3 0 4
5 3 0 0
1 1 0 0
2 1 0 2 1 3 3 1 1 0 1 3 1 3 0 0 0 0 0 0 0 0 0 0
证明: 1 , 2 , 3 线性无关.
证:设 x11 x2 2 x3 3 0, 即
( x1 x3 )1 ( x1 x2 ) 2 ( x2 x3 ) 3 0
x1 x3 0 由于 1 , 2 , 3 线性无关,于是有 x1 x2 0 x2 x3 0 解之得 x1 x2 x3 0.
§3.3 线性相关性
2013-8-8 数学与计算科学学院
2、性质
向量组之间的等价关系具有:
1) 反身性 2) 对称性 3) 传递性
§3.3 线性相关性
2013-8-8
(完整版)线性代数第四章线性方程组试题及答案.doc

充 1:当 A 列 秩 ( 或 A 可逆 ,A 在矩 乘法中有左消去律AB=0 B=0;AB=AC B=C.明B =(1,, ⋯,t ), AB = Ai =0,i=1,2, ⋯,s., , ⋯ , t 都是 AX =0212的解 . 而 A 列 秩 , AX =0 只有零解 ,i=0,i=1,2,⋯ ,s, 即 B =0.同理当 B 行 秩(或 B 可逆 ),AB 0 B T A T0 A T0A 0AB CB A C充 2如果 A 列 秩(或 A 可逆) , r( AB )=r( B ).分析 : 只用 明 次方程ABX =0 和 BX =0 同解 .( 此 矩 AB 和 B 的列向量 有相同的 性关系, 从而秩相等 .)明:是 ABX = 的解 AB = B =0( 用推 ) 是 BX = 的解 .于是 ABX =0 和 BX =0 确 同解 .同理当 B 行 秩(或B 可逆) , r( AB )=r( A ).例题一 . 填空1.A m 方 , 存在非零的 m × n 矩 B, 使 AB = 0 的充要条件是 ______.解: Ax 0 有非零解, r Am2.A n 矩 , 存在两个不相等的n 矩 B, C, 使 AB = AC 的充要条件是解: A B C 0 , B, C 不相等, Ax0 有非零解, r An3.若 n 元 性方程 有解, 且其系数矩 的秩r, 当 ______, 方程 有唯一解;当 ______ , 方程 有无 多解 .解:假 方程A m × n x = b, 矩 的秩 r ( A) r .当 r n , 方程 有惟一解 ; 当 r n , 方程 有无 多解 .4. 在 次 性方程 A m ×n x = 0 中 , 若秩 (A) = k 且 1, , ⋯ , r 是它的一个基 解2系 ,r = _____; 当 k = ______ , 此方程 只有零解。
线性代数第三章 线性方程组习题课

k1 k2 A 0, 是 否 有 非 零 解 k s
若s为奇数,则 DS 2 0 , 方程组仅有零解 k1 k S 0 ,
此时 1 , 2 ,, s 线性无关;
若s为偶数,则 DS 0 , 方程组有非零解,
5
解1
2 1 1 0 5 4 6
1 1 1 2 1 1 3 3 0 0 3 2 1 0 0 5 5 2 5 2 7 0 2 2 4 2 0 14
3 3 7 2
1 0 0 0
解
1 0 0 0
1 1 0 0
1 2 0 0
1 2 0 0
1 1 6 3a , a 0, b 2 时有解, 0 a 0 b a 2
5
1 0 0 0
1 1 0 0
1 2 0 0
1 1 0 0
1 2 0 0
1 2 0 0
这与 不能由向量组 1 , 2 , , r 1 线性表示的假设矛盾,
所以得证 r 不能由向量组 1 , 2 , , r 1 线性表示.
13
10 已 知 向 量 组
1 , 2 ,, s ( s 2) 线 性 无 关 , 设 1 1 2 , 2 2 3 , , s 1 s 1 s , s s 1 , 讨论向量组 1 , 2 ,, s 的线性相关性。
可表示成 1 , 2 , 3 , 4 的线性组合, 但表示式不唯一。
8
6 求下列向量组的一个极大无关组及秩,并把其余向量
用极大无关组线性表出。
1 (1,1,0,4) , 2 ( 2,1,5,6) , 3 (1,2,5,2) , 4 (1,1,2,0) , ( 3,0,7,14) .
《高等代数1》复习练习题(三)——第三章 线性方程组(参考解答)

《高等代数1》复习练习题(三)——第三章线性方程组(解答)(供2017级数学与应用数学专业使用)一、填空题1、设23(,2,1),(2,3,0),(1,1,1)T T T k ααα1==-=-,则当1k =-时,向量组321,,ααα线性相关. 2、设矩阵⎪⎪⎪⎭⎫⎝⎛-=403212221A ,向量(,1,1)Ta α=,已知向量组,A αα线性相关,则1a =-.3、设向量组123(,0,),(,,0),(0,,)T T T a c b c a b ααα===线性相关,则,,a b c 必满足关系式 abc=0 .4、线性方程组121232343414,,,x x a x x a x x a x x a -=-=-=-=有解的充分必要条件是_____________.5、设33⨯矩阵A 的秩()1r A =,23(1,1,2),(2,0,1),(1,2,3)T T T ααα1===是线性方程组AX β=的三个特解,则对应导出组0AX =的基础解系是121323,αααααα---中任意两个向量.6、设33⨯矩阵A 的秩()2r A =,A 的各行元素之和均为零,则齐次线性方程组0AX =的通解是(1,1,1)T k .7、若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ有非零解,则=λ1.8、设齐次线性方程组12312312300x x x x kx x kx x x ++=⎧⎪++=⎨⎪++=⎩只有零解,则k 应满足的条件是1k ≠.9、.齐次线性方程组1231231232302340x x x x ax bx x x x ++=⎧⎪++=⎨⎪++=⎩有非零解,当且仅当,a b 满足关系式1(1)2a b =+.10、若线性方程组b AX =有解,且秩()A r =,则秩()A =r .二、选择题 1、设12,,,s ααα均为n 维向量,下列结论不正确的是 ( B ).(A)若对任意一组不全为零的数12,,,s k k k ,都有1122+++≠s s k k k ααα0,则12,,,s ααα线性无关.(B)若12,,,s ααα线性相关,则对任意一组不全为零的数12,,,s k k k ,都有1122+++=s s k k k ααα0.(C)向量组12,,,s ααα线性无关的充分必要条件是此向量组的秩为s . (D)向量组12,,,s ααα线性无关的必要条件是其中任意两个向量线性无关.2、设向量组123(,2,1),(2,,0),(1,1,1)TTTt t ααα===-线性无关,则( D ).(A )3t ≠-且2t ≠. (B )3t =或2t =-. (C )3t =-或2t =. (D )3t ≠且2t ≠-.3、设向量T T T T )4,0,1,1(,)1,3,0,2(,)5,1,2,0(,)2,2,1,1(4321=-===αααα,则向量组4321,,,αααα的秩等于( C ).(A)1. (B) 2. (C)3. (D)4. 4、设12,,,m ααα是一n 维向量组,它的秩12(,,,)=<m r r m ααα,则下面说法不正确的是( A ).(A)向量组12,,,m ααα中任意一个向量都能由其余向量线性表出.(B)向量组12,,,m ααα线性相关.(C)向量组12,,,m ααα与其任一极大无关组等价.(D)向量组12,,,m ααα中任意r 个线性无关的向量都构成其极大无关组.5、设0=AX 是非齐次方程组AX β=所对应的导出组,则下列结论正确的是 ( D ).(A)若0=AX 仅有零解,则AX β=有唯一解.(B)若0=AX 有非零解,则AX β=有无穷多解. (C)若AX β=有无穷多解,则0=AX 仅有零解. (D)若AX β=有无穷多解,则0=AX 有非零解.6、若A 是n 阶方阵,β是n 维非零向量,且齐次线性方程组0=AX 有非零解,则下列结论中不会发生的是( B ).(A)AX β=无解. (B)AX β=有唯一解. (C)AX β=有无穷多解. (D)()r A n <.7、非齐次线性方程组AX β=中未知量个数为n ,方程个数为m ,()r A r =,则 ( A )(A)r m =时,AX β=有解. (B)r n =时,AX β=有唯一解. (C)m n =时,AX β=有唯一解. (D)r n <时,AX β=有无穷多解. 8、设A 为m n ⨯矩阵,且()1r A n =-,12,αα是非齐次线性方程组AX β=的两个不同的解向量,k 为任意常数,则0AX =的通解为( A ).(A )12()k αα-; (B )12()k αα+; (C )1k α; (D )2k α. 9、设12,,,s ααα均为n 维向量,下列结论正确的是( B ) .(A) 若1122s s k k k ααα+++=0,则12,,,s ααα线性相关.(B) 若对任意一组不全为零的数12,,,s k k k ,都有1122s s k k k ααα+++≠0,则12,,,s ααα线性无关.(C) 若12,,,s ααα线性相关,则对任意一组不全为零的数12,,,s k k k ,都有1122s s k k k ααα+++=0.(D) 若12000s ααα+++=0,则12,,,s ααα线性无关.三、判断题 1、如果当120n k k k ===≠时,11220n n k k k ααα+++=,则向量组12,,,nααα线性相关. ( √ )2、如果12(,,,),1,2,,i i i in a a a i s α==线性相关,则向量组1212(,,,,,,,),1,2,,i i i in i i im a a a b b b i s β==也线性相关.( X )3、若123,,,αααβ线性相关,则β可由向量组123,,ααα线性表出.( X )4、若β不能由向量组123,,ααα线性表出,则123,,,αααβ线性无关.( X )5、若向量12,,,s ααα线性相关,则其中每一个向量皆可由其余向量线性.( X )6、非齐次线性方程组的两个解的和不再是它的解. ( √ )7、方程个数小于未知量个数的线性方程组必有无穷多个解. ( X )8、设12,αα线性相关,12,ββ也线性相关,则1122,αβαβ++线性相关. ( X )9、若线性方程组AX β=有无穷多个解,则0AX =一定有非零解. ( √ ) 10、若线性方程组0AX =有非零解,则AX β=一定有无穷多解.( X ) 四、计算题1、求向量组1234(1,1,2,4),(0,3,1,2),(3,0,7,14),(1,1,2,0),T T T T αααα=-===-5(2,1,5,6)T α=的秩及一个极大线性无关组,并用极大线性无关组线性表示其余向量.解:对以12345,,,,ααααα为列的矩阵作行初等变换化为阶梯形矩阵.1234510312103121301103303(,,,,)21725011014214060224210312131203303011010000000011000440000010301011010001100000ααααα⎛⎫⎛⎫ ⎪ ⎪--⎪ ⎪=→⎪ ⎪⎪⎪--⎝⎭⎝⎭⎛⎫⎛⎫⎪⎪ ⎪ ⎪→→ ⎪ ⎪ ⎪⎪--⎝⎭⎝⎭⎛⎫⎪⎪→ ⎪⎪⎝⎭所以,向量组12345,,,,ααααα的秩是3,124,,ααα是其一个极大线性无关组,且31251243,ααααααα=+=++.2、已知向量组123(0,1,1),(,3,1),(,1,0)T TT a b βββ=-==与向量组123(1,2,3),(2,1,1),(3,0,1)T TT ααα=-=-=具有相同的秩,且3β可由123,,ααα线性表出,求,a b .解:令1231231233(,,),(,,),(,,,)A B A αααβββαααβ===则由条件可知,A 与B ,A 与A 由相同的秩.因为1233123123(,,,)2101036123110051031231231000105103510510300015b b A b b b b b b b b αααβ⎛⎫⎛⎫⎪ ⎪==→--- ⎪ ⎪⎪ ⎪--⎝⎭⎝⎭⎛⎫⎛⎫⎪ ⎪ ⎪⎪→-→ ⎪⎪⎪⎪- ⎪⎝⎭⎝⎭12300004(,,)131041041110110110110041004a b a b a b B a b βββ⎛⎫-⎪⎛⎫⎛⎫⎪ ⎪ ⎪==→→ ⎪⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭ ⎪⎝⎭⎛⎫⎪- ⎪→ ⎪ ⎪- ⎪⎝⎭所以,2=秩A =秩B =秩A ,于是10,1045a b b -=-=,故20,5a b ==. 3、设四元非齐次线性方程组=AX β的系数矩阵A 的秩为2,已知它的三个解向量为123,,ηηη,其中123(4,3,2,1),(1,3,5,1),(2,6,3,2)===-T T T ηηη,求该方程组的通解.解:因为123,,ηηη是=AX β的解,所以12(3,0,3,0)T ηη-=-,13(6,3,1,1)T ηη-=---是0AX =的解,且1213,ηηηη--线性无关.又因为()2r A =,所以0AX =的基础解系含有两个解向量,于是1213,ηηηη--是0AX =的一个基础解系.故=AX β的通解是1112213()()c c ηηηηη+-+-(12,c c F ∈)4、设向量1234,,,αααα是齐次线性方程组0AX =的一个基础解系,若112223334441,,,t t t t βααβααβααβαα=+=+=+=+,试问:当实数t 满足什么关系时,1234,,,ββββ也是0AX =的一个基础解系?解:因为1234,,,αααα是0AX =的基础解系,所以1234,,,αααα的线性组合1234,,,ββββ也是0AX =的解. 因此,当1234,,,ββββ线性无关时,1234,,,ββββ也是0AX =的一个基础解系.因为12341234100100(,,,)(,,,)010001t t t t ββββαααα⎛⎫⎪⎪= ⎪⎪⎝⎭所以,1234,,,ββββ线性无关⇔1234||0ββββ≠⇔410010010010001ttt tt=-≠⇔1t ≠±.故当1t ≠±时,1234,,,ββββ也是0AX =的一个基础解系.5、设3阶非零矩阵A 的每一个列向量都是方程组1231231232020330x x x x x ax x x x +-=⎧⎪-+=⎨⎪+ -=⎩的解,求常数a 和行列式A .解:设123(,,)A βββ=,其中123,,βββ是A 的列向量,则123,,βββ不全为零,且是已知方程组的解,于是已知方程组由非零解,从而其系数矩阵行列式为零,即11211221034120313023a a a ---=-+=-+=--所以12a =. 设已知方程组的系数矩阵为B ,则B O ≠,且123123(,,)(,,)(0,0,0)BA B B B B O ββββββ====若||0A ≠,则A 可逆,从而111()()B BE B AA BA A OA O ---=====,矛盾,所以||0A =.6、讨论常数a 为何值时,线性方程组123123123112ax x x x ax x x x ax ++=⎧⎪++=⎨⎪+ +=-⎩无解、有唯一解、有无穷多解?在有无穷多解的情况下,求出其全部解.解:对线性方程组的增广矩阵作行初等变换得22111011120024211101130113112112112112011300(2)(1)2(2)a a a a a a a A a a a a aa a a a a a a a a ⎛⎫⎛⎫--+--+⎛⎫⎪ ⎪ ⎪=→--→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭-⎛⎫ ⎪→-- ⎪ ⎪+-+⎝⎭1)当1a =时,秩1A =≠秩2A =,方程组无解. 2)当1,2a ≠-时,秩3A ==秩A ,方程组有唯一解. 3)当2a =-时,秩2A ==秩3A <,方程组有无穷多解:13231,1x x x x =+=+(3x 是自由未知量)7、已知方程组⎪⎩⎪⎨⎧=-=+++=+--330)1(31432321321x ax x a x x x x x ,问a 为何值时,此方程组:(1)有唯一解;(2)无解;(3)有无穷多解?在有无穷多解的情况下,试用其导出组的基础解系表出全部解.解:对线性方程组的增广矩阵作行初等变换得21411141114111310012101210330330233112012100(3)(1)3A a a a a a a a a a a a a a ------⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪=+→-+→-+ ⎪ ⎪ ⎪⎪ ⎪ ⎪--+-+⎝⎭⎝⎭⎝⎭-⎛⎫⎪→-+ ⎪ ⎪+-+⎝⎭1)当1,3a ≠-时,秩3A ==秩A ,方程组有唯一解.2)当1a =时,秩2A =≠秩3A =,方程组无解.3)当3a =-时,秩2A ==秩3A <,方程组有无穷多解:132314,1x x x x =-+=--(3x 是自由未知量)8、讨论常数,a b 为何值时,线性方程组1231231234324ax x x x bx x x bx x ++=⎧⎪++=⎨⎪+ +=⎩无解、有唯一解、有无穷多解?在有无穷多解的情况下,求出其全部解.解:对线性方程组的增广矩阵作行初等变换得1140114301142113113101212140010010114210121012011420014200(1)142a ab a a a a A bb b b b a a a a ab b b ab b a b ab -----⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=→→ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭--⎛⎫⎛⎫⎪ ⎪→→-- ⎪ ⎪⎪ ⎪--+--+⎝⎭⎝⎭1)当11,2a b =≠或0b =时,秩2A =≠秩3A =,方程组无解.2)当1,0a b ≠≠时,秩3A ==秩A ,方程组有唯一解. 3)当11,2a b ==时,秩2A ==秩3A <,方程组有无穷多解: 1322,2x x x =-=(3x 是自由未知量)9、对于线性方程组123123123322x x x x x x x x x λλλλ++=-⎧⎪++=-⎨⎪++=-⎩(1)λ取何值时,方程组无解、有唯一解、有无穷多解;(2)在方程组有无穷多解时,试用其对应齐次线性方程组的基础解系表示方程组通解.解:对线性方程组的增广矩阵作行初等变换得2211301133112011011211200233112011001101120(2)(1)3(1)A λλλλλλλλλλλλλλλλλλλλλλ⎛⎫----⎛⎫⎪ ⎪=-→-- ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎛⎫----⎛⎫ ⎪ ⎪→--→-- ⎪ ⎪ ⎪ ⎪--+--⎝⎭⎝⎭(1)1)当2λ=-时,秩2A =≠秩3A =,方程组无解. 2)当1,2λ≠-时,秩3A ==秩A ,方程组有唯一解. 3)当1λ=时,秩1A ==秩3A <,方程组有无穷多解.(2)在方程组有无穷多解时,与原方程组同解方程组为1232x x x ++=-,令230x x ==,得特解0(2,0,0)γ=-.与原方程组同解方程组对应的齐次线性方程组同解方程组为1230x x x ++=,所以对应的齐次线性方程组的基础解系为12(1,1,0),(1,0,1)ηη=-=-.所以原方程组的通解为:01122k k γγηη=++(12,k k 是任意数). 五、证明题1、设向量组123,,ααα线性无关,证明向量组12αα+,23αα+,31αα+也线性无关.证明:设112223331()()()0k k k αααααα+++++=则131122233()()()0k k k k k k ααα+++++=因为123,,ααα线性无关,所以131223000k k k k k k +=⎧⎪+=⎨⎪+=⎩解得1230k k k ===,故122331,,αααααα+++线性无关.2、证明向量组12233441,,,αααααααα++++线性相关. 证明:设112223334441()()()()0k k k k αααααααα+++++++=则141122233344()()()()0k k k k k k k k αααα+++++++=考虑齐次线性方程组141223340000k k k k k k k k +=⎧⎪+=⎪⎨+=⎪⎪+=⎩其系数行列式1001100110110011001111001100110010011=-=-=所以齐次线性方程组有非零解. 于是存在不全为零的数1234,,,k k k k ,使得112223334441()()()()0k k k k αααααααα+++++++=成立,故12233441,,,αααααααα++++线性相关.3、设向量组123,,ααα线性无关,证明向量组1223312,2,32αααααα---也线性无关.证明:设112223331(2)(2)(32)0k k k αααααα-+-+-=则131122233(22)()(23)0k k k k k k ααα-+-++-+=因为123,,ααα线性无关,所以1312232200230k k k k k k -=⎧⎪-+=⎨⎪-+=⎩解得1230k k k ===,故1223312,2,32αααααα---线性无关.4、设向量组123,,ααα线性无关,证明向量组123123,2322,αααααα++-+123355ααα+-线性相关.证明:设112321233123()(2322)(355)0k k k ααααααααα+++-+++-=则123112321233(23)(35)(225)0k k k k k k k k k ααα+++-+++-=因为123,,ααα线性无关,所以1231231232303502250k k k k k k k k k ++=⎧⎪-+=⎨⎪+-=⎩ 解得1323192,95k k k k =-=,取35k =,得1219,2k k =-=使得 112321233123()(2322)(355)0k k k ααααααααα+++-+++-=故123123123,2322,355ααααααααα++-++-线性相关.5、已知向量组1234,,,αααα线性无关,证明向量组12233441,,,αααααααα+++-也线性无关.证明:设112223334441()()()()0k k k k αααααααα++++++-=则141122233344()()()()0k k k k k k k k αααα-++++++=因为1234,,,αααα线性无关,所以141223340000k k k k k k k k -=⎧⎪+=⎪⎨+=⎪⎪+=⎩解得12340k k k k ====,故12233441,,,αααααααα+++-线性无关.6、设12,,,s ααα均为n 维列向量,A 是n n ⨯矩阵,试证明: (1)若12,,,s ααα线性相关,则12,,,s A A A ααα也线性相关;(2)若A 可逆,且12,,,s A A A ααα线性相关,则12,,,s ααα也线性相关.证明:(1)因为12,,,s ααα线性相关,所以存在不全为零的数12,,,s k k k ,使得1122440k k k ααα+++=从而有11221122()00s s s s k A k A k A A k k k A αααααα+++=+++==故12,,,s A A A ααα线性相关.(2)因为12,,,s A A A ααα线性相关,所以存在不全为零的数12,,,s k k k ,使得1122440k A k A k A ααα+++=从而有11221122()0s s s s A k k k k A k A k A αααααα+++=+++=由A 可逆,得1122440k k k ααα+++=.故12,,,s ααα线性相关.7、已知向量组123,,ααα与122331,,αααααα+++ (1)证明123,,ααα与122331,,αααααα+++等价;(2)证明123,,ααα线性相关的充分必要条件是122331,,αααααα+++线性相关.证明:(1)首先,122331,,αααααα+++显然可由123,,ααα线性表示. 其次,由1122331212233131223311[()()()]21[()()()]21[()()()]2ααααααααααααααααααααα⎧=+-+++⎪⎪⎪=+++-+⎨⎪⎪=-+++++⎪⎩可知,123,,ααα可由122331,,αααααα+++线性表示. 故123,,ααα与122331,,αααααα+++等价.8、已知非齐次线性方程组123423423412340221(3)21321x x x x x x x x a x x x x x bx + + +=⎧⎪ ++=⎪⎨ - +--=-⎪⎪+ ++=-⎩ 有3个线性无关的解,证明:系数矩阵A 的秩等于2,并求,a b 的值及方程组的通解.证明:设123ξξξ,,是方程组的3个线性无关解,则1213ξξξξ--,是导出组0AX =的两个解.若1213()()0k l ξξξξ-+-=,则有123()0k l k l ξξξ+--=,于是由123ξξξ,,线性无关可得0k l ==,所以1213ξξξξ--,是导出组0AX =的两个线性无关解,因此,0AX =的基础解系所含向量个数不少于2,即有4()2A -≥秩. 所以有()2A ≤秩.因为系数矩阵111101220132321A a b ⎛⎫ ⎪⎪= ⎪--- ⎪⎝⎭,有一个2阶子式111001=≠,所以有()A ≤2秩,故()=2A 秩.对增广矩阵A 做行初等变换,有313242311110111100122101221=013210132132110123111110012210010000010r r r r r r A a a b b a b -++⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪−−−→ ⎪ ⎪-------- ⎪ ⎪-----⎝⎭⎝⎭⎛⎫⎪⎪−−−→ ⎪- ⎪-⎝⎭于是由()=2A 秩,有1010a b -=⎧⎨-=⎩,即11a b =⎧⎨=⎩.因此有31324212311110111100122101221=012210122132111012211111010111012210122100000000000000000000r r r r r r r r A -++-⎛⎫⎛⎫⎪ ⎪⎪ ⎪−−−→⎪⎪--------⎪ ⎪-----⎝⎭⎝⎭---⎛⎫⎛⎫⎪⎪⎪ ⎪−−−→−−−→ ⎪ ⎪⎪⎪⎝⎭⎝⎭故方程组的通解为1342341122x x x x x x =-++⎧⎨=--⎩.9、设12,,,n ααα均为n 维线性无关列向量,A 是n n ⨯矩阵,试证明:12,,,n A A A ααα线性无关⇔A 可逆.证明:(⇒)因为12n ααα,,,线性无关,所以以12n ααα,,,为列的n n ⨯矩阵12()n B ααα=可逆.因为12,,,n A A A ααα线性无关,所以矩阵1212()()n n C A A A A AB αααααα===可逆,从而1A CB -=可逆.(⇐)若有数12n k k k ,,,,使得11220s n k A k A k A ααα+++=则有1122()0n n A k k k ααα+++=由A 可逆可得11220s n k k k ααα+++=因为12,,,n ααα线性无关.所以120n k k k ====,故12,,,nA A A ααα线性无关.。
《高等代数》课程习题 .doc

感谢你的观看《高等代数》课程习题第1章行列式习 题 1.11. 计算下列二阶行列式:(1)2345 (2)2163- (3)x x x x cos sin sin cos - (4)11123++-x x x x (5)2232ab b a a (6)ββααcos sin cos sin (7)3log log 1a b b a2. 计算下列三阶行列式:(1)341123312-- (2)00000d c b a (3)d c e ba 0000 (4)zy y x x 00002121(5)369528741 (6)01110111-- 3. 用定义计算行列式:(1)4106705330200100 (2)114300211321221---(3)500000000400030020001000 (4) dc b a 100110011001---. 4.用方程组求解公式解下列方程组:(1) ⎪⎩⎪⎨⎧=-+=--=--0520322321321321x x x x x x x x x (2)⎪⎩⎪⎨⎧=+-=-+=++232120321321321x x x x x x x x x习 题 1.21. 计算下列行列式:感谢你的观看(1)123112101 (2)15810644372---- (3)3610285140 (4)655565556 2.计算行列式(1)2341341241231234(2)12114351212734201----- (3)524222425-----a a a(4)322131399298203123- (5)0532004140013202527102135---- 3.用行列式的性质证明:(1)322)(11122b a b b a a b ab a -=+(2)3332221113333332222221111112c b a c b a c b a a c c b b a a c c b b a a c c b b a =+++++++++ 4.试求下列方程的根:(1)022223356=-+--λλλ(2)0913251323221321122=--x x5.计算下列行列式(1)8364213131524273------ (2)efcfbfde cd bdae ac ab---(3)2123548677595133634424355---------- (4)111110000000002211ΛΛΛΛΛΛΛΛΛΛn n a a a a a a ---感谢你的观看(5)xaaa x a a a xΛΛΛΛΛΛΛ (6)abb a b a b a 000000000000ΛΛΛΛΛΛΛΛΛΛ 习 题 1.31. 解下列方程组(1)⎪⎩⎪⎨⎧-=++=+--=++1024305222325321321321x x x x x x x x x (2)⎪⎪⎩⎪⎪⎨⎧=+++-=----=+-+=+++01123253224254321432143214321x x x x x x x x x x x x x x x x2. k 取何值时,下列齐次线性方程组可能有非零:(1) ⎪⎩⎪⎨⎧=+-=++-=++0200321321321x x x x kx x kx x x (2)⎪⎩⎪⎨⎧=+-=++=++0300321321321x x x x kx x x x kx 习 题 五1.41.计算下列行列式(1)3010002113005004, (2)113352063410201-- (3)222111c b a c b a(4)3351110243152113------, (5)nn n n n b a a a a a b a a a a D ++=+ΛΛΛΛΛΛΛΛ212112111112.用克莱姆法则解线性方程(1)⎪⎩⎪⎨⎧=+-=-+=--114231124342321321321x x x x x x x x x (2)⎪⎪⎩⎪⎪⎨⎧=++=+-+=+-+=++3322212543143214321321x x x x x x x x x x x x x x3.当λ为何值时,方程组⎪⎩⎪⎨⎧=+-=+-=++0020321321321x x x x x x x x x λλ可能存在非零解?4.证明下列各等式(1) 222)(11122b a b b a a b ab a -=+(2) ))()((4)2()1()2()1()2()1(222222222c b a c a b c c c b b ba a a ---=++++++ (3) ))()()()()()((111144442222d c b a d c d b c b d a c a b a d c b a d c b a d c b a+++------=5.试求一个2次多项式)(x f ,满足1)2(,1)1(,0)1(-==-=f f f .第2章矩阵 习 题 2.21.设 ⎥⎦⎤⎢⎣⎡=530142A , ⎥⎦⎤⎢⎣⎡-=502131B , ⎥⎦⎤⎢⎣⎡--=313210C , 求3A -2B +C 。
高等代数课程习题

《高等代数》课程习题第1章行列式习 题 1.11. 计算下列二阶行列式: (1)2345 (2)2163- (3)x x x x cos sin sin cos - (4)11123++-x x x x (5)2232ab ba a (6)ββααcos sin cos sin (7)3log log 1a bb a2. 计算下列三阶行列式:(1)341123312-- (2)00000d c b a (3)d c e ba 0000 (4)zy y x x 00002121(5)369528741 (6)01110111-- 3. 用定义计算行列式:(1)4106705330200100 (2)1014300211321221---(3)5000000004000300020001000 (4)dcb a 100110011001---.4.用方程组求解公式解下列方程组:(1) ⎪⎩⎪⎨⎧=-+=--=--0520322321321321x x x x x x x x x (2)⎪⎩⎪⎨⎧=+-=-+=++232120321321321x x x x x x x x x习 题 1.21. 计算下列行列式:(1)123112101 (2)15810644372---- (3)3610285140 (4)655565556 2.计算行列式(1)2341341241231234(2)12114351212734201----- (3)524222425-----a a a(4)322131399298203123- (5)0532004140013202527102135---- 3.用行列式的性质证明:(1)322)(11122b a b b a a b ab a -=+(2)3332221113333332222221111112c b a c b a c b a a c c b b a a c c b b a a c c b b a =+++++++++ 4.试求下列方程的根:(1)022223356=-+--λλλ(2)0913251323221321122=--x x5.计算下列行列式(1)8364213131524273------ (2)efcfbfde cd bdae ac ab---(3)2123548677595133634424355---------- (4)111110000000002211ΛΛΛΛΛΛΛΛΛΛn n a a a a a a ---(5)xaaa x a a a xΛΛΛΛΛΛΛ (6)abb a b a b a 000000000000ΛΛΛΛΛΛΛΛΛΛ 习 题 1.31. 解下列方程组(1)⎪⎩⎪⎨⎧-=++=+--=++1024305222325321321321x x x x x x x x x (2)⎪⎪⎩⎪⎪⎨⎧=+++-=----=+-+=+++01123253224254321432143214321x x x x x x x x x x x x x x x x2. k 取何值时,下列齐次线性方程组可能有非零:(1) ⎪⎩⎪⎨⎧=+-=++-=++0200321321321x x x x kx x kx x x (2)⎪⎩⎪⎨⎧=+-=++=++0300321321321x x x x kx x x x kx 习 题 五1.41.计算下列行列式(1)3010002113005004, (2)113352063410201-- (3)222111c b a c b a(4)335111243152113------, (5)nn n n n b a a a a a b a a a a D ++=+ΛΛΛΛΛΛΛΛ212112111112.用克莱姆法则解线性方程(1)⎪⎩⎪⎨⎧=+-=-+=--114231124342321321321x x x x x x x x x (2)⎪⎪⎩⎪⎪⎨⎧=++=+-+=+-+=++3322212543143214321321x x x x x x x x x x x x x x3.当λ为何值时,方程组⎪⎩⎪⎨⎧=+-=+-=++0020321321321x x x x x x x x x λλ可能存在非零解?4.证明下列各等式(1) 222)(11122b a b b a a b ab a -=+(2) ))()((4)2()1()2()1()2()1(222222222c b a c a b c c c b b ba a a ---=++++++ (3) ))()()()()()((111144442222d c b a d c d b c b d a c a b a d c b a d c b a d c b a+++------=5.试求一个2次多项式)(x f ,满足1)2(,1)1(,0)1(-==-=f f f .第2章矩阵 习 题 2.21.设 ⎥⎦⎤⎢⎣⎡=530142A , ⎥⎦⎤⎢⎣⎡-=502131B , ⎥⎦⎤⎢⎣⎡--=313210C , 求3A -2B +C 。
高教线性代数第三章 线性方程组课后习题答案

第三章 线性方程组1. 用消元法解下列线性方程组:123412345123451234512345354132211)234321x x x x x x x x x x x x x x x x x x x x x x x x ++-=⎧⎪++-+=-⎪⎪-+--=⎨⎪-++-=⎪⎪++-+=-⎩124512345123451234523213322)23452799616225x x x x x x x x x x x x x x x x x x x +-+=⎧⎪--+-=⎪⎨-+-+=⎪⎪-+-+=⎩ 1234234124234234433)31733x x x x x x x x x x x x x -+-=⎧⎪-+=-⎪⎨+++=⎪⎪-++=-⎩123412341234123434570233204)411131607230x x x x x x x x x x x x x x x x +-+=⎧⎪-+-=⎪⎨+-+=⎪⎪-++=-⎩123412341234123421322325)521234x x x x x x x x x x x x x x x x +-+=⎧⎪-+-=⎪⎨+-+=-⎪⎪-+-=⎩12341234123412341232313216)23122215522x x x x x x x x x x x x x x x x x x x ++-=⎧⎪++-=⎪⎪+++=⎨⎪++-=⎪⎪++=⎩ 解 1)对方程组得增广矩阵作行初等变换,有135401135401132211003212121113054312141113074512121111014812--⎡⎤⎡⎤⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥⎢⎥→------⎢⎥⎢⎥-----⎢⎥⎢⎥⎢⎥⎢⎥-----⎣⎦⎣⎦102101100101003212000212002000002000000000000000011100010100--⎡⎤⎡⎤⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥→→--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦因为()()45rank A rank B ==<,所以方程组有无穷多解,其同解方程组为1445324122200x x x x x x x -=⎧⎪+=-⎪⎨-=⎪⎪-+=⎩,解得123451022x k x k x x k x k=+⎧⎪=⎪⎪=⎨⎪=⎪⎪=--⎩ 其中k 为任意常数。
高等代数(上)_习题集(含答案)

《高等代数(上)》课程习题集一、填空题11. 若31x -整除()f x ,则(1)f =( )。
2. 如果方阵A 的行列式0=A ,则A 的行向量组线性( )关。
3. 设A 为3级方阵,*A 为A 的伴随矩阵,且31=A ,则=--1*A A ( )。
4. 若A 为方阵,则A 可逆的充要条件是——( )。
5. 已知1211A ⎡⎤=⎢⎥⎣⎦,1121B ⎡⎤=⎢⎥⎣⎦,且3AB C A B +=+,则矩阵C =( )。
6. 每一列元素之和为零的n 阶行列式D 的值等于( )。
7. 设行列式014900716=--k,则=k ( )8. 行列式22357425120403---的元素43a 的代数余子式的值为( )9. 设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=403212221A ,11k α⎛⎫⎪= ⎪ ⎪⎝⎭,若αA 与α线性相关,则=α( )10. 设A 为3阶矩阵,51=A ,则12--A =( ) 11. 已知:s ααα,,,21Λ是n 元齐次线性方程组0=Ax 的基础解系,则系数矩阵A 的秩=)(A R ( )12. 多项式)(),(x g x f 互素的充要条件是( ) 13. 多项式)(x f 没有重因式的充要条件是( )14. 若排列n j j j Λ21的逆序数为k ,则排列11j j j n n Λ-的逆序数为( )15. 当=a ( )时,线性方程组⎪⎩⎪⎨⎧=++=++=++040203221321321x a x x ax x x x x x 有零解。
16. 设A 为n n ⨯矩阵,线性方程组B AX =对任何B 都有解的充要( )17. 设00A X C ⎡⎤=⎢⎥⎣⎦,已知11,A C --存在,求1X -等于( ) 18. 如果齐次线性方程组0=AX 有非零解,则A 的列向量组线性( )关 19. )(x p 为不可约多项式,)(x f 为任意多项式,若1))(),((≠x f x p ,则( ) 20. 设A 为4级方阵,3-=A ,则=A 2( )21. 设m ααα,,,21Λ是一组n 维向量,如果n m >.,则这组向量线性( )关22. 设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=403212221A ,11k α⎛⎫⎪= ⎪ ⎪⎝⎭,若αA 与α线性相关,则k=( )。
线性代数第一章 线性方程组与矩阵 习题课 shu
上页 下页
返回 5
文档仅供参考,不能作为科学依据,请勿模仿;如有不当之处,请联系网站或本 人删除。
类 似 地 ,用 n阶 初 等 矩 阵 E(i,j)右 乘 矩 阵 A,相 当 于 对 矩 阵 A施 行 第 一 种 初 等 列 变 换 :把 A的 第i 列 与 第 j列 对 调 (ci cj).
如 果 A 中 有 一 个 非 零 的 r阶 子 式 ,则 R (A )r;
如 果 A 中 所 有 r1 阶 子 式 都 为 零 ,则 R (A )r;
R(AT)R(A);
若 A ~ B ,则 R ( A ) R ( B ) .
行阶梯形矩阵的秩等于非零行的行数.
若 A为 n阶 可 逆 矩 阵 , 则 (1) A的 最 高 阶 非 零 子 式 为 | A |;
上页 下页
返回 19
文档仅供参考,不能作为科学依据,请勿模仿;如有不当之处,请联系网站或本 人删除。
一、求矩阵的秩
求矩阵的秩有下列基本方法
(1) 计算矩阵的各阶子式, 从阶数最高的子式 开始, 找到不等于零的子式中阶数最大的一个子式, 则这个子式的阶数就是矩阵的秩.
(2) 用初等变换. 即用矩阵的初等行(或列)变换,
上页 下页
返回 11
文档仅供参考,不能作为科学依据,请勿模仿;如有不当之处,请联系网站或本 人删除。
7. 矩阵的秩
在 mn矩 阵 A 中 ,任 取 k行 和 k列 ,位 于 这 些 行 列 交 叉 处 的 k2个 元 素 ,不 改 变 它 们 在 A 中 所 处 的 位 置 次 序 而 得 到 的 k阶 行 列 式 ,称 为 矩 阵 A 的 k阶 子 式 .
