分布函数均匀分布指数分布函数.ppt
分布函数、均匀分布、指数分布函数-精品文档

X pk
3
0 .1
4
0 .3
5
0 .6
例4、 向[0,1]区间随机抛一质点,以 X表示质点坐标. 假定质点落在[0,1]区间内任一子区间内的概率与区间 长度成正比,求 X的分布函数. 解:F x P { X x } 当 x 时 0,
F x 0 ;
1, 当 x 时
F A B 0 1 1 2 A B 2 A F B 1 2
1 1 所以 F r c t a n x x a 2
例2. 已知随机变量X 的分布律为 求分布函数 F ( x )
X
pk
0 1 3
1
2
1 2
1 6
F ( x ) P { X x } 解:
F x 1
当0 时 , x 1
F ( x ) P { X x } P { 0 X x } kx
特别,令 x 1, P k 1 { 0 X 1 } k 1 1
, x0 0 F (x ) = P { X x } = , 0x1 x 1 x1 ,
F ( x ) F ( x ) P { X x } 2 1 1
同理,还可以写出 P P { x X x } { x X x }, 1 2 1 2
二、分布函数的性质
,则 F ⑴ 单调不减性: ( x ) F ( x ) 若 x 1 2 1 < x2
F ( x ) 1,且 F ( ) l i m F () x 0 , ⑵ 0
一般地,设离散型随机变量 X 的分布律为
P { X x } p , k 1 , 2 , 3 , k k
概率论随机变量的分布函数ppt课件

因此, A 是不可能事件
P{A} 0.
ppt课件
12
例1: 设随机变量X具有概率密度
ke 3 x
x0
f (x)
0 x0
(1)试确定常数k,(2)求F(x),(3)并求P{X>0.1}。
解: (1)由于
f (x)dx
ke3xdx k 1
,解得k=3.
0
3
于是X的概率密度为
f
(
x)
O
x
(3) 在 x= 处曲线有拐点,且以x轴为渐近线 ;
(4) 对固定的,改变的值,图形沿Ox轴平移;
(5) 对固定的,改变, 越小,图形越尖.
正态分布的分布函数为: F ( x)
ppt课件
1
2
e dt x
(t )2 2 2
28
标准正态分布
当=0, =1时,称X服从标准正态分布,记作X~N(0,1).
例3 设电阻值R是一个随机变量,均匀分布在800欧~1000
欧,求R的概率密度及R落在850欧~950欧的概率.
解: 由题意,R的概率密度为
1 f (r) 1000 800
, 800 r 1000
0
, 其它
950 1
而 P{850 X 950}
dr 0.5
200 ppt课件
850
18
2. 指数分布
注 (4)式及连续性随机变量分布函数的定义表示 了分布函数与概率密度间的两个关系.利用这些 关系,可以根据分布函数和概率密度中的一个推 出另一个.
ppt课件
10
连续型随机变量的分布函数与概率密度的几何意义:
1. F(x)等于曲线f(x)在(-∞,x]上的曲边梯形的面积。
均匀分布 指数分布 正态分布

均匀分布、指数分布和正态分布是概率论和统计学中常见的概率分布形式。
它们在不同的领域和问题中都有着重要的应用,因此对这三种分布形式的了解和理解是非常重要的。
在本文中,我们将分别对均匀分布、指数分布和正态分布进行介绍,并对它们的特点、应用以及相关的数学推导进行详细的阐述。
一、均匀分布1.1 均匀分布的定义均匀分布是最简单的概率分布之一,它在一个区间内的概率密度是恒定的。
具体而言,假设随机变量X服从均匀分布,记为X ~ U(a,b),其中a和b分别是区间的上下界,概率密度函数为f(x) = 1/(b-a),当a≤x≤b时,否则f(x) = 0。
这意味着在[a,b]区间内的任何值出现的概率都是相等的。
1.2 均匀分布的特点均匀分布的特点非常明显,即在相同的区间内概率密度是恒定的。
这意味着在该区间内的任何取值都有相同的概率出现,而在区间之外的取值概率为零。
均匀分布的期望值为(a+b)/2,方差为(b-a)²/12。
1.3 均匀分布的应用均匀分布在各种领域都有广泛的应用,例如在随机抽样、随机模拟、概率估计等方面。
在实际应用中,均匀分布常常被用于描述某些事件或变量在一个确定区间内出现的概率,例如在工程技术中对某一参数的可行取值范围进行建模分析。
二、指数分布2.1 指数分布的定义指数分布是描述独立随机事件发生时间间隔的概率分布。
假设随机变量X服从指数分布,记为X ~ Exp(λ),其中λ是一个称为速率参数的正数,概率密度函数为f(x) = λe^(-λx),当x≥0时,否则f(x) = 0。
指数分布通常用于描述连续随机事件的持续时间或间隔时间,是由泊松分布推导而来的。
2.2 指数分布的特点指数分布的概率密度函数呈现出递减的特点,即随着时间的增加,事件发生的概率逐渐减小。
指数分布的期望值为1/λ,方差为1/λ²。
指数分布还具有无记忆性的特点,即对任意的s,t>0,有P(X>s+t|X>s) = P(X>t),这意味着在已经发生一段时间后,事件再次发生的概率不受前一次事件发生的时间影响。
分布函数、均匀分布、指数分布函数讲解

一、连续型随机变量的定义
1. 概率密度 定义1. 设 F(x) 是随机变量 X的分布函数,若存在非负 函数 f x x , ,使对任意实数 x 有
则称 X为连续型随机变量,称 f ( x)为 X 的概率密度函 数,简称概率密度或密度函数。
对于连续型随机变量的 分布函数 F ( x)必是连续函数 .
0 1 10 F x 2 5 1
x3 3 x 4
4 x5
x5
2 1 3 P X 4 F 4 F 4 0 5 10 10
2 3 P X 5 F 5 F 4 1 5 5
130 , 0 x 30 即 f ( x) 其它 0,
为使候车时间 X 少于 5 分钟,乘客必须在7:10 到 7:15 之间,或在7:25 到 7:30 之间到达车站
P{10 X 15} P{25 X 30} 15 1 30 1 1 dx dx 10 30 25 30 3
例 2、 设连续型随机变量 X的概率密度为
求 A的值, 解:
A 1 3
1 3 x 3 0
f ( x)dx
0
A 3.
1 3
1 3 x Ae dx A( )e 3
3 x
0
f ( x ) dx
1 3 0
3e 3 x dx e
∴可以使用分布函数值描述随机变量落在区间里的概率。 (1) P{x1 X x2} (2) P{x1 X x2} 同理,还可以写出
P{X x1} P{X x1}
二、分布函数的性质
⑴ 单调不减性: ,则
16种常见概率分布概率密度函数意义及其应用

16种常见概率分布概率密度函数意义及其应用概率分布是统计学中一个重要的概念,用于描述随机变量在各个取值上的概率分布情况。
常见的概率分布有16种,它们分别是均匀分布、伯努利分布、二项分布、几何分布、泊松分布、正态分布、指数分布、负二项分布、超几何分布、Gumbel分布、Weibull分布、伽马分布、Beta分布、对数正态分布、卡方分布和三角分布。
以下将逐一介绍这些概率分布的概率密度函数、意义及其应用。
1. 均匀分布(Uniform Distribution):概率密度函数为f(x)=1/(b-a),意义是在一个区间内所有的取值具有相同的概率,应用有随机数生成、模拟实验等。
2. 伯努利分布(Bernoulli Distribution):概率密度函数为P(x)=p^x*(1-p)^(1-x),意义是在两种可能结果中,成功或失败的概率分布,应用有二分类问题的建模。
3. 二项分布(Binomial Distribution):概率密度函数为P(x)=C(n,x)*p^x*(1-p)^(n-x),意义是在n次独立重复试验中,成功次数为x的概率分布,应用有二分类问题中的n次重复试验。
4. 几何分布(Geometric Distribution):概率密度函数为P(x)=p*(1-p)^(x-1),意义是独立重复试验中,第x次成功所需的试验次数的概率分布,应用有描述一连串同样试验中第一次获得成功之前所需的试验次数。
5. 泊松分布(Poisson Distribution):概率密度函数为P(x)=(e^(-λ)*λ^x)/x!,意义是在给定时间或空间内事件发生的次数的概率分布,应用有描述单位时间或单位空间内的事件计数问题。
6. 正态分布(Normal Distribution):概率密度函数为P(x) = (1 / sqrt(2πσ^2)) * e^(-(x-μ)^2 / (2σ^2)),意义是描述连续变量的概率分布,应用广泛,例如测量误差、人口身高等。
均匀分布与指数分布

故障工作的时间 s 无关.
指数分布
例1 设顾客在某银行窗口等待服务的时间(分钟)X ~ E( 0.2 ). 某顾客在窗
口等待服务,若超过10分钟就离开. 他一个月要到银行5次,如果以Y 表示 一个月内他因未等到服务而离开窗口的次数,求Y 的分布律及 P{ Y ≥1 }.
解:任意一次未等到服务(即超过10分钟)而离开窗口的概率
t 小时的概率不 s 无关.
P X s t | X s P X s t , X s P X s t
P X s
P X s
e xdx st
ex dx s
e (st ) es
e t
PX
t
若将 X 看做某系统接连发生两次故障的时间间隔,此性质表明,在时
段(s, s+t)上无故障的概率只不时段的长度 t 有关,而不系统过去无
p PX 10
f (x)dx
1
x
e 5 dx
e
2
10
10 5
而 Y ~ B ( 5, p ). 故Y 的分布律为
P{Y k} C5ke2k (1 e2 )5k , k 0,1, 2,3, 4,5.
所以 PY 1 1 PY 0 0.5167
休息,休息一下!
等车时间丌超过2分钟的概率 p = P{ X ≤ 2 } = 2/5. 记等车丌超过2分钟的人数为 Y ,则 Y ~ B ( 3, p ).
p=?
至少有二人等车时间丌超过2分钟的概率为 :
PY 2 PY 2+PY 3 0.352.
常用的连续型分布
2. 指数分布 X ~ E( λ )
若随机变量X的概率密度为 则称X服从指数分布.
ab
x
13种常见的统计分布ppt课件

属性
✓ 连续型分布 ✓ 用于描述以方向、位置、周期性(环形)时间、角度等为测度
单位的数字特征
应用
✓ 医学领域内一些现象是以方向或时间度量,具有周期性特点, 如某疾病在一年内各月份的发生数、胎儿在一昼夜间各时点 分娩的频度
✓ 有些数据本身就是以角度来表示:如脑电阴图的上升角,气 象环境的风向玫瑰图
✓ 这些数据不能用通常的均数、标准差描述
1 二项分布 Binomial Distribution
应用 条件
✓ 各观察单位只能具有相互对立的一种结果,如阳性或阴 性,生存或死亡等,属于两分类资料
✓ 已知发生某一结果(阳性)的概率为π,其对立结果的概 率为1-π,实际工作中要求π是从大量观察中获得比较稳 定的数值。
✓ n次试验在相同条件下进行,且各个观察单位的观察结果 相互独立,即每个观察单位的观察结果不会影响到其他观 察单位的结果。如要求疾病无传染性、无家族性等。
9 F分布 F Distribution
属性
✓ 连续型分布 ✓ 用于方差Γ分布 Γ Distribution or Gamma Distribution
属性
✓ 连续型分布 ✓ 正偏态分布,常用于正偏态分布的拟合
11 圆形分布 Circular Distribution
5 均匀分布 Uniform Distribution
属性
✓ 连续型分布 ✓ 数值计算的误差分析 ✓ 任意分布的随机数
理解
✓ 均匀分布在自然情况下极为罕见,而人工栽培的有一定株 行距的植物群落即是均匀分布
✓ 均匀,表示可能性相等的含义
6 正态分布 Normal Distribution
属性
✓ 连续型分布 ✓ 自然界、人类社会、心理和教育中大量现象均按正态形式分布,
(课件)概率论与数理统计:均匀分布与指数分布

2
3
2
3
1
3 3 3
2
0
3
20 . 27
3
指数分布的概念导入
三大连续分布之指数分布
2. 指数分布 E(λ )
若连续随机变量 X 的密度函数具有形式
ex , x 0
f (x) 0,
其它
(其中 0)
那么就称该随机变量 X 服从指数分布,也称 X为指数分布变量(简称
指数量),并记为 X E ( )
在实际生活中,常用指数分布作为各种“寿命” 分布的近似。如 电子元件的寿命、动物的寿命等都假定服从指数分布。
服从指数分布的随机变量X具有一个很有趣 的性质:无记忆性。
事实上,P{ X s t | X s} P{( X s t ) ( X s)} P{ X s}
P{X s t} P{X s}
显然,不同的指数分布仅靠一个分布参数 λ 的不同取值相互区分。
指数分布 密度函数
y f (x)
的图象
指数分布 分布函数
y =F (x)
的图象
f (x)
e x , x 0
O
y f (x)
0
,x 0
x
y F (x)
F(x)
1
1 e x , x 0
0
,x 0
O
x
4
指数分布的应用举例
(1)求该电子元件寿命超过2年的概率; (2)已知该电子元件已使用了1.5年,求它还能使用超过2年的概率为多少?
解: 由题知
3e3 x x 0
f (x)
0 x 0,
(1)P( X 2) 3e3 xdx e6 ,
2
3e 3 x dx
2 P( X
均匀分布ppt课件

4.8 指数分布
设随机变量X的概率密度为 其中ג是大于0的常数。于是称X为服从参数ג的指பைடு நூலகம்分布。
它的其他性质
指数分布可以描述许多物理现象,特别是它与泊松过 程 有紧密的联系,泊松过程中两次相继发生的事件之间的 (时间,空间)间隔服从指数分布。
Thank you
此课件下载可自行编辑修改,供参考! 感谢您的支持,我们努力做得更好!
4.6 均匀分布
PPT :杨丽文
从本节开始要讨论几种重要的连续分布 设随机变量X的概率密度可表示为
则称X服从[a,b]区间内的均匀分布 它的累积分布函数为
f(x)和F(x)的形状如图4.6所示
容易算出均匀分布的数字特征 f(x)对于均值E(X)是对称的,因而所有奇数阶中心距等于0。
偶数阶中心距 均匀分布的特征函数
设任意连续随机变量Y的概率密度为g(y), 令
即x为随机变量Y的累积分布函数。x可考虑为一随 机变量,它是y的函数,根据随机变量的函数的概率密 度公式(2.3.3)
(2.3.3)
x的概率密度为
f(x)=1正是[0,1]区间均匀分布的概率密度,因此,x(即任 意连续随机变量的累积分布函数)服从[0,1]区间的均匀分布, 这一性质广泛运用于蒙特卡洛计算(见第十四章)。
均匀分布是最简单的连续随机变量,它表示在区间 [a,b]内任意等长度区间内事件出现的概率相同这样一种分 布。数字计算中的舍入误差,时钟任一时针的角度值都是 均匀分布的例子。
例如:测量结果要求保留到小数点后1位,将实测或算出的数据 第2位按四舍五入原则舍去,则存在舍入误差0.05;
它的计算极其简单,但是如下的一个重要性质使得均 匀分布具有广泛的应用:任何连续随机变量的概率密度经 过适当的变换都可转变为[0,1]区间的均匀分布 。
概率分布中的均匀分布与指数分布

概率分布中的均匀分布与指数分布概率分布是概率论和统计学中的重要概念,用于描述随机变量在不同取值下的概率分布情况。
在概率分布中,均匀分布和指数分布是两种常见的分布类型。
本文将介绍均匀分布和指数分布的特点、概率密度函数以及应用领域。
一、均匀分布均匀分布是指在一个区间内,随机变量的取值具有相同的概率。
均匀分布的特点是概率密度函数在给定区间内保持恒定。
均匀分布可以分为离散均匀分布和连续均匀分布两种类型。
1. 离散均匀分布离散均匀分布是指在有限个数的取值中,每个取值的概率相等。
例如,抛硬币的结果可以看作是一个离散均匀分布,因为硬币正面和反面出现的概率都是1/2。
离散均匀分布的概率密度函数可以表示为:P(X = x) = 1/n,其中x为取值,n为取值的总数。
2. 连续均匀分布连续均匀分布是指在一个连续的区间内,随机变量的取值概率保持恒定。
例如,某个产品的寿命服从连续均匀分布,表示在一定时间范围内,产品寿命的概率是相等的。
连续均匀分布的概率密度函数可以表示为:f(x) = 1/(b-a),其中a为区间的下界,b为区间的上界。
均匀分布的应用领域非常广泛。
例如,在随机抽样中,如果每个样本都具有相同的概率被选中,那么抽样结果就可以用均匀分布来描述。
二、指数分布指数分布是一种描述事件发生时间间隔的概率分布。
指数分布的特点是事件发生的概率密度函数在时间上是单调递减的。
指数分布常用于描述连续性事件的等待时间,例如客户到达某个服务台的时间间隔。
指数分布的概率密度函数可以表示为:f(x) = λ * exp(-λx),其中λ为事件发生率,x为时间间隔。
指数分布的期望值为1/λ,表示事件发生的平均等待时间。
指数分布在实际应用中具有重要意义。
例如,在可靠性工程中,指数分布可以用于描述设备的寿命分布。
在排队论中,指数分布可以用于描述顾客到达和服务的时间间隔。
结论通过对均匀分布和指数分布的介绍,我们了解到它们在概率分布中的不同特点和应用领域。
常见的分布函数

常见的分布函数常见的分布函数包括:1. 正态分布函数(Normal Distribution Function):也称为高斯分布函数,是最常见的概率分布函数之一,用于描述一组数据在平均值附近的分布情况。
其概率密度函数为:$$f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$。
2. 均匀分布函数(Uniform Distribution Function):是一种简单的概率分布函数,表示在一个区间内随机抽取数据的均匀分布情况。
其概率密度函数为:$$f(x)=\begin{cases}。
\frac{1}{b-a} & a\leq x \leq b \\。
0 & \text{其他}。
\end{cases}$$。
3. 伽马分布函数(Gamma Distribution Function):适用于描述正值的数据分布情况,常用于计算无线电信号的强度、生物统计学等领域。
其概率密度函数为:$$f(x)=\frac{1}{\Gamma(\alpha)\beta^\alpha}x^{\alpha-1}e^{-\frac{x}{\beta}}$$。
4. 指数分布函数(Exponential Distribution Function):是一种描述随机事件发生时间间隔的概率分布函数,常用于生物学、金融等领域。
其概率密度函数为:$$f(x)=\begin{cases}。
\lambda e^{-\lambda x} & x \geq 0 \\。
0&x<0。
\end{cases}$$。
5. 泊松分布函数(Poisson Distribution Function):用于描述事件的随机发生次数,常用于工业、生物学等领域。
其概率密度函数为:$$f(x)=\frac{\lambda^x}{x!}e^{-\lambda}$$。
分布函数、均匀分布、指数分布函数.PPT共32页

61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
谢谢!
分布函数、均匀分布、指数分布函数.
11、用道德的示范来造就一个人,显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的,对谁都一视同仁。在每件事上,她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由,因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样,法律和法律都是相互依存的。——伯克
均匀分布与指数分布

解 按题意, R的概率密度
为
p(r)
1 1100 900
,
900 r 1100,
故有
0,
其它.
P{950 R 1050}
1050
1
d r 0.5
950 200
4
2. 指数分布 设连续型随机变量X的概率密度为
p(
x)
e
x
,
x 0,
0,
x0
其中 >0为常数, 则称X服从参数为的指数分布. 容易得
016113125吴安琪016113126贾素素016113127张子琪016113130崇殿红016113106徐梦琦016113111均匀分布设连续型随机变量x具有概率密度其它则称x在区间ab上服从均匀分布记为xuab
均匀分布与指数分布
小组成员: 唐慧 016113124 吉颖 016113125 吴安琪016113126 贾素素016113127 张子琪016113130 崇殿红016113106 徐梦琦016113111
s)}
P{X s t} 1 F (s t) P{X s} 1 F (s)
e ( st ) es
et
P{X t}.
上述性质称为无记忆性.
指数分布在可靠性理论和排队论中有广泛的运用.
7
谢谢
1. 均匀分布 设连续型随机变量X具有概率密度
p(
x)
ቤተ መጻሕፍቲ ባይዱ
b
1
a
,
a x b,
0, 其它,
则称X在区间(a,b)上服从均匀分布, 记为X~U(a,b).
p(x)
1 ba
O
a
bx
2
区间 (c, c + l),且 a c < c +l
讲连续型随机变量分布及随机变量的函数的分布
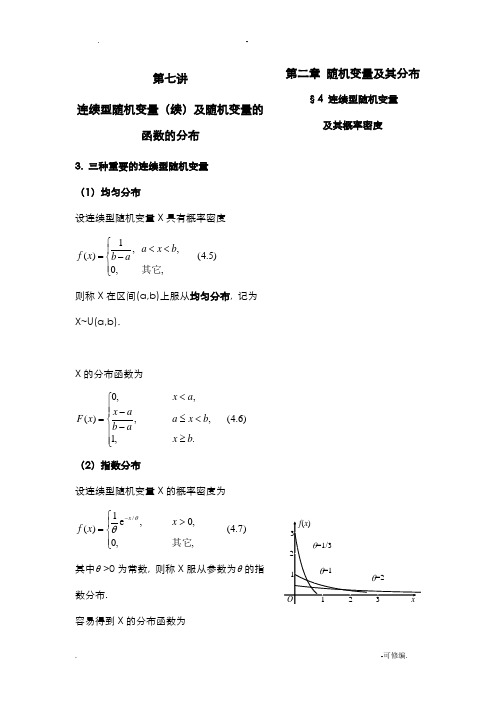
第七讲连续型随机变量(续)及随机变量的函数的分布3. 三种重要的连续型随机变量 (1)均匀分布设连续型随机变量X 具有概率密度)5.4(,,0,,1)(⎪⎩⎪⎨⎧<<-=其它b x a ab x f则称X 在区间(a,b)上服从均匀分布, 记为X~U(a,b).X 的分布函数为)6.4(.,1,,,,0)(⎪⎪⎩⎪⎪⎨⎧≥<≤--<=b x b x a a b a x a x x F(2)指数分布设连续型随机变量X 的概率密度为)7.4(,,0,0,e1)(/⎪⎩⎪⎨⎧>=-其它x x f x θθ其中θ>0为常数, 则称X 服从参数为θ的指数分布.容易得到X 的分布函数为第二章 随机变量及其分布§4 连续型随机变量及其概率密度=2)8.4(.,0,0,1)(/⎩⎨⎧>-=-其它x e x F x θ如X 服从指数分布, 则任给s,t>0, 有 P{X>s+t | X > s}=P{X > t} (4.9)事实上}.{e ee)(1)(1}{}{}{)}(){(}|{//)(t X P s F t s F s X P t s X P s X P s X t s X P s X t s X P t s t s >===-+-=>+>=>>⋂+>=>+>--+-θθθ性质(4.9)称为无记忆性.指数分布在可靠性理论和排队论中有广泛的运用. (3)正态分布设连续型随机变量X 的概率密度为)10.4(,,e21)(222)(∞<<-∞=--x x f x σμσπ其中μ,σ(σ>0)为常数, 则称X 服从参数为μ,σ的正态分布或高斯(Gauss)分布, 记为X~N(μ,2σ).显然f(x)≥0, 下面来证明1d )(=⎰+∞∞-x x f令t x =-σμ/)(, 得到dx edx et x 22)(2222121-∞+∞---∞+∞-⎰⎰=πσπσμf (x )的图形:1.5.1d 21d 21)11.4(π2d d e,,d d ,d e22)(20222/)(22/2222222======⎰⎰⎰⎰⎰⎰⎰∞∞--∞∞---∞-+∞∞-+∞∞-+-∞∞--x ex e r r I u t e I t I t x r u tt πσπθσμπ于是得转换为极坐标则有记f(x)具有的性质:(1).曲线关于x=μ对称. 这表明对于任意h>0有P{μ-h<X ≤μ}=P{μ<X ≤μ+h}. (2).当x=μ时取到最大值.π21)(σμ=f x 离μ越远, f(x)的值越小. 这表明对于同样长度的区间, 当区间离μ越远, X 落在这个区间上的概率越小。
分布函数、均匀分布、指数分布函数.32页PPT

35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确。——培根
分布函数、均匀分布、指数 分布Fra bibliotek数.31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c
cl
1 dx
l
c ba ba
由此可得,如果随机变量 X 服从区间[a,b]上的均匀
分布,则随机变量 X 在区间[a,b]上的任一子区间上取
值的概率与该子区间的长度成正比,而与该子区间的
位置无关。
例1.某公共汽车站从上午7时起,每15分钟来一班车, 即 7:00,7:15,7:30, 7:45 等时刻,如果乘客到达此站时
当 时,
当 时,
当
时,
特别,令
第五、六节
第二章
连续型随机变量及其分布
一、连续型随机变量的定义 二、常用的连续型随机变量
一、连续型随机变量的定义
1. 概率密度 定义1. 设 F(x) 是随机变量 X的分布函数,若存在非负
函数 f x x ,,使对任意实数 x 有
则称 X为连续型随机变量,称 f (x)为 X 的概率密度函 数,简称概率密度或密度函数。
例3 已知离散型随机变量 X 的分布函数为
0
1
Fx
10
2
5
1
x3 3 x4 4 x5 x5
求 X 的分布律。
解 X 的可能取值为 3,4,5。
PX 3 F 3 F 3 0 1
10
0 x 3
1
Fx
10
概率为 P{X 2 4 0} P{(X 2) ( X 2)}
P{X 2} P{X 2},
利用f
(x)
1 5
,1
x
6
4 5
0,其它
从而
P{X 2}
f (x)dx
61 dx 4 .
2
25
5
同理P{X 2} 0.
则称 X 服从 [a, b]上的均匀分布,
记作: X ~ U [a, b]
0,
分布函数为: F (x)
x
f
(t)dt
x a
b
a
,
1,
x a, a x b,
x b.
均匀分布的概率背景
因为 P{c X c l}
cl
f (x)dx
当 x 0时, {X x} F(x) 0
当 0 x 1 时, F(x) P{X x} P{X 0} 1 3
当1 x 2时,
F(x) P{X 0} P{X 1} 1 1 1
当x 2时
36 2
F(x) P{X 0} P{X 1} P{X 2} 1
2
5
1
3 x 4 4 x5 x5
PX 4 F 4 F 4 0 2 1 3
5 10 10
PX 5 F 5 F 4 1 2 3
55
所以 X 的分布律为
例4、 向[0,1]区间随机抛一质点,以 X表示质点坐标. 假定质点落在[0,1]区间内任一子区间内的概率与区间 长度成正比,求 X的分布函数. 解:
(1) P{x1 X x2}
(2) P{x1 X x2}
同理,还可以写出
P{X x1} P{X x1}
二、分布函数的性质
⑴ 单调不减性:
,则
⑵ 0 F(x) 1 ,且
⑶ 右连续性:
上述三条性质,也可以理解为判别函数是否是分布函数 的充要条件。
例1 已知 Fx Aarctan x B ,求 A、 B。
对于连续型随机变量的分布函数F ( x)必是连续函数. f (x)可积 F(x)连续
2. 概率密度的性质
⑴ 非负性 f (x) 0
⑵ f (x)dx=1 由于 F () f (x)dx=1
(3) f (x)在点x 处连续,则 f (x) F(x)
解
F A B 0
2
F A B 1
A 1
B1 2
2
所以 F x 1 arctan x 1
2
例2. 已知随机变量X 的分布律为 X 0 1 2
求分布函数 F (x)
pk
1 3
11 62
解: F(x) P{X x}
所以,
一般地,设离散型随机变量 X 的分布律为
P{X xk} pk ,k 1, 2, 3,
由概率的可列可加性得 X 的分布函数为
F x P{X x} pk P{X xk }
xk x
xk x
12 离散型的分布函数为阶梯函数;xk为间断点;
P{X xk} F (xk ) F (xk 0)
0 x 0,
例4 .电子元件的寿命X(年)服从λ=3的指数分布 (1)求该电子元件寿命超过2年的概率。 (2)已知该电子元件已使用了1.5年,求它还能使用2 年的概率为多少?
解 由已知得 X 的概率密度为
3e3x x 0 f (x)
0 x 0,
(1)P{X 2} 3e3xdx e6 2
(x)
2
1 x2 ,
1 x 1
0, 其它
解:F(x) PX x
x
f (t)dt
当x 1时, F(x) 0
求 F(x).
当1 x 1时,
F(x)
1
0 dt
x2
1 t 2 dt
1
x 1 x2 1 arcsin x 1
1 e1.
例3、 及概率密度函数 f (x)。 解:
求常数 a,b,
例4、 解:
,求A , B 及 f (x)。
注:F(x) f (x)的方法.
二、常用的连续型随机变量
1、均匀分布
定义、 若 连续型随机变量 X 的概率密度为:
f
(x)
b
1
a
,
a xb
0,
其它
的指数分布。若等待时间超过10
分钟,则他离开。假设他一个月内要来银行5次, 以 Y
表示一个月内他没有等到服务而离开窗口的次数,求Y
的分布律及至少有一次没有等到服务的概率
解 Y是离散型,Y ~ b(5, p) ,其中 p = P{X > 10}
现在 X 的概率密度为
1/ 5ex /5 x 0 f (x)
间 X 是7:00 到 7:30 之间的均匀随机变量, 试求他候车时
间少于5 分钟的概率.
解: 依题意, X ~ U (0 ,30)
即
f
(
x)
1 30
,
0,
0 x 30 其它
为使候车时间 X 少于 5 分钟,乘客必须在7:10
到 7:15 之间,或在7:25 到 7:30 之间到达车站
P{10 X 15} P{25 X 30}
15 1 dx 30 1 dx 1
10 30
25 30
3
例2、 设随机变量X 服从[1,6]上的均匀分布,求一元
二次方程t2 + X t + 1= 0 有实根的概率。
解 因为当 X 2 4 0 时,方程有实根,故所求
2
当 x 1, F(x) 1
例2、设连续型随机变量 X的概率密度为
求 A的值,
解:
f (x)dx
Ae3xdx 0 NhomakorabeaA( 1)e3x 3
0
A 1 3
A 3.
1
1
1
3 f (x)dx
3 3e3xdx
0
e3x
3 0
2 PX 3.5 X 1.5
P{X 3.5, X 1.5} P{X 1.5}
3e3xdx
3.5
3e3xdx
1.5
= e- 6
由⑴、⑵结果得:指数分布具有无记忆性,即
PX s t X s PX t (t 0)
2、 指数分布
定义:若随机变量X 的概率密度为:
f
x
e x
x0
0
x0
其中 ( 0) 为常数,则称随机变量X服从参数为的 指数分布。指数分布的分布函数为
F
x
1
0 e
x
x0 x0
例3 假设顾客在某银行窗口等待服务的时间(单位:分钟)
X 服从参数为
3、连续性随机变量的特点 (1) (2)
(3) F(x)连续。
f (x)
1 0ab x
4、密度函数f (x)的意义: 反映了随机变量 X在点x 处的密集程度。 在等长度的区间上,f的值越大,说明X在该区间内 落点的可能性越大。 f (x)
1 0ab x
例1. 设 X 的密度函数为 f (x)
f
第四节
第02章
随机变量的分布函数
一、分布函数的概念 二、分布函数的性质 三、离散型分布函数的求法
一、分布函数的概念
定义1 设 X 是一个随机变量,x 是任意实数,则称函数
为X 的分布函数。
( x )
x
分布函数 F x的函数值的含义:
表示 X 落在 (, x] 上的概率.
∴可以使用分布函数值描述随机变量落在区间里的概率。
