2020-2021天津市育贤中学高三数学下期末试题(带答案)
天津市2020〖人教版〗高三数学复习试卷第二学期综合练习高三数学文科2

天津市2020年〖人教版〗高三数学复习试卷第二学期综合练习高三数学文科 创作人:百里公地 创作日期:202X.04.01 审核人: 北堂址重 创作单位: 博恒中英学校一、选择题(共8小题)(1)已知全集U =R ,集合{}012A =,,,{}234B =,,,如图阴影部分所表示的集合为()(A ){}2 (B ){}01,(C ){}34, (D ){}0,1,2,3,4【考点】集合的运算【难度】1【答案】B【解析】由题意得:{}2A B =,由维恩图可知,阴影部分表示的集合为:U A B即在集合A 中去掉A 与B 的公共元素,所以答案为{}0,1,选B(2)若复数2()i m m m -+为纯虚数,则实数m 的值为( )(A )1- (B )0(C )1 (D )2【考点】复数综合运算【难度】1【答案】C【解析】由题意得:该复数的实部为零,虚部不为零,即:200m m m⎧-=⎨≠⎩,解得:1m =,选C(3)已知圆的方程为222610x y x y +--+=,那么圆心坐标为( )(A )(1,3)--(B )(1,3)-(C )(1,3)(D )(1,3)-【考点】圆的标准方程与一般方程【难度】1【答案】C【解析】把圆的一般方程222610x y x y +--+=进行配方可得: 22(1)(3)9x y -+-=,所以圆心坐标为:(1,3),选C(4)设点),(y x P ,则“1x =且2y =-”是“点P 在直线30l x y --=:上”的( )(A )充分而不必要条件(B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件【考点】充分条件与必要条件【难度】1【答案】A【解析】先考察充分性:把1,2x y ==-代入直线:30l x y --=,满足直线方程,所以充分性成立;再考察必要性:直线:30l x y --=上有无数个点,不一定得到:1,2x y ==-,所以必要性不成立。
2020-2021天津市育贤中学高一数学下期中试题(带答案)

2020-2021天津市育贤中学高一数学下期中试题(带答案)一、选择题1.已知定义在R 上的函数()21()x m f x m -=-为实数为偶函数,记0.5(log 3),a f =2b (log 5),c (2)f f m ==,则,,a b c ,的大小关系为( )A .a b c <<B .c a b <<C .a c b <<D .c b a <<2.设α表示平面,a ,b 表示直线,给出下列四个命题:①a α//,a b b α⊥⇒//; ②a b //,a b αα⊥⇒⊥;③a α⊥,a b b α⊥⇒⊂;④a α⊥,b a b α⊥⇒//,其中正确命题的序号是( ) A .①② B .②④ C .③④ D .①③ 3.已知直线20ax y a +-+=在两坐标轴上的截距相等,则实数(a = ) A .1B .1-C .2-或1D .2或14.从点(,3)P m 向圆22(2)(2)1x y +++=引切线,则切线长的最小值( ) A .26 B .5C .26D .42+5.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( ) A .814πB .16πC .9πD .274π6.若圆的参数方程为12cos ,32sin x y θθ=-+⎧⎨=+⎩(θ为参数),直线的参数方程为21,61x t y t =-⎧⎨=-⎩(t为参数),则直线与圆的位置关系是( ) A .相交且过圆心B .相交但不过圆心C .相切D .相离7.矩形ABCD 中,4AB =,3BC =,沿AC 将矩形ABCD 折成一个直二面角B ACD --,则四面体ABCD 的外接球的体积是( )A .12512π B .1259π C .1256π D .1253π 8.一个几何体的三视图如图所示,则该几何体的表面积为( )A .B .C .D .9.,为两个不同的平面,,为两条不同的直线,下列命题中正确的是( )①若,,则; ②若,,则; ③若,,,则④若,,,则.A .①③B .①④C .②③D .②④10.若方程21424x kx k +-=-+ 有两个相异的实根,则实数k 的取值范围是( )A .13,34⎛⎤ ⎥⎝⎦B .13,34⎛⎫ ⎪⎝⎭C .53,124⎛⎫ ⎪⎝⎭D .53,124纟çúçú棼11.α,β是两个不重合的平面,在下列条件中,可判断平面α,β平行的是( ) A .m ,n 是平面α内两条直线,且//m β,//n β B .α内不共线的三点到β的距离相等 C .α,β都垂直于平面γD .m ,n 是两条异面直线,m α⊂,n β⊂,且//m β,//n α12.如图,正方体ABCD ﹣A 1B 1C 1D 1的棱长为1,线段B 1D 1上有两个动点E 、F ,且EF=12.则下列结论中正确的个数为①AC ⊥BE ; ②EF ∥平面ABCD ;③三棱锥A ﹣BEF 的体积为定值; ④AEF ∆的面积与BEF ∆的面积相等, A .4B .3C .2D .1二、填空题13.经过两条直线2310x y ++=和340x y -+=的交点,并且平行于直线3470x y +-=的直线方程是________.14.已知四面体ABCD 的外接球球心O 在棱CD 上,3,CD=2,则A 、B 两点在四面体ABCD 的外接球上的球面距离是________. 15.如图,在四棱锥P ABCD -中,PA ⊥底面,,//,2,1ABCD AD AB AB DC AD DC AP AB ⊥====,若E 为棱PC 上一点,满足BE AC ⊥,则PEEC=__________.16.将正方形ABCD 沿对角线BD 折成直二面角A BD C --,①AB 与平面BCD 所成角的大小为60o ②ACD ∆是等边三角形 ③AB 与CD 所成的角为60o ④AC BD ⊥⑤二面角B AC D --为120︒ 则上面结论正确的为_______.17.如图,在ABC V 中,AB BC ⊥,SA ⊥平面ABC ,DE 垂直平分SC ,且分别交AC ,SC 于点D ,E ,又SA AB =,SB BC =,则二面角E BD C --的大小为_______________.18.底面边长为2的正三棱柱111ABC A B C -被不平行于底面的平面MNP 所截,其中3AM =,4BN =,5PC =,则多面体ABC MNP -体积为________19.已知棱长等于31111ABCD A B C D -,它的外接球的球心为O ﹐点E 是AB 的中点,则过点E 的平面截球O 的截面面积的最小值为________.20.在三棱锥P ABC -中,PA ⊥平面ABC ,AC BC ⊥,且三棱锥的最长的棱长为2,则此三棱锥的外接球体积为_____________.三、解答题21.已知两直线1l :240x y -+=和2l :20x y +-=的交点为P . (1)直线l 过点P 且与直线5360x y +-=垂直,求直线l 的方程; (2)圆C 过点()3,1且与1l 相切于点P ,求圆C 的方程.22.如图,在三棱锥S ABC -中,SAC ∆为等边三角形,4AC =,43BC=,BC AC ⊥,3cos SCB ∠=-,D 为AB 的中点.(1)求证:AC SD ⊥;(2)求直线SD 与平面SAC 所成角的大小.23.如图,AB 是半圆O 的直径,C 是半圆O 上除A ,B 外的一个动点,DC 垂直于半圆O 所在的平面,DC ∥EB ,DC =EB =1,AB =4.(1)证明:平面ADE ⊥平面ACD ;(2)当C 点为半圆的中点时,求二面角D ﹣AE ﹣B 的余弦值.24.如图,在正三棱柱111ABC A B C -中,点D 、E 、F 分别是BC 、1AC 、1BB 的中点.(1)求证:AD ⊥平面11BCC B ; (2)求证://EF 平面111A B C .25.如图,在三棱柱111ABC A B C -中,1CC ⊥平面ABC ,1,2AC BC AC BC CC ⊥===,点,,D E F 分别为棱11111,,AC B C BB 的中点.(1)求证://AB 平面DEF ; (2)求证:平面1ACB ⊥平面DEF ; (3)求三棱锥1E ACB -的体积.26.如图,在直三棱柱111ABC A B C -中,90ABC ︒∠=,1AB AA =,,M N 分别为AC ,11B C 的中点.(1)求证://MN 平面11ABB A ; (2)求证:1AN A B ⊥.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【解析】由()f x 为偶函数得0m =,所以0,52log 3log 32121312,a =-=-=-=2log 521514b =-=-=,0210c =-=,所以c a b <<,故选B.考点:本题主要考查函数奇偶性及对数运算.2.B【解析】 【分析】 【详解】①a ∥α,a ⊥b ⇒b 与α平行,相交或b ⊂α,故①错误; ②若a ∥b ,a ⊥α,由直线与平面垂直和判定定理得b ⊥α,故②正确; ③a ⊥α,a ⊥b ⇒b 与α平行,相交或b ⊂α,故③错误; ④若a ⊥α,b ⊥α,则由直线与平面垂直的性质得a ∥b ,故④正确. 故选B .3.D解析:D 【解析】 【分析】根据题意讨论直线它在两坐标轴上的截距为0和在两坐标轴上的截距不为0时,求出对应a 的值,即可得到答案.【详解】由题意,当2a 0-+=,即a 2=时,直线ax y 2a 0+-+=化为2x y 0+=, 此时直线在两坐标轴上的截距都为0,满足题意;当2a 0-+≠,即a 2≠时,直线ax y 2a 0+-+=化为122x y a a a+=--,由直线在两坐标轴上的截距相等,可得2a2a a-=-,解得a 1=; 综上所述,实数a 2=或a 1=. 故选:D . 【点睛】本题主要考查了直线方程的应用,以及直线在坐标轴上的截距的应用,其中解答中熟记直线在坐标轴上的截距定义,合理分类讨论求解是解答的关键,着重考查了运算与求解能力,属于基础题.4.A解析:A 【解析】 【分析】设切线长为d ,则2222(2)51(2)24d m m =++-=++再利用二次函数的图像和性质求函数的最小值得解. 【详解】设切线长为d ,则2222(2)51(2)24d m m =++-=++, min d ∴= 故选:A.本题主要考查圆的切线问题,考查直线和圆的位置关系,意在考查学生对这些知识的掌握水平和分析推理能力.5.A解析:A 【解析】 【分析】 【详解】正四棱锥P-ABCD 的外接球的球心在它的高1PO 上, 记为O ,PO=AO=R ,14PO =,1OO =4-R , 在Rt △1AOO 中,12AO =,由勾股定理()2224R R =+-得94R =, ∴球的表面积814S π=,故选A.考点:球的体积和表面积6.B解析:B 【解析】 【分析】根据题意,将圆和直线的参数方程变形为普通方程,分析可得圆心不在直线上,再利用点到直线的距离公式计算可得圆心(1,3)-到直线320y x --=的距离2d <,得到直线与圆的位置关系为相交. 【详解】根据题意,圆的参数方程为1232x cos y sin θθ=-+⎧⎨=+⎩(θ为参数),则圆的普通方程为22(1)(3)4x y ++-=,其圆心坐标为(1,3)-,半径为2.直线的方程为2161x t y t =-⎧⎨=-⎩(t 为参数),则直线的普通方程为13(1)y x +=+,即320y x --=,圆心不在直线上.∴圆心(1,3)-到直线320y x --=的距离为33(1)2210219d -⨯--==<+,即直线与圆相交. 故选A. 【点睛】本题考查直线、圆的参数方程,涉及直线与圆的位置关系,解答本题的关键是将直线与圆的参数方程变形为普通方程.7.C解析:C 【解析】 【分析】由矩形的对角线互相平分且相等即球心到四个顶点的距离相等推出球心为AC 的中点,即可求出球的半径,代入体积公式即可得解. 【详解】因为矩形对角线互相平分且相等,根据外接球性质易知外接球球心到四个顶点的距离相等,所以球心在对角线AC 上,且球的半径为AC 长度的一半,即22115222r AC AB BC ==+=,所以334451253326V r πππ⎛⎫==⋅= ⎪⎝⎭.故选:C 【点睛】本题考查球与几何体的切、接问题,二面角的概念,属于基础题.8.D解析:D 【解析】该几何体为半圆柱,底面为半径为1的半圆,高为2,因此表面积为,选D.9.B解析:B 【解析】在①中,由面面平行的性质定理得m ∥β;在②中,m 与n 平行或异面;在③中,m 与β相交、平行或m ⊂β;在④中,由n ⊥α,m ⊥α,得m ∥n ,由n ⊥β,得m ⊥β. 【详解】由α,β为两个不同的平面,m ,n 为两条不同的直线,知:在①中,若α∥β,m ⊂α,则由面面平行的性质定理得m ∥β,故①正确; 在②中,若m ∥α,n ⊂α,则m 与n 平行或异面,故②错误;在③中,若α⊥β,α∩β=n ,m ⊥n ,则m 与β相交、平行或m ⊂β,故③错误; 在④中,若n ⊥α,m ⊥α,则m ∥n , 由n ⊥β,得m ⊥β,故④正确. 故选:B . 【点睛】本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力、推理论证能力,考查化归与转化思想,是中档题.10.D解析:D 【解析】 【分析】由题意可得,曲线22(1)4(1)x y y +-=…与直线4(2)y k x -=-有2个交点,数形结合求得k 的范围. 【详解】如图所示,化简曲线得到22(1)4(1)x y y +-=…,表示以(0,1)为圆心,以2为半径的上半圆,直线化为4(2)y k x -=-,过定点(2,4)A ,设直线与半圆的切线为AD ,半圆的左端点为(2,1)B -,当AD AB k k k <…,直线与半圆有两个交点, AD 221k =+,解得512AD k =,4132(2)4AB k -==--,所以53,124k ⎛⎤∈ ⎥⎝⎦.故选:D本题考查直线与圆的位置关系,属于中档题.11.D解析:D【解析】【分析】A中,根据面面平行的判定定理可得:α∥β或者α与β相交.B中,根据面面得位置关系可得:α∥β或者α与β相交.C中,则根据面面得位置关系可得:α∥β或者α与β相交.D中,在直线n上取一点Q,过点Q作直线m 的平行线m′,所以m′与n是两条相交直线,m′⊂β,n⊂β,且m′∥β,n∥α,根据面面平行的判定定理可得α∥β,即可得到答案.【详解】由题意,对于A中,若m,n是平面α内两条直线,且m∥β,n∥β,则根据面面平行的判定定理可得:α∥β或者α与β相交.所以A错误.对于B中,若α内不共线的三点到β的距离相等,则根据面面得位置关系可得:α∥β或者α与β相交.所以B错误.对于C中,若α,β都垂直于平面γ,则根据面面得位置关系可得:α∥β或者α与β相交.所以C错误.对于D中,在直线n上取一点Q,过点Q作直线m 的平行线m′,所以m′与n是两条相交直线,m′⊂β,n⊂β,且m′∥β,n∥α,根据面面平行的判定定理可得α∥β,所以D正确.故选D.【点睛】本题主要考查了平面与平面平行的判定与性质的应用,其中解答中灵活运用平面与平面平行额判定与性质进行判定是解答的关键,着重考查学生严密的思维能力和空间想象能力,属于基础题.12.B解析:B【解析】试题分析:①中AC⊥BE,由题意及图形知,AC⊥面DD1B1B,故可得出AC⊥BE,此命题正确;②EF∥平面ABCD,由正方体ABCD-A1B1C1D1的两个底面平行,EF在其一面上,故EF与平面ABCD无公共点,故有EF∥平面ABCD,此命题正确;③三棱锥A-BEF的体积为定值,由几何体的性质及图形知,三角形BEF的面积是定值,A点到面DD1B1B距离是定值,故可得三棱锥A-BEF的体积为定值,此命题正确;④由图形可以看出,B到线段EF的距离与A到EF的距离不相等,故△AEF的面积与△BEF的面积相等不正确考点:1.正方体的结构特点;2.空间线面垂直平行的判定与性质二、填空题13.【解析】【分析】先求出两相交直线的交点设出平行于直线的直线方程根据交点在直线上求出直线方程【详解】联立直线的方程得到两直线的交点坐标平行于直线的直线方程设为则所以直线的方程为:故答案为:【点睛】本题 解析:1934011x y ++= 【解析】【分析】先求出两相交直线的交点,设出平行于直线3470x y +-=的直线方程,根据交点在直线上,求出直线方程.【详解】 联立直线的方程23103470x y x y ++=⎧⎨+-=⎩,得到两直线的交点坐标135(,)1111-, 平行于直线3470x y +-=的直线方程设为340x y c ++=, 则1353()4()+01111c ⋅-+⋅= 所以直线的方程为:1934011x y ++= 故答案为:1934011x y ++= 【点睛】 本题考查了直线的交点,以及与已知直线平行的直线方程,考查了学生概念理解,转化与划归的能力,属于基础题.14.【解析】【分析】根据球心到四个顶点距离相等可推断出O 为CD 的中点且O A =OB =OC =OD 进而在△A0B 中利用余弦定理求得cos ∠AOB 的值则∠AOB 可求进而根据弧长的计算方法求得答案【详解】解:球心 解析:23π 【解析】【分析】根据球心到四个顶点距离相等可推断出O 为CD 的中点,且OA =OB =OC =OD ,进而在△A 0B 中,利用余弦定理求得cos ∠AOB 的值,则∠AOB 可求,进而根据弧长的计算方法求得答案.【详解】解:球心到四个顶点距离相等,故球心O 在CD 中点,则OA =OB =OC =OD =1,再由AB =A 0B 中,利用余弦定理cos ∠AOB 11312112+-==-⨯⨯, 则∠AOB 23π=,则弧AB 23π=•123π=. 故答案为:23π.本题主要考查了余弦定理的应用、四面体外接球的性质等,考查了学生观察分析和基本的运算能力.15.【解析】【分析】过作交于连接根据可得平面通过解三角形求得的值也即求得的值【详解】过作交于连接根据可得平面故由于所以由于所以在直角三角形中所以而故根据前面证得可得【点睛】本小题主要考查空间点位置的确定 解析:13 【解析】 【分析】 过B 作BF AC ⊥,交AC 于F ,连接EF ,根据BE AC ⊥,可得AC ⊥平面BEF ,通过解三角形求得:AF FC 的值,也即求得PE EC 的值. 【详解】过B 作BF AC ⊥,交AC 于F ,连接EF ,根据BE AC ⊥,可得AC ⊥平面BEF ,故AC EF ⊥,由于PA AC ⊥,所以//EF PA .由于AD CD =,所以π4DAC BAC ∠=∠=.在直角三角形ABF 中,π1,4AB BAF =∠=,所以2222AF AB ==,而22AC =,故:1:3AF FC =.根据前面证得//EF PA ,可得::1:3PE EC AF FC ==.【点睛】本小题主要考查空间点位置的确定,考查线面垂直的证明,考查简单的解特殊角三角形的知识.属于基础题.16.②③④【解析】【分析】作出此直二面角的图象由图形中所给的位置关系对命题逐一判断即可得出正确结论【详解】作出如图的图象E 是BD 的中点易得∠AED =90°即为此直二面角的平面角对于命题①AB 与平面BCD解析:②③④【解析】【分析】作出此直二面角的图象,由图形中所给的位置关系对命题逐一判断,即可得出正确结论.作出如图的图象,E是BD的中点,易得∠AED=90°即为此直二面角的平面角对于命题①AB与平面BCD所成的线面角的平面角是∠ABE=45°,故AB与平面BCD成60°的角不正确;对于命题②,在等腰直角三角形AEC中AC等于正方形的边长,故△ACD是等边三角形,此命题正确;对于命题③可取AD中点F,AC的中点H,连接EF,EH,FH,则EF,FH是中位线,故∠EFH或其补角为异面直线AB与CD所成角,又EF,FH其长度为正方形边长的一半,而EH是直角三角形AEC的中线,其长度是AC的一半即正方形边长的一半,故△EFH是等边三角形,由此AB与CD所成的角为60°,此命题正确;对于命题④,BD⊥面AEC,故AC⊥BD,此命题正确;对于命题⑤,连接BH,HD,则BH⊥AC, DH⊥AC,则∠BHD为二面角B AC D--的平面角,又BH=DH=32AC,BD=2,AC cos∠BHD=-1,3故二面角B AC D--不是120︒综上知②③④是正确的故答案为②③④【点睛】本题考查与二面角有关立体几何中线线之间的角的求法,线面之间的角的求法,以及线线之间位置关系的证明方法.综合性较强,对空间立体感要求较高.17.60°【解析】【分析】首先证得是二面角的平面角解直角三角形求得的大小【详解】由于是的中点所以由于所以平面所以由于平面所以而所以平面所以所以是二面角的平面角设则所以所以在中所以所以故答案为:【点睛】本 解析:60°【解析】【分析】首先证得EDC ∠是二面角E BD C --的平面角,解直角三角形求得EDC ∠的大小.【详解】由于SB BC =,E 是SC 的中点,所以SC BE ⊥,由于,SC DE DE BE E ⊥⋂=,所以SC ⊥平面BDE ,所以SC BD ⊥.由于SA ⊥平面ABC ,所以SA BD ⊥,而SA SC S ⋂=,所以BD ⊥平面SAC ,所以,BD DC BD DE ⊥⊥,所以EDC ∠是二面角E BD C --的平面角.设1SA AB ==,则SB BC ==2SC =,所以在Rt SAC ∆中,12SA SC =,所以30SCA ∠=o ,所以60EDC ∠=o . 故答案为:60o【点睛】 本小题主要考查二面角的求法,考查空间想象能力和逻辑推理能力,属于中档题. 18.【解析】【分析】将多面体分为四棱锥与三棱锥两部分相加求和即可【详解】如图将多面体分为四棱锥与三棱锥两部分其中四棱锥的高为为梯形则故多面体体积为故答案为:【点睛】本题主要考查了多面体体积的求解方法根据解析:【解析】【分析】将多面体ABC MNP -分为四棱锥N ACPM -与三棱锥N ABC -两部分相加求和即可.【详解】如图, 将多面体ABC MNP -分为四棱锥N ACPM -与三棱锥N ABC -两部分.其中四棱锥N ACPM -的高为2sin 60⨯︒=.ACPM 为梯形.则()3521323N ACPM V -+⨯=⨯=124323N ABC V -=⨯=.故多面体ABC MNP -+=故答案为:3【点睛】本题主要考查了多面体体积的求解方法,根据多面体的特征分为两个棱锥计算即可.属于中档题.19.【解析】【分析】当过球内一点的截面与垂直时截面面积最小可求截面半径即可求出过点的平面截球的截面面积的最小值【详解】解:棱长等于的正方体它的外接球的半径为3当过点的平面与垂直时截面面积最小故答案为:【 解析:3π.【解析】【分析】当过球内一点E 的截面与OE 垂直时,截面面积最小可求截面半径,即可求出过点E 的平面截球O 的截面面积的最小值.【详解】 解:棱长等于231111ABCD A B C D -,它的外接球的半径为3,||6OE = 当过点E 的平面与OE 垂直时,截面面积最小,963r -33S ππ=⨯=, 故答案为:3π.【点睛】本题考查过点E 的平面截球O 的截面面积的最小值及接体问题,找准量化关系是关键,属于中档题.20.【解析】【分析】根据题意可得平面所以得出为三棱锥的最长边根据直角三角形的性质边的中点到三棱锥的各顶点距离都相等所以为球心球直径即为【详解】平面平面平面所以三棱锥中最长边为设中点为在中所以三棱锥的外接 解析:43π 【解析】【分析】根据题意可得,BC ⊥平面PAC ,所以BC PC ⊥,得出PB 为三棱锥的最长边,PA AB ⊥,根据直角三角形的性质,PB 边的中点到三棱锥的各顶点距离都相等,所以为球心,球直径即为PB .【详解】PA ⊥Q 平面ABC ,BC ⊂平面ABC ,PA BC ∴⊥,,,AC BC PA AC A BC ⊥=∴⊥I 平面PAC ,BC PC ⊥,,,,,PB BC PB PC PA AC PC AC PC PA ∴>>⊥∴>>,所以三棱锥中最长边为2PB =,设PB 中点为O ,在,Rt PAB Pt PBC ∆∆中,12AO CO PB ==,所以三棱锥的外接球的球心为O , 半径为41,3V π∴=. 故答案为:43π. 【点睛】 本题考查几何体的“切”“接”球问题,确定球心是解题的关键,考查空间垂直的应用,属于中档题.三、解答题21.(1)35100x y -+=;(2)()2215x y -+=.【解析】【分析】(1)联立方程组,求出直线1:240l x y -+=和2:20l x y +-=的交点,再求出直线l 的斜率,可得直线l 的方程;(2)设出圆的标准方程,求出圆心与半径,即可求得圆的方程.【详解】(1)联立方程组24020x y x y -+=⎧⎨+-=⎩,解得02x y =⎧⎨=⎩, ∴直线240x y -+=和20x y +-=的交点()0,2P , 又∵直线5360x y +-=的斜率为53-,∴直线l 的斜率为35, ∴直线l 的方程为()3205y x -=-,化为一般式可得35100x y -+=. (2)设圆的标准方程为222()()x a y b r -+-=,2222(3)(1)()5a b r ∴-+-==,1a \=,0b =,∴圆的方程为22(1)5x y -+=.【点睛】本题考查直线、圆的方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.22.(1)证明见解析;(2)6π. 【解析】【分析】(1)取AC 的中点O ,连接OS 、OD ,证明出OS AC ⊥,OD AC ⊥,利用直线与平面垂直的判定定理可得出AC ⊥平面SOD ,即可证明出AC SD ⊥;(2)延长SO ,过点D 作SO 延长线的垂线,垂足记为H ,说明直线SD 与平面SAC 所成的角为OSD ∠,求出OSD ∆三边边长,利用余弦定理求出OSD ∠,即可求出直线SD 与平面SAC 所成角的大小.【详解】(1)取AC 的中点O ,连接OS 、OD , SAC ∆Q 为等边三角形,O 为AC 的中点,SO AC ∴⊥,D Q 、O 分别为AB 、AC 的中点,//OD BC ∴,BC AC ⊥Q ,OD AC ∴⊥, SO OD O =Q I ,AC ∴⊥平面SOD ,SD ⊂Q 平面SOD ,AC SD ∴⊥; (2)延长SO ,过点D 作SO 延长线的垂线,垂足记为H ,AC ⊥Q 平面SOD ,DH ⊂平面SOD ,DH AC ∴⊥,DH SO ⊥Q ,SO AC O =I ,DH ∴⊥平面SAC ,所以,直线SD 与平面SAC 所成的角为OSD ∠,由(2)知,1232OD BC ==AC BC ⊥Q ,228AB AC BC ∴+=. SAC ∆Q 是边长为4的等边三角形,4sin233SO π∴== 在SBC ∆中,4SC =,43BC =由余弦定理得2222cos 88SB SC BC SC BC SCB =+-⋅⋅∠=,222SB ∴=由余弦定理得2221cos 28SA AB SB SAB SA AB +-∠==-⋅, 2222cos 36SD SA AD SA AD SAD ∴=+-⋅⋅∠=,6SD ∴=.在SOD ∆中,由余弦定理得222cos 22SO SD OD OSD SO SD +-∠==⋅. 0OSD π<∠<Q ,6OSD π∴∠=,因此,直线SD 与平面SAC 所成角的大小为6π. 【点睛】 本题考查利用线面垂直的性质证明线线垂直,同时也考查了直线与平面所成角的计算,涉及到利用余弦定理解三角形,考查推理能力与计算能力,属于中等题.23.(1)证明见解析(2)6-【解析】【分析】(1)由BC ⊥AC ,BC ⊥CD 得BC ⊥平面ACD ,证明四边形DCBE 是平行四边形得DE ∥BC ,故而DE ⊥平面ACD ,从而得证面面垂直;(2)建立空间坐标系,求出两半平面的法向量,计算法向量的夹角得出二面角的大小.【详解】(1)证明:∵AB 是圆O 的直径,∴AC ⊥BC ,∵DC ⊥平面ABC ,BC ⊂平面ABC ,∴DC ⊥BC ,又DC ∩AC =C ,∴BC ⊥平面ACD ,∵DC ∥EB ,DC =EB ,∴四边形DCBE 是平行四边形,∴DE ∥BC ,∴DE ⊥平面ACD ,又DE ⊂平面ADE ,∴平面ACD ⊥平面ADE.(2)当C 点为半圆的中点时,AC =BC =,以C 为原点,以CA ,CB ,CD 为坐标轴建立空间坐标系如图所示:则D (0,0,1),E (0,,1),A (,0,0),B (0,,0), ∴AB =uu u r (﹣,,0),BE =u u u r (0,0,1),DE =uuu r (0,,0),DA =u u u r (0,﹣1),设平面DAE 的法向量为m =r (x 1,y 1,z 1),平面ABE 的法向量为n =r(x 2,y 2,z 2), 则00m DA m DE ⎧⋅=⎨⋅=⎩u u u v r u u u v r ,00n AB n BE ⎧⋅=⎨⋅=⎩u u u v r u u u v r,即11100z ⎧-=⎪⎨=⎪⎩,22200z ⎧-+=⎪⎨=⎪⎩, 令x 1=1得m =r (1,0,),令x 2=1得n =r (1,1,0).∴cos2 32m nm nm n⋅===⨯r rr rr r<,>.∵二面角D﹣AE﹣B是钝二面角,∴二面角D﹣AE﹣B的余弦值为26-.【点睛】本题考查了面面垂直的判定,空间向量与二面角的计算,属于中档题.24.(1)见解析;(2)见解析.【解析】【分析】(1)可证1AD CC⊥,AD BC⊥,从而可证AD⊥平面11BCC B.(2)取11A C的中点为G,连接1,EG B G,可证1//EF B G,从而可证//EF平面111A B C.【详解】由正三棱柱111ABC A B C-可得1C C⊥平面ABC,而AD⊂平面ABC,故1AD CC⊥.因为ABC∆为等边三角形,BD DC=,故AD BC⊥,因为1BC CC C=I,BC⊂平面11BCC B,1C C⊂平面11BCC B,所以AD⊥平面11BCC B.(2)取11A C的中点为G,连接1,EG B G.在11A AC∆,因为111,A G GC AE EC==,故111//,2EG AA EG AA=.由正三棱柱111ABC A B C-可得四边形11ABB A为平行四边形,故1111,//AA BB AA BB=,而1112B F BB=,所以11111//,2B F AA B F AA=,故11//,EG B F EG B F=,故四边形1B FEG为平行四边形,1//EF B G.因为EF⊄平面111A B C,1B G⊂平面111A B C,故//EF平面111A B C.【点睛】本题考查线面垂直与线面平行的证明,前者转化为线线垂直,注意平面中的两条直线需为相交直线,后者转化为线线平行,注意一条线是平面外,另一条线是平面内,本题属于中档题.25.(1)证明见解析;(2)证明见解析;(3)23. 【解析】【分析】(1)由题意可知DE P AB ,从而得证;(2)要证平面1ACB ⊥平面DEF ,转证EF ⊥平面1ACB ,即证AC EF ⊥,1EF CB ⊥; (3)利用等积法即可得到结果.【详解】(1)证明:因为三棱柱111ABC A B C -中,11A B P AB ,又因为,D E 分别为1111,AC B C 的中点,所以DE P 11A B ,于是DE P AB , AB ⊄平面DEF ,DE ⊂平面DEF ,所以AB P 平面DEF .(2) 在三棱柱111ABC A B C -中,1CC ⊥平面ABC ,AC ⊂平面ABC ,BC ⊂平面ABC所以1CC AC ⊥,1CC BC ⊥,又AC BC ⊥,1BC CC C ⋂=,1,BC CC ⊂平面11C BC B ,所以AC ⊥平面11C BC B ,EF ⊂平面11C BC B ,所以AC EF ⊥ ,又因为12BC CC ==, 1CC BC ⊥,所以侧面11C BC B 为正方形,故11BC CB ⊥ , 而,E F 分别为111,B C BB 的中点,连结1BC ,所以EF ‖1BC , 所以1EF CB ⊥ ,又1AC CB C ⋂=,1,AC CB ⊂平面1ACB , 所以EF ⊥平面1ACB ,又EF ⊂平面DEF ,所以平面1ACB ⊥平面DEF .(3) 1111233E ACB A ECB ECB V V S AC --∆==⋅= . 【点睛】垂直、平行关系证明中应用转化与化归思想的常见类型.(1)证明线面、面面平行,需转化为证明线线平行.(2)证明线面垂直,需转化为证明线线垂直.(3)证明线线垂直,需转化为证明线面垂直.26.(1)见解析(2)见解析【解析】【分析】(1)取AB 的中点P ,连接1,PM PB ,通过中位线定理求证四边形1PMNB 是平行四边形,进而求证;(2)连接1AB ,,设法证明11A B AB ⊥,111A B B C ⊥,进而证明1A B ⊥平面1AB N ,求得1A B AN ⊥.【详解】解:(1)如图,取AB 的中点P ,连接1,PM PB ,,M P Q 分别是,AC AB 的中点,//PM BC ∴,且12PM BC =,在直三棱柱11t ABC A B C -中, 11//BC B C ,11BC B C =, N Q 是11B C 的中点,∴1PM B N =,且1//PM B N , ∴四边形1PMNB 是平行四边形,1//MN PB ∴, 而MN ⊄平面11ABB A ,1PB ⊂平面11ABB A , //MN ∴平面11ABB A .(2)如图,连接1AB ,由111ABC A B C -是直三棱柱,90ABC ︒∠=,1AB AA =可知,111B C BB ⊥,1111B C A B ⊥,1111BB B A B =I , ∴11B C ⊥平面11A B BA ,111B C A B ∴⊥, 又Q 侧面11A B BA 为正方形,11A B AB ∴⊥,1111AB B C B ⋂=,1A B ∴⊥平面11AB C , 又AN ⊂平面11AB C ,1A B AN ∴⊥【点睛】本题考查线面平行,线线垂直的证明,属于中档题.。
2020-2021天津市育贤中学九年级数学上期末试题(带答案)
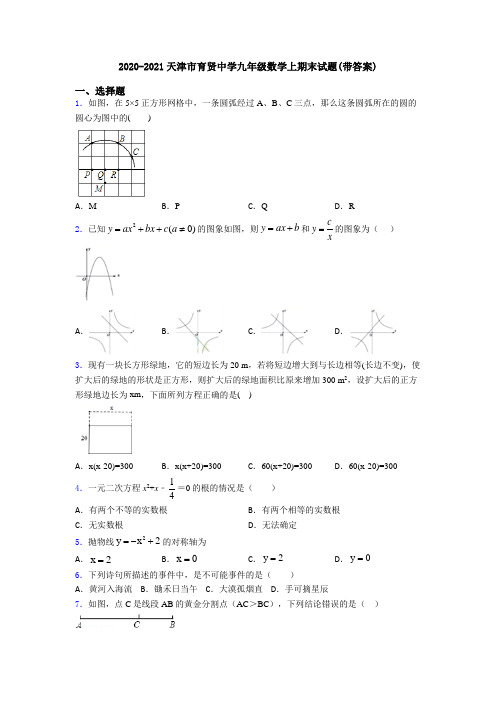
2020-2021天津市育贤中学九年级数学上期末试题(带答案)一、选择题1.如图,在5×5正方形网格中,一条圆弧经过A 、B 、C 三点,那么这条圆弧所在的圆的圆心为图中的( )A .MB .PC .QD .R2.已知2(0)y ax bx c a =++≠的图象如图,则y ax b =+和cy x=的图象为( )A .B .C .D .3.现有一块长方形绿地,它的短边长为20 m ,若将短边增大到与长边相等(长边不变),使扩大后的绿地的形状是正方形,则扩大后的绿地面积比原来增加300 m 2,设扩大后的正方形绿地边长为xm ,下面所列方程正确的是( )A .x(x-20)=300B .x(x+20)=300C .60(x+20)=300D .60(x-20)=3004.一元二次方程x 2+x ﹣14=0的根的情况是( ) A .有两个不等的实数根 B .有两个相等的实数根 C .无实数根D .无法确定5.抛物线2y x 2=-+的对称轴为 A .x 2=B .x 0=C .y 2=D .y 0=6.下列诗句所描述的事件中,是不可能事件的是( ) A .黄河入海流 B .锄禾日当午 C .大漠孤烟直 D .手可摘星辰7.如图,点C 是线段AB 的黄金分割点(AC >BC ),下列结论错误的是( )A .AC BCAB AC= B .2·BC AB BC =C .512AC AB -=D .0.618≈BCAC8.若关于x 的一元二次方程()26230a x x --+=有实数根,则整数a 的最大值是( ) A .4B .5C .6D .79.二次函数y=ax 2+bx+c (a≠0)的图象如图所示,则在下列各式子:①abc>0;②a+b+c>0;③a+c>b ;④2a+b=0;⑤∆=b 2-4ac<0中,成立的式子有( )A .②④⑤B .②③⑤C .①②④D .①③④ 10.正五边形绕着它的中心旋转后与它本身重合,最小的旋转角度数是( ) A .36°B .54°C .72°D .108°11.天虹商场一月份鞋帽专柜的营业额为100万元,三月份鞋帽专柜的营业额为150万元.设一到三月每月平均增长率为x ,则下列方程正确的是( ) A .100(1+2x )=150B .100(1+x )2=150C .100(1+x )+100(1+x )2=150D .100+100(1+x )+100(1+x )2=15012.如图,AB 是⊙O 的直径,弦CD ⊥AB ,垂足为点P ,若CD =AP =8,则⊙O 的直径为( )A .10B .8C .5D .3二、填空题13.有一人患了流感,经过两轮传染后共有169人患了流感,每轮传染中平均一个人传染了__人.14.设二次函数y =x 2﹣2x ﹣3与x 轴的交点为A ,B ,其顶点坐标为C ,则△ABC 的面积为_____.15.廊桥是我国古老的文化遗产如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面AB 高为8米的点E ,F 处要安装两盏警示灯,则这两盏灯的水平距离EF 是______米精确到1米16.从甲地到乙地有A ,B ,C 三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下: 公交车用时 公交车用时的频数 线路 3035t ≤≤ 3540t <≤ 4045t <≤ 4550t <≤ 合计A 59 151 166 124 500B 50 50 122 278 500 C4526516723500早高峰期间,乘坐_________(填“A”,“B”或“C”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.17.一个等边三角形边长的数值是方程x 2﹣3x ﹣10=0的根,那么这个三角形的周长为_____.18.关于x 的一元二次方程2ax x 10+-=有两个不相等的实数根,则实数a 的取值范围是______.19.已知x=2是关于x 的一元二次方程kx 2+(k 2﹣2)x+2k+4=0的一个根,则k 的值为_____.20.已知在同一坐标系中,抛物线y 1=ax 2的开口向上,且它的开口比抛物线y 2=3x 2+2的开口小,请你写出一个满足条件的a 值:_____.三、解答题21.如图,一农户要建一个矩形猪舍,猪舍的一边利用长为15m 的住房墙,另外三边用27m 长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m 宽的门,所围矩形猪舍的长,宽分别为多少米时,猪舍面积为96m 2?22.小明在解方程2210x x --=时出现了错误,其解答过程如下: 解:221x x -=-(第一步)22111x x -+=-+(第二步)2(1)0x -=(第三步)121x x==(第四步)(1)小明解答过程是从第几步开始出错的,写出错误原因.(2)请写出此题正确的解答过程.23.某童装店购进一批20元/件的童装,由销售经验知,每天的销售量y(件)与销售单价x(元)之间存在如图的一次函数关系.(1)求y与x之间的函数关系;(2)当销售单价定为多少时,每天可获得最大利润,最大利润是多少?24.石狮泰禾某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.(1)设每件童装降价x元时,每天可销售______ 件,每件盈利______ 元;(用x的代数式表示)(2)每件童装降价多少元时,平均每天赢利1200元.(3)要想平均每天赢利2000元,可能吗?请说明理由.25.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC 于点E,交AB的延长线于点F.(1)判断直线DE与⊙O的位置关系,并说明理由;(2)如果AB=5,BC=6,求DE的长.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】根据垂径定理的推论:弦的垂直平分线必过圆心,分别作AB,BC的垂直平分线即可得到答案.【详解】解:作AB的垂直平分线,作BC的垂直平分线,如图,它们都经过Q,所以点Q为这条圆弧所在圆的圆心.故选:C.【点睛】本题考查了垂径定理的推论:弦的垂直平分线必过圆心.这也常用来确定圆心的方法.2.C解析:C【解析】【分析】根据二次函数y=ax2+bx+c(a≠0)的图象可以得到a<0,b>0,c<0,由此可以判定y=ax+b经过一、二、四象限,双曲线cyx=在二、四象限.【详解】根据二次函数y=ax2+bx+c(a≠0)的图象,可得a<0,b>0,c<0,∴y=ax+b过一、二、四象限,双曲线cyx=在二、四象限,∴C是正确的.故选C.【点睛】此题考查一次函数,二次函数,反比例函数中系数及常数项与图象位置之间关系.3.A解析:A【解析】【分析】设扩大后的正方形绿地边长为xm,根据“扩大后的绿地面积比原来增加300m2”建立方程即可.【详解】设扩大后的正方形绿地边长为xm,根据题意得x(x-20)=300,故选A.【点睛】本题考查了由实际问题抽象出一元二次方程,解题的关键是弄清题意,并找到等量关系.4.A解析:A【解析】【分析】根据方程的系数结合根的判别式,可得出△=2>0,即可判断有两个不相等的实数根.【详解】∵△=12﹣4×1×(﹣14)=2>0,∴方程x2+x﹣14=0有两个不相等的实数根.故选:A.【点睛】本题考查了根的判别式,牢记“当△>0时,方程有两个不相等的实数根”是解题的关键.5.B解析:B【解析】【分析】根据顶点式的坐标特点,直接写出对称轴即可.【详解】解∵:抛物线y=-x2+2是顶点式,∴对称轴是直线x=0,即为y轴.故选:B.【点睛】此题考查了二次函数的性质,二次函数y=a(x-h)2+k的顶点坐标为(h,k),对称轴为直线x=h.6.D解析:D【解析】【分析】不可能事件是指在一定条件下,一定不发生的事件.【详解】A、是必然事件,故选项错误;B、是随机事件,故选项错误;C、是随机事件,故选项错误;D、是不可能事件,故选项正确.故选D.【点睛】此题主要考查了必然事件,不可能事件,随机事件的概念.理解概念是解决这类基础题的主要方法.必然事件指在一定条件下,一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.7.B解析:B 【解析】 【详解】 ∵AC >BC , ∴AC 是较长的线段,根据黄金分割的定义可知:AC BC AB AC =≈0.618, 故A 、C 、D 正确,不符合题意; AC 2=AB •BC ,故B 错误,符合题意; 故选B .8.B解析:B 【解析】 【分析】根据一元二次方程的定义和判别式的意义得到a-6≠0且△=(-2)2-4×(a-6)×3≥0,再求出两不等式的公共部分得到a ≤193且a ≠6,然后找出此范围内的最大整数即可. 【详解】根据题意得a-6≠0且△=(-2)2-4×(a-6)×3≥0, 解得a ≤193且a ≠6, 所以整数a 的最大值为5. 故选B. 【点睛】本题考查一元二次方程的定义和跟的判别式,一元二次方程的二次项系数不能为0;当一元二次方程有实数根时,△≥0.9.D解析:D 【解析】 【分析】根据二次函数的性质,利用数形结合的思想一一判断即可. 【详解】解:∵抛物线的开口向上, ∴a >0,∵对称轴在y轴的右侧,∴a,b异号,∴b<0,∵抛物线交y轴于负半轴,∴c<0,∴abc>0,故①正确,∵x=1时,y<0,∴a+b+c<0,故②错误,∵x=-1时,y>0,∴a-b+c>0,∴a+c>b,故③正确,∵对称轴x=1,∴-b2a=1,∴2a+b=0,故④正确,∵抛物线与x轴有两个交点,∴△=b2-4ac>0,故⑤错误,故选D.【点睛】本题考查二次函数的性质,解题的关键是熟练掌握基本知识,学会利用数形结合的思想解决问题,属于中考常考题型.10.C解析:C【解析】正五边形绕着它的中心旋转后与它本身重合,最小的旋转角度数是3605=72度,故选C.11.B解析:B【解析】【分析】可设每月营业额平均增长率为x,则二月份的营业额是100(1+x),三月份的营业额是100(1+x)(1+x),则可以得到方程即可.【详解】设二、三两个月每月的平均增长率是x.根据题意得:100(1+x)2=150,故选:B.【点睛】本题考查数量平均变化率问题.原来的数量为a,平均每次增长或降低的百分率为x的话,经过第一次调整,就调整到a×(1±x),再经过第二次调整就是a(1±x)(1±x)=a (1±x)2.增长用“+”,下降用“-”.12.A解析:A【解析】【分析】连接OC,先根据垂径定理求出PC的长,再根据勾股定理即可得出OC的长.【详解】连接OC,∵CD⊥AB,CD=8,∴PC=12CD=12×8=4,在Rt△OCP中,设OC=x,则OA=x,∵PC=4,OP=AP-OA=8-x,∴OC2=PC2+OP2,即x2=42+(8-x)2,解得x=5,∴⊙O的直径为10.故选A.【点睛】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.二、填空题13.12【解析】【分析】【详解】解:设平均一人传染了x人x+1+(x+1)x =169x=12或x=-14(舍去)平均一人传染12人故答案为12解析:12【解析】【分析】【详解】解:设平均一人传染了x人,x+1+(x+1)x=169x=12或x=-14(舍去).平均一人传染12人.故答案为12.14.8【解析】【分析】首先求出AB的坐标然后根据坐标求出ABCD的长再根据三角形面积公式计算即可【详解】解:∵y=x2﹣2x﹣3设y=0∴0=x2﹣2x﹣3解得:x1=3x2=﹣1即A点的坐标是(﹣10解析:8【解析】【分析】首先求出A、B的坐标,然后根据坐标求出AB、CD的长,再根据三角形面积公式计算即可.【详解】解:∵y=x2﹣2x﹣3,设y=0,∴0=x2﹣2x﹣3,解得:x1=3,x2=﹣1,即A点的坐标是(﹣1,0),B点的坐标是(3,0),∵y=x2﹣2x﹣3,=(x﹣1)2﹣4,∴顶点C的坐标是(1,﹣4),∴△ABC的面积=12×4×4=8,故答案为8.【点睛】本题考查了抛物线与x轴的交点,二次函数的性质,二次函数的三种形式的应用,主要考查学生运用性质进行计算的能力,题目比较典型,难度适中.15.85【解析】由于两盏EF距离水面都是8m因而两盏景观灯之间的水平距离就是直线y=8与抛物线两交点的横坐标差的绝对值故有-140x2+10=8即x2=80x1=45x2=-45所以两盏警示灯之间的水平解析:【解析】由于两盏E、F距离水面都是8m,因而两盏景观灯之间的水平距离就是直线y=8与抛物线两交点的横坐标差的绝对值.故有,即,,.所以两盏警示灯之间的水平距离为:16.C【解析】分析:样本容量相同观察统计表可以看出C线路上的公交车用时超过分钟的频数最小即可得出结论详解:样本容量相同C线路上的公交车用时超过分钟的频数最小所以其频率也最小故答案为C点睛:考查用频率估计解析:C【解析】分析:样本容量相同,观察统计表,可以看出C 线路上的公交车用时超过45分钟的频数最小,即可得出结论.详解:样本容量相同,C 线路上的公交车用时超过45分钟的频数最小,所以其频率也最小,故答案为C .点睛:考查用频率估计概率,读懂统计表是解题的关键.17.15【解析】【分析】先解方程求出方程的根再确定等边三角形的边长然后求等边三角形的周长【详解】解:x2﹣3x ﹣10=0(x ﹣5)(x+2)=0即x ﹣5=0或x+2=0∴x1=5x2=﹣2因为方程x2﹣解析:15【解析】【分析】先解方程求出方程的根,再确定等边三角形的边长,然后求等边三角形的周长.【详解】解:x 2﹣3x ﹣10=0,(x ﹣5)(x +2)=0,即x ﹣5=0或x +2=0,∴x 1=5,x 2=﹣2.因为方程x 2﹣3x ﹣10=0的根是等边三角形的边长,所以等边三角形的边长为5.所以该三角形的周长为:5×3=15.故答案为:15.【点睛】本题考查了一元二次方程的解法、等边三角形的周长等知识点.求出方程的解是解决本题的关键.18.且【解析】【分析】由关于x 的一元二次方程有两个不相等的实数根即可得判别式继而可求得a 的范围【详解】关于x 的一元二次方程有两个不相等的实数根解得:方程是一元二次方程的范围是:且故答案为:且【点睛】本题 解析:1a 4>-且a 0≠ 【解析】【分析】由关于x 的一元二次方程2ax x 10++=有两个不相等的实数根,即可得判别式0V >,继而可求得a 的范围.【详解】 Q 关于x 的一元二次方程2ax x 10+-=有两个不相等的实数根,()22b 4ac 14a 114a 0∴=-=-⨯⨯-=+>V , 解得:1a 4>-,Q 方程2ax 2x 10-+=是一元二次方程,a 0∴≠,a ∴的范围是:1a 4>-且a 0≠, 故答案为:1a 4>-且a 0≠. 【点睛】本题考查了一元二次方程判别式以及一元二次方程的定义,一元二次方程ax 2+bx+c=0(a ≠0)的根与△=b 2-4ac 有如下关系:(1)△>0方程有两个不相等的实数根;(2)△=0方程有两个相等的实数根;(3)△<0方程没有实数根. 19.﹣3【解析】【分析】把x=2代入kx2+(k2﹣2)x+2k+4=0得4k+2k2﹣4+2k+4=0再解关于k 的方程然后根据一元二次方程的定义确定k 的值即可【详解】把x=2代入kx2+(k2﹣2)x解析:﹣3【解析】【分析】把x=2代入kx 2+(k 2﹣2)x+2k+4=0得4k+2k 2﹣4+2k+4=0,再解关于k 的方程,然后根据一元二次方程的定义确定k 的值即可.【详解】把x=2代入kx 2+(k 2﹣2)x+2k+4=0得4k+2k 2﹣4+2k+4=0,整理得k 2+3k=0,解得k 1=0,k 2=﹣3,因为k≠0,所以k 的值为﹣3.故答案为:﹣3.【点睛】本题考查了一元二次方程的定义以及一元二次方程的解,能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.20.4【解析】【分析】由抛物线开口向上可知a >0再由开口的大小由a 的绝对值决定可求得a 的取值范围【详解】解:∵抛物线y1=ax2的开口向上∴a>0又∵它的开口比抛物线y2=3x2+2的开口小∴|a|>3解析:4【解析】【分析】由抛物线开口向上可知a >0,再由开口的大小由a 的绝对值决定,可求得a 的取值范围.【详解】解:∵抛物线y 1=ax 2的开口向上,∴a >0,又∵它的开口比抛物线y 2=3x 2+2的开口小,∴|a|>3,∴a >3,取a =4即符合题意【点睛】本题主要考查二次函数的性质,掌握二次函数的开口大小由a 的绝对值决定是解题的关键,即|a|越大,抛物线开口越小.三、解答题21.所围矩形猪舍的长为12m 、宽为8m【解析】【分析】设矩形猪舍垂直于住房墙一边长为xm 可以得出平行于墙的一边的长为(27﹣2x+1)m .根据矩形的面积公式建立方程求出其解就可以了.【详解】解:设矩形猪舍垂直于住房墙一边长为xm 可以得出平行于墙的一边的长为(27﹣2x+1)m ,由题意得x(27﹣2x+1)=96,解得:x 1=6,x 2=8,当x =6时,27﹣2x+1=16>15(舍去),当x =8时,27﹣2x+1=12.答:所围矩形猪舍的长为12m 、宽为8m .【点睛】本题考查了列一元二次方程解实际问题的运用,矩形的面积公式的运用及一元二次方程的解法的运用,解答时寻找题目的等量关系是关键.22.(1)一,移项没变号(或移项错误或等式性质用错均给分);(2)11x =21x =-【解析】【分析】(1)第一步即发生错误,移项未变号;(2)可将采用配方法解方程即可.【详解】(1)一,移项没变号(或移项错误或等式性质用错)(2)解:221x x -=22111x x -+=+()212x -=即,11x =,21x =【点睛】本题考查了解一元二次方程,熟悉各种解法的特点并灵活选择解法是解题关键.23.(1)y =﹣10x+700;(2)销售单价为45元时,每天可获得最大利润,最大利润为6250元【解析】【分析】(1)由一次函数的图象可知过(30,400)和(40,300),利用待定系数法可求得y 与x 的关系式;(2)利用x 可表示出p ,再利用二次函数的性质可求得p 的最大值.【详解】(1)设一次函数解析式为y =kx +b (k ≠0),由图象可知一次函数的过(30,400)和(40,300),代入解析式可得3040040300k b k b +=⎧⎨+=⎩, 解得:10700k b =-⎧⎨=⎩, ∴y 与x 的函数关系式为y =﹣10x +700;(2)设利润为p 元,由(1)可知每天的销售量为y 千克,∴p =y (x ﹣20)=(﹣10x +700)(x ﹣20)=﹣10x 2+900x ﹣14000=﹣10(x ﹣45)2+6250.∵﹣10<0,∴p =﹣10(x ﹣45)2+6250是开口向下的抛物线,∴当x =45时,p 有最大值,最大值为6250元,即销售单价为45元时,每天可获得最大利润,最大利润为6250元.【点睛】本题考查了二次函数的应用,求得每天的销售量y 与x 的函数关系式是解答本题的关键,注意二次函数最值的求法.24.(1)(20+2x ),(40﹣x );(2)每件童装降价20元或10元,平均每天赢利1200元;(3)不可能做到平均每天盈利2000元.【解析】【分析】(1)、根据销售量=原销售量+因价格下降而增加的数量;每件利润=原售价-进价-降价,列式即可;(2)、根据总利润=单件利润×数量,列出方程即可;(3)、根据(2)中的相关关系方程,判断方程是否有实数根即可.【详解】(1)、设每件童装降价x 元时,每天可销售20+2x 件,每件盈利40-x 元,故答案为(20+2x ),(40-x );(2)、根据题意可得:(20+2x)(40-x)=1200,解得:121020x x ==,,即每件童装降价10元或20元时,平均每天盈利1200元;(3)、(20+2x)(40-x)=2000, 230x 6000x -+=,∵此方程无解,∴不可能盈利2000元.【点睛】本题主要考查的是一元二次方程的实际应用问题,属于中等难度题型.解决这个问题的关键就是要根据题意列出方程.25.(1)相切,理由见解析;(2)DE=125. 【解析】【分析】(1)连接AD ,OD ,根据已知条件证得OD ⊥DE 即可;(2)根据勾股定理计算即可. 【详解】解:(1)相切,理由如下:连接AD ,OD ,∵AB 为⊙O 的直径,∴∠ADB=90°.∴AD ⊥BC .∵AB=AC ,∴CD=BD=12BC . ∵OA=OB ,∴OD ∥AC .∴∠ODE=∠CED .∵DE ⊥AC , ∴∠ODE=∠CED=90°. ∴OD ⊥DE .∴DE 与⊙O 相切.(2)由(1)知∠ADC=90°,∴在Rt △ADC 中,由勾股定理得, 222211()5(6)22AC BC -=-⨯=4. ∵S ACD =12AD•CD=12AC•DE , ∴12×4×3=12×5DE .∴DE=125.【点睛】本题主要考查直线与圆的位置关系,等腰三角形的性质、勾股定理等知识.正确大气层造辅助线是解题的关键.。
天津育贤中学高三数学理联考试题含解析

天津育贤中学高三数学理联考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知全集,集合,则(A)(B)(C)(D)参考答案:D,所以,选D.2. 设等差数列{a n}的前n项和为S n,若S8=32,则a2+a7=()A. 1 B. 4 C.8 D.9参考答案:考点:等差数列的前n项和.专题:等差数列与等比数列.分析:利用等差数列的通项公式和前n项和公式求解.解答:解:∵等差数列{a n}的前n项和为S n,S8=32,∴,∴a2+a7=8.故选:C.点评:本题考查等差数列的两项和的求法,是基础题,解题时要注意等差数列的性质的合理运用.3. 已知向量||=1,||=2,<,>=,则|+|为()A.9 B.7 C.3 D.参考答案:D【考点】向量的模.【分析】由向量的数量积运算得==,把已知的数据代入求解即可.【解答】解:由题意得, ====,故选:D.4. 函数f(x)=(x-3)ex的单调递增区间是()A.(-∞,2) B.(0,3) C.(1,4) D.(2,+∞)参考答案:D略5. 已知点在圆上,则函数的最小正周期和最小值分别为()A.B.C.D.参考答案:B6. 函数是奇函数,且在()内是增函数,,则不等式的解集为A.B.C.D.参考答案:D7. 已知集合A={x|x2﹣x﹣6≥0},B={x|﹣3≤x≤3},则A∩B等于()A.[﹣3,﹣2] B.[2,3] C.[﹣3,﹣2]∪{3} D.[2,3]∪{﹣3}参考答案:C【分析】根据题意,解不等式|x2﹣x﹣6≥0求出集合A,进而由交集的意义计算可得答案.【解答】解:根据题意,x2﹣x﹣6≥0?x≤﹣2或x≥3,即A={x|x2﹣x﹣6≥0}=(﹣∞,﹣2]∪[3,+∞),而B={x|﹣3≤x≤3}=[﹣3,3];A∩B=[﹣3,﹣2]∪{3};故选:C.【点评】本题考查集合的交集运算,关键是求出集合A.8. 已知椭圆与双曲线有相同的焦点F1,F2,点P 是两曲线的一个公共点,e1,e2又分别是两曲线的离心率,若PF1PF2,则的最小值为( )A. B.4 C. D.9参考答案:C【知识点】椭圆及其几何性质双曲线及其几何性质H5 H6由题意设焦距为2c,椭圆长轴长为2a1,双曲线实轴为2a2,令P在双曲线的右支上,由双曲线的定义|PF1|-|PF2|=2a2,①由椭圆定义|PF1|+|PF2|=2a1,②又∵PF1⊥PF2,∴|PF1|2+|PF2|2=4c2,③①2+②2,得|PF1|2+|PF2|2=2a12+2a22,④将④代入③,得a12+a22=2c2,∴4e12+e22=+= += +≥+2=.【思路点拨】由题意设焦距为2c,椭圆长轴长为2a1,双曲线实轴为2a2,令P在双曲线的右支上,由已知条件结合双曲线和椭圆的定义推志出a12+a22=2c2,由此能求出4e12+e22的最小值.9. 等差数列{a n}中,a4+a10+a16=30,则a18﹣2a14的值为()A.﹣20 B.﹣10 C.10 D.20参考答案:B【考点】等差数列的性质.【分析】由已知中等差数列{a n}中,a4+a10+a16=30,等差数列的性质,我们可以求出a10的值,根据等差数列的通项公式,我们即可求出a18﹣2a14的值.【解答】解:∵a4+a10+a16=30,∴3a10=30,∴a10=10,又∵a18﹣2a14=4d﹣a14=﹣a10=﹣10故选B10. 已知函数若始终存在实数,使得函数的零点不唯一,则的取值范围是()A. B. C. D.参考答案:C当a=0时,,则b=-4时, g(x)=f(x) -b的零点不唯一,选项A错误;当a=2时,,则时,g(x)=f(x) -b的零点不唯一,选项B错误;当a=3时,,函数在R上单调递增,则不存在实数b,使得函数g(x)=f(x) -b 的零点不唯一,选项D错误.本题选择C选项.点睛:分段函数中求参数范围问题:(1)问题中参数值影响变形时,往往要分类讨论,需有明确的标准、全面的考虑;(2)求解过程中,求出的参数的值或范围并不一定符合题意,因此要检验结果是否符合要求.二、填空题:本大题共7小题,每小题4分,共28分11. 已知函数若,则实数a = .参考答案:∵f[f(﹣1)]=-1,∴f[f(﹣1)]=f(2)=a?22=4a=-1∴.故答案为:.12. 等差数列{}的前n 项和为,已知,,则参考答案: 10。
天津育贤中学2021年高三数学文模拟试题含解析

天津育贤中学2021年高三数学文模拟试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 己知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是A.108cm3 B.92cm3C.84cm3D.100 cm3参考答案:D2.已知椭圆的离心率大于,是椭圆的两个焦点,若是正三角形,则点A.在椭圆外 B.在椭圆内 C.在椭圆上 D.不能确定参考答案:答案:A解析:,所以,故P在椭圆外,故选A。
3. 设函数,[x]表示不超过x的最大整数,则函数的值域是( ) A.{0,1} B.{0,-1} C.{-1,1} D.{1,1}参考答案:B略4. 设f(x)=x2-πx,α= arcsin,β=arctan,γ=arcos(-),δ=arccot(-),则(A)f(α)>f(β)>f(δ)>f(γ) (B) f(α)> f(δ)>f(β)>f(γ)(C) f(i)>f(α)>f(β)>f(γ) (D) f(δ)>f(α)>f(γ)>f(β)参考答案:B解:f(x)的对称轴为x=,易得, 0<α<<<β<<<γ<<<δ<.选B.5. 某圆的圆心在直线上,并且在两坐标轴上截得的弦长分别为4和8,则该圆的方程为 ( )A.B.C. 或D. 或参考答案:C略6. 已知满足,为导函数,且导函数的图象如图所示则的解集是()A.B. C.D.参考答案:B略7. 若函数在区间内单调递减,则的取值范围是()A .B .C .1,3) D .参考答案: C8. 若,且,则______ __.参考答案:9. 设,若对于任意,使得成立,则实数的取值范围是( )A .B .C .D .参考答案: A 略10.已知复数,则的虚部为()A 、1B 、C 、D 、参考答案: A由得,设,则,所以,解得,所以虚部为1,选A.二、 填空题:本大题共7小题,每小题4分,共28分11. 已知数列{a n }的前n 项和为S n ,且=,a 2=5,则S 6= .参考答案:722【考点】数列递推式;数列的求和.【分析】=,可得a n+1+1=3(a n +1),利用等比数列的通项公式与求和公式即可得出.【解答】解:∵ =,∴a n+1+1=3(a n +1),∴5+1=3(a 1+1),解得a 1=1.∴数列{a n +1}是等比数列,公比为3,首项为2. ∴a n +1=2×3n ﹣1,解得a n =2×3n ﹣1﹣1,则S 6=﹣6=722.故答案为:722.【点评】本题考查了等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题. 12. (在棱长为1的正方体ABCD ﹣A 1B 1C 1D 1中,点M 和N 分别是矩形ABCD 和BB 1C 1C 的中心,则过点A 、M 、N 的平面截正方体的截面面积为 _________ .参考答案:13. 过双曲线﹣=1(a >b >0)的左焦点F 作某一渐近线的垂线,分别与两渐近线相交于A ,B 两点,若,则双曲线的离心率为 .参考答案:【考点】双曲线的简单性质.【分析】方法一、运用两渐近线的对称性和条件,可得A 为BF 的中点,由垂直平分线的性质和等腰三角形的性质,可得Rt△OAB中,∠AOB=,求得渐近线的斜率,运用离心率公式即可得到;方法二、设过左焦点F作的垂线方程为,联立渐近线方程,求得交点A,B的纵坐标,由条件可得A为BF的中点,进而得到a,b的关系,可得离心率.【解答】解法一:由,可知A为BF的中点,由条件可得,则Rt△OAB中,∠AOB=,渐近线OB的斜率k==tan=,即离心率e===.解法二:设过左焦点F作的垂线方程为联立,解得,,联立,解得,,又,∴y B=﹣2y A∴3b2=a2,所以离心率.故答案为:.【点评】本题考查双曲线的性质和应用,主要是离心率的求法,解题时要认真审题,仔细解答,注意向量共线的合理运用.14. 若log2a≤1,则实数a的取值范围是.参考答案:(0,2]【考点】指、对数不等式的解法.【专题】计算题;转化思想;不等式的解法及应用.【分析】根据对数函数的性质转化为解不等式即可.【解答】解:∵底数为2大于1,是增函数,由log2a≤1,可得log2a≤log22∴a≤2.真数要大于0,即a>0.所以a的取值范围是:0<a≤2.故答案为(0,2].【点评】本题考查了对数函数的基本性质的运算.属于基础题.15. 已知一个圆锥的侧面展开图是圆心角为120°的扇形、底面圆的直径为2,则该圆锥的体积为.参考答案:π略16. 设y=f(x)为区间[0,1]上的连续函数,且恒有0≤f(x) ≤1,可以用随机模拟方法近似计算积分,先产生两组(每组N个)区间[0,1]上的均匀随机数,…,和,…,,由此得到N个点(,)(i=1,2,…,N),再数出其中满足((i=1,2,…,N))的点数,那么由随机模拟方法可得积分的近似值为 .参考答案:略17. 设点P、Q分别是曲线y=xe﹣x(e是自然对数的底数)和直线y=x+3上的动点,则P、Q两点间距离的最小值为.参考答案:考点:利用导数研究曲线上某点切线方程;两条平行直线间的距离.专题:导数的综合应用.分析:对曲线y=xe﹣x进行求导,求出点P的坐标,分析知道,过点P直线与直线y=x+2平行且与曲线相切于点P,从而求出P点坐标,根据点到直线的距离进行求解即可.解答:解:∵点P是曲线y=xe﹣x上的任意一点,和直线y=x+3上的动点Q,求P,Q两点间的距离的最小值,就是求出曲线y=xe﹣x上与直线y=x+3平行的切线与直线y=x+3之间的距离.由y′=(1﹣x)e﹣x ,令y′=(1﹣x)e﹣x =1,解得x=0,当x=0,y=0时,点P(0,0),P,Q两点间的距离的最小值,即为点P(0,0)到直线y=x+3的距离,∴d min=.故答案为:.点评:此题主要考查导数研究曲线上某点的切线方程以及点到直线的距离公式,利用了导数与斜率的关系,这是高考常考的知识点,是基础题.三、解答题:本大题共5小题,共72分。
2022年天津育贤中学高三数学文期末试卷含解析

2021-2022学年天津育贤中学高三数学文期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 现有四个函数①②③④的部分图象如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是( )A.①④②③B. ①④③②C.④①②③ D.③④②①参考答案:A2. 已知全集为R,A={x≤0},B={x|x>0},则?R(A∩B)=()A.(﹣∞,0]∪(1,+∞) B.(﹣∞,0][1,+∞) C.(﹣∞,﹣1) D.(﹣∞,﹣1]参考答案:A考点:交、并、补集的混合运算.专题:集合.分析:求出A中不等式的解集确定出A,找出A与B交集的补集即可.解答:解:由A中不等式变形得:(x﹣1)(x+1)≤0,且x+1≠0,解得:﹣1<x≤1,即A=(﹣1,1],∵B=(0,+∞),∴A∩B=(0,1],则?R(A∩B)=(﹣∞,0]∪(1,+∞),故选:A.点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.3.在抽查某产品尺寸过程中,将其尺寸分成若干组,[a,b]是其中一组,已知该组上的直方图高为h,则该组频率为()A. B. C. D.参考答案:答案:D4. 已知是双曲线的左、右焦点,过的直线与双曲线的左右两支分别交于点,若为等边三角形,则双曲线的离心率为()A.B.4 C. D.参考答案:A5. 设集合,集合,则等于A. B.C. D.参考答案:C略6. 下列函数中,在上为增函数的是A、 B、 C、 D、参考答案:B7. 已知集合A={x|1<x2<4},B={x|x﹣1≥0},则A∩B=()A.(1,2)B.[1,2)C.(﹣1,2)D.[﹣1,2)参考答案:A【考点】1E:交集及其运算.【分析】解不等式化简集合A、B,根据交集的定义写出A∩B.【解答】解:集合A={x|1<x2<4}={x|﹣2<x<﹣1或1<x<2},B={x|x﹣1≥0}={x|x≥1},则A∩B={x|1<x<2}=(1,2).故选:A.8. 若函数与图象的交点在直线的两侧,则实数t的取值范围是A. B.C. D.参考答案:B9. 已知等差数列{a n}中,a4=5,a9=17,则a14=()A. 11 B.22 C.29 D.12参考答案:考点:等差数列的通项公式.专题:等差数列与等比数列.分析:由等由差数列的性质可得2a9=a14+a4,代入数据计算可得.解答:解:∵等差数列{a n}中,a4=5,a9=17,∴由等由差数列的性质可得2a9=a14+a4,∴2×17=a14+5,解得a14=29故选:C 点评:本题考查等差数列的通项公式和性质,属基础题.10. 若函数f(x)=8x2-lnx在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k 的取值范围是()A.[1,+∞)B.[1,) C.[1, 2) D.[,2)参考答案:B二、填空题:本大题共7小题,每小题4分,共28分11. 利用分层抽样的方法在学生总数为800的年级中抽取20名同学,其中女生人数为8人,则该年级男生人数为.参考答案:480【考点】系统抽样方法.【分析】先求得分层抽样的抽取比例,根据样本中女生抽到的人数,求总体中女生数,可得总体中男生数.【解答】解由于样本容量为20,则男生的人数为12人,则该年级男生人数为×800=480,故答案为:480【点评】本题考查了分层抽样方法,熟练掌握分层抽样的特征是解答本题的关键.12. 已知D、E分别是△ABC边AB、AC上的点,且BD=2AD,AE=2EC,点P是线段DE上的任意一点,若=x+y,则xy 的最大值为.参考答案:【考点】9H:平面向量的基本定理及其意义.【分析】BD=2AD,AE=2EC,点P是线段DE上的任意一点, =x+y,可得=3x+,利用向量共线定理可得=1,再利用基本不等式的性质即可得出.【解答】解:如图所示,∵BD=2AD,AE=2EC,点P是线段DE上的任意一点, =x+y,∴=3x+,∴=1,∴2x+y=. ∵x,y >0,∵,,当且仅当y=2x=时取等号.则xy 的最大值为.故答案为:.13. 若复数(i 为虚数单位)为纯虚数,则实数m=▲ .参考答案:-114. 在三棱锥P-ABC 中,平面ABC,AB=BC=2,PB=2,则点B 到平面PAC的距离是 .参考答案:略15. 如图,在直角梯形ABCD 中,已知BC∥AD ,AB⊥AD,AB =4,BC =2,AD =4,若P 为CD 的中点,则的值为________.参考答案:建立坐标系,应用坐标运算求数量积.以点A 为坐标原点,AD 、AB 所在直线为x 、y 轴建立平面直角坐标系,则A(0,0),B(0,4),C(2,4),D(4,0),P(3,2),所以=(-3,-2)·(-3,2)=5.16. 在平面直角坐标系中,已知直线与曲线的参数方程分别为:(为参数)和:(为参数),若与相交于、两点,则.参考答案:17. 如果随机变量,且,则________.参考答案:略三、 解答题:本大题共5小题,共72分。
2020-2021高三数学下期末试题带答案(12)

2020-2021高三数学下期末试题带答案(12)一、选择题1.给出下列说法:①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线; ②有一个面是多边形,其余各面都是三角形的几何体是棱锥; ③棱台的上、下底面可以不相似,但侧棱长一定相等. 其中正确说法的个数是( ) A .0 B .1C .2D .32.()()31i 2i i --+=( )A .3i +B .3i --C .3i -+D .3i - 3.若设a 、b 为实数,且3a b +=,则22a b +的最小值是( )A .6B .8C .26D .424.设双曲线2222:1x y C a b-=(00a b >>,)的左、右焦点分别为12F F ,,过1F 的直线分别交双曲线左右两支于点M N ,,连结22MF NF ,,若220MF NF ⋅=u u u u v u u u u v,22MF NF =u u u u v u u u u v ,则双曲线C 的离心率为( ). A .2 B .3C .5D .65.设集合,,则=( )A .B .C .D .6.设F 为双曲线C :22221x y a b-=(a >0,b >0)的右焦点,O 为坐标原点,以OF 为直径的圆与圆x 2+y 2=a 2交于P 、Q 两点.若|PQ |=|OF |,则C 的离心率为 A 2 B 3C .2D 57.若双曲线22221x y a b-=3,则其渐近线方程为( )A .y=±2xB .y=2xC .12y x =±D .22y x =±8.渐近线方程为0x y ±=的双曲线的离心率是( ) A .22B .1C 2D .29.在[0,2]π内,不等式3sin x <的解集是( )A .(0)π,B .4,33ππ⎛⎫⎪⎝⎭C .45,33ππ⎛⎫⎪⎝⎭D .5,23ππ⎛⎫⎪⎝⎭10.如图所示的组合体,其结构特征是( )A .由两个圆锥组合成的B .由两个圆柱组合成的C .由一个棱锥和一个棱柱组合成的D .由一个圆锥和一个圆柱组合成的11.定义运算()()a ab a b b a b ≤⎧⊕=⎨>⎩,则函数()12xf x =⊕的图象是( ). A . B .C .D .12.在△ABC 中,AB=2,AC=3,1AB BC ⋅=u u u r u u u r则BC=______ A 3B 7C 2D 23二、填空题13.复数()1i i +的实部为 .14.已知函数()sin ([0,])f x x x π=∈和函数1()tan 2g x x =的图象交于,,A B C 三点,则ABC ∆的面积为__________.15.若函数3211()232f x x x ax =-++ 在2,3⎡⎫+∞⎪⎢⎣⎭上存在单调增区间,则实数a 的取值范围是_______.16.已知复数z=(1+i )(1+2i ),其中i 是虚数单位,则z 的模是__________ 17.若45100a b ==,则122()a b+=_____________. 18.锐角△ABC 中,若B =2A ,则ba的取值范围是__________.19.若函数2()1ln f x x x a x =-++在(0,)+∞上单调递增,则实数a 的最小值是__________.20.在区间[1,1]-上随机取一个数x ,cos2xπ的值介于1[0,]2的概率为 .三、解答题21.已知复数12i z m =-,复数21i z n =-,其中i 是虚数单位,m ,n 为实数. (1)若1m =,1n =-,求12z z +的值; (2)若212z z =,求m ,n 的值.22.设()34f x x x =-+-.(Ⅰ)求函数()2()g x f x =-的定义域;(Ⅱ)若存在实数x 满足()1f x ax ≤-,试求实数a 的取值范围.23.“微信运动”是手机APP 推出的多款健康运动软件中的一款,大学生M 的微信好友中有400位好友参与了“微信运动”.他随机抽取了40位参与“微信运动”的微信好友(女20人,男20人)在某天的走路步数,经统计,其中女性好友走路的步数情况可分为五个类别:A 、02000:步,(说明:“02000:”表示大于或等于0,小于2000,以下同理),B 、20005000:步,C 、50008000:步,D 、800010000:步,E 、1000012000:步,且A 、B 、C 三种类别的人数比例为1:4:3,将统计结果绘制如图所示的柱形图;男性好友走路的步数数据绘制如图所示的频率分布直方图.(Ⅰ)若以大学生M 抽取的微信好友在该天行走步数的频率分布,作为参与“微信运动”的所有微信好友每天走路步数的概率分布,试估计大学生M 的参与“微信运动”的400位微信好友中,每天走路步数在20008000:的人数;(Ⅱ)若在大学生M 该天抽取的步数在800010000:的微信好友中,按男女比例分层抽取6人进行身体状况调查,然后再从这6位微信好友中随机抽取2人进行采访,求其中至少有一位女性微信好友被采访的概率.24.已知等差数列{}n a 满足:12a =,且1a ,2a ,5a 成等比数列. (1)求数列{}n a 的通项公式;(2)记n S 为数列{}n a 的前n 项和,是否存在正整数n ,使得60800n S n >+ ?若存在,求n 的最小值;若不存在,说明理由.25.在直角坐标平面内,以原点O 为极点,x 轴的非负半轴为极轴建立极坐标系.已知点A ,B 的极坐标分别为()π42,,5π224⎛⎫ ⎪⎝⎭,,曲线C 的方程为r ρ=(0r >).(1)求直线AB 的直角坐标方程;(2)若直线AB 和曲线C 有且只有一个公共点,求r 的值. 26.已知0,0a b >>. (1)求证:211ab a b≥+ ;(2)若a b >,且2ab =,求证:224a b a b+≥-.【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【解析】 【分析】①②③根据定义得结论不一定正确.④画图举出反例说明题目是错误的. 【详解】解:①不一定,只有这两点的连线平行于轴时才是母线;②不一定,因为“其余各面都是三角形”并不等价于“其余各面都是有一个公共顶点的三角形”,如图(1)所示;③不一定.当以斜边所在直线为旋转轴时,其余两边旋转形成的面所围成的几何体不是圆锥,如图(2)所示,它是由两个同底圆锥组成的几何体;④错误,棱台的上、下底面是相似且对应边平行的多边形,各侧棱延长线交于一点,但是侧棱长不一定相等. 故答案为:A【点睛】(1)要想真正把握几何体的结构特征,必须多角度、全面地去分析,多观察实物,提高空间想象能力;(2)紧扣结构特征是判断的关键,熟悉空间几何体的结构特征,依据条件构建几何模型,在条件不变的情况下,变换模型中的线面关系或增加线、面等基本元素,然后再依据题意判定; (3)通过反例对结构特征进行辨析,即要说明一个命题是错误的,只要举出一个反例即可.2.B解析:B 【解析】 【分析】先分别对分子和分母用乘法公式化简,再分子分母同时乘以分母的共轭复数,化简即得最后结果. 【详解】 由题意得,复数()()()31i 2i 13i i 13i 3i i ii i--+-+⋅-+===----⋅.故应选B【点睛】本小题主要考查复数的乘法和除法的运算,乘法的运算和实数的运算类似,只需要记住2i 1=-.除法的运算记住的是分子分母同时乘以分母的共轭复数,这一个步骤称为分母实数化,分母实数化的主要目的是将分母变为实数,然后将复数的实部和虚部求出来.属于基础题.3.D解析:D 【解析】 【分析】2a b+≤转化为指数运算即可求解。
2020-2021高三数学下期末试卷(带答案)(16)

2020-2021高三数学下期末试卷(带答案)(16)一、选择题1.给出下列说法:①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线; ②有一个面是多边形,其余各面都是三角形的几何体是棱锥; ③棱台的上、下底面可以不相似,但侧棱长一定相等. 其中正确说法的个数是( ) A .0B .1C .2D .32.已知平面向量a r=(1,-3),b r=(4,-2),a b λ+rr与a r垂直,则λ是( ) A .2B .1C .-2D .-13.设ω>0,函数y=sin(ωx+3π)+2的图象向右平移43π个单位后与原图象重合,则ω的最小值是 A .23B .43C .32D .34.设01p <<,随机变量ξ的分布列如图,则当p 在()0,1内增大时,( )A .()D ξ减小B .()D ξ增大C .()D ξ先减小后增大D .()D ξ先增大后减小5.甲、乙、丙三人到三个不同的景点旅游,每人只去一个景点,设事件A 为“三个人去的景点各不相同”,事件B 为“甲独自去一个景点,乙、丙去剩下的景点”,则(A |B)P 等于( ) A .49B .29C .12D .136.已知函数()25,1,,1,x ax x f x a x x⎧---≤⎪=⎨>⎪⎩是R 上的增函数,则a 的取值范围是( )A .30a -≤<B .0a <C .2a ≤-D .32a --≤≤7.设R λ∈,则“3λ=-”是“直线2(1)1x y λλ+-=与直线()614x y λ+-=平行”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件 8.已知236a b ==,则a ,b 不可能满足的关系是() A .a b ab += B .4a b +> C .()()22112a b -+-<D .228a b +>9.已知某几何体的三视图(单位:cm )如图所示,则该几何体的体积是( )A .108cm 3B .100cm 3C .92cm 3D .84cm 310.在ABC V 中,若 13,3,120AB BC C ==∠=o ,则AC =( ) A .1 B .2C .3D .4 11.若实数满足约束条件,则的最大值是( )A .B .1C .10D .1212.在[0,2]π内,不等式3sin x <的解集是( ) A .(0)π,B .4,33ππ⎛⎫⎪⎝⎭C .45,33ππ⎛⎫⎪⎝⎭D .5,23ππ⎛⎫⎪⎝⎭二、填空题13.若双曲线22221x y a b-=()0,0a b >>两个顶点三等分焦距,则该双曲线的渐近线方程是___________.14.已知函数21,1()()1a x x f x x a x ⎧-+≤=⎨->⎩,函数()2()g x f x =-,若函数()()y f x g x =-恰有4个不同的零点,则实数a 的取值范围为______. 15.在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c ,若3A π=,3a =b=1,则c =_____________16.若9()a x x-的展开式中3x 的系数是84-,则a = .17.等边三角形ABC 与正方形ABDE 有一公共边AB ,二面角C AB D --的余弦值为33,M N ,分别是AC BC ,的中点,则EM AN ,所成角的余弦值等于 . 18.设等比数列{}n a 满足a 1+a 3=10,a 2+a 4=5,则a 1a 2…a n 的最大值为 . 19.函数()23s 34f x in x cosx =+-(0,2x π⎡⎤∈⎢⎥⎣⎦)的最大值是__________. 20.ABC △的内角,,A B C 的对边分别为,,a b c .若π6,2,3b ac B ===,则ABC △的面积为__________.三、解答题21.已知圆O 1和圆O 2的极坐标方程分别为ρ=2,ρ2-2ρcos(θ-)=2.(1)把圆O 1和圆O 2的极坐标方程化为直角坐标方程. (2)求经过两圆交点的直线的极坐标方程.22.已知菱形ABCD 的顶点A ,C 在椭圆2234x y +=上,对角线BD 所在直线的斜率为1.(1)当直线BD 过点(0,1)时,求直线AC 的方程. (2)当60ABC ∠=︒时,求菱形ABCD 面积的最大值.23.如图,在三棱柱111ABC A B C -中,H 是正方形11AA B B 的中心,122AA =,1C H ⊥平面11AA B B ,且1 5.C H =(Ⅰ)求异面直线AC 与11A B 所成角的余弦值; (Ⅱ)求二面角111A AC B --的正弦值;(Ⅲ)设N 为棱11B C 的中点,点M 在平面11AA B B 内,且MN ⊥平面111A B C ,求线段BM 的长.24.已知函数1(1)f x m x x =---+. (1)当5m =时,求不等式()2f x >的解集;(2)若二次函数223y x x =++与函数()y f x =的图象恒有公共点,求实数m 的取值范围.25.在直角坐标平面内,以原点O 为极点,x 轴的非负半轴为极轴建立极坐标系.已知点A ,B 的极坐标分别为()π42,,5π224⎛⎫ ⎪⎝⎭,,曲线C 的方程为r ρ=(0r >).(1)求直线AB 的直角坐标方程;(2)若直线AB 和曲线C 有且只有一个公共点,求r 的值. 26.商场销售某种商品的经验表明,该商品每日的销售量(单位:千克)与销售价格(单位:元/千克)满足关系式,其中,为常数,已知销售价格为5元/千克时,每日可售出该商品11千克. (1) 求的值;(2) 若商品的成品为3元/千克, 试确定销售价格的值,使商场每日销售该商品所获得的利润最大【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【解析】 【分析】①②③根据定义得结论不一定正确.④画图举出反例说明题目是错误的. 【详解】解:①不一定,只有这两点的连线平行于轴时才是母线;②不一定,因为“其余各面都是三角形”并不等价于“其余各面都是有一个公共顶点的三角形”,如图(1)所示;③不一定.当以斜边所在直线为旋转轴时,其余两边旋转形成的面所围成的几何体不是圆锥,如图(2)所示,它是由两个同底圆锥组成的几何体;④错误,棱台的上、下底面是相似且对应边平行的多边形,各侧棱延长线交于一点,但是侧棱长不一定相等. 故答案为:A【点睛】(1)要想真正把握几何体的结构特征,必须多角度、全面地去分析,多观察实物,提高空间想象能力;(2)紧扣结构特征是判断的关键,熟悉空间几何体的结构特征,依据条件构建几何模型,在条件不变的情况下,变换模型中的线面关系或增加线、面等基本元素,然后再依据题意判定; (3)通过反例对结构特征进行辨析,即要说明一个命题是错误的,只要举出一个反例即可.2.D解析:D 【解析】 【详解】试题分析:()()(),34,24,32a b λλλλλ+=-+-=+--r r ,由a b λ+r r 与a r 垂直可知()()()·0433201a b a λλλλ+=∴+---=∴=-r r r考点:向量垂直与坐标运算3.C解析:C 【解析】 函数sin 23y x πω⎛⎫=++ ⎪⎝⎭的图象向右平移43π个单位后44sin 2sin 23333w y w x wx ππππ⎡⎤⎛⎫⎛⎫=-++=+-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦所以有43332013222w k k k w w k w ππ=∴=>∴≥∴=≥Q 故选C4.D解析:D 【解析】 【分析】先求数学期望,再求方差,最后根据方差函数确定单调性. 【详解】111()0122222p p E p ξ-=⨯+⨯+⨯=+Q , 2222111111()(0)(1)(2)2222224p p D p p p p p ξ-∴=--+--+--=-++, 1(0,1)2∈Q ,∴()D ξ先增后减,因此选D. 【点睛】222111(),()(())().n n ni i i i i i i i i E x p D x E p x p E ξξξξ=====-=-∑∑∑5.C解析:C 【解析】 【分析】这是求甲独自去一个景点的前提下,三个人去的景点不同的概率,求出相应的基本事件的个数,即可得出结果. 【详解】甲独自去一个景点,则有3个景点可选,乙、丙只能在剩下的两个景点选择,根据分步乘法计数原理可得,对应的基本事件有32212⨯⨯=种;另外,三个人去不同景点对应的基本事件有3216⨯⨯=种,所以61(/)122P A B ==,故选C. 【点睛】本题主要考查条件概率,确定相应的基本事件个数是解决本题的关键.6.D解析:D 【解析】 【分析】根据分段函数的单调性特点,两段函数在各自的定义域内均单调递增,同时要考虑端点处的函数值. 【详解】要使函数在R 上为增函数,须有()f x 在(,1]-∞上递增,在(1,)+∞上递增,所以21,20,115,1aa a a ⎧-≥⎪⎪<⎨⎪⎪--⨯-≤⎩,解得32a --≤≤.故选D. 【点睛】本题考查利用分段函数的单调性求参数的取值范围,考查数形结合思想、函数与方程思想的灵活运用,求解时不漏掉端点处函数值的考虑.7.A解析:A 【解析】 【分析】当3λ=-时,两条直线是平行的,但是若两直线平行,则3λ=-或1λ=,从而可得两者之间的关系.【详解】当3λ=-时,两条直线的方程分别为:6410x y ++=,3220x y +-=,此时两条直线平行;若两条直线平行,则()()2161λλλ⨯-=--,所以3λ=-或1λ=,经检验,两者均符合,综上,“3λ=-”是“直线()211x y λλ+-=与直线()614x y λ+-=平行” 的充分不必要条件,故选A. 【点睛】充分性与必要性的判断,可以依据命题的真假来判断,若“若p 则q ”是真命题,“若q 则p ”是假命题,则p 是q 的充分不必要条件;若“若p 则q ”是真命题,“若q 则p ”是真命题,则p 是q 的充分必要条件;若“若p 则q ”是假命题,“若q 则p ”是真命题,则p 是q 的必要不充分条件;若“若p 则q ”是假命题,“若q 则p ”是假命题,则p 是q 的既不充分也不必要条件.8.C解析:C 【解析】 【分析】根据236a b ==即可得出21l 3og a =+,31l 2og b =+,根据23log log 132⋅=,33log log 222+>,即可判断出结果.【详解】 ∵236a b ==;∴226log 1og 3l a ==+,336log 1og 2l b ==+;∴2332log 2log 4a b +=++>,2332log og 42l ab =++>,故,A B 正确;()()()()2322223211log log 2log 323log 22a b =>⋅-+-+=,故C 错误;∵()()()22232223log log 2log 2323log 2a b =+++++232l 23og log 82>+=⋅,故D 正确故C . 【点睛】本题主要考查指数式和对数式的互化,对数的运算,以及基本不等式:a b +≥和不等式222a b ab +≥的应用,属于中档题9.B解析:B 【解析】试题分析:由三视图可知:该几何体是一个棱长分别为6,6,3,砍去一个三条侧棱长分别为4,4,3的一个三棱锥(长方体的一个角).据此即可得出体积.解:由三视图可知:该几何体是一个棱长分别为6,6,3,砍去一个三条侧棱长分别为4,4,3的一个三棱锥(长方体的一个角). ∴该几何体的体积V=6×6×3﹣=100.故选B .考点:由三视图求面积、体积.10.A解析:A 【解析】余弦定理2222?cos AB BC AC BC AC C =+-将各值代入 得2340AC AC +-=解得1AC =或4AC =-(舍去)选A.11.C解析:C 【解析】 【分析】本题是简单线性规划问题的基本题型,根据“画、移、解”等步骤可得解.题目难度不大题,注重了基础知识、基本技能的考查. 【详解】在平面直角坐标系内画出题中的不等式组表示的平面区域为以为顶点的三角形区域(包含边界),由图易得当目标函数经过平面区域的点时,取最大值.【点睛】解答此类问题,要求作图要准确,观察要仔细.往往由于由于作图欠准确而影响答案的准确程度,也有可能在解方程组的过程中出错.12.C解析:C【解析】【分析】根据正弦函数的图象和性质,即可得到结论.【详解】解:在[0,2π]内,若sin x3<,则43π<x53π<,即不等式的解集为(43π,53π),故选:C.【点睛】本题主要考查利用三角函数的图象与性质解不等式,考查数形结合的思想,属于基础题.二、填空题13.【解析】【分析】由题意知渐近线方程是再据得出与的关系代入渐近线方程即可【详解】∵双曲线的两个顶点三等分焦距∴又∴∴渐近线方程是故答案为【点睛】本题考查双曲线的几何性质即双曲线的渐近线方程为属于基础题解析:y =±【解析】 【分析】由题意知,渐近线方程是b y x a =±,1223a c =⨯,再据222c ab =+,得出 b 与a 的关系,代入渐近线方程即可. 【详解】∵双曲线22221x y a b-= (0,0)a b >>的两个顶点三等分焦距,∴1223a c =⨯,3c a =,又222c a b =+,∴b =∴渐近线方程是by x a=±=±,故答案为y =±. 【点睛】本题考查双曲线的几何性质即双曲线22221x y a b-= (0,0)a b >>的渐近线方程为b y xa =±属于基础题.14.【解析】【分析】由函数把函数恰有个不同的零点转化为恰有4个实数根列出相应的条件即可求解【详解】由题意函数且函数恰有个不同的零点即恰有4个实数根当时由即解得或所以解得;当时由解得或所以解得综上可得:实 解析:(]2,3【解析】 【分析】由函数()2()g x f x =-,把函数()()y f x g x =-恰有4个不同的零点,转化为()1f x =恰有4个实数根,列出相应的条件,即可求解. 【详解】由题意,函数()2()g x f x =-,且函数()()y f x g x =-恰有4个不同的零点, 即()1f x =恰有4个实数根,当1x ≤时,由11a x -+=,即110x a +=-≥,解得2=-x a 或x a =-,所以2112a a a a -≤⎧⎪-≤⎨⎪-≠-⎩,解得13a <?;当1x >时,由2()1x a -=,解得1x a =-或1x a =+,所以1111a a ->⎧⎨+>⎩,解得2a >,综上可得:实数a 的取值范围为(]2,3.【点睛】本题主要考查了函数与方程的应用,其中解答中利用条件转化为()1f x =,绝对值的定义,以及二次函数的性质求解是解答的关键,着重考查了数形结合思想,以及推理与计算能力,属于中档试题. 15.2【解析】【分析】根据条件利用余弦定理可建立关于c 的方程即可解出c 【详解】由余弦定理得即解得或(舍去)故填2【点睛】本题主要考查了利用余弦定理求三角形的边属于中档题解析:2【解析】【分析】根据条件,利用余弦定理可建立关于c 的方程,即可解出c.【详解】由余弦定理2222cos a b c bc A =+-得231c c =+-,即220c c --=,解得2c =或1c =-(舍去).故填2.【点睛】本题主要考查了利用余弦定理求三角形的边,属于中档题.16.1【解析】【分析】先求出二项式的展开式的通项公式令的指数等于求出的值即可求得展开式中的项的系数再根据的系数是列方程求解即可【详解】展开式的的通项为令的展开式中的系数为故答案为1【点睛】本题主要考查二 解析:1【解析】【分析】 先求出二项式9()ax x-的展开式的通项公式,令x 的指数等于4,求出r 的值,即可求得展开式中3x 的项的系数,再根据3x 的系数是84-列方程求解即可.【详解】9()a x x -展开式的的通项为()992199r r r r r r r a T C x C x a x --+⎛⎫=-=- ⎪⎝⎭, 令9233r r -=⇒=,9()a x x-的展开式中3x 的系数为()339841C a a -=-⇒=, 故答案为1.【点睛】本题主要考查二项展开式定理的通项与系数,属于简单题. 二项展开式定理的问题也是高考命题热点之一,关于二项式定理的命题方向比较明确,主要从以下几个方面命题:(1)考查二项展开式的通项公式1C r n r r r n T a b -+=;(可以考查某一项,也可考查某一项的系数)(2)考查各项系数和和各项的二项式系数和;(3)二项展开式定理的应用.17.【解析】【分析】【详解】设AB=2作CO⊥面ABDEOH⊥AB则CH⊥AB∠CHO 为二面角C−AB−D的平面角CH=3√OH=CHcos∠CHO=1结合等边三角形ABC与正方形ABDE可知此四棱锥为解析:16【解析】【分析】【详解】设AB=2,作CO⊥面ABDEOH⊥AB,则CH⊥AB,∠CHO为二面角C−AB−D的平面角,CH=3√,OH=CH cos∠CHO=1,结合等边三角形ABC与正方形ABDE可知此四棱锥为正四棱锥,3,11(),2212AN EM CH ANAC AB EM AC AEAN EM====+=-∴⋅=u u u ru u u r u u u r u u u u r u u u r u u u ru u u r u u u u r故EM,AN112633=⋅,18.【解析】试题分析:设等比数列的公比为由得解得所以于是当或时取得最大值考点:等比数列及其应用解析:64【解析】试题分析:设等比数列的公比为q,由132410{5a aa a+=+=得,2121(1)10{(1)5a qa q q+=+=,解得18{12aq==.所以2(1)1712(1)22212118()22n n n n n n nn a a a a q L L --++++-==⨯=,于是当3n =或4时,12n a a a L 取得最大值6264=.考点:等比数列及其应用19.1【解析】【详解】化简三角函数的解析式可得由可得当时函数取得最大值1解析:1【解析】【详解】化简三角函数的解析式,可得()22311cos cos 44f x x x x x =--=-++=2(cos 1x -+, 由[0,]2x π∈,可得cos [0,1]x ∈,当cos x =时,函数()f x 取得最大值1. 20.【解析】【分析】本题首先应用余弦定理建立关于的方程应用的关系三角形面积公式计算求解本题属于常见题目难度不大注重了基础知识基本方法数学式子的变形及运算求解能力的考查【详解】由余弦定理得所以即解得(舍去解析:【解析】【分析】本题首先应用余弦定理,建立关于c 的方程,应用,a c 的关系、三角形面积公式计算求解,本题属于常见题目,难度不大,注重了基础知识、基本方法、数学式子的变形及运算求解能力的考查.【详解】由余弦定理得2222cos b a c ac B =+-, 所以2221(2)2262c c c c +-⨯⨯⨯=, 即212c =解得c c ==-所以2a c ==11sin 22ABC S ac B ∆==⨯= 【点睛】本题涉及正数开平方运算,易错点往往是余弦定理应用有误或是开方导致错误.解答此类问题,关键是在明确方法的基础上,准确记忆公式,细心计算.三、解答题21.(1) x 2+y 2-2x-2y-2=0 (2) ρsin(θ+)=【解析】(1)∵ρ=2,∴ρ2=4,即x 2+y 2=4.∵ρ2-2ρcos(θ-)=2, ∴ρ2-2ρ (cosθcos +sinθsin )=2.∴x 2+y 2-2x-2y-2=0.(2)将两圆的直角坐标方程相减,得经过两圆交点的直线方程为x+y=1.化为极坐标方程为ρcosθ+ρsinθ=1,即ρsin(θ+)=.22.(1)20x y ++=(2)3【解析】【分析】【详解】Ⅰ)由题意得直线BD 的方程为1y x =+.因为四边形ABCD 为菱形,所以AC BD ⊥.于是可设直线AC 的方程为y x n =-+.由2234{x y y x n+==-+,得2246340x nx n -+-=. 因为A C ,在椭圆上,所以212640n ∆=-+>,解得4343n <<. 设A C ,两点坐标分别为1122()()x y x y ,,,, 则1232n x x +=,212344n x x -=,11y x n =-+,22y x n =-+. 所以122n y y +=. 所以AC 的中点坐标为344n n ⎛⎫ ⎪⎝⎭,. 由四边形ABCD 为菱形可知,点344n n ⎛⎫⎪⎝⎭,在直线1y x =+上, 所以3144n n =+,解得2n =-.所以直线AC 的方程为2y x =--,即20x y ++=.(Ⅱ)因为四边形ABCD 为菱形,且60ABC ∠=o , 所以AB BC CA ==.所以菱形ABCD的面积2S AC =. 由(Ⅰ)可得2223162-+==n AC,所以2316)S n n ⎛=-+<<⎝⎭, 故当0n =时,有max 16==S 23.(Ⅰ)3;(Ⅱ)7;(Ⅲ)4 【解析】【分析】 (Ⅰ)以B 为坐标原点,BA 所在直线为x 轴,1BB 所在直线为y 轴,建立坐标系,设异面直线AC 与11A B 所成角为α,算出11,AC A B u u u r u u u u r ,再利用cos α=11|cos ,|AC A B 〈〉u u u r u u u u r 计算即可; (Ⅱ)分别求出平面11AA C 的法向量m u r 与平面111B AC 的法向量n r ,再利用向量的夹角公式算得cos ,m n 〈〉u r r 即可;(Ⅲ)设(,,0)M a b ,由MN ⊥平面111A B C ,得111100MN A B MN A C ⎧⋅=⎪⎨⋅=⎪⎩u u u u v u u u u v u u u u v u u u u v ,进一步得到M 的坐标,再由模长公式计算BM 的长.【详解】如图所示,建立空间直角坐标系,其中点B 为坐标原点,BA 所在直线为x 轴,1BB 所在直线为y 轴,由题意,111(0,0,0),B A CA B C, (Ⅰ)11((AC A B ==-u u u ru u u u r ,所以111111cos ,||||AC A B AC A B AC A B ⋅〈〉===u u r u u u r u u u u r u u u r u u u u r , 设异面直线AC 与11A B 所成角为α,则cos α=11|cos ,|3AC A B 〈〉=u u u r u u u u r , 所以异面直线AC 与11A B所成角的余弦值为3. (Ⅱ)易知111(AA AC ==u u u r u u u u r ,设平面11AA C 的法向量(,,)m x y z =, 则11100m AC m AA ⎧⋅=⎪⎨⋅=⎪⎩u u u u v v u u u v v,即00⎧+=⎪⎨=⎪⎩,令x =z =,所以m =u r ,同理,设平面111B AC 的法向量(,,)n x y z =r , 则111100n A C n A B ⎧⋅=⎪⎨⋅=⎪⎩u u u u v v u u u u v v,即00⎧-+=⎪⎨-=⎪⎩,令y =z =n =r ,所以2cos ,7||||m n m n m n ⋅〈〉===⋅u r r u r r , 设二面角111A AC B --的大小为θ,则sin θ== 所以二面角111A AC B --. (Ⅲ)由N 为棱11B C的中点,得N ⎝⎭, 设(,,0)M a b,则,,222MN a b ⎛⎫=-- ⎪⎝⎭u u u u r , 由MN ⊥平面111A B C ,得111100MN A B MN A C ⎧⋅=⎪⎨⋅=⎪⎩u u u u v u u u u v u u u u v u u u u v ,即(02((022a a b ⎧⎛⎫-⋅-=⎪ ⎪ ⎪⎪⎝⎭⎨⎛⎫⎛⎫⎪-⋅+-⋅= ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎩,解得2224 ab⎧=⎪⎪⎨⎪=⎪⎩,故22,,024M⎛⎫⎪⎝⎭,因此22,,024BM⎛⎫= ⎪⎝⎭u u u u r,所以线段BM的长为10||4BM=u u u u r.【点睛】本题主要考查直线与平面平行、直线与平面垂直、直线与平面所成的角等基础知识,考查学生的空间想象能力、运算能力和推理论证能力.24.(Ⅰ)4,03⎛⎫- ⎪⎝⎭;(Ⅱ)4m≥【解析】试题分析:(1)当m=5时,把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.(2)由二次函数y=x2+2x+3=(x+1)2+2在x=﹣1取得最小值2,f(x)在x=﹣1处取得最大值m﹣2,故有m﹣2≥2,由此求得m的范围.试题解析:(1)当5m=时,()()()()521311521x xf x xx x⎧+<-⎪=-≤≤⎨⎪->⎩,由()2f x>得不等式的解集为3322x x⎧⎫-<<⎨⎬⎩⎭.(2)由二次函数()222312y x x x=++=++,知函数在1x=-取得最小值2,因为()()()()2121121m x xf x m xm x x⎧+<-⎪=--≤≤⎨⎪->⎩,在1x=-处取得最大值2m-,所以要是二次函数223y x x=++与函数()y f x=的图象恒有公共点.只需22m-≥,即4m≥.25.(1)340x y -+=;(2)2105 【解析】 【分析】 (1)求得()04A ,,()22B --,,问题得解. (2)利用直线AB 和曲线C 相切的关系可得:圆心到直线A B 的距离等于圆的半径r ,列方程即可得解.【详解】(1)分别将()π42A ,,()5π224B ,转化为直角坐标为()04A ,,()22B --,, 所以直线AB 的直角坐标方程为340x y -+=.(2)曲线C 的方程为r ρ=(0r >),其直角坐标方程为222x y r +=.又直线A B 和曲线C 有且只有一个公共点,即直线与圆相切,所以圆心到直线A B 的距离等于圆的半径r .又圆心到直线A B 的距离为222104531=+,即r 的值为2105. 【点睛】本题主要考查了极坐标与直角坐标互化,还考查了直线与圆相切的几何关系,考查计算能力及点到直线距离公式,属于中档题.26.(1)因为时,所以;(2)由(1)知该商品每日的销售量,所以商场每日销售该商品所获得的利润:222()(3)[10(6)]210(3)(6),363f x x x x x x x =-+-=+--<<-; /2()10[(6)2(3)(6)]30(4)(6)f x x x x x x =-+-----,令/()0f x =得4x =函数在(3,4)上递增,在(4,6)上递减,所以当时函数取得最大值 答:当销售价格时,商场每日销售该商品所获得的利润最大,最大值为42. 【解析】(1)利用销售价格为5元/千克时,每日可售出该商品11千克.把x=5,y=11代入,解关于a 的方程即可求a..(2)在(1)的基础上,列出利润关于x 的函数关系式,利润=销售量⨯(销售单价-成品单价),然后利用导数求其最值即可.。
2020-2021天津市育贤中学高一数学下期末试题(带答案)

2020-2021天津市育贤中学高一数学下期末试题(带答案)一、选择题1.若,则( )A .B .C .D .2.某空间几何体的三视图如图所示,则该几何体的体积为( )A .73B .8π3- C .83D .7π3- 3.某程序框图如图所示,若输出的S=57,则判断框内为 A .k >4? B .k >5? C .k >6?D .k >7?4.已知D ,E 是ABC V 边BC 的三等分点,点P 在线段DE 上,若AP xAB yAC =+u u u r u u u r u u u r,则xy 的取值范围是( )A .14,99⎡⎤⎢⎥⎣⎦B .11,94⎡⎤⎢⎥⎣⎦C .21,92⎡⎤⎢⎥⎣⎦D .21,94⎡⎤⎢⎥⎣⎦5.设l ,m 是两条不同的直线,α是一个平面,则下列命题正确的是 ( )A .若l m ⊥,m α⊂,则l α⊥B .若l α⊥,//l m ,则m α⊥C .若//l α,m α⊂,则//l mD .若//l α,//m α,则//l m6.若,αβ均为锐角,25sin α=,()3sin 5αβ+=,则cos β=A .25B .25C .25或25 D .2525-7.若||1OA =u u u v ,||3OB =u u u v ,0OA OB ⋅=u u u v u u u v,点C 在AB 上,且30AOC ︒∠=,设OC mOA nOBu u u v u u u v u u u v =+(,)m n R ∈,则mn的值为( ) A .13B .3C .3 D .38.设函数f (x )=cos (x +3π),则下列结论错误的是 A .f(x)的一个周期为−2π B .y=f(x)的图像关于直线x=83π对称 C .f(x+π)的一个零点为x=6π D .f(x)在(2π,π)单调递减 9.已知0,0a b >>,并且111,,2a b 成等差数列,则4a b +的最小值为( ) A .2B .4C .5D .910.在空间四边形ABCD 的边AB ,BC ,CD ,DA 上分别取E ,F ,G ,H 四点,如EF 与HG 交于点M ,那么 ( ) A .M 一定在直线AC 上 B .M 一定在直线BD 上C .M 可能在直线AC 上,也可能在直线BD 上 D .M 既不在直线AC 上,也不在直线BD 上11.如图,点N 为正方形ABCD 的中心,ECD ∆为正三角形,平面ECD ⊥平面,ABCD M 是线段ED 的中点,则( )A .BM EN =,且直线,BM EN 是相交直线B .BM EN ≠,且直线,BM EN 是相交直线C .BM EN =,且直线,BM EN 是异面直线D .BM EN ≠,且直线,BM EN 是异面直线12.设n S 为等差数列{}n a 的前n 项和,若3243S S S =+,12a =,则5a = A .12-B .10-C .10D .12二、填空题13.已知数列{}n a 前n 项和为n S ,若22nn n S a =-,则n S =__________.14.设a ,b ,c 分别为ABC ∆内角A ,B ,C 的对边.=,则222a cb ac+-的取值范围为______. 15.等边ABC ∆的边长为2,则AB u u u v 在BC uuuv 方向上的投影为________.16.已知定义在实数集R 上的偶函数()f x 在区间(],0-∞上是减函数,则不等式()()1ln f f x <的解集是________.17.已知圆的方程为x 2+y 2﹣6x ﹣8y =0,设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为18.已知函数42,0()log ,0x x f x x x ⎧≤=⎨>⎩,若1[()]2f f a =-,则a 的值是________.19.函数y =的定义域是 _________.20.设0x >,0y >,24x y +=,则(1)(21)x y xy++的最小值为__________.三、解答题21.在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等. (Ⅰ)求取出的两个球上标号为相同数字的概率; (Ⅱ)求取出的两个球上标号之积能被3整除的概率. 22.已知函数()()22f x sin x cos x x cos x x R =--∈(I )求2f 3π⎛⎫ ⎪⎝⎭的值 (II )求()f x 的最小正周期及单调递增区间.23.一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a ,b ,c .(Ⅰ)求“抽取的卡片上的数字满足a b c +=”的概率; (Ⅱ)求“抽取的卡片上的数字a ,b ,c 不完全相同”的概率.24.某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x ,y.奖励规则如下:①若3xy ≤,则奖励玩具一个; ②若8xy ≥,则奖励水杯一个; ③其余情况奖励饮料一瓶.假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动. (Ⅰ)求小亮获得玩具的概率;(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由. 25.记n S 为等差数列{}n a 的前n 项和,已知17a =-,315S =-. (1)求{}n a 的通项公式; (2)求n S ,并求n S 的最小值.26.某家庭记录了未使用节水龙头50天的日用水量数据(单位:3m )和使用了节水龙头50天的日用水量数据,得到频数分布表如下: 未使用节水龙头50天的日用水量频数分布表日用水量 [)0,0.1 [)0.1,0.2 [)0.2,0.3 [)0.3,0.4 [)0.4,0.5 [)0.5,0.6 [)0.6,0.7频数132 49 26 5使用了节水龙头50天的日用水量频数分布表 日用水量 [)0,0.1[)0.1,0.2 [)0.2,0.3 [)0.3,0.4 [)0.4,0.5 [)0.5,0.6频数151310 16 5(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:0.35m的概率;(2)估计该家庭使用节水龙头后,日用水量小于3(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【解析】试题分析:,且,故选D.【考点】三角恒等变换【名师点睛】对于三角函数的给值求值问题,关键是把待求角用已知角表示:(1)已知角为两个时,待求角一般表示为已知角的和或差.(2)已知角为一个时,待求角一般与已知角成“倍的关系”或“互余、互补”关系.2.B解析:B【解析】由三视图可知,该几何体是由一个四棱锥挖掉半个圆锥所得,故利用棱锥的体积减去半个圆锥的体积,就可求得几何体的体积. 【详解】由三视图可知,该几何体是由一个四棱锥挖掉半个圆锥所得,故其体积为21118222123233ππ-⋅⋅⋅-⋅⋅⋅⋅=.故选B. 【点睛】本小题主要考查由三视图判断几何体的结构,考查不规则几何体体积的求解方法,属于基础题.3.A解析:A 【解析】试题分析:由程序框图知第一次运行112,224k S =+==+=,第二次运行213,8311k S =+==+=,第三次运行314,22426k S =+==+=,第四次运行4154,52557k S =+=>=+=,输出57S =,所以判断框内为4?k >,故选C.考点:程序框图.4.D解析:D 【解析】 【分析】利用已知条件推出x +y =1,然后利用x ,y 的范围,利用基本不等式求解xy 的最值. 【详解】解:D ,E 是ABC V 边BC 的三等分点,点P 在线段DE 上,若AP xAB yAC =+u u u r u u u r u u u r,可得x y 1+=,x ,12y ,33⎡⎤∈⎢⎥⎣⎦,则2x y 1xy ()24+≤=,当且仅当1x y 2==时取等号,并且()2xy x 1x x x =-=-,函数的开口向下, 对称轴为:1x 2=,当1x 3=或2x 3=时,取最小值,xy 的最小值为:29.则xy 的取值范围是:21,.94⎡⎤⎢⎥⎣⎦故选D . 【点睛】本题考查函数的最值的求法,基本不等式的应用,考查转化思想以及计算能力.5.B解析:B【分析】利用,l α可能平行判断A ,利用线面平行的性质判断B ,利用//l m 或l 与m 异面判断C ,l 与m 可能平行、相交、异面,判断D . 【详解】l m ⊥,m α⊂,则,l α可能平行,A 错;l α⊥,//l m ,由线面平行的性质可得m α⊥,B 正确; //l α,m α⊂,则//l m , l 与m 异面;C 错,//l α,//m α,l 与m 可能平行、相交、异面,D 错,.故选B. 【点睛】本题主要考查线面平行的判定与性质、线面面垂直的性质,属于中档题.空间直线、平面平行或垂直等位置关系命题的真假判断,除了利用定理、公理、推理判断外,还常采用画图(尤其是画长方体)、现实实物判断法(如墙角、桌面等)、排除筛选法等;另外,若原命题不太容易判断真假,可以考虑它的逆否命题,判断它的逆否命题真假,原命题与逆否命题等价.6.B解析:B 【解析】 【分析】利用角的等量代换,β=α+β-α,只要求出α的余弦,α+β的余弦,利用复合角余弦公式展开求之. 【详解】∵α为锐角,sin 52α= s ,∴α>45°且5cos α= ,∵()3sin 5αβ+=,且13252< ,2παβπ∴+<<,∴45cosαβ+=-() , 则cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα43555525=-⨯+⨯= 故选B. 【点睛】本题考查两角和与差的正弦、余弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.7.B解析:B 【解析】利用向量的数量积运算即可算出. 【详解】解:30AOC ︒∠=Qcos ,OC OA ∴<>=u u u r u u u rOC OA OC OA⋅∴=u u u r u u u r u u u r u u u r()mOA nOB OA mOA nOBOA+⋅∴=+u u u r u u u ru u u r u u u r u u u r u u u r2= 1OA =Q,OB =,0OA OB ⋅=u u u r u u ur=229m n ∴=又C Q 在AB 上0m ∴>,0n > 3m n∴= 故选:B 【点睛】本题主要考查了向量的基本运算的应用,向量的基本定理的应用及向量共线定理等知识的综合应用.8.D解析:D 【解析】f (x )的最小正周期为2π,易知A 正确; f 8π3⎛⎫⎪⎝⎭=cos 8ππ33⎛⎫+ ⎪⎝⎭=cos3π=-1,为f (x )的最小值,故B 正确;∵f (x +π)=cos ππ3x ⎛⎫++ ⎪⎝⎭=-cos π3x ⎛⎫+ ⎪⎝⎭,∴f ππ6⎛⎫+ ⎪⎝⎭=-cos ππ63⎛⎫+ ⎪⎝⎭=-cos 2π=0,故C 正确;由于f2π3⎛⎫⎪⎝⎭=cos2ππ33⎛⎫+⎪⎝⎭=cosπ=-1,为f(x)的最小值,故f(x)在,2ππ⎛⎫⎪⎝⎭上不单调,故D错误.故选D. 9.D解析:D 【解析】∵111,,2a b成等差数列,()111144 1445529a b a ba b a ba b a b b a b a⎛⎫∴+=∴+=++=+++⋅=⎪⎝⎭,…,当且仅当a=2b即33,2a b==时“=“成立,本题选择D选项.点睛:在应用基本不等式求最值时,要把握不等式成立的三个条件,就是“一正——各项均为正;二定——积或和为定值;三相等——等号能否取得”,若忽略了某个条件,就会出现错误.10.A解析:A【解析】如图,因为EF∩HG=M,所以M∈EF,M∈HG,又EF⊂平面ABC,HG⊂平面ADC,故M∈平面ABC,M∈平面ADC,所以M∈平面ABC∩平面ADC=AC.选A.点睛:证明点在线上常用方法先找出两个平面,然后确定点是这两个平面的公共点,再确定直线是这两个平面的交线.11.B解析:B【解析】【分析】利用垂直关系,再结合勾股定理进而解决问题.【详解】如图所示, 作EO CD ⊥于O ,连接ON ,过M 作MF OD ⊥于F . 连BF ,Q 平面CDE ⊥平面ABCD .,EO CD EO ⊥⊂平面CDE ,EO ∴⊥平面ABCD ,MF ⊥平面ABCD ,MFB ∴∆与EON ∆均为直角三角形.设正方形边长为2,易知3,12EO ON EN ===,35,,72MF BF BM ==∴=.BM EN ∴≠,故选B . 【点睛】本题考查空间想象能力和计算能力, 解答本题的关键是构造直角三角性.12.B解析:B 【解析】分析:首先设出等差数列{}n a 的公差为d ,利用等差数列的求和公式,得到公差d 所满足的等量关系式,从而求得结果3d =-,之后应用等差数列的通项公式求得51421210a a d =+=-=-,从而求得正确结果.详解:设该等差数列的公差为d , 根据题中的条件可得32433(32)224222d d d ⨯⨯⨯+⋅=⨯++⨯+⋅, 整理解得3d =-,所以51421210a a d =+=-=-,故选B.点睛:该题考查的是有关等差数列的求和公式和通项公式的应用,在解题的过程中,需要利用题中的条件,结合等差数列的求和公式,得到公差d 的值,之后利用等差数列的通项公式得到5a 与1a d 和的关系,从而求得结果.二、填空题13.【解析】分析:令得当时由此推导出数列是首项为1公差为的等差数列从而得到从而得到详解:令得解得当时由)得两式相减得整理得且∴数列是首项为1公差为的等差数列可得所以点睛:本题考查数列的通项公式的求法是中解析:*2()n n S n n N =∈g【解析】分析:令1n =,得12a =,当2n ≥ 时,11122n n n S a ---=-,由此推导出数列{}2nna 是首项为1公差为12的等差数列,从而得到()112n n a n -+=,从而得到n S . 详解:令1n =,得11122a a =-,解得12a = ,当2n ≥ 时,由22n n n S a =-),得11122n n n S a ---=-,两式相减得()()1112222,n n n n n n n a S S a a ---=-=--- 整理得111222n n n n a a ---=,且111,2a = ∴数列{}2n n a 是首项为1公差为12的等差数列, ()111,22n n a n ∴=+- 可得()112,n n a n -=+ 所以()12221222.n n n n n n S a n n -⎡⎤=-=+-=⋅⎣⎦ 点睛:本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意构造法的合理运用. 14.【解析】【分析】把已知式用正弦定理化边为角由两角和的正弦公式和诱导公式化简可求得即角从而得角的范围注意由余弦定理可得结论【详解】因为所以所以即又所以则因为所以而故故答案为:【点睛】本题考查正弦与余弦解析:()()0,2U【解析】【分析】把已知式用正弦定理化边为角,由两角和的正弦公式和诱导公式化简,可求得cos C ,即C 角,从而得B 角的范围,注意2B π≠,由余弦定理可得结论. 【详解】=,所以()()2cos cos cos cos 0a C B B C =⋅≠,所以()2sin cos cos A B C C B =,即()2sin cos A C C B A +=,又sin 0A >,所以cos C =, 则6C π=,因为cos 0B ≠,所以50,,226B πππ⎛⎫⎛⎫∈ ⎪ ⎪⎝⎭⎝⎭U ,而2222cos a c b B ac +-=,故()()2223,00,2a c b ac +-∈-U . 故答案为:()()3,00,2-U .【点睛】本题考查正弦与余弦定理的应用,考查运算求解能力.本题是一个易错题,学生容易忽略cos B 不能等于0.15.【解析】【分析】建立直角坐标系结合向量的坐标运算求解在方向上的投影即可【详解】建立如图所示的平面直角坐标系由题意可知:则:且据此可知在方向上的投影为【点睛】本题主要考查平面向量数量积的坐标运算向量投 解析:1-【解析】【分析】建立直角坐标系,结合向量的坐标运算求解AB u u u r 在BC uuu r 方向上的投影即可.【详解】建立如图所示的平面直角坐标系,由题意可知:()0,0A ,()2,0B ,()1,3C , 则:()2,0AB =uu u r ,()1,3BC =-u u u v ,2AB BC ⋅=-u u u r u u u r且2AB =u u u r ,10BC =u u u v ,据此可知AB u u u r 在BC uuu r 方向上的投影为212AB BC AB ⋅-==-u u u v u u u v u u u v .【点睛】本题主要考查平面向量数量积的坐标运算,向量投影的定义与计算等知识,意在考查学生的转化能力和计算求解能力.16.【解析】由定义在实数集上的偶函数在区间上是减函数可得函数在区间上是增函数所以由不等式得即或解得或即不等式的解集是;故答案为 解析:()10,e,e ∞⎛⎫⋃+ ⎪⎝⎭【解析】由定义在实数集R 上的偶函数()f x 在区间(],0-∞上是减函数,可得函数()f x 在区间()0+∞,上是增函数,所以由不等式()()1ln f f x <得ln 1x >,即ln 1x >或ln 1x <-,解得x e >或10e x <<,即不等式()()1ln f f x <的解集是()10,e,e ∞⎛⎫⋃+ ⎪⎝⎭;故答案为()10,e,e ∞⎛⎫⋃+ ⎪⎝⎭. 17.20【解析】【分析】根据题意可知过(35)的最长弦为直径最短弦为过(35)且垂直于该直径的弦分别求出两个量然后利用对角线垂直的四边形的面积等于对角线乘积的一半求出即可【详解】解:圆的标准方程为(x ﹣解析:【解析】【分析】根据题意可知,过(3,5)的最长弦为直径,最短弦为过(3,5)且垂直于该直径的弦,分别求出两个量,然后利用对角线垂直的四边形的面积等于对角线乘积的一半求出即可.【详解】解:圆的标准方程为(x ﹣3)2+(y ﹣4)2=52,由题意得最长的弦|AC |=2×5=10,根据勾股定理得最短的弦|BD |==,且AC ⊥BD ,四边形ABCD 的面积S =|12AC |•|BD |12=⨯10×=.故答案为.【点评】考查学生灵活运用垂径定理解决数学问题的能力,掌握对角线垂直的四边形的面积计算方法为对角线乘积的一半. 18.-1或2【解析】【分析】根据函数值的正负由可得求出再对分类讨论代入解析式即可求解【详解】当时当当所以或故答案为:或【点睛】本题考查求复合函数值认真审题理解分段函数的解析式考查分类讨论思想属于中档题 解析:-1或2【解析】【分析】根据函数值的正负,由1[()]02f f a =-<,可得()0f a >,求出()f a ,再对a 分类讨论,代入解析式,即可求解.【详解】当0x ≤时,()0,f x >1[()]02f f a =-<, 411[()]log (()),()22f f a f a f a ∴==-∴=, 当410,()log ,22a f a a a >==∴=, 当10,()2,12a a f a a ≤==∴=-, 所以1a =-或2a =.故答案为:1-或2.【点睛】本题考查求复合函数值,认真审题理解分段函数的解析式,考查分类讨论思想,属于中档题. 19.【解析】【分析】由函数的解析式得到关于x 的不等式求解不等式即可确定函数的定义域【详解】函数有意义则:即求解三角不等式可得:则函数的定义域为【点睛】求函数的定义域其实质就是以函数解析式有意义为准则列出 解析:()222,233k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦【解析】【分析】由函数的解析式得到关于x 的不等式,求解不等式即可确定函数的定义域.【详解】函数有意义,则:2cos 10x +≥,即1cos 2x ≥-, 求解三角不等式可得:()222233k x k k Z ππππ-≤≤+∈, 则函数的定义域为()222,233k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦. 【点睛】求函数的定义域,其实质就是以函数解析式有意义为准则,列出不等式或不等式组,然后求出它们的解集即可. 20.【解析】【分析】把分子展开化为再利用基本不等式求最值【详解】由得得等号当且仅当即时成立故所求的最小值为【点睛】使用基本不等式求最值时一定要验证等号是否能够成立解析:92. 【解析】 【分析】 把分子展开化为(1)(21)2212552x y xy x y xy xy xy xy xy++++++===+,再利用基本不等式求最值.【详解】由24x y +=,得2422x y xy +=≥,得2xy ≤(1)(21)221255592222x y xy x y xy xy xy xy xy ++++++===+≥+=, 等号当且仅当2x y =,即2,1x y ==时成立.故所求的最小值为92. 【点睛】使用基本不等式求最值时一定要验证等号是否能够成立. 三、解答题21.(1). (2) .【解析】【分析】【详解】设从甲、乙两个盒子中各取1个球,其数字分别为x ,y .用(x ,y )表示抽取结果,则所有可能的结果有16种,即(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4).(1)设“取出的两个球上的标号相同”为事件A ,则A ={(1,1),(2,2),(3,3),(4,4)}.事件A 由4个基本事件组成,故所求概率P (A )==. (2)设“取出的两个球上标号的数字之积能被3整除”为事件B ,则B ={(1,3),(3,1),(2,3),(3,2),(3,3),(3,4),(4,3)} 事件B 由7个基本事件组成,故所求概率P (A )=.考点:古典概型的概率计算22.(I )2;(II )()f x 的最小正周期是π,2+k +k k 63Z ππππ⎡⎤∈⎢⎥⎣⎦,. 【解析】【分析】(Ⅰ)直接利用三角函数关系式的恒等变换,把函数的关系式变形成正弦型函数,进一步求出函数的值.(Ⅱ)直接利用函数的关系式,求出函数的周期和单调区间. 【详解】(Ⅰ)f (x )=sin 2x ﹣cos 2x 23-sin x cos x ,=﹣cos2x 3-sin2x ,=﹣226sin x π⎛⎫+⎪⎝⎭, 则f (23π)=﹣2sin (436ππ+)=2, (Ⅱ)因为()2sin(2)6f x x π=-+. 所以()f x 的最小正周期是π.由正弦函数的性质得3222,262k x k k Z πππππ+≤+≤+∈, 解得2,63k x k k Z ππππ+≤≤+∈, 所以,()f x 的单调递增区间是2[,]63k k k ππ+π+π∈Z ,. 【点睛】本题主要考查了三角函数的化简,以及函数的性质,是高考中的常考知识点,属于基础题,强调基础的重要性;三角函数解答题中,涉及到周期,单调性,单调区间以及最值等考点时,都属于考查三角函数的性质,首先应把它化为三角函数的基本形式即,然后利用三角函数的性质求解. 23.(1)19;(2)89. 【解析】试题分析:(1)所有的可能结果(,,)a b c 共有33327⨯⨯=种,而满足a b c +=的(,,)a b c 共计3个,由此求得“抽取的卡片上的数字满足a b c +=”的概率;(2)所有的可能结果(,,)a b c 共有33327⨯⨯=种,用列举法求得满足“抽取的卡片上的数字a 、b 、c 完全相同”的(,,)a b c 共计三个,由此求得“抽取的卡片上的数字a 、b 、c 完全相同”的概率,再用1减去此概率,即得所求.试题解析:(1) 所有的可能结果(,,)a b c 共有33327⨯⨯=种,而满足a b c +=的(,,)a b c 有(1,1,2)、(1,2,3)、(2,1,3)共计3个故“抽取的卡片上的数字满足a b c +=”的概率为31279= (2) 所有的可能结果(,,)a b c 共有33327⨯⨯=种满足“抽取的卡片上的数字a 、b 、c 完全相同”的(,,)a b c 有(1,1,1)、(2,2,2)、(3,3,3)共计三个故“抽取的卡片上的数字a 、b 、c 完全相同”的概率为31279= 所以“抽取的卡片上的数字a 、b 、c 不完全相同”的概率为18199-= 考点:独立事件的概率.【方法点睛】求复杂事件的概率通常有两种方法:一是将所求事件转化成彼此互斥的事件的和;二是先求其对立事件的概率,然后再应用公式求解.如果采用方法一,一定要将事件拆分成若干个互斥事件,不能重复和遗漏;如果采用方法二,一定要找准其对立事件,否则容易出现错误.24.(Ⅰ)516.(Ⅱ)小亮获得水杯的概率大于获得饮料的概率. 【解析】【分析】【详解】(Ⅰ)两次记录的所有结果为(1,1),(1,,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个. 满足xy≤3的有(1,1),(1,,2),(1,3),(2,1),(3,1),共5个,所以小亮获得玩具的概率为516. (Ⅱ) 满足xy≥8的有(2,4),(3,,3),(3,4),(4,2),(4,3),(4,4),共6个,所以小亮获得水杯的概率为616; 小亮获得饮料的概率为5651161616--=,所以小亮获得水杯的概率大于获得饮料的概率. 25.(1)a n =2n –9,(2)S n =n 2–8n ,最小值为–16.【解析】分析:(1)根据等差数列前n 项和公式,求出公差,再代入等差数列通项公式得结果,(2)根据等差数列前n 项和公式得n S 的二次函数关系式,根据二次函数对称轴以及自变量为正整数求函数最值.详解:(1)设{a n }的公差为d ,由题意得3a 1+3d =–15.由a 1=–7得d =2.所以{a n }的通项公式为a n =2n –9.(2)由(1)得S n =n 2–8n =(n –4)2–16.所以当n =4时,S n 取得最小值,最小值为–16.点睛:数列是特殊的函数,研究数列最值问题,可利用函数性质,但要注意其定义域为正整数集这一限制条件.26.(1)直方图见解析;(2)0.48;(3)347.45m .【解析】【分析】(1)根据题中所给的使用了节水龙头50天的日用水量频数分布表,算出落在相应区间上的频率,借助于直方图中长方形的面积表示的就是落在相应区间上的频率,从而确定出对应矩形的高,从而得到直方图;(2)结合直方图,算出日用水量小于0.35的矩形的面积总和,即为所求的频率;(3)根据组中值乘以相应的频率作和求得50天日用水量的平均值,作差乘以365天得到一年能节约用水多少3m ,从而求得结果.【详解】(1)频率分布直方图如下图所示:(2)根据以上数据,该家庭使用节水龙头后50天日用水量小于30.35m 的频率为 0.20.110.1 2.60.120.050.48⨯+⨯+⨯+⨯=;因此该家庭使用节水龙头后日用水量小于30.35m 的概率的估计值为0.48;(3)该家庭未使用节水龙头50天日用水量的平均数为()110.0510.1530.2520.3540.4590.55260.6550.4850x =⨯+⨯+⨯+⨯+⨯+⨯+⨯=. 该家庭使用了节水龙头后50天日用水量的平均数为()210.0510.1550.25130.35100.45160.5550.3550x =⨯+⨯+⨯+⨯+⨯+⨯=.估计使用节水龙头后,一年可节省水()()30.480.3536547.45m-⨯=. 【点睛】 该题考查的是有关统计的问题,涉及到的知识点有频率分布直方图的绘制、利用频率分布直方图计算变量落在相应区间上的概率、利用频率分布直方图求平均数,在解题的过程中,需要认真审题,细心运算,仔细求解,就可以得出正确结果.。
2020-2021天津市育贤中学高一数学下期末第一次模拟试卷(及答案)

2020-2021天津市育贤中学高一数学下期末第一次模拟试卷(及答案)一、选择题1.执行右面的程序框图,若输入的,,a b k 分别为1,2,3,则输出的M =( )A .203B .72C .165 D .158 2.如图,在ABC ∆中,已知5AB =,6AC =,12BD DC =u u u v u u u v ,4AD AC ⋅=u u u v u u u v,则AB BC ⋅=u u u v u u u vA .-45B .13C .-13D .-373.设集合{}1,2,4A =,{}240B x x x m =-+=.若{}1A B ⋂=,则B =( ) A .{}1,3-B .{}1,0C .{}1,3D .{}1,54.在ABC ∆中,2AB =2AC =,E 是边BC 的中点.O 为ABC ∆所在平面内一点且满足222OA OB OC ==u u u v u u u v v ,则·AE AO u u u v u u u v 的值为( )A .12B .1C .22D .325.已知定义在R 上的偶函数f (x )满足f (x -4)=f (x ),且在区间[0,2]上f (x )=x ,若关于x 的方程f (x )=log a |x |有六个不同的根,则a 的范围为( ) A .6,10B .6,22C .(2,22D .(2,4)6.为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:则y 对x 的线性回归方程为 A .y = x-1B .y = x+1C .y =88+12x D .y = 1767.要得到函数2sin 2y x x =+2sin 2y x =的图象( ) A .向左平移3π个单位 B .向右平移3π个单位 C .向左平移6π个单位 D .向右平移6π个单位 8.已知函数21(1)()2(1)a x x f x x x x x ⎧++>⎪=⎨⎪-+≤⎩在R 上单调递增,则实数a 的取值范围是 A .[]0,1B .(]0,1C .[]1,1-D .(]1,1-9.已知0,0a b >>,并且111,,2a b成等差数列,则4a b +的最小值为( ) A .2 B .4 C .5 D .9 10.函数()(1)lg(1)35f x x x x =-+--的零点个数为( )A .3B .2C .1D .011.与直线40x y --=和圆22220x y x y ++-=都相切的半径最小的圆的方程是 A .()()22112x y +++= B .()()22114x y -++= C .()()22112x y -++=D .()()22114x y +++=12.如图,点N 为正方形ABCD 的中心,ECD ∆为正三角形,平面ECD ⊥平面,ABCD M 是线段ED 的中点,则( )A .BM EN =,且直线,BM EN 是相交直线B .BM EN ≠,且直线,BM EN 是相交直线C .BM EN =,且直线,BM EN 是异面直线D .BM EN ≠,且直线,BM EN 是异面直线二、填空题13.一个空间几何体的三视图及部分数据如图所示,则这个几何体的体积是___________14.不等式2231()12x x -->的解集是______.15.已知a 0>,b 0>,且111a b +=,则b3a 2b a++的最小值等于______. 16.对于函数()f x ,()g x ,设(){}0m x f x ∈=,(){}0n x g x ∈=,若存在m ,n 使得1m n -<,则称()f x 与()g x 互为“近邻函数”.已知函数()()13log 2exf x x -=+-与()1422x x g x a +=⋅-+互为“近邻函数”,则实数a 的取值范围是______.(e 是自然对数的底数)17.设向量(12)(23)a b ==r r ,,,,若向量a b λ+r r 与向量(47)c =--r ,共线,则λ= 18.函数2cos 1y x =+的定义域是 _________.19.若()1,x ∈+∞,则131y x x =+-的最小值是_____. 20.如图,某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积为________.三、解答题21.某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[)13,14,第二组[)14,15,⋅⋅⋅,第五组[]17,18.下图是按上述分组方法得到的频率分布直方图.按上述分组方法得到的频率分布直方图.(1)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;(2)设m,n 表示该班某两位同学的百米测试成绩,且已知[)[],13,1417,18.m n ∈⋃求事件“1m n ->”发生的概率.22.已知函数()()221+0g x ax ax b a =-+>在区间[2,3]上有最大值4和最小值1.(1)求a 、b 的值; (2)设()()2g x f x x =-,若不等式()0f x k ->在x ∈(]2,5上恒成立,求实数k 的取值范围.23.已知函数f(x)=log 4(4x +1)+kx(k ∈R)是偶函数. (1)求k 的值;(2)设g(x)=log 44•23xa a ⎡⎤⎢⎥⎣⎦-,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a 的取值范围.24.已知以点C 2(,)t t(t ∈R ,t ≠0)为圆心的圆与x 轴交于点O 和点A ,与y 轴交于点O和点B ,其中O 为原点. (1)求证:△OAB 的面积为定值;(2)设直线y =-2x +4与圆C 交于点M ,N ,若OM =ON ,求圆C 的方程.25.某学校微信公众号收到非常多的精彩留言,学校从众多留言者中抽取了100人参加“学校满意度调查”,其留言者年龄集中在[]25,85之间,根据统计结果,做出频率分布直方图如下:(1)求这100位留言者年龄的平均数和中位数;(2)学校从参加调查的年龄在[)35,45和[)65,75的留言者中,按照分层抽样的方法,抽出了6人参加“精彩留言”经验交流会,赠与年龄在[)35,45的留言者每人一部价值1000元的手机,年龄在[)65,75的留言者每人一套价值700元的书,现要从这6人中选出3人作为代表发言,求这3位发言者所得纪念品价值超过2300元的概率.26.某家庭记录了未使用节水龙头50天的日用水量数据(单位:3m )和使用了节水龙头50天的日用水量数据,得到频数分布表如下: 未使用节水龙头50天的日用水量频数分布表日用水量 [)0,0.1 [)0.1,0.2 [)0.2,0.3 [)0.3,0.4 [)0.4,0.5 [)0.5,0.6 [)0.6,0.7频数132 49 26 5使用了节水龙头50天的日用水量频数分布表 日用水量 [)0,0.1[)0.1,0.2 [)0.2,0.3 [)0.3,0.4 [)0.4,0.5 [)0.5,0.6频数151310 16 5(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:(2)估计该家庭使用节水龙头后,日用水量小于30.35m 的概率;(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【解析】 【分析】 【详解】试题分析:根据题意由13≤成立,则循环,即1331,2,,2222M a b n =+====;又由23≤成立,则循环,即28382,,,33323M a b n =+====;又由33≤成立,则循环,即3315815,,,428838M a b n =+====;又由43≤不成立,则出循环,输出158M =. 考点:算法的循环结构2.D解析:D【解析】 【分析】先用AB u u u v 和AC uuu v表示出2A AB BC AB C AB ⋅=⋅-u u u v u u u v u u u v u u u v u u u v ,再根据,12BD DC =u u u v u u u v 用用AB u u u v 和AC uuu v 表示出AD u u u v,再根据4AD AC ⋅=u u u v u u u v 求出A AB C ⋅u u u v u u u v 的值,最后将A AB C ⋅u u u v u u u v 的值代入2A AB BC AB C AB ⋅=⋅-u u u v u u u v u u u v u u u v u u u v ,,从而得出答案. 【详解】()2 A =A AB BC AB C AB AB C AB ⋅=⋅-⋅-u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v ,∵12BD DC =u u u v u u u v ,∴111B C ?C B 222AD A A AD AD A AD A -=-=-+u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v(),整理可得:12 AB 33AD AC +u u u v u u u v u u u v=, 221A A 433AD AC AB C C ∴⋅⋅+=u u u v u u u v u u u v u u u v u u u v =∴ A =-12AB C ⋅u u u v u u u v , ∴2 =A =122537AB BC AB C AB ⋅⋅---=-u u u v u u u v u u u v u u u v u u u v .,故选:D . 【点睛】本题考查了平面向量数量积的运算,注意运用平面向量的基本定理,以及向量的数量积的性质,考查了运算能力,属于中档题.3.C解析:C 【解析】∵ 集合{}124A ,,=,{}2|40B x x x m =-+=,{}1A B ⋂= ∴1x =是方程240x x m -+=的解,即140m -+= ∴3m =∴{}{}{}22|40|43013B x x x m x x x =-+==-+==,,故选C4.D解析:D 【解析】 【分析】根据平面向量基本定理可知()12AE AB AC =+u u u v u u u v u u u v,将所求数量积化为1122AB AO AC AO ⋅+⋅u u uv u u u v u u u v u u u v ;由模长的等量关系可知AOB ∆和AOC ∆为等腰三角形,根据三线合一的特点可将AB AO ⋅u u u v u u u v 和AC AO ⋅u u u v u u u v 化为212AB u u uv 和212AC u u u v ,代入可求得结果.【详解】E Q 为BC 中点 ()12AE AB AC ∴=+u u u v u u u v u u u v()111222AE AO AB AC AO AB AO AC AO ∴⋅=+⋅=⋅+⋅u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v222OA OB OC ==u u u v u u u v u u u v Q AOB ∴∆和AOC ∆为等腰三角形211cos 22AB AO AB AO OAB AB AB AB ∴⋅=∠=⋅=u u u v u u u v u u u v u u u v u u u v u u u v u u u v ,同理可得:212AC AO AC ⋅=u u u v u u u v u u u v22111314422AE AO AB AC ∴⋅=+=+=u u u v u u u v u u u v u u u v本题正确选项:D 【点睛】本题考查向量数量积的求解问题,关键是能够利用模长的等量关系得到等腰三角形,从而将含夹角的运算转化为已知模长的向量的运算.5.A解析:A 【解析】由()4f x f x -=()得:4T =,当010]x ∈(,时,函数的图象如图:()()()26102f f f ===,再由关于x 的方程()log a f x x =有六个不同的根,则关于x 的方程()log a f x x =有三个不同的根,可得log 62 log 102a a<⎧⎨>⎩,解得610a ∈(,),故选A.点睛:本题主要考查了函数的周期性,奇偶性,函数的零点等基本性质,函数的图象特征,体现了数形结合的数学思想,属于中档题;首先求出()f x 的周期是4,画出函数的图象,将方程根的个数转化为函数图象交点的个数,得到关于a 的不等式,解得即可.6.C解析:C 【解析】 【分析】 【详解】试题分析:由已知可得176,176x y ==∴中心点为()176,176, 代入回归方程验证可知,只有方程y =88+12x 成立,故选C 7.C解析:C 【解析】 【分析】化简函数2sin 2y x x =+-. 【详解】依题意2ππsin 22sin 22sin 236y x x x x ⎡⎤⎛⎫⎛⎫=+=+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,故只需将函数2sin 2y x =的图象向左平移6π个单位.所以选C. 【点睛】本小题主要考查三角函数降次公式和辅助角公式,考查三角函数图象变换的知识,属于基础题.8.C解析:C 【解析】x ⩽1时,f (x )=−(x −1)2+1⩽1, x >1时,()()21,10a af x x f x x x=++'=-…在(1,+∞)恒成立, 故a ⩽x 2在(1,+∞)恒成立, 故a ⩽1,而1+a +1⩾1,即a ⩾−1, 综上,a ∈[−1,1], 本题选择C 选项.点睛:利用单调性求参数的一般方法:一是求出函数的单调区间,然后使所给区间是这个单调区间的子区间,建立关于参数的不等式组即可求得参数范围;二是直接利用函数单调性的定义:作差、变形,由f (x 1)-f (x 2)的符号确定参数的范围,另外也可分离参数转化为不等式恒成立问题.9.D解析:D【解析】 ∵111,,2a b成等差数列, ()1111441445529a b a b a b a b a b a b b a b a ⎛⎫∴+=∴+=++=+++⋅= ⎪⎝⎭,…, 当且仅当a =2b 即33,2a b ==时“=“成立, 本题选择D 选项.点睛:在应用基本不等式求最值时,要把握不等式成立的三个条件,就是“一正——各项均为正;二定——积或和为定值;三相等——等号能否取得”,若忽略了某个条件,就会出现错误.10.B解析:B 【解析】 【分析】可采用构造函数形式,令()()()35lg 1,1x h x x g x x +=+=-,采用数形结合法即可求解 【详解】由题可知,1x >-,当1x =时,()80f x =-≠, 令358()(1)lg(1)350lg(1)311x f x x x x x x x +=-+--=⇒+==+--, 令()()()35lg 1,1x h x x g x x +=+=-,画出函数图像,如图:则两函数图像有两交点,故函数()(1)lg(1)35f x x x x =-+--的零点个数为2个 故选:B 【点睛】本题考查函数零点个数的求解,数形结合思想,属于中档题11.C解析:C 【解析】圆22220x y x y ++-=的圆心坐标为()1,1-2,过圆心()1,1-与直线40x y --=垂直的直线方程为0x y +=,所求圆的圆心在此直线上,又圆心()1,1-到直线40x y --=的距离为322=,则所求圆的半径为2,设所求圆的圆心为(),a b ,且圆心在直线40x y --=的左上方,则422a b --=,且0a b +=,解得1,1a b ==-(3,3a b ==-不符合题意,舍去 ),故所求圆的方程为()()22112x y -++=.故选C .【名师点睛】本题主要考查直线与圆的位置关系,考查了数形结合的思想,考查了计算能力,属于中档题.12.B解析:B 【解析】 【分析】利用垂直关系,再结合勾股定理进而解决问题. 【详解】如图所示, 作EO CD ⊥于O ,连接ON ,过M 作MF OD ⊥于F . 连BF ,Q 平面CDE ⊥平面ABCD .,EO CD EO ⊥⊂平面CDE ,EO ∴⊥平面ABCD ,MF ⊥平面ABCD ,MFB ∴∆与EON ∆均为直角三角形.设正方形边长为2,易知3,12EO ON EN ===,35,,722MF BF BM ==∴=.BM EN ∴≠,故选B . 【点睛】本题考查空间想象能力和计算能力, 解答本题的关键是构造直角三角性.二、填空题13.【解析】【分析】先还原几何体再根据柱体体积公式求解【详解】空间几何体为一个棱柱如图底面为边长为的直角三角形高为的棱柱所以体积为【点睛】本题考查三视图以及柱体体积公式考查基本分析求解能力属基础题 解析:32【解析】 【分析】先还原几何体,再根据柱体体积公式求解 【详解】空间几何体为一个棱柱,如图,底面为边长为1,3的直角三角形,高为3的棱柱,所以体积为1313322⨯⨯⨯=【点睛】本题考查三视图以及柱体体积公式,考查基本分析求解能力,属基础题14.【解析】【分析】先利用指数函数的单调性得再解一元二次不等式即可【详解】故答案为【点睛】本题考查了指数不等式和一元二次不等式的解法属中档题 解析:()1,3-【解析】 【分析】先利用指数函数的单调性得2230x x --<,再解一元二次不等式即可. 【详解】22321 ()1230132x x x x x -->⇔--<⇔-<<. 故答案为()1,3- 【点睛】本题考查了指数不等式和一元二次不等式的解法,属中档题.15.11【解析】分析:构造基本不等式模型化简整理应用基本不等式即可得出答案详解:当且仅当时取等号的最小值等于11故答案为11点睛:本题考查基本不等式的性质与应用同时考查了整体思想与转化思想的运用解析:11 【解析】分析:构造基本不等式模型1132()(32)b ba b a b a a b a++=+++,化简整理,应用基本不等式,即可得出答案. 详解:Q111a b+=, ∴1132()(32)53()b b b a a b a b a a b a a b++=+++=++ Q 0a >,0b >,∴0b a >,0ab>, ∴2b aa b+≥,当且仅当2a b ==时取等号. 325611ba b a++≥+=. ∴32ba b a++的最小值等于11.故答案为11. 点睛:本题考查基本不等式的性质与应用,同时考查了整体思想与转化思想的运用.16.【解析】【分析】先求出的根利用等价转换的思想得到在有解并且使用分离参数方法可得结果【详解】由令所以又已知函数与互为近邻函数据题意可知:在有解则在有解即在有解令又令所以当时当时所以所以则故答案为:【点解析:10,2⎛⎤ ⎥⎝⎦.【解析】 【分析】先求出()0f x =的根,利用等价转换的思想,得到()0g x =在1m n -<有解,并且使用分离参数方法,可得结果 【详解】由()()13log 2exf x x -=+-,令()0f x =所以1x =,又已知函数()()13log 2e xf x x -=+-与()1422xx g x a +=⋅-+互为“近邻函数”据题意可知:()0g x =在11x -<有解,则()0g x =在02x <<有解即1224x x a +-=在02x <<有解,令()1224x xh x +-=,又令2x t =,()1,4t ∈,11,14t ⎛⎫∈ ⎪⎝⎭所以2222111222t y t t -⎛⎫==--+ ⎪⎝⎭ 当112t =时max 12y =当11t=时0y = 所以10,2y ⎛⎤∈ ⎥⎝⎦所以()10,2h x ⎛⎤∈ ⎥⎝⎦,则10,2a ⎛⎤∈ ⎥⎝⎦故答案为:10,2⎛⎤ ⎥⎝⎦【点睛】本题考查对新定义的理解,以及分离参数方法的应用,属中档题.17.2【解析】【分析】由题意首先求得向量然后结合向量平行的充分必要条件可得的值【详解】=由向量共线的充分必要条件有:故答案为2【点睛】本题主要考查平面向量的坐标运算向量平行的充分必要条件等知识意在考查学解析:2 【解析】 【分析】由题意首先求得向量a b λ+rr,然后结合向量平行的充分必要条件可得λ的值. 【详解】a bλ+r r =(,2(2,3)(2,23λλλλ+=++)), 由向量共线的充分必要条件有:()()(2)7(23)42λλλ+⋅-=+⋅-⇒=. 故答案为2. 【点睛】本题主要考查平面向量的坐标运算,向量平行的充分必要条件等知识,意在考查学生的转化能力和计算求解能力.18.【解析】【分析】由函数的解析式得到关于x 的不等式求解不等式即可确定函数的定义域【详解】函数有意义则:即求解三角不等式可得:则函数的定义域为【点睛】求函数的定义域其实质就是以函数解析式有意义为准则列出解析:()222,233k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ 【解析】 【分析】由函数的解析式得到关于x 的不等式,求解不等式即可确定函数的定义域. 【详解】函数有意义,则:2cos 10x +≥,即1cos 2x ≥-, 求解三角不等式可得:()222233k x k k Z ππππ-≤≤+∈, 则函数的定义域为()222,233k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦. 【点睛】求函数的定义域,其实质就是以函数解析式有意义为准则,列出不等式或不等式组,然后求出它们的解集即可.19.【解析】【分析】由已知可知然后利用基本不等式即可求解【详解】解:(当且仅当取等号)故答案为【点睛】本题主要考查了利用基本不等式求最值解题的关键是配凑积为定值属于基础试题解析:3+【解析】 【分析】由已知可知()11y 3x 3x 13x 1x 1=+=-++--,然后利用基本不等式即可求解. 【详解】解:x 1>Q ,()11y 3x 3x 13x 1x 1∴=+=-++--33≥=,(当且仅当13x =+取等号)故答案为3. 【点睛】本题主要考查了利用基本不等式求最值,解题的关键是配凑积为定值,属于基础试题.20.【解析】【分析】由三视图知几何体是半个圆锥圆锥的底面半径是1母线长是2得到圆锥的高利用圆锥体积公式得到结果【详解】由三视图知该几何体是半个圆锥圆锥的底面半径是1母线长是2∴圆锥的高是∴几何体的体积是【解析】 【分析】由三视图知几何体是半个圆锥,圆锥的底面半径是1,母线长是2,得到圆锥的高,利用圆锥体积公式得到结果. 【详解】由三视图知该几何体是半个圆锥,圆锥的底面半径是1,母线长是2,=∴几何体的体积是211132π⨯⨯⨯=,【点睛】本题考查由三视图还原几何图形,考查圆锥的体积公式,属于基础题.三、解答题21.(1)29人;(2)35.【解析】【分析】(1)根据频率分布直方图,良好即第二三两组,计算出第二三两组的频率即可算出人数;(2)结合频率分布直方图,计算出[)[]13,1417,18,两组的人数,1m n->即两位同学来自不同的两组,利用古典概型求解概率即可.【详解】(1)由直方图知,成绩在[14,16)内的人数为:500.20500.3829⨯+⨯=(人),所以该班成绩良好的人数为29人;(2)由直方图知,成绩在[13,14)的人数为500.063⨯=人;成绩在[17,18]的人数为500.042⨯=人;.事件“1m n->”发生即这两位同学来自不同的两组,此题相当于从这五人中任取2人,求这两人来自不同组的概率其概率为11232563105C CPC===.3(1)5P m n->=【点睛】此题考查用样本的频率分布估计总体分布;利用频率直方图求相关数据;古典概型及其概率的计算.22.(1)1,0a b==;(2)4k<.【解析】【分析】(1)函数()g x的对称轴方程为1x=,开口向上,则在[]2,3上单调递增,则可根据最值列出方程,可解得,a b的值.(2)由题意只需()min k f x <,则只需要求出()f x 在(]2,5上的最小值,然后运用基本不等式求最值即可. 【详解】解:(1)()g x Q 开口方向向上,且对称轴方程为 1x =,()g x ∴在[]2,3上单调递增()()()()min max 2441139614g x g a a b g x g a a b ⎧==-++=⎪∴⎨==-++=⎪⎩.解得1a =且0b =.(2)()0f x k ->Q 在(]2,5x ∈上恒成立 所以只需()min k f x <.有(1)知()()2211112222242222x x f x x x x x x x x -+==+=-++≥-⋅+=---- 当且仅当122x x -=-,即3x =时等号成立. 4k ∴<. 【点睛】本题考查二次函数的最值的求法,注意讨论对称轴和区间的位置关系,考查不等式恒成立问题的解法,注意运用参数分离和基本不等式的应用,属于中档题. 23.(1)k =-12.(2){-3}∪(1,+∞). 【解析】(1)由函数f(x)是偶函数,可知f(x)=f(-x), ∴log 4(4x +1)+kx =log 4(4-x +1)-kx.log 44141x x -++=-2kx ,即x =-2kx 对一切x ∈R 恒成立,∴k =-12.(2)函数f(x)与g(x)的图象有且只有一个公共点,即方程log 4(4x +1)-12x =log 44•23xa a ⎡⎤⎢⎥⎣⎦-有且只有一个实根,化简得方程2x +12x=a·2x-43a 有且只有一个实根.令t =2x >0,则方程(a -1)t 2-43at -1=0有且只有一个正根. ①a =1t =-34,不合题意;②a≠1时,Δ=0a =34或-3.若a =34t =-2,不合题意,若a =-3t =12;③a≠1时,Δ>0,一个正根与一个负根,即11a --<0a>1. 综上,实数a 的取值范围是{-3}∪(1,+∞).24.(1)证明见解析(2)圆C 的方程为(x -2)2+(y -1)2=5 【解析】 【分析】(1)先求出圆C 的方程(x -t )2+22)y t-(=t 2+24t ,再求出|OA|,|0B|的长,即得△OAB 的面积为定值;(2)根据212t =t 得到t =2或t =-2,再对t 分类讨论得到圆C 的方程. 【详解】(1)证明:因为圆C 过原点O ,所以OC 2=t 2+24t. 设圆C 的方程是(x -t )2+22)y t-(=t 2+24t, 令x =0,得y 1=0,y 2=4t; 令y =0,得x 1=0,x 2=2t ,所以S △OAB =12OA ·OB =12×|2t |×|4t|=4, 即△OAB 的面积为定值.(2)因为OM =ON ,CM =CN ,所以OC 垂直平分线段MN . 因为k MN =-2,所以k OC =12. 所以212t =t ,解得t =2或t =-2.当t =2时,圆心C 的坐标为(2,1),OC此时,圆心C 到直线y =-2x +4的距离dC 与直线y =-2x +4相交于两点.符合题意,此时,圆的方程为(x -2)2+(y -1)2=5.当t =-2时,圆心C 的坐标为(-2,-1),OC C 到直线y =-2x +4的距离d>.圆C 与直线y =-2x +4不相交, 所以t =-2不符合题意,舍去.所以圆C 的方程为(x -2)2+(y -1)2=5. 【点睛】本题主要考查圆的方程的求法,考查直线和圆的位置关系的求法,意在考查学生对这些知识的理解掌握水平. 25.(1)60,5607;(2)45.【解析】 【分析】(1)直接利用频率分布直方图求得平均数和中位数即可;(2)利用分层抽样可得6人中年龄在[]35,45内有2人,设为a 、b ,在[]65,86内有4人,设为1,2,3,4,写出基本事件,利用古典概型即可. 【详解】(1)这100位留言者年龄的样本平均数,300.05400.1500.15600.35700.2800.1560⨯+⨯+⨯+⨯+⨯+⨯=,年龄在[)25,55中的频率为:0.050.100.150.30++=, 年龄在[)25,65中的频率为:0.050.100.150.350.65+++=, 中位数在区间[)55,65中, 中位数为0.500.3055510600.357-+⨯=.(2)根据分层抽样原理,可知这6人中年龄在[]35,45内有2人,设为a 、b , 在[]65,86内有4人,设为1、2、3、4.设事件A 为“这3位发言者所得纪念品价值超过2300元”.从这6人中选3人的所有基本事件有:1ab 、2ab 、3ab 、4ab 、12a 、13a 、14a 、23a 、24a 、34a 、12b 、13b 、14b 、23b 、24b 、34b 、123、124、134、234,共20个.其中事件A 的对立事件即3个人都是年龄[]65,75内, 包含的有123、124、134、234,共4个. (写出事件A 的基本事件个数也可以) 所以()441205P A =-=., 【点睛】本题考查平均数、中位数,古典概型,在解题过程中要求学生算数要准确,频率分布直方图不要混淆各组数据的值,属于基础题.26.(1)直方图见解析;(2)0.48;(3)347.45m . 【解析】 【分析】(1)根据题中所给的使用了节水龙头50天的日用水量频数分布表,算出落在相应区间上的频率,借助于直方图中长方形的面积表示的就是落在相应区间上的频率,从而确定出对应矩形的高,从而得到直方图;(2)结合直方图,算出日用水量小于0.35的矩形的面积总和,即为所求的频率; (3)根据组中值乘以相应的频率作和求得50天日用水量的平均值,作差乘以365天得到一年能节约用水多少3m ,从而求得结果. 【详解】(1)频率分布直方图如下图所示:(2)根据以上数据,该家庭使用节水龙头后50天日用水量小于30.35m 的频率为0.20.110.1 2.60.120.050.48⨯+⨯+⨯+⨯=;因此该家庭使用节水龙头后日用水量小于30.35m 的概率的估计值为0.48; (3)该家庭未使用节水龙头50天日用水量的平均数为()110.0510.1530.2520.3540.4590.55260.6550.4850x =⨯+⨯+⨯+⨯+⨯+⨯+⨯=. 该家庭使用了节水龙头后50天日用水量的平均数为()210.0510.1550.25130.35100.45160.5550.3550x =⨯+⨯+⨯+⨯+⨯+⨯=. 估计使用节水龙头后,一年可节省水()()30.480.3536547.45m -⨯=.【点睛】该题考查的是有关统计的问题,涉及到的知识点有频率分布直方图的绘制、利用频率分布直方图计算变量落在相应区间上的概率、利用频率分布直方图求平均数,在解题的过程中,需要认真审题,细心运算,仔细求解,就可以得出正确结果.。
2020-2021天津市育贤中学高三数学上期末第一次模拟试卷(及答案)

2020-2021天津市育贤中学高三数学上期末第一次模拟试卷(及答案)一、选择题1.若函数y =f (x )满足:集合A ={f (n )|n ∈N *}中至少有三个不同的数成等差数列,则称函数f (x )是“等差源函数”,则下列四个函数中,“等差源函数”的个数是( ) ①y =2x +1;②y =log 2x ;③y =2x+1;④y =sin44x ππ+()A .1B .2C .3D .42.在ABC ∆中,,,a b c 分别为角,,A B C 所对的边,若 2?a bcos C =,则此三角形一定是( )A .等腰直角三角形B .直角三角形C .等腰三角形D .等腰三角形或直角三角形3.若0a b <<,则下列不等式恒成立的是 A .11a b> B .a b -> C .22a b > D .33a b <4.若正项递增等比数列{}n a 满足()()()243510a a a a R λλ+-+-=∈,则89a a λ+的最小值为( ) A .94-B .94C .274D .274-5.已知函数223log ,0(){1,0x x f x x x x +>=--≤,则不等式()5f x ≤的解集为 ( )A .[]1,1-B .[]2,4-C .(](),20,4-∞-⋃D .(][],20,4-∞-⋃ 6.已知数列{}n a 的前n 项和为n S ,1112n n a S a +=,=, 则n S =( )A .12n -B .13()2n -C .12()3n - D .112n - 7.已知等差数列{}n a 满足244a a +=,3510a a +=,则它的前10项的和10S =( ) A .138B .135C .95D .238.若a 、b 、c >0且a (a +b +c )+bc =4-,则2a +b +c 的最小值为( )A .1B .1C .+2D .29.已知等差数列{}n a ,前n 项和为n S ,5628a a +=,则10S =( ) A .140B .280C .168D .5610.已知数列{a n }满足331log 1log ()n n a a n N +++=∈且2469a a a ++=,则15793log ()a a a ++的值是( )A .-5B .-15C .5D .1511.已知变量x , y 满足约束条件13230x x y x y ≥⎧⎪+≤⎨⎪--≤⎩,则2z x y =+的最小值为( )A .1B .2C .3D .612.已知数列{}n a 中,()111,21,n n na a a n N S *+==+∈为其前n 项和,5S的值为( ) A .63B .61C .62D .57二、填空题13.关于x 的不等式a 34≤x 2﹣3x +4≤b 的解集为[a ,b ],则b -a =________. 14.已知函数1()f x x x=-,数列{}n a 是公比大于0的等比数列,且61a =,1239101()()()()()f a f a f a f a f a a +++⋅⋅⋅++=-,则1a =_______.15.已知向量()()1,,,2a x b x y ==-r r ,其中0x >,若a r 与b r 共线,则yx的最小值为__________.16.已知等差数列{}n a 的公差为()d d 0≠,前n 项和为n S,且数列也为公差为d 的等差数列,则d =______.17.已知锐角三角形的边长分别为1,3,a ,则a 的取值范围是__________. 18.若ABC ∆的三个内角45A =︒,75B =︒,60C =︒,且面积6S =+形的外接圆半径是______19.已知△ABC 中,角A 、B 、C 对应的边分别为a 、b 、c ,且bcosC ﹣ccosB 14=a 2,tanB =3tanC ,则a =_____. 20.设(3()lg f x x x =+,则对任意实数,a b ,“0a b +≥”是“()()0f a f b +≥”的_________条件.(填“充分不必要”.“必要不充分”.“充要”.“既不充分又不必要”之一)三、解答题21.已知000a b c >,>,>,函数().f x a x x b c =-+++ (1)当1a b c ===时,求不等式()3f x >的解集; (2)当()f x 的最小值为3时,求111a b c++的最小值. 22.在等差数列{}n a 中,36a =,且前7项和756T =.(1)求数列{}n a 的通项公式;(2)令3nn n b a =⋅,求数列{}n b 的前n 项和n S .23.ABC V 的内角A ,B ,C 的对边分别为a ,b ,c ,已知ABC V 的外接圆半径为R ,且sin sin cos 0A B b A --=.(1)求A ∠;(2)若tan 2tan A B =,求sin 2sin 2sin b Ca b B c C+-的值.24.已知数列{}n a 的前n 项和n S 满足231n n S a =-,其中n *∈N . (1)求数列{}n a 的通项公式;(2)设23nn n a b n n=+,求数列{}n b 的前n 项和为n T .25.在ABC ∆sin cos C c A =. (Ⅰ)求角A 的大小;(Ⅱ)若ABC S ∆,2b c +=+a 的值.26.在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且22222230a c b ac +-+=. (1)求cos B 的值; (2)求sin 24B π⎛⎫+⎪⎝⎭的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【解析】①y =2x +1,n ∈N *,是等差源函数;②因为log 21,log 22,log 24构成等差数列,所以y =log 2x 是等差源函数;③y =2x +1不是等差源函数,因为若是,则2(2p +1)=(2m +1)+(2n +1),则2p +1=2m +2n ,所以2p +1-n =2m -n +1,左边是偶数,右边是奇数,故y =2x +1不是等差源函数; ④y =sin 44x ππ⎛⎫+⎪⎝⎭是周期函数,显然是等差源函数.答案:C.2.C解析:C【解析】在ABC ∆中,222222cos ,2cos 222a b c a b c C a b C b ab abQ +-+-=∴==⋅,2222a a b c ∴=+-,,b c ∴=∴此三角形一定是等腰三角形,故选C.【方法点睛】本题主要考查利用余弦定理判断三角形形状,属于中档题.判断三角形状的常见方法是:(1)通过正弦定理和余弦定理,化边为角,利用三角变换得出三角形内角之间的关系进行判断;(2)利用正弦定理、余弦定理,化角为边,通过代数恒等变换,求出边与边之间的关系进行判断;(3)根据余弦定理确定一个内角为钝角进而知其为钝角三角形.3.D解析:D 【解析】 ∵0a b << ∴设1,1a b =-= 代入可知,,A B C 均不正确对于D ,根据幂函数的性质即可判断正确 故选D4.C解析:C 【解析】设等比数列的公比为q (q >1),1+(a 2-a 4)+λ(a 3-a 5)=0,可得λ=24531a a a a +--则a 8+λa 9=a 8+666929498385888222535353111a a a a a a a a a q q q a a a a a a a q a a q q --+=++=+-=------令21t q =-,(t >0),q 2=t+1,则设f (t )=()()()()()()3232622213112111t t t t t t q f t q t t t++-+-+=='=∴-当t >12时,f (t )递增; 当0<t <12时,f (t )递减. 可得t=12处,此时q=2f (t )取得最小值,且为274,则a 8+λa 9的最小值为274; 故选C.5.B解析:B 【解析】分析:根据分段函数,分别解不等式,再求出并集即可.详解:由于()223log ,01,0x x f x x x x +>⎧=⎨--≤⎩,当x >0时,3+log 2x≤5,即log 2x≤2=log 24,解得0<x≤4, 当x≤0时,x 2﹣x ﹣1≤5,即(x ﹣3)(x+2)≤0,解得﹣2≤x≤0, ∴不等式f (x )≤5的解集为[﹣2,4], 故选B .点睛:本题考查了分段函数以及不等式的解法和集合的运算,分段函数的值域是将各段的值域并到一起,分段函数的定义域是将各段的定义域并到一起,分段函数的最值,先取每段的最值,再将两段的最值进行比较,最终取两者较大或者较小的.6.B解析:B 【解析】 【分析】利用公式1n n n a S S -=-计算得到11323,2n n n n S S S S ++==,得到答案. 【详解】由已知1112n n a S a +==,,1n n n a S S -=- 得()12n n n S S S -=-,即11323,2n n n n S S S S ++==, 而111S a ==,所以13()2n n S -=.故选B. 【点睛】本题考查了数列前N 项和公式的求法,利用公式1n n n a S S -=-是解题的关键.7.C解析:C 【解析】试题分析:∵24354{10a a a a +=+=,∴1122{35a d a d +=+=,∴14{3a d =-=, ∴1011091040135952S a d ⨯=+⨯=-+=. 考点:等差数列的通项公式和前n 项和公式.8.D解析:D 【解析】由a (a +b +c )+bc =4-, 得(a +c )·(a +b )=4-∵a 、b 、c >0.∴(a +c )·(a +b )≤22b c 2a ++⎛⎫ ⎪⎝⎭(当且仅当a +c =b +a ,即b =c 时取“=”),∴2a +b +c=1)=-2. 故选:D点睛:在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误9.A解析:A 【解析】由等差数列的性质得,5611028a a a a +==+,∴其前10项之和为()11010102814022a a +⨯==,故选A. 10.A解析:A 【解析】试题分析:331313log 1log log log 1n n n n a a a a +++=∴-=Q 即13log 1n n a a +=13n naa +∴= ∴数列{}n a 是公比为3的等比数列335579246()393a a a q a a a ∴++=++=⨯=15793log ()5a a a ∴++=-.考点:1.等比数列的定义及基本量的计算;2.对数的运算性质.11.A解析:A 【解析】 【分析】画出可行域,平移基准直线20x y +=到可行域边界的点()1,1C -处,由此求得z 的最小值. 【详解】画出可行域如下图所示,平移基准直线20x y +=到可行域边界的点()1,1C -处,此时z 取得最小值为()2111⨯+-=. 故选:A.【点睛】本小题主要考查线性规划问题,考查数形结合的数学思想方法,属于基础题.12.D解析:D 【解析】解:由数列的递推关系可得:()11121,12n n a a a ++=++= , 据此可得:数列{}1n a + 是首项为2 ,公比为2 的等比数列,则:1122,21n n n n a a -+=⨯⇒=- ,分组求和有:()5521255712S ⨯-=-=- .本题选择D 选项.二、填空题13.4【解析】【分析】设f (x )x2﹣3x+4其函数图象是抛物线画两条与x 轴平行的直线y=a和y=b如果两直线与抛物线有两个交点得到解集应该是两个区间;此不等式的解集为一个区间所以两直线与抛物线不可能有解析:4【解析】【分析】设f(x)3 4 =x2﹣3x+4,其函数图象是抛物线,画两条与x轴平行的直线y=a和y=b,如果两直线与抛物线有两个交点,得到解集应该是两个区间;此不等式的解集为一个区间,所以两直线与抛物线不可能有两个交点,所以直线y=a应该与抛物线只有一个或没有交点,所以a小于或等于抛物线的最小值且a与b所对应的函数值相等且都等于b,利用f (b)=b求出b的值,由抛物线的对称轴求出a的值,从而求出结果.【详解】解:画出函数f(x)=34x2﹣3x+4=34(x-2)2+1的图象,如图,可得f(x)min=f(2)=1,由图象可知,若a>1,则不等式a≤34x2-3x+4≤b的解集分两段区域,不符合已知条件,因此a≤1,此时a≤x2-3x+4恒成立.又不等式a≤34x2-3x+4≤b的解集为[a,b],所以a≤1<b,f(a)=f(b)=b,可得2233443344a a bb b b⎧-+=⎪⎪⎨⎪-+=⎪⎩由34b2-3b+4=b,化为3b2-16b+16=0,解得b=43或b=4.当b=43时,由34a2-3a+4-43=0,解得a=43或a=83,不符合题意,舍去,所以b=4,此时a=0,所以b-a=4.故答案为:4【点睛】本题考查了二次函数的图象与性质的应用问题,解题时应灵活应用函数的思想解决实际问题,是中档题.14.【解析】【分析】由于是等比数列所以也是等比数列根据题目所给条件列方程解方程求得的值【详解】设数列的公比为则是首项为公比为的等比数列由得即①由得②联立①②解得【点睛】本小题主要考查等比数列的性质考查等解析:2【解析】 【分析】由于{}n a 是等比数列,所以1n a ⎧⎫⎨⎬⎩⎭也是等比数列.根据题目所给条件列方程,解方程求得1a 的值. 【详解】设数列{}n a 的公比为0q >,则1n a ⎧⎫⎨⎬⎩⎭是首项为11a ,公比为1q 的等比数列,由()()()()()1239101f a f a f a f a f a a +++⋅⋅⋅++=-得121011210111a a a a a a a ⎛⎫+++-+++=- ⎪⎝⎭L L ,即()10101111111111a q a q a q q⎛⎫-⎪-⎝⎭-=---①,由61a =,得511a q =②,联立①②解得12a =. 【点睛】本小题主要考查等比数列的性质,考查等比数列的前n 项和公式,考查运算求解能力,属于中档题.15.【解析】【分析】根据两个向量平行的充要条件写出向量的坐标之间的关系之后得出利用基本不等式求得其最小值得到结果【详解】∵其中且与共线∴即∴当且仅当即时取等号∴的最小值为【点睛】该题考查的是有关向量共线解析:【解析】 【分析】根据两个向量平行的充要条件,写出向量的坐标之间的关系,之后得出2y x x x=+,利用基本不等式求得其最小值,得到结果. 【详解】∵()1,a x =r , (),2b x y =-r ,其中0x >,且a r 与b r共线∴()12y x x ⨯-=⋅,即22y x =+∴222y x x x x x+==+≥,当且仅当2x x =即x =时取等号 ∴yx的最小值为 【点睛】该题考查的是有关向量共线的条件,涉及到的知识点有向量共线坐标所满足的条件,利用基本不等式求最值,属于简单题目.16.【解析】【分析】表示出再表示出整理并观察等式列方程组即可求解【详解】等差数列的公差为前项和为设其首项为则=又数列也为公差为的等差数列首项为所以=即:整理得:上式对任意正整数n 成立则解得:【点睛】本题 解析:12【解析】 【分析】表示出n S【详解】等差数列{}n a 的公差为()0d d ≠,前n 项和为n S ,设其首项为1a , 则n S =()112n n na d -+,又数列也为公差为d=()1n d -()1n d =-=上式对任意正整数n成立,则)2120122d d d da d d⎧=⎪=⎪-+=⎪⎩,解得:12d =,134a =- 【点睛】本题主要考查了等差数列的前n 项和及通项公式,考查了方程思想及转化思想、观察能力,属于中档题.17.【解析】由三角形中三边关系及余弦定理可得应满足解得∴实数的取值范围是答案:点睛:根据三角形的形状判断边满足的条件时需要综合考虑边的限制条件在本题中要注意锐角三角形这一条件的运用必须要考虑到三个内角的解析:a <<【解析】由三角形中三边关系及余弦定理可得a 应满足22222222224130130310a a a a <<⎧⎪+->⎪⎨+->⎪⎪+->⎩,解得a << ∴实数a的取值范围是.答案: 点睛:根据三角形的形状判断边满足的条件时,需要综合考虑边的限制条件,在本题中要注意锐角三角形这一条件的运用,必须要考虑到三个内角的余弦值都要大于零,并由此得到不等式,进一步得到边所要满足的范围.18.【解析】【分析】设三角形外接圆半径R 由三角形面积公式解方程即可得解【详解】由题:设三角形外接圆半径为R ()根据正弦定理和三角形面积公式:即解得:故答案为:【点睛】此题考查三角形面积公式和正弦定理的应解析:【解析】 【分析】设三角形外接圆半径R ,由三角形面积公式21sin 2sin sin sin 2S ab C R A B C ==解方程即可得解. 【详解】由题:1sin sin 75sin(4530)22224B =︒=︒+︒=+=设三角形外接圆半径为R (0R >),根据正弦定理和三角形面积公式:211sin 2sin 2sin sin 2sin sin sin 22S ab C R A R B C R A B C ==⋅⋅=即2622R ⨯+=,解得:R =故答案为:【点睛】此题考查三角形面积公式和正弦定理的应用,利用正弦定理对面积公式进行转化求出相关量,需要对相关公式十分熟练.19.2【解析】【分析】根据题意由tanB =3tanC 可得3变形可得sinBcosC =3sinCcosB 结合正弦定理可得sinBcosC ﹣sinCcosBsinA×a 变形可得:sinBcosC ﹣sinCc解析:2 【解析】 【分析】根据题意,由tan B =3tan C 可得sinB cosB =3sinCcosC⨯,变形可得sin B cos C =3sin C cos B ,结合正弦定理可得sin B cos C ﹣sin C cos B 14=sin A ×a ,变形可得:sin B cos C ﹣sin C cos B 14=sin (B +C )×a ,由和角公式分析可得sin B cos C ﹣sin C cos B 14=⨯a ×(sin B cos C +sin C cos B ),将sin B cos C =3sin C cos B 代入分析可得答案. 【详解】根据题意,△ABC 中,tanB =3tanC ,即sinB cosB =3sinCcosC⨯,变形可得sinBcosC =3sinCcosB , 又由bcosC ﹣ccosB 14=a 2,由正弦定理可得:sinBcosC ﹣sinCcosB 14=sinA ×a , 变形可得:sinBcosC ﹣sinCcosB 14=sin (B +C )×a , 即sinBcosC ﹣sinCcosB 14=⨯a ×(sinBcosC +sinCcosB ), 又由sinBcosC =3sinCcosB ,则2sinCcosB =sinCcosB ×a , 由题意可知:2B π≠,即sinCcosB≠0,变形可得:a =2; 故答案为:2. 【点睛】本题考查三角函数的恒等变形,涉及正弦定理的应用,考查计算能力,属于基础题.20.充要【解析】所以为奇函数又为单调递增函数所以即是的充要条件点睛:充分必要条件的三种判断方法1定义法:直接判断若则若则的真假并注意和图示相结合例如⇒为真则是的充分条件2等价法:利用⇒与非⇒非⇒与非⇒非解析:充要 【解析】33()()lg(()lg(lg10f x f x x x x x +-=++-+-== ,所以()f x 为奇函数,又()f x 为单调递增函数,所以0()()()()()()0a b a b f a f b f a f b f a f b +≥⇔≥-⇔≥-⇔≥-⇔+≥ ,即“0a b +≥”是“()()0f a f b +≥”的充要条件点睛:充分、必要条件的三种判断方法.1.定义法:直接判断“若p 则q ”、“若q 则p ”的真假.并注意和图示相结合,例如“p ⇒q ”为真,则p 是q 的充分条件.2.等价法:利用p ⇒q 与非q ⇒非p ,q ⇒p 与非p ⇒非q ,p ⇔q 与非q ⇔非p 的等价关系,对于条件或结论是否定式的命题,一般运用等价法.3.集合法:若A ⊆B ,则A 是B 的充分条件或B 是A 的必要条件;若A =B ,则A 是B 的充要条件.三、解答题21.(1){|11}x x x <->或;(2)3 【解析】 【分析】(1)通过讨论x 的范围,求出不等式的解集即可;(2)先用绝对值不等式的性质求出最小值为a +b +c =3,然后用基本不等式可得. 【详解】(1)()111f x x x =-+++, ∴1123x x ≤-⎧⎨->⎩或1133x -<<⎧⎨>⎩或1213x x ≥⎧⎨+>⎩,解得{|11}x x x 或-.(2)f x x a x b c =-+++ a x x b c a b c ≥-+++=++ 3a b c =++=,()11111113a b c a b c a b c ⎛⎫++=++++ ⎪⎝⎭ 133b a c a c b a b a c b c ⎡⎤⎛⎫⎛⎫⎛⎫=++++++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦()1322233≥+++=. 当且仅当1a b c ===时取得最小值3. 【点睛】绝对值不等式的解法:法一:利用绝对值不等式的几何意义求解,体现了数形结合的思想; 法二:利用“零点分段法”求解,体现了分类讨论的思想;法三:通过构造函数,利用函数的图象求解,体现了函数与方程的思想. 22.(1)2n a n =;(2)S n =212n -•3n +1+32【解析】 【分析】(1)等差数列{a n }的公差设为d ,运用等差数列的通项公式和求和公式,计算可得所求通项公式;(2)求得b n =2n •3n ,由数列的错位相减法求和即可.【详解】(1)等差数列{a n }的公差设为d ,a 3=6,且前7项和T 7=56. 可得a 1+2d =6,7a 1+21d =56,解得a 1=2,d =2,则a n =2n ; (2)b n =a n •3n =2n •3n ,前n 项和S n =2(1•3+2•32+3•33+…+n •3n ), 3S n =2(1•32+2•33+3•34+…+n •3n +1), 相减可得﹣2S n =2(3+32+33+ (3)﹣n •3n +1)=2•(()31313n --﹣n •3n +1),化简可得S n =212n -•3n +1+32.【点睛】本题考查等差数列和等比数列的通项公式和求和公式的运用,考查数列的错位相减法求和,以及化简运算能力,属于中档题. 23.(1)6π;(2). 【解析】 【分析】(1)由正弦定理化简已知三角等式,根据sin 0B ≠可得tan A =,即可求出角A ; (2)由(1)可得tan 6B =,利用2sin 1A =及正弦定理将分式化简,再利用余弦定理化简分式得()1tan 2A B -+,最后利用正切和角公式代入tan A ,tan B ,可求出结果. 【详解】(1)∵sin sin cos 0A B b A -=,由正弦定理得:sin sin 2sin cos 0A B R B A -=,即)sin cos 0BA A -=,∵()0,B π∈,∴sin 0B ≠,cos A A =,tan 3A =, ∵()0,A π∈,∴6A π∠=.(2)由(1)知:tan A =,tan B =,1sin 2A =,∴2sin 1A =, ∴sin 2sin sin 2sin 2sin 2sin 2sin 2sin b C Ab Ca b B c C Aa b B c C=+-+-222sin ab Ca b c =+-由余弦定理得:()sin sin 11tan tan 2sin 2sin 2cos 22b C C C A B a b Bc C C ===-++-1tan tan 3321tan tan A B A B +=-⨯=--. 【点睛】本题考查正弦定理、余弦定理、同角三角函数的基本关系等基础知识,考查学生数形结合、转化与化归以及运算求解能力,解决此类问题的关键是灵活运用正、余弦定理进行边角的互化,属于中等题. 24.(1)()1=3n n a n N -*∈ ;(2)31nn + . 【解析】 【分析】 (1)由31=22n n S a -可得113122n n S a --=-,两式相减可化为()132n n a a n -=≥从而判断出{}n a 是等比数列,进而求出数列{}n a 的通项公式;(2)利用(1),化简可得231131n b n n n n ⎛⎫==- ⎪++⎝⎭,利用裂项求和法求解即可. 【详解】 (1)()*31=22n n S a n N -∈Q ∵, ① 当11311,22n S a ==-,∴11a =, 当2n ≥,∵113122n n S a --=-, ② ①-②:13322n n n a a a -=-,即:()132n n a a n -=≥ 又,对都成立,所以是等比数列,(2)【点睛】本题主要考查等比数列的定义与通项公式,以及裂项相消法求数列的和,属于中档题. 裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,常见的裂项技巧:(1)()1111n n k k n n k ⎛⎫=- ⎪++⎝⎭;(2)n k n ++ 1n k n k=+; (3)()()1111212122121n n n n ⎛⎫=- ⎪-+-+⎝⎭;(4)()()11122n n n =++ ()()()11112n n n n ⎡⎤-⎢⎥+++⎢⎥⎣⎦;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误. 25.(1) 6A π=;(2) 2a =.【解析】试题分析:(13sin sin sin cos A C C A ⋅=⋅.消去公因式得到所以3tan A =. 进而得到角A ;(2)结合三角形的面积公式,和余弦定理得到223b c +=+式得到2a =. 解析:(I 3sin cos a C c A =,所以cos 0A ≠, 由正弦定理sin sin sin a b c A B C==, 3sin sin sin cos A C C A ⋅=⋅. 又因为 ()0,C π∈,sin 0C ≠, 所以 3tan A =. 又因为 ()0,A π∈, 所以 6A π=.(II )由11sin 324ABC S bc A bc ∆===43bc =, 由余弦定理2222cos a b c bc A =+-, 得2222cos6a b c bc π=+-,即()()222212a b c bc b c =+-=+-,因为2b c +=+ 解得 24a =. 因为 0a >, 所以 2a =. 26.(1)34-(2)16【解析】试题分析:(1)利用余弦定理表示出cosB ,将已知等式代入即可求出cosB 的值;(2)由cosB 可求出sin 2,cos 2B B 的值,然后利用两角和的余弦公式可得结果. 试题解析:(1)由22222230a c b ac +-+=,得22232a cb ac +-=-, 根据余弦定理得222332cos 224aca cb B ac ac -+-===-; (2)由3cos 4B =-,得sin B =∴sin22sin cos 8B B B ==-,21cos22cos 18B B =-=,∴1sin 2sin2cos cos2sin 4442816B B B πππ⎫⎛⎫+=+=+=⎪ ⎪⎪⎝⎭⎝⎭.。
2020-2021天津市育贤中学高一数学上期末试题(带答案)

2020-2021天津市育贤中学高一数学上期末试题(带答案) 一、选择题1.已知函数()()2,2 11,2 2xa xxf xx⎧-≥⎪=⎨⎛⎫-<⎪ ⎪⎝⎭⎩, 满足对任意的实数x1≠x2都有()()1212f x f xx x--<0成立,则实数a的取值范围为( )A.(-∞,2)B.13,8⎛⎤-∞⎥⎝⎦C.(-∞,2]D.13,28⎡⎫⎪⎢⎣⎭2.已知0.11.1x=, 1.10.9y=,234log3z=,则x,y,z的大小关系是()A.x y z>>B.y x z>>C.y z x>>D.x z y>>3.若函数f(x)=a|2x-4|(a>0,a≠1)满足f(1)=19,则f(x)的单调递减区间是( )A.(-∞,2] B.[2,+∞)C.[-2,+∞)D.(-∞,-2]4.酒驾是严重危害交通安全的违法行为.为了保障交通安全,根据国家有关规定:100mL 血液中酒精含量低于20mg的驾驶员可以驾驶汽车,酒精含量达到20~79mg的驾驶员即为酒后驾车,80mg及以上认定为醉酒驾车.假设某驾驶员喝了一定量的酒后,其血液中的酒精含量上升到了1mg/mL.如果在停止喝酒以后,他血液中酒精含量会以每小时30%的速度减少,那么他至少经过几个小时才能驾驶汽车?()(参考数据:lg0.2≈﹣0.7,1g0.3≈﹣0.5,1g0.7≈﹣0.15,1g0.8≈﹣0.1)A.1B.3C.5D.75.德国数学家狄利克在1837年时提出:“如果对于x的每一个值,y总有一个完全确定的值与之对应,则y是x的函数,”这个定义较清楚地说明了函数的内涵.只要有一个法则,使得取值范围中的每一个值,有一个确定的y和它对应就行了,不管这个对应的法则是公式、图象,表格述是其它形式已知函数f(x)由右表给出,则1102f f⎛⎫⎛⎫⎪⎪⎝⎭⎝⎭的值为()A.0B.1C.2D.36.已知131log4a=,154b=,136c=,则()A.a b c>>B.a c b>>C.c a b>>D.b c a>>7.已知定义在R上的奇函数()f x满足:(1)(3)0f x f x++-=,且(1)0f≠,若函数6()(1)cos 43g x x f x =-+⋅-有且只有唯一的零点,则(2019)f =( )A .1B .-1C .-3D .38.函数()()212ln 12f x x x =-+的图象大致是( ) A .B .C .D .9.函数f (x )是定义在R 上的偶函数,在(-∞,0]上是减函数且f (2)=0,则使f (x )<0的x 的取值范围( ) A .(-∞,2)B .(2,+∞)C .(-∞,-2)∪(2,+∞)D .(-2,2)10.函数y =11x -在[2,3]上的最小值为( ) A .2 B .12 C .13D .-1211.下列函数中,在区间(1,1)-上为减函数的是 A .11y x=- B .cos y x =C .ln(1)y x =+D .2x y -=12.已知函数()()f x g x x =+,对任意的x ∈R 总有()()f x f x -=-,且(1)1g -=,则(1)g =( )A .1-B .3-C .3D .1二、填空题13.()f x 是R 上的奇函数且满足(3)(3)f x f x -=+,若(0,3)x ∈时,()lg f x x x =+,则()f x 在(6,3)--上的解析式是______________. 14.已知()|1||1|f x x x =+--,()ag x x x=+,对于任意的m R ∈,总存在0x R ∈,使得()0f x m =或()0g x m =,则实数a 的取值范围是____________. 15.函数()()4log 521x f x x =-+-________.16.对于复数a bc d ,,,,若集合{}S a b c d =,,,具有性质“对任意x y S ∈,,必有xy S ∈”,则当221{1a b c b===,,时,b c d ++等于___________17.若存在实数(),m n m n <,使得[],x m n ∈时,函数()()2log xa f x at =+的值域也为[],m n ,其中0a >且1a ≠,则实数t 的取值范围是______.18.已知函数2,01,()1(1),13,2x x f x f x x ⎧<≤⎪=⎨-<≤⎪⎩则关于x 的方程4()0xf x k -=的所有根的和的最大值是_______.19.若幂函数()af x x =的图象经过点1(3)9,,则2a -=__________.20.()()sin cos f x x π=在区间[]0,2π上的零点的个数是______.三、解答题21.计算3221(1).log 24lglog 27lg 2log 32+-+- 326031(2).(32)(8)9⎛⎫⨯--- ⎪⎝⎭- 22.已知函数22()21x x a f x ⋅+=-是奇函数.(1)求a 的值;(2)求解不等式()4f x ≥;(3)当(1,3]x ∈时,()2(1)0f tx f x +->恒成立,求实数t 的取值范围.23.已知集合,,.(1)若,求的值; (2)若,求的取值范围.24.近年来,中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁,百般刁难并不断加大对各国的施压,拉拢他们抵制华为5G ,然而这并没有让华为却步.华为在2019年不仅净利润创下记录,海外增长同祥强劲.今年,我国华为某一企业为了进一步增加市场竞争力,计划在2020年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投人固定成本250万,每生产x (千部)手机,需另投入成本()R x 万元,且210200,040()100008019450,40x x x R x x x x ⎧+<<⎪=⎨+-⎪⎩…,由市场调研知,每部手机售价0.8万元,且全年内生产的手机当年能全部销售完.(Ⅰ)求出2020年的利润()Q x (万元)关于年产量x (千部)的函数关系式(利润=销售额-成本);(Ⅱ)2020年产量x 为多少(千部)时,企业所获利润最大?最大利润是多少? (说明:当0a >时,函数ay x x=+在单调递减,在)+∞单调递增) 25.设函数()()2log xxf x a b=-,且()()211,2log 12f f ==.(1)求a b ,的值; (2)求函数()f x 的零点;(3)设()xxg x a b =-,求()g x 在[]0,4上的值域.26.已知()log a f x x =,()()()2log 2201,1,a g x x a a a =+>+≠∈R ,()1h x x x=+. (1)当[)1,x ∈+∞时,证明:()1h x x x=+为单调递增函数; (2)当[]1,2x ∈,且()()()F x g x f x =-有最小值2时,求a 的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【解析】 【分析】 【详解】试题分析:由题意有,函数()f x 在R 上为减函数,所以有220{1(2)2()12a a -<-⨯≤-,解出138a ≤,选B. 考点:分段函数的单调性. 【易错点晴】本题主要考查分段函数的单调性,属于易错题. 从题目中对任意的实数12x x ≠,都有()()12120f x f x x x -<-成立,得出函数()f x 在R 上为减函数,减函数图象特征:从左向右看,图象逐渐下降,故在分界点2x =处,有21(2)2()12a -⨯≤-,解出138a ≤. 本题容易出错的地方是容易漏掉分界点2x =处的情况.2.A【解析】 【分析】利用指数函数、对数函数的单调性直接比较. 【详解】解:0.1x 1.1 1.11=>=Q , 1.100y 0.90.91<=<=,22334z log log 103=<<,x ∴,y ,z 的大小关系为x y z >>. 故选A . 【点睛】本题考查三个数的大小的比较,利用指数函数、对数函数的单调性等基础知识,考查运算求解能力,是基础题.3.B解析:B 【解析】 由f(1)=得a 2=, ∴a=或a=-(舍), 即f(x)=(.由于y=|2x-4|在(-∞,2]上单调递减,在[2,+∞)上单调递增,所以f(x)在(-∞,2]上单调递增,在[2,+∞)上单调递减,故选B.4.C解析:C 【解析】 【分析】根据题意先探究出酒精含量的递减规律,再根据能驾车的要求,列出模型0.70.2x ≤ 求解. 【详解】因为1小时后血液中酒精含量为(1-30%)mg /mL , x 小时后血液中酒精含量为(1-30%)x mg /mL 的,由题意知100mL 血液中酒精含量低于20mg 的驾驶员可以驾驶汽车, 所以()3002%1.x-<,0.70.2x <,两边取对数得,lg 0.7lg 0.2x < ,lg 0.214lg 0.73x >= ,所以至少经过5个小时才能驾驶汽车.【点睛】本题主要考查了指数不等式与对数不等式的解法,还考查了转化化归的思想及运算求解的能力,属于基础题.5.D解析:D 【解析】 【分析】采用逐层求解的方式即可得到结果. 【详解】∵(] 121∈-∞,,∴112f ⎛⎫= ⎪⎝⎭, 则110102f ⎛⎫=⎪⎝⎭,∴()1(())21010f f f =,又∵[)102∈+∞,,∴()103f =,故选D . 【点睛】本题主要考查函数的基础知识,强调一一对应性,属于基础题.6.C解析:C 【解析】 【分析】首先将b 表示为对数的形式,判断出0b <,然后利用中间值以及对数、指数函数的单调性比较32与,a c的大小,即可得到,,a b c 的大小关系. 【详解】因为154b=,所以551log log 104b =<=,又因为(133331log log 4log 3,log 4a ==∈,所以31,2a ⎛⎫∈ ⎪⎝⎭, 又因为131133336,82c ⎛⎫⎛⎫⎛⎫ ⎪=∈ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪⎝⎭,所以3,22c ⎛⎫∈ ⎪⎝⎭, 所以c a b >>. 故选:C. 【点睛】本题考查利用指、对数函数的单调性比较大小,难度一般.利用指、对数函数的单调性比较大小时,注意数值的正负,对于同为正或者负的情况可利用中间值进行比较.7.C【解析】 【分析】由(1)(3)0f x f x ++-=结合()f x 为奇函数可得()f x 为周期为4的周期函数,则(2019)(1)f f =-,要使函数6()(1)cos 43g x x f x =-+⋅-有且只有唯一的零点,即6(1)cos 43x f x ⋅-=只有唯一解,结合图像可得(1)3f =,即可得到答案.【详解】Q ()f x 为定义在R 上的奇函数,∴()()f x f x -=-,又Q (1)(3)0(13)(33)0f x f x f x f x ++-=⇔+++--=,(4)()0(4)()()f x f x f x f x f x ++-=⇔+=--=∴, ∴()f x 在R 上为周期函数,周期为4, ∴(2019)(50541)(1)(1)f f f f =⨯-=-=-Q 函数6()(1)cos 43g x x f x =-+⋅-有且只有唯一的零点,即6(1)cos 43x f x ⋅-=只有唯一解,令6()m x x = ,则5()6m x x '=,所以(,0)x ∈-∞为函数6()m x x =减区间,(0,)x ∈+∞为函数6()m x x =增区间,令()(1)cos 43x f x ϕ=⋅-,则()x ϕ为余弦函数,由此可得函数()m x 与函数()x ϕ的大致图像如下:由图分析要使函数()m x 与函数()x ϕ只有唯一交点,则(0)(0)m ϕ=,解得(1)3f =∴(2019)(1)3f f =-=-,故答案选C . 【点睛】本题主要考查奇函数、周期函数的性质以及函数的零点问题,解题的关键是周期函数的判定以及函数唯一零点的条件,属于中档题.8.A解析:A 【解析】函数有意义,则:10,1x x +>∴>-,由函数的解析式可得:()()21002ln 0102f =⨯-+=,则选项BD 错误; 且211111112ln 1ln ln 402222848f ⎛⎫⎛⎫⎛⎫-=⨯--⨯-+=-=+> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则选项C 错误; 本题选择A 选项.点睛:函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象.利用上述方法排除、筛选选项.9.D解析:D 【解析】 【分析】根据偶函数的性质,求出函数()0f x <在(-∞,0]上的解集,再根据对称性即可得出答案. 【详解】由函数()f x 为偶函数,所以()()220f f -==,又因为函数()f x 在(-∞,0]是减函数,所以函数()0f x <在(-∞,0]上的解集为(]2,0-,由偶函数的性质图像关于y 轴对称,可得在(0,+ ∞)上()0f x <的解集为(0,2),综上可得,()0f x <的解集为(-2,2). 故选:D. 【点睛】本题考查了偶函数的性质的应用,借助于偶函数的性质解不等式,属于基础题.10.B解析:B 【解析】 y =11x -在[2,3]上单调递减,所以x=3时取最小值为12,选B. 11.D解析:D 【解析】 试题分析:11y x=-在区间()1,1-上为增函数;cos y x =在区间()1,1-上先增后减;()ln 1y x =+在区间()1,1-上为增函数;2x y -=在区间()1,1-上为减函数,选D.考点:函数增减性12.B解析:B 【解析】由题意,f (﹣x )+f (x )=0可知f (x )是奇函数,∵()()f x g x x =+,g (﹣1)=1, 即f (﹣1)=1+1=2 那么f (1)=﹣2. 故得f (1)=g (1)+1=﹣2, ∴g (1)=﹣3, 故选:B二、填空题13.【解析】【分析】首先根据题意得到再设代入解析式即可【详解】因为是上的奇函数且满足所以即设所以所以故答案为:【点睛】本题主要考查函数的奇偶性和对称性的综合题同时考查了学生的转化能力属于中档题 解析:()6lg(6)f x x x =---+【解析】 【分析】首先根据题意得到(6)()f x f x +=-,再设(6,3)x ∈--,代入解析式即可. 【详解】因为()f x 是R 上的奇函数且满足(3)(3)f x f x -=+,所以[3(3)][3(3)]f x f x ++=-+,即(6)()()f x f x f x +=-=-. 设(6,3)x ∈--,所以6(0,3)x +∈.(6)6lg(6)()f x x x f x +=+++=-,所以()6lg(6)f x x x =---+. 故答案为:()6lg(6)f x x x =---+ 【点睛】本题主要考查函数的奇偶性和对称性的综合题,同时考查了学生的转化能力,属于中档题.14.【解析】【分析】通过去掉绝对值符号得到分段函数的解析式求出值域然后求解的值域结合已知条件推出的范围即可【详解】由题意对于任意的总存在使得或则与的值域的并集为又结合分段函数的性质可得的值域为当时可知的 解析:(,1]-∞【解析】 【分析】通过去掉绝对值符号,得到分段函数的解析式,求出值域,然后求解()ag x x x=+的值域,结合已知条件推出a 的范围即可. 【详解】由题意,对于任意的m R ∈,总存在0x R ∈,使得()0f x m =或()0g x m =,则()f x 与()g x 的值域的并集为R ,又()2,1112,112,1x f x x x x x x ≥⎧⎪=+--=-<<⎨⎪-≤-⎩,结合分段函数的性质可得,()f x 的值域为[]22-,, 当0a ≥时,可知()ag x x x=+的值域为(),⎡-∞-+∞⎣U ,所以,此时有2≤,解得01a ≤≤, 当0a <时,()ag x x x=+的值域为R ,满足题意, 综上所述,实数a 的范围为(],1-∞. 故答案为:(],1-∞. 【点睛】本题考查函数恒成立条件的转化,考查转化思想的应用,注意题意的理解是解题的关键,属于基础题.15.【解析】【分析】根据题意列出不等式组解出即可【详解】要使函数有意义需满足解得即函数的定义域为故答案为【点睛】本题主要考查了具体函数的定义域问题属于基础题;常见的形式有:1分式函数分母不能为0;2偶次 解析:[)0,5【解析】 【分析】根据题意,列出不等式组50210x x ->⎧⎨-≥⎩,解出即可.【详解】要使函数()()4log 5f x x =-+有意义,需满足50210x x ->⎧⎨-≥⎩,解得05x <≤,即函数的定义域为[)0,5,故答案为[)0,5. 【点睛】本题主要考查了具体函数的定义域问题,属于基础题;常见的形式有:1、分式函数分母不能为0;2、偶次根式下大于等于0;3、对数函数的真数部分大于0;4、0的0次方无意义;5、对于正切函数tan y x =,需满足,2x k k Z ππ≠+∈等等,当同时出现时,取其交集.16.-1【解析】由题意可得:结合集合元素的互异性则:由可得:或当时故当时故综上可得:解析:-1 【解析】由题意可得:21,1b a == ,结合集合元素的互异性,则:1b =- , 由21c b ==- 可得:c i = 或c i =- , 当c i = 时,bc i S =-∈ ,故d i =- , 当c i =- 时,bc i S =∈ ,故d i = , 综上可得:1b c d ++=- .17.【解析】【分析】由已知可构造有两不同实数根利用二次方程解出的范围即可【详解】为增函数且时函数的值域也为相当于方程有两不同实数根有两不同实根即有两解整理得:令有两个不同的正数根只需即可解得故答案为:【解析:10,4⎛⎫⎪⎝⎭【解析】 【分析】由已知可构造()2log xa a t x +=有两不同实数根,利用二次方程解出t 的范围即可.【详解】()2()log x a f x a t =+Q 为增函数,且[],x m n ∈时,函数()()2log xa f x at =+的值域也为[],m n ,(),()f m m f n n ∴==,∴相当于方程()f x x =有两不同实数根,()2log x a a t x ∴+=有两不同实根,即2x x a a t =+有两解, 整理得:20x x a a t -+=, 令,0xm a m => ,20m m t ∴-+=有两个不同的正数根, ∴只需140t t ∆=->⎧⎨>⎩即可,解得104t <<, 故答案为:10,4⎛⎫ ⎪⎝⎭【点睛】本题主要考查了对数函数的单调性,对数方程,一元二次方程有两正根,属于中档题.18.5【解析】【分析】将化简为同时设可得的函数解析式可得当k 等于8时与的交点的所有根的和的最大可得答案【详解】解:由可得:设由函数的性质与图像可得当k等于8时与的交点的所有根的和的最大此时根分别为:当时解析:5【解析】【分析】将2,01,()1(1),13,2x xfxf x x⎧<≤⎪=⎨-<≤⎪⎩化简为2,01,1()2,12,412,23,16xxxxf x xx⎧⎪<≤⎪⎪=⨯<≤⎨⎪⎪⨯<≤⎪⎩同时设4()()x f x g x=,可得()g x的函数解析式,可得当k等于8时与()g x的交点的所有根的和的最大,可得答案.【详解】解:由2,01,()1(1),13,2x xf xf x x⎧<≤⎪=⎨-<≤⎪⎩可得:2,01,1()2,12,412,23,16xxxxf x xx⎧⎪<≤⎪⎪=⨯<≤⎨⎪⎪⨯<≤⎪⎩设4()()x f x g x=,8,01,1()8,12,418,23,16xxxxg x xx⎧⎪<≤⎪⎪=⨯<≤⎨⎪⎪⨯<≤⎪⎩由()g x函数的性质与图像可得,当k等于8时与()g x的交点的所有根的和的最大,此时根分别为:当01x <≤时,188x =,11x =, 当12x <≤时,21848x ⨯=,253x =, 当23x <≤时,318816x ⨯=,373x =,此时所有根的和的最大值为:1235x x x ++=, 故答案为:5. 【点睛】本题主要考查分段函数的图像与性质,注意分段函数需分对分段区间进行讨论,属于中档题.19.【解析】由题意有:则: 解析:14【解析】 由题意有:13,29aa =∴=-, 则:()22124a--=-=. 20.5【解析】【分析】由求出的范围根据正弦函数为零确定的值再由三角函数值确定角即可【详解】时当时的解有的解有的解有故共有5个零点故答案为:5【点睛】本题主要考查了正弦函数余弦函数的三角函数值属于中档题解析:5 【解析】 【分析】由[]0,2x π∈,求出cos x π的范围,根据正弦函数为零,确定cos x 的值,再由三角函数值确定角即可. 【详解】cos x πππ-≤≤Q ,()()sin cos 0f x x π∴==时, cos 0x =,1,1-,当[]0,2x π∈时,cos 0x =的解有3,22ππ,cos 1x =-的解有π, cos 1x =的解有0,2π,故共有30,,,,222ππππ5个零点, 故答案为:5 【点睛】本题主要考查了正弦函数、余弦函数的三角函数值,属于中档题.三、解答题21.(1)32.(2)44. 【解析】 【分析】 【详解】试题分析:(1)底数相同的对数先加减运算,根号化为分数指数.(2)根号化为分数指数,再用积的乘方运算. 试题解析:223222321(1).log 24lg log lg 2log 321(log 24log 3)(lg lg 2)log 32333log 8lg13222+--=-++-=+-=-=3261(-8)9⎛⎫-- ⎪⎝⎭- 11362322(32()3)1--=⨯--9827144=⨯--=考点:1.对数运算,指数运算.2.分数指数,零指数等运算. 22.(1)2a =;(2)}{20log 3x x <≤;(3)1,4t ⎛⎫∈-∞-⎪⎝⎭【解析】 【分析】(1)由奇函数的性质得出a 的值;(2)结合()f x 的解析式可将()4f x ≥化为32021xx -≥-,解不等式即可得出答案;(3)利用函数()f x 在(1,3]x ∈上的单调性以及奇偶性将()2(1)0f tx f x +->化为21tx x <-,分离参数t 结合二次函数的性质得出实数t 的取值范围.【详解】(1)根据题意,函数222222()()211212x x x x x xa a a f x f x --⋅++⋅⋅+-===-=--- ∴2a =.(2)222()421x xf x ⋅+=≥-,即21221x x +≥-,即2132202121x x x x +--=≥-- 即()()32210210x xx ⎧--≥⎪⎨-≠⎪⎩,解得:132x <≤,得20log 3x <≤.(3)22222244()2212121x x x x xf x ⋅+⋅-+===+--- 故()f x 在(1,3]x ∈上为减函数2()(1)0f tx f x +->,即2()(1)(1)f tx f x f x >--=-即21tx x <-,221111124t x x x ⎛⎫<-=-- ⎪⎝⎭又(1,3]x ∈,11,13x ⎡⎫∈⎪⎢⎣⎭,故14t <- 综上1,4t ⎛⎫∈-∞- ⎪⎝⎭. 【点睛】本题主要考查了由函数的奇偶性求解析式以及利用单调性解不等式,属于中档题. 23.(1) 或;(2) .【解析】 试题分析:(1)由题意结合集合相等的定义分类讨论可得:的值为或. (2)由题意得到关于实数a 的不等式组,求解不等式组可得 .试题解析: (1)若,则,∴. 若,则,,∴.综上,的值为或. (2)∵,∴∴. 24.(Ⅰ)()210600250,040,100009200,40.x x x Q x x x x ⎧-+-<<⎪∴=⎨--+≥⎪⎩(Ⅱ)2020年年产量为100(千部)时,企业获得的利润最大,最大利润为9000万元. 【解析】 【分析】(Ⅰ)根据题意知利润等于销售收入减去可变成本及固定成本,分类讨论即可写出解析式(Ⅱ)利用二次函数求040x <<时函数的最大值,根据对勾函数求40x ≥时函数的最大值,比较即可得函数在定义域上的最大值. 【详解】(Ⅰ)当040x << 时,()()228001020025010600250Q x x x x x x =-+-=-+- ;当40x ≥时,()100001000080080194502509200Q x x x x x x ⎛⎫=-+--=--+ ⎪⎝⎭. ()210600250,040,100009200,40.x x x Q x x x x ⎧-+-<<⎪∴=⎨--+≥⎪⎩(Ⅱ)当040x <<时,()()210308750Q x x =--+,()()max 308750Q x Q ∴==万元;当40x ≥时,()100009200Q x x x ⎛⎫=-++ ⎪⎝⎭,当且仅当100x =时, ()()max 1009000Q x Q ==万元.所以,2020年年产量为100(千部)时,企业获得的利润最大,最大利润为9000万元. 【点睛】本题主要考查了分段函数,函数的最值,函数在实际问题中的应用,属于中档题. 25.(1)4,2a b ==(2)21log 2x +=(3)()[]0,240g x ∈ 【解析】 【分析】(1)由()()211,2log 12f f ==解出即可 (2)令()0f x =得421x x -=,即()22210xx --=,然后解出即可(3)()42xxg x =-,令2x t =,转化为二次函数 【详解】(1)由已知得()()()()222221log 12log log 12f a b f a b ⎧=-=⎪⎨=-=⎪⎩,即22212a b a b -=⎧⎨-=⎩, 解得4,2a b ==;(2)由(1)知()()2log 42xxf x =-,令()0f x =得421xx -=,即()22210xx --=,解得122x =,又20,2x x >∴=,解得2log x = (3)由(1)知()42xxg x =-,令2x t =,则()221124g t t t t ⎛⎫=-=-- ⎪⎝⎭,[]1,16t ∈, 因为()g t 在[]1,16t ∈上单调递增所以()[]0,240g x ∈, 26.(1)证明见解析(2)4a = 【解析】 【分析】(1)利用定义法证明函数的单调性,按照:设元、作差、变形、判断符号、下结论的步骤完成即可;(2)首先表示出()()()F x g x f x =-,再根据复合函数的单调性分类讨论可得。
天津高三高中数学期末考试带答案解析

天津高三高中数学期末考试班级:___________ 姓名:___________ 分数:___________一、选择题1.“”是“”的()A.充分而不必要的条件B.必要而不充分的条件C.充要条件D.既不充分也不必要的条件2.已知i是虚数单位,则复数所对应的点落在()A.第一象限B.第二象限C.第三象限D.第四象限3.已知等差数列中,,则=()A.3B.8C.14D.194.圆与直线相切于点A(3,1),则直线的方程为()A.B.C.D.5.右图是计算函数的值的程序框图,则在①、②、③处应分别填入的是()A.B.C.D.6.抛物线的焦点到双曲线的渐近线的距离为()A.1B.C.D.7.已知P是边长为2的正边BC上的动点,则()A.最大值为8B.最小值为2C.是定值6D.与P的位置有关8.设偶函数上为减函数,且,则不等式的解集为()A.B.C.D.二、填空题1.函数的定义域为。
2.一个几何体的三视图如图所示,则这个几何体的体积为。
3.设变量x,y满足约束条件目标函数的最大值为。
4.在中,若B=2A,,A= 。
5.函数在处的切线与y轴的交点为。
6.已知集合则集合等于。
三、解答题1.(本小题共13分)已知(1)求的值;(2)求函数的值域。
2.(本小题共13分)如图,矩形ABCD中,平面ABE,BE=BC,F为CE上的点,且平面ACE。
(1)求证:平面BCE;(2)求证:AE//平面BFD。
3.(本小题共13分)某学校餐厅新推出A、B、C、D四款套餐,某一天四款套餐销售情况的条形图如下。
为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:(1)若同学甲选择的是A款套餐,求甲的调查问卷被选中的概率;(2)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这两人中至少有一人选择是D款套餐的概率。
4.(本小题共13分)已知数列的前n项和为,且。
2020-2021天津市育贤中学高一数学上期末第一次模拟试卷(及答案)

2020-2021天津市育贤中学高一数学上期末第一次模拟试卷(及答案)一、选择题1.已知函数()f x 是定义在R 上的偶函数,且在[)0,∞+上是增函数,若对任意[)x 1,∞∈+,都有()()f x a f 2x 1+≤-恒成立,则实数a 的取值范围是( )A .[]2,0- B .(],8∞-- C .[)2,∞+ D .(],0∞- 2.已知()f x 是偶函数,它在[)0,+∞上是增函数.若()()lg 1f x f <-,则x 的取值范围是( )A .1,110⎛⎫ ⎪⎝⎭B .()10,10,10骣琪??琪桫C .1,1010⎛⎫ ⎪⎝⎭D .()()0,110,⋃+∞3.已知函数()ln ln(2)f x x x =+-,则 A .()f x 在(0,2)单调递增 B .()f x 在(0,2)单调递减C .()y =f x 的图像关于直线x=1对称D .()y =f x 的图像关于点(1,0)对称 4.设6log 3a =,lg5b =,14log 7c =,则,,a b c 的大小关系是( )A .a b c <<B .a b c >>C .b a c >>D .c a b >> 5.已知4213332,3,25a b c ===,则A .b a c <<B .a b c <<C .b c a <<D .c a b << 6.已知0.11.1x =, 1.10.9y =,234log 3z =,则x ,y ,z 的大小关系是( ) A .x y z >> B .y x z >>C .y z x >>D .x z y >> 7.已知二次函数()f x 的二次项系数为a ,且不等式()2f x x >-的解集为()1,3,若方程()60f x a +=,有两个相等的根,则实数a =( )A .-15B .1C .1或-15D .1-或-15 8.函数ln xy x =的图象大致是( ) A . B . C . D .9.已知全集为R ,函数()()ln 62y x x =--的定义域为集合{},|44A B x a x a =-≤≤+,且R A B ⊆ð,则a 的取值范围是( )A .210a -≤≤B .210a -<<C .2a ≤-或10a ≥D .2a <-或10a >10.已知函数f (x )=12log ,1,24,1,x x x x >⎧⎪⎨⎪+≤⎩则1(())2f f )等于( ) A .4B .-2C .2D .1 11.函数()()212ln 12f x x x =-+的图象大致是( ) A . B .C .D .12.设函数()1x2,x 12f x 1log x,x 1-≤⎧=->⎨⎩,则满足()f x 2≤的x 的取值范围是( ) A .[]1,2- B .[]0,2 C .[)1,∞+ D .[)0,∞+ 二、填空题13.若函数()(0,1)x f x a a a =>≠且在[1,2]上的最大值比最小值大2a ,则a 的值为____________.14.若函数()1f x mx x =--有两个不同的零点,则实数m 的取值范围是______.15.如果函数()22279919m m y m m x --=-+是幂函数,且图像不经过原点,则实数m =___________.16.若函数f (x )是定义在R 上的偶函数,在(-∞,0]上是减函数,且f (2)=0,则使得f (x )<0的x 的取值范围是________.17.函数()()()310310x x x f x x -⎧+<⎪=⎨-+≥⎪⎩,若函数y m =的图像与函数()y f x =的图像有公共点,则m 的取值范围是______.18.若函数()(21)()x f x x x a =+-为奇函数,则(1)f =___________. 19.若函数()121x f x a =++是奇函数,则实数a 的值是_________.20.若函数()()22f x x x a x a =+--在区间[]3,0-上不是单调函数,则实数a 的取值范围是______.三、解答题21.某种商品的销售价格会因诸多因素而上下浮动,经过调研得知:2019年9月份第x (130x ≤≤,x +∈N )天的单件销售价格(单位:元20,115()50,1530x x f x x x +≤<⎧=⎨-≤≤⎩,第x 天的销售量(单位:件)()(g x m x m =-为常数),且第20天该商品的销售收入为600元(销售收入=销售价格⨯销售量).(1)求m 的值;(2)该月第几天的销售收入最高?最高为多少?22.已知函数1()21x f x a =-+,()x R ∈. (1)用定义证明:不论a 为何实数()f x 在(,)-∞+∞上为增函数; (2)若()f x 为奇函数,求a 的值;(3)在(2)的条件下,求()f x 在区间[1,5]上的最小值.23.已知全集U =R ,集合{|25},{|121}M x x N x a x a =-=++剟剟. (Ⅰ)若1a =,求()R M N I ð;(Ⅱ)M N M ⋃=,求实数a 的取值范围.24.已知()()1 22x x f x a a R +-=+∈n .(1)若()f x 是奇函数,求a 的值,并判断()f x 的单调性(不用证明);(2)若函数()5y f x =-在区间(0,1)上有两个不同的零点,求a 的取值范围.25.已知函数()224x x a f x =-+,()()log 0,1a g x x a a =>≠. (1)若函数()f x 在区间[]1,m -上不具有单调性,求实数m 的取值范围;(2)若()()11f g =,设()112t f x =,()2t g x =,当()0,1x ∈时,试比较1t ,2t 的大小. 26.药材人工种植技术具有养殖密度高、经济效益好的特点.研究表明:人工种植药材时,某种药材在一定的条件下,每株药材的年平均生长量(v 单位:千克)是每平方米种植株数x 的函数.当x 不超过4时,v 的值为2;当420x <≤时,v 是x 的一次函数,其中当x 为10时,v 的值为4;当x 为20时,v 的值为0.()1当020x <≤时,求函数v 关于x 的函数表达式;()2当每平方米种植株数x 为何值时,每平方米药材的年生长总量(单位:千克)取得最大值?并求出这个最大值.(年生长总量=年平均生长量⨯种植株数)【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【解析】【分析】根据偶函数的性质,可知函数在(],0-∞上是减函数,根据不等式在[)1,x ∈+∞上恒成立,可得:21x a x +≤-在[)1,+∞上恒成立,可得a 的范围.【详解】 ()f x Q 为偶函数且在[)0,+∞上是增函数()f x ∴在(],0-∞上是减函数对任意[)1,x ∈+∞都有()()21f x a f x +≤-恒成立等价于21x a x +≤-2121x x a x ∴-+≤+≤- 311x a x ⇒-+≤≤-()()max min 311x a x ∴-+≤≤-当1x =时,取得两个最值3111a ∴-+≤≤- 20a ⇒-≤≤本题正确选项:A【点睛】本题考查函数奇偶性和单调性解抽象函数不等式的问题,关键在于能够通过单调性确定自变量之间的关系,得到关于自变量的不等式.2.C解析:C【解析】【分析】利用偶函数的性质将不等式()()lg 1f x f <-变形为()()lg 1f x f <,再由函数()y f x =在[)0,+∞上的单调性得出lg 1x <,利用绝对值不等式的解法和对数函数的单调性即可求出结果.【详解】由于函数()y f x =是偶函数,由()()lg 1f x f <-得()()lg 1f x f <,又Q 函数()y f x =在[)0,+∞上是增函数,则lg 1x <,即1lg 1x -<<,解得11010x <<. 故选:C.【点睛】本题考查利用函数的单调性和奇偶性解不等式,同时也涉及了对数函数单调性的应用,考查分析问题和解决问题的能力,属于中等题.3.C解析:C【解析】由题意知,(2)ln(2)ln ()f x x x f x -=-+=,所以()f x 的图象关于直线1x =对称,故C 正确,D 错误;又()ln[(2)]f x x x =-(02x <<),由复合函数的单调性可知()f x 在(0,1)上单调递增,在(1,2)上单调递减,所以A ,B 错误,故选C .【名师点睛】如果函数()f x ,x D ∀∈,满足x D ∀∈,恒有()()f a x f b x +=-,那么函数的图象有对称轴2a b x +=;如果函数()f x ,x D ∀∈,满足x D ∀∈,恒有()()f a x f b x -=-+,那么函数()f x 的图象有对称中心(,0)2a b +. 4.A解析:A【解析】【分析】构造函数()log 2xx f x =,利用单调性比较大小即可. 【详解】构造函数()21log 1log 212log x x x f x x==-=-,则()f x 在()1,+∞上是增函数, 又()6a f =,()10b f =,()14c f =,故a b c <<.故选A【点睛】本题考查实数大小的比较,考查对数函数的单调性,考查构造函数法,属于中档题.5.A解析:A【解析】【分析】【详解】 因为422233332=4,3,5a b c ===,且幂函数23y x =在(0,)+∞ 上单调递增,所以b <a <c . 故选A.点睛:本题主要考查幂函数的单调性及比较大小问题,解答比较大小问题,常见思路有两个:一是判断出各个数值所在区间(一般是看三个区间()()(),0,0,1,1,-∞+∞ );二是利用函数的单调性直接解答;数值比较多的比大小问题也可以两种方法综合应用;三是借助于中间变量比较大小.解析:A【解析】【分析】利用指数函数、对数函数的单调性直接比较.【详解】解:0.10x 1.1 1.11=>=Q , 1.100y 0.90.91<=<=,22334z log log 103=<<,x ∴,y ,z 的大小关系为x y z >>.故选A .【点睛】本题考查三个数的大小的比较,利用指数函数、对数函数的单调性等基础知识,考查运算求解能力,是基础题.7.A解析:A【解析】【分析】设()2f x ax bx c =++,可知1、3为方程()20f x x +=的两根,且0a <,利用韦达定理可将b 、c 用a 表示,再由方程()60f x a +=有两个相等的根,由0∆=求出实数a 的值.【详解】由于不等式()2f x x >-的解集为()1,3,即关于x 的二次不等式()220ax b x c +++>的解集为()1,3,则0a <. 由题意可知,1、3为关于x 的二次方程()220ax b x c +++=的两根, 由韦达定理得2134b a +-=+=,133c a=⨯=,42b a ∴=--,3c a =, ()()2423f x ax a x a ∴=-++,由题意知,关于x 的二次方程()60f x a +=有两相等的根,即关于x 的二次方程()24290ax a x a -++=有两相等的根, 则()()()224236102220a a a a ∆=+-=+-=,0a <Q ,解得15a =-,故选:A. 【点睛】 本题考查二次不等式、二次方程相关知识,考查二次不等式解集与方程之间的关系,解题的关键就是将问题中涉及的知识点进行等价处理,考查分析问题和解决问题的能力,属于中等题.8.C【解析】 分析:讨论函数ln x y x =性质,即可得到正确答案. 详解:函数ln x y x =的定义域为{|0}x x ≠ ,ln ln x x f x f x xx x --==-=-Q ()() ,∴排除B ,当0x >时,2ln ln 1-ln ,,x x x y y x x x===' 函数在()0,e 上单调递增,在(),e +∞上单调递减,故排除A,D ,故选C .点睛:本题考查了数形结合的思想应用及排除法的应用. 9.C解析:C【解析】【分析】由()()620x x -->可得{}|26=<<A x x ,{}44R C B x a x a 或=-+,再通过A 为 R C B 的子集可得结果.【详解】由()()ln 62y x x =--可知,()()62026x x x -->⇒<<,所以{}|26=<<A x x ,{}44R C B x a x a 或=-+,因为R A C B ⊆,所以6424a a 或≤-≥+,即102a a ≥≤-或,故选C.【点睛】本题考查不等式的解集和对数函数的定义域,以及集合之间的交集和补集的运算;若集合的元素已知,求解集合的交集、并集、补集时,可根据交集、并集、补集的定义求解. 10.B解析:B【解析】121242242f ⎛⎫=+=+= ⎪⎝⎭,则()1214log 422f f f ⎛⎫⎛⎫===- ⎪ ⎪⎝⎭⎝⎭,故选B. 11.A解析:A【解析】函数有意义,则:10,1x x +>∴>-,由函数的解析式可得:()()21002ln 0102f =⨯-+=,则选项BD 错误; 且211111112ln 1ln ln 402222848f ⎛⎫⎛⎫⎛⎫-=⨯--⨯-+=-=+> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则选项C 错误; 本题选择A 选项.点睛:函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象.利用上述方法排除、筛选选项.12.D解析:D【解析】【分析】分类讨论:①当x 1≤时;②当x 1>时,再按照指数不等式和对数不等式求解,最后求出它们的并集即可.【详解】当x 1≤时,1x 22-≤的可变形为1x 1-≤,x 0≥,0x 1∴≤≤.当x 1>时,21log x 2-≤的可变形为1x 2≥,x 1∴≥,故答案为[)0,∞+. 故选D .【点睛】本题主要考查不等式的转化与求解,应该转化特定的不等式类型求解. 二、填空题13.或【解析】【分析】【详解】若∴函数在区间上单调递减所以由题意得又故若∴函数在区间上单调递增所以由题意得又故答案:或 解析:12或32【解析】【分析】【详解】 若01a <<,∴函数()xf x a =在区间[1,2]上单调递减,所以2max min (),()f x a f x a ==,由题意得22a a a -=,又01a <<,故12a =.若1a >,∴函数()x f x a =在区间[1,2]上单调递增,所以2max min (),()f x a f x a ==,由题意得22a a a -=,又1a >,故32a =. 答案:12或3214.【解析】【分析】令可得从而将问题转化为和的图象有两个不同交点作出图形可求出答案【详解】由题意令则则和的图象有两个不同交点作出的图象如下图是过点的直线当直线斜率时和的图象有两个交点故答案为:【点睛】本 解析:()0,1【解析】【分析】令()0f x =,可得1mx x =-,从而将问题转化为y mx =和1y x =-的图象有两个不同交点,作出图形,可求出答案.【详解】由题意,令()10f x mx x =--=,则1mx x =-,则y mx =和1y x =-的图象有两个不同交点,作出1y x =-的图象,如下图, y mx =是过点()0,0O 的直线,当直线斜率()0,1m ∈时,y mx =和1y x =-的图象有两个交点.故答案为:()0,1.【点睛】本题考查函数零点问题,考查函数图象的应用,考查学生的计算求解能力,属于中档题. 15.3【解析】【分析】根据幂函数的概念列式解得或然后代入解析式看指数的符号负号就符合正号就不符合【详解】因为函数是幂函数所以即所以所以或当时其图象不过原点符合题意;当时其图象经过原点不合题意综上所述:故 解析:3【解析】【分析】根据幂函数的概念列式解得3m =,或6m =,然后代入解析式,看指数的符号,负号就符合,正号就不符合.【详解】因为函数()22279919m m y m m x --=-+是幂函数,所以29191m m -+=,即29180m m -+=,所以(3)(6)0m m --=,所以3m =或6m =-,当3m =时,12()f x x -=,其图象不过原点,符合题意;当5m =时,21()f x x =,其图象经过原点,不合题意.综上所述:3m =.故答案为:3【点睛】本题考查了幂函数的概念和性质,属于基础题. 16.(-22)【解析】【详解】∵函数f(x)是定义在R 上的偶函数且在(-∞0)上是增函数又f(2)=0∴f(x)在(0+∞)上是增函数且f(-2)=f(2)=0∴当-2<x <2时f(x)<0即f(x)<解析:(-2,2)【解析】【详解】∵函数f(x)是定义在R 上的偶函数,且在(-∞,0)上是增函数,又f(2)=0,∴f(x)在(0,+∞)上是增函数,且f(-2)=f(2)=0,∴当-2<x <2时,f(x)<0,即f(x)<0的解为(-2,2),即不等式的解集为(-2,2),故填(-2,2).17.【解析】【分析】作出函数的图象如下图所示得出函数的值域由图象可得m 的取值范围【详解】作出函数的图象如下图所示函数的值域为由图象可得要使函数的图像与函数的图像有公共点则m 的取值范围是故答案为:【点睛】 解析:[)()0,11,2⋃【解析】【分析】作出函数()f x 的图象如下图所示,得出函数()f x 的值域,由图象可得m 的取值范围.【详解】作出函数()f x 的图象如下图所示,函数()f x 的值域为[)()0,11,2⋃,由图象可得要使函数y m =的图像与函数()y f x =的图像有公共点,则m 的取值范围是[)()0,11,2⋃, 故答案为:[)()0,11,2⋃.【点睛】本题考查两函数图象交点问题,关键在于作出分段函数的图象,运用数形结合的思想求得范围,在作图象时,注意是开区间还是闭区间,属于基础题.18.【解析】【分析】根据函数奇偶性的定义和性质建立方程求出a 的值再将1代入即可求解【详解】∵函数为奇函数∴f (﹣x )=﹣f (x )即f (﹣x )∴(2x ﹣1)(x+a )=(2x+1)(x ﹣a )即2x2+(2 解析:23【解析】【分析】根据函数奇偶性的定义和性质建立方程求出a 的值,再将1代入即可求解【详解】∵函数()()()21xf x x x a =+-为奇函数, ∴f (﹣x )=﹣f (x ),即f (﹣x )()()()()2121x x x x a x x a -==--+--+-,∴(2x ﹣1)(x +a )=(2x +1)(x ﹣a ),即2x 2+(2a ﹣1)x ﹣a =2x 2﹣(2a ﹣1)x ﹣a ,∴2a ﹣1=0,解得a 12=.故2(1)3f = 故答案为23【点睛】本题主要考查函数奇偶性的定义和性质的应用,利用函数奇偶性的定义建立方程是解决本题的关键. 19.【解析】【分析】由函数是奇函数得到即可求解得到答案【详解】由题意函数是奇函数所以解得当时函数满足所以故答案为:【点睛】本题主要考查了利用函数的奇偶性求解参数问题其中解答中熟记奇函数的性质是解答的关键 解析:12- 【解析】【分析】由函数()f x 是奇函数,得到()010021f a =+=+,即可求解,得到答案. 【详解】由题意,函数()121x f x a =++是奇函数,所以()010021f a =+=+,解得12a =-, 当12a =-时,函数()11212x f x =-+满足()()f x f x -=-, 所以12a =-. 故答案为:12-. 【点睛】本题主要考查了利用函数的奇偶性求解参数问题,其中解答中熟记奇函数的性质是解答的关键,着重考查了推理与运算能力,属于基础题.20.【解析】【分析】将函数转化为分段函数对参数分类讨论【详解】转化为分段函数:为更好说明问题不妨设:其对称轴为;其对称轴为①当时因为的对称轴显然不在则只需的对称轴位于该区间即解得:满足题意②当时此时函数 解析:()()9,00,3-⋃【解析】【分析】将函数转化为分段函数,对参数a 分类讨论.【详解】()()22f x x x a x a =+--,转化为分段函数:()222232,2,x ax a x a f x x ax a x a ⎧-+≥=⎨+-<⎩. 为更好说明问题,不妨设:()2232h x x ax a =-+,其对称轴为3a x =; ()222g x x ax a =+-,其对称轴为x a =-.①当0a >时,因为()h x 的对称轴3a x =显然不在[]3,0-,则 只需()g x 的对称轴位于该区间,即()3,0a -∈-,解得:()0,3a ∈,满足题意.②当0a =时,()223,0,0x x f x x x ⎧≥=⎨<⎩,此时 函数在区间[]3,0-是单调函数,不满足题意.③当0a <时,因为()g x 的对称轴x a =-显然不在[]3,0-只需()h x 的对称轴位于该区间即可,即()3,03a ∈- 解得:()9,0a ∈-,满足题意.综上所述:()()9,00,3a ∈-⋃.故答案为:()()9,00,3-⋃.【点睛】本题考查分段函数的单调性,难点在于对参数a 进行分类讨论. 三、解答题21.(1)40m =;(2)当第10天时,该商品销售收入最高为900元.【解析】【分析】(1)利用分段函数,直接求解(20)(20)600f g =.推出m 的值.(2)利用分段函数分别求解函数的最大值推出结果即可.【详解】(1)销售价格20,115,()50,1530,x x f x x x +<⎧=⎨-⎩…剟第x 天的销售量(单位:件)()(g x m x m =-为常数),当20x =时,由(20)(20)(5020)(20)600f g m =--=,解得40m =.(2)当115x <…时,(20)(40)y x x =+-2220800(10)900x x x =-++=--+, 故当10x =时,900max y =,当1530x 剟时,22(50)(40)902000(45)25y x x x x x =--=-+=--, 故当15x =时,875max y =,因为875900<,故当第10天时,该商品销售收入最高为900元.【点睛】本题考查利用函数的方法解决实际问题,分段函数的应用,考查转化思想以及计算能力,是中档题.22.(1)见解析;(2)12a =;(3) 16. 【解析】【分析】【详解】 (1)()f x Q 的定义域为R, 任取12x x <, 则121211()()2121x x f x f x a a -=--+++=121222(12)(12)x x x x -++. 12x x <Q ,∴1212220,(12)(12)0x x x x -++.∴12())0(f x f x -<,即12()()f x f x <.所以不论a 为何实数()f x 总为增函数.(2)()f x Q 在x ∈R 上为奇函数,∴(0)0f =,即01021a -=+. 解得12a =. (3)由(2)知,11()221x f x =-+, 由(1) 知,()f x 为增函数,∴()f x 在区间[1,5)上的最小值为(1)f .∵111(1)236f =-=, ∴()f x 在区间[1,5)上的最小值为16. 23.(Ⅰ)(){|22R M C N x x =-≤<I 或35}x <≤(Ⅱ)2a ≤【解析】【分析】(Ⅰ)1a =时,化简集合B ,根据集合交集补集运算即可(Ⅱ)由M N M ⋃=可知N M ⊆,分类讨论N =∅,N ≠∅即可求解.【详解】(Ⅰ)当1a =时,{}|23N x x =≤≤ ,{|2R C N x x =<或}3x > .故 (){|22R M C N x x =-≤<I 或35}x <≤.(Ⅱ),M N M ⋃=QN M ∴⊆当N =∅时,121a a +>+,即0a <;当N ≠∅时,即0a ≥.N M ⊆Q ,12215a a +≥-⎧∴⎨+≤⎩解得02a ≤≤.综上:2a ≤.【点睛】本题主要考查了集合的交集,补集运算,子集的概念,分类讨论,属于中档题.24.(1)答案见解析;(2)253,8⎛⎫ ⎪⎝⎭. 【解析】试题分析:(1)函数为奇函数,则()()0f x f x -+=,据此可得2a =-,且函数()f x 在R 上单调递增;(2)原问题等价于22252x x a =-⋅+⋅在区间(0,1)上有两个不同的根,换元令2x t =,结合二次函数的性质可得a 的取值范围是253,8⎛⎫ ⎪⎝⎭. 试题解析:(1)因为是奇函数,所以()()()()1122222220x x x x x x f x f x a a a -++---+=+⋅++⋅=++=, 所以; 在上是单调递增函数; (2)在区间(0,1)上有两个不同的零点, 等价于方程在区间(0,1)上有两个不同的根, 即方程在区间(0,1)上有两个不同的根, 所以方程在区间上有两个不同的根, 画出函数在(1,2)上的图象,如下图,由图知,当直线y =a 与函数的图象有2个交点时, 所以的取值范围为. 点睛:函数零点的应用主要表现在利用零点求参数范围,若方程可解,通过解方程即可得出参数的范围,若方程不易解或不可解,则将问题转化为构造两个函数,利用两个函数图象的关系求解,这样会使得问题变得直观、简单,这也体现了数形结合思想的应用.25.(1)()1,+∞;(2)12t t >【解析】【分析】(1)根据二次函数的单调性得到答案.(2)计算得到2a =,再计算()2110x t ->=,22log 0t x =<,得到答案.【详解】(1)函数()224x x a f x =-+的对称轴为1x =, 函数()f x 在区间[]1,m -上不具有单调性,故1m >,即()1,m ∈+∞.(2)()()11f g =,即24log 10a a -+==,故2a =.当()0,1x ∈时,()()212212110x x x t f x -+=-=>=;()22log 0t g x x ==<. 故12t t >【点睛】本题考查了根据函数的单调性求参数,比较函数值大小,意在考查学生对于函数性质的综合应用. 26.(1)2,0428,4205x v x x <≤⎧⎪=⎨-+<≤⎪⎩;(2) 10株时,最大值40千克 【解析】【分析】当420x <≤时,设v ax b =+,然后代入两组数值,解二元一次方程组可得参数a 、b 的值,即可得到函数v 关于x 的函数表达式;第()2题设药材每平方米的年生长总量为()f x 千克,然后列出()f x 表达式,再分段求出()f x 的最大值,综合两段的最大值可得最终结果.【详解】(1)由题意得,当04x <≤时,2v =;当420x <≤时,设v ax b =+,由已知得200104a b a b +=⎧⎨+=⎩,解得258a b ⎧=-⎪⎨⎪=⎩,所以285v x =-+,故函数2,0428,4205x v x x <≤⎧⎪=⎨-+<≤⎪⎩. (2)设药材每平方米的年生长总量为()f x 千克,依题意及()1可得()22,0428,4205x x f x x x x <≤⎧⎪=⎨-+<≤⎪⎩, 当04x <≤时,()f x 为增函数,故()()4428max f x f ==⨯=;当420x <≤时,()()222222820(10)40555f x x x x x x =-+=--=--+,此时()()1040max f x f ==.综上所述,可知当每平方米种植10株时,药材的年生长总量取得最大值40千克.【点睛】本题主要考查应用函数解决实际问题的能力,考查了理解能力,以及实际问题转化为数学问题的能力,本题属中档题.。
2020-2021学年天津育才中学高三数学文月考试题含解析

2020-2021学年天津育才中学高三数学文月考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 设F1、F2分别是椭圆的两焦点,点P是该椭圆上一个动点,则的取值范围是A.[一2,1) B.(—2,1)C.(一2,1] D.[—2,1]参考答案:D【知识点】椭圆的应用;平面向量数量积的运算由椭圆的知F1(﹣,0),设P(x,y),则=(﹣﹣x,﹣y)(﹣x,﹣y)=x2+y2﹣3=(3x2﹣8)∵x∈[﹣2,2],∴0≤x2≤4,故∈[﹣2,1],故选D.【思路点拨】设出点P的坐标,进而可表示出,进而根据x的范围确定的范围。
2. 在中,角的对边分别为,且.则 A. B. C. D.参考答案:A略3. 如图,F是抛物线的焦点,A是抛物线E上任意一点.现给出下列四个结论:①以线段AF为直径的圆必与y轴相切;②当点A为坐标原点时,|AF|为最短;③若点B是抛物线E上异于点A的一点,则当直线AB(AB2P)过焦点F时,|AF|+|BF|取得最小值;④点B、C是抛物线E上异于点A的不同两点,若|AF|、|BF|、|CF|成等差数列,则点A、B、C的横坐标亦成等差数列.其中正确结论的个数是( )A.1个B.2个 C.3个D.4个参考答案:D4. 若某空间几何体的三视图如图所示,则该几何体的体积是()A.B.C.D.1参考答案:D略5. (5分)(2015?嘉兴二模)函数的图象可由函数y=cos2x的图象() A.向左平移而得到 B.向右平移而得到C.向左平移而得到 D.向右平移而得到参考答案:B【考点】:函数y=Asin(ωx+φ)的图象变换.【专题】:三角函数的图像与性质.【分析】:先根据诱导公式进行化函数为函数y=cos,再由左加右减上加下减的原则可确定函数y=cos2x的平移方向与单位.解:函数y=sin(2x﹣)=cos=cos(2x﹣)=cos,所以要得到函数的图象,只需将函数y=cos2x的图象向右边平移个单位即可.故选:B.【点评】:本题主要考查三角函数的平移.三角函数的平移原则为左加右减上加下减.利用诱导公式化简函数为同名函数,ω相同是今天的关键.6. 已知点M(),若的最小值为3,则的值为()A、-4B、4C、-3D、3参考答案:D略7. “a=2”是“函数f(x)=x2+2ax﹣2在区间(﹣∞,﹣2]内单调递减”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件参考答案:A【分析】由二次函数单调性和充要条件的定义可得.【解答】解:当a=2时,f(x)=x2+2ax﹣2=(x+a)2﹣a2﹣2=(x+2)2﹣6,由二次函数可知函数在区间(﹣∞,﹣2]内单调递减;若f(x)=x2+2ax﹣2=(x+a)2﹣a2﹣2在区间(﹣∞,﹣2]内单调递减,则需﹣a≥﹣2,解得a≤2,不能推出a=2,故“a=2”是“函数f(x)=x2+2ax﹣2在区间(﹣∞,﹣2]内单调递减”的充分不必要条件.故选:A.【点评】本题考查充要条件的判定,涉及二次函数的单调性,属基础题.8. 设m、n是两条不同的直线,α、β是两个不同的平面,则m⊥β的一个充分条件是()A.α⊥β且m?αB.m∥n且n⊥βC.α⊥β且m∥αD.m⊥n且n∥β参考答案:B【考点】2L:必要条件、充分条件与充要条件的判断.【分析】根据充分条件的定义,判断能由哪个选项中的条件推出m⊥β,从而得出结论.【解答】解:由选项A可得直线m也可能在平面β内,故不满足条件,故排除A.由选项B推出m⊥β,满足条件.由选项C可得直线m?β,故不满足条件.由选项D可得直线m可能在平面β内,不满足条件,故排除D.故选:B.9. 已知函数是定义在上的偶函数, 且在区间单调递增. 若实数满足, 则的取值范围是()A.B.C.D.参考答案:C略10. 已知是定义在R上的奇函数,且当x>0对,(A)(B) (C) (D)参考答案:【知识点】奇函数的性质;分段函数的应用. B4 B1C解析:因为,所以,故选 C.【思路点拨】根据奇函数的性质,以及分段函数的函数值的意义求解.二、填空题:本大题共7小题,每小题4分,共28分11. 甲烷分子由一个碳原子和四个氢原子构成,其空间结构为正四面体,碳原子位于该正四面体的中心,四个氢原子分别位于该正四面体的四个顶点上,若将碳原子和氢原子均视为一个点(体积忽略不计),设碳原子与每个氢原子的距离都是a,则该正四面体的体积为_________ .参考答案:12. 7个身高各不相同的学生排成一排照相,高个子站中间,从中间到左边一个比一个矮,从中间到右边也一个比一个矮,则共有种不同的排法(结果用数字作答).参考答案:20【知识点】排列、组合及简单计数问题.J3解析:最高个子站在中间,只需排好左右两边,第一步:先排左边,有=20种排法,第二步:排右边,有=1种,根据分步乘法计数原理,共有20×1=20种,故答案为:20.【思路点拨】最高个子站在中间,只需排好左右两边,第一步:先排左边,有=20种排法,第二步:排右边,有=1种,根据分步乘法计数原理可得结论.13. 正三棱柱ABC—A1B1C1的高为2,AB1与平面ABC所成的角为45°,则点C到平面ABC1的距离是;参考答案:答案:14. 在平面上“等边三角形内任意一点到三边的距离之和为定值”,类比猜想为:;参考答案:正四面体内任意一点到四个面的距离之和为定值15. 曲线y=x(3ln x+1)在点处的切线方程为________ 参考答案:16. 若是定义在R上的函数,则“”是“函数为奇函数”的条件(从“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中选一个).参考答案:必要不充分17. 设向量=(1,2m ),=(m+1,1),=(m,3),若(+)⊥,则||= .参考答案:【考点】9J:平面向量的坐标运算.【分析】利用平面向量坐标运算法则求出,再利用向量垂直的性质求出,由此能求出||.【解答】解:∵向量=(1,2m),=(m+1,1),=(m,3),∴+=(1+m,2m+3),∵(+)⊥,∴(1+m)(m+1)+2m+3=0,解得m=﹣2,∴=(1,﹣4),∴||==.故答案为:.【点评】本题考查向量的模的求法,是基础题,解题时要认真审题,注意平面向量运算法则的合理运用.三、解答题:本大题共5小题,共72分。
2020-2021学年天津市育贤中学高三生物下学期期末考试试卷及参考答案

2020-2021学年天津市育贤中学高三生物下学期期末考试试卷及参考答案一、选择题:本题共15小题,每小题2分,共30分。
每小题只有一个选项符合题目要求。
1. 科学家因揭秘生命的“生物钟”获得诺贝尔奖。
人体除了人脑主生物钟外,还存在肝脏、胰腺等局部生物钟,如肝脏生物钟能影响肝糖原的分解。
下列推论正确的是()A.糖尿病的发生可能与维持血糖平衡的肝脏生物钟失调有关B.与生物节律控制有关的中枢存在于脑干中,该结构还具有内分泌功能C.若小鼠肝脏生物钟基因被敲除,小鼠一定会出现高血糖D.活跃在人脑中的主生物钟基因不存在于肝脏、胰腺等组织细胞中2. 当人的下丘脑受到损伤,下列选项不受影响的是()A.性激素的分泌B.渴觉的形成C.膝跳反射D.体温的调节3. 下列与水稻叶肉细胞中ATP相关的说法,正确的是()A. 只能由细胞呼吸产生B. 细胞质基质、线粒体基质和叶绿体基质中均能合成A TPC. 分解后脱离下来的末端磷酸基团挟能量与载体蛋白结合,可使载体蛋白空间结构发生变化D. 代谢旺盛时细胞中ATP的含量明显升高4. 如图,若做向光性实验测得胚芽鞘尖端向光一侧与背光一侧生长素含量之比为1:2,则胚芽鞘尖端背光一侧的生长素浓度范围是()A. 小于2mB. 大于1m,小于2mC. 大于2mD. 无法确定5. 将同一部位紫色洋葱外表皮细胞分别浸在甲、乙、丙3种溶液中,测得原生质层的外界面与细胞壁间距离变化如图所示,下列相关分析错误的是A. 实验开始时,甲、乙溶液的浓度均大于洋葱表皮细胞细胞液浓度B. 与t0时相比,t2时乙溶液中洋葱表皮细胞的细胞液浓度未发生变化C. 实验过程中,丙溶液中有水分子进出洋葱表皮细胞D. 实验结束时,甲、乙溶液的浓度有所下降6. 我们如何找到回家的路?荣获2014年诺贝尔奖的三位科学家发现大脑里的神经细胞——“位置细胞”和“网格细胞”起到了重要作用。
下列叙述正确的是()A.“位置细胞”鲜重中质量百分比最高的元素是CB.“网格细胞”干重中质量百分比最高元素是OC.上述两种细胞鲜重中原子数量最多的元素均是HD.P和S分别是“位置细胞”中的大量元素和微量元素7. 下列经典实验不可以作为证据证明核酸是遗传物质的是()A.格里菲思肺炎双球菌体内转化实验B.艾弗里的肺炎双球菌体外转化实验C.赫尔希和蔡斯的噬菌体侵染细菌实验D.烟草花叶病毒的RNA和蛋白质分别侵染烟草的实验8. 人体造血干细胞分化存在如下过程:造血干细胞→淋巴干细胞→淋巴母细胞,淋巴母细胞转移到不同器官可分别分化为B淋巴细胞(受抗原刺激可增殖分化形成浆细胞)和T淋巴细胞(受抗原刺激可增殖分化形成效应T细胞)。
2020-2021天津市育贤中学高二数学上期中试题(带答案)

2020-2021天津市育贤中学高二数学上期中试题(带答案)一、选择题1.抛掷一枚质地均匀的骰子,记事件A 为“向上的点数是偶数”,事件B 为“向上的点数不超过3”,则概率()P A B =U ( )A .12B .13C .23 D .562.已知变量,x y 之间满足线性相关关系ˆ 1.31yx =-,且,x y 之间的相关数据如下表所示: x 1 2 3 4 y0.1m3.14则实数m =( ) A .0.8B .0.6C .1.6D .1.83.某学校10位同学组成的志愿者组织分别由李老师和张老师负责,每次献爱心活动均需该组织4位同学参加.假设李老师和张老师分别将各自活动通知的信息独立,随机地发给4位同学,且所发信息都能收到.则甲同学收到李老师或张老师所发活动通知的信息的概率为( ) A .25B .1225C .1625D .454.有5支彩笔(除颜色外无差别),颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔,则取出的2支彩笔中含有红色彩笔的概率为 A .45 B .35C .25 D .155.从甲、乙、丙三人中任选两名代表,甲被选中的概率是( ) . A .12B .13C .23D .16.某校高一1班、2班分别有10人和8人骑自行车上学,他们每天骑行路程(单位:千米)的茎叶图如图所示:则1班10人每天骑行路程的极差和2班8人每天骑行路程的中位数分别是 A .14,9.5B .9,9C .9,10D .14,97.执行如图所示的程序框图,则输出的结果是( )A .5B .7C .9D .118.如图所示是为了求出满足122222018n +++>L 的最小整数n ,和两个空白框中,可以分别填入( )A .2018S >?,输出1n -B .2018S >?,输出nC .2018S ≤?,输出1n -D .2018S ≤?,输出n9.将参加夏令营的600名学生编号为:001,002,…,600,采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到200住在第一营区,从201到500住在第二营区,从501到600住在第三营区,三个营区被抽中的人数依次为( ). A .16,26,8B .17,24,9C .16,25,9D .17,25,810.已知平面区域()20,4y x y y x ⎧⎫≥⎧⎪⎪⎪Ω=⎨⎨⎬≤-⎪⎪⎩⎩,直线2y mx m =+和曲线24y x =-两个不的交点,它们围成的平面区域为M ,向区域Ω上随机投一点A ,点A 落在区域M 内的概率为()P M .若01m ≤≤,则()P M 的取值范围为( )A .202,π-⎛⎤⎥π⎝⎦B .202,π+⎛⎤⎥π⎝⎦C .212,π+⎡⎤⎢⎥π⎣⎦D .212,π-⎡⎤⎢⎥π⎣⎦11.设点(a,b)为区域4000x y x y +-≤⎧⎪>⎨⎪>⎩内任意一点,则使函数f(x)=2ax 2bx 3-+在区间[12,+∞)上是增函数的概率为 A .13B .2 3C .1 2D .1 412.运行如图所示的程序框图,若输出S 的值为129,则判断框内可填入的条件是( )A .4?k <B .5?k <C .6?k <D .7?k < 二、填空题13.判断大小,,,,则、、、大小关系为_____________.14.如果执行如图所示的程序框图,输入正整数()2N N ≥和实数12,,...,N a a a ,输出,A B ,若输入的N 为20,12,,...,N a a a 依次为87,76,89,98,68,76,89,94,83,86,68,79,95,93,89,87,76,77,84,96,则A B =-________.15.某班按座位将学生分为两组,第一组18人,第二组27人,现采用分层抽样的方法抽取5人,再从这5人中安排两人去打扫卫生,则这两人来自同一组的概率为__________. 16.执行如图所示的流程图,则输出的的值为 .17.如左下图是一次数学考试成绩的样本频率分布直方图(样本容量n=200),若成绩不低于60分为及格,则样本中的及格人数是_________。
2020-2021天津市自立中学高三数学下期末第一次模拟试题(及答案)

2020-2021天津市自立中学高三数学下期末第一次模拟试题(及答案)一、选择题1.如图所示的圆锥的俯视图为( )A .B .C .D .2.若复数21iz =-,其中i 为虚数单位,则z = A .1+i B .1−iC .−1+iD .−1−i3.已知2a ib i i+=+ ,,a b ∈R ,其中i 为虚数单位,则+a b =( ) A .-1B .1C .2D .34.在复平面内,O 为原点,向量OA u u u v对应的复数为12i -+,若点A 关于直线y x =-的对称点为点B ,则向量OB uuu v对应的复数为( ) A .2i -+ B .2i -- C .12i +D .12i -+5.设函数()()21,04,0x log x x f x x ⎧-<=⎨≥⎩,则()()233f f log -+=( )A .9B .11C .13D .156.已知平面向量a r=(1,-3),b r=(4,-2),a b λ+rr与a r垂直,则λ是( ) A .2 B .1 C .-2 D .-1 7.设是虚数单位,则复数(1)(12)i i -+=( )A .3+3iB .-1+3iC .3+iD .-1+i8.某同学有同样的画册2本,同样的集邮册3本,从中取出4本赠送给4为朋友,每位朋友1本,则不同的赠送方法共有 A .4种 B .10种 C .18种 D .20种 9.若,,a b R i ∈为虚数单位,且()a i i b i +=+,则A .1,1a b ==B .1,1a b =-=C .1,1a b ==-D .1,1a b =-=-10.如图所示,网格纸上小正方形的边长为1,粗线画出的是由一个棱柱挖去一个棱锥后的几何体的三视图,则该几何体的体积为A .72B .64C .48D .3211.在ABC ∆中,A 为锐角,1lg lg()lgsin 2b A c+==-,则ABC ∆为( ) A .等腰三角形 B .等边三角形 C .直角三角形D .等腰直角三角形12.已知ABC V 为等边三角形,2AB =,设P ,Q 满足AP AB λ=uu u r uu u r,()()1AQ AC λλ=-∈R u u u r u u u r ,若32BQ CP ⋅=-uu u r uu r ,则λ=( )A .12B .122± C .1102± D .322± 二、填空题13.函数()23s 34f x in x cosx =-(0,2x π⎡⎤∈⎢⎥⎣⎦)的最大值是__________. 14.已知复数z=(1+i )(1+2i ),其中i 是虚数单位,则z 的模是__________ 15.ABC V 的内角A ,B ,C 的对边分别为a ,b ,c ,已知2b =,3c =,2C B =,则ABC V 的面积为______.16.371()x x+的展开式中5x 的系数是 .(用数字填写答案)17.若x ,y 满足约束条件220100x y x y y --≤⎧⎪-+≥⎨⎪≤⎩,则32z x y =+的最大值为_____________.18.锐角△ABC 中,若B =2A ,则ba的取值范围是__________. 19.从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人,组成4人服务队,要求服务队中至少有1名女生,共有__________种不同的选法.(用数字作答) 20.设α 为第四象限角,且sin3sin αα=135,则 2tan =α ________. 三、解答题21.在平面直角坐标系中,直线l 的参数方程为cos sin x t y t αα=⎧⎨=⎩(t 为参数,0≤α<π).以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为244cos 2sin ρρθρθ-=-.(Ⅰ)写出曲线C 的直角坐标方程;(Ⅱ)若直线l 与曲线C 交于A ,B 两点,且AB 的长度为25,求直线l 的普通方程. 22.设()34f x x x =-+-.(Ⅰ)求函数()2()g x f x =-的定义域;(Ⅱ)若存在实数x 满足()1f x ax ≤-,试求实数a 的取值范围. 23.已知函数2()sin()sin 3cos 2f x x x x π=--.(1)求()f x 的最小正周期和最大值; (2)求()f x 在2[,]63ππ上的单调区间24.如图:在ABC ∆中,10a =,4c =,5cos 5C =-.(1)求角A ;(2)设D 为AB 的中点,求中线CD 的长.25.如图,四棱锥P ABCD -中,//AB DC ,2ADC π∠=,122AB AD CD ===,6PD PB ==,PD BC ⊥.(1)求证:平面PBD ⊥平面PBC ;(2)在线段PC 上是否存在点M ,使得平面ABM 与平面PBD 所成锐二面角为3π?若存在,求CMCP的值;若不存在,说明理由. 26.一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a ,b ,c .(Ⅰ)求“抽取的卡片上的数字满足a b c+=”的概率;(Ⅱ)求“抽取的卡片上的数字a,b,c不完全相同”的概率.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】找到从上往下看所得到的图形即可.【详解】由圆锥的放置位置,知其俯视图为三角形.故选C.【点睛】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图,本题容易误选B,属于基础题.2.B解析:B【解析】试题分析:22(1i)1i,1i 1i(1i)(1i)z z+===+∴=---+,选B.【考点】复数的运算,复数的概念【名师点睛】本题主要考查复数的运算及复数的概念,是一道基础题目.从历年高考题目看,复数题目往往不难,一般考查复数运算与概念或复数的几何意义,也是考生必定得分的题目之一.3.B解析:B【解析】【分析】利用复数除法运算法则化简原式可得2ai b i-=+,再利用复数相等列方程求出,a b的值,从而可得结果.【详解】因为22222a i ai iai b ii i+--==-=+-,,a b∈R,所以2211b ba a==⎧⎧⇒⎨⎨-==-⎩⎩,则+1a b=,故选B.【点睛】复数是高考中的必考知识,主要考查复数的概念及复数的运算.要注意对实部、虚部的理解,掌握纯虚数、共轭复数、复数的模这些重要概念,复数的运算主要考查除法运算,通过分母实数化转化为复数的乘法,运算时特别要注意多项式相乘后的化简,防止简单问题出错,造成不必要的失分.4.A解析:A 【解析】 【分析】首先根据向量OA u u u v对应的复数为12i -+,得到点A 的坐标,结合点A 与点B 关于直线y x =-对称得到点B 的坐标,从而求得向量OB uuu v对应的复数,得到结果.【详解】复数12i -+对应的点为(1,2)A -, 点A 关于直线y x =-的对称点为(2,1)B -,所以向量OB uuu r对应的复数为2i -+.故选A . 【点睛】该题是一道复数与向量的综合题,解答本题的关键是掌握复数在平面坐标系中的坐标表示.5.B解析:B 【解析】 【分析】根据自变量所在的范围代入相应的解析式计算即可得到答案. 【详解】 ∵函数2log (1),0()4,0xx x f x x -<⎧=⎨≥⎩, ∴()2l 23og 2(3)log 3log 44f f -+=+=2+9=11.故选B . 【点睛】本题考查函数值的求法,考查指对函数的运算性质,是基础题.6.D解析:D 【解析】 【详解】试题分析:()()(),34,24,32a b λλλλλ+=-+-=+--r r ,由a b λ+r r 与a r 垂直可知()()()·0433201a b a λλλλ+=∴+---=∴=-r r r考点:向量垂直与坐标运算7.C解析:C 【解析】因为2(1)(12)1223i i i i i i -+=+--=+,故选 C. 考点:本题主要考查复数的乘法运算公式.8.B解析:B 【解析】 【分析】 【详解】分两种情况:①选2本画册,2本集邮册送给4位朋友,有C 42=6种方法;②选1本画册,3本集邮册送给4位朋友,有C 41=4种方法.所以不同的赠送方法共有6+4=10(种).9.C解析:C 【解析】 【分析】利用复数乘法的运算法则化简原式,利用复数相等的性质可得结果. 【详解】因为()a i i b i +=+, 即1ai b i -+=+,因为,,a b R i ∈为虚数单位,所以1,1a b ==-, 故选C. 【点睛】本题主要考查复数的乘法运算以及复数相等的性质,属于基础题.10.B解析:B 【解析】 【分析】由三视图可知该几何体是一个底面边长为4的正方形,高为5的正四棱柱,挖去一个底面边长为4,高为3的正四棱锥,利用体积公式,即可求解。
2022年天津育才中学高三数学理期末试题含解析

2022年天津育才中学高三数学理期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知,则= ()A.B. C.D.参考答案:答案:A2. 设复数(其中i是虚数单位),则等于A.1-2iB.1+2iC. -2iD.2i参考答案:B3. 已知等差数列的公差为,前项和为,且,则()A.0 B.1009 C.2017 D.2018参考答案:B详解:∵,∴,即,又,∴,∴,∴.故选B.4. 不等式表示的平面区域为()参考答案:A5. 已知圆截直线所得弦的长度为4,则实数的值为()A. B. C.D.参考答案:B6. 已知命题,命题,则( )A.命题是假命题B.命题是真命题C.命题是真命题D.命题是假命题参考答案:C7. 已知函数f(x)=3x+x,g(x)=x+log3x,h(x)=log3x﹣的零点分别为x1,x2,x3,则x1,x2,x3的大小关系是( )A.x1>x2>x3 B.x2>x1>x3 C.x1>x3>x2 D.x3>x2>x1参考答案:D考点:函数的零点;对数函数的单调性与特殊点.专题:计算题;函数的性质及应用.分析:函数f(x)=3x+x,g(x)=x+log3x,h(x)=log3x﹣的零点即方程3x+x=0,x+log3x=0,log3x﹣=0的根;从而比较大小.解答:解:由题意,函数f(x)=3x+x,g(x)=x+log3x,h(x)=log3x﹣的零点即方程3x+x=0,x+log3x=0,log3x﹣=0的根;易知方程3x+x=0的根小于0,方程x+log3x=0的根在(0,1)上,方程log3x﹣=0的根大于1;故x3>x2>x1;故选D.点评:本题考查了函数的零点与方程的根的关系应用,属于基础题.8. 过抛物线C:的焦点F的直线l交抛物线C于A,B两点,且,则原点到l的距离为()A. B. C. D.参考答案:C由抛物线的焦点,设直线的方程为,由,则,所以,根据抛物线定义可知,解得,当时,直线的方程为,所以原点到的距离为,当时,直线的方程为,所以原点到的距离为,所以原点到直线距离为,故选C.点睛:本题考查了抛物线的定义,点到直线的距离公式及直线与抛物线的位置关系的应用,其中对于直线与圆锥曲线问题,通常通过联立直线方程与椭圆(圆锥曲线)方程的方程组,应用一元二次方程根与系数的关系,进而求解问题,此类问题易错点是复杂式子的变形能力不足,导致错漏百出,本题能较好的考查考生的逻辑思维能力、运算求解能力、分析问题解决问题的能力等.9. 已知,那么下列命题中正确的是()A.若,则 B.若,则C.若,则 D.若,则参考答案:C略10. 在中,内角为钝角,,,,则()A.2 B.3 C.5 D.10参考答案:A二、填空题:本大题共7小题,每小题4分,共28分11. 在极坐标系中,O 为极点,设点,则的面积是.参考答案:512. 若执行如图3所示的框图,输入,,则输出的数等于参考答案:略13. 等差数列中,,记,则当=______________时,取得最大值.参考答案:9略14. 幂函数y=x a ,当a 取不同的正数时,在区间[0,1]上它们的图象是一族美丽的曲线(如图),设点A (1,0)、B (0,1),若y=x α,y=x β的图象与线段AB 分别交于M 、N ,且=,则4α+β的最小值为 _________ .参考答案:415. 已知x >0,y >0,lg2x +lg8y =lg2,则+的最小值是 .参考答案:4【考点】基本不等式在最值问题中的应用;对数的运算性质.【分析】由对数的运算性质,lg2x +lg8y =lg2x +lg23y =(x+3y )lg2,结合题意可得,x+3y=1;再利用1的代换结合基本不等式求解即可.【解答】解:lg2x+lg8y=lg2x+lg23y=(x+3y )lg2, 又由lg2x +lg8y =lg2, 则x+3y=1,进而由基本不等式的性质可得,=(x+3y )()=2+≥2+2=4,当且仅当x=3y 时取等号, 故答案为:4.【点评】本题考查基本不等式的性质与对数的运算,注意基本不等式常见的变形形式与运用,如本题中,1的代换. 16. 在等比数列中,,且,,成等差数列,则通项公式.参考答案:略17. 如图直角三角形ABC中,,点E1F分别在CA、CB上,EF∥AB,,则=______________.参考答案:-5略三、解答题:本大题共5小题,共72分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020-2021天津市育贤中学高三数学下期末试题(带答案)一、选择题1.某班上午有五节课,分別安排语文,数学,英语,物理,化学各一节课.要求语文与化学相邻,数学与物理不相邻,且数学课不排第一节,则不同排课法的种数是 A .24B .16C .8D .122.右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入,a b 分别为14,18,则输出的a =( )A .0B .2C .4D .143.若以连续掷两颗骰子分别得到的点数m ,n 作为点P 的横、纵坐标,则点P 落在圆229x y +=内的概率为( )A .536B .29C .16D .194.如果42ππα<<,那么下列不等式成立的是( )A .sin cos tan ααα<<B .tan sin cos ααα<<C .cos sin tan ααα<<D .cos tan sin ααα<<5.设01p <<,随机变量ξ的分布列如图,则当p 在()0,1内增大时,( )ξ0 1 2P12p- 122pA .()D ξ减小B .()D ξ增大C .()D ξ先减小后增大 D .()D ξ先增大后减小6.为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率是 A .13B .12C .23D .567.数列2,5,11,20,x ,47...中的x 等于( ) A .28B .32C .33D .278.已知函数()25,1,,1,x ax x f x a x x⎧---≤⎪=⎨>⎪⎩是R 上的增函数,则a 的取值范围是( )A .30a -≤<B .0a <C .2a ≤-D .32a --≤≤9.函数()sin(2)2f x x π=-的图象与函数()g x 的图象关于直线8x π=对称,则关于函数()y g x =以下说法正确的是( )A .最大值为1,图象关于直线2x π=对称B .在0,4π⎛⎫⎪⎝⎭上单调递减,为奇函数 C .在3,88ππ⎛⎫-⎪⎝⎭上单调递增,为偶函数 D .周期为π,图象关于点3,08π⎛⎫⎪⎝⎭对称 10.已知函数()3sin 2cos 2[0,]2f x x x m π=+-在上有两个零点,则m 的取值范围是A .(1,2)B .[1,2)C .(1,2]D .[l,2]11.设F 为双曲线C :22221x y a b-=(a >0,b >0)的右焦点,O 为坐标原点,以OF 为直径的圆与圆x 2+y 2=a 2交于P 、Q 两点.若|PQ |=|OF |,则C 的离心率为 A .2 B .3 C .2 D .5 12.若实数满足约束条件,则的最大值是( )A .B .1C .10D .12二、填空题13.曲线21y x x=+在点(1,2)处的切线方程为______________. 14.若过点()2,0M 3的直线与抛物线()2:0C y ax a =>的准线l 相交于点B ,与C 的一个交点为A ,若BM MA =,则a =____.15.在区间[1,1]-上随机取一个数x ,cos 2xπ的值介于1[0,]2的概率为 .16.复数()1i i +的实部为 .17.如图所示,平面BCC 1B 1⊥平面ABC ,∠ABC =120︒,四边形BCC 1B 1为正方形,且AB =BC =2,则异面直线BC 1与AC 所成角的余弦值为_____.18.已知sin cos 1αβ+=,cos sin 0αβ+=,则()sin αβ+__________.19.已知圆台的上、下底面都是球O 的截面,若圆台的高为6,上、下底面的半径分别为2,4,则球O 的表面积为__________.20.如图,长方体1111ABCD A B C D -的体积是120,E 为1CC 的中点,则三棱锥E -BCD 的体积是_____.三、解答题21.已知直线352:{132x t l y t=+=+(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为2cos ρθ=.(1)将曲线C 的极坐标方程化为直角坐标方程; (2)设点的直角坐标为3),直线l 与曲线C 的交点为A ,B ,求MA MB ⋅的值.22.已知函数2()(1)1xx f x a a x -=+>+. (1)证明:函数()f x 在(1,)-+∞上为增函数;(2)用反证法证明:()0f x =没有负数根.23.如图,四面体ABCD 中,O 、E 分别是BD 、BC 的中点,2AB AD ==2CA CB CD BD ====.(1)求证:AO ⊥平面BCD ;(2)求异面直线AB 与CD 所成角的余弦值; (3)求点E 到平面ACD 的距离.24.已知2256x ≤且21log 2x ≥,求函数22()log log 22x xf x =⋅的最大值和最小值. 25.“微信运动”是手机APP 推出的多款健康运动软件中的一款,大学生M 的微信好友中有400位好友参与了“微信运动”.他随机抽取了40位参与“微信运动”的微信好友(女20人,男20人)在某天的走路步数,经统计,其中女性好友走路的步数情况可分为五个类别:A 、02000步,(说明:“02000”表示大于或等于0,小于2000,以下同理),B 、20005000步,C 、50008000步,D 、800010000步,E 、1000012000步,且A 、B 、C 三种类别的人数比例为1:4:3,将统计结果绘制如图所示的柱形图;男性好友走路的步数数据绘制如图所示的频率分布直方图.(Ⅰ)若以大学生M 抽取的微信好友在该天行走步数的频率分布,作为参与“微信运动”的所有微信好友每天走路步数的概率分布,试估计大学生M 的参与“微信运动”的400位微信好友中,每天走路步数在20008000的人数;(Ⅱ)若在大学生M 该天抽取的步数在800010000的微信好友中,按男女比例分层抽取6人进行身体状况调查,然后再从这6位微信好友中随机抽取2人进行采访,求其中至少有一位女性微信好友被采访的概率.26.△ABC 在内角A 、B 、C 的对边分别为a ,b ,c ,已知a=bcosC+csinB . (Ⅰ)求B ;(Ⅱ)若b=2,求△ABC 面积的最大值.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】【分析】根据题意,可分三步进行分析:(1)要求语文与化学相邻,将语文与化学看成一个整体,考虑其顺序;(2)将这个整体与英语全排列,排好后,有3个空位;(3)数学课不排第一行,有2个空位可选,在剩下的2个空位中任选1个,得数学、物理的安排方法,最后利用分步计数原理,即可求解。
【详解】根据题意,可分三步进行分析:(1)要求语文与化学相邻,将语文与化学看成一个整体,考虑其顺序,有222A=种情况;(2)将这个整体与英语全排列,有222A=中顺序,排好后,有3个空位;(3)数学课不排第一行,有2个空位可选,在剩下的2个空位中任选1个,安排物理,有2中情况,则数学、物理的安排方法有224⨯=种,所以不同的排课方法的种数是22416⨯⨯=种,故选B。
【点睛】本题主要考查了排列、组合的综合应用,其中解答红注意特殊问题和相邻问题与不能相邻问题的处理方法是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题。
2.B解析:B【解析】【分析】【详解】由a=14,b=18,a<b,则b变为18﹣14=4,由a>b,则a变为14﹣4=10,由a>b,则a变为10﹣4=6,由a>b,则a变为6﹣4=2,由a<b,则b变为4﹣2=2,由a=b=2,则输出的a=2.故选B.3.D解析:D【解析】掷骰子共有36个结果,而落在圆x 2+y 2=9内的情况有(1,1),(1,2),(2,1),(2,2)这4种,∴P=41369=. 故选D4.C解析:C 【解析】 【分析】分别作出角α的正弦线、余弦线和正切线,结合图象,即可求解. 【详解】如图所示,在单位圆中分别作出α的正弦线MP 、余弦线OM 、正切线AT , 很容易地观察出OM MP AT <<,即cos sin tan ααα<<. 故选C.【点睛】本题主要考查了三角函数线的应用,其中解答中熟记三角函数的正弦线、余弦线和正切线,合理作出图象是解答的关键,着重考查了数形结合思想,以及推理与运算能力,属于基础题.5.D解析:D 【解析】 【分析】先求数学期望,再求方差,最后根据方差函数确定单调性. 【详解】111()0122222p p E p ξ-=⨯+⨯+⨯=+, 2222111111()(0)(1)(2)2222224p p D p p p p p ξ-∴=--+--+--=-++, 1(0,1)2∈,∴()D ξ先增后减,因此选D. 【点睛】222111(),()(())().nnni i i i i i i i i E x p D x E p x p E ξξξξ=====-=-∑∑∑6.C解析:C 【解析】试题分析:将4种颜色的花种任选2种种在一个花坛中,余下2种种在另一个花坛中,有6种种法,其中红色和紫色的花不在同一个花坛的种数有4种,故所求概率为23,选C. 【考点】古典概型【名师点睛】作为客观题形式出现的古典概型试题,一般难度不大,解答中的常见错误是在用列举法计数时出现重复或遗漏,避免此类错误发生的有效方法是按照一定的标准进行列举.7.B解析:B 【解析】 【分析】通过观察,得出该数列从第二项起,后一项与前一项的差分别是3的倍数,由此可求得x 的值. 【详解】因为数列的前几项为2,5,11,20,,47x , 其中5213,11523,201133-=⨯-=⨯-=⨯, 可得2043x -=⨯,解得32x =,故选B. 【点睛】本题主要考查了数列的概念及其应用,其中解答中根据题意发现数列中数字的排布规律是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.8.D解析:D 【解析】 【分析】根据分段函数的单调性特点,两段函数在各自的定义域内均单调递增,同时要考虑端点处的函数值. 【详解】要使函数在R 上为增函数,须有()f x 在(,1]-∞上递增,在(1,)+∞上递增,所以21,20,115,1a a a a ⎧-≥⎪⎪<⎨⎪⎪--⨯-≤⎩,解得32a --≤≤.故选D. 【点睛】本题考查利用分段函数的单调性求参数的取值范围,考查数形结合思想、函数与方程思想的灵活运用,求解时不漏掉端点处函数值的考虑.9.B解析:B 【解析】 【分析】先求出函数y=g(x)的解析式,再利用三角函数的图像和性质对每一个选项逐一分析判断. 【详解】设点P(x,y)是函数()y g x =图像上的任意一点,则点Q (x ,)4y π-+在函数y=f(x)的图像上,sin[2(-x+)]sin 2()42y x g x ππ=-=-=,对于选项A,函数y=g(x)的最大值为1,但是()012g π=≠±,所以图象不关于直线2x π=对称,所以该选项是错误的;对于选项B,()()g x g x -=-,所以函数g(x)是奇函数,解222+22k x k ππππ-≤≤得+44k x k ππππ-≤≤,)k Z ∈(,所以函数在0,4π⎛⎫⎪⎝⎭上单调递减,所以该选项是正确的; 对于选项C,由前面分析得函数y=g(x)的增区间为3[+,]()44k k k Z ππππ+∈,且函数y=g(x)不是偶函数,故该选项是错误;对于选项D,函数的周期为π,解2,,2k x k x ππ=∴=所以函数图像的对称中心为,0)(k Z)2k π∈(,所以该选项是错误的. 故选:B 【点睛】本题主要三角函数的解析式的求法,考查三角函数的图像和性质,意在考查学生对这些知识的理解掌握水平和分析推理能力.10.B解析:B 【解析】 【分析】 【详解】试题分析:利用辅助角公式化简函数为()3sin 2cos 2f x x x m =+-,令,则,所以此时函数即为.令有,根据题意可知在上有两个解,根据在函数图像可知,.考点:辅助角公式;;零点的判断;函数图像.11.A解析:A 【解析】 【分析】准确画图,由图形对称性得出P 点坐标,代入圆的方程得到c 与a 关系,可求双曲线的离心率. 【详解】设PQ 与x 轴交于点A ,由对称性可知PQ x ⊥轴, 又||PQ OF c ==,||,2cPA PA ∴=∴为以OF 为直径的圆的半径,A ∴为圆心||2cOA =.,22c c P ⎛⎫∴ ⎪⎝⎭,又P 点在圆222x y a +=上,22244c c a ∴+=,即22222,22c c a e a=∴==. 2e ∴=A .【点睛】本题为圆锥曲线离心率的求解,难度适中,审题时注意半径还是直径,优先考虑几何法,避免代数法从头至尾,运算繁琐,准确率大大降低,双曲线离心率问题是圆锥曲线中的重点问题,需强化练习,才能在解决此类问题时事半功倍,信手拈来.12.C解析:C【解析】【分析】本题是简单线性规划问题的基本题型,根据“画、移、解”等步骤可得解.题目难度不大题,注重了基础知识、基本技能的考查.【详解】在平面直角坐标系内画出题中的不等式组表示的平面区域为以为顶点的三角形区域(包含边界),由图易得当目标函数经过平面区域的点时,取最大值.【点睛】解答此类问题,要求作图要准确,观察要仔细.往往由于由于作图欠准确而影响答案的准确程度,也有可能在解方程组的过程中出错.二、填空题13.【解析】设则所以所以曲线在点处的切线方程为即点睛:求曲线的切线方程是导数的重要应用之一用导数求切线方程的关键在于求出斜率其求法为:设是曲线上的一点则以为切点的切线方程是若曲线在点处的切线平行于轴(即 解析:1y x =+【解析】设()y f x =,则21()2f x x x '=-,所以(1)211f '=-=, 所以曲线21y x x=+在点(1,2)处的切线方程为21(1)y x -=⨯-,即1y x =+. 点睛:求曲线的切线方程是导数的重要应用之一,用导数求切线方程的关键在于求出斜率,其求法为:设00(,)P x y 是曲线()y f x =上的一点,则以P 为切点的切线方程是000()()y y f x x x '-=-.若曲线()y f x =在点00(,())P x f x 处的切线平行于y 轴(即导数不存在)时,由切线定义知,切线方程为0x x =.14.【解析】【分析】由直线方程为与准线得出点坐标再由可得点为线段的中点由此求出点A 的坐标代入抛物线方程得出的值【详解】解:抛物线的准线方程为过点且斜率为的直线方程为联立方程组解得交点坐标为设A 点坐标为因 解析:8【解析】【分析】由直线方程为2)y x =-与准线:a l x 4=-得出点B 坐标,再由BM MA =可得,点M 为线段AB 的中点,由此求出点A 的坐标,代入抛物线方程得出a 的值.【详解】 解:抛物线()2:0C y ax a =>的准线方程为:a l x 4=- 过点()2,0M2)y x =-,联立方程组2)4y x a x ⎧=-⎪⎨=-⎪⎩,解得,交点B坐标为)(,)a a 844+-, 设A 点坐标为00(,)x y ,因为BM MA =,所以点M 为线段AB 的中点,所以00()4428)402a x a y ⎧+-⎪=⎪⎪⎨+⎪+⎪=⎪⎩,解得(a A 44+,将)()a a 8A 444++代入抛物线方程,即))()2a 8a a 444+=+, 因为0a >,解得8a =.【点睛】本题考查了抛物线的性质、向量相等等知识,解决几何问题时,往往可以转化为代数问题来进行研究,考查了数形结合的思想.15.【解析】试题分析:由题意得因此所求概率为考点:几何概型概率 解析:13【解析】 试题分析:由题意得1220cos,[1,1]112232222333xx x x x x πππππππ≤≤∈-⇒≤≤-≤≤-⇒≤≤-≤≤-或或,因此所求概率为22(1)13.1(1)3-=--考点:几何概型概率 16.【解析】复数其实部为考点:复数的乘法运算实部解析:1-【解析】复数(1)11i i i i +=-=-+,其实部为1-.考点:复数的乘法运算、实部.17.【解析】【分析】将平移到和相交的位置解三角形求得线线角的余弦值【详解】过作过作画出图像如下图所示由于四边形是平行四边形故所以是所求线线角或其补角在三角形中故【点睛】本小题主要考查空间两条直线所成角的【解析】【分析】将AC 平移到和1BC 相交的位置,解三角形求得线线角的余弦值.【详解】过B 作//BD AC ,过C 作//CD AB ,画出图像如下图所示,由于四边形ABCD 是平行四边形,故//BD AC ,所以1C BD ∠是所求线线角或其补角.在三角形1BC D 中,1122,23BC C D BD ===,故181286cos 422223C BD +-∠==⨯⨯.【点睛】本小题主要考查空间两条直线所成角的余弦值的计算,考查数形结合的数学思想方法,属于中档题.18.【解析】【详解】因为所以①因为所以②①②得即解得故本题正确答案为解析:12- 【解析】【详解】因为, 所以,① 因为, 所以,② ①②得, 即, 解得, 故本题正确答案为19.【解析】【分析】本道题结合半径这一条件利用勾股定理建立等式计算半径即可【详解】设球半径为R 球心O 到上表面距离为x 则球心到下表面距离为6-x 结合勾股定理建立等式解得所以半径因而表面积【点睛】本道题考查 解析:80π【解析】【分析】本道题结合半径这一条件,利用勾股定理,建立等式,计算半径,即可。
