大学物理课堂PPT复习资料
合集下载
大学物理大一总复习-PPT资料57页

加速度 akv2 ,式中k 为常数,试证明关闭 发动机后又行驶 x 距离时,快艇速率为:v v0ekx
证明: a d v d v d x v d v kv 2 dt dx dt dx
dv kdx v
v dv
x
k d x
v v 0
0
v ln kx
积分
求导 a(t)
积分
若aa(t)dv则dva(t)d积 t 分
在积分时
dt
常用到的 若aa(v)dv则dvd积 t 分
方法:
dt a(v)
若aa(x)dvdvdxdvdxvd则 v vdva(x)积 dx分 dt dt dx dx dt dx
例1. 一艘快艇在速率为 v 0 时关闭发动机,其
2 mg T 1 2 ma
T 2 mg ma
T 1 r Tr
1 mr 2
2
Tr
T2r
1 mr 2
2
a r
☻刚体、转动定律
联立求解:
T 11 mg / 8
例5 如图一质m量 1、为 长l的 为均匀细杆,O端 可的 绕水 过平 在沿直平面内自 。由 在转 杆动 自由下垂 弹m时 2以, 水子 平 速度a在 处垂直击中杆, 杆并 中留 ,在 求子弹入 间射
表示两个相位之差。用来比较简谐运动的步调。
相位差:表示两个相位之差。用来比较简谐运动的步调。
1)对同一简谐运动,相位差给出两运动状态间变化所需的时间.
xA co t1s () (t2 ) (t1 )
例4、一轻绳跨过两个质量均为 m、半 径均为r的均匀圆盘状定滑轮,绳的两 端分别挂着质量为m和2m的重物,如 图所示。绳与滑轮间无相对滑动,滑 轮光滑。两个定滑轮的转动惯量均为 0.5mr2。将由两个定滑轮以及质量为 m和2m的重物组成的系统从静止释放 ,求两滑轮之间绳内的张力。
证明: a d v d v d x v d v kv 2 dt dx dt dx
dv kdx v
v dv
x
k d x
v v 0
0
v ln kx
积分
求导 a(t)
积分
若aa(t)dv则dva(t)d积 t 分
在积分时
dt
常用到的 若aa(v)dv则dvd积 t 分
方法:
dt a(v)
若aa(x)dvdvdxdvdxvd则 v vdva(x)积 dx分 dt dt dx dx dt dx
例1. 一艘快艇在速率为 v 0 时关闭发动机,其
2 mg T 1 2 ma
T 2 mg ma
T 1 r Tr
1 mr 2
2
Tr
T2r
1 mr 2
2
a r
☻刚体、转动定律
联立求解:
T 11 mg / 8
例5 如图一质m量 1、为 长l的 为均匀细杆,O端 可的 绕水 过平 在沿直平面内自 。由 在转 杆动 自由下垂 弹m时 2以, 水子 平 速度a在 处垂直击中杆, 杆并 中留 ,在 求子弹入 间射
表示两个相位之差。用来比较简谐运动的步调。
相位差:表示两个相位之差。用来比较简谐运动的步调。
1)对同一简谐运动,相位差给出两运动状态间变化所需的时间.
xA co t1s () (t2 ) (t1 )
例4、一轻绳跨过两个质量均为 m、半 径均为r的均匀圆盘状定滑轮,绳的两 端分别挂着质量为m和2m的重物,如 图所示。绳与滑轮间无相对滑动,滑 轮光滑。两个定滑轮的转动惯量均为 0.5mr2。将由两个定滑轮以及质量为 m和2m的重物组成的系统从静止释放 ,求两滑轮之间绳内的张力。
归纳大学物理复习.ppt

U
P
0
E
dl
电势能
P
U P
0
q0
E
dl
q
点电荷电场的电势 U P 40r
电势的叠加原理
UP
优选文档
i
qi
4 0 ri
11
6-17 如图所示,A点有电荷+q,B 点有电荷-q,AB=2l,OCD是以B为 中心、l为半径的半圆。(1)将单位正 电荷从O点沿OCD移到D点,电场力 做功多少?(2)将单位负电荷从D 点沿AB延长线移到无穷远处,电场 力做功多少?
能量增加的 原因是因为人拉优开选文极档板做功,转化为电场能。 18
6-31 在介电常数为ε的无限大均匀电介质中,有一半径为 R的导体球带电荷Q。求电场的能量。
解:
.
优选文档
19
Chapter 7 稳恒磁场
优选文档
20
一.磁感应强度
毕奥-萨伐尔定律
dB
0
4
Idl r
r3
叠加原理
B
Ld
B
B总 Bi
优选文档
15
6-24 在一半径为a的长直导线的外面,套有内半径为b 的同轴导体薄圆筒,它们之间充以相对介电常数为εr 的均匀电介质,设导线和圆筒都均匀带电,且沿轴线单 位长度所带电荷分别为λ和- λ.(1)求空间中各点的场 强大小;(2)求导线和圆筒间的电势差.
解:(1) r a : E 0 ; r b : E 0 ;
6-5 一根玻璃棒被弯成半径为R的半圆形,其上电 荷均匀分布,总电荷量为q.求半圆中心O的场强。
解:在圆环上任取电荷元dq
y
dE
dq
4 0 R2
rˆ
大学物理PPT完整全套教学课件pptx

非弹性碰撞
碰撞后系统动能不守恒,部分机械 能转化为内能,损失了机械能。如 湿纸或橡皮泥的碰撞等。
完全非弹性碰撞
碰撞后两物体粘在一起运动,动能 损失最大,机械能损失也最大。
能量守恒定律
定律表述
自然界中的一切物质都具有能量,能量既不能创 造也不能消灭,而只能从一种形式转换成另一种 形式,从一个物体传递到另一个物体;在转化和 传递过程中能量的总量保持不变。
大学物理的学习方法和要求
掌握基本概念和基本规律
注重实验和实践
学习大学物理首先要掌握基本概念和基本 规律,理解它们的物理意义和适用范围。
大学物理实验是学习物理学的重要环节, 通过实验可以加深对物理概念和规律的理 解,培养实验技能和动手能力。
培养物理思维
拓宽知识面
学习大学物理要注重培养物理思维,即运 用物理学的方法和观点去分析和解决问题 的能力。
热力学第二定律的表述及实质
表述
实质
应用
热力学第二定律有多种表述方式,其 中最著名的是开尔文表述和克劳修斯 表述。开尔文表述指出,不可能从单 一热源吸取热量,使之完全变为有用 功而不产生其他影响。克劳修斯表述 指出,热量不可能自发地从低温物体 传到高温物体而不引起其他变化。
热力学第二定律的实质是揭示了自然 界中一切与热现象有关的宏观过程都 具有方向性,即不可逆性。这种方向 性是由系统内部的微观状态数目的变 化所决定的,也就是由系统的熵增原 理所决定的。
循环过程卡诺循环
01
02
定义
工作原理
卡诺循环是一种理想的可逆循环,由 两个等温过程和两个绝热过程组成。 它是热力学第二定律的出发点,也是 热机效率的理论极限。
卡诺循环通过高温热源吸收热量,在 低温热源放出热量,并对外作功。其 效率只与高温热源和低温热源的温度 有关,而与工作物质无关。
大学物理ppt课件完整版

03
计算机模拟和仿真
利用计算机进行数值模拟和仿真 实验,验证理论预测和实验结果 。
2024/1/25
5
物理学的发展历史
01
02
03
古代物理学
以自然哲学为主要形式, 探讨自然现象的本质和规 律,如古希腊的自然哲学 。
2024/1/25
经典物理学
以牛顿力学、电磁学等为 代表,建立了完整的经典 物理理论体系。
固体的电子论
介绍了能带理论、金属电子论、半导体电子 论等。
30
核物理和粒子物理基础
原子核的基本性质
包括核力、核子、同位素等基本概念。
放射性衰变
阐述了α衰变、β衰变、γ衰变等放射性衰变过程及 其规律。
粒子物理简介
介绍了基本粒子、相互作用、粒子加速器等基本 概念。
2024/1/25
31
THANKS
感谢观看
19
恒定电流的电场和磁场
恒定电流:电流大小和方 向均不随时间变化的电流 。
2024/1/25
毕奥-萨伐尔定律:计算 电流元在空间任一点产生 的磁场。
奥斯特-马可尼定律:描 述电流产生磁场的规律。
磁场的高斯定理和安培环 路定理:揭示磁场的基本 性质。
20
电磁感应
法拉第电磁感应定律
描述变化的磁场产生感应电动势的规律。
01
又称惯性定律,表明物体在不受外力作用时,将保持静止状态
或匀速直线运动状态。
牛顿第二定律
02
又称动量定律,表明物体加速度与作用力成正比,与物体质量
成反比。
牛顿第三定律
03
又称作用与反作用定律,表明两个物体间的作用力和反作用力
总是大小相等、方向相反、作用在同一直线上。
大学物理总复习PPT课件
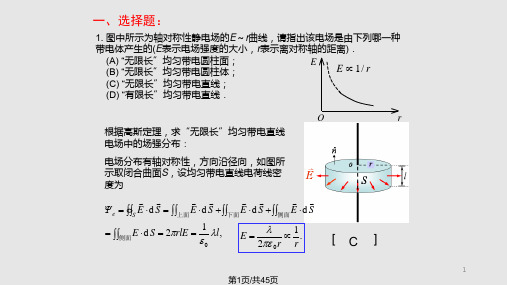
nˆ
C
P 、 -P、 0
Pn P nˆ
A P nˆ P
nˆ
B
nˆ
A
Pp
P
B P nˆ P
C P nˆ 0
20
第20页/共45页
3. 一个电流元位于直角坐标系原点,电流沿z轴方向,点
P (x,y,z)的磁感强度沿x轴的分量是:
。
(0 / 4)Iy d l /(x 2 y 2 z 2 )3/ 2
(A) 4倍和 1 / 8 ,
(B) 4倍和 1 / 2 , (C) 2倍和 1 / 4 , (D) 2倍和 1 / 2 。
B 0I
2R
Pm IS
B1
0I
2R
, B2
2
0I
2r
.
R 2r
B2 2 R 4 B1 r
Pm R2I, Pm 2r2I.
Pm Pm
2
r2 R2
1 2
[B ]
6
(A) 25 cm. (B) 50 cm. (C) 250 cm. (D) 500 cm.
p h
p
h
2
p
h
2
6.63 1034 (5 103 1010)2
103
1010
0.2652
1033(kg ms1)
px h
x
h p
6.63 1034 0.2652 1033
2.5(m)
16
第16页/共45页
i(t) 答案:( B )
S D d S q
在任何电场中,通过任意闭合曲面的电位移通量等 于闭合面内自由电荷的代数和。
S B d S 0
在任何磁场中,通过任意闭合曲面的磁通量均等 于零。
大学物理各章主要知识点总结PPT课件一等奖新名师优质课获奖比赛公开课

第四章 气体动理论
1 理想气体状态方程
PV RT M RT N RT NkT ,或P nkT
M mol
NA
其中: R 8.31J / mol K 叫普适常数
k R 1.381023 J / K 叫玻尔兹曼常数 NA
NA 6.021023 个/摩尔 叫阿伏加德罗常数
n 是分子数密度
iR 2
Cp
( i 1)R 2
Cp CV
i2 i
5 绝热过程 绝热方程
PV 恒量 V 1T 恒量 P 1T 恒量
6. 循环过程 正循环: 普遍旳热机效率计算式 逆循环: 普遍旳致冷系数计算式
A净 1 Q放
Q吸
Q吸
e Q吸 Q吸 A净 Q放 Q吸
7. 卡诺循环(两个等温过程加两个绝热过程)
. 力旳空间累积效应
r2
F
dr
r1
功、动能、动能定理、势能、机械能、
功能原理、机械能守恒定律
1 动力学问题旳解题环节: (1)拟定研究对象 (2)拟定参照系(默认大地,可不写) (3)建立坐标系 (4)分析物体旳运动或者受力情况 (5)列方程
2 主要方程:
动量守恒定律;机械能守恒定律;动量定理; 动能定理;牛顿第二定律
(2)、已知加速度和初始速度,求速度函数 已知速度函数和初始位置,求运动方程
利用积分措施
3. 圆周运动旳角量描述法
角位置 单位:rad
角速度 角加速度
d
dt
d
dt
d 2
dt 2
单位:rad/s 单位:rad/s2
4. 圆周运动旳加速度体现式
圆周运动:
a
aτ
ann
dv
dt
大学物理下册知识要点-PPT

八. 四个量子数 1.主量子数 n ( 1 , 2 , 3, …)
大体上决定了电子能量 2. 角量子数 l ( 0,1,2,…, n -1 )
决定电子的轨道角动量大小。
3. 磁量子数 ml ( 0,±1, ± 2,…, ± l ) 决定电子轨道角动量空间取向
4.自旋磁量子数 ms ( 1/2 , -1/2 ) 决定电子自旋角动量空间取向
2
中央明纹线宽度 x0 2 f tan1 2 f1 2 f λ a
其他暗纹位置
f
xk k a
2.光栅衍射
其他明纹线宽度
f xk a
光栅方程 d sin k k 0,1,2,3,
d sin k
缺级条件
asin k
k k d k 1,2,3, a
六.光的偏振
1.马吕斯定律 I I0 cos2
hh
2.估算电子的波长
1 2
me0v 2
eU
h me0
h h 1 1.225 nm
m0v 2m0e U U
六.不确定关系
不确定关系(测不准关系): 粒子在同一方向上的坐标和 动量不能同时确定。
x px 2
七.氢原子的量子力学结论
1. 能量量子化
3. 角动量空间量子化
能量
En
1 n2
主量子数 n =
激发态能量 (n 1) En E1 n2 能量是量子化的。
五.微观粒子的波粒二象性
1.一个能量为E、动量为 p 的实物粒子,同时也具有波动性, 它的波长、频率 和 E、p的关系与光子一样:
系德 布
p mv h
罗
意 关
E mc2 h
h h ─ 德布罗意波长。 p m
大学物理学复习ppt

(1)g 竖直向下; (2)0; (3)g 竖直向下; (4)(v0cosθ)2/g
静止于坐标原点、质量为4kg的物体在合外力F=3x2(N)作用下向x 轴正向运动,物体运动2m的过程中,求(1)合外力做的功;(2) 物体的末动能;(3)物体的末速度。
解:(1) A F dr Fdx 2 3x2dx x3 2 8(J)
U P E dl
• 点电荷 • (5)电势差
U q
4 0 r
b
Uab
E dl
a
• 2.基本规律 • (1)电荷守恒定律
• (2)库仑定律 • (3)高斯定理 • (4)环路定理
F 1 q1q2
40 r2
E dS q
S
0
LE dl 0
均匀带电圆环半径为R,带电量为q,求:圆环轴线上一点的场
I r2dm 质量连续分布的物体
I 1 ml 2 均质细棒对端点垂直轴 3
I 1 mR2 均质圆盘对中心垂直轴 2
2.基本规律
(1)转动定律
M I
(2)转动动能定理
A
1 2
I22
1 2
I12
(3)角动量定理(动量矩定理)
t2
t1
Mdt
L2
L1
(4)角动量守恒定律(动量矩守恒定律)
合外力矩为零时,角动量保持不变。
①× ②× ③× ④× ⑤×
细棒可绕其一端在竖直平面内自由转动,若把 棒拉至水平位置后任其自由摆动,则在向下运动过 程中,它的角速度、角加速度、转动惯量、角动量、 转动动能、动量变不变?
答案:
角速度变
角加速度变
转动惯量不变
mg
角动量变
转动动能变 动量变
静止于坐标原点、质量为4kg的物体在合外力F=3x2(N)作用下向x 轴正向运动,物体运动2m的过程中,求(1)合外力做的功;(2) 物体的末动能;(3)物体的末速度。
解:(1) A F dr Fdx 2 3x2dx x3 2 8(J)
U P E dl
• 点电荷 • (5)电势差
U q
4 0 r
b
Uab
E dl
a
• 2.基本规律 • (1)电荷守恒定律
• (2)库仑定律 • (3)高斯定理 • (4)环路定理
F 1 q1q2
40 r2
E dS q
S
0
LE dl 0
均匀带电圆环半径为R,带电量为q,求:圆环轴线上一点的场
I r2dm 质量连续分布的物体
I 1 ml 2 均质细棒对端点垂直轴 3
I 1 mR2 均质圆盘对中心垂直轴 2
2.基本规律
(1)转动定律
M I
(2)转动动能定理
A
1 2
I22
1 2
I12
(3)角动量定理(动量矩定理)
t2
t1
Mdt
L2
L1
(4)角动量守恒定律(动量矩守恒定律)
合外力矩为零时,角动量保持不变。
①× ②× ③× ④× ⑤×
细棒可绕其一端在竖直平面内自由转动,若把 棒拉至水平位置后任其自由摆动,则在向下运动过 程中,它的角速度、角加速度、转动惯量、角动量、 转动动能、动量变不变?
答案:
角速度变
角加速度变
转动惯量不变
mg
角动量变
转动动能变 动量变
《大学物理学》PPT课件

课程内容包括力学、热学、电磁学、光学和近 代物理等基础知识,涉及物质的基本性质、相 互作用和运动规律等方面。
大学物理学不仅是后续专业课程的基础,也是 培养学生科学素质、创新思维和实践能力的重 要途径。
学习目标与要求
01 掌握物理学基本概念、原理和定律,理解 物理现象的本质和规律。
02
能够运用物理学知识分析和解决实际问题 ,具备实验设计和数据处理的能力。
角动量守恒定律
在不受外力矩作用的封闭系统中,系统的总角动量保 持不变。
能量守恒定律
在封闭系统中,能量不能被创造或消灭,只能从一种 形式转化为另一种形式。
03
热学基础与热力学定律
温度与热量概念
01
温度定义
温度是表示物体冷热程度的物理量,微观上来讲是物体分子热运动的剧
烈程度。
02
热量概念
热量是指当系统状态的改变来源于热学平衡条件的破坏,也即来源于系
05
光学原理与现象解析
几何光学基础
光的直线传播
光在同种均匀介质中沿直线传 播,形成影子、日食、月食等
现象。
光的反射
光在两种物质分界面上改变传 播方向又返回原来物质中的现 象,遵循反射定律。
光的折射
光从一种透明介质斜射入另一 种透明介质时,传播方向发生 改变的现象,遵循折射定律。
透镜成像
凸透镜和凹透镜对光线的作用 及成像规律,包括放大、缩小
库仑定律与电场强度
阐述库仑定律的内容,电场强度的定义及计算 。
电势与电势能
解释电势的概念,电势差的计算,电势能的定义及性质。
稳恒电流与电路分析
1 2
电流与电阻
介绍电流的形成,电阻的定义及影响因素。
欧姆定律与焦耳定律
大学物理学不仅是后续专业课程的基础,也是 培养学生科学素质、创新思维和实践能力的重 要途径。
学习目标与要求
01 掌握物理学基本概念、原理和定律,理解 物理现象的本质和规律。
02
能够运用物理学知识分析和解决实际问题 ,具备实验设计和数据处理的能力。
角动量守恒定律
在不受外力矩作用的封闭系统中,系统的总角动量保 持不变。
能量守恒定律
在封闭系统中,能量不能被创造或消灭,只能从一种 形式转化为另一种形式。
03
热学基础与热力学定律
温度与热量概念
01
温度定义
温度是表示物体冷热程度的物理量,微观上来讲是物体分子热运动的剧
烈程度。
02
热量概念
热量是指当系统状态的改变来源于热学平衡条件的破坏,也即来源于系
05
光学原理与现象解析
几何光学基础
光的直线传播
光在同种均匀介质中沿直线传 播,形成影子、日食、月食等
现象。
光的反射
光在两种物质分界面上改变传 播方向又返回原来物质中的现 象,遵循反射定律。
光的折射
光从一种透明介质斜射入另一 种透明介质时,传播方向发生 改变的现象,遵循折射定律。
透镜成像
凸透镜和凹透镜对光线的作用 及成像规律,包括放大、缩小
库仑定律与电场强度
阐述库仑定律的内容,电场强度的定义及计算 。
电势与电势能
解释电势的概念,电势差的计算,电势能的定义及性质。
稳恒电流与电路分析
1 2
电流与电阻
介绍电流的形成,电阻的定义及影响因素。
欧姆定律与焦耳定律
(优质)大学物理总复习PPT课件

F x
Ek,max Fx0
x0 (kx mg )dx
0
Fx0
(
1 2
kx2
mgx)
很大.
(F)质点作曲线运动时,其法向加速度一般并不为零,但也有可 能在某时刻法向加速度为零.
三、计算题
1、一物体从静止开始, 在2s内被匀加速到40m/s,物体的加速度为 多少?在2s内物体运动了多大距离?
解:物体的加速度为
a
vt
v0
40 0
2
20m / s
t
2
2s内运动的距离为
x vt2 v02 402 02 40m 2a 2 20
解:质点运动过程中所受阻力为: F kv
根据牛顿第二定律:
m dv kv k dx
dt
dt
dv k dx m
当质点速度减为 v0 时, 质点走过的距离为: n
v0 n
dv
k
x1 dx
v0
m0
v0 n
v0
k m
x1
x1
m k
(n
1 n
)v0
质点所能走的总距离为:
0 dv k x2 dx
(优质)大学物理总复习PPT课件
一、填空题
已知质点的运动方程为
rr
v i
2t 2
vv j tk
,质点的速度为
,加速度为 。
二、选择题
1)根据瞬时速度矢量v 的定义,及其用直角坐标和自然坐标的表 示形式,它的大小| v |可表示为(B ,D ,F ,H )
2 )根据瞬时加速度矢量a 的定义,及其用直角坐标和自然坐标的 表示形式,它的大小| a|可表示为(A C G H )
随时间的变化规律。(2)质点上升的最大高度.
大学物理课件复习资料安培环路定理

判断下列图中结果
I1 I2 L 图1
I3
I I L 图2
I
r r 1) ∫ B⋅ dl = µo (I1 − I2 ) ) L r r 2) ∫ B⋅ dl = µo (− 2I + I ) = −µo I ) L r r 3) B⋅ dl = µo ( − 2I ) = −2µo I ) ∫
L
L 图3
l
I2 I3
r
r dl
如果环路内还有其它无限长直线电流 根据叠加原理, 根据叠加原理,可知
r r ∫ B ⋅ dl =μ0 ( I1 + I 2 − I3 )
l
3.回路不环绕电流 3.回路不环绕电流
r r ∫ B4 ⋅ dl
l
=
∫
l
µ0 I 4 cos θ 4 dl4 2π r4
I1
r
I4
=
∫
l
µ0 I 4 r4 dϕ 4 2π r4
3)环路定理适用于闭合稳恒电流的磁场。而有限电 )环路定理适用于闭合稳恒电流的磁场。 适用于闭合稳恒电流的磁场 如一段不闭合的载流导线)不适用环路定理。 流(如一段不闭合的载流导线)不适用环路定理。 4)安培环路定理说明磁场性质 —— ) 磁场是非保守场,是涡旋场。 磁场是非保守场,是涡旋场。 5)闭合回路包围电流的判断: )闭合回路包围电流的判断: 以闭合回路为边界任意做一曲面, 以闭合回路为边界任意做一曲面,电流穿过 曲面就算包围。 曲面就算包围。
L
r
v B
v dB
I
.
dI
v B
v B 的方向与 I 成右螺旋 µ 0 Ir B= 2 0 < r < R, 2π R µ0I r > R, B= 2π r
大学物理学(第二版)全套PPT课件

万有引力定律
任意两个质点通过连心线方向上的力相互吸引。 该引力大小与它们质量的乘积成正比与它们距离 的平方成反比。
机械能守恒定律
在只有重力或弹力做功的物体系统内(或者不受 其他外力的作用下),物体系统的动能和势能( 包括重力势能和弹性势能)发生相互转化,但机 械能的总能量保持不变。
04
动量守恒与能量守恒
热力学第二定律
热力学第二定律的表述
不可能从单一热源取热,使之完全转换为有用的功而不产生其他影响。
热力学第二定律的数学表达式
对于可逆过程,有dS=(dQ)/T;对于不可逆过程,有dS>(dQ)/T,其中S表示熵,T表 示热力学温度。
热力学第二定律的应用
热力学第二定律揭示了自然界中宏观过程的方向性,指出了与热现象有关的实际宏观过 程都是不可逆的。同时,它也提供了判断这些过程进行方向的原则。
刚体的定轴转动中的功与能
转动功
力矩在转动过程中所做的功叫做“转动功”,它等于力矩与角位 移的乘积。
转动动能
刚体定轴转动的动能叫做“转动动能”,它等于刚体的转动惯量与 角速度平方的一半的乘积。
机械能守恒
在只有重力或弹力做功的情况下,刚体的机械能守恒,即动能和势 能之和保持不变。
06
热学基础
温度与热量
磁场的基本概念
01
磁场的定义
磁场是一种物理场,由运动电荷或电流产生,对放入其中的磁体或电流
有力的作用。
02
磁感线
用来形象地表示磁场方向和强弱的曲线,磁感线上某点的切线方向表示
该点的磁场方向。
03
磁场的性质
磁场具有方向性、强弱性和空间分布性。
安培环路定理与毕奥-萨伐尔定律
01
大学物理复习课上册PPT课件

dt
dt
则t1=1.00s时的速度为: v 2 .0i0 4 .0 j0
切向和法向加速度分别为:
at
dv d ( dt dt
vx2 vy2)
d ( 2.002 (4.00t)2)3.58ms2 dt
an a2at2)1.7m 9s2
2、 一质点在半径为0.10m的圆周上运动,其角速度位置
2ra(d 4ras d 3)t3.求(1)在t=2.0s时质点的法向
分析:该题中虽施以“恒力”,但作
用在物体上的力的方向在不断变化。 需按功的矢量定义式来求解。 解:取图示坐标,绳索拉力对物体
30° 5N 1m
37°
所作的功为 W
x2
F
dx
x
x2 Fcosdx
x1
x1
x1
x2
0
x2 5 x dx1.69J
x1
12 x2
7、 一物体在介质中按规律x=ct3作直线运动,c为一常量,设介
dt
在t=2s时,法向加速度和切向加速度的数值分别为
an t2sr 2 2.30102ms2
at
t2s
rd4.80ms2
dt
(2)当 at a/21 2 an2at2 时,有 3at2 an2 即
3[r(24 rads3)t]2r2[1 ( 2 rads3)]4 t 1 s0.29 s 23
此时刻的角位置为
(1)物体 在空中受重力mg和空气阻力Fr=kv作 用而减速.由牛顿定律得
mgkvmdv dt
根据始末条件对上式积分,有:
t
0
dtm
dv
0
v0 mgkv
tmln1(kv0)6.1s1 k mg
大学物理PPT完整全套教学课件

温标的选择
在热力学中,常用的温标有摄氏 温标、华氏温标和热力学温标。 其中,热力学温标以绝对零度为 起点,与热量传递的方向无关, 因此更为科学。
热力学第一定律
01
热力学第一定律的表述
热量可以从一个物体传递到另一个物体,也可以与机械能 或其他能量互相转换,但是在转换过程中,能量的总值保 持不变。
02
质点运动的描述
01 位置矢量与位移
02
位置矢量描述质点在空间中的位置,位移是质点位置
的变化量
03
位移是矢量,具有大小和方向,其方向与从初位置指
向末位置的有向线段一致
质点运动的描述
速度与加速度 速度是质点运动的快慢程度,加速度是速度变化的快慢程度 速度和加速度都是矢量,具有大小和方向
圆周运动
圆周运动的描述
能量守恒定律
能量守恒定律的表述
能量既不会凭空产生,也不会凭空消失,它只会从一种形式转化为另一种形式,或者从 一个物体转移到其它物体,而能量的总量保持不变。
能量守恒定律的适用范围
无论是宏观世界还是微观世界,无论是低速运动还是高速运动,能量守恒定律都适用。
能量守恒定律的数学表达式
ΔE = W + Q,其中ΔE表示系统内能的增量,W表示外界对系统做的功,Q表示系统吸 收的热量。
通过牛顿运动定律可以预测物体 在受力后的运动状态,为物理学 研究提供基础。
非惯性系中的力学问题
01
非惯性系定义
02
惯性力概念
相对于地面做加速或减速运动的参考 系称为非惯性系。
在非惯性系中,为了解释物体的运动 ,需要引入一种假想的力,即惯性力 。
03
非惯性系中牛顿运动 定律的应用
在非惯性系中,牛顿运动定律仍然适 用,但需要考虑惯性力的影响。例如 ,在旋转的参考系中,物体受到的惯 性力会导致其偏离原来的运动轨迹。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(电流I 均匀分布在圆柱的横截面内)内外的磁场.
Example:
∫ B ⋅ dl
L
r
r
= B ∫ dl = 2πrB = µ0i
L
B out =
µ 0i 2 πr
i πr 2 πR 2
r L2 r
r B
Choose a circular loop L2 with r < R,
Solution:
Cylindrical symmetry— —P609 Choose a circular loop L1 with r > R,
B A q
(b) Potential of the shell B
VB = Q + q 4πε 0 R2
B A q
R2
R1
Potential of the sphere A
VA = q q q + Q − + 4πε 0 R 4 πε 0 R1 4πε 0 R2
oR
Q
V A = V AB + V B = q 1 1 Q + q ( − )+ 4πε 0 R R1 4πε 0R2
?
v dE v dB
v v E = ∫ dE v v B = ∫ dB
z
ˆ µ I dl × r B = ∫ dB = ∫ 0 4π r 2
x
D
I
θ2
2)外力做功 A外 = F外 d = F电d = Q ( E电 )d Q 2d = >0 2ε 0 S
σ Q = 2ε 0 2ε 0 S
B=
µ0 I (cosθ1 − cosθ 2 ) 4πr
(Right-hand rule direction)
Example: v Find B inside a “infinitely long” solenoid (载流长直螺 线管内部的磁场)(The number of turns per unit length of the solenoid n and total number of coils N). Based r on the feature of the distribution Solution: of B, we choose a rectangular loop abcd,
v v µ m µ 0 IR 2 B= 0 3 3 2πx 2x v µ0m v B= en 2 π x3 v 说明:m 的方向与圆电流 v 的单位正法矢 e n 的方向相同.
v v m = IS e n
I
S
B=
vm en
I
v
v m
v en
S
10
2 I 1 5 4 R1 * o
R2
3
B1 = 0 µ I B2 = 0 4 R2 方向垂直于纸面向里
B= µ 0 Ni µ 0 Ni = = µ 0 ni 2 πr L
R2
R1
∫LB ⋅ dl = 2πrB = µ0 Ni
B= µ 0 Ni 2 πr
v
r
It is as same as the expression of the one of long solenoid. (2) Q Bout = 0, so the magnetic field of toroid is limited in its interior.
σ 3 S + σ 4 S = QB Considering the point PB in plate B,
σ σ σ σ EB = 1 + 2 + 3 − 4 = 0 2 ε 0 2ε 0 2ε 0 2ε 0
S
σ σ σ σ EB = 1 + 2 + 3 − 4 = 0 2ε 0 2ε 0 2ε 0 2ε 0
r R
o
2
3
3
(2) letting sphere is
U ∞ = 0 , the electrical potential outside the
U =∫
r
∞
Qdr Q = 2 4 πε 4πε 0 r 0r
Example:
A conducting sphere, of radius R and charge +q, is concentric with a spherical conducting shell of inner radius R1 and outer radius R2. This shell has a net charge of Q. (a) What are the charges on the inner and outer surfaces of the shell? (b) The potential of the sphere and the shell? Solution:
2π d1
15
2. The application of Ampere’s law It plays very important role in the theory of 电磁 r 场。One can also use Ampere’s law to calculate B with symmetrical distribution of current.
o
θ1
C I B
X
P
y
E电 =
B=
µ0I 2πr
I
B
(1)若线圈有 N 匝 B =
N µ 0 IR 2
磁偶极矩
3
( 2 x + R)2
2 2
x = 0 B= ( 2)
R
µ0 I 2R
r
x
o
*p
v B
I
9
x >> R ( 3) µ IR 2 B= 0 3 , x 2x µ 0 IS B= 2 π x3
1
2014/6/13
Example
平行板 电容器带电Q,间距d ,缓慢拉动至2d
Last Time…… 静电场: 取 dq
。求:1) 电容器能量变化;2) 外力做功. 解:(1)电容器能量的变化:
Q W=W ∆ 初 = 2C 末−W
2 末
磁 场: 取 Idl Biot-Savart Law
v
−
Q2 Q 2d = 2 C 初 2ε 0 S
圆电流的磁场 σdldr dI = = σvdr = σω r dr dt v×1 dB = µ0dI µ0σω = dr 2r 2
dI dr
σ R
o
σ R o rຫໍສະໝຸດ ωωdrv σ > 0, B 向外
14
µ σω R µ σω R dr = 0 B= 0 ∫ 0 2 2 v σ < 0, B 向内
13
方向垂直于纸面向外 方向垂直于纸面向外
B3 =
µ0 I 4πR
方向垂直于纸面向外
B = B1 + B2 + B3 =
3µ 0 I µ0 I + 8R 4πR
2
2014/6/13
解法 例 半径为 R 的带电薄圆盘的电荷 面密度为 σ ,并以角 速度 ω 绕通过盘心垂 直于盘面的轴转动, 求圆盘中心的磁感强 度.
σ 3 S + σ 4 S = QB
σ1 σ 2 σ 3 σ 4
PB
σ 2 = −σ 3
σ1 = σ4 =
d
QA − QB 2S
d
Think that if the plate B is connected to the ground, then σ1= σ4 = 0
QA + QB 2S
σ 2 = −σ 3 =
Look at the description given in textbook of P608. 例 如图载流长直导线的电流为 I ,试求 通过矩形面积的磁通量. µI 解 B= 0 v B 2 πx dx µ0I dΦ = BdS = ld x 2π x l I v v µ Il d2 dx Φ = ∫S B ⋅ dS = 0 ∫d d1 d2 2π 1 x o x x Φ = µ 0 Il ln d 2
conservation of charges
Example: Two parallel-conducting-plates with same area (S>>d2). They charged QA and QB respectively. Find the surface density at each face of the plates under electrostatic equilibrium.
Main steps: (1) Symmetry analyses (由I的分布,分析分布的对称性). (2) Choose a loop (使回路上各处B相等,方向特殊,从而 可从回路积分中提出B). (3) Put into the law and calculate B.
r Find the B inside and outside a long straight wire of radius R and uniformly distributed current I over a cross section of the wire 长直圆柱形载流圆柱体
Solution: Assume surface density is σ
QA
Plot a Gauss’s surface S', we have r r σ 2 = −σ 3 ∫∫ E ⋅ dS = 0
σ 1 S + σ 2 S = QA
QA
QB
S
σ1 σ 2 σ 3 σ 4
Example:
∫ B ⋅ dl
L
r
r
= B ∫ dl = 2πrB = µ0i
L
B out =
µ 0i 2 πr
i πr 2 πR 2
r L2 r
r B
Choose a circular loop L2 with r < R,
Solution:
Cylindrical symmetry— —P609 Choose a circular loop L1 with r > R,
B A q
(b) Potential of the shell B
VB = Q + q 4πε 0 R2
B A q
R2
R1
Potential of the sphere A
VA = q q q + Q − + 4πε 0 R 4 πε 0 R1 4πε 0 R2
oR
Q
V A = V AB + V B = q 1 1 Q + q ( − )+ 4πε 0 R R1 4πε 0R2
?
v dE v dB
v v E = ∫ dE v v B = ∫ dB
z
ˆ µ I dl × r B = ∫ dB = ∫ 0 4π r 2
x
D
I
θ2
2)外力做功 A外 = F外 d = F电d = Q ( E电 )d Q 2d = >0 2ε 0 S
σ Q = 2ε 0 2ε 0 S
B=
µ0 I (cosθ1 − cosθ 2 ) 4πr
(Right-hand rule direction)
Example: v Find B inside a “infinitely long” solenoid (载流长直螺 线管内部的磁场)(The number of turns per unit length of the solenoid n and total number of coils N). Based r on the feature of the distribution Solution: of B, we choose a rectangular loop abcd,
v v µ m µ 0 IR 2 B= 0 3 3 2πx 2x v µ0m v B= en 2 π x3 v 说明:m 的方向与圆电流 v 的单位正法矢 e n 的方向相同.
v v m = IS e n
I
S
B=
vm en
I
v
v m
v en
S
10
2 I 1 5 4 R1 * o
R2
3
B1 = 0 µ I B2 = 0 4 R2 方向垂直于纸面向里
B= µ 0 Ni µ 0 Ni = = µ 0 ni 2 πr L
R2
R1
∫LB ⋅ dl = 2πrB = µ0 Ni
B= µ 0 Ni 2 πr
v
r
It is as same as the expression of the one of long solenoid. (2) Q Bout = 0, so the magnetic field of toroid is limited in its interior.
σ 3 S + σ 4 S = QB Considering the point PB in plate B,
σ σ σ σ EB = 1 + 2 + 3 − 4 = 0 2 ε 0 2ε 0 2ε 0 2ε 0
S
σ σ σ σ EB = 1 + 2 + 3 − 4 = 0 2ε 0 2ε 0 2ε 0 2ε 0
r R
o
2
3
3
(2) letting sphere is
U ∞ = 0 , the electrical potential outside the
U =∫
r
∞
Qdr Q = 2 4 πε 4πε 0 r 0r
Example:
A conducting sphere, of radius R and charge +q, is concentric with a spherical conducting shell of inner radius R1 and outer radius R2. This shell has a net charge of Q. (a) What are the charges on the inner and outer surfaces of the shell? (b) The potential of the sphere and the shell? Solution:
2π d1
15
2. The application of Ampere’s law It plays very important role in the theory of 电磁 r 场。One can also use Ampere’s law to calculate B with symmetrical distribution of current.
o
θ1
C I B
X
P
y
E电 =
B=
µ0I 2πr
I
B
(1)若线圈有 N 匝 B =
N µ 0 IR 2
磁偶极矩
3
( 2 x + R)2
2 2
x = 0 B= ( 2)
R
µ0 I 2R
r
x
o
*p
v B
I
9
x >> R ( 3) µ IR 2 B= 0 3 , x 2x µ 0 IS B= 2 π x3
1
2014/6/13
Example
平行板 电容器带电Q,间距d ,缓慢拉动至2d
Last Time…… 静电场: 取 dq
。求:1) 电容器能量变化;2) 外力做功. 解:(1)电容器能量的变化:
Q W=W ∆ 初 = 2C 末−W
2 末
磁 场: 取 Idl Biot-Savart Law
v
−
Q2 Q 2d = 2 C 初 2ε 0 S
圆电流的磁场 σdldr dI = = σvdr = σω r dr dt v×1 dB = µ0dI µ0σω = dr 2r 2
dI dr
σ R
o
σ R o rຫໍສະໝຸດ ωωdrv σ > 0, B 向外
14
µ σω R µ σω R dr = 0 B= 0 ∫ 0 2 2 v σ < 0, B 向内
13
方向垂直于纸面向外 方向垂直于纸面向外
B3 =
µ0 I 4πR
方向垂直于纸面向外
B = B1 + B2 + B3 =
3µ 0 I µ0 I + 8R 4πR
2
2014/6/13
解法 例 半径为 R 的带电薄圆盘的电荷 面密度为 σ ,并以角 速度 ω 绕通过盘心垂 直于盘面的轴转动, 求圆盘中心的磁感强 度.
σ 3 S + σ 4 S = QB
σ1 σ 2 σ 3 σ 4
PB
σ 2 = −σ 3
σ1 = σ4 =
d
QA − QB 2S
d
Think that if the plate B is connected to the ground, then σ1= σ4 = 0
QA + QB 2S
σ 2 = −σ 3 =
Look at the description given in textbook of P608. 例 如图载流长直导线的电流为 I ,试求 通过矩形面积的磁通量. µI 解 B= 0 v B 2 πx dx µ0I dΦ = BdS = ld x 2π x l I v v µ Il d2 dx Φ = ∫S B ⋅ dS = 0 ∫d d1 d2 2π 1 x o x x Φ = µ 0 Il ln d 2
conservation of charges
Example: Two parallel-conducting-plates with same area (S>>d2). They charged QA and QB respectively. Find the surface density at each face of the plates under electrostatic equilibrium.
Main steps: (1) Symmetry analyses (由I的分布,分析分布的对称性). (2) Choose a loop (使回路上各处B相等,方向特殊,从而 可从回路积分中提出B). (3) Put into the law and calculate B.
r Find the B inside and outside a long straight wire of radius R and uniformly distributed current I over a cross section of the wire 长直圆柱形载流圆柱体
Solution: Assume surface density is σ
QA
Plot a Gauss’s surface S', we have r r σ 2 = −σ 3 ∫∫ E ⋅ dS = 0
σ 1 S + σ 2 S = QA
QA
QB
S
σ1 σ 2 σ 3 σ 4
