§1.3 对称操作和点群
合集下载
点对称操作群点群(共37张PPT)

S4轴
A
A
旋转-反映操作是一个复合操作,即先经Cn旋转, 然后再经垂直Cn轴的平面的反映,可表示为Cn过程.
如:n=2时, C2=S2,由于S2效果等同于i,则S2=
C2=i;
同理, S1= C1=。
3.1.5 恒等操作E
一个分子在操作后,其取向与原来的恒等不变, 即分子中的每个原子都回到了原来的位置,我们称此操 作为恒等操作,记做E。
3.2.3 分子点群的确定
➢首先确定该分子是否属于某一特殊点群,如Td; ➢如非特殊点群,应先寻找旋转轴,如果没有旋转轴, 则寻找对称中心或反映面。
➢如有旋转轴,先指定主轴位置,再看是否存在Sn;
➢在垂直Cn轴的平面中寻找一组n重轴;
➢看分子中含有何种类型的反映面,确定分子点群。
§3.3 特征标表简介
CH4分子中4个C3操作属于同一类;
§3.2 点对称操作群(点群)
3.2.1 群的定义、群阶 3.2.2 主要点群
3.2.3 分子点群的确定
3.2.1 群的定义、群阶
我们称元素的某个集合形成一个群,群有着严格 的定义:“封闭性、结合律成立、存在恒等元素、存 在逆元素”。群中元素的个数,称作群阶。
。 旋转——第一类对称操作,或实际操作;
首先确定该分子是否属于某一特殊点群,如Td;
对称性就是物体或图像中各部分间所具有的相似性,物体以及图像的对称性可定义为经过某一不改变其中任何两点间距离的操作后能复原的性质
约化前的表示称为可约表示。 。
对称操作:使物体没有变化的操作,不改变其中任何两点间距离的操作。
绕轴旋转2π/2角,
分子可得“重现”
如果分子沿顺时针方向绕一轴旋转2π/n角后能够复
原,就称此操作为旋转操作,上述旋转所围绕的轴就称 作n次旋转轴,记做Cn。
点对称操作群(点群)

6阶群。
H2O
E, C2, v(1), v(2)
4阶群
一个分子所具有的对称操作(点对称操作)的完 全集合构成一个点群(Point Group)。每个点群具有 一个特定的符号,国际上通用的分子点群符号叫 SchÖnflies(熊夫利斯)记号。
熊夫利斯记号隐含了该点群中代表性的对称元 素符号。
例如:H2O分子,有1个C2轴,2个v反映面,所以
VI.H3BO3分子
C3h
Cl Cl
Cl
Cs
Cl
C3h
N N
N
N C4h
6. Dn点群
含有一个Cn轴和n个垂直Cn轴的C2轴。如:
[Co(en)3]3+分子具有一个C3轴和3个通过Co离子,
垂直C3轴的C2轴。
唯一的C3旋转轴 从xyz轴连成的正 三角形中心穿过, 通向Co;
D3
三条C2旋转轴分别从每个N– N键中心穿过通向Co.
图Ⅷ. P4S3
氨
C3v
三氯甲烷
C3v
IF5
C4v
5 Cnh群 :
σh .
除有一条n次旋转轴Cn外,还有与之垂直的一个镜面
C2h群: 反式二氯乙烯
C2h群: N2F2
C2垂直于荧光屏, σh 在荧光屏上
反式二氯乙烯
C2h
间苯三酚
C3h
H3BO3分子是C3h群的例子。由于B与O原子都 以Sp2杂化与其它原子成键,所以整个分子在一个 平面上。C3轴位于B原子上且垂直分子平面。(图VI)
图IV. 船式环已烷
图V. N2H4
环己烷(船式)
C2v
NH3分子(图VII)是C3v点群的典型例子。C3轴 穿过N原子和三角锥的底心,三个垂面各包括一个
H2O
E, C2, v(1), v(2)
4阶群
一个分子所具有的对称操作(点对称操作)的完 全集合构成一个点群(Point Group)。每个点群具有 一个特定的符号,国际上通用的分子点群符号叫 SchÖnflies(熊夫利斯)记号。
熊夫利斯记号隐含了该点群中代表性的对称元 素符号。
例如:H2O分子,有1个C2轴,2个v反映面,所以
VI.H3BO3分子
C3h
Cl Cl
Cl
Cs
Cl
C3h
N N
N
N C4h
6. Dn点群
含有一个Cn轴和n个垂直Cn轴的C2轴。如:
[Co(en)3]3+分子具有一个C3轴和3个通过Co离子,
垂直C3轴的C2轴。
唯一的C3旋转轴 从xyz轴连成的正 三角形中心穿过, 通向Co;
D3
三条C2旋转轴分别从每个N– N键中心穿过通向Co.
图Ⅷ. P4S3
氨
C3v
三氯甲烷
C3v
IF5
C4v
5 Cnh群 :
σh .
除有一条n次旋转轴Cn外,还有与之垂直的一个镜面
C2h群: 反式二氯乙烯
C2h群: N2F2
C2垂直于荧光屏, σh 在荧光屏上
反式二氯乙烯
C2h
间苯三酚
C3h
H3BO3分子是C3h群的例子。由于B与O原子都 以Sp2杂化与其它原子成键,所以整个分子在一个 平面上。C3轴位于B原子上且垂直分子平面。(图VI)
图IV. 船式环已烷
图V. N2H4
环己烷(船式)
C2v
NH3分子(图VII)是C3v点群的典型例子。C3轴 穿过N原子和三角锥的底心,三个垂面各包括一个
分子的对称性和群论初步

属4阶群
H3BO3分
子
C3h C31, C32 , C33 E, h , S31, S35
属6阶群 S31 hC31,S32 C32,S33 h S34 C31,S35 hC32,S36 E
Cnh Cnk (k 1,n 1), E, h , hCnl (l 1,l 1)
非全同:不能通过平移或转动等第一类对称操 作使两个图形叠合。
2.旋光异构体:一对等同而非全同的分子构成 的一对对映体。
3.手性分子:没有第二类对称元素的分子。
R(右,顺时针方向转)和 S(左,逆时针旋转) 外消旋体:等量的R和S异构体混合物一定无旋光
性方向相反
4.对称性和旋光性的关系
✓ 若分子具有反轴Ι(先旋转360°/n,再反演)的对 称性,一定无旋光性;若分子不具有反轴的对称性, 则可能出现旋光性。
元的数目有限的群称为有限群,数目无限的群 称为无限群。
点群:一个有限分子的对称操作群 ☞“点”的含义 ✔这些对称操作都是点操作,操作时分子中至少
有一个点不动。 ✔分子的对称元素至少通过一个公共点。
2.2 群的乘法表
※顺序
乘法表由行和列组成,在行坐标x和列坐标y的 交点上找到的元是yx,即先操作x,后操作y。每一 行和每一列都是元的重新排列。
C6轴: C6轴包括C2 和C3 的全部对称操作。
1.3 反演操作和对称中心 i
反演操作: 将分子的各点移到对称中心连线的延长线上,
且两边的距离相等。若分子能恢复原状,即反演操 作。
✔对称因素:对称中心 i ✔特点:延长线,等距
除位于对称中心的原子外,其余均成对出现
若对称中心位置在原点 (0,0,0)处,反演操作i的表 示矩阵为:
✓ 一重反轴=对称中心,二重反轴=镜面,独立的反 轴只有I4 。则具有这三种对称操作的无旋光性, 不具有这3种对称元素的分子都可能有旋光性。
H3BO3分
子
C3h C31, C32 , C33 E, h , S31, S35
属6阶群 S31 hC31,S32 C32,S33 h S34 C31,S35 hC32,S36 E
Cnh Cnk (k 1,n 1), E, h , hCnl (l 1,l 1)
非全同:不能通过平移或转动等第一类对称操 作使两个图形叠合。
2.旋光异构体:一对等同而非全同的分子构成 的一对对映体。
3.手性分子:没有第二类对称元素的分子。
R(右,顺时针方向转)和 S(左,逆时针旋转) 外消旋体:等量的R和S异构体混合物一定无旋光
性方向相反
4.对称性和旋光性的关系
✓ 若分子具有反轴Ι(先旋转360°/n,再反演)的对 称性,一定无旋光性;若分子不具有反轴的对称性, 则可能出现旋光性。
元的数目有限的群称为有限群,数目无限的群 称为无限群。
点群:一个有限分子的对称操作群 ☞“点”的含义 ✔这些对称操作都是点操作,操作时分子中至少
有一个点不动。 ✔分子的对称元素至少通过一个公共点。
2.2 群的乘法表
※顺序
乘法表由行和列组成,在行坐标x和列坐标y的 交点上找到的元是yx,即先操作x,后操作y。每一 行和每一列都是元的重新排列。
C6轴: C6轴包括C2 和C3 的全部对称操作。
1.3 反演操作和对称中心 i
反演操作: 将分子的各点移到对称中心连线的延长线上,
且两边的距离相等。若分子能恢复原状,即反演操 作。
✔对称因素:对称中心 i ✔特点:延长线,等距
除位于对称中心的原子外,其余均成对出现
若对称中心位置在原点 (0,0,0)处,反演操作i的表 示矩阵为:
✓ 一重反轴=对称中心,二重反轴=镜面,独立的反 轴只有I4 。则具有这三种对称操作的无旋光性, 不具有这3种对称元素的分子都可能有旋光性。
点对称操作群(点群) §3.1 对称操作与对称元素

v(2)
0 0 1 0 1 0 1 0 0
v(3)
0 1 0 1 0 0 0 0 1
Γr
C3v
E
1 2 3 2 0
C31
3 2 1 2 0 0 0 1
C32
旋转——第一类对称操作,或实际操作;
反映、反演、旋转-反映只能在想象中实现,称 作第二类对称操作或虚操作;
3.1.6 同类对称元素与同类操作
如果一个操作能使一个对称元素变成另一个对 称元素,那么这些对称元素就是同一类对称元素。 如:NH3分子中3个v反映面属于同一类; H2O分子中两个对称面不属于同一类; 对于旋转,把等价而并不恒等的旋转操作归属 于同一类,称为同类操作。 如:NH3分子中C31,C32,C33(E)中,前两个属 于同一类,2就是C3操作的阶; CH4分子中4个C3操作属于同一类;
3.4.2 分子的对称性与旋光性
分子有无旋光性就看它是否能跟它的镜像重合。 如果二者能重合,则该分子没有旋光性;反之,分 子就有旋光性。
称不具备任意次旋转-反映轴Sn的分子为不对
称分子,所有不对称分子都具有旋光性。
于C3v点群,类似的如CHCl3,NF3等。
3.2.2 主要点群
1. C1点群
H C F
Br
Cl
HCBrClF分子,无任何对称元素(除C1外),属 于C1点群,该类化合物称为非对称化合物。如: SiFClBrI、POFClBr等;
2. Cn点群
C2
H O O
H
仅含有一个Cn轴。如:H2O2仅含有一个C2轴, 该轴平分两个平面的夹角,并交于O-O键的中点, 所以,该分子属于C2点群;类似的结构如:N2H4等
第三章分子的对称性与点群优秀课件

3.群的一些相关概念 (1)群的构成:群元素可以是各种数学对象或物理
动作,可以进行某种数学运算或物理动作。 (2)群的分类:群有各种类型,如旋转群,置换群,
点群,空间群,李群…… (3)群阶:群所含的元素个数称为群阶, (4)类:群中某些对称元素在相似变换中互为共轭
元素的可分为一类。如C3v 点群中的元素可分为三类,
C
1 2
使空间某点p(x,y,z)变换到
另一个点p’(x’,y’,z’)
x' x cos sin 0x y'C2ysin cos 0y
z' z 0 0 1z
1 0 0x x 0 1 0yy
0 0 1z z
对称操作
C
1 3
使空间某点p(x,y,z)变换到另一个
点p’(x’,y’,z’)
xzy'''C31xzycsio0n22s33
2)恒等元素E 若 A G ,E G ,则 E A A A E
3)逆元素
若 AG,则必B存 G,且 在 AB BA E B为 A的逆元素 A1, B 记作
4)结合律
若 A ,B ,C G ,则 A (B ) C (A )C B
2. 群的乘法表 根据群的定义,可以得到群的乘法表
C3v点群的乘法表
E元素成一类,C31与 C32旋转成一类。三个σv
平面而成一类。 (5)子群:在一些较大的群中可以找到一些较小的
群,称为子群。例如:C3v 群中有子群 C3 。子群也 要满足群的四个要求。
一、对称点群分类
点群 Cn群 Cnv群 Cnh群 Dn群 Dnh群 Dnd群 Sn群 Td群 Oh群
C1 C2v
C 1C 1C2E
对称及点群

对称及点群
对称
对称:物体等同部分的规则重复 对称操作:借助某种几何要素,能使物体与自身重合所施行的 某种规律的动作。如旋转、镜面反射、中心反演等 对称元素:对称操作所据以进行的旋转轴、镜面、对称中心 等几何元素
对称操作及对称元素
(1) 旋转(Rotation)、旋转轴 旋转操作cn
cn
2π n
:绕过原点的轴转动
角
n 度轴:相应于cn的转动轴
n =1 , 2 , 3 , 4,6 五个值
cnn = E
C
B
A
(2) 镜面反射(Reflection)、镜面
σ
镜面反射操作σ:包含了原点的平面上的镜面反射
a. σh(horizontal):镜面是与主轴垂直的水平镜面 b. σv (vertical):镜面是包含了转轴的垂直镜面 c.该转轴的
2度轴的夹角
(3)中心反演(Inversion)与对称中心 i 中心反演操作:r →-r
(4) 旋转反映、映轴(象转轴)
Sn
旋转反映操作 sn : 绕轴转动 角后 在垂直于转轴的水平面上反射
2π n
(5)旋转反演、反轴
In
旋转反演操作In: 绕轴转2π /n接着按轴上的中心点进行反演 CH4 分子中三个相互垂直相交的 I4 轴:
σd的镜面包含主轴并平分垂直于主轴的相邻2度轴之间的夹角
立方体群 (28) T 群(正四面体群): 使正四面体自身重合的全部正当转动构成的群 (29) Td群(完全的正四面体群):使正四面体自身重合的 正当转动与非正当转动全部操作构成的群 (30)Th 群:Th = T ⊗ Ci ,不是正四面体的对称性群 (31)O 群(简立方体群/正八面体群): 使简立方体或正八面体 自身重合的全部正当转动构成的群( 24 个群元) (32) Oh 群:Oh = O ⊗ Ci ,使简立方体(或正八面体)自身重 合的一切对称操作构成的群( 48 个群元)
对称
对称:物体等同部分的规则重复 对称操作:借助某种几何要素,能使物体与自身重合所施行的 某种规律的动作。如旋转、镜面反射、中心反演等 对称元素:对称操作所据以进行的旋转轴、镜面、对称中心 等几何元素
对称操作及对称元素
(1) 旋转(Rotation)、旋转轴 旋转操作cn
cn
2π n
:绕过原点的轴转动
角
n 度轴:相应于cn的转动轴
n =1 , 2 , 3 , 4,6 五个值
cnn = E
C
B
A
(2) 镜面反射(Reflection)、镜面
σ
镜面反射操作σ:包含了原点的平面上的镜面反射
a. σh(horizontal):镜面是与主轴垂直的水平镜面 b. σv (vertical):镜面是包含了转轴的垂直镜面 c.该转轴的
2度轴的夹角
(3)中心反演(Inversion)与对称中心 i 中心反演操作:r →-r
(4) 旋转反映、映轴(象转轴)
Sn
旋转反映操作 sn : 绕轴转动 角后 在垂直于转轴的水平面上反射
2π n
(5)旋转反演、反轴
In
旋转反演操作In: 绕轴转2π /n接着按轴上的中心点进行反演 CH4 分子中三个相互垂直相交的 I4 轴:
σd的镜面包含主轴并平分垂直于主轴的相邻2度轴之间的夹角
立方体群 (28) T 群(正四面体群): 使正四面体自身重合的全部正当转动构成的群 (29) Td群(完全的正四面体群):使正四面体自身重合的 正当转动与非正当转动全部操作构成的群 (30)Th 群:Th = T ⊗ Ci ,不是正四面体的对称性群 (31)O 群(简立方体群/正八面体群): 使简立方体或正八面体 自身重合的全部正当转动构成的群( 24 个群元) (32) Oh 群:Oh = O ⊗ Ci ,使简立方体(或正八面体)自身重 合的一切对称操作构成的群( 48 个群元)
晶体的对称性与群论

z
(x,y,z)
y x
(x, y,-z)
s xy
1 0 0
0 1 0
0 x 1 0 s xy y 0 z 0 1
0 1 0
C32
?:H2O,[PtCl4 C5H5-,C6H6
]2+,
BF3分子有1C3、3C2
C3为主轴。
The principle rotation axis is the axis of the highest fold.
C6
C5
The matrix representations:
(x1,y1)
• Operation by the identity operator leaves the molecule unchanged. • All objects can be operated upon by the identity operation.
F Cl I Br
15
matrix representation of an operator
2 sin 3 2 cos 3 0
1 0 x 2 3 0 y 2 z 0 1 1 0 x 2 3 0 y 2 z 0 1
x1 x2 ˆ y y C 1 2 z z 1 2
c11 c12 c21 c22 c 31 c32
c11 c12 ˆ c C c22 21 c 31 c32
c13 c23 c33
第一章:对称性与群论
要求: 1、确定简单分子所属点群 2、解读特征标表 3、群论在无机化学中的应用 a. 对称性与分子极性 b. 分子的振动与IR、Raman光谱 c. 化学键与分子轨道等
(x,y,z)
y x
(x, y,-z)
s xy
1 0 0
0 1 0
0 x 1 0 s xy y 0 z 0 1
0 1 0
C32
?:H2O,[PtCl4 C5H5-,C6H6
]2+,
BF3分子有1C3、3C2
C3为主轴。
The principle rotation axis is the axis of the highest fold.
C6
C5
The matrix representations:
(x1,y1)
• Operation by the identity operator leaves the molecule unchanged. • All objects can be operated upon by the identity operation.
F Cl I Br
15
matrix representation of an operator
2 sin 3 2 cos 3 0
1 0 x 2 3 0 y 2 z 0 1 1 0 x 2 3 0 y 2 z 0 1
x1 x2 ˆ y y C 1 2 z z 1 2
c11 c12 c21 c22 c 31 c32
c11 c12 ˆ c C c22 21 c 31 c32
c13 c23 c33
第一章:对称性与群论
要求: 1、确定简单分子所属点群 2、解读特征标表 3、群论在无机化学中的应用 a. 对称性与分子极性 b. 分子的振动与IR、Raman光谱 c. 化学键与分子轨道等
第三章分子的对称性与点群PPT课件

C1 C2v
CCs1h
D3 D2h D2d
CSi2
Td Oh
典型类型
C2
C3
C3v
C∞v
C2h
C3h
D3h D3d
S4
D4h
D6h
D ∞h
1. Cn 点群
Cn群只有1个Cn 旋转轴。独立对称操作有n个。阶 次为n。
若分子只有n重旋转轴,它就属于Cn群,群元素为 {E,Cn1,Cn2…Cnn-1}。这是n阶循环群。
III. 1,3,5-三甲基苯
1,3,5-三甲基苯 (图III)是C3点 群的例子,若不考 虑甲基上H原子, 分子的对称性可以 很高,但整体考虑, C6H3(CH3)3只有C3 对称元素。C3轴位 于苯环中心,垂直 于苯环平面,分子 绕C3轴转动120°, 240°都能复原。
IV. CH3CCl3
如甲烷分子,一个
经过C原子的四次映转
轴S4,作用在分子上,H
1旋转到1’的位置后,
1’
经平面反映到H4的位置,
同时H2旋转到2’的位置
再反映到H3的位置……
整个分子图形不变,
S1 h ; S2 i ;
S C ; S 独立,包含C ;
3
3
h
4
2
S C ; S C i
5
5
h
6
3
即只有S4是独立的点群, 其余Sn 可化为 i, h 或 Cn i,Cn h
左图为D2对称性分子, C2主轴穿过联苯轴线,经过 2个O为水平面上的C2轴, 还有一个C2轴与这两个C2轴 垂直。
双乙二胺NH2CH2-CH2-NH2CH2-CH2-NH2可 对Co3+离子3配位 螯合,2个双乙二 胺与Co3+形成 Co(dien)2配合物, 具有D2对称性。 (右图)
立方体等的对称操作及点群讲述
群
群加上中心反演
晶体的宏观对称只有32个不同类型
01_05_晶体的宏观对称性 —— 晶体结构
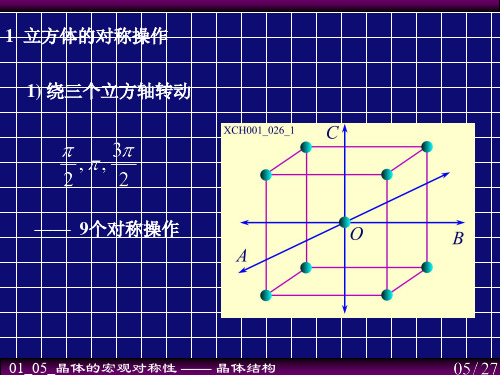
1 立方体的对称操作 1) 绕三个立方轴转动
—— 9个对称操作
01_05_晶体的宏观对称性 —— 晶体结构
2) 绕6条面对角线轴转动 3) 绕4个立方体对角线 轴转动
—— 共有6个对称操作
—— 8个对称操作 4) 单位变换
—— 1个对称操作
01_05_晶体的宏观对称性 —— 晶体结构
5) 以上24个对称操作加中心反演仍是对称操作 —— 立方体的对称操作共有48个
—— 5个
2) 绕对棱中点连线转动 —— 3个
3) 绕相对面中心连线转动
—— 3个
4) 单位变换
—— 1个
5) 以上12个对称操作加中心 反演仍是对称操作
—— 正六面柱的对称操作有24个
01_05_晶体的宏观对称性 —— 晶体结构
理论证明由10种对称素只能组成32种不同的点群 —— 晶体的宏观对称只有32个不同类型
ห้องสมุดไป่ตู้
3) 单位变换
—— 1个对称操作
01_05_晶体的宏观对称性 —— 晶体结构
4) 绕三个立方轴转动
—— 6个对称操作 5) 绕6条面对角线轴转动
加上中心反演 —— 6个对称操作
加中心反演
正四面体的对称操作共有24个
01_05_晶体的宏观对称性 —— 晶体结构
3 正六面柱的对称操作 1) 绕中心轴线转动
—— 不动操作,只含一个元素,表示没有任何对称性的晶体
回转群
只包含一个旋转轴的点群 —— 下标表示是几重旋转轴
—— 4个
双面群
包含一个n重旋转轴和n个与之对应的二重轴的点群 —— 4个
第三节分子的对称性与点群

1
6
5
6
2 Revolve 5
1 Revolve 4
6
5
3
60º
4
4
2
3
60º 3
1
2
图形不变
图形不变
空间旋转对称操作是分子对称性讨论中的重要操作之 一。任何一种分子至少可找出一种空间旋转操作。
Revolve
2π
图形不变(复原)
……
Revolve 240º
1
6
2
5
3
4
图形复原
精品资料
⑵镜像反映
当一个体系对空间平面进行反映操作时,若其图形不变,该操作称为镜 像反映对称操作。
例如: CO2 分子(直线型)
1
OC
2
i
2
O 中心反演 O C
图形不变
又如:苯分子(正六边形)
1i
O 中心反演
1
2
OC O
图形复原
1
4
CH
CH
6 CH
CH 2
i
3 CH
CH 5
中心反演
图形不变
5 CH
CH 3
2 CH
CH 6
CH
CH
4
1
精品资料
⑷像转轴 — Sn
所谓“像转”对称操作,实际上是旋转与镜面反映的复合操作。像转
轴可表示为对称轴与对称面的组合。即:
Sn = Cn +σh =σh + Cn
例如:甲烷分子中的四次像转轴 S4 = Ch +σh
C4
2
1
1
C41操作
2 反映操作
图形不变
3 4
3
点对称操作群(点群).

2 N N 1 N N D N 3 3 2 N N 1 N Cl -cis -[Co(en)2Cl2]+ Cl Cl Cl N N N 2 1 N N N 1 2 2 N 3 1 N 2 or 3 1 N N
-[Co(en)3]3+
图4–43 Δ-(–)-[Co(en)3]3+和Δ-(–)-cis–[Co(en)2Cl2]+ 的绝对构型
熊夫利斯记号隐含了该点群中代表性的对称元
素符号。 例如:H2O分子,有1个C2轴,2个v反映面,所以 属于 C2v点群,SO2,H2S也属于此点群; NH3分子,它有1个C3轴和3个v反映面,属
于C3v点群,类似的如CHCl3,NF3等。
3.2.2 主要点群
1. C1点群
H C F
Br
Cl
HCBrClF分子,无任何对称元素(除C1外),属 于C1点群,该类化合物称为非对称化合物。如: SiFClBrI、POFClBr等;
N2
D∞h
XeF4为平面四边形,属于D4h点群; CO32-离子为平面正三角形,含有对称元素 C3,3C2,3σv,σh, E,属于D3h点群; C6H6为平面正六边形,属于D6h点群;
平面乙烯属于D2h群;
环戊二烯是平面正五边形分子,为D5h点群;
以上统属于Dnh点群。此点群的特点是具有一
个Cn轴和n个垂直于主轴的C2轴,同时有h面。
一、对称操作与对称元素
1 对称性 2 旋转 3 反演与反映 4 恒等操作E
1 对称性
对称性就是物体或图像中各部分间所具有的相
似性,物体以及图像的对称性可定义为经过某一不
改变其中任何两点间距离的操作后能复原的性质。 对称元素: 对称操作中所凭借的元素(点、线、 面)。 对称操作:使物体没有变化的操作,可分为点 操作和空间操作。
三章分子对称和点群

所以 D3 的共轭类为: {e}, {d,f}, {a,b,c}
3.3 点群
• 分子的所有对称元素构成分子的点群. 这些对称元素至少保持空间中的一点(分子质心)不变, 从而成为点群.
• 如H2O的所有对称元素为: I, C2, v (xz) , v (yz)
1. Cn点群
Cn ,C2n ,C3n ,....,Cnn I
当n为偶数时, 当n为奇数时,
Snn hnCnn I Snn hnCnn h , S2nn h2nC2nn I
3.2 群的定义和基本性质
• 定义: 群 G 是一个不同元素的集合{A,B,…,R,…}, 对于一定的 乘法规则, 满足以下四个条件:
• 1) 封闭性 群中任意两个元素 R和 S的乘积等于集合中另一个元素, T=RS
y2
3 xy 2
A(d )z2 A C31 z2 C32z 2 z2
A(d )xy A C31 xy C31x C31y C32x C32 y
1 2
x
3 2
y
3 2
x
1 2
y
3 x2 4
3 y2 1 xy 42
A(d ) yz A C31 yz C31y C31z C32 y C32z
这个概念很容易推广到多个矩阵的直和。例如矩阵
b A a, B d
f
c e,
C
i
l
g h
j
k
m n
的直和是下面的六阶方阵:
a 0 0 0 0 0
0 b c 0 0 0
0 d e 0 0 0 D A B C 0 0 0 f g h
0 0 0 i j k
0 0 0 l m n
分块对角矩阵的性质:
3.3 点群
• 分子的所有对称元素构成分子的点群. 这些对称元素至少保持空间中的一点(分子质心)不变, 从而成为点群.
• 如H2O的所有对称元素为: I, C2, v (xz) , v (yz)
1. Cn点群
Cn ,C2n ,C3n ,....,Cnn I
当n为偶数时, 当n为奇数时,
Snn hnCnn I Snn hnCnn h , S2nn h2nC2nn I
3.2 群的定义和基本性质
• 定义: 群 G 是一个不同元素的集合{A,B,…,R,…}, 对于一定的 乘法规则, 满足以下四个条件:
• 1) 封闭性 群中任意两个元素 R和 S的乘积等于集合中另一个元素, T=RS
y2
3 xy 2
A(d )z2 A C31 z2 C32z 2 z2
A(d )xy A C31 xy C31x C31y C32x C32 y
1 2
x
3 2
y
3 2
x
1 2
y
3 x2 4
3 y2 1 xy 42
A(d ) yz A C31 yz C31y C31z C32 y C32z
这个概念很容易推广到多个矩阵的直和。例如矩阵
b A a, B d
f
c e,
C
i
l
g h
j
k
m n
的直和是下面的六阶方阵:
a 0 0 0 0 0
0 b c 0 0 0
0 d e 0 0 0 D A B C 0 0 0 f g h
0 0 0 i j k
0 0 0 l m n
分块对角矩阵的性质:
分子的对称性和点群

2 二面体群
(1)Dn群 2n个群元素
有一个 n 2 主轴和n个垂直于主轴 的2次旋转轴的分子
2 n1 ˆ (1) ˆ ( 2) ( n) ˆ ˆ ˆ ˆ ˆ E, Cn , Cn ,, Cn , C2 , C2 ,, C2
例
部分交错式的CH3-CH3
D3群
(2) Dnh群 除具有Dn群的对称元素外,还有一个垂 直于主轴的对称面
反演中心:进行反演所凭借的中心点称作 对称中心。
i
2 k 1 ˆ ˆ i i
(k=0,1,2,……)
2k ˆ ˆ i E
5 象转
ˆ S n
旋转和反映的复合操作
2
象转:先将分子绕某轴旋转 n 角度后, 再凭借垂直于该轴的平面进行反映后能够 产生分子等价图形的对称操作。 象转轴:进行象转所凭借的对称轴。 S n
48个对称操作分为10类
四 分子点群的确定步骤
Dh C V Td Oh Cs
Ci C1 Sn Dnh Dnd Dn Cnh CnV Cn
五 群的乘法表
“乘法”定义为一 个操作后接另一个 对称操作 NH3分子属C3v群
2 ( 1 ) ( 2 ) ( 3 ) ˆ ˆ ˆ ˆ v , ˆ v , ˆv E, C3 , C3 ,
例
丙二烯(CH2=C=CH2) D2d群 交错式乙烷(CH3-CH3) D3d群
交错式二茂铁
D5d群
3 立方群
分子有多个高次旋转轴(n3)
(1) Td群
例 CH4,CCl4,SiH4
具有正四面体构型的分子 对称元素有4个C3轴,3个C2轴,3个S4 轴(与3个C2轴重合)和6个d平面
群论 第三章

e2′
e3′ )
=
gCk
(α
)g −1(e1′
e2′
e3′ )
=
gCk
(α )(e1
e2
e3 )
( )[ ] [ ] ( ) = g e1 e2 e3 Cij = e1′ e′2 e3′ Cij 。 (2)
比较上述(1)(2)两式可见,Ck
(α
)
在
o
−
xyz
下的矩阵与
C k1
(α1
)
在
o
−
x′y′z′
1. o − xyz 为右手系,坐标向量为 e1 , e2 , e3 。
2. 点操作保持原点不动,镜面与转轴通过原点,原点即反演中心。
3. Ck (α ),σ k , Sk (α )中的 k 为单位矢。
§ 2 旋转群 SO(3)
设 T 是一个保持原点不动的点操作,即 T e j = e ′j = t1 j e1 + t2 j e2 + t3 j e3 ( j = 1 ,2 ,3),写成
所以 det M (T ) = ±1 。
定理 1 每一个点操作对应于一个行列式为 + 1 或 − 1的正交矩阵。
例如单位操作 E 、反演操作 I 分别对应于行列式为 + 1 和 − 1的正交矩阵:
M
(E
)
=
1 0
0 1
0 0 ,
0 0 1
M
(I
)
=
−1 0
0 −1
0 0 ,
0
0 1
更一般结论:
引理 2 每一个旋转对应于一个行列式为 + 1 的正交矩阵。
点对称操作群(点群)

Cs群
乙醇 邻氯吡啶
4. Cnv点群
C2
O H
H σv
σv
含有一个Cn轴和n个通过Cn轴的对称面。如:
H2O 分子具有一个C2轴和两个包含该轴的互相垂直
的对称面,故属于C2v点群。又如:NH3属于C3v点
群,XeOF4属于C4v点群,CO,HCl属于C∞v点群。
H2O C2v
与水分子类似的V型分子,如SO2、NO2、ClO2、 H2S, 船式环已烷(图IV)、N2H4(图V)等均属C2v点群。
9、Oh群
SF6
Oh 群 : 属于该群的分子,对称性与正八面体或正方体完全相同.
SF6
立方烷
10、Ih群
C60
很 多 符 号 比 如 D/L 、 R/S 和 Λ(lamtda)/Δ(delta) 都 可 以用来描述八面体配合物的绝对构型. 对于 [Co(en)3]3+这类含有三个二齿配体的配合物, Piper 建议用符号Λ/Δ来描绘鳌环在空间排布的结构差异 性.
阶群。
H2O
E, C2, v(1), v(2)
4阶群
一个分子所具有的对称操作(点对称操作)的完 全集合构成一个点群(Point Group)。每个点群具有 一个特定的符号,国际上通用的分子点群符号叫 SchÖnflies(熊夫利斯)记号。
熊夫利斯记号隐含了该点群中代表性的对称元 素符号。
例如:H2O分子,有1个C2轴,2个v反映面,所以
图Ⅷ. P4S3
氨
C3v
三氯甲烷
C3v
IF5
C4v
5 Cnh群 :
除有一条n次旋转轴Cn外,还有与之垂直的一个镜面σh .
C2h群: 反式二氯乙烯
C2h群: N2F2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间群,即有230种对称类型。 根据不同的点对称性,将晶体分为7大晶系,14种布拉维
晶格。
上页
下页
返回
结束
第一章 晶体结构
上页
下页
返回
结束
第一章 晶体结构
上页
下页
返回
结束
第一章 晶体结构
上页
下页
返回
结束
(1)旋转对称(Cn,对称素为线)
若晶体绕某一固定轴转 次(度)旋转对称轴。 下面我们计算与转动对应的变换矩阵。
上页 下页 返回 结束
2π 以后自身重合,则此轴称为n n
当OX绕Ox1转动角度时,图中
第一章 晶体结构 x3
X ( x1 , x2 , x3 )
2 3 X ( x1 , x , x )
2 2 2 2 2
2
~~ ~ ~~ ~ X AX AX XAAX XX X
上页
~ AA I
下页 返回 结束
1 I为单位矩阵,即: I 0 0
第一章 晶体结构 0 0 1 0 0 1
或者说A为正交矩阵,其矩阵行列式 A 1 。 2.简单对称操作(旋转对称、中心反映、镜象、旋转反演 对称)
( x1 , x2 , x3 ) 变为
x1 x1 x x 2 2 x x 3 3
(4)旋转--反演对称
( x1 , x2 , x3 )
1 0 0 A 0 1 0 0 0 1
A 1
第一章 晶体结构 B A
B1
A B
A1
AB AB 1 2cos θ ,
1 cos 0, ,1 2
AB 是 AB 的整数倍,
2π 2π 2π , , 4 6 1
π π , ,2π 2 3
相反若逆时针转 '角后能自身重合,则
B
A
AB AB 1 2cos θ,
称操作类型。这种对称性在宏观上表现为晶体外形的对称及物理
性质在不同方向上的对称性。所以又称宏观对称性。 如果考虑平移,还有两种情况,即螺旋轴和滑移反映面。
上页 下页 返回 结束
第一章 晶体结构 (5)n度螺旋轴:若绕轴旋转2/n角以后,再沿轴方向平
移l(T/n),晶体能自身重合,则称此轴为n度螺旋轴。其中T是
AB 是 AB 的整数倍,
上页 下页
B1
A1
A
返回
B
结束
第一章 晶体结构
1 0, ,1 cos 2
θ
π 2π , ,π 2 3
θ
2π 2π 2π , , 4 3 2
2π , n 1, , , , 2346 综合上述证明得: θ n
晶体中允许的旋转对称轴只能是1,2,3,4,6度轴。
1
2
3
4
6
上页 下页 返回 结束
第一章 晶体结构 正五边形沿竖直轴每旋转720恢
复原状,但它不能重复排列充满一个
平面而不出现空隙。因此晶体的旋转 对称轴中不存在五次轴,只有1,2, 3,4,6度旋转对称轴。 (2)中心反映(i,对称素为点) 取中心为原点,经过中心反映后,图形中任一点
( x1 , x2 , x3 ) 变为 ( x1 , x2 , x3 )
x R sin R sin cos R cos sin 3
x2 sin x3 cos
上页 下页 返回 结束
第一章 晶体结构
x1 1 0 0 x1 x 0 cos sin x 2 2 x 0 sin cos x 3 3
或C1,C2,C3,C4,C6 ,Ci,Cs,S4。
上页 下页 返回 结束
第一章 晶体结构 立方体对称性
(1)立方轴C4:
(2)体对角线C3:
(3)面对角线C2: 6个2度轴;
3个立方轴; 4个3度轴;
上页
下页
返回
结束
第一章 晶体结构
与4度轴正交的对称面
与2度轴正交的对称面
上页 下页 返回 结束
2 3 X ( x1 , x , x )
X ( x1 , x2 , x3 )
若OX在Ox2x3平面上投影的长度为R, O 则
x2
x1 x1
x2 cos x3 sin
x1
x R cos R cos cos R sin sin 2
0 1 0 A 0 cos sin 0 sin cos
晶体中允许有几度旋转对称轴呢? 设B1ABA1是晶体中某一晶
A 1
B
A
面上的一个晶列,AB为这一晶
列上相邻的两个格点。
B1
上页 下页
A B
返回
A1
结束
若晶体绕通过格点A并垂直于 纸面的u轴顺时针转角后能自身重 合,则由于晶体的周期性,通过格 点B也有一转轴u。
点对称操作:
(1)旋转对称操作:1,2,3,4,6 度旋转对称操作。 C1,C2,C3,C4,C6 (用熊夫利符号表示) (2)旋转反演对称操作: 1,2,3,4,6度旋转反演对称操作。
S1,S2,S3,S4,S6(用熊夫利符号表示)
(3)中心反映:i。
(4)镜象反映:m。
独立的对称操作有8种,即1,2,3,4,6,i,m, 4 。
x1 x1 x x 2 2 x x 3 3
1 0 0 A 0 1 0 0 0 1
上页 下页
A 1
返回 结束
第一章 晶体结构
(3)镜象(m,对称素为面)
如以x3=0面作为对称面,镜象是将图形的任何一点
1 2 1
2m
1
3
3 3i
5 1
4 2
2
上页 下页 返回 结束
6
第一章 晶体结构
6=3+m 3 3 5 1 5 1 6 2 ' 6 4 4 2
3
4
1
3
4
正四面体既无四
1
2
2
D
度轴也无对称心
4
C
B
A B
H E
D C G F
A
G
H
上页
F E
下页 返回 结束
第一章 晶体结构
2π 以后,再经过中心反演,晶体自 n 身重合,则此轴称为n次(度)旋转--反演对称轴。
若晶体绕某一固定轴转
上页
下页
返回
结束
第一章 晶体结构
旋转--反演对称轴只能有1,2,3,4,6度轴。
旋转--反演对称轴用 1, 2, 3, 4, 6 表示。 旋转--反演对称轴并不都是独立的基本对称素。如:
1i
轴方向的周期, l是小于n的整数。 n只能取1、2、3、4、6。 (6)滑移反映面:若经过某面
进行镜象操作后,再沿平行于该面
的某个方向平移T/n后,晶体能自
身重合,则称此面为滑移反映面。
T是平行方向的周期, n可取2或4。ຫໍສະໝຸດ 上页下页返回
结束
第一章 晶体结构
点对称操作加上平移操作构成空间群。全部晶体构有230种
第一章 晶体结构
a11 A a21 a 31
X ( x1 , x , x ) 2 3
X ( x1 , x2 , x3 )
O
x2
操作前后,两点间的距离保持不变, O点和X点间距与O点和 X 点间距相等。
x1
x1 x 2 x 3 x1 x x 2 3
2 3 X ( x1 , x , x ) 可以用线性变换来表示。
上页
下页
返回
结束
X AX
x1 X x2 x 3
a12 a22 a32 a13 a23 33
x1 X x 2 x x 3 3
第一章 晶体结构 1.3.2 点群 所有点对称操作都可由这8种操作或它们的组合来完成。
一个晶体的全部对称操作构成一个群,每个操作都是群的一个
元素。对称性不同的晶体属于不同的群。由旋转、中心反演、 镜象和旋转--反演点对称操作构成的群,称作点群。 理论证明,所有晶体只有32种点群,即只有32种不同的点对
第一章 晶体结构
§1.3
本节主要内容:
对称操作和点群
1.3.1 对称性与对称操作 1.3.2 点群
上页
下页
返回
结束
第一章 晶体结构
1.3.1 对称性与对称操作
对称性:经过某种动作后,晶体能够自身重合的特性。
对称操作:使晶体自身重合的动作。
对称素: 对称操作所依赖的几何要素。
1.对称操作与线性变换
经过某一对称操作,把晶体中任一点 X ( x1 , x2 , x3 ) 变为
晶格。
上页
下页
返回
结束
第一章 晶体结构
上页
下页
返回
结束
第一章 晶体结构
上页
下页
返回
结束
第一章 晶体结构
上页
下页
返回
结束
(1)旋转对称(Cn,对称素为线)
若晶体绕某一固定轴转 次(度)旋转对称轴。 下面我们计算与转动对应的变换矩阵。
上页 下页 返回 结束
2π 以后自身重合,则此轴称为n n
当OX绕Ox1转动角度时,图中
第一章 晶体结构 x3
X ( x1 , x2 , x3 )
2 3 X ( x1 , x , x )
2 2 2 2 2
2
~~ ~ ~~ ~ X AX AX XAAX XX X
上页
~ AA I
下页 返回 结束
1 I为单位矩阵,即: I 0 0
第一章 晶体结构 0 0 1 0 0 1
或者说A为正交矩阵,其矩阵行列式 A 1 。 2.简单对称操作(旋转对称、中心反映、镜象、旋转反演 对称)
( x1 , x2 , x3 ) 变为
x1 x1 x x 2 2 x x 3 3
(4)旋转--反演对称
( x1 , x2 , x3 )
1 0 0 A 0 1 0 0 0 1
A 1
第一章 晶体结构 B A
B1
A B
A1
AB AB 1 2cos θ ,
1 cos 0, ,1 2
AB 是 AB 的整数倍,
2π 2π 2π , , 4 6 1
π π , ,2π 2 3
相反若逆时针转 '角后能自身重合,则
B
A
AB AB 1 2cos θ,
称操作类型。这种对称性在宏观上表现为晶体外形的对称及物理
性质在不同方向上的对称性。所以又称宏观对称性。 如果考虑平移,还有两种情况,即螺旋轴和滑移反映面。
上页 下页 返回 结束
第一章 晶体结构 (5)n度螺旋轴:若绕轴旋转2/n角以后,再沿轴方向平
移l(T/n),晶体能自身重合,则称此轴为n度螺旋轴。其中T是
AB 是 AB 的整数倍,
上页 下页
B1
A1
A
返回
B
结束
第一章 晶体结构
1 0, ,1 cos 2
θ
π 2π , ,π 2 3
θ
2π 2π 2π , , 4 3 2
2π , n 1, , , , 2346 综合上述证明得: θ n
晶体中允许的旋转对称轴只能是1,2,3,4,6度轴。
1
2
3
4
6
上页 下页 返回 结束
第一章 晶体结构 正五边形沿竖直轴每旋转720恢
复原状,但它不能重复排列充满一个
平面而不出现空隙。因此晶体的旋转 对称轴中不存在五次轴,只有1,2, 3,4,6度旋转对称轴。 (2)中心反映(i,对称素为点) 取中心为原点,经过中心反映后,图形中任一点
( x1 , x2 , x3 ) 变为 ( x1 , x2 , x3 )
x R sin R sin cos R cos sin 3
x2 sin x3 cos
上页 下页 返回 结束
第一章 晶体结构
x1 1 0 0 x1 x 0 cos sin x 2 2 x 0 sin cos x 3 3
或C1,C2,C3,C4,C6 ,Ci,Cs,S4。
上页 下页 返回 结束
第一章 晶体结构 立方体对称性
(1)立方轴C4:
(2)体对角线C3:
(3)面对角线C2: 6个2度轴;
3个立方轴; 4个3度轴;
上页
下页
返回
结束
第一章 晶体结构
与4度轴正交的对称面
与2度轴正交的对称面
上页 下页 返回 结束
2 3 X ( x1 , x , x )
X ( x1 , x2 , x3 )
若OX在Ox2x3平面上投影的长度为R, O 则
x2
x1 x1
x2 cos x3 sin
x1
x R cos R cos cos R sin sin 2
0 1 0 A 0 cos sin 0 sin cos
晶体中允许有几度旋转对称轴呢? 设B1ABA1是晶体中某一晶
A 1
B
A
面上的一个晶列,AB为这一晶
列上相邻的两个格点。
B1
上页 下页
A B
返回
A1
结束
若晶体绕通过格点A并垂直于 纸面的u轴顺时针转角后能自身重 合,则由于晶体的周期性,通过格 点B也有一转轴u。
点对称操作:
(1)旋转对称操作:1,2,3,4,6 度旋转对称操作。 C1,C2,C3,C4,C6 (用熊夫利符号表示) (2)旋转反演对称操作: 1,2,3,4,6度旋转反演对称操作。
S1,S2,S3,S4,S6(用熊夫利符号表示)
(3)中心反映:i。
(4)镜象反映:m。
独立的对称操作有8种,即1,2,3,4,6,i,m, 4 。
x1 x1 x x 2 2 x x 3 3
1 0 0 A 0 1 0 0 0 1
上页 下页
A 1
返回 结束
第一章 晶体结构
(3)镜象(m,对称素为面)
如以x3=0面作为对称面,镜象是将图形的任何一点
1 2 1
2m
1
3
3 3i
5 1
4 2
2
上页 下页 返回 结束
6
第一章 晶体结构
6=3+m 3 3 5 1 5 1 6 2 ' 6 4 4 2
3
4
1
3
4
正四面体既无四
1
2
2
D
度轴也无对称心
4
C
B
A B
H E
D C G F
A
G
H
上页
F E
下页 返回 结束
第一章 晶体结构
2π 以后,再经过中心反演,晶体自 n 身重合,则此轴称为n次(度)旋转--反演对称轴。
若晶体绕某一固定轴转
上页
下页
返回
结束
第一章 晶体结构
旋转--反演对称轴只能有1,2,3,4,6度轴。
旋转--反演对称轴用 1, 2, 3, 4, 6 表示。 旋转--反演对称轴并不都是独立的基本对称素。如:
1i
轴方向的周期, l是小于n的整数。 n只能取1、2、3、4、6。 (6)滑移反映面:若经过某面
进行镜象操作后,再沿平行于该面
的某个方向平移T/n后,晶体能自
身重合,则称此面为滑移反映面。
T是平行方向的周期, n可取2或4。ຫໍສະໝຸດ 上页下页返回
结束
第一章 晶体结构
点对称操作加上平移操作构成空间群。全部晶体构有230种
第一章 晶体结构
a11 A a21 a 31
X ( x1 , x , x ) 2 3
X ( x1 , x2 , x3 )
O
x2
操作前后,两点间的距离保持不变, O点和X点间距与O点和 X 点间距相等。
x1
x1 x 2 x 3 x1 x x 2 3
2 3 X ( x1 , x , x ) 可以用线性变换来表示。
上页
下页
返回
结束
X AX
x1 X x2 x 3
a12 a22 a32 a13 a23 33
x1 X x 2 x x 3 3
第一章 晶体结构 1.3.2 点群 所有点对称操作都可由这8种操作或它们的组合来完成。
一个晶体的全部对称操作构成一个群,每个操作都是群的一个
元素。对称性不同的晶体属于不同的群。由旋转、中心反演、 镜象和旋转--反演点对称操作构成的群,称作点群。 理论证明,所有晶体只有32种点群,即只有32种不同的点对
第一章 晶体结构
§1.3
本节主要内容:
对称操作和点群
1.3.1 对称性与对称操作 1.3.2 点群
上页
下页
返回
结束
第一章 晶体结构
1.3.1 对称性与对称操作
对称性:经过某种动作后,晶体能够自身重合的特性。
对称操作:使晶体自身重合的动作。
对称素: 对称操作所依赖的几何要素。
1.对称操作与线性变换
经过某一对称操作,把晶体中任一点 X ( x1 , x2 , x3 ) 变为
