第十四章材料力学超静定结构
合集下载
《材料力学基础》14超静定结构

x
1
A
D
B
x
C
x
x
1
A
BD: M x
M (x) x
DC: M x
M (x) x
CA: M a
M (x) a
11
1 EI
[0a
2
x
x
dx
aa
2
x
x
dx
0aa a dx]
4 a3 3
17
11
4 3
a3
1P
11ma2 8
qa4 6
代入
11 X 1 1P 0
m
D
B
C a 2 a 2 X1
3a 2 2 EI
q
a
A
X1
B
X2
X3
(2)求 X1,X2 ,X3
代入正则方程:
11 X 1 12 X 2 13 X 3 1P 0 21 X 1 22 X 2 23 X 3 2P 0
31 X 1 32 X 2 33 X 3 3P 0
50
化简得:
8a X1 3a X 2 9 X 3 qa2 12a X1 8a X 2 12 X 3 3qa2 9a X1 3a X 2 12 X 3 qa2
q
A
解得
X
1
1 32a
(33ma
4qa2)
16.56KN
18
X
1
1 32a
(33ma
4qa2)
16.56KN
RA 16.56KN () H A 50KN () mA 92.2KN .m ( )
m
D
B
C a 2 a 2 X1
q
A
HA mA
材料力学第十四章 超静定2013

1
a a
1
M1
M2
1
1
1
M3
a
将求出的系数和常数代入正则方程,有:
8aX 1 3aX 2 9 X 3 qa 2 12aX 1 8aX 2 12 X 3 3qa
2
9aX 1 3aX 2 12 X 3 qa
qa X1 , 16
7 qa X2 , 16
BC段
B
45°
M M P X 1M
Pa Pa sin( / 4) sin 2 2 ( / 4 / 2)
A
45°
作业 • 14.4 (a),(b) • 14.8(选作)
§14. 3 对称及反对称性质的利用
1
对称结构的对称变形和反对称变形 对称结构
M i ( x) M j ( x) EI
l
dx
ji
解静不定问题的一般步骤
1) 判定静不定次数; 2) 选择静定基,得到相当系统; 3) 分解载荷:分别将外载荷、各单位载荷作 用在静定基上; 4) 画出各载荷下的内力(弯矩)图或写出内力 (弯矩)方程; 5) 用图乘法或莫尔积分等求出△iP 和 ij ; 6) 求解正则方程,解出未知力。
N0
记未知约束力偶M0为 X1, N0 用 P/2 代替。
求解静不定问题 正则方程
第十四章
超 静 定 结 构
第十四章
1 2 静不定结构
外力静不定
静不定结构
混合静不定
§14. 1 静不定结构概述
内力静不定
静不定次数的确定
静不定次数 =未知力个数 - 独立平衡方程数
(1) 外力静不定次数的确定
a a
1
M1
M2
1
1
1
M3
a
将求出的系数和常数代入正则方程,有:
8aX 1 3aX 2 9 X 3 qa 2 12aX 1 8aX 2 12 X 3 3qa
2
9aX 1 3aX 2 12 X 3 qa
qa X1 , 16
7 qa X2 , 16
BC段
B
45°
M M P X 1M
Pa Pa sin( / 4) sin 2 2 ( / 4 / 2)
A
45°
作业 • 14.4 (a),(b) • 14.8(选作)
§14. 3 对称及反对称性质的利用
1
对称结构的对称变形和反对称变形 对称结构
M i ( x) M j ( x) EI
l
dx
ji
解静不定问题的一般步骤
1) 判定静不定次数; 2) 选择静定基,得到相当系统; 3) 分解载荷:分别将外载荷、各单位载荷作 用在静定基上; 4) 画出各载荷下的内力(弯矩)图或写出内力 (弯矩)方程; 5) 用图乘法或莫尔积分等求出△iP 和 ij ; 6) 求解正则方程,解出未知力。
N0
记未知约束力偶M0为 X1, N0 用 P/2 代替。
求解静不定问题 正则方程
第十四章
超 静 定 结 构
第十四章
1 2 静不定结构
外力静不定
静不定结构
混合静不定
§14. 1 静不定结构概述
内力静不定
静不定次数的确定
静不定次数 =未知力个数 - 独立平衡方程数
(1) 外力静不定次数的确定
材料力学第十四章__超静定结构

§14.1 超静定结构概述
整理课件
本节应用能量法求解静不定系统。 应用能量法求解静不定系统,特别是对桁 架、刚架等构成的静不定系统,将更加有效 。 求解静不定问题的关键是建立补充方程。 静不定系统,按其多余约束的情况,可以 分为外力静不定系统和内力静不定系统。
整理课件
支座反力静不定 类型反力静定内力静不定
整理课件
解静不定梁的一般步骤
(4)在求出多余约束反力的基础上,根据静 力平衡条件,解出静不定梁的其它所有支 座反力。 (5)按通常的方法(已知外力求内力、应力 、变形的方法)进行所需的强度和刚度计 算。
整理课件
例:作图示梁的弯矩图 。
整理课件
解:变形协调条件为
A 0
即
MAl2Pl2 10 2 382
A
M10 1
D
P
1
2
(d)
(e)
1 P0 2M E 1 0 M P d I s2 P E 20 2 a (I 1 c
o) s (1 )d P2(a 1 ) 2 E2 I
1102M E102IdsE aI02(1)2d2EaI
上面两式代入 正则方程:
11
X 整理课1件
Pa( 2
)
求出X1后,可得图(C)
解得
MA
3Pl 16
整理课件
3Pl MA 16
11 P
5P
16
整理课件
另解:变形协调条件为
vB 0
即
RBl2
2l Pl2
5l
0
2 386
解得
5P
RB 16
整理课件
5P
5Pl/32
16
3Pl 16
材料力学 第14章 超静定结构

39
目录
例题 14-4
M1 图
M F图
1 a 2 2a a3 ⋅ = δ11 = EI 2 3 3EI ∆1F 1 a 2 qa 2 qa 4 ⋅ =− 2 8 = − 16EI EI
40
目录
例题 14-4
由力法正则方程δ11 X1 + ∆1F = 0得: 3qa X1 = 16 3qa ∴X C = ,YC = 0,M C = 0 16 qa 3qa X A (→) = X B (←) = ,YA = YB = (↑) 16 2 qa 2 M A (顺时针) = M B (逆时针) = 16
25
目录
对 称 结 构
对称结构的对称变形
26
目录
对 称 结 构
对称结构的对称变形
27
目录
对 称 结 构 对称结构的对称变形
28
目录
对 称 结 构
对称结构的对称变形
29
目录
对称结构,反对称载荷 对称结构,
判断载荷反对称的方法: 判断载荷反对称的方法:
将对称面(轴)一侧的载荷反向,若变为 将对称面( 一侧的载荷反向, 对称的,则原来的载荷便是反对称的。 对称的,则原来的载荷便是反对称的。
24
目录
对 称 结 构
对称结构的对称变形- 对称结构的对称变形-对称结构在对称载 荷作用下: 荷作用下:
约束力、内力分量以及变形和位移都是对称的; 约束力、内力分量以及变形和位移都是对称的; 反对称的内力分量必为零; 反对称的内力分量必为零; 某些对称分量也可等于零或变为已知。 某些对称分量也可等于零或变为已知
34
目录
对称结构,反对称载荷 对称结构,
第十四章 超静定结构

得: X 2 0
二、反对称载荷内力特点:
•对称面上对称内力为零。
11 X 1 12 X 2 13 X 3 1F 0 21 X 1 22 X 2 23 X 3 2 F 0 31 X 1 32 X 2 33 X 3 3 F 0
MA
5)求作弯矩图:
MC
题14.2 计算图所示桁架各杆的内力。设各杆的材料相同,横截面 积相同。 解: 为一次超静定结构。 1)确定相当系统: 2)建立正则方程:
11 X1 1F 0
3)确定系数和常数:
FNi F Nili 2(1 2) Fa 1F EAi EA F Ni F Nili 4(1 2)a 11 EAi EA
12
l
M 1 M 2 dx EI M M 1dx EI
1F
l
12 21; 13 31; 32 23
4、求未知力: 二、n次超静定结构的正则方程
1n X n 1F 0 2n X n 2 F 0 n1 X 1 n 2 X 2 nn X n nF 0 ij ji (i, j 1, 2,3 n)
二、对称载荷内力特点:
•对称面上反对称内力为零。
11 X 1 12 X 2 13 X 3 1F 0 21 X 1 22 X 2 23 X 3 2 F 0 31 X 1 32 X 2 33 X 3 3 F 0
三、基本静定系
•解除超静定结构多余约束 后得到的静定结构。 四、相当系统
•载荷和多余约束力作用下的 基本静定系称为相当系统。
§14—2 用力法解超静定结构 一、方法和步骤 1、确定相当系统: 2、建立正则方程: 由:
二、反对称载荷内力特点:
•对称面上对称内力为零。
11 X 1 12 X 2 13 X 3 1F 0 21 X 1 22 X 2 23 X 3 2 F 0 31 X 1 32 X 2 33 X 3 3 F 0
MA
5)求作弯矩图:
MC
题14.2 计算图所示桁架各杆的内力。设各杆的材料相同,横截面 积相同。 解: 为一次超静定结构。 1)确定相当系统: 2)建立正则方程:
11 X1 1F 0
3)确定系数和常数:
FNi F Nili 2(1 2) Fa 1F EAi EA F Ni F Nili 4(1 2)a 11 EAi EA
12
l
M 1 M 2 dx EI M M 1dx EI
1F
l
12 21; 13 31; 32 23
4、求未知力: 二、n次超静定结构的正则方程
1n X n 1F 0 2n X n 2 F 0 n1 X 1 n 2 X 2 nn X n nF 0 ij ji (i, j 1, 2,3 n)
二、对称载荷内力特点:
•对称面上反对称内力为零。
11 X 1 12 X 2 13 X 3 1F 0 21 X 1 22 X 2 23 X 3 2 F 0 31 X 1 32 X 2 33 X 3 3 F 0
三、基本静定系
•解除超静定结构多余约束 后得到的静定结构。 四、相当系统
•载荷和多余约束力作用下的 基本静定系称为相当系统。
§14—2 用力法解超静定结构 一、方法和步骤 1、确定相当系统: 2、建立正则方程: 由:
材料力学第十四章-超静定结构

材料力学第十四章-超静 定结构
欢迎来到材料力学第十四章的学习!本章将介绍超静定结构,我们将一起探 索它的特点、设计方法、力学分析以及应用领域。让我们开始学习吧!
超静定结构的定义
1 什么是超静定结构?
超静定结构是指具有多余约束的结构,其构件由多于所需的约束连接。
超静定结构的特点
1 多余约束的好处
超静定结构具有更高的稳定性和刚度,能够承受更大的荷载。
2 调整性能
通过改变约束条件,可以调整超静定结构的性能。
超静定结构的设计方法
1
力学方法
利用材料力学的知识和结构理论进行设计和分析。
2
优化设计
采用优化算法寻找最佳的结构设计。
3
经验和直觉
通过经验和直觉进行设计和改进。
超静定结构的力学分析
受力分析
通过受力分析了解超静定结构中力的传递和分布。
应力分析
通过应力分析研究超静定结构中的应力分布和变形。
超静定结构的应用领域
桥梁工程
超静定结构可以提高桥梁的稳定性和承载能力。
航空航天
超静定结构可以减轻飞行器的重量,提高性能。
建筑设计
超静定结构可以实现更大跨度和更复杂的建筑形 态。
机械设计
超静定结构可以提高机械设备的稳定性和准确性。
超静定结构的挑战与解决方案
1
挑战
超静定结构的设计和分析复杂,需要考虑多个因素。
2
解决方案
借助计算机辅助设计和模拟技术,提高设计和分析的效率。
3
创新思维
采用创新的方法和理念,寻找超静定结构的新应用。
总结与展望
通过本章的学习,我们了解了超静定结构的定义、特点、设计方法、力学分 析、应用领域以及面临的挑战。希望这些知识能够帮助您深入了解这一领域, 并为未来的设计和研究提供启示。
欢迎来到材料力学第十四章的学习!本章将介绍超静定结构,我们将一起探 索它的特点、设计方法、力学分析以及应用领域。让我们开始学习吧!
超静定结构的定义
1 什么是超静定结构?
超静定结构是指具有多余约束的结构,其构件由多于所需的约束连接。
超静定结构的特点
1 多余约束的好处
超静定结构具有更高的稳定性和刚度,能够承受更大的荷载。
2 调整性能
通过改变约束条件,可以调整超静定结构的性能。
超静定结构的设计方法
1
力学方法
利用材料力学的知识和结构理论进行设计和分析。
2
优化设计
采用优化算法寻找最佳的结构设计。
3
经验和直觉
通过经验和直觉进行设计和改进。
超静定结构的力学分析
受力分析
通过受力分析了解超静定结构中力的传递和分布。
应力分析
通过应力分析研究超静定结构中的应力分布和变形。
超静定结构的应用领域
桥梁工程
超静定结构可以提高桥梁的稳定性和承载能力。
航空航天
超静定结构可以减轻飞行器的重量,提高性能。
建筑设计
超静定结构可以实现更大跨度和更复杂的建筑形 态。
机械设计
超静定结构可以提高机械设备的稳定性和准确性。
超静定结构的挑战与解决方案
1
挑战
超静定结构的设计和分析复杂,需要考虑多个因素。
2
解决方案
借助计算机辅助设计和模拟技术,提高设计和分析的效率。
3
创新思维
采用创新的方法和理念,寻找超静定结构的新应用。
总结与展望
通过本章的学习,我们了解了超静定结构的定义、特点、设计方法、力学分 析、应用领域以及面临的挑战。希望这些知识能够帮助您深入了解这一领域, 并为未来的设计和研究提供启示。
第14章 超静定结构资料.

代(2)入(1)式可得:Δ1 Δ1P δ11X1 ——(3)
P
3. 建立变形协调条件, 并确定 X1
因 B 点原为一可动铰支座, 故
A
Δ1 0
即: Δ1P δ11X1 0 —(4)
B
a
4
4
O
从而:
X1
Δ1P δ11
式(4)所表示的标准式的方程式称为力法的正则方程,而
上述的解题过程中以“力 X 1 ”为基本未知量,由变形协调条件
一.力法及正则方程的概念
举例说明:曲杆如图 (a) 所示, 试求支座 B 的约束反力。
P
B
a
A
4
4
O
(a)
P
B
X1
A
4
O
(b)
解: 1. 建立基本静定系如图 (b) 所示。 2. 将静定系分解成图 (c) 和图 (d) 两种情况的叠加。
P
A
4
(c)
1P B
A O
X1
B
X1
4
O
(d)
A
4
(e)
11 若 B 点的竖向位移用 Δ1表示, 则:
并求出各个载荷单独作用下多余约束处的 变形量。 (3)根据多余约束处的变形条件,建立变形几何关系,
求出未知约束反力。
2.举例说明:
例14-1:试求图示静不定梁的约束反力。
q B
L
解:
(1)建立基本静定系统如图<a>所示 (2)将图<a>分解成图<b>和图<c>两种情况的叠加
图中:
q B
RB (a)
q
(c)
( b)
4. 平面杆系: 若杆系中各杆的轴线在同一平面内(形心主惯性平面),且
P
3. 建立变形协调条件, 并确定 X1
因 B 点原为一可动铰支座, 故
A
Δ1 0
即: Δ1P δ11X1 0 —(4)
B
a
4
4
O
从而:
X1
Δ1P δ11
式(4)所表示的标准式的方程式称为力法的正则方程,而
上述的解题过程中以“力 X 1 ”为基本未知量,由变形协调条件
一.力法及正则方程的概念
举例说明:曲杆如图 (a) 所示, 试求支座 B 的约束反力。
P
B
a
A
4
4
O
(a)
P
B
X1
A
4
O
(b)
解: 1. 建立基本静定系如图 (b) 所示。 2. 将静定系分解成图 (c) 和图 (d) 两种情况的叠加。
P
A
4
(c)
1P B
A O
X1
B
X1
4
O
(d)
A
4
(e)
11 若 B 点的竖向位移用 Δ1表示, 则:
并求出各个载荷单独作用下多余约束处的 变形量。 (3)根据多余约束处的变形条件,建立变形几何关系,
求出未知约束反力。
2.举例说明:
例14-1:试求图示静不定梁的约束反力。
q B
L
解:
(1)建立基本静定系统如图<a>所示 (2)将图<a>分解成图<b>和图<c>两种情况的叠加
图中:
q B
RB (a)
q
(c)
( b)
4. 平面杆系: 若杆系中各杆的轴线在同一平面内(形心主惯性平面),且
《材料力学》精品课程(全册)第十四章 超静定结构

,YB
9qa 16
X
A
qa 16
,
YA
7qa 16
目录
上面我们讲的是只有一个多余约束的情况! 那么当多余约束不止一个时,力法方程是什么样的呢?
P2
P2
P1
P1
P3
P3
X3
X1
X2
目录
变形协调条件 :
1 2 3 0
i 表示 X作i 用点沿着 方向X的i 位移
由叠加原理:
1 1X1 1X 2 1X3 1P 0 1 11 X 1 12 X 2 13 X 3 1P 0
C
B 11
对于线弹性结构,位移与力成正比,X1是单位力“1”的X1倍,故1X1
的X1倍,即有
1X1 11 X1
也是11
所以(*)式可变为: 11 X 1 1F 0
若:
11
l3 3EI
于是可求得
1F
Fa 2 6EI
(3l a)
X1
Fa 2 2l 3
(3l
a)
目录
例14.1:试求图示平面刚架的支座反力。已知各杆 EI=常数。
可得:
12 21 23 32 0
于是正则方程可化为
11 X 1 13 X 3 1F
31 X 1 33 X 3 3F
22 X 2 0
目录
对称结构在反对称载荷作用下的情况:
F P
F P
F
X3
X2
F
X1
X3 X2
P
P
同样用图乘法可证明
当对称结构上受反对称载荷作用时,
在对称面上对称内力等于零。
目录
例如:
该体系中多出一个外部约束,为一次超静定梁
14第十四章 超静定结构

例8:已知刚架 的抗弯刚度为E I。 试求支座 B 处的反
力。 解: M ( x1 ) x1
M ( x2 ) a
qx M ( x1 ) 6a
3 0 1
q0 a 2 M ( x2 ) 6
3 a MM 1 a 2 4 a 2 11 dx 0 x1 d x1 0 a d x2 3EI EI EI l
另解:
qa2 X1 q 2a cos45 2 qa , M A 2
例12:已知桁架各杆的拉压刚度为 EA, 求各杆的轴力。
解:
11
i 1 3
3
FNi FNi li EA EA
l 1 cos3 sin 3 EA cos Fl sin 2 EA cos
EAi
7 a 4 2 2 EA
Δ1F
i
FN i FN , i li
Fa 3 2 2 EA
由 11 X1 Δ1F 0 得
解:
例3:图示刚架 EI 为常 量,画出刚架的弯矩图。
解:
7a 3 Fa3 11 , Δ1F 24EI 4 EI
由力法正则方程 11 X1 Δ1F 0 得X 1
6F 7
M图
例4:试求图示平面刚架的支座反力。 已知各杆 EI =常数。
解:
3 1 a 2 2a 4 a 2 11 a a EI 2 3 3EI
一、外力超静定系统 由于外部的多余约束而构成的超静定系统,一般称为
外力超静定系统。 求解外力超静定系统的基本方法,是解除多余约束,
代之以多余约束反力,根据多余约束处的变形协调条件建 立补充方程进行求解。 解除多余约束后得到的静定结构,称为原超静定系统 的相当系统。
材料力学刘鸿文第十四章超静定结构

5、求B支反力
q
M=2qa2 a
2a
a 2a B
6、作刚架的弯矩图
2qa2 B
2a
2a q
8、作刚架的弯矩图
q
2a
a a
10、求C截面的挠度
P a
a
2a a C P a
11、C支座抬高δ=qa4/3EI,作刚架的弯矩图
δ a q a C
12、求C截面的转角
M=2qa2 C a 2a
13、直角拐在支座A处有一沉陷δ,求在载荷的作用
求解得到: 故:
FN 0.91F
FN 2 3 D 3 EI
0.91 50 103 8 5.05m m 6 3 24 10
变形比较法计算超静定的步骤
(1)、判定超静定次数; (2)、确定多余约束; (3)、去掉多余约束代之以反力,得到相当系统; (4)、变形协调方程; (5)、利用能量法求多余约束处的位移或转角; 此时多余约束反力作常量处理; 一般情况下,多余约束反力为力的用能量法求线位移;
2、作刚架的弯矩图
P=qa q
a
a 2a
2a
3、作刚架的弯矩图
P a a 2a
2a
4、作刚架的弯矩图
q=4KN/m B
4m
4m C
四、静不定综合
1、两根长为L=2米的竖直简支梁,在跨中用一根拉紧的金属丝 相连。左边梁的抗弯刚度为EI1=50KNm2,右边梁的抗弯刚度 为EI2=150KNm2。金属丝的横截面面积为65毫米2,E=70GPa, 求在两梁的跨中施加两个2KN的力后,金属丝内的应力。
第一类: 在结构外部存在多余约束,即支反力是静不定的;
外力超静定系统。 第二类: 仅在结构内部存在多余约束,即内力是静不定的; 内力超静定系统。 第三类:结构外部和内部均存在多余约束,即支反 力和内力是 超静定的。 混合超静定系统;
【2019年整理】材料力学刘鸿文第十四章超静定结构

13、直角拐在支座A处有一沉陷δ,求在载荷的作用
下,A处的约束反力。设GIP=4EI/5,δ=qL4/6EI
q A δ
L
C
L
B
14、直角拐的抗弯刚度为EI,拉杆CD的抗拉压刚
度相等为EA,各段的长度均为L,且I=AL2,求 CD杆的内力并作刚架的弯矩图。
D
L
C
L P
三、二次超静定问题(刚架抗弯刚度EI为常量) 1、求C截面的铅垂位移
面积为A=6.5㎜2,二者采用同种材料制成。弹性 模量E=200GPa,剪变模量G=80 GPa。CD杆 的线胀系数α=12.5×10-6,温度下降50º 。求出直 角拐的危险点的应力状态。
A 0.6m 0.3m C D B
4、图示中梁为工字型截面,梁的跨度为L=4米, 力P=40KN作用在梁的中央。对本身形心轴的惯性 矩为IZ=18.5×106mm4,求该梁的最大剪力和弯矩,
3 超静定次数 未知力的数目与独立平衡方程数目之差。
P P
4 多余约束
静不定结构中,超过维持静力平衡所必须的约束;
5 多余约束反力
与多余约束相对应的反力;
6 超静定系统的特点:
P P ①、提高构件的强度和刚度。 ②、各部分的内力分配与其各部分的刚度比相关。 ③、可以产生装配应力和温度应力。
7 超静定问题分类
16 两端固定的阶梯装杆如图所示。已知AC段和BD 段的横截面面积为A,CD段的横截面面积为2A;该 杆材料的弹性模量为E=210GPa,线膨胀系 数 121061/ C 。试求当温度升高30℃ 后,该杆各部分产生的应力。
17 两根长度各为L1和L2的梁交叉放置如图所示, 在两梁交叉点处作用有集中荷载P。两梁横截面 的惯性矩分别为I1及I2,梁的材料相同。试问在 两梁间荷载是怎样分配的。
材料力学刘鸿文第六版最新课件第十四章 超静定结构

EI 对
EI 对
EI 对
E1I1
称 E1I1 E1I1 轴
称 E1I1 E1I1 轴
称 E1I1 轴
15
正确利用对称、反对称性质,则可推知某些未知量,可大
大简化计算过程:如对称变形对称截面上,反对称内力为零;
反对称变形对称截面上,对称内力为零。
例如: 对 称
X2 X3 X3
X1 X1 X2 P
轴
X3 X3
24
[例4 ] 试用三弯矩方程作等刚度连续梁AC的弯矩图。见图(a)。
解:AC梁总共有二跨,跨
q
长l1=l2=l 。中间支座编号应 (a)A
取为1,即n=1。由于已知0,
l
2两支座上无弯矩,故
P=ql
B
C
l/2 l/2
M n1M00; M nM1M B; M n1M 20
q (b)A
MB P=ql
26
将图(d)中的单位弯矩图乘以
5 ql 2 32
便得到MB在简支梁上 产生的M图,
再与载荷引起的M 图(c)相加,
就得到梁AC的弯矩 (e) 图,见图(e)。
1 ql 2 8
1 ql 2 4
5 ql 2 32
11ql 2 64
+
+
–
5 ql 2
32
27
X1l3 5Pl 3 0 3EI 48EI
X1
5 16
P
(f)
⑥求其它约束反力
11P 16
A
3Pl 16
由平衡方程可求得A端反
力,其大小和方向见图(f)。
⑦进一步可作其他计算: 如作弯矩图可如图(g)所示
(g) –
材料力学第14章

a
M/2
X
2
EI 1 F
X1
2 1 a M a M 5a M 8 2 2 2 16
2
1F
11
15 M 14a
M/28
a F a 1 M1
11
已知:E=3G,求:F点挠度。
F/2 X1
a a 1 Fa/2 MF
1F
a
a
Fa/2
T1
2 2
Fa/2 TF
ql/2
X1
MF
2 3 EI 11 1 l ( 2 l l ) 5 l 11 X 1 12 X 2 1 F 0 2 3 6 EI 22 l 1 l 3 l 21 X 1 22 X 2 2 F 0 2 2 2 2 2 EI 12 1 l 1 l l 2 2 X1=ql/12 1 1 ql 3 l 1 ql 3 l ) 1 ql 4 EI 1 F ( 3 16 16 24 X2=ql2/36 3 3 3 EI 2 F ( 1 ql 1 1 ql ) 1 ql 16 3 16 24
1 F Fa 2 X1 ( 3l a ) 3 11 2l
F
a
a
Fa
X1
M1
a
MF
a
EI 11 1 a2 2 a 1 a3 2 3 3
Fa/2
2 3 EI1 F 1 a Fa 1 Fa 2 2
1 11 X 1 1 F 0
1 F 3 X1 F 11 2
3 3
ql
X1
1F
M1
11
2 1 ql 24
ql2/24
材料力学-第十四章 超静定结构
4 链条的一环如图所示。试求环内最大弯矩。
-3-
第十四章 超静定结构
班级
学号
姓名
5 为改善桥式起重机大梁的刚度和强度,在大梁的下方增加预应力拉杆 CD。梁的计算简 图如图 b 所示。由于 CC’′和 DD′两杆甚短,且刚度较大,其变形可以不计。试求拉杆 CD 因吊重P而增加的内力。
-4-
第十四章 超静定结构
班级
学号
姓名
6 折杆截面为圆形,直径。d=2cm,a=0.2m,l=1m,f=650N,E=200GPa,G=80GPa。试 求 F 力作用点的垂直位移。
7 求解图示超静定刚架。
-5-
第十四章 超静定结构
班级
学号
姓名
8 车床夹具如图所示,EI 已知。试求夹具 A 截面上的弯矩。
-6-
第十四章 超静定结构
班级
学号
姓名
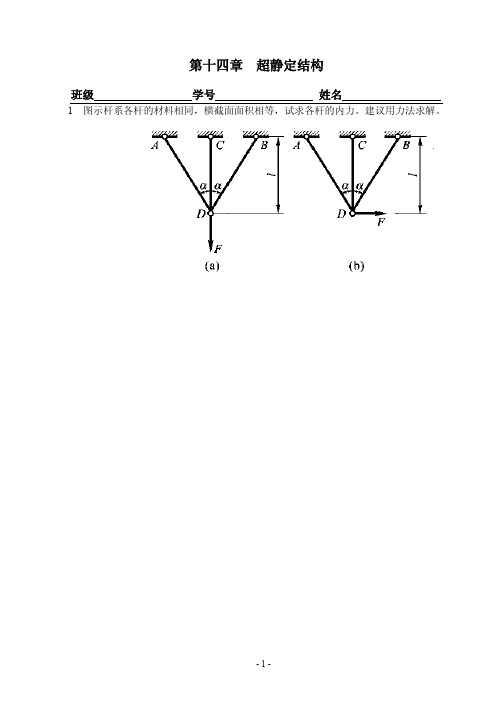
1 图示杆系各杆的材料相同,横截面面积相等,试求各杆的内力。建议用力法求解。
-1-
第十四章 超静定结构
班级
学号
2 作图示刚架的弯矩图。设刚架各杆的 EI 皆相等。
姓名
-2-
第十四章 超静定结构
班级
学号
姓名
3 刚架的A,B两点由拉杆AB相联接,拉杆的抗拉刚度为EA。试作刚架的弯矩图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
RMB B
第32次作业:习题14— 4 a,b 第33次作业:习题14—5a,14—8 第34次作业:习题14—3a,14—15 第35次作业:习题14—3b,14—11
P
x1
x1
1
1P
2 EI
a
(
0
Px2
)a2dx2
Pa 3 2EI
11
2 EI
[
a
2 0
x12dx1
a
(
0
a 2
)
2dx2
] 7 Pa 3 12 EI
则
7Pa3 Pa3 12 EI X12EI 0
6
X17P
P
P
由平衡方程求得:
RA
RB
6 7
P
H AH B P
M
A
M
B
4 7
P
a
A
B
HA
HB
RA MA
P
PP
X2 P
例3 试求图示刚架的全部约束反力。刚架EI为常数。 C
解:图示刚架有三个多余未知力。但
P
P
由于结构是对称的,而载荷反对称,
a
a
故对称轴横截面上轴力、弯矩为零,
只有一个多余未知力(剪力),只需
A
B
列出一个正则方程求解。
11X11P 0
用莫尔定理求1P和11。
P
P X1 X1
x2 x2
将上述结果代入变形协调方程得 11P
16
X1l3 5Pl 3 0 3EI 48EI
X
1
5 16
P
(f) A
3Pl
⑤求其它约束反力
16
由平衡方程可求得A端反
力,其大小和方向见图(f)。 ⑥作弯矩图,见图(g)。 ⑦求梁中点的挠度
(g) –
3Pl
16
P
B C
5P 16
5Pl。单位载荷如图(h) 。
用莫尔定理可得
P
yC
1 EI
l
2[
5
P(
l
(b)
x)P x]( x)dx
0 16 2
A
7Pl3 ()
768EI
(h)
A 注意:对于同一超静定结构,若选
取不同的多余约束,则基本静定系
A
(i)
也不同。本题中若选固定段处的转
动约束为多余约束,基本静定系是 X1
C 1 xC P
C
B X1
B
B
如图(i)所示的简支梁。
作用点沿Xi 方向的位移。
例2 试求图示刚架的全部约束反力,刚架EI为常数。
解:①刚架有两个多余约束。
a A
a
②选取并去除多余约束,代以多
q
余约束反力。
③建立力法正则方程
11X112 X 21P 0 21X1 22 X 22P 0
④计算系数ij和自由项iP
用莫尔定理求得
B q
B
A X1 X2
x2
第十四章 超静定结构
§14–1 超静定结构概述 §14–2 用力法解静不定结构 §14–3 对称及对称性质的应用
作业
§14–1 超静定结构概述
用静力学平衡方程无法确定全部约束力和内力的结构,统 称为静不定结构或系统,也称为超静定结构或系统。
在静不定结构中,超过维持静力学平衡所必须的约束称为多 余约束,多余约束相对应的反力称为多余约束反力,多余约束的 数目为结构的超静定次数。
超 第一类:仅在结构外部存在多余约束,即支反力是静
静
不定的,可称为外力超静定系统。
定 问 第二类:仅在结构内部存在多余约束,即内力是静不
题
定的,可称为内力超静定系统。
分 类 第三类:在结构外部和内部均存在多余约束,即支反
力和内力是超静定的。
分析方法 1.力法:以未知力为基本未知量的求解方法。 2.位移法:以未知位移为基本未知量的求解方法。
二、力法正则方程 上例中以未知力为未知量的变形协调方程可改写成下式
11X11P 0
变形协调方程的标准形式,即所谓的力法正则方程。
X1——多余未知量;
11——在基本静定系上, X1取单位值时引起的在X1作用点沿
X1方向的位移; 1P——在基本静定系上, 由原载荷引起的在X1作用点沿
X1方向的位移;
对于有无数多余约束反力的超静定系统的正则方程如下:
第一类
第二类
第三类
§14–2 用力法解超静定结构
一、力法的基本思路(举例说明)
例1 如图所示,梁EI为常数。 (a)
试求支座反力,作弯矩图,并 求梁中点的挠度。 解:①判定多余约束反力的数目
(一个) (b)
②选取并去除多余约束,代 以多余约束反力,列出变形 协调方程,见图(b)。
A
l 2
A
P
C
B
11X112 X 2 1n X n 1P 0
21X1 22 X 2 2n X n 2P 0
n1 X1 n2 X 2 nn X n nP0
由位移互等定理知: ij ji
ij:影响系数,表示在基本静定系上由Xj取单位值时引起的
在Xi作用点沿Xi方向的位移; iP:自由项,表示在基本静定系上, 由原载荷引起的在Xi
dx2
a3 2EI
⑤求多余约束反力 将上述结果代入力法正则方程可得
4a3
a3
qa4
3EI X12EI X 26EI 0
a3
a3
qa4
2EI
X 1 3EI
X
2
8EI
0
⑥求其它支反力
由平衡方程得其它支反力, 全部表示于图中。
X
1
1 qa() 28
X
2
3 7
qa()
A 3qa 7
q 4qa 7
1 qa B 3 qa2 28 1 28
l 2
P
C
B
X1
B 1X1 1P 0 变形协调方程
③用能量法计算 1P 和 1X1
由莫尔定理可得(图c、d、e)
(c) A
1P
1 EI
l
l P(
2
x
l 2
)xdx
5Pl3
48EI
1
1X1 EI
l 0
X
1xxdx
X1l 3 3EI
(d) A
(e) A
P
Cx
B
B x X1
B x1
④求多余约束反力
称 E1I1 E1I1 轴
称 E1I1 E1I1 轴
称 E1I1 轴
正确利用对称、反对称性质,则可推知某些未知量,可
大大简化计算过程:如对称变形对称截面上,反对称内力为
零或已知;反对称变形反对称截面上,对称内力为零或已知。
例如: 对 称 轴
X2 X3 X3
X1 X1 X2 P
X3 X3
X2
X1 X1
A x1 q
B
A
x2
x1 1
B
A
x2
x1 1
B
1P
1 EI
a
(
0
12qx22
)adx2
qa4 6EI
2
P
1 EI
a
(
0
12qx22
)x2
dx2
qa4 8EI
11
1 EI
(
0ax12dx1
a
a
0
2dx2
) 4a3 3EI
22
1 EI
a 0
x22
dx2
a3
3EI
12
21
1 EI
a
0 ax2
qa 28
§14–3 对称及对称性质的应用 一、对称结构的对称变形与反对称变形
结构几何尺寸、形状,构件材料及约束条件均对称于某一 轴,则称此结构为对称结构。当对称结构受力也对称于结构对 称轴,则此结构将产生对称变形。若外力反对称于结构对称轴, 则结构将产生反对称变形。
EI 对
EI 对
EI 对
E1I1
