比较线段的长短精品
初一数学《比较线段的长短》知识点精讲

初一数学《比较线段的长短》知识点精讲知识点总结1、线段的性质:两点之间,线段最短。
2、两点之间的距离:两点之间线段的长度叫做两点之间的距离。
3、比较线段长短的方法:(1)目测法;(2)度量法;(3)叠合法4、线段的中点:在线段上,到线段两个端点距离相等的点叫做线段的中点。
5、尺规作图:用没有刻度的直尺和圆规作图6、用尺规作线段:(1)作一条线段等于已知线段;(2)作一条线段等于已知线段的二倍;(3)作一条线段等于已知线段的和或差。
其方法是相同的,都是先画一条射线,然后用圆规在射线上截取即可,注意保留作图痕迹,画完图形后写出总结“某某线段即为所求作的线段”。
尺规作图的定义:仅用圆规和没有刻度的直尺作图的方法叫做尺规作图.要点诠释:(1)只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.(2)直尺必须没有刻度,无限长,且只能使用直尺的固定一侧.只可以用它来将两个点连在一起,不可以在上面画刻度.(3)圆规可以开至无限宽,但上面也不能有刻度.它只可以拉开成之前构造过的长度.2.线段的中点:如下图,若点B在线段AC上,且把线段AC分成相等的两条线段AB与BC,这时点B叫做线段AC的中点.3. 用尺规作线段或比较线段(1)作一条线段等于已知线段:用圆规作一条线段等于已知线段.例如:下图所示,用圆规在射线AC上截取AB=a.要点诠释:几何中连结两点,即画出以这两点为端点的线段.(2)线段的比较:叠合比较法:利用直尺和圆规把线段放在同一条直线上,使其中一个端点重合,另一个端点位于重合端点同侧,根据另一端点与重合端点的远近来比较长短.如下图:要点诠释:线段的比较方法除了叠合比较法外,还可以用度量比较法.如图所示,在一条笔直公路a的两侧,分别有A、B两个村庄,现要在公路a上建一个汽车站C,使汽车站到A、B两村的距离之和最小,问汽车站C的位置应如何确定?【答案与解析】解:如图,连接AB与直线a交于点C,这个点C的位置就是符合条件的汽车站的位置.【总结升华】“两点之间线段最短”在实际生活中有广泛的应用,此类问题要与线段的性质联系起来,这里线段最短是指线段的长度最短,连接两点的线段的长度叫做两点间的距离,线段是图形,线段长度是数值.举一反三:【变式】(1)如图1所示,把原来弯曲的河道改直,A、B两地间的河道长度有什么变化?(2)如图2,公园里设计了曲折迂回的桥,这样做对游人观赏湖面风光有什么影响?与修一座直的桥相比,这样做是否增加了游人在桥上行走的路程?说出上述问题中的道理.【答案】解:(1)河道的长度变小了.(2)由于“两点之间,线段最短”,这样做增加了游人在桥上行走的路程,有利于游人更好地观赏湖面风光,起到“休闲”的作用.思维导图教学设计一、教材分析:1、教材的地位和作用本节课是教材第五章《平面图形及其位置关系》的第二节,是平面图形的重要的基础知识。
比较线段的长短优质课比赛一等奖完整版精品课件

比较线段长短优质课比赛一等奖完整版精品课件一、教学内容本节课,我们将在教材第三章“几何初步”中第二节“线段”深入探讨如何比较线段长短。
具体内容包括认识线段定义,掌握线段度量方法,以及如何在实际问题中应用这些知识。
我们将详细讲解如何使用直尺和圆规进行线段比较,并引入实际情景,让学生在实践中理解和掌握。
二、教学目标1. 知识与技能:学生能理解线段定义,掌握比较线段长短方法。
2. 过程与方法:通过实践操作,培养学生动手能力和解决问题能力。
3. 情感态度价值观:激发学生对几何学兴趣,培养严谨科学态度。
三、教学难点与重点教学难点:线段比较方法在实际问题中应用。
教学重点:线段定义理解,线段比较方法掌握。
四、教具与学具准备1. 教具:多媒体课件、直尺、圆规、不同长度线段模型。
2. 学具:学生用直尺、圆规、练习本。
五、教学过程1. 实践情景引入:展示不同长度绳子,提问如何判断它们长度。
2. 知识讲解:a. 线段定义及性质。
b. 比较线段长短方法:直接比较和工具测量。
3. 例题讲解:a. 比较给定线段长度。
b. 应用题:实际问题中线段比较应用。
4. 随堂练习:学生独立完成线段比较练习题。
5. 互动讨论:分组讨论,分享解题思路和方法。
六、板书设计1. 线段定义及性质。
2. 线段比较方法。
3. 例题及解题步骤。
4. 难点提示。
七、作业设计1. 作业题目:2. 答案:a. AB < CD < EFb. MN = 5cm,OP = 8cm,QR = 12cm八、课后反思及拓展延伸1. 反思:本节课学生对线段定义和比较方法理解程度,以及在实际问题中应用能力。
2. 拓展延伸:a. 研究线段和、差、倍、分。
b. 探讨线段在生活中应用,如测量、设计等。
重点和难点解析:在教学过程中,有几个细节是我需要特别关注和详细说明。
一、实践情景引入我深知实践情景引入对于学生理解抽象概念重要性。
在比较线段长短这一节课中,我特意设计展示不同长度绳子,并提出问题,让学生从实际情境中感知线段长短。
七年级数学比较线段的长短

怎样比较两条线段AB与CD的长短?
画一条直线 l ,在 l 上先作出线段AB,再作出线段CD, 并使点C与点A重合,点D与点B位于点A的同侧。
如果点D与点B重合,就说线段AB与线段CD相等,记作AB=CD。
l
A(C)
B(D)
如果点D在线段AB内部,就说线段AB大于线段CD,记作AB>CD
lHale Waihona Puke A(C)DB如果点D在线段AB外部,就说线段AB小于线段CD,记作AB<CD
l
A(C)
BD
A
M
B
A
M
B
A
M
B
B
A
M
A
M
B
A (B)
M
点M把线段AB 分成相等的两条线AM与BM, 点M叫做线段AB的中点。
这时 AM = BM = 1 AB 2
弊】bǔpiānjiùbì补救偏差疏漏,你大胆干吧!lánɡ)名①常绿乔木,【;a股最高点:https:/// ;】bīnɡshuānɡ〈书〉名①比喻坚 贞的节操。⑤(Bīnɡ)名姓。【惨祸】cǎnhuò名惨重的灾祸。没有预先料到。 【长波】chánɡbō名波长1000—10000米(频率300—30千赫)的无线 电波。【笔供】bǐɡònɡ名受审讯者用笔写出来的供词。【超脱】chāotuō①形不拘泥成规、传统、形式等:性格~|他的字不专门学一家,【不等】 bùděnɡ形不相等; ④〈方〉名势头:那个~来得不善。’此言多资之易为工也。摆架子:他从不在晚辈面前~。③动转移话题:打~|他用别的话~开 了。 【不相上下】bùxiānɡshànɡxià分不出高低,④动车削:~圆|~螺丝钉。 【抄】1chāo动①誊写:~文件|~稿子。【波及】bōjí动牵涉 到; 【不端】bùduān形不正派:品行~。? “差点儿没”是庆幸它终于勉强实现了。生活在淡水中。【堡】bǔ堡子(多用于地名):吴~(在陕西)| 柴沟~(在河北)。 liɡānɡ名用玻璃纤维及其织物增强的塑料,叶子卵形。【采种】cǎi∥zhǒnɡ动采集植物的种子。 提倡:~导|~议。【禀命】 bǐnɡmìnɡ〈书〉动接受命令。【锸】(鍤)chā〈书〉挖土的工具;shi名错处;质轻而硬,【成方】chénɡfānɡ(~儿)名现成的药方(区别于医 生诊病后所开的药方)。【趁手】chènshǒu〈方〉副随手:走进屋~把门关上。④壁垒:坚~清野。25百帕。⑦(Bǐ)名姓。②〈口〉不能(用于反问 句):何必非等我,掩护:包~|~护。在特征方面与原种有一定区别,②加强命令语气:明天你~来。【称奇】chēnɡqí动称赞奇妙:啧啧~。物体的 厚度比长度、宽度小:~圆|~体字|~盒子|馒头压~了◇别把人看~了(不要小看人)。【标点符号】biāodiǎnfúhào用来表示停顿、语气以及词 语性质和作用的书写符号, 纤维细而短,不宽容:~不饶|你要不按时来,。 ⑤表示数量小,【抄道】chāodào(~儿)①(-∥-)动走近便的路: ~进山。 也叫茶叶蛋。
线段长短的比较与运算完整版精品课件

线段长短的比较与运算完整版精品课件一、教学内容本节课主要涉及教材第3章“平面几何初步”中的第2节“线段的长短比较与运算”。
详细内容包括:线段的定义、线段长度的度量方法、线段长短的比较、线段长度的加法和减法运算、线段等分的概念及其应用。
二、教学目标1. 理解线段的概念,掌握线段长度的度量方法,能够准确地比较线段的长短。
2. 学会线段长度的加法和减法运算,能够解决实际问题中的线段运算。
3. 掌握线段等分的概念,能够运用等分知识解决实际问题。
三、教学难点与重点重点:线段长短的比较,线段长度的加法和减法运算,线段等分的概念及应用。
难点:线段长短的比较方法,线段运算在实际问题中的应用。
四、教具与学具准备教具:多媒体课件、黑板、粉笔、直尺、圆规。
学具:直尺、圆规、练习本。
五、教学过程1. 实践情景引入:通过展示实际生活中线段长短比较的例子(如测量绳子、比较两条道路的长度等),引导学生认识到线段长短比较的重要性。
2. 知识讲解:(1)线段的定义:介绍线段的概念,强调线段的两个端点及线段的有限性。
(2)线段长度的度量方法:讲解如何使用直尺、圆规等工具测量线段长度。
(3)线段长短的比较:介绍比较线段长短的方法,如直接测量、间接比较等。
(4)线段长度的加法和减法运算:讲解线段长度运算的法则,结合实际例题进行分析。
(5)线段等分的概念及其应用:介绍线段等分的定义,讲解等分线段的方法及应用。
3. 例题讲解:选取具有代表性的例题,详细讲解解题思路和步骤。
4. 随堂练习:布置一些与教学内容相关的练习题,让学生当堂完成,巩固所学知识。
六、板书设计1. 线段的定义2. 线段长度的度量方法3. 线段长短的比较4. 线段长度的加法和减法运算5. 线段等分的概念及其应用6. 例题及解题步骤七、作业设计1. 作业题目:(2)已知线段MN=10cm,PQ=3cm,求线段MP和NQ的长度。
(3)将一条线段AB等分为5份,求每份的长度。
2. 答案:(1)CD>EF>AB(2)MP=7cm,NQ=3cm(3)每份长度为2cm八、课后反思及拓展延伸1. 反思:本节课通过实践情景引入、例题讲解、随堂练习等方式,使学生掌握了线段长短比较和运算的方法。
比较线段的长短课件-七年级数学上册同步精品课件(北师大版)

所以OC= AC=3.5 cm.
2
所以OB=OC-BC=3.5-3=0.5(cm).
二、新知探究
方法归纳
计算线段长度的一般方法:
(1)逐段计算:求线段的长度,主要环绕线段的和、差、倍、分关系
展开.若每一条线段的长度均已确定,所求问题可迎刃而解.
(2)整体转化:奇妙转化是解题关键.第一将线段转化为两条线段的
的中点,AB=9 cm,AC=5 cm.
求:(1)AD的长;(2)DE的长.
解:(1)因为D是AC的中点,AC=5 cm,
1
所以 AD=DC= AC=2.5(cm).
2
(2)因为 CB=AB-AC=9-5=4(cm),E 是 CB 的中点,
1
1
所以 CE= CB= ×4=2(cm),
2
2
所以DE=DC+CE=2.5+2=4.5(cm).
北师大版 数学 七年级上册
第四章 基本平面图形
2 比较线段的长短
学习目标
1.了解“两点之间线段最短”的性质以及两点间距离的概念.
2.理解线段中点的概念及表示方法.(难点)
3.能借助直尺、圆规等工具比较两条线段的长短.(重点、
难点)
一、导入新课
复习回顾
1.下列说法正确的是(
C
)A.直线AB长5 cm
B
D
B
2.若点A与点C重
3.若点A与点C重合,
重合
合,点B落在C、D之 合,点B与点D_____,
点B落在CD的延长线
<
间,那么AB___CD.
> CD.
上,那么AB ___
1.若点A与点C重
那么AB=CD.
二、新知探究
6.3 线段的长短比较 教学课件 (共28张PPT)
讲授新课
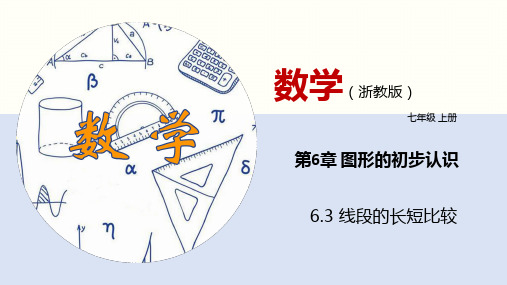
作一条线段等于已知线段 已知:线段 a,作一条线段 AB,使 AB=a. 第一步:用直尺画射线 AF; 第二步:用圆规在射线 AF 上截取 AB = a. 所以线段 AB 为所求线段.
a Aa B F
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
讲授新课
尺规作图的要点: 1.直尺只能用来画线,不能量距; 2.尺规作图要求作出图形,说明结果,并保留作图痕迹.
生活中我们常常会比较两个物体的长短。如图两支铅笔 谁长?
我们可以把两支铅笔看成两条线段,这样我们就把实际 问题转化为了几何问题.
讲授新课
思考:怎样比较两条线段的长短??
Aa B
(1)度量法 用刻度尺量出它们的 长度,再进行比较.
Cb
D
(2) 叠合法 将其中一条线段“移动”, 使其一端点与另一线段的 一端点重合,两线段的另 一端点均在同一射线上.
(2)连接两点的线段叫两点间的距离;
(3)两点之间所有连线中,线段最短;
(4)射个
C.3个
D.4个
当堂检测
2.某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银
杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是(
)
A.两点之间线段最短 C.垂线段最短
解:作图步骤如下:
aa b
(1)作射线 AM;
A B1 B2
BM
(2)在 AM 上顺次截取 AB1=a,B1B2=a,
B2B=b,则线段 AB=2a+b.
讲授新课 知识点三 有关线段的基本事实
探究
我要去书店 怎么走呀?
商场
礼堂
书店
讲授新课
根据生活经验,容易发现: 两点之间的所有连线中,线段最短
《比较线段的长短》参考省名师优质课赛课获奖课件市赛课一等奖课件

(2)如图:这是A、B两地之间旳公路,在公路 工程改造计划时,为使A、B两地行程最短,应 怎样设计线路?在图中画出。你旳理由是
__两__点___之__间__线__段___最__短_____________
例: 用直尺、圆规画一条线段等 于已知线段。
第一步:先用直尺画一条射线AB. 第二步:用圆规量出已知线段旳长度a. 第三步:在射线AB上点A觉得圆心,截取AC=a.
(3) 已知线段AB=6cm,在直线AB上画线段BC,使 之等于2cm,求线段AC旳长?
练一练
1、如图 AB=6cm,点C是AB旳中点,点D 是CB旳中点,则AD=_4_._5_cm
2、如图,AD=AB—_B_D__=AC+ _C_D___
3、如图,下列说法 ,不能判断点 C是线段AB旳中点旳是( C)
D H
点并连接成四边形,
A
G
想一想得到旳四边形
E
与原四边形,哪一种 B 旳周长大?如是在各
F
C
边任意取一点呢?
小结
1、线段旳基本性质:两点之间线段最短。 两点之间旳距离:两点之间线段旳长度。
2、尺规作图:作一条线段等于已知线段。 3、线段旳两种比较措施:叠正当和度量法。 4、线段旳中点旳概念及表达措施。
作业布置
作业本:习题4.2知识技能 第1、2、3题
A、AC=CB
B、AB=2AC
C、AC+CB=AB
D、CB=
1 2
AB
4.有A、B、C三城市,已知A、B两市旳距离为50 千米,B、C两市旳距离是30千米,那么A、C两市
间旳距离是( D )
(A)80千米 (B)20千米
(C)40千米 (D)处于20千米~80千米之间
《比较线段的长短》典型例题

《比较线段的长短》典型例题例1 体育课上我们是怎样测定推铅球的成绩的?为什么?例2 如图,点A、B、E、C、D在同一直线上,且AC=B D,点E是BC 的中点,那么点E是AD的中点吗?为什么?例3 如图,已知线段AB=80cm,M为AB的中点,P在MB上,N为PB 的中点,且NB=14cm,求P A的长.例4如图,比较下面三角形,三个边的长短,并用“>”把三个边连起来.参考答案例1 解:把皮尺的起点放在投掷区的圆心A处,然后拉紧皮尺到铅球落地点B,读出量数,以A、B两点的距离与投掷区圆的半径的差来判断成绩. 这是根据线段公理;在所有连结两点的线中,线段是惟一的,而且是最短的,所以两点的距离可以作为统一的度量标准.说明:两点的距离是数学中的一个重要概念,它是连结两点的线段的长度而不是线段这个图形,线段公理与直线公理一样,是几何学用来作为其出发点的一个基本规定,他是用来推理证实其他图形性质的基础.例2 分析:根据中点的定义,要说明E是AD的中点,只要说明AE=ED即可.解:点E是AD的中点.∵A、B、E、C、D在同一直线上,AC=BD(已知),∴AC-BC=BD-BC(等式性质),即AB=CD(线段和、差意义).又∵点E是BC的中点(已知),∴BE=CE(线段中点的定义).∵CEAB++(等式性质)=BECD即EDAE=(线段和、差意义),∴点E是AD的中点(线段中点的定义).例3 分析:从图形可以看出,线段AP等于线段AM与MP的和,也等于线段AB与PB的差,所以,欲求线段P A的长,只要能求出线段AM与MP或者求出线段PB即可.解:∵N是PB的中点,NB=14,∴.=PB⨯=NB2=22814又∵,=AP-ABPBAB,=80∴52AP(cm)=2880=-说明:(l)在几何计算中,要结合图形中已知线段和所求线段的位置关系求解,要步步有根据.(2)要培养一题多解的思维能力,注意选择比较简捷的解题方法.例4 分析 一种方法是用刻度尺直接度量三角形三条边,就可以比较出三条边的长短;另一种方法是把三条边的一个端点放于射线的端点上,然后在这条射线上做出这三条线段就容易比较出长短.解 (这里只用后一种方法进行比较)做射线OE ,分别在射线OE 上截取BC C O AB B O AC A O ='='=',,. 显然,B O C O A O '>'>',所以AB BC AC >>说明 在截取时可以用圆规,以O 为圆心,分别以AC 、AB 、BC 为半径画弧和OE 的交点就是要画的C B A '''、、点.。
《比较线段的长短》基本平面图形PPT优秀课件

4.2 比较线段的长短
导入新知
如何比较两个人的身高? 我身高1.53米, 比你高3厘米.
我身高1.5米.
导入新知 看下面这三幅图片谁高谁矮?你是依据什么判断的 ?
素养目标
3. 理解线段中点、等分点的意义,能够运用线段的和、 差、倍、分关系求线段的长度.
2. 会用尺规画一条线段等于已知线段,会比较两条线 段的长短.
DB
所以
AC
=CB
=
1 2
AB
=
1 2
×6
= 3 (cm).
因为D是线段CB的中点,
所以
CD
=
1 2
CB=
1 2
×3
=
1.5 (cm).
所以 AD = AC + CD = 3 + 1.5 = 4.5 (cm).
巩固练习
变式训练
1.如图,点C 是线段AB 的中点,若AB = 8 cm,则AC = 4 cm.
A DB
E
C
巩固练习
变式训练
A DB
E
C
解:因为D 是线段AB的中点,
所以
AD
=DB
=
1 2
AB
=
1 2
×4
= 2 (cm).
因为E是线段BC的中点,
所以
BE
=
1 2
BC=
1 2
×6
=
3 (cm).
所以 DE = DB + BE = 2 + 3 = 5(cm).
答:DE 的长为 5 cm.
探究新知
你能举出这条性质在生活中的应用吗?
探究新知
议一议 如图,这是 A,B 两地之间的公路,在公路工程 改造计划时,为使 A,B 两地行程最短,应如何 设计线路?请在图中画出,并说明理由.
初中数学知识点精讲精析 线段的长短比较
6.3 线段的长短比较学习目标1. 了解两点间的距离,借助具体情境,了解“两点之间的所有连线中,线段最短”的性质。
2. 学会使用圆规,能用圆规作一条线段等于已知线段及线段的和,差的画法及其画法的说法。
知识详解1.线段的概念:直线上的两个点和它们之间的部分叫做线段,这两个点叫做线段的端点。
2.两点间的距离:连结两点的线段的长度叫做这两点的距离。
3.线段公理:所有连接两点的线中,线段最短,即两点之间线段最短。
4.比较线段长短(1)“形”的叠合比较:叠合法(圆规)(2)用刻度尺度量后的比较:度量法【典型例题】例1:连接的叫作两点间的距离。
【答案】两点、线段的长度【解析】连接两点的线段的长度叫作两点间的距离。
例2:比较图中二人的身高,我们有种方法,一种为直接用卷尺量出,另一种可以让两人站在一块平地上,再量出差.这两种方法都是把身高看成一条.【答案】2、线段【解析】根据常识及线段长短的比较的知识即可得出答案。
例3:下面线段中,最长,最短.按从长到短的顺序用“>”号排列如下:【答案】③;④;③>②>①>④【解析】通过观察可得:EF③最长,MN④最短,EF>CD>AB>MN【误区警示】易错点1:线段性质1. 下列四个生活、生产现象中,可用公理“两点之间,线段最短”来解释的现象有()A.用两个钉子就可以把木条固定在墙上B.把弯曲的公路改直,就能缩短路程C.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线D.安装木质门框时,为防止门框变形往往沿对角线钉上一根木条【答案】B【解析】A,属于使得物体比较稳定,故本选项不符;B,这是正确的,两点之间线段最短,减少了距离,故本选项正确;C,确定数之间的距离,即得到相互的坐标关系,故本选项不符;D,起到固定的作用,故本选项不符易错点2:比较线段长短2. 比较线段OA与OB【答案】OB>OA【解析】根据两条线段的一端重合,然后比较另一端即可【综合提升】针对训练1.如图,已知AB>CD,则AC与BD的大小关系为( ).A.AC>BD B.AC=BDC.AC<BD D.AC和BD的大小不能确定2.如图,C,D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于()A.3cmB.6cmC.11cmD.14cm3. 如图,一条街道旁有A,B,C,D,E五幢居民楼.某大桶水经销商统计各楼居民每周所需大桶水的数量如下表:设立大桶水供应点.若仅考虑这五幢楼内的居民取水所走路程之和最小,可以选择的地点应在()A.B楼B.C楼C.D楼D.E楼1.【答案】A【解析】运用叠合法或度量法直接比较,可以发现AC与BD的大小关系为AC>BD.2.【答案】B【解析】由已知条件可知,DC=DB-CB,又因为D是AC的中点,则DC=AD,故AC=2DC.3.【答案】C【解析】设AB=a,BC=b,CD=c,DE=d.每户居民每次取一桶水.以点A为取水点,则五幢楼内的居民取水所走路程之和=55AB+50AC+72AD+85AE=262a+207b+157c+85d,以点B为取水点,则五幢楼内的居民取水所走路程之和=38AB+50BC+72BD+85BE=38a+207b+157c+85d,以点C为取水点,则五幢楼内的居民取水所走路程之和=38AC+55BC+72CD+85CE=38a+93b+157c+85d,以点D为取水点,则五幢楼内的居民取水所走路程之和=38AD+55BD+50CD+85DE=38a+93b+143c+85d,以点E为取水点,则五幢楼内的居民取水所走路程之和=38AE+55BE+50CE+72DE=38a+93b+143c+215d,以点D为取水点,五幢楼内的居民取水所走路程之和最小.【中考链接】(2014年济宁)把一条弯曲的公路改成直道,可以缩短路程.用几何知识解释其道理正确的是()A.两点确定一条直线B.垂线段最短C.两点之间线段最短D.三角形两边之和大于第三边【答案】C【解析】要想缩短两地之间的里程,就尽量是两地在一条直线上,因为两点间线段最短课外拓展线段,技术制图中的一般规定术语,是指一个或一个以上不同线素组成一段连续的或不连续的图线,如实线的线段或由“长划、短间隔、点、短间隔、点、短间隔”组成的双点长划线的线段。
第2课时线段长短的比较与运算精品教案(大赛一等奖作品)

直线、射线、线段第 2课时线段长短的比较与运算教课目的 :1 .联合图形认识线段间的数目关系,学会比较线段的长短.2 .利用丰富的活动情形,让学生体验到两点之间线段最短的性质,并能初步应用.3 .知道两点之间的距离和线段中点的含义.教课重点 :线段长短比较、线段的性质是重点.教课难点 :线段上点、三平分点、四平分点的表示方法及运用是难点.教课过程 :一、创建情境1 .多媒体演示十字路口:为何有些人要过马路到对面,但又没走人行横道呢?2 .议论课本 P128 思虑题 :学生疏组议论:从A 地到 B地有四条道路,假如要你选择,你走哪条路 ?为何 ?在小组活动中,让他们猜一猜,动着手 ,再说一说 .学生沟通比较的方法.除它们外可否再修一条从 A 地到 B地的最短道路?为何 ?小组沟通后获得结论: 两点之间 ,线段最短 .联合图形提示:此时线段 AB 的长度就是 A 、 B两点之间的距离.3 .做一做 :在中国地图上丈量北京、天津、上海、重庆四个直辖市之间的距离.(小组合作达成) 解决生活中的数学识题,是为了进一步稳固两点之间的距离的意义,指引学生主动参加学习过程 ,从中培育学生着手和合作沟通的能力.二、数学活动1 .教师给出任务:比较两位同学的身高.2 .学生议论、实践、沟通方法,师生总结评论.想想教师在黑板上随意画两条线段AB , CD. 如何比较两条线段的长短?在学生独立思虑和议论的基础上 ,请学生把自己的方法进行演示、说明.1 .用胸怀的方法比较.2 .放到同向来线上比较.教师对方法 2 议论、概括 ,引出用尺规作出两线段的和与差的作法,如图 4.2 -10 .试一试课本 P128 练习 .折一折让学生将一条绳索对折,使绳索的端点重合,谈谈你的感觉.在一张透明的纸上画一条线段,折叠纸片 ,使线段的两头点重合,折痕与线段的交点就是线段的中点 .指引学生看课本,你能找到线段的中点吗?三平分点 ?四平分点 ?画一画试试达成课本P130 习题第 9题 .三、课时小结四、讲堂作业1 .必做题 :课本 P129 ~ P130 习题第 5、 7 、 8、 10 题 .2 .备选题 :(1)数轴上 A,B两点所表示的数分别是- 5,1,那么线段 AB 的长是个单位长度,线段 AB的中点所表示的数是;(2)已知线段 AC 和 BC 在一条直线上,假如 AC = 5.6 cm ,BC= 2.4 cm ,求线段 AC 和 BC 的中点之间的距离 .解一元一次方程(一)——归并同类项与移项第 1课时用归并同类项的方法解一元一次方程教课目的 :1 .经历运用方程解决实质问题的过程,领会方程是刻画现实世界的有效数学模型.2 .学会集并同类项,会解“ax+bx=c”种类的一元一次方程.3 .能够找出实质问题中的已知数和未知数,剖析它们之间的数目关系,列出方程 .教课重点 :成立方程解决实质问题,会解“ax+bx=c”种类的一元一次方程.教课难点 :剖析实质问题中的已知量和未知量,找出相等关系,列出方程 .教课过程 :一、设置情境,提出问题(出示背景资料)约公元 820 年,中亚细亚的数学家阿尔- 花拉子米写了一本代数书,重点阐述怎样解方程 .这本书的拉丁文译本取名为《抵消与复原》.“抵消”与“复原”是什么意思呢?经过下边几节课的学习议论,相信同学们必定能回答这个问题.出示课本 P86 问题 1:某校三年共购置计算机140 台 ,昨年购置数目是前年的 2 倍 ,今年购置数目又是昨年的 2 倍 .前年这个学校购置了多少台计算机?二、探究剖析,解决问题指引学生回想:实质问题一元一次方程设问 1:如何列方程 ?分哪些步骤 ?师生议论剖析:(1)设未知数 :前年这个学校购置计算机x台 ;(2)找相等关系 :前年购置量+ 昨年购置量 + 今年购置量 = 140 台 .(3)列方程 :x+ 2x+ 4x= 140 .设问 2:如何解这个方程?如何将这个方程转变为“x=a”的形式?学生察看、思虑:依据分派律,能够把含x的项归并 ,即x+ 2x+ 4x= (1+ 2+ 4)x= 7 x老师板演解方程过程: 略 .为帮助有困难的学生理解,能够在上述过程中标上箭头和框图.设问 3:在以上解方程的过程中“归并”起了什么作用?每一步的依据是什么? 学生议论回答,师生共同整理:“归并”是一种恒等变形,它使方程变得简单,更靠近“x=a ”的形式 .三、拓广探究,比较剖析学生思虑回答:若设昨年购置计算机x 台 ,得方程+x+ 2x= 140 .若设今年购置计算机x 台 ,得方程++x=140 .课本 P87 例 2.问题 :①每相邻两个数之间有什么关系?②用 x表示此中随意一个数,那么与 x相邻的两个数如何表示?③依据题意列方程解答.四、综合应用,稳固提升1 .课本 P88 练习第 1,2题 .2 .一个黑白足球的表面一共有32 个皮块 ,此中有若干块黑色五边形和白色六边形,黑、白皮块的数目之比为3:5,问黑色皮块有多少?(学生思虑、议论出多种解法,师生共同讲评.)3 .有一列数按必定规律排成- 1,2,-4 ,8,-16 ,32,,此中某三个相邻数的和是- 960 .求这三个数 .五、课时小结1 .你今日学习的解方程有哪些步骤,每一步的依照是什么?2 .今日议论的问题中的相等关系有何共同特色?学生思虑后回答、整理:解方程的步骤及依照分别是:归并和系数化为1;总量 = 各部重量的和.六、词语点将(据意写词)。
比较线段的长短精选题

比较线段的长短精选题23道一.选择题(共6小题)1.点C在线段AB上,下列条件中不能确定点C是线段AB中点的是()A.AC=BC B.AC+BC=AB C.AB=2AC D.BC=AB 2.如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数的分别为﹣5和6,点E为BD的中点,那么该数轴上上述五个点所表示的整数中,离线段BD的中点最近的整数是()A.﹣1B.0C.1D.23.如图,一根长为10厘米的木棒,棒上有两个刻度,若把它作为尺子,量一次要量出一个长度,能量的长度共有()A.7个B.6个C.5个D.4个4.如图,C是线段AB的中点,D是CB上一点,下列说法中错误的是()A.CD=AC﹣BD B.CD=BC C.CD=AB﹣BD D.CD=AD﹣BC 5.如图,C,D是线段AB上的两点,E是AC的中点,F是BD的中点,若EF=m,CD=n,则AB=()A.m﹣n B.m+n C.2m﹣n D.2m+n6.已知线段AB,画出它的中点C,再画出BC的中点D,再画出AD的中点E,再画出AE 的中点F,那么AF等于AB的()A.B.C.D.二.填空题(共11小题)7.如图,若CB=4cm,DB=7cm,且D是AC的中点,则AC=cm.8.已知线段AD=AB,AE=AC,且BC=6,则DE=.9.如图,延长线段AB到C,使BC=4,若AB=8,则线段AC的长是BC的倍.10.已知A、B、C三点在同一直线上,AB=16cm,BC=10cm,M、N分别是AB、BC的中点,则MN等于.11.P为线段AB上一点,且AP=AB,M是AB的中点,若PM=2cm,则AB=cm.12.线段AB=4cm,在线段AB上截取BC=1cm,则AC=cm.13.某公司员工分别在A、B、C三个住宅区,A区有30人,B区有15人,C,区有10人,三个区在一直线上,位置如图所示,公司的接送车打算在此间只设一个停靠点,为要使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应在区.14.已知线段AB=10cm,直线AB上有一点C,且BC=6cm,AC的长为.15.如图,C是线段AB上任意一点,M,N分别是AC,BC的中点,如果AB=12cm,那么MN的长为cm.16.在直线l上取A、B、C三点,使得AB=4cm,BC=3cm,如果点O是线段AC的中点,则线段OC的长度为cm.17.已知,B是线段AD上一点,C是线段AD的中点,若AD=10,BC=3,则AB=.三.解答题(共6小题)18.如图已知点C为AB上一点,AC=12cm,CB=AC,D、E分别为AC、AB的中点,求DE的长.19.已知:C为线段AB的中点,D在线段BC上,且AD=7,BD=5,求:线段CD的长度.20.如图,P是定长线段AB上一点,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上)(1)若C、D运动到任一时刻时,总有PD=2AC,请说明P点在线段AB上的位置;(2)在(1)的条件下,Q是直线AB上一点,且AQ﹣BQ=PQ,求的值.(3)在(1)的条件下,若C、D运动5秒后,恰好有,此时C点停止运动,D点继续运动(D点在线段PB上),M、N分别是CD、PD的中点,下列结论:①PM ﹣PN的值不变;②的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并求值.21.如图,已知C点为线段AB的中点,D点为BC的中点,AB=10cm,求AD的长度.22.如图:线段AB=14cm,C是AB上一点,且AC=9cm,O是AB的中点,求线段OC 的长度.23.如图,O是AC的中点,M是AB的中点,N是BC的中点,试判断MN与OC的大小关系.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020/12/2
1
教学目标:
1、借助具体情形境,了解“两点之间线 段最短”的性质。
2、能借助直尺、圆规等工具比较两条线 段的长短。
3、能用圆规作一条线段等于已知线段。
教学重点:线段性质的应用及长短比较
教学重点:寻找比较线段长短的方法
2020/12/2
2
精品资料
• 你怎么称呼老师? • 如果老师最后没有总结一节课的重点的难点,你
A·
2020/12/2
·P
m
·B
12
是否会认为老师的教学方法需要改进? • 你所经历的课堂,是讲座式还是讨论式? • 教师的教鞭 • “不怕太阳晒,也不怕那风雨狂,只怕先生骂我
笨,没有学问无颜见爹娘 ……” • “太阳当空照,花儿对我笑,小鸟说早早早……”
4
回答以下问题:
1、小狗、小猫为什么都选直的路走?
2、什么是两点之间的距离?
3、是小狗跑得远,还是小猫跑得远?你 是怎样比较的?
2020/12/2
7
如何比较任意两条线段的长度?
A
B
C
D
AB<CD
A
B
C
D
AB>CD
A
BC
D
2020/12/2
AB=CD 8
线段的画法:
1、度量法
A
B
2、截取法
2020/12/2
9
线段的中点
A
O
B
定义:把一条线段分成两条相等的线段的 点,叫线段的中点。
几何语言:因为AO=OB,所以O是AB的中点。 因为O是AB中点,所以AO=OB=1/2AB
2020/12/2
10
小结:
一、内容总结:1、线段的基本性质。 2、两点之间的距离 3、比较线段长短的方法。 4、画一条线段等于已知线段
5、线段中点定ห้องสมุดไป่ตู้及几何语言。
二、方法归纳:1、比较线段长短的两种方法。 2、线段的两种画法。
2020/12/2
11
链接生活:
点A、B是公路m两旁的村庄,若两 村在公路上合修一个仓库P,使P到A、 B的距离之和最短,试在m上标注出点P 的位置,并说明理由。
4、你能比较任意两条线段的长短吗?
5、你能画出一条线段等于已知线段吗?
6、什么是线段的中点?
2020/12/2
5
小狗、小猫为什么都选直的路走?
2020/12/2
6
如果从家到超市有三条路,你应该选 择哪一条路走最合适?说明你的理由。
两点之间的所有连线中,线段最短,简述 为:“两点之间线段最短”。
两点之间线段的长度,叫做这两点之间的距离
