【精品】八年级数学暑假作业第12天最短路径问题新人教版

合集下载

初二数学最短路径练习题及答案

初二数学最短路径练习题及答案导言：数学中的最短路径问题是指在网络图中寻找两个顶点之间路径长度最短的问题。

该问题在实际生活中应用广泛，比如在导航系统中为我们找到最短的路线。

对于初二学生而言，在学习最短路径问题时，题目练习是非常重要的。

本文将为初二数学学习者提供一些最短路径练习题及答案，帮助他们巩固知识和提高解题能力。

练习题一：某地有4个村庄A、B、C、D，它们之间的道路如下图所示。

要求从村庄A到村庄D，经过的道路距离最短，请你找出最短路径，并计算出最短路径的长度。

解答一：根据题目所给的道路图，我们可以使用最短路径算法来求解最短路径。

以下是求解过程：1. 首先，我们需要创建一个包含4个顶点的图，并初始化每条边的权值。

将A、B、C、D顶点分别标记为1、2、3、4。

村庄A到村庄B的距离为5，即A-5-B。

村庄A到村庄C的距离为3，即A-3-C。

村庄B到村庄C的距离为2，即B-2-C。

村庄B到村庄D的距离为6，即B-6-D。

村庄C到村庄D的距离为4，即C-4-D。

2. 接下来，我们使用迪杰斯特拉算法求解最短路径。

a) 首先，我们将起始顶点A的距离设置为0，其他顶点的距离设置为无穷大。

b) 然后，我们选择距离最短的顶点，并将其标记为已访问。

c) 然后，我们更新与该顶点相邻的顶点的距离。

如果经过当前顶点到达邻接顶点的距离比已记录的最短路径更短，就更新最短路径。

d) 重复上述步骤，直到找到最短路径为止。

3. 经过计算，最短路径为A-3-C-4-D，距离为7。

练习题二：某城市有6个地点，它们之间的交通图如下所示。

请你计算从地点A到地点F的最短路径，并给出最短路径的长度。

解答二：根据题目所给的交通图，我们可以使用最短路径算法来求解最短路径。

以下是求解过程：1. 首先，我们需要创建一个包含6个顶点的图，并初始化每条边的权值。

将地点A、B、C、D、E、F分别标记为1、2、3、4、5、6。

地点A到地点B的距离为4，即A-4-B。

(word完整版)初二数学最短路径问题知识归纳+练习,推荐文档

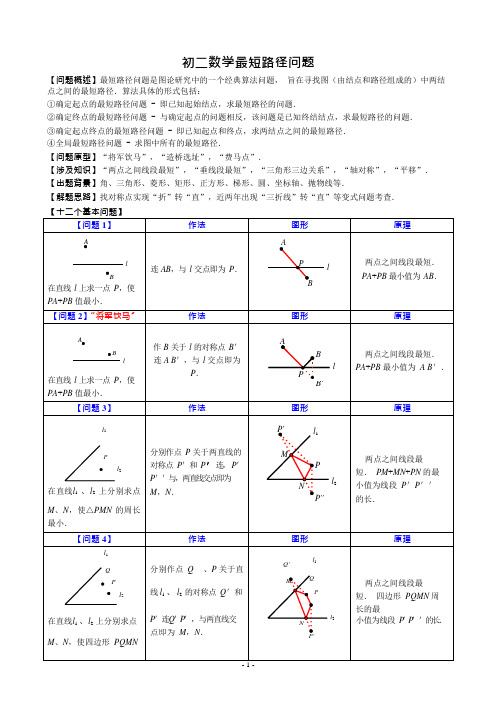
初二数学最短路径问题【问题概述】最短路径问题是图论研究中的一个经典算法问题，旨在寻找图（由结点和路径组成的）中两结点之间的最短路径．算法具体的形式包括：①确定起点的最短路径问题 - 即已知起始结点，求最短路径的问题．②确定终点的最短路径问题 - 与确定起点的问题相反，该问题是已知终结结点，求最短路径的问题．③确定起点终点的最短路径问题 - 即已知起点和终点，求两结点之间的最短路径．④全局最短路径问题 - 求图中所有的最短路径．【问题原型】“将军饮马”，“造桥选址”，“费马点”．【涉及知识】“两点之间线段最短”，“垂线段最短”，“三角形三边关系”，“轴对称”，“平移”．【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等．【解题思路】找对称点实现“折”转“直”，近两年出现“三折线”转“直”等变式问题考查．【问题1】作法图形原理AlB在直线l 上求一点P，使PA+PB 值最小．连AB，与l 交点即为P．AP lB两点之间线段最短．PA+PB 最小值为AB．【问题2】“将军饮马”作法图形原理ABl在直线l 上求一点P，使PA+PB 值最小．作B 关于l 的对称点B＇连A B＇，与l 交点即为P．ABlP两点之间线段最短．PA+PB 最小值为A B＇．B'【问题3】作法图形原理l1Pl2在直线l1、l2上分别求点M、N，使△PMN 的周长最小．分别作点P 关于两直线的对称点P＇和P＇连，P＇P＇＇与，两直线交点即为M，N．P' l1MPNl2P''两点之间线段最短．PM+MN+PN 的最小值为线段P＇P＇＇的长．【问题4】作法图形原理l1QPl2在直线l1、l2上分别求点M、N，使四边形PQMN 分别作点Q 、P 关于直线l1、l2的对称点Q＇和Q'l1M QP两点之间线段最短．四边形PQMN 周长的最P＇连Q＇P＇，与两直线交l2N 小值为线段P＇P＇＇的长．点即为M，N．P'PE3在直线 l 上求一点 P ，使直线 l 的交点即为 P ．端点的距离相等．PA - PB ＝0．PA - PB 的值最小．【问题 10】作法图形原理ABl在直线 l 上求一点 P ，使PA - PB 的值最大．作直线 AB ，与直线 l 的交点即为 P ．ABPl三角形任意两边之差小于第三边． PA - PB ≤AB ．PA - PB 的最大值＝AB ．【问题 11】作法图形原理AlB在直线 l 上求一点 P ，使PA - PB 的值最大．三角形任意两边之差小于A第三作 B 关于 l 的对称点 B ＇作直线 A B ＇，与 l 交点B'Pl边． PA - PB ≤AB ＇．即为 P ．BPA - PB 最大值＝AB ＇．【问题 12】“费马点”作法图形原理A所求点为“费马点”，即满足DBC∠APB ＝∠BPC ＝∠APC＝120°．以 AB 、AC 为APE两点之间线段最短． PA +PB +PC 最小值△ABC 中每一内角都小于边向外作等边△ABD 、△ BC＝CD ．120°，在△ABC 内求一 ACE ，连 CD 、BE 相交于点 P ，使 PA +PB +PC 值最 P ，点 P 即为所求．小．【精品练习】1. 如图所示，正方形 ABCD 的面积为 12，△ABE 是等边三角形，点 E 在正方形 ABCD 内，在对角线 AC 上有一点 P ，使 PD +PE 的和最小，则这个最小值为（）A. 2B. 2 ADC ．3D ．BC2. 如图，在边长为 2 的菱形 ABCD 中，∠ABC ＝60°，若将△ACD 绕点 A 旋转，当 AC ′、AD ′分别与 BC 、CD- 3 -662 EDM3交于点 E 、F ，则△CEF 的周长的最小值为（）A ．2B ． 2C ． 2 +D ．43. 四边形 ABCD 中，∠B ＝∠D ＝90°，∠C ＝70°，在 BC 、CD 上分别找一点 M 、N ，使△AMN 的周长最小时，∠AMN +∠ANM 的度数为（）A ．120°B ．130°C ．110°D ．140°A DBNC4. 如图，在锐角△ABC 中，AB ＝4 ，∠BAC ＝45°，∠BAC 的平分线交 BC 于点 D ，M 、N 分别是 AD 和AB 上的动点，则 BM +MN 的最小值是．A5. 如图，Rt △ABC 中，∠C ＝90°，∠B ＝30°，AB ＝6，点 E 在 AB 边上，点 D 在 BC 边上（不与点 B 、C 重合），且 ED ＝AE ，则线段 AE 的取值范围是．ACB6. 如图，∠AOB ＝30°，点 M 、N 分别在边 OA 、OB 上，且 OM ＝1，ON ＝3，点 P 、Q 分别在边 OB 、OA 上，则 MP ＋PQ ＋QN 的最小值是．（注“勾股定理”：直角三角形中两直角边的平方和等于斜边的平方，即 Rt △ABC 中，∠C ＝90°，则有 AC 2 + BC 2 = AB 2 ）- 4 -D M33 yABOxyBA OCDx7. 如图，三角形△ABC 中，∠OAB ＝∠AOB ＝15°，点 B 在 x 轴的正半轴，坐标为 B ( 6 ，0)．OC 平分∠AOB ，点 M 在 OC 的延长线上，点 N 为边 OA 上的点，则 MA ＋MN 的最小值是．8. 已知 A （2，4）、B （4，2）．C 在 y 轴上，D 在 x 轴上，则四边形 ABCD 的周长最小值为，此时 C 、D 两点的坐标分别为．9．已知 A （1，1）、B （4，2）．（1）P 为 x 轴上一动点，求 PA +PB 的最小值和此时 P 点的坐标；（2）P 为 x 轴上一动点，求 PA PB 的值最大时 P 点的坐标；（3）CD 为 x 轴上一条动线段，D 在 C 点右边且 CD ＝1，求当 AC +CD +DB 的最小值和此时 C 点的坐标；10. 点 C 为∠AOB 内一点．（1）在 OA 求作点 D ，OB 上求作点 E ，使△CDE 的周长最小，请画出图形；（2）在（1）的条件下，若∠AOB ＝30°，OC ＝10，求△CDE 周长的最小值和此时∠DCE 的度数．A- 5 -yBA OxyBA OxCO BAF11．（1）如图①，△ABD 和△ACE 均为等边三角形，BE 、CE 交于 F ，连 AF ，求证：AF +BF +CF ＝CD ；（2）在△ABC 中，∠ABC ＝30°，AB ＝6，BC ＝8，∠A ，∠C 均小于 120°，求作一点 P ，使 PA +PB +PC 的值最小，试求出最小值并说明理由．DEBC① ①① ①12．荆州护城河在 CC ＇处直角转弯，河宽相等，从 A 处到达 B 处，需经过两座桥 DD ＇、EE ＇，护城河及两桥都是东西、南北方向，桥与河岸垂直．如何确定两座桥的位置，可使 A 到 B 点路径最短？- 6 -- 7 -“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

人教版八年级数学上册课题学习《最短路径问题》课后作业

13.4 《最短路径问题》课后作业
1、问题：如图所示，要在街道旁修建一个奶站，向居民区A、B提供牛奶，奶站应建在什么地方，才能使从A、B到它的距
离之和最短．
2.如图，牧童在A处放马，其家在B处，A、B到河岸的距离分别为AC和BD，且AC=BD，若点A到河岸CD的中点的距离为500米，则牧童从A处把马牵到河边饮水再回家，最短距离是多少米？
3.如图，小河边有两个村庄A，B，要在河边建一自来水厂向
A村与B村供水．
(1)若要使厂部到A ，B 村的距离相等，则应选择在哪建厂？
(2)若要使厂部到A ，B 两村的水管最短，应建在什么地方？
4、如图,P,Q 是△ABC 边AB,AC 上的两定点,在BC 上求作一
点M,使△PMQ 的周长最短.
5、如图，在矩形ABCD 中，AB=10 , BC=5 . 若点M 、
N A
B C
分别是线段AC、AB上的两个动点，则BM+MN的最小值为
（）
A.10
B. 8
C. 5
D. 6。

八年级数学上册课题学习最短路径问题新版新人教版

(河边饮马问题)如图所示,牧马人从A地出发,到一条笔直的河边L饮马,然后到B地 .牧马人到河边的什么地方饮马,可使所走的路径最短?
第3页/共16页
如果点A和点B分别位于直线l的异侧,如何在直线l上找到一点,使得这个点到点A和点B的距离的和最短?
连接AB,与直线l相交于一点,根据“两点之间 ,线段最短”,可知这个交点即为所求.
∴∠PAB=∠PBA,∴PA=PB.
PB=PA
D.
教材第91页复习题13第15题.
点即为所求,证明时要
利用三角形三边的关如图图中所实示线,表直示线铺m表设示的一管条道河,则,点所M需,管N表道示最两短个的村方庄案,B是欲'在m(上的某) 处修建一个给水站,向两个村庄供水,现有如图所示的四种铺设管道的方案,
短”来求线段和的最小值,从而解决最短 (造桥选址问题)如图所示,A 和B 两地在一条河的两岸,现要在河上造一座桥MN. 所以AM+MN+NB<AM'+M'N'+N'B.
AC+CB<AC'+C'B? 如果点A和点B分别位于直线l的异侧,如何在直线l上找到一点,使得这个点到点A和点B的距离的和最短?
∴∠PAB=∠PBA,∴PA=PB.
对称的知识转化,利用“两点之间,线段最
【总结方法】找出解析:如图所示,作点A关于直线l的对称点A',连接A'B,与直线l的交点即为使PA+PB取得最小值的点P.
如果点A和点B位于直线l 的同侧,如何在直线l上找到一点,使得这个点到点A和点B的距离的和最短?
所以A'N+NB<AM'+N'B.

「精品」八年级数学暑假作业第12天最短路径问题新人教版

第12天最短路径问题典例在线如图，草原上两个居民点A、B在河流l的同旁，一汽车从A出发到B，途中需要到河边加水．汽车在哪一点加水，可使行驶的路程最短？在图上画出该点．【参考答案】作A关于l的对称点A′，连A′B交l于C点，则C为所求的点．如图所示：汽车在C点加水，可使行驶的路程最短．【试题解析】①作A关于直线l的对称点A′；②连接A′B交直线l于点C，则点C即为所求点．汽车在C点加水，可使行驶的路程最短．【解题必备】1．解题总思路：找点关于线的对称点实现“折”转“直”，利用平移把“折”转“直”，利用平面展开图把“折”转“直”．2．理论依据：两点之间线段最短，垂线段最短，点关于线对称，线段的平移，立体图形展开图．3．最短路径常见问题解决方法：（1）运用轴对称解决距离最短问题：利用对称的性质，通过等线段代换，将所求路线长转化为两定点之间的距离．基本思路是运用轴对称及两点之间线段最短的性质，将所求线段之和转化为一条线段的长，不论题目如何变化，运用时要抓住直线同旁有两点，这两点到直线上某点的距离和最小这个核心，所有作法都相同．注意：利用轴对称解决最值问题应注意题目要求，根据轴对称的性质，利用三角形的三边关系，通过比较来说明最值问题是常用的一种方法．解决这类最值问题时，要认真审题，不要只注意图形而忽略题意要求，审题不清导致答非所问．（2）利用平移确定最短路径选址：通过平移，除去固定部分的长，使其余几段的和正好为两定点之间的距离．选址问题的关键是把各条线段转化到一条线段上．当两点在一条直线的同侧时，过两点的直线与原直线的交点处构成线段的差最大，当两点在一条直线的异侧时，过两点的直线与原直线的交点处构成的线段的和最小，都可以用三角形三边关系来推理说明，通常根据最大值或最小值的情况取其中一个点的对称点来解决．解决连接河两岸的两个点的最短路径问题时，可以通过平移河岸的方法使河的宽度变为零，转化为求直线异侧的两点到直线上一点所连线段的和最小的问题．（3）利用展开图求立体图形表面上小虫爬行的最短路线问题：通过展开立体图形的表面或侧面，化立体为平面，化曲线或折线为直线，利用两点之间线段最短解决问题．（4）长方体问题：①将右侧面展开与下底面在同一平面内，求得其路程；②将前表面展开与上表面在同一平面内，求得其路程；③将上表面展开与左侧面在同一平面内，求得其路程．然后进行比较大小，即可得到最短路程．（5）在圆锥中，可将其侧面展开求出最短路程．试题推荐1．已知直线l同旁的两点A、B，在l上求一点P，使PA＋PB最小，则求P点的作法正确的为A．作A关于l的对称点A′，连接A′B交l与PB．AB的延长线与l交于PC．作A关于l的对称点A′，连接AA′交l与PD．以上都不对2．如图，正△ABC的边长为2，过点B的直线l⊥AB，且△ABC与△A′BC′关于直线l对称，D为直线l 上一动点，则AD+CD的最小值是A．4 B．C．D．3．如图，∠AOB=30°，∠AOB内有一定点P，且OP=10．在OA上有一点Q，OB上有一点R．若△PQR周长最小，则最小周长是A．10 B．15 C．20 D．304．如图，在锐角△ABC中，AB=6，∠BAC=60°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是A．3 B．C．D．65．知∠MON=40°，P为∠MON内一定点，OM上有一点A，ON上有一点B，当△PAB的周长取最小值时，求∠APB的度数．参考答案1．A 【解析】首先找出其中一点关于直线的对称点，然后连接对称点和另一个点与直线的交点就是点P 的位置．2．C 【解析】连接CC ′，连接A ′C 交l 于点D ，连接AD ，此时AD +CD 的值最小，如图所示．∵△ABC 与△A ′BC ′为正三角形，且△ABC 与△A ′BC ′关于直线l 对称，∴四边形CBA ′C ′为边长为2的菱形，且∠BA ′C ′=60°，∴AD +CD =A ′D +CD =A ′C A ′B ．∵OA 是PE 的垂直平分线，∴EQ =QP ；同理，OB 是PF 的垂直平分线，∴FR =RP ，∴△PQR 的周长为EF ．∵OE =OF =OP =10，且∠EOF =∠EOP +∠POF =2θ+2（30°–θ）=60°，∴△EOF 是正三角形，∴EF =10，即在OP =10的条件下，△PQR 的最小周长为10．故选A ．4．B 【解析】在AC 上取一点E ，使得AE =AB ，过E 作EN ⊥AB 于N ′，交AD 于M ，连接BM ，BE ，BE 交AD于O ，则BM +MN 最小（根据两点之间线段最短；点到直线垂直距离最短），∵AD 平分∠CAB ，AE =AB ，∴EO =OB ，AD ⊥BE ，∴AD 是BE 的垂直平分线（三线合一），∴E 和B 关于直线AD 对称，∴EM =BM ，即BM +MN ′=EM +MN ′=EN ′，∵EN ′⊥AB ，∴∠ENA =90°，∵∠CAB =60°，∴∠AEN ′=30°，∵AE =AB =6，∴AN =12AE =3，EN =BM +MN 的最小值是B ．5．100°【解析】分别作点P关于OM、ON的对称点P′、P″，连接OP′、OP″、P′P″，P′P″交OM、ON于点A、B，连接PA、PB，此时△PAB周长的最小值等于P′P″．善于思考，勤于总结！。

人教版八年级数学讲义最短路径问题(含解析)

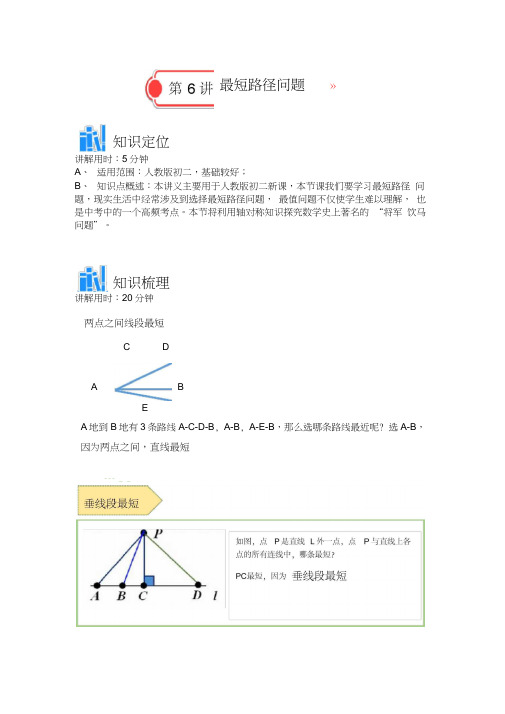
最短路径问题»知识定位讲解用时：5分钟A、适用范围：人教版初二，基础较好；B、知识点概述：本讲义主要用于人教版初二新课，本节课我们要学习最短路径问题，现实生活中经常涉及到选择最短路径问题，最值问题不仅使学生难以理解，也是中考中的一个高频考点。

本节将利用轴对称知识探究数学史上著名的“将军饮马问题”。

知识梳理讲解用时：20分钟两点之间线段最短C DA BEA地到B地有3条路线A-C-D-B, A-B, A-E-B，那么选哪条路线最近呢? 选A-B，因为两点之间，直线最短--- _ _两点在一条直线异侧相传，古希腊亚历山大里亚城里有一位久负盛名的学者，名叫海伦.有一天，位将军专程拜访海伦，求教一个百思不得其解的问题：从图中的A地出发，到一条笔直的河边I饮马，然后到B地•到河边什么地方饮马可使他所走的路线全程最短？两点在一条直线同侧作法：1、作B点关于直线L的对称点B'2、连接AB'交直线L于点C;3、点C即为所求.证明：在直线L上任意选一点C'（点C不与C重合），连接AC、BC、B' C'.在厶AB' C'中，AC +B' C' > AB'••• AC +BC > AC+BC所以AC+BC最短.【例题1】已知点A,点B都在直线I的上方，试用尺规作图在直线I上求作一点P,使得PA+PB勺值最小，则下列作法正确的是（）【答案】D【解析】根据作图的方法即可得到结论.解：作B关于直线I的对称点，连接这个对称点和A交直线I于P,则PA+PB勺值最小，••• D的作法正确，故选：D.讲解用时：3分钟解题思路：本题考查了轴对称-最短距离问题，熟练掌握轴对称的性质是解题的关键. 教学建议：学会处理两点在直线同侧的最短距离问题.难度：3 适应场景：当堂例题例题来源：无年份：2018【练习1.1】如图，直线L是一条河，P，Q是两个村庄.欲在L上的某处修建一个水泵站, 向P，Q 两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（）【答案】D【解析】利用对称的性质，通过等线段代换，将所求路线长转化为两定点之间的距离.解：作点P关于直线L的对称点P',连接QP交直线L于M根据两点之间，线段最短，可知选项D铺设的管道，则所需管道最短.故选：D.讲解用时：3分钟解题思路：本题考查了最短路径的数学问题.这类问题的解答依据是“两点之间, 线段最短”.由于所给的条件的不同，解决方法和策略上又有所差别.教学建议：学会处理两点在直线同侧的最短距离问题.难度：3 适应场景：当堂练习例题来源：无年份：2018【练习1.2 ］如图，A、B在直线I的两侧，在直线I上求一点P,使|PA-PB|的值最大.B【答案］见解析【解析］作点A关于直线I的对称点A'，则PA=PA，因而|PA- PB|=|PA'-PB|，则当A', B、P在一条直线上时，|PA- PB |的值最大.解：作点A关于直线I的对称点A'，连A B并延长交直线I于P.讲解用时：3分钟解题思路：本题考查的是作图-轴对称变换，熟知“两点之间线段最短”是解答此题的关键.教学建议：学会作对称点，通过“两点之间线段最短”进行解题•难度：4 适应场景：当堂练习例题来源：无年份：2018【例题2】如图，A、B在直线I的同侧，在直线I上求一点巳使厶PAB的周长最小.【答案】【解析】由于△ PAB的周长=PA+AB+P，而AB是定值，故只需在直线I上找一点P,使PA+PB最小.如果设A关于I的对称点为A',使PA+PB最小就是使PA +PB最小. 解：作法：作A关于I的对称点A'，连接A B交I于点P.则点P就是所要求作的点；理由：在I上取不同于P的点P',连接AP、BP .••• A和A关于直线I对称，••• PA=PA，P' A=P A，而 A ' P+BP^ A P' +BP••• PA+B R AP' +BP••• AB+AP+B R AB+AP +BP即厶ABP周长小于△ ABP周长.讲解用时：3分钟解题思路：本题考查了轴对称-最短路线问题解这类问题的关键是把两条线段的和转化为一条线段，运用三角形三边关系解决.教学建议：把三角形的周长用线段表示出来，通过转化成一条线段利用两点之间线段最短进行解题•难度：3 适应场景：当堂例题例题来源：无年份：2018【练习2.1 ］(I)如图①，点A、B在直线I两侧，请你在直线I上画出一点P,使得PA+PB 的值最小；(U)如图②，点E、F在直线I同侧，请你在直线I上画出一点P,使得PE+PF 的值最小；(川)如图③，点MN在直线I同侧，请你在直线I上画出两点OP,使得0P=1cm 且MO+OP+P的值最小.(保留作图痕迹，不写作法)【答案］见解析【解析］(I )图①，显然根据两点之间，线段最短，连接两点与直线的交点即为所求作的点；(II )图2,作E关于直线的对称点，连接FE'即可；(III )图③，画出图形，作N的对称点N',作NQ/直线I ， NQ=1cm连接MQ得出点0即可.解：（I）如图①，连接A、B两点与直线的交点即为所求作的点P,这样PA+PB 最小，理由是：两点之间，线段最短；（II ）如图②，先作点E关于直线I的对称点E'，再连接E' F交I于点P,则PE+PF=E P+PF=E F,由“两点之间，线段最短”可知，点P即为所求的点；作N关于直线I的对称点N',过N'作线段N Q//直线I，且线段N Q=1cm连接MQ交直线I于O,在直线I上截取0P=1cm如图，连接NP,则此时MO+OP+PN值最小.讲解用时：5分钟解题思路：本题考查了轴对称-最短路线问题的应用, 题目比较典型，第三小题有一定的难度，主要考查学生的理解能力和动手操作能力.教学建议：学会作对称点，通过“两点之间线段最短”进行解题• 难度：4 适应场景：当堂练习例题来源：无年份：2018【例题3】如图，等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC, AB边于E, F点.若点D为BC边的中点，点M为线段EF上一动点，求△ CDM周长的最小值.【答案】10【解析】连接AC ，由于△ ABC 是等腰三角形，点D 是BC 边的中点，故AD 丄BC ，再根据三角形的面积公式求出 AD 的长，再再根据EF 是线段AC 的垂直平分线可知，点C 关于直线EF 的对称点为点A ,故AD 的长为CM+M 的最小值，由此即可得出结论.解：连接AD •••△ ABC 是等腰三角形，点D 是BC 边的中点,• ADL BC,• - S A AB =j-BC?AD=- ••• EF 是线段AC 的垂直平分线,•••点C 关于直线EF 的对称点为点A,••• AD 的长为CM+M 的最小值，解题思路：本题考查的是轴对称-最短路线问题，熟知等腰三角形三线合一的性质是解答此题的关键.教学建议：想办法利用对称的知识将两条线段转化成一条线段，利用垂线段最短进行解题.难度：4适应场景：当堂例题例题来源：无年份：2018【练习3.1 ]如图，已知点D 点E 分别是等边三角形 ABC 中BC AB 边的中点，AD=5点F 是AD 边上的动点，求BF+EF 的最小值.【答案】5X 4X AD=16 解得AD=8X4=8+2=10.【解析】过C 作CEL AB 于E ,交AD 于F ,连接BF,贝U BF+EF 最小，证△ ADB ◎ △ CEB 得 CE=AD=,即 BF+EF=5解：过C 作CEL AB 于E ,交AD 于 F ,连接BF,则BF+EF 最小（根据两点之间线段最短；点到直线垂直距离最短），由于C 和B 关于AD 对称，则BF+EF=CF •••等边△ ABC 中, BD=CD••• ACL BC,••• AD 是 BC 的垂直平分线（三线合一）,••• C 和B 关于直线AD 对称，••• CF=BF即 BF+EF=CF+EF=CE••• AD L BC, CEL AB•••/ ADB 2 CEB=90 ,在厶 ADB?3 CEB 中,ZADB=ZCEBZABD=ZCBE ,AB=CB•••△ ADB^A CEB （AAS ,CE=AD=5即 BF+EF=5讲解用时：4分钟解题思路：本题考查的是轴对称-最短路线问题，涉及到等边三角形的性质，轴对称的性质，等腰三角形的性质、全等三角形的判定和性质等知识点的综合运用.教学建议：想办法利用对称的知识将两条线段转化成一条线段，利用垂线段最短进行解题•难度：4 适应场景：当堂练习例题来源：无年份：2018[【例题4】如图所示，在一条河的两岸有两个村庄，现要在河上建一座小桥，桥的方向与河流垂直，设河的宽度不变，试问：桥架在何处，才能使从A到B的距离最短？【答案】见解析【解析】虽然A、B两点在河两侧，但连接AB的线段不垂直于河岸•关键在于使AP+BD最短，但AP与BD未连起来，要用线段公理就要想办法使P与D重合起来，利用平行四边形的特征可以实现这一目的.解：如图，作BB'垂直于河岸GH使BB等于河宽，连接AB，与河岸EF相交于P,作PDL GH贝U PD// BB且PD=BB，于是PDBB为平行四边形，故PB =BD根据“两点之间线段最短” ，AB最短，即AP+BD最短.讲解用时：4分钟解题思路：此题考查了轴对称 —— 最短路径问题，要利用“两点之间线段最短”，但许多实际问题没这么简单，需要我们将一些线段进行转化，即用与它相等的线段替代，从而转化成两点之间线段最短的问题•目前，往往利用对称性、平行四边形的相关知识进行转化，以后还会学习一些线段转化的方法.教学建议：将3条线段进行转化成一条线段•难度：4 适应场景：当堂例题例题来源：无年份：2018【练习4.1 ］作图题(1) 如图1, 一个牧童从P 点出发，赶着羊群去河边喝水，则应当怎样选择饮水路线，才能使羊群走的路程最短？请在图中画出最短路线.(2) 如图2,在一条河的两岸有A ，B 两个村庄，现在要在河上建一座小桥，桥的方向与河岸方向垂直，桥在图中用一条线段 CD 表示•试问：桥CD 建在何处，才能使A 至U B 的路程最短呢？请在图中画出桥CD 的位【答案］见解析【解析］(1)把河岸看做一条直线, 段最短的性质即可解决问题.(2)先确定AA =CD 且AA // CD 连接BA ，与河岸的交点就是点 C,过点 C 作CD 垂直河岸，交另一河岸于点 D, CD 就是所求的桥的位置.解：(1)根据垂直线段最短的性质，即可画出这条从草地到河边最近的线路，如图1所示：利用点到直线的所有连接线段中，垂直线(2)先确定AA =CD且AA // CD连接BA，与河岸的交点就是点C,过点C作CD垂直河岸，交另一河岸于点D, CD就是所求的桥的位置•如图2,讲解用时：4分钟解题思路：此题考查了垂直线段最短的性质的在解决实际问题中的灵活应用，解题的关键是灵活运用垂直线段最短的性质作图.教学建议：掌握求最短路径的几种基本题型和方法.难度：3 适应场景：当堂练习例题来源：无年份：2018【例题5】如图，MN是等边三角形ABC的一条对称轴，D为AC的中点，点P是直线MN上的一个动点，当PC+PD最小时，/ PCD勺度数是多少？【答案】30°【解析】由于点C关于直线MN勺对称点是B,所以当B P、D三点在同一直线上时，PC+PD勺值最小解：连接PB.由题意知，••• B、C关于直线MN对称，••• PB=PC••• PC+PD=PB+PD当B、P、D三点位于同一直线时，PC+PDR最小值，连接BD交MN于P,•••△ ABC是等边三角形，D为AC的中点，••• BDL AC,••• PA=PC•••/ PCD M PAD=30讲解用时：3分钟解题思路：此题考查了线路最短的问题、等边三角形的性质等知识，解题的关键是学会利用轴对称解决最短问题，属于中考常考题型.教学建议：学会转移对称线段，利用垂线段最短进行解题•难度：3 适应场景：当堂例题例题来源：无年份：2018【练习5.1 ］已知，如图△ ABC为等边三角形，高AH=10cmP为AH上一动点，D为AB的中点，则PD+PB勺最小值为多少？【答案］10cm【解析］连接PC,根据等边三角形三线合一的性质，可得PC=BP PD+PB要取最小值，应使 D P、C三点一线.解：连接PC，•••△ ABC为等边三角形，D为AB的中点，••• PD+PB勺最小值为：PD+PB=PC+PD=CD=AH=10cm解题思路：此题主要考查有关轴对称--最短路线的问题，注意灵活应用等边三角形的性质.教学建议：学会转移对称线段，利用垂线段最短进行解题难度：3 适应场景：当堂练习例题来源：无年份：2018【例题6】如图，/ AOB 勺内部有一点P ,在射线OA OB 边上各取一点P i , B ，使得△ PRB，保留作图痕迹.【解析】作点P 关于直线OA 的对称点E ,点P 关于直线OB 的对称点F ，连接理由：••• RP=PE , RP=PF,EF 交OA 于P i ，交OB 于P 2, 连接PP , PR , △ PPP 2即为所求.解：如图，作点P 关于直线 EF 交OA 于P i ,交OB 于P 2, OA 的对称点E, 连接PP , PR , 点P 关于直线OB 的对称点F ,连接 △ PPP 2即为所求.R,叙述作图过程（作法）【答案】见解析:.△ PRF2 的周长=PR+PF2+PP=ER+p i p2+p2F=EF,根据两点之间线段最短，可知此时△ PPP2的周长最短.讲解用时：5分钟解题思路：本题考查轴对称-最短问题、两点之间线段最短等知识，解题的关键是学会利用对称解决最短问题，属于中考常考题型.教学建议：此类问题的解题技巧是做对称点，做定点关于动点所在直线的对称点• 难度：4适应场景：当堂例题例题来源：无年份：2018【练习6.1 ］知识拓展：如图2,点P在/AOB内部，试在OA 0B上分别找出两点E、F,使△ PEF周长最短（保留作图痕迹不写作法）【答案］见解析【解析］作P关于OA 0B的对称点C D,连接CD角OA 0B于E、F.此时△PEF周长有最小值；作图如下：解题思路：题主要考查了平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识，根据已知得出对称点的位置是解题关键.教学建议：此类问题的解题技巧是做对称点，做定点关于动点所在直线的对称点难度：4 适应场景：当堂练习例题来源：无年份：2018【例题7】如图，/ AOB=30，点P是/AOB内一点，PO=8在/ AOB勺两边分别有点R、Q （均不同于O）,求厶PQF周长的最小值.【答案】【解析】根据轴对称图形的性质，作出P关于OA OB的对称点M N,连接MN 根据两点之间线段最短得到最小值线段，根据等边三角形的性质解答即可.解：分别作P关于OA OB的对称点M N.连接MN交OA OB交于Q 尺则厶PQF符合条件.连接OM ON由轴对称的性质可知，OM=ON=OR=8/ MON H MOP主NOP=Z AOB=Z3O° =60°,则A MO为等边三角形，••• MN=8••• QP=QMRN=RP讲解用时：5分钟解题思路：本题考查了轴对称-最短路径问题，根据轴对称的性质作出对称点是解题的关键，掌握线段垂直平分线的性质和等边三角形的性质的灵活运用.教学建议：对称之后，角度也是相同的，做定点关于动点所在直线的对称点.难度：4 适应场景：当堂例题例题来源：无年份：2018【练习7.1 ］如图，/ AOB=30，/ AOB内有一定点P,且OP=10 0A上有一点Q, 0B上有一定点只若厶PQR周长最小，求它的最小值.【答案］10【解析］先画出图形，作PM L 0A与0A相交于M并将PM延长一倍到E,即ME=PM作PN!0B与0B相交于N,并将PN延长一倍到F,即NF=PN连接EF与0A相交于Q,与0B相交于R,再连接PQ PR则厶PQR即为周长最短的三角形.再根据线段垂直平分线的性质得出△ PQR=EF再根据三角形各角之间的关系判断出△ E0F的形状即可求解.解：设/ P0A羽，则/ P0B=30 作PML0A与0A相交于M,并将PM延长一倍至U E, 即卩ME=P M作PN10B与0B相交于N,并将PN延长一倍到F, 即卩NF=PN连接EF与0A相交于Q,与0B相交于R,再连接PQ PR则A PQR即为周长最短的三角形.v 0A是PE的垂直平分线，••• EQ=QP同理，0B是PF的垂直平分线，••• FR=RP•••△ PQR勺周长=EF.v 0E=0F=0P=1（且/ E0F M E0P# P0F=2） +2（30°-9）=60°,•••△ EOF是正三角形，••• EF=10即在保持0P=1（的条件下△ PQR勺最小周长为10.作出各点的对称点，即把求三角形周长的问题转化为求线段的长解答. 教学建议：做定点关于动点所在直线的对称点，利用轴对称的性质进行解题难度：4 适应场景：当堂练习例题来源：无年份：2018 课后作业【作业11如图，在铁路I 的同侧有A 、B 两个工厂，要在铁路边建一个货场 C,货场应建在什么地方，才能使A 、B 两厂到货场C 的距离之和最短？A * J«【答案1见解析【解析1作点B 关于直线I 的对称点B'，连接AB ，交I 于点C,则点C 即为所求点.解：如图所示：A\ ・1 ■■i I—'讲解用时：3分钟【作业2】解答此类题目的关键根据轴对称的性质难度：3 适应场景：练习题例题来源：无年份：2018故答案为：10.用三角板和直尺作图.(不写作法，保留痕迹)如图，点A, B在直线I的同侧.(1)试在直线I上取一点M使MA+M的值最小.(2)试在直线I上取一点N,使NB- NA最大.--------------------------------- 1【答案】见解析【解析】(1)作点A关于直线I的对称点，再连接解答即可；(2)连接BA延长BA交直线I于N,当N即为所求；解：(1)如图所示：「/___ 7；/M*(2)如图所示；*----- z理由：••• NB- NAC AB•••当A、B、N共线时，BN- NA的值最大.讲解用时：3分钟难度：3 适应场景：练习题例题来源：无年份：2018【作业3】如图，已知点D点E分别是等边三角形ABC中BC AB边的中点，AD=6点F 是AD 边上的动点，求BF+EF的最小值.【答案】6【解析】过C作CEL AB于E,交AD于F,连接BF,贝U BF+EF最小，证△ ADB ◎△ CEB得CE=AD=,即BF+EF=6解：过C作CEL AB于E,交AD于F,连接BF,则BF+EF最小（根据两点之间线段最短；点到直线垂直距离最短），由于C和B关于AD对称，则BF+EF=CF•••等边△ ABC中, BD=CD••• ADL BC,••• AD是BC的垂直平分线（三线合一）,••• C和B关于直线AD对称，••• CF=BF即BF+EF=CF+EF=CE••• ADL BC, CEL AB•••/ ADB2 CEB=90 ,在厶ADB?3 CEB中,fZAEB=ZCEB••• Z 阳XZCBE,I AB=CB•••△ ADB^A CEB（AAS ,••• CE=AD=6即BF+EF=6.讲解用时：3分钟难度：3 适应场景：练习题例题来源：无年份：2018【作业4】如图，点P是/ AOB内部的一点，/ AOB=30 , 0P=8cm M N是OA OB上的两个动点，则求△ MPN周长的最小值？【答案】8【解析】设点P关于0A的对称点为C,关于0B的对称点为D,当点M N在CD 上时，△ PMN勺周长最小.解：分别作点P关于OA 0B的对称点C D,连接CD分别交OA 0B于点M N, 连接OR OC OD PM PN•••点P关于0A的对称点为C,关于0B的对称点为D,••• PM=CMOP=OC / COA N POA•••点P关于0B的对称点为D,••• PN=DN OP=OD / DOB N POB••• OC=OD=OP=8cmZ COD N COA+Z POA+N POB+N DOB=N POA+2/ POB=2/ AOB=60 ,•••△ COD!等边三角形，CD=OC=OD=8cm•••△ PMN勺周长的最小值=PM+MN+PN=CM+MNCD=8cm故答案为：8.讲解用时：3分钟难度：4 适应场景：练习题例题来源：无年份：2018。

暑假作业第12天一次函数行程问题解答类(1) 人教版八年级下册

人教版8下暑假作业第12天一次函数行程问题解答类11.一天，小明从家出发匀速步行去学校上学.几分钟后，在家休假的爸爸发现小明忘带数学书，于是爸爸立即匀速跑步去追小明，爸爸追上小明后以原速原路跑回家.小明拿到快步赶往学校，并在从家出发23分钟后到校(小明被爸爸追上时交流的书后以原速的54时间忽略不计).两人之间相距的路程y(米)与小明从家出发到学校的步行时间x(分)之间的函数关系如图所示．(1)16分钟时，小明离家的距离为米;(2)设小明原先的速度为a米/分，加快速度以后的速度为，0∼11分钟小明走过的距离为，11∼16分钟小明走过的距离为;(用含a的式子表示)(3)建立方程解出(2)中的a，并说明学校距离家的距离;(4)求出爸爸追小明的速度．2.在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上，食堂离宿舍0.7km，图书馆离宿舍1km.周末，小亮从宿舍出发，匀速走了7min到食堂；在食堂停留16min吃早餐后，匀速走了5min到图书馆；在图书馆停留30min借书后，匀速走了10min返回宿舍．给出的图象反映了这个过程中小亮离宿舍的距离y km与离开宿舍的时间x min之间的对应关系．请根据相关信息，解答下列问题：(1)填表：(2)填空：①食堂到图书馆的距离为________km；②小亮从食堂到图书馆的速度为________km/min；③小亮从图书馆返回宿舍的速度为________km/min；④当小亮离宿舍的距离为0.6km时，他离开宿舍的时间为________min．(3)当0≤x≤28时，请直接写出y关于x的函数解析式．3.小泽和小帅两同学分别从甲地出发，骑自行车沿同一条路到乙地参加社会实践活动.如图，折线OAB和线段CD分别表示小泽和小帅离甲地的距离y(单位：千米)与时间x(单位：小时)之间函数关系的图象.根据图中提供的信息，解答下列问题：(1)小帅的骑车速度为千米/时;点C的坐标为;(2)求线段AB对应的函数表达式;(3)当小帅到达乙地时，小泽距乙地还有多远⋅4.在一条笔直的公路上有A、B两地，甲从A地去B地，乙从B地去A地然后立即原路返回B地，返回时的速度是原来的2倍，如图是甲、乙两人离B地的距离y(千米)和时间x(小时)之间的函数图象．请根据图象回答下列问题：(1)A、B两地的距离是______千米，a=______；(2)求P的坐标，并解释它的实际意义；(3)请直接写出当x取何值时，甲乙两人相距15千米．5.甲、乙两人开车匀速从同一地点到距离出发地480千米处的景点旅游，甲出发半小时后，乙以每小时80千米的速度沿同一路线行驶，两车分别到达目的地后停止．甲、乙两车之间的距离y(千米)与甲车行驶的时间x(小时)之间的函数关系如图所示．(1)甲行驶的速度是______千米/小时．(2)求乙车追上甲车后，y与x之间的函数关系式，并写出自变量x的取值范围．(3)求甲车出发多长时间两车相距75千米．6.甲、乙两车分别从A，B两地同时出发，沿同一条公路相向行驶，相遇后，甲车继续以原速行驶到B地，乙车立即以原速原路返回到B地．甲、乙两车距B地的路程y(km)与各自行驶的时间x(ℎ)之间的关系如图所示．(1)m=______，n=______；(2)求乙车距B地的路程y关于x的函数解析式，并写出自变量x的取值范围；(3)当甲车到达B地时，求乙车距B地的路程．7.爷爷和他的孙子小明星期天一起去爬山．来到山脚下，小明让爷爷先上山，然后追赶爷爷，如图所示，两条线段分别表示小明和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(小明开始爬山时开始计时)，请看图回答下列问题：(1)爷爷比小明先上了______米，山顶离山脚______米．(2)写出图中两条线段的交点表示的实际意义______．(3)小明在爬山过程中何时与爷爷相距20米？8.在一条笔直的公路上依次有A、C、B三地，甲、乙两人同时出发，甲从A地骑自行车匀速去B地，途经C地时因事停留1分钟，继续按原速骑行至B地，甲到达B地后，立即按原路原速返回A地；乙步行匀速从B地至A地.甲、乙两人距A地的距离y(米)与时间x(分)之间的函数关系如图所示，请结合图象解答下列问题：(1)甲的骑行速度为______ 米/分，点M的坐标为______ ；(2)求甲返回时距A地的距离y(米)与时间x(分)之间的函数解析式(不需要写出自变量的取值范围)；(3)请直接写出两人出发后，在甲返回到A地之前，______ 分钟时两人距C地的距离相等．9.已知A、B两地相距4800米，甲从A地出发步行到B地，20分钟后乙从B地出发骑自行车到A地，设甲步行的时间为x分钟，甲、乙两人离A地的距离分别为y1米、y2米，y1、y2与x的函数关系图象如图所示，根据图象解答下列问题：(1)直接写出y1、y2与x的函数关系式，并写出自变量x的取值范围；(2)求甲出发后多少分钟两人相遇，相遇时乙离A地多少米？10.小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min.小东骑自行车以300m/min的速度直接回家，两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示．(1)家与图书馆之间的路程为______m，小玲步行的速度为______m/min；(2)求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；(3)求两人相遇的时间．11.某风景区内的公路如图1所示，景区内有免费的班车，从入口处出发，沿该公路开往草甸，途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车，以后每隔10分钟有一班车从入口处发车．小聪周末到该风景区游玩，上午7：40到达入口处，因还没到班车发车时间，于是从景区入口处出发，沿该公路步行25分钟后到达塔林．离入口处的路程y(米)与时间x(分)的函数关系如图2所示．(1)求第一班车离入口处的路程y(米)与时间x(分)的函数表达式．(2)求第一班车从入口处到达塔林所需的时间．(3)小聪在塔林游玩40分钟后，想坐班车到草甸，则小聪最早能够坐上第几班车？如果他坐这班车到草甸，比他在塔林游玩结束后立即步行到草甸提早了几分钟？(假设每一班车速度均相同，小聪步行速度不变)12.周老师为锻炼身体一直坚持步行上下班．已知学校到李老师家总路程为2000米．一天，周老师下班后，以45米/分的速度从学校往家走，走到离学校900米时，正好遇到一个朋友，停下又聊了半小时，之后以110米/分的速度走回了家．周老师回家过程中，离家的路程S(米)与所用时间t(分)之间的关系如图所示．(1)求a的值．(2)b=______；c=______．(3)求周老师从学校到家的平均速度．13.一辆货车从甲地到乙地，一辆轿车从乙地到甲地，两车沿同一条公路分别从甲、乙两地同时出发，匀速行驶.已知轿车比货车每小时多行驶20km.两车相遇后休息一段时间，再同时继续行驶.两车之间的距离y(km)与货车行驶时间x(ℎ)之间的函数图象如图所示的折线AB−BC−CD−DE，结合图象回答下列问题：(1)甲、乙两地之间的距离是______ km；(2)求两车的速度分别是多少km/ℎ？(3)求线段CD的函数关系式.直接写出货车出发多长时间，与轿车相距20km？14.已知A、B两地相距240km，一辆货车从A前往B地，途中因装载货物停留一段时间.一辆轿车沿同一条公路从B地前往A地，到达A地后(在A地停留时间不计)立即原路原速返回.如图是两车距B地的距离y(km)与货车行驶时间x(ℎ)之间的函数图象，结合图象回答下列问题：(1)图中m的值是______ ；轿车的速度是______ km/ℎ；(2)求货车从A地前往B地的过程中，货车距B地的距离y(km)与行驶时间x(ℎ)之间的函数关系式；(3)直接写出轿车从B地到A地行驶过程中，轿车出发多长时间与货车相距12km？15.A，B两城市之间有一条公路相连，公路中途穿过C市，甲车从A市到B市，乙车从C市到A市，甲车的速度比乙车的速度慢20千米/小时，两车距离C市的路程y(单位：千米)与行驶的时间t(单位：小时)的函数图像如图所示，结合图像信息，解答下列问题：(1)甲车的速度是千米/小时，在图中括号内填入正确的数;(2)求图像中线段MN所在直线的函数解析式，不需要写出自变量的取值范围;(3)直接写出甲车出发后几小时，两车距C市的路程之和是460千米．16.四川省正在打造“世界最长城市中轴线”天府大道北延线德阳段，现甲乙两工程队共同承包德阳段中A，B两地之间的道路，两队分别从A，B两地相向修建．已知甲队先施工3天，乙队才开始施工，乙队施工几天后因另有紧急任务暂停施工，因考虑工期，由甲队以原速的2倍修建，乙队完成紧急任务后又以原速恢复施工，直到道路修通．甲，乙两队各自修路长度与时间之间的关系如图所示，请结合图中信息解答下列问题：(1)试问：在施工的过程中，甲队在提速前每天修道路多少米？(2)求乙队中途暂停施工的天数；(3)求A，B两地之间的道路长度．17.如图1，小刚家、学校、图书馆在同一条直线上，小刚骑自行车匀速从学校到图书馆，到达图书馆还完书后，再以相同的速度原路返回家中(上、下车时间忽略不计).小刚离家的距离y(m)与他所用的时间x(min)的函数关系如图2所示．(1)小刚家与学校的距离为______ m，小刚骑自行车的速度为______ m/min；(2)求小刚从图书馆返回家的过程中，y与x的函数表达式；(3)小刚出发35分钟时，他离家有多远？18.党的十八大以来，文山路网建设进展迅速.实现了县县通等级公路和州府通高速公路的目标.小明和爸爸为了体验高铁出行，假期间爸爸带小明从家驾车到普者黑火车站乘高铁前往昆明，他们离家的距离y(km)与出发时间t(ℎ)之间的关系如图所示．(1)小明家离普者黑火车站______ km．(2)从图中可以看出，小明和爸爸在普者黑火车站取票、检票、候车共用了______ ℎ.(3)高铁平均速度为201km/ℎ，请你计算出普者黑火车站到昆明需要多少时间？。

人教版数学八年级上册最短路径问题

原理
牧马人饮马问题
线段公理和垂线段最短轴对称知识+线段公理
人教版数学八年级上册最短路径问题
人教版数学八年级上册最短路径问题
新知应用
例2 如图，在直角坐标系中，点A，B的坐标分别为(1，4)
和(3，0)，点C是y轴上的一个动点，且A，B，C三点不在同
一条直线上，当△ABC的周长最小时点C的坐标是（ A ）
A. (0，3)
B. (0，2)
C. (0，1)
D. (0，0)
C′
解析：作B点关于y轴对称点B′，连接
最小值为（ B ）
A
A．7.5 C．4
B．5 D．不能确定
E
F
B
D
C
解析：△ABC为等边三角形，点D是BC边的中点，即点B与点
C关于直线AD对称.∵点F在AD上，故BF=CF.即BF+EF的最小
值可转化为求CF+EF的最小值，故连接CE即可，线段CE的长
即为BF+EF的最小值.
人教版数学八年级上册最短路径问题
人教版数学八年级上册最短路径问题
人教版数学八年级上册最短路径问题
新知演练
【变式3】如图，∠AOB＝30°，∠AOB内有一定点P，且OP＝ 10．若在OA、OB上分别有动点Q、R，则△PQR周长的最小值
是( A )
A．10 B．15 C．20 D．30
提示：过点P作关于OA，OB对称点P1，P2，连接 P1P2，交OA于点Q，OB于点R，此时△PQR周长的最小，连接OP1 和OP2，可证△OP1 P2为等边三角形，边长为10．
l
都保持CB 与CB′的长度相等？
利用轴对称，作出点B关于直线l的对称点B′.

人教版数学八年级最短途径问题

最新人教版数学八年级上册最短途径问题1．最短途径问题(1)求直线异侧的两点与直线上一点所连线段的和最小的问题，只要连接这两点，与直线的交点即为所求．如下图，点A，B别离是直线l异侧的两个点，在l上找一个点C，使CA＋CB最短，这时点C是直线l与AB的交点．(2)求直线同侧的两点与直线上一点所连线段的和最小的问题，只要找到其中一个点关于这条直线的对称点，连接对称点与另一个点，那么与该直线的交点即为所求．如下图，点A，B别离是直线l同侧的两个点，在l上找一个点C，使CA＋CB最短，这时先作点B关于直线l的对称点B′，那么点C是直线l与AB′的交点．为了证明点C的位置即为所求，咱们不妨在直线上另外任取一点C′，连接AC′，BC′，B′C′，证明AC＋CB＜AC′＋C′B.如下：证明：由作图可知，点B和B′关于直线l对称，因此直线l是线段BB′的垂直平分线．因为点C与C′在直线l上，因此BC＝B′C，BC′＝B′C′.在△AB′C′中，AB′＜AC′＋B′C′，因此AC＋B′C＜AC′＋B′C′，因此AC＋BC＜AC′＋C′B.【例1】在图中直线l上找到一点M，使它到A，B两点的距离和最小．分析：先确信其中一个点关于直线l的对称点，然后连接对称点和另一个点，与直线l的交点M即为所求的点．解：如下图：(1)作点B关于直线l的对称点B′；(2)连接AB′交直线l于点M.(3)那么点M即为所求的点．点拨：运用轴对称变换及性质将不在一条直线上的两条线段转化到一条直线上，然后用“两点之间线段最短”解决问题.2.运用轴对称解决距离最短问题运用轴对称及两点之间线段最短的性质，将所求线段之和转化为一条线段的长，是解决距离之和最小问题的大体思路，不论题目如何转变，运历时要抓住直线同旁有两点，这两点到直线上某点的距离和最小那个核心，所有作法都相同．警误区利用轴对称解决最值问题应注意题目要求依照轴对称的性质、利用三角形的三边关系，通过比较来讲明最值问题是经常使用的一种方式．解决这种最值问题时，要认真审题，不要只注用意形而忽略题意要求，审题不清致使答非所问．3．利用平移确信最短途径选址选址问题的关键是把各条线段转化到一条线段上．若是两点在一条直线的同侧时，过两点的直线与原直线的交点处组成线段的差最大，若是两点在一条直线的异侧时，过两点的直线与原直线的交点处组成的线段的和最小，都能够用三角形三边关系来推理说明，通常依照最大值或最小值的情形取其中一个点的对称点来解决．解决连接河两岸的两个点的最短途径问题时，能够通过平移河岸的方式使河的宽度变成零，转化为求直线异侧的两点到直线上一点所连线段的和最小的问题．在解决最短途径问题时，咱们通常利用轴对称、平移等变换把不在一条直线上的两条线段转化到一条直线上，从而作出最短途径的方式来解决问题．【例2】如图，小河边有两个村落A，B，要在河边建一自来水厂向A村与B村供水．(1)假设要使厂部到A，B村的距离相等，那么应选择在哪建厂？(2)假设要使厂部到A，B两村的水管最短，应建在什么地址？分析：(1)到A，B两点距离相等，可联想到“线段垂直平分线上的点到线段两头点的距离相等”，又要在河边，因此作AB的垂直平分线，与EF的交点即为符合条件的点．(2)要使厂部到A村、B村的距离之和最短，可联想到“两点之间线段最短”，作A(或B)点关于EF的对称点，连接对称点与B点，与EF的交点即为所求．解：(1)如图1，取线段AB的中点G，过中点G画AB的垂线，交EF于P，那么P 到A，B的距离相等．也可别离以A、B为圆心，以大于12AB为半径画弧，两弧交于两点，过这两点作直线，与EF的交点P即为所求．(2)如图2，画出点A关于河岸EF的对称点A′，连接A′B交EF于P，那么P到A，B的距离和最短．【例3】如图，从A地到B地通过一条小河(河岸平行)，今欲在河上建一座与两岸垂直的桥，应如何选择桥的位置才能使从A地到B地的路程最短？思路导引：从A到B要走的线路是A→M→N→B，如下图，而MN是定值，于是要使路程最短，只要AM＋BN最短即可．现在两线段应在同一平行方向上，平移MN到AC，从C到B应是余下的路程，连接BC的线段即为最短的，现在不难说明点N即为建桥位置，MN即为所建的桥．解：(1)如图2，过点A作AC垂直于河岸，且使AC等于河宽．(2)连接BC与河岸的一边交于点N.(3)过点N作河岸的垂线交另一条河岸于点M.则MN为所建的桥的位置．4．生活中的距离最短问题由两点之间线段最短(或三角形两边之和大于第三边)可知，求距离之和最小问题，确实是运用等量代换的方式，把几条线段的和想方法转化在一条线段上，从而解决那个问题，运用轴对称性质，能将两条线段通过类似于镜面反射的方式转化成一条线段，如图，AO＋BO＝AC的长．因此作已知点关于某直线的对称点是解决这种问题的大体方式．【例4】(实际应用题)茅坪民族中学八(2)班举行文艺晚会，桌子摆成如图a所示两直排(图中的AO，BO)，AO桌面上摆满了橘子，OB桌面上摆满了糖果，站在C处的学生小明先拿橘子再拿糖果，然后到D处座位上，请你帮忙他设计一条行走线路，使其所走的总路程最短？图a 图b解：如图b.(1)作C点关于OA的对称点C1，作D点关于OB的对称点D1，(2)连接C1D1，别离交OA，OB于P，Q，那么小明沿C→P→Q→D的线路行走，所走的总路程最短．5.运用轴对称解决距离之差最大问题利用轴对称和三角形的三边关系是解决几何中的最大值问题的关键．先做出其中一点关于对称轴的对称点，然后连接对称点和另一个点，所得直线与对称轴的交点，即为所求．依照垂直平分线的性质和三角形中两边之差小于第三边易证明这确实是最大值．破疑点解决距离的最值问题的关键运用轴对称变换及三角形三边关系是解决一些距离的最值问题的有效方式．【例5】如下图，A，B两点在直线l的双侧，在l上找一点C，使点C到点A、B 的距离之差最大．分析：此题的冲破点是作点A(或B)关于直线l的对称点A′(或B′)，作直线A′B(AB′)与直线l交于点C，把问题转化为三角形任意两边之差小于第三边来解决．解：如下图，以直线l为对称轴，作点A关于直线l的对称点A′，A′B的连线交l于点C，那么点C即为所求．理由：在直线l上任找一点C′(异于点C)，连接CA，C′A，C′A′，C′B.因为点A，A′关于直线l对称，因此l为线段AA′的垂直平分线，那么有CA＝CA′，因此CA－CB＝CA′－CB＝A′B.又因为点C′在l上，因此C′A＝C′A′.在△A′BC′中，C′A－C′B＝C′A′－C′B＜A′B，因此C′A′－C′B ＜CA－C B.点拨：依照轴对称的性质、利用三角形的三边关系，通过比较来讲明最值问题是经常使用的一种方式．。

新人教版八年级上最短路径问题ppt课件

追问2 你能用自己的语言说明这个问题的意思，并把它抽象为数学问题吗？
（3）现在的问题是怎样找出使两条线段长度之和为最
短的直线l上的点．设C 为直线上的一个动点，上
面的问题就转化为：当点C 在
B
A
C
l
本标准适用于已投入商业运行的火力发电厂纯凝式汽轮发电机组和供热汽轮发电机组的技术经济指标的统计和评价。燃机机组、余热锅炉以及联合循环机组可参照本标准执行，并增补指标。
运用新知
练习如图，一个旅游船从大桥AB 的P 处前往山脚下的Q 处接游客，然后将游客送往河岸BC 上，再返回P 处，请画出旅游船的最短路径．
C
山Q
河岸
P
A
大桥
B
本标准适用于已投入商业运行的火力发电厂纯凝式汽轮发电机组和供热汽轮发电机组的技术经济指标的统计和评价。燃机机组、余热锅炉以及联合循环机组可参照本标准执行，并增补指标。
如图，牧马人从A地出发，先到草地边某一处牧马，再到河边饮马，然后回到 B处，请画出最短路径．
解：沿AC-CD-DB路线走是最短的路线如图（1）所示：本标准适用于已投入商业运行的火力发电厂纯凝式汽轮发电机组和供热汽轮发电机组的技术经济指标的统计和评价。燃机机组、余热锅炉以及联合循环机组可参照本标准执行，并增补指标。
证明：如图，在直线l 上任取一点C′（与点C 不
重合），连接AC′，BC′，B′C′．
由轴对称的性质知，
BC =B′C，BC′=B′C′． ∴ AC +BC
= AC +B′C = AB′， AC′+BC′
= AC′+B′C′．

人教版八年级上册数学题学习最短路径问题

13.4 课题学习最短路径问题基础巩固1．有两棵树位置如图，树脚分别为A，B.地上有一只昆虫沿A —B的路径在地面上爬行．小树顶D处一只小鸟想飞下来抓住小虫后，再飞到大树的树顶C处，问小鸟飞至AB之间何处时，飞行距离最短，在图中画出该点的位置．2．已知，如图所示，甲、乙、丙三个人做传球游戏，游戏规则如下：甲将球传给乙，乙将球立刻传给丙，然后丙又立刻将球传给甲．若甲站在∠AOB内的P点，乙站在OA上，丙站在OB上，并且甲、乙、丙三人的传球速度相同．问乙和丙必须站在何处，才能使球从甲到乙、乙到丙、最后丙到甲这一轮所用的时间最少？3．如图所示，P，Q为△ABC边上的两个定点，在BC上求作一点R，使△PQR的周长最小．4．七年级(1)班同学做游戏，在活动区域边OP放了一些球(如图)，则小明按怎样的路线跑，去捡哪个位置的球，才能最快拿到球跑到目的地A?能力提升5．公园内两条小河MO，NO在O处汇合，两河形成的半岛上有一处景点P(如图所示)．现计划在两条小河上各建一座小桥Q和R，并在半岛上修三段小路，连通两座小桥与景点，这两座小桥应建在何处才能使修路费用最少？请说明理由．6．如图，牧童在A处放牛，其家在B处，A，B到河岸CD的距离分别为AC，BD，且AC＝BD，若A到河岸CD的中点的距离为500 m.(1)牧童从A处把牛牵到河边饮水后再回家，试问在何处饮水，所走路程最短？在图中作出该处，并说明理由；(2)最短路程是多少？参考答案1．解：如图，作D关于AB的对称点D′，连接CD′交AB于点E，则点E就是所求的点．2．解：如图所示，(1)分别作点P关于OA，OB的对称点P1，P2；(2)连接P1P2，与OA，OB分别相交于点M，N.因为乙站在OA上，丙站在OB上，所以乙必须站在OA上的M处，丙必须站在OB上的N处才能使传球所用时间最少．3．解：(1)作点P关于BC所在直线的对称点P′；(2)连接P′Q，交BC于点R，则点R就是所求作的点(如图所示)．4．解：如图，作小明关于活动区域边线OP的对称点A′，连接AA′交OP于点B，则小明行走的路线是小明→B→A，即在B处捡球，才能最快拿到球跑到目的地A.5．解：如图，作P关于OM的对称点P′，作P关于ON的对称点P″，连接P′P″，分别交MO，NO于Q，R，连接PQ，PR，则P′Q＝PQ，PR＝P″R，则Q，R就是小桥所在的位置．理由：在OM上任取一个异于Q的点Q′，在ON上任取一个异于R的点R′，连接PQ′，P′Q′，Q′R′，P″R′，PR′，则PQ′＝P′Q′，PR′＝P″R′，且P′Q′＋Q′R′＋R′P″＞P′Q＋QR＋RP″，所以△PQR的周长最小，故Q，R就是我们所求的小桥的位置．6．解：(1)作法：如图作点A关于CD的对称点A′；连接A′B交CD于点M.则点M即为所求的点．证明：在CD上任取一点M′，连接AM′，A′M′，BM′，AM，因为直线CD是A，A′的对称轴，M，M′在CD上，所以AM＝A′M，AM′＝A′M′，所以AM＋BM＝A′M＋BM＝A′B，在△A′M′B中，因为A′M′＋BM′＞A′B，所以AM′＋BM′＝A′M′＋BM′＞AM＋BM，即AM＋BM最小．(2)由(1)可得AM＝A′M，A′C＝AC＝BD，所以△A′CM≌△BDM，即A′M＝BM，CM＝DM，所以M为CD的中点，且A′B＝2AM，因为AM＝500 m，所以A′B＝AM＋BM＝2AM＝1 000 m．即最短路程为1 000 m.答题方法：试卷检查五法重视答案,要对结果负责不少同学都说,明明题目都会做,然而考试时却不是这里出错就是那里出错,总是拿不了高分。

初二数学最短路径问题知识归纳+练习

初二数学最短路径问题【问题概述】最短路径问题是图论研究中的一个经典算法问题，旨在寻找图（由结点和路径组成的）中两结点之间的最短路径•算法具体的形式包括：①确定起点的最短路径问题-即已知起始结点，求最短路径的问题.②确定终点的最短路径问题-与确定起点的问题相反，该问题是已知终结结点，求最短路径的问题.③确定起点终点的最短路径问题-即已知起点和终点，求两结点之间的最短路径.④全局最短路径问题-求图中所有的最短路径.【问题原型】“将军饮马”，“造桥选址”，“费马点”.【涉及知识】“两点之间线段最短”，“垂线段最短”，“三角形三边关系”，“轴对称”，“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”，近两年出现“三折线”转“直”等变式问题考查.十二个基本问题】在直线1上求一点P,使 pA PB|的值最大.作直线AB 与直线1的交点即为P.三角形任意两边之差小于第三边.PA PB < ABPA PB 的最大值=AB【问题11】作法图形原理在直线1上求一点P,使 pA PB 的值最大.作B 关于1的对称点B/ 作直线A B ，,与1交点即为P.三角形任意两边之差小于第三边.PA PB < AB\PA PB 最大值=AB^ .【问题12】“费马点”作法图形原理△ ABC 中每一内角都小于 120 °，在厶ABC 内求一点P,使PA +PBbPC 值最小.所求点为“费马点”，即满足/ APB=Z BPC=Z APC =120 ° .以 AB AC 为边向外作等边△ ABE ） △ ACE 连CD BE 相交于P,点P 即为所求.两点之间线段最短.PA +PBbPC 最小值=CD【精品练习】1如图所示，正方形 ABCD 勺面积为12,^ ABE 是等边三角形，点 P,使PDPE 的和最小，则这个最小值为（）2•如图，在边长为 2的菱形 ABCDL / ABC= 60°，若将△ ACD 绕点A 旋转，当 AC 、AD 分别与 BC CD 交于点E 、卩，则厶CEF 的周长的最小值为（）B. 2 (3)C. 2 、3E 在正方形 ABCD^，在对角线 AC 上有一点A. 2、, 3 B . 2、6 C 3D.6A. 2D . 43.四边形ABCDK / B =Z D = 90°,/ C= 70°,在BCCD 上分别找一点皿1\1,使厶AMN 勺周长最小时, 的度数为（）A. 120 ° B . 130 ° C . 110 ° D . 140 °动点，贝U BM +MN 勺最小值是5•如图，Rt △ ABC 中, / C = 90°,/ B= 30°, AB= 6,点E 在AB 边上，点 D 在BC 边上（不与点且ED=AE 则线段 AE 的取值范围是 ____________________________ .6•如图，/ AOB= 30°,点 M N 分别在边 OA OB 上，且 0晦1, ON= 3,点P 、Q 分别在边 OB+ PQ^ QN 的最小值是 _________ .（注“勾股定理”：直角三角形中两直角边的平方和等于斜边的平方，IABC 中，/ C= 90 °，则有 AC 2 BC 2 AB 2）7•如图，三角形厶 ABC 中,/ OAB=/ AOB= 15°,点B 在x 轴的正半轴，坐标为 B （ 6 3 , 0）.OC 平分/ AOB 点M 在OC 的延长线上，点 N 为边OA 上的点，贝U MAH MN 勺最小值是 _____ .8•已知A ( 2, 4)、B (4, 2). C 在y 轴上，D 在x 轴上，则四边形 ABCD 勺周长最小值为 ____________________此时C 、D 两点的坐标分别为 ___________________________ ./ AMNZ ANM4.如图，在锐角厶ABC 中, AB= 4血，/ BAC= 45°,/ BAC 的平分线交 BC 于点D, M N 分别是 AD 和 AB 上的B 、C 重合），OA 上，贝UMP IRt A9.已知A( 1，1)、B(4，2).(1) P为x轴上一动点，求PA+PB的最小值和此时P点的坐标;(2) P为x轴上一动点，求PA PB的值最大时P点的坐标;(3) CD为x轴上一条动线段，D在C点右边且CD= 1，求当AGC&DB的最小值和此时C点的坐标;10 •点C 为/ AOB内一点.(1)在0A求作点D, 0B上求作点〔，使厶CDE勺周长最小，请画岀图形；(2)在(1)的条件下，若/ AOB= 30°，OC= 10,求厶CDB周长的最小值和此时/ DCE勺度数.11. (1)如图①，△ABD^n^ ACE匀为等边三角形，BE CE交于F,连AF,求证：AF+BF+CF= CD；(2)在厶ABC中, Z ABC= 30°, AB= 6, BC= 8,Z A,/C 均小于120°,求作一点P,使PA+PB^PC的值最小，试求出最小值并说明理由.12 •荆州护城河在CC处直角转弯，河宽相等，从A处到达B处，需经过两座桥DD、EE,护城河及两桥都是东西、南北方向，桥与河岸垂直•如何确定两座桥的位置，可使A到B点路径最短？。

(最新整理)初二数学最短路径问题知识归纳+练习

作法
N A
M
l1
l2 B
作点 A 关于 l2 的对称
A 为 l1 上一定点，B 为点 A＇，作点 B 关于 l1
l2 上一定点，在 l2 上求的对称点 B＇，连 A＇
点 M，在 l1 上求点 N, B＇交l2 于 M，交 l1 于 N．
使 AM+MN+NB 的值最小．
图形
原理
B'
AN M
A'
在直线 l 上求两点 M、N A＇＇，连 A＇＇B，交直线 l
（M 在左），使 MN a ，于点 N，将 N 点向左平
并使 AM+MN+NB 的值最移 a 个单位得 M．
小．
【问题 7】
作法
A
A'
B
l MN
A''
两点之间线段最短． AM+MN+BN 的最小值为 A＇＇B+MN．
图形
原理
l1 P
【十二个基本问题】
【问题 1】
作法
图形
原理
A
l 连 AB，与 l 交点即为 P．
B
在直线 l 上求一点 P，
使 PA+PB 值最A
P
l
B
图形
两点之间线段最短． PA+PB 最小值为 AB．
原理
A
作 B 关于 l 的对称点
B
l
B＇连 A B＇，与 l 交
在直线 l 上求一点 P，
初二数学最短路径问题知识归纳+练习
初二数学最短路径问题知识归纳+练习
编辑整理：
尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（初二数学最短路径问题知识归纳+练习）的内容能够给您的工作和学习带来便利。同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为初二数学最短路径问题知识归纳+练习的全部内容。