基于灰度系统模型的原油价格预测
基于灰色理论的新疆某油田石油产量预测分析

( 1 )
第二步 : 对 【 q ’ ( f ) 作一次累加 , 求得一次累加生
成数 列
内领先 的各类试井设备和生产测井设备 ; 在测试项 目 上, 具备各类工程测井能力 ; 在测试资料解释方面, 配
( ( ) ={ X 0 ) ( 1 ) , ‘ ’ ( 2 ) , …, ‘ ( ) } ;
新 疆 石 油 科 技
2 0 1 3 年第4 5 1 J ( 第2 3 卷)
・9 ・
基 于灰 色理 论 的新 疆 某 油 田石 油 产 量 预 测 分 析
刘栋 梁
克拉玛依新科 澳石油天然气技 术股份有 限公 司,8 3 4 0 0 0 新疆 克拉玛依
摘 要 灰 色时间序列预测是对系统行为特征指标建立一组灰色预测模型, 这一模型用观察到的反映预测对象特征的时间序列
略、 石油公 司制定勘探规划等都十分关键。影响油气 储量增长趋势的影响因素很多 , 不同类型盆地油气储 量、 产 量增 长 规律 差别 也 较 大 。本文 主要 假 设在 地 下 原油储量丰富、 没有 自然因素的干扰 、 国家宏观政策没 有对原油的开采量做出调控的情况下 , 在现有技术的
基 础上 , 以过去 几年 的开采 数据作 为基 础 , 对未 来近几 年 新疆本地某 油 田的开采 量进行预 测分析 。
备 了高水平专业技术人员 , 对服务地区地质条件熟悉 并 具 有 丰富解 释 经验 , 动 态监测 综 合解 释能 力 和技术 在 国内处 于先进 水平 。 目前 , 新疆 地 区石 油 产 量 年 均增 速 为 1 3 %, 远超 全 国平 均 水平 。油 气 产量 的高 速增 加 必 然 伴 随油 田 服 务 业 务 量 的大 幅 增 长 。对 新 疆 油 田的产 油 量进 行 预测在工作中也显得十分必要。
原油价格预测的模型建立与实践

原油价格预测的模型建立与实践随着世界经济的不断发展,原油价格一直是一个备受关注的话题。
尤其是近几年,国际原油市场价格的波动幅度越来越大,为各国经济带来了很大的影响。
面对如此复杂的市场环境,我们需要建立一定的预测模型来做出合理的价格预测,以便在投资决策中作出正确的选择。
一、原油市场的重要性原油是世界能源中的重要组成部分,也是世界经济发展的重要驱动力。
在现代工业化的过程中,原油已经成为了广泛使用的一种能源,并且其在许多领域的应用也越来越广泛。
不仅如此,原油也是国际化市场上的一种重要商品,其价格波动不仅会影响到各个国家和地区的经济,还会对世界经济产生重要的影响。
二、原油价格预测的必要性由于国际原油市场的价格波动幅度较大,加之市场的复杂程度,原油价格的预测具有一定的不确定性。
因此,在进行原油交易决策之前,需要对原油价格进行较准确的预测,以达到最佳投资效果。
通过建立科学有效的模型,利用成熟的技术手段可以较为准确地预测原油价格的变化,有效指导投资者在市场中的行动。
这也是建立原油价格预测模型的必要性所在。
三、原油价格预测的方法在预测原油价格时,通常会采用以下三种方法:1、基于历史数据的时间序列分析方法时间序列分析是一种基于随时间变化而进行观测得来的数据分析方法。
它通常包括趋势分析、季节性分析和循环分析等方式,通过对历史数据进行分析,建立价格预测模型。
2、基于统计模型的回归分析方法回归分析是一种常用的预测模型,在其基础上可以建立起原油价格预测的模型。
该方法通过对原油价格的各个影响因素进行回归分析,建立多元线性回归模型,从而预测未来的价格变化。
3、基于机器学习的预测方法机器学习是一种先进的预测方法,该方法基于大数据技术和算法优化等创新技术,利用数据挖掘和预测算法来建立原油价格预测的模型。
机器学习具有高准确率、自适应性等特点,在预测精度上通常高于其他方法。
四、原油价格预测实践案例以近年来国际原油市场中的WTI原油为例,通过建立月度预测模型,进行预测实践。
原油期货价格预测模型及其应用研究

原油期货价格预测模型及其应用研究随着全球经济的不断发展和能源需求的逐步增加,原油已经成为世界上最重要的商品之一。
而原油期货作为对现货市场的衍生品,已经成为了国际原油市场上最重要的交易工具之一。
在这个日新月异的时代,任何一个决策者都需要能够对市场做出正确的判断和预测。
因此,如何通过预测模型对原油期货价格进行预测,已经成为了一个热门的研究话题。
一、背景和意义原油是一个具有复杂性和不确定性的商品,在市场价格上也存在着大量的波动。
而原油期货价格的预测对于投资者和交易者来说尤为重要。
通过预测,交易者可以获取更高的收益和更低的风险,同时把握住交易时机,掌握市场走势。
二、研究现状在目前的研究中,常见的预测方法包括统计模型、时间序列模型、人工神经网络和基于机器学习的方法等。
其中,时间序列模型被广泛应用于金融市场和商品市场价格的预测之中。
ARIMA模型作为时间序列预测的经典方法,已经在许多领域中取得了不错的预测效果。
三、预测模型及应用基于今天的量价关系,采用时间序列模型进行原油期货价格预测,并在实际应用中取得了较好的效果。
在实际应用中,通过分析历史数据,结合多种分析方法和技术手段,构建出适合原油期货市场的ARIMA模型。
在进行预测时,预测模型采用rolling-horizon方法,通过不断更新模型,预测曲线的精确度可以得到进一步提高。
四、结语在金融市场和商品市场上,原油期货价格的变化对于市场和投资者的重要性非常大。
如何通过预测模型对原油期货价格进行正确预测及时把握交易时机成为了研究者和交易者的主要问题。
通过本文的研究,我们可以看出,结合ARIMA模型的rolling-horizon方法是一种简单而有效的预测方法,在未来的市场交易中将有不小的应用前景。
灰色模型在股票价格预测中的应用——以中国石化为例

格 预 测精 度 较 长期 预 测精 度 高 ; 覃思 乾 指 出在 短
期股价预测方 面, GM ( 1 , 1 ) 模 型 优 于 ARI MA 模 型L 4 ; 夏景 明 等在 灰 色 预测模 型 的 基础 上 提 出 了组 合 灰 色 神经 网 络 预测模 型L 5 ; 王 君 等通 过 实 证分 析 了灰 色 系统 理 论在 证券 市 场 中 的应用 [ 7 ; 王 浩指 出
’
Ap p l i c a t i o n o f g r e y mo d e l i n s t o c k p r i c e f o r e c a s t i n g: Ta k i n g S i n o p e c a s a n e x a mp l e
Ke y wo r d s : GM ( 1 , 1 )mo d e l ; s t o c k f 0 r e c a s t i n g; f o r e c a s t i n g a c c u r a c y
在证 券市场 中, 对 证 券市 场 价 格 走势 进 行 预测 是一 个永恒 的课题 。随着“ 融资融 券” 的进一 步开展 及“ T+0 ” 交易 制度 的可 能设 置 , 股票 收 盘价 格 将倍
并 以 中国石 4  ̄ ( 6 0 0 0 2 8 ) 2 0 1 2 — 0 1 — 0 4至 2 0 1 2 — 1 2 — 3 1的 交易数 据 为例 进 行 了分 析 。分析 结 果表 明, 灰 色预 测模 型的平均 预测 准确度 为 9 8 . 6 3 % 。考虑到 股票 交 易规则 , 4 2 的预 测 数据 为有 效预 测 , 有
灰色方法在原油单位生产成本预测中的应用X

灰色方法在原油单位生产成本预测中的应用Ξ
吴 江 , 刘先涛
(西南石油学院经济管理学院 ,四川 南充 637001)
摘要 : 在市场经济条件下 ,企业要想在激烈的市场竞争中求得生存和发展 ,必须切实加强企业管理 ,提高生产经营活 动的经济效益 。成本管理是企业管理工作中的一项重要内容 ,而低成本策略则是企业在竞争中取得竞争优势的重要 策略之一 。从加强成本管理的角度出发 ,分析了原油单位生产成本特点 ,建立了原油单位生产成本的阶跃灰色模型 。 通过实例计算分析表明 ,给出的模型比其它模型预测结果更准确 ,更能满足实际工作的需要 。最后指出 ,成本变化的 规律不同 ,预测模型也不相同 ,在实际工作中 ,应根据实际情况选择合适的预测模型 。 关键词 :预测 ;原油 ;生产成本 ;灰色系统 中图分类号 : TE - 9 文献标识码 : A
1996 6 792. 10 889. 03
1997 7 767. 80 926. 79
1998 8 764. 29 872. 99
1999 9
852. 95
396. 70 420. 46 428. 43 504. 74 552. 46 592. 41 617. 46 635. 82
第 23 卷 第 4 期 西 南 石 油 学 院 学 报 Vol. 23 No. 4
2001 年 8 月 Journal of Sout hwest Petroleum Institute Aug 2001
文章编号 : 1000 - 2634 (2001) 04 - 0071 - 03
(2) 移动平均法较适合平稳变化序列 ,指数平 滑法较适合平稳 、线性序列 。
(3) 加权移动平均法的权数不易取得合理 ,不 便实际应用 。
中国原油进口量的灰色预测

作者: 李莉[1];徐玲蕙[1];刘仕华[1]
作者机构: [1]西南石油大学工商管理学院西南石油大学人文社科学院西南石油大学工商管理学院四川成都四川成都
出版物刊名: 中南民族大学学报:人文社会科学版
主题词: 中国;原油;进口量;灰色预测
摘要:石油作为国民经济和国家建设不可或缺的重要战略物资,具有特殊性、市场风险性、国际性、政治性和竞争激烈性等特点。
正是由于这些特点,从而决定了影响石油进口量的因素是众多的,而突发性事件更使石油进口量预测无章可寻。
鉴此,本文在结合中国历年原油进口量的基础上,利用灰色预测方法,建立了原油进口灰预测模型,并指出了2005中国原油进口量的区间。
灰色系统理论在原油管道结蜡规律预测模型的应用

21 0 0年
管 道 技 木 5 设
Pi ln Te h q a d Ee pei e c niue n
2 1 00
No 4 .
第 4期
灰 色 系统 理 论 在 原 油 管道 结蜡 规律 预 测模 型 的应 用
翁
(. 1 辽宁石油化工大学机械工程学院 , 辽宁抚顺
度 等指 标 的 实际统计数 据进 行 了灰 色动 态拟合 , 立 了相 应 的灰 色微 分方 程 和 时 间响应 函数 。结 果表 建
明 : 差 小于 2 , 型精 度 满足 工程 实 际需要 。 残 % 模
关 键词 : 油管道 ; 输 结蜡 ; 色系统 ; 型 ; 测 灰 模 预 中图分 类号 :E 3 T 82 文献标 识码 : B 文章 编 号 :0 4— 6 4 2 1 )4— 0 3一 2 10 9 1 (0 0 0 0 1 O
2 Da a ies yo eh oo y D l n16 0 , hn ) . l nUnvri f c n l , ai 10 0 C ia i t T g a
Ab t a t P o lms r ltd t x d p st n s ro syt r ae r d ie ie r n ig i ea p cso ae y e o o n s r c : rb e ea e o wa e o i o e iu l h e tn c u e p p l u n n t s e t fs ft , c n my a d i n nh
G r y Pr d ci n M o lo he Re ul rt fW a e e ito de ft g a iy o x De o iin n Cr e O i Pi ei p sto i ud l p lne
灰色系统在预测原油产量方面的应用

灰色系统在预测原油产量方面的应用
孙博年
【期刊名称】《西安石油大学学报(自然科学版)》
【年(卷),期】1996(000)004
【摘要】为了使油田能够长期稳定高产,必须编制科学合理的生产计划,而在计划编制过程中,对原油产量进行科学预测又是十分必要的。
为此,本文选定GM(1.1)模型,通过对原油生产的实际分析,建立了老井原油递减后产量的预测模型,并经过实征,具有预测精度高,计算速度快、方便实用等优点。
【总页数】1页(P54)
【作者】孙博年
【作者单位】不详;不详
【正文语种】中文
【中图分类】F426.22
【相关文献】
1.灰色系统理论GM(1,1)模型在环境质量预测方面的应用 [J], 樊智军;马建忠
2.灰色系统在赛什塘铜矿区Cu品位预测方面的应用 [J], 刘海利;朱谷昌;张普斌;夏正清
3.灰色系统理论在原油管道结蜡规律预测模型的应用 [J], 翁蕾;王爱萍
4.广西远洋渔业产量的离散灰色预测研究r——灰色系统理论应用系列论文之七[J], 朱念;梁芷铭
5.灰色系统预测在疲劳性能研究方面的应用 [J], 万德立;刘恩
因版权原因,仅展示原文概要,查看原文内容请购买。
20005971_基于灰色关联度法的中国原油期货价格影响因素分析

Liaoning Economy2018年3月26日,以人民币计价标的物为中质含硫原油的原油期货在上海能源交易中心上市,原油期货的上市引起了社会的高度关注,距今已经过去一年半的时间了,中国原油期货市场总体运行状况良好。
同其他市场一样,原油期货市场的价格是各类参与主体最为关注的因素,因此本文采用灰色关联分析法对我国原油期货的交易价格影响因素进行了实证分析,以期找出影响我国原油期货价格变化的规律性。
一、中国原油期货的价格波动及影响因素(一)原油期货的运行态势中国原油期货自上市以来,价格变动幅度不大,相对比较平稳,整体上呈下降趋势,下降幅度比较小(见图1)。
(二)影响我国原油期货价格的因素分析影响原油期货价格的因素有许多,一般来讲包括需求因素、供给因素、金融因素及国际政治因素等。
1.供给因素。
原油的根本属性是商品属性,商品属性决定了影响石油现货及期货价格波动的基础是供求规律,因而供求因素是影响其价格最直接的因素。
由于石油资源的稀缺性及不可再生性,原油供给将对原油现货乃至原油期货的价格产生重要影响。
如果产能上升,加大了全球的原油供给,则会导致期货交易者对预期价格的看跌,持有期货空头的投资者增加,从而导致原油期货价格的下降。
2.需求因素。
与供给因素相对应,需求因素也是影响原油期货价格的直接因素。
一般来讲,对原油需求量的增加会推升原油期货价格上涨。
近年来,随着亚洲经济体的发展,对能源需求量不断增加,拉动了原油价格的上升。
从需求角度看,中国是世界上最大的原油进口国,在2017年达到840万桶/日,而2017年世界原油总需求量在9700万桶/日左右,中国的原油需求量占到世界总需求量的8.7%左右,而且我国对原油的需求是逐年递增的。
3.金融因素。
从金融因素方面来看,原油期货是大宗商品,影响大宗商品价格的金融因素最主要的就是计价体制。
国际原油期货均以美元计价,美元汇率的波动会影响国际原油期货价格的变动;从理论上来看,国际原油期货价格与美元指数呈长期负相关。
国际原油价格短期预测模型、优化算法及应用

2023-10-28contents •引言•国际原油市场概述•原油价格预测模型•预测模型优化算法•预测模型优化算法应用•结论与展望目录01引言全球能源市场中的原油作为基础性能源,其价格波动对各国经济发展及国际政治局势具有重要影响。
因此,短期原油价格预测对于政策制定者、能源投资者和研究者都具有重要意义。
尽管已有许多关于原油价格预测的研究,但价格波动的复杂性和不确定性使得预测精度仍有待提高。
因此,本书旨在研究并优化原油价格短期预测模型,提高预测准确性,为相关领域提供更为准确的决策依据。
研究背景与意义本书首先对原油价格的影响因素及其波动特征进行分析,包括全球经济发展、供需变化、政治事件、货币政策等然后,本书将针对现有预测模型的不足,提出新型的优化算法。
例如,引入深度学习技术以处理更高维度的数据特征,或者结合多种方法以获得更全面的价格信息。
最后,本书将通过大量历史数据和实证分析来验证所提出优化算法的预测效果。
同时,本书还将探讨这些预测结果在能源政策制定、投资决策等方面的应用。
接着,本书将介绍并比较常见的原油价格预测方法,如时间序列分析、机器学习和神经网络等。
通过实证分析,评估各种方法的优劣和适用性。
研究内容与方法02国际原油市场概述国际原油市场现状全球化和多元化趋势01国际原油市场正逐渐向全球化和多元化方向发展,各国和地区之间的能源供需关系日益紧密。
竞争激烈02随着全球能源市场的开放和竞争加剧,国际原油市场的竞争也日趋激烈,各石油公司和企业需要提高自身的竞争力以获得更大的市场份额。
价格波动性03国际原油价格受到多种因素的影响,如供求关系、政治局势、经济状况等,价格波动性较大,这也给原油市场的短期预测带来了一定的难度。
供求关系国际原油市场的供求关系是影响价格的主要因素之一。
当供大于求时,价格下跌;当供小于求时,价格上升。
此外,各国的石油储备和战略储备也会对价格产生一定的影响。
国际原油价格影响因素政治局势政治局势的不稳定和动荡会直接影响国际原油价格。
原油价格预测模型研究

原油价格预测模型研究一、绪论原油是全球最主要的能源资源之一。
由于其价格波动的很大,原油市场一直是金融市场中最活跃的市场之一。
对于变化的原油价格进行准确的预测对于投资者和经济决策者来说具有重要的意义。
因此,本文旨在探讨原油价格预测模型的研究。
二、原油市场概述原油市场分为国际市场和国内市场两部分。
国际市场是由OPEC(石油输出国组织)和非OPEC产油国共同构成的,也是原油价格形成的主要场所。
原油价格的波动通常是由供需关系、政治风险、地缘政治事件和宏观经济指标等因素综合影响所造成的。
三、原油价格预测模型1、时间序列模型时间序列是按照特定的时间顺序排列的一系列数据,代表某个现象在时间上的变化。
时间序列模型被广泛用于原油价格预测。
常用的时间序列模型包括ARIMA模型和GARCH模型。
2、基于机器学习的模型机器学习模型被广泛应用于预测原油价格。
这些模型主要包括支持向量回归、随机森林、人工神经网络和贝叶斯网络等。
这些模型的优点在于可以使用大量的历史数据进行训练,并具有自适应性。
3、基于经济指标的模型经济指标模型将宏观经济指标作为预测原油价格的主要因素。
例如,研究发现,全球GDP、通货膨胀率和美元汇率等指标对于原油价格的影响非常显著。
四、实证研究本文通过分析历史数据和实证研究,发现政治风险和OPEC产量对于原油价格波动的影响较大。
同时,基于经济指标的模型有助于预测短期内原油价格变化的趋势。
五、结论本文对原油价格预测模型进行了综述。
时间序列模型、机器学习模型和经济指标模型是预测原油价格的主要方法。
同时,经济指标模型可以被用于预测短期内的原油价格波动趋势。
在原油市场高度复杂和不确定性较高的情况下,这些模型为投资者和经济决策者提供了预测和决策的重要依据。
基于灰色关联理论的中外石油期货价格时差

2008年3月系统工程理论与实践第3期 文章编号:100026788(2008)0320166205基于灰色关联理论的中外石油期货价格时差陈洪涛1,周德群1,韩 谊2(11南京航空航天大学经济与管理学院,南京210016;21道通期货经纪有限公司,南京210024)摘要: 运用灰色关联度平移时间法,研究了上海期货交易所(SHFE)和纽约商品期货交易所(NY MEX)、伦敦国际石油交易所(IPE)、新加坡纸货市场(SP M)和东京工业品交易所(T OC OM)前后一个月的石油期货价格之间的关联度,以发现国内外石油期货价格时差.研究表明,国内燃料油期货价格滞后于NY MEX约15天,滞后于T OC OM约26天,滞后于IPE和SP M约30天.关键词: 灰色关联度;灰色系统;石油期货;石油价格中图分类号: F206 文献标志码: A Study on the time difference between prices of China andinternational oil futures based on grey relativity theoryCHE N H ong2tao1,ZHOU De2qun1,HAN Y i2(11C ollege of Economics and Management,Nanjing University of Aeronautics and Astronautics,Nanjing210016,China;21DOT O Futures C o.,Ltd,Nanjing210024,China)Abstract: Based on the grey system theory,this paper calculated the grey relativity degree of the oil prices betweenChinese and foreign futures markets.The results dem onstrate that the fueling oil futures price in Shanghai FuturesExchange is about15days behind that in New Y ork Mercantile Exchange,about26days behind that in T oky oC omm odity Exchange and about30days behind that in International Petroleum Exchange and S ingapore Paper Market.K ey w ords: grey relativity;grey system;oil futures;oil price根据《BP世界能源统计评论(2005)》,我国石油进口量已占当年全球石油贸易量的7%,但在影响石油定价的权重上却不到011%.过去五年中,我国的石油消费年均以6%的速度增长,远远超过美国的石油消费年均增长率,在国际石油市场中处于比较重要的位置.尽管目前我国是全球第二大石油进口国和消费国,但由于缺乏配套的成熟期货市场,使得我国目前只能被动地接受国际油价.2004年,由于国际油价高企,使得我国该年度石油贸易逆差达到了300亿美元,多支付外汇70168亿美元,造成巨额损失.为争夺国际石油价格话语权,2004年8月我国在上海期货交易所(SHFE)推出180CST燃料油期货交易.本文采用灰色关联度理论,研究上海燃料油期货价格与纽约商品交易所(NY MEX)、伦敦国际石油交易所(IPE)、新加坡纸货市场(SPM)和东京工业品交易所(T OC OM)上市的各石油期货价格之间的时差,探讨我国石油期货市场效率问题.1 文献回顾在20世纪70年代以前,由于石油价格长期稳定,学术界也很少关注石油价格问题的研究.直到两次石油危机导致全球石油价格剧烈波动,给主要工业化国家带来巨大的冲击,石油价格问题才引起学术界的广泛关注.目前国外关于石油价格问题的研究可以分为石油价格波动的原因和油价预测、OPEC对国际油收稿日期:2006211221资助项目:国家自然科学基金(90510010);教育部高等学校博士点基金(20050287026);江苏省博士生创新优计划(CX07B-241r) 作者简介:陈洪涛(1981-),男,江苏盐城人,南京航空航天大学经济与管理学院博士研究生,从事能源金融工程的研究,E2mail:htchen.cumt@.价的影响以及石油价格波动对宏观经济的影响三个方面(焦建玲、范英等,2004).各石油期货市场之间的关系问题作为石油价格问题的分支,研究成果颇丰.X iaowen和T amvakis(2001)通过研究NY MEX和IPE两个市场信息的传递效应,得出NY MEX是原油价格市场的主导者的结论.Hamm oudeh等(2003)通过分析NY MEX WTI原油价格、汽油价格、燃料油价格以及鹿特丹和新加坡等国际石油市场之间的价格传递性,认为NY MEX汽油市场具有主导作用.X iaowen和T amvakis(2004)研究认为国际原油期货价格由NY MEX所主导,NY MEX WTI的期货价格反应速度相对于IPE布伦特原油价格更快,且前者对后者期货合约价格有重要影响.Hamm oudeh和Huimin(2004)研究表明亚洲金融危机没有改变NY MEX对国际原油市场的主导地位,其他国际石油期货市场价格趋同于NY MEX.由于中国燃料油期货上市时间较短且还没有其他石油期货交易品种,理论界关于石油期货问题的研究相对较少,目前该领域仅获得2项国家自然科学基金资助,研究机构主要集中于上海期货交易所博士后工作站、中国能源战略研究中心、期货经纪公司研究部等.胡政、李辉(2002)对新加坡燃料油市场对我国石油市场价格的影响做了定性分析.焦建玲、范英(2004)认为我国原油价格与国际原油价格走势基本一致,国内油价波动小于国际原油价格波动,两者间存在双向因果关系.高辉(2005)采用向量自回归的G ranger 因果关系检验以及冲击响应函数,对国内外燃料油期货价格关联度及趋势作建模预测.何凌云、范英等(2006)采用Z ipf分析方法,分析了投机者的交易时间间隔和收益预期对布伦特原油价格行为和价格形成机制的影响.相对国外,目前我国关于石油期货价格问题的研究还不成系统,针对国内外石油价格时差的研究也很少.本文借助灰色关联度模型,采用定量化的研究方法,测定中国燃料油期货价格与国际石油期货价格的时差.2 研究设计当前国际石油价格主要是由纽约商品交易所(NY MEX)、伦敦国际石油交易所(IPE)和新加坡纸货市场(SPM)三个期货市场决定.这三个交易所分别是所处地区的石油定价中心,纽约代表北美地区,伦敦代表欧洲地区,新加坡则代表包括中国在内的远东地区.日本的石油期货市场虽然起步较晚,但是发展迅速. 1999年,日本东京工业品交易所(T OC OM)推出汽油、煤油期货交易.到了2002年,以石油期货为主的东京工业品交易所交易量占日本期货交易总量的60%以上,成为亚洲地区重要的石油期货交易场所之一.本文研究时选择了NY MEX、IPE、SPM和T OC OM上述四个期货市场的油价作为国际石油价格的代表.211 研究思路根据灰色关联度理论,以中国燃料油的期货价格作为基础数列,以纽约燃料油、原油和汽油,伦敦北海布伦特原油和柴油,新加坡燃料油,东京原油、煤油和汽油的期货价格作为对比分析序列,通过计算基础数列与对比数列在不同时间点上的灰色关联度,以最大灰色关联度值对应的时间差为基准,得出国内石油期货价格和国际石油期货价格的时间差.212 研究方法传统数理统计中进行抽象系统分析的方法有很多,如主成分分析、回归分析等.传统数理统计分析要求数据量大,样本服从典型概率分布且计算复杂.灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否密切.序列曲线越接近,相应序列之间的关联度越大,反之就越小.灰色关联分析可以弥补传统数理统方法做系统分析的不足,本文选择该方法为研究工具.灰色关联分析的基本原理如下:1)行为序列构成设Xi为系统因素,k为观测对象序号,x i (k)为因素Xi关于第k个对象的观测数据,则称X i=(x i(1),x i(2),…,x i(n))为因素Xi的行为横向序列.2)始点零像化设系统行为序列Xi =(x i(1),x i(2),…,x i(n)),D为序列算子,且X i D=(x i(1)d,x i(2)d,…,x i(n)761第3期基于灰色关联理论的中外石油期货价格时差d ),其中,x 0i (k )=x i (k )d =x i (k )-x i (1),k =1,2,3,…,n .称D 为始点零化算子,X i D 为X i 的始点零化像,记为X i D =X 0i =(x 0i (1),x 0i (2),…,x 0i (n )) 3)确定|s 0|,|s i |和|s i -s o |设X 0与X 1的长度相同,且皆为12时距序列,而X 00=(x 00(1),x 00(2),…,x 00(n ))X 0i =(x 0i (1),x 0i (2),…,x 0i (n )) 分别为X 0与X 1的始点零化像,则|s 0|=∑n -1k =2x 00(k )+12x 00(n )|s i |=∑n -1k =2x 0i (k )+12x 0i (n )|s i -s 0|=∑n -1k =2(x 0i (k )-x 00(k ))+12(x 0i (n )-x 00(n )) 4)确定绝对关联度ε0iε0i =1+|s 0|+|s i |1+|s 0|+|s i |+|s i -s 0|.213 数据选择中国燃料油期货于2004年8月26日在上海期货交易所(SHFE )正式上市交易,每年按交割月份产生12种交易合约,分别是每年的1月至12月燃料油期货合约,我们选择最近期(2006年12月)交割的石油期货合约作为研究的标的合约.研究中所涉及的国内外石油期货合约分别是,沪燃油0612(代码2332)、美原油12(代码6712)、美燃油12(代码6752)、布伦特原油12(代码6562)、英柴油12(代码6582)、新FO180CST 燃油(代码2618)、日原油12(代码6832)、日煤油12(代码6852)和日汽油12(代码6812).研究选择2006Π06Π20~2006Π11Π21为研究区间,以在该区间内的上海期货交易所、纽约商品期货交易所、伦敦国际石油交易所、新加坡纸货市场和东京工业品交易所上市交易石油期货的日收盘价格为研究数据,共获得900个有效观察值.研究数据来源于道通文华财经Webstock2006资讯终端软件.3 石油期货价格时差研究结果表1 L =0时,国际石油期货产品的灰色绝对关联度期货产品灰色绝对关联度期货产品灰色绝对关联度美燃油0.530940新燃油0.572255美原油0.510951日原油0.539273美汽油0.532231日煤油0.528987布伦特原油0.745937日汽油0.529290英柴油0.527737根据灰色系统理论原理,以连续30个交易日的中国燃料油期货价格组成系统特征序列,同时以在国际石油期货市场上市的9种石油期货品种的价格组成对比分析序列.假定时间同步(步长L =0),以沪燃油—美燃油为例,计算两组不同期货市场价格序列的灰色绝对关联度.选定2006Π8Π4至2006Π9Π14连续30个交易日为基准分析区间,将中国燃料油期货价格对应于当天的美国燃料油价格,按绝对灰色关联度的原理,计算出在同一时间的中美燃料油期货价格绝对灰色关联度ε01.依此方法,再分别计算时间同步时,沪燃油—美原油、沪燃油—布伦特原油、沪燃油—英柴油、沪燃油—新燃油、沪燃油—日原油、沪燃油—日煤油和沪燃油—日汽油的绝对灰色关联度.在时间同步(L =0)时,国际各石油期货产品与中国燃料油期货价格的灰色绝对关联度汇总如表1所示.由表1可知,时间相同时,国内外石油期货价格灰色绝对关联度相近,大部分在01530上下波动.其中,国内燃料油与布伦特原油价格关联性较强,灰色关联度达到01745937.假定时间平移(步长L =±30),即861系统工程理论与实践2008年3月某日国内石油期货价格对应于前(后)L 天国外某石油产品期货价格,计算每平移一天的中国燃料油期货价格与国际能源期货价格的灰色绝对关联度.当美燃油期货价格时间向前平移一天(L =+1)时,以沪燃油—美燃油期货为例.先将中国燃料油期货价格序列分析区间固定为2006Π8Π4至2006Π9Π14,而美国燃料油期货价格向前平移一天,即对应的时间为2006Π9Π3至2006Π9Π13.按绝对灰色关联度的原理,计算时间向前平移一天后的中美燃料油期货价格绝对灰色关联度ε01(L =+1).以此类推,计算美燃料油时间向前平移30天(L =+1,…,+30)的绝对灰色关联度ε01(L =+1),n =1,2,…,30;美燃料油时间向后平移30天(L =-1,…,-30)的绝对灰色关联度ε01(L =+n ),n =1,2,…,30.在时间平移(L ≠0)后,沪燃油—美燃油期货价格的灰色绝对关联度中最大值为01535417,对应的步长为L =+19.由此可知,美国燃料油价格先行中国燃料油价格约19天.依此方法,分别计算沪燃油与其他石油期货价格的平移后灰色关联度,记为ε0i (L =±n ),其中i =2,3,…,9;n =1,2,…,30.在中国燃料油与每一种石油期货价格平移灰色关联度中,找出最大灰色关联度所对应的步长L ,即国内外石油期货价格的时差.若关联度的最大值所对应的步长L 为正数,即表示国外该石油产品期货价格先行于中国燃料油期货价格.若关联度的最大值所对应的步长L 为负数,即表示中国燃料油期货价格先行于国外该能源产品期货价格.若L 为零,表示中外能源期货价格同步.中国燃料油和国际石油期货价格灰色绝对关联度最大值及对应的L 汇总如表2所示.表2 国内外石油期货价格灰色绝对关联度最大值对应的L期货产品L 灰色绝对关联度期货产品L 灰色绝对关联度美燃油+190.535417新燃油+300.592541美原油+170.511752日原油+260.552435美汽油+160.533836日煤油+270.535573布伦特原油+300.830855日汽油+270.538492英柴油+290.5358734 结论根据灰色关联理论,通过向前(后)平移时间的方法,研究国内外石油期货价格序列的关联度及其最大值对应的时差.研究结论如下:1)我国燃料油期货价格明显滞后于国际石油价格.中外石油价格最大关联度值所对应的时间均为正数,说明国外NY MEX 、IPE 、SPM 和T OC OM 四个主要石油期货市场的价格均先行于我国燃料油期货市场.2)伦敦国际石油交易所和新加坡纸货市场石油价格先行于国内燃料油价格时间最长,约一个月.3)我国燃料油期货价格与北海布伦特原油价格的关联性最强.研究发现,上海燃料油期货价格与布伦特原油价格的关联度明显高于与其他石油期货品种之间的关联度,最大值达到01830855.4)国内外石油期货时差与所处的期货市场相关,价格关联程度具有明显的市场趋同性.纽约商品交易所与上海燃料油期货价格的时差最小,相差约15天;东京工业品交易所次之,相差约26天;伦敦国际石油交易所和新加坡纸货市场时差最长,至少30天.5)由于每份期货合约都具有到期日,且各国期货交易规则不一致导致难以按时间一一配对国内外期货价格,因此本研究最多只能考察前后一个月价格的相关性,这是本文研究的局限性.参考文献:[1] 焦建玲,范英,魏一鸣.石油价格研究综述[J ].中国能源,2004,26(4):33-39.Jiao J L ,Fan Y,Wei Y M.Review on the research of oil price[J ].Energy of China ,2004,26(4):33-39.[2] X iaowen S L ,T amvakis M N.S pillover effects in energy futures markets[J ].Energy Economics ,2001,23:43-56.[3] Hamm oundeh S ,Li H ,Jeon B.Causality and v olatility spillovers am ong petroleum prices of WTI ,gas oline and heating oil indifferent locations[J ].N orth American Journal of Economics and Finance ,2003,14:89-114.[4] X iaowen S L ,T amvakis M N.E ffects of NY MEX trading on IPE brent crude futures markets a duration analysis[J ].Energy P olicy ,961第3期基于灰色关联理论的中外石油期货价格时差071系统工程理论与实践2008年3月2004,32:77-82.[5] Hamm oudeh S,Huimin L.The impact of the Asian crisis on the behavior of US and international petroleum prices[J].EnergyEconomics,2004,26:135-160.[6] 高辉.国内外燃料油价格关联度及动态滚动预测的模型研究[J].国际石油经济,2005,13(12):24-66.G ao H.S tudy on correlation of domestic and foreign fuel oil prices and dynamic trend forecast m odeling[J].International PetroleumEconomics,2005,13(12):24-26.[7] 胡政,李辉.新加坡燃料油市场对我国的影响[J].国际石油经济,2002,10(10):15-18.Hu Z,Li H.The in fluence of S ingapore’s fuel oil market on China[J].International Petroleum Economics,2002,10(10):15-18.[8] 焦建玲,范英,张九天,等.中国原油价格与国际原油价格的互动关系研究[J].管理评论,2004,16(7):48-52.Jiao J L,Fan Y,Zhang J T,et al.S tudy on the interaction between China’s and international crude2oil prices[J].Management Review,2004,16(7):48-52.[9] 何凌云,范英,魏一鸣.基于Z ipf分析的Brent原油价格行为的实证研究[J].复杂系统与复杂性科学,2006,3(1):67-78.He L Y,Fan Y,Wei YM.Empirical study on Z ipf analysis of Brent crude oil price behaviors[J].C omplex Systems and C omplexity Science,2006,3(1):67-78.(上接第124页)[11] 徐泽水.基于不同类型残缺判断矩阵的群决策方法[J].控制与决策,2006,21(1):28-33.Xu Z S.G roup decision making method based on different types of incomplete judgment matrices[J].C ontrol and Decision,2006, 21(1):28-33.[12] 吴江,黄登仕.多属性决策中区间数偏好信息的一致化方法[J].系统工程理论方法应用,2003,12(4):359-362.Wu J,Huang D S.The uniform methods for interval number preference in formation in multi2attribute decision making[J].Systems Engineering-Theory Methodology Application,2003,12(4):359-362.[13] Mikhailov L.G roup prioritization in the AHP by fuzzy preference programming method[J].C omputers&Operations Research,2004,31(2):293-301.[14] Mikhailov L,Tsvetinov P.Evaluation of services using a fuzzy analytic hierarchy process[J].Applied S oft C omputing,2004,5(1):23-33.[15] Mikhailov L.A fuzzy approach to deriving priorities from interval pair2wise comparis on judgments[J].European Journal ofOperational Research,2004,159(3):687-704.[16] Zhu J J,Liu S X,Wang M G.Integration of weights m odel of interval numbers comparis on matrix[J].Acta Automatica S inica,2005,31(3):434-439.[17] 朱建军,刘士新,王梦光.基于遗传算法求解区间数AHP判断矩阵的权重[J].系统工程学报,2004,19(4):344-350.Zhu J J,Liu S X,Wang M G.Estimation of weight vectors of interval numbers judgment matrix in AHP using genetic alg orithm[J].Journal of Systems Engineering,2004,19(4):344-350.[18] Wang Y M,Y ang J B,Xu D L.A tw o2stage logarithmic g oal programming methods for generating weights from interval comparis onmatrices[J].Fuzzy Sets and Systems,2005,152(1):475-498.[19] 陈岩,樊治平.基于语言判断矩阵的群决策逆判问题研究[J].系统工程学报,2005,20(2):211-215.Chen Y,Fan Z P.S tudy on the adverse judgment problem for group decision making based on linguistic judgment matrices[J].Journal of Systems Engineering,2005,20(2):211-215.[20] 徐泽水.群组决策中专家赋权方法研究[J].应用数学与计算数学学报,2001,15(1):19-22.Xu Z S.Research on methods for derivign experts’weights in group decision making[J].C ommunication on Applied Mathematics and C omputation,2001,15(1):19-22.[21] 党耀国,刘思峰,刘斌.多指标区间数关联决策模型的研究[J].南京航空航天大学学报,2004,36(3):403-406.Dang Y G,Liu S F,Liu B.S tudy on incidence decision making m odel of multi2attribute interval number[J].Journal of Nanjing University of Aeronautics&Astronautics,2004,36(3):403-406.[22] R obert M,Benjamin S,Thomas L.S tatistical Methods for Engineers and Scientists[M].New Y ork:M.Dekker,1985.。
原油价格预测模型的建立与应用

原油价格预测模型的建立与应用随着全球经济的发展和科技的进步,原油已经成为全球最重要的商品之一。
原油价格的波动不仅对石油公司及相关行业有着深远的影响,也直接关系到全球能源结构和经济发展。
因此,原油价格预测成为许多行业和投资者的关注点。
1. 原油市场的复杂性原油市场的形态和价格波动是非常复杂的。
原油价格受到供需关系、政治因素、经济指标、环境和气候变化等多种影响因素的综合作用。
因此,要准确预测原油价格是非常困难的。
2. 原油价格预测模型为了更好地预测原油价格,需要建立预测模型来对价格走势进行分析。
目前,常见的原油价格预测模型有基于时间序列分析的模型、基于统计学的模型、基于机器学习的模型等。
这些模型各有优缺点,最终选择哪种模型应根据实际情况进行评估。
3. 时间序列模型时间序列模型是一种常用的原油价格预测方法。
它基于历史数据进行分析,从而预测未来价格趋势。
常见的时间序列模型包括ARIMA模型、ARCH模型、GARCH模型等。
这些模型可以对时间序列数据的方差和序列中时间相关性进行建模,从而更好地预测未来价格。
4. 统计学模型另一种常用的原油价格预测方法是基于统计学的模型。
这些模型通过分析原油价格与其他经济变量的关系来预测价格。
经济变量通常包括GDP、通货膨胀率、利率等。
通过这些变量与原油价格的历史关系,可以建立一个多元回归模型,从而预测未来的价格走势。
5. 机器学习模型机器学习模型是近年来应用于原油价格预测的新兴技术。
这些模型可以处理大量数据和非线性关系,以更准确地预测未来价格。
常见的机器学习模型包括支持向量机、人工神经网络、决策树等。
6. 模型应用建立好的原油价格预测模型可以应用于各种行业中。
石油公司可以利用预测模型来进行生产和销售计划。
金融机构可以利用预测模型作为投资决策工具。
政府也可以利用预测模型来制定能源政策。
7. 模型评估原油价格预测模型的建立不是一件容易的事情。
评估其准确性和稳定性是一项非常重要的任务,以确保模型能够有效地使用。
灰色模型与时间序列分析在成品油价格中的应用对比

( ( 】 ) ( 1 )
” 一
3 . 模 型 比较 A R I MA 模型能充分利用各项数据 , 探 索 出其 中规 律 . 且 对 数 据 动 态性 的把 握 较 好 , 精 度 较 高 。但 局 限 于短 期 预 测 且 难 以反 映 因 素 相关 关 系 。灰 色 预 测 模 型 能 将 无 规 律 的原 始 数 据 进行生成 , 得 到 规 律性 较 强 的生 成 序 列 , 精度较 高 。 但 只 适 用 于 中短 期 的 预测 ㈨
4 . 不 足 之 处
继 续 利 用 f k 十 ) = ( k + 1 ) 一 ∞ 累 减 得 到模 拟数 据 。求 得 2 叭4 年起
三个 月 的石 油 预测 价 格 为7 7 6 6 . 4 元/ 吨, 7 8 0 9 . 1 元/ 吨. 7 8 5 2 . 0 元/ 吨。 2 . 时 间 序 列 分 析 第一 步: 采集数 据 ( 数据 如上表 1 , 成 品油 2 0 0 9 — 2 0 1 3 年 各 月份价格数据 ) 第二步: 判 断 序 列 的 平 稳 性 由生 成 数 列 的 时 序 图 , 可 知 该 序 列 有 显 著 的趋 势 , 显 然 是 个非平稳序列。 第三步: 对 原 序 列 进 行差 分运 算 原 时 序 图呈 现 出 近 似 线 性 的 趋 势 , 对 序 列 进 行 一 阶 差 分 以 消 除 趋 势 的影 响 , 一 阶差 分后 序列 基 本 平 稳 。 为进 一 步 确 定 平 稳性 , 做 出 差 分 后 序 列 的 自相 关 图后 , 序 列 有 很 强 的 短 期 相 关性 , 因 此 初 步 认 为 一 阶差 分后 序 列 平 稳 。 第 四步 : 对 平 稳 的一 阶差 分 序 列 进 行 白噪声 检验 在0 . 0 5 的显 著 性 检 验 水 平 下 ,延 迟 6 阶的检验统计 量的P 值 为0 . 0 0 1 1 , 显 著 小 于0 . 0 5 , 该 差 分 序 列 不 能 视 为 白 噪声 序 列 .
基于灰色时序组合模型的油液光谱分析预测

—
X
其 中,t 8=
,
趔 髓 烂
对残差序列 E采用 A ( ) R p 模型进行建模 , 计算得
到模型参数 和 , 则残差序列的时序预测模型为
=
.
l 5
Z U
Z5
j U
取样序号
竹 +口, = 1 , , l ,… 2
图 2 时序模型预测结果
组合模型的预测结果为 二 =互 6 (一d - t 州 t = 1e 一 + )
A src : ae nteo et m a a s a cr i t eo gn ,h M mo e, R mo e a dge R b t tB sdo is c u n yi d t o a et n y f n e teG dl A dl n ryA a h lp r l s a f a p ei cm ia o o e aeue s bi ed n m cm d l f h e ue aa tecne t f rni ee g e S o bn t nm d l r sdt et lht y a i o e o em a rdd t h o tn o t n n ’ i o a s h t s , o i nh i
归模型 A ( ) , R p 翻 如下式所示
Xt =
∑ + O 12 , ,=, , 凡 … )
- 1
注 : 度 低 单 位 为 x1 浓 0
分别利用灰 色 G 1 1 , M( , )时序 A p 和灰色时 R( ) 序 组合模 型 , 表 l的数据 进行 预 测分 析 。 以前 对 P为模型阶数 ; 2 组数据为基 础进行建模 , 3 采用 M T A A L B编程 的方 ( 1 p为模型 自回归系数 ; ) 法进行计算昀 后 5 , 组数据作为验证。 灰色模型预测结果如图 l 所示, 图中可以看出, 从 为 白噪声序列( 均值为 0 方差为 :; ) 灰色模 型预测 结果很 好地 反应 了同一换 油周期 内 X t 为经过处理后的光谱测量数据 ,满足平稳 、 正 F 元素宏观上的变化趋势, e 对部分浓度值的预测误差 态分布、 零均值的要求。 较大。对后 5 组验证数据的预测平均误差为 1 4 . %。 0 利用时序对摩擦 系统动态建模 ,一般依靠计算 机编程经过模型参数识别 、 模型定 阶、 模型检验这 3 个步骤 。
石油市场预测

石油市场预测论文摘要如果说“石油是工业的血液”是对工业化时代描述的话, 那么,“石油是社会经济和生活的动力”则适合于当今世界。
事实上, 历史上从来还没有任何一种商品能像石油那样, 对人类生活产生过如此大的影响, 对国际政治经济产生过如此大的冲击。
近年来, 在国际石油价格持续上涨、屡创新高的背景下, 国内油价也持续攀升, 从而对我国社会经济发展和人民生活产生了重大影响。
日益升高的对进口石油的依存度使中国更加深刻地体会和认识到了油价的不稳定性。
本文依据历年的石油价格分析并预测出了未来石油价格的发展前景,确定影响石油价格的各个因素。
针对问题一,本文先探究不同因素对汽油、柴油价格的影响,分析得出影响较大的因素。
本文选取了替代产品的使用、估计需求、人均GDP收入这几个因素分析。
我们首先对各个因素选取可量化的指标进行分析,最后得到影响较大的因素。
由于各种因素未来的不确定性,本文选取灰色预测模型,来预测未来汽油及柴油的价格。
针对问题二,本文建立了基于灰色预测的最小二乘回归模型。
本文考察了人均国民生产总值,运营公交车数量,道路总长,人均可支配收入,汽油年均价这些指标来衡量未来汽车市场的外部环境条件。
本文将未来5年的各种车型销量为研究对象,利用因子分析对所选取的五项指标进行相关性分析,得到四个因子,运用最小二乘法将各种车型的销量与四个因子进行拟合,得到各种汽车车型销量与因子的关系表达式。
运用灰色预测对五项指标进行预测,代入回归方程得到各种车型的销量。
针对问题三,本文建立了废气排放量与油价和各种车型销量的回归拟合模型。
我们可以根据预测的油价及各种车型未来的销量,代入回归方程预测未来废气的排放量。
关键字:灰色预测相关系数因子分析问题重述2012年初,工信部公布了党政机关公务用车选用车型目录征求意见稿,在《2012年度党政机关公务用车选用车型目录(征求意见稿)》所列的412款车型中,全部为自主品牌。
车款目录型号包括轿车、多功能乘用车、越野车和新能源汽车4大类,25家入围企业均为国产自主汽车品牌,进口车与合资车全部出局。
原油价格预测模型的研究与优化

原油价格预测模型的研究与优化随着全球经济的发展和能源需求的增长,原油价格成为国际市场上备受关注的重要指标之一。
对原油价格的准确预测对于不同利益相关方来说都具有重要意义,包括石油公司、投资者和政府等。
为了满足这一需求,许多学者和分析师已经提出了各种原油价格预测模型,并对其进行了优化。
首先,为了更好地理解原油价格预测模型的研究与优化,我们需要了解原油价格的主要影响因素。
原油价格受到供求关系、宏观经济因素和地缘政治等多种因素的共同作用。
因此,在构建预测模型时,需要综合考虑这些因素,并建立相应的指标体系。
一种常见的原油价格预测模型是基于供求关系的模型。
该模型认为,原油价格的涨跌主要受到供应量和需求量的变动影响。
供应量的变动包括产量、出口和储备等方面的因素,而需求量的变动则受到经济增长、工业生产和季节因素等影响。
通过收集和分析相关数据,可以建立供求关系模型,并利用统计方法进行预测。
另一种常见的原油价格预测模型是基于宏观经济因素的模型。
宏观经济因素包括通货膨胀率、利率、汇率和国内生产总值等指标。
这些指标反映了经济的整体状况和走势,在很大程度上决定了原油需求量的变化。
通过建立宏观经济模型,可以预测原油价格的走势。
除了供求关系和宏观经济因素,地缘政治也是影响原油价格的重要因素。
例如,中东地区的地缘政治冲突和石油生产国的政策变化等都可能导致原油价格的剧烈波动。
因此,在预测模型中加入地缘政治因素,可以更准确地预测原油价格的变动。
在研究原油价格预测模型时,模型的准确性和稳定性是关键指标。
为了优化模型,我们可以采取以下几个方面的努力:首先,需要选择合适的数据集。
准确的数据是构建预测模型的基础。
在选择数据集时,需要确保数据的完整性和可靠性。
一般情况下,应选取历史数据,并确保数据能够涵盖各种影响因素的变动。
其次,需要选择合适的模型算法。
预测模型可以采用传统的统计方法,如回归分析、时间序列分析等,也可以采用机器学习和人工智能等新兴方法。
原油市场价格波动的预测模型

原油市场价格波动的预测模型原油是现今世界上最为重要的能源之一,也是世界经济最为重要的商品之一。
原油价格的波动影响着全球经济的走势和稳定,因此,对原油价格进行准确的预测显得尤为重要。
本文将探讨原油市场价格波动的预测模型。
一、宏观经济因素影响原油价格原油价格的波动受到多种宏观经济因素的影响,如供需关系、地缘政治等。
这些因素对原油价格的波动具有一定的指导作用。
供需关系是原油价格波动的最主要因素之一。
例如,OPEC(石油输出国组织)等产油国的政策对原油价格产生着深刻的影响。
OPEC等产油国的采取的减产政策将导致供给减少,从而提高原油价格。
另外,地缘政治因素也是影响原油价格波动的重要因素之一。
例如,中东局势的紧张、地区冲突等都可能导致油价波动。
此外,自然灾害和气候变化等也将对原油价格产生影响。
二、技术分析预测原油价格技术分析是原油价格波动预测的一种主要方法。
技术分析是在探究市场价格波动规律的基础上,以一定的技术手段,如趋势线、均线、相对强弱指数等,对市场价格波动进行预测的方法。
该方法的主要优势在于能够提供简单、快速的技术分析预测方法,为预测市场价格波动提供可靠性指引。
三、基本面分析预测原油价格基本面分析是对市场供求关系的分析,承认经济变化和政治风险等的影响。
基本面分析针对的是市场面临着的长期供需平衡问题,对市场的判断适用于长期市场预测。
基本面分析的主要内容包括市场目标价格、市场供给和需求的预测、市场的潜在产能和库存备货等。
通过分析市场的供求状况,预测市场的未来变化,为市场投资或者价格风险管理提供依据。
四、人工智能在原油价格预测中的应用人工智能技术是近年来兴起的,而人工智能技术对于原油价格的预测也产生了影响。
在通过机器学习算法识别变量的影响下,将原油价格预测模型应用于机器学习算法中,便能够更准确预测原油价格的变化。
例如,通过卷积神经网络(CNN)算法、长短期记忆网络(LSTM)等预测模型,可以准确预测原油价格和趋势。
国际原油价格预测(附程序)
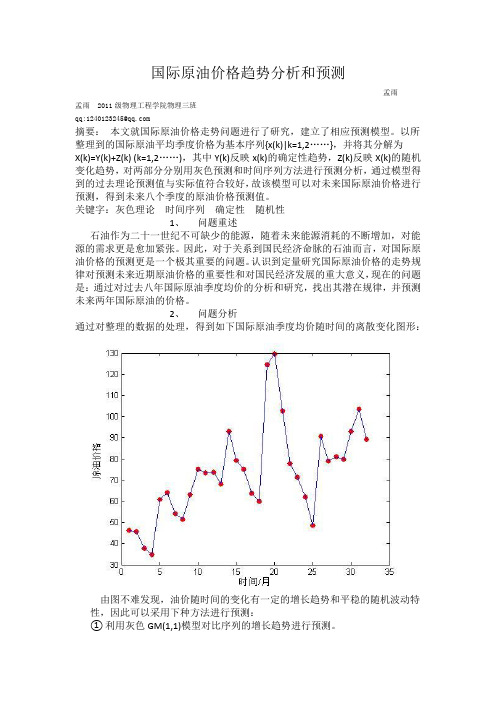
运行的 Mat lab 程序如下:
clc,clear x0=[46.18 45.72 37.81 34.82 60.71 64.21 54.08 51.43 63.23 75.04 73.40 73.81 68.24 93.01 79.13 75.08 63.69 60.03 124.65 129.59 102.60 77.93 71.37 62.12 48.47 90.81 79.00 81.07 79.71 92.95 103.47 89.25 ]; n=length(x0); lamda=x0(1:n-1)./x0(2:n); range=minmax(lamda); x1=cumsum(x0); for i=2:n z(i)=0.5*(x1(i)+x1(i-1)); end B=[-z(2:n)',ones(n-1,1)]; Y=x0(2:n)'; u=B\Y x=dsolve('Dx+a*x=b','x(0)=x0'); x=subs(x,{'a','b','x0'},{u(1),u(2),x1(1)}); yuce1=subs(x,'t',[0:n-1]); digits(6),y=vpa(x); yuce=[x0(1),diff(yuce1)] epsilon=x0-yuce delta=abs(epsilon./x0) rho=1-(1-0.5*u(1)/(1+0.5*u(1))*lamda)
1
k =
k m=1 X 0
m ,k=1、2…… 32
1
从而得到一组生成数列 X 相应的白化微分方程为: = {X ‘ 1 , X ‘ 2 … … X ‘ 32 } dx (1) + ax (1) = a dt 引入记号: − 2 ∗ (X 1 1 + X X0 (2) a ⋮ a= , y1 = , B= ⋮ u 1 1 X0 (32) − 2 ∗ (X 31 + X 利用最小二乘法得到: a = (a, u)T = [BT , B]−1 ∗ BT ∗ y1 = 于是求解微分方程得: X
塔里木油田原油单位操作成本的灰色预测

塔里木油田原油单位操作成本的灰色预测
郭一鸣
【期刊名称】《吐哈油气》
【年(卷),期】2007(012)003
【摘要】原油单位操作成本控制是石油企业进行成本预算与控制的主要手段。
市场经济条件下,企业通常采用低成本策略来提高自身竞争力。
对石油企业而言,准确的预测原油单位操作成本,可以在生产过程中采取有效的手段控制,降低成本,提高企业效益。
该文以塔里木油田1999年到2005年的原油单位操作成本数据序列为依据,利用GM(1,1)灰色模型,进行了年度操作成本预测,并得到了较好的结果。
【总页数】3页(P298-300)
【作者】郭一鸣
【作者单位】南京大学地理与海洋学院,江苏南京210000
【正文语种】中文
【中图分类】TE254.3
【相关文献】
1.C4-C8轻烃在原油地球化学研究中的应用——以塔里木盆地大宛齐油田凝析油为例 [J], 孔婷;张敏
2.塔里木油田含硫试采油井的原油密闭转运技术的应用 [J], 郭鸣;刘兴华;陈光智
3.塔里木盆地塔河油田石炭系、三叠系原油地球化学特征及成因研究 [J], 郑朝阳;柳益群;段毅;于文修;樊婷婷;张学军
4.全国最大沙漠油田塔里木哈得油田日产原油突破6000吨 [J],
5.塔里木盆地哈拉哈塘油田原油聚集过程与密度多变成因 [J], 陶小晚;张义杰;段书府;张丽娟;郑多明;田瀚;张欣欣;朱文平
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于灰度系统模型的原油价格预测专业:信息与计算科学班级:0901班组员:南柯 U200810067陈均 U200910057周巍 U200910072指导老师:徐剑2012年7月目录摘要 (I)1背景分析和问题叙述 (1)1.1背景的分析 (1)1.2问题的叙述 (1)1.3 问题的分析 (1)2模型的假设及符号说明 (2)2.1符号说明 (2)2.2 模型的假设 (2)3 问题的分析和模型的建立 (3)3.1 问题的分析 (3)N (3)3.2 灰色模型GM(1,)4模型的求解 (6)N进行预测 (6)4.1采用GM(1,)4.1.1 预测步骤 (6)4.1.2对方程进行求解 (7)4.1.3 求出预测方程 (8)4.2 编写程序求解 (8)5结果与误差分析 (11)5.1 结果表示 (11)5.2 误差分析和模型检验 (11)5.2.1结果分析 (11)5.2.2模型检验 (12)6 模型评价与改进 (13)6.1 模型的优点 (13)6.2 模型的缺点 (13)6.3 模型的推广 (13)6.4 模型的改进 (13)7 参考文献 (15)8 附录 (16)摘要原油是指直接从油井采出的天然石油,也称“黑色金子”,作为三大主要能源之一,常被用作燃油和汽油,而燃油和汽油组成目前世界上最重要的一次能源之一。
另外,原油也是许多化学工业产品——如溶剂、化肥、杀虫剂和塑料等的原料。
原油产品在社会经济发展中具有非常广泛的作用与功能,是能源的主要供应者,不仅各工业部门离不开原油产品,而且原油产品也促进了农业的发展,因此有专家认为原油是经济的命脉,关系着国民经济的发展和人民生活水平的提高。
原油价格预测有利于国民经济平稳较快的发展,有利于加快能源行业健康发展,有利于制定完善的能源规划,因此对原油价格的准确预测显得十分必要。
中国不仅是世界上最早发现和应用石油的国家,还是世界石油生产和消费大国之一。
近年来,随着国民经济的快速增长,国内石油消费大幅增加,对石油进口的依赖程度逐年加深,如何更好地对石油价格进行预测,已成为关系国民经济可持续发展的重要问题。
基于此背景,本文建立了石油价格分析预测模型。
借鉴于前辈的论文资料和实习经验,采用网站所提供的数据,我们采用灰度系统理论的分析,建立了基于微分方程算法的GM(1,N)模型,利用数学知识和C语言两种方法进行解答。
并根据所得指数函数对2012年下半年的石油价格大体趋势进行了预测,并得到了较为准确的石油价格预测结果。
关键词:原油不稳定性非线性灰色理论 GM(1,N)模型1背景分析和问题叙述1.1背景的分析能源资源是人类生存、经济发展、社会进步不可或缺的重要资源,是关系国家经济命脉和国防安全的重要战略物资。
因此,能源问题是世界各国,特别是各大国普遍关注的一个战略问题。
其中,作为三大能源(煤、石油、天然气)之一,石油是一种关系国家政治军事安全、经济发展和外交重要战略资源,其具有稀缺性和不可再生性。
石油价格不仅国际军事和政治的影响,同时受到经济和外交格局影响,其变化具有不确定性、复杂非线性,因此,石油价格的准确预测已成为世界各国研究的热点课题[1]。
1.2问题的叙述能源是世界经济增长和人类社会发展的重要物质基础,石油作为消耗能源的重要组成部分其生产和消费可以带动或阻碍经济的发展。
因此石油价格的研究和预测对我国经济和社会的可持续发展有着非常重要的意义。
接下来,就利用在长炼石化商情网[2]上找到的数据建模进行分析。
1.3 问题的分析影响石油价格水平的主要因素很多: 供求关系、重大政治事件、OPEC 组织的决策、大国动用战略储备、自然灾害、期货市场的投机炒作、季节性气候变化等。
分析所有这些影响, 从而建立包含这些影响的价格预测的公式是很困难的。
所以石油价格数据是一种高度不稳定、复杂且难以预测的时间序列数据,因为这些数据往往既隐含大量的动态特征,又受自变量的影响,同时具有高度的非线性[3]。
2模型的假设及符号说明2.1符号说明表12.2 模型的假设由于石油的价格是间断的点,所以一般是采用插值和曲线拟合等方式进行处理。
但是本问题的石油价格,受各方面影响较大,是非线性的,不稳定性大,难以预测。
(1)石油价格取每月的平均值计算:我们以长炼石化商情网上的数据为基础,以月为单位,根据2012年前半年的月度石油平均价格的数据,也就是原始始时序列数据0(),0,1,2x t t=…n,对2012年度后半年的价格进行预测。
(2)石油价格与上一年的石油价格无关:在石油价格与上一年无关的条件下,给问题求解和模型建立提供了方便。
实现通过本年前几个月的价格波动来预测后几个月的石油价格的目的。
(3)石油价格短期内不出现大幅度波动,呈现较为平稳变化趋势:石油价格短期内的大幅波动影响了模型的稳定性,这将使得求出的结果的误差过大。
3 问题的分析和模型的建立3.1 问题的分析图上是国际WTI原油在最近一个月内的走势,我们由图1可以看出,价格走势波动很大,而且没有特定的线性规律,所以用常规的一维回归方程做的价格预测可能相差很大。
针对本模型用灰色预测模型进行预测。
图13.2 灰色模型GM(1,)N灰色系统[4]产生于控制理论的研究中,在控制论中最先研究的是白色系统和黑色系统。
若一个系统的内部特征是完全已知,即系统的信息是充足完全的,我们称之为白色系统;若一个系统的内部信息是一无所知,一团漆黑,只能从它同外部的联系来观测研究,这中系统便是黑色系统。
灰色系统介于二者之间,灰色系统的一部分信息是已知的,一部分是未知的。
N模型:系统由N个变量构成,如果每个变量都有m个相互对应的GM(1,)数据,则可形成数列0(1,2x i …)ni(0)(0)(0)(0){(1),(2),()}i i i i x x x x m = (1,2,,i n = )对于上面的每一个序列都可以进行累加生成,形成n 个数列,即(1)(1)(0)(0)1()(1)()()miiii k x k x k x k x k ==-+=∑ (1,2,,i n = )(1)(1)(1)(1){(1),(2),()}i i i i x x x x m = (1,2,,i n = )对这个由n 个序列构成的系统可围绕系统主要因素(1)i x 建立微分方程:1111112231n n dx ax b x b x b x dt-+=+++ 其中^1121(,,,)()T T T n n a a b b b B B B y --==(1)(1)(1)(1)112(1)(1)(1)(1)112(1)(1)(1)(1)1121((1)(2)),(2),,(2)21((2)(3)),(3),,(3)21((1)()),(),,()2n nn x x x x x x x x B x m x m x m x m ⎡⎤-+⎢⎥⎢⎥⎢⎥-+⎢⎥=⎢⎥⎢⎥⎢⎥--+⎢⎥⎣⎦(0)(0)(0)111[(2),(3),,()]T n y x x x m =解方程得:100111112211ˆ(1)[(1)(1)](1)m m aki i i i i i xk x b x k e b x k a a ---==+=-+++∑∑ (0)(1)i i x x = (1,2,,i n = )灰色模型的误差检验:(1)(0)(1)((1))ak u ux k x e a a-+=-+(1)残差(误差)为:(1)(1)ˆ()()()q k x k x k =-(2)残差均值为:11()nk q q k n ==∑(3)原始数据的方差为:22(0)111(())n k S x k x n ==-∑其中,(0)11()n k x x k n ==∑(4)残差的方差为:22211(())n k S q k q n ==-∑(5)原验差比值为:21/C S S =(6)小误差概率为:1{|()|0.6745}P P q k q S =-<(7)检验按P 与C 的大小,可按预测精度分为好、合格、勉强、不合格,各类P 、C 值如下表所示:表2根据灰色模型原理,所编核心算法详见附录。
4模型的求解4.1采用GM(1,)N 进行预测4.1.1 预测步骤用GM(1,)N 模型对石油消费量进行预测的步骤如下:对原始时序列数据0(),0,1,2x t t = …n 做一次累加生成,得新的数列1(),x t0,1,2t =…n 。
其中,11001()(1)()()miiii k x k x k x k x k ==-+=∑将图3中WTI 原油的1-5月数据带入计算(6月用来检验)得:表3国际原油均价(1)100.32;(2)102.26;(3)106.21;(4)103.35;(5)94.72x x x x x =====。
则:10(1)(1)100.32;x x ==100(2)(1)(2)100.32102.26202.58;x x x =+=+=1000(3)(1)(2)(3)100.32102.26106.21308.79;x x x x =++=++= 10000(4)(1)(2)(3)(4)x x x x x =+++100.32102.26106.21103.35412.14;=+++=100000(5)(1)(2)(3)(4)(5)x x x x x x =++++100.32102.26106.21103.3594.72506.86;=++++=4.1.2对方程进行求解利用一次累加生成数列拟合微分方程:111dx ax u dt+= 解出参数a 和u 。
参数a 和u 用以下公式计算而得:1()T Ta B B B X u -⎡⎤=⎢⎥⎣⎦其中B 和X 分别为如下矩阵和向量:111211231111/2()11/2()11/2()1n n x x x x B x x -⎡⎤-+⎢⎥-+⎢⎥=⎢⎥⎢⎥-+⎢⎥⎣⎦2030n x x X x ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦T B 为B 的转置矩阵,1()T B B -为矩阵()T B B 的逆矩阵,n 为原始数列的数据个数。
其中:2030405102.26106.21103.3594.72x x X x x ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦11121123113411451/2(100.32202.58)1151.4511/2()11/2(202.58308.79)1255.6911/2()11/2(308.79412.14)1360.4711/2()11/2(412.14506.86)1459.5011/2()1x x x x B x x x x ⎡⎤-+--+⎡⎤⎡⎢⎥⎢⎥-+--+⎢⎥⎢⎥===⎢⎥⎢⎥-+--+⎢⎥⎢⎥-+--+⎢⎥⎣⎦⎣⎣⎦⎤⎢⎥⎢⎥⎢⎥⎢⎥⎦151.451151.451255.691255.691429393.34951227.11[]360.471360.4711227.114459.501459.501TTB B --⎡⎤⎡⎤⎢⎥⎢⎥---⎢⎥⎢⎥==⎢⎥⎢⎥---⎢⎥⎢⎥--⎣⎦⎣⎦11429393.34951227.11()[]1227.114T B B ---=-41227.111/(429393.349541227.111227.11)[]1227.11429393.3495=⨯-⨯1/529441/1731/173 2.0276⎡⎤=⎢⎥⎣⎦所以:1()T T a B B B X u -⎡⎤=⎢⎥⎣⎦1/529441/173123422.52640.02446[]1/173 2.0276406.54109.1271-⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦即:a =0.02446;u =109.12714.1.3 求出预测方程根据求解,我们可以得到所求预测方程为:1(0)(1)((1))ak u u x k x e a a-+=-+0.024464362.09864462.4185k e -=-+4.2 编写程序求解编写C 语言程序进行求解程序见附录。
