高等代数考研复习[欧氏空间]
高等代数-9第九章 欧几里得空间

(线性性)
4) ( , ) 0, 当且仅当 o 时 ( , ) 0. (非负性)
则称 ( , )为 和 的内积,称这种定义了内积的 实数域 R上的线性空间V为欧几里得空间.
§1 定义与基本性质
b
§1 定义与基本性质
线性性 ( k f lg , h) a k f ( x ) lg ( x ) h( x )dx
b
k f ( x )h( x )dx l g ( x )h( x )dx
a a
b
b
k ( f , h ) l ( g , h)
非负性 ( f , f ) f ( x ) f ( x ) dx f 2 ( x ) dx 0 a a 且 ( f , f ) 0 f ( x ) 0. 故( f , g) 为一内积, C (a , b) 构成欧氏空间.
注1 欧几里得空间 V是特殊的线性空间. (1)V为实数域 R上的线性空间; (2)V既有向量的线性运算,还有内积运算; (3) , V ,( , ) R. 注2 欧几里得空间,Euclidean Space, 简称欧氏空间. 欧几里得(Euclid,约公元前330 年—前275年),古希腊数学家,是几 何学的奠基人,被称为“几何之 父”. 他最著名的著作是《几何原本》.
b b
§1 定义与基本性质
2. 内积的运算性质 设V为欧氏空间, , , , i V , k , l , ki R
1) ( , k ) k ( , ) 2) ( , ) ( , ) ( , ) 3) ( , k l ) k ( , ) l ( , ) 4) ( k l , ) k ( , ) l ( , )
第八讲 欧氏空间

高等代数选讲
第八讲 欧氏空间
线性空间中,向量之间的基本运算只有加 法与数量乘法。作为几何空间的推广,可以发 现几何向量的度量性质,如长度、夹角等,在 线性空间的理论中没有得到反映。但是向量的 度量性质在许多问题(包括几何问题)有特殊 的地位。因此有必要在线性空间中引入度量的 概念,使其更接近于几何空间,并有更丰富的 内容与方法。
高等代数选讲 8、构造内积的方法 在实线性空间V 中构造内积使之构成欧氏空间,通 常采用如下两种方法: (1)直接构造:对任意 , V ,直接构造二元实 函数 , ,并验证其满足内积的四条公理。 (2)由正定矩阵确定内积:若V 为 n 维实线性空间, 任取V 的基 1 , 2 ,, n ,以及 n 阶正定矩阵A,定义: b1 b , a1 , a2 ,, an A 2 bn 其中 a11 a2 2 an n , b11 b2 2 bn n
高等代数选讲 欧氏空间证与内积有关的正交变换与对称变换在 现实生活中有着广泛而重要的应用,这两种变换在标 准正交基下分别对应着正交矩阵及实对称矩阵这两种 具有特殊性质的矩阵。要求掌握正交变换与对称变换 的概念及性质,能够运用它们与对应特殊矩阵之间的 关系解题对实对称矩阵A,要求能熟练地找到正交矩阵 T Q,使 Q AQ为对角阵,以及以另一种形式出现的同一 个问题,即用正交变换化实二次型为标准形。 将线性空间关于某个子空间进行直和分解是不唯 一的,但是欧氏空间关于某个子空间及其正交补空间 的直和分解是唯一的。欧氏空间的这种分解是很重要 的,要求掌握子空间的正交补的概念及基本性质,会 求某些子空间的正交补。
1 1 2 2 n n
高等代数选讲 (2) R mn --对于实矩阵 A aij mn , B bij mn 内积为
高等代数 欧式空间3

构成一个欧氏空间; 构成一个欧氏空间; (2)求 的维数; (2)求 V 的维数; (3)求使 (3)求使 的维数; tr ( A) = 0 的子空间 W 的维数;
n×n
(4)求 (4)求 W ⊥ 的维数。 的维数。 解 (1) 显然 V 是实数域上线性空间 集。若 A, B ∈ V , k ∈ ,则 的非空子
作业: 消化401-408页的内容 页的内容; 作业:1 消化401-408页的内容; 2 预习409-414页的内容。 预习409-414页的内容 页的内容。
γ 1, γ 2 , γ 3 , γ 4
1 1 T γ3 = ( 0, −1,1, 0 ) , γ 4 = 0, −1, −1, 2 . 2 2 4
(
)
α 2 = t 21β 1 + β 2 ,
1
1
................................... α n = t n1β 1 + t n 2 β 2 + L + t n ,n −1β n −1 + β n ⋅
T T T T
记
[ A, A] = ∑ i =1 ∑ j =1 a ij a ji = ∑ i =1 ∑ j =1 a ij2 ≥ 0 , 当且仅当 a = 0, i, j = 1,2,L, n ,即 A=O 时 [ A, B] = 0 . ij
n n n n
A = ( a ij )
,其中
nn
a ji = a ij , i, j = 1, 2,L , n ,则
α i , β j , i = 2,L , n, j = 1, 2,L , i − 1. 其中 t ij = β j , β j
高等代数考研复习[欧氏空间]
![高等代数考研复习[欧氏空间]](https://img.taocdn.com/s3/m/83070506763231126edb11d2.png)
即 ( , ) 0, 则称 与 正交,记为 .
非零向量组 1, 2 , , n如果满足 (i , j ) 0,(i j).
实数
称为向量 的长度,记为 0
1的向量称为单位向量.如果 长度为
则
称为
的单位化向量.长度有以下性质:
a) | | 0 当且仅当 0 时取等号; b) | k | k | |; c)
| || | | | .
夹角:欧氏空间V中向量 , 的夹角 , 定
(1 ,1 ) (1 , 2 ) ( , ) ( , ) 2 2 2 1 ( m ,1 ) ( m , 2 ) (1 , m ) ( 2 , m ) ( m , m )
则称 1, 2 , , n 是正交向量组. a)正交向量组一定是线性无关的; b) 若1, 2 , , n 是正交组,则
| 1 2 n || 1 | | 2 | | n | .
2 2 2 | | | | | | . c) 如果 , 则
为基 1, 2 , , n 的度量矩阵.
2) 度量矩阵的性质
a) 设 , 在n维欧氏空间V的基 1, 2 , , n 下的 坐标分别为 X ( x1, x2 , , xn ), Y ( y1, y2 , , yn ), 则 ( , ) X AY , 其中A是基 1, 2 , , n 的度量矩 阵.特别当 1, 2 , , n 是标准正交基时,A=E,则
高等代数考研复习
第九章 欧氏空间
高等代数课件(北大版)第九章 欧式空间§9.4

§9.4 正交变换
数学与计算科学学院
例、在欧氏空间中任取一组标准正交基 1 , 2 , , n ,
数学与计算科学学院
所以,A是正交矩阵.
" " 设 1 , 2 , , n 为V的标准正交基,且
1 , 2 , , n 1 , 2 , , n A
即, 1 , 2 , , n 1 , 2 , , n A 由于当A是正交矩阵时, 1 , 2 , , n 也是V的 标准正交基, 再由 1 即得 为正交变换.
定义线性变换 为:
1 1
i i ,
i 2, 3, n .
则 为第二类的正交变换,也称之为镜面反射.
§9.4 正交变换
数学与计算科学学院
§9.4 正交变换
数学与计算科学学院
一、一般欧氏空间中的正交变换
1.定义
欧氏空间V的线性变换 如果保持向量的内积不变, 即 , ( ), ( ) ( , ), , V 则称 为正交变换.
注:欧氏空间中的正交变换是几何空间中保持长度
不变的正交变换的推广.
1 , 2 , , n A
当 是正交变换时,由1知, 1 , 2 , , n 也是V
的标准正交基, 而由标准正交基 1 , 2 , , n 到标准
正交基 1 , 2 , , n 的过渡矩阵是正交矩阵.
§9.4 正交变换
第九章 欧氏空间
§1 定义与基本性质 §2 标准正交基 §3 同构 §4 正交变换 §5 子空间
欧氏空间复习

欧氏空间复习 一、欧氏空间定义如果V 是实数域R 上维线性空间,而且存在V 上二元实函数(,)满足: 1)(,)(,)αββα=2)(,)(,)(,)k l k l αβγαγβγ+=+3)(,)0αα≥,而且等于0的充分必要条件是0α=其中,,,,V k l R αβγ∈∈。
则称V 为具有内积(,)的欧氏空间,简称为欧氏空间。
我们有: ●(,0)0α=●1111(,)(,)rsrsi i j j i ji j i j i j k l k lαβαβ=====∑∑∑∑● 2(,)(,)(,)αβααββ≤(可以用其定义角度,证明一些不等式)如果设12,,,n εεε 为V 基,则定义(,)i j n n A εε⨯⎡⎤=⎣⎦,称其为基12,,,n εεε 的度量矩同样我们有:● 基的度量矩阵正定;● 不同基的度量矩阵合同(由此可以证明标准正交基的存在性) ●如果设1212[,,,],[,,,]n n X Y αεεεβεεε== ,则有:(,)T X AY αβ=二、标准正交基和正交补欧氏空间V 的基12,,,n εεε 称为标准正交基,如果有(,)i j ij εεδ=。
标准正交基的存在性一可以通过基的度量矩阵为正定矩阵及其正定矩阵和单位矩阵合同的性质证明。
其次可以通过施密特正交化方法证明。
我们有: ●n 维列向量12,,,n ααα 为n R 标准正交基的充分必要条件是矩阵12[,,,]n A ααα= 满足T A A E =,换句话说A 是正交矩阵。
注意一个正交矩阵决定两组正交基,一个是正交矩阵的列向量组,另外一个是正交矩阵的行向量组。
● 标准正交基的过度矩阵是正交阵。
●根据施密特正交化我们可以推出,对任意实可逆矩阵A 存在正交矩阵U 和上(或者下)三角矩阵T 使得A TU =或者A U T =。
●如果12,,,n εεε 为欧氏空间V 的标准正交基,而且:1212[,,,],[,,,]n n X Y αεεεβεεε==则有(,)T X Y αβ=。
高等代数 第7章欧式空间 7.1 欧氏空间的定义及性质

x, y
x y
例 求向量 1,2,2,3与 3,1,5,1的夹角.
18 2 解 cos 3 261. 非负性 当 x 0时, x 0;当 x 0时, x 0; 2. 齐次性 x x ; 3. 三角不等式 x y x y .
单位向量及n维向量间的夹角
1 当 x 1时, 称 x 为单位向量 .
2 当 x 0, y 0时, arccos
(4)[ x , x ] 0, 且当x 0时有[ x , x ] 0.
则称V(R)关于这个数积构成一个欧氏空间。这里 x,y为任意向量,k为任意实数。
数积的性质: (1)(x ,ky)=k(x , y) (2) (x , y+z )=(x , y)+( x , z ) (3) (x , )=0
欧氏空间的定义及性质
定义:设V(R)是实数域R上的线性空间,
在V(R)中定义了一个叫做数积的运算,即 有一定的法则,按照这个法则,对V(R)中 的任意两个向量x,y,都能确定R中唯一一个实 数,称之为x与y的数积,记作(x,y),如果这个 运算具有性质:
(1) ( 2) ( 3)
x, y y, x ; x, y x, y; x y, z x, z y, z ;
n (4) k i i 1
, l
i j 1 i
n
n,m ki l j ( i i 1, j 1
,
i
j
)
向量的长度及性质
定义2 令
x
x, x
2 2 2 x1 x2 xn ,
称 x 为n 维向量 x的长度 或 范数 .
高等代数欧氏空间的定义与基本性质

. .. . . ..
欧几里得空间的概念
注 在欧几里得空间的定义中, 对它作为线性空间的维数并无要 求,可以是有限维的,也可以是无限维的. 由内积的对称性可知,内积也满足 右齐次性 (α, kβ) = k(α, β);
因而我们也称内积满足齐次性、可加性,这两条性质合在一 起称为内积的双线性性. 即内积是实线性空间中的一个正定 对称双线性函数.
. .. . . ..
欧氏空间的度量
由欧氏空间定义中内积的正定性,有 √
(α,
α)
≥
0.
所以对于任意
的向量 α, (α, α) 是有意义的. 在几何空间中,向量的长度为
√ (α, α).
类似地,我们在一般的欧氏空间中引进:
定义 √
非负实数 (α, α) 称为向量 α 的长度,(或称范数,或称模)记 为 |α|.
. .. . . ..
欧几里得空间的概念
注 在欧几里得空间的定义中, 对它作为线性空间的维数并无要 求,可以是有限维的,也可以是无限维的. 由内积的对称性可知,内积也满足
因而我们也称内积满足齐次性、可加性,这两条性质合在一 起称为内积的双线性性. 即内积是实线性空间中的一个正定 对称双线性函数.
. . . .... .... .... . . . . .... .... .... . .
显然,向量的长度一般是正数,只有零向量的长度才是零,这样 定义的长度符合熟知的性质:
|kα| = |k||α|,
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
欧氏空间的度量
这里,k ∈ αR, α ∈ V. 事实上,
√
(完整word版)欧氏空间doc

第九章 欧氏空间9.1 基本内容与基本结论9.1.1 基本内容 1.欧几里得空间设V 是实数域R 上一线性空间,在V 上定义了一个二元实函数,称为内积,记作),(βα,它具有以下性质:(1) ),(),(αββα=; (2) ),(),(βαβαk k =; (3) ),(),(),(γβγαγβα+=+;(4) 0),(≥αα,当且仅当0=α时,0),(=αα。
这里α,β,γ是V 中任意的向量,k 是任意实数,这样的线性空间称为欧几里得空间。
2.酉空间设V 是复数域C 上一线性空间,在V 上定义了一个二元复函数,称为内积,记作),(βα,它具有以下性质:(5) ),(),(αββα=,这里),(),(αβαβ是的共轭复数; (6) ),(),(βαβαk k =; (7) ),(),(),(γβγαγβα+=+;(8) 0),(≥αα,当且仅当0=α时,0),(=αα。
这里α,β,γ是V 中任意的向量,k 是任意复数,这样的线性空间称为酉空间。
3.向量的长度非负实数),(αα称为向量α的长度,记为α。
4.向量的夹角非零向量α,β的夹角〉〈βα,规定为 βαβαβα),(arccos ,=〉〈,πβα≤〉〈≤,0。
5.向量的正交如果向量α,β的内积为零,即0),(=βα,那么称α,β正交,记为βα⊥。
6.基的度量矩阵n εεε,,,21 是n 维欧氏空间V 的一组基,令n j i j i ij ,,2,1,),,( ==εεα,称nn ij a A )(=为基n εεε,,,21 的度量矩阵。
7.正交向量组欧氏空间V 中一组非零的向量,如果它们两两正交,就称为一正交向量组。
8.正交基,标准正交基在n 维欧氏空间中,由n 个向量组成的正交向量组称为正交基,由单位向量组成的正交基称为标准正交基。
9.正交矩阵、酉矩阵n 级实矩阵称A 为正交矩阵,如果E A A T =。
n 级复矩阵称A 为酉矩阵,如果E A A T =。
高等代数欧几里得空间知识点总结

第九章 欧几里得空间( * * * )一、复习指导:在第九章中,有两个重要的考点:1.标准正交基(施密特正交化)2.实对称矩阵如何相似对角化,如何求标准形。
除此之外,欧氏空间的含义,概念,性质也要作为一个比较重要的内容来复习。
二、考点精讲:三、首师大真题: (一)欧氏空间1.设V 是是数域R 上一线性空间,在V 上定义了一个二元实函数,称为内积,记为(,)αβ,特具有一下性质: (1)(,)(,)αββα=; (2)(,)(,)k k αβαβ=(3)(,)(,)(,)αβγαγβγ+=+;(4)(,)0αα≥,当且仅当α=0时(,)αβ=0.这里,,αβγ是V 中任意的向量,k 是任意实数,这样的线性空间V 称为欧几里得空间。
2.α的长度,记为α。
3.非零向量的夹角,β规定为(,),arccos,0,ααβαβπαβ=≤≤4.如果向量,αβ的内积为零,即(,)0αβ=,那么,αβ称为正交或互相垂直,记为αβ⊥。
5.设V 是一个n 维欧几里得空间,在V 中取一组基1,2,......,n εεε令(,),(,1,2,....)ij i j a i j n εε==矩阵()ij n n A a ⨯= 称为基1,2,......,n εεε的度量矩阵。
(1)度量矩阵是正定的;(2)不同基底的度量矩阵是合同的。
6.欧氏空间V 中一组非零向量,如果它们两两正交,就称为一正交向量组。
在n 维欧氏空间中,由n 个向量组成的正交向量组称为正交基;由单位向量组成的正交基称为标准正交基。
(1)施密特正交化这是把线性无关向量组改造为单位正交向量组的方法. 以3个线性无关向量α1,α2,α3为例. ①令β1=α1,β2=α2-11112),(),(ββββα,β3=α3-11113),(),(ββββα-22223),(),(ββββα. 此时β1,β2,β3是和α1,α2,α3 等价的正交非零向量组.(二)同构1.实数域R 上欧氏空间V 与'v 称为同构,如果由V 到'v 有一个1-1上的映射σ,适合 (1)()()()σαβσασβ+=+ (2)()()k k σασα=(3)((),())(,)σασβαβ= 这里,,V k R αβ∈∈,这样的映射σ称为V 到'v 的同构映射。
高代竞赛辅导第9章欧氏空间

9.欧氏空间1.(华南理工大学2006)4R正交基,其中1111111111222211A --⎛⎫ ⎪-- ⎪= ⎪-- ⎪--⎝⎭。
解 分析:设m n A R ⨯∈的列向量为12,,,n ααα ,则12(,,,)n A ααα= , 列空间12,,,Im n W A ααα=<>= 。
0Ti i x Wx W x x αα⊥∈⇔⊥⇔⊥⇔=0Ker T TA x x A ⇔=⇔∈,从而有(Im )K er TWA A⊥⊥==,这表明:将A 改成T A ,又可以得到以上是两个非常重要的结论,在很多地方都用的上。
具体到本题:相当于求Ker TA 也就是求齐次线性方程组0T A x =的解空间的一个 标准正交基,这是一个标准问题。
先求0T A x =的一个基础解系:121331,2002αα-⎛⎫⎛⎫ ⎪ ⎪-- ⎪ ⎪==⎪ ⎪ ⎪⎪⎝⎭⎝⎭;任何将12,αα正交化、单位化得121414,14140707ββ⎛⎫⎛⎫- ⎪ ⎪ ⎪⎪ ⎪ ⎪-- ⎪⎪==⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭。
2.(中山大学2006)设由向量123(1,1,2,1),(3,1,4,1),(1,1,0,1)T T Tααα=-=-=-生成的子空间为W ,求一个线性方程组,使得它的解空间为恰好W 。
解 设矩阵()123,,A ααα=,则Im WA =()Im K er T A A⊥=。
这样问题就归结为:求齐次线性方程组0T A x =的解空间的一个基础解系1110⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭, 0101⎛⎫ ⎪- ⎪ ⎪ ⎪⎝⎭, 这个基础解系生成的空间就是Ker T A ,而它的正交补也就是W ,恰好是和以上两个向量都正交的向量全体,这正好就是齐次线性方程组123240x x x x x ++=⎧⎨-+=⎩的解空间,因此123240x x x x x ++=⎧⎨-+=⎩就是要求的线性方程组。
3.(南开大学2006)设线性方程组123451245123452303220390x x x x x x x x x x x x x x ++-+=⎧⎪+-+=⎨⎪++-+=⎩ 的解空间为V 。
高等代数欧氏空间的同构
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
(σ(α), σ(β)) = X′Y = (α, β)
定理 两个有限维欧氏空间同构当且仅当它们有相同的维数.
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
同构的性质
σ(α + β) = (X + Y)′ = X′ + Y′ = σ(α) + σ(β); σ(kα) = (kX)′ = kX′ = kσ(α);
(σ(α), σ(β)) = X′Y = (α, β)
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
同构的性质
σ(α + β) = (X + Y)′ = X′ + Y′ = σ(α) + σ(β); σ(kα) = (kX)′ = kX′ = kσ(α);
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
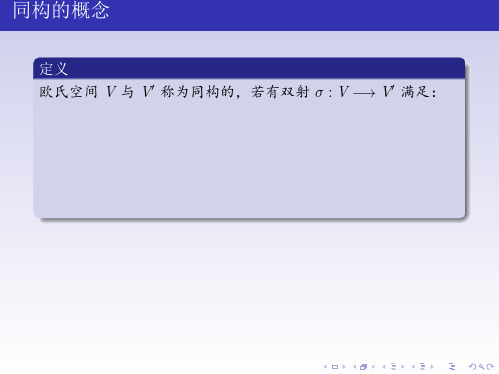
同构的概念
定义 欧氏空间 V 与 V′ 称为同构的,若有双射 σ : V −→ V′ 满足:
1 σ(α + β) = σ(α) + σ(β); 2 σ(kα) = kσ(α); 3 (σ(α), σ(β)) = (α, β).
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
同构的概念
定义 欧氏空间 V 与 V′ 称为同构的,若有双射 σ : V −→ V′ 满足:
《高等代数》第八章 欧氏空间

a11()
A(
)
ai1
(
)
a1 j ()
aij ()
a11()
0
a1 j ()
aij () a1 j () ()
的多项式,且
di() | di+1() ( i = 1, 2, … , r-1 ) .
证明 经过行列调动之后,可以使得 A() 的
左上角元素 a11() 0,如果 a11() 不能除尽 A()
的全部元素, 由引理 设可以- 矩找阵到A与(A)(的)左等上价角的元素
B1() ,它的并左且上角A(元)素中b至1(少)有 0一,个并元且素次不数能比被它除
们的乘积是 1 可以推知,它们都是零次多项式, 也就是非零的数 .
证毕
二、举例
例 1 求下列 - 矩阵的秩
2 1
(1) 1
2
1 2 2 1 2 3 2
2 1
1 ;
2
1
(2) 2
1
1
引理 设 - 矩阵A() 的左上角元素 a11() 0
并且 A() 中至少有一个元素不能被它除尽,那么 一定可以找到一个与 A() 等价的矩阵 B() ,它的 左上角元素也不为零, 但是次数比 a11() 的次数低.
证明 根据 A() 中不能被 a11() 除尽的元素
所在的位置,分三种情况来讨论:
如此下去,A() 最后就化成了所要求的形式.
北京大学数学系《高等代数》(第3版)(名校考研真题 欧几里得空间)

第9章 欧几里得空间一、分析计算题1.设B 是实数域上n×n 矩阵,,对任一大于0的常数n ,证明定义了的一个内积,使得成为欧氏空间.其中表示列向量的转置,E表示单位矩阵.[浙江大学研]证明:(1)(2)(3)(4)由于,所以由上可知,定义了上的一个内积,从而成为欧氏空间.2.设n 维欧氏空间的两个线性变换在V 的基下的矩阵分别是A 和B ,证明:,都有,则存在正定矩阵P ,使[武汉大学研]证明:由题设任给,令则同理令基的度量矩阵为,则同理因,故考虑的任意性,并结合与均为对称矩阵知3.设是n 维欧氏空间V 子空间,且的维数小于的维数,证明必有一个非零向量正交于中一切向量.[浙江大学研]证:证法1:由于恰由一切与正交的向量组成,所以只要证明即可.事实上,如,则为直和.所以又 所以 所以 所以矛盾.证法2:(1)当时,结论显然成立.(2)设,取的基的基令因为等价于(1)而方程组(1)的方程个数未知量个数s ,所以它有非零解.即使.4.设α是欧氏空间V 的线性变换,τ是V 的一个变换,且.都有(σ(α),β)=(α,τ(β)).证明:(1)τ是V 的线性变换;(2)τ的值域Imτ等于σ的核ker (σ)的正交补.[武汉大学研]证明:(1)β,α,γ∈V∈V,由题设可得由α的任意性知(1)同理,λ∈R,ξ∈V,有(2)所以由式(1)、式(2)得τ是V的线性变换.(2)可等价地证明①,有所以②如,则有所以从而结合①、②可得5.设S 是酉空间V 的一个非空集合,记证明:是子空间,且,并举例说明不一定成立.[西安交通大学研]证明:对给定的集合S ,显然V 的零元素属于,所以(复数域),对任一γ∈S 有所以即由α、β、k 、l的任意性知是V的子空间.又,由题设知可见 因此不一定成立,如在酉空间中,取S={(0,0,1)},S 不是V 的子空间,但是V 的子空间,所以6.在欧氏空间V 中(1)若向量α,β等长,证明:α+β与α-β正交,作出几何解释;(2)设V 是n 维的,S 是V 的子空间,是V 中的一切与s 正交的向量所成集合,证明:是V的子空间,且[四川大学研]证明:(1)因为,所以几何解释:表示菱形两对角线互相垂直.(2)由已知有仿上题可证是V 的予空间,且,故①成立,且故S 和是同一子空间的正交补,由正交补的惟一性,即证②.7.实矩阵A 和B ,证明:A 和B 实相似的充要条件是复相似.[复旦大学研]证明:必要性显然.下证充分性,设A 与B 复相似,即存在复可逆阵使其中M 和H 都是n 阶实方阵,由①有,此即因为故不是零多项式,它在复数域上仅有有限个根,从而存在实数a ,使,令有8.设T 是酉空间V 的一个线性变换,证明:下面四个命题互相等价.(1)T 是酉变换;(2)T 是同构映射;(3)如果是标准正交基,那么也是标准正交基;(4)T 在任一组标准正交基下的矩阵为酉矩阵.[湖南大学研] 证明:(1)=>(3)设T 是酉变换,即取为V 的一组标准正交基,且。
北京大学数学系《高等代数》(第3版)【教材精讲+考研真题解析】第9章 欧式空间 【圣才出品】

第9章欧式空间[视频讲解]9.1本章要点详解本章要点■欧式空间的定义■标准正交基■同构■正交变换■子空间■对称矩阵的标准型重难点导学一、定义与基本性质1.欧式空间的定义设V 是实数域R 上一线性空间,在V 上定义了一个二元实函数,记作(α,β),若(α,β)满足(1)(α,β)=(β,α);(2)(k α,β)=k (α,β);(3)(α+β,γ)=(α,γ)+(β,γ);(4)(α,α)≥0,当且仅当α=0时(α,α)=0.这里α,β,r 是V 中任意的向量,k 是任意实数,则称(α,β)为α和β的内积,并称线性空间V 为欧几里得空间.2.内积的简单性质V 为欧氏空间,∀α,β,γ,∀k ∈R ,则(1)(,)(,)k k =αβαβ;(2)(,)(,)(,)+=+αβγαβαγ;(3)(0,)=0β.2.欧氏空间中向量的长度(1)向量长度的定义非负实数称为向量α的长度,记为|α|.(2)关于长度的性质①零向量的长度是零;②|kα|=|k||α|;③长度为1的向量称为单位向量.如果α≠0,向量1αα就是一个单位向量,称此过程为把α单位化.3.欧氏空间中向量的夹角(1)柯西-布涅柯夫斯基不等式,即对于任意的向量α,β有|(α,β)|≤|α||β|当且仅当α,β线性相关时,等号才成立.(2)非零向量α,β的夹角<α,β>定义为(3)如果向量α,β的内积为零,即(α,β)=0,则称α,β为正交或互相垂直,记为α⊥β.注:零向量才与自己正交.(4)勾股定理:当α,β正交时,|α+β|2=|α|2+|β|2.4.有限维空间的讨论(1)度量矩阵设V是一个n维欧几里得空间,在V中取一组基ε1,ε2,…,εn,对V中任意两个向量α=x1ε1+x2ε2+…+x nεn,β=y1ε1+y2ε2+…+y nεn,由内积的性质得a ij=(εi,εj)(i,j=1,2,…,n)有a ij=a ji,则(α,β)还可写成(α,β)=X'AY,其中分别是α,β的坐标,而矩阵A=(a ij)nn称为基ε1,ε2,…,εn的度量矩阵.(2)性质①设η1,η2,…,ηn是空间V的另外一组基,而由ε1,ε2,…,εn到η1,η2,…,ηn的过渡矩阵为C,即(η1,η2,…,ηn)=(ε1,ε2,…,εn)C,于是基η1,η2,…,ηn的度量矩阵B=(b ij)=(ηi,ηj)=C'AC,则不同基的度量矩阵是合同的.②对于非零向量α,即有(α,α)=X'AX>0.因此,度量矩阵是正定的.二、标准正交基1.正交向量组欧式空间V中一组非零的向量,如果它们两两正交,称为正交向量组.按定义,由单个非零向量所成的向量组也是正交向量组.2.标准正交基(1)定义在n维欧氏空间中,由n个向量组成的正交向量组称为正交基;由单位向量组成的正交基称为标准正交基.注:①对一组正交基进行单位化就得到一组标准正交基.②一组基为标准正交基的充分必要条件是:它的度量矩阵为单位矩阵.(2)标准正交基的求法①n维欧氏空间中任一个正交向量组都能扩充成一组正交基.②对于n维欧氏空间中任意一组基ε1,ε2,…,εn,存在一组标准正交基η1,η2,…,η,使L(ε1,ε2,…,εi)=L(η1,η2,…,ηi),i=1,2,…,n.n把一组线性无关的向量变成一单位正交向量组的方法称为施密特正交化过程.3.标准正交基间的基变换设ε1,ε2,…,εn与η1,η2,…,ηn是欧氏空间V中的两组标准正交基,它们之间的过渡矩阵是A=(a ij),即因为η1,η2,…,ηn是标准正交基,所以矩阵A的各列就是η1,η2,…,ηn在标准正交基ε1,ε2,…,εn下的坐标.4.正交矩阵n级实数矩阵A称为正交矩阵,如果A'A=E.由标准正交基到标准正交基的过渡矩阵是正交矩阵;反过来,如果第一组基是标准正交基,同时过渡矩阵是正交矩阵,则第二组基一定也是标准正交基.三、同构。
高等代数--第九章 欧几里得空间

反过来,如果等号成立,由以上证明
过程可以看出,或者 0 ,或者 ( , ) 0, ( , ) 也就是说 , 线性相关。
结合具体例子来看一下这个不等式是很有意 思的。对于例1的空间Rn ,(5)式是:柯西不等式
| a1b1 a2b2 an bn |
这就是说,不同基的度量矩阵是合同的。
根据条件4),对于非零向量 ,即
0 0 X 0
有
( , ) X ' AX 0,
因此,度量矩阵是正定的。 欧几里得空间以下简称为欧氏空间。 BACK
标准正交基
定义6 欧氏空间V中一组非零的向量,如果它 们两两正交,就称为一正交向量组。 按定义,由单个非零向量所成的向量组也 是正交向量组。
即对于任意的向量 , 有
| ( , ) || || | . (5)
当且仅当 , 线性相关时,等号才成立。 证明 当 0,(5)式显然成立。以下设 0。 令t是一个实变数,作向量 t . 由4)可知,不论t取何值,一定有 ( , ) ( t , t ) 0. 即 ( , ) 2( , )t ( , )t 2 0. (6)
(m1 ,i ) ( ,i ) ki (i ,i ) (i 1,2,, m).
取
( , i ) ki (i 1,2,, m). ( i , i )
有
( i , m1 ) 0 (i 1,2,, m).
m1 0 。因此 1 , 2 ,, m , m1 由 的选择可知, 1 , 2 ,, m , 是一正交向量组,根据归纳法假定, m1 可以扩充成一正交基。于是定理得证。 定理的证明实际上也就给出了一个具体的扩 充正交向量组的方法。
高等代数-欧几里得空间

2) (, ) (, ) (, )
s
s
推广: ( , i ) ( , i )
i 1
i 1
3) (0, ) 0
§9.1 定义与基本性质
二、欧氏空间中向量的长度
1. 引入长度概念的可能性
1)在 R3向量 的长度(模) . 2) 欧氏空间V中, ,V , (, ) 0
使得 有意义.
③ ( , ) R.
§9.1 定义与基本性质
例1.在 Rn 中,对于向量
a1,a2, ,an , b1,b2, ,bn
1)定义 ( , ) a1b1 a2b2 anbn
(1)
易证 ( , ) 满足定义中的性质 1 ~ 4 .
所以, ( , ) 为内积. 这样Rn 对于内积 ( , ) 就成为一个欧氏空间.
2. 向量长度的定义
,V , ( , ) 称为向量 的长度. 特别地,当 1时,称 为单位向量.
§9.1 定义与基本性质
3. 向量长度的简单性质
1) 0; 0 0
2) k k
3)非零向量 的单位化:
1.
(3)
§9.1 定义与基本性质
三、欧氏空间中向量的夹角
1. 引入夹角概念的可能性与困难
注:
① 零向量与任意向量正交.
②
, ,
2
即 cos, 0
.
§9.1 定义与基本性质
5. 勾股定理
设V为欧氏空间, , V
2 2 2
证: 2 , , 2, ,
2 2 2
( , ) 0
.
§9.1 定义与基本性质
推广:若欧氏空间V中向量1,2 , ,m 两两正交,
当 n 3 时,1)即为几何空间 R3中内积在直角 坐标系下的表达式 . ( , )即 .
高等代数课件(北大版)第九章欧式空间§22

故
, , , 线性无关. 1 2 m
数学与计算科学学院
③ 欧氏空间中线性无关向量组未必是正交向量组.
例如: R 3 中
( 1 , 1 , 0 ) , ( 1 , 0 , 1 ) 线性无关.
1 2
但 1 , 2 不是正交向量组.
(, )1 0 . 12
④ n 维欧氏空间中正交向量组所含向量个数 n .
数学与计算科学学院
二、标准正交基
1. 几何空间 R 3 中的情况
在直角坐标系下
i ( 1 , 0 , 0 ) , j ( 0 , 1 , 0 ) , k ( 0 , 0 , 1 )
是由单位向量构成的正交向量组,即
( i , j ) ( j , k ) ( k , i )) 0 , i 1 , 2 , , m . i m 1
( , i) k , i ( , i i)
i 1 , 2 , , m ,
由归纳法假设知,对这 m 1 个向量构成的正交组 可扩充得正交基. 于是定理得证.
数学与计算科学学院
( 1 , 1 , 0 , 0 ) 1 1
正交化
再单位化
1 1 1 1 1 ( , ,0,0) | 1 | 2 2
1 1 2 1 ) 2 2 ( , , ,0 | 2 | 6 6 6
1 1 1 1 3 3 3 ( , , , ) | 3 | 1 2 1 2 1 2 1 2
④ n 维欧氏空间V中标准正交基的作用:
, , 设 为V的一组标准正交基,则 1 n
数学与计算科学学院
(i)
设
x x x V
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
且 (1,2 , ,n ) ( 1, 2 , , n )T , 则 1,2 , ,n 也是 V的标准正交基 T是正交矩阵. d) n维欧空间中任意一个正交向量组都能扩充 成一组标准正交基. 3) 标准正交基的求法:施密特(Schmidt)正交
化方法
题型分பைடு நூலகம்:
例1 设 1, 2 , , n 是欧氏空间V的基,证明:
1) 若 V 使得 ( , i ) 0, 则 0. 2) 若 1, 2 V , 对任意的 V 有 ( 1, ) ( 2 , ) 则 1 2. 例2 设 1, 2 , , m 是n维欧空间V中一组向量, 定义
高等代数考研复习
第九章 欧氏空间
2014年 8月
第九章 欧氏空间
本章主要内容为两部分: (1)欧氏空间的概念与标准正交基; (2)正交变换与对称变换. 1
欧氏空间的概念与标准正交基
欧氏空间的概念
1.1
(1)内积:
设V是实数域R上的线性空间,如果对V中任意
两个元素 , 有一个确定的实数 ( , )与之对应, 且满足: (ⅰ)交换性 ( , ) ( , ); (ⅱ)数量性 (k , ) k ( , ), k R; (ⅲ) 分配性 ( , ) ( , ) ( , ); (ⅳ) 非负性 ( , ) 0; 当且仅当 0 时取等 号.则称这种对应关系为V上的内积,记为 ( , )
( 1, 2 , , n ) (1, 2 , , n )C.
则 B CAC.
1.3 标准正交基
1) 定义:设 1, 2 , , n 是n维欧氏空间V的一组
基,如果 1, 2 , , n 两两正交,则称其为V的正
交基;单位正交基称为标准正交基.
2) 标准正交基的有关结论: a) 欧氏空间V的一组基是标准正交基的充分必 要条件是:它的度量矩阵是单位矩阵. b) 设 , V , 1, 2 , , n 是V的标准正交基,如 果 ( 1, 2 , , n ) X , ( 1, 2 , , n )Y , 则( , ) X Y .
(1 ,1 ) (1 , 2 ) ( , ) ( , ) 2 2 2 1 ( m ,1 ) ( m , 2 ) (1 , m ) ( 2 , m ) ( m , m )
( , ) X Y .
b) 度量矩阵是实对称矩阵,是正定矩阵.
c) 正交基的度量矩阵时对角矩阵,且主对角线
上元素都大于零;标准正交基的度量矩阵是
单位矩阵. d) 不同基的度量矩阵是合同的. 设 1, 2 , , n 与 1, 2 , , n分别是n维空间V的两 组基,其度量矩阵分别为A,B,且
为基 1, 2 , , n 的度量矩阵.
2) 度量矩阵的性质
a) 设 , 在n维欧氏空间V的基 1, 2 , , n 下的 坐标分别为 X ( x1, x2 , , xn ), Y ( y1, y2 , , yn ), 则 ( , ) X AY , 其中A是基 1, 2 , , n 的度量矩 阵.特别当 1, 2 , , n 是标准正交基时,A=E,则
(2) 欧氏空间:定义了内积的线性空间V称为欧
式空间.常见的欧式空间有: ⅰ) Rn 对于实向量 (a1, a2 , , an ), (b1, b2 , , bn ), 内积为 ( , ) a1b1 a2b2
1
anbn .
ⅱ) P[ x ] 对于对于多项式f(x),g(x),内积为
则称 1, 2 , , n 是正交向量组. a)正交向量组一定是线性无关的; b) 若1, 2 , , n 是正交组,则
| 1 2 n || 1 | | 2 | | n | .
2 2 2 | | | | | | . c) 如果 , 则
( , ) 义为 cos , , 0 , . | || | 正交:如果欧氏空间V中向量 , 的内积为零,
即 ( , ) 0, 则称 与 正交,记为 .
非零向量组 1, 2 , , n如果满足 (i , j ) 0,(i j).
实数
称为向量 的长度,记为 0
1的向量称为单位向量.如果 长度为
则
称为
的单位化向量.长度有以下性质:
a) | | 0 当且仅当 0 时取等号; b) | k | k | |; c)
| || | | | .
夹角:欧氏空间V中向量 , 的夹角 , 定
1.2 度量矩阵
1 , 2 , , n 是V 1)定义:设V是n维 欧氏空间,
的一组基,称矩阵
(1 ,1 ) (1 , 2 ) ( , ) ( , ) 2 2 A 2 1 ( n ,1 ) ( n , 2 ) (1 , n ) ( 2 , n ) ( n , n )
( f ( x), g ( x)) f ( x) g ( x)dx.
0
(3) 柯西-布涅科夫斯基不等式
设 , 是欧氏空间V中任意两个元素,则
| ( , ) || || |, 当且仅当 , 线性相关时取等
号. (4) 长度与夹角
V ,
| |
( , ) V是欧氏空间,对任意的 长度:设 | | 非负 ( , ).
