搞定空间几何体的外接球复习进程

合集下载

空间中的外接球进阶求法讲义-2023届高三数学一轮复习

空间中的外接球摘要：本文主要讨论一些常见空间几何体的外接球半径的求解方法，总结相应的公式。

对于更一般的几何体的外接球，用多种方法进行求解，本文引用了最新高考题以及课本中的例题，对于教师教学和学生自学都有参考作用。

一、旋转体外接球的公式在高中阶段，忧外接球的旋转体就是圆台，圆柱，圆锥，任何一个这三类旋转体，都有外接球，下面推导相应的外接球公式 1、圆台外接球半径公式的推导圆台的外接球公式为()hr r r r h h r r l l R 24242221222212212-++=+=……（1），其中l 为圆台的母线长，h 为圆台的高，1r 、2r 为圆台的上、下底面的半径，下面推导公式。

先证明一个引理：引理1：ABC ∆中，a 、b 、c 分别为角A 、B 、C 所对的边，c h 为c 边上的高线，ABC ∆外接圆半径为：ch ab R 2=。

证明：由三角形面积公式c ABC ch C ab S 21sin 21==∆，不难得到R Cc h ab 2sin ==，即ch abR 2=。

所有参数的意义如上文，设一个圆台的轴截面为等腰梯形ABCD ，其中CD AB //，12r AB =，22r CD =，l BC AD ==。

显然梯形ABCD 的高即为圆台的高h 。

由托勒密定理可得2124r r l BC AD CD AB BD AC +=⋅+⋅=⋅。

由于BD AC =，所以2124r r l AC +=。

不难得到等腰梯形ABCD 的外接圆即为圆台外接球的大圆，ABC ∆的外接圆半径与等腰梯形ABCD 半径相同，故只需求ABC ∆的外接圆半径。

而由引理1可得：hr r l l R 24212+=。

考虑等腰梯形ABCD 的腰()2212r r h l -+=，代入公式整理可得：()hr r r r hR 242221222212-++=。

例1：（2022年高考卷II 第七题）正三棱台高为1，上下底边长分别是33和34，所有顶点在同一球面上，则球的表面积是（） A 、π100 B 、π128 C 、π144 D 、π192 代入公式（1）可得圆台外接球半径为5，则外接球表面积为π100，选A 2、圆柱与圆锥的外接球半径公式若令r r r ==21，h l =，即可得到圆柱的外接球半径公式：224r l R += (2)，其中r 为底面半径，l 为母线长。

八个有趣模型——搞定空间几何体的外接球与内切球（教师版）复习过程

八个有趣模型——搞定空间几何体的外接球与内切球（教师版）复习过程八个有趣模型——搞定空间几何体的外接球与内切球一、有关定义1．球的定义：空间中到定点的距离等于定长的点的集合（轨迹）叫球面，简称球.2．外接球的定义：若一个多面体的各个顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球.3．内切球的定义：若一个多面体的各面都与一个球的球面相切，则称这个多面体是这个球的外切多面体，这个球是这个多面体的内切球.二、外接球的有关知识与方法1．性质：性质1：过球心的平面截球面所得圆是大圆，大圆的半径与球的半径相等；性质2：经过小圆的直径与小圆面垂直的平面必过球心，该平面截球所得圆是大圆；性质3：过球心与小圆圆心的直线垂直于小圆所在的平面（类比：圆的垂径定理）；性质4：球心在大圆面和小圆面上的射影是相应圆的圆心；性质5：在同一球中，过两相交圆的圆心垂直于相应的圆面的直线相交，交点是球心（类比：在同圆中，两相交弦的中垂线交点是圆心）.初图1初图22．结论：结论1：长方体的外接球的球心在体对角线的交点处，即长方体的体对角线的中点是球心；结论2：若由长方体切得的多面体的所有顶点是原长方体的顶点，则所得多面体与原长方体的外接球相同；结论3：长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心，换言之，就是：底面的一条对角线与一条高（棱）构成的直角三角形的外接圆是大圆；结论4：圆柱体的外接球球心在上下两底面圆的圆心连一段中点处；结论5：圆柱体轴截面矩形的外接圆是大圆，该矩形的对角线（外接圆直径）是球的直径；结论6：直棱柱的外接球与该棱柱外接圆柱体有相同的外接球；结论7：圆锥体的外接球球心在圆锥的高所在的直线上；结论8：圆锥体轴截面等腰三角形的外接圆是大圆，该三角形的外接圆直径是球的直径；结论9：侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.3．终极利器：勾股定理、正定理及余弦定理（解三角形求线段长度）；三、内切球的有关知识与方法1．若球与平面相切，则切点与球心连线与切面垂直.（与直线切圆的结论有一致性）.2．内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离均相等.（类比：与多边形的内切圆）.3．正多面体的内切球和外接球的球心重合.4．正棱锥的内切球和外接球球心都在高线上，但不一定重合.5．基本方法：（1）构造三角形利用相似比和勾股定理；（2）体积分割是求内切球半径的通用做法（等体积法）.四、与台体相关的，此略.五、八大模型第一讲柱体背景的模型类型一、墙角模型（三条棱两两垂直，不找球心的位置即可求出球半径）图1-1图1-2图1-3图1-4方法：找三条两两垂直的线段，直接用公式2222)2(c b a R ++=，即2222c b a R ++=，求出R 例1 （1）已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的表面积是（ C ） A ．π16 B ．π20 C ．π24 D ．π32 解： 162==h a V ，2=a ，24164442222=++=++=h a a R ，π24=S ，选C ；（2）若三棱锥的三个侧面两两垂直，且侧棱长均为3，则其外接球的表面积是π9 解：933342=++=R ，ππ942==R S ；（3）在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是.π36 解：引理：正三棱锥的对棱互相垂直.证明如下：如图（3）-1，取BC AB ,的中点E D ,，连接CD AE ,，CD AE ,交于H ，连接SH ，则H 是底面正三角形ABC 的中心，∴⊥SH 平面ABC ，∴AB SH ⊥，ΘBC AC =，BD AD =，∴AB CD ⊥，∴⊥AB 平面SCD ，∴S C AB ⊥，同理：SA BC ⊥，SB AC ⊥，即正三棱锥的对棱互垂直，本题图如图（3）-2，ΘMN AM ⊥，MN SB //，∴SB AM ⊥，ΘSB AC ⊥，∴⊥SB 平面SAC ，∴SA SB ⊥，SC SB ⊥，ΘSA SB ⊥，SA BC ⊥，∴⊥SA 平面SBC ，∴SC SA ⊥，故三棱锥ABC S -的三棱条侧棱两两互相垂直，∴36)32()32()32()2(2222=++=R ，即3642=R ，∴正三棱锥ABC S -外接球的表面积是π36.(3)题-1(引理）AC(3)题-2（解答图）AC（4）在四面体S ABC -中，ABC SA 平面⊥，,1,2,120====∠?AB AC SA BAC 则该四面体的外接球的表面积为（ D ）π11.A π7.B π310.C π340.D 解：在ABC ?中，7120cos 2222=??-+=οBC AB AB AC BC ，7=BC ，ABC ?的外接球直径为372237sin 2==∠=BAC BC r ，∴3404)372()2()2(2222=+=+=SA r R ，340π=S ，选D （5）如果三棱锥的三个侧面两两垂直，它们的面积分别为6、4、3，那么它的外接球的表面积是解：由已知得三条侧棱两两垂直，设三条侧棱长分别为c b a ,,（+ ∈R c b a ,,），则===6812ac bc ab ，∴24=abc ，∴3=a ，4=b ，2=c ，29)2(2222=++=c b a R ，ππ2942==R S ，（6）已知某几何体的三视图如图所示，三视图是腰长为1的等腰直角三角形和边长为1的正方形，则该几何体外接球的体积为解：3)2(2222=++=c b a R ，432=R ，23=Rπππ2383334343=?==R V 球，类型二、对棱相等模型（补形为长方体）题设：三棱锥（即四面体）中，已知三组对棱分别相等，求外接球半径（CD AB =，BC AD =，BD AC =）第一步：画出一个长方体，标出三组互为异面直线的对棱；第二步：设出长方体的长宽高分别为c b a ,,，x BC AD ==，y CD AB ==，z BD AC ==，列方程组，=+=+=+222222222z a c y c b x b a ?2)2(2222222z y x c b a R ++=++=，补充：图2-1中，abc abc abc V BCD A 31461=?-=-. (6)题图（6）题直观图P图2-1第三步：根据墙角模型，22222222z y x c b a R ++=++=，82222z y x R ++=，8222z y x R ++=，求出R .思考：如何求棱长为a 的正四面体体积，如何求其外接球体积？例2（1）如下图所示三棱锥A BCD -，其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为 .解：对棱相等，补形为长方体，如图2-1，设长宽高分别为c b a ,,，110493625)(2222=++=++c b a ，55222=++c b a ，5542=R ，π55=S(1)题图B（2）在三棱锥BCD A -中，2==CD AB ，3==BC AD ，4==BD AC ，则三棱锥BCD A -外接球的表面积为 .π229 解：如图2-1，设补形为长方体，三个长度为三对面的对角线长，设长宽高分别为c b a ,,，则922=+b a ，422=+c b ，1622=+a c ∴291649)(2222=++=++c b a ，291649)(2222=++=++c b a ，229222=++c b a ，22942=R ，π229=S （3）正四面体的各条棱长都为2，则该正面体外接球的体积为（3）解答题解：正四面体对棱相等的模式，放入正方体中，32=R ，23=R ，ππ2383334=?=V （4）棱长为2的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如下图，则图中三角形(正四面体的截面)的面积是 .(4)题解答图(4)题解：如解答图，将正四面体放入正方体中，截面为1PCO ?，面积是2.类型三、汉堡模型（直棱柱的外接球、圆柱的外接球）图3-1图3-2 图3-3题设：如图3-1，图3-2，图3-3,直三棱柱内接于球（同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角形）第一步：确定球心O 的位置，1O 是ABC ?的外心，则⊥1OO 平面ABC ；第二步：算出小圆1O 的半径r AO =1，h AA OO 2 12111==（h AA =1也是圆柱的高）；第三步：勾股定理：21212O O A O OA +=?222)2(r hR +=?22)2(hr R +=，解出R例3（1）一个正六棱柱的底面上正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为89，底面周长为3，则这个球的体积为解：设正六边形边长为a ，正六棱柱的高为h ，底面外接圆的半径为r ，则21=a ，正六棱柱的底面积为833)21(4362=??=S ，89833===h Sh V 柱，∴3=h ，4)3(14222=+=R 也可1)21()23( 222=+=R ），1=R ，球的体积为34π=球V ；（2）直三棱柱111ABC A B C -的各顶点都在同一球面上，若12AB AC AA ===,120BAC ∠=?，则此球的表面积等于 .解：32=BC ，4120sin 322==οr ，2=r ，5=R ，π20=S ；（3）已知EAB ?所在的平面与矩形ABCD 所在的平面互相垂直，=∠===60,2,3AEB AD EB EA ，则多面体ABCD E -的外接球的表面积为.π16 解：折叠型，法一：EAB ?的外接圆半径为31=r ，11=OO ，231=+=R ；法二：231=M O ，21322==D O r ，4413432=+=R ，2=R ，π16=表S ；法三：补形为直三棱柱，可改变直三棱柱的放置方式为立式，算法可同上，略.换一种方式，通过算圆柱的轴截面的对角线长来求球的直径：162)32()2(222=+=R ，π16=表S ；（4）在直三棱柱111C B A ABC -中，4,3,6,41====AA A AC AB π，则直三棱柱111C B A ABC -的外接球的表面积为 .π3160解：法一：282164236162=?-+=BC ，72=BC ，37423722==r ，372=r ， 3404328)2(2122=+=+=AA r R ，π3160=表S ；法二：求圆柱的轴截面的对角线长得球直径，此略.第二讲锥体背景的模型类型四、切瓜模型（两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法）图4-1图4-2图4-3图4-41．如图4-1，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径），且P 的射影是ABC ?的外心?三棱锥ABC P -的三条侧棱相等?三棱ABC P -的底面ABC ?在圆锥的底上，顶点P 点也是圆锥的顶点. 解题步骤：第一步：确定球心O 的位置，取ABC ?的外心1O ，则1,,O O P 三点共线；第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1（也是圆锥的高）；（3）题第三步：勾股定理：21212O O A O OA +=?222)(r R h R +-=，解出R ；事实上，ACP ?的外接圆就是大圆，直接用正弦定理也可求解出R .2．如图4-2，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径），且AC PA ⊥，则利用勾股定理求三棱锥的外接球半径：①222)2()2(r PA R +=?22)2(2r PA R +=；②2122OO r R +=?212OO r R +=3．如图4-3，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径） 21212O O C O OC +=?2122O O r R +=?2122O O R AC -=4．题设：如图4-4，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径）第一步：易知球心O 必是PAC ?的外心，即PAC ?的外接圆是大圆，先求出小圆的直径r AC 2=；第二步：在PAC ?中，可根据正弦定理R CcB b A a 2sin sin sin ===，求出R . 例4 （1）正四棱锥的顶点都在同一球面上，若该棱锥的高为1，底面边长为32，则该球的表面积为 . 解：法一：由正弦定理（用大圆求外接球直径）；法二：找球心联合勾股定理，72=R ，ππ4942==R S ；（2）正四棱锥ABCD S -的底面边长和各侧棱长都为2，各顶点都在同一球面上，则此球体积为解：方法一：找球心的位置，易知1=r ，1=h ，r h =，故球心在正方形的中心ABCD 处，1=R ，3 4π=V 方法二：大圆是轴截面所的外接圆，即大圆是SAC ?的外接圆，此处特殊，SAC Rt ?的斜边是球半径，22=R ，1=R ，34π=V . （3）一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是（） A ．433 B ．33 C ．43 D ．123解：高1==R h ，底面外接圆的半径为1=R ，直径为22=R ，设底面边长为a ，则260sin 2==οaR ，3=a ，433432==a S ，三棱锥的体积为4331==Sh V ；（4）在三棱锥ABC P -中，3===PC PB PA ,侧棱PA 与底面ABC 所成的角为ο60，则该三棱锥外接球的体积为（） A ．π B.3π C. 4π D.43π 解：选D ，由线面角的知识，得ABC ?的顶点C B A ,,在以23=r 为半径的圆上，在圆锥中求解，1=R ；（5）已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ?是边长为1的正三角形,SC 为球O 的直径,且2SC =，则此棱锥的体积为（）AA．6 BC．3 D．2解：36)33(12221=-=-=r R OO ，362=h ，62362433131=??==Sh V 球类型五、垂面模型（一条直线垂直于一个平面）1．题设：如图5，⊥PA 平面ABC ，求外接球半径.解题步骤：第一步：将ABC ?画在小圆面上，A 为小圆直径的一个端点，作小圆的直径AD ，连接PD ，则PD 必过球心O ；第二步：1O 为ABC ?的外心，所以⊥1OO 平面ABC ，算出小圆1O 的半径r D O =1（三角形的外接圆直径算法：利用正弦定理，得r C c B b A a 2sin sin sin ===），PA OO 211=；第三步：利用勾股定理求三棱锥的外接球半径：①222)2()2(r PA R +=?22)2(2r PA R +=；②2122OO r R +=?212OO r R +=.2．题设：如图5-1至5-8这七个图形，P 的射影是ABC ?的外心?三棱锥ABC P -的三条侧棱相等?三棱锥ABC P -的底面ABC ?在圆锥的底上，顶点P 点也是圆锥的顶点.图5-1图5-2图5-3图5-4图5-6图5-7图5-8解题步骤：第一步：确定球心O 的位置，取ABC ?的外心1O ，则1,,O O P 三点共线；第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1（也是圆锥的高）；第三步：勾股定理：21212O O A O OA +=?222)(r R h R +-=，解出R 方法二：小圆直径参与构造大圆，用正弦定理求大圆直径得球的直径. 例5 一个几何体的三视图如图所示，则该几何体外接球的表面积为( )C A ．π3 B ．π2 C ．316πD ．以上都不对解：选C ，法一：（勾股定理）利用球心的位置求球半径，球心在圆锥的高线上，221)3(R R =+-,32=R ,ππ31642==R S ；法二：（大圆法求外接球直径）如图，球心在圆锥的高线上，故圆锥的轴截面三角形PMN 的外接圆是大圆，于是3460sin 22==οR ，下略；第三讲二面角背景的模型类型六、折叠模型题设：两个全等三角形或等腰三角形拼在一起，或菱形折叠(如图6)俯视图侧视图正视图解答图图6第一步：先画出如图6所示的图形，将BCD ?画在小圆上，找出BCD ?和BD A '?的外心1H 和2H ；第二步：过1H 和2H 分别作平面BCD 和平面BD A '的垂线，两垂线的交点即为球心O ，连接OC OE ,；第三步：解1OEH ?，算出1OH ，在1OCH Rt ?中，勾股定理：22121OC CH OH =+ 注：易知21,,,H E H O 四点共面且四点共圆，证略.例6（1）三棱锥ABC P -中，平面⊥PAC 平面ABC ，△PAC 和△ABC 均为边长为2的正三角形，则三棱锥ABC P -外接球的半径为 .解：如图，3460sin 22221===οr r ，3221==r r ，312=H O ， 35343121222=+=+=r H O R ，315=R ；法二：312=H O ，311=H O ，1=AH ， 352121222=++==O O H O AH AO R ，315=R ；（2）在直角梯形ABCD 中，CD AB //，ο90=∠A ，ο45=∠C ，1==AD AB ，沿对角线BD 折成四面体BCD A -'，使平面⊥'BD A 平面BCD ，若四面体BCD A -'的顶点在同一个球面上，则该项球的表面积为π4(2)题-2(2)题-1→A(3)题解：如图，易知球心在BC的中点处，π4=表S ；（1）题（3）在四面体ABC S -中，BC AB ⊥，2==BC AB ，二面角B AC S --的余弦值为33-，则四面体ABC S -的外接球表面积为π6 解：如图，法一：33)2cos(cos 211-=+∠=∠πO OO B SO ， 33sin 21=∠O OO ，36cos 21=∠O OO ， 22cos 21211=∠=O OO O O OO ，232112=+=R ，ππ642==R S ；法二：延长1BO 到D 使111r BO DO ==，由余弦定理得6=SB ，2=SD ，大圆直径为62==SB R ；（4）在边长为32的菱形ABCD 中，ο60=∠BAD ，沿对角线BD 折成二面角C BD A --为ο120的四面体ABCD ，则此四面体的外接球表面积为π28解：如图，取BD 的中点M ，ABD ?和CBD ?的外接圆半径为221==r r ，ABD ?和CBD ?的外心21,O O 到弦BD 的距离（弦心距）为121==d d ，法一：四边形21MO OO 的外接圆直径2=OM ，7=R ，π28=S ；法二：31=OO ，7=R ；法三：作出CBD ?的外接圆直径CE ,则3==CM AM ， 4=CE ，1=ME ，7=AE ，33=AC ，72147227167cos -=??-+=∠AEC ，7233sin =∠AEC ，72723333sin 2==∠=AEC AC R ，7=R ；(4)题图(5)在四棱锥ABCD 中，ο120=∠BDA ，ο150=∠BDC ，2==BD AD ，3=CD ，二面角CBD A --的平面角的大小为ο120，则此四面体的外接球的体积为解：如图，过两小圆圆心作相应小圆所在平面的垂线确定球心，→抽象化(5)题解答图-2(5)题解答图-11B32=AB ，22=r ，弦心距32=M O ，13=BC ，131=r ，弦心距321=M O ，∴2121=O O ，72120sin 21==οO O OM ，法一：∴292222=+==OM MD OD R ，29=R ，∴329116π=球V ；法二：2522222=-=M O OM OO ，∴29222222=+==OO r OD R ，29=R ，∴329116π=球V . 类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型图7题设：如图7，ο90=∠=∠ACB APB ，求三棱锥ABC P -外接球半径（分析：取公共的斜边的中点O ，连接OC OP ,，则AB OP OC OB OA 2 1====，∴O 为三棱锥ABC P -外接球球心，然后在OCP 中求出半径），当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关，只要不是平角球半径都为定值.例7（1）在矩形ABCD 中，4=AB ，3=BC ，沿AC 将矩形ABCD 折成一个直二面角D AC B --，则四面体ABCD 的外接球的体积为（）A ．π12125B ．π9125C ．π6125D ．π3125解：（1）52==AC R ，25=R ，6125812534343πππ=?==R V ，选C（2）在矩形ABCD 中，2=AB ，3=BC ，沿BD 将矩形ABCD 折叠，连接AC ，所得三棱锥BCDA -的外接球的表面积为．解：BD 的中点是球心O ，132==BD R ，ππ1342==R S .第四讲多面体的内切球问题模型类型八、锥体的内切球问题1．题设：如图8-1，三棱锥ABC P -上正三棱锥，求其内切球的半径. 第一步：先现出内切球的截面图，H E ,分别是两个三角形的外心；第二步：求BD DH 31=，r PH PO -=，PD 是侧面ABP ?的高；第三步：由POE ?相似于PDH ?，建立等式：PDPODH OE =，解出r 2．题设：如图8-2，四棱锥ABC P -是正四棱锥，求其内切球的半径第一步：先现出内切球的截面图，H O P ,,三点共线；第二步：求BC FH 21=，r PH PO -=，PF 是侧面PCD ?的高；第三步：由POG ?相似于PFH ?，建立等式：PFPOHF OG =，解出3．题设：三棱锥ABC P -是任意三棱锥，求其的内切球半径方法：等体积法，即内切球球心与四个面构成的四个三棱锥的体积之和相等第一步：先画出四个表面的面积和整个锥体体积；第二步：设内切球的半径为r ，建立等式：PBC O PAC O PAB O ABC O ABC P V V V V V -----+++=?r S S S S r S r S r S r S V PBC PAC PAB ABC PBC PAC PAB ABC ABC P ?+++=?+?+?+?=-)(3131313131第三步：解出PBCO PAC O PAB O ABC O ABCP S S S S V r -----+++=3例8 （1）棱长为a 的正四面体的内切球表面积是 62a π，解：设正四面体内切球的半径为r ，将正四面体放入棱长为2a的正方体中（即补形为正方体），如图，则2622313133a a V V ABCP =?==-正方体，又Θr a r a Sr V ABC P 223343314314==?=-，D图8-1A图8-2∴263332a r a =，62a r =，∴内切球的表面积为6422a r S ππ==表（注：还有别的方法，此略）（2）正四棱锥ABCD S -的底面边长为2，侧棱长为37解：如图，正四棱锥ABCD S -的高7=h ，正四棱锥ABCD S -的体积为374=-ABCD S V 侧面斜高221=h ，正四棱锥ABCD S -的表面积为284+=表S ，正四棱锥ABCD S -的体积为r r S V ABCDS ?+==-328431表，∴3743284=?+r ， 771427)122(7221728474-=-=+=+=r （3）三棱锥ABC P -中，底面ABC ?是边长为2的正三角形，⊥PA 底面ABC ，2=PA ，则32解：如图，3=?ABC S ，2==??ACP ABP S S ，7=?BCP S ，743++=表S ，三棱锥ABC P -的体积为332=-ABC P V ，另一表达体积的方式是r r S V ABC P ?++==-347331表，∴3323473=?++r ，∴47332++=r习题：1．若三棱锥ABC S -的三条侧棱两两垂直，且2=SA ，4==SC SB ，则该三棱锥的外接球半径为（） A.3 B.6 C.36 D.9 解：【A 】616164)2(2=++=R ，3=R【三棱锥有一侧棱垂直于底面，且底面是直角三角形】【共两种】2．三棱锥ABC S -中，侧棱⊥SA 平面ABC ，底面ABC 是边长为3的正三角形，32=SA ，则该三棱锥的外接球体积等于 . 332π(2)题(3)题B解：260sin 32==οr ，16124)2(2=+=R ，42=R ，2=R ，外接球体积332834ππ=? 【外心法（加中垂线）找球心；正弦定理求球小圆半径】3．正三棱锥ABC S -中，底面ABC 是边长为3的正三角形，侧棱长为2，则该三棱锥的外接球体积等于 .解：ABC ?外接圆的半径为，三棱锥ABC S -的直径为3460sin 22==οR ，外接球半径32=R ，或1)3(22+-=R R ，32=R ，外接球体积2733233834343πππ===R V ， 4．三棱锥ABC P -中，平面⊥PAC 平面ABC ，△PAC 边长为2的正三角形，BC AB ⊥，则三棱锥ABC P -外接球的半径为 .解：PAC ?的外接圆是大圆，3460sin 22==οR ，32=R ， 5．三棱锥ABC P -中，平面⊥PAC 平面ABC ，2=AC ，3==PC PA ，BC AB ⊥，则三棱锥ABC P -外接球的半径为 .解：973324992cos 222=??-+=?-+=∠PC PA AC PC PA P ，81 216)97(1sin 22?=-=∠P ，924sin =∠P ，42922992422===R ，829=R 6．三棱锥ABC P -中，平面⊥PAC 平面ABC ，2=AC ，PC PA ⊥，BC AB ⊥，则三棱锥ABCP -外接球的半径为 .解：AC 是公共的斜边，AC 的中点是球心O ，球半径为1=R。

高中数学解题秘籍系列一篇文章攻克外接球

【高中数学解题秘籍系列】————一篇文章攻克外接球⚫外接球指一个空间几何图形的外接球，对于旋转体和多面体，外接球有不同的定义，广义理解为球将几何体包围，且几何体的顶点和弧面在此球上.正多面体各顶点同在一球面上，这个球叫做正多面体的外接球.⚫内切球球心到某几何体各面的距离相等且等于半径的球是几何体的内切球.如果一个球与简单多面体的各面或其延展部分都相切，且此球在多面体的内部，则称这个球为此多面体的内切球.一、外接球七大模型二、内切球万能公式(棱锥)①圆柱②直棱柱③侧棱垂直底面➢适用几何体：圆柱、直棱柱、一条侧棱垂直底面的棱锥.②和 ③ 可以通过补形转化为 ①，所以我们只需证明 ① 即可证明：设P 、O '分别为上下底面圆的圆心，O 为线段PO '的中点，( 2017•新课标 Ⅲ ) 已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( ) A ．πB ．3π4 C ．π2D ．π4由秒杀公式1得22222212=1442h R r r ⎛⎫+=+== ⎪⎝⎭，解得234r =，因此圆柱的体积233πππ144V r h =⋅=⋅⋅=，故选B.( 2017•新课标 Ⅱ ) 长方体的长、宽、高分别为3，2，1，其顶点都在球O 的球面上，则球O 的表面积为．由秒杀公式1得2222217=442h R r +=+=⎝⎭，因此球O 的表面积为274π4π14π2S R ==⋅⋅=. 本题还可用秒杀公式4可得22222223217442a b c R ++++===，因此球O 的表面积为274π4π14π2S R ==⋅⋅=. 由此可知在选用公式的时候是比较灵活的，原因在于模型之间可以相互转化.典例例题1-1例题1-2( 2012•辽宁 ) 已知点P ，A ，B ，C ，D 是球O 表面上的点，PA ⊥平面ABCD ，四边形ABCD 是边长为PA =，则OAB △的面积为．由秒杀公式1得(22222=12424h R r +=⋅+=⎝，解得R =OAB △为等边三角形，所以(2OAB S ==△( 2011•四川 ) 如图，半径为R 的球O 中有一内接圆柱．当圆柱的侧面积最大时，球的表面积与该圆柱的侧面积之差是．由秒杀公式1得222=4h R r +，于是2224=2π=4π4π2π22h r h S r h r R+⋅⋅⋅=侧，当且仅当2h r ==时不等式取“=”，于是 222=4π2π=2πSS R R R −−侧球.( 2010•辽宁 ) 已知S ，A ，B ，C 是球O 表面上的点，SA ⊥平面ABC ，AB BC ⊥，1SA AB ==，BC ，则球O 的表面积等于( )A ．4πB ．3πC ．2πD ．π由秒杀公式1得222221=144h R r +=+=⎝⎭，解得1R =，则球O 的表面积为24π4πS R ==.故选A .( 2008•浙江 ) 如图，已知球O 的面上四点A ，B ，C ，D ，DA ⊥平面ABC ，AB BC ⊥，DA AB BC ==O 的体积等于．由秒杀公式1得222229=444h R r +=+=⎝⎭，解得32R =，则球O 的体积为 334439πππ3322V R ⎛⎫==⋅⋅= ⎪⎝⎭.①圆锥 ②正棱锥➢适用几何体：圆锥、顶点在底面的射影是底面外心的棱锥(正棱锥).② 可以通过补形转化为 ①，所以我们只需证明 ① 即可心O 为PO '上一点，于是在Rt OO A '△中有解得( 2018•新课标 Ⅲ ) 设A ，B ，C ，D 是同一个半径为4的球的球面上四点，ABC △为等边三角形且面积为D ABC −体积的最大值为( ) A．B．C．D．依题意得，当三棱锥D ABC −为正三棱锥且hR 时，三棱锥D ABC −的体积最大，那么由秒杀公式2得22=42r h R h+=，①又因为ABC △为正三角形且面积为))1πsin23S =⋅⋅⋅=，解得r =①式解得2h =或6h =，又因为4hR =，所以6h =，于是()max 1=3D ABC V −⋅ 故选B .例题2-1典例( 2014•大纲版 ) 正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为( ) A ．81π4B ．16πC ．9πD ．27π4由秒杀公式2得2222+49==2244r h R h+=⋅，因此22981π=4π=4π=44S R ⎛⎫⋅ ⎪⎝⎭，故选A .( 2020•银川模拟 ) 已知圆锥的母线与底面所成的角等于60︒，且该圆锥内接于球O ，则球O 与圆锥的表面积之比等于( ) A ．4:3B ．3:4C ．16:9D ．9:16由秒杀公式2得22=2r h R h+，依题意得h =，因此R =，于是2222224164ππ4π1633=ππππ23π9r r S R S r rl r r r r ⋅===++⋅球锥. 故选C .例题2-2例题2-3( 2018秋•太原期末 ) 在三棱锥P ABC −中，顶点P 在底面ABC 的投影G 是ABC △的外心，2PB BC ==，平面PBC 与底面ABC 所成的二面角的大小为60︒，则三棱锥P ABC −的外接球的表面积为 .如图所示，作BC 的中点M ，在Rt PMB △[1]中有PM ==依题意知60PMG ∠=︒[2]，在Rt PGM △中有3sin 60cos602h PG PM GM PM ==︒==︒=，于是在Rt BGM △中有r BG =，由秒杀公式2可得224=23r h R h +=，因此264π4π9S R ==.[1] 因为顶点P 在底面ABC 的投影G 是ABC △的外心，所以PA PB PC ==. [2] 因为BC PM ⊥且BC GM ⊥，所以PMG ∠为二面角P BC A −−的平面角.( 2020•娄底模拟 ) 如图所示是某几何体的三视图，则该几何体的外接球的表面积为( )A ．25π8B ．25π4C ．25π2 D ．9π8由秒杀公式2得2222+=2r hR h+= 因此2225π=4π=4π=2S R ⋅⎝⎭，故选C .( 2019秋•东莞市期末 ) 已知球O 是正四面体A BCD −的外接球，2BC =，点E 在线段BD 上，且3BD BE =，过点E 作球O 的截面，则所得截面圆面积的最小值是( )A ．8π9B ．11π18C ．5π12 D ．4π9依题意易知3r =，3h =，由秒杀公式2得2222+=2r h R h +=，如图所示，在OBD △中，由余弦定理可得222cos 23OB BD ODOBD OB BD+−∠==⋅⋅，那么在OBE △中，由余弦定理可得222112cos 18OE OB BE OB BE OBD =+−∠=，当截面圆垂直OE 时面积最小，故截面圆的最小半径为3r '==，因此截面圆面积的最小值为()288πππ99S r '==⋅=.故选A .( 学生答疑 ) 在《九章算术》卷商功中称正四棱锥为“方锥”. 现有一“方锥”的体积为若该“方锥”的五个顶点都在球O 的球面上，则球O 表面积的最小值为 A ．18πB ．27πC ．36πD ．75π由秒杀公式2得22=2r h R h+，依题意得211=233V S h r h ⋅⋅=⋅⋅=底，即2r =2223263=32244h rh h h h R h h h ++==+⋅=4h”，即“h =”时不等式取“=”，因此 2min min 27=4π4π27π4S R =⋅=，故选B.➢适用几何体：三组线线垂直型三棱锥.证明：在三棱锥P ABC=，−中，AB AC APAB a，AC b、、两两垂直，= =，将三棱锥补成长方体，则长方体的体对角线PQ即为外接球的AP c直径，于是所以()22222R a b c=++，即( 2019•新课标 Ⅰ ) 已知三棱锥P ABC −的四个顶点在球O 的球面上，PA PB PC ==，ABC △是边长为2的正三角形，E ，F 分别是PA ，AB 的中点，90CEF ∠=︒，则球O 的体积为( ) A．B．C．D依题意得三棱锥P ABC −为正三棱锥，CE EF ⊥，因为//EF PB ，所以PB CE ⊥，由正三棱锥性质可得PB CA ⊥[1]，又因为CE ⊂面PAC ，CA ⊂面PAC ，=CE CA C ，因此PB ⊥面PAC ，因此PA PB PC ，，两两垂直[2]，由秒杀公式3得2222222++3===442a b cR ++，于是3344=π=π332V R ⎛⎫⋅⋅⋅⋅ ⎪ ⎪⎝⎭，故选D .[1] 设G 为AC 的中点，P 点在底面ABC 的投影为1O ，因为三棱锥P ABC −为正三棱锥，所以1O 为ABC △的外心，故1B O G ，，三点共线，因为1AC PO AC BG ⊥⊥，，且 11PO BG O =，所以AC ⊥平面PGB ，又因为PB ⊂平面PGB ，故PB CA ⊥.[2] PAB PAC PBC ≅≅△△△.例题3-1典例( 2012•辽宁 ) 已知正三棱锥P ABC −，点P ，A ，B ，CPA ，PB ，PC 两两垂直，则球心到截面ABC 的距离为．由秒杀公式3可得2222222344PA PB PC a b c R ++++===，由正三棱锥性质可得PA PB PC ==，解得2PA PB PC ===，则球心到截面ABC 的距离为OH ===.( 2008•福建 ) 是．由秒杀公式3可得2222944a b c R ++===，故294π4π9π4S R ==⋅=. 例题3-3( 2020•山东学业考试 ) 在三棱锥P ABC −中，PA ，PB ，PC 两两垂直，且1PA =，2PB PC ==，则该三棱锥的外接球体的体积为( )A ．9π2B ．27π2C ．9πD ．36π由秒杀公式3可得22222221229444a b c R ++++===，于是334439πππ3322V R ⎛⎫==⋅=⎪⎝⎭. 故选A .( 2019春•湖南期末 ) 已知点P 在直径为2的球面上，过点P 作球的两两相互垂直的三条弦PA ，PB ，PC ，若PA PB =，则PA PB PC ++的最大值为( )A．B ．4C．2+D ．3由秒杀公式3可得22222222221444PA PB PC PB PC a b c R +++++====，即2224PB PC +=，因此()222PAPB PC PB PC⎡++=+=⎢⎣1PC =时，即3PB PC ==时不等式取“=”，故选A .例题3-5➢适用几何体：对棱长相等的三棱锥.证明：在三棱锥P ABC −中，PA BC x ==，PB AC y ==，PC AB z ==，将三棱锥P ABC −补成如图所示长方体，设DA a =，DB b =，DC c =，于是长方体的体对角线PD 即为三棱锥P ABC −外接球，因为222222222a b z a c y b c x ⎧+=⎪+=⎨⎪+=⎩，，，所以()2222222x y z a b c ++=++，又因为那么即( 2020•红河州模拟 ) 在三棱锥A BCD −中，5AB CD AC BD ====，AD BC ==( )AB．C ．132D ．13由秒杀公式4得()((22222225+169==884x y z R +++=，解得13=2R ，故选C .( 2016•蚌埠三模 ) 在四面体ABCD 中，2AB CD ==，AC BD AD BC ==== 面体的外接球的表面积为．由秒杀公式4得()22222222+==188x y zR +++=，因此四面体外接球的表面积为24π4πS R ==.典例例题4-1例题4-2( 2019秋•路南区校级期中 ) 四面体ABCD 的四个顶点在同一球面上中，4AB BC CD DA ====，AC BD ==E 为AC 的中点，过E 作其外接球的截面，则截面面积的最大值与最小值的比为( ) A ．5:4B2CD ．5:2由秒杀公式4得()()(22222224+4==588x y z R +++=，在等腰OAE △中，OE ==当截面圆所在平面垂直OE 时面积最小，截面圆所在平面过球心O 时面积最大，因此22min maxπ2ππ5πS SR =⋅==⋅=，，于是max min 52S S =，故选D .例题4-3➢适用几何体：两全等等腰三角形折叠式棱锥.证明：在三棱锥P ABC −中，PAB CAB ≅△△，CA CB =，1O ，2O 分别是ABC △和PBC △的外心，M 为线段AB 的中点，1OO ⊥平面ABC ，2OO ⊥中有那么，在Rt MBO △中有( 2019•齐齐哈尔一模 ) 在边长为2的菱形ABCD中，BD =，将菱形ABCD 沿对角线AC 对折，使二面角B AC D −−的余弦值为13，则所得三棱锥A BCD −的外接球的表面积为.由秒杀公式5得因此三棱锥A BCD −的外接球表面积为234π4π6π2S R ==⋅=.典例例题5-1(2017•广西一模)在菱形ABCD中，60A=︒，AB=ABD∆的∆沿BD折起到PBD位置，若二面角P BD C−的外接球球心为O，BD的中−−的大小为120︒，三棱锥P BCD点为E，则(OE=)A．1B．2C D．由秒杀公式5得那么OE===，2故选B.( 原创 ) 已知空间四边形ABCD 中，2AB BD AD BC AC =====，若二面角C AB D −−的取值范围为π2π33⎡⎤⎢⎥⎣⎦，，则该几何体的外接球表面积的取值范围为．由秒杀公式5得又因为π2π33α⎡⎤∈⎢⎥⎣⎦，，所以ππ263α⎡⎤∈⎢⎥⎣⎦，，那么tan 2α∈⎣，因此213793R ⎡⎤∈⎢⎥⎣⎦，，又因为2=4πS R ，故外接球表面积的取值范围为52π28π93⎡⎤⎢⎥⎣⎦，.➢适用几何体：面面垂直型棱锥.证明：在三棱锥P ABC −中，平面ABP ⊥平面ABC ，1O ，2O 分别是ABP △和ABC △的外心，且1OO ⊥平面ABP ，2OO ⊥平面ABC ，1r ，2r 分别是ABP △和ABC △外接圆的半径，l 为线段AB 的长度，在2O BM △中有即同理所以( 原创 ) 在三棱锥S ABC −中，ABC △是边长为3的等边三角形，SA =，SB =面角S AB C −−的大小为90︒，则此三棱锥的外接球的半径为．由秒杀公式5得典例例题6-1( 2019•中卫一模 ) 一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的外接球的表面积为( ) A ．16π3B ．8π3C． D．由秒杀公式5得因此外接球的表面积为正视图侧视图俯视图( 2019•开福区校级模拟 ) 已知等腰ABC △的面积为4，AD 是底边BC 上的高，沿AD 将ABC △折成一个直二面角，则三棱锥A BCD −的外接球的表面积的最小值为．设AD x BD y ==，，因为等腰ABC △的面积为4，则=4xy ，又因为12r r ==，那么由秒杀公式5得2211242x ⋅2212x y =时，即x y ==时，不等式取“=”，故三棱锥A BCD −的外接球的表面积的最小值为2min min =4πS R .如图，三棱锥P ABC −的底面是边长为2的等边三角形，若PA PB =二面角P BA C −− 的大小为90︒，则三棱锥P ABC −的外接球的表面积等于．由秒杀公式5得因此外接球的表面积为➢适用几何体：普通三棱锥.证明：在三棱锥P ABC −中，1O ，2O 分别是ABP △和ABC △的外心，二面角12P AB C O MO α−−=∠=，M 为AB 的中点，1O M m =，2O M n =，且1OO ⊥平面ABP ，2OO ⊥平面ABC ， l 为线段AB 的长度，在四边形12OO MO 中，因为所以12OO MO 四点共圆，设四边形12OO MO 的外接圆的半径为r ，则因此( 2019秋•迎泽区校级月考 ) 在三棱锥S ABC −中，ABC △是边长为3的等边三角形，SA，SB =二面角S AB C −−的大小为120︒，则此三棱锥的外接球的半径为．由秒杀公式7得典例例题7-1( 2019春•孝感期末 ) 将边长为2的正三角形ABC 沿中线AD 折成60︒的二面角B AD C −−，则三棱锥A BDC −的外接球的表面积为．由秒杀公式7得因此外接球的表面积为( 2015秋•绍兴校级期中) 如图，三棱锥P ABC −的底面是边长为2的等边三角形，若PA PB ==P BA C −−的大小为60︒，则三棱锥P ABC −的外接球的表面积等于．由秒杀公式7得因此外接球的表面积为( 2017•葫芦岛模拟 ) 已知空间四边形ABCD 中，2AB BD AD ===，1BC =，CD =，若二面角A BD C −−的取值范围为π2π43⎡⎤⎢⎥⎣⎦，，则该几何体的外接球表面积的取值范围为．由秒杀公式7得因为π2π43α⎡⎤∈⎢⎥⎣⎦，，所以21sin 12α⎡⎤∈⎢⎥⎣⎦，，因此24533R ⎡⎤∈⎢⎥⎣⎦，，因此外接球的表面积的取值范围为➢适用几何体：所有棱锥.证明：设PAB PAC PBC ABC △、△、△、△的面积分别为1234S S S S 、、、，则那么即( 2020•来宾模拟 )已知正三棱锥的底面边长为，侧棱长为，则该正三棱锥内切球的表面积为．由秒杀公式8得所以外接球的表面积为典例例题8-1( 2020•浙江模拟 ) 几何体三视图如图所示，则该几何体的内切球表面积是．由秒杀公式8得所以外接球的表面积为( 2020•娄底模拟 ) 如图所示是某几何体的三视图，则该几何体的内切球与外接球的半径之比为( )A ．12B ．23C ．25 D ．13由秒杀公式2得2222=2r hR h++==外，由秒杀公式8得故该几何体的内切球与外接球的半径之比为故选C .。

外接球复习课

22
c2 a 2 8,
4
4
22
则由R a2 b2 c2 66
2
4
3
练习4．在三棱锥A BCD中，AB＝CD＝ 13，AD＝BC＝2 5，AC＝BD＝5，求三棱锥 A BCD外接球的体积.
D
a
b
c
c
.
b
C
a
B
A
b
B
a
c c
a
D
b
C
29
29 6.
小结：
构造长方体（正方体）的两种条件。 1.墙角结构。等价说法有“三棱锥三个侧面两
C1
所以，其外接球半径R= 3 a 2
（2）长方体的长、宽、高分别为 a,b, c ，其外接球半径
R a2 b2 c2 2
c 2R
b a
（3）正六棱柱底边长为a,高为h, R
h2 4a2 2
h
O R
，
2a
a
例1.正六棱柱的12个顶点都在一个半径为3的球
面上，当正六棱柱的底边边长为 6 时，高为 .
同一个球面上，其外接球的表面积
DCLeabharlann D2AC
2
B
A B
解：将正四面体补成正方体，正方体的边长为1，其体对
角线为 3,外接球的半径为 3，表面积为3 .
2
例5.已知三棱锥A-BCD，AB=CD=3,AC=BD=4,AD=BC= 2 2 ,三棱锥A-BCD
的外接球的半径= 。
分析：
D
a
b
c
A
c
C
b
.
a
B
A B
D
如图：AB AD, AC AD, AB AC 墙角结构又AB AC AD 3 构造正方体

(完整word版)搞定空间几何体的外接球(word文档良心出品)

图5-4图3-1专题3 搞定空间几何体的外接球与内切球一、基本方法：（1）定心：确定球心，构造直角三角形利用正余弦定理及勾股定理求解（222d r R +=）；该方法是解决外接球问题的主要的通法，但对空间想象能力、作图能力要求较高；所以熟悉以下的几种模型才能准确快速的解决外接球问题。

（2）补形：补成长方体，利用长方体对角线求解（22224c b a R ++=）；有些几何体比较难确定球心，而几何体刚好是长方体的一部分，其外接球与长方体的外接球是同一个球，故可利用长方体模型求解。

另外有些不规则的几何体还可以选择建系，设球心，利用球心到各顶点的距离相等求出球心坐标求解。

但该方法计算量大，高考一般不会考查。

高考中以模型一、二、三、四为主。

类型一：锥体模型（P 的射影是ABC ∆的外心即侧棱长相等）第一步：确定球心O 的位置，取ABC ∆的外心1O ，则1,,O O P 三点共线；第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1；第三步：勾股定理：21212O O A O OA +=⇒222)(r R h R +-=，解出R类型二：柱体模型（直棱柱、圆柱）第一步：确定球心O 的位置，1O 是ABC ∆的外心，则⊥1OO 平面ABC ；第二步：算出小圆1O 的半径r AO =1，h AA OO 212111==；第三步：勾股定理：21212O O A O OA +=⇒222)2(r h R +=⇒22)2(hr R +=，解出R第一步：将ABC ∆画在小圆面上，D 为小圆上任意的一点，；第二步：1O 为ABC ∆的外心，所以⊥1OO 平面ABC ，算出小圆1O 的半径r D O =1（三角形的外接圆直径算法：利用正弦定理，得r C cB b A a 2sin sin sin ===），PA OO d 211==；第三步：利用勾股定理求三棱锥的外接球半径：222d r R +=.图6类型四：长方体模型1.三条棱两两垂直，可补形为长方体图1-1图1-2图1-3方法：找三条两两垂直的线段，直接用公式2222)2(c b a R ++=，求出R 2.三棱锥（即四面体）中，三组对棱分别相等，亦可补形为长方体第一步：画出一个长方体，标出三组互为异面直线的对棱；第二步：设出长方体的长宽高分别为c b a ,,，x BC AD ==，y CD AB ==，z BD AC ==，第三步：由22222222z y x c b a R ++=++=，求出R .类型五：二面角模型（两个三角形拼在一起，一般为两等腰三角形或直角三角形） 1.当两等腰三角形由公共底边折叠时，第一步：先画出如图所示的图形，将BCD ∆画在小圆上，找出∆BD A '∆的外心1H 和2H ；第二步：过1H 和2H 分别作其所在平面的垂线，两垂线的交点即为球心O ，连接OC OE ,；第三步：解1OEH ∆，算出1OH ，再由勾股定理：22121OC CH OH =+，求出球的半径R 。

高中数学解题指导八个无敌模型全搞定空间几何的外接球和内切球问题

高中数学解题指导八个无敌模型全搞定空间几何的外接球和内切球问题八个有趣模型——搞定空间几何体的外接球与内切球类型一、墙角模型墙角模型是指三条线段两两垂直的几何体，通过公式(2R) = a + b + c，即2R = a^2 + b^2 + c^2，可以求出其外接球半径R。

例1：1）已知顶点都在同一球面上的正四棱柱的高为4，体积为16，求该球的表面积。

解：由V = ah = 16，得a = 2，4R = a + a + h = 4 + 4 + 16 = 24，S = 24π，答案为C。

2）若三棱锥的三个侧面两两垂直，且侧棱长均为3，求其外接球的表面积。

解：由2R = a + b + c = 3 + 3 + 3 = 9，得R = 9/4，S =4πR^2 = 9π。

3）在正三棱锥S-ABC中，M、N分别是棱SC、BC的中点，且AM⊥MN，若侧棱SA = 23，求正三棱锥S-ABC外接球的表面积。

解：由墙角模型的特点可知，正三棱锥的对棱互垂直。

连接AB、BC的中点D、E，连接AE、CD，交于H，则H是底面正三角形ABC的中心。

由AM⊥MN，SB//MN，可得AM⊥SB，AC⊥SB，故SB⊥平面SAC，SB⊥SA，SB⊥SC，即SB⊥SA，BC⊥SA，故SA⊥平面SBC，SA⊥SC。

因此，三棱锥S-ABC的三棱条侧棱两两互相垂直，由2R^2 = 23^2 + 23^2 + 23^2 = 36，得R^2 = 9，S = 36π。

类型二、棱台模型棱台模型是指上底面和下底面都是正多边形，且两底面中心连线与侧棱垂直的几何体。

通过勾股定理和相似三角形，可以求出其外接球半径R和内切球半径r。

例2：1）已知棱台的上底面和下底面都是正三角形，上底边长为3，下底边长为6，侧棱长为5，求其外接球半径R和内切球半径r。

解：由勾股定理可得棱台的高为4√3.设外接球半径为R，内切球半径为r，则有R/r = (a + b + c)/(a + b - c) = (3 + 6 +5)/(3 + 6 - 5) = 7，解得R = 7r。

几类空间几何体的外接球问题的解法

解：要使函数存在2个零点，需使ìíîïïïïf (1)=1-a +b ≥0，f (2)=4-2a +b ≥0，Δ≥0，1≤a 2≤2，绘制如图3所示的可行域（可行域为箭头所指的曲边三角形）.对z =(x -a )2+(y -b )2变形，可得z +94=a 2+æèöøb -322，则将问题转化为求点(0,32)到可行域内任意一点（a ,b ）距离的平方的最值.从图3中可以看出点(0,32)到直线1-a +b =0的距离即为(0,32)到可行域内任意一点（a ,b ）的最小距离，利用点到直线的距离公式d =||Ax 0+By 0+C A 2+B 2，得d =522.则≥522，解得z ≥78.所以a 2+b 2-3b 取值范围为éëöø78，+∞.对于目标函数为z =(x -a )2+(y -b )2型的目标函数，我们可以依据(x -a )2+(y -b )2的几何意义，把问题转化为求可行域内动点P (x ,y )与定点A (a ,b )距离的平方的最值，从而求出z 的范围.综上所述，利用线性规划模型解答含参二次函数问题有如下几个步骤:1.根据题意建立不等式组，将其视为线性约束条件;2.将所求目标设为目标函数，将其变形为直线的截距式、两点的距离;3.画出可行域；4.在可行域内寻找使得直线的纵截距、动点到定点的距离取最值的点；5.将最值点的坐标代入求得问题的答案.同学们在解题的过程中要注意根据题意建立线性规划模型，利用线性规划模型来提升解答含参二次函数问题的效率.（作者单位：宁夏育才中学）空间几何体的外接球问题是高考试卷中的重要题型，主要考查球空间几何体的性质、面积公式、体积公式.此类问题的难度系数较大，要求同学们具备较强的空间想象能力和逻辑思维能力.本文介绍几种常见空间几何体的外接球问题的题型及其解法，以帮助同学们破解此类问题.类型一：三条棱两两互相垂直的三棱锥的外接球问题该类型的三棱锥具有明显的特征：三条棱两两互相垂直.我们可以抓住该特征，将其看作长方体、正方体的一部分，构造出一个完整的长方体、正方体.将三条棱看作长方体、正方体的三条边，于是三棱锥的外接球的直径等于长方体、正方体的对角线.求出三棱锥的外接球的半径、直径，空间几何体的外接球问题便可顺利获解.类型二：一条侧棱垂直于一个底面的三棱锥的外接球问题我们可将该三棱锥看作直棱柱的一部分，将其补成一个直棱柱，再将其补成一个圆柱，如图1、2、3、4所示，那么三棱锥的外接球即为圆柱的外接球.直棱柱的上、下底面为三角形，且三角形的外接圆的直径为a sin A =b sin B =c sin C =2r ，上下底面的距离为OO 1=12PA(此时PA 垂直与底面)，则有①(2R )2=PA 2+(2r )2，即2R =PA 2+(2r )2；②R 2=r 2+OO 12，即R =r 2+OO 12，这样便建立了PA 与三棱锥的外接球之间的关系，进方法集锦图341图5图6例2.已知三棱锥S-ABC的所有顶点都在球O 球面上，SC是球O的直径.若平面SCA⊥平面SCB，SA ，SB=BC，三棱锥S-ABC的体积为9，则球O的表面积为_____．解：如图7，连接AO，OB，∵SC为球O的直径，∴O为SC的中点，∵SA=AC，SB=BC，∴AO SC，BO⊥SC，平面SCA∩平面SCB=SC的表面积为S=4πR=4π×3图7该三棱锥的两个平面相互垂直，根据已知条件证明AO⊥然后构造三角形，找出三棱锥的外接球半径与三棱锥的棱之间的关系，通过解三角形求得三根据球的表面积公式求得球由两个直角三角形构成的三棱锥的外接解答该类型问题的关键是抓住特征：.我们可以通过解直角三角形求得三图8由两个全等三角形或等腰三角形构成的三棱锥的外接球问题在求解该类型外接球问题时，我们要灵活运用全等三角形或等腰三角形的性质，关注中点为全等三角形或等腰三角形，和ΔA ′BD 的外心H 1和图9例3.三棱锥P -ABC △PAC 和△ABC 均为边长为棱锥外接球的半径.解：如图10，设O 1，O 2由题意可知O 2H =13由勾股定理可得R 2=8图11类型七：直棱柱、圆柱的外接球问题直棱柱、圆柱的外接球问题较为简单，球的球心为高线的中点，如图12所示，所以我们很容=1=1.再设小圆图12图13例4.已知三棱柱ABC -A 1B 1C 1的底面是边长为的正三角形，侧棱垂直于底面，且该三棱柱的外接球的表面积为12π，则该三棱柱的体积为______．解：设球半径为R ，上，下底面中心为M ，N ，由题意，外接球心为MN 的中点，设为O ，，得R =OA =3，由勾股定理可知，OM =1，。

空间几何体的外接球,小专题,复习专用

2
故三棱锥故三棱锥
AA11
ACD 的外接球的体积为 V ACD 的外接球的体积为 V
4 34 3
πR3 πR3
4 34 3
π π
3
3 3 4 3π . 3 4 3π .
│学习目标│➯│新课引入│➯│课本预习│➯│预习评价│➯│知识导出│➯│课堂互动│➯│课堂小结│
│课堂互动│
空间几何体的外接球问题
4．直三棱柱 ABC A1B1C1 的 6 个顶点在球O 的球面上.若 AB 3 ，
AC 4 . AB AC ， AA1 12 ，则球O 的表面积为（）
A．169 B．169 C． 288 D． 676
4
【详解】
解：将直三棱柱补形为长方体 ABEC A1B1E1C1 ，所以体对角线 BC1 的长为球O的直径.
b2 c2 10,
则该棱锥外接球的半径 R 26 ， S 球 4 R2 26 ．
2
│学习目标│➯│新课引入│➯│课本预习│➯│预习评价│➯│知识导出│➯│课堂互动│➯│课堂小结│
│课堂互动│
空间几何体的外接球问题
类型二：圆柱、直棱柱、可补形为直棱柱的(统称为圆柱型)
注：有一条侧棱垂直于底面的棱椎都可补型为直棱柱.
正方体中，则正方体的体对角线长为l 3 ，
∴三棱椎 S-ABC 外接球表面积为 4π( 3 )2 3π . 2
│学习目标│➯│新课引入│➯│课本预习│➯│预习评价│➯│知识导出│➯│课堂互动│➯│课堂小结│
│课堂互动│
空间几何体的外接球问题
类型一：补形为正方体、长方体的类型(特殊型)
8．在三棱锥 S ABC 中， SA BC 5, SB AC 17,
空间几何体的外接球问题

2020高考数学复习之空间几何体外接球和内切球解题策略

2020 年高考数学—几何体外接圆和内切球一、外接球的问题简单多面体外接球问题是立体几何中的难点和重要的考点，此类问题实质是解决球的半径尺或确定球心0 的位置问题，其中球心的确定是关键．（一）由球的定义确定球心在空间，如果一个定点与一个简单多面体的所有顶点的距离都相等，那么这个定点就是该简单多面体的外接球的球心．由上述性质，可以得到确定简单多面体外接球的球心的如下结论．结论1：正方体或长方体的外接球的球心其体对角线的中点．结论2：正棱柱的外接球的球心是上下底面中心的连线的中点．结论3：直三棱柱的外接球的球心是上下底面三角形外心的连线的中点．结论4：正棱锥的外接球的球心在其高上，具体位置可通过计算找到．结论5：若棱锥的顶点可构成共斜边的直角三角形，则公共斜边的中点就是其外接球的球心．（二）构造正方体或长方体确定球心长方体或正方体的外接球的球心是在其体对角线的中点处．以下是常见的、基本的几何体补成正方体或长方体的途径与方法．途径1：正四面体、三条侧棱两两垂直的正三棱锥、四个面都是是直角三角形的三棱锥都分别可构造正方体．途径2：同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥都分别可构造长方体和正方体．途径3：若已知棱锥含有线面垂直关系，则可将棱锥补成长方体或正方体．途径4：若三棱锥的三个侧面两两垂直，则可将三棱锥补成长方体或正方体．（三）由性质确定球心利用球心O与截面圆圆心O1 的连线垂直于截面圆及球心O 与弦中点的连线垂直于弦的性质，确定球心．二、内切球问题若一个多面体的各面都与一个球的球面相切，则称这个多面体是这个球的外切多面体，这个球是这个多面体的内切球。

1、内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离均相等。

2、正多面体的内切球和外接球的球心重合。

3、正棱锥的内切球和外接球球心都在高线上，但不重合。

4、基本方法：构造三角形利用相似比和勾股定理。

5、体积分割是求内切球半径的通用做法。

2020高考数学复习之空间几何体外接球和内切球解题策略

2020年高考数学—几何体外接圆和内切球一、外接球的问题简单多面体外接球问题是立体几何中的难点和重要的考点，此类问题实质是解决球的半径尺或确定球心0的位置问题，其中球心的确定是关键．（一）由球的定义确定球心在空间，如果一个定点与一个简单多面体的所有顶点的距离都相等，那么这个定点就是该简单多面体的外接球的球心．由上述性质，可以得到确定简单多面体外接球的球心的如下结论．结论1：正方体或长方体的外接球的球心其体对角线的中点．结论2：正棱柱的外接球的球心是上下底面中心的连线的中点．结论3：直三棱柱的外接球的球心是上下底面三角形外心的连线的中点．结论4：正棱锥的外接球的球心在其高上，具体位置可通过计算找到．结论5：若棱锥的顶点可构成共斜边的直角三角形，则公共斜边的中点就是其外接球的球心．（二）构造正方体或长方体确定球心长方体或正方体的外接球的球心是在其体对角线的中点处．以下是常见的、基本的几何体补成正方体或长方体的途径与方法．途径1：正四面体、三条侧棱两两垂直的正三棱锥、四个面都是是直角三角形的三棱锥都分别可构造正方体．途径2：同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥都分别可构造长方体和正方体．途径3：若已知棱锥含有线面垂直关系，则可将棱锥补成长方体或正方体．途径4：若三棱锥的三个侧面两两垂直，则可将三棱锥补成长方体或正方体．（三）由性质确定球心利用球心O与截面圆圆心O1的连线垂直于截面圆及球心O与弦中点的连线垂直于弦的性质，确定球心．二、内切球问题若一个多面体的各面都与一个球的球面相切，则称这个多面体是这个球的外切多面体，这个球是这个多面体的内切球。

1、内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离均相等。

2、正多面体的内切球和外接球的球心重合。

3、正棱锥的内切球和外接球球心都在高线上，但不重合。

4、基本方法：构造三角形利用相似比和勾股定理。

5、体积分割是求内切球半径的通用做法。

考点27 空间几何体的外接球(解析版)

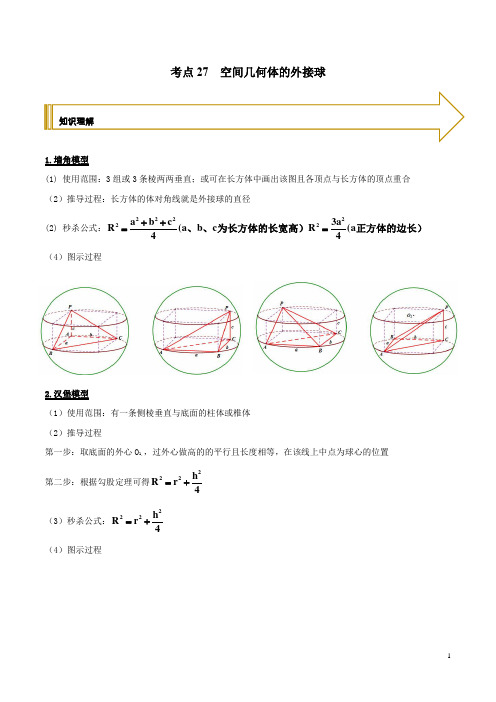
考点27 空间几何体的外接球1.墙角模型(1)使用范围：3组或3条棱两两垂直；或可在长方体中画出该图且各顶点与长方体的顶点重合（2）推导过程：长方体的体对角线就是外接球的直径(2)秒杀公式：222222a b c3aR(a b c R(a44++==、、为长方体的长宽高）正方体的边长）（4）图示过程(3)秒杀公式：2.汉堡模型（1）使用范围：有一条侧棱垂直与底面的柱体或椎体（2）推导过程第一步：取底面的外心O1,，过外心做高的的平行且长度相等，在该线上中点为球心的位置第二步：根据勾股定理可得2 22h R r4=+（3）秒杀公式：2 22h R r4=+（4）图示过程知识理解3.斗笠模型（1）使用范围：正棱锥或顶点的投影在底面的外心上（2）推导过程第一步：取底面的外心O1,，连接顶点与外心，该线为空间几何体的高h 第二步：在h上取一点作为球心O第三步：根据勾股定理22 222r h R(h R)r R2h+ =-+⇔=（3）秒杀公式：22r h R2h+ =（4）图示过程4.切瓜模型（1）使用范围：有两个平面互相垂直的棱锥（2）推导过程：第一步：分别在两个互相垂直的平面上取外心F、N，过两个外心做两个垂面的垂线，两条垂线的交点即为球心O，取BC的中点为M，连接FM、MN、OF、ON第二步：22222222212l ONMF OA AN ON AN MF R r r4∴=+=+∴=+-为矩形由勾股可得（3）秒杀公式：2 22212l R r r4 =+-（4）图示过程考向一墙角模型【例1】（2021·平罗中学高三期末）已知长方体的两个底面是边长为1的正方形，长方体的一条体对角线与底面成45角，则此长方体的外接球表面积为（）A．4πB．6πC．12πD．24π【答案】A【解析】记该长方体为1111ABCD A B C D-，1BD为该长方体的一条体对角线，其与底面所成角为45，因为在长方体1111ABCD A B C D-中，侧棱1DD⊥底面ABCD，则1D BD∠为1BD与底面所成角，即145D BD∠=，因为长方体的两个底面是边长为1的正方形，所以222BD AD AB=+=，则12DD BD==，所以1222BD=+=，又长方体的外接球直径等于其体对角线的长，即该长方体外接球的直径为12222R BD==+=，所以此长方体的外接球表面积为244S Rππ==.故选：A.考向分析【举一反三】1．（2020·天津静海区·高三月考）若棱长为2的正方体的顶点都在同一球面上，则该球的表面积为（） A ．12π B ．24πC ．36πD ．144π【答案】A【解析】因为正方体的外接球的直径2R =，所以棱长为2的正方体外接球的直径2R ==，所以该球的表面积2412R ππ=.故选：A.2．（2020·河南高三月考）已知长方体''''ABCD A B C D -中，''A B =''1B C =，'A B 与平面''ACC A）A ．4πB ．16πC ．163π D ．323π 【答案】B【解析】作BE AC ⊥，垂足为E ，连接'A E ，BE . 因为平面ABC ⊥平面''ACC A ，平面ABC平面''ACC A AC =，BE ⊂平面ABC ，所以BE ⊥平面''ACC A ，所以'BA E ∠是'A B 与平面''ACC A 所成的平面角.又2BE ==，'A B ==所以sin ''BE BA E A B ∠===，解得'AA =.4=. 设长方体的外接球的半径为R ，则24R =，解得2R =.所以该长方体的外接球的表面积为2244216S R πππ==⨯=.故选B .3．（2020·四川泸州市·高三一模）已知四棱锥A BCDE -中，四边形BCDE 是边长为2的正方形，3AB =且AB ⊥平面BCDE ，则该四棱锥外接球的表面积为（） A ．4π B ．174πC ．17πD ．8π【答案】C【解析】由题意，四棱锥A BCDE -中，四边形BCDE 是边长为2的正方形， 3AB =且AB ⊥平面BCDE ，可把四棱锥A BCDE -放置在如图所示的一个长方体内，其中长方体的长、宽、高分别为2,2,3，则四棱锥A BCDE -的外接球和长方体的外接球表示同一个球，设四棱锥A BCDE -的外接球的半径为R 2R =，解得2R =，所以该四棱锥外接球的表面积为22=4=417S R πππ⨯=. 故选：C.考向二汉堡包模型【例2】（2021·陕西西安市·高三一模）三棱柱111ABC A B C -中，棱1AB AC AA 、、两两垂直，12AA =，底面ABC 是面积为2的等腰直角三角形，若该三棱柱的顶点都在同一个球O 的表面上，则球O 的表面积为（） A ．8 B ．10πC ．12πD ．π【答案】C【解析】底面ABC 是面积为2的等腰直角三角形，所以直角边长为2，所以三棱柱111ABC A B C -可以补充成边长为2的正方体，其外接球半径为：2=，所以球O 的表面积为2412ππ=，故选：C 【举一反三】1．（2021·陕西咸阳市·高三一模）在直三棱柱111ABC A B C -中，2AB BC ==，2ABC π∠=，若该直三棱柱的外接球表面积为16π，则此直三棱柱的高为（）．A ．4B ．3C ．D ．【答案】D【解析】因为2ABC π∠=，所以将直三棱柱111ABC A B C -补成长方体1111ABCD A B C D -，则直三棱柱的外接球就是长方体的外接球，外接球的直径等于长方体的体对角线，设球的半径为R ，则2416R ππ=，解得2R =，设直三棱柱的高为h ，则2222422R h =++，即2168h =+，解得h =，所以直三棱柱的高为 D2．（2021·山西吕梁市·高三一模）四面体A BCD -中，DC ⊥面ABC ，3AB BC ==，120ABC ∠=︒，8DC =，则四面体A BCD -外接球的表面积为（）A ．100πB ．50πC ．25πD ．91π【答案】A【解析】设ABC 外接圆的圆心为1O ，四面体A BCD -外接球的球心为O ，半径为R 连接11,,O C OO OC由正弦定理可得12sin BCO C BAC =∠，即1332sin 30O C ︒==，1142OO DC ==5R OC ====即四面体A BCD -外接球的表面积为245100S ππ=⨯= 故选：A3．（2021·山东德州市·高三期末）如图，在四棱锥P ABCD -中，底面ABCD 为菱形，PD ⊥底面ABCD ，O 为对角线AC 与BD 的交点，若2PD =，3APD BAD π∠=∠=，则三棱锥P AOD -的外接球表面积为_________．【答案】16π．【解析】取PA 中点M ，DA 中点E ，连接,ME EO ，则//ME PD ，因为PD ⊥底面ABCD ，所以ME ⊥平面ABCD ，ABCD 是菱形，则AO OD ⊥，所以E 是AOD △的外心，又PD ⊥底面ABCD ，AD ⊂平面ABCD ，所以PD AD ⊥，所以M 到,,,P A D O 四点距离相等，即为三棱锥P AOD -的外接球球心．又2PD =，3APD π∠=，所以24cos3PA π==，所以2MA MP ==，所以三棱锥P AOD -的外接球表面积为24216S ππ=⨯=．故答案为：16π．考向三斗笠模型【例3】正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为（）A ．814πB ．16πC ．9πD ．274π【答案】A【解析】正四棱锥P-ABCD 的外接球的球心在它的高1PO 上，记为O ，PO=AO=R ，14PO =，1OO =4-R ，在Rt △1AOO 中，1AO =由勾股定理()2224R R =+-得94R =， ∴球的表面积814S π=，故选A.【举一反三】1．（2020·江西吉安市·高三其他模拟）正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为（）A ．812πB ．814πC ．815πD ．817π【答案】B【解析】如图示：正四棱锥S ABCD -中，高4SN =，底面正方形边长2AB =,设正四棱锥的外接球半径为R ，底面正四边形外接圆半径为r 则r BN ==由OS OB =得：()2224R R =+-，解得：94R =，∴2814ππ4V R ==. 故选：B.2．（2021·安徽芜湖市·高三期末）已知正四棱锥的体积为18，侧棱与底面所成的角为45，则该正四棱锥外接球的表面积为___________. 【答案】36π【解析】如下图所示，设正四棱锥P ABCD -的底面ABCD 的中心为E ，连接PE 、AC 、BD ，设正四棱锥P ABCD -的底面边长为a ，则AC BD ==，由于E 为正四棱锥P ABCD -的底面ABCD 的中心，则PE ⊥平面ABCD ，由于正四棱锥P ABCD -的侧棱与底面所成的角为45，则45PAC PCA ∠=∠=，所以，PAC △是以APC ∠为直角的等腰直角三角形，同理可知，PBD △是以BPD ∠为直角的等腰直角三角形，E 为AC 的中点，122PE AC a ==，2ABCD S a =正方形，23111833P ABCD ABCD V S PE a -=⋅=⨯==正方形，解得a =，23PE ==，由直角三角形的性质可得1122PE AC BD ==，即PE AE BE CE DE ====，所以，E 为正四棱锥P ABCD -外接球的球心，球E 的半径为3r PE ==，该球的表面积为2436r ππ=. 故答案为：36π.3．（2020·秦皇岛市抚宁区第一中学）已知正三棱锥S ABC -的侧棱长为6，则该正三棱锥外接球的表面积是________.【答案】64π【解析】过点S 作SE ⊥平面ABC 于点E ，记球心为O .∵在正三棱锥S ABC -中，底面边长为6，侧棱长为∴2632BE =⨯=∴6SE ==.∵球心O 到四个顶点的距离相等，均等于该正三棱锥外接球的半径长R ，∴OB R =，6OE R =-.在Rt BOE 中，222OB BE OE =+，即()22126R R =+-，解得4R =，∴外接球的表面积为2464S R ππ==.故答案为：64π.考向四切瓜模型【例4】（2021·江西高三其他模拟）已知三棱锥A -BCD 中，侧面ABC ⊥底面BCD ，三角形ABC 是边长为3的正三角形，三角形BCD 是直角三角形，且∠BCD =90°，CD =2，则此三棱锥外接球的体积等于（）A ．323πB ．643πC ．16πD ．32π【答案】A【解析】三棱锥A BCD -中，侧面ABC ⊥底面BCD ，把该三棱锥放入长方体中，如图所示；设三棱锥外接球的球心为O ，取BC 的中点M ，BD 的中点N ，三角形ABC 的重心G ，连接OG ，则AM AB ==，2233AG AM ===，112OG CD ==，所以三棱锥外接球的半径为2R OA ===，所以三棱锥外接球的体积为3344232333R V πππ⨯===．故选：A ．【举一反三】1．（2020·内蒙古赤峰市·高三月考）已知三棱锥P ABC -中，1PA =，3PB =，AB =CA CB ==面PAB ⊥面ABC ，则此三棱锥的外接球的表面积为（）A ．143πB ．283πC ．11πD ．12π【答案】B【解析】如图，1PA =，3PB =，AB =∴222PA AB PB +=，2PAB π∠=，所以ABP △的外接圆的圆心为斜边PB 的中点N ,CA CB ==∴ABC 为等腰三角形.取AB 的中点D ，连接CD ，DN ，∴CD AB ⊥，AD BD ==∴CD ==又面PAB ⊥面ABC ，面PAB ⋂面ABC AB =，CD ⊂面ABC ，∴CD ⊥面PAB ，过点N 作CD 的平行线，则球心O 一定在该直线上.设ABC 的外接圆的圆心为1O ，,则1O 点在CD 上，连接1OO ,由球的性质则，1OO ⊥平面ABC ，则1O OND 为矩形.在ABC中，cos 5CAB ∠==,则sin 5CAB ∠= 所以ABC的外接圆的半径12sin BC O A CAB ===∠所以1O A =1O D ===则1ON O D ==所以球的半径为3OP ===所以三棱锥的外接球的表面积为221284493πππ=⨯=⎝⎭故选：B2．（2020·四川泸州市·高三一模）已知三棱锥A BCD -中，BAC 和BDC 是边长为2的等边三角形，且平面ABC ⊥平面BCD ，该三棱锥外接球的表面积为（）A ．4πB ．163πC ．8πD ．203π 【答案】D【解析】取BD 的中点E ，连接,AE DE ，则,AE BC DE BC ⊥⊥，因为平面ABC ⊥平面BCD ，所以可证得AE ⊥平面BCD ，DE ⊥平面ABC ，取BCD △的外心F ，作//FM AE ，则,,,F M E A 四点共面，取ABC 的外心H ，过点H 作EF 的平行线交FM 于点O ，因为EF 垂直平面ABC ，则HO ⊥平面ABC ，所以点O 到,,,A B C D 四点的距离相等，所以点O 为三棱锥A BCD -外接球的球心，连接OC ，可求得OF HE DF ===，所以2222145333R OD OF DF ==+=+=，所以外接球的表面积为22043S R ππ==. 故选：D.3．（2021·全国高三专题练习）已知三棱锥A BCD -中，平面ABD ⊥平面BCD ，且ABD △和BCD △都是边长为2的等边三角形，则该三棱锥的外接球表面积为（）A ．4πB ．163πC ．8πD ．203π 【答案】D【解析】如图，由已知可得，ABD △与BCD △均为等边三角形，取BD 中点G ，连接AG ，CG ，则AG BD ⊥，∵平面ABD ⊥平面BCD ，则AG ⊥平面BCD ，分别取ABD △与BCD △的外心,E F ，过,E F 分别作两面的垂线，相交于O ，则O 为三棱锥A BCD -的外接球的球心，由ABD △与BCD △均为边长为2的等边三角形，可得11233OE OF CG ===⨯=，223CE ∴==，3R OC ∴====， ∴三棱锥A −BCD的外接球的表面积为2220443R πππ⨯=⨯=.故选：D.1．（2020·江西高三其他模拟（理））在三棱锥P ABC -中，AB AC ==120BAC ∠=，PB PC ==PA = ）A ．40πB ．20πC ．80πD ．60π【答案】A【解析】在BAC 中，2222cos 24BC AB AC AB AC BAC =+-⋅⋅⋅∠=，即BC =PB PC ==∴PBC 为等边三角形根据题意，有如下示意图：强化练习如图，设ABC 的外接圆的圆心为1O ，连接1O C ，1O A ，1BC O A H ⋂=，连接PH.由题意可得AH BC ⊥，且112AH O A ==12BH BC ==∴由上知：PH BC ⊥且PH ==，又222PH AH PA +=， ∴PH AH ⊥，由AH BC H =，PH ⊥平面ABC.设O 为三棱锥P ABC -外接球的球心，连接1OO ，OP ，OC 过O 作OD PH ⊥，垂足为D ，则外接球的半径R 满足()22222111()R OO CO PH OO OD =+=-+，1A C B O == 1OD O H AH ===，代入解得1OO =210R =，∴三棱锥P ABC -外接球的表面积为2440R ππ=.故选：A.2．（2020·四川泸州市·高三一模）已知四棱锥A BCDE -中，AB ⊥平面BCDE ，底面BCDE 是边长为2的正方形，且3AB =，则该四棱锥外接球的表面积为（）A ．4πB ．174πC ．17πD ．8π【答案】C【解析】由题意，四棱锥A BCDE -中，四边形BCDE 是边长为2的正方形，3AB =且AB ⊥平面BCDE ，可把四棱锥A BCDE -放置在如图所示的一个长方体内，其中长方体的长、宽、高分别为2,2,3，则四棱锥A BCDE -的外接球和长方体的外接球表示同一个球，设四棱锥A BCDE -的外接球的半径为R ，2R =，解得R =，所以该四棱锥外接球的表面积为22=4=4(172S R πππ⨯=.故选：C. 3．（2020·四川宜宾市·高三一模）已知点P ，A ，B ，C 在同一个球的球表面上，PA ⊥平面ABC ，AB ⊥AC ，PB BC PC =2，则该球的表面积为（）A ．6πB ．8πC ．12πD ．16π 【答案】A【解析】如图，三棱锥P ABC -补体在长方体中，三棱锥的外接球就是补体后长方体的外接球，长方体的外接球的直径2R ====即R =，则该球的表面积246S R ππ==.故选：A4．（2020·广东广州市·高三月考）在长方体1111ABCD A B C D -中，1AB CC ==1BC =，点M 在正方形11CDD C 内，1C M ⊥平面1ACM ，则三棱锥11M ACC -的外接球表面积为（）A ．11π2B ．7πC ．11πD ．14π【答案】C【解析】长方体1AC 中，11A D ⊥平面11CDD C ，1C M ⊂平面11CDD C ，∴111C M A D ⊥，又1C M ⊥平面1ACM ，1AC ⊂平面1ACM ，∴11C M AC ⊥， ∵1111AC AD A =，∴1C M ⊥平面11A CD ，而1CD ⊂平面11A CD ，∴11C M CD ⊥， 11CDD C 是正方形，∴M 是1CD 与1C D 交点，即为1CD 的中点，也是1C D 的中点． 1C MC △是直角三角形，设E 是1CC 中点，F 是1BB 中点，则由//EF BC 可得EF ⊥平面1MCC （长方体中棱与相交面垂直），E 是1C MC △的外心，三棱锥11A MCC -的外接球球心O 在直线EF 上（线段EF 或EF 的延长线上）．设OE h =，则22222(1)22h h ⎛⎛+=++- ⎝⎭⎝⎭，解得32h =，∴外接球半径为2r ==，表面积为21144114S r πππ==⨯=．故选：C ．5．（2020·全国高三月考）三棱柱111ABC A B C -中，1AA ⊥平面ABC ，AC AB ⊥，1AC =，AB =12AA =，则该三棱柱111ABC A B C -的外接球的体积为（）A B C D ．8π【答案】B【解析】如图，取BC 中点1O ，连1BC 交1B C 于点O ，AC AB ⊥，1O ∴为Rt ABC 的外接圆圆心， 3AB =，1AC =，2BC ∴=，ABC ∴外接圆半径为12BC =, 111////OO CC AA ，1AA ⊥平面ABC ，1OO ∴⊥平面ABC ，又1112BB OO ==，∴点O 为三棱柱111ABC A B C -的外接球球心，∴外接球半径R OB ===∴外接球体积3433V R π==. 故选：B.6．（2020·江西赣州市·高三）四面体A BCD -中，AB ⊥底面BCD ，AB BD =1CB CD ==，则四面体A BCD -的外接球表面积为（）A ．3πB ．4πC ．6πD ．12π【答案】B 【解析】如图，在四面体A BCD -中，AB ⊥底面BCD ，AB BD ==1CB CD ==，可得90BCD ∠=︒，补形为长方体，则过一个顶点的三条棱长分别为1，1，2=，则三棱锥A BCD -的外接球的半径为1．其表面积为2414ππ⨯=．故选：B ．7．（2021·天津滨海新区·高三月考）直三棱柱111ABC A B C -的所有顶点都在同一球面上，且2AB AC ==，90BAC ∠=︒，1AA = ）A ．40πB ．32πC ．10πD ．8π 【答案】A【解析】如图所示，直三棱柱111ABC A B C -的所有顶点都在同一球面上，且2AB AC ==，90BAC ∠=︒，1AA =∴可将直三棱柱111ABC A B C -补成长方体，其中2AB AC BM CM ====，11AA BB ==1CB ====r .∴球的表面积为224440S r πππ==⨯=.故选: A.8．（2020·江苏南通市·高三期中）正三棱锥S ABC -中，2SA =，AB =积为（）A ．B ．4πC ．12πD ．6π【答案】C【解析】正三棱锥S ABC -中，2SA =，AB =所以222SA SB AB +=, 故SA SB ⊥,同理可得SA SC ⊥, SB SC ⊥, 以,,SA SB SC 为棱构造正方体，则该棱锥外接球即为该正方体的外接球，如图，所以2222(2)22212R =++=，故球的表面积为2412S R ππ==, 故选：C9．（2021·安徽宣城市·高三期末（文））在三棱锥P ABC -中，PA ⊥平面ABC ，1204BAC AP AB AC ∠====，则三棱锥P ABC -的外接球的表面积是（）A ．18πB ．36πC ．40πD ．72π【答案】D【解析】如图所示，1204BAC AB AC ∠===，，取BC 中点M ，连接AM 并延长到N 使AM =MN ，则四边形ABNC 是两个等边三角形组成的菱形，AN =BN =CN ，点N 是ABC 的外接圆圆心，过N 作平面ABC 的垂线NG ，则球心一定在垂线NG 上，因为PA ⊥平面ABC ，则PA //NG ，PA 与NG 共面，在面内作PA 的中垂线，交NG 于O ，则O 是外接球球心，半径R =OA ，Rt AON 中，12ON AP ==，4AN =，故R ==故外接球的表面积2441872S R πππ==⨯=. 故选:D.10．（2020·江苏南京市第二十九中学高三期中）已知直三棱柱111ABC A B C -的顶点都在球O 上，且4AB =，16AA =，30ACB ∠=︒，则此直三棱柱的外接球O 的表面积是（）A ．25πB ．50πC ．100πD ．500π3【答案】C【解析】如图所示：设点O '为ABC 外接圆的圆心，因为30ACB ∠=︒，所以60AO B '∠=，又O A O B r ''==，所以AO B '△是等边三角形，所以4r O A O B AB ''====，又直三棱柱111ABC A B C -的顶点都在球O 上，所以外接球的半径为5R ==，所以直三棱柱的外接球O 的表面积是24100S R ππ==，故选：C11．（2021·平凉市庄浪县第一中学高三其他模拟（理））已知90ABC ∠=︒，PA ⊥平面ABC ，若1PA AB BC ===，则四面体PABC 的外接球（顶点都在球面上）的体积为（）A ．π BC ．2πD ．2【答案】D【解析】取PC 的中点O ，连接OA ，OB ，由题意得PA BC ⊥，又因为,AC BC PC AC A ⊥⋂=，所以BC ⊥平面PAC ，所以BC PB ⊥，在1,2Rt PBC OB PC ∆=，同理12OA PC =，所以12OA OB OC PC ===，因此P ，A ，B ，C 四点在以O 为球心的球面上，在Rt ABC ∆中，AC ==在Rt PAC ∆中，PC ==O 的半径12R PC ==34322π⎛= ⎝⎭，故选：D.12．（2020·甘肃省民乐县第一中学高三其他模拟（理））在四棱锥P ABCD -中，//BC AD ，AD AB ⊥，AB =6AD =，4BC =，PA PB PD ===P BCD -外接球的表面积为（） A ．60π B ．40πC ．100πD ．80π【答案】D【解析】如图，取AD 的两个三等分点1O 、E ，连接BD 、1O C 、CE ，设1BDO C H =，连接PH 、AH .则1123AO AD ==，14O D BC ∴==，又//BC AD ，1//BC O D ∴，所以，四边形1BCDO 为平行四边形，1O CBD H =，H ∴为BD 的中点，所以，1122AH BH DH BD =====由勾股定理可得14O B ===，则11O B O D =，在1Rt O AB △中，11tan ABAO B AO ∠==13AO B π∴∠=， //BC AD ，13CBO π∴∠=，又11BC O D O B ==，则1O BC △为等边三角形，1114O C O B O D ∴===，则1O 是BCD 的外接圆的圆心.因为PA PB PD ===H 为BD 的中点，PHBD ∴⊥，PA PB =，AH BH =，PH PH =，PAH PBH ∴≅△△，2PHA PHB π∴∠=∠=，PH AH ∴⊥，又PH BD ⊥，AHBD H =，PH ∴⊥平面ABCD ，且6PH ===.设O 为三棱锥P BCD -外接球的球心，连接1OO 、OP 、OD ，过O 作OF PH ⊥，垂足为F ，则外接球的半径R 满足()2222211146R OO OO O H =+=-+，设1OO x =，则()221664x x +=-+，解得2x =，从而222420R x =+=，故三棱锥P BCD -外接球的表面积为2480R ππ=. 故选：D.13．（2021·固原市第五中学高三期末（理））已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为24，则这个球的体积为____________.【答案】【解析】设正方体边长a ，正方体外接球的半径为R ，由正方体的表面积为24，所以2624a =，则2a =，又R =，所以R ，所以外接球的体积为：334433R ππ==.故答案为：.14．（2021·安徽池州市·高三期末（理））已知四棱锥A BCDE -的底面BCDE 是边长为2的正方形，DE ⊥平面ABE ，2AE =，AC =A BCDE -的外接球的表面积为___________. 【答案】283π【解析】如图所示：∵DE ⊥平面ABE ，BC ⊥平面ABE ， ∴90ABC ∠=︒，则有222AB BC AC +=，解得2AB =，又2AE =，构造正三棱柱ABE A CD '-，其上下底面边长为2，高为2，则其外接球的球心是上下中心连线的中点，设外接球半径R ，则22222113713R O E OO ⎛=+=+= ⎝⎭，所以外接球的表面积为23428S R ππ==. 故答案为：283π15．（2021·吉林四平市·高三期末）已知直三棱柱1111,2,2,ABC A BC AB AC BC AA -====其外接球的体积为____.【解析】已知AB =AC ,∴三角形ABC 为等腰三角形，取M 为BC 的中点，连接AM ,则AM ⊥BC ,由已知得BC =BM =,又2,60AB BAM =∴∠=︒,∴120BAC ∠=︒，再由正弦定理42sin BC rA ===,（r 为三角形ABC 外接圆半径），r =2, 设两底面的外接圆的圆心分别为12,O O ，外接球球心O 为12O O的中点，外接球的半径R OA ===所以球的体积为343R π=,. 16．（2021·河南郑州市·高三一模）已知A BCD -是球О的内接三棱锥，6,9,AB AC BC BD CD AD ======则球О的表面积为_______________________．【答案】84π【解析】取BC ，AD 的中点,M N ，因为6,9,AB AC BC BD CD AD ======所以AM BC ⊥，DM BC ⊥，所以BC ⊥平面AMD ，MN 既是BC ，又是AD 的垂直平分线，所以三棱锥A BCD -的外接球的球心在MN 上，且平面AMD ⊥平面BCD ，点E 是BCD △的中心，:1:2ME ED =，OE MD ⊥，且OEMN O =，AM DM ==，9AD =，所以MN ==，OMEADN，所以92OE ME OE DN MN =⇒=，解得：3OE =，则三棱锥外接球半径R OD ====，则球O 的表面积2484S R ππ==.故答案为：84π17．（2021·石嘴山市第三中学高三月考）在三棱锥D ABC -中，CD ⊥底面ABC ，,5,4AC BC AB BD BC ⊥===，则此三棱锥的外接球的表面积为______.【答案】34π【解析】因为CD ⊥底面ABC ，所以CD AC ⊥，CD BC ⊥，又AC BC ⊥，所以三棱锥D ABC -的外接球就是以,,CD CA CB为棱的长方体的外接球，其直径为长方体的对角线，因为3CD ===，3AC ===，所以外接球的直径2R ===，所以外接球的表面积为243434R πππ=⨯=. 故答案为：34π18．（2020·梅河口市第五中学高三月考）已知三棱锥A BCD-中，2AB CD AC BD ====，AD BC ==__________.【解析】由题可知，该三棱锥是由长方体的面对角线构成，如图，设长方体的棱长分别为,,a b c ，则2222225,4,3a b b c a c +=+=+=，则2226a b c ++=，设球半径为R ，则2R ==R =，则球的体积为343R π=..19．（2020·山西高三月考（文））已知正三棱柱111ABC A B C -的体积为54，6AB =，记三棱柱111ABC A B C -的外接球为球1O ，则外接球1O 的表面积是__________．【答案】60π【解析】因为正三棱柱111ABC A B C -的底面积216sin 602S =⨯⨯︒=底面外接圆半径62sin 60r ==︒所以正三棱柱111ABC A B C -的高Vh S==所以外接球1O 的半径R ==，则24π60πS R ==，故答案为：60π．20．（2020·济南市·山东省实验中学高三月考）在三棱锥P ABC -中，侧棱PA ⊥底面,120,1ABC BAC AB AC ∠===且2,PA BC =则该三棱锥的外接球的体积为__________．【答案】323π【解析】在ABC 中，由余弦定理可知：BC ===因为120,1BAC AB AC ∠===，所以ABC 是顶角为钝角的等腰三角形，设ABC 的外接圆的直径为AD ，由正弦定理可知：2sin sin120BC AD BAC ︒===∠，因为侧棱PA ⊥底面ABC ， 2PA BC ==，所以三棱锥P ABC -的外接球的直径为PD ，由勾股定理可知：4P D ===，所以三棱锥P ABC -的外接球的半径为：1422R =⨯=，所以三棱锥P ABC -的外接球的体积为：3344322.333V R πππ==⨯= 故答案为：323π。

空间向量法解外接球问题汇总(精品)

空间向量法解决几何体外接球问题汇总一、了解重要推论如上图，O为球心，O'，O''Q为球的截面圆圆心。

由球的性质知：''OO O⊥截面圆OO O⊥，''''截面圆推论1：经过球的截面圆的圆心且垂直于该截面的直线必经过球心；推论2：球的所有过截面圆圆心且垂直于该截面的直线均交于一点，该点为球心O。

二、思维转换几何体截面圆圆心相当于该截面内接图形的外心（中心），故一个几何体若存在外接球，则其各面均位于其外接球相应截面内，其外心相当于该截面圆的圆心。

我们称过几何体各面几何图形外心的法向量为外心法向量。

推论3：若几何体存在外接球，则几何体任意非平行两面的外心法向量所在直线必交于一点，此点为球心。

故，我们可由两平面的外心法向量求出球心的坐标。

推论4：若几何体存在外接球，在其非平行的两面中，其中一面的外心法向量所在直线上的一点与另一面外心相连的直线垂直于另一面的一条边，则该点为球心，且该直线垂直于该平面。

三、几何图形的外心坐标求解法以平面直角坐标系为例：其中，,12E E 为,AB AC 的中点，各点坐标如图所示，故可求得(,),(,)123564E E ，(,),(,)2244AB AC =--=-下面求外心H 的坐标，设(,)H x y 则：()()()()12023250①46440②0E H AB x y x y E H AC ⎧⋅=-+-=⎧⎪⇒⎨⎨---=⋅=⎩⎪⎩ 解得：,53x y ==，故外心坐标为(,)53H 。

注：1.根据向量还可以求直线方程，如垂直平分线方程①和②；2.在空间图形中求外心，应找出三条边的向量关系联立求出外心(,,)H x y z ，因为空间中的旋转效应，单个关系求出的是平面。

四、空间向量法求几何体外接圆半径的步骤：例：对于四面体S ABC -，求外接圆半径的步骤： ①任取两面，求外心如取面ABC 和面BCS 外心分别为(,,),(,,)11122212E E E E E E E x y z E x y z AB 中点：(,,)111中=AB x y z BC 中点：(,,)222中=BC x y z AC 中点：(,,)333中=AC x y z则有：AB E AB BC E BC AC E AC ⎧⋅=⎪⎪⋅=⎨⎪⋅=⎪⎩中1中1中1000，联立求出(,,)1111E E E E x y z ，同理可求(,,)2222E E E E x y z ②设球心坐标为(,,)H H H H x y z ,,12E H E H 分别为两面外心法向量11220①0②0③0④E H AB E H BC E H CS E H BS ⎧⋅=⎪⋅=⎪⎨⋅=⎪⎪⋅=⎩联立求出(,,)H H H H x y z ，即球心坐标。

空间几何体外接球13讲学生版_removed

第1讲长方体模型一、解题技巧归纳总结1．正方体的外接球的球心为其体对角线的中点，半径为体对角线长的一半．2．长方体的外接球的球心为其体对角线的中点，半径为体对角线长的一半．3．补成长方体（1）若三棱锥的三条侧棱两两互相垂直，则可将其放入某个长方体内，如图1所示．（2）若三棱锥的四个面均是直角三角形，则此时可构造长方体，如图2所示．（3）正四面体-P A B C 可以补形为正方体且正方体的棱长=a ，如图3所示．（4）若三棱锥的对棱两两相等．．．．．．，则可将其放入某个长方体内，如图4所示图1图2图3图4二、典型例题例1.）A ．π83B ．π2C ．π4D ．π43例2.一个正四棱柱的各个顶点在一个直径为2cm 的球面上．如果正四棱柱的底面边长为1cm ，那么该棱柱的表面积为2cm ．例3.一个长方体的各顶点均在同一球面上，且一个顶点上的三条棱的长分别为1,2,3，则此球的表面积为．例4.已知三棱锥P A B C -的顶点都在同一个球面上（球)O ，且2P A =，P B P C ==当三棱锥P A B C -的三个侧面的面积之和最大时，该三棱锥的体积与球O 的体积的比值是．三、玩转练习1．张衡(78年~139年）是中国东汉时期伟大的天文学家、文学家、数学家．他的数学著作有《算罔论》，他曾经得出结论：圆周率的平方除以十六等于八分之五．已知正方体的外接球与内切球上各有一个动点A ，B ，若线段AB 的最小值为31-，利用张衡的结论可得该正方体的外接球的表面积为()A ．30B ．1010C ．1210D ．362．棱长为2的正方体的外接球的体积为()A ．8B ．8πC ．43πD ．823π3．已知正方体的外接球的体积为323π，则该正方体的表面积为()A ．433B ．163C ．643D ．324．已知正方体的外接球的体积是323π，则这个正方体的体积是()A ．6427B 6439C ．649D 643275．已知长方体1111ABCD A B C D -的表面积为208，118AB BC AA ++=，则该长方体的外接球的表面积为()A ．116πB ．106πC ．56πD ．53π6．在长方体1111ABCD A B C D -中，2AB BC ==，1AC 与平面11BB C C 所成的角为30︒，则该长方体的外接球的表面积为()A ．8πB ．82πC ．16πD ．2π7．在长方体1111ABCD A B C D -中，2AB AD ==，12AA =，则该长方体的外接球的表面积为()A ．4πB ．8πC ．16πD ．32π8．已知长方体1111ABCD A B C D -的体积12V =，2AB =，若四面体11A B CD -的外接球的表面积为S ，则S 的最小值为()A ．8πB ．9πC ．16πD ．32π9．若正方体的外接球的体积为43π，则此正方体的棱长为．10．若某正方体的表面积为6，则该正方体的外接球的体积为．11．已知正方体的外接球的体积为43π，则该正方体的体积为．12．正方体1111ABCD A B C D -的棱长为，则此正方体的外接球的体积为．13．将一个长宽分别a ，(0)b a b <<的长方形的四个角切去四个相同的正方形，然后折成一个无盖的长方体形的盒子，若这个长方体的外接球的体积存在最小值，则ba的取值范围为．14．如图，长方体1111ABCD A B C D -中，其中AB a =，AD b =，1AA c =外接球球心为点O ，外接球体积为323π，若2214a b +的最小值为94，则A ，C 两点的球面距离为．15．已知矩形ABCD 的周长为18，把它沿图中的虚线折成正四棱柱，则这个正四棱柱的外接球表面积的最小值为．第2讲正四面体模型一、解题技巧归纳总结1．正四面体如图，设正四面体A B C D 的的棱长为a ，将其放入正方体中，则正方体的棱长为，显然正四面体和正方体有相同的外接球.正方体外接球半径为R =⋅=，即正四面体外接球半径为R =.二、典型例题例1．棱长为2的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如图，则图中三角形（正四面体的截面）的面积是（）．A．22B．32C．2D．3例2．正四面体的棱长为1，则其外接球的表面积为.三、玩转练习1．棱长为1的正四面体的外接球的半径为()A．64B．34C．1D．332．棱长为a的正四面体的外接球和内切球的体积比是()A．9:1B．4:1C．27:1D．8:13．如图所示，在正四面体A BCD-中，E是棱AD的中点，P是棱AC上一动点，BP PE+的最小值为7，则该正四面体的外接球的体积是()A6πB．6πC．3632D．3 2π4．表面积为83()A．43πB．12πC．8πD．46π5．一个正四面体的棱长为2，则这个正四面体的外接球的表面积为()A．6πB．8πC．6πD．11π6．2的正四面体的外接球中，相互垂直的两个平面分别截球面得两个圆．若两圆的圆心距为22，则两圆的公共弦长是()A．34B．34C．1D．127．如图所示，正四面体ABCD中，E是棱AD的中点，P是棱AC上一动点，BP PE+14，则该正四面体的外接球表面积是()A．12πB．32πC．8πD．24π8．已知正四面体的棱长为4，则此四面体的外接球的表面积是()A．24πB．18πC．12πD．6π9．一个棱长为6的正四面体内部有一个任意旋转的正方体，当正方体的棱长取得最大值时，正方体的外接球的表面积是()A．4πB．6πC．12πD．24π10．如图，在棱长为1的正四面体ABCD中，G为BCD∆的重心，M是线段AG的中点，则三棱锥M BCD-的外接球的表面积为()A．πB．32πC．64D6811．正四面体（四个面均为正三角形的四面体）的外接球和内切球上各有一个动点P、Q，若线段PQ长度463，则这个四面体的棱长为．12．已知正四面体ABCD的棱长为1，M为棱CD的中点，则二面角M AB D--的余弦值为；平面MAB 截此正四面体的外接球所得截面的面积为．13．已知某正四面体的内切球体积是1，则该正四面体的外接球的体积是．14．一个正四面体的展开图是边长为22的正三角形，则该四面体的外接球的表面积为．15．如图所示，正四面体ABCD中，E是棱AD的中点，P是棱AC上一动点，BP PE+14，则该正四面体的外接球的体积是．第3讲对棱相等模型一、解题技巧归纳总结1．对棱相等模型四面体A B C D 中，A B C D m ==，A C B D n ==，A D B C t ==，这种四面体叫做对棱相等四面体，可以通过构造长方体来解决这类问题.如图，设长方体的长、宽、高分别为,,a b c ，则222222222b c m a c n a b t ⎧+=⎪⎪+=⎨⎪+=⎪⎩，三式相加可得222a b c ++=222,2m n t ++而显然四面体和长方体有相同的外接球，设外接球半径为R ，则22224a b c R +=+，所以2228m n t R ++=.二、典型例题例1．三棱锥A B C D -中，已知5A B C D ==，6A D B C ==7A C B D ==，那么该三棱锥外接球的表面积为()A ．6πB ．7πC ．9πD ．12π例2．如图所示三棱锥A B C D -，其中5A B C D ==，6A C B D ==，7A D B C ==，则该三棱锥外接球的表面积为．三、玩转练习1．四面体P ABC -的一组对棱分别相等，且长度依次为25，13，5，则该四面体的外接球的表面积为()A ．294πB ．28πC ．29296πD ．29π2．在四面体ABCD 中，三组对棱棱长分别相等且依次为34，41，5则此四面体ABCD 的外接球的半径R 为()A ．52B ．5C ．522D ．43．如图，在三棱锥P ABC -中，3PA BC ==，2PB AC ==，5PC AB ==，则三棱锥P ABC -外接球的体积为()A 2πB 3πC ．6πD ．6π4．在三棱锥PABC 中，4PA BC ==，5PB AC ==，11PC AB ==，则三棱锥PABC 的外接球的表面积为()A ．26πB ．12πC ．8πD ．24π5．在四面体ABCD 34,41,5，则此四面体ABCD 的外接球的半径R 为．6．已知三棱锥A BCD -，三组对棱两两相等，且1AB CD ==，3AD BC ==，若三棱锥A BCD -的外接球表面积为92π．则AC =．7．已知四面体A BCD -中三组对棱分别相等，且长分别为257A BCD -的外接球的半径为．8．已知三棱锥A BCD -，三组对棱两两相等，即1AB CD ==，AD BC AC BD ====，则三棱锥A BCD -的外接球表面积是．9．在四面体ABCD 中，三组对棱两两相等，分别为，则该四面体外接球的表面积为．10．在四面体P ABC -中，3PA BC ==，2PB AC ==，PC AB ==，则该四面体外接球的体积为．11．三棱锥P ABC -，4PA PB BC AC ====，3PC AB ==，则它的外接球的表面积为．12．在三棱锥P ABC -中，若5PA PB BC AC ====，PC AB ==，则其的外接球的表面积为．13．在三棱锥P ABC -中，4PA BC ==，5PB AC ==，PC AB ==，则三棱锥P ABC -的外接球的表面积为．第4讲直棱柱模型一、解题技巧归纳总结1．直棱柱模型：如图1，图2，图3，直三棱柱内接于球（同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角形）图1图2图3第一步：确定球心O 的位置，1O 是A B C ∆的外心，则1O O ⊥平面A B C ；第二步：算出小圆1O 的半径1A O r =，111122O O A A h ==（1A A h =也是圆柱的高）；第三步：勾股定理：22211O A O A O O =+⇒222()2h R r =+⇒R =，解出R 二、典型例题例1.正三棱柱-111A B C A B C 内接于半径为2的球，若A ，B 两点的球面距离为π，则正三棱柱的体积为．例2.直三棱柱-111A B C A B C 的各顶点都在同一球面上，若===12A B A C A A ，∠=︒120B A C ，则此球的表面积等于．例3.一个正六棱柱的底面上正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为98，底面周长为3，则这个球的体积为.三、玩转练习1．一个直三棱柱的三视图如图所示，其中俯视图是一个顶角为120︒的等腰三角形，则该直三棱柱外接球的表面积为()A ．20πB 2053C ．25πD ．255π2．在直三棱柱111ABC A B C -中，AB BC ⊥，6AB =，8BC =，若此三棱柱外接球的半径为13，则该三棱柱的表面积为()A ．624B ．576C ．672D ．7203．在直三棱柱111ABC A B C -中．侧棱长为23，3AB BC CA ===()A ．1B 3C ．2D ．44．已知直三棱柱111ABC A B C -的底面为直角三角形，且两直角边长分别为13，此三棱柱的高为23，则该三棱柱的外接球的体积为()A ．83πB ．163πC ．323πD ．643π5．已知在直三棱柱111ABC A B C -中，3AB =120ACB ∠=︒，14AA =，则该三棱柱外接球的表面积为()A ．1623πB ．642πC ．32πD ．8π6．在直三棱柱111ABC A B C -中，2CA CB ==，90ACB ∠=︒，11CC =，则该三棱柱外接球的体积()A ．12πB ．4πC ．92πD ．8π7．直三棱柱111ABC A B C -中，AB BC ⊥，12AB BC AA ===，则该三棱柱的外接球的表面积为()A ．4πB ．8πC ．12πD ．323π8．某直三棱柱的侧棱长等于2，底面为等腰直角三角形且腰长为1，则该直三棱柱的外接球的表面积是()A ．πB ．2πC ．4πD ．6π9．正四棱柱1111ABCD A B C D -中，2AB =，二面角11A BD C --的大小为3π，则该正四棱柱外接球的表面积为()A ．12πB ．14πC ．16πD ．18π10．正六棱柱111111ABCDEF A B C D E F -的侧面是正方形，若底面的边长为a ，则该正六棱柱的外接球的表面积是()A ．24a πB ．25a πC ．28a πD ．210a π11．正六棱柱111111ABCDEF A B C D E F -的侧面是正方形，若底面的边长为1，则该正六棱柱的外接球的表面积是()A ．4πB ．5πC ．8πD ．10π12．正六棱柱的底面边长为4，高为6，则它的外接球的表面积为()A ．20πB ．25πC ．100πD ．200π13．已知矩形ABCD 的周长为18，把它沿图中的虚线折成正六棱柱，当这个正六棱柱的体积最大时，它的外接球的表面积为()A ．13πB ．12πC ．11πD ．10π14．一个直六棱柱的底面是边长为4的正六边形，侧棱长为6，则它的外接球的体积为()A ．5003πB ．500πC ．40003πD ．4000π15．棱长均为6的直三棱柱的外接球的表面积是．16．已知直三棱柱111ABC A B C -的底面为直角三角形，且两直角边长分别为13此三棱柱的高为23，则该三棱柱的外接球的体积为．17．在直三棱柱111ABC A B C -中，3BC =，120BAC ∠=︒，12AA =，则此三棱柱外接球的表面积为．18．已知在直三棱柱111ABC A B C -中，90BAC ∠=︒，11AC CC ==，则AB =19．在直三棱柱111ABC A B C -中，侧棱长为，在底面ABC ∆中，60,C AB =︒=，则此直三棱柱的外接球的表面积为．20．在直三棱柱111ABC A B C -中，AB AC ⊥，1AB =，AC =，12BB =，则该三棱柱的外接球表面积为．21．在直三棱柱111ABC A B C -中，120BAC ∠=︒且3AB AC ==，14BB =，则此三棱柱外接球的表面积为．22．在直三棱柱111ABC A B C -中，4BC =，90BAC ∠=︒，12AA =，则此三棱柱外接球的表面积为．23．已知直三棱柱111ABC A B C -的高为，BC =，120BAC ∠=︒，则该三棱柱外接球的表面积为；24．已知直三棱柱111ABC A B C -中，90BAC ∠=︒，侧面11BCC B 的面积为16，则直三棱柱111ABC A B C -外接球的半径的最小值为．25．在正四棱柱1111ABCD A B C D -中，2AB AD ==，14AA =，则正四棱柱的外接球的表面积为．26．已知矩形ABCD 的周长为18，把它沿图中的虚线折成正四棱柱，则这个正四棱柱的外接球表面积的最小值为．27．正四棱柱1111ABCD A B C D -中，AB =12AA =，设四棱柱的外接球的球心为O ，动点P 在正方形ABCD 的边长，射线OP 交球O 的表面点M ，现点P 从点A 出发，沿着A B C D A →→→→运动一次，则点M 经过的路径长为．28．在直四棱柱1111ABCD A B C D -中，AD CD =，24AB BC ==，四边形ABCD 的外接圆的圆心在线段AC 上．若四棱柱1111ABCD A B C D -的体积为36，则该四棱柱的外接球的体积为．29．已知六棱柱A BCD 1EF A -111B C D 11E F 的底面是正六边形，侧棱与底面垂直，若该六棱柱的侧面积为48，底面积为，则该六棱柱外接球的表面积等于．30．一个直六棱柱的底面是边长为2的正六边形，侧棱长为3，则它的外接球的表面积为．31．正六棱柱的底面边长为a ，高为h ，则它的外接球的表面积为．32．已知矩形A BCD 的周长为18，把它沿图中的虚线折成正六棱柱，当这个正六棱柱的体积最大时，它的外接球的表面积为．33．正六棱柱的底面边长为4，高为6，则它的外接球的表面积为．34．已知正六棱柱的高为8，侧面积为144，则它的外接球的表面积为．第5讲直棱锥模型一、解题技巧归纳总结1．直棱锥模型（一条直线垂直于一个平面）如图，P A ⊥平面A B C ，求外接球半径.解题步骤：第一步：将A B C ∆画在小圆面上，A 为小圆直径的一个端点，作小圆的直径A D ，连接P D ，则P D 必过球心O ；第二步：1O 为A B C ∆的外心，所以1O O ⊥平面A B C ，算出小圆1O 的半径1O D r =(三角形的外接圆直径算法：利用正弦定理，得2si n si n si n a b c r A B C ===)，112O O P A =；第三步：利用勾股定理求三棱锥的外接球半径：①222(2)(2)R P A r =+⇔2R =；②2221R r O O =+⇔221R r O O =+.二、典型例题例1.在《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马.若四棱锥M A B C D -为阳马，侧棱M A ⊥底面A B C D ，且2M A B C A B ===，则该阳马的外接球与内切球表面积之和为．例2.已知点P ，A ，B ，C ，D 是球O 表面上的点，⊥P A 平面A B C D ，四边形A B C D 是边长为23正方形．若=26P A ，则∆O A B 的面积为．例3.已知球O 面上的四点,,,,A B C D D A ⊥平面,,3A B C A B B C D A A B B C ⊥===，则球O 的体积等于.三、玩转练习1．已知三棱锥P ABC -中，PA ⊥平面ABC ，BC ⊥平面PAB ，若1AB BC ==，2PA =，则此三棱锥的外接球的表面积为()A ．24πB ．8πC ．6πD ．83π2．《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马．若四棱锥P ABCD -为阳马，底面ABCD 为矩形，PA ⊥平面ABCD ，2AB =，4AD =，二面角P BC A --为60︒，则四棱锥P ABCD -的外接球的表面积为()A ．16πB ．20πC ．643πD ．32π3．在三棱锥S ABC -中，SA ⊥平面ABC ，4SA =，底面ABC ∆是边长为3的正三角形，则三棱锥S ABC -的外接球的表面积为()A ．19πB ．28πC ．43πD ．76π4．三棱锥P ABC -中，PA ⊥平面ABC 且2PA =，ABC ∆3表面积为()A ．43πB ．4πC ．8πD ．20π5．三棱锥P ABC -中，AB BC ==6AC =，PC ⊥平面ABC ，2PC =，则该三棱锥的外接球表面积为()A ．253πB ．252πC ．833πD ．832π6．在三棱锥S ABC -中，侧棱SC ⊥平面ABC ，SA BC ⊥，1SC =，2AC =，3BC =，则此三棱锥的外接球的表面积为()A ．14πB ．12πC ．10πD ．8π7．在三棱锥P ABC -中，PA ⊥平面ABC ，60,2BAC AB AC PA ∠=︒===，则三棱锥P ABC -的外接球的表面积为()A ．20πB ．24πC ．28πD ．32π8．三棱锥P ABC -中，PA ⊥平面ABC ，BC CA ⊥，1AC =，2BC =，2PA =，则该三棱锥外接球的表面积为()A ．9πB ．36πC ．92πD ．94π9．在三棱锥P ABC -中，PA ⊥平面ABC ，120BAC ∠=︒，2AC =，1AB =，设D 为BC 中点，且直线PD与平面ABC ，则该三棱锥外接球的表面积为．10．如图，在三棱锥P ABC -中，PA ⊥平面ABC ，120ABC ∠=︒，4PA =．若三棱锥P ABC -外接球的半径为PC 与平面ABC 所成角的正切值为．11．在四棱锥P ABCD -中，PA ⊥平面ABCD ，2AP =，点M 是矩形ABCD 内（含边界）的动点，且1AB =，3AD =，直线PM 与平面ABCD 所成的角为4π．记点M 的轨迹长度为α，则tan α=；当三棱锥P ABM-的体积最小时，三棱锥P ABM -的外接球的表面积为．12．已知三棱锥S ABC -中，SA ⊥平面ABC ，4SA AB ==，6BC =，AC =，则三棱锥S ABC -外接球的表面积为．13．已知四面体P ABC -中，4PA PB ==，2PC =，AC =PB ⊥平面PAC ，则四面体P ABC -外接球的表面积为．14．如图，在三棱锥P ABC -中，PA ⊥平面ABC ，4PA =，1cos 3ACB ∠=，若三棱锥P ABC -外接球的表面积为52π，则三棱锥P ABC -体积的最大值为．15．已知在三棱锥P ABC -中，PA ⊥平面ABC ，2AB AC PA ===，且在ABC ∆中，120BAC ∠=︒，则三棱锥P ABC -的外接球的体积为．16．矩形ABCD 中，4AB =，2BC =，PA ⊥平面ABCD ，2PA =，E ，F 分别是AB ，DC 的中点，则四棱锥P EBCF -的外接球表面积为17．在三棱锥P ABC -中，PA ⊥平面ABC ，2PA =，3AB AC ==，又3cos 5BAC ∠=-，则该三棱锥外接球的表面积为．18．中国古代数学经典<<九章算术>>中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖臑(bi ēnào )．若三棱锥P ABC -为鳖臑，且PA ⊥平面ABC ，2PA AB ==，又该鳖臑的外接球的表面积为24π，则该鳖臑的体积为．19．三棱锥P ABC -中，PA ⊥平面ABC ，2PA AC ==1AB =，60ABC ∠=︒，则三棱锥P ABC -的外接球的表面积为．20．我国古代数学名著《九章算术》中将底面为矩形且有一侧棱垂直于底面的四棱锥称为“阳马”，现有一“阳马”如图所示，PA ⊥平面ABCD ，4PA =，AB =，1AD =，则该“阳马”外接球的表面积为．第6讲侧棱相等模型一、解题技巧归纳总结1．侧棱相等模型：如图，P 的射影是A B C ∆的外心⇔三棱锥P A B C -的三条侧棱相等⇔三棱锥P A B C -的底面A B C ∆在圆锥的底上，顶点P 点也是圆锥的顶点.解题步骤：第一步：确定球心O 的位置，取A B C ∆的外心1O ，则1,,P O O 三点共线；第二步：先算出小圆1O 的半径1A O r =，再算出棱锥的高1P O h =(也是圆锥的高)；第三步：勾股定理：22211O A O A O O =+⇒222()R h R r =-+，解出222r h R h+=.2．正棱锥外接球半径：222r h R h+=.二、典型例题例1.已知四棱锥的-P A B C D 和的矩形，则该四棱锥外接球的表面积为（）A .π18B .π323C .π36D .π48例2.体积为的正三棱锥-A B C D 的每个顶点都在半径为R 的球O 的球面上，球心O 在此三棱锥内部，且=:2:3R B C ，点E 为B D 的中点，过点E 作球O 的截面，则所得截面圆面积的最小值是.例3.在三棱锥-P A B C 中，=P A P B ====4P C A C A B ，且⊥A C A B ，则该三棱锥外接球的表面积为________.例4.在三棱锥P A B C -中，P A P B P C ===，侧棱P A 与底面A B C 所成的角为60︒，则该三棱锥外接球的体积为（）A .πB .3πC .4πD .43π例5.如图，半径为2的半球内有一内接正六棱锥-P A B C D E F ，则此正六棱锥的侧面积是．三、玩转练习1．在三棱锥P ABC -中，2PA PB PC ===，且PA ，PB ，PC 两两互相垂直，则三棱锥P ABC -的外接球的体积为()A ．B ．C ．D ．2．在三棱锥P ABC -中，6PA PB PC ===，侧棱PA 与底面ABC 所成的角为60︒，则该三棱锥外接球的表面积为()A ．12πB ．24πC ．36πD ．48π3．在三棱锥P ABC -中，PA PB PC ===2AC AB ==，且AC AB ⊥，则该三棱锥外接球的表面积为()A ．4πB ．8πC ．16πD ．9π4．在三棱锥P ABCD -中，PA PB PC ===，4AC AB ==，且AC AB ⊥，则该三棱锥外接球的表面积为()A ．4πB ．36πC ．48πD ．24π5．在三棱锥P ABC -中，PA PB PC ===1AB AC ==，BC =则该三棱锥外接球的体积为()A ．43πB ．823C ．D ．323π6．正三棱锥P ABC -中，5PA =，23AB =，则该三棱锥外接球的体积为()A ．5003πB ．100πC ．25πD ．1256π7．已知体积为3的正三棱锥P ABC -的外接球的球心为O ，若满足0OA OB OC ++=，则此三棱锥外接球的半径是()A ．2B ．2C ．32D ．348．正三棱锥底面边长为3，侧棱与底面成60︒角，则正三棱锥的外接球的体积为()A ．4πB ．16πC ．163πD ．323π9．如图，在三棱锥S ABC -中，M 、N 分别是棱SC 、BC 的中点，且MN AM ⊥，若22AB =，则此正三棱锥外接球的体积是()A ．12πB ．43πC ．433πD ．123π10．已知正四棱锥P ABCD -中，2PA =，且所有的棱长相等，则该四棱锥的外接球的表面积为()A ．16πB ．12πC ．10πD ．8π11．已知正四棱锥O ABCD -中，底面边长为2，侧棱长为3，则该四棱锥外接球的表面积为()A ．92πB ．9πC ．4πD ．π12．如图所示，正方形ABCD 的边长为2，切去阴影部分围成一个正四棱锥，则当正四棱锥体积最大时，该正四棱锥外接球的表面积为()A ．5B ．5225πC ．16925πD ．338125π13．已知正四棱锥的侧棱与底面的边长都为()A ．163πB ．323πC ．16πD ．32π142，则其外接球的表面积为()A ．16πB ．36πC ．48πD ．64π15．已知ABC ∆是等腰直角三角形，斜边2AB =，P 是平面ABC 外的一点，且满足PA PB PC ==，120APB ∠=︒，则三棱锥P ABC -外接球的表面积为．16．在ABC ∆中，8AB =，6BC =，10AC =，P 为ABC ∆外一点，满足PA PB PC ===，则三棱锥P ABC -的外接球的半径为．17．如图，在四面体P ABC -中，4PA PB PC ===，点O 是点P 在平面ABC 上的投影，且2tan 2APO ∠=，则四面体P ABC -的外接球的体积为．18．在三棱锥P ABC -中，PA PB PC ===，8AB =，6AC =．顶点P 在平面ABC 内的射影为H ，若AH AB AC λμ=+且21μλ+=，则三棱锥P ABC -的外接球的体积为．19．．在三棱锥P ABC -中，PA PB PC ===，4AC AB ==，且AC AB ⊥，则该三棱锥外接球的表面积为．20．三棱锥P ABC -中，底面ABC ∆的等边三角形，PA PB PC ==，PB ⊥平面PAC ，则三棱锥P ABC -外接球的表面积为．21．在三棱锥P ABC -中，2PA PB PC ===，AB =BC =2APC π∠=，则三棱锥P ABC -的外接球的表面积为．22．在三棱锥P ABC -中，已知PA BC ⊥，PB AC ⊥，24PA PB PC AB ====，则三棱锥P ABC -外接球的表面积为．23．如图所示，已知四棱锥P ABCD -的底面ABCD 为正方形，且PA PB PC PD ====，AB =，则四棱锥P ABCD -外接球的体积为．24．已知三棱锥P ABC -中，ABC ∆为等边三角形，2PA PB PC ===，PA PB ⊥，则三棱锥P ABC -的外接球的体积为．25．已知三棱锥P ABC -中，PA PB PC ==，ABC ∆是边长为2等边三角形，侧棱与底面所成夹角的余弦，则该三棱锥外接球的表面积为．26．已知三棱锥P ABC -的顶点P 在平面ABC 内的射影为点H ，侧棱PA PB PC ==，点O 为三棱锥P ABC -的外接球O 的球心，8AB =，6AC =，已知AO AB AC λμ=++，且1λμ+=，则球O 的表面积为．27．已知ABC ∆是等腰直角三角形，斜边3AB =，P 是平面ABC 外的一点，且满足PA PB PC ==，120APB ∠=︒，则三棱锥P ABC -外接球的半径为；该球体积为．28．在正三棱锥S ABC -中，侧棱SC ⊥侧面SAB ，侧棱SC =则此正三棱锥的外接球的表面积为．29．在六棱锥P ABCDEF -的正六边形，2PA =且与底面垂直，则该六棱锥外接球的体积等于．30．已知正六棱锥S ABCDEF -，3AB =，5SA =，则该六棱锥的外接球的表面积为．第7讲侧棱为外接球直径模型一、解题技巧归纳总结方法：找球心，然后作底面的垂线，构造直角三角形.二、典型例题例1．已知三棱锥-S A B C 的所有顶点都在球O 的表面上，∆A B C 是边长为1的正三角形，SC 为球O 的直径，且=2SC ，则此三棱锥的体积为()A ．14B ．24C ．26D ．212例2．已知点A 是以BC 为直径的圆O 上异于B ，C 的动点，P 为平面ABC 外一点，且平面PBC ⊥平面ABC ，3BC =，22PB =，5PC =，则三棱锥P ABC -外接球的表面积为．例3．三棱锥A BCD -的外接球为球O ，球O 的直径是AD ，且ABC ∆、BCD ∆都是边长为1的等边三角形，则三棱锥A BCD -的体积是．三、玩转练习1．在三棱锥ABCD 中，BC CD ⊥，Rt BCD ∆斜边上的高为1，三棱锥ABCD 的外接球的直径是AB ，若该外接球的表面积为16π，则三棱锥ABCD 体积的最大值为()A ．13B ．23C ．1D ．432．已知三棱锥S ABC -外接球的直径6SC =，且3AB BC CA ===，则三棱锥S ABC -的体积为()A ．324B ．924C ．322D ．9223．已知三棱锥S ABC -的四个顶点均在某个球面上，SC 为该球的直径，ABC ∆是边长为4的等边三角形，三棱锥S ABC -的体积为163，则此三棱锥的外接球的表面积为()A ．683πB ．163πC ．643πD ．803π4．已知三棱锥S ABC -的体积为12，1AC BC ==，120ACB ∠=︒，若SC 是其外接球的直径，则球的表面积为()A ．4πB ．6πC ．8πD ．16π5．三棱锥A BCD -的外接球为球O ，球O 的直径是AD ，且ABC ∆，BCD ∆都是边长为1的等边三角形，则三棱锥A BCD -的体积是()A ．6B ．12C ．4D ．126．已知三棱锥S ABC -的外接球为球O ，SA 为球O 的直径，且2SA =，若面SAC ⊥面SAB ，则三棱锥S ABC -的体积最大值为()A ．13B ．23C ．1D ．27．三棱锥A BCD -的外接球为球O ，球O 的直径2AD =，且ABC ∆，BCD ∆都是等边三角形，则三棱锥A BCD -的体积是()A ．13B ．24C ．23D ．128．已知三棱锥P ABC -的外接球O ，PC 为球O 的直径，且2PC =，PA PB ==，1AB =，那么顶点P到平面ABC 的距离为()A B C D 9．已知三棱锥S ABC -外接球的直径6SC =，且3AB BC CA ===，则三棱锥S ABC -的体积为．10．在三棱锥A BCD -中，底面为Rt △，且BC CD ⊥，斜边BD 上的高为1，三棱锥A BCD -的外接球的直径是AB ，若该外接球的表面积为16π，则三棱锥A BCD -的体积的最大值为．11．已知三棱锥P ABC -的四个顶点均在某球面上，PC 为该球的直径，ABC ∆是边长为4的等边三角形，三棱锥P ABC -的体积为163，则该三棱锥的外接球的表面积．12．已知三棱锥S ABC -的四个顶点均在某个球面上，SC 为该球的直径，ABC ∆是边长为4的等边三角形，三棱锥S ABC -的体积为83，则此三棱锥的外接球的表面积为．第8讲共斜边拼接模型一、解题技巧归纳总结1．共斜边拼接模型如图，在四面体A B C D 中，⊥A B A D ，⊥C B C D ，此四面体可以看成是由两个共斜边的直角三角形拼接而形成的,B D 为公共的斜边,故以“共斜边拼接模型”命名之.设点O 为公共斜边B D 的中点,根据直角三角形斜边中线等于斜边的一半的结论可知，===O A O C O B O D ，即点O 到A ，B ，C ，D 四点的距离相等,故点O 就是四面体A B C D 外接球的球心,公共的斜边B D 就是外接球的一条直径.二、典型例题例1.在矩形A B C D 中，==4,3A B B C ，沿A C 将矩形A B C D 折成一个直二面角--B A C D ，则四面体A B C D 的外接球的体积为（）A .π12512B .π1259C .π1256D .π1253例2.三棱锥-P A B C 中，平面⊥P A C 平面A B C ，=2A C ，⊥P A P C ,⊥A B B C ，则三棱锥-P A B C 的外接球的半径为三、玩转练习1．在梯形ABCD 中，//AB CD ，AD AB ⊥，4AB =，2AD CD ==，将梯形ABCD 沿对角线AC 折叠成三棱锥D ABC -，当二面角D AC B --是直二面角时，三棱锥D ABC -的外接球的表面积为()A ．4πB ．8πC ．12πD ．16π2．将边长为的正方形ABCD 沿对角线AC 折成一个直二面角B AC D --．则四面体ABCD 的外接球的体积为()A ．12πB ．23πC ．πD ．43π3．在平行四边形ABCD 中，AB BD ⊥，22421AB BD +=，将此平行四边形沿BD 折成直二面角，则三棱锥A BCD -外接球的表面积为()A ．2πB ．πC ．2πD ．4π4．在平行四边形ABCD 中，满足2AB AD AB = ，2224AB BD =- ，若将其沿BD 折成直二面角A BD C --，则三棱锥A BCD -的外接球的表面积为()A ．16πB ．8πC ．4πD ．2π5．如图，在平面四边形ABCD 中，1AB AD CD ===，AB AD ⊥，BD CD ⊥．将该四边形沿对角线BD 折成一个直二面角A BD C --，则四面体ABCD 的外接球的体积为()A ．23πB ．32πC ．2πD ．3π6．矩形ABCD 中，6AB =，8BC =，沿AC 将矩形ABCD 折成一个直二面角B AC D --，则四面体ABCD 的外接球的表面积为()A ．5003πB ．1003πC ．100πD ．400π7．如图，在平行四边形ABCD 中，222||||40AB BD +-=，90ABD ∠=︒，沿BD 折成直二面角A BD C --，则三棱锥A BCD -的外接球的表面积是()A ．16πB ．8πC ．4πD ．2π8．如图所示，在平行四边形ABCD 中，220,4|2|1AB BD AB BD ⋅=+=且，沿BD 折成直二面角A BD C --，则三棱锥A BCD -的外接球的表面积是()A ．224B ．148πC ．4πD ．2π9．平行四边形ABCD 中，0AB BD =，沿BD 将四边形折起成直二面角A 一BD C -，且222||||4AB BD += ，则三棱锥A BCD -的外接球的表面积为()A ．2πB ．4πC ．4πD ．2π10．在平行四边形ABCD 中，0AB BD =，且22240AB BD +-= ，沿BD 折成直二面角A BD C --，则三棱锥A BCD -的外接球的表面积是()A ．16πB ．8πC ．4πD ．2π11．在矩形ABCD 中，4AB =，3BC =，沿AC 将矩形ABCD 折成一个直二面角B AC D --，则四面体ABCD 的外接球的体积为()A ．12512πB ．1259πC ．1256πD ．1253π12．在平行四边形ABCD 中，0AC CB =，22240BC AC +-= ，若将其沿AC 折成直二面角D AC B --，则三棱锥D ACB -的外接球的表面积为()A ．16πB ．8πC ．4πD ．2π13．如图，二面角l αβ--满足半平面αβ⊥，半平面α内有一点A （不在l 上），半平面β内有一点C （不在l 上），A ，C 在直线l 的射影分别为B ，(D B ，D 不重合），1AB CD ==，BD =则三棱锥A BCD -外接球的表面积为．14．已知等边三角形ABC 的边长为8，D 为BC 边的中点，沿AD 将ABC ∆折成直二面角B AD C --，则三棱锥A DCB -的外接球的表面积为15．如图是两个腰长均为10cm 的等腰直角三角形拼成的一个四边形ABCD ，现将四边形ABCD 沿BD 折成直二面角A BD C --，则三棱锥A BCD -的外接球的体积为3cm ．16．在矩形ABCD 中，已知4AB =，3BC =，将该矩形沿对角线AC 折成直二面角D AC B --，则四面体ABCD 的外接球的体积为．17．将长宽分别为3和4的长方形ABCD 沿对角线AC 折成直二面角，得到四面体A BCD -，则四面体A BCD -的外接球的表面积为18ABCD 沿对角线AC 折成一个直二面角B AC D --，则四面体ABCD 的外接球的体积为．19．在平行四边形ABCD 中，220,2||||6AB BD AB BD =+= ，若将ABD ∆沿BD 折成直二面角A BD C --，则三棱锥A BCD -外接球的表面积为．第9讲最值模型一、解题技巧归纳总结这类问题是综合性问题，方法较多，常见方法有：导数法，基本不等式法，观察法等二、典型例题例1.已知A ，B 是球O 的球面上两点，90A O B ∠=︒，C 为该球面上的动点，若三棱锥O A B C -体积的最大值为36，则球O 的表面积为()A ．36πB ．64πC ．144πD ．256π例2.已知三棱锥O A B C -的顶点A ，B ，C 都在半径为2的球面上，O 是球心，120A O B ∠=︒，当A O C ∆与B O C ∆的面积之和最大时，三棱锥O A B C -的体积为()A ．32B ．233C ．23D ．13例3.体积为183的正三棱锥-A B C D 的每个顶点都在半径为R 的球O 的球面上，球心O 在此三棱锥内部，且=:2:3R B C ，点E 为B D 的中点，过点E 作球O 的截面，则所得截面圆面积的最小值是.例4.已知底面为正三角形的三棱柱内接于半径为1的球，则三棱柱的体积的最大值为．例5.已知底面为正三角形的直三棱柱内接于半径为1的球，当三棱柱的体积最大时，三棱柱的高为．三、玩转练习1．如图，四边形ABCD 的面积为22，且90ABD BDC ∠=∠=︒，把BCD ∆绕BD 旋转，使点C 运动到P ，此时向量BA 与向量DP的夹角为90︒．则四面体ABDP 外接球表面积的最小值为()。

高考数学《复习纲要》之外接球问题(2)

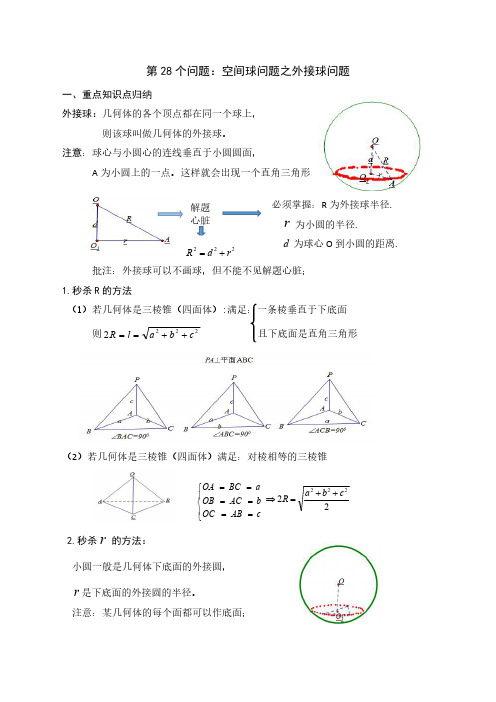
第28个问题：空间球问题之外接球问题一、重点知识点归纳外接球：几何体的各个顶点都在同一个球上，则该球叫做几何体的外接球。

注意：球心与小圆心的连线垂直于小圆圆面，A为小圆上的一点。

这样就会出现一个直角三角形：批注：外接球可以不画球，但不能不见解题心脏；1.秒杀R 的方法（2）若几何体是三棱锥（四面体）满足：对棱相等的三棱锥2.秒杀r的方法：小圆一般是几何体下底面的外接圆，r 是下底面的外接圆的半径。

注意：某几何体的每个面都可以作底面；解题心脏必须掌握：R 为外接球半径.r为小圆的半径.d 为球心O 到小圆的距离.222rd R +=（1）若这个面为直角三角形（2）若这个面为一般的三角形，则利用正弦定理。

（3）若这个面为矩形或者正方形（4）若这个面为正六边形3.秒杀d 的给法：题目中若出现“直棱柱”，则()111.2CC BB AA h hd =====侧棱长二、题型归纳题型1：秒杀方法+解题心脏例1.已知,,,S A B C 是球O 表面上的点，SA ABC ⊥平面，AB BC ⊥，1SA AB ==，BC =O 表面积等于（）A.4πB.3πC.2πD.π变式1.若三棱锥三个面两两垂直且面积分别为262322，，，则该三棱锥的外接球的体积为_____.外接圆的半径是斜边的一半。

外接圆半径是对角线的一半.正六边形的外接圆的半径等于正六边形的边长a变式2.在四面体ABCD 中,3,24======BC AD BD AC CD AB 则该四面体的外接球的体积________.变式3.设三棱柱的侧棱垂直于底面，所有棱长都为a ，顶点都在一个球面上，则该球的表面积为（）A.2a π B.273a πC.2113a π D.25aπ变式4.直三棱柱111C B A ABC -的六个顶点都在球O 的球面上，若,90,20=∠==ABC BC AB ，221=AA 则球O 的表面积为_________.题型2：顶点、球心、小圆圆心三点共线（针对椎体）解法归纳：(1).何时利用三点共线？①正棱锥（如正三棱锥,正四棱锥）②侧棱长相等的棱锥.③底面确定体积最大时（顶点无限制）(2)解题模型注意：一般建立两个方程⎩⎨⎧→=+→+=三点共线解题心脏h d R d r R 222解方程即可求出d （永远先解d ，若直接取正值；矛盾→<)(0d 11=⇒-=d d 则即若）例2.正四棱锥ABCD P -的5个顶点都在同一个球面上，若正四棱锥的底面边长为4，侧棱长为62，则此球的表面积为______.变式5.已知正三棱锥ABC P -的四个顶点均在球O 上，且,52===PC PB PA 32===AC BC AB 则球O 的表面积为（）A.π25 B.π6125 C.π25 D.π20变式6.在半径为2的球面上有不同的四个点A,B,C,D ，若2===AD AC AB ,则平面BCD 被球所截的图形的面积为__________.变式7.已知点A,B,C,D 均在球O 上，3==BC AB ，3=AC ，若三棱锥ABC D -体积的最大值为433，则球O 的表面积为（）π36.A B.π16 C.π12 D.316π类型3已知椎体的高或求高且球心不在高线上解法归纳：球心向高作“垂线”得到一个直角三角形+矩形关键问题：求l（1）若P 在下底面的投影落在下底面的顶点上，则r l =立马可以推出2hd =（2）若P 在下底面的投影不落在下底面的顶点上则；r l ≠（利用化立体为平面，只研究下底面即可来求l ）；例3.已知三棱锥ABC P -中，ABC ∆是边长为6的等边三角，ABC PA 平面⊥，且三棱锥外接球的表面积为π64，则.______=PA变式8.已知四棱锥ABCDP -的底面是正方形，223,2,==⊥∆PAB S AC ABCD PA 平面，则该四棱锥的外接球的表面积是_____.变式9.已知正方体1111D C B A ABCD -的棱长为1，点P 是线段11C A 上的动点，则三棱锥ABCD P -外接球半径R 的取值范围是________.类型4：已知某条棱是直径（SC 为直径）解法归纳：作一个球（只有这类题目）根据图象可得两个结论：①)(2到底面的距离为：S h h d =②得到两个垂直⎪⎩⎪⎨⎧=∠=∠09090SBC SAC （直径所对圆周角为90°）例4.已知三棱锥S ABC -的所有顶点都在球O 的球面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =；则此棱锥的体积为（）()A 6()B ()C ()D2变式10.已知球的直径SC =4，A ，B 是该球球面上的两点，AB =3，30=∠=∠BSC ASC ，则棱锥S —ABC 的体积为（）33.A B ．32C ．1.3D 变式11.已知三棱锥ABC S -的所有顶点都在球O 的球面上，SC 是球O 的直径，若平面SCA⊥平面SCB，SA=AC,SB=BC,三棱锥ABC S -的体积为9，则球O 的表面积为________.三、课下巩固（高考+模拟题）1.已知四面体ABC P -中，1,3,==⊥BC AC BC AC ，△PAB 是正三角形，且ABC PAB 平面平面⊥，则四面体ABC P -的外接球的半径为_______.2.在四面体ABC S -中，平面SAC ⊥平面ABC ，AB ⊥BC,AB=BC=2,0120=∠ASC ，则该四面体的外接球的表面积为______.。

空间几何体的外接球,小专题,复习

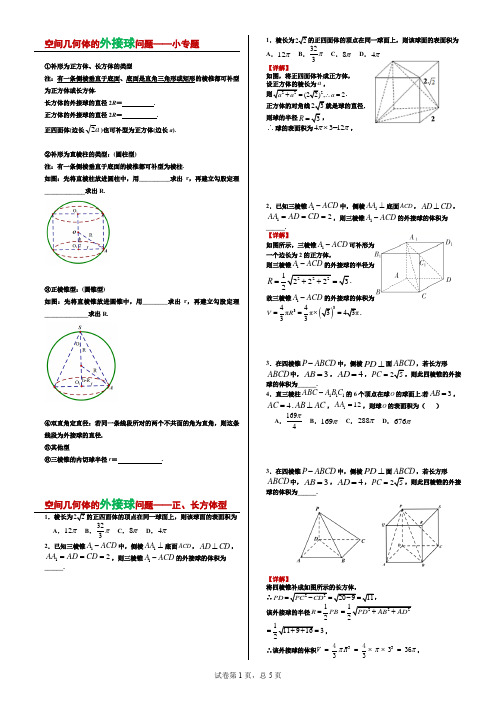
空间几何体的外接球问题——小专题①补形为正方体、长方体的类型注：有一条侧棱垂直于底面、底面是直角三角形或矩形的棱椎都可补型为正方体或长方体.长方体的外接球的直径2R ＝ . 正方体的外接球的直径2R ＝ . 正四面体(边长a 2)也可补型为正方体(边长a ).②补形为直棱柱的类型：(圆柱型)注：有一条侧棱垂直于底面的棱椎都可补型为棱柱.如图：先将直棱柱放进圆柱中，用__________求出r ，再建立勾股定理_____________求出R.③正棱锥型：(圆锥型)如图：先将直棱锥放进圆锥中，用________求出r ，再建立勾股定理______________求出R.④双直角定直径：若同一条线段所对的两个不共面的角为直角，则这条线段为外接球的直径. ⑤其他型⑥三棱锥的内切球半径r ＝ .1．棱长为22的正四面体的顶点在同一球面上，则该球面的表面积为 A ．12π B ．3π C ．8π D ．4π 2．已知三棱锥1A ACD -中，侧棱1AA ⊥底面ACD ，AD CD ⊥，12AA AD CD ===，则三棱锥1A ACD -的外接球的体积为______.1．棱长为22 A ．12π B ．323π C ．8π D ．4π 【详解】如图，将正四面体补成正方体，设正方体的棱长为a ， 222(22),2a a a +∴=. 正方体的对角线23则球的半径3R∴球的表面积为3=12π⨯，2．已知三棱锥1A ACD -中，侧棱1AA ⊥底面ACD ，AD CD ⊥，12AA AD CD ===，则三棱锥1A ACD -的外接球的体积为______. 【详解】如图所示，三棱锥1A ACD -可补形为一个边长为2的正方体，则三棱锥1A ACD -的外接球的半径为222122232R =++= 故三棱锥1A ACD -的外接球的体积为3344ππ343π33V R ==⨯=.3．在四棱锥P ABCD -中，侧棱PD ⊥面ABCD ，若长方形ABCD 中，3AB =，4=AD ，25PC =球的体积为______.4．直三棱柱111ABC A B C -的6个顶点在球O 的球面上.若3AB =，4AC =.AB AC ⊥，112AA =，则球O 的表面积为（）A ．1694πB ．169πC ．288πD ．676π3．在四棱锥P ABCD -中，侧棱PD ⊥面ABCD ，若长方形ABCD 中，3AB =，4=AD ，25PC =球的体积为______.【详解】将四棱锥补成如图所示的长方体， ∴2220911PD PC CD -- 该外接球的半径2R PB =22212PD AB AD ++11191632++， ∴该外接球的体积334433633VR πππ==⨯⨯=，4．直三棱柱111ABC A B C -的6个顶点在球O 的球面上.若3AB =，4AC =.AB AC ⊥，112AA =，则球O 的表面积为（）A ．1694πB ．169πC ．288πD ．676π 【详解】解：将直三棱柱补形为长方体1111ABEC A B E C -，所以体对角线1BC 的长为球O 的直径.因此球O 的外接圆直径为2222341213R ++，故球O 的表面积24169R ππ=.5．三棱柱111ABC A B C -中，1AA ⊥平面ABC ，90ABC ∠=︒，1AB =，3BC 12AA =其外接球的体积为_________. 6．在三棱锥S ABC -中，2AB =，2BC =，22AC =2SB =SB ⊥面ABC ，则三棱锥S ABC -的外接球半径为_______，三棱锥S ABC -的内切球半径为______.5．三棱柱111ABC A B C -中，1AA ⊥平面ABC ，90ABC ∠=︒，1AB =，3BC 12AA =其外接球的体积为_________.【详解】解：因为1AA ⊥平面ABC ，所以三棱柱111ABC A B C -为直三棱柱，90ABC ∠=︒，1AB =，3BC =12AA =，所以12BB =，则三棱柱的外接球即为以AB ，BC ，1BB 为一组邻边的长方体的外接球，设外接球的半径为R ，则()2222221212322R AB BC BB ++++=所以2R=34823V R π==，6．在三棱锥S ABC -中，2AB =，2BC=，22AC =2SB =SB ⊥面ABC ，则三棱锥S ABC -的外接球半径为_______，三棱锥S ABC -的内切球半径为______.【详解】∵222AB BC AC +=,∴AB BC ⊥，又∵SB ⊥面ABC ， ∴可以将三棱锥S ABC -放置在如图所示的长方体中，外接球的直径即为长方体的对角线. 设外接球的半径为R ，则()222222210R ++10R = 设内切球的球心为O ，半径为r ，则由S ABC O SAB O SAC O SBC O ABC V V V V V -----=+++得()42222r =解得42r -7．三棱椎S -ABC 的底面ABC 是等腰直角三角形，90ABC ∠=︒，且2SA SC AC ===3SB =S -ABC 外接球表面积为A ．2πB ．3π D ．6π 8．在三棱锥S ABC -中，5,17,SA BC SB AC ===，10SC AB == ）A ．20πB ．25πC ．26πD ．34π7．三棱椎S -ABC 的底面ABC 是等腰直角三角形，90ABC ∠=︒，且2SA SC AC ===3SB =S -ABC 外接球表面积为A ．2πB ．3π D ．6π 【详解】由题意知，可以把三棱锥S -ABC 按如图所示的位置放到棱长为1的正方体中，则正方体的体对角线长为3l ∴三棱椎S -ABC 外接球表面积为234π(3π=.8．在三棱锥S ABC -中，5,17,SA BC SB AC ===10SC AB == ）A ．20πB ．25πC ．26πD ．34π【详解】因为5,17,10SA BC SB AC SC AB ======所以可以将三棱锥S ABC -如图放置于一个长方体中，设长方体的长宽、高分别为a ，b ，c ，则有22222217,25,10,a b a c b c ⎧+=⎪+=⎨⎪+=⎩整理得22226a b c ++=，则该棱锥外接球的半径26R =S 球2426R ππ==．空间几何体的外接球问题——圆柱型1．直三棱柱ABC －111A B C 的六个顶点都在球O 的球面上．若AB ＝BC ＝2，∠ABC ＝90°，122AA ＝O 的表面积为________． 2．已知三棱锥S ABC -中，SC⊥平面ABC ，若2,120SC AB AC BAC ︒===∠=，则其外接球O 的表面积为A ．20πB 205πC ．16πD ．272π【详解】由已知，以AB ，BC ，1BB 为长，宽、高作长方体，该长方体的外接球经过直三棱柱ABC －111A B C 的六个顶点． ∵长方体的外接球直径2222221222(22)4R AB BC BB =++=++=，∴R ＝2，由此可得球的表面积2416.S R ππ＝＝故答案为16π【详解】在ABC 中，由余弦定理得2222cos 144222()122BC AB CA AB CA BAC=+-∠=+-⨯⨯⨯-= 解得23BC=，设ABC 的外接圆的半径为r ，则2324r ==，解得2r ，设外接球的半径为R ，由题得1CD =，所以222215R =+=．所以4520S ππ=⋅=球．3．如图，平面四边形ACBD 中，AB BC ⊥，3AB=，2BC =，ABD △为等边三角形，现将ABD △沿AB 翻折，使点D 移动至点P ，且PB BC ⊥，则三棱锥P ABC -的外接球的表面积为_____.4．如图，在等腰三角形ABC 中，已知3AB AC ==，2BC =.将它沿BC 边上的高AD 翻折，使B 点与C 点的距离为1，则四面体ABCD 的外接球的表面积为______.【详解】因为BC ⊥平面PAB ，将三棱锥P ABC -补形为如图所示的直三棱柱，ABP △为等边三角形，3AB =1r =．又122h BC ==，故在Rt OBE 中，222OB OE EB =+=，此即为外接球半径，从而外接球表面积为248S OB ππ=⨯=．【详解】由已知可得，翻折后1BCBD CD ===，即BCD 为等边三角形，其外接圆半径为222131332r DE ⎛⎫==-= ⎪⎝⎭，又AD DC ⊥，AD ，易得AD ⊥平面BCD ，222AD AC CD =-=，2223125236AD R ⎛⎫⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 因此25104463S R πππ==⨯=.5．已知A ，B ，C ，D 是同一球面上的四个点，120BAC ∠=︒，AB AC =，AD ⊥平面ABC ，6AD =，23AB =，则该球的表面积为______．6．在四面体ABCD 中，若1AD DC AC CB ====，则当四面体ABCD 的体积最大时，其外接球的表面积为______.【详解】由题意，设ABC 外接圆的半径为r ，120BAC ∠=︒，23AB AC ==，6BC ∴=，6243sin120r ==︒，23r =故()2222()233212AD R r =+=+=，该球的表面积为2484S R ππ==．【详解】因为1AD DC AC ===，所以底面ACD 面积为定值，因此当CB ⊥平面ACD 时，四面体ABCD 的体积最大.设ACD △外接圆半径为r ， 12sin 603r ==︒，3r =因此外接球的半径R 满足222137()()212R =+=,外接球的表面积为2743R ππ=空间几何体的问题——圆锥型1．已知扇形的面积为56π，圆心角为63π，则由该扇形围成的圆锥的外接球的表面积为_________． 2．正四棱锥V CD -AB 的五个顶点在同一个球面上，若其底面边长为4，侧棱长为26，则此球的表面积为（）A ．18πB ．36πC ．72πD ．9π【详解】设扇形的长为l ，半径为R ，则22111656222S lR R R παπ===⨯=，解得30R =，扇形弧长l 为锥底面周长2r π， ∴底面的半径5r=，∴圆锥的高为225R r -=．设外接球的半径为1R ，∴()222115(5)R R =-+，解得，13R =∴该外接球的表面积为21436R ππ=，【详解】试题分析：正方形CD AB 的对角线的交点M ，则球心在直线VM 上．122AM AC == 222484VM VA AM --，设球的半径为r ,则有()222r AM VM r =+-,即()2284r r =+-,解得3r =.∴此球的表面积为2436r ππ=．3．已知三棱锥M ABC -四个顶点均在表面积为32π的球面上，22AB BC ==4AC =，则三棱锥M ABC -体积的最大值A ．82 B ．442+ C 882+ D 1624．已知点A 、B 、C 、D 均在球O 上，3AB BC ==3AC =，若三棱锥D ABC -33O 的表面积为 A ．36π B ．16π C ．12π D ．163π【详解】设小圆的圆心为Q ，当MQ 与面ABC 垂直时，三棱锥M ABC -的体积最大，设球心为O ，半径为R ，2432R ππ=，得22R=O 到平面ABC ()222222-=，所以三棱锥MABC -体积的最大值为(188242223+⨯⨯+=【详解】试题分析：设的外接圆的半径为，，，，，，三棱锥的体积的最大值为，到平面的最大距离为，设球的半径为，则，，球的表面积为，故选B ．空间几何体的外接球问题——双直角定直径1．将长､宽分别为4和3的长方形ABCD 沿对角线AC 折起，得到四面体ABCD ，则四面体ABCD 的外接球的表面积为_____． 2．如图1所示，在直角梯形ABCD 中，AB AD ⊥，CD AD ⊥，222AB AD CD ===，将ABC ∆沿AC 折起到'ABD ∆的位置，得到图2 中的三棱锥'D ABC -，其中平面ABC ⊥平面'ACD ，则三棱锥'D ABC -的体积为_______, 其外接球的表面积为_______,3．如图所示，在平面四边形ABCD 中，AD CD ⊥，6AD CD = AC BC ⊥，o 60B ∠=，现将 ACD △沿AC 边折起，并连接BD ，当三棱锥D ABC -的体积最大时，其外接球的表面积为（） A ．4π B ．8π C ．12π D ．16π4．已知三棱锥P -ABC 中，AC =BC =22AB ，且 90=∠APB ，则三棱锥 P -ABC 的体积与三棱锥P -ABC 的外接球的体积之比的最大值为_______．空间几何体的外接球问题——其他型1．在三棱锥P ABC -中，平面PAB ⊥平面ABC ，ABC ∆是边长为237PA PB =A ．16πB ．654π C ．6516πD ．494π【详解】如图所示，取AB 中点D ，三角形的中心E 在CD 上，过点E 作平面ABC 垂线.在垂线上取一点O 为球心，因为PD AB ⊥，平面PAB ⊥平面,ABCPD ∴⊥平面ABC ，则//OE PD ，22,13CE CD DE CD CE ===-=，222PDPB BD ，设球的半径为r ,则有24OE r -作OG PD ⊥于G ，则OEDG 为矩形，222()PD DG OG PO -+=，即(2222241r r-+=,解得26516r=，故表面积为26544S r ππ==，故选B .外接球的表面积为（）A ．60πB ．40πC ．100πD ．80π【详解】如图，取BD 的中点设H ，PAHPBH ∴≅△△，， PH AH ∴⊥，又PH BD ⊥，AH BD H =，PH ∴⊥平面ABCD ，且6PH =.则外接球的半径R 满足()2222211146R OO OO O H =+=-+，设1OO x =，则()221664x x +=-+，解得2x =，从而222420R x =+=，故三棱锥P BCD -外接球的表面积为2480R ππ=.故选：D.。

2022高考数学二轮复习讲义：专题4 培优点15 空间几何体的外接球(学生版)

2022高考数学二轮复习讲义15 空间几何体的外接球【方法总结】空间几何体的外接球是高中数学的重难点．我们可以通过对几何体的割补或寻求几何体外接球的球心两大策略求解此类问题．【典例】1 半球内有一个内接正方体，则这个半球的体积与正方体的体积之比为( ) A.5π∶6 B.6π∶2 C ．π∶2 D ．5π∶12【典例】2 已知在三棱锥S －ABC 中，AB ⊥BC ，AB ＝BC ＝2，SA ＝SC ＝22，二面角B －AC －S 的大小为2π3，则三棱锥S －ABC 的外接球的表面积为( ) A.124π9 B.105π4 C.105π9 D.104π9 【典例】3 正四棱锥的顶点都在同一球面上．若该棱锥的高为4，底面边长为2，则该球的表面积为( )A.81π4 B ．16π C ．9π D.27π4 【拓展训练】1．已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( )A ．π B.3π4 C.π2 D.π42．在三棱锥P －ABC 中，△ABC 为等边三角形，PA ＝PB ＝PC ＝3，PA ⊥PB ，则三棱锥P －ABC 的外接球的体积为( )A.272π B.2732π C．273π D．27π3．已知三棱锥S－ABC的所有顶点都在球O的球面上，SC是球O的直径，若平面SCA⊥平面SCB，SA＝AC，SB＝BC，三棱锥S－ABC的体积为9，则球O的表面积为________．4．类比圆的内接四边形的概念，可得球的内接四面体的概念，已知球O的一个内接四面体A －BCD中，AB⊥BC，BD过球心O，若该四面体的体积为1，且AB＋BC＝2，则球O的表面积的最小值为________．。

搞定空间几何体的外接球复习进程

空间中的外接球进阶求法 讲义-2023届高三数学一轮复习

八个有趣模型——搞定空间几何体的外接球与内切球（教师版）复习过程

高中数学解题秘籍系列一篇文章攻克外接球

外接球复习课

(完整word版)搞定空间几何体的外接球(word文档良心出品)

高中数学解题指导八个无敌模型全搞定空间几何的外接球和内切球问题

几类空间几何体的外接球问题的解法

空间几何体的外接球,小专题,复习专用

2020高考数学复习之空间几何体外接球和内切球解题策略

2020高考数学复习之空间几何体外接球和内切球解题策略

考点27 空间几何体的外接球(解析版)

空间向量法解外接球问题汇总(精品)

空间几何体外接球13讲学生版_removed

高考数学《复习纲要》之外接球问题(2)

空间几何体的外接球,小专题,复习

2022高考数学二轮复习讲义：专题4 培优点15 空间几何体的外接球(学生版)

空间中的外接球进阶求法讲义-2023届高三数学一轮复习