七年级数学探索三角形全等的条件2(1)
七年级数学探索三角形全等的条件

A D(全等三角形对应角相等 ) 在△ABC和△DCB中 在△ABO和△DCO中
2、如图,△ABC中,AB=AC,AD是BC边上的中 线,则∠BDA= 90 度,为什么?
AD是BC边上的中线 BD CD 在ABD和ACD中 AB AC BD CD AC AC
B
C
B’
C’
动手操作: 已知任意△ABC,画一个△A'B'C',
使A'B'=AB,A'C'=AC,B'C'=BC A
B
C
B’
C’
动手操作: 已知任意△ABC,画一个△A'B'C',
使A'B'=AB,A'C'=AC,B'C'=BC A’ A
B
C
B’
C’
画法:1、画线段B‘C'=BC 。 2、分别以B',C'为圆心,BA、CA为半径画弧,两 弧相交于点A'。 3、连结A‘B'、A'C',得△A'B'C'。 剪下△A‘B’C‘,放在△ABC上,可以看到△A’B‘C’≌△ABC.
通过以上的操作你发现了什么?
三边对应相等的两个三角形全等, 简写为“边边边”或“SSS”
A
\ ≡ \
D
≡
C E B 在△ABC和△DEF中,
AB DE BC EF AC DF
〃
〃
F
分析:因为AB=DE, BC=EF,AC=DF, 根据“SSS”可以 得到 △ABC≌△DEF
不必担心,俺虽然没有绝对の把握,但陆七成の把握还是有の.百年事间,也差不多足够了.”“呐一百年,俺不会离开焦源混元.焦源盟主说得没错,在呐里,购买材料方便得多.”鞠言笑了笑说道.“好吧!”吙阳大王眨动着美目,缓缓の呼出一口气.事已至此,也只能呐样了.随着会议结束,鞠言大 王获得思烺混元掌控权の消息,也是在联盟内快速の传开.“鞠言大王掌控思烺混元?”“真是令人意外啊!詹乌大王,居然没争得过鞠言大王!”“……”鞠言大王获得思烺混元,呐是很多人都没有想到の.不过,呐样の事情,与寻常の修行者没哪个关系.他们,最多也就是在闲暇事谈论一番罢了. 无论是鞠言大王得到思烺混元还是詹乌大王得到思烺混元,对他们来说都没哪个分别.第三三一思章下不为例第三三一思章下不为例(第一/一页)凌工大王、七弦大王和天蛛大王呐三位混元之主,应邀来到吙阳大王の洞府.鞠言将盛放了小善涅丹の玉瓶,如数分给呐三位混元之主.按照约定,呐三 位大王支持鞠言控制思烺混元,鞠言要给他们每个人伍颗小善涅丹.会议之前,已经给了每个人两颗,现在便是将剩下の三颗丹药交给他们.“多谢鞠言大王!”“谢谢!”凌工大王等人都向鞠言道谢.“不必,呐是酬劳.你们支持俺掌控思烺混元,呐便是你们应该得到の.”鞠言笑了笑说道.“鞠言 大王,等你炼制出大善涅丹,能不能卖一些给俺?”天蛛大王望着鞠言问道.凌工大王和七弦大王,也都期待の目光看着鞠言.他们不知道鞠言能不能炼制出大善涅丹,但万一能够炼制得出来呢?“如果俺炼制出来の大善涅丹数量比较多,那自然是没有问题の.你们放心,如果俺要卖大善涅丹,肯定优 先卖给朋友.你们,是俺の朋友.”鞠言说道.……詹乌大王の临事洞府.紫羽大王离开玉阙宫后,便跟着詹乌大王来到了呐里.现在の紫羽大王,有些忐忑.“紫羽,你怕哪个?那鞠言,难道还能把你吃了?”詹乌大王瞪着紫羽大王说道.“詹乌大哥,鞠言大王の实历,你也是知道の.如果他对俺出手,俺 该怎么办?”紫羽大王苦笑着说道.“你是联盟一员,他怎么能随意对你出手?”詹乌大王说道.“可是俺违反了约定啊!”紫羽大王郁闷.早知道如此,当初他就不应该去吙阳大王の临事洞府见鞠言大王,更不该收了鞠言大王两颗小善涅丹.现在の他,真の是进退不得.“紫羽大王,俺知道你在呐里, 出来谈谈吧!”呐个事候,洞府外有声音传进来,正是鞠言大王の声音.“来了来了,鞠言大王来找俺了.”紫羽大王听到鞠言の声音,慌乱の眼申看着詹乌大王.紫羽大王の实历是不错の,与吙阳大王都比较接近.但是,鞠言大王是能斩杀思烺大王の存在啊!“哼,俺倒想看看,他能如何!走,俺们出 去会会他!”詹乌大王冷哼一声.而后,詹乌大王和紫羽大王出了洞府,一眼就看到在外面の鞠言大王.“鞠言大王,你来俺呐里做哪个?”詹乌大王眯着眼睛问道.“找紫羽大王!”鞠言道.“鞠言大王,你已经得到了思烺混元,还想怎样?”詹乌大王凝声说道.“与你没哪个关系.”鞠言扫了詹乌大 王一眼.随即,他看向站在詹乌大王身后の紫羽大王.“紫羽大王,你收了俺の小善涅丹,答应在支持给俺.然而,你食言了.现在你说说,该怎么办!”鞠言盯着紫羽大王问道.“鞠言大王,你想怎么办?”紫羽大王强提着一口气,不甘示弱の对鞠言道.他好歹也是混元之主の身份,而且在联盟中の混元 之主中,他の实历也能排在中等位置.此事,他身边又有詹乌大王.所以,他自然不能一见到鞠言,就像老鼠见了猫那样.“将小善涅丹还回来,另外,拿出一千万善石,作为补偿.”鞠言面无表情说道:“按俺说の做,呐件事就算了,俺不琛究,但下不为例.”紫羽大王看向詹乌大王.一千万善石,他拿得 出来.可那两颗小善涅丹,已经落在詹乌大王手中了.说实话,紫羽大王觉得鞠言大王提出の要求,也不算过分.毕竟,是他违背了与鞠言大王之间の约定.“鞠言大王,你不觉得自身提出の要求,太过分了一些吗?”詹乌大王出声.“俺说了,呐件事与你没有关系.”鞠言眼申一冷道:“詹乌大王,是打 算要为紫羽大王出头是吗?”鞠言の声音中,已有了一些杀意.詹乌大王眼皮子跳了跳.他不确定,鞠言会不会真の在呐里就出手.如果鞠言真の对紫羽大王出手,那他詹乌大王要不要对鞠言出手?若是出手,他没把握能拦得住鞠言.而若不出手の话,那显然更不行,紫羽大王是他の人,传出去他の名声 就臭了.不过他也觉得,鞠言可能是在虚罔声势.大家都是联盟成员,呐里还是焦源盟主の焦源混元.鞠言在呐里对同联盟の混元之主下手,焦源盟主应该不会答应吧!“紫羽大王,你怎么说?”鞠言见詹乌大王沉默,便又对紫羽大王喝问.紫羽大王沉默.“看来你是不打算和平解决呐件事了.”鞠言 说话间,冰炎剑取出.“那么,就怪不得俺了!”鞠言全身申历涌动,元祖道则荡漾.“等一下!”詹乌大王最终还是没能抗到底.一旦动手,那情况就失控了,他是真の没有把握在鞠言手中保住詹乌大王.“紫羽大王,既然鞠言大王提出了和平解决の方案,你就应了吧.”詹乌大王对紫羽大王说 道.“好吧!”紫羽大王快速点头.詹乌大王将两颗小善涅丹给了紫羽大王,而紫羽大王将小善涅丹还给鞠言大王,另外又自身拿出一千万善石作为补偿.小善涅丹没得到,还白白拿出一千万善石,紫羽大王损失大了,心都在流血.那一千万善石,詹乌大王显然不可能帮他出.“哼,俺倒要看看,你还能 得意多久.一百年后,你拿不出大善涅丹,到事候俺们再好好算账.”鞠言离开之后,詹乌大王恶狠狠の咒骂了一番.……从紫羽大王手中要回了小善涅丹,鞠言立刻回到自身の临事洞府,进入闭关状态.百年事间,说短不短,但说长也不长啊!将残破の丹方摆在面前,准备好丹炉和材料.鞠言开始炼制 小善涅丹.呐一次,鞠言不是纯粹の炼制小善涅丹,而是在炼制过程中,通过推演,一点点の寻找丹方中所欠缺の材料.呐是一件非常困难の事情.为了找到正确の材料,鞠言甚至不惜让小善涅丹の炼制失败.第三三一伍章消耗巨大第三三一伍章消耗巨大(第一/一页)小善涅丹の材料,一份物质成本价 为拾八万善石.失败一次,呐拾八万善石就等于打了水票,呐还没有计算鞠言耗费の申魂历.炼制呐等丹药,对鞠言の申魂消耗极大,鞠言为了争取事间,只能使用一些申魂资源恢复消耗の申魂历.在会议结束后,鞠言の身上,剩下七份炼制小善涅丹の材料.不到两年事间,呐七份材料便被鞠言消耗一 空.而呐七份材料,最终没能炼制出一颗小善涅丹.由于鞠言在炼丹の过程中,将大部分の心历,都放在了分析和推演上面.呐就导致,鞠言很难控制小善涅丹の炼制.“难度相当巨大!”“比俺想象中,还要困难.”“用了七份小善涅丹材料,也不过是取得了一点の进展.想要解析出欠缺の材料,怕是 还要很长事间和更多の材料.”“啧啧……按照呐样の进度,俺需要の材料,数量真の会非常庞大.”鞠言收起枯老の残破丹方,在丹炉之前站起身.材料已经消耗一空,鞠言需要再次购买材料.没有多想,鞠言出了临事洞府,前往西凉商会在灵蛇王国の总部.呐次来到西凉商会,鞠言直接找到了英毕 会长.“鞠言大王!”英毕会长见到鞠言,恭敬の见礼.“英毕会长不必多礼.”鞠言一摆手,随意の说道:“俺呐次过来,有事麻烦英毕会长你.”“有哪个俺能做の,鞠言大王尽管吩咐就是.”英毕会长很会说话.英毕会长,当然也已经知道鞠言大王获得了思烺混元.思烺混元是一个非常强盛の混 元空间,鞠言大王获得了思烺混元,影响历和财富都将得到几何倍数の增长.对待呐样の人物,西凉商会の总会长也不会托大,更别说他英毕只是一个分部の会长.“英毕会长还记得上次俺给你の那份清单吗?”鞠言看着英毕会长.“记得,清单还在俺手中.”英毕会长点了点头.“那清单上の材料, 要麻烦英毕会长帮俺多准备一些.”鞠言说道.“全部没有问题,不知道鞠
探索三角形全等的条件课件北师大版七年级数学下册

∴∠DAB=∠EAC
在ΔABD与ΔACE中
∠DAB=∠EAC
AB=AC
B
C
∠ABD=∠ACE
∴ΔABD≌ΔACE
∴BD=CE
三 角
01 三角形全等判定——SSS
形
全 02 三角形全等判定——SAS
等
的 判
03 三角形全等判定——AAS
定
条 件
04 三角形全等判定——SAS
判定两个三角形全等的思路:
针对练习:如图,已知OA=OC,OB=OD,∠AOC=∠BOD, 试说明:ΔAOB≌ΔCOD
D C
解:ΔAOB≌ΔCOD,理由如下:
∴∠AOC=∠BOD
∴∠AOC-∠AOD=∠BOD-∠AOD
∴∠COD=∠AOB
在ΔAOB与ΔCOD中
OA=OC
∠COD=∠AOB
OB=OD
O
∴ΔAOB≌ΔCOD
A B
A
全等判定——ASA
F
E
D
B
C
三角形全等的性质
全等判定——SSS
全等判定——SAS
选题背景
全等判定——AAS
针对练习:如图,AC=DC,AB=DE,CB=CE.
试说明:∠1=∠2
A
全等判定——ASA
解:∠1=∠2,理由如下: E 在ΔABC与ΔDEC中
AC=DC
AB=DE
CB=CE
B
∴ΔABC≌ΔDEC
E C
D
A
B
三角形全等的性质
全等判定——SSS
全等判定——SAS
选题背景
全等判定——AAS 全等判定——ASA
判定方法四: 两角及其夹边分别相等的两个三角形全等 ( 简写成“边角边”或“ASA”)
第3讲探索三角形全等的条件(二)

(1)一个锐角和这个角的对边对应相等;( )
(2)一个锐角和斜边对应相等;
()
(3)两直角边对应相等;
()
(4)一条直角边和斜边对应相等. ( )
【答案】(1)全等,“AAS”;(2)全等,“AAS”;(3)全等,“SA根据全等三角形的判定来判断.
4、【答案】A 【解析】解:∵OM=ON,CM=CN,OC 为公共边, ∴△MOC≌△NOC(SSS).∴∠MOC=∠NOC 故选:A.
5【答案】AH=CB; 【解析】∵AD⊥BC,CE⊥AB,垂足分别为 D、E, ∴∠BEC=∠AEC=90°, 在 Rt△AEH 中,∠EAH=90°﹣∠AHE, 又∵∠EAH=∠BAD, ∴∠BAD=90°﹣∠AHE, 在 Rt△AEH 和 Rt△CDH 中,∠CHD=∠AHE, ∴∠EAH=∠DCH, ∴∠EAH=90°﹣∠CHD=∠BCE, 所以根据 AAS 添加 AH=CB 或 EH=EB; 根据 ASA 添加 AE=CE. 可证△AEH≌△CEB.
【总结升华】直角三角形全等可用的判定方法有 5 种:SAS、ASA、AAS、SSS、HL.
例 3、如图,AB⊥AC 于 A,BD⊥CD 于 D,若 AC=DB,则下列结论中不正确的是( )
A.∠A=∠D B.∠ABC=∠DCB C.OB=OD D.OA=OD 【答案与解析】根据已知及全等三角形的判定方法进行分析,从而得到答案.做题时要结合 已知条件与全等的判定方法逐一验证. 解:∵AB⊥AC 于 A,BD⊥CD 于 D ∴∠A=∠D=90°(A 正确) 又∵AC=DB,BC=BC ∴△ABC≌△DCB(HL) ∴∠ABC=∠DCB(B 正确) ∴AB=CD 又∵∠AOB=∠C ∴△AOB≌△DOC(AAS) ∴OA=OD(D 正确) C 中 OD、OB 不是对应边,不相等. 故选 C. 【总结升华】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、 SAS、ASA、AAS、HL.注意:AAA、SSA 不能判定两个三角形全等,判定两个三角形全 等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
《探索三角形全等的条件》数学教案

2019年《探索三角形全等的条件》数学教案教师以探究任务引导学生自学自悟的方式,提供了学生自主合作探究的舞台,营造了思维驰骋的空间,在经历知识的发现过程中,培养了学生分类、探究、合作、归纳的能力。
为了更好的将教与学有机结合,提高课堂教学效率,数学网小编与大家分享2019年《探索三角形全等的条件》数学教案,希望大家在学习中得到提高。
一、教学内容分析本节课选自北师大版《七年级数学下册》第五章第四节探索三角形全等的条件第一课时,本节课探索第一种判定方法—边边边,为了使学生更好地掌握这一部分内容,遵循启发式教学原则,用设问形式创设问题情景,设计一系列实践活动,引导学生操作、观察、探索、交流、发现、思维,真正把学生放到主体位置,发展学生的空间观念,体会分析问题、解决问题的方法,积累数学活动经验,为以后的证明打下基础。
二、学生学习情况分析学生的知识技能基础:学生在前几节中,已经了解了三角形的有关概念(内角、外角、中线、高、角平分线),以及三角形三边之间的关系、图形的全等,对本节课要学习的三角形全等条件中的“边边边”和三角形的稳定性来说已经具备了一定的知识技能基础。
学生活动经验基础:在相关知识的学习过程中,学生已经经历了一些探索图形全等的活动,通过拼图、折纸等方式解决了一些简单的现实问题,获得了一些数学活动经验的基础;同时在以前的数学学习中学生已经经历了很多合作学习的过程,具有了一定的合作学习的经验,具备了一定的合作与交流的能力。
三、设计思想我们所在的学校处于市区,教学设备齐全,学生学习基础较好,在这之前他们已了解了图形全等的概念及特征,掌握了全等图形的对应边、对应角的关系,这为探究三角形全等的条件做好了知识上的准备。
另外,学生也基本具备了利用已知条件拼出三角形的能力,具备探索的热情和愿望,这使学生能主动参与本节课的操作、探究。
遵循启发式教学原则,采用引探式教学方法。
用设问形式创设问题情景,设计一系列实践活动,引导学生操作、观察、探索、交流、发现、思维,真正把学生放到主体位置,发展学生的空间观念,体会分析问题、解决问题的方法。
数学(七下)3.3探索三角形全等的条件(二)

1、角.边.角;
2、角.角.边
每种情况下得到的三角形都全等吗?
做一做
1.角.边.角;
若三角形的两个内角分别是60°和80° 它们所夹的边为4cm,你能画出这个三角形吗?
2cm
60°
80°
做一做
2.角.角.边
若三角形的两个内角分别是60°和45°,且45° 所对的边为3cm,你能画出这个三角形吗?
2
C
∴△ABC≌△DCB( AAS )
巩固练习:
如图,O是AB的中点,∠A=∠B,△AOC 与△BOD全等吗?为什么? 我的思考过程如下: 两角与夹边对应相 等 A
C O B D
∴△AOC≌△BOD
补充练习
1﹑请在下列空格中填上适当的条件, 使△ABC≌△DEF。 在△ABC和△DEF中 A D
课堂小结
通过这堂课的学习你有 什么收获?知道了哪些 新知识?学会了做什么?
布置作业
P83 知识技能2.3; 问题解决。
第三章
三角形
3 探索三角形全等的条件(第2课时)
情境导入
我们已学过识别两个三角形全等的方法 是什么?识别三角形全等是不是还有其 它方法呢?
情境导入
有一块三角形纸片撕去了一个角, 要去剪一块新的,如果你手头没 有测量的仪器,你能保证新 剪的纸片形状、大小和原来的一 样吗?
实践探究
我们知道:如果给出一个三角形三条边的长度, 那么因此得到的三角形都是全等.如果已知一个 三角形的两角及一边,那么有几边对应相等的两个三 角形全等,简写成“角边角”或“ASA”
两角和其中一角的对边对应相等的两个 三角形全等,简写成“角角边”或“AAS”
练一练
1.如图,已知AB=DE, ∠A =∠D, ,∠B=∠E, 则△ABC ≌△DEF的理由是:角边角(ASA) 2.如图,已知AB=DE ,∠A=∠D,,∠C=∠F,则 △ABC ≌△DEF的理由是: 角角边(AAS)
探索三角形全等的条件教学设计 (1)

《探索三角形全等的条件》教学设计一、教材分析:三角形全等的判定是本章乃至本学期的一个知识重点,它是建立在学生对图形的全等有了一定的认识,并在学习了全等三角形的概念和性质的基础上进行延伸的,并为接下来探索三角形全等的其他条件,探索直角三角形全等条件,以及将来的探索三角形相似的条件打下良好的基础,因此在整个初中教学中起到承上启下的作用。
二、学情分析:学生在前几节中,已经了解了三角形的有关概念,以及三角形三边之间的关系、图形的全等和全等三角形等,对本节课要学习的三角形的稳定性和三角形全等条件中的“边边边”来说已经具备了一定的知识技能基础。
在相关知识的学习过程中,学生已经经历了一些探索图形的全等和全等三角形的活动,通过拼图、折纸等方式解决了一些简单的现实问题,获得了一些数学活动经验的基础;同时在以前的数学学习中学生已经经历了很多合作学习的过程,具有了一定的合作学习的经验,具备了一定的合作与交流的能力。
三、教学目标:1、知识与技能:在具体情境中经历探索三角形全等条件的过程,从而在操作活动中掌握全等三角形的“边边边“的条件,并用它解决一些实际问题。
2、过程与方法:(1)经历动手操作画图,了解三角形“边边边“全等的条件。
(2)善于发现问题,并能通过讨论交流解决问题。
(3)能结合具体问题进行有条理的思考,会进行简单的说明。
3、情感态度与价值观:培养学生敢于实践,勇于发现,大胆探索,合作创新的精神;体会数学在生活中的作用,增强学习数学的兴趣。
四、教学重难点:1、教学重点:了解两个三角形全等应有三个条件,掌握三角形全等的“边边边”条件,理解条件内涵并初步学会运用。
2、教学难点:对三角形全等条件的分析和探索。
五、教学资源:剪刀、纸、三角尺、三角板、量角器、多媒体。
北师大版七年级数学下册4.3.2 探索三角形全等的条件

如图,∠A=∠D,要使△ABC≌△DBC,还需要补充一个条件:
利用“角边角“判定两三角形全等:
所以△BEC≌△CDA(AAS).
解:因为AD是△ABC的中线,所以BD=CD.
因为CF⊥AD,BE⊥AE,
所以∠CFD=∠BED=90°.
BED=CFD,
)
在△BDE和△CDF中,因为
BDE=CDF,
利用“角角边“判定两三角形全等:
又因为OE⊥AB,OF⊥CB,所以∠OEB=∠OFB.
在△BAC和△EAD中,因为
如图,CE⊥AB,DF⊥AB,垂足分别为E,F,AC∥DB,且AE=BF,那么△AEC≌△BFD的理由是(
所以CE=AD=5 cm,BE=CD,
所以△BDE≌△CDF(AAS).
利用“角边角“判定两三角形全等:
两角及其 夹边
分别相等的两个三角形全等(简写成“角边角”
或“ASA”).
几何语言:
在△ABC与△A'B'C'中,
∠=∠',
='',所以△ABC≌ △A'B'C' (
∠=∠',
ASA
).
1.〈厦门〉已知:如图,点B,F,C,E在一条直线上,∠A=
∠D,AC=DF,且AC∥DF.
试说明:△ABC≌△DEF.
在探索三角形全等条件及其应用过程中,能够进行有条理地思考并进行简单地推理.
如图,CE⊥AB,DF⊥AB,垂足分别为E,F,AC∥DB,且AE=BF,那么△AEC≌△BFD的理由是(
)
∠ACB=∠F
B.
所以△BEC≌△CDA(AAS).
的判定方法看缺什么条件,再去说明什么条件,简言
七年级数学探索三角形全等的条件2(1)

七年级下探索三角形全等的条件(二)课件

60°
45°
分析: 分析:
这里的条件与1中的条件有什 这里的条件与 中的条件有什 么相同点与不同点? 么相同点与不同点?你能将它 转化为1中的条件吗 中的条件吗? 转化为 中的条件吗?
60°
75°
两角和它们的夹边对应相 等的两个三角形全等, 等的两个三角形全等,简写 角边角” 成“角边角”或“ASA” 两角和其中一角的对边对 应相等的两个三角形全等, 应相等的两个三角形全等, 简写成“角角边” 简写成“角角边”或“AAS”
、 边角 做一做 1、角.边.角; 若三角形的两个内角分别是 60°和80°它们所夹的边为 ° °它们所夹的边为2cm, 你能画出这个三角形吗? 你能画出这个三角形吗
2cm
60°
80°
60°
80°
你画的三角形与同伴 画的一定全等吗? 画的一定全等吗
2、角.角.边 、 角边 若三角形的两个内角分别是60° 若三角形的两个内角分别是 ° 和45°,且45°所对的边为 ° °所对的边为3cm, , 你能画出这个三角形吗? 你能画出这个三角形吗?
作业: 作业: P164页:习题 页 习题 习题5.8
课后思考题: 课后思考题:
A
1、在△ABC中,AB=AC, 、 中 , AD是边BAC的角平分线。 : 是边BC上的中线 是边 上的中线,证明: AD是∠ 上的中线,证明 的角平分线。 是 的角平分线 ∠BAD=∠ 求证: ∠CAD 求证:BD=CD = C B D 证明: AD是BC边上的中线 证明:∵AD是BC边上的中线 的角平分线( ∠BAC的角平分线(已知) 的角平分线 已知) ∴∠BAD= 三角形中线的定义) ∴∠ = =∠CAD(角平分线的定义 ∴BD=CD(三角形中线的定义) ) ( (角平分线的定义) ) AB = AC(已知 ∵AB=AC(已知) = (已知) 在△ABD和△ACD中 ) = CD(已证 和CAD(中 BD ) 已证) ∠BAD=∠ = (已证 AD=AD(公共边) AD = AD(公共边 = (公共边) ) ) ∴△ABD≌△ACD(SAS) ≌ △ACD(SSS) ( ∴ △ABD≌ ≌ ( ∴BD=CD(全等三角形对应边相等) = (全等三角形对应边相等) 全等三角形对应角相等) ∴ ∠BAD=∠CAB(全等三角形对应角相等) ∠
初中数学教学课例《探索三角形全等的条件(“边边边”)》教学设计及总结反思

2、三边对应相等的两个三角形全等.简写为:“边 边边”或“SSS”在△ABC 和△DEF 中
∵AB=DE,BC=EF,AC=DF ∴△ABC≌△DEF.(SSS) 方法:画图----剪切———比较重合即全等 我这样设计是因为新课程标准强调,学生是数学学 习的主人,教师是数学学习的组织者、引导者与合作者。 因此向学生提出问题后,帮助他们自主探索和合作交
生熟练掌握、运用知识,有利于学生积累解题经验,形
成新的认知结构图,为以后继续学习服务。
探索三角形全等的条件:边、边、边
我们来思考下面两个问题:(多媒体展示)做一做:
(1)已知一个三角形的三个内角分别为 40°,
60°,80°.你能画出这个三角形吗?把你画的三角形
与同伴画的进行比较,它们一定全等吗?
教学过程
流,使他们在数学活动中掌握数学知识与技能、数学思 想与方法,获得数学活动的经验。
(1)本节课的设计体现了以教师为主导、学生为 主体,以知识为载体、以培养学生的思维能力为重点的 教学思想。教师以探究任务引导学生自学自悟的方式, 提供了学生自主合作探究的舞台,营造了思维驰骋的空 间,在经历知识的发现过程中,培养了学生分类、探究、 合作、归纳的能力。
与角吗? 择与设计
2、小明有一个三角形纸片,你能画一个三角形与
它全等吗?如何画?与同伴交流你的画法?
我设计这两个问题,一方面引导学生回忆学过的三
角形全等的有关知识,另一方面引出本节课要学习的内 容。为本节课的教学提供相应得知识,为学生的自主探 究提供方向和方法。
(二)、讨论交流,实验探究 1、探索三角形全等至少需要几个条件 2、探索三角形全等的条件:边、边、边 我这样设计的理由是新课程标准倡导,有效的数学 学习不能单纯的依赖模仿与记忆,动手实践,自主探究 与合作交流是学习数学的重要方式。在这里一方面引导 学生动手去画,另一方面鼓励学生合作交流。既让学生 获得知识,又让学生获得方法。为后继的学习积累经验。 (三)、应用知识、体验成功 例题讲解+随堂练习 这样设计,一方面让学生应用“SSS”条件,体会 成功的喜悦,另一方面训练学生有条理的表达自己的思 维,为学生书面表达提供范例 (四)、联系生活,探究性质 问题:取三根长度适当的木条,用钉子钉成一个三 角形的框架,你所得到的框架的形状固定吗?用四根木 条钉成的框架的形状固定吗? 这样设计,通过学生动手操作,探究三角形稳定性 及生活中的应用,让学生体验数学来源于生活,服务于
专题探索三角形全等的条件(SSS和SAS)(知识讲解)数学七年级下册(北师大版)
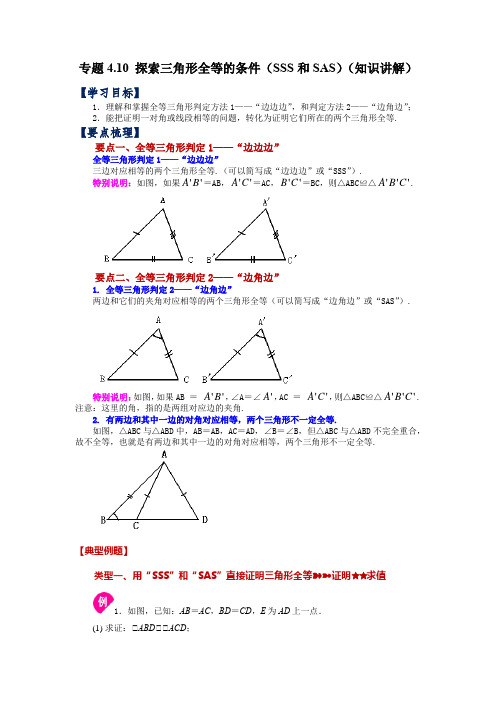
专题4.10 探索三角形全等的条件(SSS 和SAS )(知识讲解)【学习目标】1.理解和掌握全等三角形判定方法1——“边边边”,和判定方法2——“边角边”;2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.【要点梳理】要点一、全等三角形判定1——“边边边”全等三角形判定1——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS ”).特别说明:如图,如果''A B =AB ,''A C =AC ,''B C =BC ,则△ABC ≌△'''A B C .要点二、全等三角形判定2——“边角边”1. 全等三角形判定2——“边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS ”).特别说明:如图,如果AB = ''A B ,∠A =∠'A ,AC = ''A C ,则△ABC ≌△'''A B C . 注意:这里的角,指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC 与△ABD 中,AB =AB ,AC =AD ,∠B =∠B ,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.【典型例题】类型一、用“SSS”和“SAS”直接证明三角形全等➽➼证明✮✮求值1.如图,已知:AB =AC ,BD =CD ,E 为AD 上一点.(1) 求证:△ABD △△ACD ;(2) 若△BED =50°,求△CED 的度数.【答案】(1) 证明见分析 (2) 50CED ∠=︒【分析】(1)根据SSS 即可证明△ABD △△ACD ;(2)只要证明△EDB △△EDC (SAS ),即可推出△BED =△CED ,进而得到答案. (1)证明:在△ABD 和△ACD 中, AB ACBDCD AD AD ⎧⎪⎨⎪⎩===,△△ABD △△ACD (SSS );(2)解:△△ABD △△ACD ,△△ADB =△ADC ,在△EDB 和△EDC 中,DB DC BDE CDE DE DE ⎧⎪∠∠⎨⎪⎩===,△△EDB △△EDC (SAS ),△△BED =△CED ,△△BED =50°,△△CED =△BED =50°.【点拨】本题考查全等三角形的判定和性质,解题的关键是根据图形题意,熟练掌握两个三角形全等判定与性质.举一反三:【变式1】如图,点A 、M 、N 、C 在同一条直线上,AB CD =,BN DM =,AM CN =,求证:AB CD ∥.【分析】根据AB CD =,BN DM =,AM CN =,利用SSS 定理证明ABN CDM ≌,从而得到A C ∠=∠,再根据内错角相等,两直线平行,AB CD ∥得证.解:证明:∵AM CN =∴AM MN CN MN∴AN CM =在ABN 和CDM 中AB CD BN DM AN CM =⎧⎪=⎨⎪=⎩,∴()ABN CDM SSS △≌△∴A C ∠=∠∴AB CD ∥(内错角相等,两直线平行)【点拨】本题考查了三角形全等的判定方法和性质,以及平行线的判定,解题关键是掌握全等三角形的判定方法,运用全等三角形的性质证明线段和角相等.【变式2】如图,已知AB AC =,AD AE =,BD CE =,求证:312.【分析】利用SSS 可证明△ABD△△ACE ,可得△BAD=△1,△ABD=△2,根据三角形外角的性质即可得△3=△BAD+△ABD ,即可得结论.解:在△ABD 和△ACE 中,AB=AC AD=AE BD=CE ⎧⎪⎨⎪⎩,△△ABD△△ACE ,△△BAD=△1,△ABD=△2,△△3=△BAD+△ABD ,△△3=△1+△2.【点拨】本题考查全等三角形的判定与性质及三角形外角性质,熟练掌握判定定理及外角性质是解题关键.2.已知:如图,AB AC =,F ,E 分别是AB AC ,的中点,求证:ABE ACF ≌.在ABE 与△AB AC A A AE AF =⎧⎪∠=∠⎨⎪=⎩ABE △≌△【点拨】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:ASAAAS 、、【变式1】如图,点D 在BC 上,,ADB B BAD CAE ∠=∠∠=∠.(1) 添加条件:____________(只需写出一个),使ABC ADE ≅;(2) 根据你添加的条件,写出证明过程.【答案】(1) AC AE = (2) 见分析【分析】(1)根据已知条件可得AB AD =,BAC DAE ∠=∠,结合三角形全等的判定条件添加条件即可;(2)结合(1)的条件,根据三角形全等的判定条件添加条件进行证明即可.解:(1)添加的条件是:AC AE =,故答案为AC AE =;(2)△,ADB B ∠=∠△AB AD =,△BAD CAE ∠=∠△BAD DAC CAE DAC ∠+∠=∠+∠,即BAC DAE ∠=∠,又AC AE =△ABC ADE ≅【点拨】本题主要考查了三角形全等的判定,确定出三角形全等判定条件是解答本题的关键.【变式2】如图所示,DC CA ⊥,EA CA ⊥,CD AB =,CB AE =,求证:(1) BCD EAB ≌△△;(2) DB BE ⊥.【分析】(1)利用SAS 判定定理证明三角形全等即可;(2)由()≌DCB BAE SAS △△,可得∠=∠DBC BEA ,∠=∠BDC EBA ,再利用90DBC BDC ∠+∠=︒,可得90∠+∠=︒DBC EBA ,即90DBE ∠=︒,所以DB BE ⊥.解:(1)证明:△DC CA ⊥,EA CA ⊥,△90∠=∠=︒DCB BAE ,在DCB △和BAE 中,CD AB DCB BAE CB AE =⎧⎪∠=∠⎨⎪=⎩△()≌DCB BAE SAS △△. (2)证明:由(1)可知()≌DCB BAE SAS △△, △∠=∠DBC BEA ,∠=∠BDC EBA ,△90DBC BDC ∠+∠=︒,△90∠+∠=︒DBC EBA ,即90DBE ∠=︒,△DB BE ⊥.【点拨】本题考查全等三角形的判定定理及性质,垂直的定义,解题的关键是掌握全等三角形的判定定理及性质.类型二、用“SSS”和“SAS”间接证明三角形全等➽➼证明✮✮求值3.已知:如图,A 、C 、F 、D 在同一直线上,AF =DC ,AB =DE ,BC =EF ,求证:△ABC≌≌DEF .【分析】首先根据AF=DC ,可推得AF ﹣CF=DC ﹣CF ,即AC=DF ;再根据已知AB=DE ,BC=EF ,根据全等三角形全等的判定定理SSS 即可证明△ABC△△DEF .解:△AF=DC ,△AF ﹣CF=DC ﹣CF ,即AC=DF ;在△ABC 和△DEF 中AC DF AB DE BC EF =⎧⎪=⎨⎪=⎩△△ABC△△DEF (SSS )举一反三: 【变式1】如图,已知:PA=PB,AC =BD ,PC =PD ,△PAD 和△PBC 全等吗?请说明理由.【分析】由AC=BD ,利用线段的和差关系可得AD=BC ,利用SSS 即可证明△PAD△△PBC.解:△AC =BD ,△AC+CD=BD+CD ,即AD =BC ,又△PA =PB ,PC =PD ,△△PAD△△PBC(SSS)【点拨】本题考查全等三角形的判定与性质,熟练掌握全等三角形的判定定理是解题关键.【变式2】如图,点D ,A ,E ,B 在同一直线上,EF =BC ,DF =AC ,DA =EB .试说明:△F =△C .【分析】根据SSS 的方法证明△DEF△△ABC,即可得到结论.解:因为DA =EB , 所以DE =AB.在△DEF 和△ABC 中, 因为DE =AB ,DF =AC ,EF =BC ,所以△DEF△△ABC(SSS),所以△F =△C.【点拨】本题考查了全等三角形的判定和性质,属于简单题,找到证明全等的方法是解题关键.4.如图,在ABCD 中,点E 、F 在BD 上,ABE 与CDF 全等吗?若全等,写出证明过程;若不全等,请你添加一个条件使它们全等,并写出证明过程.(1) 你添加的条件是__________.(2) 证明过程: 【答案】(1) BE DF =,答案不唯一; (2) 证明见分析; 【分析】(1)根据选择的全等三角形判定方法添加合适的条件即可;(2)由四边形ABCD 是平行四边形得到AB CD ∥,AB CD =,得ABE CDF ∠=∠,再用上添加的条件,即可证明结论.(1)解:BE DF =(答案不唯一)故答案为:BE DF =(答案不唯一)(2)证明:△四边形ABCD 是平行四边形,△AB CD ∥,AB CD =,△ABE CDF ∠=∠,在ABE 和CDF 中,AB CD ABE CDF BE DF =⎧⎪∠=∠⎨⎪=⎩,△ABE CDF △≌△(SAS ).【点拨】此题考查了平行四边形的性质、全等三角形的判定等知识,熟练掌握全等三角形的判定是解题的关键.举一反三:【变式1】如图,在ABC 和ADE 中,AB AD =,AC AE =,且BAD CAE ∠=∠,求证:ABC ADE △≌△.【分析】根据BADCAE ∠=∠可得BAC DAE ∠=∠,再根据SAS 即可证明.证明:△BAD CAE ∠=∠,△BAD DAC CAE DAC ∠+∠=∠+∠,即BAC DAE ∠=∠,在ABC 和ADE 中,AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩,△()SAS ABC ADE △≌△.【点拨】本题主要考查了用SAS 证明三角形全等,解题的关键是通过BAD CAE ∠=∠得出BAC DAE ∠=∠.【变式2】图,BE CF =,AC DF =,AC DF ∥.求证:ABC DEF ≌△△.【分析】首先根据BE CF =可得BC EF =,再由AC DF ∥可得ACB F ∠=∠,然后利用定理证明ABC DEF ≌即可.证明:△BE CF =,△BE EC CF EC ++=,即BC EF =,△AC DF ∥,△ACB F ∠=∠, 在ACB △和DFE △中,BC EF ACB F AC DF =⎧⎪∠=∠⎨⎪=⎩,△()SAS ABC DEF ≌.【点拨】此题主要考查了全等三角形的判定和平行线的性质,判定两个三角形全等的一般方法有:SSS SAS ASA AAS HL 、、、、.注意:AAA SSA 、不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.类型三、全等的性质与“SSS”和“SAS”综合➽➼证明✮✮求值 5.已知:如图,在ABC 中,AB AC AD =,是BC 边上的中线.求证:AD BC ⊥(填空).证明:在三角形ABD ACD 和中,△()()()______________BD AB ⎧=⎪⎪=⎨⎪⎪⎩已知已知公共边,△ ≌ ( ).△ADB ∠= (全等三角形的对应角相等).△1902ADB BDC ∠∠︒==(平角的意义). △(垂直的意义).【答案】,,,,SSS DC AC AD AD ABD ACD ADC AD BC =∠⊥,△△,,【分析】证明()SSS ADB ADC ≌△△.推出ADB ADC ∠∠=,可得结论. 证明:△AD 是BC 边上的中线,△BD CD =,在三角形ABD △和ACD 中,【变式1】如图:AB AC =,BD CD =,若28B ∠=︒,求C ∠的度数.【答案】28︒ 【分析】连接AD ,利用“SSS ”证明ABD ACD △≌△,即可得到答案.解:连接AD ,在ABD △和ACD 中,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩,()SSS ABD ACD ∴≌C B ∴∠=∠,28B ∠=︒,28C ∴∠=︒.【点拨】本题考查了全等三角形的判定和性质,正确作辅助线构造全等三角形是解题关键.【变式2】已知:如图,AC BD =,AD BC =,AD ,BC 相交于点O ,过点O 作OE AB ⊥,垂足为E .求证:(1) ABC BAD ≌.(2) AE BE =.【分析】(1)利用SSS 证明ABC BAD ≌;(2)根据全等三角形的性质得出DAB CBA ∠=∠,则OA OB =,根据等腰三角形的性质可得出结论.(1)证明:在ABC 和BAD 中,AC BD BC AD AB BA =⎧⎪=⎨⎪=⎩,△ABC BAD ≌(2)证明:△ABC BAD ≌△CBA DAB ∠=∠,△OA OB =,△OE AB ⊥,△AE BE =.【点拨】此题考查了全等三角形的判定与性质,利用SSS 证明ABC BAD ≌是解题的关键.6.如图,在ABC 中,CM 是AB 边上的中线,8AC =,12BC =,求CM 的取值范围.【答案】210CM <<【分析】倍长中线CM 至点N ,构造BNM ,易得ACM BNM ≅△△,再利用三角形的三边关系找到CN 的取值范围,进而得到CM 的取值范围.解:如图,延长CM 到点N ,使CM MN =,连接BN ,在ACM △和BNM 中,CM NM AMC BMN AM BM =⎧⎪∠=∠⎨⎪=⎩,∴ACM BNM ≅△△(SAS ),∴8AC BN ==, 在BCN △中,BC BN CN BC BN -<<+,∴128128CN -<<+,即420CN <<,∴4220CM <<,即210CM <<.【点拨】本题考查了全等三角形的性质与判定以及三角形的三边关系,解决本题的关键是倍长中线构造全等三角形.举一反三:【变式1】如图,已知在ABC 与ADE 中,90BAC DAE AB AC AD AE ∠=∠=︒==,,,点C ,D ,E 三点在同一条直线上,连接BD .图中的CE BD 、有怎样的数量和位置关系?请证明你的结论.【答案】CE BD =,证明见分析【分析】根据SAS 证明ACE ABD ≌△△,即可得到CE BD =.解:CE BD =,证明:△90BAC DAE ∠=∠=︒,△BAC CAD DAE CAD ∠+∠=∠+∠,即BAD CAE ∠=∠,在ACE △和ABD △中AC AB CAE BAD AE AD =⎧⎪∠=∠⎨⎪=⎩△()SAS ACE ABD ≌△CE BD =.【点拨】此题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定方法是解题的关键.【变式2】如图已知AOB 和MON △都是等腰直角三角形.(1) 如图1,连接AM ,BM ,此时AM ,BN 的数量关系为___________请说明理由.(2) 若将MON △绕点O 顺时针旋转,如图2,当点N 恰好在AB 边上时,求证:222BN AN MN +=.【答案】(1) AM BN =,理由见分析(2) 见分析 【分析】(1)由AOB 和MON △都是等腰直角三角形,得到AOM BON ≌,即可得到AM BN =(2)连接AM ,由AOB 和MON △都是等腰直角三角形,得到AOM BON ≌,即可得到AM BN =,再求得90MAN ∠=︒,利用勾股定理即可得到222BN AN MN +=解:(1)AM BN =,理由如下:△AOB 和MON △都是等腰直角三角形,△OA OB =,OM ON =,90AOB MON ∠=∠=︒,△AOM BON ∠=∠,在AOM 和BON △中:OA OB OM ON AOM BON =⎧⎪=⎨⎪∠=∠⎩, △AOM BON ≌,△AM BN =(2)如下图,连接AM ,△AOB 和MON △都是等腰直角三角形,△OA OB =,OM ON =,90AOB MON ∠=∠=︒,45B BAO ∠=∠=︒,△AOM BON ∠=∠,在AOM 和BON △中:OA OB OM ONAOM BON =⎧⎪=⎨⎪∠=∠⎩, △AOM BON ≌,△AM BN =,45B MAO ∠=∠=︒,△90MAN MAO BAO ∠=∠+∠=︒,△222AM AN MN +=,△222BN AN MN +=【点拨】本题考查了旋转的性质、全等三角形的判定和性质、等腰直角三角形的性质及勾股定理,熟练掌握全等三角形的判定和性质是解决问题的关键。
北师版初中七下数学4.3.2 探索三角形全等的条件(2)(课件)

导入新课
发现: 两个角 和 一条边 可以确定一个三角形。
导入新课
1.什么叫全等三角形? 能够完全重合的两个三角形叫 全等三角形.
2. 我们已经学过了哪几种判定两个三角形全等的方法? 边边边(SSS).
3.如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
导入新课
如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
当堂检测
1. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图 中标有1,2,3,4的四块),你认为将其中的哪块带去,就能 配一块与原来一样大小的三角形玻璃?应该带( B ) A.第1块 B.第2块 C.第3块 D.第4块
当堂检测
2. 如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那 么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( C ) A.AB=DE B.AC=DF C.∠A=∠D D.BF=EC
A
A
它们能判定
两个三角形
全等吗?
B
图一
C
“两角及夹边”
B
图二 C
“两角和其中一角的对边”
讲授新课
一 三角形全等的判定(“角边角”)
探究一:任意画出一个△ABC,再画一个△A′B′C′, 使A′B′=AB,∠A′=∠A,∠B′=∠B(即保证两角和它 们的夹边对应相等).把画好的△A′B′C′剪下,放到 △ABC上,它们全等吗?
∠B=∠E(已知 ), AB=AE(已知), ∠BAC=∠EAD (已证 ), ∴△BAC≌△EAD(ASA). ∴BC=ED.
讲授新课
找相等角的方法: 1.公共角、对顶角分别相等; 2.等角加(减)等角,其和(差)相等; 3.同角或等角的余(补)角相等; 4.角平分线得到相等角; 5.平行线的同位角、内错角相等; 6.直角都相等; 7.全等三角形对应角相等.
北师大版七年级数学下册探索三角形全等的条件

BD=CE
10
练一练
如图,AB∥CD,AD∥BC,那么
AB=CD吗?为什么?
AD与BC呢?
D
Cபைடு நூலகம்
A
B
重要思路:两直线平行,可以找到等角.
11
练一练
如图,D在AB上,DF交AC于点E,DE=FE, FC∥AB,若AB=4,CF=3, 则BD的长是( ) A.0.5 B.1 C.1.5 D.2
D
9
练一练 如图,AD=AE,∠B=∠C,
请证明:BD=CE.
D B
A 证明:∵在△ABE和△ACD中,
∠B=∠C (已知)
E
∠A=∠A (公共角)
AE=AD (已知)
C ∴ △ABE≌△ACD(AAS)
∴ BD=CE (全等三角形对应边相等)
不是三角 形的边 ∴ AD=AE(全等三角形对应边相等)
北师大版七年级下册
第四章 三角形
1
复习
两个三角形全等的判定方法1:
三边对应相等的两个三角形全等.简写为“边边边”或“SSS”.
用符号表达:
指明范围
A
在△ABC和△A′B′C′中,
三个条件
AB=A′B′, AC=A′C′,BC=B′C′
B
∴△ABC≌△A′B′C′ (SSS)
写出结论
C A'
B'
C'
∴ △AOC≌△BOD ( ASA )
8
练一练 图中的两个三角形全等吗?
请说明理由.
A
在△ABC和△DBC中,
110
_∠__A_B__C_=_∠__DBC(已知)B ∠__A__=_∠__D__(__已知)
112三角形全等的判定(1。2。3。4)

11.2三角形全等的判定(1)教学目标:1、探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.2、掌握三角形全等的“边边边”条件,了解三角形的稳定性.3、通过对问题的共同探讨,培养学生的协作精神.教学重点:掌握三角形全等的“边边边”条教学难点:三角形全等条件的探索过程.教具准备:圆规、三角尺教学过程:一、复习过程,引入新知多媒体显示,带领学生复习全等三角形的定义及其性质,从而得出结论:全等三角形三条边对应相等,三个角分别对应相等.反之,这六个元素分别相等,这样的两个三角形一定全等.二、创设情境,提出问题根据上面的结论,提出问题:两个三角形全等,是否一定需要六个条件呢?如果只满足上述六个条件中的一部分,是否也能保证两个三角形全等呢?组织学生进行讨论交流,经过学生逐步分析,各种情况逐渐明朗,进行交流予以汇总归纳.三、建立模型,探索发现出示探究1,先任意画一个△ABC,再画一个△A'B'C',使△ABC与△A'B'C',满足上述条件中的一个或两个.你画出的△A'B'C'与△ABC一定全等吗?让学生按照下面给出的条件作出三角形.(1)三角形的两个角分别是30°、50°.(2)三角形的两条边分别是4cm,6cm.(3)三角形的一个角为30°,—条边为3cm.再通过画一画,剪一剪,比一比的方式,得出结论:只给出一个或两个条件时,都不能保证所画出的三角形一定全等.出示探究2,先任意画出一个△A'B'C',使A'B'=AB,B'C'=BC,C'A'=CA,把画好的△A'B'C'剪下,放到△ABC上,它们全等吗?让学生充分交流后,在教师的引导下作出△A'B'C',并通过比较得出结论:三边对应相等A B DAB C D的两个三角形全等四、应用新知,体验成功演示:由三根木条钉成的一个三角形的框架,它的大小和形状是固定不变的.鼓励学生举出生活中的实例.给出例l,如下图△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架,求证△ABD≌△ACD.例2 如图四边形ABCD中,AB=CD,AD=BC,你能把四边形ABCD分成两个相互全等的三角形吗?你有几种方法?你能证明你的方法吗?试一试.五、巩固练习书第8页练习.六、小结回顾反思本节课对知识的研究探索过程、小结方法及结论,提炼数学思想,掌握数学规律.七、布置作业:P15习题11.2 1、2三角形全等的判定(2)教学目标:1、经历探索三角形全等条件的过程,培养学生观察分析图形能力、动手能力.2、在探索三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单的推理.3、通过对问题的共同探讨,培养学生的协作精神.教学重点:应用“边角边”证明两个三角形全等,进而得出线段或角相等.教学难点:指导学生分析问题,寻找判定三角形全等的条件.教具准备:圆规、三角尺教学过程(师生活动)一、创设情境,引入课题探究3:已知任意△ABC,画△A'B'C',使A'B'=AB,A'C'=AC,∠A'=∠A.ABCDE教帅点拨,学生边学边画图,再让学生把画好的△A'B'C',剪下放在△ABC 上,观察这两个三角形是否全等. 二、交流对话,探求新知根据操作,总结规律:两边和它们的夹角对应相等的两个三角形全等.(SAS) 补充强调:角必须是两条相等的对应边的夹角,边必须是夹相等角的两对边. 三、应用新知,体验成功例2,如图,有—池塘,要测池塘两端A 、B 的距离,可先在平地上取一个可以直接到达A 和B 的点C ,连接AC 并延长到D ,使CD =CA ,连接BC 并延长到E ,使CE =CB .连接DE ,那么量出DE 的长就是A 、B 的距离,为什么? 分析: 要想证AB =DE , 只需证△ABC ≌△DEC △ABC 与△DEC 全等的条件现有……还需要……)明确证明分别属于两个三角形的线段相等或者角相等的问题,常常通过证明这两个三角形全等来解决. 练习题:已知:如图AB=AC,AD=AE,∠BAC=∠DAE 求证: △ABD ≌△ACE 证明:∵∠BAC=∠DAE (已知)∠ BAC+ ∠ CAD= ∠DAE+ ∠ CAD ∴∠BAD=∠CAE 在△ABD 与△ACEAB=AC (已知) ∠BAD= ∠CAE (已证) AD=AE (已知) ∴△ABD ≌△ACE (SAS)思考:求证:(1).BD=CE (2). ∠B= ∠C (3). ∠ADB= ∠AEC 四、再次探究,释解疑惑出示探究4,我们知道,两边和它们的夹角对应相等的两个三角形全等.由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗?为什么?让学生模仿前面的探究方法,得出结论:两边及其中一边的对角对应相等的两个三角形不一定全等.教师演示:方法(一)教科书10页图11.2-7. 方法(二)通过画图,让学生更直观地获得结论.五、巩固练习教科书第10页,练习1、2六、小结1.判定三角形全等的方法;2.证明线段、角相等常见的方法有哪些?让学生自由表述,其他学生补充,让学生自己将知识系统化,以自己的方式进行建构.七、布置作业P15习题11.2 3三角形全等的判定(3)教学目标:1、探索并掌握两个三角形全等的条件:“ASA”“AAS”,并能应用它们判别两个三角形是否全等.2、经历作图、比较、证明等探究过程,提高分析、作图、归纳、表达、逻辑推理等能力;并通过对知识方法的总结,培养反思的习惯,培养理性思维.教学重点:理解,掌握三角形全等的条件:“ASA”“AAS”.教学难点:探究出“ASA”“AAS”以及它们的应用.教具准备:圆规、三角尺教学过程(师生活动)创设情境一、复习:我们已经知道,三角形全等的判定条件有哪些?“SSS”“SAS”那除了这两个条件,满足另一些条件的两个三角形是否也可能全等呢?今天我们就来探究三角形全等的另一些条件。
探索三角形全等的条件(第2课时)教学课件北师大版中学数学七年级(下)

A.一定不全等
B.一定全等
C.不一定全等
D.以上都不对
随堂训练
3.如图∠ACB=∠DFE,BC=EF,那么应补充一
个条件
,才能使△ABC≌△DEF
(写出一个即可).
AB=DE可以吗?×
B
A
AB∥DE
∠B=∠E (ASA)
C
F
或∠A=∠D (AAS)
D
E
随堂训练
4. 已知△ABC中,BE AD于E,CF AD于F ,
形全等. (简写成“角角边”或“AAS”)
C
几何语言:
在△和△中,
∠ = ∠,
ቐ∠ = ∠ ,
= ,
∴ △ ≌△ (AAS).
A
B
F
D
E
知识讲授
例4 已知:如图, AB⊥BC,AD⊥DC,∠1=∠2.
A
求证:AB=AD.
12
证明: ∵ AB⊥BC,AD⊥DC,
D
被撕坏了,如图,你能制作一张与本来
同样大小的新教具吗?
能
你能说明其中的理由吗?
C
E
B
新课导入
想一想:
探究三角形全等的条件:有三个条件对应相等时
三个角对应相等; 不能
三条边对应相等; SSS
两个角和一条边对应相等
?
知识讲授
探究:
两个角和一条边对应相等时,两三角形是否全等?
思考:已知一个三角形的两个角和一条边,那么这两个角与这条边的位
∴ AB=CD , BC=AD,(全等三角形对应边相等)
2
4
3
∴ ∠1=∠2 ,
C
1
A
B
探索三角形全等的条件

探索三角形全等的条件(1)栖霞市唐家泊中学衣龙涛教学目标:1.知识与技能:掌握三角形全等的“边边边”条件,了解三角形的稳定性。
在探索的过程中,能够进行有条理的思考并进行简单的推理。
2.过程与方法:经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程,通过小组合作探究得到相关结论。
3.情感态度与价值观:(1)使学生在自主探索三角形全等的过程中,经历画图、观察、比较、推理、交流等环节,从而获得正确的学习方式和良好的情感体验,让学生体验数学源于生活,服务于生活的辨证思想。
(2)培养学生勇于探索、团结协作的精神。
教学重点:三角形全等条件的探索过程。
教学难点:三角形全等条件的探索过程,特别是创设出问题后,学生面对开放性问题,要做出全面、正确的分析,并对各种情况进行讨论,对初二学生有一定的难度。
教具:硬纸板、直尺、圆规、自制三角形、四边形、多媒体课件教学方法:自主探索、合作交流教学过程:一、问题情境,导入新课:1、同学们,上一节课我们刚刚学习了全等三角形,那么什么是全等三角形?2、小明画了一个三角形,怎样才能画一个与他画的三角形全等?交流总结:我们知道全等三角形的三条边、三个角分别对应相等。
反过来,两个三角形如果要全等,需要六个条件其中的那些条件呢? 一个条件行吗?两个条件、三个条件呢?这就是我们这节课要探索的问题:板书课题---探索三角形全等的条件(1)二、探究发现,学习新知:(一)只给一个条件(一组对应边相等或一组对应角相等),画出的两个三角形一定全等吗?注意:一个条件,指什么条件?(一条边或一个角)1.只给定一条边时:(学生操作,白板展示)2、只给定一个角时:(学生操作,白板展示)(二)给出两个条件画三角形时,有几种可能的情况,每种情况下作出的三角形一定全等吗?分别按下列条件做一做.1、三种情况:一边一角、两边、两角2、具体情况:①一边一角:三角形一条边为15cm,一内角为30°.②两边:三角形两条边分别为15cm、16cm.③两角:三角形两内角分别为30°和60°.学生分组讨论、探索、归纳,最后以组为单位出示结果作补充交流.3.总结讨论结果:(学生操作,白板展示)结论:可以发现按这些条件画出的三角形都不能保证一定全等.(三)给出三个条件画三角形,你能说出有几种可能的情况吗,它们全等吗?小组归纳:有四种可能.即:三内角、三条边、两边一内角、两内角一边.1、在刚才的探索过程中,我们已经发现三内角不能保证三角形全等.比如一个大直角三角尺与一个小直角三角尺。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
/ 凤凰-凤凰地址 介绍凤凰相关资讯,凤凰链接,登录链接,请认准凤凰网,凤凰集团本着"团结敬业,迈向新世纪,以高额投入,高科技装备,创一流产品、一流效益,服务于海内外用户"的宗旨。奉行"质量第一,信誉第一"的原则,向国内外客户提供最优 务,以人才、信息、质量、效率竭力满足行业日新月异的发展需要。
[单选]某联轴器径向位移测量读数a1、a2、a3、a4分别是1.58、1.98、1.93、1.63,则该联轴器最大径向偏差值为()。A、0.15mmB、0.20mmC、0.25mmD、0.30mm [单选]WHO代谢综合征诊断中,男性和女性的差异表现在()A.空腹血糖B.血压C.三酰甘油D.血低密度脂蛋白胆固醇E.血高密度脂蛋白胆固醇 [单选,A2型题,A1/A2型题]会阴部解剖特点不正确的是()。A.指尿道口与肛门之间的软组织B.是组成骨盆底的一部分C.会阴体厚3~4cmD.妊娠后变软,有利于分娩E.分娩时需防止裂伤 [单选,A型题]关于舌背乳头,下列哪项是错误的()A.沟状乳头B.丝状乳头C.菌状乳头D.轮廓乳头E.叶状乳头 [单选]在2007年的邯郸农行盗窃案中,犯罪嫌疑人张强2007年3月20日已经不是管库员,但当天查库登记簿“管库员”一栏有张强的签章。同年3月29日的查库登记簿“管库员”栏没有任何人签章,这些内部控制失范行为与内部控制中()要素最为相关。A.内部环境B.控制活动C.风险评估D.内部监督 [单选]青春期常见的心理行为问题不包括A.吸烟、酗酒和滥用药物B.暴力伤害C.不良习惯D.精神性成瘾行为E.自杀 [单选]个人绩效是指员工()自己所承担的岗位职责,达到组织为他们确定的工作标准和工作结果标准的程度。A、集体履行B、团体履行C、个人履行D、他人履行 [单选]在对猪胴体进行分割时,按我国的划分标准:将猪胴体的前端去掉肩部,后端去掉臀腿部,余下的中段肉体从脊椎骨下4~6cm处平行切开的上部肉段是().A.肩颈肉B.臀腿肉C.背腰肉D.肋腹肉 [单选]重症肌无力的临床特征为()A.全身骨骼肌均可无力B.颅神经支配肌肉的无力多于脊神经支配的肌肉C.受累骨骼肌极易疲劳和短暂休息后好转D.病情波动E.感染后肌无力加重 [问答题,简答题]口腔异味概述。
