新编【2018年中考试题分类汇编】-中考数学:图形的相似
【精品】2018年全国各地中考数学经典真题分类汇编:图形的相似(含答案)

中考数学真题汇编 :图形的相像一、选择题1.已知,以下变形错误的选项是()A. B. C. D.【答案】 B2.已知与相像,且相像比为,则与的面积比()A. B. C. D.【答案】 D3.要制作两个形状同样的三角形框架,此中一个三角形的三边长分别为,和,另一个三角形的最短边长为 2.5 cm,则它的最长边为()A. 3cmB. 4cmC. 4.5cmD. 5cm【答案】 C4.在平面直角坐标系中,线段AB 两个端点的坐标分别为A(6,8), B(10, 2),若以原点O 为位似中心,在第一象限内将线段AB 缩短为本来的后获得线段CD,则点 A 的对应点 C 的坐标为()A. ( 5, 1)B(.4, 3)C(. 3,4)D(. 1, 5)【答案】 C5.如图,△ ACB和△ ECD都是等腰直角三角形,CA=CB, CE=CD,△ ACB的极点 A 在△ ECD的斜边 DE 上,若 AE=, AD=,则两个三角形重叠部分的面积为()A. B. C. D.【答案】 D6.在平面直角坐标系中,点是线段上一点,以原点为位似中心把放大到本来的两倍,则点的对应点的坐标为( )A. B.或 C. D.或【答案】 B7.如图,点在线段上,在的同侧作等腰和等腰,与、分别交于点、确的是(.关于以下结论:①);②;③.此中正∵∠ BEA=∠ CDA∠PME=∠ AMD∴P、 E、 D、 A 四点共圆∴∠ APD=AED=90°∵∠ CAE=180°-∠BAC-∠ EAD=90°∴△ CAP∽△ CMA∴AC2 =CP?CM∵ AC=AB∴2CB2=CP?CM因此③正确A. ①②③B①. C①②. D②③.【答案】 A8.如图,将沿边上的中线平移到的地点,已知的面积为9,暗影部分三角形的面积为 4.若,则等于()A.2B.3C.D.【答案】 A9.学校门口的栏杆如下图,栏杆从水平地点绕点旋转到地点,已知,,垂足分别为,,,,,则栏杆端应降落的垂直距离为( )A. B. C. D.【答案】 C10.如图,在△ ABC中,点 D 在 AB 边上, DE∥BC,与边 AC 交于点 E,连接 BE,记△ ADE,△ BCE的面积分别为S1,S2,()A. 若C. 若,则,则B若.D若.,则,则【答案】 D11.如图,菱形ABCD的对角线AC、 BD 订交于点O,点 E 为边CD的中点,若菱形ABCD的周长为16,∠ BAD=60°,则△ OCE的面积是()。
2018年最新中考数学分类汇编___相似(超经典)

相似一.选择题1.如图,在四边形ABCD 中,DC ∥AB ,CB ⊥AB ,AB=AD ,CD=AB ,点E 、F 分别为AB 、AD 的中点,则△AEF 与多边形BCDFE 的面积之比为( )A .B .C .D .2.如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O 为位似中心,相似比为31,在第一象限内把线段AB 缩小后得到线段CD ,则点C 的坐标为( )A .(2,1)B .(2,0)C .(3,3)D .(3,1)3.如图,已知AB 、CD 、EF 都与BD 垂直,垂足分别是B 、D 、F ,且AB =1,CD =3,那么EF 的长是 ( )A .13 B .23 C .34 D .45第7题图FE BDA C4.如图所示,△ABC 中,DE ∥BC ,若,则下列结论中正确的是( )A .B .C .D .5.(2015•甘肃武威,第9题3分)如图,D 、E 分别是△ABC 的边AB 、BC 上的点,DE ∥AC ,若S △BDE :S △CDE =1:3,则S △DOE :S △AOC 的值为( )A .B .C .D .6.如图,在△ABC 中,AB=CB ,以AB 为直径的⊙O 交AC 于点D .过点C 作CF ∥AB ,在CF 上取一点E ,使DE=CD ,连接AE .对于下列结论:①AD=DC ;②△CBA ∽△CDE ;③=;④AE 为⊙O 的切线,一定正确的结论全部包含其中的选项是( )A.①②B.①②③C.①④D.①②④7.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是()A.∠ABP=∠C B.∠APB=∠ABC C.=D.=10. 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为l:2,∠OCD=90°,CO=CD.若B(1,0),则点C[中国^的坐标为( )yxDC BAOA.(1,2)B.(1,1)C.(2, 2)D.(2,1)11.如图,在ABC ∆中,BC DE //,6=AD ,3=DB ,4=AE ,则EC 的长为(A )1 (B )2 (C )3 (D )412.如图,∥∥,两条直线与这三条平行线分别交于点A 、B 、C 和D 、E 、F .已知,则的值为( )A .B .C .D .13.如图,AD∥BE∥CF,直线l1、l2这与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则EF的长为()A. 4 B. 5 C. 6 D. 814.如图,在矩形ABCD中,AB=10 , BC=5 .若点M、N分别是线段AC AB上的两个动点,则BM+MN的最小值为()A. 10 B. 8 C. 53 D. 615.若,则的值为()A.1 B. C. D.16.如图,在Rt△ABC中,∠ABC=90°,AB=BC.点D是线段AB上的一点,连结CD,过点B 作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①;②若点D是AB的中点,则AF=AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若,则.其中正确的结论序号是()A.①② B.③④ C.①②③ D.①②③④17.如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于AD的长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF.若BD=6,AF=4,CD=3,则BE的长是()A. 2 B. 4 C. 6 D. 8考点:平行线分线段成比例;菱形的判定与性质;作图—基本作图..分析:根据已知得出MN是线段AD的垂直平分线,推出AE=DE,AF=DF,求出DE∥AC,DF ∥AE,得出四边形AEDF是菱形,根据菱形的性质得出AE=DE=DF=AF,根据平行线分线段成比例定理得出=,代入求出即可.解答:解:∵根据作法可知:MN是线段AD的垂直平分线,∴AE=DE,AF=DF,∴∠EAD=∠EDA,∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠EDA=∠CAD,∴DE∥AC,同理DF∥AE,∴四边形AEDF是菱形,∴AE=DE=DF=AF,∵AF=4,∴AE=DE=DF=AF=4,∵DE∥AC,∴=,∵BD=6,AE=4,CD=3,∴=,∴BE=8,故选D.点评:本题考查了平行线分线段成比例定理,菱形的性质和判定,线段垂直平分线性质,等腰三角形的性质的应用,能根据定理四边形AEDF是菱形是解此题的关键,注意:一组平行线截两条直线,所截得的对应线段成比例.……依次顺延18.(2015•甘肃兰州,第5题,4分)如图,线段CD两个端点的坐标分别为C(1,2),D (2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(5,0),则点A的坐标为A.(2,5)B.(2.5,5)C. (3,5)D.(3,6)【答案】B【考点解剖】本题考查了坐标和相似的有关知识【思路点拔】根据题意:AO:CO=BO:DO=5:2,而位似中心恰好是坐标原点O,所以点A的横、纵坐标都是点C横、纵坐标的2.5倍,因此选B。
专题5.2 图形的相似(第01期)-2018年中考数学试题分项版解析汇编(解析版)

专题5.2 图形的相似(第01期)-2018年中考数学试题分项版解析汇编(解析版)一、单选题1.学校门口的栏杆如图所示,栏杆从水平位置绕点旋转到位置,已知,,垂足分别为,,,,,则栏杆端应下降的垂直距离为( )A.B.C.D.【来源】2018年浙江省绍兴市中考数学试卷解析【答案】C【点评】考查了相似三角形的判定与性质,掌握相似三角形的判定方法是解题的关键.2.在平面直角坐标系中,点是线段上一点,以原点为位似中心把放大到原来的两倍,则点的对应点的坐标为( )A. B. 或C.D.或【来源】山东省潍坊市2018年中考数学试题【答案】B【解析】分析:根据位似变换的性质计算即可.详解:点P(m,n )是线段AB 上一点,以原点O 为位似中心把△AOB 放大到原来的两倍,则点P 的对应点的坐标为(m×2,n×2)或(m×(-2),n×(-2)),即(2m,2n )或(-2m,-2n),故选B.点睛:本题考查的是位似变换、坐标与图形的性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.3.如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )A. 2B. 3C.D.【来源】四川省宜宾市2018年中考数学试题【答案】A【解析】分析:由S△ABC=9、S△A′EF=4且AD为BC边的中线知S△A′DE=S△A′EF=2,S△ABD=S△ABC=,根据△DA′E∽△DAB知,据此求解可得.详解:如图,点睛:本题主要平移的性质,解题的关键是熟练掌握平移变换的性质与三角形中线的性质、相似三角形的判定与性质等知识点.学科#网4.在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为( )A. (5,1)B. (4,3)C. (3,4)D. (1,5)【来源】山东省滨州市2018年中考数学试题【答案】C点睛:此题主要考查了位似图形的性质,利用两图形的位似比得出对应点横纵坐标关系是解题关键.5.如图,点在线段上,在的同侧作等腰和等腰,与、分别交于点、.对于下列结论:①;②;③.其中正确的是()A. ①②③B. ①C. ①②D. ②③【来源】江苏省扬州市2018年中考数学试题【答案】A【解析】分析:(1)由等腰Rt△ABC和等腰Rt△ADE三边份数关系可证;(2)通过等积式倒推可知,证明△PAM∽△EMD即可;(3)2CB2转化为AC2,证明△ACP∽△MCA,问题可证.详解:由已知:AC=AB,AD=AE点睛:本题考查了相似三角形的性质和判断.在等积式和比例式的证明中应注意应用倒推的方法寻找相似三角形进行证明,进而得到答案.6.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为,和,另一个三角形的最短边长为2.5 cm,则它的最长边为( )A. 3cmB. 4cmC. 4.5cmD. 5cm【来源】【全国省级联考】2018年重庆市中考数学试卷(A卷)【答案】C【解析】【分析】根据相似三角形三边对应成比例进行求解即可得.【详解】设另一个三角形的最长边为xcm,由题意得5:2.5=9:x,解得:x=4.5,故选C.【点睛】本题考查了相似三角形的性质,熟知相似三角形对应边成比例是解题的关键.7.如图,是等边三角形,是等腰直角三角形,,于点,连分别交,于点,,过点作交于点,则下列结论:①;②;③;④;⑤.A. 5B. 4C. 3D. 2【来源】湖北省孝感市2018年中考数学试题【答案】B详解:∵△ABC为等边三角形,△ABD为等腰直角三角形,∴∠BAC=60°、∠BAD=90°、AC=AB=AD,∠ADB=∠ABD=45°,∴△CAD是等腰三角形,且顶角∠CAD=150°,∴∠ADC=15°,故①正确;∵AE⊥BD,即∠AED=90°,∴∠DAE=45°,∴∠AFG=∠ADC+∠DAE=60°,∠FAG=45°,∴∠AGF=75°,由∠AFG≠∠AGF知AF≠AG,故②错误;记AH与CD的交点为P,由AH⊥CD且∠AFG=60°知∠FAP=30°,则∠BAH=∠ADC=15°,设EF=a,∵△ADF≌△BAH,∴BH=AF=2x,△ABE中,∵∠AEB=90°、∠ABE=45°,∴BE=AE=AF+EF=a+2x,∴EH=BE-BH=a+2x-2x=a,∵∠APF=∠AEH=90°,∠FAP=∠HAE,∴△PAF∽△EAH,∴,即,整理,得:2x2=(-1)ax,由x≠0得2x=(-1)a,即AF=(-1)EF,故⑤正确;故选:B.点睛:本题主要考查相似三角形的判定与性质,解题的关键是掌握等腰三角形与等边三角形的性质、全等三角形与相似三角形的判定与性质等知识点.二、填空题8.如图,△ABC中,点D、E分別在AB、AC上,DE∥BC,AD:DB=1:2,则△ADE与△ABC的面积的比为__________.【来源】江苏省连云港市2018年中考数学试题【答案】1:9点睛:本题考查的是相似三角形的判定与性质,熟知相似三角形面积的比等于相似比的平方是解答此题的关键.9.已知且,则=__________.【来源】四川省凉山州2018年中考数学试题【答案】【解析】分析:根据相似三角形的面积比等于相似比的平方求解即可.详解:∵△ABC∽△A′B′C′,∴S△ABC:S△A′B′C′=AB2:A′B′2=1:2,∴AB:A′B′=1:.点睛:本题的关键是理解相似三角形的面积比等于相似比的平方.10.如图,直线,直线交,,于点,,;直线交,,于点,,.已知,则__________.【来源】2018年浙江省舟山市中考数学试题【答案】2【点评】考查平行线分线段成比例定理,熟练掌握定理是解题的关键.11.如图,E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,连接AC、HE、EC,GA,GF.已知AG⊥GF,AC=,则AB的长为__________.【来源】江苏省连云港市2018年中考数学试题【答案】2【解析】分析:连接BD.由△ADG∽△GCF,设CF=BF=a,CG=DG=b,可得,推出,可得b=a,在Rt△GCF中,利用勾股定理求出b,即可解决问题;详解:如图,连接BD.∵四边形ABCD是矩形,∴∠ADC=∠DCB=90°,AC=BD=,∵CG=DG,CF=FB,∴GF=BD=,点睛:本题考查中点四边形、矩形的性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.学科#网12.如图,中,,于点,于点,于点,,则__________.【来源】湖南省娄底市2018年中考数学试题【答案】6【解析】【分析】由等腰三角形的性质可得∠C =∠ABC, BD=DC=BC,再根据∠BED=∠CFB=90°,可证△BED∽△CFB,根据相似三角形的对应边成比例即可求得.【点睛】本题考查了等腰三角形的性质、相似三角形的判定与性质,得到△BED∽△CFB是解本题的关键.13.矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.【来源】安徽省2018年中考数学试题【答案】3或1.2【解析】【分析】由△PBE∽△DBC,可得∠PBE=∠DBC,继而可确定点P在BD上,然后再根据△APD是等腰三角形,分DP=DA、AP=DP两种情况进行讨论即可得.【详解】∵四边形ABCD是矩形,∴∠BAD=∠C=90°,CD=AB=6,∴BD=10,如图2,当AP=DP时,此时P为BD中点,∵△PBE∽△DBC,∴PE:CD=PB:DB=1:2,∴PE:6=1:2,∴PE=3;综上,PE的长为1.2或3,故答案为:1.2或3.【点睛】本题考查了相似三角形的性质,等腰三角形的性质,矩形的性质等,确定出点P在线段BD上是解题的关键.14.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图,是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门位于的中点,南门位于的中点,出东门15步的处有一树木,求出南门多少步恰好看到位于处的树木(即点在直线上)?请你计算的长为__________步.【来源】山东省泰安市2018年中考数学试题【答案】点睛:本题考查了相似三角形的应用.解题的关键是证明△CKD∽△DHA.15.如图,在直角△ABC中,∠C=90°,AC=6,BC=8,P、Q分别为边BC、AB上的两个动点,若要使△APQ是等腰三角形且△BPQ是直角三角形,则AQ =________.【来源】江苏省盐城市2018年中考数学试题【答案】或【解析】分析:分两种情形分别求解:①如图1中,当AQ=PQ,∠QPB=90°时,②当AQ=PQ,∠PQB=90°时;详解:①如图1中,当AQ=PQ,∠QPB=90°时,设AQ=PQ=x,②当AQ=PQ,∠PQB=90°时,如图2,设AQ=PQ=y.∵△BQP∽△BCA,∴,∴,∴y=.综上所述,满足条件的AQ的值为或.点睛:本题考查勾股定理、等腰三角形的性质、相似三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题.三、解答题16.如图,在方格纸中.(1)请在方格纸上建立平面直角坐标系,使,,并求出点坐标;(2)以原点为位似中心,相似比为2,在第一象限内将放大,画出放大后的图形;(3)计算的面积.【来源】四川省凉山州2018年中考数学试题【答案】(1)作图见解析;.(2)作图见解析;(3)16.详解:(1)如图所示,即为所求的直角坐标系;B(2,1);(2)如图:△A'B'C'即为所求;(3)S△A'B'C'=×4×8=16.点睛:此题主要考查了位似变换以及三角形面积求法,正确得出对应点位置是解题的关键.画位似图形的一般步骤为:①确定位似中心;②分别连接并延长位似中心和关键点;③根据位似比,确定位似图形的关键点;④顺次连接上述各点,得到放大或缩小的图形.17.如图,在中,为上一点,以为圆心,长为半径作圆,与相切于点,过点作交的延长线于点,且.(1)求证:为的切线;(2)若, ,求的长.【来源】江西省2018年中等学校招生考试数学试题【答案】(1)证明见解析;(2)【详解】(1)作OE⊥AB于点E,∵切BC于点C,∴OC⊥BC,∠ACB=90°,∵AD⊥BD,∴∠D=90°,∴∠ABD+∠BAD =90°,∠CBD+∠BOC=90°,∵∠BOC=∠AOD,∠AOD=∠BAD,∴∠BOC=∠BAD,∴∠ABD=∠CBD在△OBC和△OBE中,∴△OBC≌△OBE,∴OE=OC,∴OE是⊙O的半径,∵OE⊥AB ,∴AB为⊙O的切线;【点睛】本题考查了切线的判定与性质,相似三角形的判定与性质等,熟练掌握相关的判定与性质定理是解题的关键.18.如图,在中,=8,=4,=6,,是的平分线,交于点,求的长.【来源】江西省2018年中等学校招生考试数学试题【答案】4【解析】【分析】由已知条件先求得CD=BC=4,然后再证明△ABE∽△CDE,根据相似三角形对应边成比例结合CE+AE=AC=6即可求得AE的长.【详解】∵BD是∠ABC的平分线,∴∠ABD=∠CBD,【点睛】本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质定理是解题的关键.19.已知,中,,是边上一点,作,分别交边,于点,.(1)若(如图1),求证:.(2)若,过点作,交(或的延长线)于点.试猜想:线段,和之间的数量关系,并就情形(如图2)说明理由.(3)若点与重合(如图3),,且.①求的度数;②设,,,试证明:.【来源】2018年浙江省舟山市中考数学试题【答案】(1)证明见解析;(2)猜想:,理由见解析;(3)①;②证明见解析.【解析】【分析】(1)根据平行线的判定,得到,,证明.即可证明.(2)过点作的平行线交的延长线于点,证明≌得到.证明四边形是平行四边形,即可得到.(3)①设,,根据三角形的内角和列出方程,求解即可.②延长至,使,连结,证明.根据相似三角形的性质得到,即可证明.【解答】(1)∵,,,∴,,∴,,,∴.∴.(3)①设,∵,,∴,又,即,∴,即.【点评】考查平行四边形的判定与性质,全等三角形的判定与性质,相似三角形的判定与性质,综合性比较强,对学生综合能力要求较高.学科#网20.(1)(发现)如图①,已知等边△ABC,将直角三角形的60°角顶点D任意放在BC边上(点D不与点B、C重合),使两边分别交线段AB、AC于点E、F.①若AB=6,AE=4,BD=2,则CF =________;②求证:△EBD∽△DCF.(2)(思考)若将图①中的三角板的顶点D在BC边上移动,保持三角板与AB、AC的两个交点E、F都存在,连接EF,如图②所示.问点D是否存在某一位置,使ED平分∠BEF且FD平分∠CFE?若存在,求出的值;若不存在,请说明理由.(3)(探索)如图③,在等腰△ABC中,AB=AC,点O为BC边的中点,将三角形透明纸板的一个顶点放在点O处(其中∠MON=∠B),使两条边分别交边AB、AC于点E、F(点E、F均不与△ABC的顶点重合),连接EF.设∠B=α,则△AEF与△ABC的周长之比为________(用含α的表达式表示).【来源】江苏省盐城市2018年中考数学试题【答案】(1)①4;②证明见解析;(2)存在;(3)1-cosα.(3)【探索】由已知不难求得C△ABC=AB+BC+CA=2AB+2OB=2(m+mcosα),则需要用m和α的三角函数表示出C△AEF,C△AEF=AE+EF+AF;题中直接已知O是BC的中点,应用(2)题的方法和结论,作OG⊥BE,OD⊥EF,OH⊥CF,可得EG=ED,FH=DF,则C△AEF=AE+EF+AF=AG+AH=2AG,而AG=AB-OB,从而可求得.②证明:∵∠EDF=60°,∠B=60°∴∠CDF+∠BDE=120°,∠BED+∠BDE=120°,∴∠BED=∠CDF,又∵∠B=∠C,∴△EBD∽△DCF(2)存在.如图,作DM⊥BE,DG⊥EF,DN⊥CF,垂足分别为M,G,N,∵ED平分∠BEF且FD平分∠CFE,∴DM=DG=DN,又∵∠B=∠C=60°,∠BMD=∠CND=90°,∴△BDM≅△CDN,∴BD=CD,即点D是BC的中点,∴;( 3 )连结AO,作OG⊥BE,OD⊥EF,OH⊥CF,垂足分别为G,D,H,点睛:本题考查了角平分线的定义,等边三角形的性质,全等三角形以及相似三角形的判定和性质等知识点.难度较大.21.如图1,在中,于点的垂直平分线交于点,交于点,,.(1)如图2,作于点,交于点,将沿方向平移,得到,连接.①求四边形的面积;②直线上有一动点,求周长的最小值.(2)如图3.延长交于点.过点作,过边上的动点作,并与交于点,将沿直线翻折,使点的对应点恰好落在直线上,求线段的长.【来源】山东省潍坊市2018年中考数学试题【答案】(1)①;②周长的最小值为9;(2)的长为或.根据平移的性质,MM'=CD=6,连接BM,如图1,四边形BHMM′的面积=×6×1.5+×4×1.5=7.5;②连接CM交直线EF于点N,连接DN,如图2,(2)∵BF∥CE,∴,∴QF=2,∴PK=PK'=6,过点K'作E'F'∥EF,分别交CD于点E',交QK于点F',如图3,当点P在线段CE上时,在Rt△PK'E'中,PE'2=PK'2-E'K'2,∴PE′=2,∵Rt△PE'K'∽Rt△K'F'Q,综上所述,CP的长为或.点睛:此题考查四边形的综合题,关键是根据相似三角形的性质和平移的性质解答,注意(2)分两种情况分析.学科#网22.如图,在菱形ABCD中,AC与BD交于点O,E是BD上一点,EF//AB,∠EAB=∠EBA,过点B作DA的垂线,交DA的延长线于点G.(1)∠DEF和∠AEF是否相等?若相等,请证明;若不相等,请说明理由;(2)找出图中与ΔAGB相似的三角形,并证明;(3)BF的延长线交CD的延长线于点H,交AC于点M.求证:BM2=MF⋅MH.【来源】山东省泰安市2018年中考数学试题【答案】(1),理由见解析;(2),证明见解析;(3)证明见解析.详解:(1)∠DEF=∠AEF,理由如下:∵EF∥AB,∴∠DEF=∠EBA,∠AEF=∠EAB.∵∠EAB=∠EBA,∴∠DEF=∠AEF;(2)△EOA∽△AGB,理由如下:∵四边形ABCD是菱形,∴AB=AD,AC⊥BD,∴∠GAB=∠ABE+∠ADB=2∠ABE.∵∠AEO=∠ABE+∠BAE=2∠ABE.∵∠GAB=∠AEO,∠GAB=∠AOE=90°,∴△EOA∽△AGB;(3)如图,连接DM.∵四边形ABCD是菱形,由对称性可知,BM=DM,∠ADM=∠ABM.∵AB∥CH,∴∠ABM=∠H,∴∠ADM=∠H.∵∠DMH=∠FMD,∴△MFD∽△MDH,∴,∴DM2=MF•MH,∴BM2=MF•MH.点睛:本题是相似形综合题,主要考查了菱形的性质,对称性,相似三角形的判定和性质,判断出△EOA∽△AGB是解答本题的关键.。
专题5.2 图形的相似2018年中考数学试题分项版解析汇编(原卷版)

北师大版七年级数学上册学校:___________姓名:___________班级:___________考号:___________ 一、单选题1.学校门口的栏杆如图所示,栏杆从水平位置 绕 点旋转到 位置,已知,别为 , ,,,,则栏杆 端应下降的垂直距离 为( ),垂足分A.B.C.2.在平面直角坐标系中,点对应点的坐标为( )A.B.或D. 是线段 上一点,以原点 为位似中心把放大到原来的两倍,则点 的C.D.或3.如图,将△ABC 沿 BC 边上的中线 AD 平移到△A'B'C'的位置,已知△ABC 的面积为 9,阴影部分三角形的面积为 4.若 AA'=1,则 A'D 等于( )A. 2 B. 3 C.D.4.在平面直角坐标系中,线段 AB 两个端点的坐标分别为 A(6,8),B(10,2),若以原点 O 为位似中心,在第一象限内将线段 AB 缩短为原来的 后得到线段 CD,则点 A 的对应点 C 的坐标为( ) A. (5,1) B. (4,3) C. (3,4) D. (1,5)5.如图,点 在线段 上,在 的同侧作等腰和等腰, 与 、 分别交于点 、 .对于下列结论:①;②;③.其中正确的是( )1北师大版七年级数学上册A. ①②③ B. ① C. ①② D. ②③ 6.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为 , 和 ,另一个三角形的最短边长为 2.5 cm,则它的最长边为( ) A. 3cm B. 4cm C. 4.5cm D. 5cm7.如图,是等边三角形,是等腰直角三角形,于点 , ,过点 作交 于点 ,则下列结论:,于点 ,连 分别交 ,①;②;③;④;⑤.A. 5 B. 4 C. 3 D. 2二、填空题 8.如图,△ABC 中,点 D、E 分別在 AB、AC 上,DE∥BC,AD:DB=1:2,则△ADE 与△ABC 的面积的比 为__________.9.已知且,则=__________.2北师大版七年级数学上册10.如图,直线,直线 交 , , 于点 , , ;直线 交 , , 于点 , , .已知,则 __________.11.如图,E、F、G、H 分别为矩形 ABCD 的边 AB、BC、CD、DA 的中点,连接 AC、HE、EC,GA,GF.已 知 AG⊥GF,AC= ,则 AB 的长为__________.12 . 如 图 ,中,,于 点,于点 ,于点 ,__________ .,则13.矩形 ABCD 中,AB=6,BC=8.点 P 在矩形 ABCD 的内部,点 E 在边 BC 上,满足△PBE∽△DBC,若 △APD 是等腰三角形,则 PE 的长为数___________. 14.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开 门,出东门十五步有木,问:出南门几步而见木?” 用今天的话说,大意是:如图, 是一座边长为 200 步(“步”是古代的长度单位)的正方形小城,东门 位于 的中点,南门 位于 的中点,出东门 15 步的 处有一树木,求出南门多少步恰好看到位于 处的 树木(即点 在直线 上)?请你计算 的长为__________步.3北师大版七年级数学上册15.如图,在直角△ABC 中,∠C=90°,AC=6,BC=8,P、Q 分别为边 BC、AB 上的两个动点,若要使△APQ 是等腰三角形且△BPQ 是直角三角形,则 AQ =________.三、解答题 16.如图,在方格纸中.(1)请在方格纸上建立平面直角坐标系,使,,并求出 点坐标;(2)以原点 为位似中心,相似比为 2,在第一象限内将 放大,画出放大后的图形;(3)计算的面积 .17.如图,在中, 为 上一点,以 为圆心, 长为半径作圆,与 相切于点 ,过点 作交 的延长线于点 ,且.(1)求证: 为 的切线;(2)若,,求 的长.4北师大版七年级数学上册18.如图,在中, =8, =4, =6,, 是 的平分线, 交 于点 ,求 的长.19.已知, 中,, 是 边上一点,作,分别交边 , 于点 , .(1)若(如图 1),求证:.(2)若,过点 作,交 (或 的延长线)于点 .试猜想:线段 , 和 之间的数量关系,并就情形(如图 2)说明理由.(3)若点 与 重合(如图 3), ①求 的度数;,且.②设,,,试证明:.20.(1)(发现)如图①,已知等边△ABC,将直角三角形的 60°角顶点 D 任意放在 BC 边上(点 D 不与点 B、C 重合),使两边分别交线段 AB、AC 于点 E、F.5北师大版七年级数学上册①若 AB=6,AE=4,BD=2,则 CF =________; ②求证:△EBD∽△DCF. (2)(思考)若将图①中的三角板的顶点 D 在 BC 边上移动,保持三角板与 AB、AC 的两个交点 E、F 都存 在,连接 EF,如图②所示.问点 D 是否存在某一位置,使 ED 平分∠BEF 且 FD 平分∠CFE?若存在,求出 的值;若不存在,请说明理由. (3)(探索)如图③,在等腰△ABC 中,AB=AC,点 O 为 BC 边的中点,将三角形透明纸板的一个顶点放 在点 O 处(其中∠MON=∠B),使两条边分别交边 AB、AC 于点 E、F(点 E、F 均不与△ABC 的顶点重合), 连接 EF.设∠B=α,则△AEF 与△ABC 的周长之比为________(用含 α 的表达式表示).21 . 如 图 1, 在中,,,.于点的垂直平分线交 于点 ,交 于点(1)如图 2,作 ①求四边形于点 ,交 于点 ,将 的面积;沿 方向平移,得到,连接 .6。
2018版中考数学《6.3图形的相似》导向(含答案)

§6.3 图形的相似一、选择题 1.(改编题)如图,△ABC 中,DE ∥BC ,AD =5,BD =10,AE =3,则CE 的值为 () A .9 B .6C .3D .4解析 ∵DE ∥BC ,∴AD BD =AE CE ,即510=3CE .解得CE =6.故选B.答案 B2.(原创题)如图,平行四边形ABCD 中,E 为AD 的中点,已知△DEF 的面积为S ,则四边形ABCE 的面积为 ( )A .8SB .9SC .10SD .11S解析 ∵DE ∥BC ,BC =2DE ,∴EF CF =DE BC =12,∴S △DEF S △DCF =12,S △DEF S △BCF =14.∵S △DEF=S ,∴S △BCF =4S ,S △DCF =2S .∴S 四边形ABCE =S 四边形ABCD -S △DEC =9S .故选B. 答案 B3.(改编题)如图,点D ,E ,F 分别是△ABC (AB >AC )各边的中点,下列说法错误的是 ( )A .AD 平分∠BACB .△AEF ∽△ABCC .EF 与AD 互相平分D .△DFE 是△ABC 的位似图形解析 由中位线定理可知EF ∥BC ,∴△AEF ∽△ABC ,故B 正确;由中位线定理可得DE ∥AC ,DF ∥AB ,∴四边形AEDF 是平行四边形,∴EF 与AD 互相平分,故C 正确;∵DE ∥AC ,EF ∥BC ,DF ∥AB ,∴△DFE ∽△ABC .又AD ,BF ,CE 相交于一点,∴△DFE 是△ABC 的位似图形,故D 正确.综上所述,排除B ,C ,D ,故选A.答案 A4. (改编题)在▱ABCD 中,E 为靠近点D 的AD 的三等分点,连结BE ,交AC 于点F ,AC =12,则AF 为( )A .4B .4.8C .5.2D .6解析 ∵E 是AD 的三等分点,∴AE =23AD ,∴AE =23BC .∵AD ∥BC ,∴△AEF ∽△CBF .∴AE CB =AF CF =23.设AF =2x ,则CF =3x ,由题意得,2x +3x =12,x =2.4,∴AF =4.8,故选B.答案 B5.(原创题)如图,已知∠ACB =∠CDB =90°,若添加一个条件,使得△BDC 与△ABC 相似,则下列条件中不符合要求的是( ) A .∠ABC =∠BCDB .∠ABC =∠CBD C.AC BC =AB BD D .AB ∥CD解析 由两角对应相等的两个三角形相似得出A 、B 都符合要求;由AB ∥CD 可得∠ABC =∠BCD ,故D 也符合要求;而C 中给出的四条线段不是两个三角形的对应边,故C 不符合要求.故选C.答案 C二、填空题6.(改编题)如图,▱ABCD 中,点E 是边AD 的中点,EC 交对角线BD 于点F ,则EF ∶FC 等于________.解析 ▱ABCD 中,点E 是边AD 的中点,则ED ∶BC=1∶2,△DEF ∽△BCF ,所以EF ∶FC =ED ∶BC=1∶2.答案 1∶2 7.(原创题)如图,D ,E 分别是AB ,AC 上的两点,添加_______,使得△ADE 和△ACB 相似(添加一个即可).解析 由图可知,∠A 是公共角,故添加∠ADE =∠C或∠AED =∠B ,都可以由两角对应相等得出△ADE ∽△ACB ;添加∠ADE =∠B 或∠AED =∠C ,都可以由两角对应相等得出△ADE ∽△ABC ;添加AD AC =AE AB ,由两对应边的比相等且夹角相等可得△ADE ∽△ACB ;添加AD AB =AE AC ,由两对应边的比相等且夹角相等可得△ADE ∽△ABC ;添加DE ∥BC ,也可得△ADE ∽△ABC ;综上所述,可添加:∠ADE =∠C 或∠AED =∠B 或∠ADE =∠B 或∠AED =∠C 或AD AC =AE AB 或AD AB =AE AC 或DE ∥BC .答案 答案不唯一,如:∠ADE =∠C (或∠AED =∠B 或∠ADE =∠B 或∠AED=∠C 或AD AC =AE AB 或AD AB =AE AC 或DE ∥BC )三、解答题8.(原创题)如图,△ABC 中,AB =8厘米,AC =16厘米,点P 从A 出发,以每秒2厘米的速度向B 运动,点Q 从C 同时出发,以每秒3厘米的速度向A 运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A ,P ,Q 为顶点的三角形与△ABC 相似时,运动时间是多少?解 当△APQ ∽△ABC 时,AP AB =AQ AC .设用t 秒时,以A ,P ,Q 为顶点的三角形与△ABC 相似,则AP =2t ,CQ =3t ,AQ =16-3t .于是2t 8=16-3t 16,解得,t =167.当△APQ∽△ACB时,APAC=AQAB.设用t秒时,以A,P,Q为顶点的三角形与△ABC 相似,则AP=2t,CQ=3t,AQ=16-3t.于是2t16=16-3t8,解得t=4.故答案为:t=167或t=4.。
2018年中考数学《图形的相似》专题练习含答案
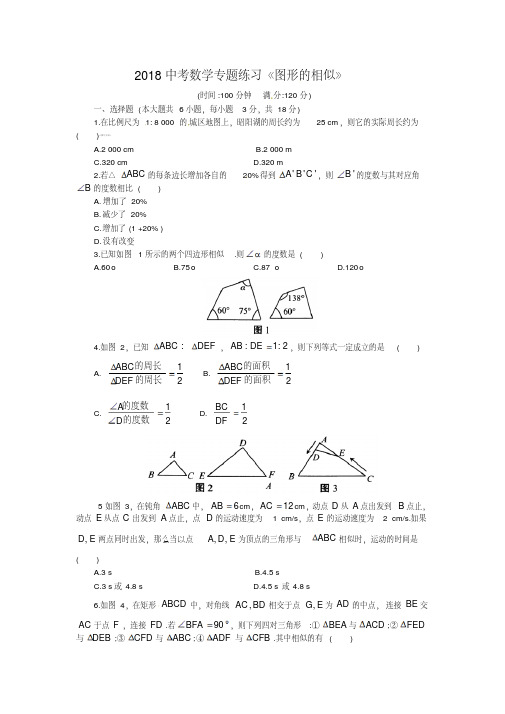
2018中考数学专题练习《图形的相似》(时间:100分钟满分:120分)一、选择题(本大题共6小题,每小题3分,共18分)1.在比例尺为1: 8 000的城区地图上,昭阳湖的周长约为25 cm ,则它的实际周长约为()[来源学科网]A.2 000 cmB.2 000 mC.320 cmD.320 m 2.若△ABC 的每条边长增加各自的20%得到'''A B C ,则'B 的度数与其对应角B 的度数相比()A.增加了20%B.减少了20%C.增加了(1 +20% )D.没有改变3.已知如图1所示的两个四边形相似.则的度数是( )A.60oB.75oC.87 oD.120o4.如图2,已知ABC DEF :,:1:2AB DE,则下列等式一定成立的是( )A.12ABC DEF 的周长的周长 B.12ABC DEF 的面积的面积C. 12A D 的度数的度数D.12BC DF5如图3,在钝角ABC 中,6AB cm ,12AC cm ,动点D 从A 点出发到B 点止,动点E 从点C 出发到A 点止,点D 的运动速度为 1 cm/s ,点E 的运动速度为 2 cm/s.如果,D E 两点同时出发,那么当以点,,A D E 为顶点的三角形与ABC 相似时,运动的时间是() A.3 s B.4.5 s C.3 s 或4.8 sD.4.5 s 或4.8 s6.如图4,在矩形ABCD 中,对角线,AC BD 相交于点,G E 为AD 的中点,连接BE 交AC 于点F ,连接FD .若90BFA ,则下列四对三角形:①BEA 与ACD ;②FED与DEB ;③CFD 与ABC ;④ADF 与CFB .其中相似的有( )。
2018年中考数学专题复习卷:图形的相似(含解析)

图形的相似一、选择题1.已知,下列变形错误的是()A. B.C.D.【答案】B【解析】由得,3a=2b,A. 由得,所以变形正确,故不符合题意;B. 由得3a=2b,所以变形错误,故符合题意;C. 由可得,所以变形正确,故不符合题意;D.3a=2b变形正确,故不符合题意.故答案为:B.【分析】根据已知比例式可得出3a=2b,再根据比例的基本性质对各选项逐一判断即可。
2.如图,已知直线a∥b∥c,直线m分别交直线a、b、c于点A,B,C,直线n分别交直线a、b、c于点D,E,F,若, ,则的值应该()A. 等于B. 大于C. 小于D. 不能确定【答案】B【解析】:如图,过点A作AN∥DF,交BE于点M,交CF于点N∵a∥b∥c∴AD=ME=NF=4(平行线中的平行线段相等)∵AC=AB+BC=2+4=6∴设MB=x,CN=3x∴BE=x+4,CF=3x+4∵∵x>0∴故答案为:B【分析】过点A作AN∥DF,交BE于点M,交CF于点N,根据已知及平行线中的平行线段相等,可得出AD=ME=NF=4,再根据平行线分线段成比例得出BM和CN的关系,设MB=x,CN=3x,分别表示出BE、CF,再求出它们的比,利用求差法比较大小,即可求解。
3.在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为()A. (5,1) B. (4,3) C. (3,4) D. (1,5)【答案】C【解析】:∵以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,∴端点C的横坐标和纵坐标都变为A点的横坐标和纵坐标的一半,又∵A(6,8),∴端点C的坐标为(3,4).故答案为:C.【分析】根据位似图形的性质,位似图形上一个点的坐标等于原图形上对应点的横纵坐标分别乘以位似比,或位似比的相反数。
4.如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE,记△ADE,△BCE的面积分别为S1, S2,()A. 若,则B. 若,则C. 若,则D. 若,则【答案】D【解析】 :如图,过点D作DF⊥AC于点F,过点B作BM⊥AC于点M∴DF∥BM,设DF=h1, BM=h2∴∵DE∥BC∴∴∵若∴设=k<0.5(0<k<0.5)∴AE=AC∙k,CE=AC-AE=AC(1-k),h1=h2k∵S1= AE∙h1= AC∙k∙h1, S2= CE∙h2= AC(1-k)h2∴3S1= k2ACh2, 2S2=(1-K)∙ACh2∵0<k<0.5∴k2<(1-K)∴3S1<2S2故答案为:D【分析】过点D作DF⊥AC于点F,过点B作BM⊥AC于点M,可得出DF∥BM,设DF=h1, BM=h2,再根据DE∥BC,可证得,若,设=k<0.5(0<k<0.5),再分别求出3S1和2S2,根据k的取值范围,即可得出答案。
2018年全国中考数学试卷解析分类汇编(第一期)专题26图形的相似与位似

图形的相似与位似一.选择题1. (2018?淄博第8题,4分)如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD,CD=AB,点E、F分别为AB、AD的中点,则△AEF与多边形BCDFE的面积之比为()A.B.C.D.考点:相似三角形的判定与性质;三角形的面积;三角形中位线定理..专题:压轴题.分析:根据三角形的中位线求出EF=BD,EF∥BD,推出△AEF∽△ABD,得出=,求出==,即可求出△AEF与多边形BCDFE的面积之比.解答:解:连接BD ,∵F 、E 分别为AD 、AB 中点,∴EF=BD ,EF ∥BD ,∴△AEF ∽△ABD ,∴==,∴△AEF 的面积:四边形EFDB 的面积=1:3,∵CD=AB ,CB ⊥DC ,AB ∥CD ,∴==,∴△AEF 与多边形BCDFE 的面积之比为1:(3+2)=1:5,故选C .点评:本题考查了三角形的面积,三角形的中位线等知识点的应用,主要考查学生运用性质进行推理和计算的能力,题目比较典型,难度适中.2.(2018·湖北省武汉市,第6题3分)如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O 为位似中心,相似比为31,在第一象限内把线段AB 缩小后得到线段CD ,则点C 的坐标为()A .(2,1)B .(2,0)C .(3,3)D .(3,1)1.A【解析】∵线段CD 和线段AB 关于原点位似,∴△ODC ∽△OBA ,∴31OBABCD OD ,即3136CD OD ,∴CD =1,OD=2,∴C (2,1).。
6.5图形的相似(第1部分)-2018年中考数学试题分类汇编(word解析版)

第六部分图形的变化6.5 图形的相似【一】知识点清单1、图形的相似比例的性质(补充);比例线段(补充);黄金分割(删);相似图形;相似多边形的性质;相似多边形的判定2、相似三角形平行线分线段成比例;相似三角形的判定;相似三角形的性质;相似三角形的判定与性质;作图—相似变换(删);射影定理(删);3、位似位似变换;作图-位似变换;平面直角坐标系中的位似变换【二】分类试题及参考答案与解析一、选择题1.(2018年重庆A卷-第5题-4分)要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,6cm和9cm,另一个三角形的最短边长为2.5cm,则它的最长边为()A.3cm B.4cm C.4.5cm D.5cm【知识考点】相似三角形的性质.【思路分析】根据相似三角形的对应边成比例求解可得.【解答过程】解:设另一个三角形的最长边长为xcm,根据题意,得:=,解得:x=4.5,即另一个三角形的最长边长为4.5cm,故选:C.【总结归纳】本题主要考查相似三角形的性质,解题的关键是掌握相似三角形的对应角相等,对应边的比相等.2.(2018年广东省-第7题-3分)在△ABC中,点D、E分别为边AB、AC的中点,则△ADE与△ABC 的面积之比为()A.12B.13C.14D.16【知识考点】相似三角形的判定与性质;三角形中位线定理.【思路分析】由点D、E分别为边AB、AC的中点,可得出DE为△ABC的中位线,进而可得出DE∥BC及△ADE∽△ABC,再利用相似三角形的性质即可求出△ADE与△ABC的面积之比.【解答过程】解:∵点D、E分别为边AB、AC的中点,∴DE为△ABC的中位线,∴DE∥BC,∴△ADE∽△ABC,∴=()2=.故选:C.【总结归纳】本题考查了相似三角形的判定与性质以及三角形中位线定理,利用三角形的中位线定理找出DE∥BC是解题的关键.二、填空题1.(2018年北京-第13题-2分)如图,在矩形ABCD中,E是边AB的中点,连接DE交对角线AC 于点F,若AB=4,AD=3,则CF的长为.【知识考点】矩形的性质;相似三角形的判定与性质.【思路分析】根据矩形的性质可得出AB∥CD,进而可得出∠FAE=∠FCD,结合∠AFE=∠CFD(对顶角相等)可得出△AFE∽△CFD,利用相似三角形的性质可得出==2,利用勾股定理可求出AC的长度,再结合CF=•AC,即可求出CF的长.【解答过程】解:∵四边形ABCD为矩形,∴AB=CD,AD=BC,AB∥CD,∴∠FAE=∠FCD,又∵∠AFE=∠CFD,∴△AFE∽△CFD,∴==2.∵AC==5,∴CF=•AC=×5=.故答案为:.【总结归纳】本题考查了相似三角形的判定与性质、矩形的性质以及勾股定理,利用相似三角形的性质找出CF=2AF是解题的关键.2.(2018年宁夏-第12题-3分)已知:23ab=,则22a ba b-+的值是.【知识考点】比例的性质.【思路分析】根据等式的性质,可用a表示b,根据分式的性质,可得答案.【解答过程】解:由=,得b=a.则==﹣,故答案为:﹣.【总结归纳】本题考查了比例的性质,利用等式的性质得出b=a是解题关键,又利用了分式的性质.3.(2018年青海省-第7题-2分)如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且43OEEA=,则FGBC=.【知识考点】位似变换.【思路分析】直接利用位似图形的性质结合位似比等于相似比得出答案.【解答过程】解:∵四边形ABCD与四边形EFGH位似,其位似中心为点O,且=,∴=,则==.故答案为:.【总结归纳】此题主要考查了位似变换,正确掌握位似图形的性质是解题关键.4.(2018年云南省-第5题-3分)如图,已知AB∥CD,若14ABCD=,则OAOC=.。
【精编】2018年中考数学真题汇编 图形的相似

中考数学真题汇编:图形的相似一、选择题1.已知,下列变形错误的是()A. B. C. D.【答案】B2.已知与相似,且相似比为,则与的面积比()A. B. C. D.【答案】D3.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为,和,另一个三角形的最短边长为2.5 cm,则它的最长边为()A. 3cmB. 4cmC. 4.5cmD. 5cm【答案】C4.在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为()A. (5,1)B. (4,3)C. (3,4)D. (1,5)【答案】C5.如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上,若AE= ,AD= ,则两个三角形重叠部分的面积为()A. B. C. D.【答案】D6.在平面直角坐标系中,点是线段上一点,以原点为位似中心把放大到原来的两倍,则点的对应点的坐标为( )A. B. 或 C. D. 或【答案】B7.如图,点在线段上,在的同侧作等腰和等腰,与、分别交于点、.对于下列结论:①;②;③.其中正确的是()∵∠BEA=∠CDA∠PME=∠AMD∴P、E、D、A四点共圆∴∠APD=AED=90°∵∠CAE=180°-∠BAC-∠EAD=90°∴△CAP∽△CMA∴AC2=CP•CM∵AC= AB∴2CB2=CP•CM所以③正确A. ①②③B. ①C. ①②D. ②③【答案】A8.如图,将沿边上的中线平移到的位置,已知的面积为9,阴影部分三角形的面积为4.若,则等于()A. 2B. 3C.D.【答案】A9.学校门口的栏杆如图所示,栏杆从水平位置绕点旋转到位置,已知,,垂足分别为,,,,,则栏杆端应下降的垂直距离为( )A. B. C. D.【答案】C10.如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE,记△ADE,△BCE的面积分别为S1,S2,()A. 若,则B. 若,则C. 若,则D. 若,则【答案】D11.如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是()。
2018年全国各地中考数学真题汇编:图形的相似(含答案)

中考数学真题汇编:图形的相似一、选择题.已知,下列变形错误的是(). . . .【答案】.已知与相似,且相似比为,则与的面积比(). . . .【答案】.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为,和,另一个三角形的最短边长为,则它的最长边为(). . . .【答案】.在平面直角坐标系中,线段两个端点的坐标分别为(,),(,),若以原点为位似中心,在第一象限内将线段缩短为原来的后得到线段,则点的对应点的坐标为(). (,) . (,) . (,) . (,)【答案】.如图,△和△都是等腰直角三角形,,,△的顶点在△的斜边上,若,,则两个三角形重叠部分的面积为().【答案】.在平面直角坐标系中,点是线段上一点,以原点为位似中心把放大到原来的两倍,则点的对应点的坐标为( ). . 或 . . 或【答案】.如图,点在线段上,在的同侧作等腰和等腰,与、分别交于点、.对于下列结论:①;②;③.其中正确的是()∵∠∠∠∠∴、、、四点共圆∴∠°∵∠°∠∠°∴△∽△∴•∵∴•所以③正确. ①②③ . ① . ①② . ②③【答案】.如图,将沿边上的中线平移到的位置,已知的面积为,阴影部分三角形的面积为.若,则等于(). . . .【答案】.学校门口的栏杆如图所示,栏杆从水平位置绕点旋转到位置,已知,,垂足分别为,,,,,则栏杆端应下降的垂直距离为( ). . . .【答案】.如图,在△中,点在边上,∥,与边交于点,连结,记△,△的面积分别为,,(). 若,则 . 若,则. 若,则. 若,则【答案】.如图,菱形的对角线、相交于点,点为边的中点,若菱形的周长为,∠=°,则△的面积是()。
. . . .【答案】.如图,已知是的直径,点在的延长线上,与相切于点,过点作的垂线交的延长线于点,若的半径为,,则的长为(). . . .【答案】二、填空题.如图,△中,点、分别在、上,∥,:=:,则△与△的面积的比为.【答案】.如图,在边长为的小正方形网格中,点、、、都在这些小正方形的顶点上,、相交于点,则∠.【答案】.矩形中,,.点在矩形的内部,点在边上,满足△∽△,若△是等腰三角形,则的长为数.【答案】或.如图,在矩形中,,,点、分别在、上,若,∠°,则的长为.【答案】.如图,、、、分别为矩形的边、、、的中点,连接、、、、,已知⊥,=,则的长为.【答案】.在△中∠°,平分∠平分∠、相交于点,且,则.【答案】.如图,在矩形中,,点为线段上的动点,将沿折叠,使点落在矩形内点处.下列结论正确的是. (写出所有正确结论的序号)①当为线段中点时,;②当为线段中点时,;③当三点共线时,;④当三点共线时,.【答案】①③④.如图,在△中,,,若,边上的中线垂直相交于点,则.【答案】三、解答题.为了测量竖直旗杆的高度,某综合实践小组在地面处竖直放置标杆,并在地面上水平放置个平面镜,使得,,在同一水平线上,如图所示.该小组在标杆的处通过平面镜恰好观测到旗杆顶(此时∠∠).在处测得旗杆顶的仰角为°,平面镜的俯角为°,米,问旗杆的高度约为多少米? (结果保留整数)(参考数据:°≈,°≈)【答案】解:如图,∵,∴∠∠°,∵∠∠,∴∠°,∴∠°,∵∠∠°,∴△∽△,∴,在△中,∠∠∠°°°,°,∴,∴×≈,答:旗杆高约米..如图,在正方形中,点在边上(不与点,重合),连接,作⊥,于点,⊥于点,设。
2018年中考数学试题分项版解析汇编(第02期)专题5.2 图形的相似(含解析)

专题5.2 图形的相似一、单选题1.两三角形的相似比是2:3,则其面积之比是()A.: B. 2:3 C. 4:9 D. 8:27【来源】广西壮族自治区玉林市2018年中考数学试卷【答案】C【解析】【分析】根据相似三角形的面积比等于相似比的平方计算即可.【详解】∵两三角形的相似比是2:3,∴其面积之比是4:9,故选C.【点睛】本题考查了相似三角形的性质,熟练掌握相似三角形的面积比等于相似比的平方是解题的关键. 2.已知△ABC∽△DEF,相似比为2,且△ABC的面积为16,则△DEF的面积为()A. 32 B. 8 C. 4 D. 16【来源】贵州省铜仁市2018年中考数学试题【答案】C点睛:此题考查了相似三角形的性质.此题比较简单,注意掌握相似三角形的面积的比等于相似比的平方的性质的应用.3.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为()A.五丈 B.四丈五尺 C.一丈 D.五尺【来源】吉林省长春市2018年中考数学试卷【答案】B【点睛】本题考查了相似三角形的应用举例,熟知同一时刻物髙与影长成正比是解答此题的关键.4.如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是()A. B. C. D.【来源】黑龙江省哈尔滨市2018年中考数学试题【答案】D【解析】分析:由GE∥BD、GF∥AC可得出△AEG∽△ABD、△DFG∽△DCA,根据相似三角形的性质即可找出,此题得解.详解:∵GE∥BD,GF∥AC,∴△AEG∽△ABD,△DFG∽△DCA,∴,,∴.故选:D.点睛:本题考查了相似三角形的判定与性质,利用相似三角形的性质找出是解题的关键.5.如图,四边形ABCD为平行四边形,E、F为CD边的两个三等分点,连接AF、BE交于点G,则S△EFG:S△ABG=()A. 1:3 B. 3:1 C. 1:9 D. 9:1【来源】湖北省荆门市2018年中考数学试卷【答案】C【点睛】本题考查了平行四边形的性质、相似三角形的判定与性质等知识,熟练掌握和灵活运用平行四边形的性质、相似三角形的判定与性质是解题的关键.6.如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则的值为()A. B. C. D. 1【来源】四川省达州市2018年中考数学试题【答案】C【解析】分析:首先证明AG:AB=CH:BC=1:3,推出GH∥AC,推出△BGH∽△BAC,可得,,由此即可解决问题.点睛:本题考查平行四边形的性质、相似三角形的判定和性质、全等三角形的判定和性质、等高模型等知识,解题的关键是灵活运用所学知识解决问题,属于中考选择题中的压轴题.7.如图所示,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O 为位似中心缩小为原图形的,得到△COD,则CD的长度是()A. 2 B. 1 C. 4 D. 2【来源】湖南省邵阳市2018年中考数学试卷【答案】A【点睛】本题主要考查了位似变换以及坐标与图形的性质,正确把握位似图形的性质是解题关键.8.如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则的值为()A. 1 B. C.-1 D.+1【来源】湖北省随州市2018年中考数学试卷【答案】C【解析】【分析】由DE∥BC可得出△ADE∽△ABC,利用相似三角形的性质结合S△ADE=S四边形BCED,可得出,结合BD=AB﹣AD即可求出的值.【详解】∵DE∥BC,∴∠ADE=∠B,∠AED=∠C,∴△ADE∽△ABC,∴,∵S△ADE=S四边形BCED,S△ABC=S△ADE+S四边形BCED,∴,∴,故选C.【点睛】本题考查了相似三角形的判定与性质,牢记相似三角形的面积比等于相似比的平方是解题的关键.9.如图,在平面直角坐标系中,M、N、C三点的坐标分别为(,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是()A. B. C. D.【来源】广西壮族自治区桂林市2018年中考数学试题【答案】A【解析】分析:分两种情形:当A与点N、M重合时来确定b的最大与最小值即可.详解:如图1,当点A与点N重合时,CA⊥AB,∴MN是直线AB的一部分,∵N(3,1)∴OB=1,此时b=1;当点A与点M重合时,如图2,延长NM交y轴于点D,易证△MCN∽△BMD∴∵MN=3-=,DM=,CN=1∴BD=∴OB=BD-OD=-1=,即b=-,∴b的取值范围是.故选A.点睛:此题考查了坐标与图形,灵活运用相似三角形的判定与性质是解此题的关键..10.如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD =60°,则△OCE的面积是()A. B. 2 C. D. 4【来源】江苏省宿迁市2018年中考数学试卷【答案】A【详解】∵菱形ABCD的周长为16,∴菱形ABCD的边长为4,∵∠BAD=60°,∴△ABD是等边三角形,又∵O是菱形对角线AC、BD的交点,∴AC⊥BD,【点睛】本题考查了相似三角形的判定与性质,等边三角形的判定与性质,勾股定理,菱形的性质,结合图形熟练应用相关性质是解题的关键.11.如图,在△ABC中,EF∥BC,AB=3AE,若S四边形BCFE=16,则S△ABC=()A. 16 B. 18 C. 20 D. 24【来源】广西壮族自治区贵港市2018年中考数学试卷【答案】B【解析】【分析】由EF∥BC,可证明△AEF∽△ABC,利用相似三角形的性质即可求出S△ABC的值.【详解】∵EF∥BC,∴△AEF∽△ABC,∵AB=3AE,∴AE:AB=1:3,∴S△AEF:S△ABC=1:9,设S△AEF=x,∵S四边形BCFE=16,∴,解得:x=2,∴S△ABC=18,故选B.【点睛】本题考查了相似三角形的判定与性质,熟练掌握相似三角形的面积比等于相似比的平方是解本题的关键.12.在△ABC中,点D、E分别为边AB、AC的中点,则△ADE与△ABC的面积之比为()A. B. C. D.【来源】广东省2018年中考数学试题【答案】C【点睛】本题考查了相似三角形的判定与性质、三角形中位线定理,利用三角形的中位线定理找出DE∥BC 是解题的关键.二、填空题13.已知:如图,△ABC的面积为12,点D、E分别是边AB、AC的中点,则四边形BCED的面积为_____.【来源】四川省资阳市2018年中考数学试卷【答案】9【解析】【分析】设四边形BCED的面积为x,则S△ADE=12﹣x,由题意知DE∥BC且DE=BC,从而得,据此建立关于x的方程,解之可得.【点睛】本题主要考查相似三角形的判定与性质,解题的关键是掌握中位线定理及相似三角形的面积比等于相似比的平方的性质.14.如图,在△ABC中,BC=6,BC边上的高为4,在△ABC的内部作一个矩形EFGH,使EF在BC边上,另外两个顶点分别在AB、AC边上,则对角线EG长的最小值为_____.【来源】贵州省贵阳市2018年中考数学试卷【答案】【解析】【分析】作AQ⊥BC于点Q,交DG于点P,设GF=PQ=x,则AP=4﹣x,证△ADG∽△ABC得,据此知EF=DG=(4﹣x),由EG=即可求得答案.【详解】如图,作AQ⊥BC于点Q,交DG于点P,【点睛】本题主要考查相似三角形的判定与性质,解题的关键是掌握矩形的性质、相似三角形的判定与性质及二次函数的性质及勾股定理.15.如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是_____.【来源】上海市2018年中考数学试卷【答案】【详解】作AH⊥BC于H,交GF于M,如图,∵△ABC的面积是6,∴BC•AH=6,∴AH==3,设正方形DEFG的边长为x,则GF=x,MH=x,AM=3﹣x,∵GF∥BC,∴△AGF∽△ABC,∴,即,解得x=,即正方形DEFG的边长为,故答案为:.【点睛】本题考查了相似三角形的判定与性质,正确添加辅助线求出BC边上的高是解题的关键.16.如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120m,则乙楼的高CD是_____m(结果保留根号)【来源】广西钦州市2018年中考数学试卷【答案】40【点睛】此题主要考查了解直角三角形的应用,正确得出tan∠CDA=tan30°=是解题关键.17.如图所示,点E是平行四边形ABCD的边BC延长线上一点,连接AE,交CD于点F,连接BF.写出图中任意一对相似三角形:_____.【来源】湖南省邵阳市2018年中考数学试卷【答案】△ADF∽△ECF【解析】【分析】利用平行四边形的性质得到AD∥CE,则根据相似三角形的判定方法可判断△ADF∽△ECF.【详解】∵四边形ABCD为平行四边形,∴AD∥CE,∴△ADF∽△ECF,故答案为:△ADF∽△ECF.【点睛】本题考查了平行四边形的性质、相似三角形的判定,熟练掌握平行四边形的性质和相似三角形的判定是解题的关键.18.如图,在矩形中,是边的中点,连接交对角线于点,若,,则的长为________.【来源】北京市2018年中考数学试卷【答案】点睛:考查矩形的性质,勾股定理,相似三角形的性质及判定,熟练掌握相似三角形的判定方法和性质是解题的关键.19.如图,与是以点为位似中心的位似图形,相似比为,,,若点的坐标是,则点的坐标是__________.【来源】山东省菏泽市2018年中考数学试题【答案】(2,2)详解:与是以点为位似中心的位似图形,,,若点的坐标是,过点作交于点E.点的坐标为:与的相似比为,点的坐标为:即点的坐标为:故答案为:点睛:考查位似图形的性质,熟练掌握位似图形的性质是解题的关键.三、解答题20.周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.【来源】陕西省2018年中考数学试题【答案】河宽为17米.【解析】【分析】由题意先证明∆ABC∽∆ADE,再根据相似三角形的对应边成比例即可求得AB的长.【点睛】本题考查了相似三角形的应用,熟记相似三角形的判定与性质是解题的关键.21.已知正方形中与交于点,点在线段上,作直线交直线于,过作于,设直线交于.(1)如图,当在线段上时,求证:;(2)如图2,当在线段上,连接,当时,求证:;(3)在图3,当在线段上,连接,当时,求证:.【来源】湖南省常德市2018年中考数学试卷【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.【详解】(1)∵正方形ABCD的对角线AC,BD相交于O,∴OD=OA,∠AOM=∠DON=90°,∴∠OND+∠ODN=90°,∵∠ANH=∠OND,∴∠ANH+∠ODN=90°,∵DH⊥AE,∴∠DHM=90°,∴∠ANH+∠OAM=90°,∴∠ODN=∠OAM,∴△DON≌△AOM,∴OM=ON;∵DN⊥AE,∴▱DENM是菱形,∴DE=EN,∴∠EDN=∠END,∵EN∥BD,∴∠END=∠BDN,∴∠EDN=∠BDN,∵∠BDC=45°,∴∠BDN=22.5°,∵∠AHD=90°,∴∠AMB=∠DME=90°﹣∠BDN=67.5°,∵∠ABM=45°,∴∠BAM=67.5°=∠AMB,∴BM=AB;(3)设CE=a(a>0)∵EN⊥CD,∴∠CEN=90°,∵∠ACD=45°,∴∠CNE=45°=∠ACD,∴EN=CE=a,∴CN=a,∴a=b(已舍去不符合题意的)∴CN=a=b,AC=(a+b)=b,∴AN=AC﹣CN=b,∴AN2=2b2,AC•CN=b•b=2b2∴AN2=AC•CN.【点睛】本题是相似形综合题,涉及到的知识点有正方形的性质、平行四边形、菱形的判定、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理等,判断出四边形DENM是菱形是解(2)的关键,判断出△DEN∽△ADE是解(3)的关键.22.如图①,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,点M为BC中点,N为线段AM上的点,且MB=MN.(1)求证:BN平分∠ABE;(2)若BD=1,连结DN,当四边形DNBC为平行四边形时,求线段BC的长;(3)如图②,若点F为AB的中点,连结FN、FM,求证:△MFN∽△BDC.【来源】四川省眉山市2018年中考数学试题【答案】(1)证明见解析;(2);(3)证明见解析.详解:(1)∵AB=AC,∴∠ABC=∠ACB,∵M为BC的中点,∴AM⊥BC,在Rt△ABM中,∠MAB+∠ABC=90°,在Rt△CBE中,∠EBC+∠ACB=90°,∴∠MAB=∠EBC,又∵MB=MN,∴△MBN为等腰直角三角形,∴∠MNB=∠MBN=45°,∴∠EBC+∠NBE=45°,∠MAB+∠ABN=∠MNB=45°,∴∠NBE=∠ABN,即BN平分∠ABE;(2)设BM=CM=MN=a,∵四边形DNBC是平行四边形,∴DN=BC=2a,在△ABN和△DBN中,∵,∴△ABN≌△DBN(SAS),∴AN=DN=2a,在Rt△ABM中,由AM2+MB2=AB2可得(2a+a)2+a2=1,解得:a=±(负值舍去),∴BC=2a=;点睛:本题主要考查相似形的综合问题,解题的关键是掌握等腰三角形三线合一的性质、直角三角形和平行四边形的性质及全等三角形与相似三角形的判定与性质等知识点.23.在△ABC中,∠ABC=90°.(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN;(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=,求tanC的值;(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=,,直接写出tan∠CEB的值.【来源】湖北省武汉市2018年中考数学试卷【答案】(1)证明见解析;(2);(3).【详解】(1)∵AM⊥MN,CN⊥MN,∴∠AMB=∠BNC=90°,∴∠BAM+∠ABM=90°,∵∠ABC=90°,∴∠ABM+∠CBN=90°,∴∠BAM=∠CBN,∵∠AMB=∠NBC,∴△ABM∽△BCN;(2)如图,过点P作PF⊥AP交AC于F,在Rt△AFP中,tan∠PAC=,同(1)的方法得,△ABP∽△PQF,∴,设AB=a,PQ=2a,BP=b,FQ=2b(a>0,b>0),∵∠BAP=∠C,∠B=∠CQF=90°,∴△ABP∽△CQF,∴,∴CQ==2a,(3)在Rt△ABC中,sin∠BAC=,如图,过点A作AG⊥BE于G,过点C作CH⊥BE交EB的延长线于H,∵∠DEB=90°,∴CH∥AG∥DE,∴,同(1)的方法得,△ABG∽△BCH,∴=,设BG=4m,CH=3m,AG=4n,BH=3n,∵AB=AE,AG⊥BE,∴EG=BG=4m,∴GH=BG+BH=4m+3n,∴,∴n=2m,∴EH=EG+GH=4m+4m+3n=8m+3n=8m+6m=14m,在Rt△CEH中,tan∠BEC=.【点睛】本题是相似形综合题,主要考查了同角的余角相等,相似三角形的判定和性质,锐角三角函数,平行线分线段成比例定理,根据题意添加辅助线构造出图1中的相似三角形模型是解本题的关键.24.如图1所示,在四边形ABCD中,点O,E,F,G分别是AB,BC,CD,AD的中点,连接OE,EF,FG,GO,GE.(1)证明:四边形OEFG是平行四边形;(2)将△OGE绕点O顺时针旋转得到△OMN,如图2所示,连接GM,EN.①若OE=,OG=1,求的值;②试在四边形ABCD中添加一个条件,使GM,EN的长在旋转过程中始终相等.(不要求证明)【来源】湖南省邵阳市2018年中考数学试卷【答案】(1)证明见解析;(2)①;②添加AC=BD.【解析】【分析】(1)连接AC,由四个中点可知OE∥AC、OE=AC,GF∥AC、GF=AC,据此得出OE=GF、OE//GF,即可得证;(2)①由旋转性质知OG=OM、OE=ON,∠GOM=∠EON,据此可证△OGM∽△OEN得;②连接AC、BD,根据①知△OGM∽△OEN,若要GM=EN只需使△OGM≌△OEN,添加使AC=BD的条件均可以满足此条件.【详解】(1)如图1,连接AC,(2)①∵△OGE绕点O顺时针旋转得到△OMN,∴OG=OM、OE=ON,∠GOM=∠EON,∴,∴△OGM∽△OEN,∴;②添加AC=BD,如图2,连接AC、BD,∵点O、E、F、G分别是AB、BC、CD、AD的中点,∴OG=EF=BD、OE=GF=BD,∵AC=BD,【点睛】本题主要考查相似形的综合题,解题的关键是熟练掌握中位线定义及其定理、平行四边形的判定、旋转的性质、相似三角形与全等三角形的判定与性质等知识点.25.如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= °;(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.【来源】江苏省淮安市2018年中考数学试题【答案】(1)15°;(2)BE=.(3)AC=20.【解析】分析:(1)根据“准互余三角形”的定义构建方程即可解决问题;(2)只要证明△CAE∽△CBA,可得CA2=CE•CB,由此即可解决问题;(3)如图②中,将△BCD沿BC翻折得到△BCF.只要证明△FCB∽△FAC,可得CF2=FB•FA,设FB=x,则有:x(x+7)=122,推出x=9或﹣16(舍弃),再利用勾股定理求出AC即可;详解:(1)∵△ABC是“准互余三角形”,∠C>90°,∠A=60°,∴2∠B+∠A=60°,解得,∠B=15°;(2)如图①中,(3)如图②中,将△BCD沿BC翻折得到△BCF.则有:x(x+7)=122,∴x=9或﹣16(舍去),∴AF=7+9=16,在Rt△ACF中,AC=.点睛:本题考查四边形综合题、相似三角形的判定和性质、“准互余三角形”的定义等知识,解题的关键是理解题意,学会利用翻折变换添加辅助线,构造相似三角形解决问题,学会利用已知模型构建辅助线解决问题,属于中考压轴题.26.在△ABC中,E、F分别为线段AB、AC上的点(不与A、B、C重合).(1)如图1,若EF∥BC,求证:(2)如图2,若EF不与BC平行,(1)中的结论是否仍然成立?请说明理由;(3)如图3,若EF上一点G恰为△ABC的重心,,求的值.【来源】湖北省黄石市2018年中考数学试卷【答案】(1)证明见解析;(2)证明见解析;(3)详解:(1)∵EF∥BC,∴△AEF∽△ABC,∴,∴==;(2)若EF不与BC平行,(1)中的结论仍然成立,分别过点F、C作AB的垂线,垂足分别为N、H,∵FN⊥AB、CH⊥AB,∴FN∥CH,∴△AFN∽△ACH,∴,∴==;(3)连接AG并延长交BC于点M,连接BG并延长交AC于点N,连接MN,而==a,∴+ a =a,解得:a=,∴=×=.点睛:本题主要考查相似形的综合问题,解题的关键是熟练掌握相似三角形的判定与性质和三角形重心的定义及其性质等知识点.27.(1)(发现)如图①,已知等边△ABC,将直角三角板的60°角顶点D任意放在BC边上(点D不与点B、C重合),使两边分别交线段AB、AC于点E、F.①若AB=6,AE=4,BD=2,则CF =________;②求证:△EBD∽△DCF.(2)(思考)若将图①中的三角板的顶点D在BC边上移动,保持三角板与边AB、AC的两个交点E、F都存在,连接EF,如图②所示.问点D是否存在某一位置,使ED平分∠BEF且FD平分∠CFE?若存在,求出的值;若不存在,请说明理由.(3)(探索)如图③,在等腰△ABC中,AB=AC,点O为BC边的中点,将三角形透明纸板的一个顶点放在点O处(其中∠MON=∠B),使两条边分别交边AB、AC于点E、F(点E、F均不与△ABC的顶点重合),连接EF.设∠B=α,则△AEF与△ABC的周长之比为________(用含α的表达式表示).【来源】江苏省盐城市2018年中考数学试题【答案】(1)①4;②证明见解析;(2)存在;(3)1-cosα.(1)①先求出BE的长度后发现BE=BD,又∠B=60°,可知△BDE是等边三角形,可得∠BDE=60°,【解析】分析:另外∠EDF=60°,可证得△CDF是等边三角形,从而CF=CD=BC-BD;②证明△EBD∽△DCF,这个模型可称为“一线三等角相似模型”,根据“AA”判定相似;(2)【思考】由平分线可联系到角平分线的性质“角平分线上的点到角两边的距离相等”,可过D作DM⊥BE,DG⊥EF,DN⊥CF,则DM=DG=DN,从而通过证明△BDM≅△CDN可得BD=CD;详解:(1)①∵△ABC是等边三角形,∴AB=BC=AC=6,∠B=∠C=60°,∵AE=4,∴BE=2,则BE=BD,∴△BDE是等边三角形,∴∠BDE=60°,又∵∠EDF=60°,∴∠CDF=180°-∠EDF-∠B=60°,则∠CDF =∠C=60°,∴△CDF是等边三角形,∴CF=CD=BC-BD=6-2=4;②证明:∵∠EDF=60°,∠B=60°∴∠CDF+∠BDE=120°,∠BED+∠BDE=120°,∴∠BED=∠CDF,又∵∠B=∠C,∴△EBD∽△DCF(2)存在.如图,作DM⊥BE,DG⊥EF,DN⊥CF,垂足分别为M,G,N,( 3 )连结AO,作OG⊥BE,OD⊥EF,OH⊥CF,垂足分别为G,D,H,则∠BGO=∠CHO=90°,∵AB=AC,O是BC的中点∴∠B=∠C,OB=OC,∴△OBG≅△OCH,∴OG=OH,GB=CH,∠BOG=∠COH=90°−α,则∠GOH=180°-(∠BOG+∠COH)=2α,∵∠EOF=∠B=α,则∠GOH=2∠EOF=2α,由(2)题可猜想应用EF=ED+DF=EG+FH,则 C△AEF=AE+EF+AF=AE+EG+FH+AF=AG+AH=2AG,设AB=m,则OB=mcosα,GB=mcos2α,.点睛:本题考查了角平分线的定义,等边三角形的性质,全等三角形以及相似三角形的判定和性质等知识点.难度较大.28.如图①,在四边形BCDE中,BC⊥CD,DE⊥CD,AB⊥AE,垂足分别为C,D,A,BC≠AC,点M,N,F分别为AB,AE,BE的中点,连接MN,MF,NF.(1)如图②,当BC=4,DE=5,tan∠FMN=1时,求的值;(2)若tan∠FMN=,BC=4,则可求出图中哪些线段的长?写出解答过程;(3)连接CM,DN,CF,DF.试证明△FMC与△DNF全等;(4)在(3)的条件下,图中还有哪些其它的全等三角形?请直接写出.【来源】山东省威海市2018年中考数学试题【答案】(1);(2)可求线段AD的长;(3)证明见解析;(4)△BMF≌△NFM≌△MAN≌△FNE.(3)根据△ABC和△ADE都是直角三角形,M,N分别是AB,AE的中点,即可得到BM=CM,NA=ND,进而得出∠4=2∠1,∠5=2∠3,根据∠4=∠5,即可得到∠FMC=∠FND,再根据FM=DN,CM=NF,可得△FMC≌△DNF;(4)由BM=AM=FN,MF=AN=NE,∠FMB=∠MFN=∠MAN=∠ENF=90°,即可得到:△BMF≌△NFM≌△MAN≌△FNE.详解:(1)∵点M,N,F分别为AB,AE,BE的中点,∴MF,NF都是△ABE的中位线,∴MF=AE=AN,NF=AB=AM,∴四边形ANFM是平行四边形,又∵AB⊥AE,∴四边形ANFM是矩形,又∵tan∠FMN=1,∴FN=FM,∴矩形ANFM是正方形,AB=AE,(2)可求线段AD的长.由(1)可得,四边形MANF为矩形,MF=AE,NF=AB,∵tan∠FMN=,即=,∴=,∵∠1=∠3,∠C=∠D=90°,∴△ABC∽△EAD,∴==,∵BC=4,∴AD=8;(3)∵BC⊥CD,DE⊥CD,∴△ABC和△ADE都是直角三角形,(4)在(3)的条件下,BM=AM=FN,MF=AN=NE,∠FMB=∠MFN=∠MAN=∠ENF=90°,∴图中有:△BMF≌△NFM≌△MAN≌△FNE.点睛:本题属于相似形综合题,主要考查了全等三角形的判定与性质,相似三角形的判定与性质,直角三角形的性质以及矩形的判定与性质的综合运用,解决问题的关键是判定全等三角形或相似三角形,利用全等三角形的对应边相等,相似三角形的对应边成比例得出有关结论.29.(1)某学校“智慧方园”数学社团遇到这样一个题目:如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=,BO:CO=1:3,求AB的长.经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).请回答:∠ADB= °,AB= .(2)请参考以上解决思路,解决问题:如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.【来源】山东省东营市2018年中考数学试题【答案】(1)75;4;(2)CD=4.详解:(1)∵BD∥AC,∴∠ADB=∠O AC=75°.∵∠BOD=∠COA,∴△BOD∽△COA,∴.又∵AO=3,∴OD=AO=,∴AD=AO+OD=4.∵∠BAD=30°,∠ADB=75°,∴∠ABD=180°-∠BAD-∠ADB=75°=∠ADB,∴AB=AD=4.(2)过点B作BE∥AD交AC于点E,如图所示.∵AC⊥AD,BE∥AD,∴∠DAC=∠BEA=90°.∵∠AOD=∠EOB,∴△AOD∽△EOB,∴.∵BO:OD=1:3,∴.∵AO=3,∴EO=,∴AE=4.∵∠ABC=∠ACB=75°,∴∠BAC=30°,AB=AC,∴AB=2BE.点睛:本题考查了相似三角形的性质、等腰三角形的判定与性质、勾股定理以及平行线的性质,解题的关键是:(1)利用相似三角形的性质求出OD的值;(2)利用勾股定理求出BE、CD的长度.30.如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将△ADP沿AP翻折得到△AD′P,PD′的延长线交边AB于点M,过点B作BN∥MP交DC于点N.(1)求证:AD2=DP•PC;(2)请判断四边形PMBN的形状,并说明理由;(3)如图2,连接AC ,分别交PM ,PB 于点E ,F .若=,求的值.【来源】云南省昆明市2018年中考数学试题【答案】(1)证明见解析;(2)四边形PMBN 是菱形,理由见解析;(3)(3)由于,可设DP=k ,AD=2k ,由(1)可知:AG=DP=k ,PG=AD=2k ,从而求出GB=PC=4k ,AB=AG+GB=5k ,由于CP ∥AB ,从而可证△PCF ∽△BAF ,△PCE ∽△MAE ,从而可得,,从而可求出EF=AF-AE=AC-AC =AC ,从而可得.详解:(1)过点P 作PG ⊥AB 于点G ,∴易知四边形DPGA ,四边形PCBG 是矩形, ∴AD=PG ,DP=AG ,GB=PC ∵∠APB=90°,∴∠APG+∠GPB=∠GPB+∠PBG=90°, ∴∠APG=∠PBG , ∴△APG ∽△PBG ,∴,∴PG 2=AG•GB, 即AD 2=DP•PC; (2)∵DP ∥AB ,∴∠DPA=∠PAM,由题意可知:∠DPA=∠APM,∴∠PAM=∠APM,∵∠APB-∠PAM=∠APB-∠APM,即∠ABP=∠MPB∴AM=PM,PM=MB,∴PM=MB,又易证四边形PMBN是平行四边形,∴四边形PMBN是菱形;又易证:△PCE∽△MAE,AM=AB=,∴∴,∴EF=AF-AE=AC-AC=AC,∴.点睛:本题考查相似三角形的综合问题,涉及相似三角形的性质与判定,菱形的判定,直角三角形斜边上的中线的性质等知识,综合程度较高,需要学生灵活运用所学知识.41。
6.5图形的相似(第3部分)-2018年中考数学试题分类汇编(word解析版)

第六部分 图形的变化 6.5 图形的相似【一】知识点清单 1、图形的相似相似图形;相似多边形的性质;相似多边形的判定 比例的性质(补充);比例线段(补充); 黄金分割(删); 2、相似三角形平行线分线段成比例;相似三角形的判定;相似三角形的性质;相似三角形的判定与性质;作图—相似变换(删);射影定理(删) 3、位似位似变换;作图-位似变换;平面直角坐标系中的位似变换【二】分类试题汇编及参考答案与解析一、选择题1.(2018年贵州省铜仁市-第6题-4分)已知△ABC ∽△DEF ,相似比为2,且△ABC 的面积为16,则△DEF 的面积为( ) A .32B .8C .4D .16【知识考点】相似三角形的性质.【思路分析】由△ABC ∽△DEF ,相似比为2,根据相似三角形的面积的比等于相似比的平方,即可得△ABC 与△DEF 的面积比为4,又由△ABC 的面积为16,即可求得△DEF 的面积. 【解答过程】解:∵△ABC ∽△DEF ,相似比为2, ∴△ABC 与△DEF 的面积比为4, ∵△ABC 的面积为16, ∴△DEF 的面积为:16×=4. 故选:C .【总结归纳】此题考查了相似三角形的性质.此题比较简单,注意掌握相似三角形的面积的比等于相似比的平方的性质的应用.2.(2018年甘肃省白银市/酒泉市/张掖市/武威市/定西市/陇南市-第4题-3分)已知23a b=(a≠0,b≠0),下列变形错误的是( ) A .23a b = B .2a=3b C .32b a = D .3a=2b【知识考点】比例的性质.【思路分析】根据两内项之积等于两外项之积对各选项分析判断即可得解. 【解答过程】解:由23a b=得,3a=2b ,A、由原式可得:3a=2b,正确;B、由原式可得2a=3b,错误;C、由原式可得:3a=2b,正确;D、由原式可得:3a=2b,正确;故选:B.【总结归纳】本题考查了比例的性质,主要利用了两内项之积等于两外项之积.3.(2018年湖南邵阳市-第8题-3分)如图所示,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的12,得到△COD,则CD的长度是()A.2 B.1 C.4 D.【知识考点】位似变换;坐标与图形性质.【思路分析】直接利用位似图形的性质以及结合A点坐标直接得出点C的坐标,即可得出答案.【解答过程】解:∵点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的,得到△COD,∴C(1,2),则CD的长度是:2.故选:A.【总结归纳】此题主要考查了位似变换以及坐标与图形的性质,正确把握位似图形的性质是解题关键.4.(2018年山东省潍坊市-第8题-3分)在平面直角坐标系中,点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB放大到原来的两倍,则点P的对应点的坐标为()A.(2m,2n)B.(2m,2n)或(﹣2m,﹣2n)C.11, 22 m n⎛⎫ ⎪⎝⎭D.11,22m n⎛⎫⎪⎝⎭或11,22m n⎛⎫--⎪⎝⎭【知识考点】位似变换;坐标与图形性质.【思路分析】根据位似变换的性质计算即可.【解答过程】解:点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB放大到原来的两倍,则点P的对应点的坐标为(m×2,n×2)或(m×(﹣2),n×(﹣2)),即(2m,2n)或(﹣2m,﹣2n),故选:B.【总结归纳】本题考查的是位似变换、坐标与图形的性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k ,那么位似图形对应点的坐标的比等于k 或﹣k . 5.(2018年四川省巴中市-第6题-3分)如图,在△ABC 中,点D ,E 分别是边AC ,AB 的中点,BD 与CE 交于点O ,连接DE .下列结论:①OE OD OB OC =;②12DE BC =;③12DOE BOCS S =;④13DOE DBES S=.其中正确的个数有( )A .1个B .2个C .3个D .4个【知识考点】三角形中位线定理;相似三角形的判定与性质.【思路分析】由点D ,E 分别是边AC ,AB 的中点知DE 是△ABC 的中位线,据此知DE ∥BC 且=,从而得△ODE ∽△OBC ,根据相似三角形的性质逐一判断可得.【解答过程】解:∵点D ,E 分别是边AC ,AB 的中点, ∴DE 是△ABC 的中位线, ∴DE ∥BC 且=,②正确;∴∠ODE=∠OBC 、∠OED=∠OCB , ∴△ODE ∽△OBC , ∴===,①错误;=()2=,③错误;∵===,∴=,④正确;故选:B .【总结归纳】本题主要考查相似三角形的判定与性质,解题的关键是掌握中位线定理及相似三角形的判定与性质.二、填空题1.(2018年湖南邵阳市-第12题-3分)如图所示,点E 是平行四边形ABCD 的边BC 延长线上一点,连接AE,交CD于点F,连接BF.写出图中任意一对相似三角形:.【知识考点】相似三角形的判定;平行四边形的性质.【思路分析】利用平行四边形的性质得到AD∥CE,则根据相似三角形的判定方法可判断△ADF∽△ECF.【解答过程】解:∵四边形ABCD为平行四边形,∴AD∥CE,∴△ADF∽△ECF.故答案为△ADF∽△ECF.【总结归纳】本题考查了相似三角形的判定:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;有两组角对应相等的两个三角形相似.也考查了平行四边形的性质.2.(2018年辽宁省锦州市-第12题-3分)如图,在平面直角坐标系中,每个小方格都是边长为1个单位长度的正方形,已知△AOB与△A1OB1位似,位似中心为原点O,且相似比为3:2,点A,B 都在格点上,则点B1的坐标为.【知识考点】坐标与图形性质;位似变换.【思路分析】把B的横纵坐标分别乘以﹣得到B′的坐标.【解答过程】解:由题意得:△AOB与△A1OB1位似,位似中心为原点O,且相似比为3:2,又∵B(3,1)∴B′的坐标是[3×(﹣),1×(﹣)],即B′的坐标是(﹣2,﹣);故答案为:(﹣2,﹣).【总结归纳】本题考查了位似变换:先确定点的坐标,及相似比,再分别把横纵坐标与相似比相乘即可,注意原图形与位似图形是同侧还是异侧,来确定所乘以的相似比的正负.3.(2018年四川省南充市-第15题-3分)如图,在△ABC中,DE∥BC,BF平分∠ABC,交DE的延长线于点F.若AD=1,BD=2,BC=4,则EF=.【知识考点】相似三角形的判定与性质;等腰三角形的判定与性质.【思路分析】由DE∥BC可得出△ADE∽△ABC,根据相似三角形的性质和平行线的性质解答即可.【解答过程】解:∵DE∥BC,∴∠F=∠FBC,∵BF平分∠ABC,∴∠DBF=∠FBC,∴∠F=∠DBF,∴DB=DF,∵DE∥BC,∴△ADE∽△ABC,∴,即,解得:DE=,∵DF=DB=2,∴EF=DF﹣DE=2﹣,故答案为:【总结归纳】此题考查相似三角形的判定和性质,关键是由DE∥BC可得出△ADE∽△ABC.4.(2018年浙江省嘉兴市舟山市-第12题-4分)如图,直线l1∥l2∥l3,直线AC交l1,l2,l3于点A,B,C;直线DF交l1,l2,l3于点D,E,F,已知13ABAC,则EFDE=.【知识考点】平行线分线段成比例.【思路分析】根据题意求出,根据平行线分线段成比例定理解答.【解答过程】解:∵=,∴=2,∵l1∥l2∥l3,∴==2,故答案为:2.【总结归纳】本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.三、解答题1.(2018年四川省巴中市-第25题-8分)在如图所示的平面直角坐标系中,已知点A(﹣3,﹣3),点B(﹣1,﹣3),点C(﹣1,﹣1).(1)画出△ABC;(2)画出△ABC关于x轴对称的△A1B1C1,并写出A1点的坐标:;(3)以O为位似中心,在第一象限内把△ABC扩大到原来的两倍,得到△A2B2C2,并写出A2点的坐标:.【知识考点】作图﹣轴对称变换;作图﹣位似变换.【思路分析】(1)根据A、B、C三点坐标画出图形即可;(2)作出A、B、C关于轴的对称点A1、B1、C1即可;(3)延长OC到C2,使得OC2=2OC,同法作出A2,B2即可;【解答过程】解:(1)△ABC如图所示;(2)△A1B1C1如图所示;A1(﹣3,3),(3)△A2B2C2如图所示;A2(6,6).故答案为(﹣3,3),(6,6).【总结归纳】本题考查作图﹣位似变换,轴对称变换等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.。
教育最新K122018年中考数学真题汇编 图形的相似

中考数学真题汇编:图形的相似一、选择题1.已知,下列变形错误的是()A. B.C.D.【答案】B2.已知与相似,且相似比为,则与的面积比()A. B.C.D.【答案】D3.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为,和,另一个三角形的最短边长为2.5 cm,则它的最长边为()A. 3cmB. 4cmC. 4.5cmD. 5cm【答案】C4.在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为()A. (5,1)B. (4,3) C. (3,4) D. (1,5)【答案】C5.如图,△ACB 和△ECD 都是等腰直角三角形,CA=CB ,CE=CD ,△ACB 的顶点A 在△ECD 的斜边DE 上,若AE=,AD=,则两个三角形重叠部分的面积为( )A. B. C. D.【答案】D6.在平面直角坐标系中,点是线段上一点,以原点 为位似中心把放大到原来的两倍,则点 的对应点的坐标为( )A.B. 或C.D.或【答案】B 7.如图,点 在线段 上,在的同侧作等腰和等腰, 与、分别交于点 、.对于下列结论:①;②;③.其中正确的是( )∵∠BEA=∠CDA ∠PME=∠AMD∴P 、E 、D 、A 四点共圆 ∴∠APD=AED=90°∵∠CAE=180°-∠BAC-∠EAD=90° ∴△CAP ∽△CMA ∴AC 2=CP•CM ∵AC=AB∴2CB 2=CP•CM所以③正确A. ①②③B. ①C. ①②D. ②③【答案】A8.如图,将沿边上的中线平移到的位置,已知的面积为9,阴影部分三角形的面积为4.若,则等于()A. 2B. 3C.D.【答案】A9.学校门口的栏杆如图所示,栏杆从水平位置绕点旋转到位置,已知,,垂足分别为,,,,,则栏杆端应下降的垂直距离为( )A. B.C.D.【答案】C10.如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE,记△ADE,△BCE的面积分别为S1, S2,()A. 若,则B. 若,则C. 若,则D. 若,则【答案】D11.如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD =60°,则△OCE的面积是()。
【2018中考数学真题+分类汇编】一期26图形的相似与位似试题含解析377【2018数学中考真题分项汇编系列】

图形的相似与位似一、选择题1..(2018•山东枣庄•3分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF 平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为()A.B.C.D.【分析】根据三角形的内角和定理得出∠CAF+∠CFA=90°,∠FAD+∠AED=90°,根据角平分线和对顶角相等得出∠CEF=∠CFE,即可得出EC=FC,再利用相似三角形的判定与性质得出答案.【解答】解:过点F作FG⊥AB于点G,∵∠ACB=90°,CD⊥AB,∴∠CDA=90°,∴∠CAF+∠CFA=90°,∠FAD+∠AED=90°,∵AF平分∠CAB,∴∠CAF=∠FAD,∴∠CFA=∠AED=∠CEF,∴CE=CF,∵AF平分∠CAB,∠ACF=∠AGF=90°,∴FC=FG,∵∠B=∠B,∠FGB=∠ACB=90°,∴△BFG∽△BAC,∴=,∵AC=3,AB=5,∠ACB=90°,∴BC=4,∴=,∵FC=FG,∴=,解得:FC=,即CE的长为.故选:A.【点评】本题考查了直角三角形性质、等腰三角形的性质和判定,三角形的内角和定理以及相似三角形的判定与性质等知识,关键是推出∠CEF=∠CFE.2.(2018•山东滨州•3分)在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为()A.(5,1)B.(4,3)C.(3,4)D.(1,5)【分析】利用位似图形的性质,结合两图形的位似比进而得出C点坐标.【解答】解:∵以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,∴端点C的横坐标和纵坐标都变为A点的横坐标和纵坐标的一半,又∵A(6,8),∴端点C的坐标为(3,4).故选:C.【点评】此题主要考查了位似图形的性质,利用两图形的位似比得出对应点横纵坐标关系是解题关键.3 (2018•江苏扬州•3分)如图,点A在线段BD上,在BD的同侧做等腰Rt△ABC和等腰Rt △ADE,CD与BE、AE分别交于点P,M.对于下列结论:①△BAE∽△CAD;②MP•MD=MA•ME;③2CB2=CP•CM.其中正确的是()A.①②③B.①C.①② D.②③【分析】(1)由等腰Rt△ABC和等腰Rt△ADE三边份数关系可证;(2)通过等积式倒推可知,证明△PAM∽△EMD即可;(3)2CB2转化为AC2,证明△ACP∽△MCA,问题可证.【解答】解:由已知:AC=AB,AD=AE∴∵∠BAC=∠EAD∴∠BAE=∠CAD∴△BAE∽△CAD所以①正确∵△BAE∽△CAD∴∠BEA=∠CDA∵∠PME=∠AMD∴△PME∽△AMD∴∴MP•MD=MA•ME所以②正确∵∠BEA=∠CDA∠PME=∠AMD∴P、E、D、A四点共圆∴∠APD=∠EAD=90°∵∠CAE=180°﹣∠BAC﹣∠EAD=90°∴△CAP∽△CMA∴AC2=CP•CM∵AC=AB∴2CB2=CP•CM所以③正确故选:A.【点评】本题考查了相似三角形的性质和判断.在等积式和比例式的证明中应注意应用倒推的方法寻找相似三角形进行证明,进而得到答案.4 (2018·山东临沂·3分)如图.利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,测得AB=1.6m.BC=12.4m.则建筑物CD的高是()A.9.3m B.10.5m C.12.4m D.14m【分析】先证明∴△ABE∽△ACD,则利用相似三角形的性质得=,然后利用比例性质求出CD即可.【解答】解:∵EB∥CD,∴△ABE∽△ACD,∴=,即=,∴CD=10.5(米).故选:B.【点评】本题考查了相似三角形的应用:借助标杆或直尺测量物体的高度.利用杆或直尺测量物体的高度就是利用杆或直尺的高(长)作为三角形的边,利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.5(2018·山东潍坊·3分)在平面直角坐标系中,点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB放大到原来的两倍,则点P的对应点的坐标为()A.(2m,2n)B.(2m,2n)或(﹣2m,﹣2n)C.(m,n)D.(m,n)或(﹣m,﹣n)【分析】根据位似变换的性质计算即可.【解答】解:点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB放大到原来的两倍,则点P的对应点的坐标为(m×2,n×2)或(m×(﹣2),n×(﹣2)),即(2m,2n)或(﹣2m,﹣2n),故选:B.【点评】本题考查的是位似变换、坐标与图形的性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.6.(2018•湖南省永州市•4分)如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为()A.2 B.4 C.6 D.8【分析】只要证明△ADC∽△ACB,可得=,即AC2=AD•AB,由此即可解决问题;【解答】解:∵∠A=∠A,∠ADC=∠ACB,∴△ADC∽△ACB,∴=,∴AC2=AD•AB=2×8=16,∵AC>0,∴AC=4,故选:B.【点评】本题考查相似三角形的判定和性质、解题的关键是正确寻找相似三角形解决问题,属于中考常考题型.7 (2018·四川宜宾·3分)如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于()A.2 B.3 C.D.【考点】Q2:平移的性质.【分析】由S△ABC=9、S△A′EF=4且AD为BC边的中线知S△A′DE=S△A′EF=2,S△ABD=S△ABC=,根据△DA′E∽△DAB知()2=,据此求解可得.【解答】解:如图,∵S△ABC=9、S△A′EF=4,且AD为BC边的中线,∴S△A′DE=S△A′EF=2,S△ABD=S△ABC=,∵将△ABC沿BC边上的中线AD平移得到△A'B'C',∴A′E∥AB,∴△DA′E∽△DAB,则()2=,即()2=,解得A′D=2或A′D=﹣(舍),故选:A.【点评】本题主要平移的性质,解题的关键是熟练掌握平移变换的性质与三角形中线的性质、相似三角形的判定与性质等知识点.8(2018·四川自贡·4分)如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积为4,则△ABC的面积为()A.8 B.12 C.14 D.16【分析】直接利用三角形中位线定理得出DE∥BC,DE=BC,再利用相似三角形的判定与性质得出答案.【解答】解:∵在△ABC中,点D、E分别是AB、AC的中点,∴DE∥BC,DE=BC,∴△ADE∽△ABC,∵=,∴=,∵△ADE的面积为4,∴△ABC的面积为:16,故选:D.【点评】此题主要考查了三角形的中位线以及相似三角形的判定与性质,正确得出△ADE∽△ABC是解题关键.9(2018·台湾·分)小柔要榨果汁,她有苹果、芭乐、柳丁三种水果,且其颗数比为9:7:6,小柔榨完果汁后,苹果、芭乐、柳丁的颗数比变为6:3:4,已知小柔榨果汁时没有使用柳丁,关于她榨果汁时另外两种水果的使用情形,下列叙述何者正确?()A.只使用苹果B.只使用芭乐C.使用苹果及芭乐,且使用的苹果颗数比使用的芭乐颗数多D.使用苹果及芭乐,且使用的芭乐颗数比使用的苹果颗数多【分析】根据三种水果的颗数的关系,设出三种水果的颗数,再根据榨果汁后的颗数的关系,求出榨果汁后,苹果和芭乐的颗数,进而求出苹果,芭乐的用量,即可得出结论.【解答】解:∵苹果、芭乐、柳丁三种水果,且其颗数比为9:7:6,∴设苹果为9x颗,芭乐7x颗,铆钉6x颗(x是正整数),∵小柔榨果汁时没有使用柳丁,∴设小柔榨完果汁后,苹果a颗,芭乐b颗,∵小柔榨完果汁后,苹果、芭乐、柳丁的颗数比变为6:3:4,∴,,∴a=9x,b=x,∴苹果的用量为9x﹣a=9x﹣9x=0,芭乐的用量为7x﹣b=7x﹣x=x>0,∴她榨果汁时,只用了芭乐,故选:B.【点评】此题是推理与论证题目,主要考查了根据比例的关系,比例的性质,求出榨汁后苹果和芭乐的数量是解本题的关键.10 (2018·台湾·分)如图,△ABC、△FGH中,D、E两点分别在AB、AC上,F点在DE上,G、H两点在BC上,且DE∥BC,FG∥AB,FH∥AC,若BG:GH:HC=4:6:5,则△ADE与△FGH 的面积比为何?()A.2:1 B.3:2 C.5:2 D.9:4【分析】只要证明△ADE∽△FGH,可得=()2,由此即可解决问题;【解答】解:∵BG:GH:HC=4:6:5,可以假设BG=4k,GH=6k,HC=5k,∵DE∥BC,FG∥AB,FH∥AC,∴四边形BGFD是平行四边形,四边形EFHC是平行四边形,∴DF=BG=4k,EF=HC=5k,DE=DF+EF=9k,∠FGH=∠B=∠ADE,∠FHG=∠C=∠AED,∴△ADE∽△FGH,∴=()2=()2=.故选:D.【点评】本题考查相似三角形的判定和性质,平行四边形的判定和性质等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.11.(2018•湖北荆门•3分)如图,四边形ABCD为平行四边形,E、F为CD边的两个三等分点,连接AF、BE交于点G,则S△EFG:S△ABG=()A.1:3 B.3:1 C.1:9 D.9:1【分析】利用相似三角形的性质面积比等于相似比的平方即可解决问题;【解答】解:∵四边形ABCD是平行四边形,∴CD=AB,CD∥AB,∵DE=EF=FC,∴EF:AB=1:3,∴△EFG∽△BAG,∴=()2=,故选:C.【点评】本题考查平行四边形的性质、相似三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.12.(2018•湖北恩施•3分)如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点.已知FG=2,则线段AE的长度为()A.6 B.8 C.10 D.12【分析】根据正方形的性质可得出AB∥CD,进而可得出△ABF∽△GDF,根据相似三角形的性质可得出==2,结合FG=2可求出AF、AG的长度,由CG∥AB、AB=2CG可得出CG为△EAB的中位线,再利用三角形中位线的性质可求出AE的长度,此题得解.【解答】解:∵四边形ABCD为正方形,∴AB=CD,AB∥CD,∴∠ABF=∠GDF,∠BAF=∠DGF,∴△ABF∽△GDF,∴==2,∴AF=2GF=4,∴AG=6.∵CG∥AB,AB=2CG,∴CG为△EAB的中位线,∴AE=2AG=12.故选:D.【点评】本题考查了相似三角形的判定与性质、正方形的性质以及三角形的中位线,利用相似三角形的性质求出AF的长度是解题的关键.13. (2018·浙江临安·3分)如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是()A.B.C.D.【考点】相似三角形的判定,【分析】根据正方形的性质求出∠ACB,根据相似三角形的判定定理判断即可.【解答】解:由正方形的性质可知,∠ACB=180°﹣45°=135°,A、C、D图形中的钝角都不等于135°,由勾股定理得,BC=,AC=2,对应的图形B中的边长分别为1和,∵=,∴图B中的三角形(阴影部分)与△ABC相似,故选:B.【点评】本题考查的是相似三角形的判定,掌握两组对应边的比相等且夹角对应相等的两个三角形相似是解题的关键.14(2018·浙江临安·3分)如图,在△ABC中,DE∥BC,DE分别与AB,AC相交于点D,E,若AD=4,DB=2,则DE:BC的值为()A.B.C.D.【考点】相似三角形的判定和相似三角形的性质【分析】根据平行于三角形一边的直线和其他两边相交,所截得的三角形与原三角形相似,再根据相似三角形的对应边成比例解则可.【解答】解:∵DE∥BC,∴△ADE∽△ABC,∴===.故选:A.【点评】本题考查了相似三角形的判定和相似三角形的性质,对应边不要搞错.15(2018·重庆(A)·4分)要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,6cm和9cm,另一个三角形的最短边长为2.5cm,则它的最长边为A. 3cmB. 4cmC. 4.5cmD. 5cm【考点】相似三角形的性质【解析】利用相似三角形三边对应成比例解出即可。
【2018中考数学真题+分类汇编】三期26图形的相似与位似试题含解析391【2018数学中考真题分项汇编系列】

图形的相似与位似一.选择题1. (2018·广西梧州·3分)如图,AG:GD=4:1,BD:DC=2:3,则AE:EC的值是()A.3:2 B.4:3 C.6:5 D.8:5【分析】过点D作DF∥CA交BE于F,如图,利用平行线分线段成比例定理,由DF∥CE得到==,则CE=DF,由DF∥AE得到===,则AE=4DF,然后计算的值.【解答】解:过点D作DF∥CA交BE于F,如图,∵DF∥CE,∴=,而BD:DC=2:3,∴=,则CE=DF,∵DF∥A E,∴=,∵AG:GD=4:1,∴=,则AE=4DF,∴==.故选:D.【点评】本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.2.(2018·四川省攀枝花·3分)如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作Rt△ABC,使∠BAC=90°,∠ACB=30°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是()A.B.C.D.解:如图所示:过点C作CD⊥y轴于点D.∵∠BAC=90°,∴∠DAC+∠OAB=90°.∵∠DCA+∠DAC=90°,∴∠DCA=∠OAB.又∵∠CDA=∠AOB=90°,∴△CDA∽△AOB,∴===tan30°,则=,故y=x+1(x>0),则选项C符合题意.故选C.3.(2018·重庆市B卷)(4.00分)制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是()A.360元B.720元C.1080元D.2160元【分析】根据题意求出长方形广告牌每平方米的成本,根据相似多边形的性质求出扩大后长方形广告牌的面积,计算即可.【解答】解:3m×2m=6m2,∴长方形广告牌的成本是120÷6=20元/m2,将此广告牌的四边都扩大为原来的3倍,则面积扩大为原来的9倍,∴扩大后长方形广告牌的面积=9×6=54m2,∴扩大后长方形广告牌的成本是54×20=1080m2,故选:C.【点评】本题考查的是相似多边形的性质,掌握相似多边形的面积比等于相似比的平方是解题的关键.4.(2018·辽宁省盘锦市)如图,已知在▱ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F,则下列选项中的结论错误的是()A.FA:FB=1:2 B.AE:BC=1:2C.BE:CF=1:2 D.S△ABE:S△FBC=1:4【解答】解:∵四边形ABCD是平行四边形,∴CD∥AB,CD=AB,∴△DEC∽△AEF,∴==.∵E为AD的中点,∴CD=AF,FE=EC,∴FA:FB=1:2,A说法正确,不符合题意;∵FE=EC,FA=AB,∴AE:BC=1:2,B说法正确,不符合题意;∵∠FBC不一定是直角,∴BE:CF不一定等于1:2,C说法错误,符合题意;∵AE∥BC,AE=BC,∴S△ABE:S△FBC=1:4,D说法正确,不符合题意;故选C.5. (2018•乐山•3分)如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是()A.EG=4GC B.EG=3GC C.EG=GC D.EG=2GC解:∵DE∥FG∥BC,DB=4FB,∴.故选B.6. (2018•莱芜•3分)如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:①AE=BC②AF=CF③BF2=FG•FC④EG•AE=BG•AB其中正确的个数是()A.1 B.2 C.3 D.4【分析】①只要证明△ADE为直角三角形即可②只要证明△AEF≌△CBF(SAS)即可;③假设BF2=FG•FC,则△FBG∽△FCB,推出∠FBG=∠FCB=45°,由∠ACF=45°,推出∠ACB=90°,显然不可能,故③错误,④由△ADF∽△GBF,可得==,由EG∥CD,推出==,推出=,由AD=AE,EG•AE=BG•AB,故④正确,【解答】解:①DE平分∠ADC,∠ADC为直角,∴∠ADE=×90°=45°,∴△ADE为直角三角形∴AD=AE,又∵四边形ABCD矩形,∴AD=BC,∴AE=BC②∵∠BFE=90°,∠BFE=∠AED=45°,∴△BFE为等腰直角三角形,∴则有EF=BF又∵∠AEF=∠DFB+∠ABF=135°,∠CBF=∠ABC+∠ABF=135°,∴∠AEF=∠CBF在△AEF和△CBF中,AE=BC,∠AEF=∠CBF,EF=BF,∴△AEF≌△CBF(SAS)∴AF=CF③假设BF2=FG•FC,则△FBG∽△FCB,∴∠FBG=∠FCB=45°,∵∠ACF=45°,∴∠ACB=90°,显然不可能,故③错误,④∵∠BGF=180°﹣∠CGB,∠DAF=90°+∠EAF=90°+(90°﹣∠AGF)=180°﹣∠AGF,∠AGF=∠BGC,∴∠DAF=∠BGF,∵∠ADF=∠FBG=45°,∴△ADF∽△GBF,∴==,∵EG∥CD,∴==,∴=,∵AD=AE,∴EG•AE=BG•AB,故④正确,故选:C.【点评】本题考查相似三角形的判定和性质、矩形的性质、等腰直角三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.7.(2018·吉林长春·3分)《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为()A.五丈 B.四丈五尺 C.一丈 D.五尺【分析】根据同一时刻物高与影长成正比可得出结论.【解答】解:设竹竿的长度为x尺,∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,∴,解得x=45(尺).故选:B.【点评】本题考查的是相似三角形的应用,熟知同一时刻物髙与影长成正比是解答此题的关键.二.填空题1. (2018·广西贺州·3分)如图,正方形ABCD的边长为12,点E在边AB上,BE=8,过点E作EF∥BC,分别交BD.CD于G、F两点.若点P、Q分别为DG、CE的中点,则PQ的长为.【解答】解:作QM⊥EF于点M,作PN⊥EF于点N,作QH⊥PN交PN的延长线于点H,如右图所示,∵正方形ABCD的边长为12,BE=8,EF∥BC,点P、Q分别为DG、CE的中点,∴DF=4,CF=8,EF=12,∴MQ=4,PN=2,MF=6,∵QM⊥EF,PN⊥EF,BE=8,DF=4,∴△EGB∽△FGD,∴,即,解得,FG=4,∴FN=2,∴MN=6﹣2=4,∴QH=4,∵PH=PN+QM,∴PH=6,∴PQ==,故答案为:2.2. (2018·广西梧州·3分)如图,点C为Rt△ACB与Rt△DCE的公共点,∠ACB=∠DCE=90°,连接AD.BE,过点C作CF⊥AD于点F,延长FC交BE于点G.若AC=BC=25,CE=15,DC=20,则的值为.【分析】过E作EH⊥GF于H,过B作BP⊥GF于P,依据△EHG∽△BPG,可得=,再根据△DCF∽△CEH,△ACF∽△CBP,即可得到EH=CF,BP=CF,进而得出=.【解答】解:如图,过E作EH⊥GF于H,过B作BP⊥GF于P,则∠EHG=∠BPG=90°,又∵∠EGH=∠BGP,∴△EHG∽△BPG,∴=,∵CF⊥AD,∴∠DFC=∠AFC=90°,∴∠DFC=∠CHF,∠AFC=∠CPB,又∵∠ACB=∠DCE=90°,∴∠CDF=∠ECH,∠FAC=∠PCB,∴△DCF∽△CEH,△ACF∽△CBP,∴==,==1,∴EH=CF,BP=CF,∴=,∴=,故答案为:.【点评】本题主要考查了相似三角形的判定与性质,解决问题的关键是作辅助线构造相似三角形,利用相似三角形的对应边成比例进行推算.3.(2018·云南省·3分)如图,已知AB∥CD,若=,则= .【分析】利用相似三角形的性质即可解决问题;【解答】解:∵AB∥CD,∴△AOB∽△COD,∴==,故答案为.【点评】本题考查平行线的性质,相似三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.4.(2018·辽宁省沈阳市)(3.00分)如图,△ABC是等边三角形,AB=,点D是边BC上一点,点H是线段AD上一点,连接BH、CH.当∠BHD=60°,∠AHC=90°时,DH= .【分析】作AE⊥BH于E,BF⊥AH于F,如图,利用等边三角形的性质得AB=AC,∠BAC=60°,再证明∠ABH=∠CAH,则可根据“AAS”证明△ABE≌△CAH,所以BE=AH,AE=CH,在Rt△AHE 中利用含30度的直角三角形三边的关系得到HE=AH,AE=AH,则CH=AH,于是在Rt △AHC中利用勾股定理可计算出AH=2,从而得到BE=2,HE=1,AE=CH=,BH=1,接下来在Rt△BFH中计算出HF=,BF=,然后证明△CHD∽△BFD,利用相似比得到=2,从而利用比例性质可得到DH的长.【解答】解:作AE⊥BH于E,BF⊥AH于F,如图,∵△ABC是等边三角形,∴AB=AC,∠BAC=60°,∵∠BHD=∠ABH+∠BAH=60°,∠BAH+∠CAH=60°,∴∠ABH=∠CAH,在△ABE和△CAH中,∴△ABE≌△CAH,∴BE=AH,AE=CH,在Rt△AHE中,∠AHE=∠BHD=60°,∴sin∠AHE=,HE=AH,∴AE=AH•sin60°=AH,∴CH=AH,在Rt△AHC中,AH2+(AH)2=AC2=()2,解得AH=2,∴BE=2,HE=1,AE=CH=,∴BH=BE﹣HE=2﹣1=1,在Rt△BFH中,HF=BH=,BF=,∵BF∥CH,∴△CHD∽△BFD,∴===2,∴DH=HF=×=.故答案为.【点评】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了全等三角形的判定与性质和等边三角形的性质.5.(2018·辽宁省抚顺市)(3.00分)如图,△AOB三个顶点的坐标分别为A(8,0),O(0,0),B(8,﹣6),点M为OB的中点.以点O为位似中心,把△AOB缩小为原来的,得到△A′O′B′,点M′为O′B′的中点,则MM′的长为或.【分析】分两种情形画出图形,即可解决问题;【解答】解:如图,在Rt△AOB中,OB==10,①当△A′OB′在第三象限时,MM′=.②当△A″OB″在第二象限时,MM′=,故答案为或.【点评】本题考查位似变换,坐标与图形的性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.6.(2018·江苏常州·2分)如图,在△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,过点P沿直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么AP长的取值范围是3≤AP<4 .【分析】分四种情况讨论,依据相似三角形的对应边成比例,即可得到AP的长的取值范围.【解答】解:如图所示,过P作PD∥AB交BC于D或PE∥BC交AB于E,则△PCD∽△ACB 或△APE∽△ACB,此时0<AP<4;如图所示,过P作∠APF=∠B交AB于F,则△APF∽△ABC,此时0<AP≤4;如图所示,过P作∠CPG=∠CBA交BC于G,则△CPG∽△CBA,此时,△CPG∽△CBA,当点G与点B重合时,CB2=CP×CA,即22=CP×4,∴CP=1,AP=3,∴此时,3≤AP<4;综上所述,AP长的取值范围是3≤AP<4.故答案为:3≤AP<4.【点评】本题主要考查了相似三角形的性质,相似三角形的对应角相等,对应边的比相等.三.解答题1.(2018·广西梧州·10分)如图,AB是⊙M的直径,BC是⊙M的切线,切点为B,C是BC 上(除B点外)的任意一点,连接CM交⊙M于点G,过点C作DC⊥BC交BG的延长线于点D,连接AG并延长交BC于点E.(1)求证:△ABE∽△BCD;(2)若MB=BE=1,求CD的长度.【分析】(1)根据直径所对圆周角和切线性质,证明三角形相似;(2)利用勾股定理和面积法得到AG、GE,根据三角形相似求得GH,得到MB.GH和CD的数量关系,求得CD.【解答】(1)证明:∵BC为⊙M切线∴∠ABC=90°∵DC⊥BC∴∠BCD=90°∴∠ABC=∠BCD∵AB是⊙M的直径∴∠AGB=90°即:BG⊥AE∴∠CBD=∠A∴△ABE∽△BCD(2)解:过点G作GH⊥BC于H∵MB=BE=1∴AB=2∴AE=由(1)根据面积法AB•BE=BG•AE∴BG=由勾股定理:AG=,GE=∵GH∥AB∴∴∴GH=又∵GH∥AB①同理:②①+②,得∴∴CD=【点评】本题是几何综合题,综合考察了圆周角定理、切线性质和三角形相似.解答时,注意根据条件构造相似三角形.2. (2018·湖北十堰·8分)如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作FG⊥AC于点F,交AB的延长线于点G.(1)求证:FG是⊙O的切线;(2)若tanC=2,求的值.【分析】(1)欲证明FG是⊙O的切线,只要证明OD⊥FG;(2)由△GDB∽△GAD,设BG=a.可得===,推出DG=2a,AG=4a,由此即可解决问题;【解答】(1)证明:连接AD.OD.∵AB是直径,∴∠ADB=90°,即AD⊥BC,∵AC=AB,∴CD=BD,∵OA=OB,∴OD∥AC,∵DF⊥AC,∴OD⊥DF,∴FG是⊙O的切线.(2)解:∵tanC==2,BD=CD,∴BD:AD=1:2,∵∠GDB+∠ODB=90°,∠ADO+∠ODB=90°,∵OA=OD,∴∠OAD=∠ODA,∴∠GDB=∠GAD,∵∠G=∠G,∴△GDB∽△GAD,设BG=a.∴===,∴DG=2a,AG=4a,∴BG:GA=1:4.【点评】本题考查相似三角形的判定和性质、等腰三角形的性质、三角形中位线定理、圆周角定理、切线的判定等知识,解题的关键是学会添加常用辅助线,构造三角形中位线或相似三角形解决问题,属于中考常考题型.3. (2018•乐山•10分)如图,P是⊙O外的一点,PA.PB是⊙O的两条切线,A.B是切点,PO交AB于点F,延长BO交⊙O于点C,交PA的延长交于点Q,连结AC.(1)求证:AC∥PO;(2)设D为PB的中点,QD交AB于点E,若⊙O的半径为3,CQ=2,求的值.(1)证明:∵P A.PB是⊙O的两条切线,A.B是切点,∴PA=PB,且PO平分∠BPA,∴PO⊥AB.∵BC是直径,∴∠CAB=90°,∴AC⊥AB,∴AC∥PO;(2)解:连结OA.DF,如图,∵P A.PB是⊙O的两条切线,A.B是切点,∴∠OAQ=∠PBQ=90°.在Rt△OAQ中,OA=OC=3,∴OQ=5.由QA2+OA2=OQ2,得QA=4.在Rt△PBQ中,PA=PB,QB=OQ+OB=8,由QB2+PB2=PQ2,得82+PB2=(PB+4)2,解得PB=6,∴PA=PB=6.∵OP⊥AB,∴BF=AF=AB.又∵D为PB的中点,∴DF∥AP,DF=PA=3,∴△DFE∽△QEA,∴ ==,设AE=4t,FE=3t,则AF=AE+FE=7t,∴BE=BF+FE=AF+FE=7t+3t=10t,∴ ==.4. (2018•莱芜•9分)已知△ABC中,AB=AC,∠BAC=90°,D.E分别是AB.AC的中点,将△ADE绕点A按顺时针方向旋转一个角度α(0°<α<90°)得到△AD'E′,连接BD′、CE′,如图1.(1)求证:BD′=CE';(2)如图2,当α=60°时,设AB与D′E′交于点F,求的值.(1)首先依据旋转的性质和中点的定义证明AD′=AE′,然后再利用SAS证明△BD′A 【分析】≌△CE′A,最后,依据全等三角形的性质进行证明即可;(2)连接DD′,先证明△ADD′为等边三角形,然后再证明△△ABD′为直角三角形,接下来,再证明△BFD′∽△AFE′,最后,依据相似三角形的性质求解即可.【解答】解:(1)证明:∵AB=AC,D.E分别是AB.AC的中点,∴AD=BD=AE=EC.由旋转的性质可知:∠DAD′=∠EAE′=α,AD′=AD,AE′=AE.∴AD′=AE′,∴△BD′A≌△CE′A,∴BD′=CE′.(2)连接DD′.∵∠DAD′=60°,AD=AD′,∴△ADD′是等边三角形.∴∠ADD′=∠AD′D=60°,DD′=DA=DB.∴∠DBD′=∠DD′B=30°,∴∠BD′A=90°.∵∠D′AE′=90°,∴∠BAE′=30°,∴∠BAE′=∠ABD′,又∵∠BFD′=∠AFE′,∴△BFD′∽△AFE′,∴.∵在Rt△ABD′中,tan∠BAD′==,∴=.【点评】本题主要考查的是全等三角形的判定和性质、相似三角形的性质和判定、旋转的性质,发现△BFD′∽△AFE′是解题的关键.5. (2018•陕西•7分)周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C.A共线.已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.【答案】河宽为17米.【解析】【分析】由题意先证明∆ABC∽∆ADE,再根据相似三角形的对应边成比例即可求得AB的长.【详解】∵CB⊥AD,ED⊥AD,∴∠CBA=∠EDA=90°,∵∠CAB=∠EAD,∴∆ABC∽∆ADE,∴,又∵AD=AB+BD,BD=8.5,BC=1,DE=1.5,∴,∴AB=17,即河宽为17米.【点睛】本题考查了相似三角形的应用,熟记相似三角形的判定与性质是解题的关键.。
2018年中考数学专题复习卷:图形的相似(含解析)

图形的相似一、选择题1.已知,下列变形错误的是()A. B.C.D.【答案】B【解析】由得,3a=2b,A. 由得,所以变形正确,故不符合题意;B. 由得3a=2b,所以变形错误,故符合题意;C. 由可得,所以变形正确,故不符合题意;D.3a=2b变形正确,故不符合题意.故答案为:B.【分析】根据已知比例式可得出3a=2b,再根据比例的基本性质对各选项逐一判断即可。
2.如图,已知直线a∥b∥c,直线m分别交直线a、b、c于点A,B,C,直线n分别交直线a、b、c于点D,E,F,若, ,则的值应该()A. 等于B. 大于C. 小于D. 不能确定【答案】B【解析】:如图,过点A作AN∥DF,交BE于点M,交CF于点N∵a∥b∥c∴AD=ME=NF=4(平行线中的平行线段相等)∵AC=AB+BC=2+4=6∴设MB=x,CN=3x∴BE=x+4,CF=3x+4∵∵x>0∴故答案为:B【分析】过点A作AN∥DF,交BE于点M,交CF于点N,根据已知及平行线中的平行线段相等,可得出AD=ME=NF=4,再根据平行线分线段成比例得出BM和CN的关系,设MB=x,CN=3x,分别表示出BE、CF,再求出它们的比,利用求差法比较大小,即可求解。
3.在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为()A. (5,1)B. (4,3) C. (3,4) D. (1,5)【答案】C【解析】:∵以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,∴端点C的横坐标和纵坐标都变为A点的横坐标和纵坐标的一半,又∵A(6,8),∴端点C的坐标为(3,4).故答案为:C.【分析】根据位似图形的性质,位似图形上一个点的坐标等于原图形上对应点的横纵坐标分别乘以位似比,或位似比的相反数。
4.如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE,记△ADE,△BCE的面积分别为S1, S2,()A. 若,则B. 若,则C. 若,则D. 若,则【答案】D【解析】 :如图,过点D作DF⊥AC于点F,过点B作BM⊥AC于点M∴DF∥BM,设DF=h1, BM=h2∴∵DE∥BC∴∴∵若∴设=k<0.5(0<k<0.5)∴AE=AC∙k,CE=AC-AE=AC(1-k),h1=h2k∵S1= AE∙h1= AC∙k∙h1, S2= CE∙h2= AC(1-k)h2∴3S1= k2ACh2, 2S2=(1-K)∙ACh2∵0<k<0.5∴k2<(1-K)∴3S1<2S2故答案为:D【分析】过点D作DF⊥AC于点F,过点B作BM⊥AC于点M,可得出DF∥BM,设DF=h1, BM=h2,再根据DE∥BC,可证得,若,设=k<0.5(0<k<0.5),再分别求出3S1和2S2,根据k的取值范围,即可得出答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学真题汇编:图形的相似一、选择题1.已知,下列变形错误的是()A. B. C. D.【答案】B2.已知与相似,且相似比为,则与的面积比()A. B. C. D.【答案】D3.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为,和,另一个三角形的最短边长为2.5 cm,则它的最长边为()A. 3cmB. 4cmC. 4.5cmD. 5cm【答案】C4.在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为()A. (5,1)B. (4,3)C. (3,4)D. (1,5)【答案】C5.如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上,若AE= ,AD= ,则两个三角形重叠部分的面积为()A. B. C. D.【答案】D6.在平面直角坐标系中,点是线段上一点,以原点为位似中心把放大到原来的两倍,则点的对应点的坐标为( )A. B. 或 C. D. 或【答案】B7.如图,点在线段上,在的同侧作等腰和等腰,与、分别交于点、.对于下列结论:①;②;③.其中正确的是()∵∠BEA=∠CDA∠PME=∠AMD∴P、E、D、A四点共圆∴∠APD=AED=90°∵∠CAE=180°-∠BAC-∠EAD=90°∴△CAP∽△CMA∴AC2=CP•CM∵AC= AB∴2CB2=CP•CM所以③正确A. ①②③B. ①C. ①②D. ②③【答案】A8.如图,将沿边上的中线平移到的位置,已知的面积为9,阴影部分三角形的面积为4.若,则等于()A. 2B. 3C.D.【答案】A9.学校门口的栏杆如图所示,栏杆从水平位置绕点旋转到位置,已知,,垂足分别为,,,,,则栏杆端应下降的垂直距离为( )A. B. C. D.【答案】C10.如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE,记△ADE,△BCE的面积分别为S1,S2,()A. 若,则B. 若,则C. 若,则D. 若,则【答案】D11.如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD 的周长为16,∠BAD=60°,则△OCE的面积是()。
A. B. 2 C. D. 4【答案】A12.如图,已知AB是的直径,点P在BA的延长线上,PD与相切于点D,过点B作PD的垂线交PD的延长线于点C,若的半径为4,,则PA的长为()A. 4B.C. 3D. 2.5【答案】A二、填空题13.如图,△ABC中,点D、E分别在AB、AC上,DE∥BC,AD:DB=1:2,则△ADE 与△ABC的面积的比为________.【答案】1:914.如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则tan∠AOD=________.【答案】215.矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE ∽△DBC,若△APD是等腰三角形,则PE的长为数________.【答案】3或1.216.如图,在矩形ABCD中,AB=2,BC=4,点E、F分别在BC、CD上,若AE= ,∠EAF=45°,则AF的长为________.【答案】17.如图,E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,连接AC、HE、EC、GA、GF,已知AG⊥GF,AC=,则AB的长为________.【答案】218.在Rt△ABC中∠C=90°,AD平分∠CAB,BE平分∠CBA,AD、BE相交于点F,且AF=4,EF= ,则AC=________.【答案】19.如图,在矩形中,,点为线段上的动点,将沿折叠,使点落在矩形内点处.下列结论正确的是________. (写出所有正确结论的序号)①当为线段中点时,;②当为线段中点时,;③当三点共线时,;④当三点共线时,.【答案】①③④20.如图,在△ABC中,AC=3,BC=4,若AC,BC边上的中线BE,AD垂直相交于点O,则AB=________.【答案】三、解答题21.为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米? (结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)【答案】解:如图,∵FM//BD,∴∠FED=∠MFE=45°,∵∠DEF=∠BEA,∴∠AEB=45°,∴∠FEA=90°,∵∠FDE=∠ABE=90°,∴△FDE∽△ABE,∴,在Rt△FEA中,∠AFE=∠MFE+∠MFA=45°+39.3°=84.3°,tan84.3°= ,∴,∴AB=1.8×10.02≈18,答:旗杆AB高约18米.22.如图,在正方形ABCD中,点G在边BC上(不与点B,C重合),连接AG,作DE⊥AG,于点E,BF⊥AG于点F,设。
(1)求证:AE=BF;(2)连接BE,DF,设∠EDF= ,∠EBF= 求证:(3)设线段AG与对角线BD交于点H,△AHD和四边形CDHG的面积分别为S1和S2,求的最大值.【答案】(1)因为四边形ABCD是正方形,所以∠BAF+∠EAD=90°,又因为DE⊥AG,所以∠EAD+∠ADE=90°,所以∠ADE=∠BAF,又因为BF⊥AG,所以∠DEA=∠AFB=90°,又因为AD=AB所以Rt△DAE≌Rt△ABF,所以AE=BF(2)易知Rt△BFG∽Rt△DEA,所以在Rt△DEF和Rt△BEF中,tanα= ,tanβ=所以ktanβ= = = = =tanα所以(3)设正方形ABCD的边长为1,则BG=k,所以△ABG的面积等于k因为△ABD的面积等于=又因为=k,所以S1所以S=1- k- =2所以=-k2+k+1= ≤因为0<k<1,所以当k= ,即点G为BC中点时,有最大值23.如图,以的直角边为直径作交斜边于点,过圆心作,交于点,连接.(1)判断与的位置关系并说明理由;(2)求证:;(3)若,,求的长.【答案】(1)解:DE是圆O的切线证明:连接OD∵OE∥AC∴∠1=∠3,∠2=∠A∵OA=OD∴∠1=∠A∴∠2=∠3在△BOE和△DOE中OE=OD,∠2=∠3,OE=OE∴△BOE≌△DOE(SAS)∴∠ODE=∠OBE=90°∴OD⊥DE∴DE是圆O的切线(2)解:证明:连接BD∵AB是直径∴∠BDC=∠ADB=∠ABC=90°∵OE∥AC,O是AB的中点∴OE是△ABC的中位线∴AC=2OE∵∠BDC=∠ABC,∠C=∠C∴△ABC∽△BDC∴∴BC2=2CD•OE∵BC=2DE,∴(2DE)2=2CD•OE∴(3)解:∵设:BD=4x,CD=3x∵在△BDC中,,∴BC=2DE=5∴(4x)2+(3x)2=25解之:x=1,x=-1(舍去)∴BD=4∵∠ABD=∠C∴AD=BD•tan∠ABD=24.若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.(1)已知△ABC是比例三角形,AB=2,BC=3.请直接写出所有满足条件的AC的长;(2)如图1,在四边形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAC=∠ADC.求证:△ABC是比例三角形;(3)如图2,在(2)的条件下,当∠ADC=90°时,求的值。
【答案】(1)或或.(2)证明:∵AD∥BC,∴∠ACB =∠CAD,又∵∠BAC=∠ADC,∴△ABC∽△DCA,∴= ,即CA2=BC·AD,又∵AD∥BC,∴∠ADB=∠CBD,∵BD平分∠ABC,∴∠ABD=∠CBD,∴∠ADB=∠ABD,∴AB=AD,∴CA2=BC·AB,∴△ABC是比例三角形.(3)解:如图,过点A作AH⊥BD于点H,∵AB=AD,∴BH= BD,∴AD∥BC,∠ADC=90°,∴∠BHA=∠BCD=90°,又∵∠ABH=∠DBC,∴△ABH∽△DBC,∴= ,∴AB·BC=DB·BH,∴AB·BC= BD2,又∵AB·BC=AC2,∴BD2=AC2,∴= .。
