双曲线(一等奖课件)
合集下载
双曲线及其标准方程(公开课)公开课一等奖

详细描述
双曲线的焦点距离公式是根据双曲线的标准方程中的系数计算得出的。这个公式可以帮助我们了解双 曲线的形状和大小,以及焦点在双曲线上的位置。通过焦点距离公式,我们可以进一步研究双曲线的 性质和特点。
05 双曲线与其他曲线的对比
CHAPTER
与椭圆的对比
01 02
形状
双曲线和椭圆都是二次曲线,但它们的形状和结构有所不同。双曲线有 两个分支,分别向两个方向无限延伸,而椭圆则是一个封闭的形状,由 两个焦点和连接它们的线段所形成。
此时,双曲线的两个顶点位于y轴上,坐标分别为 $(0, -a)$ 和 $(0, a)$。
双曲线的焦距为 $2c$,其中 $c = sqrt{a^2 + b^2}$。
双曲线标准方程的推导
通过平面几何的方法,我们可以推导出双曲线的标准方程。
首先,设双曲线的焦点到任一点 $P(x, y)$ 的距离之差为常数 $2a$,即 $|PF_1 - PF_2| = 2a$。
此时,双曲线的两个顶点位于x轴上, 坐标分别为 $(-a, 0)$ 和 $(a, 0)$。
双曲线的焦距为 $2c$,其中 $c = sqrt{a^2 + b^2}$。
焦点在y轴上
焦点在y轴上时,双曲线的标准方程为 $frac{y^2}{a^2} frac{x^2}{b^2} = 1$,其中 $a$ 和 $b$ 是常数,分别表示双曲线的实 半轴和虚半轴的长度。
根据平面几何的性质和勾股定理,我们可以推导出双曲线的标准方程为 $frac{x^2}{a^2} frac{y^2}{b^2} = 1$ 或 $frac{y^2}{a^2} - frac{x^2}{b^2} = 1$。
03 双曲线的应用
CHAPTER
双曲线的焦点距离公式是根据双曲线的标准方程中的系数计算得出的。这个公式可以帮助我们了解双 曲线的形状和大小,以及焦点在双曲线上的位置。通过焦点距离公式,我们可以进一步研究双曲线的 性质和特点。
05 双曲线与其他曲线的对比
CHAPTER
与椭圆的对比
01 02
形状
双曲线和椭圆都是二次曲线,但它们的形状和结构有所不同。双曲线有 两个分支,分别向两个方向无限延伸,而椭圆则是一个封闭的形状,由 两个焦点和连接它们的线段所形成。
此时,双曲线的两个顶点位于y轴上,坐标分别为 $(0, -a)$ 和 $(0, a)$。
双曲线的焦距为 $2c$,其中 $c = sqrt{a^2 + b^2}$。
双曲线标准方程的推导
通过平面几何的方法,我们可以推导出双曲线的标准方程。
首先,设双曲线的焦点到任一点 $P(x, y)$ 的距离之差为常数 $2a$,即 $|PF_1 - PF_2| = 2a$。
此时,双曲线的两个顶点位于x轴上, 坐标分别为 $(-a, 0)$ 和 $(a, 0)$。
双曲线的焦距为 $2c$,其中 $c = sqrt{a^2 + b^2}$。
焦点在y轴上
焦点在y轴上时,双曲线的标准方程为 $frac{y^2}{a^2} frac{x^2}{b^2} = 1$,其中 $a$ 和 $b$ 是常数,分别表示双曲线的实 半轴和虚半轴的长度。
根据平面几何的性质和勾股定理,我们可以推导出双曲线的标准方程为 $frac{x^2}{a^2} frac{y^2}{b^2} = 1$ 或 $frac{y^2}{a^2} - frac{x^2}{b^2} = 1$。
03 双曲线的应用
CHAPTER
高三一轮复习双曲线名师公开课获奖课件百校联赛一等奖课件

研究双曲线几何性质时的两个注意点: (1)实半轴、虚半轴所构成的直角三角形是值得关注的一个重点; (2)由于 e=ac是一个比值,故只需根据条件得到关于 a,b,c 的 一个关系式,利用 b2=c2-a2 消去 b,然后变形即可求 e,并注 意 e>1.
栏目 导引
第八章 平面解析几何
3.(1)(2014·云南省昆明市高三调研测试)已知 F(c,0)是双曲线 C:xa22-by22=1(a>0,b>0)的右焦点,若双曲线 C 的渐近线与圆 F: (x-c)2+y2=12c2 相切,则双曲线 C 的离心率为____2____; (2)(2012·高考天津卷)已知双曲线 C1:xa22-by22=1(a>0,b>0)与双 曲线 C2:x42-1y62 =1 有相同的渐近线,且 C1 的右焦点为 F( 5, 0),则 a=____1____,b=_____2___.
栏目 导引
第八章 平面解析几何
2.求适合下列条件的双曲线的标准方程: (1)虚轴长为 12,离心率为54; (2)焦距为 26,且经过点 M(0,12). 【解】(1)设双曲线的标准方程为 xa22-yb22=1 或ay22-xb22=1(a>0,b>0).
栏目 导引
第八章 平面解析几何
由题意知,2b=12,e=ca=54,∴b=6,c=10,a=8.∴双曲 线的标准方程为6x42-3y62 =1 或6y42 -3x62=1. (2)∵双曲线经过点 M(0,12),∴M(0,12)为双曲线的一个 顶点, 故焦点在 y 轴上,且 a=12.
则双曲线xa22-yb22=1
的离心率
13 e=____3____.
5.设 F1,F2 是双曲线 x2-2y42 =1 的两个焦点,P 是双曲线
栏目 导引
第八章 平面解析几何
3.(1)(2014·云南省昆明市高三调研测试)已知 F(c,0)是双曲线 C:xa22-by22=1(a>0,b>0)的右焦点,若双曲线 C 的渐近线与圆 F: (x-c)2+y2=12c2 相切,则双曲线 C 的离心率为____2____; (2)(2012·高考天津卷)已知双曲线 C1:xa22-by22=1(a>0,b>0)与双 曲线 C2:x42-1y62 =1 有相同的渐近线,且 C1 的右焦点为 F( 5, 0),则 a=____1____,b=_____2___.
栏目 导引
第八章 平面解析几何
2.求适合下列条件的双曲线的标准方程: (1)虚轴长为 12,离心率为54; (2)焦距为 26,且经过点 M(0,12). 【解】(1)设双曲线的标准方程为 xa22-yb22=1 或ay22-xb22=1(a>0,b>0).
栏目 导引
第八章 平面解析几何
由题意知,2b=12,e=ca=54,∴b=6,c=10,a=8.∴双曲 线的标准方程为6x42-3y62 =1 或6y42 -3x62=1. (2)∵双曲线经过点 M(0,12),∴M(0,12)为双曲线的一个 顶点, 故焦点在 y 轴上,且 a=12.
则双曲线xa22-yb22=1
的离心率
13 e=____3____.
5.设 F1,F2 是双曲线 x2-2y42 =1 的两个焦点,P 是双曲线
双曲线的性质市公开课一等奖省赛课微课金奖PPT课件

∴
双曲线焦点在
x
轴上,∴设双曲线方程为
x2 a2
y2 b2
1 (a>0,b>0),
∴
b4 a3 (3)2
a2
(2
3 b2
)2
解之得
a2
9 4
,∴
1
b2 4
双曲线方程为 x2 9 4
y2 4
1
法二:巧设方程,利用待定系数法. ⑴设双曲线方程为 x2 y2 ( 0) ,
(3)2 (2
第7页
二、导出双曲线 y2 a2
x2 b2
1(a
0,b 0)
的简单几何性质
y
(1)范围: y a, y a
(2)对称性: 关于x轴、y轴、原点都对称
a
(3)顶点: (0,-a)、(0,a)
(4)渐近线: y a x
b
(5)离心率: e c a
-b o b x -a
第8页
小结
性 质 图象
顶点是A1(a, 0)、A2 (a, 0) 只有两个!
(2)线段A1 A2 :双曲线实轴,长为2a,
a:实半轴长;
线段B1B2 :双曲线虚轴,长为2b,
b:虚半轴长
y
b B2
(3)实轴与虚轴等长双曲线 叫等轴双曲线
x2 y 2 m(m 0)
A1 -a o a A2
x
-b B1
第4页
4、渐近线
双曲线性质
第1页
定义 图象
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
y
y
M
M
F2
F1 o F2 x
x
F1
方程
双曲线及其标准方程市公开课一等奖省赛课获奖课件

第17页
变式训练
1.求适合下列条件的双曲线的标准方程. (1)焦点分别为 F1(-10,0),F2(10,0),且经过点(3 5,- 4(2));经过点(3,0),(-6,-3). 解:(1)由题设知双曲线的焦点在 x 轴上,且 c=10.所以可 设它的标准方程为xa22-by22=1(a>0,b>0).从而将双曲线 的标准方程化为100x-2 b2-by22=1,将点(3 5,-4)代入并 化简整理,得 b4-39b2-1 600=0,解得 b2=64 或 b2=- 25(舍去),故所求双曲线的标准方程为3x62-6y42 =1.
第20页
变式训练
2.设双曲线x2-y2= 49
1,
F1、
F2
是其两个焦点,点
M
在双
曲线上.
(1)若∠F1MF2=90°,求△F1MF2 的面积; (2)若∠F1MF2=60°时,△F1MF2 的面积是多少?
第21页
解:(1)由双曲线方程知 a=2,b=3,c= 13, 设|MF1|=r1,|MF2|=r2(r1>r2). 由双曲线定义得 r1-r2=2a=4, 两边平方得 r21+r22-2r1·r2=16, 即|F1F2|2-4S△F1MF2=16, 即 4S△F1MF2=52-16, ∴S△F1MF2=9. (2)若∠F1MF2=60°,在△F1MF2 中, 由余弦定理得|F1F2|2=r21+r22-2r1r2cos 60°, |F1F2|2=(r1-r2)2+r1r2, ∴r1r2=36, 则 S△F1MF2=12r1r2sin 60°=9 3.
第24页
第18页
(2)设双曲线的方程为 mx2+ny2=1(mn<0), ∵双曲线经过点(3,0),(-6,-3), ∴9m+0=1,
变式训练
1.求适合下列条件的双曲线的标准方程. (1)焦点分别为 F1(-10,0),F2(10,0),且经过点(3 5,- 4(2));经过点(3,0),(-6,-3). 解:(1)由题设知双曲线的焦点在 x 轴上,且 c=10.所以可 设它的标准方程为xa22-by22=1(a>0,b>0).从而将双曲线 的标准方程化为100x-2 b2-by22=1,将点(3 5,-4)代入并 化简整理,得 b4-39b2-1 600=0,解得 b2=64 或 b2=- 25(舍去),故所求双曲线的标准方程为3x62-6y42 =1.
第20页
变式训练
2.设双曲线x2-y2= 49
1,
F1、
F2
是其两个焦点,点
M
在双
曲线上.
(1)若∠F1MF2=90°,求△F1MF2 的面积; (2)若∠F1MF2=60°时,△F1MF2 的面积是多少?
第21页
解:(1)由双曲线方程知 a=2,b=3,c= 13, 设|MF1|=r1,|MF2|=r2(r1>r2). 由双曲线定义得 r1-r2=2a=4, 两边平方得 r21+r22-2r1·r2=16, 即|F1F2|2-4S△F1MF2=16, 即 4S△F1MF2=52-16, ∴S△F1MF2=9. (2)若∠F1MF2=60°,在△F1MF2 中, 由余弦定理得|F1F2|2=r21+r22-2r1r2cos 60°, |F1F2|2=(r1-r2)2+r1r2, ∴r1r2=36, 则 S△F1MF2=12r1r2sin 60°=9 3.
第24页
第18页
(2)设双曲线的方程为 mx2+ny2=1(mn<0), ∵双曲线经过点(3,0),(-6,-3), ∴9m+0=1,
双曲线及其标准方程 公开课 公开课 一等奖

③ 列式
M1FM2F2a
2020/3/22
④化简
将上述方程化为: x c 2 y 2x c 2 y 2 2 a
移项两边平方后整理得:c xa2axc2y2
两边再平方后整理得: c 2 a 2 x 2 a 2 y 2 a 2 c 2 a 2
两边同时除以 a2c2a2 得:
x2
y2
题后反思:
变式训练 若|PF1|-|PF2|=8呢?
x2 y2 1(x 0) 16 9
求标准方程要做 到先定型,后定 量。
2020/3/22
x 求焦点在 轴上,经过点 ( 2, 3),( 15, 2) 3 的双曲线的标准方程 .
知识迁移 深化认知
例2 :
方程 x2 y2 1 表示焦点在y轴双曲线时, 2m m1
3 a 2 , b 2 , c 6( 0 ,6 ) . ( 0 , 6 )
4 a 3 ,b 2 ,c 5 (5 ,0 ) ,( 5 ,0 )
2020/3/22
例1、已知双曲线的焦点 F1(-5,0), F2(5,0),双曲线上 一点P到焦点的距离差的绝对值等于8,求双曲线的
标准方程。
y2x2 1(a0,b0) a2 b2
y M
F2 x
O
F1
如果 x 2的系数是正的,则焦点在 x轴上;如果
y 2 的系数是正的,则焦点在 y轴上。
2020/3/22
感受标准方程
通过描点大致画出图像
x2- y 2 =1 4
同学们:恭喜通过第三关
①
开普勒
③
2020/3/22
华罗庚
②
伽利略
④
牛顿
第4关:
则m的取值范围___m_______2___.
高中数学新人教A版选修精品双曲线的参数方程市公开课一等奖省优质课获奖课件.pptx
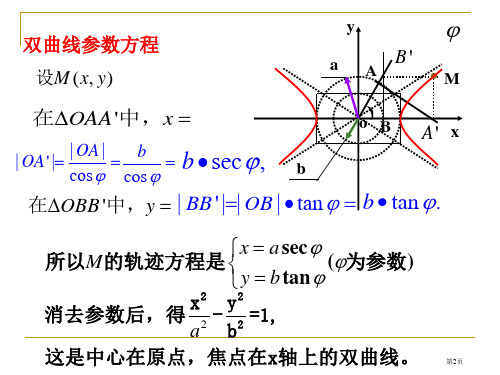
双曲线参数方程
设M (x, y)
y
a
B'
A
•M
在OAA'中,x
| OA' | | OA | b b • sec,
cos cos
b
o B A' x
在OBB '中,y | BB ' || OB | • tan b • tan.
所以M的轨迹方程是
x y
a b
sec tan
(为参数)
消去参数后,得 x2 - y2 =1,
解:双曲线的渐近线方程为:y b x.
a
不妨设M为双曲线右支上一点,其坐标为(asec,btan),
ቤተ መጻሕፍቲ ባይዱ
y
则直线MA的方程为:y b tan b (x a sec).
将y=
b
a x代入①,解得点A的横坐标为
同设理A可aOx得=,,x点则A =Bta2(的ans横ec坐b标.为taxnB =)a2(. sec tan).
a2 b2
这是中心在原点,焦点在x轴上的双曲线。 第2页
双曲线参数方程
x2 - y2 =1(a>0,b>0)的参数方程为: a2 b2
y
a
A B' • M
x
y
a b
sec tan
(为参数)
通常规定 [o,2 )且
,
3
b
。
22
说明:
o B A' x
⑴ 这里参数 叫做双曲线离心角与直线OM倾斜角不一样.
⑵se双c2曲线参1数t方an程2 能相够比由较方而程得到,ax22所以by22双与曲1三线角参恒数等方式程
实质是三角代换.
设M (x, y)
y
a
B'
A
•M
在OAA'中,x
| OA' | | OA | b b • sec,
cos cos
b
o B A' x
在OBB '中,y | BB ' || OB | • tan b • tan.
所以M的轨迹方程是
x y
a b
sec tan
(为参数)
消去参数后,得 x2 - y2 =1,
解:双曲线的渐近线方程为:y b x.
a
不妨设M为双曲线右支上一点,其坐标为(asec,btan),
ቤተ መጻሕፍቲ ባይዱ
y
则直线MA的方程为:y b tan b (x a sec).
将y=
b
a x代入①,解得点A的横坐标为
同设理A可aOx得=,,x点则A =Bta2(的ans横ec坐b标.为taxnB =)a2(. sec tan).
a2 b2
这是中心在原点,焦点在x轴上的双曲线。 第2页
双曲线参数方程
x2 - y2 =1(a>0,b>0)的参数方程为: a2 b2
y
a
A B' • M
x
y
a b
sec tan
(为参数)
通常规定 [o,2 )且
,
3
b
。
22
说明:
o B A' x
⑴ 这里参数 叫做双曲线离心角与直线OM倾斜角不一样.
⑵se双c2曲线参1数t方an程2 能相够比由较方而程得到,ax22所以by22双与曲1三线角参恒数等方式程
实质是三角代换.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分析:依题意画出图形(如图)
直觉巨响点的位置情况.
只要能把巨响点满足的两个曲线 方程求出来.那么解方程组就可以确 定巨响点的位置.
P
yC
A
o
B
x
要求曲线的方程,恰当的建立坐 标系是一个关键.
解:如图,以接报中心为原点 O,正东、正北方向为 x 轴、y 轴正向,建立直角坐标系. 设 A、B、C 分别是西、东、北观测点, 则 A(-1020,0) B(1020,0) , ,C(0,1020). 设 P(x,y)为巨响点, 由 A、C 同时听到巨响声,得|PA|=|PC|, 故 P 在 AC 的垂直平分线 PO 上,PO 的方程为 y =-x,
如图所示,建立直角坐标系xOy, 使A、B两点在x轴上,并 且点O与线段AB的中点重合 y P 设爆炸点P的坐标为(x,y), 则 PA PB 340 2 680 A o B x 即 2a=680,a=340 AB 800 2c 800, c 400, b2 c 2 a 2 44400 800 PA PB 680 0 , x 0 x 2 y2 1( x 0) 因此炮弹爆炸点的轨迹方程为 115600 44400
用 y=-x 代入上式,得 x 680 5 ,∵|PB|>|PA|, x 680 5, y 680 5, 即P(680 5,680 5), 故PO 680 10 答:巨响发生在接报中心的西偏北 450 距中心 680 10m 处.
课堂练习
1.已 知在 △ ABC 中 , B(5, 0) , C(5, 0) ,点 A 运 动时满足 3 sin B sin C sin A ,求点 A 的轨迹方程. 5 2 2
(1)双曲线的焦点位置和方程形式
有什么对应关系? 看X2 、Y2前的系数,哪一个为正,焦点 就在那根轴上。椭圆呢?
(2)双曲线的标准方程与椭圆的标准 方程有何区别与联系?
双曲线与椭圆之间的区别与联系 椭
定义
圆
双曲线
||MF1|-|MF2||=2a
|MF1|+|MF2|=2a
方程
x2 y 2 x2 y 2 2 1(a b 0) 2 1(a 0, b 0) 2 2 a b a b y 2 x2 y 2 x2 2 1(a b 0) 2 1(a 0, b 0) 2 2 a b a b
思考 1:若在 A,B 两地同时听到炮弹爆炸声,则炮弹爆 炸点的轨迹是什么?
答: 爆炸点的轨迹是线段 AB 的垂直平分线.
思考 2:根据两个不同的观测点测得同一炮弹爆炸声的 时间差,可以确定爆炸点在某条曲线上,但不能确定 爆炸点的准确位置. 而现实生活中为了安全,我们最 关心的是炮弹爆炸点的准确位置,怎样才能确定爆炸 点的准确位置呢?
2.课本 P 62 习题 2.3 A 组第 5 题 如图,圆 O 的半径为定长 r ,A 是圆 O 外一定点,P 是圆上任意一点, 线段 AP 的垂直平分线 l 和直线 OP 相交于点 Q,当点 P 在圆 O 上运动时, 点 Q 的轨迹是什么?为什么?
x y 1( x 3) 9 16
P62组第5题.gsp演示第2题的轨迹
双曲线定义
平面内与两个定点F1,F2的距离的差的绝对值 等于常数(小于︱F1F2︱)的点的轨迹叫做双曲线.
| |MF1| - |MF2| | = 2a ( 0<2a< |F1F2|) 点M的轨迹是双曲线
① 两个定点F1、F2——双曲线的焦点; ② |F1F2|=2c ——焦距.
M
注意: 0<2a<2c ;
x y ∴可设双曲线方程为: 2 2 1 (a>0,b>0). a b 2 2 2 ∵2a=6,2c=10,∴a=3,c=5.∴b =5 -3 =16.
x2 y2 1 ( x ≥ 3) . 所以点 P 的轨迹方程为 9 16
2 2
练习
写出适合下列条件的双曲线的标准方程
1.a=4,b=3,焦点在x轴上;
答:再增设一个观测点C,利用B、C(或A、C)两 处测得的爆炸声的时间差,可以求出另一个双曲线的 方程,解这两个方程组成的方程组,就能确定爆炸点 的准确位置.这是双曲线的一个重要应用.
思考 3: (2004 年高考题)某中心接到其正东、正西、正 北方向三个观测点的报告:正西、正北两个观测点同时 听到了一声巨响,正东观测点听到的时间比其他两观测 点晚 4s. 已知各观测点到该中心的距离都是 1020m. 试 确定该巨响发生的位置.(假定当时声音传播的速度为 340m/s,相关各点均在同一平面上)
PF1 PF2 6
变式训练 1:已知两定点 F1 (5,0) , F2 (5,0) ,动点 P 满足
PF1 PF2 10 ,求动点 P 的轨迹方程.
解: ∵ F1F2 10 ,
PF1 PF2 10
∴ 点 P 的轨迹是两条射线,
轨迹方程为 y 0( x ≥ 5 或x ≤ 5) .
课时小结: 本节课主要是进一步了解双曲线的定义 及其标准方程,并运用双曲线的定义及其标 准方程解决问题, 体会双曲线在实际生活中 的一个重要应用. 其实全球定位系统就是根 据例 2 这个原理来定位的. 运用定义及现成的模型思考,这是一个 相当不错的思考方向.即把不熟悉的问题往 熟悉的方向转化,定义模型是最原始,也是最 容易想到的地方.
因 B 点比 A 点晚 4s 听到爆炸声,故|PB|-|PA|=340×4=1360, x2 y2 由双曲线定义知 P 点在以 A、B 为焦点的双曲线 2 2 1 的一支上, a b 依题意得 a = 680, c = 1020, b2 c 2 a 2 10202 6802 5 3402 x2 y2 1 ∴双曲线的方程为 2 2 680 5 340
课外作业
P61 A组2、5、B组2
:
2.焦点为(0,-6),(0,6),过点(2,5)
例2.已知A,B两地相距800m,在A地听到炮弹爆炸声比在B 地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.
解: 由声速及在A地听到炮弹爆炸声比在B地晚2s,可知A地与爆炸点
的距离比B地与爆炸点的距离远680m.因为|AB|>680m,所以爆炸点 的轨迹是以A、B为焦点的双曲线在靠近B处的一支上.
c2 a 2 b2
x2 a2
b 2 1(a 0, b 0)
y2
此即为 焦点在x 轴上的 双曲线 的标准 方程
若建系时,焦点在y轴上呢?
y
M
y
M F2 x
F1
O
F2
x
O
F1
x y 2 1 2 a b
2
2
y x 2 1 2 a b
2
2
(a 0,b 0)
思考:
讨论: (2)若2a=2c,则轨迹是什么?(2)两条射线
F1 o F2
(1) 若|MF1| - |MF2| = 2a或-2a,则轨迹是什么? (1)双曲线的一支
(3)若2a>2c,则轨迹是什么?(3)不表示任何轨迹 (4)若2a=0,则轨迹是什么? (4)线段F1F2的垂直平分线
2.按照求曲线方程的步骤建立双曲线标准方程 y
焦点
F(±c,0)
F(±c,0)
F(0,±c)
a.b.c的关 系
F(0,±c)
a>0,b>0,但a不一 定大于b,c2=a2+b2
a>b>0,a2=b2+c2
典型应用
例 1(参考课本 P54 例 ) 已 知 两 定 点 F1 (5, 0) , F2 (5, 0) , 动 点 P 满 足
PF1 PF2 6 , 求动点 P 的轨迹方程.
1
F2
1. 类比椭圆探究出双曲线定义: 平面内与两定点F1、F2的距离的 差 等于常数 的点的轨迹是什么呢? 拉链画双曲线
①如图(A),
|MF1|-|MF2|=|F2F|=2a
②如图(B), |MF2|-|MF1|=|F1F|=2a 由①②可得: | |MF1|-|MF2| | = 2a (差的绝对值) 上面 两条合起来叫做双曲线 用几何画板演示双曲线.gsp
2.3.1双曲线及其标准方程 (第二课时)
学习目标
1、熟练掌握双曲线的定义、标准方 程。 2、了解双曲线在生活中的应用。 重点、难点:双曲线的应用。
复习引入
说出椭圆定义的内涵和外延
平面内与两定点F1、F2的距离的 和 等于常数 2a ( 2a>|F1F2|=2c>0) 的点的轨迹叫做椭圆.即 |MF1|+|MF2|=2a( 2a>2c>0) 点M的轨迹是椭圆 Y 若2a=2c,点M的轨迹是线段F1F2; M x, y O 若2a<2c,点M的轨迹不存在。 c, 0 c, 0 X F
∴ 由双曲线的定义可知,点 P 的轨迹是一条双曲线,
∵焦点为 F1 (5,0), F2 (5,0)
x2 y2 ∴可设所求方程为: 2 2 1 (a>0,b>0). a b ∵2a=6,2c=10,∴a=3,c=5. x2 y2 1. 所以点 P 的轨迹方程为 9 16
解:∵ F1F2 10 >6,
变式训练 2:已知两定点 F1 (5,0) , F2 (5,0) ,动点 P 满足
PF1 PF2 6 ,求动点 P 的轨迹方程. 解: ∵ F1F2 10 >6, PF1 PF2 6
∴ 由双曲线的定义可知, 点 P 的轨迹是双曲线的一支 (右支), ∵焦点为 F1 (5,0), F2 (5,0)
( x c) y ( x c) y 2a
2 2 2 2
( x c)
